Graphen

Graphen ist ein hexagonales Gitter auf atomarer Ebene, das aus Kohlenstoffatomen besteht. ⓘ

Graphen (/ˈɡræfiːn/) ist ein Allotrop des Kohlenstoffs, das aus einer einzigen Schicht von Atomen besteht, die in einer zweidimensionalen Wabengitter-Nanostruktur angeordnet sind. Der Name leitet sich von "Graphit" und dem Suffix -ene ab, was die Tatsache widerspiegelt, dass das Graphit-Allotrop des Kohlenstoffs zahlreiche Doppelbindungen enthält. ⓘ

Jedes Atom in einem Graphenblatt ist mit seinen drei nächsten Nachbarn durch eine starke σ-Bindung verbunden und trägt zu einem Valenzband mit einem Elektron bei, das sich über das gesamte Blatt erstreckt. Dies ist die gleiche Art von Bindung wie in Kohlenstoff-Nanoröhren und polyzyklischen aromatischen Kohlenwasserstoffen sowie (teilweise) in Fullerenen und glasartigem Kohlenstoff. Das Valenzband wird von einem Leitungsband berührt, was Graphen zu einem Halbmetall mit ungewöhnlichen elektronischen Eigenschaften macht, die am besten durch Theorien für masselose relativistische Teilchen beschrieben werden. Ladungsträger in Graphen zeigen eine lineare und nicht eine quadratische Abhängigkeit der Energie vom Impuls, und es können Feldeffekttransistoren mit Graphen hergestellt werden, die bipolar leiten. Der Ladungstransport ist über große Entfernungen ballistisch; das Material weist große Quantenoszillationen und einen großen und nichtlinearen Diamagnetismus auf. Graphen leitet Wärme und Elektrizität sehr effizient entlang seiner Ebene. Das Material absorbiert stark Licht aller sichtbaren Wellenlängen, was die schwarze Farbe von Graphit erklärt; dennoch ist ein einzelnes Graphenblatt aufgrund seiner extremen Dünnheit nahezu transparent. Das Material ist etwa 100-mal so stark wie der stärkste Stahl mit derselben Dicke. ⓘ

Foto einer aufgehängten Graphenmembran im Durchlicht. Dieses ein Atom dicke Material kann mit bloßem Auge gesehen werden, da es etwa 2,3 % des Lichts absorbiert. ⓘ

Wissenschaftler haben jahrzehntelang über die mögliche Existenz und Herstellung von Graphen spekuliert. Wahrscheinlich wird es schon seit Jahrhunderten unwissentlich in kleinen Mengen durch die Verwendung von Bleistiften und anderen ähnlichen Anwendungen von Graphit hergestellt. Möglicherweise wurde es 1962 in Elektronenmikroskopen beobachtet, aber nur untersucht, wenn es auf Metalloberflächen aufgebracht war. ⓘ

Im Jahr 2004 wurde das Material von Andre Geim und Konstantin Novoselov an der Universität Manchester wiederentdeckt, isoliert und untersucht. Im Jahr 2010 erhielten Geim und Novoselov den Nobelpreis für Physik für ihre "bahnbrechenden Experimente zum zweidimensionalen Material Graphen". Hochwertiges Graphen ließ sich erstaunlich leicht isolieren. ⓘ

Graphen ist zu einem wertvollen und nützlichen Nanomaterial geworden, da es eine außergewöhnlich hohe Zugfestigkeit, elektrische Leitfähigkeit und Transparenz aufweist und das dünnste zweidimensionale Material der Welt ist. Der Weltmarkt für Graphen belief sich im Jahr 2012 auf 9 Millionen US-Dollar, wobei der größte Teil der Nachfrage aus der Forschung und Entwicklung in den Bereichen Halbleiter, Elektronik, elektrische Batterien und Verbundwerkstoffe stammt. ⓘ

Die IUPAC (Internationale Union für reine und angewandte Chemie) empfiehlt, den Namen "Graphit" für das dreidimensionale Material zu verwenden und "Graphen" nur dann, wenn die Reaktionen, die strukturellen Beziehungen oder andere Eigenschaften der einzelnen Schichten diskutiert werden. Eine engere Definition von "isoliertem oder freistehendem Graphen" setzt voraus, dass die Schicht ausreichend von ihrer Umgebung isoliert ist, würde aber auch Schichten einschließen, die auf Siliziumdioxid oder Siliziumkarbid aufgehängt oder übertragen sind. ⓘ

Valenzstrichformel

Graphen [gʁa'feːn] (Betonung auf der zweiten Silbe: Graphen; französisch graphène, englisch graphene) ist die Bezeichnung für eine Modifikation des Kohlenstoffs mit zweidimensionaler Struktur, in der jedes Kohlenstoffatom im Winkel von 120° von drei weiteren umgeben ist, sodass sich ein bienenwabenförmiges Muster ausbildet. Da Kohlenstoff vierwertig ist, müssen dabei je „Wabe“ zwei Doppelbindungen auftreten, die jedoch nicht lokalisiert sind. Es handelt sich um eine Verkettung von Benzolringen, wie sie in aromatischen Verbindungen oft auftritt. Obwohl ein einzelner Benzolring in der Darstellungsweise der Valenzstrichformeln drei Doppelbindungen hat, haben zusammenhängende Benzolringe in dieser Darstellungsweise rein formal nur zwei Doppelbindungen pro Ring. Deshalb lässt sich die Struktur besser beschreiben, indem man die delokalisierten Bindungen als großen Kreis im Benzolring darstellt. Die Bindungsverhältnisse im Graphen sind in der Graphenstruktur beschrieben. Graphen lässt sich als polycyclischer aromatischer Kohlenwasserstoff beschreiben. Am „Rande“ des Wabengitters müssen andere Atomgruppen angedockt sein, die aber – je nach dessen Größe – die Eigenschaften des Graphens kaum verändern. ⓘ

Graphen-Modell ⓘ

Einführender (und gleichzeitig zusammenfassender) Animationsfilm (Text in Englischer Sprache): Elektronische Bandstruktur und Dirac-Kegel; Gitter-Effekte ⓘ

In der Theorie wurden einlagige Kohlenstoffschichten, Graphene, zum ersten Mal verwendet, um den Aufbau und die elektronischen Eigenschaften komplexer aus Kohlenstoff bestehender Materialien beschreiben zu können. ⓘ

Unendlich ausgedehnte und überall flache strikt zweidimensionale Strukturen sind allerdings aufgrund eines rigorosen mathematischen Theorems, des Mermin-Wagner-Theorems und seiner Varianten, nicht möglich, da sie nachweislich thermodynamisch instabil sind. ⓘ

Deshalb herrschte bei Chemikern und Physikern allgemeines Erstaunen, als Konstantin Novoselov, Andre Geim und ihre Mitarbeiter 2004 die Darstellung freier, einschichtiger Graphenkristalle bekannt gaben. Deren unerwartete Stabilität könnte durch die Existenz metastabiler Zustände oder durch Ausbildung einer unregelmäßigen Welligkeit (engl. crumpling) der Graphenschicht erklärt werden. ⓘ

Geschichte

Ein Klumpen Graphit, ein Graphen-Transistor und ein Klebebandspender. 2010 von Andre Geim und Konstantin Novoselov an das Nobelmuseum in Stockholm gespendet. ⓘ

Struktur von Graphit und seinen Einlagerungsverbindungen

1859 stellte Benjamin Brodie die stark lamellare Struktur von thermisch reduziertem Graphitoxid fest. Im Jahr 1916 bestimmten Peter Debye und Paul Scherrer die Struktur von Graphit durch Röntgenpulverbeugung. Die Struktur wurde 1918 von V. Kohlschütter und P. Haenni eingehender untersucht, die auch die Eigenschaften von Graphitoxidpapier beschrieben. Seine Struktur wurde 1924 durch Einkristallbeugung bestimmt. ⓘ

Die Theorie von Graphen wurde erstmals 1947 von P. R. Wallace als Ausgangspunkt für das Verständnis der elektronischen Eigenschaften von 3D-Graphit erforscht. Die emergente masselose Dirac-Gleichung wurde erstmals 1984 von Gordon Walter Semenoff sowie von David P. DiVincenzo und Eugene J. Mele getrennt aufgezeigt. Semenoff betonte das Auftreten eines elektronischen Landau-Niveaus in einem Magnetfeld genau am Dirac-Punkt. Dieses Niveau ist für den anomalen ganzzahligen Quanten-Hall-Effekt verantwortlich. ⓘ

Beobachtungen von dünnen Graphitschichten und verwandten Strukturen

Transmissionselektronenmikroskopische (TEM) Bilder von dünnen Graphitproben, die aus einigen Graphenschichten bestehen, wurden 1948 von G. Ruess und F. Vogt veröffentlicht. Später wurden auch einzelne Schichten direkt beobachtet. Einzelne Graphitschichten wurden auch durch Transmissionselektronenmikroskopie in Massenmaterialien beobachtet, insbesondere in Ruß, der durch chemisches Exfolieren gewonnen wurde. ⓘ

1961-1962 veröffentlichte Hanns-Peter Boehm eine Studie über extrem dünne Graphitflocken und prägte den Begriff Graphen" für die hypothetische einlagige Struktur. In dieser Arbeit wird von Graphitplättchen berichtet, die ein zusätzliches Kontrastäquivalent von bis zu ~0,4 nm oder 3 Atomschichten amorphen Kohlenstoffs ergeben. Dies war die bestmögliche Auflösung für TEMs von 1960. Weder damals noch heute lässt sich jedoch sagen, wie viele Schichten in diesen Flocken enthalten waren. Heute wissen wir, dass der TEM-Kontrast von Graphen sehr stark von den Fokussierungsbedingungen abhängt. So ist es beispielsweise unmöglich, anhand des TEM-Kontrasts zwischen schwebendem einschichtigem und mehrschichtigem Graphen zu unterscheiden, und die einzige bekannte Möglichkeit besteht darin, die relativen Intensitäten verschiedener Beugungsflecken zu analysieren. Die ersten zuverlässigen TEM-Beobachtungen von Monolagen finden sich wahrscheinlich in den Artikeln. 24 und 26 in der Übersichtsarbeit von Geim und Novoselov aus dem Jahr 2007. ⓘ

In den 1970er Jahren beschrieben C. Oshima und andere einzelne Schichten aus Kohlenstoffatomen, die epitaktisch auf anderen Materialien aufgewachsen waren. Dieses "epitaktische Graphen" besteht aus einem einatomig dicken hexagonalen Gitter aus sp²-gebundenen Kohlenstoffatomen, wie bei freistehendem Graphen. Es findet jedoch ein erheblicher Ladungstransfer zwischen den beiden Materialien statt, und in einigen Fällen kommt es zu einer Hybridisierung zwischen den d-Orbitalen der Substratatome und den π-Orbitalen des Graphens, wodurch sich die elektronische Struktur im Vergleich zu der des freistehenden Graphens erheblich verändert. ⓘ

Der Begriff "Graphen" wurde 1987 erneut verwendet, um einzelne Graphitblätter als Bestandteil von Graphiteinlagerungsverbindungen zu beschreiben, die als kristalline Salze des Einlagerungsstoffs und von Graphen angesehen werden können. Es wurde auch bei der Beschreibung von Kohlenstoff-Nanoröhren durch R. Saito und Mildred und Gene Dresselhaus im Jahr 1992 und von polyzyklischen aromatischen Kohlenwasserstoffen im Jahr 2000 durch S. Wang und andere verwendet. ⓘ

Die Bemühungen um die Herstellung dünner Graphitfilme durch mechanische Exfoliation begannen 1990. Bei den ersten Versuchen wurden Exfoliationstechniken eingesetzt, die dem Ziehverfahren ähneln. Es wurden mehrschichtige Proben mit einer Dicke von bis zu 10 nm hergestellt. ⓘ

Im Jahr 2002 meldeten Robert B. Rutherford und Richard L. Dudman in den USA ein Patent für ein Verfahren zur Herstellung von Graphen an, bei dem wiederholt Schichten von einer auf einem Substrat haftenden Graphitflocke abgeschält werden, wobei eine Graphitdicke von 0,00001 Zoll (2,5×10-7 Meter) erreicht wird. Der Schlüssel zum Erfolg war die visuelle Erkennung von Graphen mit hohem Durchsatz auf einem richtig gewählten Substrat, das einen kleinen, aber spürbaren optischen Kontrast bietet. ⓘ

Ein weiteres US-Patent wurde im selben Jahr von Bor Z. Jang und Wen C. Huang für ein Verfahren zur Herstellung von Graphen auf der Grundlage von Exfoliation und anschließender Abrasion angemeldet. ⓘ

Im Jahr 2014 meldete der Erfinder Larry Fullerton ein Verfahren zur Herstellung einlagiger Graphenblätter an. ⓘ

Vollständige Isolierung und Charakterisierung

Andre Geim und Konstantin Novoselov auf der Pressekonferenz der Nobelpreisträger, Königlich Schwedische Akademie der Wissenschaften, 2010. ⓘ

Graphen wurde 2004 von Andre Geim und Konstantin Novoselov an der Universität Manchester vollständig isoliert und charakterisiert. Sie zogen Graphenschichten mit einem gewöhnlichen Klebeband aus Graphit in einem Prozess, der entweder mikromechanische Spaltung oder Scotch-Tape-Technik genannt wird. Die Graphenflocken wurden dann auf eine dünne Siliziumdioxidschicht (Silica) auf einer Siliziumplatte ("Wafer") übertragen. Das Siliziumdioxid isolierte das Graphen elektrisch und ging mit ihm eine schwache Wechselwirkung ein, wodurch nahezu ladungsneutrale Graphenschichten entstanden. Das Silizium unter dem SiO
₂ konnte als "Backgate"-Elektrode verwendet werden, um die Ladungsdichte im Graphen in einem weiten Bereich zu variieren. ⓘ

Für diese Arbeit erhielten die beiden im Jahr 2010 den Nobelpreis für Physik "für bahnbrechende Experimente zum zweidimensionalen Material Graphen". Ihre Veröffentlichung und die von ihnen beschriebene, überraschend einfache Präparationsmethode lösten einen "Graphen-Goldrausch" aus. Die Forschung weitete sich aus und spaltete sich in viele verschiedene Teilbereiche auf, in denen unterschiedliche außergewöhnliche Eigenschaften des Materials erforscht wurden - quantenmechanische, elektrische, chemische, mechanische, optische, magnetische usw. ⓘ

Erforschung kommerzieller Anwendungen

Seit Anfang der 2000er Jahre arbeiten eine Reihe von Unternehmen und Forschungslabors an der Entwicklung kommerzieller Anwendungen von Graphen. Im Jahr 2014 wurde zu diesem Zweck an der Universität Manchester ein Nationales Graphen-Institut gegründet, das mit einer Anschubfinanzierung von 60 Mio. GBP ausgestattet wurde. In Nordostengland haben zwei kommerzielle Hersteller, Applied Graphene Materials und Thomas Swan Limited, die Produktion aufgenommen. Cambridge Nanosystems ist eine groß angelegte Graphenpulver-Produktionsanlage in East Anglia. ⓘ

Struktur

Alle Kohlenstoffatome von Graphen sind sp²-hybridisiert, das heißt, jedes Kohlenstoffatom kann drei gleichwertige σ-Bindungen zu anderen C-Atomen ausbilden. Daraus resultiert eine auch aus den Schichten des Graphits bekannte Waben-Struktur. Die Kohlenstoff-Kohlenstoff-Bindungslängen sind alle gleich und betragen 142 pm. Die dritten, nicht hybridisierten 2p-Orbitale stehen wie auch im Graphit senkrecht zur Graphenebene und bilden ein delokalisiertes π-Bindungssystem aus. ⓘ

Graphen besteht folglich aus zwei äquivalenten Untergittern A und B, denen die Kohlenstoffatome zugeordnet sind. Die Untergitter sind um die Bindungslänge $a_{b}$ gegeneinander verschoben. Die zweiatomige Einheitszelle wird durch die Gittervektoren ${\vec {a}}_{1}$ und ${\vec {a}}_{2}$ aufgespannt. Diese zeigen dabei auf die jeweils übernächsten Nachbarn. Die Länge der Vektoren und damit die Gitterkonstante $a$ lässt sich berechnen zu ⓘ

$a=|{\vec {a}}_{1}|=|{\vec {a}}_{2}|={\sqrt {3}}\cdot a_{b}\approx 2{,}46\,\mathrm {\AA} =246\,\mathrm {pm}$. ⓘ

Graphen kann einerseits als Einkristall, andererseits als riesiges Molekül verstanden werden. Ebenso können kleinere Moleküle wie z. B. Benzol, Hexabenzocoronen oder Naphthalin als wasserstoffsubstituierte Graphenfragmente gesehen werden. ⓘ

Bindung

Die Kohlenstofforbitale 2s, 2p_x, 2p_y bilden das Hybridorbital sp² mit drei Hauptkeulen bei 120°. Das verbleibende Orbital, p_z, ragt aus der Ebene des Graphens heraus. ⓘ

Sigma- und pi-Bindungen in Graphen. Sigma-Bindungen entstehen durch eine Überlappung von sp²-Hybridorbitalen, während pi-Bindungen durch Tunnelbildung zwischen den hervorstehenden pz-Orbitalen entstehen. ⓘ

Drei der vier Elektronen der äußeren Schale jedes Atoms in einer Graphenschicht besetzen drei sp²-Hybridorbitale - eine Kombination der Orbitale s, p_x und py -, die mit den drei nächstgelegenen Atomen geteilt werden und σ-Bindungen bilden. Die Länge dieser Bindungen beträgt etwa 0,142 Nanometer. ⓘ

Das verbleibende Elektron in der äußeren Schale nimmt ein pz-Orbital ein, das senkrecht zur Ebene ausgerichtet ist. Diese Orbitale hybridisieren miteinander und bilden zwei halbgefüllte Bänder aus frei beweglichen Elektronen, π und π∗, die für die meisten der bemerkenswerten elektronischen Eigenschaften von Graphen verantwortlich sind. Neuere quantitative Schätzungen der aromatischen Stabilisierung und der Grenzgröße, die aus den Hydrierungsenthalpien (ΔH_hydro) abgeleitet wurden, stimmen gut mit den Literaturberichten überein. ⓘ

Graphenblätter stapeln sich zu Graphit mit einem Interplanarabstand von 0,335 nm (3,35 Å). ⓘ

Graphenblätter in fester Form zeigen in der Regel in der Beugung Anzeichen für die (002)-Schichtung von Graphit. Dies ist bei einigen einwandigen Nanostrukturen der Fall. Im Kern von präsolaren Graphitzwiebeln wurde jedoch ungeschichtetes Graphen mit nur (hk0)-Ringen gefunden. TEM-Studien zeigen Facettierungen an Defekten in flachen Graphenblättern und deuten auf eine Rolle bei der zweidimensionalen Kristallisation aus einer Schmelze hin. ⓘ

Geometrie

Rastersondenmikroskopische Aufnahme von Graphen ⓘ

Die hexagonale Gitterstruktur von isoliertem, einlagigem Graphen lässt sich mit der Transmissionselektronenmikroskopie (TEM) von Graphenblättern, die zwischen Stäben eines Metallgitters aufgehängt sind, direkt erkennen. Einige dieser Bilder zeigen ein "Kräuseln" des flachen Blattes mit einer Amplitude von etwa einem Nanometer. Diese Kräuselungen können materialimmanent sein und auf die Instabilität zweidimensionaler Kristalle zurückzuführen sein, aber auch auf den allgegenwärtigen Schmutz, der auf allen TEM-Bildern von Graphen zu sehen ist. Rückstände von Fotolack, die entfernt werden müssen, um Bilder mit atomarer Auflösung zu erhalten, könnten die "Adsorbate" sein, die in TEM-Bildern zu sehen sind und die beobachtete Welligkeit erklären könnten. ⓘ

Die hexagonale Struktur ist auch in Rastertunnelmikroskop-Bildern (STM) von Graphen auf Siliziumdioxid-Substraten zu sehen. Die in diesen Bildern zu sehende Welligkeit wird durch die Anpassung von Graphen an das Gitter des Substrats verursacht und ist nicht intrinsisch. ⓘ

Stabilität

Ab-Initio-Berechnungen zeigen, dass ein Graphenblatt thermodynamisch instabil ist, wenn seine Größe weniger als 20 nm beträgt, und erst bei Molekülen mit mehr als 24 000 Atomen zum stabilsten Fulleren (wie bei Graphit) wird. ⓘ

Eigenschaften

Elektronisch

Elektronische Bandstruktur von Graphen. Valenz- und Leitungsbänder treffen sich an den sechs Spitzen der hexagonalen Brillouin-Zone und bilden linear verlaufende Dirac-Kegel. ⓘ

Graphen ist ein Halbleiter mit Null-Lücke, da sich seine Leitungs- und Valenzbänder an den Dirac-Punkten treffen. Die Dirac-Punkte sind sechs Orte im Impulsraum am Rand der Brillouin-Zone, die in zwei nicht-äquivalente Gruppen von drei Punkten unterteilt sind. Die beiden Gruppen werden mit K und K' bezeichnet. Die Gruppen verleihen Graphen eine Tal-Entartung von gv = 2. Im Gegensatz dazu ist bei herkömmlichen Halbleitern der wichtigste Punkt im Allgemeinen Γ, wo der Impuls gleich Null ist. Vier elektronische Eigenschaften unterscheiden sie von anderen Systemen kondensierter Materie. ⓘ

Wenn die Richtung in der Ebene jedoch nicht mehr unendlich, sondern begrenzt ist, würde sich seine elektronische Struktur ändern. Sie werden als Graphen-Nanobänder bezeichnet. Wenn sie "zick-zack" sind, ist die Bandlücke immer noch Null. Bei einem "Sessel" wäre die Bandlücke ungleich Null. ⓘ

Das hexagonale Gitter von Graphen kann als zwei ineinandergreifende Dreiecksgitter betrachtet werden. Diese Sichtweise wurde erfolgreich genutzt, um die Bandstruktur für eine einzelne Graphitschicht unter Verwendung einer Annäherung durch enge Bindung zu berechnen. ⓘ

Elektronisches Spektrum

Elektronen, die sich durch das Wabengitter von Graphen ausbreiten, verlieren effektiv ihre Masse und erzeugen Quasiteilchen, die durch ein 2D-Analogon der Dirac-Gleichung und nicht durch die Schrödinger-Gleichung für Spin-1/2-Teilchen beschrieben werden. ⓘ

Dispersionsbeziehung

Elektronische Bandstruktur und Dirac-Kegel, mit Wirkung der Dotierung ⓘ

Die Spalttechnik führte 2005 direkt zur ersten Beobachtung des anomalen Quanten-Hall-Effekts in Graphen durch die Gruppe von Geim sowie Philip Kim und Yuanbo Zhang. Dieser Effekt lieferte den direkten Beweis für die theoretisch vorhergesagte Berry-Phase masseloser Dirac-Fermionen in Graphen und den ersten Beweis für die Dirac-Fermion-Natur der Elektronen. Diese Effekte waren 2003-2004 von Yakov Kopelevich, Igor A. Luk'yanchuk und anderen in massivem Graphit beobachtet worden. ⓘ

Wenn die Atome auf dem hexagonalen Graphengitter angeordnet sind, ist die Überlappung zwischen den pz(π)-Orbitalen und den s- oder den px- und py-Orbitalen aufgrund der Symmetrie gleich Null. Die pz-Elektronen, die die π-Bänder in Graphen bilden, können daher unabhängig behandelt werden. Im Rahmen dieser π-Band-Näherung und unter Verwendung eines konventionellen Tight-Binding-Modells lautet die Dispersionsrelation (die sich nur auf Wechselwirkungen zwischen den ersten und nächsten Nachbarn beschränkt), die die Energie der Elektronen mit dem Wellenvektor k erzeugt ⓘ

$E(k_{x},k_{y})=\pm \,\gamma _{0}{\sqrt {1+4\cos ^{2}{{\tfrac {1}{2}}ak_{x}}+4\cos {{\tfrac {1}{2}}ak_{x}}\cdot \cos {{\tfrac {\sqrt {3}}{2}}ak_{y}}}}$ ⓘ

mit der Sprungenergie der nächsten Nachbarn (π-Orbitale) γ₀ ≈ 2,8 eV und der Gitterkonstante a ≈ 2,46 Å. Die Leitungs- bzw. Valenzbänder entsprechen den unterschiedlichen Vorzeichen. Mit einem pz-Elektron pro Atom ist in diesem Modell das Valenzband voll besetzt, während das Leitungsband unbesetzt ist. Die beiden Bänder berühren sich an den Zonenecken (dem K-Punkt in der Brillouin-Zone), wo es eine Zustandsdichte von Null, aber keine Bandlücke gibt. Das Graphenblatt weist somit einen halbmetallischen Charakter (oder einen Halbleiter mit Null-Lücke) auf, auch wenn dies von einem zu einem Kohlenstoff-Nanoröhrchen gerollten Graphenblatt aufgrund seiner Krümmung nicht gesagt werden kann. Zwei der sechs Dirac-Punkte sind unabhängig, während die übrigen durch Symmetrie gleichwertig sind. In der Nähe der K-Punkte hängt die Energie linear vom Wellenvektor ab, ähnlich wie bei einem relativistischen Teilchen. Da eine Elementarzelle des Gitters eine Basis aus zwei Atomen hat, hat die Wellenfunktion eine effektive 2-Spinor-Struktur. ⓘ

Infolgedessen können die Elektronen bei niedrigen Energien, selbst wenn man den echten Spin vernachlässigt, durch eine Gleichung beschrieben werden, die formal der masselosen Dirac-Gleichung entspricht. Daher werden die Elektronen und Löcher als Dirac-Fermionen bezeichnet. Diese pseudo-relativistische Beschreibung ist auf das chirale Limit beschränkt, d. h. auf die verschwindende Ruhemasse M₀, was zu interessanten zusätzlichen Eigenschaften führt:

$v_{F}\,{\vec {\sigma }}\cdot \nabla \psi (\mathbf {r} )\,=\,E\psi (\mathbf {r} ).$ ⓘ

Hier ist v_F ~ 10⁶ m/s (.003 c) die Fermi-Geschwindigkeit in Graphen, die in der Dirac-Theorie die Lichtgeschwindigkeit ersetzt; ${\vec {\sigma }}$ ist der Vektor der Pauli-Matrizen, $\psi (\mathbf {r} )$ ist die Zweikomponenten-Wellenfunktion der Elektronen, und E ist ihre Energie. ⓘ

Die Gleichung, die die lineare Dispersionsbeziehung der Elektronen beschreibt, lautet ⓘ

$E(q)=\hbar v_{F}q$ ⓘ

wobei der Wellenvektor q vom Scheitelpunkt K der Brillouin-Zone aus gemessen wird, $q=\left|\mathbf {k} -\mathrm {K} \right|$gemessen wird und der Nullpunkt der Energie mit dem Dirac-Punkt zusammenfällt. Die Gleichung verwendet eine Pseudospin-Matrixformel, die zwei Untergitter des Bienenwabengitters beschreibt. ⓘ

Energie der Elektronen in Graphen als Funktion ihrer Wellenzahl $\mathbf {k} =(k_{x},k_{y})$ in Tight-Binding-Näherung.
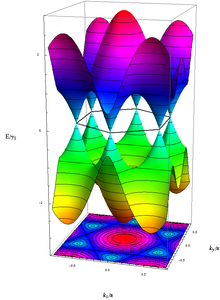
Die „besetzten“ bzw. „unbesetzten“ Zustände („gelb-grün“ bzw. „blau-rot“) berühren einander ohne Lücke genau an den im Text erwähnten sechs k-Werten. ⓘ

$E=\pm {\sqrt {\gamma _{0}^{2}\left(1+4\cos ^{2}{\pi k_{y}a}+4\cos {\pi k_{y}a}\cdot \cos {\pi k_{x}{\sqrt {3}}a}\right)}}$, ⓘ

Ausbreitung von Ein-Atom-Wellen

Elektronenwellen in Graphen breiten sich innerhalb einer einatomigen Schicht aus, was sie empfindlich gegenüber der Nähe anderer Materialien wie hoch-κ-Dielektrika, Supraleitern und Ferromagneten macht. ⓘ

Ambipolarer Elektronen- und Löchertransport

Wenn die Gate-Spannung in einem Feldeffekt-Graphen-Bauelement von positiv auf negativ geändert wird, schaltet die Leitung von Elektronen auf Löcher um. Die Ladungsträgerkonzentration ist proportional zu der angelegten Spannung. Bei einer Gatespannung von Null ist Graphen neutral, und der Widerstand ist wegen des Mangels an Ladungsträgern am höchsten. Der schnelle Abfall des Widerstandes, wenn Ladungsträger injiziert werden, zeigt ihre hohe Mobilität, hier in der Größenordnung von 5000 cm²/Vs. n-Si/SiO₂-Substrat, T=1K. ⓘ

Graphen weist bei Raumtemperatur eine bemerkenswerte Elektronenbeweglichkeit auf, mit berichteten Werten von über 15000 cm²⋅V-1⋅s-1. Die Beweglichkeit von Löchern und Elektronen ist nahezu gleich. Die Mobilität ist zwischen 10 K und 100 K temperaturunabhängig und ändert sich auch bei Raumtemperatur (300 K) nur wenig, was darauf schließen lässt, dass der dominierende Streuungsmechanismus die Defektstreuung ist. Die Streuung an den akustischen Phononen von Graphen begrenzt die Mobilität bei Raumtemperatur in freistehendem Graphen auf 200000 cm²⋅V-1⋅s-1 bei einer Trägerdichte von 10¹² cm-2. ⓘ

Der entsprechende spezifische Widerstand von Graphenblättern würde 10-6 Ω⋅cm betragen. Dies ist weniger als der spezifische Widerstand von Silber, der niedrigste, der bei Raumtemperatur bekannt ist. Auf SiO
₂-Substraten ist jedoch die Streuung der Elektronen an den optischen Phononen des Substrats ein größerer Effekt als die Streuung an den grapheneigenen Phononen. Dies begrenzt die Mobilität auf 40000 cm²⋅V-1⋅s-1. ⓘ

Der Ladungstransport ist aufgrund der Adsorption von Verunreinigungen wie Wasser und Sauerstoffmolekülen sehr problematisch. Dies führt zu nicht wiederholbaren und hysteresebehafteten I-U-Kennlinien. Die Forscher müssen die elektrischen Messungen im Vakuum durchführen. Der Schutz der Graphenoberfläche durch eine Beschichtung mit Materialien wie SiN, PMMA, h-BN usw. wurde von Forschern diskutiert. Im Januar 2015 wurde über den ersten stabilen Betrieb eines Graphen-Bauteils an der Luft über mehrere Wochen berichtet, dessen Oberfläche durch Aluminiumoxid geschützt war. Im Jahr 2015 zeigte lithiumbeschichtetes Graphen Supraleitfähigkeit, ein Novum für Graphen. ⓘ

Der elektrische Widerstand in 40 Nanometer breiten Nanobändern aus epitaktischem Graphen ändert sich in diskreten Schritten. Die Leitfähigkeit der Bänder übertrifft die Vorhersagen um das 10-fache. Die Bänder können sich eher wie optische Wellenleiter oder Quantenpunkte verhalten, so dass die Elektronen reibungslos entlang der Bandkanten fließen können. In Kupfer steigt der Widerstand proportional zur Länge, wenn die Elektronen auf Verunreinigungen treffen. ⓘ

Der Transport wird von zwei Modi dominiert. Der eine ist ballistisch und temperaturunabhängig, während der andere thermisch aktiviert ist. Ballistische Elektronen ähneln denen in zylindrischen Kohlenstoff-Nanoröhrchen. Bei Raumtemperatur steigt der Widerstand bei einer bestimmten Länge abrupt an - der ballistische Modus bei 16 Mikrometern und der andere bei 160 Nanometern (1 % der ersten Länge). ⓘ

Graphenelektronen können selbst bei Raumtemperatur Mikrometerdistanzen ohne Streuung zurücklegen. ⓘ

Trotz einer Trägerdichte von Null in der Nähe der Dirac-Punkte weist Graphen eine minimale Leitfähigkeit in der Größenordnung von $4e^{2}/h$. Der Ursprung dieser minimalen Leitfähigkeit ist noch unklar. Eine Welligkeit der Graphenschicht oder ionisierte Verunreinigungen im SiO
₂-Substrat können jedoch zu lokalen Pfützen von Ladungsträgern führen, die eine Leitfähigkeit ermöglichen. Mehrere Theorien legen nahe, dass die Mindestleitfähigkeit bei $4e^{2}/{(\pi }h)$betragen sollte; die meisten Messungen liegen jedoch in der Größenordnung $4e^{2}/h$ oder höher und hängen von der Konzentration der Verunreinigungen ab. ⓘ

Graphen weist bei einer Ladungsträgerdichte nahe Null eine positive Lichtleitfähigkeit und bei hoher Ladungsträgerdichte eine negative Lichtleitfähigkeit auf. Dies wird durch das Zusammenspiel von fotoinduzierten Änderungen des Drude-Gewichts und der Ladungsträgerstreuungsrate bestimmt. ⓘ

Graphen, das mit verschiedenen gasförmigen Spezies (sowohl Akzeptoren als auch Donatoren) dotiert ist, kann durch sanftes Erhitzen im Vakuum in einen undotierten Zustand zurückgeführt werden. Selbst bei Dotierungskonzentrationen von mehr als 10¹² cm-2 zeigt die Ladungsträgerbeweglichkeit keine erkennbare Veränderung. Mit Kalium dotiertes Graphen kann im Ultrahochvakuum bei niedriger Temperatur die Mobilität um das 20-fache verringern. Die Verringerung der Mobilität ist reversibel, wenn das Graphen erhitzt wird, um das Kalium zu entfernen. ⓘ

Aufgrund der zwei Dimensionen von Graphen wird angenommen, dass eine Ladungsfraktionierung (bei der die scheinbare Ladung einzelner Pseudopartikel in niedrigdimensionalen Systemen weniger als ein einzelnes Quant beträgt) auftritt. Graphen könnte daher ein geeignetes Material für den Bau von Quantencomputern mit anyonischen Schaltkreisen sein. ⓘ

Chiraler halb-ganzzahliger Quanten-Hall-Effekt

Landau-Niveaus in Graphen treten bei Energien auf, die proportional zu √N sind, im Gegensatz zur Standardsequenz, die als N+1/2 verläuft. ⓘ

Der Quanten-Hall-Effekt ist eine quantenmechanische Version des Hall-Effekts, d. h. der Erzeugung von Querleitfähigkeit (senkrecht zum Hauptstrom) in Gegenwart eines Magnetfelds. Die Quantisierung des Hall-Effekts $\sigma _{xy}$ bei ganzzahligen Vielfachen (dem "Landau-Niveau") der Basisgröße $e^{2}/h$ (wobei e die elektrische Elementarladung und h die Plancksche Konstante ist). Er kann normalerweise nur in sehr reinen Silizium- oder Galliumarsenid-Festkörpern bei Temperaturen um 3 K und sehr hohen Magnetfeldern beobachtet werden. ⓘ

Graphen zeigt den Quanten-Hall-Effekt in Bezug auf die Quantisierung der Leitfähigkeit: Der Effekt ist insofern ungewöhnlich, als die Abfolge der Schritte gegenüber der Standardabfolge um 1/2 verschoben ist und einen zusätzlichen Faktor von 4 aufweist. Die Hall-Leitfähigkeit von Graphen ist $\sigma _{xy}=\pm {4\cdot \left(N+1/2\right)e^{2}}/h$wobei N das Landau-Niveau ist und die doppelte Tal- und doppelte Spin-Entartung den Faktor 4 ergibt. Diese Anomalien treten nicht nur bei extrem niedrigen Temperaturen auf, sondern auch bei Raumtemperatur, d. h. bei etwa 20 °C (293 K). ⓘ

Dieses Verhalten ist eine direkte Folge der chiralen, masselosen Dirac-Elektronen von Graphen. In einem Magnetfeld hat ihr Spektrum ein Landau-Niveau mit einer Energie genau am Dirac-Punkt. Dieses Niveau ist eine Folge des Atiyah-Singer-Index-Theorems und ist in neutralem Graphen zur Hälfte gefüllt, was zu den "+1/2" in der Hall-Leitfähigkeit führt. Zweischichtiges Graphen zeigt ebenfalls den Quanten-Hall-Effekt, allerdings nur mit einer der beiden Anomalien (d. h. $\sigma _{xy}=\pm {4\cdot N\cdot e^{2}}/h$). Bei der zweiten Anomalie ist das erste Plateau bei N=0 nicht vorhanden, was darauf hindeutet, dass zweischichtiges Graphen am Neutralitätspunkt metallisch bleibt. ⓘ

Chiraler halb-ganzzahliger Quanten-Hall-Effekt in Graphen. Plateaus in der transversalen Leitfähigkeit erscheinen bei halben Ganzzahlen von 4e²/h. ⓘ

Im Gegensatz zu normalen Metallen zeigt der Längswiderstand von Graphen bei Messungen der Shubnikov-de Haas-Oszillationen eher Maxima als Minima für ganzzahlige Werte des Landau-Füllfaktors, wodurch der Begriff integraler Quanten-Hall-Effekt entsteht. Diese Oszillationen weisen eine Phasenverschiebung von π auf, die als Berry-Phase bezeichnet wird. Die Berry-Phase entsteht aufgrund der Chiralität oder der Abhängigkeit (Locking) der Pseudospin-Quantenzahl vom Impuls der niederenergetischen Elektronen in der Nähe der Dirac-Punkte. Die Temperaturabhängigkeit der Oszillationen zeigt, dass die Ladungsträger eine Zyklotronmasse ungleich Null haben, obwohl ihre effektive Masse im Dirac-Ferion-Formalismus gleich Null ist. ⓘ

Graphenproben, die auf Nickelschichten und sowohl auf der Silizium- als auch auf der Kohlenstoffseite von Siliziumkarbid präpariert wurden, zeigen den anomalen Effekt direkt in elektrischen Messungen. Graphitische Schichten auf der Kohlenstoffseite von Siliziumkarbid zeigen in winkelaufgelösten Photoemissionsexperimenten ein deutliches Dirac-Spektrum, und der Effekt wird in Zyklotronresonanz- und Tunnelexperimenten beobachtet. ⓘ

Starke Magnetfelder

In Magnetfeldern von mehr als 10 Tesla oder so werden zusätzliche Plateaus der Hall-Leitfähigkeit bei σ_xy = νe²/h mit ν = 0, ±1, ±4 beobachtet. Ein Plateau bei ν = 3 und der fraktionierte Quanten-Hall-Effekt bei ν = 1/3 wurden ebenfalls beobachtet. ⓘ

Diese Beobachtungen mit ν = 0, ±1, ±3, ±4 deuten darauf hin, dass die vierfache Entartung (zwei Tal- und zwei Spin-Freiheitsgrade) der Landau-Energieniveaus teilweise oder vollständig aufgehoben ist. ⓘ

Casimir-Effekt

Der Casimir-Effekt ist eine Wechselwirkung zwischen unverbundenen neutralen Körpern, die durch die Fluktuationen des elektrodynamischen Vakuums hervorgerufen wird. Mathematisch lässt er sich erklären, indem man die Normalmoden elektromagnetischer Felder betrachtet, die ausdrücklich von den Randbedingungen (oder Anpassungsbedingungen) auf den Oberflächen der wechselwirkenden Körper abhängen. Da die Wechselwirkung zwischen Graphen und elektromagnetischen Feldern für ein Material mit einer Dicke von einem Atom sehr stark ist, ist der Casimir-Effekt von wachsendem Interesse. ⓘ

Van-der-Waals-Kraft

Die Van-der-Waals-Kraft (oder Dispersionskraft) ist ebenfalls ungewöhnlich, da sie einem inversen kubischen, asymptotischen Potenzgesetz gehorcht, im Gegensatz zum üblichen inversen Quartzgesetz. ⓘ

Massive" Elektronen

Die Einheitszelle von Graphen hat zwei identische Kohlenstoffatome und zwei Null-Energie-Zustände: in einem befindet sich das Elektron auf Atom A, in dem anderen auf Atom B. Sind die beiden Atome in der Einheitszelle jedoch nicht identisch, ändert sich die Situation. Hunt et al. zeigen, dass der Kontakt von hexagonalem Bornitrid (h-BN) mit Graphen das Potenzial zwischen Atom A und Atom B so weit verändern kann, dass die Elektronen eine Masse und damit eine Bandlücke von etwa 30 meV [0,03 Elektronenvolt (eV)] entwickeln. ⓘ

Die Masse kann positiv oder negativ sein. Eine Anordnung, die die Energie eines Elektrons auf Atom A relativ zu Atom B leicht erhöht, verleiht ihm eine positive Masse, während eine Anordnung, die die Energie von Atom B erhöht, eine negative Elektronenmasse erzeugt. Die beiden Versionen verhalten sich gleich und sind durch optische Spektroskopie nicht zu unterscheiden. Ein Elektron, das sich von einem Bereich mit positiver Masse zu einem Bereich mit negativer Masse bewegt, muss einen Zwischenbereich durchqueren, in dem seine Masse wieder zu Null wird. Dieser Bereich ist lückenlos und daher metallisch. Metallische Moden, die halbleitende Bereiche mit entgegengesetztem Massenvorzeichen begrenzen, sind ein Kennzeichen einer topologischen Phase und weisen weitgehend dieselbe Physik auf wie topologische Isolatoren. ⓘ

Wenn die Masse in Graphen kontrolliert werden kann, können Elektronen auf masselose Bereiche beschränkt werden, indem man sie mit massiven Bereichen umgibt, was die Strukturierung von Quantenpunkten, Drähten und anderen mesoskopischen Strukturen ermöglicht. Außerdem entstehen eindimensionale Leiter entlang der Grenze. Diese Drähte wären gegen Rückstreuung geschützt und könnten Ströme ohne Verlust leiten. ⓘ

Die Dielektrizitätskonstante

Die Permittivität von Graphen variiert mit der Frequenz. In einem Bereich von Mikrowellen- bis Millimeterwellenfrequenzen beträgt sie etwa 3,3. Diese Dielektrizitätskonstante in Verbindung mit der Fähigkeit, sowohl Leiter als auch Isolatoren zu sein, bedeutet, dass kompakte Kondensatoren aus Graphen theoretisch große Mengen an elektrischer Energie speichern könnten. ⓘ

Optisch

Die einzigartigen optischen Eigenschaften von Graphen führen zu einer unerwartet hohen Opazität für eine atomare Monolage im Vakuum, die πα ≈ 2,3 % des Lichts vom sichtbaren bis zum Infrarotbereich absorbiert. Dabei ist α die Feinstrukturkonstante. Dies ist eine Folge der "ungewöhnlichen niederenergetischen elektronischen Struktur von einlagigem Graphen, die konische Bänder von Elektronen und Löchern aufweist, die sich am Dirac-Punkt treffen... [die] sich qualitativ von den häufigeren quadratischen massiven Bändern unterscheidet." Auf der Grundlage des Slonczewski-Weiss-McClure (SWMcC)-Bandmodells von Graphit heben sich der interatomare Abstand, der Sprungwert und die Frequenz auf, wenn die optische Leitfähigkeit unter Verwendung der Fresnel-Gleichungen in der Dünnschichtgrenze berechnet wird. ⓘ

Obwohl experimentell bestätigt, ist die Messung nicht genau genug, um andere Techniken zur Bestimmung der Feinstrukturkonstante zu verbessern. ⓘ

Mit Hilfe der multiparametrischen Oberflächenplasmonenresonanz wurden sowohl die Dicke als auch der Brechungsindex von durch chemische Gasphasenabscheidung (CVD) hergestellten Graphenfilmen bestimmt. Der gemessene Brechungsindex und der Extinktionskoeffizient bei 670 nm (6,7×10-7 m) Wellenlänge betragen 3,135 bzw. 0,897. Die Dicke wurde auf einer Fläche von 0,5 mm mit 3,7 Å bestimmt, was mit den 3,35 Å übereinstimmt, die für den Abstand der Kohlenstoffatome von Schicht zu Schicht bei Graphitkristallen angegeben werden. Die Methode kann auch für markierungsfreie Echtzeit-Wechselwirkungen von Graphen mit organischen und anorganischen Substanzen verwendet werden. Darüber hinaus wurde die Existenz von unidirektionalen Oberflächenplasmonen in den nicht reziproken gyrotropen Grenzflächen auf Graphenbasis theoretisch nachgewiesen. Durch die effiziente Steuerung des chemischen Potenzials von Graphen kann die unidirektionale Arbeitsfrequenz kontinuierlich von THz bis zum nahen Infrarot und sogar im sichtbaren Bereich eingestellt werden. Insbesondere kann die unidirektionale Frequenzbandbreite bei gleichem Magnetfeld um 1 bis 2 Größenordnungen größer sein als die in Metall, was auf die Überlegenheit der extrem kleinen effektiven Elektronenmasse in Graphen zurückzuführen ist. ⓘ

Die Bandlücke von Graphen kann durch Anlegen einer Spannung an einen Graphen-Feldeffekttransistor (FET) mit zwei Gates bei Raumtemperatur von 0 bis 0,25 eV (etwa 5 Mikrometer Wellenlänge) eingestellt werden. Die optische Reaktion von Graphen-Nanobändern ist durch ein angelegtes Magnetfeld bis in den Terahertzbereich abstimmbar. Graphen/Graphenoxid-Systeme zeigen ein elektrochromes Verhalten, das eine Abstimmung sowohl der linearen als auch der ultraschnellen optischen Eigenschaften ermöglicht. ⓘ

Ein auf Graphen basierendes Bragg-Gitter (eindimensionaler photonischer Kristall) wurde hergestellt und seine Fähigkeit zur Anregung elektromagnetischer Oberflächenwellen in der periodischen Struktur unter Verwendung eines 633 nm (6,33×10-7 m) He-Ne-Lasers als Lichtquelle nachgewiesen. ⓘ

Sättigbare Absorption

Diese einzigartige Absorption kann gesättigt werden, wenn die optische Eingangsintensität über einem Schwellenwert liegt. Dieses nichtlineare optische Verhalten wird als sättigbare Absorption bezeichnet, und der Schwellenwert wird als Sättigungsfluenz bezeichnet. Aufgrund der universellen optischen Absorption und der Null-Bandlücke kann Graphen bei starker Anregung im sichtbaren bis nahen Infrarotbereich leicht gesättigt werden. Dies ist von Bedeutung für die Modenverriegelung von Faserlasern, bei denen eine Vollband-Modenverriegelung durch einen sättigbaren Absorber auf Graphenbasis erreicht wurde. Aufgrund dieser besonderen Eigenschaft findet Graphen eine breite Anwendung in der ultraschnellen Photonik. Außerdem kann die optische Reaktion von Graphen/Graphenoxid-Schichten elektrisch abgestimmt werden. ⓘ

Die sättigbare Absorption in Graphen kann aufgrund seiner breitbandigen optischen Absorptionseigenschaft im Mikrowellen- und Terahertzband auftreten. Die sättigbare Mikrowellenabsorption in Graphen zeigt die Möglichkeit von Mikrowellen- und Terahertz-Photonikgeräten aus Graphen auf, wie z. B. ein sättigbarer Mikrowellenabsorber, Modulator, Polarisator, Mikrowellensignalverarbeitung und drahtlose Breitbandzugangsnetze. ⓘ

Nichtlinearer Kerr-Effekt

Bei intensiverer Laserbeleuchtung könnte Graphen aufgrund des optischen nichtlinearen Kerr-Effekts auch eine nichtlineare Phasenverschiebung aufweisen. Ausgehend von einer typischen z-Scan-Messung mit offener und geschlossener Apertur besitzt Graphen einen riesigen nichtlinearen Kerr-Koeffizienten von 10-7 cm²⋅W-1, der fast neun Größenordnungen größer ist als der von Massendielektrika. Dies deutet darauf hin, dass Graphen ein leistungsfähiges nichtlineares Kerr-Medium sein könnte, in dem eine Vielzahl von nichtlinearen Effekten beobachtet werden kann, von denen das Soliton der wichtigste ist. ⓘ

Exzitonisch

Es werden First-Principle-Berechnungen mit Quasiteilchenkorrekturen und Vielteilcheneffekten durchgeführt, um die elektronischen und optischen Eigenschaften von Materialien auf Graphenbasis zu untersuchen. Der Ansatz wird in drei Stufen beschrieben. Mit GW-Berechnungen werden die Eigenschaften von Materialien auf Graphenbasis genau untersucht, einschließlich Bulk-Graphen, Nanobändern, funktionalisierten Sessel-Orbändern an Kanten und Oberflächen, wasserstoffgesättigten Sesselbändern, Josephson-Effekt in Graphen-SNS-Übergängen mit einem einzigen lokalisierten Defekt und Sesselband-Skalierungseigenschaften. ⓘ

Spin-Transport

Graphen gilt als ideales Material für die Spintronik, da es nur eine geringe Spin-Bahn-Wechselwirkung und so gut wie keine magnetischen Kernmomente in Kohlenstoff (sowie eine schwache Hyperfeinwechselwirkung) aufweist. Die Injektion und der Nachweis von elektrischem Spinstrom wurden bis zu Raumtemperatur nachgewiesen. Es wurde eine Spinkohärenzlänge von über 1 Mikrometer bei Raumtemperatur beobachtet, und die Steuerung der Polarität des Spinstroms mit einem elektrischen Gate wurde bei niedriger Temperatur beobachtet. ⓘ

Magnetische Eigenschaften

Starke Magnetfelder

Der Quanten-Hall-Effekt von Graphen in Magnetfeldern von mehr als 10 Tesla zeigt weitere interessante Eigenschaften. Zusätzliche Plateaus der Hall-Leitfähigkeit bei $\sigma _{xy}=\nu e^{2}/h$ mit $\nu =0,\pm {1},\pm {4}$ werden beobachtet. Auch die Beobachtung eines Plateaus bei $\nu =3$ und der fraktionierte Quanten-Hall-Effekt bei $\nu =1/3$ wurden berichtet. ⓘ

Diese Beobachtungen bei $\nu =0,\pm 1,\pm 3,\pm 4$ deuten darauf hin, dass die vierfache Entartung (zwei Tal- und zwei Spin-Freiheitsgrade) der Landau-Energieniveaus teilweise oder vollständig aufgehoben ist. Eine Hypothese ist, dass die magnetische Katalyse der Symmetriebrechung für die Aufhebung der Entartung verantwortlich ist. ⓘ

Spintronische und magnetische Eigenschaften können in Graphen gleichzeitig vorhanden sein. Graphen-Nanomeshes mit geringen Defekten, die mit einer nicht-lithografischen Methode hergestellt wurden, weisen sogar bei Raumtemperatur Ferromagnetismus mit großer Amplitude auf. Darüber hinaus wird ein Spin-Pumping-Effekt für Felder gefunden, die parallel zu den Ebenen von ferromagnetischen Nanomeshes mit wenigen Schichten angelegt werden, während eine Magnetowiderstands-Hystereseschleife bei senkrechten Feldern beobachtet wird. ⓘ

Magnetische Substrate

Im Jahr 2014 magnetisierten Forscher Graphen, indem sie es auf eine atomar glatte Schicht aus magnetischem Yttrium-Eisen-Granat legten. Die elektronischen Eigenschaften von Graphen wurden dadurch nicht beeinträchtigt. Bei früheren Ansätzen wurde Graphen mit anderen Substanzen dotiert. Die Anwesenheit des Dotierstoffs wirkte sich negativ auf die elektronischen Eigenschaften aus. ⓘ

Thermische Leitfähigkeit

Der Wärmetransport in Graphen ist ein aktives Forschungsgebiet, das aufgrund des Potenzials für Wärmemanagementanwendungen Aufmerksamkeit erregt hat. In Anlehnung an die Vorhersagen für Graphen und verwandte Kohlenstoff-Nanoröhren ergaben frühe Messungen der Wärmeleitfähigkeit von suspendiertem Graphen eine außergewöhnlich hohe Wärmeleitfähigkeit von bis zu 5300 W⋅m-1⋅K-1, verglichen mit der Wärmeleitfähigkeit von pyrolytischem Graphit von etwa 2000 W⋅m-1⋅K-1 bei Raumtemperatur. Spätere Studien, die hauptsächlich mit besser skalierbarem, aber stärker defektem Graphen durchgeführt wurden, das durch chemische Gasphasenabscheidung gewonnen wurde, waren jedoch nicht in der Lage, solch hohe Wärmeleitfähigkeitsmessungen zu reproduzieren, und ergaben eine große Bandbreite von Wärmeleitfähigkeiten zwischen 1500 und 2500 W⋅m-1⋅K-1 für suspendiertes einlagiges Graphen. Die große Bandbreite der gemeldeten Wärmeleitfähigkeit kann durch große Messunsicherheiten sowie durch Schwankungen in der Graphenqualität und den Verarbeitungsbedingungen verursacht werden. Darüber hinaus ist bekannt, dass die Wärmeleitfähigkeit von einlagigem Graphen, das auf einem amorphen Material aufgebracht ist, bei Raumtemperatur aufgrund der Streuung der Graphen-Gitterwellen durch das Substrat auf etwa 500 - 600 W⋅m-1⋅K-1 sinkt und bei in amorphem Oxid eingeschlossenem Graphen mit wenigen Lagen sogar noch niedriger sein kann. Ebenso können polymere Rückstände zu einer ähnlichen Abnahme der Wärmeleitfähigkeit von suspendiertem Graphen auf etwa 500 - 600 W⋅m-1⋅K-1 für zweischichtiges Graphen beitragen. ⓘ

Es wurde vermutet, dass die Isotopenzusammensetzung, das Verhältnis von ¹²C zu ¹³C, einen erheblichen Einfluss auf die Wärmeleitfähigkeit hat. So hat beispielsweise isotopenreines ¹²C-Graphen eine höhere Wärmeleitfähigkeit als ein 50:50-Isotopenverhältnis oder das natürlich vorkommende 99:1-Verhältnis. Mit Hilfe des Wiedemann-Franz-Gesetzes lässt sich zeigen, dass die Wärmeleitung phononendominiert ist. Bei einem Graphenstreifen mit Gates kann jedoch eine angelegte Gatespannung, die eine Fermi-Energieverschiebung verursacht, die viel größer als kBT ist, dazu führen, dass der elektronische Beitrag zunimmt und bei niedrigen Temperaturen über den Phononenbeitrag dominiert. Die ballistische Wärmeleitfähigkeit von Graphen ist isotrop. ⓘ

Das Potenzial für diese hohe Leitfähigkeit wird deutlich, wenn man Graphit betrachtet, eine 3D-Version von Graphen mit einer Wärmeleitfähigkeit in der Basalebene von über 1000 W⋅m-1⋅K-1 (vergleichbar mit Diamant). Bei Graphit ist die Wärmeleitfähigkeit in der c-Achse (außerhalb der Ebene) aufgrund der schwachen Bindungskräfte zwischen den Basalebenen sowie des größeren Gitterabstands um einen Faktor von ~100 geringer. Darüber hinaus wird gezeigt, dass die ballistische Wärmeleitfähigkeit von Graphen die untere Grenze der ballistischen Wärmeleitfähigkeit pro Umfangseinheit von Kohlenstoffnanoröhren darstellt. ⓘ

Trotz seiner 2-D-Natur hat Graphen 3 akustische Phononmoden. Die beiden Modi innerhalb der Ebene (LA, TA) haben eine lineare Dispersionsbeziehung, während der Modus außerhalb der Ebene (ZA) eine quadratische Dispersionsbeziehung aufweist. Aus diesem Grund wird der T²-abhängige Beitrag der linearen Moden zur Wärmeleitfähigkeit bei niedrigen Temperaturen durch den T1,5-Beitrag der Mode außerhalb der Ebene dominiert. Einige Graphen-Phononenbänder weisen negative Grüneisen-Parameter auf. Bei niedrigen Temperaturen (wo die meisten optischen Moden mit positiven Grüneisen-Parametern noch nicht angeregt sind) ist der Beitrag der negativen Grüneisen-Parameter dominant und der Wärmeausdehnungskoeffizient (der direkt proportional zu den Grüneisen-Parametern ist) negativ. Die niedrigsten negativen Grüneisen-Parameter entsprechen den niedrigsten transversalen akustischen ZA-Moden. Die Phononenfrequenzen für solche Moden nehmen mit dem in der Ebene liegenden Gitterparameter zu, da sich die Atome in der Schicht bei der Streckung weniger frei in z-Richtung bewegen können. Dies ist vergleichbar mit dem Verhalten einer Saite, die, wenn sie gedehnt wird, Schwingungen mit kleinerer Amplitude und höherer Frequenz aufweist. Dieses Phänomen, das als "Membraneffekt" bezeichnet wird, wurde 1952 von Lifshitz vorhergesagt. ⓘ

2016 wurde ein sogenanntes hydrodynamisches („flüssigkeitsähnliches“) Verhalten der Elektronen im Graphen festgestellt, jedoch mit außergewöhnlichen Eigenschaften: So ist z. B. das sonst für metallische Systeme gültige Wiedemann-Franz-Gesetz, das das Verhältnis von thermischer und elektrischer Leitfähigkeit, geteilt durch die Kelvintemperatur T, bei metallischen Systemen gleich einer universellen Konstante ist, bei Graphen verletzt, indem bei Annäherung der Fermi-Energie an den Überschneidungspunkt die Wärmeleitfähigkeit viel zu groß wird (der spezifische Wärmewiderstand also viel zu klein). Darüber hinaus beobachtet man in dieser Elektronenflüssigkeit (Fachausdruck: Dirac-Flüssigkeit) eine ungewöhnliche Tendenz zur Ausbildung von Wirbelstrukturen. ⓘ

Mechanische

Die (zweidimensionale) Dichte von Graphen beträgt 0,763 mg pro Quadratmeter. ⓘ

Graphen ist das stärkste jemals getestete Material mit einer intrinsischen Zugfestigkeit von 130 GPa (19.000.000 psi) (mit einer repräsentativen technischen Zugfestigkeit von ~50-60 GPa für das Strecken von großflächigem, freistehendem Graphen) und einem Elastizitätsmodul (Steifigkeit) von fast 1 TPa (150.000.000 psi). In der Nobelankündigung wurde dies mit der Aussage illustriert, dass eine 1 m² große Graphen-Hängematte eine 4 kg schwere Katze tragen würde, aber nur so viel wiegt wie ein Schnurrhaar der Katze, nämlich 0,77 mg (etwa 0,001 % des Gewichts von 1 m² Papier). ⓘ

Die Graphen-Monolage wurde mit vernachlässigbarer Dehnung in einem großen Winkel gebogen, was die mechanische Robustheit der zweidimensionalen Kohlenstoff-Nanostruktur zeigt. Selbst bei extremer Verformung kann die ausgezeichnete Ladungsträgerbeweglichkeit in der Graphen-Monolage erhalten bleiben. ⓘ

Die Federkonstante der aufgehängten Graphenblätter wurde mit einem Rasterkraftmikroskop (AFM) gemessen. Die Graphenblätter wurden über SiO
₂-Hohlräumen aufgehängt, wo eine AFM-Spitze verwendet wurde, um eine Spannung auf das Blatt auszuüben, um seine mechanischen Eigenschaften zu testen. Die Federkonstante lag im Bereich von 1-5 N/m und die Steifigkeit bei 0,5 TPa, was sich von derjenigen von Bulk-Graphit unterscheidet. Diese intrinsischen Eigenschaften könnten zu Anwendungen wie NEMS als Drucksensoren und Resonatoren führen. Aufgrund der großen Oberflächenenergie und der Duktilität außerhalb der Ebene sind flache Graphenblätter instabil in Bezug auf das Scrollen, d. h. das Biegen in eine zylindrische Form, was ihren energieärmeren Zustand darstellt. ⓘ

Wie bei allen Materialien unterliegen auch die Graphenbereiche thermischen und Quantenfluktuationen in der relativen Verschiebung. Obwohl die Amplitude dieser Fluktuationen in 3D-Strukturen begrenzt ist (selbst im Grenzfall unendlicher Größe), zeigt das Mermin-Wagner-Theorem, dass die Amplitude langwelliger Fluktuationen logarithmisch mit dem Maßstab einer 2D-Struktur wächst und daher in Strukturen unendlicher Größe unbegrenzt sein würde. Die lokale Verformung und die elastische Dehnung werden durch diese weiträumige Divergenz in der relativen Verschiebung vernachlässigbar beeinflusst. Man geht davon aus, dass sich eine ausreichend große 2D-Struktur bei fehlender Seitenspannung verbiegt und zerknittert, um eine fluktuierende 3D-Struktur zu bilden. Forscher haben Wellen in schwebenden Graphenschichten beobachtet, und es wurde vorgeschlagen, dass die Wellen durch thermische Fluktuationen im Material verursacht werden. Als Folge dieser dynamischen Verformungen ist es fraglich, ob Graphen wirklich eine 2D-Struktur ist. Kürzlich wurde gezeigt, dass diese Wellen, wenn sie durch die Einführung von Leerstellen verstärkt werden, dem Graphen eine negative Poissonzahl verleihen können, was zum dünnsten bisher bekannten auxetischen Material führt. ⓘ

Graphen-Nanoblätter wurden durch ein Beschichtungsverfahren in eine Ni-Matrix eingearbeitet, um Ni-Graphen-Verbundwerkstoffe auf einem Zielsubstrat zu bilden. Die Verbesserung der mechanischen Eigenschaften der Verbundwerkstoffe wird auf die hohe Wechselwirkung zwischen Ni und Graphen und die Verhinderung des Versetzungsgleitens in der Ni-Matrix durch das Graphen zurückgeführt. ⓘ

Bruchzähigkeit

2014 wiesen Forscher der Rice University und des Georgia Institute of Technology darauf hin, dass Graphen trotz seiner Festigkeit auch relativ spröde ist, mit einer Bruchzähigkeit von etwa 4 MPa√m. Dies deutet darauf hin, dass unvollkommenes Graphen wahrscheinlich wie keramische Werkstoffe spröde bricht, im Gegensatz zu vielen metallischen Werkstoffen, deren Bruchzähigkeit eher im Bereich von 15-50 MPa√m liegt. Später im Jahr 2014 gab das Rice-Team bekannt, dass Graphen die Kraft eines Aufpralls besser verteilen kann als jedes andere bekannte Material, nämlich zehnmal stärker als Stahl pro Gewichtseinheit. Die Kraft wurde mit einer Geschwindigkeit von 22,2 Kilometern pro Sekunde übertragen (13,8 mi/s). ⓘ

Polykristallines Graphen

Für die Herstellung von Graphen in großem Maßstab, das für Bauelemente benötigt wird, wurden verschiedene Methoden entwickelt, insbesondere die chemische Gasphasenabscheidung (CVD), die im folgenden Abschnitt beschrieben wird. Bei solchen Verfahren wird häufig polykristallines Graphen synthetisiert. Die mechanischen Eigenschaften von polykristallinem Graphen werden durch die Art der im System vorhandenen Defekte, wie z. B. Korngrenzen (GB) und Leerstellen, und die durchschnittliche Korngröße beeinflusst. Wie sich die mechanischen Eigenschaften in Abhängigkeit von solchen Defekten verändern, wurde von Forschern theoretisch und experimentell untersucht. ⓘ

Graphen-Korngrenzen enthalten typischerweise Heptagon-Fünfeck-Paare. Die Anordnung solcher Defekte hängt davon ab, ob die GB in Zick-Zack- oder in Sesselrichtung angeordnet sind. Außerdem hängt sie vom Neigungswinkel der GB ab. Im Jahr 2010 haben Forscher der Brown University rechnerisch vorausgesagt, dass mit zunehmendem Neigungswinkel auch die Festigkeit der Korngrenzen zunimmt. Sie zeigten, dass das schwächste Glied in der Korngrenze an den kritischen Bindungen der Heptagonringe liegt. Wenn der Korngrenzenwinkel zunimmt, nimmt die Spannung in diesen Heptagonringen ab, so dass die Korngrenze stärker ist als bei niedrigeren Winkeln. Sie schlugen vor, dass die Festigkeit der Korngrenze bei einem ausreichend großen Winkel der Korngrenze in der Tat mit der von reinem Graphen vergleichbar ist. Im Jahr 2012 wurde außerdem gezeigt, dass die Festigkeit je nach der detaillierten Anordnung der Defekte zunehmen oder abnehmen kann. Diese Vorhersagen wurden seitdem durch experimentelle Beweise untermauert. In einer Studie aus dem Jahr 2013 unter der Leitung der Gruppe von James Hone untersuchten die Forscher die elastische Steifigkeit und Festigkeit von CVD-gewachsenem Graphen durch eine Kombination aus Nanoindentation und hochauflösendem TEM. Sie fanden heraus, dass die elastische Steifigkeit identisch und die Festigkeit nur geringfügig niedriger ist als bei ursprünglichem Graphen. Im selben Jahr untersuchten Forscher der UC Berkeley und der UCLA bi-kristallines Graphen mit TEM und AFM. Sie fanden heraus, dass die Stärke der Korngrenzen tatsächlich mit dem Neigungswinkel zunimmt. ⓘ

Obwohl das Vorhandensein von Leerstellen nicht nur in polykristallinem Graphen vorkommt, können Leerstellen erhebliche Auswirkungen auf die Festigkeit von Graphen haben. Es herrscht allgemeiner Konsens darüber, dass die Festigkeit mit zunehmender Dichte der Leerstellen abnimmt. Tatsächlich haben verschiedene Studien gezeigt, dass sich die Festigkeit von Graphen mit einer ausreichend geringen Dichte an Leerstellen nicht wesentlich von derjenigen von reinem Graphen unterscheidet. Andererseits kann eine hohe Dichte von Leerstellen die Festigkeit von Graphen stark verringern. ⓘ

Im Vergleich zu den recht gut verstandenen Auswirkungen von Korngrenzen und Leerstellen auf die mechanischen Eigenschaften von Graphen gibt es keinen klaren Konsens über die allgemeinen Auswirkungen der durchschnittlichen Korngröße auf die Festigkeit von polykristallinem Graphen. In der Tat haben drei bemerkenswerte theoretische/rechnerische Studien zu diesem Thema zu drei unterschiedlichen Schlussfolgerungen geführt. Erstens untersuchten Kotakoski und Myer im Jahr 2012 die mechanischen Eigenschaften von polykristallinem Graphen mit einem "realistischen atomistischen Modell" unter Verwendung von Molekulardynamiksimulationen (MD). Um den Wachstumsmechanismus der CVD nachzuahmen, wählten sie zunächst zufällig Keimstellen aus, die mindestens 5A (willkürlich gewählt) von anderen Stellen entfernt sind. Aus diesen Keimstellen wurde polykristallines Graphen erzeugt, das anschließend bei 3000 K getempert und dann abgeschreckt wurde. Auf der Grundlage dieses Modells stellten sie fest, dass Risse an den Korngrenzen entstehen, die Korngröße jedoch keinen wesentlichen Einfluss auf die Festigkeit hat. Zweitens untersuchten Z. Song et al. im Jahr 2013 mit Hilfe von MD-Simulationen die mechanischen Eigenschaften von polykristallinem Graphen mit gleich großen hexagonalen Körnern. Die hexagonalen Körner waren in verschiedenen Gitterrichtungen ausgerichtet, und die GBs bestanden nur aus heptagonalen, pentagonalen und hexagonalen Kohlenstoffringen. Die Motivation für dieses Modell war, dass ähnliche Systeme experimentell in Graphenflocken beobachtet worden waren, die auf der Oberfläche von flüssigem Kupfer gewachsen waren. Sie stellten außerdem fest, dass Risse typischerweise an den Dreifachübergängen entstehen und dass die Streckgrenze von Graphen mit abnehmender Korngröße zunimmt. Auf der Grundlage dieser Erkenntnis schlugen sie vor, dass polykristallines Graphen einer Pseudo-Hall-Petch-Beziehung folgt. Drittens untersuchten Z. D. Sha et al. im Jahr 2013 die Auswirkungen der Korngröße auf die Eigenschaften von polykristallinem Graphen, indem sie die Kornfelder mit Hilfe der Voronoi-Konstruktion modellierten. Die GBs in diesem Modell bestanden aus Heptagon, Pentagon und Hexagon sowie aus Quadraten, Achtecken und Leerstellen. Durch MD-Simulationen fanden sie im Gegensatz zur vorgenannten Studie eine umgekehrte Hall-Petch-Beziehung, bei der die Festigkeit von Graphen mit zunehmender Korngröße steigt. Experimentelle Beobachtungen und andere theoretische Vorhersagen führten ebenfalls zu unterschiedlichen Schlussfolgerungen, ähnlich wie die drei oben genannten. Diese Diskrepanzen zeigen die Komplexität der Auswirkungen, die die Korngröße, die Anordnung der Defekte und die Art der Defekte auf die mechanischen Eigenschaften von polykristallinem Graphen haben. ⓘ

Chemisch

Graphen hat eine theoretische spezifische Oberfläche (SSA) von 2630 m²/g. Dies ist viel größer als die bisher für Ruß (in der Regel kleiner als 900 m²/g) oder für Kohlenstoff-Nanoröhren (CNT) gemeldete Fläche von ≈100 bis 1000 m²/g und ähnelt der von Aktivkohle. Graphen ist die einzige Form von Kohlenstoff (oder festem Material), bei der jedes Atom von zwei Seiten für eine chemische Reaktion zur Verfügung steht (aufgrund der 2D-Struktur). Die Atome an den Rändern eines Graphenblattes haben eine besondere chemische Reaktionsfähigkeit. Graphen hat den höchsten Anteil an Randatomen aller Allotrope. Defekte innerhalb eines Blatts erhöhen seine chemische Reaktivität. Die Anfangstemperatur der Reaktion zwischen der Basalebene von einlagigem Graphen und Sauerstoffgas liegt unter 260 °C (530 K). Graphen verbrennt bei sehr niedrigen Temperaturen (z. B. 350 °C (620 K)). Graphen wird üblicherweise mit sauerstoff- und stickstoffhaltigen funktionellen Gruppen modifiziert und mittels Infrarotspektroskopie und Röntgenphotoelektronenspektroskopie analysiert. Die Bestimmung der Strukturen von Graphen mit sauerstoff- und stickstoffhaltigen funktionellen Gruppen erfordert jedoch, dass die Strukturen gut kontrolliert werden. ⓘ

Im Jahr 2013 berichteten Physiker der Stanford University, dass einlagiges Graphen hundertmal reaktionsfähiger ist als dickere mehrlagige Schichten. ⓘ

Graphen kann Löcher in seinen Schichten selbst reparieren, wenn es kohlenstoffhaltigen Molekülen, wie z. B. Kohlenwasserstoffen, ausgesetzt wird. Werden sie mit reinen Kohlenstoffatomen beschossen, ordnen sich die Atome perfekt zu Sechsecken an und füllen die Löcher vollständig aus. ⓘ

Biologisch

Trotz der vielversprechenden Ergebnisse verschiedener Zellstudien und Proof-of-Concept-Studien ist die vollständige Biokompatibilität von Materialien auf Graphenbasis noch nicht vollständig geklärt. Verschiedene Zelllinien reagieren unterschiedlich, wenn sie Graphen ausgesetzt werden, und es hat sich gezeigt, dass die laterale Größe der Graphenflocken, die Form und die Oberflächenchemie bei ein und derselben Zelllinie unterschiedliche biologische Reaktionen hervorrufen können. ⓘ

Es gibt Hinweise darauf, dass Graphen ein vielversprechendes Material für die Interaktion mit Nervenzellen ist; Studien an kultivierten Nervenzellen zeigen jedoch nur begrenzten Erfolg. ⓘ

Graphen hat auch einen gewissen Nutzen in der Osteogenik. Forscher des Graphen-Forschungszentrums an der National University of Singapore (NUS) entdeckten 2011 die Fähigkeit von Graphen, die osteogene Differenzierung menschlicher mesenchymaler Stammzellen ohne biochemische Induktoren zu beschleunigen. ⓘ

Graphen kann in Biosensoren verwendet werden; 2015 zeigten Forscher, dass ein Sensor auf Graphenbasis zum Nachweis eines Biomarkers für das Krebsrisiko verwendet werden kann. Durch die Verwendung von epitaktischem Graphen auf Siliziumkarbid konnten sie insbesondere 8-Hydroxydeoxyguanosin (8-OHdG), einen Biomarker für DNA-Schäden, nachweisen. ⓘ

Trägersubstrat

Die elektronischen Eigenschaften von Graphen können durch das Trägersubstrat erheblich beeinflusst werden. Es wurden Untersuchungen von Graphen-Monolagen auf sauberen und Wasserstoff(H)-passivierten Silizium(100)-Oberflächen (Si(100)/H) durchgeführt. Die Si(100)/H-Oberfläche stört die elektronischen Eigenschaften von Graphen nicht, während die Wechselwirkung zwischen der reinen Si(100)-Oberfläche und Graphen die elektronischen Zustände von Graphen erheblich verändert. Dieser Effekt resultiert aus der kovalenten Bindung zwischen C- und Oberflächen-Si-Atomen, die das π-Orbitale-Netzwerk der Graphenschicht verändert. Die lokale Zustandsdichte zeigt, dass die gebundenen C- und Si-Oberflächenzustände in der Nähe der Fermi-Energie stark gestört sind. ⓘ

Steifigkeit und Temperaturabhängigkeit

Graphen ist in Schichtrichtung extrem steif, weil die sp²-Bindung zwischen benachbarten Atomen von der Stärke her mit der sp³-Bindung von Diamant vergleichbar ist. Dementsprechend erwartet man generell – und das entspricht dem Experiment –, dass die für die Anwendung interessanten Eigenschaften von Graphen nicht nur am absoluten Temperaturnullpunkt gelten, d. h. bei −273,15 °C, sondern bei Zimmertemperatur gültig bleiben. ⓘ

Eine solche Eigenschaft ist die Thermoelektrizität: Ein Temperaturgradient in Graphen-Ebenen verursacht eine elektrische Feldstärke aufgrund einer Entkopplung der Temperatur der Elektronen von der des Gitters. Elektrische Spannung bei Beleuchtung von Graphen war schon früher beobachtet worden, aber als Ursache wurde die Photovoltaik vermutet. Dass die Entkopplung noch bei Zimmertemperatur beobachtet werden kann, liegt an der Steifigkeit des Gitters: Die elementaren Schwingungsanregungen des Gitters (Phononen) sind so hochenergetisch, dass die Elektronen selten ein solches Phonon erzeugen. ⓘ

Elastisches Verhalten und Pseudo-Magnetfeld

Im Juli 2010 wurde in einer Veröffentlichung in der amerikanischen Wissenschaftszeitschrift Science von extrem starken Pseudo-Magnetfeldern berichtet. Durch elastische Verformung wurden in Graphen winzige dreieckige Bläschen von 4 Nanometer bis 10 Nanometer Größe erzeugt, in denen sich die Elektronen so bewegten, als würde ein etwa 300 Tesla starkes Magnetfeld auf sie einwirken. Es zeigte sich, dass der beobachtete Effekt, im Gegensatz zur Auswirkung eines echten Magnetfeldes, den eigentlichen Spin des Elektrons nicht beeinflusst, sondern dass stattdessen der gerade erwähnte Pseudo-Spin beeinflusst wird, der mit der Existenz zweier verschiedener äquivalenter Basis-Atome in der Bienenwaben-Struktur zusammenhängt. Dieser Pseudospin hat eine ähnliche Wechselwirkung mit dem Pseudo-Magnetfeld wie echte Spins mit echten Magnetfeldern, weil auch diese „Zwei-Niveau-Systeme“ generieren. Die Experimente um den so erzeugten „Pseudo-Quanten-Hall-Effekt“ basierten auf theoretischen Vorhersagen, die damit bestätigt wurden. ⓘ

Spinströme

Im April 2011 haben A. Geim und Mitarbeiter einen Artikel veröffentlicht, in dem sie starke Spinströme und strominduzierten Magnetismus in der Nähe des Dirac-Punktes beschreiben, d. h. in der Nähe des Treffpunktes von Leitungsband und Valenzband. Das eröffnet die Aussicht auf Anwendungen in der Spintronik. ⓘ

Chemische Funktionalisierung und EU-Großprojekt

2013 hat die EU ein neues Großprojekt („flagship project“) über Graphene angekündigt, an dem Forscher in vielen Mitgliedstaaten zusammenarbeiten werden, vor allem Physiker und Chemiker. Man kann z. B. Doppelbindungen des Graphens – jede zweite Bindung ist eine solche – „aufbrechen“ und durch zwei Einzelbindungen ersetzen, an die man dann verschiedene organische Moleküle anheftet: Dadurch kann man die Eigenschaften des Systems gezielt beeinflussen. ⓘ

Bildet

Einlagige Blätter

Im Jahr 2013 stellte eine Gruppe polnischer Wissenschaftler eine Produktionsanlage vor, die die Herstellung von kontinuierlichen Monolagen ermöglicht. Der Prozess basiert auf dem Wachstum von Graphen auf einer flüssigen Metallmatrix. Das Produkt dieses Prozesses wurde als hochfestes metallurgisches Graphen bezeichnet. In einer neuen Studie, die in Nature veröffentlicht wurde, haben die Forscher eine einlagige Graphenelektrode und eine neuartige oberflächensensitive nichtlineare Spektroskopietechnik verwendet, um die oberste Wasserschicht an der elektrochemisch geladenen Oberfläche zu untersuchen. Sie fanden heraus, dass die Reaktion des Grenzflächenwassers auf ein angelegtes elektrisches Feld asymmetrisch in Bezug auf die Art des angelegten Feldes ist. ⓘ

Zweischicht-Graphen

Zweischichtiges Graphen zeigt den anomalen Quanten-Hall-Effekt, eine abstimmbare Bandlücke und das Potenzial für exzitonische Kondensation, was es zu einem vielversprechenden Kandidaten für optoelektronische und nanoelektronische Anwendungen macht. Zweischichtiges Graphen kommt typischerweise entweder in verdrehten Konfigurationen vor, bei denen die beiden Schichten relativ zueinander gedreht sind, oder in graphitischen Bernal-Stapelkonfigurationen, bei denen die Hälfte der Atome in einer Schicht auf der Hälfte der Atome in der anderen Schicht liegt. Die Anordnung und Ausrichtung der Stapelung bestimmen die optischen und elektronischen Eigenschaften von zweischichtigem Graphen. ⓘ

Eine Möglichkeit zur Synthese von zweischichtigem Graphen ist die chemische Gasphasenabscheidung, mit der große zweischichtige Bereiche erzeugt werden können, die fast ausschließlich einer Bernal-Stapelgeometrie entsprechen. ⓘ

Es hat sich gezeigt, dass die beiden Graphenschichten erheblichen Dehnungen oder Dotierungsfehlanpassungen standhalten können, was letztlich zu ihrer Exfoliation führen sollte. ⓘ

Turbostratisches Graphen

Turbostratisches Graphen weist eine schwache Kopplung zwischen den Schichten auf, und der Abstand ist im Vergleich zu Bernal-gestapeltem mehrlagigem Graphen größer. Durch die Rotationsverschiebung bleibt die elektronische 2D-Struktur erhalten, wie die Raman-Spektroskopie bestätigt. Der D-Peak ist sehr schwach, während die 2D- und G-Peaks deutlich sichtbar bleiben. Eine Besonderheit ist, dass das I_2D/IG-Verhältnis 10 übersteigen kann. Am wichtigsten ist jedoch, dass der M-Peak, der von der AB-Stapelung herrührt, nicht vorhanden ist, während die TS₁- und TS₂-Moden im Raman-Spektrum sichtbar sind. Das Material entsteht durch die Umwandlung von nicht-graphenhaltigem Kohlenstoff in graphenhaltigen Kohlenstoff, ohne dass genügend Energie zur Verfügung steht, um die Reorganisation benachbarter Graphenschichten zu kristallinen graphitischen Strukturen zu ermöglichen. ⓘ

Graphen-Übergitter

Periodisch gestapeltes Graphen und seine isolierende Isomorphie stellen ein faszinierendes Strukturelement für die Realisierung hochfunktionaler Übergitter auf atomarer Ebene dar, die Möglichkeiten für die Entwicklung nanoelektronischer und photonischer Bauelemente bieten. Durch Stapeln von Graphen und seinen verwandten Formen lassen sich verschiedene Arten von Übergittern herstellen. Es hat sich gezeigt, dass das Energieband in schichtgestapelten Übergittern empfindlicher auf die Barrierenbreite reagiert als in herkömmlichen III-V-Halbleiterübergittern. Wenn in jeder Periode mehr als eine Atomschicht zur Barriere hinzugefügt wird, kann die Kopplung elektronischer Wellenfunktionen in benachbarten Potenzialtöpfen erheblich reduziert werden, was zu einer Degeneration kontinuierlicher Teilbänder in quantisierte Energieniveaus führt. Wenn man die Breite der Potentialtöpfe variiert, verhalten sich die Energieniveaus in den Potentialtöpfen entlang der L-M-Richtung deutlich anders als in der K-H-Richtung. ⓘ

Ein Übergitter entspricht einer periodischen oder quasi-periodischen Anordnung verschiedener Materialien und kann durch eine Übergitterperiode beschrieben werden, die dem System eine neue Translationssymmetrie verleiht, die sich auf die Phononendispersion und damit auf die Wärmetransporteigenschaften auswirkt. Kürzlich wurden einheitliche einlagige Graphen-HBN-Strukturen durch lithografische Strukturierung in Verbindung mit chemischer Gasphasenabscheidung (CVD) erfolgreich synthetisiert. Darüber hinaus sind Übergitter aus Graphen und HBN ideale Modellsysteme für die Realisierung und das Verständnis des kohärenten (wellenartigen) und inkohärenten (teilchenartigen) Phononentransports. ⓘ

Graphen-Nanobänder

Bezeichnungen für Graphen-Kantentopologien ⓘ

GNR Elektronische Bandstruktur von Graphenstreifen unterschiedlicher Breite in Zick-Zack-Ausrichtung. Tight-binding-Berechnungen zeigen, dass sie alle metallisch sind. ⓘ

GNR Elektronische Bandstruktur von Graphenstreifen unterschiedlicher Breite in der Armchair-Orientierung. Tight-binding-Berechnungen zeigen, dass sie je nach Breite (Chiralität) halbleitend oder metallisch sind. ⓘ

Graphen-Nanobänder ("Nanostreifen" in der "Zick-Zack"-Orientierung) zeigen bei niedrigen Temperaturen spinpolarisierte metallische Kantenströme, was auch Anwendungen im neuen Bereich der Spintronik nahelegt. (In der "Armchair"-Orientierung verhalten sich die Kanten wie Halbleiter). ⓘ

Graphen-Quantenpunkte

Ein Graphen-Quantenpunkt (GQD) ist ein Graphenfragment mit einer Größe von weniger als 100 nm. Die Eigenschaften von GQDs unterscheiden sich aufgrund der Quanteneinschränkungseffekte, die erst bei einer Größe von weniger als 100 nm sichtbar werden, von denen von "normalem" Graphen. ⓘ

Graphenoxid

Graphenoxid wird in der Regel durch chemische Exfoliation von Graphit hergestellt. Ein besonders beliebtes Verfahren ist die verbesserte Hummer-Methode. Bei der Papierherstellung mit dispergiertem, oxidiertem und chemisch behandeltem Graphit in Wasser bilden die einlagigen Flocken eine einzige Schicht und gehen starke Bindungen ein. Diese Blätter, Graphenoxidpapier genannt, haben einen gemessenen Zugmodul von 32 GPa. Die chemische Eigenschaft von Graphitoxid hängt mit den funktionellen Gruppen zusammen, die an die Graphenblätter gebunden sind. Diese können den Polymerisationspfad und ähnliche chemische Prozesse verändern. Graphenoxid-Flocken in Polymeren weisen verbesserte photoleitende Eigenschaften auf. Graphen ist normalerweise hydrophob und undurchlässig für alle Gase und Flüssigkeiten (vakuumdicht). Wenn es jedoch zu einer Kapillarmembran auf Graphenoxidbasis geformt wird, fließen sowohl flüssiges Wasser als auch Wasserdampf so schnell hindurch, als ob die Membran nicht vorhanden wäre. ⓘ

Chemische Modifikation

Foto von einlagigem Graphenoxid, das einer chemischen Behandlung bei hoher Temperatur unterzogen wird, was zu einer Faltung der Blätter und zum Verlust der Carboxylfunktionalität führt, oder das durch eine Carbodiimid-Behandlung bei Raumtemperatur zu sternförmigen Clustern kollabiert.

Lösliche Graphenfragmente können im Labor durch chemische Modifikation von Graphit hergestellt werden. Zunächst wird mikrokristalliner Graphit mit einem Säuregemisch aus Schwefelsäure und Salpetersäure behandelt. Durch eine Reihe von Oxidations- und Exfoliationsschritten entstehen kleine Graphenplättchen mit Carboxylgruppen an ihren Rändern. Diese werden durch Behandlung mit Thionylchlorid in Säurechloridgruppen umgewandelt; anschließend werden sie durch Behandlung mit Octadecylamin in das entsprechende Graphenamid umgewandelt. Das resultierende Material (kreisförmige Graphenschichten von 5,3 Å oder 5,3×10-10 m Dicke) ist in Tetrahydrofuran, Tetrachlormethan und Dichlorethan löslich. ⓘ

Das Rückfließenlassen von einlagigem Graphenoxid (SLGO) in Lösungsmitteln führt zu einer Verkleinerung und Faltung der einzelnen Schichten sowie zum Verlust der Carboxylgruppenfunktionalität um bis zu 20 %, was auf thermische Instabilitäten der SLGO-Schichten in Abhängigkeit von der Herstellungsmethode hinweist. Bei Verwendung von Thionylchlorid entstehen Acylchloridgruppen, die dann aliphatische und aromatische Amide mit einer Reaktivitätsumsetzung von etwa 70-80 % bilden können. ⓘ

Boehm-Titrationsergebnisse für verschiedene chemische Reaktionen von einlagigem Graphenoxid, die die Reaktivität der Carboxylgruppen und die daraus resultierende Stabilität der SLGO-Folien nach der Behandlung zeigen. ⓘ

Hydrazinrückfluss wird üblicherweise für die Reduktion von SLGO zu SLG(R) verwendet, aber Titrationen zeigen, dass nur etwa 20-30 % der Carboxylgruppen verloren gehen, so dass eine beträchtliche Anzahl für chemische Bindungen zur Verfügung steht. Die Analyse von SLG(R), das auf diesem Weg erzeugt wurde, zeigt, dass das System instabil ist, und die Verwendung eines Rührens bei Raumtemperatur mit HCl (< 1,0 M) führt zu einem Verlust von etwa 60 % der COOH-Funktionalität. Die Behandlung von SLGO mit Carbodiimiden bei Raumtemperatur führt zum Zusammenbruch der einzelnen Blätter zu sternförmigen Clustern, die anschließend eine schlechte Reaktivität mit Aminen aufweisen (ca. 3-5 % Umwandlung des Zwischenprodukts in das endgültige Amid). Es ist offensichtlich, dass die herkömmliche chemische Behandlung von Carboxylgruppen auf SLGO zu morphologischen Veränderungen der einzelnen Schichten führt, die eine Verringerung der chemischen Reaktivität zur Folge haben, was ihre Verwendung bei der Synthese von Verbundwerkstoffen möglicherweise einschränkt. Daher wurden verschiedene Arten chemischer Reaktionen erforscht. SLGO wurde auch mit Polyallylamin gepfropft, das durch Epoxidgruppen vernetzt ist. Wenn sie in Graphenoxidpapier gefiltert werden, weisen diese Verbundstoffe eine höhere Steifigkeit und Festigkeit auf als unmodifiziertes Graphenoxidpapier. ⓘ

Eine vollständige Hydrierung von beiden Seiten der Graphenfolie führt zu Graphan, eine partielle Hydrierung hingegen zu hydriertem Graphen. In ähnlicher Weise führt die beidseitige Fluorierung von Graphen (oder die chemische und mechanische Exfoliation von Graphitfluorid) zu Fluorgraphen (Graphenfluorid), während die partielle Fluorierung (im Allgemeinen die Halogenierung) zu fluoriertem (halogeniertem) Graphen führt. ⓘ

Graphen-Ligand/Komplex

Graphen kann als Ligand dienen, um Metalle und Metallionen durch Einführung funktioneller Gruppen zu koordinieren. Die Strukturen von Graphen-Liganden ähneln z. B. Metall-Porphyrin-Komplexen, Metall-Phthalocyanin-Komplexen und Metall-Phenanthrolin-Komplexen. Kupfer- und Nickel-Ionen können mit Graphen-Liganden koordiniert werden. ⓘ

Graphen-Faser

Im Jahr 2011 berichteten Forscher über einen neuartigen und dennoch einfachen Ansatz zur Herstellung von Graphenfasern aus durch chemische Gasphasenabscheidung hergestellten Graphenfilmen. Die Methode war skalierbar und kontrollierbar und ermöglichte eine einstellbare Morphologie und Porenstruktur durch die Kontrolle der Verdampfung von Lösungsmitteln mit geeigneter Oberflächenspannung. Flexible Festkörper-Superkondensatoren, die auf diesen Graphenfasern basieren, wurden 2013 demonstriert. ⓘ

Im Jahr 2015 wurden durch Einlagerung kleiner Graphenfragmente in die von größeren, aufgerollten Graphenblättern gebildeten Lücken nach dem Ausglühen Wege für die Leitung geschaffen, während die Fragmente zur Verstärkung der Fasern beitrugen. Die so entstandenen Fasern boten eine bessere thermische und elektrische Leitfähigkeit und mechanische Festigkeit. Die Wärmeleitfähigkeit erreichte 1.290 W/m/K (1.290 Watt pro Meter pro Kelvin), während die Zugfestigkeit 1.080 MPa (157.000 psi) erreichte. ⓘ

2016 wurden kontinuierliche Graphenfasern im Kilometermaßstab mit herausragenden mechanischen Eigenschaften und ausgezeichneter elektrischer Leitfähigkeit durch Nassspinnen von Graphenoxid-Flüssigkristallen mit hohem Durchsatz und anschließender Graphitierung mittels einer synergetischen Defektstrategie in großem Maßstab hergestellt. Die Graphenfasern mit überlegenen Leistungen versprechen breite Anwendungen in Funktionstextilien, leichten Motoren, mikroelektronischen Geräten usw. ⓘ

Die Tsinghua-Universität in Peking unter der Leitung von Wei Fei vom Fachbereich Chemieingenieurwesen behauptet, eine Kohlenstoffnanoröhrenfaser mit einer Zugfestigkeit von 80 GPa (12.000.000 psi) herstellen zu können. ⓘ

3D-Graphen

Im Jahr 2013 wurde eine dreidimensionale Wabe aus hexagonal angeordnetem Kohlenstoff als 3D-Graphen bezeichnet, und es wurde auch selbsttragendes 3D-Graphen hergestellt. 3D-Graphenstrukturen können entweder durch CVD- oder lösungsbasierte Verfahren hergestellt werden. Eine Übersicht von Khurram und Xu et al. aus dem Jahr 2016 enthält eine Zusammenfassung des damaligen Stands der Technik für die Herstellung der 3D-Struktur von Graphen und anderen verwandten zweidimensionalen Materialien. Im Jahr 2013 berichteten Forscher der Stony Brook University über eine neuartige, durch Radikale initiierte Vernetzungsmethode zur Herstellung poröser, freistehender 3D-Architekturen aus Graphen und Kohlenstoffnanoröhren unter Verwendung von Nanomaterialien als Bausteine ohne Polymermatrix als Träger. Diese 3D-Graphengerüste/Schaumstoffe können in verschiedenen Bereichen wie Energiespeicherung, Filtration, Wärmemanagement und biomedizinische Geräte und Implantate eingesetzt werden. ⓘ

Im Jahr 2016 wurde über eine kastenförmige Graphen-Nanostruktur (BSG) berichtet, die nach der mechanischen Spaltung von pyrolytischem Graphit entsteht. Die entdeckte Nanostruktur ist ein mehrschichtiges System paralleler hohler Nanokanäle, die sich entlang der Oberfläche befinden und einen viereckigen Querschnitt aufweisen. Die Dicke der Kanalwände beträgt etwa 1 nm. Zu den potenziellen Anwendungsbereichen von BSG gehören: ultraempfindliche Detektoren, hochleistungsfähige katalytische Zellen, Nanokanäle für die DNA-Sequenzierung und -Manipulation, hochleistungsfähige wärmeableitende Oberflächen, wiederaufladbare Batterien mit erhöhter Leistung, nanomechanische Resonatoren, Elektronenvervielfältigungskanäle in nanoelektronischen Emissionsgeräten, hochkapazitive Sorptionsmittel für die sichere Wasserstoffspeicherung. ⓘ

Es wurde auch über dreidimensionales zweischichtiges Graphen berichtet. ⓘ

Säulenförmiges Graphen

Graphen in Säulenform ist eine hybride Kohlenstoffstruktur, die aus einer orientierten Anordnung von Kohlenstoffnanoröhren besteht, die an jedem Ende mit einer Graphenschicht verbunden sind. Es wurde erstmals 2008 von George Froudakis und Kollegen von der Universität Kreta in Griechenland theoretisch beschrieben. Säulenförmiges Graphen wurde bisher noch nicht im Labor synthetisiert, aber es gibt Hinweise darauf, dass es nützliche elektronische Eigenschaften haben oder als Wasserstoffspeicher dienen könnte. ⓘ

Verstärktes Graphen

Graphen, das mit eingebetteten Verstärkungsstäben aus Kohlenstoffnanoröhrchen ("rebar") verstärkt ist, lässt sich leichter handhaben und verbessert gleichzeitig die elektrischen und mechanischen Eigenschaften beider Materialien. ⓘ

Funktionalisierte ein- oder mehrwandige Kohlenstoffnanoröhren werden auf Kupferfolien aufgeschleudert und dann erhitzt und abgekühlt, wobei die Nanoröhren selbst als Kohlenstoffquelle dienen. Beim Erhitzen zerfallen die funktionellen Kohlenstoffgruppen in Graphen, während sich die Nanoröhren teilweise aufspalten und in der Ebene kovalente Bindungen mit dem Graphen eingehen, was die Festigkeit erhöht. Die Nanoröhren können sich überlappen, wodurch das Material ein besserer Leiter ist als herkömmliches CVD-gewachsenes Graphen. Die Nanoröhren überbrücken effektiv die Korngrenzen, die in herkömmlichem Graphen zu finden sind. Die Technik beseitigt die Spuren des Substrats, auf dem die später getrennten Schichten mittels Epitaxie abgeschieden wurden. ⓘ

Stapel von wenigen Schichten wurden als kostengünstiger und physikalisch flexibler Ersatz für Indiumzinnoxid (ITO) vorgeschlagen, das in Displays und Photovoltaikzellen verwendet wird. ⓘ

Geformtes Graphen

Im Jahr 2015 entwickelten Forscher der University of Illinois in Urbana-Champaign (UIUC) einen neuen Ansatz zur Herstellung von 3D-Formen aus flachen 2D-Graphenschichten. Ein Graphenfilm, der in Lösungsmittel getränkt wurde, um ihn aufzuquellen und verformbar zu machen, wurde auf ein darunter liegendes Substrat gelegt, den "Former". Das Lösungsmittel verdampfte mit der Zeit und hinterließ eine Graphenschicht, die die Form der darunter liegenden Struktur angenommen hatte. Auf diese Weise konnten sie eine Reihe relativ komplizierter mikrostruktureller Formen herstellen. Die Merkmale variieren von 3,5 bis 50 μm. Reines Graphen und mit Gold verziertes Graphen wurden jeweils erfolgreich in das Substrat integriert. ⓘ

Graphen-Aerogel

Ein Aerogel aus Graphenschichten, die durch Kohlenstoffnanoröhren getrennt sind, wurde mit 0,16 Milligramm pro Kubikzentimeter gemessen. Eine Lösung aus Graphen und Kohlenstoff-Nanoröhrchen in einer Form wird gefriergetrocknet, um die Lösung zu dehydrieren, so dass das Aerogel entsteht. Das Material hat eine hervorragende Elastizität und Absorption. Es kann sich nach einer Kompression von mehr als 90 % vollständig erholen und bis zum 900-fachen seines Gewichts an Öl aufnehmen, und zwar mit einer Geschwindigkeit von 68,8 Gramm pro Sekunde. ⓘ

Graphen-Nanospule

Im Jahr 2015 wurde eine gewundene Form von Graphen in graphitischem Kohlenstoff (Kohle) entdeckt. Der Spiraleffekt entsteht durch Defekte im sechseckigen Gitter des Materials, die dazu führen, dass es sich entlang seiner Kante spiralförmig windet und so eine Riemannsche Fläche nachahmt, wobei die Graphenoberfläche ungefähr senkrecht zur Achse steht. Wenn an eine solche Spule eine Spannung angelegt wird, fließt Strom um die Spirale und erzeugt ein Magnetfeld. Das Phänomen gilt für Spiralen mit Zickzack- oder Sesselmuster, allerdings mit unterschiedlichen Stromverteilungen. Computersimulationen ergaben, dass eine herkömmliche Spiralspule mit einem Durchmesser von 205 Mikrometern durch eine nur 70 Nanometer breite Nanospule mit einer Feldstärke von bis zu 1 Tesla ausgeglichen werden kann. ⓘ

Die in Rice mit Hilfe von Computermodellen analysierten Nano-Solenoide sollten laut Yakobson und seinem Team in der Lage sein, starke Magnetfelder von etwa 1 Tesla zu erzeugen, was in etwa der Feldstärke der Spulen in typischen Lautsprechern entspricht - und etwa der Feldstärke einiger MRT-Geräte. Sie fanden heraus, dass das Magnetfeld in dem hohlen, nanometerbreiten Hohlraum in der Mitte der Spirale am stärksten ist. ⓘ

Ein Solenoid mit einer solchen Spule verhält sich wie ein Quantenleiter, dessen Stromverteilung zwischen dem Kern und der Außenseite mit der angelegten Spannung variiert, was zu einer nichtlinearen Induktivität führt. ⓘ

Zerknittertes Graphen

Im Jahr 2016 stellte die Brown University eine Methode zum "Zerknittern" von Graphen vor, bei der dem Material Falten im Nanobereich hinzugefügt werden. Dazu wurden Schichten von Graphenoxid auf eine Schrumpffolie aufgebracht, die dann geschrumpft wurde, wobei sich die Folie auflöste, bevor sie auf einer anderen Folie erneut geschrumpft wurde. Das zerknitterte Graphen wurde superhydrophob, und bei der Verwendung als Batterieelektrode wurde gezeigt, dass das Material die elektrochemische Stromdichte um bis zu 400 % erhöhen kann. ⓘ

Herstellung

Es wurde eine rasch wachsende Zahl von Produktionstechniken entwickelt, um die Verwendung von Graphen in kommerziellen Anwendungen zu ermöglichen. ⓘ

Isolierte 2D-Kristalle können durch chemische Synthese nicht einmal im Prinzip über kleine Größen hinaus gezüchtet werden, da die rasche Zunahme der Phononendichte mit zunehmender lateraler Größe die 2D-Kristallite zwingt, sich in die dritte Dimension zu biegen. In jedem Fall muss Graphen an ein Substrat gebunden werden, um seine zweidimensionale Form beizubehalten. ⓘ

Kleine Graphenstrukturen, wie Graphen-Quantenpunkte und Nanobänder, können mit "Bottom-up"-Methoden hergestellt werden, bei denen das Gitter aus organischen Molekülmonomeren (z. B. Zitronensäure, Glukose) zusammengesetzt wird. Bei "Top-down"-Methoden hingegen werden Graphit- und Graphen-Materialien mit starken Chemikalien (z. B. Mischsäuren) geschnitten. ⓘ

Mechanische

Mechanische Exfoliation

Geim und Novoselov verwendeten zunächst Klebeband, um Graphenblätter von Graphit abzuziehen. Um einzelne Schichten zu erhalten, sind normalerweise mehrere Exfoliationsschritte erforderlich. Nach dem Exfolieren werden die Flocken auf einem Siliziumwafer abgelagert. Es können Kristallite erhalten werden, die größer als 1 mm und mit bloßem Auge sichtbar sind. ⓘ

Im Jahr 2014 wurde durch Exfoliation Graphen mit der geringsten Anzahl von Defekten und der höchsten Elektronenbeweglichkeit hergestellt. ⓘ

Alternativ dringt ein scharfer einkristalliner Diamantkeil in die Graphitquelle ein, um Schichten zu spalten. ⓘ

Im Jahr 2014 wurden defektfreie, nicht oxidierte graphenhaltige Flüssigkeiten aus Graphit mit Hilfe von Mischern hergestellt, die lokale Scherraten von mehr als 10×10⁴ erzeugen. ⓘ

Die Scher-Exfoliation ist eine weitere Methode, die durch den Einsatz von Rotor-Stator-Mischern die skalierbare Herstellung von defektfreiem Graphen ermöglicht. Da für die mechanische Exfoliation keine Turbulenzen erforderlich sind, hat sich das Kugelmahlen mit niedriger Geschwindigkeit als effektiv für die Herstellung von wasserlöslichem Graphen mit hoher Ausbeute erwiesen. ⓘ

Exfoliation mit Ultraschall

Durch Dispergieren von Graphit in einem flüssigen Medium kann Graphen durch Beschallung und anschließende Zentrifugation hergestellt werden, wobei Konzentrationen von 2,1 mg/ml in N-Methylpyrrolidon erreicht werden. Bei Verwendung einer geeigneten ionischen Flüssigkeit als Dispergiermedium wurden Konzentrationen von 5,33 mg/ml erzielt. Das Umstapeln ist bei dieser Technik ein Problem. ⓘ

Die Zugabe eines Tensids zu einem Lösungsmittel vor der Beschallung verhindert das Restacking durch Adsorption an der Graphenoberfläche. Dies führt zu einer höheren Graphenkonzentration, aber die Entfernung des Tensids erfordert chemische Behandlungen. ⓘ

Die Beschallung von Graphit an der Grenzfläche zweier nicht mischbarer Flüssigkeiten, vor allem Heptan und Wasser, führte zur Herstellung makroskopischer Graphenfilme. Die Graphenblätter werden an der energiereichen Grenzfläche zwischen den Materialien adsorbiert und daran gehindert, sich neu zu stapeln. Die Schichten sind zu etwa 95 % transparent und leitfähig. ⓘ

Mit bestimmten Spaltparametern kann die kastenförmige Graphen-Nanostruktur (BSG) auf einem Graphitkristall hergestellt werden. ⓘ

Spaltung von einlagigem Kohlenstoff

Schneiden von Nanoröhren

Graphen kann durch Öffnen von Kohlenstoff-Nanoröhren durch Schneiden oder Ätzen hergestellt werden. Bei einem solchen Verfahren werden mehrwandige Kohlenstoff-Nanoröhren in Lösung durch Einwirkung von Kaliumpermanganat und Schwefelsäure aufgeschnitten. ⓘ

Im Jahr 2014 wurde mit Kohlenstoffnanoröhrchen verstärktes Graphen durch Schleuderbeschichtung und Ausglühen funktionalisierter Kohlenstoffnanoröhrchen hergestellt. ⓘ

Fulleren-Aufspaltung

Bei einem anderen Ansatz werden Buckyballs mit Überschallgeschwindigkeit auf ein Substrat gespritzt. Die Kugeln brechen beim Aufprall auf, und die entstehenden Käfige verbinden sich zu einem Graphenfilm. ⓘ

Chemisch

Reduktion von Graphitoxid

Das meistversprechende Verfahren ist die Herstellung von Graphen durch Reduktion von Graphenoxid. So berichtete beispielsweise das California Nanosystems Institute (CNSI) im Jahr 2008 über ein „Massenproduktionsverfahren“, das auf der Reduktion von Graphitoxid in flüssigem Hydrazin basiert. Auf diese Weise konnten Graphen-Monolagen der Größe 20 µm × 40 µm erzeugt werden. Daneben wurde auch über den schrittweisen Aufbau aus polyzyklischen Aromaten sowie eine chemische Abblätterung aus Graphit durch organische Lösungsmittel berichtet. ⓘ

Im Grammmaßstab lässt sich Graphen auch in einer zweistufigen Reaktion herstellen. Dabei werden im ersten Schritt in einer Solvothermalsynthese Natrium und Ethanol miteinander umgesetzt. Unter mehrstündigem Erhitzen unter hohem Druck entsteht dabei ein komplexes Gemisch mit Natriumethoxid als Hauptbestandteil. Im zweiten Schritt wird das Reaktionsgemisch unter Luftausschluss stark erhitzt (Pyrolyse), wobei man nach einer abschließenden Ultraschallbehandlung unter anderem Graphen isolieren kann. ⓘ

Größere Mengen können durch die Pyrolyse von Graphitoxid erhalten werden. Durch plötzliches Erhitzen auf Temperaturen zwischen 600 und 1000 °C wird dabei die Schichtstruktur des Edukts vom abgespaltenen Gas aufgesprengt, während sich in den Schichten das hexagonale Graphengitter spontan neu bildet. Die dabei typisch erhaltene spezifische Oberfläche des Materials entspricht einer Stapelhöhe von durchschnittlich 2–3 Graphenlagen. ⓘ

P. Boehm berichtete 1962 über die Herstellung einlagiger Flocken aus reduziertem Graphenoxid. Durch schnelles Erhitzen von Graphitoxid und Exfoliation erhält man hochdisperses Kohlenstoffpulver mit einigen Prozent Graphenflocken. ⓘ

Eine andere Methode ist die Reduktion von Graphitoxid-Monolayer-Filmen, z. B. durch Hydrazin mit Glühen in Argon/Wasserstoff, wobei ein nahezu intaktes Kohlenstoffgerüst entsteht, das eine effiziente Entfernung funktioneller Gruppen ermöglicht. Die gemessene Ladungsträgerbeweglichkeit überstieg 1000 cm/Vs (10m/Vs). ⓘ

Beim Brennen einer mit Graphitoxid beschichteten DVD entstand ein leitfähiger Graphenfilm (1738 Siemens pro Meter) mit einer spezifischen Oberfläche (1520 Quadratmeter pro Gramm), der sehr widerstandsfähig und formbar war. ⓘ

Eine dispergierte Suspension von reduziertem Graphenoxid wurde in Wasser durch eine hydrothermale Dehydratisierungsmethode ohne Verwendung eines Tensids synthetisiert. Der Ansatz ist einfach, industriell anwendbar, umweltfreundlich und kosteneffizient. Viskositätsmessungen bestätigten, dass die kolloidale Graphen-Suspension (Graphen-Nanofluid) ein Newtonsches Verhalten aufweist, wobei die Viskosität der von Wasser sehr ähnlich ist. ⓘ

Geschmolzene Salze

Graphitpartikel können in geschmolzenen Salzen korrodiert werden, um eine Vielzahl von Kohlenstoff-Nanostrukturen einschließlich Graphen zu bilden. In geschmolzenem Lithiumchlorid gelöste Wasserstoffkationen können an kathodisch polarisierten Graphitstäben entladen werden, die dann interkalieren und Graphenblätter abschälen. Die hergestellten Graphen-Nanoblätter weisen eine einkristalline Struktur mit einer lateralen Größe von mehreren hundert Nanometern auf und besitzen einen hohen Grad an Kristallinität und thermischer Stabilität. ⓘ

Elektrochemische Synthese

Die elektrochemische Synthese kann Graphen exfolieren. Die Variation einer gepulsten Spannung steuert die Dicke, die Flockenfläche und die Anzahl der Defekte und beeinflusst die Eigenschaften. Der Prozess beginnt mit dem Eintauchen des Graphits in ein Lösungsmittel zur Interkalation. Der Prozess kann durch Überwachung der Transparenz der Lösung mit einer LED und einer Fotodiode verfolgt werden. ⓘ

Hydrothermale Selbstmontage

Graphen wurde mit Hilfe eines Zuckers (z. B. Glukose, Zucker, Fruktose usw.) hergestellt. Diese substratfreie "Bottom-up"-Synthese ist sicherer, einfacher und umweltfreundlicher als die Exfoliation. Mit dieser Methode lässt sich die Schichtdicke steuern, die von Mono- bis zu Multischichten reicht und als "Tang-Lau-Methode" bekannt ist. ⓘ

Natriumethoxid-Pyrolyse

Gram-Mengen wurden durch die Reaktion von Ethanol mit Natriummetall hergestellt, gefolgt von Pyrolyse und Waschen mit Wasser. ⓘ

Mikrowellen-unterstützte Oxidation

Im Jahr 2012 wurde berichtet, dass Graphen mit Hilfe von Mikrowellenenergie direkt in einem Schritt synthetisiert werden kann. Dieser Ansatz vermeidet die Verwendung von Kaliumpermanganat in der Reaktionsmischung. Es wurde auch berichtet, dass mit Hilfe von Mikrowellenstrahlung Graphenoxid mit oder ohne Löcher synthetisiert werden kann, indem die Mikrowellenzeit gesteuert wird. Durch Erhitzen mit Mikrowellen kann die Reaktionszeit drastisch von Tagen auf Sekunden verkürzt werden. ⓘ

Graphen kann auch durch mikrowellenunterstützte hydrothermale Pyrolyse hergestellt werden. ⓘ

Thermische Zersetzung von Siliziumkarbid

Durch Erhitzen von Siliciumcarbid (SiC) auf hohe Temperaturen (1100 °C) unter niedrigem Druck (ca. 10-6 Torr oder 10-4 Pa) wird es zu Graphen reduziert. ⓘ

Chemische Gasphasenabscheidung

Epitaxie

Epitaktisches Graphenwachstum auf Siliziumkarbid ist eine Technik zur Herstellung von Graphen im Wafermaßstab. Epitaktisches Graphen kann so schwach an Oberflächen gekoppelt sein (durch die aktiven Valenzelektronen, die Van-der-Waals-Kräfte erzeugen), dass die zweidimensionale elektronische Bandstruktur von isoliertem Graphen erhalten bleibt. ⓘ

Ein normaler Siliziumwafer, der mit einer Germaniumschicht (Ge) beschichtet ist, die in verdünnte Flusssäure getaucht wird, entfernt die sich natürlich bildenden Germaniumoxidgruppen, wodurch wasserstoffterminiertes Germanium entsteht. Durch CVD kann dieses mit Graphen beschichtet werden. ⓘ

Die direkte Synthese von Graphen auf dem Isolator TiO₂ mit hoher Dielektrizitätskonstante (highκ). In einem zweistufigen CVD-Verfahren wird gezeigt, dass Graphen direkt auf TiO₂-Kristallen oder TiO₂-Nanoblättern wachsen kann, ohne dass ein Metallkatalysator verwendet wird. ⓘ

Metallsubstrate

CVD-Graphen kann auf Metallsubstraten wie Ruthenium, Iridium, Nickel und Kupfer gezüchtet werden. ⓘ

Rolle-zu-Rolle

Im Jahr 2014 wurde ein zweistufiges Rolle-zu-Rolle-Verfahren angekündigt. Im ersten Schritt der Rolle-zu-Rolle-Fertigung wird das Graphen durch chemische Gasphasenabscheidung hergestellt. Im zweiten Schritt wird das Graphen auf einem Substrat fixiert. ⓘ

Großflächiges Raman-Mapping von CVD-Graphen auf abgeschiedenen Cu-Dünnschichten auf 150-mm-SiO₂/Si-Wafern zeigt eine Kontinuität der Monolagen von >95 % und einen Durchschnittswert von ~2,62 für I_2D/IG. Der Maßstab ist 200 μm. ⓘ

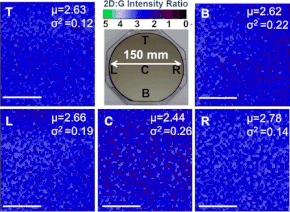
Kalte Wand

Das Wachsen von Graphen in einem industriellen CVD-System mit Widerstandsheizung an der kalten Wand soll Graphen 100-mal schneller herstellen als herkömmliche CVD-Systeme, die Kosten um 99 % senken und Material mit verbesserten elektronischen Eigenschaften erzeugen. ⓘ

CVD-Graphen im Wafer-Maßstab

CVD-Graphen ist skalierbar und wurde auf einem Axitron-Black-Magic-System auf 100- bis 300-mm-Standard-Si/SiO₂-Wafern auf Cu-Dünnschichtkatalysatoren gezüchtet. Auf 100- bis 300-mm-Wafersubstraten wird eine einschichtige Graphenbedeckung von >95 % mit vernachlässigbaren Defekten erreicht, was durch umfangreiche Raman-Kartierungen bestätigt wird. ⓘ

Lösungsmittel-Grenzflächen-Fangmethode (SITM)

Wie eine Gruppe unter der Leitung von D. H. Adamson berichtet, kann Graphen aus natürlichem Graphit hergestellt werden, wobei die Integrität der Schichten durch die SITM-Methode (Solvent Interface Trapping) erhalten bleibt. Bei der SITM-Methode wird eine energiereiche Grenzfläche, z. B. Öl und Wasser, verwendet, um Graphit zu Graphen abzuschälen. Der gestapelte Graphit löst sich an der Öl-Wasser-Grenzfläche ab, um in einem thermodynamisch günstigen Prozess Graphen mit wenigen Schichten zu erzeugen, ähnlich wie sich kleine Molekül-Tenside ausbreiten, um die Grenzflächenenergie zu minimieren. Auf diese Weise verhält sich Graphen wie ein 2D-Tensid. SITM wurde für eine Vielzahl von Anwendungen wie leitfähige Polymer-Graphen-Schäume, leitfähige Polymer-Graphen-Mikrokugeln, leitfähige dünne Filme und leitfähige Tinten beschrieben. ⓘ

Reduzierung von Kohlendioxid

In einer stark exothermen Reaktion wird Magnesium in einer Oxidations-Reduktionsreaktion mit Kohlendioxid verbrannt, wobei Kohlenstoffnanopartikel wie Graphen und Fullerene entstehen. ⓘ

Überschallspray

Die Überschallbeschleunigung von Tröpfchen durch eine Laval-Düse wurde genutzt, um reduziertes Graphenoxid auf einem Substrat abzuscheiden. Die Energie des Aufpralls ordnet die Kohlenstoffatome zu makellosem Graphen um. ⓘ

Laser

Im Jahr 2014 wurde ein CO
₂-Infrarotlaser verwendet, um aus handelsüblichen Polymerfolien strukturierte poröse dreidimensionale Netzwerke aus laserinduziertem Graphen (LIG) herzustellen. Das resultierende Material weist eine hohe elektrische Leitfähigkeit und Oberfläche auf. Das Laserinduktionsverfahren ist mit Rolle-zu-Rolle-Herstellungsverfahren kompatibel. Ein ähnliches Material, laserinduzierte Graphenfasern (LIGF), wurde 2018 vorgestellt. ⓘ

Flash-Joule-Erwärmung

Im Jahr 2019 wurde die Flash-Joule-Erhitzung (transiente elektrothermische Hochtemperaturerhitzung) als Methode zur Synthese von turbostratischem Graphen in Pulverform entdeckt. Bei dieser Methode werden verschiedene Kohlenstoffquellen wie Ruß, Kohle und Lebensmittelabfälle elektrothermisch in mikroskopisch kleine Graphenflocken umgewandelt. In neueren Arbeiten wurde die Verwendung von gemischten Kunststoffabfällen, Altreifen und Pyrolyse-Asche als Kohlenstoffrohstoffe nachgewiesen. Der Graphenisierungsprozess wird kinetisch gesteuert, und die Energiedosis wird so gewählt, dass der Kohlenstoff in seinem graphenartigen Zustand erhalten bleibt (ein übermäßiger Energieeintrag führt zu einer anschließenden Graphitisierung durch Ausglühen). ⓘ

Ionenimplantation

Durch die Beschleunigung von Kohlenstoffionen in einem elektrischen Feld in einen Halbleiter aus dünnen Nickelschichten auf einem SiO₂/Si-Substrat wird bei einer relativ niedrigen Temperatur von 500 °C eine falten-, riss- und rückstandsfreie Graphenschicht im Wafermaßstab (4 Zoll (100 mm)) erzeugt. ⓘ

CMOS-kompatibles Graphen

Die Integration von Graphen in den weit verbreiteten CMOS-Fertigungsprozess erfordert seine übertragungsfreie Direktsynthese auf dielektrischen Substraten bei Temperaturen unter 500 °C. Auf der IEDM 2018 demonstrierten Forscher der University of California, Santa Barbara, einen neuartigen CMOS-kompatiblen Graphen-Syntheseprozess bei 300 °C, der sich für Back-End-of-Line-Anwendungen (BEOL) eignet. Der Prozess beinhaltet eine druckunterstützte Festkörperdiffusion von Kohlenstoff durch einen dünnen Film eines Metallkatalysators. Es wurde gezeigt, dass die synthetisierten großflächigen Graphenfilme eine hohe Qualität (über Raman-Charakterisierung) und ähnliche Widerstandswerte aufweisen, wenn man sie mit bei hoher Temperatur durch CVD synthetisierten Graphenfilmen desselben Querschnitts bis zu einer Breite von 20 nm vergleicht. ⓘ

Mechanisch

Einer der ersten Graphentransistoren, die Geim und Novoselov hergestellt haben. Das Graphen wurde dabei mit Klebeband von HOPG abgelöst ⓘ

Die ersten Graphenflocken wurden von Novoselov durch Abblätterung (Exfoliation) von HOPG (englisch Highly Oriented Pyrolytic Graphite, dt. hochgeordneter pyrolytischer Graphit) gewonnen. Das eingesetzte Verfahren ähnelt dem sogenannten Klebebandtest; dabei wird ein Klebeband auf eine Fläche gedrückt – in diesem Fall auf einen Graphitblock – und anschließend schnell abgezogen, so dass herauslösbare Elemente (hier Graphit) im Klebstoff zurückbleiben. Dieses Klebeband wird dann auf einen mit Fotolack beschichteten Silicium-Wafer gedrückt und nochmals abgezogen. Nach dem Entfernen des Klebebands bleiben dünne Graphitpartikel auf der Oberfläche der Fotolackschicht zurück. Anschließend wird die Fotolackschicht mit Aceton aufgelöst und dann der Wafer mit Wasser und 2-Propanol gespült. Bei Auflösen der Fotolackschicht haften einige Graphitpartikel an der Waferoberfläche, die zusätzlich dünn mit Siliciumdioxid beschichtet sein kann. Auf diese Weise lassen sich lokal dünne Graphitfilme herstellen. Die für Graphenuntersuchungen interessanten Schichten, welche dünner als 50 nm sind, sind optisch fast transparent. Die zusätzliche Schicht verändert die Reflexionseigenschaften des Substrates, so dass sich die durch Interferenzeffekte bedingte violette Farbe der Siliciumdioxidschicht nach Blau verändert. An den Rändern dieser 50-nm-Schichten kann man dann mit dem Rastertunnel- oder Rasterkraftmikroskop nach dünnerem Graphen suchen. ⓘ

Bei einer anderen Exfoliationsmethode werden vor dem Exfoliationsprozess mit einem Sauerstoffplasma Vertiefungen in das HOPG geätzt, die isolierte Plateaus (Mesas) stehen lassen. Danach wird ein mit Klebstoff benetzter Glasträger auf die Oberfläche gedrückt und abgezogen. Die im Klebstoff haftenden Mesas werden nun ebenfalls so lange mit Klebestreifen abgezogen, bis nur noch ein Rest übrig bleibt. Danach wird der Klebstoff in Propanon aufgelöst und die im Propanon suspendierten Graphenflocken mit einem Siliciumwafer herausgefischt und wiederum mit optischem Mikroskop und Rastertunnel- oder Rasterkraftmikroskop abgesucht. ⓘ

Bei diesen beiden Methoden handelt es sich um sehr zeitaufwendige Verfahren, bei denen man zwar hochwertige, aber nur sehr wenige Proben erhält. ⓘ

Im April 2014 wurde eine Methode bekannt, bei der sich mittels eines starken Mixers in einem Gemisch aus Wasser, Geschirrspülmittel und Graphitpulver große Mengen hochwertiges Graphen erzeugen lassen. Das Graphitpulver wird hierbei in etwa 100 Nanometer große und 1 Nanometer dicke Graphenflocken gespalten. ⓘ

Epitaktisches Wachstum

Graphen kann epitaktisch auf metallischen Substraten wachsen. Eine in der Literatur vorgestellte Methode ist die Zersetzung von Ethen auf Iridium. In einem weiteren Verfahren wird die Löslichkeit von Kohlenstoff in Übergangsmetallen verwendet. Beim Erhitzen löst sich der Kohlenstoff im Metall, tritt beim Abkühlen wieder heraus und ordnet sich als Graphen auf der Oberfläche an. ⓘ

Eine weitere Möglichkeit der Darstellung einzelner Graphenlagen ist die thermische Zersetzung hexagonaler Siliciumcarbid-Oberflächen. Bei Temperaturen oberhalb des Schmelzpunktes von Silicium verdampft das Silicium aufgrund seines (im Vergleich zu Kohlenstoff) höheren Dampfdrucks. Auf der Oberfläche bilden sich dann dünne Schichten einkristallinen Graphits, die aus wenigen Graphenmonolagen bestehen. Dieses Verfahren ist geeignet für Anlassprozesse im Vakuum und in einer Inertgasatmosphäre aus Argon. Die Dicke und Struktur des epitaktisch gewachsenen Graphens hängt dabei empfindlich von den eingestellten Prozessparametern ab, insbesondere von der Wahl der Atmosphäre und der Struktur der Substratoberfläche sowie der Polarisation der Siliciumcarbid-Oberfläche. ⓘ

Große Flächen aus Graphen stellt man dadurch her, dass man eine monoatomare Schicht aus Kohlenstoff auf eine Folie aus inertem Trägermaterial, wie zum Beispiel Kupfer, durch chemische Gasphasenabscheidung (CVD, von engl. "Chemical Vapour Deposition) aufbringt und dann das Trägermaterial auflöst, oder indem man das Graphen mechanisch vom Wachstumssubstrat abhebt. Dies geschieht oft mittels elektrochemischer Delamination ("Bubbling"), wobei eine Spannung angelegt wird, um durch Elektrolyse Gas unter dem Graphen herzustellen. Man verbindet die Kupferfolie als Elektrode mit einer Spannungsquelle; die zweite Elektrode wird in einer Salzlösung befestigt. Beim folgenden Eintauchen der Folie entstehen Blasen unter dem Graphen, welches sich so vom Kupfer löst und dann gereinigt werden kann. Damit die dünne Graphenschicht nicht zerstört wird, wird sie üblicherweise vorher mit einem Kunststoff beschichtet, der die Stabilität beim Ablösen erhöht. Kupferfolien sind für CVD besonders geeignet, da sich kaum Kohlenstoff im Metallgitter zu lösen vermag (also die Oberfläche kaum durchdringt). Die Schwache Wechselwirkung zwischen Graphen und Kupfer ist ein weiterer großer Vorteil. Die Geschwindigkeit dieses Prozesses kann durch eine schwache Sauerstoffzufuhr, zum Beispiel durch Erhitzen eines SiO-Gitters drastisch erhöht werden. ⓘ

Simulation

Neben der experimentellen Untersuchung von Graphen und graphenbasierten Bauelementen ist auch deren numerische Modellierung und Simulation ein wichtiges Forschungsthema gewesen. Die Kubo-Formel liefert einen analytischen Ausdruck für die Leitfähigkeit von Graphen und zeigt, dass diese von mehreren physikalischen Parametern wie Wellenlänge, Temperatur und chemischem Potenzial abhängt. Darüber hinaus wurde ein Oberflächenleitfähigkeitsmodell vorgeschlagen, das Graphen als eine unendlich dünne (zweiseitige) Schicht mit einer lokalen und isotropen Leitfähigkeit beschreibt. Dieses Modell ermöglicht die Ableitung analytischer Ausdrücke für das elektromagnetische Feld in Gegenwart einer Graphenschicht in Form einer dyadischen Green-Funktion (dargestellt mit Sommerfeld-Integralen) und eines anregenden elektrischen Stroms. Obwohl diese analytischen Modelle und Methoden Ergebnisse für mehrere kanonische Probleme zu Vergleichszwecken liefern können, sind viele praktische Probleme mit Graphen, wie z. B. der Entwurf von beliebig geformten elektromagnetischen Geräten, analytisch nicht lösbar. Mit den jüngsten Fortschritten auf dem Gebiet der computergestützten Elektromagnetik (CEM) sind verschiedene genaue und effiziente numerische Methoden für die Analyse elektromagnetischer Feld-Wellen-Wechselwirkungen auf Graphenschichten und/oder Graphen-basierten Geräten verfügbar geworden. Es wird eine umfassende Zusammenfassung der Berechnungswerkzeuge vorgeschlagen, die für die Analyse von Graphen-basierten Geräten/Systemen entwickelt wurden. ⓘ

Graphen-Analoga

Graphenanaloga (auch als "künstliches Graphen" bezeichnet) sind zweidimensionale Systeme, die ähnliche Eigenschaften wie Graphen aufweisen. Graphenanaloga werden seit der Entdeckung von Graphen im Jahr 2004 intensiv erforscht. Man versucht, Systeme zu entwickeln, in denen die Physik leichter zu beobachten und zu manipulieren ist als in Graphen. In diesen Systemen sind nicht immer Elektronen die Teilchen, die verwendet werden. Es können auch optische Photonen, Mikrowellenphotonen, Plasmonen, Mikrokavitätspolaritonen oder sogar Atome sein. Auch die Wabenstruktur, in der sich diese Teilchen entwickeln, kann von anderer Natur sein als die Kohlenstoffatome in Graphen. Es kann sich um einen photonischen Kristall, eine Anordnung von Metallstäben, metallische Nanopartikel, ein Gitter aus gekoppelten Mikrokavitäten oder ein optisches Gitter handeln. ⓘ

Anwendungen

(a) Die typische Struktur eines Berührungssensors in einem Touchscreen. (Bild mit freundlicher Genehmigung von Synaptics, Incorporated) (b) Ein aktuelles Beispiel für den transparenten Graphen-Touchscreen der 2D Carbon Graphene Material Co.,Ltd, der in (c) einem kommerziellen Smartphone eingesetzt wird. ⓘ

Graphen ist ein transparenter und flexibler Leiter, der vielversprechend für verschiedene Material-/Geräteanwendungen ist, darunter Solarzellen, Leuchtdioden (LED), Touchpanels und intelligente Fenster oder Telefone. Smartphone-Produkte mit Graphen-Touchscreens sind bereits auf dem Markt. ⓘ

Im Jahr 2013 kündigte Head eine neue Reihe von Graphen-Tennisschlägern an. ⓘ

Seit 2015 gibt es ein Produkt für die kommerzielle Nutzung: ein mit Graphen durchsetztes Druckerpulver. Viele weitere Verwendungsmöglichkeiten für Graphen wurden vorgeschlagen oder befinden sich in der Entwicklung, u. a. in den Bereichen Elektronik, Biotechnik, Filtration, leichte/starke Verbundwerkstoffe, Photovoltaik und Energiespeicherung. Graphen wird häufig als Pulver und als Dispersion in einer Polymermatrix hergestellt. Diese Dispersion eignet sich vermutlich für fortschrittliche Verbundwerkstoffe, Farben und Beschichtungen, Schmiermittel, Öle und funktionelle Flüssigkeiten, Kondensatoren und Batterien, Wärmemanagementanwendungen, Display-Materialien und Verpackungen, Solarzellen, Tinten und Materialien für 3D-Drucker sowie Barrieren und Folien. ⓘ

Am 2. August 2016 wurde das neue Modell Mono von BAC vorgestellt, das sowohl als erstes Rennauto mit Straßenzulassung als auch als Serienfahrzeug aus Graphen hergestellt werden soll. ⓘ

Im Januar 2018 wurden an der University of California, Santa Barbara, unter der Leitung von Kaustav Banerjee erstmals spiralförmige Induktoren auf Graphenbasis demonstriert, die die kinetische Induktivität bei Raumtemperatur nutzen. Es wurde vorhergesagt, dass diese Induktoren eine erhebliche Miniaturisierung bei integrierten Hochfrequenzschaltungen ermöglichen würden. ⓘ

Das Potenzial von epitaktischem Graphen auf SiC für die Metrologie wurde 2010 mit einer Quantisierungsgenauigkeit des Quanten-Hall-Widerstands von drei Teilen pro Milliarde bei einlagigem epitaktischem Graphen nachgewiesen. Im Laufe der Jahre wurden Genauigkeiten von Teilen pro Billion bei der Quantisierung des Hall-Widerstands und riesige Quanten-Hall-Plateaus nachgewiesen. Entwicklungen bei der Verkapselung und Dotierung von epitaktischem Graphen haben zur Kommerzialisierung von Quantenwiderstandsnormalen aus epitaktischem Graphen geführt. ⓘ

Im Jahr 2021 wurde nachgewiesen, dass mit Tensiden funktionalisiertes Graphenpulver, wenn es Beton zugesetzt wird, die Druck-, Zug- und Biegefestigkeit verbessert. ⓘ

Toxizität

Eine 2016 von Lalwani et al. veröffentlichte Übersicht über die Toxizität von Graphen fasst die In-vitro-, In-vivo-, antimikrobiellen und Umwelteffekte zusammen und hebt die verschiedenen Mechanismen der Graphen-Toxizität hervor. Eine weitere, 2016 von Ou et al. veröffentlichte Übersichtsarbeit konzentrierte sich auf Nanomaterialien aus der Graphen-Familie (GFN) und zeigte mehrere typische Mechanismen wie physikalische Zerstörung, oxidativen Stress, DNA-Schäden, Entzündungsreaktion, Apoptose, Autophagie und Nekrose auf. ⓘ

Eine Studie aus dem Jahr 2020 zeigte, dass die Toxizität von Graphen von mehreren Faktoren abhängt, wie Form, Größe, Reinheit, Verarbeitungsschritte nach der Herstellung, oxidativer Zustand, funktionelle Gruppen, Dispersionszustand, Synthesemethoden, Verabreichungsweg und -dosis sowie Expositionszeiten. ⓘ

Im Jahr 2014 zeigten Forschungen an der Stony Brook University, dass Graphen-Nanobänder, Graphen-Nanoplättchen und Graphen-Nanozwiebeln bei Konzentrationen von bis zu 50 μg/ml nicht toxisch sind. Diese Nanopartikel verändern nicht die Differenzierung menschlicher Stammzellen aus dem Knochenmark in Osteoblasten (Knochen) oder Adipozyten (Fett), was darauf hindeutet, dass Graphen-Nanopartikel in niedrigen Dosen für biomedizinische Anwendungen sicher sind. Im Jahr 2013 fanden Forscher der Brown University heraus, dass 10 μm kleine Graphenflocken in der Lage sind, Zellmembranen in Lösung zu durchdringen. Es wurde beobachtet, dass sie zunächst über scharfe und gezackte Spitzen eindringen, so dass Graphen in die Zelle aufgenommen werden kann. Die physiologischen Auswirkungen dieses Vorgangs sind noch unbekannt, und es handelt sich um ein relativ unerforschtes Gebiet. ⓘ

Verallgemeinerungen

Verallgemeinerungen sind naheliegend. Einige durch Faltung oder Rollprozesse entstehende Strukturen, darunter die Kohlenstoffnanoröhren (englisch carbon nanotubes) und die Fullerene, wurden bereits erwähnt. Aber näherliegend ist es, zunächst Zweilagensysteme aus Graphen zu untersuchen. Diese haben interessante zusätzliche Eigenschaften: Sie zeigen halbleitendes Verhalten analog zu Silicium, aber mit einer Bandlücke, die durch elektrische Felder systematisch verändert werden kann. ⓘ

Graphan

Mit Hilfe von atomarem Wasserstoff, der durch eine elektrische Entladung in einem Wasserstoff-Argon-Gemisch erzeugt wird, lässt sich Graphen in Graphan umwandeln. In Graphan ist jedem Kohlenstoffatom ein Wasserstoffatom zugeordnet, und die Bindungsstruktur ähnelt dem sesselförmigen Cyclohexan. Graphan zerfällt oberhalb von 450 °C in Graphen und Wasserstoff. Graphan ist im Gegensatz zum Graphen ein elektrischer Isolator. ⓘ

Doppelschicht-Graphen

Hier ergeben sich je nach Ausrichtung der beiden Gitter zueinander Moiré-Muster mit entsprechender stärkerer Kopplung der Bänder in beiden Schichten und neuen Transportphänomenen je nach Drehwinkel, was 2011 zur Vorhersage einer neuen Art von Supraleitung durch Allan H. MacDonald und Rafi Bistritzer bei einem bestimmten Drehwinkel führte, experimentell bestätigt durch ein Team am Massachusetts Institute of Technology unter Pablo Jarillo-Herrero 2017. MacDonald, Bistritzer und Jarillo-Herrero erhielten dafür 2020 den Wolf-Preis in Physik. ⓘ

Grundlagenforschung und mögliche Anwendung

Wegen der hohen elektrischen Leitfähigkeit von Graphen wird derzeit an der Frage geforscht, ob Graphen Silicium als Transistormaterial ablösen könnte. Erste Erfolge wie die Darstellung eines Graphit-Microchips konnten bereits verbucht werden. Mit graphenbasierten Transistoren sollten Taktraten im Bereich von 500 bis 1000 GHz möglich sein. IBM gelang es Anfang 2010, erstmals einen 100-GHz-Transistor auf Graphenbasis herzustellen. Nach Untersuchungen von Yanqing Wu und Mitarbeitern vom April 2011 scheint Kohlenstoff mit Diamantstruktur geeignete Substrate zu ergeben. ⓘ

In der Grundlagenforschung dient Graphen als Modellsubstanz für zweidimensionale Kristalle: Es ist schwierig, das System in Form von Einzelschichten zu erhalten; erst im Jahre 2004 konnten die ersten kontaktierbaren „Graphen-Flocken“ erhalten werden. ⓘ

• Eventueller Einsatz in Superkondensatoren und Akkus
• Als Graphenoxid ist es gasdicht und gleichzeitig permeabel für H₂O-Moleküle. Dadurch ist ein Einsatz als Wasserfilter, Destillator und Dichtmittel vor allem als hermetische Versiegelung (sogar dicht für Helium) geeignet.
• Eventueller Einsatz in der Photovoltaik als Solarzelle der dritten Generation mit einem Wirkungsgrad bis zu 60 %. Jedoch erscheint dieser Ansatz nach neuerer Forschung nicht möglich.
• Realisierung einer stabilen und haltbaren Speicherzelle für künstliche neuronale Netze mit Zwischenzuständen statt binären Werten ⓘ

Die Europäische Kommission hat 2013 im Rahmen der European Flagship Initiative beschlossen, die Erforschung von Graphen mit einer Milliarde Euro zu fördern. ⓘ

Im November 2016 wird über eine neue Möglichkeit berichtet, Graphen als eine Art mechanisches Pixel für die Entwicklung neuartiger energieeffizienter Farbdisplays zu nutzen. Eine Membran aus Graphen über einer Luftkammer wölbt sich bei Druckunterschieden und einfallendes Licht wird in unterschiedlichen Farben reflektiert. Die Forscher glauben, dass man auf der Basis eine reflektive Displaytechnik entwickeln kann, die auf interferometrischer Modulation beruht. ⓘ

Dem Fraunhofer-Institut für Organische Elektronik, Elektronenstrahl- und Plasmatechnik (FEP) ist es 2016/17 erstmals gelungen, OLED-Elektroden aus Graphen herzustellen. Das Verfahren wurde im EU-geförderten Projekt „Gladiator“ (Graphene Layers: Production, Characterization and Integration) gemeinsam mit Partnern aus Industrie und Forschung entwickelt und optimiert. ⓘ

Das australische Unternehmen Talga entwickelt einen neuartigen Beton, der unter anderem die Elektromobilität vorantreiben soll. Der Beton ist mit Graphen versetzt. Das soll induktives Laden von Elektroautos oder das Beheizen der Straße ermöglichen. ⓘ

Auswirkungen auf Mensch und Umwelt

Mit Stand 2014 wurden bislang nur sehr geringe Mengen an Graphen produziert – meist in Kleinstmengen zu rein wissenschaftlichen Zwecken. Die Toxizität von Graphen wurde bislang noch nicht tiefergehend untersucht, ebenso wenig die möglichen Auswirkungen auf die Umwelt. Wissenschaftler der University of California, Riverside sehen die Forschungen hinsichtlich der von Graphen ausgehenden Gefahren auf dem Stand, den die Wissenschaft bezüglich Pharmazeutika und Chemikalien vor 30 Jahren erreicht hatte. Erste Veröffentlichungen zu diesem Thema lassen unter anderem erwarten, dass Graphen im Grundwasser eine hohe Mobilität aufweist und sich daher schnell verbreiten könnte. ⓘ