Sechseck

Regelmäßiges Sechseck ⓘ
Regelmäßiges Sechseck ⓘ
	Ein regelmäßiges Sechseck
Typ	Regelmäßiges Vieleck
Kanten und Scheitelpunkte	6
Schläfli-Symbol	{6}, t{3}
Coxeter-Dynkin-Diagramme	;
Symmetrie-Gruppe	Dihedral (D6), Ordnung 2×6
Innenwinkel (Grad)	120°
Eigenschaften	Konvex, zyklisch, gleichseitig, isogonal, isotoxisch

In der Geometrie ist ein Sechseck (von griechisch ἕξ, hex, d.h. "sechs", und γωνία, gonía, d.h. "Ecke, Winkel") ein sechsseitiges Polygon oder 6-Gon. Die Summe der Innenwinkel eines einfachen (sich nicht selbst überschneidenden) Sechsecks beträgt 720°. ⓘ

Regelmäßiges Sechseck

Ein regelmäßiges Sechseck hat das Schläfli-Symbol {6} und kann auch als abgestumpftes gleichseitiges Dreieck, t{3}, konstruiert werden, bei dem sich zwei Arten von Kanten abwechseln. ⓘ

Eine Schritt-für-Schritt-Animation der Konstruktion eines regelmäßigen Sechsecks mit Zirkel und Lineal nach Euklids Elementen, Buch IV, Satz 15: Dies ist möglich, da 6

=

2 × 3, ein Produkt aus einer Zweierpotenz und verschiedenen Fermat-Primzahlen.

Wenn die Seitenlänge AB gegeben ist, ergibt das Ziehen eines Kreisbogens von Punkt A und Punkt B den Schnittpunkt M, den Mittelpunkt des Umkreises. Man überträgt die Strecke AB viermal auf den umschriebenen Kreis und verbindet die Eckpunkte. ⓘ

Ein regelmäßiges Sechseck ist definiert als ein Sechseck, das sowohl gleichseitig als auch gleichwinklig ist. Es ist bizentrisch, d.h. es ist sowohl zyklisch (hat einen Umkreis) als auch tangential (hat einen Inkreis). ⓘ

Die gemeinsame Länge der Seiten ist gleich dem Radius des Inkreises oder Umkreises, der gleich ist ${\tfrac {2}{\sqrt {3}}}$ mal dem Apothemus (Radius des Inkreises). Alle Innenwinkel betragen 120 Grad. Ein regelmäßiges Sechseck hat sechs Rotationssymmetrien (Rotationssymmetrie der Ordnung sechs) und sechs Reflexionssymmetrien (sechs Symmetrielinien), die die Flächengruppe D₆ bilden. Die längsten Diagonalen eines regelmäßigen Sechsecks, die diametral gegenüberliegende Eckpunkte verbinden, sind doppelt so lang wie eine Seite. Daraus ergibt sich, dass ein Dreieck, dessen Scheitelpunkt in der Mitte des regelmäßigen Sechsecks liegt und das eine Seite mit dem Sechseck teilt, gleichseitig ist, und dass das regelmäßige Sechseck in sechs gleichseitige Dreiecke unterteilt werden kann. ⓘ

Wie Quadrate und gleichseitige Dreiecke passen regelmäßige Sechsecke lückenlos zusammen, um die Ebene zu kacheln (drei Sechsecke treffen sich an jedem Scheitelpunkt), und sind daher nützlich für die Konstruktion von Mosaiken. Die Zellen einer Bienenwabe sind aus diesem Grund sechseckig und weil diese Form den Raum und das Baumaterial effizient nutzt. Das Voronoi-Diagramm eines regelmäßigen Dreiecksgitters ist das Wabenmosaik aus Sechsecken. Es wird normalerweise nicht als Triambus betrachtet, obwohl es gleichseitig ist. ⓘ

Ein reguläres Sechseck lässt sich als Konstruktion mit Zirkel und Lineal sehr einfach aus einem Kreis darstellen, indem der Radius des Kreises sechsmal auf dem Kreisrand abgetragen wird (siehe Konstruktion 1). Die erhaltenen Punkte sind die Ecken des Sechsecks. Alternativ genügt nach Euklid das zweimalige Abtragen auf dem Kreisrand. Die fehlenden Ecken können dann über die Geraden durch den Mittelpunkt des Umkreises und die bereits bekannten Ecken konstruiert werden (siehe Konstruktion 2 nach Euklid, als animierte Grafik). ⓘ

Konstruktion 1
Konstruktion 2 nach Euklid, als animierte Grafik ⓘ

Parameter

Der maximale Durchmesser (der der langen Diagonale des Sechsecks entspricht), D, ist das Doppelte des maximalen Radius oder Umfangsradius, R, der der Seitenlänge, t, entspricht. Der minimale Durchmesser oder der Durchmesser des Inkreises (Abstand der parallelen Seiten, Flach-zu-Flach-Abstand, kurze Diagonale oder Höhe, wenn er auf einer flachen Unterlage ruht), d, ist das Doppelte des minimalen Radius oder Inradius, r. Die Maxima und Minima sind durch denselben Faktor verbunden:

{\frac {1}{2}}d=r=\cos(30^{\circ })R={\frac {\sqrt {3}}{2}}R={\frac {\sqrt {3}}{2}}t

und, in ähnlicher Weise,

d={\frac {\sqrt {3}}{2}}D.

ⓘ

Der Flächeninhalt eines regelmäßigen Sechsecks

{\begin{aligned}A&={\frac {3{\sqrt {3}}}{2}}R^{2}=3Rr=2{\sqrt {3}}r^{2}\\[3pt]&={\frac {3{\sqrt {3}}}{8}}D^{2}={\frac {3}{4}}Dd={\frac {\sqrt {3}}{2}}d^{2}\\[3pt]&\approx 2.598R^{2}\approx 3.464r^{2}\\&\approx 0.6495D^{2}\approx 0.866d^{2}.\end{aligned}}

ⓘ

Für jedes regelmäßige Vieleck kann die Fläche auch durch den Apothemus a und den Umfang p ausgedrückt werden. Für das regelmäßige Sechseck sind diese durch a = r und p ${}=6R=4r{\sqrt {3}}$ , also

{\begin{aligned}A&={\frac {ap}{2}}\\&={\frac {r\cdot 4r{\sqrt {3}}}{2}}=2r^{2}{\sqrt {3}}\\&\approx 3.464r^{2}.\end{aligned}}

ⓘ

Das regelmäßige Sechseck füllt den Bruchteil ${\tfrac {3{\sqrt {3}}}{2\pi }}\approx 0.8270$ seines umschriebenen Kreises aus. ⓘ

Hat ein regelmäßiges Sechseck die aufeinanderfolgenden Eckpunkte A, B, C, D, E, F und ist P ein beliebiger Punkt auf dem Umkreis zwischen B und C, dann ist PE + PF = PA + PB + PC + PD. ⓘ

Aus dem Verhältnis von Umfangsradius zu Innenradius folgt, dass das Verhältnis von Höhe zu Breite eines regelmäßigen Sechsecks 1:1,1547005 beträgt, d. h. ein Sechseck mit einer langen Diagonale von 1,0000000 hat einen Abstand von 0,8660254 zwischen parallelen Seiten. ⓘ

Punkt in der Ebene

Für einen beliebigen Punkt in der Ebene eines regelmäßigen Sechsecks mit Umfangsradius $R$ , dessen Abstände zum Schwerpunkt des regelmäßigen Sechsecks und zu seinen sechs Scheitelpunkten sind $L$ und $d_{i}$ sind, gilt ⓘ

d_{1}^{2}+d_{4}^{2}=d_{2}^{2}+d_{5}^{2}=d_{3}^{2}+d_{6}^{2}=2\left(R^{2}+L^{2}\right),

d_{1}^{2}+d_{3}^{2}+d_{5}^{2}=d_{2}^{2}+d_{4}^{2}+d_{6}^{2}=3\left(R^{2}+L^{2}\right),

d_{1}^{4}+d_{3}^{4}+d_{5}^{4}=d_{2}^{4}+d_{4}^{4}+d_{6}^{4}=3\left(\left(R^{2}+L^{2}\right)^{2}+2R^{2}L^{2}\right).

ⓘ

Wenn $d_{i}$ die Abstände von den Scheitelpunkten eines regelmäßigen Sechsecks zu einem beliebigen Punkt auf seinem Umkreis sind, dann gilt ⓘ

\left(\sum _{i=1}^{6}d_{i}^{2}\right)^{2}=4\sum _{i=1}^{6}d_{i}^{4}.

ⓘ

Symmetrie

Beispiel für Sechsecke durch Symmetrie ⓘ

d6 isotoxisch	g6 gerichtet	p6 isogonal		d2	g2 allgemein Parallelogon	p2
	r12 regelmäßig				i4
	g3				a1

Die sechs Spiegelungslinien eines regelmäßigen Sechsecks mit Dih₆- oder r12-Symmetrie, Ordnung 12. ⓘ

Die Flächensymmetrien sind unterteilt, je nachdem, ob sie durch Eckpunkte (d für Diagonale) oder Kanten (p für Senkrechte) verlaufen. Die zyklischen Symmetrien in der mittleren Spalte sind mit g für ihre zentrale Gyrationsordnung gekennzeichnet. Die vollständige Symmetrie der regelmäßigen Form ist r12 und keine Symmetrie ist mit a1 gekennzeichnet. ⓘ

Das regelmäßige Sechseck hat die Symmetrie D₆. Es gibt 16 Untergruppen. Davon sind 8 isomorph: die Gruppe selbst (D₆), 2 zweiflächige: (D_3, D₂), 4 zyklische: (Z₆, Z₃, Z₂, Z₁) und die triviale (e) ⓘ

Diese Symmetrien drücken neun verschiedene Symmetrien eines regelmäßigen Sechsecks aus. John Conway bezeichnet diese mit einem Buchstaben und einer Gruppenordnung. r12 ist eine vollständige Symmetrie, und a1 ist keine Symmetrie. p6, ein isogonales Sechseck, das durch drei Spiegel konstruiert wird, kann abwechselnd lange und kurze Kanten haben, und d6, ein isotoxisches Sechseck, das mit gleichen Kantenlängen konstruiert wird, aber die Eckpunkte haben abwechselnd zwei verschiedene Innenwinkel. Diese beiden Formen sind Duale von einander und haben die halbe Symmetrieordnung des regulären Sechsecks. Die i4-Formen sind reguläre Sechsecke, die entlang einer Symmetrierichtung abgeflacht oder gestreckt sind. Es kann als verlängerte Raute gesehen werden, während d2 und p2 als horizontal und vertikal verlängerte Drachen gesehen werden können. g2-Sechsecke, deren gegenüberliegende Seiten parallel sind, werden auch hexagonale Parallelogone genannt. ⓘ

Jede Untergruppensymmetrie lässt einen oder mehrere Freiheitsgrade für unregelmäßige Formen zu. Nur die Untergruppe g6 hat keine Freiheitsgrade, sondern kann als gerichtete Kanten gesehen werden. ⓘ

Sechsecke der Symmetrie g2, i4 und r12 können als Parallelogone die euklidische Ebene durch Translation tesselieren. Andere Sechseckformen können die Ebene mit unterschiedlichen Ausrichtungen tesselieren. ⓘ

p6m (*632)	cmm (2*22)	p2 (2222)	p31m (3*3)	pmg (22*)		pg (××) ⓘ
r12	i4	g2	d2	d2	p2	a1
Dih₆	Dih₂	Z₂	Dih₁			Z₁

A2- und G2-Gruppen

Wurzeln der Gruppe A2	G2-Gruppenwurzeln

Die 6 Wurzeln der einfachen Lie-Gruppe A2, dargestellt durch ein Dynkin-Diagramm dargestellt sind, liegen in einem regelmäßigen sechseckigen Muster. Die beiden einfachen Wurzeln haben einen Winkel von 120° zwischen sich. ⓘ

Die 12 Wurzeln der außergewöhnlichen Lie-Gruppe G2, dargestellt durch ein Dynkin-Diagramm sind ebenfalls hexagonal angeordnet. Die beiden einfachen Wurzeln zweier Längen haben einen Winkel von 150° zwischen sich. ⓘ

Zerlegung

6-Würfel-Projektion	12-Rauten-Dissektion ⓘ

Coxeter sagt, dass jedes Zonogon (ein 2m-Eck, dessen gegenüberliegende Seiten parallel und gleich lang sind) in 1⁄2m(m - 1) Parallelogramme zerlegt werden kann. Dies gilt insbesondere für regelmäßige Polygone mit gleich vielen Seiten; in diesem Fall sind die Parallelogramme alle Rauten. Diese Zerlegung eines regelmäßigen Sechsecks basiert auf einer Petrie-Polygonprojektion eines Würfels mit 3 von 6 quadratischen Flächen. Andere Parallelogramme und Projektionsrichtungen des Würfels werden in rechteckige Quader zerlegt. ⓘ

Zerlegung von Sechsecken in drei Rhomben und Parallelogramme ⓘ
2D	Rauten	Parallelogramme

	Regelmäßige {6}	Sechseckige Parallelogramme
3D	Quadratische Flächen		Rechteckige Flächen

	Würfel		Rechtwinkliger Quader

Sechseckige Strukturen

Giant's Causeway in Großaufnahme ⓘ

Von den Bienenwaben bis zum Giant's Causeway - sechseckige Muster sind in der Natur aufgrund ihrer Effizienz weit verbreitet. In einem sechseckigen Gitter ist jede Linie so kurz wie möglich, wenn eine große Fläche mit möglichst wenigen Sechsecken gefüllt werden soll. Das bedeutet, dass die Waben weniger Wachs benötigen, um gebaut zu werden, und dass sie unter Druck viel an Festigkeit gewinnen. ⓘ

Unregelmäßige Sechsecke mit parallelen gegenüberliegenden Kanten werden Parallelogone genannt und können die Ebene auch durch Verschiebung kacheln. In drei Dimensionen werden sechseckige Prismen mit parallelen gegenüberliegenden Flächen Paralleloeder genannt, die den 3-Raum durch Translation tesselieren können. ⓘ

Sechseckige Prismenmosaike
Formular	Sechseckige Kacheln	Sechseckige prismatische Honigwabe ⓘ
Regelmäßig
Parallelogonal

Mosaike aus Sechsecken

Neben dem regelmäßigen Sechseck, das ein eindeutiges Mosaik der Ebene ergibt, kann jedes unregelmäßige Sechseck, das das Conway-Kriterium erfüllt, die Ebene kacheln. ⓘ

In einen Kegelschnitt eingeschriebenes Sechseck

Das Pascalsche Theorem (auch bekannt als "Hexagrammum Mysticum Theorem") besagt, dass, wenn ein beliebiges Sechseck in einen Kegelschnitt eingeschrieben ist und Paare gegenüberliegender Seiten verlängert werden, bis sie sich treffen, die drei Schnittpunkte auf einer Geraden liegen, der "Pascalschen Linie" dieser Konfiguration. ⓘ

Zyklisches Sechseck

Das Lemoine-Sechseck ist ein zyklisches Sechseck (ein in einen Kreis eingeschriebenes Sechseck), dessen Eckpunkte durch die sechs Schnittpunkte der Kanten eines Dreiecks und die drei zu den Kanten parallelen Linien gegeben sind, die durch seinen Symmetriepunkt gehen. ⓘ

Wenn die aufeinanderfolgenden Seiten eines zyklischen Sechsecks a, b, c, d, e, f sind, dann schneiden sich die drei Hauptdiagonalen nur dann in einem einzigen Punkt, wenn ace = bdf ist. ⓘ

Wenn für jede Seite eines zyklischen Sechsecks die benachbarten Seiten bis zu ihrem Schnittpunkt verlängert werden und so ein Dreieck außerhalb der jeweiligen Seite bilden, dann sind die Segmente, die die Umfänge der gegenüberliegenden Dreiecke verbinden, deckungsgleich. ⓘ

Wenn ein Sechseck auf dem Umkreis eines spitzen Dreiecks an den sechs Punkten (einschließlich der drei Eckpunkte des Dreiecks), an denen die erweiterten Höhen des Dreiecks auf den Umkreis treffen, Spitzen hat, dann ist der Flächeninhalt des Sechsecks doppelt so groß wie der des Dreiecks. ⓘ

Sechseck tangential zu einem Kegelschnitt

ABCDEF sei ein Sechseck, das von sechs Tangenten eines Kegelschnitts gebildet wird. Dann besagt der Satz von Brianchon, dass sich die drei Hauptdiagonalen AD, BE und CF in einem einzigen Punkt schneiden. ⓘ

In einem Sechseck, das tangential zu einem Kreis liegt und dessen Seiten a, b, c, d, e und f aufeinander folgen, ⓘ

a+c+e=b+d+f.

ⓘ

Gleichseitige Dreiecke auf den Seiten eines beliebigen Sechsecks

Gleichseitige Dreiecke auf den Seiten eines beliebigen Sechsecks ⓘ

Wenn auf jeder Seite eines Sechsecks ein gleichseitiges Dreieck konstruiert wird, dann bilden die Mittelpunkte der Segmente, die die Mittelpunkte der gegenüberliegenden Dreiecke verbinden, ein weiteres gleichseitiges Dreieck. ⓘ

Schräges Sechseck

Ein regelmäßiges schräges Sechseck, gesehen als Kanten (schwarz) eines dreieckigen Antiprismas, Symmetrie D_3d, [2⁺,6], (2*3), Ordnung 12. ⓘ

Ein schräges Sechseck ist ein schräges Polygon mit sechs Ecken und Kanten, das jedoch nicht in derselben Ebene liegt. Das Innere eines solchen Sechsecks ist im Allgemeinen nicht definiert. Ein schräges Zickzack-Sechseck hat Scheitelpunkte, die zwischen zwei parallelen Ebenen wechseln. ⓘ

Ein regelmäßiges schräges Sechseck ist scheitelpunkttransitiv mit gleichen Kantenlängen. In drei Dimensionen ist es ein schräges Zickzack-Sechseck und kann in den Ecken und Seitenkanten eines dreieckigen Antiprismas mit der gleichen D_3d, [2⁺,6]-Symmetrie, Ordnung 12, gesehen werden. ⓘ

Der Würfel und das Oktaeder (wie das dreieckige Antiprisma) haben regelmäßige schiefe Sechsecke als Petrie-Polygone. ⓘ

Schiefe Sechsecke auf 3-fachen Achsen ⓘ
Würfel	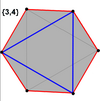Oktaeder

Petrie-Polygone

Das regelmäßige schiefe Sechseck ist das Petrie-Polygon für diese höherdimensionalen regelmäßigen, gleichmäßigen und dualen Polyeder und Polytope, die in diesen schrägen orthogonalen Projektionen dargestellt sind:

4D		5D ⓘ
3-3-Duoprisma	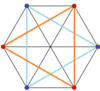3-3-Duopyramide	5-Simplex

Konvexes gleichseitiges Sechseck

Eine Hauptdiagonale eines Sechsecks ist eine Diagonale, die das Sechseck in Vierecke unterteilt. In jedem konvexen gleichseitigen Sechseck (das alle Seiten gleich lang sind) mit einer gemeinsamen Seite a gibt es eine Hauptdiagonale d₁, so dass ⓘ

{\frac {d_{1}}{a}}\leq 2

ⓘ

und eine Hauptdiagonale d₂, die so beschaffen ist, dass ⓘ

{\frac {d_{2}}{a}}>{\sqrt {3}}.

ⓘ

Polyeder mit Sechsecken

Es gibt keinen platonischen Körper, der nur aus regelmäßigen Sechsecken besteht, da die Sechsecke mosaikartig angeordnet sind, so dass sich das Ergebnis nicht "zusammenfalten" lässt. Die archimedischen Körper mit einigen sechseckigen Flächen sind das abgestumpfte Tetraeder, das abgestumpfte Oktaeder, das abgestumpfte Ikosaeder (berühmt für Fußbälle und Fullerene), das abgestumpfte Kuboktaeder und das abgestumpfte Ikosidodekaeder. Diese Sechsecke können als abgeschnittene Dreiecke betrachtet werden, mit Coxeter-Diagrammen der Form und . ⓘ

Hexagone in archimedischen Körpern ⓘ
Tetraeder	Oktaedrisch		Ikosaedrisch

abgestumpftes Tetraeder	abgestumpftes Oktaeder	abgestumpftes Kuboktaeder	abgestumpftes Ikosaeder	abgestumpftes Ikosidodekaeder

Es gibt auch andere Symmetriepolyeder mit gestreckten oder abgeflachten Sechsecken, wie das Goldberg-Polyeder G(2,0):

Sechsecke in Goldberg-Polyedern ⓘ
Tetraeder	Oktaedrisch	Ikosaedrisch
Abgeflachtes Tetraeder	Abgeschrägter Würfel	Abgeschrägtes Dodekaeder

Es gibt auch 9 Johnson-Körper mit regelmäßigen Sechsecken:

Johnson-Körper mit Sechsecken ⓘ
dreieckige Kuppel	verlängerter dreieckiger Kuppelkörper	kreiselverlängerte dreieckige Kuppel
augmentiertes sechseckiges Prisma	parabiaugmentiertes sechseckiges Prisma	metabiaugmentiertes sechseckiges Prisma	triaugmentiertes hexagonales Prisma
augmentiertes abgestumpftes Tetraeder	dreieckiger Hebesphenorotunda	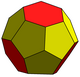Abgestumpftes Triakis-Tetraeder

Prismoide mit Sechsecken ⓘ
Sechseckiges Prisma	Sechseckiges Antiprisma	Sechseckige Pyramide

Tilings mit regelmäßigen Sechsecken ⓘ
Regelmäßig	1-gleichförmig
{6,3}	r{6,3}	rr{6,3}	tr{6,3}

2-uniforme Tilings

Galerie der natürlichen und künstlichen Sechsecke

Die ideale kristalline Struktur von Graphen ist ein hexagonales Gitter.
Zusammengebaute E-ELT-Spiegelsegmente
Eine Bienenwabe
Die Schuppen eines Schildkrötenpanzers
Das Hexagon des Saturn, ein sechseckiges Wolkenmuster um den Nordpol des Planeten
Mikroskopische Aufnahme einer Schneeflocke
Benzol, die einfachste aromatische Verbindung mit hexagonaler Form.
Sechseckige Anordnung von Blasen in einem Schaum.
Kristallstruktur eines molekularen Sechsecks, das aus sechseckigen aromatischen Ringen besteht.
Natürlich geformte Basaltsäulen vom Giant's Causeway in Nordirland; große Massen müssen langsam abkühlen, um ein polygonales Bruchmuster zu bilden
Ein Luftbild von Fort Jefferson im Dry Tortugas National Park
Der Spiegel des James Webb-Weltraumteleskops besteht aus 18 sechseckigen Segmenten.
Das französische Mutterland hat eine vage sechseckige Form. Im Französischen bezieht sich l'Hexagone auf das europäische Festland von Frankreich.
Hexagonaler Hanksit-Kristall, eines von vielen Mineralen des hexagonalen Kristallsystems
Hexagonale Scheune
Das Hexagon, ein sechseckiges Theater in Reading, Berkshire
Władysław Glińskis sechseckiges Schachspiel
Pavillon in den Botanischen Gärten von Taiwan
Sechseckiges Fenster ⓘ

Polyeder mit regelmäßigen Sechsecken

Einige Polyeder haben regelmäßige Sechsecke als Seitenflächen, zum Beispiel der Tetraederstumpf, der Oktaederstumpf, das Große Rhombenkuboktaeder, der Ikosaederstumpf und das Große Rhombenikosidodekaeder. Die genannten Polyeder sind archimedische Körper. ⓘ

Tetraederstumpf
Oktaederstumpf
Großes Rhombenkuboktaeder
Ikosaederstumpf (Fußballkörper)
Großes Rhombenikosidodekaeder ⓘ

Vorkommen von Sechsecken und hexagonalen Strukturen

Hexagonale Kristallstruktur des Graphit ⓘ

Regelmäßige Sechsecke sind in Kunst, Kultur, Natur und Technik häufig anzutreffen. Die folgende Liste zeigt nur einige Beispiele. ⓘ

Kunst und Kultur

Luftbild von Fort Jefferson auf den Florida Keys ⓘ

Kapelle mit sechseckiger Grundfläche auf der Comburg ⓘ

In der Architektur, Malerei und Grafik des Judentums und des Christentums liegt bei der Verwendung des Hexagons die Symbolik der Zahl 6 zugrunde, deren Bedeutung sich aus der Summe der ersten drei Zahlen (1+2+3) und deren Zahlensymbolik ergibt. Sie und damit das gleichseitige Hexagon symbolisieren in beiden Religionen die Allmacht Gottes. Sie stehen aber auch für Gleichgewicht und Harmonie des Göttlichen und Weltlichen, die zudem in der Gleichseitigkeit des Hexagons sowie in dessen Zusammensetzung aus sechs gedachten oder geometrisch sichtbaren gleichseitigen Dreiecken liegen, also auch die Symbolik der Zahl 3 enthalten. Die Zahl 6 und das Hexagon können, je nach Zusammenhang, auch Symbol des Sechstagewerks der Schöpfung (1. Buch Mose) sein. ⓘ

Ein Beispiel aus der christlichen Malerei des Spätmittelalters ist der hexagonale Tisch im „Paradiesgärtlein“ des Oberrheinischen Meisters (um 1410; Frankfurt, Städelsches Kunstinstitut): Er beherrscht farblich leuchtend in Form und Symbolkraft des Sechsecks das Bild und ist entscheidender Faktor zum Verständnis des Bildes, der auch durch seine Rolle in der Bildkomposition betont wird. ⓘ

Weitere Beispiele der Verwendung des Hexagons, jedoch nur eingeschränkt von symbolischer Bedeutung:

Architektur: In vielen Kulturen ist das Hexagon ein grundlegendes Element zur Gestaltung von Fenstern, Fliesen und Mosaiken. Beispiele sind Fresken am Dom zu Pisa oder Mauerelemente mancher Gebäude in Pompeji; ebenso befindet sich die Glastonbury Abbey innerhalb eines (gedachten) Hexagons. Bei der Privatvilla Kentuck Knob von Architekt Frank Lloyd Wright ist das Sechseck das durchgehende Konstruktionsprinzip, der Lantern Tower in Schottland erhebt sich über einem sechseckigen Grundriss, ebenso der Musentempel im Schlosspark Tiefurt in Thüringen wie der Wasserturm Zörbig in Sachsen-Anhalt. Mehrere Sechsecke bilden den Grundriss des Düsseldorfer Rank-Xerox-Hauses. ⓘ

M. C. Escher: Viele seiner Mosaik-Variationen basieren auf Sechsecken.
Frankreich: Aufgrund seiner ungefähr sechseckigen Form wird das auf dem europäischen Festland gelegene Territorium Frankreichs auch als l'hexagone bezeichnet. Daher befindet sich auf der Rückseite der französischen 1- und 2-Euro-Münzen ein stilisierter Baum in einem Hexagon, und der Marschall von Frankreich trägt seine sieben Sterne auf den Schulterstücken im Sechseck angeordnet.
Musikelektronik: Die ersten kommerziellen elektronischen Schlagzeuge der britischen Firma Simmons waren hexagonal geformt. ⓘ

Technik

Schraube mit Innensechskant ⓘ

Die Köpfe von Schrauben sind häufig sechseckig, entweder als Außensechskant oder als Innensechskant (Inbus). Auch Sechskantmuttern sind verbreitet.
Eine Sandwichplatte mit Wabenkern, also eine Verbundkonstruktion mit einem wabenförmigen Stützkern, wird bei Konstruktionen eingesetzt, bei denen es auf eine hohe Festigkeit bei geringem Gewicht oder Materialverbrauch ankommt.
Stützstrukturen vieler 3D-Drucker, die auf dem Verfahren Fused Deposition Modeling basieren, können bei vielen Modellen unter anderem als Wabenstruktur gedruckt werden, welche ähnlich der vorher genannten Sandwichbauweise eine hohe Stabilität mit geringem Gewicht und Filamentverbrauch kombiniert.
Die Spiegelsegmente moderner Großteleskope sind meist hexagonal-ellipsoidisch geformt. Die hexagonale Form hat beispielsweise beim James-Webb-Weltraumteleskop den Vorteil, dass neben der Zwischenraum-freien Anordnung, lediglich 3 Segmenttypen unter 18 Segmenten für die Anordnung konstruiert bzw. gefertigt werden müssen, da sie äquidistant zur zentralen optischen Achse sind und alle durch eine Linie ausgehend vom Zentrum der Gesamtanordnung symmetrisch zerschnitten werden können. Dies gilt bei einer zum Magischen Sechseck analogen Anordnung für N≤3. ⓘ

Spiele

Bei vielen Spielen, besonders bei Konfliktsimulationsspielen, besteht der Spielplan aus einem Sechseckraster. Dadurch können unter anderem Entfernungen zwischen zwei Feldern einfacher bestimmt werden als bei einem Quadratraster (zum Beispiel einem Schachbrett). Als besonders prominent gilt hier das Spiel Die Siedler von Catan, bei dem sowohl das Spielbrett selbst als auch die einzelnen Landschaftsplättchen die Sechseckform aufweisen. ⓘ