Wellenfunktion

Vergleich der Konzepte des klassischen und des Quanten-Harmonischen Oszillators für ein einzelnes spinloses Teilchen. Die beiden Prozesse unterscheiden sich stark. Der klassische Prozess (A-B) wird als Bewegung eines Teilchens entlang einer Trajektorie dargestellt. Der Quantenprozess (C-H) hat keine solche Flugbahn. Vielmehr wird er als Welle dargestellt; hier zeigt die vertikale Achse den Realteil (blau) und den Imaginärteil (rot) der Wellenfunktion. In den Feldern (C-F) sind vier verschiedene Lösungen der Schrödinger-Gleichung als stehende Welle dargestellt. Die Felder (G-H) zeigen außerdem zwei verschiedene Wellenfunktionen, die Lösungen der Schrödinger-Gleichung, aber keine stehenden Wellen sind. ⓘ

Eine Wellenfunktion in der Quantenphysik ist eine mathematische Beschreibung des Quantenzustands eines isolierten Quantensystems. Die Wellenfunktion ist eine komplexwertige Wahrscheinlichkeitsamplitude, aus der sich die Wahrscheinlichkeiten für die möglichen Ergebnisse von Messungen am System ableiten lassen. Die gebräuchlichsten Symbole für eine Wellenfunktion sind die griechischen Buchstaben ψ und Ψ (Kleinbuchstaben bzw. Großbuchstaben). ⓘ

Die Wellenfunktion ist eine Funktion der Freiheitsgrade, die einer Maximalmenge kommutabler Observablen entspricht. Sobald eine solche Darstellung gewählt ist, kann die Wellenfunktion aus dem Quantenzustand abgeleitet werden. ⓘ

Für ein gegebenes System ist die Wahl der zu verwendenden kommutierenden Freiheitsgrade nicht eindeutig, und dementsprechend ist auch der Bereich der Wellenfunktion nicht eindeutig. So kann die Wellenfunktion beispielsweise als Funktion aller Positionskoordinaten der Teilchen im Positionsraum oder der Impulse aller Teilchen im Impulsraum betrachtet werden; beide sind durch eine Fouriertransformation miteinander verbunden. Einige Teilchen, wie Elektronen und Photonen, haben einen Spin ungleich Null, und die Wellenfunktion für solche Teilchen enthält den Spin als intrinsischen, diskreten Freiheitsgrad; andere diskrete Variablen können ebenfalls einbezogen werden, z. B. der Isospin. Wenn ein System interne Freiheitsgrade hat, ordnet die Wellenfunktion an jedem Punkt der kontinuierlichen Freiheitsgrade (z. B. einem Punkt im Raum) eine komplexe Zahl für jeden möglichen Wert der diskreten Freiheitsgrade zu (z. B. die z-Komponente des Spins) - diese Werte werden häufig in einer Spaltenmatrix dargestellt (z. B. ein 2 × 1-Spaltenvektor für ein nichtrelativistisches Elektron mit Spin 1⁄2). ⓘ

Nach dem Überlagerungsprinzip der Quantenmechanik können Wellenfunktionen addiert und mit komplexen Zahlen multipliziert werden, um neue Wellenfunktionen und einen Hilbert-Raum zu bilden. Das innere Produkt zwischen zwei Wellenfunktionen ist ein Maß für die Überlappung zwischen den entsprechenden physikalischen Zuständen und wird in der grundlegenden probabilistischen Interpretation der Quantenmechanik, der Bornschen Regel, verwendet, die Übergangswahrscheinlichkeiten mit inneren Produkten in Beziehung setzt. Die Schrödinger-Gleichung bestimmt, wie sich Wellenfunktionen im Laufe der Zeit entwickeln, und eine Wellenfunktion verhält sich qualitativ wie andere Wellen, z. B. Wasserwellen oder Wellen auf einer Schnur, da die Schrödinger-Gleichung mathematisch gesehen eine Art von Wellengleichung ist. Dies erklärt den Namen "Wellenfunktion" und führt zum Welle-Teilchen-Dualismus. Die Wellenfunktion in der Quantenmechanik beschreibt jedoch eine Art von physikalischem Phänomen, das sich grundlegend von dem der klassischen mechanischen Wellen unterscheidet und noch immer für verschiedene Interpretationen offen ist. ⓘ

In der statistischen Interpretation von Born in der nichtrelativistischen Quantenmechanik, ist der quadrierte Modul der Wellenfunktion, |ψ|², eine reelle Zahl, die als Wahrscheinlichkeitsdichte der Messung eines Teilchens an einem bestimmten Ort - oder mit einem bestimmten Impuls - zu einem bestimmten Zeitpunkt interpretiert wird und möglicherweise bestimmte Werte für diskrete Freiheitsgrade hat. Das Integral dieser Größe über alle Freiheitsgrade des Systems muss gemäß der Wahrscheinlichkeitsinterpretation 1 sein. Diese allgemeine Anforderung, die eine Wellenfunktion erfüllen muss, wird als Normalisierungsbedingung bezeichnet. Da die Wellenfunktion komplexwertig ist, können nur ihre relative Phase und ihr relativer Betrag gemessen werden - ihr Wert sagt für sich genommen nichts über die Größen oder Richtungen der messbaren Größen aus; man muss Quantenoperatoren, deren Eigenwerte den Mengen möglicher Messergebnisse entsprechen, auf die Wellenfunktion ψ anwenden und die statistischen Verteilungen für die messbaren Größen berechnen. ⓘ

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt. ⓘ

Die Wellenfunktion $\psi ({\vec {x}},t)$ beziehungsweise ${\tilde {\psi }}({\vec {p}},t)$ beschreibt den quantenmechanischen Zustand eines Elementarteilchens oder eines Systems von Elementarteilchen im Orts- oder im Impulsraum. Grundlage der Beschreibung ist hierbei die Wellenmechanik von Erwin Schrödinger. Ihr Betragsquadrat bestimmt die Wahrscheinlichkeitsdichte für den Ort beziehungsweise den Impuls des Teilchens. Nach der Kopenhagener Deutung der Quantenmechanik enthält die Wellenfunktion eine Beschreibung aller Informationen einer Entität oder eines ganzen Systems. ⓘ

Bei Teilchensystemen (z. B. mit mehreren ununterscheidbaren Teilchen) bezeichnet man eine solche Lösung als Vielteilchen-Wellenfunktion. Wegen der Wechselwirkung der Teilchen untereinander lassen sich diese Lösungen jedoch meist nicht mehr ohne die modernere Methodik der Quantenfeldtheorie berechnen. ⓘ

Historischer Hintergrund

Im Jahr 1905 postulierte Albert Einstein die Proportionalität zwischen der Frequenz $f$ eines Photons und seiner Energie $E$, $E=hf$, und 1916 die entsprechende Beziehung zwischen dem Impuls eines Photons $p$ und Wellenlänge $\lambda$, $\lambda ={\frac {h}{p}}$, wobei $h$ die Planck-Konstante ist. Im Jahr 1923 war De Broglie der erste, der vorschlug, dass die Beziehung $\lambda ={\frac {h}{p}}$(heute De-Broglie-Relation) für massive Teilchen gilt, wobei der wichtigste Hinweis die Lorentz-Invarianz ist, und dies kann als Ausgangspunkt für die moderne Entwicklung der Quantenmechanik angesehen werden. Die Gleichungen stellen den Welle-Teilchen-Dualismus sowohl für masselose als auch für massive Teilchen dar. ⓘ

In den 1920er und 1930er Jahren wurde die Quantenmechanik mit Hilfe der Infinitesimalrechnung und der linearen Algebra entwickelt. Zu denjenigen, die die Techniken der Infinitesimalrechnung verwendeten, gehörten Louis de Broglie, Erwin Schrödinger und andere, die die "Wellenmechanik" entwickelten. Zu denjenigen, die die Methoden der linearen Algebra anwandten, gehörten Werner Heisenberg, Max Born und andere, die die "Matrixmechanik" entwickelten. Schrödinger zeigte später, dass die beiden Ansätze gleichwertig sind. ⓘ

Im Jahr 1926 veröffentlichte Schrödinger die berühmte Wellengleichung, die heute nach ihm benannt ist, die Schrödinger-Gleichung. Diese Gleichung beruhte auf der klassischen Energieerhaltung unter Verwendung von Quantenoperatoren und den de Broglie-Beziehungen, und die Lösungen der Gleichung sind die Wellenfunktionen für das Quantensystem. Allerdings war niemandem klar, wie sie zu interpretieren war. Zunächst dachten Schrödinger und andere, dass die Wellenfunktionen Teilchen darstellen, die sich ausbreiten, wobei sich der größte Teil des Teilchens dort befindet, wo die Wellenfunktion groß ist. Dies erwies sich als unvereinbar mit der elastischen Streuung eines Wellenpakets (das ein Teilchen darstellt) an einem Ziel; es breitet sich in alle Richtungen aus. Ein gestreutes Teilchen kann zwar in alle Richtungen streuen, aber es zerfällt nicht und fliegt nicht in alle Richtungen davon. Im Jahr 1926 stellte Born die Perspektive der Wahrscheinlichkeitsamplitude vor. Damit werden die Berechnungen der Quantenmechanik direkt mit den experimentellen Beobachtungen der Wahrscheinlichkeitsrechnung verknüpft. Sie wird als Teil der Kopenhagener Interpretation der Quantenmechanik akzeptiert. Es gibt viele andere Interpretationen der Quantenmechanik. 1927 unternahmen Hartree und Fock den ersten Schritt zur Lösung der N-Körper-Wellenfunktion und entwickelten den Selbstkonsistenzzyklus: einen iterativen Algorithmus zur Annäherung an die Lösung. Heute ist er auch als Hartree-Fock-Methode bekannt. Die Slater-Determinante und die Permanenz (einer Matrix) waren Teil der Methode, die von John C. Slater bereitgestellt wurde. ⓘ

Schrödinger stieß auf eine Gleichung für die Wellenfunktion, die die relativistische Energieerhaltung erfüllte, bevor er die nichtrelativistische veröffentlichte, verwarf sie aber, da sie negative Wahrscheinlichkeiten und negative Energien vorhersagte. Im Jahr 1927 fanden Klein, Gordon und Fock die Wellenfunktion ebenfalls, berücksichtigten aber die elektromagnetische Wechselwirkung und bewiesen, dass sie Lorentz-invariant ist. De Broglie kam 1928 ebenfalls zu dieser Gleichung. Diese relativistische Wellengleichung ist heute vor allem als Klein-Gordon-Gleichung bekannt. ⓘ

1927 fand Pauli phänomenologisch eine nichtrelativistische Gleichung zur Beschreibung von Spin-1/2-Teilchen in elektromagnetischen Feldern, die heute als Pauli-Gleichung bezeichnet wird. Pauli fand heraus, dass die Wellenfunktion nicht durch eine einzige komplexe Funktion von Raum und Zeit beschrieben werden kann, sondern zwei komplexe Zahlen benötigt, die jeweils den Spin-1/2- und -1/2-Zuständen des Fermions entsprechen. Bald darauf, im Jahr 1928, fand Dirac eine Gleichung aus der ersten erfolgreichen Vereinheitlichung der speziellen Relativitätstheorie und der Quantenmechanik, die auf das Elektron angewandt wurde und heute als Dirac-Gleichung bezeichnet wird. Darin ist die Wellenfunktion ein Spinor, der aus vier komplexwertigen Komponenten besteht: zwei für das Elektron und zwei für das Antiteilchen des Elektrons, das Positron. Im nichtrelativistischen Grenzfall ähnelt die Dirac-Wellenfunktion der Pauli-Wellenfunktion für das Elektron. Später wurden weitere relativistische Wellengleichungen gefunden. ⓘ

Wellenfunktionen und Wellengleichungen in modernen Theorien

Alle diese Wellengleichungen sind von bleibender Bedeutung. Die Schrödinger-Gleichung und die Pauli-Gleichung sind unter vielen Umständen ausgezeichnete Näherungen der relativistischen Varianten. Sie sind bei praktischen Problemen wesentlich einfacher zu lösen als die relativistischen Gegenstücke. ⓘ

Die Klein-Gordon-Gleichung und die Dirac-Gleichung sind zwar relativistisch, stellen aber keine vollständige Versöhnung von Quantenmechanik und spezieller Relativitätstheorie dar. Der Zweig der Quantenmechanik, in dem diese Gleichungen auf die gleiche Weise wie die Schrödinger-Gleichung untersucht werden und der oft als relativistische Quantenmechanik bezeichnet wird, ist zwar sehr erfolgreich, hat aber auch seine Grenzen (siehe z. B. die Lamb-Verschiebung) und konzeptionelle Probleme (siehe z. B. das Dirac-Meer). ⓘ

Die Relativitätstheorie macht es unvermeidlich, dass die Anzahl der Teilchen in einem System nicht konstant ist. Für eine vollständige Versöhnung ist die Quantenfeldtheorie erforderlich. In dieser Theorie haben die Wellengleichungen und die Wellenfunktionen ihren Platz, allerdings in einem etwas anderen Gewand. Das Hauptinteresse gilt nicht den Wellenfunktionen, sondern den Operatoren, den so genannten Feldoperatoren (oder einfach nur Feldern, wo "Operator" verstanden wird) auf dem Hilbert-Raum der Zustände (die im nächsten Abschnitt beschrieben werden). Es stellt sich heraus, dass die ursprünglichen relativistischen Wellengleichungen und ihre Lösungen immer noch benötigt werden, um den Hilbert-Raum aufzubauen. Darüber hinaus stellt sich heraus, dass die Operatoren freier Felder, d. h. wenn keine Wechselwirkungen angenommen werden, (formal) dieselbe Gleichung erfüllen wie die Felder (Wellenfunktionen) in vielen Fällen. ⓘ

So bleiben die Klein-Gordon-Gleichung (Spin 0) und die Dirac-Gleichung (Spin 1⁄2) in dieser Form in der Theorie erhalten. Zu den Analoga für höhere Spins gehören die Proca-Gleichung (Spin 1), die Rarita-Schwinger-Gleichung (Spin 3⁄2) und, allgemeiner, die Bargmann-Wigner-Gleichungen. Für masselose freie Felder sind zwei Beispiele die Maxwell-Gleichung für freie Felder (Spin 1) und die Einstein-Gleichung für freie Felder (Spin 2) für die Feldoperatoren. Alle diese Gleichungen sind im Wesentlichen eine direkte Folge der Forderung nach Lorentz-Invarianz. Ihre Lösungen müssen sich unter der Lorentz-Transformation auf eine vorgeschriebene Weise transformieren, d.h. unter einer bestimmten Darstellung der Lorentz-Gruppe, und das zusammen mit einigen anderen vernünftigen Forderungen, z.B. der Eigenschaft der Cluster-Zerlegung, mit Auswirkungen auf die Kausalität ausreicht, um die Gleichungen zu fixieren. ⓘ

Dies gilt für freie Feldgleichungen; Wechselwirkungen werden nicht berücksichtigt. Wenn eine Lagrange-Dichte (einschließlich Wechselwirkungen) verfügbar ist, liefert der Lagrange-Formalismus eine Bewegungsgleichung auf der klassischen Ebene. Diese Gleichung kann sehr komplex sein und lässt sich nicht lösen. Jede Lösung würde sich auf eine feste Anzahl von Teilchen beziehen und den Begriff "Wechselwirkung", auf den in diesen Theorien Bezug genommen wird, nicht berücksichtigen, da es sich dabei um die Erzeugung und Vernichtung von Teilchen handelt und nicht um externe Potenziale wie in der gewöhnlichen "ersten quantisierten" Quantentheorie. ⓘ

In der Stringtheorie bleibt die Situation analog. So hat eine Wellenfunktion im Impulsraum die Rolle eines Fourier-Expansionskoeffizienten in einem allgemeinen Zustand eines Teilchens (Strings) mit einem nicht scharf definierten Impuls. ⓘ

Definition (ein spinloses Teilchen in einer Dimension)

Stehende Wellen für ein Teilchen in einem Kasten, Beispiele für stationäre Zustände.

Laufende Wellen eines freien Teilchens.

Die Realteile der Ortswellenfunktion Ψ(x) und der Impulswellenfunktion Φ(p) sowie die entsprechenden Wahrscheinlichkeitsdichten |Ψ(x)|² und |Φ(p)|² für ein spinloses Teilchen in einer x- oder p-Dimension. Die Farbtrübung der Teilchen entspricht der Wahrscheinlichkeitsdichte (nicht der Wellenfunktion), das Teilchen an der Position x oder dem Impuls p zu finden. ⓘ

Betrachten wir zunächst den einfachen Fall eines nichtrelativistischen Einzelteilchens ohne Spin in einer Raumdimension. Allgemeinere Fälle werden weiter unten erörtert. ⓘ

Der dreidimensionale Fall ist analog zum Eindimensionalen; Die Wellenfunktion ist eine komplexe Funktion $\psi (x,y,z)\,$ definiert über dem dreidimensionalen Raum, und ihr Betragsquadrat wird als dreidimensionale Wahrscheinlichkeitsdichte interpretiert. Die Wahrscheinlichkeit, bei einer Messung das Teilchen im Volumen $R$ zu finden, ist deshalb ⓘ

$\int _{R}|\psi (x,y,z)|^{2}\,\mathrm {d} V$. ⓘ

Die Normierungsbedingung ist analog zum eindimensionalen Fall ⓘ

$\int |\psi (x,y,z)|^{2}\,\mathrm {d} V=1$ ⓘ

wobei das Integral sich über den gesamten Raum erstreckt. ⓘ

Orts-Raum-Wellenfunktionen

Der Zustand eines solchen Teilchens wird vollständig durch seine Wellenfunktion beschrieben,

$$\Psi (x,t)\,,$$

wobei x die Position und t die Zeit ist. Diese ist eine komplexwertige Funktion zweier reeller Variablen x und t. ⓘ

Wird die Wellenfunktion für ein spinloses Teilchen in einer Dimension als Wahrscheinlichkeitsamplitude interpretiert, so wird der quadratische Modul der Wellenfunktion, die positive reelle Zahl

$$\left|\Psi (x,t)\right|^{2}=\Psi ^{*}(x,t)\Psi (x,t)=\rho (x,t),$$

als Wahrscheinlichkeitsdichte dafür interpretiert, dass sich das Teilchen bei x befindet. Das Sternchen gibt die konjugierte komplexe Zahl an. Wenn die Position des Teilchens gemessen wird, kann sein Ort nicht aus der Wellenfunktion bestimmt werden, sondern wird durch eine Wahrscheinlichkeitsverteilung beschrieben. ⓘ

Normalisierungsbedingung

Die Wahrscheinlichkeit, dass seine Position x im Intervall a ≤ x ≤ b liegt, ist das Integral der Dichte über dieses Intervall:

$$P_{a\leq x\leq b}(t)=\int _{a}^{b}\,|\Psi (x,t)|^{2}dx$$

Dabei ist t die Zeit, zu der das Teilchen gemessen wurde. Daraus ergibt sich die Normalisierungsbedingung:

$$\int _{-\infty }^{\infty }\,|\Psi (x,t)|^{2}dx=1\,,$$

Denn wenn das Teilchen gemessen wird, befindet es sich mit 100%iger Wahrscheinlichkeit irgendwo. ⓘ

Für ein gegebenes System bildet die Menge aller möglichen normalisierbaren Wellenfunktionen (zu einem bestimmten Zeitpunkt) einen abstrakten mathematischen Vektorraum, d. h. es ist möglich, verschiedene Wellenfunktionen zu addieren und Wellenfunktionen mit komplexen Zahlen zu multiplizieren (siehe Vektorraum für weitere Einzelheiten). Technisch gesehen bilden die Wellenfunktionen aufgrund der Normalisierungsbedingung eher einen projektiven Raum als einen gewöhnlichen Vektorraum. Dieser Vektorraum ist unendlich-dimensional, da es keine endliche Menge von Funktionen gibt, die in verschiedenen Kombinationen addiert werden können, um alle möglichen Funktionen zu erzeugen. Außerdem ist er ein Hilbert-Raum, weil das innere Produkt zweier Wellenfunktionen Ψ₁ und Ψ₂ als komplexe Zahl (zum Zeitpunkt t) definiert werden kann

$$(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)dx.$$

ⓘ

Weitere Einzelheiten sind unten angegeben. Obwohl das innere Produkt von zwei Wellenfunktionen eine komplexe Zahl ist, ist das innere Produkt einer Wellenfunktion Ψ mit sich selbst,

$$(\Psi ,\Psi )=\|\Psi \|^{2}\,,$$

ist immer eine positive reelle Zahl. Die Zahl ||Ψ| (nicht ||Ψ||²) nennt man die Norm der Wellenfunktion Ψ. ⓘ

Wenn (Ψ, Ψ) = 1 ist, dann ist Ψ normiert. Wenn Ψ nicht normiert ist, dann ergibt die Division durch seine Norm die normierte Funktion Ψ/||Ψ||. Zwei Wellenfunktionen Ψ₁ und Ψ₂ sind orthogonal, wenn (Ψ₁, Ψ₂) = 0. Wenn sie normiert und orthogonal sind, sind sie orthonormal. Die Orthogonalität (also auch die Orthonormalität) von Wellenfunktionen ist keine notwendige Bedingung, die Wellenfunktionen erfüllen müssen, aber es ist aufschlussreich, sie zu betrachten, da sie die lineare Unabhängigkeit der Funktionen garantiert. In einer Linearkombination von orthogonalen Wellenfunktionen Ψn haben wir,

$$\Psi =\sum _{n}a_{n}\Psi _{n}\,,\quad a_{n}={\frac {(\Psi _{n},\Psi )}{(\Psi _{n},\Psi _{n})}}$$

ⓘ

Wären die Wellenfunktionen Ψn nicht orthogonal, wären die Koeffizienten weniger einfach zu erhalten. ⓘ

Quantenzustände als Vektoren

In der Kopenhagener Deutung ergibt das Modulusquadrat des inneren Produkts (eine komplexe Zahl) eine reelle Zahl

$$\left|(\Psi _{1},\Psi _{2})\right|^{2}=P\left(\Psi _{2}\rightarrow \Psi _{1}\right)\,,$$

die unter der Annahme, dass beide Wellenfunktionen normalisiert sind, als die Wahrscheinlichkeit interpretiert wird, dass die Wellenfunktion Ψ₂ bei der Messung einer Beobachtungsgröße, deren Eigenwerte die möglichen Ergebnisse der Messung sind, zur neuen Wellenfunktion Ψ₁ "kollabiert", wobei Ψ₁ ein Eigenvektor des resultierenden Eigenwerts ist. Dies ist die Bornsche Regel, eines der grundlegenden Postulate der Quantenmechanik. ⓘ

Zu einem bestimmten Zeitpunkt sind alle Werte der Wellenfunktion Ψ(x, t) Komponenten eines Vektors. Es gibt unendlich viele davon, und anstelle der Summation wird die Integration verwendet. In der Bra-ket-Schreibweise wird dieser Vektor geschrieben

$$|\Psi (t)\rangle =\int \Psi (x,t)|x\rangle dx$$

und wird als "Quantenzustandsvektor" oder einfach "Quantenzustand" bezeichnet. Es hat mehrere Vorteile, Wellenfunktionen als Elemente eines abstrakten Vektorraums zu verstehen:

• Alle leistungsfähigen Werkzeuge der linearen Algebra können verwendet werden, um Wellenfunktionen zu manipulieren und zu verstehen. Ein Beispiel:
  • Die lineare Algebra erklärt, wie einem Vektorraum eine Basis gegeben werden kann, und dann kann jeder Vektor im Vektorraum in dieser Basis ausgedrückt werden. Dies erklärt die Beziehung zwischen einer Wellenfunktion im Ortsraum und einer Wellenfunktion im Impulsraum und deutet darauf hin, dass es auch andere Möglichkeiten gibt.
  • Die Bra-ket-Notation kann zur Manipulation von Wellenfunktionen verwendet werden.
• Die Vorstellung, dass Quantenzustände Vektoren in einem abstrakten Vektorraum sind, ist in allen Aspekten der Quantenmechanik und der Quantenfeldtheorie völlig allgemein, während die Vorstellung, dass Quantenzustände komplexwertige "Wellen"-Funktionen des Raums sind, nur in bestimmten Situationen wahr ist. ⓘ

Der Zeitparameter wird oft unterdrückt, so auch im Folgenden. Die x-Koordinate ist ein kontinuierlicher Index. Die |x⟩ sind die Basisvektoren, die orthonormal sind, so dass ihr inneres Produkt eine Deltafunktion ist;

$$\langle x'|x\rangle =\delta (x'-x)$$

daher

$$\langle x'|\Psi \rangle =\int \Psi (x)\langle x'|x\rangle dx=\Psi (x')$$

und

$$|\Psi \rangle =\int |x\rangle \langle x|\Psi \rangle dx=\left(\int |x\rangle \langle x|dx\right)|\Psi \rangle$$

was den Identitätsoperator beleuchtet

$$I=\int |x\rangle \langle x|dx\,.$$

ⓘ

Die Suche nach dem Identitätsoperator in einer Basis ermöglicht es, den abstrakten Zustand explizit in einer Basis auszudrücken, und mehr (das innere Produkt zwischen zwei Zustandsvektoren und andere Operatoren für Beobachtungsgrößen können in der Basis ausgedrückt werden). ⓘ

Momentum-Raum-Wellenfunktionen

Das Teilchen hat auch eine Wellenfunktion im Impulsraum:

$$\Phi (p,t)$$

Dabei ist p der Impuls in einer Dimension, der jeden Wert von -∞ bis +∞ annehmen kann, und t die Zeit. ⓘ

Analog zum Ortsfall kann das innere Produkt zweier Wellenfunktionen Φ₁(p, t) und Φ₂(p, t) wie folgt definiert werden:

$$(\Phi _{1},\Phi _{2})=\int _{-\infty }^{\infty }\,\Phi _{1}^{*}(p,t)\Phi _{2}(p,t)dp\,.$$

ⓘ

Eine besondere Lösung der zeitunabhängigen Schrödingergleichung ist

$$\Psi _{p}(x)=e^{ipx/\hbar },$$

eine ebene Welle, die zur Beschreibung eines Teilchens mit dem Impuls genau p verwendet werden kann, da sie eine Eigenfunktion des Impulsoperators ist. Diese Funktionen sind nicht auf die Einheit normalisierbar (sie sind nicht quadratintegrierbar), so dass sie nicht wirklich Elemente des physikalischen Hilbert-Raums sind. Die Menge

$$\{\Psi _{p}(x,t),-\infty \leq p\leq \infty \}$$

bildet die so genannte Impulsbasis. Diese "Basis" ist keine Basis im üblichen mathematischen Sinne. Da die Funktionen nicht normalisierbar sind, werden sie stattdessen auf eine Deltafunktion normalisiert,

$$(\Psi _{p},\Psi _{p'})=\delta (p-p').$$

ⓘ

Zum anderen sind sie zwar linear unabhängig, aber es gibt zu viele von ihnen (sie bilden eine nicht abzählbare Menge) für eine Basis für den physikalischen Hilbert-Raum. Sie können dennoch verwendet werden, um alle Funktionen in diesem Raum mit Hilfe von Fourier-Transformationen auszudrücken, wie im Folgenden beschrieben. ⓘ

Beziehungen zwischen Positions- und Impulsdarstellungen

Die x- und p-Darstellungen sind

$${\begin{aligned}|\Psi \rangle =I|\Psi \rangle &=\int |x\rangle \langle x|\Psi \rangle dx=\int \Psi (x)|x\rangle dx,\\|\Psi \rangle =I|\Psi \rangle &=\int |p\rangle \langle p|\Psi \rangle dp=\int \Phi (p)|p\rangle dp.\end{aligned}}$$

ⓘ

Projizieren Sie nun den Zustand Ψ auf die Eigenfunktionen des Impulses, indem Sie den letzten Ausdruck der beiden Gleichungen verwenden,

$$\int \Psi (x)\langle p|x\rangle dx=\int \Phi (p')\langle p|p'\rangle dp'=\int \Phi (p')\delta (p-p')dp'=\Phi (p).$$

ⓘ

Unter Verwendung des bekannten Ausdrucks für geeignet normierte Eigenzustände des Impulses in der Ortsdarstellung erhält man dann Lösungen der freien Schrödingergleichung

$$\langle x|p\rangle =p(x)={\frac {1}{\sqrt {2\pi \hbar }}}e^{{\frac {i}{\hbar }}px}\Rightarrow \langle p|x\rangle ={\frac {1}{\sqrt {2\pi \hbar }}}e^{-{\frac {i}{\hbar }}px},$$

erhält man

$$\Phi (p)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Psi (x)e^{-{\frac {i}{\hbar }}px}dx\,.$$

ⓘ

Gleichermaßen erhält man unter Verwendung von Eigenfunktionen der Position,

$$\Psi (x)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Phi (p)e^{{\frac {i}{\hbar }}px}dp\,.$$

ⓘ

Die Orts- und Impuls-Raum-Wellenfunktionen sind also Fourier-Transformationen voneinander. Die beiden Wellenfunktionen enthalten die gleiche Information, und eine der beiden Funktionen allein reicht aus, um jede Eigenschaft des Teilchens zu berechnen. Als Repräsentanten von Elementen des abstrakten physikalischen Hilbert-Raums, dessen Elemente die möglichen Zustände des betrachteten Systems darstellen, repräsentieren sie denselben Zustandsvektor und damit identische physikalische Zustände, sind aber im Allgemeinen nicht gleich, wenn man sie als quadratisch-integrable Funktionen betrachtet. ⓘ

In der Praxis wird die Orts-Raum-Wellenfunktion viel häufiger verwendet als die Impuls-Raum-Wellenfunktion. Das Potential, das in die betreffende Gleichung eingeht (Schrödinger, Dirac usw.), bestimmt, in welcher Basis die Beschreibung am einfachsten ist. Für den harmonischen Oszillator treten x und p symmetrisch ein, so dass es hier keine Rolle spielt, welche Beschreibung man verwendet. Es ergibt sich die gleiche Gleichung (modulo Konstanten). Daraus folgt, mit ein wenig Nachdenken, ein Faktum: Die Lösungen der Wellengleichung des harmonischen Oszillators sind Eigenfunktionen der Fourier-Transformation in L². ⓘ

Definitionen (andere Fälle)

Es folgen die allgemeinen Formen der Wellenfunktion für Systeme in höheren Dimensionen und mit mehr Teilchen sowie mit anderen Freiheitsgraden als Positionskoordinaten oder Impulskomponenten. ⓘ

Ein-Teilchen-Zustände im 3d-Positionsraum

Die Positions-Raum-Wellenfunktion eines einzelnen Teilchens ohne Spin in drei Raumdimensionen ist ähnlich wie im obigen Fall einer Raumdimension:

$$\Psi (\mathbf {r} ,t)$$

Dabei ist r der Ortsvektor im dreidimensionalen Raum und t die Zeit. Wie immer ist Ψ(r, t) eine komplexwertige Funktion von reellen Variablen. Als ein einzelner Vektor in Dirac-Notation

$$|\Psi (t)\rangle =\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r} ,t)\,|\mathbf {r} \rangle$$

ⓘ

Alle bisherigen Ausführungen zu inneren Produkten, Impulsraum-Wellenfunktionen, Fourier-Transformationen usw. lassen sich auf höhere Dimensionen übertragen. ⓘ

Für ein Teilchen mit Spin ist die Wellenfunktion - ohne Berücksichtigung der Ortsfreiheitsgrade - nur eine Funktion des Spins (die Zeit ist ein Parameter);

$$\xi (s_{z},t)$$

wobei sz die Quantenzahl der Spinprojektion entlang der z-Achse ist. (Die z-Achse ist eine willkürliche Wahl; andere Achsen können stattdessen verwendet werden, wenn die Wellenfunktion entsprechend transformiert wird, siehe unten.) Der Parameter sz ist im Gegensatz zu r und t eine diskrete Variable. Zum Beispiel kann sz für ein Spin-1/2-Teilchen nur +1/2 oder -1/2 sein, und keinen anderen Wert annehmen. (Für den Spin s kann sz im Allgemeinen s, s - 1, ..., -s + 1, -s sein). Wenn man jede Quantenzahl einsetzt, erhält man eine komplexwertige Funktion von Raum und Zeit, von denen es 2s + 1 gibt. Diese können in einem Spaltenvektor angeordnet werden ⓘ

$$\xi ={\begin{bmatrix}\xi (s,t)\\\xi (s-1,t)\\\vdots \\\xi (-(s-1),t)\\\xi (-s,t)\\\end{bmatrix}}=\xi (s,t){\begin{bmatrix}1\\0\\\vdots \\0\\0\\\end{bmatrix}}+\xi (s-1,t){\begin{bmatrix}0\\1\\\vdots \\0\\0\\\end{bmatrix}}+\cdots +\xi (-(s-1),t){\begin{bmatrix}0\\0\\\vdots \\1\\0\\\end{bmatrix}}+\xi (-s,t){\begin{bmatrix}0\\0\\\vdots \\0\\1\\\end{bmatrix}}$$

ⓘ

In der Braket-Schreibweise lassen sich diese leicht zu den Komponenten eines Vektors anordnen

$$|\xi (t)\rangle =\sum _{s_{z}=-s}^{s}\xi (s_{z},t)\,|s_{z}\rangle$$

ⓘ

Der gesamte Vektor ξ ist eine Lösung der Schrödinger-Gleichung (mit einem geeigneten Hamiltonian), die sich zu einem gekoppelten System von 2s + 1 gewöhnlichen Differentialgleichungen mit den Lösungen ξ(s, t), ξ(s - 1, t), ..., ξ(-s, t) entfaltet. Einige Autoren verwenden den Begriff "Spinfunktion" anstelle von "Wellenfunktion". Dies steht im Gegensatz zu den Lösungen von Positionsraum-Wellenfunktionen, bei denen die Positionskoordinaten kontinuierliche Freiheitsgrade sind, da die Schrödinger-Gleichung dann die Form einer Wellengleichung hat. ⓘ

Allgemeiner ausgedrückt, kann die Wellenfunktion für ein Teilchen in 3D mit beliebigem Spin im "Positions-Spin-Raum" wie folgt geschrieben werden:

$$\Psi (\mathbf {r} ,s_{z},t)$$

und diese können auch in einem Spaltenvektor angeordnet werden

$$\Psi (\mathbf {r} ,t)={\begin{bmatrix}\Psi (\mathbf {r} ,s,t)\\\Psi (\mathbf {r} ,s-1,t)\\\vdots \\\Psi (\mathbf {r} ,-(s-1),t)\\\Psi (\mathbf {r} ,-s,t)\\\end{bmatrix}}$$

angeordnet werden, in dem die Spin-Abhängigkeit bei der Indizierung der Einträge berücksichtigt wird, und die Wellenfunktion ist eine komplexe vektorielle Funktion von Raum und Zeit. ⓘ

Alle Werte der Wellenfunktion, nicht nur für diskrete, sondern auch für kontinuierliche Variablen, werden in einem einzigen Vektor zusammengefasst

$$|\Psi (t)\rangle =\sum _{s_{z}}\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r} ,s_{z},t)\,|\mathbf {r} ,s_{z}\rangle$$

ⓘ

Für ein einzelnes Teilchen ergibt das Tensorprodukt ⊗ seines Positionszustandsvektors |ψ⟩ und seines Spin-Zustandsvektors |ξ⟩ den zusammengesetzten Positions-Spin-Zustandsvektor

$$|\psi (t)\rangle \!\otimes \!|\xi (t)\rangle =\sum _{s_{z}}\int d^{3}\!\mathbf {r} \,\psi (\mathbf {r} ,t)\,\xi (s_{z},t)\,|\mathbf {r} \rangle \!\otimes \!|s_{z}\rangle$$

mit den Identifikationen

$$|\Psi (t)\rangle =|\psi (t)\rangle \!\otimes \!|\xi (t)\rangle$$

$$\Psi (\mathbf {r} ,s_{z},t)=\psi (\mathbf {r} ,t)\,\xi (s_{z},t)$$

$$|\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle \!\otimes \!|s_{z}\rangle$$

ⓘ

Die Faktorisierung mit dem Tensorprodukt ist nur möglich, wenn die Bahn- und Spin-Drehimpulse des Teilchens im Hamilton-Operator, der der Dynamik des Systems zugrunde liegt, trennbar sind (mit anderen Worten, der Hamilton-Operator kann in die Summe der Bahn- und Spin-Terme zerlegt werden). Die Zeitabhängigkeit kann in einem der beiden Faktoren untergebracht werden, und die zeitliche Entwicklung jedes Faktors kann separat untersucht werden. Die Faktorisierung ist nicht möglich für Wechselwirkungen, bei denen ein äußeres Feld oder eine raumabhängige Größe an den Spin koppelt; Beispiele sind ein Teilchen in einem Magnetfeld und die Spin-Bahn-Kopplung. ⓘ

Die vorangegangene Diskussion ist nicht auf den Spin als diskrete Variable beschränkt, der Gesamtdrehimpuls J kann ebenfalls verwendet werden. Andere diskrete Freiheitsgrade, wie der Isospin, können ähnlich ausgedrückt werden wie der obige Spin. ⓘ

Die Bedeutung der Komponenten des Vektors hängt von der verwendeten Basis ab, typischerweise entsprechen $c_{1}$ und $c_{2}$ den Koeffizienten für eine Ausrichtung des Spins in $z$-Richtung (spin up) und entgegen der $z$-Richtung (spin down). In der Dirac-Notation ist dies:

$|\psi \rangle =c_{1}|{\mathord {\uparrow }}_{z}\rangle +c_{2}|{\mathord {\downarrow }}_{z}\rangle$ B._Elektron) ⓘ

Die Werte $|c_{1}|^{2}\,$ und $|c_{2}|^{2}\,$ werden dann als die Wahrscheinlichkeiten interpretiert, dass der Spin bei einer Messung in $z$-Richtung oder entgegen der $z$-Richtung orientiert ist. B._Elektron) ⓘ

Dies führt zur Normierungsbedingung B._Elektron) ⓘ

$|c_{1}|^{2}+|c_{2}|^{2}=1\,$. B._Elektron) ⓘ

Vielteilchenzustände im 3d-Positionsraum

Wanderwellen von zwei freien Teilchen, wobei zwei der drei Dimensionen unterdrückt sind. Oben die Positionsraum-Wellenfunktion, unten die Impulsraum-Wellenfunktion mit den entsprechenden Wahrscheinlichkeitsdichten. ⓘ

Wenn es viele Teilchen gibt, gibt es im Allgemeinen nur eine Wellenfunktion und nicht für jedes Teilchen eine eigene Wellenfunktion. Die Tatsache, dass eine Wellenfunktion viele Teilchen beschreibt, macht die Quantenverschränkung und das EPR-Paradoxon möglich. Die Positions-Raum-Wellenfunktion für N Teilchen wird wie folgt geschrieben:

$$\Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t)$$

wobei ri die Position des i-ten Teilchens im dreidimensionalen Raum und t die Zeit ist. Insgesamt handelt es sich um eine komplexwertige Funktion von 3N + 1 reellen Variablen. ⓘ

In der Quantenmechanik gibt es eine grundlegende Unterscheidung zwischen identischen Teilchen und unterscheidbaren Teilchen. So sind beispielsweise zwei beliebige Elektronen identisch und grundsätzlich nicht voneinander unterscheidbar; die Gesetze der Physik machen es unmöglich, einem bestimmten Elektron eine "Identifikationsnummer" aufzudrücken, um es zu identifizieren. Dies bedeutet eine Anforderung an die Wellenfunktion für ein System identischer Teilchen:

$$\Psi \left(\ldots \mathbf {r} _{a},\ldots ,\mathbf {r} _{b},\ldots \right)=\pm \Psi \left(\ldots \mathbf {r} _{b},\ldots ,\mathbf {r} _{a},\ldots \right)$$

wobei das Vorzeichen + auftritt, wenn die Teilchen alle Bosonen sind, und das Vorzeichen -, wenn sie alle Fermionen sind. Mit anderen Worten: Die Wellenfunktion ist entweder total symmetrisch in den Positionen der Bosonen oder total antisymmetrisch in den Positionen der Fermionen. Der physikalische Austausch von Teilchen entspricht einem mathematischen Austausch von Argumenten in der Wellenfunktion. Die Antisymmetrie der fermionischen Wellenfunktionen führt zum Pauli-Prinzip. Im Allgemeinen sind bosonische und fermionische Symmetrieanforderungen Ausdruck der Teilchenstatistik und finden sich auch in anderen Quantenzustandsformalismen. ⓘ

Für N unterscheidbare Teilchen (von denen keine zwei identisch sind, d. h. keine zwei denselben Satz von Quantenzahlen haben) muss die Wellenfunktion weder symmetrisch noch antisymmetrisch sein. ⓘ

Für eine Ansammlung von Teilchen, von denen einige identisch sind mit den Koordinaten r₁, r₂, ... und andere unterscheidbar x₁, x₂, ... (nicht identisch miteinander und nicht identisch mit den zuvor erwähnten identischen Teilchen), ist die Wellenfunktion nur in den identischen Teilchenkoordinaten ri symmetrisch oder antisymmetrisch:

$$\Psi \left(\ldots \mathbf {r} _{a},\ldots ,\mathbf {r} _{b},\ldots ,\mathbf {x} _{1},\mathbf {x} _{2},\ldots \right)=\pm \Psi \left(\ldots \mathbf {r} _{b},\ldots ,\mathbf {r} _{a},\ldots ,\mathbf {x} _{1},\mathbf {x} _{2},\ldots \right)$$

ⓘ

Für die unterscheidbaren Teilchenkoordinaten xi gibt es wiederum keine Symmetrieanforderung. ⓘ

Die Wellenfunktion für N Teilchen mit jeweils einem Spin ist die komplexwertige Funktion

$$\Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},s_{z\,1},s_{z\,2}\cdots s_{z\,N},t)$$

ⓘ

Akkumulation all dieser Komponenten in einem einzigen Vektor, ⓘ

$$|\Psi \rangle =\overbrace {\sum _{s_{z\,1},\ldots ,s_{z\,N}}} ^{\text{discrete labels}}\overbrace {\int _{R_{N}}d^{3}\mathbf {r} _{N}\cdots \int _{R_{1}}d^{3}\mathbf {r} _{1}} ^{\text{continuous labels}}\;\underbrace {{\Psi }(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},s_{z\,1},\ldots ,s_{z\,N})} _{\begin{array}{c}{\text{wave function (component of }}\\{\text{ state vector along basis state)}}\end{array}}\;\underbrace {|\mathbf {r} _{1},\ldots ,\mathbf {r} _{N},s_{z\,1},\ldots ,s_{z\,N}\rangle } _{\text{basis state (basis ket)}}\,.$$

ⓘ

Für identische Teilchen gelten die Symmetrieanforderungen sowohl für die Positions- als auch für die Spin-Argumente der Wellenfunktion, so dass sie insgesamt die richtige Symmetrie aufweist. ⓘ

Die Formeln für die inneren Produkte sind Integrale über alle Koordinaten oder Momente und Summen über alle Spinquantenzahlen. Für den allgemeinen Fall von N Teilchen mit Spin in 3-d,

$$(\Psi _{1},\Psi _{2})=\sum _{s_{z\,N}}\cdots \sum _{s_{z\,2}}\sum _{s_{z\,1}}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{1}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{2}\cdots \int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r} _{N}\Psi _{1}^{*}\left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)\Psi _{2}\left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)$$

sind dies insgesamt N dreidimensionale Volumenintegrale und N Summen über die Spins. Die differentiellen Volumenelemente d³ri werden auch "dVi" oder "dxi dyi dzi" geschrieben. ⓘ

Die mehrdimensionalen Fourier-Transformationen der Positions- oder Positions-Spin-Raum-Wellenfunktionen ergeben die Impuls- oder Impuls-Spin-Raum-Wellenfunktionen. ⓘ

In diesem Fall ist die Wellenfunktion eine komplexe Funktion von sechs Raumvariablen, ⓘ

$\psi (x_{1},y_{1},z_{1},x_{2},y_{2},z_{2})\,$, ⓘ

und $|\psi |^{2}\,$ ist die gemeinsame Wahrscheinlichkeitsdichtefunktion der Positionen beider Teilchen. Die Wahrscheinlichkeit einer Positionsmessung beider Teilchen in den beiden jeweiligen Regionen R und S ist dann ⓘ

$\int _{R}\int _{S}|\psi |^{2}\,\mathrm {d} V_{2}\,\mathrm {d} V_{1}$ ⓘ

wobei $\mathrm {d} V_{1}=\mathrm {d} x_{1}\mathrm {d} y_{1}\mathrm {d} z_{1}$ und ebenso für $\mathrm {d} V_{2}$. Die Normierungsbedingung ist deshalb ⓘ

$\int |\psi |^{2}\,\mathrm {d} V_{2}\,\mathrm {d} V_{1}=1$, ⓘ

wobei das vorgestellte Integral über den gesamten Bereich aller sechs Variablen reicht. ⓘ

Wahrscheinlichkeitsinterpretation

Für den allgemeinen Fall von N Teilchen mit Spin in 3d, wenn Ψ als eine Wahrscheinlichkeitsamplitude interpretiert wird, ist die Wahrscheinlichkeitsdichte

$$\rho \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)=\left|\Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)\right|^{2}$$

ⓘ

und die Wahrscheinlichkeit, dass sich das Teilchen 1 in der Region R₁ mit dem Spin s_z1 = m₁ und das Teilchen 2 in der Region R₂ mit dem Spin s_z2 = m₂ usw. zum Zeitpunkt t befindet, ist das Integral der Wahrscheinlichkeitsdichte über diese Regionen und bewertet bei diesen Spin-Zahlen:

$$P_{\mathbf {r} _{1}\in R_{1},s_{z\,1}=m_{1},\ldots ,\mathbf {r} _{N}\in R_{N},s_{z\,N}=m_{N}}(t)=\int _{R_{1}}d^{3}\mathbf {r} _{1}\int _{R_{2}}d^{3}\mathbf {r} _{2}\cdots \int _{R_{N}}d^{3}\mathbf {r} _{N}\left|\Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},m_{1}\cdots m_{N},t\right)\right|^{2}$$

ⓘ

Zeitabhängigkeit

Für Systeme in zeitunabhängigen Potentialen kann die Wellenfunktion immer als Funktion der Freiheitsgrade multipliziert mit einem zeitabhängigen Phasenfaktor geschrieben werden, dessen Form durch die Schrödinger-Gleichung gegeben ist. Für N Teilchen, wobei nur ihre Positionen betrachtet und andere Freiheitsgrade unterdrückt werden,

$$\Psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N},t)=e^{-iEt/\hbar }\,\psi (\mathbf {r} _{1},\mathbf {r} _{2},\ldots ,\mathbf {r} _{N})\,,$$

wobei E der Energieeigenwert des Systems ist, der dem Eigenzustand Ψ entspricht. Wellenfunktionen dieser Form werden als stationäre Zustände bezeichnet. ⓘ

Die Zeitabhängigkeit des Quantenzustands und der Operatoren kann durch unitäre Transformationen der Operatoren und Zustände bestimmt werden. Für jeden Quantenzustand |Ψ⟩ und Operator O ändert sich im Schrödinger-Bild |Ψ(t)⟩ mit der Zeit gemäß der Schrödinger-Gleichung, während O konstant ist. Im Heisenberg-Bild ist es umgekehrt: |Ψ⟩ ist konstant, während sich O(t) gemäß der Heisenberg-Bewegungsgleichung mit der Zeit entwickelt. Das Dirac-Bild (oder Wechselwirkungsbild) ist eine Zwischenform, bei der die Zeitabhängigkeit sowohl bei den Operatoren als auch bei den Zuständen, die sich gemäß den Bewegungsgleichungen entwickeln, gegeben ist. Es ist vor allem für die Berechnung der Elemente der S-Matrix nützlich. ⓘ

Nicht-relativistische Beispiele

Im Folgenden werden Lösungen der Schrödingergleichung für ein nichtrelativistisches spinloses Teilchen dargestellt. ⓘ

Endliche Potentialbarriere

Streuung an einer endlichen Potentialbarriere der Höhe V₀. Die Amplituden und die Richtung der sich nach links und rechts bewegenden Wellen sind angegeben. In Rot die Wellen, die für die Ableitung der Reflexions- und Transmissionsamplitude verwendet wurden. E > V₀ für diese Abbildung. ⓘ

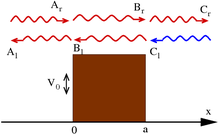
Eines der hervorstechendsten Merkmale der Wellenmechanik ist die Möglichkeit, dass ein Teilchen einen Ort mit einem (in der klassischen Mechanik) prohibitiven Kraftpotenzial erreichen kann. Ein gängiges Modell ist die "Potentialbarriere", im eindimensionalen Fall ist das Potential

$$V(x)={\begin{cases}V_{0}&|x|<a\\0&|x|\geq a\end{cases}}$$

und die stationären Lösungen der Wellengleichung haben die Form (für einige Konstanten k, κ)

$$\Psi (x)={\begin{cases}A_{\mathrm {r} }e^{ikx}+A_{\mathrm {l} }e^{-ikx}&x<-a,\\B_{\mathrm {r} }e^{\kappa x}+B_{\mathrm {l} }e^{-\kappa x}&|x|\leq a,\\C_{\mathrm {r} }e^{ikx}+C_{\mathrm {l} }e^{-ikx}&x>a.\end{cases}}$$

ⓘ

Man beachte, dass diese Wellenfunktionen nicht normalisiert sind; siehe Streutheorie zur Diskussion. ⓘ

Die Standardinterpretation ist die eines Teilchenstroms, der von links (der Richtung des negativen x) auf die Stufe geschossen wird: Ar = 1 bedeutet, dass die Teilchen einzeln geschossen werden; die Terme, die Ar und Cr enthalten, bedeuten Bewegung nach rechts, während Al und Cl - nach links. Bei dieser Strahlinterpretation ist Cl = 0 zu setzen, da keine Teilchen von rechts kommen. Durch Anwendung der Kontinuität der Wellenfunktionen und ihrer Ableitungen an den Grenzen ist es somit möglich, die oben genannten Konstanten zu bestimmen. ⓘ

3D-Wellenfunktionen von eingeschlossenen Elektronen in einem Quantenpunkt. Hier sind rechteckige und dreieckige Quantenpunkte dargestellt. Die Energiezustände in rechteckigen Punkten sind eher vom s- und p-Typ. In einem dreieckigen Punkt hingegen sind die Wellenfunktionen aufgrund der Einschluss-Symmetrie gemischt. (Klicken Sie für die Animation) ⓘ

In einem Halbleiterkristallit, dessen Radius kleiner ist als der Bohrradius seines Exzitons, werden die Exzitonen zusammengepresst, was zu Quanteneinschluss führt. Die Energieniveaus können dann mit dem Teilchen-im-Kasten-Modell modelliert werden, bei dem die Energie der verschiedenen Zustände von der Länge des Kastens abhängt. ⓘ

Harmonischer Quantenoszillator

Die Wellenfunktionen für den harmonischen Quantenoszillator können durch Hermite-Polynome Hn ausgedrückt werden, die wie folgt lauten

$$\Psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)$$

mit n = 0, 1, 2, .... ⓘ

Die Elektronenwahrscheinlichkeitsdichte für die ersten paar Elektronenorbitale des Wasserstoffatoms, dargestellt als Querschnitte. Diese Orbitale bilden eine orthonormale Basis für die Wellenfunktion des Elektrons. Die verschiedenen Orbitale sind in verschiedenen Maßstäben dargestellt. ⓘ

Wasserstoffatom

Die Wellenfunktionen eines Elektrons in einem Wasserstoffatom werden durch sphärische Harmonische und verallgemeinerte Laguerre-Polynome ausgedrückt (diese werden von verschiedenen Autoren unterschiedlich definiert - siehe Hauptartikel über sie und das Wasserstoffatom). ⓘ

Es ist zweckmäßig, Kugelkoordinaten zu verwenden, und die Wellenfunktion kann in Funktionen für jede Koordinate zerlegt werden,

$$\Psi _{n\ell m}(r,\theta ,\phi )=R(r)\,\,Y_{\ell }^{m}\!(\theta ,\phi )$$

wobei R radiale Funktionen sind und Y^m
_ℓ(θ, φ) sind sphärische Harmonische vom Grad ℓ und der Ordnung m. Dies ist das einzige Atom, für das die Schrödinger-Gleichung exakt gelöst wurde. Für Atome mit mehreren Elektronen sind Näherungsmethoden erforderlich. Die Familie der Lösungen lautet:

$$\Psi _{n\ell m}(r,\theta ,\phi )={\sqrt {{\left({\frac {2}{na_{0}}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell )!]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )$$

wobei a₀ = 4πε₀ħ²/mee² der Bohr-Radius ist, L^{2ℓ + 1}
n - ℓ - 1 sind die verallgemeinerten Laguerre-Polynome vom Grad n - ℓ - 1, n = 1, 2, ... ist die Hauptquantenzahl, ℓ = 0, 1, ..., n - 1 die azimutale Quantenzahl, m = -ℓ, -ℓ + 1, ..., ℓ - 1, ℓ die magnetische Quantenzahl. Für wasserstoffähnliche Atome gibt es sehr ähnliche Lösungen. ⓘ

Bei dieser Lösung wird der Spin des Elektrons nicht berücksichtigt. ⓘ

In der Abbildung der Wasserstofforbitale sind die 19 Teilbilder Bilder von Wellenfunktionen im Ortsraum (ihre Norm im Quadrat). Die Wellenfunktionen stellen den abstrakten Zustand dar, der durch das Tripel der Quantenzahlen (n, ℓ, m) unten rechts in jedem Bild charakterisiert ist. Dabei handelt es sich um die Hauptquantenzahl, die Bahndrehimpulsquantenzahl und die magnetische Quantenzahl. Zusammen mit einer Spin-Projektionsquantenzahl des Elektrons ist dies ein vollständiger Satz von Beobachtungsgrößen. ⓘ

Die Abbildung kann zur Veranschaulichung einiger weiterer Eigenschaften der Funktionsräume von Wellenfunktionen dienen.

• In diesem Fall sind die Wellenfunktionen quadratisch integrierbar. Man kann den Funktionsraum zunächst als den Raum der quadratisch integrierbaren Funktionen betrachten, der üblicherweise mit L² bezeichnet wird.
• Die dargestellten Funktionen sind Lösungen der Schrödinger-Gleichung. Offensichtlich erfüllt nicht jede Funktion in L² die Schrödingergleichung für das Wasserstoffatom. Der Funktionsraum ist also ein Unterraum von L².
• Die dargestellten Funktionen bilden einen Teil einer Basis für den Funktionsraum. Zu jedem Tripel (n, ℓ, m) gehört eine Basiswellenfunktion. Berücksichtigt man den Spin, so gibt es für jedes Tripel zwei Basisfunktionen. Der Funktionsraum hat also eine abzählbare Basis.
• Die Basisfunktionen sind zueinander orthonormal. ⓘ

Wellenfunktionen und Funktionsräume

Das Konzept der Funktionsräume kommt natürlich in der Diskussion über Wellenfunktionen vor. Ein Funktionsraum ist eine Menge von Funktionen, gewöhnlich mit einigen definierenden Anforderungen an die Funktionen (im vorliegenden Fall, dass sie quadratisch integrierbar sind), manchmal mit einer algebraischen Struktur auf der Menge (im vorliegenden Fall eine Vektorraumstruktur mit einem inneren Produkt), zusammen mit einer Topologie auf der Menge. Letztere wird hier nur spärlich verwendet, sie wird nur benötigt, um eine genaue Definition dessen zu erhalten, was es bedeutet, dass eine Teilmenge eines Funktionsraums geschlossen ist. Im Folgenden wird festgestellt, dass der Funktionsraum der Wellenfunktionen ein Hilbert-Raum ist. Diese Feststellung ist die Grundlage der vorherrschenden mathematischen Formulierung der Quantenmechanik. ⓘ

Struktur des Vektorraums

Eine Wellenfunktion ist ein Element eines Funktionsraums, der teilweise durch die folgenden konkreten und abstrakten Beschreibungen gekennzeichnet ist.

• Die Schrödinger-Gleichung ist linear. Das bedeutet, dass die Lösungen der Gleichung, die Wellenfunktionen, addiert und mit Skalaren multipliziert werden können, um eine neue Lösung zu bilden. Die Menge der Lösungen der Schrödinger-Gleichung ist ein Vektorraum.
• Das Überlagerungsprinzip der Quantenmechanik. Wenn Ψ und Φ zwei Zustände im abstrakten Raum der Zustände eines quantenmechanischen Systems sind und a und b zwei beliebige komplexe Zahlen sind, dann ist aΨ + bΦ ebenfalls ein gültiger Zustand. (Ob der Nullvektor als gültiger Zustand gilt ("kein System vorhanden"), ist eine Frage der Definition. Der Nullvektor beschreibt jedenfalls nicht den Vakuumzustand in der Quantenfeldtheorie.) Die Menge der zulässigen Zustände ist ein Vektorraum. ⓘ

Diese Ähnlichkeit ist natürlich nicht zufällig. Es gibt auch eine Unterscheidung zwischen den Räumen, die man im Auge behalten sollte. ⓘ

Darstellungen

Grundzustände werden durch eine Menge von Quantenzahlen charakterisiert. Dabei handelt es sich um eine Menge von Eigenwerten einer maximalen Menge von kommutativen Observablen. Physikalische Observablen werden durch lineare Operatoren, auch Observablen genannt, im Vektorraum dargestellt. Maximalität bedeutet, dass der Menge keine weiteren algebraisch unabhängigen Observablen hinzugefügt werden können, die mit den bereits vorhandenen kommutieren. Die Wahl einer solchen Menge kann als Wahl der Darstellung bezeichnet werden. ⓘ

• Ein Postulat der Quantenmechanik besagt, dass eine physikalisch beobachtbare Größe eines Systems, wie Position, Impuls oder Spin, durch einen linearen hermiteschen Operator im Zustandsraum dargestellt wird. Die möglichen Ergebnisse der Messung der Größe sind die Eigenwerte des Operators. Auf einer tieferen Ebene ergeben sich die meisten, vielleicht sogar alle, Observablen als Generatoren von Symmetrien.
• Die physikalische Interpretation ist, dass eine solche Menge das darstellt, was - theoretisch - gleichzeitig mit beliebiger Genauigkeit gemessen werden kann. Die Heisenbergsche Unschärferelation verbietet die gleichzeitige exakte Messung von zwei nicht-kommutierenden Observablen.
• Die Menge ist nicht eindeutig. Für ein Ein-Teilchen-System kann sie z. B. die Position und die Spin-Z-Projektion (x, S_z) oder den Impuls und die Spin-Y-Projektion (p, Sy) darstellen. In diesem Fall sind der Operator, der der Position entspricht (ein Multiplikationsoperator in der Positionsdarstellung), und der Operator, der dem Impuls entspricht (ein Differentialoperator in der Positionsdarstellung), nicht kommutabel.
• Sobald eine Darstellung gewählt ist, bleibt die Willkür bestehen. Es bleibt die Wahl eines Koordinatensystems. Dies kann z. B. die Wahl der x-, y- und z-Achse sein oder die Wahl von gekrümmten Koordinaten, wie sie z. B. bei den Kugelkoordinaten für die Wasserstoff-Atomwellenfunktionen verwendet werden. Diese letzte Wahl legt auch eine Basis im abstrakten Hilbert-Raum fest. Die Grundzustände werden mit den Quantenzahlen bezeichnet, die dem maximalen Satz von kommutierenden Observablen und einem geeigneten Koordinatensystem entsprechen. ⓘ

Die abstrakten Zustände sind nur insofern "abstrakt", als eine willkürliche Wahl, die für eine bestimmte explizite Beschreibung erforderlich ist, nicht gegeben ist. Dies ist dasselbe, als würde man sagen, dass keine Wahl der maximalen Menge von kommutierenden Observablen getroffen wurde. Dies ist vergleichbar mit einem Vektorraum ohne festgelegte Basis. Wellenfunktionen, die einem Zustand entsprechen, sind daher nicht eindeutig. Diese Nicht-Einzigartigkeit spiegelt die Nicht-Einzigartigkeit bei der Wahl einer maximalen Menge von kommutierenden Observablen wider. Für ein Spin-Teilchen in einer Dimension gibt es für einen bestimmten Zustand zwei Wellenfunktionen, Ψ(x, Sz) und Ψ(p, Sy), die beide denselben Zustand beschreiben.

• Für jede Wahl maximaler Mengen von Beobachtungswerten für den abstrakten Zustandsraum gibt es eine entsprechende Darstellung, die mit einem Funktionsraum von Wellenfunktionen verbunden ist.
• Zwischen all diesen verschiedenen Funktionsräumen und dem abstrakten Zustandsraum gibt es Eins-zu-Eins-Entsprechungen (hier ohne Berücksichtigung von Normalisierung und unbeobachtbaren Phasenfaktoren), wobei der gemeinsame Nenner ein bestimmter abstrakter Zustand ist. Die Beziehung zwischen den Impuls- und Positionsraum-Wellenfunktionen, die denselben Zustand beschreiben, ist zum Beispiel die Fourier-Transformation. ⓘ

Jede Wahl der Darstellung sollte als Spezifizierung eines eindeutigen Funktionsraums betrachtet werden, in dem die Wellenfunktionen, die dieser Wahl der Darstellung entsprechen, leben. Diese Unterscheidung wird am besten beibehalten, auch wenn man argumentieren könnte, dass zwei solcher Funktionsräume mathematisch gleich sind, z. B. die Menge der quadratisch integrierbaren Funktionen. Man kann sich dann die Funktionsräume als zwei verschiedene Kopien dieser Menge vorstellen. ⓘ

Inneres Produkt

Es gibt eine zusätzliche algebraische Struktur auf den Vektorräumen der Wellenfunktionen und dem abstrakten Zustandsraum.

• Physikalisch gesehen überschneiden sich verschiedene Wellenfunktionen bis zu einem gewissen Grad. Ein System, das sich in einem Zustand Ψ befindet, der sich nicht mit einem Zustand Φ überschneidet, kann bei einer Messung nicht als im Zustand Φ befindlich erkannt werden. Wenn aber Φ₁, Φ₂, ... Ψ zu einem gewissen Grad überlappen, besteht die Chance, dass die Messung eines durch Ψ beschriebenen Systems in den Zuständen Φ₁, Φ₂, .... gefunden wird. Auch Selektionsregeln sind zu beachten. Diese werden meist in der Erhaltung einiger Quantenzahlen formuliert. Das bedeutet, dass bestimmte Prozesse, die unter bestimmten Gesichtspunkten zulässig sind (z. B. Energie- und Impulserhaltung), nicht auftreten, weil sich die anfänglichen und endgültigen Gesamtwellenfunktionen nicht überschneiden.
• Mathematisch stellt sich heraus, dass Lösungen der Schrödinger-Gleichung für bestimmte Potentiale in gewisser Weise orthogonal sind, was gewöhnlich durch ein Integral beschrieben wird
  $$\int \Psi _{m}^{*}\Psi _{n}w\,dV=\delta _{nm},$$
  wobei m, n (Mengen von) Indizes (Quantenzahlen) sind, die verschiedene Lösungen kennzeichnen, die streng positive Funktion w wird als Gewichtsfunktion bezeichnet, und δ_mn ist das Kronecker-Delta. Die Integration wird über den gesamten relevanten Raum durchgeführt. ⓘ

Dies motiviert die Einführung eines inneren Produkts auf dem Vektorraum der abstrakten Quantenzustände, das mit den obigen mathematischen Beobachtungen beim Übergang zu einer Darstellung vereinbar ist. Es wird mit (Ψ, Φ) bezeichnet, oder in der Bra-ket-Notation ⟨Ψ|Φ⟩. Es ergibt eine komplexe Zahl. Mit dem inneren Produkt ist der Funktionsraum ein Innenproduktraum. Das explizite Aussehen des inneren Produkts (in der Regel ein Integral oder eine Summe von Integralen) hängt von der Wahl der Darstellung ab, die komplexe Zahl (Ψ, Φ) jedoch nicht. Ein Großteil der physikalischen Interpretation der Quantenmechanik geht auf die Bornsche Regel zurück. Sie besagt, dass die Wahrscheinlichkeit p, bei einer Messung den Zustand Φ zu finden, wenn sich das System im Zustand Ψ befindet, wie folgt ist

$$p=|(\Phi ,\Psi )|^{2},$$

wobei Φ und Ψ als normalisiert angenommen werden. Betrachten wir ein Streuungsexperiment. Wenn in der Quantenfeldtheorie Φ_out einen Zustand in der "fernen Zukunft" (e_inen "out-Zustand") beschreibt, nachdem die Wechselwirkungen zwischen den streuenden Teilchen aufgehört haben, und Ψin einen "_in-Zustand" _in der "fernen Vergangenheit", dann werden die Größen (Φ_out, Ψin), wobei Φ_out und Ψin über eine vollständige Menge von in-Zuständen bzw. out-Zuständen variieren, als S-Matrix oder Streumatrix bezeichnet. Die Kenntnis dieser Matrix bedeutet, dass die vorliegende Theorie gelöst ist, zumindest was die Vorhersagen angeht. Messbare Größen wie Zerfallsraten und Streuquerschnitte lassen sich anhand der S-Matrix berechnen. ⓘ

Hilbert-Raum

Die obigen Ausführungen fassen das Wesen der Funktionsräume zusammen, deren Elemente die Wellenfunktionen sind. Die Beschreibung ist jedoch noch nicht vollständig. Es gibt eine weitere technische Anforderung an den Funktionsraum, nämlich die der Vollständigkeit, die es erlaubt, Grenzwerte von Sequenzen im Funktionsraum zu betrachten und sicher zu sein, dass der Grenzwert, wenn er existiert, ein Element des Funktionsraums ist. Ein vollständiger innerer Produktraum wird Hilbert-Raum genannt. Die Eigenschaft der Vollständigkeit ist bei fortgeschrittenen Behandlungen und Anwendungen der Quantenmechanik von entscheidender Bedeutung. So hängt beispielsweise die Existenz von Projektionsoperatoren oder orthogonalen Projektionen von der Vollständigkeit des Raums ab. Diese Projektionsoperatoren wiederum sind für die Behauptung und den Beweis vieler nützlicher Theoreme, z. B. des Spektralsatzes, unerlässlich. In der einführenden Quantenmechanik ist dies nicht sehr wichtig, und technische Details und Links können in Fußnoten wie der folgenden gefunden werden. Der Raum L² ist ein Hilbert-Raum, dessen inneres Produkt später vorgestellt wird. Der Funktionsraum des Beispiels in der Abbildung ist ein Unterraum von L². Ein Unterraum eines Hilbert-Raums ist ein Hilbert-Raum, wenn er abgeschlossen ist. ⓘ

Zusammenfassend lässt sich sagen, dass die Menge aller möglichen normalisierbaren Wellenfunktionen für ein System mit einer bestimmten Wahl der Basis zusammen mit dem Nullvektor einen Hilbert-Raum bilden. ⓘ

Nicht alle Funktionen, die von Interesse sind, sind Elemente eines Hilbert-Raums, beispielsweise L². Das krasseste Beispiel ist die Menge der Funktionen e2πip - x⁄h. Dabei handelt es sich um ebene Wellenlösungen der Schrödingergleichung für ein freies Teilchen, die jedoch nicht normalisierbar sind und daher nicht in L² liegen. Sie sind aber dennoch grundlegend für die Beschreibung. Man kann mit ihnen Funktionen ausdrücken, die mit Wellenpaketen normalisierbar sind. Sie sind in gewissem Sinne eine Basis (aber weder eine Hilbert-Raum-Basis noch eine Hamel-Basis), in der Wellenfunktionen von Interesse ausgedrückt werden können. Es gibt auch das Artefakt "Normierung auf eine Deltafunktion", das häufig aus Gründen der Vereinfachung der Notation verwendet wird, siehe weiter unten. Die Deltafunktionen selbst sind auch nicht quadratisch integrierbar. ⓘ

Die obige Beschreibung des Funktionsraums, der die Wellenfunktionen enthält, ist größtenteils mathematisch motiviert. Die Funktionsräume sind aufgrund der Vollständigkeit in gewissem Sinne sehr groß. Nicht alle Funktionen sind realistische Beschreibungen eines physikalischen Systems. Im Funktionsraum L² findet man zum Beispiel die Funktion, die für alle rationalen Zahlen den Wert 0 und für die Irrationalen im Intervall [0, 1] den Wert -i annimmt. Diese ist quadratisch integrabel, kann aber kaum einen physikalischen Zustand darstellen. ⓘ

Gemeinsame Hilbert-Räume

Während der Raum der Lösungen als Ganzes ein Hilbert-Raum ist, gibt es viele andere Hilbert-Räume, die häufig als Bestandteile auftreten.

• Quadratisch integrable komplexwertige Funktionen auf dem Intervall [0, 2π]. Die Menge {e^int/2π, n ∈ ℤ} ist eine Hilbert-Raumbasis, d.h. eine maximale Orthonormalmenge.
• Die Fourier-Transformation bringt Funktionen im obigen Raum zu Elementen von l²(ℤ), dem Raum der quadratisch summierbaren Funktionen ℤ → ℂ. Der letztgenannte Raum ist ein Hilbert-Raum und die Fourier-Transformation ist ein Isomorphismus von Hilbert-Räumen. Seine Basis ist {ei, i ∈ ℤ} mit ei(j) = δ_ij, i, j ∈ ℤ.
• Das einfachste Beispiel für übergreifende Polynome ist der Raum der quadratisch integrierbaren Funktionen auf dem Intervall [-1, 1], für den die Legendre-Polynome eine Hilbert-Raumbasis (vollständige Orthonormalmenge) sind.
• Die quadratisch integrierbaren Funktionen auf der Einheitskugel S² sind ein Hilbert-Raum. Die Basisfunktionen sind in diesem Fall die sphärischen Harmonischen. Die Legendre-Polynome sind Bestandteile der sphärischen Harmonischen. Die meisten Probleme mit Rotationssymmetrie haben "dieselbe" (bekannte) Lösung in Bezug auf diese Symmetrie, so dass das ursprüngliche Problem auf ein Problem mit geringerer Dimensionalität reduziert wird.
• Die zugehörigen Laguerre-Polynome erscheinen im Problem der Wasserstoffwellenfunktion, nachdem die sphärischen Harmonischen herausgerechnet wurden. Diese umfassen den Hilbert-Raum der quadratisch integrierbaren Funktionen auf dem halbunendlichen Intervall [0, ∞). ⓘ

Ganz allgemein kann man eine einheitliche Behandlung aller Polynomlösungen zweiter Ordnung für die Sturm-Liouville-Gleichungen im Hilbert-Raum in Betracht ziehen. Dazu gehören die Legendre- und Laguerre-Polynome sowie die Tschebyscheff-Polynome, Jacobi-Polynome und Hermite-Polynome. Alle diese Polynome tauchen tatsächlich in physikalischen Problemen auf, letztere im harmonischen Oszillator, und was sonst ein verwirrendes Labyrinth von Eigenschaften spezieller Funktionen ist, wird zu einer organisierten Sammlung von Fakten. Siehe dazu Byron & Fuller (1992, Kapitel 5). ⓘ

Es gibt auch endlich-dimensionale Hilbert-Räume. Der Raum ℂn ist ein Hilbert-Raum der Dimension n. Das innere Produkt ist das innere Standardprodukt auf diesen Räumen. In ihm befindet sich der "Spin-Teil" der Wellenfunktion eines einzelnen Teilchens.

• Bei der nichtrelativistischen Beschreibung eines Elektrons ist n = 2 und die gesamte Wellenfunktion ist eine Lösung der Pauli-Gleichung.
• Bei der entsprechenden relativistischen Behandlung ist n = 4 und die Wellenfunktion löst die Dirac-Gleichung. ⓘ

Bei mehr Teilchen ist die Situation komplizierter. Man muss Tensorprodukte verwenden und die Darstellungstheorie der beteiligten Symmetriegruppen (die Rotationsgruppe bzw. die Lorentzgruppe) nutzen, um aus dem Tensorprodukt die Räume zu extrahieren, in denen sich die (totalen) Spinwellenfunktionen befinden. (Weitere Probleme ergeben sich im relativistischen Fall, wenn die Teilchen nicht frei sind. Siehe die Bethe-Salpeter-Gleichung.) Entsprechende Bemerkungen gelten für das Konzept des Isospins, für das die Symmetriegruppe SU(2) ist. Die Modelle der Kernkräfte aus den sechziger Jahren (die auch heute noch nützlich sind, siehe Kernkraft) verwendeten die Symmetriegruppe SU(3). Auch in diesem Fall befindet sich der Teil der Wellenfunktionen, der den inneren Symmetrien entspricht, in einigen ℂn oder Unterräumen von Tensorprodukten solcher Räume. ⓘ

• In der Quantenfeldtheorie ist der zugrunde liegende Hilbert-Raum der Fock-Raum. Er wird aus freien Einzelteilchenzuständen gebildet, d. h. aus Wellenfunktionen, wenn eine Darstellung gewählt wird, und kann eine beliebige endliche, nicht notwendigerweise zeitlich konstante Anzahl von Teilchen aufnehmen. Die interessante (oder besser gesagt die nachvollziehbare) Dynamik liegt nicht in den Wellenfunktionen, sondern in den Feldoperatoren, die auf den Fockraum wirken. Daher ist das Heisenberg-Bild die häufigste Wahl (konstante Zustände, zeitlich variierende Operatoren). ⓘ

Aufgrund der unendlichen Dimension des Systems sind die geeigneten mathematischen Werkzeuge Studienobjekte der Funktionalanalysis. ⓘ

Vereinfachte Beschreibung

Stetigkeit der Wellenfunktion und ihrer ersten räumlichen Ableitung (in x-Richtung, y- und z-Koordinaten nicht dargestellt) zu einem bestimmten Zeitpunkt t. ⓘ

Nicht alle einführenden Lehrbücher gehen den langen Weg und führen die vollständige Hilbert-Raum-Maschinerie ein, sondern der Schwerpunkt liegt auf der nichtrelativistischen Schrödinger-Gleichung in Ortsdarstellung für bestimmte Standardpotentiale. Damit die Berechnungen und die physikalische Interpretation sinnvoll sind, werden die folgenden Einschränkungen für die Wellenfunktion manchmal explizit formuliert:

• Die Wellenfunktion muss quadratisch integrierbar sein. Dies ist durch die Kopenhagener Interpretation der Wellenfunktion als Wahrscheinlichkeitsamplitude motiviert.
• Sie muss überall kontinuierlich und überall kontinuierlich differenzierbar sein. Dies ist durch das Auftreten der Schrödinger-Gleichung für die meisten physikalisch sinnvollen Potentiale begründet. ⓘ

Es ist möglich, diese Bedingungen für spezielle Zwecke etwas zu lockern. Wenn diese Bedingungen nicht erfüllt sind, ist es nicht möglich, die Wellenfunktion als Wahrscheinlichkeitsamplitude zu interpretieren. ⓘ

Dies ändert nichts an der Struktur des Hilbert-Raums, den diese speziellen Wellenfunktionen bewohnen, aber der Unterraum der quadratisch-integrablen Funktionen L², der ein Hilbert-Raum ist und die zweite Bedingung erfüllt, ist nicht in L² geschlossen, also kein Hilbert-Raum an sich. Die Funktionen, die die Anforderungen nicht erfüllen, werden sowohl aus technischen als auch aus praktischen Gründen weiterhin benötigt. ⓘ

Mehr über Wellenfunktionen und abstrakte Zustandsräume

Wie bereits gezeigt wurde, stellt die Menge aller möglichen Wellenfunktionen in einer bestimmten Darstellung für ein System einen im Allgemeinen unendlich-dimensionalen Hilbert-Raum dar. Aufgrund der vielfältigen Möglichkeiten, die Darstellungsbasis zu wählen, sind diese Hilberträume nicht eindeutig. Man spricht daher von einem abstrakten Hilbert-Raum, dem Zustandsraum, bei dem die Wahl der Darstellung und der Basis unbestimmt bleibt. Genauer gesagt, wird jeder Zustand als abstrakter Vektor im Zustandsraum dargestellt. Ein Quantenzustand |Ψ⟩ in einer beliebigen Darstellung wird im Allgemeinen als ein Vektor ausgedrückt

$$|\Psi \rangle =\sum _{\boldsymbol {\alpha }}\int d^{m}\!{\boldsymbol {\omega }}\,\,\Psi ({\boldsymbol {\alpha }},{\boldsymbol {\omega }},t)\,|{\boldsymbol {\alpha }},{\boldsymbol {\omega }}\rangle$$

wobei

• |α, ω⟩ die Basisvektoren der gewählten Darstellung
• dmω = dω₁dω₂...dωm ein "Differentialvolumenelement" in den kontinuierlichen Freiheitsgraden
• Ψ(α, ω, t) eine Komponente des Vektors |Ψ⟩, genannt die Wellenfunktion des Systems
• α = (α₁, α₂, ..., αn) dimensionslose diskrete Quantenzahlen
• ω = (ω₁, ω₂, ..., ω_m) kontinuierliche Variablen (nicht unbedingt dimensionslos) ⓘ

Diese Quantenzahlen indizieren die Komponenten des Zustandsvektors. Außerdem befinden sich alle α in einer n-dimensionalen Menge A = A₁ × A₂ × ... × An, wobei jedes Ai die Menge der zulässigen Werte für αi ist; alle ω befinden sich in einem m-dimensionalen "Volumen" Ω ⊆ ℝ^m, wobei Ω = Ω₁ × Ω₂ × ... × Ω_m und jedes Ωi ⊆ R die Menge der zulässigen Werte für ωi ist, eine Teilmenge der reellen Zahlen R. Aus Gründen der Allgemeinheit sind n und m nicht unbedingt gleich. ⓘ

Beispiel:

1. Für ein einzelnes Teilchen in 3D mit dem Spin s, unter Vernachlässigung anderer Freiheitsgrade und unter Verwendung kartesischer Koordinaten, könnten wir α = (sz) für die Spinquantenzahl des Teilchens entlang der z-Richtung und ω = (x, y, z) für die Positionskoordinaten des Teilchens nehmen. Dabei ist A = {-s, -s + 1, ..., s - 1, s} die Menge der zulässigen Spinquantenzahlen und Ω = R³ ist die Menge aller möglichen Teilchenpositionen im 3d-Positionsraum.
2. Eine alternative Wahl ist α = (s_y) für die Spinquantenzahl entlang der y-Richtung und ω = (p_x, p_y, pz) für die Impulskomponenten des Teilchens. In diesem Fall sind A und Ω die gleichen wie zuvor. ⓘ

Die Wahrscheinlichkeitsdichte für das Auffinden des Systems zum Zeitpunkt $t$im Zustand |α, ω⟩ ist

$$\rho _{\alpha ,\omega }(t)=|\Psi ({\boldsymbol {\alpha }},{\boldsymbol {\omega }},t)|^{2}$$

ⓘ

Die Wahrscheinlichkeit, ein System mit α in einigen oder allen möglichen Konfigurationen mit diskreten Variablen, D ⊆ A, und ω in einigen oder allen möglichen Konfigurationen mit kontinuierlichen Variablen, C ⊆ Ω, zu finden, ist die Summe und das Integral über die Dichte,

$$P(t)=\sum _{{\boldsymbol {\alpha }}\in D}\int _{C}\rho _{\alpha ,\omega }(t)\,\,d^{m}\!{\boldsymbol {\omega }}$$

ⓘ

Da die Summe aller Wahrscheinlichkeiten 1 sein muss, muss die Normalisierungsbedingung

$$1=\sum _{{\boldsymbol {\alpha }}\in A}\int _{\Omega }\rho _{\alpha ,\omega }(t)\,d^{m}\!{\boldsymbol {\omega }}$$

zu jeder Zeit während der Entwicklung des Systems gelten. ⓘ

Die Normalisierungsbedingung erfordert, dass ρ dmω dimensionslos ist, d. h. Ψ muss nach der Dimensionsanalyse die gleichen Einheiten haben wie (ω₁ω₂...ωm)-1/2. ⓘ

Ontologie

Die Frage, ob die Wellenfunktion wirklich existiert und was sie darstellt, ist eine der wichtigsten Fragen bei der Interpretation der Quantenmechanik. Viele berühmte Physiker einer früheren Generation wie Schrödinger, Einstein und Bohr haben über dieses Problem gerätselt. Einige vertreten Formulierungen oder Varianten der Kopenhagener Deutung (z. B. Bohr, Wigner und von Neumann), während andere, wie Wheeler oder Jaynes, den eher klassischen Ansatz verfolgen und die Wellenfunktion als eine Information im Kopf des Beobachters betrachten, d. h. als ein Maß für unser Wissen über die Realität. Einige, darunter Schrödinger, Bohm und Everett und andere, vertraten die Ansicht, dass die Wellenfunktion eine objektive, physikalische Existenz haben muss. Einstein war der Ansicht, dass sich eine vollständige Beschreibung der physikalischen Realität direkt auf den physikalischen Raum und die Zeit beziehen sollte, im Gegensatz zur Wellenfunktion, die sich auf einen abstrakten mathematischen Raum bezieht. ⓘ

Siehe auch

• Boson
• de Broglie-Bohm-Theorie
• Doppelspaltexperiment
• Faradaysche Welle
• Fermion
• Phasenraum-Formulierung
• Schrödinger-Gleichung
• Kollaps der Wellenfunktion
• Wellenpaket ⓘ

Allgemeine Quellen

• Arons, A. B.; Peppard, M. B. (1965). "Einsteins Vorschlag des Photonenkonzepts: Eine Übersetzung des Artikels in den Annalen der Physik von 1905" (PDF). American Journal of Physics. 33 (5): 367. Bibcode:1965AmJPh..33..367A. doi:10.1119/1.1971542.
• Atkins, P. W. (1974). Quanta: A Handbook of Concepts. ISBN 978-0-19-855494-3.
• Bohr, N. (1985). Kalckar, J. (Hrsg.). Niels Bohr - Gesammelte Werke: Grundlagen der Quantenphysik I (1926 - 1932). Bd. 6. Amsterdam: Nord-Holland. ISBN 978-044453289-3.
• Born, M. (1926a). "Zur Quantenmechanik der Stoßvorgange". Z. Phys. 37 (12): 863-867. Bibcode:1926ZPhy...37..863B. doi:10.1007/bf01397477. S2CID 119896026.
• Born, M. (1926b). "Quantenmechanik der Stoßvorgange". Z. Phys. 38 (11-12): 803-827. Bibcode:1926ZPhy...38..803B. doi:10.1007/bf01397184. S2CID 126244962.
• Born, M. (1927). "Physikalische Aspekte der Quantenmechanik". Nature. 119 (2992): 354-357. Bibcode:1927Natur.119..354B. doi:10.1038/119354a0.
• Born, M. (11. Dezember 1954). "Die statistische Interpretation der Quantenmechanik". Nobelvorlesung. Nobel-Stiftung. 122 (3172): 675–9. doi:10.1126/science.122.3172.675. PMID 17798674.
• de Broglie, L. (1923). "Radiations-Ondes et quanta" [Strahlung - Wellen und Quanten]. Comptes Rendus (in français). 177: 507-510, 548, 630. Online-Kopie (Französisch) Online-Kopie (Englisch)
• de Broglie, L. (1960). Nichtlineare Wellenmechanik: eine kausale Interpretation. Amsterdam: Elsevier - über Internet Archive.
• Byron, F. W.; Fuller, R. W. (1992) [Erstmals veröffentlicht 1969]. Mathematics of Classical and Quantum Physics. Dover Books on Physics (überarbeitete Auflage). Dover Veröffentlichungen. ISBN 978-0-486-67164-2 - über Internet Archive.
• Camilleri, K. (2009). Heisenberg und die Interpretation der Quantenmechanik: der Physiker als Philosoph. Cambridge UK: Cambridge University Press. ISBN 978-0-521-88484-6.
• Conway, J. B. (1990). Ein Kurs in Funktionalanalysis. Graduate Texts in Mathematics. Vol. 96. Springer Verlag. ISBN 978-0-387-97245-9.
• Dirac, P. A. M. (1939). "Eine neue Notation für die Quantenmechanik". Mathematical Proceedings of the Cambridge Philosophical Society. 35 (3): 416-418. Bibcode:1939PCPS...35..416D. doi:10.1017/S0305004100021162.
• Dirac, P. A. M. (1982). Die Prinzipien der Quantenmechanik. Die internationale Reihe der Monographien zur Physik (4. Aufl.). Oxford University Press. ISBN 0-19-852011-5.
• Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt". Annalen der Physik (in Deutsch). 17 (6): 132-148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607.
• Einstein, A. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gesellschaft Zürich. 18: 47-62.
• Einstein, A. (1917). "Zur Quantentheorie der Strahlung". Physikalische Zeitschrift (in Deutsch). 18: 121-128. Bibcode:1917PhyZ...18..121E.
• Einstein, A. (1998). Schilpp, P. A. (Hrsg.). Albert Einstein: Philosopher-Scientist. Die Bibliothek der lebenden Philosophen. Vol. VII (3. Aufl.). La Salle Publishing Company, Illinois: Open Court. ISBN 978-0-87548-133-3.
• Eisberg, Robert Martin; Resnick, Robert (1985). Quantenphysik der Atome, Moleküle, Festkörper, Kerne und Teilchen (2. Aufl.). John Wiley & Sons. ISBN 978-0-471-87373-0 - über Internet Archive.
• Greiner, W.; Reinhardt, J. (2008). Quantenelektrodynamik (4. Aufl.). springer. ISBN 978-354087560-4.
• Griffiths, D. J. (2004). Einführung in die Quantenmechanik (2. Aufl.). Essex England: Pearson Education. ISBN 978-013111892-8.
• Griffiths, David (2008). Einführung in die Elementarteilchen. Wiley-VCH. S. 162ff. ISBN 978-3-527-40601-2.
• ter Haar, D. (1967). Die alte Quantentheorie. Pergamon Press. S. 167-183. LCCN 66029628 - über Internet Archive.
• Hanle, P.A. (1977), "Erwin Schrödingers Reaktion auf Louis de Broglies Thesen zur Quantentheorie", Isis, 68 (4): 606-609, doi:10.1086/351880, S2CID 121913205
• Heisenberg, W. (1958). Physik und Philosophie: die Revolution in der modernen Wissenschaft. New York: Harper & Row - über Internet Archive.
• Jaynes, E. T. (2003). Larry, G. (Hrsg.). Wahrscheinlichkeitsrechnung: Die Logik der Wissenschaft. Cambridge University Press. ISBN 978-0-521 59271-0.
• Landau, L. D.; Lifshitz, E. M. (1977). Quantenmechanik: Non-Relativistic Theory. Vol. 3 (3. Aufl.). Pergamon Press. ISBN . 978-0-08-020940-1. Online-Kopie
• Lerner, R.G.; Trigg, G.L. (1991). Enzyklopädie der Physik (2. Aufl.). VHC Verlag. ISBN 978-0-89573-752-6 - über Internet Archive.
• Ludwig, G. (1968). Wellenmechanik. Oxford UK: Pergamon Press. ISBN 978-0-08-203204-5. LCCN 66-30631 - über Internet Archive.
• Martin, B.R.; Shaw, G. (2008). Teilchenphysik. Manchester Physics Series (3. Aufl.). John Wiley & Sons. ISBN 978-0-470-03294-7.
• Murdoch, D. (1987). Niels Bohrs Philosophie der Physik. Cambridge UK: Cambridge University Press. ISBN 978-0-521-33320-7 - über Internet Archive.
• Newton, R.G. (2002). Quantenphysik: ein Text für Doktoranden. New York: Springer. ISBN 978-0-387-95473-8.
• Pauli, Wolfgang (1927). "Zur Quantenmechanik des magnetischen Elektrons". Zeitschrift für Physik (in Deutsch). 43 (9-10): 601-623. Bibcode:1927ZPhy...43..601P. doi:10.1007/bf01397326. S2CID 128228729.
• Peleg, Y.; Pnini, R.; Zaarur, E.; Hecht, E. (2010). Quantenmechanik. Schaum's outlines (2nd ed.). McGraw Hill. ISBN . 978-0-07-162358-2.
• Rae, A.I.M. (2008). Quantenmechanik. Vol. 2 (5. Aufl.). Taylor & Francis Gruppe. ISBN 978-1-5848-89700.
• Schrödinger, E. (1926). "Eine wellenförmige Theorie der Mechanik von Atomen und Molekülen" (PDF). Physical Review. 28 (6): 1049-1070. Bibcode:1926PhRv...28.1049S. doi:10.1103/PhysRev.28.1049. Archiviert vom Original (PDF) am 17. Dezember 2008.
• Shankar, R. (1994). Grundlagen der Quantenmechanik (2. Aufl.). ISBN 978-030644790-7.
• Tipler, P. A.; Mosca, G.; Freeman (2008). Physik für Wissenschaftler und Ingenieure - mit moderner Physik (6. Aufl.). ISBN 978-0-7167-8964-2.
• Weinberg, S. (2002), Die Quantentheorie der Felder, Bd. 1, Cambridge University Press, ISBN 978-0-521-55001-7 - über Internet Archive
• Weinberg, S. (2013), Vorlesungen in Quantenmechanik, Cambridge University Press, ISBN 978-1-107-02872-2
• Wheeler, J.A.; Zurek, W.H. (1983). Quantentheorie und Messung. Princeton NJ: Princeton University Press.
• Young, H. D.; Freedman, R. A. (2008). Pearson (Hrsg.). Sears' and Zemansky's University Physics (12. Auflage). Addison-Wesley. ISBN 978-0-321-50130-1.
• Zettili, N. (2009). Quantenmechanik: Konzepte und Anwendungen (2. Aufl.). ISBN 978-0-470-02679-3.
• Zwiebach, Barton (2009). Ein erster Kurs in Stringtheorie. Cambridge University Press. ISBN 978-0-521-88032-9. ⓘ

Quantenteilchen als Welle

Da die Bewegungsgleichungen im komplexen Raum definiert sind, benötigen sie zur allgemeinen Lösung eine Funktion, deren Funktionswerte ebenfalls im komplexen Raum liegen. Daher ist die Wellenfunktion nicht reell, sondern komplexwertig. Dies spiegelt sich u. a. darin wider, dass $\psi ({\vec {r}},t)$ nicht unbedingt eine reale physikalische Bedeutung zukommt. Sie ist in der Regel nicht messbar, sondern dient nur der mathematischen Beschreibung des quantenmechanischen Zustands eines physikalischen Systems. Aus ihr lässt sich jedoch das zu erwartende Ergebnis einer Messung durch komplexe Konjugation berechnen. ⓘ

Zum Vergleich: Auch die elektrische Feldstärke ${\vec {E}}({\vec {r}},t)$ einer Radiowelle ist die Lösung einer (klassischen) elektrodynamischen Wellengleichung. Die elektrische Feldstärke ist jedoch z. B. durch eine Antenne und einen Radioempfänger messbar. ⓘ

Teilchen mit inneren Eigenschaften (wie zum Beispiel dem Spin eines gebundenen Elektrons oder dem Drehimpuls eines Photons) werden durch Wellenfunktionen mit mehreren Komponenten beschrieben. Je nach dem Transformationsverhalten der Wellenfunktionen bei Lorentztransformationen unterscheidet man in der relativistischen Quantenfeldtheorie skalare, tensorielle und spinorielle Wellenfunktionen bzw. Felder. ⓘ

Definition

Entwicklungskoeffizienten des Zustandsvektors

Formal betrachtet sind die Wellenfunktionen die Entwicklungskoeffizienten des quantenmechanischen Zustandsvektors im Orts- beziehungsweise Impulsraum. Es ist in Dirac-Notation

${\begin{aligned}\psi ({\vec {x}},t)&=\langle x|\psi (t)\rangle \\{\tilde {\psi }}({\vec {p}},t)&=\langle p|\psi (t)\rangle \end{aligned}}$

mit

• dem Zustandsvektor $|\psi \rangle$
• den Ortseigenkozuständen $\langle x|$
• den Impulseigenkozuständen $\langle p|$

sodass gilt:

$|\psi \rangle =\int \mathrm {d} ^{3}{\vec {x}}\,|x\rangle \langle x|\psi \rangle =\int \mathrm {d} ^{3}{\vec {x}}\,|x\rangle \psi ({\vec {x}})$

$|\psi \rangle =\int \mathrm {d} ^{3}{\vec {p}}\,|p\rangle \langle p|\psi \rangle =\int \mathrm {d} ^{3}{\vec {p}}\,|p\rangle {\tilde {\psi }}({\vec {p}})$

Die Orts- und Impulseigenzustände sind die Eigenzustände des Ortsoperators ${\hat {x}}$ beziehungsweise Impulsoperators ${\hat {p}}$, für die ${\hat {x}}|x\rangle =x|x\rangle$ und ${\hat {p}}|p\rangle =p|p\rangle$ gilt. Aus der Definition wird offensichtlich, dass die Wellenfunktion im Orts- sowie im Impulsraum einer Normierungsbedingung folgen, da der Zustandsvektor bereits normiert ist:

$1=\langle \psi |\psi \rangle =\int \mathrm {d} ^{3}{\vec {x}}\,\psi ^{\dagger }({\vec {x}})\psi ({\vec {x}})=\int \mathrm {d} ^{3}{\vec {p}}\,{\tilde {\psi }}^{\dagger }({\vec {p}}){\tilde {\psi }}({\vec {p}})$ ⓘ

Wellenfunktion im Impulsraum

Die Wellenfunktion im Impulsraum ${\tilde {\psi }}({\vec {p}})$ ist mit der Wellenfunktion im Ortsraum $\psi ({\vec {x}})$ über eine Fourier-Transformation verknüpft. Es gilt

${\tilde {\psi }}({\vec {p}},t)=\int \mathrm {d} ^{3}{\vec {x}}\,\psi ({\vec {x}},t)e^{-\mathrm {i} {\vec {p}}\cdot {\vec {x}}}$

nebst der Ersetzung ${\vec {p}}=\hbar {\vec {k}}$. Aufgrund des Satzes von Plancherel ist die Fouriertransformation mit der Normierung verträglich, sodass die Wellenfunktion im Impulsraum ebenso normiert ist wie die Wellenfunktion im Ortsraum. ⓘ

Beispiel: Freies Teilchen

Die Wellenfunktion $\psi ({\vec {x}},t)$ eines freien Teilchens kann als Fourierreihe über ebene Wellen dargestellt werden:

$\psi ({\vec {x}},t)=\int {\frac {\mathrm {d} ^{3}{\vec {k}}}{(2\pi )^{3}}}A({\vec {k}})e^{\mathrm {i} (\omega t-{\vec {k}}\cdot {\vec {x}})}$ ⓘ

mit

• dem Ortsvektor ${\vec {x}}$
• dem Wellenvektor ${\vec {k}}$, der Richtung und Wellenlänge der Welle festlegt
• den vom Wellenvektor abhängigen komplexwertigen Amplituden $A({\vec {k}})$
• der Kreisfrequenz $\omega ({\vec {k}})$, die die Schwingungsperiode der Welle beschreibt und mit dem Wellenvektor über eine Dispersionsrelation verknüpft ist. ⓘ

Die Amplituden müssen so gewählt werden, dass die Normierung der Wellenfunktion gewährleistet ist. Das Betragsquadrat der Wellenfunktion ist durch

${\begin{aligned}|\psi ({\vec {x}},t)|^{2}&=\psi ^{\dagger }({\vec {x}},t)\,\psi ({\vec {x}},t)\\&=\int {\frac {\mathrm {d} ^{3}{\vec {k}}}{(2\pi )^{3}}}\int {\frac {\mathrm {d} ^{3}{\vec {k}}'}{(2\pi )^{3}}}A^{\dagger }({\vec {k}})A({\vec {k}}')e^{\mathrm {i} ({\vec {k}}-{\vec {k}}')\cdot {\vec {x}}}e^{-\mathrm {i} (\omega -\omega ')t}\end{aligned}}$

gegeben. Eine Integration über das gesamte Volumen ergibt mit der Darstellung der Dirac-Distribution $\textstyle \int \mathrm {d} ^{3}x\,e^{i{\vec {k}}\cdot {\vec {x}}}=\delta ^{(3)}({\vec {k}})$:

$\int \mathrm {d} ^{3}{\vec {x}}\,|\psi ({\vec {x}},t)|^{2}=\int {\frac {\mathrm {d} ^{3}{\vec {k}}}{(2\pi )^{3}}}A^{\dagger }({\vec {k}})A({\vec {k}})=1$. ⓘ

Praktisch kann dies beispielsweise durch eine gaußförmige Einhüllende

$A({\vec {k}})=\left[{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {{\vec {k}}^{2}}{2\sigma ^{2}}}}\right]^{1/2}$

realisiert werden. Durch die Wahl dieser Einhüllenden wird ein Teilchen mit minimaler Orts-Impuls-Unschärfe und einem Erwartungswert des Impulses bei ${\vec {p}}_{0}=0$ beschrieben. $\sigma$ ist dabei die Breite des Wellenpakets, die gewissermaßen angibt, wie sich die Unschärfe auf den Orts- und Impulserwartungswert verteilt. ⓘ

Messungen in der Wellenmechanik

Eine Aussage im quantenmechanischen Messprozess lautet, bei einer Messung kollabiert die Wellenfunktion instantan auf einen Eigenwert des zur Messung zugehörigen Operators. Dieser Eigenwert ist das Ergebnis der Messung. Die Wahrscheinlichkeit, auf einen dieser Eigenwerte zu kollabieren, ist in der Matrizenmechanik durch

$P=\|\langle \phi |\psi \rangle \|^{2}$

gegeben, wobei $|\phi \rangle$ der zum Eigenwert $\phi$ gehörige Eigenzustand eines Operators $\Phi$ sei. In der Wellenmechanik entspricht dies der Formulierung

$P=\left\|\int \mathrm {d} ^{3}{\vec {x}}\,\langle \phi |x\rangle \langle x|\psi \rangle \right\|^{2}=\left\|\int \mathrm {d} ^{3}{\vec {x}}\,\phi ^{\dagger }(x)\psi (x)\right\|^{2}$.

Das Skalarprodukt des Hilbertraums entspricht also einer Integration über den gesamten Raumbereich im Ortsraum. Zwei Wellenfunktionen heißen orthogonal, wenn das Integral über den gesamten Ortsraum ihres Produkts verschwindet. Die Wahrscheinlichkeit, den Messwert $\phi$ zu erhalten, wenn das System durch die Wellenfunktion $\psi (x)$ beschrieben wird und $\phi (x)$ und $\psi (x)$ orthogonal sind, ist dementsprechend Null. ⓘ

Der Erwartungswert einer Messung im Zustand $|\psi \rangle$ wird in der Matrizenmechanik durch

$\langle \Phi \rangle =\langle \psi |\Phi |\psi \rangle$

beschrieben. Dies übersetzt sich in der Wellenmechanik zu:

$\langle \Phi \rangle =\int \mathrm {d} ^{3}{\vec {x}}\int \mathrm {d} ^{3}{\vec {x}}'\,\langle \psi |x\rangle \langle x|\Phi |x'\rangle \langle x'|\psi \rangle =\int \mathrm {d} ^{3}{\vec {x}}\int \mathrm {d} ^{3}{\vec {x}}'\,\psi ^{\dagger }({\vec {x}})\Phi (x,x')\psi ({\vec {x}}')$

Dabei ist $\Phi (x,x')$ der Operator in Ortsdarstellung. Für lokale Operatoren gilt $\Phi ({\vec {x}},{\vec {x}}')=\Phi ({\vec {x}})\delta ^{(3)}({\vec {x}}-{\vec {x}}')$ und die doppelte Integration reduziert sich auf eine einfache:

$\langle \Phi \rangle =\int \mathrm {d} ^{3}{\vec {x}}\,\psi ^{\dagger }({\vec {x}})\Phi ({\vec {x}})\psi ({\vec {x}})$ ⓘ

Teilcheninterpretation

Die physikalische Interpretation einer Wellenfunktion ist kontextabhängig. Mehrere Beispiele werden unten angeführt, gefolgt von einer Interpretation der oben beschriebenen drei Fälle. ⓘ