Polarisation

Zirkulare Polarisation auf Gummifaden, umgewandelt in lineare Polarisation ⓘ

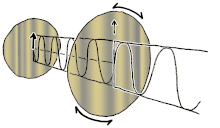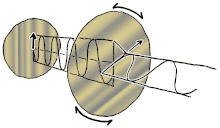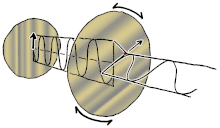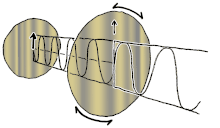
Polarisation ist eine Eigenschaft von Transversalwellen, die die geometrische Ausrichtung der Schwingungen angibt. Bei einer Transversalwelle steht die Richtung der Schwingung senkrecht zur Bewegungsrichtung der Welle. Ein einfaches Beispiel für eine polarisierte Transversalwelle sind Schwingungen, die sich entlang einer gespannten Saite ausbreiten (siehe Abbildung), zum Beispiel bei einem Musikinstrument wie einer Gitarrensaite. Je nachdem, wie die Saite gezupft wird, können die Schwingungen in vertikaler oder horizontaler Richtung oder in einem beliebigen Winkel senkrecht zur Saite verlaufen. Im Gegensatz dazu erfolgt bei Longitudinalwellen, wie Schallwellen in einer Flüssigkeit oder einem Gas, die Verschiebung der Teilchen bei der Schwingung immer in Ausbreitungsrichtung, so dass diese Wellen keine Polarisation aufweisen. Zu den transversalen Wellen, die eine Polarisation aufweisen, gehören elektromagnetische Wellen wie Licht und Radiowellen, Gravitationswellen und transversale Schallwellen (Scherwellen) in Festkörpern. ⓘ

Eine elektromagnetische Welle wie Licht besteht aus einem gekoppelten oszillierenden elektrischen und einem magnetischen Feld, die immer senkrecht zueinander stehen; vereinbarungsgemäß bezieht sich die "Polarisation" elektromagnetischer Wellen auf die Richtung des elektrischen Feldes. Bei linearer Polarisation schwingen die Felder in einer einzigen Richtung. Bei der zirkularen oder elliptischen Polarisation rotieren die Felder mit einer konstanten Rate in einer Ebene, während sich die Welle ausbreitet. Die Drehung kann in zwei Richtungen erfolgen: Drehen sich die Felder in Bezug auf die Ausbreitungsrichtung der Welle nach rechts, spricht man von zirkularer Polarisation nach rechts, drehen sich die Felder nach links, spricht man von zirkularer Polarisation nach links. ⓘ

Licht oder andere elektromagnetische Strahlung aus vielen Quellen, wie z. B. der Sonne, Flammen und Glühlampen, besteht aus kurzen Wellenzügen mit einer gleichmäßigen Mischung von Polarisationen; dies wird als unpolarisiertes Licht bezeichnet. Polarisiertes Licht kann erzeugt werden, indem unpolarisiertes Licht durch einen Polarisator geleitet wird, der nur Wellen einer bestimmten Polarisation durchlässt. Die gebräuchlichsten optischen Materialien haben keinen Einfluss auf die Polarisation des Lichts, aber einige Materialien, die Doppelbrechung, Dichroismus oder optische Aktivität aufweisen, beeinflussen das Licht je nach seiner Polarisation unterschiedlich. Einige dieser Materialien werden zur Herstellung von Polarisationsfiltern verwendet. Licht wird auch teilweise polarisiert, wenn es in einem bestimmten Winkel von einer Oberfläche reflektiert wird. ⓘ

Nach der Quantenmechanik können elektromagnetische Wellen auch als Teilchenströme, so genannte Photonen, betrachtet werden. So gesehen wird die Polarisation einer elektromagnetischen Welle durch eine quantenmechanische Eigenschaft der Photonen bestimmt, die als ihr Spin bezeichnet wird. Ein Photon hat einen von zwei möglichen Spins: Es kann sich entweder rechtsherum oder linksherum um seine Bewegungsrichtung drehen. Zirkular polarisierte elektromagnetische Wellen bestehen aus Photonen mit nur einer Art von Spin, entweder rechts- oder linksdrehend. Linear polarisierte Wellen bestehen aus Photonen, die sich in einer Überlagerung von rechts und links zirkular polarisierten Zuständen befinden, mit gleicher Amplitude und Phase, die so synchronisiert sind, dass sie in einer Ebene schwingen. ⓘ

Die Polarisation ist ein wichtiger Parameter in Bereichen der Wissenschaft, die sich mit transversalen Wellen befassen, wie Optik, Seismologie, Radio und Mikrowellen. Besonders betroffen sind Technologien wie Laser, drahtlose und faseroptische Telekommunikation und Radar. ⓘ

Polarisation einer stehenden Welle auf einem Gummifaden. Im Vordergrund wird das Ende des Fadens durch das Futter einer Bohrmaschine im Kreis geführt. Dadurch entsteht eine zirkuläre Schwingung. Zwei parallele Metallstangen erlauben eine freie Bewegung des Gummis in waagerechter, nicht aber in senkrechter Richtung. Dadurch schwingt das Gummi hinter den Stangen nur noch in einer Ebene. Dies entspricht linearer Polarisation. ⓘ

Zirkulare Polarisation: Auslenkung (z. B. einer Seilwelle) in x- und y-Richtung (in Ausbreitungsrichtung beträgt sie Null) in Abhängigkeit von der Zeit und von der z-Komponente des Ortes. Rot und blau die Komponenten der Auslenkung, schwarz die 3D-Ansicht. Der Pfeil illustriert den umlaufenden Auslenkungsvektor für einen Raumpunkt. ⓘ

Einführung

Wellenausbreitung und Polarisation

kreuzlinear polarisiert ⓘ

Die meisten Lichtquellen werden als inkohärent und unpolarisiert (oder nur "teilweise polarisiert") eingestuft, da sie aus einer zufälligen Mischung von Wellen mit unterschiedlichen räumlichen Eigenschaften, Frequenzen (Wellenlängen), Phasen und Polarisationszuständen bestehen. Für das Verständnis elektromagnetischer Wellen und insbesondere der Polarisation ist es jedoch einfacher, nur kohärente ebene Wellen zu betrachten; das sind sinusförmige Wellen mit einer bestimmten Richtung (oder einem bestimmten Wellenvektor), einer bestimmten Frequenz, Phase und einem bestimmten Polarisationszustand. Die Charakterisierung eines optischen Systems in Bezug auf eine ebene Welle mit diesen Parametern kann dann zur Vorhersage seiner Reaktion auf einen allgemeineren Fall verwendet werden, da eine Welle mit einer bestimmten räumlichen Struktur in eine Kombination von ebenen Wellen (ihr so genanntes Winkelspektrum) zerlegt werden kann. Inkohärente Zustände können stochastisch als gewichtete Kombination solcher unkorrelierter Wellen mit einer bestimmten Verteilung von Frequenzen (ihrem Spektrum), Phasen und Polarisationen modelliert werden. ⓘ

Transversale elektromagnetische Wellen

Bei einer "vertikal polarisierten" elektromagnetischen Welle der Wellenlänge λ oszilliert der elektrische Feldvektor E (rot) in vertikaler Richtung. Das magnetische Feld B (oder H) steht immer im rechten Winkel dazu (blau), und beide stehen senkrecht zur Ausbreitungsrichtung (z). ⓘ

Elektromagnetische Wellen (wie z. B. Licht), die sich im freien Raum oder einem anderen homogenen, isotropen, nicht dämpfenden Medium ausbreiten, werden korrekt als Transversalwellen beschrieben, d. h. der elektrische Feldvektor E und das magnetische Feld H einer ebenen Welle stehen jeweils in einer Richtung senkrecht (oder "quer") zur Ausbreitungsrichtung der Welle; E und H stehen auch senkrecht zueinander. Konventionell wird die "Polarisationsrichtung" einer elektromagnetischen Welle durch ihren elektrischen Feldvektor angegeben. Betrachten wir eine monochromatische ebene Welle der optischen Frequenz f (Licht der Vakuumwellenlänge λ hat eine Frequenz von f = c/λ, wobei c die Lichtgeschwindigkeit ist), so ist die Ausbreitungsrichtung die z-Achse. Da es sich um eine Transversalwelle handelt, müssen die Felder E und H nur Komponenten in x- und y-Richtung enthalten, während Ez = Hz = 0 ist. Unter Verwendung der komplexen (oder Phasor-) Notation werden die momentanen physikalischen elektrischen und magnetischen Felder durch die Realteile der komplexen Größen in den folgenden Gleichungen angegeben. Als Funktion der Zeit t und der räumlichen Position z (da für eine ebene Welle in +z-Richtung die Felder keine Abhängigkeit von x oder y haben) können diese komplexen Felder wie folgt geschrieben werden

${\vec {E}}(z,t)={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{\lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}e_{x}\\e_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$ ⓘ

und

${\vec {H}}(z,t)={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i2\pi \left({\frac {z}{\lambda }}-{\frac {t}{T}}\right)}={\begin{bmatrix}h_{x}\\h_{y}\\0\end{bmatrix}}\;e^{i(kz-\omega t)}$ ⓘ

wobei λ = λ₀/n die Wellenlänge im Medium (dessen Brechungsindex n ist) und T = 1/f die Periode der Welle ist. Dabei sind ex, ey, hx und hy komplexe Zahlen. In der zweiten, kompakteren Form, in der diese Gleichungen üblicherweise ausgedrückt werden, werden diese Faktoren durch die Wellenzahl $k=2\pi n/\lambda _{0}$ und der Winkelfrequenz (oder "Radiantfrequenz") $\omega =2\pi f$. In einer allgemeineren Formulierung, bei der die Ausbreitung nicht auf die +z-Richtung beschränkt ist, wird die räumliche Abhängigkeit kz ersetzt durch ${\vec {k}}\cdot {\vec {r}}$ wobei ${\vec {k}}$ den Wellenvektor bezeichnet, dessen Betrag die Wellenzahl ist. ⓘ

Somit enthalten die Leitvektoren e und h jeweils bis zu zwei (komplexe) Komponenten ungleich Null, die die Amplitude und Phase der x- und y-Polarisationskomponenten der Welle beschreiben (auch hier kann es keine z-Polarisationskomponente für eine transversale Welle in +z-Richtung geben). Für ein gegebenes Medium mit einer charakteristischen Impedanz $\eta$ist h mit e durch verbunden:

$h_{y}={\frac {e_{x}}{\eta }}$ ⓘ

und

$h_{x}=-{\frac {e_{y}}{\eta }}$. ⓘ

In einem Dielektrikum ist η real und hat den Wert η₀/n, wobei n der Brechungsindex und η₀ die Impedanz des freien Raums ist. In einem leitenden Medium ist die Impedanz komplex. Man beachte, dass aufgrund dieser Beziehung das Punktprodukt von E und H gleich Null sein muss:

${\vec {E}}\left({\vec {r}},t\right)\cdot {\vec {H}}\left({\vec {r}},t\right)=e_{x}h_{x}+e_{y}h_{y}+e_{z}h_{z}=e_{x}\left(-{\frac {e_{y}}{\eta }}\right)+e_{y}\left({\frac {e_{x}}{\eta }}\right)+0\cdot 0=0$ ⓘ

Das bedeutet, dass diese Vektoren erwartungsgemäß orthogonal (rechtwinklig zueinander) sind. ⓘ

Wenn man also die Ausbreitungsrichtung (in diesem Fall +z) und η kennt, kann man die Welle genauso gut nur mit ex und ey beschreiben, die das elektrische Feld beschreiben. Der Vektor, der ex und ey enthält (aber ohne die z-Komponente, die bei einer transversalen Welle notwendigerweise Null ist), wird als Jones-Vektor bezeichnet. Ein allgemeiner Jones-Vektor gibt nicht nur den Polarisationszustand der Welle an, sondern auch den Gesamtbetrag und die Phase dieser Welle. Konkret ist die Intensität der Lichtwelle proportional zur Summe der quadrierten Beträge der beiden elektrischen Feldkomponenten:

$I=\left(\left|e_{x}\right|^{2}+\left|e_{y}\right|^{2}\right)\,{\frac {1}{2\eta }}$ ⓘ

Der Polarisationszustand der Welle ist jedoch nur vom (komplexen) Verhältnis von ey zu e_x abhängig. Betrachten wir also nur Wellen, bei denen |e_x|² + |ey|² = 1 ist; dies entspricht zufällig einer Intensität von etwa 0,00133 Watt pro Quadratmeter im freien Raum (wobei $\eta =$ $\eta _{0}$). Und da die absolute Phase einer Welle bei der Erörterung ihres Polarisationszustandes unwichtig ist, legen wir fest, dass die Phase von e_x gleich Null ist, mit anderen Worten: e_x ist eine reelle Zahl, während ey komplex sein kann. Unter diesen Einschränkungen können e_x und ey wie folgt dargestellt werden:

$e_{x}={\sqrt {\frac {1+Q}{2}}}$

$e_{y}={\sqrt {\frac {1-Q}{2}}}\,e^{i\phi }$ ⓘ

wobei der Polarisationszustand nun vollständig durch den Wert von Q (-1 < Q < 1) und die relative Phase parametrisiert ist $\phi$. ⓘ

Nicht-transversale Wellen

Neben den transversalen Wellen gibt es viele Wellenbewegungen, bei denen die Schwingung nicht auf Richtungen senkrecht zur Ausbreitungsrichtung beschränkt ist. Diese Fälle gehen weit über den Rahmen des vorliegenden Artikels hinaus, der sich auf transversale Wellen (wie die meisten elektromagnetischen Wellen in Volumenmedien) konzentriert. Man sollte sich jedoch der Fälle bewusst sein, in denen die Polarisation einer kohärenten Welle nicht einfach durch einen Jones-Vektor beschrieben werden kann, wie wir es gerade getan haben. ⓘ

Bei der Betrachtung elektromagnetischer Wellen ist zu beachten, dass die vorangegangenen Ausführungen ausschließlich für ebene Wellen in einem homogenen, isotropen, nicht dämpfenden Medium gelten, während das elektrische oder magnetische Feld in einem anisotropen Medium (z. B. in doppelbrechenden Kristallen, wie unten beschrieben) sowohl longitudinale als auch transversale Komponenten haben kann. In diesen Fällen gehorchen die elektrische Verschiebung D und die magnetische Flussdichte B immer noch der obigen Geometrie, aber aufgrund der Anisotropie der elektrischen Suszeptibilität (oder der magnetischen Permeabilität), die jetzt durch einen Tensor gegeben ist, kann die Richtung von E (oder H) von der von D (oder B) abweichen. Selbst in isotropen Medien können sogenannte inhomogene Wellen in ein Medium eindringen, dessen Brechungsindex einen signifikanten Imaginärteil (oder "Extinktionskoeffizient") aufweist, wie z. B. Metalle; diese Felder sind ebenfalls nicht streng transversal. Oberflächenwellen oder Wellen, die sich in einem Wellenleiter (z. B. einer optischen Faser) ausbreiten, sind im Allgemeinen keine Transversalwellen, sondern können als elektrische oder magnetische Transversalmode oder als Hybridmode beschrieben werden. ⓘ

Selbst im freien Raum können longitudinale Feldkomponenten in fokalen Bereichen erzeugt werden, in denen die Annäherung an ebene Wellen nicht mehr gilt. Ein extremes Beispiel ist radial oder tangential polarisiertes Licht, in dessen Brennpunkt das elektrische bzw. magnetische Feld vollständig longitudinal (entlang der Ausbreitungsrichtung) ist. ⓘ

Bei Longitudinalwellen wie Schallwellen in Flüssigkeiten liegt die Schwingungsrichtung definitionsgemäß in der Ausbreitungsrichtung, so dass die Frage der Polarisation normalerweise gar nicht gestellt wird. Andererseits können Schallwellen in einem Festkörper sowohl transversal als auch longitudinal sein, so dass es insgesamt drei Polarisationskomponenten gibt. In diesem Fall ist die transversale Polarisation mit der Richtung der Scherspannung und der Verschiebung in Richtungen senkrecht zur Ausbreitungsrichtung verbunden, während die longitudinale Polarisation die Kompression des Festkörpers und die Schwingung entlang der Ausbreitungsrichtung beschreibt. Die unterschiedliche Ausbreitung von transversaler und longitudinaler Polarisation ist in der Seismologie von Bedeutung. ⓘ

Zustand der Polarisation

Oszillation des elektrischen Feldes ⓘ

Polarisation lässt sich am besten verstehen, wenn man zunächst nur reine Polarisationszustände und eine kohärente Sinuswelle mit einer bestimmten optischen Frequenz betrachtet. Der Vektor im nebenstehenden Diagramm könnte die Oszillation des elektrischen Feldes beschreiben, das von einem Monomode-Laser ausgesendet wird (dessen Oszillationsfrequenz typischerweise 10¹⁵-mal schneller ist). Das Feld oszilliert in der x-y-Ebene, entlang der Seite, wobei sich die Welle in z-Richtung, senkrecht zur Seite, ausbreitet. Die ersten beiden Diagramme unten zeichnen den elektrischen Feldvektor über einen kompletten Zyklus für lineare Polarisation bei zwei verschiedenen Ausrichtungen nach; diese werden jeweils als ein bestimmter Polarisationszustand (SOP) betrachtet. Beachten Sie, dass die lineare Polarisation bei 45° auch als Addition einer horizontal linear polarisierten Welle (wie in der Abbildung ganz links) und einer vertikal polarisierten Welle mit derselben Amplitude und derselben Phase betrachtet werden kann. ⓘ

Animation mit vier verschiedenen Polarisationszuständen und drei orthogonalen Projektionen. ⓘ

Eine zirkular polarisierte Welle als Summe von zwei linear polarisierten Komponenten, die um 90° phasenverschoben sind ⓘ

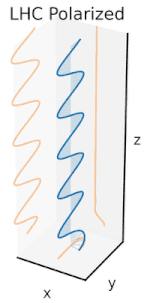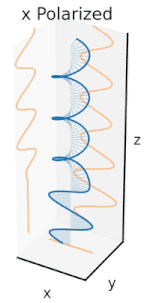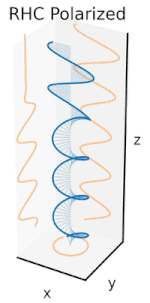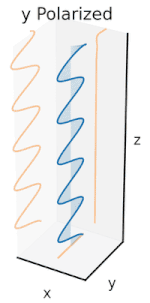
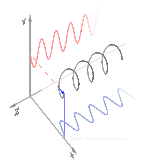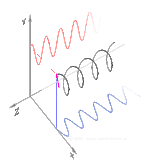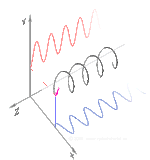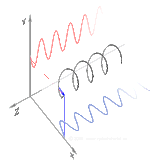
Wenn man nun eine Phasenverschiebung zwischen diesen horizontalen und vertikalen Polarisationskomponenten einführt, erhält man im Allgemeinen eine elliptische Polarisation, wie in der dritten Abbildung dargestellt. Wenn die Phasenverschiebung genau ±90° beträgt, entsteht eine zirkulare Polarisation (vierte und fünfte Abbildung). Auf diese Weise wird in der Praxis zirkulare Polarisation erzeugt, wenn man von linear polarisiertem Licht ausgeht und eine Viertelwellenplatte verwendet, um eine solche Phasenverschiebung einzuführen. Das Ergebnis zweier solcher phasenverschobener Komponenten, die einen rotierenden elektrischen Feldvektor erzeugen, ist in der Animation rechts dargestellt. Beachten Sie, dass eine zirkulare oder elliptische Polarisation entweder eine Drehung des Feldes im oder gegen den Uhrzeigersinn bedeuten kann. Diese entsprechen unterschiedlichen Polarisationszuständen, wie die beiden oben gezeigten zirkularen Polarisationen. ⓘ

Natürlich ist die Orientierung der x- und y-Achsen in dieser Beschreibung willkürlich. Die Wahl eines solchen Koordinatensystems und die Betrachtung der Polarisationsellipse in Bezug auf die x- und y-Polarisationskomponenten entspricht der Definition des Jones-Vektors (siehe unten) in Bezug auf diese Basispolarisationen. Normalerweise wählt man die Achsen so, dass sie zu einem bestimmten Problem passen, z. B. wenn x in der Einfallsebene liegt. Da es separate Reflexionskoeffizienten für die linearen Polarisationen in und orthogonal zur Einfallsebene gibt (p- und s-Polarisationen, siehe unten), vereinfacht diese Wahl die Berechnung der Reflexion einer Welle an einer Oberfläche erheblich. ⓘ

Außerdem kann man als Basisfunktionen jedes Paar orthogonaler Polarisationszustände verwenden, nicht nur lineare Polarisationen. Die Wahl von rechten und linken zirkularen Polarisationen als Basisfunktionen vereinfacht zum Beispiel die Lösung von Problemen, die zirkulare Doppelbrechung (optische Aktivität) oder zirkularen Dichroismus beinhalten. ⓘ

Polarisationsellipse

Betrachten wir eine rein polarisierte monochromatische Welle. Zeichnet man den Vektor des elektrischen Feldes über einen Schwingungszyklus auf, so erhält man im Allgemeinen eine Ellipse, wie sie in der Abbildung dargestellt ist, die einem bestimmten Zustand elliptischer Polarisation entspricht. Man beachte, dass die lineare und die zirkulare Polarisation als Spezialfälle der elliptischen Polarisation betrachtet werden können. ⓘ

Ein Polarisationszustand kann dann in Abhängigkeit von den geometrischen Parametern der Ellipse und ihrer "Händigkeit" beschrieben werden, d. h. ob die Drehung um die Ellipse im oder gegen den Uhrzeigersinn erfolgt. Eine Parametrisierung der elliptischen Figur spezifiziert den Orientierungswinkel ψ, definiert als der Winkel zwischen der Hauptachse der Ellipse und der x-Achse zusammen mit der Elliptizität ε = a/b, dem Verhältnis zwischen der Haupt- und der Nebenachse der Ellipse. (auch als Achsenverhältnis bezeichnet). Der Elliptizitätsparameter ist eine alternative Parametrisierung der Exzentrizität einer Ellipse ${\textstyle e={\sqrt {1-b^{2}/a^{2}}},}$ oder des Elliptizitätswinkels, ${\textstyle \chi =\arctan b/a}$ ${\textstyle =\arctan 1/\varepsilon }$ wie in der Abbildung zu sehen ist. Der Winkel χ ist auch insofern von Bedeutung, als der Breitengrad (Winkel vom Äquator) des Polarisationszustandes, wie er auf der Poincaré-Kugel (siehe unten) dargestellt wird, gleich ±2χ ist. Die Sonderfälle der linearen und zirkularen Polarisation entsprechen einer Elliptizität ε von unendlich bzw. eins (oder χ von null bzw. 45°). ⓘ

Jones-Vektor

Vollständige Informationen über einen vollständig polarisierten Zustand liefern auch die Amplitude und die Phase der Schwingungen in zwei Komponenten des elektrischen Feldvektors in der Polarisationsebene. Diese Darstellung wurde oben verwendet, um zu zeigen, dass verschiedene Polarisationszustände möglich sind. Die Amplituden- und Phaseninformation kann bequem als zweidimensionaler komplexer Vektor (der Jones-Vektor) dargestellt werden:

$\mathbf {e} ={\begin{bmatrix}a_{1}e^{i\theta _{1}}\\a_{2}e^{i\theta _{2}}\end{bmatrix}}.$ ⓘ

Hier $a_{1}$ und $a_{2}$ die Amplitude der Welle in den beiden Komponenten des elektrischen Feldvektors, während $\theta _{1}$ und $\theta _{2}$ die Phasen darstellen. Das Produkt eines Jones-Vektors mit einer komplexen Zahl mit Einheitsmodul ergibt einen anderen Jones-Vektor, der dieselbe Ellipse und damit denselben Polarisationszustand darstellt. Das physikalische elektrische Feld, der Realteil des Jones-Vektors, würde sich ändern, aber der Polarisationszustand selbst ist unabhängig von der absoluten Phase. Die zur Darstellung des Jones-Vektors verwendeten Basisvektoren müssen keine linearen Polarisationszustände darstellen (d. h. real sein). Im Allgemeinen können zwei beliebige orthogonale Zustände verwendet werden, wobei ein orthogonales Vektorpaar formal als ein Paar mit einem inneren Produkt von Null definiert ist. Eine gängige Wahl sind linke und rechte zirkulare Polarisationen, um beispielsweise die unterschiedliche Ausbreitung von Wellen in zwei solchen Komponenten in zirkular doppelbrechenden Medien (siehe unten) oder Signalwege von kohärenten Detektoren, die auf zirkulare Polarisation empfindlich sind, zu modellieren. ⓘ

Koordinatenrahmen

Unabhängig davon, ob der Polarisationszustand durch geometrische Parameter oder Jones-Vektoren dargestellt wird, ist die Orientierung des Koordinatensystems implizit in der Parametrisierung enthalten. Dies ermöglicht einen Freiheitsgrad, nämlich die Drehung um die Ausbreitungsrichtung. Bei der Betrachtung von Licht, das sich parallel zur Erdoberfläche ausbreitet, werden häufig die Begriffe "horizontale" und "vertikale" Polarisation verwendet, wobei erstere mit der ersten Komponente des Jones-Vektors bzw. dem Azimutwinkel Null assoziiert wird. In der Astronomie hingegen wird im Allgemeinen das äquatoriale Koordinatensystem verwendet, wobei der Null-Azimut (oder Positionswinkel, wie er in der Astronomie üblicherweise genannt wird, um Verwechslungen mit dem horizontalen Koordinatensystem zu vermeiden) dem Nordpol entspricht. ⓘ

s- und p-Bezeichnungen

Elektromagnetische Vektoren für ${\textstyle {\textbf {E}}}$, ${\textstyle {\textbf {B}}}$ und ${\textstyle {\textbf {k}}}$ mit ${\textstyle {\textbf {E}}={\textbf {E}}(x,y)}$ zusammen mit 3 planaren Projektionen und einer Deformationsfläche des gesamten elektrischen Feldes. Das Licht ist immer s-polarisiert in der xy-Ebene. ${\textstyle \theta }$ ist der Polarwinkel von ${\textstyle {\textbf {k}}}$ und ${\textstyle \varphi _{E}}$ ist der azimutale Winkel von ${\textstyle {\textbf {E}}}$. ⓘ

Ein weiteres häufig verwendetes Koordinatensystem bezieht sich auf die Einfallsebene. Dies ist die Ebene, die von der einfallenden Ausbreitungsrichtung und dem Vektor senkrecht zur Ebene einer Grenzfläche gebildet wird, mit anderen Worten, die Ebene, in der der Strahl vor und nach der Reflexion oder Brechung verläuft. Die Komponente des elektrischen Feldes, die parallel zu dieser Ebene verläuft, wird als p-artig (parallel) und die Komponente, die senkrecht zu dieser Ebene steht, als s-artig (von senkrecht, deutsch für senkrecht) bezeichnet. Polarisiertes Licht, dessen elektrisches Feld entlang der Einfallsebene verläuft, wird daher als p-polarisiert bezeichnet, während Licht, dessen elektrisches Feld senkrecht zur Einfallsebene verläuft, als s-polarisiert bezeichnet wird. Die P-Polarisation wird gemeinhin als transversal-magnetisch (TM) bezeichnet und wird auch als pi-polarisiert oder tangentiale Polarisation bezeichnet. Die S-Polarisation wird auch als transversal-elektrisch (TE) bezeichnet, ebenso wie die Sigma-Polarisation oder die Polarisation in der Sagittalebene. ⓘ

Unpolarisiertes und teilweise polarisiertes Licht

Definition

Natürliches Licht ist wie die meisten anderen sichtbaren Lichtquellen inkohärent: Die Strahlung wird unabhängig voneinander von einer großen Anzahl von Atomen oder Molekülen erzeugt, deren Emissionen unkorreliert sind und im Allgemeinen eine zufällige Polarisation aufweisen. In diesem Fall wird das Licht als unpolarisiert bezeichnet. Dieser Begriff ist etwas ungenau, da die elektrischen und magnetischen Felder zu jedem Zeitpunkt an einem Ort eine bestimmte Richtung haben, aber er impliziert, dass sich die Polarisation so schnell ändert, dass sie nicht gemessen werden kann oder für das Ergebnis eines Experiments relevant ist. Ein so genannter Depolarisator wirkt auf einen polarisierten Strahl ein, um einen Strahl zu erzeugen, der eigentlich an jedem Punkt vollständig polarisiert ist, bei dem sich die Polarisation jedoch so schnell über den Strahl hinweg ändert, dass sie in den vorgesehenen Anwendungen ignoriert werden kann. ⓘ

Unpolarisiertes Licht kann als eine Mischung aus zwei unabhängigen, entgegengesetzt polarisierten Strömen beschrieben werden, die jeweils die Hälfte der Intensität aufweisen. Man spricht von teilpolarisiertem Licht, wenn einer der beiden Ströme mehr Leistung aufweist als der andere. Bei einer bestimmten Wellenlänge kann teilpolarisiertes Licht statistisch als Überlagerung einer völlig unpolarisierten Komponente und einer völlig polarisierten Komponente beschrieben werden. Dann kann man das Licht durch den Grad der Polarisation und die Parameter der polarisierten Komponente beschreiben. Diese polarisierte Komponente kann, wie oben beschrieben, durch einen Jones-Vektor oder eine Polarisationsellipse beschrieben werden. Um jedoch auch den Grad der Polarisation zu beschreiben, verwendet man normalerweise Stokes-Parameter (siehe unten), um einen Zustand partieller Polarisation zu spezifizieren. ⓘ

Begründung

Die Übertragung von ebenen Wellen durch ein homogenes Medium wird vollständig durch Jones-Vektoren und 2×2 Jones-Matrizen beschrieben. In der Praxis gibt es jedoch Fälle, in denen das gesamte Licht aufgrund von räumlichen Inhomogenitäten oder dem Vorhandensein von inkohärenten Wellen nicht auf diese einfache Weise dargestellt werden kann. Die so genannte Depolarisation lässt sich beispielsweise nicht mit Jones-Matrizen beschreiben. In diesen Fällen ist es üblich, stattdessen eine 4×4-Matrix zu verwenden, die auf den Stokes-4-Vektor wirkt. Solche Matrizen wurden erstmals 1929 von Paul Soleillet verwendet, obwohl sie heute als Mueller-Matrizen bekannt sind. Während zu jeder Jones-Matrix eine Mueller-Matrix gehört, ist dies umgekehrt nicht der Fall. Mueller-Matrizen werden dann verwendet, um die beobachteten Polarisationseffekte bei der Streuung von Wellen an komplexen Oberflächen oder Teilchengruppen zu beschreiben, wie im Folgenden dargestellt werden soll. ⓘ

Kohärenzmatrix

Der Jones-Vektor beschreibt perfekt den Polarisations- und Phasenzustand einer einzelnen monochromatischen Welle, die einen reinen Polarisationszustand wie oben beschrieben darstellt. Ein Gemisch von Wellen unterschiedlicher Polarisation (oder sogar unterschiedlicher Frequenzen) entspricht jedoch nicht einem Jones-Vektor. Bei der so genannten teilpolarisierten Strahlung sind die Felder stochastisch, und die Variationen und Korrelationen zwischen den Komponenten des elektrischen Feldes können nur statistisch beschrieben werden. Eine solche Darstellung ist die Kohärenzmatrix:

${\begin{aligned}\mathbf {\Psi } &=\left\langle \mathbf {e} \mathbf {e} ^{\dagger }\right\rangle \\&=\left\langle {\begin{bmatrix}e_{1}e_{1}^{*}&e_{1}e_{2}^{*}\\e_{2}e_{1}^{*}&e_{2}e_{2}^{*}\end{bmatrix}}\right\rangle \\&=\left\langle {\begin{bmatrix}a_{1}^{2}&a_{1}a_{2}e^{i\left(\theta _{1}-\theta _{2}\right)}\\a_{1}a_{2}e^{-i\left(\theta _{1}-\theta _{2}\right)}&a_{2}^{2}\end{bmatrix}}\right\rangle \end{aligned}}$ ⓘ

wobei eckige Klammern die Mittelung über viele Wellenzyklen bezeichnen. Es wurden mehrere Varianten der Kohärenzmatrix vorgeschlagen: Die Wiener Kohärenzmatrix und die spektrale Kohärenzmatrix von Richard Barakat messen die Kohärenz einer spektralen Zerlegung des Signals, während die Wolf-Kohärenzmatrix einen Mittelwert über alle Zeit/Frequenzen bildet. ⓘ

Die Kohärenzmatrix enthält alle statistischen Informationen zweiter Ordnung über die Polarisation. Diese Matrix kann in die Summe zweier idempotenter Matrizen zerlegt werden, die den Eigenvektoren der Kohärenzmatrix entsprechen und jeweils einen Polarisationszustand darstellen, der orthogonal zum anderen ist. Eine alternative Zerlegung ist die in vollständig polarisierte (Null-Determinante) und unpolarisierte (skalierte Identitätsmatrix) Komponenten. In beiden Fällen entspricht die Summierung der Komponenten der inkohärenten Überlagerung der Wellen der beiden Komponenten. Im letzteren Fall spricht man vom "Polarisationsgrad", d. h. dem Anteil der vollständig polarisierten Komponente an der Gesamtintensität. ⓘ

Stokes-Parameter

Die Kohärenzmatrix ist nicht einfach zu visualisieren, daher ist es üblich, inkohärente oder teilweise polarisierte Strahlung durch die Gesamtintensität (I), den (gebrochenen) Polarisationsgrad (p) und die Formparameter der Polarisationsellipse zu beschreiben. Eine alternative und mathematisch bequeme Beschreibung ist durch die Stokes-Parameter gegeben, die von George Gabriel Stokes 1852 eingeführt wurden. Die Beziehung zwischen den Stokes-Parametern und den Parametern der Intensitäts- und Polarisationsellipse ist in den nachstehenden Gleichungen und der Abbildung dargestellt. ⓘ

$S_{0}=I\,$

$S_{1}=Ip\cos 2\psi \cos 2\chi \,$

$S_{2}=Ip\sin 2\psi \cos 2\chi \,$

$S_{3}=Ip\sin 2\chi \,$ ⓘ

Dabei sind Ip, 2ψ und 2χ die sphärischen Koordinaten des Polarisationszustandes im dreidimensionalen Raum der letzten drei Stokes-Parameter. Man beachte die Zweierfaktoren vor ψ und χ, die der Tatsache entsprechen, dass eine Polarisationsellipse nicht von einer um 180° gedrehten Ellipse oder einer Ellipse mit vertauschten Halbachsenlängen und einer 90°-Drehung unterschieden werden kann. Die Stokes-Parameter werden manchmal mit I, Q, U und V bezeichnet. ⓘ

Die vier Stokes-Parameter reichen aus, um die 2D-Polarisation einer paraxialen Welle zu beschreiben, nicht aber die 3D-Polarisation einer allgemeinen nicht-paraxialen Welle oder eines evaneszenten Feldes. ⓘ

Poincaré-Kugel

Vernachlässigt man den ersten Stokes-Parameter S₀ (oder I), können die drei anderen Stokes-Parameter direkt in dreidimensionalen kartesischen Koordinaten aufgetragen werden. Für eine gegebene Leistung in der polarisierten Komponente, die durch

$P={\sqrt {S_{1}^{2}+S_{2}^{2}+S_{3}^{2}}}$ ⓘ

gegebene Potenz der polarisierten Komponente wird die Menge aller Polarisationszustände dann auf Punkte auf der Oberfläche der so genannten Poincaré-Kugel (allerdings mit dem Radius P) abgebildet, wie in der nebenstehenden Abbildung dargestellt. ⓘ

Poincaré-Kugel, auf oder unter der die drei Stokes-Parameter [S₁, S₂, S₃] (oder [Q, U, V]) in kartesischen Koordinaten aufgetragen sind ⓘ

Darstellung der Polarisationszustände auf der Poincaré-Kugel ⓘ

In diesem Fall wird ein normierter Stokes-Vektor verwendet, indem der Stokes-Vektor durch die Gesamtintensität S₀ geteilt wird:

$\mathbf {S'} ={\frac {1}{S_{0}}}{\begin{bmatrix}S_{0}\\S_{1}\\S_{2}\\S_{3}\end{bmatrix}}.$ ⓘ

Der normalisierte Stokes-Vektor $\mathbf {S'}$ hat dann eine einheitliche Leistung ($S'_{0}=1$) und die drei signifikanten Stokes-Parameter, die in drei Dimensionen aufgetragen werden, liegen auf der Poincaré-Kugel mit dem Radius Eins für reine Polarisationszustände (wobei $P'_{0}=1$). Teilweise polarisierte Zustände liegen innerhalb der Poincaré-Kugel in einem Abstand von $P'={\sqrt {S_{1}'^{2}+S_{2}'^{2}+S_{3}'^{2}}}$ vom Ursprung. Wenn die nichtpolarisierte Komponente nicht von Interesse ist, kann der Stokes-Vektor weiter normalisiert werden, um

$\mathbf {S} ={\frac {1}{P'}}{\begin{bmatrix}1\\S'_{1}\\S'_{2}\\S'_{3}\end{bmatrix}}={\frac {1}{P}}{\begin{bmatrix}S_{0}\\S_{1}\\S_{2}\\S_{3}\end{bmatrix}}.$ ⓘ

Wird dieser Punkt aufgetragen, so liegt er auf der Oberfläche der Poincaré-Kugel mit dem Radius 1 und gibt den Polarisationszustand der polarisierten Komponente an. ⓘ

Zwei beliebige antipodische Punkte auf der Poincaré-Kugel beziehen sich auf orthogonale Polarisationszustände. Die Überlappung zwischen zwei beliebigen Polarisationszuständen hängt nur von der Entfernung zwischen ihren Standorten auf der Kugel ab. Diese Eigenschaft, die nur wahr sein kann, wenn reine Polarisationszustände auf einer Kugel abgebildet werden, ist die Motivation für die Erfindung der Poincaré-Kugel und die Verwendung von Stokes-Parametern, die somit auf (oder unter) der Kugel aufgetragen werden. ⓘ

Beachten Sie, dass das IEEE die Begriffe RHCP und LHCP anders definiert als die von Physikern verwendeten. In der IEEE-Norm für Antennen von 1979 wird RHCP auf dem Südpol der Poincare-Sphäre dargestellt. Die IEEE definiert RHCP mit der rechten Hand, wobei der Daumen in die Senderichtung zeigt und die Finger die Drehrichtung des E-Feldes mit der Zeit anzeigen. Der Grund für die unterschiedlichen Konventionen, die von Physikern und Ingenieuren verwendet werden, ist, dass bei astronomischen Beobachtungen die eintreffende Welle immer auf den Beobachter zukommt, während man bei den meisten Ingenieuren davon ausgeht, dass sie hinter dem Sender stehen und die Welle beobachten, die sich von ihnen weg bewegt. In diesem Artikel wird nicht die IEEE-Antennennorm von 1979 verwendet und auch nicht die in IEEE-Arbeiten übliche +t-Konvention. ⓘ

Auswirkungen auf Reflexion und Ausbreitung

Polarisation bei der Wellenausbreitung

In einem Vakuum breiten sich die Komponenten des elektrischen Feldes mit Lichtgeschwindigkeit aus, so dass sich die Phase der Welle in Raum und Zeit ändert, der Polarisationszustand jedoch nicht. Das heißt, der elektrische Feldvektor e einer ebenen Welle in der Richtung +z folgt:

$\mathbf {e} (z+\Delta z,t+\Delta t)=\mathbf {e} (z,t)e^{ik(c\Delta t-\Delta z)},$ ⓘ

wobei k die Wellenzahl ist. Wie bereits erwähnt, ist das momentane elektrische Feld der Realteil des Produkts aus dem Jones-Vektor mal dem Phasenfaktor $e^{-i\omega t}$. Wenn eine elektromagnetische Welle mit Materie in Wechselwirkung tritt, wird ihre Ausbreitung entsprechend dem (komplexen) Brechungsindex des Materials verändert. Wenn der Real- oder Imaginärteil dieses Brechungsindexes vom Polarisationszustand einer Welle abhängt - Eigenschaften, die als Doppelbrechung bzw. Polarisationsdichroismus (oder Dämpfung) bekannt sind -, dann wird der Polarisationszustand einer Welle im Allgemeinen verändert. ⓘ

In solchen Medien kann eine elektromagnetische Welle mit einem bestimmten Polarisationszustand in zwei orthogonal polarisierte Komponenten zerlegt werden, die auf unterschiedliche Ausbreitungskonstanten treffen. Die Auswirkung der Ausbreitung über einen bestimmten Pfad auf diese beiden Komponenten lässt sich am einfachsten in Form einer komplexen 2×2-Transformationsmatrix J, der so genannten Jones-Matrix, beschreiben:

$\mathbf {e'} =\mathbf {J} \mathbf {e} .$ ⓘ

Die Jones-Matrix beim Durchgang durch ein transparentes Material ist sowohl von der Ausbreitungsdistanz als auch von der Doppelbrechung abhängig. Die Doppelbrechung (ebenso wie der durchschnittliche Brechungsindex) ist im Allgemeinen dispersiv, d. h. sie variiert in Abhängigkeit von der optischen Frequenz (Wellenlänge). Bei nicht doppelbrechenden Materialien ist die 2×2-Jones-Matrix jedoch die Identitätsmatrix (multipliziert mit einem skalaren Phasenfaktor und einem Dämpfungsfaktor), was bedeutet, dass sich die Polarisation während der Ausbreitung nicht ändert. ⓘ

Für Ausbreitungseffekte in zwei orthogonalen Moden kann die Jones-Matrix geschrieben werden als ⓘ

$\mathbf {J} =\mathbf {T} {\begin{bmatrix}g_{1}&0\\0&g_{2}\end{bmatrix}}\mathbf {T} ^{-1},$ ⓘ

wobei g₁ und g₂ komplexe Zahlen sind sind, die die Phasenverzögerung und möglicherweise die Amplitudendämpfung aufgrund der Ausbreitung in jeder der beiden Polarisationseigenmoden beschreiben. T ist eine Einheitsmatrix, die eine Änderung der Basis von diesen Ausbreitungsmoden zum linearen System darstellt, das für die Jones-Vektoren verwendet wird; im Fall von linearer Doppelbrechung oder Dämpfung sind die Moden selbst lineare Polarisationszustände, so dass T und T-1 weggelassen werden können, wenn die Koordinatenachsen entsprechend gewählt wurden. ⓘ

Doppelbrechung

In sogenannten doppelbrechenden Medien, in denen die Amplituden unverändert sind, aber eine differentielle Phasenverzögerung auftritt, ist die Jones-Matrix eine Einheitsmatrix: |g₁| = |g₂| = 1. Als diattenuierend (oder dichroitisch im Sinne der Polarisation) bezeichnete Medien, bei denen nur die Amplituden der beiden Polarisationen unterschiedlich beeinflusst werden, können mit einer hermitschen Matrix (im Allgemeinen multipliziert mit einem gemeinsamen Phasenfaktor) beschrieben werden. Da jede Matrix als Produkt von unitären und positiven hermiteschen Matrizen geschrieben werden kann, lässt sich die Lichtausbreitung durch eine beliebige Folge von polarisationsabhängigen optischen Komponenten als Produkt dieser beiden grundlegenden Arten von Transformationen beschreiben. ⓘ

Farbmuster einer Kunststoffbox, die zwischen zwei gekreuzten Polarisatoren eine spannungsinduzierte Doppelbrechung zeigt. ⓘ

In doppelbrechenden Medien gibt es keine Dämpfung, aber zwei Moden erhalten eine unterschiedliche Phasenverzögerung. Bekannte Erscheinungsformen der linearen Doppelbrechung (d. h., bei denen die Basispolarisationen orthogonale lineare Polarisationen sind) treten in optischen Wellenplatten/-verzögerern und vielen Kristallen auf. Wenn linear polarisiertes Licht ein doppelbrechendes Material durchläuft, ändert sich im Allgemeinen sein Polarisationszustand, es sei denn, seine Polarisationsrichtung ist mit einer dieser Basispolarisationen identisch. Da die Phasenverschiebung und damit die Änderung des Polarisationszustandes in der Regel wellenlängenabhängig ist, können solche Objekte, die unter weißem Licht zwischen zwei Polarisatoren betrachtet werden, zu farbigen Effekten führen, wie auf dem nebenstehenden Foto zu sehen. ⓘ

Zirkulare Doppelbrechung wird auch als optische Aktivität bezeichnet, insbesondere in chiralen Flüssigkeiten, oder als Faraday-Rotation, wenn sie auf das Vorhandensein eines Magnetfeldes in Ausbreitungsrichtung zurückzuführen ist. Wird linear polarisiertes Licht durch ein solches Objekt geleitet, so tritt es zwar immer noch linear polarisiert, aber mit gedrehter Polarisationsachse aus. Eine Kombination aus linearer und zirkularer Doppelbrechung hat als Basispolarisationen zwei orthogonale elliptische Polarisationen; der Begriff "elliptische Doppelbrechung" wird jedoch selten verwendet. ⓘ

Ausbreitungswege von Vektoren auf der Poincaré-Kugel bei Doppelbrechung. Die Ausbreitungsmodi (Rotationsachsen) sind durch rote, blaue und gelbe Linien dargestellt, die Ausgangsvektoren durch dicke schwarze Linien und die Wege, die sie nehmen, durch farbige Ellipsen (die Kreise in drei Dimensionen darstellen). ⓘ

Man kann sich den Fall der linearen Doppelbrechung (mit zwei orthogonalen linearen Ausbreitungsmoden) mit einer ankommenden Welle vorstellen, die in einem Winkel von 45° zu diesen Moden linear polarisiert ist. Mit zunehmender Phasendifferenz wird die Polarisation elliptisch, geht schließlich in eine rein zirkulare Polarisation über (90° Phasendifferenz), dann in eine elliptische und schließlich in eine lineare Polarisation (180° Phase) senkrecht zur ursprünglichen Polarisation, dann wieder zirkular (270° Phase), dann elliptisch mit dem ursprünglichen Azimutwinkel und schließlich wieder in den ursprünglichen linear polarisierten Zustand (360° Phase), wo der Zyklus von neuem beginnt. Im Allgemeinen ist die Situation komplizierter und kann als eine Drehung der Poincaré-Kugel um die durch die Ausbreitungsmodi definierte Achse beschrieben werden. Beispiele für lineare (blau), zirkulare (rot) und elliptische (gelb) Doppelbrechung sind in der Abbildung links dargestellt. Die Gesamtintensität und der Polarisationsgrad bleiben davon unberührt. Wenn die Weglänge im doppelbrechenden Medium ausreichend ist, können die beiden Polarisationskomponenten eines kollimierten Strahls (oder Strahlenbündels) mit einem Positionsversatz aus dem Material austreten, obwohl ihre endgültigen Ausbreitungsrichtungen gleich sind (vorausgesetzt, die Eintritts- und Austrittsfläche sind parallel). Dies wird häufig bei Kalzitkristallen beobachtet, die dem Betrachter zwei leicht versetzte Bilder eines Objekts hinter dem Kristall in entgegengesetzter Polarisation zeigen. Dieser Effekt war der Grund für die erste Entdeckung der Polarisation durch Erasmus Bartholinus im Jahr 1669. ⓘ

Dichroismus

Medien, bei denen die Durchlässigkeit einer Polarisationsmode bevorzugt reduziert ist, werden als dichroitisch oder diattenuierend bezeichnet. Wie bei der Doppelbrechung kann die Abschwächung in Bezug auf lineare Polarisationsmoden (in einem Kristall) oder zirkulare Polarisationsmoden (normalerweise in einer Flüssigkeit) erfolgen. ⓘ

Geräte, die fast die gesamte Strahlung in einer Mode blockieren, werden als Polarisationsfilter oder einfach als "Polarisatoren" bezeichnet. Dies entspricht g₂=0 in der obigen Darstellung der Jones-Matrix. Der Ausgang eines idealen Polarisators ist ein bestimmter Polarisationszustand (in der Regel lineare Polarisation) mit einer Amplitude, die der ursprünglichen Amplitude der Eingangswelle in diesem Polarisationsmodus entspricht. Die Leistung im anderen Polarisationsmodus wird eliminiert. Wenn also unpolarisiertes Licht durch einen idealen Polarisator geleitet wird (mit g₁=1 und g₂=0), bleibt genau die Hälfte der ursprünglichen Leistung erhalten. Praktische Polarisatoren, insbesondere preiswerte Blattpolarisatoren, haben zusätzliche Verluste, so dass g₁ < 1. In vielen Fällen ist jedoch der Polarisationsgrad oder das Auslöschungsverhältnis des Polarisators die relevantere Kennzahl, die einen Vergleich von g₁ mit g₂ beinhaltet. Da sich die Jones-Vektoren auf die Amplituden der Wellen (und nicht auf die Intensität) beziehen, beträgt bei der Beleuchtung mit unpolarisiertem Licht die verbleibende Leistung in der unerwünschten Polarisation (g₂/g₁)² der Leistung in der gewünschten Polarisation. ⓘ

Spiegelbildliche Reflexion

Zusätzlich zur Doppelbrechung und zum Dichroismus in ausgedehnten Medien können Polarisationseffekte, die mit Jones-Matrizen beschrieben werden können, auch an (reflektierenden) Grenzflächen zwischen zwei Materialien mit unterschiedlichem Brechungsindex auftreten. Diese Effekte werden durch die Fresnel-Gleichungen behandelt. Ein Teil der Welle wird transmittiert und ein Teil wird reflektiert; für ein gegebenes Material sind diese Anteile (und auch die Phase der Reflexion) vom Einfallswinkel abhängig und für die s- und p-Polarisation unterschiedlich. Daher wird der Polarisationszustand des reflektierten Lichts (auch wenn es ursprünglich unpolarisiert war) im Allgemeinen verändert. ⓘ

Ein Stapel von Platten im Brewster-Winkel zu einem Strahl reflektiert an jeder Oberfläche einen Teil des s-polarisierten Lichts, so dass (nach vielen solcher Platten) ein hauptsächlich p-polarisierter Strahl übrig bleibt. ⓘ

Jedes Licht, das unter einem speziellen Einfallswinkel, dem so genannten Brewster-Winkel, auf eine Oberfläche trifft, an der der Reflexionskoeffizient für die p-Polarisation gleich Null ist, wird so reflektiert, dass nur noch die s-Polarisation übrig bleibt. Dieses Prinzip wird im so genannten "Plattenstapel-Polarisator" (siehe Abbildung) angewandt, bei dem ein Teil der s-Polarisation durch Reflexion an jeder Brewster-Winkel-Oberfläche entfernt wird, so dass nach der Übertragung durch viele solcher Oberflächen nur die p-Polarisation übrig bleibt. Der im Allgemeinen geringere Reflexionskoeffizient der p-Polarisation ist auch die Grundlage für polarisierte Sonnenbrillen; durch die Blockierung der s-Polarisation (horizontal) wird der größte Teil der Blendung durch Reflexion, z. B. auf einer nassen Straße, entfernt. ⓘ

In dem wichtigen Spezialfall der Reflexion bei senkrechtem Einfall (ohne anisotrope Materialien) gibt es keine besondere s- oder p-Polarisation. Sowohl die x- als auch die y-Polarisationskomponente werden identisch reflektiert, so dass die Polarisation der reflektierten Welle mit der der einfallenden Welle identisch ist. Bei zirkularer (oder elliptischer) Polarisation wird die Händigkeit des Polarisationszustandes jedoch umgekehrt, da diese per Konvention relativ zur Ausbreitungsrichtung festgelegt wird. Die zirkulare Drehung des elektrischen Feldes um die x-y-Achse, die für eine Welle in +z-Richtung "rechtshändig" genannt wird, ist für eine Welle in -z-Richtung "linkshändig". Für den allgemeinen Fall der Reflexion an einem Einfallswinkel ungleich Null kann eine solche Verallgemeinerung jedoch nicht vorgenommen werden. So ist beispielsweise rechtszirkular polarisiertes Licht, das von einer dielektrischen Oberfläche unter einem streifenden Winkel reflektiert wird, immer noch rechtshändig (aber elliptisch) polarisiert. Linear polarisiertes Licht, das von einem Metall unter nicht normalem Einfall reflektiert wird, wird im Allgemeinen elliptisch polarisiert. Diese Fälle werden mit Jones-Vektoren behandelt, auf die die unterschiedlichen Fresnel-Koeffizienten für die s- und p-Polarisationskomponenten einwirken. ⓘ

Messtechniken mit Polarisation

Einige optische Messtechniken basieren auf der Polarisation. Bei vielen anderen optischen Verfahren ist die Polarisation von entscheidender Bedeutung oder muss zumindest berücksichtigt und kontrolliert werden; diese Beispiele sind zu zahlreich, um sie hier aufzuführen. ⓘ

Messung von Spannungen

Spannungen in Kunststoffgläsern ⓘ

In der Technik ermöglicht das Phänomen der spannungsinduzierten Doppelbrechung die einfache Beobachtung von Spannungen in transparenten Materialien. Wie oben erwähnt und auf dem nebenstehenden Foto zu sehen, erzeugt die Doppelbrechung bei Betrachtung zwischen zwei Polarisatoren typischerweise farbige Muster. Wenn äußere Kräfte auf das Material einwirken, werden dadurch innere Spannungen im Material sichtbar. Darüber hinaus wird Doppelbrechung häufig aufgrund von Spannungen beobachtet, die zum Zeitpunkt der Herstellung "eingefroren" wurden. Dies ist bekanntlich bei Zellophanband zu beobachten, dessen Doppelbrechung auf die Dehnung des Materials während des Herstellungsprozesses zurückzuführen ist. ⓘ

Ellipsometrie

Die Ellipsometrie ist eine leistungsfähige Technik zur Messung der optischen Eigenschaften einer einheitlichen Oberfläche. Dabei wird der Polarisationszustand des Lichts nach spiegelnder Reflexion an einer solchen Oberfläche gemessen. Dies geschieht in der Regel als Funktion des Einfallswinkels oder der Wellenlänge (oder beidem). Da die Ellipsometrie auf der Reflexion beruht, ist es nicht erforderlich, dass die Probe lichtdurchlässig ist oder dass ihre Rückseite zugänglich ist. ⓘ

Die Ellipsometrie kann zur Modellierung des (komplexen) Brechungsindexes einer Oberfläche eines Schüttguts verwendet werden. Sie ist auch sehr nützlich bei der Bestimmung der Parameter einer oder mehrerer dünner Schichten, die auf einem Substrat aufgebracht sind. Aufgrund ihrer Reflexionseigenschaften werden nicht nur die vorhergesagten Größen der p- und s-Polarisationskomponenten, sondern auch ihre relativen Phasenverschiebungen bei der Reflexion mit Messungen mit einem Ellipsometer verglichen. Ein normales Ellipsometer misst nicht den tatsächlichen Reflexionskoeffizienten (was eine sorgfältige photometrische Kalibrierung des Beleuchtungsstrahls erfordert), sondern das Verhältnis der p- und s-Reflexionen sowie die Änderung der Polarisationselliptizität (daher der Name), die durch die Reflexion an der untersuchten Oberfläche verursacht wird. Neben der Verwendung in Wissenschaft und Forschung werden Ellipsometer auch vor Ort eingesetzt, um beispielsweise Produktionsprozesse zu kontrollieren. ⓘ

Geologie

Mikroskopische Aufnahme eines vulkanischen Sandkorns; oberes Bild ist planpolarisiertes Licht, unteres Bild ist kreuzpolarisiertes Licht, Skalenfeld links in der Mitte ist 0,25 Millimeter. ⓘ

Die Eigenschaft der (linearen) Doppelbrechung ist in kristallinen Mineralien weit verbreitet und war sogar ausschlaggebend für die erste Entdeckung der Polarisation. In der Mineralogie wird diese Eigenschaft häufig mit Hilfe von Polarisationsmikroskopen zur Identifizierung von Mineralien ausgenutzt. Siehe optische Mineralogie für weitere Einzelheiten. ⓘ

Schallwellen in festen Materialien weisen eine Polarisation auf. Die unterschiedliche Ausbreitung der drei Polarisationen durch die Erde ist für die Seismologie von entscheidender Bedeutung. Horizontal und vertikal polarisierte seismische Wellen (Scherwellen) werden als SH und SV bezeichnet, während Wellen mit longitudinaler Polarisation (Kompressionswellen) als P-Wellen bezeichnet werden. ⓘ

Chemie

Wir haben gesehen (siehe oben), dass die Doppelbrechung einer Kristallart nützlich ist, um sie zu identifizieren, und daher ist der Nachweis der linearen Doppelbrechung besonders nützlich in der Geologie und Mineralogie. Bei linear polarisiertem Licht ändert sich im Allgemeinen der Polarisationszustand beim Durchgang durch einen solchen Kristall, so dass es bei der Betrachtung zwischen zwei gekreuzten Polarisatoren hervorsticht, wie auf dem Foto oben zu sehen. Auch in der Chemie kann die Drehung der Polarisationsachsen in einer flüssigen Lösung ein nützliches Messinstrument sein. In einer Flüssigkeit ist eine lineare Doppelbrechung unmöglich, jedoch kann eine zirkulare Doppelbrechung auftreten, wenn sich ein chirales Molekül in Lösung befindet. Wenn die rechts- und linkshändigen Enantiomere eines solchen Moleküls in gleicher Anzahl vorhanden sind (ein so genanntes racemisches Gemisch), heben sich ihre Auswirkungen auf. Liegt jedoch nur ein Enantiomer vor (oder überwiegt eines), wie es bei organischen Molekülen häufiger der Fall ist, wird eine zirkuläre Nettodoppelbrechung (oder optische Aktivität) beobachtet, die das Ausmaß dieses Ungleichgewichts (oder die Konzentration des Moleküls selbst, wenn davon ausgegangen werden kann, dass nur ein Enantiomer vorhanden ist) offenbart. Dies wird mit einem Polarimeter gemessen, bei dem polarisiertes Licht durch eine Röhre mit der Flüssigkeit geleitet wird, an deren Ende sich ein weiterer Polarisator befindet, der gedreht wird, um die Lichtdurchlässigkeit aufzuheben. ⓘ

Astronomie

In vielen Bereichen der Astronomie ist die Untersuchung der polarisierten elektromagnetischen Strahlung aus dem Weltraum von großer Bedeutung. Obwohl die Polarisation in der Regel bei der Wärmestrahlung von Sternen keine Rolle spielt, ist sie auch in der Strahlung kohärenter astronomischer Quellen (z. B. Hydroxyl- oder Methanolmaser) und inkohärenter Quellen wie den großen Radiokeulen in aktiven Galaxien und der Radiostrahlung von Pulsaren (die, so wird spekuliert, manchmal kohärent sein kann) vorhanden und wird dem Sternenlicht auch durch Streuung am interstellaren Staub aufgezwungen. Die Polarisation liefert nicht nur Informationen über die Strahlungsquellen und die Streuung, sondern ist über die Faraday-Rotation auch ein Indikator für das interstellare Magnetfeld. Die Polarisation des kosmischen Mikrowellenhintergrunds wird genutzt, um die Physik des sehr frühen Universums zu untersuchen. Synchrotronstrahlung ist von Natur aus polarisiert. Es wird vermutet, dass astronomische Quellen die Chiralität biologischer Moleküle auf der Erde verursacht haben. ⓘ

Anwendungen und Beispiele

Polarisierte Sonnenbrillen

Wirkung eines Polarisators auf die Reflexion von Watten. Im Bild links lässt der horizontal ausgerichtete Polarisator diese Reflexionen bevorzugt durch; dreht man den Polarisator um 90° (rechts), wie man es mit einer polarisierten Sonnenbrille tun würde, wird fast das gesamte spiegelnd reflektierte Sonnenlicht blockiert. ⓘ

Man kann testen, ob eine Sonnenbrille polarisiert ist, indem man durch zwei Brillen schaut, von denen eine senkrecht zur anderen steht. Wenn beide polarisiert sind, wird das gesamte Licht blockiert. ⓘ

Unpolarisiertes Licht, das von einer spiegelnden (glänzenden) Oberfläche reflektiert wird, erhält im Allgemeinen einen gewissen Grad an Polarisierung. Dieses Phänomen wurde 1808 von dem Mathematiker Étienne-Louis Malus beobachtet, nach dem das Malus-Gesetz benannt ist. Polarisierende Sonnenbrillen machen sich diesen Effekt zunutze, um die Blendung durch Reflexionen von horizontalen Flächen zu verringern, insbesondere von der Straße, auf die man im Streifwinkel blickt. ⓘ

Träger von polarisierten Sonnenbrillen beobachten gelegentlich unbeabsichtigte Polarisationseffekte wie farbabhängige Doppelbrechungseffekte, z. B. bei gehärtetem Glas (z. B. Autoscheiben) oder Gegenständen aus transparentem Kunststoff, in Verbindung mit natürlicher Polarisation durch Reflexion oder Streuung. Das polarisierte Licht von LCD-Monitoren (siehe unten) ist sehr auffällig, wenn diese getragen werden. ⓘ

Himmelspolarisation und Fotografie

Die Auswirkungen eines Polarisationsfilters (rechtes Bild) auf den Himmel in einer Fotografie ⓘ

Die Polarisation wird im Licht des Himmels beobachtet, da das Sonnenlicht beim Durchgang durch die Erdatmosphäre an Aerosolen gestreut wird. Das gestreute Licht erzeugt die Helligkeit und die Farbe des klaren Himmels. Diese partielle Polarisation des Streulichts kann genutzt werden, um den Himmel auf Fotos abzudunkeln und den Kontrast zu erhöhen. Dieser Effekt ist am stärksten an Punkten des Himmels zu beobachten, die einen 90°-Winkel zur Sonne bilden. Polfilter machen sich diese Effekte zunutze, um die Ergebnisse beim Fotografieren von Szenen zu optimieren, bei denen es zu Reflexionen oder Streuungen am Himmel kommt. ⓘ

Farbige Streifen im Embassy Gardens Sky Pool bei Betrachtung durch einen Polarisator, die auf spannungsinduzierte Doppelbrechung im Oberlicht zurückzuführen sind ⓘ

Die Polarisation des Himmels wurde zur Orientierung in der Navigation verwendet. Der Himmelskompass von Pfund wurde in den 1950er Jahren für die Navigation in der Nähe der Pole des Erdmagnetfeldes verwendet, wenn weder Sonne noch Sterne sichtbar waren (z. B. bei Bewölkung oder Dämmerung). Es wird vermutet, dass die Wikinger bei ihren ausgedehnten Expeditionen über den Nordatlantik im 9. bis 11. Jahrhundert ein ähnliches Gerät (den "Sonnenstein") benutzten, bevor der Magnetkompass im 12. Jahrhundert aus Asien nach Europa kam. Mit dem Himmelskompass verwandt ist die "Polaruhr", die Charles Wheatstone im späten 19. ⓘ

Display-Technologien

Das Prinzip der Flüssigkristallanzeige (LCD) beruht auf der Drehung der Achse der linearen Polarisation durch die Flüssigkristallanordnung. Das Licht der Hintergrundbeleuchtung (oder der rückseitigen Reflexionsschicht bei Geräten ohne Hintergrundbeleuchtung) durchläuft zunächst eine linear polarisierende Folie. Dieses polarisierte Licht durchläuft die eigentliche Flüssigkristallschicht, die in Pixeln (für ein Fernsehgerät oder einen Computermonitor) oder in einem anderen Format, z. B. einer Sieben-Segment-Anzeige oder einer Anzeige mit kundenspezifischen Symbolen für ein bestimmtes Produkt, organisiert sein kann. Die Flüssigkristallschicht wird mit einer konsistenten rechts- (oder links-) händigen Chiralität hergestellt, die im Wesentlichen aus winzigen Helices besteht. Dies bewirkt eine zirkulare Doppelbrechung und ist so konstruiert, dass der lineare Polarisationszustand um 90 Grad gedreht wird. Wenn jedoch eine Spannung an die Zelle angelegt wird, richten sich die Moleküle auf, wodurch die zirkuläre Doppelbrechung verringert wird oder ganz verloren geht. Auf der Betrachtungsseite des Bildschirms befindet sich eine weitere linear polarisierende Folie, die in der Regel um 90 Grad versetzt zu der Folie hinter der aktiven Schicht angeordnet ist. Wenn die zirkuläre Doppelbrechung durch Anlegen einer ausreichenden Spannung aufgehoben wird, bleibt die Polarisation des durchgelassenen Lichts im rechten Winkel zum vorderen Polarisator, und das Pixel erscheint dunkel. Ohne Spannung bewirkt die 90-Grad-Drehung der Polarisation jedoch, dass sie genau mit der Achse des vorderen Polarisators übereinstimmt und das Licht durchgelassen wird. Zwischenspannungen bewirken eine mittlere Drehung der Polarisationsachse, und das Pixel hat eine mittlere Intensität. Bildschirme, die auf diesem Prinzip beruhen, sind weit verbreitet und werden heute in den meisten Fernsehgeräten, Computermonitoren und Videoprojektoren eingesetzt, so dass die frühere Röhrentechnologie im Wesentlichen überflüssig geworden ist. Der Einsatz der Polarisation beim Betrieb von LCD-Displays ist für jemanden, der eine polarisierte Sonnenbrille trägt, sofort erkennbar und macht das Display oft unlesbar. ⓘ

In einem ganz anderen Sinne ist die Polarisationskodierung die führende (aber nicht die einzige) Methode, um in stereoskopischen Displays für 3D-Filme getrennte Bilder für das linke und das rechte Auge zu liefern. Dabei werden getrennte Bilder für jedes Auge entweder von zwei verschiedenen Projektoren mit orthogonal ausgerichteten Polarisationsfiltern projiziert oder, was typischer ist, von einem einzigen Projektor mit zeitlich gemultiplexter Polarisation (einem Gerät mit schnell wechselnder Polarisation für aufeinanderfolgende Bilder). Polarisierte 3D-Brillen mit geeigneten Polarisationsfiltern sorgen dafür, dass jedes Auge nur das gewünschte Bild empfängt. In der Vergangenheit wurde bei solchen Systemen die lineare Polarisationskodierung verwendet, da sie kostengünstig war und eine gute Trennung bot. Die zirkulare Polarisation macht die Trennung der beiden Bilder jedoch unempfindlich gegen eine Neigung des Kopfes und ist heute in der 3D-Filmvorführung weit verbreitet, wie z. B. das System von RealD. Für die Projektion solcher Bilder sind Bildschirme erforderlich, die die Polarisation des projizierten Lichts bei Reflexion beibehalten (z. B. Silberbildschirme); ein normaler diffuser weißer Projektionsschirm verursacht eine Depolarisierung der projizierten Bilder und ist daher für diese Anwendung ungeeignet. ⓘ

Obwohl inzwischen überholt, litten CRT-Computerbildschirme unter der Reflexion durch die Glashülle, was zu Blendung durch Raumlicht und folglich zu einem schlechten Kontrast führte. Um dieses Problem zu beheben, wurden verschiedene Antireflexionslösungen eingesetzt. Eine Lösung nutzte das Prinzip der Reflexion von zirkular polarisiertem Licht. Ein zirkularer Polarisationsfilter vor der Leinwand lässt (sagen wir) nur rechts zirkular polarisiertes Raumlicht durch. Bei rechtszirkular polarisiertem Licht (je nach verwendeter Konvention) dreht sich die Richtung des elektrischen (und magnetischen) Feldes im Uhrzeigersinn, während es sich in +z-Richtung ausbreitet. Bei der Reflexion hat das Feld immer noch dieselbe Drehrichtung, aber die Ausbreitung erfolgt nun in -z-Richtung, so dass die reflektierte Welle links zirkular polarisiert ist. Mit dem rechtszirkularen Polarisationsfilter vor dem reflektierenden Glas wird das unerwünschte Licht, das vom Glas reflektiert wird, in einem sehr polarisierten Zustand sein, der durch diesen Filter blockiert wird, wodurch das Problem der Reflexion beseitigt wird. Die Umkehrung der zirkularen Polarisation bei der Reflexion und die Beseitigung von Reflexionen auf diese Weise kann leicht beobachtet werden, indem man in einen Spiegel schaut, während man eine 3-D-Filmbrille trägt, die in den beiden Gläsern links- und rechtsseitige zirkulare Polarisation verwendet. Schließt man ein Auge, so sieht das andere Auge eine Reflexion, in der es sich selbst nicht sehen kann; diese Linse erscheint schwarz. Die andere Linse (des geschlossenen Auges) hat jedoch die richtige zirkuläre Polarisation, so dass das geschlossene Auge vom offenen Auge leicht gesehen werden kann. ⓘ

Funkübertragung und -empfang

Alle Radio- (und Mikrowellen-) Antennen, die zum Senden oder Empfangen verwendet werden, sind von Natur aus polarisiert. Sie senden in einer bestimmten Polarisation (bzw. empfangen Signale) und sind völlig unempfindlich gegenüber der entgegengesetzten Polarisation; in bestimmten Fällen ist diese Polarisation eine Funktion der Richtung. Die meisten Antennen sind nominell linear polarisiert, aber auch elliptische und zirkulare Polarisation ist möglich. Wie in der Optik üblich, bezieht sich die "Polarisation" einer Funkwelle auf die Polarisation ihres elektrischen Feldes, wobei das Magnetfeld bei einer linear polarisierten Welle um 90 Grad gedreht ist. ⓘ

Die große Mehrheit der Antennen ist linear polarisiert. Aus Symmetrieüberlegungen lässt sich nämlich zeigen, dass eine Antenne, die vollständig in einer Ebene liegt, die auch den Beobachter einschließt, nur in Richtung dieser Ebene polarisiert sein kann. Dies gilt für viele Fälle, so dass man leicht auf die Polarisation einer solchen Antenne in einer bestimmten Ausbreitungsrichtung schließen kann. So ist eine typische Yagi- oder logarithmisch-periodische Dachantenne mit horizontalen Leitern von einer zweiten Station aus gesehen in Richtung des Horizonts notwendigerweise horizontal polarisiert. Eine vertikale "Peitschenantenne" oder ein AM-Sendeturm, der als Antennenelement verwendet wird (wiederum für Beobachter, die horizontal davon entfernt sind), sendet jedoch in vertikaler Polarisation. Eine Drehkreuzantenne mit ihren vier Armen in der horizontalen Ebene sendet ebenfalls horizontal polarisierte Strahlung in Richtung des Horizonts. Wird dieselbe Drehkreuzantenne jedoch in der "axialen Betriebsart" (nach oben, für dieselbe horizontal ausgerichtete Struktur) verwendet, ist ihre Strahlung zirkular polarisiert. In mittleren Höhen ist sie elliptisch polarisiert. ⓘ

Die Polarisation ist in der Funkkommunikation wichtig, denn wenn man beispielsweise versucht, eine horizontal polarisierte Antenne für den Empfang einer vertikal polarisierten Übertragung zu verwenden, wird die Signalstärke erheblich reduziert (oder unter sehr kontrollierten Bedingungen auf Null reduziert). Dieses Prinzip wird beim Satellitenfernsehen genutzt, um die Kanalkapazität in einem festen Frequenzband zu verdoppeln. Ein und derselbe Frequenzkanal kann für zwei Signale verwendet werden, die in entgegengesetzter Polarisation ausgestrahlt werden. Indem die Empfangsantenne auf die eine oder andere Polarisation eingestellt wird, kann eines der beiden Signale ausgewählt werden, ohne dass das andere gestört wird. ⓘ

Vor allem aufgrund des Bodens gibt es einige Unterschiede bei der Ausbreitung (und auch bei den Reflexionen, die für das TV-Geisterbild verantwortlich sind) zwischen horizontaler und vertikaler Polarisation. Beim AM- und FM-Rundfunk wird in der Regel die vertikale Polarisation verwendet, beim Fernsehen die horizontale Polarisation. Vor allem bei niedrigen Frequenzen wird die horizontale Polarisation vermieden. Das liegt daran, dass sich die Phase einer horizontal polarisierten Welle bei der Reflexion am Boden umkehrt. Ein entfernter Sender in horizontaler Richtung empfängt sowohl die direkte als auch die reflektierte Welle, die sich somit gegenseitig aufheben. Dieses Problem wird bei vertikaler Polarisation vermieden. Die Polarisation spielt auch bei der Übertragung von Radarimpulsen und dem Empfang von Radarreflexionen durch dieselbe oder eine andere Antenne eine Rolle. So kann beispielsweise die Rückstreuung von Radarimpulsen durch Regentropfen durch zirkulare Polarisation vermieden werden. So wie die Spiegelreflexion von zirkular polarisiertem Licht die Händigkeit der Polarisation umkehrt (siehe oben), gilt das gleiche Prinzip für die Streuung an Objekten, die viel kleiner als eine Wellenlänge sind, wie z. B. Regentropfen. Andererseits führt die Reflexion dieser Welle an einem unregelmäßigen Metallobjekt (z. B. einem Flugzeug) in der Regel zu einer Änderung der Polarisation und zum (teilweisen) Empfang der zurückkommenden Welle durch dieselbe Antenne. ⓘ

Der Effekt der freien Elektronen in der Ionosphäre verursacht in Verbindung mit dem Erdmagnetfeld die Faraday-Rotation, eine Art zirkuläre Doppelbrechung. Dies ist derselbe Mechanismus, der die Achse der linearen Polarisation durch Elektronen im interstellaren Raum drehen kann (siehe unten). Das Ausmaß der durch ein solches Plasma verursachten Faraday-Drehung ist bei niedrigeren Frequenzen stark übertrieben, so dass der Effekt bei den von Satelliten verwendeten höheren Mikrowellenfrequenzen minimal ist. Mittel- oder Kurzwellenübertragungen, die nach der Brechung durch die Ionosphäre empfangen werden, sind jedoch stark betroffen. Da der Weg einer Welle durch die Ionosphäre und der Vektor des Erdmagnetfeldes entlang dieses Weges nicht vorhersehbar sind, hat eine mit vertikaler (oder horizontaler) Polarisation gesendete Welle beim Empfänger im Allgemeinen eine Polarisation in beliebiger Richtung zur Folge. ⓘ

Zirkulare Polarisation durch ein Kunststofffenster eines Flugzeugs, 1989 ⓘ

Polarisation und Sehen

Viele Tiere sind in der Lage, einige der Komponenten der Polarisation von Licht wahrzunehmen, z. B. linear horizontal polarisiertes Licht. Dies wird im Allgemeinen zu Navigationszwecken genutzt, da die lineare Polarisation des Himmelslichts immer senkrecht zur Sonnenrichtung steht. Diese Fähigkeit ist bei Insekten, einschließlich Bienen, sehr verbreitet, die diese Information zur Orientierung bei ihren Kommunikationstänzen nutzen. Polarisationsempfindlichkeit wurde auch bei Tintenfischen, Kalmaren, Tintenfischen und Fangschreckenkrebsen beobachtet. Im letzteren Fall misst eine Art alle sechs orthogonalen Komponenten der Polarisation und verfügt vermutlich über eine optimale Polarisationssicht. Die schnell wechselnden, lebhaft gefärbten Hautmuster von Tintenfischen, die zur Kommunikation genutzt werden, enthalten ebenfalls Polarisationsmuster, und bei Fangschreckenkrebsen ist bekannt, dass sie polarisationsselektives reflektierendes Gewebe besitzen. Man nahm an, dass Tauben die Polarisation des Himmels wahrnehmen können und dass dies eine ihrer Orientierungshilfen ist, aber Untersuchungen zeigen, dass dies ein weit verbreiteter Mythos ist. ⓘ

Das bloße menschliche Auge ist nur schwach polarisationsempfindlich, ohne dass ein Filter dazwischengeschaltet werden muss. Polarisiertes Licht erzeugt in der Nähe des Zentrums des Gesichtsfeldes ein sehr schwaches Muster, den so genannten Haidinger-Pinsel. Dieses Muster ist sehr schwer zu erkennen, aber mit etwas Übung kann man lernen, polarisiertes Licht mit dem bloßen Auge zu erkennen. ⓘ

Drehimpuls durch zirkulare Polarisation

Es ist bekannt, dass elektromagnetische Strahlung einen gewissen linearen Impuls in Ausbreitungsrichtung hat. Zusätzlich trägt das Licht aber auch einen gewissen Drehimpuls, wenn es zirkular (oder teilweise) polarisiert ist. Im Vergleich zu niedrigeren Frequenzen, wie z. B. Mikrowellen, ist der Drehimpuls des Lichts, selbst bei reiner zirkularer Polarisation, im Vergleich zum linearen Impuls (oder Strahlungsdruck) der gleichen Welle sehr gering und schwer zu messen. In einem Experiment wurde er jedoch genutzt, um Geschwindigkeiten von bis zu 600 Millionen Umdrehungen pro Minute zu erreichen. ⓘ

Polarisationsarten

lineare Polarisation

Die Richtung der Schwingung ist konstant. Die Auslenkung aus der Ruhelage (im Fall der mechanischen Welle eine Verschiebung senkrecht zur Ausbreitungsrichtung) ändert periodisch ihren Betrag und ihr Vorzeichen. Die Richtung in Bezug auf eine bestimmte Ebene kann als Winkel angegeben werden (bei seismischen Wellen üblich) oder als Anteil der beiden Komponenten parallel bzw. senkrecht. Für elektromagnetische Wellen siehe das folgende Kapitel.

zirkulare Polarisation

(im 19. Jahrhundert als drehende Polarisation bezeichnet) Der Betrag der Auslenkung ist (abgesehen von Modulation) konstant, ihre Richtung ändert sich innerhalb der senkrecht zum Wellenvektor stehenden Ebene (der xy-Ebene im Bild) mit konstanter Winkelgeschwindigkeit. Für den Drehsinn siehe Helizität. Allerdings wird in der Literatur, besonders der älteren, häufig rechtszirkular polarisiert als Umlauf im Uhrzeigersinn bei Blickrichtung gegen die Ausbreitungsrichtung definiert (entsprechend einer Linksschraube). Abkürzungen: RHCP und LHCP für rechts- oder linkshändige Polarisation (eng. Right Hand Circular Polarization und Left Hand Circular Polarization).

elliptische Polarisation

Ist die Mischform der beiden oben genannten und bei der die die Auslenkung eine Ellipse beschreibt. ⓘ

Polarisation elektromagnetischer Wellen

Wahrnehmung von polarisiertem Licht

Viele Insekten können linear polarisiertes Licht nach seiner Polarisationsrichtung unterscheiden und nutzen diesen Effekt, um sich zu orientieren. Bei der Honigbiene wurde dies durch Karl von Frisch erforscht. ⓘ

Auch Fangschreckenkrebse, die Wasserwanze Notonecta glauca, Große Mausohren (Myotis myotis) und Wüstenameisen sind dazu in der Lage, sowie Menschen, allerdings mit sehr geringem Kontrast (Haidinger-Büschel-Phänomen). ⓘ