Mathematik
 | ||
| Mathematik | ||
|---|---|---|
|
|
||
| Artikel | ||
|
||
| Wissenschaftler | ||
|
||
| Navigation | ||
|
||
Die Mathematik (von altgriechisch μάθημα; máthēma: "Wissen, Studium, Lernen") ist ein Wissensgebiet, das Themen wie Zahlen (Arithmetik, Zahlentheorie), Formeln und verwandte Strukturen (Algebra), Formen und die Räume, in denen sie enthalten sind (Geometrie), sowie Mengen und ihre Veränderungen (Kalkül und Analysis) umfasst. ⓘ
Bei den meisten mathematischen Aktivitäten geht es um die Entdeckung und den Nachweis von Eigenschaften abstrakter Objekte durch reines Denken. Bei diesen Objekten handelt es sich entweder um Abstraktionen aus der Natur, wie z. B. natürliche Zahlen oder Linien, oder - in der modernen Mathematik - um Entitäten, die mit bestimmten Eigenschaften, den so genannten Axiomen, festgelegt sind. Ein Beweis besteht aus einer Abfolge von Anwendungen einiger deduktiver Regeln auf bereits bekannte Ergebnisse, einschließlich bereits bewiesener Theoreme, Axiome und (im Falle der Abstraktion von der Natur) einiger grundlegender Eigenschaften, die als wahre Ausgangspunkte der betrachteten Theorie angesehen werden. Das Ergebnis eines Beweises wird als Theorem bezeichnet. ⓘ
Die Mathematik wird in der Wissenschaft häufig zur Modellierung von Phänomenen verwendet. Auf diese Weise lassen sich quantitative Vorhersagen aus experimentellen Gesetzen ableiten. So lässt sich beispielsweise die Bewegung der Planeten mit Hilfe des Newtonschen Gravitationsgesetzes in Verbindung mit mathematischen Berechnungen genau vorhersagen. Die Unabhängigkeit der mathematischen Wahrheit von Experimenten bedeutet, dass die Genauigkeit solcher Vorhersagen nur von der Angemessenheit des Modells zur Beschreibung der Realität abhängt. Ungenaue Vorhersagen bedeuten, dass die mathematischen Modelle verbessert oder geändert werden müssen, nicht dass die Mathematik in den Modellen selbst falsch ist. So lässt sich beispielsweise die Perihelpräzession des Merkurs nicht durch das Newtonsche Gravitationsgesetz erklären, wohl aber durch die allgemeine Relativitätstheorie von Einstein. Diese experimentelle Bestätigung von Einsteins Theorie zeigt, dass das Newtonsche Gravitationsgesetz nur eine Annäherung ist, auch wenn es in der täglichen Anwendung genau ist. ⓘ
Mathematik ist in vielen Bereichen unverzichtbar, darunter Naturwissenschaften, Technik, Medizin, Finanzen, Informatik und Sozialwissenschaften. Einige Bereiche der Mathematik, wie z. B. Statistik und Spieltheorie, werden in engem Zusammenhang mit ihren Anwendungen entwickelt und werden häufig unter dem Begriff angewandte Mathematik zusammengefasst. Andere mathematische Bereiche werden unabhängig von einer Anwendung entwickelt (und werden daher als reine Mathematik bezeichnet), aber praktische Anwendungen werden oft erst später entdeckt. Ein passendes Beispiel ist das Problem der ganzzahligen Faktorisierung, das auf Euklid zurückgeht, aber vor seiner Verwendung im RSA-Kryptosystem (für die Sicherheit von Computernetzwerken) keine praktische Anwendung hatte. ⓘ
Historisch gesehen taucht das Konzept eines Beweises und die damit verbundene mathematische Strenge erstmals in der griechischen Mathematik auf, vor allem in Euklids Elementen. Von Anfang an war die Mathematik im Wesentlichen in Geometrie und Arithmetik (Umgang mit natürlichen Zahlen und Brüchen) unterteilt, bis im 16. und 17. Jahrhundert Algebra und Infinitesimalrechnung als neue Bereiche eingeführt wurden. Seitdem hat die Wechselwirkung zwischen mathematischen Innovationen und wissenschaftlichen Entdeckungen zu einem raschen Anstieg der Entwicklung der Mathematik geführt. Am Ende des 19. Jahrhunderts führte die Gründungskrise der Mathematik zur Systematisierung der axiomatischen Methode. Dies wiederum führte zu einem dramatischen Anstieg der Zahl der mathematischen Gebiete und ihrer Anwendungsbereiche. Ein Beispiel dafür ist die Klassifikation der mathematischen Fächer, in der mehr als sechzig Gebiete der ersten Stufe der Mathematik aufgeführt sind. ⓘ
Die Mathematik (bundesdeutsches Hochdeutsch: [matemaˈtiːk], [matemaˈtik]; österreichisches Hochdeutsch: [mateˈmaːtik]; altgriechisch μαθηματικὴ τέχνη mathēmatikē téchnē ‚die Kunst des Lernens‘) ist eine Formalwissenschaft, die aus der Untersuchung von geometrischen Figuren und dem Rechnen mit Zahlen entstand. Für Mathematik gibt es keine allgemein anerkannte Definition; heute wird sie üblicherweise als eine Wissenschaft beschrieben, die durch logische Definitionen selbstgeschaffene abstrakte Strukturen mittels der Logik auf ihre Eigenschaften und Muster untersucht. ⓘ

Bereiche der Mathematik
Vor der Renaissance war die Mathematik in zwei Hauptbereiche unterteilt: die Arithmetik, die sich mit dem Umgang mit Zahlen befasst, und die Geometrie, die sich mit dem Studium der Formen beschäftigt. Einige Pseudowissenschaften, wie Numerologie und Astrologie, wurden damals nicht klar von der Mathematik abgegrenzt. ⓘ
In der Renaissance kamen zwei weitere Bereiche hinzu. Die mathematische Notation führte zur Algebra, die, grob gesagt, aus dem Studium und der Manipulation von Formeln besteht. Die Kalkulation, bestehend aus den beiden Teilgebieten Infinitesimalrechnung und Integralrechnung, ist die Lehre von den stetigen Funktionen, die die typischerweise nichtlinearen Beziehungen zwischen unterschiedlichen Größen (Variablen) modellieren. Diese Unterteilung in vier Hauptbereiche - Arithmetik, Geometrie, Algebra, Kalkül - blieb bis zum Ende des 19. Jahrhunderts bestehen. Jahrhunderts. Bereiche wie die Himmelsmechanik und die Festkörpermechanik wurden damals oft als Teil der Mathematik betrachtet, werden aber heute als Teil der Physik angesehen. Einige Themen, die in dieser Zeit entwickelt wurden, gehen der Mathematik voraus und werden in Bereiche wie die Wahrscheinlichkeitstheorie und die Kombinatorik unterteilt, die erst später als eigenständige Bereiche betrachtet wurden. ⓘ
Ende des 19. Jahrhunderts führten die Gründungskrise der Mathematik und die daraus resultierende Systematisierung der axiomatischen Methode zu einer explosionsartigen Zunahme neuer Gebiete der Mathematik. Heute umfasst die Klassifikation der mathematischen Fächer nicht weniger als vierundsechzig Gebiete der ersten Stufe. Einige dieser Bereiche entsprechen der älteren Einteilung, wie z. B. die Zahlentheorie (die moderne Bezeichnung für die höhere Arithmetik) und die Geometrie. (Mehrere andere Bereiche der ersten Ebene tragen jedoch "Geometrie" in ihrem Namen oder werden anderweitig allgemein als Teil der Geometrie betrachtet.) Algebra und Infinitesimalrechnung erscheinen nicht als Bereiche der ersten Stufe, sondern sind jeweils in mehrere Bereiche der ersten Stufe unterteilt. Andere Bereiche der ersten Ebene sind im 20. Jahrhundert entstanden (z. B. Kategorientheorie, homologische Algebra und Informatik) oder wurden zuvor nicht als Mathematik betrachtet, wie z. B. Mathematische Logik und Grundlagen (einschließlich Modelltheorie, Berechenbarkeitstheorie, Mengenlehre, Beweistheorie und algebraische Logik). ⓘ

Kennzeichnend für die Mathematik ist weiterhin die Weise, wie sie durch das Bearbeiten von „eigentlich zu schweren“ Problemen voranschreitet. ⓘ
Sobald ein Grundschüler das Addieren natürlicher Zahlen gelernt hat, ist er in der Lage, folgende Frage zu verstehen und durch Probieren zu beantworten: „Welche Zahl muss man zu 3 addieren, um 5 zu erhalten?“ Die systematische Lösung solcher Aufgaben aber erfordert die Einführung eines neuen Konzepts: der Subtraktion. Die Frage lässt sich dann umformulieren zu: „Was ist 5 minus 3?“ Sobald aber die Subtraktion definiert ist, kann man auch die Frage stellen: „Was ist 3 minus 5?“, die auf eine negative Zahl und damit bereits über die Grundschulmathematik hinaus führt. ⓘ
Ebenso wie in diesem elementaren Beispiel beim individuellen Erlernen ist die Mathematik auch in ihrer Geschichte fortgeschritten: auf jedem erreichten Stand ist es möglich, wohldefinierte Aufgaben zu stellen, zu deren Lösung weitaus anspruchsvollere Mittel nötig sind. Oft sind zwischen der Formulierung eines Problems und seiner Lösung viele Jahrhunderte vergangen und ist mit der Problemlösung schließlich ein völlig neues Teilgebiet begründet worden: so konnten mit der Infinitesimalrechnung im 17. Jahrhundert Probleme gelöst werden, die seit der Antike offen waren. ⓘ
Auch eine negative Antwort, der Beweis der Unlösbarkeit eines Problems, kann die Mathematik voranbringen: so ist aus gescheiterten Versuchen zur Auflösung algebraischer Gleichungen die Gruppentheorie entstanden. ⓘ
Zahlentheorie

Die Zahlentheorie begann mit der Manipulation von Zahlen, d. h. den natürlichen Zahlen und wurde später erweitert auf ganze Zahlen und rationale Zahlen Früher wurde die Zahlentheorie als Arithmetik bezeichnet, aber heute wird dieser Begriff meist für numerische Berechnungen verwendet. ⓘ
Viele einfach formulierte Zahlenprobleme lassen sich nur mit anspruchsvollen Methoden aus der gesamten Mathematik lösen. Ein bekanntes Beispiel ist der letzte Satz von Fermat. Diese Vermutung wurde 1637 von Pierre de Fermat aufgestellt, aber erst 1994 von Andrew Wiles bewiesen, der Werkzeuge wie die Schematheorie der algebraischen Geometrie, die Kategorientheorie und die homologische Algebra verwendete. Ein weiteres Beispiel ist die Goldbachsche Vermutung, die besagt, dass jede gerade ganze Zahl größer als 2 die Summe zweier Primzahlen ist. Sie wurde 1742 von Christian Goldbach aufgestellt und ist trotz erheblicher Anstrengungen bis heute unbewiesen. ⓘ
Die Zahlentheorie umfasst mehrere Teilbereiche, darunter die analytische Zahlentheorie, die algebraische Zahlentheorie, die Geometrie der Zahlen (methodenorientiert), diophantische Gleichungen und die Transzendenztheorie (problemorientiert). ⓘ
Geometrie
Die Geometrie ist einer der ältesten Zweige der Mathematik. Sie begann mit empirischen Rezepten für Formen wie Linien, Winkel und Kreise, die vor allem für die Bedürfnisse des Vermessungswesens und der Architektur entwickelt wurden, hat sich aber inzwischen auf viele andere Teilgebiete ausgedehnt. ⓘ
Eine grundlegende Neuerung war die Einführung des Konzepts der Beweise durch die alten Griechen, das besagt, dass jede Behauptung bewiesen werden muss. So reicht es beispielsweise nicht aus, durch Messung festzustellen, dass zwei Längen gleich sind; ihre Gleichheit muss durch Schlussfolgerungen aus zuvor akzeptierten Ergebnissen (Theoremen) und einigen grundlegenden Aussagen bewiesen werden. Die Grundaussagen müssen nicht bewiesen werden, weil sie selbstverständlich sind (Postulate) oder zur Definition des Untersuchungsgegenstandes gehören (Axiome). Dieses für die gesamte Mathematik grundlegende Prinzip wurde zunächst für die Geometrie ausgearbeitet und von Euklid um 300 v. Chr. in seinem Buch Elemente systematisiert. ⓘ
Die daraus resultierende euklidische Geometrie ist die Lehre von den Formen und ihren Anordnungen aus Linien, Ebenen und Kreisen in der euklidischen Ebene (ebene Geometrie) und dem (dreidimensionalen) euklidischen Raum. ⓘ
Die euklidische Geometrie wurde ohne Änderung der Methoden oder des Umfangs bis zum 17. Jahrhundert entwickelt, als René Descartes das einführte, was heute als kartesische Koordinaten bezeichnet wird. Dies war ein bedeutender Paradigmenwechsel, denn anstatt reelle Zahlen als Längen von Linienabschnitten zu definieren (siehe Zahlengerade), erlaubte es die Darstellung von Punkten durch ihre Koordinaten (die Zahlen sind). Dies ermöglichte die Verwendung von Algebra (und später von Kalkül) zur Lösung geometrischer Probleme. Dadurch wurde die Geometrie in zwei neue Teilgebiete aufgeteilt: die synthetische Geometrie, die sich rein geometrischer Methoden bedient, und die analytische Geometrie, die Koordinaten systematisch verwendet. ⓘ
Die analytische Geometrie ermöglicht die Untersuchung von Kurven, die nicht mit Kreisen und Linien verbunden sind. Solche Kurven können als Graphen von Funktionen definiert werden (deren Untersuchung zur Differentialgeometrie führte). Sie können auch als implizite Gleichungen, häufig Polynomgleichungen, definiert werden (woraus die algebraische Geometrie hervorging). Die analytische Geometrie ermöglicht es auch, Räume mit mehr als drei Dimensionen zu betrachten. ⓘ
Im 19. Jahrhundert entdeckten die Mathematiker nicht-euklidische Geometrien, die nicht dem Parallelitätspostulat folgen. Diese Entdeckung stellt den Wahrheitsgehalt des Postulats in Frage und offenbart zusammen mit dem Russel-Paradoxon die Gründungskrise der Mathematik. Dieser Aspekt der Krise wurde durch die Systematisierung der axiomatischen Methode und die Annahme, dass die Wahrheit der gewählten Axiome kein mathematisches Problem darstellt, gelöst. Die axiomatische Methode wiederum ermöglicht die Untersuchung verschiedener Geometrien, die entweder durch eine Änderung der Axiome oder durch die Berücksichtigung von Eigenschaften, die unter bestimmten Transformationen des Raums invariant sind, gewonnen werden. ⓘ
Zu den Teilbereichen der Geometrie gehören heute:
- Die projektive Geometrie, die im 16. Jahrhundert von Girard Desargues eingeführt wurde, erweitert die euklidische Geometrie um Punkte im Unendlichen, in denen sich parallele Linien schneiden. Dadurch werden viele Aspekte der klassischen Geometrie vereinfacht, da die Behandlung von sich schneidenden und parallelen Linien vereinheitlicht wird.
- Affine Geometrie, die Untersuchung von Eigenschaften in Bezug auf Parallelität und unabhängig vom Konzept der Länge.
- Differentialgeometrie, die Untersuchung von Kurven, Flächen und deren Verallgemeinerungen, die durch differenzierbare Funktionen definiert sind
- Vervielfältigungstheorie, die Untersuchung von Formen, die nicht unbedingt in einen größeren Raum eingebettet sind
- Riemannsche Geometrie, die Lehre von den Abstandseigenschaften in gekrümmten Räumen
- Algebraische Geometrie, die Lehre von Kurven, Flächen und ihren Verallgemeinerungen, die mit Hilfe von Polynomen definiert werden
- Topologie, die Untersuchung von Eigenschaften, die bei kontinuierlichen Verformungen erhalten bleiben
- Algebraische Topologie, die Anwendung algebraischer Methoden in der Topologie, insbesondere der homologischen Algebra
- Diskrete Geometrie, Studium der endlichen Konfigurationen in der Geometrie
- Konvexe Geometrie, die Lehre von den konvexen Mengen, die ihre Bedeutung aus ihren Anwendungen in der Optimierung bezieht
- Komplexe Geometrie, die Geometrie, die man erhält, wenn man die reellen Zahlen durch komplexe Zahlen ersetzt ⓘ
Algebra
Die Algebra ist die Kunst der Handhabung von Gleichungen und Formeln. Diophantus (3. Jahrhundert) und al-Khwarizmi (9. Jahrhundert) waren die beiden wichtigsten Vorläufer der Algebra. Der erste löste einige Gleichungen mit unbekannten natürlichen Zahlen, indem er neue Beziehungen ableitete, bis er die Lösung erhielt. Der zweite führte systematische Methoden zur Umformung von Gleichungen ein (z. B. das Verschieben eines Terms von einer Seite einer Gleichung auf die andere Seite). Der Begriff Algebra leitet sich von dem arabischen Wort ab, das er für die Bezeichnung einer dieser Methoden im Titel seiner Hauptabhandlung verwendete. ⓘ

Die Algebra wurde erst mit François Viète (1540-1603) zu einem eigenständigen Gebiet, der die Verwendung von Buchstaben (Variablen) zur Darstellung unbekannter oder unbestimmter Zahlen einführte. Dies ermöglicht es den Mathematikern, die Operationen, die mit den dargestellten Zahlen durchgeführt werden müssen, durch mathematische Formeln zu beschreiben. ⓘ
Bis zum 19. Jahrhundert bestand die Algebra hauptsächlich aus dem Studium linearer Gleichungen (heute lineare Algebra) und Polynomgleichungen mit einer einzigen Unbekannten, die als algebraische Gleichungen bezeichnet wurden (ein Begriff, der immer noch in Gebrauch ist, obwohl er zweideutig sein kann). Im 19. Jahrhundert begannen die Mathematiker, Variablen zu verwenden, um andere Dinge als Zahlen darzustellen (z. B. Matrizen, modulare ganze Zahlen und geometrische Transformationen), für die häufig Verallgemeinerungen der arithmetischen Operationen gelten. Das Konzept der algebraischen Struktur geht darauf ein und besteht aus einer Menge, deren Elemente nicht spezifiziert sind, aus Operationen, die auf die Elemente der Menge wirken, und aus Regeln, denen diese Operationen folgen müssen. Aufgrund dieses Wandels erweiterte sich der Anwendungsbereich der Algebra um die Untersuchung algebraischer Strukturen. Dieser Gegenstand der Algebra wurde moderne Algebra oder abstrakte Algebra genannt. (Der letztgenannte Begriff taucht vor allem im Bildungskontext auf, im Gegensatz zur elementaren Algebra, die sich mit der älteren Art der Manipulation von Formeln befasst). ⓘ

Einige Arten von algebraischen Strukturen haben nützliche und oft grundlegende Eigenschaften in vielen Bereichen der Mathematik. Ihr Studium wurde zu einem eigenständigen Teil der Algebra und umfasst:
- Gruppentheorie;
- Feldtheorie;
- Vektorräume, deren Untersuchung im Wesentlichen dieselbe ist wie die der linearen Algebra
- die Ringtheorie;
- die kommutative Algebra, d. h. die Lehre von den kommutativen Ringen, die auch die Lehre von den Polynomen umfasst und einen grundlegenden Teil der algebraischen Geometrie darstellt;
- homologische Algebra
- Lie-Algebra und Theorie der Lie-Gruppen;
- Boolesche Algebra, die weithin für die Untersuchung der logischen Struktur von Computern verwendet wird. ⓘ
Die Untersuchung der Arten algebraischer Strukturen als mathematische Objekte ist Gegenstand der universellen Algebra und der Kategorientheorie. Letztere gilt für jede mathematische Struktur (nicht nur für algebraische). Ursprünglich wurde sie zusammen mit der homologischen Algebra eingeführt, um die algebraische Untersuchung von nicht-algebraischen Objekten wie topologischen Räumen zu ermöglichen; dieses spezielle Anwendungsgebiet wird algebraische Topologie genannt. ⓘ
Kalkül und Analysis
Die Infinitesimalrechnung wurde von den Mathematikern Newton und Leibniz im 17. Jahrhundert unabhängig voneinander und gleichzeitig eingeführt. Jahrhundert unabhängig voneinander und gleichzeitig von den Mathematikern Newton und Leibniz eingeführt und befasst sich im Wesentlichen mit der Beziehung zwischen voneinander abhängigen Variablen. Die Infinitesimalrechnung wurde im 18. Jahrhundert von Euler mit der Einführung des Begriffs der Funktion und vielen anderen Ergebnissen erweitert. Heutzutage bezieht sich der Begriff "Kalkül" hauptsächlich auf den elementaren Teil dieser Theorie, während der Begriff "Analysis" üblicherweise für fortgeschrittene Teile verwendet wird. ⓘ
Die Analysis wird weiter unterteilt in die reelle Analysis, bei der die Variablen reelle Zahlen darstellen, und die komplexe Analysis, bei der die Variablen komplexe Zahlen darstellen. Die Analysis umfasst viele Teilbereiche, die sie teilweise mit anderen Bereichen der Mathematik teilt; dazu gehören
- Multivariable Kalkulation
- Funktionalanalysis, bei der die Variablen unterschiedliche Funktionen darstellen;
- Integration, Maßtheorie und Potentialtheorie, die alle eng mit der Wahrscheinlichkeitsrechnung verbunden sind;
- Gewöhnliche Differentialgleichungen;
- Partielle Differentialgleichungen;
- Numerische Analyse, die sich hauptsächlich mit der Berechnung von Lösungen gewöhnlicher und partieller Differentialgleichungen auf Computern befasst, die in vielen Anwendungen vorkommen. ⓘ
Diskrete Mathematik
Diskrete Mathematik ist im weitesten Sinne das Studium endlicher mathematischer Objekte. Da es sich hier um diskrete Objekte handelt, sind die Methoden der Infinitesimalrechnung und der mathematischen Analyse nicht direkt anwendbar. Algorithmen - insbesondere ihre Implementierung und ihre Rechenkomplexität - spielen in der diskreten Mathematik eine wichtige Rolle. ⓘ
Diskrete Mathematik umfasst:
- Kombinatorik, die Kunst, mathematische Objekte aufzuzählen, die bestimmte Bedingungen erfüllen. Ursprünglich handelte es sich bei diesen Objekten um Elemente oder Teilmengen einer bestimmten Menge; dies wurde auf verschiedene Objekte ausgedehnt, wodurch eine enge Verbindung zwischen der Kombinatorik und anderen Teilen der diskreten Mathematik hergestellt wird. So umfasst die diskrete Geometrie beispielsweise das Zählen von Konfigurationen geometrischer Formen
- Graphentheorie und Hypergraphen
- Codierungstheorie, einschließlich fehlerkorrigierender Codes und eines Teils der Kryptographie
- Matroidentheorie
- Diskrete Geometrie
- Diskrete Wahrscheinlichkeitsverteilungen
- Spieltheorie (obwohl auch kontinuierliche Spiele untersucht werden, sind die meisten gängigen Spiele, wie Schach und Poker, diskret)
- Diskrete Optimierung, einschließlich kombinatorische Optimierung, ganzzahlige Programmierung, Programmierung mit Einschränkungen ⓘ
Das Vier-Farben-Theorem und die optimale Kugelpackung waren zwei wichtige Probleme der diskreten Mathematik, die in der zweiten Hälfte des 20. Jahrhunderts gelöst wurden. Das P-versus-NP-Problem, das bis heute offen geblieben ist, ist auch für die diskrete Mathematik von Bedeutung, da seine Lösung einen Großteil der Mathematik beeinflussen würde. ⓘ
Mathematische Logik und Mengenlehre
Die beiden Fächer mathematische Logik und Mengenlehre gehören beide seit dem Ende des 19. Vor dieser Zeit wurden Mengen nicht als mathematische Objekte betrachtet, und die Logik, obwohl sie für mathematische Beweise verwendet wurde, gehörte zur Philosophie und wurde nicht speziell von Mathematikern studiert. ⓘ
Vor Cantors Studie über unendliche Mengen zögerten die Mathematiker, tatsächlich unendliche Sammlungen in Betracht zu ziehen, und betrachteten Unendlichkeit als das Ergebnis endloser Aufzählung. Cantors Arbeit stieß viele Mathematiker vor den Kopf, da er nicht nur tatsächlich unendliche Mengen betrachtete, sondern auch zeigte, dass dies unterschiedliche Größen der Unendlichkeit impliziert (siehe Cantors Diagonalargument) und dass es mathematische Objekte gibt, die nicht berechnet oder sogar explizit beschrieben werden können (z. B. Hamel-Basen der reellen Zahlen über den rationalen Zahlen). Dies führte zu der Kontroverse über Cantors Mengenlehre. ⓘ
Im gleichen Zeitraum kamen verschiedene Bereiche der Mathematik zu dem Schluss, dass die früheren intuitiven Definitionen der grundlegenden mathematischen Objekte nicht ausreichten, um mathematische Strenge zu gewährleisten. Beispiele für solche intuitiven Definitionen sind "eine Menge ist eine Sammlung von Objekten", "die natürliche Zahl ist das, was zum Zählen verwendet wird", "ein Punkt ist eine Form mit einer Nulllänge in jeder Richtung", "eine Kurve ist eine Spur, die von einem sich bewegenden Punkt hinterlassen wird" usw. ⓘ
Dies wurde zur Gründungskrise der Mathematik. Sie wurde schließlich in der Mainstream-Mathematik durch die Systematisierung der axiomatischen Methode innerhalb einer formalisierten Mengenlehre gelöst. Grob gesagt, wird jedes mathematische Objekt durch die Menge aller ähnlichen Objekte und die Eigenschaften, die diese Objekte haben müssen, definiert. In der Peano-Arithmetik sind die natürlichen Zahlen beispielsweise definiert durch "Null ist eine Zahl", "jede Zahl hat einen eindeutigen Nachfolger", "jede Zahl außer Null hat einen eindeutigen Vorgänger" und einige Regeln für die Argumentation. Die "Natur" der auf diese Weise definierten Objekte ist ein philosophisches Problem, das die Mathematiker den Philosophen überlassen, auch wenn viele Mathematiker eine Meinung zu dieser Natur haben und ihre Meinung - manchmal auch "Intuition" genannt - als Leitfaden für ihre Studien und Beweise verwenden. ⓘ
Dieser Ansatz ermöglicht es, "Logiken" (d. h. Mengen zulässiger Ableitungsregeln), Theoreme, Beweise usw. als mathematische Objekte zu betrachten und Theoreme über sie zu beweisen. Die Unvollständigkeitssätze von Gödel beispielsweise besagen, grob gesagt, dass es in jeder Theorie, die die natürlichen Zahlen enthält, Theoreme gibt, die wahr (d. h. in einer größeren Theorie beweisbar), aber innerhalb der Theorie nicht beweisbar sind. ⓘ
Dieser Ansatz der Grundlagen der Mathematik wurde in der ersten Hälfte des 20. Jahrhunderts von Mathematikern unter der Führung von Brouwer in Frage gestellt, der die intuitionistische Logik propagierte, die das Gesetz der ausgeschlossenen Mitte ausdrücklich nicht kennt. ⓘ
Diese Probleme und Debatten führten zu einer umfassenden Erweiterung der mathematischen Logik mit Teilbereichen wie der Modelltheorie (Modellierung einiger logischer Theorien innerhalb anderer Theorien), der Beweistheorie, der Typentheorie, der Theorie der Berechenbarkeit und der Theorie der rechnerischen Komplexität. Obwohl diese Aspekte der mathematischen Logik vor dem Aufkommen von Computern eingeführt wurden, trug ihre Verwendung beim Entwurf von Compilern, bei der Programmzertifizierung, bei Beweisassistenten und anderen Aspekten der Informatik ihrerseits zur Erweiterung dieser logischen Theorien bei. ⓘ
Angewandte Mathematik
Angewandte Mathematik ist die Lehre von den mathematischen Methoden, die in Wissenschaft, Technik, Wirtschaft und Industrie eingesetzt werden. Die "angewandte Mathematik" ist also eine mathematische Wissenschaft mit Spezialwissen. Der Begriff "Angewandte Mathematik" beschreibt auch das Fachgebiet, in dem Mathematiker an praktischen Problemen arbeiten; als ein auf praktische Probleme ausgerichtetes Fachgebiet konzentriert sich die Angewandte Mathematik auf die "Formulierung, Untersuchung und Verwendung mathematischer Modelle". ⓘ
In der Vergangenheit haben praktische Anwendungen die Entwicklung mathematischer Theorien motiviert, die dann zum Gegenstand des Studiums in der reinen Mathematik wurden, wo die Mathematik in erster Linie um ihrer selbst willen entwickelt wird. Daher ist die angewandte Mathematik eng mit der Forschung in der reinen Mathematik verbunden. ⓘ
Statistik und andere Entscheidungswissenschaften
Die angewandte Mathematik weist erhebliche Überschneidungen mit der Statistik auf, deren Theorie mathematisch formuliert ist, insbesondere die Wahrscheinlichkeitstheorie. Statistiker erstellen (im Rahmen eines Forschungsprojekts) mit Hilfe von Zufallsstichproben und randomisierten Experimenten "sinnvolle Daten"; der Entwurf einer statistischen Stichprobe oder eines Experiments legt die Analyse der Daten fest (bevor die Daten verfügbar sind). Bei der Überprüfung von Daten aus Experimenten und Stichproben oder bei der Analyse von Daten aus Beobachtungsstudien machen Statistiker "Sinn aus den Daten", indem sie die Kunst der Modellierung und die Theorie der Schlussfolgerungen anwenden - mit Modellauswahl und Schätzung; die geschätzten Modelle und die daraus folgenden Vorhersagen sollten an neuen Daten getestet werden. ⓘ
Die statistische Theorie befasst sich mit Entscheidungsproblemen wie der Minimierung des Risikos (erwarteter Verlust) einer statistischen Maßnahme, z. B. der Verwendung eines Verfahrens zur Parameterschätzung, Hypothesentests und der Auswahl des besten. In diesen traditionellen Bereichen der mathematischen Statistik wird ein statistisches Entscheidungsproblem durch die Minimierung einer Zielfunktion, z. B. des erwarteten Verlusts oder der Kosten, unter bestimmten Einschränkungen formuliert: Beim Entwurf einer Umfrage geht es zum Beispiel oft darum, die Kosten für die Schätzung eines Mittelwerts der Grundgesamtheit mit einem bestimmten Vertrauensniveau zu minimieren. Aufgrund ihrer Verwendung von Optimierungsverfahren überschneidet sich die mathematische Theorie der Statistik mit anderen Entscheidungswissenschaften wie Operations Research, Kontrolltheorie und mathematischer Ökonomie. ⓘ
Computermathematik
Die Computermathematik befasst sich mit mathematischen Problemen, die in der Regel zu groß für menschliche Rechenkapazitäten sind. Die numerische Analyse befasst sich mit Methoden für Analyseprobleme unter Verwendung der Funktionsanalyse und der Approximationstheorie; die numerische Analyse umfasst im Allgemeinen die Untersuchung der Approximation und Diskretisierung mit besonderem Schwerpunkt auf Rundungsfehlern. Die numerische Analyse und im weiteren Sinne das wissenschaftliche Rechnen befassen sich auch mit nichtanalytischen Themen der mathematischen Wissenschaft, insbesondere mit der algorithmischen Matrix- und Graphentheorie. Andere Bereiche der Computermathematik umfassen Computeralgebra und symbolische Berechnungen. ⓘ
Geschichte
Die Geschichte der Mathematik ist eine ständig wachsende Reihe von Abstraktionen. Evolutionär gesehen war die erste Abstraktion, die jemals entdeckt wurde und die viele Tiere teilen, wahrscheinlich die der Zahlen: die Erkenntnis, dass z. B. eine Sammlung von zwei Äpfeln und eine Sammlung von zwei Orangen etwas gemeinsam haben, nämlich dass es zwei von ihnen gibt. Wie aus den auf Knochen gefundenen Zahlenreihen hervorgeht, wussten die prähistorischen Völker möglicherweise nicht nur, wie man physische Objekte zählt, sondern auch, wie man abstrakte Größen wie Zeit - Tage, Jahreszeiten oder Jahre - zählt. ⓘ

Belege für eine komplexere Mathematik gibt es erst um 3000 v. Chr., als die Babylonier und Ägypter begannen, Arithmetik, Algebra und Geometrie für Steuer- und andere Finanzberechnungen, für das Bauwesen und die Astronomie zu verwenden. Die ältesten mathematischen Texte aus Mesopotamien und Ägypten stammen aus der Zeit von 2000 bis 1800 vor Christus. In vielen frühen Texten werden pythagoreische Dreiergruppen erwähnt, so dass der Satz des Pythagoras das älteste und am weitesten verbreitete mathematische Konzept nach den Grundrechenarten und der Geometrie zu sein scheint. In der babylonischen Mathematik tauchen die Grundrechenarten (Addition, Subtraktion, Multiplikation und Division) erstmals in den archäologischen Aufzeichnungen auf. Die Babylonier besaßen auch ein Stellenwertsystem und verwendeten ein sexagesimales Zahlensystem, das noch heute zur Messung von Winkeln und Zeit verwendet wird. ⓘ

Mit der griechischen Mathematik begannen die alten Griechen im 6. Jahrhundert v. Chr. mit den Pythagoräern ein systematisches Studium der Mathematik als eigenständiges Fach. Um 300 v. Chr. führte Euklid die axiomatische Methode ein, die noch heute in der Mathematik verwendet wird und aus Definition, Axiom, Lehrsatz und Beweis besteht. Sein Buch, die Elemente, gilt weithin als das erfolgreichste und einflussreichste Lehrbuch aller Zeiten. Als größter Mathematiker der Antike wird oft Archimedes (ca. 287-212 v. Chr.) aus Syrakus angesehen. Er entwickelte Formeln zur Berechnung der Oberfläche und des Volumens von Rotationskörpern und benutzte die Methode der Erschöpfung, um die Fläche unter dem Bogen einer Parabel mit der Summierung einer unendlichen Reihe zu berechnen, auf eine Weise, die der modernen Infinitesimalrechnung nicht allzu unähnlich ist. Weitere bemerkenswerte Errungenschaften der griechischen Mathematik sind Kegelschnitte (Apollonius von Perga, 3. Jahrhundert v. Chr.), Trigonometrie (Hipparchus von Nicäa, 2. Jahrhundert v. Chr.) und die Anfänge der Algebra (Diophantus, 3. Jahrhundert n. Chr.). ⓘ

Das hinduistisch-arabische Zahlensystem und die Regeln für seine Operationen, die heute in der ganzen Welt verwendet werden, entwickelten sich im Laufe des ersten Jahrtausends nach Christus in Indien und wurden über die islamische Mathematik in die westliche Welt übertragen. Zu den weiteren bemerkenswerten Entwicklungen der indischen Mathematik gehören die moderne Definition und Annäherung von Sinus und Kosinus sowie eine frühe Form der unendlichen Reihe. ⓘ


Während des Goldenen Zeitalters des Islam, insbesondere im 9. und 10. Jahrhundert, erlebte die Mathematik viele wichtige Innovationen, die auf der griechischen Mathematik aufbauten. Die bemerkenswerteste Errungenschaft der islamischen Mathematik war die Entwicklung der Algebra. Zu den weiteren Errungenschaften der islamischen Periode gehören Fortschritte in der sphärischen Trigonometrie und die Hinzufügung des Dezimalpunkts zum arabischen Zahlensystem. Viele bemerkenswerte Mathematiker aus dieser Zeit waren Perser, wie Al-Khwarismi, Omar Khayyam und Sharaf al-Dīn al-Ṭūsī. ⓘ
In der frühen Neuzeit begann sich die Mathematik in Westeuropa immer schneller zu entwickeln. Die Entwicklung des Kalküls durch Isaac Newton und Gottfried Leibniz im 17. Jahrhundert revolutionierte die Mathematik. Leonhard Euler war der bedeutendste Mathematiker des 18. Jahrhunderts, der zahlreiche Theoreme und Entdeckungen beisteuerte. Der vielleicht bedeutendste Mathematiker des 19. Jahrhunderts war der deutsche Mathematiker Carl Gauß, der zahlreiche Beiträge zu Bereichen wie Algebra, Analysis, Differentialgeometrie, Matrixtheorie, Zahlentheorie und Statistik leistete. Zu Beginn des 20. Jahrhunderts veränderte Kurt Gödel die Mathematik durch die Veröffentlichung seiner Unvollständigkeitssätze, die zum Teil zeigen, dass jedes konsistente axiomatische System - wenn es stark genug ist, um die Arithmetik zu beschreiben - wahre Sätze enthält, die nicht bewiesen werden können. ⓘ
Seitdem ist die Mathematik stark erweitert worden, und es hat eine fruchtbare Interaktion zwischen Mathematik und Wissenschaft stattgefunden, von der beide profitieren. Bis zum heutigen Tag werden mathematische Entdeckungen gemacht. In der Januar-Ausgabe 2006 des Bulletin of the American Mathematical Society schreibt Mikhail B. Sevryuk: "Die Zahl der seit 1940 (dem ersten Betriebsjahr von MR) in die Datenbank von Mathematical Reviews aufgenommenen Arbeiten und Bücher beläuft sich inzwischen auf mehr als 1,9 Millionen, und jedes Jahr kommen mehr als 75 000 Artikel hinzu. Die überwältigende Mehrheit der Werke in diesem Ozean enthält neue mathematische Theoreme und ihre Beweise." ⓘ
Etymologie
Das Wort Mathematik stammt aus dem Altgriechischen máthēma () und bedeutet "das, was man lernt", "das, was man kennenlernt", also auch "Studium" und "Wissenschaft". Das Wort für "Mathematik" hatte schon in der Antike die engere und technischere Bedeutung "mathematische Studie". Sein Adjektiv ist mathēmatikós (), was so viel bedeutet wie "mit dem Lernen verbunden" oder "fleißig", was sich ebenfalls zu "mathematisch" weiterentwickelte. Insbesondere bedeutete mathēmatikḗ tékhnē (; ) "die mathematische Kunst". ⓘ
In ähnlicher Weise war eine der beiden wichtigsten Denkschulen des Pythagoras als mathēmatikoi (μαθηματικοί) bekannt, was damals eher "Lernende" als "Mathematiker" im heutigen Sinne bedeutete. ⓘ
Im Lateinischen und im Englischen bis etwa 1700 bedeutete der Begriff mathematics eher "Astrologie" (oder manchmal "Astronomie") als "Mathematik"; die Bedeutung änderte sich allmählich zu der heutigen von etwa 1500 bis 1800. Dies hat zu mehreren Fehlübersetzungen geführt. So wird beispielsweise die Warnung des heiligen Augustinus, die Christen sollten sich vor den mathematici, d. h. den Astrologen, in Acht nehmen, manchmal falsch als Verurteilung der Mathematiker übersetzt. ⓘ
Die offensichtliche Pluralform im Englischen, wie auch die französische Pluralform (und die weniger gebräuchliche Singularableitung), geht auf den lateinischen Neutrumplural (Cicero) zurück, der auf dem griechischen Plural ta mathēmatiká () basiert, der von Aristoteles (384-322 v. Chr.) verwendet wurde und in etwa "alle mathematischen Dinge" bedeutet, obwohl es plausibel ist, dass das Englische nur das Adjektiv mathematic(al) entlehnt und das Substantiv Mathematik neu gebildet hat, nach dem Muster der Physik und Metaphysik, die aus dem Griechischen übernommen wurden. Im Englischen wird das Substantiv mathematics mit einem Verb im Singular verwendet. Es wird oft zu maths oder, in Nordamerika, math verkürzt. ⓘ
Vorgeschlagene Definitionen
Es besteht kein allgemeiner Konsens über die genaue Definition oder den erkenntnistheoretischen Status der Mathematik. Viele Berufsmathematiker sind nicht an einer Definition der Mathematik interessiert oder halten sie für undefinierbar. Es gibt nicht einmal einen Konsens darüber, ob die Mathematik eine Kunst oder eine Wissenschaft ist. Manche sagen einfach: "Mathematik ist das, was Mathematiker tun". ⓘ
Aristoteles definierte die Mathematik als "Wissenschaft von der Menge", und diese Definition galt bis ins 18. Aristoteles stellte jedoch auch fest, dass die Konzentration auf die Quantität allein die Mathematik nicht von Wissenschaften wie der Physik unterscheidet; seiner Ansicht nach unterscheiden sich die Mathematik durch Abstraktion und das Studium der Quantität als eine Eigenschaft, die "im Denken" von realen Vorgängen getrennt werden kann. ⓘ
Im 19. Jahrhundert, als das Studium der Mathematik an Strenge zunahm und sich mit abstrakten Themen wie der Gruppentheorie und der projektiven Geometrie zu befassen begann, die keinen eindeutigen Bezug zu Quantität und Messung haben, begannen Mathematiker und Philosophen, eine Vielzahl neuer Definitionen vorzuschlagen. Bis heute befassen sich Philosophen mit Fragen der Philosophie der Mathematik, z. B. mit dem Wesen des mathematischen Beweises. ⓘ
Logische Argumentation
Mathematiker bemühen sich, ihre Ergebnisse mit systematischer Argumentation zu entwickeln, um falsche "Theoreme" zu vermeiden. Diese falschen Beweise entstehen oft aus fehlbaren Intuitionen und sind in der Geschichte der Mathematik weit verbreitet gewesen. Um deduktives Denken zu ermöglichen, müssen einige Grundannahmen ausdrücklich als Axiome zugelassen werden. Traditionell wurden diese Axiome auf der Grundlage des gesunden Menschenverstands ausgewählt, aber moderne Axiome drücken in der Regel formale Garantien für primitive Begriffe wie einfache Objekte und Beziehungen aus. ⓘ
Die Gültigkeit eines mathematischen Beweises ist grundsätzlich eine Frage der Strenge, und ein falsches Verständnis von Strenge ist eine bemerkenswerte Ursache für einige verbreitete Missverständnisse über Mathematik. Die mathematische Sprache kann gewöhnlichen Wörtern wie oder und nur mehr Präzision verleihen als in der Alltagssprache. Anderen Wörtern wie "offen" und "Feld" werden für bestimmte mathematische Konzepte neue Bedeutungen verliehen. Manchmal prägen Mathematiker sogar ganz neue Wörter (z. B. Homöomorphismus). Dieses Fachvokabular ist sowohl präzise als auch kompakt und ermöglicht es, komplexe Ideen geistig zu verarbeiten. Mathematiker bezeichnen diese Präzision von Sprache und Logik als "Strenge". ⓘ
Die von der Mathematik erwartete Strenge hat sich im Laufe der Zeit verändert: Die alten Griechen erwarteten detaillierte Argumente, aber zur Zeit Isaac Newtons waren die angewandten Methoden weniger streng (nicht wegen einer anderen Auffassung von Mathematik, sondern wegen des Fehlens der mathematischen Methoden, die zum Erreichen der Strenge erforderlich sind). Die mit dem Newtonschen Ansatz verbundenen Probleme wurden erst in der zweiten Hälfte des 19. Jahrhunderts mit den formalen Definitionen der reellen Zahlen, der Grenzwerte und der Integrale gelöst. Später, zu Beginn des 20. Jahrhunderts, veröffentlichten Bertrand Russell und Alfred North Whitehead ihre Principia Mathematica, in denen sie zu zeigen versuchten, dass alle mathematischen Konzepte und Aussagen definiert und dann ausschließlich durch symbolische Logik bewiesen werden können. Dies war Teil eines umfassenderen philosophischen Programms, das als Logizismus bekannt ist und die Mathematik in erster Linie als eine Erweiterung der Logik betrachtet. ⓘ
Trotz der Prägnanz der Mathematik erfordern viele Beweise Hunderte von Seiten, um sie zu formulieren. Das Aufkommen computergestützter Beweise hat dazu geführt, dass die Länge der Beweise weiter zunimmt. Assistierte Beweise können fehlerhaft sein, wenn die Beweissoftware Mängel aufweist und wenn sie langwierig und schwer zu überprüfen sind. Andererseits ermöglichen Beweisassistenten die Überprüfung von Details, die in einem handschriftlichen Beweis nicht angegeben werden können, und bieten Sicherheit für die Korrektheit langer Beweise wie dem 255 Seiten umfassenden Feit-Thompson-Theorem. ⓘ
Symbolische Notation

Neben einer speziellen Sprache macht die moderne Mathematik auch viel Gebrauch von einer speziellen Notation. Diese Symbole tragen ebenfalls zur Strenge bei, indem sie den Ausdruck mathematischer Ideen vereinfachen und Routineoperationen ermöglichen, die einheitlichen Regeln folgen. Die moderne Notation macht die Mathematik für Versierte viel effizienter, für Anfänger kann sie jedoch entmutigend sein. ⓘ
Die meisten der heute gebräuchlichen mathematischen Notationen wurden nach dem 15. Jahrhundert erfunden, wobei viele Beiträge insbesondere von Leonhard Euler (1707-1783) stammen. Davor wurden mathematische Argumente in der Regel in Worten ausgedrückt, was die mathematische Entdeckung einschränkte. ⓘ
Ab dem 19. Jahrhundert entwickelte sich eine Denkschule, die als Formalismus bekannt ist. Für einen Formalisten geht es in der Mathematik in erster Linie um formale Systeme von Symbolen und Regeln für deren Kombination. Aus dieser Sicht sind selbst Axiome nur privilegierte Formeln in einem axiomatischen System, die ohne verfahrenstechnische Ableitung aus anderen Elementen des Systems gegeben sind. Eine Maximalinstanz des Formalismus war David Hilberts Forderung aus dem frühen 20. Jahrhundert, die oft als Hilberts Programm bezeichnet wird, die gesamte Mathematik auf diese Weise zu kodieren. ⓘ
Kurt Gödel bewies mit seinen Unvollständigkeitssätzen, dass dieses Ziel grundsätzlich unmöglich ist. Er zeigte, dass jedes formale System, das reichhaltig genug ist, um selbst einfache arithmetische Berechnungen zu beschreiben, seine eigene Vollständigkeit oder Konsistenz nicht garantieren kann. Nichtsdestotrotz haben formalistische Konzepte weiterhin großen Einfluss auf die Mathematik, bis zu dem Punkt, an dem standardmäßig erwartet wird, dass Aussagen in mengentheoretischen Formeln ausgedrückt werden können. Nur ganz außergewöhnliche Ergebnisse werden akzeptiert, wenn sie nicht in das eine oder andere axiomatische System passen. ⓘ
Sonderrolle unter den Wissenschaften

Eine Sonderrolle unter den Wissenschaften nimmt die Mathematik bezüglich der Gültigkeit ihrer Erkenntnisse und der Strenge ihrer Methoden ein. Während beispielsweise alle naturwissenschaftlichen Erkenntnisse durch neue Experimente falsifiziert werden können und daher prinzipiell vorläufig sind, werden mathematische Aussagen durch reine Gedankenoperationen auseinander hervorgebracht oder aufeinander zurückgeführt und brauchen nicht empirisch überprüfbar zu sein. Dafür muss aber für mathematische Erkenntnisse ein streng logischer Beweis gefunden werden, bevor sie als mathematischer Satz anerkannt werden. In diesem Sinn sind mathematische Sätze prinzipiell endgültige und allgemeingültige Wahrheiten, sodass die Mathematik als die exakte Wissenschaft betrachtet werden kann. Gerade diese Exaktheit ist für viele Menschen das Faszinierende an der Mathematik. So sagte David Hilbert auf dem Internationalen Mathematiker-Kongress 1900 in Paris:
„Wir erörtern noch kurz, welche berechtigten allgemeinen Forderungen an die Lösung eines mathematischen Problems zu stellen sind: ich meine vor allem die, daß es gelingt, die Richtigkeit der Antwort durch eine endliche Anzahl von Schlüssen darzutun, und zwar auf Grund einer endlichen Anzahl von Voraussetzungen, welche in der Problemstellung liegen und die jedesmal genau zu formulieren sind. Diese Forderung der logischen Deduktion mittels einer endlichen Anzahl von Schlüssen ist nichts anderes als die Forderung der Strenge in der Beweisführung. In der Tat, die Forderung der Strenge, die in der Mathematik bekanntlich von sprichwörtlicher Bedeutung geworden ist, entspricht einem allgemeinen philosophischen Bedürfnis unseres Verstandes, und andererseits kommt durch ihre Erfüllung allein erst der gedankliche Inhalt und die Fruchtbarkeit des Problems zur vollen Geltung. Ein neues Problem, zumal, wenn es aus der äußeren Erscheinungswelt stammt, ist wie ein junges Reis, welches nur gedeiht und Früchte trägt, wenn es auf den alten Stamm, den sicheren Besitzstand unseres mathematischen Wissens, sorgfältig und nach den strengen Kunstregeln des Gärtners aufgepfropft wird.“ ⓘ
Joseph Weizenbaum vom Massachusetts Institute of Technology bezeichnete die Mathematik als die Mutter aller Wissenschaften. ⓘ
„Ich behaupte aber, daß in jeder besonderen Naturlehre nur so viel eigentliche Wissenschaft angetroffen werden könne, als darin Mathematik anzutreffen ist.“
Die Mathematik ist daher auch eine kumulative Wissenschaft. Man kennt heute über 2000 mathematische Fachzeitschriften. Dies birgt jedoch auch eine Gefahr: durch neuere mathematische Gebiete geraten ältere Gebiete in den Hintergrund. Neben sehr allgemeinen Aussagen gibt es auch sehr spezielle Aussagen, für die keine echte Verallgemeinerung bekannt ist. Donald E. Knuth schreibt dazu im Vorwort seines Buches Concrete Mathematics: ⓘ
“The course title ‘Concrete Mathematics’ was originally intended as an antidote to ‘Abstract Mathematics’, since concrete classical results were rapidly being swept out of the modern mathematical curriculum by a new wave of abstract ideas popularly called the ‘New Math’. Abstract mathematics is a wonderful subject, and there’s nothing wrong with it: It’s beautiful, general and useful. But its adherents had become deluded that the rest of mathematics was inferior and no longer worthy of attention. The goal of generalization had become so fashionable that a generation of mathematicians had become unable to relish beauty in the particular, to enjoy the challenge of solving quantitative problems, or to appreciate the value of technique. Abstract mathematics was becoming inbred and losing touch with reality; mathematical education needed a concrete counterweight in order to restore a healthy balance.”
„Der Veranstaltungstitel ‚Konkrete Mathematik‘ war ursprünglich als Gegenpol zur ‚Abstrakten Mathematik‘ gedacht, denn konkrete, klassische Errungenschaften wurden von einer neuen Welle abstrakter Vorstellungen – gemeinhin ‚New Math‘ (‚neue Mathematik‘) genannt – in rasantem Tempo aus den Lehrplänen gespült. Abstrakte Mathematik ist eine wunderbare Sache, an der nichts auszusetzen ist: Sie ist schön, allgemeingültig und nützlich. Aber ihre Anhänger gelangten zu der irrigen Ansicht, dass die übrige Mathematik minderwertig und nicht mehr beachtenswert sei. Das Ziel der Verallgemeinerung kam dermaßen in Mode, dass eine ganze Generation von Mathematikern nicht mehr im Stande war, Schönheit im Speziellen zu erkennen, die Lösung von quantitativen Problemen als Herausforderung zu begreifen oder den Wert mathematischer Techniken zu schätzen. Die abstrakte Mathematik drehte sich nur noch um sich selbst und verlor den Kontakt zur Realität; in der mathematischen Ausbildung war ein konkretes Gegengewicht notwendig, um wieder ein stabiles Gleichgewicht herzustellen.“ ⓘ
Es kommt somit der älteren mathematischen Literatur eine besondere Bedeutung zu. ⓘ
Der Mathematiker Claus Peter Ortlieb kritisiert die – seiner Ansicht nach – zu wenig reflektierte Anwendung der modernen Mathematik:
„Man muss sich bewusst machen, dass die Erfassung der Welt durch Mathematik Grenzen hat. Die Annahme, sie funktioniere allein nach mathematischen Gesetzen, führt dazu, dass man nur noch nach diesen Gesetzen Ausschau hält. Natürlich werde ich sie in den Naturwissenschaften auch finden, doch ich muss mir im Klaren darüber sein, dass ich die Welt durch eine Brille hindurch betrachte, die von vornherein große Teile ausblendet. […] Die mathematische Methode ist längst von Wissenschaftlern fast aller Disziplinen übernommen worden und wird in allen möglichen Bereichen angewandt, wo sie eigentlich nichts zu suchen hat. […] Bedenklich sind Zahlen immer dann, wenn sie zu Normierungen führen, obwohl niemand mehr nachvollziehen kann, wie die Zahlen zustande gekommen sind.“ ⓘ
In der Praxis werden Mathematiker in der Regel mit Naturwissenschaftlern zusammengefasst, und die Mathematik hat vieles mit den Naturwissenschaften gemeinsam, vor allem das deduktive Schließen aus Annahmen. Mathematiker entwickeln mathematische Hypothesen, so genannte Vermutungen, durch Versuch und Irrtum und Intuition, ähnlich wie Wissenschaftler. Auch die experimentelle Mathematik und Berechnungsmethoden wie die Simulation gewinnen in der Mathematik immer mehr an Bedeutung. ⓘ
Alle Wissenschaften werfen heute Probleme auf, die von Mathematikern untersucht werden, und umgekehrt führen Ergebnisse aus der Mathematik oft zu neuen Fragen und Erkenntnissen in den Wissenschaften. Der Physiker Richard Feynman beispielsweise kombinierte mathematische Überlegungen und physikalische Erkenntnisse, um die Pfadintegralformulierung der Quantenmechanik zu entwickeln. Die Stringtheorie wiederum ist ein vorgeschlagener Rahmen für die Vereinheitlichung eines Großteils der modernen Physik, der neue Techniken und Ergebnisse in der Mathematik inspiriert hat. ⓘ

Der deutsche Mathematiker Carl Friedrich Gauß nannte die Mathematik "die Königin der Wissenschaften", und in jüngerer Zeit hat Marcus du Sautoy die Mathematik als "die Hauptantriebskraft für wissenschaftliche Entdeckungen" bezeichnet. Einige Autoren betonen jedoch, dass sich die Mathematik in einem wesentlichen Punkt von der modernen Vorstellung von Wissenschaft unterscheidet: Sie stützt sich nicht auf empirische Beweise. ⓘ
Das mathematische Wissen hat sich seit der wissenschaftlichen Revolution explosionsartig ausgebreitet, und wie in anderen Studienbereichen hat dies zu einer Spezialisierung geführt. In der neuesten Mathematics Subject Classification der American Mathematical Society (2010) werden Hunderte von Teilgebieten aufgeführt, wobei die vollständige Klassifizierung 46 Seiten umfasst. In der Regel können viele Konzepte in einem Teilgebiet auf unbestimmte Zeit von anderen Zweigen der Mathematik isoliert bleiben; Ergebnisse können in erster Linie als Gerüst dienen, um andere Theoreme und Techniken zu unterstützen, oder sie können keine klare Beziehung zu etwas außerhalb des Teilgebiets haben. ⓘ
Die Mathematik zeigt jedoch eine bemerkenswerte Tendenz, sich weiterzuentwickeln, und mit der Zeit entdecken Mathematiker oft überraschende Anwendungen oder Verbindungen zwischen Konzepten. Ein sehr einflussreiches Beispiel dafür war das Erlanger Programm von Felix Klein, das innovative und tiefgreifende Verbindungen zwischen Geometrie und Algebra herstellte. Dies wiederum öffnete beide Gebiete für eine größere Abstraktion und brachte völlig neue Teilgebiete hervor. ⓘ
Häufig wird zwischen der angewandten Mathematik und der reinen Mathematik unterschieden, die sich ganz auf abstrakte Fragen und Konzepte konzentriert. Wie bei anderen Teilgebieten der Mathematik ist die Grenze jedoch fließend. Ideen, die zunächst mit Blick auf eine bestimmte Anwendung entwickelt wurden, werden später oft verallgemeinert und in den allgemeinen Bestand mathematischer Konzepte aufgenommen. Einige Bereiche der angewandten Mathematik haben sich sogar mit praktischen Bereichen zu eigenständigen Disziplinen zusammengeschlossen, wie z. B. Statistik, Operations Research und Computerwissenschaften. ⓘ
Vielleicht noch überraschender ist es, wenn Ideen in die andere Richtung fließen und selbst die "reinste" Mathematik zu unerwarteten Vorhersagen oder Anwendungen führt. So nimmt beispielsweise die Zahlentheorie einen zentralen Platz in der modernen Kryptographie ein, und in der Physik haben Ableitungen aus den Maxwellschen Gleichungen den experimentellen Nachweis von Radiowellen und der Konstanz der Lichtgeschwindigkeit vorweggenommen. Der Physiker Eugene Wigner hat dieses Phänomen die "unvernünftige Wirksamkeit der Mathematik" genannt. ⓘ
Die unheimliche Verbindung zwischen abstrakter Mathematik und materieller Realität hat mindestens seit Pythagoras zu philosophischen Debatten geführt. Der antike Philosoph Platon argumentierte, dies sei möglich, weil die materielle Realität abstrakte Objekte widerspiegelt, die außerhalb der Zeit existieren. Daher wird die Ansicht, dass mathematische Objekte in gewisser Weise eigenständig und abstrakt existieren, oft als Platonismus bezeichnet. Obwohl sich die meisten Mathematiker in der Regel nicht mit den vom Platonismus aufgeworfenen Fragen befassen, bezeichnen sich einige philosophisch orientierte Mathematiker als Platoniker, auch in der heutigen Zeit. ⓘ

Über die Frage, zu welcher Kategorie der Wissenschaften die Mathematik gehört, wird seit langer Zeit kontrovers diskutiert. ⓘ
Viele mathematische Fragestellungen und Begriffe sind durch die Natur betreffende Fragen motiviert, beispielsweise aus der Physik oder den Ingenieurwissenschaften, und die Mathematik wird als Hilfswissenschaft in nahezu allen Naturwissenschaften herangezogen. Jedoch ist sie selbst keine Naturwissenschaft im eigentlichen Sinne, da ihre Aussagen nicht von Experimenten oder Beobachtungen abhängen. Dennoch wird in der neueren Philosophie der Mathematik davon ausgegangen, dass auch die Methodik der Mathematik immer mehr derjenigen der Naturwissenschaft entspricht. Im Anschluss an Imre Lakatos wird eine „Renaissance des Empirismus“ vermutet, wonach auch Mathematiker Hypothesen aufstellen und für diese Bestätigungen suchen. ⓘ
Die Mathematik hat methodische und inhaltliche Gemeinsamkeiten mit der Philosophie; beispielsweise ist die Logik ein Überschneidungsbereich der beiden Wissenschaften. Damit könnte man die Mathematik zu den Geisteswissenschaften rechnen, aber auch die Einordnung der Philosophie ist umstritten. ⓘ
Auch aus diesen Gründen kategorisieren einige die Mathematik – neben anderen Disziplinen wie der Informatik – als Strukturwissenschaft bzw. Formalwissenschaft. ⓘ
An deutschen Universitäten gehört die Mathematik meistens zur selben Fakultät wie die Naturwissenschaften, und so wird Mathematikern nach der Promotion in der Regel der akademische Grad eines Dr. rer. nat. (Doktor der Naturwissenschaft) verliehen. Im Gegensatz dazu erreicht im englischen Sprachraum der Hochschulabsolvent die Titel „Bachelor of Arts“ bzw. „Master of Arts“, die eigentlich an Geisteswissenschaftler vergeben werden. ⓘ
Kreativität und Intuition
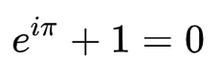
Die Notwendigkeit von Korrektheit und Strenge bedeutet nicht, dass in der Mathematik kein Platz für Kreativität ist. Im Gegenteil, die meisten mathematischen Arbeiten, die über das Auswendigrechnen hinausgehen, erfordern kluge Problemlösungen und das intuitive Erforschen neuer Perspektiven. ⓘ
Mathematisch Interessierte sehen in der Mathematik oft nicht nur Kreativität, sondern auch einen ästhetischen Wert, der gemeinhin als Eleganz bezeichnet wird. Eigenschaften wie Einfachheit, Symmetrie, Vollständigkeit und Allgemeinheit werden bei Beweisen und Techniken besonders geschätzt. G. H. Hardy vertrat in A Mathematician's Apology die Ansicht, dass diese ästhetischen Erwägungen an sich ausreichen, um das Studium der reinen Mathematik zu rechtfertigen. Er nannte auch andere Kriterien wie Bedeutung, Unerwartetheit und Unvermeidbarkeit, die zur mathematischen Ästhetik beitragen. ⓘ
Paul Erdős drückte dieses Gefühl eher ironisch aus, indem er von "dem Buch" sprach, einer angeblich göttlichen Sammlung der schönsten Beweise. Das 1998 erschienene Buch Proofs from THE BOOK, das von Erdős inspiriert wurde, ist eine Sammlung von besonders prägnanten und aufschlussreichen mathematischen Argumenten. Einige Beispiele für besonders elegante Ergebnisse sind Euklids Beweis, dass es unendlich viele Primzahlen gibt, und die schnelle Fourier-Transformation für die harmonische Analyse. ⓘ
Manche sind der Meinung, dass die Mathematik als Wissenschaft zu betrachten, bedeutet, ihre Kunstfertigkeit und Geschichte in den sieben traditionellen freien Künsten herunterzuspielen. Diese Meinungsverschiedenheit zeigt sich unter anderem in der philosophischen Debatte darüber, ob mathematische Ergebnisse geschaffen (wie in der Kunst) oder entdeckt (wie in der Wissenschaft) werden. Die Beliebtheit der Freizeitmathematik ist ein weiteres Zeichen für das Vergnügen, das viele beim Lösen mathematischer Fragen empfinden. ⓘ
Im 20. Jahrhundert initiierte der Mathematiker L. E. J. Brouwer sogar eine philosophische Perspektive, die als Intuitionismus bekannt ist und die Mathematik in erster Linie mit bestimmten kreativen Prozessen im Geist in Verbindung bringt. Der Intuitionismus ist wiederum eine Spielart des Konstruktivismus, der einen mathematischen Gegenstand nur dann als gültig ansieht, wenn er direkt konstruiert und nicht nur indirekt durch die Logik garantiert werden kann. Dies führt dazu, dass engagierte Konstruktivisten bestimmte Ergebnisse ablehnen, insbesondere Argumente wie Existenzbeweise, die auf dem Gesetz der ausgeschlossenen Mitte beruhen. ⓘ
Letztendlich haben weder der Konstruktivismus noch der Intuitionismus die klassische Mathematik verdrängt oder sich im Mainstream durchgesetzt. Diese Programme haben jedoch bestimmte Entwicklungen motiviert, wie die intuitionistische Logik und andere grundlegende Erkenntnisse, die für sich genommen geschätzt werden. ⓘ
In der Gesellschaft
Die Mathematik hat eine bemerkenswerte Fähigkeit, kulturelle Grenzen und Zeiträume zu überwinden. Als menschliche Aktivität hat die Ausübung der Mathematik eine soziale Seite, die Bildung, Karriere, Anerkennung, Popularisierung usw. umfasst. ⓘ
Auszeichnungen und Preisprobleme
Die prestigeträchtigste Auszeichnung in der Mathematik ist die Fields-Medaille, die 1936 ins Leben gerufen wurde und alle vier Jahre (außer während des Zweiten Weltkriegs) an bis zu vier Personen verliehen wird. Sie gilt als das mathematische Pendant zum Nobelpreis. ⓘ
Weitere angesehene Mathematikpreise sind:
- der Abel-Preis, der 2002 ins Leben gerufen und 2003 erstmals verliehen wurde
- die Chern-Medaille für das Lebenswerk, die 2009 eingeführt und 2010 erstmals verliehen wurde
- Der Wolf-Preis für Mathematik, ebenfalls für das Lebenswerk, der 1978 eingeführt wurde ⓘ
Der deutsche Mathematiker David Hilbert stellte im Jahr 1900 eine berühmte Liste von 23 offenen Problemen zusammen, die so genannten "Hilbertschen Probleme". Diese Liste hat unter Mathematikern große Berühmtheit erlangt, und bis zum Jahr 2022 wurden mindestens dreizehn der Probleme (je nachdem, wie einige interpretiert werden) gelöst. ⓘ
Im Jahr 2000 wurde eine neue Liste mit sieben wichtigen Problemen veröffentlicht, die den Titel "Millennium Prize Problems" trägt. Nur eines davon, die Riemann-Hypothese, ist eine Wiederholung eines der Hilbert-Probleme. Für die Lösung eines dieser Probleme ist eine Belohnung von 1 Million Dollar ausgesetzt. Bis heute ist nur eines dieser Probleme, die Poincaré-Vermutung, gelöst worden. ⓘ
Mathematik in der Gesellschaft

Das vom Bundesministerium für Bildung und Forschung (BMBF) seit dem Jahr 2000 jährlich ausgerichtete Wissenschaftsjahr war 2008 das Jahr der Mathematik. ⓘ
Mathematik in der Schule
Mathematik spielt in der Schule eine wichtige Rolle als Pflichtfach. Mathematikdidaktik ist die Wissenschaft, die sich mit dem Lehren und Lernen von Mathematik beschäftigt. In den Klassen 5–10 geht es vor allem um das Erlernen von Rechenfertigkeiten. In deutschen Gymnasien werden in der Oberstufe, also ab Klasse 11, dann Differential- und Integralrechnung sowie Analytische Geometrie / Lineare Algebra eingeführt und dazu Stochastik weitergeführt. ⓘ
Große Verbreitung an Schulen hat der Wettbewerb Känguru der Mathematik gefunden: Von 200 Teilnehmern im Jahr 1995 stieg die Anzahl auf 968.000 im Jahr 2019. Es ist ein Multiple-Choice-Wettbewerb mit Aufgaben zum Knobeln, zum Rechnen und zum Schätzen, der vor allem Freude an der Beschäftigung mit Mathematik wecken soll. Die Aufgaben erfordern keine schriftliche Begründung. ⓘ
Mathematik als Studienfach und Beruf
Menschen, die sich beruflich mit der Entwicklung und der Anwendung der Mathematik beschäftigen, nennt man Mathematiker. ⓘ
Neben dem Mathematikstudium, in dem man seine Schwerpunkte auf reine und/oder angewandte Mathematik setzen kann, sind in neuerer Zeit vermehrt interdisziplinäre Studiengänge wie Technomathematik, Wirtschaftsmathematik, Computermathematik oder Biomathematik eingerichtet worden. Ferner ist das Lehramt an weiterführenden Schulen und Hochschulen ein wichtiger mathematischer Berufszweig. An deutschen Universitäten wurde im Rahmen des Bologna-Prozesses das Diplom auf Bachelor/Master-Studiengänge umgestellt. Eine gewisse Anzahl an Semesterwochenstunden müssen auch angehende Informatiker, Chemiker, Biologen, Physiker, Geologen und Ingenieure belegen. ⓘ
Die häufigsten Arbeitgeber für Mathematiker sind Versicherungen, Banken und Unternehmensberatungen, insbesondere im Bereich mathematischer Finanzmodelle und Consulting, aber auch im IT-Bereich. Darüber hinaus werden Mathematiker in fast allen Branchen eingesetzt. ⓘ
Mathematische Museen und Sammlungen
Mathematik ist eine der ältesten Wissenschaften und auch eine experimentelle Wissenschaft. Diese beiden Aspekte lassen sich durch Museen und historische Sammlungen sehr gut verdeutlichen. ⓘ
Die älteste Einrichtung dieser Art in Deutschland ist der 1728 gegründete Mathematisch-Physikalische Salon in Dresden. Das Arithmeum in Bonn am dortigen Institut für diskrete Mathematik geht in die 1970er Jahre zurück und beruht auf der Sammlung von Rechengeräten des Mathematikers Bernhard Korte. Das Heinz Nixdorf MuseumsForum (Abkürzung „HNF“) in Paderborn ist das größte deutsche Museum zur Entwicklung der Rechentechnik (insbesondere des Computers), und das Mathematikum in Gießen wurde 2002 von Albrecht Beutelspacher gegründet und wird von ihm laufend weiterentwickelt. Im Museumsquartier in Wien befindet sich das von Rudolf Taschner geleitete Math.space, welches die Mathematik im Kontext zu Kultur und Zivilisation zeigt. ⓘ
Darüber hinaus sind zahlreiche Spezialsammlungen an Universitäten untergebracht, aber auch in umfassenderen Sammlungen wie zum Beispiel im Deutschen Museum in München oder im Museum für Technikgeschichte in Berlin (Rechner von Konrad Zuse entwickelt und gebaut). ⓘ




