Polynom
In der Mathematik ist ein Polynom ein Ausdruck, der aus unbestimmten Zahlen (auch Variablen genannt) und Koeffizienten besteht und nur die Operationen Addition, Subtraktion, Multiplikation und nichtnegative ganzzahlige Potenzierung von Variablen umfasst. Ein Beispiel für ein Polynom mit einer einzigen unbestimmten Zahl x ist x2 - 4x + 7. Ein Beispiel mit drei Variablen ist x3 + 2xyz2 - yz + 1. ⓘ
Polynome kommen in vielen Bereichen der Mathematik und Wissenschaft vor. Sie werden beispielsweise zur Bildung von Polynomgleichungen verwendet, die eine Vielzahl von Problemen kodieren, von elementaren Wortproblemen bis hin zu komplizierten wissenschaftlichen Problemen; sie werden zur Definition von Polynomfunktionen verwendet, die in Bereichen wie Chemie und Physik bis hin zu Wirtschafts- und Sozialwissenschaften vorkommen; sie werden in der Infinitesimalrechnung und der numerischen Analyse verwendet, um andere Funktionen zu approximieren. In der fortgeschrittenen Mathematik werden Polynome verwendet, um Polynomringe und algebraische Varietäten zu konstruieren, die zentrale Konzepte in der Algebra und der algebraischen Geometrie darstellen. ⓘ
Ein Polynom summiert die Vielfachen von Potenzen einer Variablen bzw. Unbestimmten:
oder kurz mit dem Summenzeichen:
Dabei ist das Summenzeichen, die Zahlen sind die Koeffizienten (das können beispielsweise reelle Zahlen oder allgemeiner Elemente aus einem beliebigen Ring sein) und ist die Unbestimmte. ⓘ
Exponenten der Potenzen sind natürliche Zahlen. Die Summe ist außerdem stets endlich. Unendliche Summen von Vielfachen von Potenzen mit natürlichzahligen Exponenten einer Unbestimmten heißen formale Potenzreihen. ⓘ
Für Mathematik und Physik gibt es einige wichtige spezielle Polynome. ⓘ
In der elementaren Algebra identifiziert man diesen Ausdruck mit einer Funktion in (einer Polynomfunktion). In der abstrakten Algebra unterscheidet man streng zwischen einer Polynomfunktion und einem Polynom als Element eines Polynomrings. In der Schulmathematik wird eine Polynomfunktion oft auch als ganzrationale Funktion bezeichnet. ⓘ
Dieser Artikel erklärt außerdem die mathematischen Begriffe: Leitkoeffizient, Normieren eines Polynoms und Absolutglied. ⓘ
Etymologie
Das Wort Polynom bedeutet so viel wie „mehrnamig“. Es entstammt dem griech. πολύ polý „viel“ und όνομα onoma „Name“. Diese Bezeichnung geht zurück bis auf Euklids Elemente. In Buch X nennt er eine zweigliedrige Summe ἐκ δύο ὀνομάτων (ek dýo onomátōn): „aus zwei Namen (bestehend)“. Die Bezeichnung Polynom geht auf Viëta zurück: In seiner Isagoge (1591) verwendet er den Ausdruck polynomia magnitudo für eine mehrgliedrige Größe. ⓘ
Das Wort Polynom setzt sich aus zwei verschiedenen Wurzeln zusammen: dem griechischen poly, was so viel wie "viele" bedeutet, und dem lateinischen nomen, was "Name" bedeutet. Es wurde aus dem Begriff Binom abgeleitet, indem die lateinische Wurzel bi- durch das griechische poly- ersetzt wurde. Das heißt, es bedeutet eine Summe von vielen Termen (viele Monomiale). Das Wort Polynom wurde erstmals im 17. Jahrhundert verwendet. ⓘ
Notation und Terminologie

Das x, das in einem Polynom vorkommt, wird allgemein als Variable oder Unbestimmte bezeichnet. Betrachtet man das Polynom als einen Ausdruck, so ist x ein festes Symbol, das keinen Wert hat (sein Wert ist "unbestimmt"). Betrachtet man jedoch die durch das Polynom definierte Funktion, so stellt x das Argument der Funktion dar und wird daher als "Variable" bezeichnet. Viele Autoren verwenden diese beiden Begriffe synonym. ⓘ
Ein Polynom P in der unbestimmten Zahl x wird im Allgemeinen entweder als P oder als P(x) bezeichnet. Formal heißt das Polynom P und nicht P(x), aber die Verwendung der funktionalen Schreibweise P(x) stammt aus einer Zeit, als die Unterscheidung zwischen einem Polynom und der zugehörigen Funktion unklar war. Außerdem ist die funktionale Notation oft nützlich, um in einem einzigen Satz ein Polynom und seine Unbestimmtheit zu spezifizieren. Zum Beispiel ist "P(x) sei ein Polynom" eine Kurzform für "P sei ein Polynom in der Unbestimmten x". Andererseits sind viele Formeln, bei denen es nicht notwendig ist, den Namen der Unbestimmten hervorzuheben, viel einfacher und leichter zu lesen, wenn der Name der Unbestimmten nicht bei jedem Vorkommen des Polynoms erscheint. ⓘ
Die Mehrdeutigkeit von zwei Schreibweisen für ein und dasselbe mathematische Objekt kann formal gelöst werden, indem man die allgemeine Bedeutung der funktionalen Schreibweise für Polynome betrachtet. Wenn a eine Zahl, eine Variable, ein anderes Polynom oder ganz allgemein einen beliebigen Ausdruck bezeichnet, dann bezeichnet P(a) gemäß der Konvention das Ergebnis der Ersetzung von x durch a in P. Das Polynom P definiert also die Funktion
die die zu P gehörende Polynomfunktion ist. Häufig wird bei der Verwendung dieser Schreibweise angenommen, dass a eine Zahl ist. Man kann sie jedoch für jeden Bereich verwenden, in dem Addition und Multiplikation definiert sind (d. h. für jeden Ring). Insbesondere wenn a ein Polynom ist, ist P(a) auch ein Polynom. ⓘ
Genauer gesagt, wenn a die unbestimmte Zahl x ist, dann ist das Bild von x durch diese Funktion das Polynom P selbst (die Ersetzung von x durch x ändert nichts). Mit anderen Worten,
was formal die Existenz von zwei Bezeichnungen für dasselbe Polynom rechtfertigt. ⓘ
Definition
Ein Polynomausdruck ist ein Ausdruck, der aus Konstanten und Symbolen, die Variablen oder Unbestimmte genannt werden, durch Addition, Multiplikation und Potenzierung zu einer nichtnegativen ganzen Zahl gebildet werden kann. Bei den Konstanten handelt es sich in der Regel um Zahlen, aber auch um beliebige Ausdrücke, die keine Unbestimmten enthalten und mathematische Objekte darstellen, die addiert und multipliziert werden können. Zwei Polynomausdrücke gelten als dasselbe Polynom, wenn sie durch Anwendung der üblichen Eigenschaften der Kommutativität, Assoziativität und Distributivität der Addition und Multiplikation ineinander umgewandelt werden können. Zum Beispiel und zwei Polynomausdrücke, die das gleiche Polynom darstellen; man schreibt also ⓘ
Ein Polynom mit einer einzigen unbestimmten Zahl x kann immer in der Form geschrieben (oder umgeschrieben) werden
wobei Konstanten sind, die als die Koeffizienten des Polynoms bezeichnet werden, und die Unbestimmtheit ist. Das Wort "unbestimmt" bedeutet, dass keinen bestimmten Wert darstellt, obwohl er durch jeden beliebigen Wert ersetzt werden kann. Die Abbildung, die das Ergebnis dieser Substitution mit dem substituierten Wert verknüpft, ist eine Funktion, die Polynomfunktion genannt wird. ⓘ
Dies kann durch die Verwendung der Summenschreibweise prägnanter ausgedrückt werden:
Das heißt, ein Polynom kann entweder Null sein oder als Summe einer endlichen Anzahl von Termen geschrieben werden, die nicht Null sind. Jeder Term besteht aus dem Produkt einer Zahl - dem sogenannten Koeffizienten des Terms - und einer endlichen Anzahl von unbestimmten Potenzen, die auf nichtnegative ganze Zahlen erhöht werden. ⓘ
Klassifizierung
Der Exponent einer Unbestimmten in einem Term wird als Grad dieser Unbestimmten in diesem Term bezeichnet; der Grad des Terms ist die Summe der Grade der Unbestimmten in diesem Term, und der Grad eines Polynoms ist der größte Grad jedes Terms mit einem Koeffizienten ungleich Null. Da x = x1 ist, ist der Grad einer unbestimmten Zahl ohne geschriebenen Exponenten eins. ⓘ
Ein Term ohne Unbestimmte und ein Polynom ohne Unbestimmte nennt man einen konstanten Term bzw. ein konstantes Polynom. Der Grad eines konstanten Terms und eines konstanten Polynoms ungleich Null ist 0. Der Grad des Null-Polynoms 0 (das überhaupt keine Terme hat) wird im Allgemeinen als nicht definiert behandelt (siehe jedoch unten). ⓘ
Zum Beispiel:
ist ein Term. Der Koeffizient ist -5, die Indeterminaten sind x und y, der Grad von x ist zwei, der Grad von y ist eins. Der Grad des gesamten Terms ist die Summe der Grade der einzelnen Unbestimmten, in diesem Beispiel ist der Grad also 2 + 1 = 3. ⓘ
Die Bildung einer Summe aus mehreren Termen ergibt ein Polynom. Zum Beispiel ist das folgende ein Polynom:
Es besteht aus drei Termen: Der erste hat den Grad zwei, der zweite den Grad eins und der dritte den Grad null. ⓘ
Polynome kleinen Grades haben spezielle Namen erhalten. Ein Polynom vom Grad Null ist ein konstantes Polynom oder einfach eine Konstante. Polynome ersten, zweiten oder dritten Grades sind lineare Polynome, quadratische Polynome bzw. kubische Polynome. Für Polynome höheren Grades werden die spezifischen Bezeichnungen im Allgemeinen nicht verwendet, obwohl das quartische Polynom (für den vierten Grad) und das quintische Polynom (für den fünften Grad) manchmal verwendet werden. Die Namen für die Grade können auf das Polynom oder auf seine Terme angewendet werden. Zum Beispiel ist der Term 2x in x2 + 2x + 1 ein linearer Term in einem quadratischen Polynom. ⓘ
Das Polynom 0, das als Polynom ohne Terme betrachtet werden kann, wird als Nullpolynom bezeichnet. Im Gegensatz zu anderen konstanten Polynomen ist sein Grad nicht Null. Vielmehr wird der Grad des Nullpolynoms entweder ausdrücklich unbestimmt gelassen oder als negativ definiert (entweder -1 oder -∞). Das Nullpolynom ist auch insofern einzigartig, als es das einzige Polynom in einer Unbestimmten ist, das eine unendliche Anzahl von Wurzeln hat. Der Graph des Nullpolynoms, f(x) = 0, ist die x-Achse. ⓘ
Bei Polynomen in mehr als einer Unbestimmten heißt ein Polynom homogen vom Grad n, wenn alle seine Nicht-Null-Terme den Grad n haben. Das Nullpolynom ist homogen, und als homogenes Polynom ist sein Grad unbestimmt. Zum Beispiel ist x3y2 + 7x2y3 - 3x5 homogen vom Grad 5. Für weitere Einzelheiten siehe Homogenes Polynom. ⓘ
Das Kommutativgesetz der Addition kann verwendet werden, um die Terme in eine beliebige Reihenfolge zu bringen. Bei Polynomen mit einer unbestimmten Zahl werden die Terme in der Regel nach dem Grad geordnet, entweder in "absteigenden Potenzen von x", wobei der Term mit dem höchsten Grad an erster Stelle steht, oder in "aufsteigenden Potenzen von x". Das Polynom 3x2 - 5x + 4 wird in absteigenden Potenzen von x geschrieben. Der erste Term hat den Koeffizienten 3, die unbestimmte Zahl x und den Exponenten 2. Im zweiten Term ist der Koeffizient -5. Der dritte Term ist eine Konstante. Da der Grad eines Polynoms, das nicht Null ist, der größte Grad eines beliebigen Terms ist, hat dieses Polynom den Grad zwei. ⓘ
Zwei Terme mit denselben Indeterminaten, die auf dieselben Potenzen erhöht werden, nennt man "ähnliche Terme" oder "gleichartige Terme", und sie können mit Hilfe des Distributivgesetzes zu einem einzigen Term zusammengefasst werden, dessen Koeffizient die Summe der Koeffizienten der kombinierten Terme ist. Es kann vorkommen, dass der Koeffizient 0 ist. Polynome können nach der Anzahl der Terme mit Koeffizienten ungleich Null klassifiziert werden, so dass ein Polynom mit einem Term als Monomial, ein Polynom mit zwei Termen als Binomial und ein Polynom mit drei Termen als Trinomial bezeichnet wird. Für ein Polynom mit vier Termen wird gelegentlich der Begriff "Quadrinom" verwendet. ⓘ
Ein reelles Polynom ist ein Polynom mit reellen Koeffizienten. Wenn es zur Definition einer Funktion verwendet wird, ist der Bereich nicht so eingeschränkt. Eine reelle Polynomfunktion ist jedoch eine Funktion von den reellen Werten zu den reellen Werten, die durch ein reelles Polynom definiert ist. In ähnlicher Weise ist ein ganzzahliges Polynom ein Polynom mit ganzzahligen Koeffizienten und ein komplexes Polynom ist ein Polynom mit komplexen Koeffizienten. ⓘ
Ein Polynom mit einer Unbestimmtheit wird als univariates Polynom bezeichnet, ein Polynom mit mehr als einer Unbestimmtheit als multivariates Polynom. Ein Polynom mit zwei Unbestimmtheiten wird als bivariates Polynom bezeichnet. Diese Begriffe beziehen sich eher auf die Art der Polynome, mit denen man im Allgemeinen arbeitet, als auf einzelne Polynome; wenn man beispielsweise mit univariaten Polynomen arbeitet, schließt man konstante Polynome (die sich aus der Subtraktion von nicht konstanten Polynomen ergeben können) nicht aus, obwohl konstante Polynome streng genommen überhaupt keine Unbestimmten enthalten. Es ist möglich, multivariate Polynome weiter in bivariate, trivariate usw. Polynome zu klassifizieren, je nachdem, wie viele Unbestimmtheiten maximal zulässig sind. Damit die Menge der betrachteten Objekte bei der Subtraktion geschlossen bleibt, werden bei der Untersuchung von trivariaten Polynomen in der Regel bivariate Polynome zugelassen usw. Es ist auch üblich, einfach "Polynome in x, y und z" zu sagen und die zulässigen Unbestimmten aufzulisten. ⓘ
Die Auswertung eines Polynoms besteht darin, dass für jede unbestimmte Zahl ein numerischer Wert eingesetzt wird und die angegebenen Multiplikationen und Additionen durchgeführt werden. Bei Polynomen mit einer Unbestimmtheit ist die Auswertung nach der Horner-Methode in der Regel effizienter (geringere Anzahl von Rechenoperationen):
Durch ⓘ
Arithmetik
Addition und Subtraktion
Polynome können nach dem Assoziativgesetz addiert werden (indem alle Terme zu einer einzigen Summe zusammengefasst werden), möglicherweise gefolgt von einer Umordnung (unter Anwendung des Kommutativgesetzes) und der Kombination gleicher Terme. Zum Beispiel, wenn
- und
dann kann die Summe
neu geordnet und umgruppiert werden kann als
und dann vereinfacht zu
Wenn Polynome addiert werden, ist das Ergebnis ein weiteres Polynom. ⓘ
Die Subtraktion von Polynomen ist ähnlich. ⓘ
Multiplikation
Polynome können auch multipliziert werden. Um das Produkt zweier Polynome zu einer Summe von Termen zu erweitern, wird das Distributivgesetz wiederholt angewendet, was dazu führt, dass jeder Term des einen Polynoms mit jedem Term des anderen multipliziert wird. Zum Beispiel, wenn
dann
Die Durchführung der Multiplikation in jedem Term ergibt
Das Kombinieren ähnlicher Terme ergibt
was vereinfacht werden kann zu
Wie in diesem Beispiel ist das Produkt von Polynomen immer ein Polynom. ⓘ
Komposition
Gegeben ein Polynom mit einer einzigen Variablen und einem anderen Polynom g mit einer beliebigen Anzahl von Variablen erhält man die Zusammensetzung erhält man, indem man jede Kopie der Variablen des ersten Polynoms durch das zweite Polynom ersetzt. Zum Beispiel, wenn und dann
Division
Bei der Division eines Polynoms durch ein anderes handelt es sich in der Regel nicht um ein Polynom. Stattdessen sind solche Verhältnisse eine allgemeinere Familie von Objekten, die je nach Kontext rationale Brüche, rationale Ausdrücke oder rationale Funktionen genannt werden. Dies ist vergleichbar mit der Tatsache, dass das Verhältnis zweier ganzer Zahlen eine rationale Zahl ist, nicht unbedingt eine ganze Zahl. Der Bruch 1/(x2 + 1) ist zum Beispiel kein Polynom und kann nicht als endliche Summe von Potenzen der Variablen x geschrieben werden. ⓘ
Für Polynome in einer Variablen gibt es einen Begriff der euklidischen Division von Polynomen, der die euklidische Division von ganzen Zahlen verallgemeinert. Dieser Begriff der Division a(x)/b(x) führt zu zwei Polynomen, einem Quotienten q(x) und einem Rest r(x), so dass a = b q + r und Grad(r) < Grad(b) ist. Der Quotient und der Rest können mit einem von mehreren Algorithmen berechnet werden, einschließlich der langen Polynomdivision und der synthetischen Division. ⓘ
Wenn der Nenner b(x) monisch und linear ist, d. h. b(x) = x - c für eine Konstante c, dann besagt der Polynom-Rest-Satz, dass der Rest der Division von a(x) durch b(x) die Bewertung a(c) ist. In diesem Fall kann der Quotient mit der Ruffini-Regel berechnet werden, einem Spezialfall der synthetischen Division. ⓘ
Faktorisierung
Alle Polynome mit Koeffizienten in einem eindeutigen Faktorisierungsbereich (z. B. die ganzen Zahlen oder ein Feld) haben auch eine faktorisierte Form, in der das Polynom als Produkt von irreduziblen Polynomen und einer Konstanten geschrieben wird. Diese faktorisierte Form ist bis auf die Ordnung der Faktoren und ihre Multiplikation mit einer invertierbaren Konstante eindeutig. Im Fall des Feldes der komplexen Zahlen sind die irreduziblen Faktoren linear. Über den reellen Zahlen haben sie entweder den Grad eins oder zwei. Über den ganzen Zahlen und den rationalen Zahlen können die irreduziblen Faktoren jeden Grad haben. Zum Beispiel ist die faktorisierte Form von
ist
über den ganzen Zahlen und den reellen Zahlen, und
über den komplexen Zahlen. ⓘ
Die Berechnung der faktorisierten Form, die so genannte Faktorisierung, ist im Allgemeinen zu schwierig, um sie von Hand zu berechnen. Effiziente Algorithmen zur Faktorisierung von Polynomen sind jedoch in den meisten Computeralgebrasystemen verfügbar. ⓘ
Berechnungen
Die Berechnung von Ableitungen und Integralen von Polynomen ist im Vergleich zu anderen Arten von Funktionen besonders einfach. Die Ableitung des Polynoms
Für Polynome, deren Koeffizienten aus abstrakteren Zusammenhängen stammen (z. B. wenn die Koeffizienten ganze Zahlen modulo einer Primzahl p oder Elemente eines beliebigen Rings sind), kann die Formel für die Ableitung immer noch formal interpretiert werden, wobei der Koeffizient kak als die Summe von k Kopien von ak verstanden wird. Zum Beispiel ist die Ableitung des Polynoms xp + x über die ganzen Zahlen modulo p das Polynom 1. ⓘ
Polynomielle Funktionen
Eine Polynomfunktion ist eine Funktion, die durch Auswertung eines Polynoms definiert werden kann. Genauer gesagt ist eine Funktion f mit einem Argument aus einem gegebenen Bereich eine Polynomfunktion, wenn es ein Polynom gibt
existiert, das sich zu für alle x im Bereich von f auswertet (hier ist n eine nichtnegative ganze Zahl und a0, a1, a2, ..., an sind konstante Koeffizienten). Im Allgemeinen haben Polynomfunktionen, sofern nicht anders angegeben, komplexe Koeffizienten, Argumente und Werte. Insbesondere definiert ein Polynom, das nur reelle Koeffizienten haben darf, eine Funktion von den komplexen Zahlen zu den komplexen Zahlen. Wenn der Bereich dieser Funktion ebenfalls auf die reellen Zahlen beschränkt ist, ist die resultierende Funktion eine reelle Funktion, die reelle Zahlen auf reelle Zahlen abbildet. ⓘ
Zum Beispiel ist die Funktion f, definiert durch
definiert ist, ist eine Polynomfunktion mit einer Variablen. Polynomfunktionen mehrerer Variablen werden auf ähnliche Weise definiert, wobei Polynome in mehr als einer Unbestimmten verwendet werden, wie in
Gemäß der Definition von Polynomfunktionen kann es Ausdrücke geben, die offensichtlich keine Polynome sind, aber dennoch Polynomfunktionen definieren. Ein Beispiel ist der Ausdruck der die gleichen Werte annimmt wie das Polynom auf dem Intervall annimmt und somit beide Ausdrücke die gleiche Polynomfunktion auf diesem Intervall definieren. ⓘ
Jede Polynomfunktion ist stetig, glatt und ganz. ⓘ
Graphen
Eine Polynomfunktion in einer reellen Variable kann durch einen Graphen dargestellt werden.
-
Der Graph des Nullpolynoms
f(x) = 0ist die x-Achse.
-
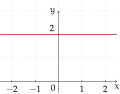
Der Graph eines Polynoms vom Grad 0
f(x) = a0, wobei a0 ≠ 0,ist eine horizontale Linie mit dem y-Achsenabschnitt a0
-
Der Graph eines Polynoms vom Grad 1 (oder einer linearen Funktion)
f(x) = a0 + a1x, mit a1 ≠ 0,ist eine schräge Linie mit y-Achsenabschnitt a0 und Steigung a1.
-
Der Graph eines Polynoms vom Grad 2
f(x) = a0 + a1x + a2x2, mit a2 ≠ 0ist eine Parabel.
-
Der Graph eines Polynoms vom Grad 3
f(x) = a0 + a1x + a2x2 + a3x3, mit a3 ≠ 0eine kubische Kurve ist.
-
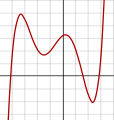
Der Graph eines beliebigen Polynoms vom Grad 2 oder höher
f(x) = a0 + a1x + a2x2 + ⋯ + anxn, wobei an ≠ 0 und n ≥ 2eine stetige nichtlineare Kurve ist. ⓘ
Eine nicht konstante Polynomfunktion tendiert gegen unendlich, wenn die Variable (in absoluten Werten) unendlich ansteigt. Wenn der Grad größer als eins ist, hat der Graph keine Asymptote. Er hat zwei parabolische Zweige mit vertikaler Richtung (ein Zweig für positive x und einer für negative x). ⓘ
Polynomgraphen werden in der Infinitesimalrechnung mit Hilfe von Schnittpunkten, Steigungen, Konkavität und Endverhalten analysiert. ⓘ
Gleichungen
Eine Polynomgleichung, auch algebraische Gleichung genannt, ist eine Gleichung der Form
zum Beispiel,
ist eine Polynomgleichung. ⓘ
Bei der Betrachtung von Gleichungen werden die Unbestimmten (Variablen) von Polynomen auch als Unbekannte bezeichnet, und die Lösungen sind die möglichen Werte der Unbekannten, für die die Gleichheit gilt (im Allgemeinen kann es mehr als eine Lösung geben). Eine Polynomgleichung steht im Gegensatz zu einer Polynomidentität wie (x + y)(x - y) = x2 - y2, bei der beide Ausdrücke dasselbe Polynom in unterschiedlichen Formen darstellen, und folglich ergibt jede Auswertung beider Glieder eine gültige Gleichheit. ⓘ
In der elementaren Algebra werden Methoden wie die quadratische Formel zum Lösen aller Polynomgleichungen ersten und zweiten Grades in einer Variablen gelehrt. Es gibt auch Formeln für kubische und quartische Gleichungen. Für höhere Polynome besagt das Abel-Ruffini-Theorem, dass es keine allgemeine Formel in Radikalen geben kann. Mit Hilfe von Wurzelfindungsalgorithmen lassen sich jedoch numerische Näherungen für die Wurzeln eines Polynomausdrucks beliebigen Grades finden. ⓘ
Die Anzahl der Lösungen einer Polynomgleichung mit reellen Koeffizienten darf den Grad nicht überschreiten und ist gleich dem Grad, wenn die komplexen Lösungen mit ihrer Multiplizität gezählt werden. Diese Tatsache wird als Fundamentalsatz der Algebra bezeichnet. ⓘ
Lösen von Gleichungen
Eine Wurzel eines univariaten Polynoms P, das nicht Null ist, ist ein Wert a von x, so dass P(a) = 0 ist. Mit anderen Worten, eine Wurzel von P ist eine Lösung der Polynomgleichung P(x) = 0 oder eine Nullstelle der durch P definierten Polynomfunktion. Im Fall des Nullpolynoms ist jede Zahl eine Nullstelle der entsprechenden Funktion, und der Begriff der Wurzel wird nur selten verwendet. ⓘ
Eine Zahl a ist dann und nur dann eine Wurzel eines Polynoms P, wenn das lineare Polynom x - a P teilt, d. h. wenn es ein anderes Polynom Q gibt, so dass P = (x - a) Q ist. Es kann vorkommen, dass eine Potenz (größer als 1) von x - a P teilt; in diesem Fall ist a eine mehrfache Wurzel von P, und ansonsten ist a eine einfache Wurzel von P. Wenn P ein Polynom ungleich Null ist, gibt es eine höchste Potenz m, so dass (x - a)m P teilt, was als Vielfachheit von a als Wurzel von P bezeichnet wird. Die Anzahl der Wurzeln eines Polynoms P ungleich Null, gezählt mit ihren jeweiligen Vielfachheiten, kann den Grad von P nicht überschreiten und ist gleich diesem Grad, wenn alle komplexen Wurzeln berücksichtigt werden (dies ist eine Folge des Fundamentalsatzes der Algebra. Die Koeffizienten eines Polynoms und seine Wurzeln sind durch die Formeln von Vieta miteinander verbunden. ⓘ
Einige Polynome, wie z. B. x2 + 1, haben keine Wurzeln unter den reellen Zahlen. Erweitert man jedoch die Menge der akzeptierten Lösungen auf die komplexen Zahlen, so hat jedes nicht konstante Polynom mindestens eine Wurzel; dies ist der fundamentale Satz der Algebra. Durch sukzessives Herausdividieren der Faktoren x - a sieht man, dass jedes Polynom mit komplexen Koeffizienten als eine Konstante (sein Leitkoeffizient) mal ein Produkt solcher Polynomfaktoren vom Grad 1 geschrieben werden kann; folglich ist die Anzahl der (komplexen) Wurzeln, gezählt mit ihren Vielfachen, genau gleich dem Grad des Polynoms. ⓘ
Das Lösen einer Gleichung" kann mehrere Bedeutungen haben. Man kann die Lösungen als explizite Zahlen ausdrücken; zum Beispiel ist die einzige Lösung von 2x - 1 = 0 1/2. Leider ist dies im Allgemeinen für Gleichungen vom Grad größer als eins unmöglich, und seit der Antike haben Mathematiker versucht, die Lösungen als algebraische Ausdrücke auszudrücken; der Goldene Schnitt ist die einzige positive Lösung von In der Antike gelang dies nur für die Grade eins und zwei. Für quadratische Gleichungen liefert die quadratische Formel solche Ausdrücke für die Lösungen. Seit dem 16. Jahrhundert sind ähnliche Formeln (die neben den Quadratwurzeln auch Kubikwurzeln verwenden), wenn auch wesentlich komplizierter, für Gleichungen dritten und vierten Grades bekannt (siehe kubische Gleichung und quartische Gleichung). Formeln für Gleichungen ab dem 5. Grad blieben den Forschern jedoch mehrere Jahrhunderte lang verborgen. Im Jahr 1824 bewies Niels Henrik Abel das erstaunliche Ergebnis, dass es Gleichungen vom Grad 5 gibt, deren Lösungen nicht durch eine (endliche) Formel ausgedrückt werden können, die nur arithmetische Operationen und Radikale umfasst (siehe Abel-Ruffini-Theorem). Im Jahr 1830 bewies Évariste Galois, dass die meisten Gleichungen höheren Grades als vier nicht durch Radikale gelöst werden können, und zeigte, dass man für jede Gleichung entscheiden kann, ob sie durch Radikale lösbar ist, und wenn ja, sie lösen kann. Dieses Ergebnis markierte den Beginn der Galois-Theorie und der Gruppentheorie, zweier wichtiger Zweige der modernen Algebra. Galois selbst wies darauf hin, dass die mit seiner Methode verbundenen Berechnungen nicht durchführbar waren. Dennoch wurden Formeln für lösbare Gleichungen 5. und 6. Grades veröffentlicht (siehe quintische Funktion und sextische Gleichung). ⓘ
Wenn es keinen algebraischen Ausdruck für die Wurzeln gibt und wenn ein solcher Ausdruck zwar existiert, aber zu kompliziert ist, um nützlich zu sein, besteht die einzige Möglichkeit, die Gleichung zu lösen, darin, numerische Näherungen der Lösungen zu berechnen. Dafür gibt es viele Methoden; einige sind auf Polynome beschränkt, andere können auf jede kontinuierliche Funktion angewendet werden. Die effizientesten Algorithmen ermöglichen die einfache Lösung (auf einem Computer) von Polynomgleichungen mit einem Grad von mehr als 1.000 (siehe Wurzelfindungsalgorithmus). ⓘ
Bei Polynomen mit mehr als einer unbestimmten Zahl werden die Kombinationen von Werten für die Variablen, für die die Polynomfunktion den Wert Null annimmt, im Allgemeinen als Nullstellen und nicht als "Wurzeln" bezeichnet. Die Untersuchung der Nullstellenmengen von Polynomen ist Gegenstand der algebraischen Geometrie. Für eine Menge von Polynomgleichungen mit mehreren Unbekannten gibt es Algorithmen, um zu entscheiden, ob sie eine endliche Anzahl komplexer Lösungen haben, und, wenn diese Anzahl endlich ist, um die Lösungen zu berechnen. Siehe System von Polynomgleichungen. ⓘ
Der Spezialfall, in dem alle Polynome vom Grad 1 sind, wird als System linearer Gleichungen bezeichnet, für das es eine Reihe weiterer unterschiedlicher Lösungsmethoden gibt, darunter die klassische Gaußsche Elimination. ⓘ
Eine Polynomgleichung, bei der man sich nur für die Lösungen interessiert, die ganzzahlig sind, wird Diophantische Gleichung genannt. Das Lösen diophantischer Gleichungen ist im Allgemeinen eine sehr schwierige Aufgabe. Es wurde bewiesen, dass es keinen allgemeinen Algorithmus gibt, um sie zu lösen oder auch nur zu entscheiden, ob die Lösungsmenge leer ist (siehe Hilberts zehntes Problem). Einige der berühmtesten Probleme, die in den letzten fünfzig Jahren gelöst wurden, haben mit diophantischen Gleichungen zu tun, wie z. B. Fermats letzter Satz. ⓘ
Polynomielle Ausdrücke
Polynome, bei denen die unbestimmten Zahlen durch andere mathematische Objekte ersetzt werden, werden häufig betrachtet und haben manchmal einen besonderen Namen. ⓘ
Trigonometrische Polynome
Ein trigonometrisches Polynom ist eine endliche Linearkombination der Funktionen sin(nx) und cos(nx), wobei n die Werte einer oder mehrerer natürlicher Zahlen annimmt. Bei reellwertigen Funktionen können die Koeffizienten als reelle Zahlen angenommen werden. ⓘ
Erweitert man sin(nx) und cos(nx) durch sin(x) und cos(x), so wird ein trigonometrisches Polynom zu einem Polynom in den beiden Variablen sin(x) und cos(x) (mit List of trigonometric identities#Multiple-angle formulae). Umgekehrt kann jedes Polynom in sin(x) und cos(x) mit Hilfe von Produkt-zu-Summe-Identitäten in eine Linearkombination der Funktionen sin(nx) und cos(nx) umgewandelt werden. Diese Äquivalenz erklärt, warum Linearkombinationen als Polynome bezeichnet werden. ⓘ
Für komplexe Koeffizienten gibt es keinen Unterschied zwischen einer solchen Funktion und einer endlichen Fourier-Reihe. ⓘ
Trigonometrische Polynome sind weit verbreitet, zum Beispiel bei der trigonometrischen Interpolation zur Interpolation periodischer Funktionen. Sie werden auch bei der diskreten Fourier-Transformation verwendet. ⓘ
Matrix-Polynome
Ein Matrixpolynom ist ein Polynom mit quadratischen Matrizen als Variablen. Bei einem gewöhnlichen, skalarwertigen Polynom
ist dieses Polynom, das mit einer Matrix A ausgewertet wird
wobei I die Identitätsmatrix ist. ⓘ
Eine Matrixpolynomgleichung ist eine Gleichheit zwischen zwei Matrixpolynomen, die für die betreffenden Matrizen gilt. Eine Matrixpolynom-Identität ist eine Matrixpolynom-Gleichung, die für alle Matrizen A in einem bestimmten Matrixring Mn(R) gilt. ⓘ
Bezeichnung spezieller Polynomfunktionen
Polynome des Grades
- 0 werden konstante Funktionen genannt (z. B. ).
- 1 werden lineare Funktionen oder genauer affin lineare Funktionen genannt (z. B. ).
- 2 werden quadratische Funktionen genannt (z. B. ).
- 3 werden kubische Funktionen genannt (z. B. ).
- 4 werden quartische Funktionen genannt (z. B. ). ⓘ
Ein bivariates Polynom, bei dem die zweite Variable durch eine auf die erste Variable angewandte Exponentialfunktion ersetzt wird, z. B. P(x, ex), kann als Exponentialpolynom bezeichnet werden. ⓘ
Verwandte Konzepte
Rationale Funktionen
Ein rationaler Bruch ist der Quotient (algebraischer Bruch) von zwei Polynomen. Jeder algebraische Ausdruck, der in einen rationalen Bruch umgeschrieben werden kann, ist eine rationale Funktion. ⓘ
Während Polynomfunktionen für alle Werte der Variablen definiert sind, ist eine rationale Funktion nur für die Werte der Variablen definiert, für die der Nenner nicht Null ist. ⓘ
Die rationalen Brüche schließen die Laurentschen Polynome ein, beschränken aber die Nenner nicht auf Potenzen einer unbestimmten Zahl. ⓘ
Posynomialfunktionen
Lässt man mehrere Variablen und beliebige reelle Potenzen zu, so erhält man den Begriff der Posynomialfunktion. ⓘ
Laurentische Polynome sind wie Polynome, lassen aber negative Potenzen der Variablen zu. ⓘ
Potenzreihen
Formale Potenzreihen sind wie Polynome, lassen jedoch unendlich viele Terme ungleich Null zu, so dass sie keinen endlichen Grad haben. Im Gegensatz zu Polynomen können sie im Allgemeinen nicht explizit und vollständig aufgeschrieben werden (genauso wenig wie irrationale Zahlen), aber die Regeln für die Manipulation ihrer Terme sind die gleichen wie bei Polynomen. Nicht-formale Potenzreihen verallgemeinern ebenfalls Polynome, aber die Multiplikation von zwei Potenzreihen konvergiert möglicherweise nicht. ⓘ
Geht man zu unendlichen Reihen der Form
- Lies: „f (ist) gleich die Summe von i gleich Null bis Unendlich von a-i (mal) (Groß-) x hoch i“
über, erhält man formale Potenzreihen. ⓘ
Polynomialer Ring
Ein Polynom f über einem kommutativen Ring R ist ein Polynom, dessen Koeffizienten alle zu R gehören. Es lässt sich leicht nachweisen, dass die Polynome in einer gegebenen Menge von Indeterminaten über R einen kommutativen Ring bilden, der als Polynomring in diesen Indeterminaten bezeichnet wird, und zwar mit für den univariaten Fall und im multivariaten Fall. ⓘ
Man hat
Der größte Teil der Theorie des multivariaten Falls lässt sich also auf einen iterierten univariaten Fall reduzieren. ⓘ
Die Karte von R zu R[x], die r zu sich selbst als konstantes Polynom schickt, ist ein injektiver Ringhomomorphismus, durch den R als Unterring von R[x] betrachtet wird. Insbesondere ist R[x] eine Algebra über R. ⓘ
Man kann sich den Ring R[x] so vorstellen, dass er sich aus R ergibt, indem man ein neues Element x zu R hinzufügt und sich minimal zu einem Ring erweitert, in dem x keine anderen Beziehungen als die obligatorischen und die Kommutation mit allen Elementen von R erfüllt (d. h. xr = rx). Dazu muss man alle Potenzen von x und auch deren Linearkombinationen hinzufügen. ⓘ
Die Bildung des Polynomrings und die Bildung von Faktorenringen durch Ausklammern von Idealen sind wichtige Hilfsmittel, um aus bekannten Ringen neue zu konstruieren. Ein Beispiel dafür ist der Ring (bzw. das Feld) der komplexen Zahlen, der aus dem Polynomring R[x] über den reellen Zahlen durch Ausklammern des Ideals der Vielfachen des Polynoms x2 + 1 gebildet werden kann. Ein weiteres Beispiel ist die Konstruktion von endlichen Feldern, die in ähnlicher Weise abläuft, wobei man mit dem Feld der ganzen Zahlen modulo einer Primzahl als Koeffizientenring R beginnt (siehe modulare Arithmetik). ⓘ
Wenn R kommutativ ist, kann man jedem Polynom P in R[x] eine Polynomfunktion f zuordnen, deren Bereich gleich R ist. (Allgemeiner ausgedrückt, können Bereich und Domäne jede beliebige unitale assoziative Algebra über R sein.) Man erhält den Wert f(r) durch Ersetzen des Symbols x in P durch den Wert r. Ein Grund für die Unterscheidung zwischen Polynomen und Polynomfunktionen ist, dass über einigen Ringen verschiedene Polynome zu derselben Polynomfunktion führen können (siehe Fermats kleiner Satz für ein Beispiel, bei dem R die ganzen Zahlen modulo p ist). Dies ist nicht der Fall, wenn R die reellen oder komplexen Zahlen sind, weshalb die beiden Konzepte in der Analysis nicht immer unterschieden werden. Ein noch wichtigerer Grund für die Unterscheidung zwischen Polynomen und Polynomfunktionen ist, dass viele Operationen mit Polynomen (wie die euklidische Division) die Betrachtung der Zusammensetzung eines Polynoms als Ausdruck erfordern, anstatt es bei einem konstanten Wert für x zu bewerten. ⓘ
Teilbarkeit
Wenn R ein ganzzahliger Bereich ist und f und g Polynome in R[x] sind, sagt man, dass f g teilt oder f ein Teiler von g ist, wenn es ein Polynom q in R[x] gibt, für das f q = g ist. dann ist a eine Wurzel von f, wenn und nur wenn dividiert f. In diesem Fall kann der Quotient mit Hilfe der langen Polynomdivision berechnet werden. ⓘ
Wenn F ein Feld ist und f und g Polynome in F[x] mit g ≠ 0 sind, dann gibt es eindeutige Polynome q und r in F[x] mit
und so, dass der Grad von r kleiner ist als der Grad von g (unter Verwendung der Konvention, dass das Polynom 0 einen negativen Grad hat). Die Polynome q und r sind eindeutig durch f und g bestimmt. Dies wird als euklidische Division, Division mit Rest oder polynomiale Langdivision bezeichnet und zeigt, dass der Ring F[x] ein euklidischer Bereich ist. ⓘ
Analog dazu können Primzahlpolynome (richtiger: irreduzible Polynome) als Polynome definiert werden, die nicht Null sind und nicht in das Produkt zweier nicht konstanter Polynome faktorisiert werden können. Im Falle von Koeffizienten in einem Ring muss "nicht konstant" durch "nicht konstant oder nicht einheitlich" ersetzt werden (beide Definitionen stimmen im Falle von Koeffizienten in einem Feld überein). Jedes Polynom kann in das Produkt einer invertierbaren Konstanten mit einem Produkt von irreduziblen Polynomen zerlegt werden. Gehören die Koeffizienten zu einem Feld oder einem eindeutigen Faktorisierungsbereich, so ist diese Zerlegung bis auf die Reihenfolge der Faktoren und die Multiplikation jedes nicht einheitsbezogenen Faktors mit einer Einheit (und die Division des Einheitsfaktors durch dieselbe Einheit) eindeutig. Wenn die Koeffizienten zu ganzen Zahlen, rationalen Zahlen oder einem endlichen Feld gehören, gibt es Algorithmen zur Prüfung der Irreduzibilität und zur Berechnung der Faktorisierung in irreduzible Polynome (siehe Faktorisierung von Polynomen). Diese Algorithmen sind für die handschriftliche Berechnung nicht praktikabel, stehen aber in jedem Computeralgebrasystem zur Verfügung. In einigen Fällen kann auch das Eisenstein-Kriterium zur Bestimmung der Irreduzibilität verwendet werden. ⓘ
Anwendungen
Positionale Notation
In modernen Positionszahlensystemen, wie dem Dezimalsystem, sind die Ziffern und ihre Positionen in der Darstellung einer ganzen Zahl, z. B. 45, eine Kurzschreibweise für ein Polynom in der Radix oder Basis, in diesem Fall 4 × 101 + 5 × 100. Ein weiteres Beispiel: Im Radix 5 bezeichnet eine Ziffernfolge wie 132 die (Dezimal-)Zahl 1 × 52 + 3 × 51 + 2 × 50 = 42. Diese Darstellung ist eindeutig. Ist b eine positive ganze Zahl größer als 1, so lässt sich jede positive ganze Zahl a eindeutig darstellen in der Form ⓘ
wobei m eine nichtnegative ganze Zahl ist und die rs ganze Zahlen sind, so dass ⓘ
- 0 < rm < b und 0 ≤ ri < b für i = 0, 1, . . . , m - 1. ⓘ
Interpolation und Approximation
Die einfache Struktur von Polynomfunktionen macht sie für die Analyse allgemeiner Funktionen mit Hilfe von Polynomapproximationen sehr nützlich. Ein wichtiges Beispiel in der Infinitesimalrechnung ist der Satz von Taylor, der grob besagt, dass jede differenzierbare Funktion lokal wie eine Polynomfunktion aussieht, und der Satz von Stone-Weierstraß, der besagt, dass jede stetige Funktion, die auf einem kompakten Intervall der reellen Achse definiert ist, auf dem gesamten Intervall so genau wie gewünscht durch eine Polynomfunktion angenähert werden kann. Zu den praktischen Methoden der Annäherung gehören die polynomiale Interpolation und die Verwendung von Splines. ⓘ
Andere Anwendungen
Polynome werden häufig verwendet, um Informationen über ein anderes Objekt zu kodieren. Das charakteristische Polynom einer Matrix oder eines linearen Operators enthält Informationen über die Eigenwerte des Operators. Das minimale Polynom eines algebraischen Elements erfasst die einfachste algebraische Beziehung, die dieses Element erfüllt. Das chromatische Polynom eines Graphen zählt die Anzahl der richtigen Färbungen dieses Graphen. ⓘ
Der Begriff "Polynom" kann als Adjektiv auch für Mengen oder Funktionen verwendet werden, die in polynomieller Form geschrieben werden können. In der Komplexitätstheorie bedeutet der Begriff Polynomzeit beispielsweise, dass die Zeit, die für die Ausführung eines Algorithmus benötigt wird, durch eine Polynomfunktion einer Variablen, z. B. der Größe der Eingabe, begrenzt ist. ⓘ
Geschichte
Die Bestimmung der Wurzeln von Polynomen oder das "Lösen algebraischer Gleichungen" ist eines der ältesten Probleme der Mathematik. Die elegante und praktische Notation, die wir heute verwenden, entwickelte sich jedoch erst ab dem 15. Davor wurden die Gleichungen in Worten ausgedrückt. Eine Algebra-Aufgabe aus der chinesischen Arithmetik in neun Abschnitten, die um 200 v. Chr. entstand, beginnt zum Beispiel so: "Drei Garben gutes Getreide, zwei Garben mittelmäßiges Getreide und eine Garbe schlechtes Getreide werden für 29 Dou verkauft. Wir würden 3x + 2y + z = 29 schreiben. ⓘ
Geschichte der Notation
Die früheste bekannte Verwendung des Gleichheitszeichens findet sich in Robert Recorde's The Whetstone of Witte, 1557. Die Zeichen + für Addition, - für Subtraktion und die Verwendung eines Buchstabens für eine Unbekannte erscheinen in Michael Stifels Arithemetica integra, 1544. René Descartes führte in La géometrie, 1637, das Konzept des Graphen einer Polynomgleichung ein. Er machte die Verwendung von Buchstaben am Anfang des Alphabets zur Bezeichnung von Konstanten und von Buchstaben am Ende des Alphabets zur Bezeichnung von Variablen populär, wie oben in der allgemeinen Formel für ein Polynom mit einer Variablen zu sehen ist, wobei die a's für Konstanten und x für eine Variable stehen. Descartes führte die Verwendung von hochgestellten Buchstaben ein, um auch Exponenten zu bezeichnen. ⓘ
Polynome in der abstrakten Algebra
Definition
In der abstrakten Algebra definiert man ein Polynom als ein Element eines Polynomringes . Dieser wiederum ist die Erweiterung des Koeffizientenringes durch ein unbestimmtes, (algebraisch) freies Element . Damit enthält die Potenzen , und deren Linearkombinationen mit . Dies sind auch schon alle Elemente, d. h., jedes Polynom ist eindeutig durch die Folge
seiner Koeffizienten charakterisiert. ⓘ
Konstruktion
Umgekehrt kann ein Modell des Polynomrings durch die Menge der endlichen Folgen in konstruiert werden. Dazu wird auf eine Addition „“ als gliedweise Summe der Folgen und eine Multiplikation „“ durch Faltung der Folgen definiert. Ist also und , so ist
und
mit diesen Verknüpfungen ist nun selbst ein kommutativer Ring, der Polynomring (in einer Unbestimmten) über . ⓘ
Identifiziert man die Unbestimmte als Folge , so dass , etc., so kann jede Folge wieder im intuitiven Sinne als Polynom dargestellt werden als














































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)




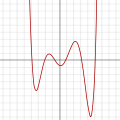













![{\displaystyle R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce54622cb380383ab3a42441b056626ea0d2440)
![{\displaystyle R[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c388e003e234e12fb55533e35a211c8cf295e5)
![{\displaystyle R[x_{1},\ldots ,x_{n}]=\left(R[x_{1},\ldots ,x_{n-1}]\right)[x_{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0bbfe1bccac6aa10e3a7daba9b95381c6f05bd)




![{\displaystyle R[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afeccd52deabb878398a8485755c3ceea80caf9a)

















![{\displaystyle (a_{0},a_{1},a_{2},\dotsc )\in R[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e53ddb980d40bc739046a179cfcb53c05e8bd2b)
