Primzahl

Zusammengesetzte Zahlen können in Rechtecken angeordnet werden, Primzahlen jedoch nicht ⓘ

Eine Primzahl (oder Primzahl) ist eine natürliche Zahl größer als 1, die kein Produkt zweier kleinerer natürlicher Zahlen ist. Eine natürliche Zahl größer als 1, die keine Primzahl ist, nennt man eine zusammengesetzte Zahl. Zum Beispiel ist 5 eine Primzahl, weil die einzigen Möglichkeiten, sie als Produkt zu schreiben, 1 × 5 oder 5 × 1, die 5 selbst beinhalten. 4 hingegen ist zusammengesetzt, weil sie ein Produkt (2 × 2) ist, bei dem beide Zahlen kleiner als 4 sind. Primzahlen spielen in der Zahlentheorie aufgrund des Fundamentalsatzes der Arithmetik eine zentrale Rolle: Jede natürliche Zahl größer als 1 ist entweder selbst eine Primzahl oder kann als Produkt von Primzahlen faktorisiert werden, das bis zu ihrer Reihenfolge eindeutig ist. ⓘ

Die Eigenschaft, eine Primzahl zu sein, wird als Primärität bezeichnet. Eine einfache, aber langsame Methode zur Überprüfung der Primzahl einer bestimmten Zahl $n$, genannt Probedivision, prüft, ob $n$ ein Vielfaches einer beliebigen ganzen Zahl zwischen 2 und ${\sqrt {n}}$. Zu den schnelleren Algorithmen gehören der Miller-Rabin-Primatitätstest, der schnell ist, aber eine geringe Fehlerwahrscheinlichkeit aufweist, und der AKS-Primatitätstest, der in polynomialer Zeit immer die richtige Antwort liefert, aber zu langsam ist, um praktikabel zu sein. Besonders schnelle Methoden gibt es für Zahlen mit besonderen Formen, wie die Mersenne-Zahlen. Die größte bekannte Primzahl ist eine Mersenne-Primzahl mit 24.862.048 Dezimalstellen (Stand Dezember 2018). ⓘ

Es gibt unendlich viele Primzahlen, wie Euklid um 300 v. Chr. gezeigt hat. Es ist keine einfache Formel bekannt, die Primzahlen von zusammengesetzten Zahlen trennt. Allerdings lässt sich die Verteilung der Primzahlen innerhalb der natürlichen Zahlen im Großen statistisch modellieren. Das erste Ergebnis in dieser Richtung ist der Primzahlensatz, der Ende des 19. Jahrhunderts bewiesen wurde und besagt, dass die Wahrscheinlichkeit, dass eine zufällig ausgewählte große Zahl eine Primzahl ist, umgekehrt proportional zu ihrer Stellenzahl, d. h. zu ihrem Logarithmus ist. ⓘ

Mehrere historische Fragen zu Primzahlen sind immer noch ungelöst. Dazu gehören die Goldbachsche Vermutung, dass jede gerade ganze Zahl größer als 2 als Summe zweier Primzahlen ausgedrückt werden kann, und die Zwillingsprimzahlvermutung, dass es unendlich viele Paare von Primzahlen gibt, zwischen denen nur eine gerade Zahl liegt. Diese Fragen gaben den Anstoß für die Entwicklung verschiedener Zweige der Zahlentheorie, die sich auf analytische oder algebraische Aspekte der Zahlen konzentrieren. Primzahlen werden in verschiedenen Verfahren der Informationstechnologie verwendet, z. B. in der Kryptographie mit öffentlichen Schlüsseln, die auf der Schwierigkeit beruht, große Zahlen in ihre Primfaktoren zu zerlegen. In der abstrakten Algebra gehören zu den Objekten, die sich in verallgemeinerter Form wie Primzahlen verhalten, auch Primfaktoren und Primideale. ⓘ

$\mathbb {P}$ ⓘ

Die Menge der Primzahlen wird in der Regel mit dem Symbol $\mathbb {P}$ bezeichnet. Man weiß durch den Satz des Euklid seit der Antike, dass es unendlich viele Primzahlen gibt. Mit $\mathbb {P}$ verknüpft ist die Folge $\left(p_{n}\right)_{n\in \mathbb {N} }$ der nach ihrer Größe geordneten Primzahlen, die man auch Primzahlfolge nennt. Es ist demnach ⓘ

$\mathbb {N} \supset \mathbb {P} =\{p_{n}\mid n\in \mathbb {N} \}$ ⓘ

mit ⓘ

$\left(p_{n}\right)_{n\in \mathbb {N} }=\left(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,\dotsc \right)$ (Folge A000040 in OEIS). ⓘ

Primzahlfolge in der Teilerfläche ⓘ

Diese Eigenschaften werden in der Algebra für Verallgemeinerungen des Primzahlbegriffs genutzt. ⓘ

Primzahlen und ihre Eigenschaften spielen in der Kryptographie eine große Rolle, weil Primfaktoren auch mit dem Aufkommen elektronischer Rechenmaschinen nicht effizient gefunden werden können. Andererseits ermöglichen diese Maschinen eine effiziente Verschlüsselung sowie, wenn man den Schlüssel kennt, Entschlüsselung auch langer Texte. ⓘ

Definition und Beispiele

Eine natürliche Zahl (1, 2, 3, 4, 5, 6 usw.) wird als Primzahl (oder Primfaktor) bezeichnet, wenn sie größer als 1 ist und nicht als Produkt zweier kleinerer natürlicher Zahlen geschrieben werden kann. Die Zahlen, die größer als 1 und nicht prim sind, werden zusammengesetzte Zahlen genannt. Mit anderen Worten, $n$ ist eine Primzahl, wenn $n$ Punkte nicht in kleinere, gleich große Gruppen von mehr als einem Punkt aufgeteilt werden können, oder wenn es nicht möglich ist, die $n$ Punkte in einem rechteckigen Gitter anzuordnen, das mehr als einen Punkt breit und mehr als einen Punkt hoch ist. Zum Beispiel sind von den Zahlen 1 bis 6 die Zahlen 2, 3 und 5 die Primzahlen, da es keine anderen Zahlen gibt, die sie gleichmäßig (ohne Rest) teilen. 1 ist keine Primzahl, da sie in der Definition ausdrücklich ausgeschlossen ist. 4 = 2 × 2 und 6 = 2 × 3 sind beide zusammengesetzt. ⓘ

Demonstration mit Cuisenaire-Stäben, dass 7 eine Primzahl ist, da sie durch keine der Zahlen 2, 3, 4, 5 oder 6 gleichmäßig teilbar ist ⓘ

Die Teiler einer natürlichen Zahl $n$ sind die natürlichen Zahlen, die sich $n$ gleichmäßig teilen. Jede natürliche Zahl hat sowohl 1 als auch sich selbst als Teiler. Wenn sie einen anderen Teiler hat, kann sie nicht prim sein. Diese Idee führt zu einer anderen, aber gleichwertigen Definition der Primzahlen: Sie sind die Zahlen mit genau zwei positiven Teilern, 1 und die Zahl selbst. Eine weitere Möglichkeit, das Gleiche auszudrücken, ist, dass eine Zahl $n$ eine Primzahl ist, wenn sie größer als eins ist und wenn keine der Zahlen $2,3,\dots ,n-1$ die Zahl teilt. $n$ gleichmäßig teilt. ⓘ

Die ersten 25 Primzahlen (alle Primzahlen kleiner als 100) sind:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 (Folge A000040 im OEIS). ⓘ

Keine gerade Zahl $n$ größer als 2 ist eine Primzahl, denn jede solche Zahl lässt sich als das Produkt $2\times n/2$. Daher ist jede Primzahl außer 2 eine ungerade Zahl und wird als ungerade Primzahl bezeichnet. In ähnlicher Weise enden alle Primzahlen, die größer als 5 sind, im üblichen Dezimalsystem auf 1, 3, 7 oder 9. Die Zahlen, die mit anderen Ziffern enden, sind alle zusammengesetzt: Dezimalzahlen, die auf 0, 2, 4, 6 oder 8 enden, sind gerade, und Dezimalzahlen, die auf 0 oder 5 enden, sind durch 5 teilbar. ⓘ

Die Menge aller Primzahlen wird manchmal mit $\mathbf {P}$ (ein fettgedrucktes großes P) oder durch $\mathbb {P}$ (ein fettes großes P auf der Tafel) bezeichnet. ⓘ

Geschichte

Der mathematische Papyrus von Rhind ⓘ

Der mathematische Papyrus von Rhind aus der Zeit um 1550 v. Chr. enthält ägyptische Bruchausdehnungen verschiedener Formen für Primzahlen und zusammengesetzte Zahlen. Die frühesten erhaltenen Aufzeichnungen über das explizite Studium der Primzahlen stammen jedoch aus der antiken griechischen Mathematik. Euklids Elemente (ca. 300 v. Chr.) beweist die Unendlichkeit der Primzahlen und den Fundamentalsatz der Arithmetik und zeigt, wie man aus einer Mersenne-Primzahl eine perfekte Zahl konstruieren kann. Eine andere griechische Erfindung, das Sieb des Eratosthenes, wird immer noch zur Erstellung von Primzahllisten verwendet. ⓘ

Um 1000 n. Chr. fand der islamische Mathematiker Ibn al-Haytham (Alhazen) das Wilsonsche Theorem, das die Primzahlen als die Zahlen charakterisiert $n$ die sich gleichmäßig durch $(n-1)!+1$. Er vermutete auch, dass alle geraden perfekten Zahlen aus Euklids Konstruktion mit Mersenne-Primzahlen stammen, konnte dies aber nicht beweisen. Ein anderer islamischer Mathematiker, Ibn al-Banna' al-Marrakushi, stellte fest, dass das Sieb des Eratosthenes beschleunigt werden kann, indem nur die Teiler bis zur Quadratwurzel der größten zu prüfenden Zahl geprüft werden. Fibonacci brachte die Innovationen der islamischen Mathematik zurück nach Europa. In seinem Buch Liber Abaci (1202) beschrieb er erstmals die Probedivision zur Prüfung der Primzahl, wobei er wiederum nur Teiler bis zur Quadratwurzel verwendete. ⓘ

Im Jahr 1640 stellte Pierre de Fermat (ohne Beweis) den kleinen Satz von Fermat auf (später von Leibniz und Euler bewiesen). Fermat untersuchte auch die Primärität der Fermatschen Zahlen $2^{2^{n}}+1$und Marin Mersenne untersuchte die Mersenne-Primzahlen, Primzahlen der Form $2^{p}-1$ mit $p$ selbst eine Primzahl ist. Christian Goldbach formulierte 1742 in einem Brief an Euler die Goldbachsche Vermutung, dass jede gerade Zahl die Summe von zwei Primzahlen ist. Euler bewies die Vermutung von Alhazen (heute das Euklid-Euler-Theorem), dass alle geraden perfekten Zahlen aus Mersenne-Primzahlen konstruiert werden können. Mit seinen Beweisen für die Unendlichkeit der Primzahlen und die Divergenz der Summe der Kehrwerte der Primzahlen führte er Methoden der mathematischen Analyse in dieses Gebiet ein ${\tfrac {1}{2}}+{\tfrac {1}{3}}+{\tfrac {1}{5}}+{\tfrac {1}{7}}+{\tfrac {1}{11}}+\cdots$. Zu Beginn des 19. Jahrhunderts stellten Legendre und Gauß die Vermutung auf, dass die Anzahl der Primzahlen $x$ gegen unendlich tendiert, die Anzahl der Primzahlen bis zu $x$ asymptotisch ist zu $x/\log x$, wobei $\log x$ ist der natürliche Logarithmus von $x$. Eine schwächere Konsequenz dieser hohen Dichte an Primzahlen war Bertrands Postulat, dass es für jede $n>1$ gibt es eine Primzahl zwischen $n$ und $2n$, bewiesen 1852 von Pafnuty Tschebyschow. Die Ideen von Bernhard Riemann in seinem 1859 erschienenen Aufsatz über die Zeta-Funktion skizzierten eine Möglichkeit, die Vermutung von Legendre und Gauß zu beweisen. Obwohl die eng verwandte Riemannsche Hypothese unbewiesen blieb, wurde Riemanns Skizze 1896 von Hadamard und de la Vallée Poussin vervollständigt, und das Ergebnis ist heute als Primzahlensatz bekannt. Ein weiteres wichtiges Ergebnis aus dem 19. Jahrhundert war Dirichlets Theorem über arithmetische Progressionen, das besagt, dass bestimmte arithmetische Progressionen unendlich viele Primzahlen enthalten. ⓘ

Viele Mathematiker haben an Primzahltests für Zahlen gearbeitet, die größer sind als diejenigen, bei denen die Probedivision praktisch anwendbar ist. Zu den Methoden, die sich auf bestimmte Zahlenformen beschränken, gehören der Pépin-Test für Fermat-Zahlen (1877), das Proth-Theorem (ca. 1878), der Lucas-Lehmer-Primatitätstest (entstanden 1856) und der verallgemeinerte Lucas-Primatitätstest. ⓘ

Seit 1951 wurden alle größten bekannten Primzahlen mit Hilfe dieser Tests auf Computern gefunden. Die Suche nach immer größeren Primzahlen hat auch außerhalb mathematischer Kreise Interesse geweckt, etwa durch die Great Internet Mersenne Prime Search und andere verteilte Computerprojekte. Die Vorstellung, dass Primzahlen außerhalb der reinen Mathematik nur wenige Anwendungen haben, wurde in den 1970er Jahren erschüttert, als die Kryptographie mit öffentlichen Schlüsseln und das RSA-Kryptosystem erfunden wurden, die Primzahlen als Grundlage verwenden. ⓘ

Die zunehmende praktische Bedeutung der computergestützten Primzahlprüfung und Faktorisierung führte zur Entwicklung verbesserter Methoden, die mit großen Zahlen von unbeschränkter Form umgehen können. Die mathematische Theorie der Primzahlen machte ebenfalls Fortschritte mit dem Green-Tao-Theorem (2004), das besagt, dass es beliebig lange arithmetische Reihen von Primzahlen gibt, und dem Beweis von Yitang Zhang (2013), dass es unendlich viele Primzahllücken mit begrenzter Größe gibt. ⓘ

Primzahl der Eins

Die meisten frühen Griechen hielten die 1 nicht einmal für eine Zahl, so dass sie ihre Primzahl nicht in Betracht ziehen konnten. Einige wenige Gelehrte in der griechischen und später römischen Tradition, darunter Nikomachos, Iamblichus, Boethius und Cassiodorus, betrachteten die Primzahlen ebenfalls als Unterteilung der ungeraden Zahlen, so dass sie auch 2 nicht als Primzahl betrachteten. Euklid und die Mehrheit der anderen griechischen Mathematiker betrachteten 2 jedoch als Primzahl. Die mittelalterlichen islamischen Mathematiker folgten weitgehend den Griechen und betrachteten 1 nicht als Zahl. Im Mittelalter und in der Renaissance begannen die Mathematiker, 1 als Zahl zu betrachten, und einige von ihnen setzten sie als erste Primzahl ein. Mitte des 18. Jahrhunderts führte Christian Goldbach in seinem Briefwechsel mit Leonhard Euler die 1 als Primzahl auf; Euler selbst hielt die 1 jedoch nicht für eine Primzahl. Im 19. Jahrhundert hielten viele Mathematiker die 1 immer noch für eine Primzahl, und noch bis 1956 wurden Listen von Primzahlen veröffentlicht, die die 1 enthielten. ⓘ

Würde man die Definition einer Primzahl dahingehend ändern, dass 1 eine Primzahl ist, müssten viele Aussagen, die sich auf Primzahlen beziehen, auf umständlichere Weise umformuliert werden. So müsste beispielsweise der Fundamentalsatz der Arithmetik in Form von Faktorisierungen in Primzahlen größer als 1 umformuliert werden, da jede Zahl mehrere Faktorisierungen mit einer unterschiedlichen Anzahl von Kopien von 1 aufweisen würde. Auch das Sieb des Eratosthenes würde nicht korrekt funktionieren, wenn es 1 als Primzahl behandeln würde, da es alle Vielfachen von 1 (d. h. alle anderen Zahlen) eliminieren und nur die einzige Zahl 1 ausgeben würde. Auch einige andere, eher technische Eigenschaften von Primzahlen gelten nicht für die Zahl 1: So sind beispielsweise die Formeln für die Eulersche Totientenfunktion oder für die Summe der Teilerfunktionen für Primzahlen anders als für 1. Zu Beginn des 20. Jahrhunderts waren sich die Mathematiker einig, dass die 1 nicht als Primzahl, sondern in einer eigenen Kategorie als "Einheit" aufgeführt werden sollte. ⓘ

Elementare Eigenschaften

Eindeutige Faktorisierung

Schreibt man eine Zahl als Produkt von Primzahlen, so spricht man von einer Primfaktorzerlegung der Zahl. Ein Beispiel:

${\begin{aligned}34866&=2\times 3\times 3\times 13\times 149\\&=2\times 3^{2}\times 13\times 149.\end{aligned}}$

Die Terme im Produkt werden Primfaktoren genannt. Ein und derselbe Primfaktor kann mehrmals vorkommen; in diesem Beispiel gibt es zwei Kopien des Primfaktors $3.$ Wenn eine Primzahl mehrfach vorkommt, kann die Potenzierung verwendet werden, um mehrere Kopien derselben Primzahl zusammenzufassen: zum Beispiel in der zweiten Schreibweise des Produkts oben, $3^{2}$ für das Quadrat oder die zweite Potenz von $3.$ ⓘ

Die zentrale Bedeutung der Primzahlen für die Zahlentheorie und die Mathematik im Allgemeinen ergibt sich aus dem Fundamentalsatz der Arithmetik. Dieser Satz besagt, dass jede ganze Zahl, die größer als 1 ist, als Produkt aus einer oder mehreren Primzahlen geschrieben werden kann. Noch stärker, Dieses Produkt ist einzigartig in dem Sinne, dass zwei Primfaktorzerlegungen der gleichen Zahl die gleiche Anzahl von Kopien der gleichen Primzahlen haben, obwohl ihre Reihenfolge unterschiedlich sein kann. Obwohl es also viele verschiedene Möglichkeiten gibt, eine Faktorisierung mit einem ganzzahligen Faktorisierungsalgorithmus zu finden, müssen sie alle das gleiche Ergebnis liefern. Die Primzahlen können somit als die "Grundbausteine" der natürlichen Zahlen betrachtet werden. ⓘ

Einige Beweise für die Einzigartigkeit von Primfaktorzerlegungen beruhen auf dem Euklidschen Lemma: Wenn $p$ eine Primzahl ist und $p$ dividiert ein Produkt $ab$ von ganzen Zahlen $a$ und $b,$ dann $p$ die Zahl teilt. $a$ oder $p$ die Zahl teilt. $b$ (oder beide). Umgekehrt, wenn eine Zahl $p$ die Eigenschaft hat, dass sie, wenn sie ein Produkt teilt, immer mindestens einen Faktor des Produkts teilt, dann $p$ eine Primzahl sein. ⓘ

Unendlichkeit

Es gibt unendlich viele Primzahlen. Eine andere Möglichkeit, dies zu sagen, ist, dass die Folge

2, 3, 5, 7, 11, 13, ...

der Primzahlen niemals endet. Diese Aussage wird zu Ehren des antiken griechischen Mathematikers Euklid als Euklids Theorem bezeichnet, da ihm der erste bekannte Beweis für diese Aussage zugeschrieben wird. Es sind viele weitere Beweise für die Unendlichkeit der Primzahlen bekannt, darunter ein analytischer Beweis von Euler, Goldbachs Beweis auf der Grundlage der Fermat-Zahlen, Furstenbergs Beweis mit Hilfe der allgemeinen Topologie und Kummers eleganter Beweis. ⓘ

Der Beweis von Euklid zeigt, dass jede endliche Liste von Primzahlen unvollständig ist. Der Kerngedanke besteht darin, die Primzahlen einer beliebigen Liste miteinander zu multiplizieren und zu addieren $1.$ Besteht die Liste aus den Primzahlen $p_{1},p_{2},\ldots ,p_{n},$ ergibt dies die Zahl

$N=1+p_{1}\cdot p_{2}\cdots p_{n}.$

Durch den Fundamentalsatz, $N$ eine Primfaktorzerlegung

$N=p'_{1}\cdot p'_{2}\cdots p'_{m}$

mit einem oder mehreren Primfaktoren. $N$ ist gleichmäßig durch jeden dieser Faktoren teilbar, aber $N$ hat einen Rest von eins, wenn sie durch eine der Primzahlen in der gegebenen Liste geteilt wird, so dass keine der Primfaktoren von $N$ in der gegebenen Liste sein kann. Da es keine endliche Liste mit allen Primzahlen gibt, muss es unendlich viele Primzahlen geben. ⓘ

Die Zahlen, die durch Addition von eins zu den Produkten der kleinsten Primzahlen gebildet werden, heißen Euklidische Zahlen. Die ersten fünf von ihnen sind Primzahlen, aber die sechste,

$1+{\big (}2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13{\big )}=30031=59\cdot 509,$

ist eine zusammengesetzte Zahl. ⓘ

Formeln für Primzahlen

Es ist keine effiziente Formel für Primzahlen bekannt. Es gibt zum Beispiel kein nicht konstantes Polynom, auch nicht in mehreren Variablen, das nur Primzahlen annimmt. Es gibt jedoch zahlreiche Ausdrücke, die alle Primzahlen oder nur Primzahlen kodieren. Eine mögliche Formel basiert auf dem Wilson-Theorem und erzeugt die Zahl 2 viele Male und alle anderen Primzahlen genau einmal. Es gibt auch eine Reihe von diophantischen Gleichungen mit neun Variablen und einem Parameter, die folgende Eigenschaft haben: Der Parameter ist nur dann eine Primzahl, wenn das resultierende Gleichungssystem eine Lösung über die natürlichen Zahlen hat. Auf diese Weise kann man eine einzige Formel erhalten, die die Eigenschaft hat, dass alle ihre positiven Werte Primzahlen sind. ⓘ

Weitere Beispiele für primzahlgenerierende Formeln stammen aus dem Satz von Mills und einem Satz von Wright. Diese besagen, dass es reelle Konstanten gibt $A>1$ und $\mu$ so dass

$\left\lfloor A^{3^{n}}\right\rfloor {\text{ and }}\left\lfloor 2^{\cdots ^{2^{2^{\mu }}}}\right\rfloor$

prim sind für jede natürliche Zahl $n$ in der ersten Formel und eine beliebige Anzahl von Exponenten in der zweiten Formel. Hier steht $\lfloor {}\cdot {}\rfloor$ für die Floor-Funktion, also die größte ganze Zahl, die kleiner oder gleich der betreffenden Zahl ist. Diese sind jedoch nicht nützlich, um Primzahlen zu erzeugen, da die Primzahlen zuerst erzeugt werden müssen, um die Werte von $A$ oder $\mu .$ ⓘ

Offene Fragen

Es wurden viele Vermutungen über Primzahlen aufgestellt, die sich um diese drehen. Viele dieser oft elementar formulierten Vermutungen sind seit Jahrzehnten unbeweisbar: Alle vier Landau-Probleme aus dem Jahr 1912 sind immer noch ungelöst. Eine davon ist die Goldbachsche Vermutung, die besagt, dass jede gerade ganze Zahl $n$ größer als 2 als Summe von zwei Primzahlen geschrieben werden kann. Im Jahr 2014 wurde diese Vermutung für alle Zahlen bis zu 2 bewiesen. $n=4\cdot 10^{18}.$ Es wurden auch schwächere Aussagen bewiesen, z. B. das Vinogradov-Theorem, das besagt, dass jede ausreichend große ungerade ganze Zahl als Summe von drei Primzahlen geschrieben werden kann. Das Theorem von Chen besagt, dass jede hinreichend große gerade Zahl als Summe einer Primzahl und einer Halbprimzahl (dem Produkt zweier Primzahlen) ausgedrückt werden kann. Außerdem lässt sich jede gerade Zahl größer als 10 als Summe von sechs Primzahlen darstellen. Der Zweig der Zahlentheorie, der solche Fragen untersucht, heißt additive Zahlentheorie. ⓘ

Eine andere Art von Problemen betrifft die Primzahllücken, d. h. die Differenzen zwischen aufeinanderfolgenden Primzahlen. Dass es beliebig große Primzahllücken gibt, wird deutlich, wenn man feststellt, dass die Folge $n!+2,n!+3,\dots ,n!+n$ besteht aus $n-1$ zusammengesetzten Zahlen besteht, für jede natürliche Zahl $n.$ Große Primzahllücken treten jedoch viel früher auf, als dieses Argument zeigt. Zum Beispiel liegt die erste Primzahllücke der Länge 8 zwischen den Primzahlen 89 und 97, also viel kleiner als $8!=40320.$ Es wird vermutet, dass es unendlich viele Zwillingsprimzahlen gibt, d. h. Paare von Primzahlen mit der Differenz 2; dies ist die Zwillingsprimzahlvermutung. Die Polignac-Vermutung besagt ganz allgemein, dass es für jede positive ganze Zahl $k,$ unendlich viele Paare von aufeinanderfolgenden Primzahlen gibt, die sich durch $2k.$ Die Andrica-Vermutung, die Brocard-Vermutung, die Legendre-Vermutung und die Oppermann-Vermutung besagen alle, dass die größten Abstände zwischen Primzahlen von $1$ bis $n$ höchstens annähernd so groß sein sollten wie ${\sqrt {n}},$ ein Ergebnis, das bekanntlich aus der Riemann-Hypothese folgt, während die viel stärkere Cramér-Vermutung die größte Lückengröße auf $O((\log n)^{2}).$ Primzahllücken können auf Primzahl $k$-Tupel, Muster in den Differenzen zwischen mehr als zwei Primzahlen. Ihre Unendlichkeit und Dichte sind Gegenstand der ersten Hardy-Littlewood-Vermutung, die mit der Heuristik begründet werden kann, dass sich die Primzahlen ähnlich wie eine zufällige Zahlenfolge verhalten, deren Dichte durch den Primzahlensatz gegeben ist. ⓘ

Analytische Eigenschaften

Die analytische Zahlentheorie befasst sich mit der Zahlentheorie unter dem Blickwinkel von stetigen Funktionen, Grenzwerten, unendlichen Reihen und der damit verbundenen Mathematik des Unendlichen und Infinitesimalen. ⓘ

Dieser Studienbereich begann mit Leonhard Euler und seinem ersten wichtigen Ergebnis, der Lösung des Basler Problems. Das Problem fragte nach dem Wert der unendlichen Summe $1+{\tfrac {1}{4}}+{\tfrac {1}{9}}+{\tfrac {1}{16}}+\dots ,$ die man heute als den Wert der $\zeta (2)$ der Riemannschen Zeta-Funktion. Diese Funktion ist eng mit den Primzahlen und einem der bedeutendsten ungelösten Probleme der Mathematik, der Riemannschen Hypothese, verbunden. Euler zeigte, dass $\zeta (2)=\pi ^{2}/6$. Der Kehrwert dieser Zahl, $6/\pi ^{2}$ist die Grenzwahrscheinlichkeit, dass zwei gleichmäßig aus einem großen Bereich ausgewählte Zufallszahlen relativ prim sind (keine gemeinsamen Faktoren haben). ⓘ

Die Verteilung der Primzahlen im Großen, z. B. die Frage, wie viele Primzahlen kleiner sind als ein bestimmter, großer Schwellenwert, wird durch den Primzahlensatz beschrieben, aber es ist keine effiziente Formel für die $n$-te Primzahl bekannt. Der Satz von Dirichlet über arithmetische Progressionen besagt in seiner Grundform, dass lineare Polynome

$p(n)=a+bn$

mit relativ primen ganzen Zahlen $a$ und $b$ unendlich viele Primwerte annehmen. Stärkere Formen des Satzes besagen, dass die Summe der Kehrwerte dieser Primwerte divergiert und dass verschiedene lineare Polynome mit denselben $b$ ungefähr den gleichen Anteil an Primzahlen haben. Es wurden zwar Vermutungen über den Anteil der Primzahlen in Polynomen höheren Grades formuliert, diese bleiben jedoch unbewiesen, und es ist unbekannt, ob es ein quadratisches Polynom gibt, das (bei ganzzahligen Argumenten) unendlich oft Primzahlen hat. ⓘ

Analytischer Beweis des Satzes von Euklid

Eulers Beweis, dass es unendlich viele Primzahlen gibt, betrachtet die Summen der Kehrwerte von Primzahlen, ⓘ

${\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots +{\frac {1}{p}}.$ ⓘ

Euler zeigte, dass es für jede beliebige reelle Zahl $x$eine Primzahl existiert $p$ existiert, für die diese Summe größer ist als $x$. Dies zeigt, dass es unendlich viele Primzahlen gibt, denn wenn es endlich viele Primzahlen gäbe, würde die Summe ihren Maximalwert bei der größten Primzahl erreichen und nicht über jede $x$. Die Wachstumsrate dieser Summe wird durch das zweite Theorem von Mertens genauer beschrieben. Zum Vergleich: Die Summe ⓘ

${\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}$ ⓘ

nicht ins Unendliche wächst, wenn $n$ gegen unendlich geht (siehe das Basler Problem). In diesem Sinne kommen Primzahlen häufiger vor als Quadrate von natürlichen Zahlen, obwohl beide Mengen unendlich sind. Der Satz von Brun besagt, dass die Summe der Kehrwerte von Zwillingsprimzahlen, ⓘ

$\left({{\frac {1}{3}}+{\frac {1}{5}}}\right)+\left({{\frac {1}{5}}+{\frac {1}{7}}}\right)+\left({{\frac {1}{11}}+{\frac {1}{13}}}\right)+\cdots ,$

endlich ist. Aufgrund des Bruns Theorems ist es nicht möglich, die Eulersche Methode zur Lösung der Zwillingsprimzahl-Vermutung, dass es unendlich viele Zwillingsprimzahlen gibt, zu verwenden. ⓘ

(2b)

${\frac {n}{\ln(n)-{\frac {1}{2}}}}<\pi (n)<{\frac {n}{\ln(n)-{\frac {3}{2}}}}$ für $n\geq 67$ ⓘ

erfüllt ist. ⓘ

Anzahl der Primzahlen unterhalb einer bestimmten Grenze

Der relative Fehler von ${\tfrac {n}{\log n}}$ und dem logarithmischen Integral $\operatorname {Li} (n)$ als Annäherungen an die Primzahl-Zählfunktion. Beide relativen Fehler sinken gegen Null, wenn $n$ wächst, aber die Konvergenz gegen Null ist für das logarithmische Integral viel schneller. ⓘ

Die Primzahl-Zählfunktion $\pi (n)$ ist definiert als die Anzahl der Primzahlen, die nicht größer sind als $n$. Ein Beispiel, $\pi (11)=5$, da es fünf Primzahlen gibt, die kleiner oder gleich 11 sind. Methoden wie der Meissel-Lehmer-Algorithmus können die exakten Werte von $\pi (n)$ schneller berechnen, als es möglich wäre, jede Primzahl bis zu $n$. Das Primzahltheorem besagt, dass $\pi (n)$ asymptotisch ist zu $n/\log n$, was als

$\pi (n)\sim {\frac {n}{\log n}},$

bezeichnet wird und bedeutet, dass das Verhältnis von $\pi (n)$ zum rechten Bruch gegen 1 geht, wenn $n$ ins Unendliche wächst. Dies bedeutet, dass die Wahrscheinlichkeit, dass eine zufällig gewählte Zahl kleiner als $n$ eine Primzahl ist, (ungefähr) umgekehrt proportional zur Anzahl der Ziffern in $n$. Es bedeutet auch, dass die $n$Primzahl proportional ist zu $n\log n$ ist und daher die durchschnittliche Größe einer Primzahllücke proportional ist zu $\log n$. Eine genauere Schätzung für $\pi (n)$ ergibt sich aus dem versetzten logarithmischen Integral

$\pi (n)\sim \operatorname {Li} (n)=\int _{2}^{n}{\frac {dt}{\log t}}.$ ⓘ

Arithmetische Progressionen

Eine arithmetische Progression ist eine endliche oder unendliche Folge von Zahlen, bei der die aufeinanderfolgenden Zahlen in der Folge alle die gleiche Differenz aufweisen. Diese Differenz wird als Modulus der Progression bezeichnet. Ein Beispiel,

3, 12, 21, 30, 39, ...,

ist eine unendliche arithmetische Progression mit dem Modulus 9. In einer arithmetischen Progression haben alle Zahlen den gleichen Rest, wenn sie durch den Modulus geteilt werden; in diesem Beispiel ist der Rest 3. Da sowohl der Modulus 9 als auch der Rest 3 Vielfache von 3 sind, ist dies auch für jedes Element der Folge der Fall. Daher enthält diese Folge nur eine einzige Primzahl, nämlich 3 selbst. Im Allgemeinen ist die unendliche Folge

$a,a+q,a+2q,a+3q,\dots$

kann nur dann mehr als eine Primzahl enthalten, wenn ihr Rest $a$ und der Modulus $q$ relativ prim sind. Wenn sie relativ prim sind, besagt der Satz von Dirichlet über arithmetische Progressionen, dass die Progression unendlich viele Primzahlen enthält.

Primzahlen in den arithmetischen Progressionen modulo 9. Jede Zeile des dünnen horizontalen Bandes zeigt eine der neun möglichen Progressionen modulo 9, wobei die Primzahlen rot markiert sind. Die Zahlenfolgen 0, 3 oder 6 modulo 9 enthalten höchstens eine Primzahl (die Zahl 3); die übrigen Zahlenfolgen 2, 4, 5, 7 und 8 modulo 9 haben unendlich viele Primzahlen, wobei die Anzahl der Primzahlen in jeder Folge ähnlich ist.

Das Green-Tao-Theorem zeigt, dass es beliebig lange endliche arithmetische Progressionen gibt, die nur aus Primzahlen bestehen. ⓘ

Primzahlen von quadratischen Polynomen

Die Ulam-Spirale. Primzahlen (rot) häufen sich auf einigen Diagonalen und nicht auf anderen. Die Primzahlen von $4n^{2}-2n+41$ sind in blau dargestellt. ⓘ

Euler stellte fest, dass die Funktion

$n^{2}-n+41$

Primzahlen liefert für $1\leq n\leq 40$liefert, obwohl unter den späteren Werten auch zusammengesetzte Zahlen auftreten. Die Suche nach einer Erklärung für dieses Phänomen führte zu der tiefen algebraischen Zahlentheorie der Heegner-Zahlen und dem Klassenzahlproblem. Die Hardy-Littlewood-Vermutung F sagt die Dichte der Primzahlen unter den Werten von quadratischen Polynomen mit ganzzahligen Koeffizienten in Bezug auf das logarithmische Integral und die Polynomkoeffizienten. Für kein quadratisches Polynom ist bewiesen, dass es unendlich viele Primzahlen hat. ⓘ

Die Ulam-Spirale ordnet die natürlichen Zahlen in einem zweidimensionalen Gitter spiralförmig in konzentrischen Quadraten um den Ursprung an, wobei die Primzahlen hervorgehoben sind. Die Primzahlen scheinen sich auf bestimmten Diagonalen zu häufen und nicht auf anderen, was darauf hindeutet, dass einige quadratische Polynome häufiger Primwerte annehmen als andere. ⓘ

Weitere spezielle Arten von Primzahlen finden sich in der :Kategorie:Primzahl. ⓘ

Zeta-Funktion und die Riemann-Hypothese

Darstellung der absoluten Werte der Zeta-Funktion, die einige ihrer Merkmale zeigt ⓘ

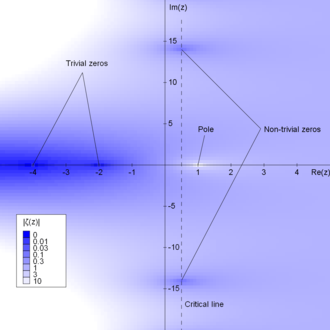
Eine der berühmtesten ungelösten Fragen der Mathematik, die auf das Jahr 1859 zurückgeht und zu den Problemen des Millenniumspreises gehört, ist die Riemannsche Hypothese, die fragt, wo die Nullstellen der Riemannschen Zeta-Funktion $\zeta (s)$ zu finden sind. Diese Funktion ist eine analytische Funktion auf den komplexen Zahlen. Für komplexe Zahlen $s$ mit Realteil größer als eins ist sie sowohl eine unendliche Summe über alle ganzen Zahlen als auch ein unendliches Produkt über die Primzahlen,

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}=\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}}.$

Diese von Euler entdeckte Gleichheit zwischen einer Summe und einem Produkt wird als Euler-Produkt bezeichnet. Das Euler-Produkt lässt sich aus dem Fundamentalsatz der Arithmetik ableiten und zeigt die enge Verbindung zwischen der Zeta-Funktion und den Primzahlen. Es führt zu einem weiteren Beweis, dass es unendlich viele Primzahlen gibt: Gäbe es nur endlich viele, dann wäre die Gleichheit von Summe und Produkt auch bei $s=1$gelten, aber die Summe würde divergieren (es ist die harmonische Reihe $1+{\tfrac {1}{2}}+{\tfrac {1}{3}}+\dots$), während das Produkt endlich wäre, was ein Widerspruch ist. ⓘ

Die Riemannsche Hypothese besagt, dass die Nullstellen der Zeta-Funktion alle entweder negative gerade Zahlen oder komplexe Zahlen sind, deren Realteil gleich 1/2 ist. Der ursprüngliche Beweis des Primzahlensatzes basierte auf einer schwachen Form dieser Hypothese, nämlich dass es keine Nullen mit einem Realteil gleich 1 gibt, obwohl auch andere, elementarere Beweise gefunden wurden. Die Primzahlfunktion kann durch die explizite Formel von Riemann als eine Summe ausgedrückt werden, bei der jeder Term von einer der Nullstellen der Zeta-Funktion stammt; der Hauptterm dieser Summe ist das logarithmische Integral, und die übrigen Terme bewirken, dass die Summe über und unter dem Hauptterm schwankt. In diesem Sinne bestimmen die Nullstellen, wie regelmäßig die Primzahlen verteilt sind. Wenn die Riemann-Hypothese zutrifft, sind diese Schwankungen gering, und die asymptotische Verteilung der Primzahlen, die durch den Primzahlensatz gegeben ist, gilt auch für viel kürzere Intervalle (mit einer Länge von etwa der Quadratwurzel aus $x$ für Intervalle in der Nähe einer Zahl $x$). ⓘ

Abstrakte Algebra

Modulare Arithmetik und endliche Felder

Die modulare Arithmetik modifiziert die gewöhnliche Arithmetik, indem sie nur die Zahlen $\{0,1,2,\dots ,n-1\}$, für eine natürliche Zahl $n$ genannt Modulus. Jede andere natürliche Zahl kann in dieses System übertragen werden, indem man sie durch ihren Rest nach der Division durch $n$. Modulare Summen, Differenzen und Produkte werden berechnet, indem man die gleiche Ersetzung durch den Rest auf das Ergebnis der üblichen Summe, Differenz oder des Produkts ganzer Zahlen. Die Gleichheit von ganzen Zahlen entspricht der Kongruenz in der modularen Arithmetik: $x$ und $y$ sind kongruent (geschrieben $x\equiv y$ mod $n$), wenn sie denselben Rest nach der Division durch $n$. Allerdings ist in diesem Zahlensystem die Division durch alle Zahlen ungleich Null nur dann möglich, wenn der Modulus prim ist. Zum Beispiel mit der Primzahl $7$ als Modulus, ist die Division durch $3$ möglich: $2/3\equiv 3{\bmod {7}}$Denn die Verrechnung der Nenner durch Multiplikation beider Seiten mit $3$ ergibt die gültige Formel $2\equiv 9{\bmod {7}}$. Bei dem zusammengesetzten Modul $6$ist die Division durch $3$ unmöglich. Es gibt keine gültige Lösung für $2/3\equiv x{\bmod {6}}$: Die Verrechnung der Nenner durch Multiplikation mit $3$ wird die linke Seite zu $2$ und die rechte Seite wird entweder $0$ oder $3$. In der Terminologie der abstrakten Algebra bedeutet die Fähigkeit zur Division, dass die modulare Arithmetik modulo einer Primzahl ein Feld oder, genauer gesagt, ein endliches Feld bildet, während andere Moduli nur einen Ring, aber kein Feld ergeben. ⓘ

Mehrere Theoreme über Primzahlen können mit Hilfe der modularen Arithmetik formuliert werden. So besagt beispielsweise der kleine Satz von Fermat, dass, wenn $a\not \equiv 0$ (mod $p$), dann $a^{p-1}\equiv 1$ (mod $p$). Summiert man dies über alle Auswahlmöglichkeiten von $a$ ergibt die Gleichung

$\sum _{a=1}^{p-1}a^{p-1}\equiv (p-1)\cdot 1\equiv -1{\pmod {p}},$

die immer dann gilt, wenn $p$ prim ist. Die Giuga-Vermutung besagt, dass diese Gleichung auch eine hinreichende Bedingung dafür ist, dass $p$ prim sein muss. Wilsons Theorem besagt, dass eine ganze Zahl $p>1$ dann und nur dann prim ist, wenn die Faktorielle $(p-1)!$ kongruent ist zu $-1$ mod $p$. Für eine zusammengesetzte Zahl $\;n=r\cdot s\;$ kann dies nicht gelten, da einer ihrer Faktoren sowohl n als auch $(n-1)!$teilt und somit $(n-1)!\equiv -1{\pmod {n}}$ unmöglich ist. ⓘ

p-adische Zahlen

Die $p$-adische Ordnung $\nu _{p}(n)$ einer ganzen Zahl $n$ ist die Anzahl der Kopien von $p$ in der Primfaktorzerlegung von $n$. Dasselbe Konzept kann von ganzen Zahlen auf rationale Zahlen erweitert werden, indem man die $p$-adische Ordnung eines Bruchs $m/n$ zu definieren als $\nu _{p}(m)-\nu _{p}(n)$. Die $p$-adische Absolutwert $|q|_{p}$ einer beliebigen rationalen Zahl $q$ ist dann definiert als $|q|_{p}=p^{-\nu _{p}(q)}$. Die Multiplikation einer ganzen Zahl mit ihrem $p$-adischen Absolutwert werden die Faktoren von $p$ in ihrer Faktorisierung und es bleiben nur die anderen Primzahlen übrig. So wie der Abstand zwischen zwei reellen Zahlen durch den Absolutwert ihres Abstands gemessen werden kann, kann der Abstand zwischen zwei rationalen Zahlen durch ihren $p$-adischen Abstand, dem $p$-adische Absolutwert ihrer Differenz. Bei dieser Definition des Abstands sind zwei Zahlen nahe beieinander (sie haben einen kleinen Abstand), wenn ihre Differenz durch eine hohe Potenz von ... teilbar ist. $p$. Genauso wie die reellen Zahlen aus den rationalen Zahlen und ihren Abständen gebildet werden können, indem man zusätzliche Grenzwerte hinzufügt, um ein vollständiges Feld zu bilden, können die rationalen Zahlen mit dem $p$-adischen Abstand zu einem anderen vollständigen Feld erweitert werden können, den $p$-adischen Zahlen. ⓘ

Dieses Bild einer Ordnung, eines Absolutwerts und eines daraus abgeleiteten vollständigen Feldes lässt sich auf algebraische Zahlenkörper und ihre Bewertungen (bestimmte Abbildungen von der multiplikativen Gruppe des Feldes auf eine total geordnete additive Gruppe, auch Ordnungen genannt), Absolutwerte (bestimmte multiplikative Abbildungen vom Feld auf die reellen Zahlen, auch Normen genannt) und Orte (Erweiterungen zu vollständigen Feldern, in denen das gegebene Feld eine dichte Menge ist, auch Vervollständigungen genannt) verallgemeinern. Die Erweiterung von den rationalen Zahlen zu den reellen Zahlen ist zum Beispiel eine Stelle, in der der Abstand zwischen den Zahlen der übliche absolute Wert ihrer Differenz ist. Die entsprechende Abbildung auf eine additive Gruppe wäre der Logarithmus des Absolutwerts, obwohl dies nicht alle Anforderungen an eine Bewertung erfüllt. Nach dem Satz von Ostrowski sind bis zu einem natürlichen Begriff der Äquivalenz die reellen Zahlen und $p$-adische Zahlen mit ihren Ordnungen und absoluten Werten die einzigen Wertungen, absoluten Werte und Stellen der rationalen Zahlen. Das lokal-globale Prinzip ermöglicht es, bestimmte Probleme mit den rationalen Zahlen zu lösen, indem man die Lösungen von jeder ihrer Stellen zusammensetzt, was wiederum die Bedeutung der Primzahlen für die Zahlentheorie unterstreicht. ⓘ

Primzahl-Elemente in Ringen

Die Gaußschen Primzahlen mit einer Norm kleiner als 500 ⓘ

Ein kommutativer Ring ist eine algebraische Struktur, in der Addition, Subtraktion und Multiplikation definiert sind. Die ganzen Zahlen sind ein Ring, und die Primzahlen in den ganzen Zahlen wurden auf zwei verschiedene Arten auf Ringe verallgemeinert: Primzahlenelemente und nicht reduzierbare Elemente. Ein Element $p$ eines Rings $R$ wird als prim bezeichnet, wenn es ungleich Null ist, keine multiplikative Umkehrung hat (d. h. keine Einheit ist) und die folgende Bedingung erfüllt: Wenn $p$ das Produkt $xy$ von zwei Elementen von $R$dividiert, dividiert es auch mindestens eines von $x$ oder $y$. Ein Element ist irreduzibel, wenn es weder eine Einheit noch das Produkt von zwei anderen Elementen ist, die keine Einheit sind. Im Ring der ganzen Zahlen bilden die Primzahlen und die irreduziblen Elemente die gleiche Menge,

$\{\dots ,-11,-7,-5,-3,-2,2,3,5,7,11,\dots \}\,.$

In einem beliebigen Ring sind alle Primzahlenelemente irreduzibel. Der Umkehrschluss gilt nicht allgemein, aber für eindeutige Faktorisierungsbereiche. ⓘ

Der Fundamentalsatz der Arithmetik gilt (per Definition) auch für eindeutige Faktorisierungsbereiche. Ein Beispiel für einen solchen Bereich sind die Gaußschen Zahlen $\mathbb {Z} [i]$, der Ring der komplexen Zahlen der Form $a+bi$ wobei $i$ die imaginäre Einheit bezeichnet und $a$ und $b$ beliebige ganze Zahlen sind. Seine Primzahlen werden als Gaußsche Primzahlen bezeichnet. Nicht jede Zahl, die unter den ganzen Zahlen eine Primzahl ist, bleibt auch in den Gaußschen Zahlen eine Primzahl; zum Beispiel kann die Zahl 2 als Produkt der beiden Gaußschen Primzahlen geschrieben werden $1+i$ und $1-i$. Rationale Primzahlen (die Primzahlen in den ganzen Zahlen), die kongruent zu 3 mod 4 sind, sind Gaußsche Primzahlen, aber rationale Primzahlen, die kongruent zu 1 mod 4 sind, sind es nicht. Dies ist eine Folge des Fermatschen Satzes über die Summen zweier Quadrate, der besagt, dass eine ungerade Primzahl $p$ als Summe von zwei Quadraten darstellbar ist, $p=x^{2}+y^{2}$und daher faktorisierbar als $p=(x+iy)(x-iy)$, genau dann, wenn $p$ 1 mod 4 ist. ⓘ

Primzahlideale

Nicht jeder Ring ist ein eindeutiger Faktorisierungsbereich. Zum Beispiel im Ring der Zahlen $a+b{\sqrt {-5}}$ (für ganze Zahlen $a$ und $b$) hat die Zahl $21$ zwei Faktorisierungen $21=3\cdot 7=(1+2{\sqrt {-5}})(1-2{\sqrt {-5}})$, wobei keiner der vier Faktoren weiter reduziert werden kann, so dass es keine eindeutige Faktorisierung gibt. Um die eindeutige Faktorisierung auf eine größere Klasse von Ringen auszudehnen, kann der Begriff einer Zahl durch den eines Ideals ersetzt werden, eine Teilmenge der Elemente eines Rings, die alle Summen von Paaren seiner Elemente und alle Produkte seiner Elemente mit Ringelementen enthält. Primzahlideale, die die Primzahlen in dem Sinne verallgemeinern, dass das von einer Primzahl erzeugte Hauptideal ein Primzahlideal ist, sind ein wichtiges Instrument und Studienobjekt in der kommutativen Algebra, der algebraischen Zahlentheorie und der algebraischen Geometrie. Die Primideale des Rings der ganzen Zahlen sind die Ideale (0), (2), (3), (5), (7), (11), ... Der Fundamentalsatz der Arithmetik verallgemeinert sich zum Lasker-Noether-Theorem, das jedes Ideal in einem noetherschen kommutativen Ring als Schnittpunkt von Primidealen ausdrückt, die die entsprechenden Verallgemeinerungen von Primzahlen sind. ⓘ

Das Spektrum eines Rings ist ein geometrischer Raum, dessen Punkte die Primideale des Rings sind. Auch die arithmetische Geometrie profitiert von diesem Begriff, und viele Konzepte gibt es sowohl in der Geometrie als auch in der Zahlentheorie. So hat beispielsweise die Faktorisierung oder Verzweigung von Primidealen, wenn sie auf ein Erweiterungsfeld übertragen werden, ein grundlegendes Problem der algebraischen Zahlentheorie, eine gewisse Ähnlichkeit mit der Verzweigung in der Geometrie. Diese Konzepte können sogar bei zahlentheoretischen Fragen helfen, die sich ausschließlich mit ganzen Zahlen befassen. So können beispielsweise Primzahlideale im Ring ganzer quadratischer Zahlenfelder zum Nachweis der quadratischen Reziprozität verwendet werden, einer Aussage, die die Existenz von Quadratwurzeln modulo ganzer Primzahlen betrifft. Frühe Versuche, Fermats letzten Satz zu beweisen, führten zu Kummers Einführung von regulären Primzahlen, ganzzahligen Primzahlen, die mit dem Scheitern der eindeutigen Faktorisierung in den zyklotomischen Zahlen zusammenhängen. Die Frage, wie viele ganzzahlige Primzahlen ein Produkt aus mehreren Primzahlidealen in einem algebraischen Zahlenfeld bilden, wird durch den Satz von Tschebotarew über die Dichte beantwortet, der (wenn er auf die zyklotomischen Zahlen angewandt wird) Dirichlets Satz über Primzahlen in arithmetischen Progressionen als Spezialfall enthält. ⓘ

Gruppentheorie

In der Theorie der endlichen Gruppen besagen die Sylow-Theoreme, dass, wenn eine Potenz einer Primzahl $p^{n}$ die Ordnung einer Gruppe teilt, dann hat die Gruppe eine Untergruppe der Ordnung $p^{n}$. Nach dem Lagrange-Theorem ist jede Gruppe mit Primzahlordnung eine zyklische Gruppe, und nach dem Burnside-Theorem ist jede Gruppe, deren Ordnung durch nur zwei Primzahlen teilbar ist, lösbar. ⓘ

Berechnungsmethoden

Das kleine Zahnrad in diesem landwirtschaftlichen Gerät hat 13 Zähne, eine Primzahl, und das mittlere Zahnrad hat 21 Zähne, eine relative Primzahl zu 13 ⓘ

Lange Zeit galt die Zahlentheorie im Allgemeinen und das Studium der Primzahlen im Besonderen als das Paradebeispiel der reinen Mathematik, das außer der Verwendung von Primzahlzähnen zur gleichmäßigen Verteilung des Verschleißes keine Anwendungen außerhalb der Mathematik hatte. Insbesondere Zahlentheoretiker wie der britische Mathematiker G. H. Hardy rühmten sich, Arbeiten zu verfassen, die absolut keine militärische Bedeutung hatten. ⓘ

Diese Vorstellung von der Reinheit der Zahlentheorie wurde in den 1970er Jahren erschüttert, als öffentlich bekannt wurde, dass Primzahlen als Grundlage für die Entwicklung von Kryptographiealgorithmen mit öffentlichen Schlüsseln verwendet werden können. Diese Anwendungen haben dazu geführt, dass Algorithmen für das Rechnen mit Primzahlen und insbesondere die Primzahlprüfung, d. h. Methoden zur Feststellung, ob eine bestimmte Zahl eine Primzahl ist, eingehend untersucht wurden. Die grundlegendste Primzahlprüfungsroutine, die Probedivision, ist zu langsam, um für große Zahlen nützlich zu sein. Eine Gruppe moderner Primzahltests ist auf beliebige Zahlen anwendbar, während es für Zahlen spezieller Typen effizientere Tests gibt. Die meisten Primzahltests sagen nur, ob ihr Argument eine Primzahl ist oder nicht. Routinen, die auch einen Primfaktor zusammengesetzter Argumente (oder alle ihre Primfaktoren) liefern, werden Faktorisierungsalgorithmen genannt. Primzahlen werden auch bei der Berechnung von Prüfsummen, Hashtabellen und Pseudozufallszahlengeneratoren verwendet. ⓘ

Versuchsweise Division

Die grundlegendste Methode zur Überprüfung der Primzahl einer gegebenen ganzen Zahl $n$ wird Probedivision genannt. Diese Methode teilt $n$ durch jede ganze Zahl von 2 bis zur Quadratwurzel von $n$. Jede solche ganze Zahl, die $n$ gleichmäßig teilt, ergibt $n$ als zusammengesetzt; andernfalls ist sie prim. Ganzzahlen, die größer als die Quadratwurzel sind, brauchen nicht geprüft zu werden, da immer, wenn $n=a\cdot b$einer der beiden Faktoren $a$ und $b$ kleiner als oder gleich der Quadratwurzel von $n$. Eine weitere Optimierung besteht darin, nur Primzahlen als Faktoren in diesem Bereich zu prüfen. Um beispielsweise zu prüfen, ob 37 eine Primzahl ist, wird diese Zahl durch die Primzahlen im Bereich von 2 bis ${\sqrt {37}}$die 2, 3 und 5 sind. Jede Division ergibt einen Rest ungleich Null, so dass 37 tatsächlich eine Primzahl ist. ⓘ

Obwohl diese Methode einfach zu beschreiben ist, ist sie für die Prüfung der Primzahl großer ganzer Zahlen unpraktisch, da die Anzahl der durchgeführten Tests in Abhängigkeit von der Anzahl der Ziffern dieser ganzen Zahlen exponentiell ansteigt. Dennoch wird die Probedivision mit einer kleineren Grenze als der Quadratwurzel für die Größe des Divisors verwendet, um schnell zusammengesetzte Zahlen mit kleinen Faktoren zu entdecken, bevor kompliziertere Methoden auf die Zahlen angewendet werden, die diesen Filter passieren. ⓘ

Siebe

Das Sieb des Eratosthenes beginnt mit allen unmarkierten (grauen) Zahlen. Es findet wiederholt die erste unmarkierte Zahl, markiert sie als Primzahl (dunkle Farben) und markiert ihr Quadrat und alle späteren Vielfachen als zusammengesetzt (hellere Farben). Nach der Markierung der Vielfachen von 2 (rot), 3 (grün), 5 (blau) und 7 (gelb) sind alle Primzahlen bis zur Quadratwurzel der Tabellengröße abgearbeitet, und alle verbleibenden unmarkierten Zahlen (11, 13 usw.) werden als Primzahlen markiert (magenta). ⓘ

Vor der Einführung von Computern wurden häufig mathematische Tabellen gedruckt, in denen alle Primzahlen oder Primfaktorzerlegungen bis zu einer bestimmten Grenze aufgeführt waren. Die älteste Methode zur Erstellung einer Liste von Primzahlen ist das Sieb des Eratosthenes. Die Animation zeigt eine optimierte Variante dieser Methode. Eine andere, asymptotisch effizientere Siebmethode für dasselbe Problem ist das Sieb von Atkin. In der fortgeschrittenen Mathematik wendet die Siebtheorie ähnliche Methoden auf andere Probleme an. ⓘ

Primzahltest versus Primzahlbeweis

Einige der schnellsten modernen Tests zur Feststellung, ob eine beliebige Zahl $n$ Primzahlen sind probabilistische (oder Monte-Carlo-) Algorithmen, d. h., sie haben eine geringe Zufallswahrscheinlichkeit, eine falsche Antwort zu liefern. Der Solovay-Strassen-Primatitätstest für eine gegebene Zahl zum Beispiel $p$ wählt eine Zahl $a$ zufällig aus $2$ durch $p-2$ und prüft durch modulare Potenzierung ob $a^{(p-1)/2}\pm 1$ teilbar ist durch $p$. Wenn ja, antwortet er mit Ja, andernfalls mit Nein. Wenn $p$ wirklich eine Primzahl ist, antwortet es immer mit ja, aber wenn $p$ zusammengesetzt ist, antwortet es mit einer Wahrscheinlichkeit von höchstens 1/2 mit Ja und mit einer Wahrscheinlichkeit von mindestens 1/2 mit Nein. Wenn dieser Test wiederholt wird $n$ für dieselbe Zahl wiederholt, ist die Wahrscheinlichkeit, dass eine zusammengesetzte Zahl den Test jedes Mal besteht, höchstens $1/2^{n}$. Da dieser Wert exponentiell mit der Anzahl der Tests abnimmt, ist es sehr wahrscheinlich (wenn auch nicht sicher), dass eine Zahl, die den wiederholten Test besteht, eine Primzahl ist. Schlägt der Test hingegen jemals fehl, dann ist die Zahl mit Sicherheit zusammengesetzt. Eine zusammengesetzte Zahl, die einen solchen Test besteht, wird als Pseudoprimzahl bezeichnet. ⓘ

Im Gegensatz dazu garantieren einige andere Algorithmen, dass ihre Antwort immer richtig ist: Primzahlen werden immer als Primzahlen und zusammengesetzte Zahlen immer als zusammengesetzte Zahlen bestimmt. Dies gilt zum Beispiel für die Probedivision. Zu den Algorithmen mit garantiert korrekter Ausgabe gehören sowohl deterministische (nicht zufällige) Algorithmen wie der AKS-Primzahltest, als auch randomisierte Las-Vegas-Algorithmen, bei denen die vom Algorithmus getroffenen Zufallsentscheidungen keinen Einfluss auf die endgültige Antwort haben, wie z. B. einige Varianten des Elliptikkurven-Primatitätsnachweises. Wenn die Elliptische-Kurven-Methode zu dem Schluss kommt, dass eine Zahl prim ist, liefert sie eine Primzahlbescheinigung, die schnell überprüft werden kann. Der Elliptische-Kurven-Primatitätstest ist in der Praxis der schnellste der garantiert korrekten Primzahltests, aber seine Laufzeitanalyse basiert auf heuristischen Argumenten und nicht auf strengen Beweisen. Der AKS-Primalitätstest hat eine mathematisch bewiesene Zeitkomplexität, ist aber in der Praxis langsamer als der elliptische Kurven-Primatitätsbeweis. Diese Methoden können verwendet werden, um große zufällige Primzahlen zu erzeugen, indem Zufallszahlen erzeugt und getestet werden, bis eine Primzahl gefunden wird; Dabei kann ein schneller probabilistischer Test die meisten zusammengesetzten Zahlen schnell eliminieren, bevor ein garantiert korrekter Algorithmus verwendet wird, um zu überprüfen, ob die verbleibenden Zahlen Primzahlen sind. ⓘ

In der folgenden Tabelle sind einige dieser Tests aufgeführt. Ihre Laufzeit ist angegeben in Form von $n$der zu prüfenden Zahl und, bei probabilistischen Algorithmen, der Anzahl $k$ der durchgeführten Tests. Außerdem, $\varepsilon$ eine beliebig kleine positive Zahl, und log ist der Logarithmus zu einer unbestimmten Basis. Die Notation big O bedeutet, dass jede Zeitschranke mit einem konstanten Faktor multipliziert werden muss, um sie von dimensionslosen Einheiten in Zeiteinheiten umzuwandeln; dieser Faktor hängt von Implementierungsdetails ab, z. B. von der Art des für die Ausführung des Algorithmus verwendeten Computers, nicht aber von den Eingabeparametern $n$ und $k$. ⓘ

Test	Entwickelt in	Typ	Laufende Zeit	Anmerkungen	Referenzen ⓘ
AKS-Primalitätstest	2002	deterministisch	$O((\log n)^{6+\varepsilon })$
Elliptische Kurven-Primalitätsbeweise	1986	Las Vegas	$O((\log n)^{4+\varepsilon })$ heuristisch
Baillie-PSW-Primalitätstest	1980	Monte Carlo	$O((\log n)^{2+\varepsilon })$
Miller-Rabin-Primatitätstest	1980	Monte Carlo	$O(k(\log n)^{2+\varepsilon })$	Fehlerwahrscheinlichkeit $4^{-k}$
Solovay-Strassen-Primalitätstest	1977	Monte Carlo	$O(k(\log n)^{2+\varepsilon })$	Fehlerwahrscheinlichkeit $2^{-k}$

Ob eine beliebige natürliche Zahl prim ist, kann mit einem Primzahltest herausgefunden werden. Es gibt mehrere solcher Verfahren, die sich auf besondere Eigenschaften von Primzahlen stützen. In der Praxis wird der Miller-Rabin-Test am häufigsten verwendet, der eine extrem kurze Laufzeit hat, allerdings mit kleiner Wahrscheinlichkeit falsch-positive Ergebnisse liefert. Mit dem AKS-Primzahltest ist es möglich, über die Primalität ohne Gefahr eines Irrtums in polynomieller Laufzeit zu entscheiden. Allerdings ist er in der Praxis deutlich langsamer als der Miller-Rabin-Test. ⓘ

Spezialalgorithmen und die größte bekannte Primzahl

Zusätzlich zu den oben genannten Tests, die für jede natürliche Zahl gelten, können einige Zahlen einer speziellen Form schneller auf ihre Primzahl geprüft werden. Mit dem Lucas-Lehmer-Primzahltest lässt sich zum Beispiel deterministisch feststellen, ob eine Mersenne-Zahl (eine Zahl kleiner als eine Zweierpotenz) prim ist, in der gleichen Zeit wie eine einzige Iteration des Miller-Rabin-Tests. Aus diesem Grund ist seit 1992 (Stand Dezember 2018) die größte bekannte Primzahl immer eine Mersenne-Primzahl gewesen. Es wird vermutet, dass es unendlich viele Mersenne-Primzahlen gibt. ⓘ

Die folgende Tabelle enthält die größten bekannten Primzahlen verschiedener Typen. Einige dieser Primzahlen wurden durch verteiltes Rechnen gefunden. Im Jahr 2009 wurde das Projekt Great Internet Mersenne Prime Search mit einem Preis in Höhe von 100 000 US-Dollar für die erste Entdeckung einer Primzahl mit mindestens 10 Millionen Ziffern ausgezeichnet. Die Electronic Frontier Foundation bietet außerdem 150.000 $ und 250.000 $ für Primzahlen mit mindestens 100 Millionen bzw. 1 Milliarde Ziffern. ⓘ

Typ	Primzahl	Anzahl der Dezimalziffern	Datum	Gefunden von ⓘ
Mersenne-Primzahl	282,589,933 − 1	24,862,048	7. Dezember 2018	Patrick Laroche, Große Internet-Mersenne-Primzahl-Suche
Proth prime	10,223 × 231,172,165 + 1	9,383,761	Oktober 31, 2016	Péter Szabolcs, PrimeGrid
faktorielle Primzahl	208,003! − 1	1,015,843	Juli 2016	Sou Fukui
primorial prime	1,098,133# − 1	476,311	März 2012	James P. Burt, PrimeGrid
Zwillings-Primzahlen	2,996,863,034,895  × 21,290,000 ± 1	388,342	September 2016	Tom Greer, PrimeGrid

Ganzzahlige Faktorisierung

Gegeben eine zusammengesetzte ganze Zahl $n$wird die Aufgabe, einen (oder alle) Primfaktoren zu liefern, als Faktorisierung von $n$. Sie ist wesentlich schwieriger als die Primzahlprüfung, und obwohl viele Faktorisierungsalgorithmen bekannt sind, sind sie langsamer als die schnellsten Methoden der Primzahlprüfung. Trial Division und Pollard's rho Algorithmus können verwendet werden, um sehr kleine Faktoren von $n$zu finden, und die elliptische Kurvenfaktorisierung kann effektiv sein, wenn $n$ Faktoren von mittlerer Größe hat. Zu den Methoden, die für beliebig große Zahlen geeignet sind und nicht von der Größe der Faktoren abhängen, gehören das quadratische Sieb und das allgemeine Zahlenfeldsieb. Wie bei der Primzahlprüfung gibt es auch Faktorisierungsalgorithmen, bei denen die Eingabe eine spezielle Form haben muss, wie z. B. das spezielle Zahlenfeldsieb. Im Dezember 2019 ist die größte bekannte Zahl, die durch einen allgemeinen Algorithmus faktorisiert wurde, RSA-240, die 240 Dezimalstellen (795 Bits) hat und das Produkt zweier großer Primzahlen ist. ⓘ

Shors Algorithmus kann jede ganze Zahl in einer polynomialen Anzahl von Schritten auf einem Quantencomputer faktorisieren. Mit der derzeitigen Technologie kann dieser Algorithmus jedoch nur für sehr kleine Zahlen ausgeführt werden. Im Oktober 2012 war die größte Zahl, die von einem Quantencomputer mit Shors Algorithmus faktorisiert wurde, 21. ⓘ

Andere rechnerische Anwendungen

Mehrere Kryptoalgorithmen für öffentliche Schlüssel, wie RSA und der Diffie-Hellman-Schlüsselaustausch, basieren auf großen Primzahlen (2048-Bit-Primzahlen sind üblich). RSA beruht auf der Annahme, dass es viel einfacher (d. h. effizienter) ist, die Multiplikation von zwei (großen) Zahlen $x$ und $y$ als zu berechnen $x$ und $y$ (als Primzahl angenommen), wenn nur das Produkt $xy$ bekannt ist. Der Diffie-Hellman-Schlüsselaustausch beruht auf der Tatsache, dass es effiziente Algorithmen für die modulare Potenzierung (Berechnung von $a^{b}{\bmod {c}}$) gibt, während die umgekehrte Operation (der diskrete Logarithmus) als schwieriges Problem gilt. ⓘ

Primzahlen werden häufig für Hashtabellen verwendet. So basierte die ursprüngliche Methode von Carter und Wegman für universelles Hashing auf der Berechnung von Hash-Funktionen durch die Wahl zufälliger linearer Funktionen modulo großer Primzahlen. Carter und Wegman verallgemeinerten diese Methode zu $k$-unabhängiges Hashing durch die Verwendung von Polynomen höheren Grades, wiederum modulo großer Primzahlen. Wie bei der Hash-Funktion werden auch bei Hash-Tabellen, die auf quadratischer Sondierung basieren, Primzahlen für die Größe der Hash-Tabelle verwendet, um sicherzustellen, dass die Sondierungssequenz die gesamte Tabelle abdeckt. ⓘ

Einige Prüfsummenverfahren beruhen auf der Mathematik der Primzahlen. Die Prüfsummen, die in den internationalen Standardbuchnummern verwendet werden, werden beispielsweise definiert, indem der Rest der Zahl modulo 11, einer Primzahl, genommen wird. Da 11 eine Primzahl ist, kann diese Methode sowohl einstellige Fehler als auch Vertauschungen benachbarter Ziffern erkennen. Eine andere Prüfsummenmethode, Adler-32, verwendet die Arithmetik modulo 65521, die größte Primzahl kleiner als $2^{16}$. Primzahlen werden auch in Pseudozufallszahlengeneratoren verwendet, z. B. in linearen kongruenten Generatoren und dem Mersenne Twister. ⓘ

Andere Anwendungen

Primzahlen sind von zentraler Bedeutung für die Zahlentheorie, haben aber auch viele Anwendungen in anderen Bereichen der Mathematik, einschließlich abstrakter Algebra und elementarer Geometrie. So ist es zum Beispiel möglich, Primzahlen von Punkten in einem zweidimensionalen Gitter so zu platzieren, dass keine drei Punkte in einer Linie liegen oder dass jedes Dreieck, das von drei Punkten gebildet wird, eine große Fläche hat. Ein weiteres Beispiel ist das Eisenstein-Kriterium, ein Test, ob ein Polynom irreduzibel ist, der auf der Teilbarkeit seiner Koeffizienten durch eine Primzahl und ihr Quadrat beruht. ⓘ

Die zusammenhängende Summe von zwei Primzahlknoten ⓘ

Das Konzept der Primzahl ist so wichtig, dass es in verschiedenen Zweigen der Mathematik auf unterschiedliche Weise verallgemeinert wurde. Im Allgemeinen bedeutet "Primzahl" Minimalität oder Unzerlegbarkeit in einem geeigneten Sinne. Beispielsweise ist das Primzahlfeld eines bestimmten Feldes dessen kleinstes Teilfeld, das sowohl 0 als auch 1 enthält. Es ist entweder das Feld der rationalen Zahlen oder ein endliches Feld mit einer Primzahl von Elementen, daher der Name. Oftmals wird mit dem Wort Primzahl eine zweite, zusätzliche Bedeutung gemeint, nämlich dass jedes Objekt im Wesentlichen eindeutig in seine Primzahlkomponenten zerlegt werden kann. In der Knotentheorie ist ein Primzahlknoten beispielsweise ein Knoten, der in dem Sinne unzerlegbar ist, dass er nicht als zusammenhängende Summe zweier nicht-trivialer Knoten geschrieben werden kann. Jeder Knoten lässt sich eindeutig als eine zusammenhängende Summe von Primzahlknoten darstellen. Die Primzahlzerlegung von 3-Mannigfaltigkeiten ist ein weiteres Beispiel für diesen Typ. ⓘ

Außerhalb der Mathematik und der Datenverarbeitung haben Primzahlen potenzielle Verbindungen zur Quantenmechanik und wurden in der Kunst und Literatur metaphorisch verwendet. Sie wurden auch in der Evolutionsbiologie verwendet, um die Lebenszyklen von Zikaden zu erklären. ⓘ

Konstruierbare Polygone und Polygonpartitionen

Konstruktion eines regelmäßigen Fünfecks mit Lineal und Zirkel. Dies ist nur möglich, weil 5 eine Fermat-Primzahl ist. ⓘ

Fermat-Primzahlen sind Primzahlen der Form

$F_{k}=2^{2^{k}}+1,$

mit $k$ eine nichtnegative ganze Zahl. Sie sind nach Pierre de Fermat benannt, der vermutete, dass alle diese Zahlen Primzahlen sind. Die ersten fünf dieser Zahlen - 3, 5, 17, 257 und 65.537 - sind Primzahlen, aber $F_{5}$ ist zusammengesetzt, und das gilt auch für alle anderen Fermat-Zahlen, die seit 2017 verifiziert wurden. Ein regelmäßiges $n$-Eck ist nur dann mit Lineal und Zirkel konstruierbar, wenn die ungeraden Primfaktoren von $n$ (falls vorhanden) eindeutige Fermat-Primzahlen sind. Ebenso kann ein regelmäßiges $n$-Eck mit Hilfe von Lineal, Zirkel und einer Winkeldreieckskurve konstruiert werden, wenn die Primfaktoren von $n$ eine beliebige Anzahl von Kopien von 2 oder 3 sind, zusammen mit einer (möglicherweise leeren) Menge verschiedener Pierpont-Primzahlen, Primzahlen der Form $2^{a}3^{b}+1$. ⓘ

Es ist möglich, jedes konvexe Polygon zu unterteilen in $n$ kleinere konvexe Polygone gleicher Fläche und gleichen Umfangs, wenn $n$ eine Potenz einer Primzahl ist, aber dies ist nicht bekannt für andere Werte von $n$. ⓘ

Quantenmechanik

Beginnend mit den Arbeiten von Hugh Montgomery und Freeman Dyson in den 1970er Jahren haben Mathematiker und Physiker spekuliert, dass die Nullstellen der Riemannschen Zeta-Funktion mit den Energieniveaus von Quantensystemen zusammenhängen. Primzahlen sind auch in der Quanteninformationswissenschaft von Bedeutung, und zwar dank mathematischer Strukturen wie wechselseitig unverzerrten Basen und symmetrischen, informationsmäßig vollständigen, positiv-operatorwertigen Maßen. ⓘ

Biologie

Die evolutionäre Strategie der Zikaden der Gattung Magicicada macht sich Primzahlen zunutze. Diese Insekten verbringen die meiste Zeit ihres Lebens als Larven unter der Erde. Erst nach 7, 13 oder 17 Jahren verpuppen sie sich und schlüpfen aus ihren Höhlen. Dann fliegen sie umher, pflanzen sich fort und sterben nach höchstens ein paar Wochen. Biologen stellen die Theorie auf, dass sich diese primär nummerierten Brutzyklen entwickelt haben, um zu verhindern, dass sich Raubtiere mit diesen Zyklen synchronisieren. Im Gegensatz dazu wird angenommen, dass es sich bei den mehrjährigen Zeiträumen zwischen den Blütezeiten von Bambuspflanzen um glatte Zahlen handelt, die nur kleine Primzahlen in ihrer Faktorisierung enthalten. ⓘ

Kunst und Literatur

Primzahlen haben viele Künstler und Schriftsteller beeinflusst. Der französische Komponist Olivier Messiaen nutzte Primzahlen, um ametrische Musik durch "natürliche Phänomene" zu schaffen. In Werken wie La Nativité du Seigneur (1935) und Quatre études de rythme (1949-50) verwendet er gleichzeitig Motive mit Längen, die durch verschiedene Primzahlen gegeben sind, um unvorhersehbare Rhythmen zu schaffen: Die Primzahlen 41, 43, 47 und 53 erscheinen in der dritten Etüde, "Neumes rythmiques". Messiaen zufolge wurde diese Art zu komponieren "von den Bewegungen der Natur inspiriert, Bewegungen von freier und ungleicher Dauer". ⓘ

In seinem Science-Fiction-Roman Contact schlug der Wissenschaftler Carl Sagan vor, dass die Primfaktorzerlegung als Mittel zur Herstellung zweidimensionaler Bildebenen bei der Kommunikation mit Außerirdischen verwendet werden könnte, eine Idee, die er 1975 erstmals informell mit dem amerikanischen Astronomen Frank Drake entwickelt hatte. In dem Roman The Curious Incident of the Dog in the Night-Time von Mark Haddon ordnet der Erzähler die Abschnitte der Geschichte nach aufeinanderfolgenden Primzahlen an, um den geistigen Zustand der Hauptfigur, eines mathematisch begabten Teenagers mit Asperger-Syndrom, zu vermitteln. Primzahlen werden als Metapher für Einsamkeit und Isolation in Paolo Giordanos Roman Die Einsamkeit der Primzahlen verwendet, in dem sie als "Außenseiter" unter den ganzen Zahlen dargestellt werden. ⓘ

Eigenschaften von Primzahlen

Der kleine Satz von Fermat

Es sei $p$ eine Primzahl. Für jede ganze Zahl $a$, die nicht durch $p$ teilbar ist, gilt (für die Notation siehe Kongruenz):

$a^{p-1}\equiv 1\mod p$ ⓘ

Für nicht durch $p$ teilbare Zahlen $a$ ist die folgende Formulierung äquivalent:

$a^{p}\equiv a\mod p$ ⓘ

Es gibt Zahlen $n$, die keine Primzahlen sind, sich aber dennoch zu einer Basis $a$ wie Primzahlen verhalten, d. h., es ist $a^{n-1}\equiv 1{\bmod {n}}$. Solche $n$ nennt man Fermatsche Pseudoprimzahlen zur Basis $a$. Ein $n$, das Fermatsche Pseudoprimzahl bezüglich aller zu ihm teilerfremden Basen $a$ ist, nennt man Carmichael-Zahl. ⓘ

In diesem Zusammenhang zeigt sich die Problematik Fermatscher Pseudoprimzahlen: Sie werden von einem Primzahltest, der den kleinen Satz von Fermat nutzt (Fermatscher Primzahltest), fälschlicherweise für Primzahlen gehalten. Wenn allerdings ein Verschlüsselungsverfahren wie RSA eine zusammengesetzte Zahl statt einer Primzahl verwendet, ist die Verschlüsselung nicht mehr sicher. Deshalb müssen bei solchen Verfahren bessere Primzahltests verwendet werden. ⓘ

Euler und das Legendre-Symbol

Eine einfache Folge aus dem kleinen Satz von Fermat ist: Für jede ungerade Primzahl $p$ und jede ganze Zahl $a$, die nicht durch $p$ teilbar ist, gilt entweder ⓘ

$a^{\frac {p-1}{2}}\equiv 1\mod p$ ⓘ

oder ⓘ

$a^{\frac {p-1}{2}}\equiv -1\mod p.$ ⓘ

Man kann zeigen, dass der erste Fall genau dann eintritt, wenn es eine Quadratzahl gibt, die kongruent zu $a$ modulo $p$ ist, siehe Legendre-Symbol. ⓘ

Binomialkoeffizient

Für Primzahlen $p$ und $1\leq k<p$ gilt ⓘ

$p\,{\Big |}{p \choose k}.$ ⓘ

Zusammen mit dem binomischen Satz folgt daraus ⓘ

$(a+b)^{p}\equiv a^{p}+b^{p}\mod p.$ ⓘ

Für ganze Zahlen $a,b$ folgt diese Aussage auch direkt aus dem kleinen Fermatschen Satz, aber sie ist beispielsweise auch für Polynome mit ganzzahligen Koeffizienten anwendbar; im allgemeinen Kontext entspricht sie der Tatsache, dass die Abbildung $x\mapsto x^{p}$ in Ringen der Charakteristik $p$ ein Homomorphismus ist, der sogenannte Frobenius-Homomorphismus. ⓘ

Aus dem Satz von Wilson ($p$ ist genau dann eine Primzahl, wenn $(p-1)!\equiv -1{\pmod {p}}$ ist) folgt, dass für jede Primzahl $p$ und jede natürliche Zahl $n$ die Kongruenz ⓘ

${{np-1} \choose {p-1}}\equiv 1{\pmod {p}}$ ⓘ

erfüllt ist. ⓘ

Charles Babbage bewies 1819, dass für jede Primzahl $p>2$ diese Kongruenz gilt:

${{2p-1} \choose {p-1}}\equiv 1{\pmod {p^{2}}}$ ⓘ

Der Mathematiker Joseph Wolstenholme (1829–1891) bewies dann 1862, dass für jede Primzahl $p>3$ die folgende Kongruenz gilt:

${{2p-1} \choose {p-1}}\equiv 1{\pmod {p^{3}}}$ ⓘ

Lineare Rekursionen

Den kleinen Fermatschen Satz kann man auch in der Form lesen: In der Folge $a^{n}-a$ ist für eine Primzahl $p$ das $p$-te Folgenglied stets durch $p$ teilbar. Ähnliche Eigenschaften besitzen auch andere Folgen von exponentiellem Charakter, wie die Lucas-Folge ($p\mid L_{p}-1$) und die Perrin-Folge ($p\mid P_{p}$). Für andere lineare Rekursionen gelten analoge, aber kompliziertere Aussagen, beispielsweise für die Fibonacci-Folge $(f_{n})_{n=0,1,2,\dotsc }=0,1,1,2,3,5,\dotsc$: Ist $p$ eine Primzahl, so ist $f_{p}-\left({\frac {p}{5}}\right)$ durch $p$ teilbar. Dabei ist ⓘ

$\left({\frac {p}{5}}\right)={\begin{cases}1&p\equiv 1,4\mod 5\\-1&p\equiv 2,3\mod 5\\0&p=5\end{cases}}$ ⓘ

das Legendre-Symbol. ⓘ

Divergenz der Summe der Kehrwerte

Die Reihe der Kehrwerte der Primzahlen ist divergent. Somit gilt:

$\sum _{i=1}^{\infty }{\frac {1}{p_{i}}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+\dotsb =\infty$ ⓘ

Das ist gleichbedeutend mit der Aussage, dass die durch $\textstyle a_{n}=\sum _{i=1}^{n}{\frac {1}{p_{i}}}$ definierte Folge keinen endlichen Grenzwert besitzt, was wiederum bedeutet, dass sich für ein genügend groß gewähltes $n$ jede erdenkliche reelle Zahl übertreffen lässt. Dies ist zunächst einmal verblüffend, da die Primzahllücken im Schnitt immer weiter zunehmen. Der Satz von Mertens trifft eine Aussage über das genaue Wachstumsverhalten dieser divergenten Reihe. ⓘ

Primzahlzertifikat

Herauszufinden, ob eine natürliche Zahl prim ist oder nicht, kann sehr aufwändig sein. Zu jeder Primzahl lässt sich aber eine Kette von Behauptungen angeben, die alle unmittelbar nachvollziehbar sind, zusammen die Primalität belegen und deren Gesamtlänge höchstens proportional ist zum Quadrat der Länge der Primzahl. Ein solcher Beleg wird Zertifikat (engl. primality certificate) genannt. ⓘ

Bei der Zusammengesetztheit (Nichtprimalität) einer Zahl ist der Unterschied zwischen Beleg und Finden eines Belegs noch augenfälliger: Als Beleg genügen zwei Faktoren, deren Produkt die zusammengesetzte Zahl ergibt; das Finden eines echten Teilers kann aber sehr viel Aufwand bedeuten. ⓘ

Liste der Rekordprimzahlen nach Jahren

Zahl	Anzahl der Dezimalziffern	Jahr	Entdecker (genutzter Computer) ⓘ
217−1	6	1588	Cataldi
219−1	6	1588	Cataldi
231−1	10	1772	Euler
(259−1)/179.951	13	1867	Landry
2127−1	39	1876	Lucas
(2148+1)/17	44	1951	Ferrier
180·(2127−1)2+1	79	1951	Miller & Wheeler (EDSAC1)
2521−1	157	1952	Robinson (SWAC)
2607−1	183	1952	Robinson (SWAC)
21.279−1	386	1952	Robinson (SWAC)
22.203−1	664	1952	Robinson (SWAC)
22.281−1	687	1952	Robinson (SWAC)
23.217−1	969	1957	Riesel (BESK)
24.423−1	1.332	1961	Hurwitz (IBM7090)
29.689−1	2.917	1963	Gillies (ILLIAC 2)
29.941−1	2.993	1963	Gillies (ILLIAC 2)
211.213−1	3.376	1963	Gillies (ILLIAC 2)
219.937−1	6.002	1971	Tuckerman (IBM360/91)
221.701−1	6.533	1978	Noll & Nickel (CDC Cyber 174)
223.209−1	6.987	1979	Noll (CDC Cyber 174)
244.497−1	13.395	1979	Nelson & Slowinski (Cray 1)
286.243−1	25.962	1982	Slowinski (Cray 1)
2132.049−1	39.751	1983	Slowinski (Cray X-MP)
2216.091−1	65.050	1985	Slowinski (Cray X-MP/24)
391.581·2216.193−1	65.087	1989	„Amdahler Sechs“ (Amdahl 1200)
2756.839−1	227.832	1992	Slowinski & Gage (Cray 2)
2859.433−1	258.716	1994	Slowinski & Gage (Cray C90)
21.257.787−1	378.632	1996	Slowinski & Gage (Cray T94)
21.398.269−1	420.921	1996	Armengaud, Woltman (GIMPS, Pentium 90 MHz)
22.976.221−1	895.932	1997	Spence, Woltman (GIMPS, Pentium 100 MHz)
23.021.377−1	909.526	1998	Clarkson, Woltman, Kurowski (GIMPS, Pentium 200 MHz)
26.972.593−1	2.098.960	1999	Hajratwala, Woltman, Kurowski (GIMPS, Pentium 350 MHz)
213.466.917−1	4.053.946	2001	Cameron, Woltman, Kurowski (GIMPS, Athlon 800 MHz)
220.996.011−1	6.320.430	2003	Shafer (GIMPS, Pentium 4 2 GHz)
224.036.583−1	7.235.733	2004	Findley (GIMPS, Pentium 4 2,4 GHz)
225.964.951−1	7.816.230	2005	Nowak (GIMPS, Pentium 4 2,4 GHz)
230.402.457−1	9.152.052	2005	Cooper, Boone (GIMPS, Pentium 4 3 GHz)
232.582.657−1	9.808.358	2006	Cooper, Boone (GIMPS, Pentium 4 3 GHz)
243.112.609−1	12.978.189	2008	Smith, Woltman, Kurowski et al. (GIMPS, Core 2 Duo 2,4 GHz)
257.885.161−1	17.425.170	2013	Cooper, Woltman, Kurowski et al. (GIMPS, Core2 Duo E8400 @ 3,00 GHz)
274.207.281−1	22.338.618	2016	Cooper, Woltman, Kurowski et al. (GIMPS, Intel i7-4790 @ 3,60 GHz)
277.232.917−1	23.249.425	2017	Jonathan Pace et al. (GIMPS, Intel i5-6600 @ 3,30 GHz)
282.589.933−1	24.862.048	2018	Patrick Laroche et al. (GIMPS, Intel i5-4590T @ 2.0 GHz)

Verteilung und Wachstum

Schranken

Die (bewiesene) Bonsesche Ungleichung garantiert, dass das Quadrat einer Primzahl kleiner ist als das Produkt aller kleineren Primzahlen (ab der fünften Primzahl). ⓘ

Nach der (unbewiesenen) Andricaschen Vermutung ist die Differenz der Wurzeln der $n$-ten und der $(n+1)$-ten Primzahl kleiner als 1. ⓘ

Abschätzungen zu Primzahlen und Folgerungen aus dem Primzahlsatz

Im Folgenden sei die Folge der Primzahlen mit $(p_{n})_{n\in \mathbb {N} }$ bezeichnet. ⓘ

Abschätzungen

Für Indizes $n\in \mathbb {N}$ gelten folgende Abschätzungen:

(1a)

$p_{n}<p_{n+1}<2\cdot p_{n}$ ⓘ

(1b)

${p_{n+1}}^{2}\leq 2\cdot {p_{n}}^{2}$ für $n\geq 5$ ⓘ

(1c)

$p_{n}<2^{n}$ für $n\geq 2$ ⓘ

(1d)

$p_{n}>n\cdot \ln(n)$ ⓘ

(1e)

$\sum _{k=2}^{n}{\frac {1}{p_{k}}}>{\frac {1}{36}}\cdot {\ln {\ln(n+1)}}$ für $n\geq 2$ ⓘ

Primzahlen in der Informatik

Bei der Informationssicherheit und insbesondere bei der Verschlüsselung von Nachrichten (siehe Kryptographie) spielen Primzahlen eine wichtige Rolle. Sie werden oft in asymmetrischen Kryptosystemen wie etwa Public-Key-Verschlüsselungsverfahren eingesetzt. Wichtige Beispiele sind der Diffie-Hellman-Schlüsselaustausch, das RSA-Kryptosystem, das unter anderem bei OpenPGP zum Einsatz kommt, das Elgamal-Kryptosystem und das Rabin-Kryptosystem. Dabei werden die Schlüssel aus großen, zufällig erzeugten Primzahlen berechnet, die geheim bleiben müssen. ⓘ

Solche Algorithmen basieren auf Einwegfunktionen, die schnell ausführbar sind, deren Umkehrung aber mit der aktuell bekannten Technologie praktisch unmöglich zu berechnen ist. Neue Informationstechnologien, zum Beispiel Quantencomputer, könnten das aber ändern. Das ungelöste P-NP-Problem steht damit in Zusammenhang. ⓘ

Primzahlen in der Natur

Manche Tier- und Pflanzenarten (z. B. bestimmte Zikaden oder Fichten) vermehren sich in Zyklen von Primzahlen (etwa alle 11, 13 oder 17 Jahre) besonders stark, um es Fressfeinden zu erschweren, sich auf das massenhafte Auftreten einzustellen. ⓘ