Kryptographie

Kryptografie oder Kryptologie (von altgriechisch κρυπτός, romanisiert: kryptós "verborgen, geheim"; und γράφειν graphein "schreiben" bzw. -λογία -logia "studieren") ist die Praxis und das Studium von Techniken zur sicheren Kommunikation in Gegenwart von Gegnern. Ganz allgemein geht es bei der Kryptografie um die Konstruktion und Analyse von Protokollen, die verhindern, dass Dritte oder die Öffentlichkeit private Nachrichten lesen können; verschiedene Aspekte der Informationssicherheit wie Datenvertraulichkeit, Datenintegrität, Authentifizierung und Nichtabstreitbarkeit sind für die moderne Kryptografie von zentraler Bedeutung. Die moderne Kryptografie liegt an der Schnittstelle zwischen den Disziplinen Mathematik, Informatik, Elektrotechnik, Kommunikationswissenschaft und Physik. Zu den Anwendungen der Kryptografie gehören der elektronische Handel, chipbasierte Zahlungskarten, digitale Währungen, Computerpasswörter und die militärische Kommunikation. ⓘ
Vor der Moderne war Kryptografie praktisch ein Synonym für Verschlüsselung, d. h. die Umwandlung von Informationen aus einem lesbaren Zustand in unverständlichen Unsinn. Der Absender einer verschlüsselten Nachricht teilt die Entschlüsselungstechnik nur mit den vorgesehenen Empfängern, um den Zugriff von Gegnern auszuschließen. In der kryptographischen Literatur werden häufig die Namen Alice ("A") für den Absender, Bob ("B") für den vorgesehenen Empfänger und Eve ("Lauscher") für den Gegner verwendet. Seit der Entwicklung von Rotor-Chiffriermaschinen im Ersten Weltkrieg und dem Aufkommen von Computern im Zweiten Weltkrieg sind die Methoden der Kryptografie immer komplexer und ihre Anwendungen immer vielfältiger geworden. ⓘ
Die moderne Kryptografie basiert in hohem Maße auf der mathematischen Theorie und der Praxis der Informatik; kryptografische Algorithmen werden auf der Grundlage von Annahmen über die rechnerische Härte entwickelt, so dass solche Algorithmen in der Praxis für jeden Gegner schwer zu knacken sind. Es ist zwar theoretisch möglich, in ein gut konzipiertes System einzubrechen, in der Praxis ist dies jedoch nicht möglich. Solche Systeme werden daher als "rechnerisch sicher" bezeichnet, wenn sie gut konzipiert sind. Theoretische Fortschritte (z. B. Verbesserungen bei den Algorithmen zur ganzzahligen Faktorisierung) und eine schnellere Rechentechnik machen es erforderlich, diese Entwürfe ständig neu zu bewerten und gegebenenfalls anzupassen. Informationstheoretisch sichere Verfahren, die selbst mit unbegrenzter Rechenleistung nachweislich nicht geknackt werden können, wie z. B. das One-Time-Pad, sind in der Praxis viel schwieriger zu verwenden als die besten theoretisch knackbaren, aber rechnerisch sicheren Verfahren. ⓘ
Die Entwicklung der Kryptotechnik hat im Informationszeitalter eine Reihe von Rechtsfragen aufgeworfen. Das Potenzial der Kryptographie, als Werkzeug für Spionage und Aufruhr eingesetzt zu werden, hat viele Regierungen dazu veranlasst, sie als Waffe einzustufen und ihre Verwendung und Ausfuhr einzuschränken oder sogar zu verbieten. In einigen Ländern, in denen der Einsatz von Kryptografie legal ist, können Ermittler per Gesetz die Offenlegung von Verschlüsselungsschlüsseln für Dokumente erzwingen, die für eine Untersuchung relevant sind. Die Kryptografie spielt auch eine wichtige Rolle bei der Verwaltung digitaler Rechte und bei Streitigkeiten über Urheberrechtsverletzungen im Zusammenhang mit digitalen Medien. ⓘ
Terminologie
Die erste Verwendung des Begriffs "Kryptograph" (im Gegensatz zu "Kryptogramm") geht auf das 19. Jahrhundert zurück und geht auf "The Gold-Bug", eine Geschichte von Edgar Allan Poe, zurück. ⓘ
Bis in die Neuzeit bezog sich die Kryptografie fast ausschließlich auf die "Verschlüsselung", d. h. die Umwandlung gewöhnlicher Informationen (Klartext genannt) in eine unverständliche Form (Chiffretext genannt). Die Entschlüsselung ist der umgekehrte Vorgang, d. h. die Rückverwandlung des unverständlichen Chiffretextes in den Klartext. Eine Chiffre (oder Chiffrierung) ist ein Paar von Algorithmen, die die Verschlüsselung und die umgekehrte Entschlüsselung durchführen. Die genaue Funktionsweise einer Chiffre wird sowohl durch den Algorithmus als auch in jedem Fall durch einen "Schlüssel" gesteuert. Der Schlüssel ist ein Geheimnis (das idealerweise nur den Beteiligten bekannt ist), in der Regel eine Zeichenfolge (idealerweise kurz, damit der Benutzer sie sich merken kann), die zur Entschlüsselung des Chiffriertextes benötigt wird. In formaler mathematischer Hinsicht ist ein "Kryptosystem" eine geordnete Liste von Elementen mit endlich möglichen Klartexten, endlich möglichen Chiffretexten, endlich möglichen Schlüsseln und den Ver- und Entschlüsselungsalgorithmen, die jedem Schlüssel entsprechen. Schlüssel sind sowohl formal als auch in der Praxis wichtig, da Chiffren ohne variable Schlüssel trivialerweise nur mit der Kenntnis der verwendeten Chiffre gebrochen werden können und daher für die meisten Zwecke nutzlos (oder sogar kontraproduktiv) sind. In der Vergangenheit wurden Chiffren oft direkt zur Ver- oder Entschlüsselung verwendet, ohne zusätzliche Verfahren wie Authentifizierung oder Integritätsprüfungen. ⓘ
Es gibt zwei Haupttypen von Kryptosystemen: symmetrische und asymmetrische. Bei symmetrischen Systemen, den einzigen, die bis in die 1970er Jahre bekannt waren, verschlüsselt und entschlüsselt derselbe geheime Schlüssel eine Nachricht. Die Datenmanipulation in symmetrischen Systemen ist wesentlich schneller als in asymmetrischen Systemen. Asymmetrische Systeme verwenden einen "öffentlichen Schlüssel" zum Verschlüsseln einer Nachricht und einen dazugehörigen "privaten Schlüssel" zum Entschlüsseln der Nachricht. Der Vorteil asymmetrischer Systeme besteht darin, dass der öffentliche Schlüssel frei veröffentlicht werden kann, so dass die Parteien eine sichere Kommunikation aufbauen können, ohne einen gemeinsamen geheimen Schlüssel zu haben. In der Praxis werden asymmetrische Systeme verwendet, um zunächst einen geheimen Schlüssel auszutauschen, und dann erfolgt die sichere Kommunikation über ein effizienteres symmetrisches System unter Verwendung dieses Schlüssels. Beispiele für asymmetrische Systeme sind der Diffie-Hellman-Schlüsselaustausch, RSA (Rivest-Shamir-Adleman), ECC (Elliptic Curve Cryptography) und die Post-Quantum-Kryptografie. Zu den sicheren symmetrischen Algorithmen gehört der weit verbreitete AES (Advanced Encryption Standard), der den älteren DES (Data Encryption Standard) ersetzt hat. Zu den unsicheren symmetrischen Algorithmen gehören Kindersprachverschlüsselungssysteme wie Schweinelatein oder andere Cant und alle historischen kryptografischen Systeme, egal wie ernsthaft sie gemeint waren, vor der Erfindung des One-Time-Pad Anfang des 20. ⓘ
In der Umgangssprache wird der Begriff "Code" oft für jede Methode der Verschlüsselung oder Verschleierung von Bedeutung verwendet. In der Kryptographie hat Code jedoch eine spezifischere Bedeutung: die Ersetzung einer Einheit des Klartextes (d. h. eines bedeutungsvollen Wortes oder Satzes) durch ein Codewort (z. B. "Wallaby" ersetzt "Angriff im Morgengrauen"). Eine Chiffre hingegen ist ein Schema zum Ändern oder Ersetzen eines Elements unterhalb einer solchen Ebene (ein Buchstabe, eine Silbe oder ein Buchstabenpaar usw.), um einen Chiffretext zu erzeugen. ⓘ
Kryptoanalyse ist die Bezeichnung für die Untersuchung von Methoden, mit denen die Bedeutung verschlüsselter Informationen ermittelt werden kann, ohne dass man Zugang zu dem normalerweise dafür erforderlichen Schlüssel hat; d. h. es ist die Untersuchung, wie man Verschlüsselungsalgorithmen oder ihre Implementierungen "knacken" kann. ⓘ
Einige verwenden die Begriffe "Kryptographie" und "Kryptologie" im Englischen synonym, während andere (einschließlich der US-Militärpraxis im Allgemeinen) "Kryptographie" speziell für die Verwendung und Anwendung kryptographischer Techniken und "Kryptologie" für das kombinierte Studium von Kryptographie und Kryptoanalyse verwenden. Das Englische ist flexibler als mehrere andere Sprachen, in denen "Kryptologie" (von Kryptologen) immer im zweiten Sinne verwendet wird. RFC 2828 weist darauf hin, dass Steganografie manchmal zur Kryptologie gezählt wird. ⓘ
Die Untersuchung von Merkmalen von Sprachen, die in der Kryptografie oder Kryptologie Anwendung finden (z. B. Häufigkeitsdaten, Buchstabenkombinationen, universelle Muster usw.), wird als Kryptolinguistik bezeichnet. ⓘ
Geschichte der Kryptografie und Kryptoanalyse
Vor der Neuzeit konzentrierte sich die Kryptografie auf die Vertraulichkeit von Nachrichten (d. h. die Verschlüsselung), d. h. die Umwandlung von Nachrichten von einer verständlichen in eine unverständliche Form und am anderen Ende wieder zurück, so dass sie für Abfangjäger oder Lauscher ohne geheimes Wissen (d. h. den für die Entschlüsselung der Nachricht erforderlichen Schlüssel) unlesbar werden. Mit der Verschlüsselung wurde versucht, die Geheimhaltung der Kommunikation, z. B. von Spionen, Militärs und Diplomaten, zu gewährleisten. In den letzten Jahrzehnten hat sich das Gebiet über Vertraulichkeitsaspekte hinaus ausgeweitet und umfasst u. a. Techniken zur Integritätsprüfung von Nachrichten, zur Authentifizierung der Identität von Absendern und Empfängern, digitale Signaturen, interaktive Beweise und sichere Berechnungen. ⓘ
Klassische Kryptographie

Die wichtigsten klassischen Chiffren sind Transpositions-Chiffren, bei denen die Reihenfolge der Buchstaben in einer Nachricht geändert wird (z. B. wird "Hallo Welt" zu "ehlol owrdl" in einem trivial einfachen Umordnungsschema), und Substitutions-Chiffren, bei denen Buchstaben oder Buchstabengruppen systematisch durch andere Buchstaben oder Buchstabengruppen ersetzt werden (z. B. wird "fly at once" zu "gmz bu podf", indem jeder Buchstabe durch den darauf folgenden im lateinischen Alphabet ersetzt wird). Einfache Versionen der beiden Chiffrierverfahren haben nie viel Schutz vor findigen Gegnern geboten. Eine frühe Substitutions-Chiffre war die Caesar-Chiffre, bei der jeder Buchstabe des Klartextes durch einen Buchstaben ersetzt wurde, der eine bestimmte Anzahl von Positionen weiter unten im Alphabet stand. Sueton berichtet, dass Julius Cäsar diese Chiffre mit einer Verschiebung von drei Buchstaben für die Kommunikation mit seinen Generälen verwendete. Atbash ist ein Beispiel für eine frühe hebräische Chiffre. Die früheste bekannte Anwendung der Kryptographie ist ein in Stein gemeißelter Geheimtext in Ägypten (ca. 1900 v. Chr.), aber dies geschah möglicherweise eher zur Belustigung gebildeter Beobachter als zum Verbergen von Informationen. ⓘ
Die Griechen der Antike sollen Chiffren gekannt haben (z. B. die Scytale-Transpositions-Chiffre, die angeblich vom spartanischen Militär verwendet wurde). Auch die Steganografie (d. h. das Verbergen der Existenz einer Nachricht, um sie vertraulich zu halten) wurde bereits in der Antike entwickelt. Ein frühes Beispiel von Herodot war eine Nachricht, die auf den rasierten Kopf eines Sklaven tätowiert und unter dem nachwachsenden Haar versteckt wurde. Zu den moderneren Beispielen der Steganografie gehört die Verwendung von unsichtbarer Tinte, Mikropunkten und digitalen Wasserzeichen zur Verschleierung von Informationen. ⓘ
In Indien spricht das 2000 Jahre alte Kamasutra von Vātsyāyana von zwei verschiedenen Arten von Chiffren namens Kautiliyam und Mulavediya. Bei der Kautiliyam basieren die Buchstabenersetzungen auf phonetischen Beziehungen, z. B. werden Vokale zu Konsonanten. Im Mulavediya besteht das Chiffrieralphabet aus der Paarung von Buchstaben und der Verwendung der wechselseitigen Buchstaben. ⓘ
Dem muslimischen Autor Ibn al-Nadim zufolge gab es im sassanidischen Persien zwei Geheimschriften: die šāh-dabīrīya (wörtlich "Königsschrift"), die für die offizielle Korrespondenz verwendet wurde, und die rāz-saharīya, die zur Übermittlung geheimer Nachrichten an andere Länder diente. ⓘ
David Kahn stellt in seinem Buch The Codebreakers fest, dass die moderne Kryptologie ihren Ursprung bei den Arabern hat, die als erstes Volk systematisch kryptoanalytische Methoden dokumentierten. Al-Khalil (717-786) schrieb das Buch der kryptografischen Botschaften, in dem erstmals Permutationen und Kombinationen verwendet wurden, um alle möglichen arabischen Wörter mit und ohne Vokale aufzulisten. ⓘ

Chiffretexte, die von einer klassischen Chiffre (und einigen modernen Chiffren) erzeugt werden, geben statistische Informationen über den Klartext preis, und diese Informationen können oft verwendet werden, um die Chiffre zu knacken. Nach der Entdeckung der Frequenzanalyse durch den arabischen Mathematiker und Universalgelehrten Al-Kindi (auch bekannt als Alkindus) im 9. Jahrhundert konnten fast alle dieser Chiffren von einem informierten Angreifer geknackt werden. Solche klassischen Chiffren erfreuen sich auch heute noch großer Beliebtheit, wenn auch meist als Rätsel (siehe Kryptogramm). Al-Kindi schrieb ein Buch über Kryptografie mit dem Titel Risalah fi Istikhraj al-Mu'amma (Manuskript zur Entschlüsselung kryptografischer Nachrichten), in dem die erste bekannte Anwendung von Kryptoanalysetechniken der Frequenzanalyse beschrieben wird. ⓘ


Die Häufigkeit der Sprachbuchstaben ist für einige erweiterte historische Verschlüsselungstechniken wie die homophone Chiffre, die dazu neigen, die Häufigkeitsverteilung zu verflachen, wenig hilfreich. Für diese Chiffren können die Häufigkeiten von Sprachbuchstabengruppen (oder n-Grammen) einen Angriff darstellen. ⓘ
Bis zur Entwicklung der polyalphabetischen Chiffre, die eindeutig von Leon Battista Alberti um das Jahr 1467 entwickelt wurde, obwohl es Hinweise darauf gibt, dass sie bereits Al-Kindi bekannt war, blieben im Wesentlichen alle Chiffren für die Kryptoanalyse mit Hilfe der Frequenzanalyse anfällig. Albertis Innovation bestand darin, verschiedene Chiffren (d. h. Substitutionsalphabete) für verschiedene Teile einer Nachricht zu verwenden (vielleicht für jeden aufeinander folgenden Klartextbuchstaben an der Grenze). Er erfand auch das wahrscheinlich erste automatische Chiffriergerät, ein Rad, das eine Teilrealisierung seiner Erfindung darstellte. Bei der Vigenère-Chiffre, einer polyalphabetischen Chiffre, wird zur Verschlüsselung ein Schlüsselwort verwendet, das die Buchstabenersetzung steuert, je nachdem, welcher Buchstabe des Schlüsselworts verwendet wird. Mitte des 19. Jahrhunderts zeigte Charles Babbage, dass die Vigenère-Chiffre durch die Kasiski-Prüfung angreifbar ist, doch wurde diese erst etwa zehn Jahre später von Friedrich Kasiski veröffentlicht. ⓘ
Obwohl die Frequenzanalyse eine leistungsfähige und allgemeine Technik gegen viele Chiffren sein kann, war die Verschlüsselung in der Praxis dennoch oft effektiv, da viele Möchtegern-Kryptoanalytiker die Technik nicht kannten. Um eine Nachricht ohne Frequenzanalyse zu knacken, musste man im Wesentlichen die verwendete Chiffre und vielleicht auch den Schlüssel kennen, was Spionage, Bestechung, Einbruch, Überlistung usw. für kryptoanalytisch Unkundige attraktiver machte. Im 19. Jahrhundert wurde schließlich ausdrücklich anerkannt, dass die Geheimhaltung des Algorithmus einer Chiffre keine sinnvolle und praktische Garantie für die Sicherheit von Nachrichten ist; es wurde sogar erkannt, dass jedes angemessene kryptografische System (einschließlich Chiffren) auch dann sicher sein sollte, wenn der Gegner den Algorithmus der Chiffre selbst vollständig kennt. Die Sicherheit des verwendeten Schlüssels allein sollte für eine gute Chiffre ausreichen, um die Vertraulichkeit bei einem Angriff zu wahren. Dieses Grundprinzip wurde erstmals 1883 von Auguste Kerckhoffs explizit formuliert und wird allgemein als Kerckhoffs'sches Prinzip bezeichnet; alternativ und unverblümter wurde es von Claude Shannon, dem Erfinder der Informationstheorie und der Grundlagen der theoretischen Kryptographie, als Shannons Maxime - "der Feind kennt das System" - neu formuliert. ⓘ
Es wurden verschiedene physikalische Geräte und Hilfsmittel zur Unterstützung von Chiffren verwendet. Eines der frühesten Hilfsmittel dürfte die Sense aus dem antiken Griechenland gewesen sein, ein Stab, der angeblich von den Spartanern als Hilfsmittel für eine Transpositions-Chiffre verwendet wurde. Im Mittelalter wurden weitere Hilfsmittel erfunden, wie z. B. das Chiffriergitter, das auch für eine Art von Steganografie verwendet wurde. Mit der Erfindung polyalphabetischer Chiffren kamen ausgefeiltere Hilfsmittel wie Albertis eigene Chiffrierscheibe, Johannes Trithemius' Tabula-Recta-Schema und Thomas Jeffersons Radchiffre (nicht öffentlich bekannt und von Bazeries um 1900 unabhängig neu erfunden). Zu Beginn des 20. Jahrhunderts wurden zahlreiche mechanische Ver- und Entschlüsselungsgeräte erfunden und einige davon patentiert, darunter Rotormaschinen, darunter die Enigma-Maschine, die von der deutschen Regierung und dem Militär ab den späten 1920er Jahren und während des Zweiten Weltkriegs verwendet wurde. Die Chiffren, die von den besseren Exemplaren dieser Maschinenkonstruktionen implementiert wurden, führten nach dem Ersten Weltkrieg zu einem erheblichen Anstieg der kryptoanalytischen Schwierigkeiten. ⓘ
Das Computerzeitalter
Vor dem frühen 20. Jahrhundert befasste sich die Kryptografie hauptsächlich mit linguistischen und lexikografischen Mustern. Seitdem hat sich der Schwerpunkt verlagert, und die Kryptografie macht nun ausgiebigen Gebrauch von der Mathematik, einschließlich Aspekten der Informationstheorie, der Komplexität von Berechnungen, der Statistik, der Kombinatorik, der abstrakten Algebra, der Zahlentheorie und der endlichen Mathematik, im Allgemeinen beginnend mit der bahnbrechenden Arbeit New direction in cryptography. Die Kryptographie ist auch ein Zweig der Ingenieurwissenschaften, allerdings ein ungewöhnlicher, da sie sich mit aktiven, intelligenten und böswilligen Gegnern befasst; andere Ingenieurwissenschaften (z. B. Bau- oder Chemieingenieurwesen) müssen sich nur mit neutralen Naturkräften befassen. Auch die Beziehung zwischen kryptographischen Problemen und der Quantenphysik wird aktiv erforscht. ⓘ
Die Entwicklung von Digitalcomputern und Elektronik half der Kryptoanalyse und ermöglichte viel komplexere Chiffren. Darüber hinaus ermöglichten Computer die Verschlüsselung jeglicher Art von Daten, die in einem beliebigen Binärformat darstellbar sind, im Gegensatz zu klassischen Chiffren, die nur geschriebene Texte verschlüsselten; dies war neu und bedeutsam. Der Einsatz von Computern hat somit die linguistische Kryptographie verdrängt, sowohl bei der Entwicklung von Chiffren als auch bei der Kryptoanalyse. Viele Computerchiffren lassen sich dadurch charakterisieren, dass sie mit binären Bitfolgen (manchmal in Gruppen oder Blöcken) arbeiten, im Gegensatz zu klassischen und mechanischen Verfahren, die im Allgemeinen herkömmliche Zeichen (d. h. Buchstaben und Ziffern) direkt verarbeiten. Allerdings haben Computer auch die Kryptoanalyse unterstützt, was die erhöhte Komplexität der Chiffren bis zu einem gewissen Grad kompensiert hat. Dennoch sind gute moderne Chiffren der Kryptoanalyse immer einen Schritt voraus; in der Regel ist die Verwendung einer hochwertigen Chiffre sehr effizient (d. h. sie ist schnell und erfordert nur wenige Ressourcen wie Speicher oder CPU-Kapazität), während das Brechen der Chiffre einen Aufwand erfordert, der um viele Größenordnungen größer ist als der für eine klassische Chiffre erforderliche Aufwand, so dass eine Kryptoanalyse so ineffizient und unpraktisch ist, dass sie praktisch unmöglich ist. ⓘ
Aufkommen der modernen Kryptographie
Die Kryptoanalyse der neuen mechanischen Geräte erwies sich als schwierig und mühsam. Im Vereinigten Königreich gaben die kryptoanalytischen Bemühungen in Bletchley Park während des Zweiten Weltkriegs den Anstoß zur Entwicklung effizienterer Mittel für die Durchführung der sich wiederholenden Aufgaben. Dies gipfelte in der Entwicklung des Colossus, des weltweit ersten vollelektronischen, digitalen, programmierbaren Computers, der bei der Entschlüsselung von Chiffren half, die von der Lorenz SZ40/42-Maschine der deutschen Armee erzeugt wurden. ⓘ
Umfangreiche offene akademische Forschungen im Bereich der Kryptografie sind relativ neu und begannen Mitte der 1970er Jahre. In den frühen 1970er Jahren entwickelten IBM-Mitarbeiter den Data Encryption Standard (DES)-Algorithmus, der zum ersten Kryptographiestandard der US-Regierung wurde. Im Jahr 1976 veröffentlichten Whitfield Diffie und Martin Hellman den Diffie-Hellman-Schlüsselaustauschalgorithmus. Im Jahr 1977 wurde der RSA-Algorithmus in Martin Gardners Scientific American-Kolumne veröffentlicht. Seitdem hat sich die Kryptografie zu einem weit verbreiteten Werkzeug in der Kommunikation, in Computernetzen und in der Computersicherheit im Allgemeinen entwickelt. ⓘ
Einige moderne kryptografische Verfahren können ihre Schlüssel nur dann geheim halten, wenn bestimmte mathematische Probleme unlösbar sind, z. B. das Problem der ganzzahligen Faktorisierung oder das Problem des diskreten Logarithmus, so dass eine enge Verbindung zur abstrakten Mathematik besteht. Es gibt nur sehr wenige Kryptosysteme, die nachweislich bedingungslos sicher sind. Das One-Time-Pad ist eines davon und wurde von Claude Shannon als solches nachgewiesen. Es gibt einige wichtige Algorithmen, die unter bestimmten Annahmen als sicher erwiesen wurden. Die Unmöglichkeit, extrem große ganze Zahlen zu faktorisieren, ist beispielsweise die Grundlage für die Annahme, dass RSA und einige andere Systeme sicher sind, aber selbst dann ist der Beweis der Unknackbarkeit nicht möglich, da das zugrunde liegende mathematische Problem offen bleibt. In der Praxis sind diese Systeme weit verbreitet und werden von den meisten kompetenten Beobachtern für unknackbar gehalten. Es gibt RSA-ähnliche Systeme, wie z. B. das von Michael O. Rabin, die nachweislich sicher sind, vorausgesetzt, die Faktorisierung von n = pq ist unmöglich; es ist in der Praxis ziemlich unbrauchbar. Das Problem des diskreten Logarithmus ist die Grundlage für die Annahme, dass einige andere Kryptosysteme sicher sind, und auch hier gibt es verwandte, weniger praktische Systeme, die in Bezug auf das Problem der Lösbarkeit oder Unlösbarkeit des diskreten Logarithmus nachweislich sicher sind. ⓘ
Die Entwickler von kryptographischen Algorithmen und Systemen müssen nicht nur die Geschichte der Kryptographie kennen, sondern auch die wahrscheinlichen zukünftigen Entwicklungen berücksichtigen, während sie an ihren Entwürfen arbeiten. So hat beispielsweise die ständige Verbesserung der Rechenleistung von Computern die Möglichkeiten von Brute-Force-Angriffen vergrößert, so dass bei der Festlegung von Schlüssellängen die erforderlichen Schlüssellängen ebenfalls zunehmen. Die potenziellen Auswirkungen der Quanteninformatik werden von einigen Entwicklern kryptografischer Systeme, die Post-Quantum-Kryptografie entwickeln, bereits berücksichtigt. Die Ankündigung, dass es bald kleine Implementierungen dieser Maschinen geben wird, könnte dazu führen, dass die Notwendigkeit einer vorbeugenden Vorsicht mehr als nur spekulativ ist. ⓘ
Moderne Kryptographie
Kryptographie mit symmetrischen Schlüsseln

Die Kryptographie mit symmetrischem Schlüssel bezieht sich auf Verschlüsselungsmethoden, bei denen Sender und Empfänger denselben Schlüssel verwenden (oder, seltener, bei denen ihre Schlüssel zwar unterschiedlich sind, aber in einem leicht berechenbaren Zusammenhang stehen). Dies war die einzige Art der Verschlüsselung, die bis Juni 1976 öffentlich bekannt war. ⓘ

Symmetrische Schlüsselchiffren werden entweder als Blockchiffren oder als Stromchiffren implementiert. Eine Blockchiffre verschlüsselt die Eingabe in Blöcken von Klartext, im Gegensatz zu einzelnen Zeichen, der Eingabeform, die von einer Stromchiffre verwendet wird. ⓘ
Der Data Encryption Standard (DES) und der Advanced Encryption Standard (AES) sind Blockchiffrierungen, die von der US-Regierung als Kryptografiestandards eingestuft wurden (obwohl die Einstufung von DES schließlich zurückgezogen wurde, nachdem der AES eingeführt wurde). Trotz seiner Ausmusterung als offizieller Standard ist DES (insbesondere seine immer noch zugelassene und wesentlich sicherere Triple-DES-Variante) nach wie vor sehr beliebt; er wird in einer Vielzahl von Anwendungen eingesetzt, von der Verschlüsselung von Geldautomaten bis hin zum Schutz von E-Mails und sicherem Fernzugriff. Viele andere Blockchiffren wurden entwickelt und auf den Markt gebracht, wobei die Qualität sehr unterschiedlich ist. Viele, sogar einige, die von fähigen Praktikern entwickelt wurden, sind gründlich geknackt worden, wie z. B. FEAL. ⓘ
Im Gegensatz zu den Blockchiffren wird bei Stromchiffren ein beliebig langer Strom von Schlüsselmaterial erzeugt, der mit dem Klartext Bit für Bit oder Zeichen für Zeichen kombiniert wird, ähnlich wie bei einem One-Time-Pad. Bei einer Stromchiffre wird der Ausgabestrom auf der Grundlage eines verborgenen internen Zustands erzeugt, der sich während des Betriebs der Chiffre ändert. Dieser interne Zustand wird zunächst mit Hilfe des geheimen Schlüsselmaterials hergestellt. RC4 ist eine weit verbreitete Stromchiffre. Blockchiffren können als Stromchiffren verwendet werden, indem Blöcke eines Schlüsselstroms (anstelle eines Pseudozufallszahlengenerators) erzeugt werden und eine XOR-Operation auf jedes Bit des Klartextes mit jedem Bit des Schlüsselstroms angewendet wird. ⓘ
Nachrichtenauthentifizierungscodes (MACs) sind kryptografischen Hash-Funktionen sehr ähnlich, mit dem Unterschied, dass ein geheimer Schlüssel verwendet werden kann, um den Hash-Wert beim Empfang zu authentifizieren; diese zusätzliche Komplikation blockiert ein Angriffsschema gegen Bare-Digest-Algorithmen und wurde daher als lohnenswert erachtet. Kryptographische Hash-Funktionen sind eine dritte Art von kryptographischen Algorithmen. Sie nehmen eine Nachricht beliebiger Länge als Eingabe und geben einen kurzen Hash mit fester Länge aus, der z. B. für eine digitale Signatur verwendet werden kann. Bei guten Hash-Funktionen kann ein Angreifer keine zwei Nachrichten finden, die denselben Hash ergeben. MD4 ist eine seit langem genutzte Hash-Funktion, die jetzt gebrochen ist; MD5, eine verstärkte Variante von MD4, ist ebenfalls weit verbreitet, aber in der Praxis gebrochen. Die Nationale Sicherheitsbehörde der USA hat eine Reihe von MD5-ähnlichen Hash-Funktionen entwickelt, den Secure Hash Algorithm: SHA-0 war ein fehlerhafter Algorithmus, der von der Behörde zurückgezogen wurde; SHA-1 ist weit verbreitet und sicherer als MD5, aber Kryptoanalytiker haben Angriffe gegen ihn festgestellt; die SHA-2-Familie verbessert SHA-1, ist aber seit 2011 anfällig für Konflikte; und die US-Normenbehörde hielt es aus Sicherheitsgründen für "klug", einen neuen Standard zu entwickeln, um "die Robustheit des gesamten NIST-Hash-Algorithmus-Toolkits deutlich zu verbessern". Daher wurde ein Wettbewerb zur Entwicklung von Hash-Funktionen ausgeschrieben, um bis 2012 einen neuen nationalen US-Standard mit der Bezeichnung SHA-3 auszuwählen. Der Wettbewerb endete am 2. Oktober 2012, als das NIST bekannt gab, dass Keccak der neue SHA-3-Hash-Algorithmus sein wird. Im Gegensatz zu Block- und Stromchiffren, die invertierbar sind, erzeugen kryptografische Hash-Funktionen eine gehashte Ausgabe, die nicht zum Abrufen der ursprünglichen Eingabedaten verwendet werden kann. Kryptografische Hash-Funktionen werden verwendet, um die Authentizität von Daten zu überprüfen, die von einer nicht vertrauenswürdigen Quelle abgerufen wurden, oder um eine zusätzliche Sicherheitsebene zu schaffen. ⓘ
Kryptographie mit öffentlichem Schlüssel

Bei symmetrischen Kryptosystemen wird derselbe Schlüssel für die Ver- und Entschlüsselung einer Nachricht verwendet, obwohl eine Nachricht oder eine Gruppe von Nachrichten einen anderen Schlüssel haben kann als andere. Ein erheblicher Nachteil symmetrischer Verschlüsselungen ist die für ihre sichere Verwendung erforderliche Schlüsselverwaltung. Jedes einzelne Paar von kommunizierenden Parteien muss im Idealfall einen anderen Schlüssel haben, und vielleicht auch für jeden ausgetauschten Chiffretext. Die Anzahl der erforderlichen Schlüssel steigt mit dem Quadrat der Anzahl der Netzmitglieder, was sehr schnell komplexe Schlüsselverwaltungssysteme erfordert, um sie alle konsistent und geheim zu halten. ⓘ
In einer bahnbrechenden Arbeit aus dem Jahr 1976 schlugen Whitfield Diffie und Martin Hellman den Begriff der Public-Key-Kryptographie (auch allgemeiner als asymmetrischer Schlüssel bezeichnet) vor, bei der zwei unterschiedliche, aber mathematisch verwandte Schlüssel verwendet werden - ein öffentlicher und ein privater Schlüssel. Ein System mit öffentlichem Schlüssel ist so aufgebaut, dass die Berechnung des einen Schlüssels (des "privaten Schlüssels") aus dem anderen (dem "öffentlichen Schlüssel") rechnerisch nicht möglich ist, obwohl sie notwendigerweise miteinander verbunden sind. Stattdessen werden beide Schlüssel als ein zusammengehöriges Paar heimlich erzeugt. Der Historiker David Kahn bezeichnete die Public-Key-Kryptografie als "das revolutionärste neue Konzept auf diesem Gebiet seit der Entstehung der polyalphabetischen Substitution in der Renaissance". ⓘ
In Kryptosystemen mit öffentlichem Schlüssel kann der öffentliche Schlüssel frei verteilt werden, während der dazugehörige private Schlüssel geheim bleiben muss. In einem Verschlüsselungssystem mit öffentlichem Schlüssel wird der öffentliche Schlüssel zur Verschlüsselung verwendet, während der private oder geheime Schlüssel zur Entschlüsselung verwendet wird. Diffie und Hellman konnten zwar kein solches System finden, zeigten aber mit dem Diffie-Hellman-Schlüsselaustauschprotokoll, das heute in der sicheren Kommunikation weit verbreitet ist, dass die Verschlüsselung mit öffentlichen Schlüsseln möglich ist. Der X.509-Standard definiert das am häufigsten verwendete Format für Zertifikate für öffentliche Schlüssel. ⓘ
Die Veröffentlichung von Diffie und Hellman löste weitreichende akademische Bemühungen aus, ein praktisches Verschlüsselungssystem mit öffentlichen Schlüsseln zu finden. Dieses Rennen wurde schließlich 1978 von Ronald Rivest, Adi Shamir und Len Adleman gewonnen, deren Lösung seitdem als RSA-Algorithmus bekannt ist. ⓘ
Der Diffie-Hellman- und der RSA-Algorithmus sind nicht nur die ersten öffentlich bekannten Beispiele für hochwertige Public-Key-Algorithmen, sondern gehören auch zu den am häufigsten verwendeten. Andere asymmetrische Schlüsselalgorithmen sind das Cramer-Shoup-Kryptosystem, die ElGamal-Verschlüsselung und verschiedene Elliptische-Kurven-Verfahren. ⓘ
Aus einem 1997 veröffentlichten Dokument des britischen Geheimdienstes Government Communications Headquarters (GCHQ) geht hervor, dass die Kryptographen des GCHQ mehrere akademische Entwicklungen vorweggenommen haben. Berichten zufolge hatte James H. Ellis um 1970 die Grundsätze der asymmetrischen Kryptographie entwickelt. 1973 erfand Clifford Cocks eine Lösung, die dem RSA-Konzept sehr ähnlich war. Im Jahr 1974 soll Malcolm J. Williamson den Diffie-Hellman-Schlüsselaustausch entwickelt haben. ⓘ

Die Kryptographie mit öffentlichen Schlüsseln wird auch für die Implementierung digitaler Signaturverfahren verwendet. Eine digitale Signatur erinnert an eine gewöhnliche Unterschrift; beide haben die Eigenschaft, dass sie für einen Benutzer leicht zu erstellen, aber für jeden anderen schwer zu fälschen sind. Digitale Signaturen können auch dauerhaft mit dem Inhalt der zu unterzeichnenden Nachricht verknüpft werden; sie können dann nicht von einem Dokument zum anderen "verschoben" werden, da jeder Versuch nachweisbar ist. Bei digitalen Unterschriftsverfahren gibt es zwei Algorithmen: einen für die Unterzeichnung, bei dem ein geheimer Schlüssel verwendet wird, um die Nachricht zu verarbeiten (oder ein Hash der Nachricht oder beides), und einen für die Überprüfung, bei dem der passende öffentliche Schlüssel zusammen mit der Nachricht verwendet wird, um die Gültigkeit der Unterschrift zu überprüfen. RSA und DSA sind zwei der bekanntesten digitalen Signaturverfahren. Digitale Signaturen sind von zentraler Bedeutung für den Betrieb von Public-Key-Infrastrukturen und vielen Netzsicherheitsverfahren (z. B. SSL/TLS, viele VPNs usw.). ⓘ
Public-Key-Algorithmen basieren meist auf der Rechenkomplexität "harter" Probleme, oft aus der Zahlentheorie. Die Schwierigkeit von RSA hängt beispielsweise mit dem Problem der ganzzahligen Faktorisierung zusammen, während Diffie-Hellman und DSA mit dem Problem des diskreten Logarithmus verbunden sind. Die Sicherheit der Kryptographie mit elliptischen Kurven basiert auf zahlentheoretischen Problemen mit elliptischen Kurven. Aufgrund der Schwierigkeit der zugrundeliegenden Probleme beinhalten die meisten Public-Key-Algorithmen Operationen wie modulare Multiplikation und Potenzierung, die sehr viel rechenintensiver sind als die in den meisten Blockchiffren verwendeten Techniken, insbesondere bei typischen Schlüsselgrößen. Daher handelt es sich bei Kryptosystemen mit öffentlichem Schlüssel in der Regel um hybride Kryptosysteme, bei denen ein schneller, qualitativ hochwertiger symmetrischer Verschlüsselungsalgorithmus für die Nachricht selbst verwendet wird, während der entsprechende symmetrische Schlüssel mit der Nachricht versandt wird, jedoch mit einem Algorithmus mit öffentlichem Schlüssel verschlüsselt wird. In ähnlicher Weise werden häufig hybride Signaturverfahren verwendet, bei denen eine kryptografische Hash-Funktion berechnet wird und nur der daraus resultierende Hash-Wert digital signiert wird. ⓘ
Die Sicherheit der faktorisierungsbasierten Public-Key-Kryptographie liegt in der Verwendung eines Produkts aus großen Primzahlen, welches als öffentlicher Schlüssel dient. Der private Schlüssel besteht aus den dazugehörenden Primfaktoren bzw. davon abgeleiteten Werten. Die Zerlegung einer hinreichend großen Zahl gilt aufgrund der sehr aufwendigen Faktorisierung als nicht praktikabel. ⓘ
Beispiel zur Faktorisierung
Anschaulich gesprochen ist es trotz ausgefeilter Faktorisierungsverfahren schwierig, zu einer gegebenen Zahl, die das Produkt zweier großer Primfaktoren ist, z. B. der Zahl 805963, einen dieser Faktoren zu finden. Der Berechnungsaufwand zum Finden eines Faktors wächst dabei mit zunehmender Länge der Zahl sehr schnell, was bei genügend großen Zahlen dazu führt, dass die Faktorisierung auch auf einem Supercomputer tausende Jahre dauern würde. In der Praxis werden daher Zahlen mit mehreren hundert Dezimalstellen verwendet. Für die Multiplikation großer Zahlen existieren hingegen effiziente Algorithmen; es ist also leicht, aus zwei Faktoren (919 und 877) das Produkt (805963) zu berechnen. Diese Asymmetrie im Aufwand von Multiplikation und Faktorisierung macht man sich in bei faktorisierungsbasierten Public-Key-Verfahren zu Nutze. Kryptographisch sichere Verfahren sind dann solche, für die es keine bessere Methode zum Brechen der Sicherheit als das Faktorisieren einer großen Zahl gibt, insbesondere kann der private nicht aus dem öffentlichen Schlüssel errechnet werden. ⓘ
Kryptografische Hash-Funktionen
Kryptografische Hash-Funktionen sind kryptografische Algorithmen, mit denen bestimmte Schlüssel zur Verschlüsselung von Daten für die symmetrische oder asymmetrische Verschlüsselung erzeugt und verwendet werden können, wobei diese Funktionen selbst als Schlüssel betrachtet werden können. Sie nehmen eine Nachricht beliebiger Länge als Eingabe und geben einen kurzen Hash mit fester Länge aus, der z. B. für eine digitale Signatur verwendet werden kann. Bei guten Hash-Funktionen kann ein Angreifer keine zwei Nachrichten finden, die denselben Hash ergeben. MD4 ist eine seit langem genutzte Hash-Funktion, die jetzt gebrochen ist; MD5, eine verstärkte Variante von MD4, ist ebenfalls weit verbreitet, aber in der Praxis gebrochen. Die Nationale Sicherheitsbehörde der USA hat eine Reihe von MD5-ähnlichen Hash-Funktionen, den Secure Hash Algorithm, entwickelt: SHA-0 war ein fehlerhafter Algorithmus, der von der Behörde zurückgezogen wurde; SHA-1 ist weit verbreitet und sicherer als MD5, aber Kryptoanalytiker haben Angriffe gegen ihn festgestellt; die SHA-2-Familie verbessert SHA-1, ist aber seit 2011 anfällig für Konflikte; und die US-Normenbehörde hielt es aus Sicherheitsgründen für "klug", einen neuen Standard zu entwickeln, um "die Robustheit des gesamten NIST-Hash-Algorithmus-Toolkits deutlich zu verbessern". Daher wurde ein Wettbewerb zur Entwicklung von Hash-Funktionen ausgeschrieben, um bis 2012 einen neuen nationalen US-Standard mit der Bezeichnung SHA-3 auszuwählen. Der Wettbewerb endete am 2. Oktober 2012, als das NIST bekannt gab, dass Keccak der neue SHA-3-Hash-Algorithmus sein wird. Im Gegensatz zu Block- und Stromchiffren, die invertierbar sind, erzeugen kryptografische Hash-Funktionen eine gehashte Ausgabe, die nicht zum Abrufen der ursprünglichen Eingabedaten verwendet werden kann. Kryptografische Hash-Funktionen werden verwendet, um die Authentizität von Daten zu überprüfen, die von einer nicht vertrauenswürdigen Quelle abgerufen wurden, oder um eine zusätzliche Sicherheitsebene zu schaffen. ⓘ
Kryptoanalyse

Das Ziel der Kryptoanalyse besteht darin, eine Schwachstelle oder Unsicherheit in einem kryptografischen System zu finden, die eine Umgehung oder Umgehung des Systems ermöglicht. ⓘ
Es ist ein weit verbreiteter Irrglaube, dass jede Verschlüsselungsmethode geknackt werden kann. Im Zusammenhang mit seiner Arbeit in den Bell Labs im Zweiten Weltkrieg hat Claude Shannon bewiesen, dass die Chiffre mit dem One-Time-Pad unknackbar ist, vorausgesetzt, das Schlüsselmaterial ist wirklich zufällig, wird nie wiederverwendet, wird vor allen möglichen Angreifern geheim gehalten und ist gleich lang oder länger als die Nachricht. Die meisten Chiffren, abgesehen vom One-Time-Pad, können mit ausreichendem Rechenaufwand durch Brute-Force-Angriffe geknackt werden, aber der erforderliche Aufwand kann exponentiell von der Schlüsselgröße abhängen, verglichen mit dem Aufwand, der für die Nutzung der Chiffre erforderlich ist. In solchen Fällen kann eine wirksame Sicherheit erreicht werden, wenn bewiesen wird, dass der erforderliche Aufwand (d. h. der "Arbeitsfaktor" nach Shannon) jenseits der Fähigkeiten eines jeden Gegners liegt. Das heißt, es muss gezeigt werden, dass keine effiziente Methode (im Gegensatz zur zeitaufwändigen Brute-Force-Methode) gefunden werden kann, um die Chiffre zu knacken. Da ein solcher Beweis bis heute nicht erbracht wurde, bleibt das One-Time-Pad die einzige theoretisch unknackbare Chiffre. Obwohl eine gut implementierte One-Time-Pad-Verschlüsselung nicht geknackt werden kann, ist eine Verkehrsanalyse dennoch möglich. ⓘ
Es gibt eine Vielzahl von kryptoanalytischen Angriffen, die auf verschiedene Arten klassifiziert werden können. Eine gängige Unterscheidung hängt davon ab, was Eve (ein Angreifer) weiß und welche Möglichkeiten ihr zur Verfügung stehen. Bei einem reinen Chiffretext-Angriff hat Eve nur Zugriff auf den Chiffretext (gute moderne Kryptosysteme sind in der Regel effektiv immun gegen reine Chiffretext-Angriffe). Bei einem Angriff mit bekanntem Klartext hat Eve Zugriff auf einen Chiffretext und den dazugehörigen Klartext (oder auf viele solcher Paare). Bei einem Angriff mit ausgewähltem Klartext kann Eve einen Klartext auswählen und den entsprechenden Chiffretext (vielleicht viele Male) erfahren; ein Beispiel ist die Gartenarbeit, die von den Briten im Zweiten Weltkrieg verwendet wurde. Bei einem Angriff mit gewähltem Chiffretext kann Eve möglicherweise Chiffretexte wählen und die entsprechenden Klartexte erfahren. Bei einem Man-in-the-Middle-Angriff schließlich schaltet sich Eve zwischen Alice (den Absender) und Bob (den Empfänger), greift auf den Datenverkehr zu, verändert ihn und leitet ihn dann an den Empfänger weiter. Ebenfalls von Bedeutung, wenn auch oft von überragender Bedeutung, sind Fehler (im Allgemeinen bei der Entwicklung oder Verwendung eines der beteiligten Protokolle). ⓘ
Bei der Kryptoanalyse von symmetrischen Chiffren wird in der Regel nach Angriffen auf die Block- oder Stromchiffren gesucht, die effizienter sind als jeder Angriff, der gegen eine perfekte Chiffre möglich wäre. Ein einfacher Brute-Force-Angriff gegen DES erfordert beispielsweise einen bekannten Klartext und 255 Entschlüsselungen, wobei etwa die Hälfte der möglichen Schlüssel ausprobiert wird, um einen Punkt zu erreichen, an dem die Chancen besser als gleich sind, dass der gesuchte Schlüssel gefunden wurde. Dies ist jedoch möglicherweise nicht sicher genug; ein linearer Kryptoanalyse-Angriff auf DES erfordert 243 bekannte Klartexte (mit den entsprechenden Chiffretexten) und etwa 243 DES-Operationen. Dies ist eine erhebliche Verbesserung gegenüber Brute-Force-Angriffen. ⓘ
Die Algorithmen für öffentliche Schlüssel basieren auf der Rechenschwierigkeit verschiedener Probleme. Die berühmtesten davon sind die Schwierigkeit der ganzzahligen Faktorisierung von Semiprimzahlen und die Schwierigkeit der Berechnung diskreter Logarithmen, von denen noch nicht bewiesen ist, dass sie in Polynomialzeit (P) nur mit einem klassischen Turing-Computer lösbar sind. Ein Großteil der Kryptoanalyse von öffentlichen Schlüsseln befasst sich mit der Entwicklung von Algorithmen in P, die diese Probleme lösen können, oder mit der Verwendung anderer Technologien, wie z. B. Quantencomputern. So sind beispielsweise die bekanntesten Algorithmen zur Lösung der auf elliptischen Kurven basierenden Version des diskreten Logarithmus sehr viel zeitaufwändiger als die bekanntesten Algorithmen zum Faktorisieren, zumindest für Probleme von mehr oder weniger gleicher Größe. Um eine gleichwertige Verschlüsselungsstärke zu erreichen, benötigen Techniken, die auf der Schwierigkeit der Faktorisierung großer zusammengesetzter Zahlen beruhen, wie z. B. das RSA-Kryptosystem, daher größere Schlüssel als Techniken mit elliptischen Kurven. Aus diesem Grund sind Kryptosysteme mit öffentlichen Schlüsseln, die auf elliptischen Kurven basieren, seit ihrer Erfindung Mitte der 1990er Jahre sehr beliebt geworden. ⓘ
Während die reine Kryptoanalyse Schwachstellen in den Algorithmen selbst nutzt, basieren andere Angriffe auf Kryptosysteme auf der tatsächlichen Verwendung der Algorithmen in realen Geräten und werden als Seitenkanalangriffe bezeichnet. Wenn ein Kryptoanalytiker beispielsweise Zugriff auf die Zeit hat, die das Gerät für die Verschlüsselung einer Reihe von Klartexten oder für die Meldung eines Fehlers in einem Kennwort oder PIN-Zeichen benötigt hat, kann er unter Umständen einen Zeitangriff durchführen, um eine Chiffre zu knacken, die ansonsten gegen eine Analyse resistent ist. Ein Angreifer könnte auch das Muster und die Länge von Nachrichten untersuchen, um daraus wertvolle Informationen abzuleiten; dies ist als Verkehrsanalyse bekannt und kann für einen aufmerksamen Angreifer recht nützlich sein. Eine schlechte Verwaltung eines Kryptosystems, z. B. das Zulassen zu kurzer Schlüssel, macht jedes System angreifbar, unabhängig von anderen Vorzügen. Social Engineering und andere Angriffe auf Menschen (z.B. Bestechung, Erpressung, Spionage, Folter, ...) werden in der Regel eingesetzt, da sie im Vergleich zur reinen Kryptoanalyse deutlich kostengünstiger und in angemessener Zeit durchführbar sind. ⓘ
Kryptographische Primitive
Ein großer Teil der theoretischen Arbeit in der Kryptographie betrifft kryptographische Primitive - Algorithmen mit grundlegenden kryptographischen Eigenschaften - und ihre Beziehung zu anderen kryptographischen Problemen. Aus diesen grundlegenden Primitiven werden dann kompliziertere kryptografische Werkzeuge entwickelt. Diese Primitive liefern grundlegende Eigenschaften, die zur Entwicklung komplexerer Werkzeuge, so genannter Kryptosysteme oder kryptografischer Protokolle, verwendet werden, die eine oder mehrere hochrangige Sicherheitseigenschaften garantieren. Beachten Sie jedoch, dass die Unterscheidung zwischen kryptografischen Primitiven und Kryptosystemen recht willkürlich ist; so wird beispielsweise der RSA-Algorithmus manchmal als Kryptosystem und manchmal als Primitiv betrachtet. Typische Beispiele für kryptografische Primitive sind Pseudozufallsfunktionen, Einwegfunktionen usw. ⓘ
Kryptosysteme
Ein oder mehrere kryptografische Primitive werden häufig zur Entwicklung eines komplexeren Algorithmus verwendet, der als kryptografisches System oder Kryptosystem bezeichnet wird. Kryptosysteme (z. B. El-Gamal-Verschlüsselung) sind so konzipiert, dass sie eine bestimmte Funktionalität (z. B. Verschlüsselung mit öffentlichem Schlüssel) bieten und gleichzeitig bestimmte Sicherheitseigenschaften garantieren (z. B. Sicherheit bei chosen-plaintext attack (CPA) im Zufallsorakelmodell). Kryptosysteme nutzen die Eigenschaften der zugrunde liegenden kryptografischen Primitive, um die Sicherheitseigenschaften des Systems zu unterstützen. Da die Unterscheidung zwischen Primitiven und Kryptosystemen etwas willkürlich ist, kann ein hochentwickeltes Kryptosystem aus einer Kombination von mehreren primitiveren Kryptosystemen abgeleitet werden. In vielen Fällen beinhaltet die Struktur des Kryptosystems eine Hin- und Her-Kommunikation zwischen zwei oder mehreren Parteien im Raum (z. B. zwischen dem Absender einer sicheren Nachricht und ihrem Empfänger) oder über die Zeit (z. B. kryptografisch geschützte Sicherungsdaten). Solche Kryptosysteme werden manchmal als kryptographische Protokolle bezeichnet. ⓘ
Einige weithin bekannte Kryptosysteme sind RSA, Schnorr-Signatur, ElGamal-Verschlüsselung und Pretty Good Privacy (PGP). Zu den komplexeren Kryptosystemen gehören elektronische Geldsysteme, Unterschriftenverschlüsselungssysteme usw. Zu den eher "theoretischen" Kryptosystemen gehören interaktive Beweissysteme (z. B. Zero-Knowledge-Beweise), Systeme zur gemeinsamen Nutzung von Geheimnissen usw. ⓘ
Leichtgewichtige Kryptographie
Die leichtgewichtige Kryptografie (LWC) betrifft kryptografische Algorithmen, die für ein streng begrenztes Umfeld entwickelt wurden. Das Wachstum des Internets der Dinge (IoT) hat die Forschung zur Entwicklung von leichtgewichtigen Algorithmen, die für diese Umgebung besser geeignet sind, vorangetrieben. Eine IoT-Umgebung erfordert strenge Beschränkungen in Bezug auf Stromverbrauch, Verarbeitungsleistung und Sicherheit. Algorithmen wie PRESENT, AES und SPECK sind Beispiele für die vielen LWC-Algorithmen, die entwickelt wurden, um den vom National Institute of Standards and Technology festgelegten Standard zu erreichen. ⓘ
Anwendungen
Im Allgemeinen
Die Kryptografie wird im Internet häufig eingesetzt, um Benutzerdaten zu schützen und Abhörmaßnahmen zu verhindern. Um die Geheimhaltung während der Übertragung zu gewährleisten, verwenden viele Systeme die Kryptografie mit privaten Schlüsseln, um die übertragenen Informationen zu schützen. Mit Public-Key-Systemen kann man die Geheimhaltung ohne einen Hauptschlüssel oder eine große Anzahl von Schlüsseln aufrechterhalten. Einige Algorithmen wie Bitlocker und Veracrypt sind jedoch im Allgemeinen keine Private-Public-Key-Kryptografie. Veracrypt z. B. verwendet einen Kennwort-Hash, um den einzigen privaten Schlüssel zu erzeugen. Er kann jedoch so konfiguriert werden, dass er in Systemen mit öffentlich-privatem Schlüssel läuft. Die quelloffene C++-Verschlüsselungsbibliothek OpenSSL bietet freie und quelloffene Verschlüsselungssoftware und -werkzeuge. Das am häufigsten verwendete Verschlüsselungsverfahren ist AES, da es über eine Hardwarebeschleunigung für alle x86-basierten Prozessoren verfügt, die AES-NI unterstützen. Ein enger Konkurrent ist ChaCha20-Poly1305, eine Stromchiffre, die jedoch in der Regel für mobile Geräte verwendet wird, da diese auf ARM basieren und keine AES-NI-Befehlssatzerweiterung aufweisen. ⓘ
In der Cybersicherheit
Kryptografie kann zur Sicherung der Kommunikation durch Verschlüsselung eingesetzt werden. Websites verwenden die Verschlüsselung über HTTPS. Die "Ende-zu-Ende"-Verschlüsselung, bei der nur Absender und Empfänger Nachrichten lesen können, wird für E-Mails in Pretty Good Privacy und für sichere Nachrichtenübermittlung im Allgemeinen in WhatsApp, Signal und Telegram eingesetzt. ⓘ
Betriebssysteme verwenden Verschlüsselung, um Passwörter geheim zu halten, Teile des Systems zu verbergen und sicherzustellen, dass Software-Updates wirklich vom Systemhersteller stammen. Anstatt Passwörter im Klartext zu speichern, speichern Computersysteme Hashes davon. Wenn sich ein Benutzer anmeldet, lässt das System das eingegebene Passwort durch eine kryptografische Hash-Funktion laufen und vergleicht es mit dem Hash-Wert in der Datei. Auf diese Weise hat weder das System noch ein Angreifer zu irgendeinem Zeitpunkt Zugriff auf das Passwort im Klartext. ⓘ
Die Verschlüsselung wird manchmal dazu verwendet, das gesamte Laufwerk zu verschlüsseln. Das University College London hat beispielsweise BitLocker (ein Programm von Microsoft) implementiert, um Laufwerksdaten undurchsichtig zu machen, ohne dass sich die Benutzer anmelden müssen. ⓘ
Rechtliche Fragen
Verbote
Die Kryptografie ist seit langem für Geheimdienste und Strafverfolgungsbehörden von Interesse. Geheime Kommunikation kann kriminell oder sogar verräterisch sein. Wegen der Erleichterung des Schutzes der Privatsphäre und der mit dem Verbot einhergehenden Beeinträchtigung der Privatsphäre ist die Kryptografie auch für Bürgerrechtsaktivisten von großem Interesse. Dementsprechend gab es in der Vergangenheit immer wieder kontroverse rechtliche Fragen im Zusammenhang mit der Kryptografie, insbesondere seit dem Aufkommen preiswerter Computer, die einen breiten Zugang zu hochwertiger Kryptografie ermöglichen. ⓘ
In einigen Ländern ist bzw. war sogar die Verwendung von Kryptographie im Inland eingeschränkt. Bis 1999 schränkte Frankreich die Verwendung von Kryptographie im Inland erheblich ein, hat aber seitdem viele dieser Vorschriften gelockert. In China und im Iran ist für die Verwendung von Kryptographie nach wie vor eine Lizenz erforderlich. Viele Länder haben strenge Beschränkungen für den Einsatz von Kryptographie. Zu den restriktivsten gehören die Gesetze in Belarus, Kasachstan, der Mongolei, Pakistan, Singapur, Tunesien und Vietnam. ⓘ
In den Vereinigten Staaten ist die Kryptographie für den Inlandsgebrauch legal, aber es hat viele Konflikte über rechtliche Fragen im Zusammenhang mit der Kryptographie gegeben. Ein besonders wichtiges Thema war die Ausfuhr von Kryptographie und kryptographischer Software und Hardware. Wahrscheinlich aufgrund der Bedeutung der Kryptoanalyse im Zweiten Weltkrieg und der Erwartung, dass die Kryptografie auch weiterhin für die nationale Sicherheit wichtig sein würde, haben viele westliche Regierungen die Ausfuhr von Kryptografie zu einem bestimmten Zeitpunkt streng geregelt. Nach dem Zweiten Weltkrieg war es in den USA illegal, Verschlüsselungstechnologie nach Übersee zu verkaufen oder zu vertreiben; tatsächlich wurde Verschlüsselung als militärische Hilfsausrüstung eingestuft und auf die Munitionsliste der Vereinigten Staaten gesetzt. Bis zur Entwicklung von Personalcomputern, asymmetrischen Schlüsselalgorithmen (d. h. Public-Key-Techniken) und dem Internet war dies nicht besonders problematisch. Mit der Entwicklung des Internets und der zunehmenden Verbreitung von Computern wurden jedoch hochwertige Verschlüsselungstechniken auf der ganzen Welt bekannt. ⓘ
Ausfuhrkontrollen
In den 1990er Jahren wurden die US-Ausfuhrbestimmungen für Kryptografie mehrfach in Frage gestellt. Nachdem der Quellcode des Verschlüsselungsprogramms Pretty Good Privacy (PGP) von Philip Zimmermann im Juni 1991 seinen Weg ins Internet gefunden hatte, führte eine Beschwerde von RSA Security (damals RSA Data Security, Inc.) zu einer langwierigen strafrechtlichen Untersuchung gegen Zimmermann durch die US-Zollbehörde und das FBI, obwohl nie Anklage erhoben wurde. Daniel J. Bernstein, damals Doktorand an der UC Berkeley, reichte Klage gegen die US-Regierung ein, um einige Aspekte der Beschränkungen aus Gründen der Meinungsfreiheit anzufechten. Der Fall Bernstein gegen die Vereinigten Staaten aus dem Jahr 1995 führte schließlich zu einem Urteil aus dem Jahr 1999, wonach der gedruckte Quellcode für kryptografische Algorithmen und Systeme durch die Verfassung der Vereinigten Staaten als freie Meinungsäußerung geschützt ist. ⓘ
1996 unterzeichneten neununddreißig Länder das Wassenaar-Arrangement, ein Rüstungskontrollabkommen, das sich mit der Ausfuhr von Waffen und "Dual-Use"-Technologien wie der Kryptografie befasst. In diesem Vertrag wurde festgelegt, dass die Verwendung von Kryptographie mit kurzen Schlüssellängen (56 Bit für symmetrische Verschlüsselung, 512 Bit für RSA) nicht länger der Exportkontrolle unterliegt. Die Ausfuhr von Kryptographie aus den USA wurde im Jahr 2000 stark gelockert; es gibt nicht mehr viele Beschränkungen für die Schlüssellängen von in die USA exportierter Software für den Massenmarkt. Seit dieser Lockerung der US-Ausfuhrbeschränkungen und weil die meisten an das Internet angeschlossenen PCs mit Webbrowsern aus den USA wie Firefox oder Internet Explorer ausgestattet sind, hat fast jeder Internetnutzer weltweit über seinen Browser potenziell Zugang zu hochwertiger Kryptografie (z. B. über Transport Layer Security). Die E-Mail-Client-Programme Mozilla Thunderbird und Microsoft Outlook können ebenfalls E-Mails über TLS übertragen und empfangen sowie mit S/MIME verschlüsselte E-Mails senden und empfangen. Vielen Internetnutzern ist nicht bewusst, dass ihre Basisanwendungssoftware so umfangreiche Kryptosysteme enthält. Diese Browser und E-Mail-Programme sind so allgegenwärtig, dass selbst Regierungen, die die zivile Nutzung von Kryptografie regeln wollen, es im Allgemeinen nicht für sinnvoll halten, die Verbreitung oder Nutzung von Kryptografie dieser Qualität zu kontrollieren. ⓘ
Beteiligung der NSA

Ein weiteres umstrittenes Thema im Zusammenhang mit der Kryptografie in den Vereinigten Staaten ist der Einfluss der Nationalen Sicherheitsbehörde (NSA) auf die Entwicklung von Chiffriergeräten und die entsprechende Politik. Die NSA war an der Entwicklung von DES beteiligt, als es bei IBM entwickelt und vom National Bureau of Standards als möglicher Bundesstandard für Kryptografie in Betracht gezogen wurde. DES wurde so konzipiert, dass es gegen die differentielle Kryptoanalyse resistent ist, eine leistungsfähige und allgemeine kryptoanalytische Technik, die der NSA und IBM bekannt war, aber erst öffentlich bekannt wurde, als sie in den späten 1980er Jahren wiederentdeckt wurde. Laut Steven Levy entdeckte IBM die differentielle Kryptoanalyse, hielt die Technik aber auf Wunsch der NSA geheim. Die Technik wurde erst öffentlich bekannt, als Biham und Shamir sie einige Jahre später wiederentdeckten und bekannt gaben. Die ganze Angelegenheit zeigt, wie schwierig es ist, festzustellen, über welche Ressourcen und Kenntnisse ein Angreifer tatsächlich verfügt. ⓘ
Ein weiteres Beispiel für die Beteiligung der NSA war die Clipper-Chip-Affäre von 1993, ein Verschlüsselungs-Mikrochip, der Teil der Capstone-Initiative zur Kontrolle der Kryptographie sein sollte. Clipper wurde von Kryptographen aus zwei Gründen stark kritisiert. Der Chiffrieralgorithmus (Skipjack genannt) war damals als geheim eingestuft (die Freigabe erfolgte 1998, lange nachdem die Clipper-Initiative ausgelaufen war). Die geheime Chiffre gab Anlass zu der Befürchtung, dass die NSA die Chiffre absichtlich schwach gemacht hatte, um ihre geheimdienstlichen Bemühungen zu unterstützen. Die gesamte Initiative wurde auch wegen ihres Verstoßes gegen das Kerckhoffsche Prinzip kritisiert, da das System einen speziellen Treuhandschlüssel enthielt, der von der Regierung zur Verwendung durch die Strafverfolgungsbehörden (d. h. zum Abhören) gehalten wurde. ⓘ
Verwaltung digitaler Rechte
Die Kryptografie ist ein zentrales Element der digitalen Rechteverwaltung (DRM), einer Gruppe von Techniken zur technischen Kontrolle der Nutzung von urheberrechtlich geschütztem Material, die auf Betreiben einiger Urheberrechtsinhaber in großem Umfang eingeführt und genutzt wird. 1998 unterzeichnete US-Präsident Bill Clinton den Digital Millennium Copyright Act (DMCA), der die Herstellung, Verbreitung und Verwendung bestimmter kryptoanalytischer Techniken und Technologien (die heute bekannt sind oder später entdeckt wurden) unter Strafe stellte, insbesondere solcher, die zur Umgehung von DRM-Technologien verwendet werden können. Dies hatte spürbare Auswirkungen auf die Kryptographie-Forschungsgemeinschaft, da man argumentieren kann, dass jegliche kryptoanalytische Forschung gegen das DMCA verstößt. Ähnliche Gesetze sind seitdem in mehreren Ländern und Regionen erlassen worden, einschließlich der Umsetzung in der EU-Urheberrechtsrichtlinie. Ähnliche Beschränkungen werden in Verträgen gefordert, die von den Mitgliedsstaaten der Weltorganisation für geistiges Eigentum unterzeichnet wurden. ⓘ
Das US-Justizministerium und das FBI haben das DMCA nicht so rigoros durchgesetzt, wie einige befürchtet hatten, aber das Gesetz bleibt dennoch umstritten. Niels Ferguson, ein angesehener Kryptographieforscher, hat öffentlich erklärt, dass er einige seiner Forschungsergebnisse zu einem Intel-Sicherheitsdesign aus Angst vor einer strafrechtlichen Verfolgung nach dem DMCA nicht veröffentlichen wird. Der Kryptologe Bruce Schneier hat argumentiert, dass das DMCA die Bindung an einen bestimmten Anbieter fördert und tatsächliche Maßnahmen zur Cybersicherheit behindert. Sowohl Alan Cox (langjähriger Linux-Kernel-Entwickler) als auch Edward Felten (und einige seiner Studenten in Princeton) sind auf Probleme im Zusammenhang mit dem Gesetz gestoßen. Dmitry Sklyarov wurde während eines Besuchs aus Russland in den USA verhaftet und wegen angeblicher Verstöße gegen das DMCA im Zusammenhang mit seiner Arbeit in Russland, wo diese legal war, für fünf Monate ins Gefängnis gesteckt. Im Jahr 2007 wurden die kryptografischen Schlüssel, die für die Verschlüsselung von Blu-ray- und HD-DVD-Inhalten verantwortlich sind, entdeckt und im Internet veröffentlicht. In beiden Fällen verschickte die Motion Picture Association of America zahlreiche DMCA-Abmahnungen, und es kam zu einer massiven Gegenreaktion im Internet, die durch die wahrgenommenen Auswirkungen solcher Meldungen auf die faire Nutzung und die Redefreiheit ausgelöst wurde. ⓘ
Erzwungene Offenlegung von Verschlüsselungscodes
Im Vereinigten Königreich gibt der Regulation of Investigatory Powers Act der Polizei die Befugnis, Verdächtige zu zwingen, Dateien zu entschlüsseln oder Passwörter zum Schutz von Verschlüsselungscodes herauszugeben. Die Nichtbefolgung ist ein eigenständiger Straftatbestand, der bei einer Verurteilung mit einer zweijährigen Haftstrafe oder in Fällen, in denen es um die nationale Sicherheit geht, mit bis zu fünf Jahren bestraft werden kann. Es gab bereits erfolgreiche Strafverfolgungen auf der Grundlage des Gesetzes; die erste im Jahr 2009 endete mit einer Freiheitsstrafe von 13 Monaten. Ähnliche Gesetze zur erzwungenen Offenlegung in Australien, Finnland, Frankreich und Indien zwingen einzelne Verdächtige, gegen die ermittelt wird, zur Herausgabe von Verschlüsselungsschlüsseln oder Passwörtern während einer strafrechtlichen Untersuchung. ⓘ
In den Vereinigten Staaten ging es in dem Bundesstrafverfahren Vereinigte Staaten gegen Fricosu um die Frage, ob eine Person durch einen Durchsuchungsbefehl gezwungen werden kann, eine Verschlüsselungspassphrase oder ein Passwort preiszugeben. Die Electronic Frontier Foundation (EFF) argumentierte, dass dies einen Verstoß gegen den im fünften Verfassungszusatz verankerten Schutz vor Selbstbezichtigung darstellt. Im Jahr 2012 entschied das Gericht, dass der Angeklagte gemäß dem All Writs Act verpflichtet sei, dem Gericht eine unverschlüsselte Festplatte vorzulegen. ⓘ
In vielen Gerichtsbarkeiten ist der rechtliche Status der erzwungenen Offenlegung nach wie vor unklar. ⓘ
Im Verschlüsselungsstreit zwischen dem FBI und Apple aus dem Jahr 2016 geht es um die Möglichkeit der Gerichte in den Vereinigten Staaten, die Unterstützung der Hersteller bei der Entsperrung von Mobiltelefonen zu erzwingen, deren Inhalt kryptografisch geschützt ist. ⓘ
Als mögliche Gegenmaßnahme zur erzwungenen Offenlegung unterstützt einige kryptografische Software die plausible Bestreitbarkeit, bei der die verschlüsselten Daten nicht von unbenutzten Zufallsdaten zu unterscheiden sind (z. B. von denen eines Laufwerks, das sicher gelöscht wurde). ⓘ
Abgrenzung zur Steganographie
Sowohl Kryptographie als auch Steganographie haben zum Ziel, die Vertraulichkeit einer Nachricht zu schützen. Allerdings unterscheiden sie sich im Ansatzpunkt der Verfahren:
- Kryptographie verschlüsselt die Nachricht. Somit sorgt sie dafür, dass eine unbeteiligte dritte Person, die die (verschlüsselten) Daten zu Gesicht bekommt, die Bedeutung nicht erfassen kann.
- Steganographische Verfahren verbergen den Kanal, über den kommuniziert wird. Eine unbeteiligte dritte Person bleibt dadurch in Unkenntnis der Kommunikation. ⓘ
Kryptographische und steganographische Verfahren können kombiniert werden. Beispielsweise führt eine Verschlüsselung (Kryptographie) einer Nachricht, die über einen verdeckten Kanal kommuniziert wird (Steganographie), dazu, dass selbst nach dem Entdecken und erfolgreichen Auslesen des Kanals der Inhalt der Nachricht geheim bleibt. ⓘ
Ziele der Kryptographie
Die moderne Kryptographie hat vier Hauptziele zum Schutz von Datenbeständen, Nachrichten und/oder Übertragungskanälen:
- Vertraulichkeit/Zugriffsschutz: Nur dazu berechtigte Personen sollen in der Lage sein, die Daten oder die Nachricht zu lesen oder Informationen über ihren Inhalt zu erlangen.
- Integrität/Änderungsschutz: Die Daten müssen nachweislich vollständig und unverändert sein.
- Authentizität/Fälschungsschutz: Der Urheber der Daten oder der Absender der Nachricht soll eindeutig identifizierbar sein, und seine Urheberschaft sollte nachprüfbar sein.
- Verbindlichkeit/Nichtabstreitbarkeit: Der Urheber der Daten oder Absender einer Nachricht soll nicht in der Lage sein, seine Urheberschaft zu bestreiten, d. h., sie sollte sich gegenüber Dritten nachweisen lassen. ⓘ
Kryptographische Verfahren und Systeme dienen nicht notwendigerweise gleichzeitig allen der hier aufgelisteten Ziele. ⓘ
Geschichte der Kryptographie
Klassische Kryptographie
Der früheste belegte Einsatz von Kryptographie findet sich im dritten Jahrtausend v. Chr. in der altägyptischen Kryptographie des Alten Reiches. Hebräische Gelehrte benutzten im Mittelalter einfache Zeichentausch-Algorithmen (wie beispielsweise die Atbasch-Verschlüsselung). Im Mittelalter waren in ganz Europa vielfältige Geheimschriften zum Schutz des diplomatischen Briefverkehrs in Gebrauch, so etwa das Alphabetum Kaldeorum. Auch für heilkundliche Texte waren Geheimschriften in Gebrauch, etwa zur Niederschrift von Rezepten gegen die ab 1495 sich ausbreitende Syphilis. ⓘ
Ende des 19. Jahrhunderts kam es aufgrund der weiten Verbreitung des Telegrafen (den man auf einfache Weise anzapfen und abhören konnte) zu neuen Überlegungen in der Kryptographie. So formulierte Auguste Kerckhoffs von Nieuwenhof mit Kerckhoffs’ Prinzip einen Grundsatz der Kryptographie, wonach die Sicherheit eines kryptographischen Verfahrens nur von der Geheimhaltung des Schlüssels und nicht von der des Verfahrens abhängen soll. Das Verfahren selbst kann vielmehr veröffentlicht und von Experten auf seine Tauglichkeit untersucht werden. ⓘ
Kryptographie im Zweiten Weltkrieg

Im Zweiten Weltkrieg wurden mechanische und elektromechanische Schlüsselmaschinen, wie T52 oder SZ 42, zahlreich eingesetzt, auch wenn in Bereichen, wo dies nicht möglich war, weiterhin Handschlüssel wie der Doppelkastenschlüssel verwendet wurden. In dieser Zeit wurden große Fortschritte in der mathematischen Kryptographie gemacht. Notwendigerweise geschah dies jedoch nur im Geheimen. Die deutschen Militärs machten regen Gebrauch von einer als ENIGMA bekannten Maschine, die ab 1932 durch polnische und ab 1939 durch britische Codeknacker gebrochen wurde. ⓘ
Moderne Kryptographie
Beginn moderner Kryptographie
Das Zeitalter moderner Kryptographie begann mit Claude Shannon, möglicherweise dem Vater der mathematischen Kryptographie. 1949 veröffentlichte er den Artikel Communication Theory of Secrecy Systems. Dieser Artikel, zusammen mit seinen anderen Arbeiten über Informations- und Kommunikationstheorie, begründete eine starke mathematische Basis der Kryptographie. Hiermit endete auch eine Phase der Kryptographie, die auf die Geheimhaltung des Verfahrens setzte, um eine Entschlüsselung durch Dritte zu verhindern oder zu erschweren. Statt dieser – auch Security by obscurity genannten – Taktik müssen sich kryptografische Verfahren nun dem offenen wissenschaftlichen Diskurs stellen. ⓘ
Data Encryption Standard (DES)
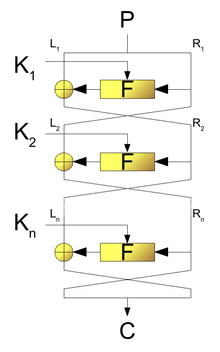
1976 gab es zwei wichtige Fortschritte. Erstens war dies der DES (Data Encryption Standard)-Algorithmus, entwickelt von IBM und der National Security Agency (NSA), um einen sicheren einheitlichen Standard für die behördenübergreifende Verschlüsselung zu schaffen (DES wurde 1977 unter dem Namen FIPS 46-2 (Federal Information Processing Standard) veröffentlicht). DES und sicherere Varianten davon (3DES) werden bis heute z. B. für Bankdienstleistungen eingesetzt. DES wurde 2001 durch den neuen FIPS-197-Standard AES ersetzt. ⓘ
Homomorphe Verschlüsselung
Ein homomorphes Verschlüsselungsverfahren erlaubt es, Berechnungen auf verschlüsselten Daten durchzuführen. Dem Kryptologen Craig Gentry gelang es 2009 nachzuweisen, dass ein Verschlüsselungsverfahren existiert, das beliebige Berechnungen auf verschlüsselten Daten zulässt. Eine homomorphe Verschlüsselung spielt eine wichtige Rolle beim Cloud-Computing. Um Datenmissbrauch bei der Verarbeitung sensibler Daten zu vermeiden, ist es wünschenswert, dass der Dienstleister nur auf den verschlüsselten Daten rechnet und die Klartexte nie zu Gesicht bekommt. ⓘ
Kryptographie und Mathematik
Die Sicherheit der meisten asymmetrischen Kryptosysteme beruht auf der Schwierigkeit von Problemen, die in der algorithmischen Zahlentheorie untersucht werden. Die bekanntesten dieser Probleme sind die Primfaktorzerlegung und das Finden diskreter Logarithmen. ⓘ
Weitere Anwendungen der Zahlentheorie
Außer dem Faktorisierungsproblem finden sowohl das Problem des Diskreten Logarithmus (Elgamal-Kryptosystem) als auch fortgeschrittene Methoden der algebraischen Zahlentheorie, wie etwa die Verschlüsselung über elliptische Kurven (ECC) breite Anwendung. ⓘ
Ein weiteres Anwendungsgebiet ist die Kodierungstheorie, die sich in ihrer modernen Form auf die Theorie der algebraischen Funktionenkörper stützt. ⓘ
Zukünftige Entwicklungen
Die derzeit wichtigsten Public-Key-Verfahren (RSA), Verfahren, die auf dem Diskreten Logarithmus in endlichen Körpern beruhen (z. B. DSA oder Diffie-Hellman), und Elliptic Curve Cryptography könnten theoretisch durch so genannte Quantencomputer in Polynomialzeit gebrochen werden und somit ihre Sicherheit verlieren. ⓘ
Kryptographie und Gesellschaft
In Zeiten des Internets wurde der Ruf auch nach privater Verschlüsselung laut. Bislang waren es Regierungen und globale Großunternehmen, die die RSA-Verschlüsselung aufgrund notwendiger, leistungsstarker Computer einsetzen konnten. Der amerikanische Physiker Phil Zimmermann entwickelte daraufhin eine RSA-Verschlüsselung für die breite Öffentlichkeit, die er Pretty Good Privacy (PGP) nannte und im Juni 1991 im Usenet veröffentlichte. Neu bei diesem Verfahren war die Möglichkeit, eine E-Mail mit einer digitalen Unterschrift zu unterzeichnen, die den Urheber der Nachricht eindeutig ausweist. ⓘ
Kryptographie und Recht
Da es moderne, computergestützte Verfahren jedem möglich machen, Informationen sicher zu verschlüsseln, besteht seitens der Regierungen ein Bedürfnis, diese Informationen entschlüsseln zu können. Die US-Regierung prüfte im Jahr 1996, ob ein Verfahren gegen den Erfinder von PGP, Phil Zimmermann, wegen illegalen Waffenexports eingeleitet werden könne. Sie stellte das Verfahren jedoch nach öffentlichen Protesten ein. In den USA unterliegt Kryptographie, wie auch in vielen anderen Ländern, einem Exportbeschränkungsgesetz. In den USA regelt der Arms Export Control Act und die International Traffic in Arms Regulations den Export von Kryptographietechniken. ⓘ
Oft gelingt Untersuchungsbehörden die Entschlüsselung eines Beweisstücks nur mit Hilfe des privaten Schlüssels. Es gibt in verschiedenen Ländern Mitwirkungspflichten bei der Entschlüsselung von Beweismaterial. Teilweise wird dabei auch vom Verdächtigten verlangt, den Schlüssel preiszugeben. In Großbritannien wurden Zuwiderhandlungen schon mit langen Haftstrafen geahndet. Nach Ansicht von Kritikern widerspricht dies dem Aussageverweigerungsrecht. ⓘ
In Frankreich gab es von 1990 bis 1996 ein Gesetz, das zum Deponieren dieses Schlüssels bei einer „vertrauenswürdigen Behörde“ verpflichtete. Damit verbunden war ein Verbot anderer Verfahren und Schlüssel. Einem Journalisten, der dies praktizieren wollte, ist es allerdings nicht gelungen, eine dafür zuständige Behörde zu finden. Nach einer Lockerung des Gesetzes 1996 ist die Verwendung bestimmter Kryptographieverfahren genehmigungspflichtig. Auch in Deutschland und in der EU gibt es seit Jahren Debatten über gesetzliche Kontrolle der Kryptographie. Ein Verbot der Kryptographie ist nicht praktikabel, da die Algorithmen bekannt sind und jeder mit den notwendigen Programmierkenntnissen ein entsprechendes Programm selbst schreiben könnte. Web-Anwendungen wie z. B. elektronisches Banking oder Shopping sind ohne Kryptographie nicht denkbar. ⓘ
Im Rahmen der digitalen Rechteverwaltung werden Kryptographieverfahren eingesetzt, deren Umgehung (mittels Kryptoanalyse) unter Strafe gestellt ist. ⓘ

