Lichtgeschwindigkeit

Geschwindigkeit des Lichts ⓘ

Im Durchschnitt braucht das Sonnenlicht etwa 8 Minuten und 17 Sekunden, um von der Sonne zur Erde zu gelangen.
Genaue Werte
Meter pro Sekunde	299792458
Ungefähre Werte (auf drei signifikante Stellen)
Kilometer pro Stunde	1080000000
Meilen pro Sekunde	186000
Meilen pro Stunde	671000000
Astronomische Einheiten pro Tag	173
Parsecs pro Jahr	0.307
Ungefähre Laufzeiten von Lichtsignalen
Entfernung	Zeit
ein Fuß	1,0 ns
ein Meter	3,3 ns
von der geostationären Umlaufbahn zur Erde	119 ms
die Länge des Äquators der Erde	134 ms
vom Mond zur Erde	1.3 s
von der Sonne zur Erde (1 AU)	8,3 min
ein Lichtjahr	1,0 Jahr
ein Parsec	3,26 Jahre
vom nächstgelegenen Stern zur Sonne (1,3 pc)	4,2 Jahre
von der nächstgelegenen Galaxie zur Erde	25000 Jahre
quer durch die Milchstraße	100000 Jahre
von der Andromeda-Galaxie bis zur Erde	2,5 Millionen Jahre

Die Lichtgeschwindigkeit im Vakuum, gemeinhin als c bezeichnet, ist eine universelle physikalische Konstante, die in vielen Bereichen der Physik von Bedeutung ist. Ihr genauer Wert ist definiert als 299792458 Meter pro Sekunde (etwa 300000 km/s oder 186000 mi/s). Nach der speziellen Relativitätstheorie ist c die Obergrenze für die Geschwindigkeit, mit der sich herkömmliche Materie, Energie oder jedes Signal, das Informationen trägt, durch den Raum bewegen kann. ⓘ

Alle Formen der elektromagnetischen Strahlung - nicht nur das sichtbare Licht - bewegen sich mit Lichtgeschwindigkeit. Für viele praktische Zwecke scheinen sich Licht und andere elektromagnetische Wellen augenblicklich auszubreiten, aber bei großen Entfernungen und sehr empfindlichen Messungen hat ihre endliche Geschwindigkeit spürbare Auswirkungen. Das auf der Erde gesehene Sternenlicht hat die Sterne schon vor vielen Jahren verlassen, so dass die Menschen die Geschichte des Universums durch die Betrachtung entfernter Objekte studieren können. Bei der Kommunikation mit weit entfernten Raumsonden kann es Minuten bis Stunden dauern, bis eine Nachricht zwischen der Erde und dem Raumfahrzeug übermittelt wird. In der Datenverarbeitung legt die Lichtgeschwindigkeit die ultimative Mindestverzögerung für die Kommunikation zwischen Computern, im Computerspeicher und innerhalb einer CPU fest. Die Lichtgeschwindigkeit kann zusammen mit der Laufzeitmessung verwendet werden, um große Entfernungen mit hoher Präzision zu messen. ⓘ

Ole Rømer wies 1676 erstmals nach, dass sich Licht mit einer endlichen Geschwindigkeit (nicht sofort) bewegt, indem er die scheinbare Bewegung des Jupitermondes Io untersuchte. In den folgenden Jahrhunderten wurden immer genauere Messungen der Lichtgeschwindigkeit vorgenommen. In einer 1865 veröffentlichten Arbeit schlug James Clerk Maxwell vor, dass Licht eine elektromagnetische Welle ist und sich daher mit der Geschwindigkeit c ausbreitet. 1905 postulierte Albert Einstein, dass die Lichtgeschwindigkeit c in Bezug auf ein beliebiges Inertialsystem eine Konstante ist und unabhängig von der Bewegung der Lichtquelle gilt. Er untersuchte die Konsequenzen dieses Postulats, indem er die Relativitätstheorie ableitete und dabei zeigte, dass der Parameter c auch außerhalb des Kontextes von Licht und Elektromagnetismus von Bedeutung ist. ⓘ

Massenlose Teilchen und Feldstörungen wie Gravitationswellen bewegen sich im Vakuum ebenfalls mit der Geschwindigkeit c. Solche Teilchen und Wellen bewegen sich mit c unabhängig von der Bewegung der Quelle oder dem Inertialsystem des Beobachters. Teilchen mit einer Ruhemasse ungleich Null können sich c nähern, es aber nie erreichen, unabhängig davon, in welchem Bezugssystem ihre Geschwindigkeit gemessen wird. In der speziellen und der allgemeinen Relativitätstheorie steht c im Zusammenhang mit Raum und Zeit und kommt auch in der berühmten Gleichung der Masse-Energie-Äquivalenz, E = mc2, vor. In einigen Fällen scheinen sich Objekte oder Wellen schneller als das Licht fortzubewegen (z. B. Phasengeschwindigkeiten von Wellen, das Auftreten bestimmter astronomischer Hochgeschwindigkeitsobjekte und bestimmte Quanteneffekte). Es wird davon ausgegangen, dass die Ausdehnung des Universums ab einer bestimmten Grenze die Lichtgeschwindigkeit übersteigt. ⓘ

Die Geschwindigkeit, mit der sich Licht durch transparente Materialien wie Glas oder Luft ausbreitet, ist kleiner als c; ebenso ist die Geschwindigkeit der elektromagnetischen Wellen in Kabeln langsamer als c. Das Verhältnis zwischen c und der Geschwindigkeit v, mit der sich Licht in einem Material ausbreitet, wird als Brechungsindex n des Materials bezeichnet (n = c/v). Für sichtbares Licht liegt der Brechungsindex von Glas beispielsweise typischerweise bei 1,5, was bedeutet, dass sich das Licht in Glas mit c/1,5 ≈ 200000 km/s ausbreitet; der Brechungsindex von Luft für sichtbares Licht beträgt etwa 1,0003, so dass die Lichtgeschwindigkeit in Luft etwa 90 km/s langsamer als c ist. ⓘ

Physikalische Konstante ⓘ
Name	Lichtgeschwindigkeit (im Vakuum)
Formelzeichen	$c,\,c_{0}$
Größenart	Geschwindigkeit
Wert
SI	299792458 $\textstyle {\frac {\mathrm {m} }{\mathrm {s} }}$
Unsicherheit (rel.)	(exakt)
CGS	2.99792458e10 $\textstyle {\frac {\mathrm {cm} }{\mathrm {s} }}$
Planck-Einheiten	1
Bezug zu anderen Konstanten
$c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}$ (in SI und Planck) $\varepsilon _{0}\,$ – Elektrische Feldkonstante $\mu _{0}\,$ – Magnetische Feldkonstante
Quellen und Anmerkungen
Quelle für den SI-Wert: CODATA 2014 (Direktlink)

Unter der Lichtgeschwindigkeit $c$ ($c$ nach lat. celeritas: Schnelligkeit) versteht man meist die Ausbreitungsgeschwindigkeit von Licht im Vakuum. Neben Licht breiten sich auch alle anderen elektromagnetischen Wellen sowie auch Gravitationswellen mit dieser Geschwindigkeit aus. Sie ist eine fundamentale Naturkonstante, deren Bedeutung in der speziellen und allgemeinen Relativitätstheorie weit über die Beschreibung der elektromagnetischen Wellenausbreitung hinausgeht. ⓘ

Zahlenwert, Notation und Einheiten

Die Lichtgeschwindigkeit im Vakuum wird in der Regel mit einem kleinen c für "konstant" oder dem lateinischen Wort celeritas (für "Schnelligkeit") bezeichnet. Im Jahr 1856 hatten Wilhelm Eduard Weber und Rudolf Kohlrausch c für eine andere Konstante verwendet, von der sich später herausstellte, dass sie dem √2-Fachen der Lichtgeschwindigkeit im Vakuum entspricht. Historisch gesehen wurde das Symbol V als alternatives Symbol für die Lichtgeschwindigkeit verwendet, das 1865 von James Clerk Maxwell eingeführt wurde. Im Jahr 1894 definierte Paul Drude c in seiner modernen Bedeutung neu. Einstein verwendete V in seinen deutschsprachigen Originalarbeiten zur Speziellen Relativitätstheorie im Jahr 1905, wechselte aber 1907 zu c, das inzwischen das Standardsymbol für die Lichtgeschwindigkeit geworden war. ⓘ

Manchmal wird c für die Wellengeschwindigkeit in einem beliebigen materiellen Medium verwendet, und c₀ für die Lichtgeschwindigkeit im Vakuum. Diese tiefgestellte Schreibweise, die in der offiziellen SI-Literatur übernommen wurde, hat die gleiche Form wie andere verwandte Konstanten: μ₀ für die Permeabilität oder magnetische Konstante des Vakuums, ε₀ für die Permittivität oder elektrische Konstante des Vakuums und Z₀ für die Impedanz des freien Raums. In diesem Artikel wird c ausschließlich für die Lichtgeschwindigkeit im Vakuum verwendet. ⓘ

Seit 1983 ist das Meter im Internationalen Einheitensystem (SI) als die Strecke definiert, die das Licht im Vakuum in 1⁄299792458 einer Sekunde zurücklegt. Diese Definition legt die Lichtgeschwindigkeit im Vakuum auf genau 299792458 m/s fest. Als dimensionale physikalische Konstante ist der numerische Wert von c für verschiedene Einheitssysteme unterschiedlich. So beträgt die Lichtgeschwindigkeit in britischen Maßeinheiten etwa 186282 Meilen pro Sekunde, also etwa 1 Fuß pro Nanosekunde. In Zweigen der Physik, in denen c häufig vorkommt, wie z. B. in der Relativitätstheorie, ist es üblich, Systeme mit natürlichen Maßeinheiten oder das geometrische Einheitensystem zu verwenden, in dem c = 1 ist. In diesen Einheiten wird c nicht explizit angegeben, da die Multiplikation oder Division mit 1 das Ergebnis nicht beeinflusst. Die Einheit Lichtsekunde pro Sekunde ist immer noch relevant, auch wenn sie weggelassen wird. ⓘ

Grundlegende Rolle in der Physik

Die Geschwindigkeit, mit der sich Lichtwellen im Vakuum ausbreiten, ist sowohl von der Bewegung der Wellenquelle als auch vom Inertialsystem des Beobachters unabhängig. Diese Invarianz der Lichtgeschwindigkeit wurde 1905 von Einstein postuliert, nachdem er durch die Maxwellsche Theorie des Elektromagnetismus und den fehlenden Beweis für den leuchtenden Äther motiviert worden war; sie wurde seitdem durch zahlreiche Experimente immer wieder bestätigt. Es ist nur möglich, experimentell zu überprüfen, dass die Geschwindigkeit des Lichts in beiden Richtungen (z. B. von einer Quelle zu einem Spiegel und wieder zurück) rahmenunabhängig ist, da es unmöglich ist, die Geschwindigkeit des Lichts in einer Richtung (z. B. von einer Quelle zu einem weit entfernten Detektor) zu messen, ohne eine Konvention darüber zu haben, wie die Uhren an der Quelle und am Detektor synchronisiert werden sollten. Nimmt man jedoch die Einstein-Synchronisation für die Uhren an, so ist die Einweg-Lichtgeschwindigkeit per Definition gleich der Zweiweg-Lichtgeschwindigkeit. Die spezielle Relativitätstheorie untersucht die Folgen dieser Invarianz von c unter der Annahme, dass die physikalischen Gesetze in allen Inertialsystemen gleich sind. Eine Folge davon ist, dass c die Geschwindigkeit ist, mit der sich alle masselosen Teilchen und Wellen, einschließlich Licht, im Vakuum bewegen müssen. ⓘ

Der Lorentz-Faktor γ als Funktion der Geschwindigkeit. Er beginnt bei 1 und nähert sich der Unendlichkeit, wenn v sich c nähert. ⓘ

Die spezielle Relativitätstheorie hat viele kontraintuitive und experimentell überprüfte Implikationen. Dazu gehören die Äquivalenz von Masse und Energie (E = mc²), die Längenkontraktion (bewegte Objekte verkürzen sich) und die Zeitdilatation (bewegte Uhren laufen langsamer). Der Faktor γ, um den die Längenkontraktion und die Zeitdilatation erfolgen, wird als Lorentz-Faktor bezeichnet und ist gegeben durch γ = (1 - v²/c²)-1/2, wobei v die Geschwindigkeit des Objekts ist. Der Unterschied von γ zu 1 ist vernachlässigbar für Geschwindigkeiten, die viel langsamer als c sind, wie z. B. die meisten Alltagsgeschwindigkeiten - in diesem Fall wird die spezielle Relativitätstheorie durch die galileische Relativitätstheorie sehr gut angenähert -, aber er nimmt bei relativistischen Geschwindigkeiten zu und divergiert gegen unendlich, wenn v sich c nähert. Ein Zeitdilatationsfaktor von γ = 2 tritt beispielsweise bei einer Relativgeschwindigkeit von 86,6 % der Lichtgeschwindigkeit (v = 0,866 c) auf. In ähnlicher Weise tritt ein Zeitdilatationsfaktor von γ = 10 bei v = 99,5% c auf. ⓘ

Die Ergebnisse der speziellen Relativitätstheorie lassen sich dadurch zusammenfassen, dass Raum und Zeit als eine einheitliche Struktur behandelt werden, die als Raumzeit bezeichnet wird (wobei c die Einheiten von Raum und Zeit miteinander in Beziehung setzt), und dass physikalische Theorien einer speziellen Symmetrie genügen müssen, die Lorentz-Invarianz genannt wird und deren mathematische Formulierung den Parameter c enthält. Als solcher ist der Parameter c in der modernen Physik allgegenwärtig und taucht in vielen Zusammenhängen auf, die nichts mit Licht zu tun haben. Die allgemeine Relativitätstheorie sagt zum Beispiel voraus, dass c auch die Geschwindigkeit der Gravitation und der Gravitationswellen ist, und die Beobachtungen von Gravitationswellen stimmen mit dieser Vorhersage überein. In nicht-inertialen Bezugssystemen (gravitativ gekrümmte Raumzeit oder beschleunigte Bezugssysteme) ist die lokale Lichtgeschwindigkeit konstant und gleich c, aber die Lichtgeschwindigkeit entlang einer Bahn von endlicher Länge kann von c abweichen, je nachdem, wie Entfernungen und Zeiten definiert sind. ⓘ

Im Allgemeinen wird davon ausgegangen, dass fundamentale Konstanten wie c in der gesamten Raumzeit den gleichen Wert haben, d. h., dass sie nicht vom Ort abhängen und sich nicht mit der Zeit verändern. In verschiedenen Theorien wird jedoch vermutet, dass sich die Lichtgeschwindigkeit im Laufe der Zeit verändert haben könnte. Es wurden keine schlüssigen Beweise für solche Veränderungen gefunden, aber sie sind Gegenstand laufender Forschungen. ⓘ

Außerdem wird allgemein davon ausgegangen, dass die Lichtgeschwindigkeit isotrop ist, d. h. dass sie unabhängig von der Richtung, in der sie gemessen wird, den gleichen Wert hat. Beobachtungen der Emissionen von Kernenergieniveaus in Abhängigkeit von der Ausrichtung der emittierenden Kerne in einem Magnetfeld (siehe Hughes-Drever-Experiment) und von rotierenden optischen Resonatoren (siehe Resonatorexperimente) haben der möglichen Anisotropie in zwei Richtungen enge Grenzen gesetzt. ⓘ

Obere Grenze für Geschwindigkeiten

Nach der Speziellen Relativitätstheorie ist die Energie eines Objekts mit der Ruhemasse m und der Geschwindigkeit v gegeben durch γmc², wobei γ der oben definierte Lorentz-Faktor ist. Wenn v gleich null ist, ist γ gleich eins, was zu der berühmten Formel E = mc² für die Äquivalenz von Masse und Energie führt. Der Faktor γ nähert sich der Unendlichkeit, wenn v sich c nähert, und man bräuchte eine unendliche Menge an Energie, um ein Objekt mit Masse auf Lichtgeschwindigkeit zu beschleunigen. Die Lichtgeschwindigkeit ist die Obergrenze für die Geschwindigkeit von Objekten mit positiver Ruhemasse, und einzelne Photonen können sich nicht schneller als mit Lichtgeschwindigkeit fortbewegen. Dies wurde in vielen Tests zu relativistischer Energie und relativistischem Impuls experimentell nachgewiesen. ⓘ

Das Ereignis A geht B im roten Raum voraus, ist gleichzeitig mit B im grünen Raum und folgt B im blauen Raum. ⓘ

Ganz allgemein ist es unmöglich, dass sich Signale oder Energie schneller als c bewegen. Ein Argument dafür ergibt sich aus der kontraintuitiven Implikation der Speziellen Relativitätstheorie, der so genannten Relativität der Gleichzeitigkeit. Wenn der räumliche Abstand zwischen zwei Ereignissen A und B größer ist als das Zeitintervall zwischen ihnen multipliziert mit c, dann gibt es Bezugssysteme, in denen A vor B liegt, andere, in denen B vor A liegt, und wieder andere, in denen sie gleichzeitig stattfinden. Würde sich also etwas schneller als c relativ zu einem Inertialsystem bewegen, würde es sich relativ zu einem anderen System in der Zeit rückwärts bewegen, und die Kausalität wäre verletzt. In einem solchen Bezugssystem könnte eine "Wirkung" vor ihrer "Ursache" beobachtet werden. Eine solche Verletzung der Kausalität wurde noch nie beobachtet und würde zu Paradoxien wie dem tachyonischen Antitelefon führen. ⓘ

Beobachtungen und Experimente, die schneller als das Licht sind

Es gibt Situationen, in denen es den Anschein hat, dass sich Materie, Energie oder informationstragende Signale mit Geschwindigkeiten größer als c bewegen, was jedoch nicht der Fall ist. Wie im Abschnitt über die Ausbreitung von Licht in einem Medium weiter unten erörtert wird, können viele Wellengeschwindigkeiten c überschreiten. Die Phasengeschwindigkeit von Röntgenstrahlen durch die meisten Gläser kann routinemäßig c überschreiten, aber die Phasengeschwindigkeit bestimmt nicht die Geschwindigkeit, mit der Wellen Informationen übertragen. ⓘ

Wird ein Laserstrahl schnell über ein entferntes Objekt geschwenkt, kann sich der Lichtfleck schneller als c bewegen, obwohl die anfängliche Bewegung des Flecks wegen der Zeit, die das Licht braucht, um mit der Geschwindigkeit c zum entfernten Objekt zu gelangen, verzögert ist. In ähnlicher Weise kann ein Schatten, der auf ein entferntes Objekt projiziert wird, mit einer zeitlichen Verzögerung schneller als c bewegt werden. In keinem der beiden Fälle bewegt sich Materie, Energie oder Information schneller als das Licht. ⓘ

Die Änderungsrate des Abstands zwischen zwei Objekten in einem Bezugsrahmen, in dem sich beide bewegen (ihre Annäherungsgeschwindigkeit), kann einen Wert von mehr als c haben. ⓘ

Bestimmte Quanteneffekte scheinen augenblicklich und damit schneller als c übertragen zu werden, wie im EPR-Paradoxon. Ein Beispiel sind die Quantenzustände zweier Teilchen, die verschränkt sein können. Solange eines der Teilchen nicht beobachtet wird, befinden sie sich in einer Überlagerung von zwei Quantenzuständen. Wenn die Teilchen getrennt werden und der Quantenzustand des einen Teilchens beobachtet wird, wird der Quantenzustand des anderen Teilchens sofort bestimmt. Es ist jedoch unmöglich zu kontrollieren, welchen Quantenzustand das erste Teilchen annimmt, wenn es beobachtet wird, so dass auf diese Weise keine Informationen übertragen werden können. ⓘ

Ein weiterer Quanteneffekt, der das Auftreten von Überlichtgeschwindigkeiten vorhersagt, ist der so genannte Hartman-Effekt: Unter bestimmten Bedingungen ist die Zeit, die ein virtuelles Teilchen benötigt, um durch eine Barriere zu tunneln, konstant, unabhängig von der Dicke der Barriere. Dies könnte dazu führen, dass ein virtuelles Teilchen einen großen Spalt schneller als das Licht durchquert. Allerdings können mit diesem Effekt keine Informationen übertragen werden. ⓘ

Sogenannte superluminale Bewegungen sind bei bestimmten astronomischen Objekten zu beobachten, etwa bei den relativistischen Jets von Radiogalaxien und Quasaren. Diese Jets bewegen sich jedoch nicht mit Geschwindigkeiten, die über der Lichtgeschwindigkeit liegen: Die scheinbare Superluminalbewegung ist ein Projektionseffekt, der durch Objekte verursacht wird, die sich nahe der Lichtgeschwindigkeit bewegen und sich der Erde in einem kleinen Winkel zur Sichtlinie nähern: Da das Licht, das ausgesendet wurde, als der Jet weiter entfernt war, länger brauchte, um die Erde zu erreichen, entspricht die Zeit zwischen zwei aufeinanderfolgenden Beobachtungen einer längeren Zeit zwischen den Zeitpunkten, an denen die Lichtstrahlen ausgesendet wurden. ⓘ

Ein Bericht aus dem Jahr 2011 über Neutrinos, die sich scheinbar schneller als das Licht bewegen, erwies sich als experimenteller Fehler. ⓘ

In Modellen des expandierenden Universums driften Galaxien umso schneller auseinander, je weiter sie voneinander entfernt sind. Dieses Auseinanderdriften ist nicht auf die Bewegung durch den Raum zurückzuführen, sondern auf die Ausdehnung des Raums selbst. So scheinen sich beispielsweise weit von der Erde entfernte Galaxien mit einer Geschwindigkeit von der Erde wegzubewegen, die proportional zu ihrer Entfernung ist. Jenseits einer Grenze, die Hubble-Sphäre genannt wird, wird die Geschwindigkeit, mit der sich ihre Entfernung von der Erde vergrößert, größer als die Lichtgeschwindigkeit. ⓘ

Ausbreitung des Lichts

In der klassischen Physik wird das Licht als eine Art elektromagnetische Welle beschrieben. Das klassische Verhalten des elektromagnetischen Feldes wird durch die Maxwellschen Gleichungen beschrieben, die vorhersagen, dass die Geschwindigkeit c, mit der sich elektromagnetische Wellen (wie Licht) im Vakuum ausbreiten, mit der verteilten Kapazität und Induktivität des Vakuums, die auch als elektrische Konstante ε₀ bzw. magnetische Konstante μ₀ bezeichnet werden, durch die Gleichung ⓘ

$c={\frac {1}{\sqrt {\varepsilon _{0}\mu _{0}}}}\ .$ ⓘ

In der modernen Quantenphysik wird das elektromagnetische Feld durch die Theorie der Quantenelektrodynamik (QED) beschrieben. In dieser Theorie wird das Licht durch die fundamentalen Anregungen (oder Quanten) des elektromagnetischen Feldes, die sogenannten Photonen, beschrieben. In der QED sind Photonen masselose Teilchen und bewegen sich daher gemäß der speziellen Relativitätstheorie mit Lichtgeschwindigkeit im Vakuum. ⓘ

Es wurden Erweiterungen der QED erwogen, in denen das Photon eine Masse hat. In einer solchen Theorie würde seine Geschwindigkeit von seiner Frequenz abhängen, und die invariante Geschwindigkeit c der Speziellen Relativitätstheorie wäre dann die obere Grenze der Lichtgeschwindigkeit im Vakuum. Bei strengen Tests wurde keine Veränderung der Lichtgeschwindigkeit mit der Frequenz beobachtet, was die Masse des Photons stark einschränkt. Die erhaltene Grenze hängt vom verwendeten Modell ab: Wenn das massive Photon durch die Proca-Theorie beschrieben wird, liegt die experimentelle Obergrenze für seine Masse bei etwa 10-57 Gramm; wenn die Photonenmasse durch einen Higgs-Mechanismus erzeugt wird, ist die experimentelle Obergrenze weniger scharf, m ≤ 10-14 eV/c² (etwa 2 × 10-47 g). ⓘ

Ein weiterer Grund dafür, dass die Lichtgeschwindigkeit mit der Frequenz variiert, wäre das Versagen der Speziellen Relativitätstheorie, auf beliebig kleine Skalen anwendbar zu sein, wie es von einigen vorgeschlagenen Theorien der Quantengravitation vorhergesagt wird. Im Jahr 2009 wurde bei der Beobachtung des Gammastrahlenausbruchs GRB 090510 kein Hinweis auf eine Abhängigkeit der Photonengeschwindigkeit von der Energie gefunden, was in bestimmten Modellen der Quantisierung der Raumzeit enge Grenzen für die Beeinflussung dieser Geschwindigkeit durch die Photonenenergie bei Energien nahe der Planck-Skala setzt. ⓘ

In einem Medium

In einem Medium breitet sich das Licht in der Regel nicht mit der Geschwindigkeit c aus; außerdem bewegen sich verschiedene Arten von Lichtwellen mit unterschiedlichen Geschwindigkeiten. Die Geschwindigkeit, mit der sich die einzelnen Wellenberge und -täler einer ebenen Welle (eine Welle, die den gesamten Raum mit nur einer Frequenz ausfüllt) ausbreiten, wird als Phasengeschwindigkeit vp bezeichnet. Ein physikalisches Signal mit endlicher Ausdehnung (ein Lichtimpuls) breitet sich mit einer anderen Geschwindigkeit aus. Die Gesamteinhüllende des Impulses bewegt sich mit der Gruppengeschwindigkeit vg, und sein frühester Teil bewegt sich mit der Frontgeschwindigkeit vf. ⓘ

Der blaue Punkt bewegt sich mit der Geschwindigkeit der Wellen, der Phasengeschwindigkeit; der grüne Punkt bewegt sich mit der Geschwindigkeit der Hülle, der Gruppengeschwindigkeit; und der rote Punkt bewegt sich mit der Geschwindigkeit des vordersten Teils des Pulses, der Frontgeschwindigkeit. ⓘ

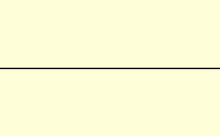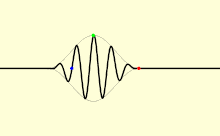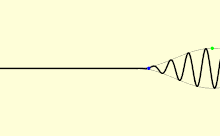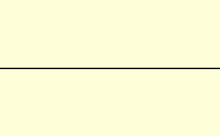
Die Phasengeschwindigkeit ist wichtig, um zu bestimmen, wie sich eine Lichtwelle durch ein Material oder von einem Material zu einem anderen bewegt. Sie wird oft in Form eines Brechungsindexes dargestellt. Der Brechungsindex eines Materials ist definiert als das Verhältnis von c zur Phasengeschwindigkeit vp im Material: größere Brechungsindizes bedeuten geringere Geschwindigkeiten. Der Brechungsindex eines Materials kann von der Frequenz, der Intensität, der Polarisation oder der Ausbreitungsrichtung des Lichts abhängen; in vielen Fällen kann er jedoch als eine materialabhängige Konstante behandelt werden. Der Brechungsindex von Luft beträgt etwa 1,0003. Dichtere Medien wie Wasser, Glas und Diamant haben Brechungsindizes von etwa 1,3, 1,5 bzw. 2,4 für sichtbares Licht. In exotischen Materialien wie Bose-Einstein-Kondensaten nahe dem absoluten Nullpunkt kann die effektive Lichtgeschwindigkeit nur wenige Meter pro Sekunde betragen. Dabei handelt es sich jedoch um eine Absorptions- und Rückstrahlungsverzögerung zwischen den Atomen, wie bei allen Geschwindigkeiten, die langsamer als c sind, in materiellen Stoffen. Als extremes Beispiel für die "Verlangsamung" des Lichts in der Materie behaupteten zwei unabhängige Physikerteams, das Licht zum "völligen Stillstand" gebracht zu haben, indem sie es durch ein Bose-Einstein-Kondensat des Elements Rubidium leiteten. Die populäre Beschreibung, dass das Licht in diesen Experimenten "angehalten" wurde, bezieht sich jedoch nur darauf, dass das Licht in den angeregten Zuständen der Atome gespeichert und zu einem beliebigen späteren Zeitpunkt, angeregt durch einen zweiten Laserimpuls, wieder emittiert wird. In der Zeit, in der es "angehalten" wurde, hatte es aufgehört, Licht zu sein. Dieses Verhalten trifft mikroskopisch gesehen im Allgemeinen auf alle transparenten Medien zu, die die Lichtgeschwindigkeit "verlangsamen". ⓘ

In transparenten Materialien ist der Brechungsindex im Allgemeinen größer als 1, d. h. die Phasengeschwindigkeit ist kleiner als c. In anderen Materialien ist es möglich, dass der Brechungsindex für einige Frequenzen kleiner als 1 wird; in einigen exotischen Materialien kann der Brechungsindex sogar negativ werden. Die Bedingung, dass die Kausalität nicht verletzt wird, bedeutet, dass der Real- und der Imaginärteil der Dielektrizitätskonstante eines beliebigen Materials, die dem Brechungsindex bzw. dem Dämpfungskoeffizienten entsprechen, durch die Kramers-Kronig-Beziehung miteinander verbunden sind. In der Praxis bedeutet dies, dass die Welle in einem Material mit einem Brechungsindex kleiner als 1 schnell absorbiert wird. ⓘ

Ein Impuls mit unterschiedlichen Gruppen- und Phasengeschwindigkeiten (was der Fall ist, wenn die Phasengeschwindigkeit nicht für alle Frequenzen des Impulses gleich ist) verschmiert mit der Zeit, ein Vorgang, der als Dispersion bezeichnet wird. Bestimmte Materialien haben eine außergewöhnlich niedrige (oder sogar null) Gruppengeschwindigkeit für Lichtwellen, ein Phänomen, das als langsames Licht bezeichnet wird. Das Gegenteil, Gruppengeschwindigkeiten von mehr als c, wurde 1993 theoretisch vorgeschlagen und im Jahr 2000 experimentell erreicht. Es sollte sogar möglich sein, dass die Gruppengeschwindigkeit unendlich oder negativ wird, wobei sich die Impulse augenblicklich oder rückwärts in der Zeit bewegen. ⓘ

Keine dieser Möglichkeiten erlaubt es jedoch, Informationen schneller als mit c zu übertragen. Es ist unmöglich, Informationen mit einem Lichtimpuls schneller als mit der Geschwindigkeit des frühesten Teils des Impulses (der Frontgeschwindigkeit) zu übertragen. Es kann gezeigt werden, dass diese (unter bestimmten Annahmen) immer gleich c ist. ⓘ

Es ist möglich, dass sich ein Teilchen durch ein Medium schneller als die Phasengeschwindigkeit des Lichts in diesem Medium bewegt (aber immer noch langsamer als c). Wenn ein geladenes Teilchen dies in einem dielektrischen Material tut, wird das elektromagnetische Äquivalent einer Stoßwelle, die so genannte Cherenkov-Strahlung, emittiert. ⓘ

In einem Medium werden die beiden Feldkonstanten durch das Material geändert, was durch die Faktoren relative Permittivität $\varepsilon _{\mathrm {r} }$ und relative Permeabilität $\mu _{\mathrm {r} }$ berücksichtigt wird. Beide hängen von der Frequenz $\omega$ ab. Die Lichtgeschwindigkeit im Medium ist dementsprechend

$c_{\text{medium}}(\omega )={\frac {1}{\sqrt {\varepsilon (\omega )\,\mu (\omega )}}}={\frac {1}{\sqrt {\varepsilon _{0}\,\varepsilon _{\mathrm {r} }(\omega )\,\mu _{0}\,\mu _{\mathrm {r} }(\omega )}}}={\frac {c}{\sqrt {\varepsilon _{\mathrm {r} }(\omega )\,\mu _{\mathrm {r} }(\omega )}}}$.

Das Verhältnis der Lichtgeschwindigkeit in Vakuum zu der in einem Medium ist der (frequenzabhängige) Brechungsindex $n$ des Mediums. Der Zusammenhang des Brechungsindex mit der relativen Permittivität und der relativen Permeabilität heißt auch maxwellsche Relation:

$n(\omega )={\frac {c}{c_{\text{medium}}(\omega )}}={\sqrt {\varepsilon _{\mathrm {r} }(\omega )\,\mu _{\mathrm {r} }(\omega )}}$ ⓘ

Wegen der im Allgemeinen gegebenen Abhängigkeit von $\varepsilon _{\mathrm {r} }$ und $\mu _{\mathrm {r} }$ von der Frequenz der Welle ist zu beachten, dass $c_{\mathrm {medium} }$ die Phasengeschwindigkeit im Medium bezeichnet, mit der Punkte gleicher Phase (z. B. Minima oder Maxima) einer ebenen Welle mit konstanter Amplitude fortschreiten. Die Hüllkurve eines räumlich begrenzten Wellenpakets pflanzt sich hingegen mit der Gruppengeschwindigkeit fort. In Medien weichen diese beiden Geschwindigkeiten mehr oder weniger voneinander ab. Insbesondere bedeutet ein Brechungsindex $n<1$ lediglich, dass sich die Wellenberge schneller als $c$ ausbreiten. Wellenpakete, mit denen Information und Energie transportiert werden, sind weiterhin langsamer als $c$. ⓘ

Praktische Auswirkungen der Endlichkeit

Die Lichtgeschwindigkeit ist für die Kommunikation von Bedeutung: Die Verzögerungszeit für die Hin- und Rückreise ist größer als Null. Dies gilt von kleinen bis zu astronomischen Größenordnungen. Andererseits hängen einige Techniken von der endlichen Lichtgeschwindigkeit ab, zum Beispiel bei Entfernungsmessungen. ⓘ

Kleine Maßstäbe

In Supercomputern stellt die Lichtgeschwindigkeit eine Grenze für die Geschwindigkeit dar, mit der Daten zwischen Prozessoren übertragen werden können. Wenn ein Prozessor mit 1 Gigahertz arbeitet, kann ein Signal in einem einzigen Zyklus nur maximal 30 Zentimeter weit übertragen werden. Die Prozessoren müssen daher nahe beieinander platziert werden, um die Kommunikationslatenzen zu minimieren; dies kann zu Schwierigkeiten bei der Kühlung führen. Wenn die Taktfrequenzen weiter steigen, wird die Lichtgeschwindigkeit schließlich zu einem begrenzenden Faktor für das interne Design einzelner Chips. ⓘ

Große Entfernungen auf der Erde

Wenn man davon ausgeht, dass der Äquatorumfang der Erde etwa 40075 km beträgt und dass c etwa 300000 km/s ist, beträgt die theoretisch kürzeste Zeit, in der eine Information die halbe Erdkugel entlang der Oberfläche umläuft, etwa 67 Millisekunden. Wenn das Licht in einer Glasfaser um den Globus reist, ist die tatsächliche Laufzeit länger, unter anderem weil die Lichtgeschwindigkeit in einer Glasfaser je nach Brechungsindex n um etwa 35 % langsamer ist. Außerdem gibt es in globalen Kommunikationssituationen selten gerade Linien, und es kommt zu Verzögerungen, wenn das Signal einen elektronischen Schalter oder einen Signalregenerator passiert. ⓘ

Raumfahrt und Astronomie

Ein Lichtstrahl, der sich zwischen Erde und Mond bewegt, wird in der Zeit dargestellt, die ein Lichtimpuls benötigt, um sich zwischen ihnen zu bewegen: 1,255 Sekunden bei ihrem mittleren Umlaufabstand (Oberfläche zu Oberfläche). Die relativen Größen und Abstände des Erde-Mond-Systems sind maßstabsgetreu dargestellt. ⓘ

Auch die Kommunikation zwischen der Erde und dem Raumschiff erfolgt nicht sofort. Es gibt eine kurze Verzögerung zwischen der Quelle und dem Empfänger, die mit zunehmender Entfernung immer deutlicher wird. Diese Verzögerung war bei der Kommunikation zwischen der Bodenkontrollstation und Apollo 8, dem ersten Raumschiff mit Besatzung, das den Mond umkreiste, erheblich: Bei jeder Frage musste die Bodenkontrollstation mindestens drei Sekunden auf die Antwort warten. Die Verzögerung bei der Kommunikation zwischen Erde und Mars kann je nach der relativen Position der beiden Planeten zwischen fünf und zwanzig Minuten variieren. Wenn also ein Roboter auf der Marsoberfläche auf ein Problem stößt, würden seine menschlichen Kontrolleure erst mindestens fünf Minuten später davon erfahren, möglicherweise sogar bis zu zwanzig Minuten später; es würde dann weitere fünf bis zwanzig Minuten dauern, bis die Anweisungen von der Erde zum Mars gelangen. ⓘ

Der Empfang von Licht und anderen Signalen von weit entfernten astronomischen Quellen kann sogar noch viel länger dauern. So hat es beispielsweise 13 Milliarden (13×10⁹) Jahre gedauert, bis das Licht von den fernen Galaxien, die auf den Hubble-Ultra-Deep-Field-Aufnahmen zu sehen sind, zur Erde gelangt ist. Diese heute aufgenommenen Bilder zeigen die Galaxien so, wie sie vor 13 Milliarden Jahren erschienen, als das Universum weniger als eine Milliarde Jahre alt war. Die Tatsache, dass weiter entfernte Objekte aufgrund der endlichen Lichtgeschwindigkeit jünger erscheinen, ermöglicht es den Astronomen, Rückschlüsse auf die Entwicklung der Sterne, der Galaxien und des Universums selbst zu ziehen. ⓘ

Astronomische Entfernungen werden manchmal in Lichtjahren ausgedrückt, insbesondere in populärwissenschaftlichen Veröffentlichungen und Medien. Ein Lichtjahr ist die Entfernung, die das Licht in einem julianischen Jahr zurücklegt, etwa 9461 Milliarden Kilometer, 5879 Milliarden Meilen oder 0,3066 Parsec. In runden Zahlen ausgedrückt, entspricht ein Lichtjahr fast 10 Billionen Kilometern oder fast 6 Billionen Meilen. Proxima Centauri, der der Erde nach der Sonne am nächsten gelegene Stern, ist etwa 4,2 Lichtjahre entfernt. ⓘ

Entfernungsmessung

Radarsysteme messen die Entfernung zu einem Ziel anhand der Zeit, die ein Radiowellenimpuls benötigt, um zur Radarantenne zurückzukehren, nachdem er vom Ziel reflektiert wurde: Die Entfernung zum Ziel ist die Hälfte der Hin- und Rücklaufzeit multipliziert mit der Lichtgeschwindigkeit. Ein GPS-Empfänger (Global Positioning System) misst seine Entfernung zu den GPS-Satelliten auf der Grundlage der Zeit, die ein Funksignal von jedem Satelliten benötigt, und errechnet aus diesen Entfernungen die Position des Empfängers. Da Licht in einer Sekunde etwa 300000 Kilometer zurücklegt, müssen diese Messungen für kleine Sekundenbruchteile sehr genau sein. Das Lunar Laser Ranging Experiment, die Radarastronomie und das Deep Space Network bestimmen die Entfernungen zum Mond, zu den Planeten bzw. zu Raumfahrzeugen durch Messung der Umlaufzeiten. ⓘ

Hochfrequenzhandel

Die Lichtgeschwindigkeit ist beim Hochfrequenzhandel wichtig geworden, bei dem Händler versuchen, sich einen winzigen Vorteil zu verschaffen, indem sie ihre Geschäfte Bruchteile einer Sekunde vor anderen Händlern an die Börsen bringen. So sind die Händler beispielsweise auf Mikrowellenkommunikation zwischen den Handelsplätzen umgestiegen, da Mikrowellen, die sich in der Luft fast mit Lichtgeschwindigkeit bewegen, einen Vorteil gegenüber Glasfasersignalen haben, die sich 30-40 % langsamer bewegen. ⓘ

Messung

Es gibt verschiedene Möglichkeiten, den Wert von c zu bestimmen. Eine Möglichkeit besteht darin, die tatsächliche Ausbreitungsgeschwindigkeit von Lichtwellen zu messen, was in verschiedenen astronomischen und erdgebundenen Versuchsanordnungen durchgeführt werden kann. Es ist jedoch auch möglich, c aus anderen physikalischen Gesetzen zu bestimmen, in denen es vorkommt, z. B. durch die Bestimmung der Werte der elektromagnetischen Konstanten ε₀ und μ₀ und die Verwendung ihrer Beziehung zu c. Historisch gesehen wurden die genauesten Ergebnisse durch die getrennte Bestimmung der Frequenz und der Wellenlänge eines Lichtstrahls erzielt, wobei ihr Produkt gleich c ist. ⓘ

1983 wurde das Meter definiert als "die Länge des Weges, den das Licht im Vakuum während eines Zeitintervalls von 1⁄299792458 einer Sekunde zurücklegt", wobei der Wert der Lichtgeschwindigkeit, wie unten beschrieben, per Definition auf 299792458 m/s festgelegt wurde. Folglich führen genaue Messungen der Lichtgeschwindigkeit eher zu einer genauen Darstellung des Meters als zu einem genauen Wert von c. ⓘ

Astronomische Messungen

Messung der Lichtgeschwindigkeit anhand der Verfinsterung von Io durch Jupiter ⓘ

Der Weltraum eignet sich aufgrund seiner Größe und seines nahezu perfekten Vakuums gut für die Messung der Lichtgeschwindigkeit. Normalerweise misst man die Zeit, die das Licht benötigt, um eine bestimmte Referenzdistanz im Sonnensystem zu durchlaufen, z. B. den Radius der Erdumlaufbahn. In der Vergangenheit konnten solche Messungen recht genau durchgeführt werden, je nachdem, wie genau die Länge der Referenzstrecke in erdgebundenen Einheiten bekannt ist. ⓘ

Ole Christensen Rømer nutzte eine astronomische Messung, um im Jahr 1676 die erste quantitative Schätzung der Lichtgeschwindigkeit vorzunehmen. Von der Erde aus gemessen, sind die Umlaufzeiten von Monden, die einen fernen Planeten umkreisen, kürzer, wenn sich die Erde dem Planeten nähert, als wenn sie sich von ihm entfernt. Die Entfernung, die das Licht vom Planeten (oder seinem Mond) zur Erde zurücklegt, ist kürzer, wenn sich die Erde an dem Punkt ihrer Umlaufbahn befindet, der ihrem Planeten am nächsten ist, als wenn sie sich an dem am weitesten entfernten Punkt ihrer Umlaufbahn befindet, wobei der Unterschied in der Entfernung dem Durchmesser der Erdbahn um die Sonne entspricht. Die beobachtete Änderung der Umlaufzeit des Mondes wird durch den Unterschied in der Zeit verursacht, die das Licht benötigt, um die kürzere oder längere Strecke zu überwinden. Rømer beobachtete diesen Effekt bei Jupiters innerstem Mond Io und schloss daraus, dass das Licht 22 Minuten braucht, um den Durchmesser der Erdbahn zu durchqueren. ⓘ

Aberration des Lichts: Das Licht einer weit entfernten Quelle scheint für ein sich bewegendes Teleskop aufgrund der endlichen Lichtgeschwindigkeit von einem anderen Ort zu kommen. ⓘ

Eine andere Methode ist die Nutzung der Aberration des Lichts, die im 18. Jahrhundert von James Bradley entdeckt und erklärt wurde. Dieser Effekt ergibt sich aus der vektoriellen Addition der Geschwindigkeit des von einer weit entfernten Quelle (z. B. einem Stern) eintreffenden Lichts und der Geschwindigkeit des Beobachters (siehe Diagramm rechts). Ein sich bewegender Beobachter sieht also das Licht aus einer etwas anderen Richtung kommen und sieht die Quelle folglich an einer gegenüber ihrer ursprünglichen Position verschobenen Stelle. Da sich die Richtung der Erdgeschwindigkeit auf der Umlaufbahn der Erde um die Sonne ständig ändert, bewirkt dieser Effekt, dass sich die scheinbare Position der Sterne verschiebt. Aus dem Winkelunterschied in der Position der Sterne (maximal 20,5 Bogensekunden) lässt sich die Lichtgeschwindigkeit in Form der Geschwindigkeit der Erde um die Sonne ausdrücken, die mit der bekannten Länge eines Jahres in die Zeit umgerechnet werden kann, die für den Weg von der Sonne zur Erde benötigt wird. Mit dieser Methode leitete Bradley 1729 ab, dass sich das Licht 10210-mal schneller als die Erde auf ihrer Bahn bewegt (die moderne Zahl liegt bei 10066-mal schneller) oder dass das Licht 8 Minuten und 12 Sekunden braucht, um von der Sonne zur Erde zu gelangen. ⓘ

Astronomische Einheit

Eine Astronomische Einheit (AE) ist ungefähr die durchschnittliche Entfernung zwischen der Erde und der Sonne. Sie wurde 2012 mit genau 149597870700 m neu definiert. Zuvor basierte die AE nicht auf dem Internationalen Einheitensystem, sondern auf der von der Sonne im Rahmen der klassischen Mechanik ausgeübten Gravitationskraft. Die aktuelle Definition verwendet den empfohlenen Wert in Metern für die frühere Definition der astronomischen Einheit, die durch Messung ermittelt wurde. Diese Neudefinition ist analog zu der des Meters und hat ebenfalls zur Folge, dass die Lichtgeschwindigkeit auf einen exakten Wert in astronomischen Einheiten pro Sekunde festgelegt wird (über die exakte Lichtgeschwindigkeit in Metern pro Sekunde). ⓘ

Früher wurde der Kehrwert von c, ausgedrückt in Sekunden pro astronomischer Einheit, durch den Vergleich der Zeit gemessen, die Radiosignale benötigen, um verschiedene Raumfahrzeuge im Sonnensystem zu erreichen, wobei deren Position anhand der Gravitationswirkung der Sonne und der verschiedenen Planeten berechnet wurde. Durch die Kombination vieler solcher Messungen konnte ein bestmöglicher Wert für die Lichtzeit pro Entfernungseinheit ermittelt werden. Die beste Schätzung, die von der Internationalen Astronomischen Union (IAU) im Jahr 2009 genehmigt wurde, war zum Beispiel:

Lichtzeit für eine Entfernungseinheit: t_au = 499,004783836(10) s

c = 0,00200398880410(4) AU/s = 173,144632674(3) AU/Tag.

Die relative Unsicherheit dieser Messungen beträgt 0,02 Teile pro Milliarde (2×10-11), was der Unsicherheit der Längenmessung auf der Erde durch Interferometrie entspricht. Da der Meter als die vom Licht in einem bestimmten Zeitintervall zurückgelegte Länge definiert ist, kann die Messung der Lichtzeit im Sinne der früheren Definition der astronomischen Einheit auch als Messung der Länge einer AE (alte Definition) in Metern interpretiert werden. ⓘ

Flugzeittechniken

Eine der letzten und genauesten Laufzeitmessungen, das Experiment von Michelson, Pease und Pearson aus den Jahren 1930-35, verwendete einen rotierenden Spiegel und eine 1,6 km lange Vakuumkammer, die der Lichtstrahl zehnmal durchlief. Dabei wurde eine Genauigkeit von ±11 km/s erreicht. ⓘ

Schema des Fizeau-Apparats ⓘ

Eine Methode zur Messung der Lichtgeschwindigkeit besteht darin, die Zeit zu messen, die das Licht benötigt, um zu einem Spiegel in bekannter Entfernung und zurück zu gelangen. Dies ist das Funktionsprinzip des Fizeau-Foucault-Apparats, der von Hippolyte Fizeau und Léon Foucault auf der Grundlage eines Vorschlags von François Arago entwickelt wurde. ⓘ

Der von Fizeau verwendete Aufbau besteht aus einem Lichtstrahl, der auf einen 8 km entfernten Spiegel gerichtet ist. Auf dem Weg von der Quelle zum Spiegel durchläuft der Strahl ein rotierendes Zahnrad. Bei einer bestimmten Umdrehungsgeschwindigkeit passiert der Strahl auf dem Hinweg eine Lücke und auf dem Rückweg eine weitere, aber bei etwas höheren oder niedrigeren Geschwindigkeiten trifft der Strahl auf einen Zahn und geht nicht durch das Rad. Wenn man den Abstand zwischen Rad und Spiegel, die Anzahl der Zähne des Rades und die Umdrehungsgeschwindigkeit kennt, kann man die Lichtgeschwindigkeit berechnen. ⓘ

Bei der Methode von Foucault wird das Zahnrad durch einen rotierenden Spiegel ersetzt. Da sich der Spiegel weiterdreht, während das Licht zum entfernten Spiegel und zurück wandert, wird das Licht vom rotierenden Spiegel auf dem Hinweg in einem anderen Winkel reflektiert als auf dem Rückweg. Aus diesem Winkelunterschied, der bekannten Drehgeschwindigkeit und der Entfernung zum entfernten Spiegel lässt sich die Lichtgeschwindigkeit berechnen. ⓘ

Mit Hilfe von Oszilloskopen mit einer Zeitauflösung von weniger als einer Nanosekunde kann die Lichtgeschwindigkeit heute direkt gemessen werden, indem man die Verzögerung eines Lichtimpulses eines Lasers oder einer von einem Spiegel reflektierten LED misst. Diese Methode ist weniger genau (mit Fehlern in der Größenordnung von 1 %) als andere moderne Techniken, wird aber manchmal als Laborexperiment im Physikunterricht an Hochschulen eingesetzt. ⓘ

Elektromagnetische Konstanten

Eine Möglichkeit zur Ableitung von c, die nicht direkt von einer Messung der Ausbreitung elektromagnetischer Wellen abhängt, ist die Verwendung der Beziehung zwischen c und der Dielektrizitätskonstante des Vakuums ε₀ und der Permeabilität des Vakuums μ₀, die in der Maxwellschen Theorie festgelegt ist: c² = 1/(ε₀μ₀). Die Dielektrizitätskonstante des Vakuums kann durch Messung der Kapazität und der Abmessungen eines Kondensators bestimmt werden, während der Wert der Vakuumpermeabilität durch die Definition des Ampere auf genau 4π×10-7 H⋅m-1 festgelegt ist. Rosa und Dorsey verwendeten diese Methode 1907, um einen Wert von 299710±22 km/s zu ermitteln. ⓘ

Hohlraumresonanz

Elektromagnetische stehende Wellen in einem Hohlraum ⓘ

Eine andere Möglichkeit, die Lichtgeschwindigkeit zu messen, besteht darin, die Frequenz f und die Wellenlänge λ einer elektromagnetischen Welle im Vakuum unabhängig voneinander zu messen. Der Wert von c kann dann mit Hilfe der Beziehung c = fλ ermittelt werden. Eine Möglichkeit ist die Messung der Resonanzfrequenz eines Hohlraumresonators. Sind auch die Abmessungen des Resonanzraumes bekannt, kann man daraus die Wellenlänge der Welle bestimmen. Im Jahr 1946 bestimmten Louis Essen und A.C. Gordon-Smith die Frequenz für eine Reihe von Normalmoden von Mikrowellen in einem Mikrowellenhohlraum mit genau bekannten Abmessungen. Die Abmessungen wurden mit einer Genauigkeit von etwa ±0,8 μm mit Hilfe von interferometrisch kalibrierten Messgeräten ermittelt. Da die Wellenlänge der Moden aus der Geometrie des Hohlraums und aus der elektromagnetischen Theorie bekannt war, ermöglichte die Kenntnis der zugehörigen Frequenzen eine Berechnung der Lichtgeschwindigkeit. ⓘ

Das Ergebnis von Essen-Gordon-Smith, 299792±9 km/s, war wesentlich präziser als die mit optischen Verfahren ermittelten Werte. Bis 1950 ergaben wiederholte Messungen von Essen ein Ergebnis von 299792,5±3,0 km/s. ⓘ

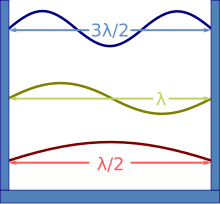
Diese Technik lässt sich im Haushalt mit einem Mikrowellenherd und Lebensmitteln wie Marshmallows oder Margarine demonstrieren: Wenn der Drehteller entfernt wird, damit sich die Lebensmittel nicht bewegen, werden sie an den Antinodes (den Punkten, an denen die Wellenamplitude am größten ist) am schnellsten gegart und beginnen dort zu schmelzen. Der Abstand zwischen zwei solchen Punkten ist die halbe Wellenlänge der Mikrowellen; durch Messung dieses Abstands und Multiplikation der Wellenlänge mit der Mikrowellenfrequenz (normalerweise auf der Rückseite des Ofens angegeben, typischerweise 2450 MHz) kann der Wert von c berechnet werden, "oft mit weniger als 5 % Fehler". ⓘ

Interferometrie

Eine interferometrische Bestimmung der Länge. Links: konstruktive Interferenz; rechts: destruktive Interferenz. ⓘ

Die Interferometrie ist eine weitere Methode zur Bestimmung der Wellenlänge elektromagnetischer Strahlung für die Bestimmung der Lichtgeschwindigkeit. Ein kohärenter Lichtstrahl (z. B. von einem Laser) mit einer bekannten Frequenz (f) wird auf zwei Wege aufgeteilt und anschließend wieder zusammengeführt. Durch Verstellen der Weglänge unter Beobachtung des Interferenzmusters und sorgfältige Messung der Änderung der Weglänge kann die Wellenlänge des Lichts (λ) bestimmt werden. Die Lichtgeschwindigkeit wird dann mit der Gleichung c = λf berechnet. ⓘ

Vor dem Aufkommen der Lasertechnik wurden kohärente Funkquellen für interferometrische Messungen der Lichtgeschwindigkeit verwendet. Die interferometrische Bestimmung der Wellenlänge wird jedoch mit zunehmender Wellenlänge ungenauer, so dass die Experimente durch die große Wellenlänge (~4 mm) der Radiowellen in ihrer Genauigkeit eingeschränkt waren. Die Genauigkeit kann durch die Verwendung von Licht mit einer kürzeren Wellenlänge verbessert werden, aber dann wird es schwierig, die Frequenz des Lichts direkt zu messen. Eine Möglichkeit, dieses Problem zu umgehen, besteht darin, mit einem niederfrequenten Signal zu beginnen, dessen Frequenz genau gemessen werden kann, und aus diesem Signal nach und nach höherfrequente Signale zu synthetisieren, deren Frequenz dann mit dem ursprünglichen Signal verknüpft werden kann. Ein Laser kann dann auf die Frequenz eingestellt werden, und seine Wellenlänge kann mit Hilfe der Interferometrie bestimmt werden. Diese Technik geht auf eine Gruppe des National Bureau of Standards (das später zum National Institute of Standards and Technology wurde) zurück. Mit ihr wurde 1972 die Lichtgeschwindigkeit im Vakuum mit einem Unsicherheitsfaktor von 3,5×10-9 gemessen. ⓘ

Geschichte

Geschichte der Messungen von c (in km/s) ⓘ

<1638	Galileo, bedeckte Laternen	nicht schlüssig
<1667	Accademia del Cimento, bedeckte Laternen	nicht schlüssig
1675	Rømer und Huygens, Monde des Jupiters	220000	-27% Fehler
1729	James Bradley, Aberration des Lichts	301000	+0,40% Fehler
1849	Hippolyte Fizeau, Zahnrad	315000	+5,1% Fehler
1862	Léon Foucault, Drehspiegel	298000±500	-0,60% Fehler
1907	Rosa und Dorsey, EM-Konstanten	299710±30	-280 ppm Fehler
1926	Albert A. Michelson, rotierender Spiegel	299796±4	+12 ppm Fehler
1950	Essen und Gordon-Smith, Hohlraumresonator	299792.5±3.0	+0,14 ppm Fehler
1958	K.D. Froome, Radio-Interferometrie	299792.50±0.10	+0,14 ppm Fehler
1972	Evenson et al., Laserinterferometrie	299792.4562±0.0011	-0,006 ppm Fehler
1983	17. CGPM, Definition des Meters	299792.458 (genau)	genau, wie definiert

Bis in die frühe Neuzeit war nicht bekannt, ob sich das Licht augenblicklich oder mit einer sehr schnellen endlichen Geschwindigkeit ausbreitet. Die erste überlieferte Untersuchung zu diesem Thema stammt aus dem antiken Griechenland. Die alten Griechen, muslimische Gelehrte und klassische europäische Wissenschaftler diskutierten lange darüber, bis Rømer die erste Berechnung der Lichtgeschwindigkeit vornahm. Einsteins Spezielle Relativitätstheorie ergab, dass die Lichtgeschwindigkeit unabhängig vom Bezugssystem konstant ist. Seitdem haben die Wissenschaftler immer genauere Messungen vorgenommen. ⓘ

Frühe Geschichte

Historisch vermutete Höhe der Lichtgeschwindigkeit ⓘ

Jahr (etwa)	Forscher	Lichtgeschwindigkeit
450 v. Chr.	Empedokles	endlich
350 v. Chr.	Aristoteles	unendlich
100	Heron von Alexandria	unendlich
1000	Avicenna/Alhazen	endlich
1350	Sayana	endlich
1600	Johannes Kepler	unendlich
1620	René Descartes	unendlich
1620	Galileo Galilei	endlich

Die Frage, ob das Licht sich unendlich schnell ausbreitet oder ob es eine endliche Geschwindigkeit besitzt, war bereits in der Philosophie der Antike von Interesse. Licht legt einen Kilometer in nur drei Mikrosekunden zurück. Mit den Beobachtungsmöglichkeiten der Antike ist somit unweigerlich ein Lichtstrahl scheinbar in dem Moment seines Entstehens gleichzeitig bereits an seinem Ziel. ⓘ

Trotzdem glaubte bereits Empedokles (um 450 v. Chr.), Licht sei etwas, das sich in Bewegung befinde und daher Zeit brauche, um Entfernungen zurückzulegen. Aristoteles meinte dagegen, Licht komme von der bloßen Anwesenheit von Objekten her, sei aber nicht in Bewegung. Er führte an, dass die Geschwindigkeit andernfalls so enorm groß sein müsse, dass sie jenseits der menschlichen Vorstellungskraft liege. Aufgrund seines Ansehens und Einflusses fand Aristoteles’ Theorie allgemeine Akzeptanz. ⓘ

Eine altertümliche Theorie des Sehens ging davon aus, dass das zum Sehen benötigte Licht vom Auge emittiert wird. Ein Objekt sollte demnach zu sehen sein, wenn die Lichtstrahlen aus dem Auge darauf träfen. Aufbauend auf dieser Vorstellung, befürwortete auch Heron von Alexandria die aristotelische Theorie. Er führte an, dass die Lichtgeschwindigkeit unendlich groß sein müsse, da man selbst die weit entfernten Sterne sehen kann, sobald man die Augen öffnet. ⓘ

In der orientalischen Welt war dagegen auch die Idee einer endlichen Lichtgeschwindigkeit verbreitet. Insbesondere glaubten die persischen Philosophen und Wissenschaftler Avicenna und Alhazen (beide um das Jahr 1000), dass das Licht eine endliche Geschwindigkeit besitzt. Ihre Unterstützer waren aber gegenüber der Anhängerschaft der aristotelischen Theorie in der Minderheit. ⓘ

Zu Beginn des 17. Jahrhunderts glaubte der Astronom Johannes Kepler, dass die Lichtgeschwindigkeit zumindest im Vakuum unendlich sei, da der leere Raum für Licht kein Hindernis darstelle. Hier scheint schon die Idee auf, dass die Geschwindigkeit eines Lichtstrahls vom durchquerten Medium abhängig sein könnte. ⓘ

Francis Bacon argumentierte, dass das Licht nicht notwendigerweise unendlich schnell sein müsse, sondern vielleicht nur schneller als wahrnehmbar. ⓘ

René Descartes ging von einer unendlich großen Lichtgeschwindigkeit aus. Sonne, Mond und Erde liegen während einer Sonnenfinsternis in einer Linie. Descartes argumentierte, dass diese Himmelskörper für einen Beobachter zu diesem Zeitpunkt scheinbar nicht in Reihe stünden, wenn die Lichtgeschwindigkeit endlich sei. Da ein solcher Effekt nie beobachtet wurde, sah er sich in seiner Annahme bestätigt. Descartes glaubte derart stark an eine unendlich große Lichtgeschwindigkeit, dass er überzeugt war, sein Weltbild würde zusammenbrechen, wenn sie endlich wäre. ⓘ

Dem standen um das Jahr 1700 die Theorien von Isaac Newton und Christiaan Huygens mit endlicher Lichtgeschwindigkeit gegenüber. Newton sah Licht als einen Strom von Teilchen an, während Huygens Licht als eine Welle deutete. Beide konnten das Brechungsgesetz erklären, indem sie die Lichtgeschwindigkeit proportional (Newton) bzw. umgekehrt proportional (Huygens) zum Brechungsindex ansetzten. Newtons Vorstellung galt als widerlegt, seitdem im 19. Jahrhundert Interferenz und Beugung beobachtet und die Geschwindigkeit in Medien gemessen werden konnten. ⓘ

Da es zu Huygens’ Zeit die erste Messung der Lichtgeschwindigkeit gab, die seiner Meinung nach viel zu hoch war, als dass Körper mit Masse diese erreichen könnten, schlug er mit dem Äther ein elastisches (weder sicht- noch messbares) Hintergrundmedium vor, das die Ausbreitung von Wellen gestatte, ähnlich dem Schall in der Luft. ⓘ

Im 13. Jahrhundert argumentierte Roger Bacon mit philosophischen Argumenten, die sich auf die Schriften von Alhazen und Aristoteles stützten, dass die Lichtgeschwindigkeit in der Luft nicht unendlich ist. In den 1270er Jahren zog Witelo die Möglichkeit in Betracht, dass sich das Licht im Vakuum mit unendlicher Geschwindigkeit ausbreitet, sich aber in dichteren Körpern verlangsamt. ⓘ

Erste Messversuche

1629 schlug Isaac Beeckman ein Experiment vor, bei dem eine Person den Blitz einer Kanone beobachtete, der von einem etwa 1,6 km entfernten Spiegel reflektiert wurde. Im Jahr 1638 schlug Galileo Galilei ein Experiment vor, von dem er behauptete, es bereits einige Jahre zuvor durchgeführt zu haben, um die Lichtgeschwindigkeit zu messen, indem er die Verzögerung zwischen dem Aufdecken einer Laterne und ihrer Wahrnehmung in einiger Entfernung beobachtete. Er war nicht in der Lage zu unterscheiden, ob sich das Licht augenblicklich fortbewegt oder nicht, kam aber zu dem Schluss, dass es, wenn dies nicht der Fall ist, dennoch außerordentlich schnell sein muss. Im Jahr 1667 berichtete die Accademia del Cimento in Florenz, dass sie Galileis Experiment durchgeführt hatte, wobei die Laternen etwa eine Meile voneinander entfernt waren, aber keine Verzögerung beobachtet wurde. Die tatsächliche Verzögerung bei diesem Experiment hätte etwa 11 Mikrosekunden betragen. ⓘ

Rømers Beobachtungen der Bedeckungen von Io von der Erde aus ⓘ

Die erste quantitative Schätzung der Lichtgeschwindigkeit wurde 1676 von Ole Rømer vorgenommen. Aus der Beobachtung, dass die Perioden von Jupiters innerstem Mond Io kürzer zu sein schienen, wenn sich die Erde dem Jupiter näherte, als wenn sie sich von ihm entfernte, schloss er, dass sich das Licht mit einer endlichen Geschwindigkeit bewegt, und schätzte, dass es 22 Minuten braucht, um den Durchmesser der Erdbahn zu durchqueren. Christiaan Huygens kombinierte diese Schätzung mit einer Schätzung des Durchmessers der Erdumlaufbahn, um eine geschätzte Lichtgeschwindigkeit von 220000 km/s zu erhalten, die 26 % unter dem tatsächlichen Wert liegt. ⓘ

Isaac Newton berichtete in seinem 1704 erschienenen Buch Opticks über Römers Berechnungen der endlichen Lichtgeschwindigkeit und gab für die Zeit, die das Licht für den Weg von der Sonne zur Erde benötigt, einen Wert von "sieben oder acht Minuten" an (der moderne Wert beträgt 8 Minuten 19 Sekunden). Newton erkundigte sich, ob die Schatten der Sonnenfinsternis von Rømer farbig waren; als er hörte, dass dies nicht der Fall war, schloss er daraus, dass die verschiedenen Farben sich mit derselben Geschwindigkeit fortbewegten. Im Jahr 1729 entdeckte James Bradley die stellare Aberration. Aus diesem Effekt ermittelte er, dass sich das Licht 10.210 Mal schneller als die Erde auf ihrer Umlaufbahn bewegen muss (die moderne Zahl ist 10.066 Mal schneller) oder dass das Licht 8 Minuten und 12 Sekunden braucht, um von der Sonne zur Erde zu gelangen. ⓘ

Verbindungen zum Elektromagnetismus

Im 19. Jahrhundert entwickelte Hippolyte Fizeau eine Methode zur Bestimmung der Lichtgeschwindigkeit auf der Grundlage von Lichtlaufzeitmessungen auf der Erde und gab einen Wert von 315000 km/s an. Seine Methode wurde von Léon Foucault verbessert, der im Jahr 1862 einen Wert von 298000 km/s ermittelte. Im Jahr 1856 maßen Wilhelm Eduard Weber und Rudolf Kohlrausch das Verhältnis der elektromagnetischen und elektrostatischen Ladungseinheiten, 1/√ε₀μ₀, durch Entladung eines Leydener Gefäßes und stellten fest, dass der numerische Wert sehr nahe an der von Fizeau direkt gemessenen Lichtgeschwindigkeit lag. Im folgenden Jahr berechnete Gustav Kirchhoff, dass sich ein elektrisches Signal in einem widerstandslosen Draht mit dieser Geschwindigkeit entlang des Drahtes ausbreitet. Anfang der 1860er Jahre zeigte Maxwell, dass sich elektromagnetische Wellen nach der von ihm erarbeiteten Theorie des Elektromagnetismus im leeren Raum mit einer Geschwindigkeit ausbreiten, die dem oben genannten Weber/Kohlrausch-Verhältnis entspricht, und unter Hinweis auf die numerische Nähe dieses Wertes zur von Fizeau gemessenen Lichtgeschwindigkeit schlug er vor, dass Licht tatsächlich eine elektromagnetische Welle ist. ⓘ

Der "leuchtende Äther"

Hendrik Lorentz (rechts) mit Albert Einstein ⓘ

Damals ging man davon aus, dass der leere Raum mit einem Hintergrundmedium, dem "leuchtenden Äther", gefüllt ist, in dem das elektromagnetische Feld existiert. Einige Physiker waren der Meinung, dass dieser Äther als bevorzugter Bezugsrahmen für die Ausbreitung des Lichts diente und es daher möglich sein sollte, die Bewegung der Erde in Bezug auf dieses Medium zu messen, indem man die Isotropie der Lichtgeschwindigkeit misst. Ab den 1880er Jahren wurden mehrere Experimente durchgeführt, um diese Bewegung nachzuweisen. Das berühmteste ist das von Albert A. Michelson und Edward W. Morley 1887 durchgeführte Experiment. Die festgestellte Bewegung war stets geringer als der Beobachtungsfehler. Moderne Experimente zeigen, dass die Geschwindigkeit des Lichts in beiden Richtungen mit einer Genauigkeit von 6 Nanometern pro Sekunde isotrop (in jeder Richtung gleich) ist. Aufgrund dieses Experiments schlug Hendrik Lorentz vor, dass die Bewegung des Apparats durch den Äther dazu führen kann, dass sich der Apparat entlang seiner Länge in Bewegungsrichtung zusammenzieht, und er nahm ferner an, dass sich auch die Zeitvariable für bewegte Systeme entsprechend ändern muss ("Ortszeit"), was zur Formulierung der Lorentz-Transformation führte. Auf der Grundlage der Lorentz'schen Äthertheorie zeigte Henri Poincaré (1900), dass diese Ortszeit (erster Ordnung in v/c) von Uhren angezeigt wird, die sich im Äther bewegen und unter der Annahme einer konstanten Lichtgeschwindigkeit synchronisiert sind. 1904 spekulierte er, dass die Lichtgeschwindigkeit eine Grenzgeschwindigkeit in der Dynamik sein könnte, vorausgesetzt, die Annahmen der Lorentz-Theorie werden alle bestätigt. 1905 brachte Poincaré die Lorentz'sche Äthertheorie in vollem Einklang mit dem Relativitätsprinzip. ⓘ

Spezielle Relativitätstheorie

Einstein postulierte 1905 von Anfang an, dass die von einem unbeschleunigten Beobachter gemessene Lichtgeschwindigkeit im Vakuum unabhängig von der Bewegung der Quelle oder des Beobachters ist. Daraus und aus dem Relativitätsprinzip leitete er die spezielle Relativitätstheorie ab, in der die Lichtgeschwindigkeit im Vakuum c als fundamentale Konstante auch in Zusammenhängen auftaucht, die nichts mit Licht zu tun haben. Dies machte das Konzept des stationären Äthers (an dem Lorentz und Poincaré noch festhielten) unbrauchbar und revolutionierte die Konzepte von Raum und Zeit. ⓘ

Höhere Genauigkeit von c und Neudefinition von Meter und Sekunde

In der zweiten Hälfte des 20. Jahrhunderts wurden große Fortschritte bei der genaueren Messung der Lichtgeschwindigkeit erzielt, zunächst durch Hohlraumresonanztechniken und später durch Laserinterferometertechniken. Dies wurde durch neue, präzisere Definitionen des Meters und der Sekunde unterstützt. 1950 bestimmte Louis Essen die Geschwindigkeit mit Hilfe der Hohlraumresonanz auf 299792,5±3,0 km/s. Dieser Wert wurde von der 12. Generalversammlung der Radio-Scientific Union im Jahr 1957 angenommen. Im Jahr 1960 wurde das Meter durch die Wellenlänge einer bestimmten Spektrallinie von Krypton-86 neu definiert, und 1967 wurde die Sekunde durch die Hyperfeinübergangsfrequenz des Grundzustands von Cäsium-133 neu definiert. ⓘ

1972 bestimmte eine Gruppe des US National Bureau of Standards in Boulder, Colorado, mit Hilfe der Laserinterferometermethode und den neuen Definitionen die Lichtgeschwindigkeit im Vakuum mit c = 299792456,2±1,1 m/s. Dies war 100-mal weniger unsicher als der zuvor akzeptierte Wert. Die verbleibende Unsicherheit hing hauptsächlich mit der Definition des Meters zusammen. Da ähnliche Experimente vergleichbare Ergebnisse für c ergaben, empfahl die 15. Allgemeine Konferenz für Maß und Gewicht 1975, den Wert 299792458 m/s für die Lichtgeschwindigkeit zu verwenden. ⓘ

Definiert als explizite Konstante

Tagung der Generalkonferenz für Maß und Gewicht (CGPM) im Jahr 1983 stellte fest, dass Wellenlängen aus Frequenzmessungen und ein bestimmter Wert für die Lichtgeschwindigkeit besser reproduzierbar sind als die vorherige Norm. Die Definition der Sekunde aus dem Jahr 1967 wurde beibehalten, so dass die Cäsium-Hyperfeinfrequenz nun sowohl die Sekunde als auch das Meter bestimmt. Zu diesem Zweck definierten sie das Meter neu als "die Länge des Weges, den das Licht im Vakuum während eines Zeitintervalls von 1/299792458 einer Sekunde zurücklegt". Infolge dieser Definition beträgt der Wert der Lichtgeschwindigkeit im Vakuum genau 299792458 m/s und ist zu einer definierten Konstante im SI-Einheitensystem geworden. Verbesserte experimentelle Techniken, mit denen vor 1983 die Lichtgeschwindigkeit gemessen wurde, wirken sich nicht mehr auf den bekannten Wert der Lichtgeschwindigkeit in SI-Einheiten aus, sondern ermöglichen stattdessen eine präzisere Umsetzung des Meters durch genauere Messung der Wellenlänge von Krypton-86 und anderen Lichtquellen. ⓘ

Im Jahr 2011 erklärte die CGPM ihre Absicht, alle sieben SI-Basiseinheiten neu zu definieren, indem sie die "explizite Konstantenformulierung" verwendet, bei der jede "Einheit indirekt durch die explizite Angabe eines exakten Werts für eine gut anerkannte Grundkonstante definiert wird", wie dies bei der Lichtgeschwindigkeit der Fall war. Sie schlug eine neue, aber völlig gleichwertige Formulierung für die Definition des Meters vor: "Das Meter, Symbol m, ist die Einheit der Länge; seine Größe wird festgelegt, indem der Zahlenwert der Lichtgeschwindigkeit im Vakuum auf genau 299792458 festgelegt wird, wenn er in der SI-Einheit m s-1 ausgedrückt wird." Dies war eine der Änderungen, die in die Neudefinition der SI-Basiseinheiten im Jahr 2019 einflossen, die auch als das Neue SI bezeichnet wird. ⓘ

Lichtgeschwindigkeit und Elektrodynamik

Aus den Maxwell-Gleichungen folgt, dass elektrische und magnetische Felder schwingen können und dabei Energie durch den leeren Raum transportieren. Dabei gehorchen die Felder einer Wellengleichung, ähnlich der für mechanische Wellen und für Wasserwellen. Die elektromagnetischen Wellen übertragen Energie und Information, was in technischen Anwendungen für Radio, Radar oder Laser genutzt wird. ⓘ

Ebene Welle oder Kugelwelle im Vakuum

Die Geschwindigkeit von ebenen oder kugelförmigen elektromagnetischen Wellen im Vakuum ist den Maxwell-Gleichungen zufolge der Kehrwert der Wurzel des Produkts der elektrischen Feldkonstanten $\varepsilon _{0}$ und der magnetischen Feldkonstanten $\mu _{0}\colon$ ⓘ

$c={\frac {1}{\sqrt {\varepsilon _{0}\,\mu _{0}}}}$ ⓘ

Daraus berechnete Maxwell 1865 mit den damals bekannten Werten für $\varepsilon _{0}$ und $\mu _{0}$ den Wert von $310\,740\;{\text{km/s}}$ und folgerte:

„Diese Geschwindigkeit ist so nahe an der Lichtgeschwindigkeit, sodass wir einen starken Grund zu der Annahme haben, dass das Licht selbst (einschließlich Wärmestrahlung und anderer Strahlung, falls es sie gibt), eine elektromagnetische Welle ist.“

Maxwells Annahme ist in allen Beobachtungen an elektromagnetischer Strahlung bestätigt worden. ⓘ

Transversal modulierte Welle im Vakuum

Nach den Maxwell-Gleichungen ergibt sich die von der Wellenlänge unabhängige Lichtgeschwindigkeit $c=1/{\sqrt {\varepsilon _{0}\,\mu _{0}}}$ u. a. für den Fall einer im Vakuum unendlich ausgedehnten ebenen Welle mit einer wohldefinierten Fortpflanzungsrichtung. Demgegenüber hat jede praktisch realisierbare Lichtwelle immer ein gewisses Strahlprofil. Wird dies als Überlagerung von ebenen Wellen mit leicht veränderten Fortpflanzungsrichtungen dargestellt, haben die einzelnen ebenen Wellen zwar alle die Vakuumlichtgeschwindigkeit $c$, jedoch gilt dies nicht notwendig für die durch die Überlagerung entstehende Welle. Es resultiert eine leicht verlangsamte Welle. Das konnte an speziell geformten Bessel-Strahlen von Mikrowellen und sichtbarem Licht auch nachgewiesen werden, sogar für die Geschwindigkeit einzelner Photonen. Bei allen praktisch realisierbaren Lichtwellen, auch bei scharf gebündelten Laserstrahlen, ist dieser Effekt aber vernachlässigbar klein. ⓘ

Überlichtgeschwindigkeit

Es gibt Spekulationen über Teilchen, die sich schneller als mit Lichtgeschwindigkeit bewegen. Ein Beispiel sind als Tachyonen bezeichnete, hypothetische Teilchen. Nach der Relativitätstheorie könnten Tachyonen nicht mit normaler Materie wechselwirken: Sonst könnte man nicht, für alle Beobachter gleich, zwischen Ursache und Wirkung unterscheiden. Die theoretischen Grundlagen des Tachyonen-Konzepts sind umstritten. Ein experimenteller Nachweis von Tachyonen gelang bisher nicht. ⓘ

Darüber hinaus erregten in den vergangenen Jahren Veröffentlichungen besonderes Aufsehen, in denen die Beobachtung von Überlichtgeschwindigkeit behauptet wurde. Doch entweder konnte gezeigt werden, dass die scheinbar überlichtschnelle Signalübermittlung durch eine Fehlinterpretation der Daten entstand (überlichtschnelle Jets, superluminares Tunneln), oder die Messungen konnten nicht reproduziert werden und stellten sich schließlich als fehlerhaft heraus (siehe beispielsweise Messungen der Neutrinogeschwindigkeit). ⓘ

Historische Hintergründe

Zur Konstanz der Lichtgeschwindigkeit

Erste Überlegungen

James Bradley konnte mit seinen Untersuchungen zur Aberration von 1728 nicht nur die Lichtgeschwindigkeit selbst bestimmen, sondern auch erstmals Aussagen über ihre Konstanz treffen. Er beobachtete, dass die Aberration für alle Sterne in der gleichen Blickrichtung während eines Jahres in identischer Weise variiert. Daraus schloss er, dass die Geschwindigkeit, mit der Sternenlicht auf der Erde eintrifft, im Rahmen seiner Messgenauigkeit von etwa einem Prozent für alle Sterne gleich ist. ⓘ

Um zu klären, ob diese Eintreffgeschwindigkeit davon abhängt, ob sich die Erde auf ihrem Weg um die Sonne auf einen Stern zu oder von ihm weg bewegt, reichte diese Messgenauigkeit allerdings nicht aus. Diese Frage untersuchte zuerst François Arago 1810 anhand der Messung des Ablenkwinkels von Sternenlicht in einem Glasprisma. Nach der damals akzeptierten Korpuskulartheorie des Lichtes erwartete er eine Veränderung dieses Winkels in einer messbaren Größenordnung, da sich die Geschwindigkeit des einfallenden Sternenlichts zu der Geschwindigkeit der Erde auf ihrem Weg um die Sonne addieren sollte. Es zeigten sich jedoch im Jahresverlauf keine messbaren Schwankungen des Ablenkwinkels. Arago erklärte dieses Ergebnis mit der These, dass Sternenlicht ein Gemisch aus verschiedenen Geschwindigkeiten sei, während das menschliche Auge daraus nur eine einzige wahrnehmen könne. Aus heutiger Sicht kann seine Messung jedoch als erster experimenteller Nachweis der Konstanz der Lichtgeschwindigkeit betrachtet werden. ⓘ

Mit dem Aufkommen der Vorstellung von Licht als Wellenphänomen formulierte Augustin Fresnel 1818 eine andere Interpretation des Arago-Experiments. Danach schloss die Analogie zwischen mechanischen Wellen und Lichtwellen die Vorstellung ein, dass sich Lichtwellen in einem gewissen Medium ausbreiten müssen, dem sogenannten Äther, so wie sich auch Wasserwellen im Wasser ausbreiten. Der Äther sollte dabei den Bezugspunkt für ein bevorzugtes Inertialsystem darstellen. Fresnel erklärte das Ergebnis von Arago durch die Annahme, dass dieser Äther im Inneren von Materie teilweise mitgeführt werde, in diesem Fall im verwendeten Prisma. Dabei würde der Grad der Mitführung in geeigneter Weise vom Brechungsindex abhängen. ⓘ

Unabhängigkeit von der Quelle

Mit dem Michelson-Morley-Experiment wurde zwar die Konstanz der Lichtgeschwindigkeit für einen mit der Lichtquelle mitbewegten Beobachter bestätigt, jedoch keineswegs für einen nicht mit der Quelle mitbewegten Beobachter. Denn das Experiment kann auch mit einer Emissionstheorie erklärt werden, wonach die Lichtgeschwindigkeit in allen Bezugssystemen lediglich konstant relativ zur Emissionsquelle ist (das heißt, in Systemen, wo sich die Quelle mit ±v bewegt, würde sich das Licht folglich mit c ± v ausbreiten). Auch Albert Einstein zog vor 1905 eine solche Hypothese kurz in Betracht, was auch der Grund war, dass er in seinen Schriften das MM-Experiment zwar immer als Bestätigung des Relativitätsprinzips, aber nicht als Bestätigung der Lichtkonstanz verwendete. ⓘ

Jedoch würde eine Emissionstheorie eine völlige Reformulierung der Elektrodynamik erfordern, wogegen der große Erfolg von Maxwells Theorie sprach. Die Emissionstheorie wurde auch experimentell widerlegt. Beispielsweise müssten die von der Erde aus beobachteten Bahnen von Doppelsternen bei unterschiedlichen Lichtgeschwindigkeiten verzerrt ausfallen, was jedoch nicht beobachtet wurde. Beim Zerfall von sich mit annähernd $c$ bewegenden π⁰-Mesonen hätten die dabei entstehenden Photonen die Geschwindigkeit der Mesonen übernehmen und sich annähernd mit doppelter Lichtgeschwindigkeit bewegen sollen, was jedoch nicht der Fall war. Auch der Sagnac-Effekt demonstriert die Unabhängigkeit der Lichtgeschwindigkeit von der Bewegung der Quelle. Alle diese Experimente finden ihre Erklärung in der Speziellen Relativitätstheorie, die u. a. aussagt: Licht überholt nicht Licht. ⓘ

Variable Lichtgeschwindigkeit und Konstanz im beobachtbaren Universum

Obwohl die Konstanz der Lichtgeschwindigkeit experimentell nachgewiesen wurde, gibt es bis jetzt keine ausreichend überzeugende Erklärung für ihre Konstanz und ihren speziellen Wert. Die Schleifenquantengravitation beispielsweise diktiert, dass die Geschwindigkeit eines Photons nicht als Konstante definiert werden kann, sondern dass ihr Wert von der Photonfrequenz abhängt. Tatsächlich gibt es Theorien, dass die Lichtgeschwindigkeit sich mit dem Alter des Universums ändert und dass sie im frühen Universum nicht konstant war. Albrecht und Magueijo zeigen, dass die kosmologischen Evolutionsgleichungen zusammen mit einer variablen Lichtgeschwindigkeit die Probleme des Horizonts, der Flachheit und der kosmologischen Konstante lösen können. Die Annahme einer Raumzeit mit drei Raum- und zwei Zeitdimensionen gibt eine natürliche Erklärung für die Konstanz der Lichtgeschwindigkeit im beobachtbaren Universum und auch dafür, dass die Lichtgeschwindigkeit im frühen Universum variierte. ⓘ