Trigonometrie
| Trigonometrie ⓘ |
|---|
 |
|
| Referenz |
|
| Gesetze und Theoreme |
|
| Kalkül |
|
Die Trigonometrie (von altgriechisch τρίγωνον (trígōnon) "Dreieck" und μέτρον (métron) "Maß") ist ein Teilgebiet der Mathematik, das sich mit den Beziehungen zwischen Seitenlängen und Winkeln von Dreiecken befasst. Das Fachgebiet entwickelte sich in der hellenistischen Welt im 3. Jahrhundert v. Chr. aus der Anwendung der Geometrie auf astronomische Studien. Die Griechen konzentrierten sich auf die Berechnung von Akkorden, während Mathematiker in Indien die frühesten bekannten Wertetabellen für trigonometrische Verhältnisse (auch trigonometrische Funktionen genannt) wie den Sinus erstellten. ⓘ
Im Laufe der Geschichte wurde die Trigonometrie in Bereichen wie Geodäsie, Vermessung, Himmelsmechanik und Navigation eingesetzt. ⓘ
Die Trigonometrie ist für ihre vielen Identitäten bekannt. Diese trigonometrischen Identitäten werden häufig verwendet, um trigonometrische Ausdrücke umzuschreiben, um einen Ausdruck zu vereinfachen, eine nützlichere Form eines Ausdrucks zu finden oder eine Gleichung zu lösen. ⓘ

Geschichte

Die sumerischen Astronomen untersuchten das Winkelmaß anhand einer Einteilung der Kreise in 360 Grad. Sie und später die Babylonier untersuchten das Verhältnis der Seiten ähnlicher Dreiecke und entdeckten einige Eigenschaften dieser Verhältnisse, machten daraus aber keine systematische Methode zur Bestimmung von Seiten und Winkeln von Dreiecken. Die alten Nubier verwendeten eine ähnliche Methode. ⓘ
Im 3. Jahrhundert v. Chr. untersuchten hellenistische Mathematiker wie Euklid und Archimedes die Eigenschaften von Sehnen und eingeschriebenen Winkeln in Kreisen, und sie bewiesen Theoreme, die den modernen trigonometrischen Formeln entsprechen, obwohl sie sie geometrisch und nicht algebraisch darstellten. 140 v. Chr. gab Hipparchus (aus Nicaea, Kleinasien) die ersten Tabellen der Sehnen an, die den modernen Tabellen der Sinuswerte entsprechen, und nutzte sie zur Lösung von Problemen der Trigonometrie und der sphärischen Trigonometrie. Im 2. Jahrhundert n. Chr. erstellte der griechisch-ägyptische Astronom Ptolemäus (aus Alexandria, Ägypten) in Buch 1, Kapitel 11 seines Almagest detaillierte trigonometrische Tabellen (Ptolemäus' Akkordtabelle). Ptolemäus verwendete die Sehnenlänge, um seine trigonometrischen Funktionen zu definieren, was einen kleinen Unterschied zu der heute verwendeten Sinuskonvention darstellt. (Der Wert, den wir als sin(θ) bezeichnen, lässt sich ermitteln, indem man die Sehnenlänge für den doppelten Winkel (2θ) in Ptolemäus' Tabelle nachschlägt und dann diesen Wert durch zwei teilt). Es vergingen Jahrhunderte, bis detailliertere Tabellen erstellt wurden, und Ptolemäus' Abhandlung blieb für die Durchführung trigonometrischer Berechnungen in der Astronomie während der nächsten 1200 Jahre in der mittelalterlichen byzantinischen, islamischen und später westeuropäischen Welt in Gebrauch. ⓘ
Die moderne Sinuskonvention wird erstmals im Surya Siddhanta beschrieben, und ihre Eigenschaften wurden von dem indischen Mathematiker und Astronomen Aryabhata im 5. Diese griechischen und indischen Werke wurden von mittelalterlichen islamischen Mathematikern übersetzt und erweitert. Bis zum 10. Jahrhundert verwendeten islamische Mathematiker alle sechs trigonometrischen Funktionen, hatten ihre Werte tabellarisch erfasst und wandten sie auf Probleme der sphärischen Geometrie an. Der persische Universalgelehrte Nasir al-Din al-Tusi gilt als Begründer der Trigonometrie als eigenständige mathematische Disziplin. Nasīr al-Dīn al-Tūsī war der erste, der die Trigonometrie als eine von der Astronomie unabhängige mathematische Disziplin behandelte, und er entwickelte die sphärische Trigonometrie in ihrer heutigen Form. Er führte die sechs verschiedenen Fälle eines rechtwinkligen Dreiecks in der sphärischen Trigonometrie auf, und in seinem Werk On the Sector Figure gab er das Sinusgesetz für ebene und sphärische Dreiecke an, entdeckte das Tangentengesetz für sphärische Dreiecke und lieferte Beweise für diese beiden Gesetze. Das Wissen über trigonometrische Funktionen und Methoden gelangte über lateinische Übersetzungen des griechischen Almagest des Ptolemäus sowie über die Werke persischer und arabischer Astronomen wie Al Battani und Nasir al-Din al-Tusi nach Westeuropa. Eines der frühesten Werke eines nordeuropäischen Mathematikers über Trigonometrie ist De Triangulis des deutschen Mathematikers Regiomontanus aus dem 15. Jahrhundert, der von dem byzantinischen griechischen Gelehrten Kardinal Basilios Bessarion, mit dem er mehrere Jahre zusammenlebte, zum Schreiben angeregt wurde und eine Kopie des Almagest erhielt. Zur gleichen Zeit wurde eine weitere Übersetzung des Almagest aus dem Griechischen ins Lateinische von dem Kreter Georg von Trebizond fertiggestellt. Die Trigonometrie war im Nordeuropa des 16. Jahrhunderts noch so wenig bekannt, dass Nikolaus Kopernikus in De revolutionibus orbium coelestium zwei Kapitel der Erklärung ihrer Grundbegriffe widmete. ⓘ
Aufgrund der Anforderungen der Navigation und des wachsenden Bedarfs an genauen Karten großer geografischer Gebiete entwickelte sich die Trigonometrie zu einem wichtigen Zweig der Mathematik. Bartholomaeus Pitiscus war der erste, der das Wort verwendete und veröffentlichte 1595 seine Trigonometria. Gemma Frisius beschrieb zum ersten Mal die Methode der Triangulation, die noch heute in der Vermessung verwendet wird. Es war Leonhard Euler, der die komplexen Zahlen vollständig in die Trigonometrie einbezog. Die Arbeiten der schottischen Mathematiker James Gregory im 17. Jahrhundert und Colin Maclaurin im 18. Jahrhundert waren für die Entwicklung trigonometrischer Reihen von großer Bedeutung. Ebenfalls im 18. Jahrhundert definierte Brook Taylor die allgemeine Taylor-Reihe. ⓘ
Der Begriff Trigonometrie wurde durch Bartholomäus Pitiscus in seinem Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus von 1595 eingeführt. ⓘ
Trigonometrische Verhältnisse
Trigonometrische Verhältnisse sind die Verhältnisse zwischen den Kanten eines rechtwinkligen Dreiecks. Diese Verhältnisse sind durch die folgenden trigonometrischen Funktionen des bekannten Winkels A gegeben, wobei sich a, b und h auf die Längen der Seiten in der nebenstehenden Abbildung beziehen:
- Sinusfunktion (sin), definiert als das Verhältnis zwischen der dem Winkel gegenüberliegenden Seite und der Hypotenuse.
- Kosinusfunktion (cos), definiert als das Verhältnis zwischen dem angrenzenden Schenkel (der Seite des Dreiecks, die den Winkel mit dem rechten Winkel verbindet) und der Hypotenuse.
- Tangensfunktion (tan), definiert als das Verhältnis zwischen dem gegenüberliegenden Schenkel und dem angrenzenden Schenkel. ⓘ
Die Hypotenuse ist die Seite, die dem 90-Grad-Winkel in einem rechtwinkligen Dreieck gegenüberliegt; sie ist die längste Seite des Dreiecks und eine der beiden Seiten, die an den Winkel A angrenzt. Der angrenzende Schenkel ist die andere Seite, die an den Winkel A angrenzt. Die gegenüberliegende Seite ist die Seite, die dem Winkel A gegenüberliegt. Siehe unten unter Mnemotechnik. ⓘ
Da zwei rechtwinklige Dreiecke mit demselben spitzen Winkel A ähnlich sind, hängt der Wert eines trigonometrischen Verhältnisses nur vom Winkel A ab. ⓘ
Die Kehrwerte dieser Funktionen werden als Kosekans (csc), Sekans (sec) bzw. Kotangens (cot) bezeichnet:
Kosinus, Kotangens und Kosekans sind so benannt, weil sie jeweils der Sinus, der Tangens und der Sekans des Komplementärwinkels sind, abgekürzt als "Co". ⓘ
Mit diesen Funktionen lassen sich praktisch alle Fragen zu beliebigen Dreiecken mit Hilfe des Sinus- und des Kosinussatzes beantworten. Mit diesen Gesetzen lassen sich die übrigen Winkel und Seiten eines beliebigen Dreiecks berechnen, sobald zwei Seiten und ihr zugehöriger Winkel oder zwei Winkel und eine Seite oder drei Seiten bekannt sind. ⓘ
Mnemotechnik
Mnemotechniken werden häufig verwendet, um sich Fakten und Beziehungen in der Trigonometrie zu merken. So kann man sich beispielsweise die Verhältnisse von Sinus, Kosinus und Tangens in einem rechtwinkligen Dreieck merken, indem man sie und die entsprechenden Seiten als Buchstabenkombinationen darstellt. Eine Gedächtnisstütze ist zum Beispiel SOH-CAH-TOA:
- Sinus = Gegenüberliegend ÷ Hypotenuse
- Kosinus = Angrenzend ÷ Hypotenuse
- Tangente = Gegenüberliegend ÷ Angrenzend ⓘ
Eine Möglichkeit, sich die Buchstaben zu merken, besteht darin, sie phonetisch auszusprechen (z. B. ähnlich wie Krakatoa). Eine andere Methode besteht darin, die Buchstaben zu einem Satz zusammenzusetzen, z. B. "Some Old Hippie Caught Another Hippie Trippin' On Acid". ⓘ
Der Einheitskreis und gängige trigonometrische Werte


Trigonometrische Verhältnisse können auch mit Hilfe des Einheitskreises dargestellt werden, d. h. eines Kreises mit dem Radius 1 und dem Ursprung in der Ebene. In diesem Fall schneidet die Endseite eines Winkels A, der sich in der Standardposition befindet, den Einheitskreis in einem Punkt (x,y), wobei und . Diese Darstellung ermöglicht die Berechnung häufig vorkommender trigonometrischer Werte, wie z. B. die in der folgenden Tabelle aufgeführten:
| Funktion | 0 | ⓘ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sinus | |||||||||
| Kosinus | |||||||||
| Tangens | undefiniert | ||||||||
| Sekante | undefiniert | ||||||||
| Kosekans | undefiniert | undefiniert | |||||||
| Kotangens | undefiniert | undefiniert |
Trigonometrische Funktionen von reellen oder komplexen Variablen
Mit Hilfe des Einheitskreises können die Definitionen der trigonometrischen Verhältnisse auf alle positiven und negativen Argumente ausgedehnt werden (siehe trigonometrische Funktion). ⓘ
Graphen der trigonometrischen Funktionen
Die folgende Tabelle gibt einen Überblick über die Eigenschaften der Graphen der sechs wichtigsten trigonometrischen Funktionen:
| Funktion | Periode | Bereich | Bereich | Graph ⓘ |
|---|---|---|---|---|
| Sinus | 
| |||
| Kosinus | 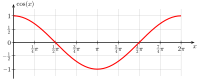
| |||
| Tangens | 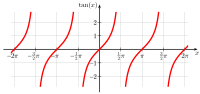
| |||
| Sekante | 
| |||
| Kosekans | 
| |||
| Kotangens | 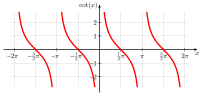
|
Inverse trigonometrische Funktionen
Da die sechs wichtigsten trigonometrischen Funktionen periodisch sind, sind sie nicht injektiv (oder 1 zu 1) und somit nicht invertierbar. Durch Einschränkung des Bereichs einer trigonometrischen Funktion können sie jedoch invertierbar gemacht werden. ⓘ
Die Namen der inversen trigonometrischen Funktionen sowie ihr Bereich und ihre Reichweite sind der folgenden Tabelle zu entnehmen:
| Name . | Übliche Schreibweise | Definition | Bereich von x für reelles Ergebnis | Bereich des üblichen Hauptwerts (Bogenmaß) |
Bereich des üblichen Hauptwerts (Grad) ⓘ |
|---|---|---|---|---|---|
| Arkussinus | y = arcsin(x) | x = sin(y) | -1 ≤ x ≤ 1 | - ≤ y ≤ | -90° ≤ y ≤ 90° |
| Arkosinus | y = arccos(x) | x = cos(y) | -1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0° ≤ y ≤ 180° |
| Arkustangens | y = arctan(x) | x = tan(y) | alle reellen Zahlen | - < y < | -90° < y < 90° |
| Arkotangens | y = arccot(x) | x = cot(y) | alle reellen Zahlen | 0 < y < π | 0° < y < 180° |
| Arkussekans | y = arcsec(x) | x = sec(y) | x ≤ -1 oder 1 ≤ x | 0 ≤ y < oder < y ≤ π | 0° ≤ y < 90° oder 90° < y ≤ 180° |
| arccosecant | y = arccsc(x) | x = csc(y) | x ≤ -1 oder 1 ≤ x | - ≤ y < 0 oder 0 < y ≤ | -90° ≤ y < 0° oder 0° < y ≤ 90° |
Darstellungen von Potenzreihen
Betrachtet man die trigonometrischen Verhältnisse als Funktionen einer reellen Variablen, so können sie durch eine unendliche Reihe dargestellt werden. Für Sinus und Kosinus gibt es zum Beispiel folgende Darstellungen:
Mit diesen Definitionen können die trigonometrischen Funktionen für komplexe Zahlen definiert werden. Wenn sie als Funktionen reeller oder komplexer Variablen erweitert werden, gilt die folgende Formel für die komplexe Exponentialfunktion:
Diese komplexe Exponentialfunktion, die in Form von trigonometrischen Funktionen geschrieben ist, ist besonders nützlich. ⓘ
Berechnung trigonometrischer Funktionen
Trigonometrische Funktionen gehörten zu den frühesten Anwendungen von mathematischen Tabellen. Solche Tabellen wurden in Mathematiklehrbücher aufgenommen, und den Schülern wurde beigebracht, Werte nachzuschlagen und zwischen den aufgeführten Werten zu interpolieren, um eine höhere Genauigkeit zu erzielen. Rechenschieber hatten spezielle Skalen für trigonometrische Funktionen. ⓘ
Wissenschaftliche Taschenrechner haben Tasten für die Berechnung der wichtigsten trigonometrischen Funktionen (sin, cos, tan und manchmal cis und ihre Umkehrungen). Die meisten erlauben eine Auswahl an Winkelmessmethoden: Grad, Bogenmaß und manchmal auch Grad. Die meisten Computerprogrammiersprachen bieten Funktionsbibliotheken, die die trigonometrischen Funktionen enthalten. Die Fließkommaeinheit, die in den Mikroprozessorchips der meisten Personalcomputer eingebaut ist, verfügt über integrierte Befehle zur Berechnung trigonometrischer Funktionen. ⓘ
Andere trigonometrische Funktionen
Neben den sechs oben genannten Verhältnissen gibt es noch weitere trigonometrische Funktionen, die historisch wichtig waren, aber heute nur noch selten verwendet werden. Dazu gehören der Akkord (crd(θ) = 2 sin()), der Versinus (versin(θ) = 1 - cos(θ) = 2 sin2()) (der in den frühesten Tabellen auftaucht), der Coversinus (coversin(θ) = 1 - sin(θ) = versin( - θ)), der Haversinus (haversin(θ) = versin(θ) = sin2()), die Exsecante (exsec(θ) = sec(θ) - 1) und die Excosecante (excsc(θ) = exsec( - θ) = csc(θ) - 1). Siehe Liste der trigonometrischen Identitäten für weitere Beziehungen zwischen diesen Funktionen. ⓘ
Anwendungen
Astronomie
Seit Jahrhunderten wird die sphärische Trigonometrie zur Bestimmung von Sonnen-, Mond- und Sternpositionen, zur Vorhersage von Finsternissen und zur Beschreibung der Planetenbahnen verwendet. ⓘ
In der heutigen Zeit wird die Triangulation in der Astronomie zur Messung der Entfernung zu nahen Sternen sowie in Satellitennavigationssystemen eingesetzt. ⓘ

Historisch gesehen wurde die Trigonometrie zur Bestimmung von Breiten- und Längengraden von Segelschiffen, zum Zeichnen von Kursen und zur Berechnung von Entfernungen während der Navigation verwendet. ⓘ
Die Trigonometrie wird auch heute noch in der Navigation eingesetzt, z. B. im Global Positioning System und in der künstlichen Intelligenz für autonome Fahrzeuge. ⓘ
Vermessung
In der Landvermessung wird die Trigonometrie bei der Berechnung von Längen, Flächen und relativen Winkeln zwischen Objekten eingesetzt. ⓘ
In größerem Maßstab wird die Trigonometrie in der Geografie verwendet, um Entfernungen zwischen Landmarken zu messen. ⓘ
Periodische Funktionen

Die Sinus- und Kosinusfunktionen sind grundlegend für die Theorie periodischer Funktionen, wie z. B. derjenigen, die Schall- und Lichtwellen beschreiben. Fourier entdeckte, dass jede kontinuierliche, periodische Funktion als unendliche Summe von trigonometrischen Funktionen beschrieben werden kann. ⓘ
Auch nichtperiodische Funktionen können durch die Fourier-Transformation als Integral von Sinus- und Kosinusfunktionen dargestellt werden. Dies findet u. a. in der Quantenmechanik und der Kommunikation Anwendung. ⓘ
Optik und Akustik
Die Trigonometrie ist in vielen physikalischen Wissenschaften nützlich, unter anderem in der Akustik und der Optik. In diesen Bereichen wird sie zur Beschreibung von Schall- und Lichtwellen und zur Lösung von Grenzwert- und Übertragungsproblemen verwendet. ⓘ
Andere Anwendungen
Weitere Bereiche, in denen Trigonometrie oder trigonometrische Funktionen verwendet werden, sind Musiktheorie, Geodäsie, Audiosynthese, Architektur, Elektronik, Biologie, medizinische Bildgebung (CT-Scans und Ultraschall), Chemie, Zahlentheorie (und damit Kryptologie), Seismologie, Meteorologie, Ozeanografie, Bildkompression, Phonetik, Wirtschaftswissenschaften, Elektrotechnik, Maschinenbau, Bauingenieurwesen, Computergrafik, Kartografie, Kristallografie und Spieleentwicklung. ⓘ
Identitäten

Die Trigonometrie ist bekannt für ihre vielen Identitäten, d. h. Gleichungen, die für alle möglichen Eingaben wahr sind. ⓘ
Identitäten, die nur Winkel betreffen, werden als trigonometrische Identitäten bezeichnet. Andere Gleichungen, die so genannten Dreiecksgleichungen, beziehen sich sowohl auf die Seiten als auch auf die Winkel eines bestimmten Dreiecks. ⓘ
Dreiecksgleichungen
Die folgenden Zahlenwerte sind abgerundet. In einem Dreieck ABC sind folgende Größen gegeben:
Aus diesen Angaben soll die Seitenlänge c ermittelt werden. Da die Ankathete von bekannt und die Hypotenuse gesucht ist, wird die Kosinus-Funktion verwendet. ⓘ
Sinusgesetz
Das Sinusgesetz (auch bekannt als "Sinusregel") für ein beliebiges Dreieck besagt
wobei die Fläche des Dreiecks und R der Radius des Umkreises des Dreiecks ist:
Kosinussatz
Der Kosinussatz (auch bekannt als Kosinusformel oder "Kosinusregel") ist eine Erweiterung des Satzes von Pythagoras auf beliebige Dreiecke:
oder äquivalent dazu:
Gesetz der Tangens
Das von François Viète entwickelte Tangentengesetz ist eine Alternative zum Kosinussatz, wenn es darum geht, die unbekannten Kanten eines Dreiecks zu bestimmen, und ermöglicht einfachere Berechnungen bei der Verwendung trigonometrischer Tabellen. Es ist gegeben durch:
Fläche
Bei zwei Seiten a und b und dem Winkel zwischen den Seiten C ist der Flächeninhalt des Dreiecks gegeben durch die Hälfte des Produkts aus den Längen der beiden Seiten und dem Sinus des Winkels zwischen den beiden Seiten: Die Heronsche Formel ist eine weitere Methode zur Berechnung des Flächeninhalts eines Dreiecks. Diese Formel besagt, dass, wenn ein Dreieck die Seitenlängen a, b und c hat und der Halbmesser ⓘ
dann ist der Flächeninhalt des Dreiecks:
- ,
wobei R der Radius des Umkreises des Dreiecks ist. ⓘ
Trigonometrische Identitäten
Pythagoreische Identitäten
Die folgenden trigonometrischen Identitäten beziehen sich auf den Satz des Pythagoras und gelten für jeden Wert:
Die zweite und dritte Gleichung ergeben sich aus der Division der ersten Gleichung durch und abgeleitet. ⓘ
Eulersche Formel
Die Eulersche Formel, die besagt, dass ergibt die folgenden analytischen Identitäten für Sinus, Kosinus und Tangens in Abhängigkeit von e und der imaginären Einheit i:
Andere trigonometrische Identitäten
Weitere häufig verwendete trigonometrische Identitäten sind die Halbwinkelidentitäten, die Winkelsummen- und -differenzidentitäten sowie die Produkt-Summen-Identitäten. ⓘ







































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![{\displaystyle (-\infty ,-1]\cup [1,\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e3448e2de68557e598967fb8b1f8900260c4a64)















![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan \left[{\tfrac {1}{2}}(A-B)\right]}{\tan \left[{\tfrac {1}{2}}(A+B)\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1da4e06eb6f25cd7f7fc1a7784a11a82ae53f9f)









