Spieltheorie
| Komplexe Systeme ⓘ |
|---|
| Themen |
| Teil einer Serie über ⓘ |
| Wirtschaftswissenschaften |
|---|
|
|
|
Die Spieltheorie befasst sich mit mathematischen Modellen für strategische Interaktionen zwischen rationalen Akteuren. Sie findet in allen Bereichen der Sozialwissenschaften sowie in der Logik, Systemwissenschaft und Informatik Anwendung. Ursprünglich befasste sie sich mit Zwei-Personen-Nullsummenspielen, bei denen die Gewinne oder Verluste jedes Teilnehmers durch die Gewinne oder Verluste der anderen Teilnehmer genau ausgeglichen werden. Im 21. Jahrhundert wird die Spieltheorie auf ein breites Spektrum von Verhaltensbeziehungen angewandt; sie ist jetzt ein Oberbegriff für die Wissenschaft der logischen Entscheidungsfindung bei Menschen, Tieren und Computern. ⓘ
Die moderne Spieltheorie begann mit der Idee von Gleichgewichten mit gemischten Strategien in Zwei-Personen-Nullsummenspielen und deren Beweis durch John von Neumann. Von Neumanns ursprünglicher Beweis verwendete das Brouwersche Fixpunkttheorem für kontinuierliche Abbildungen auf kompakte konvexe Mengen, das zu einer Standardmethode in der Spieltheorie und der mathematischen Ökonomie wurde. Auf seine Arbeit folgte 1944 das gemeinsam mit Oskar Morgenstern verfasste Buch Theory of Games and Economic Behavior, in dem kooperative Spiele mit mehreren Spielern untersucht wurden. Die zweite Auflage dieses Buches lieferte eine axiomatische Theorie des erwarteten Nutzens, die es mathematischen Statistikern und Wirtschaftswissenschaftlern ermöglichte, Entscheidungsprozesse unter Unsicherheit zu behandeln. ⓘ
Die Spieltheorie wurde in den 1950er Jahren von vielen Gelehrten umfassend entwickelt. Sie wurde in den 1970er Jahren ausdrücklich auf die Evolution angewandt, obwohl ähnliche Entwicklungen mindestens bis in die 1930er Jahre zurückreichen. Die Spieltheorie ist als wichtiges Instrument in vielen Bereichen anerkannt. Mit der Verleihung des Nobelpreises für Wirtschaftswissenschaften an die Spieltheoretiker Paul Milgrom und Robert B. Wilson im Jahr 2020 haben fünfzehn Spieltheoretiker den Nobelpreis für Wirtschaftswissenschaften erhalten. John Maynard Smith erhielt den Crafoord-Preis für seine Anwendung der evolutionären Spieltheorie. ⓘ
Die Spieltheorie ist eine mathematische Theorie, in der Entscheidungssituationen modelliert werden, in denen mehrere Beteiligte miteinander interagieren. Sie versucht dabei unter anderem, das rationale Entscheidungsverhalten in sozialen Konfliktsituationen davon abzuleiten. Die Spieltheorie ist originär ein Teilgebiet der Mathematik. Sie bedient mannigfaltige Anwendungsfelder. ⓘ
In diesem Artikel wird die nicht-kooperative Spieltheorie behandelt, die von der kooperativen Spieltheorie zu unterscheiden ist. Unten finden sich einige Bemerkungen zu den Unterschieden. ⓘ
Geschichte
Vorläufer
Die Diskussionen über die Mathematik der Spiele begannen lange vor der Entstehung der modernen mathematischen Spieltheorie. Cardanos Werk über Glücksspiele in Liber de ludo aleae (Buch über Glücksspiele), das um 1564 geschrieben, aber erst 1663 posthum veröffentlicht wurde, formulierte einige der grundlegenden Ideen auf diesem Gebiet. In den 1650er Jahren entwickelten Pascal und Huygens das Konzept der Erwartung, um über die Struktur von Glücksspielen nachzudenken, und Huygens veröffentlichte 1657 sein Glücksspielkalkül in De ratiociniis in ludo aleæ (Über das Rechnen im Glücksspiel). ⓘ
Im Jahr 1713 wurde in einem Schreiben, das Charles Waldegrave zugeschrieben wird, ein Spiel namens "le Her" analysiert. Er war ein aktiver Jakobiner und Onkel von James Waldegrave, einem britischen Diplomaten. In diesem Brief lieferte Waldegrave eine minimale gemischte Strategielösung für eine Zwei-Personen-Version des Kartenspiels le Her, und das Problem ist heute als Waldegrave-Problem bekannt. In seinen Recherches sur les principes mathématiques de la théorie des richesses (Forschungen über die mathematischen Prinzipien der Theorie des Reichtums) von 1838 betrachtete Antoine Augustin Cournot ein Duopol und präsentierte eine Lösung, die das Nash-Gleichgewicht des Spiels darstellt. ⓘ
Im Jahr 1913 veröffentlichte Ernst Zermelo Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels, in der er nachwies, dass die optimale Schachstrategie streng festgelegt ist. Dies ebnete den Weg für allgemeinere Theoreme. ⓘ
1938 bewies der dänische Wirtschaftsmathematiker Frederik Zeuthen mit Hilfe des Brouwerschen Fixpunktsatzes, dass das mathematische Modell eine Gewinnstrategie hat. In seinem 1938 erschienenen Buch Applications aux Jeux de Hasard und früheren Notizen bewies Émile Borel ein Minimax-Theorem für Zwei-Personen-Nullsummen-Matrixspiele nur dann, wenn die Auszahlungsmatrix symmetrisch ist, und lieferte eine Lösung für ein nichttriviales unendliches Spiel (im Englischen als Blotto-Spiel bekannt). Borel vermutete die Nichtexistenz von Gleichgewichten mit gemischten Strategien in endlichen Zwei-Personen-Nullsummenspielen, eine Vermutung, die von Neumann als falsch erwiesen wurde. ⓘ
Geburt und frühe Entwicklungen

Die Spieltheorie existierte nicht als eigenständiges Gebiet, bis John von Neumann 1928 die Arbeit On the Theory of Games of Strategy veröffentlichte. Von Neumanns ursprünglicher Beweis verwendete Brouwers Fixpunkttheorem über kontinuierliche Abbildungen auf kompakten konvexen Mengen, das zu einer Standardmethode in der Spieltheorie und der mathematischen Ökonomie wurde. Auf seine Arbeit folgte 1944 sein Buch Theory of Games and Economic Behavior, das er gemeinsam mit Oskar Morgenstern verfasste. Die zweite Auflage dieses Buches enthielt eine axiomatische Theorie des Nutzens, die Daniel Bernoullis alte Theorie des Nutzens (des Geldes) als eigenständige Disziplin wieder aufleben ließ. Von Neumanns Arbeit an der Spieltheorie gipfelte in diesem Buch von 1944. Dieses grundlegende Werk enthält die Methode zur Suche nach gegenseitig konsistenten Lösungen für Zwei-Personen-Nullsummenspiele. Nachfolgende Arbeiten konzentrierten sich vor allem auf die kooperative Spieltheorie, die optimale Strategien für Gruppen von Individuen analysiert, wobei davon ausgegangen wird, dass sie untereinander Vereinbarungen über geeignete Strategien durchsetzen können. ⓘ

1950 erschien die erste mathematische Erörterung des Gefangenendilemmas, und ein Experiment wurde von den bekannten Mathematikern Merrill M. Flood und Melvin Dresher im Rahmen der Untersuchungen der RAND Corporation zur Spieltheorie durchgeführt. RAND verfolgte die Studien wegen möglicher Anwendungen auf die globale Nuklearstrategie. Etwa zur gleichen Zeit entwickelte John Nash ein Kriterium für die gegenseitige Übereinstimmung der Strategien der Spieler, das so genannte Nash-Gleichgewicht, das auf eine größere Anzahl von Spielen anwendbar ist als das von Neumann und Morgenstern vorgeschlagene Kriterium. Nash bewies, dass jedes nicht-kooperative Spiel mit endlich n Spielern und ohne Nullsumme (nicht nur mit zwei Spielern und ohne Nullsumme) ein so genanntes Nash-Gleichgewicht mit gemischten Strategien aufweist. ⓘ
Die Spieltheorie erlebte in den 1950er Jahren einen Aufschwung, in dem die Konzepte des Kerns, des extensiven Spiels, des fiktiven Spiels, der wiederholten Spiele und des Shapley-Werts entwickelt wurden. In den 1950er Jahren gab es auch die ersten Anwendungen der Spieltheorie in der Philosophie und der Politikwissenschaft. ⓘ
Ein Spiel im Sinne der Spieltheorie ist eine Entscheidungssituation mit mehreren Beteiligten, die sich mit ihren Entscheidungen gegenseitig beeinflussen. Im Unterschied zur klassischen Entscheidungstheorie modelliert diese Theorie also Situationen, in denen der Erfolg des Einzelnen nicht nur vom eigenen Handeln, sondern auch von dem anderer abhängt (interdependente Entscheidungssituation). ⓘ
Der Begriff Spieltheorie (engl. game theory) entstand aus zuvor von den Begründern verwendeten Begriffsumschreibungen wie Theorie der Gesellschaftsspiele (1928) bzw. theory of games (1944). Obwohl bereits in den Publikationen von 1928 und 1944 ökonomische Anwendungen als primäre Zielsetzung formuliert wurden, befinden sich dort mehrfache Hinweise auf Implikationen für Gesellschaftsspiele wie Schach, das Bluffen beim Poker, Baccara und das Signalisieren beim Bridge. Auch späteren Autoren dienten Gesellschaftsspiele als Beispiele, etwa für John Forbes Nash in seiner Dissertation von 1950, in der er im Anschluss an einen Existenzbeweis für das nachfolgend nach ihm benannte Gleichgewicht als einfaches Beispiel eine Berechnung für ein Drei-Personen-Poker durchführte. In späterer Zeit wurde im deutschen Sprachraum wiederholt der Begriff Interaktive Entscheidungstheorie für treffender als Spieltheorie befunden. Aufgrund der weiten Verbreitung des Begriffs Spieltheorie konnten sich solche Vorschläge aber nicht durchsetzen. ⓘ
Der Begriff Spieltheorie taucht wiederum auch in anderen Gebieten der theoretischen Behandlung von Spielen auf – siehe Spielwissenschaft, Spielpädagogik, Ludologie oder Homo ludens. ⓘ
Preisgekrönte Leistungen
1965 führte Reinhard Selten sein Lösungskonzept der subgame perfect equilibria ein, das das Nash-Gleichgewicht weiter verfeinerte. Später führte er auch die Perfektion der zittrigen Hand ein. 1994 wurden Nash, Selten und Harsanyi für ihre Beiträge zur ökonomischen Spieltheorie mit dem Nobelpreis für Wirtschaftswissenschaften ausgezeichnet. ⓘ
In den 1970er Jahren wurde die Spieltheorie in großem Umfang in der Biologie angewandt, was vor allem auf die Arbeit von John Maynard Smith und seine evolutionär stabile Strategie zurückzuführen ist. Darüber hinaus wurden die Konzepte des korrelierten Gleichgewichts, der Perfektion der zitternden Hand und des gemeinsamen Wissens eingeführt und analysiert. ⓘ
Im Jahr 2005 folgten die Spieltheoretiker Thomas Schelling und Robert Aumann auf Nash, Selten und Harsanyi als Nobelpreisträger. Schelling arbeitete an dynamischen Modellen, frühen Beispielen der evolutionären Spieltheorie. Aumann leistete einen größeren Beitrag zur Gleichgewichtsschule, indem er Gleichgewichtsvergröberung und korrelierte Gleichgewichte einführte und eine umfassende formale Analyse der Annahme gemeinsamen Wissens und ihrer Folgen entwickelte. ⓘ
Im Jahr 2007 erhielten Leonid Hurwicz, Eric Maskin und Roger Myerson den Nobelpreis für Wirtschaftswissenschaften "für die Schaffung der Grundlagen der Theorie des Mechanismusdesigns". Zu Myersons Beiträgen gehören der Begriff des angemessenen Gleichgewichts und ein wichtiges Lehrbuch für Studenten: Game Theory, Analysis of Conflict. Hurwicz führte das Konzept der Anreizkompatibilität ein und formalisierte es. ⓘ
Im Jahr 2012 erhielten Alvin E. Roth und Lloyd S. Shapley den Nobelpreis für Wirtschaftswissenschaften "für die Theorie stabiler Allokationen und die Praxis der Marktgestaltung". Im Jahr 2014 ging der Nobelpreis an den Spieltheoretiker Jean Tirole. ⓘ
Ausgangspunkt
Historischer Ausgangspunkt der Spieltheorie ist die Analyse des Homo oeconomicus, insbesondere durch Daniel Bernoulli, Joseph Bertrand, Antoine-Augustin Cournot (1838), Francis Ysidro Edgeworth (1881), Frederik Ludvig Bang von Zeuthen und Heinrich Freiherr von Stackelberg. Diese spieltheoretischen Analysen waren jedoch immer Antworten auf spezifische Fragestellungen, ohne dass eine allgemeinere Theorie zur Analyse strategischer Interaktion daraus entwickelt worden wäre. Die ersten allgemeinen Überlegungen stellte Émile Borel 1921 an. ⓘ
Weitere Entwicklung
Seit 1970 ist eine sehr stürmische Entwicklung der Spieltheorie und ein Ausufern in andere Disziplinen zu beobachten. In diesem Sinne entstanden seit damals die Kombinatorische und die Algorithmische Spieltheorie als sehr mathematisch orientierte Zweige sowie die Evolutionäre Spieltheorie, die am stärksten von der Annahme bewusster Entscheidungen abrückt. ⓘ
Spieltypen
Kooperativ / nicht-kooperativ
Ein Spiel ist kooperativ, wenn die Spieler in der Lage sind, verbindliche Verpflichtungen einzugehen, die von außen durchgesetzt werden (z. B. durch Vertragsrecht). Ein Spiel ist nicht-kooperativ, wenn die Spieler keine Allianzen bilden können oder wenn alle Vereinbarungen selbst erzwungen werden müssen (z. B. durch glaubwürdige Drohungen). ⓘ
Kooperative Spiele werden häufig im Rahmen der kooperativen Spieltheorie analysiert, die sich auf die Vorhersage der Koalitionsbildung, der gemeinsamen Handlungen der Gruppen und der daraus resultierenden kollektiven Auszahlungen konzentriert. Dies steht im Gegensatz zur traditionellen nicht-kooperativen Spieltheorie, die sich auf die Vorhersage der Handlungen und Auszahlungen der einzelnen Spieler und die Analyse von Nash-Gleichgewichten konzentriert. Die Konzentration auf individuelle Auszahlungen kann zu einem Phänomen führen, das als Tragödie der Allmende bekannt ist und bei dem Ressourcen in einem kollektiv ineffizienten Umfang genutzt werden. Das Fehlen formeller Verhandlungen führt zu einer Verschlechterung der öffentlichen Güter durch Übernutzung und Unterversorgung, die auf private Anreize zurückzuführen ist. ⓘ
Die kooperative Spieltheorie bietet einen Ansatz auf hohem Niveau, da sie nur die Struktur, die Strategien und die Auszahlungen von Koalitionen beschreibt, während die nicht-kooperative Spieltheorie auch untersucht, wie sich Verhandlungsverfahren auf die Verteilung der Auszahlungen innerhalb jeder Koalition auswirken. Da die nicht-kooperative Spieltheorie allgemeiner ist, können kooperative Spiele mit Hilfe des Ansatzes der nicht-kooperativen Spieltheorie analysiert werden (der Umkehrschluss gilt nicht), sofern genügend Annahmen getroffen werden, um alle möglichen Strategien zu erfassen, die den Spielern aufgrund der Möglichkeit der externen Durchsetzung der Kooperation zur Verfügung stehen. Die Verwendung einer einzigen Theorie mag zwar wünschenswert sein, aber in vielen Fällen stehen nicht genügend Informationen zur Verfügung, um die formalen Verfahren, die während des strategischen Verhandlungsprozesses zur Verfügung stehen, genau zu modellieren, oder das resultierende Modell wäre zu komplex, um in der realen Welt ein praktisches Instrument zu sein. In solchen Fällen bietet die kooperative Spieltheorie einen vereinfachten Ansatz, der die Analyse des Spiels als Ganzes ermöglicht, ohne dass Annahmen über die Verhandlungsmacht getroffen werden müssen. ⓘ

Generell wird die nicht-kooperative von der kooperativen Spieltheorie so unterschieden: Können die Spieler bindende Verträge abschließen, so spricht man von kooperativer Spieltheorie. Sind hingegen alle Verhaltensweisen (also auch eine mögliche Kooperation zwischen Spielern) self-enforcing, d. h., sie ergeben sich aus dem Eigeninteresse der Spieler, ohne dass bindende Verträge abgeschlossen werden können, so spricht man von nicht-kooperativer Spieltheorie. ⓘ
Die nicht-kooperative Spieltheorie spielt in der universitären Lehre eine größere Rolle als die kooperative Spieltheorie. Es gibt viele Lehrbücher zur Spieltheorie und es gibt an Universitäten viele Veranstaltungen mit dem Titel Spieltheorie, in denen die kooperative Spieltheorie gar nicht oder nur am Rande behandelt wird. Obwohl die Alfred-Nobel-Gedächtnispreisträger Robert J. Aumann und John Forbes Nash Jr. beide entscheidende Beiträge zur kooperativen Spieltheorie geleistet haben, wurde der Preis vom Nobelpreiskomitee ausdrücklich für ihre Beiträge zur nicht-kooperativen Spieltheorie vergeben. ⓘ
Dennoch wird in der aktuellen Forschung weiterhin die kooperative Spieltheorie untersucht, und ein Großteil neuer spieltheoretischer wissenschaftlicher Artikel sind der kooperativen Spieltheorie zuzuordnen. Die weiterhin große Bedeutung der kooperativen Spieltheorie in der Forschung ist auch daran abzulesen, dass in der wissenschaftlichen Diskussion sehr präsente Forschungsfelder wie die Verhandlungstheorie und die Matchingtheorie zu einem großen Teil mit den Mitteln der kooperativen Spieltheorie analysiert werden. ⓘ
Symmetrisch / asymmetrisch
| E | F ⓘ | |
| E | 1, 2 | 0, 0 |
| F | 0, 0 | 1, 2 |
| Ein asymmetrisches Spiel | ||
Ein symmetrisches Spiel ist ein Spiel, bei dem die Auszahlungen für das Spielen einer bestimmten Strategie nur von den anderen verwendeten Strategien abhängen, nicht aber davon, wer sie spielt. Das heißt, ein Spiel ist symmetrisch, wenn die Identität der Spieler geändert werden kann, ohne dass sich die Auszahlung für die Strategien ändert. Viele der üblicherweise untersuchten 2×2-Spiele sind symmetrisch. Die Standarddarstellungen von Huhn, das Gefangenendilemma und die Hirschjagd sind allesamt symmetrische Spiele. Einige Wissenschaftler würden auch bestimmte asymmetrische Spiele als Beispiele für diese Spiele ansehen. Die häufigsten Auszahlungen für jedes dieser Spiele sind jedoch symmetrisch. ⓘ
Die am häufigsten untersuchten asymmetrischen Spiele sind Spiele, bei denen die Strategien der beiden Spieler nicht identisch sind. Beim Ultimatumspiel und auch beim Diktatorspiel gibt es beispielsweise für jeden Spieler unterschiedliche Strategien. Es ist jedoch auch möglich, dass ein Spiel für beide Spieler identische Strategien aufweist und dennoch asymmetrisch ist. Das in der Grafik dieses Abschnitts dargestellte Spiel ist beispielsweise asymmetrisch, obwohl beide Spieler identische Strategien haben. ⓘ
Nullsummenspiel / Nicht-Nullsummenspiel
| A | B ⓘ | |
| A | –1, 1 | 3, –3 |
| B | 0, 0 | –2, 2 |
| Ein Nullsummenspiel | ||
Nullsummenspiele (allgemeiner: Konstantsummenspiele) sind Spiele, bei denen die Entscheidungen der Spieler die verfügbaren Ressourcen weder erhöhen noch verringern können. Bei Nullsummenspielen addiert sich der Gesamtnutzen für alle Spieler in einem Spiel für jede Kombination von Strategien immer zu Null (informeller ausgedrückt: ein Spieler profitiert nur auf Kosten der anderen). Poker ist ein Beispiel für ein Nullsummenspiel (abgesehen von der Möglichkeit des Hausanteils), da man genau den Betrag gewinnt, den die Gegner verlieren. Zu den anderen Nullsummenspielen gehören das Spiel mit Pfennigen und die meisten klassischen Brettspiele wie Go und Schach. ⓘ
Viele Spiele, die von Spieltheoretikern untersucht werden (darunter das berühmte Gefangenendilemma), sind Nicht-Nullsummenspiele, weil das Ergebnis ein Nettoergebnis größer oder kleiner als Null hat. Bei Nicht-Nullsummenspielen geht ein Gewinn eines Spielers nicht unbedingt mit einem Verlust eines anderen Spielers einher. ⓘ
Konstantsummenspiele entsprechen Aktivitäten wie Diebstahl und Glücksspiel, aber nicht der grundlegenden wirtschaftlichen Situation, in der es potenzielle Gewinne aus dem Handel gibt. Es ist möglich, jedes Konstantsummenspiel in ein (möglicherweise asymmetrisches) Nullsummenspiel umzuwandeln, indem ein Dummy-Spieler (oft "das Brett" genannt) hinzugefügt wird, dessen Verluste die Nettogewinne der Spieler ausgleichen. ⓘ
Simultan / sequentiell
Simultanspiele sind Spiele, bei denen beide Spieler gleichzeitig am Zug sind oder bei denen die späteren Spieler nichts von den Aktionen der früheren Spieler wissen (so dass sie effektiv simultan sind). Sequentielle Spiele (oder dynamische Spiele) sind Spiele, bei denen die späteren Spieler etwas über die früheren Aktionen wissen. Dabei muss es sich nicht um perfekte Informationen über jede Aktion der früheren Spieler handeln; es kann sich auch um sehr wenig Wissen handeln. Ein Spieler kann zum Beispiel wissen, dass ein früherer Spieler eine bestimmte Aktion nicht ausgeführt hat, während er nicht weiß, welche der anderen verfügbaren Aktionen der erste Spieler tatsächlich ausgeführt hat. ⓘ
Der Unterschied zwischen simultanen und sequentiellen Spielen zeigt sich in den oben erwähnten unterschiedlichen Darstellungen. Häufig wird die Normalform zur Darstellung von simultanen Spielen verwendet, während die extensive Form zur Darstellung von sequentiellen Spielen verwendet wird. Die Umwandlung der extensiven Form in die Normalform ist eine Einbahnstraße, was bedeutet, dass mehrere Spiele in extensiver Form derselben Normalform entsprechen. Folglich sind Gleichgewichtsvorstellungen für simultane Spiele unzureichend, um über sequentielle Spiele zu argumentieren; siehe Subgame-Perfektion. ⓘ
Kurz gesagt, die Unterschiede zwischen sequentiellen und simultanen Spielen sind wie folgt:
| Sequentiell | Simultan ⓘ | |
|---|---|---|
| Normalerweise bezeichnet durch | Entscheidungsbäume | Auszahlungsmatrizen |
Vorwissen über den Zug des Gegners? |
Ja | Nein |
| Zeitachse? | Ja | Nein |
| Auch bekannt als | Spiel mit extensiver Form Extensives Spiel |
Strategisches Spiel
Strategisches Spiel |
Cournot-Wettbewerb
Beim Cournot-Wettbewerbsmodell entscheiden sich die Spieler für eine bestimmte Menge eines homogenen Produkts, das sie unabhängig voneinander und gleichzeitig produzieren, wobei die Grenzkosten für jedes Unternehmen unterschiedlich sein können und die Auszahlung für das Unternehmen der Gewinn ist. Die Produktionskosten sind öffentlich bekannt, und die Unternehmen versuchen, ihre gewinnmaximierende Menge auf der Grundlage dessen zu finden, was sie glauben, dass die anderen Unternehmen produzieren werden, und verhalten sich wie Monopolisten. In diesem Spiel wollen die Unternehmen die Monopolmenge produzieren, aber es besteht ein großer Anreiz, davon abzuweichen und mehr zu produzieren, wodurch der markträumende Preis sinkt. So könnten die Unternehmen beispielsweise versucht sein, von der Monopolmenge abzuweichen, wenn die Monopolmenge niedrig und der Preis hoch ist, um die Produktion zu steigern und den Gewinn zu maximieren. Diese Option bietet jedoch nicht den höchsten Gewinn, da die Fähigkeit eines Unternehmens, seinen Gewinn zu maximieren, von seinem Marktanteil und der Elastizität der Marktnachfrage abhängt. Das Cournot-Gleichgewicht ist erreicht, wenn jedes Unternehmen nach seiner eigenen Reaktionsfunktion handelt und keinen Anreiz hat, davon abzuweichen, da es auf der Grundlage der Produktion der anderen Unternehmen die beste Antwort hat. Innerhalb des Spiels erreichen die Unternehmen das Nash-Gleichgewicht, wenn das Cournot-Gleichgewicht erreicht ist. ⓘ
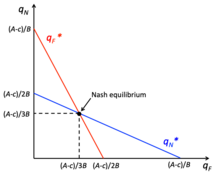
Bertrand-Wettbewerb
Der Bertrand-Wettbewerb geht von homogenen Produkten und konstanten Grenzkosten aus, und die Akteure wählen die Preise. Das Gleichgewicht des Preiswettbewerbs besteht darin, dass der Preis gleich den Grenzkosten ist, wobei vollständige Informationen über die Kosten der Wettbewerber vorausgesetzt werden. Daher haben die Unternehmen einen Anreiz, vom Gleichgewicht abzuweichen, da ein homogenes Produkt mit einem niedrigeren Preis den gesamten Marktanteil gewinnen wird, was als Kostenvorteil bekannt ist. ⓘ
Perfekte Informationen und unvollständige Informationen
Entscheidend für Darstellung und Lösung ist der Informationsstand der Spieler. Unterschieden werden hierbei drei Begriffe: Vollständige, perfekte (bzw. vollkommene) Information und perfektes Erinnerungsvermögen, je nachdem, ob der Spieler über die Spielregeln, die Züge der anderen Spieler und die eigenen Informationen aus der Vergangenheit informiert ist. Standard ist das Spiel mit vollständiger Information sowie perfektem Erinnerungsvermögen. Perfekte Information gehört nicht zu den Standardannahmen, da sie hinderlich bei der Erklärung zahlreicher einfacher Konflikte wäre. ⓘ
Vollständige Information, die Kenntnis aller Spieler über die Spielregeln, ist eine Annahme, die man beim Spiel im klassischen Wortsinn (vgl. Spiel) gemeinhin als Voraussetzung für gemeinsames Spielen betrachten wird. Unstimmigkeiten über die Spielregeln, etwa, ob bei Mensch ärgere Dich nicht die Pflicht besteht, einen gegnerischen Kegel zu schlagen, wenn dies im betreffenden Zug möglich ist, oder ob bei Mau Mau eine gezogene Karte sofort gelegt werden darf, wenn sie passt, werden in der Regel als ernsthafte Störung betrachtet, wenn sie nicht vor dem Spiel geklärt wurden. Andererseits wird die Spieltheorie auf viele Situationen angewendet, für die dieses Informationserfordernis zu rigide wäre, da mit dem Vorhandensein gewisser Informationen nicht gerechnet werden kann (z. B. bei politischen Entscheidungen). Darum ist es sinnvoll, die klassische Spieltheorie, die mit vollständiger Information arbeitet, um die Möglichkeit unvollständiger Information zu erweitern. Andererseits ist dieses Feld dadurch begrenzt, weil sich für jedes Spiel mit unvollständiger Information ein Spiel mit vollständiger Information konstruieren lässt, das strategisch äquivalent ist. ⓘ
Perfekte Information, also die Kenntnis sämtlicher Spieler über sämtliche Züge sämtlicher Spieler, ist eine rigorose Forderung, die in vielen klassischen Spielen nicht erfüllt ist: Sie ist beispielsweise in den meisten Kartenspielen verletzt, weil zu Spielbeginn der Zug des Zufallsspielers und die Verteilung der Blätter unbekannt ist, da man jeweils nur die eigenen Karten einsehen kann. Darum wird in spieltheoretischen Modellen meist nicht von perfekter Information ausgegangen. Erfüllt ein Spiel das Kriterium perfekter Information, ist es in der Regel vom Prinzip her einfacher zu lösen; auch wenn sich in der Realität wie beim Schach aufgrund der Komplexität große Hürden ergeben. ⓘ
Perfektes Erinnerungsvermögen ist das Wissen jedes Spielers über sämtliche Informationen, die ihm bereits in der Vergangenheit zugänglich waren. Obwohl diese Annahme zumindest vom Prinzip her auf den ersten Blick immer erfüllt zu sein scheint, gibt es Gegenbeispiele: Handelt es sich bei einem Spiel um ein Team kooperierender Akteure wie beim Skat, kennt „der“ einzelne Spieler zum Zeitpunkt einer eigenen Entscheidung nicht mehr den Informationskontext vergangener Züge, die ein Partner aufgrund seiner Karten getroffen hat. ⓘ

Bayessches Spiel
Eine der Annahmen des Nash-Gleichgewichts ist, dass jeder Spieler korrekte Annahmen über die Aktionen der anderen Spieler hat. In der Spieltheorie gibt es jedoch viele Situationen, in denen die Teilnehmer die Eigenschaften ihrer Gegner nicht vollständig kennen. Verhandlungsführer können die Bewertung des Verhandlungsgegenstandes durch den Gegner nicht kennen, Unternehmen können die Kostenfunktionen des Gegners nicht kennen, Kämpfer können die Stärken des Gegners nicht kennen, und Geschworene können die Interpretation der Beweise durch ihren Kollegen nicht kennen. In manchen Fällen kennen die Teilnehmer zwar den Charakter ihres Gegners gut, wissen aber nicht, wie gut ihr Gegner seinen eigenen Charakter kennt. ⓘ
Ein Bayes'sches Spiel ist ein strategisches Spiel mit unvollständigen Informationen. In einem strategischen Spiel sind die Entscheidungsträger Spieler, und jeder Spieler hat eine Gruppe von Aktionen. Ein zentraler Bestandteil der unvollständigen Informationsspezifikation ist die Menge der Zustände. Jeder Zustand beschreibt vollständig eine Sammlung von Merkmalen, die für den Spieler relevant sind, wie z. B. seine Präferenzen und Details über ihn. Es muss einen Zustand für jeden Satz von Merkmalen geben, von denen ein Spieler glaubt, dass sie existieren könnten. ⓘ
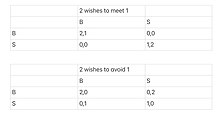
Beispiel: Spieler 1 ist sich nicht sicher, ob Spieler 2 lieber mit ihr ausgehen oder von ihr weggehen möchte, während Spieler 2 die Präferenzen von Spieler 1 nach wie vor kennt. Um genau zu sein, nehmen wir an, dass Spielerin 1 glaubt, dass Spielerin 2 mit einer Wahrscheinlichkeit von 1/2 mit ihr ausgehen und mit einer Wahrscheinlichkeit von 1/2 von ihr weggehen möchte (diese Einschätzung stammt wahrscheinlich aus der Erfahrung von Spielerin 1: sie sieht sich in diesem Fall zur Hälfte mit Spielern konfrontiert, die mit ihr ausgehen wollen, und zur Hälfte mit Spielern, die ihr aus dem Weg gehen wollen). Aufgrund der Wahrscheinlichkeit erfordert die Analyse dieser Situation, dass man die Präferenz des Spielers für das Unentschieden versteht, auch wenn man sich nur für das reine strategische Gleichgewicht interessiert. ⓘ
Kombinatorische Spiele
Spiele, bei denen die Schwierigkeit, eine optimale Strategie zu finden, aus der Vielzahl der möglichen Züge resultiert, werden als kombinatorische Spiele bezeichnet. Beispiele hierfür sind Schach und Go. Auch Spiele mit unvollkommener Information können einen stark kombinatorischen Charakter haben, wie z. B. Backgammon. Es gibt keine einheitliche Theorie, die sich mit kombinatorischen Elementen in Spielen befasst. Es gibt jedoch mathematische Werkzeuge, mit denen bestimmte Probleme gelöst und allgemeine Fragen beantwortet werden können. ⓘ
Spiele mit perfekter Information wurden in der kombinatorischen Spieltheorie untersucht, die neuartige Darstellungen, z. B. surreale Zahlen, sowie kombinatorische und algebraische (und manchmal nicht-konstruktive) Beweismethoden entwickelt hat, um Spiele bestimmter Typen zu lösen, einschließlich "loopy" Spiele, die zu unendlich langen Zugfolgen führen können. Diese Methoden befassen sich mit Spielen, die eine höhere kombinatorische Komplexität aufweisen als diejenigen, die normalerweise in der traditionellen (oder "wirtschaftlichen") Spieltheorie betrachtet werden. Ein typisches Spiel, das auf diese Weise gelöst wurde, ist Hex. Ein verwandtes Forschungsgebiet, das sich auf die Komplexitätstheorie stützt, ist die Spielkomplexität, bei der es darum geht, die rechnerischen Schwierigkeiten bei der Suche nach optimalen Strategien abzuschätzen. ⓘ
Die Forschung im Bereich der künstlichen Intelligenz hat sich sowohl mit Spielen mit vollkommener als auch mit unvollkommener Information befasst, die sehr komplexe kombinatorische Strukturen aufweisen (wie Schach, Go oder Backgammon) und für die keine nachweisbaren optimalen Strategien gefunden wurden. Zu den praktischen Lösungen gehören rechnerische Heuristiken wie Alpha-Beta-Beschneidung oder die Verwendung künstlicher neuronaler Netze, die durch Verstärkungslernen trainiert werden und die Spiele in der rechnerischen Praxis besser handhabbar machen. ⓘ
Unendlich lange Spiele
Spiele, wie sie von Wirtschaftswissenschaftlern und Spielern in der realen Welt untersucht werden, sind im Allgemeinen nach endlich vielen Zügen beendet. Reine Mathematiker sind nicht so eingeschränkt, und insbesondere Mengentheoretiker untersuchen Spiele, die unendlich viele Züge dauern, wobei der Gewinner (oder eine andere Auszahlung) erst bekannt ist, wenn alle diese Züge abgeschlossen sind. ⓘ
Das Hauptaugenmerk liegt in der Regel nicht so sehr auf der Frage, wie ein solches Spiel am besten zu spielen ist, sondern ob ein Spieler eine Gewinnstrategie hat. (Mit Hilfe des Auswahlaxioms kann bewiesen werden, dass es Spiele gibt - selbst bei perfekter Information und wenn die einzigen Ergebnisse "gewinnen" oder "verlieren" sind -, bei denen keiner der Spieler eine Gewinnstrategie hat.) Das Vorhandensein solcher Strategien für geschickt konzipierte Spiele hat wichtige Konsequenzen für die deskriptive Mengenlehre. ⓘ
Diskrete und kontinuierliche Spiele
Ein Großteil der Spieltheorie befasst sich mit endlichen, diskreten Spielen, die eine endliche Anzahl von Spielern, Zügen, Ereignissen, Ergebnissen usw. haben. Viele Konzepte können jedoch erweitert werden. Bei kontinuierlichen Spielen können die Spieler eine Strategie aus einer kontinuierlichen Strategiemenge wählen. So wird beispielsweise der Cournot-Wettbewerb in der Regel so modelliert, dass die Strategien der Spieler beliebige nichtnegative Größen sind, einschließlich gebrochener Größen. ⓘ
Differentielle Spiele
Differentialspiele wie das kontinuierliche Verfolgungs- und Ausweichspiel sind kontinuierliche Spiele, bei denen die Entwicklung der Zustandsvariablen der Spieler durch Differentialgleichungen bestimmt wird. Das Problem, eine optimale Strategie in einem Differentialspiel zu finden, ist eng mit der Theorie der optimalen Steuerung verbunden. Insbesondere gibt es zwei Arten von Strategien: Die Strategien mit offenem Regelkreis werden mit Hilfe des Pontryagin-Maximum-Prinzips gefunden, während die Strategien mit geschlossenem Regelkreis mit der Methode der dynamischen Programmierung nach Bellman gefunden werden. ⓘ
Ein Sonderfall der Differentialspiele sind die Spiele mit einem zufälligen Zeithorizont. In solchen Spielen ist die Endzeit eine Zufallsvariable mit einer bestimmten Wahrscheinlichkeitsverteilungsfunktion. Daher maximieren die Spieler den mathematischen Erwartungswert der Kostenfunktion. Es wurde gezeigt, dass das modifizierte Optimierungsproblem als diskontiertes Differentialspiel über ein unendliches Zeitintervall umformuliert werden kann. ⓘ
Evolutionäre Spieltheorie
Die evolutionäre Spieltheorie untersucht Spieler, die ihre Strategien im Laufe der Zeit nach Regeln anpassen, die nicht unbedingt rational oder weitsichtig sind. Im Allgemeinen wird die Entwicklung von Strategien im Laufe der Zeit gemäß solchen Regeln als Markov-Kette mit einer Zustandsvariablen wie dem aktuellen Strategieprofil oder der Art und Weise, wie das Spiel in der jüngsten Vergangenheit gespielt wurde, modelliert. Solche Regeln können Nachahmung, Optimierung oder das Überleben des Stärkeren beinhalten. ⓘ
In der Biologie können solche Modelle die Evolution darstellen, bei der die Nachkommen die Strategien ihrer Eltern übernehmen und die Eltern, die erfolgreichere Strategien spielen (d. h. höhere Gewinne erzielen), eine größere Anzahl von Nachkommen haben. In den Sozialwissenschaften stellen solche Modelle typischerweise strategische Anpassungen von Spielern dar, die ein Spiel viele Male im Laufe ihres Lebens spielen und dabei bewusst oder unbewusst ihre Strategien gelegentlich anpassen. ⓘ
Stochastische Ergebnisse (und Beziehung zu anderen Bereichen)
Individuelle Entscheidungsprobleme mit stochastischen Ergebnissen werden manchmal als "Ein-Spieler-Spiele" bezeichnet. Sie können mit ähnlichen Werkzeugen in den verwandten Disziplinen der Entscheidungstheorie, des Operations Research und in Bereichen der künstlichen Intelligenz modelliert werden, insbesondere in der KI-Planung (mit Unsicherheit) und in Multi-Agenten-Systemen. Auch wenn diese Bereiche unterschiedliche Motivationen haben, sind die mathematischen Grundlagen im Wesentlichen dieselben, z. B. die Verwendung von Markov-Entscheidungsprozessen (MDP). ⓘ
Stochastische Ergebnisse können auch im Sinne der Spieltheorie modelliert werden, indem man einen zufällig agierenden Spieler hinzufügt, der "zufällige Züge" macht ("moves by nature"). Dieser Spieler wird in der Regel nicht als dritter Spieler in einem ansonsten aus zwei Spielern bestehenden Spiel betrachtet, sondern dient lediglich dazu, die Würfel zu werfen, wenn es das Spiel erfordert. ⓘ
Bei einigen Problemen können unterschiedliche Ansätze zur Modellierung stochastischer Ergebnisse zu unterschiedlichen Lösungen führen. Der Unterschied zwischen MDPs und der Minimax-Lösung besteht zum Beispiel darin, dass letztere den ungünstigsten Fall über eine Reihe von gegnerischen Zügen betrachtet, anstatt eine Erwartung über diese Züge angesichts einer festen Wahrscheinlichkeitsverteilung zu entwickeln. Der Minimax-Ansatz kann vorteilhaft sein, wenn keine stochastischen Modelle der Ungewissheit zur Verfügung stehen, kann aber auch extrem unwahrscheinliche (aber teure) Ereignisse überschätzen und die Strategie in solchen Szenarien dramatisch beeinflussen, wenn angenommen wird, dass ein Gegner ein solches Ereignis erzwingen kann. (Siehe die Theorie des schwarzen Schwans für weitere Erörterungen zu dieser Art von Modellierungsproblemen, insbesondere im Zusammenhang mit der Vorhersage und Begrenzung von Verlusten im Investmentbanking). ⓘ
Es wurden auch allgemeine Modelle untersucht, die alle Elemente von stochastischen Ergebnissen, Gegnern und teilweiser oder verrauschter Beobachtbarkeit (von Zügen anderer Spieler) umfassen. Als "Goldstandard" gilt das teilweise beobachtbare stochastische Spiel (POSG), aber nur wenige realistische Probleme sind in der POSG-Darstellung rechnerisch machbar. ⓘ
Metaspiele
Dies sind Spiele, deren Spiel die Entwicklung der Regeln für ein anderes Spiel, das Ziel- oder Gegenstandsspiel, ist. Metaspiele zielen darauf ab, den Nutzwert des entwickelten Regelsatzes zu maximieren. Die Theorie der Metaspiele ist mit der Theorie des Mechanismusdesigns verwandt. ⓘ
Der Begriff Metaspiel-Analyse wird auch für einen von Nigel Howard entwickelten praktischen Ansatz verwendet, bei dem eine Situation als strategisches Spiel betrachtet wird, in dem die Beteiligten versuchen, ihre Ziele mit Hilfe der ihnen zur Verfügung stehenden Optionen zu erreichen. Spätere Entwicklungen haben zur Formulierung der Konfrontationsanalyse geführt. ⓘ
Pooling-Spiele
Dies sind Spiele, die in allen Gesellschaftsformen vorherrschen. Bei Pooling-Spielen handelt es sich um wiederholte Spiele mit wechselnden Auszahlungstabellen im Allgemeinen über einen erfahrenen Pfad, und ihre Gleichgewichtsstrategien nehmen in der Regel die Form einer evolutionären sozialen Konvention und einer wirtschaftlichen Konvention an. Die Theorie des Pooling-Spiels wurde entwickelt, um die Interaktion zwischen der optimalen Wahl in einem Spiel und dem Auftauchen des nächsten Auszahlungstabellen-Aktualisierungspfads formal zu erkennen, die Existenz von Invarianz und Robustheit zu identifizieren und die Varianz über die Zeit vorherzusagen. Die Theorie basiert auf der Klassifizierung der topologischen Transformation der Aktualisierung der Auszahlungstabelle im Laufe der Zeit, um die Varianz und Invarianz vorherzusagen, und fällt auch in den Bereich des Rechengesetzes der erreichbaren Optimalität für geordnete Systeme. ⓘ
Mean-Field-Spieltheorie
Die Mean-Field-Spieltheorie befasst sich mit der strategischen Entscheidungsfindung in sehr großen Populationen von kleinen interagierenden Akteuren. Diese Klasse von Problemen wurde in der wirtschaftswissenschaftlichen Literatur von Boyan Jovanovic und Robert W. Rosenthal, in der technischen Literatur von Peter E. Caines und von den Mathematikern Pierre-Louis Lions und Jean-Michel Lasry untersucht. ⓘ
Darstellung von Spielen
Die in der Spieltheorie untersuchten Spiele sind wohldefinierte mathematische Objekte. Um vollständig definiert zu sein, muss ein Spiel die folgenden Elemente enthalten: die Spieler des Spiels, die Informationen und Aktionen, die jedem Spieler an jedem Entscheidungspunkt zur Verfügung stehen, und die Auszahlungen für jedes Ergebnis. (Eric Rasmusen bezeichnet diese vier "wesentlichen Elemente" mit dem Akronym "PAPI"). Ein Spieltheoretiker verwendet diese Elemente in der Regel zusammen mit einem Lösungskonzept seiner Wahl, um eine Reihe von Gleichgewichtsstrategien für jeden Spieler abzuleiten, so dass, wenn diese Strategien eingesetzt werden, kein Spieler durch einseitiges Abweichen von seiner Strategie profitieren kann. Diese Gleichgewichtsstrategien bestimmen ein Gleichgewicht für das Spiel - einen stabilen Zustand, in dem entweder ein Ergebnis oder eine Reihe von Ergebnissen mit bekannter Wahrscheinlichkeit eintritt. ⓘ
Die meisten kooperativen Spiele werden in der charakteristischen Funktionsform dargestellt, während die extensive und die normale Form verwendet werden, um nicht-kooperative Spiele zu definieren. ⓘ
Extensive Form

Die extensive Form kann verwendet werden, um Spiele mit einer zeitlichen Abfolge von Zügen zu formalisieren. Spiele werden hier auf Bäumen gespielt (wie hier abgebildet). Hier stellt jeder Scheitelpunkt (oder Knoten) einen Punkt der Wahl für einen Spieler dar. Der Spieler wird durch eine Nummer angegeben, die am Scheitelpunkt steht. Die Linien, die vom Scheitelpunkt ausgehen, stellen eine mögliche Aktion für diesen Spieler dar. Die Auszahlungen werden am unteren Ende des Baums angegeben. Die extensive Form kann als eine Verallgemeinerung eines Entscheidungsbaums für mehrere Spieler betrachtet werden. Um ein Spiel der extensiven Form zu lösen, muss die Rückwärtsinduktion angewendet werden. Dabei wird der Spielbaum rückwärts abgearbeitet, um festzustellen, was ein rationaler Spieler am letzten Scheitelpunkt des Baums tun würde, was der Spieler mit dem vorherigen Zug tun würde, wenn der Spieler mit dem letzten Zug rational ist, und so weiter, bis der erste Scheitelpunkt des Baums erreicht ist. ⓘ
Das abgebildete Spiel besteht aus zwei Spielern. So wie dieses Spiel strukturiert ist (d. h. mit sequentieller Entscheidungsfindung und perfekter Information), "zieht" Spieler 1 zuerst, indem er entweder F oder U (fair oder unfair). Als Nächstes wählt Spieler 2, der nun den Zug von Spieler 1 gesehen hat, entweder A oder R. Sobald Spieler 2 seine Wahl getroffen hat, gilt das Spiel als beendet, und jeder Spieler erhält seine jeweilige Auszahlung. Angenommen, Spieler 1 wählt U und dann wählt Spieler 2 A: Spieler 1 erhält dann eine Auszahlung von "acht" (was in der realen Welt auf viele Arten interpretiert werden kann, am einfachsten in Form von Geld, aber auch Dinge wie acht Tage Urlaub oder acht eroberte Länder oder sogar acht weitere Gelegenheiten, das gleiche Spiel gegen andere Spieler zu spielen, bedeuten könnte) und Spieler 2 erhält eine Auszahlung von "zwei". ⓘ
Die extensive Form kann auch Spiele mit gleichzeitigen Zügen und Spiele mit unvollkommener Information erfassen. Um sie darzustellen, verbindet entweder eine gepunktete Linie verschiedene Eckpunkte, um sie als Teil derselben Informationsmenge darzustellen (d. h. die Spieler wissen nicht, an welchem Punkt sie sich befinden), oder es wird eine geschlossene Linie um sie herum gezogen. (Siehe Beispiel im Abschnitt über unvollkommene Informationen). ⓘ
Normale Form
| Spieler 2 wählt Links |
Spieler 2 wählt Rechts ⓘ | |
| Spieler 1 wählt oben |
4, 3 | –1, –1 |
| Spieler 1 wählt unten |
0, 0 | 3, 4 |
| Normalform oder Auszahlungsmatrix eines Spiels mit 2 Spielern und 2 Strategien | ||
Die Normalform (oder strategische Form) eines Spiels wird in der Regel durch eine Matrix dargestellt, die die Spieler, Strategien und Auszahlungen zeigt (siehe das Beispiel rechts). Allgemeiner kann es durch eine beliebige Funktion dargestellt werden, die jeder möglichen Kombination von Handlungen eine Auszahlung für jeden Spieler zuordnet. Im nebenstehenden Beispiel gibt es zwei Spieler; einer wählt die Zeile und der andere die Spalte. Jeder Spieler hat zwei Strategien, die durch die Anzahl der Zeilen und die Anzahl der Spalten festgelegt sind. Die Auszahlungsbeträge sind im Inneren angegeben. Die erste Zahl ist die Auszahlung, die der Zeilenspieler (in unserem Beispiel Spieler 1) erhält; die zweite ist die Auszahlung für den Spaltenspieler (in unserem Beispiel Spieler 2). Angenommen, Spieler 1 spielt oben und Spieler 2 spielt links. Dann erhält Spieler 1 eine Auszahlung von 4, und Spieler 2 erhält 3. ⓘ
Wenn ein Spiel in normaler Form dargestellt wird, wird davon ausgegangen, dass jeder Spieler gleichzeitig oder zumindest ohne Kenntnis der Aktionen der anderen Spieler handelt. Wenn die Spieler einige Informationen über die Entscheidungen der anderen Spieler haben, wird das Spiel normalerweise in extensiver Form dargestellt. ⓘ
Zu jedem Spiel in extensiver Form gibt es ein äquivalentes Spiel in Normalform. Die Umwandlung in die Normalform kann jedoch zu einer exponentiellen Vergrößerung der Darstellung führen, was sie rechnerisch unpraktisch macht. ⓘ
Charakteristische Funktionsform
Bei Spielen mit abnehmbarem Nutzen gibt es keine separaten Belohnungen, sondern die charakteristische Funktion bestimmt die Auszahlung für jede Einheit. Die Idee ist, dass die Einheit, die sozusagen "leer" ist, überhaupt keine Belohnung erhält. ⓘ
Der Ursprung dieser Form ist in dem Buch von John von Neumann und Oskar Morgenstern zu finden; bei der Betrachtung dieser Fälle vermuteten sie, dass, wenn eine Einheit auftritt, wirkt sie gegen die Fraktion als ob zwei Individuen ein normales Spiel spielen würden. Die ausgeglichene Auszahlung von C ist eine grundlegende Funktion. Obwohl es verschiedene Beispiele gibt, die helfen, Koalitionsbeträge aus normalen Spielen zu bestimmen, erscheinen nicht alle, die in ihrer Funktionsform von solchen abgeleitet werden können. ⓘ
Formal wird eine charakteristische Funktion gesehen als: (N,v), wobei N die Gruppe der Personen darstellt und ein normaler Nutzen ist. ⓘ
Solche charakteristischen Funktionen haben sich erweitert, um Spiele zu beschreiben, bei denen es keinen entfernbaren Nutzen gibt. ⓘ
Alternative Spieldarstellungen
Alternative Spieldarstellungen werden für einige Unterklassen von Spielen verwendet oder an die Bedürfnisse der interdisziplinären Forschung angepasst. Zusätzlich zu den klassischen Spielrepräsentationen kodieren einige der alternativen Repräsentationen auch zeitbezogene Aspekte. ⓘ
| Name | Jahr | Mittel | Art der Spiele | Zeit ⓘ |
|---|---|---|---|---|
| Überlastungsspiel | 1973 | Funktionen | Teilmenge der n-Personen-Spiele, gleichzeitige Züge | Nein |
| Sequentielle Form | 1994 | Matrizen | 2-Personen-Spiele mit unvollkommener Information | Nein |
| Zeitlich begrenzte Spiele | 1994 | Funktionen | 2-Personen-Spiele | Ja |
| Gala | 1997 | Logik | n-Personen-Spiele mit unvollkommener Information | Nein |
| Spiele mit lokalem Effekt | 2003 | Funktionen | Teilmenge der n-Personen-Spiele, gleichzeitige Züge | Nein |
| GDL | 2005 | Logik | deterministische n-Personen-Spiele, gleichzeitige Züge | Nein |
| Spiel Petri-Netze | 2006 | Petri-Netz | deterministische n-Personen-Spiele, gleichzeitige Züge | Nein |
| Kontinuierliche Spiele | 2007 | Funktionen | Teilmenge der 2-Personen-Spiele mit unvollkommener Information | Ja |
| PNSI | 2008 | Petri-Netz | n-Personen-Spiele mit unvollkommener Information | Ja |
| Aktionsgraphen-Spiele | 2012 | Graphen, Funktionen | n-Personen-Spiele, gleichzeitige Züge | Nein |
| Grafische Spiele | 2015 | Graphen, Funktionen | n-Personen-Spiele, gleichzeitige Züge | Nein |
Allgemeine und angewandte Anwendungen
Als eine Methode der angewandten Mathematik wurde die Spieltheorie zur Untersuchung einer Vielzahl von menschlichen und tierischen Verhaltensweisen eingesetzt. Ursprünglich wurde sie in den Wirtschaftswissenschaften entwickelt, um eine große Anzahl wirtschaftlicher Verhaltensweisen zu verstehen, einschließlich des Verhaltens von Unternehmen, Märkten und Verbrauchern. Die erste Anwendung der spieltheoretischen Analyse erfolgte durch Antoine Augustin Cournot im Jahr 1838 mit seiner Lösung des Cournot-Duopols. Die Anwendung der Spieltheorie in den Sozialwissenschaften hat sich ausgeweitet, und die Spieltheorie wurde auch auf politische, soziologische und psychologische Verhaltensweisen angewandt. ⓘ
Obwohl Naturforscher wie Charles Darwin bereits vor dem 20. Jahrhundert spieltheoretische Aussagen machten, begann die Anwendung spieltheoretischer Analysen in der Biologie mit Ronald Fishers Studien zum Tierverhalten in den 1930er Jahren. Diese Arbeit war älter als der Name "Spieltheorie", weist aber viele wichtige Gemeinsamkeiten mit diesem Bereich auf. Die Entwicklungen in der Wirtschaftswissenschaft wurden später vor allem von John Maynard Smith in seinem 1982 erschienenen Buch Evolution and the Theory of Games auf die Biologie angewandt. ⓘ
Die Spieltheorie wird nicht nur zur Beschreibung, Vorhersage und Erklärung von Verhalten verwendet, sondern auch zur Entwicklung von Theorien über ethisches oder normatives Verhalten und zur Vorschreibung solchen Verhaltens. In den Wirtschaftswissenschaften und der Philosophie haben Wissenschaftler die Spieltheorie angewandt, um das Verständnis von gutem oder richtigem Verhalten zu fördern. Spieltheoretische Argumente dieser Art lassen sich bereits bei Platon finden. Eine alternative Version der Spieltheorie, die so genannte chemische Spieltheorie, stellt die Entscheidungen des Spielers als metaphorische chemische Reaktionsmoleküle, so genannte "Wissensmoleküle", dar. Die chemische Spieltheorie berechnet dann die Ergebnisse als Gleichgewichtslösungen für ein System von chemischen Reaktionen. ⓘ
Beschreibung und Modellierung

Die Spieltheorie dient in erster Linie der Beschreibung und Modellierung des Verhaltens menschlicher Populationen. Einige Wissenschaftler sind der Ansicht, dass sie durch die Ermittlung von Spielgleichgewichten vorhersagen können, wie sich menschliche Populationen verhalten werden, wenn sie mit Situationen konfrontiert werden, die dem untersuchten Spiel entsprechen. Diese spezielle Sichtweise der Spieltheorie ist kritisiert worden. Es wird argumentiert, dass die von Spieltheoretikern getroffenen Annahmen bei der Anwendung auf reale Situationen häufig verletzt werden. Spieltheoretiker gehen in der Regel davon aus, dass die Spieler rational handeln, aber in der Praxis weicht das menschliche Verhalten oft von diesem Modell ab. Die Spieltheoretiker reagieren darauf, indem sie ihre Annahmen mit denen der Physik vergleichen. Obwohl ihre Annahmen nicht immer zutreffen, können sie die Spieltheorie als ein vernünftiges wissenschaftliches Ideal betrachten, das den von Physikern verwendeten Modellen ähnelt. Empirische Untersuchungen haben jedoch gezeigt, dass bei einigen klassischen Spielen, wie dem Tausendfüßler-Spiel, dem Raten von 2/3 des Durchschnittsspiels und dem Diktatorspiel, regelmäßig keine Nash-Gleichgewichte auftreten. Es gibt eine anhaltende Debatte über die Bedeutung dieser Experimente und darüber, ob die Analyse der Experimente alle Aspekte der relevanten Situation vollständig erfasst. ⓘ
Einige Spieltheoretiker haben sich, in Anlehnung an die Arbeiten von John Maynard Smith und George R. Price, der evolutionären Spieltheorie zugewandt, um diese Fragen zu klären. Diese Modelle gehen entweder von keiner Rationalität oder von einer begrenzten Rationalität auf Seiten der Spieler aus. Trotz des Namens geht die evolutionäre Spieltheorie nicht unbedingt von einer natürlichen Selektion im biologischen Sinne aus. Die evolutionäre Spieltheorie umfasst sowohl die biologische als auch die kulturelle Evolution und auch Modelle des individuellen Lernens (z. B. fiktive Spieldynamik). ⓘ
Präskriptive oder normative Analyse
| Kooperieren | Defekt ⓘ | |
| Kooperieren | -1, -1 | -10, 0 |
| Defekt | 0, -10 | -5, -5 |
| Das Gefangenendilemma | ||
Einige Wissenschaftler betrachten die Spieltheorie nicht als ein Instrument zur Vorhersage des menschlichen Verhaltens, sondern als einen Vorschlag, wie sich Menschen verhalten sollten. Da eine Strategie, die einem Nash-Gleichgewicht eines Spiels entspricht, die beste Antwort auf die Handlungen der anderen Spieler darstellt - vorausgesetzt, sie befinden sich im (gleichen) Nash-Gleichgewicht -, erscheint es angemessen, eine Strategie zu spielen, die Teil eines Nash-Gleichgewichts ist. Diese normative Anwendung der Spieltheorie ist auch in die Kritik geraten. ⓘ
Wirtschaft und Unternehmen
Die Spieltheorie ist eine wichtige Methode, die in der mathematischen Ökonomie und in der Wirtschaft zur Modellierung des konkurrierenden Verhaltens interagierender Akteure eingesetzt wird. Die Anwendungen umfassen ein breites Spektrum wirtschaftlicher Phänomene und Ansätze wie Auktionen, Verhandlungen, Preisgestaltung bei Fusionen und Übernahmen, faire Aufteilung, Duopole, Oligopole, Bildung sozialer Netze, agentenbasierte Computerökonomie, allgemeines Gleichgewicht, Entwurf von Mechanismen und Wahlsysteme sowie so unterschiedliche Bereiche wie experimentelle Ökonomie, Verhaltensökonomie, Informationsökonomie, industrielle Organisation und politische Ökonomie. ⓘ
Diese Forschung konzentriert sich in der Regel auf bestimmte Gruppen von Strategien, die als "Lösungskonzepte" oder "Gleichgewichte" bekannt sind. Eine gängige Annahme ist, dass die Spieler rational handeln. Bei nicht-kooperativen Spielen ist das berühmteste dieser Konzepte das Nash-Gleichgewicht. Ein Satz von Strategien ist ein Nash-Gleichgewicht, wenn jede Strategie die beste Antwort auf die anderen Strategien darstellt. Wenn alle Spieler die Strategien in einem Nash-Gleichgewicht spielen, haben sie keinen einseitigen Anreiz, davon abzuweichen, da ihre Strategie die beste ist, die sie in Anbetracht dessen, was die anderen tun, tun können. ⓘ
Die Auszahlungen des Spiels werden im Allgemeinen als der Nutzen der einzelnen Spieler angesehen. ⓘ
Ein typischer Aufsatz zur Spieltheorie in den Wirtschaftswissenschaften beginnt mit der Darstellung eines Spiels, das eine Abstraktion einer bestimmten wirtschaftlichen Situation ist. Es werden ein oder mehrere Lösungskonzepte gewählt, und der Autor zeigt auf, welche Strategiesätze in dem vorgestellten Spiel Gleichgewichte des entsprechenden Typs darstellen. Ökonomen und Wirtschaftsprofessoren schlagen zwei primäre Verwendungszwecke vor (siehe oben): beschreibend und präskriptiv. ⓘ
Das Chartered Institute of Procurement & Supply (CIPS) fördert die Kenntnis und den Einsatz der Spieltheorie im Zusammenhang mit der Unternehmensbeschaffung. CIPS und TWS Partners haben eine Reihe von Umfragen durchgeführt, um das Verständnis, das Bewusstsein und die Anwendung der Spieltheorie unter Beschaffungsfachleuten zu untersuchen. Einige der wichtigsten Ergebnisse der dritten jährlichen Umfrage (2019) sind:
- Die Anwendung der Spieltheorie auf die Beschaffungsaktivitäten hat zugenommen - zum Zeitpunkt der Umfrage lag sie bei 19 % aller Befragten.
- 65 % der Teilnehmer sagen voraus, dass die Anwendung der Spieltheorie zunehmen wird.
- 70% der Befragten geben an, dass sie "nur ein grundlegendes oder weniger grundlegendes Verständnis" der Spieltheorie haben
- 20 % der Teilnehmer haben eine berufsbegleitende Ausbildung in Spieltheorie absolviert.
- 50% der Befragten gaben an, dass neue oder verbesserte Softwarelösungen wünschenswert wären
- 90% der Befragten gaben an, dass sie nicht über die Software verfügen, die sie für ihre Arbeit benötigen. ⓘ
Projektleitung
Eine vernünftige Entscheidungsfindung ist entscheidend für den Erfolg von Projekten. Im Projektmanagement wird die Spieltheorie verwendet, um den Entscheidungsprozess von Akteuren wie Investoren, Projektmanagern, Auftragnehmern, Unterauftragnehmern, Regierungen und Kunden zu modellieren. Häufig haben diese Akteure konkurrierende Interessen, und manchmal sind ihre Interessen direkt nachteilig für andere Akteure, so dass sich Projektmanagement-Szenarien gut für die Modellierung durch die Spieltheorie eignen. ⓘ
Piraveenan (2019) nennt in seinem Überblick mehrere Beispiele, in denen die Spieltheorie zur Modellierung von Projektmanagement-Szenarien verwendet wird. So hat ein Investor in der Regel mehrere Investitionsoptionen, und jede Option wird wahrscheinlich zu einem anderen Projekt führen, so dass eine der Investitionsoptionen gewählt werden muss, bevor die Projektcharta erstellt werden kann. Ähnlich verhält es sich bei jedem Großprojekt, an dem Unterauftragnehmer beteiligt sind, z. B. bei einem Bauprojekt. Hier gibt es ein komplexes Zusammenspiel zwischen dem Hauptauftragnehmer (dem Projektleiter) und den Unterauftragnehmern bzw. zwischen den Unterauftragnehmern selbst, das in der Regel mehrere Entscheidungspunkte umfasst. Gibt es beispielsweise eine Unklarheit im Vertrag zwischen dem Hauptauftragnehmer und dem Subunternehmer, muss jeder entscheiden, wie stark er seinen Standpunkt vertreten will, ohne das gesamte Projekt und damit seinen eigenen Anteil daran zu gefährden. Wenn Projekte von konkurrierenden Unternehmen auf den Weg gebracht werden, muss das Marketing-Personal entscheiden, welches der beste Zeitpunkt und die beste Strategie für die Vermarktung des Projekts bzw. des daraus resultierenden Produkts oder der Dienstleistung ist, damit das Projekt angesichts der Konkurrenz ein Maximum an Zugkraft gewinnen kann. In jedem dieser Szenarien hängen die erforderlichen Entscheidungen von den Entscheidungen anderer Akteure ab, die in gewisser Weise konkurrierende Interessen zu den Interessen des Entscheidungsträgers haben, und können daher idealerweise mit Hilfe der Spieltheorie modelliert werden. ⓘ
Piraveenan fasst zusammen, dass für die Modellierung von Projektmanagement-Szenarien überwiegend Spiele mit zwei Spielern verwendet werden, und je nach Identität dieser Spieler werden im Projektmanagement fünf verschiedene Arten von Spielen verwendet. ⓘ
- Spiele zwischen Staat und Privatsektor (Spiele, die öffentlich-private Partnerschaften modellieren)
- Auftragnehmer-Auftragnehmer-Spiele
- Spiele zwischen Auftragnehmer und Unterauftragnehmer
- Spiele zwischen Unterauftragnehmern und Unterauftragnehmern
- Spiele mit anderen Spielern ⓘ
Bei den Spieltypen werden sowohl kooperative als auch nicht-kooperative, Normalform- und Extensivform- sowie Nullsummen- und Nicht-Nullsummenspiele zur Modellierung verschiedener Projektmanagement-Szenarien verwendet. ⓘ
Politikwissenschaft
Die Anwendung der Spieltheorie auf die Politikwissenschaft konzentriert sich auf die sich überschneidenden Bereiche der gerechten Aufteilung, der politischen Ökonomie, der öffentlichen Wahl, der Kriegsverhandlungen, der positiven politischen Theorie und der Theorie der sozialen Wahl. In jedem dieser Bereiche haben Forscher spieltheoretische Modelle entwickelt, bei denen die Spieler oft Wähler, Staaten, spezielle Interessengruppen und Politiker sind. ⓘ
Frühe Beispiele für die Anwendung der Spieltheorie in der Politikwissenschaft stammen von Anthony Downs. In seinem Buch An Economic Theory of Democracy aus dem Jahr 1957 wendet er das Hotelling-Modell der Firmenstandorte auf den politischen Prozess an. Im Downs'schen Modell verpflichten sich die politischen Kandidaten zu Ideologien in einem eindimensionalen politischen Raum. Downs zeigt zunächst, wie die politischen Kandidaten zu der vom Medianwähler bevorzugten Ideologie konvergieren, wenn die Wähler vollständig informiert sind, argumentiert dann aber, dass die Wähler sich dafür entscheiden, rational unwissend zu bleiben, was eine Divergenz der Kandidaten ermöglicht. Die Spieltheorie wurde 1962 auf die Kubakrise während der Präsidentschaft von John F. Kennedy angewandt. ⓘ
Es wurde auch vorgeschlagen, dass die Spieltheorie die Stabilität jeder Form von politischer Regierung erklärt. Im einfachsten Fall einer Monarchie zum Beispiel kann der König, der nur eine Person ist, seine Autorität nicht dadurch aufrechterhalten, dass er persönlich die physische Kontrolle über alle oder auch nur eine nennenswerte Anzahl seiner Untertanen ausübt. Die Kontrolle des Souveräns erklärt sich stattdessen dadurch, dass jeder Bürger anerkennt, dass alle anderen Bürger voneinander erwarten, dass sie den König (oder eine andere etablierte Regierung) als die Person ansehen, deren Befehle befolgt werden. Eine koordinierte Kommunikation zwischen den Bürgern mit dem Ziel, den Souverän zu ersetzen, ist faktisch ausgeschlossen, da eine Verschwörung zur Ersetzung des Souveräns im Allgemeinen als Verbrechen geahndet wird. In einem Prozess, der durch Varianten des Gefangenendilemmas modelliert werden kann, wird es daher in Zeiten der Stabilität kein Bürger für rational halten, den Souverän zu ersetzen, selbst wenn alle Bürger wissen, dass sie besser dran wären, wenn sie alle gemeinsam handeln würden. ⓘ
Eine spieltheoretische Erklärung für den demokratischen Frieden ist, dass öffentliche und offene Debatten in Demokratien anderen Staaten klare und zuverlässige Informationen über ihre Absichten vermitteln. Im Gegensatz dazu ist es schwierig, die Absichten nicht-demokratischer Führer zu kennen, zu wissen, welche Auswirkungen Zugeständnisse haben werden und ob Versprechen eingehalten werden. Daher wird es Misstrauen und mangelnde Bereitschaft zu Zugeständnissen geben, wenn mindestens eine der Streitparteien eine Nicht-Demokratie ist. ⓘ
Die Spieltheorie sagt jedoch voraus, dass zwei Länder auch dann in den Krieg ziehen können, wenn sich ihre Führer der Kosten eines Kampfes bewusst sind. Ein Krieg kann aus asymmetrischen Informationen resultieren; zwei Länder können Anreize haben, die Menge der ihnen zur Verfügung stehenden militärischen Ressourcen falsch darzustellen, so dass sie nicht in der Lage sind, Streitigkeiten einvernehmlich beizulegen, ohne auf Kämpfe zurückzugreifen. Darüber hinaus kann Krieg aufgrund von Verpflichtungsproblemen entstehen: Wenn zwei Länder einen Streit mit friedlichen Mitteln beilegen wollen, aber jedes Land die Bedingungen dieser Einigung nicht einhalten will, haben sie möglicherweise keine andere Wahl, als auf Krieg zu setzen. Schließlich kann ein Krieg auch aus der Unteilbarkeit von Problemen resultieren. ⓘ
Die Spieltheorie könnte auch dabei helfen, die Reaktionen einer Nation vorherzusagen, wenn eine neue Regel oder ein neues Gesetz auf diese Nation angewendet werden soll. Ein Beispiel ist die Forschung von Peter John Wood (2013), der untersucht hat, was Nationen tun könnten, um den Klimawandel einzudämmen. Wood war der Meinung, dass dies durch den Abschluss von Verträgen mit anderen Ländern zur Reduzierung der Treibhausgasemissionen erreicht werden könnte. Er kam jedoch zu dem Schluss, dass diese Idee nicht funktionieren kann, weil sie die Nationen in ein Gefangenendilemma bringen würde. ⓘ
Biologie
| Falke | Taube ⓘ | |
| Falke | 20, 20 | 80, 40 |
| Taube | 40, 80 | 60, 60 |
| Das Falke-Taube-Spiel | ||
Anders als in der Ökonomie werden die Auszahlungen für Spiele in der Biologie oft so interpretiert, dass sie der Fitness entsprechen. Darüber hinaus liegt der Schwerpunkt weniger auf Gleichgewichten, die einer Vorstellung von Rationalität entsprechen, als vielmehr auf solchen, die durch evolutionäre Kräfte aufrechterhalten werden können. Das bekannteste Gleichgewicht in der Biologie ist die evolutionär stabile Strategie (ESS), die erstmals in (Maynard Smith & Price 1973) vorgestellt wurde. Obwohl ihre ursprüngliche Motivation keine der mentalen Anforderungen des Nash-Gleichgewichts beinhaltete, ist jedes ESS ein Nash-Gleichgewicht. ⓘ
In der Biologie wurde die Spieltheorie als Modell verwendet, um viele verschiedene Phänomene zu verstehen. Sie wurde erstmals verwendet, um die Entwicklung (und Stabilität) des ungefähren Geschlechterverhältnisses von 1:1 zu erklären. (Fisher 1930) schlug vor, dass das Geschlechterverhältnis von 1:1 das Ergebnis von evolutionären Kräften ist, die auf Individuen einwirken, die versuchen, die Anzahl ihrer Enkel zu maximieren. ⓘ
Darüber hinaus haben Biologen die evolutionäre Spieltheorie und das ESS genutzt, um die Entstehung der Tierkommunikation zu erklären. Die Analyse von Signalisierungsspielen und anderen Kommunikationsspielen hat Einblicke in die Evolution der Kommunikation unter Tieren gegeben. So scheint das Mobbing-Verhalten vieler Arten, bei dem eine große Anzahl von Beutetieren ein größeres Raubtier angreift, ein Beispiel für eine spontan entstandene Organisation zu sein. Auch bei Ameisen hat sich gezeigt, dass sie ein der Mode ähnliches Feed-forward-Verhalten zeigen (siehe Paul Ormerods Butterfly Economics). ⓘ
Biologen haben das Spiel "Huhn" zur Analyse von Kampfverhalten und Territorialität verwendet. ⓘ
Maynard Smith schreibt im Vorwort zu Evolution and the Theory of Games: "Paradoxerweise hat sich herausgestellt, dass die Spieltheorie leichter auf die Biologie anwendbar ist als auf das Gebiet des wirtschaftlichen Verhaltens, für das sie ursprünglich entwickelt wurde". Die evolutionäre Spieltheorie wurde verwendet, um viele scheinbar unvereinbare Phänomene in der Natur zu erklären. ⓘ
Ein solches Phänomen ist als biologischer Altruismus bekannt. Dabei handelt es sich um eine Situation, in der ein Organismus so zu handeln scheint, dass er anderen Organismen nützt und sich selbst schadet. Dies unterscheidet sich von den traditionellen Vorstellungen von Altruismus, da solche Handlungen nicht bewusst sind, sondern offenbar evolutionäre Anpassungen zur Steigerung der allgemeinen Fitness darstellen. Beispiele dafür finden sich bei verschiedenen Arten, von Vampirfledermäusen, die das Blut, das sie bei einer nächtlichen Jagd gewonnen haben, wieder auswürgen und es Gruppenmitgliedern geben, die nicht gefüttert wurden, über Arbeitsbienen, die sich ihr ganzes Leben lang um die Bienenkönigin kümmern und sich nie paaren, bis hin zu Grünen Meerkatzen, die Gruppenmitglieder vor einem herannahenden Raubtier warnen, selbst wenn dies die Überlebenschancen des Einzelnen gefährdet. All diese Handlungen erhöhen die Gesamtfitness einer Gruppe, allerdings zu einem Preis, der dem Einzelnen entsteht. ⓘ
Die evolutionäre Spieltheorie erklärt diesen Altruismus mit der Idee der Verwandtenselektion. Altruisten unterscheiden zwischen den Individuen, denen sie helfen, und bevorzugen Verwandte. Die Hamilton-Regel erklärt das evolutionäre Grundprinzip hinter dieser Auswahl mit der Gleichung c < b × r, wobei die Kosten c für den Altruisten geringer sein müssen als der Nutzen b für den Empfänger, multipliziert mit dem Verwandtschaftskoeffizienten r. Je näher zwei Organismen miteinander verwandt sind, desto häufiger tritt Altruismus auf, da sie viele der gleichen Allele teilen. Das bedeutet, dass das altruistische Individuum, indem es dafür sorgt, dass die Allele seines nahen Verwandten durch das Überleben seiner Nachkommen weitergegeben werden, auf die Option verzichten kann, selbst Nachkommen zu haben, da die gleiche Anzahl von Allelen weitergegeben wird. So hat beispielsweise die Hilfe für Geschwister (bei diploiden Tieren) einen Koeffizienten von 1⁄2, weil ein Individuum (im Durchschnitt) die Hälfte der Allele in den Nachkommen seiner Geschwister teilt. Wenn sichergestellt wird, dass genügend Nachkommen eines Geschwisters bis zum Erwachsenenalter überleben, ist es nicht notwendig, dass das altruistische Individuum Nachkommen produziert. Die Werte der Koeffizienten hängen stark vom Umfang des Spielfelds ab; wenn beispielsweise die Entscheidung, wen man bevorzugt, alle genetischen Lebewesen und nicht nur alle Verwandten einschließt und wir davon ausgehen, dass die Diskrepanz zwischen allen Menschen nur etwa 1 % der Vielfalt im Spielfeld ausmacht, wird ein Koeffizient, der im kleineren Feld 1⁄2 war, zu 0,995. Ähnlich verhält es sich, wenn man davon ausgeht, dass andere als genetische Informationen (z. B. Epigenetik, Religion, Wissenschaft usw.) im Laufe der Zeit erhalten geblieben sind, dann wird das Spielfeld noch größer und die Diskrepanzen kleiner. ⓘ
Computerwissenschaft und Logik
Die Spieltheorie spielt in der Logik und in der Informatik eine immer wichtigere Rolle. Mehrere logische Theorien stützen sich auf die Semantik von Spielen. Darüber hinaus haben Informatiker Spiele verwendet, um interaktive Berechnungen zu modellieren. Außerdem liefert die Spieltheorie eine theoretische Grundlage für den Bereich der Multiagentensysteme. ⓘ
Unabhängig davon hat die Spieltheorie eine Rolle bei Online-Algorithmen gespielt, insbesondere bei der k-Server-Problem, das in der Vergangenheit als Spiele mit beweglichen Kosten und Anfrage-Antwort-Spiele bezeichnet wurde. Das Yao-Prinzip ist eine spieltheoretische Technik, mit der sich untere Schranken für die Rechenkomplexität von randomisierten Algorithmen, insbesondere Online-Algorithmen, nachweisen lassen. ⓘ
Das Aufkommen des Internets hat die Entwicklung von Algorithmen zur Ermittlung von Gleichgewichten in Spielen, Märkten, Computerauktionen, Peer-to-Peer-Systemen sowie Sicherheits- und Informationsmärkten motiviert. Die algorithmische Spieltheorie und damit auch das Design algorithmischer Mechanismen verbindet das Design von Algorithmen und die Analyse komplexer Systeme mit der Wirtschaftstheorie. ⓘ
Philosophie
| Hirsch | Hase ⓘ | |
| Hirsch | 3, 3 | 0, 2 |
| Hase | 2, 0 | 2, 2 |
| Hirschjagd | ||
Die Spieltheorie ist in der Philosophie mehrfach eingesetzt worden. Als Reaktion auf zwei Arbeiten von W.V.O. Quine (1960, 1967) entwickelte Lewis (1969) mit Hilfe der Spieltheorie eine philosophische Darstellung der Konvention. Auf diese Weise lieferte er die erste Analyse des gemeinsamen Wissens und setzte sie bei der Analyse von Koordinationsspielen ein. Außerdem schlug er zum ersten Mal vor, dass man Bedeutung in Form von Signalisierungsspielen verstehen kann. Dieser Vorschlag wurde seit Lewis von mehreren Philosophen weiterverfolgt. In Anlehnung an Lewis (1969) spieltheoretische Darstellung von Konventionen haben Edna Ullmann-Margalit (1977) und Bicchieri (2006) Theorien über soziale Normen entwickelt, die sie als Nash-Gleichgewichte definieren, die sich aus der Umwandlung eines gemischtmotivischen Spiels in ein Koordinationsspiel ergeben. ⓘ
Die Spieltheorie hat Philosophen auch dazu herausgefordert, in Begriffen der interaktiven Erkenntnistheorie zu denken: Was bedeutet es für ein Kollektiv, gemeinsame Überzeugungen oder gemeinsames Wissen zu haben, und welche Konsequenzen hat dieses Wissen für die sozialen Ergebnisse, die sich aus den Interaktionen der Akteure ergeben. Zu den Philosophen, die in diesem Bereich gearbeitet haben, gehören Bicchieri (1989, 1993), Skyrms (1990) und Stalnaker (1999). ⓘ
In der Ethik haben einige Autoren (vor allem David Gauthier, Gregory Kavka und Jean Hampton) versucht, Thomas Hobbes' Projekt der Ableitung der Moral aus dem Eigeninteresse zu verfolgen. Da Spiele wie das Gefangenendilemma einen offensichtlichen Konflikt zwischen Moral und Eigeninteresse darstellen, ist die Erklärung, warum Kooperation durch Eigeninteresse erforderlich ist, ein wichtiger Bestandteil dieses Projekts. Diese allgemeine Strategie ist Bestandteil der allgemeinen Sichtweise des Gesellschaftsvertrags in der politischen Philosophie (für Beispiele siehe Gauthier (1986) und Kavka (1986)). ⓘ
Andere Autoren haben versucht, die evolutionäre Spieltheorie zu nutzen, um die Entstehung menschlicher Einstellungen zur Moral und entsprechender tierischer Verhaltensweisen zu erklären. Diese Autoren betrachten verschiedene Spiele, darunter das Gefangenendilemma, die Hirschjagd und das Nash-Verhandlungsspiel, als Erklärung für die Entstehung von Moralvorstellungen (siehe z. B. Skyrms (1996, 2004) und Sober und Wilson (1998)). ⓘ
Preisgestaltung im Einzelhandel und bei Konsumgütern
Anwendungen der Spieltheorie werden häufig bei den Preisstrategien des Einzelhandels und der Verbrauchermärkte eingesetzt, insbesondere beim Verkauf unelastischer Güter. Da die Einzelhändler ständig miteinander um Marktanteile konkurrieren, ist es für sie üblich geworden, auf bestimmte Waren zeitweise Rabatte zu gewähren, in der Hoffnung, die Kundenfrequenz in den Ladengeschäften (bzw. die Besucherzahlen auf den Websites von E-Commerce-Händlern) zu erhöhen oder den Absatz von Zusatz- oder Ergänzungsprodukten zu steigern. ⓘ
Der Schwarze Freitag, ein beliebter Shopping-Feiertag in den USA, ist für viele Einzelhändler der Zeitpunkt, an dem sie sich auf optimale Preisstrategien konzentrieren, um den Markt für das Weihnachtsgeschäft zu erobern. Im Szenario des Schwarzen Freitags stellen sich Einzelhändler, die die Spieltheorie anwenden, in der Regel die Frage: "Wie wird der dominante Wettbewerber auf mich reagieren?" In einem solchen Szenario gibt es zwei Spieler: den Einzelhändler und den Verbraucher. Der Einzelhändler konzentriert sich auf eine optimale Preisstrategie, während der Verbraucher auf das beste Angebot aus ist. In diesem geschlossenen System gibt es oft keine dominante Strategie, da beide Spieler alternative Möglichkeiten haben. Das heißt, der Einzelhändler kann sich einen anderen Kunden suchen, und der Verbraucher kann bei einem anderen Einzelhändler einkaufen. Angesichts des Marktwettbewerbs an diesem Tag besteht die dominante Strategie der Einzelhändler jedoch darin, ihre Konkurrenten zu übertreffen. Das offene System geht von mehreren Einzelhändlern aus, die ähnliche Waren verkaufen, und von einer endlichen Anzahl von Verbrauchern, die die Waren zu einem optimalen Preis nachfragen. Ein Blog eines Professors der Cornell University lieferte ein Beispiel für eine solche Strategie, als Amazon einen Samsung-Fernseher 100 Dollar unter dem Einzelhandelspreis anbot und damit die Konkurrenz unterbot. Amazon machte einen Teil der Differenz wieder wett, indem es den Preis für HDMI-Kabel erhöhte, da festgestellt wurde, dass die Verbraucher beim Verkauf von Sekundärartikeln weniger preisdiskriminierend sind. ⓘ
Die Einzelhandelsmärkte entwickeln weiterhin Strategien und Anwendungen der Spieltheorie, wenn es um die Preisgestaltung von Konsumgütern geht. Die wichtigsten Erkenntnisse, die zwischen Simulationen in einer kontrollierten Umgebung und realen Einzelhandelserfahrungen gefunden wurden, zeigen, dass die Anwendungen solcher Strategien komplexer sind, da jeder Einzelhändler ein optimales Gleichgewicht zwischen Preisgestaltung, Lieferantenbeziehungen, Markenimage und dem Potenzial, den Verkauf von profitableren Artikeln zu kannibalisieren, finden muss. ⓘ
Epidemiologie
Da die Entscheidung, sich gegen eine bestimmte Krankheit impfen zu lassen, häufig von Einzelpersonen getroffen wird, die bei dieser Entscheidung eine Reihe von Faktoren und Parametern berücksichtigen können (z. B. das Auftreten und die Häufigkeit der Krankheit, das wahrgenommene und das tatsächliche Risiko, sich mit der Krankheit anzustecken, die Sterblichkeitsrate, das wahrgenommene und das tatsächliche Risiko der Impfung sowie die finanziellen Kosten der Impfung), wurde die Spieltheorie zur Modellierung und Vorhersage der Impfrate in einer Gesellschaft verwendet. ⓘ
In der Populärkultur
- Basierend auf dem Buch von Sylvia Nasar aus dem Jahr 1998 wurde die Lebensgeschichte des Spieltheoretikers und Mathematikers John Nash 2001 in dem Biopic A Beautiful Mind mit Russell Crowe als Nash in der Hauptrolle verfilmt.
- Im militärischen Science-Fiction-Roman Starship Troopers von Robert A. Heinlein aus dem Jahr 1959 werden die Begriffe "Spieltheorie" und "Theorie der Spiele" erwähnt. Im gleichnamigen Film von 1997 bezeichnete die Figur Carl Jenkins seinen Auftrag beim militärischen Geheimdienst als "Spiele und Theorie".
- Der Film Dr. Strangelove aus dem Jahr 1964 persifliert spieltheoretische Ideen zur Abschreckungstheorie. So hängt beispielsweise die nukleare Abschreckung von der Drohung ab, katastrophale Vergeltungsmaßnahmen zu ergreifen, wenn ein nuklearer Angriff entdeckt wird. Ein Spieltheoretiker könnte argumentieren, dass solche Drohungen nicht glaubwürdig sein können, da sie zu subgame imperfect equilibria führen können. Der Film geht noch einen Schritt weiter, indem sich die Sowjetunion unwiderruflich zu einer katastrophalen nuklearen Reaktion verpflichtet, ohne diese Drohung öffentlich zu machen.
- Die Power-Pop-Band Game Theory aus den 1980er Jahren wurde von dem Sänger/Songwriter Scott Miller gegründet, der den Bandnamen als Anspielung auf "das Studium der Berechnung der geeignetsten Aktion angesichts eines Gegners ... um sich selbst das Minimum an Misserfolg zu ermöglichen" beschrieb.
- Liar Game, ein japanischer Manga aus dem Jahr 2005 und eine Fernsehserie aus dem Jahr 2007, stellt die Hauptfiguren in jeder Episode vor ein Spiel oder ein Problem, das typischerweise aus der Spieltheorie stammt, wie die von den Figuren angewandten Strategien zeigen.
- Der Roman Spy Story von Len Deighton aus dem Jahr 1974 untersucht Elemente der Spieltheorie im Zusammenhang mit Armeeübungen im Kalten Krieg.
- Der Roman The Dark Forest von Liu Cixin aus dem Jahr 2008 erforscht die Beziehung zwischen außerirdischem Leben, der Menschheit und der Spieltheorie.
- Der Hauptantagonist Joker im Film The Dark Knight stellt spieltheoretische Konzepte vor - insbesondere das Gefangenendilemma in einer Szene, in der er die Passagiere zweier Fähren auffordert, die andere zu bombardieren, um ihre eigene zu retten. ⓘ
Siehe auch
- Angewandte Ethik
- Spiel um die gemeinsame Nutzung von Bandbreiten
- Kettenladen-Paradoxon
- Kollektive Intentionalität
- Glossar der Spieltheorie
- Haushaltsinterne Verhandlung
- Königsmacher-Szenario
- Recht und Wirtschaft
- Grundzüge der künstlichen Intelligenz
- Parrondos Paradoxon
- Vorsorgeprinzip
- Quanten-Schiedsspiel
- Risikomanagement
- Selbstbestätigendes Gleichgewicht
- Tragödie der Allmende
- Wilson-Doktrin (Wirtschaftswissenschaften) ⓘ
Verzeichnisse
- Liste der kognitiven Verzerrungen
- Liste der aufkommenden Technologien
- Liste der Spiele in der Spieltheorie ⓘ
Referenzen und weiterführende Literatur
Lehrbücher und allgemeine Referenzen
- Aumann, Robert J (1987), "Spieltheorie", The New Palgrave: A Dictionary of Economics, Bd. 2, S. 460-82.
- Camerer, Colin (2003), "Einführung", Behavioral Game Theory: Experiments in Strategic Interaction, Russell Sage Foundation, S. 1-25, ISBN 978-0-691-09039-9, archiviert vom Original am 14. Mai 2011, abgerufen am 9. Februar 2011, Beschreibung.
- Dutta, Prajit K. (1999), Strategien und Spiele: Theorie und Praxis, MIT Press, ISBN 978-0-262-04169-0. Geeignet für Studenten im Grundstudium und Wirtschaftsstudenten. https://b-ok.org/book/2640653/e56341.
- Fernandez, L. F.; Bierman, H. S. (1998), Spieltheorie mit wirtschaftlichen Anwendungen, Addison-Wesley, ISBN 978-0-201-84758-1. Geeignet für Studenten der Oberstufe.
- Gibbons, Robert D. (1992), Spieltheorie für angewandte Wirtschaftswissenschaftler, Princeton University Press, ISBN 978-0-691-00395-5. Geeignet für fortgeschrittene Undergraduates.
- In Europa veröffentlicht als Gibbons, Robert (2001), A Primer in Game Theory, London: Harvester Wheatsheaf, ISBN 978-0-7450-1159-2.
- Gintis, Herbert (2000), Game theory evolving: a problem-centered introduction to modeling strategic behavior, Princeton University Press, ISBN 978-0-691-00943-8
- Green, Jerry R.; Mas-Colell, Andreu; Whinston, Michael D. (1995), Mikroökonomische Theorie, Oxford University Press, ISBN 978-0-19-507340-9. Stellt die Spieltheorie in einer formalen Weise dar, die sich für Hochschulabsolventen eignet.
- Joseph E. Harrington (2008), Games, strategies, and decision making, Worth, ISBN 0-7167-6630-2. Lehrbuch, geeignet für Studenten in angewandten Bereichen; zahlreiche Beispiele, weniger Formalismen in der Konzeptdarstellung.
- Howard, Nigel (1971), Paradoxes of Rationality: Games, Metagames, and Political Behavior, Cambridge, MA: The MIT Press, ISBN 978-0-262-58237-7
- Isaacs, Rufus (1999), Differential Games: A Mathematical Theory With Applications to Warfare and Pursuit, Control and Optimization, New York: Dover Publications, ISBN 978-0-486-40682-4
- Maschler, Michael; Solan, Eilon; Zamir, Shmuel (2013), Game Theory, Cambridge University Press, ISBN 978-1-108-49345-1. Lehrbuch für Grundschüler.
- Miller, James H. (2003), Game theory at work: how to use game theory to outthink and outmaneuver your competition, New York: McGraw-Hill, ISBN 978-0-07-140020-6. Geeignet für ein allgemeines Publikum.
- Osborne, Martin J. (2004), Eine Einführung in die Spieltheorie, Oxford University Press, ISBN 978-0-19-512895-6. Lehrbuch für Grundschüler.
- Osborne, Martin J.; Rubinstein, Ariel (1994), Ein Kurs in Spieltheorie, MIT Press, ISBN 978-0-262-65040-3. Eine moderne Einführung für Hochschulabsolventen.
- Shoham, Yoav; Leyton-Brown, Kevin (2009), Multiagentensysteme: Algorithmic, Game-Theoretic, and Logical Foundations, New York: Cambridge University Press, ISBN 978-0-521-89943-7, abgerufen am 8. März 2016
- Watson, Joel (2013), Strategy: An Introduction to Game Theory (3. Auflage), New York: W.W. Norton and Co, ISBN 978-0-393-91838-0. Ein führendes Lehrbuch für das fortgeschrittene Undergraduate-Niveau.
- McCain, Roger A. (2010), Roger McCain's Game Theory: Eine nicht-technische Einführung in die Analyse von Strategien (überarbeitete Auflage), ISBN 978-981-4289-65-8
- Webb, James N. (2007), Spieltheorie: Entscheidungen, Interaktion und Evolution, Mathematik für Grundschüler, Springer, ISBN 978-1-84628-423-6 Konsistente Behandlung von Spieltypen, die normalerweise von verschiedenen angewandten Bereichen beansprucht werden, z. B. Markov-Entscheidungsprozesse. ⓘ
Historisch wichtige Texte
- Aumann, R. J.; Shapley, L. S. (1974), Values of Non-Atomic Games, Princeton University Press
- Cournot, A. Augustin (1838), "Recherches sur les principles mathematiques de la théorie des richesses", Libraire des Sciences Politiques et Sociales
- Edgeworth, Francis Y. (1881), Mathematische Hellseher, London: Kegan Paul
- Farquharson, Robin (1969), Theory of Voting, Blackwell (Yale U.P. in den U.S.A.), ISBN 978-0-631-12460-3
- Luce, R. Duncan; Raiffa, Howard (1957), Games and decisions: introduction and critical survey, New York: Wiley
- nachgedruckte Ausgabe: R. Duncan Luce; Howard Raiffa (1989), Games and decisions: introduction and critical survey, New York: Dover Publications, ISBN 978-0-486-65943-5: CS1 maint: mehrere Namen: Autorenliste (Link)
- Maynard Smith, John (1982), Evolution and the theory of games, Cambridge University Press, ISBN 978-0-521-28884-2
- Maynard Smith, John; Price, George R. (1973), "The logic of animal conflict", Nature, 246 (5427): 15-18, Bibcode:1973Natur.246...15S, doi:10.1038/246015a0, S2CID 4224989
- Nash, John (1950), "Equilibrium points in n-person games", Proceedings of the National Academy of Sciences of the United States of America, 36 (1): 48-49, Bibcode:1950PNAS...36...48N, doi:10.1073/pnas.36.1.48, PMC 1063129, PMID 16588946
- Shapley, L.S. (1953), A Value for n-person Games, In: Beiträge zur Theorie der Spiele Band II, H. W. Kuhn und A. W. Tucker (Hrsg.)
- Shapley, L.S. (1953), Stochastic Games, Proceedings of National Academy of Science Vol. 39, S. 1095-1100.
- von Neumann, John (1928), "Zur Theorie der Gesellschaftsspiele", Mathematische Annalen, 100 (1): 295-320, doi:10.1007/bf01448847, S2CID 122961988 Englische Übersetzung: "On the Theory of Games of Strategy," in A. W. Tucker and R. D. Luce, ed. (1959), Contributions to the Theory of Games, v. 4, p. 42. Princeton University Press.
- von Neumann, John; Morgenstern, Oskar (1944), "Theory of games and economic behavior", Nature, Princeton University Press, 157 (3981): 172, Bibcode:1946Natur.157..172R, doi:10.1038/157172a0, S2CID 29754824
- Zermelo, Ernst (1913), "Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels", Proceedings of the Fifth International Congress of Mathematicians, 2: 501-4 ⓘ
Andere gedruckte Referenzen
- Ben David, S.; Borodin, Allan; Karp, Richard; Tardos, G.; Wigderson, A. (1994), "On the Power of Randomization in On-line Algorithms" (PDF), Algorithmica, 11 (1): 2-14, doi:10.1007/BF01294260, S2CID 26771869
- Downs, Anthony (1957), Eine ökonomische Theorie der Demokratie, New York: Harper
- Gauthier, David (1986), Moral durch Vereinbarung, Oxford University Press, ISBN 978-0-19-824992-4
- Allan Gibbard, "Manipulation of voting schemes: a general result", Econometrica, Vol. 41, No. 4 (1973), S. 587-601.
- Grim, Patrick; Kokalis, Trina; Alai-Tafti, Ali; Kilb, Nicholas; St Denis, Paul (2004), "Making meaning happen", Journal of Experimental & Theoretical Artificial Intelligence, 16 (4): 209-243, doi:10.1080/09528130412331294715, S2CID 5737352
- Harper, David; Maynard Smith, John (2003), Tierische Signale, Oxford University Press, ISBN 978-0-19-852685-8
- Lewis, David (1969), Konvention: Eine philosophische Studie, ISBN 978-0-631-23257-5 (Ausgabe 2002)
- McDonald, John (1950-1996), Strategie in Poker, Wirtschaft und Krieg, W. W. Norton, ISBN 978-0-393-31457-1. Eine Einführung für den Laien.
- Papayoanou, Paul (2010), Spieltheorie für Unternehmen: A Primer in Strategic Gaming, Probabilistic, ISBN 978-0-9647938-7-3.
- Quine, W.v.O (1967), "Truth by Convention", Philosophica Essays for A.N. Whitehead, Russel and Russel Publishers, ISBN 978-0-8462-0970-6
- Quine, W.v.O (1960), "Carnap und die logische Wahrheit", Synthese, 12 (4): 350-374, doi:10.1007/BF00485423, S2CID 46979744
- Satterthwaite, Mark A. (April 1975), "Strategy-proofness and Arrow's Conditions: Existence and Correspondence Theorems for Voting Procedures and Social Welfare Functions" (PDF), Journal of Economic Theory, 10 (2): 187–217, doi:10.1016/0022-0531(75)90050-2
- Siegfried, Tom (2006), Eine schöne Mathematik, Joseph Henry Press, ISBN 978-0-309-10192-9
- Skyrms, Brian (1990), Die Dynamik der rationalen Entscheidungsfindung, Harvard University Press, ISBN 978-0-674-21885-7
- Skyrms, Brian (1996), Evolution des Gesellschaftsvertrags, Cambridge University Press, ISBN 978-0-521-55583-8
- Skyrms, Brian (2004), The stag hunt and the evolution of social structure, Cambridge University Press, ISBN 978-0-521-53392-8
- Sober, Elliott; Wilson, David Sloan (1998), Unto others: the evolution and psychology of unselfish behavior, Harvard University Press, ISBN 978-0-674-93047-6
- Thrall, Robert M.; Lucas, William F. (1963), "-person games in partition function form", Naval Research Logistics Quarterly, 10 (4): 281–298, doi:10.1002/nav.3800100126
- Dolev, Shlomi; Panagopoulou, Panagiota; Rabie, Mikael; Schiller, Elad Michael; Spirakis, Paul (2011), "Rationality authority for provable rational behavior", Proceedings of the 30th annual ACM SIGACT-SIGOPS symposium on Principles of distributed computing, pp. 289-290, doi:10.1145/1993806.1993858, ISBN 978-1-4503-0719-2, S2CID 8974307
- Chastain, Erick; Livnat, Adi; Papadimitriou, Christos; Vazirani, Umesh (Juni 2014), "Algorithms, games, and evolution", Proceedings of the National Academy of Sciences of the United States of America, 111 (29): 10620-10623, Bibcode:2014PNAS..11110620C, doi:10.1073/pnas.1406556111, PMC 4115542, PMID 24979793 ⓘ
Anwendung
Die Spieltheorie ist weniger eine zusammenhängende Theorie als mehr ein Satz von Analyseinstrumenten. Anwendungen findet die Spieltheorie vor allem im Operations Research, in den Wirtschaftswissenschaften (sowohl Volkswirtschaftslehre als auch Betriebswirtschaftslehre), in der Ökonomischen Analyse des Rechts (law and economics) als Teilbereich der Rechtswissenschaften, in der Politikwissenschaft, in der Soziologie, in der Psychologie, in der Informatik, in der linguistischen Textanalyse und seit den 1980ern auch in der Biologie (insb. die evolutionäre Spieltheorie). ⓘ
Rezeption
Die Spieltheorie erlaubt es, soziale Konfliktsituationen, die strategische Spiele genannt werden, facettenreich abzubilden und mathematisch streng zu lösen. Aufgrund der unrealistischen Modellannahmen wird die empirische Erklärungskraft der Spieltheorie in der Regel in Abrede gestellt. Kein Mensch wird jemals so rational sein, wie es den Spielern durch die spieltheoretischen Lösungskonzepte unterstellt wird. Menschen unterliegen stets kognitiven Beschränkungen, die perfekt rationales Verhalten in komplexen Spielen ausschließen. Indes muss nach Auffassung des Bamberger Politikwissenschaftlers Reinhard Zintl zwischen dem Anwendungsfall als Verhaltenstheorie und demjenigen als Verfassungstheorie unterschieden werden; und es sei je nach Erklärungsproblem auch eine inkonsistente Verwendung einzelner Akteursmodelle durchaus gestattet und zweckmäßig. ⓘ
Beispiele
Berühmte Probleme
- Gefangenendilemma
- Feiglingsspiel (englisch chicken game)
- Hirschjagd
- Falke-Taube-Spiel
- Kampf der Geschlechter
- Ultimatumspiel
- Eisverkäufer-am-Strand-Problem (Hotellings Gesetz)
- Beauty Contest
- Triell
- Braess-Paradoxon
- Teilungsproblem
- Vertrauensspiel
- Tragik der Allmende
- Dollarauktion
- Matching Pennies ⓘ
Berühmte Strategien
Trigger-Strategien:
- Tit for Tat (Quid pro quo)
- Tit for Two Tats
- Grim ⓘ



