Stringtheorie
| String-Theorie ⓘ |
|---|
 |
| Grundlegende Objekte |
|
| Störungsspezifische Theorie |
|
| Nicht-störende Ergebnisse |
|
| Phänomenologie |
|
| Mathematik |
|
|
In der Physik ist die Stringtheorie ein theoretischer Rahmen, in dem die punktförmigen Teilchen der Teilchenphysik durch eindimensionale Objekte, so genannte Strings, ersetzt werden. Die Stringtheorie beschreibt, wie sich diese Strings durch den Raum ausbreiten und miteinander wechselwirken. Auf Entfernungsskalen, die größer sind als die Stringskala, sieht ein String wie ein gewöhnliches Teilchen aus, dessen Masse, Ladung und andere Eigenschaften durch den Schwingungszustand des Strings bestimmt werden. In der Stringtheorie entspricht einer der vielen Schwingungszustände des Strings dem Graviton, einem quantenmechanischen Teilchen, das die Gravitationskraft trägt. Die Stringtheorie ist also eine Theorie der Quantengravitation. ⓘ
Die Stringtheorie ist ein breit gefächertes und vielfältiges Thema, das versucht, eine Reihe tiefgreifender Fragen der fundamentalen Physik zu beantworten. Die Stringtheorie hat zu einer Reihe von Fortschritten in der mathematischen Physik beigetragen, die auf eine Vielzahl von Problemen in der Physik Schwarzer Löcher, der Kosmologie des frühen Universums, der Kernphysik und der Physik kondensierter Materie angewandt wurden, und sie hat eine Reihe wichtiger Entwicklungen in der reinen Mathematik angeregt. Da die Stringtheorie potenziell eine einheitliche Beschreibung der Schwerkraft und der Teilchenphysik liefert, ist sie ein Kandidat für eine Theorie von allem, ein in sich geschlossenes mathematisches Modell, das alle grundlegenden Kräfte und Formen der Materie beschreibt. Trotz zahlreicher Arbeiten zu diesen Problemen ist nicht bekannt, inwieweit die Stringtheorie die reale Welt beschreibt oder wie viel Freiheit sie bei der Wahl ihrer Details lässt. ⓘ
Die Stringtheorie wurde erstmals in den späten 1960er Jahren als Theorie der starken Kernkraft untersucht, bevor sie zugunsten der Quantenchromodynamik aufgegeben wurde. Später erkannte man, dass gerade die Eigenschaften, die die Stringtheorie als Theorie der Kernphysik ungeeignet machten, sie zu einem vielversprechenden Kandidaten für eine Quantentheorie der Gravitation machten. Die früheste Version der Stringtheorie, die bosonische Stringtheorie, umfasste nur die Klasse der als Bosonen bekannten Teilchen. Später entwickelte sie sich zur Superstringtheorie, die eine Supersymmetrie genannte Verbindung zwischen Bosonen und der Teilchenklasse der Fermionen voraussetzt. Fünf konsistente Versionen der Superstring-Theorie wurden entwickelt, bevor Mitte der 1990er Jahre vermutet wurde, dass es sich bei allen um verschiedene Grenzfälle einer einzigen Theorie in 11 Dimensionen handelt, die als M-Theorie bekannt ist. Ende 1997 entdeckten Theoretiker eine wichtige Beziehung, die so genannte Anti-De-Sitter/Konforme-Feldtheorie-Korrespondenz (AdS/CFT-Korrespondenz), die die Stringtheorie mit einer anderen Art von physikalischer Theorie, der Quantenfeldtheorie, verbindet. ⓘ
Eine der Herausforderungen der Stringtheorie besteht darin, dass die vollständige Theorie nicht unter allen Umständen eine zufriedenstellende Definition hat. Ein weiteres Problem besteht darin, dass die Theorie eine riesige Landschaft möglicher Universen beschreibt, was die Entwicklung von Theorien der Teilchenphysik auf der Grundlage der Stringtheorie erschwert hat. Diese Probleme haben dazu geführt, dass einige in der Gemeinschaft diese physikalischen Ansätze kritisieren und den Wert der weiteren Forschung zur Vereinheitlichung der Stringtheorie in Frage stellen. ⓘ
Die Stringtheorie führte zu einem bis dahin beispiellos engen Austausch zwischen verschiedenen Gebieten der Mathematik und theoretischen Physik, die zu grundlegenden neuen Einsichten führten und zu Umwälzungen in der Betrachtung von Quantenfeldtheorien (wie das holografische Prinzip in AdS/CFT). Strings fanden darüber hinaus auch schon viele Anwendungen in anderen Gebieten der Physik wie der Beschreibung von Anregungen in der Festkörperphysik und der Theorie der starken Wechselwirkung (Quantenchromodynamik). Sie führte auch zu zahlreichen Entwicklungen in der reinen Mathematik. ⓘ
Die Stringtheorie ist gegenwärtig weder experimentell bestätigt noch widerlegt. Dies liegt unter anderem daran, dass die Vereinigung der Naturkräfte erst auf Energieskalen erwartet wird (siehe Planck-Skala), die in absehbarer Zeit nicht erreichbar sind. Die Stringtheorie wird daher seit den 2000er Jahren sowohl innerhalb als auch außerhalb der Physik kritisiert. Die Kritik richtet sich dabei auch auf die einseitige und außergewöhnliche Bindung von Forschungsressourcen in Gebieten, die Anwendungen fern stehen, und erfolgte besonders dezidiert von Theoretikern, die alternative Theorien der Quantengravitation verfolgen (wie der Schleifenquantengravitation). Zudem tauchten bei der konkreten mathematischen Durcharbeitung der Stringtheorie unerwartet viele Varianten auf, die die Erfolgsaussichten, alle Naturkräfte über die Stringtheorie zu vereinheitlichen, in weite Ferne rücken. ⓘ
Grundlagen

Überblick
Im 20. Jahrhundert entstanden zwei theoretische Rahmenwerke zur Formulierung der physikalischen Gesetze. Der erste ist Albert Einsteins allgemeine Relativitätstheorie, eine Theorie, die die Schwerkraft und die Struktur der Raumzeit auf der Makroebene erklärt. Die andere ist die Quantenmechanik, eine völlig andere Formulierung, die bekannte Wahrscheinlichkeitsprinzipien verwendet, um physikalische Phänomene auf der Mikroebene zu beschreiben. In den späten 1970er Jahren hatten sich diese beiden Konzepte als ausreichend erwiesen, um die meisten der beobachteten Merkmale des Universums zu erklären, von den Elementarteilchen über die Atome bis hin zur Entwicklung der Sterne und des Universums als Ganzes. ⓘ
Trotz dieser Erfolge gibt es noch viele Probleme, die gelöst werden müssen. Eines der tiefgreifendsten Probleme der modernen Physik ist das Problem der Quantengravitation. Die allgemeine Relativitätstheorie ist im Rahmen der klassischen Physik formuliert, während die anderen fundamentalen Kräfte im Rahmen der Quantenmechanik beschrieben werden. Um die allgemeine Relativitätstheorie mit den Grundsätzen der Quantenmechanik in Einklang zu bringen, ist eine Quantentheorie der Gravitation erforderlich, doch ergeben sich Schwierigkeiten, wenn man versucht, die üblichen Vorschriften der Quantentheorie auf die Gravitationskraft anzuwenden. Neben dem Problem, eine konsistente Theorie der Quantengravitation zu entwickeln, gibt es viele weitere grundlegende Probleme in der Physik der Atomkerne, der schwarzen Löcher und des frühen Universums. ⓘ
Die Stringtheorie ist ein theoretischer Rahmen, der versucht, diese und viele andere Fragen zu beantworten. Ausgangspunkt der Stringtheorie ist die Idee, dass die punktförmigen Teilchen der Teilchenphysik auch als eindimensionale Objekte, so genannte Strings, modelliert werden können. Die Stringtheorie beschreibt, wie sich Strings durch den Raum ausbreiten und miteinander wechselwirken. In einer bestimmten Version der Stringtheorie gibt es nur eine Art von String, der wie eine kleine Schleife oder ein Segment eines gewöhnlichen Strings aussieht und auf unterschiedliche Weise schwingen kann. Auf Entfernungsskalen, die größer sind als die Stringskala, sieht ein String wie ein gewöhnliches Teilchen aus, dessen Masse, Ladung und andere Eigenschaften durch den Schwingungszustand des Strings bestimmt werden. Auf diese Weise können alle verschiedenen Elementarteilchen als schwingende Strings betrachtet werden. In der Stringtheorie entsteht aus einem der Schwingungszustände des Strings das Graviton, ein quantenmechanisches Teilchen, das die Gravitationskraft überträgt. Die Stringtheorie ist also eine Theorie der Quantengravitation. ⓘ
Eine der wichtigsten Entwicklungen der letzten Jahrzehnte in der Stringtheorie war die Entdeckung bestimmter "Dualitäten", mathematischer Transformationen, die eine physikalische Theorie mit einer anderen identifizieren. Physiker, die sich mit der Stringtheorie befassen, haben eine Reihe dieser Dualitäten zwischen verschiedenen Versionen der Stringtheorie entdeckt, was zu der Vermutung geführt hat, dass alle konsistenten Versionen der Stringtheorie in einem einzigen Rahmen zusammengefasst sind, der als M-Theorie bekannt ist. ⓘ
Studien zur Stringtheorie haben auch zu einer Reihe von Ergebnissen über die Natur schwarzer Löcher und die Gravitationswechselwirkung geführt. Bei dem Versuch, die Quantenaspekte Schwarzer Löcher zu verstehen, treten bestimmte Paradoxien auf, und die Arbeit an der Stringtheorie hat versucht, diese Fragen zu klären. Ende 1997 gipfelte diese Arbeit in der Entdeckung der Korrespondenz zwischen Anti-de-Sitter und konformer Feldtheorie (AdS/CFT). Dabei handelt es sich um ein theoretisches Ergebnis, das die Stringtheorie mit anderen physikalischen Theorien in Beziehung setzt, die theoretisch besser verstanden werden. Die AdS/CFT-Korrespondenz hat Auswirkungen auf die Untersuchung von schwarzen Löchern und der Quantengravitation und wurde auf andere Themen angewandt, darunter die Kernphysik und die Physik kondensierter Materie. ⓘ
Da die Stringtheorie alle grundlegenden Wechselwirkungen, einschließlich der Schwerkraft, umfasst, hoffen viele Physiker, dass sie irgendwann so weit entwickelt sein wird, dass sie unser Universum vollständig beschreibt und zu einer Theorie von allem wird. Eines der Ziele der aktuellen Forschung im Bereich der Stringtheorie ist es, eine Lösung der Theorie zu finden, die das beobachtete Spektrum der Elementarteilchen reproduziert, mit einer kleinen kosmologischen Konstante, die dunkle Materie und einen plausiblen Mechanismus für die kosmische Inflation enthält. Obwohl es Fortschritte in Richtung dieser Ziele gibt, ist nicht bekannt, inwieweit die Stringtheorie die reale Welt beschreibt oder wie viel Freiheit die Theorie bei der Wahl der Details lässt. ⓘ
Eine der Herausforderungen der Stringtheorie besteht darin, dass die vollständige Theorie nicht unter allen Umständen eine zufriedenstellende Definition hat. Die Streuung von Strings lässt sich am einfachsten mit den Techniken der Störungstheorie definieren, aber es ist nicht allgemein bekannt, wie man die Stringtheorie nicht-perturbativ definieren kann. Es ist auch nicht klar, ob es ein Prinzip gibt, nach dem die Stringtheorie ihren Vakuumzustand auswählt, den physikalischen Zustand, der die Eigenschaften unseres Universums bestimmt. Diese Probleme haben einige Wissenschaftler dazu veranlasst, diese Ansätze zur Vereinheitlichung der Physik zu kritisieren und den Wert der weiteren Forschung an diesen Problemen in Frage zu stellen. ⓘ
Strings

Die Anwendung der Quantenmechanik auf physikalische Objekte wie das elektromagnetische Feld, die in Raum und Zeit ausgedehnt sind, wird als Quantenfeldtheorie bezeichnet. In der Teilchenphysik bilden die Quantenfeldtheorien die Grundlage für unser Verständnis der Elementarteilchen, die als Anregungen in den Grundfeldern modelliert werden. ⓘ
In der Quantenfeldtheorie werden die Wahrscheinlichkeiten verschiedener physikalischer Ereignisse in der Regel mit Hilfe der Störungstheorie berechnet. Die von Richard Feynman und anderen in der ersten Hälfte des 20. Jahrhunderts entwickelte Störungstheorie verwendet spezielle Diagramme, die sogenannten Feynman-Diagramme, um Berechnungen zu organisieren. Man stellt sich vor, dass diese Diagramme die Bahnen von punktförmigen Teilchen und deren Wechselwirkungen darstellen. ⓘ
Der Ausgangspunkt für die Stringtheorie ist die Idee, dass die punktförmigen Teilchen der Quantenfeldtheorie auch als eindimensionale Objekte, so genannte Strings, modelliert werden können. Die Wechselwirkung von Strings lässt sich am einfachsten durch eine Verallgemeinerung der in der gewöhnlichen Quantenfeldtheorie verwendeten Störungstheorie definieren. Auf der Ebene der Feynman-Diagramme bedeutet dies, dass das eindimensionale Diagramm, das den Weg eines Punktteilchens darstellt, durch eine zweidimensionale (2D) Fläche ersetzt wird, die die Bewegung eines Strings darstellt. Anders als in der Quantenfeldtheorie gibt es in der Stringtheorie keine vollständige nicht-perturbative Definition, so dass viele der theoretischen Fragen, die Physiker gerne beantworten würden, unerreichbar bleiben. ⓘ
In den auf der Stringtheorie basierenden Theorien der Teilchenphysik wird angenommen, dass die charakteristische Längenskala von Strings in der Größenordnung der Planck-Länge oder 10-35 Meter liegt, der Skala, bei der die Auswirkungen der Quantengravitation vermutlich signifikant werden. Auf viel größeren Längenskalen, wie den in Physiklabors sichtbaren Skalen, wären solche Objekte nicht von nulldimensionalen Punktteilchen zu unterscheiden, und der Schwingungszustand des Strings würde die Art des Teilchens bestimmen. Einer der Schwingungszustände eines Strings entspricht dem Graviton, einem quantenmechanischen Teilchen, das die Gravitationskraft trägt. ⓘ
Die ursprüngliche Version der Stringtheorie war die bosonische Stringtheorie, die jedoch nur Bosonen beschrieb, eine Klasse von Teilchen, die Kräfte zwischen den Materieteilchen, den Fermionen, übertragen. Die bosonische Stringtheorie wurde schließlich von Theorien abgelöst, die als Superstringtheorien bezeichnet werden. Diese Theorien beschreiben sowohl Bosonen als auch Fermionen und beinhalten eine theoretische Idee namens Supersymmetrie. In Theorien mit Supersymmetrie hat jedes Boson ein Gegenstück, das ein Fermion ist, und andersherum. ⓘ
Es gibt mehrere Versionen der Superstringtheorie: Typ I, Typ IIA, Typ IIB und zwei Varianten der heterotischen Stringtheorie (SO(32) und E8×E8). Die verschiedenen Theorien erlauben unterschiedliche Arten von Strings, und die Teilchen, die bei niedrigen Energien entstehen, weisen unterschiedliche Symmetrien auf. So umfasst die Theorie vom Typ I sowohl offene Strings (d. h. Segmente mit Endpunkten) als auch geschlossene Strings (die geschlossene Schleifen bilden), während die Typen IIA, IIB und heterotisch nur geschlossene Strings umfassen. ⓘ
Zusätzliche Dimensionen

Im täglichen Leben gibt es drei bekannte Raumdimensionen (3D): Höhe, Breite und Länge. In Einsteins allgemeiner Relativitätstheorie wird die Zeit als eine den drei Raumdimensionen gleichgestellte Dimension behandelt; in der allgemeinen Relativitätstheorie werden Raum und Zeit nicht als getrennte Einheiten modelliert, sondern zu einer vierdimensionalen (4D) Raumzeit vereinigt. In diesem Rahmen wird das Phänomen der Schwerkraft als eine Folge der Geometrie der Raumzeit betrachtet. ⓘ
Obwohl das Universum durch die 4D-Raumzeit gut beschrieben ist, gibt es mehrere Gründe, warum Physiker Theorien in anderen Dimensionen in Betracht ziehen. In einigen Fällen wird eine Theorie durch die Modellierung der Raumzeit in einer anderen Anzahl von Dimensionen mathematisch besser nachvollziehbar, und man kann leichter Berechnungen durchführen und allgemeine Erkenntnisse gewinnen. Es gibt auch Situationen, in denen Theorien in zwei oder drei Raumzeitdimensionen für die Beschreibung von Phänomenen in der Physik der kondensierten Materie nützlich sind. Und schließlich gibt es Szenarien, in denen es tatsächlich mehr als 4D der Raumzeit geben könnte, die sich jedoch der Entdeckung entzogen haben. ⓘ
Die Stringtheorien benötigen zusätzliche Raumzeitdimensionen für ihre mathematische Konsistenz. In der bosonischen Stringtheorie ist die Raumzeit 26-dimensional, während sie in der Superstringtheorie 10-dimensional und in der M-Theorie 11-dimensional ist. Um reale physikalische Phänomene mit Hilfe der Stringtheorie beschreiben zu können, muss man sich daher Szenarien vorstellen, in denen diese zusätzlichen Dimensionen in Experimenten nicht beobachtet werden können. ⓘ

Die Verdichtung ist eine Möglichkeit, die Anzahl der Dimensionen in einer physikalischen Theorie zu verändern. Bei der Verdichtung wird davon ausgegangen, dass sich einige der zusätzlichen Dimensionen in sich selbst "schließen" und Kreise bilden. Im Grenzfall, in dem diese aufgerollten Dimensionen sehr klein werden, erhält man eine Theorie, in der die Raumzeit effektiv eine geringere Anzahl von Dimensionen hat. Eine Standardanalogie hierfür ist die Betrachtung eines mehrdimensionalen Objekts wie eines Gartenschlauchs. Wenn man den Schlauch aus ausreichender Entfernung betrachtet, scheint er nur eine Dimension zu haben, nämlich seine Länge. Nähert man sich jedoch dem Schlauch, stellt man fest, dass er eine zweite Dimension hat, nämlich seinen Umfang. Eine Ameise, die auf der Oberfläche des Schlauchs krabbelt, würde sich also in zwei Dimensionen bewegen. ⓘ
Durch Verdichtung lassen sich Modelle konstruieren, in denen die Raumzeit tatsächlich vierdimensional ist. Allerdings führt nicht jede Art der Verdichtung der zusätzlichen Dimensionen zu einem Modell mit den richtigen Eigenschaften, um die Natur zu beschreiben. In einem brauchbaren Modell der Teilchenphysik müssen die kompakten Extradimensionen wie eine Calabi-Yau-Mannigfaltigkeit geformt sein. Eine Calabi-Yau-Mannigfaltigkeit ist ein spezieller Raum, der in Anwendungen auf die Stringtheorie in der Regel als sechsdimensional angesehen wird. Er ist nach den Mathematikern Eugenio Calabi und Shing-Tung Yau benannt. ⓘ
Ein weiterer Ansatz zur Verringerung der Anzahl der Dimensionen ist das sogenannte Brane-World-Szenario. Bei diesem Ansatz gehen die Physiker davon aus, dass das beobachtbare Universum ein vierdimensionaler Unterraum eines höherdimensionalen Raums ist. In solchen Modellen entstehen die krafttragenden Bosonen der Teilchenphysik aus offenen Strings, deren Endpunkte mit dem vierdimensionalen Unterraum verbunden sind, während die Gravitation aus geschlossenen Strings entsteht, die sich durch den größeren Umgebungsraum ausbreiten. Diese Idee spielt eine wichtige Rolle bei den Versuchen, Modelle der realen Physik auf der Grundlage der Stringtheorie zu entwickeln, und sie liefert eine natürliche Erklärung für die Schwäche der Gravitation im Vergleich zu den anderen fundamentalen Kräften. ⓘ
Dualitäten
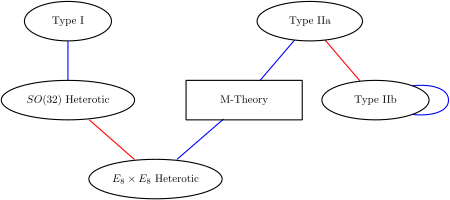
Eine bemerkenswerte Tatsache bei der Stringtheorie ist, dass die verschiedenen Versionen der Theorie alle auf höchst untriviale Weise miteinander verbunden sind. Eine der Beziehungen, die zwischen verschiedenen Stringtheorien bestehen können, wird S-Dualität genannt. Dabei handelt es sich um eine Beziehung, die besagt, dass eine Ansammlung von stark wechselwirkenden Teilchen in einer Theorie in einigen Fällen als eine Ansammlung von schwach wechselwirkenden Teilchen in einer völlig anderen Theorie betrachtet werden kann. Grob gesagt wird eine Ansammlung von Teilchen als stark wechselwirkend bezeichnet, wenn sie sich häufig verbinden und zerfallen, und als schwach wechselwirkend, wenn sie dies nur selten tun. Die Stringtheorie vom Typ I erweist sich durch S-Dualität als äquivalent zur heterotischen Stringtheorie SO(32). In ähnlicher Weise ist die Stringtheorie vom Typ IIB durch S-Dualität auf eine nichttriviale Weise mit sich selbst verbunden. ⓘ
Eine weitere Beziehung zwischen verschiedenen Stringtheorien ist die T-Dualität. Hier betrachtet man Strings, die sich um eine kreisförmige Extradimension ausbreiten. Die T-Dualität besagt, dass ein String, der sich um einen Kreis mit dem Radius R ausbreitet, äquivalent zu einem String ist, der sich um einen Kreis mit dem Radius 1/R ausbreitet, und zwar in dem Sinne, dass alle beobachtbaren Größen in einer Beschreibung mit den Größen in der dualen Beschreibung identisch sind. Ein String hat beispielsweise einen Impuls, wenn er sich um einen Kreis ausbreitet, und er kann sich auch ein oder mehrere Male um den Kreis winden. Die Anzahl der Windungen der Saite um einen Kreis wird als Windungszahl bezeichnet. Wenn ein String in einer Beschreibung den Impuls p und die Windungszahl n hat, hat er in der dualen Beschreibung den Impuls n und die Windungszahl p. So ist beispielsweise die Stringtheorie vom Typ IIA über die T-Dualität äquivalent zur Stringtheorie vom Typ IIB, und auch die beiden Versionen der heterotischen Stringtheorie sind über die T-Dualität miteinander verbunden. ⓘ
Im Allgemeinen bezieht sich der Begriff Dualität auf eine Situation, in der sich zwei scheinbar unterschiedliche physikalische Systeme auf nicht-triviale Weise als äquivalent erweisen. Zwei Theorien, die durch eine Dualität verbunden sind, müssen keine Stringtheorien sein. So ist die Montonen-Olive-Dualität ein Beispiel für eine S-Dualität zwischen Quantenfeldtheorien. Die AdS/CFT-Korrespondenz ist ein Beispiel für eine Dualität, die die Stringtheorie mit einer Quantenfeldtheorie verbindet. Wenn zwei Theorien durch eine Dualität miteinander verbunden sind, bedeutet dies, dass die eine Theorie auf irgendeine Weise so transformiert werden kann, dass sie am Ende genauso aussieht wie die andere Theorie. Man sagt dann, dass die beiden Theorien unter dieser Transformation zueinander dual sind. Anders ausgedrückt: Die beiden Theorien sind mathematisch unterschiedliche Beschreibungen desselben Phänomens. ⓘ
Zweige

In der Stringtheorie und anderen verwandten Theorien ist eine Brane ein physikalisches Objekt, das den Begriff des Punktteilchens auf höhere Dimensionen verallgemeinert. So kann beispielsweise ein Punktteilchen als Brane der Dimension Null betrachtet werden, während ein String als Brane der Dimension Eins betrachtet werden kann. Es ist auch möglich, höherdimensionale Branen zu betrachten. In der Dimension p werden diese als p-Branen bezeichnet. Das Wort Brane kommt von dem Wort "Membran", das sich auf eine zweidimensionale Brane bezieht. ⓘ
Branes sind dynamische Objekte, die sich nach den Regeln der Quantenmechanik durch die Raumzeit ausbreiten können. Sie haben eine Masse und können auch andere Eigenschaften wie eine Ladung haben. Eine p-Brane erstreckt sich über ein (p+1)-dimensionales Volumen in der Raumzeit, das Weltvolumen genannt wird. Physiker untersuchen häufig Felder, die dem elektromagnetischen Feld entsprechen und im Weltvolumen einer Brane leben. ⓘ
In der Stringtheorie sind D-Branen eine wichtige Klasse von Branen, die entstehen, wenn man offene Strings betrachtet. Wenn sich ein offener String durch die Raumzeit ausbreitet, müssen seine Endpunkte auf einer D-Brane liegen. Der Buchstabe "D" in D-Brane bezieht sich auf eine bestimmte mathematische Bedingung für das System, die sogenannte Dirichlet-Randbedingung. Die Untersuchung von D-Branen in der Stringtheorie hat zu wichtigen Ergebnissen wie der AdS/CFT-Korrespondenz geführt, die Licht in viele Probleme der Quantenfeldtheorie gebracht hat. ⓘ
Verzweigungen werden häufig aus rein mathematischer Sicht untersucht und als Objekte bestimmter Kategorien beschrieben, wie z. B. die abgeleitete Kategorie kohärenter Garben auf einer komplexen algebraischen Vielfalt oder die Fukaya-Kategorie einer symplektischen Mannigfaltigkeit. Die Verbindung zwischen dem physikalischen Begriff einer Brane und dem mathematischen Begriff einer Kategorie hat zu wichtigen mathematischen Erkenntnissen auf den Gebieten der algebraischen und symplektischen Geometrie und der Darstellungstheorie geführt. ⓘ
M-Theorie
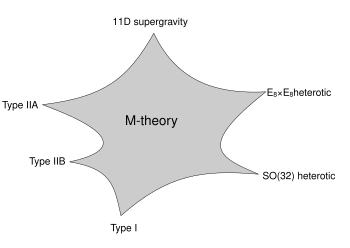
Vor 1995 glaubten Theoretiker, dass es fünf konsistente Versionen der Superstringtheorie gibt (Typ I, Typ IIA, Typ IIB und zwei Versionen der heterotischen Stringtheorie). Dieses Verständnis änderte sich 1995, als Edward Witten vorschlug, dass die fünf Theorien nur spezielle Grenzfälle einer elfdimensionalen Theorie namens M-Theorie sind. Wittens Vermutung beruhte auf der Arbeit einer Reihe anderer Physiker, darunter Ashoke Sen, Chris Hull, Paul Townsend und Michael Duff. Seine Ankündigung führte zu einer Flut von Forschungsaktivitäten, die heute als zweite Superstring-Revolution bekannt sind. ⓘ
Vereinheitlichung der Superstring-Theorien
In den 1970er Jahren interessierten sich viele Physiker für Supergravitationstheorien, die die allgemeine Relativitätstheorie mit der Supersymmetrie kombinieren. Während die allgemeine Relativitätstheorie in jeder beliebigen Anzahl von Dimensionen Sinn macht, setzt die Supergravitation der Anzahl der Dimensionen eine Obergrenze. Im Jahr 1978 zeigte Werner Nahm in einer Arbeit, dass die maximale Raumzeitdimension, in der eine konsistente supersymmetrische Theorie formuliert werden kann, elf ist. Im selben Jahr zeigten Eugene Cremmer, Bernard Julia und Joël Scherk von der École Normale Supérieure, dass die Supergravitation nicht nur bis zu elf Dimensionen zulässt, sondern in dieser maximalen Anzahl von Dimensionen sogar am elegantesten ist. ⓘ
Ursprünglich hofften viele Physiker, dass es durch die Verdichtung der elfdimensionalen Supergravitation möglich sein würde, realistische Modelle unserer vierdimensionalen Welt zu konstruieren. Die Hoffnung war, dass solche Modelle eine einheitliche Beschreibung der vier fundamentalen Kräfte der Natur liefern würden: Elektromagnetismus, die starke und schwache Kernkraft und die Schwerkraft. Das Interesse an der elfdimensionalen Supergravitation ließ bald nach, als verschiedene Schwachstellen in diesem Modell entdeckt wurden. Eines der Probleme bestand darin, dass die physikalischen Gesetze anscheinend zwischen dem Uhrzeigersinn und dem Gegenuhrzeigersinn unterscheiden, ein Phänomen, das als Chiralität bekannt ist. Edward Witten und andere stellten fest, dass sich diese Chiralitätseigenschaft nicht ohne weiteres durch Verdichtung von elf Dimensionen ableiten lässt. ⓘ
Im Zuge der ersten Superstring-Revolution im Jahr 1984 wandten sich viele Physiker der Stringtheorie zu, um eine einheitliche Theorie der Teilchenphysik und der Quantengravitation zu entwickeln. Im Gegensatz zur Supergravitationstheorie war die Stringtheorie in der Lage, die Chiralität des Standardmodells zu berücksichtigen, und sie lieferte eine Theorie der Gravitation, die mit Quanteneffekten vereinbar ist. Ein weiteres Merkmal der Stringtheorie, das in den 1980er und 1990er Jahren viele Physiker anzog, war ihr hoher Grad an Eindeutigkeit. In gewöhnlichen Teilchentheorien kann man jede beliebige Ansammlung von Elementarteilchen betrachten, deren klassisches Verhalten durch eine beliebige Lagrange beschrieben wird. In der Stringtheorie sind die Möglichkeiten sehr viel eingeschränkter: In den 1990er Jahren argumentierten die Physiker, dass es nur fünf konsistente supersymmetrische Versionen der Theorie gibt. ⓘ
Obwohl es nur eine Handvoll konsistenter Superstringtheorien gab, blieb es ein Rätsel, warum es nicht nur eine einzige konsistente Formulierung gab. Als die Physiker jedoch begannen, die Stringtheorie genauer zu untersuchen, stellten sie fest, dass diese Theorien auf komplizierte und nichttriviale Weise miteinander verbunden sind. Sie fanden heraus, dass ein System stark wechselwirkender Strings in einigen Fällen als ein System schwach wechselwirkender Strings betrachtet werden kann. Dieses Phänomen ist als S-Dualität bekannt. Es wurde von Ashoke Sen im Zusammenhang mit heterotischen Strings in vier Dimensionen und von Chris Hull und Paul Townsend im Zusammenhang mit der Theorie vom Typ IIB untersucht. Die Theoretiker fanden auch heraus, dass verschiedene Stringtheorien durch T-Dualität miteinander verbunden sein können. Diese Dualität impliziert, dass Strings, die sich auf völlig unterschiedlichen Raumzeitgeometrien ausbreiten, physikalisch äquivalent sein können. ⓘ
Etwa zur gleichen Zeit, als viele Physiker die Eigenschaften von Strings untersuchten, befasste sich eine kleine Gruppe von Physikern mit den möglichen Anwendungen höherdimensionaler Objekte. Im Jahr 1987 zeigten Eric Bergshoeff, Ergin Sezgin und Paul Townsend, dass die elfdimensionale Supergravitation zweidimensionale Branes enthält. Intuitiv sehen diese Objekte wie Blätter oder Membranen aus, die sich durch die elfdimensionale Raumzeit ausbreiten. Kurz nach dieser Entdeckung betrachteten Michael Duff, Paul Howe, Takeo Inami und Kellogg Stelle eine besondere Verdichtung der elfdimensionalen Supergravitation, bei der eine der Dimensionen zu einem Kreis zusammengerollt ist. In diesem Fall kann man sich vorstellen, dass die Membran um die kreisförmige Dimension gewickelt ist. Wenn der Radius des Kreises ausreichend klein ist, sieht diese Membran wie ein String in der zehndimensionalen Raumzeit aus. Duff und seine Mitarbeiter zeigten, dass diese Konstruktion genau die Strings reproduziert, die in der Superstringtheorie vom Typ IIA vorkommen. ⓘ
Auf einer Stringtheorie-Konferenz im Jahr 1995 machte Edward Witten den überraschenden Vorschlag, dass alle fünf Superstringtheorien in Wirklichkeit nur verschiedene Grenzfälle einer einzigen Theorie in elf Raumzeitdimensionen sind. Wittens Ankündigung fasste alle bisherigen Ergebnisse zur S- und T-Dualität und zum Auftreten höherdimensionaler Branes in der Stringtheorie zusammen. In den Monaten nach Wittens Ankündigung erschienen im Internet Hunderte von neuen Arbeiten, die verschiedene Teile seines Vorschlags bestätigten. Heute ist diese Flut von Arbeiten als die zweite Superstring-Revolution bekannt. ⓘ
Anfänglich schlugen einige Physiker vor, dass die neue Theorie eine fundamentale Theorie der Membranen sei, aber Witten war skeptisch, was die Rolle der Membranen in der Theorie betraf. In einem Papier aus dem Jahr 1996 schrieben Hořava und Witten: "Da vorgeschlagen wurde, dass die elfdimensionale Theorie eine Supermembrantheorie ist, es aber einige Gründe gibt, an dieser Interpretation zu zweifeln, werden wir sie unverbindlich M-Theorie nennen und die Beziehung von M zu Membranen der Zukunft überlassen." In Ermangelung eines Verständnisses der wahren Bedeutung und Struktur der M-Theorie hat Witten vorgeschlagen, dass das M je nach Geschmack für "Magie", "Mysterium" oder "Membran" stehen sollte, und dass die wahre Bedeutung des Titels entschieden werden sollte, wenn eine fundamentalere Formulierung der Theorie bekannt ist. ⓘ
Matrix-Theorie
In der Mathematik ist eine Matrix eine rechteckige Anordnung von Zahlen oder anderen Daten. In der Physik ist ein Matrixmodell eine besondere Art von physikalischer Theorie, deren mathematische Formulierung den Begriff der Matrix in einer wichtigen Weise einbezieht. Ein Matrixmodell beschreibt das Verhalten einer Reihe von Matrizen im Rahmen der Quantenmechanik. ⓘ
Ein wichtiges Beispiel für ein Matrixmodell ist das BFSS-Matrixmodell, das 1997 von Tom Banks, Willy Fischler, Stephen Shenker und Leonard Susskind vorgeschlagen wurde. Diese Theorie beschreibt das Verhalten eines Satzes von neun großen Matrizen. In ihrer Originalarbeit zeigten die Autoren unter anderem, dass die Niedrigenergiegrenze dieses Matrixmodells durch elfdimensionale Supergravitation beschrieben wird. Diese Berechnungen führten sie zu dem Vorschlag, dass das BFSS-Matrixmodell genau der M-Theorie entspricht. Das BFSS-Matrixmodell kann daher als Prototyp für eine korrekte Formulierung der M-Theorie und als Werkzeug zur Untersuchung der Eigenschaften der M-Theorie in einem relativ einfachen Rahmen verwendet werden. ⓘ
Die Entwicklung der Matrixmodell-Formulierung der M-Theorie hat Physiker dazu veranlasst, verschiedene Verbindungen zwischen der Stringtheorie und einem Zweig der Mathematik, der nichtkommutativen Geometrie, zu untersuchen. Dabei handelt es sich um eine Verallgemeinerung der gewöhnlichen Geometrie, in der Mathematiker neue geometrische Begriffe mit Hilfe von Werkzeugen der nichtkommutativen Algebra definieren. In einer Arbeit aus dem Jahr 1998 zeigten Alain Connes, Michael R. Douglas und Albert Schwarz, dass einige Aspekte von Matrixmodellen und der M-Theorie durch eine nichtkommutative Quantenfeldtheorie beschrieben werden, eine spezielle Art von physikalischer Theorie, in der die Raumzeit mathematisch mit Hilfe der nichtkommutativen Geometrie beschrieben wird. Damit wurde eine Verbindung zwischen Matrixmodellen und der M-Theorie einerseits und der nicht-kommutativen Geometrie andererseits hergestellt. Dies führte schnell zur Entdeckung weiterer wichtiger Verbindungen zwischen nichtkommutativer Geometrie und verschiedenen physikalischen Theorien. ⓘ
Schwarze Löcher
In der allgemeinen Relativitätstheorie ist ein Schwarzes Loch definiert als eine Region der Raumzeit, in der das Gravitationsfeld so stark ist, dass kein Teilchen oder keine Strahlung entkommen kann. In den gegenwärtig akzeptierten Modellen der Sternentwicklung geht man davon aus, dass Schwarze Löcher entstehen, wenn massereiche Sterne einen Gravitationskollaps erleiden, und man nimmt an, dass viele Galaxien in ihrem Zentrum supermassive Schwarze Löcher enthalten. Schwarze Löcher sind auch aus theoretischen Gründen wichtig, denn sie stellen Theoretiker, die versuchen, die Quantenaspekte der Gravitation zu verstehen, vor große Herausforderungen. Die Stringtheorie hat sich als wichtiges Instrument zur Untersuchung der theoretischen Eigenschaften von Schwarzen Löchern erwiesen, da sie einen Rahmen bietet, in dem Theoretiker ihre Thermodynamik untersuchen können. ⓘ
Bekenstein-Hawking-Formel
In dem als statistische Mechanik bezeichneten Zweig der Physik ist die Entropie ein Maß für die Zufälligkeit oder Unordnung eines physikalischen Systems. Dieses Konzept wurde in den 1870er Jahren von dem österreichischen Physiker Ludwig Boltzmann erforscht, der zeigte, dass die thermodynamischen Eigenschaften eines Gases aus den kombinierten Eigenschaften der vielen Moleküle, aus denen es besteht, abgeleitet werden können. Boltzmann argumentierte, dass man makroskopische Eigenschaften wie Volumen, Temperatur und Druck verstehen kann, wenn man das Verhalten der verschiedenen Moleküle eines Gases mittelt. Außerdem führte diese Sichtweise dazu, dass er die Entropie als den natürlichen Logarithmus der Anzahl der verschiedenen Zustände der Moleküle (auch Mikrozustände genannt), die zu denselben makroskopischen Eigenschaften führen, genau definierte. ⓘ
Im zwanzigsten Jahrhundert begannen die Physiker, die gleichen Konzepte auf schwarze Löcher anzuwenden. In den meisten Systemen, z. B. Gasen, steigt die Entropie mit dem Volumen. In den 1970er Jahren schlug der Physiker Jacob Bekenstein vor, dass die Entropie eines Schwarzen Lochs stattdessen proportional zur Fläche seines Ereignishorizonts ist, der Grenze, jenseits derer Materie und Strahlung durch die Anziehungskraft des Lochs verloren gehen. In Verbindung mit den Ideen des Physikers Stephen Hawking führte Bekensteins Arbeit zu einer präzisen Formel für die Entropie eines Schwarzen Lochs. Die Bekenstein-Hawking-Formel drückt die Entropie S wie folgt aus ⓘ
wobei c die Lichtgeschwindigkeit, k die Boltzmann-Konstante, ħ die reduzierte Planck-Konstante, G die Newton-Konstante und A die Fläche des Ereignishorizonts ist. ⓘ
Wie jedes physikalische System hat auch ein Schwarzes Loch eine Entropie, die durch die Anzahl der verschiedenen Mikrozustände definiert ist, die zu denselben makroskopischen Eigenschaften führen. Die Bekenstein-Hawking-Entropieformel gibt den Erwartungswert der Entropie eines Schwarzen Lochs an, aber bis in die 1990er Jahre fehlte den Physikern noch eine Ableitung dieser Formel durch Zählen von Mikrozuständen in einer Theorie der Quantengravitation. Eine solche Ableitung dieser Formel zu finden, wurde als wichtiger Test für die Lebensfähigkeit einer Theorie der Quantengravitation wie der Stringtheorie angesehen. ⓘ
Ableitung innerhalb der Stringtheorie
In einer Arbeit aus dem Jahr 1996 zeigten Andrew Strominger und Cumrun Vafa, wie sich die Beckenstein-Hawking-Formel für bestimmte Schwarze Löcher in der Stringtheorie ableiten lässt. Ihre Berechnung basierte auf der Beobachtung, dass D-Brane - die bei schwacher Wechselwirkung wie fluktuierende Membranen aussehen - bei starker Wechselwirkung zu dichten, massiven Objekten mit Ereignishorizonten werden. Mit anderen Worten: Ein System aus stark wechselwirkenden D-Branen ist in der Stringtheorie nicht von einem Schwarzen Loch zu unterscheiden. Strominger und Vafa analysierten solche D-Branensysteme und berechneten die Anzahl der verschiedenen Möglichkeiten, D-Branen so in der Raumzeit zu platzieren, dass ihre kombinierte Masse und Ladung gleich einer bestimmten Masse und Ladung für das resultierende Schwarze Loch ist. Ihre Berechnung gab die Bekenstein-Hawking-Formel exakt wieder, einschließlich des Faktors 1/4. Spätere Arbeiten von Strominger, Vafa und anderen verfeinerten die ursprünglichen Berechnungen und lieferten die genauen Werte der "Quantenkorrekturen", die zur Beschreibung sehr kleiner schwarzer Löcher erforderlich sind. ⓘ
Die schwarzen Löcher, die Strominger und Vafa in ihrer ursprünglichen Arbeit betrachteten, unterschieden sich erheblich von den tatsächlichen astrophysikalischen schwarzen Löchern. Ein Unterschied bestand darin, dass Strominger und Vafa nur extreme Schwarze Löcher betrachteten, um die Berechnung nachvollziehbar zu machen. Diese sind definiert als Schwarze Löcher mit der kleinstmöglichen Masse, die mit einer gegebenen Ladung vereinbar ist. Außerdem beschränkten sich Strominger und Vafa auf schwarze Löcher in der fünfdimensionalen Raumzeit mit unphysikalischer Supersymmetrie. ⓘ
Obwohl die Entropieberechnung von Strominger und Vafa ursprünglich in diesem sehr speziellen und physikalisch unrealistischen Kontext der Stringtheorie entwickelt wurde, hat sie zu einem qualitativen Verständnis darüber geführt, wie die Entropie Schwarzer Löcher in jeder Theorie der Quantengravitation berücksichtigt werden kann. Tatsächlich argumentierte Strominger 1998, dass das ursprüngliche Ergebnis auf eine beliebige konsistente Theorie der Quantengravitation verallgemeinert werden kann, ohne sich auf Strings oder Supersymmetrie zu stützen. In Zusammenarbeit mit mehreren anderen Autoren zeigte er 2010, dass einige Ergebnisse zur Entropie Schwarzer Löcher auf nicht extreme astrophysikalische Schwarze Löcher ausgedehnt werden können. ⓘ
AdS/CFT-Korrespondenz
Einen Ansatz zur Formulierung der Stringtheorie und zur Untersuchung ihrer Eigenschaften bietet die Korrespondenz zwischen der Anti-De-Sitter- und der konformen Feldtheorie (AdS/CFT). Dies ist ein theoretisches Ergebnis, das besagt, dass die Stringtheorie in einigen Fällen einer Quantenfeldtheorie entspricht. Die AdS/CFT-Korrespondenz bietet nicht nur Einblicke in die mathematische Struktur der Stringtheorie, sondern hat auch viele Aspekte der Quantenfeldtheorie in Bereichen beleuchtet, in denen herkömmliche Berechnungsmethoden unwirksam sind. Die AdS/CFT-Korrespondenz wurde erstmals Ende 1997 von Juan Maldacena vorgeschlagen. Wichtige Aspekte der Korrespondenz wurden in Artikeln von Steven Gubser, Igor Klebanov und Alexander Markovich Polyakov sowie von Edward Witten ausgearbeitet. Bis 2010 wurde Maldacenas Artikel mit über 7000 Zitaten zum meistzitierten Artikel auf dem Gebiet der Hochenergiephysik. ⓘ
Überblick über die Korrespondenz

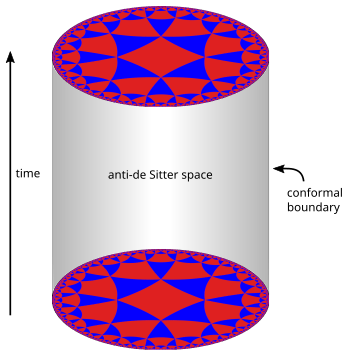
In der AdS/CFT-Korrespondenz wird die Geometrie der Raumzeit durch eine bestimmte Vakuumlösung der Einsteinschen Gleichung, den so genannten Anti-De-Sitter-Raum, beschrieben. Ganz elementar ausgedrückt ist der Anti-de-Sitter-Raum ein mathematisches Modell der Raumzeit, in dem sich der Begriff des Abstands zwischen Punkten (die Metrik) von dem Begriff des Abstands in der gewöhnlichen euklidischen Geometrie unterscheidet. Er ist eng mit dem hyperbolischen Raum verwandt, der als Scheibe betrachtet werden kann (siehe Abbildung links). Dieses Bild zeigt ein Mosaik einer Scheibe aus Dreiecken und Quadraten. Man kann den Abstand zwischen den Punkten dieser Scheibe so definieren, dass alle Dreiecke und Quadrate gleich groß sind und die kreisförmige äußere Begrenzung unendlich weit von jedem Punkt im Inneren entfernt ist. ⓘ
Man kann sich einen Stapel hyperbolischer Scheiben vorstellen, wobei jede Scheibe den Zustand des Universums zu einem bestimmten Zeitpunkt darstellt. Das resultierende geometrische Objekt ist der dreidimensionale Anti-de-Sitter-Raum. Er sieht aus wie ein massiver Zylinder, in dem jeder Querschnitt eine Kopie der hyperbolischen Scheibe ist. In diesem Bild verläuft die Zeit in vertikaler Richtung. Die Oberfläche dieses Zylinders spielt eine wichtige Rolle in der AdS/CFT-Korrespondenz. Wie die hyperbolische Ebene ist auch der Anti-de-Sitter-Raum so gekrümmt, dass jeder Punkt im Inneren tatsächlich unendlich weit von dieser Grenzfläche entfernt ist. ⓘ
Diese Konstruktion beschreibt ein hypothetisches Universum mit nur zwei Raumdimensionen und einer Zeitdimension, kann aber auf eine beliebige Anzahl von Dimensionen verallgemeinert werden. Tatsächlich kann der hyperbolische Raum mehr als zwei Dimensionen haben, und man kann Kopien des hyperbolischen Raums "stapeln", um höherdimensionale Modelle des Anti-de-Sitter-Raums zu erhalten. ⓘ
Ein wichtiges Merkmal des Anti-De-Sitter-Raums ist seine Grenze (die im Falle des dreidimensionalen Anti-De-Sitter-Raums wie ein Zylinder aussieht). Eine Eigenschaft dieser Grenze ist, dass sie innerhalb einer kleinen Region auf der Oberfläche um einen beliebigen Punkt herum genauso aussieht wie der Minkowski-Raum, das Modell der Raumzeit, das in der Nicht-Gravitationsphysik verwendet wird. Man kann also eine Hilfstheorie in Betracht ziehen, in der die "Raumzeit" durch die Grenze des Anti-De-Sitter-Raums gegeben ist. Diese Beobachtung ist der Ausgangspunkt für die AdS/CFT-Korrespondenz, die besagt, dass die Grenze des Anti-de-Sitter-Raums als "Raumzeit" für eine Quantenfeldtheorie angesehen werden kann. Die Behauptung ist, dass diese Quantenfeldtheorie einer Gravitationstheorie, wie z. B. der Stringtheorie, im Anti-de-Sitter-Raum in dem Sinne äquivalent ist, dass es ein "Wörterbuch" für die Übersetzung von Entitäten und Berechnungen in der einen Theorie in ihre Entsprechungen in der anderen Theorie gibt. So kann beispielsweise ein einzelnes Teilchen in der Gravitationstheorie einer Ansammlung von Teilchen in der Grenzwerktheorie entsprechen. Darüber hinaus sind die Vorhersagen in den beiden Theorien quantitativ identisch, d. h. wenn zwei Teilchen in der Gravitationstheorie eine 40-prozentige Chance haben, miteinander zu kollidieren, dann haben auch die entsprechenden Ansammlungen in der Grenzwerktheorie eine 40-prozentige Chance, miteinander zu kollidieren. ⓘ
Anwendungen auf die Quantengravitation
Die Entdeckung der AdS/CFT-Korrespondenz war ein großer Fortschritt für das Verständnis der Stringtheorie und der Quantengravitation. Ein Grund dafür ist, dass die Korrespondenz eine Formulierung der Stringtheorie in Form der Quantenfeldtheorie liefert, die im Vergleich dazu gut verstanden wird. Ein weiterer Grund ist, dass die Korrespondenz einen allgemeinen Rahmen bietet, in dem Physiker die Paradoxa Schwarzer Löcher untersuchen und versuchen können, sie zu lösen. ⓘ
1975 veröffentlichte Stephen Hawking eine Berechnung, die nahelegte, dass Schwarze Löcher nicht völlig schwarz sind, sondern aufgrund von Quanteneffekten in der Nähe des Ereignishorizonts eine schwache Strahlung abgeben. Zunächst stellte Hawkings Ergebnis ein Problem für die Theoretiker dar, da es nahelegte, dass Schwarze Löcher Informationen zerstören. Genauer gesagt schien Hawkings Berechnung im Widerspruch zu einem der grundlegenden Postulate der Quantenmechanik zu stehen, das besagt, dass sich physikalische Systeme in der Zeit gemäß der Schrödinger-Gleichung weiterentwickeln. Diese Eigenschaft wird gewöhnlich als Einheitlichkeit der zeitlichen Entwicklung bezeichnet. Der scheinbare Widerspruch zwischen Hawkings Berechnung und dem Unitaritätspostulat der Quantenmechanik wurde als das Informationsparadoxon des Schwarzen Lochs bekannt. ⓘ
Die AdS/CFT-Korrespondenz löst das Informationsparadoxon des Schwarzen Lochs zumindest bis zu einem gewissen Grad auf, weil sie zeigt, wie sich ein Schwarzes Loch in einer Weise entwickeln kann, die in einigen Kontexten mit der Quantenmechanik vereinbar ist. Tatsächlich kann man Schwarze Löcher im Kontext der AdS/CFT-Korrespondenz betrachten, und jedes solche Schwarze Loch entspricht einer Konfiguration von Teilchen an der Grenze des Anti-De-Sitter-Raums. Diese Teilchen gehorchen den üblichen Regeln der Quantenmechanik und entwickeln sich insbesondere einheitlich, so dass sich auch das Schwarze Loch einheitlich entwickeln muss, wobei die Grundsätze der Quantenmechanik zu beachten sind. Im Jahr 2005 verkündete Hawking, dass das Paradoxon durch die AdS/CFT-Korrespondenz zugunsten der Informationserhaltung gelöst worden sei, und er schlug einen konkreten Mechanismus vor, durch den Schwarze Löcher Informationen erhalten könnten. ⓘ
Anwendungen in der Kernphysik
Neben der Anwendung auf theoretische Probleme der Quantengravitation wurde die AdS/CFT-Korrespondenz auch auf eine Vielzahl von Problemen der Quantenfeldtheorie angewandt. Ein physikalisches System, das mithilfe der AdS/CFT-Korrespondenz untersucht wurde, ist das Quark-Gluon-Plasma, ein exotischer Materiezustand, der in Teilchenbeschleunigern erzeugt wird. Dieser Materiezustand entsteht für kurze Augenblicke, wenn schwere Ionen wie Gold- oder Bleikerne bei hohen Energien zusammenstoßen. Bei solchen Kollisionen zerfallen die Quarks, aus denen die Atomkerne bestehen, bei Temperaturen von etwa zwei Billionen Kelvin, also unter Bedingungen, wie sie etwa 10-11 Sekunden nach dem Urknall herrschten. ⓘ
Die Physik des Quark-Gluon-Plasmas wird von einer Theorie namens Quantenchromodynamik beherrscht, die jedoch bei Problemen, die das Quark-Gluon-Plasma betreffen, mathematisch schwer zu lösen ist. In einem 2005 erschienenen Artikel zeigten Đàm Thanh Sơn und seine Mitarbeiter, dass die AdS/CFT-Korrespondenz genutzt werden kann, um einige Aspekte des Quark-Gluon-Plasmas zu verstehen, indem es in der Sprache der Stringtheorie beschrieben wird. Durch Anwendung der AdS/CFT-Korrespondenz waren Sơn und seine Mitarbeiter in der Lage, das Quark-Gluon-Plasma in Form von schwarzen Löchern in der fünfdimensionalen Raumzeit zu beschreiben. Die Berechnungen zeigten, dass das Verhältnis zweier mit dem Quark-Gluon-Plasma verbundener Größen, der Scherviskosität und der Volumendichte der Entropie, ungefähr gleich einer bestimmten universellen Konstante sein sollte. Im Jahr 2008 wurde der vorhergesagte Wert dieses Verhältnisses für das Quark-Gluon-Plasma am Relativistic Heavy Ion Collider im Brookhaven National Laboratory bestätigt. ⓘ
Anwendungen in der Physik der kondensierten Materie
Die AdS/CFT-Korrespondenz wurde auch genutzt, um Aspekte der Physik der kondensierten Materie zu untersuchen. Im Laufe der Jahrzehnte haben experimentelle Physiker der kondensierten Materie eine Reihe von exotischen Materiezuständen entdeckt, darunter Supraleiter und Supraflüssigkeiten. Diese Zustände werden mit dem Formalismus der Quantenfeldtheorie beschrieben, aber einige Phänomene lassen sich mit den Standardmethoden der Feldtheorie nur schwer erklären. Einige Theoretiker der kondensierten Materie, darunter Subir Sachdev, hoffen, dass die AdS/CFT-Korrespondenz es ermöglichen wird, diese Systeme in der Sprache der Stringtheorie zu beschreiben und mehr über ihr Verhalten zu erfahren. ⓘ
Bisher ist es gelungen, mit Methoden der Stringtheorie den Übergang eines Suprafluids zu einem Isolator zu beschreiben. Ein Suprafluid ist ein System aus elektrisch neutralen Atomen, das ohne Reibung fließt. Solche Systeme werden häufig im Labor mit flüssigem Helium erzeugt, aber in jüngster Zeit haben Experimentatoren neue Wege zur Erzeugung künstlicher Supraflüssigkeiten entwickelt, indem sie Billionen kalter Atome in ein Gitter aus sich kreuzenden Lasern schütten. Diese Atome verhalten sich zunächst wie ein Suprafluid, aber wenn die Experimentatoren die Intensität der Laser erhöhen, werden sie weniger beweglich und gehen dann plötzlich in einen isolierenden Zustand über. Während dieses Übergangs verhalten sich die Atome auf ungewöhnliche Weise. So verlangsamen sich die Atome mit einer Geschwindigkeit, die von der Temperatur und der Planckschen Konstante abhängt, dem grundlegenden Parameter der Quantenmechanik, der bei der Beschreibung der anderen Phasen nicht berücksichtigt wird. Dieses Verhalten wurde kürzlich durch die Betrachtung einer dualen Beschreibung verstanden, bei der die Eigenschaften der Flüssigkeit in Form eines höherdimensionalen schwarzen Lochs beschrieben werden. ⓘ
Phänomenologie
Die Stringtheorie ist nicht nur eine Idee von großem theoretischen Interesse, sondern bietet auch einen Rahmen für die Konstruktion von Modellen der realen Physik, die die allgemeine Relativitätstheorie und die Teilchenphysik miteinander verbinden. Die Phänomenologie ist der Zweig der theoretischen Physik, in dem Physiker aus abstrakteren theoretischen Ideen realistische Modelle der Natur konstruieren. Die String-Phänomenologie ist der Teil der Stringtheorie, der versucht, realistische oder halb-realistische Modelle auf der Grundlage der Stringtheorie zu konstruieren. ⓘ
Zum Teil wegen theoretischer und mathematischer Schwierigkeiten und zum Teil wegen der extrem hohen Energien, die erforderlich sind, um diese Theorien experimentell zu testen, gibt es bisher keine experimentellen Beweise, die eindeutig darauf hindeuten würden, dass eines dieser Modelle eine korrekte fundamentale Beschreibung der Natur ist. Dies hat einige in der Gemeinschaft dazu veranlasst, diese Vereinigungsansätze zu kritisieren und den Wert der weiteren Forschung an diesen Problemen in Frage zu stellen. ⓘ
Teilchenphysik
Die derzeit akzeptierte Theorie zur Beschreibung der Elementarteilchen und ihrer Wechselwirkungen ist als Standardmodell der Teilchenphysik bekannt. Diese Theorie liefert eine einheitliche Beschreibung von drei der grundlegenden Kräfte der Natur: Elektromagnetismus sowie die starke und schwache Kernkraft. Trotz seines bemerkenswerten Erfolgs bei der Erklärung eines breiten Spektrums physikalischer Phänomene kann das Standardmodell keine vollständige Beschreibung der Realität sein. Dies liegt daran, dass das Standardmodell die Schwerkraft nicht einbezieht und Probleme wie das Hierarchieproblem und die Unfähigkeit, die Struktur der Fermionenmassen oder der dunklen Materie zu erklären, aufwirft. ⓘ
Die Stringtheorie wurde verwendet, um eine Vielzahl von Modellen der Teilchenphysik zu konstruieren, die über das Standardmodell hinausgehen. Typischerweise beruhen solche Modelle auf der Idee der Verdichtung. Ausgehend von der zehn- oder elfdimensionalen Raumzeit der String- oder M-Theorie postulieren die Physiker eine Form für die zusätzlichen Dimensionen. Durch geeignete Wahl dieser Form können sie Modelle konstruieren, die in etwa dem Standardmodell der Teilchenphysik entsprechen, mit zusätzlichen unentdeckten Teilchen. Eine beliebte Methode, um aus der Stringtheorie eine realistische Physik abzuleiten, besteht darin, von der heterotischen Theorie in zehn Dimensionen auszugehen und anzunehmen, dass die sechs zusätzlichen Dimensionen der Raumzeit die Form einer sechsdimensionalen Calabi-Yau-Mannigfaltigkeit haben. Solche Verdichtungen bieten viele Möglichkeiten, realistische Physik aus der Stringtheorie zu extrahieren. Andere ähnliche Methoden können verwendet werden, um realistische oder halb-realistische Modelle unserer vierdimensionalen Welt auf der Grundlage der M-Theorie zu konstruieren. ⓘ
Kosmologie

Die Urknalltheorie ist das vorherrschende kosmologische Modell für das Universum von den frühesten bekannten Perioden bis zu seiner späteren großräumigen Entwicklung. Trotz ihres Erfolgs bei der Erklärung vieler beobachteter Merkmale des Universums, einschließlich der galaktischen Rotverschiebungen, der relativen Häufigkeit leichter Elemente wie Wasserstoff und Helium und der Existenz eines kosmischen Mikrowellenhintergrunds, gibt es mehrere Fragen, die unbeantwortet bleiben. So erklärt das Standard-Urknallmodell beispielsweise nicht, warum das Universum in allen Richtungen gleich zu sein scheint, warum es auf sehr großen Entfernungsskalen flach erscheint oder warum bestimmte angenommene Teilchen wie magnetische Monopole in Experimenten nicht beobachtet werden. ⓘ
Derzeit ist der führende Kandidat für eine Theorie, die über den Urknall hinausgeht, die Theorie der kosmischen Inflation. Die von Alan Guth und anderen in den 1980er Jahren entwickelte Inflationstheorie postuliert eine Periode extrem schneller Expansion des Universums vor der Expansion, die von der Standard-Urknalltheorie beschrieben wird. Die Theorie der kosmischen Inflation bewahrt die Erfolge des Urknalls und bietet gleichzeitig eine natürliche Erklärung für einige der rätselhaften Eigenschaften des Universums. Die Theorie wird auch durch Beobachtungen des kosmischen Mikrowellenhintergrunds, der Strahlung, die den Himmel seit etwa 380.000 Jahren nach dem Urknall erfüllt, eindrucksvoll unterstützt. ⓘ
In der Inflationstheorie wird die rasche anfängliche Ausdehnung des Universums durch ein hypothetisches Teilchen namens Inflaton verursacht. Die genauen Eigenschaften dieses Teilchens sind in der Theorie nicht festgelegt, sondern sollten letztlich aus einer grundlegenderen Theorie wie der Stringtheorie abgeleitet werden. In der Tat gab es eine Reihe von Versuchen, ein Inflaton im Spektrum der von der Stringtheorie beschriebenen Teilchen zu identifizieren und die Inflation mit Hilfe der Stringtheorie zu untersuchen. Auch wenn diese Ansätze letztendlich durch Beobachtungsdaten wie die Messungen des kosmischen Mikrowellenhintergrunds unterstützt werden könnten, befindet sich die Anwendung der Stringtheorie auf die Kosmologie noch in einem frühen Stadium. ⓘ
Verbindungen zur Mathematik
Die Stringtheorie hat nicht nur die Forschung in der theoretischen Physik beeinflusst, sondern auch eine Reihe von wichtigen Entwicklungen in der reinen Mathematik angeregt. Wie viele sich entwickelnde Ideen in der theoretischen Physik verfügt die Stringtheorie derzeit nicht über eine mathematisch strenge Formulierung, in der alle ihre Konzepte genau definiert werden können. Daher lassen sich Physiker, die sich mit der Stringtheorie beschäftigen, oft von ihrer physikalischen Intuition leiten und stellen Vermutungen über die Beziehungen zwischen den scheinbar unterschiedlichen mathematischen Strukturen an, die zur Formalisierung verschiedener Teile der Theorie verwendet werden. Diese Vermutungen werden später von Mathematikern bewiesen, und auf diese Weise dient die Stringtheorie als Quelle für neue Ideen in der reinen Mathematik. ⓘ
Spiegelsymmetrie

Nachdem Calabi-Yau-Mannigfaltigkeiten in die Physik Einzug gehalten hatten, um zusätzliche Dimensionen in der Stringtheorie zu verdichten, begannen viele Physiker, diese Mannigfaltigkeiten zu untersuchen. In den späten 1980er Jahren stellten mehrere Physiker fest, dass es bei einer solchen Verdichtung der Stringtheorie nicht möglich ist, eine entsprechende Calabi-Yau-Mannigfaltigkeit eindeutig zu rekonstruieren. Stattdessen können zwei verschiedene Versionen der Stringtheorie, Typ IIA und Typ IIB, auf völlig unterschiedlichen Calabi-Yau-Mannigfaltigkeiten kompaktiert werden, was zu derselben Physik führt. In diesem Fall werden die Mannigfaltigkeiten als Spiegelmannigfaltigkeiten bezeichnet, und die Beziehung zwischen den beiden physikalischen Theorien wird als Spiegelsymmetrie bezeichnet. ⓘ
Unabhängig davon, ob Calabi-Yau-Verdichtungen der Stringtheorie eine korrekte Beschreibung der Natur liefern, hat die Existenz der Spiegeldualität zwischen verschiedenen Stringtheorien bedeutende mathematische Konsequenzen. Die Calabi-Yau-Mannigfaltigkeiten, die in der Stringtheorie verwendet werden, sind für die reine Mathematik von Interesse, und die Spiegelsymmetrie ermöglicht es Mathematikern, Probleme in der enumerativen Geometrie zu lösen, einem Zweig der Mathematik, der sich mit dem Zählen der Lösungen geometrischer Fragen beschäftigt. ⓘ
Die enumerative Geometrie untersucht eine Klasse von geometrischen Objekten, die algebraischen Varietäten genannt werden und durch das Verschwinden von Polynomen definiert sind. Der rechts abgebildete Clebsch-Kubus ist beispielsweise eine algebraische Varietät, die durch ein bestimmtes Polynom dritten Grades in vier Variablen definiert ist. Ein berühmtes Ergebnis der Mathematiker Arthur Cayley und George Salmon aus dem 19. Jahrhundert besagt, dass es genau 27 Geraden gibt, die vollständig auf einer solchen Fläche liegen. ⓘ
Wenn man dieses Problem verallgemeinert, kann man fragen, wie viele Geraden auf einer quintischen Calabi-Yau-Mannigfaltigkeit, wie der oben abgebildeten, die durch ein Polynom vom Grad 5 definiert ist, gezogen werden können. Dieses Problem wurde von dem deutschen Mathematiker Hermann Schubert im 19. Jahrhundert gelöst, der herausfand, dass es genau 2.875 solcher Linien gibt. Im Jahr 1986 bewies der Geometer Sheldon Katz, dass die Anzahl der Kurven, wie z. B. Kreise, die durch Polynome zweiten Grades definiert sind und vollständig in der Quinte liegen, 609.250 beträgt. ⓘ
Bis zum Jahr 1991 waren die meisten klassischen Probleme der enumerativen Geometrie gelöst, und das Interesse an der enumerativen Geometrie hatte nachgelassen. Das Feld wurde im Mai 1991 wiederbelebt, als die Physiker Philip Candelas, Xenia de la Ossa, Paul Green und Linda Parks zeigten, dass die Spiegelsymmetrie dazu verwendet werden kann, schwierige mathematische Fragen zu einer Calabi-Yau-Mannigfaltigkeit in einfachere Fragen zu ihrem Spiegel zu übersetzen. Insbesondere nutzten sie die Spiegelsymmetrie, um zu zeigen, dass eine sechsdimensionale Calabi-Yau-Mannigfaltigkeit genau 317.206.375 Kurven dritten Grades enthalten kann. Neben der Zählung von Kurven dritten Grades erzielten Candelas und seine Mitarbeiter eine Reihe allgemeinerer Ergebnisse für die Zählung rationaler Kurven, die weit über die von Mathematikern erzielten Ergebnisse hinausgingen. ⓘ
Ursprünglich wurden diese Ergebnisse von Candelas mit physikalischen Gründen begründet. Mathematiker bevorzugen jedoch im Allgemeinen strenge Beweise, die keine Berufung auf physikalische Intuition erfordern. Angeregt durch die Arbeiten der Physiker zur Spiegelsymmetrie haben die Mathematiker daher ihre eigenen Argumente konstruiert, die die enumerativen Vorhersagen der Spiegelsymmetrie beweisen. Heute ist die Spiegelsymmetrie ein aktives Forschungsgebiet in der Mathematik, und Mathematiker arbeiten daran, ein vollständigeres mathematisches Verständnis der Spiegelsymmetrie auf der Grundlage der Intuition der Physiker zu entwickeln. Zu den wichtigsten Ansätzen zur Spiegelsymmetrie gehören das homologische Spiegelsymmetrieprogramm von Maxim Kontsevich und die SYZ-Vermutung von Andrew Strominger, Shing-Tung Yau und Eric Zaslow. ⓘ
Monströser Mondschein

Die Gruppentheorie ist der Zweig der Mathematik, der das Konzept der Symmetrie untersucht. Als Beispiel kann man eine geometrische Form wie ein gleichseitiges Dreieck betrachten. Es gibt verschiedene Operationen, die man an diesem Dreieck durchführen kann, ohne seine Form zu verändern. Man kann es um 120°, 240° oder 360° drehen oder an einer der Linien spiegeln, die in der Abbildung mit S0, S1 oder S2 bezeichnet sind. Jede dieser Operationen wird als Symmetrie bezeichnet, und die Sammlung dieser Symmetrien erfüllt bestimmte technische Eigenschaften, die sie zu dem machen, was Mathematiker eine Gruppe nennen. In diesem speziellen Beispiel wird die Gruppe als Dihedralgruppe der Ordnung 6 bezeichnet, weil sie sechs Elemente hat. Eine allgemeine Gruppe kann endlich viele oder unendlich viele Symmetrien beschreiben; wenn es nur endlich viele Symmetrien gibt, nennt man sie eine endliche Gruppe. ⓘ
Mathematiker bemühen sich oft um eine Klassifizierung (oder Liste) aller mathematischen Objekte eines bestimmten Typs. Es wird allgemein angenommen, dass endliche Gruppen zu vielfältig sind, um eine sinnvolle Klassifizierung zu ermöglichen. Ein bescheideneres, aber immer noch anspruchsvolles Problem ist die Klassifizierung aller endlichen einfachen Gruppen. Dabei handelt es sich um endliche Gruppen, die als Bausteine für die Konstruktion beliebiger endlicher Gruppen verwendet werden können, so wie Primzahlen zur Konstruktion beliebiger ganzer Zahlen durch Bildung von Produkten verwendet werden können. Eine der wichtigsten Errungenschaften der modernen Gruppentheorie ist die Klassifikation der endlichen einfachen Gruppen, ein mathematischer Satz, der eine Liste aller möglichen endlichen einfachen Gruppen enthält. ⓘ
Dieses Klassifikationstheorem identifiziert mehrere unendliche Gruppenfamilien sowie 26 weitere Gruppen, die in keine Familie passen. Die letztgenannten Gruppen werden als "sporadische" Gruppen bezeichnet, und jede von ihnen verdankt ihre Existenz einer bemerkenswerten Kombination von Umständen. Die größte sporadische Gruppe, die so genannte Monstergruppe, enthält über 1053 Elemente, mehr als das Tausendfache der Anzahl der Atome in der Erde. ⓘ
Eine scheinbar nicht verwandte Konstruktion ist die j-Funktion der Zahlentheorie. Dieses Objekt gehört zu einer speziellen Klasse von Funktionen, die als modulare Funktionen bezeichnet werden und deren Graphen eine bestimmte Art von sich wiederholenden Mustern bilden. Obwohl diese Funktion in einem Zweig der Mathematik auftaucht, der sich von der Theorie der endlichen Gruppen stark zu unterscheiden scheint, erweisen sich die beiden Themen als eng miteinander verbunden. In den späten 1970er Jahren bemerkten die Mathematiker John McKay und John Thompson, dass bestimmte Zahlen, die in der Analyse der Monstergruppe auftauchen (nämlich die Dimensionen ihrer irreduziblen Darstellungen), mit Zahlen verwandt sind, die in einer Formel für die j-Funktion erscheinen (nämlich die Koeffizienten ihrer Fourier-Reihe). Diese Beziehung wurde von John Horton Conway und Simon Norton weiterentwickelt, die sie als "monstrous moonshine" bezeichneten, weil sie so weit hergeholt schien. ⓘ
Im Jahr 1992 schlug Richard Borcherds eine Brücke zwischen der Theorie der modularen Funktionen und endlichen Gruppen und erklärte dabei die Beobachtungen von McKay und Thompson. Borcherds' Arbeit nutzte Ideen aus der Stringtheorie in einer wesentlichen Weise und erweiterte frühere Ergebnisse von Igor Frenkel, James Lepowsky und Arne Meurman, die die Monstergruppe als die Symmetrien einer bestimmten Version der Stringtheorie erkannt hatten. Im Jahr 1998 wurde Borcherds für seine Arbeit mit der Fields-Medaille ausgezeichnet. ⓘ
Seit den 1990er Jahren hat die Verbindung zwischen Stringtheorie und Mondschein zu weiteren Ergebnissen in Mathematik und Physik geführt. Im Jahr 2010 entdeckten die Physiker Tohru Eguchi, Hirosi Ooguri und Yuji Tachikawa Verbindungen zwischen einer anderen sporadischen Gruppe, der Mathieu-Gruppe M24, und einer bestimmten Version der Stringtheorie. Miranda Cheng, John Duncan und Jeffrey A. Harvey schlugen eine Verallgemeinerung dieses Mondscheinphänomens vor, die sie umbralen Mondschein nannten, und ihre Vermutung wurde von Duncan, Michael Griffin und Ken Ono mathematisch bewiesen. Witten hat auch spekuliert, dass die Version der Stringtheorie, die in monströsem Mondschein auftritt, mit einem bestimmten vereinfachten Modell der Gravitation in drei Raumzeitdimensionen zusammenhängen könnte. ⓘ
Geschichte
Frühe Ergebnisse
Einige der von der Stringtheorie wieder eingeführten Strukturen sind bereits viel früher im Rahmen des von Albert Einstein begonnenen Programms der klassischen Vereinheitlichung entstanden. Der erste, der eine fünfte Dimension zu einer Theorie der Gravitation hinzufügte, war Gunnar Nordström im Jahr 1914, der feststellte, dass die Gravitation in fünf Dimensionen sowohl die Gravitation als auch den Elektromagnetismus in vier Dimensionen beschreibt. Nordström versuchte, den Elektromagnetismus mit seiner Gravitationstheorie zu vereinheitlichen, die jedoch 1919 von Einsteins allgemeiner Relativitätstheorie verdrängt wurde. Danach kombinierte der deutsche Mathematiker Theodor Kaluza die fünfte Dimension mit der allgemeinen Relativitätstheorie, und nur Kaluza wird gewöhnlich die Idee zugeschrieben. Im Jahr 1926 gab der schwedische Physiker Oskar Klein eine physikalische Interpretation der nicht beobachtbaren zusätzlichen Dimension - sie ist in einen kleinen Kreis eingewickelt. Einstein führte einen nicht-symmetrischen metrischen Tensor ein, während Brans und Dicke viel später der Gravitation eine skalare Komponente hinzufügten. Diese Ideen wurden in der Stringtheorie wiederbelebt, wo sie von den Konsistenzbedingungen gefordert werden. ⓘ

Die Stringtheorie wurde ursprünglich in den späten 1960er und frühen 1970er Jahren als eine nie vollständig erfolgreiche Theorie der Hadronen entwickelt, also der subatomaren Teilchen wie Proton und Neutron, die die starke Wechselwirkung spüren. In den 1960er Jahren entdeckten Geoffrey Chew und Steven Frautschi, dass die Mesonen Familien bilden, die Regge-Trajektorien genannt werden und deren Massen mit den Spins in einer Weise zusammenhängen, die später von Yoichiro Nambu, Holger Bech Nielsen und Leonard Susskind als die von rotierenden Strings erwartete Beziehung verstanden wurde. Chew plädierte dafür, eine Theorie für die Wechselwirkungen dieser Trajektorien zu entwickeln, die nicht voraussetzt, dass sie aus fundamentalen Teilchen bestehen, sondern ihre Wechselwirkungen aus Selbstkonsistenzbedingungen der S-Matrix konstruiert. Der S-Matrix-Ansatz wurde von Werner Heisenberg in den 1940er Jahren entwickelt, um eine Theorie zu konstruieren, die sich nicht auf die lokalen Begriffe von Raum und Zeit stützt, von denen Heisenberg glaubte, dass sie auf der nuklearen Skala zusammenbrechen. Obwohl der Maßstab um viele Größenordnungen verschoben wurde, war der von ihm vertretene Ansatz ideal für eine Theorie der Quantengravitation geeignet. ⓘ
Anhand von experimentellen Daten entwickelten R. Dolen, D. Horn und C. Schmid einige Summenregeln für den Hadronenaustausch. Wenn ein Teilchen und ein Antiteilchen streuen, können virtuelle Teilchen auf zwei qualitativ unterschiedliche Arten ausgetauscht werden. Im s-Kanal annihilieren die beiden Teilchen und bilden temporäre Zwischenzustände, die in die Teilchen des Endzustands zerfallen. Im t-Kanal tauschen die Teilchen Zwischenzustände durch Emission und Absorption aus. In der Feldtheorie addieren sich die beiden Beiträge, wobei der eine einen kontinuierlichen Hintergrundbeitrag und der andere Spitzenwerte bei bestimmten Energien ergibt. In den Daten wurde deutlich, dass die Spitzen aus dem Hintergrund gestohlen wurden - die Autoren interpretierten dies so, dass der t-Kanal-Beitrag dual zum s-Kanal-Beitrag war, d. h. beide beschrieben die gesamte Amplitude und schlossen den anderen ein. ⓘ

Das Ergebnis wurde von Murray Gell-Mann weithin bekannt gemacht, was Gabriele Veneziano dazu veranlasste, eine Streuungsamplitude zu konstruieren, die die Eigenschaft der Dolen-Horn-Schmid-Dualität aufwies, die später in World-Sheet-Dualität umbenannt wurde. Die Amplitude benötigte Pole dort, wo die Teilchen auf geradlinigen Bahnen erscheinen, und es gibt eine spezielle mathematische Funktion, deren Pole gleichmäßig auf der Hälfte der reellen Linie verteilt sind - die Gamma-Funktion - die in der Regge-Theorie weit verbreitet war. Durch die Manipulation von Kombinationen von Gamma-Funktionen gelang es Veneziano, eine konsistente Streuungsamplitude mit Polen auf geraden Linien und überwiegend positiven Resten zu finden, die der Dualität gehorcht und bei hoher Energie die entsprechende Regge-Skalierung aufweist. Die Amplitude passte zu Nahstrahl-Streudaten ebenso gut wie zu anderen Regge-Typ-Anpassungen und hatte eine suggestive integrale Darstellung, die zur Verallgemeinerung verwendet werden konnte. ⓘ
In den folgenden Jahren arbeiteten Hunderte von Physikern daran, das Bootstrap-Programm für dieses Modell zu vervollständigen, was zu vielen Überraschungen führte. Veneziano selbst entdeckte, dass das leichteste Teilchen ein Tachyon sein muss, damit die Streuamplitude die Streuung eines Teilchens beschreibt, das in der Theorie vorkommt - eine offensichtliche Bedingung für die Selbstkonsistenz. Miguel Virasoro und Joel Shapiro fanden eine andere Amplitude, die heute als die von geschlossenen Strings verstanden wird, während Ziro Koba und Holger Nielsen Venezianos integrale Darstellung auf die Mehrteilchenstreuung verallgemeinerten. Veneziano und Sergio Fubini führten einen Operatorformalismus für die Berechnung der Streuamplituden ein, der ein Vorläufer der konformen Theorie des Weltenblatts war, während Virasoro verstand, wie man die Pole mit Resten falschen Vorzeichens mit Hilfe einer Einschränkung der Zustände entfernen kann. Claud Lovelace berechnete eine Schleifenamplitude und stellte fest, dass es eine Inkonsistenz gibt, wenn die Dimension der Theorie nicht 26 ist. Charles Thorn, Peter Goddard und Richard Brower bewiesen daraufhin, dass es in Dimensionen kleiner oder gleich 26 keine Zustände gibt, die sich mit falschem Vorzeichen fortpflanzen. ⓘ
In den Jahren 1969-70 erkannten Yoichiro Nambu, Holger Bech Nielsen und Leonard Susskind, dass die Theorie in Raum und Zeit mit Hilfe von Strings beschrieben werden kann. Die Streuamplituden wurden von Peter Goddard, Jeffrey Goldstone, Claudio Rebbi und Charles Thorn systematisch aus dem Wirkungsprinzip abgeleitet, wodurch die von Veneziano und Fubini eingeführten Vertex-Operatoren ein Raum-Zeit-Bild erhielten und die Virasoro-Bedingungen eine geometrische Interpretation. ⓘ
Im Jahr 1971 fügte Pierre Ramond dem Modell Fermionen hinzu, was ihn dazu veranlasste, eine zweidimensionale Supersymmetrie zu formulieren, um die Zustände mit falschem Vorzeichen aufzuheben. John Schwarz und André Neveu fügten der Fermi-Theorie kurze Zeit später einen weiteren Sektor hinzu. In den Fermi-Theorien war die kritische Dimension 10. Stanley Mandelstam formulierte sowohl für die Bose- als auch für die Fermi-Theorie eine konforme Weltblatt-Theorie, die ein zweidimensionales feldtheoretisches Pfadintegral zur Erzeugung des Operatorformalismus liefert. Michio Kaku und Keiji Kikkawa formulierten den bosonischen String anders, nämlich als String-Feldtheorie mit unendlich vielen Teilchentypen und mit Feldern, die nicht auf Punkten, sondern auf Schleifen und Kurven Werte annehmen. ⓘ
1974 entdeckte Tamiaki Yoneya, dass alle bekannten Stringtheorien ein masseloses Spin-Zwei-Teilchen enthielten, das den korrekten Ward-Identitäten gehorchte und ein Graviton war. John Schwarz und Joël Scherk kamen zu demselben Schluss und wagten die These, dass die Stringtheorie eine Theorie der Gravitation und keine Theorie der Hadronen sei. Sie führten die Kaluza-Klein-Theorie wieder ein, um den zusätzlichen Dimensionen einen Sinn zu geben. Gleichzeitig wurde die Quantenchromodynamik als die korrekte Theorie der Hadronen anerkannt, was die Aufmerksamkeit der Physiker auf sich lenkte und das Bootstrap-Programm scheinbar in den Mülleimer der Geschichte beförderte. ⓘ
Die Stringtheorie schaffte es schließlich aus dem Mülleimer, aber in den folgenden zehn Jahren wurde die Arbeit an dieser Theorie völlig ignoriert. Dennoch entwickelte sich die Theorie dank der Arbeit einer Handvoll von Anhängern in einem stetigen Tempo weiter. Ferdinando Gliozzi, Joël Scherk und David Olive erkannten 1977, dass die ursprünglichen Ramond- und Neveu-Schwarz-Strings nicht miteinander vereinbar waren und kombiniert werden mussten. Die daraus resultierende Theorie enthielt kein Tachyon und wurde 1984 von John Schwarz und Michael Green als raumzeitliche Supersymmetrie nachgewiesen. Im selben Jahr gab Alexander Polyakov der Theorie eine moderne Pfadintegralformulierung und entwickelte die konforme Feldtheorie umfassend weiter. 1979 zeigte Daniel Friedan, dass die Bewegungsgleichungen der Stringtheorie, die Verallgemeinerungen der Einstein-Gleichungen der allgemeinen Relativitätstheorie sind, aus den Gleichungen der Renormierungsgruppe für die zweidimensionale Feldtheorie hervorgehen. Schwarz und Green entdeckten die T-Dualität und konstruierten zwei Superstringtheorien - IIA und IIB, die durch T-Dualität miteinander verbunden sind, und Theorien vom Typ I mit offenen Strings. Die Konsistenzbedingungen waren so stark, dass die gesamte Theorie mit nur wenigen diskreten Auswahlmöglichkeiten nahezu eindeutig bestimmt war. ⓘ
Erste Superstring-Revolution

In den frühen 1980er Jahren entdeckte Edward Witten, dass die meisten Theorien der Quantengravitation chirale Fermionen wie das Neutrino nicht berücksichtigen konnten. Daraufhin untersuchte er in Zusammenarbeit mit Luis Álvarez-Gaumé Verletzungen der Erhaltungssätze in Gravitationstheorien mit Anomalien und kam zu dem Schluss, dass Stringtheorien vom Typ I inkonsistent sind. Green und Schwarz entdeckten einen Beitrag zur Anomalie, den Witten und Alvarez-Gaumé übersehen hatten und der die Eichgruppe der Stringtheorie vom Typ I auf SO(32) beschränkte. Als Edward Witten diese Berechnung verstand, war er davon überzeugt, dass die Stringtheorie wirklich eine konsistente Theorie der Schwerkraft ist, und er wurde zu einem profilierten Befürworter. Nach Wittens Vorbild begannen zwischen 1984 und 1986 Hunderte von Physikern, auf diesem Gebiet zu arbeiten, was manchmal als die erste Superstring-Revolution bezeichnet wird. ⓘ
Während dieser Zeit entdeckten David Gross, Jeffrey Harvey, Emil Martinec und Ryan Rohm heterotische Strings. Die Eichgruppe dieser geschlossenen Strings bestand aus zwei Kopien von E8, und beide Kopien konnten problemlos und auf natürliche Weise das Standardmodell enthalten. Philip Candelas, Gary Horowitz, Andrew Strominger und Edward Witten fanden heraus, dass die Calabi-Yau-Mannigfaltigkeiten die Verdichtungen sind, die ein realistisches Maß an Supersymmetrie bewahren, während Lance Dixon und andere die physikalischen Eigenschaften von Orbifolds, charakteristischen geometrischen Singularitäten, die in der Stringtheorie zulässig sind, herausarbeiteten. Cumrun Vafa verallgemeinerte die T-Dualität von Kreisen auf beliebige Mannigfaltigkeiten und schuf damit das mathematische Gebiet der Spiegelsymmetrie. Daniel Friedan, Emil Martinec und Stephen Shenker entwickelten die kovariante Quantisierung des Superstrings mit Techniken der konformen Feldtheorie weiter. David Gross und Vipul Periwal entdeckten, dass die String-Störungstheorie divergent ist. Stephen Shenker zeigte, dass sie viel schneller divergiert als die Feldtheorie, was darauf hindeutet, dass neue nicht-perturbative Objekte fehlen. ⓘ

In den 1990er Jahren entdeckte Joseph Polchinski, dass die Theorie höherdimensionale Objekte, die so genannten D-Branen, benötigt, und identifizierte diese mit den Lösungen der Schwarzen Löcher der Supergravitation. Diese wurden als die neuen Objekte verstanden, die von den störungsbedingten Divergenzen vorgeschlagen wurden, und sie eröffneten ein neues Gebiet mit einer reichen mathematischen Struktur. Schnell wurde klar, dass nicht nur Strings, sondern auch D-Branen und andere p-Branen den materiellen Inhalt der Stringtheorien bildeten, und die physikalische Interpretation der Strings und Branes wurde enthüllt - sie sind eine Art Schwarzes Loch. Leonard Susskind hatte das holographische Prinzip von Gerardus 't Hooft in die Stringtheorie aufgenommen und die langen, hoch angeregten String-Zustände mit gewöhnlichen thermischen Zuständen Schwarzer Löcher identifiziert. Wie von 't Hooft vorgeschlagen, beschreiben die Fluktuationen des Horizonts des Schwarzen Lochs, die Weltblatt- oder Weltvolumentheorie, nicht nur die Freiheitsgrade des Schwarzen Lochs, sondern auch alle Objekte in der Nähe. ⓘ
Zweite Superstring-Revolution
1995 hielt Edward Witten auf der jährlichen Konferenz der Stringtheoretiker an der University of Southern California (USC) einen Vortrag über die Stringtheorie, der im Wesentlichen die fünf damals existierenden Stringtheorien vereinte und eine neue 11-dimensionale Theorie namens M-Theorie hervorbrachte. Die M-Theorie wurde auch in der Arbeit von Paul Townsend etwa zur gleichen Zeit angedeutet. Die rege Tätigkeit, die zu dieser Zeit begann, wird manchmal als die zweite Superstring-Revolution bezeichnet. ⓘ

In dieser Zeit formulierten Tom Banks, Willy Fischler, Stephen Shenker und Leonard Susskind die Matrixtheorie, eine vollständige holographische Beschreibung der M-Theorie mit IIA-D0-Branen. Dies war die erste Definition der Stringtheorie, die vollständig nicht-perturbativ war und eine konkrete mathematische Umsetzung des holografischen Prinzips darstellte. Sie ist ein Beispiel für eine Dualität zwischen Eichtheorie und Gravitation und wird heute als Spezialfall der AdS/CFT-Korrespondenz verstanden. Andrew Strominger und Cumrun Vafa berechneten die Entropie bestimmter Konfigurationen von D-Branen und fanden eine Übereinstimmung mit der semiklassischen Antwort für extrem geladene schwarze Löcher. Petr Hořava und Witten fanden die elfdimensionale Formulierung der heterotischen Stringtheorien und zeigten, dass Orbifalten das Chiralitätsproblem lösen. Witten stellte fest, dass die effektive Beschreibung der Physik von D-Branen bei niedrigen Energien durch eine supersymmetrische Eichtheorie erfolgt, und fand geometrische Interpretationen von mathematischen Strukturen in der Eichtheorie, die er und Nathan Seiberg zuvor in Bezug auf die Lage der Branes entdeckt hatten. ⓘ
1997 stellte Juan Maldacena fest, dass die niederenergetischen Anregungen einer Theorie in der Nähe eines Schwarzen Lochs aus Objekten in der Nähe des Horizonts bestehen, der für extrem geladene Schwarze Löcher wie ein Anti-De-Sitter-Raum aussieht. Er stellte fest, dass in dieser Grenze die Eichtheorie die String-Anregungen in der Nähe der Branes beschreibt. Daher stellte er die Hypothese auf, dass die Stringtheorie in einer horizontnahen Geometrie extrem geladener Schwarzer Löcher, einem Anti-de-Sitter-Raum mal einer Kugel mit Fluss, ebenso gut durch die limitierende Eichtheorie bei niedriger Energie, die supersymmetrische Yang-Mills-Theorie N = 4, beschrieben wird. Diese Hypothese, die als AdS/CFT-Korrespondenz bezeichnet wird, wurde von Steven Gubser, Igor Klebanov und Alexander Polyakov sowie von Edward Witten weiterentwickelt und ist heute allgemein anerkannt. Sie ist eine konkrete Umsetzung des holografischen Prinzips, das weitreichende Auswirkungen auf Schwarze Löcher, Lokalität und Information in der Physik sowie auf die Natur der Gravitationswechselwirkung hat. Durch diese Beziehung hat sich gezeigt, dass die Stringtheorie mit Eichtheorien wie der Quantenchromodynamik zusammenhängt, was zu einem besseren quantitativen Verständnis des Verhaltens von Hadronen geführt hat und die Stringtheorie zu ihren Wurzeln zurückbringt. ⓘ
Kritik
An der Stringtheorie entzündete sich seit den 2000er-Jahren eine zum Teil heftige Kritik. Der Nobelpreisträger und Festkörperphysiker Robert Laughlin, der vor allem die starke Bindung von Forschungsressourcen auf einem den Anwendungen fernstehenden Gebiet kritisiert, fasst es wie folgt zusammen: „Weit entfernt von einer wunderbaren technologischen Hoffnung auf eine bessere Zukunft ist die Stringtheorie die tragische Konsequenz eines überholten Glaubenssystems.“ (“Far from a wonderful technological hope for a greater tomorrow, string theory is the tragic consequence of an obsolete belief system.”) Der Nobelpreisträger Gerard ’t Hooft (2013) kritisiert wie Vertreter konkurrierender Theorien zur Quantengravitation (wie der Schleifenquantengravitation, Carlo Rovelli, Lee Smolin), dass die Stringtheorie zu sehr konventionellen Auffassungen der Rolle der Raumzeit in der Quantenmechanik verhaftet ist. Carlo Rovelli kritisiert an der Stringtheorie, dass sie sich als nicht funktionsfähig erweise und dennoch auch nach Jahrzehnten mit einem Aufwand, der seinesgleichen sucht, noch daran weitergearbeitet werde (“it does not work, therefore let’s develop it further”). Einige Kritiker gehen sogar so weit, dass sie der Stringtheorie die Rolle einer falsifizierbaren wissenschaftlichen Theorie absprechen. Peter Woit verwendete dafür ein bekanntes Zitat des für seine Scharfzüngigkeit bekannten Nobelpreisträgers Wolfgang Pauli, der grundsätzlich experimentell nicht überprüfbare (und auch nicht falsifizierbare) Theorien für physikalische Phänomene so charakterisierte, dass sie nicht einmal falsch seien (englisch not even wrong, der Titel von Woits Buch). ⓘ
Anzahl der Lösungen
Um Modelle der Teilchenphysik auf der Grundlage der Stringtheorie zu konstruieren, legen Physiker in der Regel zunächst eine Form für die zusätzlichen Dimensionen der Raumzeit fest. Jede dieser verschiedenen Formen entspricht einem anderen möglichen Universum oder "Vakuumzustand" mit einer anderen Ansammlung von Teilchen und Kräften. Nach dem derzeitigen Verständnis der Stringtheorie gibt es eine enorme Anzahl von Vakuumzuständen, die in der Regel auf etwa 10500 geschätzt wird, und diese könnten so vielfältig sein, dass sie fast jedes Phänomen, das bei niedrigen Energien beobachtet werden kann, berücksichtigen. ⓘ
Viele Kritiker der Stringtheorie haben Bedenken hinsichtlich der großen Zahl möglicher Universen geäußert, die die Stringtheorie beschreibt. In seinem Buch Not Even Wrong hat Peter Woit, Dozent an der Fakultät für Mathematik der Columbia University, argumentiert, dass die große Anzahl verschiedener physikalischer Szenarien die Stringtheorie als Rahmen für die Konstruktion von Modellen der Teilchenphysik unbrauchbar macht. Laut Woit, ⓘ
Die mögliche Existenz von, sagen wir, 10500 verschiedenen konsistenten Vakuumzuständen für die Superstringtheorie zerstört wahrscheinlich die Hoffnung, mit der Theorie irgendetwas vorhersagen zu können. Wenn man aus dieser großen Menge nur diejenigen Zustände auswählt, deren Eigenschaften mit den gegenwärtigen experimentellen Beobachtungen übereinstimmen, ist es wahrscheinlich, dass es immer noch eine so große Anzahl dieser Zustände gibt, dass man für die Ergebnisse jeder neuen Beobachtung so ziemlich jeden gewünschten Wert erhalten kann. ⓘ
Einige Physiker sind der Meinung, dass diese große Anzahl von Lösungen sogar ein Vorteil ist, weil sie eine natürliche anthropische Erklärung für die beobachteten Werte der physikalischen Konstanten, insbesondere den kleinen Wert der kosmologischen Konstante, ermöglichen kann. Das anthropische Prinzip besagt, dass einige der in den physikalischen Gesetzen vorkommenden Zahlen nicht durch ein fundamentales Prinzip festgelegt sind, sondern mit der Entwicklung intelligenten Lebens vereinbar sein müssen. 1987 veröffentlichte Steven Weinberg einen Artikel, in dem er argumentierte, dass die kosmologische Konstante nicht zu groß gewesen sein kann, da sich sonst keine Galaxien und kein intelligentes Leben hätten entwickeln können. Weinberg schlug vor, dass es eine riesige Anzahl möglicher konsistenter Universen geben könnte, jedes mit einem anderen Wert der kosmologischen Konstante, und dass Beobachtungen nur deshalb auf einen kleinen Wert der kosmologischen Konstante hindeuten, weil die Menschen zufällig in einem Universum leben, das intelligentes Leben und damit Beobachter zugelassen hat. ⓘ
Der Stringtheoretiker Leonard Susskind hat argumentiert, dass die Stringtheorie eine natürliche anthropische Erklärung für den kleinen Wert der kosmologischen Konstante liefert. Nach Susskind könnten die verschiedenen Vakuumzustände der Stringtheorie als verschiedene Universen innerhalb eines größeren Multiversums realisiert werden. Die Tatsache, dass das beobachtete Universum eine kleine kosmologische Konstante hat, ist nur eine tautologische Folge der Tatsache, dass ein kleiner Wert für die Existenz von Leben erforderlich ist. Viele prominente Theoretiker und Kritiker sind mit den Schlussfolgerungen von Susskind nicht einverstanden. Laut Woit ist "in diesem Fall [die anthropische Argumentation] nichts anderes als eine Ausrede für das Scheitern. Spekulative wissenschaftliche Ideen scheitern nicht nur, wenn sie falsche Vorhersagen machen, sondern auch, wenn sie sich als nichtssagend und unfähig erweisen, etwas vorherzusagen." ⓘ
Kompatibilität mit dunkler Energie
Es ist nach wie vor unbekannt, ob die Stringtheorie mit einer metastabilen, positiven kosmologischen Konstante vereinbar ist. Es gibt einige mutmaßliche Beispiele für solche Lösungen, wie das von Kachru et al. im Jahr 2003 beschriebene Modell. Im Jahr 2018 stellte eine Gruppe von vier Physikern eine kontroverse Vermutung auf, die besagt, dass ein solches Universum nicht existiert. Dies steht im Widerspruch zu einigen populären Modellen der dunklen Energie wie dem Λ-CDM, das eine positive Vakuumenergie voraussetzt. Die Stringtheorie ist jedoch wahrscheinlich mit bestimmten Arten von Quintessenz vereinbar, bei denen die dunkle Energie durch ein neues Feld mit exotischen Eigenschaften verursacht wird. ⓘ
Unabhängigkeit des Hintergrunds
Eine der grundlegenden Eigenschaften von Einsteins allgemeiner Relativitätstheorie ist, dass sie hintergrundunabhängig ist, d. h., dass die Formulierung der Theorie in keiner Weise eine bestimmte Raumzeitgeometrie bevorzugt. ⓘ
Einer der Hauptkritikpunkte an der Stringtheorie war von Anfang an, dass sie nicht offenkundig hintergrundunabhängig ist. In der Stringtheorie muss man in der Regel eine feste Referenzgeometrie für die Raumzeit angeben, und alle anderen möglichen Geometrien werden als Störungen dieser festen Geometrie beschrieben. In seinem Buch The Trouble With Physics behauptet der Physiker Lee Smolin vom Perimeter Institute for Theoretical Physics, dass dies die Hauptschwäche der Stringtheorie als Theorie der Quantengravitation sei, da die Stringtheorie diese wichtige Erkenntnis der allgemeinen Relativitätstheorie nicht berücksichtigt habe. ⓘ
Andere haben Smolins Charakterisierung der Stringtheorie nicht zugestimmt. In einer Rezension von Smolins Buch schreibt der Stringtheoretiker Joseph Polchinski ⓘ
[Smolin] verwechselt einen Aspekt der verwendeten mathematischen Sprache mit einem der beschriebenen Physik. Neue physikalische Theorien werden oft mit einer mathematischen Sprache entdeckt, die nicht die geeignetste für sie ist... Bei der Stringtheorie war immer klar, dass die Physik unabhängig vom Hintergrund ist, auch wenn die verwendete Sprache es nicht ist, und die Suche nach einer geeigneteren Sprache geht weiter. Wie Smolin mit Verspätung feststellt, bietet [AdS/CFT] tatsächlich eine unerwartete und leistungsstarke Lösung für dieses Problem. ⓘ
Polchinski stellt fest, dass ein wichtiges offenes Problem in der Quantengravitation darin besteht, holographische Beschreibungen der Gravitation zu entwickeln, die nicht erfordern, dass das Gravitationsfeld asymptotisch anti-de Sitter sein muss. Smolin antwortete darauf, dass die AdS/CFT-Korrespondenz, so wie sie derzeit verstanden wird, möglicherweise nicht stark genug ist, um alle Bedenken hinsichtlich der Hintergrundunabhängigkeit auszuräumen. ⓘ
Soziologie der Wissenschaft
Seit den Superstring-Revolutionen der 1980er und 1990er Jahre ist die Stringtheorie eines der dominierenden Paradigmen der theoretischen Hochenergiephysik. Einige Stringtheoretiker haben die Ansicht vertreten, dass es keine ebenso erfolgreiche alternative Theorie gibt, die sich mit den tiefen Fragen der fundamentalen Physik befasst. In einem Interview aus dem Jahr 1987 äußerte sich der Nobelpreisträger David Gross kontrovers zu den Gründen für die Popularität der Stringtheorie:
Der wichtigste [Grund] ist, dass es keine anderen guten Ideen gibt. Das ist es, was die meisten Leute dazu bringt, sich damit zu beschäftigen. Als die Leute anfingen, sich für die Stringtheorie zu interessieren, wussten sie noch gar nichts darüber. Tatsächlich ist die erste Reaktion der meisten Menschen, dass die Theorie extrem hässlich und unangenehm ist, zumindest war das vor ein paar Jahren der Fall, als das Verständnis der Stringtheorie noch nicht so weit entwickelt war. Es war schwierig für die Menschen, etwas darüber zu erfahren und sich dafür zu begeistern. Ich glaube, der eigentliche Grund, warum die Leute sich von ihr angezogen fühlen, ist, dass es keine andere Möglichkeit gibt. Alle anderen Ansätze zur Konstruktion großer vereinheitlichter Theorien, die anfangs eher konservativ waren und erst nach und nach immer radikaler wurden, sind gescheitert, und dieses Spiel ist noch nicht gescheitert. ⓘ
Mehrere andere hochrangige Theoretiker und Kommentatoren haben sich ähnlich geäußert und darauf hingewiesen, dass es keine brauchbaren Alternativen zur Stringtheorie gibt. ⓘ
Viele Kritiker der Stringtheorie haben sich zu diesem Stand der Dinge geäußert. In seinem Buch zur Kritik der Stringtheorie betrachtet Peter Woit den Status der Stringtheorie-Forschung als ungesund und schädlich für die Zukunft der Grundlagenphysik. Er argumentiert, dass die extreme Popularität der Stringtheorie unter theoretischen Physikern teilweise eine Folge der finanziellen Struktur der akademischen Welt und des harten Wettbewerbs um knappe Ressourcen ist. In seinem Buch The Road to Reality äußert sich der mathematische Physiker Roger Penrose ähnlich: "Der oft hektische Wettbewerb, den diese einfache Kommunikation hervorruft, führt zu Mitläufereffekten, bei denen Forscher befürchten, zurückzubleiben, wenn sie nicht mitmachen." Penrose behauptet auch, dass die technische Schwierigkeit der modernen Physik junge Wissenschaftler dazu zwingt, sich auf die Vorlieben etablierter Forscher zu verlassen, anstatt eigene neue Wege zu beschreiten. Lee Smolin vertritt in seiner Kritik eine etwas andere Position. Er behauptet, die Stringtheorie sei aus einer Tradition der Teilchenphysik hervorgegangen, die von Spekulationen über die Grundlagen der Physik abrate, während sein bevorzugter Ansatz, die Schleifenquantengravitation, zu radikalerem Denken ermutige. Smolin meint dazu, ⓘ
Die Stringtheorie ist eine starke, gut motivierte Idee und verdient einen Großteil der Arbeit, die ihr gewidmet wurde. Wenn sie bisher gescheitert ist, liegt das vor allem daran, dass die ihr innewohnenden Schwächen eng mit ihren Stärken verbunden sind - und natürlich ist die Geschichte noch nicht zu Ende, denn die Stringtheorie könnte sich durchaus als Teil der Wahrheit erweisen. Die eigentliche Frage ist nicht, warum wir so viel Energie auf die Stringtheorie verwandt haben, sondern warum wir nicht annähernd genug auf alternative Ansätze verwandt haben. ⓘ
Smolin schlägt eine Reihe von Rezepten vor, wie Wissenschaftler eine größere Vielfalt von Ansätzen in der Quantengravitationsforschung fördern könnten. ⓘ
Arten von Strings
Orientierung
Strings können auch eine „Orientierung“ besitzen, die man sich als stringinternen Pfeil denken kann, der sie von Strings mit der entgegengesetzten Orientierung unterscheidet. Im Gegensatz dazu gibt es auch den „nichtorientierten String“, dem kein solcher Pfeil zugewiesen werden kann. ⓘ
Bosonische Stringtheorie
Nambu-Goto-Wirkung
Die Nambu-Goto-Wirkung ist die einfachste Form der Wirkung einer Stringtheorie, beschreibt eine bosonische Stringtheorie (ohne Fermionen) und wurde um 1970 von Yōichirō Nambu und Tetsuo Gotō eingeführt. Da die Lichtkegelquantisierung der Nambu-Goto-Wirkung nicht manifest kovariant ist, bietet sich hier die äquivalente, aber kompliziertere Polyakov-Wirkung an. Ein Punktteilchen, das sich durch die Raumzeit bewegt, beschreibt eine eindimensionale Kurve, auch Weltlinie genannt. Analog dazu beschreibt ein eindimensionaler String, der sich durch die Raumzeit bewegt, eine zweidimensionale Weltfläche. Die Weltfläche eines Strings wird beschrieben durch eine Parametrisierung mit , wobei als Zeitparameter interpretiert werden kann und den String parametrisiert, für geschlossene Strings gilt . Sei nun der Tangentialraum der Weltfläche aufgespannt durch die Vektoren und . Um die Weltfläche zu beschreiben, kann vom Analogon der bekannten euklidischen Flächenformel ausgegangen werden:

Da der Radikand im Fall der Strings negativ ist (höherdimensionaler Minkowskiraum, eine der Richtungen der Strings zeitartig, die andere raumartig), muss noch das Vorzeichen geändert werden, indem einfach die Terme vertauscht werden; setzt man nun die Tangentialvektoren ein, führt dies auf ⓘ
mit dem metrischen Tensor und der Determinantenbildung bezüglich . ⓘ
Nach der Multiplikation mit entsprechenden Einheiten, um das Funktional konsistent mit einer physikalischen Wirkung zu machen, erhält man nun die Nambu-Goto-Wirkung für geschlossene und offene relativistische Strings in einer -dimensionalen Raumzeit, wobei die Lichtgeschwindigkeit ist und die oben eingeführte Stringspannung:
- mit
- und
- ⓘ
Die Impulsdichten ergeben sich zu:
Die Nambu-Goto-Wirkung kann auch in manifester reparametrisierungsinvarianter Form geschrieben werden, wobei , im Detail . Dies führt auf:
Die Form dieser Wirkung eignet sich auch zur Verallgemeinerung auf Objekte, die eine höhere Dimensionalität als Strings haben, wie z. B. D-Brane. ⓘ
Im Vergleich dazu war die Wirkung für ein relativistisches Punktteilchen (wobei das Vorzeichen für den Term unter dem Wurzelzeichen so gewählt wird, dass der Term unter der Wurzel für zeitartige Weltlinien positiv ist). ⓘ
Polyakov-Wirkung
Die Quadratwurzel der Nambu-Goto Wirkung hat entscheidende Nachteile bei der Quantisierung, eine einfachere Form ist die Polyakov-Wirkung, auch String-Sigma-Modell genannt:
- , ⓘ
wobei eine zusätzliche Weltflächenmetrik ist (). Reparametrisierungsinvarianz und Skalierungsinvarianz erlauben es, das Hilfsfeld als zu wählen, worauf sich die Polyakov-Wirkung vereinfacht zu ⓘ
für Bewegungsgleichungen in einer flachen Minkowski-Raumzeit. ⓘ
Symmetrien der Polyakov-Wirkung
- Poincaré-Transformation: Globale Symmetrie der Weltflächen-Felder mit mit . ⓘ
- Reparametrisierungen: Die Polyakov-Wirkung ist klassisch äquivalent zur Nambu-Goto-Wirkung und daher auch lokal reparametrisierungsinvariant unter und . ⓘ
- Weyl-Transformationen: Lokal invariant unter Reskalierung und . ⓘ
Lösung der Bewegungsgleichungen
Um Lösungen der Bewegungsgleichungen zu finden, bietet sich eine Formulierung in Lichtkegel-Koordinaten an mit ⓘ
- mit Ableitungen und Wellengleichung . ⓘ
Geschlossener String
Die allgemeine Lösung der Wellengleichung mit Randbedingungen für geschlossene Strings ist gegeben durch ⓘ
- , ⓘ
wobei der Parameter für zur Vereinfachung gesetzt wurde. bezeichnet man bei einem geschlossenen String als Rechts-Beweger und als Links-Beweger. ⓘ
Offener String
Die allgemeine Lösung für offene Strings mit Neumann-Randbedigungen ist gegeben durch ⓘ
- . ⓘ
ist die Position des Massenschwerpunktes und der Gesamtimpuls des Strings; der exponentielle Term beschreibt die angeregten Zustände. ⓘ