Phonon
| Physik der kondensierten Materie ⓘ |
|---|
|
|
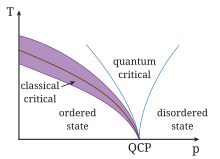
Phasen - Phasenübergang - QCP |
|
In der Physik ist ein Phonon eine kollektive Anregung in einer periodischen, elastischen Anordnung von Atomen oder Molekülen in kondensierter Materie, insbesondere in Festkörpern und einigen Flüssigkeiten. Als eine Art Quasiteilchen ist ein Phonon ein angeregter Zustand in der quantenmechanischen Quantisierung der Schwingungsmoden für elastische Strukturen von wechselwirkenden Teilchen. Phononen kann man sich als quantisierte Schallwellen vorstellen, ähnlich wie Photonen als quantisierte Lichtwellen. ⓘ
Die Untersuchung von Phononen ist ein wichtiger Teil der Physik der kondensierten Materie. Sie spielen eine wichtige Rolle bei vielen physikalischen Eigenschaften von Systemen aus kondensierter Materie, z. B. bei der Wärmeleitfähigkeit und der elektrischen Leitfähigkeit, und spielen eine grundlegende Rolle bei Modellen der Neutronenstreuung und verwandten Effekten. ⓘ
Das Konzept der Phononen wurde 1932 von dem sowjetischen Physiker Igor Tamm eingeführt. Der Name Phonon leitet sich vom griechischen Wort φωνή (phonē) ab, das mit Klang oder Stimme übersetzt werden kann, da langwellige Phononen einen Klang erzeugen. Der Name ist analog zum Wort Photon. ⓘ
Der Begriff Phonon (nach griechisch φωνή phonē, deutsch ‚Klang‘) wurde in Analogie zu den Schwingungsquanten des elektromagnetischen Feldes, den Photonen, gewählt und zum ersten Mal von J. I. Frenkel 1932 in seinem Buch Wave Mechanics, Elementary Theory verwendet. ⓘ
Definition
Ein Phonon ist die quantenmechanische Beschreibung einer elementaren Schwingungsbewegung, bei der ein Gitter aus Atomen oder Molekülen gleichmäßig mit einer einzigen Frequenz schwingt. In der klassischen Mechanik bezeichnet man damit eine Normalmode der Schwingung. Normalmoden sind wichtig, weil jede beliebige Gitterschwingung als Überlagerung dieser elementaren Schwingungsmoden betrachtet werden kann (vgl. Fourier-Analyse). Während Normalmoden in der klassischen Mechanik wellenartige Phänomene sind, haben Phononen auch teilchenartige Eigenschaften, was mit dem Welle-Teilchen-Dualismus der Quantenmechanik zusammenhängt. ⓘ
Gitterdynamik
Die Gleichungen in diesem Abschnitt verwenden keine Axiome der Quantenmechanik, sondern Beziehungen, für die es eine direkte Entsprechung in der klassischen Mechanik gibt. ⓘ
Ein Beispiel: Ein starres, regelmäßiges, kristallines (nicht amorphes) Gitter besteht aus N Teilchen. Diese Teilchen können Atome oder Moleküle sein. N ist eine große Zahl, etwa in der Größenordnung von 1023, oder in der Größenordnung der Avogadro-Zahl für eine typische Probe eines Festkörpers. Da das Gitter starr ist, müssen die Atome Kräfte aufeinander ausüben, um jedes Atom in der Nähe seiner Gleichgewichtslage zu halten. Bei diesen Kräften kann es sich um Van-der-Waals-Kräfte, kovalente Bindungen, elektrostatische Anziehungskräfte und andere handeln, die letztlich alle auf die elektrische Kraft zurückzuführen sind. Magnetische und Gravitationskräfte sind im Allgemeinen vernachlässigbar. Die Kräfte zwischen den einzelnen Atompaaren lassen sich durch eine potenzielle Energiefunktion V beschreiben, die vom Abstand zwischen den Atomen abhängt. Die potenzielle Energie des gesamten Gitters ist die Summe aller paarweisen potenziellen Energien, multipliziert mit dem Faktor 1/2, um Doppelzählungen auszugleichen:
wobei ri die Position des i-ten Atoms und V die potenzielle Energie zwischen zwei Atomen ist. ⓘ
Es ist schwierig, dieses Vielkörperproblem explizit zu lösen, weder in der klassischen noch in der Quantenmechanik. Um die Aufgabe zu vereinfachen, werden in der Regel zwei wichtige Näherungswerte festgelegt. Erstens: Die Summe wird nur über benachbarte Atome gebildet. Obwohl sich die elektrischen Kräfte in realen Festkörpern bis ins Unendliche erstrecken, ist diese Näherung immer noch gültig, da die von weit entfernten Atomen erzeugten Felder effektiv abgeschirmt werden. Zweitens werden die Potentiale V als harmonische Potentiale behandelt. Dies ist zulässig, solange die Atome in der Nähe ihrer Gleichgewichtslage bleiben. Formal wird dies durch eine Taylor-Erweiterung von V um seinen Gleichgewichtswert zu einer quadratischen Ordnung erreicht, wodurch V proportional zur Verschiebung x2 und die elastische Kraft einfach proportional zu x ist. Der Fehler beim Ignorieren von Termen höherer Ordnung bleibt gering, wenn x nahe an der Gleichgewichtsposition bleibt. ⓘ
Das resultierende Gitter kann als ein System von Kugeln dargestellt werden, die durch Federn verbunden sind. Die folgende Abbildung zeigt ein kubisches Gitter, das ein gutes Modell für viele Arten von kristallinen Festkörpern ist. Zu den anderen Gittern gehört eine lineare Kette, ein sehr einfaches Gitter, das wir in Kürze für die Modellierung von Phononen verwenden werden. (Zu anderen gängigen Gittern siehe Kristallstruktur). ⓘ
Die potenzielle Energie des Gitters kann nun wie folgt geschrieben werden ⓘ
Dabei ist ω die Eigenfrequenz der harmonischen Potentiale, die als gleich angenommen werden, da das Gitter regelmäßig ist. Ri ist die Positionskoordinate des i-ten Atoms, die wir nun von seiner Gleichgewichtsposition aus messen. Die Summe über die nächsten Nachbarn wird als (nn) bezeichnet. ⓘ
Gitterwellen

Aufgrund der Verbindungen zwischen den Atomen führt die Verschiebung eines oder mehrerer Atome aus ihrer Gleichgewichtslage zu einer Reihe von Schwingungswellen, die sich durch das Gitter ausbreiten. Eine solche Welle ist in der Abbildung rechts zu sehen. Die Amplitude der Welle ist durch die Verschiebungen der Atome aus ihren Gleichgewichtspositionen gegeben. Die Wellenlänge λ ist markiert. ⓘ
Es gibt eine minimal mögliche Wellenlänge, die durch das Doppelte des Gleichgewichtsabstands a zwischen den Atomen gegeben ist. Jede Wellenlänge, die kürzer ist als diese, kann aufgrund der Periodizität des Gitters auf eine Wellenlänge abgebildet werden, die länger als 2a ist. Dies kann als eine Folge des Nyquist-Shannon-Abtasttheorems betrachtet werden, wobei die Gitterpunkte als "Abtastpunkte" einer kontinuierlichen Welle angesehen werden. ⓘ
Nicht jede mögliche Gitterschwingung hat eine wohldefinierte Wellenlänge und Frequenz. Die Normalmoden besitzen jedoch wohldefinierte Wellenlängen und Frequenzen. ⓘ
Eindimensionales Gitter

Um die für ein dreidimensionales Atomgitter erforderliche Analyse zu vereinfachen, ist es sinnvoll, ein eindimensionales Gitter oder eine lineare Kette zu modellieren. Dieses Modell ist komplex genug, um die wichtigsten Merkmale von Phononen darzustellen. ⓘ
Klassische Behandlung
Die Kräfte zwischen den Atomen werden als linear und als nächste Nachbarn angenommen und durch eine elastische Feder dargestellt. Jedes Atom wird als Punktteilchen angenommen und der Kern und die Elektronen bewegen sich im Gleichschritt (adiabatischer Satz):
- n - 1 n n + 1 ← a →. ⓘ
···o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o··· ⓘ
- →→ → →→→
- un - 1 un un + 1 ⓘ
Dabei bezeichnet n das n-te Atom von insgesamt N, a ist der Abstand zwischen den Atomen, wenn sich die Kette im Gleichgewicht befindet, und un die Verschiebung des n-ten Atoms aus seiner Gleichgewichtslage. ⓘ
Wenn C die Elastizitätskonstante der Feder und m die Masse des Atoms ist, dann lautet die Bewegungsgleichung des n-ten Atoms ⓘ
Es handelt sich um eine Reihe von gekoppelten Gleichungen. ⓘ
Da zu erwarten ist, dass die Lösungen oszillieren, werden neue Koordinaten durch eine diskrete Fourier-Transformation definiert, um sie zu entkoppeln. ⓘ
Setzen Sie ⓘ
Hier entspricht na der kontinuierlichen Variablen x der Skalarfeldtheorie und entwickelt sich zu dieser. Die Qk werden als Normalkoordinaten bezeichnet, Kontinuumsfeldmoden φk. ⓘ
Die Substitution in die Bewegungsgleichung ergibt die folgenden entkoppelten Gleichungen (dies erfordert eine erhebliche Manipulation unter Verwendung der Orthonormalitäts- und Vollständigkeitsbeziehungen der diskreten Fourier-Transformation), ⓘ
- Dies sind die Gleichungen für entkoppelte harmonische Oszillatoren, die die folgende Lösung haben
- ⓘ
Jede Normalkoordinate Qk steht für eine unabhängige Schwingungsmode des Gitters mit der Wellenzahl k, die als Normalmode bezeichnet wird. ⓘ
Die zweite Gleichung für ωk ist als Dispersionsbeziehung zwischen der Kreisfrequenz und der Wellenzahl bekannt. ⓘ
Im Kontinuumslimit ist a→0, N→∞, wobei Na fest gehalten wird, un → φ(x), ein skalares Feld, und . Dies entspricht der klassischen freien Skalarfeldtheorie, einer Anordnung unabhängiger Oszillatoren. ⓘ
Quantenmechanische Behandlung
Eine eindimensionale quantenmechanische harmonische Kette besteht aus N identischen Atomen. Dies ist das einfachste quantenmechanische Modell eines Gitters, aus dem Phononen entstehen können. Der Formalismus für dieses Modell ist leicht auf zwei und drei Dimensionen verallgemeinerbar. ⓘ
Im Gegensatz zum vorigen Abschnitt werden die Positionen der Massen nicht mit ui bezeichnet, sondern mit x1, x2..., gemessen von ihren Gleichgewichtspositionen (d. h. xi = 0, wenn sich das Teilchen i in seiner Gleichgewichtsposition befindet). In zwei oder mehr Dimensionen sind die xi Vektorgrößen. Der Hamiltonian für dieses System lautet ⓘ
wobei m die Masse eines jeden Atoms ist (unter der Annahme, dass sie für alle gleich ist), und xi und pi die Positions- bzw. Impulsoperatoren für das i-te Atom sind und die Summe über die nächsten Nachbarn (nn) gebildet wird. Man erwartet jedoch, dass in einem Gitter auch Wellen auftreten können, die sich wie Teilchen verhalten. Es ist üblich, Wellen im Fourier-Raum zu behandeln, der die Normalmoden des Wellenvektors als Variablen anstelle der Koordinaten der Teilchen verwendet. Die Anzahl der Normalmoden ist gleich der Anzahl der Teilchen. Der Fourier-Raum ist jedoch angesichts der Periodizität des Systems sehr nützlich. ⓘ
Es kann ein Satz von N "Normalkoordinaten" Qk eingeführt werden, die als diskrete Fourier-Transformationen von xk definiert sind, und N "konjugierte Momente" Πk, die als Fourier-Transformationen von pk definiert sind:
Die Größe kn erweist sich als die Wellenzahl des Phonons, d. h. 2π geteilt durch die Wellenlänge. ⓘ
Durch diese Wahl bleiben die gewünschten Kommutationsbeziehungen sowohl im reellen Raum als auch im Wellenvektorraum erhalten ⓘ
Aus dem allgemeinen Ergebnis ⓘ
Der Term der potentiellen Energie ist ⓘ
wobei ⓘ
Der Hamiltonian kann im Wellenvektorraum geschrieben werden als ⓘ
Die Kopplungen zwischen den Positionsvariablen wurden wegtransformiert; wären Q und Π hermitesch (was sie nicht sind), würde der transformierte Hamiltonian N ungekoppelte harmonische Oszillatoren beschreiben. ⓘ
Die Form der Quantisierung hängt von der Wahl der Randbedingungen ab; der Einfachheit halber werden periodische Randbedingungen eingeführt, die das (N + 1)-te Atom als äquivalent zum ersten Atom definieren. Physikalisch entspricht dies der Verbindung der Kette an ihren Enden. Die resultierende Quantisierung ist ⓘ
Die obere Grenze für n ergibt sich aus der minimalen Wellenlänge, die, wie oben erläutert, das Doppelte des Gitterabstands a beträgt. ⓘ
Die Eigenwerte oder Energieniveaus des harmonischen Oszillators für den Modus ωk sind:
Die Niveaus sind gleichmäßig verteilt bei:
wobei 1/2ħω die Nullpunktenergie eines quantenharmonischen Oszillators ist. ⓘ
Dem Gitter des harmonischen Oszillators muss eine exakte Menge an Energie ħω zugeführt werden, um ihn auf das nächste Energieniveau zu bringen. Im Vergleich zum Fall des Photons, bei dem das elektromagnetische Feld quantisiert ist, wird das Quant der Schwingungsenergie als Phonon bezeichnet. ⓘ
Alle Quantensysteme weisen gleichzeitig wellenartige und teilchenartige Eigenschaften auf. Die teilchenartigen Eigenschaften des Phonons lassen sich am besten mit den später beschriebenen Methoden der zweiten Quantisierung und der Operatortechniken verstehen. ⓘ
Dreidimensionales Gitter
Dies kann auf ein dreidimensionales Gitter verallgemeinert werden. Die Wellenzahl k wird durch einen dreidimensionalen Wellenvektor k ersetzt. Außerdem ist jedes k jetzt mit drei Normalkoordinaten verbunden. ⓘ
Die neuen Indizes s = 1, 2, 3 bezeichnen die Polarisation der Phononen. Im eindimensionalen Modell konnten sich die Atome nur entlang der Linie bewegen, so dass die Phononen den Longitudinalwellen entsprachen. In drei Dimensionen sind die Schwingungen nicht auf die Ausbreitungsrichtung beschränkt, sondern können auch in den senkrechten Ebenen auftreten, wie Transversalwellen. Daraus ergeben sich die zusätzlichen Normalkoordinaten, die wir, wie die Form der Hamiltonschen Beziehung zeigt, als unabhängige Phononenarten betrachten können. ⓘ
Ausbreitungsverhältnis



Für eine eindimensionale alternierende Anordnung von zwei Arten von Ionen oder Atomen der Masse m1, m2, die sich periodisch in einem Abstand a wiederholen und durch Federn der Federkonstante K verbunden sind, ergeben sich zwei Schwingungsmoden:
Dabei ist k der Wellenvektor der Schwingung, der mit der Wellenlänge durch . ⓘ
Der Zusammenhang zwischen Frequenz und Wellenvektor, ω = ω(k), wird als Dispersionsrelation bezeichnet. Das Pluszeichen ergibt den sogenannten optischen Modus, das Minuszeichen den akustischen Modus. Im optischen Modus bewegen sich zwei benachbarte unterschiedliche Atome gegeneinander, während sie sich im akustischen Modus gemeinsam bewegen. ⓘ
Die Ausbreitungsgeschwindigkeit eines akustischen Phonons, die auch die Schallgeschwindigkeit im Gitter ist, wird durch die Steigung der akustischen Dispersionsrelation ∂ωk/∂k bestimmt (siehe Gruppengeschwindigkeit). Bei niedrigen Werten von k (d. h. bei großen Wellenlängen) ist die Dispersionsrelation nahezu linear, und die Schallgeschwindigkeit beträgt ungefähr ωa, unabhängig von der Phononfrequenz. Infolgedessen können sich Phononenpakete mit unterschiedlichen (aber langen) Wellenlängen über große Entfernungen durch das Gitter ausbreiten, ohne auseinanderzubrechen. Dies ist der Grund dafür, dass sich Schall ohne nennenswerte Verzerrung durch Festkörper ausbreitet. Dieses Verhalten versagt bei großen Werten von k, d. h. bei kurzen Wellenlängen, aufgrund der mikroskopischen Details des Gitters. ⓘ
Für einen Kristall mit mindestens zwei Atomen in seiner Urzelle weisen die Dispersionsbeziehungen zwei Arten von Phononen auf, nämlich optische und akustische Moden, die der oberen blauen bzw. unteren roten Kurve im Diagramm entsprechen. Die vertikale Achse ist die Energie oder Frequenz des Phonons, während die horizontale Achse der Wellenvektor ist. Die Grenzen bei -π/a und π/a sind die Grenzen der ersten Brillouin-Zone. Ein Kristall mit N ≥ 2 verschiedenen Atomen in der Urzelle weist drei akustische Moden auf: eine longitudinale akustische Mode und zwei transversale akustische Moden. Die Anzahl der optischen Moden beträgt 3N - 3. Die untere Abbildung zeigt die Dispersionsbeziehungen für mehrere Phononenmoden in GaAs als Funktion des Wellenvektors k in den Hauptrichtungen der Brillouin-Zone. ⓘ
Viele Phononendispersionskurven wurden durch inelastische Neutronenstreuung gemessen. ⓘ
Die Physik des Schalls in Flüssigkeiten unterscheidet sich von der Physik des Schalls in Festkörpern, obwohl es sich in beiden Fällen um Dichtewellen handelt: Schallwellen in Flüssigkeiten haben nur longitudinale Komponenten, während Schallwellen in Festkörpern longitudinale und transversale Komponenten haben. Dies liegt daran, dass Flüssigkeiten keine Scherspannungen aufnehmen können (siehe jedoch viskoelastische Flüssigkeiten, die nur für hohe Frequenzen gelten). ⓘ
- , ⓘ
Für niedrige Werte von lautet der Ausdruck näherungsweise ⓘ
- . ⓘ
ist die Schallgeschwindigkeit. An den Zonengrenzen gilt ⓘ
Die Gruppengeschwindigkeit, also die Geschwindigkeit des Energietransports im Medium, ergibt sich zu ⓘ
- . ⓘ
Interpretation von Phononen mit Hilfe von Techniken der zweiten Quantisierung
Der oben abgeleitete Hamiltonian mag wie eine klassische Hamiltonfunktion aussehen, aber wenn er als Operator interpretiert wird, beschreibt er eine Quantenfeldtheorie von nicht wechselwirkenden Bosonen. Die zweite Quantisierungstechnik, die der Leiteroperator-Methode ähnelt, die für harmonische Quantenoszillatoren verwendet wird, ist ein Mittel zur Extraktion von Energieeigenwerten ohne direkte Lösung der Differentialgleichungen. Gegeben sei der Hamiltonian, sowie die konjugierte Position, und konjugierter Impuls die im obigen Abschnitt zur Quantenbehandlung definiert wurden, können wir Erzeugungs- und Vernichtungsoperatoren definieren:
- und ⓘ
Die folgenden Kommutatoren lassen sich durch Einsetzen der kanonischen Kommutationsbeziehung leicht ermitteln:
Auf diese Weise können die Operatoren bk† und bk invertiert werden, um die konjugierte Position und den konjugierten Impuls neu zu definieren:
- und ⓘ
Durch direkte Substitution dieser Definitionen für und in den Wellenvektorraum-Hamiltonian, wie er oben definiert ist, und vereinfacht, ergibt sich der Hamiltonian in der Form:
Dies ist die zweite Quantisierungstechnik, auch bekannt als Besetzungszahlformulierung, wobei nk = bk†bk die Besetzungszahl ist. Dies kann als eine Summe von N unabhängigen Oszillator-Hamiltonianen gesehen werden, jeder mit einem eindeutigen Wellenvektor, und ist mit den Methoden kompatibel, die für den harmonischen Quantenoszillator verwendet werden (beachten Sie, dass nk hermitisch ist). Wenn ein Hamiltonian als Summe von kommutierenden Sub-Hamiltonians geschrieben werden kann, sind die Energieeigenzustände durch die Produkte der Eigenzustände der einzelnen Sub-Hamiltonians gegeben. Das entsprechende Energiespektrum ist dann durch die Summe der einzelnen Eigenwerte der Sub-Hamiltonianer gegeben. ⓘ
Wie beim quantenharmonischen Oszillator kann man zeigen, dass bk† und bk eine einzige Feldanregung, ein Phonon, mit einer Energie von ħωk erzeugen bzw. zerstören. ⓘ
Drei wichtige Eigenschaften von Phononen lassen sich aus dieser Technik ableiten. Erstens sind Phononen Bosonen, da durch wiederholte Anwendung des Erzeugungsoperators bk† eine beliebige Anzahl identischer Anregungen erzeugt werden kann. Zweitens ist jedes Phonon ein "kollektiver Modus", der durch die Bewegung jedes Atoms im Gitter verursacht wird. Dies geht aus der Tatsache hervor, dass die Erzeugungs- und Vernichtungsoperatoren, die hier im Impulsraum definiert sind, Summen über die Positions- und Impulsoperatoren jedes Atoms enthalten, wenn sie im Positionsraum geschrieben werden (siehe Positions- und Impulsraum). Schließlich lässt sich anhand der Positions-Positions-Korrelationsfunktion zeigen, dass Phononen als Wellen der Gitterverschiebung wirken. ⓘ
Diese Technik lässt sich leicht auf drei Dimensionen verallgemeinern, wo der Hamiltonian die Form annimmt:
Diese kann als Summe von 3N unabhängigen Oszillator-Hamiltonianen interpretiert werden, eine für jeden Wellenvektor und jede Polarisation. ⓘ
Akustische und optische Phononen
Festkörper mit mehr als einem Atom in der kleinsten Einheitszelle weisen zwei Arten von Phononen auf: akustische Phononen und optische Phononen. ⓘ
Akustische Phononen sind kohärente Bewegungen von Atomen des Gitters aus ihrer Gleichgewichtslage heraus. Erfolgt die Verschiebung in Ausbreitungsrichtung, so liegen die Atome in einigen Bereichen näher beieinander, in anderen weiter auseinander, wie bei einer Schallwelle in Luft (daher der Name akustisch). Eine Verschiebung senkrecht zur Ausbreitungsrichtung ist vergleichbar mit Wellen auf einer Saite. Wenn die Wellenlänge der akustischen Phononen ins Unendliche geht, entspricht dies einer einfachen Verschiebung des gesamten Kristalls, und diese kostet null Verformungsenergie. Akustische Phononen weisen eine lineare Beziehung zwischen Frequenz und Phononwellenvektor für große Wellenlängen auf. Die Frequenzen der akustischen Phononen tendieren bei größeren Wellenlängen gegen Null. Akustische Längs- und Querphononen werden häufig als LA- bzw. TA-Phononen abgekürzt. ⓘ
Optische Phononen sind phasenverschobene Bewegungen der Atome im Gitter, wobei sich ein Atom nach links und sein Nachbar nach rechts bewegt. Dies geschieht, wenn die Gitterbasis aus zwei oder mehr Atomen besteht. Sie werden als optisch bezeichnet, weil in ionischen Kristallen, wie z. B. Natriumchlorid, Verschiebungsschwankungen eine elektrische Polarisation erzeugen, die an das elektromagnetische Feld koppelt. Daher können sie durch Infrarotstrahlung angeregt werden, wobei das elektrische Feld des Lichts jedes positive Natrium-Ion in Richtung des Feldes und jedes negative Chlorid-Ion in die andere Richtung bewegt, wodurch der Kristall in Schwingung versetzt wird. ⓘ
Optische Phononen haben eine Frequenz ungleich Null in der Mitte der Brillouin-Zone und zeigen keine Dispersion in der Nähe dieser langwelligen Grenze. Das liegt daran, dass sie einem Schwingungsmodus entsprechen, bei dem positive und negative Ionen an benachbarten Gitterplätzen gegeneinander schwingen und ein zeitlich veränderliches elektrisches Dipolmoment erzeugen. Optische Phononen, die auf diese Weise mit Licht wechselwirken, werden als infrarotaktiv bezeichnet. Optische Phononen, die Raman-aktiv sind, können auch indirekt mit Licht wechselwirken, nämlich durch Raman-Streuung. Optische Phononen werden oft als LO- und TO-Phononen abgekürzt, für die longitudinalen bzw. transversalen Moden; die Aufteilung zwischen LO- und TO-Frequenzen wird oft durch die Lyddane-Sachs-Teller-Beziehung genau beschrieben. ⓘ
Bei der experimentellen Messung der optischen Phononenenergie werden die optischen Phononenfrequenzen manchmal in der spektroskopischen Wellenzahlnotation angegeben, wobei das Symbol ω für die gewöhnliche Frequenz (nicht die Winkelfrequenz) steht und in cm-1 ausgedrückt wird. Den Wert erhält man, indem man die Frequenz durch die Lichtgeschwindigkeit im Vakuum dividiert. Mit anderen Worten: Die Wellenzahl in der Einheit cm-1 entspricht dem Kehrwert der Wellenlänge eines Photons im Vakuum, das die gleiche Frequenz wie das gemessene Phonon hat. ⓘ
Kristallimpuls

In Analogie zu Photonen und Materiewellen wurden Phononen mit dem Wellenvektor k so behandelt, als ob er einen Impuls ħk hätte; dies ist jedoch nicht ganz korrekt, denn ħk ist eigentlich kein physikalischer Impuls; er wird als Kristallimpuls oder Pseudomoment bezeichnet. Dies liegt daran, dass k nur bis zur Addition von konstanten Vektoren (den reziproken Gittervektoren und ganzzahligen Vielfachen davon) bestimmt wird. Im eindimensionalen Modell sind zum Beispiel die Normalkoordinaten Q und Π so definiert, dass ⓘ
wobei ⓘ
für jede ganze Zahl n. Ein Phonon mit der Wellenzahl k entspricht somit einer unendlichen Familie von Phononen mit den Wellenzahlen k ± 2π/a, k ± 4π/a usw. Physikalisch gesehen wirken die reziproken Gittervektoren wie zusätzliche Impulsstücke, die das Gitter dem Phonon verleihen kann. Für Bloch-Elektronen gelten ähnliche Einschränkungen. ⓘ

In der Regel ist es sinnvoll, die Phononwellenvektoren k zu betrachten, die den kleinsten Betrag |k| in ihrer "Familie" haben. Die Menge aller solcher Wellenvektoren definiert die erste Brillouin-Zone. Weitere Brillouin-Zonen können als Kopien der ersten Zone definiert werden, die um einen reziproken Gittervektor verschoben sind. ⓘ
Thermodynamik
Die thermodynamischen Eigenschaften eines Festkörpers stehen in direktem Zusammenhang mit seiner Phononenstruktur. Die Gesamtheit aller möglichen Phononen, die durch die Phononendispersionsbeziehungen beschrieben werden, bilden die so genannte Phononendichte, die die Wärmekapazität eines Kristalls bestimmt. Es liegt in der Natur dieser Verteilung, dass die Wärmekapazität durch den hochfrequenten Teil der Verteilung dominiert wird, während die Wärmeleitfähigkeit in erster Linie das Ergebnis des niederfrequenten Bereichs ist. ⓘ
Bei absoluter Nulltemperatur befindet sich ein Kristallgitter in seinem Grundzustand und enthält keine Phononen. Ein Gitter mit einer Temperatur ungleich Null hat eine Energie, die nicht konstant ist, sondern zufällig um einen Mittelwert schwankt. Diese Energieschwankungen werden durch zufällige Gitterschwingungen verursacht, die als Phononengas betrachtet werden können. Da diese Phononen durch die Temperatur des Gitters erzeugt werden, werden sie manchmal als thermische Phononen bezeichnet. ⓘ
Thermische Phononen können durch zufällige Energiefluktuationen erzeugt und zerstört werden. In der Sprache der statistischen Mechanik bedeutet dies, dass das chemische Potenzial für das Hinzufügen eines Phonons gleich Null ist. Dieses Verhalten ist eine Erweiterung des harmonischen Potenzials in den anharmonischen Bereich. Das Verhalten thermischer Phononen ähnelt dem von einem elektromagnetischen Hohlraum erzeugten Photonengas, in dem Photonen von den Hohlraumwänden emittiert oder absorbiert werden können. Diese Ähnlichkeit ist nicht zufällig, denn es stellt sich heraus, dass sich das elektromagnetische Feld wie eine Reihe von harmonischen Oszillatoren verhält, was zu Schwarzer-Körper-Strahlung führt. Beide Gase gehorchen der Bose-Einstein-Statistik: Im thermischen Gleichgewicht und innerhalb des harmonischen Regimes ist die Wahrscheinlichkeit, Phononen oder Photonen in einem bestimmten Zustand mit einer bestimmten Winkelfrequenz zu finden, gleich:
wobei ωk,s die Frequenz der Phononen (oder Photonen) in dem Zustand, kB die Boltzmann-Konstante und T die Temperatur ist. ⓘ
Phononentunnelung
Phononen zeigen nachweislich das Verhalten des Quantentunnelns (oder Phononentunnelns), bei dem über Lücken von bis zu einem Nanometer Breite Wärme über Phononen fließen kann, die zwischen zwei Materialien "tunneln". Diese Art der Wärmeübertragung funktioniert über Entfernungen, die zu groß sind, um Wärmeleitung zu ermöglichen, aber zu klein, um Strahlung zuzulassen, und kann daher nicht durch klassische Wärmeübertragungsmodelle erklärt werden. ⓘ
Operator-Formalismus
Der Phonon-Hamiltonian ist gegeben durch ⓘ
In Bezug auf die Erzeugungs- und Vernichtungsoperatoren sind diese gegeben durch ⓘ
Bei der Darstellung der Hamiltonfunktion im Operatorformalismus haben wir den 1/2ħωq-Term nicht berücksichtigt, da sich die 1/2ħωq-Terme bei einem Kontinuum oder einem unendlichen Gitter zu einem unendlichen Term addieren würden. Daher wird er "renormiert", indem der Faktor 1/2ħωq auf 0 gesetzt wird, mit dem Argument, dass der Energieunterschied das ist, was wir messen, und nicht der absolute Wert davon. Daher fehlt der Faktor 1/2ħωq im formalisierten Ausdruck des Operators für den Hamiltonian. ⓘ
Der Grundzustand, auch "Vakuumzustand" genannt, ist der Zustand, in dem es keine Phononen gibt. Daher ist die Energie des Grundzustands 0. Befindet sich ein System im Zustand |n1n2n3...⟩, so gibt es nα Phononen vom Typ α, wobei nα die Besetzungszahl der Phononen ist. Die Energie eines einzelnen Phonons vom Typ α ist gegeben durch ħωq und die Gesamtenergie eines allgemeinen Phononensystems ist gegeben durch n1ħω1 + n2ħω2 +.... Da es keine Querterme gibt (z. B. n1ħω2), werden die Phononen als nicht wechselwirkend bezeichnet. Die Wirkung der Erzeugungs- und Annihilationsoperatoren ist gegeben durch:
und, ⓘ
Der Erzeugungsoperator aα† erzeugt ein Phonon vom Typ α, während aα ein Phonon annihiliert. Sie sind also die Erzeugungs- bzw. Vernichtungsoperatoren für Phononen. Analog zum Fall des quantenharmonischen Oszillators können wir den Teilchenzahloperator wie folgt definieren ⓘ
Der Zahlenoperator pendelt mit einer Kette von Produkten der Erzeugungs- und Vernichtungsoperatoren nur dann, wenn die Anzahl der Erzeugungsoperatoren gleich der Anzahl der Vernichtungsoperatoren ist. ⓘ
Es kann gezeigt werden, dass Phononen unter Austausch symmetrisch sind (d.h. |α,β⟩ = |β,α⟩), so dass sie als Bosonen betrachtet werden. ⓘ
Nichtlinearität
Ebenso wie Photonen können auch Phononen über parametrische Abwärtskonversion wechselwirken und gequetschte kohärente Zustände bilden. ⓘ
Vorausgesagte Eigenschaften
Jüngste Forschungsarbeiten haben gezeigt, dass Phononen und Rotonen eine nicht zu vernachlässigende Masse haben und von der Schwerkraft genauso beeinflusst werden können wie normale Teilchen. Insbesondere wird vorhergesagt, dass Phononen eine Art negative Masse und negative Schwerkraft haben. Dies lässt sich dadurch erklären, dass sich Phononen in dichteren Materialien bekanntermaßen schneller bewegen. Da der Teil eines Materials, der in Richtung einer Gravitationsquelle zeigt, näher am Objekt ist, wird er an diesem Ende dichter. Daraus lässt sich ableiten, dass die Phononen abgelenkt werden, wenn sie den Dichteunterschied bemerken, was die Eigenschaften eines negativen Gravitationsfeldes zeigt. Obwohl der Effekt zu gering wäre, um ihn zu messen, ist es möglich, dass zukünftige Geräte zu erfolgreichen Ergebnissen führen könnten. ⓘ
Phononen wird auch eine Schlüsselrolle bei der Supraleitung in Materialien und der Vorhersage von supraleitenden Verbindungen zugeschrieben. ⓘ
2019 gelang es Forschern erstmals, einzelne Phononen zu isolieren, ohne sie zu zerstören. ⓘ
Nachweis
Die Phononendispersion, d. h. der Zusammenhang zwischen Energie und Impuls der Gitterschwingungen, kann durch die inelastische Neutronenstreuung, die inelastische Röntgenstreuung sowie durch die hochauflösende Elektronenenergieverlustspektroskopie (HREELS) untersucht werden. Phononen mit kleinem Impuls, d. h. im Zentrum der Brillouin-Zone, können durch Raman-, Infrarot-Spektroskopie oder Brillouin-Streuung nachgewiesen werden. Die erste Phononen-Dispersionskurve wurde 1955 am Chalk River Reaktor von Bertram Brockhouse mit Neutronenstreuung an einem Aluminiumeinkristall aufgenommen. ⓘ
Dispersion
Die Dispersionsrelation gibt die Abhängigkeit der Energie bzw. Kreisfrequenz vom Impuls bzw. Wellenzahl an. Bei Phononen ergibt sich diese Beziehung aus der Newtonschen Bewegungsgleichung. Dazu nimmt man an, dass sich die Atome in einem periodischen Potential befinden, in dem sie Schwingungen ausführen. ⓘ
Zwei benachbarte Atome haben einen Phasenunterschied von , wobei der Abstand zweier benachbarter Atome in der Ruhelage ist. Ein Phasenunterschied von entspricht einem von Null; höhere Phasenunterschiede sind dementsprechend äquivalent mit einem Wert zwischen und . Aus Symmetriegründen betrachtet man das Intervall zwischen und . Das entspricht -Werten aus der ersten Brillouin-Zone, also . Dadurch hat man alle physikalisch relevanten Wellenzahlen abgedeckt. ⓘ

