Gas

Driftende Rauchpartikel zeigen die Bewegung des umgebenden Gases an. ⓘ

Gas ist einer der vier Grundzustände der Materie (die anderen sind fest, flüssig und plasmatisch). ⓘ

Ein reines Gas kann aus einzelnen Atomen bestehen (z. B. ein Edelgas wie Neon), aus elementaren Molekülen, die aus einer Art von Atom bestehen (z. B. Sauerstoff), oder aus zusammengesetzten Molekülen, die aus einer Vielzahl von Atomen bestehen (z. B. Kohlendioxid). Ein Gasgemisch, wie z. B. Luft, enthält eine Vielzahl von reinen Gasen. Was ein Gas von Flüssigkeiten und Feststoffen unterscheidet, ist die weitgehende Trennung der einzelnen Gasteilchen. Durch diese Trennung wird ein farbloses Gas für den menschlichen Beobachter normalerweise unsichtbar. ⓘ

Der gasförmige Zustand der Materie liegt zwischen dem flüssigen und dem Plasmazustand, wobei letzterer die obere Temperaturgrenze für Gase darstellt. Am unteren Ende der Temperaturskala liegen degenerative Quantengase, die immer mehr Aufmerksamkeit erregen. Atomare Gase mit hoher Dichte, die auf sehr tiefe Temperaturen unterkühlt sind, werden aufgrund ihres statistischen Verhaltens entweder als Bose-Gase oder als Fermi-Gase klassifiziert. Eine umfassende Auflistung dieser exotischen Materiezustände finden Sie unter Liste der Materiezustände. ⓘ

Teilchenmodell eines Gases ⓘ

Neben fest und flüssig ist gasförmig einer der drei klassischen Aggregatzustände. Eine Substanz ist dann ein Gas, wenn sich ihre Teilchen in großem Abstand voneinander frei bewegen und den verfügbaren Raum kontinuierlich ausfüllen. Unter Normalbedingungen nimmt ein Gas im Vergleich zu einem Festkörper oder einer Flüssigkeit gleicher Masse den rund tausend- bis zweitausendfachen Raum ein. ⓘ

Zusammen mit den Flüssigkeiten zählen Gase zu den Fluiden. ⓘ

Elementare Gase

Die einzigen chemischen Elemente, die bei STP als zweiatomige homonukleare Moleküle stabil sind, sind Wasserstoff (H₂), Stickstoff (N₂), Sauerstoff (O₂) und zwei Halogene: Fluor (F₂) und Chlor (Cl₂). Zusammen mit den einatomigen Edelgasen - Helium (He), Neon (Ne), Argon (Ar), Krypton (Kr), Xenon (Xe) und Radon (Rn) - werden diese Gase als Elementargase" bezeichnet. ⓘ

Etymologie

Die Herkunft des Wortes Gas war lange Zeit unklar. Zwar war mehr oder weniger bekannt, dass das Wort als Fachbegriff im 17. Jahrhundert durch den flämischen Arzt und Naturforscher Johan Baptista van Helmont († 1644) in Brüssel eingeführt wurde, über die Etymologie bestand jedoch Unsicherheit, und es wurde Herkunft u. a. aus dem Hebräischen, aus niederl. geest („Geist“), aus niederl. gisten („gären“) oder aus deutsch gäsen (bei Paracelsus für „gären“), gäscht („Schaum“ auf gärender Flüssigkeit) vermutet. Die Klärung wurde 1859 durch den Sprachwissenschaftler Matthias de Vries herbeigeführt, der eine Aussage aus van Helmonts Ortus Medicinae (Amsterdam 1648) beibrachte, wonach dieser das Wort speziell für den durch Kälte entstandenen Dunst des Wassers bewusst neugeschaffen und hierbei eine Anlehnung an das griechische, im Niederländischen sehr ähnlich ausgesprochene Wort χάος („Chaos“) bezweckt hatte: „ideo paradoxi licentia, in nominis egestate, halitum illum gas vocavi, non longe a chao veterum secretum“ („In Ermangelung eines Namens habe ich mir die Freiheit zum Ungewöhnlichen genommen, diesen Hauch Gas zu nennen, da er sich vom Chaos der Alten nur wenig unterscheidet.“). ⓘ

Eine andere Geschichte besagt, dass der Begriff von Van Helmont von "gahst (oder geist)" abgeleitet wurde, was so viel wie "Gespenst oder Geist" bedeutet. Diese Geschichte wird von den Herausgebern des Oxford English Dictionary nicht anerkannt. Der französisch-amerikanische Historiker Jacques Barzun vermutet dagegen, dass Van Helmont das Wort aus dem deutschen Gäscht entlehnt hat, was so viel bedeutet wie Schaum, der bei der Gärung entsteht. ⓘ

Physikalische Eigenschaften

Da die meisten Gase nur schwer direkt beobachtet werden können, werden sie mit Hilfe von vier physikalischen Eigenschaften oder makroskopischen Merkmalen beschrieben: Druck, Volumen, Anzahl der Teilchen (die Chemiker gruppieren sie nach Molen) und Temperatur. Diese vier Eigenschaften wurden von Wissenschaftlern wie Robert Boyle, Jacques Charles, John Dalton, Joseph Gay-Lussac und Amedeo Avogadro wiederholt für eine Vielzahl von Gasen in unterschiedlichen Umgebungen beobachtet. Ihre detaillierten Studien führten schließlich zu einer mathematischen Beziehung zwischen diesen Eigenschaften, die durch das ideale Gasgesetz ausgedrückt wird (siehe Abschnitt über vereinfachte Modelle unten). ⓘ

Gaspartikel sind weit voneinander entfernt und haben daher schwächere intermolekulare Bindungen als Flüssigkeiten oder Feststoffe. Diese intermolekularen Kräfte resultieren aus elektrostatischen Wechselwirkungen zwischen den Gasteilchen. Gleich geladene Bereiche verschiedener Gasteilchen stoßen sich ab, während sich entgegengesetzt geladene Bereiche verschiedener Gasteilchen gegenseitig anziehen; Gase, die permanent geladene Ionen enthalten, werden als Plasmen bezeichnet. Gasförmige Verbindungen mit polaren kovalenten Bindungen weisen ein dauerhaftes Ladungsungleichgewicht auf und unterliegen daher relativ starken zwischenmolekularen Kräften, obwohl das Molekül und die Nettoladung der Verbindung neutral bleiben. Zwischen unpolaren kovalenten Bindungen von Molekülen bestehen vorübergehende, zufällig induzierte Ladungen, und die durch sie verursachten elektrostatischen Wechselwirkungen werden als Van-der-Waals-Kräfte bezeichnet. Die Wechselwirkung dieser zwischenmolekularen Kräfte variiert innerhalb einer Substanz, was viele der physikalischen Eigenschaften bestimmt, die für jedes Gas einzigartig sind. Ein Vergleich der Siedepunkte von Verbindungen, die durch ionische und kovalente Bindungen entstehen, führt uns zu dieser Schlussfolgerung. Die schwebenden Rauchpartikel auf dem Bild geben einen Einblick in das Verhalten von Niederdruckgasen. ⓘ

Im Vergleich zu den anderen Aggregatzuständen haben Gase eine geringe Dichte und Viskosität. Druck und Temperatur beeinflussen die Teilchen innerhalb eines bestimmten Volumens. Diese Variation der Teilchentrennung und -geschwindigkeit wird als Kompressibilität bezeichnet. Diese Teilchentrennung und -größe beeinflusst die optischen Eigenschaften von Gasen, wie aus der folgenden Liste der Brechungsindizes hervorgeht. Schließlich breiten sich die Gasteilchen aus oder diffundieren, um sich gleichmäßig in jedem Behälter zu verteilen. ⓘ

Makroskopische Ansicht von Gasen

Shuttle-Bilder der Wiedereintrittsphase ⓘ

Bei der Beobachtung eines Gases ist es üblich, einen Bezugsrahmen oder eine Längenskala anzugeben. Ein größerer Längenmaßstab entspricht einem makroskopischen oder globalen Blickwinkel auf das Gas. Dieser Bereich (als Volumen bezeichnet) muss so groß sein, dass er eine große Stichprobe von Gasteilchen enthält. Die daraus resultierende statistische Analyse dieser Stichprobengröße ergibt das "durchschnittliche" Verhalten (d. h. Geschwindigkeit, Temperatur oder Druck) aller Gasteilchen innerhalb des Bereichs. Im Gegensatz dazu entspricht eine kleinere Längenskala einer mikroskopischen oder partikulären Sichtweise. ⓘ

Makroskopisch werden die Gaseigenschaften entweder in Bezug auf die Gasteilchen selbst (Geschwindigkeit, Druck oder Temperatur) oder in Bezug auf ihre Umgebung (Volumen) gemessen. Robert Boyle beispielsweise beschäftigte sich während eines kleinen Teils seiner Karriere mit der pneumatischen Chemie. Eines seiner Experimente bezog sich auf die makroskopischen Eigenschaften von Druck und Volumen eines Gases. Boyle schloss ein inertes Gas im geschlossenen Ende des Reagenzglases mit einer Quecksilbersäule ein, wodurch die Anzahl der Teilchen und die Temperatur konstant gehalten wurden. Er beobachtete, dass sich das Volumen des eingeschlossenen Gases verringerte, wenn der Druck im Gas durch Hinzufügen von mehr Quecksilber zur Säule erhöht wurde (dies ist als inverse Beziehung bekannt). Wenn Boyle den Druck und das Volumen jeder Beobachtung multiplizierte, war das Produkt konstant. Diese Beziehung galt für jedes Gas, das Boyle beobachtete, was zu dem Gesetz (PV=k) führte, das zu Ehren seiner Arbeit auf diesem Gebiet benannt wurde. ⓘ

Für die Analyse von Gaseigenschaften gibt es viele mathematische Hilfsmittel. Da Gase extremen Bedingungen ausgesetzt sind, werden diese Hilfsmittel immer komplexer, von den Euler-Gleichungen für die nichtviskose Strömung bis hin zu den Navier-Stokes-Gleichungen, die die viskosen Effekte vollständig berücksichtigen. Diese Gleichungen werden an die Bedingungen des jeweiligen Gassystems angepasst. Boyles Laborausrüstung erlaubte die Verwendung von Algebra, um seine analytischen Ergebnisse zu erhalten. Seine Ergebnisse waren möglich, weil er Gase in Situationen mit relativ niedrigem Druck untersuchte, in denen sie sich auf "ideale" Weise verhielten. Diese idealen Beziehungen gelten für Sicherheitsberechnungen für eine Vielzahl von Flugbedingungen auf den verwendeten Materialien. Die heute verwendeten Hightech-Geräte wurden entwickelt, um uns bei der sicheren Erforschung exotischerer Betriebsumgebungen zu helfen, in denen sich die Gase nicht mehr "ideal" verhalten. Diese fortgeschrittene Mathematik, einschließlich Statistik und Multivariablenrechnung, ermöglicht die Lösung solch komplexer dynamischer Situationen wie dem Wiedereintritt von Raumfahrzeugen. Ein Beispiel ist die Analyse des Wiedereintritts der Raumfähre, um sicherzustellen, dass die Materialeigenschaften unter diesen Belastungsbedingungen angemessen sind. In diesem Flugzustand verhält sich das Gas nicht mehr ideal. ⓘ

Druck

Das Symbol zur Darstellung des Drucks in Gleichungen ist "p" oder "P" mit SI-Einheiten in Pascal. ⓘ

Bei der Beschreibung eines Gasbehälters bezieht sich der Begriff Druck (oder Absolutdruck) auf die durchschnittliche Kraft pro Flächeneinheit, die das Gas auf die Oberfläche des Behälters ausübt. Innerhalb dieses Volumens ist es manchmal einfacher, sich die Gasteilchen in geraden Linien zu bewegen, bis sie mit dem Behälter zusammenstoßen (siehe Diagramm am Anfang des Artikels). Die Kraft, die ein Gasteilchen während dieses Zusammenstoßes auf den Behälter ausübt, ist die Änderung des Impulses des Teilchens. Bei einem Zusammenstoß ändert sich nur die Normalkomponente der Geschwindigkeit. Ein Teilchen, das sich parallel zur Wand bewegt, ändert seinen Impuls nicht. Daher muss die durchschnittliche Kraft auf eine Oberfläche die durchschnittliche Änderung des linearen Impulses aus all diesen Gaspartikelkollisionen sein. ⓘ

Der Druck ist die Summe aller Normalkomponenten der Kraft, die von den auf die Wände des Behälters auftreffenden Teilchen ausgeübt wird, geteilt durch den Oberflächenbereich der Wand. ⓘ

Temperatur

Luftballon schrumpft nach Eintauchen in flüssigen Stickstoff ⓘ

Das Symbol zur Darstellung der Temperatur in Gleichungen ist T mit der SI-Einheit Kelvin. ⓘ

Die Geschwindigkeit eines Gasteilchens ist proportional zu seiner absoluten Temperatur. Das Volumen des Ballons im Video schrumpft, wenn sich die Geschwindigkeit der eingeschlossenen Gasteilchen durch die Zugabe von extrem kaltem Stickstoff verringert. Die Temperatur eines jeden physikalischen Systems hängt mit den Bewegungen der Teilchen (Moleküle und Atome) zusammen, aus denen das [Gas-]System besteht. In der statistischen Mechanik ist die Temperatur das Maß für die durchschnittliche kinetische Energie, die in einem Molekül gespeichert ist (auch als thermische Energie bezeichnet). Die Art und Weise, wie diese Energie gespeichert wird, hängt von den Freiheitsgraden des Moleküls selbst ab (Energiemoden). Wird einem Gas oder einer Flüssigkeit thermische (kinetische) Energie zugeführt (ein endothermer Prozess), entstehen Translations-, Rotations- und Vibrationsbewegungen. Im Gegensatz dazu kann ein Festkörper seine innere Energie nur durch die Anregung zusätzlicher Schwingungsmoden erhöhen, da die Kristallgitterstruktur sowohl Translations- als auch Rotationsbewegungen verhindert. Diese erhitzten Gasmoleküle haben einen größeren Geschwindigkeitsbereich (breitere Geschwindigkeitsverteilung) mit einer höheren Durchschnitts- oder Mittelgeschwindigkeit. Die Varianz dieser Verteilung ist darauf zurückzuführen, dass die Geschwindigkeiten der einzelnen Teilchen aufgrund wiederholter Zusammenstöße mit anderen Teilchen ständig variieren. Der Geschwindigkeitsbereich kann durch die Maxwell-Boltzmann-Verteilung beschrieben werden. Die Verwendung dieser Verteilung setzt ideale Gase nahe dem thermodynamischen Gleichgewicht für das betrachtete System von Teilchen voraus. ⓘ

Spezifisches Volumen

Das Symbol, das zur Darstellung des spezifischen Volumens in Gleichungen verwendet wird, ist "v" mit den SI-Einheiten Kubikmeter pro Kilogramm. ⓘ

Das Symbol zur Darstellung des Volumens in Gleichungen ist "V" mit SI-Einheiten von Kubikmetern. ⓘ

Bei der Durchführung einer thermodynamischen Analyse ist es üblich, von intensiven und extensiven Eigenschaften zu sprechen. Eigenschaften, die von der Gasmenge abhängen (entweder von der Masse oder vom Volumen), werden als extensive Eigenschaften bezeichnet, während Eigenschaften, die nicht von der Gasmenge abhängen, als intensive Eigenschaften bezeichnet werden. Das spezifische Volumen ist ein Beispiel für eine intensive Eigenschaft, denn es ist das Verhältnis des Volumens, das von einer Masseneinheit eines Gases eingenommen wird, das in einem System im Gleichgewicht identisch ist. 1000 Atome eines Gases nehmen bei einer gegebenen Temperatur und einem gegebenen Druck den gleichen Raum ein wie alle anderen 1000 Atome. Dieses Konzept ist bei Festkörpern wie Eisen, die im Vergleich zu Gasen inkompressibel sind, leichter zu veranschaulichen. Allerdings ist das Volumen selbst --- nicht spezifisch --- eine umfassende Eigenschaft. ⓘ

Dichte

Das Symbol zur Darstellung der Dichte in Gleichungen ist ρ (rho) mit den SI-Einheiten Kilogramm pro Kubikmeter. Dieser Term ist der Kehrwert des spezifischen Volumens. ⓘ

Da sich Gasmoleküle innerhalb eines Behälters frei bewegen können, wird ihre Masse normalerweise durch die Dichte charakterisiert. Die Dichte ist die Menge der Masse pro Volumeneinheit eines Stoffes oder der Kehrwert des spezifischen Volumens. Bei Gasen kann die Dichte in einem weiten Bereich variieren, da sich die Teilchen frei bewegen können, wenn sie durch Druck oder Volumen eingeschränkt werden. Diese Schwankung der Dichte wird als Kompressibilität bezeichnet. Wie Druck und Temperatur ist auch die Dichte eine Zustandsvariable eines Gases, und die Änderung der Dichte während eines Prozesses unterliegt den Gesetzen der Thermodynamik. Bei einem statischen Gas ist die Dichte im gesamten Behälter gleich. Die Dichte ist daher eine skalare Größe. Mit Hilfe der kinetischen Theorie lässt sich zeigen, dass die Dichte umgekehrt proportional zur Größe des Behälters ist, in dem sich eine feste Masse von Gas befindet. In diesem Fall einer festen Masse nimmt die Dichte mit zunehmendem Volumen ab. ⓘ

Mikroskopische Betrachtung von Gasen

Die Teilchen der Gasphase (Atome, Moleküle oder Ionen) bewegen sich frei, wenn kein elektrisches Feld angelegt ist.

Wenn man ein Gas unter einem leistungsstarken Mikroskop beobachten könnte, würde man eine Ansammlung von Teilchen ohne bestimmte Form oder Volumen sehen, die sich mehr oder weniger zufällig bewegen. Diese Gasteilchen ändern ihre Richtung nur, wenn sie mit einem anderen Teilchen oder mit den Seiten des Behälters zusammenstoßen. Diese mikroskopische Sicht des Gases wird durch die statistische Mechanik gut beschrieben, kann aber durch viele verschiedene Theorien beschrieben werden. Die kinetische Theorie der Gase, die davon ausgeht, dass diese Zusammenstöße vollkommen elastisch sind, berücksichtigt nicht die intermolekularen Anziehungs- und Abstoßungskräfte. ⓘ

Kinetische Theorie der Gase

Die kinetische Theorie gibt Aufschluss über die makroskopischen Eigenschaften von Gasen, indem sie deren molekulare Zusammensetzung und Bewegung berücksichtigt. Ausgehend von den Definitionen von Impuls und kinetischer Energie kann man die Impulserhaltung und die geometrischen Beziehungen eines Würfels nutzen, um makroskopische Systemeigenschaften wie Temperatur und Druck mit der mikroskopischen Eigenschaft der kinetischen Energie pro Molekül in Beziehung zu setzen. Die Theorie liefert gemittelte Werte für diese beiden Eigenschaften. ⓘ

Mit Hilfe der kinetischen Theorie der Gase lässt sich erklären, wie das System (die betrachtete Ansammlung von Gasteilchen) auf Temperaturänderungen mit einer entsprechenden Änderung der kinetischen Energie reagiert. ⓘ

Ein Beispiel: Stellen Sie sich vor, Sie haben einen versiegelten Behälter mit einer festen Größe (einem konstanten Volumen), der eine feste Anzahl von Gasteilchen enthält; ausgehend vom absoluten Nullpunkt (der theoretischen Temperatur, bei der Atome oder Moleküle keine thermische Energie haben, d. h. sich nicht bewegen oder vibrieren), beginnen Sie, dem System Energie zuzuführen, indem Sie den Behälter erhitzen, so dass Energie auf die Teilchen im Inneren übertragen wird. Sobald ihre innere Energie über der Nullpunktenergie liegt, d. h. ihre kinetische Energie (auch als thermische Energie bezeichnet) ungleich Null ist, beginnen sich die Gasteilchen im Behälter zu bewegen. Wenn der Behälter weiter erhitzt wird (wenn mehr Energie zugeführt wird), erhöhen die einzelnen Teilchen ihre Durchschnittsgeschwindigkeit, da die gesamte innere Energie des Systems zunimmt. Die höhere Durchschnittsgeschwindigkeit aller Teilchen führt zu einer höheren Kollisionsrate (d. h. einer größeren Anzahl von Kollisionen pro Zeiteinheit), sowohl zwischen den Teilchen und dem Behälter als auch zwischen den Teilchen selbst. ⓘ

Die makroskopische, messbare Größe des Drucks ist das direkte Ergebnis dieser mikroskopischen Teilchenkollisionen mit der Oberfläche, über die einzelne Moleküle eine kleine Kraft ausüben, von denen jedes zur Gesamtkraft beiträgt, die auf einen bestimmten Bereich wirkt. (Lesen Sie "Druck" im obigen Abschnitt "Makroskopische Betrachtung von Gasen"). ⓘ

Ebenso ist die makroskopisch messbare Größe Temperatur eine Quantifizierung des Gesamtbetrags der Bewegung oder der kinetischen Energie, die die Teilchen aufweisen. (Lesen Sie "Temperatur" im obigen Abschnitt "Makroskopische Betrachtung von Gasen"). ⓘ

Thermische Bewegung und statistische Mechanik

In der kinetischen Theorie der Gase wird davon ausgegangen, dass die kinetische Energie lediglich aus linearen Translationen entsprechend einer Geschwindigkeitsverteilung der Teilchen im System besteht. In realen Gasen und anderen realen Stoffen sind die Bewegungen, die die kinetische Energie eines Systems definieren (und die insgesamt die Temperatur bestimmen), jedoch aufgrund der komplexeren Struktur von Molekülen im Vergleich zu einzelnen Atomen, die sich ähnlich wie Punktmassen verhalten, viel komplexer als einfache lineare Translationen. In realen thermodynamischen Systemen spielen Quantenphänomene eine große Rolle bei der Bestimmung thermischer Bewegungen. Die zufälligen, thermischen Bewegungen (kinetische Energie) in Molekülen sind eine Kombination aus einer endlichen Anzahl möglicher Bewegungen, einschließlich Translation, Rotation und Vibration. Dieser endliche Bereich möglicher Bewegungen führt zusammen mit der endlichen Anzahl von Molekülen im System zu einer endlichen Anzahl von Mikrozuständen innerhalb des Systems; wir nennen die Menge aller Mikrozustände ein Ensemble. Speziell für atomare oder molekulare Systeme gibt es je nach Situation drei verschiedene Arten von Ensembles: mikrokanonische Ensembles, kanonische Ensembles oder große kanonische Ensembles. Durch spezifische Kombinationen von Mikrozuständen innerhalb eines Ensembles können wir den Makrozustand des Systems (Temperatur, Druck, Energie usw.) wirklich definieren. Dazu müssen wir zunächst alle Mikrozustände mit Hilfe einer Partitionsfunktion zählen. Die Verwendung der statistischen Mechanik und der Verteilungsfunktion ist ein wichtiges Instrument in der gesamten physikalischen Chemie, denn sie ist der Schlüssel zur Verbindung zwischen den mikroskopischen Zuständen eines Systems und den makroskopischen Variablen, die wir messen können, wie Temperatur, Druck, Wärmekapazität, innere Energie, Enthalpie und Entropie, um nur einige zu nennen. (Lesen: Verteilungsfunktion - Bedeutung und Aussagekraft) ⓘ

Die Verwendung der Verteilungsfunktion zur Ermittlung der Energie eines Moleküls oder eines Systems von Molekülen kann manchmal durch das Gleichverteilungs-Theorem angenähert werden, was die Berechnung stark vereinfacht. Bei dieser Methode wird jedoch davon ausgegangen, dass alle molekularen Freiheitsgrade gleichmäßig besetzt sind und daher gleichmäßig zur Speicherung von Energie im Molekül genutzt werden. Dies würde bedeuten, dass sich die innere Energie linear mit der Temperatur ändert, was nicht der Fall ist. Dabei wird die Tatsache ignoriert, dass sich die Wärmekapazität mit der Temperatur ändert, da bestimmte Freiheitsgrade bei niedrigeren Temperaturen nicht erreichbar sind (auch bekannt als "eingefroren"). Wenn die innere Energie der Moleküle zunimmt, steigt auch die Fähigkeit, Energie in zusätzlichen Freiheitsgraden zu speichern. Je mehr Freiheitsgrade zur Speicherung von Energie zur Verfügung stehen, desto höher ist die molare Wärmekapazität der Substanz.

Die zufällige Bewegung von Gasteilchen führt zur Diffusion. ⓘ

Brownsche Bewegung

Die Brownsche Bewegung ist das mathematische Modell, mit dem die zufällige Bewegung von in einer Flüssigkeit schwebenden Teilchen beschrieben wird. Die Gaspartikelanimation mit rosa und grünen Partikeln veranschaulicht, wie dieses Verhalten zur Ausbreitung von Gasen führt (Entropie). Auch diese Vorgänge werden durch die Teilchentheorie beschrieben. ⓘ

Da die Beobachtung einzelner Gasteilchen (Atome oder Moleküle) mit dem heutigen Stand der Technik nicht möglich ist, können nur theoretische Berechnungen Aufschluss darüber geben, wie sie sich bewegen. Ihre Bewegung unterscheidet sich jedoch von der Brownschen Bewegung, denn bei der Brownschen Bewegung handelt es sich um einen gleichmäßigen Luftwiderstand aufgrund der Reibungskraft vieler Gasmoleküle, der durch heftige Zusammenstöße eines einzelnen (oder mehrerer) Gasmoleküle mit dem Teilchen unterbrochen wird. Das Teilchen (das im Allgemeinen aus Millionen oder Milliarden von Atomen besteht) bewegt sich also in einer zackigen Bahn, die jedoch nicht so zackig ist, wie es bei der Untersuchung eines einzelnen Gasmoleküls zu erwarten wäre. ⓘ

Zwischenmolekulare Kräfte - der Hauptunterschied zwischen realen und idealen Gasen

Kräfte zwischen zwei oder mehr Molekülen oder Atomen, die entweder anziehend oder abstoßend wirken, werden als intermolekulare Kräfte bezeichnet. Zwischenmolekulare Kräfte wirken auf Moleküle, wenn sie sich in räumlicher Nähe zueinander befinden. Diese Kräfte sind für die korrekte Modellierung molekularer Systeme sehr wichtig, da sie das mikroskopische Verhalten der Moleküle in jedem System genau vorhersagen und daher für die genaue Vorhersage der physikalischen Eigenschaften von Gasen (und Flüssigkeiten) unter sehr unterschiedlichen physikalischen Bedingungen notwendig sind. ⓘ

Eine der bekanntesten zwischenmolekularen Kräfte in der gesamten Physik, die sich aus dem Studium der physikalischen Chemie ergibt, sind die Van-der-Waals-Kräfte. Van-der-Waals-Kräfte spielen eine Schlüsselrolle bei der Bestimmung fast aller physikalischen Eigenschaften von Flüssigkeiten wie Viskosität, Fließgeschwindigkeit und Gasdynamik (siehe Abschnitt Physikalische Eigenschaften). Die Van-der-Waals-Wechselwirkungen zwischen den Gasmolekülen sind der Grund dafür, dass die Modellierung eines "realen Gases" mathematisch schwieriger ist als die eines "idealen Gases". Wenn man diese von der Nähe abhängigen Kräfte ignoriert, kann ein reales Gas wie ein ideales Gas behandelt werden, was die Berechnungen erheblich vereinfacht. ⓘ

Isotherme Kurven, die die Nicht-Idealität eines realen Gases veranschaulichen. Die Änderungen des Volumens (dargestellt durch Z, Kompressibilitätsfaktor), die bei der Änderung des Drucks auftreten. Der Kompressibilitätsfaktor Z ist gleich dem Verhältnis Z = PV/nRT. Ein ideales Gas mit dem Kompressibilitätsfaktor Z = 1 wird durch die horizontale Linie beschrieben, bei der die y-Achse gleich 1 ist. Die Nicht-Idealität kann als die Abweichung eines Gases über oder unter Z = 1 beschrieben werden. ⓘ

Die zwischenmolekularen Anziehungen und Abstoßungen zwischen zwei Gasmolekülen sind abhängig vom Abstand zwischen ihnen. Die kombinierten Anziehungen und Abstoßungen werden durch das Lennard-Jones-Potenzial gut modelliert, das zu den am besten untersuchten interatomaren Potenzialen gehört, die die potenzielle Energie von Molekülsystemen beschreiben. Das Lennard-Jones-Potenzial zwischen Molekülen lässt sich in zwei separate Komponenten aufteilen: eine Anziehung über große Entfernungen aufgrund der Londoner Dispersionskraft und eine Abstoßung über kurze Entfernungen aufgrund der Elektron-Elektron-Austauschwechselwirkung (die mit dem Pauli-Ausschlussprinzip zusammenhängt). ⓘ

Wenn zwei Moleküle relativ weit voneinander entfernt sind (d. h. sie haben eine hohe potenzielle Energie), erfahren sie eine schwache Anziehungskraft, die sie veranlasst, sich aufeinander zuzubewegen, wodurch ihre potenzielle Energie sinkt. Wenn die Moleküle jedoch zu weit voneinander entfernt sind, erfahren sie keine nennenswerte Anziehungskraft. Wenn sich die Moleküle jedoch zu nahe kommen, stoßen sie zusammen und erfahren eine sehr starke Abstoßungskraft (modelliert durch harte Kugeln), die viel stärker ist als die Anziehungskraft, so dass jegliche Anziehung aufgrund der Nähe vernachlässigt wird. ⓘ

Wenn sich zwei Moleküle einander nähern, und zwar aus einer Entfernung, die weder zu groß noch zu klein ist, nimmt ihre Anziehungskraft zu, da der Betrag ihrer potenziellen Energie zunimmt (sie wird negativer) und ihre gesamte innere Energie sinkt. Die Anziehung, die eine Annäherung der Moleküle bewirkt, kann nur dann stattfinden, wenn die Moleküle für die Dauer der Annäherung in der Nähe bleiben. Daher sind die Anziehungskräfte am stärksten, wenn sich die Moleküle mit geringer Geschwindigkeit bewegen. Das bedeutet, dass die Anziehungskraft zwischen den Molekülen bei niedrigen Gastemperaturen erheblich ist. Wenn man jedoch dieses kalte Gas isotherm in einem kleinen Volumen komprimiert, die Moleküle in die Nähe zwingt und den Druck erhöht, beginnen die Abstoßungskräfte gegenüber den Anziehungskräften zu dominieren, da die Geschwindigkeit, mit der Zusammenstöße stattfinden, erheblich zunimmt. Daher ist bei niedrigen Temperaturen und niedrigem Druck die Anziehung die vorherrschende zwischenmolekulare Wechselwirkung. ⓘ

Wenn sich zwei Moleküle mit hoher Geschwindigkeit in beliebige Richtungen auf sich nicht überschneidenden Bahnen bewegen, verbringen sie nicht genug Zeit in ihrer Nähe, um von der anziehenden London-Zerstreuungskraft beeinflusst zu werden. Wenn die beiden Moleküle kollidieren, bewegen sie sich zu schnell und ihre kinetische Energie ist viel größer als die anziehende potenzielle Energie, so dass sie sich beim Zusammenstoß nur abstoßen. Daher kann die Anziehung zwischen Molekülen bei hohen Temperaturen aufgrund der hohen Geschwindigkeiten vernachlässigt werden. Bei hohen Temperaturen und hohem Druck ist die Abstoßung die vorherrschende intermolekulare Wechselwirkung. ⓘ

Unter Berücksichtigung der oben genannten Effekte, die diese Anziehung und Abstoßung verursachen, unterscheiden sich reale Gase vom idealen Gasmodell durch die folgende Verallgemeinerung:

• Bei niedrigen Temperaturen und niedrigem Druck ist das von einem realen Gas eingenommene Volumen kleiner als das vom idealen Gasgesetz vorhergesagte Volumen.
• Bei hohen Temperaturen und hohen Drücken ist das von einem realen Gas eingenommene Volumen größer als das vom idealen Gasgesetz vorhergesagte Volumen. ⓘ

Mathematische Modelle

Eine Zustandsgleichung (für Gase) ist ein mathematisches Modell, das zur groben Beschreibung oder Vorhersage der Zustandseigenschaften eines Gases verwendet wird. Gegenwärtig gibt es keine einzige Zustandsgleichung, die die Eigenschaften aller Gase unter allen Bedingungen genau vorhersagt. Daher wurde eine Reihe von sehr viel genaueren Zustandsgleichungen für Gase in bestimmten Temperatur- und Druckbereichen entwickelt. Die am häufigsten diskutierten "Gasmodelle" sind "perfektes Gas", "ideales Gas" und "reales Gas". Jedes dieser Modelle beruht auf einer Reihe von Annahmen, die die Analyse eines bestimmten thermodynamischen Systems erleichtern. Mit jedem weiteren Modell wird der Temperaturbereich, auf den es anwendbar ist, ausgeweitet. ⓘ

Ideales und perfektes Gas

Die Zustandsgleichung für ein ideales oder perfektes Gas ist das ideale Gasgesetz und lautet

$PV=nRT,$

wobei P der Druck, V das Volumen, n die Gasmenge (in Mol-Einheiten), R die universelle Gaskonstante, 8,314 J/(mol K), und T die Temperatur ist. Auf diese Weise geschrieben, wird es manchmal als "Chemiker-Version" bezeichnet, da es die Anzahl der Moleküle n betont.

$P=\rho R_{s}T,$

wobei $R_{s}$ die spezifische Gaskonstante für ein bestimmtes Gas in der Einheit J/(kg K) ist und ρ = m/V die Dichte ist. Diese Schreibweise ist die Version der "Gasdynamiker", die bei der Modellierung von Gasströmen mit Beschleunigung ohne chemische Reaktionen praktischer ist. ⓘ

Das Gesetz des idealen Gases macht keine Annahmen über die spezifische Wärme eines Gases. Im allgemeinsten Fall ist die spezifische Wärme eine Funktion sowohl der Temperatur als auch des Drucks. Wenn die Druckabhängigkeit (und möglicherweise auch die Temperaturabhängigkeit) in einer bestimmten Anwendung vernachlässigt wird, wird das Gas manchmal als ideales Gas bezeichnet, obwohl die genauen Annahmen je nach Autor und/oder Wissenschaftsgebiet variieren können. ⓘ

Für ein ideales Gas gilt das ideale Gasgesetz ohne Einschränkungen hinsichtlich der spezifischen Wärme. Ein ideales Gas ist ein vereinfachtes "echtes Gas" mit der Annahme, dass der Kompressibilitätsfaktor Z auf 1 gesetzt wird, was bedeutet, dass dieses pneumatische Verhältnis konstant bleibt. Bei einem Kompressibilitätsfaktor von 1 müssen auch die vier Zustandsgrößen dem idealen Gasgesetz folgen. ⓘ

Diese Annäherung eignet sich besser für Anwendungen in der Technik, obwohl einfachere Modelle verwendet werden können, um einen "ungefähren" Bereich zu ermitteln, in dem die tatsächliche Lösung liegen sollte. Ein Beispiel, bei dem die "Idealgasannäherung" geeignet wäre, wäre die Brennkammer eines Düsentriebwerks. Es kann auch nützlich sein, die Elementarreaktionen und chemischen Dissoziationen für die Berechnung der Emissionen beizubehalten. ⓘ

Reales Gas

Ausbruch des Mount Redoubt, Alaska, am 21. April 1990, zur Veranschaulichung echter Gase, die sich nicht im thermodynamischen Gleichgewicht befinden. ⓘ

Jede der unten aufgeführten Annahmen erhöht die Komplexität der Lösung des Problems. Da die Dichte eines Gases mit steigendem Druck zunimmt, spielen die zwischenmolekularen Kräfte eine größere Rolle im Gasverhalten, was dazu führt, dass das ideale Gasgesetz keine "vernünftigen" Ergebnisse mehr liefert. Am oberen Ende der Motortemperaturbereiche (z. B. Brennkammerbereiche - 1300 K) nehmen die komplexen Brennstoffteilchen durch Rotationen und Vibrationen innere Energie auf, so dass ihre spezifische Wärme von derjenigen der zweiatomigen Moleküle und Edelgase abweicht. Bei mehr als dem Doppelten dieser Temperatur beginnt die elektronische Anregung und Dissoziation der Gasteilchen, wodurch sich der Druck an eine größere Anzahl von Teilchen anpasst (Übergang vom Gas zum Plasma). Schließlich wurde bei allen thermodynamischen Prozessen davon ausgegangen, dass es sich um gleichförmige Gase handelt, deren Geschwindigkeiten gemäß einer festen Verteilung variieren. Die Verwendung einer Nicht-Gleichgewichtssituation impliziert, dass das Strömungsfeld auf irgendeine Weise charakterisiert werden muss, um eine Lösung zu ermöglichen. Einer der ersten Versuche, die Grenzen des idealen Gasgesetzes zu erweitern, bestand darin, verschiedene thermodynamische Prozesse zu berücksichtigen, indem man die Gleichung so anpasste, dass sie pVn = konstant lautet, und dann das n durch verschiedene Werte wie das spezifische Wärmeverhältnis γ variierte. ⓘ

Wirkliche Gaseffekte umfassen die Anpassungen, die vorgenommen wurden, um eine größere Bandbreite des Gasverhaltens zu berücksichtigen:

• Kompressibilitätseffekte (Z darf von 1,0 abweichen)
• Variable Wärmekapazität (spezifische Wärmewerte variieren mit der Temperatur)
• Van-der-Waals-Kräfte (bezogen auf die Kompressibilität, kann andere Zustandsgleichungen ersetzen)
• Thermodynamische Nicht-Gleichgewichts-Effekte
• Probleme mit molekularer Dissoziation und Elementarreaktionen mit variabler Zusammensetzung. ⓘ

Für die meisten Anwendungen ist eine solch detaillierte Analyse übertrieben. Beispiele, bei denen reale Gaseffekte erhebliche Auswirkungen hätten, wären der Wiedereintritt des Space Shuttle, bei dem extrem hohe Temperaturen und Drücke herrschen, oder die Gase, die bei geologischen Ereignissen entstehen, wie im Bild des Ausbruchs des Mount Redoubt 1990. ⓘ

Permanentes Gas

Als Permanentgas wird ein Gas bezeichnet, dessen kritische Temperatur unterhalb des für den Menschen bewohnbaren Temperaturbereichs liegt und das daher nicht durch Druck innerhalb dieses Bereichs verflüssigt werden kann. In der Vergangenheit ging man davon aus, dass solche Gase nicht verflüssigt werden können und daher dauerhaft im gasförmigen Zustand verbleiben würden. Der Begriff bezieht sich auf die Lagerung und den Transport von Gasen bei Umgebungstemperatur unter hohem Druck. ⓘ

Historische Forschung

Boyle'sches Gesetz

Boyle's Ausrüstung ⓘ

Das Boyle'sche Gesetz war vielleicht der erste Ausdruck einer Zustandsgleichung. Im Jahr 1662 führte Robert Boyle eine Reihe von Experimenten mit einem J-förmigen Glasrohr durch, das an einem Ende verschlossen war. Dem Rohr wurde Quecksilber zugesetzt, wodurch eine bestimmte Menge Luft in dem kurzen, verschlossenen Ende des Rohrs eingeschlossen wurde. Dann wurde das Gasvolumen sorgfältig gemessen, während weiteres Quecksilber in das Rohr gegeben wurde. Der Druck des Gases konnte durch die Differenz zwischen dem Quecksilberspiegel im kurzen Ende des Rohrs und dem im langen, offenen Ende bestimmt werden. Das Bild von Boyles Ausrüstung zeigt einige der exotischen Werkzeuge, die Boyle bei seinen Gasuntersuchungen verwendete. ⓘ

Bei diesen Experimenten stellte Boyle fest, dass der Druck, den ein Gas bei konstanter Temperatur ausübt, umgekehrt proportional zum Volumen des Gases ist. Wird beispielsweise das Volumen halbiert, verdoppelt sich der Druck, und wird das Volumen verdoppelt, halbiert sich der Druck. Angesichts des umgekehrten Verhältnisses zwischen Druck und Volumen ist das Produkt aus Druck (P) und Volumen (V) eine Konstante (k) für eine bestimmte Masse eines eingeschlossenen Gases, solange die Temperatur konstant ist. In einer Formel ausgedrückt heißt das:

$PV=k$ ⓘ

Da die Volumina und Drücke vor und nach der festen Gasmenge bei gleichen Temperaturen vor und nach der Gasmenge gleich der Konstante k sind, können sie durch die Gleichung in Beziehung gesetzt werden: $\qquad P_{1}V_{1}=P_{2}V_{2}.$ ⓘ

Charles'sches Gesetz

Im Jahr 1787 stellte der französische Physiker und Ballonpionier Jacques Charles fest, dass sich Sauerstoff, Stickstoff, Wasserstoff, Kohlendioxid und Luft innerhalb eines Intervalls von 80 Kelvin in gleichem Maße ausdehnen. Er stellte fest, dass bei einem idealen Gas mit konstantem Druck das Volumen direkt proportional zur Temperatur ist:

${\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}$ ⓘ

Gay-Lussac'sches Gesetz

Im Jahr 1802 veröffentlichte Joseph Louis Gay-Lussac die Ergebnisse ähnlicher, wenn auch umfangreicherer Experimente. Gay-Lussac würdigte die frühere Arbeit von Charles, indem er das Gesetz zu seinen Ehren benannte. Gay-Lussac selbst wird das Gesetz zur Beschreibung des Drucks zugeschrieben, das er 1809 fand. Es besagt, dass der Druck, den ein ideales Gas auf die Seitenwände eines Behälters ausübt, proportional zu seiner Temperatur ist.

${\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}\,$ ⓘ

Das Avogadrosche Gesetz

Im Jahr 1811 wies Amedeo Avogadro nach, dass gleiche Volumina reiner Gase die gleiche Anzahl von Teilchen enthalten. Seine Theorie wurde erst 1858 allgemein anerkannt, als ein anderer italienischer Chemiker, Stanislao Cannizzaro, die nicht idealen Ausnahmen erklären konnte. Für seine Arbeit mit Gasen ein Jahrhundert zuvor steht die nach ihm benannte Avogadro-Konstante für die Anzahl der Atome in 12 Gramm elementarem Kohlenstoff-12 (6,022×10²³ mol-1). Diese spezifische Anzahl von Gasteilchen nimmt bei Standardtemperatur und -druck (ideales Gasgesetz) 22,40 Liter ein, was als molares Volumen bezeichnet wird. ⓘ

Das Avogadrosche Gesetz besagt, dass das von einem idealen Gas eingenommene Volumen proportional zur Anzahl der Mole (oder Moleküle) im Behälter ist. Daraus ergibt sich das molare Volumen eines Gases, das bei STP 22,4 dm³ (oder Liter) beträgt. Die Beziehung ist gegeben durch ⓘ

${\frac {V_{1}}{n_{1}}}={\frac {V_{2}}{n_{2}}}\,$ ⓘ

Dabei ist n gleich der Molzahl des Gases (Anzahl der Moleküle geteilt durch die Avogadrosche Zahl). ⓘ

Daltonsches Gesetz

Dalton'sche Notation. ⓘ

Im Jahr 1801 veröffentlichte John Dalton das Gesetz der Partialdrücke, das sich aus seiner Arbeit mit dem idealen Gasgesetz ableitet: Der Druck eines Gemischs nichtreaktiver Gase ist gleich der Summe der Drücke der einzelnen Gaskomponenten. Mathematisch kann dies für n Arten wie folgt dargestellt werden:

DruckGesamt = Druck₁ + Druck₂ + ... + Druck ⓘ

Die Abbildung von Daltons Tagebuch zeigt die Symbolik, die er als Abkürzung für die Aufzeichnung des von ihm eingeschlagenen Weges verwendete. Zu seinen wichtigsten Beobachtungen, die er beim Mischen von nicht reaktionsfähigen "elastischen Flüssigkeiten" (Gasen) machte, gehörten die folgenden:

• Anders als Flüssigkeiten drifteten schwerere Gase beim Mischen nicht auf den Boden.
• Die Identität der Gasteilchen spielte bei der Bestimmung des Enddrucks keine Rolle (sie verhielten sich, als ob ihre Größe vernachlässigbar wäre). ⓘ

Besondere Themen

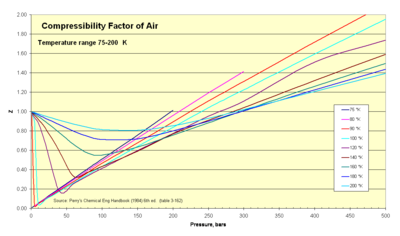
Komprimierbarkeit

Komprimierbarkeitsfaktoren für Luft. ⓘ

Thermodynamiker verwenden diesen Faktor (Z) zur Änderung der idealen Gasgleichung, um die Kompressibilitätseffekte von realen Gasen zu berücksichtigen. Dieser Faktor stellt das Verhältnis zwischen dem tatsächlichen und dem idealen spezifischen Volumen dar. Er wird manchmal auch als "Fudge-Faktor" oder Korrektur bezeichnet, um den nützlichen Bereich des idealen Gasgesetzes für Konstruktionszwecke zu erweitern. Normalerweise liegt dieser Z-Wert sehr nahe bei Eins. Die Abbildung des Kompressibilitätsfaktors veranschaulicht, wie Z über einen Bereich von sehr kalten Temperaturen variiert. ⓘ

Reynolds-Zahl

In der Strömungsmechanik ist die Reynoldszahl das Verhältnis von Trägheitskräften (vsρ) zu viskosen Kräften (μ/L). Sie ist eine der wichtigsten dimensionslosen Zahlen in der Strömungsmechanik und wird in der Regel zusammen mit anderen dimensionslosen Zahlen als Kriterium für die Bestimmung der dynamischen Ähnlichkeit verwendet. Die Reynolds-Zahl ist somit das Bindeglied zwischen den Modellierungsergebnissen (Entwurf) und den tatsächlichen Bedingungen im Originalmaßstab. Sie kann auch zur Charakterisierung der Strömung verwendet werden. ⓘ

Viskosität

Die Satellitenansicht der Wetterlage in der Nähe der Robinson Crusoe Inseln am 15. September 1999 zeigt ein turbulentes Wolkenmuster, das als Kármán-Wirbelstraße bezeichnet wird ⓘ

Die Viskosität, eine physikalische Eigenschaft, ist ein Maß dafür, wie gut benachbarte Moleküle aneinander haften. Ein Festkörper kann aufgrund der Stärke dieser klebrigen intermolekularen Kräfte einer Scherkraft standhalten. Eine Flüssigkeit verformt sich kontinuierlich, wenn sie einer ähnlichen Belastung ausgesetzt ist. Die Viskosität eines Gases ist zwar geringer als die einer Flüssigkeit, aber sie ist dennoch eine beobachtbare Eigenschaft. Hätten Gase keine Viskosität, würden sie nicht an der Oberfläche eines Flügels haften und eine Grenzschicht bilden. Eine Untersuchung des Deltaflügels im Schlierenbild zeigt, dass die Gasteilchen aneinander haften (siehe Abschnitt Grenzschicht). ⓘ

Turbulenz

Deltaflügel im Windkanal. Die Schatten bilden sich, weil sich die Brechungsindizes im Gas ändern, wenn es sich an der Vorderkante dieses Flügels zusammenzieht. ⓘ

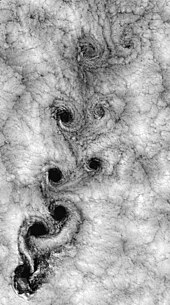
In der Strömungsdynamik ist die Turbulenz oder turbulente Strömung ein Strömungszustand, der durch chaotische, stochastische Veränderungen der Eigenschaften gekennzeichnet ist. Dazu gehören die Diffusion mit geringem Impuls, die Konvektion mit hohem Impuls und die schnelle Veränderung von Druck und Geschwindigkeit in Raum und Zeit. Die Satellitenansicht des Wetters um die Robinson-Crusoe-Inseln ist ein Beispiel dafür. ⓘ

Grenzschicht

Partikel "kleben" an der Oberfläche eines Objekts, das sich durch sie bewegt. Diese Partikelschicht wird als Grenzschicht bezeichnet. An der Oberfläche des Objekts ist sie aufgrund der Reibung der Oberfläche im Wesentlichen statisch. Das Objekt mit seiner Grenzschicht ist praktisch die neue Form des Objekts, die der Rest der Moleküle "sieht", wenn sich das Objekt nähert. Diese Grenzschicht kann sich von der Oberfläche ablösen, wodurch im Wesentlichen eine neue Oberfläche entsteht und sich der Strömungsweg völlig verändert. Das klassische Beispiel hierfür ist ein überzogenes Tragflächenprofil. Das Bild eines Deltaflügels zeigt deutlich, wie sich die Grenzschicht verdickt, wenn das Gas von rechts nach links entlang der Vorderkante strömt. ⓘ

Prinzip der maximalen Entropie

Wenn die Gesamtzahl der Freiheitsgrade gegen unendlich geht, befindet sich das System in dem Makrozustand, der der höchsten Multiplizität entspricht. Zur Veranschaulichung dieses Prinzips kann man die Hauttemperatur eines gefrorenen Metallstabs betrachten. Notieren Sie anhand eines Wärmebildes der Hauttemperatur die Temperaturverteilung auf der Oberfläche. Diese erste Beobachtung der Temperatur stellt einen "Mikrozustand" dar. Zu einem späteren Zeitpunkt ergibt sich aus einer zweiten Beobachtung der Hauttemperatur ein zweiter Mikrozustand. Wenn man diesen Beobachtungsprozess fortsetzt, kann man eine Reihe von Mikrozuständen erzeugen, die die thermische Geschichte der Oberfläche des Stabes veranschaulichen. Die Charakterisierung dieser historischen Reihe von Mikrozuständen ist möglich, indem man den Makrozustand wählt, der sie alle erfolgreich in eine einzige Gruppierung einordnet. ⓘ

Thermodynamisches Gleichgewicht

Wenn ein System keine Energie mehr überträgt, wird dieser Zustand als thermodynamisches Gleichgewicht bezeichnet. Normalerweise bedeutet dieser Zustand, dass das System und die Umgebung die gleiche Temperatur haben, so dass keine Wärme mehr zwischen ihnen übertragen wird. Es bedeutet auch, dass die äußeren Kräfte ausgeglichen sind (das Volumen ändert sich nicht) und alle chemischen Reaktionen innerhalb des Systems abgeschlossen sind. Der Zeitrahmen für diese Ereignisse variiert je nach System. Das Schmelzen eines Eisbehälters bei Raumtemperatur dauert Stunden, während bei Halbleitern die Wärmeübertragung beim Übergang von einem ein- zu einem ausgeschalteten Zustand in der Größenordnung von einigen Nanosekunden liegen kann. ⓘ

Phasenübergänge der Materie () ⓘ

Zu Von	Fest	Flüssigkeit	Gas	Plasma
Fest		Schmelzen	Sublimation
Flüssigkeit	Gefrieren		Verdampfen
Gas	Ablagerung	Kondensation		Ionisierung
Plasma			Rekombination

Der Aggregatzustand gasförmig

Der Aggregatzustand „gasförmig“ entsteht aus der „festen“ oder „flüssigen“ Form durch Energiezufuhr (Wärme). Für einige Elemente und Verbindungen genügen bereits die Standardbedingungen (Temperatur 20 °C, Druck 101325 Pa), um als Gas vorzuliegen; bei ausreichend hohen Temperaturen wird jedoch jede Materie in den gasförmigen Zustand versetzt. Die dabei zugeführte Energie wird zur Bewegungsenergie der einzelnen Teilchen (je nach Temperatur mit Geschwindigkeiten im Bereich um 500 m/s), was den gasförmigen Zustand mit vollständigem Ausfüllen des vorgegebenen Raumes mit statistischer Gleichverteilung der Gasteilchen bewirkt. Hierbei strebt das Gesamtsystem den Zustand höchster Entropie an (zweiter Hauptsatz der Thermodynamik). Dass dies der wahrscheinlichste Zustand ist, kann man auf folgende Weise anschaulich machen: Unterteilt man gedanklich das einem Gas zur Verfügung stehende Volumen in Raumzellen von etwa der Größe eines Moleküls, dann gibt es viel mehr Möglichkeiten, die Moleküle auf die vielen Zellen des ganzen Volumens zu verteilen als auf einen kleinen Bruchteil. Der Makrozustand der raumerfüllenden Verteilung weist die meisten Anordnungsmöglichkeiten (Mikrozustände) für die Teilchen auf und damit auch die höchste Entropie. Die Zahl der Mikrozustände, das statistische Gewicht, kann berechnet werden. Genaueres unter Entropie (Thermodynamik) /Beispiele. ⓘ

Zustandsübergänge

Gaskessel der Stadtwerke Esslingen ⓘ

Den Übergang vom flüssigen in den gasförmigen Aggregatzustand bezeichnet man als Verdampfung (oberhalb des Siedepunktes) oder Verdunstung (unterhalb des Siedepunktes), den umgekehrten Übergang vom gasförmigen in den flüssigen Aggregatzustand als Kondensation. Der direkte Übergang vom festen in den gasförmigen Aggregatzustand ist die Sublimation, der umgekehrte Übergang vom gasförmigen in den festen Aggregatzustand heißt Resublimation. ⓘ

Lagerung

Um eine möglichst große Menge an Gas in einem Behälter zu speichern, also eine hohe Dichte zu erhalten, wird das Gas stark komprimiert (siehe auch Druckgas). Zwecks hoher Druckbelastbarkeit der Gasbehälter werden meist zylinderförmige oder kugelförmige Druckbehälter (z. B. Gasflaschen) eingesetzt. Gaskessel oder Gasometer sind Niederdruckspeicher mit großem geometrischen Volumen. Aufgrund des geringen Drucks (< 1 bar) ist die gespeicherte Menge aber unbedeutend. Gasversorger speichern das Gas üblicherweise im Leitungsnetz (Gasnetz), indem sie Hochdruckleitungen großer Nennweite einsetzen. ⓘ

Verwandte Themen

• Angabe der Stoffreinheit bei technischen Gasen
• Dampf ist ein historisch älterer Begriff und bezeichnet einen Stoff im gasförmigen Aggregatzustand, der unter Normalbedingungen als Flüssigkeit vorhanden ist (siehe z. B. Wasserdampf).
• Dampfbildung durch Kavitation
• Elektronengas
• Erdgas (Energieträger und Wirtschaftsfaktor)
• Flüssiggas
• Ideales Fermigas
• Gastransport
• Gaswolke
• Linde-Verfahren zur Verflüssigung von Gasen
• Nachweis von Gasen
• Physikalische Eigenschaften von Gasen, siehe Gasgesetze
• Spezielle Arten von Gasen und Gasgemischen, siehe :Kategorie:Gas
• Stadtgas ⓘ