Bose-Einstein-Kondensat
| Physik der kondensierten Materie ⓘ |
|---|
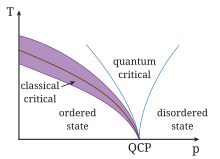 |
| Phasen - Phasenübergang - QCP |
|
In der Physik der kondensierten Materie ist ein Bose-Einstein-Kondensat (BEC) ein Materiezustand, der typischerweise entsteht, wenn ein Gas von Bosonen mit sehr geringer Dichte auf Temperaturen nahe dem absoluten Nullpunkt (-273,15 °C oder -459,67 °F) abgekühlt wird. Unter solchen Bedingungen nimmt ein großer Teil der Bosonen den niedrigsten Quantenzustand ein, in dem mikroskopische quantenmechanische Phänomene, insbesondere die Interferenz von Wellenfunktionen, makroskopisch sichtbar werden. Ein BEC entsteht durch die Abkühlung eines Gases mit extrem niedriger Dichte (etwa 100.000-mal weniger dicht als normale Luft) auf extrem niedrige Temperaturen. ⓘ
Dieser Zustand wurde erstmals 1924-1925 von Albert Einstein in Anlehnung an eine bahnbrechende Arbeit von Satyendra Nath Bose über das neue Gebiet, das heute als Quantenstatistik bekannt ist, allgemein vorhergesagt. ⓘ
Das Bose-Einstein-Kondensat (nach Satyendranath Bose und Albert Einstein; Abkürzung BEK, englisch BEC) ist ein extremer Aggregatzustand eines Systems ununterscheidbarer Teilchen, in dem sich der überwiegende Anteil der Teilchen im selben quantenmechanischen Zustand befindet. Das ist nur möglich, wenn die Teilchen Bosonen sind und somit der Bose-Einstein-Statistik unterliegen. ⓘ
Bose-Einstein-Kondensate sind makroskopische Quantenobjekte, in denen die einzelnen Bosonen vollständig delokalisiert sind. Dies wird auch als makroskopischer Quantenzustand bezeichnet. Die Bosonen sind vollständig ununterscheidbar. Der Zustand kann daher durch eine einzige Wellenfunktion beschrieben werden. ⓘ
Daraus resultierende Eigenschaften sind Suprafluidität, Supraleitung, Suprasolidität oder Kohärenz über makroskopische Entfernungen. Letztere erlaubt Interferenzexperimente mit Bose-Einstein-Kondensaten sowie die Herstellung eines Atomlasers, den man durch kontrollierte Auskopplung eines Teils der Materiewelle aus der das Kondensat haltenden Falle erhalten kann. ⓘ
Geschichte

Bose schickte Einstein zunächst einen Aufsatz über die Quantenstatistik von Lichtquanten (heute Photonen genannt), in dem er das Plancksche Quantenstrahlungsgesetz ohne jeden Bezug zur klassischen Physik ableitete. Einstein war beeindruckt, übersetzte die Arbeit selbst vom Englischen ins Deutsche und reichte sie für Bose bei der Zeitschrift für Physik ein, die sie 1924 veröffentlichte. (Das verschollen geglaubte Einstein-Manuskript wurde 2005 in einer Bibliothek der Universität Leiden gefunden). Einstein dehnte die Ideen von Bose in zwei weiteren Arbeiten auf die Materie aus. Das Ergebnis ihrer Bemühungen ist das Konzept des Bose-Gases, das der Bose-Einstein-Statistik unterliegt, welche die statistische Verteilung identischer Teilchen mit ganzzahligem Spin beschreibt, die jetzt Bosonen genannt werden. Bosonen, zu denen sowohl das Photon als auch Atome wie Helium-4 (4
He
), dürfen sich einen Quantenzustand teilen. Einstein schlug vor, dass bosonische Atome, wenn man sie auf eine sehr niedrige Temperatur abkühlt, in den niedrigsten zugänglichen Quantenzustand fallen (oder "kondensieren"), was zu einer neuen Form von Materie führt. ⓘ
1938 schlug Fritz London das BEC als einen Mechanismus für Suprafluidität in 4
He
und Supraleitfähigkeit vor. ⓘ
Das Bestreben, ein Bose-Einstein-Kondensat im Labor herzustellen, wurde durch einen 1976 von zwei Programmdirektoren der National Science Foundation (William Stwalley und Lewis Nosanow) veröffentlichten Aufsatz angeregt. Daraufhin verfolgten vier unabhängige Forschungsgruppen unter der Leitung von Isaac Silvera (Universität Amsterdam), Walter Hardy (University of British Columbia), Thomas Greytak (Massachusetts Institute of Technology) und David Lee (Cornell University) die Idee weiter. ⓘ
Am 5. Juni 1995 wurde das erste gasförmige Kondensat von Eric Cornell und Carl Wieman im NIST-JILA-Labor der Universität von Colorado in Boulder in einem auf 170 Nanokelvin (nK) gekühlten Gas aus Rubidiumatomen erzeugt. Kurz darauf erzeugte Wolfgang Ketterle am MIT ein Bose-Einstein-Kondensat in einem Gas aus Natriumatomen. Für ihre Leistungen erhielten Cornell, Wieman und Ketterle 2001 den Nobelpreis für Physik. Diese frühen Studien begründeten das Gebiet der ultrakalten Atome, und Hunderte von Forschungsgruppen auf der ganzen Welt erzeugen heute routinemäßig BECs aus verdünnten Atomdämpfen in ihren Labors. ⓘ
Seit 1995 wurden viele andere Atomsorten kondensiert, und BECs wurden auch mit Molekülen, Quasiteilchen und Photonen realisiert. ⓘ
Kritische Temperatur
Der Übergang zum BEC findet unterhalb einer kritischen Temperatur statt, die für ein gleichförmiges dreidimensionales Gas, das aus nicht wechselwirkenden Teilchen ohne offensichtliche innere Freiheitsgrade besteht, wie folgt angegeben wird:
wobei:
ist die kritische Temperatur, die Teilchendichte, die Masse pro Boson, die reduzierte Planck-Konstante, die Boltzmann-Konstante und die Riemannsche Zetafunktion;
Wechselwirkungen verschieben den Wert und die Korrekturen können mit Hilfe der Mean-Field-Theorie berechnet werden. Diese Formel ergibt sich aus der Bestimmung der Gasentartung im Bose-Gas unter Verwendung der Bose-Einstein-Statistik. ⓘ
Ableitung
Ideales Bose-Gas
Für ein ideales Bose-Gas haben wir die Zustandsgleichung:
wobei das Volumen pro Teilchen ist, die Wärmewellenlänge, die Fugazität und
Es ist auffällig, dass eine monoton wachsende Funktion von in ist, da dies die einzigen Werte sind, für die die Reihen konvergieren. Da der zweite Term auf der rechten Seite den Ausdruck für die durchschnittliche Besetzungszahl des Grundzustands enthält enthält, kann die Zustandsgleichung wie folgt umgeschrieben werden ⓘ
Da der linke Term der zweiten Gleichung immer positiv sein muss, und weil ist eine stärkere Bedingung ⓘ
die einen Übergang zwischen einer Gasphase und einer kondensierten Phase definiert. Im kritischen Bereich ist es möglich, eine kritische Temperatur und eine thermische Wellenlänge zu definieren:
Die kritischen Werte sind so, dass, wenn die Temperatur der kondensierten Phase positiv ist. Die kritischen Werte sind so, dass wenn oder in der Gegenwart eines Bose-Einstein-Kondensats befinden. Es ist wichtig zu verstehen, was mit dem Anteil der Teilchen auf der fundamentalen Ebene geschieht. Schreiben Sie also die Zustandsgleichung für und erhalten damit ⓘ
- und äquivalent dazu . ⓘ
Wenn also der Bruchteil und wenn der Bruchteil . Bei Temperaturen nahe dem absoluten Wert 0 neigen die Teilchen dazu, im fundamentalen Zustand zu kondensieren, d. h. dem Zustand mit dem Impuls . ⓘ
Modelle
Bose-Einsteins nicht wechselwirkendes Gas
Man betrachte eine Ansammlung von N nicht wechselwirkenden Teilchen, die sich jeweils in einem von zwei Quantenzuständen befinden können, und . Wenn die beiden Zustände die gleiche Energie haben, ist jede unterschiedliche Konfiguration gleich wahrscheinlich. ⓘ
Wenn wir sagen können, welches Teilchen welches ist, gibt es verschiedene Konfigurationen, denn jedes Teilchen kann sich in oder unabhängig sein kann. In fast allen Konfigurationen befindet sich etwa die Hälfte der Teilchen in und die andere Hälfte in . Das Gleichgewicht ist ein statistischer Effekt: Die Zahl der Konfigurationen ist am größten, wenn die Teilchen gleichmäßig verteilt sind. ⓘ
Wenn die Teilchen jedoch nicht unterscheidbar sind, gibt es nur N+1 verschiedene Konfigurationen. Wenn es K Teilchen im Zustand befinden, gibt es N - K Teilchen im Zustand . Ob sich ein bestimmtes Teilchen im Zustand oder im Zustand ist, kann nicht bestimmt werden, so dass jeder Wert von K einen eindeutigen Quantenzustand für das gesamte System bestimmt. ⓘ
Nehmen wir nun an, dass die Energie des Zustands etwas größer ist als die Energie des Zustands um einen Betrag E. Bei der Temperatur T hat ein Teilchen eine geringere Wahrscheinlichkeit, sich im Zustand durch . Im unterscheidbaren Fall wird die Teilchenverteilung leicht in Richtung des Zustands . Da im Fall der Ununterscheidbarkeit jedoch kein statistischer Druck in Richtung einer gleichen Anzahl besteht, ist das wahrscheinlichste Ergebnis, dass die meisten Teilchen in den Zustand . ⓘ
Im Fall der Unterscheidbarkeit kann für große N der Anteil im Zustand errechnet werden. Es ist dasselbe wie das Werfen einer Münze mit einer Wahrscheinlichkeit proportional zu p = exp(-E/T), um Schwanz zu erhalten. ⓘ
Im Fall der Ununterscheidbarkeit ist jeder Wert von K ein einzelner Zustand, der seine eigene Boltzmann-Wahrscheinlichkeit hat. Die Wahrscheinlichkeitsverteilung ist also exponentiell:
Für große N ist die Normalisierungskonstante C (1 - p). Die erwartete Gesamtzahl der Teilchen, die sich nicht im niedrigsten Energiezustand befinden, ist im Grenzwert von ist gleich
Sie wächst nicht, wenn N groß ist, sondern nähert sich lediglich einer Konstante. Dies wird ein vernachlässigbarer Bruchteil der Gesamtzahl der Teilchen sein. Eine Ansammlung von genügend Bose-Teilchen im thermischen Gleichgewicht wird sich also größtenteils im Grundzustand befinden und nur wenige in einem angeregten Zustand, egal wie klein der Energieunterschied ist. ⓘ
Betrachten wir nun ein Gas von Teilchen, die sich in verschiedenen Impulszuständen befinden können, mit der Bezeichnung . Wenn die Anzahl der Teilchen geringer ist als die Anzahl der thermisch zugänglichen Zustände, befinden sich die Teilchen bei hohen Temperaturen und geringen Dichten alle in verschiedenen Zuständen. In diesem Grenzfall handelt es sich um ein klassisches Gas. Wenn die Dichte zunimmt oder die Temperatur sinkt, wird die Anzahl der zugänglichen Zustände pro Teilchen kleiner, und irgendwann werden mehr Teilchen in einen einzigen Zustand gezwungen, als die statistische Gewichtung für diesen Zustand maximal zulässt. Von diesem Zeitpunkt an geht jedes zusätzliche Teilchen in den Grundzustand über. ⓘ
Um die Übergangstemperatur bei einer beliebigen Dichte zu berechnen, integriert man über alle Impulszustände den Ausdruck für die maximale Anzahl der angeregten Teilchen, p/(1 - p):
Wenn das Integral (auch Bose-Einstein-Integral genannt) mit Faktoren von und ℏ durch Dimensionsanalyse wiederhergestellt wird, ergibt sich die Formel für die kritische Temperatur aus dem vorangegangenen Abschnitt. Dieses Integral definiert also die kritische Temperatur und die Teilchenzahl, die den Bedingungen eines vernachlässigbaren chemischen Potentials entsprechen . In der Bose-Einstein-Statistik ist die Verteilung, für BECs tatsächlich immer noch ungleich Null ist; allerdings ist jedoch kleiner als die Grundzustandsenergie. Es sei denn, man spricht speziell über den Grundzustand, kann für die meisten Energie- oder Impulszustände angenähert werden als . ⓘ
Bogoliubov-Theorie für schwach wechselwirkendes Gas
Nikolay Bogoliubov betrachtete Störungen an der Grenze des verdünnten Gases und fand einen endlichen Druck bei einer Temperatur von Null und einem positiven chemischen Potenzial. Dies führt zu Korrekturen für den Grundzustand. Der Bogoliubov-Zustand hat Druck (T = 0): . ⓘ
Das ursprüngliche wechselwirkende System kann in ein System von nicht wechselwirkenden Teilchen mit einem Dispersionsgesetz umgewandelt werden. ⓘ
Gross-Pitaevskii-Gleichung
In einigen einfachsten Fällen kann der Zustand kondensierter Teilchen mit einer nichtlinearen Schrödingergleichung beschrieben werden, die auch als Gross-Pitaevskii-Gleichung oder Ginzburg-Landau-Gleichung bekannt ist. Die Gültigkeit dieses Ansatzes ist jedoch auf den Fall ultrakalter Temperaturen beschränkt, was für die meisten Experimente mit Alkaliatomen gut passt. ⓘ
Dieser Ansatz geht von der Annahme aus, dass der Zustand des BEC durch die eindeutige Wellenfunktion des Kondensats beschrieben werden kann . Für ein System dieser Art, als die Teilchendichte interpretiert, so dass die Gesamtzahl der Atome ⓘ
Unter der Voraussetzung, dass sich im Wesentlichen alle Atome im Kondensat befinden (d. h. zum Grundzustand kondensiert sind) und die Bosonen mit Hilfe der Theorie des mittleren Feldes behandelt werden, ist die mit dem Zustand verbundene Energie (E) ist:
Die Minimierung dieser Energie in Bezug auf infinitesimale Variationen in zu minimieren und die Anzahl der Atome konstant zu halten, ergibt die Gross-Pitaevski-Gleichung (GPE) (auch eine nichtlineare Schrödinger-Gleichung):
wobei:
ⓘist die Masse der Bosonen, ist das äußere Potential, und steht für die Wechselwirkungen zwischen den Teilchen.
Im Fall eines externen Potenzials von Null ist das Dispersionsgesetz wechselwirkender Bose-Einstein-kondensierter Teilchen durch das so genannte Bogoliubov-Spektrum gegeben (für ):
Die Gross-Pitaevskii-Gleichung (GPE) liefert eine relativ gute Beschreibung des Verhaltens von atomaren BECs. Die GPE berücksichtigt jedoch nicht die Temperaturabhängigkeit der dynamischen Variablen und ist daher nur gültig für . Sie ist z. B. nicht anwendbar für die Kondensate von Exzitonen, Magnonen und Photonen, deren kritische Temperatur mit der Raumtemperatur vergleichbar ist. ⓘ
Numerische Lösung
Die Gross-Pitaevskii-Gleichung ist eine partielle Differentialgleichung in Raum- und Zeitvariablen. Normalerweise hat sie keine analytische Lösung und verschiedene numerische Methoden, wie z. B. Split-step Crank-Nicolson und Fourier-Spektralverfahren, werden zu ihrer Lösung verwendet. Es gibt verschiedene Fortran- und C-Programme zu ihrer Lösung für die Kontaktwechselwirkung und langreichweitige dipolare Wechselwirkung, die frei verwendet werden können. ⓘ
Schwachstellen des Gross-Pitaevskii-Modells
Das Gross-Pitaevskii-Modell von BEC ist eine physikalische Näherung, die für bestimmte Klassen von BECs gilt. Das GPE beruht auf folgenden Vereinfachungen: Es geht davon aus, dass die Wechselwirkungen zwischen den Kondensatteilchen vom Typ Kontakt-Zweikörper sind, und vernachlässigt außerdem anomale Beiträge zur Eigenenergie. Diese Annahmen sind vor allem für verdünnte dreidimensionale Kondensate geeignet. Wenn man eine dieser Annahmen lockert, erhält die Gleichung für die Kondensat-Wellenfunktion die Terme, die Potenzen höherer Ordnung der Wellenfunktion enthalten. Bei einigen physikalischen Systemen erweist sich die Anzahl solcher Terme als unendlich, so dass die Gleichung im Wesentlichen nicht mehr polynomial ist. Beispiele hierfür sind die Bose-Fermi-Verbundkondensate, effektiv niederdimensionale Kondensate, dichte Kondensate und superfluide Cluster und Tröpfchen. Es wird festgestellt, dass man über die Gross-Pitaevskii-Gleichung hinausgehen muss. Zum Beispiel ist der logarithmische Term aus der logarithmischen Schrödinger-Gleichung zusammen mit einem Ginzburg-Sobyanin-Beitrag zur Gross-Pitaevskii-Gleichung hinzugefügt werden, um korrekt zu bestimmen, dass die Schallgeschwindigkeit als Kubikwurzel des Drucks für Helium-4 bei sehr niedrigen Temperaturen skaliert, und zwar in enger Übereinstimmung mit dem Experiment. ⓘ
Andere
Es ist jedoch klar, dass im allgemeinen Fall das Verhalten des Bose-Einstein-Kondensats durch gekoppelte Evolutionsgleichungen für die Kondensatdichte, die Supraflüssigkeitsgeschwindigkeit und die Verteilungsfunktion der Elementaranregungen beschrieben werden kann. Dieses Problem wurde 1977 von Peletminskii et al. in einem mikroskopischen Ansatz gelöst. Die Peletminskii-Gleichungen gelten für alle endlichen Temperaturen unterhalb des kritischen Punktes. Jahre später, im Jahr 1985, erhielten Kirkpatrick und Dorfman ähnliche Gleichungen mit einem anderen mikroskopischen Ansatz. Die Peletminskii-Gleichungen reproduzieren auch die hydrodynamischen Gleichungen von Chalatnikov für Superfluid als Grenzfall. ⓘ
Superfluidität von BEC und Landau-Kriterium
Die Phänomene der Suprafluidität eines Bose-Gases und der Supraleitung eines stark korrelierten Fermi-Gases (ein Gas aus Cooper-Paaren) sind eng mit der Bose-Einstein-Kondensation verbunden. Unter entsprechenden Bedingungen, unterhalb der Temperatur des Phasenübergangs, wurden diese Phänomene in Helium-4 und verschiedenen Klassen von Supraleitern beobachtet. In diesem Sinne wird die Supraleitung oft als die Suprafluidität des Fermi-Gases bezeichnet. In der einfachsten Form lässt sich der Ursprung der Suprafluidität aus dem Modell der schwach wechselwirkenden Bosonen ableiten. ⓘ
Experimentelle Beobachtung
Suprafluides Helium-4
1938 entdeckten Pjotr Kapitsa, John Allen und Don Misener, dass Helium-4 bei Temperaturen unter 2,17 K (dem Lambda-Punkt) zu einer neuen Art von Flüssigkeit wird, die heute als Suprafluid bezeichnet wird. Supraflüssiges Helium hat viele ungewöhnliche Eigenschaften, darunter eine Viskosität von Null (die Fähigkeit, ohne Energieverlust zu fließen) und die Existenz von quantisierten Wirbeln. Schnell glaubte man, dass die Suprafluidität auf die partielle Bose-Einstein-Kondensation der Flüssigkeit zurückzuführen sei. Tatsächlich treten viele Eigenschaften des supraflüssigen Heliums auch in den von Cornell, Wieman und Ketterle erzeugten gasförmigen Kondensaten auf (siehe unten). Supraflüssiges Helium-4 ist eher eine Flüssigkeit als ein Gas, was bedeutet, dass die Wechselwirkungen zwischen den Atomen relativ stark sind; die ursprüngliche Theorie der Bose-Einstein-Kondensation muss stark modifiziert werden, um sie zu beschreiben. Die Bose-Einstein-Kondensation bleibt jedoch grundlegend für die superfluiden Eigenschaften von Helium-4. Man beachte, dass Helium-3, ein Fermion, ebenfalls in eine superfluide Phase eintritt (bei einer viel niedrigeren Temperatur), was durch die Bildung bosonischer Cooper-Paare aus zwei Atomen erklärt werden kann (siehe auch fermionisches Kondensat). ⓘ
Verdünnte atomare Gase
Das erste "reine" Bose-Einstein-Kondensat wurde am 5. Juni 1995 von Eric Cornell, Carl Wieman und Kollegen am JILA erzeugt. Sie kühlten einen verdünnten Dampf aus etwa zweitausend Rubidium-87-Atomen mit einer Kombination aus Laserkühlung (eine Technik, für die ihre Erfinder Steven Chu, Claude Cohen-Tannoudji und William D. Phillips 1997 den Nobelpreis für Physik erhielten) und magnetischer Verdampfungskühlung auf unter 170 nK. Etwa vier Monate später kondensierte Natrium-23 in einem unabhängigen Versuch unter der Leitung von Wolfgang Ketterle am MIT. Ketterles Kondensat hatte hundertmal mehr Atome und ermöglichte wichtige Ergebnisse wie die Beobachtung quantenmechanischer Interferenzen zwischen zwei verschiedenen Kondensaten. Cornell, Wieman und Ketterle erhielten 2001 den Nobelpreis für Physik für ihre Leistungen. ⓘ
Eine Gruppe unter der Leitung von Randall Hulet an der Rice University kündigte nur einen Monat nach der JILA-Arbeit ein Kondensat aus Lithiumatomen an. Lithium hat anziehende Wechselwirkungen, so dass das Kondensat instabil ist und bis auf wenige Atome zusammenbricht. Hulets Team zeigte anschließend, dass das Kondensat durch Quantendruck für bis zu 1000 Atome stabilisiert werden kann. Seitdem sind verschiedene Isotope kondensiert worden. ⓘ
Diagramm der Geschwindigkeitsverteilungsdaten
In der Abbildung zu diesem Artikel zeigen die Geschwindigkeitsverteilungsdaten die Bildung eines Bose-Einstein-Kondensats aus einem Gas von Rubidiumatomen. Die Falschfarben geben die Anzahl der Atome bei den einzelnen Geschwindigkeiten an, wobei rot für die wenigsten und weiß für die meisten steht. Die Bereiche, die weiß und hellblau erscheinen, liegen bei den niedrigsten Geschwindigkeiten. Aufgrund der Heisenberg'schen Unschärferelation ist der Peak nicht unendlich schmal: räumlich begrenzte Atome haben eine minimale Breite in der Geschwindigkeitsverteilung. Diese Breite ist durch die Krümmung des magnetischen Potenzials in der jeweiligen Richtung gegeben. In engeren Richtungen ist die Breite der ballistischen Geschwindigkeitsverteilung größer. Diese Anisotropie der Spitze auf der rechten Seite ist ein rein quantenmechanischer Effekt und kommt in der thermischen Verteilung auf der linken Seite nicht vor. Dieses Diagramm diente 1999 als Titelbild für das Lehrbuch Thermische Physik von Ralph Baierlein. ⓘ
Quasiteilchen
Die Bose-Einstein-Kondensation gilt auch für Quasiteilchen in Festkörpern. Magnonen, Exzitonen und Polaritonen haben einen ganzzahligen Spin, d. h. sie sind Bosonen, die Kondensate bilden können. ⓘ
Magnonen, Elektronenspinwellen, können durch ein Magnetfeld gesteuert werden. Dichten von der Grenze eines verdünnten Gases bis hin zu einer stark wechselwirkenden Bose-Flüssigkeit sind möglich. Die magnetische Ordnung ist das Analogon zur Suprafluidität. Im Jahr 1999 wurde die Kondensation in antiferromagnetischem TlCuCl
3 bei Temperaturen von bis zu 14 K nachgewiesen. Die hohe Übergangstemperatur (im Vergleich zu atomaren Gasen) ist auf die geringe Masse der Magnonen (nahe der eines Elektrons) und die größere erreichbare Dichte zurückzuführen. Im Jahr 2006 wurde die Kondensation in einem ferromagnetischen Yttrium-Eisen-Granat-Dünnfilm sogar bei Raumtemperatur und mit optischem Pumpen beobachtet. ⓘ
Boer et al. sagten 1961 voraus, dass Exzitonen, Elektron-Loch-Paare, bei niedriger Temperatur und hoher Dichte kondensieren können. In Experimenten mit Doppelschichtsystemen wurde die Kondensation erstmals 2003 durch das Verschwinden der Hall-Spannung nachgewiesen. Die schnelle Erzeugung optischer Exzitonen wurde 2005 zur Bildung von Kondensaten in Sub-Kelvin-Cu
2O im Jahr 2005. ⓘ
Die Kondensation von Polaritonen wurde erstmals für Exziton-Polaritonen in einem bei 5 K gehaltenen Quantentopf-Mikrokavität nachgewiesen. ⓘ
In der Schwerelosigkeit
Im Juni 2020 gelang es dem Cold Atom Laboratory-Experiment an Bord der Internationalen Raumstation, ein BEC aus Rubidiumatomen zu erzeugen und über eine Sekunde lang im freien Fall zu beobachten. Obwohl es sich zunächst nur um einen Funktionsnachweis handelte, zeigten frühe Ergebnisse, dass sich in der Mikrogravitationsumgebung der ISS etwa die Hälfte der Atome zu einer magnetisch unempfindlichen haloartigen Wolke um den Hauptkörper des BECs formte. ⓘ
Eigenartige Eigenschaften
Quantisierte Wirbel
Wie in vielen anderen Systemen können auch in BECs Wirbel existieren. Wirbel können z. B. durch "Rühren" des Kondensats mit Lasern erzeugt werden, durch Rotation der Einschlussfalle, oder durch schnelles Abkühlen über den Phasenübergang. Der erzeugte Wirbel ist ein Quantenwirbel, dessen Kernform durch die Wechselwirkungen bestimmt wird. Die Flüssigkeitszirkulation um einen beliebigen Punkt ist aufgrund des einwertigen Charakters des BEC-Ordnungsparameters oder der Wellenfunktion quantisiert, die in der Form wobei und sind wie im zylindrischen Koordinatensystem, und ist die Winkelquantenzahl (auch bekannt als die "Ladung" des Wirbels). Da die Energie eines Wirbels proportional zum Quadrat seines Drehimpulses ist, können in trivialer Topologie nur Wirbel im stationären Zustand existieren; Wirbel mit höherer Ladung haben die Tendenz, sich in Wirbel aufzuspalten, wenn die Topologie der Geometrie dies zulässt. ⓘ
Ein axialsymmetrisches (z. B. harmonisches) Begrenzungspotential wird üblicherweise für die Untersuchung von Wirbeln in BEC verwendet. Zur Bestimmung von zu bestimmen, muss die Energie von minimiert werden, und zwar gemäß der Randbedingung . Dies geschieht in der Regel auf rechnerische Weise, doch in einem gleichförmigen Medium zeigt die folgende analytische Form das korrekte Verhalten und stellt eine gute Annäherung dar:
Hier, die Dichte fern vom Wirbel und , wobei die Heilungslänge des Kondensats ist. ⓘ
Ein einfach geladener Wirbel () befindet sich im Grundzustand, wobei seine Energie gegeben durch ⓘ
wobei (Um eine wohldefinierte Energie zu erhalten, ist es notwendig, diese Grenze mit einzubeziehen. .) ⓘ
Für mehrfach geladene Wirbel () wird die Energie angenähert durch ⓘ
die größer ist als die Energie von einfach geladene Wirbel, was darauf hindeutet, dass diese mehrfach geladenen Wirbel instabil sind und nicht zerfallen. Forschungsergebnisse deuten jedoch darauf hin, dass es sich um metastabile Zustände handelt, die eine relativ lange Lebensdauer haben können. ⓘ
In engem Zusammenhang mit der Entstehung von Wirbeln in BECs steht die Erzeugung so genannter dunkler Solitonen in eindimensionalen BECs. Diese topologischen Objekte weisen einen Phasengradienten über ihre Knotenebene auf, der ihre Form auch bei Ausbreitung und Wechselwirkung stabilisiert. Obwohl Solitonen keine Ladung tragen und daher für den Zerfall anfällig sind, wurden relativ langlebige dunkle Solitonen erzeugt und ausgiebig untersucht. ⓘ
Anziehende Wechselwirkungen
Experimente unter der Leitung von Randall Hulet an der Rice University von 1995 bis 2000 zeigten, dass Lithiumkondensate mit anziehenden Wechselwirkungen bis zu einer kritischen Atomzahl stabil existieren können. Beim Abschrecken des Gases beobachteten sie, wie das Kondensat wuchs und dann kollabierte, als die Anziehungskraft die Nullpunktenergie des einschließenden Potenzials überwältigte, und zwar in einem Ausbruch, der an eine Supernova erinnerte, mit einer Explosion, der eine Implosion vorausging. ⓘ
Weitere Arbeiten über anziehende Kondensate wurden im Jahr 2000 vom JILA-Team, bestehend aus Cornell, Wieman und Mitarbeitern, durchgeführt. Ihre Instrumente ließen sich nun besser steuern, so dass sie natürlich anziehende Rubidium-85-Atome (mit negativer Atom-Atom-Streulänge) verwendeten. Mit Hilfe der Feshbach-Resonanz, bei der ein Schwenken des Magnetfelds zu Spin-Flip-Kollisionen führt, senkten sie die charakteristischen, diskreten Energien, bei denen sich Rubidium bindet, wodurch ihre Rb-85-Atome abstoßend werden und ein stabiles Kondensat entsteht. Der umkehrbare Wechsel von Anziehung zu Abstoßung ist auf Quanteninterferenz zwischen den wellenförmigen Kondensatatomen zurückzuführen. ⓘ
Als das JILA-Team die Magnetfeldstärke weiter erhöhte, kehrte das Kondensat plötzlich zur Anziehung zurück, implodierte und schrumpfte bis zur Unkenntlichkeit, dann explodierte es und stieß etwa zwei Drittel seiner 10.000 Atome aus. Etwa die Hälfte der Atome des Kondensats schien aus dem Experiment verschwunden zu sein und war weder im kalten Überrest noch in der expandierenden Gaswolke zu sehen. Carl Wieman erklärte, dass diese Eigenschaft des Bose-Einstein-Kondensats nach der gegenwärtigen Atomtheorie nicht erklärt werden kann, da der Energiezustand eines Atoms nahe dem absoluten Nullpunkt nicht ausreichen sollte, um eine Implosion auszulösen; es wurden jedoch spätere Mittelfeldtheorien vorgeschlagen, um dies zu erklären. Höchstwahrscheinlich bildeten sie Moleküle aus zwei Rubidiumatomen; die durch diese Bindung gewonnene Energie verleiht ihnen eine ausreichende Geschwindigkeit, um die Falle unbemerkt zu verlassen. ⓘ
Der Prozess der Bildung eines molekularen Bose-Kondensats während des Durchlaufs des Magnetfelds durch die Feshbach-Resonanz sowie der umgekehrte Prozess werden durch ein exakt lösbares Modell beschrieben, das viele experimentelle Beobachtungen erklären kann. ⓘ
Aktuelle Forschung
Wie können wir die Existenz von Bose-Einstein-Kondensaten für allgemein wechselwirkende Systeme rigoros beweisen?
Im Vergleich zu häufiger anzutreffenden Materiezuständen sind Bose-Einstein-Kondensate extrem zerbrechlich. Die geringste Wechselwirkung mit der äußeren Umgebung kann ausreichen, um sie über die Kondensationsschwelle hinaus zu erwärmen, so dass ihre interessanten Eigenschaften verschwinden und ein normales Gas entsteht. ⓘ
Nichtsdestotrotz haben sie sich als nützlich erwiesen, um eine breite Palette von Fragen der Grundlagenphysik zu erforschen, und in den Jahren seit den ersten Entdeckungen der JILA- und MIT-Gruppen ist eine Zunahme der experimentellen und theoretischen Aktivitäten zu verzeichnen. Beispiele hierfür sind Experimente, die die Interferenz zwischen Kondensaten aufgrund des Welle-Teilchen-Dualismus nachgewiesen haben, die Untersuchung von Suprafluidität und quantisierten Wirbeln, die Erzeugung heller Materiewellen-Solitonen aus Bose-Kondensaten, die auf eine Dimension beschränkt sind, und die Verlangsamung von Lichtimpulsen auf sehr niedrige Geschwindigkeiten durch elektromagnetisch induzierte Transparenz. Wirbel in Bose-Einstein-Kondensaten sind derzeit auch Gegenstand der analogen Gravitationsforschung, bei der die Möglichkeit untersucht wird, Schwarze Löcher und damit verbundene Phänomene in solchen Umgebungen im Labor zu modellieren. Experimentatoren haben auch "optische Gitter" realisiert, bei denen das Interferenzmuster von sich überlappenden Lasern ein periodisches Potential liefert. Diese wurden verwendet, um den Übergang zwischen einem Suprafluid und einem Mott-Isolator zu erforschen, und können bei der Untersuchung der Bose-Einstein-Kondensation in weniger als drei Dimensionen, z. B. dem Tonks-Girardeau-Gas, nützlich sein. Darüber hinaus wurde die Empfindlichkeit des Pinning-Übergangs von stark wechselwirkenden Bosonen, die in einem flachen eindimensionalen optischen Gitter eingeschlossen sind, das ursprünglich von Haller beobachtet wurde, durch eine Veränderung des primären optischen Gitters durch ein sekundäres schwächeres erforscht. So wurde für ein resultierendes schwaches bichromatisches optisches Gitter festgestellt, dass der Pinning-Übergang robust ist gegenüber der Einführung des schwächeren sekundären optischen Gitters robust ist. Untersuchungen von Wirbeln in uneinheitlichen Bose-Einstein-Kondensaten sowie von Exzitatonen dieser Systeme durch bewegliche abstoßende oder anziehende Hindernisse wurden ebenfalls durchgeführt. In diesem Zusammenhang wurden die Bedingungen für Ordnung und Chaos in der Dynamik eines gefangenen Bose-Einstein-Kondensats durch die Anwendung sich bewegender blau- und rot-abgestimmter Laserstrahlen über die zeitabhängige Gross-Pitaevskii-Gleichung erforscht. ⓘ
Es wurden Bose-Einstein-Kondensate aus einer breiten Palette von Isotopen hergestellt. ⓘ
Durch das Abkühlen von Fermionen auf extrem niedrige Temperaturen wurden entartete Gase erzeugt, die dem Pauli-Ausschlussprinzip unterliegen. Für die Bose-Einstein-Kondensation müssen sich die Fermionen "paaren", um bosonische Verbundteilchen zu bilden (z. B. Moleküle oder Cooper-Paare). Die ersten molekularen Kondensate wurden im November 2003 von den Gruppen von Rudolf Grimm an der Universität Innsbruck, Deborah S. Jin an der University of Colorado in Boulder und Wolfgang Ketterle am MIT erzeugt. Jin schuf kurz darauf das erste fermionische Kondensat, indem sie mit demselben System arbeitete, jedoch außerhalb des molekularen Bereichs. ⓘ
1999 leitete die dänische Physikerin Lene Hau ein Team der Harvard University, das einen Lichtstrahl mithilfe eines Superfluids auf etwa 17 Meter pro Sekunde verlangsamte. Hau und ihre Mitarbeiter haben seitdem eine Gruppe von Kondensatatomen dazu gebracht, von einem Lichtpuls zurückzustoßen, so dass sie die Phase und Amplitude des Lichts aufzeichneten, die von einem zweiten nahegelegenen Kondensat wiedergewonnen wurden, was sie als "durch langsames Licht vermittelte atomare Materiewellenverstärkung" unter Verwendung von Bose-Einstein-Kondensaten bezeichnen: Einzelheiten werden in Nature diskutiert. ⓘ
Ein weiteres aktuelles Forschungsinteresse gilt der Erzeugung von Bose-Einstein-Kondensaten in der Mikrogravitation, um deren Eigenschaften für die hochpräzise Atominterferometrie zu nutzen. Die erste Demonstration eines BEC in Schwerelosigkeit gelang 2008 in einem Fallturm in Bremen, Deutschland, durch ein Forscherkonsortium unter der Leitung von Ernst M. Rasel von der Leibniz Universität Hannover. Dasselbe Team demonstrierte 2017 die erste Erzeugung eines Bose-Einstein-Kondensats im Weltraum, und es ist auch Gegenstand von zwei bevorstehenden Experimenten auf der Internationalen Raumstation. ⓘ
Forscher auf dem neuen Gebiet der Atomtronik nutzen die Eigenschaften von Bose-Einstein-Kondensaten, wenn sie Gruppen identischer kalter Atome mit Lasern manipulieren. ⓘ
BECs wurden 1970 von Emmanuel David Tannenbaum für die Anti-Tarnkappentechnik vorgeschlagen. ⓘ
Im Jahr 2020 berichteten Forscher über die Entwicklung supraleitender BEC und dass es offenbar einen "fließenden Übergang" zwischen BEC und Bardeen-Cooper-Shrieffer-Regime gibt. ⓘ
Kontinuierliche Bose-Einstein-Kondensation
Die Beschränkungen der Verdampfungskühlung haben atomare BECs auf einen "gepulsten" Betrieb beschränkt, der einen äußerst ineffizienten Arbeitszyklus beinhaltet, bei dem mehr als 99 % der Atome verworfen werden, um BEC zu erreichen. Das Erreichen einer kontinuierlichen BEC war ein wichtiges offenes Problem der experimentellen BEC-Forschung, das von den gleichen Beweggründen wie die Entwicklung kontinuierlicher optischer Laser angetrieben wurde: Materiewellen mit hohem Fluss und hoher Kohärenz, die kontinuierlich erzeugt werden, würden neue Sensoranwendungen ermöglichen. ⓘ
Kontinuierliches BEC wurde zum ersten Mal 2022 erreicht. ⓘ
Dunkle Materie
P. Sikivie und Q. Yang zeigten, dass kalte Axionen aus dunkler Materie durch Thermalisierung aufgrund gravitativer Selbstwechselwirkungen ein Bose-Einstein-Kondensat bilden. Die Existenz von Axionen konnte bisher nicht bestätigt werden. Die wichtige Suche nach ihnen wurde jedoch mit der Fertigstellung der Erweiterungen des Axion Dark Matter Experiment (ADMX) an der University of Washington Anfang 2018 erheblich verbessert. ⓘ
Im Jahr 2014 wurde am Forschungszentrum Jülich ein potenzielles Dibaryon bei etwa 2380 MeV nachgewiesen. Das Zentrum behauptete, dass die Messungen die Ergebnisse aus dem Jahr 2011 bestätigen, und zwar mit einer besser reproduzierbaren Methode. Das Teilchen existierte für 10-23 Sekunden und wurde d*(2380) genannt. Es wird angenommen, dass dieses Teilchen aus drei Up- und drei Down-Quarks besteht. Es wird vermutet, dass Gruppen von d-Sternen aufgrund der vorherrschenden niedrigen Temperaturen im frühen Universum Bose-Einstein-Kondensate bilden könnten, und dass sich BECs aus solchen Hexaquarks mit eingeschlossenen Elektronen wie dunkle Materie verhalten könnten. ⓘ
Isotope
Der Effekt wurde hauptsächlich bei Alkaliatomen beobachtet, deren Kerneigenschaften sich besonders gut für die Arbeit mit Fallen eignen. Seit 2012 können bei ultratiefen Temperaturen von oder darunter Bose-Einstein-Kondensate für eine Vielzahl von Isotopen, hauptsächlich von Alkali- und Erdalkalimetallen, erhalten,
und Lanthanidatomen (7
Li
, 23
Na
, 39
K
, 41
K
, 85
Rb
, 87
Rb
, 133
Cs
, 52
Cr
, 40
Ca
, 84
Sr
, 86
Sr
, 88
Sr
, 174
Yb
, 164
Dy
, und 168
Er
). Mit Hilfe der neu entwickelten Methode der "Verdunstungskühlung" gelang es schließlich, Wasserstoff zu erforschen. Dagegen ist der supraflüssige Zustand von 4
He
unterhalb von 2,17 K kein gutes Beispiel, weil die Wechselwirkung zwischen den Atomen zu stark ist. Nur 8 % der Atome befinden sich im Grundzustand der Falle in der Nähe des absoluten Nullpunkts und nicht die 100 % eines echten Kondensats. ⓘ
Das bosonische Verhalten einiger dieser alkalischen Gase erscheint auf den ersten Blick seltsam, weil ihre Kerne einen halbzahligen Gesamtspin haben. Es ergibt sich aus einem subtilen Zusammenspiel von Elektronen- und Kernspins: Bei ultratiefen Temperaturen und entsprechenden Anregungsenergien sind der halbzahlige Gesamtspin der Elektronenhülle und der halbzahlige Gesamtspin des Kerns durch eine sehr schwache Hyperfeinwechselwirkung gekoppelt. Der Gesamtspin des Atoms, der sich aus dieser Kopplung ergibt, ist ein ganzzahliger kleinerer Wert. Die Chemie von Systemen bei Raumtemperatur wird durch die elektronischen Eigenschaften bestimmt, die im Wesentlichen fermionisch sind, da thermische Anregungen bei Raumtemperatur typische Energien haben, die viel höher sind als die Hyperfeinwerte. ⓘ
In der Fiktion
- Film Spectral 2016 - US-Militär kämpft gegen mysteriöse feindliche Kreaturen, die aus Bose-Einstein-Kondensat bestehen
- Die Wissenschaft von Spectral: Verhält sich das Bose-Einstein-Kondensat wirklich so? Ein echter Wissenschaftler, der sich mit Bose-Einstein-Kondensat beschäftigt, gibt einen Überblick über die Wissenschaft von Spectral. Und der Regisseur des Films, Nic Mathieu, antwortet. Thilo Stöferle. July 18, 2017. Ars Technica. Accessed June 4, 2021.
- Blind Lake 2003 Roman - Wissenschaftler beobachten empfindungsfähiges Leben auf einem 51 Lichtjahre entfernten Planeten mit Teleskopen, die von Quantencomputern auf der Basis von Bose-Einstein-Kondensaten angetrieben werden.
- In Mass Effect gibt es kryonische Munition, die laut Aromatext mit Bose-Einstein-Kondensaten gefüllt ist. Beim Aufprall zerplatzen die Kugeln und versprühen eine superkalte Flüssigkeit auf den Feind. ⓘ
Experimenteller Nachweis

Der Nachweis, dass tatsächlich ein Bose-Einstein-Kondensat erzeugt wurde, erfolgt bei atomaren Gasen meistens mit Hilfe von Absorptions-Abbildungen nach einer Flugzeit. ⓘ
Dazu wird die Falle, in der das Gas gefangen war, schlagartig abgeschaltet. Daraufhin expandiert die Gaswolke und wird nach einer Flugzeit mit resonantem Laserlicht bestrahlt. Die Photonen des Strahls werden von den Atomen der Gaswolke gestreut, der Strahl also effektiv geschwächt. Der entstandene (Halb-)Schatten kann mit einer empfindlichen CCD-Kamera aufgenommen werden, aus seinem Bild lässt sich die Dichteverteilung der Gaswolke rekonstruieren. ⓘ
Diese ist für Bose-Einstein-Kondensate anisotrop, während ein klassisches Gas im thermischen Gleichgewicht immer isotrop expandiert. In vielen Fällen ist die Dichteverteilung parabelförmig, was sich als Konsequenz der Wechselwirkung zwischen den Atomen verstehen lässt und das Bose-Einstein-Kondensat von einem idealen Bosegas unterscheidet. ⓘ
Ähnliche Effekte
- Beim Fermionen-Kondensat basiert der Effekt ebenfalls auf Bosonen. Aufgrund des Pauli-Prinzips ist es nicht möglich, dass sich Fermionen im selben Zustand befinden. Dies gilt aber nicht für sich paarweise zu Bosonen zusammenschließende Fermionen, die dann als Bosonen ein Kondensat bilden können. ⓘ














![{\displaystyle f\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41c57ac0222bfe2602c3c23d82a400772087d030)


































![{\displaystyle E=\int d{\vec {r}}\left[{\frac {\hbar ^{2}}{2m}}|\nabla \psi ({\vec {r}})|^{2}+V({\vec {r}})|\psi ({\vec {r}})|^{2}+{\frac {1}{2}}U_{0}|\psi ({\vec {r}})|^{4}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1da50aafaf10d7bc40d6f6323837bb787e441da)






















