Wellenlänge

Die Wellenlänge einer Sinuswelle, λ, kann zwischen zwei beliebigen Punkten mit der gleichen Phase gemessen werden, z. B. zwischen Scheitelpunkten (oben) oder Tiefpunkten (unten) oder entsprechenden Nulldurchgängen, wie dargestellt. ⓘ

In der Physik ist die Wellenlänge die räumliche Periode einer periodischen Welle - der Abstand, über den sich die Form der Welle wiederholt. Sie ist der Abstand zwischen aufeinanderfolgenden Punkten gleicher Phase auf der Welle, z. B. zwei benachbarten Wellenbergen, Wellentälern oder Nulldurchgängen, und ist ein Merkmal sowohl von Wanderwellen als auch von stehenden Wellen sowie von anderen räumlichen Wellenmustern. Der Kehrwert der Wellenlänge wird als Raumfrequenz bezeichnet. Die Wellenlänge wird im Allgemeinen mit dem griechischen Buchstaben Lambda (λ) bezeichnet. Der Begriff Wellenlänge wird manchmal auch auf modulierte Wellen und auf die sinusförmigen Hüllkurven modulierter Wellen oder auf Wellen, die durch Interferenz mehrerer Sinuskurven entstehen, angewandt. ⓘ

Geht man von einer Sinuswelle aus, die sich mit einer festen Wellengeschwindigkeit bewegt, so ist die Wellenlänge umgekehrt proportional zur Frequenz der Welle: Wellen mit höheren Frequenzen haben kürzere Wellenlängen, und Wellen mit niedrigeren Frequenzen haben längere Wellenlängen. ⓘ

Die Wellenlänge hängt von dem Medium (z. B. Vakuum, Luft oder Wasser) ab, durch das sich eine Welle bewegt. Beispiele für Wellen sind Schallwellen, Licht, Wasserwellen und periodische elektrische Signale in einem Leiter. Eine Schallwelle ist eine Veränderung des Luftdrucks, während bei Licht und anderen elektromagnetischen Strahlungen die Stärke des elektrischen und des magnetischen Feldes variiert. Wasserwellen sind Schwankungen in der Höhe eines Gewässers. Bei den Schwingungen eines Kristallgitters variieren die Positionen der Atome. ⓘ

Der Bereich der Wellenlängen oder Frequenzen von Wellenphänomenen wird als Spektrum bezeichnet. Die Bezeichnung stammt ursprünglich vom Spektrum des sichtbaren Lichts, kann aber heute auf das gesamte elektromagnetische Spektrum sowie auf ein Schall- oder Schwingungsspektrum angewendet werden. ⓘ

Sinusförmige Wellen

In linearen Medien kann jedes Wellenmuster durch die unabhängige Ausbreitung sinusförmiger Komponenten beschrieben werden. Die Wellenlänge λ einer sinusförmigen Wellenform, die sich mit konstanter Geschwindigkeit ausbreitet $v$ ist gegeben durch ⓘ

$\lambda ={\frac {v}{f}}\,\,,$ ⓘ

wobei $v$ die Phasengeschwindigkeit (Betrag der Phasengeschwindigkeit) der Welle ist und $f$ die Frequenz der Welle ist. In einem dispersiven Medium hängt die Phasengeschwindigkeit selbst von der Frequenz der Welle ab, wodurch die Beziehung zwischen Wellenlänge und Frequenz nichtlinear ist. ⓘ

Bei elektromagnetischer Strahlung - wie z. B. Licht - ist die Phasengeschwindigkeit im freien Raum gleich der Lichtgeschwindigkeit, d. h. etwa 3×10⁸ m/s. Die Wellenlänge einer elektromagnetischen (Radio-)Welle von 100 MHz beträgt also etwa: 3×10⁸ m/s geteilt durch 10⁸ Hz = 3 Meter. Die Wellenlänge des sichtbaren Lichts reicht von tiefrot, etwa 700 nm, bis violett, etwa 400 nm (weitere Beispiele siehe elektromagnetisches Spektrum). ⓘ

Für Schallwellen in der Luft beträgt die Schallgeschwindigkeit 343 m/s (bei Raumtemperatur und atmosphärischem Druck). Die Wellenlängen der für das menschliche Ohr hörbaren Schallfrequenzen (20 Hz-20 kHz) liegen also zwischen etwa 17 m und 17 mm. Fledermäuse verwenden etwas höhere Frequenzen, damit sie Ziele, die kleiner als 17 mm sind, auflösen können. Die Wellenlängen des hörbaren Schalls sind viel länger als die des sichtbaren Lichts. ⓘ

Sinusförmige stehende Wellen in einem Kasten, der die Endpunkte zu Knoten macht, haben eine ganzzahlige Anzahl von halben Wellenlängen, die in den Kasten passen. ⓘ

Eine stehende Welle (schwarz), dargestellt als Summe von zwei sich ausbreitenden Wellen, die sich in entgegengesetzte Richtungen ausbreiten (rot und blau) ⓘ

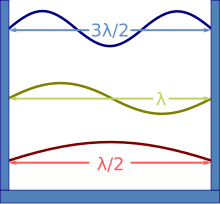
Stehende Wellen

Eine stehende Welle ist eine wellenförmige Bewegung, die an einem Ort bleibt. Eine sinusförmige stehende Welle enthält stationäre Punkte ohne Bewegung, die als Knotenpunkte bezeichnet werden, und die Wellenlänge ist das Doppelte des Abstands zwischen den Knotenpunkten. ⓘ

Die obere Abbildung zeigt drei stehende Wellen in einem Kasten. Die Wände des Kastens werden als Voraussetzung dafür betrachtet, dass die Welle Knoten an den Wänden des Kastens haben muss (ein Beispiel für Randbedingungen), die bestimmen, welche Wellenlängen zulässig sind. Wenn der Kasten beispielsweise ideale Metallwände hat, ergibt sich für eine elektromagnetische Welle die Bedingung für Knoten an den Wänden, weil die Metallwände kein tangentiales elektrisches Feld tragen können, was die Welle zwingt, an der Wand eine Amplitude von Null zu haben. ⓘ

Die stehende Welle kann als Summe von zwei sich ausbreitenden Sinuswellen mit entgegengesetzten Geschwindigkeiten betrachtet werden. Folglich stehen Wellenlänge, Periode und Wellengeschwindigkeit in der gleichen Beziehung wie bei einer sich ausbreitenden Welle. Die Lichtgeschwindigkeit lässt sich zum Beispiel aus der Beobachtung stehender Wellen in einem Metallkasten mit idealem Vakuum bestimmen. ⓘ

Mathematische Darstellung

Sich ausbreitende Sinuswellen werden häufig mathematisch durch ihre Geschwindigkeit v (in x-Richtung), ihre Frequenz f und ihre Wellenlänge λ wie folgt dargestellt:

$y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)$ ⓘ

Dabei ist y der Wert der Welle an einer beliebigen Position x und zum Zeitpunkt t und A ist die Amplitude der Welle. Sie werden auch üblicherweise durch die Wellenzahl k (2π-facher Kehrwert der Wellenlänge) und die Winkelfrequenz ω (2π-fache der Frequenz) ausgedrückt als:

$y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)$ ⓘ

wobei die Wellenlänge und die Wellenzahl mit der Geschwindigkeit und der Frequenz wie folgt zusammenhängen:

$k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},$ ⓘ

oder ⓘ

$\lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.$ ⓘ

In der zweiten oben angegebenen Form wird die Phase (kx - ωt) oft zu (k-r - ωt) verallgemeinert, indem die Wellenzahl k durch einen Wellenvektor ersetzt wird, der die Richtung und Wellenzahl einer ebenen Welle im 3-Raum angibt, die durch den Positionsvektor r parametrisiert wird. In diesem Fall steht die Wellenzahl k, der Betrag von k, immer noch in derselben Beziehung zur Wellenlänge wie oben gezeigt, wobei v als skalare Geschwindigkeit in Richtung des Wellenvektors interpretiert wird. Die erste Form, bei der die reziproke Wellenlänge in der Phase verwendet wird, lässt sich nicht so leicht auf eine Welle in einer beliebigen Richtung verallgemeinern. ⓘ

Verallgemeinerungen auf Sinuskurven mit anderen Phasen und auf komplexe Exponentiale sind ebenfalls üblich; siehe ebene Welle. Die typische Konvention, bei der Beschreibung einer Welle die Kosinusphase anstelle der Sinusphase zu verwenden, beruht auf der Tatsache, dass der Kosinus der Realteil des komplexen Exponentials in der Welle ist

$Ae^{i\left(kx-\omega t\right)}.$ ⓘ

Allgemeine Medien

Die Wellenlänge verringert sich in einem Medium mit langsamerer Ausbreitung. ⓘ

Brechung: Beim Eintritt in ein Medium, in dem die Geschwindigkeit geringer ist, ändert die Welle ihre Richtung. ⓘ

Trennung von Farben durch ein Prisma (Klicken für Animation) ⓘ

Die Geschwindigkeit einer Welle hängt von dem Medium ab, in dem sie sich ausbreitet. Insbesondere ist die Lichtgeschwindigkeit in einem Medium geringer als im Vakuum, was bedeutet, dass die gleiche Frequenz in einem Medium einer kürzeren Wellenlänge entspricht als im Vakuum, wie in der Abbildung rechts dargestellt. ⓘ

Diese Geschwindigkeitsänderung beim Eintritt in ein Medium bewirkt eine Brechung oder eine Richtungsänderung von Wellen, die in einem Winkel auf die Grenzfläche zwischen Medien treffen. Bei elektromagnetischen Wellen wird diese Änderung des Ausbreitungswinkels durch das Snellsche Gesetz bestimmt. ⓘ

Die Wellengeschwindigkeit in einem Medium kann sich nicht nur von der in einem anderen unterscheiden, sondern die Geschwindigkeit variiert in der Regel auch mit der Wellenlänge. Folglich ändert sich die Richtungsänderung beim Eintritt in ein anderes Medium mit der Wellenlänge der Welle. ⓘ

Für elektromagnetische Wellen wird die Geschwindigkeit in einem Medium durch dessen Brechungsindex bestimmt, und zwar gemäß

$v={\frac {c}{n(\lambda _{0})}},$

wobei c die Lichtgeschwindigkeit im Vakuum und n(λ₀) der Brechungsindex des Mediums bei der Wellenlänge λ₀ ist, wobei letzterer im Vakuum und nicht im Medium gemessen wird. Die entsprechende Wellenlänge im Medium ist

$\lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.$ ⓘ

Wenn Wellenlängen elektromagnetischer Strahlung angegeben werden, ist in der Regel die Wellenlänge im Vakuum gemeint, es sei denn, die Wellenlänge wird ausdrücklich als die Wellenlänge in einem anderen Medium angegeben. In der Akustik, wo ein Medium für die Existenz der Wellen unerlässlich ist, wird der Wellenlängenwert für ein bestimmtes Medium angegeben. ⓘ

Die Änderung der Lichtgeschwindigkeit in Abhängigkeit von der Wellenlänge wird als Dispersion bezeichnet und ist auch für das bekannte Phänomen verantwortlich, dass Licht durch ein Prisma in die einzelnen Farben getrennt wird. Die Trennung erfolgt, wenn der Brechungsindex im Prisma mit der Wellenlänge variiert, so dass sich verschiedene Wellenlängen mit unterschiedlichen Geschwindigkeiten im Prisma ausbreiten und in verschiedenen Winkeln gebrochen werden. Die mathematische Beziehung, die beschreibt, wie die Geschwindigkeit des Lichts in einem Medium mit der Wellenlänge variiert, wird als Dispersionsrelation bezeichnet. ⓘ

Uneinheitliche Medien

Verschiedene lokale Wellenlängen in einer Meereswelle, die sich dem Ufer nähert, von Wellenberg zu Wellenberg ⓘ

Die Wellenlänge kann auch dann ein nützliches Konzept sein, wenn die Welle im Raum nicht periodisch ist. Bei einer Meereswelle, die sich dem Ufer nähert, wie in der Abbildung dargestellt, hat die ankommende Welle eine unterschiedliche lokale Wellenlänge, die zum Teil von der Tiefe des Meeresbodens im Vergleich zur Wellenhöhe abhängt. Die Analyse der Welle kann auf dem Vergleich der lokalen Wellenlänge mit der lokalen Wassertiefe basieren. ⓘ

Eine sinusförmige Welle, die sich in einem ungleichförmigen Medium ausbreitet, mit Verlust ⓘ

Wellen, die zeitlich sinusförmig sind, sich aber durch ein Medium ausbreiten, dessen Eigenschaften mit der Position variieren (ein inhomogenes Medium), können sich mit einer Geschwindigkeit ausbreiten, die mit der Position variiert, und sind daher möglicherweise nicht sinusförmig im Raum. Die Abbildung rechts zeigt ein Beispiel. Wenn sich die Welle verlangsamt, wird die Wellenlänge kürzer und die Amplitude nimmt zu; nach einer Stelle mit maximaler Reaktion ist die kurze Wellenlänge mit einem hohen Verlust verbunden und die Welle stirbt ab. ⓘ

Die Analyse der Differentialgleichungen solcher Systeme erfolgt häufig näherungsweise mit der WKB-Methode (auch bekannt als Liouville-Green-Methode). Bei dieser Methode wird die Phase durch den Raum integriert, wobei eine lokale Wellenzahl verwendet wird, die als "lokale Wellenlänge" der Lösung in Abhängigkeit von Zeit und Raum interpretiert werden kann. Bei dieser Methode wird das System lokal so behandelt, als wäre es gleichförmig mit den lokalen Eigenschaften; insbesondere ist die mit einer Frequenz verbundene lokale Wellengeschwindigkeit das Einzige, was zur Schätzung der entsprechenden lokalen Wellenzahl oder Wellenlänge benötigt wird. Darüber hinaus berechnet die Methode eine sich langsam ändernde Amplitude, um andere Bedingungen der Gleichungen oder des physikalischen Systems zu erfüllen, wie z. B. die Erhaltung der Energie in der Welle. ⓘ

Kristalle

Eine Welle auf einer Linie von Atomen kann entsprechend einer Vielzahl von Wellenlängen interpretiert werden. ⓘ

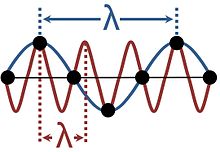
Wellen in kristallinen Festkörpern sind nicht kontinuierlich, da sie aus den Schwingungen diskreter Teilchen bestehen, die in einem regelmäßigen Gitter angeordnet sind. Dies führt zu Aliasing, da ein und dieselbe Schwingung als eine Vielzahl unterschiedlicher Wellenlängen betrachtet werden kann, wie in der Abbildung dargestellt. Beschreibungen, die mehr als eine dieser Wellenlängen verwenden, sind redundant; es ist üblich, die längste Wellenlänge zu wählen, die dem Phänomen entspricht. Der Bereich der Wellenlängen, der ausreicht, um alle möglichen Wellen in einem kristallinen Medium zu beschreiben, entspricht den Wellenvektoren, die auf die Brillouin-Zone beschränkt sind. ⓘ

Diese Unbestimmtheit der Wellenlänge in Festkörpern ist wichtig für die Analyse von Wellenphänomenen wie Energiebändern und Gitterschwingungen. Sie ist mathematisch gleichbedeutend mit dem Aliasing eines Signals, das in diskreten Intervallen abgetastet wird. ⓘ

Allgemeinere Wellenformen

Nahezu periodische Wellen über flachem Wasser ⓘ

Das Konzept der Wellenlänge wird am häufigsten auf sinusförmige oder nahezu sinusförmige Wellen angewandt, da in einem linearen System die Sinuskurve die einzige Form ist, die sich ohne Formänderung ausbreitet - nur mit einer Phasenänderung und möglicherweise einer Amplitudenänderung. Die Wellenlänge (oder alternativ die Wellenzahl oder der Wellenvektor) ist eine Charakterisierung der Welle im Raum, die funktional mit ihrer Frequenz zusammenhängt, wie sie durch die Physik des Systems eingeschränkt wird. Sinuskurven sind die einfachsten Wanderwellenlösungen, und komplexere Lösungen können durch Überlagerung aufgebaut werden. ⓘ

Im Sonderfall dispersionsfreier und gleichförmiger Medien breiten sich andere Wellen als Sinuswellen mit unveränderter Form und konstanter Geschwindigkeit aus. Unter bestimmten Umständen können Wellen mit unveränderlicher Form auch in nichtlinearen Medien auftreten; die Abbildung zeigt beispielsweise Meereswellen in flachem Wasser, die schärfere Wellenberge und flachere Wellentäler als eine Sinuswelle aufweisen, was typisch für eine Cnoidalwelle ist, eine Wanderwelle, die so genannt wird, weil sie durch die elliptische Jacobi-Funktion m-ter Ordnung beschrieben wird, die gewöhnlich als cn(x; m) bezeichnet wird. Ozeanwellen mit großer Amplitude und bestimmten Formen können sich aufgrund der Eigenschaften des nichtlinearen Oberflächenwellenmediums unverändert ausbreiten. ⓘ

Wellenlänge einer periodischen, aber nicht sinusförmigen Wellenform. ⓘ

Wenn eine sich ausbreitende Welle eine feste Form hat, die sich im Raum oder in der Zeit wiederholt, handelt es sich um eine periodische Welle. Solche Wellen werden manchmal als Wellenlänge betrachtet, auch wenn sie nicht sinusförmig sind. Wie in der Abbildung dargestellt, wird die Wellenlänge zwischen aufeinanderfolgenden entsprechenden Punkten auf der Wellenform gemessen. ⓘ

Wellenpakete

Ein sich ausbreitendes Wellenpaket ⓘ

Lokale Wellenpakete, "Ausbrüche" von Wellenbewegungen, bei denen sich jedes Wellenpaket als Einheit ausbreitet, finden in vielen Bereichen der Physik Anwendung. Ein Wellenpaket hat eine Hüllkurve, die die Gesamtamplitude der Welle beschreibt; innerhalb der Hüllkurve wird der Abstand zwischen benachbarten Spitzen oder Tälern manchmal als lokale Wellenlänge bezeichnet. Ein Beispiel ist in der Abbildung dargestellt. Im Allgemeinen bewegt sich die Einhüllende des Wellenpakets mit einer anderen Geschwindigkeit als die Wellen, aus denen es besteht. ⓘ

Mit Hilfe der Fourier-Analyse können Wellenpakete in unendliche Summen (oder Integrale) von Sinuswellen mit unterschiedlichen Wellenzahlen oder Wellenlängen zerlegt werden. ⓘ

Louis de Broglie postulierte, dass alle Teilchen mit einem bestimmten Impulswert p eine Wellenlänge λ = h/p haben, wobei h die Plancksche Konstante ist. Diese Hypothese bildete die Grundlage der Quantenmechanik. Heutzutage wird diese Wellenlänge als de Broglie-Wellenlänge bezeichnet. Die Elektronen in einem CRT-Display haben beispielsweise eine De-Broglie-Wellenlänge von etwa 10-13 m. Um zu verhindern, dass sich die Wellenfunktion eines solchen Teilchens über den gesamten Raum ausbreitet, schlug de Broglie die Verwendung von Wellenpaketen zur Darstellung von Teilchen vor, die im Raum lokalisiert sind. Die räumliche Ausbreitung des Wellenpakets und die Ausbreitung der Wellenzahlen der Sinusschwingungen, aus denen das Paket besteht, entsprechen den Unsicherheiten der Position und des Impulses des Teilchens, deren Produkt durch die Heisenbergsche Unschärferelation begrenzt ist. ⓘ

Dabei ist h das Plancksche Wirkungsquantum, c die Lichtgeschwindigkeit, m die Masse und v die Geschwindigkeit des Teilchens. ⓘ

Interferenz und Beugung

Doppelspalt-Interferenz

Muster der Lichtintensität auf einem Schirm für Licht, das durch zwei Spaltöffnungen fällt. Die Beschriftungen auf der rechten Seite beziehen sich auf die Differenz der Weglängen der beiden Spaltöffnungen, die hier als Punktquellen idealisiert werden. ⓘ

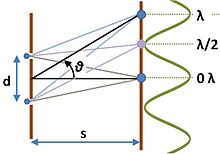
Wenn sich sinusförmige Wellenformen addieren, können sie sich je nach ihrer relativen Phase gegenseitig verstärken (konstruktive Interferenz) oder aufheben (destruktive Interferenz). Dieses Phänomen wird im Interferometer genutzt. Ein einfaches Beispiel ist ein auf Young zurückgehendes Experiment, bei dem Licht durch zwei Schlitze geleitet wird. Wie in der Abbildung dargestellt, wird das Licht durch zwei Schlitze geleitet und scheint auf einen Schirm. Der Weg des Lichts zu einer Position auf dem Schirm ist für die beiden Schlitze unterschiedlich und hängt von dem Winkel θ ab, den der Weg mit dem Schirm bildet. Wenn wir annehmen, dass der Schirm weit genug von den Spaltöffnungen entfernt ist (d. h. s ist groß im Vergleich zum Spaltabstand d), dann sind die Wege nahezu parallel, und die Wegdifferenz ist einfach d sin θ. Dementsprechend lautet die Bedingung für konstruktive Interferenz:

$d\sin \theta =m\lambda \ ,$ ⓘ

wobei m eine ganze Zahl ist, und für destruktive Interferenz gilt:

$d\sin \theta =(m+1/2)\lambda \ .$ ⓘ

Wenn also die Wellenlänge des Lichts bekannt ist, kann der Spaltabstand anhand des Interferenzmusters oder der Interferenzstreifen bestimmt werden, und umgekehrt. ⓘ

Bei Mehrfachspalten ist das Muster

$I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,$

wobei q die Anzahl der Spaltöffnungen und g die Gitterkonstante ist. Der erste Faktor, I₁, ist das Einzelspaltergebnis, das den sich schneller ändernden zweiten Faktor moduliert, der von der Anzahl der Spaltöffnungen und deren Abstand abhängt. In der Abbildung wurde I₁ auf Eins gesetzt, was eine sehr grobe Annäherung darstellt. ⓘ

Die Interferenz bewirkt eine Umverteilung des Lichts, so dass die im Licht enthaltene Energie nicht verändert wird, sondern nur der Ort, an dem sie auftritt. ⓘ

Beugung am Einzelspalt

Das Beugungsmuster eines Doppelspalts hat eine Einspalthülle. ⓘ

Der Begriff der Wegdifferenz und der konstruktiven oder destruktiven Interferenz, der oben für das Doppelspaltexperiment verwendet wurde, gilt auch für die Darstellung von Licht, das von einem einzigen Spalt auf einem Bildschirm aufgefangen wird. Das Hauptergebnis dieser Interferenz ist die Ausbreitung des Lichts aus dem schmalen Spalt in ein breiteres Bild auf dem Bildschirm. Diese Verteilung der Wellenenergie wird als Beugung bezeichnet. ⓘ

Je nach dem Abstand zwischen der Quelle und dem Schirm werden zwei Arten der Beugung unterschieden: Fraunhofer-Beugung oder Fernfeldbeugung bei großen Abständen und Fresnel-Beugung oder Nahfeldbeugung bei geringen Abständen. ⓘ

Bei der Analyse des Einzelspalts wird die von Null abweichende Breite des Spalts berücksichtigt, und jeder Punkt in der Öffnung wird als Quelle eines Beitrags zum Lichtstrahl betrachtet (Huygens'sche Wellenformen). Auf dem Bildschirm hat das Licht, das von jeder Position innerhalb des Spalts eintrifft, eine andere Weglänge, wenn auch möglicherweise nur eine sehr geringe Differenz. Folglich kommt es zu Interferenzen. ⓘ

Im Fraunhofer-Beugungsmuster, das weit genug von einem einzelnen Spalt entfernt ist, ist die Intensitätsstreuung S im Rahmen einer Kleinwinkelnäherung über eine quadrierte Sinusfunktion mit der Position x verbunden:

$S(u)=\mathrm {sinc} ^{2}(u)=\left({\frac {\sin \pi u}{\pi u}}\right)^{2}\ ;$  mit  $u={\frac {xL}{\lambda R}}\ ,$ ⓘ

wobei L die Spaltbreite, R der Abstand des Musters (auf dem Schirm) vom Spalt und λ die Wellenlänge des verwendeten Lichts ist. Die Funktion S hat Nullstellen, wenn u eine ganze Zahl ungleich Null ist, wobei die x-Werte in einem Abstand proportional zur Wellenlänge liegen. ⓘ

Beugungsbegrenzte Auflösung

Die Beugung ist die grundlegende Begrenzung des Auflösungsvermögens optischer Instrumente, wie z. B. Teleskope (einschließlich Radioteleskope) und Mikroskope. Für eine kreisförmige Öffnung wird der beugungsbegrenzte Bildpunkt als Airy-Scheibe bezeichnet; der Abstand x in der Formel für die Beugung durch einen einzelnen Spalt wird durch den radialen Abstand r und der Sinus durch 2J₁ ersetzt, wobei J₁ eine Besselfunktion erster Ordnung ist. ⓘ

Die auflösbare räumliche Größe von Objekten, die durch ein Mikroskop betrachtet werden, ist nach dem Rayleigh-Kriterium, dem Radius zur ersten Nullstelle der Airy-Scheibe, auf eine Größe proportional zur Wellenlänge des verwendeten Lichts und abhängig von der numerischen Apertur begrenzt:

$r_{Airy}=1.22{\frac {\lambda }{2\mathrm {NA} }}\ ,$ ⓘ

wobei die numerische Apertur definiert ist als $\mathrm {NA} =n\sin \theta \;$ wobei θ der Halbwinkel des vom Mikroskopobjektiv aufgenommenen Strahlenkegels ist. ⓘ

Die Winkelgröße des zentralen hellen Teils (Radius bis zur ersten Nullstelle der Airy-Scheibe) des Bildes, das durch eine kreisförmige Öffnung gebeugt wird, ein Maß, das am häufigsten für Teleskope und Kameras verwendet wird, ist:

$\delta =1.22{\frac {\lambda }{D}}\ ,$ ⓘ

wobei λ die Wellenlänge der Wellen ist, die für die Abbildung fokussiert werden, D der Durchmesser der Eintrittspupille des Abbildungssystems in denselben Einheiten und die Winkelauflösung δ in Radiant. ⓘ

Wie bei anderen Beugungsmustern skaliert das Muster im Verhältnis zur Wellenlänge, so dass kürzere Wellenlängen zu einer höheren Auflösung führen können. ⓘ

Subwellenlänge

Der Begriff Subwellenlänge wird verwendet, um ein Objekt zu beschreiben, das eine oder mehrere Dimensionen kleiner ist als die Länge der Welle, mit der das Objekt wechselwirkt. So bezeichnet der Begriff Lichtwellenleiter mit Subwellenlängen-Durchmesser einen Lichtwellenleiter, dessen Durchmesser kleiner ist als die Wellenlänge des sich durch ihn ausbreitenden Lichts. ⓘ

Ein Teilchen mit geringer Wellenlänge ist ein Teilchen, das kleiner ist als die Wellenlänge des Lichts, mit dem es wechselwirkt (siehe Rayleigh-Streuung). Subwellenlängen-Aperturen sind Löcher, die kleiner sind als die Wellenlänge des sich durch sie ausbreitenden Lichts. Solche Strukturen finden unter anderem in der außergewöhnlichen optischen Übertragung und in Nullmoden-Wellenleitern Anwendung. ⓘ

Der Begriff "Subwellenlänge" kann sich auch auf ein Phänomen beziehen, das Objekte im Subwellenlängenbereich betrifft, z. B. die Bildgebung im Subwellenlängenbereich. ⓘ

Winkelförmige Wellenlänge

Beziehung zwischen Wellenlänge, Winkelwellenlänge und anderen Welleneigenschaften. ⓘ

Eine Größe, die mit der Wellenlänge zusammenhängt, ist die Winkelwellenlänge (auch als reduzierte Wellenlänge bezeichnet), üblicherweise symbolisiert durch ƛ (Lambda-Balken). Sie ist gleich der "regulären" Wellenlänge, "reduziert" um den Faktor 2π (ƛ = λ/2π). Sie wird in der Regel in der Quantenmechanik in Kombination mit der reduzierten Planck-Konstante (Symbol ħ, h-Bar) und der Winkelfrequenz (Symbol ω) oder der Winkelwellenzahl (Symbol k) verwendet. ⓘ