Transversalwelle

Mechanische Welle

                  |

___________________|___________________ | | Transversalwelle Longitudinalwelle ⓘ

Illustration einer einfachen (ebenen) Transversalwelle, die sich in einem elastischen Medium in horizontaler Richtung ausbreitet, wobei die Teilchen in vertikaler Richtung verschoben werden. Es ist nur eine Schicht des Materials dargestellt. ⓘ

Darstellung der elektrischen (rot) und magnetischen (blau) Felder entlang eines Strahls bei einer einfachen Lichtwelle. Für jede Ebene, die senkrecht zum Strahl verläuft, hat jedes Feld an allen Punkten der Ebene den gleichen Wert. ⓘ

Ausbreitung einer transversalen Kugelwelle in einem 2d-Gitter (empirisches Modell) ⓘ

In der Physik ist eine Transversalwelle eine Welle, deren Schwingungen senkrecht zur Ausbreitungsrichtung der Welle verlaufen. Dies steht im Gegensatz zu einer Longitudinalwelle, die sich in der Richtung ihrer Schwingungen ausbreitet. Die Wasserwelle ist ein Beispiel für eine Transversalwelle. ⓘ

Ein einfaches Beispiel sind die Wellen, die auf einer horizontalen Schnur erzeugt werden können, indem man ein Ende verankert und das andere Ende auf und ab bewegt. Ein anderes Beispiel sind die Wellen, die auf der Membran einer Trommel entstehen. Die Wellen breiten sich in Richtungen aus, die parallel zur Membranebene liegen, aber die Membran selbst wird senkrecht zu dieser Ebene nach oben und unten verschoben. Licht ist ein weiteres Beispiel für eine Transversalwelle, bei der die Schwingungen die elektrischen und magnetischen Felder sind, die im rechten Winkel zu den idealen Lichtstrahlen stehen, die die Ausbreitungsrichtung beschreiben. ⓘ

Transversalwellen treten häufig in elastischen Festkörpern aufgrund der erzeugten Scherspannung auf; die Schwingungen sind in diesem Fall die Verschiebung der Festkörperteilchen aus ihrer entspannten Position in Richtungen, die senkrecht zur Ausbreitung der Welle stehen. Diese Verschiebungen entsprechen einer lokalen Scherverformung des Materials. Daher wird eine Transversalwelle dieser Art als Scherwelle bezeichnet. Da Flüssigkeiten im Ruhezustand keinen Scherkräften widerstehen können, ist die Ausbreitung von Transversalwellen in der Masse von Flüssigkeiten nicht möglich. In der Seismologie werden Scherwellen auch als Sekundärwellen oder S-Wellen bezeichnet. ⓘ

Transversalwellen stehen im Gegensatz zu Longitudinalwellen, bei denen die Schwingungen in der Richtung der Welle auftreten. Das Standardbeispiel für eine Longitudinalwelle ist eine Schallwelle oder "Druckwelle" in Gasen, Flüssigkeiten oder Festkörpern, deren Schwingungen eine Kompression und Ausdehnung des Materials verursachen, durch das sich die Welle ausbreitet. Druckwellen werden in der Geophysik als "Primärwellen" oder "P-Wellen" bezeichnet. ⓘ

Mathematische Formulierung

Mathematisch gesehen ist die einfachste Art der Transversalwelle eine ebene, linear polarisierte Sinuswelle. "Ebene" bedeutet hier, dass die Ausbreitungsrichtung unveränderlich und über das gesamte Medium gleich ist; "linear polarisiert" bedeutet, dass die Richtung der Verschiebung ebenfalls unveränderlich und über das gesamte Medium gleich ist; und der Betrag der Verschiebung ist eine sinusförmige Funktion nur der Zeit und der Position entlang der Ausbreitungsrichtung. ⓘ

Die Bewegung einer solchen Welle lässt sich mathematisch wie folgt ausdrücken. Sei d die Ausbreitungsrichtung (ein Vektor mit Einheitslänge) und o ein beliebiger Bezugspunkt im Medium. Sei u die Richtung der Schwingungen (ein weiterer Vektor mit Einheitslänge, der senkrecht zu d steht). Die Verschiebung eines Teilchens an einem beliebigen Punkt p des Mediums und zu einem beliebigen Zeitpunkt t (Sekunden) ist

$$S(p,t)=Au\sin \left({\frac {t-(p-o){\frac {d}{v}}}{T}}+\phi \right)$$

wobei A die Amplitude oder Stärke der Welle ist, T ihre Periode, v die Ausbreitungsgeschwindigkeit und φ ihre Phase bei o. Alle diese Parameter sind reelle Zahlen. Das Symbol "-" bezeichnet das innere Produkt von zwei Vektoren. ⓘ

Nach dieser Gleichung breitet sich die Welle in der Richtung d aus, und die Schwingungen erfolgen hin und her entlang der Richtung u. Man sagt, die Welle sei in der Richtung u linear polarisiert. ⓘ

Ein Beobachter, der auf einen festen Punkt p blickt, wird sehen, dass sich das dortige Teilchen in einer einfachen harmonischen (sinusförmigen) Bewegung mit einer Periode von T Sekunden bewegt, mit einer maximalen Teilchenverschiebung A in jeder Richtung, d. h. mit einer Frequenz von f = 1/T vollen Schwingungszyklen pro Sekunde. Eine Momentaufnahme aller Teilchen zu einem festen Zeitpunkt t zeigt für alle Teilchen in jeder Ebene senkrecht zu d die gleiche Verschiebung, wobei die Verschiebungen in den aufeinanderfolgenden Ebenen ein sinusförmiges Muster bilden, wobei sich jeder volle Zyklus entlang d um die Wellenlänge λ = v T = v/f erstreckt. Das gesamte Muster bewegt sich mit der Geschwindigkeit V in Richtung d. ⓘ

Dieselbe Gleichung beschreibt eine ebene, linear polarisierte sinusförmige Lichtwelle, mit dem Unterschied, dass die "Verschiebung" S(p, t) das elektrische Feld am Punkt p und zur Zeit t ist. (Das magnetische Feld wird durch dieselbe Gleichung beschrieben, jedoch mit einer "Verschiebungs"-Richtung, die sowohl senkrecht zu d als auch zu u ist, und einer anderen Amplitude). ⓘ

Überlagerungsprinzip

In einem homogenen, linearen Medium lassen sich komplexe Schwingungen (Schwingungen in einem Material oder Lichtströme) als Überlagerung vieler einfacher Sinuswellen beschreiben, entweder in Quer- oder in Längsrichtung. ⓘ

Die Schwingungen einer Geigensaite beispielsweise lassen sich als Summe vieler Transversalwellen unterschiedlicher Frequenzen analysieren, die die Saite entweder nach oben oder unten oder von links nach rechts verschieben. Die Wellen in einem Teich können als eine Kombination von Transversal- und Longitudinalwellen (Schwerewellen) analysiert werden, die sich gemeinsam ausbreiten. ⓘ

Zirkulare Polarisation

Wenn das Medium linear ist und mehrere unabhängige Ausbreitungsrichtungen für dieselbe Ausbreitungsrichtung d zulässt, können wir zwei zueinander senkrechte Polarisationsrichtungen wählen und jede Welle, die in einer anderen Richtung linear polarisiert ist, als eine lineare Kombination (Mischung) dieser beiden Wellen darstellen. ⓘ

Kombiniert man zwei Wellen mit gleicher Frequenz, Geschwindigkeit und Ausbreitungsrichtung, aber mit unterschiedlichen Phasen und unabhängigen Ausbreitungsrichtungen, erhält man eine zirkulär oder elliptisch polarisierte Welle. In einer solchen Welle beschreiben die Teilchen kreisförmige oder elliptische Bahnen, anstatt sich hin und her zu bewegen. ⓘ

Es mag zum Verständnis beitragen, das oben erwähnte Gedankenexperiment mit einer gespannten Schnur noch einmal zu betrachten. Beachten Sie, dass Sie auch Wellen auf der Schnur auslösen können, indem Sie Ihre Hand nach rechts und links bewegen, anstatt nach oben und unten. Dies ist ein wichtiger Punkt. Es gibt zwei unabhängige (orthogonale) Richtungen, in die sich die Wellen bewegen können. (Dies gilt für zwei beliebige, rechtwinklig zueinander stehende Richtungen, wobei zur Verdeutlichung oben und unten sowie rechts und links gewählt wurden.) Alle Wellen, die durch eine geradlinige Handbewegung ausgelöst werden, sind linear polarisierte Wellen. ⓘ

Stellen Sie sich nun aber vor, Sie bewegen Ihre Hand im Kreis. Ihre Bewegung wird eine spiralförmige Welle auf der Saite auslösen. Sie bewegen Ihre Hand gleichzeitig sowohl nach oben und unten als auch von einer Seite zur anderen. Die Maxima der seitlichen Bewegung liegen eine Viertelwellenlänge (oder ein Viertel einer Kreisbahn, d. h. 90 Grad oder π/2 Radiant) von den Maxima der Auf- und Abwärtsbewegung entfernt. An jedem beliebigen Punkt entlang der Saite beschreibt die Auslenkung der Saite denselben Kreis wie Ihre Hand, allerdings verzögert um die Ausbreitungsgeschwindigkeit der Welle. Beachten Sie auch, dass Sie Ihre Hand wahlweise im oder gegen den Uhrzeigersinn bewegen können. Diese abwechselnden Kreisbewegungen erzeugen rechts und links zirkular polarisierte Wellen. ⓘ

In dem Maße, in dem Ihr Kreis unvollkommen ist, wird eine regelmäßige Bewegung eine Ellipse beschreiben und elliptisch polarisierte Wellen erzeugen. Bei extremer Exzentrizität wird die Ellipse zu einer geraden Linie, die eine lineare Polarisation entlang der Hauptachse der Ellipse erzeugt. Eine elliptische Bewegung kann immer in zwei orthogonale lineare Bewegungen mit ungleicher Amplitude und 90 Grad Phasenverschiebung zerlegt werden, wobei die zirkulare Polarisation der Spezialfall ist, bei dem die beiden linearen Bewegungen die gleiche Amplitude haben. ⓘ

Mechanisch auf einem Gummifaden erzeugte zirkulare Polarisation, die durch einen mechanischen Polarisationsfilter in lineare Polarisation umgewandelt wird. ⓘ

Eine Transversalwelle schwingt senkrecht zu ihrer Ausbreitungsrichtung. Die Welle lässt sich anhand eines Seils veranschaulichen, bei dem ein Ende in der Hand gehalten wird. Indem man die Hand auf- und abbewegt, lässt sich das Seil aus seiner Ruheposition auslenken und diese Auslenkung pflanzt sich entlang des Seils fort. Es handelt sich hierbei um eine Transversalwelle, da sich die Welle waagerecht entlang des Seils ausbreitet, die Auslenkung des Seils aus seiner Ruhelage jedoch nach oben und unten geschieht. Der Wellenvektor, der die Ausbreitungsrichtung der Welle kennzeichnet ist damit senkrecht zu der Amplitude der Seilschwingung. ⓘ

Anstelle einer Auf- und Abbewegung lässt sich eine ähnliche Welle auch durch Handbewegungen von rechts nach links erzeugen, oder einer Kombination beider Richtungen. Solche Wellen sind ebenfalls Transversalwellen, unterscheiden sich jedoch in der Schwingungsrichtung. Diese Schwingungsrichtung der Transversalwelle wird Polarisation genannt. ⓘ

Leistung in einer Transversalwelle in einem Faden

(Die lineare Massendichte der Saite sei μ.) ⓘ

Die kinetische Energie eines Massenelements in einer Transversalwelle ist gegeben durch:

$$dK={\frac {1}{2}}\ dm\ v_{y}^{2}={\frac {1}{2}}\ \mu dx\ A^{2}\omega ^{2}\cos ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)$$

ⓘ

In einer Wellenlänge, kinetische Energie

$$K={\frac {1}{2}}\mu A^{2}\omega ^{2}\int _{0}^{\lambda }\cos ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)dx={\frac {1}{4}}\mu A^{2}\omega ^{2}\lambda$$

ⓘ

Unter Anwendung des Hooke'schen Gesetzes ist die potentielle Energie im Massenelement

$$dU={\frac {1}{2}}\ dm\omega ^{2}\ y^{2}={\frac {1}{2}}\ \mu dx\omega ^{2}\ A^{2}\sin ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)$$

ⓘ

Und die potentielle Energie für eine Wellenlänge

$$U={\frac {1}{2}}\mu A^{2}\omega ^{2}\int _{0}^{\lambda }\sin ^{2}\left({\frac {2\pi x}{\lambda }}-\omega t\right)dx={\frac {1}{4}}\mu A^{2}\omega ^{2}\lambda$$

ⓘ

Gesamtenergie in einer Wellenlänge ${\textstyle K+U={\frac {1}{2}}\mu A^{2}\omega ^{2}\lambda }$ ⓘ

Daher ist die durchschnittliche Leistung ${\textstyle {\frac {1}{2}}\mu A^{2}\omega ^{2}v_{x}}$ ⓘ

Eigenschaften

Elastische Wellen

Aus der Navier-Stokes-Gleichung lässt sich für die Bewegung von dissipationsfreien elastischen Wellen in einem Festkörper die Differentialgleichung

$\rho {\frac {\partial ^{2}\mathbf {u} }{\partial t^{2}}}=\mu \nabla ^{2}\mathbf {u} +(\lambda +\mu )\nabla (\nabla \cdot \mathbf {u} )$

für die zeit- und ortsabhängige Auslenkung $\mathbf {u} (\mathbf {x} ,t)$ herleiten. Dabei sind $\rho$, $\mu$ und $\lambda$ konstante Materialparameter. Das Vektorfeld $\mathbf {u}$ lässt sich, wie jedes Vektorfeld, in einen rotations- und einen divergenzfreien Teil aufspalten:

$\mathbf {u} =\mathbf {u} _{\mathrm {L} }+\mathbf {u} _{\mathrm {T} }$

wobei für den rotationsfreien Teil gilt

${\begin{aligned}\nabla \times \mathbf {u} _{\mathrm {L} }&=0\\\nabla \times (\nabla \times \mathbf {u} _{\mathrm {L} })&=\nabla (\nabla \cdot \mathbf {u} _{\mathrm {L} })-\nabla ^{2}\mathbf {u} _{\mathrm {L} }=0\end{aligned}}$

und für den divergenzfreien

${\begin{aligned}\nabla \cdot \mathbf {u} _{\mathrm {T} }&=0\\\nabla (\nabla \cdot \mathbf {u} _{\mathrm {T} })&=0\end{aligned}}$

Damit erhält man zwei getrennte Wellengleichungen für den transversalen und longitudinalen Teil der Welle:

${\begin{aligned}0&=\left(\rho {\frac {\partial ^{2}}{\partial t^{2}}}-(\lambda +2\mu )\nabla ^{2}\right)\mathbf {u} _{\mathrm {L} }\\0&=\left(\rho {\frac {\partial ^{2}}{\partial t^{2}}}-\mu \nabla ^{2}\right)\mathbf {u} _{\mathrm {T} }\end{aligned}}$

mit unterschiedlichen Phasengeschwindigkeiten $c_{\mathrm {L} }={\sqrt {(\lambda +2\mu )/\rho }}$ für die Longitudinalwelle und $c_{\mathrm {T} }={\sqrt {\mu /\rho }}$ für die Transversalwelle. Im selben Medium ist die Geschwindigkeit von Transversalwellen stets kleiner als die von Longitudinalwellen. ⓘ

Beispiele

• 

  Ebener Transversalwellenzug

• 

  Transversalwellenzug als Zylinder- oder Kugelwelle

• 

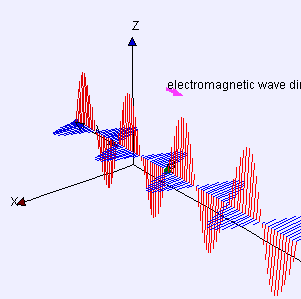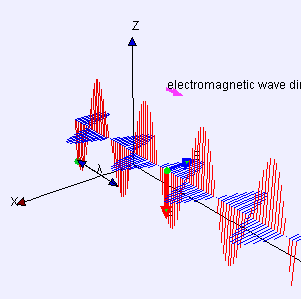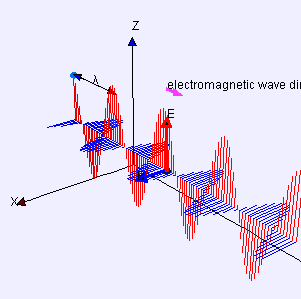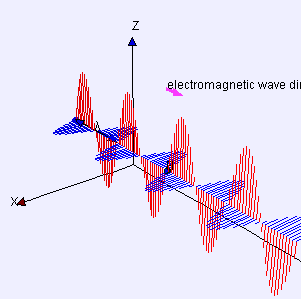
  Fernfeld einer linear polarisierten, elektromagnetischen Welle im Vakuum, die sich in x-Richtung ausbreitet. Die elektrische Feldstärke ${\vec {E}}$ (in blau) und die magnetische Flussdichte ${\vec {B}}$ (in rot) sind senkrecht dazu. ⓘ

Mediengebunden

• dilatationsfreie Wellen in einem inkompressiblen elastischen Medium (Festkörper)
• Oberflächenwellen auf Flüssigkeiten, wie Wasserwellen, sind keine reinen Transversalwellen, sondern bilden eine Mischform aus Transversalwelle und Longitudinalwelle
• Alfvénwellen oder transversale Plasmawellen
• Ultraschall in Festkörpern hat wegen der auftretenden Schubspannungen neben dem Longitudinalwellenanteil zusätzlich auch einen Anteil von Transversalwellen, benutzt wird das beispielsweise beim Schrägschallverfahren
• La-Ola-Welle in einem Fußballstadion ⓘ

Nicht mediengebunden

• Elektromagnetische Wellen
• Gravitationswellen ⓘ