Quantenfeldtheorie
| Quantenfeldtheorie ⓘ |
|---|
 |
| Geschichte |
In der theoretischen Physik ist die Quantenfeldtheorie (QFT) ein theoretischer Rahmen, der die klassische Feldtheorie, die spezielle Relativitätstheorie und die Quantenmechanik kombiniert. Die QFT wird in der Teilchenphysik verwendet, um physikalische Modelle subatomarer Teilchen zu konstruieren, und in der Physik kondensierter Materie, um Modelle von Quasiteilchen zu konstruieren. ⓘ
In der QFT werden Teilchen als angeregte Zustände (auch Quanten genannt) ihrer zugrunde liegenden Quantenfelder behandelt, die fundamentaler sind als die Teilchen. Die Wechselwirkungen zwischen den Teilchen werden durch Wechselwirkungsterme in der Lagrange beschrieben, an denen die entsprechenden Quantenfelder beteiligt sind. Jede Wechselwirkung kann durch Feynman-Diagramme gemäß der Störungstheorie der Quantenmechanik visuell dargestellt werden. ⓘ
Die Methoden der Quantenfeldtheorie kommen vor allem in der Elementarteilchenphysik und in der statistischen Mechanik zur Anwendung. Man unterscheidet dabei zwischen relativistischen Quantenfeldtheorien, die die spezielle Relativitätstheorie berücksichtigen und häufig in der Elementarteilchenphysik Anwendung finden, und nicht-relativistischen Quantenfeldtheorien, die beispielsweise in der Festkörperphysik relevant sind. ⓘ
Die Objekte und Methoden der QFT sind physikalisch motiviert, auch wenn viele Teilbereiche der Mathematik zum Einsatz kommen. Die Axiomatische Quantenfeldtheorie versucht dabei, Grundlagen und Konzepte in einen mathematisch rigorosen Rahmen zu fassen. ⓘ
Geschichte
Die Quantenfeldtheorie ist das Ergebnis der Arbeit von Generationen theoretischer Physiker, die einen Großteil des 20. Ihre Entwicklung begann in den 1920er Jahren mit der Beschreibung der Wechselwirkungen zwischen Licht und Elektronen und gipfelte in der ersten Quantenfeldtheorie, der Quantenelektrodynamik. Ein großes theoretisches Hindernis folgte bald mit dem Auftreten und Fortbestehen verschiedener Unendlichkeiten in Störungsrechnungen, ein Problem, das erst in den 1950er Jahren mit der Erfindung des Renormierungsverfahrens gelöst wurde. Ein zweites großes Hindernis war die offensichtliche Unfähigkeit der QFT, die schwache und starke Wechselwirkung zu beschreiben, was einige Theoretiker dazu veranlasste, den feldtheoretischen Ansatz aufzugeben. Die Entwicklung der Eichtheorie und die Fertigstellung des Standardmodells in den 1970er Jahren führten zu einer Renaissance der Quantenfeldtheorie. ⓘ
Theoretischer Hintergrund

Die Quantenfeldtheorie ergibt sich aus der Kombination der klassischen Feldtheorie, der Quantenmechanik und der speziellen Relativitätstheorie. Es folgt ein kurzer Überblick über diese theoretischen Vorläufer. ⓘ
Die früheste erfolgreiche klassische Feldtheorie ist diejenige, die aus Newtons Gesetz der universellen Gravitation hervorging, obwohl das Konzept der Felder in seiner Abhandlung Philosophiæ Naturalis Principia Mathematica von 1687 überhaupt nicht vorkommt. Die von Newton beschriebene Schwerkraft ist eine "Fernwirkung" - ihre Auswirkungen auf weit entfernte Objekte treten unabhängig von der Entfernung sofort ein. In einem Briefwechsel mit Richard Bentley stellte Newton jedoch fest, dass "es unvorstellbar ist, dass unbelebte tierische Materie ohne die Vermittlung von etwas anderem, das nicht materiell ist, auf andere Materie einwirkt und diese ohne gegenseitige Berührung beeinflusst". Erst im 18. Jahrhundert entdeckten die mathematischen Physiker eine praktische Beschreibung der Schwerkraft auf der Grundlage von Feldern - eine numerische Größe (ein Vektor im Falle des Gravitationsfeldes), die jedem Punkt im Raum zugeordnet ist und die Wirkung der Schwerkraft auf jedes Teilchen an diesem Punkt angibt. Dies wurde jedoch lediglich als mathematischer Trick betrachtet. ⓘ
Mit der Entwicklung des Elektromagnetismus im 19. Jahrhundert begannen die Felder, eine eigene Existenz zu entwickeln. Michael Faraday prägte im Jahr 1845 den englischen Begriff "field". Er führte Felder als Eigenschaften des Raums (auch ohne Materie) mit physikalischen Wirkungen ein. Er argumentierte gegen "Fernwirkung" und schlug vor, dass Wechselwirkungen zwischen Objekten über raumfüllende "Kraftlinien" stattfinden. Diese Beschreibung von Feldern hat bis heute Bestand. ⓘ
Die Theorie des klassischen Elektromagnetismus wurde 1864 mit den Maxwellschen Gleichungen vervollständigt, die die Beziehung zwischen dem elektrischen Feld, dem magnetischen Feld, dem elektrischen Strom und der elektrischen Ladung beschrieben. Die Maxwellschen Gleichungen implizierten die Existenz elektromagnetischer Wellen, ein Phänomen, bei dem sich elektrische und magnetische Felder mit einer endlichen Geschwindigkeit, die sich als Lichtgeschwindigkeit herausstellt, von einem Raumpunkt zu einem anderen ausbreiten. Die Fernwirkung war damit endgültig widerlegt. ⓘ
Trotz des enormen Erfolgs des klassischen Elektromagnetismus konnte dieser weder die diskreten Linien in den Atomspektren noch die Verteilung der Schwarzkörperstrahlung in verschiedenen Wellenlängen erklären. Max Plancks Untersuchung der Schwarzkörperstrahlung markierte den Beginn der Quantenmechanik. Er behandelte Atome, die elektromagnetische Strahlung absorbieren und aussenden, als winzige Oszillatoren mit der entscheidenden Eigenschaft, dass ihre Energie nicht kontinuierlich, sondern nur eine Reihe von diskreten Werten annehmen kann. Diese werden als harmonische Quantenoszillatoren bezeichnet. Dieser Prozess der Beschränkung von Energien auf diskrete Werte wird als Quantisierung bezeichnet. Auf dieser Idee aufbauend schlug Albert Einstein 1905 eine Erklärung für den photoelektrischen Effekt vor: Licht besteht aus einzelnen Energiepaketen, den so genannten Photonen (den Lichtquanten). Dies bedeutete, dass die elektromagnetische Strahlung zwar Wellen im klassischen elektromagnetischen Feld sind, aber auch in Form von Teilchen existieren. ⓘ
1913 führte Niels Bohr das Bohrsche Modell der Atomstruktur ein, wonach die Elektronen in den Atomen nur eine Reihe diskreter, nicht aber kontinuierlicher Energien annehmen können. Dies ist ein weiteres Beispiel für die Quantisierung. Das Bohrsche Modell erklärte erfolgreich die diskrete Natur der atomaren Spektrallinien. 1924 stellte Louis de Broglie die Hypothese des Welle-Teilchen-Dualismus auf, wonach mikroskopische Teilchen unter verschiedenen Umständen sowohl wellenartige als auch teilchenartige Eigenschaften aufweisen. Durch die Zusammenführung dieser verstreuten Ideen wurde zwischen 1925 und 1926 eine kohärente Disziplin, die Quantenmechanik, formuliert, zu der Max Planck, Louis de Broglie, Werner Heisenberg, Max Born, Erwin Schrödinger, Paul Dirac und Wolfgang Pauli wichtige Beiträge leisteten. ⓘ
Im selben Jahr wie seine Arbeit über den photoelektrischen Effekt veröffentlichte Einstein seine spezielle Relativitätstheorie, die auf dem Maxwellschen Elektromagnetismus aufbaut. Es wurden neue Regeln, die so genannten Lorentz-Transformationen, für die Art und Weise aufgestellt, wie sich die Zeit- und Raumkoordinaten eines Ereignisses bei Änderungen der Geschwindigkeit des Beobachters ändern, und die Unterscheidung zwischen Zeit und Raum wurde verwischt. Es wurde vorgeschlagen, dass alle physikalischen Gesetze für Beobachter mit unterschiedlichen Geschwindigkeiten gleich sein müssen, d. h. dass die physikalischen Gesetze unter Lorentz-Transformationen invariant sind. ⓘ
Zwei Schwierigkeiten blieben bestehen. Die Schrödinger-Gleichung, die der Quantenmechanik zugrunde liegt, konnte zwar die stimulierte Emission von Strahlung aus Atomen erklären, bei der ein Elektron unter der Einwirkung eines äußeren elektromagnetischen Feldes ein neues Photon aussendet, aber sie war nicht in der Lage, die spontane Emission zu erklären, bei der ein Elektron spontan an Energie verliert und auch ohne Einwirkung eines äußeren elektromagnetischen Feldes ein Photon aussendet. Theoretisch konnte die Schrödinger-Gleichung keine Photonen beschreiben und war mit den Grundsätzen der speziellen Relativitätstheorie unvereinbar, da sie die Zeit als gewöhnliche Zahl behandelt und die Raumkoordinaten zu linearen Operatoren macht. ⓘ
Quantenelektrodynamik
Die Quantenfeldtheorie begann natürlich mit der Untersuchung der elektromagnetischen Wechselwirkungen, da das elektromagnetische Feld in den 1920er Jahren das einzige bekannte klassische Feld war. ⓘ
Durch die Arbeiten von Born, Heisenberg und Pascual Jordan in den Jahren 1925-1926 wurde eine Quantentheorie des freien elektromagnetischen Feldes (eines Feldes ohne Wechselwirkungen mit der Materie) durch kanonische Quantisierung entwickelt, indem das elektromagnetische Feld als eine Menge von harmonischen Quantenoszillatoren behandelt wurde. Durch den Ausschluss von Wechselwirkungen war eine solche Theorie jedoch noch nicht in der Lage, quantitative Vorhersagen über die reale Welt zu machen. ⓘ
In seiner bahnbrechenden Arbeit Die Quantentheorie der Emission und Absorption von Strahlung aus dem Jahr 1927 prägte Dirac den Begriff Quantenelektrodynamik (QED), eine Theorie, die zu den Termen, die das freie elektromagnetische Feld beschreiben, einen zusätzlichen Wechselwirkungsterm zwischen der elektrischen Stromdichte und dem elektromagnetischen Vektorpotential hinzufügt. Mit Hilfe der Störungstheorie erster Ordnung gelang es ihm, das Phänomen der spontanen Emission zu erklären. Nach der Unschärferelation der Quantenmechanik können harmonische Quantenoszillatoren nicht stationär bleiben, sondern sie haben ein Energieminimum ungleich Null und müssen immer schwingen, selbst im niedrigsten Energiezustand (dem Grundzustand). Daher bleibt auch im perfekten Vakuum ein oszillierendes elektromagnetisches Feld mit Nullpunktenergie bestehen. Diese Quantenfluktuation der elektromagnetischen Felder im Vakuum ist es, die die spontane Strahlungsemission der Elektronen in den Atomen "anregt". Diracs Theorie war sehr erfolgreich bei der Erklärung der Emission und Absorption von Strahlung durch Atome; durch Anwendung der Störungstheorie zweiter Ordnung konnte sie die Streuung von Photonen, die Resonanzfluoreszenz und die nichtrelativistische Compton-Streuung erklären. Die Anwendung der Störungstheorie höherer Ordnung war jedoch mit problematischen Unendlichkeiten in den Berechnungen behaftet. ⓘ
Im Jahr 1928 schrieb Dirac eine Wellengleichung auf, die relativistische Elektronen beschrieb - die Dirac-Gleichung. Sie hatte folgende wichtige Konsequenzen: Der Spin eines Elektrons ist 1/2, der g-Faktor des Elektrons ist 2, sie führte zur korrekten Sommerfeld-Formel für die Feinstruktur des Wasserstoffatoms und konnte zur Ableitung der Klein-Nishina-Formel für relativistische Compton-Streuung verwendet werden. Obwohl die Ergebnisse fruchtbar waren, implizierte die Theorie anscheinend auch die Existenz negativer Energiezustände, was dazu führen würde, dass Atome instabil wären, da sie immer durch die Emission von Strahlung in niedrigere Energiezustände zerfallen könnten. ⓘ
Damals herrschte die Ansicht vor, dass die Welt aus zwei sehr unterschiedlichen Bestandteilen zusammengesetzt ist: materiellen Teilchen (wie Elektronen) und Quantenfeldern (wie Photonen). Materielle Teilchen galten als ewig und ihr physikalischer Zustand wurde durch die Wahrscheinlichkeit beschrieben, dass sich jedes Teilchen in einer bestimmten Region des Raums oder in einem bestimmten Geschwindigkeitsbereich befindet. Photonen hingegen galten lediglich als angeregte Zustände des zugrunde liegenden quantisierten elektromagnetischen Feldes und konnten frei erzeugt oder zerstört werden. Zwischen 1928 und 1930 entdeckten Jordan, Eugene Wigner, Heisenberg, Pauli und Enrico Fermi, dass materielle Teilchen auch als angeregte Zustände von Quantenfeldern betrachtet werden können. So wie Photonen angeregte Zustände des gequantelten elektromagnetischen Feldes sind, hatte jede Art von Teilchen ihr entsprechendes Quantenfeld: ein Elektronenfeld, ein Protonenfeld usw. Mit genügend Energie wäre es nun möglich, materielle Teilchen zu erzeugen. Aufbauend auf dieser Idee schlug Fermi 1932 eine Erklärung für den Betazerfall vor, die als Fermi-Wechselwirkung bekannt wurde. Atomkerne enthalten an sich keine Elektronen, aber beim Zerfallsprozess wird ein Elektron aus dem umgebenden Elektronenfeld erzeugt, analog zu dem Photon, das beim Strahlungszerfall eines angeregten Atoms aus dem umgebenden elektromagnetischen Feld entsteht. ⓘ
1929 erkannten Dirac und andere, dass die in der Dirac-Gleichung implizierten negativen Energiezustände beseitigt werden konnten, indem die Existenz von Teilchen mit der gleichen Masse wie die Elektronen, aber mit entgegengesetzter elektrischer Ladung angenommen wurde. Dies gewährleistete nicht nur die Stabilität der Atome, sondern war auch der erste Vorschlag für die Existenz von Antimaterie. Der Beweis für Positronen wurde 1932 von Carl David Anderson in der kosmischen Strahlung entdeckt. Bei ausreichender Energie, z. B. durch Absorption eines Photons, konnte ein Elektron-Positron-Paar entstehen, ein Prozess, der als Paarbildung bezeichnet wird; der umgekehrte Prozess, die Annihilation, konnte auch durch die Emission eines Photons erfolgen. Dies zeigte, dass die Anzahl der Teilchen während einer Wechselwirkung nicht festgelegt sein muss. Historisch gesehen wurden Positronen jedoch zunächst als "Löcher" in einem unendlichen Elektronenmeer betrachtet und nicht als eine neue Art von Teilchen, und diese Theorie wurde als Dirac-Loch-Theorie bezeichnet. Die QFT bezog natürlich auch Antiteilchen in ihren Formalismus ein. ⓘ
Die klassische Quantenmechanik befasste sich zunächst mit Atomen, Molekülen oder Festkörpern, d. h. mit Systemen mit einer vorgegebenen Zahl von Teilchen. Dabei wurden die Schrödingergleichung und ein von Wellenfunktionen aufgespannter Hilbertraum verwendet. ⓘ
Zu einer Quantenfeldtheorie gelangt man beim konsequenten Übergang von einer Wellenfunktions- zu einer Teilchenzahl-Darstellung, der zweiten Quantisierung. Genauer bedeutet dies, dass sich ein solcher Vielteilchen-Hilbertraum nach Wahl eines Satzes von Ein-Teilchen-Funktionen durch alle möglichen (erlaubten) Produkte von Ein-Teilchen-Funktionen (z. B. Slater-Determinanten) aufspannen lässt. Ein vollständiger Satz solcher Basisvektoren ist dann allein durch die Besetzungszahlen der Einteilchen-Zustände charakterisierbar. ⓘ
Eine Streuung von einem Teilchen an einem Potential erscheint in einer solchen Teilchenzahl-Darstellung als eine Änderung von Besetzungszahlen: der dem Impuls des einlaufenden Teilchens entsprechende Zustand enthält nach der Streuung ein Teilchen weniger, der dem Impuls des auslaufenden Teilchens entsprechende Zustand enthält nach der Streuung ein Teilchen mehr. Dies interpretiert man natürlicherweise als Vernichtung und Erzeugung von Teilchen gewisser Einteilchenzustände. Die grundlegenden Operatoren sind dann Teilchen-Erzeugungs- und Vernichtungsoperatoren, der Hilbertraum wird zu einem Fockraum. Der resultierende Formalismus ist eine Quantenfeldtheorie. ⓘ
Quantenfeldtheorien sind i. d. R. das adäquate Mittel zur Beschreibung quantenmechanischer Vielteilchensysteme. Die richtige Vertauschungssymmetrie der Wellenfunktion ist dann implizit, und für das Pauli-Prinzip und das allgemeinere Spin-Statistik-Theorem ergeben sich einfache Begründungen oder Herleitungen. ⓘ
Ein essentieller Aspekt der Quantenfeldtheorien ist, dass sich Teilchenzahlen ändern können. Die grundlegenden Operatoren sind dann nicht mehr die Teilchenkoordinaten und -Impulse, sondern Quantenfelder wie oder , welche ein Teilchen (oder Antiteilchen) am Ort vernichten oder erzeugen. ⓘ
Sobald die Relativitätstheorie ins Spiel kommt, können entsprechend der Äquivalenz von Energie und Masse Teilchen entstehen oder verschwinden, und in der Elementarteilchenphysik ist der Quantenfeldtheorie-Formalismus daher das Mittel der Wahl. Klein-Gordon-Gleichung und Dirac-Gleichung erhalten eine neue Interpretation, und die im klassischen Formalismus mit Antiteilchen auftretenden Komplikationen verschwinden. ⓘ
Unendlichkeiten und Renormierung
Robert Oppenheimer zeigte 1930, dass Störungsberechnungen höherer Ordnung in der QED immer unendliche Größen ergaben, wie die Elektroneneigenenergie und die Vakuum-Nullpunktenergie der Elektronen- und Photonenfelder, was darauf hindeutet, dass die damaligen Berechnungsmethoden Wechselwirkungen mit Photonen mit extrem hohen Impulsen nicht richtig behandeln konnten. Erst 20 Jahre später wurde ein systematischer Ansatz zur Beseitigung solcher Unendlichkeiten entwickelt. ⓘ
Ernst Stueckelberg veröffentlichte zwischen 1934 und 1938 eine Reihe von Arbeiten, in denen er eine relativistisch invariante Formulierung der QFT aufstellte. Im Jahr 1947 entwickelte Stueckelberg unabhängig davon auch ein vollständiges Renormierungsverfahren. Leider wurden diese Leistungen von der theoretischen Gemeinschaft nicht verstanden und anerkannt. ⓘ
Angesichts dieser Unendlichkeiten schlugen John Archibald Wheeler und Heisenberg 1937 bzw. 1943 vor, die problematische QFT durch die so genannte S-Matrix-Theorie zu ersetzen. Da die spezifischen Details mikroskopischer Wechselwirkungen für Beobachtungen unzugänglich sind, sollte die Theorie nur versuchen, die Beziehungen zwischen einer kleinen Anzahl von Beobachtungsgrößen (z. B. die Energie eines Atoms) in einer Wechselwirkung zu beschreiben, anstatt sich mit den mikroskopischen Details der Wechselwirkung zu befassen. 1945 schlugen Richard Feynman und Wheeler kühn vor, die QFT ganz aufzugeben und schlugen als Mechanismus für die Teilchenwechselwirkung die Aktion-auf-Entfernung vor. ⓘ
1947 maßen Willis Lamb und Robert Retherford den winzigen Unterschied zwischen den Energieniveaus 2S1/2 und 2P1/2 des Wasserstoffatoms, auch Lamb-Verschiebung genannt. Durch die Vernachlässigung des Beitrags von Photonen, deren Energie die Elektronenmasse übersteigt, gelang es Hans Bethe, den numerischen Wert der Lamb-Verschiebung zu schätzen. In der Folge bestätigten Norman Myles Kroll, Lamb, James Bruce French und Victor Weisskopf diesen Wert erneut, indem sie einen Ansatz verwendeten, bei dem Unendlichkeiten andere Unendlichkeiten aufhoben, um endliche Größen zu erhalten. Diese Methode war jedoch umständlich und unzuverlässig und konnte nicht für andere Berechnungen verallgemeinert werden. ⓘ
Der Durchbruch gelang schließlich um 1950, als Julian Schwinger, Richard Feynman, Freeman Dyson und Shinichiro Tomonaga eine robustere Methode zur Eliminierung von Unendlichkeiten entwickelten. Die Hauptidee besteht darin, die berechneten Werte von Masse und Ladung, so unendlich sie auch sein mögen, durch ihre endlichen Messwerte zu ersetzen. Dieses systematische Berechnungsverfahren ist als Renormierung bekannt und kann in der Störungstheorie auf jede beliebige Ordnung angewendet werden. Wie Tomonaga in seiner Nobelvorlesung sagte:
Da die Teile der veränderten Masse und Ladung, die auf Feldreaktionen zurückzuführen sind, [unendlich werden], ist es unmöglich, sie mit der Theorie zu berechnen. Die in Experimenten beobachtete Masse und Ladung sind jedoch nicht die ursprüngliche Masse und Ladung, sondern die durch Feldreaktionen veränderte Masse und Ladung, und diese sind endlich. Andererseits sind die Masse und die Ladung, die in der Theorie erscheinen, ... die durch Feldreaktionen veränderten Werte. Da dies so ist, und vor allem, da die Theorie nicht in der Lage ist, die modifizierte Masse und Ladung zu berechnen, können wir das Verfahren der Substitution von experimentellen Werten für sie phänomenologisch übernehmen... Dieses Verfahren wird Renormierung von Masse und Ladung genannt... Nach langen, mühsamen Berechnungen, die weniger geschickt waren als die von Schwinger, erhielten wir ein Ergebnis... das mit dem der Amerikaner übereinstimmte. ⓘ
Durch Anwendung des Renormierungsverfahrens wurden schließlich Berechnungen durchgeführt, um das anomale magnetische Moment des Elektrons (die Abweichung des g-Faktors des Elektrons von 2) und die Vakuumpolarisation zu erklären. Diese Ergebnisse stimmen in bemerkenswerter Weise mit den experimentellen Messungen überein und markieren das Ende des "Krieges gegen die Unendlichkeit". ⓘ
Zur gleichen Zeit führte Feynman die Pfadintegralformulierung der Quantenmechanik und Feynman-Diagramme ein. Letztere können zur visuellen und intuitiven Organisation und zur Berechnung von Termen in der Störungsexpansion verwendet werden. Jedes Diagramm kann als Pfade von Teilchen in einer Wechselwirkung interpretiert werden, wobei jeder Scheitelpunkt und jede Linie einen entsprechenden mathematischen Ausdruck hat, und das Produkt dieser Ausdrücke ergibt die Streuungsamplitude der durch das Diagramm dargestellten Wechselwirkung. ⓘ
Mit der Erfindung des Renormierungsverfahrens und der Feynman-Diagramme wurde die QFT schließlich zu einem vollständigen theoretischen Rahmen. ⓘ
Nicht-Renormalisierbarkeit
Angesichts des enormen Erfolgs der QED glaubten viele Theoretiker in den wenigen Jahren nach 1949, dass die QFT bald ein Verständnis aller mikroskopischen Phänomene liefern könnte, nicht nur der Wechselwirkungen zwischen Photonen, Elektronen und Positronen. Entgegen diesem Optimismus trat die QFT in eine weitere Depressionsphase ein, die fast zwei Jahrzehnte lang andauerte. ⓘ
Das erste Hindernis war die begrenzte Anwendbarkeit des Renormierungsverfahrens. Bei Störungsrechnungen in der QED konnten alle unendlichen Größen durch die Neudefinition einer kleinen (endlichen) Anzahl physikalischer Größen (nämlich der Masse und Ladung des Elektrons) eliminiert werden. Dyson bewies 1949, dass dies nur für eine kleine Klasse von Theorien möglich ist, die "renormierbare Theorien" genannt werden und zu denen die QED gehört. Die meisten Theorien, einschließlich der Fermi-Theorie der schwachen Wechselwirkung, sind jedoch "nicht renormierbar". Jede Störungsrechnung in diesen Theorien, die über die erste Ordnung hinausgeht, würde zu Unendlichkeiten führen, die nicht durch die Neudefinition einer endlichen Anzahl von physikalischen Größen beseitigt werden können. ⓘ
Das zweite große Problem ergab sich aus der begrenzten Gültigkeit der Feynman-Diagramm-Methode, die auf einer Reihenentwicklung in der Störungstheorie beruht. Damit die Reihe konvergiert und Berechnungen niedriger Ordnung eine gute Annäherung darstellen, muss die Kopplungskonstante, in der die Reihe expandiert wird, eine ausreichend kleine Zahl sein. Die Kopplungskonstante in der QED ist die Feinstrukturkonstante α ≈ 1/137, die so klein ist, dass nur die einfachsten Feynman-Diagramme niedrigster Ordnung in realistischen Berechnungen berücksichtigt werden müssen. Im Gegensatz dazu liegt die Kopplungskonstante der starken Wechselwirkung etwa in der Größenordnung von eins, so dass komplizierte Feynman-Diagramme höherer Ordnung ebenso wichtig sind wie einfache Diagramme. Es gab also keine Möglichkeit, zuverlässige quantitative Vorhersagen für die starke Wechselwirkung mit perturbativen QFT-Methoden abzuleiten. ⓘ
Angesichts dieser Schwierigkeiten begannen viele Theoretiker, sich von der QFT abzuwenden. Einige konzentrierten sich auf Symmetrieprinzipien und Erhaltungssätze, während andere die alte S-Matrix-Theorie von Wheeler und Heisenberg aufgriffen. Die QFT wurde heuristisch als Leitprinzipien verwendet, aber nicht als Grundlage für quantitative Berechnungen. ⓘ
Schwinger schlug jedoch einen anderen Weg ein. Mehr als ein Jahrzehnt lang waren er und seine Schüler fast die einzigen Vertreter der Feldtheorie gewesen, aber 1966 fand er mit einer neuen Methode, die er Quellentheorie nannte, einen Weg, das Problem der Unendlichkeiten zu umgehen. Die Entwicklungen in der Pionenphysik, in der die neue Sichtweise am erfolgreichsten angewandt wurde, überzeugten ihn von den großen Vorteilen der mathematischen Einfachheit und begrifflichen Klarheit, die ihre Anwendung mit sich brachte. ⓘ
In der Quellentheorie gibt es keine Divergenzen und keine Renormierung. Sie kann als das Rechenwerkzeug der Feldtheorie betrachtet werden, ist aber allgemeiner. Mit Hilfe der Quellentheorie konnte Schwinger das anomale magnetische Moment des Elektrons berechnen, was er bereits 1947 getan hatte, diesmal jedoch ohne "ablenkende Bemerkungen" über unendliche Größen. ⓘ
Schwinger wandte die Quellentheorie auch auf seine QFT-Theorie der Schwerkraft an und konnte alle vier klassischen Ergebnisse Einsteins reproduzieren: die gravitative Rotverschiebung, die Ablenkung und Verlangsamung des Lichts durch die Schwerkraft und die Perihelpräzession des Merkurs. Die Vernachlässigung der Quellentheorie durch die Physikgemeinschaft war für Schwinger eine große Enttäuschung:
Die mangelnde Anerkennung dieser Fakten durch andere war deprimierend, aber verständlich. -J. Schwinger ⓘ
Standard-Modell

1954 verallgemeinerten Yang Chen-Ning und Robert Mills die lokale Symmetrie der QED, was zu nicht-Abelschen Eichtheorien (auch als Yang-Mills-Theorien bekannt) führte, die auf komplizierteren lokalen Symmetriegruppen beruhen. In der QED wechselwirken (elektrisch) geladene Teilchen durch den Austausch von Photonen, während in der nicht-Abelschen Eichtheorie Teilchen mit einer neuen Art von "Ladung" durch den Austausch von masselosen Eichbosonen wechselwirken. Im Gegensatz zu Photonen tragen diese Eichbosonen selbst eine Ladung. ⓘ
Sheldon Glashow entwickelte 1960 eine nicht-Abelsche Eichtheorie, die die elektromagnetische und die schwache Wechselwirkung vereinte. Im Jahr 1964 gelangten Abdus Salam und John Clive Ward auf einem anderen Weg zur gleichen Theorie. Diese Theorie war jedoch nicht renormierbar. ⓘ
Peter Higgs, Robert Brout, François Englert, Gerald Guralnik, Carl Hagen und Tom Kibble schlugen in ihren berühmten Physical Review Letters vor, dass die Eichsymmetrie in Yang-Mills-Theorien durch einen Mechanismus namens spontane Symmetriebrechung gebrochen werden könnte, wodurch ursprünglich masselose Eichbosonen Masse erhalten könnten. ⓘ
Indem er die frühere Theorie von Glashow, Salam und Ward mit der Idee der spontanen Symmetriebrechung kombinierte, schrieb Steven Weinberg 1967 eine Theorie nieder, die die elektroschwachen Wechselwirkungen zwischen allen Leptonen und die Auswirkungen des Higgs-Bosons beschreibt. Seine Theorie wurde zunächst weitgehend ignoriert, bis sie 1971 durch den Beweis von Gerard 't Hooft, dass nicht-Abelsche Eichtheorien renormierbar sind, wieder ans Licht gebracht wurde. Die elektroschwache Theorie von Weinberg und Salam wurde 1970 von Glashow, John Iliopoulos und Luciano Maiani von den Leptonen auf die Quarks ausgedehnt, womit sie abgeschlossen war. ⓘ
Harald Fritzsch, Murray Gell-Mann und Heinrich Leutwyler entdeckten 1971, dass bestimmte Phänomene, die mit der starken Wechselwirkung zusammenhängen, auch mit der nicht-Abelschen Eichtheorie erklärt werden können. Die Quantenchromodynamik (QCD) war geboren. 1973 zeigten David Gross, Frank Wilczek und Hugh David Politzer, dass nicht-Abelsche Eichtheorien "asymptotisch frei" sind, was bedeutet, dass die Kopplungskonstante der starken Wechselwirkung unter Renormierung mit steigender Wechselwirkungsenergie abnimmt. (Ähnliche Entdeckungen waren bereits zuvor mehrfach gemacht worden, wurden aber weitgehend ignoriert). Daher wird die Kopplungskonstante in der QCD zumindest bei hochenergetischen Wechselwirkungen hinreichend klein, um eine gestörte Reihenentwicklung zu rechtfertigen, wodurch quantitative Vorhersagen für die starke Wechselwirkung möglich werden. ⓘ
Diese theoretischen Durchbrüche führten zu einer Renaissance der QFT. Die vollständige Theorie, die die elektroschwache Theorie und die Chromodynamik umfasst, wird heute als das Standardmodell der Elementarteilchen bezeichnet. Das Standardmodell beschreibt erfolgreich alle fundamentalen Wechselwirkungen mit Ausnahme der Gravitation, und seine zahlreichen Vorhersagen wurden in den folgenden Jahrzehnten auf bemerkenswerte Weise experimentell bestätigt. Das Higgs-Boson, das für den Mechanismus der spontanen Symmetriebrechung von zentraler Bedeutung ist, wurde schließlich 2012 am CERN nachgewiesen, womit die Existenz aller Bestandteile des Standardmodells vollständig bestätigt wurde. ⓘ
Andere Entwicklungen
In den 1970er Jahren wurden nicht-perturbative Methoden in nicht-Abelschen Eichtheorien entwickelt. Der 't Hooft-Polyakov-Monopol wurde theoretisch von 't Hooft und Alexander Polyakov entdeckt, Flux-Tubes von Holger Bech Nielsen und Poul Olesen und Instantons von Polyakov und anderen Autoren. Diese Objekte sind für die Störungstheorie unzugänglich. ⓘ
Im gleichen Zeitraum entstand auch die Supersymmetrie. Die erste supersymmetrische QFT in vier Dimensionen wurde 1970 von Yuri Golfand und Evgeny Likhtman aufgestellt, aber ihr Ergebnis stieß aufgrund des Eisernen Vorhangs nicht auf großes Interesse. Erst nach der Arbeit von Julius Wess und Bruno Zumino im Jahr 1973 wurde die Supersymmetrie in der theoretischen Gemeinschaft bekannt. ⓘ
Von den vier fundamentalen Wechselwirkungen bleibt die Gravitation die einzige, für die es keine konsistente QFT-Beschreibung gibt. Verschiedene Versuche einer Theorie der Quantengravitation führten zur Entwicklung der Stringtheorie, die ihrerseits eine Art zweidimensionale QFT mit konformer Symmetrie darstellt. Joël Scherk und John Schwarz schlugen 1974 erstmals vor, dass die Stringtheorie die Quantentheorie der Gravitation sein könnte. ⓘ
Physik der kondensierten Materie
Obwohl die Quantenfeldtheorie aus dem Studium der Wechselwirkungen zwischen Elementarteilchen hervorgegangen ist, wurde sie erfolgreich auf andere physikalische Systeme angewendet, insbesondere auf Vielteilchensysteme in der Physik der kondensierten Materie. ⓘ
Historisch gesehen war der Higgs-Mechanismus der spontanen Symmetriebrechung ein Ergebnis von Yoichiro Nambus Anwendung der Supraleitertheorie auf Elementarteilchen, während das Konzept der Renormierung aus der Untersuchung von Phasenübergängen zweiter Ordnung in Materie hervorging. ⓘ
Kurz nach der Einführung der Photonen führte Einstein das Quantisierungsverfahren für Schwingungen in einem Kristall durch, was zu den ersten Quasiteilchen, den Phononen, führte. Lev Landau behauptete, dass niederenergetische Anregungen in vielen Systemen kondensierter Materie durch die Wechselwirkungen zwischen einer Reihe von Quasiteilchen beschrieben werden können. Die Feynman-Diagramm-Methode der QFT war von Natur aus gut geeignet für die Analyse verschiedener Phänomene in Systemen mit kondensierter Materie. ⓘ
Die Eichtheorie wird verwendet, um die Quantisierung des magnetischen Flusses in Supraleitern, den spezifischen Widerstand beim Quanten-Hall-Effekt sowie die Beziehung zwischen Frequenz und Spannung beim Wechselstrom-Josephson-Effekt zu beschreiben. ⓘ
Grundsätze
Der Einfachheit halber werden in den folgenden Abschnitten natürliche Einheiten verwendet, in denen sowohl die reduzierte Planck-Konstante ħ als auch die Lichtgeschwindigkeit c auf eins gesetzt werden. ⓘ
Klassische Felder
Ein klassisches Feld ist eine Funktion von Raum- und Zeitkoordinaten. Beispiele sind das Gravitationsfeld der Newtonschen Gravitation g(x, t) sowie das elektrische Feld E(x, t) und das magnetische Feld B(x, t) im klassischen Elektromagnetismus. Ein klassisches Feld kann man sich als eine numerische Größe vorstellen, die jedem Punkt im Raum zugeordnet ist und sich mit der Zeit ändert. Es hat also unendlich viele Freiheitsgrade. ⓘ
Viele Phänomene, die quantenmechanische Eigenschaften aufweisen, lassen sich nicht allein durch klassische Felder erklären. Phänomene wie der photoelektrische Effekt lassen sich am besten durch diskrete Teilchen (Photonen) und nicht durch ein räumlich kontinuierliches Feld erklären. Das Ziel der Quantenfeldtheorie ist es, verschiedene quantenmechanische Phänomene mit Hilfe eines modifizierten Feldkonzepts zu beschreiben. ⓘ
Kanonische Quantisierung und Pfadintegrale sind zwei gängige Formulierungen der QFT. Um die Grundlagen der QFT zu erläutern, folgt ein Überblick über die klassische Feldtheorie. ⓘ
Das einfachste klassische Feld ist ein reelles Skalarfeld - eine reelle Zahl an jedem Punkt im Raum, die sich in der Zeit ändert. Es wird als ϕ(x, t) bezeichnet, wobei x der Ortsvektor und t die Zeit ist. Angenommen, die Lagrange des Feldes, ist
wobei die Lagrangesche Dichte ist, ist die Zeitableitung des Feldes, ∇ ist der Gradientenoperator, und m ist ein reeller Parameter (die "Masse" des Feldes). Anwendung der Euler-Lagrange-Gleichung auf die Lagrangesche:
erhält man die Bewegungsgleichungen für das Feld, die beschreiben, wie es sich in Zeit und Raum verändert:
Dies wird als Klein-Gordon-Gleichung bezeichnet. ⓘ
Da es sich bei der Klein-Gordon-Gleichung um eine Wellengleichung handelt, lassen sich ihre Lösungen wie folgt als Summe von Normalmoden (durch Fourier-Transformation erhalten) darstellen:
Dabei ist a eine komplexe Zahl (nach Konvention normiert), * bedeutet komplexe Konjugation und ωp ist die Frequenz der Normalmode:
Somit kann jeder Normalmodus, der einem einzelnen p entspricht, als ein klassischer harmonischer Oszillator mit der Frequenz ωp angesehen werden. ⓘ
Kanonische Quantisierung
Das Quantisierungsverfahren für das oben beschriebene klassische Feld in ein Quantenoperatorfeld ist analog zur Promotion eines klassischen harmonischen Oszillators in einen quantenharmonischen Oszillator. ⓘ
Die Verschiebung eines klassischen harmonischen Oszillators wird beschrieben durch
wobei a eine komplexe Zahl (normiert nach Konvention) und ω die Frequenz des Oszillators ist. Man beachte, dass x die Verschiebung eines Teilchens in einfacher harmonischer Bewegung aus der Gleichgewichtslage ist, nicht zu verwechseln mit der räumlichen Bezeichnung x eines Quantenfeldes. ⓘ
Für einen harmonischen Quantenoszillator wird x(t) zu einem linearen Operator :
Die komplexen Zahlen a und a* werden ersetzt durch den Annihilationsoperator und den Erzeugungsoperator ersetzt, wobei † die hermitsche Konjugation bezeichnet. Die Kommutationsbeziehung zwischen den beiden ist
Der Hamiltonian des einfachen harmonischen Oszillators kann wie folgt geschrieben werden
Der Vakuumzustand , der Zustand mit der niedrigsten Energie, ist definiert durch
und hat die Energie Man kann leicht überprüfen, dass was bedeutet, dass die Energie des einfachen harmonischen Oszillators um . Zum Beispiel ist der Zustand ist ein Eigenzustand der Energie . Jeder Energieeigenzustand eines einfachen harmonischen Oszillators kann erhalten werden aus durch sukzessive Anwendung des Erzeugungsoperators und jeder Zustand des Systems lässt sich als Linearkombination der Zustände
Ein ähnliches Verfahren kann auf das reelle Skalarfeld ϕ angewendet werden, indem es zu einem Quantenfeldoperator , während der Annihilationsoperator , der Erzeugungsoperator und die Winkelfrequenz nun für ein bestimmtes p sind:
Ihre Kommutierungsbeziehungen sind:
wobei δ die Dirac-Delta-Funktion ist. Der Vakuumzustand ist definiert durch
Jeder Quantenzustand des Feldes kann erhalten werden aus durch aufeinanderfolgende Anwendung von Erzeugungsoperatoren (oder durch eine Linearkombination solcher Zustände), z. B.
Während der Zustandsraum eines einzelnen harmonischen Quantenoszillators alle diskreten Energiezustände eines einzelnen schwingenden Teilchens enthält, enthält der Zustandsraum eines Quantenfeldes die diskreten Energieniveaus einer beliebigen Anzahl von Teilchen. Der letztgenannte Raum wird als Fock-Raum bezeichnet, der der Tatsache Rechnung trägt, dass die Teilchenzahl in relativistischen Quantensystemen nicht festgelegt ist. Der Prozess der Quantisierung einer beliebigen Anzahl von Teilchen anstelle eines einzelnen Teilchens wird oft auch als zweite Quantisierung bezeichnet. ⓘ
Das oben beschriebene Verfahren ist eine direkte Anwendung der nichtrelativistischen Quantenmechanik und kann zur Quantisierung von (komplexen) Skalarfeldern, Dirac-Feldern, Vektorfeldern (z. B. dem elektromagnetischen Feld) und sogar Strings verwendet werden. Allerdings sind die Erzeugungs- und Vernichtungsoperatoren nur in den einfachsten Theorien, die keine Wechselwirkungen enthalten (so genannte freie Theorien), gut definiert. Im Falle des reellen Skalarfeldes war die Existenz dieser Operatoren eine Folge der Zerlegung der Lösungen der klassischen Bewegungsgleichungen in eine Summe von Normalmoden. Um Berechnungen für jede realistische wechselwirkende Theorie durchzuführen, ist die Störungstheorie erforderlich. ⓘ
Die Lagrange eines jeden Quantenfeldes in der Natur würde zusätzlich zu den Termen der freien Theorie auch Wechselwirkungsterme enthalten. Zum Beispiel könnte ein quartischer Wechselwirkungsterm in die Lagrange des reellen Skalarfeldes eingeführt werden:
wobei μ ein Raumzeitindex ist, , usw. Die Summation über den Index μ wurde in Anlehnung an die Einstein-Notation weggelassen. Wenn der Parameter λ hinreichend klein ist, kann die durch die obige Lagrange beschriebene wechselwirkende Theorie als eine kleine Störung der freien Theorie betrachtet werden. ⓘ
Pfadintegrale
Bei der Pfadintegralformulierung der QFT geht es um die direkte Berechnung der Streuungsamplitude eines bestimmten Wechselwirkungsprozesses und nicht um die Aufstellung von Operatoren und Zustandsräumen. Zur Berechnung der Wahrscheinlichkeitsamplitude für die Entwicklung eines Systems von einem Anfangszustand zum Zeitpunkt t = 0 in einen Endzustand Bei t = T wird die Gesamtzeit T in N kleine Intervalle unterteilt. Die Gesamtamplitude ist das Produkt aus der Amplitude der Entwicklung innerhalb jedes Intervalls, integriert über alle Zwischenzustände. Sei H der Hamiltonian (d. h. der Generator der Zeitentwicklung), dann
Für den Grenzwert N → ∞ wird das obige Produkt der Integrale zum Feynman-Pfadintegral:
wobei L die Lagrange mit ϕ und ihren Ableitungen nach Raum- und Zeitkoordinaten ist, die aus dem Hamiltonian H durch Legendre-Transformation gewonnen wird. Die Anfangs- und Endbedingungen des Pfadintegrals sind jeweils
Mit anderen Worten: Die Gesamtamplitude ist die Summe der Amplituden aller möglichen Pfade zwischen dem Anfangs- und dem Endzustand, wobei die Amplitude eines Pfades durch den Exponentialwert des Integranden gegeben ist. ⓘ
Zwei-Punkt-Korrelationsfunktion
Bei Berechnungen stößt man häufig auf Ausdrücke wie
Die freie Zweipunktfunktion, die auch als Feynman-Propagator bezeichnet wird, kann für das reelle Skalarfeld entweder durch kanonische Quantisierung oder durch Pfadintegrale wie folgt bestimmt werden
In einer wechselwirkenden Theorie, in der die Lagrange oder der Hamiltonian Terme enthält oder enthält, die Wechselwirkungen beschreiben, ist die Zweipunktfunktion schwieriger zu definieren. Mit Hilfe der kanonischen Quantisierungsformulierung und der Pfadintegralformulierung ist es jedoch möglich, sie durch eine unendliche Störungsreihe der freien Zweipunktfunktion auszudrücken. ⓘ
Bei kanonischer Quantisierung kann die Zweipunkt-Korrelationsfunktion wie folgt geschrieben werden:
wobei ε eine infinitesimale Zahl und ϕI der Feldoperator im Rahmen der freien Theorie ist. Dabei ist die Exponentialfunktion als ihre Potenzreihenentwicklung zu verstehen. Zum Beispiel, in -Theorie ist der Wechselwirkungsterm des Hamiltonian und die Entwicklung des Zwei-Punkt-Korrelators in Form von wird
Bei der Pfadintegralformulierung kann die Zweipunktkorrelationsfunktion wie folgt geschrieben werden
wobei ist die Lagrangesche Dichte. Wie im vorangegangenen Abschnitt kann die Exponentialfunktion als Reihe in λ erweitert werden, wodurch die wechselwirkende Zweipunktfunktion auf Größen der freien Theorie reduziert wird. ⓘ
Das Wick'sche Theorem reduziert außerdem jede n-Punkt-Korrelationsfunktion in der freien Theorie auf eine Summe von Produkten von Zweipunkt-Korrelationsfunktionen. Ein Beispiel,
Da wechselwirkende Korrelationsfunktionen durch freie Korrelationsfunktionen ausgedrückt werden können, müssen nur letztere ausgewertet werden, um alle physikalischen Größen in der (perturbativen) wechselwirkenden Theorie zu berechnen. Dies macht den Feynman-Propagator zu einer der wichtigsten Größen in der Quantenfeldtheorie. ⓘ
Feynman-Diagramm
Korrelationsfunktionen in der Wechselwirkungstheorie können als Störungsreihe geschrieben werden. Jeder Term in der Reihe ist ein Produkt von Feynman-Propagatoren in der freien Theorie und kann visuell durch ein Feynman-Diagramm dargestellt werden. Der λ1-Term in der Zweipunkt-Korrelationsfunktion in der ϕ4-Theorie ist zum Beispiel
Nach Anwendung des Satzes von Wick ist einer der Terme
Dieser Term lässt sich stattdessen aus dem Feynman-Diagramm ableiten ⓘ
 . ⓘ
. ⓘ
Das Diagramm besteht aus ⓘ
- äußeren Punkten, die mit einer Kante verbunden sind und durch Punkte dargestellt werden (hier beschriftet und ).
- internen Scheitelpunkten, die mit vier Kanten verbunden sind und durch Punkte dargestellt werden (hier beschriftet mit ).
- Kanten, die die Eckpunkte verbinden und durch Linien dargestellt werden. ⓘ
Jeder Scheitelpunkt entspricht einem einzelnen Feldfaktor an dem entsprechenden Punkt in der Raumzeit, während die Kanten den Propagatoren zwischen den Raumzeitpunkten entsprechen. Den Term in der Störungsreihe, der dem Diagramm entspricht, erhält man durch Aufschreiben des Ausdrucks, der aus den sogenannten Feynman-Regeln folgt:
- Für jeden inneren Scheitelpunkt schreiben Sie einen Faktor .
- Für jede Kante, die zwei Scheitelpunkte miteinander verbindet und schreiben Sie einen Faktor .
- Dividieren Sie durch den Symmetriefaktor des Diagramms. ⓘ
Mit dem Symmetriefaktor Befolgt man diese Regeln, so erhält man genau den obigen Ausdruck. Durch Fourier-Transformation des Propagators lassen sich die Feynman-Regeln vom Ortsraum in den Impulsraum umformulieren. ⓘ
Um die n-Punkt-Korrelationsfunktion bis zur k-ten Ordnung zu berechnen, listet man alle gültigen Feynman-Diagramme mit n externen Punkten und k oder weniger Scheitelpunkten auf und verwendet dann die Feynman-Regeln, um den Ausdruck für jeden Term zu erhalten. Um genau zu sein,
ist gleich der Summe aller zusammenhängenden Diagramme mit n äußeren Punkten (Ausdrücke, die ihnen entsprechen). (Zusammenhängende Diagramme sind solche, in denen jeder Scheitelpunkt mit einem externen Punkt durch Linien verbunden ist. Komponenten, die keine Verbindung zu externen Linien haben, werden manchmal als "Vakuumblasen" bezeichnet.) In der oben diskutierten ϕ4-Wechselwirkungstheorie muss jeder Scheitelpunkt vier Beine haben. ⓘ
In realistischen Anwendungen kann die Streuungsamplitude einer bestimmten Wechselwirkung oder die Zerfallsrate eines Teilchens aus der S-Matrix berechnet werden, die ihrerseits mit der Methode des Feynman-Diagramms ermittelt werden kann. ⓘ
Feynman-Diagramme ohne "Schleifen" werden Tree-Level-Diagramme genannt, die die Wechselwirkungsprozesse niedrigster Ordnung beschreiben; solche, die n Schleifen enthalten, werden als n-Schleifen-Diagramme bezeichnet, die Beiträge höherer Ordnung oder Strahlungskorrekturen zur Wechselwirkung beschreiben. Linien, deren Endpunkte Scheitelpunkte sind, können als die Ausbreitung virtueller Teilchen betrachtet werden. ⓘ
Renormierung
Feynman-Regeln können verwendet werden, um Diagramme auf Baumebene direkt auszuwerten. Eine naive Berechnung von Schleifendiagrammen wie dem oben gezeigten führt jedoch zu divergierenden Impulsintegralen, was zu bedeuten scheint, dass fast alle Terme in der Störungsexpansion unendlich sind. Das Renormierungsverfahren ist ein systematischer Prozess zur Beseitigung solcher Unendlichkeiten. ⓘ
Parameter, die in der Lagrange erscheinen, wie die Masse m und die Kopplungskonstante λ, haben keine physikalische Bedeutung - m, λ und die Feldstärke ϕ sind keine experimentell messbaren Größen und werden hier als bloße Masse, bloße Kopplungskonstante bzw. bloßes Feld bezeichnet. Die physikalische Masse und die Kopplungskonstante werden in einem Wechselwirkungsprozess gemessen und unterscheiden sich im Allgemeinen von den nackten Größen. Bei der Berechnung der physikalischen Größen aus diesem Wechselwirkungsprozess kann man den Bereich der divergenten Impulsintegrale so begrenzen, dass er unterhalb eines Impulsgrenzwertes Λ liegt, Ausdrücke für die physikalischen Größen erhalten und dann den Grenzwert Λ → ∞ annehmen. Dies ist ein Beispiel für Regularisierung, eine Klasse von Methoden zur Behandlung von Divergenzen in der QFT, wobei Λ der Regulator ist. ⓘ
Der oben dargestellte Ansatz wird als nackte Störungstheorie bezeichnet, da die Berechnungen nur die nackten Größen wie Masse und Kopplungskonstante umfassen. Ein anderer Ansatz, die so genannte renormierte Störungstheorie, besteht darin, von Anfang an physikalisch sinnvolle Größen zu verwenden. Im Fall der ϕ4-Theorie wird zunächst die Feldstärke neu definiert:
Dabei ist ϕ das bloße Feld, ϕr das renormierte Feld und Z eine noch zu bestimmende Konstante. Die Lagrangesche Dichte wird zu:
wobei mr und λr die experimentell messbare, renormierte Masse bzw. Kopplungskonstante sind und
sind zu bestimmende Konstanten. Die ersten drei Terme sind die ϕ4-Lagrangedichte, die in Form der renormierten Größen geschrieben wird, während die letzten drei Terme als "Gegenterme" bezeichnet werden. Da die Lagrange nun mehr Terme enthält, sollten die Feynman-Diagramme zusätzliche Elemente enthalten, die jeweils ihre eigenen Feynman-Regeln haben. Das Verfahren ist wie folgt skizziert. Wählen Sie zunächst ein Regularisierungsschema (z. B. die oben eingeführte Cut-Off-Regularisierung oder die dimensionale Regularisierung); nennen Sie den Regler Λ. Berechnen Sie Feynman-Diagramme, in denen divergente Terme von Λ abhängen. Definieren Sie dann δZ, δm und δλ so, dass Feynman-Diagramme für die Gegenterme die divergenten Terme in den normalen Feynman-Diagrammen genau aufheben, wenn der Grenzwert Λ → ∞ genommen wird. Auf diese Weise erhält man sinnvolle endliche Größen. ⓘ
Nur in renormierbaren Theorien ist es möglich, alle Unendlichkeiten zu eliminieren, um ein endliches Ergebnis zu erhalten, während in nicht renormierbaren Theorien Unendlichkeiten nicht durch die Neudefinition einer kleinen Anzahl von Parametern entfernt werden können. Das Standardmodell der Elementarteilchen ist eine renormierbare QFT, während die Quantengravitation nicht renormierbar ist. ⓘ
Renormierungsgruppe
Die von Kenneth Wilson entwickelte Renormierungsgruppe ist ein mathematischer Apparat, mit dem die Veränderungen der physikalischen Parameter (Koeffizienten in der Lagrange) untersucht werden können, wenn das System auf verschiedenen Skalen betrachtet wird. Die Art und Weise, in der sich jeder Parameter mit der Skala ändert, wird durch seine β-Funktion beschrieben. Die Korrelationsfunktionen, die den quantitativen physikalischen Vorhersagen zugrunde liegen, ändern sich mit der Skala gemäß der Callan-Symanzik-Gleichung. ⓘ
Zum Beispiel hat die Kopplungskonstante in der QED, nämlich die Elementarladung e, die folgende β-Funktion:
wobei Λ die Energieskala ist, unter der die Messung von e durchgeführt wird. Diese Differentialgleichung impliziert, dass die beobachtete Elementarladung mit zunehmender Skala steigt. Die renormierte Kopplungskonstante, die sich mit der Energieskala ändert, wird auch als laufende Kopplungskonstante bezeichnet. ⓘ
Die Kopplungskonstante g in der Quantenchromodynamik, einer nicht-Abelschen Eichtheorie, die auf der Symmetriegruppe SU(3) basiert, hat die folgende β-Funktion:
wobei Nf die Anzahl der Quark-Flavours ist. Für den Fall, dass Nf ≤ 16 ist (das Standardmodell hat Nf = 6), nimmt die Kopplungskonstante g mit zunehmender Energieskala ab. Während also die starke Wechselwirkung bei niedrigen Energien stark ist, wird sie bei hohen Energien sehr schwach, ein Phänomen, das als asymptotische Freiheit bekannt ist. ⓘ
Konforme Feldtheorien (CFTs) sind spezielle QFTs, die konforme Symmetrie zulassen. Sie sind unempfindlich gegenüber Änderungen der Skala, da alle ihre Kopplungskonstanten eine verschwindende β-Funktion haben. (Das Gegenteil ist jedoch nicht der Fall - das Verschwinden aller β-Funktionen impliziert nicht die konforme Symmetrie der Theorie). Beispiele hierfür sind die Stringtheorie und die N = 4 supersymmetrische Yang-Mills-Theorie. ⓘ
Nach Wilsons Bild ist jede QFT grundsätzlich von ihrem Energie-Cut-off Λ begleitet, d.h. dass die Theorie bei Energien oberhalb von Λ nicht mehr gültig ist und alle Freiheitsgrade oberhalb der Skala Λ weggelassen werden müssen. Der Grenzwert könnte zum Beispiel der Kehrwert des Atomabstands in einem System aus kondensierter Materie sein, und in der Elementarteilchenphysik könnte er mit der grundlegenden "Körnigkeit" der Raumzeit in Verbindung gebracht werden, die durch Quantenfluktuationen in der Gravitation verursacht wird. Die Grenzskala der Theorien über Teilchenwechselwirkungen liegt weit jenseits der derzeitigen Experimente. Selbst wenn die Theorie auf dieser Skala sehr kompliziert wäre, muss sie bei niedrigen Energien durch eine renormierbare effektive Feldtheorie beschrieben werden, solange ihre Kopplungen ausreichend schwach sind. Der Unterschied zwischen renormierbaren und nicht renormierbaren Theorien besteht darin, dass erstere unempfindlich gegenüber Details bei hohen Energien sind, während letztere von ihnen abhängen. Nach dieser Auffassung sind nicht renormierbare Theorien als niederenergetische effektive Theorien einer fundamentaleren Theorie zu betrachten. Die Tatsache, dass es in einer solchen Theorie nicht gelingt, den Cut-Off Λ aus den Berechnungen zu entfernen, deutet lediglich darauf hin, dass auf Skalen oberhalb von Λ neue physikalische Phänomene auftreten, für die eine neue Theorie erforderlich ist. ⓘ
Andere Theorien
Die in den vorangegangenen Abschnitten beschriebenen Quantisierungs- und Renormierungsverfahren werden für die freie Theorie und die ϕ4-Theorie des reellen Skalarfeldes durchgeführt. Ein ähnlicher Prozess kann für andere Arten von Feldern durchgeführt werden, einschließlich des komplexen Skalarfeldes, des Vektorfeldes und des Dirac-Feldes, sowie für andere Arten von Wechselwirkungsterminen, einschließlich der elektromagnetischen Wechselwirkung und der Yukawa-Wechselwirkung. ⓘ
Die Quantenelektrodynamik enthält beispielsweise ein Dirac-Feld ψ, das das Elektronenfeld darstellt, und ein Vektorfeld Aμ, das das elektromagnetische Feld (Photonenfeld) darstellt. (Trotz seines Namens entspricht das elektromagnetische "Feld" der Quantenelektrodynamik eigentlich dem klassischen elektromagnetischen Vierer-Potential und nicht den klassischen elektrischen und magnetischen Feldern). Die vollständige QED-Lagrangedichte ist:
wobei γμ Dirac-Matrizen sind, und ist die elektromagnetische Feldstärke. Die Parameter in dieser Theorie sind die (bloße) Elektronenmasse m und die (bloße) Elementarladung e. Der erste und zweite Term in der Lagrangeschen Dichte entsprechen dem freien Dirac-Feld bzw. den freien Vektorfeldern. Der letzte Term beschreibt die Wechselwirkung zwischen dem Elektronen- und dem Photonenfeld, die als Störung der freien Theorien behandelt wird. ⓘ
Die obige Abbildung zeigt ein Beispiel für ein Feynman-Diagramm auf Baumebene in der QED. Es beschreibt die Annihilation eines Elektrons und eines Positrons, wobei ein Photon außerhalb der Schale entsteht, das dann in ein neues Paar aus Elektron und Positron zerfällt. Die Zeit läuft von links nach rechts. Vorwärts gerichtete Pfeile stehen für die Ausbreitung von Positronen, während rückwärts gerichtete Pfeile für die Ausbreitung von Elektronen stehen. Eine gewellte Linie stellt die Ausbreitung eines Photons dar. Jeder Scheitelpunkt in QED-Feynman-Diagrammen muss einen eingehenden und einen ausgehenden Fermionenschenkel (Positron/Elektron) sowie einen Photonenschenkel haben. ⓘ
Eichen-Symmetrie
Wenn die folgende Transformation der Felder an jedem Raumzeitpunkt x (eine lokale Transformation) durchgeführt wird, bleibt die QED-Lagrange unverändert bzw. invariant:
wobei α(x) eine beliebige Funktion der Raumzeitkoordinaten ist. Wenn die Lagrange einer Theorie (oder genauer gesagt die Wirkung) unter einer bestimmten lokalen Transformation invariant ist, dann wird diese Transformation als Eichsymmetrie der Theorie bezeichnet. Eichsymmetrien bilden in jedem Raumzeitpunkt eine Gruppe. Im Fall der QED ist die aufeinanderfolgende Anwendung von zwei verschiedenen lokalen Symmetrietransformationen und ist eine weitere Symmetrietransformation . Für jedes α(x), ein Element der U(1)-Gruppe, daher spricht man bei der QED von einer U(1)-Eichsymmetrie. Das Photonenfeld Aμ kann als U(1)-Eichboson bezeichnet werden. ⓘ
U(1) ist eine abelsche Gruppe, was bedeutet, dass das Ergebnis unabhängig von der Reihenfolge, in der ihre Elemente angewendet werden, dasselbe ist. QFTs können auch auf nicht-abelschen Gruppen aufgebaut werden, was zu nicht-abelschen Eichtheorien (auch als Yang-Mills-Theorien bekannt) führt. Die Quantenchromodynamik, die die starke Wechselwirkung beschreibt, ist eine nicht-Abelsche Eichtheorie mit einer SU(3)-Eichsymmetrie. Sie enthält drei Dirac-Felder ψi, i = 1,2,3, die Quark-Felder darstellen, sowie acht Vektorfelder Aa,μ, a = 1,...,8, die Gluonen-Felder darstellen, die die SU(3)-Eichbosonen sind. Die QCD-Lagrangedichte ist:
wobei Dμ die eichkovariante Ableitung ist:
wobei g die Kopplungskonstante ist, ta die acht Generatoren von SU(3) in der fundamentalen Darstellung (3×3-Matrizen) sind,
und fabc sind die Strukturkonstanten von SU(3). Die sich wiederholenden Indizes i,j,a werden implizit nach der Einstein-Notation summiert. Diese Lagrange ist invariant unter der Transformation:
wobei U(x) an jedem Raumzeitpunkt x ein Element von SU(3) ist:
Die vorangegangene Diskussion der Symmetrien bezieht sich auf die Ebene der Lagrange. Mit anderen Worten, es handelt sich um "klassische" Symmetrien. Nach der Quantisierung weisen einige Theorien ihre klassischen Symmetrien nicht mehr auf, ein Phänomen, das Anomalie genannt wird. In der Pfadintegralformulierung beispielsweise ist trotz der Invarianz der Lagrangeschen Dichte unter einer bestimmten lokalen Transformation der Felder das Maß des Pfadintegrals ändern kann. Damit eine Theorie, die die Natur beschreibt, konsistent ist, darf sie keine Anomalie in ihrer Eichsymmetrie enthalten. Das Standardmodell der Elementarteilchen ist eine Eichtheorie, die auf der Gruppe SU(3) × SU(2) × U(1) basiert, in der sich alle Anomalien exakt aufheben. ⓘ
Die theoretische Grundlage der allgemeinen Relativitätstheorie, das Äquivalenzprinzip, kann auch als eine Form der Eichsymmetrie verstanden werden, was die allgemeine Relativitätstheorie zu einer auf der Lorentz-Gruppe basierenden Eichtheorie macht. ⓘ
Das Noether-Theorem besagt, dass jede kontinuierliche Symmetrie, d. h. der Parameter in der Symmetrietransformation ist kontinuierlich und nicht diskret, zu einem entsprechenden Erhaltungssatz führt. Zum Beispiel impliziert die U(1)-Symmetrie der QED die Ladungserhaltung. ⓘ
Eichtransformationen setzen keine unterschiedlichen Quantenzustände in Beziehung. Vielmehr werden zwei gleichwertige mathematische Beschreibungen desselben Quantenzustands miteinander in Beziehung gesetzt. Ein Beispiel: Das Photonenfeld Aμ hat als Vierervektor vier scheinbare Freiheitsgrade, aber der tatsächliche Zustand eines Photons wird durch seine zwei Freiheitsgrade beschrieben, die der Polarisation entsprechen. Die verbleibenden zwei Freiheitsgrade werden als "redundant" bezeichnet - scheinbar unterschiedliche Schreibweisen von Aμ können durch eine Eichtransformation miteinander in Beziehung gesetzt werden und beschreiben tatsächlich denselben Zustand des Photonenfeldes. In diesem Sinne ist die Eichtransformation keine "echte" Symmetrie, sondern ein Spiegelbild der "Redundanz" der gewählten mathematischen Beschreibung. ⓘ
Um die Eichredundanz in der Pfadintegralformulierung zu berücksichtigen, muss man das so genannte Faddeev-Popov-Eichungsfixierungsverfahren durchführen. In nicht-Abelschen Eichtheorien führt ein solches Verfahren neue Felder ein, die "Geister" genannt werden. Teilchen, die den Geisterfeldern entsprechen, werden als Geisterteilchen bezeichnet, die von außen nicht nachgewiesen werden können. Eine strengere Verallgemeinerung des Faddejew-Popow-Verfahrens ist durch die BRST-Quantisierung gegeben. ⓘ
Spontane Symmetriebrechung
Spontane Symmetriebrechung ist ein Mechanismus, bei dem die Symmetrie der Lagrange durch das von ihr beschriebene System verletzt wird. ⓘ
Zur Veranschaulichung des Mechanismus betrachten wir ein lineares Sigma-Modell mit N reellen Skalarfeldern, das durch die Lagrangesche Dichte beschrieben wird:
wobei μ und λ reelle Parameter sind. Die Theorie lässt eine globale O(N)-Symmetrie zu:
Der niedrigste Energiezustand (Grundzustand oder Vakuumzustand) der klassischen Theorie ist ein beliebiges einheitliches Feld ϕ0, das folgende Bedingungen erfüllt
Ohne Verlust an Allgemeinheit sei der Grundzustand in der N-ten Richtung:
Die ursprünglichen N Felder können umgeschrieben werden als:
und die ursprüngliche Lagrangesche Dichte als:
mit k = 1, ..., N - 1. Die ursprüngliche globale O(N)-Symmetrie ist nicht mehr vorhanden, so dass nur die Untergruppe O(N - 1) übrig bleibt. Die größere Symmetrie vor dem spontanen Symmetriebrechen wird als "versteckt" oder spontan gebrochen bezeichnet. ⓘ
Das Goldstone-Theorem besagt, dass bei spontaner Symmetriebrechung jede gebrochene kontinuierliche globale Symmetrie zu einem masselosen Feld, dem Goldstone-Boson, führt. Im obigen Beispiel hat O(N) N(N - 1)/2 kontinuierliche Symmetrien (die Dimension seiner Lie-Algebra), während O(N - 1) (N - 1)(N - 2)/2 hat. Die Anzahl der gebrochenen Symmetrien ist ihre Differenz, N - 1, die den N - 1 masselosen Feldern πk entspricht. ⓘ
Wird hingegen eine Eichsymmetrie (im Gegensatz zu einer globalen Symmetrie) spontan gebrochen, wird das resultierende Goldstone-Boson vom entsprechenden Eichboson "gefressen", indem es zu einem zusätzlichen Freiheitsgrad für das Eichboson wird. Das Goldstone-Bosonen-Äquivalenztheorem besagt, dass bei hoher Energie die Amplitude für die Emission oder Absorption eines longitudinal polarisierten massiven Eichbosons gleich der Amplitude für die Emission oder Absorption des Goldstone-Bosons ist, das von dem Eichboson gefressen wurde. ⓘ
In der QFT des Ferromagnetismus kann das spontane Brechen der Symmetrie die Ausrichtung der magnetischen Dipole bei niedrigen Temperaturen erklären. Im Standardmodell der Elementarteilchen erhalten die W- und Z-Bosonen, die ansonsten aufgrund der Eichsymmetrie masselos wären, ihre Masse durch spontane Symmetriebrechung des Higgs-Bosons, ein Prozess, der als Higgs-Mechanismus bezeichnet wird. ⓘ
Supersymmetrie
Alle experimentell bekannten Symmetrien in der Natur beziehen Bosonen auf Bosonen und Fermionen auf Fermionen. Theoretiker haben die Hypothese aufgestellt, dass es eine Art von Symmetrie, die so genannte Supersymmetrie, gibt, die Bosonen und Fermionen miteinander verbindet. ⓘ
Das Standardmodell gehorcht der Poincaré-Symmetrie, deren Generatoren die Raumzeittranslationen Pμ und die Lorentz-Transformationen Jμν sind. Zusätzlich zu diesen Generatoren umfasst die Supersymmetrie in (3+1)-Dimensionen weitere Generatoren Qα, die so genannten Superladungen, die ihrerseits als Weyl-Fermionen transformiert werden. Die Symmetriegruppe, die von all diesen Generatoren erzeugt wird, ist als Super-Poincaré-Gruppe bekannt. Im Allgemeinen kann es mehr als einen Satz von Supersymmetrie-Generatoren geben, QαI, I = 1, ..., N, die die entsprechende N = 1 Supersymmetrie, N = 2 Supersymmetrie und so weiter erzeugen. Die Supersymmetrie kann auch in anderen Dimensionen konstruiert werden, insbesondere in (1+1) Dimensionen für ihre Anwendung in der Superstringtheorie. ⓘ
Die Lagrange einer supersymmetrischen Theorie muss unter der Wirkung der Super-Poincaré-Gruppe invariant sein. Beispiele für solche Theorien sind: Minimales supersymmetrisches Standardmodell (MSSM), N = 4 supersymmetrische Yang-Mills-Theorie und Superstringtheorie. In einer supersymmetrischen Theorie hat jedes Fermion einen bosonischen Superpartner und umgekehrt. ⓘ
Wenn die Supersymmetrie zu einer lokalen Symmetrie erhoben wird, ist die daraus resultierende Eichtheorie eine Erweiterung der allgemeinen Relativitätstheorie, die Supergravitation genannt wird. ⓘ
Die Supersymmetrie ist eine mögliche Lösung für viele aktuelle Probleme der Physik. So kann beispielsweise das Hierarchieproblem des Standardmodells - warum die Masse des Higgs-Bosons nicht auf einer sehr hohen Skala wie der großen vereinheitlichten Skala oder der Planck-Skala strahlungskorrigiert ist - gelöst werden, indem man das Higgs-Feld und seinen Superpartner, das Higgsino, in Beziehung setzt. Strahlungskorrekturen aufgrund von Higgs-Boson-Schleifen in Feynman-Diagrammen werden durch entsprechende Higgsino-Schleifen aufgehoben. Die Supersymmetrie bietet auch Antworten auf die große Vereinheitlichung aller Eichkopplungskonstanten im Standardmodell sowie auf die Natur der dunklen Materie. ⓘ
Bis zum Jahr 2018 haben Experimente jedoch noch keine Beweise für die Existenz supersymmetrischer Teilchen erbracht. Wenn die Supersymmetrie eine echte Symmetrie der Natur wäre, dann müsste sie gebrochen werden, und die Energie des Symmetriebrechens müsste höher sein als die, die mit heutigen Experimenten erreicht werden kann. ⓘ
Andere Raumzeiten
Die ϕ4-Theorie, die QED, die QCD sowie das gesamte Standardmodell gehen alle von einem (3+1)-dimensionalen Minkowski-Raum (3 Raum- und 1 Zeitdimension) als Hintergrund aus, auf dem die Quantenfelder definiert werden. Die QFT legt jedoch a priori weder die Anzahl der Dimensionen noch die Geometrie der Raumzeit fest. ⓘ
In der Physik der kondensierten Materie wird die QFT verwendet, um (2+1)-dimensionale Elektronengase zu beschreiben. In der Hochenergiephysik ist die Stringtheorie eine Form der (1+1)-dimensionalen QFT, während die Kaluza-Klein-Theorie die Schwerkraft in zusätzlichen Dimensionen nutzt, um Eichtheorien in niedrigeren Dimensionen zu erzeugen. ⓘ
Im Minkowski-Raum wird die flache Metrik ημν verwendet, um Raumzeitindizes in der Lagrange zu erhöhen und zu senken, z. B.
wobei ημν der Kehrwert von ημν ist, der ημρηρν = δμν erfüllt. Für QFTs in gekrümmter Raumzeit wird dagegen eine allgemeine Metrik (wie die Schwarzschild-Metrik, die ein Schwarzes Loch beschreibt) verwendet:
Dabei ist gμν der Kehrwert von gμν. Für ein reelles Skalarfeld ist die Lagrangesche Dichte in einer allgemeinen Raumzeit
wobei g = det(gμν) ist und ∇μ die kovariante Ableitung bezeichnet. Die Lagrange einer QFT und damit ihre Berechnungsergebnisse und physikalischen Vorhersagen hängen von der Geometrie des Raumzeithintergrunds ab. ⓘ
Topologische Quantenfeldtheorie
Die Korrelationsfunktionen und physikalischen Vorhersagen einer QFT hängen von der Raumzeitmetrik gμν ab. Für eine spezielle Klasse von QFTs, die topologischen Quantenfeldtheorien (TQFTs), sind alle Korrelationsfunktionen unabhängig von kontinuierlichen Änderungen der Raumzeitmetrik. QFTs in gekrümmter Raumzeit ändern sich im Allgemeinen entsprechend der Geometrie (lokalen Struktur) des Raumzeit-Hintergrunds, während TQFTs unter Raumzeit-Diffeomorphismen invariant sind, aber auf die Topologie (globale Struktur) der Raumzeit reagieren. Das bedeutet, dass alle Berechnungsergebnisse von TQFTs topologische Invarianten der zugrunde liegenden Raumzeit sind. Die Chern-Simons-Theorie ist ein Beispiel für eine TQFT und wurde verwendet, um Modelle der Quantengravitation zu konstruieren. Zu den Anwendungen der TQFT gehören der fraktionale Quanten-Hall-Effekt und topologische Quantencomputer. Die Weltlinienbahn fraktionierter Teilchen (bekannt als Anyons) kann eine Link-Konfiguration in der Raumzeit bilden, was die Flechtstatistik von Anyons in der Physik mit den Link-Invarianten in der Mathematik. Zu den topologischen Quantenfeldtheorien (TQFTs), die für die Pionierforschung im Bereich der topologischen Quantenmaterie geeignet sind, gehören die Chern-Simons-Witten-Eichtheorien in 2+1 Raumzeitdimensionen und andere neue exotische TQFTs in 3+1 Raumzeitdimensionen und darüber hinaus. ⓘ
Störende und nicht-störende Methoden
Mit Hilfe der Störungstheorie kann die Gesamtwirkung eines kleinen Wechselwirkungsterms Ordnung für Ordnung durch eine Reihenentwicklung in der Anzahl der an der Wechselwirkung beteiligten virtuellen Teilchen angenähert werden. Jeder Term in der Expansion kann als eine mögliche Art und Weise verstanden werden, wie (physikalische) Teilchen über virtuelle Teilchen miteinander wechselwirken können, was durch ein Feynman-Diagramm veranschaulicht wird. Die elektromagnetische Kraft zwischen zwei Elektronen in der QED wird (in der Störungstheorie erster Ordnung) durch die Ausbreitung eines virtuellen Photons dargestellt. In ähnlicher Weise sind die W- und Z-Bosonen Träger der schwachen Wechselwirkung und die Gluonen Träger der starken Wechselwirkung. Die Interpretation einer Wechselwirkung als eine Summe von Zwischenzuständen, die den Austausch verschiedener virtueller Teilchen beinhalten, ist nur im Rahmen der Störungstheorie sinnvoll. Im Gegensatz dazu behandeln nicht-perturbative Methoden in der QFT die wechselwirkende Lagrange als Ganzes ohne jegliche Reihenentwicklung. Anstelle von Teilchen, die Wechselwirkungen tragen, haben diese Methoden Konzepte wie den 't Hooft-Polyakov-Monopol, die Domänenwand, die Flussröhre und den Instanton hervorgebracht. Beispiele für QFTs, die vollständig nicht-perturbativ lösbar sind, sind Minimalmodelle der konformen Feldtheorie und das Thirring-Modell. ⓘ
Mathematische Strenge
Trotz ihres überwältigenden Erfolgs in der Teilchenphysik und der Physik der kondensierten Materie fehlt der QFT selbst eine formale mathematische Grundlage. Nach dem Haag-Theorem gibt es beispielsweise kein wohldefiniertes Wechselwirkungsbild für die QFT, was bedeutet, dass die Störungstheorie der QFT, die der gesamten Feynman-Diagramm-Methode zugrunde liegt, grundlegend unklar ist. ⓘ
Die Störungstheorie der Quantenfeldtheorie, die nur verlangt, dass die Größen als formale Potenzreihen ohne Konvergenzanforderungen berechenbar sind, kann jedoch streng mathematisch behandelt werden. Insbesondere Kevin Costellos Monographie Renormalization and Effective Field Theory bietet eine rigorose Formulierung der perturbativen Renormierung, die sowohl die effektivfeldtheoretischen Ansätze von Kadanoff, Wilson und Polchinski als auch den Batalin-Vilkovisky-Ansatz zur Quantisierung von Eichtheorien kombiniert. Darüber hinaus können perturbative Pfadintegralmethoden, die typischerweise als formale Berechnungsmethoden verstanden werden, die von der endlichdimensionalen Integrationstheorie inspiriert sind, durch ihre endlichdimensionalen Analoga eine solide mathematische Interpretation erhalten. ⓘ
Seit den 1950er Jahren haben theoretische Physiker und Mathematiker versucht, alle QFTs in einer Reihe von Axiomen zu organisieren, um die Existenz konkreter Modelle der relativistischen QFT auf mathematisch strenge Weise nachzuweisen und ihre Eigenschaften zu untersuchen. Diese Studienrichtung wird als konstruktive Quantenfeldtheorie bezeichnet, ein Teilgebiet der mathematischen Physik, das zu Ergebnissen wie dem CPT-Theorem, dem Spin-Statistik-Theorem und dem Goldstone-Theorem sowie zu mathematisch strengen Konstruktionen vieler wechselwirkender QFTs in zwei und drei Raumzeitdimensionen geführt hat, z. B. zweidimensionale Skalarfeldtheorien mit beliebigen polynomialen Wechselwirkungen, dreidimensionale Skalarfeldtheorien mit einer quartischen Wechselwirkung usw. ⓘ
Im Vergleich zur gewöhnlichen QFT sind die topologische Quantenfeldtheorie und die konforme Feldtheorie mathematisch besser abgesichert - beide können in den Rahmen der Darstellungen von Kobordismen eingeordnet werden. ⓘ
Die algebraische Quantenfeldtheorie ist ein weiterer Ansatz zur Axiomatisierung der QFT, bei dem die grundlegenden Objekte lokale Operatoren und die algebraischen Beziehungen zwischen ihnen sind. Zu den axiomatischen Systemen, die diesem Ansatz folgen, gehören die Wightman-Axiome und die Haag-Kastler-Axiome. Eine Möglichkeit, Theorien zu konstruieren, die den Wightman-Axiomen genügen, besteht in der Verwendung der Osterwalder-Schrader-Axiome, die die notwendigen und hinreichenden Bedingungen dafür liefern, dass eine Theorie der realen Zeit aus einer Theorie der imaginären Zeit durch analytische Fortführung (Wick-Rotation) gewonnen werden kann. ⓘ
Yang-Mills-Existenz und Massenlücke, eines der Millenniumspreis-Probleme, betrifft die wohldefinierte Existenz von Yang-Mills-Theorien, wie sie durch die oben genannten Axiome dargelegt sind. Die vollständige Problemstellung lautet wie folgt.
Beweisen Sie, dass für jede kompakte einfache Eichgruppe G eine nichttriviale Quanten-Yang-Mills-Theorie existiert auf existiert und eine Massenlücke Δ > 0 hat. Die Existenz beinhaltet die Feststellung axiomatischer Eigenschaften, die mindestens so stark sind wie die in Streater & Wightman (1964), Osterwalder & Schrader (1973) und Osterwalder & Schrader (1975) genannten. ⓘ
Die Axiomatische Quantenfeldtheorie versucht, ausgehend von einem Satz möglichst weniger, als mathematisch oder physikalisch unumgänglich angesehener Axiome, eine konsistente Beschreibung der Quantenfeldtheorie zu erzielen. ⓘ
Etliche konkrete Ergebnisse konnten mit dieser Herangehensweise erzielt werden, zum Beispiel die Herleitung des Spin-Statistik-Theorems und des CPT-Theorems alleine aus den Axiomen, d. h. unabhängig von einer speziellen Quantenfeldtheorie. Ein früher Erfolg war die 1955 von Lehmann, Symanzik und Zimmermann entwickelte LSZ-Reduktionsformel für die S-Matrix. Außerdem existiert ein von Bogoliubov, Medvedev und Polianov begründeter funktionalanalytischer Zugang zur S-Matrix-Theorie (auch BMP-Theorie genannt). ⓘ
Weitere Anwendungen im Bereich der klassischen Statistik und der Quantenstatistik sind schon sehr weit fortgeschritten. Sie reichen von der allgemeinen Ableitung der Existenz thermodynamischer Größen, Satz von Gibbs, Zustandsgrößen wie Druck, innerer Energie und Entropie bis zum Beweis der Existenz von Phasenübergängen und der exakten Behandlung wichtiger Vielteilchensysteme:
- des Bardeen-Cooper-Schrieffer-Modells der Supraleitfähigkeit
- des Heisenbergschen Ferromagneten
- des idealen Bose-Gases. ⓘ
Grundlagen
Die Quantenfeldtheorien sind ursprünglich als relativistische Streutheorien entwickelt worden. In gebundenen Systemen sind die Teilchenenergien im Allgemeinen deutlich kleiner als die Massenenergien mc2. Daher ist es in solchen Fällen meist ausreichend genau, in der nichtrelativistischen Quantenmechanik mit der Störungstheorie zu arbeiten. Bei Kollisionen zwischen kleinen Teilchen können jedoch sehr viel höhere Energien auftreten, so dass relativistische Effekte berücksichtigt werden müssen. ⓘ
Im folgenden Abschnitt wird erklärt, welche Schritte zur Entwicklung einer relativistischen Streutheorie nötig sind. Zunächst wird dazu die Lagrangedichte aufgestellt, dann werden die Felder quantisiert. Zuletzt wird mit den quantisierten Feldern eine Streutheorie beschrieben und ein dabei auftretendes Problem durch die Renormierung gelöst. ⓘ
Feldquantisierung
Bisher wurde noch keine Aussage über die Eigenschaften der Felder gemacht. Bei starken Feldern mit einer großen Zahl von Bosonen-Anregungen können diese halbklassisch behandelt werden, im Allgemeinen muss man aber zunächst einen Mechanismus entwickeln, um die Auswirkungen der Quantennatur der Felder zu beschreiben. Die Entwicklung eines solchen Mechanismus bezeichnet man als Feldquantisierung und sie ist der erste Schritt, um das Verhalten der Felder berechenbar zu machen. Es gibt dabei zwei verschiedene Formalismen, die unterschiedliches Vorgehen beinhalten. ⓘ
- Der ältere kanonische Formalismus lehnt sich an den Formalismus der Quantenmechanik an. Er deutet die dort auftretenden Ein-Teilchen-Wellengleichungen als die Beschreibungen von Amplituden einer klassischen Feldtheorie, welche ihrerseits einer Quantisierung gemäß der kanonischen Vertauschungsregeln der Quantenmechanik bedürfen. Der Formalismus eignet sich damit, um fundamentale Eigenschaften der Felder, wie das Spin-Statistik-Theorem zu zeigen. Sein Nachteil ist jedoch, dass viele Aspekte in diesem Formalismus recht willkürlich wirken. Außerdem sind die Berechnung von Wechselwirkungsamplituden und die Feldquantisierung bei nicht-abelschen Eichtheorien recht kompliziert.
- Der neuere Pfadintegral-Formalismus baut auf dem Prinzip der kleinsten Wirkung auf, das heißt, es wird über alle Feldkonfigurationen integriert, sich nicht aufhebende Beiträge kommen aber bei schwacher Kopplung nur von Pfaden in der Nähe der Minima der Wirkung. Der Vorteil dieses Formalismus ist, dass sich die Berechnung von Wechselwirkungsamplituden als vergleichsweise einfach darstellt und die Symmetrien der Felder klar zum Ausdruck kommen. Der aus mathematischer Sicht schwerwiegende Mangel dieses Formalismus ist, dass die Konvergenz des Pfadintegrals und damit das Funktionieren der Methoden des Formalismus nicht mathematisch streng bewiesen ist. Er wird daher besonders in der mathematischen Physik teilweise als heuristisch und „unpräzise“ bzw. „nichtkonstruktiv“ abgelehnt, obwohl er zugleich als Ausgangspunkt der Gittereichtheorien dient, die eines der Hauptwerkzeuge der numerischen Behandlung von Quantenfeldtheorien sind. ⓘ
Im Folgenden werden die Grundlagen der Feldquantisierung für freie Felder in beiden Formalismen erklärt. ⓘ
Kanonischer Formalismus
Für die Feldquantisierung im kanonischen Formalismus benutzt man den Hamilton-Formalismus der klassischen Mechanik. Man ordnet dabei jedem Feld ( bzw. ) ein kanonisch konjugiertes Feld analog dem kanonischen Impuls zu. Das Feld und sein kanonisch konjugiertes Feld sind dann im Sinne der Quantenmechanik konjugierte Operatoren, sogenannte Feldoperatoren, und erfüllen eine Unschärferelation, wie Ort und Impuls in der Quantenmechanik. Die Unschärferelation kann entweder durch eine Kommutatorrelation (für Bosonen nach dem Spin-Statistik-Theorem) oder eine Antikommutatorrelation (für Fermionen) analog zum Kommutator von Ort und Impuls realisiert werden. Den Hamilton-Operator, der die Energie des Systems charakterisiert, erhält man, indem man die Hamilton-Funktion bildet und darin die Felder durch die Feldoperatoren ersetzt. Er ist in der Regel positiv definit oder darf zumindest keine unbeschränkt negativen Eigenwerte haben, da ein solches System unter beliebig großer Energieabgabe an die Umgebung in immer tiefere Energieeigenzustände fallen würde. ⓘ
Skalare Felder
Für skalare Felder erhält man als kanonisch konjugiertes Feld zu und als kanonisch konjugiertes Feld zu . Die geforderte Kommutatorrelation lautet
Es ist in Quantenfeldtheorien üblich, im Impulsraum zu rechnen. Dazu betrachtet man die Fourier-Darstellung des Feldoperators, die für das Skalarfeld lautet
Dabei sind der Impuls und die Stufenfunktion, die bei negativem Argument 0 und sonst 1 ist. Da und Operatoren sind, trifft dies auch auf , , und zu. Ihre Kommutatoren folgen aus dem Kommutator der Feldoperatoren. Der Operator kann als Operator interpretiert werden, der ein Teilchen mit Impuls erzeugt, während ein Antiteilchen mit Impuls erzeugt. Entsprechend können und als Operatoren interpretiert werden, die ein Teilchen oder Antiteilchen mit Impuls vernichten. Die Verwendung der Kommutatorrelationen führt wie gewünscht zu einem positiv definiten Hamilton-Operator. Es können beliebig viele Skalarfelder im selben Zustand sein (Bose-Einstein-Statistik). ⓘ
Spinorfelder
Wenn man für ein Spinorfeld analog vorgeht, erhält man als kanonisch konjugiertes Feld zu und als kanonisch konjugiertes Feld zu . Damit ergeben sich die geforderten (Anti-)Kommutatorrelationen zu
Dabei sind und Spinorindizes. Man betrachtet dann wieder analog die Fourier-Darstellung des Feldoperators und berechnet den Hamilton-Operator. Einen positiven Hamilton-Operator erhält man beim Spinorfeld jedoch nur, wenn man Antikommutatoren benutzt. Diese werden mit geschweiften Klammern geschrieben, was in den obigen Formeln bereits vorweggenommen wurde. Aufgrund dieser Antikommutatoren ergibt die zweimalige Anwendung desselben Erzeugungsoperators auf einen Zustand den Nullzustand. Das bedeutet, dass nie zwei Spin-1/2-Teilchen im selben Zustand sein können (Pauli-Prinzip). Spinorfelder gehorchen daher der Fermi-Dirac-Statistik. ⓘ
Eichfelder
Für Eichfelder lauten die geforderten Kommutatorrelationen
wobei die Komponenten der Minkowski-Metrik bezeichnet. Allerdings erhält man aus der Lagrangedichte , was die geforderte Kommutatorrelation nicht erfüllen kann. Die Quantisierung von Eichfeldern ist daher nur bei Festlegung einer Eichbedingung möglich. Die Festlegung einer geeigneten Eichbedingung, die den Zugang über Kommutatorrelationen von Feldern ermöglicht und gleichzeitig die Lorentzinvarianz der Lagrangedichte erhält, ist kompliziert. ⓘ
Man verwendet meist eine Abwandlung der Lorenz-Eichung, um sinnvoll ein kanonisch konjugiertes Feld definieren zu können. Der Formalismus wird nach seinen Entwicklern Suraj N. Gupta und Konrad Bleuler als Gupta-Bleuler-Formalismus bezeichnet. ⓘ
Eine Alternative stellt eine physikalische Eichung wie z. B. die temporale plus eine weitere Eichbedingung dar. Hier werden zwei der vier Polarisationen des Eichfeldes als physikalische Freiheitsgrade direkt durch die Wahl der Eichung sowie durch die anschließende Implementierung des Gaußschen Gesetzes als Bedingung an die physikalischen Zustände eliminiert. Der wesentliche Vorteil ist die Reduzierung des Hilbertraumes auf ausschließlich physikalische, transversale Freiheitsgrade. Dem steht als Nachteil der Verlust einer manifest kovarianten Formulierung gegenüber. ⓘ
Antiteilchen
Ein spezielles Gebiet der relativistischen Quantenmechanik betrifft Lösungen der relativistischen Klein-Gordon-Gleichung und der Dirac-Gleichung mit negativer Energie. Dies würde es Teilchen erlauben, zu unendlicher negativer Energie abzusteigen, was in der Realität nicht beobachtet wird. In der Quantenmechanik löst man dieses Problem, indem man die entsprechenden Lösungen willkürlich als Entitäten mit positiver Energie interpretiert, die sich rückwärts in der Zeit bewegen; man überträgt also in der Wellenfunktion das negative Vorzeichen von der Energie E auf die Zeit t, was wegen der Beziehung naheliegend ist ( h ist die Plancksche Konstante und das der Energiedifferenz zugeordnete Frequenzintervall). ⓘ
Paul Dirac interpretierte diese rückwärts bewegten Lösungen als Antiteilchen. ⓘ
Konkrete Quantenfeldtheorien
Standardmodell
Durch Kombination des elektroschwachen Modells mit der Quantenchromodynamik entsteht eine vereinte Quantenfeldtheorie, das so genannte Standardmodell der Elementarteilchenphysik. Es enthält alle bekannten Teilchen und kann die meisten bekannten Vorgänge erklären. ⓘ
Gleichzeitig ist aber bekannt, dass das Standardmodell nicht die endgültige Theorie sein kann. Zum einen ist die Gravitation nicht enthalten, zum anderen gibt es eine Reihe von Beobachtungen (Neutrinooszillationen, Dunkle Materie), nach denen eine Erweiterung des Standardmodells notwendig scheint. Außerdem enthält das Standardmodell viele willkürliche Parameter und erklärt z. B. das sehr unterschiedliche Massenspektrum der Elementarteilchenfamilien nicht. ⓘ
Die im Folgenden erläuterten Quantenfeldtheorien sind alle im Standardmodell enthalten. ⓘ
ϕ4-Theorie
Die Lagrangedichte der -Theorie lautet
Diese Quantenfeldtheorie besitzt große theoretische Bedeutung, da sie die einfachste denkbare Quantenfeldtheorie mit einer Wechselwirkung ist und hier im Gegensatz zu realistischeren Modellen einige exakte mathematische Aussagen über ihre Eigenschaften gemacht werden können. Sie beschreibt ein selbstwechselwirkendes reelles oder komplexes Skalarfeld. ⓘ
In der statistischen Physik spielt sie eine Rolle als einfachstes Kontinuumsmodell für die (sehr allgemeine) Landau-Theorie der Phasenübergänge zweiter Ordnung und der kritischen Phänomene. Von der statistischen Interpretation aus bekommt man zugleich einen neuen und konstruktiven Zugang zum Renormierungsproblem, indem gezeigt wird, dass die Renormierung der Massen, Ladungen und Vertex-Funktionen durch Eliminierung kurzwelliger Wellenphänomene aus der sog. Zustandssumme (englisch: „Partition Function“) erreicht werden kann. Auch das Higgsfeld des Standardmodells hat eine -Selbstwechselwirkung, die allerdings noch um Wechselwirkungen mit den anderen Feldern des Standardmodells ergänzt wird. In diesen Fällen ist die Kopplungskonstante m2 negativ, was einer imaginären Masse entspräche. Diese Felder werden daher als tachyonische Felder bezeichnet. Diese Bezeichnung bezieht sich jedoch auf das Higgsfeld und nicht auf das Higgs-Teilchen, das sogenannte Higgs-Boson, welches kein Tachyon, sondern ein gewöhnliches Teilchen mit reeller Masse ist. Das Higgsteilchen wird auch nicht durch das Higgsfeld beschrieben, sondern nur durch einen bestimmten Anteil dieses Feldes. ⓘ
Schwache Wechselwirkung
Die schwache Wechselwirkung, deren bekanntester Effekt der Betazerfall ist, nimmt eine physikalisch geschlossene Formulierung nach Vereinheitlichung mit der QED im elektroschwachen Standardmodell an. Die Wechselwirkung wird hier durch Photonen, W- und Z-Bosonen vermittelt. ⓘ
Quantenchromodynamik
Ein anderes Beispiel einer QFT ist die Quantenchromodynamik (QCD), welche die Starke Wechselwirkung beschreibt. In ihr wird ein Teil der im Atomkern auftretenden Wechselwirkungen zwischen Protonen und Neutronen auf die subnukleare Wechselwirkung zwischen Quarks und Gluonen reduziert. ⓘ
Interessant ist in der QCD, dass die Gluonen, welche die Wechselwirkung vermitteln, selbst miteinander wechselwirken. (Das wäre am Beispiel der QED etwa so, als ob sich zwei durchdringende Lichtstrahlen direkt beeinflussen würden.) Eine Konsequenz dieser gluonischen Selbstwechselwirkung ist, dass die elementaren Quarks nicht einzeln beobachtet werden können, sondern immer in Form von Quark-Antiquark-Zuständen oder Zuständen dreier Quarks (oder Antiquarks) auftreten (Confinement). Auf der anderen Seite folgt daraus, dass die Kopplungskonstante bei hohen Energien nicht zunimmt, sondern abnimmt. Dieses Verhalten wird als asymptotische Freiheit bezeichnet. ⓘ
Verhältnis zu anderen Theorien
Versuche, diese Quantenfeldtheorien mit der allgemeinen Relativitätstheorie (Gravitation) zur Quantengravitation zu vereinen, sind bisher ohne Erfolg geblieben. Nach Ansicht vieler Forscher erfordert die Quantisierung der Gravitation neue, über die Quantenfeldtheorie hinausgehende Konzepte, da hier der Raum-Zeit-Hintergrund selbst dynamisch wird. Beispiele aus der aktuellen Forschung sind die Stringtheorie, die M-Theorie und die Loop-Quantengravitation. Weiter liefern die Supersymmetrie, die Twistor-Theorie, die Finite Quantenfeldtheorie und die Topologische Quantenfeldtheorie wichtige konzeptionelle Ideen, die zurzeit in der Fachwelt diskutiert werden. ⓘ
Auch in der Festkörpertheorie finden sich Anwendungen der (nicht-relativistischen) Quantenfeldtheorie, und zwar hauptsächlich in der Vielteilchentheorie. ⓘ




![{\displaystyle L=\int d^{3}x\,{\mathcal {L}}=\int d^{3}x\,\left[{\frac {1}{2}}{\dot {\phi }}^{2}-{\frac {1}{2}}(\nabla \phi )^{2}-{\frac {1}{2}}m^{2}\phi ^{2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c9ce91f7eb79d2c06f42cc431ab9bbca59ca89)


![{\displaystyle {\frac {\partial }{\partial t}}\left[{\frac {\partial {\mathcal {L}}}{\partial (\partial \phi /\partial t)}}\right]+\sum _{i=1}^{3}{\frac {\partial }{\partial x^{i}}}\left[{\frac {\partial {\mathcal {L}}}{\partial (\partial \phi /\partial x^{i})}}\right]-{\frac {\partial {\mathcal {L}}}{\partial \phi }}=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b60bbe90a93512487bc5805c9f9c6753483396)








![{\displaystyle \left[{\hat {a}},{\hat {a}}^{\dagger }\right]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac6a25fa663fd271e485103c5f5510df6bfe657e)




![{\displaystyle [{\hat {H}},{\hat {a}}^{\dagger }]=\hbar \omega ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b89bfb22d3caa3ad1448848733895617ac1d197)









![{\displaystyle \left[{\hat {a}}_{\mathbf {p} },{\hat {a}}_{\mathbf {q} }^{\dagger }\right]=(2\pi )^{3}\delta (\mathbf {p} -\mathbf {q} ),\quad \left[{\hat {a}}_{\mathbf {p} },{\hat {a}}_{\mathbf {q} }\right]=\left[{\hat {a}}_{\mathbf {p} }^{\dagger },{\hat {a}}_{\mathbf {q} }^{\dagger }\right]=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e717bcbc4eacc629e354ccb1313c85c8d7d1f030)


















![{\displaystyle \langle \Omega |T\{\phi (x)\phi (y)\}|\Omega \rangle =\lim _{T\to \infty (1-i\epsilon )}{\frac {\left\langle 0\left|T\left\{\phi _{I}(x)\phi _{I}(y)\exp \left[-i\int _{-T}^{T}dt\,H_{I}(t)\right]\right\}\right|0\right\rangle }{\left\langle 0\left|T\left\{\exp \left[-i\int _{-T}^{T}dt\,H_{I}(t)\right]\right\}\right|0\right\rangle }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5da3c13010e11cdcfa46460fe31c93cda1ea9e28)





![{\displaystyle \langle \Omega |T\{\phi (x)\phi (y)\}|\Omega \rangle =\lim _{T\to \infty (1-i\epsilon )}{\frac {\int {\mathcal {D}}\phi \,\phi (x)\phi (y)\exp \left[i\int _{-T}^{T}d^{4}z\,{\mathcal {L}}\right]}{\int {\mathcal {D}}\phi \,\exp \left[i\int _{-T}^{T}d^{4}z\,{\mathcal {L}}\right]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a53cf57879d423ddf41fcff180629b0917de9fa)



















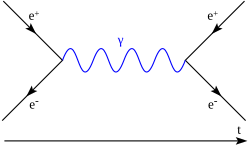



![{\displaystyle e^{i[\alpha (x)+\alpha '(x)]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/171b083b739b394140c10da874c3e4c7d23fe601)



![{\displaystyle \psi ^{i}(x)\to U^{ij}(x)\psi ^{j}(x),\quad A_{\mu }^{a}(x)t^{a}\to U(x)\left[A_{\mu }^{a}(x)t^{a}+ig^{-1}\partial _{\mu }\right]U^{\dagger }(x),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08c1ca05167f65c0cba1f6243946464914e11ab3)

![{\displaystyle {\mathcal {L}}[\phi ,\partial _{\mu }\phi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/562e89f35d6535c06ecb8c3cc70aa8da84920ed5)

















![{\displaystyle [\phi ({\vec {x}},t),\pi ({\vec {y}},t)]=[\phi ^{\dagger }({\vec {x}},t),\pi ^{\dagger }({\vec {y}},t)]=i\delta ^{(3)}({\vec {x}}-{\vec {y}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8ba3270714452ad7e0ca18658b03af09619a115)
![{\displaystyle \phi (x)=\int {\frac {\mathrm {d} ^{4}k}{(2\pi )^{4}}}2\pi \delta (k^{2}-m^{2})\theta (k_{0})\left[a(k)e^{-ikx}+b^{\dagger }(k)e^{ikx}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/279cd5c96c678195663a29e383bc528ad0cadd38)















![{\displaystyle [A_{\mu }({\vec {x}},t),\pi _{\nu }({\vec {y}},t)]=ig_{\mu \nu }\delta ^{(3)}({\vec {x}}-{\vec {y}}),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43f78bc6529b3b2d6c98097bf69c7ebdc463fd82)








