Paramagnetismus

Wenn flüssiger Sauerstoff aus einem Becher in einen starken Magneten gegossen wird, wird der Sauerstoff aufgrund seines Paramagnetismus vorübergehend zwischen den Magnetpolen eingeschlossen. ⓘ

Paramagnetismus ist eine Form des Magnetismus, bei der einige Materialien von einem von außen angelegten Magnetfeld schwach angezogen werden und interne, induzierte Magnetfelder in Richtung des angelegten Magnetfelds bilden. Im Gegensatz dazu werden diamagnetische Materialien von Magnetfeldern abgestoßen und bilden induzierte Magnetfelder, die der Richtung des angelegten Magnetfeldes entgegengesetzt sind. Zu den paramagnetischen Materialien gehören die meisten chemischen Elemente und einige Verbindungen; sie haben eine relative magnetische Permeabilität von etwas mehr als 1 (d. h. eine geringe positive magnetische Suszeptibilität) und werden daher von Magnetfeldern angezogen. Das durch das angelegte Feld induzierte magnetische Moment ist linear zur Feldstärke und eher schwach. In der Regel ist eine empfindliche analytische Waage erforderlich, um diesen Effekt festzustellen. Moderne Messungen an paramagnetischen Materialien werden häufig mit einem SQUID-Magnetometer durchgeführt. ⓘ

Paramagnetismus ist auf das Vorhandensein ungepaarter Elektronen im Material zurückzuführen, so dass die meisten Atome mit unvollständig gefüllten Atomorbitalen paramagnetisch sind, obwohl es Ausnahmen wie Kupfer gibt. Aufgrund ihres Spins haben ungepaarte Elektronen ein magnetisches Dipolmoment und wirken wie kleine Magnete. Ein äußeres Magnetfeld bewirkt, dass sich die Spins der Elektronen parallel zum Feld ausrichten, was eine Nettoanziehung bewirkt. Zu den paramagnetischen Materialien gehören Aluminium, Sauerstoff, Titan und Eisenoxid (FeO). Daher wird in der Chemie eine einfache Faustregel verwendet, um festzustellen, ob ein Teilchen (Atom, Ion oder Molekül) paramagnetisch oder diamagnetisch ist: Wenn alle Elektronen in dem Teilchen gepaart sind, dann ist die aus diesem Teilchen bestehende Substanz diamagnetisch; wenn sie ungepaarte Elektronen hat, dann ist die Substanz paramagnetisch. ⓘ

Im Gegensatz zu Ferromagneten behalten paramagnetische Stoffe bei Abwesenheit eines von außen angelegten Magnetfeldes keine Magnetisierung bei, da die thermische Bewegung die Spinausrichtung zufällig verändert. (Einige paramagnetische Materialien behalten sogar am absoluten Nullpunkt ihre Spin-Unordnung bei, was bedeutet, dass sie im Grundzustand, d. h. ohne thermische Bewegung, paramagnetisch sind). Daher sinkt die Gesamtmagnetisierung auf Null, wenn das angelegte Feld entfernt wird. Selbst in Gegenwart des Feldes gibt es nur eine geringe induzierte Magnetisierung, da nur ein kleiner Teil der Spins durch das Feld ausgerichtet wird. Dieser Anteil ist proportional zur Feldstärke, was die lineare Abhängigkeit erklärt. Die Anziehung, die ferromagnetische Materialien erfahren, ist nicht linear und viel stärker, so dass sie z. B. bei der Anziehung zwischen einem Kühlschrankmagneten und dem Eisen des Kühlschranks selbst leicht zu beobachten ist. ⓘ

Vereinfachter Vergleich der Permeabilitäten von ferromagnetischen (μ_f) , paramagnetischen (μ_p) und diamagnetischen Materialien (μ_d) zu Vakuum (μ₀) . Dabei ist μ jeweils die Steigung der Kurven B(H).
H: Feldstärke des äußeren Feldes
B: Flussdichte des induzierten Feldes ⓘ

Die magnetische Permeabilität $\textstyle \mu _{r}$ ist bei Paramagneten größer als 1 (bzw. die magnetische Suszeptibilität $\chi =\textstyle \mu _{r}-1$ positiv). In der physikalischen Klassifikation gelten alle Materialien, die dieser Bedingung genügen und keine persistierende magnetische Ordnung aufweisen, als paramagnetisch. ⓘ

Beziehung zu Elektronenspins

Paramagnetismus, Ferromagnetismus und Spinwellen ⓘ

Die Atome oder Moleküle von paramagnetischen Materialien besitzen ein permanentes magnetisches Moment (Dipol), auch wenn kein Feld angelegt ist. Das permanente Moment ist im Allgemeinen auf den Spin der ungepaarten Elektronen in atomaren oder molekularen Elektronenorbitalen zurückzuführen (siehe Magnetisches Moment). Im reinen Paramagnetismus treten die Dipole nicht miteinander in Wechselwirkung und sind in Abwesenheit eines äußeren Feldes aufgrund der thermischen Bewegung zufällig ausgerichtet, was zu einem magnetischen Moment von Null führt. Wenn ein Magnetfeld angelegt wird, neigen die Dipole dazu, sich nach dem angelegten Feld auszurichten, was zu einem magnetischen Nettomoment in Richtung des angelegten Feldes führt. In der klassischen Beschreibung kann diese Ausrichtung als Folge eines Drehmoments verstanden werden, das durch ein angelegtes Feld auf die magnetischen Momente ausgeübt wird und das versucht, die Dipole parallel zum angelegten Feld auszurichten. Der wahre Ursprung der Ausrichtung kann jedoch nur über die quantenmechanischen Eigenschaften von Spin und Drehimpuls verstanden werden. ⓘ

Wenn zwischen benachbarten Dipolen ein ausreichender Energieaustausch stattfindet, treten sie in Wechselwirkung und können sich spontan ausrichten oder gegeneinander ausrichten und magnetische Domänen bilden, was zu Ferromagnetismus (Permanentmagneten) bzw. Antiferromagnetismus führt. Paramagnetisches Verhalten kann auch bei ferromagnetischen Materialien oberhalb ihrer Curie-Temperatur und bei Antiferromagneten oberhalb ihrer Néel-Temperatur beobachtet werden. Bei diesen Temperaturen überwindet die verfügbare Wärmeenergie einfach die Wechselwirkungsenergie zwischen den Spins. ⓘ

Im Allgemeinen sind die paramagnetischen Effekte recht gering: Die magnetische Suszeptibilität liegt bei den meisten Paramagneten in der Größenordnung von 10-3 bis 10-5, kann aber bei synthetischen Paramagneten wie Ferrofluiden bis zu 10-1 betragen. ⓘ

Delokalisierung

Ausgewählte Pauli-paramagnetische Metalle

Werkstoff	Magnetische Suszeptibilität, $\chi _{v}$ [10−5] (SI-Einheiten) ⓘ
Wolfram	6.8
Cäsium	5.1
Aluminium	2.2
Lithium	1.4
Magnesium	1.2
Natrium	0.72

In leitenden Materialien sind die Elektronen delokalisiert, d. h. sie bewegen sich mehr oder weniger als freie Elektronen durch den Festkörper. Die Leitfähigkeit kann in einem Bandstrukturbild als Folge der unvollständigen Füllung von Energiebändern verstanden werden. In einem gewöhnlichen nichtmagnetischen Leiter ist das Leitungsband für Spin-up- und Spin-down-Elektronen identisch. Wenn ein Magnetfeld angelegt wird, spaltet sich das Leitungsband in ein Spin-up- und ein Spin-down-Band auf, was auf den Unterschied in der magnetischen potentiellen Energie für Spin-up- und Spin-down-Elektronen zurückzuführen ist. Da das Fermi-Niveau für beide Bänder identisch sein muss, bedeutet dies, dass in dem Band, das sich nach unten bewegt hat, ein kleiner Überschuss der Spinart vorhanden ist. Dieser Effekt ist eine schwache Form des Paramagnetismus, die als Pauli-Paramagnetismus bezeichnet wird. ⓘ

Der Effekt konkurriert immer mit einer diamagnetischen Reaktion mit entgegengesetztem Vorzeichen, die auf alle Kernelektronen der Atome zurückzuführen ist. Stärkere Formen des Magnetismus erfordern in der Regel lokalisierte und nicht wandernde Elektronen. In einigen Fällen kann sich jedoch eine Bandstruktur ergeben, in der es zwei delokalisierte Teilbänder mit Zuständen entgegengesetzten Spins gibt, die unterschiedliche Energien haben. Wenn ein Teilband gegenüber dem anderen bevorzugt besetzt ist, kann eine itinerante ferromagnetische Ordnung vorliegen. Diese Situation tritt normalerweise nur in relativ schmalen (d-)Bändern auf, die schlecht delokalisiert sind. ⓘ

s- und p-Elektronen

Im Allgemeinen bedeutet eine starke Delokalisierung in einem Festkörper aufgrund einer großen Überlappung mit benachbarten Wellenfunktionen, dass es eine große Fermi-Geschwindigkeit gibt; dies bedeutet, dass die Anzahl der Elektronen in einem Band weniger empfindlich auf Verschiebungen der Energie dieses Bandes reagiert, was einen schwachen Magnetismus bedeutet. Aus diesem Grund sind Metalle vom s- und p-Typ in der Regel entweder Pauli-Paramagnetismus oder, wie im Falle von Gold, sogar Diamagnetismus. Im letzteren Fall überwiegt der diamagnetische Beitrag der inneren Elektronen der geschlossenen Schale einfach den schwachen paramagnetischen Term der fast freien Elektronen. ⓘ

d- und f-Elektronen

Stärkere magnetische Effekte werden typischerweise nur beobachtet, wenn d- oder f-Elektronen beteiligt sind. Insbesondere letztere sind in der Regel stark lokalisiert. Darüber hinaus kann das magnetische Moment eines Lanthanidatoms recht groß sein, da es im Fall von Gadolinium(III) bis zu sieben ungepaarte Elektronen tragen kann (daher seine Verwendung in der MRT). Die hohen magnetischen Momente der Lanthanide sind ein Grund dafür, dass superstarke Magnete in der Regel auf Elementen wie Neodym oder Samarium basieren. ⓘ

Molekulare Lokalisierung

Das obige Bild ist eine Verallgemeinerung, da es sich auf Materialien mit einem ausgedehnten Gitter und nicht mit einer Molekularstruktur bezieht. Auch die molekulare Struktur kann zu einer Lokalisierung von Elektronen führen. Obwohl es in der Regel energetische Gründe dafür gibt, dass eine Molekülstruktur so beschaffen ist, dass sie keine teilweise gefüllten Orbitale (d. h. ungepaarte Spins) aufweist, gibt es in der Natur einige Verbindungen mit nicht geschlossener Schale. Molekularer Sauerstoff ist ein gutes Beispiel dafür. Selbst im gefrorenen Festkörper enthält er zweiradikalische Moleküle, die sich paramagnetisch verhalten. Die ungepaarten Spins befinden sich in Orbitalen, die von Sauerstoff-p-Wellenfunktionen abgeleitet sind, aber die Überlappung ist auf einen Nachbarn in den O₂-Molekülen beschränkt. Die Abstände zu anderen Sauerstoffatomen im Gitter bleiben zu groß, um zu einer Delokalisierung zu führen, und die magnetischen Momente bleiben ungepaart. ⓘ

Theorie

Das Bohr-Van Leeuwen-Theorem beweist, dass es in einem rein klassischen System weder Diamagnetismus noch Paramagnetismus geben kann. Die paramagnetische Reaktion hat dann zwei mögliche Quantenursprünge, die entweder von den permanenten magnetischen Momenten der Ionen oder von der räumlichen Bewegung der Leitungselektronen im Inneren des Materials herrühren. Beide Beschreibungen werden im Folgenden gegeben. ⓘ

Curie'sches Gesetz

Bei niedrigen Magnetisierungsgraden folgt die Magnetisierung von Paramagneten zumindest näherungsweise dem so genannten Curie-Gesetz. Dieses Gesetz besagt, dass die Suszeptibilität, $\chi$von paramagnetischen Materialien umgekehrt proportional zu ihrer Temperatur ist, d. h., dass Materialien bei niedrigeren Temperaturen magnetischer werden. Der mathematische Ausdruck lautet:

$$\mathbf {M} =\chi \mathbf {H} ={\frac {C}{T}}\mathbf {H}$$

wobei:

• $\mathbf {M}$ die resultierende Magnetisierung ist, gemessen in Ampere/Meter (A/m),
• $\chi$ die volumenmagnetische Suszeptibilität (dimensionslos) ist,
• $H$ das magnetische Hilfsfeld (A/m) ist,
• $T$ ist die absolute Temperatur, gemessen in Kelvin (K),
• $C$ ist eine materialspezifische Curie-Konstante (K). ⓘ

Das Curie-Gesetz gilt unter den üblichen Bedingungen niedriger Magnetisierung (μBH ≲ kBT), gilt jedoch nicht für den Bereich mit hohem Feld und niedriger Temperatur, in dem eine Sättigung der Magnetisierung auftritt (μBH ≳ kBT) und alle magnetischen Dipole auf das angelegte Feld ausgerichtet sind. Wenn die Dipole ausgerichtet sind, führt eine Erhöhung des externen Feldes nicht zu einer Erhöhung der Gesamtmagnetisierung, da es keine weitere Ausrichtung geben kann. ⓘ

Für ein paramagnetisches Ion mit nicht wechselwirkenden magnetischen Momenten mit dem Drehimpuls J ist die Curie-Konstante mit den magnetischen Momenten der einzelnen Ionen verknüpft,

$$C={\frac {n}{3k_{\mathrm {B} }}}\mu _{\mathrm {eff} }^{2}{\text{ where }}\mu _{\mathrm {eff} }=g_{J}\mu _{\mathrm {B} }{\sqrt {J(J+1)}}.$$

ⓘ

wobei n die Anzahl der Atome pro Volumeneinheit ist. Der Parameter μ_eff wird als das effektive magnetische Moment pro paramagnetischem Ion interpretiert. Verwendet man eine klassische Behandlung mit molekularen magnetischen Momenten, die als diskrete magnetische Dipole, μ, dargestellt werden, so ergibt sich ein Curie-Gesetz-Ausdruck derselben Form, wobei μ anstelle von μ_eff erscheint. ⓘ

Ableitung

Das Curie-Gesetz lässt sich ableiten, wenn man eine Substanz mit nicht wechselwirkenden magnetischen Momenten mit dem Drehimpuls J betrachtet. Wenn die orbitalen Beiträge zum magnetischen Moment vernachlässigbar sind (was häufig der Fall ist), gilt im Folgenden J = S. Wenn wir ein Magnetfeld entlang der so genannten z-Achse anlegen, erfahren die Energieniveaus jedes paramagnetischen Zentrums eine Zeeman-Aufspaltung ihrer Energieniveaus, jeweils mit einer z-Komponente, die mit M_J (oder nur MS für den rein spinmagnetischen Fall) bezeichnet wird. Unter Anwendung der semiklassischen Boltzmann-Statistik ergibt sich für die Magnetisierung einer solchen Substanz folgende Formel

$$n{\bar {m}}={\frac {n\sum \limits _{M_{J}=-J}^{J}{\mu _{M_{J}}e^{{-E_{M_{J}}}/{k_{\mathrm {B} }T}\;}}}{\sum \limits _{M_{J}=-J}^{J}{e^{{-E_{M_{J}}}/{k_{\mathrm {B} }T}\;}}}}={\frac {n\sum \limits _{M_{J}=-J}^{J}{M_{J}g_{J}\mu _{\mathrm {B} }e^{{M_{J}g_{J}\mu _{\mathrm {B} }H}/{k_{\mathrm {B} }T}\;}}}{\sum \limits _{M_{J}=-J}^{J}{e^{{M_{J}g_{J}\mu _{\mathrm {B} }H}/{k_{\mathrm {B} }T}\;}}}}.$$

Dabei ist $\mu _{M_{J}}$ die z-Komponente des magnetischen Moments für jedes Zeeman-Niveau ist, so dass $\mu _{M_{J}}=M_{J}g_{J}\mu _{\mathrm {B} }-\mu _{\mathrm {B} }$ wird als Bohr-Magneton bezeichnet und g_J ist der Landé-g-Faktor, der sich auf den g-Faktor für freie Elektronen, g_S, reduziert, wenn J = S. (Bei dieser Behandlung wird davon ausgegangen, dass sich die über alle Moleküle gemittelten x- und y-Komponenten der Magnetisierung aufheben, da das entlang der z-Achse angelegte Feld die Moleküle zufällig orientiert). Die Energie der einzelnen Zeeman-Niveaus ist $E_{M_{J}}=-M_{J}g_{J}\mu _{\mathrm {B} }H$. Für Temperaturen über einigen K, $M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\ll 1$und wir können die Approximation $e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}\simeq 1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;$:

$${\bar {m}}={\frac {\sum \limits _{M_{J}=-J}^{J}{M_{J}g_{J}\mu _{\mathrm {B} }e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}}}{\sum \limits _{M_{J}=-J}^{J}e^{M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;}}}\simeq g_{J}\mu _{\mathrm {B} }{\frac {\sum \limits _{M_{J}=-J}^{J}M_{J}\left(1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;\right)}{\sum \limits _{M_{J}=-J}^{J}\left(1+M_{J}g_{J}\mu _{\mathrm {B} }H/k_{\mathrm {B} }T\;\right)}}={\frac {g_{J}^{2}\mu _{\mathrm {B} }^{2}H}{k_{\mathrm {B} }T}}{\frac {\sum \limits _{-J}^{J}M_{J}^{2}}{\sum \limits _{M_{J}=-J}^{J}{(1)}}},$$

anwenden, was zu folgenden Ergebnissen führt:

$${\bar {m}}={\frac {g_{J}^{2}\mu _{\mathrm {B} }^{2}H}{3k_{\mathrm {B} }T}}J(J+1).$$

Die Volumenmagnetisierung ist dann $M=n{\bar {m}}={\frac {n}{3k_{\mathrm {B} }T}}\left[g_{J}^{2}J(J+1)\mu _{\mathrm {B} }^{2}\right]H,$ und die Suszeptibilität ist gegeben durch

$$\chi ={\frac {\partial M_{\rm {m}}}{\partial H}}={\frac {n}{3k_{\rm {B}}T}}\mu _{\mathrm {eff} }^{2}{\text{ ; and }}\mu _{\mathrm {eff} }=g_{J}{\sqrt {J(J+1)}}\mu _{\mathrm {B} }.$$

ⓘ

Wenn die Beiträge des Orbitaldrehimpulses zum magnetischen Moment klein sind, wie es bei den meisten organischen Radikalen oder bei oktaedrischen Übergangsmetallkomplexen mit d³- oder hochspinigen d⁵-Konfigurationen der Fall ist, hat das effektive magnetische Moment die Form ( mit g-Faktor ge = 2,0023... ≈ 2),

$$\mu _{\mathrm {eff} }\simeq 2{\sqrt {S(S+1)}}\mu _{\mathrm {B} }={\sqrt {N_{\rm {u}}(N_{\rm {u}}+2)}}\mu _{\mathrm {B} },$$

wobei Nu die Anzahl der ungepaarten Elektronen ist. Bei anderen Übergangsmetallkomplexen ergibt dies eine nützliche, wenn auch etwas grobe Schätzung. ⓘ

Wenn die Curie-Konstante Null ist, können Effekte zweiter Ordnung, die den Grundzustand mit den angeregten Zuständen koppeln, auch zu einer von der Temperatur unabhängigen paramagnetischen Suszeptibilität führen, die als Van-Vleck-Suszeptibilität bezeichnet wird. ⓘ

Pauli-Paramagnetismus

Bei einigen Alkalimetallen und Edelmetallen sind die Leitungselektronen schwach wechselwirkend und im Raum delokalisiert und bilden ein Fermi-Gas. Bei diesen Materialien stammt ein Beitrag zur magnetischen Reaktion aus der Wechselwirkung zwischen den Elektronenspins und dem Magnetfeld, die als Pauli-Paramagnetismus bekannt ist. Für ein kleines Magnetfeld $\mathbf {H}$ist die zusätzliche Energie pro Elektron durch die Wechselwirkung zwischen einem Elektronenspin und dem Magnetfeld wie folgt gegeben

$\Delta E=-\mu _{0}\mathbf {H} \cdot {\boldsymbol {\mu }}_{e}=-\mu _{0}\mathbf {H} \cdot \left(-g_{e}{\frac {\mu _{\mathrm {B} }}{\hbar }}\mathbf {S} \right)=\pm \mu _{0}\mu _{\mathrm {B} }H,$ ⓘ

wobei $\mu _{0}$ die Permeabilität des Vakuums ist, ${\boldsymbol {\mu }}_{e}$ das magnetische Moment des Elektrons ist, $\mu _{\rm {B}}$ das Bohrsche Magneton ist, $\hbar$ die reduzierte Planck-Konstante ist, und der g-Faktor sich mit dem Spin aufhebt $\mathbf {S} =\pm \hbar /2$. Die $\pm$ zeigt an, dass das Vorzeichen positiv (negativ) ist, wenn die Spin-Komponente des Elektrons in Richtung von $\mathbf {H}$ parallel (antiparallel) zum Magnetfeld ist. ⓘ

In einem Metall erhöht das Anlegen eines äußeren Magnetfeldes die Dichte der Elektronen mit zum Feld antiparallelen Spins und verringert die Dichte der Elektronen mit entgegengesetztem Spin. Hinweis: Die Pfeile in diesem Bild zeigen die Spinrichtung an, nicht das magnetische Moment. ⓘ

Bei niedrigen Temperaturen in Bezug auf die Fermi-Temperatur $T_{\rm {F}}$ (etwa 10⁴ Kelvin für Metalle) ist die Zahl der Elektronen $n_{\uparrow }$ ($n_{\downarrow }$), die parallel (antiparallel) zum Magnetfeld zeigen, wie folgt geschrieben werden:

$n_{\uparrow }\approx {\frac {n_{e}}{2}}-{\frac {\mu _{0}\mu _{\mathrm {B} }}{2}}g(E_{\mathrm {F} })H\quad ;\quad \left(n_{\downarrow }\approx {\frac {n_{e}}{2}}+{\frac {\mu _{0}\mu _{\mathrm {B} }}{2}}g(E_{\mathrm {F} })H\right),$ ⓘ

mit $n_{e}$ die Gesamtdichte der freien Elektronen und $g(E_{\mathrm {F} })$ die elektronische Zustandsdichte (Anzahl der Zustände pro Energie pro Volumen) bei der Fermi-Energie $E_{\mathrm {F} }$. ⓘ

In dieser Näherung ist die Magnetisierung gegeben als das magnetische Moment eines Elektrons mal der Differenz der Dichten:

$M=\mu _{\mathrm {B} }(n_{\downarrow }-n_{\uparrow })=\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} })H,$ ⓘ

Daraus ergibt sich eine positive paramagnetische Suszeptibilität unabhängig von der Temperatur:

$\chi _{\mathrm {P} }=\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} }).$ ⓘ

Die paramagnetische Suszeptibilität nach Pauli ist ein makroskopischer Effekt und muss der diamagnetischen Suszeptibilität nach Landau gegenübergestellt werden, die minus ein Drittel der Pauli-Suszeptibilität beträgt und ebenfalls von delokalisierten Elektronen herrührt. Die Pauli-Suszeptibilität entsteht durch die Spin-Wechselwirkung mit dem Magnetfeld, während die Landau-Suszeptibilität durch die räumliche Bewegung der Elektronen entsteht und unabhängig vom Spin ist. In dotierten Halbleitern ändert sich das Verhältnis zwischen der Landau- und der Pauli-Suszeptibilität, da die effektive Masse der Ladungsträger $m^{*}$ von der Elektronenmasse abweichen kann $m_{e}$. ⓘ

Die für ein Elektronengas berechnete magnetische Reaktion ist nicht vollständig, da die von den Ionen herrührende magnetische Suszeptibilität berücksichtigt werden muss. Außerdem können diese Formeln bei eingeschlossenen Systemen, die sich von der Masse unterscheiden, wie Quantenpunkte, oder bei hohen Feldern versagen, wie der De Haas-Van Alphen-Effekt zeigt. ⓘ

Der Pauli-Paramagnetismus ist nach dem Physiker Wolfgang Pauli benannt. Vor Paulis Theorie war das Fehlen eines starken Curie-Paramagnetismus in Metallen ein offenes Problem, da das führende Drude-Modell diesen Beitrag ohne die Verwendung von Quantenstatistik nicht erklären konnte. Der Pauli-Paramagnetismus und der Landau-Diamagnetismus sind im Wesentlichen Anwendungen des Spin- und des Freie-Elektronen-Modells, wobei der erste auf den intrinsischen Spin der Elektronen zurückzuführen ist und der zweite auf ihre Orbitalbewegung. ⓘ

Beispiele für Paramagnete

Als "Paramagnete" werden meist Materialien bezeichnet, die zumindest in einem nennenswerten Temperaturbereich magnetische Suszeptibilitäten aufweisen, die den Gesetzen von Curie oder Curie-Weiss entsprechen. Im Prinzip kann jedes System, das Atome, Ionen oder Moleküle mit ungepaarten Spins enthält, als Paramagnet bezeichnet werden, aber die Wechselwirkungen zwischen ihnen müssen sorgfältig berücksichtigt werden. ⓘ

Systeme mit minimalen Wechselwirkungen

Die engste Definition wäre: ein System mit ungepaarten Spins, die nicht miteinander wechselwirken. In diesem engsten Sinne ist der einzige reine Paramagnet ein verdünntes Gas aus einatomigen Wasserstoffatomen. Jedes Atom hat ein ungepaartes Elektron, das nicht miteinander wechselwirkt. ⓘ

Ein Gas aus Lithiumatomen besitzt bereits zwei gepaarte Kernelektronen, die eine diamagnetische Reaktion mit entgegengesetztem Vorzeichen erzeugen. Streng genommen ist Li also ein gemischtes System, obwohl die diamagnetische Komponente zugegebenermaßen schwach ist und oft vernachlässigt wird. Bei schwereren Elementen gewinnt der diamagnetische Beitrag an Bedeutung, und bei metallischem Gold dominiert er die Eigenschaften. Das Element Wasserstoff wird praktisch nie als "paramagnetisch" bezeichnet, weil das einatomige Gas nur bei extrem hohen Temperaturen stabil ist; H-Atome verbinden sich zu molekularem H₂, und dabei gehen die magnetischen Momente verloren (gelöscht), weil sich die Spins paaren. Wasserstoff ist also diamagnetisch, und das Gleiche gilt für viele andere Elemente. Obwohl die elektronische Konfiguration der einzelnen Atome (und Ionen) der meisten Elemente ungepaarte Spins enthält, sind sie nicht unbedingt paramagnetisch, denn bei Umgebungstemperatur ist das Quenchen eher die Regel als die Ausnahme. Die Quenching-Tendenz ist bei f-Elektronen am geringsten, da f-Orbitale (insbesondere 4f-Orbitale) radial kontrahiert sind und sich nur schwach mit Orbitalen benachbarter Atome überlappen. Folglich sind die Lanthanidenelemente mit unvollständig gefüllten 4f-Orbitalen paramagnetisch oder magnetisch geordnet. ⓘ

μ_eff-Werte für typische d³- und d⁵-Übergangsmetallkomplexe.

Werkstoff	μeff/μB ⓘ
[Cr(NH3)6]Br3	3.77
K3[Cr(CN)6]	3.87
K3[MoCl6]	3.79
K4[V(CN)6]	3.78
[Mn(NH3)6]Cl2	5.92
(NH4)2[Mn(SO4)2]·6H2O	5.92
NH4[Fe(SO4)2]-12H2O	5.89

Paramagnete in kondensierter Phase sind also nur möglich, wenn die Wechselwirkungen der Spins, die entweder zum Quenchen oder zur Ordnung führen, durch strukturelle Isolierung der magnetischen Zentren in Schach gehalten werden. Es gibt zwei Klassen von Materialien, für die dies gilt:

• Molekulare Materialien mit einem (isolierten) paramagnetischen Zentrum.
  • Gute Beispiele sind Koordinationskomplexe von d- oder f-Metallen oder Proteine mit solchen Zentren, z.B. Myoglobin. In solchen Materialien wirkt der organische Teil des Moleküls wie eine Hülle, die die Spins von ihren Nachbarn abschirmt.
  • Kleine Moleküle können in radikalischer Form stabil sein, Sauerstoff O₂ ist ein gutes Beispiel. Solche Systeme sind recht selten, da sie eher reaktiv sind.
• Verdünnte Systeme.
  • Löst man eine paramagnetische Spezies in einem diamagnetischen Gitter in geringer Konzentration, z. B. Nd³⁺ in CaCl₂, so werden die Neodym-Ionen in ausreichend großem Abstand voneinander getrennt, so dass sie nicht miteinander wechselwirken. Solche Systeme sind von größter Bedeutung für die wohl empfindlichste Methode zur Untersuchung paramagnetischer Systeme: EPR. ⓘ

Systeme mit Wechselwirkungen

Idealisiertes Curie-Weiss-Verhalten; Anm.: TC=θ, aber TN ist nicht θ. Die paramagnetischen Bereiche sind durch durchgezogene Linien gekennzeichnet. In der _Nähe von T_N oder TC weicht das Verhalten normalerweise vom Ideal ab. ⓘ

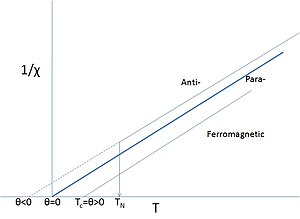
Wie bereits erwähnt, behalten viele Materialien, die d- oder f-Elemente enthalten, nicht gelöschte Spins. Salze solcher Elemente zeigen oft paramagnetisches Verhalten, aber bei ausreichend niedrigen Temperaturen können sich die magnetischen Momente ordnen. Es ist nicht unüblich, solche Materialien als "Paramagnete" zu bezeichnen, wenn man sich auf ihr paramagnetisches Verhalten oberhalb des Curie- oder Néel-Punktes bezieht, insbesondere wenn diese Temperaturen sehr niedrig sind oder nie richtig gemessen wurden. Selbst bei Eisen ist es nicht unüblich zu sagen, dass es oberhalb seines relativ hohen Curie-Punktes zu einem Paramagneten wird. In diesem Fall wird der Curie-Punkt als ein Phasenübergang zwischen einem Ferromagneten und einem "Paramagneten" angesehen. Der Begriff Paramagnet bezieht sich nun lediglich auf die lineare Reaktion des Systems auf ein angelegtes Feld, dessen Temperaturabhängigkeit eine geänderte Version des Curie'schen Gesetzes, das so genannte Curie-Weiss-Gesetz, erfordert:

$\mathbf {M} ={\frac {C}{T-\theta }}\mathbf {H}$ ⓘ

Dieses geänderte Gesetz enthält einen Term θ, der die Austauschwechselwirkung beschreibt, die vorhanden ist, aber durch die thermische Bewegung überwunden wird. Das Vorzeichen von θ hängt davon ab, ob ferro- oder antiferromagnetische Wechselwirkungen vorherrschen, und es ist selten genau Null, außer in den oben erwähnten verdünnten, isolierten Fällen. ⓘ

Offensichtlich ist die paramagnetische Curie-Weiss-Beschreibung oberhalb von TN oder T_C eine etwas andere Interpretation des Wortes "Paramagnet", da sie nicht die Abwesenheit von Wechselwirkungen impliziert, sondern eher, dass die magnetische Struktur in Abwesenheit eines externen Feldes bei diesen ausreichend hohen Temperaturen zufällig ist. Selbst wenn θ nahe Null ist, bedeutet dies nicht, dass es keine Wechselwirkungen gibt, sondern nur, dass sich die ausrichtenden ferro- und die anti-ausrichtenden antiferromagnetischen Wechselwirkungen aufheben. Eine zusätzliche Komplikation besteht darin, dass die Wechselwirkungen oft in verschiedenen Richtungen des Kristallgitters unterschiedlich sind (Anisotropie), was zu komplizierten magnetischen Strukturen führt, sobald sie geordnet sind. ⓘ

Die Zufälligkeit der Struktur gilt auch für die vielen Metalle, die über einen breiten Temperaturbereich hinweg eine paramagnetische Reaktion zeigen. Sie folgen jedoch nicht dem Curie'schen Gesetz als Funktion der Temperatur, sondern sind oft mehr oder weniger temperaturunabhängig. Diese Art von Verhalten ist ein Wanderverhalten und sollte besser als Pauli-Paramagnetismus bezeichnet werden, aber es ist nicht ungewöhnlich, dass z. B. das Metall Aluminium als "Paramagnet" bezeichnet wird, obwohl die Wechselwirkungen stark genug sind, um diesem Element eine sehr gute elektrische Leitfähigkeit zu verleihen. ⓘ

Superparamagnete

Einige Materialien zeigen ein induziertes magnetisches Verhalten, das dem Curie-Gesetz folgt, jedoch mit außergewöhnlich großen Werten für die Curie-Konstanten. Diese Materialien werden als Superparamagnete bezeichnet. Sie zeichnen sich durch eine starke ferromagnetische oder ferrimagnetische Kopplung in Domänen begrenzter Größe aus, die sich unabhängig voneinander verhalten. Die Volumeneigenschaften eines solchen Systems ähneln denen eines Paramagneten, aber auf mikroskopischer Ebene sind sie geordnet. Die Materialien weisen eine Ordnungstemperatur auf, oberhalb derer das Verhalten zum gewöhnlichen Paramagnetismus (mit Wechselwirkung) zurückkehrt. Ferrofluide sind ein gutes Beispiel, aber das Phänomen kann auch in Festkörpern auftreten, z. B. wenn verdünnte paramagnetische Zentren in ein starkes, wanderndes Medium mit ferromagnetischer Kopplung eingebracht werden, wie z. B. bei der Substitution von Fe in TlCu₂Se₂ oder in der Legierung AuFe. Solche Systeme enthalten ferromagnetisch gekoppelte Cluster, die bei niedrigeren Temperaturen ausfrieren. Sie werden auch als Miktomagnete bezeichnet. ⓘ

Arten

Magnetische Momente von Atomen im Grundzustand (Langevin-Paramagnetismus)

Der Gesamtdrehimpuls eines Atoms im Grundzustand lässt sich theoretisch über die sogenannten Hundschen Regeln bestimmen. Wichtigste Essenz daraus ist, dass sich der Gesamtdrehimpuls ${\vec {J}}$ einer abgeschlossenen Schale immer zu Null addiert. In allen anderen Fällen besitzt das Atom ein magnetisches Moment. ⓘ

Die Temperaturabhängigkeit dieses Beitrags wird durch das Curiesche Gesetz

$\chi _{\mathrm {Langevin} }={\frac {C}{T}}\sim 10^{-3\ldots -2}$

beschrieben, dabei ist $C$ die Curie-Konstante (eine Materialkonstante). ⓘ

Eine genauere Analyse des Langevin-Paramagnetismus geschieht mit Hilfe der Langevin- und der Brillouin-Funktion. ⓘ

Magnetische Momente von Atomen in angeregten Zuständen (Van-Vleck-Paramagnetismus)

Auch wenn der Gesamtdrehimpuls eines Atoms in seinem Grundzustand Null ist, so muss das nicht für angeregte Zustände gelten. Bei einer endlichen Temperatur sind immer einige Atome in einem angeregten Zustand, daher kommt dieser Beitrag bei allen Stoffen vor. Von nennenswerter Größe ist er allerdings nur in Molekülkristallen; dort kann er den Langevin-Paramagnetismus sogar an Stärke übertreffen. Die Größe dieses Beitrages zu berechnen ist aber gerade für Moleküle recht aufwändig. ⓘ

Vergleich der Größenordnungen

$\chi ^{\text{van Vleck}}\approx \chi ^{\text{Pauli}}\approx \left|\chi ^{\text{Diamag.}}\right|\approx 10^{-6\ldots -5}\ll \chi ^{\text{Langevin}}\approx 10^{-3\ldots -2}$ ⓘ

Superparamagnetismus

Die magnetischen Eigenschaften von gekörnten ferromagnetischen Festkörpern sind abhängig von der Korngröße. Bei Verkleinerung der Korngröße nimmt die Anzahl der magnetischen Bezirke (Weiss-Bezirk) pro Korn ab. Unterhalb einer kritischen Größe ist es energetisch ungünstig, mehrere dieser Bereiche auszubilden. Es existiert also nur noch ein Weiss-Bezirk pro Korn, d. h., alle atomaren magnetischen Momente eines Korns sind parallel zueinander angeordnet. Unterhalb einer weiteren kritischen Größe ist bei endlichen Temperaturen eine stabile Ausrichtung des magnetischen Gesamtmoments nicht mehr möglich, da die zur Ummagnetisierung benötigte Energie kleiner als die thermische Energie wird. Der Festkörper als Ganzes verhält sich nun paramagnetisch mit der Besonderheit, dass die magnetischen Momente nicht einzeln, sondern in Blöcken auf externe Magnetfelder reagieren. Diese besondere Form des Paramagnetismus wird als Superparamagnetismus bezeichnet. ⓘ

Anwendung

Der Paramagnetismus von Sauerstoff wird bei der physikalischen Gasanalyse genutzt. ⓘ

Beispiele

Alkalimetalle

Die Elektronenhülle der Alkalimetalle besteht aus einer Edelgaskonfiguration und einem zusätzlichen s-Elektron. Nach den Hundschen Regeln besitzen die Atome im Grundzustand also ein magnetisches Moment. Dies ist der erste Fall (s. o.), der einen starken Beitrag zur Suszeptibilität liefert. Die Alkalimetalle sind demnach paramagnetisch. ⓘ

Erdalkalimetalle

Im Gegensatz zu den Alkalimetallen besitzen die Erdalkalimetalle zwei s-Elektronen und damit eine abgeschlossene Unterschale. Jedoch gehören sie zu den Metallen und betreffen damit den zweiten Fall (magnetisch ausgerichtete Leitungselektronen des Pauli-Paramagnetismus). Mit Ausnahme von Beryllium überwiegt dieser Beitrag den diamagnetischen, womit die Erdalkalimetalle schwach paramagnetisch sind. ⓘ

Seltene Erden

Die Metalle der Seltenen Erden gehören zu den technisch wichtigsten Materialien für Legierungen in Permanentmagneten. Die Ursache liegt darin, dass die entscheidende nicht vollständig besetzte Schale im Inneren der Elektronenhülle liegt (f-Elektronen) und somit praktisch keinen Einfluss auf die chemischen Eigenschaften der Atome hat. Fast alle diese Metalle sind daher paramagnetisch (nach dem ersten Fall), jedoch variiert die Stärke des Paramagnetismus sehr; Gadolinium ist sogar ferromagnetisch. Das macht sie zu idealen Kandidaten in Legierungen mit ferromagnetischen Metallen, wodurch sehr starke Permanentmagnete hergestellt werden können. ⓘ

Moleküle

Da Moleküle häufig eine abgeschlossene Elektronenkonfiguration haben und keine Metalle sind, zeigen sie nur einen Beitrag nach dem dritten Fall. Einige Beispiele für paramagnetische Substanzen sind:

• Stickstoffdioxid
• Sauerstoff ⓘ

Ältere Messverfahren für Gaskonzentrationen paramagnetischer Gase beruhten darauf, dass Gasgemische, z. B. Luft mit enthaltenem Sauerstoff, eine Doppel-Rohrschleife innerhalb eines starken Permanent-Magnetfeldes durchströmten. Beim Einströmen teilte sich der Gastrom gleichmäßig zwischen linkem und rechtem Rohr auf. Die Rohre waren jeweils zu einem Halbring gebogen, die sich letztlich wieder vereinigten vor dem Gasaustritt. Ein Querrohr innerhalb dieses Magnetfeldes verband beide Halbbogen-Rohre mittig. Das paramagnetische Gasmolekül wurde in das Magnetfeld des Querrohres hineingezogen. Je nach Gehalt des paramagnetischen Gases im Gasgemisch strömte im Querrohr entweder kein Gas (kein paramagnetisches Gas im Gasgemisch enthalten), oder viel Gas (wenn der Volumenanteil an paramagnetischem Gas groß war). Der Gastrom im Querrohr wurde gemessen über die durch ihn verursachte Abkühlung eines mit Konstantstrom beheizten Thermistors (Kaltleiter oder Heißleiter). Die Spannung am Thermistor war dabei eine Funktion des Gasstromes im Querrohr und damit ein Maß für den Volumenanteil an paramagnetischem Gas. ⓘ