Tunneleffekt

Quantentunneln, auch als Tunneln (US) bezeichnet, ist ein quantenmechanisches Phänomen, bei dem sich eine Wellenfunktion durch eine Potenzialbarriere ausbreiten kann. ⓘ

Die Übertragung durch die Barriere kann endlich sein und hängt exponentiell von der Höhe und der Breite der Barriere ab. Die Wellenfunktion kann auf der einen Seite verschwinden und auf der anderen Seite wieder auftauchen. Die Wellenfunktion und ihre erste Ableitung sind stetig. Im stationären Zustand ist der Wahrscheinlichkeitsfluss in Vorwärtsrichtung räumlich gleichmäßig. Es geht kein Teilchen und keine Welle verloren. Tunneling tritt bei Barrieren mit einer Dicke von 1-3 nm und weniger auf. ⓘ

Einige Autoren bezeichnen auch das bloße Eindringen der Wellenfunktion in die Barriere, ohne Übertragung auf der anderen Seite, als Tunneleffekt. Quanten-Tunneln wird von den Gesetzen der klassischen Mechanik nicht vorhergesagt, da die Überwindung einer potenziellen Barriere potenzielle Energie erfordert. ⓘ

Quantentunneln spielt eine wesentliche Rolle bei physikalischen Phänomenen wie der Kernfusion und dem radioaktiven Zerfall von Atomkernen. Er findet Anwendung in der Tunneldiode, im Quantencomputer und im Rastertunnelmikroskop. ⓘ

Der Effekt wurde im frühen 20. Jahrhundert vorhergesagt. Jahrhunderts vorhergesagt, aber erst Mitte des Jahrhunderts wurde er als allgemeines physikalisches Phänomen anerkannt. ⓘ

Quanten-Tunneling begrenzt die Mindestgröße von Bauelementen, die in der Mikroelektronik verwendet werden, da Elektronen leicht durch isolierende Schichten und Transistoren tunneln, die dünner als etwa 1 nm sind. ⓘ

Das Tunneln lässt sich mit der Heisenbergschen Unschärferelation erklären, die besagt, dass ein Quantenobjekt sowohl als Welle als auch als Teilchen bekannt sein kann. Mit anderen Worten: Die Ungewissheit über den genauen Ort von Lichtteilchen ermöglicht es diesen Teilchen, die Regeln der klassischen Mechanik zu brechen und sich im Raum zu bewegen, ohne die potenzielle Energiebarriere zu überwinden. ⓘ

Aufenthaltswahrscheinlichkeit eines Elektrons, das auf eine Potentialbarriere trifft. Mit geringer Wahrscheinlichkeit geht es durch die Barriere hindurch, was nach der klassischen Physik nicht möglich wäre. ⓘ

Tunneleffekt ist in der Physik eine veranschaulichende Bezeichnung dafür, dass ein Teilchen eine Potentialbarriere von endlicher Höhe auch dann überwinden kann, wenn seine Energie geringer als die „Höhe“ der Barriere ist. Nach den Vorstellungen der klassischen Physik wäre dies unmöglich, aber nach der Quantenmechanik ist es möglich. Mit Hilfe des Tunneleffekts wird unter anderem der Alpha-Zerfall von Atomkernen erklärt. Technische Anwendungen sind beispielsweise das Rastertunnelmikroskop und der Flash-Speicher. ⓘ

Geschichte

Das Quantentunneln wurde aus der Untersuchung der Radioaktivität entwickelt, die 1896 von Henri Becquerel entdeckt wurde. Die Radioaktivität wurde von Marie Curie und Pierre Curie weiter untersucht, wofür sie 1903 den Nobelpreis für Physik erhielten. Ernest Rutherford und Egon Schweidler untersuchten die Natur der Radioaktivität, die später von Friedrich Kohlrausch empirisch verifiziert wurde. Die Idee der Halbwertszeit und die Möglichkeit, den Zerfall vorherzusagen, gehen auf ihre Arbeit zurück. ⓘ

1901 entdeckte Robert Francis Earhart ein unerwartetes Leitungssystem, als er die Leitung von Gasen zwischen eng beieinander liegenden Elektroden mit dem Michelson-Interferometer untersuchte. J. J. Thomson kommentierte, dass diese Entdeckung weitere Untersuchungen rechtfertige. In den Jahren 1911 und 1914 nahm der damalige Doktorand Franz Rother direkte Messungen der Emissionsströme in einem konstanten Feld vor. Er verwendete Earharts Methode zur Kontrolle und Messung des Elektrodenabstands, allerdings mit einem empfindlichen Plattformgalvanometer. Im Jahr 1926 maß Rother die Feldemissionsströme in einem "harten" Vakuum zwischen eng beieinander liegenden Elektroden. ⓘ

Quanten-Tunnelbau wurde erstmals 1927 von Friedrich Hund bei der Berechnung des Grundzustands des Doppelwandpotentials festgestellt. Leonid Mandelstam und Mikhail Leontovich entdeckten ihn unabhängig voneinander im selben Jahr. Sie untersuchten die Auswirkungen der damals neuen Schrödinger-Wellengleichung. ⓘ

Ihre erste Anwendung war eine mathematische Erklärung für den Alphazerfall, die 1928 von George Gamow (der die Erkenntnisse von Mandelstam und Leontovich kannte) und unabhängig davon von Ronald Gurney und Edward Condon entwickelt wurde. Die letztgenannten Forscher lösten gleichzeitig die Schrödinger-Gleichung für ein Modell-Kernpotential und leiteten eine Beziehung zwischen der Halbwertszeit des Teilchens und der Energie der Emission ab, die direkt von der mathematischen Wahrscheinlichkeit der Tunnelung abhing. ⓘ

Nach dem Besuch eines Gamow-Seminars erkannte Max Born die Allgemeingültigkeit des Tunnelns. Er erkannte, dass sie nicht auf die Kernphysik beschränkt war, sondern ein allgemeines Ergebnis der Quantenmechanik darstellte, das für viele verschiedene Systeme galt. Kurz darauf betrachteten beide Gruppen den Fall von Teilchen, die in den Kern tunneln. Die Untersuchung von Halbleitern und die Entwicklung von Transistoren und Dioden führten dazu, dass 1957 das Tunneln von Elektronen in Festkörpern akzeptiert wurde. Leo Esaki, Ivar Giaever und Brian Josephson sagten das Tunneln von supraleitenden Cooper-Paaren voraus, wofür sie 1973 den Nobelpreis für Physik erhielten. Im Jahr 2016 wurde das Quantentunneln von Wasser entdeckt. ⓘ

Einführung in das Konzept

Animation, die den Tunneleffekt und seine Anwendung auf ein STM zeigt ⓘ

Quantentunneln fällt in den Bereich der Quantenmechanik: die Untersuchung von Vorgängen auf der Quantenskala. Der Tunneleffekt kann nicht direkt wahrgenommen werden. Ein Großteil seines Verständnisses wird durch die mikroskopische Welt geprägt, die die klassische Mechanik nicht erklären kann. Um das Phänomen zu verstehen, kann man Teilchen, die versuchen, eine Potenzialbarriere zu überwinden, mit einem Ball vergleichen, der versucht, über einen Hügel zu rollen. ⓘ

Quantenmechanik und klassische Mechanik unterscheiden sich in der Behandlung dieses Szenarios. Die klassische Mechanik sagt voraus, dass Teilchen, die nicht genug Energie haben, um eine Barriere zu überwinden, die andere Seite nicht erreichen können. Eine Kugel, die nicht genügend Energie hat, um den Berg zu überwinden, würde also wieder hinunterrollen. Ein Ball, dem die Energie fehlt, um eine Wand zu durchdringen, prallt zurück. Alternativ dazu kann der Ball auch Teil der Wand werden (Absorption). ⓘ

In der Quantenmechanik können diese Teilchen mit einer geringen Wahrscheinlichkeit auf die andere Seite tunneln und so die Barriere überwinden. Der Ball leiht sich gewissermaßen Energie aus seiner Umgebung, um die Wand zu durchqueren. Anschließend gibt sie diese Energie zurück, indem sie die reflektierten Elektronen energiereicher macht, als sie es sonst gewesen wären. ⓘ

Der Grund für diesen Unterschied liegt darin, dass die Materie Eigenschaften von Wellen und Teilchen besitzt. Eine Interpretation dieser Dualität beinhaltet die Heisenbergsche Unschärferelation, die eine Grenze dafür setzt, wie genau die Position und der Impuls eines Teilchens gleichzeitig bekannt sein können. Dies bedeutet, dass keine Lösung eine Wahrscheinlichkeit von genau Null (oder Eins) hat, auch wenn sie sich der Unendlichkeit nähern kann. Würde beispielsweise die Berechnung der Position mit einer Wahrscheinlichkeit von 1 erfolgen, müsste die Geschwindigkeit unendlich sein (ein Ding der Unmöglichkeit). Die Wahrscheinlichkeit, dass ein bestimmtes Teilchen auf der gegenüberliegenden Seite einer Barriere existiert, ist also ungleich Null, und solche Teilchen werden auf der "anderen" Seite (ein semantisch schwieriges Wort in diesem Fall) im Verhältnis zu dieser Wahrscheinlichkeit erscheinen. ⓘ

Das Tunneling-Problem

Eine Simulation eines Wellenpakets, das auf eine potenzielle Barriere trifft. In relativen Einheiten ist die Energie der Barriere 20, größer als die mittlere Energie des Wellenpakets von 14. Ein Teil des Wellenpakets durchdringt die Barriere. ⓘ

Die Wellenfunktion eines Teilchens fasst alles zusammen, was man über ein physikalisches System wissen kann. Daher wird bei Problemen der Quantenmechanik die Wellenfunktion des Systems analysiert. Mithilfe mathematischer Formulierungen wie der Schrödinger-Gleichung lässt sich die Wellenfunktion ableiten. Das Quadrat des Absolutwerts dieser Wellenfunktion steht in direktem Zusammenhang mit der Wahrscheinlichkeitsverteilung für die Position des Teilchens, die die Wahrscheinlichkeit beschreibt, dass sich das Teilchen an einem bestimmten Ort befindet. Je breiter die Barriere und je höher die Barrierenergie, desto geringer ist die Wahrscheinlichkeit des Tunnelns. ⓘ

Ein einfaches Modell einer Tunnelbarriere, wie z. B. die rechteckige Barriere, kann analysiert und algebraisch gelöst werden. In der kanonischen Feldtheorie wird das Tunneln durch eine Wellenfunktion beschrieben, die innerhalb des Tunnels eine Amplitude ungleich Null hat; der Strom ist dort jedoch Null, weil die relative Phase der Amplitude der konjugierten Wellenfunktion (die zeitliche Ableitung) orthogonal zu ihr ist. ⓘ

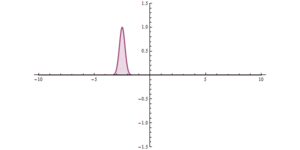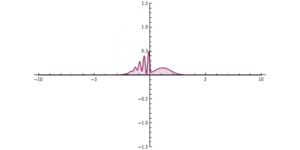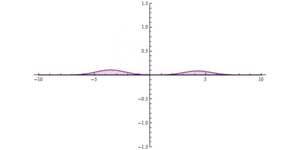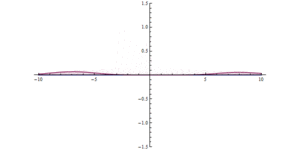
Die Simulation zeigt ein solches System. ⓘ

Ein Elektronenwellenpaket, das auf eine Potentialbarriere gerichtet ist. Man beachte den dunklen Fleck auf der rechten Seite, der die tunnelnden Elektronen darstellt. ⓘ

Die 2. Illustration zeigt die Unschärferelation bei der Arbeit. Eine Welle trifft auf die Barriere; die Barriere zwingt sie dazu, höher und schmaler zu werden. Die Welle ist nun auf beiden Seiten der Barriere zu finden, sie ist auf beiden Seiten breiter und ihre maximale Amplitude ist geringer, aber die Gesamtamplitude ist gleich. In beiden Abbildungen führt die Lokalisierung der Welle im Raum zu einer Lokalisierung der Wirkung der Barriere in der Zeit, wodurch die Energie/der Impuls der Welle gestreut wird. ⓘ

Probleme im wirklichen Leben haben oft keine solche Barriere, so dass "semiklassische" oder "quasiklassische" Methoden entwickelt wurden, um Näherungslösungen anzubieten, wie z. B. die WKB-Näherung. Wahrscheinlichkeiten können mit beliebiger Genauigkeit, die durch die Rechenressourcen begrenzt ist, über die Feynmansche Pfadintegralmethode abgeleitet werden. Eine solche Genauigkeit ist in der technischen Praxis selten erforderlich. ⓘ

Dynamisches Tunneln

Quanten-Tunnel-Oszillationen der Wahrscheinlichkeit in einer integrierbaren Doppelmulde des Potentials, gesehen im Phasenraum. ⓘ

Das Konzept des Quantentunnelns kann auf Situationen ausgedehnt werden, in denen es einen Quantentransport zwischen Regionen gibt, die klassischerweise nicht miteinander verbunden sind, auch wenn es keine zugehörige Potenzialbarriere gibt. Dieses Phänomen wird als dynamisches Tunneln bezeichnet. ⓘ

Tunneln im Phasenraum

Das Konzept des dynamischen Tunnelns ist besonders geeignet, um das Problem des Quantentunnelns in hohen Dimensionen (d>1) zu lösen. Im Falle eines integrierbaren Systems, in dem begrenzte klassische Trajektorien auf Tori im Phasenraum beschränkt sind, kann Tunneln als Quantentransport zwischen halbklassischen Zuständen verstanden werden, die auf zwei unterschiedlichen, aber symmetrischen Tori aufgebaut sind. ⓘ

Chaos-unterstütztes Tunneln

Chaos-unterstützte Tunnel-Oszillationen zwischen zwei regelmäßigen Tori, die in einem chaotischen Meer eingebettet sind, gesehen im Phasenraum ⓘ

Im wirklichen Leben sind die meisten Systeme nicht integrabel und weisen verschiedene Grade von Chaos auf. Die klassische Dynamik wird dann als gemischt bezeichnet, und der Phasenraum des Systems besteht in der Regel aus Inseln regulärer Bahnen, die von einem großen Meer chaotischer Bahnen umgeben sind. Das Vorhandensein eines chaotischen Sees zwischen den beiden symmetrischen Tori, in dem der Transport klassischerweise erlaubt ist, unterstützt dann das Tunneln zwischen den beiden. Dieses Phänomen wird als chaosunterstütztes Tunneln bezeichnet und ist durch scharfe Resonanzen der Tunnelrate gekennzeichnet, wenn ein Systemparameter variiert wird. ⓘ

Resonanz-unterstütztes Tunneln

Wenn $\hbar$ klein gegenüber der Größe der regelmäßigen Inseln ist, spielt die Feinstruktur des klassischen Phasenraums eine Schlüsselrolle beim Tunneln. Insbesondere sind die beiden symmetrischen Tori "über eine Reihe von klassisch verbotenen Übergängen über nichtlineare Resonanzen" gekoppelt, die die beiden Inseln umgeben. ⓘ

Ähnliche Phänomene

Mehrere Phänomene zeigen das gleiche Verhalten wie das Tunneln von Quanten und können durch Tunneln genau beschrieben werden. Beispiele sind das Tunneln einer klassischen Welle-Teilchen-Assoziation, die evaneszente Wellenkopplung (die Anwendung der Maxwellschen Wellengleichung auf Licht) und die Anwendung der nichtdispersiven Wellengleichung aus der Akustik auf "Wellen auf Saiten". Die evaneszente Wellenkopplung wurde bis vor kurzem nur in der Quantenmechanik als "Tunneln" bezeichnet; jetzt wird sie in anderen Zusammenhängen verwendet. ⓘ

Diese Effekte werden ähnlich wie bei der rechteckigen Potentialbarriere modelliert. In diesen Fällen gibt es ein Übertragungsmedium, durch das sich die Welle ausbreitet und das überall gleich oder fast gleich ist, und ein zweites Medium, durch das sich die Welle anders ausbreitet. Dies kann als ein dünner Bereich des Mediums B zwischen zwei Bereichen des Mediums A beschrieben werden. Die Analyse einer rechteckigen Barriere mit Hilfe der Schrödinger-Gleichung kann an diese anderen Effekte angepasst werden, sofern die Wellengleichung Wanderwellenlösungen im Medium A, aber reelle Exponentiallösungen im Medium B hat. ⓘ

In der Optik ist Medium A ein Vakuum und Medium B ist Glas. In der Akustik kann Medium A eine Flüssigkeit oder ein Gas und Medium B ein Festkörper sein. In beiden Fällen ist Medium A ein Bereich des Raums, in dem die Gesamtenergie des Teilchens größer ist als seine potenzielle Energie, und Medium B ist die potenzielle Barriere. Diese haben eine eintreffende Welle und resultierende Wellen in beide Richtungen. Es kann mehrere Medien und Barrieren geben, und die Barrieren müssen nicht diskret sein. Näherungen sind in diesem Fall nützlich. ⓘ

Flash-Speicher-Medien wie USB-Sticks und Speicherkarten verwenden Floating-Gate-(MOS)FETs und beruhen somit ebenfalls auf dem Tunneleffekt. ⓘ

Anwendungen

Das Tunneln ist die Ursache für einige wichtige makroskopische physikalische Phänomene. Quanten-Tunneling hat wichtige Auswirkungen auf die Funktionsweise der Nanotechnologie. ⓘ

Elektronik

Tunnelbau ist eine Quelle von Leckströmen in der VLSI-Elektronik (Very Large Scale Integration) und führt zu einem erheblichen Stromverbrauch und zu Erwärmungseffekten, die solche Geräte plagen. Sie gilt als die untere Grenze für die Herstellung mikroelektronischer Bauelemente. Tunneling ist eine grundlegende Technik, die zur Programmierung der Floating Gates von Flash-Speichern verwendet wird. ⓘ

Kaltemission

Die kalte Emission von Elektronen ist in der Halbleiter- und Supraleiterphysik von Bedeutung. Sie ähnelt der thermionischen Emission, bei der Elektronen zufällig von der Oberfläche eines Metalls springen, um einer Vorspannung zu folgen, weil sie durch zufällige Zusammenstöße mit anderen Teilchen statistisch gesehen mehr Energie haben als die Barriere. Wenn das elektrische Feld sehr groß ist, wird die Barriere dünn genug, damit die Elektronen aus dem atomaren Zustand heraus tunneln können, was zu einem Strom führt, der ungefähr exponentiell mit dem elektrischen Feld variiert. Diese Materialien sind wichtig für Flash-Speicher, Vakuumröhren und einige Elektronenmikroskope. ⓘ

Tunnelübergang

Eine einfache Barriere kann durch die Trennung von zwei Leitern mit einem sehr dünnen Isolator erzeugt werden. Es handelt sich dabei um Tunnelübergänge, für deren Erforschung das Verständnis des Quantentunnelns erforderlich ist. Josephson-Übergänge nutzen die Vorteile des Quantentunnelns und der Supraleitung, um den Josephson-Effekt zu erzeugen. Dies findet Anwendung bei Präzisionsmessungen von Spannungen und Magnetfeldern sowie bei der Mehrfachsolarzelle. ⓘ

Zelluläre Quantenpunkt-Automaten

QCA ist eine molekulare, binäre Logiksynthesetechnologie, die mit dem Elektronentunnelsystem zwischen Inseln arbeitet. Es handelt sich um ein sehr stromsparendes und schnelles Gerät, das mit einer Höchstfrequenz von 15 PHz arbeiten kann. ⓘ

Tunneldiode

Ein Funktionsmechanismus einer resonanten Tunneldiode, der auf dem Phänomen des Quantentunnelns durch Potentialbarrieren beruht. ⓘ

Dioden sind elektrische Halbleiterbauelemente, die den elektrischen Stromfluss in eine Richtung stärker als in die andere Richtung zulassen. Das Bauelement ist auf eine Verarmungsschicht zwischen N- und P-Halbleitern angewiesen, um seinen Zweck zu erfüllen. Wenn diese stark dotiert sind, kann die Verarmungsschicht dünn genug für das Tunneln sein. Wenn eine kleine Vorwärtsspannung angelegt wird, ist der durch Tunneln verursachte Strom erheblich. Er hat ein Maximum an dem Punkt, an dem die Vorspannung so groß ist, dass das Energieniveau des p- und des n-Leitungsbandes gleich ist. Wenn die Vorspannung erhöht wird, stimmen die beiden Leitungsbänder nicht mehr überein und die Diode verhält sich typisch. ⓘ

Da der Tunnelstrom schnell abfällt, können Tunneldioden hergestellt werden, die einen Spannungsbereich aufweisen, in dem der Strom mit steigender Spannung abnimmt. Diese besondere Eigenschaft wird bei einigen Anwendungen genutzt, z. B. bei Hochgeschwindigkeitsgeräten, bei denen sich die charakteristische Tunnelwahrscheinlichkeit ebenso schnell ändert wie die Vorspannung. ⓘ

Die resonante Tunneldiode nutzt das Quanten-Tunneln auf eine ganz andere Weise, um ein ähnliches Ergebnis zu erzielen. Diese Diode hat eine Resonanzspannung, bei der viel Strom eine bestimmte Spannung begünstigt, was dadurch erreicht wird, dass zwei dünne Schichten mit einem hochenergetischen Leitfähigkeitsbereich nahe beieinander liegen. Dadurch entsteht ein Quantenpotentialtopf mit einem diskreten niedrigsten Energieniveau. Wenn dieses Energieniveau höher ist als das der Elektronen, findet kein Tunneln statt und die Diode befindet sich in Sperrspannung. Sobald sich die beiden Spannungsenergien angleichen, fließen die Elektronen wie ein offener Draht. Wenn die Spannung weiter ansteigt, wird das Tunneln unwahrscheinlich und die Diode verhält sich wieder wie eine normale Diode, bevor ein zweites Energieniveau spürbar wird. ⓘ

Tunnel-Feldeffekttransistoren

Im Rahmen eines europäischen Forschungsprojekts wurden Feldeffekttransistoren entwickelt, bei denen das Gate (der Kanal) nicht durch thermische Injektion, sondern durch Quantentunneln gesteuert wird, wodurch die Gate-Spannung von ≈1 Volt auf 0,2 Volt gesenkt und der Stromverbrauch um das bis zu 100-fache reduziert werden konnte. Wenn diese Transistoren in VLSI-Chips eingesetzt werden können, würden sie die Leistung pro Stromverbrauch von integrierten Schaltungen verbessern. ⓘ

Kernfusion

Quanten-Tunneling ist ein wesentliches Phänomen für die Kernfusion. Die Temperatur in Sternkernen reicht im Allgemeinen nicht aus, um die Coulomb-Barriere zu überwinden und eine thermonukleare Fusion zu erreichen. Das Quantentunneln erhöht die Wahrscheinlichkeit, dass diese Barriere durchbrochen wird. Obwohl diese Wahrscheinlichkeit immer noch gering ist, reicht die extrem große Anzahl von Atomkernen im Kern eines Sterns aus, um eine ständige Fusionsreaktion aufrechtzuerhalten. ⓘ

Druck und Temperatur in der Sonne und anderen Sternen würden, energetisch betrachtet, nicht für eine thermonukleare Fusion von Atomkernen ausreichen, die die Quelle der emittierten Strahlung ist. Durch den Tunneleffekt wird das Coulomb-Potential jedoch mit einer gewissen Wahrscheinlichkeit quantenmechanisch überwunden. Der Tunneleffekt ist insofern mitentscheidend für das Leben auf der Erde. ⓘ

Radioaktiver Zerfall

Radioaktiver Zerfall ist der Prozess der Emission von Teilchen und Energie aus dem instabilen Kern eines Atoms zur Bildung eines stabilen Produkts. Dies geschieht durch das Tunneln eines Teilchens aus dem Kern (ein Elektron, das in den Kern tunnelt, ist ein Elektroneneinfang). Dies war die erste Anwendung des Quantentunnelns. Der radioaktive Zerfall ist für die Astrobiologie von Bedeutung, da diese Folge des Quantentunnelns eine konstante Energiequelle über einen großen Zeitraum für Umgebungen außerhalb der zirkumstellaren bewohnbaren Zone schafft, in denen eine Sonneneinstrahlung nicht möglich oder nicht wirksam wäre (unterirdische Ozeane). ⓘ

Quanten-Tunneling könnte einer der Mechanismen des hypothetischen Protonenzerfalls sein. ⓘ

Chemische Reaktionen

Der Tunneleffekt von Atomen bei chemischen Reaktionen führt dazu, dass diese schneller und bei tieferen Temperaturen ablaufen können, als durch klassische Bewegung über die Aktivierungsenergie. Bei Raumtemperatur spielt er vor allem bei Wasserstoffübertragungsreaktionen eine Rolle. Bei tiefen Temperaturen sind aber durch Einbeziehung des Tunneleffekts viele astrochemische Synthesen von Molekülen in interstellaren Dunkelwolken erklärbar, u. a. die Synthese von molekularem Wasserstoff, Wasser (Eis) und dem präbiotisch wichtigen Formaldehyd. ⓘ

Quantenbiologie

Das Quantentunneln gehört zu den zentralen nicht-trivialen Quanteneffekten in der Quantenbiologie. Hier ist er sowohl als Elektronentunnelung als auch als Protonentunnelung von Bedeutung. Elektronentunneln ist ein Schlüsselfaktor bei vielen biochemischen Redoxreaktionen (Photosynthese, Zellatmung) sowie bei der enzymatischen Katalyse. Protonentunnelung ist ein Schlüsselfaktor bei spontanen DNA-Mutationen. ⓘ

Eine Spontanmutation tritt auf, wenn eine normale DNA-Replikation stattfindet, nachdem ein besonders wichtiges Proton getunnelt wurde. Eine Wasserstoffbrücke verbindet DNA-Basenpaare. Ein Doppelmuldenpotenzial entlang einer Wasserstoffbrückenbindung trennt eine potenzielle Energiebarriere. Man geht davon aus, dass das Doppelmuldenpotenzial asymmetrisch ist, wobei eine Mulde tiefer liegt als die andere, so dass das Proton normalerweise in der tieferen Mulde ruht. Damit es zu einer Mutation kommt, muss das Proton in die flachere Senke getunnelt sein. Die Bewegung des Protons aus seiner normalen Position wird als tautomerer Übergang bezeichnet. Findet die DNA-Replikation in diesem Zustand statt, kann die Basenpaarungsregel für die DNA gefährdet sein und eine Mutation verursachen. Per-Olov Lowdin war der erste, der diese Theorie der spontanen Mutation innerhalb der Doppelhelix entwickelte. Andere Fälle von durch Quanten-Tunneling ausgelösten Mutationen in der Biologie werden als Ursache für Alterung und Krebs angesehen. ⓘ

Der Tunneleffekt ist einer der zentralen Effekte in der Quantenbiologie. So ist der genetische Code unter anderem durch das Auftreten von Protonen-Tunneln in der DNA nicht vollständig stabil. Dadurch ist der Tunneleffekt mitverantwortlich für das Auftreten von Spontan-Mutationen. Elektronentunneln spielt dagegen bei vielen biochemischen Redox- und Katalysereaktionen eine wichtige Rolle. ⓘ

Quantenleitfähigkeit

Während das Drude-Lorentz-Modell der elektrischen Leitfähigkeit hervorragende Vorhersagen über die Art der leitenden Elektronen in Metallen macht, kann es durch die Verwendung von Quantentunneln erweitert werden, um die Art der Kollisionen der Elektronen zu erklären. Wenn ein freies Elektronenwellenpaket auf eine lange Reihe gleichmäßig verteilter Barrieren trifft, interferiert der reflektierte Teil des Wellenpakets gleichmäßig mit dem übertragenen Teil zwischen allen Barrieren, so dass eine 100%ige Übertragung möglich wird. Die Theorie sagt voraus, dass, wenn positiv geladene Kerne eine perfekt rechteckige Anordnung bilden, die Elektronen als freie Elektronen durch das Metall tunneln, was zu einer extrem hohen Leitfähigkeit führt, und dass Verunreinigungen im Metall diese erheblich stören. ⓘ

Rastertunnelmikroskop

Das von Gerd Binnig und Heinrich Rohrer erfundene Rastertunnelmikroskop (STM) kann die Abbildung einzelner Atome auf der Oberfläche eines Materials ermöglichen. Es funktioniert, indem es die Beziehung zwischen Quantentunnelung und Abstand ausnutzt. Wenn die Spitze der STM-Nadel in die Nähe einer leitenden Oberfläche gebracht wird, an der eine Vorspannung anliegt, kann durch Messung des Elektronenstroms, der zwischen der Nadel und der Oberfläche tunnelt, der Abstand zwischen der Nadel und der Oberfläche ermittelt werden. Durch die Verwendung von piezoelektrischen Stäben, die sich bei Anlegen einer Spannung in ihrer Größe verändern, kann die Höhe der Spitze so eingestellt werden, dass der Tunnelstrom konstant bleibt. Die zeitlich veränderlichen Spannungen, die an diese Stäbe angelegt werden, können aufgezeichnet und zur Abbildung der Oberfläche des Leiters verwendet werden. STMs sind bis auf 0,001 nm genau, das entspricht etwa 1 % des Atomdurchmessers. ⓘ

Kinetischer Isotopeneffekt

In der chemischen Kinetik führt die Substitution eines leichten Isotops eines Elements durch ein schwereres normalerweise zu einer langsameren Reaktionsgeschwindigkeit. Dies wird im Allgemeinen auf Unterschiede in den Nullpunktsschwingungsenergien für chemische Bindungen zurückgeführt, die das leichtere und das schwerere Isotop enthalten, und wird im Allgemeinen durch die Theorie der Übergangszustände modelliert. In bestimmten Fällen werden jedoch große Isotopeneffekte beobachtet, die nicht durch eine semiklassische Behandlung erklärt werden können, und es ist Quanten-Tunneling erforderlich. R. P. Bell entwickelte eine modifizierte Behandlung der Arrhenius-Kinetik, die üblicherweise zur Modellierung dieses Phänomens verwendet wird. ⓘ

Schneller als Licht

Einige Physiker haben behauptet, dass sich Spin-Null-Teilchen beim Tunneln schneller als mit Lichtgeschwindigkeit fortbewegen können. Dies scheint gegen das Kausalitätsprinzip zu verstoßen, da dann ein Bezugssystem existiert, in dem das Teilchen ankommt, bevor es es verlassen hat. Im Jahr 1998 hat Francis E. Low das Phänomen des Nullzeittunnelns kurz beschrieben. In jüngerer Zeit wurden von Günter Nimtz experimentelle Daten zur Tunnelzeit von Phononen, Photonen und Elektronen veröffentlicht. ⓘ

Andere Physiker, wie Herbert Winful, bestritten diese Behauptungen. Winful argumentierte, dass sich das Wellenpaket eines tunnelnden Teilchens lokal ausbreitet, so dass ein Teilchen die Barriere nicht nichtlokal durchtunneln kann. Winful argumentierte auch, dass die Experimente, die angeblich eine nichtlokale Ausbreitung zeigen, falsch interpretiert wurden. Insbesondere misst die Gruppengeschwindigkeit eines Wellenpakets nicht seine Geschwindigkeit, sondern hängt mit der Zeit zusammen, die das Wellenpaket in der Barriere gespeichert ist. Das Problem bleibt jedoch, dass die Wellenfunktion innerhalb der Barriere an allen Punkten gleichzeitig ansteigt. Mit anderen Worten: In jedem Bereich, der für Messungen unzugänglich ist, ist die nichtlokale Ausbreitung immer noch mathematisch sicher. ⓘ

Ein Experiment, das 2020 unter der Leitung von Aephraim Steinberg durchgeführt wurde, zeigte, dass Teilchen in der Lage sein sollten, mit scheinbaren Geschwindigkeiten schneller als das Licht zu tunneln. ⓘ

Mathematische Diskussion

Quantentunneln durch eine Barriere. Die Energie des getunnelten Teilchens bleibt gleich, aber die Wahrscheinlichkeits-Amplitude wird verringert. ⓘ

Die Schrödinger-Gleichung

Die zeitunabhängige Schrödinger-Gleichung für ein Teilchen in einer Dimension kann wie folgt geschrieben werden

$$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}}{dx^{2}}}\Psi (x)+V(x)\Psi (x)=E\Psi (x)$$

oder

$${\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)\Psi (x)\equiv {\frac {2m}{\hbar ^{2}}}M(x)\Psi (x),$$

ⓘ

wobei

• $\hbar$ die reduzierte Plancksche Konstante ist,
• m die Masse des Teilchens ist,
• x die in der Bewegungsrichtung des Teilchens gemessene Entfernung ist,
• Ψ ist die Schrödinger-Wellenfunktion,
• V ist die potenzielle Energie des Teilchens (gemessen in Bezug auf ein beliebiges geeignetes Referenzniveau),
• E ist die Energie des Teilchens, die mit der Bewegung in der x-Achse verbunden ist (gemessen relativ zu V),
• M(x) ist eine durch V(x) - E definierte Größe, die in der Physik keinen anerkannten Namen hat. ⓘ

Die Lösungen der Schrödinger-Gleichung nehmen für verschiedene Werte von x unterschiedliche Formen an, je nachdem, ob M(x) positiv oder negativ ist. Wenn M(x) konstant und negativ ist, kann die Schrödinger-Gleichung in folgender Form geschrieben werden ⓘ

${\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)=-k^{2}\Psi (x),\qquad {\text{where}}\quad k^{2}=-{\frac {2m}{\hbar ^{2}}}M.$ ⓘ

Die Lösungen dieser Gleichung stellen Wanderwellen mit der Phasenkonstante +k oder -k dar. Wenn M(x) konstant und positiv ist, kann die Schrödingergleichung auch in folgender Form formuliert werden ⓘ

${\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)={\kappa }^{2}\Psi (x),\qquad {\text{where}}\quad {\kappa }^{2}={\frac {2m}{\hbar ^{2}}}M.$ ⓘ

Die Lösungen dieser Gleichung sind steigende und fallende Exponentiale in Form von evaneszenten Wellen. Wenn M(x) mit der Position variiert, tritt der gleiche Unterschied im Verhalten auf, je nachdem ob M(x) negativ oder positiv ist. Daraus folgt, dass das Vorzeichen von M(x) die Art des Mediums bestimmt, wobei ein negatives M(x) dem Medium A und ein positives M(x) dem Medium B entspricht. Daraus folgt, dass eine evaneszente Wellenkopplung auftreten kann, wenn ein Bereich mit positivem M(x) zwischen zwei Bereichen mit negativem M(x) liegt und somit eine potenzielle Barriere entsteht. ⓘ

Die mathematische Behandlung der Situation, in der M(x) mit x variiert, ist schwierig, außer in speziellen Fällen, die in der Regel nicht der physikalischen Realität entsprechen. Eine vollständige mathematische Behandlung findet sich in der Monographie von Fröman und Fröman aus dem Jahr 1965. Ihre Ideen wurden nicht in die Physiklehrbücher aufgenommen, aber ihre Korrekturen haben kaum quantitative Auswirkungen. ⓘ

Die WKB-Approximation

Die Wellenfunktion wird als Exponentialfunktion einer Funktion ausgedrückt:

$$\Psi (x)=e^{\Phi (x)},$$

wobei

$$\Phi (x)+\Phi '(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).$$

ⓘ

$\Phi '(x)$ wird dann in einen realen und einen imaginären Teil zerlegt:

$$\Phi '(x)=A(x)+iB(x),$$

wobei A(x) und B(x) reellwertige Funktionen sind. ⓘ

Setzt man die zweite Gleichung in die erste ein und nutzt die Tatsache, dass der Imaginärteil 0 sein muss, ergibt sich folgendes:

$$A'(x)+A(x)^{2}-B(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).$$

Quantentunneln in der Phasenraumformulierung der Quantenmechanik. Wigner-Funktion für das Tunneln durch die Potentialbarriere $U(x)=8e^{-0.25x^{2}}$ in atomaren Einheiten (a.u.). Die durchgezogenen Linien stellen den Niveausatz des Hamiltonianers $H(x,p)=p^{2}/2+U(x)$. ⓘ

Um diese Gleichung mit Hilfe der semiklassischen Näherung zu lösen, muss jede Funktion als Potenzreihe erweitert werden in $\hbar$. Aus den Gleichungen geht hervor, dass die Potenzreihe mindestens mit einer Ordnung von $\hbar ^{-1}$ beginnen, um den Realteil der Gleichung zu erfüllen; für einen guten klassischen Grenzwert ist es besser, mit der höchstmöglichen Potenz der Planckschen Konstante zu beginnen, was zu

$$A(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}A_{k}(x)$$

und

$$B(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}B_{k}(x),$$

mit den folgenden Beschränkungen für die Terme niedrigster Ordnung,

$$A_{0}(x)^{2}-B_{0}(x)^{2}=2m\left(V(x)-E\right)$$

und

$$A_{0}(x)B_{0}(x)=0.$$

ⓘ

An dieser Stelle können zwei Extremfälle betrachtet werden. ⓘ

Fall 1 ⓘ

Wenn sich die Amplitude im Vergleich zur Phase langsam ändert $A_{0}(x)=0$ und

$$B_{0}(x)=\pm {\sqrt {2m\left(E-V(x)\right)}}$$

was der klassischen Bewegung entspricht. Die Auflösung der nächsten Expansionsordnung führt zu

$$\Psi (x)\approx C{\frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}+\theta }}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}}$$

ⓘ

Fall 2 ⓘ

Wenn die Phase im Vergleich zur Amplitude langsam variiert, $B_{0}(x)=0$ und

$$A_{0}(x)=\pm {\sqrt {2m\left(V(x)-E\right)}}$$

was dem Tunneln entspricht. Die Auflösung der nächsten Ordnung der Ausdehnung ergibt

$$\Psi (x)\approx {\frac {C_{+}e^{+\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}+C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}$$

ⓘ

In beiden Fällen ist aus dem Nenner ersichtlich, dass beide Näherungslösungen in der Nähe der klassischen Wendepunkte schlecht sind $E=V(x)$. In der Nähe des Potentialbergs verhält sich das Teilchen wie eine freie, oszillierende Welle; unterhalb des Potentialbergs erfährt das Teilchen exponentielle Amplitudenänderungen. Durch Betrachtung des Verhaltens an diesen Grenzen und klassischen Wendepunkten kann eine globale Lösung gefunden werden. ⓘ

Zu Beginn wird ein klassischer Wendepunkt gewählt, $x_{1}$ gewählt und ${\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)$ wird in einer Potenzreihe über $x_{1}$:

$${\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})+v_{2}(x-x_{1})^{2}+\cdots$$

ⓘ

Wenn man nur den Term erster Ordnung beibehält, ist die Linearität gewährleistet:

$${\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1}).$$

ⓘ

Mit dieser Näherung wird die Gleichung bei $x_{1}$ zu einer Differentialgleichung:

$${\frac {d^{2}}{dx^{2}}}\Psi (x)=v_{1}(x-x_{1})\Psi (x).$$

ⓘ

Diese kann mit Airy-Funktionen als Lösungen gelöst werden. ⓘ

$$\Psi (x)=C_{A}Ai\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)+C_{B}Bi\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)$$

ⓘ

Nimmt man diese Lösungen für alle klassischen Wendepunkte, kann eine globale Lösung gebildet werden, die die Grenzlösungen miteinander verbindet. Sind die beiden Koeffizienten auf der einen Seite eines klassischen Wendepunkts gegeben, können die beiden Koeffizienten auf der anderen Seite eines klassischen Wendepunkts bestimmt werden, indem diese lokale Lösung verwendet wird, um sie zu verbinden. ⓘ

Folglich werden die Lösungen der Airy-Funktionen in den richtigen Grenzwerten zu Sinus-, Kosinus- und Exponentialfunktionen asymptotisch. Die Beziehungen zwischen $C,\theta$ und $C_{+},C_{-}$ sind ⓘ

$$C_{+}={\frac {1}{2}}C\cos {\left(\theta -{\frac {\pi }{4}}\right)}$$

und

Quanten-Tunnelbau durch eine Barriere. Am Ursprung (x = 0) befindet sich eine sehr hohe, aber schmale Potentialbarriere. Es ist ein signifikanter Tunneleffekt zu beobachten.

$C_{-}=-C\sin {\left(\theta -{\frac {\pi }{4}}\right)}$ ⓘ

Mit den gefundenen Koeffizienten kann die globale Lösung gefunden werden. Der Transmissionskoeffizient für ein Teilchen, das durch eine einzelne Potentialbarriere tunnelt, ist also ⓘ

$$T(E)=e^{-2\int _{x_{1}}^{x_{2}}dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left[V(x)-E\right]}}},$$

ⓘ

wobei $x_{1},x_{2}$ sind die beiden klassischen Wendepunkte für die Potentialbarriere. ⓘ

Für eine rechteckige Barriere vereinfacht sich dieser Ausdruck zu:

$$T(E)=e^{-2{\sqrt {{\frac {2m}{\hbar ^{2}}}(V_{0}-E)}}(x_{2}-x_{1})}={\tilde {V}}_{0}^{-(x_{2}-x_{1})}.$$

ⓘ

Entdeckung

1897 beobachtete Robert Williams Wood den Effekt in einem Experiment bei der Feldemission von Elektronen im Vakuum, ohne ihn deuten zu können. ⓘ

1926/1927 hat Friedrich Hund den später so genannten Tunneleffekt (dessen Entdeckung oft George Gamow zugeschrieben wird) zuerst bei isomeren Molekülen entdeckt und beschrieben. ⓘ

1926 legten Gregor Wentzel, Hendrik Anthony Kramers und Léon Brillouin mit der nach ihnen benannten WKB-Methode den Grundstein für die quantenmechanische Erklärung von Tunnelprozessen. Mit dieser Methode konnten 1928 George Gamow bei seinem Aufenthalt bei Max Born in Göttingen sowie Ronald W. Gurney und Edward U. Condon den Alphazerfall erklären. Gleichzeitig gelang Ralph Howard Fowler und Lothar Wolfgang Nordheim die Erklärung der Feldemission von Elektronen. ⓘ

Der schwedische Physiker Oskar Klein gab 1929 eine verfeinerte Theorie der Durchtunnelung von Barrieren durch sehr schnelle Teilchen an (Klein-Paradox, englisch Klein tunneling). Voraussagen dieser Theorie konnten 2020 bestätigt werden. ⓘ

Auftreten und Anwendungen

Alphazerfall

Auf dem Tunneleffekt beruht unter anderem der Alphazerfall von Atomkernen. Nach der klassischen Physik dürfte der Kern wegen der anziehenden starken Wechselwirkung nicht zerfallen. Jedoch kommt es durch den Tunneleffekt zu einer von Null verschiedenen Wahrscheinlichkeit pro Zeiteinheit (Zerfallswahrscheinlichkeit) dafür, dass das Alphateilchen den Kern verlässt, denn die quantenmechanische Aufenthaltswahrscheinlichkeit des Alphateilchens ist auch jenseits der Energiebarriere nicht gleich Null; befindet sich das positiv geladene Alphateilchen einmal außerhalb der Barriere, verlässt es durch Abstoßung vom ebenfalls positiv geladenen Rest des Kerns diesen endgültig. Aus der Zerfallswahrscheinlichkeit ergibt sich für diesen stochastischen Vorgang eine Halbwertszeit. ⓘ

Zwei-Elektroden-Tunneln

1933 berechneten Hans Bethe und Arnold Sommerfeld näherungsweise die Tunnelstromdichte zwischen zwei Elektroden mit geringer Potentialdifferenz und trapezförmiger Potentialbarriere. Eine etwas bessere Näherung konnte dann 1935 von R. Holm und B. Kirschstein angegeben werden, die die Form der Potentialbarriere mit einer Parabel approximierten. Holm verfeinerte 1951 seine Theorie dahingehend, dass er die Tunnelstromdichte auch für Potentialdifferenzen angeben konnte, die in der Größenordnung der Austrittsarbeit von üblichen Elektrodenmaterialien liegt. Erst 1963 konnte J. Simmons eine generalisierte Formel angeben, mit der die Tunnelstromdichte für alle Potentialdifferenzen zwischen zwei Elektroden ausgerechnet werden kann, wobei dann auch die Feldemission mit eingeschlossen ist. ⓘ

Feldelektronen- und Feldionenmikroskop

Eine wichtige Anwendung fand der Tunneleffekt bei den hochauflösenden Mikroskopen, die Erwin Wilhelm Müller in Berlin entwickelt hat. 1936 beschrieb er das Feldelektronenmikroskop und 1951 dann das Feldionenmikroskop, das als erstes Instrument eine atomare Auflösung ermöglichte. ⓘ

Tunneldiode

1957 entwickelte Leo Esaki die erste Tunneldiode, ein elektronisches Hochfrequenz-Halbleiterbauelement mit negativem differentiellen Widerstand. Er bekam dafür 1973 den Nobelpreis für Physik. ⓘ

Rastertunnelmikroskop

Gerd Binnig und Heinrich Rohrer entwickelten ein Verfahren, mit dem erstmals das kontrollierte Zwei-Elektroden-Tunneln im Vakuum möglich wurde, das schließlich zur Erfindung des Rastertunnelmikroskops führte. Das Patent für diese Technik wurde 1979 beantragt. Sie bekamen dafür 1986 zusammen mit Ernst Ruska den Physik-Nobelpreis verliehen. ⓘ

Magnetischer Tunnelwiderstand

Beim magnetischen Tunnelwiderstand wird die Tatsache ausgenutzt, dass sich der Tunnelstrom zwischen zwei an einem magnetischen Tunnelkontakt durch einen dünnen Isolator getrennten Ferromagnetika durch ein äußeres Magnetfeld ändert. Dieser Effekt wird zum Beispiel beim Auslesen der Daten in modernen Festplatten ausgenutzt (TMR-Effekt). ⓘ

Messung des Zeitbedarfs

Obige Gleichungen geben keine Auskunft, wie lange das Teilchen braucht, um von einem Ende des Tunnels zum anderen zu gelangen. Die Schätzungen für Elektronen lagen zwischen Null und etwa 500·10⁻¹⁸ Sekunden. Aktuelle Experimente an der ETH Zürich (2008) haben einen Zeitbedarf von maximal 34·10⁻¹⁸ s ergeben, das ist die Messgenauigkeit der Anordnung. Im Experiment wurde ein zirkular polarisierter Laserpuls von nur 5·10⁻¹⁵ s Dauer (während dieser Zeit rotiert der elektrische Feldvektor einmal um 360°) auf ein Elektron geschossen, das „hinter“ einem Potentialwall von 24,6 eV an ein Heliumatom gebunden war. Die Durchtrittswahrscheinlichkeit des Elektrons ist bei dieser Wallhöhe so gering, dass keine spontane Ionisation des He-Atoms beobachtet wird. ⓘ

Durch den kurzen Laserpuls verringerte sich die Höhe des Potentialwalls für eine definierte Zeit so weit, dass eines der beiden Elektronen das Atom verlassen konnte. Dann wurde es vom elektrischen Feld des Lichtpulses beschleunigt und vom He⁺-Ion entfernt. Aus der Abflugrichtung konnte der Zeitverlauf berechnet werden. Nach Ansicht der Forscher ist das Elektron unmittelbar nach seinem „Verschwinden“ auf der Innenseite des Potentialwalls wieder außen aufgetaucht. Bei dem Versuch handelte es sich nicht um eine Photoionisation, weil dazu eine Photonenenergie im UV-Bereich notwendig gewesen wäre. Der verwendete Femtosekundenlaser hat zwar keine exakt definierbare Wellenlänge, der Schwerpunkt seines breitbandigen Bereiches liegt jedoch eindeutig im IR-Bereich. Hier reicht die Photonenenergie nicht aus, um Helium zu ionisieren. ⓘ