Fourier-Transformation

Eine Fourier-Transformation (FT) ist eine mathematische Transformation, die Funktionen, die von Raum oder Zeit abhängen, in Funktionen zerlegt, die von der Raum- oder Zeitfrequenz abhängen. Dieser Vorgang wird auch als Analyse bezeichnet. Ein Anwendungsbeispiel wäre die Zerlegung der Wellenform eines musikalischen Akkords in die Intensität der einzelnen Tonhöhen. Der Begriff Fourier-Transformation bezieht sich sowohl auf die Darstellung im Frequenzbereich als auch auf die mathematische Operation, die die Darstellung im Frequenzbereich mit einer Funktion in Raum oder Zeit verbindet. ⓘ
Die Fourier-Transformation einer Funktion ist eine komplexwertige Funktion, die die komplexen Sinusschwingungen darstellt, aus denen die ursprüngliche Funktion besteht. Für jede Frequenz stellt der Betrag (Absolutwert) des komplexen Wertes die Amplitude einer komplexen Sinuskurve mit dieser Frequenz dar, und das Argument des komplexen Wertes stellt die Phasenverschiebung der komplexen Sinuskurve dar. Wenn eine Frequenz nicht vorhanden ist, hat die Transformation den Wert 0 für diese Frequenz. Die Fourier-Transformation ist nicht auf Zeitfunktionen beschränkt, aber der Bereich der ursprünglichen Funktion wird gemeinhin als Zeitbereich bezeichnet. Das Fourier-Inversions-Theorem bietet einen Syntheseprozess, der die ursprüngliche Funktion aus ihrer Darstellung im Frequenzbereich wiederherstellt. ⓘ
| Fourier-Transformationen ⓘ |
|---|
|
Funktionen, die im Zeitbereich lokalisiert sind, haben Fourier-Transformationen, die sich über den Frequenzbereich ausbreiten und umgekehrt, ein Phänomen, das als Unschärfeprinzip bekannt ist. Der kritische Fall für dieses Prinzip ist die Gauß-Funktion, die in der Wahrscheinlichkeitstheorie und Statistik sowie bei der Untersuchung physikalischer Phänomene mit Normalverteilung (z. B. Diffusion) von großer Bedeutung ist. Die Fourier-Transformation einer Gaußschen Funktion ist eine weitere Gaußsche Funktion. Joseph Fourier führte die Fourier-Transformation in seiner Studie über die Wärmeübertragung ein, in der Gauß-Funktionen als Lösungen der Wärmegleichung erscheinen. ⓘ
Die Fourier-Transformation kann formal als ein uneigentliches Riemann-Integral definiert werden, was sie zu einer Integraltransformation macht, obwohl diese Definition für viele Anwendungen, die eine anspruchsvollere Integrationstheorie erfordern, nicht geeignet ist. Viele relativ einfache Anwendungen verwenden zum Beispiel die Dirac-Delta-Funktion, die formal so behandelt werden kann, als wäre sie eine Funktion, aber die Begründung erfordert eine mathematisch anspruchsvollere Sichtweise. ⓘ
Die Fourier-Transformation kann auch auf Funktionen mehrerer Variablen im euklidischen Raum verallgemeinert werden, indem eine Funktion des dreidimensionalen "Positionsraums" in eine Funktion des dreidimensionalen Impulses (oder eine Funktion von Raum und Zeit in eine Funktion des 4-Momentes) umgewandelt wird. Dieser Gedanke macht die räumliche Fourier-Transformation zu einer sehr natürlichen Methode bei der Untersuchung von Wellen und in der Quantenmechanik, wo es wichtig ist, Wellenlösungen entweder als Funktionen der Position oder des Impulses und manchmal als beides darstellen zu können. Im Allgemeinen sind die Funktionen, auf die Fourier-Methoden anwendbar sind, komplexwertig und möglicherweise vektorwertig. Eine weitere Verallgemeinerung ist auf Funktionen auf Gruppen möglich, wozu neben der ursprünglichen Fourier-Transformation auf R oder Rn (als Gruppen unter Addition betrachtet) insbesondere die zeitdiskrete Fourier-Transformation (DTFT, Gruppe = Z), die diskrete Fourier-Transformation (DFT, Gruppe = Z mod N) und die Fourier-Reihe oder zirkuläre Fourier-Transformation (Gruppe = S1, der Einheitskreis ≈ geschlossenes endliches Intervall mit identifizierten Endpunkten) gehören. Letztere wird routinemäßig verwendet, um periodische Funktionen zu behandeln. Die schnelle Fourier-Transformation (FFT) ist ein Algorithmus zur Berechnung der DFT. ⓘ
Definition
Es gibt mehrere gängige Konventionen für die Definition der Fourier-Transformation einer integrierbaren Funktion . Einer von ihnen ist:
|
(Gleichung 1) ⓘ |
Die Transformation der Funktion bei der Frequenz ist gegeben durch die komplexe Zahl . Die Auswertung von Gl.1 für alle Werte von ergibt die Funktion im Frequenzbereich. Die Fourier-Transformation wird hier durch Hinzufügen eines Zirkumflexes zum Symbol der Funktion angegeben. Wenn die unabhängige Variable die Zeit darstellt (oft bezeichnet mit anstelle von ), steht die Transformationsvariable für die Frequenz (oft bezeichnet mit anstelle von ). Wenn z. B. die Zeit in Sekunden gemessen wird, dann ist die Frequenz in Hertz. ⓘ
Bei reellwertigen Gleichung 1 hat die Symmetrieeigenschaft Sie kann daher reduziert werden auf:
was bedeutet, dass negative Werte der Frequenz, in diesem Zusammenhang unnötig sind. ⓘ
Unter geeigneten Bedingungen kann als eine Rekombination von komplexen Exponentialen aller möglichen Frequenzen dargestellt werden:
|
(Gleichung.2) ⓘ |
das für reellwertige Werte reduziert auf:
Die komplexe Zahl, vermittelt sowohl die Amplitude als auch die Phase der Frequenz . Gleichung 2 ist als Fourier-Inversionstheorem bekannt und wurde erstmals in Fouriers Analytischer Wärmetheorie eingeführt, obwohl ein Beweis nach modernen Maßstäben erst viel später erbracht wurde. Die Funktionen und werden oft als Fourier-Integralpaar oder Fourier-Transformationspaar bezeichnet. Eine gebräuchliche Notation für die Bezeichnung von Transformationspaaren ist:
- . ⓘ
Für andere gängige Konventionen und Notationen, einschließlich der Verwendung der Winkelfrequenz ω anstelle der gewöhnlichen Frequenz ξ, siehe Andere Konventionen und Andere Notationen weiter unten. Die Fourier-Transformation im euklidischen Raum wird gesondert behandelt, wobei die Variable x häufig für Position und ξ-Impuls steht. Die in diesem Artikel gewählten Konventionen sind die der harmonischen Analyse und werden als die einzigen Konventionen charakterisiert, bei denen die Fourier-Transformation sowohl unitär auf L2 als auch ein Algebra-Homomorphismus von L1 nach L∞ ist, ohne das Lebesgue-Maß zu renormalisieren. ⓘ
Es gibt viele andere Charakterisierungen der Fourier-Transformation. Zum Beispiel verwendet man das Stone-von-Neumann-Theorem: Die Fourier-Transformation ist der einzige unitäre Intertwiner für die symplektischen und euklidischen Schrödinger-Darstellungen der Heisenberg-Gruppe. ⓘ
Geschichte
Im Jahr 1822 behauptete Fourier (siehe Joseph Fourier § The Analytic Theory of Heat), dass jede Funktion, ob kontinuierlich oder diskontinuierlich, in eine Reihe von Sinuskurven erweitert werden kann. Diese wichtige Arbeit wurde von anderen korrigiert und erweitert und bildet die Grundlage für die verschiedenen Formen der Fourier-Transformation, die seitdem verwendet werden. ⓘ
Einführung

Obwohl Fourier-Reihen periodische Wellenformen als Summe harmonisch zusammenhängender Sinusschwingungen darstellen können, können Fourier-Reihen keine nicht-periodischen Wellenformen darstellen. Die Fourier-Transformation ist jedoch in der Lage, auch nicht-periodische Wellenformen darzustellen. Dies wird dadurch erreicht, dass die Periode einer beliebigen Wellenform durch einen Begrenzungsprozess bis ins Unendliche verlängert wird und dann als periodische Wellenform behandelt wird. ⓘ
Bei der Untersuchung von Fourier-Reihen stellen die Fourier-Koeffizienten die Amplitude jeder harmonisch verwandten Sinuskurve in der Fourier-Reihe einer periodischen Funktion f dar. ⓘ
Die Fourier-Transformation verwendet ein Integral (oder eine "kontinuierliche Summe"), das die Eigenschaften von Sinus und Kosinus ausnutzt, um die Amplitude und Phase jeder Sinuskurve in einer Fourier-Reihe wiederherzustellen. Bei der inversen Fourier-Transformation werden diese Wellen mithilfe eines ähnlichen Integrals rekombiniert, um die ursprüngliche Funktion zu reproduzieren. ⓘ
Verwendung komplexer Sinusschwingungen zur Darstellung reeller Sinusschwingungen
Zur Vereinfachung der Mathematik ist es wünschenswert, die Fourier-Reihe als eine Summe komplexer Exponentiale zu schreiben (siehe Fourier-Reihe § Exponentialform). Jedes komplexe Exponential oder komplexe Sinusoid der Frequenz ξ kann mit der Eulerschen Formel als Summe einer Kosinuswelle der Frequenz ξ für die reelle Komponente und einer Sinuswelle ebenfalls der Frequenz ξ für die imaginäre Komponente ausgedrückt werden:
Wenn man reelle Sinusschwingungen als komplexe Sinusschwingungen ausdrückt, müssen die Fourier-Koeffizienten komplexwertig sein, was jedoch den Vorteil hat, dass alle notwendigen Informationen über jede Frequenz kompakt dargestellt werden. Die übliche Interpretation dieser komplexen Zahl ist, dass (ihr Betrag) die Amplitude angibt und (sein Argument) die Phase der komplexen Sinuskurve für diesen Koeffizienten angibt. ⓘ

Diese komplexen Exponentiale können eine negative Frequenz haben. Beispielsweise durchlaufen die beiden komplexen Sinuskurven e2πiξx und e-2πiξx einen Zyklus pro Einheit x, aber die erste steht für eine positive Frequenz, während die zweite für eine negative Frequenz steht. Eine positive Frequenz kann als Drehung gegen den Uhrzeigersinn um die komplexe Ebene verstanden werden, während eine negative Frequenz als Drehung im Uhrzeigersinn um die komplexe Ebene verstanden werden kann. Wenn komplexe Sinuskurven als dreidimensionale Spirale interpretiert werden (wobei die dritte Dimension die imaginäre Komponente ist), ändert die Negierung der Frequenz einfach die Händigkeit der Spirale. ⓘ
Reale Sinus- und Kosinuswellen lassen sich aus der komplexen Exponentialdarstellung von Sinuskurven ableiten. So lassen sich beispielsweise Kosinus- und Sinuswellen über eine Folge der Eulerschen Formel entweder als Real- oder Imaginärteil einer komplexen Sinuskurve oder als gewichtete Summe zweier komplexer Sinuskurven mit entgegengesetzter Frequenz ausdrücken:
Folglich kann eine allgemeine Form jeder reellen Sinuskurve (mit Frequenz ξ, Phasenverschiebung θ und Amplitude A) als Summe zweier komplexer Sinuskurven mit entgegengesetzter Frequenz (ξ und -ξ), aber gleichem Betrag (A/2) und mit der Phasenverschiebung θ in ihren beiden komplexen Koeffizienten ausgedrückt werden:
Man kann also davon ausgehen, dass jede reelle Sinuskurve (und jedes reelle Signal) aus einer positiven und einer negativen Frequenz besteht, deren imaginäre Komponenten sich aufheben, deren reelle Komponenten aber gleichermaßen zur Bildung des reellen Signals beitragen. ⓘ
Um die Verwendung komplexer Zahlen und negativer Frequenzen zu vermeiden, können die Sinus- und die Kosinustransformation zusammen als gleichwertige alternative Form der Fouriertransformation verwendet werden. ⓘ
Fourier-Transformation für Funktionen, die außerhalb eines Intervalls Null sind
Es besteht ein enger Zusammenhang zwischen der Definition von Fourier-Reihen und der Fourier-Transformation für Funktionen f, die außerhalb eines Intervalls null sind. Für eine solche Funktion können wir ihre Fourier-Reihe auf jedem Intervall berechnen, das die Punkte einschließt, in denen f nicht Null ist. Die Fourier-Transformierte ist ebenfalls für eine solche Funktion definiert. Mit zunehmender Länge des Intervalls, in dem wir die Fourier-Reihe berechnen, beginnen die Koeffizienten der Fourier-Reihe der Fourier-Transformation zu ähneln, und die Summe der Fourier-Reihe von f beginnt, der inversen Fourier-Transformation zu ähneln. Genauer gesagt: Nehmen wir an, T ist groß genug, dass das Intervall [-T/2, T/2] das Intervall enthält, in dem f nicht Null ist. Dann ist der n-te Reihenkoeffizient cn gegeben durch:
Vergleicht man dies mit der Definition der Fourier-Transformation, so ergibt sich, dass
da f(x) außerhalb von [-T/2, T/2] Null ist. Die Fourier-Koeffizienten sind also gleich den Werten der Fourier-Transformierten, die auf einem Gitter der Breite 1/T abgetastet wurden, multipliziert mit der Gitterbreite 1/T. ⓘ
Unter geeigneten Bedingungen ist die Fourier-Reihe von f gleich der Funktion f. Mit anderen Worten: f kann geschrieben werden:
wobei die letzte Summe einfach die erste Summe ist, die mit den Definitionen ξn = n/T und Δξ = n + 1/T - n/T = 1/T umgeschrieben wird. ⓘ
Diese zweite Summe ist eine Riemannsche Summe. Mit T → ∞ konvergiert sie gegen das Integral der inversen Fourier-Transformation, wie oben angegeben. Unter geeigneten Bedingungen kann dieses Argument präzisiert werden. ⓘ
Beispiel
Die folgenden Abbildungen veranschaulichen, wie die Fourier-Transformation misst, ob eine Frequenz in einer bestimmten Funktion vorhanden ist. Die dargestellte Funktion f(t) = cos(6πt) e-πt2 schwingt mit 3 Hz (wenn t Sekunden misst) und tendiert schnell gegen 0. (Der zweite Faktor in dieser Gleichung ist eine Hüllfunktion, die die kontinuierliche Sinuskurve zu einem kurzen Impuls formt. Ihre allgemeine Form ist eine Gaußsche Funktion). Diese Funktion wurde speziell so gewählt, dass sie eine reelle Fourier-Transformation hat, die leicht aufgezeichnet werden kann. Das erste Bild enthält den Graphen dieser Funktion. Um zu berechnen zu berechnen, müssen wir e-2πi(3t)f(t) integrieren. Das zweite Bild zeigt die Darstellung der Real- und Imaginärteile dieser Funktion. Der Realteil des Integranden ist fast immer positiv, denn wenn f(t) negativ ist, ist auch der Realteil von e-2πi(3t) negativ. Da sie mit der gleichen Geschwindigkeit schwingen, ist der Realteil von e-2πi(3t) positiv, wenn f(t) positiv ist. Das Ergebnis ist, dass man bei der Integration des Realteils des Integranden eine relativ große Zahl erhält (in diesem Fall 1/2). Versucht man hingegen, eine Frequenz zu messen, die nicht vorhanden ist, wie in dem Fall, in dem wir uns mit sieht man, dass sowohl die reale als auch die imaginäre Komponente dieser Funktion schnell zwischen positiven und negativen Werten schwankt, wie im dritten Bild dargestellt. In diesem Fall oszilliert der Integrand also schnell genug, so dass das Integral sehr klein ist und der Wert der Fourier-Transformation für diese Frequenz nahezu Null ist. ⓘ
Die allgemeine Situation mag etwas komplizierter sein, aber so misst die Fourier-Transformation, wie viel von einer einzelnen Frequenz in einer Funktion f(t) vorhanden ist. ⓘ
Betrag der Fourier-Transformation, mit Kennzeichnung von 3 und 5 Hz. ⓘ
Eigenschaften der Fourier-Transformation
Hier nehmen wir an, dass f(x), g(x) und h(x) ganzzahlige Funktionen sind: Lebesgue-messbar auf der reellen Linie befriedigend:
Wir bezeichnen die Fourier-Transformationen dieser Funktionen als f̂(ξ), ĝ(ξ) bzw. ĥ(ξ). ⓘ
Grundlegende Eigenschaften
Die Fourier-Transformierte hat die folgenden grundlegenden Eigenschaften: ⓘ
Linearität
- Für beliebige komplexe Zahlen a und b, wenn h(x) = af (x) + bg(x), dann ĥ(ξ) = a - f̂(ξ) + b - ĝ(ξ). ⓘ
Translation / Zeitverschiebung

- Für jede reelle Zahl x0, wenn h(x) = f(x - x0), dann ĥ(ξ) = e-2πix0ξ f̂(ξ). ⓘ
Modulation / Frequenzverschiebung
- Für jede reelle Zahl ξ0, wenn h(x) = e2πixξ0 f(x), dann ĥ(ξ) = f̂(ξ - ξ0). ⓘ
Zeitliche Skalierung
- Für eine reelle Zahl a ungleich Null, wenn h(x) = f(ax), dann
- Der Fall a = -1 führt zur Eigenschaft der Zeitumkehrung, die besagt: Wenn h(x) = f(-x), dann ist ĥ(ξ) = f̂(-ξ). ⓘ
Konjugation
- Wenn h(x) = f(x), dann
- Insbesondere wenn f reell ist, dann hat man die Realitätsbedingung
- das heißt, f̂ ist eine hermitesche Funktion. Und wenn f rein imaginär ist, dann
- ⓘ
Real- und Imaginärteil in der Zeit
- Wenn , dann .
- Wenn , dann . ⓘ
Die Nullfrequenzkomponente
- Setzt man ξ = 0 in die Definition ein, so erhält man
- Das ist dasselbe wie das Integral von f über sein gesamtes Gebiet und wird auch als Mittelwert oder DC-Bias der Funktion bezeichnet. ⓘ
Invertierbarkeit und Periodizität
Unter geeigneten Bedingungen für die Funktion kann sie aus ihrer Fourier-Transformation zurückgewonnen werden . Bezeichnet man den Fourier-Transformierten-Operator nämlich mit , so , dann wird bei geeigneten Funktionen durch die zweimalige Anwendung der Fourier-Transformation die Funktion einfach gespiegelt: , was als "Umkehrung der Zeit" interpretiert werden kann. Da die Umkehrung der Zeit zweiperiodisch ist, ergibt sich bei zweimaliger Anwendung Der Fourier-Transformationsoperator ist also vierperiodisch, und in ähnlicher Weise kann die inverse Fourier-Transformation durch dreimaliges Anwenden der Fourier-Transformation ermittelt werden: . Insbesondere ist die Fourier-Transformation (unter geeigneten Bedingungen) invertierbar. ⓘ
Genauer gesagt, definiert man den Paritätsoperator so, dass ist, haben wir:
Diese Gleichheiten von Operatoren erfordern eine sorgfältige Definition des betreffenden Funktionsraums, die Definition der Gleichheit von Funktionen (Gleichheit in jedem Punkt? Gleichheit fast überall?) und die Definition der Gleichheit von Operatoren - d. h. die Definition der Topologie des betreffenden Funktions- und Operatorraums. Diese sind nicht für alle Funktionen wahr, aber unter verschiedenen Bedingungen, die den Inhalt der verschiedenen Formen des Fourier-Inversionssatzes bilden. ⓘ
Diese vierfache Periodizität der Fourier-Transformation ähnelt einer Drehung der Ebene um 90°, zumal die zweifache Iteration eine Umkehrung ergibt, und in der Tat kann diese Analogie präzisiert werden. Während die Fourier-Transformation einfach als Umschaltung zwischen dem Zeit- und dem Frequenzbereich interpretiert werden kann, wobei die inverse Fourier-Transformation die beiden Bereiche wieder zurückschaltet, kann sie geometrisch als Drehung um 90° im Zeit-Frequenz-Bereich interpretiert werden (wobei die Zeit als x-Achse und die Frequenz als y-Achse betrachtet wird), und die Fourier-Transformation kann zur fraktionalen Fourier-Transformation verallgemeinert werden, die Drehungen um andere Winkel beinhaltet. Dies kann weiter zu linearen kanonischen Transformationen verallgemeinert werden, die als Wirkung der speziellen linearen Gruppe SL2(R) auf die Zeit-Frequenz-Ebene dargestellt werden können, wobei die erhaltene symplektische Form der Unschärferelation entspricht (siehe unten). Dieser Ansatz wird insbesondere in der Signalverarbeitung im Rahmen der Zeit-Frequenz-Analyse untersucht. ⓘ
Einheiten und Dualität
Die Frequenzvariable muss inverse Einheiten zu den Einheiten des ursprünglichen Funktionsbereichs haben (typischerweise t oder x genannt). Wenn beispielsweise t in Sekunden gemessen wird, sollte ξ in Zyklen pro Sekunde angegeben werden. Wenn die Zeit in 2π Sekunden gemessen wird, wird stattdessen ein anderer griechischer Buchstabe ω verwendet, um die Winkelfrequenz (mit ω = 2πξ) in Bogenmaß pro Sekunde anzugeben. Wenn x für Längeneinheiten verwendet wird, muss ξ in inversen Längeneinheiten angegeben werden, z. B. in Wellenzahlen. Das heißt, es gibt zwei Versionen der reellen Linie: eine, die der Bereich von t ist und in Einheiten von t gemessen wird, und die andere, die der Bereich von ξ ist und in inversen Einheiten zu den Einheiten von t gemessen wird. Diese beiden unterschiedlichen Versionen der reellen Linie können nicht miteinander gleichgesetzt werden. Daher geht die Fourier-Transformation von einem Raum von Funktionen in einen anderen Raum von Funktionen: Funktionen, die einen anderen Definitionsbereich haben. ⓘ
Im Allgemeinen muss ξ immer als lineare Form auf dem Raum ihrer Domäne betrachtet werden, d. h. die zweite reelle Linie ist der Dualraum der ersten reellen Linie. Für eine formale Erklärung und weitere Details siehe den Artikel über lineare Algebra. Dieser Gesichtspunkt wird bei der Verallgemeinerung der Fourier-Transformation auf allgemeine Symmetriegruppen, einschließlich des Falls der Fourier-Reihen, wichtig. ⓘ
Die Tatsache, dass es keinen bevorzugten Weg (oft sagt man "keinen kanonischen Weg") gibt, um die beiden Versionen der reellen Linie, die an der Fourier-Transformation beteiligt sind, zu vergleichen - die Fixierung der Einheiten auf einer Linie erzwingt nicht die Skalierung der Einheiten auf der anderen Linie -, ist der Grund für die Fülle konkurrierender Konventionen zur Definition der Fourier-Transformation. Die verschiedenen Definitionen, die sich aus der unterschiedlichen Wahl der Einheiten ergeben, unterscheiden sich durch verschiedene Konstanten. ⓘ
Sei sei die Form der Fourier-Transformierten in Form der gewöhnlichen Frequenz ξ. ⓘ
Da ist die alternative Form (die Fourier-Transformierte § Andere Konventionen nennt die nicht-unitäre Form in Winkelfrequenz) hat keinen Faktor in ihrer Definition ⓘ
hat aber einen Faktor von in der entsprechenden Umkehrformel ⓘ
Eine alternative Form (die Fourier-Transformation § Andere Konventionen nennt die unitäre Form in der Winkelfrequenz) hat einen Faktor von in seiner Definition ⓘ
und hat auch denselben Faktor von in der entsprechenden Umkehrformel, wodurch sich eine symmetrische Beziehung ergibt ⓘ
In anderen Konventionen hat die Fourier-Transformation i im Exponenten anstelle von -i, und umgekehrt für die Inversionsformel. Das definiert effektiv als negative Frequenz, denn die entsprechende Spektralkomponente ist Aber viele der Identitäten, die die Fourier-Transformation beinhalten, bleiben in diesen Konventionen gültig, vorausgesetzt, dass alle Terme, die explizit i beinhalten, durch -i ersetzt werden. Um noch mehr Verwirrung zu stiften, sollte man sich bewusst sein, dass Elektrotechniker den Buchstaben i für den Strom verwenden und ihre Form der Transformation normalerweise den Buchstaben j für die imaginäre Einheit anstelle von i verwendet. ⓘ
Bei der Verwendung dimensionsloser Einheiten werden die konstanten Faktoren möglicherweise nicht einmal in der Transformationsdefinition angegeben. In der Wahrscheinlichkeitstheorie wird beispielsweise die charakteristische Funktion Φ der Wahrscheinlichkeitsdichtefunktion f einer Zufallsvariablen X vom kontinuierlichen Typ ohne ein negatives Vorzeichen im Exponential definiert, und da die Einheiten von x ignoriert werden, gibt es auch kein 2π:
(In der Wahrscheinlichkeitstheorie und in der mathematischen Statistik wird die Fourier-Stieltjes-Transformation bevorzugt, weil so viele Zufallsvariablen nicht kontinuierlich sind und keine Dichtefunktion besitzen und man nicht mit Funktionen, sondern mit Verteilungen, d. h. mit Maßen, die "Atome" besitzen, arbeiten muss). ⓘ
Unter dem höheren Gesichtspunkt der Gruppencharaktere, der viel abstrakter ist, verschwinden alle diese willkürlichen Entscheidungen, wie in einem späteren Abschnitt dieses Artikels erläutert wird, der den Begriff der Fourier-Transformation einer Funktion auf einer lokal kompakten abelschen Gruppe behandelt. ⓘ
Gleichmäßige Stetigkeit und das Riemann-Lebesgue-Lemma


Die Fourier-Transformation kann in einigen Fällen für nicht-ganzzahlige Funktionen definiert werden, aber die Fourier-Transformationen von ganzzahligen Funktionen haben mehrere starke Eigenschaften. ⓘ
Die Fouriertransformation f̂ einer beliebigen integrierbaren Funktion f ist gleichmäßig stetig und
Durch das Riemann-Lebesgue-Lemma,
Jedoch, nicht unbedingt integrierbar sein. Zum Beispiel ist die Fourier-Transformation der Rechteckfunktion, die integrierbar ist, die Sinc-Funktion, die nicht Lebesgue-integrierbar ist, weil ihre uneigentlichen Integrale sich analog zu den alternierenden harmonischen Reihen verhalten, indem sie zu einer Summe konvergieren, ohne absolut konvergent zu sein. ⓘ
Es ist im Allgemeinen nicht möglich, die inverse Transformation als Lebesgue-Integral zu schreiben. Wenn jedoch sowohl f als auch integrierbar sind, ist die umgekehrte Gleichheit ⓘ
fast überall gilt. Das heißt, die Fourier-Transformation ist injektiv auf L1(R). (Aber wenn f stetig ist, dann gilt die Gleichheit für jedes x.) ⓘ
Plancherel-Theorem und Parseval's Theorem
Seien f(x) und g(x) ganzzahlig und seien f̂(ξ) und ĝ(ξ) ihre Fouriertransformationen. Wenn f(x) und g(x) auch quadratisch integrabel sind, dann folgt die Parseval-Formel:
wobei der Balken die komplexe Konjugation bezeichnet. ⓘ
Das Plancherel-Theorem, das aus dem oben Gesagten folgt, besagt, dass ⓘ
Das Theorem von Plancherel ermöglicht es, die Fourier-Transformation durch ein Kontinuitätsargument zu einem unitären Operator auf L2(R) zu erweitern. Auf L1(R) ∩ L2(R) stimmt diese Erweiterung mit der ursprünglichen, auf L1(R) definierten Fourier-Transformation überein und vergrößert somit den Bereich der Fourier-Transformation auf L1(R) + L2(R) (und folglich auf Lp(R) für 1 ≤ p ≤ 2). Der Satz von Plancherel hat in den Naturwissenschaften die Bedeutung, dass die Fourier-Transformation die Energie der ursprünglichen Größe bewahrt. Die Terminologie dieser Formeln ist nicht ganz einheitlich. Der Satz von Parseval wurde nur für Fourier-Reihen bewiesen und wurde zuerst von Lyapunov bewiesen. Die Parseval-Formel ist jedoch auch für die Fourier-Transformation sinnvoll, und obwohl sie im Zusammenhang mit der Fourier-Transformation von Plancherel bewiesen wurde, wird sie häufig als Parseval-Formel, Parseval-Relation oder sogar als Parseval-Theorem bezeichnet. ⓘ
Siehe Pontryagin-Dualismus für eine allgemeine Formulierung dieses Konzepts im Zusammenhang mit lokal kompakten abelschen Gruppen. ⓘ
Poisson-Summenformel
Die Poisson-Summationsformel (PSF) ist eine Gleichung, die die Fourier-Reihenkoeffizienten der periodischen Summation einer Funktion mit den Werten der kontinuierlichen Fourier-Transformation der Funktion in Beziehung setzt. Die Poisson-Summationsformel besagt, dass für hinreichend regelmäßige Funktionen f, ⓘ
Es gibt eine Vielzahl nützlicher Formen, die von der Grundformel durch Anwendung der Skalierungs- und Zeitverschiebungseigenschaften der Fouriertransformation abgeleitet werden. Die Formel findet Anwendung in der Technik, der Physik und der Zahlentheorie. Das Dual der Standard-Poisson-Summenformel im Frequenzbereich wird auch als zeitdiskrete Fourier-Transformation bezeichnet. ⓘ
Die Poisson-Summation wird im Allgemeinen mit der Physik periodischer Medien in Verbindung gebracht, z. B. der Wärmeleitung auf einem Kreis. Die fundamentale Lösung der Wärmegleichung auf einem Kreis wird als Thetafunktion bezeichnet. Sie wird in der Zahlentheorie verwendet, um die Transformationseigenschaften von Thetafunktionen zu beweisen, die sich als eine Art modulare Form erweisen, und sie ist allgemeiner mit der Theorie der automorphen Formen verbunden, wo sie auf einer Seite der Selberg-Spurformel erscheint. ⓘ
Differenzierung
Angenommen, f(x) ist eine absolut stetige differenzierbare Funktion, und sowohl f als auch seine Ableitung f′ sind integrierbar. Dann ist die Fourier-Transformation der Ableitung gegeben durch
Allgemeiner ausgedrückt, ist die Fourier-Transformation der n-ten Ableitung f(n) gegeben durch
Durch Anwendung der Fourier-Transformation und unter Verwendung dieser Formeln können einige gewöhnliche Differentialgleichungen in algebraische Gleichungen umgewandelt werden, die viel einfacher zu lösen sind. Aus diesen Formeln ergibt sich auch die Faustregel "f(x) ist dann und nur dann glatt, wenn f̂(ξ) für |ξ| → ∞ schnell auf 0 fällt." Wenn man die analogen Regeln für die inverse Fourier-Transformation anwendet, kann man auch sagen: "f(x) fällt schnell auf 0 für |x| → ∞, wenn und nur wenn f̂(ξ) glatt ist." ⓘ
Satz über die Faltung
Die Fourier-Transformation ist eine Umrechnung zwischen Faltung und Multiplikation von Funktionen. Wenn f(x) und g(x) integrierbare Funktionen mit Fourier-Transformationen f̂(ξ) bzw. ĝ(ξ) sind, dann ist die Fourier-Transformation der Faltung durch das Produkt der Fourier-Transformationen f̂(ξ) und ĝ(ξ) gegeben (bei anderen Konventionen für die Definition der Fourier-Transformation kann ein konstanter Faktor auftreten). ⓘ
Dies bedeutet, dass wenn
wobei ∗ die Faltungsoperation bezeichnet, dann:
In der Theorie linearer zeitinvarianter Systeme (LTI) ist es üblich, g(x) als die Impulsantwort eines LTI-Systems mit dem Eingang f(x) und dem Ausgang h(x) zu interpretieren, da der Ersatz des Einheitsimpulses für f(x) h(x) = g(x) ergibt. In diesem Fall stellt ĝ(ξ) die Frequenzantwort des Systems dar. ⓘ
Lässt sich umgekehrt f(x) als Produkt zweier quadratisch integrierbarer Funktionen p(x) und q(x) zerlegen, so ist die Fourier-Transformierte von f(x) durch die Faltung der jeweiligen Fourier-Transformierten p̂(ξ) und q̂(ξ) gegeben. ⓘ
Kreuzkorrelationstheorem
Auf analoge Weise kann gezeigt werden, dass, wenn h(x) die Kreuzkorrelation von f(x) und g(x) ist:
dann ist die Fourier-Transformierte von h(x):
Als Spezialfall ist die Autokorrelation der Funktion f(x):
wofür ⓘ
Eigenfunktionen
Eine wichtige Wahl einer orthonormalen Basis für L2(R) ist durch die Hermite-Funktionen gegeben ⓘ
wobei Hen(x) die Hermite-Polynome des "Probabilisten" sind, definiert als ⓘ
Nach dieser Konvention für die Fourier-Transformation ergibt sich, dass ⓘ
- . ⓘ
Mit anderen Worten, die Hermite-Funktionen bilden ein vollständiges orthonormales System von Eigenfunktionen für die Fourier-Transformation auf L2(R). Diese Wahl der Eigenfunktionen ist jedoch nicht eindeutig. Es gibt nur vier verschiedene Eigenwerte der Fourier-Transformation (±1 und ±i) und jede Linearkombination von Eigenfunktionen mit demselben Eigenwert ergibt eine andere Eigenfunktion. Daraus folgt, dass L2(R) als direkte Summe von vier Räumen H0, H1, H2 und H3 zerlegt werden kann, wobei die Fourier-Transformation auf Hek einfach durch Multiplikation mit ik wirkt. ⓘ
Da die vollständige Menge der Hermite-Funktionen eine Auflösung der Identität bietet, kann die Fourier-Transformation durch eine solche Summe von Termen dargestellt werden, die mit den oben genannten Eigenwerten gewichtet sind, und diese Summen können explizit summiert werden. Dieser Ansatz zur Definition der Fourier-Transformation wurde erstmals von Norbert Wiener verfolgt. Hermite-Funktionen haben unter anderem die Eigenschaft, dass sie sowohl im Frequenz- als auch im Zeitbereich exponentiell schnell abfallen, und werden daher zur Definition einer Verallgemeinerung der Fourier-Transformation verwendet, nämlich der fraktionalen Fourier-Transformation, die in der Zeit-Frequenz-Analyse verwendet wird. In der Physik wurde diese Transformation von Edward Condon eingeführt. ⓘ
Zusammenhang mit der Heisenberg-Gruppe
Die Heisenberg-Gruppe ist eine bestimmte Gruppe von unitären Operatoren auf dem Hilbert-Raum L2(R) von quadratisch integrierbaren komplexwertigen Funktionen f auf der reellen Linie, die durch die Translationen (Ty f)(x) = f (x + y) und die Multiplikation mit e2πixξ, (Mξ f)(x) = e2πixξ f (x) erzeugt werden. Diese Operatoren sind nicht kommutabel, da ihr (Gruppen-)Kommutator
der die Multiplikation mit der (von x unabhängigen) Konstanten e2πiyξ ∈ U(1) (die Kreisgruppe der komplexen Einheitsmodulzahlen) ist. Als abstrakte Gruppe ist die Heisenberg-Gruppe die dreidimensionale Lie-Gruppe der Tripel (x, ξ, z) ∈ R2 × U(1), mit dem Gruppengesetz
Bezeichnen Sie die Heisenberg-Gruppe mit H1. Das obige Verfahren beschreibt nicht nur die Gruppenstruktur, sondern auch eine standardmäßige unitäre Darstellung von H1 auf einem Hilbert-Raum, die wir mit ρ : H1 → B(L2(R)) bezeichnen. Definieren Sie den linearen Automorphismus von R2 durch
so dass J2 = -I. Dieser J kann zu einem eindeutigen Automorphismus von H1 erweitert werden:
Nach dem Stone-von-Neumann-Theorem sind die unitären Darstellungen ρ und ρ ∘ j unitär äquivalent, so dass es einen eindeutigen Intertwiner W ∈ U(L2(R)) gibt, für den gilt
Dieser Operator W ist die Fourier-Transformation. ⓘ
Viele der Standardeigenschaften der Fourier-Transformation sind unmittelbare Folgen dieses allgemeineren Rahmens. Zum Beispiel ist das Quadrat der Fourier-Transformation, W2, ein Intertwiner, der mit J2 = -I assoziiert ist, und daher ist (W2f)(x) = f (-x) die Spiegelung der ursprünglichen Funktion f. ⓘ
Komplexer Bereich
Das Integral für die Fourier-Transformation
kann für komplexe Werte ihres Arguments ξ untersucht werden. Je nach den Eigenschaften von f kann es sein, dass diese Funktion überhaupt nicht gegen die reelle Achse konvergiert, oder dass sie für alle Werte von ξ = σ + iτ zu einer komplexen analytischen Funktion konvergiert, oder etwas dazwischen. ⓘ
Das Paley-Wiener-Theorem besagt, dass f dann und nur dann glatt (d. h. n-fach differenzierbar für alle positiven ganzen Zahlen n) und kompakt unterstützt ist, wenn f̂ (σ + iτ) eine holomorphe Funktion ist, für die eine Konstante a > 0 existiert, so dass für jede ganze Zahl n ≥ 0,
für irgendeine Konstante C. (In diesem Fall ist f auf [-a, a] gestützt.) Dies kann ausgedrückt werden, indem man sagt, dass f̂ eine ganze Funktion ist, die in σ schnell abnimmt (für feste τ) und in τ exponentiell wächst (gleichmäßig in σ). ⓘ
(Wenn f nicht glatt, sondern nur L2 ist, gilt die Aussage immer noch, sofern n = 0.) Der Raum solcher Funktionen einer komplexen Variablen heißt Paley-Wiener-Raum. Dieses Theorem wurde auf halbeinfache Lie-Gruppen verallgemeinert. ⓘ
Wenn f auf der Halbgeraden t ≥ 0 gestützt wird, dann wird f als "kausal" bezeichnet, da die Impulsantwortfunktion eines physikalisch realisierbaren Filters diese Eigenschaft haben muss, da keine Wirkung ihrer Ursache vorausgehen kann. Paley und Wiener zeigten, dass sich f̂ zu einer holomorphen Funktion auf der komplexen unteren Halbebene τ < 0 ausdehnt, die gegen Null tendiert, wenn τ gegen unendlich geht. Der umgekehrte Fall ist falsch, und es ist nicht bekannt, wie man die Fourier-Transformation einer kausalen Funktion charakterisieren kann. ⓘ
Laplace-Transformation
Die Fourier-Transformation f̂(ξ) ist verwandt mit der Laplace-Transformation F(s), die auch zur Lösung von Differentialgleichungen und zur Analyse von Filtern verwendet wird. ⓘ
Es kann vorkommen, dass eine Funktion f, für die das Fourier-Integral überhaupt nicht auf der reellen Achse konvergiert, dennoch eine komplexe Fourier-Transformation hat, die in einem Bereich der komplexen Ebene definiert ist. ⓘ
Wenn zum Beispiel f(t) exponentiell wächst, d. h.,
für einige Konstanten C, a ≥ 0, dann
konvergent für alle 2πτ < -a, ist die zweiseitige Laplace-Transformation von f. ⓘ
Die üblichere ("einseitige") Version der Laplace-Transformation ist
Wenn f auch kausal und analytisch ist, dann: Die Erweiterung der Fourier-Transformation auf den komplexen Bereich bedeutet also, dass sie die Laplace-Transformation als Spezialfall im Fall von kausalen Funktionen enthält - allerdings mit dem Variablenwechsel s = 2πiξ. ⓘ
Aus einem anderen, vielleicht klassischeren Blickwinkel betrachtet, beinhaltet die Laplace-Transformation aufgrund ihrer Form einen zusätzlichen exponentiellen Regulierungsterm, der sie außerhalb der imaginären Linie konvergieren lässt, auf der die Fourier-Transformation definiert ist. Als solche kann sie für höchstens exponentiell divergente Reihen und Integrale konvergieren, während die ursprüngliche Fourier-Zerlegung dies nicht kann, was die Analyse von Systemen mit divergenten oder kritischen Elementen ermöglicht. Zwei besondere Beispiele aus der linearen Signalverarbeitung sind die Konstruktion von Allpass-Filternetzwerken aus kritischen Kämmen und die Abschwächung von Filtern durch exakte Pol-Nullpunkt-Auslöschung auf dem Einheitskreis. Solche Konstruktionen sind in der Audioverarbeitung üblich, wo ein hochgradig nichtlineares Phasenverhalten gefragt ist, wie z. B. beim Hall. ⓘ
Wenn darüber hinaus für die Signalverarbeitung ausgedehnte impulsartige Impulsantworten gesucht werden, ist es am einfachsten, eine Schaltung zu haben, die eine divergente Zeitantwort erzeugt, und dann deren Divergenz durch eine verzögerte entgegengesetzte und kompensatorische Antwort aufzuheben. In diesem Fall lässt nur die dazwischen liegende Verzögerungsschaltung eine klassische Fourier-Beschreibung zu, was entscheidend ist. Die beiden Schaltkreise an der Seite sind instabil und lassen keine konvergente Fourier-Zerlegung zu. Sie lassen jedoch eine Beschreibung im Laplace-Bereich zu, mit identischen Halbebenen der Konvergenz in der komplexen Ebene (oder im diskreten Fall in der Z-Ebene), in der sich ihre Auswirkungen aufheben. ⓘ
In der modernen Mathematik wird die Laplace-Transformation üblicherweise unter dem Begriff Fourier-Methoden subsumiert. Beide werden unter dem weitaus allgemeineren und abstrakteren Begriff der harmonischen Analyse subsumiert. ⓘ
Umkehrung
Wenn f̂ komplex analytisch ist für a ≤ τ ≤ b, dann ⓘ
durch den Integralsatz von Cauchy. Daher kann die Fourier-Inversionsformel die Integration entlang verschiedener Linien, parallel zur reellen Achse, verwenden. ⓘ
Theorem: Wenn f(t) = 0 für t < 0, und |f(t)| < Cea|t| für einige Konstanten C, a > 0, dann
für jedes τ < -a/2π. ⓘ
Dieses Theorem impliziert die Mellin-Inversionsformel für die Laplace-Transformation,
für beliebige b > a, wobei F(s) die Laplace-Transformation von f(t) ist. ⓘ
Die Hypothesen können wie in den Ergebnissen von Carleman und Hunt dahingehend abgeschwächt werden, dass f(t) e-at L1 ist, vorausgesetzt, dass f in einer geschlossenen Nachbarschaft von t eine beschränkte Variation aufweist (vgl. Satz von Dirichlet-Dini), dass der Wert von f bei t als arithmetisches Mittel der linken und rechten Grenzwerte betrachtet wird und dass die Integrale im Sinne der Cauchy-Hauptwerte betrachtet werden. ⓘ
L2-Versionen dieser Inversionsformeln sind ebenfalls verfügbar. ⓘ
Fourier-Transformation im euklidischen Raum
Die Fourier-Transformation kann in beliebig vielen Dimensionen n definiert werden. Wie im eindimensionalen Fall gibt es viele Konventionen. Für eine integrierbare Funktion f(x) wird in diesem Artikel die Definition verwendet:
Dabei sind x und ξ n-dimensionale Vektoren, und x - ξ ist das Punktprodukt der Vektoren. Alternativ kann ξ als zum dualen Vektorraum gehörig betrachtet werden In diesem Fall wird das Punktprodukt zur Kontraktion von x und ξ, gewöhnlich geschrieben als ⟨x, ξ⟩. ⓘ
Alle oben aufgeführten grundlegenden Eigenschaften gelten für die n-dimensionale Fourier-Transformation, ebenso wie das Theorem von Plancherel und Parseval. Wenn die Funktion integrierbar ist, ist die Fourier-Transformation immer noch gleichmäßig stetig und das Riemann-Lebesgue-Lemma gilt. ⓘ
Unschärferelation
Im Allgemeinen gilt: Je konzentrierter f(x) ist, desto breiter muss seine Fouriertransformation f̂(ξ) sein. Die Skalierungseigenschaft der Fourier-Transformierten besagt: Wenn man eine Funktion in x zusammendrückt, dehnt sich ihre Fourier-Transformierte in ξ aus. Es ist nicht möglich, sowohl eine Funktion als auch ihre Fourier-Transformierte beliebig zu konzentrieren. ⓘ
Der Kompromiss zwischen der Verdichtung einer Funktion und ihrer Fourier-Transformierten kann in Form einer Unschärferelation formalisiert werden, indem man eine Funktion und ihre Fourier-Transformierte als konjugierte Variablen in Bezug auf die symplektische Form im Zeit-Frequenz-Bereich betrachtet: Aus der Sicht der linearen kanonischen Transformation ist die Fourier-Transformierte eine Drehung um 90° im Zeit-Frequenz-Bereich und bewahrt die symplektische Form. ⓘ
Nehmen wir an, f(x) sei eine integrierbare und quadratisch-integrable Funktion. Ohne Verlust der Allgemeinheit nehmen wir an, dass f(x) normalisiert ist:
Aus dem Plancherel-Theorem folgt, dass f̂(ξ) ebenfalls normalisiert ist. ⓘ
Die Streuung um x = 0 kann durch die Streuung um Null gemessen werden, die durch ⓘ
In der Wahrscheinlichkeitsrechnung ist dies das zweite Moment von |f(x)|2 um Null. ⓘ
Die Unschärferelation besagt, dass, wenn f(x) absolut stetig ist und die Funktionen x-f(x) und f′(x) quadratisch integrabel sind, dann ⓘ
- . ⓘ
Die Gleichheit wird nur in dem Fall erreicht ⓘ
wobei σ > 0 willkürlich ist und C1 = 4√2/√σ, so dass f L2-normalisiert ist. Mit anderen Worten: f ist eine (normalisierte) Gaußfunktion mit Varianz σ2, zentriert bei Null, und ihre Fouriertransformierte ist eine Gaußfunktion mit Varianz σ-2. ⓘ
Tatsächlich impliziert diese Ungleichung, dass:
für jedes x0, ξ0 ∈ R. ⓘ
In der Quantenmechanik sind die Impuls- und Positionswellenfunktionen Fourier-Transformationspaare, und zwar bis auf einen Faktor der Planckschen Konstante. Unter Berücksichtigung dieser Konstante wird die obige Ungleichung zur Aussage der Heisenbergschen Unschärferelation. ⓘ
Eine stärkere Unschärferelation ist die Hirschmansche Unschärferelation, die wie folgt ausgedrückt wird:
wobei H(p) die differentielle Entropie der Wahrscheinlichkeitsdichtefunktion p(x) ist:
wobei die Logarithmen eine beliebige Basis haben können, die konsistent ist. Die Gleichheit wird für einen Gauß erreicht, wie im vorherigen Fall. ⓘ
Sinus- und Kosinustransformationen
In Fouriers ursprünglicher Formulierung der Transformation wurden keine komplexen Zahlen verwendet, sondern Sinus und Kosinus. Statistiker und andere verwenden immer noch diese Form. Eine absolut integrierbare Funktion f, für die die Fourier-Inversion gilt, kann in Form echter Frequenzen (unter Vermeidung negativer Frequenzen, die manchmal als physikalisch schwer zu interpretieren gelten) λ erweitert werden durch ⓘ
Dies wird als trigonometrisches Integral oder Fourier-Integral-Expansion bezeichnet. Die Koeffizientenfunktionen a und b können mit Hilfe von Varianten der Fourier-Kosinus-Transformation und der Fourier-Sinus-Transformation ermittelt werden (die Normierungen sind wiederum nicht genormt):
und ⓘ
In der älteren Literatur wird von den beiden Transformationsfunktionen, der Fourier-Kosinus-Transformation a und der Fourier-Sinus-Transformation b, gesprochen. ⓘ
Die Funktion f lässt sich aus der Sinus- und Kosinustransformation wie folgt wiederherstellen ⓘ
zusammen mit trigonometrischen Identitäten. Dies wird als Fouriersche Integralformel bezeichnet. ⓘ
Sphärische Harmonische
Die Menge der homogenen harmonischen Polynome vom Grad k auf Rn sei mit Ak bezeichnet. Die Menge Ak besteht aus den festen sphärischen Harmonischen des Grades k. Die festen sphärischen Harmonischen spielen in höheren Dimensionen eine ähnliche Rolle wie die Hermite-Polynome in der ersten Dimension. Genauer gesagt, wenn f(x) = e-π|x|2P(x) für irgendein P(x) in Ak, dann ist f̂(ξ) = i-k f(ξ). Die Menge Hk sei die Hülle in L2(Rn) von Linearkombinationen von Funktionen der Form f(|x|)P(x), wobei P(x) in Ak liegt. Der Raum L2(Rn) ist dann eine direkte Summe der Räume Hk und die Fourier-Transformation bildet jeden Raum Hk auf sich selbst ab und es ist möglich, die Wirkung der Fourier-Transformation auf jeden Raum Hk zu charakterisieren. ⓘ
Sei f(x) = f0(|x|)P(x) (mit P(x) in Ak), dann ⓘ
wobei ⓘ
Dabei bezeichnet J(n + 2k - 2)/2 die Besselfunktion erster Art mit der Ordnung n + 2k - 2/2. Für k = 0 ergibt sich daraus eine nützliche Formel für die Fourier-Transformation einer Radialfunktion. Dies ist im Wesentlichen die Hankel-Transformation. Außerdem gibt es eine einfache Rekursion für die Fälle n + 2 und n, mit der man z. B. die dreidimensionale Fourier-Transformation einer Radialfunktion aus der eindimensionalen berechnen kann. ⓘ
Restriktionsprobleme
In höheren Dimensionen wird es interessant, Restriktionsprobleme für die Fourier-Transformation zu untersuchen. Die Fourier-Transformation einer integrierbaren Funktion ist stetig und die Einschränkung dieser Funktion auf eine beliebige Menge ist definiert. Für eine quadratisch integrierbare Funktion könnte die Fourier-Transformierte jedoch eine allgemeine Klasse von quadratisch integrierbaren Funktionen sein. Die Restriktion der Fourier-Transformierten einer L2(Rn)-Funktion kann also nicht auf Mengen mit dem Maß 0 definiert werden. Es ist immer noch ein aktives Forschungsgebiet, Restriktionsprobleme in Lp für 1 < p < 2 zu verstehen. Überraschenderweise ist es in einigen Fällen möglich, die Restriktion einer Fourier-Transformierten auf eine Menge S zu definieren, vorausgesetzt S hat eine Krümmung ungleich Null. Der Fall, dass S die Einheitskugel in Rn ist, ist von besonderem Interesse. In diesem Fall besagt der Tomas-Stein-Beschränkungssatz, dass die Beschränkung der Fourier-Transformierten auf die Einheitskugel in Rn ein beschränkter Operator auf Lp ist, sofern 1 ≤ p ≤ 2n + 2/n + 3. ⓘ
Ein bemerkenswerter Unterschied zwischen der Fourier-Transformation in einer Dimension und in höheren Dimensionen betrifft den Partialsummenoperator. Man betrachte eine wachsende Sammlung messbarer Mengen ER, die durch R ∈ (0,∞) indiziert sind: z. B. Kugeln mit dem Radius R, die im Ursprung zentriert sind, oder Würfel mit der Seite 2R. Für eine gegebene integrierbare Funktion f sei die Funktion fR definiert durch:
Nehmen wir außerdem an, dass f ∈ Lp(Rn). Für n = 1 und 1 < p < ∞, wenn man ER = (-R, R) nimmt, dann konvergiert fR gegen f in Lp, wenn R gegen unendlich tendiert, durch die Beschränktheit der Hilbert-Transformation. Naiverweise kann man hoffen, dass dies auch für n > 1 gilt. Wenn man ER als Würfel mit der Seitenlänge R annimmt, dann gilt die Konvergenz immer noch. Ein weiterer natürlicher Kandidat ist die euklidische Kugel ER = {ξ : |ξ| < R}. Damit dieser Partialsummenoperator konvergieren kann, muss der Multiplikator für die Einheitskugel in Lp(Rn) beschränkt sein. Für n ≥ 2 ist es ein berühmtes Theorem von Charles Fefferman, dass der Multiplikator für die Einheitskugel niemals begrenzt ist, es sei denn, p = 2. Wenn p ≠ 2 ist, zeigt dies nicht nur, dass fR nicht zu f in Lp konvergieren kann, sondern dass für einige Funktionen f ∈ Lp(Rn) fR nicht einmal ein Element von Lp ist. ⓘ
Fourier-Transformation auf Funktionsräumen
Auf Lp-Räumen
Auf L1
Die Definition der Fourier-Transformation durch die Integralformel ⓘ
gilt für Lebesgue-integrierbare Funktionen f, d. h. f ∈ L1(Rn). ⓘ
Die Fouriertransformation F : L1(Rn) → L∞(Rn) ist ein beschränkter Operator. Dies folgt aus der Beobachtung, dass ⓘ
was zeigt, dass ihre Operatornorm durch 1 begrenzt ist. Tatsächlich ist sie gleich 1, was man zum Beispiel an der Transformation der Rektfunktion sehen kann. Das Bild von L1 ist eine Teilmenge des Raums C0(Rn) der stetigen Funktionen, die im Unendlichen gegen Null tendieren (Riemann-Lebesgue-Lemma), obwohl es nicht der gesamte Raum ist. In der Tat gibt es keine einfache Charakterisierung des Bildes. ⓘ
Auf L2
Da kompakt gestützte glatte Funktionen integrierbar und dicht in L2(Rn) sind, erlaubt uns das Plancherel-Theorem, die Definition der Fourier-Transformation durch Kontinuitätsargumente auf allgemeine Funktionen in L2(Rn) zu erweitern. Die Fourier-Transformierte in L2(Rn) ist nicht mehr durch ein gewöhnliches Lebesgue-Integral gegeben, obwohl sie durch ein uneigentliches Integral berechnet werden kann, was hier bedeutet, dass für eine L2-Funktion f, ⓘ
wobei der Grenzwert im L2-Sinn genommen wird. (Allgemeiner ausgedrückt: Man kann eine Folge von Funktionen nehmen, die im Schnittpunkt von L1 und L2 liegen und in der L2-Norm zu f konvergieren, und die Fourier-Transformierte von f als die L2-Grenze der Fourier-Transformierten dieser Funktionen definieren). ⓘ
Viele der Eigenschaften der Fourier-Transformierten in L1 lassen sich durch ein geeignetes Grenzwertargument auf L2 übertragen. ⓘ
Außerdem ist F : L2(Rn) → L2(Rn) ein unitärer Operator. Damit ein Operator unitär ist, genügt es zu zeigen, dass er bijektiv ist und das innere Produkt bewahrt. In diesem Fall folgt dies aus dem Fourier-Inversionssatz in Verbindung mit der Tatsache, dass für jedes f, g ∈ L2(Rn) gilt ⓘ
Insbesondere ist das Bild von L2(Rn) selbst unter der Fouriertransformation. ⓘ
Auf anderen Lp
Die Definition der Fourier-Transformation kann auf Funktionen in Lp(Rn) für 1 ≤ p ≤ 2 ausgedehnt werden, indem solche Funktionen in einen fetten Schwanzteil in L2 und einen fetten Körperteil in L1 zerlegt werden. In jedem dieser Räume liegt die Fourier-Transformierte einer Funktion in Lp(Rn) in Lq(Rn), wobei q = p/p - 1 die Hölder-Konjugierte von p ist (gemäß der Hausdorff-Young-Ungleichung). Außer für p = 2 ist das Bild jedoch nicht leicht zu charakterisieren. Weitere Erweiterungen sind eher technischer Natur. Die Fourier-Transformation von Funktionen in Lp für den Bereich 2 < p < ∞ erfordert die Untersuchung von Verteilungen. In der Tat kann gezeigt werden, dass es Funktionen in Lp mit p > 2 gibt, so dass die Fourier-Transformierte nicht als Funktion definiert ist. ⓘ
Temperierte Verteilungen
Man könnte erwägen, den Bereich der Fourier-Transformation von L1 + L2 zu erweitern, indem man verallgemeinerte Funktionen oder Verteilungen betrachtet. Eine Verteilung auf Rn ist eine kontinuierliche lineare Funktion auf dem Raum Cc(Rn) der kompakt unterstützten glatten Funktionen, die mit einer geeigneten Topologie ausgestattet ist. Die Strategie besteht dann darin, die Wirkung der Fourier-Transformation auf Cc(Rn) zu betrachten und durch Dualität zu Verteilungen überzugehen. Das Hindernis dabei ist, dass die Fourier-Transformation Cc(Rn) nicht auf Cc(Rn) abbildet. Tatsächlich kann die Fourier-Transformation eines Elements in Cc(Rn) auf einer offenen Menge nicht verschwinden; siehe die obige Diskussion über die Unschärferelation. Der richtige Raum ist hier der etwas größere Raum der Schwartz-Funktionen. Die Fourier-Transformation ist ein Automorphismus auf dem Schwartz-Raum als topologischem Vektorraum und induziert somit einen Automorphismus auf seinem Dual, dem Raum der temperierten Verteilungen. Zu den temperierten Verteilungen gehören alle oben erwähnten integrierbaren Funktionen sowie gut verhaltene Funktionen mit polynomialem Wachstum und Verteilungen mit kompakter Unterstützung. ⓘ
Zur Definition der Fourier-Transformierten einer temperierten Verteilung seien f und g ganzzahlige Funktionen und f̂ bzw. ĝ ihre Fourier-Transformierten. Dann gehorcht die Fourier-Transformierte der folgenden Multiplikationsformel, ⓘ
Jede integrierbare Funktion f definiert (induziert) eine Verteilung Tf durch die Beziehung ⓘ
für alle Schwartz-Funktionen φ. Es ist also sinnvoll, die Fourier-Transformation T̂f von Tf zu definieren durch ⓘ
für alle Schwartz-Funktionen φ. Erweitert man dies auf alle temperierten Verteilungen T, so erhält man die allgemeine Definition der Fourier-Transformation. ⓘ
Verteilungen können differenziert werden, und die oben erwähnte Kompatibilität der Fourier-Transformation mit Differenzierung und Faltung gilt auch für temperierte Verteilungen. ⓘ
Verallgemeinerungen
Fourier-Stieltjes-Transformation
Die Fourier-Transformation eines endlichen Borel-Maßes μ auf Rn ist gegeben durch:
Diese Transformation besitzt weiterhin viele der Eigenschaften der Fourier-Transformation von integrierbaren Funktionen. Ein bemerkenswerter Unterschied ist, dass das Riemann-Lebesgue-Lemma für Maße versagt. Für den Fall, dass dμ = f(x) dx ist, reduziert sich die obige Formel auf die übliche Definition für die Fourier-Transformation von f. Für den Fall, dass μ die mit einer Zufallsvariablen X verbundene Wahrscheinlichkeitsverteilung ist, ist die Fourier-Stieltjes-Transformation eng mit der charakteristischen Funktion verwandt, aber die typischen Konventionen in der Wahrscheinlichkeitstheorie nehmen eixξ statt e-2πixξ. Für den Fall, dass die Verteilung eine Wahrscheinlichkeitsdichtefunktion hat, reduziert sich diese Definition auf die Fourier-Transformation, die auf die Wahrscheinlichkeitsdichtefunktion angewendet wird, wiederum mit einer anderen Wahl der Konstanten. ⓘ
Die Fourier-Transformation kann verwendet werden, um eine Charakterisierung der Maße zu geben. Der Satz von Bochner charakterisiert, welche Funktionen als Fourier-Stieltjes-Transformation eines positiven Maßes auf dem Kreis auftreten können. ⓘ
Außerdem ist die Dirac-Delta-Funktion, obwohl sie keine Funktion ist, ein endliches Borel-Maß. Ihre Fouriertransformation ist eine konstante Funktion (deren spezifischer Wert von der Form der verwendeten Fouriertransformation abhängt). ⓘ
Örtlich kompakte abelsche Gruppen
Die Fourier-Transformation kann auf jede lokal kompakte abelsche Gruppe verallgemeinert werden. Eine lokal kompakte abelsche Gruppe ist eine abelsche Gruppe, die gleichzeitig ein lokal kompakter topologischer Hausdorff-Raum ist, so dass die Gruppenoperation kontinuierlich ist. Wenn G eine lokal kompakte abelsche Gruppe ist, hat sie ein translationsinvariantes Maß μ, das Haar-Maß. Für eine lokal kompakte abelsche Gruppe G wird die Menge der irreduziblen, d. h. eindimensionalen, unitären Darstellungen als ihre Charaktere bezeichnet. Mit ihrer natürlichen Gruppenstruktur und der Topologie der punktweisen Konvergenz ist die Menge der Charaktere Ĝ selbst eine lokal kompakte abelsche Gruppe, das Pontryagin-Dual von G. Für eine Funktion f in L1(G) ist ihre Fourier-Transformation definiert durch ⓘ
In diesem Fall gilt das Riemann-Lebesgue-Lemma; f̂(ξ) ist eine im Unendlichen verschwindende Funktion auf Ĝ. ⓘ
Die Fourier-Transformation auf T=R/Z ist ein Beispiel; hier ist T eine lokal kompakte abelsche Gruppe, und das Haar-Maß μ auf T kann als das Lebesgue-Maß auf [0,1] betrachtet werden. Betrachten wir die Darstellung von T auf der komplexen Ebene C, die ein 1-dimensionaler komplexer Vektorraum ist. Es gibt eine Gruppe von Darstellungen (die irreduzibel sind, da C 1-dim ist) wobei für . ⓘ
Der Charakter einer solchen Darstellung, d.h. die Spur von für jedes und , ist selbst. Im Fall der Darstellung einer endlichen Gruppe ist die Zeichentabelle der Gruppe G eine Reihe von Vektoren, so dass jede Reihe das Zeichen einer irreduziblen Darstellung von G ist, und diese Vektoren bilden eine Orthonormalbasis des Raums der Klassenfunktionen, die durch das Schursche Lemma von G auf C abgebildet werden. Nun ist die Gruppe T nicht mehr endlich, aber immer noch kompakt, und die Orthonormalität der Zeichentabelle bleibt erhalten. Jede Zeile der Tabelle ist die Funktion von und das innere Produkt zwischen zwei Klassenfunktionen (alle Funktionen sind Klassenfunktionen, da T abelsch ist) ist definiert als mit dem Normierungsfaktor . Die Folge ist eine Orthonormalbasis des Raums der Klassenfunktionen . ⓘ
Für jede Darstellung V einer endlichen Gruppe G, ausgedrückt werden als die Spanne ( sind die Irrepse von G), so dass . Ähnlich für und , . Das Pontriagin-Dual ist und für , ist seine Fourier-Transformierte für . ⓘ
Gelfand-Transformation
Die Fourier-Transformation ist ebenfalls ein Spezialfall der Gelfand-Transformation. In diesem speziellen Zusammenhang ist sie eng mit der oben definierten Pontryagin-Dualitätskarte verwandt. ⓘ
Bei einer abelschen lokal kompakten topologischen Hausdorff-Gruppe G betrachten wir wie zuvor den Raum L1(G), der durch ein Haar-Maß definiert ist. Mit Faltung als Multiplikation ist L1(G) eine abelsche Banach-Algebra. Sie hat auch eine Involution *, die gegeben ist durch ⓘ
Nimmt man die Vervollständigung in Bezug auf die größte mögliche C*-Norm, so erhält man ihre einhüllende C*-Algebra, die so genannte Gruppen-C*-Algebra C*(G) von G. (Jede C*-Norm auf L1(G) ist durch die L1-Norm begrenzt, daher existiert ihr Supremum). ⓘ
Bei einer beliebigen abelschen C*-Algebra A ergibt die Gelfand-Transformation einen Isomorphismus zwischen A und C0(A^), wobei A^ die multiplikativen linearen Funktionale, d. h. eindimensionale Darstellungen, auf A mit der schwachen*-Topologie ist. Die Abbildung ist einfach gegeben durch ⓘ
Es stellt sich heraus, dass die multiplikativen linearen Funktionale von C*(G) nach geeigneter Identifikation genau die Zeichen von G sind, und die Gelfand-Transformation, wenn sie auf die dichte Teilmenge L1(G) beschränkt ist, ist die Fourier-Pontryagin-Transformation. ⓘ
Kompakte nicht-abelsche Gruppen
Die Fourier-Transformation kann auch für Funktionen auf einer nicht-abelschen Gruppe definiert werden, vorausgesetzt, die Gruppe ist kompakt. Lässt man die Annahme außer Acht, dass die zugrunde liegende Gruppe abelsch ist, so müssen irreduzible unitäre Darstellungen nicht immer eindimensional sein. Das bedeutet, dass die Fourier-Transformierte auf einer nicht-abelschen Gruppe Werte als Hilbert-Raum-Operatoren annimmt. Die Fourier-Transformation auf kompakten Gruppen ist ein wichtiges Werkzeug in der Darstellungstheorie und der nichtkommutativen harmonischen Analyse. ⓘ
Sei G eine kompakte topologische Hausdorff-Gruppe. Σ sei die Sammlung aller Isomorphismenklassen der endlich-dimensionalen irreduziblen unitären Darstellungen, zusammen mit einer bestimmten Wahl der Darstellung U(σ) auf dem Hilbert-Raum Hσ endlicher Dimension dσ für jedes σ ∈ Σ. Wenn μ ein endliches Borel-Maß auf G ist, dann ist die Fourier-Stieltjes-Transformation von μ der Operator auf Hσ, der durch ⓘ
wobei U(σ) die komplex-konjugierte Darstellung von U(σ) ist, die auf Hσ wirkt. Wenn μ absolut stetig ist in Bezug auf das linksinvariante Wahrscheinlichkeitsmaß λ auf G, dargestellt als ⓘ
für irgendein f ∈ L1(λ), identifiziert man die Fourier-Transformation von f mit der Fourier-Stieltjes-Transformation von μ. ⓘ
Die Abbildung
definiert einen Isomorphismus zwischen dem Banachraum M(G) endlicher Borelmaße (siehe rca-Raum) und einem geschlossenen Unterraum des Banachraums C∞(Σ), der aus allen durch Σ indizierten Folgen E = (Eσ) von (beschränkten) linearen Operatoren Eσ : Hσ → Hσ besteht, für die die Norm ⓘ
endlich ist. Das "Faltungs-Theorem" besagt, dass dieser Isomorphismus von Banach-Räumen in der Tat ein isometrischer Isomorphismus von C*-Algebren in einen Unterraum von C∞(Σ) ist. Die Multiplikation auf M(G) ist gegeben durch die Faltung von Maßen und die Involution *, definiert durch ⓘ
und C∞(Σ) hat eine natürliche C*-Algebra-Struktur als Hilbert-Raum-Operatoren. ⓘ
Das Peter-Weyl-Theorem gilt, und es folgt eine Version der Fourier-Inversionsformel (Plancherel-Theorem): wenn f ∈ L2(G), dann ⓘ
wobei die Summation als konvergent im Sinne von L2 verstanden wird. ⓘ
Die Verallgemeinerung der Fourier-Transformation auf die nicht-kommutative Situation hat zum Teil auch zur Entwicklung der nicht-kommutativen Geometrie beigetragen. In diesem Zusammenhang ist eine kategoriale Verallgemeinerung der Fourier-Transformation auf nicht-kommutative Gruppen die Tannaka-Krein-Dualität, die die Gruppe der Zeichen durch die Kategorie der Darstellungen ersetzt. Allerdings geht dabei der Zusammenhang mit harmonischen Funktionen verloren. ⓘ
Alternativen
In der Signalverarbeitung ist eine Funktion (der Zeit) eine Darstellung eines Signals mit perfekter Zeitauflösung, aber ohne Frequenzinformation, während die Fourier-Transformierte eine perfekte Frequenzauflösung, aber keine Zeitinformation hat: Der Betrag der Fourier-Transformierten an einem Punkt gibt an, wie viel Frequenzinhalt vorhanden ist, aber der Ort wird nur durch die Phase (Argument der Fourier-Transformierten an einem Punkt) angegeben, und stehende Wellen sind zeitlich nicht lokalisiert - eine Sinuswelle setzt sich ins Unendliche fort, ohne abzufallen. Dies schränkt die Nützlichkeit der Fourier-Transformation für die Analyse von zeitlich begrenzten Signalen ein, insbesondere von Transienten oder anderen Signalen mit endlicher Ausdehnung. ⓘ
Als Alternative zur Fourier-Transformation werden in der Zeit-Frequenz-Analyse Zeit-Frequenz-Transformationen oder Zeit-Frequenz-Verteilungen verwendet, um Signale in einer Form darzustellen, die sowohl Zeit- als auch Frequenzinformationen enthält - gemäß der Unschärferelation besteht ein Kompromiss zwischen diesen beiden. Dabei kann es sich um Verallgemeinerungen der Fourier-Transformation handeln, wie z. B. die Kurzzeit-Fourier-Transformation oder die fraktionierte Fourier-Transformation, oder um andere Funktionen zur Darstellung von Signalen, wie z. B. Wavelet-Transformationen und Chirplet-Transformationen, wobei das Wavelet-Analogon der (kontinuierlichen) Fourier-Transformation die kontinuierliche Wavelet-Transformation ist. ⓘ
Anwendungen
Lineare Operationen, die in einem Bereich (Zeit oder Frequenz) durchgeführt werden, haben entsprechende Operationen im anderen Bereich, die manchmal einfacher durchzuführen sind. Die Operation der Differenzierung im Zeitbereich entspricht der Multiplikation mit der Frequenz, so dass einige Differentialgleichungen im Frequenzbereich leichter zu analysieren sind. Auch die Faltung im Zeitbereich entspricht der einfachen Multiplikation im Frequenzbereich (siehe Faltungssatz). Nachdem die gewünschten Operationen durchgeführt wurden, kann das Ergebnis in den Zeitbereich zurücktransformiert werden. Die harmonische Analyse ist die systematische Untersuchung der Beziehung zwischen dem Frequenz- und dem Zeitbereich, einschließlich der Arten von Funktionen oder Operationen, die im einen oder anderen Bereich "einfacher" sind, und hat tiefe Verbindungen zu vielen Bereichen der modernen Mathematik. ⓘ
Analyse von Differentialgleichungen
Die vielleicht wichtigste Anwendung der Fourier-Transformation ist die Lösung partieller Differentialgleichungen. Viele der Gleichungen der mathematischen Physik des neunzehnten Jahrhunderts können auf diese Weise behandelt werden. Fourier untersuchte die Wärmegleichung, die in einer Dimension und in dimensionslosen Einheiten wie folgt lautet ⓘ
Das etwas schwierigere Beispiel ist die Wellengleichung in einer Dimension, ⓘ
Wie üblich besteht das Problem nicht darin, eine Lösung zu finden: es gibt unendlich viele. Das Problem ist das so genannte "Randproblem": Finden Sie eine Lösung, die die "Randbedingungen" erfüllt ⓘ
Hier sind f und g gegebene Funktionen. Für die Wärmegleichung kann nur eine Randbedingung erforderlich sein (normalerweise die erste). Aber für die Wellengleichung gibt es immer noch unendlich viele Lösungen y, die die erste Randbedingung erfüllen. Wenn man jedoch beide Bedingungen auferlegt, gibt es nur eine mögliche Lösung. ⓘ
Es ist einfacher, die Fourier-Transformation ŷ der Lösung zu finden, als die Lösung direkt zu finden. Das liegt daran, dass die Fourier-Transformation die Differenzierung in eine Multiplikation mit der Fourier-Dualvariablen umwandelt, so dass eine partielle Differentialgleichung, die auf die ursprüngliche Funktion angewendet wird, in eine Multiplikation mit Polynomfunktionen der Dualvariablen umgewandelt wird, die auf die transformierte Funktion angewendet wird. Nachdem ŷ bestimmt ist, können wir die inverse Fourier-Transformation anwenden, um y zu finden. ⓘ
Die Fourier-Methode ist wie folgt. Zunächst ist zu beachten, dass jede Funktion der Formen ⓘ
erfüllt die Wellengleichung. Diese werden die elementaren Lösungen genannt. ⓘ
Zweitens ist zu beachten, dass daher jedes Integral ⓘ
(für beliebige a+, a-, b+, b-) erfüllt die Wellengleichung. (Dieses Integral ist nur eine Art kontinuierliche Linearkombination, und die Gleichung ist linear). ⓘ
Dies ähnelt nun der Formel für die Fourier-Synthese einer Funktion. Tatsächlich handelt es sich um die reelle inverse Fourier-Transformation von a± und b± in der Variablen x. ⓘ
Der dritte Schritt besteht darin, zu untersuchen, wie man die spezifischen unbekannten Koeffizientenfunktionen a± und b± findet, die dazu führen, dass y die Randbedingungen erfüllt. Wir interessieren uns für die Werte dieser Lösungen bei t = 0. Wir setzen also t = 0. Unter der Annahme, dass die Bedingungen für die Fourier-Inversion erfüllt sind, können wir dann die Fourier-Transformationen von Sinus und Kosinus (in der Variablen x) beider Seiten finden und erhalten ⓘ
und ⓘ
Die Ableitung von y nach t und die Anwendung der Fourier-Sinus- und -Kosinus-Transformationen führt zu ⓘ
und ⓘ
Dies sind vier lineare Gleichungen für die vier Unbekannten a± und b± in Form der Fourier-Sinus- und Cosinus-Transformationen der Randbedingungen, die mit elementarer Algebra leicht zu lösen sind, sofern diese Transformationen gefunden werden können. ⓘ
Zusammenfassend lässt sich sagen, dass wir eine Reihe von elementaren Lösungen gewählt haben, die durch ξ parametrisiert sind und deren allgemeine Lösung eine (kontinuierliche) Linearkombination in Form eines Integrals über den Parameter ξ ist. Dieses Integral hatte jedoch die Form eines Fourier-Integrals. Der nächste Schritt bestand darin, die Randbedingungen in Form dieser Integrale auszudrücken und sie mit den gegebenen Funktionen f und g gleichzusetzen. Der letzte Schritt bestand darin, die Fourier-Inversion auszunutzen, indem man die Fourier-Transformation auf beide Seiten anwendet und so Ausdrücke für die Koeffizientenfunktionen a± und b± in Bezug auf die gegebenen Randbedingungen f und g erhält. ⓘ
Von einem höheren Standpunkt aus betrachtet, kann das Fourier-Verfahren konzeptionell umformuliert werden. Da es zwei Variablen gibt, werden wir die Fourier-Transformation sowohl in x als auch in t verwenden, anstatt wie Fourier zu arbeiten, der nur in den räumlichen Variablen transformierte. Man beachte, dass ŷ im Sinne einer Verteilung betrachtet werden muss, da y(x, t) nicht L1 sein wird: Als Welle bleibt sie über die Zeit bestehen und ist somit kein flüchtiges Phänomen. Sie ist jedoch begrenzt und ihre Fourier-Transformation kann daher als Verteilung definiert werden. Die operationellen Eigenschaften der Fourier-Transformation, die für diese Gleichung relevant sind, bestehen darin, dass sie die Differenzierung in x zur Multiplikation mit 2πiξ und die Differenzierung in Bezug auf t zur Multiplikation mit 2πif führt, wobei f die Frequenz ist. Dann wird die Wellengleichung zu einer algebraischen Gleichung in ŷ:
Dies ist gleichbedeutend mit der Forderung, dass ŷ(ξ, f) = 0 ist, es sei denn, ξ = ±f. Dies erklärt sofort, warum die Wahl der elementaren Lösungen, die wir zuvor getroffen haben, so gut funktioniert hat: Offensichtlich sind f̂ = δ(ξ ± f) Lösungen. Wenn wir die Fourier-Inversion auf diese Deltafunktionen anwenden, erhalten wir die elementaren Lösungen, die wir zuvor ausgewählt haben. Aber von einem höheren Standpunkt aus betrachtet man nicht die elementaren Lösungen, sondern den Raum aller Verteilungen, die auf der (entarteten) Kegelform ξ2 - f2 = 0 liegen. ⓘ
Wir können auch die Verteilungen auf der Kegelschnittfläche betrachten, die durch Verteilungen einer Variablen auf der Geraden ξ = f plus Verteilungen auf der Geraden ξ = -f gegeben sind, und zwar wie folgt: wenn Φ eine beliebige Testfunktion ist, ⓘ
wobei s+, und s-, Verteilungen einer Variablen sind. ⓘ
Dann ergibt die Fourier-Inversion für die Randbedingungen etwas sehr Ähnliches wie das, was wir weiter oben konkretisiert hatten (setzen Sie Φ(ξ, f) = e2πi(xξ+tf), was eindeutig polynomiales Wachstum ist):
und ⓘ
Wendet man nun die einvariable Fourier-Transformation in der Variablen x auf diese Funktionen von x an, so erhält man, wie zuvor, zwei Gleichungen in den beiden unbekannten Verteilungen s± (die als gewöhnliche Funktionen betrachtet werden können, wenn die Randbedingungen L1 oder L2 sind). ⓘ
Aus rechnerischer Sicht besteht der Nachteil natürlich darin, dass man zunächst die Fourier-Transformationen der Randbedingungen berechnen, dann die Lösung aus diesen zusammensetzen und anschließend eine inverse Fourier-Transformation berechnen muss. Geschlossene Formeln sind selten, es sei denn, es gibt eine geometrische Symmetrie, die ausgenutzt werden kann, und die numerischen Berechnungen sind wegen der oszillierenden Natur der Integrale schwierig, was die Konvergenz langsam und schwer abschätzbar macht. Für praktische Berechnungen werden daher häufig andere Methoden verwendet. ⓘ
Im zwanzigsten Jahrhundert wurden diese Methoden auf alle linearen partiellen Differentialgleichungen mit Polynomkoeffizienten und durch die Erweiterung des Begriffs der Fourier-Transformation auf Fourier-Integraloperatoren auch auf einige nichtlineare Gleichungen ausgedehnt. ⓘ
Fourier-Transformationsspektroskopie
Die Fourier-Transformation wird auch in der kernmagnetischen Resonanz (NMR) und in anderen Arten der Spektroskopie verwendet, z. B. in der Infrarot-Spektroskopie (FTIR). Bei der NMR wird ein exponentiell geformtes Signal des freien Induktionsabfalls (FID) im Zeitbereich erfasst und im Frequenzbereich durch Fourier-Transformation in eine Lorentzsche Linienform gebracht. Die Fourier-Transformation wird auch in der Magnetresonanztomographie (MRT) und der Massenspektrometrie verwendet. ⓘ
Quantenmechanik
Die Fourier-Transformation ist in der Quantenmechanik in zweierlei Hinsicht nützlich. Zunächst einmal postuliert die grundlegende konzeptionelle Struktur der Quantenmechanik die Existenz von Paaren komplementärer Variablen, die durch die Heisenbergsche Unschärferelation miteinander verbunden sind. So kann beispielsweise die räumliche Variable q eines Teilchens in einer Dimension nur durch den quantenmechanischen "Positionsoperator" gemessen werden, was mit einem Informationsverlust über den Impuls p des Teilchens einhergeht. Daher kann der physikalische Zustand des Teilchens entweder durch eine Funktion, die so genannte "Wellenfunktion", von q oder durch eine Funktion von p beschrieben werden, aber nicht durch eine Funktion von beiden Variablen. Die Variable p wird als konjugierte Variable zu q bezeichnet. In der klassischen Mechanik wäre der physikalische Zustand eines Teilchens (das der Einfachheit halber in einer Dimension existiert) dadurch gegeben, dass sowohl p als auch q gleichzeitig bestimmte Werte zugewiesen werden. Die Menge aller möglichen physikalischen Zustände ist also der zweidimensionale reelle Vektorraum mit einer p-Achse und einer q-Achse, der sogenannte Phasenraum. ⓘ
Im Gegensatz dazu wählt die Quantenmechanik eine Polarisierung dieses Raums in dem Sinne, dass sie einen Unterraum mit der halben Dimension wählt, z. B. nur die q-Achse, aber statt nur Punkte zu betrachten, die Menge aller komplexwertigen "Wellenfunktionen" auf dieser Achse nimmt. Dennoch ist die Wahl der p-Achse eine ebenso gültige Polarisation, die eine andere Darstellung der Menge der möglichen physikalischen Zustände des Teilchens ergibt, die mit der ersten Darstellung durch die Fourier-Transformation verbunden ist ⓘ
Physikalisch realisierbare Zustände sind L2, und daher sind nach dem Plancherel-Theorem auch ihre Fourier-Transformationen L2. (Da q in Entfernungseinheiten und p in Impulseinheiten angegeben ist, macht das Vorhandensein der Planckschen Konstante im Exponenten diesen dimensionslos, wie es auch sein sollte). ⓘ
Daher kann die Fourier-Transformation verwendet werden, um von einer Art der Darstellung des Zustands des Teilchens, durch eine Wellenfunktion der Position, zu einer anderen Art der Darstellung des Zustands des Teilchens überzugehen: durch eine Wellenfunktion des Impulses. Es sind unendlich viele verschiedene Polarisationen möglich, und alle sind gleichermaßen gültig. Die Möglichkeit, Zustände von einer Darstellung in eine andere zu transformieren, ist manchmal sehr praktisch. ⓘ
Die andere Anwendung der Fourier-Transformation in der Quantenmechanik und der Quantenfeldtheorie ist die Lösung der geltenden Wellengleichung. In der nichtrelativistischen Quantenmechanik lautet Schrödingers Gleichung für eine zeitlich veränderliche Wellenfunktion in einer Dimension, die keinen äußeren Kräften unterliegt, wie folgt ⓘ
Dies ist die gleiche Gleichung wie die Wärmegleichung, mit Ausnahme der imaginären Einheit i. Zur Lösung dieser Gleichung können Fourier-Methoden verwendet werden. ⓘ
Bei Vorhandensein eines Potentials, das durch die potentielle Energiefunktion V(x) gegeben ist, wird die Gleichung ⓘ
Die "elementaren Lösungen", wie wir sie oben genannt haben, sind die so genannten "stationären Zustände" des Teilchens, und der Fourier-Algorithmus, wie oben beschrieben, kann immer noch verwendet werden, um das Randwertproblem der zukünftigen Entwicklung von ψ zu lösen, wenn die Werte für t = 0 gegeben sind. Randwertprobleme und die zeitliche Entwicklung der Wellenfunktion sind von geringem praktischem Interesse: Am wichtigsten sind die stationären Zustände. ⓘ
In der relativistischen Quantenmechanik wird die Schrödingergleichung zu einer Wellengleichung, wie sie in der klassischen Physik üblich war, mit dem Unterschied, dass komplexwertige Wellen betrachtet werden. Ein einfaches Beispiel ohne Wechselwirkungen mit anderen Teilchen oder Feldern ist die freie eindimensionale Klein-Gordon-Schrödinger-Fock-Gleichung, dieses Mal in dimensionslosen Einheiten, ⓘ
Dies ist aus mathematischer Sicht dasselbe wie die oben gelöste Wellengleichung der klassischen Physik (allerdings mit einer komplexwertigen Welle, was für die Methoden keinen Unterschied macht). Dies ist in der Quantenfeldtheorie von großem Nutzen: Jede separate Fourier-Komponente einer Welle kann als separater harmonischer Oszillator behandelt und dann quantisiert werden, ein Verfahren, das als "zweite Quantisierung" bekannt ist. Fourier-Methoden wurden angepasst, um auch nicht-triviale Wechselwirkungen zu behandeln. ⓘ
Signalverarbeitung
Die Fourier-Transformation wird für die Spektralanalyse von Zeitreihen verwendet. Bei der statistischen Signalverarbeitung wird die Fourier-Transformation jedoch in der Regel nicht auf das Signal selbst angewendet. Selbst wenn ein reales Signal tatsächlich instationär ist, hat es sich in der Praxis als ratsam erwiesen, ein Signal durch eine Funktion (oder alternativ einen stochastischen Prozess) zu modellieren, die in dem Sinne stationär ist, dass ihre charakteristischen Eigenschaften über die gesamte Zeit konstant sind. Die Fourier-Transformierte einer solchen Funktion existiert nicht im üblichen Sinne, und es hat sich für die Analyse von Signalen als nützlicher erwiesen, stattdessen die Fourier-Transformierte ihrer Autokorrelationsfunktion zu verwenden. ⓘ
Die Autokorrelationsfunktion R einer Funktion f ist definiert durch ⓘ
Diese Funktion ist eine Funktion der Zeitspanne τ, die zwischen den zu korrelierenden Werten von f verstreicht. ⓘ
Für die meisten in der Praxis vorkommenden Funktionen f ist R eine begrenzte gerade Funktion der Zeitverzögerung τ und für typische verrauschte Signale erweist sie sich als gleichmäßig stetig mit einem Maximum bei τ = 0. ⓘ
Die Autokorrelationsfunktion, die korrekter als Autokovarianzfunktion bezeichnet wird, sofern sie nicht in geeigneter Weise normiert ist, misst die Stärke der Korrelation zwischen den durch eine Zeitverzögerung getrennten Werten von f. Auf diese Weise wird nach der Korrelation von f mit seiner eigenen Vergangenheit gesucht. Sie ist auch für andere statistische Aufgaben als die Analyse von Signalen nützlich. Wenn zum Beispiel f(t) die Temperatur zum Zeitpunkt t darstellt, erwartet man eine starke Korrelation mit der Temperatur mit einer Zeitverzögerung von 24 Stunden. ⓘ
Sie besitzt eine Fourier-Transformation, ⓘ
Diese Fourier-Transformation wird als Leistungsspektraldichtefunktion von f bezeichnet. (Wenn nicht zuvor alle periodischen Komponenten aus f herausgefiltert werden, wird dieses Integral divergieren, aber es ist einfach, solche Periodizitäten herauszufiltern). ⓘ
Das Leistungsspektrum, das durch diese Dichtefunktion P angegeben wird, misst den Anteil der Frequenz ξ an der Varianz der Daten. Bei elektrischen Signalen ist die Varianz proportional zur durchschnittlichen Leistung (Energie pro Zeiteinheit), und so beschreibt das Leistungsspektrum, wie viel die verschiedenen Frequenzen zur durchschnittlichen Leistung des Signals beitragen. Dieses Verfahren wird als Spektralanalyse von Zeitreihen bezeichnet und ist analog zur üblichen Varianzanalyse von Daten, die keine Zeitreihen sind (ANOVA). ⓘ
Die Kenntnis darüber, welche Frequenzen in diesem Sinne "wichtig" sind, ist für den richtigen Entwurf von Filtern und für die richtige Bewertung von Messgeräten entscheidend. Es kann auch für die wissenschaftliche Analyse der Phänomene nützlich sein, die für die Erzeugung der Daten verantwortlich sind. ⓘ
Das Leistungsspektrum eines Signals kann auch näherungsweise direkt gemessen werden, indem die durchschnittliche Leistung gemessen wird, die in einem Signal verbleibt, nachdem alle Frequenzen außerhalb eines schmalen Bandes herausgefiltert wurden. ⓘ
Die Spektralanalyse wird auch für visuelle Signale durchgeführt. Das Leistungsspektrum ignoriert alle Phasenbeziehungen, was für viele Zwecke gut genug ist, aber für Videosignale müssen auch andere Arten der Spektralanalyse verwendet werden, wobei immer noch die Fourier-Transformation als Werkzeug verwendet wird. ⓘ
Andere Notationen
Andere gängige Bezeichnungen für f̂(ξ) sind:
Die Bezeichnung der Fourier-Transformation mit einem Großbuchstaben, der dem Buchstaben der zu transformierenden Funktion entspricht (z. B. f(x) und F(ξ)), ist besonders in den Natur- und Ingenieurwissenschaften üblich. In der Elektronik wird oft Omega (ω) anstelle von ξ verwendet, da es als Winkelfrequenz interpretiert wird. Manchmal wird es als F(jω) geschrieben, wobei j die imaginäre Einheit ist, um die Beziehung zur Laplace-Transformation zu verdeutlichen, und manchmal wird es informell als F(2πf) geschrieben, um die gewöhnliche Frequenz zu verwenden. In einigen Kontexten wie der Teilchenphysik wird das gleiche Symbol verwendet. sowohl für eine Funktion als auch für ihre Fourier-Transformation verwendet werden, wobei sich die beiden nur durch ihr Argument unterscheiden: würde sich wegen des Impulsarguments auf die Fouriertransformation beziehen, während sich aufgrund des Positionsarguments auf die ursprüngliche Funktion beziehen würde. Obwohl Tilden verwendet werden können wie in verwendet werden, um Fourier-Transformationen anzuzeigen, können Tilden auch verwendet werden, um eine Modifikation einer Größe mit einer Lorentz-invarianteren Form anzuzeigen, z. B. , ist also Vorsicht geboten. ⓘ
Die Interpretation der komplexen Funktion f̂(ξ) kann erleichtert werden, indem man sie in Polarkoordinatenform ausdrückt ⓘ
in Form der beiden reellen Funktionen A(ξ) und φ(ξ) ausgedrückt wird, wobei:
ist die Phase (siehe arg-Funktion). ⓘ
Dann kann die inverse Transformation geschrieben werden:
die eine Rekombination aller Frequenzkomponenten von f(x) ist. Jede Komponente ist eine komplexe Sinuskurve der Form e2πixξ, deren Amplitude A(ξ) ist und deren anfänglicher Phasenwinkel (bei x = 0) φ(ξ) ist. ⓘ
Die Fourier-Transformation kann als eine Abbildung auf Funktionsräume betrachtet werden. Diese Abbildung wird hier mit F bezeichnet, und F(f) bezeichnet die Fourier-Transformierte der Funktion f. Diese Abbildung ist linear, was bedeutet, dass F auch als lineare Transformation auf dem Funktionsraum betrachtet werden kann, und impliziert, dass die Standardnotation in der linearen Algebra für die Anwendung einer linearen Transformation auf einen Vektor (hier die Funktion f) verwendet werden kann, um F f anstelle von F(f) zu schreiben. Da das Ergebnis der Anwendung der Fourier-Transformation wiederum eine Funktion ist, können wir uns für den Wert dieser Funktion interessieren, der bei dem Wert ξ für ihre Variable ausgewertet wird, und dieser wird entweder als F f(ξ) oder als (F f)(ξ) bezeichnet. Dabei ist zu beachten, dass im ersten Fall implizit davon ausgegangen wird, dass F zuerst auf f angewendet und dann die resultierende Funktion nach ξ ausgewertet wird und nicht umgekehrt. ⓘ
In der Mathematik und verschiedenen angewandten Wissenschaften ist es oft notwendig, zwischen einer Funktion f und dem Wert von f zu unterscheiden, wenn seine Variable gleich x ist, bezeichnet als f(x). Dies bedeutet, dass eine Schreibweise wie F(f(x)) formal als Fourier-Transformation der Werte von f bei x interpretiert werden kann. Trotz dieses Mangels wird die vorherige Schreibweise häufig verwendet, wenn eine bestimmte Funktion oder eine Funktion einer bestimmten Variablen transformiert werden soll. Ein Beispiel, ⓘ
wird manchmal verwendet, um auszudrücken, dass die Fourier-Transformierte einer Rechteckfunktion eine Sinc-Funktion ist, oder ⓘ
wird verwendet, um die Verschiebungseigenschaft der Fouriertransformation auszudrücken. ⓘ
Beachten Sie, dass das letzte Beispiel nur unter der Annahme korrekt ist, dass die transformierte Funktion eine Funktion von x und nicht von x0 ist. ⓘ
Andere Konventionen
Die Fourier-Transformierte kann auch in Form der Winkelfrequenz geschrieben werden:
wobei die Einheit Radiant pro Sekunde ist. ⓘ
Die Substitution von ξ = ω/2π in den obigen Formeln führt zu dieser Konvention:
Unter dieser Konvention wird die inverse Transformation zu:
Im Gegensatz zur Konvention in diesem Artikel ist die Fourier-Transformation, wenn sie auf diese Weise definiert wird, nicht mehr eine unitäre Transformation auf L2(Rn). Es besteht auch weniger Symmetrie zwischen den Formeln für die Fourier-Transformation und ihre Umkehrung. ⓘ
Eine andere Konvention besteht darin, den Faktor von (2π)n gleichmäßig auf die Fourier-Transformation und ihre Inverse aufzuteilen, was zu Definitionen führt:
Unter dieser Konvention ist die Fouriertransformation wieder eine unitäre Transformation auf L2(Rn). Sie stellt auch die Symmetrie zwischen der Fouriertransformation und ihrer Inversen wieder her. ⓘ
Variationen aller drei Konventionen lassen sich durch Konjugation des komplex-exponentiellen Kerns sowohl der Vorwärts- als auch der Rückwärtstransformation erzeugen. Die Vorzeichen müssen dabei entgegengesetzt sein. Ansonsten ist die Wahl (wieder) eine Frage der Konvention. ⓘ
| gewöhnliche Frequenz ξ (Hz) | einheitlich | |
|---|---|---|
| Winkelfrequenz ω (rad/s) | einheitlich | |
| nicht-einheitlich |
| gewöhnliche Frequenz ξ (Hz) | einheitlich | |
|---|---|---|
| Winkelfrequenz ω (rad/s) | einheitlich | |
| nicht-einheitlich |
Wie oben erläutert, ist die charakteristische Funktion einer Zufallsvariablen dasselbe wie die Fourier-Stieltjes-Transformation ihres Verteilungsmaßes, aber in diesem Zusammenhang ist es typisch, eine andere Konvention für die Konstanten zu verwenden. Typischerweise ist die charakteristische Funktion definiert als
Wie bei der obigen Konvention der "nicht-einheitlichen Winkelfrequenz" erscheint der Faktor 2π weder in der Normierungskonstante noch im Exponenten. Im Gegensatz zu den oben genannten Konventionen wird bei dieser Konvention das umgekehrte Vorzeichen im Exponenten verwendet. ⓘ
Berechnungsmethoden
Die geeignete Berechnungsmethode hängt weitgehend davon ab, wie die ursprüngliche mathematische Funktion dargestellt wird und wie die gewünschte Form der Ausgangsfunktion aussieht. ⓘ
Da die grundlegende Definition einer Fourier-Transformation ein Integral ist, werden Funktionen, die als geschlossene Ausdrücke ausgedrückt werden können, üblicherweise berechnet, indem das Integral analytisch bearbeitet wird, um einen geschlossenen Ausdruck in der konjugierten Variablen der Fourier-Transformation als Ergebnis zu erhalten. Diese Methode wird verwendet, um Tabellen von Fourier-Transformationen zu erstellen, einschließlich derjenigen in der folgenden Tabelle (Fourier-Transformation#Tabellen wichtiger Fourier-Transformationen). ⓘ
Viele Computeralgebra-Systeme wie Matlab und Mathematica, die zur symbolischen Integration fähig sind, können Fourier-Transformationen analytisch berechnen. Um beispielsweise die Fourier-Transformierte von f(t) = cos(6πt) e-πt2 zu berechnen, könnte man den folgenden Befehl eingeben integriere cos(6*pi*t) exp(-pi*t^2) exp(-i*2*pi*f*t) von -inf bis inf in Wolfram Alpha eingeben. ⓘ
Numerische Integration von Funktionen in geschlossener Form
Wenn die Eingangsfunktion in geschlossener Form vorliegt und die gewünschte Ausgangsfunktion eine Reihe von geordneten Paaren (z. B. eine Wertetabelle, aus der ein Graph erzeugt werden kann) über einen bestimmten Bereich ist, dann kann die Fourier-Transformation durch numerische Integration bei jedem Wert der konjugierten Fourier-Variablen (z. B. Frequenz), für die ein Wert der Ausgangsvariablen gewünscht wird, erzeugt werden. Beachten Sie, dass bei dieser Methode für jeden Frequenzwert, für den ein Wert der Fourier-Transformation gewünscht wird, eine separate numerische Integration berechnet werden muss. Der Ansatz der numerischen Integration funktioniert bei einer viel breiteren Klasse von Funktionen als der analytische Ansatz, da er Ergebnisse für Funktionen liefert, die keine geschlossene Form von Fourier-Transformierten-Integralen haben. ⓘ
Numerische Integration einer Reihe von geordneten Paaren
Wenn die Eingangsfunktion eine Reihe von geordneten Paaren ist (z. B. eine Zeitreihe aus der wiederholten Messung einer Ausgangsvariablen über ein Zeitintervall), dann muss auch die Ausgangsfunktion eine Reihe von geordneten Paaren sein (z. B. eine komplexe Zahl im Vergleich zur Frequenz über einen bestimmten Frequenzbereich), es sei denn, es werden bestimmte Annahmen und Näherungen gemacht, die es ermöglichen, die Ausgangsfunktion durch einen Ausdruck in geschlossener Form zu approximieren. Im allgemeinen Fall, in dem davon ausgegangen wird, dass die verfügbaren Eingangsreihen geordneter Paare Abtastwerte sind, die eine kontinuierliche Funktion über ein Intervall darstellen (z. B. Amplitude gegen Zeit), können die Reihen geordneter Paare, die die gewünschte Ausgangsfunktion darstellen, durch numerische Integration der Eingangsdaten über das verfügbare Intervall bei jedem Wert der konjugierten Fourier-Variablen (z. B. Frequenz), für die der Wert der Fourier-Transformation gewünscht wird, erhalten werden. ⓘ
Die explizite numerische Integration über die geordneten Paare kann den Fourier-Transformationsausgangswert für jeden gewünschten Wert der konjugierten Fourier-Transformationsvariablen (z. B. Frequenz) ergeben, so dass ein Spektrum bei jeder gewünschten Schrittgröße und über jeden gewünschten Variablenbereich für die genaue Bestimmung von Amplituden, Frequenzen und Phasen entsprechend isolierten Spitzenwerten erzeugt werden kann. Im Gegensatz zu den Einschränkungen der DFT- und FFT-Methoden kann die explizite numerische Integration eine beliebige Schrittweite haben und die Fourier-Transformation über einen beliebigen Bereich der konjugierten Fourier-Transformationsvariablen (z. B. die Frequenz) berechnen. ⓘ
Diskrete Fourier-Transformationen und schnelle Fourier-Transformationen
Wenn die geordneten Paare, die die ursprüngliche Eingangsfunktion repräsentieren, in ihrer Eingangsvariablen in gleichen Abständen angeordnet sind (z. B. gleiche Zeitschritte), dann wird die Fourier-Transformation als diskrete Fourier-Transformation (DFT) bezeichnet, die entweder durch explizite numerische Integration, durch explizite Auswertung der DFT-Definition oder durch schnelle Fourier-Transformationsmethoden (FFT) berechnet werden kann. Im Gegensatz zur expliziten Integration der Eingabedaten führt die Verwendung der DFT- und FFT-Methoden zu Fourier-Transformationen, die durch geordnete Paare mit einer Schrittweite beschrieben werden, die dem Kehrwert des ursprünglichen Abtastintervalls entspricht. Wenn beispielsweise die Eingangsdaten alle 10 Sekunden abgetastet werden, hat die Ausgabe der DFT- und FFT-Methoden einen Frequenzabstand von 0,1 Hz. ⓘ
Tabellen mit wichtigen Fourier-Transformationen
Die folgenden Tabellen enthalten einige Fourier-Transformationen in geschlossener Form. Für die Funktionen f(x), g(x) und h(x) werden ihre Fourier-Transformationen mit f̂, ĝ bzw. ĥ bezeichnet. Es werden nur die drei gebräuchlichsten Konventionen berücksichtigt. Es mag nützlich sein, zu bemerken, dass Eintrag 105 eine Beziehung zwischen der Fourier-Transformierten einer Funktion und der ursprünglichen Funktion angibt, was als Beziehung zwischen der Fourier-Transformierten und ihrer Inversen angesehen werden kann. ⓘ
Funktionale Beziehungen, eindimensional
Die Fourier-Transformationen in dieser Tabelle sind in Erdélyi (1954) oder Kammler (2000, Anhang) zu finden. ⓘ
| Funktion | Fourier-Transformierte unitär, gewöhnliche Frequenz |
Fourier-Transformierte unitär, Winkelfrequenz |
Fourier-Transformierte nicht-unitäre, Winkelfrequenz |
Bemerkungen ⓘ | |
|---|---|---|---|---|---|
| Definition | |||||
| 101 | Linearität | ||||
| 102 | Verschiebung im Zeitbereich | ||||
| 103 | Verschiebung im Frequenzbereich, Dual von 102 | ||||
| 104 | a| groß ist, dann ist f(ax) um 0 konzentriert und breitet sich aus und flacht ab. | ||||
| 105 | Dualität. Hier muss f̂ nach der gleichen Methode wie die Fourier-Transformations-Spalte berechnet werden. Ergibt sich aus dem Vertauschen der "Dummy"-Variablen von x und ξ oder ω oder ν. | ||||
| 106 | da f eine Schwartz-Funktion ist | ||||
| 107 | Dies ist das Dual von 106 | ||||
| 108 | Die Schreibweise f ∗ g bezeichnet die Faltung von f und g - diese Regel ist das Faltungs-Theorem | ||||
| 109 | Dies ist das Dual von 108 | ||||
| 110 | Für f(x) rein reell | Hermitsche Symmetrie. z bezeichnet die komplex Konjugierte. | |||
| 111 | Für f(x) rein reell und gerade | f̂(ξ), f̂(ω) und f̂(ν) sind rein reelle gerade Funktionen. | |||
| 112 | Für f(x) rein reell und ungerade | f̂(ξ), f̂(ω) und f̂(ν) sind rein imaginäre ungerade Funktionen. | |||
| 113 | Für f(x) rein imaginär | z bezeichnet die konjugierte komplexe Funktion. | |||
| 114 | Komplexe Konjugation, Verallgemeinerung von 110 und 113 | ||||
| 115 | Dies folgt aus den Regeln 101 und 103 unter Verwendung der Eulerschen Formel: | ||||
| 116 | Dies folgt aus 101 und 103 unter Verwendung der Eulerschen Formel: | ||||
Quadratisch-integrable Funktionen, eindimensional
Die Fourier-Transformationen in dieser Tabelle können in Campbell & Foster (1948), Erdélyi (1954) oder Kammler (2000, Anhang) nachgelesen werden. ⓘ
| Funktion | Fourier-Transformierte unitär, gewöhnliche Frequenz |
Fourier-Transformierte unitär, Winkelfrequenz |
Fourier-Transformierte nicht-unitäre, Winkelfrequenz |
Bemerkungen ⓘ | |
|---|---|---|---|---|---|
| 201 | Der Rechteckimpuls und die normalisierte sinc-Funktion, hier definiert als sinc(x) = sin(πx)/πx | ||||
| 202 | Dual der Regel 201. Die Rechteckfunktion ist ein idealer Tiefpassfilter, und die sinc-Funktion ist die nicht kausale Impulsantwort eines solchen Filters. Die sinc-Funktion ist hier definiert als sinc(x) = sin(πx)/πx | ||||
| 203 | Die Funktion tri(x) ist die Dreiecksfunktion | ||||
| 204 | Dual der Regel 203. | ||||
| 205 | Die Funktion u(x) ist die Heaviside-Einheitsschrittfunktion und a > 0. | ||||
| 206 | Dies zeigt, dass für die unitäre Fourier-Transformation die Gaußsche Funktion e-αx2 ihre eigene Fourier-Transformation für eine bestimmte Wahl von α ist. Damit sie integrabel ist, muss Re(α) > 0 sein. | ||||
| 207 | Dies wird als komplexe Sinuskurve mit quadratischer Phase oder als "Chirp"-Funktion bezeichnet. | ||||
| 208 | Für Re(a) > 0, d. h. die Fourier-Transformierte einer zweiseitig abklingenden Exponentialfunktion ist eine Lorentzsche Funktion. | ||||
| 209 | Die hyperbolische Sekante ist ihre eigene Fouriertransformation | ||||
| 210 | Hn ist das Hermite-Polynom n-ter Ordnung. Wenn a = 1 ist, sind die Gauß-Hermite-Funktionen Eigenfunktionen des Fourier-Transformierten. Für eine Herleitung siehe Hermite-Polynom. Die Formel reduziert sich auf 206 für n = 0. |
Verteilungen, eindimensional
Die Fourier-Transformationen in dieser Tabelle sind in Erdélyi (1954) oder Kammler (2000, Anhang) zu finden. ⓘ
| Funktion | Fourier-Transformierte unitär, gewöhnliche Frequenz |
Fourier-Transformierte unitär, Winkelfrequenz |
Fourier-Transformierte nicht-unitäre, Winkelfrequenz |
Bemerkungen ⓘ | |
|---|---|---|---|---|---|
| 301 | Die Verteilung δ(ξ) bezeichnet die Dirac-Delta-Funktion. | ||||
| 302 | Dual der Regel 301. | ||||
| 303 | Dies folgt aus 103 und 301. | ||||
| 304 | Dies folgt aus den Regeln 101 und 303 unter Verwendung der Eulerschen Formel: | ||||
| 305 | Dies folgt aus 101 und 303 unter Verwendung von | ||||
| 306 | Dies folgt aus 101 und 207 unter Verwendung von | ||||
| 307 | Dies folgt aus 101 und 207 unter Verwendung von | ||||
| 308 | Hier ist n eine natürliche Zahl und δ(n)(ξ) die n-te Verteilungsableitung der Dirac-Deltafunktion. Diese Regel ergibt sich aus den Regeln 107 und 301. Kombiniert man diese Regel mit 101, kann man alle Polynome umformen. | ||||
| Dual der Regel 308. δ(n)(ξ) ist die n-te Verteilungsableitung der Dirac-Delta-Funktion. Diese Regel folgt aus 106 und 302. | |||||
| 309 | Hier ist sgn(ξ) die Vorzeichenfunktion. Man beachte, dass 1/x keine Verteilung ist. Es ist notwendig, den Cauchy-Hauptwert zu verwenden, wenn man gegen Schwartz-Funktionen testet. Diese Regel ist bei der Untersuchung der Hilbert-Transformation nützlich. | ||||
| 310 | 1/xn ist die homogene Verteilung, die durch die Verteilungsableitung definiert ist | ||||
| 311 | x|α ist eine lokal integrierbare Funktion und damit eine temperierte Verteilung. Die Funktion α ↦ |x|α ist eine holomorphe Funktion von der rechten Halbebene zum Raum der temperierten Verteilungen. Sie lässt eine eindeutige meromorphe Erweiterung zu einer temperierten Verteilung zu, auch bezeichnet als |x|α für α ≠ -1, -3, ... (Siehe homogene Verteilung.) | ||||
| Spezialfall von 311. | |||||
| 312 | Das Dual der Regel 309. Diesmal müssen die Fourier-Transformationen als Cauchy-Hauptwert betrachtet werden. | ||||
| 313 | Die Funktion u(x) ist die Heaviside-Einheitsschrittfunktion; dies folgt aus den Regeln 101, 301 und 312. | ||||
| 314 | Diese Funktion ist als Dirac-Kamm-Funktion bekannt. Dieses Ergebnis lässt sich aus 302 und 102 ableiten, zusammen mit der Tatsache, dass als Verteilungen. | ||||
| 315 | Die Funktion J0(x) ist die Besselfunktion der ersten Art nullter Ordnung. | ||||
| 316 | Dies ist eine Verallgemeinerung von 315. Die Funktion Jn(x) ist die Besselfunktion erster Art n-ter Ordnung. Die Funktion Tn(x) ist das Tschebyscheff-Polynom der ersten Art. | ||||
| 317 | ξ|,1/|ω|,1/|ν| gegen Schwartz-Funktionen. Die Details können den Koeffizienten der Deltafunktion verändern. | ||||
| 318 | Diese Formel gilt für 1 > α > 0. Verwenden Sie die Differenzierung, um die Formel für höhere Exponenten abzuleiten. u ist die Heaviside-Funktion. |
Zweidimensionale Funktionen
| Funktion | Fourier-Transformierte unitär, gewöhnliche Frequenz |
Fourier-Transformierte unitär, Winkelfrequenz |
Fourier-Transformierte nicht-unitäre, Winkelfrequenz |
Bemerkungen ⓘ | |
|---|---|---|---|---|---|
| 400 | Die Variablen ξx, ξy, ωx, ωy, νx, νy sind reelle Zahlen. Die Integrale werden über die gesamte Ebene genommen. | ||||
| 401 | Beide Funktionen sind Gauß-Funktionen, die nicht unbedingt ein Einheitsvolumen haben. | ||||
| 402 | Die Funktion ist definiert durch circ(r) = 1 für 0 ≤ r ≤ 1, und ist ansonsten 0. Das Ergebnis ist die Amplitudenverteilung der Airy-Scheibe und wird durch J1 (die Bessel-Funktion erster Ordnung) ausgedrückt. | ||||
| 403 | Dies ist die Hankel-Transformation von r-1, eine 2-D-Fourier-"Selbsttransformation". | ||||
| 404 |
Formeln für allgemeine n-dimensionale Funktionen
| Funktion | Fourier-Transformierte unitär, gewöhnliche Frequenz |
Fourier-Transformierte unitär, Winkelfrequenz |
Fourier-Transformierte nicht-unitäre, Winkelfrequenz |
Bemerkungen ⓘ | |
|---|---|---|---|---|---|
| 500 | |||||
| 501 | Die Funktion χ[0, 1] ist die Indikatorfunktion des Intervalls [0, 1]. Die Funktion Γ(x) ist die Gammafunktion. Die Funktion Jn/2 + δ ist eine Besselfunktion erster Art mit der Ordnung n/2 + δ. Nimmt man n = 2 und δ = 0, so erhält man 402. | ||||
| 502 | Siehe Riesz-Potenzial, wobei die Konstante gegeben ist durch Die Formel gilt auch für alle α ≠ n, n + 2, ... durch analytische Fortsetzung, aber dann müssen die Funktion und ihre Fourier-Transformierten als geeignet regularisierte temperierte Verteilungen verstanden werden. Siehe homogene Verteilung. | ||||
| 503 | Dies ist die Formel für eine auf 1 normierte multivariate Normalverteilung mit einem Mittelwert von 0. Die fettgedruckten Variablen sind Vektoren oder Matrizen. In Anlehnung an die Notation der vorgenannten Seite ist Σ = σ σT und Σ-1 = σ-T σ-1 | ||||
| 504 | Hier Re(α) > 0 |
Anwendungsfälle
Kompressionsverfahren für die digitale Kommunikation
Die Kompression von digitalen Daten auf Basis der Fourier-Transformation ist eine zentrale Technologie für Kommunikation, Datenaustausch und Streaming von Medien im (mobilen) Internet. ⓘ
Beispielsweise wird zur Kompression von Audio-Daten (etwa um eine MP3 Datei zu erzeugen) das Audio-Signal in den Frequenz-Raum transformiert. Die Transformation erfolgt über das Verfahren der (modifizierten) diskreten Kosinustransformation, welches der schnellen Fourier-Transformation ähnelt. Im Frequenzraum werden dann alle Frequenzen, die Menschen nicht hören können oder die nur wenig zum subjektiven Empfinden des Klangs beitragen, entfernt. Das Ergebnis wird im letzten Schritt aus dem Frequenz-Raum rücktransformiert – daraus erhält man, auf Grund des verringerten Frequenzumfangs, eine deutlich kleinere (komprimierte) Audio-Datei. ⓘ
In vergleichbaren Verfahren können Bilder (JPEG Kompression) oder Filme (MPEG-4) komprimiert werden. ⓘ
Signalanalyse
In der Signalanalyse werden mittels Fourier-Transformation Frequenzanalysen von Signalen durchgeführt. Hierzu wird das Verfahren der diskreten Fourier-Transformation bzw. der schnellen Fourier-Transformation genutzt. Ein Beispiel für die Vielzahl von technischen Anwendungen ist die Nutzung der Signalanalyse bei der Erstellung von Bildern mittels Magnetresonanztomographie. ⓘ
Beispiel Signalanalyse in der Akustik
Der reine Kammerton ist eine Sinuswelle mit der Frequenz 440 Hz, also 440 Schwingungen pro Sekunde. Eine ideale Stimmgabel gibt genau dieses Sinussignal ab. Der gleiche Ton gespielt mit einem anderen Musikinstrument (nicht-ideale Stimmgabel), ist eine Zusammensetzung/Überlagerung aus Wellen verschiedener Wellenlängen. Diese sind bezüglich ihrer Frequenz normalerweise ganzzahlige Vielfache der Frequenz des Grundtons. Die Zusammensetzung und jeweilige Amplitude dieser Wellen ist bestimmend für die Klangfarbe jedes Musikinstruments. Nur die Welle mit der größten Wellenlänge, der Grundton des Signals, hat dabei die Frequenz 440 Hz. Die anderen Wellen, die Obertöne, haben höhere Frequenzen. ⓘ
An der Fourier-Transformierten des Tonsignals kann man direkt die verschiedenen Frequenzen/Wellenlängen der Wellenzusammensetzung ablesen. Diese Eigenschaft kann man beispielsweise für die automatische Erkennung von Tonhöhen und Musikinstrumenten in einem Tonsignal ausnutzen. ⓘ
Fourier-Transformation von L2-Funktionen
Differentiationsregel
Falls die Funktion schwach differenzierbar ist, gibt es eine Differentiationsregel analog zu denen für Schwarzfunktionen. Sei also eine k-mal schwach differenzierbare L2-Funktion und ein Multiindex mit . Dann gilt
- . ⓘ





































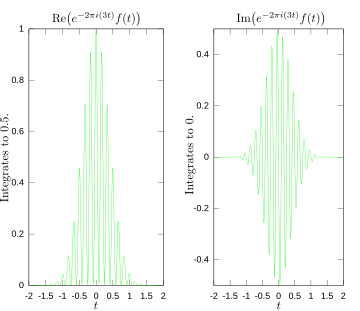
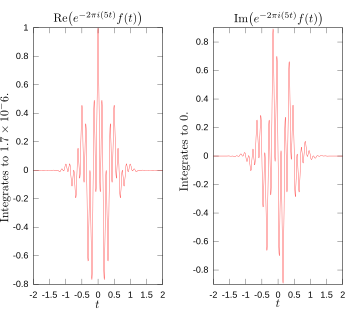














































![{\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\mathrm {He} _{n}\left(2x{\sqrt {\pi }}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9121f54a3fdbb0eedecf2aef5a379bdfae414b7)































































































































































































































































































































![{\displaystyle \chi _{[0,1]}(|\mathbf {x} |)\left(1-|\mathbf {x} |^{2}\right)^{\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1f3e6c1f52f0ee9366c40ee6f67c65f11dbd03a)





















