Doppelspaltexperiment

Photonen oder Materieteilchen (wie ein Elektron) erzeugen ein Wellenmuster, wenn zwei Spaltöffnungen verwendet werden

Licht eines grünen Lasers, das durch zwei Spaltöffnungen von 0,4 mm Breite und 0,1 mm Abstand fällt

In der modernen Physik ist das Doppelspaltexperiment ein Beweis dafür, dass Licht und Materie sowohl Eigenschaften von klassisch definierten Wellen als auch von Teilchen aufweisen können; außerdem zeigt es die grundsätzlich wahrscheinlichkeitsorientierte Natur quantenmechanischer Phänomene. Diese Art von Experiment wurde erstmals 1802 von Thomas Young mit Licht durchgeführt, um das Wellenverhalten des Lichts zu demonstrieren. Damals ging man davon aus, dass Licht entweder aus Wellen oder aus Teilchen besteht. Mit dem Beginn der modernen Physik, etwa hundert Jahre später, erkannte man, dass Licht tatsächlich sowohl das Verhalten von Wellen als auch von Teilchen zeigen kann. Im Jahr 1927 wiesen Davisson und Germer nach, dass Elektronen dasselbe Verhalten zeigen, was später auf Atome und Moleküle ausgedehnt wurde. Thomas Youngs Lichtexperiment war Teil der klassischen Physik, lange bevor die Quantenmechanik und das Konzept des Welle-Teilchen-Dualismus entwickelt wurden. Er glaubte, damit den Beweis für die Richtigkeit der Wellentheorie des Lichts erbracht zu haben, und sein Experiment wird manchmal auch als Youngs Experiment oder Youngs Spalt bezeichnet. ⓘ

Das Experiment gehört zu einer allgemeinen Klasse von "Doppelweg"-Experimenten, bei denen eine Welle in zwei separate Wellen aufgespalten wird (die Welle besteht in der Regel aus vielen Photonen und wird besser als Wellenfront bezeichnet (nicht zu verwechseln mit den Welleneigenschaften des einzelnen Photons)), die sich später zu einer einzigen Welle vereinigen. Änderungen der Weglängen der beiden Wellen führen zu einer Phasenverschiebung, wodurch ein Interferenzmuster entsteht. Eine andere Variante ist das Mach-Zehnder-Interferometer, bei dem der Strahl mit einem Strahlteiler geteilt wird.

In der Grundversion dieses Experiments beleuchtet eine kohärente Lichtquelle, z. B. ein Laserstrahl, eine von zwei parallelen Schlitzen durchbrochene Platte, und das durch die Schlitze hindurchtretende Licht wird auf einem Schirm hinter der Platte beobachtet. Die Wellennatur des Lichts führt dazu, dass die Lichtwellen, die durch die beiden Schlitze laufen, interferieren und helle und dunkle Streifen auf dem Bildschirm erzeugen - ein Ergebnis, das nicht zu erwarten wäre, wenn das Licht aus klassischen Teilchen bestünde. Es zeigt sich jedoch, dass das Licht immer an diskreten Punkten auf dem Schirm absorbiert wird, und zwar als einzelne Teilchen (nicht als Wellen); das Interferenzmuster entsteht durch die unterschiedliche Dichte dieser Teilchentreffer auf dem Schirm. Bei Versionen des Experiments mit Detektoren an den Spaltöffnungen wird außerdem festgestellt, dass jedes detektierte Photon einen Spalt durchläuft (wie ein klassisches Teilchen) und nicht beide Spaltöffnungen (wie eine Welle). Solche Experimente zeigen jedoch, dass die Teilchen kein Interferenzmuster bilden, wenn man feststellt, durch welchen Spalt sie laufen. Diese Ergebnisse belegen das Prinzip des Welle-Teilchen-Dualismus. ⓘ

Andere Teilchen auf atomarer Ebene, wie z. B. Elektronen, zeigen das gleiche Verhalten, wenn sie auf einen Doppelspalt geschossen werden. Darüber hinaus wird beobachtet, dass die Erkennung einzelner diskreter Stöße inhärent probabilistisch ist, was mit klassischer Mechanik nicht erklärbar ist. ⓘ

Das Experiment kann mit Einheiten durchgeführt werden, die viel größer sind als Elektronen und Photonen, obwohl es mit zunehmender Größe immer schwieriger wird. Die größten Einheiten, für die das Doppelspaltexperiment durchgeführt wurde, waren Moleküle, die jeweils 2000 Atome umfassten (deren Gesamtmasse 25.000 atomare Masseneinheiten betrug). ⓘ

Das Doppelspaltexperiment (und seine Variationen) ist aufgrund seiner Klarheit bei der Darstellung der zentralen Rätsel der Quantenmechanik zu einem Klassiker geworden. Richard Feynman bezeichnete es als "ein Phänomen, das unmöglich [...] auf klassische Weise erklärt werden kann und in dem das Herz der Quantenmechanik steckt", weil es die grundlegende Begrenztheit der Fähigkeit des Beobachters zur Vorhersage von Versuchsergebnissen demonstriert. In Wirklichkeit enthält es das einzige Geheimnis [der Quantenmechanik]." ⓘ

Doppelspaltexperiment ⓘ

Überblick

Dieselbe Doppelspaltanordnung (0,7 mm zwischen den Spaltöffnungen); im oberen Bild ist ein Spalt geschlossen. Im Einzelspaltbild bildet sich ein Beugungsmuster (die schwachen Flecken auf beiden Seiten des Hauptbandes) aufgrund der von Null abweichenden Breite des Spaltes. Dieses Beugungsmuster ist auch im Doppelspaltbild zu sehen, allerdings mit vielen kleineren Interferenzstreifen. ⓘ

Wenn das Licht ausschließlich aus gewöhnlichen oder klassischen Teilchen bestünde und diese Teilchen in einer geraden Linie durch einen Spalt geschossen würden und auf der anderen Seite auf einen Schirm treffen würden, würde man erwarten, ein Muster zu sehen, das der Größe und Form des Spaltes entspricht. Wenn dieses "Einspaltexperiment" jedoch tatsächlich durchgeführt wird, ist das Muster auf dem Schirm ein Beugungsmuster, bei dem das Licht gestreut wird. Je kleiner der Spalt ist, desto größer ist der Streuwinkel. Der obere Teil des Bildes zeigt den zentralen Teil des Musters, der entsteht, wenn ein roter Laser einen Spalt beleuchtet, und, wenn man genau hinsieht, zwei schwache Seitenstreifen. Mit einem feineren Gerät kann man mehr Bänder erkennen. Die Beugung erklärt das Muster als das Ergebnis der Interferenz von Lichtwellen am Spalt. ⓘ

Simulation der Wellenfunktion eines Teilchens: Doppelspaltexperiment. Die weiße Unschärfe stellt die Welle dar. Je weißer das Pixel ist, desto größer ist die Wahrscheinlichkeit, ein Teilchen an dieser Stelle zu finden, wenn es gemessen wird. ⓘ

Beleuchtet man zwei parallele Spaltöffnungen, interferiert das Licht der beiden Spaltöffnungen erneut. Hier ist die Interferenz ein ausgeprägteres Muster mit einer Reihe von abwechselnd hellen und dunklen Streifen. Die Breite der Streifen ist eine Eigenschaft der Frequenz des beleuchtenden Lichts. (Als Thomas Young (1773-1829) dieses Phänomen erstmals nachwies, deutete es darauf hin, dass das Licht aus Wellen besteht, da die Helligkeitsverteilung durch die abwechselnd additive und subtraktive Interferenz von Wellenfronten erklärt werden kann. Youngs Experiment, das Anfang des 19. Jahrhunderts durchgeführt wurde, spielte eine entscheidende Rolle für das Verständnis der Wellentheorie des Lichts und verdrängte die von Isaac Newton vorgeschlagene korpuskulare Theorie des Lichts, die im 17. und 18. Die spätere Entdeckung des photoelektrischen Effekts zeigte jedoch, dass sich das Licht unter verschiedenen Umständen so verhalten kann, als bestünde es aus einzelnen Teilchen. Diese scheinbar widersprüchlichen Entdeckungen machten es notwendig, über die klassische Physik hinauszugehen und die Quantennatur des Lichts zu berücksichtigen. ⓘ

Feynman sagte gern, dass sich die gesamte Quantenmechanik aus dem sorgfältigen Nachdenken über die Auswirkungen dieses einzigen Experiments ableiten lässt. Er schlug auch vor (als Gedankenexperiment), dass das Interferenzmuster verschwinden würde, wenn vor jedem Spalt Detektoren angebracht wären. ⓘ

Die Englert-Greenberger-Dualitätsbeziehung bietet eine detaillierte Behandlung der Mathematik der Doppelspaltinterferenz im Kontext der Quantenmechanik. ⓘ

Ein Doppelspaltexperiment mit geringer Intensität wurde erstmals 1909 von G. I. Taylor durchgeführt, indem er die Intensität des einfallenden Lichts verringerte, bis sich die Emissions-/Absorptionsereignisse der Photonen größtenteils nicht mehr überlappten. ⓘ

Ein Doppelspaltexperiment wurde erst 1961 mit etwas anderem als Licht durchgeführt, als Claus Jönsson von der Universität Tübingen es mit Elektronenstrahlen durchführte. Im Jahr 1974 wiederholten die italienischen Physiker Pier Giorgio Merli, Gian Franco Missiroli und Giulio Pozzi das Experiment mit einzelnen Elektronen und einem Biprisma (anstelle eines Spalts) und zeigten, dass jedes Elektron mit sich selbst interferiert, wie es die Quantentheorie vorhersagt. Im Jahr 2002 wurde die Ein-Elektronen-Version des Experiments von den Lesern der Zeitschrift Physics World zum "schönsten Experiment" gewählt. ⓘ

2012 führten Stefano Frabboni und seine Mitarbeiter schließlich das Doppelspaltexperiment mit Elektronen und echten Spaltöffnungen nach dem von Feynman vorgeschlagenen Originalschema durch. Sie schickten einzelne Elektronen auf nanofabrizierte Schlitze (ca. 100 nm breit) und konnten durch Auffangen der übertragenen Elektronen mit einem Einzelelektronendetektor den Aufbau eines Doppelspalt-Interferenzmusters zeigen. ⓘ

Im Jahr 2019 wurde die Einzelteilcheninterferenz von Marco Giammarchi und Mitarbeitern für Antimaterie nachgewiesen. ⓘ

Thomas Young ⓘ

Variationen des Experiments

Interferenz von Einzelteilchen

Aufbau eines Interferenzmusters aus einzelnen Teilchendetektionen ⓘ

Eine wichtige Variante dieses Experiments betrifft einzelne Teilchen. Schickt man ein Teilchen nach dem anderen durch einen Doppelspaltapparat, so erscheinen erwartungsgemäß einzelne Teilchen auf dem Bildschirm. Bemerkenswerterweise entsteht jedoch ein Interferenzmuster, wenn man diese Teilchen nacheinander aufbaut (siehe nebenstehendes Bild). Dies demonstriert den Welle-Teilchen-Dualismus, der besagt, dass alle Materie sowohl Wellen- als auch Teilcheneigenschaften aufweist: Das Teilchen wird als einzelner Impuls an einer einzigen Stelle gemessen, während die Welle die Wahrscheinlichkeit beschreibt, dass das Teilchen an einer bestimmten Stelle des Bildschirms absorbiert wird. Dieses Phänomen ist bei Photonen, Elektronen, Atomen und sogar einigen Molekülen nachgewiesen worden. Ein Erfolg wurde mit Buckminsterfulleren (C
₆₀) im Jahr 2001, wobei 2 Moleküle mit 430 Atomen (C
₆₀(C
₁₂F
₂₅)
₁₀ und C
₁₆₈H
₉₄F
₁₅₂O
₈N
₄S
₄) im Jahr 2011 und mit Molekülen von bis zu 2000 Atomen im Jahr 2019. ⓘ

Die Nachweiswahrscheinlichkeit ist das Quadrat der Amplitude der Welle und kann mit klassischen Wellen berechnet werden (siehe unten). Seit den Anfängen der Quantenmechanik haben einige Theoretiker nach Möglichkeiten gesucht, zusätzliche Determinanten oder "verborgene Variablen" einzubeziehen, die, wenn sie bekannt würden, den Ort jedes einzelnen Stoßes mit dem Ziel erklären würden. ⓘ

Mach-Zehnder-Interferometer

Photonen in einem Mach-Zehnder-Interferometer zeigen eine wellenförmige Interferenz und einen teilchenförmigen Nachweis in Einzelphotonendetektoren. ⓘ

Das Mach-Zehnder-Interferometer kann als eine vereinfachte Version des Doppelspaltexperiments angesehen werden. Anstatt sich nach den beiden Spaltöffnungen durch den freien Raum auszubreiten und jede beliebige Stelle eines ausgedehnten Bildschirms zu treffen, können sich die Photonen im Interferometer nur über zwei Pfade ausbreiten und zwei diskrete Photodetektoren treffen. Dadurch ist es möglich, das Interferometer durch einfache lineare Algebra in der Dimension 2 und nicht durch Differentialgleichungen zu beschreiben. ⓘ

Ein vom Laser ausgesandtes Photon trifft auf den ersten Strahlteiler und befindet sich dann in einer Überlagerung zwischen den beiden möglichen Pfaden. Im zweiten Strahlteiler überlagern sich diese Wege, so dass das Photon mit der Wahrscheinlichkeit 1 auf den Photodetektor rechts und mit der Wahrscheinlichkeit 0 auf den Photodetektor unten trifft. Es ist interessant zu überlegen, was passieren würde, wenn das Photon definitiv in einem der Pfade zwischen den Strahlteilern wäre. Dies lässt sich erreichen, indem man einen der Pfade blockiert oder indem man die Anwesenheit eines Photons dort nachweist. In beiden Fällen gibt es keine Interferenz mehr zwischen den Pfaden, und beide Photodetektoren werden mit der Wahrscheinlichkeit 1/2 getroffen. Daraus lässt sich schließen, dass das Photon nach dem ersten Strahlteiler weder den einen noch den anderen Weg einschlägt, sondern dass es sich in einer echten Quantenüberlagerung der beiden Wege befindet. ⓘ

Experimente zum "Wohin" und das Prinzip der Komplementarität

Ein bekanntes Gedankenexperiment besagt, dass das Interferenzmuster verschwindet, wenn an den Schlitzen Teilchendetektoren angebracht werden, die zeigen, durch welchen Schlitz ein Photon geht. Dieses Experiment veranschaulicht das Komplementaritätsprinzip, wonach Photonen sich entweder als Teilchen oder als Wellen verhalten können, aber nicht als beides gleichzeitig beobachtet werden können. Trotz der Bedeutung dieses Gedankenexperiments in der Geschichte der Quantenmechanik (siehe z. B. die Diskussion über Einsteins Version dieses Experiments) wurden bis in die 1970er Jahre keine technisch machbaren Realisierungen dieses Experiments vorgeschlagen. (Naive Umsetzungen des Gedankenexperiments aus dem Lehrbuch sind nicht möglich, da Photonen nicht nachgewiesen werden können, ohne dass das Photon absorbiert wird). Gegenwärtig sind mehrere Experimente durchgeführt worden, die verschiedene Aspekte der Komplementarität veranschaulichen. ⓘ

Ein 1987 durchgeführter Versuch brachte Ergebnisse, die zeigten, dass man Informationen über den Weg eines Teilchens erhalten kann, ohne die Interferenz ganz zu zerstören. Dies zeigte die Wirkung von Messungen, die die Teilchen auf ihrem Weg weniger stark störten und dadurch das Interferenzmuster nur in vergleichbarem Maße beeinflussten. Mit anderen Worten: Wenn man nicht darauf besteht, dass die Methode, mit der bestimmt wird, welchen Spalt jedes Photon durchläuft, völlig zuverlässig ist, kann man immer noch ein (verschlechtertes) Interferenzmuster erkennen. ⓘ

Verzögerte Wahl und Quantenradiervarianten

Ein Diagramm von Wheelers Delayed-Choice-Experiment, das das Prinzip der Bestimmung des Weges des Photons nach dem Durchgang durch den Spalt zeigt ⓘ

Wheelers Delayed-Choice-Experimente zeigen, dass die Gewinnung von Informationen über den Weg eines Teilchens nach dessen Durchgang durch den Spalt sein vorheriges Verhalten am Spalt scheinbar rückwirkend ändern kann. ⓘ

Experimente mit Quantenlöschern zeigen, dass das Wellenverhalten wiederhergestellt werden kann, indem die "Welcher-Weg"-Information gelöscht oder auf andere Weise dauerhaft unzugänglich gemacht wird. ⓘ

Eine einfache Veranschaulichung des Quantenradiergummi-Phänomens wurde in einem Artikel im Scientific American gegeben. Bringt man vor jedem Spalt Polarisatoren an, deren Achsen orthogonal zueinander stehen, wird das Interferenzmuster eliminiert. Die Polarisatoren können so betrachtet werden, dass sie jedem Strahl die Information über den Weg hinzufügen. Die Einführung eines dritten Polarisators vor dem Detektor mit einer Achse von 45° relativ zu den anderen Polarisatoren "löscht" diese Information aus, so dass das Interferenzmuster wieder auftaucht. Dies lässt sich auch erklären, wenn man das Licht als klassische Welle betrachtet, sowie bei der Verwendung von Zirkularpolarisatoren und einzelnen Photonen. Für die Implementierung der Polarisatoren mit verschränkten Photonenpaaren gibt es keine klassische Erklärung. ⓘ

Schwache Messung

In einem viel beachteten Experiment aus dem Jahr 2012 behaupteten Forscher, den Weg jedes Teilchens identifiziert zu haben, ohne dass das von den Teilchen erzeugte Interferenzmuster in irgendeiner Weise beeinträchtigt wurde. Dazu verwendeten sie einen Aufbau, bei dem die Teilchen nicht von einer punktförmigen Quelle, sondern von einer Quelle mit zwei Intensitätsmaxima auf den Bildschirm kamen. Kommentatoren wie Svensson haben jedoch darauf hingewiesen, dass zwischen den schwachen Messungen, die in dieser Variante des Doppelspaltexperiments durchgeführt wurden, und der Heisenbergschen Unschärferelation eigentlich kein Widerspruch besteht. Die schwache Messung mit anschließender Nachselektion ermöglichte nicht die gleichzeitige Messung von Position und Impuls für jedes einzelne Teilchen, sondern die Messung der durchschnittlichen Flugbahn der Teilchen, die an verschiedenen Positionen ankamen. Mit anderen Worten: Die Experimentatoren erstellten eine statistische Karte der gesamten Bahnlandschaft. ⓘ

Andere Varianten

Eine Labor-Doppelspaltanordnung; Abstand zwischen den oberen Pfosten ca. 2,5 cm (ein Zoll). ⓘ

Nahfeld-Intensitätsverteilungsmuster für plasmonische Schlitze mit gleicher Breite (A) und ungleicher Breite (B). ⓘ

1967 demonstrierten Pfleegor und Mandel die Zwei-Quellen-Interferenz mit zwei separaten Lasern als Lichtquellen. ⓘ

Im Jahr 1972 wurde experimentell gezeigt, dass bei einem Doppelspaltsystem, bei dem immer nur ein Spalt geöffnet war, dennoch Interferenz beobachtet werden konnte, sofern der Wegunterschied so groß war, dass das detektierte Photon von einem der beiden Spalte stammen konnte. Die experimentellen Bedingungen waren so beschaffen, dass die Photonendichte im System viel kleiner als eins war. ⓘ

1999 wurde ein Quanteninterferenzexperiment (unter Verwendung eines Beugungsgitters anstelle von zwei Spaltöffnungen) mit Buckyball-Molekülen (die jeweils 60 Kohlenstoffatome enthalten) erfolgreich durchgeführt. Ein Buckyball ist groß genug (Durchmesser ca. 0,7 nm, fast eine halbe Million Mal größer als ein Proton), um unter einem Elektronenmikroskop gesehen zu werden. ⓘ

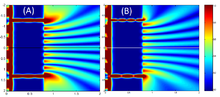
Im Jahr 2005 stellte E. R. Eliel eine experimentelle und theoretische Studie über die optische Übertragung eines dünnen Metallschirms vor, der von zwei Schlitzen im Subwellenlängenbereich durchbrochen ist, die durch viele optische Wellenlängen getrennt sind. Es wurde gezeigt, dass die Gesamtintensität des Fernfeld-Doppelspaltmusters in Abhängigkeit von der Wellenlänge des einfallenden Lichtstrahls verringert oder erhöht wird. ⓘ

Im Jahr 2012 führten Forscher an der University of Nebraska-Lincoln das von Richard Feynman beschriebene Doppelspaltexperiment mit Elektronen durch, wobei sie neue Instrumente einsetzten, die eine Kontrolle der Übertragung der beiden Spaltöffnungen und die Überwachung von Einzel-Elektronennachweisen ermöglichten. Die Elektronen wurden von einer Elektronenkanone abgefeuert und durch einen oder zwei Schlitze von 62 nm Breite × 4 μm Höhe geleitet. ⓘ

Im Jahr 2013 wurde ein Quanteninterferenzexperiment (unter Verwendung von Beugungsgittern anstelle von zwei Spaltöffnungen) erfolgreich mit Molekülen durchgeführt, die jeweils 810 Atome (mit einer Gesamtmasse von über 10.000 atomaren Masseneinheiten) enthielten. Im Jahr 2019 wurde der Rekord auf 2000 Atome (25.000 amu) erhöht. ⓘ

Hydrodynamische Pilotwellen-Analoga

Es wurden hydrodynamische Analoga entwickelt, die verschiedene Aspekte quantenmechanischer Systeme nachbilden können, darunter die Interferenz einzelner Teilchen durch einen Doppelspalt. Ein Silikonöltröpfchen, das an der Oberfläche einer Flüssigkeit abprallt, treibt sich selbst durch resonante Wechselwirkungen mit seinem eigenen Wellenfeld an. Das Tröpfchen schwappt bei jedem Aufprall sanft in die Flüssigkeit. Gleichzeitig beeinflussen die Wellen vergangener Sprünge seinen Kurs. Die Wechselwirkung des Tropfens mit seinen eigenen Wellen, die eine so genannte Pilotwelle bilden, veranlasst ihn zu Verhaltensweisen, von denen man bisher annahm, dass sie den Elementarteilchen eigen sind - darunter auch Verhaltensweisen, die üblicherweise als Beweis dafür gelten, dass sich Elementarteilchen wie Wellen im Raum ausbreiten, ohne einen bestimmten Ort zu haben, bis sie gemessen werden. ⓘ

Zu den Verhaltensweisen, die durch dieses hydrodynamische Pilotwellensystem nachgeahmt werden, gehören Quanteneinzelteilchenbeugung, Tunnelbildung, gequantelte Orbits, Aufspaltung von Orbitalniveaus, Spin und multimodale Statistik. Es ist auch möglich, Unschärferelationen und Ausschlussprinzipien abzuleiten. Es sind Videos verfügbar, die verschiedene Merkmale dieses Systems veranschaulichen. (Siehe Externe Links.) ⓘ

Kompliziertere Systeme, bei denen sich zwei oder mehr Teilchen in Überlagerung befinden, lassen sich jedoch nicht so einfach und klassisch intuitiv erklären. Dementsprechend wurde noch kein hydrodynamisches Analogon der Verschränkung entwickelt. Dennoch sind optische Analogien möglich. ⓘ

Klassische wellenoptische Formulierung

Doppelspalt-Beugungsmuster durch eine ebene Welle ⓘ

Foto der Doppelspaltinterferenz von Sonnenlicht. ⓘ

Zwei Spaltöffnungen werden durch eine ebene Welle beleuchtet. ⓘ

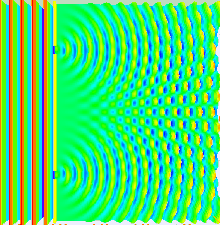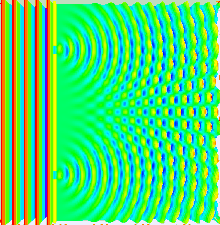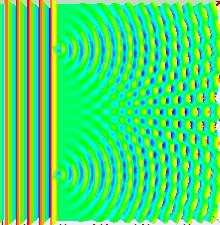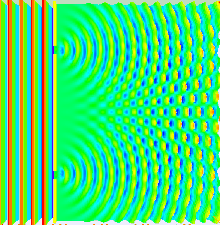
Ein Großteil des Verhaltens von Licht lässt sich mit der klassischen Wellentheorie modellieren. Das Huygens-Fresnel-Prinzip ist ein solches Modell; es besagt, dass jeder Punkt auf einer Wellenfront ein sekundäres Wavelet erzeugt und dass die Störung an jedem nachfolgenden Punkt durch Summierung der Beiträge der einzelnen Wavelets an diesem Punkt ermittelt werden kann. Bei dieser Summierung müssen sowohl die Phase als auch die Amplitude der einzelnen Wavelets berücksichtigt werden. Gemessen werden kann nur die Intensität eines Lichtfeldes - sie ist proportional zum Quadrat der Amplitude. ⓘ

Beim Doppelspaltexperiment werden die beiden Spaltöffnungen mit dem quasi monochromatischen Licht eines einzigen Lasers beleuchtet. Wenn die Breite der Spaltöffnungen klein genug ist (viel kleiner als die Wellenlänge des Laserlichts), brechen die Spaltöffnungen das Licht in Zylinderwellen. Diese beiden zylindrischen Wellenfronten überlagern sich, und die Amplitude und damit die Intensität an einem beliebigen Punkt der kombinierten Wellenfronten hängt sowohl von der Größe als auch von der Phase der beiden Wellenfronten ab. Der Phasenunterschied zwischen den beiden Wellen wird durch den Unterschied in der von den beiden Wellen zurückgelegten Entfernung bestimmt. ⓘ

Wenn der Betrachtungsabstand groß ist im Vergleich zum Abstand der Spaltöffnungen (Fernfeld), kann die Phasendifferenz mit Hilfe der in der Abbildung unten rechts dargestellten Geometrie ermittelt werden. Die Wegdifferenz zwischen zwei Wellen, die sich unter einem Winkel θ bewegen, ist gegeben durch:

$d\sin \theta \approx d\theta$ ⓘ

Dabei ist d der Abstand zwischen den beiden Spaltöffnungen. Wenn die beiden Wellen gleichphasig sind, d. h. die Wegdifferenz ist gleich einer ganzen Anzahl von Wellenlängen, ist die summierte Amplitude und damit die summierte Intensität maximal, und wenn sie gegenphasig sind, d. h. die Wegdifferenz ist gleich einer halben Wellenlänge, anderthalb Wellenlängen usw., dann heben sich die beiden Wellen auf und die summierte Intensität ist Null. Dieser Effekt wird als Interferenz bezeichnet. Die Maxima des Interferenzstreifens treten bei Winkeln auf ⓘ

$~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots$ ⓘ

wobei λ die Wellenlänge des Lichts ist. Der Winkelabstand der Streifen, θf, ist gegeben durch ⓘ

$\theta _{f}\approx \lambda /d$ ⓘ

Der Abstand der Streifen in einem Abstand z von den Spaltöffnungen ist gegeben durch ⓘ

$~w=z\theta _{f}=z\lambda /d$ ⓘ

Wenn beispielsweise zwei Schlitze einen Abstand von 0,5 mm (d) haben und mit einem Laser mit einer Wellenlänge von 0,6 μm (λ) beleuchtet werden, beträgt der Abstand der Streifen in einer Entfernung von 1 m (z) 1,2 mm. ⓘ

Wenn die Spaltbreite b im Vergleich zur Wellenlänge beträchtlich ist, wird die Fraunhofer-Beugungsgleichung benötigt, um die Intensität des gebeugten Lichts wie folgt zu bestimmen:

${\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi b\sin \theta }{\lambda }}\right]\end{aligned}}$ ⓘ

Dabei ist die sinc-Funktion definiert als sinc(x) = sin(x)/x für x ≠ 0, und sinc(0) = 1. ⓘ

Dies wird in der obigen Abbildung veranschaulicht, wobei das erste Muster das Beugungsmuster eines einzelnen Spalts darstellt, das durch die sinc-Funktion in dieser Gleichung gegeben ist, und die zweite Abbildung die kombinierte Intensität des von den beiden Spaltöffnungen gebeugten Lichts zeigt, wobei die cos-Funktion die Feinstruktur darstellt und die gröbere Struktur die Beugung durch die einzelnen Spaltöffnungen, die durch die sinc-Funktion beschrieben wird. ⓘ

Ähnliche Berechnungen für das Nahfeld können mit Hilfe der Fresnelschen Beugungsgleichung durchgeführt werden, die besagt, dass mit zunehmender Annäherung der Beobachtungsebene an die Ebene, in der sich die Spaltöffnungen befinden, die mit den einzelnen Spaltöffnungen assoziierten Beugungsmuster kleiner werden, so dass der Bereich, in dem Interferenzen auftreten, kleiner wird und sogar ganz verschwinden kann, wenn sich die beiden Beugungsmuster nicht überlappen. ⓘ

Interpretationen des Experiments

Wie das Gedankenexperiment zu Schrödingers Katze wird auch das Doppelspaltexperiment häufig verwendet, um die Unterschiede und Gemeinsamkeiten zwischen den verschiedenen Interpretationen der Quantenmechanik zu verdeutlichen. ⓘ

Kopenhagener Deutung

Die Kopenhagener Deutung, die von einigen der Pioniere der Quantenmechanik vertreten wird, besagt, dass es nicht wünschenswert ist, etwas zu behaupten, das über die mathematischen Formeln und die Art der physikalischen Apparate und Reaktionen hinausgeht, die es uns ermöglichen, ein gewisses Wissen über die Vorgänge auf atomarer Ebene zu erlangen. Eines der mathematischen Konstrukte, das es den Experimentatoren ermöglicht, bestimmte Versuchsergebnisse sehr genau vorherzusagen, wird manchmal als Wahrscheinlichkeitswelle bezeichnet. In ihrer mathematischen Form entspricht sie der Beschreibung einer physikalischen Welle, aber ihre "Wellenberge" und "Wellentäler" geben den Grad der Wahrscheinlichkeit für das Auftreten bestimmter Phänomene an (z. B. ein Lichtfunke an einem bestimmten Punkt auf einem Detektorschirm), die in der Makrowelt der normalen menschlichen Erfahrung beobachtet werden können. ⓘ

Man kann sagen, dass die Wahrscheinlichkeitswelle "durch den Raum geht", weil die Wahrscheinlichkeitswerte, die man aus ihrer mathematischen Darstellung berechnen kann, von der Zeit abhängen. Man kann nicht sagen, wo sich ein Teilchen, wie z. B. ein Photon, zwischen dem Zeitpunkt seiner Aussendung und dem Zeitpunkt seiner Entdeckung befindet, denn um sagen zu können, dass sich etwas zu einem bestimmten Zeitpunkt irgendwo befindet, muss man es entdecken. Die Voraussetzung für das Auftreten eines Interferenzmusters ist, dass Teilchen emittiert werden und dass es einen Schirm mit mindestens zwei verschiedenen Wegen gibt, die das Teilchen vom Sender zum Detektionsschirm nehmen kann. In Experimenten wird nichts zwischen dem Zeitpunkt der Emission des Teilchens und seiner Ankunft auf dem Detektionsschirm beobachtet. Wenn man nun eine Strahlenverfolgung durchführt, als ob eine Lichtwelle (im Sinne der klassischen Physik) breit genug wäre, um beide Wege zu nehmen, dann wird diese Strahlenverfolgung das Auftreten von Maxima und Minima auf dem Detektorschirm genau vorhersagen, wenn viele Teilchen den Apparat durchlaufen und nach und nach das erwartete Interferenzmuster "malen". ⓘ

Pfadintegrale Formulierung

Einer von unendlich vielen gleich wahrscheinlichen Pfaden, die im Feynman-Pfadintegral verwendet werden (siehe auch: Wiener-Prozess) ⓘ

Die Kopenhagener Interpretation ähnelt der Pfadintegralformulierung der Quantenmechanik von Feynman. Die Pfadintegralformulierung ersetzt die klassische Vorstellung einer einzigen, eindeutigen Trajektorie für ein System durch eine Summe über alle möglichen Trajektorien. Die Trajektorien werden durch funktionale Integration addiert. ⓘ

Jede Bahn wird als gleich wahrscheinlich angesehen und trägt daher den gleichen Betrag bei. Die Phase dieses Beitrags an einem bestimmten Punkt entlang des Pfades wird jedoch durch die Aktion entlang des Pfades bestimmt:

$$A_{\text{path}}(x,y,z,t)=e^{iS(x,y,z,t)}$$

ⓘ

Alle diese Beiträge werden dann addiert, und der Betrag des Endergebnisses wird quadriert, um die Wahrscheinlichkeitsverteilung für die Position eines Teilchens zu erhalten:

$$p(x,y,z,t)\propto \left\vert \int _{\text{all paths}}e^{iS(x,y,z,t)}\right\vert ^{2}$$

ⓘ

Wie immer bei der Berechnung von Wahrscheinlichkeiten müssen die Ergebnisse dann durch Auferlegung normalisiert werden:

$$\iiint _{\text{all space}}p(x,y,z,t)\,dV=1$$

ⓘ

Zusammenfassend lässt sich sagen, dass die Wahrscheinlichkeitsverteilung des Ergebnisses das normalisierte Quadrat der Norm der Überlagerung über alle Pfade vom Ausgangspunkt zum Endpunkt von Wellen ist, die sich proportional zur Aktion entlang jedes Pfades ausbreiten. Die Unterschiede in der kumulativen Wirkung entlang der verschiedenen Pfade (und damit die relativen Phasen der Beiträge) erzeugen das Interferenzmuster, das beim Doppelspaltexperiment beobachtet wird. Feynman betonte, dass es sich bei seiner Formulierung lediglich um eine mathematische Beschreibung handelt und nicht um den Versuch, einen realen Prozess zu beschreiben, den wir messen können. ⓘ

Relationale Interpretation

Ein Beispiel für das Unschärfeprinzip im Zusammenhang mit der relationalen Interpretation. Je mehr man über die Position eines Teilchens weiß, desto weniger weiß man über seine Geschwindigkeit und umgekehrt. ⓘ

Nach der relationalen Interpretation der Quantenmechanik, die erstmals von Carlo Rovelli vorgeschlagen wurde, resultieren Beobachtungen wie die im Doppelspaltexperiment speziell aus der Wechselwirkung zwischen dem Beobachter (Messgerät) und dem beobachteten Objekt (mit dem physisch interagiert wird), nicht aus einer absoluten Eigenschaft des Objekts. Wenn ein Elektron zunächst an einem bestimmten Spalt "beobachtet" wird, dann enthält die Wechselwirkung zwischen Beobachter und Teilchen (Photon und Elektron) Informationen über die Position des Elektrons. Dadurch wird die letztendliche Position des Teilchens auf dem Bildschirm teilweise eingeschränkt. Wird es nicht an einem bestimmten Spalt "beobachtet" (mit einem Photon gemessen), sondern am Bildschirm, dann gibt es keine Information über den "Weg" als Teil der Wechselwirkung, so dass die "beobachtete" Position des Elektrons auf dem Bildschirm ausschließlich durch seine Wahrscheinlichkeitsfunktion bestimmt wird. Damit ist das resultierende Muster auf dem Bildschirm dasselbe, als ob jedes einzelne Elektron durch beide Schlitze gegangen wäre. ⓘ

Viele-Welten-Interpretation

Der Physiker David Deutsch argumentiert in seinem Buch The Fabric of Reality, dass das Doppelspaltexperiment ein Beweis für die Viele-Welten-Interpretation ist. Da jedoch jede Interpretation der Quantenmechanik empirisch ununterscheidbar ist, sind einige Wissenschaftler skeptisch gegenüber dieser Behauptung. ⓘ

De Broglie-Bohm-Theorie

Die De-Broglie-Bohm-Theorie ist eine Alternative zum Standardverständnis der Quantenmechanik und besagt, dass die Teilchen jederzeit einen genauen Ort haben und dass ihre Geschwindigkeiten durch die Wellenfunktion definiert sind. Während also ein einzelnes Teilchen im Doppelspaltexperiment einen bestimmten Spalt durchläuft, durchläuft die sogenannte "Pilotwelle", die es beeinflusst, beide. Die de Broglie-Bohm-Trajektorien für den Doppelspalt wurden erstmals von Chris Dewdney in Zusammenarbeit mit Chris Philippidis und Basil Hiley am Birkbeck College (London) berechnet. Die de Broglie-Bohm-Theorie liefert die gleichen statistischen Ergebnisse wie die Standard-Quantenmechanik, lässt aber viele ihrer konzeptionellen Schwierigkeiten außer Acht. ⓘ

Bohmsche Trajektorien

Trajektorien von Teilchen unter der De Broglie-Bohm-Theorie im Doppelspaltexperiment.

100 Trajektorien, die von der Wellenfunktion gesteuert werden. In der De Broglie-Bohm-Theorie wird ein Teilchen jederzeit durch eine Wellenfunktion und eine Position (Massenschwerpunkt) dargestellt. Dies ist eine Art erweiterter Realität im Vergleich zur Standardinterpretation.

Numerische Simulation des Doppelspaltexperiments mit Elektronen. Abbildung links: Entwicklung (von links nach rechts) der Intensität des Elektronenstrahls am Ausgang des Spalts (links) bis zum Detektionsschirm 10 cm nach dem Spalt (rechts). Je höher die Intensität, desto hellblauer ist die Farbe - Abbildung in der Mitte: Einschläge der Elektronen, die auf dem Bildschirm beobachtet werden - Abbildung rechts: Intensität der Elektronen in der Fernfeldnäherung (auf dem Bildschirm). Numerische Daten aus dem Experiment von Claus Jönsson (1961). Photonen, Atome und Moleküle folgen einer ähnlichen Entwicklung. ⓘ

Das Experiment in der Lehre

Bei der Vermittlung von Wellenphänomenen im Physikunterricht hat das Doppelspaltexperiment einen festen Platz. Schon mit einfacher Geometrie und Algebra kann hierbei das Zustandekommen der Interferenzstreifen und deren Stärke erläutert werden. In den Lehrbüchern von Robert Wichard Pohl werden ausführliche Demonstrationsexperimente zur Veranschaulichung der Interferenzen mit Wasserwellen in einem Wellentrog beschrieben. Solche Demonstrationen werden auch per Video präsentiert, beispielsweise von der ETH Zürich. Die Beugung von Licht am Doppelspalt ist ein Standardversuch in Physik-Praktika. ⓘ

In einigen Lehrbüchern, wie etwa Feynman-Vorlesungen über Physik, stehen Gedankenexperimente mit dem Doppelspalt an prominenter Stelle als Einstieg in die Quantenphysik. Nach Feynman trägt der Doppelspaltversuch „das Herz der Quantenmechanik“ in sich; „Er enthält das einzige Geheimnis“. In diesen Lehrbüchern wird mit dem Doppelspalt anschaulich erklärt, wie in der Mikrophysik sowohl die Methoden der Wellentheorie als auch die Teilchentheorie genutzt werden müssen, um die Bewegung von einzelnen Elektronen und Atomen und ihr jedes Mal punktförmiges Signal auf dem Schirm zu beschreiben, und dass keine der beiden Theorien alleine die Beobachtungen erklären kann. Die konkrete Durchführung von Experimenten zur Beugung von Materiewellen an einem Doppelspalt ist allerdings aufwendig und schwierig, da die Wellenlänge von Mikroteilchen von subatomarer Größe ist. Bei dem Doppelspaltexperiment mit Elektronenwellen von C. Jönsson war die Wellenlänge 5 pm, also etwa 100 mal kleiner als die typische Ausdehnung eines Atoms. ⓘ

Experimentelle Beobachtung

Interferenzmuster eines Doppelspaltexperiments mit wachsender Anzahl N der am Schirm angekommenen Elektronen:   b:N= 200,  c:N= 6 000,  d:N= 40 000,  e:N= 140 000 Elektronen ⓘ

• Die beiden interferierenden Wellen müssen eine feste Phasenbeziehung zueinander haben, damit Interferenzstreifen beobachtet werden können. Ausreichende räumliche Kohärenz ist gegeben, wenn die Breite der Quelle (bei Young ein Eintrittsspalt) aus Sicht des Doppelspaltes nicht aufgelöst werden kann (siehe Rayleigh-Kriterium). Die Anforderung an die zeitliche Kohärenz hängt davon ab, wie viele Streifen man neben dem zentralen Streifen erkennen will.
• Eine Ergänzung der Apparatur, deren Messergebnis die Information ist, durch welchen der beiden Spalte ein Teilchen den Detektor erreicht hat („Welcher-Weg“-Experiment), bewirkt unvermeidlich, dass die Interferenzstreifen verschwinden. (Bei Photonen kann die Welcher-Weg-Information auch einfach durch Polarisationsfilter realisiert sein. Platziert man vor (oder hinter) einem Spalt ein Filter mit einer bestimmten Polarisationsebene und bei dem anderen Spalt genauso eins mit dazu orthogonaler Polarisationsebene, so entscheidet die Polarisation des Photons darüber, welchen Weg das Photon nimmt. In diesem Fall tritt keine Interferenz am Schirm auf.) Die Auslöschung der Interferenz gilt auch dann, wenn die Messergebnisse dieser Zusatzapparatur unberücksichtigt bleiben, weil sie z. B. gar nicht abgelesen werden; es genügt schon die physikalische Möglichkeit dazu. Umgekehrt zeigen Aufbauten, bei denen es physikalisch unmöglich ist herauszufinden, welcher Spalt genommen wurde, immer ein Interferenzmuster.
• Die beiden vorhergehenden Aussagen gelten selbst dann, wenn die Entscheidung, ob die Information über den Weg eines Teilchens durch ein Messergebnis festgehalten wird, erst getroffen wird, nachdem es die Spalte passiert hat. Die Entscheidung, den Weg nicht zu ermitteln, führt dann dazu, dass auf dem Schirm das Interferenzmuster beobachtet wird. Das kann man so deuten, dass die schon gewonnene Information über den genommenen Weg nachträglich gelöscht („ausradiert“) wird. Daher wird ein solcher Aufbau Quantenradierer genannt.
• Das Interferenzmuster hängt nicht von der Anzahl der beteiligten Teilchen oder dem gleichzeitigen Durchtritt durch den Doppelspalt ab. Bei niedrigerer Intensität baut sich das Interferenzmuster lediglich langsamer beim Detektor auf, bleibt aber in der Gestalt gleich. Das passiert selbst dann, wenn sich zu jedem Zeitpunkt höchstens ein Teilchen zwischen Quelle und Detektor befindet. Daher muss auch die Verteilung der Wahrscheinlichkeit des Ankommens an den Positionen auf dem Detektor bei jedem einzelnen Durchflug entstehen. Dieses Phänomen lässt sich als Interferenz der Teilchen mit sich selbst umschreiben. ⓘ

Berechnung des Interferenzmusters

Einfluss von Spaltgeometrie und Wellenlänge

Setzt man die Ausdrücke für $\gamma$ und $\delta$ in die Gleichung des Interferenzmusters ein, so werden die Einflüsse von Spaltgeometrie und Wellenlänge des einfallenden Lichtes auf das Aussehen des Interferenzmusters deutlich:

$I(\alpha )=I_{0}\cdot \left({\frac {\sin \left({\frac {k}{2}}b\sin \alpha \right)}{{\frac {k}{2}}b\sin \alpha }}\right)^{\!2}\cdot \cos ^{2}\left({\frac {k}{2}}a\sin \alpha \right)$ ⓘ

mit $k=2\pi /\lambda$. ⓘ

• Eine Änderung der Spaltbreite $b$ führt zu einer Änderung der Lage der Extrema des Einfachspaltes, dessen Intensitätsverteilung (im Bild blau) die Hüllkurve der Intensitätsverteilung des Doppelspalts bildet (im Bild rot)

→ Je breiter der Spalt, desto enger wird die Hüllkurve

• Eine Änderung des Spaltabstandes $a$ führt zu einer Änderung der Lage der Extrema des Doppelspalts innerhalb der konstant bleibenden Hüllkurve

→ Je größer der Spaltabstand, desto enger liegen die Extrema des Doppelspalts beieinander

• Eine Änderung der Wellenlänge $\lambda$ wirkt sich sowohl auf die Hüllkurve als auch auf die Intensitätsverteilung des Doppelspalts aus

→ Je größer die Wellenlänge, desto breiter werden Hüllkurve und die Interferenzabstände des Doppelspalts ⓘ

Berechnung mit Fourier-Optik

Das Interferogramm einer Spaltkonstellation lässt sich auch mit Hilfe der Fourier-Optik berechnen. Dabei wird ausgenutzt, dass im Falle der Fraunhofer-Beugung das Beugungsmuster der Fouriertransformierten der Autokorrelation der Blendenfunktion entspricht. Der Vorteil dieses Ansatzes ist, dass sich auch das Beugungsbild komplizierterer Mehrfachspalte und Gitter schnell berechnen lässt. Wesentlich ist dabei die Ausnutzung des Faltungstheorems. ⓘ

Das Koordinatensystem wird so gelegt, dass die zwei Einzelspalte einen Abstand $a$ haben und symmetrisch zum Schnitt der Koordinatenachsen liegen. Die Blendenfunktion der zwei identischen Spalte mit Breite $b$ im Ortsraum lautet ⓘ

$(\delta (x+a/2)+\delta (x-a/2))*\operatorname {rect} _{b}(x)$ ⓘ

wobei $*$ den Faltungsoperator und $\operatorname {rect} _{b}(x)$ die Rechteckfunktion bezeichnet. ⓘ

Die Fouriertransformierte der gegebenen Blendenfunktion ist nach dem Faltungstheorem das Produkt aus der Fouriertransformierten der Rechteckfunktion und der Fouriertransformierten der zwei Delta-Distributionen. ⓘ

${\mathcal {F}}[\operatorname {rect} _{b}(x)](k_{x})=b\cdot \operatorname {si} \left({\frac {b}{2}}k_{x}\right)=b{\frac {\sin \left({\frac {k_{x}}{2}}b\right)}{{\frac {k_{x}}{2}}b}}={\frac {\sin \left({\frac {k_{x}}{2}}b\right)}{\frac {k_{x}}{2}}}$ ⓘ

${\mathcal {F}}[\delta (x\pm d)](k_{x})=\cos(a\cdot k_{x}/2)$ ⓘ

Daraus folgt für die Intensität am Schirm ein Cosinus mit einer Sinc-Funktion als Einhüllende. Die Funktion weist die charakteristischen $N-1=1$ Nebenmaxima eines $N=2$-fach-Spaltes auf (siehe auch Optisches Gitter). ⓘ

$I(k)=I_{0}\left({\frac {\sin \left({\frac {k_{x}}{2}}b\right)}{{\frac {k_{x}}{2}}b}}\cdot \cos({\frac {k_{x}}{2}}a)\right)^{2}$ ⓘ

Mit $I_{0}$ als Intensitätskonstante. ⓘ

Für $k_{x}=k\cdot \sin \alpha$ folgt die oben bereits gezeigte Beziehung für $I(\alpha )$. ⓘ