Quantenzahl
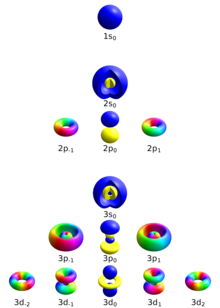
| Teil einer Reihe von Artikeln über ⓘ |
| Quantenmechanik |
|---|
|
In der Quantenphysik und -chemie beschreiben die Quantenzahlen die Werte der konservierten Größen in der Dynamik eines Quantensystems. Quantenzahlen entsprechen den Eigenwerten von Operatoren, die mit dem Hamiltonschen Operator kommutieren - Größen, die gleichzeitig mit der Energie des Systems genau bekannt sind - und ihren entsprechenden Eigenräumen. Zusammengenommen charakterisieren alle Quantenzahlen eines Quantensystems einen Basiszustand des Systems vollständig und können im Prinzip zusammen gemessen werden. ⓘ
Ein wichtiger Aspekt der Quantenmechanik ist die Quantisierung vieler beobachtbarer Größen von Interesse. Dies führt insbesondere zu Quantenzahlen, die Werte in diskreten Mengen ganzer oder halber Zahlen annehmen, obwohl sie sich in einigen Fällen der Unendlichkeit nähern können. Dies unterscheidet die Quantenmechanik von der klassischen Mechanik, in der die Werte, die das System charakterisieren, wie Masse, Ladung oder Impuls, alle kontinuierlich variieren. Quantenzahlen beschreiben häufig speziell die Energieniveaus von Elektronen in Atomen, aber es gibt auch andere Möglichkeiten wie Drehimpuls, Spin usw. Eine wichtige Familie sind die Geschmacksquantenzahlen - interne Quantenzahlen, die die Art eines Teilchens und seine Wechselwirkungen mit anderen Teilchen durch die fundamentalen Kräfte bestimmen. Jedes Quantensystem kann eine oder mehrere Quantenzahlen haben; es ist daher schwierig, alle möglichen Quantenzahlen aufzulisten. ⓘ
Für ein bestimmtes System benötigte Quantenzahlen
Die Anzahl der Quantenzahlen ist von System zu System unterschiedlich und lässt sich nicht allgemein beantworten. Daher müssen diese Parameter für jedes zu untersuchende System gefunden werden. Ein quantisiertes System benötigt mindestens eine Quantenzahl. Die Dynamik (d. h. die zeitliche Entwicklung) eines jeden Quantensystems wird durch einen Quantenoperator in Form eines Hamiltonianers H beschrieben. Es gibt eine Quantenzahl des Systems, die der Energie des Systems entspricht, d. h. einem der Eigenwerte des Hamiltonianers. Außerdem gibt es eine Quantenzahl für jeden linear unabhängigen Operator O, der mit dem Hamiltonianer kommutiert. Ein vollständiger Satz von kommutierenden Observablen (CSCO), die mit dem Hamiltonian kommutieren, charakterisiert das System mit all seinen Quantenzahlen. Es besteht eine Eins-zu-Eins-Beziehung zwischen den Quantenzahlen und den Operatoren der CSCO, wobei jede Quantenzahl einen der Eigenwerte des entsprechenden Operators annimmt. Aufgrund der unterschiedlichen Basis, die beliebig gewählt werden kann, um einen vollständigen Satz von kommutierenden Operatoren zu bilden, können unterschiedliche Sätze von Quantenzahlen für die Beschreibung desselben Systems in unterschiedlichen Situationen verwendet werden. ⓘ
Elektron in einem Atom
Nachstehend werden im Einzelnen die Quantenzahlen beschrieben, die zur vollständigen Beschreibung des einfachsten Atoms, des Wasserstoffatoms, gebraucht werden. Die Eigenzustände des gebundenen Elektrons und seine Wellenfunktion im Wasserstoffatom werden durch vier Quantenzahlen beschrieben:
- als Zustandsvektor: , bzw. als Wellenfunktion: .
Dieser Satz von Quantenzahlen wurde von Wolfgang Pauli erstmals 1924 gefunden. Da sie jeweils einen einzigen Zustand eines Elektrons festlegen, konnte er das nach ihm benannte Pauli-Prinzip so formulieren: Keine zwei Elektronen des Atoms können in allen vier Quantenzahlen übereinstimmen. ⓘ
Die Spin-Orbital-Wechselwirkung setzt diese Zahlen jedoch in Beziehung. So kann eine vollständige Beschreibung des Systems mit weniger Quantenzahlen gegeben werden, wenn orthogonale Entscheidungen für diese Basisvektoren getroffen werden. ⓘ
Spezifität
Verschiedene Elektronen in einem System haben unterschiedliche Quantenzahlen. So ist beispielsweise das Elektron mit dem höchsten besetzten Orbital, das eigentliche Unterscheidungselektron (d. h. das Elektron, das ein Element vom vorhergehenden unterscheidet), r das Unterscheidungselektron nach der Aufbaunäherung. Zur weiteren Veranschaulichung: Bei Lanthan befinden sich die beteiligten Elektronen in den Orbitalen 6s, 5d und 4f. In diesem Fall sind die Hauptquantenzahlen 6, 5 und 4. ⓘ
Gemeinsame Terminologie
Das hier verwendete Modell beschreibt die Elektronen mit den vier Quantenzahlen n, ℓ, mℓ, ms, die im Folgenden aufgeführt sind. Dies ist auch die übliche Nomenklatur bei der klassischen Beschreibung von Kernteilchenzuständen (z. B. Protonen und Neutronen). Eine Quantenbeschreibung von Molekülorbitalen erfordert andere Quantenzahlen, da der Hamiltonian und seine Symmetrien unterschiedlich sind. ⓘ
Prinzipielle Quantenzahl
Die Hauptquantenzahl beschreibt die Elektronenhülle bzw. das Energieniveau eines Elektrons. Der Wert von n reicht von 1 bis zu der Schale, die das äußerste Elektron des Atoms enthält, d. h.
- n = 1, 2, ... ⓘ
Bei Cäsium (Cs) beispielsweise befindet sich das äußerste Valenzelektron in der Schale mit dem Energieniveau 6, so dass ein Elektron in Cäsium einen n-Wert von 1 bis 6 haben kann. ⓘ
Für Teilchen in einem zeitunabhängigen Potenzial (siehe Schrödinger-Gleichung) bezeichnet sie auch den n-ten Eigenwert der Hamiltonschen Gleichung (H), d. h. die Energie E, wobei der Beitrag des Drehimpulses (der Term, der J2 einbezieht) weggelassen wird. Diese Zahl hängt also nur vom Abstand zwischen dem Elektron und dem Kern ab (d. h. von der radialen Koordinate r). Der durchschnittliche Abstand nimmt mit n zu. Daher sagt man, dass Quantenzustände mit unterschiedlichen Hauptquantenzahlen zu verschiedenen Schalen gehören. ⓘ
Azimutale Quantenzahl
Die azimutale Quantenzahl, auch bekannt als Drehimpulsquantenzahl oder Orbitalquantenzahl, beschreibt die Unterschale und gibt die Größe des Bahndrehimpulses durch die folgende Beziehung an ⓘ
- L2 = ħ2 ℓ (ℓ + 1) ⓘ
In der Chemie und Spektroskopie wird ℓ = 0 als s-Orbital, ℓ = 1 als p-Orbital, ℓ = 2 als d-Orbital und ℓ = 3 als f-Orbital bezeichnet. ⓘ
Der Wert von ℓ reicht von 0 bis n - 1, so dass das erste p-Orbital (ℓ = 1) in der zweiten Elektronenschale (n = 2), das erste d-Orbital (ℓ = 2) in der dritten Schale (n = 3) und so weiter erscheint:
- ℓ = 0, 1, 2,..., n - 1 ⓘ
Eine Quantenzahl, die mit n = 3 beginnt, ℓ = 0, beschreibt ein Elektron im s-Orbital der dritten Elektronenschale eines Atoms. In der Chemie ist diese Quantenzahl sehr wichtig, da sie die Form eines Atomorbitals angibt und chemische Bindungen und Bindungswinkel stark beeinflusst. Die azimutale Quantenzahl kann auch die Anzahl der in einem Orbital vorhandenen Winkelknoten angeben. Bei p-Orbitalen beispielsweise ist ℓ = 1 und damit die Anzahl der Winkelknoten in einem p-Orbital gleich 1. ⓘ
Die Form des Orbitals wird auch durch die azimutale Quantenzahl angegeben. ⓘ
Magnetische Quantenzahl
Die magnetische Quantenzahl beschreibt das spezifische Orbital (oder die "Wolke") innerhalb dieser Unterschale und ergibt die Projektion des Orbitaldrehimpulses entlang einer bestimmten Achse:
- Lz = mℓ ħ ⓘ
Die Werte von mℓ reichen von -ℓ bis ℓ, mit ganzzahligen Intervallen. ⓘ
Die s-Unterschale (ℓ = 0) enthält nur ein Orbital, so dass das mℓ eines Elektrons in einem s-Orbital immer 0 ist. Die p-Unterschale (ℓ = 1) enthält drei Orbitale (in manchen Systemen als drei "hantelförmige" Wolken dargestellt), so dass das mℓ eines Elektrons in einem p-Orbital -1, 0 oder 1 ist. Die d-Unterschale (ℓ = 2) enthält fünf Orbitale mit mℓ-Werten von -2, -1, 0, 1 und 2. ⓘ
Spinquantenzahl
Die Spinquantenzahl beschreibt den Eigendrehimpuls des Elektrons in jedem Orbital und gibt die Projektion des Spin-Drehimpulses S entlang der angegebenen Achse an:
- Sz = ms ħ. ⓘ
Im Allgemeinen reichen die Werte von ms von -s bis s, wobei s die Spinquantenzahl ist, die mit dem Eigendrehimpuls des Teilchens verbunden ist:
- ms = -s, -s + 1, -s + 2, ..., s - 2, s - 1, s. ⓘ
Ein Elektron hat die Spin-Zahl s = 1/2, folglich ist ms ±1/2, was sich auf die Zustände "spin up" und "spin down" bezieht. Aufgrund des Pauli-Ausschlussprinzips muss jedes Elektron in jedem einzelnen Orbital eine andere Quantenzahl haben, daher enthält ein Orbital nie mehr als zwei Elektronen. ⓘ
hat, gibt es für seine z-Komponente nur zwei mögliche Werte:
Regeln
Es gibt keine allgemeingültigen festen Werte für mℓ und ms. Vielmehr sind die mℓ- und ms-Werte willkürlich. Die einzige Einschränkung bei der Wahl dieser Konstanten besteht darin, dass das in einem bestimmten Satz von Berechnungen oder Beschreibungen verwendete Benennungsschema konsistent sein muss (z. B. das Orbital, das vom ersten Elektron in einem p-Orbital besetzt ist, kann als mℓ = -1 oder mℓ = 0 oder mℓ = 1 beschrieben werden, aber der mℓ-Wert des nächsten ungepaarten Elektrons in diesem Orbital muss anders sein; die mℓ-Werte, die den Elektronen in anderen Orbitalen zugeordnet sind, können wiederum mℓ = -1 oder mℓ = 0 oder mℓ = 1 sein). ⓘ
Diese Regeln lassen sich wie folgt zusammenfassen:
ⓘName Symbol Bedeutung Wertebereich Wertebeispiele Hauptquantenzahl n Schale 1 ≤ n n = 1, 2, 3, ... Azimutale Quantenzahl (Drehimpuls) ℓ Unterschale (s-Orbital wird als 0, p-Orbital als 1 usw. aufgeführt) 0 ≤ ℓ ≤ n - 1 für n = 3:
ℓ = 0, 1, 2 (s, p, d)Magnetische Quantenzahl (Projektion des Drehimpulses) mℓ Orbital (Orientierung des Orbitals) -ℓ ≤ mℓ ≤ ℓ für ℓ = 2:
mℓ = -2, -1, 0, 1, 2Spinquantenzahl ms Spin des Elektrons (-1/2 = "spin down", 1/2 = "spin up") -s ≤ ms ≤ s für ein Elektron s = 1/2,
also ms = -1/2, +1/2
Beispiel: Die Quantenzahlen für die äußersten Valenzelektronen eines Kohlenstoffatoms (C), die sich im 2p-Atomorbital befinden, lauten: n = 2 (2. Elektronenschale), ℓ = 1 (p-Orbital-Unterschale), mℓ = 1, 0, -1, ms = 1/2 (parallele Spins). ⓘ
Die Ergebnisse der Spektroskopie zeigen, dass bis zu zwei Elektronen ein einziges Orbital besetzen können. Allerdings können zwei Elektronen nach den Hund'schen Regeln, die das Pauli-Ausschlussprinzip berücksichtigen, niemals denselben exakten Quantenzustand oder dieselbe Menge von Quantenzahlen haben. Eine vierte Quantenzahl, die den Spin mit zwei möglichen Werten repräsentiert, wurde als Ad-hoc-Annahme hinzugefügt, um den Konflikt zu lösen; diese Annahme sollte später durch die relativistische Quantenmechanik und die Ergebnisse des berühmten Stern-Gerlach-Experiments im Detail erklärt werden. ⓘ
Hintergrund
Im Laufe der Geschichte der Quantenmechanik wurden viele verschiedene Modelle vorgeschlagen, aber das bekannteste Nomenklatursystem entstand aus der Hund-Mulliken-Molekülorbitaltheorie von Friedrich Hund, Robert S. Mulliken und Beiträgen von Schrödinger, Slater und John Lennard-Jones. In dieses Nomenklatursystem flossen die Bohr'schen Energieniveaus, die Hund-Mulliken-Orbital-Theorie und die auf der Spektroskopie und den Hund'schen Regeln beruhenden Beobachtungen zum Elektronenspin ein. ⓘ
Gesamtdrehimpulszahlen
Gesamtdrehimpuls eines Teilchens
Berücksichtigt man die Spin-Bahn-Wechselwirkung, so sind die L- und S-Operatoren nicht mehr mit der Hamiltonformel vertauschbar, und ihre Eigenwerte ändern sich daher mit der Zeit. Daher sollte ein anderer Satz von Quantenzahlen verwendet werden. Dieser Satz umfasst ⓘ
- Die Gesamtdrehimpuls-Quantenzahl:
- j = |ℓ ± s|
woraus sich der Gesamtdrehimpuls durch die Beziehung
- J2 = ħ2 j (j + 1)
- Die Projektion des Gesamtdrehimpulses entlang einer bestimmten Achse:
- mj = -j, -j + 1, -j + 2, ..., j - 2, j - 1, j
analog zur obigen Beziehung ergibt und die folgende Bedingung erfüllt
- mj = mℓ + ms und |mℓ + ms| ≤ j
- Parität
Dies ist der Eigenwert unter Reflexion: positiv (+1) für Zustände, die von geraden ℓ stammen und negativ (-1) für Zustände, die von ungeraden ℓ stammen. Erstere wird auch als gerade Parität und letztere als ungerade Parität bezeichnet und ist gegeben durch
- P = (-1)ℓ ⓘ
Betrachten wir zum Beispiel die folgenden 8 Zustände, die durch ihre Quantenzahlen definiert sind:
ⓘn ℓ mℓ ms ℓ + s ℓ - s mℓ + ms (1) 2 1 1 +1/2 3/2 1/23/2 (2) 2 1 1 -1/2 3/2 1/2 1/2 (3) 2 1 0 +1/2 3/2 1/2 1/2 (4) 2 1 0 -1/2 3/2 1/2 -1/2 (5) 2 1 -1 +1/2 3/2 1/2 -1/2 (6) 2 1 -1 -1/2 3/2 1/2-3/2 (7) 2 0 0 +1/2 1/2 -1/2 1/2 (8) 2 0 0 -1/2 1/2 -1/2 -1/2
Die Quantenzustände im System können als Linearkombination dieser 8 Zustände beschrieben werden. Wenn man jedoch bei Vorhandensein einer Spin-Bahn-Wechselwirkung dasselbe System durch 8 Zustände beschreiben will, die Eigenvektoren des Hamiltonian sind (d. h. jeder stellt einen Zustand dar, der sich im Laufe der Zeit nicht mit anderen mischt), sollten wir die folgenden 8 Zustände betrachten:
ⓘj mj Parität align=rechts | 3/2| align=rechts | ungerade kommend von Zustand (1) oben align=rechts | 1/2 ungerade kommend von Zustand (2) und (3) oben align=rechts | -1/2 ungerade aus den Zuständen (4) und (5) oben kommend align=rechts | -3/2| align=rechts | ungerade kommend von Zustand (6) oben align=rechts | 1/2 ungerade aus den Zuständen (2) und (3) oben kommend align=rechts | -1/2 ungerade aus den Zuständen (4) und (5) oben kommend align=rechts | 1/2 gerade kommend von Zustand (7) oben align=right | -1/2 even kommend von Zustand (8) oben
Quantenzahlen des Kerndrehimpulses
Wenn der Gesamtdrehimpuls eines Neutrons jn = ℓ + s und der eines Protons jp = ℓ + s ist (wobei s für Protonen und Neutronen zufällig wieder 1/2 ist (siehe Anmerkung)), dann sind die Kerndrehimpulsquantenzahlen I gegeben durch:
- I = |jn - jp|, |jn - jp| + 1, |jn - jp| + 2, ..., (jn + jp) - 2, (jn + jp) - 1, (jn + jp) ⓘ
Anmerkung: Die Bahndrehimpulse der Kern- (und Atom-) Zustände sind alle ganzzahlige Vielfache von ħ, während die Eigendrehimpulse von Neutron und Proton halbzahlige Vielfache sind. Es sollte unmittelbar einleuchten, dass die Kombination der Eigendrehimpulse der Nukleonen mit ihrer Bahnbewegung immer halbzahlige Werte für den Gesamtspin I eines jeden ungeraden A-Kerns und ganzzahlige Werte für jeden geraden A-Kern ergibt. ⓘ
Die Parität mit der Zahl I wird zur Kennzeichnung von Kerndrehimpulszuständen verwendet. Beispiele für einige Isotope von Wasserstoff (H), Kohlenstoff (C) und Natrium (Na) sind; ⓘ
ⓘ1
1HI = (1/2)+ 9
6CI = (3/2)- 20
11NaI = 2+ 2
1HI = 1+ 10
6CI = 0+ 21
11NaI = (3/2)+ 3
1HI = (1/2)+ 11
6C22
11NaI = 3+ 12
6CI = 0+ 23
11NaI = (3/2)+ 13
6CI = (1/2)- 24
11NaI = 4+ 14
6CI = 0+ 25
11NaI = (5/2)+ 15
6CI = (1/2)+ 26
11NaI = 3+
Der Grund für die ungewöhnlichen Schwankungen von I, selbst bei Unterschieden von nur einem Nukleon, liegt in der ungeraden und geraden Anzahl von Protonen und Neutronen - Nukleonenpaare haben einen Gesamtdrehimpuls von Null (genau wie Elektronen in Orbitalen), so dass eine ungerade oder gerade Anzahl ungepaarter Nukleonen übrig bleibt. Die Eigenschaft des Kernspins ist ein wichtiger Faktor für den Betrieb der NMR-Spektroskopie in der organischen Chemie und der MRT in der Nuklearmedizin, da das magnetische Moment des Kerns mit einem äußeren Magnetfeld wechselwirkt. ⓘ
Elementarteilchen
Elementarteilchen enthalten viele Quantenzahlen, von denen man gewöhnlich annimmt, dass sie ihnen innewohnen. Die Elementarteilchen sind jedoch Quantenzustände des Standardmodells der Teilchenphysik, und daher stehen die Quantenzahlen dieser Teilchen in der gleichen Beziehung zum Hamiltonian dieses Modells wie die Quantenzahlen des Bohr-Atoms zu seinem Hamiltonian. Mit anderen Worten, jede Quantenzahl steht für eine Symmetrie des Problems. In der Quantenfeldtheorie ist es sinnvoller, zwischen Raumzeit- und internen Symmetrien zu unterscheiden. ⓘ
Typische Quantenzahlen, die sich auf Raumzeitsymmetrien beziehen, sind der Spin (bezogen auf die Rotationssymmetrie), die Parität, die C-Parität und die T-Parität (bezogen auf die Poincaré-Symmetrie der Raumzeit). Typische interne Symmetrien sind Leptonenzahl und Baryonenzahl oder die elektrische Ladung. (Eine vollständige Liste der Quantenzahlen dieser Art finden Sie im Artikel über den Geschmack). ⓘ
Multiplikative Quantenzahlen
Die meisten erhaltenen Quantenzahlen sind additiv, so dass bei einer Elementarteilchenreaktion die Summe der Quantenzahlen vor und nach der Reaktion gleich sein sollte. Einige jedoch, die gewöhnlich als Parität bezeichnet werden, sind multiplikativ, d. h. ihr Produkt bleibt erhalten. Alle multiplikativen Quantenzahlen gehören zu einer Symmetrie (wie die Parität), bei der die zweimalige Anwendung der Symmetrietransformation gleichbedeutend ist mit der Nichtanwendung (Involution). ⓘ
Nebenquantenzahl
Die Nebenquantenzahl (auch Bahnquantenzahl oder Drehimpulsquantenzahl) kennzeichnet die Form des Atomorbitals in einem Atom. Bei gegebenem kann ihr Wert jede kleinere natürliche Zahl (einschließlich Null) sein:
- . ⓘ
Der Name „Drehimpulsquantenzahl“ verweist darauf, dass der Eigenwert des Quadrats des Drehimpulsoperators ist. ⓘ
Im laufenden Text wird der Wert von oft durch bestimmte, historisch festgelegte Buchstaben gekennzeichnet:
- s für (ursprünglich für ‚scharf‘, z. B. „s-Zustand“)
- p für (ursprünglich für engl. ‚principal‘, ‚Haupt‘-Zustand)
- d für (ursprünglich für ‚diffus‘)
- f für (ursprünglich für ‚fundamental‘)
- g für
und entsprechend alphabetisch weiter. Die gleiche Bezeichnungsweise wird z. B. auch für die Partialwellen bei Streuung, Kernreaktionen usw. verwendet. ⓘ
Magnetische Quantenzahl des Bahndrehimpulses
Die magnetische Quantenzahl des Drehimpulses wird mit bezeichnet und beschreibt die räumliche Orientierung des Elektronen-Bahndrehimpulses, genauer: die Größe seiner z-Komponente in Einheiten . Deshalb wird sie gelegentlich auch als bezeichnet. Sie kann betragsmäßig nicht größer als die Nebenquantenzahl sein, aber auch negative ganzzahlige Werte annehmen (siehe auch Richtungsquantelung):
Sie heißt Magnetquantenzahl, weil sie die zusätzliche potentielle Energie des Elektrons charakterisiert, die bei Anlegen eines Magnetfeldes in z-Richtung auftritt (Zeeman-Effekt). Durch seine Bewegung erzeugt das Elektron ein magnetisches Moment. Bei (dem Betrag nach) maximaler z-Komponente zeigt sein Bahndrehimpuls die maximal mögliche parallele oder antiparallele Ausrichtung zur z-Achse, und das mit ihm verbundene magnetische Moment bewirkt die im angelegten Feld maximal mögliche Energieerhöhung bzw. -verminderung. Bei ist die z-Komponente des Bahndrehimpulses null und bleibt ohne Einfluss auf die Energie des Elektrons. ⓘ
Weitere Quantenzahlen
Neben den Isospin- und Strangeness-Quantenzahlen bei Elementarteilchen sind einige andere Beispiele für weitere Quantenzahlen (meist zusammengesetzt bzw. abgeleitet): ⓘ
Paritätsquantenzahl
Die Paritätsquantenzahl bezeichnet das Symmetrieverhalten des Zustands unter Raumspiegelung. Sie kann die Werte und annehmen und hat keine Entsprechung in der klassischen Physik. Bis auf wenige Ausnahmen haben alle Energieeigenzustände der verschiedenen quantenmechanischen Systeme in sehr guter Näherung eine dieser beiden Quantenzahlen. ⓘ
Kernspinquantenzahl
Die Kernspinquantenzahl , auch kurz Kernspin genannt, beschreibt den Drehimpuls eines ganzen Atomkerns. Dieser setzt sich zusammen aus den Spins und den Bahndrehimpulsen der einzelnen Protonen und Neutronen, weshalb er folgende Werte annehmen kann:
- ganzzahlig, wenn die Nukleonenzahl gerade ist, z. B.
- halbzahlig, wenn die Nukleonenzahl ungerade ist, z. B. ⓘ
Gesamtdrehimpulsquantenzahl des Atoms
Die Gesamtdrehimpulsquantenzahl des Atoms beschreibt den Gesamtdrehimpuls eines ganzen Atoms. Dieser setzt sich aus dem Gesamtdrehimpuls J aller Elektronen und dem Kernspin I zusammen:
Für seinen Betrag gilt:
Dabei nimmt F (für ein J) folgende Werte an:
Radiale Quantenzahl
Die radiale Quantenzahl ist die Anzahl der Nullstellen (Knoten) im radialen Anteil der Wellenfunktion eines gebundenen Teilchens:
mit
- : Hauptquantenzahl
- : Anzahl der Knoten insgesamt
- : Nebenquantenzahl = Anzahl der Knoten im winkelabhängigen Teil der Wellenfunktion:
| Schale | = Anz. Knoten insgesamt |
Nebenquantenzahl = Anz. Knoten im winkelabh. Teil der WF |
radiale Quantenzahl = Anz. Knoten im radiusabh. Teil der WF ⓘ |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 |
| 1 | 0 | ||
| 3 | 2 | 0 | 2 |
| 1 | 1 | ||
| 2 | 0 |
usw. ⓘ



































