Säurekonstante
| Säuren und Basen ⓘ |
|---|
 |
|
| Säuren-Typen |
|
| Basen-Typen |
|
Die Säuredissoziationskonstante Ka (auch als Säurekonstante oder Säure-Ionisationskonstante bezeichnet) ist ein quantitatives Maß für die Stärke einer Säure in Lösung. Sie ist die Gleichgewichtskonstante für eine chemische Reaktion
Die Dissoziationskonstante ist definiert durch
wobei die Mengen in eckigen Klammern die Konzentrationen der Spezies im Gleichgewicht darstellen. ⓘ
Die Säurekonstante KS ist eine Stoffkonstante, die Aufschluss darüber gibt, in welchem Maße ein Stoff in einer Gleichgewichtsreaktion mit Wasser unter Protolyse reagiert:
- .
Dabei steht HA für eine Brønsted-Säure (nach Johannes Nicolaus Brønsted), die ein Proton H+ an ein Lösungsmittel wie Wasser abgeben kann, wobei ein Anion A− zurückbleibt. Allgemeiner gilt die Brønsted'sche Definition auch für nichtwässrige Systeme, hier gilt für ein beliebiges, protonierbares Lösungsmittel Y:
- . ⓘ
Theoretischer Hintergrund
Die Säuredissoziationskonstante einer Säure ist eine direkte Folge der zugrundeliegenden Thermodynamik der Dissoziationsreaktion; der pKa-Wert ist direkt proportional zur Standardänderung der freien Gibbs-Energie für die Reaktion. Der Wert von pKa ändert sich mit der Temperatur und kann auf der Grundlage des Le Châtelier-Prinzips qualitativ verstanden werden: Wenn die Reaktion endotherm ist, nimmt Ka zu und pKa nimmt mit steigender Temperatur ab; bei exothermen Reaktionen ist das Gegenteil der Fall. ⓘ
Der Wert von pKa hängt auch in vielerlei Hinsicht von der Molekularstruktur der Säure ab. Pauling schlug beispielsweise zwei Regeln vor: eine für die aufeinanderfolgenden pKa-Werte von polyprotischen Säuren (siehe Polyprotische Säuren unten) und eine für die Schätzung des pKa-Werts von Oxysäuren auf der Grundlage der Anzahl der =O- und -OH-Gruppen (siehe Faktoren, die die pKa-Werte beeinflussen unten). Weitere strukturelle Faktoren, die die Größe der Säuredissoziationskonstante beeinflussen, sind induktive Effekte, mesomere Effekte und Wasserstoffbrückenbindungen. Hammett-Gleichungen wurden häufig zur Schätzung von pKa verwendet. ⓘ
Das quantitative Verhalten von Säuren und Basen in Lösung kann nur verstanden werden, wenn ihre pKa-Werte bekannt sind. Insbesondere kann der pH-Wert einer Lösung vorhergesagt werden, wenn die analytische Konzentration und die pKa-Werte aller Säuren und Basen bekannt sind; umgekehrt ist es möglich, die Gleichgewichtskonzentration der Säuren und Basen in Lösung zu berechnen, wenn der pH-Wert bekannt ist. Diese Berechnungen finden in vielen verschiedenen Bereichen der Chemie, Biologie, Medizin und Geologie Anwendung. So sind zum Beispiel viele Verbindungen, die für Medikamente verwendet werden, schwache Säuren oder Basen, und die Kenntnis der pKa-Werte kann zusammen mit dem Octanol-Wasser-Verteilungskoeffizienten verwendet werden, um abzuschätzen, inwieweit die Verbindung in den Blutkreislauf gelangt. Säuredissoziationskonstanten sind auch in der Wasserchemie und der chemischen Ozeanographie von Bedeutung, wo der Säuregrad des Wassers eine grundlegende Rolle spielt. In lebenden Organismen hängen die Säure-Basen-Homöostase und die Enzymkinetik von den pKa-Werten der vielen in der Zelle und im Körper vorhandenen Säuren und Basen ab. In der Chemie ist die Kenntnis der pKa-Werte notwendig für die Herstellung von Pufferlösungen und auch Voraussetzung für ein quantitatives Verständnis der Wechselwirkung zwischen Säuren oder Basen und Metallionen zur Bildung von Komplexen. Experimentell können pKa-Werte durch potentiometrische (pH-)Titration bestimmt werden, aber für pKa-Werte unter etwa 2 oder über etwa 11 sind aufgrund praktischer Schwierigkeiten bei der pH-Messung möglicherweise spektrophotometrische oder NMR-Messungen erforderlich. ⓘ
Begriffsbestimmungen
Nach der ursprünglichen molekularen Definition von Arrhenius ist eine Säure eine Substanz, die in wässriger Lösung dissoziiert und dabei das Wasserstoffion H+ (ein Proton) freisetzt:
- HA ⇌ A- + H+. ⓘ
Die Gleichgewichtskonstante für diese Dissoziationsreaktion wird als Dissoziationskonstante bezeichnet. Das freigesetzte Proton verbindet sich mit einem Wassermolekül zu einem Hydronium- (oder Oxonium-) Ion H3O+ (nackte Protonen gibt es in Lösung nicht), so dass Arrhenius später vorschlug, die Dissoziation als Säure-Base-Reaktion zu schreiben:
- HA + H2O ⇌ A- + H3O+. ⓘ
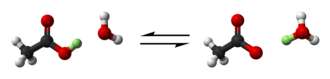
Brønsted und Lowry verallgemeinerten dies weiter zu einer Protonenaustauschreaktion:
- Säure + Base ⇌ konjugierte Base + konjugierte Säure. ⓘ
Die Säure verliert ein Proton und hinterlässt eine konjugierte Base; das Proton wird auf die Base übertragen, wodurch eine konjugierte Säure entsteht. Bei wässrigen Lösungen einer Säure HA ist die Base Wasser, die konjugierte Base ist A- und die konjugierte Säure ist das Hydroniumion. Die Brønsted-Lowry-Definition gilt auch für andere Lösungsmittel, z. B. Dimethylsulfoxid: Das Lösungsmittel S wirkt als Base, nimmt ein Proton auf und bildet die konjugierte Säure SH+.
- HA + S ⇌ A- + SH+. ⓘ
In der Lösungschemie ist es üblich, H+ als Abkürzung für das solvatisierte Wasserstoffion zu verwenden, unabhängig vom Lösungsmittel. In wässriger Lösung bezeichnet H+ ein solvatisiertes Hydronium-Ion und nicht ein Proton. ⓘ
Die Bezeichnung einer Säure oder Base als "konjugiert" hängt vom jeweiligen Kontext ab. Die konjugierte Säure BH+ einer Base B dissoziiert nach der Formel
- BH+ + OH- ⇌ B + H2O ⓘ
was die Umkehrung des Gleichgewichts ist
- H2O (Säure) + B (Base) ⇌ OH- (konjugierte Base) + BH+ (konjugierte Säure). ⓘ
Das Hydroxidion OH-, eine wohlbekannte Base, fungiert hier als konjugierte Base der Säure Wasser. Säuren und Basen werden also einfach als Donatoren bzw. Akzeptoren von Protonen betrachtet. ⓘ
Eine umfassendere Definition der Säuredissoziation schließt die Hydrolyse ein, bei der Protonen durch die Spaltung von Wassermolekülen entstehen. Borsäure (B(OH)3) zum Beispiel erzeugt H3O+, als wäre sie ein Protonendonator, aber es wurde durch Raman-Spektroskopie bestätigt, dass dies auf das Hydrolysegleichgewicht zurückzuführen ist:
- B(OH)3 + 2 H2O ⇌ B(OH)4- + H3O+. ⓘ
In ähnlicher Weise bewirkt die Hydrolyse von Metallionen, dass sich Ionen wie [Al(H2O)6]3+ wie schwache Säuren verhalten:
- [Al(H2O)6]3+ + H2O ⇌ [Al(H2O)5(OH)]2+ + H3O+. ⓘ
Nach der ursprünglichen Lewis-Definition ist eine Säure ein Stoff, der ein Elektronenpaar aufnimmt, um eine koordinative kovalente Bindung zu bilden. ⓘ
Gleichgewichtskonstante
Eine Säuredissoziationskonstante ist ein besonderes Beispiel für eine Gleichgewichtskonstante. Die Dissoziation einer monoprotischen Säure, HA, in verdünnter Lösung kann wie folgt beschrieben werden
- HA ⇌ A- + H+ ⓘ
Die thermodynamische Gleichgewichtskonstante, kann definiert werden durch
wobei {X} die Aktivität der chemischen Spezies X im Gleichgewicht darstellt. ist dimensionslos, da die Aktivität dimensionslos ist. Die Aktivitäten der Dissoziationsprodukte stehen im Zähler, die Aktivitäten der Reaktanten im Nenner. Siehe Aktivitätskoeffizient für eine Herleitung dieses Ausdrucks. ⓘ

Da die Aktivität das Produkt aus Konzentration und Aktivitätskoeffizient (γ) ist, kann die Definition auch wie folgt geschrieben werden
Um die mit der Verwendung von Aktivitäten verbundenen Komplikationen zu vermeiden, werden die Dissoziationskonstanten nach Möglichkeit in einem Medium mit hoher Ionenstärke bestimmt, d. h. unter Bedingungen, bei denen immer als konstant angenommen werden kann. Das Medium könnte zum Beispiel eine Lösung von 0,1 molarem (M) Natriumnitrat oder 3 M Kaliumperchlorat sein. Mit dieser Annahme,
Kumulative und stufenweise Konstanten
Eine kumulative Gleichgewichtskonstante, bezeichnet mit steht in Beziehung zu dem Produkt der Stufenkonstanten, bezeichnet mit . Für eine zweibasige Säure ist die Beziehung zwischen stufenweisen und Gesamtkonstanten wie folgt
Man beachte, dass im Zusammenhang mit der Bildung von Metall-Ligand-Komplexen die Gleichgewichtskonstanten für die Bildung von Metallkomplexen in der Regel als Assoziationskonstanten definiert werden. In diesem Fall werden auch die Gleichgewichtskonstanten für die Ligandenprotonierung als Assoziationskonstanten definiert. Die Nummerierung der Assoziationskonstanten ist umgekehrt zur Nummerierung der Dissoziationskonstanten; in diesem Beispiel ⓘ
Assoziations- und Dissoziationskonstanten
Bei der Erörterung der Eigenschaften von Säuren ist es üblich, die Gleichgewichtskonstanten als Säuredissoziationskonstanten (Ka) zu bezeichnen, wobei die Zahlenwerte mit dem Symbol pKa angegeben werden.
Für Basen hingegen werden Assoziationskonstanten verwendet.
Allgemeine Computerprogramme, die zur Ableitung von Gleichgewichtskonstanten aus experimentellen Daten verwendet werden, verwenden jedoch Assoziationskonstanten sowohl für Säuren als auch für Basen. Da die Stabilitätskonstanten für einen Metall-Liganden-Komplex immer als Assoziationskonstanten angegeben werden, muss auch die Ligandenprotonierung als Assoziationsreaktion angegeben werden. Aus den Definitionen geht hervor, dass der Wert einer Säuredissoziationskonstante der Kehrwert des Wertes der entsprechenden Assoziationskonstante ist.
- Kdissoc = 1 / Kassoc
- log Kdissoc = -log Kassoc
- pKdissoc = log Kassoc ⓘ
Anmerkungen
- Für eine bestimmte Säure oder Base ist pKa + pKb = pKw, die Selbstionisationskonstante von Wasser.
- Die Assoziationskonstante für die Bildung eines supramolekularen Komplexes kann als Ka bezeichnet werden; in diesen Fällen steht "a" für "Assoziation" und nicht für "Säure".
- Bei polyprotischen Säuren ist die Nummerierung der stufenweisen Assoziationskonstanten umgekehrt wie die Nummerierung der Dissoziationskonstanten. Zum Beispiel für Phosphorsäure (Einzelheiten unter #polyprotische Säuren, unten) ⓘ
Temperaturabhängigkeit
Alle Gleichgewichtskonstanten variieren mit der Temperatur gemäß der van 't Hoff-Gleichung
R ist die Gaskonstante und T ist die absolute Temperatur. Bei exothermen Reaktionen ist die Standard-Enthalpieänderung also negativ, negativ und K nimmt mit der Temperatur ab. Für endotherme Reaktionen, positiv, und K nimmt mit der Temperatur zu. ⓘ
Die Standard-Enthalpieänderung für eine Reaktion ist nach dem Kirchhoffschen Gesetz der Thermochemie selbst eine Funktion der Temperatur:
Dimensionalität
In der Gleichung
Ka scheint die Dimension der Konzentration zu haben. Da jedoch die Gleichgewichtskonstante ist, keine physikalische Dimension haben. Dieses scheinbare Paradoxon kann auf verschiedene Weise aufgelöst werden.
- Nehmen wir an, dass der Quotient der Aktivitätskoeffizienten den Zahlenwert 1 hat, so dass den gleichen numerischen Wert hat wie die thermodynamische Gleichgewichtskonstante .
- Man drückt jeden Konzentrationswert als das Verhältnis c/c0 aus, wobei c0 die Konzentration in einem [hypothetischen] Standardzustand ist, der per Definition den Zahlenwert 1 hat.
- Drücken Sie die Konzentrationen auf der Skala des Molenbruchs aus. Da der Molenbruch keine Dimension hat, ist der Quotient der Konzentrationen per Definition eine reine Zahl. ⓘ
Die Verfahren (1) und (2) liefern identische numerische Werte für eine Gleichgewichtskonstante. Da außerdem eine Konzentration, einfach proportional zum Molenbruch ist, und der Dichte,
In der Biochemie ist es üblich, einen Wert mit einer Dimension anzugeben, z. B. "Ka = 30 mM", um die Skala, millimolar (mM) oder mikromolar (μM), der für seine Berechnung verwendeten Konzentrationswerte anzugeben. ⓘ
Starke Säuren und Basen
Eine Säure wird als "stark" eingestuft, wenn die Konzentration ihrer undissoziierten Spezies zu gering ist, um gemessen zu werden. Jede wässrige Säure mit einem pKa-Wert von weniger als 0 ist fast vollständig deprotoniert und gilt als starke Säure. Alle diese Säuren geben ihre Protonen an Wasser ab und bilden die Kationenspezies des Lösungsmittels (H3O+ in wässriger Lösung), so dass sie alle im Wesentlichen den gleichen Säuregrad haben, ein Phänomen, das als Solvent Leveling bekannt ist. Sie gelten in wässriger Lösung als vollständig dissoziiert, da die Menge der undissoziierten Säure im Gleichgewicht mit den Dissoziationsprodukten unterhalb der Nachweisgrenze liegt. Ebenso wird jede wässrige Base mit einer Assoziationskonstante pKb kleiner als etwa 0, entsprechend einem pKa größer als etwa 14, zu OH- nivelliert und gilt als starke Base. ⓘ
Salpetersäure mit einem pK-Wert von ca. -1,7 verhält sich in wässrigen Lösungen mit einem pH-Wert von mehr als 1 wie eine starke Säure, bei niedrigeren pH-Werten wie eine schwache Säure. ⓘ
Die pKa-Werte für starke Säuren wurden mit theoretischen Mitteln geschätzt. Der pKa-Wert von wässrigem HCl wurde beispielsweise auf -9,3 geschätzt. ⓘ
Monoprotische Säuren

Wenn man den Ausdruck zur Definition von Ka umformt und pH = -log10[H+] einsetzt, erhält man ⓘ
Dies ist die Henderson-Hasselbalch-Gleichung, aus der die folgenden Schlussfolgerungen gezogen werden können.
- Bei Halbneutralisation ist das Verhältnis [A-]/[HA] = 1; da log(1) = 0 ist, ist der pH-Wert bei Halbneutralisation numerisch gleich pKa. Umgekehrt ist bei pH = pKa die Konzentration von HA gleich der Konzentration von A-.
- Der Pufferbereich erstreckt sich über den ungefähren Bereich pKa ± 2. Außerhalb des Bereichs pKa ± 1 ist die Pufferung schwach. Bei pH ≤ pKa - 2 gilt die Substanz als vollständig protoniert und bei pH ≥ pKa + 2 als vollständig dissoziiert (deprotoniert).
- Wenn der pH-Wert bekannt ist, kann das Verhältnis berechnet werden. Dieses Verhältnis ist unabhängig von der analytischen Konzentration der Säure. ⓘ
In Wasser reichen die messbaren pKa-Werte von etwa -2 für eine starke Säure bis etwa 12 für eine sehr schwache Säure (oder starke Base). ⓘ
Eine Pufferlösung mit einem gewünschten pH-Wert kann als Mischung aus einer schwachen Säure und ihrer konjugierten Base hergestellt werden. In der Praxis kann die Mischung durch Auflösen der Säure in Wasser und Zugabe der erforderlichen Menge einer starken Säure oder Base hergestellt werden. Wenn der pKa-Wert und die analytische Konzentration der Säure bekannt sind, lassen sich das Ausmaß der Dissoziation und der pH-Wert einer Lösung einer einwertigen Säure mit Hilfe einer ICE-Tabelle leicht berechnen. ⓘ
Polyprotische Säuren

Eine polyprotische Säure ist eine Verbindung, die mehr als 1 Proton verlieren kann. Schrittweise Dissoziationskonstanten werden jeweils für den Verlust eines einzelnen Protons definiert. Die Konstante für die Dissoziation des ersten Protons kann als Ka1 bezeichnet werden und die Konstanten für die Dissoziation der nachfolgenden Protonen als Ka2 usw. Phosphorsäure, H3PO4, ist ein Beispiel für eine polyprotische Säure, da sie drei Protonen verlieren kann.
ⓘGleichgewicht pK Definition und Wert H
3PO
4 ⇌ H
2PO-
4 + H+H
2PO-
4 ⇌ HPO2-
4 + H+HPO2-
4 ⇌ PO3-
4 + H+
Wenn der Unterschied zwischen aufeinanderfolgenden pK-Werten etwa vier oder mehr beträgt, wie in diesem Beispiel, kann jede Spezies als eigenständige Säure betrachtet werden; in der Tat können Salze von H
2PO-
4 können aus einer Lösung kristallisiert werden, indem der pH-Wert auf etwa 5,5 eingestellt wird, und Salze von HPO2-
4 können aus der Lösung kristallisiert werden, wenn der pH-Wert auf etwa 10 eingestellt wird. Das Diagramm der Speziesverteilung zeigt, dass die Konzentrationen der beiden Ionen bei pH 5,5 und 10 maximal sind. ⓘ
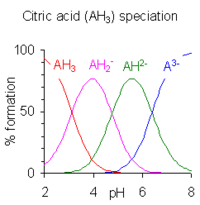
Wenn der Unterschied zwischen aufeinanderfolgenden pK-Werten weniger als vier beträgt, überschneiden sich die pH-Bereiche, in denen die Spezies im Gleichgewicht existieren. Je kleiner die Differenz ist, desto größer ist die Überlappung. Der Fall der Zitronensäure ist rechts dargestellt; Lösungen von Zitronensäure sind über den gesamten Bereich von pH 2,5 bis 7,5 gepuffert. ⓘ
Nach der ersten Pauling-Regel steigen die pK-Werte einer bestimmten Säure nacheinander an (pKa2 > pKa1). Bei Sauerstoffsäuren mit mehr als einem ionisierbaren Wasserstoff am selben Atom steigen die pKa-Werte oft um etwa 5 Einheiten für jedes entfernte Proton, wie im obigen Beispiel der Phosphorsäure. ⓘ
Aus der obigen Tabelle ist ersichtlich, dass das zweite Proton aus einer negativ geladenen Spezies entfernt wird. Da das Proton eine positive Ladung trägt, ist zusätzliche Arbeit erforderlich, um es zu entfernen. Aus diesem Grund ist pKa2 größer als pKa1. pKa3 ist größer als pKa2, da eine weitere Ladungstrennung stattfindet. Wenn eine Ausnahme von der Paulingschen Regel gefunden wird, deutet dies darauf hin, dass auch eine größere Strukturänderung stattfindet. Im Fall von VO2+ (aq.) ist das Vanadium oktaedrisch und 6-koordiniert, während die Vanadinsäure tetraedrisch und 4-koordiniert ist. Dies bedeutet, dass bei der ersten Dissoziation vier "Teilchen" freigesetzt werden, bei den anderen Dissoziationen jedoch nur zwei "Teilchen", was zu einem viel größeren Entropiebeitrag zur Standard-Gibbs-Energieänderung für die erste Reaktion führt als für die anderen.
ⓘGleichgewicht pKa [VO2(H2O)4]+ ⇌ H3VO4 + H+ + 2H2O H3VO4 ⇌ H
2VO-
4 + H+H
2VO-
4 ⇌ HVO2-
4 + H+HVO2-
4 ⇌ VO3-
4 + H+
Isoelektrischer Punkt
Für Stoffe in Lösung ist der isoelektrische Punkt (pI) definiert als der pH-Wert, bei dem die nach Ladungswert gewichtete Summe der Konzentrationen der positiv geladenen Spezies gleich der gewichteten Summe der Konzentrationen der negativ geladenen Spezies ist. Gibt es von jeder Art nur eine Spezies, so lässt sich der isoelektrische Punkt direkt aus den pK-Werten ableiten. Nehmen wir das Beispiel von Glycin, definiert als AH. Es sind zwei Dissoziationsgleichgewichte zu berücksichtigen.
- AH+
2 ⇌ AH + H+; [AH][H+] = K1[AH+
2] - AH ⇌ A- + H+; [A-][H+] = K2[AH] ⓘ
Setzen Sie den Ausdruck für [AH] aus der zweiten Gleichung in die erste Gleichung ein
- [A-][H+]2 = K1K2[AH+
2] ⓘ
Am isoelektrischen Punkt ist die Konzentration der positiv geladenen Spezies, AH2+, gleich der Konzentration der negativ geladenen Spezies, A-, also
- [H+]2 = K1K2 ⓘ
Der pH-Wert ergibt sich daher, wenn man kologarithmiert, wie folgt
Die pI-Werte für Aminosäuren sind unter Proteinogene Aminosäure aufgeführt. Wenn mehr als zwei geladene Spezies miteinander im Gleichgewicht sind, kann eine vollständige Speziationsberechnung erforderlich sein. ⓘ
Basen und Basizität
Die Gleichgewichtskonstante Kb für eine Base ist in der Regel definiert als die Assoziationskonstante für die Protonierung der Base B unter Bildung der konjugierten Säure HB+.
- B + H2O ⇌ HB+ + OH- ⓘ
Mit einer ähnlichen Argumentation wie zuvor
Kb ist mit Ka für die konjugierte Säure verbunden. In Wasser ist die Konzentration des Hydroxid-Ions [OH-] mit der Konzentration des Wasserstoff-Ions durch Kw = [H+][OH-] verknüpft, daher
Die Substitution des Ausdrucks für [OH-] in den Ausdruck für Kb ergibt
Wenn Ka, Kb und Kw unter den gleichen Bedingungen (Temperatur und Ionenstärke) bestimmt werden, ergibt sich durch Umrechnen, dass pKb = pKw - pKa. In wässrigen Lösungen bei 25 °C beträgt pKw 13,9965, also
mit ausreichender Genauigkeit für die meisten praktischen Zwecke. Eigentlich ist es nicht nötig, pKb getrennt von pKa zu definieren, aber es wird hier getan, da in der älteren Literatur oft nur pKb-Werte zu finden sind. ⓘ
Für ein hydrolysiertes Metallion kann Kb auch als eine stufenweise Dissoziationskonstante definiert werden
Dies ist der Kehrwert einer Assoziationskonstante für die Bildung des Komplexes. ⓘ
Basizität ausgedrückt als Dissoziationskonstante der konjugierten Säure
Da die Beziehung pKb = pKw - pKa nur für wässrige Lösungen gilt (obwohl analoge Beziehungen für andere amphotere Lösungsmittel gelten), verwenden Teildisziplinen der Chemie wie die organische Chemie, die sich gewöhnlich mit nichtwässrigen Lösungen befassen, im Allgemeinen nicht pKb als Maß für die Basizität. Stattdessen wird der pKa der konjugierten Säure (pKaH) angegeben, wenn die Basizität quantifiziert werden muss. Für die Base B und ihre konjugierte Säure BH+, die sich im Gleichgewicht befinden, ist dies definiert als
Ein höherer Wert für pKaH entspricht einer stärkeren Base. So bedeuten beispielsweise die Werte pKaH(C5H5N) = 5,25 und pKaH((CH3CH2)3N) = 10,75, dass (CH3CH2)3N (Triethylamin) eine stärkere Base ist als C5H5N (Pyridin). ⓘ
Amphotere Stoffe
Eine amphotere Substanz ist eine Substanz, die je nach pH-Wert als Säure oder als Base wirken kann. Wasser (unten) ist eine amphotere Substanz. Ein weiteres Beispiel für ein amphoteres Molekül ist das Bicarbonat-Ion HCO-
3, das die konjugierte Base des Kohlensäuremoleküls H2CO3 im Gleichgewicht ist
- H2CO3 + H2O ⇌ HCO-
3 + H3O+ ⓘ
sondern auch die konjugierte Säure des Carbonat-Ions CO2-
3 in (der Umkehrung des) Gleichgewichts
- HCO-
3 + OH- ⇌ CO2-
3 + H2O.oder
Kohlensäuregleichgewichte sind wichtig für die Säure-Basen-Homöostase im menschlichen Körper. ⓘ
Eine Aminosäure ist ebenfalls amphoter, mit der zusätzlichen Komplikation, dass das neutrale Molekül einem internen Säure-Basen-Gleichgewicht unterliegt, bei dem die basische Aminogruppe das Proton der sauren Carboxylgruppe anzieht und bindet, wodurch ein Zwitterion entsteht.
- NH2CHRCO2H ⇌ NH+
3CHRCO-
2 ⓘ
Bei einem pH-Wert von weniger als 5 sind sowohl die Carboxylatgruppe als auch die Aminogruppe protoniert. Mit steigendem pH-Wert dissoziiert die Säure nach der Formel
- NH+
3CHRCO
2H ⇌ NH+
3CHRCO-
2 + H+ ⓘ
Bei hohem pH-Wert kann eine zweite Dissoziation stattfinden.
- NH+
3CHRCO-
2 ⇌ NH
2CHRCO-
2 + H+ ⓘ
Das Aminosäuremolekül ist also amphoter, da es entweder protoniert oder deprotoniert werden kann. ⓘ
Selbstionisierung von Wasser
Das Wassermolekül kann entweder ein Proton gewinnen oder verlieren. Man sagt, es sei amphiprotisch. Das Ionisierungsgleichgewicht kann wie folgt beschrieben werden
- H2O ⇌ OH- + H+ ⓘ
wobei H+ in wässriger Lösung ein solvatisiertes Proton bezeichnet. Häufig wird dies als Hydronium-Ion H3O+ geschrieben, aber diese Formel ist nicht exakt, da in der Tat mehr als ein Wassermolekül solvatisiert ist und auch Spezies wie H5O2+, H7O3+ und H9O4+ vorhanden sind. ⓘ
Die Gleichgewichtskonstante ist gegeben durch
Bei Lösungen, in denen die Konzentrationen der gelösten Stoffe nicht sehr hoch sind, kann die Konzentration [H2O] als konstant angenommen werden, unabhängig von den gelösten Stoffen; dieser Ausdruck kann dann ersetzt werden durch
Die Selbstionisationskonstante von Wasser, Kw, ist also nur ein Spezialfall einer Säuredissoziationskonstante. Es kann auch eine logarithmische Form analog zu pKa definiert werden
| T (°C) | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| pKw | 14.943 | 14.734 | 14.535 | 14.346 | 14.167 | 13.997 | 13.830 | 13.680 | 13.535 | 13.396 | 13.262 |
Diese Daten können an eine Parabel angepasst werden mit
- pKw = 14,94 - 0,04209T + 0,0001718T2 ⓘ
Aus dieser Gleichung ergibt sich pKw = 14 bei 24,87 °C. Bei dieser Temperatur haben sowohl Wasserstoff- als auch Hydroxid-Ionen eine Konzentration von 10-7 M. ⓘ
Azidität in nichtwässrigen Lösungen
Ein Lösungsmittel begünstigt die Ionisierung eines gelösten sauren Moleküls unter den folgenden Umständen eher:
- Es ist ein protisches Lösungsmittel, das in der Lage ist, Wasserstoffbrücken zu bilden.
- Es hat eine hohe Donorzahl und ist damit eine starke Lewis-Base.
- Es hat eine hohe Dielektrizitätskonstante (relative Dielektrizitätskonstante), was es zu einem guten Lösungsmittel für ionische Stoffe macht.
Die pKa-Werte von organischen Verbindungen werden häufig mit den aprotischen Lösungsmitteln Dimethylsulfoxid (DMSO) und Acetonitril (ACN) ermittelt. ⓘ
| Lösungsmittel | Donatorzahl | Dielektrizitätskonstante |
|---|---|---|
| Acetonitril | 14 | 37 |
| Dimethylsulfoxid | 30 | 47 |
| Wasser | 18 | 78 |
DMSO wird häufig als Alternative zu Wasser verwendet, da es eine niedrigere Dielektrizitätskonstante als Wasser hat und weniger polar ist, so dass es unpolare, hydrophobe Substanzen leichter auflöst. Es hat einen messbaren pKa-Bereich von etwa 1 bis 30. Acetonitril ist weniger basisch als DMSO, so dass Säuren in diesem Lösungsmittel im Allgemeinen schwächer und Basen stärker sind. Einige pKa-Werte bei 25 °C für Acetonitril (ACN) und Dimethylsulfoxid (DMSO) sind in den folgenden Tabellen aufgeführt. Zum Vergleich sind die Werte für Wasser angegeben. ⓘ
| HA ⇌ A- + H+ | ACN | DMSO | Wasser |
|---|---|---|---|
| p-Toluolsulfonsäure | 8.5 | 0.9 | Starke |
| 2,4-Dinitrophenol | 16.66 | 5.1 | 3.9 |
| Benzoesäure | 21.51 | 11.1 | 4.2 |
| Essigsäure | 23.51 | 12.6 | 4.756 |
| Phenol | 29.14 | 18.0 | 9.99 |
| BH+ ⇌ B + H+ | ACN | DMSO | Wasser |
| Pyrrolidin | 19.56 | 10.8 | 11.4 |
| Triethylamin | 18.82 | 9.0 | 10.72 |
| Protonenschwamm | 18.62 | 7.5 | 12.1 |
| Pyridin | 12.53 | 3.4 | 5.2 |
| Anilin | 10.62 | 3.6 | 4.6 |
Die Ionisierung von Säuren ist in einem sauren Lösungsmittel geringer als in Wasser. Chlorwasserstoff ist beispielsweise eine schwache Säure, wenn er in Essigsäure aufgelöst ist. Der Grund dafür ist, dass Essigsäure eine viel schwächere Base ist als Wasser.
- HCl + CH3CO2H ⇌ Cl- + CH
3C(OH)+
2 - Säure + Base ⇌ konjugierte Base + konjugierte Säure ⓘ
Vergleichen Sie diese Reaktion mit dem, was passiert, wenn Essigsäure in dem saureren Lösungsmittel reine Schwefelsäure gelöst wird
H2SO4 + CH3CO2H ⇌ HSO-
4 + CH
3C(OH)+
2 ⓘ

Die unwahrscheinliche geminale Diolart CH
3C(OH)+
2 ist in diesen Umgebungen stabil. Für wässrige Lösungen ist die pH-Skala die am besten geeignete Säurefunktion. Für nichtwässrige Medien wurden andere Säurefunktionen vorgeschlagen, vor allem die Hammett-Säurefunktion H0 für supersaure Medien und ihre modifizierte Version H- für superbasische Medien. ⓘ
In aprotischen Lösungsmitteln können Oligomere, wie das bekannte Essigsäure-Dimer, durch Wasserstoffbrückenbindungen gebildet werden. Eine Säure kann auch Wasserstoffbrücken mit ihrer konjugierten Base bilden. Dieser Prozess, der als Homokonjugation bezeichnet wird, bewirkt, dass der Säuregehalt von Säuren erhöht und ihr effektiver pKa-Wert gesenkt wird, indem die konjugierte Base stabilisiert wird. Homokonjugation erhöht die protonenspendende Kraft von Toluolsulfonsäure in Acetonitrillösung um einen Faktor von fast 800. ⓘ
In wässrigen Lösungen findet keine Homokonjugation statt, da Wasser stärkere Wasserstoffbrückenbindungen mit der konjugierten Base bildet als die Säure. ⓘ
Gemischte Lösungsmittel
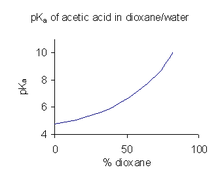
Wenn eine Verbindung nur begrenzt in Wasser löslich ist, ist es üblich (z. B. in der pharmazeutischen Industrie), die pKa-Werte in einem Lösungsmittelgemisch wie Wasser/Dioxan oder Wasser/Methanol zu bestimmen, in dem die Verbindung besser löslich ist. In dem rechts dargestellten Beispiel steigt der pKa-Wert mit zunehmendem Anteil an Dioxan steil an, da die Dielektrizitätskonstante des Gemischs abnimmt. ⓘ
Ein in einem gemischten Lösungsmittel erhaltener pKa-Wert kann nicht direkt für wässrige Lösungen verwendet werden. Der Grund dafür ist, dass die Aktivität des Lösungsmittels im Standardzustand als eins definiert ist. So ist beispielsweise der Standardzustand eines Wasser-Dioxan-Gemischs mit einem Mischungsverhältnis von 9:1 genau dieses Lösungsmittelgemisch, dem keine gelösten Stoffe zugesetzt sind. Um den pKa-Wert für die Verwendung mit wässrigen Lösungen zu erhalten, muss er aus den Werten, die aus verschiedenen Gemischen von Co-Lösungsmitteln erhalten wurden, auf eine Co-Lösungsmittelkonzentration von Null extrapoliert werden. ⓘ
Diese Tatsachen werden dadurch verschleiert, dass das Lösungsmittel aus dem Ausdruck, der normalerweise zur Definition von pKa verwendet wird, weggelassen wird, aber pKa-Werte, die in einem bestimmten gemischten Lösungsmittel erhalten wurden, können miteinander verglichen werden und ergeben relative Säurestärken. Das Gleiche gilt für pKa-Werte, die in einem bestimmten nichtwässrigen Lösungsmittel wie DMSO erhalten wurden. ⓘ
Eine universelle, lösungsmittelunabhängige Skala für Säuredissoziationskonstanten wurde nicht entwickelt, da es keine bekannte Möglichkeit gibt, die Standardzustände von zwei verschiedenen Lösungsmitteln zu vergleichen. ⓘ
Faktoren, die den pKa-Wert beeinflussen
Die zweite Regel von Pauling besagt, dass der Wert des ersten pKa für Säuren der Formel XOm(OH)n in erster Linie von der Anzahl der Oxogruppen m abhängt und annähernd unabhängig von der Anzahl der Hydroxygruppen n und auch vom Zentralatom X ist. Alternativ dazu wurden verschiedene numerische Formeln vorgeschlagen, darunter pKa = 8 - 5m (bekannt als Bellsche Regel), pKa = 7 - 5m oder pKa = 9 - 7m. Die Abhängigkeit von m korreliert mit der Oxidationsstufe des Zentralatoms X: je höher die Oxidationsstufe, desto stärker die Oxycarbonsäure. Zum Beispiel ist pKa für HClO 7,2, für HClO2 2,0, für HClO3 -1 und HClO4 ist eine starke Säure (pKa ≪ 0). Die zunehmende Acidität beim Hinzufügen einer Oxogruppe ist auf die Stabilisierung der konjugierten Base durch Verlagerung ihrer negativen Ladung auf ein zusätzliches Sauerstoffatom zurückzuführen. Diese Regel kann bei der Zuordnung der Molekülstruktur helfen: Phosphorsäure (H3PO3) hat beispielsweise einen pKa-Wert nahe 2, was darauf hindeutet, dass es sich um HPO(OH)2 handelt, wie später durch NMR-Spektroskopie bestätigt wurde, und nicht um P(OH)3, das einen pKa-Wert nahe 8 haben müsste. ⓘ



Bei organischen Säuren beeinflussen induktive Effekte und mesomere Effekte die pKa-Werte. Ein einfaches Beispiel dafür ist die Wirkung des Ersatzes der Wasserstoffatome in Essigsäure durch das elektronegativere Chloratom. Die elektronenziehende Wirkung des Substituenten erleichtert die Ionisierung, so dass die pKa-Werte in den Reihen 4,7, 2,8, 1,4 und 0,7 abnehmen, wenn 0, 1, 2 oder 3 Chloratome vorhanden sind. Die Hammett-Gleichung liefert einen allgemeinen Ausdruck für die Wirkung von Substituenten.
- log(Ka) = log(K0
a) + ρσ. ⓘ
Ka ist die Dissoziationskonstante einer substituierten Verbindung, K0
a ist die Dissoziationskonstante, wenn der Substituent Wasserstoff ist, ρ ist eine Eigenschaft der unsubstituierten Verbindung und σ hat einen bestimmten Wert für jeden Substituenten. Eine Darstellung von log(Ka) gegen σ ist eine Gerade mit dem Achsenabschnitt log(K0
a) und der Steigung ρ. Dies ist ein Beispiel für eine lineare Beziehung zur freien Energie, da log(Ka) proportional zur Standardänderung der freien Energie ist. Hammett formulierte die Beziehung ursprünglich anhand von Daten von Benzoesäure mit verschiedenen Substituenten in ortho- und para-Position: einige numerische Werte sind in der Hammett-Gleichung enthalten. Diese und andere Studien ermöglichten es, die Substituenten nach ihrer elektronenziehenden oder elektronenabgebenden Kraft zu ordnen und zwischen induktiven und mesomeren Effekten zu unterscheiden. ⓘ
Alkohole verhalten sich in Wasser normalerweise nicht wie Säuren, aber das Vorhandensein einer Doppelbindung neben der OH-Gruppe kann den pKa-Wert durch den Mechanismus der Keto-Enol-Tautomerie erheblich senken. Ascorbinsäure ist ein Beispiel für diesen Effekt. Das Diketon 2,4-Pentandion (Acetylaceton) ist aufgrund des Keto-Enol-Gleichgewichts ebenfalls eine schwache Säure. Bei aromatischen Verbindungen wie Phenol, die einen OH-Substituenten aufweisen, erhöht die Konjugation mit dem aromatischen Ring als Ganzes die Stabilität der deprotonierten Form erheblich. ⓘ
Auch strukturelle Effekte können von Bedeutung sein. Der Unterschied zwischen Fumarsäure und Maleinsäure ist ein klassisches Beispiel. Bei der Fumarsäure handelt es sich um (E)-1,4-But-2-ensäure, ein trans-Isomer, während Maleinsäure das entsprechende cis-Isomer, d. h. (Z)-1,4-But-2-ensäure, ist (siehe cis-trans-Isomerie). Fumarsäure hat pKa-Werte von etwa 3,0 und 4,5. Im Gegensatz dazu hat Maleinsäure pKa-Werte von etwa 1,5 und 6,5. Der Grund für diesen großen Unterschied liegt darin, dass beim Entfernen eines Protons aus dem cis-Isomer (Maleinsäure) eine starke intramolekulare Wasserstoffbrücke mit der in der Nähe verbleibenden Carboxylgruppe gebildet wird. Dies begünstigt die Bildung des H+-Maleats und steht der Entfernung des zweiten Protons aus dieser Verbindung entgegen. Im trans-Isomer sind die beiden Carboxylgruppen immer weit voneinander entfernt, so dass keine Wasserstoffbrückenbindung beobachtet wird. ⓘ
Der Protonenschwamm, 1,8-Bis(dimethylamino)naphthalin, hat einen pKa-Wert von 12,1. Es ist eine der stärksten bekannten Aminbasen. Die hohe Basizität wird auf die Entlastung bei der Protonierung und die starke interne Wasserstoffbrückenbindung zurückgeführt. ⓘ
Die Auswirkungen des Lösungsmittels und der Solvatation sollten in diesem Abschnitt ebenfalls erwähnt werden. Es stellt sich heraus, dass diese Einflüsse subtiler sind als die des oben erwähnten dielektrischen Mediums. Zum Beispiel wird die erwartete (durch elektronische Effekte der Methylsubstituenten) und in der Gasphase beobachtete Reihenfolge der Basizität von Methylaminen, Me3N > Me2NH > MeNH2 > NH3, durch Wasser in Me2NH > MeNH2 > Me3N > NH3 geändert. Neutrale Methylaminmoleküle sind mit Wassermolekülen hauptsächlich über eine Akzeptorwechselwirkung, N-HOH, und nur gelegentlich über eine weitere Donatorbindung, NH-OH2, wasserstoffgebunden. Daher werden Methylamine unabhängig von der Anzahl der Methylgruppen in etwa gleichem Maße durch Hydratation stabilisiert. In krassem Gegensatz dazu nutzen die entsprechenden Methylammoniumkationen immer alle verfügbaren Protonen für die NH-OH2-Donor-Bindung. Die relative Stabilisierung von Methylammonium-Ionen nimmt also mit der Anzahl der Methylgruppen ab, was die Reihenfolge der Wasserbasizität von Methylaminen erklärt. ⓘ
Bei organischen Säuren entscheiden vor allem drei Struktureigenschaften über die Säurestärke:
- Stabilisierung des entstehenden Anions durch Mesomerie: So sind z. B. Carbonsäuren saurer als Alkohole. Mesomere Effekte spielen hierbei eine entscheidende Rolle: Ein −M-Effekt (etwa einer Nitrogruppe –NO2) erhöht die Säurestärke, ein +M-Effekt verringert sie.
- Hybridisierung des Kohlenstoffatoms: Mit steigendem s-Gehalt nimmt die Stärke zu. So hat Ethin (sp-Hybridorbital) einen niedrigeren pKS-Wert als Ethen (sp2-Hybridorbital) und dieses einen niedrigeren als Ethan (sp3-Hybridorbital), es gilt also für den pKS-Wert: sp < sp2 < sp3; die Werte betragen für Ethin 25, für Ethen 44 und für Ethan 50.
- Induktive Effekte: Die Säurestärke steigt, wenn elektronenziehende Gruppen vorhanden sind, z. B. Halogene wie Fluor und Chlor oder Sauerstoff. Trichloressigsäure ist beispielsweise eine stärkere Säure als Essigsäure. ⓘ
Einige Substituenten besitzen sowohl mesomere als auch induktive Effekte, etwa die Halogene oder Nitrogruppen. Halogene weisen einen starken −I-, aber einen schwachen +M-Effekt auf; die Nitrogruppe wirkt sowohl elektronenanziehend (−I-Effekt) als auch über einen −M-Effekt, d. h. beide Effekte wirken in dieselbe Richtung. ⓘ
Thermodynamik
Eine Gleichgewichtskonstante ist mit der Standard-Gibbs-Energieänderung für die Reaktion verbunden, so dass für eine Säuredissoziationskonstante
- . ⓘ
R ist die Gaskonstante und T ist die absolute Temperatur. Man beachte, dass pKa = -log(Ka) und 2,303 ≈ ln(10). Bei 25 °C ist ΔG⊖ in kJ-mol-1 ≈ 5,708 pKa (1 kJ-mol-1 = 1000 Joule pro Mol). Die freie Energie setzt sich aus einem Enthalpie- und einem Entropie-Term zusammen.
Die Standard-Enthalpieänderung kann kalorimetrisch oder mit Hilfe der van 't Hoff-Gleichung bestimmt werden, wobei die kalorimetrische Methode vorzuziehen ist. Wenn sowohl die Standard-Enthalpieänderung als auch die Säure-Dissoziationskonstante bestimmt worden sind, lässt sich die Standard-Entropieänderung anhand der obigen Gleichung leicht berechnen. In der folgenden Tabelle werden die Entropieterme aus den experimentellen Werten von pKa und ΔH⊖ berechnet. Die Daten wurden kritisch ausgewählt und beziehen sich auf 25 °C und die Ionenstärke Null, in Wasser. ⓘ
| Verbindung | Gleichgewicht | pKa | ΔG⊖ (kJ-mol-1) | ΔH⊖ (kJ-mol-1) | -TΔS⊖ (kJ-mol-1) ⓘ |
|---|---|---|---|---|---|
| HA = Essigsäure | HA ⇌ H+ + A- | 4.756 | 27.147 | −0.41 | 27.56 |
| H2A+ = GlycinH+ | H2A+ ⇌ HA + H+ | 2.351 | 13.420 | 4.00 | 9.419 |
| HA ⇌ H+ + A- | 9.78 | 55.825 | 44.20 | 11.6 | |
| H2A = Maleinsäure | H2A ⇌ HA- + H+ | 1.92 | 10.76 | 1.10 | 9.85 |
| HA- ⇌ H+ + A2- | 6.27 | 35.79 | −3.60 | 39.4 | |
| H3A = Zitronensäure | H3A ⇌ H2A- + H+ | 3.128 | 17.855 | 4.07 | 13.78 |
| H2A- ⇌ HA2- + H+ | 4.76 | 27.176 | 2.23 | 24.9 | |
| HA2- ⇌ A3- + H+ | 6.40 | 36.509 | −3.38 | 39.9 | |
| H3A = Borsäure | H3A ⇌ H2A- + H+ | 9.237 | 52.725 | 13.80 | 38.92 |
| H3A = Phosphorsäure | H3A ⇌ H2A- + H+ | 2.148 | 12.261 | −8.00 | 20.26 |
| H2A- ⇌ HA2- + H+ | 7.20 | 41.087 | 3.60 | 37.5 | |
| HA2- ⇌ A3- + H+ | 12.35 | 80.49 | 16.00 | 54.49 | |
| HA- = Hydrogensulfat | HA- ⇌ A2- + H+ | 1.99 | 11.36 | −22.40 | 33.74 |
| H2A = Oxalsäure | H2A ⇌ HA- + H+ | 1.27 | 7.27 | −3.90 | 11.15 |
| HA- ⇌ A2- + H+ | 4.266 | 24.351 | −7.00 | 31.35 |
| Verbindung | Gleichgewicht | pKa | ΔH⊖ (kJ-mol-1) | -TΔS⊖ (kJ-mol-1) ⓘ |
|---|---|---|---|---|
| B = Ammoniak | HB+ ⇌ B + H+ | 9.245 | 51.95 | 0.8205 |
| B = Methylamin | HB+ ⇌ B + H+ | 10.645 | 55.34 | 5.422 |
| B = Triethylamin | HB+ ⇌ B + H+ | 10.72 | 43.13 | 18.06 |
Erstens ist zu beachten, dass bei einem positiven pKa-Wert auch die Standardänderung der freien Energie für die Dissoziationsreaktion positiv ist. Zweitens sind einige Reaktionen exotherm und andere endotherm, aber wenn ΔH⊖ negativ ist, ist TΔS⊖ der dominierende Faktor, der bestimmt, dass ΔG⊖ positiv ist. Schließlich ist der Entropiebeitrag bei diesen Reaktionen immer ungünstig (ΔS⊖ < 0). Ionen in wässriger Lösung neigen dazu, die sie umgebenden Wassermoleküle auszurichten, wodurch die Lösung geordnet wird und die Entropie sinkt. Der Beitrag eines Ions zur Entropie ist die partielle molare Entropie, die häufig negativ ist, insbesondere bei kleinen oder stark geladenen Ionen. Bei der Ionisierung einer neutralen Säure bilden sich zwei Ionen, so dass die Entropie abnimmt (ΔS⊖ < 0). Bei der zweiten Ionisierung derselben Säure sind nun drei Ionen vorhanden und das Anion ist geladen, so dass die Entropie erneut abnimmt. ⓘ
Man beachte, dass die Standardänderung der freien Energie für die Reaktion die Änderungen von den Reaktanten in ihren Standardzuständen zu den Produkten in ihren Standardzuständen betrifft. Die Änderung der freien Energie im Gleichgewicht ist gleich Null, da die chemischen Potenziale von Reaktanten und Produkten im Gleichgewicht gleich sind. ⓘ
Experimentelle Bestimmung
Die experimentelle Bestimmung der pKa-Werte erfolgt in der Regel durch Titration in einem Medium mit hoher Ionenstärke und bei konstanter Temperatur. Ein typisches Verfahren sieht wie folgt aus. Eine Lösung der Verbindung in dem Medium wird mit einer starken Säure angesäuert, bis die Verbindung vollständig protoniert ist. Anschließend wird die Lösung mit einer starken Base titriert, bis alle Protonen entfernt wurden. An jedem Punkt der Titration wird der pH-Wert mit einer Glaselektrode und einem pH-Meter gemessen. Die Gleichgewichtskonstanten werden durch Anpassung der berechneten pH-Werte an die beobachteten Werte mit Hilfe der Methode der kleinsten Quadrate ermittelt. ⓘ
Das Gesamtvolumen der zugegebenen starken Base sollte im Vergleich zum Ausgangsvolumen der Titrierlösung gering sein, um die Ionenstärke nahezu konstant zu halten. Dadurch wird sichergestellt, dass der pKa-Wert während der Titration konstant bleibt. ⓘ
Eine berechnete Titrationskurve für Oxalsäure ist rechts abgebildet. Oxalsäure hat pKa-Werte von 1,27 und 4,27. Daher werden die Pufferbereiche bei etwa pH 1,3 und pH 4,3 zentriert sein. Die Pufferbereiche enthalten die Informationen, die notwendig sind, um die pKa-Werte zu erhalten, da sich die Konzentrationen von Säure und konjugierter Base entlang eines Pufferbereichs ändern. ⓘ
Zwischen den beiden Pufferbereichen gibt es einen Endpunkt oder Äquivalenzpunkt bei etwa pH 3. Dieser Endpunkt ist nicht scharf und typisch für eine diprotische Säure, deren Pufferbereiche sich geringfügig überlappen: pKa2 - pKa1 beträgt in diesem Beispiel etwa drei. (Wäre der Unterschied in den pK-Werten etwa zwei oder weniger, würde der Endpunkt nicht auffallen.) Der zweite Endpunkt beginnt bei etwa pH 6,3 und ist scharf. Dies zeigt an, dass alle Protonen entfernt wurden. In diesem Fall ist die Lösung nicht gepuffert und der pH-Wert steigt bei Zugabe einer kleinen Menge einer starken Base steil an. Der pH-Wert steigt jedoch nicht unbegrenzt weiter an. Bei etwa pH 11 (pKw - 3) beginnt ein neuer Pufferbereich, in dem die Selbstionisierung des Wassers wichtig wird. ⓘ
Es ist sehr schwierig, pH-Werte von weniger als zwei in wässriger Lösung mit einer Glaselektrode zu messen, da die Nernst-Gleichung bei solch niedrigen pH-Werten zusammenbricht. Zur Bestimmung von pK-Werten von weniger als etwa 2 oder mehr als etwa 11 können spektrophotometrische oder NMR-Messungen anstelle von oder in Kombination mit pH-Messungen verwendet werden. ⓘ
Wenn die Glaselektrode nicht verwendet werden kann, wie bei nichtwässrigen Lösungen, werden häufig spektrophotometrische Methoden eingesetzt. Dabei kann es sich um Absorptions- oder Fluoreszenzmessungen handeln. In beiden Fällen wird angenommen, dass die gemessene Menge proportional zur Summe der Beiträge der einzelnen photoaktiven Spezies ist; bei Absorptionsmessungen wird das Beer-Lambert-Gesetz angenommen. ⓘ
Mit Hilfe der isothermischen Titrationskalorimetrie (ITC) können sowohl ein pK-Wert als auch die entsprechende Standardenthalpie für die Säuredissoziation bestimmt werden. Die Software zur Durchführung der Berechnungen wird von den Geräteherstellern für einfache Systeme geliefert. ⓘ
Wässrige Lösungen mit normalem Wasser können für 1H-NMR-Messungen nicht verwendet werden, stattdessen muss schweres Wasser, D2O, eingesetzt werden. 13C-NMR-Daten können jedoch mit normalem Wasser verwendet werden, und 1H-NMR-Spektren können mit nichtwässrigen Medien verwendet werden. Bei den mit NMR gemessenen Größen handelt es sich um zeitlich gemittelte chemische Verschiebungen, da der Protonenaustausch auf der NMR-Zeitskala schnell ist. Andere chemische Verschiebungen, wie z. B. die von 31P, können gemessen werden. ⓘ
Mikrokonstanten

Bei einigen Molekülen kann die Dissoziation (oder Assoziation) an mehr als einer nicht-äquivalenten Stelle stattfinden, und die beobachtete makroskopische Gleichgewichtskonstante oder Makrokonstante ist eine Kombination von Mikrokonstanten, die verschiedene Arten betreffen. Wenn ein Reaktant zwei Produkte parallel bildet, ist die Makrokonstante eine Summe aus zwei Mikrokonstanten, . Dies gilt zum Beispiel für die Deprotonierung der Aminosäure Cystein, die in Lösung als neutrales Zwitterion HS-CH2-CH(NH3+)-COO- vorliegt. Die beiden Mikrokonstanten stehen für die Deprotonierung entweder am Schwefel oder am Stickstoff, und die Summe der Makrokonstanten ist hier die Säuredissoziationskonstante Ka = Ka(-SH) + Ka(-NH3+). ⓘ
Auch eine Base wie Spermin hat mehr als eine Stelle, an der eine Protonierung stattfinden kann. So kann beispielsweise eine Monoprotonierung an einer endständigen -NH2-Gruppe oder an internen -NH-Gruppen erfolgen. Die Kb-Werte für die Dissoziation von Spermin, das an der einen oder anderen Stelle protoniert ist, sind Beispiele für Mikrokonstanten. Sie können nicht direkt durch pH-, Absorptions-, Fluoreszenz- oder NMR-Messungen bestimmt werden; ein gemessener Kb-Wert ist die Summe der K-Werte für die Mikroreaktionen.
Da der Ort der Protonierung jedoch für die biologische Funktion sehr wichtig ist, wurden mathematische Methoden zur Bestimmung der Mikrokonstanten entwickelt. ⓘ
Wenn zwei Reaktanten parallel ein einziges Produkt bilden, ist die Makrokonstante . Zum Beispiel kann das oben erwähnte Gleichgewicht für Spermin in Form von Ka-Werten zweier tautomerer konjugierter Säuren betrachtet werden, wobei die Makrokonstante In diesem Fall . Dies ist äquivalent zu dem vorhergehenden Ausdruck, da proportional ist zu . ⓘ
Wenn ein Reaktant zwei Reaktionen in Serie durchläuft, ist die Makrokonstante für die kombinierte Reaktion das Produkt der Mikrokonstanten für die beiden Schritte. Zum Beispiel kann das oben erwähnte Cystein-Zwitterion zwei Protonen verlieren, eine vom Schwefel und eine vom Stickstoff, und die Gesamtmakrokonstante für den Verlust von zwei Protonen ist das Produkt der beiden Dissoziationskonstanten K = Ka(-SH) Ka(-NH3+). Dies kann auch in Form von logarithmischen Konstanten geschrieben werden als pK = pKa(-SH) + pKa(-NH3+). ⓘ
Anwendungen und Bedeutung
Die Kenntnis der pKa-Werte ist wichtig für die quantitative Behandlung von Systemen mit Säure-Base-Gleichgewichten in Lösung. Es gibt zahlreiche Anwendungen in der Biochemie; so sind die pKa-Werte von Proteinen und Aminosäureseitenketten von großer Bedeutung für die Aktivität von Enzymen und die Stabilität von Proteinen. Die pKa-Werte von Proteinen lassen sich nicht immer direkt messen, sondern können mit theoretischen Methoden berechnet werden. Pufferlösungen werden in großem Umfang verwendet, um Lösungen bei oder nahe dem physiologischen pH-Wert für die Untersuchung biochemischer Reaktionen bereitzustellen; die Gestaltung dieser Lösungen hängt von der Kenntnis der pKa-Werte ihrer Bestandteile ab. Wichtige Pufferlösungen sind MOPS, das eine Lösung mit einem pH-Wert von 7,2 liefert, und Tricin, das bei der Gelelektrophorese verwendet wird. Die Pufferung ist ein wesentlicher Bestandteil der Säure-Basen-Physiologie, einschließlich der Säure-Basen-Homöostase, und ist der Schlüssel zum Verständnis von Störungen wie der Säure-Basen-Störung. Der isoelektrische Punkt eines bestimmten Moleküls ist eine Funktion seiner pK-Werte, so dass verschiedene Moleküle unterschiedliche isoelektrische Punkte haben. Dies ermöglicht eine Technik namens isoelektrische Fokussierung, die für die Trennung von Proteinen durch 2-D-Polyacrylamid-Gelelektrophorese verwendet wird. ⓘ
Pufferlösungen spielen auch in der analytischen Chemie eine wichtige Rolle. Sie werden immer dann verwendet, wenn der pH-Wert einer Lösung auf einen bestimmten Wert festgelegt werden soll. Im Vergleich zu einer wässrigen Lösung ist der pH-Wert einer Pufferlösung relativ unempfindlich gegenüber der Zugabe einer kleinen Menge einer starken Säure oder einer starken Base. Die Pufferkapazität einer einfachen Pufferlösung ist am größten, wenn pH = pKa. Bei der Säure-Base-Extraktion kann die Effizienz der Extraktion einer Verbindung in eine organische Phase, z. B. einen Ether, optimiert werden, indem der pH-Wert der wässrigen Phase mit einem geeigneten Puffer eingestellt wird. Bei optimalem pH-Wert ist die Konzentration der elektrisch neutralen Spezies maximiert; eine solche Spezies ist in organischen Lösungsmitteln mit niedriger Dielektrizitätskonstante besser löslich als in Wasser. Diese Technik wird für die Reinigung von schwachen Säuren und Basen verwendet. ⓘ
Ein pH-Indikator ist eine schwache Säure oder eine schwache Base, die im pH-Übergangsbereich, der etwa pKa ± 1 beträgt, ihre Farbe ändert. Die Entwicklung eines Universalindikators erfordert eine Mischung von Indikatoren, deren benachbarte pKa-Werte sich um etwa zwei unterscheiden, so dass sich ihre pH-Übergangsbereiche gerade überschneiden. ⓘ
In der Pharmakologie verändert die Ionisierung einer Verbindung ihr physikalisches Verhalten und ihre Makroeigenschaften wie Löslichkeit und Lipophilie (log p). Beispielsweise erhöht die Ionisierung einer Verbindung die Löslichkeit in Wasser, verringert aber die Lipophilie. Dies wird in der Arzneimittelentwicklung ausgenutzt, um die Konzentration einer Verbindung im Blut zu erhöhen, indem der pKa-Wert einer ionisierbaren Gruppe angepasst wird. ⓘ
Die Kenntnis der pKa-Werte ist wichtig für das Verständnis von Koordinationskomplexen, die durch die Wechselwirkung eines Metallions, Mm+, das als Lewis-Säure wirkt, mit einem Liganden, L, der als Lewis-Base wirkt, gebildet werden. Der Ligand kann jedoch auch Protonierungsreaktionen eingehen, so dass die Bildung eines Komplexes in wässriger Lösung symbolisch durch die folgende Reaktion dargestellt werden könnte
- [M(H2O)n]m+ + LH ⇌ [M(H2O)n-1L](m-1)+ + H3O+ ⓘ
Um die Gleichgewichtskonstante für diese Reaktion, bei der der Ligand ein Proton verliert, zu bestimmen, muss der pKa-Wert des protonierten Liganden bekannt sein. In der Praxis kann der Ligand polyprotisch sein, z. B. kann EDTA4- vier Protonen aufnehmen; in diesem Fall müssen alle pKa-Werte bekannt sein. Darüber hinaus unterliegt das Metallion der Hydrolyse, d. h. es verhält sich wie eine schwache Säure, so dass die pK-Werte für die Hydrolysereaktionen ebenfalls bekannt sein müssen. ⓘ
Die Bewertung der mit einer Säure oder Base verbundenen Gefahr kann die Kenntnis der pKa-Werte erfordern. Beispielsweise ist Blausäure ein sehr giftiges Gas, weil das Cyanid-Ion das eisenhaltige Enzym Cytochrom c-Oxidase hemmt. Cyanwasserstoff ist in wässriger Lösung eine schwache Säure mit einem pKa-Wert von etwa 9. In stark alkalischen Lösungen, z. B. oberhalb von pH 11, ist Natriumcyanid folglich "vollständig dissoziiert", so dass die Gefahr durch das Cyanwasserstoffgas wesentlich geringer ist. Eine saure Lösung hingegen ist sehr gefährlich, da das gesamte Cyanid in seiner sauren Form vorliegt. Das Verschlucken von Cyanid durch den Mund ist unabhängig vom pH-Wert potenziell tödlich, da es mit der Cytochrom-C-Oxidase reagiert. ⓘ
In der Umweltwissenschaft sind Säure-Base-Gleichgewichte für Seen und Flüsse von Bedeutung; so sind beispielsweise Huminsäuren wichtige Bestandteile natürlicher Gewässer. Ein weiteres Beispiel kommt aus der chemischen Ozeanographie: Um die Löslichkeit von Eisen(III) in Meerwasser bei verschiedenen Salzgehalten zu quantifizieren, wurden die pKa-Werte für die Bildung der Eisen(III)-Hydrolyseprodukte Fe(OH)2+, Fe(OH)+
2 und Fe(OH)3 sowie das Löslichkeitsprodukt von Eisenhydroxid bestimmt. ⓘ
Werte für gängige Substanzen
Es gibt mehrere Techniken zur Bestimmung des pKa-Wertes einer Chemikalie, was zu einigen Diskrepanzen zwischen verschiedenen Quellen führt. Gut gemessene Werte liegen in der Regel innerhalb von 0,1 Einheiten voneinander. Die hier vorgestellten Daten wurden bei 25 °C in Wasser gemessen. Weitere Werte finden Sie im Abschnitt Thermodynamik (siehe oben). Eine Tabelle der pKa-Werte von Carbonsäuren, gemessen in DMSO, ist auf der Seite über Carbanionen zu finden. ⓘ
| Chemisch | Gleichgewicht | pKa ⓘ |
|---|---|---|
| BH = Adenin | BH ⇌ B- + H+ | 4.17 |
| BH+ 2 ⇌ BH + H+ |
9.65 | |
| H3A = Arsensäure | H3A ⇌ H2A- + H+ | 2.22 |
| H2A- ⇌ HA2- + H+ | 6.98 | |
| HA2- ⇌ A3- + H+ | 11.53 | |
| HA = Benzoesäure | HA ⇌ H+ + A- | 4.204 |
| HA = Buttersäure | HA ⇌ H+ + A- | 4.82 |
| H2A = Chromsäure | H2A ⇌ HA- + H+ | 0.98 |
| HA- ⇌ A2- + H+ | 6.5 | |
| B = Kodein | BH+ ⇌ B + H+ | 8.17 |
| HA = Kresol | HA ⇌ H+ + A- | 10.29 |
| HA = Ameisensäure | HA ⇌ H+ + A- | 3.751 |
| HA = Fluorwasserstoffsäure | HA ⇌ H+ + A- | 3.17 |
| HA = Cyanwasserstoffsäure | HA ⇌ H+ + A- | 9.21 |
| HA = Selenwasserstoff | HA ⇌ H+ + A- | 3.89 |
| HA = Wasserstoffperoxid (90%) | HA ⇌ H+ + A- | 11.7 |
| HA = Milchsäure | HA ⇌ H+ + A- | 3.86 |
| HA = Propionsäure | HA ⇌ H+ + A- | 4.87 |
| HA = Phenol | HA ⇌ H+ + A- | 9.99 |
| H2A = L-(+)-Ascorbinsäure | H2A ⇌ HA- + H+ | 4.17 |
| HA- ⇌ A2- + H+ | 11.57 |
Herleitung der Säurekonstanten
Die Säurekonstante leitet sich als Gleichgewichtskonstante einer chemischen Reaktion aus der Gibbs-Energie (auch Freie Enthalpie) her. Ist diese bekannt, so gilt für die Gleichgewichtskonstante einer beliebigen chemischen Reaktion:
- , ⓘ
wobei die Universelle Gaskonstante, die Temperatur und die eulersche Zahl ist. Die Formel beschreibt so auch die beobachtbare Temperaturabhängigkeit der Säurekonstanten. ⓘ
ist dabei als Produkt der Aktivitäten definiert und ist eine Größe der Dimension Zahl. Werden Mischungseffekte vernachlässigt, gilt . Dies ist in Lösungen bis 1 mmol/l ohne größere Fehler möglich. Konstanten können daher mit den Aktivitäten wie auch mit den Konzentrationen aufgestellt werden. Sie besitzen jedoch einen anderen Zahlenwert. Bedingt durch die historische Entwicklung der Chemie aus einer praktischen Wissenschaft werden meist die konzentrationsbezogenen Konstanten angegeben, da diese experimentell vor der thermodynamischen Begründung gefunden wurden. ⓘ
Säurestärke
Ursachen der verschiedenen Säurestärken
Die Säurestärke eines Moleküls kann an verschiedenen Faktoren abgeschätzt werden. ⓘ
Eine Säure ist umso stärker bzw. gibt umso leichter ein Proton ab, ⓘ
- wenn ein induktiver Elektronenzug vorhanden ist (−I-Effekt).
- je stabiler die korrespondierende Base ist, das heißt je schwächer die korrespondierende Base ist.
- wenn das elektronegativere Atom das dissoziierbare Wasserstoffatom trägt (bei Atomen gleicher Größe).
- wenn das größere Atom das Wasserstoffatom trägt (bei Atomen verschiedener Größe).
- je niedriger die Standardbildungsenthalpie ist.
- je instabiler das Säure-Molekül ist. ⓘ
Mehrprotonige Säuren

| H3PO4 | H2PO4− | HPO42− ⓘ |
| PO43− | H+ | OH− |

| H2SO4 | HSO4− | SO42− ⓘ |
| H+ | OH− |
Bei einer mehrprotonigen Säure besteht eine schrittweise Protolyse. Für jede Protolysationsstufe liegt eine eigene Säurekonstante bzw. pKS-Wert vor. Für die einzelnen Protolyseschritte gilt im Allgemeinen: KS1 > KS2 > KS3 (bzw. pKS1 < pKS2 < pKS3), da aus der steigenden Ionenladung des entstehenden Säurerestanions die weiterführende Protolyse weniger energetisch begünstigt ist. ⓘ
Als Beispiel gilt für die Phosphorsäure:
Beim pH-Wert 7,20 liegen näherungsweise gleich große Konzentrationen an Dihydrogen- und Hydrogenphosphat-Ionen vor, die Konzentrationen an undissoziierter Phosphorsäure und Phosphationen sind millionenfach kleiner. Diese Zusammenhänge macht man sich in Phosphatpuffern zu Nutze. ⓘ
Schwefelsäure ist um fünf Größenordnungen acider als Phosphorsäure:
Konzentrierte Schwefelsäure wird in Blei-Akkumulatoren als Elektrolyt verwendet. Unter diesen Gleichgewichtsbedingungen existieren keine freien Sulfat-Ionen mehr. ⓘ

pKS- und pKB-Werte einiger Verbindungen
Die folgende Tabelle listet pKS- und pKB-Werte einiger Säuren und Basen bei Standardbedingungen:
| Säurestärke | pKS | Säure + H2O H3O+ + Base | pKB | Basenstärke ⓘ | |
|---|---|---|---|---|---|
| sehr stark | −17 | H[SbF6] | [SbF6]− | 31 | |
| −10 | HClO4 | ClO4− | 24 | sehr schwach | |
| −10 | HI | I− | 24 | ||
| −8,9 | HBr | Br− | 22,9 | ||
| −6 | HCl | Cl− | 20 | ||
| −3 | H2SO4 | HSO4− | 17 | ||
| −1,32 | HNO3 | NO3− | 15,32 | ||
| stark | 0,00 | H3O+ | H2O | 14,00 | schwach |
| 1,92 | HSO4− | SO42− | 12,08 | ||
| 2,13 | H3PO4 | H2PO4− | 11,87 | ||
| 2,22 | [Fe(H2O)6]3+ | [Fe(OH)(H2O)5]2+ | 11,78 | ||
| 3,14 | HF | F− | 10,86 | ||
| 3,75 | HCOOH | HCOO− | 10,25 | ||
| mittelstark | 4,75 | CH3COOH | CH3COO− | 9,25 | mittelstark |
| 4,85 | [Al(H2O)6]3+ | [Al(OH)(H2O)5]2+ | 9,15 | ||
| 6,52 | H2CO3 | HCO3− | 7,48 | ||
| 6,92 | H2S | HS− | 7,08 | ||
| 7,20 | H2PO4− | HPO42− | 6,80 | ||
| schwach | 9,25 | NH4+ | NH3 | 4,75 | stark |
| 9,40 | HCN | CN− | 4,60 | ||
| 9,8 | Trimethyl-Ammonium | Trimethylamin | 4,2 | ||
| 10,40 | HCO3− | CO32− | 3,60 | ||
| 10,6 | Methyl-Ammonium | Methylamin | 3,4 | ||
| 10,73 | Dimethyl-Ammonium | Dimethylamin | 3,27 | ||
| 12,36 | HPO42− | PO43− | 1,64 | ||
| 13,00 | HS− | S2− | 1,00 | ||
| 14,00 | H2O | OH− | 0,00 | ||
| sehr schwach | 15,90 | CH3-CH2-OH | CH3-CH2-O− | −1,90 | sehr stark |
| 23 | NH3 | NH2− | −9 | ||
| 48 | CH4 | CH3− | −34 | ||

![{\displaystyle K_{\text{a}}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cdd9efda0e3a32060020b5c9e5b2c78981b2a93)
![{\displaystyle \mathrm {p} K_{{\ce {a}}}=-\log _{10}K_{\text{a}}=\log _{10}{\frac {{\ce {[HA]}}}{[{\ce {A^-}}][{\ce {H+}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7af05bf129db2f9bc618fe809660b6e4ff8dce9)





![{\displaystyle K^{\ominus }={{\frac {[{\ce {A^-}}][{\ce {H+}}]}{{\ce {[HA]}}}}\Gamma },\quad \Gamma ={\frac {\gamma _{{\ce {A^-}}}\ \gamma _{{\ce {H+}}}}{\gamma _{{\ce {HA}}}\ }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e9373db7091aeb4f51a26757a677b420f0a8418)

![{\displaystyle K_{\text{a}}={\frac {K^{\ominus }}{\Gamma }}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a5a59c740de89347ec4c96d982292fc05c64b2f)
![{\displaystyle \mathrm {p} K_{{\ce {a}}}=-\log _{10}{\frac {[{\ce {A^-}}][{\ce {H^+}}]}{[{\ce {HA}}]}}=\log _{10}{\frac {{\ce {[HA]}}}{[{\ce {A^-}}][{\ce {H+}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bed5fbab82167a42994a6d735931d08b06f1e7a5)



![{\displaystyle \beta _{2}={\frac {{\ce {[H_2A]}}}{[{\ce {A^{2-}}}][{\ce {H+}}]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3306fbf9ccf8d12352eab96dfb5461897f2c3a15)


![{\displaystyle K_{\text{dissoc}}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} :\mathrm {p} K_{\text{a}}=-\log K_{\text{dissoc}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5f9c1efd45de9edf690ebf6a72cc806eb2b0331)
![{\displaystyle K_{\text{assoc}}=\mathrm {\frac {[HA]}{[A^{-}][H^{+}]}} :\mathrm {p} K_{\text{b}}=-\log K_{\text{assoc}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a0453338b1d420214ac7c127d3faa13374fce0)




![{\displaystyle K_{\mathrm {a} }=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df1424aa532585fc7ad6dd660a596705ee31a2b)







![{\displaystyle \mathrm {pH} =\mathrm {p} K_{\text{a}}+\log \mathrm {\frac {[A^{-}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e874f2b8ea8e4127605788c356393cfd7fff37)
![{\displaystyle \mathrm {p} K_{{\ce {a1}}}=\log _{10}{\frac {[{\ce {H_3PO_4}}]}{[{\ce {H_2PO_4^{-}}}][{\ce {H^+}}]}}=2.14}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff6e67381cb8a691b8873fbf884dad30b001352)
![{\displaystyle \mathrm {p} K_{{\ce {a2}}}=\log _{10}{\frac {[{\ce {H_2PO_4^{-}}}]}{[{\ce {HPO_4^{2-}}}][{\ce {H^+}}]}}=7.2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efe9f5a620a62c8de4a6567f58faf01e66829903)
![{\displaystyle \mathrm {p} K_{{\ce {a3}}}=\log _{10}{\frac {[{\ce {HPO_4^{2-}}}]}{[{\ce {PO_4^{3-}}}][{\ce {H^+}}]}}=12.37}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf6cf97c1d47ba55db3a383374b9d8cd4eda22ee)





![{\displaystyle {\begin{aligned}K_{\text{b}}&=\mathrm {\frac {[HB^{+}][OH^{-}]}{[B]}} \\\mathrm {p} K_{\text{b}}&=-\log _{10}\left(K_{\text{b}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dea1aac629a595476e18c042a8f4365a50f0efc)
![{\displaystyle \mathrm {[OH^{-}]} ={\frac {K_{\mathrm {w} }}{\mathrm {[H^{+}]} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7f583da9f8b50145990ffa4342919930edfa16)
![{\displaystyle K_{\text{b}}={\frac {[\mathrm {HB^{+}} ]K_{\text{w}}}{\mathrm {[B][H^{+}]} }}={\frac {K_{\text{w}}}{K_{\text{a}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/921c3abd37a1c5c00c31831509d3b090394c0d47)


![{\displaystyle K_{\mathrm {b} }={\frac {[\mathrm {M} _{p}(\mathrm {OH} )_{q-1}^{+}][\mathrm {OH} ^{-}]}{[\mathrm {M} _{p}(\mathrm {OH} )_{q}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb70331666676f62afda8017ff13fd1e941241a)
![{\displaystyle \mathrm {p} K_{\mathrm {aH} }(\mathrm {B} )=\mathrm {p} K_{\mathrm {a} }(\mathrm {BH} ^{+})=-\log _{10}{\Big (}{\frac {[\mathrm {B} ][\mathrm {H^{+}} ]}{[\mathrm {BH} ^{+}]}}{\Big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa04a34c3fecca06d502586ca2f7c523c391233a)
![{\displaystyle K_{\text{a}}=\mathrm {\frac {[H^{+}][OH^{-}]}{[H_{2}O]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdc540ad193c8f1661c1897698be93153fc5fb84)
![{\displaystyle K_{\text{w}}=[\mathrm {H} ^{+}][\mathrm {OH} ^{-}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0039f77db244ea2f6d03d3475dc7a232a8ccb16)
































