Nernst-Gleichung

Die Nernst-Gleichung ist eine fundamentale Gleichung der Elektrochemie. Sie beschreibt die Abhängigkeit des Elektrodenpotentials eines Redox-Paares ${\rm {{Ox}+z_{\mathrm {e} }\ e^{-}\rightleftharpoons \ {\rm {Red}}}}$ von den Konzentrationen der beteiligten Substanzen und der Temperatur. Die Gleichung ist nach dem deutschen Chemie Nobelpreisträger Walther Nernst benannt. Die ausführliche Form der Nernst-Gleichung lautet:

$E=E^{0}+{\frac {RT}{z_{e}F}}\ln {\bigg (}{\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}{\bigg )}$ ⓘ

$E$	Elektrodenpotential ⓘ
$E^{0}$	Standardelektrodenpotential
$R$	Universelle oder molare Gaskonstante: $R=8,31447\ \mathrm {J\cdot {mol}^{-1}\cdot {K}^{-1}} =8,31447\ \mathrm {C\cdot V\cdot {mol}^{-1}\cdot {K}^{-1}}$
$T$	absolute Temperatur (= Temperatur in Kelvin)
$z_{\mathrm {e} }$	Anzahl der übertragenen Elektronen (auch Äquivalentzahl)
$F$	Faraday-Konstante: $F=96485\ \mathrm {C\cdot {mol}^{-1}} =96485\ \mathrm {J\cdot V^{-1}\cdot {mol}^{-1}}$
$a$	Aktivität des betreffenden Redox-Partners (für verdünnte Lösungen kann auch die Stoffmengenkonzentration $c$ eingesetzt werden)

Nimmt man an, dass eine Temperatur von $T=25{}^{\circ }\mathrm {C}$ vorliegt, kann man die Nernst-Gleichung vereinfachen zu:

$E=E^{0}+{\frac {0,059\ \mathrm {V} }{z_{e}}}\lg {\bigg (}{\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}{\bigg )}$ ⓘ

Man beachte, dass in dieser Form der Nernst-Gleichung der dekadische Logarithmus $\lg$ und nicht der natürliche Logarithmus $\ln$ steht. ⓘ

Mathematische Herleitung der vereinfachten Nernst-Gleichung   ⓘ

Die Nernst-Gleichung in allgemeiner Form $E=E^{0}+{\frac {RT}{z_{e}F}}\ln {\bigg (}{\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}{\bigg )}$ kann vereinfacht werden. Hierzu nimmt man an, dass eine Temperatur von $T=25{}^{\circ }{\rm {{C}=298\ \mathrm {K} }}$ vorherrscht. Setzt man nun die allgemeine Gaskonstante $R$ und die Faraday-Konstante $F$ ein, erhält man: $E=E^{0}+{\frac {8,314\ {\frac {\rm {J\cdot mol}}{\rm {K}}}\cdot 298\ {\rm {K}}}{z_{e}\cdot \ 96485\ {\frac {\rm {C}}{\rm {mol}}}}}\ln {\bigg (}{\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}{\bigg )}$ Nun soll der natürliche Logarithmus in einen dekadischen Logarithmus umgeformt werden. Hierfür ist folgende Basisumformung notwendig: $\lg {\bigg (}{\frac {a_{\mathrm {Red} }}{a_{\mathrm {Ox} }}}{\bigg )}={\frac {\ln {\big (}{\frac {a_{\mathrm {Red} }}{a_{\mathrm {Ox} }}}{\big )}}{\ln(10)}}\ \Rightarrow \ \ln {\bigg (}{\frac {a_{\mathrm {Red} }}{a_{\mathrm {Ox} }}}{\bigg )}=\ln(10)\cdot \lg {\bigg (}{\frac {a_{\mathrm {Red} }}{a_{\mathrm {Ox} }}}{\bigg )}$ Durch Zusammenfassen der Konstanten erhält man: ${\frac {8,314\ {\frac {\rm {J\cdot mol}}{\rm {K}}}\cdot 298\ {\rm {K\cdot \ln(10)}}}{96485\ {\rm {\frac {C}{mol}}}}}=0,059\ {\rm {V}}$ Somit erhält man die Nernst-Gleichung in vereinfachter Form: $E=E^{0}+{\frac {0,059\ \mathrm {V} }{z_{e}}}\lg {\bigg (}{\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}{\bigg )}$

Mathematische Anmerkung zur Nernst-Gleichung   ⓘ

Allgemein kann man das Vorzeichen eines Logarithmus umdrehen, wenn man Zähler und Nenner im Quotienten vertauscht: $\log {\bigg (}{\frac {a}{b}}{\bigg )}=-\ \log {\bigg (}{\frac {b}{a}}{\bigg )}$ Somit gilt: $E=E^{0}+{\frac {RT}{z_{e}F}}\ln {\bigg (}{\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}{\bigg )}$ $E=E^{0}-{\frac {RT}{z_{e}F}}\ln {\bigg (}{\frac {a_{\mathrm {Red} }}{a_{\mathrm {Ox} }}}{\bigg )}$ Und auch: $E=E^{0}+{\frac {0,059\ \mathrm {V} }{z_{e}}}\lg {\bigg (}{\frac {a_{\mathrm {Ox} }}{a_{\mathrm {Red} }}}{\bigg )}$ $E=E^{0}-{\frac {0,059\ \mathrm {V} }{z_{e}}}\lg {\bigg (}{\frac {a_{\mathrm {Red} }}{a_{\mathrm {Ox} }}}{\bigg )}$

Ausdruck

Allgemeine Form mit chemischen Aktivitäten

Wenn ein Oxidationsmittel (Ox) eine Anzahl z von Elektronen ( e-) aufnimmt, um in seine reduzierte Form (Red) umgewandelt zu werden, wird die Halbreaktion wie folgt ausgedrückt: ⓘ

Ox + z e- → Rot ⓘ

Der Reaktionsquotient (Qr), oft auch als Ionenaktivitätsprodukt (IAP) bezeichnet, ist das Verhältnis zwischen den chemischen Aktivitäten (a) der reduzierten Form (des Reduktionsmittels, a_Red) und der oxidierten Form (des Oxidationsmittels, aOx). Die chemische Aktivität einer gelösten Spezies entspricht ihrer tatsächlichen thermodynamischen Konzentration, wobei die elektrischen Wechselwirkungen zwischen allen in der Lösung vorhandenen Ionen bei hohen Konzentrationen berücksichtigt werden. Für eine bestimmte gelöste Art ist ihre chemische Aktivität (a) das Produkt aus ihrem Aktivitätskoeffizienten (γ) und ihrer molaren (mol/l Lösung) oder molalen (mol/kg Wasser) Konzentration (C): a = γ C. Wenn also die Konzentration (C, im Folgenden auch mit eckigen Klammern [ ] bezeichnet) aller gelösten Spezies, die von Interesse sind, hinreichend niedrig ist und ihre Aktivitätskoeffizienten nahe bei Eins liegen, können ihre chemischen Aktivitäten durch ihre Konzentrationen angenähert werden, wie dies üblicherweise bei der Vereinfachung oder Idealisierung einer Reaktion zu didaktischen Zwecken geschieht: ⓘ

$Q_{r}={\frac {a_{\text{Red}}}{a_{\text{Ox}}}}={\frac {[Red]}{[Ox]}}$ ⓘ

Im chemischen Gleichgewicht ist das Verhältnis Qr zwischen de_r Aktivität des Reaktionsprodukts (a_Red) und der Aktivität des Reagenz (a_Ox) gleich der Gleichgewichtskonstante K der Halbreaktion: ⓘ

$K={\frac {a_{\text{Red}}}{a_{\text{Ox}}}}$ ⓘ

Die Standardthermodynamik besagt auch, dass die tatsächliche freie Gibbs-Energie ΔG mit der freien Energieänderung im Standardzustand ΔGo verbunden ist
durch die Beziehung:

$$\Delta G=\Delta G^{\ominus }+RT\ln Q_{r}$$

wobei Qr der Reaktionsquotient ist. Das mit der elektrochemischen Reaktion verbundene Zellpotenzial E ist definiert als die Abnahme der freien Gibbs-Energie pro übertragenem Coulomb der Ladung, was zu folgender Beziehung führt

$$\Delta G=-zFE.$$

Die Konstante F (die Faraday-Konstante) ist ein Einheitsumrechnungsfaktor F = N_Aq, wobei N_A die Avogadro-Konstante und q die fundamentale Elektronenladung ist. Daraus ergibt sich unmittelbar die Nernst-Gleichung, die für eine elektrochemische Halbzelle lautet

$$E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {a_{\text{Red}}}{a_{\text{Ox}}}}.$$

Für eine vollständige elektrochemische Reaktion (Vollzelle) kann die Gleichung wie folgt geschrieben werden

$$E_{\text{cell}}=E_{\text{cell}}^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}$$

ⓘ

wobei:

• E_red ist das Reduktionspotential der Halbzelle bei der interessierenden Temperatur,
• E^o
  rot ist das Standard-Halbzellen-_Reduktionspotential,
• E_cell ist das Zellpotential (elektromotorische Kraft) bei der interessierenden Temperatur,
• E^o
  Zelle ist das Standard-Zellpotential,
• R ist die universelle Gaskonstante: R = 8,31446261815324 J K-1 mol-1,
• T ist die Temperatur in Kelvin,
• z ist die Anzahl der bei der Zellreaktion oder Halbreaktion übertragenen Elektronen,
• F ist die Faraday-Konstante, die Anzahl der Coulomb pro Mol Elektronen: F = 96485.3321233100184 C mol-1,
• Qr ist der Reaktionsquotient der Zellreaktion, und
• a ist die chemische Aktivität der betreffenden Spezies, wobei a_Red die Aktivität der reduzierten Form und a_Ox die Aktivität der oxidierten Form ist. ⓘ

Thermische Spannung

Bei Raumtemperatur (25 °C) beträgt die Thermospannung $V_{T}={\frac {RT}{F}}$ ungefähr 25,693 mV. Die Nernst-Gleichung wird häufig als Logarithmus zur Basis 10 (d. h. als gewöhnlicher Logarithmus) und nicht als natürlicher Logarithmus ausgedrückt; in diesem Fall wird sie wie folgt geschrieben

$$E=E^{\ominus }-{\frac {V_{T}}{z}}\ln {\frac {a_{\text{Red}}}{a_{\text{Ox}}}}=E^{\ominus }-{\frac {\lambda V_{T}}{z}}\log _{10}{\frac {a_{\text{Red}}}{a_{\text{Ox}}}}.$$

ⓘ

wobei λ = ln(10) ≈ 2,3026 und λV_T ≈ 0,05916 Volt. ⓘ

Form mit Aktivitätskoeffizienten und Konzentrationen

Ähnlich wie die Gleichgewichtskonstanten werden die Aktivitäten immer in Bezug auf den Standardzustand gemessen (1 mol/L für gelöste Stoffe, 1 atm für Gase und T = 298,15 K, d. h. 25 °C oder 77 °F). Die chemische Aktivität einer Spezies i, ai, ist mit der gemessenen Konzentration Ci über die Beziehung ai = γi Ci verbunden, wobei γi der Aktivitätskoeffizient der Spezies i ist. Da die Aktivitätskoeffizienten bei niedrigen Konzentrationen gegen Eins tendieren oder bei mittleren und hohen Konzentrationen unbekannt oder schwer zu bestimmen sind, werden die Aktivitäten in der Nernst-Gleichung häufig durch einfache Konzentrationen ersetzt und dann formale Standardreduktionspotenziale $E_{\text{red}}^{\ominus '}$ verwendet. ⓘ

Unter Berücksichtigung der Aktivitätskoeffizienten ($\gamma$) wird die Nernst-Gleichung wie folgt: ⓘ

$$E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln \left({\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}{\frac {C_{\text{Red}}}{C_{\text{Ox}}}}\right)$$

ⓘ

$$E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\left(\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}+\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}\right)$$

ⓘ

$$E_{\text{red}}=\underbrace {\left(E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}\right)} _{E_{\text{red}}^{\ominus '}}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}$$

ⓘ

Wobei der erste Term, der die Aktivitätskoeffizienten ($\gamma$) bezeichnet wird mit $E_{\text{red}}^{\ominus '}$ bezeichnet und als formales Standardreduktionspotenzial bezeichnet, so dass $E_{\text{red}}$ direkt ausgedrückt werden kann als eine Funktion von $E_{\text{red}}^{\ominus '}$ und den Konzentrationen in der einfachsten Form der Nernst-Gleichung ausgedrückt werden kann:

$$E_{\text{red}}=E_{\text{red}}^{\ominus '}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}$$

ⓘ

Formales Standardreduktionspotential

Wenn man anstelle von Aktivitäten einfache Konzentrationen verwenden möchte, die Aktivitätskoeffizienten aber weit von der Einheit entfernt sind und nicht mehr vernachlässigt werden können, weil sie unbekannt oder zu schwierig zu bestimmen sind, kann es zweckmäßig sein, den Begriff des "so genannten" formalen Standardreduktionspotenzials ($E_{\text{red}}^{\ominus '}$) einzuführen, das mit dem Standard-Reduktionspotential wie folgt zusammenhängt:

$$E_{\text{red}}^{\ominus '}=E_{\text{red}}^{\ominus }-{\frac {RT}{zF}}\ln {\frac {\gamma _{\text{Red}}}{\gamma _{\text{Ox}}}}$$

So kann die Nernst-Gleichung für die Halbzellenreaktion formal korrekt in Form von Konzentrationen geschrieben werden als:

$$E_{\text{red}}=E_{\text{red}}^{\ominus '}-{\frac {RT}{zF}}\ln {\frac {C_{\text{Red}}}{C_{\text{Ox}}}}$$

und ebenso für den Ausdruck der Vollzelle. ⓘ

Nach Wenzel (2020) ist ein formales Reduktionspotential $E_{\text{red}}^{\ominus '}$ das Reduktionspotenzial, das für eine Halbreaktion unter bestimmten Bedingungen gilt, wie z. B. pH-Wert, Ionenstärke oder Konzentration der Komplexbildner. ⓘ

Das formale Reduktionspotenzial $E_{\text{red}}^{\ominus '}$ ist häufig eine zweckmäßigere, aber bedingte Form des Standard-Reduktionspotenzials, bei der Aktivitätskoeffizienten und spezifische Bedingungen für das Reaktionsmedium berücksichtigt werden. Daher ist sein Wert ein bedingter Wert, d. h., er hängt von den Versuchsbedingungen ab, und die Ionenstärke beeinflusst die Aktivitätskoeffizienten, $E_{\text{red}}^{\ominus '}$ von Medium zu Medium variieren wird. In der Literatur finden sich mehrere Definitionen des formalen Reduktionspotenzials, je nach dem verfolgten Ziel und den durch das untersuchte System auferlegten experimentellen Beschränkungen. Die allgemeine Definition von $E_{\text{red}}^{\ominus '}$ bezieht sich auf seinen Wert, der bestimmt wird, wenn ${\frac {C_{\text{red}}}{C_{\text{ox}}}}=1$. Ein speziellerer Fall ist, wenn $E_{\text{red}}^{\ominus '}$ auch bei pH 7 bestimmt wird, wie z. B. bei Redoxreaktionen, die in der Biochemie oder in biologischen Systemen wichtig sind. ⓘ

Bestimmung des formalen Standardreduktionspotentials bei Cred/Cox = 1

Das formale Standardreduktionspotential $E_{\text{red}}^{\ominus '}$ kann definiert werden als das gemessene Reduktionspotential $E_{\text{red}}$ der Halbreaktion bei einem Konzentrationsverhältnis der oxidierten und reduzierten Spezies von eins (d. h. wenn C_red/C_ox = 1) unter gegebenen Bedingungen. ⓘ

In der Tat: ⓘ

as, $E_{\text{red}}=E_{\text{red}}^{\ominus }$, wenn ${\frac {a_{\text{red}}}{a_{\text{ox}}}}=1$, ⓘ

$E_{\text{red}}=E_{\text{red}}^{\ominus '}$, wenn ${\frac {C_{\text{red}}}{C_{\text{ox}}}}=1$, ⓘ

weil $\ln {1}=0$, und dass der Term ${\frac {\gamma _{\text{red}}}{\gamma _{\text{ox}}}}$ enthalten ist in $E_{\text{red}}^{\ominus '}$. ⓘ

Das formale Reduktionspotential ermöglicht es, einfacher mit molaren (mol/L, M) oder molalen (mol/kg H₂O, m) Konzentrationen anstelle von Aktivitäten zu arbeiten. Da molare und molale Konzentrationen früher als formale Konzentrationen bezeichnet wurden, könnte dies den Ursprung des Adjektivs formal in dem Ausdruck formales Potenzial erklären. ⓘ

Das formale Potenzial ist also das reversible Potenzial einer Elektrode im Gleichgewicht, die in eine Lösung eingetaucht ist, in der die Reaktanten und Produkte die gleiche Konzentration haben. Wenn eine kleine inkrementelle Änderung des Potenzials eine Änderung der Reaktionsrichtung bewirkt, d. h. von Reduktion zu Oxidation oder umgekehrt, ist das System nahe am Gleichgewicht, reversibel und befindet sich auf seinem formalen Potenzial. Wenn das formale Potenzial unter Standardbedingungen gemessen wird (d. h. die Aktivität jeder gelösten Spezies beträgt 1 mol/L, T = 298,15 K = 25 °C = 77 °F, P_gas = 1 bar), wird es de facto zu einem Standardpotenzial.
Nach Brown und Swift (1949): ⓘ

"Ein formales Potential ist definiert als das Potential einer Halbzelle, gemessen gegen die Standard-Wasserstoffelektrode, wenn die Gesamtkonzentration jeder Oxidationsstufe eine formale ist". ⓘ

In diesem Fall, wie auch bei den Standard-Reduktionspotentialen, bleiben die Konzentrationen der gelösten Spezies gleich einem Mol (M) oder einem Molal (m) und werden daher als ein Formal (F) bezeichnet. Die Konzentration C wird also in der Molarität M (1 mol/L) ausgedrückt: ⓘ

${\frac {C_{\text{red}}}{C_{\text{ox}}}}={\frac {1\,\mathrm {M} _{\text{red}}}{1\,\mathrm {M} _{\text{ox}}}}=1$ ⓘ

Der Begriff der formalen Konzentration (F) wird in der aktuellen Literatur weitgehend ignoriert und kann im Allgemeinen mit der molaren Konzentration (M) oder der Molalität (m) im Falle thermodynamischer Berechnungen gleichgesetzt werden. ⓘ

Das formale Potenzial befindet sich ebenfalls auf halbem Weg zwischen den beiden Spitzen in einem zyklischen Voltammogramm, wo die Konzentration von Ox (der oxidierten Spezies) und Red (der reduzierten Spezies) an der Elektrodenoberfläche gleich ist. ⓘ

Die Aktivitätskoeffizienten $\gamma _{red}$ und $\gamma _{ox}$ sind in das formale Potenzial $E_{\text{red}}^{\ominus '}$enthalten und hängen von den Versuchsbedingungen wie Temperatur, Ionenstärke und pH-Wert ab, $E_{\text{red}}^{\ominus '}$ kann nicht als unveränderliches Standardpotenzial bezeichnet werden, sondern muss systematisch für jeden spezifischen Satz von Versuchsbedingungen bestimmt werden. ⓘ

Formale Reduktionspotenziale werden verwendet, um die Berechnungen eines betrachteten Systems unter bestimmten Bedingungen und die Interpretation der Messungen zu vereinfachen. Die Versuchsbedingungen, unter denen sie bestimmt werden, und ihre Beziehung zu den Standard-Reduktionspotenzialen müssen klar beschrieben werden, damit sie nicht mit den Standard-Reduktionspotenzialen verwechselt werden. ⓘ

Formales Standard-Reduktionspotenzial bei pH 7

Formale Standardreduktionspotentiale ($E_{\text{red}}^{\ominus '}$) werden in der Biochemie und Zellbiologie auch häufig für Standard-Reduktionspotenziale verwendet, die bei pH 7 gemessen werden, einem Wert, der dem pH-Wert der meisten physiologischen und intrazellulären Flüssigkeiten näher kommt als der Standard-pH-Wert von 0. Der Vorteil besteht darin, dass eine angemessenere Redox-Skala definiert wird, die den realen Bedingungen besser entspricht als der Standardzustand. Formale Standardreduktionspotentiale ($E_{\text{red}}^{\ominus '}$) ermöglichen es, leichter abzuschätzen, ob eine Redoxreaktion, die in einem Stoffwechselprozess oder als Brennstoff für mikrobielle Aktivität unter bestimmten Bedingungen stattfinden soll, durchführbar ist oder nicht. ⓘ

Standardreduktionspotenziale beziehen sich immer auf die Standard-Wasserstoffelektrode (SHE), wobei [ H⁺] = 1 M einem pH-Wert von 0 entspricht und $E_{\text{red H+}}^{\ominus }$ willkürlich auf Null gesetzt werden, ist dies bei einem pH-Wert von 7 nicht mehr der Fall. Dann ist das Reduktionspotenzial $E_{\text{red}}$ einer Wasserstoff-Elektrode, die bei pH 7 arbeitet, -0,413 V gegenüber der Standard-Wasserstoffelektrode (SHE). ⓘ

Ausdruck der Nernst-Gleichung in Abhängigkeit vom pH-Wert

Die $E_{h}$ und der pH-Wert einer Lösung sind durch die Nernst-Gleichung miteinander verbunden, die üblicherweise durch ein Pourbaix-Diagramm dargestellt wird ($E_{h}$ - pH-Diagramm). $E_{h}$ bezeichnet ausdrücklich $E_{\text{red}}$ ausgedrückt gegen die Standard-Wasserstoffelektrode (SHE). Für eine Halbzellengleichung, die üblicherweise als Reduktionsreaktion geschrieben wird (d. h. Elektronenaufnahme durch ein Oxidationsmittel auf der linken Seite):

$a\,A+b\,B+h\,{\ce {H+}}+z\,e^{-}\quad {\ce {<=>}}\quad c\,C+d\,D$ ⓘ

Das Halbzellen-Standard-Reduktionspotenzial $E_{\text{red}}^{\ominus }$ ist gegeben durch ⓘ

$E_{\text{red}}^{\ominus }({\text{volt}})=-{\frac {\Delta G^{\ominus }}{zF}}$ ⓘ

wobei $\Delta G^{\ominus }$ die freie Standard-Gibbs-Energieänderung, z die Anzahl der beteiligten Elektronen und F die Faraday-Konstante ist. Die Nernst-Gleichung setzt den pH-Wert und $E_{h}$ wie folgt:

$E_{h}=E_{\text{red}}=E_{\text{red}}^{\ominus }-{\frac {0.05916}{z}}\log \left({\frac {\{C\}^{c}\{D\}^{d}}{\{A\}^{a}\{B\}^{b}}}\right)-{\frac {0.05916\,h}{z}}{\text{pH}}$   ⓘ

wobei die geschweiften Klammern die Aktivitäten angeben und die Exponenten in der üblichen Weise dargestellt werden. Diese Gleichung ist die Gleichung einer Geraden für $E_{\text{red}}$ in Abhängigkeit vom pH-Wert mit einer Steigung von $-0.05916\,\left({\frac {h}{z}}\right)$ volt (pH hat keine Einheiten). ⓘ

Diese Gleichung sagt niedrigere $E_{\text{red}}$ bei höheren pH-Werten. Dies wird für die Reduktion von O₂ zu H₂O oder OH- und für die Reduktion von H⁺ zu H₂ beobachtet. $E_{\text{red}}$ wird dann oft als $E_{h}$ angegeben, um darauf hinzuweisen, dass sie sich auf die Standard-Wasserstoffelektrode (SHE) bezieht, deren $E_{\text{red}}$ = 0 unter Standardbedingungen (T = 298,15 K = 25 °C = 77 F, P_gas = 1 atm (1,013 bar), Konzentrationen = 1 M und damit pH = 0). ⓘ

Hauptfaktoren, die die formalen Standardreduktionspotentiale beeinflussen

Der Hauptfaktor, der die formalen Reduktionspotenziale in biochemischen oder biologischen Prozessen beeinflusst, ist meist der pH-Wert. Um Näherungswerte für formale Reduktionspotenziale zu bestimmen, muss die Nernst-Gleichung angewandt werden, wobei Änderungen der Aktivitätskoeffizienten aufgrund der Ionenstärke zunächst vernachlässigt werden, wobei darauf zu achten ist, dass die Beziehung zunächst als Funktion des pH-Werts ausgedrückt wird. Der zweite Faktor, der zu berücksichtigen ist, sind die Werte der Konzentrationen, die in die Nernst-Gleichung eingehen. Um ein formales Reduktionspotenzial für eine biochemische Reaktion zu definieren, müssen der pH-Wert, die Konzentrationswerte und die Hypothesen zu den Aktivitätskoeffizienten immer ausdrücklich angegeben werden. Wenn mehrere formale Reduktionspotenziale verwendet oder verglichen werden, müssen sie auch in sich konsistent sein. ⓘ

Probleme können auftreten, wenn verschiedene Datenquellen mit unterschiedlichen Konventionen oder Näherungswerten (d. h. mit unterschiedlichen zugrunde liegenden Hypothesen) gemischt werden. Bei Arbeiten im Grenzbereich zwischen anorganischen und biologischen Prozessen (z. B. beim Vergleich von abiotischen und biotischen Prozessen in der Geochemie, wenn in dem System auch mikrobielle Aktivität am Werk sein könnte) muss darauf geachtet werden, dass Standard-Reduktionspotenziale gegen SHE (pH = 0) nicht versehentlich direkt mit formalen Reduktionspotenzialen (pH = 7) vermischt werden. Definitionen müssen klar formuliert und sorgfältig kontrolliert werden, insbesondere wenn die Datenquellen unterschiedlich sind und aus verschiedenen Bereichen stammen (z. B. wenn Daten aus Lehrbüchern der klassischen Elektrochemie und der Mikrobiologie ausgewählt und gemischt werden, ohne auf die unterschiedlichen Konventionen zu achten, auf denen sie beruhen). ⓘ

Beispiele mit einem Pourbaix-Diagramm

Pourbaix-Diagramm für Wasser, einschließlich der Stabilitätsbereiche für Wasser, Sauerstoff und Wasserstoff bei Standardtemperatur und -druck (STP). Die vertikale Skala (Ordinate) ist das Elektrodenpotenzial im Verhältnis zu einer SHE-Elektrode. Die horizontale Skala (Abszisse) ist der pH-Wert des Elektrolyten (ansonsten keine Wechselwirkung). Oberhalb der oberen Linie perlt der Sauerstoff von der Elektrode ab, bis das Wasser vollständig verbraucht ist. Unterhalb der unteren Linie perlt Wasserstoff von der Elektrode ab, bis das Wasser vollständig verbraucht ist. ⓘ

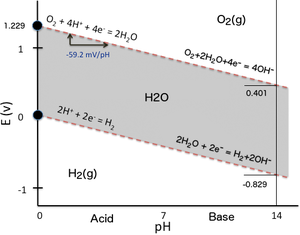
Zur Veranschaulichung der Abhängigkeit des Reduktionspotenzials vom pH-Wert kann man einfach die beiden Oxidations-Reduktions-Gleichgewichte, die den Stabilitätsbereich des Wassers bestimmen, in einem Pourbaix-Diagramm (Eh-pH-Plot) darstellen. Bei der Elektrolyse von Wasser durch Anlegen einer ausreichenden Differenz des elektrischen Potenzials zwischen zwei in Wasser getauchten Elektroden entsteht an der Kathode Wasserstoff (Reduktion von Wasserprotonen), während an der Anode Sauerstoff gebildet wird (Oxidation von Sauerstoffatomen des Wassers). Das Gleiche kann geschehen, wenn ein Reduktionsmittel, das stärker als Wasserstoff ist (z. B. metallisches Na), oder ein Oxidationsmittel, das stärker als Sauerstoff ist (z. B. F₂), mit Wasser in Kontakt kommt und mit diesem reagiert. In der nebenstehenden Eh-pH-Darstellung (der einfachsten Version eines Pourbaix-Diagramms) wird der Bereich der Wasserstabilität (graue Fläche) in Bezug auf das Redoxpotenzial durch zwei geneigte rote gestrichelte Linien begrenzt: ⓘ

• Untere Stabilitätslinie mit Wasserstoffgasentwicklung aufgrund der Protonenreduktion bei sehr niedrigem Eh:

2 H⁺ + 2 e- ⇌ H₂ (Kathode: Reduktion) ⓘ

• Höhere Stabilitätslinie mit Sauerstoffgasentwicklung aufgrund der Sauerstoffoxidation von Wasser bei sehr hohem E_h-Wert:

2 H₂O ⇌ O₂ + 4 H⁺ + 4 e- (Anode: Oxidation) ⓘ

Bei der Lösung der Nernst-Gleichung für jede entsprechende Reduktionsreaktion (die Oxidationsreaktion von Wasser, bei der Sauerstoff entsteht, muss rückgängig gemacht werden) haben beide Gleichungen eine ähnliche Form, da die Anzahl der Protonen und die Anzahl der Elektronen, die an einer Reaktion beteiligt sind, gleich sind und ihr Verhältnis eins ist (2 H⁺/2 e- für H₂ bzw. 4 H⁺/4 e- bei O₂), was die Lösung der Nernst-Gleichung in Abhängigkeit vom pH-Wert vereinfacht. ⓘ

Das Ergebnis lässt sich numerisch wie folgt ausdrücken: ⓘ

$E_{\text{red}}=E_{\text{red}}^{\ominus }-0.05916\ pH$ ⓘ

Man beachte, dass die Steigungen der beiden oberen und unteren Linien des Wasserstabilitätsbereichs gleich sind (-59,16 mV/pH-Einheit), so dass sie in einem Pourbaix-Diagramm parallel sind. Da die Steigungen negativ sind, erfordert sowohl die Wasserstoff- als auch die Sauerstoffentwicklung bei hohem pH-Wert ein viel niedrigeres Reduktionspotenzial als bei niedrigem pH-Wert. ⓘ

Für die Reduktion von H⁺ zu H₂ ergibt sich die oben genannte Beziehung: ⓘ

$E_{\text{red}}=-0.05916\ pH$
weil nach Konvention $E_{\text{red}}^{\ominus }$ = 0 V für die Standard-Wasserstoffelektrode (SHE: pH = 1).
Also, bei pH = 7, $E_{\text{red}}$ = -0,414 V für die Reduktion von Protonen. ⓘ

Für die Reduktion von O₂ zu 2 H₂O ergibt sich die oben genannte Beziehung: ⓘ

$E_{\text{red}}=1.229-0.05916\ pH$
weil $E_{\text{red}}^{\ominus }$ = +1,229 V in Bezug auf die Standard-Wasserstoffelektrode (SHE: pH = 1).
Also, bei pH = 7, $E_{\text{red}}$ = +0,815 V für die Reduktion von Sauerstoff. ⓘ

Der Offset von -414 mV in $E_{\text{red}}$ ist für beide Reduktionsreaktionen gleich, da sie die gleiche lineare Beziehung in Abhängigkeit vom pH-Wert aufweisen und die Steigungen ihrer Linien gleich sind. Dies lässt sich direkt in einem Pourbaix-Diagramm nachweisen. Bei anderen Reduktionsreaktionen hängt der Wert des formalen Reduktionspotenzials bei einem pH-Wert von 7, wie er für biochemische Reaktionen üblich ist, ebenfalls von der Steigung der entsprechenden Linie in einem Pourbaix-Diagramm ab, d. h. vom Verhältnis h⁄z der Anzahl der an der Reduktionsreaktion beteiligten H⁺ zur Anzahl der e- und damit von der Stöchiometrie der Halbreaktion. Die Bestimmung des formalen Reduktionspotentials bei pH = 7 für eine gegebene biochemische Halbreaktion erfordert also, es mit der entsprechenden Nernst-Gleichung als Funktion des pH-Wertes zu berechnen. Man kann nicht einfach einen Offset von -414 mV auf den Eh-Wert (SHE) anwenden, wenn das Verhältnis h⁄z von 1 abweicht. ⓘ

Anwendungen in der Biologie

Neben wichtigen Redoxreaktionen in der Biochemie und Mikrobiologie wird die Nernst-Gleichung auch in der Physiologie zur Berechnung des elektrischen Potenzials einer Zellmembran in Bezug auf eine Ionenart verwendet. Sie kann mit der Säuredissoziationskonstante verknüpft werden. ⓘ

Nernst-Potenzial

Die Nernst-Gleichung wird in der Physiologie zur Berechnung des Potenzials eines Ions der Ladung z durch eine Membran verwendet. Dieses Potenzial wird anhand der Konzentration des Ions sowohl innerhalb als auch außerhalb der Zelle bestimmt:

$$E={\frac {RT}{zF}}\ln {\frac {[{\text{ion outside cell}}]}{[{\text{ion inside cell}}]}}=2.3026{\frac {RT}{zF}}\log _{10}{\frac {[{\text{ion outside cell}}]}{[{\text{ion inside cell}}]}}.$$

ⓘ

Wenn sich die Membran im thermodynamischen Gleichgewicht befindet (d. h. kein Nettofluss von Ionen) und die Zelle nur für ein Ion durchlässig ist, dann muss das Membranpotenzial gleich dem Nernst-Potenzial für dieses Ion sein. ⓘ

Goldman-Gleichung

Wenn die Membran für mehr als ein Ion durchlässig ist, was zwangsläufig der Fall ist, kann das Ruhepotenzial anhand der Goldman-Gleichung bestimmt werden, die eine Lösung der G-H-K-Einstromgleichung unter der Bedingung ist, dass die durch die elektrochemische Kraft angetriebene Gesamtstromdichte Null ist:

$$E_{\mathrm {m} }={\frac {RT}{F}}\ln {\left({\frac {\displaystyle \sum _{i}^{N}P_{\mathrm {M} _{i}^{+}}\left[\mathrm {M} _{i}^{+}\right]_{\mathrm {out} }+\displaystyle \sum _{j}^{M}P_{\mathrm {A} _{j}^{-}}\left[\mathrm {A} _{j}^{-}\right]_{\mathrm {in} }}{\displaystyle \sum _{i}^{N}P_{\mathrm {M} _{i}^{+}}\left[\mathrm {M} _{i}^{+}\right]_{\mathrm {in} }+\displaystyle \sum _{j}^{M}P_{\mathrm {A} _{j}^{-}}\left[\mathrm {A} _{j}^{-}\right]_{\mathrm {out} }}}\right)},$$

ⓘ

wobei ⓘ

• E_m ist das Membranpotential (in Volt, äquivalent zu Joule pro Coulomb),
• P_ion ist die Permeabilität für dieses Ion (in Metern pro Sekunde),
• [ion]_out ist die extrazelluläre Konzentration dieses Ions (in Mol pro Kubikmeter, um mit den anderen SI-Einheiten übereinzustimmen, obwohl die Einheiten eigentlich keine Rolle spielen, da die Ionenkonzentrationsterme zu einem dimensionslosen Verhältnis werden),
• [ion]_in ist die intrazelluläre Konzentration dieses Ions (in Molen pro Kubikmeter),
• R ist die ideale Gaskonstante (Joule pro Kelvin pro Mol),
• T ist die Temperatur in Kelvin,
• F ist die Faradaysche Konstante (Coulomb pro Mol). ⓘ

Das Potenzial an der Zellmembran, das der Nettodiffusion eines bestimmten Ions durch die Membran genau entgegenwirkt, wird als Nernst-Potenzial für dieses Ion bezeichnet. Wie oben dargestellt, wird die Größe des Nernst-Potenzials durch das Verhältnis der Konzentrationen dieses spezifischen Ions auf den beiden Seiten der Membran bestimmt. Je größer dieses Verhältnis ist, desto größer ist die Tendenz des Ions, in eine Richtung zu diffundieren, und desto größer ist daher das Nernst-Potenzial, das erforderlich ist, um die Diffusion zu verhindern. Es gibt einen ähnlichen Ausdruck, der r (den absoluten Wert des Transportverhältnisses) einschließt. Damit werden Transporter mit ungleichen Austauschverhältnissen berücksichtigt. Siehe: Natrium-Kalium-Pumpe, bei der das Transportverhältnis 2/3 beträgt, so dass r in der unten stehenden Formel gleich 1,5 ist. Der Grund, warum wir hier einen Faktor r = 1,5 einfügen, ist, dass die Stromdichte durch elektrochemische Kraft J_e.c.(Na⁺) + J_e.c.(K⁺) nicht mehr Null ist, sondern J_e.c.(Na⁺) + 1,5J_e.c.(K⁺) = 0 (da für beide Ionen der Fluss durch elektrochemische Kraft durch den durch die Pumpe kompensiert wird, d.h. J_e.c. = -J_pump), wodurch sich die Bedingungen für die Anwendung der GHK-Gleichung ändern. Die anderen Variablen sind die gleichen wie oben. Das folgende Beispiel enthält zwei Ionen: Kalium (K⁺) und Natrium (Na⁺). Es wird angenommen, dass sich Chlorid im Gleichgewicht befindet.

$$E_{m}={\frac {RT}{F}}\ln {\left({\frac {rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {out} }}{rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {in} }}}\right)}.$$

ⓘ

Wenn Chlorid (Cl-) berücksichtigt wird, ⓘ

$$E_{m}={\frac {RT}{F}}\ln {\left({\frac {rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {out} }+P_{\mathrm {Cl} ^{-}}\left[\mathrm {Cl} ^{-}\right]_{\mathrm {in} }}{rP_{\mathrm {K} ^{+}}\left[\mathrm {K} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Na} ^{+}}\left[\mathrm {Na} ^{+}\right]_{\mathrm {in} }+P_{\mathrm {Cl} ^{-}}\left[\mathrm {Cl} ^{-}\right]_{\mathrm {out} }}}\right)}.$$

ⓘ

Ableitung

Verwendung des Boltzmann-Faktors

Der Einfachheit halber betrachten wir eine Lösung mit redoxaktiven Molekülen, die eine reversible Ein-Elektronen-Reaktion eingehen ⓘ

Ox + e- ⇌ Rot ⓘ

und die ein Standardpotential von Null haben, und in der die Aktivitäten gut durch die Konzentrationen repräsentiert sind (d. h. Einheitsaktivitätskoeffizient). Das chemische Potenzial μc dieser Lösung ist die Differenz zwischen den Energiebarrieren für die Aufnahme von Elektronen aus der Arbeitselektrode und für die Abgabe von Elektronen an die Arbeitselektrode, die das elektrochemische Potenzial der Lösung bestimmt. Das Verhältnis von oxidierten zu reduzierten Molekülen, [Ox]/[Red], entspricht der Wahrscheinlichkeit, oxidiert zu werden (Elektronen abzugeben), gegenüber der Wahrscheinlichkeit, reduziert zu werden (Elektronen aufzunehmen), was wir als Boltzmann-Faktor für diese Prozesse schreiben können:

$${\begin{aligned}{\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}&={\frac {\exp \left(-[{\text{barrier for gaining an electron}}]/kT\right)}{\exp \left(-[{\text{barrier for losing an electron}}]/kT\right)}}\\[6px]&=\exp \left({\frac {\mu _{\mathrm {c} }}{kT}}\right).\end{aligned}}$$

ⓘ

Wenn man den natürlichen Logarithmus beider Seiten nimmt, erhält man

$$\mu _{\mathrm {c} }=kT\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.$$

ⓘ

Wenn μ_c ≠ 0 bei [Ox]/[Red] = 1 ist, müssen wir diese zusätzliche Konstante einfügen:

$$\mu _{\mathrm {c} }=\mu _{\mathrm {c} }^{\ominus }+kT\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.$$

ⓘ

Dividiert man die Gleichung durch e, um von chemischen Potenzialen in Elektrodenpotenziale umzuwandeln, und erinnert sich daran, dass k/e = R/F ist, erhält man die Nernst-Gleichung für den Ein-Elektronen-Prozess Ox + e- ⇌ Red :

$${\begin{aligned}E&=E^{\ominus }-{\frac {kT}{e}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{F}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}.\end{aligned}}$$

ⓘ

Anwendung der Thermodynamik (chemisches Potential)

Die Mengen werden hier pro Molekül und nicht pro Mol angegeben, daher werden die Boltzmann-Konstante k und die Elektronenladung e anstelle der Gaskonstante R und der Faraday-Konstante F verwendet. Zur Umrechnung in die in den meisten Chemie-Lehrbüchern angegebenen molaren Mengen muss lediglich mit der Avogadro-Konstante multipliziert werden: R = kN_A und F = eN_A. Die Entropie eines Moleküls ist definiert als ⓘ

$$S\ {\stackrel {\mathrm {def} }{=}}\ k\ln \Omega ,$$

ⓘ

wobei Ω die Anzahl der Zustände ist, die dem Molekül zur Verfügung stehen. Die Anzahl der Zustände muss linear mit dem Volumen V des Systems variieren (zum besseren Verständnis wird hier ein idealisiertes System betrachtet, so dass die Aktivitäten sehr nahe an den tatsächlichen Konzentrationen liegen. Ein grundlegender statistischer Nachweis der erwähnten Linearität würde den Rahmen dieses Abschnitts sprengen, aber um zu sehen, dass dies wahr ist, ist es einfacher, einen üblichen isothermen Prozess für ein ideales Gas zu betrachten, bei dem die Entropieänderung ΔS = nR ln(V₂/V1) stattfindet. Aus der Definition der Entropie und der Bedingung einer konstanten Temperatur und Gasmenge n folgt, dass die Änderung der Anzahl der Zustände proportional zur relativen Änderung des Volumens V₂/V1 sein muss. In diesem Sinne gibt es keinen Unterschied in den statistischen Eigenschaften idealer Gasatome im Vergleich zu den gelösten Spezies einer Lösung mit Aktivitätskoeffizienten gleich 1: die Teilchen "hängen" frei herum und füllen das vorgesehene Volumen aus), die umgekehrt proportional zur Konzentration c ist, so dass wir die Entropie auch schreiben können als

$$S=k\ln \ (\mathrm {constant} \times V)=-k\ln \ (\mathrm {constant} \times c).$$

ⓘ

Die Änderung der Entropie von einem Zustand 1 zu einem anderen Zustand 2 ist also

$$\Delta S=S_{2}-S_{1}=-k\ln {\frac {c_{2}}{c_{1}}},$$

so dass die Entropie des Zustands 2 beträgt

$$S_{2}=S_{1}-k\ln {\frac {c_{2}}{c_{1}}}.$$

ⓘ

Wenn sich der Zustand 1 unter Standardbedingungen befindet, bei denen c₁ eine Einheit ist (z. B. 1 atm oder 1 M), hebt er lediglich die Einheiten von c₂ auf. Wir können daher die Entropie eines beliebigen Moleküls A schreiben als

$$S(\mathrm {A} )=S^{\ominus }(\mathrm {A} )-k\ln[\mathrm {A} ],$$

wobei $S^{\ominus }$ ist die Entropie bei Standardbedingungen und [A] bezeichnet die Konzentration von A. Die Entropieänderung bei einer Reaktion ⓘ

aA + bB → yY + zZ

ist dann gegeben durch

$$\Delta S_{\mathrm {rxn} }={\big (}yS(\mathrm {Y} )+zS(\mathrm {Z} ){\big )}-{\big (}aS(\mathrm {A} )+bS(\mathrm {B} ){\big )}=\Delta S_{\mathrm {rxn} }^{\ominus }-k\ln {\frac {[\mathrm {Y} ]^{y}[\mathrm {Z} ]^{z}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}}.$$

ⓘ

Wir definieren das Verhältnis im letzten Term als den Reaktionsquotienten:

$$Q_{r}={\frac {\displaystyle \prod _{j}a_{j}^{\nu _{j}}}{\displaystyle \prod _{i}a_{i}^{\nu _{i}}}}\approx {\frac {[\mathrm {Z} ]^{z}[\mathrm {Y} ]^{y}}{[\mathrm {A} ]^{a}[\mathrm {B} ]^{b}}},$$

wobei der Zähler ein Produkt der Aktivitäten der Reaktionsprodukte aj ist, die jeweils mit einem stöchiometrischen Koeffizienten νj potenziert werden, und der Nenner ein ähnliches Produkt der Aktivitäten der Reaktanten ist. Alle Aktivitäten beziehen sich auf eine Zeit t. Unter bestimmten Umständen (siehe chemisches Gleichgewicht) ist jeder Aktivitätsterm wie a^νj
_j kann durch einen Konzentrationsterm [A] ersetzt werden. In einer elektrochemischen Zelle ist das Zellpotenzial E das durch Redoxreaktionen verfügbare chemische Potenzial (E = μc/e). E ist mit der Gibbsschen freien Energieänderung ΔG nur durch eine Konstante verbunden: ΔG = -zFE, wobei n die Anzahl der übertragenen Elektronen und F die Faraday-Konstante ist. Das Vorzeichen ist negativ, weil eine spontane Reaktion eine negative freie Gibbs-Energie ΔG und ein positives Potenzial E hat. Die freie Gibbs-Energie ist mit der Entropie durch G = H - TS verbunden, wobei H die Enthalpie und T die Temperatur des Systems ist. Unter Verwendung dieser Beziehungen können wir nun die Änderung der freien Gibbs-Energie schreiben,

$$\Delta G=\Delta H-T\Delta S=\Delta G^{\ominus }+kT\ln Q_{r},$$

und das Zellpotential,

$$E=E^{\ominus }-{\frac {kT}{ze}}\ln Q_{r}.$$

ⓘ

Dies ist die allgemeinere Form der Nernst-Gleichung. ⓘ

Für die Redoxreaktion Ox + z e- → Red,

$$Q_{r}={\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}},$$

und wir haben:

$${\begin{aligned}E&=E^{\ominus }-{\frac {kT}{ze}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{zF}}\ln {\frac {[\mathrm {Red} ]}{[\mathrm {Ox} ]}}\\&=E^{\ominus }-{\frac {RT}{zF}}\ln Q_{r}.\end{aligned}}$$

ⓘ

Das Zellpotenzial bei Standardtemperatur und -druck (STP) $E^{\ominus }$ wird häufig durch das formale Potenzial $E^{\ominus '}$ersetzt, das die Aktivitätskoeffizienten der gelösten Spezies unter gegebenen Versuchsbedingungen (T, P, Ionenstärke, pH-Wert und Komplexbildner) enthält und das tatsächlich in einer elektrochemischen Zelle gemessene Potenzial darstellt. ⓘ

Beziehung zum chemischen Gleichgewicht

Die freie Standard-Gibbs-Energie $\Delta G^{\ominus }$ ist wie folgt mit der Gleichgewichtskonstante K verknüpft: ⓘ

$\Delta G^{\ominus }=-RT\ln {K}$ ⓘ

Zugleich $\Delta G^{\ominus }$ auch gleich dem Produkt aus der während der Reaktion übertragenen Gesamtladung (zF) und dem Zellpotential ($E_{cell}^{\ominus }$):

$\Delta G^{\ominus }=-zFE_{cell}^{\ominus }$ ⓘ

Das Vorzeichen ist negativ, da das betrachtete System Arbeit verrichtet und somit Energie freisetzt. ⓘ

Also, ⓘ

$-zFE_{cell}^{\ominus }=-RT\ln {K}$ ⓘ

Und deshalb: ⓘ

$E_{cell}^{\ominus }={\frac {RT}{zF}}\ln {K}$ ⓘ

Ausgehend von der Nernst-Gleichung kann man die gleiche Beziehung auch in umgekehrter Weise aufzeigen. ⓘ

Im chemischen oder thermodynamischen Gleichgewicht ist das elektrochemische Potenzial (E) = 0, und daher erreicht der Reaktionsquotient (Qr) den speziellen Wert, der als Gleichgewichtskonstante (K_eq) bezeichnet wird:

Qr = K_{eq ⓘ}

Daraus folgt, ⓘ

$${\begin{aligned}0&=E^{\ominus }-{\frac {RT}{zF}}\ln K\\{\frac {RT}{zF}}\ln K&=E^{\ominus }\\\ln K&={\frac {zFE^{\ominus }}{RT}}\end{aligned}}$$

ⓘ

Oder im Normalzustand, ⓘ

$$\log _{10}K={\frac {zE^{\ominus }}{\lambda V_{T}}}={\frac {zE^{\ominus }}{0.05916{\text{ V}}}}\quad {\text{at }}T=298.15~{\text{K}}$$

ⓘ

Wir haben also einen Zusammenhang zwischen dem Standard-Elektrodenpotential und der Gleichgewichtskonstante einer Redoxreaktion hergestellt. ⓘ

Beschränkungen

In verdünnten Lösungen kann die Nernst-Gleichung direkt in Form von Konzentrationen ausgedrückt werden (da die Aktivitätskoeffizienten nahe bei Eins liegen). Bei höheren Konzentrationen müssen jedoch die tatsächlichen Aktivitäten der Ionen verwendet werden. Dies erschwert die Anwendung der Nernst-Gleichung, da die Schätzung der nicht idealen Aktivitäten der Ionen im Allgemeinen experimentelle Messungen erfordert. Die Nernst-Gleichung gilt auch nur, wenn kein Nettostrom durch die Elektrode fließt. Die Aktivität der Ionen an der Elektrodenoberfläche ändert sich, wenn ein Stromfluss stattfindet, und es gibt zusätzliche Überspannungs- und Widerstandsverlustterme, die zum gemessenen Potenzial beitragen. ⓘ

Bei sehr niedrigen Konzentrationen der potenzialbestimmenden Ionen nähert sich das durch die Nernst-Gleichung vorhergesagte Potenzial ±∞ an. Dies ist physikalisch bedeutungslos, da unter solchen Bedingungen die Austauschstromdichte sehr gering wird und möglicherweise kein thermodynamisches Gleichgewicht besteht, das für die Einhaltung der Nernst-Gleichung erforderlich ist. Die Elektrode wird in einem solchen Fall als unpolarisiert bezeichnet. Andere Effekte neigen dazu, die Kontrolle über das elektrochemische Verhalten des Systems zu übernehmen, wie z. B. die Beteiligung des solvatisierten Elektrons an der Stromübertragung und den Elektrodengleichgewichten, wie von Alexander Frumkin und B. Damaskin, Sergio Trasatti usw. analysiert. ⓘ

Zeitabhängigkeit des Potentials

Der Ausdruck der Zeitabhängigkeit wurde von Karaoglanoff aufgestellt. ⓘ

Bedeutung in anderen wissenschaftlichen Bereichen

Die Nernst-Gleichung wurde in die wissenschaftliche Kontroverse über die kalte Fusion einbezogen. Fleischmann und Pons, die behaupteten, dass es die kalte Fusion geben könnte, berechneten, dass eine Palladiumkathode, die in eine Elektrolysezelle mit schwerem Wasser eingetaucht ist, einen Druck von bis zu 10²⁷ Atmosphären innerhalb des Kristallgitters des Kathodenmetalls erreichen könnte, was ausreichen würde, um eine spontane Kernfusion zu bewirken. In Wirklichkeit wurden nur 10.000-20.000 Atmosphären erreicht. Der amerikanische Physiker John R. Huizenga behauptete, die ursprüngliche Berechnung sei durch eine Fehlinterpretation der Nernst-Gleichung beeinflusst worden. Er zitierte eine Arbeit über Pd-Zr-Legierungen. ⓘ

Die Nernst-Gleichung ermöglicht die Berechnung des Ausmaßes der Reaktion zwischen zwei Redox-Systemen und kann z. B. verwendet werden, um zu beurteilen, ob eine bestimmte Reaktion zu Ende geht oder nicht. Im chemischen Gleichgewicht sind die elektromotorischen Kräfte (EMK) der beiden Halbzellen gleich. Dadurch lässt sich die Gleichgewichtskonstante K der Reaktion und damit das Ausmaß der Reaktion berechnen. ⓘ

Interpretation und Bedeutung

Galvanische Zelle ⓘ

Jede Kombination von zwei Elektroden nennt man Galvanische Zelle (z. B. Batterien, Akkus oder auch biologische Zellen). Ihre Leerlaufspannung U₀ (historisch: Elektromotorische Kraft) ist gleich der Potentialdifferenz ΔE der Elektroden, die bei Anwendung der Nernst-Gleichung auf die Halbzellen als U₀ = ΔE = E_Akzeptor − E_Donator berechnet werden kann. Analog erlaubt sie die Berechnung der sich einstellenden Gleichgewichtsaktivitäten, wenn an die Halbzellen eine Spannung angelegt wird. ⓘ

Die Nernst-Gleichung besitzt zentrale Bedeutung in der Elektrochemie, Galvanik und Elektroanalytik, weil sie die elektrische Größe Spannung (bzw. Elektrodenpotential) mit der chemischen Größe Konzentration verbindet. Sie ist streng genommen nur gültig für Zellen ohne Überführung und stromlose Vorgänge, bietet aber einen Ausgangspunkt für die Herleitung von Gleichungen in stromdurchflossenen elektrochemischen Systemen. Das Nernstpotential U₀ multipliziert mit der Ladung z·F für einen molaren Stoffumsatz z·F·U₀ ergibt die Gibbsenergie. ∆G = −z·F·U₀. Das Nernstpotential gibt demnach die chemische Energie der elektrochemischen Reaktion, geteilt durch die beteiligte Ladung an. ⓘ

Alternative Formulierungen

Die Bezeichnung Nernst-Gleichung wird je nach Anwendung für verschiedene abgeleitete oder erweiterte Gleichungen benutzt. ⓘ

Spezielle (historische) Nernst-Gleichung

Die ursprüngliche Form leitete im Jahr 1889 der deutsche Physiker und Chemiker Walther Nernst unter Verwendung von Konzentrationen c ab. ⓘ

$E=E^{0}+{\frac {RT}{z_{\mathrm {e} }F}}\ln {\frac {c_{\mathrm {Ox} }}{c_{\mathrm {Red} }}}$ ⓘ

Der Faktor R T / z_e F wird Nernst-Faktor oder Elektrodensteilheit genannt; eine Wertetabelle für R T / z_e F bei verschiedenen Temperaturen befindet sich im Artikel zur Elektrodensteilheit. ⓘ

Allgemeine Nernst-Gleichung (Herleitung)

Für die Änderung der Gibbs-Energie (Freien Enthalpie) $\Delta _{\mathrm {R} }G$ einer chemischen Reaktion, an der $k$ Stoffe $A_{1},\dots ,A_{k}$ gemäß

$\nu _{1}A_{1}+\nu _{2}A_{2}+\dots \longrightarrow \dots +\nu _{k-1}A_{k-1}+\nu _{k}A_{k}$

beteiligt sind, gilt ⓘ

$\Delta _{\mathrm {R} }G=\Delta _{\mathrm {R} }G^{0}+RT\,\ln \prod _{i=1}^{k}a_{i}^{\nu _{i}}$ ⓘ

$a_{i}$	auf die Standardaktivität bezogene Aktivität des Stoffes $i$ ⓘ
$\nu _{i}$	stöchiometrischer Koeffizient des Stoffes $i$ in der Reaktionsgleichung (negativ für Edukte)

Der Zusammenhang zwischen $\Delta _{\mathrm {R} }G$ und dem Logarithmus ist plausibel, da einerseits $\Delta _{\mathrm {R} }G$ proportional zur Teilchenzahl (oder der Schreibweise der chemischen Gleichung) ist, andererseits in den Aktivitätsquotienten die einzelnen Aktivitäten mit der Potenz der stöchiometrischen Koeffizienten eingehen. Der Logarithmus wandelt den Exponenten in einen Faktor um. ⓘ

$\mathrm {2\,H_{2}+O_{2}\longrightarrow 2\,H_{2}O}$ ergibt pro $\mathrm {H_{2}O}$ dasselbe (elektro-)chemische Potential wie $\mathrm {H_{2}+{1 \over 2}\ O_{2}\longrightarrow H_{2}O} \qquad$. ⓘ

$\Delta _{\mathrm {R} }G$ ist die bei konstantem Druck und konstanter Temperatur aus der Reaktion maximal gewinnbare Arbeit, die vollständig in nutzbare elektrische Arbeit umgewandelt werden kann. Aufgrund des Energieerhaltungssatzes gilt ⓘ

$\Delta _{\mathrm {R} }G=-z_{e}\,F\,\Delta E$ ⓘ

was in der allgemeinen Nernst-Gleichung resultiert ⓘ

$\Delta E=\Delta E^{0}-{\frac {RT}{z_{e}F}}\,\ln \prod _{i=1}^{k}a_{i}^{\nu _{i}}$ ⓘ

Die allgemeine Nernst-Gleichung erlaubt für die betrachtete Reaktion die Berechnung der Gleichgewichtskonstanten (für $\Delta E=0$), Richtung (freiwillig für $\Delta E>0$, erzwungen für $\Delta E<0$) und Spannung $\Delta E$, die die Reaktion liefert, wenn man ihre Redox-Teilreaktionen in getrennten Halbzellen ablaufen lässt. ⓘ

siehe auch: chemisches Potential, elektrochemisches Potential ⓘ

Anwendung

Die Nernst-Gleichung findet in der potentiometrischen Titration Verwendung. Beispielsweise wird eine Messelektrode in eine Probelösung eingetaucht und muss auf das zu bestimmende Ion reagieren, das heißt, das Potential dieser Elektrode muss abhängig von der Konzentration des zu bestimmenden Ions sein. Diese Abhängigkeit wird durch die Nernst-Gleichung beschrieben. Bei dem Versuch ist darauf zu achten, dass die Messung stromlos erfolgt, da sich sonst durch Elektrolyse die Potentiale verfälschen würden. Man verwendete daher zur Messung eine Spannungs-Kompensationsschaltung. ⓘ

Reduktion

Für die Reduktion

$\mathrm {Ox+{\mathit {z}}_{\mathit {e}}e^{-}\longrightarrow Red}$

geht die allgemeine Form unmittelbar in die erstgenannte Gleichung über. Diese Identität hat zwei praktische Bedeutungen:

• Die elektrochemische Spannungsreihe listet prinzipiell Reduktionen.
• Da man jede chemische Reaktion in Oxidations- und Reduktionsteilreaktionen von Redox-Paaren zerlegen kann, ist ΔE die Summe der mit den zugehörigen stöchiometrischen Koeffizienten multiplizierten Nernst-Gleichungen für die Teilreaktionen. Dabei gehen die Oxidationsteilreaktionen mit negativem stöchiometrischen Koeffizienten ein. ⓘ

Knallgasreaktion

Die Teilreaktionen der so genannten Knallgasreaktion

$\mathrm {2\ H_{2}+O_{2}\longrightarrow 2\ H_{2}O}$

laufen als Oxidation

$\mathrm {2\ H_{2}\longrightarrow 4\ H^{+}+4\ e^{-}}$

bzw. Reduktion

$\mathrm {O_{2}+4\ e^{-}\longrightarrow 2\ O^{2-}}$

räumlich getrennt in Wasserstoff-Sauerstoff-Brennstoffzellen ab. Die damit erzielbare Spannung kann mit der Nernst-Gleichung berechnet werden und beträgt unter Standardbedingungen ΔE⁰ = 1,23 V. ⓘ

Konzentrationselemente

Kupfer-Konzentrationselement ⓘ

Ein Konzentrationselement besteht aus zwei Halbzellen, die Elektrolyte mit den gleichen Bestandteilen enthalten, aber mit unterschiedlicher Ionenkonzentration. Es eignet sich daher besonders zur Demonstration der Nernst-Gleichung. ⓘ

Ein Beispiel ist ein Kupfer-Konzentrationselement aus zwei Kupferelektroden und zwei Kupfersulfatlösungen, die sich nur in der Konzentration unterscheiden. Bei Stromfluss gleichen sich dann die Konzentrationen in den Zellen an, denn es laufen dann folgende Reaktionen ab: Die Reduktion in der Halbzelle mit der größeren Kupferionenkonzentration c_g:

$\mathrm {Cu^{2+}({\mathit {c}}_{g})+2\ e^{-}\longrightarrow Cu}$

Die Oxidation in der Halbzelle mit der kleineren Kupferionenkonzentration c_k:

$\mathrm {Cu\longrightarrow Cu^{2+}({\mathit {c}}_{k})+2\ e^{-}}$

Anhand der Nernst-Gleichungen für die Teilreaktionen oder mit der allgemeinen Nernst-Gleichung der Gesamtreaktion erhält man für die Spannung ΔE des Kupfer-Konzentrationselements:

$\Delta E={\frac {RT}{2F}}\ln {\frac {c_{\mathrm {g} }(\mathrm {Cu} ^{2+})}{c_{\mathrm {k} }(\mathrm {Cu} ^{2+})}}$

Allgemein gilt für die Spannung eines Konzentrationselements:

$\Delta E={\frac {RT}{z_{e}F}}\ln {\frac {a_{\mathrm {g} }}{a_{\mathrm {k} }}}$.

Im Temperaturbereich von 22 bis 26 °C gilt:

$\Delta E={\frac {0{,}059V}{z_{e}}}\lg {\frac {a_{\mathrm {g} }}{a_{\mathrm {k} }}}$. ⓘ

Konzentrationselemente mit verschiedenen Elementen

Bei Konzentrationselementen mit unterschiedlichen Elementen und Konzentrationen, die von den Normalbedingungen abweichen, wird folgende Formel verwendet:

$E=E^{0}+{\frac {0{,}059V}{z_{e}}}\lg {\frac {(c_{\mathrm {ox} })^{a}}{(c_{\mathrm {red} })^{b}}}$. ⓘ

• a = Vorfaktor der Oxidationsseite (Beispiel: 4 $\mathrm {H} ^{+}$)
• b = Vorfaktor der Reduktionsseite (Beispiel: 2 $\mathrm {H_{2}O}$) ⓘ

Lambdasonden

Bei einer Lambdasonde, deren Sensorelement für Sauerstoffionen leitfähig ist, stellt sich aufgrund des Konzentrationsgefälles des Sauerstoffes zwischen Luft und Abgas eine Spannung ein, die benutzt wird, um mit der Lambdaregelung ein gewünschtes Gemisch einzustellen. ⓘ

Nernst-Gleichung in der Biologie und Physiologie

In biologischen Systemen trennen Zellmembranen Bereiche unterschiedlicher Ionenkonzentrationen ab. Ist die Membran für ein bestimmtes Ion selektiv permeabel, wird es entlang des Konzentrationsgradienten diffundieren, gleichzeitig entsteht aber, da das Ion geladen ist, eine Spannung (Ruhemembranpotential). Mit der Nernst-Gleichung lässt sich die Gleichgewichtslage dieses Vorgangs beschreiben. ⓘ

Gebräuchlich ist eine vereinfachte Form der Gleichung, bei der R, F und T (310 K) sowie der Umrechnungsfaktor zum dekadischen Logarithmus in eine Konstante gefasst werden:

$E={\frac {61{,}51\,\mathrm {mV} }{z_{e}}}\lg {\frac {c_{\mathrm {aussen} }}{c_{\mathrm {innen} }}}$ ⓘ

Siehe auch: Goldman-Gleichung ⓘ