Viskosität

Viskosität ⓘ
Viskosität ⓘ
	Eine Simulation von Flüssigkeiten mit unterschiedlicher Viskosität. Die Flüssigkeit auf der linken Seite hat eine geringere Viskosität als die Flüssigkeit auf der rechten Seite.
Allgemeine Symbole	η, μ
Ableitungen von; anderen Größen	μ = G-t

Die Viskosität einer Flüssigkeit ist ein Maß für ihren Widerstand gegen Verformung bei einer bestimmten Geschwindigkeit. Bei Flüssigkeiten entspricht sie dem informellen Konzept der "Dicke": Sirup hat zum Beispiel eine höhere Viskosität als Wasser. ⓘ

Die Viskosität quantifiziert die innere Reibungskraft zwischen benachbarten Flüssigkeitsschichten, die sich relativ zueinander bewegen. Wenn beispielsweise eine viskose Flüssigkeit durch ein Rohr gedrückt wird, fließt sie in der Nähe der Rohrachse schneller als in der Nähe der Wände. Experimente zeigen, dass eine gewisse Spannung (z. B. ein Druckunterschied zwischen den beiden Enden des Rohrs) erforderlich ist, um die Strömung aufrechtzuerhalten. Dies liegt daran, dass eine Kraft erforderlich ist, um die Reibung zwischen den Schichten der Flüssigkeit zu überwinden, die sich relativ zueinander bewegen. Bei einem Rohr mit konstanter Durchflussrate ist die Stärke der Ausgleichskraft proportional zur Viskosität der Flüssigkeit. ⓘ

Im Allgemeinen hängt die Viskosität vom Zustand der Flüssigkeit ab, z. B. von der Temperatur, dem Druck und der Verformungsgeschwindigkeit. Die Abhängigkeit von einigen dieser Eigenschaften ist jedoch in bestimmten Fällen vernachlässigbar. So variiert die Viskosität einer Newtonschen Flüssigkeit nicht wesentlich mit der Verformungsgeschwindigkeit. Eine Viskosität von Null (kein Widerstand gegen Scherspannung) wird nur bei sehr niedrigen Temperaturen in Supraflüssigkeiten beobachtet; ansonsten verlangt der zweite Hauptsatz der Thermodynamik, dass alle Flüssigkeiten eine positive Viskosität haben. Ein Fluid mit einer Viskosität von Null wird als ideal oder inviskid bezeichnet. ⓘ

Physikalische Größe ⓘ

Name

dynamische Viskosität

Formelzeichen

\eta

,

\mu

Größen- und Einheitensystem	Einheit	Dimension
SI	Pa·s = N·s·m⁻² = kg·m⁻¹·s⁻¹	M·L⁻¹·T⁻¹
cgs	P	M·L⁻¹·T⁻¹

Physikalische Größe ⓘ

Name

kinematische Viskosität

Formelzeichen

\nu

Größen- und Einheitensystem	Einheit	Dimension
SI	m²·s⁻¹	L²·T⁻¹
cgs	St	L²·T⁻¹

Die Viskosität bezeichnet die Zähflüssigkeit oder Zähigkeit von Flüssigkeiten und Gasen (Fluiden). Je höher die Viskosität ist, desto dickflüssiger (weniger fließfähig) ist das Fluid; je niedriger die Viskosität, desto dünnflüssiger (fließfähiger) ist es. ⓘ

Ohne weitere Angaben ist der Widerstand des Fluids gegenüber Scherung gemeint. Sie wird daher als Scherviskosität bezeichnet, zur Abgrenzung gegenüber der Dehnviskosität bei Dehnung sowie der Volumenviskosität bei gleichmäßigem Druck. Des Weiteren wird zwischen der dynamischen Viskosität und der kinematischen Viskosität unterschieden. Die dynamische Viskosität ist das Verhältnis von Schubspannung und Geschwindigkeitsgradient. Der Kehrwert der dynamischen Viskosität ist die Fluidität. Die dynamische Viskosität $\eta$ und die kinematische Viskosität $\nu$ stehen über die Dichte $\rho$ in direktem Zusammenhang, ⓘ

\eta =\nu \cdot \rho

. ⓘ

Teilchen zäher Flüssigkeiten sind stärker aneinander gebunden und somit weniger beweglich; man spricht von der inneren Reibung. Sie resultiert nicht nur aus den Anziehungskräften zwischen den Teilchen des Fluids (Kohäsion). Bei dünnflüssigeren Fluiden resultiert die Viskosität aus einem Impulsfluss im Fluid. Die Viskosität von Feststoffen ist vergleichsweise hoch und damit schwer bestimmbar. Statt Viskosität werden Begriffe wie Verlustfaktor, Speicher- und Verlustmodul verwendet. ⓘ

Das Wort Viskosität geht auf den typisch zähflüssigen Saft der Beeren in der Pflanzengattung Misteln (Viscum) zurück. Aus solchen Misteln wurde Vogelleim gewonnen. „Viskos“ bedeutet „zäh wie Vogelleim“. ⓘ

Die blaugrüne Flüssigkeit links ist niederviskos wie Wasser, die orange rechts hochviskos wie Honig. ⓘ

Die Viskosität taucht in der Berechnung des viskosen Spannungstensors auf. ⓘ

Etymologie

Das Wort "Viskosität" leitet sich vom lateinischen viscum ("Mistel") ab. Viscum bezeichnete auch einen zähflüssigen Klebstoff, der aus Mistelbeeren gewonnen wird. ⓘ

Definition

Dynamische Viskosität

Illustration einer ebenen Couette-Strömung. Da der Scherströmung die Reibung zwischen benachbarten Flüssigkeitsschichten (die sich relativ zueinander bewegen) entgegenwirkt, ist eine Kraft erforderlich, um die Bewegung der oberen Platte aufrechtzuerhalten. Die relative Stärke dieser Kraft ist ein Maß für die Viskosität der Flüssigkeit. ⓘ

Bei einer allgemeinen Parallelströmung ist die Schubspannung proportional zum Geschwindigkeitsgefälle. ⓘ

In der Materialwissenschaft und -technik ist man oft daran interessiert, die Kräfte oder Spannungen zu verstehen, die bei der Verformung eines Materials auftreten. Wäre das Material beispielsweise eine einfache Feder, so würde die Antwort auf diese Frage durch das Hooke'sche Gesetz gegeben, das besagt, dass die Kraft, die eine Feder erfährt, proportional zum Abstand ist, den sie vom Gleichgewicht entfernt. Spannungen, die auf die Verformung eines Materials aus einem bestimmten Ruhezustand zurückzuführen sind, werden als elastische Spannungen bezeichnet. In anderen Materialien gibt es Spannungen, die auf die Änderungsrate der Verformung im Laufe der Zeit zurückzuführen sind. Diese werden als viskose Spannungen bezeichnet. In einer Flüssigkeit wie Wasser zum Beispiel hängen die Spannungen, die beim Scheren der Flüssigkeit entstehen, nicht von der Strecke ab, über die die Flüssigkeit geschert wurde, sondern davon, wie schnell die Scherung erfolgt. ⓘ

Die Viskosität ist die Materialeigenschaft, die die viskosen Spannungen in einem Material mit der Änderungsrate einer Verformung (der Dehnungsrate) in Beziehung setzt. Obwohl sie für allgemeine Strömungen gilt, lässt sie sich bei einer einfachen Scherströmung, wie der planaren Couette-Strömung, leicht veranschaulichen und definieren. ⓘ

Bei der Couette-Strömung ist ein Fluid zwischen zwei unendlich großen Platten eingeschlossen, von denen eine feststeht und die andere sich parallel mit konstanter Geschwindigkeit bewegt $u$ (siehe Abbildung rechts). Wenn die Geschwindigkeit der oberen Platte niedrig genug ist (um Turbulenzen zu vermeiden), bewegen sich die Flüssigkeitsteilchen im stationären Zustand parallel zu ihr, und ihre Geschwindigkeit variiert von $0$ an der Unterseite bis $u$ an der Oberseite. Jede Flüssigkeitsschicht bewegt sich schneller als die darunter liegende, und die Reibung zwischen ihnen erzeugt eine Kraft, die ihrer relativen Bewegung entgegenwirkt. Insbesondere übt die Flüssigkeit auf die obere Platte eine Kraft aus, die ihrer Bewegung entgegengesetzt ist, und eine gleiche, aber entgegengesetzte Kraft auf die untere Platte. Es ist also eine äußere Kraft erforderlich, um die obere Platte mit konstanter Geschwindigkeit in Bewegung zu halten. ⓘ

Bei vielen Flüssigkeiten wird beobachtet, dass die Strömungsgeschwindigkeit linear von Null am Boden bis $u$ an der Oberseite. Außerdem wird die Größe der Kraft, $F$ die auf die obere Platte wirkt, proportional zu der Geschwindigkeit $u$ und der Fläche $A$ der einzelnen Platten und umgekehrt proportional zu ihrem Abstand $y$ :

F=\mu A{\frac {u}{y}}.

Der Proportionalitätsfaktor ist die dynamische Viskosität der Flüssigkeit, die oft einfach als Viskosität bezeichnet wird. Sie wird mit dem griechischen Buchstaben mu ( $μ$ ) bezeichnet. Die dynamische Viskosität hat die Dimensionen $\mathrm {(mass/length)/time}$ Daher ergeben sich die SI-Einheiten und die abgeleiteten Einheiten:

[\mu ]={\frac {\rm {kg}}{\rm {m\cdot s}}}={\frac {\rm {N}}{\rm {m^{2}}}}\cdot s={\rm {Pa\cdot s}}=

Druck multipliziert mit Zeit. ⓘ

Das vorgenannte Verhältnis $u/y$ wird als Scherdeformationsrate oder Schergeschwindigkeit bezeichnet und ist die Ableitung der Flüssigkeitsgeschwindigkeit in der Richtung senkrecht zu den Platten (siehe Abbildungen rechts). Wenn sich die Geschwindigkeit nicht linear mit $y$ variiert, dann lautet die entsprechende Verallgemeinerung:

\tau =\mu {\frac {\partial u}{\partial y}},

wobei $\tau =F/A$ , und $\partial u/\partial y$ die lokale Schergeschwindigkeit ist. Dieser Ausdruck wird als Newtonsches Gesetz der Viskosität bezeichnet. In Scherströmungen mit planarer Symmetrie definiert es $\mu$ . Es ist ein Spezialfall der allgemeinen Definition der Viskosität (siehe unten), die in koordinatenfreier Form ausgedrückt werden kann. ⓘ

Die Verwendung des griechischen Buchstabens mu ( $\mu$ ) für die dynamische Viskosität (manchmal auch als absolute Viskosität bezeichnet) ist unter Maschinenbau- und Chemieingenieuren sowie unter Mathematikern und Physikern üblich. Allerdings wird der griechische Buchstabe eta ( $\eta$ ) wird jedoch auch von Chemikern, Physikern und der IUPAC verwendet. Die Viskosität $\mu$ wird manchmal auch als Scherviskosität bezeichnet. Mindestens ein Autor rät jedoch von der Verwendung dieser Terminologie ab und weist darauf hin, dass $\mu$ nicht nur in Scherströmungen, sondern auch in Nicht-Scherströmungen auftreten kann. ⓘ

Kinematische Viskosität

In der Fluiddynamik ist es manchmal angemessener, mit der kinematischen Viskosität (manchmal auch Impulsdiffusivität genannt) zu arbeiten, die als das Verhältnis der dynamischen Viskosität ( $μ$ ) zur Dichte der Flüssigkeit ( $ρ$ ) definiert ist. Sie wird gewöhnlich mit dem griechischen Buchstaben nu ( $ν$ ) bezeichnet:

\nu ={\frac {\mu }{\rho }},

ⓘ

und hat die Dimensionen $\mathrm {(length)^{2}/time}$ Daher ergeben sich die SI-Einheiten und die abgeleiteten Einheiten:

[\nu ]={\frac {\rm {m^{2}}}{\rm {s}}}=\mathrm {{\frac {\rm {N\cdot m}}{\rm {kg}}}\cdot s} =\mathrm {{\frac {\rm {J}}{\rm {kg}}}\cdot s} =

spezifische Energie multipliziert mit der Zeit. ⓘ

Allgemeine Definition

Ganz allgemein sind die viskosen Spannungen in einem Fluid definiert als die Spannungen, die sich aus der relativen Geschwindigkeit der verschiedenen Fluidteilchen ergeben. Daher müssen die viskosen Spannungen von den räumlichen Gradienten der Strömungsgeschwindigkeit abhängen. Wenn die Geschwindigkeitsgradienten klein sind, dann hängen die viskosen Spannungen in erster Näherung nur von den ersten Ableitungen der Geschwindigkeit ab. (Für Newtonsche Flüssigkeiten ist dies ebenfalls eine lineare Abhängigkeit.) In kartesischen Koordinaten kann die allgemeine Beziehung dann wie folgt geschrieben werden ⓘ

\tau _{ij}=\sum _{k}\sum _{\ell }\mu _{ijk\ell }{\frac {\partial v_{k}}{\partial r_{\ell }}},

ⓘ

wobei $\mu _{ijk\ell }$ ist ein Viskositätstensor, der den Geschwindigkeitsgradiententensor $\partial v_{k}/\partial r_{\ell }$ auf den viskosen Spannungstensor $\tau _{ij}$ . Da die Indizes in diesem Ausdruck von 1 bis 3 variieren können, gibt es insgesamt 81 "Viskositätskoeffizienten" $\mu _{ijkl}$ insgesamt. Geht man jedoch davon aus, dass der Viskositätsrang-4-Tensor isotrop ist, reduzieren sich diese 81 Koeffizienten auf drei unabhängige Parameter $\alpha$ , $\beta$ , $\gamma$ :

\mu _{ijk\ell }=\alpha \delta _{ij}\delta _{k\ell }+\beta \delta _{ik}\delta _{j\ell }+\gamma \delta _{i\ell }\delta _{jk},

und außerdem wird angenommen, dass keine viskosen Kräfte auftreten, wenn das Fluid einer einfachen Starrkörperrotation unterliegt, so dass $\beta =\gamma$ verbleiben nur zwei unabhängige Parameter. Die gebräuchlichste Zerlegung ist die in die Standardviskosität (skalar) $\mu$ und der Volumenviskosität $\kappa$ so dass $\alpha =\kappa -{\tfrac {2}{3}}\mu$ und $\beta =\gamma =\mu$ . In Vektorschreibweise erscheint dies als:

{\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\dagger }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,

wobei $\mathbf {\delta }$ ist der Einheitstensor, und der Dolch $\dagger$ steht für die Transponierung. Diese Gleichung kann als eine verallgemeinerte Form des Newtonschen Viskositätsgesetzes betrachtet werden. ⓘ

Die Volumenviskosität (auch Volumenviskosität genannt) drückt eine Art von innerer Reibung aus, die der scherungsfreien Kompression oder Expansion einer Flüssigkeit widersteht. Die Kenntnis von $\kappa$ ist bei fluiddynamischen Problemen häufig nicht erforderlich. Ein inkompressibles Fluid erfüllt zum Beispiel die Bedingung $\nabla \cdot \mathbf {v} =0$ und daher entfällt der Term, der $\kappa$ entfällt. Außerdem, $\kappa$ für Gase oft als vernachlässigbar angesehen, da er $0$ in einem einatomigen idealen Gas. Eine Situation, in der $\kappa$ wichtig sein kann, ist die Berechnung des Energieverlusts bei Schall- und Stoßwellen, die durch das Stokes'sche Gesetz der Schalldämpfung beschrieben werden, da diese Phänomene mit schnellen Ausdehnungen und Kompressionen einhergehen. ⓘ

Die Definitionsgleichungen für die Viskosität sind keine grundlegenden Naturgesetze, so dass ihre Nützlichkeit sowie die Methoden zur Messung oder Berechnung der Viskosität mit separaten Mitteln ermittelt werden müssen. Ein potenzielles Problem besteht darin, dass die Viskosität im Prinzip vom vollständigen mikroskopischen Zustand der Flüssigkeit abhängt, der die Positionen und Momente aller Teilchen im System umfasst. Derart detaillierte Informationen sind in der Regel in realistischen Systemen nicht verfügbar. Unter bestimmten Bedingungen kann jedoch gezeigt werden, dass die meisten dieser Informationen vernachlässigbar sind. Insbesondere für Newtonsche Flüssigkeiten in der Nähe des Gleichgewichts und weit entfernt von Grenzen (Bulk-Zustand) hängt die Viskosität nur von raum- und zeitabhängigen makroskopischen Feldern (wie Temperatur und Dichte) ab, die das lokale Gleichgewicht definieren. ⓘ

Dennoch kann die Viskosität eine nicht zu vernachlässigende Abhängigkeit von mehreren Systemeigenschaften aufweisen, wie Temperatur, Druck sowie Amplitude und Frequenz eines externen Einflusses. Daher sind Präzisionsmessungen der Viskosität nur definiert in Bezug auf einen bestimmten Flüssigkeitszustand definiert. Um Vergleiche zwischen Experimenten und theoretischen Modellen zu standardisieren, werden die Viskositätsdaten manchmal auf ideale Grenzfälle extrapoliert, wie z. B. die Null-Schergrenze oder (bei Gasen) die Null-Dichte-Grenze. ⓘ

Impulstransport

Die Transporttheorie bietet eine alternative Interpretation der Viskosität im Hinblick auf den Impulstransport: Die Viskosität ist die Materialeigenschaft, die den Impulstransport in einer Flüssigkeit charakterisiert, so wie die Wärmeleitfähigkeit den Wärmetransport und die (Massen-)Diffusivität den Massentransport charakterisiert. Diese Sichtweise ist im Newtonschen Viskositätsgesetz implizit enthalten, $\tau =\mu (\partial u/\partial y)$ weil die Schubspannung $\tau$ Einheiten hat, die einem Impulsfluss entsprechen, d. h. Impuls pro Zeiteinheit pro Flächeneinheit. Daher $\tau$ so interpretiert werden, dass es den Impulsfluss in der $y$ Richtung von einer Flüssigkeitsschicht zur nächsten. Nach dem Newtonschen Gesetz der Viskosität erfolgt dieser Impulsfluss über ein Geschwindigkeitsgefälle, und die Größe des entsprechenden Impulsflusses wird durch die Viskosität bestimmt. ⓘ

Die Analogie zum Wärme- und Stofftransport kann deutlich gemacht werden. So wie die Wärme von einer hohen Temperatur zu einer niedrigen Temperatur und die Masse von einer hohen Dichte zu einer niedrigen Dichte fließt, fließt der Impuls von einer hohen Geschwindigkeit zu einer niedrigen Geschwindigkeit. Diese Verhaltensweisen werden alle durch kompakte Ausdrücke beschrieben, die als konstitutive Beziehungen bezeichnet werden und deren eindimensionale Formen hier angegeben sind:

{\begin{aligned}\mathbf {J} &=-D{\frac {\partial \rho }{\partial x}}&&{\text{(Fick's law of diffusion)}}\\[5pt]\mathbf {q} &=-k_{t}{\frac {\partial T}{\partial x}}&&{\text{(Fourier's law of heat conduction)}}\\[5pt]\tau &=\mu {\frac {\partial u}{\partial y}}&&{\text{(Newton's law of viscosity)}}\end{aligned}}

wobei $\rho$ ist die Dichte, $\mathbf {J}$ und $\mathbf {q}$ sind die Massen- und Wärmeströme, und $D$ und $k_{t}$ sind die Massendiffusivität und die Wärmeleitfähigkeit. Die Tatsache, dass der Transport von Masse, Impuls und Energie (Wärme) zu den wichtigsten Prozessen in der Kontinuumsmechanik gehört, ist kein Zufall: Es handelt sich um eine der wenigen physikalischen Größen, die auf mikroskopischer Ebene bei Kollisionen zwischen Teilchen erhalten bleiben. Ihre Dynamik wird also nicht durch die schnelle und komplexe mikroskopische Wechselwirkungszeitskala bestimmt, sondern findet auf makroskopischen Zeitskalen statt, wie sie durch die verschiedenen Gleichungen der Transporttheorie und der Hydrodynamik beschrieben werden. ⓘ

Newtonsche und nicht-newtonsche Fluide

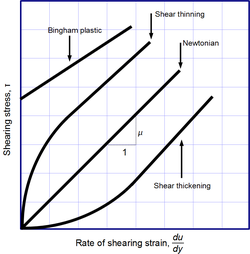
Die Viskosität, die Steigung jeder Linie, ist von Material zu Material unterschiedlich. ⓘ

Das Newtonsche Viskositätsgesetz ist kein fundamentales Naturgesetz, sondern eine konstitutive Gleichung (wie das Hooke'sche Gesetz, das Fick'sche Gesetz und das Ohm'sche Gesetz), die zur Definition der Viskosität dient $\mu$ . Ihre Form ist durch Experimente motiviert, die zeigen, dass die Viskosität für ein breites Spektrum von Flüssigkeiten $\mu$ unabhängig von der Dehnungsgeschwindigkeit ist. Solche Flüssigkeiten werden als Newtonsche Flüssigkeiten bezeichnet. Gase, Wasser und viele gängige Flüssigkeiten können unter normalen Bedingungen und in normalen Zusammenhängen als newtonsche Flüssigkeiten betrachtet werden. Es gibt jedoch viele nicht-newtonsche Flüssigkeiten, die erheblich von diesem Verhalten abweichen. Zum Beispiel:

Scherverdickende (dilatante) Flüssigkeiten, deren Viskosität mit der Scherdehnung zunimmt.
Scherverdünnende Flüssigkeiten, deren Viskosität mit der Rate der Scherbelastung abnimmt.
Thixotrope Flüssigkeiten, deren Viskosität mit der Zeit abnimmt, wenn sie geschüttelt, gerührt oder anderweitig belastet werden.
Rheopektische Flüssigkeiten, die bei Schütteln, Rühren oder anderer Beanspruchung mit der Zeit zähflüssiger werden.
Bingham-Kunststoffe, die sich bei geringen Spannungen wie ein Festkörper verhalten, bei hohen Spannungen jedoch wie eine viskose Flüssigkeit fließen. ⓘ

Das Trouton-Verhältnis ist das Verhältnis der Dehnungsviskosität zur Scherviskosität. Für ein Newtonsches Fluid beträgt das Trouton-Verhältnis 3. Scherverdünnende Flüssigkeiten werden sehr häufig, aber irreführend, als thixotrop bezeichnet. ⓘ

Selbst bei einer Newtonschen Flüssigkeit hängt die Viskosität in der Regel von ihrer Zusammensetzung und Temperatur ab. Bei Gasen und anderen kompressiblen Flüssigkeiten hängt sie von der Temperatur ab und variiert nur sehr langsam mit dem Druck. Die Viskosität einiger Flüssigkeiten kann von anderen Faktoren abhängen. Eine magnetorheologische Flüssigkeit zum Beispiel wird dicker, wenn sie einem Magnetfeld ausgesetzt wird, und verhält sich dann möglicherweise wie ein Festkörper. ⓘ

In Festkörpern

Die viskosen Kräfte, die beim Fließen von Flüssigkeiten auftreten, unterscheiden sich von den elastischen Kräften, die in einem Festkörper als Reaktion auf Scher-, Druck- oder Dehnungsspannungen auftreten. Während bei letzteren die Spannung proportional zum Ausmaß der Scherverformung ist, ist sie bei einer Flüssigkeit proportional zur Verformungsrate über die Zeit. Aus diesem Grund verwendete Maxwell für die Viskosität von Flüssigkeiten den Begriff der flüchtigen Elastizität. ⓘ

Viele Flüssigkeiten (einschließlich Wasser) reagieren jedoch kurzzeitig wie elastische Festkörper, wenn sie einer plötzlichen Belastung ausgesetzt werden. Umgekehrt fließen viele "Feststoffe" (sogar Granit) wie Flüssigkeiten, wenn auch sehr langsam, selbst bei beliebig geringer Belastung. Solche Materialien werden am besten als viskoelastisch bezeichnet, d. h. sie besitzen sowohl Elastizität (Reaktion auf Verformung) als auch Viskosität (Reaktion auf die Verformungsgeschwindigkeit). ⓘ

Viskoelastische Feststoffe können sowohl eine Scherviskosität als auch eine Volumenviskosität aufweisen. Die Dehnungsviskosität ist eine lineare Kombination aus Scher- und Volumenviskosität, die die Reaktion eines festen elastischen Materials auf Dehnung beschreibt. Sie wird häufig zur Charakterisierung von Polymeren verwendet. ⓘ

In der Geologie werden Erdmaterialien, die eine viskose Verformung aufweisen, die mindestens drei Größenordnungen größer ist als ihre elastische Verformung, manchmal als rheid bezeichnet. ⓘ

Messung

Die Viskosität wird mit verschiedenen Arten von Viskosimetern und Rheometern gemessen. Ein Rheometer wird für Flüssigkeiten verwendet, die nicht durch einen einzigen Viskositätswert definiert werden können und daher mehr Parameter zur Einstellung und Messung erfordern als bei einem Viskosimeter. Um genaue Messungen zu erhalten, ist eine genaue Temperaturkontrolle der Flüssigkeit erforderlich, insbesondere bei Materialien wie Schmierstoffen, deren Viskosität sich bei einer Änderung von nur 5 °C verdoppeln kann. ⓘ

Bei einigen Flüssigkeiten ist die Viskosität über einen großen Bereich von Schergeschwindigkeiten konstant (Newtonsche Flüssigkeiten). Flüssigkeiten ohne konstante Viskosität (nicht-newtonsche Flüssigkeiten) lassen sich nicht mit einer einzigen Zahl beschreiben. Nicht-newtonsche Flüssigkeiten weisen eine Vielzahl unterschiedlicher Korrelationen zwischen Scherspannung und Schergeschwindigkeit auf. ⓘ

Eines der gängigsten Instrumente zur Messung der kinematischen Viskosität ist das Glaskapillarviskosimeter. ⓘ

In der Beschichtungsindustrie kann die Viskosität mit einem Becher gemessen werden, in dem die Ausflusszeit gemessen wird. Es gibt verschiedene Arten von Bechern, wie z. B. den Zahn-Becher und den Ford-Viskositätsbecher, wobei die Verwendung der einzelnen Typen hauptsächlich von der jeweiligen Branche abhängt. ⓘ

Das Stormer-Viskosimeter, das auch bei Beschichtungen verwendet wird, bestimmt die Viskosität durch lastabhängige Rotation. Die Viskosität wird in Krebs-Einheiten (KU) angegeben, die es nur bei Stormer-Viskosimetern gibt. ⓘ

Vibrationsviskosimeter können ebenfalls zur Messung der Viskosität verwendet werden. Resonanz- oder Vibrationsviskosimeter arbeiten durch die Erzeugung von Scherwellen in der Flüssigkeit. Bei dieser Methode wird der Sensor in die Flüssigkeit getaucht und bei einer bestimmten Frequenz zum Schwingen gebracht. Wenn die Oberfläche des Sensors durch die Flüssigkeit schert, geht aufgrund ihrer Viskosität Energie verloren. Diese Energie wird dann gemessen und in einen Viskositätswert umgewandelt. Eine höhere Viskosität bedeutet einen größeren Energieverlust. ⓘ

Die Dehnungsviskosität kann mit verschiedenen Rheometern gemessen werden, die eine Dehnungsspannung ausüben. ⓘ

Die Volumenviskosität kann mit einem akustischen Rheometer gemessen werden. ⓘ

Die scheinbare Viskosität ist eine Berechnung, die sich aus Tests mit Bohrspülungen ergibt, die bei der Erschließung von Öl- oder Gasbohrungen verwendet werden. Diese Berechnungen und Tests helfen den Ingenieuren, die Eigenschaften der Bohrspülung entsprechend den erforderlichen Spezifikationen zu entwickeln und zu erhalten. ⓘ

Die Nanoviskosität (von Nanosonden erfasste Viskosität) kann durch Fluoreszenzkorrelationsspektroskopie gemessen werden. ⓘ

Einheiten

Die SI-Einheit der dynamischen Viskosität ist die Newton-Sekunde pro Quadratmeter (N-s/m²), die häufig auch in den äquivalenten Formen Pascal-Sekunde (Pa-s), Kilogramm pro Meter pro Sekunde (kg-m-1-s-1) und Poiseuilli (Pl) angegeben wird. Die CGS-Einheit ist das Poise (P, oder g-cm-1-s-1 = 0,1 Pa-s), benannt nach Jean Léonard Marie Poiseuille. Sie wird üblicherweise, insbesondere in ASTM-Normen, als Centipoise (cP) angegeben. Die Angabe in Centipoise ist zweckmäßig, da die Viskosität von Wasser bei 20 °C etwa 1 cP beträgt, und ein Centipoise entspricht der SI-Einheit Millipascalsekunde (mPa-s). ⓘ

Die SI-Einheit der kinematischen Viskosität ist Quadratmeter pro Sekunde (m²/s), während die CGS-Einheit für die kinematische Viskosität Stokes (St, oder cm²-s-1 = 0,0001 m²-s-1) ist, benannt nach Sir George Gabriel Stokes. Im amerikanischen Sprachgebrauch wird Stoke manchmal als Singularform verwendet. Häufig wird stattdessen der Teiler Centistokes (cSt) verwendet, 1 cSt = 1 mm²-s-1 = 10-6 m²-s-1. Die kinematische Viskosität von Wasser bei 20 °C beträgt etwa 1 cSt. ⓘ

Die am häufigsten verwendeten Systeme der US-Gewohnheits- oder imperialen Einheiten sind das britische Gravitationssystem (BG) und das englische Ingenieurssystem (EE). Im BG-System hat die dynamische Viskosität die Einheit Pfund-Sekunden pro Quadratfuß (lb-s/ft²), im EE-System die Einheit Pfund-Kraft-Sekunden pro Quadratfuß (lbf-s/ft²). Das Pfund und die Pfund-Kraft sind gleichwertig; die beiden Systeme unterscheiden sich nur in der Definition von Kraft und Masse. Im BG-System ist das Pfund eine Basiseinheit, von der aus die Einheit der Masse (das Geschoss) durch das Zweite Newtonsche Gesetz definiert wird, während im EE-System die Einheiten von Kraft und Masse (die Pfund-Kraft bzw. Pfund-Masse) unabhängig voneinander durch das Zweite Gesetz unter Verwendung der Proportionalitätskonstante gc definiert werden. ⓘ

Die kinematische Viskosität hat sowohl im BG- als auch im EE-System die Einheit Quadratfuß pro Sekunde (ft²/s). ⓘ

Zu den nicht genormten Einheiten gehört das reyn, eine britische Einheit der dynamischen Viskosität. In der Automobilindustrie wird der Viskositätsindex verwendet, um die Veränderung der Viskosität mit der Temperatur zu beschreiben. ⓘ

Der Kehrwert der Viskosität ist die Fließfähigkeit, üblicherweise symbolisiert durch $\phi =1/\mu$ oder $F=1/\mu$ je nach Konvention, gemessen in reziproken Poise (P-1 oder cm-s-g-1), manchmal auch Rhe genannt. Die Fließfähigkeit wird in der technischen Praxis nur selten verwendet. ⓘ

In der Erdölindustrie wurde die kinematische Viskosität früher mit dem Saybolt-Viskosimeter gemessen und in der Einheit Saybolt-Sekunde (SUS) angegeben. Manchmal werden auch andere Abkürzungen wie SSU (Saybolt seconds universal) oder SUV (Saybolt universal viscosity) verwendet. Die kinematische Viskosität in Zentistokes kann aus SUS gemäß der Arithmetik und der Referenztabelle in ASTM D 2161 umgerechnet werden. ⓘ

Molekulare Ursprünge

Der Impulstransport in Gasen erfolgt durch diskrete Molekülstöße und in Flüssigkeiten durch Anziehungskräfte, die die Moleküle eng aneinander binden. Aus diesem Grund sind die dynamischen Viskositäten von Flüssigkeiten in der Regel viel größer als die von Gasen. Darüber hinaus nimmt die Viskosität bei Gasen mit der Temperatur zu und bei Flüssigkeiten ab. ⓘ

Oberhalb des kritischen Flüssigkeits-Gas-Punktes werden die flüssige und die gasförmige Phase durch eine einzige überkritische Phase ersetzt. In diesem Bereich interpolieren die Mechanismen des Impulstransports zwischen flüssigkeits- und gasähnlichem Verhalten. Entlang einer überkritischen Isobare (Oberfläche mit konstantem Druck) nimmt beispielsweise die kinematische Viskosität bei niedriger Temperatur ab und bei hoher Temperatur zu, wobei ein Minimum dazwischen liegt. Eine grobe Schätzung für den Wert am Minimum ist

\nu _{\text{min}}={\frac {1}{4\pi }}{\frac {\hbar }{\sqrt {m_{e}m}}}

wobei $\hbar$ ist die Plancksche Konstante, $m_{e}$ ist die Elektronenmasse, und $m$ die Molekülmasse ist. ⓘ

Im Allgemeinen hängt die Viskosität eines Systems jedoch im Detail davon ab, wie die Moleküle, aus denen das System besteht, interagieren, und es gibt keine einfachen, aber korrekten Formeln für sie. Die einfachsten exakten Ausdrücke sind die Green-Kubo-Beziehungen für die lineare Scherviskosität oder die von Evans und Morriss (1988) abgeleiteten Ausdrücke für die transiente Zeitkorrelationsfunktion. Obwohl diese Ausdrücke jeweils exakt sind, erfordert die Berechnung der Viskosität einer dichten Flüssigkeit unter Verwendung dieser Beziehungen derzeit den Einsatz von Computersimulationen der Molekulardynamik. Für ein verdünntes Gas können etwas mehr Fortschritte erzielt werden, da elementare Annahmen darüber, wie sich Gasmoleküle bewegen und interagieren, zu einem grundlegenden Verständnis der molekularen Ursprünge der Viskosität führen. Anspruchsvollere Behandlungen können durch eine systematische Grobkörnigkeit der Bewegungsgleichungen der Gasmoleküle erstellt werden. Ein Beispiel für eine solche Behandlung ist die Chapman-Enskog-Theorie, die aus der Boltzmann-Gleichung Ausdrücke für die Viskosität eines verdünnten Gases ableitet. ⓘ

Reine Gase

Elementare Berechnung der Viskosität für ein verdünntes Gas

Betrachten Sie ein verdünntes Gas, das sich parallel zur $x$ -Achse mit der Geschwindigkeit $u(y)$ die nur von der $y$ Koordinate abhängt. Um die Diskussion zu vereinfachen, wird angenommen, dass das Gas eine gleichmäßige Temperatur und Dichte hat. ⓘ

Unter diesen Annahmen ist die $x$ Geschwindigkeit eines Moleküls, das durch $y=0$ gleich der Geschwindigkeit, die das Molekül hatte, als seine mittlere freie Weglänge $\lambda$ begann. Da $\lambda$ im Vergleich zu makroskopischen Größenordnungen typischerweise klein ist, hat die durchschnittliche $x$ Geschwindigkeit eines solchen Moleküls die Form ⓘ

u(0)\pm \alpha \lambda {\frac {du}{dy}}(0),

ⓘ

wobei $\alpha$ ist eine numerische Konstante in der Größenordnung von $1$ . (Einige Autoren schätzen $\alpha =2/3$ ; eine sorgfältigere Berechnung für starre elastische Kugeln ergibt dagegen $\alpha \simeq 0.998$ .) Da sich die Hälfte der Moleküle auf beiden Seiten in Richtung $y=0$ und dies im Durchschnitt mit der Hälfte der durchschnittlichen Molekulargeschwindigkeit $(8k_{\text{B}}T/\pi m)^{1/2}$ ist der Impulsfluss von beiden Seiten ⓘ

{\frac {1}{4}}\rho \cdot {\sqrt {\frac {8k_{\text{B}}T}{\pi m}}}\cdot \left(u(0)\pm \alpha \lambda {\frac {du}{dy}}(0)\right).

Der Nettodrehimpulsfluss bei $y=0$ ist die Differenz der beiden Werte:

-{\frac {1}{2}}\rho \cdot {\sqrt {\frac {8k_{\text{B}}T}{\pi m}}}\cdot \alpha \lambda {\frac {du}{dy}}(0).

ⓘ

Nach der Definition der Viskosität sollte dieser Impulsfluss gleich sein $-\mu {\frac {du}{dy}}(0)$ sein, was zu ⓘ

\mu =\alpha \rho \lambda {\sqrt {\frac {2k_{\text{B}}T}{\pi m}}}.

ⓘ

Die Viskosität in Gasen ergibt sich hauptsächlich aus der molekularen Diffusion, die den Impuls zwischen den Strömungsschichten transportiert. Eine elementare Berechnung für ein verdünntes Gas bei Temperatur $T$ und Dichte $\rho$ ergibt

\mu =\alpha \rho \lambda {\sqrt {\frac {2k_{\text{B}}T}{\pi m}}},

ⓘ

wobei $k_{\text{B}}$ ist die Boltzmann-Konstante, $m$ die Molekülmasse und $\alpha$ eine numerische Konstante in der Größenordnung von $1$ . Die Größe $\lambda$ , die mittlere freie Weglänge, misst die durchschnittliche Entfernung, die ein Molekül zwischen Kollisionen zurücklegt. Auch ohne a priori Kenntnis von $\alpha$ hat dieser Ausdruck nicht-triviale Auswirkungen. Insbesondere, da $\lambda$ in der Regel umgekehrt proportional zur Dichte ist und mit der Temperatur zunimmt, $\mu$ selbst mit der Temperatur ansteigen und bei fester Temperatur unabhängig von der Dichte sein. Tatsächlich bleiben beide Vorhersagen auch bei anspruchsvolleren Behandlungen bestehen und beschreiben die experimentellen Beobachtungen genau. Im Gegensatz dazu nimmt die Viskosität von Flüssigkeiten normalerweise mit der Temperatur ab. ⓘ

Für starre elastische Kugeln mit dem Durchmesser $\sigma$ , $\lambda$ errechnet werden und ergibt ⓘ

\mu ={\frac {\alpha }{\pi ^{3/2}}}{\frac {\sqrt {k_{\text{B}}mT}}{\sigma ^{2}}}.

ⓘ

In diesem Fall ist $\lambda$ unabhängig von der Temperatur ist, also $\mu \propto T^{1/2}$ . Für kompliziertere molekulare Modelle jedoch $\lambda$ auf nicht-triviale Weise von der Temperatur ab, und einfache kinetische Argumente, wie sie hier verwendet werden, sind unzureichend. Grundlegender ist, dass der Begriff des mittleren freien Weges für Teilchen, die über einen endlichen Bereich interagieren, ungenau wird, was die Nützlichkeit des Konzepts für die Beschreibung realer Gase einschränkt. ⓘ

Chapman-Enskog-Theorie

Eine von Sydney Chapman und David Enskog in den frühen 1900er Jahren entwickelte Technik ermöglicht eine verfeinerte Berechnung von $\mu$ . Sie basiert auf der Boltzmann-Gleichung, die eine statistische Beschreibung eines verdünnten Gases in Form von zwischenmolekularen Wechselwirkungen liefert. Die Technik ermöglicht die genaue Berechnung von $\mu$ für Molekülmodelle, die realistischer sind als starre elastische Kugeln, z. B. solche, die intermolekulare Anziehung beinhalten. Dies ist notwendig, um die korrekte Temperaturabhängigkeit von $\mu$ zu reproduzieren, die Experimenten zufolge schneller ansteigt als der $T^{1/2}$ Trend, der für starr-elastische Kugeln vorhergesagt wird. Die Chapman-Enskog-Analyse zeigt in der Tat, dass die vorhergesagte Temperaturabhängigkeit durch Variation der Parameter in verschiedenen Molekülmodellen angepasst werden kann. Ein einfaches Beispiel ist das Sutherland-Modell, das starre elastische Kugeln mit schwacher gegenseitiger Anziehung beschreibt. In einem solchen Fall kann die Anziehungskraft perturbativ behandelt werden, was zu einem einfachen Ausdruck für $\mu$ :

\mu ={\frac {5}{16\sigma ^{2}}}\left({\frac {k_{\text{B}}mT}{\pi }}\right)^{1/2}\left(1+{\frac {S}{T}}\right)^{-1},

wobei $S$ ist unabhängig von der Temperatur und wird nur durch die Parameter der intermolekularen Anziehung bestimmt. Um eine Verbindung zum Experiment herzustellen, ist es zweckmäßig, die Formel umzuschreiben in

\mu =\mu _{0}\left({\frac {T}{T_{0}}}\right)^{3/2}{\frac {T_{0}+S}{T+S}},

wobei $\mu _{0}$ ist die Viskosität bei der Temperatur $T_{0}$ . Wenn $\mu$ aus Experimenten bekannt ist bei $T=T_{0}$ und mindestens einer anderen Temperatur bekannt ist, dann kann $S$ berechnet werden. Die Ausdrücke für $\mu$ die auf diese Weise erhalten werden, sind für eine Reihe einfacher Gase qualitativ genau. Etwas anspruchsvollere Modelle, wie das Lennard-Jones-Potenzial, können eine bessere Übereinstimmung mit Experimenten liefern, allerdings nur um den Preis einer undurchsichtigeren Abhängigkeit von der Temperatur. In einigen Systemen muss auch die Annahme der Kugelsymmetrie aufgegeben werden, wie dies bei Dämpfen mit stark polaren Molekülen wie H₂O der Fall ist. In diesen Fällen ist die Chapman-Enskog-Analyse wesentlich komplizierter. ⓘ

Bulk-Viskosität

Nach dem kinetisch-molekularen Bild entsteht in Gasen immer dann eine von Null abweichende Volumenviskosität, wenn es nicht vernachlässigbare Relaxationszeitskalen gibt, die den Energieaustausch zwischen der Translationsenergie der Moleküle und ihrer inneren Energie, z. B. Rotations- und Vibrationsenergie, bestimmen. Daher ist die Volumenviskosität $0$ für ein einatomiges ideales Gas, in dem die innere Energie der Moleküle vernachlässigbar ist, ist jedoch ungleich Null für ein Gas wie Kohlendioxid, dessen Moleküle sowohl Rotations- als auch Schwingungsenergie besitzen. ⓘ

Reine Flüssigkeiten

Video mit drei Flüssigkeiten mit unterschiedlicher Viskosität ⓘ

Experiment, das das Verhalten einer viskosen Flüssigkeit mit blauem Farbstoff zur Sichtbarmachung zeigt ⓘ

Im Gegensatz zu Gasen gibt es kein einfaches, aber genaues Bild für die molekularen Ursachen der Viskosität in Flüssigkeiten. ⓘ

Auf der einfachsten Beschreibungsebene wird die relative Bewegung benachbarter Schichten in einer Flüssigkeit hauptsächlich durch anziehende molekulare Kräfte die an der Schichtgrenze wirken. In diesem Bild erwartet man (richtigerweise), dass die Viskosität mit steigender Temperatur abnimmt. Dies ist darauf zurückzuführen, dass mit steigender Temperatur die zufällige thermische Bewegung der Moleküle zunimmt, was es ihnen leichter macht, ihre anziehenden Wechselwirkungen zu überwinden. ⓘ

Aufbauend auf dieser Veranschaulichung kann eine einfache Theorie in Analogie zur diskreten Struktur eines Festkörpers aufgestellt werden: Gruppen von Molekülen in einer Flüssigkeit werden als "Käfige" visualisiert, die einzelne Moleküle umgeben und einschließen. Diese Käfige können besetzt oder unbesetzt sein, und stärkere molekulare Anziehungskraft entspricht stärkeren Käfigen. Aufgrund der zufälligen thermischen Bewegung "hüpft" ein Molekül zwischen den Käfigen mit einer Geschwindigkeit, die umgekehrt zur Stärke der molekularen Anziehung ist. Im Gleichgewicht sind diese "Sprünge" in keine Richtung voreingenommen. Damit sich jedoch zwei benachbarte Schichten relativ zueinander bewegen können, müssen die "Sprünge" in die Richtung der Relativbewegung ausgerichtet sein. Die Kraft, die erforderlich ist, um diese gerichtete Bewegung aufrechtzuerhalten, kann für eine gegebene Scherrate geschätzt werden und führt zu ⓘ

\mu \approx {\frac {N_{A}h}{V}}\operatorname {exp} \left(3.8{\frac {T_{b}}{T}}\right),

(1) ⓘ

wobei $N_{A}$ ist die Avogadro-Konstante, $h$ ist die Planck-Konstante, $V$ ist das Volumen eines Mols einer Flüssigkeit und $T_{b}$ ist der normale Siedepunkt. Dieses Ergebnis hat die gleiche Form wie die bekannte empirische Beziehung ⓘ

\mu =Ae^{B/T},

(2) ⓘ

wobei $A$ und $B$ sind Konstanten, die aus den Daten angepasst werden. Andererseits äußern mehrere Autoren Vorsicht in Bezug auf dieses Modell. Bei der Verwendung von Gleichung (1) kann es zu Fehlern von bis zu 30 % kommen, verglichen mit der Anpassung von Gleichung (2) an experimentelle Daten. Grundsätzlich wurden die physikalischen Annahmen, die Gleichung (1) zugrunde liegen, kritisiert. Es wurde auch argumentiert, dass die exponentielle Abhängigkeit in Gleichung (1) die experimentellen Beobachtungen nicht unbedingt genauer beschreibt als einfachere, nicht-exponentielle Ausdrücke. ⓘ

In Anbetracht dieser Unzulänglichkeiten ist die Entwicklung eines weniger ad-hoc-Modells von praktischem Interesse. Indem man auf Einfachheit zugunsten von Präzision verzichtet, ist es möglich, ausgehend von den grundlegenden Bewegungsgleichungen für Moleküle strenge Ausdrücke für die Viskosität zu schreiben. Ein klassisches Beispiel für diesen Ansatz ist die Irving-Kirkwood-Theorie. Andererseits werden solche Ausdrücke als Mittelwerte über Korrelationsfunktionen mehrerer Teilchen angegeben und sind daher in der Praxis nur schwer anwendbar. ⓘ

Im Allgemeinen scheinen empirisch abgeleitete Ausdrücke (auf der Grundlage vorhandener Viskositätsmessungen) die einzige durchweg zuverlässige Methode zur Berechnung der Viskosität in Flüssigkeiten zu sein. ⓘ

Gemische und Verschnitte

Gasförmige Gemische

Das gleiche molekularkinetische Bild eines Einkomponentengases kann auch auf ein Gasgemisch angewendet werden. So kann beispielsweise mit dem Chapman-Enskog-Ansatz die Viskosität $\mu _{\text{mix}}$ eines binären Gasgemischs in Form der Viskositäten der einzelnen Komponenten geschrieben werden $\mu _{1,2}$ , ihren jeweiligen Volumenanteilen und den zwischenmolekularen Wechselwirkungen. Wie bei dem Einkomponentengas ist die Abhängigkeit von $\mu _{\text{mix}}$ von den Parametern der zwischenmolekularen Wechselwirkungen durch verschiedene Kollisionsintegrale, die möglicherweise nicht in Form von Elementarfunktionen ausgedrückt werden können. Um brauchbare Ausdrücke für $\mu _{\text{mix}}$ zu erhalten, die mit den experimentellen Daten einigermaßen übereinstimmen, müssen die Kollisionsintegrale in der Regel mit einer Kombination aus analytischer Berechnung und empirischer Anpassung bewertet werden. Ein Beispiel für ein solches Verfahren ist der oben beschriebene Sutherland-Ansatz für ein Einkomponentengas. ⓘ

Mischungen von Flüssigkeiten

Wie bei reinen Flüssigkeiten lässt sich auch die Viskosität eines Flüssigkeitsgemischs nur schwer anhand molekularer Prinzipien vorhersagen. Eine Methode besteht darin, die oben für eine reine Flüssigkeit vorgestellte molekulare "Käfigtheorie" zu erweitern. Dies kann auf unterschiedlichem Niveau geschehen. Ein Ausdruck, der sich aus einer solchen Analyse ergibt, ist die Lederer-Roegiers-Gleichung für ein binäres Gemisch:

\ln \mu _{\text{blend}}={\frac {x_{1}}{x_{1}+\alpha x_{2}}}\ln \mu _{1}+{\frac {\alpha x_{2}}{x_{1}+\alpha x_{2}}}\ln \mu _{2},

ⓘ

wobei $\alpha$ ist ein empirischer Parameter, und $x_{1,2}$ und $\mu _{1,2}$ sind die jeweiligen Molenbrüche und Viskositäten der Flüssigkeitsanteile. ⓘ

Da das Mischen ein wichtiger Prozess in der Schmierstoff- und Ölindustrie ist, gibt es eine Vielzahl von empirischen und eigenen Gleichungen zur Vorhersage der Viskosität einer Mischung. ⓘ

Lösungen und Suspensionen

Wässrige Lösungen

Je nach gelöstem Stoff und Konzentrationsbereich kann eine wässrige Elektrolytlösung im Vergleich zu reinem Wasser bei gleicher Temperatur und gleichem Druck eine größere oder kleinere Viskosität aufweisen. So hat beispielsweise eine 20%ige Kochsalzlösung (Natriumchlorid) eine Viskosität, die mehr als das 1,5-fache der Viskosität von reinem Wasser beträgt, während eine 20%ige Kaliumjodidlösung eine Viskosität aufweist, die etwa das 0,91-fache der Viskosität von reinem Wasser beträgt. ⓘ

Ein idealisiertes Modell für verdünnte elektrolytische Lösungen führt zu folgender Vorhersage für die Viskosität $\mu _{s}$ einer Lösung:

{\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}},

wobei $\mu _{0}$ ist die Viskosität des Lösungsmittels, $c$ ist die Konzentration, und $A$ ist eine positive Konstante, die sowohl von den Eigenschaften des Lösungsmittels als auch der gelösten Substanz abhängt. Dieser Ausdruck ist jedoch nur für sehr verdünnte Lösungen gültig, die $c$ weniger als 0,1 mol/L. Für höhere Konzentrationen sind zusätzliche Terme erforderlich, die die molekularen Korrelationen höherer Ordnung berücksichtigen:

{\frac {\mu _{s}}{\mu _{0}}}=1+A{\sqrt {c}}+Bc+Cc^{2},

wobei $B$ und $C$ Die Terme werden aus den Daten angepasst. Insbesondere kann ein negativer Wert von $B$ den in einigen Lösungen beobachteten Rückgang der Viskosität erklären. Die geschätzten Werte dieser Konstanten sind nachstehend für Natriumchlorid und Kaliumiodid bei einer Temperatur von 25 °C angegeben (Mol = Mol, L = Liter). ⓘ

Gelöster Stoff	$A$ (mol-1/2 L^1/2)	$B$ (mol-1 L)	$C$ (mol-2 L²) ⓘ
Natriumchlorid (NaCl)	0.0062	0.0793	0.0080
Kaliumjodid (KI)	0.0047	−0.0755	0.0000

Suspensionen

In einer Suspension von Feststoffteilchen (z. B. mikroskopisch kleine Kugeln in Öl) kann die effektive Viskosität $\mu _{\text{eff}}$ in Form von Spannungs- und Dehnungskomponenten definiert werden, die über ein Volumen gemittelt werden, das im Vergleich zum Abstand zwischen den suspendierten Teilchen groß, im Hinblick auf makroskopische Dimensionen jedoch klein ist. Solche Suspensionen weisen im Allgemeinen ein nicht-newtonsches Verhalten auf. Für verdünnte Systeme in stationären Strömungen ist das Verhalten jedoch newtonsch und die Ausdrücke für $\mu _{\text{eff}}$ können direkt aus der Teilchendynamik abgeleitet werden. In einem sehr verdünnten System, mit einem Volumenanteil $\phi \lesssim 0.02$ können Wechselwirkungen zwischen den Schwebeteilchen vernachlässigt werden. In einem solchen Fall kann man das Strömungsfeld um jedes Teilchen unabhängig voneinander explizit berechnen und die Ergebnisse kombinieren, um Folgendes zu erhalten $\mu _{\text{eff}}$ . Für Kugeln ergibt sich daraus die Einstein-Gleichung:

\mu _{\text{eff}}=\mu _{0}\left(1+{\frac {5}{2}}\phi \right),

ⓘ

wobei $\mu _{0}$ ist die Viskosität der suspendierenden Flüssigkeit. Die lineare Abhängigkeit von $\phi$ ist eine Folge der Vernachlässigung der Wechselwirkungen zwischen den Teilchen. Für verdünnte Systeme erwartet man im Allgemeinen $\mu _{\text{eff}}$ die Form ⓘ

\mu _{\text{eff}}=\mu _{0}\left(1+B\phi \right),

ⓘ

wobei der Koeffizient $B$ von der Teilchenform abhängen kann (z. B. Kugeln, Stäbe, Scheiben). Die experimentelle Bestimmung des genauen Wertes von $B$ ist jedoch schwierig: Selbst die Vorhersage $B=5/2$ für Kugeln ist nicht abschließend validiert worden, wobei in verschiedenen Experimenten Werte im Bereich von $1.5\lesssim B\lesssim 5$ . Diese Unzulänglichkeit wird auf die Schwierigkeiten bei der Kontrolle der Versuchsbedingungen zurückgeführt. ⓘ

In dichteren Suspensionen, $\mu _{\text{eff}}$ eine nichtlineare Abhängigkeit von $\phi$ an, was auf die Bedeutung der Wechselwirkungen zwischen den Partikeln hinweist. Es gibt verschiedene analytische und halb-empirische Verfahren zur Erfassung dieses Systems. Auf der grundlegendsten Ebene wird ein Term quadratisch in $\phi$ addiert zu $\mu _{\text{eff}}$ :

\mu _{\text{eff}}=\mu _{0}\left(1+B\phi +B_{1}\phi ^{2}\right),

ⓘ

und der Koeffizient $B_{1}$ wird aus experimentellen Daten abgeleitet oder aus der mikroskopischen Theorie approximiert. Einige Autoren raten jedoch zur Vorsicht bei der Anwendung solcher einfachen Formeln, da nicht-newtonsches Verhalten in dichten Suspensionen ( $\phi \gtrsim 0.25$ für Kugeln) oder in Suspensionen mit länglichen oder flexiblen Teilchen auftritt. ⓘ

Man unterscheidet zwischen einer Suspension fester Teilchen, wie oben beschrieben, und einer Emulsion. Letztere ist eine Suspension aus winzigen Tröpfchen, die selbst eine innere Zirkulation aufweisen können. Das Vorhandensein einer internen Zirkulation kann die beobachtete effektive Viskosität verringern, und es müssen verschiedene theoretische oder halb-empirische Modelle verwendet werden. ⓘ

Amorphe Materialien

Übliche Glasviskositätskurven ⓘ

Im Hoch- und Tieftemperaturbereich hat das viskose Fließen in amorphen Materialien (z. B. in Gläsern und Schmelzen) die Arrhenius-Form:

\mu =Ae^{Q/(RT)},

ⓘ

wobei $Q$ eine relevante Aktivierungsenergie ist, die in Form von molekularen Parametern angegeben wird; T ist die Temperatur; $R$ ist die molare Gaskonstante; und A ist ungefähr eine Konstante. Die Aktivierungsenergie $Q$ nimmt einen anderen Wert an, je nachdem, ob die Hoch- oder Tieftemperaturgrenze betrachtet wird: Sie ändert sich von einem hohen Wert $Q H$ bei niedrigen Temperaturen (im glasartigen Zustand) zu einem niedrigen Wert $Q L$ bei hohen Temperaturen (im flüssigen Zustand). ⓘ

Gemeinsamer Logarithmus der Viskosität in Abhängigkeit von der Temperatur für B₂O₃, der zwei Regime zeigt ⓘ

Für mittlere Temperaturen, $Q$ nicht trivial mit der Temperatur und die einfache Arrhenius-Form versagt. Auf der anderen Seite liefert die Zwei-Exponential-Gleichung ⓘ

\mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\right],

ⓘ

wobei $A$ , $B$ , $C$ , $D$ alle Konstanten sind, bietet eine gute Anpassung an die experimentellen Daten über den gesamten Temperaturbereich, während sie gleichzeitig im Niedrig- und Hochtemperaturbereich auf die korrekte Arrhenius-Form reduziert wird. Dieser Ausdruck lässt sich aus verschiedenen theoretischen Modellen für amorphe Materialien auf atomarer Ebene ableiten. ⓘ

Eine Zwei-Exponential-Gleichung für die Viskosität kann im Rahmen des Dyre-Schubmodells für unterkühlte Flüssigkeiten abgeleitet werden, wobei die Arrhenius-Energieschranke mit dem hochfrequenten Schermodul mal einem charakteristischen Schubvolumen identifiziert wird. Wenn man die Temperaturabhängigkeit des Schermoduls über die thermische Ausdehnung und über den abstoßenden Teil des intermolekularen Potenzials angibt, erhält man eine weitere Zwei-Exponential-Gleichung:

\mu =\exp {\left\{{\frac {V_{c}C_{G}}{k_{B}T}}\exp {\left[(2+\lambda )\alpha _{T}T_{g}\left(1-{\frac {T}{T_{g}}}\right)\right]}\right\}}

ⓘ

wobei $C_{G}$ bezeichnet den hochfrequenten Schermodul des Materials bei einer Temperatur, die gleich der Glasübergangstemperatur ist $T_{g}$ , $V_{c}$ ist das so genannte Schubvolumen, d. h. das charakteristische Volumen der Gruppe von Atomen, die am Schubvorgang beteiligt sind, durch den ein Atom/Molekül aus dem Käfig der nächsten Nachbarn entkommt, typischerweise in der Größenordnung des von wenigen Atomen eingenommenen Volumens. Außerdem $\alpha _{T}$ der Wärmeausdehnungskoeffizient des Materials, $\lambda$ ist ein Parameter, der die Steilheit des Potenzgesetz-Anstiegs der ansteigenden Flanke des ersten Peaks der radialen Verteilungsfunktion misst und in einem quantitativen Zusammenhang mit dem abstoßenden Teil des interatomaren Potenzials steht. Und schließlich, $k_{B}$ die Boltzmann-Konstante. ⓘ

Wirbelviskosität

Bei der Untersuchung von Turbulenzen in Flüssigkeiten besteht eine gängige praktische Strategie darin, die kleinräumigen Wirbel (oder Wirbel) in der Bewegung zu ignorieren und eine großräumige Bewegung mit einer effektiven Viskosität, der so genannten "Wirbelviskosität", zu berechnen, die den Transport und die Dissipation von Energie in der kleinräumigen Strömung charakterisiert (siehe Simulation großer Wirbel). Im Gegensatz zur Viskosität der Flüssigkeit selbst, die nach dem zweiten Hauptsatz der Thermodynamik positiv sein muss, kann die Wirbelviskosität negativ sein. ⓘ

Vorhersage

Da die Viskosität kontinuierlich von Temperatur und Druck abhängt, kann sie nicht durch eine endliche Anzahl experimenteller Messungen beschrieben werden. Vorhersageformeln werden notwendig, wenn keine experimentellen Werte für die für die interessierenden Temperaturen und Drücke vorliegen. Diese Fähigkeit ist wichtig für thermophysikalische Simulationen, bei denen die Temperatur und der Druck eines Fluids kontinuierlich mit Raum und Zeit variieren können. Eine ähnliche Situation ergibt sich bei Mischungen reiner Flüssigkeiten, bei denen die Viskosität kontinuierlich von den Konzentrationsverhältnissen der einzelnen Komponenten abhängt ⓘ

Für die einfachsten Flüssigkeiten, wie verdünnte einatomige Gase und ihre Gemische, können ab initio quantenmechanische Berechnungen die Viskosität genau vorhersagen in Form von fundamentaler atomarer Konstanten vorhersagen, d. h. ohne Bezugnahme auf bestehende Viskositätsmessungen. Für den speziellen Fall des verdünnten Heliums, sind die Unsicherheiten bei der ab initio berechneten Viskosität um zwei Größenordnungen geringer als die Unsicherheiten bei experimentellen Werten. ⓘ

Für die meisten Flüssigkeiten sind solche hochpräzisen Berechnungen nach den ersten Grundsätzen nicht durchführbar. Vielmehr müssen theoretische oder empirische Ausdrücke an die vorhandenen Viskositätsmessungen angepasst werden. Wird ein solcher Ausdruck über einen großen Temperatur- und Druckbereich hinweg an hochgenaue Daten angepasst und Druck angepasst werden kann, wird er als "Referenzkorrelation" für dieses Fluid bezeichnet. Referenzkorrelationen sind veröffentlicht worden für Für viele reine Flüssigkeiten wurden Referenzkorrelationen veröffentlicht; einige Beispiele sind Wasser, Kohlendioxid, Ammoniak, Benzol und Xenon. Viele dieser Korrelationen decken Temperatur- und Druckbereiche ab, die gasförmige, flüssige und überkritische Phasen umfassen. ⓘ

Thermophysikalische Modellierungssoftware stützt sich häufig auf Referenzkorrelationen zur Vorhersage der Viskosität bei benutzerdefinierten Temperaturen und Drücken. Diese Korrelationen können urheberrechtlich geschützt sein. Beispiele sind REFPROP (proprietär) und CoolProp (Open-Source). ⓘ

Die Viskosität kann auch mit Hilfe von Formeln berechnet werden, die die Viskosität in Form von Statistiken der einzelnen Partikel Trajektorien ausdrücken. Zu diesen Formeln gehören die Green-Kubo-Beziehungen für die lineare Scherviskosität und die transiente Zeitkorrelationsfunktion die von Evans und Morriss (1988) abgeleitet wurden. Der Vorteil dieser Ausdrücke ist, dass sie formal exakt sind und für allgemeine Systeme gelten. Der Nachteil ist, dass sie eine detaillierte Kenntnis Der Nachteil ist, dass sie eine detaillierte Kenntnis der Partikelbahnen erfordern, die nur in rechenintensiven Simulationen wie der Molekulardynamik verfügbar ist. Außerdem ist ein genaues Modell für die Wechselwirkungen zwischen den Teilchen erforderlich, das für komplexe Moleküle schwer zu erhalten sein kann. ⓘ

Ausgewählte Substanzen

Im Pechtropfenexperiment der University of Queensland tropft seit 1927 langsam Pech durch einen Trichter, und zwar etwa alle zehn Jahre ein Tropfen. Auf diese Weise wurde ermittelt, dass die Viskosität von Pech etwa 230 Milliarden (2,3×10¹¹) Mal so groß ist wie die von Wasser. ⓘ

Die beobachteten Werte der Viskosität schwanken selbst bei gewöhnlichen Stoffen um mehrere Größenordnungen (siehe die Tabelle der Größenordnungen unten). So hat beispielsweise eine 70%ige Saccharose (Zucker)-Lösung eine Viskosität, die mehr als 400 Mal so hoch ist wie die von Wasser und 26000 Mal so hoch wie die von Luft. Noch dramatischer ist, dass die Viskosität von Pech schätzungsweise das 230-Milliardenfache der Viskosität von Wasser beträgt. ⓘ

Wasser

Die dynamische Viskosität $\mu$ von Wasser beträgt etwa 0,89 mPa-s bei Raumtemperatur (25 °C). Als Funktion der Temperatur in Kelvin kann die Viskosität anhand der halbempirischen Vogel-Fulcher-Tammann-Gleichung geschätzt werden:

\mu =A\exp \left({\frac {B}{T-C}}\right)

wobei A = 0,02939 mPa-s, B = 507,88 K und C = 149,3 K. Experimentell ermittelte Werte der Viskosität sind ebenfalls in der nachstehenden Tabelle aufgeführt. Die Werte bei 20 °C sind ein nützlicher Anhaltspunkt: dort beträgt die dynamische Viskosität etwa 1 cP und die kinematische Viskosität etwa 1 cSt. ⓘ

Viskosität von Wasser
bei verschiedenen Temperaturen ⓘ
Temperatur (°C)	Viskosität (mPa-s oder cP)
10	1.3059
20	1.0016
30	0.79722
50	0.54652
70	0.40355
90	0.31417

Luft

Unter atmosphärischen Standardbedingungen (25 °C und einem Druck von 1 bar) beträgt die dynamische Viskosität von Luft 18,5 μPa-s und ist damit etwa 50 Mal kleiner als die Viskosität von Wasser bei derselben Temperatur. Außer bei sehr hohem Druck hängt die Viskosität von Luft hauptsächlich von der Temperatur ab. Unter den vielen möglichen Näherungsformeln für die Temperaturabhängigkeit (siehe Temperaturabhängigkeit der Viskosität) ist eine:

\eta _{\text{air}}=2.791\cdot 10^{-7}\cdot T^{0.7355}

ⓘ

die im Bereich von -20 °C bis 400 °C genau ist. Damit diese Formel gültig ist, muss die Temperatur in Kelvin angegeben werden; $\eta _{\text{air}}$ entspricht dann der Viskosität in Pa-s. ⓘ

Honig beim Beträufeln ⓘ

Andere übliche Stoffe

Stoff	Viskosität (mPa-s)	Temperatur (°C)
Benzol	0.604	25
Wasser	1.0016	20
Quecksilber	1.526	25
Vollmilch	2.12	20
Dunkles Bier	2.53	20
Olivenöl	56.2	26
Honig	$\approx$ 2000–10000	20
Ketchup	$\approx$ 5000–20000	25
Erdnussbutter	$\approx$ 10⁴–10⁶
Stellplatz	2.3×10¹¹	10-30 (variabel)

Schätzungen der Größenordnung

Die folgende Tabelle veranschaulicht die Bandbreite der Viskositätswerte gängiger Stoffe. Sofern nicht anders angegeben, wird eine Temperatur von 25 °C und ein Druck von 1 Atmosphäre angenommen. ⓘ

Bei den aufgeführten Werten handelt es sich lediglich um repräsentative Schätzungen, da sie Messunsicherheiten, Schwankungen in den Materialdefinitionen oder nicht-newtonsches Verhalten nicht berücksichtigen. ⓘ

Faktor (Pa-s)	Beschreibung	Beispiele	Werte (Pa-s)
10⁻⁶	Unterer Bereich der Viskosität von Gasen	Butan	7.49 × 10⁻⁶
10⁻⁶	Unterer Bereich der Viskosität von Gasen	Wasserstoff	8.8 × 10⁻⁶
10⁻⁵	Oberer Bereich der gasförmigen Viskosität	Krypton	2.538 × 10⁻⁵
10⁻⁵	Oberer Bereich der gasförmigen Viskosität	Neon	3.175 × 10⁻⁵
10⁻⁴	Unterer Bereich der flüssigen Viskosität	Pentan	2.24 × 10⁻⁴
		Benzin	6 × 10⁻⁴
		Wasser	8.90 × 10⁻⁴
10⁻³	Typischer Bereich für kleinmolekulare Newtonsche Flüssigkeiten	Ethanol	1.074 × 10⁻³
		Quecksilber	1.526 × 10⁻³
		Vollmilch (20 °C)	2.12 × 10⁻³
		Blut	3 × 10-3 bis 6 × 10-3
		Flüssiger Stahl (1550 °C)	6 × 10⁻³
10⁻² – 10⁰	Öle und langkettige Kohlenwasserstoffe	Leinsamenöl	0.028
		Ölsäure	0.036
		Olivenöl	0.084
		SAE 10 Motoröl	0,085 bis 0,14
		Rizinusöl	0.1
		SAE 20 Motoröl	0,14 bis 0,42
		SAE 30 Motoröl	0,42 bis 0,65
		SAE 40 Motoröl	0,65 bis 0,90
		Glyzerin	1.5
		Pfannkuchensirup	2.5
10¹ – 10³	Pasten, Gele und andere Halbflüssigkeiten (im Allgemeinen nicht-newtonsch)	Ketchup	≈ 10¹
		Senf	≈ 10¹
		Saure Sahne	≈ 10²
		Erdnussbutter	≈ 10²
		Schmalz	≈ 10³
≈10⁸	Viskoelastische Polymere	Stellplatz	2.3×10⁸
≈10²¹	Bestimmte Feststoffe unter einer viskoelastischen Beschreibung	Mantel (Geologie)	≈ 10¹⁹ bis 10²⁴

Viskosität von Flüssigkeiten

Abbildung 2: Modellvorstellung zur Viskosität: Links eine Veranschaulichung zum Geschwindigkeitsgradient (2), sowie die Form des Gradienten für den Betrag der Geschwindigkeit (gestrichelt). Für den genauen Verlauf siehe Korkenzieherströmung. Rechts eine Veranschaulichung für die verzahnten Molekülschichten (1). ⓘ

Den Effekt innerer Reibung kann man sich vereinfacht durch die Bewegung zweier übereinander liegender, verzahnter Molekülschichten vorstellen (siehe Abb. 2, Punkt 1). Beim Fließen gleiten die Moleküle aneinander vorbei, und um die Verzahnung zu überwinden, benötigt man eine gewisse Kraft. Den Zusammenhang zwischen dieser Kraft und den Eigenschaften des vorliegenden Fluids definiert die Viskosität. Erkennbar wird dieser Zusammenhang besonders gut an der homologen Reihe der Alkane (kettenförmige Kohlenwasserstoffe), hier steigt die Viskosität mit der Kettenlänge und damit den zunehmenden intermolekular wirkenden Van-der-Waals-Kräften kontinuierlich an. Bei den mittleren Alkanen (ab Nonan, neun C-Atome) hat sie bereits einen Wert ähnlich dem von Wasser. ⓘ

Sehr gut veranschaulichen kann man sich die Viskosität auch an folgendem Beispiel: gleitet Wind über das Wasser eines Ozeans, erzeugt dies eine Bewegung der Wasserschicht an der Oberfläche. Je tiefer man nun taucht, desto ruhiger wird das Wasser, bis man einen Punkt erreicht, wo keine Strömung herrscht. Die einzelnen Flüssigkeitsschichten bewegen sich mit unterschiedlicher Geschwindigkeit $v$ , es entsteht ein Geschwindigkeitsgradient (siehe Abb. 2, Punkt 2). ⓘ

Newtonsche Fluide

Handelt es sich um sehr dünne Fluidschichten, so ist der Geschwindigkeitsverlauf linear, wie in obiger Herleitung. Dieser Zusammenhang wurde bereits 1687 von Isaac Newton unterstellt:

“The resistance which arises from the lack of slipperiness originating in a fluid – other things being equal – is proportional to the velocity by which the parts of the fluid are being separated from each other.”

„Der Widerstand, der durch den Mangel an Gleitfähigkeit innerhalb einer Flüssigkeit entsteht, ist – vorausgesetzt, dass alle anderen Bedingungen gleich bleiben – proportional zu der Geschwindigkeit, mit der die Flüssigkeitsteilchen voneinander getrennt werden.“

– Isaac Newton: Philosophiae Naturalis Principia Mathematica ⓘ

Abbildung 3: Schubspannungs-Schergeschwindigkeits-Diagramm:
1: Scherverzähendes (dilatantes) Fluid
2: Newtonsches Fluid
3: Scherverdünnendes (pseudoplastisches) Fluid
4: Bingham-plastisches Fluid
5: Casson-plastisches Fluid
Nach rechts ist die Schergeschwindigkeit und nach oben die daraus resultierende Schubspannung angetragen. ⓘ

Flüssigkeiten, die diesem linearen Zusammenhang folgen, werden deswegen als Newtonsche Fluide bezeichnet. Ist $\eta$ von $v$ abhängig, so bezeichnet man die Flüssigkeit als nicht-newtonsch oder nichtnewtonsch. Beim Newtonschen Viskositätsgesetz wird stets laminare Strömung sowie Temperatur- und Druckunabhängigkeit der Flüssigkeitseigenschaften angenommen. Für diese Stoffe stellt sich das im Schubspannungs-Schergeschwindigkeits-Diagramm gezeigte, lineare Geschwindigkeitsprofil ein (Abb. 3, Kurve 2: Newtonsches Fluid). ⓘ

In den rheologischen Modellen wird das Newtonsche Verhalten durch das Newton-Element, einem Dämpfungszylinder ähnlich einem Stoßdämpfer, dargestellt. ⓘ

Nicht-Newtonsche Fluide

Viele Substanzen folgen diesem Gesetz jedoch nicht, sondern zeigen ein zeit- oder schergeschwindigkeitsabhängiges Verhalten. Dabei unterscheidet man verschiedene Arten der Abweichung:

Fließgrenze, es muss erst eine gewisse Mindestschubspannung vorhanden sein, um ein Fließen zu erreichen (plastisches Fließen). Diese Art Fluid wird auch als Bingham-Fluid bezeichnet
Strukturviskosität / Dilatanz, dabei ist die Viskosität $\eta$ keine Konstante, sondern ändert sich mit dem Schergefälle ${\dot {\gamma }}$
Thixotropie / Rheopexie, hierbei zeigen sich zeitabhängige Strukturveränderungen, so dass je nach Zeitdauer seit der letzten Fließbewegung andere Viskositätswerte zu finden sind. ⓘ

Im allgemeinen Fall muss das Schergefälle ${\dot {\gamma }}$ aus dem Scherwinkel in der Flüssigkeit berechnet werden und nicht über den Geschwindigkeitsgradienten. Das Verhältnis ${\frac {\tau }{\dot {\gamma }}}$ wird in diesem Fall auch scheinbare Viskosität genannt. ⓘ

Viskoelastische Materialien können mit der komplexen Viskosität, bei der von einer sinusförmigen Scherung ausgegangen wird, beschrieben werden. ⓘ

Typische Nicht-Newtonsche Fluide sind zusammengesetzte Substanzen wie Blut und Ketchup. Da Blut sowohl aus den festen Substanzen des Hämatokrits als auch des Blutplasmas besteht, das Mischungsverhältnis jedoch stark variiert, verändert sich auch die Viskosität. Bei hohem Anteil der festen Substanzen ist z. B. die Leistungsfähigkeit in Ausdauer-Sportarten deutlich erhöht, bei zu hohen durch Doping kann dies zum Tod führen. ⓘ

Temperaturabhängigkeit

Die dynamische Viskosität der meisten Flüssigkeiten nimmt mit steigender Temperatur ab und kann oft mit der Arrhenius-Andrade-Beziehung beschrieben werden:

\eta =\eta _{0}\cdot \exp \left({\frac {E_{\mathrm {A} }}{R\cdot T}}\right)

ⓘ

mit

$\eta _{0}$ eine Materialkonstante
$E_{\mathrm {A} }$ die Aktivierungsenergie (auch Platzwechselenergie)
$R$ die allgemeine Gaskonstante
$T$ die absolute Temperatur.

Bei Flüssigkeiten in der Nähe (d. h. bis ca. 100 K über) der Glasübergangstemperatur gilt meist die WLF-Beziehung. Hier dominiert nämlich das sehr geringe freie Volumen, das in der Nähe der Glasübergangstemperatur viel stärker von der Temperatur abhängt als die Kettenbeweglichkeit, die hinter der Arrhenius-Andrade-Beziehung steht. ⓘ

Die Abhängigkeit der kinematischen Viskosität von der Temperatur wird bei Ölen durch den Viskositätsindex beschrieben. ⓘ

Speziell für Wasser lässt sich die Viskosität im Temperaturbereich zwischen 0 °C und 100 °C mit nachfolgend angegebener Gebrauchsformel ermitteln. Dabei ist die Temperatur in der Einheit Kelvin einzusetzen. Der damit berechnete Wert entspricht der dynamischen Viskosität in der Einheit Pa·s. ⓘ

\eta _{\text{Wasser}}={\frac {1}{0{,}1\cdot T^{2}-34{,}335\cdot T+2472}}

ⓘ

Messung

Messanordnungen von links nach rechts: koaxiale Zylinder, Platte-Platte, Kegel-Platte; bewegter Teil in Orange, unbewegter Teil in blassem Violett, Fluid in Hellblau ⓘ

Die Viskosität von Flüssigkeiten kann mit einem Viskosimeter z. B. gemäß EN ISO 3219 gemessen werden. Ein Rheometer ermöglicht es, darüber hinaus noch weitere rheologische Eigenschaften, auch von Festkörpern, zu bestimmen. Bei beiden Gerätetypen wird entsprechend der Viskositätsdefinition die zu messende Probe im Spalt zwischen zwei Körpern (z. B. zwei koaxialen Zylindern oder zwei parallelen Platten) eingebracht. Ein Teil der Anordnung rotiert oder oszilliert mit definierter Geschwindigkeit, während der andere ruht. Aus der Geometrie der Messanordnung und der Geschwindigkeit des bewegten Teiles ergibt sich die Schergeschwindigkeit. Das zur Aufrechterhaltung der Bewegung notwendige Drehmoment wird gemessen, woraus sich dann die Schubspannung und damit die Viskosität ermitteln lässt. ⓘ

Eine schnelle und einfache, aber auch sehr ungenaue Methode der Viskositätsbestimmung ist der Auslaufbecher. ⓘ

Viskosität von Gasen

Bei Fluiden mit niedriger Viskosität entspricht das Bild der inneren Reibung „nicht den physikalisch korrekten Vorstellungen über molekülbedingte Transportvorgänge in Fluiden“. Stattdessen resultiert hier die Viskosität im Fluid aus einem Impulsfluss, der mit dem folgenden Bild veranschaulicht werden kann: Die Stromfäden in der Strömung werden durch Züge versinnbildlicht, die mit unterschiedlicher Geschwindigkeit parallel nebeneinanderher fahren und mit Sandsäcken beladen sind. Die Sandsäcke entsprechen den Fluidelementen im Stromfaden. Personen auf den Zügen werfen die Sandsäcke auf den jeweils anderen Zug, was der zufälligen thermischen Bewegung der Fluidelemente zwischen den Stromfäden gleichkommt. Landet ein Sack des langsameren Zuges auf dem schnelleren, dann nimmt der Sandsack Impuls auf, den der schnellere Zug an ihn abgibt und so selbst langsamer wird. Wenn umgekehrt ein Sack des schnelleren Zuges auf dem langsameren landet, nimmt der Zug den Impuls des Sandsacks auf und wird so selbst schneller. Durch diesen Impulsaustausch wird der schnellere Zug abgebremst und der langsamere beschleunigt. ⓘ

Viskosität stellt demnach einen Impulsfluss von einem schneller fließenden Stromfaden auf einen langsamer fließenden dar. In einer Kontinuumsströmung tauschen die Fluidelemente Impulse über die zwischen ihnen wirkenden Spannungen aus. Zwischen den unterschiedlich schnell nebeneinanderher fließenden Stromfäden kommt es zu Schubspannungen, die sich makroskopisch als Viskosität bemerkbar machen. ⓘ

Kinetische Gastheorie

Nach Hirschfelder kann die Viskosität reiner Gase mit Hilfe der kinetischen Gastheorie in einem großen Temperaturbereich (etwa von 200 bis 3000 Kelvin) berechnet werden. ⓘ

\eta ={\frac {5\cdot {\sqrt {\pi \cdot m\cdot k_{\mathrm {B} }\cdot T}}}{16\cdot \pi \cdot \sigma ^{2}\cdot \Omega ^{(2,2)^{\star }}}}

ⓘ

Hierbei ist $m$ die Molekülmasse, $k_{\mathrm {B} }$ die Boltzmann-Konstante, $T$ die Temperatur, $\sigma$ der Lennard-Jones-Stoßdurchmesser und $\Omega ^{(2,2)^{\star }}$ das reduzierte Stoßintegral, das von der reduzierten Temperatur $T^{\star }=k_{\mathrm {B} }T/\epsilon$ abhängt. $\epsilon$ ist die Energie des Lennard-Jones-Potentials. Werte für die Lennard-Jones-Parameter und das reduzierte Stoßintegral sind in Lienhards Lehrbuch zur Wärmeübertragung in Kapitel 11 aufgeführt. Das reduzierte Stoßintegral $\Omega ^{(2,2)^{\star }}$ ist so definiert, dass für ein ideales Gas, bei dem Teilchenwechselwirkungen wie Stöße harter Kugeln betrachtet werden, $\Omega ^{(2,2)^{\star }}=1$ gilt. ⓘ

Physik des Reibungstensors

Die Viskosität begründet sich aus dem Experiment, nach dem zur Aufrechterhaltung einer Scherströmung eine Kraft erforderlich ist. Diese Kraft bewirkt einen Impulsaustausch innerhalb der Strömung bzw. mit dem Rand, weshalb sie zur Kategorie der Oberflächenkräfte zählt. Kontinuumsströmungen tauschen Impuls über mechanische Spannungen aus, wobei ein Spannungsanstieg eine Beschleunigung bewirkt. Im Kontinuum lässt sich die beschleunigende Kraft in der allgemeinsten Form als Divergenz eines Tensors formulieren:

{\vec {F}}=\nabla \cdot \mathbf {S} =\operatorname {div} \mathbf {S} ,

ⓘ

wobei $\mathbf {S}$ die Komponente des Spannungstensors auf Grund der Viskosität ist und zäher Spannungstensor oder Reibungstensor heißt. Der Nabla-Operator $\nabla$ bildet hier die Divergenz div des Reibungstensors. ⓘ

Aus dem Experiment folgt unmittelbar, dass der Reibungstensor eine Funktion der räumlichen Änderung der Strömungsgeschwindigkeit ist:

\mathbf {S} =\mathbf {S} (\operatorname {grad} {\vec {v}})

ⓘ

Der Operator grad bildet aus der Geschwindigkeit ${\vec {v}}$ den Geschwindigkeitsgradient. Da kein Impulsfluss bei homogener Strömung $({\vec {v}}={\text{const.}}$ oder $\operatorname {grad} {\vec {v}}=\mathbf {0} ),$ enthält der Reibungstensor keine Komponenten, die unabhängig vom Geschwindigkeitsgefälle sind. In Newtonschen Fluiden sind die Spannungen linear in den Geschwindigkeitsgradienten, eine Annahme, die gerechtfertigt ist, wenn der Geschwindigkeitsgradient im Sinne der Hydrodynamik klein ist. ⓘ

Weiterhin tritt keine Viskosität auf, wenn sich die Strömung in starrer Rotation ( ${\vec {v}}={\vec {\Omega }}\times {\vec {r}}$ mit dem Abstandsvektor ${\vec {r}}$ von der Drehachse) befindet, wobei ${\vec {\Omega }}$ die Winkelgeschwindigkeit ist, die aus dem schiefsymmetrischen Anteil des Geschwindigkeitsgradienten resultiert, siehe Kinematik in der Strömungsmechanik. Dieser schiefsymmetrische Anteil hat mithin keinen Einfluss auf die Spannungen, weswegen allein der symmetrische Anteil D des Geschwindigkeitsgradienten ⓘ

\mathbf {D} :={\frac {1}{2}}[\operatorname {grad} {\vec {v}}+(\operatorname {grad} {\vec {v}})^{\top }]={\frac {1}{2}}{\begin{pmatrix}2{\frac {\partial v_{x}}{\partial x}}&{\frac {\partial v_{x}}{\partial y}}+{\frac {\partial v_{y}}{\partial x}}&{\frac {\partial v_{x}}{\partial z}}+{\frac {\partial v_{z}}{\partial x}}\\&2{\frac {\partial v_{y}}{\partial y}}&{\frac {\partial v_{y}}{\partial z}}+{\frac {\partial v_{z}}{\partial y}}\\{\text{sym.}}&&2{\frac {\partial v_{z}}{\partial z}}\end{pmatrix}}

ⓘ

Spannungen verursacht. Das hochgestellte T bildet die Transposition. Mit der weiteren Annahme einer isotropen Flüssigkeit werden die unmittelbaren Stoffeigenschaften durch skalare Größen beschrieben. Damit wird der Reibungstensor:

\mathbf {S} =2\eta \left[\mathbf {D} -{\frac {1}{3}}\operatorname {Sp} (\mathbf {D} )\mathbf {1} \right]+\zeta \operatorname {Sp} (\mathbf {D} )\mathbf {1} \quad {\text{bzw.}}\quad S_{ij}=\eta \left({\frac {\partial v_{i}}{\partial x_{j}}}+{\frac {\partial v_{j}}{\partial x_{i}}}-{\frac {2}{3}}\delta _{ij}\sum _{k=1}^{3}{\frac {\partial v_{k}}{\partial x_{k}}}\right)+\zeta \delta _{ij}\ \sum _{k=1}^{3}{\frac {\partial v_{k}}{\partial x_{k}}}.

ⓘ

Darin ist $\delta$ das Kronecker-Delta, $\zeta =\lambda +{\tfrac {2}{3}}\eta$ die Volumenviskosität, $\lambda$ die erste Lamé-Konstante, $\operatorname {Sp}$ der Spur-Operator und $\mathbf {1}$ ist der Einheitstensor. Der erste Term beschreibt die Viskosität durch volumentreue Deformation (der Tensor in den eckigen Klammern ist spurfrei oder deviatorisch). Der zweite Term stellt die Viskosität durch Volumenänderung dar. Dieser Term wird bei Inkompressibilität verschwinden, denn dann ist $\operatorname {Sp} (\mathbf {D} )=\operatorname {div} {\vec {v}}=0$ . ⓘ

Viskosität ⓘ
Eine Simulation von Flüssigkeiten mit unterschiedlicher Viskosität. Die Flüssigkeit auf der linken Seite hat eine geringere Viskosität als die Flüssigkeit auf der rechten Seite.
Allgemeine Symbole	$η$ , $μ$
Ableitungen von anderen Größen	$μ = G - t$