Oberflächenspannung

Regenwasserabfluss von einem Vordach. Zu den Kräften, die die Tropfenbildung bestimmen, gehören: Oberflächenspannung, Kohäsion, Van-der-Waals-Kraft, Plateau-Rayleigh-Instabilität. ⓘ

Bei diesem Versuch, ein Wassertröpfchen zu zerschneiden, wirken Oberflächenspannung und Hydrophobie zusammen. ⓘ

Experimentelle Demonstration der Oberflächenspannung mit Seife ⓘ

Unter Oberflächenspannung versteht man die Tendenz von Flüssigkeitsoberflächen in Ruhe, sich auf die kleinstmögliche Oberfläche zusammenzuziehen. Die Oberflächenspannung ermöglicht es Objekten mit einer höheren Dichte als Wasser wie Rasierklingen und Insekten (z. B. Wasserläufer), auf einer Wasseroberfläche zu schwimmen, ohne auch nur teilweise unterzutauchen. ⓘ

An den Grenzflächen zwischen Flüssigkeit und Luft ist die Oberflächenspannung darauf zurückzuführen, dass die Flüssigkeitsmoleküle sich gegenseitig stärker anziehen (aufgrund der Kohäsion) als die Moleküle in der Luft (aufgrund der Adhäsion). ⓘ

Es gibt zwei Hauptmechanismen, die dabei eine Rolle spielen. Der eine ist eine nach innen gerichtete Kraft auf die Oberflächenmoleküle, die eine Kontraktion der Flüssigkeit bewirkt. Der zweite ist eine tangentiale Kraft parallel zur Oberfläche der Flüssigkeit. Diese tangentiale Kraft wird allgemein als Oberflächenspannung bezeichnet. Im Endeffekt verhält sich die Flüssigkeit so, als ob ihre Oberfläche mit einer gespannten elastischen Membran bedeckt wäre. Diese Analogie darf jedoch nicht zu weit getrieben werden, da die Spannung in einer elastischen Membran vom Ausmaß der Verformung der Membran abhängt, während die Oberflächenspannung eine inhärente Eigenschaft der Grenzfläche zwischen Flüssigkeit und Luft oder Flüssigkeit und Dampf ist. ⓘ

Aufgrund der relativ starken Anziehung der Wassermoleküle zueinander durch ein Netz von Wasserstoffbrückenbindungen hat Wasser eine höhere Oberflächenspannung (72,8 Millinewton (mN) pro Meter bei 20 °C) als die meisten anderen Flüssigkeiten. Die Oberflächenspannung ist ein wichtiger Faktor für das Phänomen der Kapillarität. ⓘ

Die Oberflächenspannung hat die Dimension einer Kraft pro Längeneinheit oder einer Energie pro Flächeneinheit. Beide sind gleichwertig, aber wenn man sich auf die Energie pro Flächeneinheit bezieht, ist es üblich, den Begriff Oberflächenenergie zu verwenden, der insofern allgemeiner ist, als er auch für Feststoffe gilt. ⓘ

In der Materialwissenschaft wird die Oberflächenspannung entweder für die Oberflächenspannung oder die Oberflächenenergie verwendet. ⓘ

Wasser bildet im freien Fall aufgrund der Oberflächenspannung Tropfen, die annähernd kugelförmig sind. ⓘ

Wasserläuferpaar nutzt die Oberflächenspannung ⓘ

Die Oberflächenspannung (Formelsymbol: $\sigma$, $\gamma$) ist also eine Grenzflächenspannung, die zwischen Flüssigkeiten und Gasphasen auftritt. Gemessen wird sie in den SI-Einheiten kg/s², gleichbedeutend mit N/m. ⓘ

Verursacht

Schematische Darstellung der Kohäsionskräfte an den Molekülen einer Flüssigkeit ⓘ

Aufgrund der Kohäsionskräfte wird ein von der Oberfläche entferntes Molekül von den benachbarten Flüssigkeitsmolekülen in alle Richtungen gleichermaßen angezogen, so dass die Nettokraft gleich Null ist. Die Moleküle an der Oberfläche haben nicht auf allen Seiten die gleichen Moleküle und werden daher nach innen gezogen. Dadurch entsteht ein gewisser Innendruck, der die Flüssigkeitsoberfläche dazu zwingt, sich auf die kleinste Fläche zusammenzuziehen. ⓘ

Aufgrund der Kohäsion der Wassermoleküle gibt es auch eine Spannung parallel zur Oberfläche an der Grenzfläche zwischen Flüssigkeit und Luft, die einer äußeren Kraft widersteht. ⓘ

Die Anziehungskräfte, die zwischen Molekülen desselben Typs wirken, werden als Kohäsionskräfte bezeichnet, während die Kräfte, die zwischen Molekülen unterschiedlichen Typs wirken, als Adhäsionskräfte bezeichnet werden. Das Gleichgewicht zwischen der Kohäsion der Flüssigkeit und ihrer Adhäsion am Material des Behälters bestimmt den Grad der Benetzung, den Kontaktwinkel und die Form des Meniskus. Wenn die Kohäsion überwiegt (d. h. die Adhäsionsenergie weniger als die Hälfte der Kohäsionsenergie beträgt), ist die Benetzung gering und der Meniskus ist an einer senkrechten Wand konvex (wie bei Quecksilber in einem Glasbehälter). Wenn hingegen die Adhäsion dominiert (Adhäsionsenergie mehr als die Hälfte der Kohäsionsenergie), ist die Benetzung hoch und der entsprechende Meniskus ist konkav (wie bei Wasser in einem Glas). ⓘ

Die Oberflächenspannung ist für die Form von Flüssigkeitstropfen verantwortlich. Obwohl sie leicht verformbar sind, neigen Wassertropfen dazu, durch das Ungleichgewicht der Kohäsionskräfte der Oberflächenschicht in eine kugelförmige Form gezogen zu werden. Gäbe es keine anderen Kräfte, wären die Tropfen praktisch aller Flüssigkeiten annähernd kugelförmig. Die kugelförmige Form minimiert die nach dem Laplace-Gesetz erforderliche "Wandspannung" der Oberflächenschicht. ⓘ

Wassertropfen, der auf einem Damast liegt. Die Oberflächenspannung ist hoch genug, um ein Durchsickern durch das Textil zu verhindern. ⓘ

Eine weitere Möglichkeit, die Oberflächenspannung zu betrachten, ist die Betrachtung der Energie. Ein Molekül, das mit einem Nachbarn in Kontakt ist, befindet sich in einem niedrigeren Energiezustand als wenn es allein wäre. Die Innenmoleküle haben so viele Nachbarn wie möglich, aber den Grenzmolekülen fehlen (im Vergleich zu den Innenmolekülen) Nachbarn und sie haben daher eine höhere Energie. Damit die Flüssigkeit ihren Energiezustand minimieren kann, muss die Anzahl der Grenzmoleküle mit höherer Energie minimiert werden. Die minimierte Anzahl der Grenzmoleküle führt zu einer minimalen Oberfläche. Infolge der Oberflächenminimierung nimmt eine Oberfläche die glatteste Form an, die sie annehmen kann (der mathematische Beweis, dass "glatte" Formen die Oberfläche minimieren, beruht auf der Euler-Lagrange-Gleichung). Da jede Krümmung in der Oberflächenform zu einer größeren Fläche führt, ergibt sich auch eine höhere Energie. ⓘ

Auswirkungen der Oberflächenspannung

Wasser

Verschiedene Auswirkungen der Oberflächenspannung lassen sich bei gewöhnlichem Wasser beobachten:

1. Abperlen des Regenwassers auf einer wachshaltigen Oberfläche, z. B. einem Blatt. Das Wasser haftet nur schwach am Wachs und stark an sich selbst, so dass sich das Wasser zu Tropfen zusammenballt. Die Oberflächenspannung verleiht ihnen ihre nahezu kugelförmige Form, da eine Kugel das kleinstmögliche Verhältnis von Oberfläche zu Volumen aufweist.
2. Die Bildung von Tropfen erfolgt, wenn eine Flüssigkeitsmasse gedehnt wird. Die Animation (unten) zeigt, wie das am Wasserhahn haftende Wasser an Masse gewinnt, bis es bis zu einem Punkt gedehnt wird, an dem die Oberflächenspannung den Tropfen nicht mehr mit dem Wasserhahn verbinden kann. Dann trennt er sich und die Oberflächenspannung formt den Tropfen zu einer Kugel. Würde ein Wasserstrahl aus dem Wasserhahn fließen, würde er während seines Falles in Tropfen zerfallen. Die Schwerkraft dehnt den Strahl aus, und die Oberflächenspannung drückt ihn in Kugeln zusammen.
3. Der Auftrieb von Objekten, die dichter als Wasser sind, erfolgt, wenn das Objekt nicht benetzbar ist und sein Gewicht klein genug ist, um von den Kräften der Oberflächenspannung getragen zu werden. So nutzen beispielsweise Wasserläufer die Oberflächenspannung, um auf der Oberfläche eines Teiches zu laufen, und zwar auf folgende Weise. Die Nichtbenetzbarkeit des Beins des Wasserläufers bedeutet, dass es keine Anziehung zwischen den Molekülen des Beins und den Molekülen des Wassers gibt. Wenn das Bein auf das Wasser drückt, versucht die Oberflächenspannung des Wassers lediglich, seine Ebenheit durch die Verformung durch das Bein wiederherzustellen. Dieses Verhalten des Wassers drückt den Wasserläufer nach oben, so dass er auf der Wasseroberfläche stehen kann, solange seine Masse klein genug ist, dass das Wasser ihn tragen kann. Die Wasseroberfläche verhält sich wie ein elastischer Film: Die Füße des Insekts verursachen Vertiefungen in der Wasseroberfläche, wodurch die Oberfläche vergrößert wird und die Tendenz zur Minimierung der Oberflächenkrümmung (also der Fläche) des Wassers die Füße des Insekts nach oben drückt.
4. Die Trennung von Öl und Wasser (in diesem Fall von Wasser und flüssigem Wachs) wird durch eine Oberflächenspannung zwischen ungleichen Flüssigkeiten verursacht. Diese Art der Oberflächenspannung wird als "Grenzflächenspannung" bezeichnet, aber die Chemie ist dieselbe.
5. Unter Weintränen versteht man die Bildung von Tropfen und Rinnsalen an der Seite eines Glases, das ein alkoholisches Getränk enthält. Die Ursache ist eine komplexe Wechselwirkung zwischen den unterschiedlichen Oberflächenspannungen von Wasser und Ethanol; sie wird durch eine Kombination aus der Veränderung der Oberflächenspannung von Wasser durch Ethanol und der Tatsache, dass Ethanol schneller verdampft als Wasser, hervorgerufen. ⓘ

• 

  A. Wasser perlt auf einem Blatt ab

• 

  B. Aus einem Wasserhahn tropfendes Wasser

• 

  C. Wasserläufer bleiben aufgrund der Oberflächenspannung an der Oberfläche einer Flüssigkeit

• 

  D. Lavalampe mit Wechselwirkung zwischen ungleichen Flüssigkeiten: Wasser und flüssiges Wachs

• 

  E. Foto, das das Phänomen der "Weintränen" zeigt. ⓘ

Tenside

Die Oberflächenspannung ist auch bei anderen gängigen Phänomenen zu beobachten, insbesondere wenn Tenside zu ihrer Verringerung eingesetzt werden:

• Seifenblasen haben eine sehr große Oberfläche bei sehr geringer Masse. Blasen in reinem Wasser sind instabil. Der Zusatz von Tensiden kann jedoch eine stabilisierende Wirkung auf die Blasen haben (siehe Marangoni-Effekt). Beachten Sie, dass Tenside die Oberflächenspannung von Wasser um das Dreifache oder mehr verringern.
• Emulsionen sind eine Art von Kolloiden, bei denen die Oberflächenspannung eine Rolle spielt. Winzige Ölfragmente, die in reinem Wasser suspendiert sind, fügen sich spontan zu viel größeren Massen zusammen. Durch das Vorhandensein eines Tensids wird die Oberflächenspannung jedoch herabgesetzt, so dass winzige Öltröpfchen in der Wassermasse stabil bleiben (oder umgekehrt). ⓘ

Physik

Physikalische Einheiten

Die Oberflächenspannung, dargestellt durch das Symbol γ (alternativ σ oder T), wird als Kraft pro Längeneinheit gemessen. Ihre SI-Einheit ist Newton pro Meter, aber auch die cgs-Einheit Dyne pro Zentimeter wird verwendet. Ein Beispiel,

$$\gamma =1~\mathrm {\frac {dyn}{cm}} =1~\mathrm {\frac {erg}{cm^{2}}} =1~\mathrm {\frac {10^{-7}\,m\cdot N}{10^{-4}\,m^{2}}} =0.001~\mathrm {\frac {N}{m}} =0.001~\mathrm {\frac {J}{m^{2}}} .$$

ⓘ

Wachstum der Oberfläche

Dieses Diagramm veranschaulicht die Kraft, die zur Vergrößerung der Oberfläche erforderlich ist. Diese Kraft ist proportional zur Oberflächenspannung. ⓘ

Die Oberflächenspannung kann in Form von Kraft oder Energie definiert werden. ⓘ

In Bezug auf die Kraft

Die Oberflächenspannung γ einer Flüssigkeit ist die Kraft pro Längeneinheit. In der Abbildung rechts besteht der rechteckige Rahmen aus drei unbeweglichen Seiten (schwarz), die eine "U"-Form bilden, und einer vierten beweglichen Seite (blau), die nach rechts gleiten kann. Die Oberflächenspannung zieht den blauen Balken nach links; die Kraft F, die erforderlich ist, um die bewegliche Seite zu halten, ist proportional zur Länge L der unbeweglichen Seite. Das Verhältnis F/L hängt also nur von den intrinsischen Eigenschaften der Flüssigkeit ab (Zusammensetzung, Temperatur usw.), nicht von ihrer Geometrie. Hätte der Rahmen beispielsweise eine kompliziertere Form, so wäre das Verhältnis F/L, wobei L die Länge der beweglichen Seite und F die Kraft ist, die erforderlich ist, um sie am Gleiten zu hindern, für alle Formen gleich. Wir definieren daher die Oberflächenspannung als ⓘ

$$\gamma ={\frac {F}{2L}}.$$

Der Grund für die Zahl 1/2 liegt darin, dass die Folie zwei Seiten (zwei Oberflächen) hat, von denen jede in gleichem Maße zur Kraft beiträgt; die Kraft, die von einer einzelnen Seite ausgeht, ist also γL = F/2. ⓘ

In Bezug auf die Energie

Die Oberflächenspannung γ einer Flüssigkeit ist das Verhältnis zwischen der Änderung der Energie der Flüssigkeit und der Änderung der Flüssigkeitsoberfläche (die zur Änderung der Energie geführt hat). Dies lässt sich leicht mit der vorangegangenen Definition in Bezug auf die Kraft in Verbindung bringen: Wenn F die Kraft ist, die erforderlich ist, um die Seite daran zu hindern, ins Rutschen zu kommen, dann ist dies auch die Kraft, die die Seite bei konstanter Geschwindigkeit (gemäß dem zweiten Newtonschen Gesetz) im Zustand des Rutschens halten würde. Bewegt sich die Seite jedoch nach rechts (in Richtung der aufgebrachten Kraft), dann vergrößert sich die Oberfläche der gestreckten Flüssigkeit, während die aufgebrachte Kraft Arbeit an der Flüssigkeit verrichtet. Das bedeutet, dass die Vergrößerung der Oberfläche die Energie des Films erhöht. Die Arbeit, die durch die Kraft F bei der Bewegung der Seite um die Strecke Δx verrichtet wird, ist W = FΔx; gleichzeitig vergrößert sich die Gesamtfläche des Films um ΔA = 2LΔx (der Faktor 2 kommt daher, dass die Flüssigkeit zwei Seiten, zwei Oberflächen hat). Multipliziert man also sowohl den Zähler als auch den Nenner von γ = 1/2F/L mit Δx, erhält man

$$\gamma ={\frac {F}{2L}}={\frac {F\Delta x}{2L\Delta x}}={\frac {W}{\Delta A}}.$$

Diese Arbeit W wird mit den üblichen Argumenten als gespeicherte potenzielle Energie interpretiert. Folglich kann die Oberflächenspannung auch im SI-System als Joule pro Quadratmeter und im cgs-System als Ergs pro cm² gemessen werden. Da mechanische Systeme versuchen, einen Zustand minimaler potenzieller Energie zu erreichen, nimmt ein freier Flüssigkeitstropfen naturgemäß eine kugelförmige Gestalt an, die bei einem gegebenen Volumen die geringste Oberfläche aufweist. Die Äquivalenz zwischen der Messung der Energie pro Flächeneinheit und der Kraft pro Längeneinheit kann durch Dimensionsanalyse nachgewiesen werden. ⓘ

Oberflächenkrümmung und Druck

Oberflächenspannungskräfte, die auf einen winzigen (differentiellen) Fleck der Oberfläche wirken. δθ_x und δθ_y geben den Betrag der Krümmung über die Abmessungen des Flecks an. Das Gleichgewicht zwischen den Spannungskräften und dem Druck führt zu der Young-Laplace-Gleichung ⓘ

Wirkt keine Kraft senkrecht auf eine gespannte Fläche, muss die Fläche flach bleiben. Unterscheidet sich jedoch der Druck auf einer Seite der Oberfläche vom Druck auf der anderen Seite, so ergibt die Druckdifferenz mal Fläche eine Normalkraft. Damit die Oberflächenspannungskräfte die Druckkraft aufheben können, muss die Oberfläche gekrümmt sein. Das Diagramm zeigt, wie die Oberflächenkrümmung eines winzigen Flächenstücks zu einer Nettokomponente der Oberflächenspannungskräfte führt, die senkrecht zur Mitte des Stücks wirken. Wenn alle Kräfte ausgeglichen sind, ist die resultierende Gleichung als Young-Laplace-Gleichung bekannt:

$$\Delta p=\gamma \left({\frac {1}{R_{x}}}+{\frac {1}{R_{y}}}\right)$$

wobei:

• Δp ist die Druckdifferenz, die als Laplace-Druck bezeichnet wird.
• γ ist die Oberflächenspannung.
• R_x und R_y sind die Krümmungsradien in jeder der zur Oberfläche parallelen Achsen.

Die Größe in Klammern auf der rechten Seite ist die (doppelte) mittlere Krümmung der Oberfläche (je nach Normierung). Die Lösungen dieser Gleichung bestimmen die Form von Wassertropfen, Pfützen, Menisken, Seifenblasen und alle anderen Formen, die durch die Oberflächenspannung bestimmt werden (z. B. die Form der Abdrücke, die die Füße eines Wasserläufers auf der Oberfläche eines Teichs hinterlassen). Die folgende Tabelle zeigt, wie der Innendruck eines Wassertropfens mit abnehmendem Radius zunimmt. Bei nicht sehr kleinen Tropfen ist der Effekt unauffällig, aber der Druckunterschied wird enorm, wenn sich die Tropfengröße der Molekülgröße nähert. (Im Grenzfall eines einzelnen Moleküls wird das Konzept bedeutungslos.) ⓘ

Δp für Wassertropfen mit unterschiedlichen Radien bei STP ⓘ

Radius des Tropfens	1 mm	0,1 mm	1 μm	10 nm
Δp (atm)	0.0014	0.0144	1.436	143.6

Schwebende Objekte

Querschnitt einer Nadel, die auf der Wasseroberfläche schwimmt. F_w ist da_s Gewicht und Fs sind die resultierenden Kräfte der Oberflächenspannung. ⓘ

Wenn ein Gegenstand auf eine Flüssigkeit gesetzt wird, drückt sein Gewicht Fw auf die Oberfläche, und wenn die Oberflächenspannung und die nach unten gerichtete Kraft gleich sind, wird sie durch die Oberflächenspannungskräfte auf beiden Seiten Fs ausgeglichen, die jeweils parallel zur Wasseroberfläche an den Stellen verlaufen, an denen sie den Gegenstand berühren. Beachten Sie, dass kleine Bewegungen des Körpers dazu führen können, dass der Gegenstand sinkt. Mit abnehmendem Berührungswinkel nimmt auch die Oberflächenspannung ab. Die horizontalen Komponenten der beiden Fs-Pfeile zeigen in entgegengesetzte Richtungen und heben sich daher gegenseitig auf, aber die vertikalen Komponenten zeigen in dieselbe Richtung und addieren sich daher zum Gleichgewicht Fw. Die Oberfläche des Objekts darf nicht benetzbar sein, damit dies geschieht, und sein Gewicht muss so gering sein, dass die Oberflächenspannung es tragen kann. Bezeichnet m die Masse der Nadel und g die Erdbeschleunigung, so ergibt sich ⓘ

$$F_{\mathrm {w} }=2F_{\mathrm {s} }\sin \theta \quad \Leftrightarrow \quad mg=2\gamma L\sin \theta$$

ⓘ

Flüssige Oberfläche

Minimale Oberfläche ⓘ

Die Form der minimalen Oberfläche, die von einem beliebig geformten Rahmen begrenzt wird, mit rein mathematischen Mitteln zu bestimmen, kann eine entmutigende Aufgabe sein. Wenn man jedoch einen Rahmen aus Draht herstellt und ihn in eine Seifenlösung taucht, erscheint in dem entstehenden Seifenfilm innerhalb von Sekunden eine lokale minimale Oberfläche. ⓘ

Der Grund dafür ist, dass der Druckunterschied an einer Flüssigkeitsgrenzfläche proportional zur mittleren Krümmung ist, wie aus der Young-Laplace-Gleichung hervorgeht. Bei einem offenen Seifenfilm ist die Druckdifferenz gleich Null, so dass die mittlere Krümmung gleich Null ist, und minimale Oberflächen haben die Eigenschaft der mittleren Krümmung Null. ⓘ

Kontaktwinkel

Die Oberfläche einer beliebigen Flüssigkeit ist eine Grenzfläche zwischen dieser Flüssigkeit und einem anderen Medium. Die Oberfläche eines Teiches beispielsweise ist eine Grenzfläche zwischen dem Teichwasser und der Luft. Die Oberflächenspannung ist also keine Eigenschaft der Flüssigkeit allein, sondern eine Eigenschaft der Grenzfläche der Flüssigkeit zu einem anderen Medium. Befindet sich eine Flüssigkeit in einem Behälter, so gibt es neben der Grenzfläche zwischen Flüssigkeit und Luft an der Oberfläche auch eine Grenzfläche zwischen der Flüssigkeit und den Wänden des Behälters. Die Oberflächenspannung zwischen der Flüssigkeit und der Luft ist in der Regel anders (größer) als die Oberflächenspannung zwischen der Flüssigkeit und den Wänden eines Behälters. Und dort, wo die beiden Oberflächen aufeinandertreffen, muss ihre Geometrie so beschaffen sein, dass sich alle Kräfte ausgleichen. ⓘ

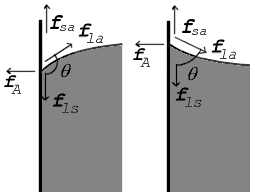Kräfte an der Berührungsstelle für Kontaktwinkel größer als 90° (links) und kleiner als 90° (rechts) ⓘ

Wo sich die beiden Oberflächen treffen, bilden sie einen Kontaktwinkel θ, der der Winkel ist, den die Tangente an die Oberfläche mit der festen Oberfläche bildet. Beachten Sie, dass der Winkel durch die Flüssigkeit gemessen wird, wie in den obigen Diagrammen dargestellt. Das Diagramm auf der rechten Seite zeigt zwei Beispiele. Die Spannungskräfte sind für die Grenzfläche Flüssigkeit-Luft, die Grenzfläche Flüssigkeit-Festkörper und die Grenzfläche Festkörper-Luft dargestellt. Im linken Beispiel ist die Differenz zwischen der Oberflächenspannung Flüssigkeit-Festkörper und Festkörper-Luft, γls - γ_sa, kleiner als die Oberflächenspannung Flüssigkeit-Luft, γ_la, aber dennoch positiv, d. h. ⓘ

$$\gamma _{\mathrm {la} }>\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }>0$$

ⓘ

Im Diagramm müssen sich sowohl die vertikalen als auch die horizontalen Kräfte genau an der Kontaktstelle aufheben, was als Gleichgewicht bezeichnet wird. Die horizontale Komponente von f_la wird durch die Adhäsionskraft, fA, aufgehoben. ⓘ

$$f_{\mathrm {A} }=f_{\mathrm {la} }\sin \theta$$

ⓘ

Das aufschlussreichere Kräftegleichgewicht liegt jedoch in der vertikalen Richtung. Die vertikale Komponente von fla muss die Differenz der Kräfte ent_lang der festen Oberfläche, f_ls - f_sa, genau aufheben. ⓘ

$$f_{\mathrm {ls} }-f_{\mathrm {sa} }=-f_{\mathrm {la} }\cos \theta$$

ⓘ

Einige Kontaktwinkel zwischen Flüssigkeit und Festkörper ⓘ

Flüssigkeit	Festkörper	Kontakt winkel
Wasser	Natron-Kalk-Glas Bleiglas geschmolzener Quarz	0°
Ethanol
Diethyläther
Tetrachlorkohlenstoff
Glycerin
Essigsäure
Wasser	Paraffinwachs	107°
	Silber	90°
Methyljodid	Natron-Kalk-Glas	29°
	Bleiglas	30°
	geschmolzener Quarz	33°
Quecksilber	Natron-Kalk-Glas	140°

Da die Kräfte in direktem Verhältnis zu den jeweiligen Oberflächenspannungen stehen, gilt auch hier:

$$\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }=-\gamma _{\mathrm {la} }\cos \theta$$

ⓘ

wobei

• γ_ls die Oberflächenspannung zwischen Flüssigkeit und Festkörper ist,
• γ_la die Flüssigkeits-Luft-Oberflächenspannung ist,
• γ_sa die Oberflächenspannung Festkörper-Luft ist,
• θ ist der Kontaktwinkel, wobei ein konkaver Meniskus einen Kontaktwinkel von weniger als 90° und ein konvexer Meniskus einen Kontaktwinkel von mehr als 90° hat. ⓘ

Das bedeutet, dass die Differenz zwischen der Oberflächenspannung Flüssigkeit-Festkörper und Festkörper-Luft, γls - γ_sa, zwar schwer direkt zu messen ist, aber aus der Oberflächenspannung Flüssigkeit-Luft, γ_la, und dem Gleichgewichts-Kontaktwinkel, θ, abgeleitet werden kann, der eine Funktion des leicht messbaren fortschreitenden und zurückweichenden Kontaktwinkels ist (siehe Hauptartikel Kontaktwinkel). ⓘ

Die gleiche Beziehung besteht auch im Diagramm auf der rechten Seite. In diesem Fall sieht man jedoch, dass die Oberflächenspannungsdifferenz zwischen Flüssigkeit und Feststoff bzw. Feststoff und Luft negativ sein muss, da der Kontaktwinkel kleiner als 90° ist:

$$\gamma _{\mathrm {la} }>0>\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }$$

ⓘ

Spezielle Kontaktwinkel

Beachten Sie, dass im Sonderfall einer Wasser-Silber-Grenzfläche, bei der der Kontaktwinkel gleich 90° ist, die Oberflächenspannungsdifferenz zwischen Flüssigkeit und Festkörper bzw. Festkörper und Luft genau null ist. ⓘ

Ein weiterer Sonderfall liegt vor, wenn der Kontaktwinkel genau 180° beträgt. Wasser mit speziell präpariertem Teflon nähert sich diesem Wert. Ein Kontaktwinkel von 180° liegt vor, wenn die Oberflächenspannung zwischen Flüssigkeit und Festkörper genau gleich der Oberflächenspannung zwischen Flüssigkeit und Luft ist. ⓘ

$$\gamma _{\mathrm {la} }=\gamma _{\mathrm {ls} }-\gamma _{\mathrm {sa} }>0\qquad \theta =180^{\circ }$$

ⓘ

Methoden der Messung

Krafttensiometer verwenden die Du Noüy-Ringmethode und die Wilhelmy-Plattenmethode. ⓘ

Da sich die Oberflächenspannung in verschiedenen Effekten äußert, bietet sie eine Reihe von Möglichkeiten zu ihrer Messung. Welche Methode optimal ist, hängt von der Art der zu messenden Flüssigkeit, den Bedingungen, unter denen ihre Spannung gemessen werden soll, und der Stabilität ihrer Oberfläche bei Verformung ab. Ein Gerät, das die Oberflächenspannung misst, heißt Tensiometer. ⓘ

• Du-Noüy-Ring-Methode: Die traditionelle Methode zur Messung der Ober- oder Grenzflächenspannung. Die Benetzungseigenschaften der Oberfläche oder Grenzfläche haben wenig Einfluss auf diese Messtechnik. Gemessen wird die maximale Zugkraft, die von der Oberfläche auf den Ring ausgeübt wird.
• Wilhelmy-Platten-Methode: Eine universelle Methode, die sich besonders zur Überprüfung der Oberflächenspannung über lange Zeiträume eignet. Eine vertikale Platte mit bekanntem Umfang wird an einer Waage befestigt, und die Kraft, die durch die Benetzung entsteht, wird gemessen.
• Spinning-Drop-Methode: Dieses Verfahren ist ideal für die Messung niedriger Grenzflächenspannungen. Der Durchmesser eines Tropfens in einer schweren Phase wird gemessen, während beide in Rotation versetzt werden.
• Methode des hängenden Tropfens: Oberflächen- und Grenzflächenspannung können mit dieser Technik auch bei erhöhten Temperaturen und Drücken gemessen werden. Die Geometrie eines Tropfens wird optisch analysiert. Bei hängenden Tropfen wurden der maximale Durchmesser und das Verhältnis zwischen diesem Parameter und dem Durchmesser im Abstand des maximalen Durchmessers von der Tropfenspitze zur Bewertung der Größen- und Formparameter verwendet, um die Oberflächenspannung zu bestimmen.
• Blasendruckmethode (Jaeger-Methode): Ein Messverfahren zur Bestimmung der Oberflächenspannung bei kurzen Oberflächenzeiten. Gemessen wird der maximale Druck jeder einzelnen Blase.
• Tropfenvolumen-Methode: Eine Methode zur Bestimmung der Grenzflächenspannung als Funktion des Grenzflächenalters. Eine Flüssigkeit mit einer bestimmten Dichte wird in eine zweite Flüssigkeit mit einer anderen Dichte gepumpt, und die Zeit zwischen den erzeugten Tropfen wird gemessen.
• Kapillaraufstiegsmethode: Das Ende einer Kapillare wird in die Lösung getaucht. Die Höhe, die die Lösung im Inneren der Kapillare erreicht, wird durch die unten beschriebene Gleichung mit der Oberflächenspannung in Beziehung gesetzt.
  

  Die Oberflächenspannung kann mit der Methode des hängenden Tropfens auf einem Goniometer gemessen werden.
• Stalagmometrische Methode: Eine Methode zum Wiegen und Ablesen eines Flüssigkeitstropfens.
• Methode des hängenden Tropfens: Eine Methode zur Bestimmung der Oberflächenspannung und der Dichte durch Aufsetzen eines Tropfens auf ein Substrat und Messung des Kontaktwinkels (siehe Sessile-Drop-Methode).
• Du Noüy-Padday-Methode: Eine minimierte Version der Du Noüy-Methode verwendet eine Metallnadel mit kleinem Durchmesser anstelle eines Rings in Kombination mit einer hochempfindlichen Mikrowaage zur Aufzeichnung der maximalen Zugkraft. Der Vorteil dieser Methode besteht darin, dass sehr kleine Probenvolumina (bis hinunter zu einigen zehn Mikrolitern) mit sehr hoher Präzision gemessen werden können, ohne dass eine Auftriebskorrektur erforderlich ist (bei einer Nadel oder besser einem Stab mit geeigneter Geometrie). Außerdem kann die Messung sehr schnell durchgeführt werden, mindestens in etwa 20 Sekunden.
• Schwingungsfrequenz der schwebenden Tropfen: Die Eigenfrequenz der Schwingungen von magnetisch schwebenden Tropfen wurde zur Messung der Oberflächenspannung von supraflüssigem ⁴He verwendet. Dieser Wert wird auf 0,375 dyn/cm bei T = 0 K geschätzt.
• Resonanzschwingungen von kugelförmigen und halbkugelförmigen Flüssigkeitstropfen: Die Technik basiert auf der Messung der Resonanzfrequenz von kugelförmigen und halbkugelförmigen Pendeltropfen, die durch ein moduliertes elektrisches Feld in Schwingungen versetzt werden. Die Oberflächenspannung und die Viskosität können anhand der erhaltenen Resonanzkurven bewertet werden.
• Drop-Bounce-Verfahren: Diese Methode basiert auf aerodynamischem Schweben mit einer teilbaren Düse. Nach dem Abwurf eines stabilen schwebenden Tropfens auf eine Plattform verformt sich die Probe und prallt zurück, wobei sie in der Luft oszilliert und versucht, ihre Oberfläche zu verkleinern. Durch dieses Schwingungsverhalten können die Oberflächenspannung und die Viskosität der Flüssigkeit gemessen werden.
• Mit dem Smartphone: Einige Smartphones können zur Messung der Oberflächenspannung einer transparenten Flüssigkeit verwendet werden. Die Methode basiert auf der Messung der Wellenlänge von Kapillarwellen mit bekannter Frequenz. Das Smartphone wird auf einen Becher mit der Flüssigkeit gelegt. Dann regt der Vibrationsmotor des Smartphones (durch die Tasse hindurch) Kapillarwellen auf der Oberfläche der Flüssigkeit an, die von der Kamera des Smartphones erfasst werden. ⓘ

Auswirkungen

Flüssigkeit in einem vertikalen Rohr

Schema eines Quecksilberbarometers ⓘ

Ein Quecksilberbarometer alter Bauart besteht aus einer vertikalen Glasröhre mit einem Durchmesser von etwa 1 cm, die teilweise mit Quecksilber gefüllt ist und in deren ungefülltem Volumen ein Vakuum (das so genannte Torricelli-Vakuum) herrscht (siehe Abbildung rechts). Man beachte, dass der Quecksilberspiegel in der Mitte der Röhre höher ist als an den Rändern, so dass die Oberseite des Quecksilbers kuppelförmig ist. Der Massenschwerpunkt der gesamten Quecksilbersäule wäre etwas niedriger, wenn die Oberseite des Quecksilbers über den gesamten Querschnitt der Röhre flach wäre. Die kuppelförmige Oberseite bietet jedoch eine etwas geringere Oberfläche für die gesamte Quecksilbermasse. Auch hier wirken beide Effekte zusammen, um die gesamte potenzielle Energie zu minimieren. Eine solche Oberflächenform wird als konvexer Meniskus bezeichnet. ⓘ

Wir betrachten die Oberfläche der gesamten Quecksilbermasse, einschließlich des Teils der Oberfläche, der mit dem Glas in Berührung kommt, da Quecksilber überhaupt nicht am Glas haftet. Die Oberflächenspannung des Quecksilbers wirkt also über die gesamte Oberfläche, auch dort, wo es mit dem Glas in Kontakt ist. Wäre die Röhre nicht aus Glas, sondern aus Kupfer, sähe die Situation ganz anders aus. Quecksilber haftet aggressiv an Kupfer. In einer Kupferröhre ist der Quecksilberspiegel in der Mitte der Röhre also niedriger als an den Rändern (d. h. es würde sich ein konkaver Meniskus bilden). In einer Situation, in der die Flüssigkeit an den Wänden ihres Behälters haftet, betrachten wir den Teil der Flüssigkeitsoberfläche, der mit dem Behälter in Kontakt ist, als eine negative Oberflächenspannung. Die Flüssigkeit ist dann bestrebt, die Kontaktfläche zu maximieren. In diesem Fall führt eine Vergrößerung der Kontaktfläche mit dem Behälter also eher zu einer Verringerung als zu einer Erhöhung der potenziellen Energie. Diese Verringerung reicht aus, um die erhöhte potenzielle Energie auszugleichen, die mit dem Anheben der Flüssigkeit in der Nähe der Behälterwände verbunden ist. ⓘ

Veranschaulichung des kapillaren Aufstiegs und Falls. Rot=Kontaktwinkel kleiner als 90°; blau=Kontaktwinkel größer als 90° ⓘ

Wenn ein Rohr ausreichend eng ist und die Flüssigkeit ausreichend stark an den Wänden haftet, kann die Oberflächenspannung die Flüssigkeit durch ein als Kapillarwirkung bekanntes Phänomen das Rohr hinaufziehen. Die Höhe, auf die die Säule angehoben wird, ist durch das Jurinsche Gesetz gegeben:

$$h={\frac {2\gamma _{\mathrm {la} }\cos \theta }{\rho gr}}$$

ⓘ

wobei ⓘ

• h ist die Höhe, um die die Flüssigkeit angehoben wird,
• γ_la die Flüssigkeits-Luft-Oberflächenspannung ist,
• ρ ist die Dichte der Flüssigkeit,
• r ist der Radius der Kapillare,
• g ist die Beschleunigung durch die Schwerkraft,
• θ ist der oben beschriebene Kontaktwinkel. Wenn θ größer als 90° ist, wie z. B. bei Quecksilber in einem Glasbehälter, wird die Flüssigkeit eher abgesenkt als angehoben. ⓘ

Pfützen auf einer Oberfläche

Profilkurve des Randes einer Pfütze, bei der der Kontaktwinkel 180° beträgt. Die Kurve ergibt sich aus der Formel:

$$x-x_{0}={\frac {1}{2}}H\cosh ^{-1}\left({\frac {H}{h}}\right)-H{\sqrt {1-{\frac {h^{2}}{H^{2}}}}}$$

wobei ${\textstyle H=2{\sqrt {{\gamma }/{g\rho }}}}$ ⓘ

Kleine Wasserpfützen auf einer glatten, sauberen Oberfläche haben eine wahrnehmbare Dicke. ⓘ

Gießt man Quecksilber auf eine waagerechte, flache Glasplatte, so entsteht eine Pfütze mit einer wahrnehmbaren Dicke. Die Pfütze breitet sich nur bis zu dem Punkt aus, an dem sie etwas weniger als einen halben Zentimeter dick ist, und nicht dünner. Dies ist wiederum auf die starke Oberflächenspannung des Quecksilbers zurückzuführen. Die flüssige Masse flacht ab, weil dadurch ein möglichst großer Teil des Quecksilbers auf ein möglichst niedriges Niveau gebracht wird, aber gleichzeitig wirkt die Oberflächenspannung, um die Gesamtoberfläche zu verringern. Das Ergebnis dieses Kompromisses ist eine Pfütze mit einer nahezu festen Dicke. ⓘ

Dieselbe Oberflächenspannungsdemonstration kann mit Wasser, Kalkwasser oder sogar Kochsalzlösung durchgeführt werden, allerdings nur auf einer Oberfläche aus einer Substanz, an der Wasser nicht haftet. Wachs ist ein solcher Stoff. Wasser, das auf eine glatte, flache, horizontale Wachsoberfläche, z. B. eine gewachste Glasplatte, gegossen wird, verhält sich ähnlich wie Quecksilber, das auf Glas gegossen wird. ⓘ

Die Dicke einer Flüssigkeitspfütze auf einer Oberfläche, deren Kontaktwinkel 180° beträgt, ist gegeben durch:

$$h=2{\sqrt {\frac {\gamma }{g\rho }}}$$

ⓘ

wobei ⓘ

• h ist die Tiefe der Pfütze in Zentimetern oder Metern.
• γ ist die Oberflächenspannung der Flüssigkeit in dyn pro Zentimeter oder Newton pro Meter.
• g ist die Erdbeschleunigung und ist gleich 980 cm/s² oder 9,8 m/s²
• ρ ist die Dichte der Flüssigkeit in Gramm pro Kubikzentimeter oder Kilogramm pro Kubikmeter ⓘ

Veranschaulichung, wie ein geringerer Kontaktwinkel zu einer Verringerung der Pfützentiefe führt ⓘ

In der Realität wird die Dicke der Pfützen etwas geringer sein, als es die obige Formel vorhersagt, da nur sehr wenige Oberflächen einen Kontaktwinkel von 180° mit einer Flüssigkeit haben. Wenn der Kontaktwinkel weniger als 180° beträgt, ist die Dicke durch gegeben:

$$h={\sqrt {\frac {2\gamma _{\mathrm {la} }\left(1-\cos \theta \right)}{g\rho }}}.$$

ⓘ

Für Quecksilber auf Glas: γ_Hg = 487 dyn/cm, ρ_Hg = 13,5 g/cm³ und θ = 140°, was h_Hg = 0,36 cm ergibt. Für Wasser auf Paraffin bei 25 °C gilt γ = 72 dyn/cm, ρ = 1,0 g/cm³ und θ = 107°, was h_H2O = 0,44 cm ergibt. ⓘ

Die Formel sagt auch voraus, dass sich die Flüssigkeit bei einem Kontaktwinkel von 0° in einer mikrodünnen Schicht auf der Oberfläche ausbreitet. Eine solche Oberfläche gilt als vollständig von der Flüssigkeit benetzbar. ⓘ

Das Aufbrechen von Strömen in Tropfen

Aufbrechen eines langgestreckten Wasserstrahls in Tropfen aufgrund der Oberflächenspannung. ⓘ

Im täglichen Leben können wir alle beobachten, dass ein Wasserstrahl, der aus einem Wasserhahn kommt, in Tropfen zerfällt, ganz gleich, wie gleichmäßig er aus dem Wasserhahn austritt. Dies ist auf ein Phänomen zurückzuführen, das als Plateau-Rayleigh-Instabilität bezeichnet wird und ausschließlich auf die Auswirkungen der Oberflächenspannung zurückzuführen ist. ⓘ

Die Erklärung für diese Instabilität beginnt mit der Existenz winziger Störungen in der Strömung. Diese sind immer vorhanden, unabhängig davon, wie glatt die Strömung ist. Wenn man die Störungen in sinusförmige Komponenten auflöst, stellt man fest, dass einige Komponenten mit der Zeit wachsen, während andere mit der Zeit abklingen. Unter den Komponenten, die mit der Zeit wachsen, wachsen einige schneller als andere. Ob eine Komponente ab- oder zunimmt und wie schnell sie zunimmt, hängt ganz von ihrer Wellenzahl (ein Maß für die Anzahl der Spitzen und Täler pro Zentimeter) und den Radien des ursprünglichen zylindrischen Stroms ab. ⓘ

Thermodynamik

Thermodynamische Theorien der Oberflächenspannung

J.W. Gibbs entwickelte die thermodynamische Theorie der Kapillarität auf der Grundlage der Kapillarität, die auf der Idee der Diskontinuitätsflächen beruht. Gibbs betrachtete den Fall einer scharfen mathematischen Oberfläche, die sich irgendwo innerhalb der mikroskopisch unscharfen physikalischen Grenzfläche zwischen zwei homogenen Substanzen befindet. Da er erkannte, dass die genaue Wahl des Ortes, an dem sich die Oberfläche befindet, etwas willkürlich war, ließ er sie flexibel. Da sich die Grenzfläche im thermischen und chemischen Gleichgewicht mit den sie umgebenden Stoffen befindet (mit der Temperatur T und den chemischen Potenzialen μi), betrachtete Gibbs den Fall, dass die Oberfläche überschüssige Energie, überschüssige Entropie und überschüssige Teilchen aufweisen kann, und stellte fest, dass die natürliche freie Energiefunktion in diesem Fall wie folgt lautet $U-TS-\mu _{1}N_{1}-\mu _{2}N_{2}\cdots$eine Größe, die später als das große Potenzial bezeichnet und mit dem Symbol $\Omega$. ⓘ

Gibbs' Einordnung einer präzisen mathematischen Oberfläche in eine unscharfe physikalische Schnittstelle. ⓘ

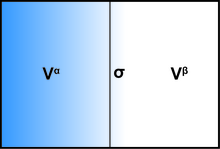
Betrachtet man ein bestimmtes Teilvolumen $V$ das eine Diskontinuitätsfläche enthält, wird das Volumen durch die mathematische Oberfläche in zwei Teile A und B mit den Volumina $V_{\text{A}}$ und $V_{\text{B}}$mit $V=V_{\text{A}}+V_{\text{B}}$ genau. Wenn nun die beiden Teile A und B homogene Fluide (mit Drücken $p_{\text{A}}$, $p_{\text{B}}$) wären und bis zur mathematischen Grenze vollkommen homogen blieben, ohne Oberflächeneffekte, wäre das gesamte große Potenzial dieses Volumens einfach $-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}$. Die interessierenden Oberflächeneffekte sind eine Abwandlung davon, und sie können alle in einem Term der freien Oberflächenenergie zusammengefasst werden $\Omega _{\text{S}}$ zusammengefasst werden, so dass das gesamte große Potenzial des Volumens gleich ist:

$$\Omega =-p_{\text{A}}V_{\text{A}}-p_{\text{B}}V_{\text{B}}+\Omega _{\text{S}}.$$

ⓘ

Für hinreichend makroskopische und leicht gekrümmte Oberflächen muss die freie Oberflächenenergie einfach proportional zum Oberflächenbereich sein:

$$\Omega _{\text{S}}=\gamma A,$$

für die Oberflächenspannung $\gamma$ und Oberflächenbereich $A$. ⓘ

Wie bereits erwähnt, bedeutet dies, dass die zur Vergrößerung einer Oberfläche A erforderliche mechanische Arbeit dW = γ dA ist, vorausgesetzt, die Volumina auf beiden Seiten ändern sich nicht. Die Thermodynamik verlangt, dass für Systeme mit konstantem chemischem Potenzial und konstanter Temperatur alle spontanen Zustandsänderungen mit einer Abnahme dieser freien Energie einhergehen $\Omega$d. h. eine Zunahme der Gesamtentropie unter Berücksichtigung der möglichen Bewegung von Energie und Teilchen von der Oberfläche in die umgebenden Fluide. Daher ist es leicht zu verstehen, warum die Verkleinerung der Oberfläche einer Flüssigkeitsmasse immer spontan erfolgt, sofern sie nicht mit anderen Energieänderungen verbunden ist. Daraus folgt, dass zur Vergrößerung der Oberfläche eine bestimmte Menge an Energie zugeführt werden muss. ⓘ

Gibbs und andere Wissenschaftler haben mit der Willkürlichkeit der genauen mikroskopischen Anordnung der Oberfläche gerungen. Bei mikroskopischen Oberflächen mit sehr engen Krümmungen ist es nicht korrekt anzunehmen, dass die Oberflächenspannung unabhängig von der Größe ist, und Themen wie die Tolman-Länge kommen ins Spiel. Für eine makroskopische Oberfläche (und ebene Oberflächen) hat die Anordnung der Oberfläche keine signifikante Auswirkung auf γ, aber sie hat eine sehr starke Auswirkung auf die Werte der Oberflächenentropie, der Oberflächenüberschußdichte und der inneren Energie der Oberfläche, die die partiellen Ableitungen der Oberflächenspannungsfunktion sind $\gamma (T,\mu _{1},\mu _{2},\cdots )$. ⓘ

Gibbs betonte, dass bei Festkörpern die freie Oberflächenenergie völlig anders sein kann als die Oberflächenspannung (die er als Oberflächenspannung bezeichnete): Die freie Oberflächenenergie ist die Arbeit, die erforderlich ist, um die Oberfläche zu bilden, während die Oberflächenspannung die Arbeit ist, die erforderlich ist, um die Oberfläche zu dehnen. Bei einer Grenzfläche zwischen zwei Flüssigkeiten gibt es keine Unterscheidung zwischen Verformung und Dehnung, da die Flüssigkeiten und die Oberfläche ihre Natur vollständig erneuern, wenn die Oberfläche gedehnt wird. Bei einem Festkörper führt die Dehnung der Oberfläche, selbst wenn sie elastisch ist, zu einer grundlegend veränderten Oberfläche. Außerdem ist die Oberflächenspannung auf einem Festkörper eine gerichtete Größe (ein Spannungstensor), während die Oberflächenenergie skalar ist. ⓘ

Fünfzehn Jahre nach Gibbs entwickelte J.D. van der Waals die Theorie der Kapillareffekte, die auf der Hypothese einer kontinuierlichen Veränderung der Dichte beruht. Er fügte der Energiedichte den Term $c(\nabla \rho )^{2},$ wobei c der Kapillaritätskoeffizient und ρ die Dichte ist. Für Mehrphasengleichgewichte stimmen die Ergebnisse des van-der-Waals-Ansatzes praktisch mit den Gibbs-Formeln überein, aber für die Modellierung der Dynamik von Phasenübergängen ist der van-der-Waals-Ansatz wesentlich geeigneter. Die van-der-Waals-Kapillaritätsenergie wird heute in den Phasenfeldmodellen von Mehrphasenströmungen häufig verwendet. Solche Terme werden auch in der Dynamik von Nicht-Gleichgewichtsgasen entdeckt. ⓘ

Thermodynamik von Blasen

Der Druck im Inneren einer idealen kugelförmigen Blase lässt sich aus Überlegungen zur thermodynamischen freien Energie ableiten. Die oben genannte freie Energie kann wie folgt geschrieben werden:

$$\Omega =-\Delta PV_{\text{A}}-p_{\text{B}}V+\gamma A$$

wobei $\Delta P=p_{\text{A}}-p_{\text{B}}$ ist der Druckunterschied zwischen dem Inneren (A) und dem Äußeren (B) der Blase, und $V_{\text{A}}$ ist das Volumen der Blase. Im Gleichgewicht ist dΩ = 0, und so,

$$\Delta P\,dV_{\text{A}}=\gamma \,dA.$$

ⓘ

Für eine kugelförmige Blase sind das Volumen und der Oberflächenbereich einfach gegeben durch

$$V_{\text{A}}={\tfrac {4}{3}}\pi R^{3}\quad \rightarrow \quad dV_{\text{A}}=4\pi R^{2}\,dR,$$

und

$$A=4\pi R^{2}\quad \rightarrow \quad dA=8\pi R\,dR.$$

ⓘ

Setzt man diese Beziehungen in den vorhergehenden Ausdruck ein, so erhält man

$$\Delta P={\frac {2}{R}}\gamma ,$$

was der Young-Laplace-Gleichung entspricht, wenn R_x = R_y ist. ⓘ

Einfluss der Temperatur

Temperaturabhängigkeit der Oberflächenspannung zwischen der flüssigen und der dampfförmigen Phase von reinem Wasser ⓘ

Temperaturabhängigkeit der Oberflächenspannung von Benzol ⓘ

Die Oberflächenspannung ist von der Temperatur abhängig. Aus diesem Grund muss bei der Angabe eines Wertes für die Oberflächenspannung einer Grenzfläche die Temperatur explizit angegeben werden. Im Allgemeinen nimmt die Oberflächenspannung mit steigender Temperatur ab und erreicht bei der kritischen Temperatur einen Wert von 0. Für weitere Einzelheiten siehe Eötvös-Regel. Es gibt nur empirische Gleichungen für den Zusammenhang zwischen Oberflächenspannung und Temperatur:

• Eötvös:
  $$\gamma V^{2/3}=k(T_{\mathrm {C} }-T).$$
  Dabei ist V das molare Volumen eines Stoffes, T_C die kritische Temperatur und k eine für fast alle Stoffe gültige Konstante. Ein typischer Wert ist k = 2,1×10-7 J K-1 mol-2⁄3. Für Wasser kann man weiterhin V = 18 ml/mol und T_C = 647 K (374 °C) verwenden. Eine Variante von Eötvös wird von Ramay und Shields beschrieben:
  $$\gamma V^{2/3}=k\left(T_{\mathrm {C} }-T-6\right)$$
  Der Temperatur-Offset von 6 K verleiht der Formel eine bessere Übereinstimmung mit der Realität bei niedrigeren Temperaturen.
• Guggenheim-Katayama:
  $$\gamma =\gamma ^{\circ }\left(1-{\frac {T}{T_{\mathrm {C} }}}\right)^{n}$$
  γ° ist eine Konstante für jede Flüssigkeit und n ist ein empirischer Faktor, dessen Wert 11/9 für organische Flüssigkeiten ist. Diese Gleichung wurde auch von van der Waals vorgeschlagen, der darüber hinaus vorschlug, dass γ° durch den folgenden Ausdruck gegeben werden könnte
  $$K_{2}T_{\mathrm {C} }^{1/3}P_{\mathrm {C} }^{2/3},$$
  wobei K₂ eine universelle Konstante für alle Flüssigkeiten und P_C der kritische Druck der Flüssigkeit ist (obwohl spätere Experimente ergaben, dass K₂ in gewissem Maße von einer Flüssigkeit zur anderen variiert). ⓘ

Sowohl Guggenheim-Katayama als auch Eötvös berücksichtigen die Tatsache, dass die Oberflächenspannung bei der kritischen Temperatur den Wert 0 erreicht, während Ramay und Shields an diesem Endpunkt der Realität nicht gerecht werden. ⓘ

Einfluss der Konzentration gelöster Stoffe

Gelöste Stoffe können je nach Beschaffenheit der Oberfläche und des gelösten Stoffes unterschiedliche Auswirkungen auf die Oberflächenspannung haben:

• Geringe oder keine Wirkung, z. B. Zucker bei Wasser/Luft, die meisten organischen Verbindungen bei Öl/Luft
• Erhöhung der Oberflächenspannung, die meisten anorganischen Salze bei Wasser|Luft
• Nicht-monotone Änderung, die meisten anorganischen Säuren an Wasser/Luft
• Verminderung der Oberflächenspannung progressiv, wie bei den meisten Amphiphilen, z.B. Alkohole an Wasser/Luft
• Verminderung der Oberflächenspannung bis zu einer bestimmten kritischen Konzentration, danach keine Wirkung mehr: Tenside, die Mizellen bilden ⓘ

Erschwerend kommt hinzu, dass ein gelöster Stoff an der Oberfläche eines Lösungsmittels in einer anderen Konzentration vorliegen kann als in seiner Masse. Dieser Unterschied variiert von einer Lösungsmittel-Lösungsmittel-Kombination zur anderen. ⓘ

Die Gibbs-Isotherme besagt Folgendes:

$$\Gamma =-{\frac {1}{RT}}\left({\frac {\partial \gamma }{\partial \ln C}}\right)_{T,P}$$

ⓘ

• Γ ist als Oberflächenkonzentration bekannt und stellt den Überschuss des gelösten Stoffes pro Flächeneinheit der Oberfläche gegenüber der Konzentration dar, die vorhanden wäre, wenn die Massenkonzentration bis zur Oberfläche vorherrschen würde. Sie hat die Einheit mol/m²
• C ist die Konzentration der Substanz in der Gesamtlösung.
• R ist die Gaskonstante und T die Temperatur. ⓘ

Bei ihrer Herleitung werden bestimmte Annahmen getroffen, daher kann die Gibbs-Isotherme nur auf ideale (sehr verdünnte) Lösungen mit zwei Komponenten angewendet werden. ⓘ

Einfluss der Partikelgröße auf den Dampfdruck

Die Clausius-Clapeyron-Beziehung führt zu einer weiteren Gleichung, die ebenfalls auf Kelvin zurückgeht, nämlich der Kelvin-Gleichung. Sie erklärt, warum aufgrund der Oberflächenspannung der Dampfdruck für kleine Flüssigkeitströpfchen in Suspension größer ist als der Standarddampfdruck der gleichen Flüssigkeit, wenn die Grenzfläche flach ist. Das heißt, wenn eine Flüssigkeit kleine Tröpfchen bildet, ist die Gleichgewichtskonzentration ihres Dampfes in der Umgebung größer. Dies ist darauf zurückzuführen, dass der Druck im Inneren des Tröpfchens größer ist als außerhalb. ⓘ

$$P_{\mathrm {v} }^{\mathrm {fog} }=P_{\mathrm {v} }^{\circ }e^{V2\gamma /(RTr_{\mathrm {k} })}$$

ⓘ

Die Moleküle auf der Oberfläche eines winzigen Tröpfchens (links) haben im Durchschnitt weniger Nachbarn als die Moleküle auf einer flachen Oberfläche (rechts). Daher sind sie schwächer an das Tröpfchen gebunden als Moleküle auf einer ebenen Oberfläche. ⓘ

• P_v° ist der Standard-Dampfdruck für diese Flüssigkeit bei dieser Temperatur und diesem Druck.
• V ist das molare Volumen.
• R ist die Gaskonstante
• rk ist der Kelvin-Radius, also der Radius der Tröpfchen. ⓘ

Der Effekt erklärt die Übersättigung von Dämpfen. In Ermangelung von Keimbildungsstellen müssen sich winzige Tröpfchen bilden, bevor sie sich zu größeren Tröpfchen entwickeln können. Dazu ist ein Dampfdruck erforderlich, der ein Vielfaches des Dampfdrucks am Phasenübergangspunkt beträgt. ⓘ

Diese Gleichung wird auch in der Katalysatorchemie verwendet, um die Mesoporosität von Feststoffen zu bewerten. ⓘ

Der Effekt kann in Form der durchschnittlichen Anzahl der molekularen Nachbarn der Oberflächenmoleküle betrachtet werden (siehe Diagramm). ⓘ

Die Tabelle zeigt einige berechnete Werte dieses Effekts für Wasser bei verschiedenen Tropfengrößen:

P/P0 für Wassertropfen mit verschiedenen Radien bei STP ⓘ
Tröpfchenradius (nm)	1000	100	10	1
P/P0	1.001	1.011	1.114	2.95

Der Effekt wird bei sehr kleinen Tropfengrößen deutlich, da sich in einem Tropfen mit einem Radius von 1 nm etwa 100 Moleküle befinden, eine Menge, die klein genug ist, um eine quantenmechanische Analyse zu erfordern. ⓘ

Oberflächenspannung von Wasser und Meerwasser

Die beiden auf der Erde am häufigsten vorkommenden Flüssigkeiten sind Süßwasser und Meerwasser. In diesem Abschnitt werden Korrelationen von Referenzdaten für die Oberflächenspannung von beiden angegeben. ⓘ

Oberflächenspannung von Wasser

Die Oberflächenspannung von reinem, flüssigem Wasser in Kontakt mit dem Wasserdampf wird vom IAPWS wie folgt angegeben ⓘ

$$\gamma _{\text{w}}=235.8\left(1-{\frac {T}{T_{\text{C}}}}\right)^{1.256}\left[1-0.625\left(1-{\frac {T}{T_{\text{C}}}}\right)\right]~{\text{mN/m}},$$

ⓘ

wobei sowohl T als auch die kritische Temperatur T_C = 647,096 K in Kelvin angegeben sind. Der Gültigkeitsbereich umfasst die gesamte Dampf-Flüssigkeits-Sättigungskurve, vom Tripelpunkt (0,01 °C) bis zum kritischen Punkt. Sie liefert auch vernünftige Ergebnisse, wenn sie auf metastabile (unterkühlte) Bedingungen extrapoliert wird, und zwar bis zu mindestens -25 °C. Diese Formulierung wurde ursprünglich 1976 vom IAPWS angenommen und 1994 an die Internationale Temperaturskala von 1990 angepasst. ⓘ

Die Unsicherheit dieser Formulierung wird von IAPWS für den gesamten Temperaturbereich angegeben. Für Temperaturen unter 100 °C beträgt die Unsicherheit ±0,5 %. ⓘ

Oberflächenspannung von Meerwasser

Nayar et al. veröffentlichten Referenzdaten für die Oberflächenspannung von Meerwasser über den Salzgehalt von 20 ≤ S ≤ 131 g/kg und einen Temperaturbereich von 1 ≤ t ≤ 92 °C bei atmosphärischem Druck. Der Temperatur- und Salzgehaltsbereich umfasst sowohl den ozeanographischen Bereich als auch den Bereich der Bedingungen, die bei thermischen Entsalzungstechnologien anzutreffen sind. Die Unsicherheit der Messungen lag zwischen 0,18 und 0,37 mN/m, wobei die durchschnittliche Unsicherheit 0,22 mN/m betrug. ⓘ

Nayar et al. korrelierten die Daten mit der folgenden Gleichung

$$\gamma _{\mathrm {sw} }=\gamma _{\mathrm {w} }\left(1+3.766\times 10^{-4}S+2.347\times 10^{-6}St\right)$$

wobei γ_sw die Oberflächenspannung von Meerwasser in mN/m, γ_w die Oberflächenspannung von Wasser in mN/m, S der Bezugssalzgehalt in g/kg und t die Temperatur in Grad Celsius ist. Die durchschnittliche absolute prozentuale Abweichung zwischen den Messungen und der Korrelation betrug 0,19 %, während die maximale Abweichung 0,60 % betrug. ⓘ

Die International Association for the Properties of Water and Steam (IAPWS) hat diese Korrelation als internationale Standardrichtlinie angenommen. ⓘ

Tabelle der Daten

Oberflächenspannung von verschiedenen Flüssigkeiten in dyn/cm gegen Luft
Die mit "%" bezeichneten Mischungszusammensetzungen sind Massenanteile
dyn/cm ist äquivalent zu den SI-Einheiten mN/m (Millinewton pro Meter) ⓘ

Flüssigkeit	Temperatur (°C)	Oberflächenspannung, γ
Essigsäure	20	27.60
Essigsäure (45,1%) + Wasser	30	40.68
Essigsäure (10,0%) + Wasser	30	54.56
Aceton	20	23.70
Blut	22	55.89
Diethylether	20	17.00
Ethanol	20	22.27
Ethanol (40%) + Wasser	25	29.63
Ethanol (11,1%) + Wasser	25	46.03
Glycerin	20	63.00
n-Hexan	20	18.40
Salzsäure 17,7 M wässrige Lösung	20	65.95
Isopropanol	20	21.70
Flüssiges Helium II	−273	0.37
Flüssiger Stickstoff	−196	8.85
Flüssiger Sauerstoff	−182	13.2
Quecksilber	15	487.00
Methanol	20	22.60
Geschmolzenes Silberchlorid	650	163
Geschmolzenes Natriumchlorid/Calciumchlorid (47/53 Mol-%)	650	139
n-Oktan	20	21.80
Natriumchlorid 6,0 M wässrige Lösung	20	82.55
Saccharose (55%) + Wasser	20	76.45
Wasser	0	75.64
Wasser	25	71.97
Wasser	50	67.91
Wasser	100	58.85
Toluol	25	27.73

Wasser hat also eine vergleichsweise hohe Oberflächenspannung (siehe auch Drucktabellen Wasser in WikiBooks). ⓘ

Galerie der Effekte

• 

  Auflösung eines sich bewegenden Wasserstrahls, der an einem Löffel abprallt.

• 

  Foto von fließendem Wasser, das an einer Hand haften bleibt. Die Oberflächenspannung erzeugt die Wasserschicht zwischen der Strömung und der Hand.

• 

  Eine Seifenblase gleicht die Kräfte der Oberflächenspannung mit dem inneren pneumatischen Druck aus.

• 

  Die Oberflächenspannung verhindert, dass eine Münze untergeht: Die Münze ist unbestreitbar dichter als Wasser, also muss sie ein größeres Volumen als ihr eigenes verdrängen, damit der Auftrieb die Masse ausgleicht.

• 

  Eine Aluminiummünze schwimmt bei 10 °C auf der Wasseroberfläche. Jedes zusätzliche Gewicht würde die Münze auf den Grund sinken lassen.

• 

  Ein Gänseblümchen. Die Gesamtheit der Blüte liegt unter dem Niveau der (ungestörten) freien Oberfläche. Das Wasser steigt sanft um den Rand der Blüte herum auf. Die Oberflächenspannung verhindert, dass das Wasser die Luft zwischen den Blütenblättern verdrängt und die Blume möglicherweise unter Wasser setzt.

• 

  Eine Büroklammer aus Metall schwimmt auf dem Wasser. In der Regel können mehrere vorsichtig hinzugefügt werden, ohne dass das Wasser überläuft.

• 

  Eine Büroklammer aus Metall schwimmt auf dem Wasser. Ein Gitter vor dem Licht hat die "Konturlinien" erzeugt, die die durch die Metallbüroklammer verursachte Verformung der Wasseroberfläche zeigen. ⓘ

Messung

Bügelmethode

Messung der Oberflächenspannung mit der Bügelmethode ⓘ

Bügel in der Flüssigkeit ⓘ

Bei der Bügelmethode (auch als Abreißmethode bekannt) wird ein Bügel mit einem darin eingelöteten extrem dünnen Draht (meist aus Platin) in die Flüssigkeit gehängt, sodass dieser gerade in die Flüssigkeit eintaucht und von dieser benetzt wird. Mit einer Präzisionsfederwaage wird dann die Zugkraft am Bügel nach und nach erhöht. Der Draht wird dann aus der Flüssigkeit gezogen und zieht einen Flüssigkeitsfilm mit. An einem bestimmten Punkt reißt dieser Film ab. ⓘ

Durch das Ziehen am Bügel wird Arbeit gegen die Oberflächenspannung verrichtet. Aus der maximal möglichen Zugkraft am Bügel, bevor der Flüssigkeitsfilm abreißt, den Abmessungen des Bügels und der Dichte der Flüssigkeit kann dann die Oberflächenspannung berechnet werden. ⓘ

Bei Flüssigkeiten wie Ethanol und Drahtlängen von 2–3 cm bei einem Radius von 0,1 mm liegt der Erwartungswert für die Masse im zwei- bis dreistelligen Milligramm-Bereich. Es sind also sehr präzise Waagen nötig. Bei einer Messunsicherheit der Waage von 5 mg und einer Vermessung des Drahtes auf 1 µm genau beträgt der größte Fehler des Endergebnisses bereits 8 bis 12 %. ⓘ

Messung mit dem Kapillareffekt

Kapillare in der Messflüssigkeit ⓘ

Bei dieser Messmethode macht man sich den Kapillareffekt zunutze, also, dass Flüssigkeiten in dünnen Röhren nach oben steigen. Man benötigt ein Gefäß (etwa eine Küvette) und eine möglichst dünne Kapillare. Diese wird dann einfach in die Flüssigkeit gestellt und die Steighöhe wird gemessen. ⓘ

Da die Flüssigkeit theoretisch unendlich lange braucht, um ihren Endstand zu erreichen, zieht man die Flüssigkeit zunächst in der Kapillare (etwa mit einer Spritze) nach oben und lässt sie anschließend wieder absinken. Die Oberflächenspannung kann dann direkt aus der Steighöhe abgelesen werden, wenn die Dichte der Flüssigkeit und der Kapillarradius bekannt sind. Da dessen Messung recht schwierig ist, nimmt man Einmalmikropipetten und misst deren Länge. Da das Volumen bekannt ist, lässt sich so der Innenradius berechnen. ⓘ

Wasser erreicht in Kapillaren mit einem Radius von 0,2 mm Steighöhen von bis zu 7 cm. Für die möglichst exakte Messung der Steighöhe eignet sich beispielsweise ein Kathetometer. Ist die Dichte der Flüssigkeit genau bekannt und kann man die Steighöhe auf 0,1 mm genau ablesen, liegt der Fehler im unteren einstelligen Prozentbereich. ⓘ

Historisches

Der Begriff der Oberflächenspannung wurde erstmals 1629 von Niccolò Cabeo verwendet und 1751 von Johann Andreas von Segner klarer gefasst. Zur Theorie wurde 1805 von Thomas Young, 1806 von Pierre-Simon Laplace, 1830 von Siméon Denis Poisson (siehe auch Young-Laplace-Gleichung, Youngsche Gleichung) und 1842 bis 1868 von Joseph Plateau Wertvolles beigetragen. ⓘ