Schmelzpunkt

Schmelzpunkt Θ (Theta) einiger Substanzen bei Normaldruck von 1013 Hektopascal ⓘ

Material	°C	K
Helium (bei 26 bar)	−272,2	0000,955
Wasserstoff	−259	0014
Deuterium	−254	0019
Tritium	−253	0020
Neon	−248	0025
Sauerstoff	−218	0055
Stickstoff	−210	0063
Ozon	−193	0080
Ethanol (C2H5OH)	−114	0159
Chlor	−102	0171
Motorenbenzin	0−40	0233
Quecksilber	0−38,36	0234,795
Glykoldinitrat	0−22	0251
Wasser	0000	0273,152
Nitroglycerin	0002	0275,95
Benzol	0005,5	0278,7
Kerzenwachs	0055	0328
Naphthalin	0080	0353
Trinitrotoluol	0080,35	0353,20
Schwefel (rhombisch)	0113	0386
Schwefel (monoklin)	0119	0392
Zucker	0160	0433
Lithium	0180	0453
Zinn	0231	0504
Blei	0327,4	0600,6
Zink	0419,5	0692,7
Aluminium	0660,32	0933,48
Kochsalz	0801	1074
Silber	0960,8	1234,0
Gold	1064	1337
Kupfer	1084	1357
Beryllium	1287	1560
Eisen	1536	1809
Platin	1773,5	2046,7
Bor	2076	2349
Thoriumoxid (ThO2)	3390	3663
Wolfram	3422	3695
Hafniumcarbid (HfC)	3890	4163
Tantalcarbid	3942	4215
Tantalhafniumcarbid	4215	4488

Als Schmelztemperatur (vulgo Schmelzpunkt (Smp.), engl. Melting point (Mp.)) bezeichnet man die Temperatur, bei der ein Stoff schmilzt, das heißt vom festen in den flüssigen Aggregatzustand übergeht. Die Schmelztemperatur ist abhängig vom Stoff, im Gegensatz zur Siedetemperatur aber nur sehr wenig vom Druck (Schmelzdruck). Schmelztemperatur und Druck werden zusammen als Schmelzpunkt bezeichnet, wobei dieser den Zustand eines Reinstoffes beschreibt und Teil der Schmelzkurve im Phasendiagramm des Stoffes ist. Manche Stoffe können nicht schmelzen, weil sie vorher chemisch zerfallen, und andere können bei Normalbedingungen nur sublimieren. ⓘ

Für reine chemische Elemente ist der Schmelzpunkt identisch mit dem Gefrierpunkt und bleibt während des gesamten Schmelzvorganges konstant. Durch Verunreinigungen bzw. bei Gemischen wird die Schmelztemperatur in der Regel erniedrigt (Schmelzpunkterniedrigung), außerdem kann die Temperatur während des Schmelzvorganges steigen, wodurch man es mit einem Schmelz-Bereich zu tun hat. Die Schmelzpunkterniedrigung (Kryoskopie) durch gelöste Substanzen ist ein Grund, warum Eis durch Salz geschmolzen werden kann. ⓘ

Im Unterschied zu chemischen Elementen kann es auch bei reinen chemischen Verbindungen zu Abweichungen zwischen Schmelzpunkt und Gefrierpunkt kommen. Falls die Gefrierpunktstemperatur unterhalb der Schmelzpunkttemperatur liegt, spricht man von einer thermischen Hysterese. Dies ist zum Beispiel bei reinem Wasser der Fall; ohne Nukleationskeime und unter einem Druck von 1 bar gefriert Wasser bei ca. −40 °C und schmilzt bei ca. 0 °C. Bei amorphen Werkstoffen wie z. B. Gläsern und einigen Kunststoffen spricht man von der Übergangstemperatur. Auch die Definition einer Erweichungstemperatur ist möglich. ⓘ

Die Schmelztemperatur zählt mit der Dichte, Risszähigkeit, Festigkeit, Duktilität und der Härte, zu den Werkstoffeigenschaften eines Werkstoffes. ⓘ

Den größten flüssigen Bereich von 630 °C bis 3900 °C, also über 3270 °C, besitzt das Element Neptunium. Den kleinsten Flüssigbereich von −248,6 °C bis −246,3 °C hat das Edelgas Neon mit 2,3 °C. ⓘ

Betrachtet man ihn als die Temperatur des umgekehrten Übergangs von der flüssigen in die feste Phase, so spricht man vom Gefrierpunkt oder Kristallisationspunkt. Aufgrund der Fähigkeit von Stoffen zur Unterkühlung kann der Gefrierpunkt leicht unter seinem tatsächlichen Wert liegen. Bei der Bestimmung des "charakteristischen Gefrierpunkts" einer Substanz ist die eigentliche Methodik fast immer "das Prinzip der Beobachtung des Verschwindens und nicht der Bildung von Eis, d. h. der Schmelzpunkt". ⓘ

Beispiele

Schmelzpunkte (in blau) und Siedepunkte (in rosa) der ersten acht Carbonsäuren (°C) ⓘ

Bei den meisten Stoffen sind die Schmelz- und Gefrierpunkte ungefähr gleich. Der Schmelz- und Gefrierpunkt von Quecksilber liegt beispielsweise bei 234,32 Kelvin (-38,83 °C; -37,89 °F). Bestimmte Stoffe weisen jedoch unterschiedliche Fest-Flüssig-Übergangstemperaturen auf. Agar zum Beispiel schmilzt bei 85 °C (185 °F; 358 K) und erstarrt ab 31 °C (88 °F; 304 K); diese Richtungsabhängigkeit wird als Hysterese bezeichnet. Der Schmelzpunkt von Eis bei 1 Atmosphäre Druck liegt sehr nahe bei 0 °C (32 °F; 273 K); er wird auch als Eispunkt bezeichnet. In Gegenwart von Keimbildnern ist der Gefrierpunkt von Wasser nicht immer mit dem Schmelzpunkt identisch. In Abwesenheit von Keimbildnern kann Wasser als unterkühlte Flüssigkeit bis zu -48,3 °C (-54,9 °F; 224,8 K) existieren, bevor es gefriert. ⓘ

Das Metall mit dem höchsten Schmelzpunkt ist Wolfram mit 3.414 °C (6.177 °F; 3.687 K); aufgrund dieser Eigenschaft eignet sich Wolfram hervorragend zur Verwendung als elektrischer Glühfaden in Glühlampen. Der oft zitierte Kohlenstoff schmilzt nicht bei Umgebungsdruck, sondern sublimiert bei etwa 3.700 °C (6.700 °F; 4.000 K); eine flüssige Phase existiert erst oberhalb eines Drucks von 10 MPa (99 atm) und geschätzten 4.030-4.430 °C (7.290-8.010 °F; 4.300-4.700 K) (siehe Kohlenstoff-Phasendiagramm). Tantal-Hafnium-Karbid (Ta₄HfC₅) ist eine feuerfeste Verbindung mit einem sehr hohen Schmelzpunkt von 4.215 K (3.942 °C; 7.127 °F). Quantenmechanische Computersimulationen haben vorausgesagt, dass die Legierung HfN_0.38C_0.51 einen noch höheren Schmelzpunkt (etwa 4400 K) haben wird, was sie zum Stoff mit dem höchsten Schmelzpunkt bei Umgebungsdruck machen würde. Diese Vorhersage wurde später durch Experimente bestätigt. Am anderen Ende der Skala gefriert Helium bei normalem Druck selbst bei Temperaturen, die willkürlich nahe dem absoluten Nullpunkt liegen, überhaupt nicht; dazu ist ein Druck erforderlich, der mehr als das Zwanzigfache des normalen atmosphärischen Drucks beträgt. ⓘ

Liste der gebräuchlichen Chemikalien ⓘ
Chemikalie	Dichte (g/cm3)	Schmelze (K)	Siedepunkt (K)
Wasser @STP	1	273	373
Lötmittel (Pb60Sn40)		456
Kakaobutter		307.2	-
Paraffinwachs	0.9	310	643
Wasserstoff	0.00008988	14.01	20.28
Helium	0.0001785	—	4.22
Beryllium	1.85	1560	2742
Kohlenstoff	2.267	—	4000
Stickstoff	0.0012506	63.15	77.36
Sauerstoff	0.001429	54.36	90.20
Natrium	0.971	370.87	1156
Magnesium	1.738	923	1363
Aluminium	2.698	933.47	2792
Schwefel	2.067	388.36	717.87
Chlor	0.003214	171.6	239.11
Kalium	0.862	336.53	1032
Titan	4.54	1941	3560
Eisen	7.874	1811	3134
Nickel	8.912	1728	3186
Kupfer	8.96	1357.77	2835
Zink	7.134	692.88	1180
Gallium	5.907	302.9146	2673
Silber	10.501	1234.93	2435
Cadmium	8.69	594.22	1040
Indium	7.31	429.75	2345
Jod	4.93	386.85	457.4
Tantal	16.654	3290	5731
Wolfram	19.25	3695	5828
Platin	21.46	2041.4	4098
Gold	19.282	1337.33	3129
Quecksilber	13.5336	234.43	629.88
Blei	11.342	600.61	2022
Wismut	9.807	544.7	1837
Anmerkungen

Schmelzpunktmessungen

Eine ungefähre Messung ist mit einem Thermometer durch Aufschmelzen der Probe und Ablesen der Schmelztemperatur möglich. ⓘ

Für die exakte Messung des Schmelzpunktes stehen unterschiedliche Methoden zur Verfügung:

• Apparatur nach Thiele, bei der die Probe in einem gerührten oder durch Konvektion strömenden Ölbad geschmolzen wird
• Apparatur nach DAB, mit Normschliff 29/32, bestehend aus Kolben von ca. 100 ml und Einsatzrohr mit Entlüftungsloch
• Apparatur nach Dr. C. F. Linström (oft fälschlich auch Lindström geschrieben), hierbei wird die Probe in einem Kupferblock bis zum Schmelzpunkt erwärmt
• Heiztischapparatur nach Kofler (siehe auch Kofler-Heizbank), Tottoli
• Dynamische Differenzkalorimetrie (DSC)
• Bei der Kapillarmethode wird die zu untersuchende Substanz in eine Glaskapillare eingebracht. Diese wird in einen vorgeheizten Heizblock eingesetzt und die Temperatur langsam erhöht. Als Schmelztemperatur gilt hierbei die Temperatur, bei der das letzte feste Teilchen schmilzt. ⓘ

• 

  Schmelzpunktbestimmungsapparat nach Thiele

• 

  Koflerbank mit Proben zum Kalibrieren

• 

  Automatisches Schmelz­punktmessgerät M5000 ⓘ

Meist werden die Messwerte damit gekennzeichnet, dass sie nicht korrigiert sind. Diese Angabe bezieht sich auf den (geringen) Fehler, der dadurch entsteht, dass von einem Flüssigkeitsthermometer nur dessen Reservoir in das zu bestimmende Medium taucht, wodurch der in der Kapillare aufsteigende Teil der Thermometerflüssigkeit eine andere Temperatur und Ausdehnung hat. ⓘ

Im praktischen Laborbetrieb finden heute meist automatische Schmelzpunktmessgeräte Verwendung, die das Ergebnis in kurzer Zeit digital liefern. ⓘ

Kofler-Bank mit Proben zur Kalibrierung ⓘ

Für die Bestimmung von Schmelzpunkten gibt es viele Labortechniken. Eine Kofler-Bank ist ein Metallstreifen mit einem Temperaturgradienten (von Raumtemperatur bis 300 °C). Eine beliebige Substanz kann auf einen Abschnitt des Streifens gelegt werden, wodurch ihr thermisches Verhalten bei der Temperatur an diesem Punkt sichtbar wird. Die Differential-Scanning-Kalorimetrie liefert Informationen über den Schmelzpunkt und die Schmelzenthalpie. ⓘ

Eine einfache Schmelzpunktapparatur für die Analyse kristalliner Feststoffe besteht aus einem Ölbad mit einem durchsichtigen Fenster (einfachste Ausführung: ein Thiele-Rohr) und einer einfachen Lupe. Mehrere Körner eines Feststoffs werden in ein dünnes Glasrohr gegeben und teilweise in das Ölbad getaucht. Das Ölbad wird erhitzt (und gerührt) und mit Hilfe der Lupe (und einer externen Lichtquelle) kann das Schmelzen der einzelnen Kristalle bei einer bestimmten Temperatur beobachtet werden. Anstelle eines Ölbads kann auch ein Metallblock verwendet werden. Einige moderne Geräte verfügen über eine automatische optische Erkennung. ⓘ

Die Messung kann auch kontinuierlich während eines Betriebsprozesses durchgeführt werden. In Ölraffinerien wird beispielsweise der Gefrierpunkt von Dieselkraftstoff "online" gemessen, d. h. die Probe wird aus dem Prozess genommen und automatisch gemessen. Dies ermöglicht häufigere Messungen, da die Probe nicht manuell entnommen und in ein entferntes Labor gebracht werden muss. ⓘ

Techniken für feuerfeste Materialien

Bei feuerfesten Materialien (z. B. Platin, Wolfram, Tantal, einige Karbide und Nitride usw.) kann der extrem hohe Schmelzpunkt (der üblicherweise bei über 1800 °C liegt) durch Erhitzen des Materials in einem Schwarzkörperofen und Messung der Schwarzkörpertemperatur mit einem optischen Pyrometer bestimmt werden. Bei den höchstschmelzenden Materialien kann dies eine Extrapolation um mehrere hundert Grad erfordern. Es ist bekannt, dass die spektrale Strahldichte eines glühenden Körpers eine Funktion seiner Temperatur ist. Ein optisches Pyrometer gleicht die Strahldichte eines zu untersuchenden Körpers mit der Strahldichte einer Quelle ab, die zuvor als Funktion der Temperatur kalibriert worden ist. Auf diese Weise erübrigt sich die Messung des absoluten Betrags der Strahlungsintensität. Zur Bestimmung der Kalibrierung des Pyrometers müssen jedoch bekannte Temperaturen verwendet werden. Für Temperaturen, die über dem Kalibrierungsbereich der Quelle liegen, muss eine Extrapolationstechnik angewendet werden. Diese Extrapolation wird mit Hilfe des Planckschen Strahlungsgesetzes durchgeführt. Die Konstanten in dieser Gleichung sind nicht mit ausreichender Genauigkeit bekannt, so dass die Fehler bei der Extrapolation bei höheren Temperaturen größer werden. Es wurden jedoch Standardtechniken entwickelt, um diese Extrapolation durchzuführen. ⓘ

Nehmen wir den Fall, dass Gold als Quelle verwendet wird (mp = 1063 °C). Bei dieser Technik wird der Strom durch die Glühwendel des Pyrometers so eingestellt, dass die Lichtintensität der Glühwendel der eines schwarzen Körpers am Schmelzpunkt von Gold entspricht. Damit ist die primäre Kalibriertemperatur festgelegt, die durch den Strom durch die Pyrometerlampe ausgedrückt werden kann. Mit der gleichen Stromeinstellung wird das Pyrometer auf einen anderen schwarzen Körper mit einer höheren Temperatur gerichtet. Zwischen Pyrometer und Schwarzem Strahler wird ein absorbierendes Medium mit bekannter Transmission eingefügt. Die Temperatur des schwarzen Strahlers wird dann so lange eingestellt, bis die Intensität des schwarzen Strahlers mit der des Pyrometerfadens übereinstimmt. Die tatsächliche höhere Temperatur des schwarzen Körpers wird dann anhand des Planckschen Gesetzes bestimmt. Dann wird das absorbierende Medium entfernt und der Strom durch den Glühfaden so eingestellt, dass die Intensität des Glühfadens mit der des schwarzen Körpers übereinstimmt. Damit wird ein zweiter Kalibrierungspunkt für das Pyrometer festgelegt. Dieser Schritt wird wiederholt, um die Kalibrierung auf höhere Temperaturen zu übertragen. Nun sind die Temperaturen und die entsprechenden Pyrometer-Fadenströme bekannt, und es kann eine Kurve der Temperatur in Abhängigkeit vom Strom erstellt werden. Diese Kurve kann dann auf sehr hohe Temperaturen extrapoliert werden. ⓘ

Um den Schmelzpunkt einer feuerfesten Substanz mit dieser Methode zu bestimmen, müssen entweder Schwarzkörperbedingungen herrschen oder der Emissionsgrad des zu messenden Materials bekannt sein. Das Einschließen des hochschmelzenden Materials im flüssigen Zustand kann zu experimentellen Schwierigkeiten führen. So wurden die Schmelztemperaturen einiger hochschmelzender Metalle durch Beobachtung der Strahlung aus einem Hohlraum eines schwarzen Körpers in festen Metallproben gemessen, die viel länger als breit waren. Um einen solchen Hohlraum zu bilden, wird ein Loch senkrecht zur Längsachse in der Mitte eines Stabes aus dem Material gebohrt. Diese Stäbe werden dann erhitzt, indem ein sehr starker Strom durch sie geleitet wird, und die aus dem Loch austretende Strahlung wird mit einem optischen Pyrometer beobachtet. Der Schmelzpunkt wird durch die Verdunkelung des Lochs angezeigt, wenn die flüssige Phase erscheint und die Bedingungen des schwarzen Körpers zerstört werden. Heute werden behälterlose Laserheiztechniken in Verbindung mit schnellen Pyrometern und Spektralpyrometern eingesetzt, um die Zeit, in der die Probe auf extremen Temperaturen gehalten wird, genau zu steuern. Mit solchen Experimenten von weniger als einer Sekunde Dauer lassen sich einige der Probleme lösen, die mit herkömmlichen Schmelzpunktmessungen bei sehr hohen Temperaturen verbunden sind, z. B. die Verdampfung der Probe und die Reaktion mit dem Behälter. ⓘ

Thermodynamik

Druckabhängigkeit des Wasserschmelzpunkts. ⓘ

Damit ein Feststoff schmelzen kann, ist Wärme erforderlich, um seine Temperatur auf den Schmelzpunkt zu erhöhen. Damit das Schmelzen stattfinden kann, muss jedoch weitere Wärme zugeführt werden: Dies wird als Schmelzwärme bezeichnet und ist ein Beispiel für latente Wärme. ⓘ

Aus thermodynamischer Sicht ist am Schmelzpunkt die Änderung der freien Gibbs-Energie (ΔG) des Materials gleich Null, aber die Enthalpie (H) und die Entropie (S) des Materials nehmen zu (ΔH, ΔS > 0). Das Phänomen des Schmelzens tritt auf, wenn die freie Gibbs-Energie des flüssigen Materials niedriger ist als die des festen Materials. Bei verschiedenen Drücken geschieht dies bei einer bestimmten Temperatur. Es kann auch gezeigt werden, dass:

$\Delta S={\frac {\Delta H}{T}}$ ⓘ

Hier sind T, ΔS und ΔH die Temperatur am Schmelzpunkt, die Änderung der Schmelzentropie und die Änderung der Schmelzenthalpie. ⓘ

Der Schmelzpunkt reagiert empfindlich auf extrem große Druckänderungen, aber im Allgemeinen ist diese Empfindlichkeit um Größenordnungen geringer als beim Siedepunkt, da der Übergang vom festen zum flüssigen Zustand nur eine kleine Volumenänderung darstellt. Wenn, wie in den meisten Fällen zu beobachten, eine Substanz im festen Zustand dichter ist als im flüssigen Zustand, steigt der Schmelzpunkt mit zunehmendem Druck an. Andernfalls ist das Verhalten genau umgekehrt. Dies ist insbesondere bei Wasser der Fall, wie in der Grafik rechts dargestellt, aber auch bei Si, Ge, Ga und Bi. Bei extrem großen Druckschwankungen werden erhebliche Änderungen des Schmelzpunkts beobachtet. So liegt der Schmelzpunkt von Silizium bei Umgebungsdruck (0,1 MPa) bei 1415 °C, bei einem Druck von mehr als 10 GPa sinkt er jedoch auf 1000 °C. ⓘ

Schmelzpunkte werden häufig zur Charakterisierung von organischen und anorganischen Verbindungen und zur Feststellung ihrer Reinheit verwendet. Der Schmelzpunkt einer reinen Substanz ist immer höher und hat einen kleineren Bereich als der Schmelzpunkt einer unreinen Substanz oder allgemeiner von Gemischen. Je höher die Menge der anderen Bestandteile ist, desto niedriger ist der Schmelzpunkt und desto breiter ist der Schmelzpunktbereich, der oft als "pastöser Bereich" bezeichnet wird. Die Temperatur, bei der ein Gemisch zu schmelzen beginnt, wird als "Solidus" bezeichnet, während die Temperatur, bei der das Schmelzen abgeschlossen ist, als "Liquidus" bezeichnet wird. Eutektika sind besondere Arten von Gemischen, die sich wie einzelne Phasen verhalten. Sie schmelzen bei einer konstanten Temperatur scharf und bilden eine Flüssigkeit mit derselben Zusammensetzung. Alternativ dazu erstarrt eine Flüssigkeit mit der eutektischen Zusammensetzung beim Abkühlen als gleichmäßig verteilte, kleine (feinkörnige) Mischkristalle mit der gleichen Zusammensetzung. ⓘ

Im Gegensatz zu kristallinen Festkörpern haben Gläser keinen Schmelzpunkt; Beim Erhitzen gehen sie fließend in eine viskose Flüssigkeit über. Bei weiterer Erwärmung werden sie allmählich weicher, was durch bestimmte Erweichungspunkte charakterisiert werden kann. ⓘ

Gefrierpunktserniedrigung

Der Gefrierpunkt eines Lösungsmittels wird durch Zugabe einer anderen Verbindung herabgesetzt, so dass eine Lösung einen niedrigeren Gefrierpunkt hat als ein reines Lösungsmittel. Dieses Phänomen wird in technischen Anwendungen genutzt, um das Einfrieren zu vermeiden, z. B. durch Zugabe von Salz oder Ethylenglykol zu Wasser. ⓘ

Carnelley'sche Regel

In der organischen Chemie besagt die 1882 von Thomas Carnelley aufgestellte Carnelley-Regel, dass eine hohe molekulare Symmetrie mit einem hohen Schmelzpunkt verbunden ist. Carnelley stützte seine Regel auf die Untersuchung von 15.000 chemischen Verbindungen. So steigt beispielsweise bei drei Strukturisomeren mit der Summenformel C₅H₁₂ der Schmelzpunkt in der Reihe Isopentan -160 °C (113 K), n-Pentan -129,8 °C (143 K) und Neopentan -16,4 °C (256,8 K). Auch bei Xylolen und Dichlorbenzolen steigt der Schmelzpunkt in der Reihenfolge meta, ortho und dann para an. Pyridin hat eine niedrigere Symmetrie als Benzol und daher einen niedrigeren Schmelzpunkt, aber der Schmelzpunkt steigt bei Diazinen und Triazinen wieder an. Viele käfigartige Verbindungen wie Adamantan und Cuban mit hoher Symmetrie haben relativ hohe Schmelzpunkte. ⓘ

Ein hoher Schmelzpunkt resultiert aus einer hohen Schmelzwärme, einer niedrigen Schmelzentropie oder einer Kombination aus beidem. Bei hochsymmetrischen Molekülen ist die Kristallphase dicht gepackt mit vielen effizienten intermolekularen Wechselwirkungen, was zu einer höheren Enthalpieänderung beim Schmelzen führt. ⓘ

Wie viele hochsymmetrische Verbindungen hat auch Tetrakis(trimethylsilyl)silan einen sehr hohen Schmelzpunkt (m.p.) von 319-321 °C. Da es zum Sublimieren neigt, muss die Probe zur Bestimmung des Schmelzpunkts in einem Röhrchen verschlossen werden. ⓘ

Vorhersage des Schmelzpunkts von Substanzen (Lindemann-Kriterium)

Ein Versuch zur Vorhersage des Schmelzpunkts von kristallinen Stoffen wurde erstmals 1910 von Frederick Lindemann unternommen. Der Gedanke hinter dieser Theorie war die Beobachtung, dass die durchschnittliche Amplitude thermischer Schwingungen mit steigender Temperatur zunimmt. Das Schmelzen beginnt, wenn die Amplitude der Schwingungen so groß wird, dass benachbarte Atome teilweise den gleichen Raum einnehmen. Das Lindemann-Kriterium besagt, dass ein Schmelzen zu erwarten ist, wenn die mittlere quadratische Amplitude der Schwingungen einen Schwellenwert überschreitet. ⓘ

Unter der Annahme, dass alle Atome in einem Kristall mit der gleichen Frequenz ν schwingen, kann die durchschnittliche Wärmeenergie mit Hilfe des Äquipartitionstheorems wie folgt geschätzt werden

$E=4\pi ^{2}m\nu ^{2}~u^{2}=k_{\rm {B}}T$

wobei m die Atommasse, ν die Frequenz, u die durchschnittliche Schwingungsamplitude, k_B die Boltzmann-Konstante und T die absolute Temperatur ist. Wenn der Schwellenwert von u² gleich c²a² ist, wobei c die Lindemann-Konstante und a der Atomabstand ist, dann wird der Schmelzpunkt geschätzt als

$T_{\rm {m}}={\cfrac {4\pi ^{2}m\nu ^{2}c^{2}a^{2}}{k_{\rm {B}}}}.$

Je nach Schätzung der durchschnittlichen thermischen Energie lassen sich mehrere andere Ausdrücke für die geschätzte Schmelztemperatur erhalten. Ein weiterer häufig verwendeter Ausdruck für das Lindemann-Kriterium ist

$T_{\rm {m}}={\cfrac {4\pi ^{2}m\nu ^{2}c^{2}a^{2}}{2k_{\rm {B}}}}.$

Aus dem Ausdruck für die Debye-Frequenz für ν ergibt sich

$T_{\rm {m}}={\cfrac {2\pi mc^{2}a^{2}\theta _{\rm {D}}^{2}k_{\rm {B}}}{h^{2}}}$

wobei θD die Debye-Temperatur und h die Planck-Konstante ist. Die Werte für c liegen für die meisten Materialien zwischen 0,15 und 0,3. ⓘ

Vorhersage des Schmelzpunkts

Im Februar 2011 hat Alfa Aesar über 10 000 Schmelzpunkte von Verbindungen aus seinem Katalog als offene Daten veröffentlicht. Anhand dieses Datensatzes wurde ein Random-Forest-Modell für die Schmelzpunktvorhersage erstellt, das nun frei verfügbar ist. Offene Schmelzpunktdaten sind auch bei Nature Precedings verfügbar. Hochwertige Daten, die aus Patenten gewonnen wurden, sowie Modelle, die mit diesen Daten entwickelt wurden, wurden von Tetko et al. veröffentlicht. ⓘ

Schmelzpunkt der Elemente

Schmelzpunkt der Elemente im Periodensystem ⓘ
Gruppe →	1	2		3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
↓ Periode
1	H2 13,99 K (-259.16 °C)																		He0,95 K (-272.20 °C)
2	Li453,65 K (180.50 °C)	Be1560 K (1287 °C)												B 2349 K (2076 °C)	C	N2 63,23 K (-209.86 °C)	O2 54,36 K (-218.79 °C)	F2 53,48 K (-219.67 °C)	Ne24,56 K (-248.59 °C)
3	Na370,944 K (97.794 °C)	Mg923 K (650 °C)												Al933,47 K (660.32 °C)	Si1687 K (1414 °C)	P 317,3 K (44.15 °C)	S 388,36 K (115.21 °C)	Cl2171,6 K (-101.5 °C)	Ar83,81 K (-189.34 °C)
4	K 336,7 K (63.5 °C)	Ca1115 K (842 °C)		Sc1814 K (1541 °C)	Ti1941 K (1668 °C)	V 2183 K (1910 °C)	Cr2180 K (1907 °C)	Mn1519 K (1246 °C)	Fe1811 K (1538 °C)	Co1768 K (1495 °C)	Ni1728 K (1455 °C)	Cu1357.77 K (1084.62 °C)	Zn692,68 K (419.53 °C)	Ga302,9146 K (29.7646 °C)	Ge1211,40 K (938.25 °C)	As	Se494 K (221 °C)	Br2265,8 K (-7.2 °C)	Kr115,78 K (-157.37 °C)
5	Rb312,45 K (39.30 °C)	Sr1050 K (777 °C)		Y 1799 K (1526 °C)	Zr2128 K (1855 °C)	Nb2750 K (2477 °C)	Mo2896 K (2623 °C)	Tc2430 K (2157 °C)	Ru2607 K (2334 °C)	Rh2237 K (1964 °C)	Pd1828.05 K (1554.9 °C)	Ag1234,93 K (961.78 °C)	Cd594,22 K (321.07 °C)	In429,7485 K (156.5985 °C)	Sn505,08 K (231.93 °C)	Sb903,78 K (630.63 °C)	Te722,66 K (449.51 °C)	I2 386,85 K (113.7 °C)	Xe161,40 K (-111.75 °C)
6	Cs301,7 K (28.5 °C)	Ba1000 K (727 °C)		Lu1925 K (1652 °C)	Hf2506 K (2233 °C)	Ta3290 K (3017 °C)	W 3695 K (3422 °C)	Re3459 K (3186 °C)	Os3306 K (3033 °C)	Ir2719 K (2446 °C)	Pt2041,4 K (1768.3 °C)	Au1337,33 K (1064.18 °C)	Hg234,3210 K (-38.8290 °C)	Tl577 K (304 °C)	Pb600,61 K (327.46 °C)	Bi544,7 K (271.5 °C)	Po527 K (254 °C)	At575 K (302 °C)	Rn202 K (-71 °C)
7	Fr300 K (27 °C)	Ra973 K (700 °C)		Lr1900 K (1627 °C)	Rf2400 K (2100 °C)	Db	Sg	Bh	Hs	Mt	Ds	Rg	Cn283±11 K (10±11 °C)	Nh700 K (430 °C)	Fl200 K (-73 °C)	Mc670 K (400 °C)	Lv637-780 K (364-507 °C)	Ts623-823 K (350-550 °C)	Og325±15 K (52±15 °C)
				La1193 K (920 °C)	Ce1068 K (795 °C)6	Pr1208 K (935 °C)	Nd1297 K (1024 °C)	Pm1315 K (1042 °C)	Sm1345 K (1072 °C)	Eu1099 K (826 °C)	Gd1585 K (1312 °C)	Tb1629 K (1356 °C)	Dy1680 K (1407 °C)	Ho1734 K (1461 °C)	Er1802 K (1529 °C)	Tm1818 K (1545 °C)	Yb1097 K (824 °C)
				Ac1500 K (1227 °C)	Th2023 K (1750 °C)	Pa1841 K (1568 °C)	U 1405,3 K (1132.2 °C)	Np912±3 K (639±3 °C)	Pu912,5 K (639.4 °C)	Am1449 K (1176 °C)	Cm1613 K (1340 °C)	Bk1259 K (986 °C)	Cf1173 K (900 °C)	Es1133 K (860 °C)	Fm1800 K (1527 °C)	Md1100 K (827 °C)	Nr1100 K (827 °C)
Legende
Die Werte sind in Kelvin K und Celsius °C angegeben, gerundet.
Für das Äquivalent in Fahrenheit °F, siehe: Schmelzpunkte der Elemente (Datenseite)
Einige Werte sind Vorhersagen
Primordial Vom Zerfall Synthetischer Rand zeigt natürliches Vorkommen des Elements s-Block g-Block f-Block d-Block p-Block

Druckabhängigkeit

Analytik

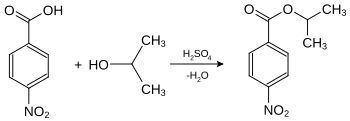
Die Bestimmung des Schmelzpunkts einer Substanz ist auch von großer Bedeutung in der qualitativen Analytik, einschließlich der Identitätsprüfung, da viele Substanzen über ihren Schmelzpunkt identifiziert werden können. Die Reinheit von Stoffen kann qualitativ ebenfalls über den Schmelzpunkt gemessen werden. Verunreinigungen haben niedrigere Schmelzpunkte zur Folge. Flüssige Substanzen oder solche mit niedrigem Schmelzpunkt werden dazu in leicht kristallisierende Derivate umgewandelt: Alkohole können beispielsweise durch die Messung der Schmelzpunkte ihrer Ester der 4-Nitrobenzoesäure oder der 3,5-Dinitrobenzoesäure identifiziert werden. Hierzu wird die zu analysierende Substanz in Gegenwart geringer Mengen Schwefelsäure umgesetzt. Die Schmelzpunkte dieser Derivate sind in der Regel scharf. ⓘ

Nachweis von Isopropanol als Derivat der 4-Nitrobenzoesäure: 4-Nitrobenzoesäure-2-propylester (Smp.: 100,5 °C)	Nachweis von Isopropanol als Derivat der 3,5-Dinitrobenzoesäure: 3,5-Dinitrobenzoesäure-2-propylester (Smp.: 123 °C)

Die Derivate der 3,5-Dinitrobenzoesäure besitzen in der Regel höhere Schmelzpunkte als die der 4-Nitrobenzoesäure. Sie werden dann bevorzugt gewählt, wenn der Schmelzpunkt mit der 4-Nitrobenzoesäure zu niedrig ist und keine genaue Bestimmung mehr möglich wird. ⓘ

Umfangreiche Tabellenwerke mit Angaben zu Schmelzpunkten organischer Verbindungen, als wichtige Hilfsmittel für Analytiker, liegen vor. Schmelzpunkte von Derivaten einzelner Stoffklassen werden in den einschlägigen Lehrbüchern der organischen Analytik gelistet. ⓘ