Brechungsindex

Ein Lichtstrahl wird in einem Kunststoffblock gebrochen ⓘ

In der Optik ist der Brechungsindex (auch Brechungsindex genannt) eines optischen Mediums eine dimensionslose Zahl, die das Lichtbeugungsvermögen dieses Mediums angibt. ⓘ

Brechung eines Lichtstrahls ⓘ

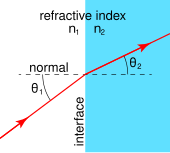
Der Brechungsindex bestimmt, wie stark der Weg des Lichts beim Eintritt in ein Material gebogen oder gebrochen wird. Dies wird durch das Snellsche Brechungsgesetz beschrieben: n₁ sin θ₁ = n₂ sin θ₂, wobei θ₁ und θ₂ die Einfalls- bzw. Brechungswinkel eines Strahls sind, der die Grenzfläche zwischen zwei Medien mit den Brechungsindizes n₁ und n₂ passiert. Die Brechungsindizes bestimmen auch die Lichtmenge, die beim Erreichen der Grenzfläche reflektiert wird, sowie den kritischen Winkel für die innere Totalreflexion, ihre Intensität (Fresnelsche Gleichungen) und den Brewster-Winkel. ⓘ

Der Brechungsindex kann als der Faktor angesehen werden, um den die Geschwindigkeit und die Wellenlänge der Strahlung im Vergleich zu ihren Werten im Vakuum reduziert werden: Die Lichtgeschwindigkeit in einem Medium ist v = c/n, und die Wellenlänge in diesem Medium ist λ = λ₀/n, wobei λ₀ die Wellenlänge des Lichts im Vakuum ist. Dies impliziert, dass das Vakuum einen Brechungsindex von 1 hat, und setzt voraus, dass die Frequenz (f = v/λ) der Welle nicht vom Brechungsindex beeinflusst wird. ⓘ

Der Brechungsindex kann mit der Wellenlänge variieren. Dies führt dazu, dass sich weißes Licht bei der Brechung in die einzelnen Farben aufspaltet. Dies wird als Dispersion bezeichnet. Dieser Effekt kann bei Prismen und Regenbögen sowie als chromatische Aberration bei Linsen beobachtet werden. Die Lichtausbreitung in absorbierenden Materialien kann mit einem komplexwertigen Brechungsindex beschrieben werden. Der Imaginärteil ist dann für die Abschwächung zuständig, während der Realteil für die Brechung verantwortlich ist. Bei den meisten Materialien ändert sich der Brechungsindex mit der Wellenlänge um einige Prozent über das sichtbare Spektrum. Dennoch werden die Brechungsindizes für Materialien in der Regel mit einem einzigen Wert für n angegeben, der in der Regel bei 633 nm gemessen wird. ⓘ

Das Konzept des Brechungsindexes gilt für das gesamte elektromagnetische Spektrum, von Röntgenstrahlen bis zu Radiowellen. Es kann auch auf Wellenphänomene wie Schall angewendet werden. In diesem Fall wird die Schallgeschwindigkeit anstelle der Lichtgeschwindigkeit verwendet, und es muss ein anderes Referenzmedium als das Vakuum gewählt werden. ⓘ

Bei Linsen (z. B. Brillen) ist eine Linse aus einem Material mit hohem Brechungsindex dünner und damit leichter als eine herkömmliche Linse mit einem niedrigeren Brechungsindex. Solche Linsen sind in der Regel teurer in der Herstellung als herkömmliche Linsen. ⓘ

Beachte, dass mit „optische Dichte“ zuweilen auch ein Maß für die Extinktion bezeichnet wird. ⓘ

Definition

Der relative Brechungsindex eines optischen Mediums 2 in Bezug auf ein anderes Referenzmedium 1 (n₂₁) ist durch das Verhältnis der Lichtgeschwindigkeit in Medium 1 zu derjenigen in Medium 2 gegeben. Dies kann wie folgt ausgedrückt werden:

$n_{21}={\frac {v_{1}}{v_{2}}}.$

Wenn das Referenzmedium 1 das Vakuum ist, dann wird der Brechungsindex des Mediums 2 in Bezug auf das Vakuum betrachtet. Er wird einfach als n₂ dargestellt und als absoluter Brechungsindex des Mediums 2 bezeichnet. ⓘ

Der absolute Brechungsindex n eines optischen Mediums ist definiert als das Verhältnis zwischen der Lichtgeschwindigkeit im Vakuum, c = 299792458 m/s, und der Phasengeschwindigkeit v des Lichts im Medium,

$n={\frac {c}{v}}.$

Die Phasengeschwindigkeit ist die Geschwindigkeit, mit der sich der Scheitelpunkt oder die Phase der Welle bewegt, die sich von der Gruppengeschwindigkeit, der Geschwindigkeit, mit der sich der Lichtimpuls oder die Hülle der Welle bewegt, unterscheiden kann. In der Vergangenheit war Luft mit einem standardisierten Druck und einer standardisierten Temperatur als Referenzmedium üblich. ⓘ

Geschichte

Thomas Young prägte den Begriff des Brechungsindexes. ⓘ

Thomas Young war vermutlich derjenige, der 1807 zum ersten Mal die Bezeichnung "Brechungsindex" verwendete und erfand. Gleichzeitig änderte er diesen Wert der Brechkraft in eine einzige Zahl, anstelle des traditionellen Verhältnisses von zwei Zahlen. Das Verhältnis hatte den Nachteil, dass es unterschiedlich aussah. Newton, der es als "Verhältnis der Sinuskurven von Einfall und Brechung" bezeichnete, schrieb es als Verhältnis von zwei Zahlen, wie "529 zu 396" (oder "fast 4 zu 3"; für Wasser). Hauksbee, der es "Verhältnis der Brechung" nannte, schrieb es als Verhältnis mit einem festen Zähler, wie "10000 zu 7451,9" (für Urin). Hutton schrieb es als Verhältnis mit einem festen Nenner, z. B. 1,3358 zu 1 (Wasser). ⓘ

Young benutzte 1807 noch kein Symbol für den Brechungsindex. In den folgenden Jahren begannen andere, verschiedene Symbole zu verwenden: n, m und µ. Das Symbol n setzte sich allmählich durch. ⓘ

Typische Werte

Diamanten haben einen sehr hohen Brechungsindex von 2,417. ⓘ

Der Brechungsindex hängt auch von der Wellenlänge des Lichts ab, wie aus der Cauchy-Gleichung hervorgeht: Die allgemeinste Form der Cauchy'schen Gleichung lautet ⓘ

$n(\lambda )=A+{\frac {B}{\lambda ^{2}}}+{\frac {C}{\lambda ^{4}}}+\cdots ,$ ⓘ

wobei n der Brechungsindex, λ die Wellenlänge, A, B, C usw. Koeffizienten sind, die für ein Material durch Anpassung der Gleichung an gemessene Brechungsindizes bei bekannten Wellenlängen bestimmt werden können. Die Koeffizienten werden gewöhnlich für λ als Vakuumwellenlänge in Mikrometern angegeben. ⓘ

In der Regel reicht es aus, eine zweigliedrige Form der Gleichung zu verwenden:

$n(\lambda )=A+{\frac {B}{\lambda ^{2}}},$ ⓘ

wobei die Koeffizienten A und B speziell für diese Form der Gleichung bestimmt werden. ⓘ

Ausgewählte Brechungsindizes bei λ=589 nm. Für Referenzen siehe die erweiterte Liste der Brechungsindizes.

Werkstoff	n ⓘ
Vakuum	1
Gase bei 0 °C und 1 atm
Luft	1.000293
Helium	1.000036
Wasserstoff	1.000132
Kohlendioxid	1.00045
Flüssigkeiten bei 20 °C
Wasser	1.333
Ethanol	1.36
Olivenöl	1.47
Feststoffe
Eis	1.31
Quarzglas (Quarz)	1.46
PMMA (Acryl, Plexiglas, Luzit, Plexiglas)	1.49
Fensterglas	1.52
Polycarbonat (Lexan™)	1.58
Flintglas (typisch)	1.69
Saphir	1.77
Kubischer Zirkoniumdioxid	2.15
Diamant	2.42
Moissanit	2.65

Für sichtbares Licht haben die meisten transparenten Medien Brechungsindizes zwischen 1 und 2. Einige Beispiele sind in der nebenstehenden Tabelle aufgeführt. Diese Werte werden bei der gelben D-Linie von Natrium mit einer Wellenlänge von 589 Nanometern gemessen, wie es üblich ist. Gase haben bei Atmosphärendruck aufgrund ihrer geringen Dichte einen Brechungsindex nahe bei 1. Fast alle festen und flüssigen Stoffe haben einen Brechungsindex von über 1,3, wobei Aerogel eine deutliche Ausnahme bildet. Aerogel ist ein Feststoff mit sehr geringer Dichte, der mit einem Brechungsindex zwischen 1,002 und 1,265 hergestellt werden kann. Moissanit liegt mit einem Brechungsindex von bis zu 2,65 am anderen Ende der Skala. Die meisten Kunststoffe haben Brechungsindizes im Bereich von 1,3 bis 1,7, aber einige Polymere mit hohem Brechungsindex können Werte von bis zu 1,76 erreichen. ⓘ

Für infrarotes Licht können die Brechungsindizes erheblich höher sein. Germanium ist im Wellenlängenbereich von 2 bis 14 µm durchsichtig und hat einen Brechungsindex von etwa 4. Kürzlich wurde eine neue Art von Materialien gefunden, die als "topologische Isolatoren" bezeichnet werden und einen hohen Brechungsindex von bis zu 6 im nahen bis mittleren Infrarotbereich haben. Außerdem sind topologische Isolatoren transparent, wenn sie eine Dicke im Nanobereich haben. Diese Eigenschaften sind für Anwendungen in der Infrarotoptik potenziell wichtig. ⓘ

Brechungsindex unter Eins

Nach der Relativitätstheorie kann sich keine Information schneller als mit Lichtgeschwindigkeit im Vakuum fortbewegen, aber das bedeutet nicht, dass der Brechungsindex nicht kleiner als 1 sein kann. Der Brechungsindex misst die Phasengeschwindigkeit des Lichts, das keine Information trägt. Die Phasengeschwindigkeit ist die Geschwindigkeit, mit der sich die Wellenberge bewegen, und kann schneller sein als die Lichtgeschwindigkeit im Vakuum, was zu einem Brechungsindex unter 1 führen kann. Im Röntgenbereich liegen die Brechungsindizes unter, aber sehr nahe bei 1 (Ausnahmen in der Nähe einiger Resonanzfrequenzen). Zum Beispiel hat Wasser einen Brechungsindex von 0,99999974 = 1 - 2,6×10-7 für Röntgenstrahlung bei einer Photonenenergie von 30 keV (0,04 nm Wellenlänge). ⓘ

Ein Beispiel für ein Plasma mit einem Brechungsindex kleiner als eins ist die Ionosphäre der Erde. Da der Brechungsindex der Ionosphäre (eines Plasmas) kleiner als 1 ist, werden elektromagnetische Wellen, die sich durch das Plasma ausbreiten, "weg von der Normalen" gebogen (siehe Geometrische Optik), so dass die Radiowelle zur Erde zurückgebrochen wird, was Funkverbindungen über große Entfernungen ermöglicht. Siehe auch Funkausbreitung und Skywave. ⓘ

Geschichte

1968 beschrieb der sowjetische Physiker Wiktor Wesselago das seltsame Verhalten von Materialien mit negativem Brechungsindex: „Würde die Herstellung gelingen, könnte man damit Linsen fertigen, deren Auflösungsvermögen weit besser wäre als das von Linsen aus gewöhnlichen optischen Werkstoffen“. ⓘ

1999 schlug Sir John Pendry ein Design für Metamaterialien mit negativem Brechungsindex für Mikrowellen vor, das kurz darauf realisiert wurde. ⓘ

2003 hat eine Gruppe um Yong Zhang in Colorado entdeckt, dass Kristalle aus Yttrium-Vanadat (YVO₄), einer Verbindung von Yttrium, Vanadium und Sauerstoff, auch ohne Weiterverarbeitung einen negativen Brechungsindex für Lichtwellen eines großen Frequenzbereichs aufweisen. Der Kristall besteht aus zwei ineinandergeschachtelten Kristallgittern mit symmetrischen optischen Achsen. Die negative Lichtbrechung tritt aber nur in einem gewissen Winkelbereich des Einfallswinkels auf. In künftigen Experimenten wollen die Forscher weitere vermutete Eigenschaften der negativen Brechung prüfen – wie etwa die Umkehrung des Dopplereffekts und der Tscherenkow-Strahlung. ⓘ

2007 stellten Vladimir Shalaev und seine Kollegen von der Purdue-Universität ein Metamaterial mit negativem Brechungsindex für Strahlung im nahen Infrarotbereich vor. ⓘ

2007 ist es Physikern um Ulf Leonhardt von der Universität St Andrews unter Verwendung von Metamaterial mit negativem Brechungsindex („linkshändiges Material“) gelungen, den sogenannten Casimir-Effekt umzukehren (reverser Casimir-Effekt, auch Quanten-Levitation genannt). Dies eröffnet die Zukunftsperspektive auf eine (nahezu) reibungslose Nanotechnologie. ⓘ

Eine Resonatoranordnung mit geteiltem Ring, die einen negativen Brechungsindex für Mikrowellen erzeugt ⓘ

Neuere Forschungen haben auch gezeigt, dass es Materialien mit negativem Brechungsindex gibt, wenn Permittivität und Permeabilität gleichzeitig negative Werte aufweisen. Dies kann mit periodisch aufgebauten Metamaterialien erreicht werden. Die daraus resultierende negative Brechung (d. h. eine Umkehrung des Snellschen Gesetzes) bietet die Möglichkeit, die Superlinse und andere neue Phänomene mit Hilfe von Metamaterialien aktiv zu entwickeln. ⓘ

Mikroskopische Erklärung

In der optischen Mineralogie werden Dünnschliffe zur Untersuchung von Gesteinen verwendet. Die Methode beruht auf den unterschiedlichen Brechungsindizes der verschiedenen Mineralien. ⓘ

Auf atomarer Ebene wird die Phasengeschwindigkeit einer elektromagnetischen Welle in einem Material verlangsamt, weil das elektrische Feld eine Störung der Ladungen der einzelnen Atome (hauptsächlich der Elektronen) verursacht, die proportional zur elektrischen Suszeptibilität des Mediums ist. (In ähnlicher Weise erzeugt das magnetische Feld eine Störung, die proportional zur magnetischen Suszeptibilität ist). Wenn die elektromagnetischen Felder in der Welle schwingen, werden die Ladungen im Material mit derselben Frequenz hin- und hergeschüttelt". Die Ladungen strahlen somit ihre eigene elektromagnetische Welle mit der gleichen Frequenz ab, allerdings in der Regel mit einer Phasenverzögerung, da sich die Ladungen mit der sie antreibenden Kraft phasenverschoben bewegen können (siehe sinusförmig angetriebener harmonischer Oszillator). Die Lichtwelle, die sich im Medium ausbreitet, ist die makroskopische Überlagerung (Summe) aller derartigen Beiträge im Material: die ursprüngliche Welle plus die von allen bewegten Ladungen abgestrahlten Wellen. Bei dieser Welle handelt es sich in der Regel um eine Welle mit der gleichen Frequenz, aber kürzerer Wellenlänge als die ursprüngliche Welle, was zu einer Verlangsamung der Phasengeschwindigkeit der Welle führt. Der größte Teil der Strahlung der schwingenden materiellen Ladungen modifiziert die eintreffende Welle und verändert ihre Geschwindigkeit. Ein Teil der Nettoenergie wird jedoch in andere Richtungen oder sogar mit anderen Frequenzen abgestrahlt (siehe Streuung). ⓘ

Je nach der relativen Phase der ursprünglichen Antriebswelle und der von der Ladungsbewegung abgestrahlten Wellen gibt es verschiedene Möglichkeiten:

• Wenn die Elektronen eine Lichtwelle aussenden, die um 90° phasenverschoben zu der sie erschütternden Lichtwelle ist, führt dies dazu, dass sich die gesamte Lichtwelle langsamer ausbreitet. Dies ist die normale Brechung von transparenten Materialien wie Glas oder Wasser und entspricht einem realen Brechungsindex größer als 1.
• Wenn die Elektronen eine Lichtwelle aussenden, die um 270° phasenverschoben zu der Lichtwelle ist, die sie durchschüttelt, wird die Welle schneller laufen. Dies wird "anomale Brechung" genannt und wird in der Nähe von Absorptionslinien (typischerweise in Infrarotspektren), bei Röntgenstrahlen in gewöhnlichen Materialien und bei Radiowellen in der Ionosphäre der Erde beobachtet. Sie entspricht einer Dielektrizitätskonstante von weniger als 1, was dazu führt, dass der Brechungsindex ebenfalls kleiner als 1 ist und die Phasengeschwindigkeit des Lichts größer als die Lichtgeschwindigkeit im Vakuum c ist (beachten Sie, dass die Signalgeschwindigkeit immer noch kleiner als c ist, wie oben beschrieben). Wenn die Reaktion ausreichend stark und phasenverschoben ist, ergibt sich ein negativer Wert für die Dielektrizitätskonstante und den imaginären Brechungsindex, wie er in Metallen oder Plasmen beobachtet wird.
• Wenn die Elektronen eine Lichtwelle aussenden, die um 180° phasenverschoben zu der sie durchschüttelnden Lichtwelle ist, kommt es zu einer destruktiven Interferenz mit dem ursprünglichen Licht, wodurch die Gesamtlichtintensität verringert wird. Dies ist die Lichtabsorption in undurchsichtigen Materialien und entspricht einem imaginären Brechungsindex.
• Wenn die Elektronen eine Lichtwelle aussenden, die mit der sie erschütternden Lichtwelle in Phase ist, wird die Lichtwelle verstärkt. Dies ist selten, kommt aber bei Lasern durch stimulierte Emission vor. Dies entspricht einem imaginären Brechungsindex, der das umgekehrte Vorzeichen wie bei der Absorption hat.

Bei den meisten Materialien liegt die Phase bei den Frequenzen des sichtbaren Lichts zwischen 90° und 180°, was einer Kombination aus Brechung und Absorption entspricht. ⓘ

Jede linear polarisierte Welle kann als Überlagerung zweier zirkularer Wellen mit entgegengesetztem Umlaufsinn interpretiert werden. Verläuft die Ausbreitungsrichtung parallel zu den Magnetfeldlinien, ergeben sich für die Brechzahlen n folgende Formeln:

$n_{\text{links}}={\sqrt {1-{\frac {f_{P}^{2}}{f(f+f_{B})}}}}$ ⓘ

$n_{\text{rechts}}={\sqrt {1-{\frac {f_{P}^{2}}{f(f-f_{B})}}}}$ ⓘ

Dabei ist $f$ die Frequenz der Welle, $f_{P}$ die Plasmafrequenz der freien Elektronen im Plasma und $f_{B}$ die Gyrationsfrequenz dieser Elektronen. Der Unterschied beider Formeln verschwindet, falls der Wellenvektor mit der Richtung des Magnetfeldes einen rechten Winkel einschließt, weil dann $f_{B}=0$ ist. ⓘ

Streuung

Licht verschiedener Farben hat in Wasser leicht unterschiedliche Brechungsindizes und erscheint daher an verschiedenen Stellen des Regenbogens. ⓘ

In einem Prisma führt die Dispersion dazu, dass sich die verschiedenen Farben in unterschiedlichen Winkeln brechen und weißes Licht in einen Regenbogen von Farben aufgespalten wird. ⓘ

Die Veränderung des Brechungsindex mit der Wellenlänge für verschiedene Gläser. Der schattierte Bereich zeigt den Bereich des sichtbaren Lichts. ⓘ

Der Brechungsindex von Materialien ändert sich mit der Wellenlänge (und der Frequenz) des Lichts. Dies wird als Dispersion bezeichnet und bewirkt, dass Prismen und Regenbögen weißes Licht in seine einzelnen Spektralfarben aufteilen. Da der Brechungsindex mit der Wellenlänge variiert, ändert sich auch der Brechungswinkel, wenn das Licht von einem Material zum anderen gelangt. Die Dispersion führt auch dazu, dass die Brennweite von Linsen von der Wellenlänge abhängig ist. Dies ist eine Art von chromatischer Aberration, die in bildgebenden Systemen häufig korrigiert werden muss. In Bereichen des Spektrums, in denen das Material kein Licht absorbiert, nimmt der Brechungsindex mit zunehmender Wellenlänge tendenziell ab und somit mit der Frequenz zu. Dies wird als "normale Dispersion" bezeichnet, im Gegensatz zur "anomalen Dispersion", bei der der Brechungsindex mit der Wellenlänge zunimmt. Für sichtbares Licht bedeutet normale Dispersion, dass der Brechungsindex für blaues Licht höher ist als für rotes. ⓘ

Für Optiken im sichtbaren Bereich wird die Dispersion eines Linsenmaterials häufig durch die Abbe-Zahl quantifiziert:

$V={\frac {n_{\mathrm {yellow} }-1}{n_{\mathrm {blue} }-n_{\mathrm {red} }}}.$

Für eine genauere Beschreibung der Wellenlängenabhängigkeit des Brechungsindexes kann die Sellmeier-Gleichung verwendet werden. Dabei handelt es sich um eine empirische Formel, die sich gut zur Beschreibung der Dispersion eignet. Sellmeier-Koeffizienten werden in Tabellen oft anstelle des Brechungsindexes angegeben. ⓘ

Wegen der Dispersion ist es in der Regel wichtig, die Vakuumwellenlänge des Lichts anzugeben, für die ein Brechungsindex gemessen wird. Typischerweise werden Messungen bei verschiedenen wohldefinierten spektralen Emissionslinien durchgeführt; so bezeichnet nD in der Regel den Brechungsindex bei der Fraunhofer-Linie "D", dem Zentrum der gelben Natrium-Doppelemission bei 589,29 nm Wellenlänge. ⓘ

Komplexer Brechungsindex

Beim Durchgang von Licht durch ein Medium wird immer ein Teil des Lichts absorbiert. Dies lässt sich bequem durch die Definition eines komplexen Brechungsindexes berücksichtigen,

${\underline {n}}=n-i\kappa .$ ⓘ

Dabei ist der Realteil n der Brechungsindex und gibt die Phasengeschwindigkeit an, während der Imaginärteil κ als Extinktions- oder Absorptionskoeffizient bezeichnet wird - obwohl sich κ auch auf den Massendämpfungskoeffizienten beziehen kann - und das Ausmaß der Dämpfung angibt, wenn sich die elektromagnetische Welle durch das Material ausbreitet. ⓘ

Dass κ der Absorption entspricht, wird deutlich, wenn man diesen Brechungsindex in den Ausdruck für das elektrische Feld einer ebenen elektromagnetischen Welle einsetzt, die sich in x-Richtung ausbreitet. Dazu wird die komplexe Wellenzahl k mit dem komplexen Brechungsindex n durch k = 2πn/λ₀ in Beziehung gesetzt, wobei λ₀ die Vakuumwellenlänge ist; dies kann in den Ausdruck für eine ebene Welle, die sich in x-Richtung ausbreitet, wie folgt eingesetzt werden:

$\mathbf {E} (s,t)=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i({\underline {k}}x-\omega t)}\right]=\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i(2\pi (n+i\kappa )x/\lambda _{0}-\omega t)}\right]=e^{-2\pi \kappa x/\lambda _{0}}\operatorname {Re} \!\left[\mathbf {E} _{0}e^{i(kx-\omega t)}\right].$ ⓘ

Hier sehen wir, dass κ einen exponentiellen Zerfall ergibt, wie vom Beer-Lambert-Gesetz erwartet. Da die Intensität proportional zum Quadrat des elektrischen Feldes ist, hängt die Intensität von der Tiefe des Materials ab als ⓘ

$I(x)=I_{0}e^{-4\pi \kappa x/\lambda _{0}}.$ ⓘ

und somit ist der Absorptionskoeffizient α = 4πκ/λ₀, und die Eindringtiefe (die Entfernung, nach der die Intensität um den Faktor 1/e abnimmt) ist δp = 1/α = λ₀/4πκ. ⓘ

Sowohl n als auch κ sind von der Frequenz abhängig. In den meisten Fällen ist κ > 0 (das Licht wird absorbiert) oder κ = 0 (das Licht wandert für immer ohne Verlust). In besonderen Situationen, insbesondere im Verstärkungsmedium von Lasern, ist es auch möglich, dass κ < 0 ist, was einer Verstärkung des Lichts entspricht. ⓘ

Eine alternative Konvention verwendet n = n + iκ anstelle von n = n - iκ, wobei aber κ > 0 immer noch einem Verlust entspricht. Diese beiden Konventionen sind also nicht miteinander vereinbar und sollten nicht verwechselt werden. Der Unterschied hängt mit der Definition der sinusförmigen Zeitabhängigkeit als Re[exp(-iωt)] gegenüber Re[exp(+iωt)] zusammen. Siehe Mathematische Beschreibungen der Trübung. ⓘ

Dielektrischer Verlust und eine von Null abweichende Gleichstromleitfähigkeit in Materialien verursachen Absorption. Gute dielektrische Materialien wie Glas haben eine extrem niedrige Gleichstromleitfähigkeit, und bei niedrigen Frequenzen ist auch der dielektrische Verlust vernachlässigbar, was zu fast keiner Absorption führt. Bei höheren Frequenzen (z. B. bei sichtbarem Licht) kann der dielektrische Verlust die Absorption jedoch deutlich erhöhen und die Transparenz des Materials für diese Frequenzen verringern. ⓘ

Der Realteil n und der Imaginärteil κ des komplexen Brechungsindexes sind durch die Kramers-Kronig-Beziehungen miteinander verbunden. 1986 leiteten A.R. Forouhi und I. Bloomer eine Gleichung ab, die κ als Funktion der Photonenenergie E beschreibt und für amorphe Materialien gilt. Forouhi und Bloomer wandten dann die Kramers-Kronig-Beziehung an, um die entsprechende Gleichung für n als Funktion von E abzuleiten. 1988 wurde derselbe Formalismus von Forouhi und Bloomer auf kristalline Materialien angewandt. ⓘ

Der Brechungsindex und der Extinktionskoeffizient, n und κ, werden in der Regel anhand von Größen gemessen, die von ihnen abhängen, wie z. B. der Reflexionsgrad, R, oder der Transmissionsgrad, T, oder die ellipsometrischen Parameter, ψ und δ. Die Bestimmung von n und κ anhand solcher gemessenen Größen erfordert die Entwicklung eines theoretischen Ausdrucks für R oder T bzw. ψ und δ in Form eines gültigen physikalischen Modells für n und κ. Durch Anpassung des theoretischen Modells an das gemessene R oder T bzw. ψ und δ mittels Regressionsanalyse können n und κ abgeleitet werden. ⓘ

Röntgenstrahlung und extremes UV

Bei Röntgen- und extremer UV-Strahlung weicht der komplexe Brechungsindex nur geringfügig von der Einheit ab und hat in der Regel einen Realteil kleiner als 1. Er wird daher normalerweise als n = 1 - δ + iβ geschrieben (oder n = 1 - δ - iβ mit der oben erwähnten alternativen Konvention). Weit oberhalb der Atomresonanzfrequenz lässt sich delta wie folgt angeben

$\delta ={\frac {r_{0}\lambda ^{2}n_{e}}{2\pi }}$ ⓘ

wobei $r_{0}$ der klassische Elektronenradius ist, $\lambda$ die Wellenlänge der Röntgenstrahlung ist und $n_{e}$ die Elektronendichte ist. Man kann annehmen, dass die Elektronendichte einfach die Anzahl der Elektronen pro Atom Z multipliziert mit der atomaren Dichte ist, aber für eine genauere Berechnung des Brechungsindexes muss Z durch den komplexen atomaren Formfaktor ersetzt werden $f=Z+f'+if$. Daraus folgt, dass

$\delta ={\frac {r_{0}\lambda ^{2}}{2\pi }}(Z+f')n_{\text{atom}}$

$\beta ={\frac {r_{0}\lambda ^{2}}{2\pi }}fn_{\text{atom}}$ ⓘ

mit $\delta$ und $\beta$ typischerweise in der Größenordnung von 10-5 und 10-6 liegen. ⓘ

Beziehungen zu anderen Größen

Optische Weglänge

Die Farben einer Seifenblase werden durch die optische Weglänge durch den dünnen Seifenfilm bestimmt, ein Phänomen, das als Dünnfilminterferenz bezeichnet wird. ⓘ

Die optische Weglänge (OPL) ist das Produkt aus der geometrischen Länge d des Weges, den das Licht durch ein System zurücklegt, und dem Brechungsindex des Mediums, durch das es sich ausbreitet,

${\text{OPL}}=nd.$

Dies ist ein wichtiges Konzept in der Optik, weil es die Phase des Lichts bestimmt und die Interferenz und Beugung des Lichts bei seiner Ausbreitung regelt. Nach dem Fermat'schen Prinzip lassen sich Lichtstrahlen als diejenigen Kurven charakterisieren, die die optische Weglänge optimieren. ⓘ

Brechung

Brechung des Lichts an der Grenzfläche zwischen zwei Medien mit unterschiedlichem Brechungsindex, wobei n₂ > n₁ ist. Da die Phasengeschwindigkeit im zweiten Medium geringer ist (v₂ < v₁), ist der Brechungswinkel θ₂ kleiner als der Einfallswinkel θ₁, d. h. der Strahl im Medium mit dem höheren Index liegt näher an der Normalen. ⓘ

Wenn sich Licht von einem Medium in ein anderes bewegt, ändert es seine Richtung, d. h. es wird gebrochen. Bewegt es sich von einem Medium mit dem Brechungsindex n₁ zu einem Medium mit dem Brechungsindex n₂, mit einem Einfallswinkel zur Oberflächennormalen von θ₁, kann der Brechungswinkel θ₂ aus dem Snellschen Gesetz berechnet werden:

$n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}.$ ⓘ

Wenn Licht in ein Material mit höherem Brechungsindex eintritt, ist der Brechungswinkel kleiner als der Einfallswinkel, und das Licht wird zur Normalen der Oberfläche hin gebrochen. Je höher der Brechungsindex ist, desto mehr nähert sich das Licht der Normalenrichtung. Beim Durchgang durch ein Medium mit niedrigerem Brechungsindex wird das Licht stattdessen von der Normalen weg zur Oberfläche hin gebrochen. ⓘ

Innere Totalreflexion

Die innere Totalreflexion tritt an der Luft-Wasser-Grenze auf. ⓘ

Wenn es keinen Winkel θ₂ gibt, der das Snellsche Gesetz erfüllt, d. h.,

${\frac {n_{1}}{n_{2}}}\sin \theta _{1}>1,$

kann das Licht nicht durchgelassen werden und wird stattdessen intern total reflektiert. Dies geschieht nur, wenn es auf ein optisch weniger dichtes Material trifft, d. h. ein Material mit niedrigerem Brechungsindex. Um die Totalreflexion zu erreichen, muss der Einfallswinkel θ₁ größer sein als der kritische Winkel

$\theta _{\mathrm {c} }=\arcsin \!\left({\frac {n_{2}}{n_{1}}}\right)\!.$ ⓘ

Reflexionsvermögen

Neben dem durchgelassenen Licht gibt es auch einen reflektierten Teil. Der Reflexionswinkel ist gleich dem Einfallswinkel, und die Menge des reflektierten Lichts wird durch das Reflexionsvermögen der Oberfläche bestimmt. Das Reflexionsvermögen kann aus dem Brechungsindex und dem Einfallswinkel mit den Fresnel-Gleichungen berechnet werden, die sich für normalen Einfall auf ⓘ

$R_{0}=\left|{\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}\right|^{2}\!.$ ⓘ

Für gewöhnliches Glas in Luft ist n₁ = 1 und n₂ = 1,5, so dass etwa 4 % der einfallenden Leistung reflektiert wird. Bei anderen Einfallswinkeln hängt das Reflexionsvermögen auch von der Polarisation des einfallenden Lichts ab. Bei einem bestimmten Winkel, dem Brewster-Winkel, wird p-polarisiertes Licht (Licht mit dem elektrischen Feld in der Einfallsebene) vollständig durchgelassen. Der Brewster-Winkel lässt sich aus den beiden Brechungsindizes der Grenzfläche wie folgt berechnen

$\theta _{\mathrm {B} }=\arctan \!\left({\frac {n_{2}}{n_{1}}}\right)\!.$ ⓘ

Linsen

Die Leistung einer Lupe wird durch die Form und den Brechungsindex der Linse bestimmt. ⓘ

Die Brennweite einer Linse wird durch ihren Brechungsindex n und die Krümmungsradien R₁ und R₂ ihrer Oberflächen bestimmt. Die Brechkraft einer dünnen Linse in Luft ist durch die Lensmaker-Formel gegeben:

${\frac {1}{f}}=(n-1)\!\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right)\!,$

wobei f die Brennweite der Linse ist. ⓘ

Auflösung des Mikroskops

Die Auflösung eines guten optischen Mikroskops wird hauptsächlich durch die numerische Apertur (NA) des Objektivs bestimmt. Die numerische Apertur wiederum wird bestimmt durch den Brechungsindex n des Mediums, das den Raum zwischen der Probe und der Linse ausfüllt, und den halben Lichtsammelwinkel θ gemäß

$\mathrm {NA} =n\sin \theta .$ ⓘ

Aus diesem Grund wird zur Erzielung einer hohen Auflösung in der Mikroskopie in der Regel die Ölimmersion verwendet. Bei dieser Technik wird das Objektiv in einen Tropfen Immersionsöl mit hohem Brechungsindex auf die zu untersuchende Probe getaucht. ⓘ

Relative Dielektrizitätskonstante und Permeabilität

Der Brechungsindex der elektromagnetischen Strahlung ist gleich

$n={\sqrt {\varepsilon _{\mathrm {r} }\mu _{\mathrm {r} }}},$

Dabei ist εr die relative Dielektrizitätskonstante des Materials und μr seine relative Permeabilität. Der Brechungsindex wird in der Optik in den Fresnel-Gleichungen und dem Snellschen Gesetz verwendet, während die relative Dielektrizitätskonstante und die relative Permeabilität in den Maxwell-Gleichungen und der Elektronik verwendet werden. Die meisten natürlich vorkommenden Materialien sind bei optischen Frequenzen nicht magnetisch, d. h. μr liegt sehr nahe bei 1, daher ist n ungefähr √εr. In diesem besonderen Fall folgen die komplexe relative Dielektrizitätskonstante εr, mit den Real- und Imaginärteilen εr und ɛ̃r, und der komplexe Brechungsindex n, mit den Real- und Imaginärteilen n und κ (letzterer wird als "Extinktionskoeffizient" bezeichnet), der Beziehung

${\underline {\varepsilon }}_{\mathrm {r} }=\varepsilon _{\mathrm {r} }+i{\tilde {\varepsilon }}_{\mathrm {r} }={\underline {n}}^{2}=(n+i\kappa )^{2},$

und ihre Komponenten sind miteinander verbunden durch:

$\varepsilon _{\mathrm {r} }=n^{2}-\kappa ^{2},$

${\tilde {\varepsilon }}_{\mathrm {r} }=2n\kappa ,$

und:

$n={\sqrt {\frac {|{\underline {\varepsilon }}_{\mathrm {r} }|+\varepsilon _{\mathrm {r} }}{2}}},$

$\kappa ={\sqrt {\frac {|{\underline {\varepsilon }}_{\mathrm {r} }|-\varepsilon _{\mathrm {r} }}{2}}}.$

wobei $|{\underline {\varepsilon }}_{\mathrm {r} }|={\sqrt {\varepsilon _{\mathrm {r} }^{2}+{\tilde {\varepsilon }}_{\mathrm {r} }^{2}}}$ ist der komplexe Modulus. ⓘ

Wellenwiderstand

Die Wellenimpedanz einer ebenen elektromagnetischen Welle in einem nichtleitenden Medium ist gegeben durch

$Z={\sqrt {\frac {\mu }{\varepsilon }}}={\sqrt {\frac {\mu _{\mathrm {0} }\mu _{\mathrm {r} }}{\varepsilon _{\mathrm {0} }\varepsilon _{\mathrm {r} }}}}={\sqrt {\frac {\mu _{\mathrm {0} }}{\varepsilon _{\mathrm {0} }}}}{\sqrt {\frac {\mu _{\mathrm {r} }}{\varepsilon _{\mathrm {r} }}}}=Z_{0}{\sqrt {\frac {\mu _{\mathrm {r} }}{\varepsilon _{\mathrm {r} }}}}=Z_{0}{\frac {\mu _{\mathrm {r} }}{n}}$

wobei $Z_{0}$ ist der Wellenwiderstand des Vakuums, μ und ϵ sind die absolute Permeabilität und Permittivität des Mediums, εr ist die relative Permittivität des Materials, und μr ist seine relative Permeabilität. ⓘ

In nichtmagnetischen Medien mit $\mu _{\mathrm {r} }=1$,

$Z={\frac {Z_{0}}{n}},$ ⓘ

$n={\frac {Z_{0}}{Z}}.$ ⓘ

Der Brechungsindex in einem nichtmagnetischen Medium ist also das Verhältnis zwischen dem Wellenwiderstand des Vakuums und dem Wellenwiderstand des Mediums. ⓘ

Das Reflexionsvermögen $R_{0}$ zwischen zwei Medien kann also sowohl durch die Wellenwiderstände als auch durch die Brechungsindizes ausgedrückt werden als

$R_{0}=\left|{\frac {n_{1}-n_{2}}{n_{1}+n_{2}}}\right|^{2}\!=\left|{\frac {Z_{2}-Z_{1}}{Z_{2}+Z_{1}}}\right|^{2}\!.$ ⓘ

Dichte

Die Beziehung zwischen dem Brechungsindex und der Dichte von Silikat- und Borosilikatgläsern ⓘ

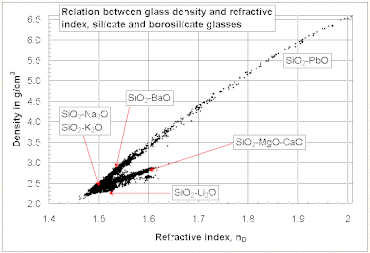
Im Allgemeinen nimmt der Brechungsindex eines Glases mit seiner Dichte zu. Es besteht jedoch nicht für alle Silikat- und Borosilikatgläser ein allgemeiner linearer Zusammenhang zwischen dem Brechungsindex und der Dichte. Ein relativ hoher Brechungsindex und eine niedrige Dichte lassen sich bei Gläsern erzielen, die Leichtmetalloxide wie Li₂O und MgO enthalten, während bei Gläsern, die PbO und BaO enthalten, der umgekehrte Trend zu beobachten ist, wie im Diagramm rechts zu sehen ist. ⓘ

Viele Öle (wie z. B. Olivenöl) und Ethanol sind Beispiele für Flüssigkeiten, die entgegen der allgemeinen Korrelation zwischen Dichte und Brechungsindex eine höhere Brechkraft, aber eine geringere Dichte als Wasser aufweisen. ⓘ

Für Luft ist n - 1 proportional zur Dichte des Gases, solange sich die chemische Zusammensetzung nicht ändert. Für ideale Gase ist er daher auch proportional zum Druck und umgekehrt proportional zur Temperatur. ⓘ

Gruppenindex

Manchmal wird ein "Gruppengeschwindigkeits-Brechungsindex" definiert, der gewöhnlich als Gruppenindex bezeichnet wird:

$n_{\mathrm {g} }={\frac {\mathrm {c} }{v_{\mathrm {g} }}},$

wobei vg die Gruppengeschwindigkeit ist. Dieser Wert ist nicht mit n zu verwechseln, das immer in Bezug auf die Phasengeschwindigkeit definiert ist. Wenn die Dispersion klein ist, kann die Gruppengeschwindigkeit mit der Phasengeschwindigkeit durch die folgende Beziehung verknüpft werden

$v_{\mathrm {g} }=v-\lambda {\frac {\mathrm {d} v}{\mathrm {d} \lambda }},$

wobei λ die Wellenlänge im Medium ist. In diesem Fall lässt sich der Gruppenindex in Bezug auf die Wellenlängenabhängigkeit des Brechungsindexes wie folgt ausdrücken

$n_{\mathrm {g} }={\frac {n}{1+{\frac {\lambda }{n}}{\frac {\mathrm {d} n}{\mathrm {d} \lambda }}}}.$ ⓘ

Wenn der Brechungsindex eines Mediums als Funktion der Vakuumwellenlänge (anstelle der Wellenlänge im Medium) bekannt ist, lauten die entsprechenden Ausdrücke für die Gruppengeschwindigkeit und den Index (für alle Werte der Dispersion)

$v_{\mathrm {g} }=\mathrm {c} \!\left(n-\lambda _{0}{\frac {\mathrm {d} n}{\mathrm {d} \lambda _{0}}}\right)^{-1}\!,$

$n_{\mathrm {g} }=n-\lambda _{0}{\frac {\mathrm {d} n}{\mathrm {d} \lambda _{0}}},$

wobei λ₀ die Wellenlänge im Vakuum ist. ⓘ

Andere Beziehungen

Wie im Fizeau-Experiment gezeigt wurde, ist die Geschwindigkeit des Lichts in einem sich bewegenden Medium relativ zu einem Beobachter, der sich mit der Geschwindigkeit v in dieselbe Richtung wie das Licht bewegt, gleich:

$V={\frac {\mathrm {c} }{n}}+{\frac {v\left(1-{\frac {1}{n^{2}}}\right)}{1+{\frac {v}{cn}}}}\approx {\frac {\mathrm {c} }{n}}+v\left(1-{\frac {1}{n^{2}}}\right)\ .$ ⓘ

Der Brechungsindex eines Stoffes kann mit seiner Polarisierbarkeit durch die Lorentz-Lorenz-Gleichung oder mit den molaren Brechungsgraden seiner Bestandteile durch die Gladstone-Dale-Beziehung in Beziehung gesetzt werden. ⓘ

Brechungsvermögen

In atmosphärischen Anwendungen wird die Brechzahl als N = n - 1 definiert, oft skaliert als N = 10⁶(n - 1) oder N = 10⁸(n - 1); die Multiplikationsfaktoren werden verwendet, weil der Brechungsindex für Luft, n, höchstens um einige Teile pro Zehntausend von der Einheit abweicht. ⓘ

Die molare Brechzahl hingegen ist ein Maß für die gesamte Polarisierbarkeit eines Mols einer Substanz und kann aus dem Brechungsindex wie folgt berechnet werden

$A={\frac {M}{\rho }}{\frac {n^{2}-1}{n^{2}+2}},$

wobei ρ die Dichte und M die molare Masse ist. ⓘ

Nichtskalare, nichtlineare oder inhomogene Brechung

Bislang haben wir angenommen, dass die Brechung durch lineare Gleichungen mit einem räumlich konstanten, skalaren Brechungsindex gegeben ist. Diese Annahmen können auf verschiedene Arten zusammenbrechen, die in den folgenden Unterabschnitten beschrieben werden. ⓘ

Doppelbrechung

Ein Kalzitkristall auf einem Papier mit einigen Buchstaben, die Doppelbrechung zeigen ⓘ

Doppelbrechende Materialien können Farben erzeugen, wenn sie zwischen gekreuzten Polarisatoren liegen. Dies ist die Grundlage für die Photoelastizität. ⓘ

Bei einigen Materialien hängt der Brechungsindex von der Polarisation und der Ausbreitungsrichtung des Lichts ab. Dies wird als Doppelbrechung oder optische Anisotropie bezeichnet. ⓘ

In der einfachsten Form, der uniaxialen Doppelbrechung, gibt es nur eine spezielle Richtung im Material. Diese Achse wird als die optische Achse des Materials bezeichnet. Licht mit linearer Polarisation senkrecht zu dieser Achse erfährt einen gewöhnlichen Brechungsindex no, während parallel polarisiertes Licht einen außerordentlichen Brechungsindex ne erfährt. Die Doppelbrechung des Materials ist die Differenz zwischen diesen Brechungsindizes, Δn = ne - no. Licht, das sich in Richtung der optischen Achse ausbreitet, wird von der Doppelbrechung nicht beeinflusst, da der Brechungsindex nicht von der Polarisation abhängt. Bei anderen Ausbreitungsrichtungen wird das Licht in zwei linear polarisierte Strahlen aufgeteilt. Für Licht, das sich senkrecht zur optischen Achse ausbreitet, haben die Strahlen die gleiche Richtung. Dies kann genutzt werden, um die Polarisationsrichtung von linear polarisiertem Licht zu ändern oder mit Wellenplatten zwischen linearer, zirkularer und elliptischer Polarisation zu wechseln. ⓘ

Viele Kristalle sind von Natur aus doppelbrechend, aber auch isotrope Materialien wie Kunststoffe und Glas können oft doppelbrechend gemacht werden, indem man ihnen eine Vorzugsrichtung gibt, z. B. durch eine äußere Kraft oder ein elektrisches Feld. Dieser Effekt wird als Photoelastizität bezeichnet und kann genutzt werden, um Spannungen in Strukturen aufzudecken. Das doppelbrechende Material wird zwischen gekreuzten Polarisatoren angeordnet. Eine Änderung der Doppelbrechung verändert die Polarisation und damit den Anteil des Lichts, der durch den zweiten Polarisator durchgelassen wird. ⓘ

Im allgemeineren Fall der doppelbrechenden Materialien, der im Bereich der Kristalloptik beschrieben wird, ist die Dielektrizitätskonstante ein Tensor vom Rang 2 (eine 3 x 3-Matrix). In diesem Fall kann die Ausbreitung des Lichts nicht einfach durch den Brechungsindex beschrieben werden, außer für Polarisationen entlang der Hauptachsen. ⓘ

Nichtlinearität

Das starke elektrische Feld von Licht hoher Intensität (z. B. das eines Lasers) kann dazu führen, dass sich der Brechungsindex eines Mediums beim Durchgang des Lichts ändert, was zu einer nichtlinearen Optik führt. Ändert sich der Index quadratisch mit dem Feld (linear mit der Intensität), spricht man vom optischen Kerr-Effekt, der Phänomene wie Selbstfokussierung und Selbstphasenmodulation verursacht. Ändert sich der Index linear mit dem Feld (ein nicht-trivialer linearer Koeffizient ist nur bei Materialien möglich, die keine Inversionssymmetrie besitzen), spricht man vom Pockels-Effekt. ⓘ

Inhomogenität

Eine Linse mit Gradientenindex, bei der sich der Brechungsindex (n) mit dem radialen Abstand (x) parabolisch ändert. Die Linse bündelt das Licht auf die gleiche Weise wie eine herkömmliche Linse. ⓘ

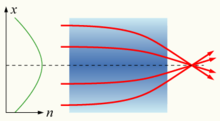
Wenn der Brechungsindex eines Mediums nicht konstant ist, sondern sich allmählich mit der Position ändert, wird das Material als Gradientenindex- oder GRIN-Medium bezeichnet und durch die Gradientenindexoptik beschrieben. Licht, das sich durch ein solches Medium bewegt, kann gebogen oder fokussiert werden, und dieser Effekt kann zur Herstellung von Linsen, einigen optischen Fasern und anderen Geräten genutzt werden. Die Einführung von GRIN-Elementen in den Entwurf eines optischen Systems kann das System erheblich vereinfachen und die Anzahl der Elemente um bis zu einem Drittel reduzieren, während die Gesamtleistung erhalten bleibt. Die kristalline Linse des menschlichen Auges ist ein Beispiel für eine GRIN-Linse mit einem Brechungsindex, der von etwa 1,406 im inneren Kern bis zu etwa 1,386 im weniger dichten Kortex reicht. Einige häufige Luftspiegelungen werden durch einen räumlich variierenden Brechungsindex der Luft verursacht. ⓘ

Messung des Brechungsindexes

Homogene Medien

Das Prinzip vieler Refraktometer ⓘ

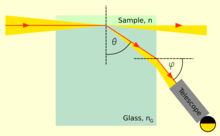
Der Brechungsindex von Flüssigkeiten oder Festkörpern kann mit Refraktometern gemessen werden. Sie messen in der Regel einen bestimmten Brechungswinkel oder den kritischen Winkel für die innere Totalreflexion. Die ersten im Handel erhältlichen Laborrefraktometer wurden Ende des 19. Jahrhunderts von Ernst Abbe entwickelt. Die gleichen Prinzipien werden auch heute noch verwendet. Bei diesem Instrument wird eine dünne Schicht der zu messenden Flüssigkeit zwischen zwei Prismen gelegt. Das Licht wird unter Einfallswinkeln bis zu 90° durch die Flüssigkeit gestrahlt, d. h. die Lichtstrahlen verlaufen parallel zur Oberfläche. Das zweite Prisma sollte einen höheren Brechungsindex als die Flüssigkeit haben, damit das Licht nur unter Winkeln in das Prisma einfällt, die kleiner als der kritische Winkel für die Totalreflexion sind. Dieser Winkel kann dann entweder durch ein Fernrohr oder mit einem digitalen Photodetektor in der Brennebene eines Objektivs gemessen werden. Der Brechungsindex n der Flüssigkeit kann dann aus dem maximalen Transmissionswinkel θ als n = n_G sin θ berechnet werden, wobei n_G der Brechungsindex des Prismas ist. ⓘ

Ein tragbares Refraktometer zur Messung des Zuckergehalts von Früchten ⓘ

Diese Art von Geräten wird häufig in chemischen Labors zur Identifizierung von Substanzen und zur Qualitätskontrolle verwendet. Handgehaltene Varianten werden in der Landwirtschaft eingesetzt, z. B. von Winzern zur Bestimmung des Zuckergehalts im Traubensaft, und Inline-Prozessrefraktometer werden z. B. in der chemischen und pharmazeutischen Industrie zur Prozesskontrolle verwendet. ⓘ

In der Gemmologie wird eine andere Art von Refraktometer verwendet, um den Brechungsindex und die Doppelbrechung von Edelsteinen zu messen. Der Edelstein wird auf ein Prisma mit hohem Brechungsindex gelegt und von unten beleuchtet. Eine Kontaktflüssigkeit mit hohem Brechungsindex wird verwendet, um den optischen Kontakt zwischen dem Edelstein und dem Prisma herzustellen. Bei kleinen Einfallswinkeln wird der größte Teil des Lichts in den Edelstein durchgelassen, aber bei großen Winkeln kommt es zu einer internen Totalreflexion im Prisma. Der kritische Winkel wird normalerweise durch ein Fernrohr gemessen. ⓘ

Variationen des Brechungsindex

Differentialinterferenzkontrastmikroskopische Aufnahme von Hefezellen ⓘ

Ungefärbte biologische Strukturen erscheinen in der Hellfeldmikroskopie meist transparent, da die meisten zellulären Strukturen keine nennenswerten Mengen an Licht abschwächen. Dennoch entspricht die Variation der Materialien, aus denen diese Strukturen bestehen, auch einer Variation des Brechungsindexes. Die folgenden Techniken wandeln diese Variationen in messbare Amplitudendifferenzen um: Um die räumliche Variation des Brechungsindexes in einer Probe zu messen, werden Phasenkontrast-Bildgebungsverfahren eingesetzt. Diese Verfahren messen die Phasenvariationen der aus der Probe austretenden Lichtwelle. Die Phase ist proportional zur optischen Weglänge, die der Lichtstrahl durchlaufen hat, und liefert somit ein Maß für das Integral des Brechungsindexes entlang des Strahlengangs. Die Phase kann bei optischen oder höheren Frequenzen nicht direkt gemessen werden und muss daher durch Interferenz mit einem Referenzstrahl in Intensität umgewandelt werden. Im visuellen Spektrum geschieht dies mit der Zernike-Phasenkontrastmikroskopie, der differentiellen Interferenzkontrastmikroskopie (DIC) oder der Interferometrie. ⓘ

Bei der Zernike-Phasenkontrastmikroskopie werden die niederfrequenten Komponenten des Bildes durch einen phasenverschobenen Ring in der Fourierebene der Probe phasenverschoben, so dass hochfrequente Teile des Bildes mit dem niederfrequenten Referenzstrahl interferieren können. Bei der DIC wird die Beleuchtung in zwei Strahlen aufgeteilt, die unterschiedliche Polarisationen erhalten, unterschiedlich phasenverschoben sind und mit leicht unterschiedlichen Beträgen quer verschoben werden. Nach der Probe werden die beiden Teile zur Interferenz gebracht, wodurch ein Bild der Ableitung der optischen Weglänge in Richtung der Differenz der Querverschiebung entsteht. Bei der Interferometrie wird die Beleuchtung durch einen teilreflektierenden Spiegel in zwei Strahlen aufgeteilt. Einer der beiden Strahlen wird durch die Probe geleitet, bevor sie zur Interferenz gebracht werden und ein direktes Bild der Phasenverschiebungen liefern. Wenn die Unterschiede in der optischen Weglänge mehr als eine Wellenlänge betragen, enthält das Bild Streifen. ⓘ

Es gibt mehrere Phasenkontrast-Röntgenbildgebungsverfahren zur Bestimmung der räumlichen 2D- oder 3D-Verteilung des Brechungsindex von Proben im Röntgenbereich. ⓘ

Anwendungen

Der Brechungsindex ist eine wichtige Eigenschaft der Komponenten eines jeden optischen Instruments. Er bestimmt die Fokussierungskraft von Linsen, das Dispersionsvermögen von Prismen, das Reflexionsvermögen von Linsenbeschichtungen und die Lichtleitfähigkeit von Lichtleitfasern. Da der Brechungsindex eine grundlegende physikalische Eigenschaft einer Substanz ist, wird er häufig verwendet, um eine bestimmte Substanz zu identifizieren, ihre Reinheit zu bestätigen oder ihre Konzentration zu messen. Der Brechungsindex wird zur Messung von Feststoffen, Flüssigkeiten und Gasen verwendet. Am häufigsten wird er verwendet, um die Konzentration eines gelösten Stoffes in einer wässrigen Lösung zu messen. Der Brechungsindex kann auch als nützliches Instrument zur Unterscheidung zwischen verschiedenen Edelsteinarten verwendet werden, da jeder einzelne Stein eine einzigartige Chatoyanz aufweist. Ein Refraktometer ist ein Instrument zur Messung des Brechungsindexes. Bei einer Zuckerlösung kann der Brechungsindex verwendet werden, um den Zuckergehalt zu bestimmen (siehe Brix). ⓘ

Der Brechungsindex ist eine der zentralen Bestimmungsgrößen für optische Linsen. Die Kunst der Optikrechnung zur Auslegung optischer Instrumente (Objektive, Messinstrumente, Belichtungsanlagen der Fotolithografie) beruht auf der Kombination verschiedener brechender Linsenoberflächen mit passenden Glassorten. ⓘ

In der Chemie und Pharmazie wird der Brechungsindex bei einer bestimmten Temperatur oft eingesetzt, um flüssige Substanzen zu charakterisieren. Die Temperatur und die Wellenlänge, bei der der Brechungsindex bestimmt wurde, werden dabei dem Symbol für den Brechungsindex angefügt, für 20 °C und die Natrium-D-Linie z. B. $n_{D}^{20}$. ⓘ

Die Bestimmung des Brechungsindex erlaubt eine einfache Bestimmung des Gehaltes einer bestimmten Substanz in einem Lösungsmittel:

• Zucker in Wein, siehe Grad Brix und Grad Oechsle
• Harz in Lösungsmittel
• Gefrierschutzmittel (meist Ethylenglycol) im Kühlwasser von Verbrennungsmotoren oder thermischen Solaranlagen ⓘ

Physikalische Grundlagen

Einfluss des komplexen Brechungs­index eines Materials $n+\mathrm {i} k$ auf das Refle­xions­verhalten eines Lichtstrahls beim Auftreffen auf die Grenzfläche Luft/Material ⓘ

Verlauf des wellenlängenabhängigen komplexen Brechungsindex im visuellen Bereich für Halbleiter mit Band­über­gängen in diesem Bereich ⓘ

Die Bezeichnung „Brechungsindex“ kommt vom Begriff Brechung und seinem Auftreten im Snelliusschen Brechungsgesetz. Der Brechungsindex $n$ ist eine Größe der Dimension Zahl. Er gibt das Verhältnis der Vakuumlichtgeschwindigkeit $c_{0}$ zur Ausbreitungsgeschwindigkeit $c_{\mathrm {M} }$ des Lichts im Medium an:

$n={\frac {c_{0}}{c_{\mathrm {M} }}}$ ⓘ

Komplexer Brechungsindex

Anisotroper Brechungsindex

In anisotropen Medien ist der Brechungsindex kein Skalar, sondern ein Tensor zweiter Stufe. Wellenvektor und Ausbreitungsrichtung stimmen dann nicht mehr überein. ⓘ

Brechungsindex der Luft und anderer Stoffe

Brechungsindex ausgewählter Stoffe bei der Wellenlänge 589 nm (gelb-orange) der Natrium-D-Linie. ⓘ

Material	Brechungs- index n
Vakuum	exakt 1
Helium (Normbed.)	1,000 034 911
Luft (Normbed.)	1,000 292
Schwefelhexafluorid (Normbed.)	1,000 729
Aerogel	1,007 … 1,24
Eis	1,31
Wasser (liqu.) 20 °C	1,3330
menschl. Augenlinse	1,35 … 1,42
Ethanol (liqu.)	1,3614
Flussspat (Calciumfluorid)	1,43
menschliche Epidermis	1,45
Quarzglas	1,46
Glycerin (liqu.)	1,473 99
PMMA (Plexiglas)	1,49
Kronglas	1,46 … 1,65
Benzol (liqu.)	1,5011
Fensterglas	1,52
Mikroskopische Deckgläser	1,523
Quarz	1,54
Halit (Steinsalz)	1,54
Polystyrol (PS)	1,58
Polycarbonat (PC)	1,585
Epoxidharz	1,55 … 1,63
Flintglas	1,56 … 1,93
Schwefelkohlenstoff (CS2) (liqu.)	1,6319
Kunststoffglas für Brillen	bis 1,76
Diiodmethan (liqu.)	1,7425
Rubin (Aluminiumoxid)	1,76
Mineralglas für Brillen (polarisierend)	bis 1,9 (1,5)
Glas	1,45 … 2,14
Bleikristall	bis 1,93
Zirkon	1,92
Diamant	2,42
Titandioxid (Anatas)	2,52
Siliciumcarbid	2,65 … 2,69
Titandioxid (Rutil)	3,10

Luft

Der Brechungsindex für sichtbares Licht von Luft beträgt auf Meeresniveau 1,00028 (trockene Luft bei Normatmosphäre). Er hängt von der Dichte und damit von der Temperatur der Luft ab, sowie von der speziellen Zusammensetzung der Luft – insbesondere der Luftfeuchtigkeit. Da die Luftdichte nach oben – entsprechend den Gasgesetzen in einem Schwerefeld, siehe barometrische Höhenformel – exponentiell abnimmt, beträgt der Brechungsindex in 8 km Höhe nur mehr 1,00011. Durch diese astronomische Refraktion scheinen Sterne höher zu stehen, als das ohne Atmosphäre der Fall wäre. Im technischen Bereich wird manchmal zur Vereinfachung der Brechungsindex der Materialien auf den von Luft bezogen. ⓘ

Faraday-Effekt

Falls $n$ positiv ist, lässt sich damit die Phasengeschwindigkeit der Welle

$v_{\text{phase}}={\frac {c}{n}}$

und damit wiederum die Wellenlänge

$\lambda ={\frac {c}{nf}}$

berechnen. Weil sich die rechts- bzw. linksdrehenden zirkularen Wellen in ihren Wellenlängen unterscheiden, ist eine davon nach einer gewissen Weglänge um einen kleinen Winkel weiter gedreht als die andere. Der resultierende Vektor (und damit die Polarisationsebene) als Summe der beiden Komponenten wird deshalb beim Durchlaufen des Plasmas gedreht, was man als Faraday-Rotation bezeichnet. Nach einer längeren Strecke kann die Gesamtdrehung sehr groß sein und ändert sich wegen der Bewegung der Ionosphäre ständig. Eine Sendung in vertikaler Polarisation kann den Empfänger in unregelmäßigen Zeitabständen auch horizontal polarisiert erreichen. Falls die Empfangsantenne darauf nicht reagiert, ändert sich die Signalstärke sehr drastisch, was als Fading bezeichnet wird. ⓘ

Beim Funkverkehr mit Satelliten unterscheiden sich $n_{\text{links}}$ und $n_{\text{rechts}}$ wegen der wesentlich höheren Frequenzen nur geringfügig, entsprechend geringer ist auch die Faradayrotation. ⓘ

Messung im optischen Bereich

Zur experimentellen Bestimmung des Brechungsindex eines Mediums mit $\mu _{r2}\ ({\text{med}})=\mu _{r1}\ ({\text{Luft}})$ (zum Beispiel nicht magnetisch) $n_{\text{med}}$ kann man zum Beispiel den Brewster-Winkel beim Übergang von Luft in dieses Medium messen. Für diesen Fall gilt ⓘ

$\tan(\alpha _{\text{Brewster}})={\frac {n_{\text{med}}}{n_{\text{Luft}}}}\approx n_{\text{med}}$. ⓘ

Für die Messung wird ein Refraktometer angewandt. ⓘ

Eine Abschätzung des Brechungsindexes ist mit der sogenannten Immersionsmethode durch das Eintauchen eines Gegenstands in durchsichtige Flüssigkeiten mit verschiedener Dichte möglich. Wenn der Brechungsindex von Gegenstand und Flüssigkeit identisch sind, verschwinden die Konturen des Gegenstands. Dieses Verfahren kann leicht eingesetzt werden, um zum Beispiel Rubine oder Saphire mit einem Brechungsindex von rund 1,76 zu identifizieren, indem sie in eine geeignete Schwerflüssigkeit eingetaucht werden, wie beispielsweise Diiodmethan (Brechungsindex = 1,74). ⓘ