Chaosforschung

Eine Darstellung des Lorenz-Attraktors für die Werte r = 28, σ = 10, b = 8/3 ⓘ

Eine Animation eines Doppelstabpendels bei einer Zwischenenergie, die chaotisches Verhalten zeigt. Würde man das Pendel von einer geringfügig anderen Ausgangssituation aus starten, würde sich eine ganz andere Flugbahn ergeben. Das Doppelstabpendel ist eines der einfachsten dynamischen Systeme mit chaotischen Lösungen. ⓘ

Die Chaostheorie ist eine interdisziplinäre wissenschaftliche Theorie und ein Zweig der Mathematik, der sich mit den zugrundeliegenden Mustern und deterministischen Gesetzen dynamischer Systeme beschäftigt, die sehr empfindlich auf die Anfangsbedingungen reagieren und von denen man früher annahm, dass sie völlig zufällige Zustände der Unordnung und Unregelmäßigkeiten aufweisen. Die Chaostheorie besagt, dass der scheinbaren Zufälligkeit chaotischer komplexer Systeme Muster, Zusammenhänge, ständige Rückkopplungsschleifen, Wiederholungen, Selbstähnlichkeit, Fraktale und Selbstorganisation zugrunde liegen. Der Schmetterlingseffekt, ein dem Chaos zugrunde liegendes Prinzip, beschreibt, wie eine kleine Änderung in einem Zustand eines deterministischen nichtlinearen Systems zu großen Unterschieden in einem späteren Zustand führen kann (was bedeutet, dass es eine empfindliche Abhängigkeit von den Anfangsbedingungen gibt). Eine Metapher für dieses Verhalten ist, dass ein Schmetterling, der in Brasilien mit den Flügeln schlägt, in Texas einen Tornado verursachen kann. ⓘ

Kleine Unterschiede in den Anfangsbedingungen, die beispielsweise auf Messfehler oder Rundungsfehler bei numerischen Berechnungen zurückzuführen sind, können bei solchen dynamischen Systemen zu stark voneinander abweichenden Ergebnissen führen, was eine langfristige Vorhersage ihres Verhaltens im Allgemeinen unmöglich macht. Dies kann passieren, obwohl diese Systeme deterministisch sind, d. h. ihr zukünftiges Verhalten folgt einer eindeutigen Entwicklung und ist vollständig durch ihre Ausgangsbedingungen bestimmt, ohne dass Zufallselemente beteiligt sind. Mit anderen Worten: Die deterministische Natur dieser Systeme macht sie nicht vorhersehbar. Dieses Verhalten wird als deterministisches Chaos oder einfach als Chaos bezeichnet. Die Theorie wurde von Edward Lorenz wie folgt zusammengefasst:

Chaos: Wenn die Gegenwart die Zukunft bestimmt, aber die ungefähre Gegenwart die Zukunft nicht annähernd bestimmt. ⓘ

Chaotisches Verhalten kommt in vielen natürlichen Systemen vor, z. B. in der Strömung von Flüssigkeiten, in Unregelmäßigkeiten des Herzschlags, im Wetter und im Klima. Es tritt auch spontan in einigen Systemen mit künstlichen Komponenten auf, z. B. an der Börse und im Straßenverkehr. Dieses Verhalten kann durch die Analyse eines chaotischen mathematischen Modells oder durch analytische Techniken wie Rekursionsdiagramme und Poincaré-Karten untersucht werden. Die Chaostheorie findet in einer Vielzahl von Disziplinen Anwendung, darunter Meteorologie, Anthropologie, Soziologie, Umweltwissenschaften, Informatik, Ingenieurwesen, Wirtschaft, Ökologie und Krisenmanagement bei Pandemien. Die Theorie bildete die Grundlage für Studienbereiche wie komplexe dynamische Systeme, Randbereiche der Chaostheorie und Selbstorganisationsprozesse. ⓘ

Die Chaosforschung oder Chaostheorie bezeichnet ein nicht klar umgrenztes Teilgebiet der nichtlinearen Dynamik bzw. der dynamischen Systeme, welches der mathematischen Physik oder angewandten Mathematik zugeordnet ist. ⓘ

Als einführendes Beispiel wird oft auf das magnetische Pendel oder das Doppelpendel verwiesen. Andere Beispiele sind der Schmetterlingseffekt beim Wetter, Turbulenzen, Wirtschaftskreisläufe, bestimmte Musterbildungsprozesse, wie beispielsweise Erosion, die Entstehung eines Verkehrsstaus, neuronale Netze sowie Laser. ⓘ

Die Chaosforschung basiert unter anderem auf Arbeiten von Henri Poincaré, Edward N. Lorenz, Benoît Mandelbrot und Mitchell Feigenbaum. Die hier dargestellten Phänomene entsprechen dem Minimalkonsens darüber, was thematisch zur Chaosforschung zählt. ⓘ

Einführung

Die Chaostheorie befasst sich mit deterministischen Systemen, deren Verhalten prinzipiell vorhersagbar ist. Chaotische Systeme sind eine Zeit lang vorhersehbar und werden dann "scheinbar" zufällig. Wie lange das Verhalten eines chaotischen Systems tatsächlich vorhergesagt werden kann, hängt von drei Faktoren ab: davon, wie viel Unsicherheit bei der Vorhersage toleriert werden kann, wie genau der aktuelle Zustand gemessen werden kann, und von einer Zeitskala, die von der Dynamik des Systems abhängt, der so genannten Lyapunov-Zeit. Einige Beispiele für Lyapunov-Zeiten sind: chaotische elektrische Schaltkreise, etwa 1 Millisekunde; Wettersysteme, einige Tage (unbewiesen); das innere Sonnensystem, 4 bis 5 Millionen Jahre. In chaotischen Systemen nimmt die Unsicherheit einer Vorhersage mit der verstrichenen Zeit exponentiell zu. Daher wird die proportionale Unsicherheit der Vorhersage durch die Verdoppelung der Vorhersagezeit mathematisch mehr als quadriert. In der Praxis bedeutet dies, dass eine aussagekräftige Vorhersage nicht über ein Intervall von mehr als dem Zwei- oder Dreifachen der Ljapunow-Zeit möglich ist. Wenn keine sinnvollen Vorhersagen gemacht werden können, erscheint das System zufällig. ⓘ

Die Chaostheorie ist eine Methode der qualitativen und quantitativen Analyse zur Untersuchung des Verhaltens dynamischer Systeme, die nicht durch einzelne Datenbeziehungen erklärt und vorhergesagt werden können, sondern durch ganze, kontinuierliche Datenbeziehungen erklärt und vorhergesagt werden müssen. ⓘ

Chaotische Dynamik

Die Karte, die durch x → 4 x (1 - x) und y → (x + y) mod 1 definiert ist, reagiert empfindlich auf die anfänglichen x-Positionen. Hier divergieren zwei Reihen von x- und y-Werten im Laufe der Zeit deutlich von einer winzigen Anfangsdifferenz. ⓘ

Im allgemeinen Sprachgebrauch bedeutet "Chaos" "ein Zustand der Unordnung". In der Chaostheorie wird der Begriff jedoch genauer definiert. Obwohl es keine allgemein anerkannte mathematische Definition von Chaos gibt, besagt eine häufig verwendete Definition, die ursprünglich von Robert L. Devaney formuliert wurde, dass ein dynamisches System die folgenden Eigenschaften aufweisen muss, um als chaotisch eingestuft zu werden:

1. Es muss empfindlich auf die Anfangsbedingungen reagieren,
2. Sie muss topologisch transitiv sein,
3. sie muss dichte periodische Orbits haben. ⓘ

In einigen Fällen hat sich gezeigt, dass die letzten beiden oben genannten Eigenschaften tatsächlich eine Empfindlichkeit gegenüber den Anfangsbedingungen implizieren. Im Fall der diskreten Zeit ist dies für alle kontinuierlichen Karten auf metrischen Räumen der Fall. In diesen Fällen ist dies zwar oft die praktisch bedeutsamste Eigenschaft, aber die "Empfindlichkeit gegenüber Anfangsbedingungen" muss nicht in der Definition angegeben werden. ⓘ

Wenn die Aufmerksamkeit auf Intervalle beschränkt wird, impliziert die zweite Eigenschaft die beiden anderen. Eine alternative und im Allgemeinen schwächere Definition von Chaos verwendet nur die ersten beiden Eigenschaften in der obigen Liste. ⓘ

Empfindlichkeit gegenüber Anfangsbedingungen

Lorenz-Gleichungen, die zur Erstellung von Diagrammen für die Variable y verwendet werden. Die Anfangsbedingungen für x und z wurden beibehalten, aber die für y wurden zwischen 1,001, 1,0001 und 1,00001 geändert. Die Werte für $\rho$, $\sigma$ und $\beta$ waren 45,92, 16 bzw. 4. Wie aus dem Diagramm ersichtlich ist, führt selbst der geringste Unterschied bei den Anfangswerten in den drei Fällen zu signifikanten Änderungen nach etwa 12 Sekunden der Entwicklung. Dies ist ein Beispiel für die empfindliche Abhängigkeit von den Anfangsbedingungen. ⓘ

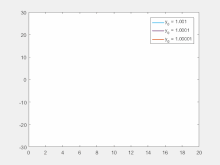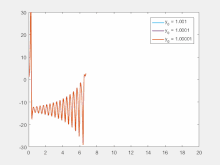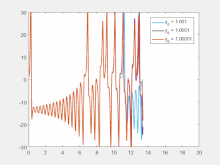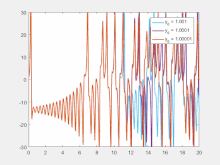
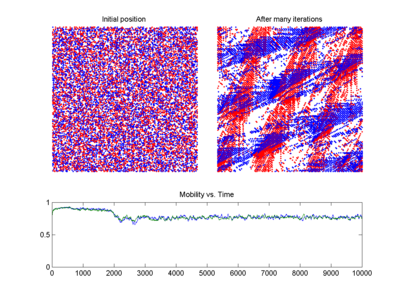
Empfindlichkeit gegenüber den Anfangsbedingungen bedeutet, dass jeder Punkt in einem chaotischen System durch andere Punkte, die deutlich unterschiedliche zukünftige Pfade oder Bahnen aufweisen, beliebig stark angenähert wird. So kann eine beliebig kleine Änderung oder Störung der aktuellen Trajektorie zu einem deutlich anderen zukünftigen Verhalten führen. ⓘ

Die Empfindlichkeit gegenüber den Anfangsbedingungen ist im Volksmund als "Schmetterlingseffekt" bekannt, so genannt wegen des Titels eines Vortrags, den Edward Lorenz 1972 vor der American Association for the Advancement of Science in Washington, D.C., mit dem Titel Predictability: Löst der Flügelschlag eines Schmetterlings in Brasilien einen Tornado in Texas aus? Der Flügelschlag stellt eine kleine Änderung des Ausgangszustands des Systems dar, die eine Kette von Ereignissen auslöst, die die Vorhersagbarkeit großräumiger Phänomene verhindert. Hätte der Schmetterling nicht mit den Flügeln geschlagen, wäre die Flugbahn des Gesamtsystems möglicherweise ganz anders verlaufen. ⓘ

Wie Lorenz in seinem 1993 erschienenen Buch "The Essence of Chaos" (Das Wesen des Chaos) vorschlägt, kann "empfindliche Abhängigkeit als akzeptable Definition von Chaos dienen". In demselben Buch definiert Lorenz den Schmetterlingseffekt wie folgt: "Das Phänomen, dass eine kleine Änderung im Zustand eines dynamischen Systems dazu führt, dass sich die nachfolgenden Zustände stark von den Zuständen unterscheiden, die ohne die Änderung eingetreten wären."  Die obige Definition steht im Einklang mit der empfindlichen Abhängigkeit der Lösungen von den Anfangsbedingungen (SDIC). Es wurde ein idealisiertes Skimodell entwickelt, um die Empfindlichkeit von zeitlich veränderlichen Pfaden gegenüber den Ausgangslagen zu veranschaulichen. Ein Vorhersagehorizont kann vor dem Einsetzen von SDIC bestimmt werden (d. h. vor einer signifikanten Trennung der anfänglichen, nahe beieinander liegenden Trajektorien). ⓘ

Eine Folge der Empfindlichkeit gegenüber den Anfangsbedingungen ist, dass das System ab einer bestimmten Zeit nicht mehr vorhersagbar ist, wenn wir mit einer begrenzten Menge an Informationen über das System beginnen (wie es in der Praxis normalerweise der Fall ist). Dies ist vor allem beim Wetter der Fall, das im Allgemeinen nur etwa eine Woche im Voraus vorhersehbar ist. Das bedeutet nicht, dass man keine Aussagen über weit in der Zukunft liegende Ereignisse machen kann, sondern nur, dass das System einigen Einschränkungen unterliegt. Wir wissen zum Beispiel, dass die Temperatur der Erdoberfläche auf der Erde (während der gegenwärtigen geologischen Ära) weder 100 °C erreichen noch unter -130 °C fallen wird, aber wir können nicht genau vorhersagen, welcher Tag die heißeste Temperatur des Jahres haben wird. ⓘ

Mathematisch ausgedrückt, misst der Lyapunov-Exponent die Empfindlichkeit gegenüber den Anfangsbedingungen in Form der Exponentialabweichung von den gestörten Anfangsbedingungen. Genauer gesagt, bei zwei Ausgangstrajektorien im Phasenraum, die unendlich nahe beieinander liegen, mit anfänglichem Abstand $\delta \mathbf {Z} _{0}$sind, divergieren die beiden Trajektorien schließlich mit einer Rate, die durch ⓘ

$|\delta \mathbf {Z} (t)|\approx e^{\lambda t}|\delta \mathbf {Z} _{0}|,$ ⓘ

wobei $t$ die Zeit ist und $\lambda$ der Lyapunov-Exponent ist. Die Trennungsrate hängt von der Ausrichtung des anfänglichen Trennungsvektors ab, so dass ein ganzes Spektrum von Lyapunov-Exponenten existieren kann. Die Anzahl der Lyapunov-Exponenten ist gleich der Anzahl der Dimensionen des Phasenraums, obwohl es üblich ist, sich nur auf den größten zu beziehen. So wird beispielsweise der maximale Lyapunov-Exponent (MLE) am häufigsten verwendet, da er die Gesamtvorhersagbarkeit des Systems bestimmt. Ein positiver MLE wird in der Regel als Hinweis darauf gewertet, dass das System chaotisch ist. ⓘ

Neben der oben genannten Eigenschaft gibt es noch weitere Eigenschaften, die mit der Empfindlichkeit der Anfangsbedingungen zusammenhängen. Dazu gehören z. B. die maßtheoretische Vermischung (wie in der Ergodentheorie erörtert) und die Eigenschaften eines K-Systems. ⓘ

Nicht-Periodizität

Ein chaotisches System kann Sequenzen von Werten für die sich entwickelnde Variable aufweisen, die sich exakt wiederholen und ein periodisches Verhalten ausgehend von einem beliebigen Punkt in dieser Sequenz ergeben. Solche periodischen Sequenzen sind jedoch eher abstoßend als anziehend, d. h. wenn die sich entwickelnde Variable außerhalb der Sequenz liegt, egal wie nahe sie daran ist, tritt sie nicht in die Sequenz ein, sondern weicht sogar von ihr ab. Für fast alle Ausgangsbedingungen entwickelt sich die Variable also chaotisch mit nicht-periodischem Verhalten. ⓘ

Topologische Vermischung

Sechs Iterationen eines Satzes von Zuständen $[x,y]$ durchlaufen die logistische Karte. Die erste Iteration (blau) ist die Anfangsbedingung, die im Wesentlichen einen Kreis bildet. Die Animation zeigt die erste bis sechste Iteration der kreisförmigen Anfangsbedingungen. Es ist zu erkennen, dass mit fortschreitender Iteration eine Vermischung stattfindet. Die sechste Iteration zeigt, dass die Punkte fast vollständig im Phasenraum verstreut sind. Wären wir in den Iterationen weiter fortgeschritten, wäre die Durchmischung homogen und unumkehrbar gewesen. Die logistische Karte hat die Gleichung $x_{k+1}=4x_{k}(1-x_{k})$. Um den Zustandsraum der logistischen Karte in zwei Dimensionen zu erweitern, wurde ein zweiter Zustand erzeugt, $y$erstellt als $y_{k+1}=x_{k}+y_{k}$, wenn $x_{k}+y_{k}<1$ und $y_{k+1}=x_{k}+y_{k}-1$ andernfalls. ⓘ

Die durch x → 4 x (1 - x) und y → (x + y) mod 1 definierte Karte zeigt ebenfalls eine topologische Mischung. Hier wird die blaue Region durch die Dynamik zunächst in die violette Region, dann in die rosa und rote Region und schließlich in eine Wolke aus vertikalen Linien verwandelt, die über den Raum verstreut sind. ⓘ

Topologische Durchmischung (oder die schwächere Bedingung der topologischen Transitivität) bedeutet, dass sich das System im Laufe der Zeit so entwickelt, dass sich jede beliebige Region oder offene Menge seines Phasenraums schließlich mit jeder anderen beliebigen Region überschneidet. Dieses mathematische Konzept der "Vermischung" entspricht der üblichen Intuition, und die Vermischung von Farbstoffen oder Flüssigkeiten ist ein Beispiel für ein chaotisches System. ⓘ

Die topologische Vermischung wird in den gängigen Darstellungen des Chaos oft ausgelassen, die Chaos nur mit der Empfindlichkeit gegenüber den Anfangsbedingungen gleichsetzen. Eine empfindliche Abhängigkeit von den Anfangsbedingungen allein bedeutet jedoch noch kein Chaos. Betrachten wir zum Beispiel ein einfaches dynamisches System, das durch wiederholtes Verdoppeln eines Anfangswertes entsteht. Dieses System ist überall empfindlich von den Anfangsbedingungen abhängig, da jedes Paar nahe beieinander liegender Punkte schließlich weit voneinander entfernt wird. In diesem Beispiel gibt es jedoch keine topologische Vermischung und somit auch kein Chaos. Vielmehr ist das Verhalten sehr einfach: Alle Punkte außer 0 tendieren zu positiver oder negativer Unendlichkeit. ⓘ

Topologische Transitivität

Eine Abbildung $f:X\to X$ wird als topologisch transitiv bezeichnet, wenn für jedes Paar nicht leerer offener Mengen $U,V\subset X$gibt es $k>0$ derart, dass $f^{k}(U)\cap V\neq \emptyset$. Die topologische Transitivität ist eine schwächere Version der topologischen Mischung. Wenn eine Karte topologisch transitiv ist, dann gibt es für einen Punkt x und eine Region V einen Punkt y in der Nähe von x, dessen Bahn durch V verläuft. Dies impliziert, dass es unmöglich ist, das System in zwei offene Mengen zu zerlegen. ⓘ

Ein wichtiges verwandtes Theorem ist das Birkhoffsche Transitivitäts-Theorem. Es ist leicht zu erkennen, dass die Existenz eines dichten Orbits topologische Transitivität impliziert. Das Birkhoffsche Transitivitäts-Theorem besagt, dass, wenn X ein zweiter abzählbarer, vollständiger metrischer Raum ist, die topologische Transitivität die Existenz einer dichten Menge von Punkten in X impliziert, die dichte Orbits haben. ⓘ

Dichte der periodischen Bahnen

Wenn ein chaotisches System dichte periodische Bahnen hat, bedeutet dies, dass jeder Punkt im Raum beliebig dicht von periodischen Bahnen umkreist wird. Die eindimensionale logistische Karte, definiert durch x → 4 x (1 - x), ist eines der einfachsten Systeme mit einer hohen Dichte periodischer Bahnen. Ein Beispiel, ${\tfrac {5-{\sqrt {5}}}{8}}$ → ${\tfrac {5+{\sqrt {5}}}{8}}$ → ${\tfrac {5-{\sqrt {5}}}{8}}$ (oder ungefähr 0,3454915 → 0,9045085 → 0,3454915) eine (instabile) Bahn der Periode 2, und ähnliche Bahnen gibt es für die Perioden 4, 8, 16 usw. (in der Tat für alle im Sharkovskii-Theorem genannten Perioden). ⓘ

Das Sharkovskii-Theorem ist die Grundlage für den Beweis von Li und Yorke (1975), dass jedes kontinuierliche eindimensionale System, das einen regelmäßigen Zyklus der Periode 3 aufweist, auch regelmäßige Zyklen jeder anderen Länge sowie vollständig chaotische Bahnen aufweist. ⓘ

Seltsame Attraktoren

Der Lorenz-Attraktor zeigt chaotisches Verhalten. Diese beiden Diagramme zeigen, wie empfindlich die Abhängigkeit von den Anfangsbedingungen in dem vom Attraktor eingenommenen Bereich des Phasenraums ist. ⓘ

Einige dynamische Systeme, wie die eindimensionale logistische Karte, die durch x → 4 x (1 - x) definiert ist, sind überall chaotisch, aber in vielen Fällen ist chaotisches Verhalten nur in einer Teilmenge des Phasenraums zu finden. Am interessantesten sind die Fälle, in denen sich das chaotische Verhalten auf einem Attraktor abspielt, da dann ein großer Satz von Anfangsbedingungen zu Bahnen führt, die zu dieser chaotischen Region konvergieren. ⓘ

Eine einfache Möglichkeit zur Veranschaulichung eines chaotischen Attraktors besteht darin, mit einem Punkt im Anziehungsbereich des Attraktors zu beginnen und dann einfach seine nachfolgende Umlaufbahn aufzuzeichnen. Aufgrund der Bedingung der topologischen Transitivität ergibt dies wahrscheinlich ein Bild des gesamten endgültigen Attraktors, und in der Tat geben die beiden in der Abbildung rechts dargestellten Bahnen ein Bild der allgemeinen Form des Lorenz-Attraktors. Dieser Attraktor ergibt sich aus einem einfachen dreidimensionalen Modell des Lorenz-Wettersystems. Der Lorenz-Attraktor ist vielleicht eines der bekanntesten Diagramme chaotischer Systeme, wahrscheinlich weil es nicht nur eines der ersten, sondern auch eines der komplexesten ist und als solches ein sehr interessantes Muster ergibt, das mit ein wenig Fantasie wie die Flügel eines Schmetterlings aussieht. ⓘ

Im Gegensatz zu den Festpunkt-Attraktoren und den Grenzzyklen sind die Attraktoren, die in chaotischen Systemen entstehen, die so genannten seltsamen Attraktoren, sehr detailliert und komplex. Seltsame Attraktoren treten sowohl in kontinuierlichen dynamischen Systemen (wie dem Lorenz-System) als auch in einigen diskreten Systemen (wie der Hénon-Karte) auf. Andere diskrete dynamische Systeme haben eine abstoßende Struktur, die Julia-Menge genannt wird und sich an der Grenze zwischen den Anziehungsbereichen der Fixpunkte bildet. Julia-Mengen können als seltsame Abstoßer betrachtet werden. Sowohl seltsame Attraktoren als auch Julia-Mengen haben typischerweise eine fraktale Struktur, und die fraktale Dimension kann für sie berechnet werden. ⓘ

Minimale Komplexität eines chaotischen Systems

Bifurkationsdiagramm der logistischen Karte x → r x (1 - x). Jeder vertikale Schnitt zeigt den Attraktor für einen bestimmten Wert von r. Das Diagramm zeigt eine Verdoppelung der Periode mit zunehmendem r, was schließlich zum Chaos führt. Dunklere Punkte werden häufiger besucht. ⓘ

Diskrete chaotische Systeme, wie die logistische Karte, können unabhängig von ihrer Dimensionalität seltsame Attraktoren aufweisen. Die Universalität von eindimensionalen Karten mit parabolischen Maxima und Feigenbaum-Konstanten $\delta =4.669201...$,$\alpha =2.502907...$ ist gut sichtbar bei einer Karte, die als Spielzeugmodell Modell für diskrete Laserdynamik: $x\rightarrow Gx(1-\mathrm {tanh} (x))$, wobei $x$ für die Amplitude des elektrischen Feldes steht, $G$ die Laserverstärkung als Bifurkationsparameter ist. Der allmähliche Anstieg von $G$ im Intervall $[0,\infty )$ ändert sich die Dynamik von einer regulären zu einer chaotischen mit qualitativ demselben Bifurkationsdiagramm wie bei der logistischen Karte. ⓘ

Im Gegensatz dazu zeigt das Poincaré-Bendixson-Theorem bei kontinuierlichen dynamischen Systemen, dass ein seltsamer Attraktor nur in drei oder mehr Dimensionen auftreten kann. Endlich-dimensionale lineare Systeme sind niemals chaotisch; damit ein dynamisches System chaotisches Verhalten zeigt, muss es entweder nichtlinear oder unendlich-dimensional sein. ⓘ

Das Poincaré-Bendixson-Theorem besagt, dass eine zweidimensionale Differentialgleichung ein sehr regelmäßiges Verhalten aufweist. Der unten beschriebene Lorenz-Attraktor wird durch ein System von drei Differentialgleichungen erzeugt, wie z. B.:

${\begin{aligned}{\frac {\mathrm {d} x}{\mathrm {d} t}}&=\sigma y-\sigma x,\\{\frac {\mathrm {d} y}{\mathrm {d} t}}&=\rho x-xz-y,\\{\frac {\mathrm {d} z}{\mathrm {d} t}}&=xy-\beta z.\end{aligned}}$

wobei $x$, $y$, und $z$ bilden den Systemzustand, $t$ ist die Zeit, und $\sigma$, $\rho$, $\beta$ sind die Systemparameter. Fünf der Terme auf der rechten Seite sind linear, während zwei quadratisch sind; insgesamt sind es sieben Terme. Ein weiterer bekannter chaotischer Attraktor wird durch die Rössler-Gleichungen erzeugt, die nur einen von sieben nichtlinearen Termen aufweisen. Sprott fand ein dreidimensionales System mit nur fünf Termen, das nur einen nichtlinearen Term aufweist, der für bestimmte Parameterwerte Chaos zeigt. Zhang und Heidel zeigten, dass zumindest für dissipative und konservative quadratische Systeme dreidimensionale quadratische Systeme mit nur drei oder vier Termen auf der rechten Seite kein chaotisches Verhalten zeigen können. Der Grund dafür ist, einfach ausgedrückt, dass die Lösungen solcher Systeme asymptotisch zu einer zweidimensionalen Fläche sind und sich die Lösungen daher gut verhalten. ⓘ

Während das Poincaré-Bendixson-Theorem zeigt, dass ein kontinuierliches dynamisches System in der euklidischen Ebene nicht chaotisch sein kann, können zweidimensionale kontinuierliche Systeme mit nicht-euklidischer Geometrie chaotisches Verhalten zeigen. Es mag überraschen, dass Chaos auch in linearen Systemen auftreten kann, sofern sie unendlich dimensional sind. Eine Theorie des linearen Chaos wird derzeit in einem Zweig der mathematischen Analyse entwickelt, der als funktionale Analyse bekannt ist. ⓘ

Unendlich dimensionale Karten

Die einfache Verallgemeinerung der gekoppelten diskreten Karten basiert auf dem Faltungsintegral, das die Interaktion zwischen räumlich verteilten Karten vermittelt: $\psi _{n+1}({\vec {r}},t)=\int K({\vec {r}}-{\vec {r}}^{,},t)f[\psi _{n}({\vec {r}}^{,},t)]d{\vec {r}}^{,}$, ⓘ

wobei Kernel $K({\vec {r}}-{\vec {r}}^{,},t)$ ein Propagator ist, der als grüne Funktion eines relevanten physikalischen Systems abgeleitet ist, $f[\psi _{n}({\vec {r}},t)]$ kann sowohl eine logistische Karte $\psi \rightarrow G\psi [1-\tanh(\psi )]$ oder eine komplexe Karte sein. Beispiele für komplexe Karten sind die Julia-Menge $f[\psi ]=\psi ^{2}$ oder die Ikeda-Karte $\psi _{n+1}=A+B\psi _{n}e^{i(|\psi _{n}|^{2}+C)}$ dienen können. Bei Wellenausbreitungsproblemen in der Entfernung $L=ct$ mit Wellenlänge $\lambda =2\pi /k$ betrachtet werden, kann der Kernel $K$ kann die Form einer Greenschen Funktion für die Schrödinger-Gleichung haben:. ⓘ

$K({\vec {r}}-{\vec {r}}^{,},L)={\frac {ik\exp[ikL]}{2\pi L}}\exp[{\frac {ik|{\vec {r}}-{\vec {r}}^{,}|^{2}}{2L}}]$. ⓘ

Ruckartige Systeme

In der Physik ist der Ruck die dritte Ableitung der Position nach der Zeit. Als solche sind Differentialgleichungen der Form

$J\left({\overset {...}{x}},{\ddot {x}},{\dot {x}},x\right)=0$

werden manchmal als Ruck-Gleichungen bezeichnet. Es hat sich gezeigt, dass eine Ruckgleichung, die einem System von drei gewöhnlichen, nichtlinearen Differentialgleichungen erster Ordnung entspricht, in gewissem Sinne die Minimalvoraussetzung für Lösungen mit chaotischem Verhalten ist. Dies motiviert das mathematische Interesse an Rucksystemen. Systeme, die eine vierte oder höhere Ableitung enthalten, werden dementsprechend Hyperrucksysteme genannt. ⓘ

Das Verhalten eines Rucksystems wird durch eine Ruckgleichung beschrieben, und für bestimmte Ruckgleichungen können einfache elektronische Schaltungen Lösungen modellieren. Diese Schaltungen werden als Ruckschaltungen bezeichnet. ⓘ

Eine der interessantesten Eigenschaften von Ruckschaltungen ist die Möglichkeit eines chaotischen Verhaltens. Bestimmte bekannte chaotische Systeme, wie der Lorenz-Attraktor und die Rössler-Karte, werden üblicherweise als ein System von drei Differentialgleichungen erster Ordnung beschrieben, die sich zu einer einzigen (wenn auch recht komplizierten) Ruckgleichung zusammenfügen lassen. Ein weiteres Beispiel für eine Ruckgleichung mit Nichtlinearität in der Größe von $x$ ist:

${\frac {\mathrm {d} ^{3}x}{\mathrm {d} t^{3}}}+A{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+{\frac {\mathrm {d} x}{\mathrm {d} t}}-|x|+1=0.$ ⓘ

Hier ist A ein einstellbarer Parameter. Diese Gleichung hat eine chaotische Lösung für A=3/5 und kann mit der folgenden Ruckschaltung realisiert werden; die erforderliche Nichtlinearität wird durch die beiden Dioden hervorgerufen:

In der obigen Schaltung sind alle Widerstände gleich groß, außer $R_{A}=R/A=5R/3$, und alle Kondensatoren sind gleich groß. Die dominante Frequenz ist $1/2\pi RC$. Der Ausgang des Operationsverstärkers 0 entspricht der Variablen x, der Ausgang von 1 entspricht der ersten Ableitung von x und der Ausgang von 2 entspricht der zweiten Ableitung. ⓘ

Ähnliche Schaltungen benötigen nur eine Diode oder gar keine Dioden. ⓘ

Siehe auch die bekannte Schaltung von Chua, eine Grundlage für chaotische echte Zufallszahlengeneratoren. Die einfache Konstruktion dieser Schaltung hat sie zu einem allgegenwärtigen Beispiel für ein chaotisches System gemacht. ⓘ

Spontane Ordnung

Unter den richtigen Bedingungen entwickelt sich das Chaos spontan zu einem Gleichgewichtsmuster. Nach dem Kuramoto-Modell genügen vier Bedingungen, um in einem chaotischen System eine Synchronisation zu erreichen. Beispiele sind die gekoppelte Schwingung des Pendels von Christiaan Huygens, Glühwürmchen, Neuronen, die Resonanz der Londoner Millennium Bridge und große Anordnungen von Josephson-Kontakten. ⓘ

Geschichte

Barnsley-Farn, der mit Hilfe des Chaos-Spiels erzeugt wurde. Natürliche Formen (Farne, Wolken, Berge usw.) können durch ein iteriertes Funktionssystem (IFS) nachgebildet werden. ⓘ

Ein früher Befürworter der Chaostheorie war Henri Poincaré. In den 1880er Jahren stellte er bei der Untersuchung des Dreikörperproblems fest, dass es Umlaufbahnen geben kann, die nicht periodisch sind, aber auch nicht ewig zunehmen oder sich einem festen Punkt nähern. 1898 veröffentlichte Jacques Hadamard eine einflussreiche Studie über die chaotische Bewegung eines freien Teilchens, das reibungslos auf einer Oberfläche mit konstanter negativer Krümmung gleitet, das so genannte "Hadamardsche Billard". Hadamard konnte zeigen, dass alle Flugbahnen instabil sind, da alle Teilchenbahnen exponentiell voneinander abweichen, mit einem positiven Lyapunov-Exponenten. ⓘ

Die Chaostheorie nahm ihren Anfang im Bereich der Ergodentheorie. Spätere Studien, auch zum Thema nichtlineare Differentialgleichungen, wurden von George David Birkhoff, Andrey Nikolaevich Kolmogorov, Mary Lucy Cartwright und John Edensor Littlewood sowie Stephen Smale durchgeführt. Mit Ausnahme von Smale wurden diese Studien alle direkt von der Physik inspiriert: das Dreikörperproblem im Fall von Birkhoff, Turbulenzen und astronomische Probleme im Fall von Kolmogorov und Radiotechnik im Fall von Cartwright und Littlewood. Obwohl chaotische Planetenbewegungen nicht beobachtet worden waren, hatten Experimentatoren Turbulenzen in der Flüssigkeitsbewegung und nichtperiodische Schwingungen in Radiokreisläufen entdeckt, ohne eine Theorie zu haben, die erklären konnte, was sie sahen. ⓘ

Trotz erster Erkenntnisse in der ersten Hälfte des 20. Jahrhunderts wurde die Chaostheorie als solche erst nach der Jahrhundertmitte formalisiert, als einigen Wissenschaftlern klar wurde, dass die lineare Theorie, die damals vorherrschende Systemtheorie, das beobachtete Verhalten bestimmter Experimente wie das der logistischen Karte einfach nicht erklären konnte. Was bis dahin der Ungenauigkeit von Messungen und einfachem "Rauschen" zugeschrieben worden war, wurde von den Chaostheoretikern als vollständiger Bestandteil der untersuchten Systeme betrachtet. ⓘ

Der wichtigste Katalysator für die Entwicklung der Chaostheorie war der elektronische Computer. Ein Großteil der Mathematik der Chaostheorie beinhaltet die wiederholte Iteration einfacher mathematischer Formeln, die von Hand nicht durchführbar wären. Elektronische Computer machten diese wiederholten Berechnungen praktisch, während Zahlen und Bilder es ermöglichten, diese Systeme zu visualisieren. Als Doktorand im Labor von Chihiro Hayashi an der Universität Kyoto experimentierte Yoshisuke Ueda mit Analogrechnern und bemerkte am 27. November 1961 etwas, das er "zufällige Übergangsphänomene" nannte. Sein Berater war damals jedoch nicht mit seinen Schlussfolgerungen einverstanden und erlaubte ihm erst 1970, über seine Ergebnisse zu berichten. ⓘ

Turbulenz im Spitzenwirbel eines Flugzeugflügels. Studien über den kritischen Punkt, jenseits dessen ein System Turbulenzen erzeugt, waren wichtig für die Chaostheorie und wurden zum Beispiel von dem sowjetischen Physiker Lev Landau analysiert, der die Landau-Hopf-Theorie der Turbulenz entwickelte. David Ruelle und Floris Takens sagten später im Gegensatz zu Landau voraus, dass Flüssigkeitsturbulenzen durch einen seltsamen Attraktor entstehen können, ein Hauptkonzept der Chaostheorie. ⓘ

Edward Lorenz war ein früher Pionier dieser Theorie. Sein Interesse an der Chaostheorie wurde zufällig durch seine Arbeit an der Wettervorhersage im Jahr 1961 geweckt. Lorenz benutzte einen einfachen Digitalcomputer, einen Royal McBee LGP-30, um seine Wettersimulationen durchzuführen. Um Zeit zu sparen, startete er die Simulation in der Mitte ihres Verlaufs, als er eine Folge von Daten erneut sehen wollte. Zu diesem Zweck gab er einen Ausdruck der Daten ein, die den Bedingungen in der Mitte der ursprünglichen Simulation entsprachen. Zu seiner Überraschung war das Wetter, das die Maschine vorherzusagen begann, völlig anders als in der vorherigen Berechnung. Lorenz führte dies auf den Computerausdruck zurück. Der Computer arbeitete mit 6-stelliger Genauigkeit, aber der Ausdruck rundete Variablen auf eine 3-stellige Zahl ab, so dass ein Wert wie 0,506127 als 0,506 gedruckt wurde. Dieser Unterschied ist winzig, und man war sich damals einig, dass er keine praktische Auswirkung haben sollte. Lorenz entdeckte jedoch, dass kleine Änderungen der Ausgangsbedingungen große Änderungen der langfristigen Ergebnisse bewirken. Die Entdeckung von Lorenz, die den Lorenz-Attraktoren ihren Namen gab, zeigte, dass selbst detaillierte Atmosphärenmodelle im Allgemeinen keine genauen langfristigen Wettervorhersagen machen können. ⓘ

1963 fand Benoit Mandelbrot in Daten über Baumwollpreise wiederkehrende Muster auf allen Ebenen. Zuvor hatte er sich mit der Informationstheorie befasst und war zu dem Schluss gekommen, dass Rauschen wie eine Cantor-Menge strukturiert ist: Auf jeder Skala ist das Verhältnis von rauschbehafteten Perioden zu fehlerfreien Perioden eine Konstante - Fehler sind also unvermeidlich und müssen durch den Einbau von Redundanz eingeplant werden. Mandelbrot beschrieb sowohl den "Noah-Effekt" (bei dem es zu plötzlichen diskontinuierlichen Veränderungen kommen kann) als auch den "Joseph-Effekt" (bei dem ein Wert eine Zeit lang bestehen bleiben kann, sich danach aber plötzlich ändert). Dies stellte die Vorstellung in Frage, dass Preisänderungen normal verteilt sind. Im Jahr 1967 veröffentlichte er "How long is the coast of Britain? Statistical self-similarity and fractional dimension" (Statistische Selbstähnlichkeit und fraktionale Dimension), in der er zeigte, dass die Länge einer Küstenlinie mit dem Maßstab des Messinstruments variiert, sich in allen Maßstäben ähnelt und für ein unendlich kleines Messinstrument unendlich lang ist. Er argumentierte, dass ein Garnknäuel aus der Ferne betrachtet als Punkt (0-dimensional), aus der Nähe betrachtet als Kugel (3-dimensional) oder als gekrümmter Strang (1-dimensional) erscheint, und argumentierte, dass die Dimensionen eines Objekts relativ zum Beobachter sind und gebrochen sein können. Ein Objekt, dessen Unregelmäßigkeit über verschiedene Maßstäbe hinweg konstant ist ("Selbstähnlichkeit"), ist ein Fraktal (Beispiele sind der Menger-Schwamm, die Sierpiński-Dichtung und die Koch-Kurve oder Schneeflocke, die unendlich lang ist, aber einen endlichen Raum umschließt und eine fraktale Dimension von etwa 1,2619 hat). Im Jahr 1982 veröffentlichte Mandelbrot das Buch The Fractal Geometry of Nature, das zu einem Klassiker der Chaostheorie wurde. ⓘ

Im Dezember 1977 veranstaltete die New Yorker Akademie der Wissenschaften das erste Symposium zum Thema Chaos, an dem David Ruelle, Robert May, James A. Yorke (der den Begriff "Chaos" in der Mathematik geprägt hat), Robert Shaw und der Meteorologe Edward Lorenz teilnahmen. Im folgenden Jahr veröffentlichten Pierre Coullet und Charles Tresser "Itérations d'endomorphismes et groupe de renormalisation", und Mitchell Feigenbaums Artikel "Quantitative Universality for a Class of Nonlinear Transformations" erschien nach drei Jahren der Ablehnung durch die Gutachter endlich in einer Zeitschrift. So entdeckten Feigenbaum (1975) und Coullet & Tresser (1978) die Universalität im Chaos, was die Anwendung der Chaostheorie auf viele verschiedene Phänomene ermöglichte. ⓘ

1979 präsentierte Albert J. Libchaber auf einem von Pierre Hohenberg organisierten Symposium in Aspen seine experimentelle Beobachtung der Bifurkationskaskade, die zu Chaos und Turbulenz in Rayleigh-Bénard-Konvektionssystemen führt. Zusammen mit Mitchell J. Feigenbaum wurde er 1986 mit dem Wolf-Preis für Physik für ihre inspirierenden Leistungen ausgezeichnet. ⓘ

1986 organisierte die New Yorker Akademie der Wissenschaften gemeinsam mit dem National Institute of Mental Health und dem Office of Naval Research die erste wichtige Konferenz über Chaos in Biologie und Medizin. Dort präsentierte Bernardo Huberman ein mathematisches Modell der Augenbewegungsstörung bei Menschen mit Schizophrenie. Dies führte in den 1980er Jahren zu einer Erneuerung der Physiologie durch die Anwendung der Chaostheorie, zum Beispiel bei der Untersuchung pathologischer Herzzyklen. ⓘ

1987 veröffentlichten Per Bak, Chao Tang und Kurt Wiesenfeld in der Zeitschrift Physical Review Letters eine Arbeit, in der sie zum ersten Mal die selbstorganisierte Kritikalität (SOC) beschrieben, die als einer der Mechanismen gilt, durch die in der Natur Komplexität entsteht. ⓘ

Neben weitgehend laborgestützten Ansätzen wie dem Bak-Tang-Wiesenfeld-Sandhaufen haben sich viele andere Untersuchungen auf große natürliche oder soziale Systeme konzentriert, von denen bekannt ist (oder vermutet wird), dass sie skaleninvariantes Verhalten zeigen. Obwohl diese Ansätze (zumindest anfangs) von den Fachleuten in den untersuchten Bereichen nicht immer begrüßt wurden, hat sich die SOC dennoch als ein starker Kandidat für die Erklärung einer Reihe von Naturphänomenen etabliert, darunter Erdbeben (die lange vor der Entdeckung der SOC als Quelle skaleninvarianten Verhaltens bekannt waren, wie das Gutenberg-Richter-Gesetz, das die statistische Verteilung der Erdbebengröße beschreibt, und das Omori-Gesetz, das die Häufigkeit von Nachbeben beschreibt), Sonneneruptionen, Fluktuationen in Wirtschaftssystemen wie den Finanzmärkten (Verweise auf die SOC sind in der Wirtschaftsphysik üblich), Landschaftsbildung, Waldbrände, Erdrutsche, Epidemien und biologische Evolution (wo die SOC beispielsweise als dynamischer Mechanismus hinter der von Niles Eldredge und Stephen Jay Gould aufgestellten Theorie der "punktuellen Gleichgewichte" angeführt wurde). Angesichts der Implikationen einer skalenfreien Verteilung von Ereignisgrößen haben einige Forscher vorgeschlagen, dass ein weiteres Phänomen, das als Beispiel für SOC betrachtet werden sollte, das Auftreten von Kriegen ist. Diese Untersuchungen des SOC umfassten sowohl Modellierungsversuche (entweder die Entwicklung neuer Modelle oder die Anpassung bestehender Modelle an die Besonderheiten eines bestimmten natürlichen Systems) als auch umfangreiche Datenanalysen, um das Vorhandensein und/oder die Merkmale natürlicher Skalierungsgesetze zu ermitteln. ⓘ

Im selben Jahr veröffentlichte James Gleick das Buch Chaos: Making a New Science, das zu einem Bestseller wurde und die allgemeinen Grundsätze der Chaostheorie sowie ihre Geschichte einer breiten Öffentlichkeit vorstellte. Zunächst war die Chaostheorie die Domäne einiger weniger, isolierter Personen, doch nach und nach entwickelte sie sich zu einer transdisziplinären und institutionellen Disziplin, vor allem unter dem Namen Analyse nichtlinearer Systeme. In Anspielung auf Thomas Kuhns Konzept eines Paradigmenwechsels, das in The Structure of Scientific Revolutions (1962) dargelegt wurde, behaupteten viele "Chaologen" (wie sich einige selbst bezeichneten), dass diese neue Theorie ein Beispiel für einen solchen Wechsel sei, eine These, die von Gleick vertreten wurde. ⓘ

Die Verfügbarkeit von billigeren, leistungsfähigeren Computern erweitert die Anwendbarkeit der Chaostheorie. Gegenwärtig ist die Chaostheorie nach wie vor ein aktives Forschungsgebiet, an dem viele verschiedene Disziplinen beteiligt sind, z. B. Mathematik, Topologie, Physik, soziale Systeme, Bevölkerungsmodellierung, Biologie, Meteorologie, Astrophysik, Informationstheorie, Computational Neuroscience, Krisenmanagement bei Pandemien usw. ⓘ

Ende des 19. Jahrhunderts gewann Henri Poincaré einen Preis mit dem Lösungsansatz für die Frage, ob das Sonnensystem stabil sei. Manche Quellen geben dies als die Geburtsstunde der Chaosforschung an, es dauerte jedoch bis in die Mitte des 20. Jahrhunderts, bis der Lösungsansatz von Poincaré mit Hilfe von Computern brauchbar umgesetzt werden konnte. ⓘ

Chaotische Phänomene sind schon seit langem bekannt, wie beispielsweise das Dreikörperproblem oder Turbulenz. Lange Zeit wurden diese Phänomene als eher weniger verbreitete Spezialfälle angesehen. Da eine angemessene Untersuchung ohne Computer wenig erfolgversprechend schien, und kaum jemand besondere Erkenntnisse erwartete, da die Phänomene vollständig auf den Konzepten der klassischen Physik beruhen, wurden sie wenig beachtet. Das änderte sich erst mit dem Aufkommen schneller Computer. ⓘ

Robert May simulierte 1976 eine Fischpopulation $P$ mit einer Wachstumsrate $R$ mit der Formel $P_{\text{neu}}=R\cdot P_{\text{alt}}\cdot (1-P_{\text{alt}}),$ um mit dem Term $1-P_{\text{alt}}$ begrenzte Ressourcen abzubilden. Er wählte für seine rechnerische Simulation eine sehr kleine Anfangspopulation von 2 % und entdeckte, dass bei einer Wachstumsrate $R$ um $3{,}8$ ein chaotisches Verhalten seiner Modellrechnung einsetzt. ⓘ

In den 1970er bis 1980er Jahren entdeckte Mitchell Feigenbaum die Phänomene der logistischen Gleichung und die nach ihm benannte Feigenbaum-Konstante. Diese Gleichung korrespondiert mit der von Benoit Mandelbrot 1980 untersuchten Mandelbrot-Menge, da sie ebenfalls auf einer quadratischen Gleichung beruht. ⓘ

Etwa zur selben Zeit arbeiteten Siegfried Großmann in Marburg und Hermann Haken in Stuttgart an der Formulierung ihrer Theorien, die bald von den Ideen um Mandelbrot und Feigenbaum inspiriert wurden. Großmann formulierte eine Beschreibung des Lasers mit Hilfe der nichtlinearen Dynamik, und Haken gilt als Begründer der Synergetik und Entdecker des sogenannten Versklavungsprinzips. Die Mandelbrot-Menge, populär „Apfelmännchen“ genannt, gilt als eines der formenreichsten Fraktale, das überhaupt bekannt ist. ⓘ

Ab den 1980er Jahren wurden an vielen Universitäten Arbeitsgruppen eingerichtet, wie z. B. in Graz, Wien oder Regensburg. In München wirkte die „Chaosgruppe der TU München“ unter der Leitung von Alfred Hübler mit zahlreichen Forschungsprojekten am Lehrstuhl Physik E13 (Edgar Lüscher). Sie organisierte sich nach dem Tod Lüschers in einem Forschungsverein und veranstaltete eine Ringvorlesung und mehrere Jahrestagungen, bei denen versucht wurde, die gesamte Bandbreite der Chaosforschung zu repräsentieren und einen interdisziplinären Dialog zu ermöglichen. Es entstanden auch große Forschungsinstitute wie z. B. das Santa Fe Institute (USA) oder das Institut für nichtlineare Dynamik in Potsdam. ⓘ

Die aktuelle Forschung befasst sich eher mit einem uneinheitlichen Satz von Phänomenen und Theorien. Viele Forscher, die sich heute noch mit der Thematik beschäftigen, würden sich selbst nicht mehr als Chaosforscher bezeichnen. ⓘ

Anwendungen

Eine Conus-Textilhülle, die der Regel 30 ähnelt, einem zellulären Automaten mit chaotischem Verhalten. ⓘ

Obwohl die Chaostheorie aus der Beobachtung von Wettermustern entstanden ist, lässt sie sich inzwischen auf eine Vielzahl anderer Situationen anwenden. Einige Bereiche, die heute von der Chaostheorie profitieren, sind Geologie, Mathematik, Biologie, Informatik, Wirtschaft, Technik, Finanzen, Meteorologie, Philosophie, Anthropologie, Physik, Politik, Bevölkerungsdynamik und Robotik. Nachfolgend sind einige Kategorien mit Beispielen aufgeführt, doch ist diese Liste keineswegs vollständig, da immer wieder neue Anwendungen hinzukommen. ⓘ

Kryptographie

Die Chaostheorie wird seit vielen Jahren in der Kryptographie eingesetzt. In den letzten Jahrzehnten wurden Chaos und nichtlineare Dynamik bei der Entwicklung von Hunderten von kryptografischen Primitiven eingesetzt. Zu diesen Algorithmen gehören Bildverschlüsselungsalgorithmen, Hash-Funktionen, sichere Pseudozufallszahlengeneratoren, Stromchiffren, Wasserzeichen und Steganografie. Die meisten dieser Algorithmen basieren auf uni-modalen chaotischen Karten, und ein großer Teil dieser Algorithmen verwendet die Kontrollparameter und den Anfangszustand der chaotischen Karten als ihre Schlüssel. Aus einer breiteren Perspektive, ohne Verlust der Allgemeingültigkeit, sind die Ähnlichkeiten zwischen den chaotischen Karten und den kryptographischen Systemen die Hauptmotivation für den Entwurf von chaotischen kryptographischen Algorithmen. Eine Art der Verschlüsselung, der geheime oder symmetrische Schlüssel, beruht auf Diffusion und Verwirrung, die durch die Chaostheorie gut modelliert wird. Eine andere Art der Datenverarbeitung, die DNA-Datenverarbeitung, bietet in Verbindung mit der Chaostheorie eine Möglichkeit, Bilder und andere Informationen zu verschlüsseln. Viele der DNA-Chaos-Verschlüsselungsalgorithmen haben sich entweder als nicht sicher erwiesen, oder die angewandte Technik ist nicht effizient. ⓘ

Robotik

Die Robotik ist ein weiterer Bereich, der in letzter Zeit von der Chaostheorie profitiert hat. Anstelle von Robotern, die nach dem Prinzip von Versuch und Irrtum mit ihrer Umgebung interagieren, wurde die Chaostheorie zur Erstellung eines Vorhersagemodells verwendet. Eine chaotische Dynamik wurde bei passiv gehenden zweibeinigen Robotern beobachtet. ⓘ

Biologie

Seit über hundert Jahren verfolgen Biologen die Entwicklung von Populationen verschiedener Arten mit Hilfe von Populationsmodellen. Die meisten Modelle sind kontinuierlich, aber in letzter Zeit ist es Wissenschaftlern gelungen, chaotische Modelle in bestimmten Populationen zu implementieren. So zeigte eine Studie über Modelle des kanadischen Luchses ein chaotisches Verhalten beim Populationswachstum. Chaos ist auch in ökologischen Systemen wie der Hydrologie zu finden. Ein chaotisches Modell für die Hydrologie hat zwar seine Unzulänglichkeiten, aber man kann dennoch viel lernen, wenn man die Daten durch die Brille der Chaostheorie betrachtet. Eine weitere biologische Anwendung findet sich in der Kardiotokographie. Die Überwachung des Fötus ist ein heikles Unterfangen, bei dem es darum geht, genaue Informationen zu erhalten und gleichzeitig so wenig invasiv wie möglich zu sein. Durch die chaotische Modellierung lassen sich bessere Modelle für die Warnzeichen einer fötalen Hypoxie erstellen. ⓘ

Wirtschaft

Es ist möglich, dass auch Wirtschaftsmodelle durch Anwendung der Chaostheorie verbessert werden können, aber die Vorhersage des Zustands eines Wirtschaftssystems und der Faktoren, die es am meisten beeinflussen, ist eine äußerst komplexe Aufgabe. Wirtschafts- und Finanzsysteme unterscheiden sich grundlegend von denen der klassischen Naturwissenschaften, da erstere von Natur aus stochastisch sind, da sie aus den Interaktionen von Menschen resultieren, und es daher unwahrscheinlich ist, dass rein deterministische Modelle eine genaue Darstellung der Daten liefern. Die empirische Literatur, in der auf Chaos in den Wirtschafts- und Finanzwissenschaften getestet wird, liefert sehr gemischte Ergebnisse, was zum Teil darauf zurückzuführen ist, dass spezifische Tests für Chaos und allgemeinere Tests für nichtlineare Beziehungen verwechselt werden. ⓘ

In den Wirtschaftswissenschaften konnte das Chaos mit Hilfe der Rekurrenzquantifizierungsanalyse nachgewiesen werden. Tatsächlich konnten Orlando et al. mit Hilfe des so genannten Rekursionsquantifizierungs-Korrelationsindex versteckte Veränderungen in Zeitreihen aufspüren. Anschließend wurde dieselbe Technik eingesetzt, um Übergänge von laminaren (regelmäßigen) zu turbulenten (chaotischen) Phasen sowie Unterschiede zwischen makroökonomischen Variablen zu erkennen und verborgene Merkmale der wirtschaftlichen Dynamik hervorzuheben. Schließlich könnte das Chaos bei der Modellierung der Funktionsweise der Wirtschaft sowie bei der Einbettung von Schocks aufgrund von externen Ereignissen wie COVID-19 helfen. Ein aktueller Bericht über die Instrumente und Ergebnisse der empirischen Kalibrierung und Prüfung deterministischer chaotischer Modelle (z. B. Kaldor-Kalecki, Goodwin, Harrod) findet sich in Orlando et al. ⓘ

Andere Bereiche

In der Chemie ist die Vorhersage der Gaslöslichkeit für die Herstellung von Polymeren von entscheidender Bedeutung, aber Modelle, die mit Hilfe der Partikelschwarmoptimierung (PSO) arbeiten, konvergieren oft zu den falschen Punkten. Durch die Einführung von Chaos wurde eine verbesserte Version von PSO geschaffen, die dafür sorgt, dass die Simulationen nicht stecken bleiben. In der Himmelsmechanik, insbesondere bei der Beobachtung von Asteroiden, führt die Anwendung der Chaostheorie zu besseren Vorhersagen darüber, wann sich diese Objekte der Erde und anderen Planeten nähern werden. Vier der fünf Monde des Pluto drehen sich chaotisch. In der Quantenphysik und der Elektrotechnik hat die Untersuchung großer Anordnungen von Josephson-Übergängen stark von der Chaostheorie profitiert. In der näheren Umgebung sind Kohlebergwerke seit jeher gefährliche Orte, an denen häufige Erdgaslecks zu vielen Todesfällen führen. Bis vor kurzem gab es keine zuverlässige Methode, um vorherzusagen, wann sie auftreten würden. Aber diese Gaslecks haben chaotische Tendenzen, die sich bei richtiger Modellierung ziemlich genau vorhersagen lassen. ⓘ

Die Chaostheorie kann auch außerhalb der Naturwissenschaften angewandt werden, aber in der Vergangenheit litten fast alle derartigen Studien unter mangelnder Reproduzierbarkeit, schlechter externer Validität und/oder mangelnder Beachtung der Kreuzvalidierung, was zu einer schlechten Vorhersagegenauigkeit führte (wenn überhaupt eine Vorhersage außerhalb der Stichprobe versucht wurde). Glass und Mandell und Selz haben festgestellt, dass bisher keine EEG-Studie auf das Vorhandensein von seltsamen Attraktoren oder anderen Anzeichen für chaotisches Verhalten hingewiesen hat. ⓘ

Die Forscher haben die Chaostheorie weiterhin auf die Psychologie angewandt. Bei der Modellierung des Gruppenverhaltens, bei dem sich heterogene Mitglieder so verhalten können, als ob sie in unterschiedlichem Maße teilen, was in der Theorie von Wilfred Bion eine Grundannahme ist, haben die Forscher beispielsweise festgestellt, dass die Gruppendynamik das Ergebnis der individuellen Dynamik der Mitglieder ist: Jedes Individuum reproduziert die Gruppendynamik in einem anderen Ausmaß, und das chaotische Verhalten der Gruppe spiegelt sich in jedem Mitglied wider. ⓘ

Redington und Reidbord (1992) versuchten zu zeigen, dass das menschliche Herz chaotische Züge aufweisen kann. Sie beobachteten die Veränderungen in den Intervallen zwischen den Herzschlägen einer einzelnen Psychotherapie-Patientin, während sie während einer Therapiesitzung Phasen unterschiedlicher emotionaler Intensität durchlief. Die Ergebnisse waren zugegebenermaßen nicht schlüssig. Es gab nicht nur Unklarheiten in den verschiedenen Diagrammen, die die Autoren erstellten, um angeblich Beweise für eine chaotische Dynamik zu liefern (Spektralanalyse, Phasentrajektorie und Autokorrelationsdiagramme), sondern auch, als sie versuchten, einen Lyapunov-Exponenten als definitivere Bestätigung für chaotisches Verhalten zu berechnen, stellten die Autoren fest, dass sie dies nicht zuverlässig tun konnten. ⓘ

In ihrer Arbeit von 1995 behaupteten Metcalf und Allen, dass sie im Verhalten von Tieren ein Muster der Periodenverdopplung entdeckt hätten, das zu Chaos führe. Die Autoren untersuchten eine bekannte Reaktion, die so genannte zeitplanbedingte Polydipsie, bei der ein Tier, das über einen bestimmten Zeitraum kein Futter erhält, ungewöhnlich viel Wasser trinkt, wenn das Futter endlich angeboten wird. Der Kontrollparameter (r), der hier zum Einsatz kam, war die Länge des Intervalls zwischen den wiederaufgenommenen Fütterungen. Die Autoren haben darauf geachtet, eine große Anzahl von Tieren zu testen und viele Wiederholungen einzubeziehen, und sie haben ihr Experiment so angelegt, dass die Wahrscheinlichkeit ausgeschlossen ist, dass Veränderungen in den Reaktionsmustern durch unterschiedliche Ausgangspunkte für r verursacht wurden. ⓘ

Zeitreihen und erste Verzögerungsdiagramme bieten die beste Unterstützung für die aufgestellten Behauptungen und zeigen einen ziemlich klaren Übergang von Periodizität zu Unregelmäßigkeit, wenn die Fütterungszeiten erhöht wurden. Die verschiedenen Phasentrajektorien und Spektralanalysen stimmen dagegen nicht gut genug mit den anderen Diagrammen oder der allgemeinen Theorie überein, um unweigerlich zu einer chaotischen Diagnose zu führen. Beispielsweise zeigen die Phasenverläufe keine eindeutige Progression hin zu immer größerer Komplexität (und weg von der Periodizität); der Prozess scheint ziemlich verworren. Wo Metcalf und Allen in ihren Spektraldiagrammen Perioden von zwei und sechs sahen, gibt es auch Raum für alternative Interpretationen. All diese Unklarheiten machen eine gewundene Post-hoc-Erklärung erforderlich, um zu zeigen, dass die Ergebnisse zu einem chaotischen Modell passen. ⓘ

Durch die Anpassung eines Modells der Karriereberatung, das eine chaotische Interpretation der Beziehung zwischen Arbeitnehmern und dem Arbeitsmarkt beinhaltet, fanden Amundson und Bright heraus, dass Menschen, die mit Karriereentscheidungen zu kämpfen haben, bessere Vorschläge gemacht werden können. Moderne Organisationen werden zunehmend als offene, komplexe, adaptive Systeme mit grundlegenden natürlichen, nichtlinearen Strukturen betrachtet, die internen und externen Kräften unterliegen, die zum Chaos beitragen können. So werden beispielsweise Teambildung und Gruppenentwicklung zunehmend als inhärent unvorhersehbares System erforscht, da die Ungewissheit des ersten Zusammentreffens verschiedener Individuen die Entwicklung des Teams ungewiss macht. ⓘ

Manche sagen, dass die Chaos-Metapher, die in verbalen Theorien verwendet wird, die auf mathematischen Modellen und psychologischen Aspekten des menschlichen Verhaltens beruhen bietet hilfreiche Einsichten zur Beschreibung der Komplexität von kleinen Arbeitsgruppen, die über die Metapher selbst hinausgehen. ⓘ

Die Verkehrsprognose kann von der Anwendung der Chaostheorie profitieren. Bessere Vorhersagen darüber, wann der Verkehr auftreten wird, würden es ermöglichen, Maßnahmen zu ergreifen, um ihn zu zerstreuen, bevor er überhaupt entstanden ist. Die Kombination von Prinzipien der Chaostheorie mit einigen anderen Methoden hat zu einem genaueren Modell für kurzfristige Vorhersagen geführt (siehe die Darstellung des BML-Verkehrsmodells rechts). ⓘ

Die Chaostheorie wurde auf Umweltdaten des Wasserkreislaufs (auch hydrologische Daten) wie Niederschlag und Wassermenge angewandt. Diese Studien haben zu kontroversen Ergebnissen geführt, da die Methoden zur Feststellung einer chaotischen Signatur oft relativ subjektiv sind. Frühe Studien neigten dazu, "erfolgreich" Chaos zu finden, während spätere Studien und Meta-Analysen diese Studien in Frage stellten und Erklärungen dafür lieferten, warum diese Datensätze wahrscheinlich keine niedrigdimensionale chaotische Dynamik aufweisen. ⓘ

Grundlagen

Quantentheorie, Determinismus und Unschärfe

Im Folgenden wird die Determiniertheit der Quantenmechanik (und ihre Grenzen durch die Heisenbergsche Unschärferelation) auf Grundlage der Kopenhagener Deutung erläutert. Für alle anderen Interpretationen der Quantenmechanik, beispielsweise die De-Broglie-Bohm-Theorie, ist der folgende Abschnitt nur begrenzt korrekt. ⓘ

Während im Sinne der klassischen Physik die Vorhersagbarkeit realer komplexer Systeme an praktisch nie vollkommen exakten Messungen der Anfangsbedingungen scheitert, zeigt die Berücksichtigung der Erkenntnisse der Quantenphysik, dass deren Verhalten prinzipiell nicht determiniert ist. So besagt die Heisenbergsche Unschärferelation, dass Ort und Impuls eines Objektes nicht gleichzeitig beliebig genau bestimmbar sind; diese Einschränkung bezieht sich nicht auf Unzulänglichkeiten des Beobachtungsvorgangs (z. B. ungenaue Messung), sondern ist prinzipieller Natur. Diese Unschärfe ist bei makroskopischen Systemen gewöhnlich vernachlässigbar. Da ihre Auswirkungen bei chaotischen Systemen jedoch beliebig wachsen, nehmen sie früher oder später makroskopische Dimensionen an (vgl. Schmetterlingseffekt). Bei dem Gerät zur Ziehung der Lottozahlen mit Kugeln ist das bereits nach etwa 20 Stößen der Fall. Die Vorhersagbarkeit chaotischer Systeme scheitert daher spätestens an der Unschärferelation (weil sie verbietet, dass die Anfangsbedingungen beliebig genau gemessen werden können). Das bedeutet, dass reale Systeme – im Gegensatz zu den sie beschreibenden mathematischen Modellen – prinzipiell nicht im klassischen Sinn deterministisch sein können. ⓘ

Nichtlineare Systeme

Chaotisches Verhalten kann nur in Systemen auftreten, deren Dynamik durch nichtlineare Gleichungen beschrieben wird. Solche Gleichungen sind meist nicht analytisch, d. h. nicht durch Angabe expliziter Größen, sondern nur numerisch lösbar. Ursache des exponentiellen Wachstums von Unterschieden in den Anfangsbedingungen sind dabei oft Mechanismen von Selbstverstärkung beispielsweise durch Rückkopplungen. ⓘ

Ist durch Reibung hinreichend Dissipation im Spiel, so kann sich in der Regel kein chaotisches Verhalten ausbilden. So könnten beispielsweise bei Jahrmarktsfahrgeschäften, die konstruktionsbedingt zu chaotischem Verhalten neigen, ohne entsprechende Bremsmaßnahmen unerwartete und unzumutbare Beschleunigungsspitzen auftreten. ⓘ

Dass dissipative Terme nicht ausschließlich stabilisierend wirken, zeigt sich am Beispiel einer Grenzschicht. Mit der linearen Stabilitätstheorie lässt sich zeigen, dass erst der Einfluss der Reibung das Wachstum kleiner Störungen ermöglicht. Dieses exponentielle Anwachsen stellt die erste Phase des laminar-turbulenten Umschlags dar. ⓘ

Phänomene

Ein wesentliches Ergebnis der Chaosforschung ist die Entdeckung, dass chaotische Systeme trotz ihres langfristig nicht vorhersagbaren, scheinbar irregulären Verhaltens bestimmte typische Verhaltensmuster zeigen. Da sie bei völlig unterschiedlichen Systemen beobachtet werden, sind sie von universeller Bedeutung. ⓘ

Seltsame Attraktoren

Phasenraumdiagramme

Phasenraumdiagramme bieten einen anschaulichen Überblick über die Dynamik eines Systems. Der Zustand des Systems wird dabei zu jedem Zeitpunkt durch einen Punkt in einem Raum dargestellt, dessen Koordinatenachsen durch den Satz von unabhängigen Zustandsgrößen des Systems und deren Geschwindigkeiten gegeben sind. Die Dynamik lässt sich damit als die Bahn dieses Punktes im Phasenraum interpretieren. So wird beispielsweise der Phasenraum eines Pendels durch den Auslenkwinkel und die zugehörige Winkelgeschwindigkeit aufgespannt, und eine periodische Pendelbewegung entspricht einer geschlossenen Kurve um den Koordinatenursprung. Mathematisch lässt sich die Gesamtheit aller möglichen Verhaltensweisen als Strömungsfeld im Phasenraum interpretieren. ⓘ

Störungen und Resonanzen

Systeme können sehr empfindlich auf Störungen reagieren und dadurch schnell ins Chaos übergehen. Erst das KAM-Theorem hat gezeigt, dass regelmäßige Einflüsse an sensiblen Stellen im Phasenraum nicht zwingend chaotisches Verhalten hervorrufen müssen. Sensibel sind z. B. rationale (ganzzahlige) Verhältnisse zwischen einer ungestörten Schwingung (z. B. eines Doppelpendels) zu einer periodischen Anregung. Diese rufen nämlich Resonanzen hervor (ähnlich wie bei Bahnresonanzen), weshalb für das Theorem nur irrationale Verhältnisse betrachtet werden. ⓘ

Aus mathematischer Sicht, gerade bei normalerweise vorherrschenden Messungenauigkeiten, kann man jede irrationale Zahl durch Brüche approximieren (Kettenbruchentwicklung). Daher scheint die Überlegung praktisch sinnlos zu sein. Man muss aber bedenken, dass sich ein System umso schneller durch Resonanzen aufschaukeln wird, je näher das Frequenzverhältnis an einem rationalen Wert liegt. Das heißt, die erwarteten Werte weichen noch schneller von den gemessenen ab, als es sonst der Fall wäre. ⓘ

Besonders stabil gegenüber Störungen (zeitlich gesehen) sind daher irrationale Verhältnisse, die sich nur schlecht durch Brüche annähern lassen. Allgemein spricht man in diesem Zusammenhang von edlen Zahlen, wobei ein Verhältnis namens Goldener Schnitt die Zahl ist, die sich am schlechtesten mittels Kettenbruchentwicklung annähern lässt und somit am stabilsten gegen chaotische Einflüsse ist. ⓘ

Der Übergang ins Chaos

Nichtlineare dynamische Systeme können neben Chaos auch andere Verhaltensweisen zeigen, wie beispielsweise Konvergenz gegen einen Ruhezustand oder gegen einen periodischen Grenzzyklus. Welches Verhalten auftritt, kann von den Anfangsbedingungen oder auch von anderen Kontrollparametern abhängen. Eine grafische Darstellung der entsprechenden Einzugsgebiete für bestimmte Verhaltensweisen als Funktion dieser Parameter ist oft fraktal. Der Übergangsbereich zu chaotischem Verhalten zeichnet sich dabei durch bestimmte Eigenschaften aus, wie beispielsweise plötzliche qualitative Änderungen des Verhaltens, die auch als Bifurkation bezeichnet werden. ⓘ

Periodenverdopplung

Bifurkationsdiagramm der Zahlenfolge zur logistischen Gleichung. Dargestellt sind die Häufungspunkte x der Folge als Funktion des Kontrollparameters r. Links konvergiert die Folge, rechts ist sie chaotisch, dazwischen periodisch. An den Verzweigungsstellen im Übergangsbereich findet jeweils eine Periodenverdopplung statt. ⓘ

Beim Übergang von periodischem Verhalten zum Chaos kann ein Phänomen auftreten, das als Periodenverdopplung oder Feigenbaum-Szenario bezeichnet wird. Dabei nimmt zum chaotischen Bereich hin die Oszillationsperiode stufenweise um den Faktor zwei zu ($\Delta r_{n}\propto 2^{n},$ in nebenstehender Zeichnung). Die zugehörigen Parameterintervalle $\Delta x_{n}$ werden mit zunehmender Periode immer kürzer ($\Delta x_{n}\propto 1/2^{\delta _{n}}$): Das Verhältnis der Längen aufeinander folgender Parameterintervalle ergibt im Limes $n\to \infty$ die Feigenbaum-Konstante $\delta \approx 4{,}669,$ eine irrationale Zahl. Dabei ist der chaotische Bereich auf fraktale Weise immer wieder von Intervallen mit periodischem Verhalten durchbrochen, die jeweils wiederum über Periodenverdopplung in das benachbarte Chaos übergehen. Dieses Verhalten und das zugehörige Zahlenverhältnis hängen nicht von den Details des mathematischen oder physikalischen nichtlinearen Systems ab. Sie sind eine Gemeinsamkeit vieler chaotischer Systeme. ⓘ

Intermittenz

Neben der Periodenverdopplung werden auch andere Formen des Übergangs ins Chaos beobachtet, wie beispielsweise die sogenannte Intermittenz. Dabei wechseln sich bei einem Parameterwert im Übergangsbereich quasiperiodisches und chaotisches Verhalten ständig ab, wobei zu chaotischen Parameterwerten hin der chaotische Anteil ständig zunimmt. ⓘ

Beispiele für chaotische Systeme

Naturwissenschaftliche Beispiele

Den meisten Vorgängen in der Natur liegen nichtlineare Prozesse zugrunde. Entsprechend vielfältig sind die Systeme, die chaotisches Verhalten zeigen können. Hier einige wichtige oder bekannte Beispiele:

• Das Wetter. Zurzeit ist die Zuverlässigkeit der Wettervorhersage durch die grobe Kenntnis des Ausgangszustandes begrenzt. Aber auch bei vollständiger Information würde eine langfristige Wettervorhersage letztlich am chaotischen Charakter des meteorologischen Geschehens scheitern. Die Stabilität des Wetters kann stark schwanken. So sind bei bestimmten Wetterlagen Vorhersagen für eine Woche durchaus möglich, bei anderen dagegen kaum für 24 Stunden.
• Das Doppelpendel. Da es sich aufgrund von nur zwei unabhängigen Freiheitsgraden leicht modellieren und auch leicht herstellen lässt, ist es ein beliebtes Demonstrationsobjekt für überraschende Wechsel im chaotischen Bewegungsablauf. In Computersimulationen und bei den Versuchen lassen sich bestimmte Klassen von Systemverhalten identifizieren, wie beispielsweise die maximal mögliche Anzahl von Überschlägen in Abhängigkeit von der anfänglichen Energie und der Reibung. Bei der schwingenden atwoodschen Maschine liegen ebenfalls zwei Freiheitsgrade vor, aber nur ein Körper schwingt wie ein Pendel.
• Das magnetische Pendel, bei dem eine an einem Faden aufgehängte Eisenkugel über mehreren Magneten pendelt.
• Systeme mit stoßenden Kugeln. Wichtig ist, dass die Kugeln entweder kollidieren oder an gekrümmten Hindernissen reflektiert werden, damit Störungen exponentiell anwachsen. Beispiele sind das Gerät zur Ziehung der Lottozahlen, der Flipperautomat und Billard.
• Das Dreikörperproblem und damit auch unser Sonnensystem oder Sternsysteme aus drei oder mehr Sternen wie beispielsweise Sternhaufen.
• In der Medizin sind die Entstehung tödlicher Embolien bei Arterienverkalkung, der Ausfall bestimmter Hirnfunktionen beim Schlaganfall oder die Entstehung bösartiger Tumoren nach Mutationen von Suppressor-Genen typische Beispiele für chaotisches Verhalten.
• Der Herzrhythmus wurde zeitweise als chaotisches Signal angesehen. Je nach Gesundheitszustand lässt sich der Herzrhythmus über chaostheoretische Kriterien klassifizieren. Die dabei berechneten Parameter stellen jedoch lediglich empirische Größen dar. Anwendungsgebiete sind die Vorhersage des plötzlichen Herztodes oder allgemein gesprochen die Diagnose von Erkrankungen, die durch das vegetative Nervensystem vermittelt werden. Hierbei wird angenommen, dass das System umso stabiler ist, je chaotischer das Verhalten ist. Die Betrachtung des Herz-Kreislauf-Systems als „chaotisch“ ist jedoch in verschiedener Hinsicht problematisch.
• Turbulenz wie beispielsweise beim Bénard-Experiment zur Konvektion.
• Die Belousov-Zhabotinsky-Reaktion, eine chemische Reaktion.
• Die Populationsdynamik in Räuber-Beute-Modellen.
• Die Bäcker-Transformation, ein diskretes System, das den Ort einer Rosine im Kuchenteig beim abwechselnden Auswalzen und Falten des Teigs betrachtet. ⓘ

Geistes- und sozialwissenschaftliche Beispiele

Neben diesen naturwissenschaftlichen Beispielen wird die Chaosforschung auch in verschiedenen Geistes- und Sozialwissenschaften genutzt, um chaotisches Verhalten zu beschreiben und zu erklären. Hier einige Beispiele:

• Börsenkurse und Konjunkturentwicklung. Bereits Mandelbrot hatte darauf hingewiesen, dass zahlreiche Verlaufskurven von Wirtschaftsdaten nichtlineare Eigenschaften haben und sich mit Hilfe von Fraktalen und Intermittenzen beschreiben lassen.
• In der Geschichtswissenschaft wird die Chaosforschung vor allem zur Beschreibung und Erklärung von Krisen und Übergangszuständen genutzt.
• In der Kommunikationswissenschaft wird die Chaosforschung im Bereich der Nachrichtenforschung verwendet, um die Auswahl und Gestaltung von Nachrichten besser zu erklären.
• In der Psychologie dient die Chaosforschung als Ansatz, um beispielsweise sprachpsychologische Befunde zum Stottern oder die Ursachen für kriminelle Affekttaten (wie Amokläufe) zu erklären. ⓘ

Allerdings wird in manchen Fällen die Verwendung von chaostheoretischen Begriffen in Geistes- und Sozialwissenschaften kritisiert. Der Vorwurf lautet, dass dabei Begriffe und Ergebnisse der Chaostheorie zur jeweiligen Argumentation herangezogen werden, obwohl die mathematische/physikalische Definition eines chaotischen Systems nicht oder nur teilweise erfüllt ist. Es wird also das Ansehen von Mathematik und Physik in Anspruch genommen, ohne dass ein inhaltlicher Zusammenhang besteht, ähnlich dem Vorgang des Namedropping in der Wissenschaft. ⓘ