Schmetterlingseffekt

Ein Diagramm des Lorenzschen seltsamen Attraktors für die Werte ρ=28, σ = 10, β = 8/3. Der Schmetterlingseffekt oder die empfindliche Abhängigkeit von den Anfangsbedingungen ist die Eigenschaft eines dynamischen Systems, dass ausgehend von einer beliebigen Anzahl von beliebig nahe beieinander liegenden alternativen Anfangsbedingungen auf dem Attraktor die iterierten Punkte willkürlich voneinander entfernt werden. ⓘ

Experimentelle Demonstration des Schmetterlingseffekts mit verschiedenen Aufnahmen desselben Doppelpendels. Bei jeder Aufzeichnung beginnt das Pendel mit nahezu dem gleichen Ausgangszustand. Mit der Zeit wachsen die Unterschiede in der Dynamik von fast unmerklich bis drastisch. ⓘ

In der Chaostheorie bezeichnet der Schmetterlingseffekt die empfindliche Abhängigkeit von den Anfangsbedingungen, bei der eine kleine Änderung in einem Zustand eines deterministischen nichtlinearen Systems zu großen Unterschieden in einem späteren Zustand führen kann. ⓘ

Der Begriff ist eng mit der Arbeit des Mathematikers und Meteorologen Edward Norton Lorenz verbunden. Er stellte fest, dass sich der Schmetterlingseffekt von dem metaphorischen Beispiel ableitet, dass die Details eines Tornados (der genaue Zeitpunkt seiner Entstehung, der genaue Weg, den er nimmt) durch geringfügige Störungen beeinflusst werden, z. B. durch einen entfernten Schmetterling, der einige Wochen zuvor mit den Flügeln schlägt. Lorenz verwendete ursprünglich eine Möwe, die einen Sturm auslöst, ließ sich aber 1972 dazu überreden, es mit der Verwendung von Schmetterling und Tornado poetischer zu gestalten. Lorenz entdeckte den Effekt, als er Läufe seines Wettermodells mit scheinbar unbedeutend gerundeten Anfangsbedingungen beobachtete. Er stellte fest, dass das Wettermodell die Ergebnisse von Läufen mit ungerundeten Anfangsbedingungen nicht reproduzieren konnte. Eine sehr kleine Änderung der Ausgangsbedingungen hatte ein deutlich anderes Ergebnis zur Folge. ⓘ

Die Idee, dass kleine Ursachen große Auswirkungen auf das Wetter haben können, wurde bereits von dem französischen Mathematiker und Ingenieur Henri Poincaré erkannt. Auch der amerikanische Mathematiker und Philosoph Norbert Wiener trug zu dieser Theorie bei. Lorenz' Arbeit stellte das Konzept der Instabilität der Erdatmosphäre auf eine quantitative Grundlage und verknüpfte das Konzept der Instabilität mit den Eigenschaften großer Klassen dynamischer Systeme, die eine nichtlineare Dynamik und ein deterministisches Chaos durchlaufen. ⓘ

Das Konzept des Schmetterlingseffekts wird seither außerhalb der Wetterkunde als allgemeiner Begriff für jede Situation verwendet, in der eine kleine Veränderung die Ursache für größere Auswirkungen sein soll. ⓘ

Geschichte

In Die Berufung des Menschen (1800) sagt Johann Gottlieb Fichte: "Man könnte kein einziges Sandkorn von seinem Platz entfernen, ohne dadurch ... etwas in allen Teilen des unermesslichen Ganzen zu verändern". ⓘ

Die Chaostheorie und die empfindliche Abhängigkeit von den Anfangsbedingungen wurden in zahlreichen Formen der Literatur beschrieben. Dies wird durch den Fall des Dreikörperproblems von Poincaré im Jahr 1890 belegt. Später schlug er vor, dass solche Phänomene zum Beispiel in der Meteorologie vorkommen könnten. ⓘ

Im Jahr 1898 stellte Jacques Hadamard eine allgemeine Divergenz von Flugbahnen in Räumen mit negativer Krümmung fest. Pierre Duhem erörterte 1908 die mögliche allgemeine Bedeutung dieses Phänomens. ⓘ

Die Idee, dass der Tod eines Schmetterlings weitreichende Auswirkungen auf nachfolgende historische Ereignisse haben könnte, taucht erstmals in "A Sound of Thunder" auf, einer Kurzgeschichte von Ray Bradbury aus dem Jahr 1952. In "A Sound of Thunder" geht es um Zeitreisen. ⓘ

Im Jahr 1961 ließ Lorenz ein numerisches Computermodell laufen, um eine Wettervorhersage aus der Mitte des vorherigen Laufs als Abkürzung zu wiederholen. Er gab die Anfangsbedingung 0,506 aus dem Ausdruck ein, anstatt den genauen Wert 0,506127 einzugeben. Das Ergebnis war ein völlig anderes Wetterszenario. ⓘ

Lorenz schrieb:

An einem Punkt beschloss ich, einige der Berechnungen zu wiederholen, um die Vorgänge genauer zu untersuchen. Ich hielt den Computer an, tippte eine Reihe von Zahlen ein, die er kurz zuvor ausgedruckt hatte, und ließ ihn wieder laufen. Ich ging in den Flur, um eine Tasse Kaffee zu trinken, und kehrte nach etwa einer Stunde zurück, in der der Computer etwa zwei Monate Wetter simuliert hatte. Die Zahlen, die gedruckt wurden, entsprachen nicht den alten. Ich vermutete sofort eine schwache Vakuumröhre oder ein anderes Computerproblem, was nicht ungewöhnlich war, aber bevor ich den Kundendienst anrief, beschloss ich, nachzusehen, wo genau der Fehler aufgetreten war, da ich wusste, dass dies den Wartungsprozess beschleunigen könnte. Statt eines plötzlichen Bruchs stellte ich fest, dass die neuen Werte zunächst die alten wiederholten, aber bald darauf um eine und dann um mehrere Einheiten in der letzten [Dezimal-]Stelle abwichen, und dann begannen sie, sich in der vorletzten Stelle und dann in der Stelle davor zu unterscheiden. Tatsächlich verdoppelten sich die Differenzen mehr oder weniger alle vier Tage, bis irgendwann im zweiten Monat jede Ähnlichkeit mit der ursprünglichen Ausgabe verschwand. Das reichte aus, um mir zu sagen, was passiert war: Die Zahlen, die ich eingegeben hatte, waren nicht die exakten Originalzahlen, sondern die gerundeten Werte, die im Originalausdruck erschienen waren. Die anfänglichen Rundungsfehler waren die Übeltäter; sie wurden immer größer, bis sie die Lösung dominierten.

- E. N. Lorenz, Das Wesen des Chaos, U. Washington Press, Seattle (1993), Seite 134 ⓘ

1963 veröffentlichte Lorenz eine theoretische Studie dieses Effekts in einer viel zitierten, bahnbrechenden Arbeit mit dem Titel Deterministic Nonperiodic Flow (die Berechnungen wurden auf einem Royal McBee LGP-30 Computer durchgeführt). An anderer Stelle erklärte er:

Ein Meteorologe bemerkte, dass, wenn die Theorie richtig wäre, ein einziger Flügelschlag einer Möwe ausreichen würde, um den Verlauf des Wetters für immer zu verändern. Die Kontroverse ist noch nicht beigelegt, aber die jüngsten Beweise scheinen für die Möwen zu sprechen. ⓘ

Auf Anregung von Kollegen verwendete Lorenz in späteren Reden und Abhandlungen den poetischeren Schmetterling. Als er keinen Titel für einen Vortrag fand, den er 1972 auf der 139. Tagung der American Association for the Advancement of Science halten sollte, dachte sich Philip Merilees den Titel Does the flap of a butterfly's wings in Brazil set off a tornado in Texas? aus, so Lorenz. Obwohl der Flügelschlag eines Schmetterlings bei der Formulierung dieses Begriffs konstant geblieben ist, haben sich der Ort des Schmetterlings, die Folgen und der Ort der Folgen stark verändert. ⓘ

Der Begriff bezieht sich auf die Vorstellung, dass die Flügel eines Schmetterlings winzige Veränderungen in der Atmosphäre bewirken können, die letztlich den Weg eines Tornados verändern oder das Auftreten eines Tornados an einem anderen Ort verzögern, beschleunigen oder sogar verhindern können. Der Schmetterling treibt den Tornado nicht an oder erzeugt ihn direkt, aber der Begriff soll andeuten, dass der Flügelschlag des Schmetterlings den Tornado verursachen kann: in dem Sinne, dass der Flügelschlag ein Teil der Anfangsbedingungen eines miteinander verbundenen komplexen Netzes ist; eine Reihe von Bedingungen führt zu einem Tornado, die andere Reihe von Bedingungen nicht. Der Flügelschlag stellt eine kleine Veränderung der Ausgangsbedingungen des Systems dar, die kaskadenartig zu großräumigen Veränderungen der Ereignisse führt (vgl. Dominoeffekt). Hätte der Schmetterling nicht mit den Flügeln geschlagen, wäre die Flugbahn des Systems möglicherweise ganz anders verlaufen - es ist aber auch möglich, dass die Bedingungen ohne den Flügelschlag des Schmetterlings zu einem Tornado führen. ⓘ

Der Schmetterlingseffekt stellt eine offensichtliche Herausforderung für die Vorhersage dar, da die Anfangsbedingungen für ein System wie das Wetter nie mit absoluter Genauigkeit bekannt sein können. Dieses Problem war der Grund für die Entwicklung der Ensemble-Vorhersage, bei der eine Reihe von Vorhersagen auf der Grundlage von gestörten Ausgangsbedingungen gemacht werden. ⓘ

Einige Wissenschaftler haben seitdem argumentiert, dass das Wettersystem nicht so empfindlich auf die Anfangsbedingungen reagiert, wie bisher angenommen. David Orrell vertritt die Auffassung, dass der größte Anteil an den Fehlern in der Wettervorhersage auf Modellfehler zurückzuführen ist und die Empfindlichkeit gegenüber den Anfangsbedingungen eine relativ geringe Rolle spielt. Stephen Wolfram weist auch darauf hin, dass die Lorenz-Gleichungen stark vereinfacht sind und keine Terme enthalten, die viskose Effekte darstellen; er glaubt, dass diese Terme dazu neigen würden, kleine Störungen zu dämpfen. Jüngste Studien mit verallgemeinerten Lorenz-Modellen, die zusätzliche dissipative Terme und Nichtlinearität enthalten, deuten darauf hin, dass ein größerer Erwärmungsparameter für den Ausbruch von Chaos erforderlich ist. ⓘ

Während der "Schmetterlingseffekt" häufig als Synonym für die empfindliche Abhängigkeit von den Anfangsbedingungen erklärt wird, wie sie Lorenz in seinem Aufsatz von 1963 beschrieb (und zuvor von Poincaré beobachtet wurde), wurde die Schmetterlingsmetapher ursprünglich auf eine Arbeit angewandt, die er 1969 veröffentlichte und die die Idee einen Schritt weiter führte. Lorenz schlug ein mathematisches Modell dafür vor, wie sich winzige Bewegungen in der Atmosphäre auf größere Systeme auswirken. Er fand heraus, dass die Systeme in diesem Modell nur bis zu einem bestimmten Punkt in der Zukunft vorhergesagt werden konnten, und darüber hinaus würde eine Verringerung des Fehlers in den Anfangsbedingungen die Vorhersagbarkeit nicht erhöhen (solange der Fehler nicht Null ist). Damit wurde nachgewiesen, dass ein deterministisches System in Bezug auf die Vorhersagbarkeit von einem nicht-deterministischen System durch Beobachtung nicht zu unterscheiden ist. Jüngste Überprüfungen dieses Papiers legen nahe, dass es eine bedeutende Herausforderung für die Vorstellung darstellt, dass unser Universum deterministisch ist, vergleichbar mit den Herausforderungen, die die Quantenphysik bietet. ⓘ

In dem 1993 erschienenen Buch "The Essence of Chaos" definiert Lorenz den Schmetterlingseffekt wie folgt: "Das Phänomen, dass eine kleine Änderung des Zustands eines dynamischen Systems dazu führt, dass sich nachfolgende Zustände stark von den Zuständen unterscheiden, die ohne die Änderung eingetreten wären." Diese Eigenschaft entspricht der empfindlichen Abhängigkeit der Lösungen von den Anfangsbedingungen (SDIC) in . Im selben Buch wandte Lorenz die Aktivität des Skifahrens an und entwickelte ein idealisiertes Skimodell, um die Empfindlichkeit zeitlich veränderlicher Pfade gegenüber den Anfangsstellungen aufzuzeigen. Ein Vorhersagehorizont wird vor dem Auftreten von SDIC festgelegt. ⓘ

Abbildung

Der Schmetterlingseffekt im Lorenz-Attraktor
Zeit 0 ≤ t ≤ 30 (größer)		z-Koordinate (größer)
Diese Abbildungen zeigen zwei Segmente der dreidimensionalen Entwicklung zweier Trajektorien (eine in blau, die andere in gelb) für denselben Zeitraum im Lorenz-Attraktor, ausgehend von zwei Anfangspunkten, die sich in der x-Koordinate nur um 10-5 unterscheiden. Anfänglich scheinen die beiden Bahnen übereinzustimmen, wie die geringe Differenz zwischen der z-Koordinate der blauen und der gelben Bahn zeigt, aber für t > 23 ist die Differenz so groß wie der Wert der Bahn. Die Endposition der Kegel zeigt, dass die beiden Bahnen bei t = 30 nicht mehr übereinstimmen.
Eine Animation des Lorenz-Attraktors zeigt die kontinuierliche Entwicklung.

ⓘ

Theorie und mathematische Definition

Rekursion, die ungefähre Rückkehr eines Systems zu seinen Anfangsbedingungen, und die empfindliche Abhängigkeit von den Anfangsbedingungen sind die beiden Hauptmerkmale chaotischer Bewegungen. Sie haben die praktische Konsequenz, dass komplexe Systeme, wie z. B. das Wetter, nach einer bestimmten Zeitspanne (im Falle des Wetters etwa eine Woche) nur schwer vorhergesagt werden können, da es unmöglich ist, die atmosphärischen Ausgangsbedingungen völlig genau zu messen. ⓘ

Ein dynamisches System zeigt eine empfindliche Abhängigkeit von den Anfangsbedingungen, wenn sich beliebig nahe beieinander liegende Punkte im Laufe der Zeit mit exponentieller Geschwindigkeit voneinander entfernen. Die Definition ist nicht topologisch, sondern im Wesentlichen metrisch. Lorenz definierte die empfindliche Abhängigkeit wie folgt: Die Eigenschaft, die eine Bahn (d. h. eine Lösung) kennzeichnet, wenn die meisten anderen Bahnen, die zu einem bestimmten Zeitpunkt nahe an ihr vorbeiziehen, mit fortschreitender Zeit nicht in ihrer Nähe bleiben. ⓘ

Wenn M der Zustandsraum für die Karte $f^{t}$ist, dann $f^{t}$ eine empfindliche Abhängigkeit von den Anfangsbedingungen, wenn es für ein beliebiges x in M und ein beliebiges δ > 0 y in M gibt, deren Abstand d(. , .) so ist, dass $0<d(x,y)<\delta$ und so, dass

$d(f^{\tau }(x),f^{\tau }(y))>\mathrm {e} ^{a\tau }\,d(x,y)$ ⓘ

Die Definition erfordert nicht, dass sich alle Punkte einer Nachbarschaft vom Basispunkt x trennen, aber sie erfordert einen positiven Lyapunov-Exponenten. Zusätzlich zu einem positiven Lyapunov-Exponenten ist die Begrenztheit ein weiteres wichtiges Merkmal chaotischer Systeme. ⓘ

Der einfachste mathematische Rahmen, der eine empfindliche Abhängigkeit von den Anfangsbedingungen aufweist, wird durch eine bestimmte Parametrisierung der logistischen Karte bereitgestellt:

$x_{n+1}=4x_{n}(1-x_{n}),\quad 0\leq x_{0}\leq 1,$ ⓘ

die, anders als die meisten chaotischen Karten, eine geschlossene Lösung hat:

$x_{n}=\sin ^{2}(2^{n}\theta \pi )$ ⓘ

wobei der Parameter der Anfangsbedingungen $\theta$ gegeben ist durch $\theta ={\tfrac {1}{\pi }}\sin ^{-1}(x_{0}^{1/2})$. Für rationale $\theta$geht nach einer endlichen Anzahl von Iterationen $x_{n}$ in eine periodische Folge über. Aber fast alle $\theta$ sind irrational, und für irrationale $\theta$, $x_{n}$ wiederholt sich nie - sie ist nicht periodisch. Diese Lösungsgleichung zeigt deutlich die beiden Hauptmerkmale des Chaos - Streckung und Faltung: Der Faktor 2n zeigt das exponentielle Wachstum der Streckung, was zu einer empfindlichen Abhängigkeit von den Anfangsbedingungen führt (der Schmetterlingseffekt), während die quadrierte Sinusfunktion $x_{n}$ die Faltung innerhalb des Bereichs [0, 1] hält. ⓘ

In physikalischen Systemen

Im Wetter

Am bekanntesten ist der Schmetterlingseffekt im Zusammenhang mit dem Wetter; er lässt sich beispielsweise in Standard-Wettervorhersagemodellen leicht nachweisen. Die Klimaforscher James Annan und William Connolley erklären, dass das Chaos bei der Entwicklung von Wettervorhersagemethoden wichtig ist; die Modelle reagieren empfindlich auf die Anfangsbedingungen. Sie fügen den Vorbehalt hinzu: "Natürlich hat die Existenz eines unbekannten Schmetterlings, der mit den Flügeln schlägt, keine direkte Auswirkung auf die Wettervorhersage, da es viel zu lange dauert, bis eine so kleine Störung zu einer signifikanten Größe heranwächst, und wir uns um viel mehr unmittelbare Unwägbarkeiten zu kümmern haben. Daher ist die direkte Auswirkung dieses Phänomens auf die Wettervorhersage oft etwas falsch. Die beiden Arten von Schmetterlingseffekten, einschließlich der empfindlichen Abhängigkeit von den Anfangsbedingungen und der Fähigkeit einer winzigen Störung, eine organisierte Zirkulation über große Entfernungen zu erzeugen, sind nicht genau dasselbe. Ein Vergleich der beiden Arten von Schmetterlingseffekten und der dritten Art von Schmetterlingseffekten ist dokumentiert worden. ⓘ

Durch die Entdeckung nebeneinander existierender chaotischer und nicht-chaotischer Attraktoren in Lorenz-Modellen schlugen Shen und seine Kollegen eine überarbeitete Sichtweise vor, die besagt, dass "das Wetter Chaos und Ordnung besitzt", im Gegensatz zu der herkömmlichen Sichtweise "das Wetter ist chaotisch". Infolgedessen tritt die empfindliche Abhängigkeit von den Anfangsbedingungen (SDIC) nicht immer auf. SDIC tritt nämlich auf, wenn zwei Bahnen (d. h. Lösungen) zum chaotischen Attraktor werden; sie tritt nicht auf, wenn sich zwei Bahnen auf denselben Punktattraktor zubewegen. Die obige Animation für die Bewegung eines Doppelpendels liefert eine Analogie. Bei großen Schwenkwinkeln ist die Bewegung des Pendels oft chaotisch. Im Vergleich dazu sind die Bewegungen bei kleinen Schwenkwinkeln nicht chaotisch. ⓘ

In der Quantenmechanik

Das Potenzial für eine empfindliche Abhängigkeit von den Anfangsbedingungen (der Schmetterlingseffekt) wurde in einer Reihe von Fällen in der semiklassischen und Quantenphysik untersucht, darunter Atome in starken Feldern und das anisotrope Kepler-Problem. Einige Autoren haben argumentiert, dass eine extreme (exponentielle) Abhängigkeit von den Anfangsbedingungen bei reinen Quantenbehandlungen nicht zu erwarten ist; die empfindliche Abhängigkeit von den Anfangsbedingungen, die bei klassischen Bewegungen nachgewiesen wurde, ist jedoch in den von Martin Gutzwiller und John B. Delos und Mitarbeitern entwickelten semiklassischen Behandlungen enthalten. Die Zufallsmatrixtheorie und Simulationen mit Quantencomputern beweisen, dass einige Versionen des Schmetterlingseffekts in der Quantenmechanik nicht existieren. ⓘ

Andere Autoren vermuten, dass der Schmetterlingseffekt in Quantensystemen beobachtet werden kann. Zbyszek P. Karkuszewski et al. betrachten die zeitliche Entwicklung von Quantensystemen, die leicht unterschiedliche Hamiltonianer haben. Sie untersuchen, wie empfindlich Quantensysteme auf kleine Änderungen in ihren gegebenen Hamiltonianen reagieren. David Poulin et al. stellten einen Quantenalgorithmus zur Messung des Treuezerfalls vor, der "die Geschwindigkeit misst, mit der identische Ausgangszustände auseinanderlaufen, wenn sie einer leicht unterschiedlichen Dynamik unterworfen werden". Sie betrachten den Treuezerfall als "das engste Quantenanalogon zum (rein klassischen) Schmetterlingseffekt". Während der klassische Schmetterlingseffekt die Auswirkung einer kleinen Änderung der Position und/oder Geschwindigkeit eines Objekts in einem gegebenen Hamilton-System berücksichtigt, betrachtet der Quantenschmetterlingseffekt die Auswirkung einer kleinen Änderung des Hamilton-Systems mit einer gegebenen Anfangsposition und -geschwindigkeit. Dieser Quantenschmetterlingseffekt ist experimentell nachgewiesen worden. Quanten- und semiklassische Behandlungen der Empfindlichkeit von Systemen gegenüber Anfangsbedingungen sind als Quantenchaos bekannt. ⓘ

Beispiele

Meteorologie

Da die Anfangsbedingungen experimentell immer nur mit endlicher Genauigkeit bestimmt werden können, ist eine Konsequenz dieses Effekts für solche Systeme, dass es unmöglich ist, ihr Verhalten für längere Zeit vorherzusagen. Zum Beispiel kann das Wetter für einen Tag relativ genau prognostiziert werden, während eine Vorhersage für einen Monat kaum möglich ist. Selbst wenn die ganze Erdoberfläche mit Sensoren bedeckt wäre, diese nur geringfügig voneinander entfernt lägen, bis in die höchsten Lagen der Erdatmosphäre reichten und exakte Daten lieferten, wäre auch ein unbegrenzt leistungsfähiger Computer nicht in der Lage, langfristig exakte Prognosen der Wetterentwicklung zu machen. Da das Computermodell die Räume zwischen den Sensoren nicht erfasst, kommt es zu geringfügigen Divergenzen zwischen Modell und Realität, die sich dann positiv verstärken und zu großen Unterschieden führen. ⓘ

Beispielsweise lassen sich aus den Daten von 1000 Wetterstationen einigermaßen zuverlässige Prognosen über einen Zeitraum von vier Tagen machen. Für entsprechende Vorhersagen über elf Tage bräuchte man bereits 100 Millionen gleichmäßig über die Erde verteilte Messstationen. Absurd wird das Vorhaben, wenn sich die Vorhersage über einen Monat erstrecken soll; denn dann wären 10²⁰ Wetterstationen erforderlich, das heißt je eine auf je fünf Quadratmillimeter Erdoberfläche (Lit.: Heiden). ⓘ

Allerdings ist das Lorenz-Modell eigentlich viel chaotischer als der tatsächliche Wetterverlauf. Die Gleichungen sind viel instabiler als die grundlegenden physikalischen Gleichungen. Der Mathematiker Wladimir Igorewitsch Arnold gibt als eine prinzipielle obere Schranke für die Wettervorhersage zwei Wochen an. ⓘ

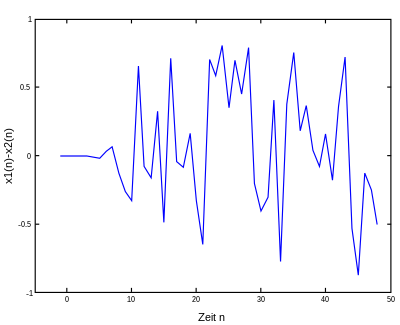
Zeltabbildung

Ein minimales Beispiel für den Schmetterlingseffekt ist die Zeltabbildung.

Im Diagramm wird die Differenz zwischen den Werten zweier solcher Abbildungen mit leicht unterschiedlichem Startparameter (hier: 0,506 und 0,506127) über der Anzahl der Iterationen (im Diagramm dargestellt als „Zeit“) aufgetragen. Beide Abbildungen haben den gleichen Kontrollparameter, der so gewählt wurde, dass die Zeltabbildung chaotisches Verhalten zeigt (erkennbar im entsprechenden Bifurkationsdiagramm). Die maximal mögliche Abweichung ist ± 1. Die beiden Abbildungen sind demnach schon nach wenigen Iterationen völlig verschieden. ⓘ

Planetenbahnen

Wenn mehr als zwei Himmelskörper gravitativ aneinander gebunden sind, können minimale Änderungen der Ausgangssituation im Laufe der Zeit zu großen nichtvorhersagbaren Änderungen der Bahnen und Positionen führen. Dieses Verhalten ist Thema des Dreikörperproblems. ⓘ

Künstlerische Verarbeitungen

Vor dem Hinzufügen neuer Einträge in diesem Abschnitt beachte bitte die aktuellen und vorangegeangenen Diskussionen und diskutiere erst, bevor du änderst. Möglicherweise wurden dein beabsichtigter Eintrag und seine Relevanz für das Lemma bereits diskutiert. Auf der sicheren Seite bist du, wenn du eine taugliche Quelle nennst, die den Bezug belegt. ⓘ

Belletristik

• Ray Bradburys Kurzgeschichte Ferner Donner aus dem Jahr 1952 befasst sich gut zehn Jahre vor der Entstehung des Begriffs mit der Auswirkung kleiner Veränderungen auf die Zukunft.
• Stephen King nutzt den Schmetterlingseffekt in seinem Roman Der Anschlag, wo ein Zeitreisender die Auswirkungen seiner Eingriffe nicht abzuschätzen vermag.
• Michael Crichton verarbeitet in seinem Roman DinoPark dieses Prinzip.
• Nick McDonell erwähnt den Schmetterlingseffekt in seinem Roman Zwölf.
• Stephen Fry bezieht sich mit seinem Buch Geschichte machen auf den Schmetterlingseffekt.
• Jussi Adler-Olsen zitiert den Begriff abgewandelt schon im Titel seines Thrillers Erwartung. Der Marco-Effekt und bezieht sich ausdrücklich darauf. ⓘ

Film

• Der Zufall möglicherweise aus dem Jahre 1981
• Lola rennt aus dem Jahr 1998
• Sie liebt ihn – sie liebt ihn nicht aus dem Jahr 1998
• Donnie Darko aus dem Jahr 2001
• Minority Report mit Tom Cruise von Steven Spielberg aus dem Jahr 2002
• Böse Zellen aus dem Jahr 2003
• Category 6 – Der Tag des Tornado aus dem Jahr 2004
• Butterfly Effect, Butterfly Effect 2 und Butterfly Effect 3 – Die Offenbarung aus den Jahren 2004, 2006 und 2009
• A Sound of Thunder aus dem Jahr 2005
• Chaos aus dem Jahr 2005
• Babel aus dem Jahr 2006
• Oxford Murders aus dem Jahr 2008
• Mr. Nobody aus dem Jahr 2009
• Parallelwelten aus dem Jahr 2019 ⓘ

Dokumentationen

• Boom und Crash – Wie Spekulation ins Chaos führt, aus dem Jahr 2021 ⓘ

Fernsehserien

• Erased, "Die Stadt, in der es mich nicht gibt" aus dem Jahr 2016
• Scrubs, Folge Mein Schmetterling (Staffel 3, Folge 16)
• Heroes, Folge Der Schmetterlingseffekt (Staffel 3, Folge 2)
• How I Met Your Mother, Folge Zur richtigen Zeit am richtigen Ort (Staffel 4, Folge 22)
• Dexter, Folge Schmetterlingseffekt (Staffel 3, Folge 8)
• Die Simpsons Treehouse of Horror V, Folge Zeit und Strafe
• Family Guy, Folge Gestatten, Lois Quagmire (Staffel 5, Folge 18)
• Fringe – Grenzfälle des FBI, Folge Das Glühwürmchen (Staffel 3, Folge 10)
• Community, Folge Remedial Chaos Theory (Staffel 3, Folge 4)
• Guilty Crown, Folge Die Konvergenz des Schmetterlingseffekt (Staffel 1, Folge 22)
• Die fantastische Welt von Gumball, Folge Der Schmetterling (Staffel 3, Folge 27)
• Raumschiff Enterprise – Das nächste Jahrhundert, Folge Parallelen (Staffel 7, Folge 11) ⓘ

Videospiele

• Life Is Strange
• Until Dawn
• The Dark Pictures Anthology ⓘ