Resonanz

Resonanz (von lateinisch resonare „widerhallen“) ist in Physik und Technik das verstärkte Mitschwingen eines schwingfähigen Systems, wenn es einer zeitlich veränderlichen Einwirkung unterliegt. Dabei kann das System um ein Vielfaches stärker ausschlagen als beim konstanten Einwirken der Anregung mit ihrer maximalen Stärke. Bei periodischer Anregung muss die Anregungsfrequenz oder ein ganzzahliges Vielfaches davon in der Nähe einer Resonanzfrequenz des Systems liegen. Das Phänomen kann bei allen schwingfähigen physikalischen und technischen Systemen auftreten und kommt auch im Alltag häufig vor. Resonanzen werden in der Technik oft ausgenutzt, um eine bestimmte Frequenz herauszufiltern oder zu verstärken. Wo eine Verstärkung nicht gewünscht ist, müssen unerwünschte Resonanzen jedoch vermieden werden. ⓘ

Die im Resonanzfall anwachsenden Ausschläge entstehen dadurch, dass das System bei jeder Schwingung erneut Energie aufnimmt und speichert. Um zu verhindern, dass das System durch zu große Ausschläge aus dem schwingfähigen Amplitudenbereich austritt (Resonanzkatastrophe) oder zerstört wird, kann seine Dämpfung erhöht, seine Eigenfrequenz oder die Anregungsfrequenz verändert, oder die Stärke der Anregung verringert werden. Das anfängliche Anwachsen der Ausschläge wird dadurch begrenzt, dass die zugeführte Energie zunehmend von der Dämpfung (z. B. Reibung) aufgezehrt wird, oder dadurch, dass sich bei zu großem Unterschied zwischen Resonanz- und Anregungsfrequenz der Energiefluss immer wieder umkehrt, weil Anregung und schwingendes System „aus dem Takt“ geraten. ⓘ

Als Folge stellt sich im Laufe der Zeit der Zustand der eingeschwungenen Schwingung her, bei dem die Amplitude konstant bleibt und die Schwingungsfrequenz mit der Anregungsfrequenz übereinstimmt. Die weiterhin in jeder Schwingung zugeführte Energie wird dann vollständig von der Dämpfung aufgezehrt. Nach Abschalten der Anregung kommt das System in Form einer gedämpften Schwingung mit seiner Eigenfrequenz allmählich zur Ruhe. ⓘ

Das Phänomen der Resonanz spielt in Physik und Technik auf vielen Gebieten eine wichtige Rolle, zum Beispiel in der Mechanik, Akustik, Baudynamik, Elektrizitätslehre, Geowissenschaft, Astronomie, Optik und Quantenphysik. In der modernen Quantenphysik gilt die Gleichung $E=hf$, die jedem Energiebetrag $E$ vermittels der Planckschen Konstante $h$ die Frequenz $f$ einer Schwingung zuordnet. Anstelle der Resonanz bei einer bestimmten Frequenz betrachtet man hier die Resonanz bei einer bestimmten Energie, die der Differenz der Energien von zwei verschiedenen Anregungszuständen des betrachteten Systems entspricht. ⓘ

Zunahme der Amplitude bei abnehmender Dämpfung und Annäherung der Frequenz an die Resonanzfrequenz eines angetriebenen gedämpften einfachen harmonischen Oszillators. ⓘ

Der Begriff Resonanz (von lateinisch resonantia, 'Echo', von resonare, 'widerhallen') stammt aus dem Bereich der Akustik, insbesondere die bei Musikinstrumenten beobachtete sympathische Resonanz, z. B. wenn eine Saite zu schwingen beginnt und einen Ton erzeugt, nachdem eine andere Saite angeschlagen wurde. ⓘ

Überblick

Resonanz tritt auf, wenn ein System in der Lage ist, Energie zu speichern und leicht zwischen zwei oder mehr verschiedenen Speichermodi zu übertragen (z. B. kinetische Energie und potenzielle Energie im Falle eines einfachen Pendels). Allerdings kommt es von Zyklus zu Zyklus zu gewissen Verlusten, die als Dämpfung bezeichnet werden. Wenn die Dämpfung gering ist, entspricht die Resonanzfrequenz ungefähr der Eigenfrequenz des Systems, d. h. der Frequenz der nicht erzwungenen Schwingungen. Manche Systeme haben mehrere, unterschiedliche Resonanzfrequenzen. ⓘ

Beispiele

Das Anschieben einer Person auf einer Schaukel ist ein gängiges Beispiel für Resonanz. Die belastete Schaukel, ein Pendel, hat eine Eigenschwingungsfrequenz, ihre Resonanzfrequenz, und wehrt sich dagegen, schneller oder langsamer geschoben zu werden. ⓘ

Ein bekanntes Beispiel ist eine Spielplatzschaukel, die als Pendel wirkt. Wenn man eine Person in der Schaukel im Takt des natürlichen Intervalls der Schaukel (ihrer Resonanzfrequenz) anschiebt, wird die Schaukel immer höher (maximale Amplitude), während Versuche, die Schaukel in einem schnelleren oder langsameren Tempo anzuschieben, kleinere Bögen erzeugen. Das liegt daran, dass die Energie, die die Schaukel aufnimmt, maximiert wird, wenn die Stöße mit den natürlichen Schwingungen der Schaukel übereinstimmen. ⓘ

Resonanz ist in der Natur weit verbreitet und wird in vielen Geräten ausgenutzt. Sie ist der Mechanismus, durch den praktisch alle sinusförmigen Wellen und Schwingungen erzeugt werden. Viele Geräusche, die wir hören, wenn z. B. harte Gegenstände aus Metall, Glas oder Holz angeschlagen werden, werden durch kurze Resonanzschwingungen im Gegenstand verursacht. Licht und andere kurzwellige elektromagnetische Strahlung wird durch Resonanz auf atomarer Ebene erzeugt, z. B. bei Elektronen in Atomen. Weitere Beispiele für Resonanz:

• Zeitmessmechanismen moderner Uhren, z. B. die Unruh in einer mechanischen Uhr und der Quarzkristall in einer Quarzuhr
• Gezeitenresonanz in der Bay of Fundy
• Akustische Resonanzen von Musikinstrumenten und des menschlichen Vokaltrakts
• Zerspringen eines Kristallweinglases, wenn es einem Musikton mit der richtigen Tonhöhe (seiner Resonanzfrequenz) ausgesetzt wird
• Reibungstöne, z. B. wenn man einen Glasgegenstand (Glas, Flasche, Vase) durch Reiben mit der Fingerspitze am Rand zum Schwingen bringt
• Elektrische Resonanz von Schwingkreisen in Radios und Fernsehern, die einen selektiven Empfang von Radiofrequenzen ermöglichen
• Erzeugung von kohärentem Licht durch optische Resonanz in einem Laserresonator
• Orbitalresonanz, wie sie bei einigen Monden der Gasriesen des Sonnensystems auftritt
• Materialresonanzen auf atomarer Ebene bilden die Grundlage für verschiedene spektroskopische Techniken, die in der Physik der kondensierten Materie eingesetzt werden
  • Elektronen-Spin-Resonanz
  • Mössbauer-Effekt
  • Magnetische Kernresonanz ⓘ

Lineare Systeme

Resonanz äußert sich in vielen linearen und nichtlinearen Systemen als Schwingungen um einen Gleichgewichtspunkt. Wenn das System durch einen sinusförmigen externen Eingang angetrieben wird, kann ein gemessener Ausgang des Systems als Reaktion darauf oszillieren. Das Verhältnis der Amplitude der stationären Schwingungen des Ausgangs zu den Schwingungen des Eingangs wird als Verstärkung bezeichnet, und die Verstärkung kann eine Funktion der Frequenz des sinusförmigen externen Eingangs sein. Spitzenwerte in der Verstärkung bei bestimmten Frequenzen entsprechen Resonanzen, bei denen die Amplitude der gemessenen Ausgangsschwingungen überproportional groß ist. ⓘ

Da viele lineare und nichtlineare Systeme, die schwingen, als harmonische Oszillatoren in der Nähe ihrer Gleichgewichte modelliert werden, beginnt dieser Abschnitt mit einer Ableitung der Resonanzfrequenz für einen angetriebenen, gedämpften harmonischen Oszillator. Anschließend werden anhand einer RLC-Schaltung die Zusammenhänge zwischen Resonanz und der Übertragungsfunktion eines Systems, dem Frequenzgang, den Polen und den Nullstellen veranschaulicht. Aufbauend auf dem Beispiel der RLC-Schaltung werden diese Beziehungen für lineare Systeme höherer Ordnung mit mehreren Eingängen und Ausgängen verallgemeinert. ⓘ

Der angetriebene, gedämpfte harmonische Oszillator

Betrachten Sie eine gedämpfte Masse an einer Feder, die durch eine sinusförmige, von außen angelegte Kraft angetrieben wird. Das zweite Newtonsche Gesetz hat die Form ⓘ

$m{\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-kx-c{\frac {\mathrm {d} x}{\mathrm {d} t}},$

(1) ⓘ

wobei m die Masse, x die Verschiebung der Masse aus dem Gleichgewichtspunkt, F₀ die Antriebsamplitude, ω die Antriebswinkelfrequenz, k die Federkonstante und c der viskose Dämpfungskoeffizient ist. Dies kann in die folgende Form umgeschrieben werden ⓘ

${\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+2\zeta \omega _{0}{\frac {\mathrm {d} x}{\mathrm {d} t}}+\omega _{0}^{2}x={\frac {F_{0}}{m}}\sin(\omega t),$

(2)

wobei

$\omega _{0}={\sqrt {\frac {k}{m}}}$ die ungedämpfte Winkelfrequenz des Oszillators oder die Eigenfrequenz genannt wird,

$\zeta ={\frac {c}{2{\sqrt {mk}}}}$ das Dämpfungsverhältnis ist. ⓘ

Viele Quellen bezeichnen ω₀ auch als Resonanzfrequenz. Wie unten gezeigt, liegt die Resonanzfrequenz bei der Analyse von Schwingungen der Verschiebung x(t) jedoch in der Nähe von ω₀, ist aber nicht identisch mit dieser. Im Allgemeinen liegt die Resonanzfrequenz in der Nähe der Eigenfrequenz, ist aber nicht unbedingt mit ihr identisch. Das Beispiel der RLC-Schaltung im nächsten Abschnitt gibt Beispiele für unterschiedliche Resonanzfrequenzen für dasselbe System. ⓘ

Die allgemeine Lösung von Gleichung (2) ist die Summe aus einer instationären Lösung, die von den Anfangsbedingungen abhängt, und einer stationären Lösung, die unabhängig von den Anfangsbedingungen ist und nur von der Antriebsamplitude F₀, der Antriebsfrequenz ω, der ungedämpften Kreisfrequenz ω₀ und dem Dämpfungsverhältnis ζ abhängt. Die instationäre Lösung klingt in relativ kurzer Zeit ab, so dass es zur Untersuchung der Resonanz ausreicht, die stationäre Lösung zu betrachten. ⓘ

Es ist möglich, die stationäre Lösung für x(t) als eine Funktion proportional zur treibenden Kraft mit einer induzierten Phasenänderung φ zu schreiben, ⓘ

$x(t)={\frac {F_{0}}{m{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}}\sin(\omega t+\varphi ),$

(3) ⓘ

wobei

$\varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi .$ ⓘ

Der Phasenwert wird in der Regel zwischen -180° und 0 angenommen, so dass er sowohl für positive als auch für negative Werte des arctan-Arguments eine Phasenverschiebung darstellt. ⓘ

Stationäre Variation der Amplitude mit der relativen Frequenz $\omega /\omega _{0}$ und Dämpfung $\zeta$ eines angetriebenen einfachen harmonischen Oszillators ⓘ

Resonanz tritt auf, wenn bei bestimmten Antriebsfrequenzen die stationäre Amplitude von x(t) groß ist im Vergleich zu ihrer Amplitude bei anderen Antriebsfrequenzen. Bei einer Masse auf einer Feder entspricht Resonanz physikalisch gesehen den Schwingungen der Masse, die bei bestimmten Antriebsfrequenzen große Auslenkungen aus der Gleichgewichtslage der Feder aufweisen. Betrachtet man die Amplitude von x(t) in Abhängigkeit von der Antriebsfrequenz ω, so ist die Amplitude maximal bei der Antriebsfrequenz ⓘ

$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.$ ⓘ

ωr ist die Resonanzfrequenz für dieses System. Auch hier ist zu beachten, dass die Resonanzfrequenz nicht gleich der ungedämpften Winkelfrequenz ω₀ des Oszillators ist. Sie sind proportional, und wenn das Dämpfungsverhältnis gegen Null geht, sind sie gleich, aber bei einer Dämpfung ungleich Null sind sie nicht die gleiche Frequenz. Wie in der Abbildung dargestellt, kann die Resonanz auch bei anderen Frequenzen in der Nähe der Resonanzfrequenz auftreten, einschließlich ω₀, aber die maximale Reaktion liegt bei der Resonanzfrequenz. ⓘ

Beachten Sie auch, dass ωr nur dann real und ungleich Null ist, wenn $\zeta <1/{\sqrt {2}}$Dieses System kann also nur in Resonanz treten, wenn der harmonische Oszillator deutlich unterdämpft ist. Bei Systemen mit einem sehr kleinen Dämpfungsverhältnis und einer Antriebsfrequenz nahe der Resonanzfrequenz können die stationären Schwingungen sehr groß werden. ⓘ

Das Pendel

Für andere angetriebene, gedämpfte harmonische Oszillatoren, deren Bewegungsgleichungen nicht genau wie das Beispiel der Masse an einer Feder aussehen, bleibt die Resonanzfrequenz

$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}},$ ⓘ

aber die Definitionen von ω₀ und ζ ändern sich je nach der Physik des Systems. Für ein Pendel der Länge l und einen kleinen Auslenkungswinkel θ wird Gleichung (1) zu

$ml{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-mg\theta -cl{\frac {\mathrm {d} \theta }{\mathrm {d} t}}$ ⓘ

und daher

$\omega _{0}={\sqrt {\frac {g}{l}}},$

$\zeta ={\frac {c}{2m}}{\sqrt {\frac {l}{g}}}.$ ⓘ

RLC-Reihenschaltungen

Eine RLC-Reihenschaltung ⓘ

Betrachten wir eine Schaltung, die aus einem Widerstand mit dem Widerstand R, einer Induktivität mit der Induktivität L und einem Kondensator mit der Kapazität C besteht, die mit dem Strom i(t) in Reihe geschaltet sind und von einer Spannungsquelle mit der Spannung vin(t) betrieben werden. Der Spannungsabfall in der Schaltung ist

$L{\frac {di(t)}{dt}}+Ri(t)+V(0)+{\frac {1}{C}}\int _{0}^{t}i(\tau )d\tau =v_{in}(t).$

(4) ⓘ

Anstatt eine mögliche Lösung dieser Gleichung zu analysieren, wie im obigen Beispiel der Masse an einer Feder, wird in diesem Abschnitt der Frequenzgang dieser Schaltung untersucht. Nehmen Sie die Laplace-Transformation von Gleichung (4),

$sLI(s)+RI(s)+{\frac {1}{sC}}I(s)=V_{in}(s),$ ⓘ

wobei I(s) und Vin(s) die Laplace-Transformierten des Stroms bzw. der Eingangsspannung sind und s ein komplexer Frequenzparameter im Laplace-Bereich ist. Umstellen der Terme,

$I(s)={\frac {s}{s^{2}L+Rs+{\frac {1}{C}}}}V_{in}(s).$ ⓘ

Spannung über dem Kondensator

Bei einer RLC-Schaltung in Reihe gibt es mehrere Möglichkeiten, wo die Ausgangsspannung gemessen werden kann. Angenommen, die Ausgangsspannung, die von Interesse ist, ist der Spannungsabfall über dem Kondensator. Wie oben gezeigt, ist diese Spannung im Laplace-Bereich

$V_{out}(s)={\frac {1}{sC}}I(s)$ ⓘ

oder

$V_{out}={\frac {1}{LC(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{in}(s).$ ⓘ

Definieren Sie für diese Schaltung eine Eigenfrequenz und ein Dämpfungsverhältnis,

$\omega _{0}={\frac {1}{\sqrt {LC}}},$

$\zeta ={\frac {R}{2}}{\sqrt {\frac {C}{L}}}.$ ⓘ

Das Verhältnis der Ausgangsspannung zur Eingangsspannung ist

$H(s)\triangleq {\frac {V_{out}(s)}{V_{in}(s)}}={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}$ ⓘ

H(s) ist die Übertragungsfunktion zwischen der Eingangsspannung und der Ausgangsspannung. Beachten Sie, dass diese Übertragungsfunktion zwei Pole hat - Wurzeln des Polynoms im Nenner der Übertragungsfunktion - bei

$s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}}$

(5) ⓘ

und keine Nullstellen-Wurzeln des Polynoms im Zähler der Übertragungsfunktion. Außerdem ist zu beachten, dass für ζ ≤ 1 die Größe dieser Pole die Eigenfrequenz ω₀ ist und dass für ζ < 1/${\sqrt {2}}$, unserer Bedingung für Resonanz im Beispiel des harmonischen Oszillators, die Pole näher an der imaginären als an der reellen Achse liegen. ⓘ

Bewertet man H(s) entlang der imaginären Achse s = iω, so beschreibt die Übertragungsfunktion den Frequenzgang dieser Schaltung. Äquivalent dazu kann der Frequenzgang analysiert werden, indem man anstelle der Laplace-Transformation die Fourier-Transformation von Gleichung (4) verwendet. Die Übertragungsfunktion, die ebenfalls komplex ist, kann als Verstärkung und Phase geschrieben werden,

$H(i\omega )=G(\omega )e^{i\Phi (\omega )}.$ ⓘ

Bode-Magnituden-Diagramm für die Spannung über den Elementen einer RLC-Reihenschaltung. Eigenfrequenz ω₀ = 1 rad/s, Dämpfungsverhältnis ζ = 0,4. Die Kondensatorspannung erreicht Spitzenwerte unterhalb der Eigenfrequenz der Schaltung, die Induktionsspannung erreicht Spitzenwerte oberhalb der Eigenfrequenz, und die Widerstandsspannung erreicht Spitzenwerte bei der Eigenfrequenz mit einer Spitzenverstärkung von 1. Die Verstärkung der Spannung am Kondensator und an der Induktivität in Reihe zeigt Antiresonanz, wobei die Verstärkung bei der Eigenfrequenz gegen Null geht. ⓘ

Eine sinusförmige Eingangsspannung mit der Frequenz ω führt zu einer Ausgangsspannung mit der gleichen Frequenz, die mit G(ω) skaliert ist und eine Phasenverschiebung Φ(ω) aufweist. Die Verstärkung und die Phase können in einem Bode-Diagramm über der Frequenz aufgetragen werden. Für die Kondensatorspannung der RLC-Schaltung beträgt die Verstärkung der Übertragungsfunktion H(iω)

$G(\omega )={\frac {\omega _{0}^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$

(6) ⓘ

Man beachte die Ähnlichkeit zwischen der Verstärkung hier und der Amplitude in Gleichung (3). Auch hier ist die Verstärkung bei der Resonanzfrequenz maximiert

$\omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.$ ⓘ

In diesem Fall entspricht die Resonanz physikalisch gesehen einer relativ großen Amplitude für die stationären Schwingungen der Spannung am Kondensator im Vergleich zu ihrer Amplitude bei anderen Antriebsfrequenzen. ⓘ

Spannung an der Spule

Die Resonanzfrequenz muss nicht immer die in den obigen Beispielen angegebene Form annehmen. Nehmen wir stattdessen an, dass die Ausgangsspannung des RLC-Schaltkreises die Spannung an der Spule ist. Wie oben gezeigt, ist die Spannung an der Spule im Laplace-Bereich

$V_{out}(s)=sLI(s),$

$V_{out}(s)={\frac {s^{2}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{in}(s),$

$V_{out}(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}V_{in}(s),$ ⓘ

unter Verwendung der gleichen Definitionen für ω₀ und ζ wie im vorherigen Beispiel. Die Übertragungsfunktion zwischen Vin(s) und dieser neuen Spannung V_out(s) an der Spule ist

$H(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$ ⓘ

Man beachte, dass diese Übertragungsfunktion die gleichen Pole wie die Übertragungsfunktion im vorherigen Beispiel hat, aber auch zwei Nullstellen im Zähler bei s = 0. Bewertet man H(s) entlang der imaginären Achse, so ergibt sich folgende Verstärkung

$G(\omega )={\frac {\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$ ⓘ

Verglichen mit der Verstärkung in Gleichung (6), bei der die Kondensatorspannung als Ausgang verwendet wird, hat diese Verstärkung einen Faktor von ω² im Zähler und weist daher eine andere Resonanzfrequenz auf, die die Verstärkung maximiert. Diese Frequenz ist

$\omega _{r}={\frac {\omega _{0}}{\sqrt {1-2\zeta ^{2}}}},$ ⓘ

Für denselben RLC-Kreis, aber mit der Spannung an der Spule als Ausgang, ist die Resonanzfrequenz nun größer als die Eigenfrequenz, obwohl sie immer noch zur Eigenfrequenz tendiert, wenn das Dämpfungsverhältnis gegen Null geht. Die Tatsache, dass ein und derselbe Stromkreis bei unterschiedlicher Wahl des Ausgangs unterschiedliche Resonanzfrequenzen haben kann, ist kein Widerspruch. Wie aus Gleichung (4) hervorgeht, wird der Spannungsabfall im Stromkreis auf die drei Elemente des Stromkreises aufgeteilt, und jedes Element hat eine andere Dynamik. Die Spannung des Kondensators wächst langsam durch die Integration des Stroms über die Zeit und reagiert daher empfindlicher auf niedrigere Frequenzen, während die Spannung der Spule wächst, wenn sich der Strom schnell ändert, und daher empfindlicher auf höhere Frequenzen reagiert. Während der Stromkreis als Ganzes eine Eigenfrequenz hat, bei der er zum Schwingen neigt, führt die unterschiedliche Dynamik der einzelnen Elemente des Stromkreises dazu, dass jedes Element mit einer etwas anderen Frequenz schwingt. ⓘ

Spannung über dem Widerstand

Angenommen, die Ausgangsspannung, die uns interessiert, ist die Spannung am Widerstand. Im Laplace-Bereich ist die Spannung über dem Widerstand

$V_{out}(s)=RI(s),$

$V_{out}(s)={\frac {Rs}{L(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{in}(s),$ ⓘ

und unter Verwendung der gleichen Eigenfrequenz und des gleichen Dämpfungsverhältnisses wie im Kondensatorbeispiel lautet die Übertragungsfunktion

$H(s)={\frac {2\zeta \omega _{0}s}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$ ⓘ

Man beachte, dass diese Übertragungsfunktion die gleichen Pole aufweist wie die vorangegangenen Beispiele für RLC-Schaltungen, aber nur eine Nullstelle im Zähler bei s = 0. Für diese Übertragungsfunktion beträgt die Verstärkung

$G(\omega )={\frac {2\zeta \omega _{0}\omega }{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$ ⓘ

Die Resonanzfrequenz, die diese Verstärkung maximiert, ist

$\omega _{r}=\omega _{0},$ ⓘ

und die Verstärkung ist bei dieser Frequenz gleich 1, so dass die Spannung am Widerstand bei der Eigenfrequenz der Schaltung mitschwingt und die Amplitude der Spannung am Widerstand bei dieser Frequenz gleich der Amplitude der Eingangsspannung ist. ⓘ

Antiresonanz

Einige Systeme weisen eine Antiresonanz auf, die auf die gleiche Weise analysiert werden kann wie die Resonanz. Bei der Antiresonanz ist die Amplitude der Reaktion des Systems bei bestimmten Frequenzen unverhältnismäßig klein, anstatt unverhältnismäßig groß zu sein. Im Beispiel der RLC-Schaltung kann dieses Phänomen beobachtet werden, indem sowohl die Induktivität als auch der Kondensator zusammen analysiert werden. ⓘ

Nehmen wir an, dass die Ausgangsspannung, die in der RLC-Schaltung von Interesse ist, die Spannung an der Induktivität und dem in Reihe geschalteten Kondensator ist. Gleichung (4) hat gezeigt, dass die Summe der Spannungen an den drei Schaltungselementen der Eingangsspannung entspricht, so dass die Messung der Ausgangsspannung als Summe der Spannungen an der Induktivität und am Kondensator dasselbe ist wie vin minus dem Spannungsabfall am Widerstand. Das vorangegangene Beispiel hat gezeigt, dass bei der Eigenfrequenz des Systems die Amplitude des Spannungsabfalls über dem Widerstand gleich der Amplitude von vin ist und daher die Spannung über der Induktivität und dem Kondensator zusammen die Amplitude Null hat. Wir können dies anhand der Übertragungsfunktion zeigen. ⓘ

Die Summe der Spannungen von Induktor und Kondensator ist

$V_{out}(s)=(sL+{\frac {1}{sC}})I(s),$

$V_{out}(s)={\frac {s^{2}+{\frac {1}{LC}}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{in}(s).$ ⓘ

Mit den gleichen Eigenfrequenzen und Dämpfungsverhältnissen wie in den vorangegangenen Beispielen ergibt sich folgende Übertragungsfunktion

$H(s)={\frac {s^{2}+\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.$ ⓘ

Man beachte, dass diese Übertragungsfunktion die gleichen Pole wie in den vorherigen Beispielen hat, aber Nullstellen bei

$s=\pm i\omega _{0}.$

(7) ⓘ

Bewertet man die Übertragungsfunktion entlang der imaginären Achse, so ergibt sich die folgende Verstärkung

$G(\omega )={\frac {\omega _{0}^{2}-\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.$ ⓘ

Anstatt nach Resonanz, d. h. nach Spitzen der Verstärkung zu suchen, ist zu beachten, dass die Verstärkung bei ω = ω₀ auf Null geht, was unsere Analyse der Widerstandsspannung ergänzt. Dies wird als Antiresonanz bezeichnet, die den gegenteiligen Effekt der Resonanz hat. Anstatt bei dieser Frequenz einen überproportionalen Ausgang zu haben, reagiert die Schaltung bei dieser Wahl des Ausgangs bei dieser Frequenz überhaupt nicht. Die herausgefilterte Frequenz entspricht genau den Nullstellen der Übertragungsfunktion, die in Gleichung (7) dargestellt wurden und auf der imaginären Achse lagen. ⓘ

Beziehungen zwischen Resonanz und Frequenzgang im Beispiel der RLC-Reihenschaltung

Diese RLC-Schaltungsbeispiele veranschaulichen, wie die Resonanz mit dem Frequenzgang des Systems zusammenhängt. Diese Beispiele veranschaulichen insbesondere:

• wie Resonanzfrequenzen gefunden werden können, indem man nach Spitzen in der Verstärkung der Übertragungsfunktion zwischen dem Eingang und dem Ausgang des Systems sucht, z. B. in einer Bode-Magnitude-Darstellung
• wie die Resonanzfrequenz für ein einzelnes System bei unterschiedlicher Wahl des Systemausgangs unterschiedlich sein kann
• Der Zusammenhang zwischen der Eigenfrequenz des Systems, dem Dämpfungsverhältnis des Systems und der Resonanzfrequenz des Systems
• Der Zusammenhang zwischen der Eigenfrequenz des Systems und der Größe der Pole der Übertragungsfunktion, der in Gleichung (5) aufgezeigt wird, und somit ein Zusammenhang zwischen den Polen und der Resonanzfrequenz
• eine Verbindung zwischen den Nullstellen der Übertragungsfunktion und der Form der Verstärkung in Abhängigkeit von der Frequenz und damit eine Verbindung zwischen den Nullstellen und der Resonanzfrequenz, die die Verstärkung maximiert
• Ein Zusammenhang zwischen den Nullstellen der Übertragungsfunktion und der Antiresonanz ⓘ

Im nächsten Abschnitt werden diese Konzepte auf die Resonanz in einem allgemeinen linearen System ausgedehnt. ⓘ

Verallgemeinerung von Resonanz und Antiresonanz für lineare Systeme

Betrachten wir nun ein beliebiges lineares System mit mehreren Eingängen und Ausgängen. In der Zustandsraumdarstellung könnte ein lineares zeitinvariantes System dritter Ordnung mit drei Eingängen und zwei Ausgängen zum Beispiel wie folgt geschrieben werden

${\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\\{\dot {x}}_{3}\end{bmatrix}}=A{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+B{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},$

${\begin{bmatrix}y_{1}(t)\\y_{2}(t)\end{bmatrix}}=C{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+D{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},$ ⓘ

wobei ui(t) die Eingänge, xi(t) die Zustandsvariablen, yi(t) die Ausgänge und A, B, C und D Matrizen sind, die die Dynamik zwischen den Variablen beschreiben. ⓘ

Dieses System hat eine Übertragungsfunktionsmatrix, deren Elemente die Übertragungsfunktionen zwischen den verschiedenen Eingängen und Ausgängen sind. Ein Beispiel,

${\begin{bmatrix}Y_{1}(s)\\Y_{2}(s)\end{bmatrix}}={\begin{bmatrix}H_{11}(s)&H_{12}(s)&H_{13}(s)\\H_{21}(s)&H_{22}(s)&H_{23}(s)\end{bmatrix}}{\begin{bmatrix}U_{1}(s)\\U_{2}(s)\\U_{3}(s)\end{bmatrix}}.$ ⓘ

Jedes H_ij(s) ist eine skalare Übertragungsfunktion, die einen der Eingänge mit einem der Ausgänge verbindet. Die obigen Beispiele für RLC-Schaltungen hatten eine Eingangsspannung und zeigten vier mögliche Ausgangsspannungen - über den Kondensator, über die Induktivität, über den Widerstand und über den Kondensator und die Induktivität in Reihe - jede mit ihrer eigenen Übertragungsfunktion. Wenn die RLC-Schaltung so eingerichtet wäre, dass sie alle vier Ausgangsspannungen messen könnte, hätte das System eine 4×1-Übertragungsfunktionsmatrix, die den einzelnen Eingang mit jedem der vier Ausgänge verbindet. ⓘ

Entlang der imaginären Achse ausgewertet, kann jedes H_ij(iω) als Verstärkung und Phasenverschiebung geschrieben werden,

$H_{ij}(i\omega )=G_{ij}(\omega )e^{i\Phi _{ij}(\omega )}.$ ⓘ

Spitzen in der Verstärkung bei bestimmten Frequenzen entsprechen Resonanzen zwischen dem Eingang und dem Ausgang der jeweiligen Übertragungsfunktion, vorausgesetzt, das System ist stabil. ⓘ

Jede Übertragungsfunktion H_ij(s) kann auch als ein Bruch geschrieben werden, dessen Zähler und Nenner Polynome von s sind.

$H_{ij}(s)={\frac {N_{ij}(s)}{D_{ij}(s)}}.$ ⓘ

Die komplexen Wurzeln des Zählers werden als Nullstellen, die komplexen Wurzeln des Nenners als Pole bezeichnet. Bei einem stabilen System geben die Positionen dieser Pole und Nullstellen in der komplexen Ebene Aufschluss darüber, ob das System in Resonanz oder Antiresonanz treten kann und bei welchen Frequenzen. Insbesondere kann jedes stabile oder geringfügig stabile, komplex konjugierte Polpaar mit imaginären Komponenten als Eigenfrequenz und Dämpfungsverhältnis geschrieben werden als

$s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}},$ ⓘ

wie in Gleichung (5). Die Eigenfrequenz ω₀ dieses Pols ist die Größe der Position des Pols auf der komplexen Ebene, und das Dämpfungsverhältnis dieses Pols bestimmt, wie schnell diese Schwingung abklingt. Ganz allgemein,

• Komplexe konjugierte Polpaare in der Nähe der imaginären Achse entsprechen einer Spitze oder Resonanz im Frequenzgang in der Nähe der Eigenfrequenz des Pols. Liegt das Polpaar auf der imaginären Achse, ist die Verstärkung bei dieser Frequenz unendlich.
• Komplexe konjugierte Nullenpaare in der Nähe der imaginären Achse entsprechen einer Kerbe oder Antiresonanz im Frequenzgang in der Nähe der Frequenz der Null, d. h. der Frequenz, die dem Betrag der Null entspricht. Liegt das Nullstellenpaar auf der imaginären Achse, ist die Verstärkung bei dieser Frequenz gleich Null. ⓘ

Im Beispiel der RLC-Schaltung wird die erste Verallgemeinerung, die die Pole mit der Resonanz verbindet, in Gleichung (5) beobachtet. Die zweite Verallgemeinerung, die Nullstellen mit Antiresonanz in Verbindung bringt, ist in Gleichung (7) zu finden. In den Beispielen des harmonischen Oszillators, der Kondensatorspannung der RLC-Schaltung und der Induktionsspannung der RLC-Schaltung entsprechen "Pole nahe der imaginären Achse" dem deutlich unterdämpften Zustand ζ < 1/${\sqrt {2}}$. ⓘ

Stehende Wellen

Eine Masse auf einer Feder hat eine Eigenfrequenz, da sie nur einen einzigen Freiheitsgrad hat. ⓘ

Ein physikalisches System kann so viele Eigenfrequenzen haben, wie es Freiheitsgrade hat, und kann in der Nähe jeder dieser Eigenfrequenzen in Resonanz treten. Eine Masse an einer Feder, die einen Freiheitsgrad hat, hat eine Eigenfrequenz. Ein Doppelpendel, das zwei Freiheitsgrade hat, kann zwei Eigenfrequenzen haben. Je mehr harmonische Oszillatoren miteinander gekoppelt sind, desto länger dauert es, bis die Energie von einem zum nächsten übertragen wird. Systeme mit einer sehr großen Anzahl von Freiheitsgraden können als kontinuierlich und nicht als Systeme mit diskreten Oszillatoren betrachtet werden. ⓘ

Die Energieübertragung von einem Oszillator zum nächsten erfolgt in Form von Wellen. So kann beispielsweise die Saite einer Gitarre oder die Wasseroberfläche in einer Schüssel als ein Kontinuum kleiner gekoppelter Oszillatoren modelliert werden, entlang derer sich Wellen ausbreiten können. In vielen Fällen haben diese Systeme das Potenzial, bei bestimmten Frequenzen in Resonanz zu treten und an festen Positionen stehende Wellen mit großen Schwingungsamplituden zu bilden. Resonanz in Form stehender Wellen liegt vielen bekannten Phänomenen zugrunde, z. B. dem von Musikinstrumenten erzeugten Klang, elektromagnetischen Hohlräumen, die in Lasern und Mikrowellenherden verwendet werden, und Energieniveaus von Atomen. ⓘ

Stehende Wellen auf einer Saite

Eine stehende Welle (in schwarz), die entsteht, wenn zwei Wellen, die sich von links und rechts bewegen, aufeinander treffen und sich überlagern ⓘ

Wenn eine Saite fester Länge mit einer bestimmten Frequenz angesteuert wird, breitet sich entlang der Saite eine Welle mit der gleichen Frequenz aus. Die Wellen werden an den Enden der Saite reflektiert, und schließlich wird ein stabiler Zustand erreicht, in dem sich die Wellen in beide Richtungen ausbreiten. Die Wellenform ist die Überlagerung der Wellen. ⓘ

Bei bestimmten Frequenzen scheint sich die stationäre Wellenform nicht entlang der Saite zu bewegen. An festen Positionen, den so genannten Knotenpunkten, wird die Saite nie verschoben. Zwischen den Knotenpunkten schwingt die Saite, und genau auf halbem Weg zwischen den Knotenpunkten - an Positionen, die als Anti-Knotenpunkte bezeichnet werden - haben die Schwingungen ihre größte Amplitude. ⓘ

Stehende Wellen in einer Saite - die Grundschwingung und die ersten 5 Oberschwingungen. ⓘ

Bei einer Saite der Länge $L$ mit festen Enden, ist die Auslenkung $y(x,t)$ der Saite senkrecht zur $x$-Achse zum Zeitpunkt $t$ ist

$y(x,t)=2y_{\text{max}}\sin(kx)\cos(2\pi ft),$ ⓘ

wobei

• $y_{\text{max}}$ ist die Amplitude der links- und rechtslaufenden Wellen, die zur stehenden Welle interferieren,
• $k$ ist die Wellenzahl,
• $f$ ist die Frequenz. ⓘ

Die Frequenzen, die in Resonanz treten und stehende Wellen bilden, hängen mit der Länge der Saite wie folgt zusammen

$f={\frac {nv}{2L}}$,

$n=1,2,3,\dots$ ⓘ

wobei $v$ ist die Geschwindigkeit der Welle und die ganze Zahl $n$ bezeichnet verschiedene Moden oder Harmonische. Die stehende Welle mit $n$ = 1 schwingt mit der Grundfrequenz und hat eine Wellenlänge, die doppelt so groß ist wie die Länge der Saite. Die möglichen Schwingungsformen bilden eine harmonische Reihe. ⓘ

Arten

Mechanisch und akustisch

Schulversuch zur Resonanzmasse ⓘ

Mechanische Resonanz ist die Tendenz eines mechanischen Systems, mehr Energie zu absorbieren, wenn die Frequenz seiner Schwingungen mit der natürlichen Schwingungsfrequenz des Systems übereinstimmt, als bei anderen Frequenzen. Dies kann bei unsachgemäß konstruierten Strukturen wie Brücken, Gebäuden, Zügen und Flugzeugen zu heftigen Schwingungen und sogar zu katastrophalem Versagen führen. Bei der Konstruktion von Objekten müssen Ingenieure sicherstellen, dass die mechanischen Resonanzfrequenzen der Bauteile nicht mit den Antriebsschwingungsfrequenzen von Motoren oder anderen schwingenden Teilen übereinstimmen, ein Phänomen, das als Resonanzkatastrophe bekannt ist. ⓘ

Die Vermeidung von Resonanzkatastrophen ist ein Hauptanliegen bei jedem Gebäude-, Turm- und Brückenbauprojekt. Als Gegenmaßnahme können Stoßdämpfer installiert werden, die Resonanzfrequenzen absorbieren und so die absorbierte Energie ableiten. Das Gebäude Taipei 101 basiert auf einem 660-Tonnen-Pendel (730-Short-Ton) - einem abgestimmten Massendämpfer -, um Resonanzen auszugleichen. Außerdem ist das Bauwerk so konzipiert, dass es bei einer Frequenz schwingt, die normalerweise nicht auftritt. Gebäude in erdbebengefährdeten Gebieten werden oft so konstruiert, dass die Schwingungsfrequenzen der zu erwartenden Bodenbewegungen berücksichtigt werden. Darüber hinaus müssen Ingenieure, die Objekte mit Motoren konstruieren, sicherstellen, dass die mechanischen Resonanzfrequenzen der Bauteile nicht mit den Antriebsschwingungsfrequenzen der Motoren oder anderer stark schwingender Teile übereinstimmen. ⓘ

Uhren halten die Zeit durch mechanische Resonanz in einer Unruh, einem Pendel oder einem Quarzkristall. ⓘ

Es wurde angenommen, dass die Trittfrequenz von Läufern aufgrund der Resonanz zwischen der in den unteren Gliedmaßen gespeicherten elastischen Energie und der Masse des Läufers energetisch günstig ist. ⓘ

Die akustische Resonanz ist ein Teilgebiet der mechanischen Resonanz, das sich mit den mechanischen Schwingungen im Frequenzbereich des menschlichen Gehörs, also dem Schall, befasst. Das menschliche Gehör ist normalerweise auf Frequenzen zwischen etwa 20 Hz und 20.000 Hz (20 kHz) beschränkt. Viele Gegenstände und Materialien wirken als Resonatoren mit Resonanzfrequenzen in diesem Bereich, und wenn sie angeschlagen werden, vibrieren sie mechanisch und drücken auf die umgebende Luft, wodurch Schallwellen entstehen. Dies ist die Quelle vieler perkussiver Klänge, die wir hören. ⓘ

Akustische Resonanz ist ein wichtiger Aspekt für Instrumentenbauer, da die meisten akustischen Instrumente Resonatoren verwenden, wie z. B. die Saiten und der Korpus einer Geige, die Länge des Rohrs einer Flöte und die Form und Spannung der Membran einer Trommel. ⓘ

Wie die mechanische Resonanz kann auch die akustische Resonanz zu einem katastrophalen Versagen des Objekts bei der Resonanz führen. Das klassische Beispiel hierfür ist das Zerbrechen eines Weinglases durch Schall, der genau die Resonanzfrequenz des Glases trifft, obwohl dies in der Praxis schwierig ist. ⓘ

Internationale Raumstation

Die Raketentriebwerke für die Internationale Raumstation (ISS) werden von einem Autopiloten gesteuert. Normalerweise sorgen hochgeladene Parameter zur Steuerung des Triebwerkskontrollsystems für das Zvezda-Modul dafür, dass die Raketentriebwerke die Internationale Raumstation auf eine höhere Umlaufbahn bringen. Die Raketentriebwerke sind an Scharnieren befestigt, und normalerweise bemerkt die Besatzung diesen Vorgang nicht. Am 14. Januar 2009 führten die hochgeladenen Parameter jedoch dazu, dass der Autopilot die Raketentriebwerke in immer stärkeren Schwingungen mit einer Frequenz von 0,5 Hz schwang. Diese Schwingungen wurden auf Video aufgezeichnet und hielten 142 Sekunden lang an. ⓘ

Elektrisch

Animation zur Veranschaulichung der elektrischen Resonanz in einem abgestimmten Stromkreis, der aus einem Kondensator (C) und einer Induktionsspule (L) besteht, die miteinander verbunden sind. Ladung fließt zwischen den Kondensatorplatten durch die Spule hin und her. Die Energie pendelt zwischen dem elektrischen Feld (E) des Kondensators und dem magnetischen Feld (B) der Spule hin und her. ⓘ

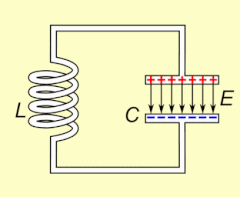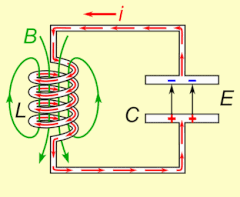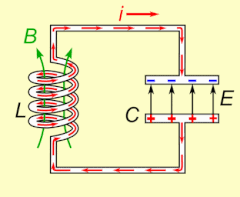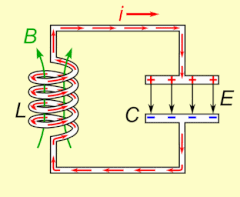
Elektrische Resonanz tritt in einem elektrischen Stromkreis bei einer bestimmten Resonanzfrequenz auf, wenn die Impedanz des Stromkreises bei einer Reihenschaltung ein Minimum und bei einer Parallelschaltung ein Maximum erreicht (in der Regel, wenn die Übertragungsfunktion ihren absoluten Höchstwert erreicht). Resonanz in Schaltkreisen wird sowohl für die Übertragung als auch für den Empfang von drahtloser Kommunikation wie Fernsehen, Mobiltelefonen und Radio genutzt. ⓘ

Optische

Ein optischer Hohlraum, auch optischer Resonator genannt, ist eine Anordnung von Spiegeln, die einen Stehwellen-Hohlraumresonator für Lichtwellen bildet. Optische Resonatoren sind ein wichtiger Bestandteil von Lasern, da sie das Verstärkungsmedium umgeben und für die Rückkopplung des Laserlichts sorgen. Sie werden auch in optischen parametrischen Oszillatoren und einigen Interferometern verwendet. Das im Hohlraum eingeschlossene Licht wird mehrfach reflektiert und erzeugt bei bestimmten Resonanzfrequenzen stehende Wellen. Die erzeugten stehenden Wellenmuster werden als "Moden" bezeichnet. Die longitudinalen Moden unterscheiden sich nur in der Frequenz, während die transversalen Moden sich für verschiedene Frequenzen unterscheiden und unterschiedliche Intensitätsmuster über den Querschnitt des Strahls aufweisen. Ringresonatoren und Flüstergalerien sind Beispiele für optische Resonatoren, die keine stehenden Wellen bilden. ⓘ

Die verschiedenen Resonatortypen unterscheiden sich durch die Brennweiten der beiden Spiegel und den Abstand zwischen ihnen; flache Spiegel werden wegen der Schwierigkeit, sie genau auszurichten, nicht häufig verwendet. Die Geometrie (Resonatortyp) muss so gewählt werden, dass der Strahl stabil bleibt, d. h. dass die Strahlgröße nicht bei jeder Reflexion weiter zunimmt. Die Resonatortypen müssen auch andere Kriterien erfüllen, z. B. eine minimale Strahltaille oder keinen Brennpunkt (und damit intensives Licht an diesem Punkt) im Inneren des Hohlraums haben. ⓘ

Optische Hohlräume sind so konstruiert, dass sie einen sehr großen Q-Faktor haben. Ein Strahl wird sehr oft mit geringer Dämpfung reflektiert, so dass die Frequenzlinienbreite des Strahls im Vergleich zur Frequenz des Lasers gering ist. ⓘ

Weitere optische Resonanzen sind die Resonanz geführter Moden und die Oberflächenplasmonenresonanz, die zu anomaler Reflexion und hohen evaneszenten Feldern bei Resonanz führen. In diesem Fall handelt es sich bei den resonanten Moden um geführte Moden eines Wellenleiters oder um Oberflächenplasmonenmoden einer dielektrisch-metallischen Grenzfläche. Diese Moden werden in der Regel durch ein Sub-Wellenlängen-Gitter angeregt. ⓘ

Orbital

In der Himmelsmechanik tritt eine Orbitalresonanz auf, wenn zwei sich umkreisende Körper einen regelmäßigen, periodischen Gravitationseinfluss aufeinander ausüben, der in der Regel darauf zurückzuführen ist, dass ihre Umlaufperioden durch ein Verhältnis von zwei kleinen ganzen Zahlen miteinander verbunden sind. Orbitalresonanzen verstärken den gegenseitigen gravitativen Einfluss der Körper erheblich. In den meisten Fällen führt dies zu einer instabilen Wechselwirkung, bei der die Körper ihren Impuls austauschen und ihre Bahnen verschieben, bis die Resonanz nicht mehr besteht. Unter bestimmten Umständen kann ein Resonanzsystem stabil sein und sich selbst korrigieren, so dass die Körper in Resonanz bleiben. Beispiele hierfür sind die 1:2:4-Resonanz der Jupitermonde Ganymed, Europa und Io sowie die 2:3-Resonanz zwischen Pluto und Neptun. Instabile Resonanzen mit den inneren Monden des Saturn führen zu Lücken in den Ringen des Saturn. Der Sonderfall der 1:1-Resonanz (zwischen Körpern mit ähnlichen Bahnradien) führt dazu, dass große Körper des Sonnensystems die Umgebung ihrer Bahnen räumen, indem sie fast alles andere um sich herum ausstoßen; dieser Effekt wird in der aktuellen Definition eines Planeten verwendet. ⓘ

Atome, Teilchen und Moleküle

NMR-Magnet bei HWB-NMR, Birmingham, UK. In seinem starken 21,2-Tesla-Feld liegt die Protonenresonanz bei 900 MHz. ⓘ

Kernspinresonanz (NMR) ist die Bezeichnung für ein physikalisches Resonanzphänomen, das die Beobachtung spezifischer quantenmechanischer magnetischer Eigenschaften eines Atomkerns in Gegenwart eines angelegten externen Magnetfeldes beinhaltet. Viele wissenschaftliche Techniken nutzen NMR-Phänomene zur Untersuchung von Molekülphysik, Kristallen und nichtkristallinen Materialien durch NMR-Spektroskopie. NMR wird auch routinemäßig in fortschrittlichen medizinischen Bildgebungsverfahren eingesetzt, wie z. B. in der Magnetresonanztomographie (MRT). ⓘ

Alle Kerne mit einer ungeraden Anzahl von Nukleonen haben ein eigenes magnetisches Moment und einen Eigendrehimpuls. Ein wesentliches Merkmal der NMR ist, dass die Resonanzfrequenz einer bestimmten Substanz direkt proportional zur Stärke des angelegten Magnetfelds ist. Wird eine Probe in ein ungleichmäßiges Magnetfeld gelegt, so hängen die Resonanzfrequenzen der Kerne der Probe davon ab, wo sie sich in diesem Feld befinden. Daher kann das Teilchen anhand seiner Resonanzfrequenz ziemlich genau lokalisiert werden. ⓘ

Die paramagnetische Elektronenresonanz, auch bekannt als Elektronenspinresonanz (ESR), ist eine spektroskopische Technik, die der NMR ähnelt, aber stattdessen ungepaarte Elektronen verwendet. Die Materialien, auf die sich diese Technik anwenden lässt, sind sehr viel begrenzter, da das Material sowohl einen ungepaarten Spin haben als auch paramagnetisch sein muss. ⓘ

Der Mössbauer-Effekt ist die resonante und rückstoßfreie Emission und Absorption von Gammastrahlenphotonen durch Atome in fester Form. ⓘ

In der Teilchenphysik treten Resonanzen unter ähnlichen Bedingungen auf wie in der klassischen Physik auf der Ebene der Quantenmechanik und der Quantenfeldtheorie. Resonanzen können auch als instabile Teilchen betrachtet werden, wobei die Formel im Abschnitt Universelle Resonanzkurve dieses Artikels gilt, wenn Γ die Zerfallsrate des Teilchens und Ω die Masse M des Teilchens ist. In diesem Fall stammt die Formel aus dem Propagator des Teilchens, wobei seine Masse durch die komplexe Zahl M + iΓ ersetzt wird. Die Formel ist ferner durch das optische Theorem mit der Zerfallsrate des Teilchens verbunden. ⓘ

Benachteiligungen

Eine Kolonne von Soldaten, die im Gleichschritt auf einer schmalen und strukturell flexiblen Brücke marschiert, kann diese in gefährlich große Amplitudenschwingungen versetzen. Am 12. April 1831 stürzte die Broughton-Hängebrücke in der Nähe von Salford, England, ein, während eine Gruppe britischer Soldaten darüber marschierte. Seitdem hat die britische Armee eine ständige Anweisung für Soldaten, beim Überqueren von Brücken den Schritt zu unterbrechen, um zu vermeiden, dass sich die Resonanz ihres regelmäßigen Marschierens auf die Brücke überträgt. ⓘ

Die Schwingungen eines Motors können Resonanzschwingungen in den tragenden Strukturen hervorrufen, wenn deren Eigenfrequenz in der Nähe der Schwingungen des Motors liegt. Ein gängiges Beispiel ist das klappernde Geräusch einer Buskarosserie, wenn der Motor im Leerlauf läuft. ⓘ

Strukturelle Resonanz einer Hängebrücke, die durch Winde ausgelöst wird, kann zu ihrem katastrophalen Einsturz führen. Mehrere frühe Hängebrücken in Europa und den USA wurden durch strukturelle Resonanz, die durch mäßigen Wind verursacht wurde, zerstört. Der Einsturz der Tacoma Narrows Bridge am 7. November 1940 wird in der Physik als ein klassisches Beispiel für Resonanz bezeichnet. Robert H. Scanlan und andere haben argumentiert, dass die Zerstörung stattdessen durch aeroelastisches Flattern verursacht wurde, eine komplizierte Wechselwirkung zwischen der Brücke und dem Wind, der durch sie hindurchging - ein Beispiel für eine Eigenschwingung oder eine Art "selbsterhaltende Schwingung", wie sie in der nichtlinearen Schwingungstheorie beschrieben wird. ⓘ

Q-Faktor

Hoher und niedriger Q-Faktor ⓘ

Der Q-Faktor oder Qualitätsfaktor ist ein dimensionsloser Parameter, der beschreibt, wie wenig gedämpft ein Oszillator oder Resonator ist, und der die Bandbreite eines Resonators relativ zu seiner Mittenfrequenz charakterisiert. Ein hoher Wert für Q bedeutet einen geringeren Energieverlust im Verhältnis zur gespeicherten Energie, d. h. das System ist leicht gedämpft. Der Parameter wird durch die folgende Gleichung definiert:

$Q=2\pi {\text{ }}{\frac {\text{ maximum energy stored}}{\text{total energy lost per cycle at resonance}}}$. ⓘ

Je höher der Q-Faktor ist, desto größer ist die Amplitude bei der Resonanzfrequenz und desto kleiner ist die Bandbreite, d. h. der Frequenzbereich, in dem die Resonanz auftritt. Bei elektrischer Resonanz ist ein Kreislauf mit hohem Q-Faktor in einem Radioempfänger schwieriger abzustimmen, hat aber eine größere Selektivität und kann daher Signale anderer Sender besser herausfiltern. Oszillatoren mit hohem Q-Faktor sind stabiler. ⓘ

Beispiele mit einem niedrigen Q-Faktor sind Türschließer (Q=0,5). Systeme mit hohem Q-Faktor sind Stimmgabeln (Q=1000), Atomuhren und Laser (Q≈10¹¹). ⓘ

Universelle Resonanzkurve

"Universelle Resonanzkurve", eine symmetrische Annäherung an die normierte Antwort eines Schwingkreises; Abszissenwerte sind die Abweichung von der Mittenfrequenz, in Einheiten der Mittenfrequenz geteilt durch 2Q; Ordinate ist die relative Amplitude und die Phase in Zyklen; gestrichelte Kurven vergleichen die Bandbreite der Antworten realer zweipoliger Schaltungen für einen Q-Wert von 5; für höhere Q-Werte gibt es weniger Abweichungen von der universellen Kurve. Die Kreuze markieren die Ränder der 3-dB-Bandbreite (Verstärkung 0,707, Phasenverschiebung 45° oder 0,125 Zyklen). ⓘ

Das genaue Verhalten einer Resonanz, insbesondere bei Frequenzen, die weit von der Resonanzfrequenz entfernt sind, hängt von den Details des physikalischen Systems ab und ist in der Regel nicht genau symmetrisch um die Resonanzfrequenz, wie oben für den einfachen harmonischen Oszillator dargestellt. Für einen leicht gedämpften linearen Oszillator mit einer Resonanzfrequenz Ω wird die Intensität der Schwingungen I, wenn das System mit einer Antriebsfrequenz ω angetrieben wird, normalerweise durch eine Formel angenähert, die symmetrisch zur Resonanzfrequenz ist:

$I(\omega )\equiv |\chi |^{2}\propto {\frac {1}{(\omega -\Omega )^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}.$ ⓘ

Wobei die Suszeptibilität $\chi (\omega )$ die Amplitude des Oszillators mit der Antriebskraft im Frequenzraum verknüpft: $x(\omega )=\chi (\omega )F(\omega )$ ⓘ

Die Intensität ist definiert als das Quadrat der Amplitude der Oszillationen. Es handelt sich um eine Lorentzsche Funktion oder Cauchy-Verteilung, und diese Reaktion findet sich in vielen physikalischen Situationen mit resonanten Systemen. Γ ist ein Parameter, der von der Dämpfung des Oszillators abhängt und als Linienstärke der Resonanz bekannt ist. Stark gedämpfte Oszillatoren neigen zu großen Linienbreiten und reagieren auf einen größeren Bereich von Antriebsfrequenzen um die Resonanzfrequenz. Die Linienbreite ist umgekehrt proportional zum Q-Faktor, der ein Maß für die Schärfe der Resonanz ist. ⓘ

In der Funktechnik und Elektronik ist diese annähernd symmetrische Reaktion als universelle Resonanzkurve bekannt, ein Konzept, das 1932 von Frederick E. Terman eingeführt wurde, um die annähernde Analyse von Funkschaltungen mit einer Reihe von Mittenfrequenzen und Q-Werten zu vereinfachen ⓘ

Geschichte

Der Begriff Resonanz stammt aus der Akustik, wo er von altersher das deutlich bemerkbare Mitschwingen von Saiten bei Tönen geeigneter Tonhöhe bezeichnet. Die Anregung großer Schwingungen durch periodisch wirkende Kräfte der richtigen Frequenz wurde schon in Galileis Untersuchungen 1602 und 1638 zu Pendeln und Saiten beschrieben, die am Beginn der neuzeitlichen Naturwissenschaft standen. Allerdings nahm er auch an, Schwingungen mit anderer als der Eigenfrequenz ließen sich überhaupt nicht anregen. Eine entsprechende Bewegungsgleichung für einen Massenpunkt (ohne Dämpfung der Bewegung) wurde 1739 von Leonhard Euler erstmals aufgestellt. Seine allgemeine Lösung enthielt bereits das Mitschwingen mit der Frequenz der anregenden Kraft in Überlagerung mit einer Schwingung mit der Eigenfrequenz, sowie im Falle der Gleichheit beider Frequenzen das unbegrenzte Anwachsen der Schwingungsweite. Er sah diese Ergebnisse, die sich aus der Rechnung ergaben, allerdings als „wunderliche“ theoretische Voraussage an. 1823 behandelte Thomas Young im Zusammenhang mit den Gezeiten die mechanische Resonanz einschließlich Dämpfung und gab erstmals die vollständige Berechnung von Resonanzkurve und Phasenverschiebung an. Im Zusammenhang mit der Erzeugung und dem Nachweis elektrischer und magnetischer Schwingungen fand Anton Oberbeck für den elektrischen Schwingkreis dieselben Erscheinungen, worauf er die Bedeutung des Begriffs „Resonanz“ entsprechend erweiterte. Die Entdeckung der elektromagnetischen Wellen durch Heinrich Hertz, sowie deren Nutzung zur drahtlosen Telegraphie durch Guglielmo Marconi ab 1895, verschafften der elektromagnetischen Resonanz dann schnell eine große Bedeutung in Wissenschaft und Technik. ⓘ

Jedoch wurde die mechanische Resonanz im Wesentlichen erst ab Anfang des 20. Jahrhunderts richtig gewürdigt, nachdem der Physiker und Mathematiker Arnold Sommerfeld – als erster Professor für Technische Mechanik, der nicht vorher Ingenieur gewesen war – darauf hingewiesen hatte. Damals waren Hängebrücken mit marschierenden Soldaten oder schnell fahrenden Dampflokomotiven schon durch Resonanz eingestürzt, und bei den langen Antriebswellen von größeren Dampfschiffen waren bei bestimmten Geschwindigkeiten bereits unerwartet starke Schwingungen aufgetreten, die mehrfach schon zu Zerstörungen geführt hatten. ⓘ

Alltagsbeispiele

Resonanz kommt im Alltag häufig vor. Allerdings sind nicht alle Schwingungen Folge einer Resonanz. ⓘ

Beim wiederholten Anschwingen einer Kinderschaukel gibt man der Schaukel immer dann einen Schubs, wenn diese nach vorne schwingt. Die Anregungsstöße erfolgen dabei periodisch und offensichtlich gerade mit der Frequenz der Schaukelschwingung: es handelt sich also um Resonanz. Man beachte, dass die Krafteinwirkung bei den anregenden Schubsen keineswegs wie eine Sinuskurve verläuft, es reicht aus, dass sie periodisch erfolgt. Dabei kann die Anregungsfrequenz auch einen ganzzahligen Bruchteil der Schwingungsfrequenz betragen, wenn man z. B. nur jedes zweite oder dritte Mal anschubst. ⓘ

Anders ist das bei einem ruhenden Pendel, wenn man ihm einen einmaligen Stoß gibt. Auch wenn das Ergebnis ähnlich ist, nämlich dass das Pendel nun schwingt, so liegt keine periodische Anregung vor und es handelt sich nicht um Resonanz. ⓘ

Jeder kennt die Situation in der Kantine: man trägt einen Teller Suppe auf dem Tablett. Stimmt die Frequenz, mit der die Suppe im Teller hin- und herschwappt, gerade mit der eigenen Schrittfrequenz überein, so schaukelt sich diese Schwingung mit jedem Schritt auf, bis die Suppe überschwappt, oder man eben langsamer bzw. schneller geht. Doch nicht bei jedem Überschwappen handelt es sich um Resonanz: Die Frequenz, mit der Kaffee in einer Kaffeetasse hin- und herschwappt (die Eigenfrequenz des Kaffees in der Tasse), liegt deutlich höher als die gewöhnliche Schrittfrequenz, nämlich ungefähr zwei- bis dreimal so hoch. Dennoch passiert es ebenfalls, dass wenn plötzlich jemand um die Ecke kommt, man abrupt anhalten muss und dabei der Kaffee überschwappt. Hier liegt keine periodische Anregung und somit keine Resonanz vor. Der Kaffee schwappt – analog zum nur einmal angestoßenen Pendel – aufgrund von Impulserhaltung über. ⓘ

Der Drehknopf bei einem Transistorradio mag im Zeitalter der Radios mit automatischer Senderauswahl und vorprogrammierten Programmknöpfen schon etwas in Vergessenheit geraten: mit ihm wird der Drehkondensator in einem LC-Schwingkreis verändert, so dass der Schwingkreis auf eine bestimmte Frequenz eingestellt ist. Radiowellen dieser Frequenz können nun verstärkt werden und die ihnen aufmodulierten kleinen Amplituden- oder Frequenzänderungen (siehe Amplitudenmodulation und Frequenzmodulation) können in das übertragene akustische Signal umgewandelt werden. Die im LC-Schwingkreis eingestellte Resonanzfrequenz filtert dabei gerade die Radiowellen heraus, die auf einer bestimmten Frequenz übertragen wurden. ⓘ

Die Trommel in einer Waschmaschine ist mit Federn aufgehängt, die mit einer bestimmten Frequenz schwingen können. Ist diese Schwingung schlecht gedämpft, oder bleibt die Waschmaschine -möglicherweise wegen Überladung- beim Anlaufen des Schleudergangs mit ihrer Drehzahl zu lange im Frequenzbereich dieser Schwingung, so schaukelt sich diese aufgrund von Resonanz auf und die ganze Waschmaschine beginnt zu rütteln. Erst wenn eine höhere Drehzahl erreicht ist (und keine Resonanz mehr vorliegt) beruhigt sich dieses Rütteln (aufgrund der Dämpfung), bis am Ende des Schleudergangs wieder der entsprechende Frequenzbereich durchlaufen wird und die Maschine wegen Resonanz erneut zu rütteln beginnt. Typischerweise ist die Wäsche am Ende des Schleudergangs jedoch trockener, erzeugt somit eine geringere Unwucht und das Rütteln am Ende des Schleudergangs ist deutlich schwächer. ⓘ

Auch lockere Teile in oder an Motoren können eine bestimmte Eigenfrequenz haben. Liegt die Drehzahl des Motors gerade bei dieser Frequenz, so ist das Wackeln solcher Teile oft sehr laut hörbar, was bei anderen Drehzahlen wieder verschwindet. ⓘ

Resonanz am Beispiel des harmonischen Oszillators

Bewegungsgleichung

Konstante Kraft

Eine statische konstante Kraft $F(t)=F_{0}$ eines Erregers hätte eine konstante Auslenkung aus der Ruhelage um $A_{\text{E}}=F_{0}/k$ zur Folge. ⓘ

Phasenresonanz und Energiefluss

Bei $\omega =\omega _{0}$ eilt die eingeschwungene Schwingung $x(t)$ der erregenden Kraft um genau 1/4 Periode hinterher (Phasengang −90°, auch als Phasenresonanz bezeichnet). Daher sind Geschwindigkeit ${\dot {x}}(t)$ und Kraft $F(t)$ genau in Phase, sodass die Kraft stets in Richtung der momentanen Geschwindigkeit wirkt. Die Energie fließt dann ständig in das System hinein, während sie bei anderen Frequenzen zweimal pro Periode die Richtung wechselt, weil die Phasendifferenz bei $\omega <\omega _{0}$ kleiner als 90° und bei höherer Frequenz größer als 90° (und bis 180°) ist. Die kinetische Energie des eingeschwungenen Zustands erreicht in der Phasenresonanz ihr Maximum. Sie ist dann so groß wie der gesamte Energieeintrag während der letzten $Q/(2\pi )$ Schwingungen. ⓘ

Halbwertsbreite und Gütefaktor

Als Halbwertsbreite $\Delta f_{\text{FWHM}}$ (engl. full width at half maximum) der Resonanz wird der Bereich von Frequenzen $f=\omega /2\pi$ um die Resonanzfrequenz $f_{\text{res}}=\omega _{0}/2\pi$ bezeichnet, in dem für die Amplitude gilt: $A^{2}\geq {\tfrac {1}{2}}A_{\text{res}}^{2}$. Im interessierenden Bereich geringer Dämpfung liegen nach der Näherungsformel für die Lorentzkurve diese Grenzen bei $\eta =1\pm D$. Umgerechnet auf die Frequenzachse ergibt sich die Halbwertsbreite

$\Delta f_{\text{FWHM}}=2D{\frac {\omega _{0}}{2\pi }}\equiv {\frac {\gamma }{\pi }}$.

Die Schärfe der Resonanz kann mit der Dämpfung oder mit dem Gütefaktor

${\frac {\Delta f_{\text{FWHM}}}{f_{\text{res}}}}=2D={\frac {1}{Q}}$

angegeben werden. ⓘ

Nach der oben angegebenen Bedeutung des Gütefaktors kann man einen Zeitraum von $Q$ Perioden der Eigenfrequenz als charakteristisch für das Abklingen einer gedämpften Eigenschwingung ansehen, also auch charakteristisch für die Dauer des Einschwingvorgangs oder im übertragenen Sinn für das „Gedächtnis des Oszillators“. Analysiert man eine Schwingung mit Frequenz $f_{0}$ mithilfe einer Reihe von Resonatoren zu verschiedenen Resonanzfrequenzen $f$, dann erfordert die Bestimmung der Resonanzamplitude also die Zeit $\Delta t=Q/f_{0}$ und liefert die Resonanzfrequenz mit der Genauigkeit $\Delta f_{\text{FWHM}}$. Unterscheiden sich zwei Oszillatoren in der Frequenz um $\Delta f_{\text{FWHM}}$, dann macht in diesem Zeitraum $\Delta t$ der schnellere gerade eine Schwingung mehr als der langsamere. Es folgt $\Delta t\cdot \Delta f_{\text{FWHM}}=1$: je genauer die Frequenz einer Schwingung bestimmt werden soll, desto länger muss man sie auf einen Resonator einwirken lassen. Das ist eine frühe Form der Frequenz-Zeit-Unschärferelation. ⓘ

Beispiele für das Auftreten von Resonanz

Mechanik

Zungenfrequenzmesser (Ablesung: f ≈ 49,9 Hz) ⓘ

• Bei einem Zungenfrequenzmesser wird derjenige von vielen Biegeschwingern, der mit der Erregerfrequenz in Resonanz ist, zu besonders großer Schwingungsamplitude angeregt.
• Kommt eine Brücke in Resonanz mit der Schrittfrequenz von marschierenden Fußgängermassen, kann sich die Konstruktion gefährlich aufschaukeln, Beispiel Millennium Bridge (London)
• Fahrzeugkarosserien neigen bei bestimmten Motordrehzahlen zu starken Vibrationen (Dröhnen)
• Bahnresonanz kann bei Planeten dafür sorgen, dass ein Himmelskörper auf Kollisionskurs mit einem anderen gerät. An Lagrange-Punkten kann diese Resonanz stabilisierend wirken, beispielsweise bleibt der Sonnenbeobachtungssatellit SOHO seit 1995 immer in der Nähe des inneren Lagrange-Punktes L₁.
• Zur Erzeugung von Ultraschall für medizinische oder technische Anwendungen werden elektromechanische, meist piezoelektrische, Wandler zu resonanten Schwingungen angeregt.
• Ein Ultraschallbohrer bringt das zu bohrende Gestein in Resonanz, wodurch das Gestein zerbröselt. ⓘ

Hydromechanik

• Tideresonanz
• Wellenresonanz ⓘ

Akustik

Betrag der akustischen Flussimpedanz eines luftgefüllten kurzen, dünnen Rohres als Funktion der Frequenz. Einheit der vertikalen Skala ist Pa·s/m³ ⓘ

• die Tonerzeugung bei Musikinstrumenten (Streich- und Blasinstrumenten), siehe z. B. Holzblasinstrument, Resonanzboden
• das Mitschwingen einer nicht gespielten Saite, wenn ein gleichgestimmtes Instrument ertönt (z. B. Resonanzsaite)
• In geschlossenen Räumen kann es bei bestimmten Frequenzen zu störender Raumresonanz kommen.
• Ein Resonanzauspuff ermöglicht bei Zweitakt-Motoren bei einer ganz bestimmten Drehzahl eine gewisse Leistungssteigerung. ⓘ

Akustische Resonanz spielt beispielsweise bei fast allen Musikinstrumenten eine Rolle, oft durch Bildung einer stehenden Welle. ⓘ

Misst man am Ende eines beiderseits offenen, zylindrischen Rohres mit geeigneten Mikrophonen Schalldruck und Schallschnelle, kann man bei Kenntnis des Rohrquerschnitts die akustische Flussimpedanz berechnen. Diese zeigt Mehrfachresonanzen, wie man sie auch bei der Ausbreitung elektromagnetischer Wellen entlang Drähten als Sonderfall λ/2 kennt. Das Messergebnis im Bild zeigt mehrere scharfe Minima der Flussimpedanz bei Vielfachen der Frequenz 500 Hz. Eine Überprüfung mit der Rohrlänge von 325 mm und der Schallgeschwindigkeit in Luft ergibt den Sollwert 528 Hz. ⓘ

Weil der Messwert des tiefsten Minimums mit etwa 40000 Pa·s/m³ von der Schallkennimpedanz der umgebenden Luft (413,5 Pa·s/m³) erheblich abweicht, liegt eine Fehlanpassung vor und die schwingende Luftsäule im Rohr ist nur leise hörbar. Dieser geringe Energieverlust drückt sich in einem hohen Gütefaktor des Resonators aus. ⓘ

Elektrotechnik

Ohne Resonanz gäbe es keine Funktechnik mit den bekannten Teilgebieten Fernsehen, Mobiltelefon, Radar, Funkfernsteuerung und Radioastronomie, weil es ohne die Möglichkeit, Sendefrequenzen voneinander zu trennen, weltweit nur wenige vereinzelte Sender mit ausreichenden Abständen geben könnte. Im überwiegenden Teil aller Oszillatorschaltungen und elektrischen Filter werden Schwingkreise verwendet, denen die Thomsonsche Schwingungsgleichung zur Resonanzfrequenz ⓘ

$\omega _{0}={\frac {1}{\sqrt {LC}}}$ ⓘ

zu Grunde liegt. Der Wirkungsgrad von Antennen und Tesla-Transformatoren wird durch Resonanz drastisch gesteigert. ⓘ

Die Sicherheit im Eisenbahnnetz wird durch die induktive Zugbeeinflussung verbessert. Dabei tritt ein am Fahrzeug angebrachter Schwingkreis in resonante Wechselwirkung mit einem am Gleis angebrachten Schwingkreis, dessen Frequenz je nach Stellung des nächsten Bahnsignals verschieden ist; bei Signalstellung „Halt“ wird eine Zwangsbremsung ausgelöst. ⓘ

Die großen Teilchenbeschleuniger der Elementarteilchenphysik beruhen auf Resonanzeffekten, ebenso die Kernspinresonanzspektroskopie in der Chemie und die Magnetresonanztomographie in der Medizin. ⓘ

RFIDs, umgangssprachlich auch Funketiketten genannt, ermöglicht die automatische Identifizierung und Lokalisierung von Gegenständen und Lebewesen. Dabei wird die Betriebsenergie durch Resonanz auf das RFID übertragen und dieses sendet seine Information auf gleichem Weg zurück. ⓘ

Ein Absorptionsfrequenzmesser wirkt bei Resonanz wie ein selektives Voltmeter. ⓘ

Ein Magnetron erzeugt nur dann Schwingungen, wenn die Umlaufgeschwindigkeit mit der Eigenfrequenz der Hohlraumresonatoren übereinstimmt. ⓘ

Atom- und Molekülphysik

Schematische Darstellung eines Zweizustandssystems, das mit elektromagnetischer Strahlung wechselwirkt. ⓘ

Termschema des Wasserstoffatoms: Die durch Pfeile angedeuteten Übergänge können mit zu ihrer Energiedifferenz resonantem Licht angeregt werden ⓘ

Empfindlichkeit der Zapfen des menschlichen Auges. S:Blau, M:Grün, L:Rot, Z: Gesamt ⓘ

In der Atom- und Molekülphysik spricht man von Resonanz, wenn ein Photon der Energie $E_{\gamma }=h\cdot \nu$ (h: Plancksches Wirkungsquantum, ν: Frequenz des Lichtes) in der Hülle des Atoms absorbiert wird. Dies ist nur möglich, wenn $E_{\gamma }$ gerade gleich der Energiedifferenz $\Delta E_{\mathrm {GA} }=E_{\mathrm {A} }-E_{\mathrm {G} }$ zwischen zwei Zuständen G und A der Elektronenhülle ist. Ein Elektron wird dann vom Zustand G in den Zustand A angehoben. Die Anregungswahrscheinlichkeit $p_{\mathrm {GA} }(E_{\gamma })$ eines solchen Überganges wird durch eine Lorentzkurve beschrieben:

$p_{\mathrm {GA} }(E_{\gamma })\propto {\frac {1}{\left|(1+(E_{\gamma }/\Delta E_{\mathrm {GA} })^{2})\right|}}$ ⓘ

Der Vorgang heißt Resonanzabsorption. Er erklärt beispielsweise die Fraunhoferlinien im Spektrum des Sonnenlichts. ⓘ

Meist fällt nun das Elektron aus dem angeregten Zustand zurück in den Grundzustand, wobei wieder ein Photon der Energie $E_{\gamma }=E_{\mathrm {GA} }$ ausgesandt wird. Dies geschieht entweder spontan (spontane Emission, Fluoreszenz, Phosphoreszenz) oder durch Stoß eines zweiten eingestrahlten Photons der gleichen Energie (stimulierte Emission, ausgenutzt beim Laser). ⓘ

Aus dem Grundzustand kann das Atom nun wieder angeregt werden. Es kann also eine Besetzungszahloszillation zwischen den Zuständen G und A ausführen, die als Rabi-Oszillation bezeichnet wird. Die Oszillation tritt, wie erwähnt, nur dann auf, wenn die eingestrahlten Photonen in Resonanz mit den Energieniveaus eines Atoms sind. Solche Resonanzen können z. B. zur Identifizierung von Gasen in der Spektroskopie verwendet werden, da sie das Vermessen der atom- oder molekültypischen Energieniveaus erlauben. ⓘ

Im menschlichen Auge gibt es drei verschiedene Arten von Zapfen (Farbrezeptoren). Die darin enthaltenen Opsin-Moleküle unterscheiden sich durch ihre spektrale Empfindlichkeit und setzen bei Resonanz mit Photonen geeigneter Wellenlänge intrazelluläre Signalkaskaden in Gang (s. Phototransduktion). Es werden elektrische Signale gebildet, die über die Ganglienzellen an das Gehirn weitergegeben werden. Dort entsteht aus den übermittelten Signalen ein Farbeindruck (s. Farbwahrnehmung). ⓘ

Weitere Resonanzphänomene treten bei der Kopplung des magnetischen Moments eines Atoms, Atomkerns, Moleküls oder Elektrons (Spin) an ein Magnetfeld auf, zum Beispiel Elektronenspinresonanz und Kernspinresonanz. Dabei regt ein mit passender Frequenz oszillierendes Magnetfeld das Umklappen des Spins zwischen zwei diskreten Zuständen verschiedener Energie an. Auch dieser Effekt kann entsprechend den Rabi-Oszillationen beschrieben werden und wird z. B. in der Medizintechnik und zu Materialuntersuchungen eingesetzt (siehe z. B. Magnetresonanztomographie). ⓘ

Kernphysik

Resonanz bedeutet in der Kernphysik, dass bei einem Stoßvorgang mit bestimmter kinetischer Energie die beiden Partner sich zu einem kurzzeitig gebundenen System, dem Compoundkern, in einem seiner möglichen Energiezustände vereinigen. Der Wirkungsquerschnitt zeigt bei dieser Stoßenergie ein Maximum von der Form einer Breit-Wigner-Kurve, die der für Resonanzen typischen Lorentzkurve gleicht. ⓘ

Ein solches System kann nicht stabil sein, sondern zerfällt nach kurzer Zeit wieder, z. B. in die beiden Teilchen, aus denen es gebildet wurde. Doch lässt sich aus der Zerfallsbreite der Kurve entnehmen, dass es wesentlich länger existiert hat, als einer Reaktion der Teilchen im Vorbeiflug entsprechen würde. ⓘ

Alle größeren Kerne zeigen die Riesenresonanz, einen angeregten Zustand, bei dem die Protonen gemeinsam gegenüber den Neutronen schwingen. ⓘ

Die Resonanzabsorption von Gammaquanten ermöglicht durch Ausnutzung des Dopplereffekts den Vergleich von Anregungsenergien mit einer Genauigkeit von mehr als 10¹². Atomkerne sind Resonatoren mit z. T. extrem hohen Gütefaktoren von 10¹² und aufwärts (z. B. Gütefaktor von ⁹⁹Tc: 6,8·10²⁴). ⓘ

Teilchenphysik

Ähnlich wie bei der Compoundkernbildung kann aus zwei Stoßpartnern ein instabiles, aber vergleichsweise langlebiges gebundenes System oder sogar ein einziges, andersartiges Teilchen entstehen, wenn die Stoßenergie im Schwerpunktsystem gerade dazu ausreicht. Dieser Fall wird auch als Resonanzproduktion bezeichnet. Die Anregungsfunktion des Stoßprozesses, also sein Wirkungsquerschnitt aufgetragen als Funktion der Energie, zeigt dann bei dieser Energie ein Maximum mit der für eine Resonanz typischen Kurvenform. So gebildete Systeme werden häufig als Resonanz oder Resonanzteilchen bezeichnet. Aus der Halbwertsbreite der Kurve (siehe Zerfallsbreite) kann die – für eine direkte Messung zu kurze – Lebensdauer des entstandenen Teilchens bestimmt werden. ⓘ