Fraktal

Die Mandelbrot-Menge: Ihr Rand ist eine fraktale Kurve mit der Hausdorff-Dimension 2 ⓘ

Vergrößerung des Randes der Mandelbrot-Menge ⓘ

In der Mathematik wird der Begriff Fraktal verwendet, um geometrische Formen zu beschreiben, die in beliebig kleinen Maßstäben eine detaillierte Struktur aufweisen und in der Regel eine fraktale Dimension haben, die streng über der topologischen Dimension liegt. Viele Fraktale sehen in verschiedenen Maßstäben ähnlich aus, wie die aufeinander folgenden Vergrößerungen der Mandelbrot-Menge zeigen. Dieses Auftreten ähnlicher Muster in immer kleineren Maßstäben wird als Selbstähnlichkeit bezeichnet, auch bekannt als expandierende Symmetrie oder sich entfaltende Symmetrie; wenn diese Wiederholung in jedem Maßstab genau gleich ist, wie beim Menger-Schwamm, wird die Form als affine Selbstähnlichkeit bezeichnet. Die fraktale Geometrie gehört zum mathematischen Zweig der Maßtheorie. ⓘ

Fraktale unterscheiden sich von endlichen geometrischen Figuren unter anderem dadurch, wie sie skalieren. Die Verdoppelung der Kantenlängen eines gefüllten Polygons multipliziert dessen Fläche mit vier, was zwei (das Verhältnis zwischen der neuen und der alten Seitenlänge) hoch zwei (die konventionelle Dimension des gefüllten Polygons) ist. Wird der Radius einer gefüllten Kugel verdoppelt, so vergrößert sich ihr Volumen um acht, was zwei (das Verhältnis zwischen dem neuen und dem alten Radius) hoch drei (die konventionelle Dimension der gefüllten Kugel) entspricht. Wenn jedoch alle eindimensionalen Längen eines Fraktals verdoppelt werden, skaliert der räumliche Inhalt des Fraktals um eine Potenz, die nicht notwendigerweise eine ganze Zahl ist und im Allgemeinen größer ist als seine konventionelle Dimension. Diese Potenz wird als fraktale Dimension des geometrischen Objekts bezeichnet, um sie von der konventionellen Dimension zu unterscheiden (die formell als topologische Dimension bezeichnet wird). ⓘ

Analytisch sind viele Fraktale nirgends differenzierbar. Eine unendliche fraktale Kurve kann anders als eine gewöhnliche Linie durch den Raum gewunden werden - obwohl sie topologisch immer noch 1-dimensional ist, zeigt ihre fraktale Dimension an, dass sie den Raum lokal effizienter ausfüllt als eine gewöhnliche Linie. ⓘ

Sierpinski-Teppich (bis Stufe 6), ein Fraktal mit einer topologischen Dimension von 1 und einer Hausdorff-Dimension von 1,893 ⓘ

Ein Liniensegment ähnelt einem eigenen Teil seiner selbst, ist aber kaum ein Fraktal. ⓘ

Jahrhundert mit den Begriffen der Rekursion, haben sich Fraktale durch eine zunehmend strengere mathematische Behandlung zur Untersuchung kontinuierlicher, aber nicht differenzierbarer Funktionen im 19. Jahrhundert durch die bahnbrechenden Arbeiten von Bernard Bolzano, Bernhard Riemann und Karl Weierstraß entwickelt, und weiter zur Prägung des Wortes Fraktal im 20. ⓘ

Unter Mathematikern herrscht Uneinigkeit darüber, wie das Konzept eines Fraktals formal zu definieren ist. Mandelbrot selbst fasste es so zusammen: "Schön, verdammt schwierig, zunehmend nützlich. Das sind Fraktale." Formal definierte Mandelbrot 1982 Fraktale wie folgt: "Ein Fraktal ist per Definition eine Menge, deren Hausdorff-Besicovitch-Dimension die topologische Dimension strikt überschreitet." Später, als er dies als zu restriktiv ansah, vereinfachte und erweiterte er die Definition wie folgt: "Ein Fraktal ist eine grobe oder fragmentierte geometrische Form, die in Teile zerlegt werden kann, von denen jeder (zumindest annähernd) eine verkleinerte Kopie des Ganzen ist." Noch später schlug Mandelbrot vor, "das Fraktal ohne pedantische Definition zu verwenden, die fraktale Dimension als Oberbegriff zu verwenden, der für alle Varianten gilt". ⓘ

Unter Mathematikern herrscht Einigkeit darüber, dass theoretische Fraktale unendlich viele selbstähnliche, iterierte und detaillierte mathematische Konstrukte sind, für die bereits zahlreiche Beispiele formuliert und untersucht wurden. Fraktale sind nicht auf geometrische Muster beschränkt, sondern können auch zeitliche Prozesse beschreiben. Fraktale Muster mit verschiedenen Graden der Selbstähnlichkeit wurden in visuellen, physikalischen und akustischen Medien dargestellt oder untersucht und finden sich in Natur, Technik, Kunst, Architektur und Recht. Fraktale sind auf dem Gebiet der Chaostheorie von besonderer Bedeutung, da sie in den geometrischen Darstellungen der meisten chaotischen Prozesse auftauchen (typischerweise entweder als Attraktoren oder als Grenzen zwischen Anziehungsbereichen). ⓘ

Fraktal ist ein vom Mathematiker Benoît Mandelbrot 1975 geprägter Begriff (lateinisch fractus ‚gebrochen‘, von lateinisch frangere‚ (in Stücke zer-)‚brechen‘), der bestimmte natürliche oder künstliche Gebilde oder geometrische Muster bezeichnet. ⓘ

Diese Gebilde oder Muster besitzen im Allgemeinen keine ganzzahlige Hausdorff-Dimension, sondern eine gebrochene – daher der Name – und weisen zudem einen hohen Grad von Skaleninvarianz bzw. Selbstähnlichkeit auf. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst besteht. Geometrische Objekte dieser Art unterscheiden sich in wesentlichen Aspekten von gewöhnlichen glatten Figuren. ⓘ

Etymologie

Der Begriff "Fraktal" wurde 1975 von dem Mathematiker Benoît Mandelbrot geprägt. Mandelbrot leitete ihn vom lateinischen frāctus ab, was "gebrochen" oder "zerbrochen" bedeutet, und verwendete ihn, um das Konzept der theoretischen Bruchdimensionen auf geometrische Muster in der Natur auszuweiten. ⓘ

Einführung

Ein einfacher fraktaler Baum ⓘ

Ein fraktaler "Baum" mit elf Iterationen ⓘ

Das Wort "Fraktal" hat für Laien oft eine andere Bedeutung als für Mathematiker, die eher mit fraktaler Kunst vertraut sind als mit dem mathematischen Konzept. Das mathematische Konzept ist selbst für Mathematiker schwer formal zu definieren, aber die wichtigsten Merkmale lassen sich mit ein wenig mathematischem Hintergrundwissen verstehen. ⓘ

Das Merkmal der "Selbstähnlichkeit" beispielsweise lässt sich leicht verstehen, wenn man eine Analogie zum Heranzoomen mit einem Objektiv oder einem anderen Gerät herstellt, das digitale Bilder vergrößert, um feinere, zuvor unsichtbare, neue Strukturen zu entdecken. Bei Fraktalen erscheint jedoch kein neues Detail; es ändert sich nichts, und dasselbe Muster wiederholt sich immer wieder, oder bei manchen Fraktalen taucht fast dasselbe Muster immer wieder auf. Selbstähnlichkeit an sich ist nicht unbedingt kontraintuitiv (z. B. haben die Menschen informell über Selbstähnlichkeit nachgedacht, wie beim unendlichen Regress in parallelen Spiegeln oder dem Homunkulus, dem kleinen Mann im Kopf des kleinen Mannes im Kopf ...). Der Unterschied bei Fraktalen besteht darin, dass das reproduzierte Muster detailliert sein muss. ⓘ

Diese Idee der Detailliertheit bezieht sich auf eine andere Eigenschaft, die ohne viel mathematischen Hintergrund verstanden werden kann: Die Tatsache, dass die fraktale Dimension größer ist als die topologische Dimension, bezieht sich beispielsweise darauf, wie ein Fraktal skaliert, verglichen mit der Wahrnehmung geometrischer Formen. Eine gerade Linie beispielsweise wird üblicherweise als eindimensional aufgefasst; wenn eine solche Figur in Stücke von je 1/3 der Länge des Originals zerlegt wird, gibt es immer drei gleiche Stücke. Ein eindimensionales Quadrat wird als zweidimensional verstanden; wenn eine solche Figur in Stücke zerlegt wird, die in beiden Dimensionen jeweils um den Faktor 1/3 verkleinert sind, gibt es insgesamt 3² = 9 Stücke. ⓘ

Bei gewöhnlichen selbstähnlichen Objekten bedeutet n-dimensional, dass es insgesamt rn Teile gibt, wenn es in Stücke zerlegt wird, die jeweils um den Skalierungsfaktor 1/r verkleinert sind. Betrachten wir nun die Koch-Kurve. Sie kann in vier Teilkopien zerlegt werden, die jeweils um den Skalierungsfaktor 1/3 verkleinert werden. In strenger Analogie können wir also die "Dimension" der Koch-Kurve als die einzige reelle Zahl D betrachten, die 3D = 4 erfüllt. Diese Zahl nennen die Mathematiker die fraktale Dimension der Koch-Kurve; sie ist sicherlich nicht das, was man üblicherweise als die Dimension einer Kurve wahrnimmt (diese Zahl ist nicht einmal eine ganze Zahl!). Eine Schlüsseleigenschaft von Fraktalen ist im Allgemeinen, dass sich die fraktale Dimension von der konventionell verstandenen Dimension (formell topologische Dimension genannt) unterscheidet. ⓘ

Computergeneriertes 3D-Fraktal ⓘ

Dies führt auch zum Verständnis einer dritten Eigenschaft, nämlich dass Fraktale als mathematische Gleichungen "nirgends differenzierbar" sind. Konkret bedeutet dies, dass Fraktale nicht auf herkömmliche Weise gemessen werden können. Wenn man versucht, die Länge einer gewellten, nicht fraktalen Kurve zu bestimmen, könnte man gerade Segmente eines Messwerkzeugs finden, die klein genug sind, um sie über die Wellen zu legen, wobei die Stücke so klein werden könnten, dass sie als der Kurve entsprechend angesehen werden können, wie es bei der normalen Messung mit einem Maßband der Fall ist. Bei der Messung einer unendlich "wackeligen" fraktalen Kurve wie der Schneeflocke von Koch würde man jedoch niemals ein gerades Segment finden, das klein genug wäre, um sich der Kurve anzupassen, da das gezackte Muster immer wieder auftauchen würde, und zwar in beliebig kleinen Maßstäben, wodurch jedes Mal, wenn man versuchte, das Maßband enger und enger an die Kurve anzupassen, etwas mehr von der gemessenen Gesamtlänge abgezogen würde. Das Ergebnis ist, dass man unendlich viel Maßband braucht, um die gesamte Kurve perfekt abzudecken, d. h. die Schneeflocke hat einen unendlichen Umfang. ⓘ

Geschichte

Eine Koch-Schneeflocke ist ein Fraktal, das mit einem gleichseitigen Dreieck beginnt und dann das mittlere Drittel jedes Liniensegments durch ein Paar von Liniensegmenten ersetzt, die einen gleichseitigen Höcker bilden ⓘ

Cantor-Menge (ternär). ⓘ

Die Geschichte der Fraktale reicht von theoretischen Studien bis hin zu modernen Anwendungen in der Computergrafik, wobei mehrere bemerkenswerte Persönlichkeiten kanonische Fraktalformen beigesteuert haben. Ein häufiges Thema in der traditionellen afrikanischen Architektur ist die Verwendung fraktaler Skalierung, wobei kleine Teile der Struktur dazu neigen, größeren Teilen ähnlich zu sehen, wie z. B. ein kreisförmiges Dorf, das aus runden Häusern besteht. Pickover zufolge nahm die den Fraktalen zugrunde liegende Mathematik im 17. Jahrhundert Gestalt an, als der Mathematiker und Philosoph Gottfried Leibniz über rekursive Selbstähnlichkeit nachdachte (auch wenn er den Fehler beging, zu glauben, dass nur die gerade Linie in diesem Sinne selbstähnlich sei). ⓘ

In seinen Schriften verwendete Leibniz den Begriff "Bruchteilexponenten", beklagte aber, dass die "Geometrie" diese noch nicht kannte. Verschiedenen historischen Berichten zufolge beschäftigten sich danach nur wenige Mathematiker mit diesem Thema, und die Arbeit derjenigen, die es taten, blieb weitgehend im Dunkeln, weil man sich gegen solch ungewohnte neue Konzepte sträubte, die manchmal als mathematische "Monster" bezeichnet wurden. So dauerte es zwei Jahrhunderte, bis Karl Weierstraß am 18. Juli 1872 in der Königlich-Preußischen Akademie der Wissenschaften die erste Definition einer Funktion mit einem Graphen vorstellte, den man heute als Fraktal bezeichnen würde und der die nicht intuitive Eigenschaft hat, überall stetig, aber nirgends differenzierbar zu sein. ⓘ

Darüber hinaus wird die Quotientendifferenz mit zunehmendem Summationsindex beliebig groß. Nicht lange danach, im Jahr 1883, veröffentlichte Georg Cantor, der Vorlesungen von Weierstraß besucht hatte, Beispiele für Untermengen der reellen Linie, die als Cantor-Mengen bekannt sind und ungewöhnliche Eigenschaften aufweisen und heute als Fraktale anerkannt sind. Ebenfalls in der letzten Hälfte dieses Jahrhunderts führten Felix Klein und Henri Poincaré eine Kategorie von Fraktalen ein, die heute als "selbst-inverse" Fraktale bezeichnet werden. ⓘ

Eine Julia-Menge, ein mit der Mandelbrot-Menge verwandtes Fraktal ⓘ

Eine Sierpinski-Dichtung kann durch einen fraktalen Baum erzeugt werden. ⓘ

Einer der nächsten Meilensteine kam 1904, als Helge von Koch, der die Ideen von Poincaré weiterführte und mit der abstrakten und analytischen Definition von Weierstraß unzufrieden war, eine geometrischere Definition vorlegte, die auch handgezeichnete Bilder einer ähnlichen Funktion enthielt, die heute als Kochsche Schneeflocke bezeichnet wird. Ein weiterer Meilenstein folgte ein Jahrzehnt später im Jahr 1915, als Wacław Sierpiński sein berühmtes Dreieck und ein Jahr später seinen Teppich konstruierte. 1918 kamen zwei französische Mathematiker, Pierre Fatou und Gaston Julia, die unabhängig voneinander arbeiteten, im Wesentlichen gleichzeitig zu Ergebnissen, die das beschreiben, was heute als fraktales Verhalten im Zusammenhang mit der Abbildung komplexer Zahlen und iterativer Funktionen angesehen wird, und die zu weiteren Ideen über Attraktoren und Repelloren (d. h. Punkte, die andere Punkte anziehen oder abstoßen) führten, die für die Untersuchung von Fraktalen sehr wichtig geworden sind. ⓘ

Sehr kurz nach dieser Arbeit, im März 1918, erweiterte Felix Hausdorff die Definition von "Dimension", was für die Entwicklung der Definition von Fraktalen von großer Bedeutung war, um Mengen mit nicht-ganzzahligen Dimensionen zu ermöglichen. Die Idee der selbstähnlichen Kurven wurde von Paul Lévy weiterentwickelt, der 1938 in seinem Aufsatz Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole eine neue fraktale Kurve beschrieb, die Lévy-C-Kurve. ⓘ

Ein seltsamer Attraktor, der eine multifraktale Skalierung aufweist ⓘ

Dreiecksfraktal mit gleichmäßigem Massenzentrum ⓘ

2x 120 Grad rekursives IFS ⓘ

Verschiedene Forscher haben postuliert, dass die frühen Forscher ohne die Hilfe moderner Computergrafik auf das beschränkt waren, was sie in manuellen Zeichnungen darstellen konnten, so dass ihnen die Mittel fehlten, um die Schönheit zu visualisieren und einige der Implikationen vieler der von ihnen entdeckten Muster zu schätzen (die Julia-Menge beispielsweise konnte nur durch einige Iterationen als sehr einfache Zeichnungen visualisiert werden). Das änderte sich jedoch in den 1960er Jahren, als Benoit Mandelbrot begann, über Selbstähnlichkeit zu schreiben, z. B. in How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension (Statistische Selbstähnlichkeit und fraktionale Dimension), die auf früheren Arbeiten von Lewis Fry Richardson aufbauten. ⓘ

Im Jahr 1975 verfestigte Mandelbrot Hunderte von Jahren des Denkens und der mathematischen Entwicklung, indem er das Wort "Fraktal" prägte und seine mathematische Definition mit eindrucksvollen, am Computer konstruierten Visualisierungen illustrierte. Diese Bilder, wie z. B. die kanonische Mandelbrot-Menge, beflügelten die Phantasie der Menschen; viele von ihnen basierten auf Rekursion, was zur populären Bedeutung des Begriffs "Fraktal" führte. ⓘ

1980 hielt Loren Carpenter einen Vortrag auf der SIGGRAPH, in dem er seine Software zur Erzeugung und Darstellung fraktaler Landschaften vorstellte. ⓘ

Definition und Merkmale

Eine oft zitierte Beschreibung, die Mandelbrot zur Beschreibung geometrischer Fraktale veröffentlichte, lautet: "eine grobe oder fragmentierte geometrische Form, die in Teile zerlegt werden kann, von denen jeder (zumindest annähernd) eine verkleinerte Kopie des Ganzen ist"; dies ist im Allgemeinen hilfreich, aber begrenzt. Die Autoren sind sich über die genaue Definition von Fraktalen uneinig, aber die meisten gehen auf die grundlegenden Ideen der Selbstähnlichkeit und der ungewöhnlichen Beziehung von Fraktalen zu dem Raum, in den sie eingebettet sind, ein. ⓘ

Einig ist man sich darüber, dass fraktale Muster durch fraktale Dimensionen charakterisiert werden, doch während diese Zahlen die Komplexität quantifizieren (d. h. sich ändernde Details bei wechselndem Maßstab), beschreiben sie weder eindeutig noch spezifizieren sie Details, wie bestimmte fraktale Muster konstruiert werden können. Als Mandelbrot 1975 das Wort "fraktal" prägte, tat er dies, um ein Objekt zu bezeichnen, dessen Hausdorff-Besicovitch-Dimension größer ist als seine topologische Dimension. Diese Bedingung wird jedoch von raumfüllenden Kurven wie der Hilbert-Kurve nicht erfüllt. ⓘ

Aufgrund der Schwierigkeiten, eine einheitliche Definition für Fraktale zu finden, argumentieren einige, dass Fraktale überhaupt nicht streng definiert werden sollten. Nach Falconer sollten Fraktale nur allgemein durch eine Gestalt der folgenden Merkmale charakterisiert werden; ⓘ

Selbstähnlichkeit, die Folgendes umfassen kann:

Exakte Selbstähnlichkeit: in allen Maßstäben identisch, wie z. B. die Koch'sche Schneeflocke
Quasi-Selbstähnlichkeit: nähert sich demselben Muster in verschiedenen Maßstäben an; kann kleine Kopien des gesamten Fraktals in verzerrter und entarteter Form enthalten; z. B. sind die Satelliten der Mandelbrot-Menge Annäherungen an die gesamte Menge, aber keine exakten Kopien.
Statistische Selbstähnlichkeit: stochastische Wiederholung eines Musters, so dass numerische oder statistische Maße über Skalen hinweg erhalten bleiben; z. B. zufällig erzeugte Fraktale wie das bekannte Beispiel der Küstenlinie Großbritanniens, bei dem man nicht erwarten würde, ein Segment zu finden, das so sauber skaliert und wiederholt ist wie die wiederholte Einheit, die Fraktale wie die Schneeflocke von Koch definiert.
Qualitative Selbstähnlichkeit: wie bei einer Zeitreihe
Multifraktale Skalierung: gekennzeichnet durch mehr als eine fraktale Dimension oder Skalierungsregel

Feine oder detaillierte Struktur auf beliebig kleinen Skalen. Eine Folge dieser Struktur ist, dass Fraktale emergente Eigenschaften haben können (im Zusammenhang mit dem nächsten Kriterium in dieser Liste).
Lokale und globale Unregelmäßigkeiten, die sich in der Sprache der traditionellen euklidischen Geometrie nur als Grenzwert einer rekursiv definierten Abfolge von Stufen beschreiben lassen. Bei Bildern von fraktalen Mustern wurde dies durch Ausdrücke wie "sich sanft auftürmende Oberflächen" und "Strudel über Strudel" ausgedrückt; siehe Allgemeine Techniken zur Erzeugung von Fraktalen ⓘ

Als Gruppe bilden diese Kriterien Leitlinien für den Ausschluss bestimmter Fälle, z. B. solcher, die selbstähnlich sind, ohne andere typische fraktale Merkmale aufzuweisen. Eine gerade Linie beispielsweise ist zwar selbstähnlich, aber nicht fraktal, weil sie keine Details aufweist und sich leicht in der euklidischen Sprache beschreiben lässt, ohne dass eine Rekursion erforderlich ist. ⓘ

Gängige Techniken zur Erzeugung von Fraktalen

Selbstähnliches Verzweigungsmuster, modelliert in silico nach den Prinzipien des L-Systems ⓘ

Bilder von Fraktalen können durch Fraktal-Generierungsprogramme erstellt werden. Aufgrund des Schmetterlingseffekts kann eine kleine Änderung einer einzelnen Variablen zu einem unvorhersehbaren Ergebnis führen. ⓘ

Iterierte Funktionssysteme (IFS) - verwenden feste geometrische Ersetzungsregeln; können stochastisch oder deterministisch sein; z. B. Koch-Schneeflocke, Cantor-Menge, Haferman-Teppich, Sierpinski-Teppich, Sierpinski-Dichtung, Peano-Kurve, Harter-Heighway-Drachenkurve, T-Quadrat, Menger-Schwamm
Seltsame Attraktoren - Iterationen einer Karte oder Lösungen eines Systems von Anfangswert-Differential- oder Differenzgleichungen, die Chaos aufweisen (siehe z. B. das multifraktale Bild oder die logistische Karte)
L-Systeme - verwenden die Umschreibung von Zeichenketten; können Verzweigungsmustern ähneln, wie in Pflanzen, biologischen Zellen (z. B. Neuronen und Zellen des Immunsystems), Blutgefäßen, Lungenstrukturen usw. oder Schildkrötengrafikmustern wie raumfüllenden Kurven und Kacheln
Escape-Time-Fraktale - verwenden eine Formel oder eine Rekursionsrelation an jedem Punkt eines Raums (z. B. der komplexen Ebene); in der Regel quasi selbstähnlich; auch bekannt als "Orbit"-Fraktale; z. B. die Mandelbrot-Menge, die Julia-Menge, das Burning Ship-Fraktal, das Nova-Fraktal und das Lyapunov-Fraktal. Die 2D-Vektorfelder, die durch ein oder zwei Iterationen von Escape-Time-Formeln erzeugt werden, ergeben ebenfalls eine fraktale Form, wenn Punkte (oder Pixeldaten) wiederholt durch dieses Feld geführt werden.
Zufallsfraktale - verwenden stochastische Regeln; z. B. Lévy-Flug, Perkolationscluster, selbstausweichende Spaziergänge, fraktale Landschaften, Trajektorien der Brownschen Bewegung und der Brownsche Baum (d. h. dendritische Fraktale, die durch Modellierung diffusionsbegrenzter Aggregationscluster oder reaktionsbegrenzter Aggregationscluster entstehen). ⓘ

Ein Fraktal, das durch eine endliche Unterteilungsregel für eine alternierende Verbindung erzeugt wird ⓘ

Finite Unterteilungsregeln - verwenden einen rekursiven topologischen Algorithmus zur Verfeinerung von Kacheln und sind dem Prozess der Zellteilung ähnlich. Die iterativen Prozesse, die bei der Erstellung der Cantor-Menge und des Sierpinski-Teppichs verwendet werden, sind Beispiele für endliche Unterteilungsregeln, ebenso wie die baryzentrische Unterteilung. ⓘ

Anwendungen

Durch ihren Formenreichtum und den damit verbundenen ästhetischen Reiz spielen sie in der digitalen Kunst eine Rolle und haben dort das Genre der Fraktalkunst hervorgebracht. Ferner werden sie bei der computergestützten Simulation formenreicher Strukturen, beispielsweise realitätsnaher Landschaften, eingesetzt. Um in der Funktechnik verschiedene Frequenzbereiche zu empfangen, werden Fraktalantennen genutzt. ⓘ

Simulierte Fraktale

Fraktale Muster sind in großem Umfang modelliert worden, wenn auch aufgrund der praktischen Grenzen von Raum und Zeit in der Physik nicht unendlich, sondern in einer Reihe von Maßstäben. Modelle können theoretische Fraktale oder natürliche Phänomene mit fraktalen Merkmalen simulieren. Die Ergebnisse des Modellierungsprozesses können sehr künstlerische Darstellungen, Untersuchungsergebnisse oder Benchmarks für die fraktale Analyse sein. Einige spezifische Anwendungen von Fraktalen in der Technik sind an anderer Stelle aufgeführt. Bilder und andere Ergebnisse der Modellierung werden in der Regel als "Fraktale" bezeichnet, auch wenn sie keine streng fraktalen Merkmale aufweisen, z. B. wenn es möglich ist, in einen Bereich des fraktalen Bildes zu zoomen, der keine fraktalen Eigenschaften aufweist. Außerdem können sie Berechnungs- oder Darstellungsartefakte enthalten, die keine Merkmale echter Fraktale sind. ⓘ

Modellierte Fraktale können Töne, digitale Bilder, elektrochemische Muster, zirkadiane Rhythmen usw. sein. Fraktale Muster wurden im physischen 3-dimensionalen Raum und virtuell rekonstruiert, was oft als "in silico"-Modellierung bezeichnet wird. Modelle von Fraktalen werden in der Regel mit fraktaler Software erstellt, die Techniken wie die oben beschriebenen einsetzt. So können beispielsweise Bäume, Farne, Zellen des Nervensystems, Blut- und Lungengefäße und andere Verzweigungsmuster in der Natur mit Hilfe von rekursiven Algorithmen und L-Systemen auf dem Computer modelliert werden. ⓘ

Der rekursive Charakter einiger Muster ist bei bestimmten Beispielen offensichtlich - ein Zweig eines Baumes oder ein Farnwedel ist ein Miniaturabbild des Ganzen: nicht identisch, aber von Natur aus ähnlich. In ähnlicher Weise wurden zufällige Fraktale verwendet, um viele hochgradig unregelmäßige Objekte der realen Welt zu beschreiben bzw. zu erschaffen. Eine Einschränkung bei der Modellierung von Fraktalen besteht darin, dass die Ähnlichkeit eines fraktalen Modells mit einem natürlichen Phänomen nicht beweist, dass das modellierte Phänomen durch einen ähnlichen Prozess wie die Modellierungsalgorithmen entstanden ist. ⓘ

Natürliche Phänomene mit fraktalen Merkmalen

Näherungsweise Fraktale, die in der Natur vorkommen, zeigen Selbstähnlichkeit über weite, aber endliche Skalenbereiche. Die Verbindung zwischen Fraktalen und Blättern wird beispielsweise derzeit genutzt, um den Kohlenstoffgehalt von Bäumen zu bestimmen. Zu den Phänomenen, die bekanntermaßen fraktale Merkmale aufweisen, gehören: ⓘ

Aktin-Zytoskelett
Algen
Färbemuster von Tieren
Blutgefäße und Pulmonalgefäße
Wolken und Niederschlagsgebiete
Küstenlinien
Krater
Kristalle
DNA
Erdbeben
Verwerfungslinien
Geometrische Optik
Herzfrequenzen
Herztöne
Seeufer und -gebiete
Blitze
Hörner von Bergziegen
Netzwerke
Polymere
Perkolation
Gebirgsketten
Ozeanwellen
Ananas
Proteine
Die Ringe des Saturn
Flussnetze
Romanesco-Brokkoli
Schneeflocken
Bodenporen
Oberflächen in turbulenten Strömungen
Bäume
Staubkörner
Brownsche Bewegung (erzeugt durch einen eindimensionalen Wiener-Prozess). ⓘ

Frostkristalle, die auf kaltem Glas natürlich vorkommen, bilden fraktale Muster
Fraktale Beckenbegrenzung in einem geometrischen optischen System
Ein Fraktal entsteht beim Auseinanderziehen zweier mit Klebstoff beschichteter Acrylplatten
Hochspannungsdurchbruch in einem Acrylglasblock erzeugt eine fraktale Lichtenberg-Figur
Romanesco-Brokkoli, der eine selbstähnliche Form aufweist, die einem natürlichen Fraktal nahe kommt
Fraktale Auftaumuster, polarer Mars. Die Muster werden durch Sublimation von gefrorenem CO₂ gebildet. Die Breite des Bildes beträgt etwa einen Kilometer.
Schleimpilz Brefeldia maxima wächst fraktal auf Holz ⓘ

Fraktale in der Zellbiologie

Fraktale treten häufig im Bereich der lebenden Organismen auf, wo sie durch Verzweigungsprozesse und andere komplexe Musterbildung entstehen. Ian Wong und seine Mitarbeiter haben gezeigt, dass wandernde Zellen durch Anhäufung und Verzweigung Fraktale bilden können. Nervenzellen funktionieren durch Prozesse an der Zelloberfläche, deren Phänomene durch eine starke Vergrößerung des Verhältnisses von Oberfläche zu Volumen noch verstärkt werden. Infolgedessen bilden Nervenzellen häufig fraktale Muster. Diese Prozesse sind für die Zellphysiologie und verschiedene Pathologien von entscheidender Bedeutung. ⓘ

Es wird auch festgestellt, dass sich mehrere subzelluläre Strukturen zu Fraktalen zusammensetzen. Diego Krapf hat gezeigt, dass sich die Aktinfilamente in menschlichen Zellen durch Verzweigungsprozesse zu fraktalen Mustern zusammensetzen. In ähnlicher Weise zeigte Matthias Weiss, dass das endoplasmatische Retikulum fraktale Merkmale aufweist. Nach heutigem Verständnis sind Fraktale in der Zellbiologie allgegenwärtig, von Proteinen über Organellen bis hin zu ganzen Zellen. ⓘ

In kreativen Arbeiten

Seit 1999 haben zahlreiche wissenschaftliche Gruppen Fraktalanalysen an über 50 Gemälden von Jackson Pollock (1912-1956) durchgeführt, indem sie Farbe direkt auf horizontale Leinwände schütteten. ⓘ

Kürzlich wurde mit Hilfe der Fraktalanalyse eine Erfolgsquote von 93 % bei der Unterscheidung zwischen echten und nachgemachten Pollocks erreicht. Kognitive Neurowissenschaftler haben gezeigt, dass Pollocks Fraktale beim Betrachter den gleichen Stressabbau hervorrufen wie computergenerierte Fraktale und Fraktale der Natur. ⓘ

Die Dekalkomanie, eine von Künstlern wie Max Ernst angewandte Technik, kann fraktalähnliche Muster erzeugen. Dabei wird Farbe zwischen zwei Oberflächen gepresst und diese auseinandergezogen. ⓘ

Der Kybernetiker Ron Eglash hat vorgeschlagen, dass fraktale Geometrie und Mathematik in der afrikanischen Kunst, in Spielen, in der Wahrsagerei, im Handel und in der Architektur weit verbreitet sind. Kreisförmige Häuser erscheinen in Kreisen von Kreisen, rechteckige Häuser in Rechtecken von Rechtecken und so weiter. Solche Skalierungsmuster finden sich auch in afrikanischen Textilien, Skulpturen und sogar in Cornrow-Frisuren. Hokky Situngkir wies auch auf ähnliche Eigenschaften in der traditionellen indonesischen Kunst, in der Batik und in den Ornamenten der traditionellen Häuser hin. ⓘ

Der Ethnomathematiker Ron Eglash hat sich mit dem geplanten Grundriss der Stadt Benin befasst und dabei Fraktale als Grundlage verwendet, und zwar nicht nur in der Stadt selbst und in den Dörfern, sondern sogar in den Räumen der Häuser. Als die Europäer zum ersten Mal nach Afrika kamen, hielten sie die Architektur für sehr unorganisiert und damit für primitiv. Es kam ihnen nie in den Sinn, dass die Afrikaner eine Form der Mathematik verwendet haben könnten, die sie noch gar nicht entdeckt hatten." ⓘ

In einem Interview mit Michael Silverblatt aus dem Jahr 1996 gab David Foster Wallace zu, dass die Struktur des ersten Entwurfs von Infinite Jest, den er seinem Lektor Michael Pietsch übergab, von Fraktalen inspiriert war, insbesondere vom Sierpinski-Dreieck (auch bekannt als Sierpinski-Dichtung), dass aber der überarbeitete Roman "eher einer schiefen Sierpinski-Dichtung" gleicht. ⓘ

Einige Werke des niederländischen Künstlers M. C. Escher, wie z. B. Circle Limit III, enthalten Formen, die sich bis ins Unendliche wiederholen und immer kleiner werden, je näher sie den Rändern kommen, in einem Muster, das bei einer Vergrößerung immer gleich aussehen würde. ⓘ

Ein Fraktal, das die Oberfläche eines Berges modelliert (Animation)
Rekursives 3D-Bild
Rekursives fraktales Schmetterlingsbild
Eine fraktale Flamme ⓘ

Physiologische Reaktionen

Der Mensch scheint besonders gut an die Verarbeitung fraktaler Muster mit D-Werten zwischen 1,3 und 1,5 angepasst zu sein. Wenn Menschen fraktale Muster mit D-Werten zwischen 1,3 und 1,5 betrachten, führt dies tendenziell zu einer Verringerung des physiologischen Stresses. ⓘ

Anwendungen in der Technik

Fraktale Antennen
Fraktale Transistoren
Fraktale Wärmetauscher
Digitale Bildgebung
Architektur
Städtisches Wachstum
Klassifizierung von histopathologischen Präparaten
Fraktale Landschaft oder Komplexität von Küstenlinien
Aufspüren von "Leben, wie wir es nicht kennen" durch fraktale Analyse
Enzyme (Michaelis-Menten-Kinetik)
Erzeugung von neuer Musik
Signal- und Bildkompression
Erstellung digitaler fotografischer Vergrößerungen
Fraktal in der Bodenmechanik
Entwurf von Computer- und Videospielen
Computergrafik
Organische Umgebungen
Prozedurale Erzeugung
Fraktographie und Bruchmechanik
Theorie der Kleinwinkelstreuung von fraktal rauen Systemen
T-Shirts und andere Modeartikel
Generierung von Mustern für die Tarnung, z. B. MARPAT
Digitale Sonnenuhr
Technische Analyse von Preisreihen
Fraktale in Netzwerken
Medizin
Neurowissenschaften
Diagnostische Bildgebung
Pathologie
Geologie
Geographie
Archäologie
Bodenmechanik
Seismologie
Suche und Rettung
Technische Analyse
Morton-Ordnungsraum-Füllkurven für GPU-Cache-Kohärenz bei der Texturabbildung, Rasterisierung und Indizierung von Turbulenzdaten. ⓘ

Begriff und Umfeld

Der Begriff Fraktal kann sowohl substantivisch als auch adjektivisch verwendet werden. Das Gebiet der Mathematik, in dem Fraktale und ihre Gesetzmäßigkeiten untersucht werden, heißt fraktale Geometrie und ragt in mehrere andere Bereiche hinein, wie Funktionentheorie, Berechenbarkeitstheorie und dynamische Systeme. Wie der Name schon andeutet, wird der klassische Begriff der euklidischen Geometrie erweitert, was sich auch in den gebrochenen und nicht natürlichen Dimensionen vieler Fraktale widerspiegelt. Neben Mandelbrot gehören Wacław Sierpiński und Gaston Maurice Julia zu den namensgebenden Mathematikern. ⓘ

Verfahren zur Erzeugung von Fraktalen

Fraktale können auf viele verschiedene Arten erzeugt werden, doch alle Verfahren enthalten ein rekursives Vorgehen:

Die Iteration von Funktionen ist die einfachste und bekannteste Art, Fraktale zu erzeugen; die Mandelbrot-Menge entsteht so. Eine besondere Form dieses Verfahrens sind IFS-Fraktale (Iterierte Funktionensysteme), bei denen mehrere Funktionen kombiniert werden. So lassen sich natürliche Gebilde erstellen.
Dynamische Systeme erzeugen fraktale Gebilde, sogenannte seltsame Attraktoren.
L-Systeme, die auf wiederholter Textersetzung beruhen, eignen sich gut zur Modellierung natürlicher Gebilde wie Pflanzen und Zellstrukturen. ⓘ

Es gibt fertige Programme, sogenannte Fraktalgeneratoren, mit denen Computeranwender auch ohne Kenntnis der mathematischen Grundlagen und Verfahren Fraktale darstellen lassen können. ⓘ

Einfache und regelmäßige Fraktale mit Abbildungen

Fraktal	L-System	Winkel	Strecken-Verhältnis	Visualisierung	Anzahl der Spiegelachsen	Punktsymmetrie	Drehsymmetrie	Dimensionen	Hausdorff-Dimension des Randes ⓘ
Drachenkurve	F → R oder F → L R → +R--L+ L → -R++L-	$45^{\circ }$	$1:1/{\sqrt {2}}$		0	nein	keine	2
Gosper-Kurve	F → R oder F → L R → R+L++L-R--RR-L+ L → -R+LL++L+R--R-L	$60^{\circ }$	$1:1/{\sqrt {7}}$		0	ja	6-zählig	2
Hilbert-Kurve	X X → -YF+XFX+FY- Y → +XF-YFY-FX+	$90^{\circ }$	$1:1/2$		1	nein	keine	2
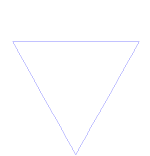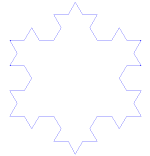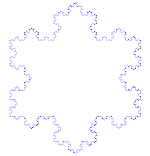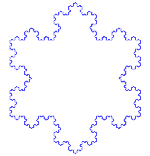
Koch-Flocke	F--F--F F → F+F--F+F	$60^{\circ }$	$1:1/3$		12	ja	6-zählig	2	${\frac {\log(4)}{\log(3)}}\approx 1{,}262$
Peano-Kurve	X X → XFYFX+F+YFXFY-F-XFYFX Y → YFXFY-F-XFYFX+F+YFXFY	$90^{\circ }$			0	ja	2-zählig	2
Peano-Kurve	F F → F-F+F+F+F-F-F-F+F	$90^{\circ }$	$1:1/3$		0	ja	2-zählig	2
Penta Plexity	F++F++F++F++F F → F++F++F\|F-F++F	$36^{\circ }$	$1:1/\left({\frac {{\sqrt {5}}+1}{2}}\right)^{2}$		10	nein	5-zählig	2
Pfeilspitze	F → R oder F → L R → -L+R+L- L → +R-L-R+	$60^{\circ }$	$1:1/2$		1	nein	keine	2
Sierpinski-Dreieck	FXF--FF--FF X → --FXF++FXF++FXF-- F → FF	$60^{\circ }$			6	nein	3-zählig	2	${\frac {\log(3)}{\log(2)}}\approx 1{,}585$
Sierpinski-Dreieck, 2. Variante	F--F--F F → F--F--F--ff f → ff	$60^{\circ }$	$1:1/3$		6	nein	3-zählig	2	${\frac {\log(3)}{\log(2)}}\approx 1{,}585$
Sierpinski-Teppich	F F → F+F-F-FF-F-F-fF f → fff	$90^{\circ }$	$1:1/3$		8	ja	4-zählig	2
Lévy-C-Kurve	F F → +F--F+	$45^{\circ }$	$1:1/{\sqrt {2}}$		1	nein	keine	2	$\approx 1{,}9340$

Erklärung des L-Systems

Das optionale, also nicht notwendige F wird im Allgemeinen als Strecke benutzt, die durch eine Anweisungsfolge ersetzt wird. Wie das F stehen auch andere groß geschriebene Buchstaben wie R und L für einen Streckenabschnitt, der ersetzt wird. + und − stehen für einen bestimmten Winkel, der im Uhrzeigersinn oder gegen den Uhrzeigersinn läuft. Das Symbol | bezeichnet eine Kehrtwendung des Zeichenstiftes, also eine Drehung um 180°. Gegebenenfalls setzt man dafür ein entsprechendes Vielfaches des Drehwinkels ein. ⓘ

Beispiel Drachenkurve

 F → R
 R → +R--L+
 L → -R++L- ⓘ

F ist eine einfache Strecke zwischen zwei Punkten. F → R heißt, dass die Strecke F durch R ersetzt wird. Dieser Schritt ist notwendig, da es zwei rekursive Ersetzungen R und L besitzt, die sich gegenseitig enthalten. Im Weiteren wird wie folgt ersetzt:

 R
 +R--L+
 +(+R--L+)--(-R++L-)+
 +(+(+R--L+)--(-R++L-)+)--(-(+R--L+)++(-R++L-)-)+
 .
 .
 . ⓘ

Ab einem bestimmten Abschnitt muss dieser Ersetzungsprozess abgebrochen werden, um eine Grafik zu bekommen:

 +(+(+r--l+)--(-r++l-)+)--(-(+r--l+)++(-r++l-)-)+ ⓘ

Dabei stellen r und l jeweils eine fest vorgegebene Strecke dar. ⓘ

Zufallsfraktale

Daneben spielen in der Natur auch „Zufallsfraktale“ eine große Rolle. Diese werden nach probabilistischen Regeln erzeugt. Dies kann etwa durch Wachstumsprozesse geschehen, wobei man beispielsweise diffusionsbegrenztes Wachstum (Witten und Sander) und „Tumorwachstum“ unterscheidet. Im ersten Fall entstehen baumartige Strukturen, im letzten Fall Strukturen mit runder Form, je nachdem, in welcher Weise man die neu hinzukommenden Teilchen an die schon vorhandenen Aggregate anlagert. Wenn die fraktalen Exponenten nicht konstant sind, sondern z. B. von der Entfernung von einem zentralen Punkt des Aggregats abhängen, spricht man von sog. Multifraktalen. ⓘ