Hilbertraum

Der Zustand einer schwingenden Saite kann als Punkt in einem Hilbert-Raum modelliert werden. Die Zerlegung einer schwingenden Saite in ihre Schwingungen in verschiedenen Obertönen ist durch die Projektion des Punktes auf die Koordinatenachsen des Raums gegeben. ⓘ

In der Mathematik ermöglichen Hilbert-Räume (benannt nach David Hilbert) die Verallgemeinerung der Methoden der linearen Algebra und der Infinitesimalrechnung von (endlich-dimensionalen) euklidischen Vektorräumen auf Räume, die unendlich-dimensional sein können. Ein Hilbert-Raum ist ein Vektorraum, der mit einem inneren Produkt ausgestattet ist, das eine Abstandsfunktion definiert, für die er ein vollständiger metrischer Raum ist. Hilbert-Räume kommen in der Mathematik und Physik häufig vor, in der Regel als Funktionsräume. ⓘ

Die ersten Hilbert-Räume wurden unter diesem Gesichtspunkt im ersten Jahrzehnt des 20. Jahrhunderts von David Hilbert, Erhard Schmidt und Frigyes Riesz untersucht. Jahrhunderts von David Hilbert, Erhard Schmidt und Frédéric Riesz untersucht. Sie sind unverzichtbare Werkzeuge in den Theorien der partiellen Differentialgleichungen, der Quantenmechanik, der Fourier-Analyse (mit Anwendungen in der Signalverarbeitung und der Wärmeübertragung) und der Ergodentheorie (die die mathematische Grundlage der Thermodynamik bildet). John von Neumann prägte den Begriff Hilbert-Raum für das abstrakte Konzept, das vielen dieser vielfältigen Anwendungen zugrunde liegt. Der Erfolg der Hilbert-Raum-Methoden läutete eine sehr fruchtbare Ära für die Funktionsanalyse ein. Neben den klassischen euklidischen Vektorräumen sind Beispiele für Hilbert-Räume Räume mit quadratisch-integrablen Funktionen, Räume mit Folgen, Sobolev-Räume, die aus verallgemeinerten Funktionen bestehen, und Hardy-Räume mit holomorphen Funktionen. ⓘ

Geometrische Intuition spielt in vielen Aspekten der Hilbert-Raum-Theorie eine wichtige Rolle. Exakte Entsprechungen des Satzes von Pythagoras und des Parallelogrammgesetzes gelten in einem Hilbert-Raum. Auf einer tieferen Ebene spielt die senkrechte Projektion auf einen linearen Unterraum oder einen Unterraum (das Analogon zum "Fallenlassen der Höhe" eines Dreiecks) eine wichtige Rolle bei Optimierungsproblemen und anderen Aspekten der Theorie. Ein Element eines Hilbert-Raums kann durch seine Koordinaten in Bezug auf eine orthonormale Basis eindeutig spezifiziert werden, in Analogie zu den kartesischen Koordinaten in der klassischen Geometrie. Wenn diese Basis abzählbar unendlich ist, ermöglicht sie die Identifizierung des Hilbert-Raums mit dem Raum der unendlichen Folgen, die quadratsummierbar sind. Der letztgenannte Raum wird in der älteren Literatur oft als Hilbert-Raum bezeichnet. ⓘ

Im mathematischen Teilgebiet der Funktionalanalysis ist ein Hilbertraum (Hilbert‧raum, auch Hilbert-Raum, Hilbertscher Raum), benannt nach dem deutschen Mathematiker David Hilbert, ein Vektorraum über dem Körper der reellen oder komplexen Zahlen, versehen mit einem Skalarprodukt – und damit Winkel- und Längenbegriffen –, der vollständig bezüglich der vom Skalarprodukt induzierten Norm (des Längenbegriffs) ist. Ein Hilbertraum ist ein Banachraum, dessen Norm durch ein Skalarprodukt induziert ist. Lässt man die Bedingung der Vollständigkeit fallen, spricht man von einem Prähilbertraum. ⓘ

Die Struktur eines Hilbertraums ist eindeutig festgelegt durch seine Hilbertraumdimension. Diese kann eine beliebige Kardinalzahl sein. Ist die Dimension endlich und betrachtet man als Körper die reellen Zahlen, so handelt es sich um einen euklidischen Raum. In vielen Gebieten, etwa in der mathematischen Beschreibung der Quantenmechanik, ist „der“ Hilbertraum mit abzählbarer Dimension, d. h. mit der kleinstmöglichen unendlichen Dimension, von besonderer Bedeutung. Ein Element eines Hilbertraums kann als eine Familie einer der Dimension entsprechenden Anzahl reeller bzw. komplexer Werte (im Endlichdimensionalen kartesische Koordinaten genannt) aufgefasst werden. Analog zu Vektorräumen, deren Elemente stets nur in endlich vielen Koordinaten einer Hamelbasis ungleich null sind, ist jedes Element eines Hilbertraums nur in abzählbar vielen Koordinaten einer Orthonormalbasis ungleich null und die Koordinatenfamilie ist quadratsummabel. ⓘ

Hilberträume tragen durch ihr Skalarprodukt eine topologische Struktur. Dadurch sind hier im Gegensatz zu allgemeinen Vektorräumen Grenzwertprozesse möglich. Hilberträume sind abgeschlossen unter abzählbaren Summen von orthogonalen Elementen mit einer quadratsummablen Folge von Normen bzw. von parallelen Elementen mit einer absolutsummablen Folge von Normen. ⓘ

Definition und Veranschaulichung

Motivierendes Beispiel: Euklidischer Vektorraum

Eines der bekanntesten Beispiele für einen Hilbert-Raum ist der euklidische Vektorraum, der aus dreidimensionalen Vektoren besteht, mit R³ bezeichnet wird und mit dem Punktprodukt ausgestattet ist. Das Punktprodukt nimmt zwei Vektoren x und y und erzeugt eine reelle Zahl x ⋅ y. Werden x und y in kartesischen Koordinaten dargestellt, so ist das Punktprodukt definiert durch

$${\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}\,.$$

ⓘ

Das Punktprodukt erfüllt die folgenden Eigenschaften:

1. Es ist symmetrisch in x und y: x ⋅ y = y ⋅ x.
2. Es ist linear in seinem ersten Argument: (ax₁ + bx₂) ⋅ y = a(x₁ ⋅ y) + b(x₂ ⋅ y) für beliebige Skalare a, b und Vektoren x₁, x₂ und y.
3. Sie ist positiv definit: für alle Vektoren x, x ⋅ x ≥ 0 , mit Gleichheit, wenn und nur wenn x = 0. ⓘ

Eine Operation auf Paaren von Vektoren, die wie das Punktprodukt diese drei Eigenschaften erfüllt, wird als (reelles) inneres Produkt bezeichnet. Ein Vektorraum, der mit einem solchen inneren Produkt ausgestattet ist, wird als (reeller) Innenproduktraum bezeichnet. Jeder endlich-dimensionale Innenproduktraum ist auch ein Hilbert-Raum. Die grundlegende Eigenschaft des Punktprodukts, die es mit der euklidischen Geometrie verbindet, besteht darin, dass es sowohl mit der Länge (oder Norm) eines Vektors, bezeichnet als ||x||, als auch mit dem Winkel θ zwischen zwei Vektoren x und y durch die folgende Formel verbunden ist

$$\mathbf {x} \cdot \mathbf {y} =\left\|\mathbf {x} \right\|\left\|\mathbf {y} \right\|\,\cos \theta \,.$$

ⓘ

Vollständigkeit bedeutet, dass ein Teilchen, das sich entlang der gebrochenen Bahn (in blau) bewegt und dabei eine endliche Gesamtstrecke zurücklegt, eine wohldefinierte Nettoverschiebung (in orange) hat. ⓘ

Die multivariable Infinitesimalrechnung im euklidischen Raum setzt die Fähigkeit voraus, Grenzwerte zu berechnen und nützliche Kriterien für die Feststellung der Existenz von Grenzwerten zu haben. Eine mathematische Reihe

$$\sum _{n=0}^{\infty }\mathbf {x} _{n}$$

bestehend aus Vektoren in R³ ist absolut konvergent, sofern die Summe der Längen als gewöhnliche Reihe reeller Zahlen konvergiert:

$$\sum _{k=0}^{\infty }\|\mathbf {x} _{k}\|<\infty \,.$$

ⓘ

Genau wie bei einer Reihe von Skalaren konvergiert eine absolut konvergente Reihe von Vektoren auch zu einem Grenzvektor L im euklidischen Raum in dem Sinne, dass

$$\left\|\mathbf {L} -\sum _{k=0}^{N}\mathbf {x} _{k}\right\|\to 0\quad {\text{as }}N\to \infty \,.$$

ⓘ

Diese Eigenschaft drückt die Vollständigkeit des euklidischen Raums aus: dass eine Reihe, die absolut konvergiert, auch im gewöhnlichen Sinne konvergiert. ⓘ

Hilbert-Räume werden oft über den komplexen Zahlen betrachtet. Die mit C bezeichnete komplexe Ebene ist mit einem Größenbegriff ausgestattet, dem komplexen Modulus |z|, der als Quadratwurzel aus dem Produkt von z mit seiner komplexen Konjugierten definiert ist:

$$|z|^{2}=z{\overline {z}}\,.$$

ⓘ

Wenn z = x + iy eine Zerlegung von z in seinen Real- und Imaginärteil ist, dann ist der Modulus die übliche euklidische zweidimensionale Länge:

$$|z|={\sqrt {x^{2}+y^{2}}}\,.$$

ⓘ

Das innere Produkt eines Paares komplexer Zahlen z und w ist das Produkt von z mit dem komplex Konjugierten von w:

$$\langle z,w\rangle =z{\overline {w}}\,.$$

ⓘ

Es ist komplexwertig. Der Realteil von ⟨z, w⟩ ergibt das übliche zweidimensionale euklidische Punktprodukt. ⓘ

Ein zweites Beispiel ist der Raum C², dessen Elemente Paare von komplexen Zahlen z = (z₁, z₂) sind. Dann ist das innere Produkt von z mit einem anderen solchen Vektor w = (w₁, w₂) gegeben durch

$$\langle z,w\rangle =z_{1}{\overline {w_{1}}}+z_{2}{\overline {w_{2}}}\,.$$

ⓘ

Der Realteil von ⟨z, w⟩ ist dann das zweidimensionale euklidische Punktprodukt. Dieses innere Produkt ist hermitesch symmetrisch, was bedeutet, dass das Ergebnis der Vertauschung von z und w das komplex Konjugierte ist:

$$\langle w,z\rangle ={\overline {\langle z,w\rangle }}\,.$$

ⓘ

Definition

A Hilbert-Raum H ist ein reeller oder komplexer Raum mit innerem Produkt, der auch ein vollständiger metrischer Raum in Bezug auf die durch das innere Produkt induzierte Abstandsfunktion ist. ⓘ

Um zu sagen, dass H ein komplexer Innenproduktraum bedeutet, dass H ein komplexer Vektorraum ist, in dem es ein inneres Produkt gibt $\langle x,y\rangle$ gibt, das jedem Paar von Elementen eine komplexe Zahl zuordnet $x,y$ von H zugeordnet ist, das die folgenden Eigenschaften erfüllt:

1. Das innere Produkt ist konjugiert-symmetrisch, d.h. das innere Produkt eines Paares von Elementen ist gleich dem konjugiert-komplexen inneren Produkt der vertauschten Elemente:
   $$\langle y,x\rangle ={\overline {\langle x,y\rangle }}\,.$$
   Wichtig ist, dass dies impliziert, dass $\langle x,x\rangle$ eine reelle Zahl ist.
2. Das innere Produkt ist linear in seinem ersten Argument. Für alle komplexen Zahlen $a$ und $b,$
   $$\langle ax_{1}+bx_{2},y\rangle =a\langle x_{1},y\rangle +b\langle x_{2},y\rangle \,.$$
3. Das innere Produkt eines Elements mit sich selbst ist positiv definit:
   $${\begin{alignedat}{4}\langle x,x\rangle >0&\quad {\text{ if }}x\neq 0,\\\langle x,x\rangle =0&\quad {\text{ if }}x=0\,.\end{alignedat}}$$
   ⓘ

Aus den Eigenschaften 1 und 2 folgt, dass ein komplexes inneres Produkt antilinear, auch genannt konjugiert lineargenannt, in seinem zweiten Argument ist, was bedeutet, dass

$$\langle x,ay_{1}+by_{2}\rangle ={\bar {a}}\langle x,y_{1}\rangle +{\bar {b}}\langle x,y_{2}\rangle \,.$$

ⓘ

A reeller innerer Produktraum ist auf dieselbe Weise definiert, nur dass H ein reeller Vektorraum ist und das innere Produkt reelle Werte annimmt. Ein solches inneres Produkt ist eine bilineare Abbildung und $(H,H,\langle \cdot ,\cdot \rangle )$ bildet ein duales System. ⓘ

Die Norm ist die reellwertige Funktion

$$\|x\|={\sqrt {\langle x,x\rangle }}\,,$$

und der Abstand $d$ zwischen zwei Punkten $x,y$ in H ist in Bezug auf die Norm definiert durch

$$d(x,y)=\|x-y\|={\sqrt {\langle x-y,x-y\rangle }}\,.$$

ⓘ

Dass diese Funktion eine Abstandsfunktion ist, bedeutet erstens, dass sie symmetrisch ist in $x$ und $y,$ zweitens, dass der Abstand zwischen $x$ und sich selbst Null ist, und andernfalls der Abstand zwischen $x$ und $y$ positiv sein muss, und schließlich, dass die Dreiecksungleichung gilt, was bedeutet, dass die Länge eines Schenkels eines Dreiecks xyz nicht größer sein kann als die Summe der Längen der beiden anderen Schenkel:

$$d(x,z)\leq d(x,y)+d(y,z)\,.$$

Diese letzte Eigenschaft ist letztlich eine Folge der grundlegenderen Cauchy-Schwarz-Ungleichung, die besagt

$$\left|\langle x,y\rangle \right|\leq \|x\|\|y\|$$

mit Gleichheit, wenn und nur wenn $x$ und $y$ linear abhängig sind. ⓘ

Mit einer auf diese Weise definierten Abstandsfunktion ist jeder innere Produktraum ein metrischer Raum und wird manchmal auch als Hausdorff-Prä-Hilbert-Raum. Jeder Prä-Hilbert-Raum, der zusätzlich auch ein vollständiger Raum ist, ist ein Hilbert-Raum. ⓘ

Die Vollständigkeit von H wird durch eine Form des Cauchy-Kriteriums für Folgen in H ausgedrückt: Ein Prä-Hilbert-Raum H ist vollständig, wenn jede Cauchy-Folge in Bezug auf diese Norm zu einem Element des Raums konvergiert. Die Vollständigkeit kann durch die folgende äquivalente Bedingung charakterisiert werden: Wenn eine Reihe von Vektoren

$$\sum _{k=0}^{\infty }u_{k}$$

absolut konvergiert in dem Sinne, dass

$$\sum _{k=0}^{\infty }\|u_{k}\|<\infty \,,$$

konvergiert, dann konvergiert die Reihe in H in dem Sinne, dass die Teilsummen zu einem Element von H konvergieren. ⓘ

Als vollständiger normierter Raum sind Hilbert-Räume per Definition auch Banach-Räume. Als solche sind sie topologische Vektorräume, in denen topologische Begriffe wie die Offenheit und Geschlossenheit von Teilmengen gut definiert sind. Von besonderer Bedeutung ist der Begriff eines geschlossenen linearen Unterraums eines Hilbert-Raums, der mit dem durch die Restriktion induzierten inneren Produkt ebenfalls vollständig (als geschlossene Menge in einem vollständigen metrischen Raum) und damit ein eigenständiger Hilbert-Raum ist. ⓘ

Zweites Beispiel: Sequenzräume

Der Sequenzraum l² besteht aus allen unendlichen Folgen z = (z₁, z₂, ...) komplexer Zahlen, so dass die Reihe

$$\sum _{n=1}^{\infty }|z_{n}|^{2}$$

ⓘ

konvergiert. Das innere Produkt auf l² ist definiert durch

$$\langle \mathbf {z} ,\mathbf {w} \rangle =\sum _{n=1}^{\infty }z_{n}{\overline {w_{n}}}\,,$$

ⓘ

wobei die letztgenannte Reihe als Folge der Cauchy-Schwarz-Ungleichung und der Konvergenz der vorhergehenden Reihe konvergiert. ⓘ

Die Vollständigkeit des Raums ist gegeben, wenn eine Reihe von Elementen aus l² absolut (in der Norm) konvergiert, dann konvergiert sie zu einem Element von l². Der Beweis ist grundlegend für die mathematische Analyse und ermöglicht es, mathematische Reihen von Elementen des Raums mit der gleichen Leichtigkeit zu handhaben wie Reihen komplexer Zahlen (oder Vektoren in einem endlich-dimensionalen euklidischen Raum). ⓘ

Geschichte

David Hilbert ⓘ

Vor der Entwicklung der Hilbert-Räume waren den Mathematikern und Physikern andere Verallgemeinerungen der euklidischen Räume bekannt. Insbesondere die Idee eines abstrakten linearen Raums (Vektorraum) hatte gegen Ende des 19. Jahrhunderts an Zugkraft gewonnen: Es handelt sich um einen Raum, dessen Elemente addiert und mit Skalaren (wie reellen oder komplexen Zahlen) multipliziert werden können, ohne dass diese Elemente notwendigerweise mit "geometrischen" Vektoren, wie Positions- und Impulsvektoren in physikalischen Systemen, identifiziert werden. Andere Objekte, die von Mathematikern an der Wende zum 20. Jahrhundert untersucht wurden, insbesondere Räume von Folgen (einschließlich Reihen) und Räume von Funktionen, können natürlich als lineare Räume betrachtet werden. Funktionen können beispielsweise addiert oder mit konstanten Skalaren multipliziert werden, und diese Operationen gehorchen den algebraischen Gesetzen, die für die Addition und Skalarmultiplikation von Raumvektoren gelten. ⓘ

Im ersten Jahrzehnt des 20. Jahrhunderts führten parallele Entwicklungen zur Einführung von Hilbert-Räumen. Jahrhunderts führten parallele Entwicklungen zur Einführung von Hilbert-Räumen. Die erste davon war die Beobachtung, die während David Hilberts und Erhard Schmidts Studium der Integralgleichungen entstand, dass zwei quadratisch integrierbare reellwertige Funktionen f und g auf einem Intervall [a, b] ein inneres Produkt haben ⓘ

$\langle f,g\rangle =\int _{a}^{b}f(x)g(x)\,\mathrm {d} x$ ⓘ

haben, das viele der bekannten Eigenschaften des euklidischen Punktprodukts aufweist. Insbesondere ist die Idee einer orthogonalen Familie von Funktionen von Bedeutung. Schmidt nutzte die Ähnlichkeit dieses inneren Produkts mit dem üblichen Punktprodukt, um ein Analogon der Spektralzerlegung für einen Operator der Form ⓘ

$f(x)\mapsto \int _{a}^{b}K(x,y)f(y)\,\mathrm {d} y$ ⓘ

wobei K eine kontinuierliche Funktion ist, die symmetrisch zu x und y ist. Die sich daraus ergebende Eigenfunktionserweiterung drückt die Funktion K als eine Reihe der Form ⓘ

$K(x,y)=\sum _{n}\lambda _{n}\varphi _{n}(x)\varphi _{n}(y)$ ⓘ

wobei die Funktionen φn orthogonal sind in dem Sinne, dass ⟨φn, φm⟩ = 0 für alle n ≠ m. Die einzelnen Terme in dieser Reihe werden manchmal als elementare Produktlösungen bezeichnet. Es gibt jedoch Eigenfunktionserweiterungen, die nicht in einem geeigneten Sinne zu einer quadratisch integrierbaren Funktion konvergieren: Die fehlende Komponente, die die Konvergenz gewährleistet, ist die Vollständigkeit. ⓘ

Die zweite Entwicklung war das Lebesgue-Integral, eine Alternative zum Riemann-Integral, das 1904 von Henri Lebesgue eingeführt wurde. Das Lebesgue-Integral ermöglichte die Integration einer viel breiteren Klasse von Funktionen. Im Jahr 1907 bewiesen Frigyes Riesz und Ernst Sigismund Fischer unabhängig voneinander, dass der Raum L² der quadratischen Lebesgue-integrierbaren Funktionen ein vollständiger metrischer Raum ist. Als Folge des Zusammenspiels zwischen Geometrie und Vollständigkeit konnten die Ergebnisse von Joseph Fourier, Friedrich Bessel und Marc-Antoine Parseval aus dem 19. Jahrhundert über trigonometrische Reihen leicht auf diese allgemeineren Räume übertragen werden, was zu einem geometrischen und analytischen Apparat führte, der heute gewöhnlich als Riesz-Fischer-Theorem bekannt ist. ⓘ

Im frühen 20. Jahrhundert wurden weitere grundlegende Ergebnisse bewiesen. Das Rieszsche Repräsentationstheorem wurde beispielsweise 1907 von Maurice Fréchet und Frigyes Riesz unabhängig voneinander aufgestellt. John von Neumann prägte den Begriff des abstrakten Hilbert-Raums in seiner Arbeit über unbeschränkte hermitesche Operatoren. Obwohl andere Mathematiker wie Hermann Weyl und Norbert Wiener bestimmte Hilbert-Räume bereits sehr detailliert untersucht hatten, oft von einem physikalisch motivierten Standpunkt aus, gab von Neumann die erste vollständige und axiomatische Behandlung von ihnen. Von Neumann verwendete sie später in seinem bahnbrechenden Werk über die Grundlagen der Quantenmechanik und in seiner weiteren Arbeit mit Eugene Wigner. Der Name "Hilbert-Raum" wurde bald von anderen übernommen, zum Beispiel von Hermann Weyl in seinem Buch über Quantenmechanik und Gruppentheorie. ⓘ

Die Bedeutung des Konzepts eines Hilbert-Raums wurde durch die Erkenntnis unterstrichen, dass er eine der besten mathematischen Formulierungen der Quantenmechanik bietet. Kurz gesagt, die Zustände eines quantenmechanischen Systems sind Vektoren in einem bestimmten Hilbert-Raum, die Beobachtungsgrößen sind hermitsche Operatoren auf diesem Raum, die Symmetrien des Systems sind unitäre Operatoren und Messungen sind orthogonale Projektionen. Die Beziehung zwischen quantenmechanischen Symmetrien und unitären Operatoren gab den Anstoß für die Entwicklung der Theorie der unitären Darstellung von Gruppen, die 1928 von Hermann Weyl begründet wurde. Andererseits wurde in den frühen 1930er Jahren deutlich, dass die klassische Mechanik mit Hilfe des Hilbert-Raums beschrieben werden kann (klassische Mechanik nach Koopman-von Neumann) und dass bestimmte Eigenschaften klassischer dynamischer Systeme mit Hilfe von Hilbert-Raum-Techniken im Rahmen der Ergodentheorie analysiert werden können. ⓘ

Die Algebra der Observablen in der Quantenmechanik ist natürlich eine Algebra von Operatoren, die auf einem Hilbert-Raum definiert sind, gemäß Werner Heisenbergs matrixmechanischer Formulierung der Quantentheorie. Von Neumann begann in den 1930er Jahren mit der Untersuchung von Operatoralgebren als Ringe von Operatoren in einem Hilbert-Raum. Die Art von Algebren, die von Neumann und seinen Zeitgenossen untersucht wurden, sind heute als von-Neumann-Algebren bekannt. In den 1940er Jahren definierten Israel Gelfand, Mark Naimark und Irving Segal eine Art von Operatoralgebren, die C*-Algebren, die einerseits keinen Bezug zu einem zugrundeliegenden Hilbert-Raum hatten und andererseits viele der nützlichen Eigenschaften der zuvor untersuchten Operatoralgebren extrapolierten. Insbesondere das Spektraltheorem für selbstadjungierte Operatoren, das einem Großteil der bestehenden Hilbert-Raum-Theorie zugrunde liegt, wurde auf C*-Algebren verallgemeinert. Diese Techniken sind nun grundlegend für die abstrakte harmonische Analyse und die Darstellungstheorie. ⓘ

Beispiele

Lebesgue-Räume

Lebesgue-Räume sind Funktionsräume, die mit Maßräumen (X, M, μ) assoziiert sind, wobei X eine Menge, M eine σ-Algebra von Teilmengen von X und μ ein abzählbares additives Maß auf M ist. L²(X, μ) sei der Raum derjenigen komplexwertigen messbaren Funktionen auf X, für die das Lebesgue-Integral des Quadrats des Absolutwerts der Funktion endlich ist, d. h. für eine Funktion f in L²(X, μ),

$$\int _{X}|f|^{2}\mathrm {d} \mu <\infty \,,$$

und für die Funktionen nur dann identisch sind, wenn sie sich nur auf einer Menge mit dem Maß Null unterscheiden. ⓘ

Das innere Produkt der Funktionen f und g in L²(X, μ) ist dann definiert als

$$\langle f,g\rangle =\int _{X}f(t){\overline {g(t)}}\,\mathrm {d} \mu (t)$$

oder

$$\langle f,g\rangle =\int _{X}{\overline {f(t)}}g(t)\,\mathrm {d} \mu (t)\,,$$

ⓘ

wobei die zweite Form (Konjugation des ersten Elements) in der Literatur zur theoretischen Physik häufig zu finden ist. Für f und g in L² existiert das Integral aufgrund der Cauchy-Schwarz-Ungleichung und definiert ein inneres Produkt in diesem Raum. Ausgestattet mit diesem inneren Produkt ist L² tatsächlich vollständig. Das Lebesgue-Integral ist unerlässlich, um die Vollständigkeit zu gewährleisten: Auf Gebieten mit reellen Zahlen sind beispielsweise nicht genügend Funktionen Riemann-integrierbar. ⓘ

Die Lebesgue-Räume kommen in vielen natürlichen Situationen vor. Die Räume L²(R) und L²([0,1]) der quadratisch integrierbaren Funktionen in Bezug auf das Lebesgue-Maß auf der reellen Linie bzw. dem Einheitsintervall sind natürliche Gebiete, auf denen die Fourier-Transformation und Fourier-Reihen definiert werden können. In anderen Situationen kann das Maß etwas anderes sein als das gewöhnliche Lebesgue-Maß auf der reellen Linie. Wenn beispielsweise w eine beliebige positive messbare Funktion ist, wird der Raum aller messbaren Funktionen f auf dem Intervall [0, 1], die die Bedingung

$$\int _{0}^{1}{\bigl |}f(t){\bigr |}^{2}w(t)\,\mathrm {d} t<\infty$$

erfüllt, wird der gewichtete L²-Raum L²
w([0, 1]), und w wird als Gewichtsfunktion bezeichnet. Das innere Produkt ist definiert durch

$$\langle f,g\rangle =\int _{0}^{1}f(t){\overline {g(t)}}w(t)\,\mathrm {d} t\,.$$

ⓘ

Der gewichtete Raum L²
_w([0, 1]) ist identisch mit dem Hilbert-Raum L²([0, 1], μ), in dem das Maß μ einer Lebesgue-meßbaren Menge A definiert ist durch

$$\mu (A)=\int _{A}w(t)\,\mathrm {d} t\,.$$

ⓘ

Solche gewichteten L²-Räume werden häufig zur Untersuchung orthogonaler Polynome verwendet, da verschiedene Familien orthogonaler Polynome bezüglich verschiedener Gewichtungsfunktionen orthogonal sind. ⓘ

Sobolev-Räume

Sobolev-Räume, die mit Hs oder W^{s, 2} bezeichnet werden, sind Hilbert-Räume. Sie sind eine besondere Art von Funktionsräumen, in denen eine Differenzierung möglich ist, die aber (im Gegensatz zu anderen Banach-Räumen wie den Hölder-Räumen) die Struktur eines inneren Produkts unterstützen. Da die Differenzierung erlaubt ist, eignen sich Sobolev-Räume gut für die Theorie der partiellen Differentialgleichungen. Sie bilden auch die Grundlage für die Theorie der direkten Methoden in der Variationsrechnung. ⓘ

Für s eine nichtnegative ganze Zahl und Ω ⊂ Rn enthält der Sobolev-Raum Hs(Ω) L²-Funktionen, deren schwache Ableitungen der Ordnung bis s ebenfalls L² sind. Das innere Produkt in Hs(Ω) ist

$$\langle f,g\rangle =\int _{\Omega }f(x){\bar {g}}(x)\,\mathrm {d} x+\int _{\Omega }Df(x)\cdot D{\bar {g}}(x)\,\mathrm {d} x+\cdots +\int _{\Omega }D^{s}f(x)\cdot D^{s}{\bar {g}}(x)\,\mathrm {d} x$$

wobei der Punkt das Punktprodukt im euklidischen Raum der partiellen Ableitungen der jeweiligen Ordnung angibt. Sobolev-Räume können auch definiert werden, wenn s keine ganze Zahl ist. ⓘ

Sobolev-Räume werden auch unter dem Gesichtspunkt der Spektraltheorie untersucht, wobei man sich insbesondere auf die Struktur des Hilbert-Raums stützt. Wenn Ω ein geeignetes Gebiet ist, kann man den Sobolev-Raum Hs(Ω) als den Raum der Bessel-Potentiale definieren; ungefähr,

$$H^{s}(\Omega )=\left.\left\{(1-\Delta )^{-{\frac {s}{2}}}f\;\right|\,f\in L^{2}(\Omega )\right\}\,.$$

ⓘ

Dabei ist Δ der Laplacian und (1 - Δ)-s/2 wird im Sinne des Spektralabbildungssatzes verstanden. Diese Definition bietet nicht nur eine brauchbare Definition von Sobolev-Räumen für nicht-ganzzahlige s, sondern hat auch besonders wünschenswerte Eigenschaften unter der Fourier-Transformation, die sie ideal für die Untersuchung von Pseudodifferentialoperatoren machen. Wenn man diese Methoden auf einer kompakten Riemannschen Mannigfaltigkeit anwendet, kann man beispielsweise die Hodge-Zerlegung erhalten, die die Grundlage der Hodge-Theorie ist. ⓘ

Räume mit holomorphen Funktionen

Hardy-Räume

Die Hardy-Räume sind Funktionsräume, die in der komplexen Analyse und der harmonischen Analyse vorkommen und deren Elemente bestimmte holomorphe Funktionen in einem komplexen Gebiet sind. Bezeichne U die Einheitsscheibe in der komplexen Ebene. Dann ist der Hardy-Raum H²(U) definiert als der Raum der holomorphen Funktionen f auf U, so dass die Mittelwerte ⓘ

$$M_{r}(f)={\frac {1}{2\pi }}\int _{0}^{2\pi }\left|f\left(re^{i\theta }\right)\right|^{2}\,\mathrm {d} \theta$$

ⓘ

für r < 1 begrenzt bleiben. Die Norm auf diesem Hardy-Raum ist definiert durch

$$\left\|f\right\|_{2}=\lim _{r\to 1}{\sqrt {M_{r}(f)}}\,.$$

ⓘ

Hardy-Räume in der Scheibe sind mit Fourier-Reihen verwandt. Eine Funktion f ist in H²(U), wenn und nur wenn

$$f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}$$

wobei

$$\sum _{n=0}^{\infty }|a_{n}|^{2}<\infty \,.$$

ⓘ

H²(U) besteht also aus denjenigen Funktionen, die auf dem Kreis L² sind und deren Fourier-Koeffizienten mit negativer Frequenz verschwinden. ⓘ

Bergman-Räume

Die Bergman-Räume sind eine weitere Familie von Hilbert-Räumen für holomorphe Funktionen. Sei D eine begrenzte offene Menge in der komplexen Ebene (oder ein höherdimensionaler komplexer Raum) und sei L^{2, h}(D) der Raum der holomorphen Funktionen f in D, die auch in L²(D) sind in dem Sinne, dass

$$\|f\|^{2}=\int _{D}|f(z)|^{2}\,\mathrm {d} \mu (z)<\infty \,,$$

ⓘ

wobei das Integral in Bezug auf das Lebesgue-Maß in D genommen wird. Offensichtlich ist L^{2, h}(D) ein Unterraum von L²(D); tatsächlich ist er ein geschlossener Unterraum und somit ein eigenständiger Hilbert-Raum. Dies ist eine Folge der für kompakte Teilmengen K von D gültigen Schätzung, dass

$$\sup _{z\in K}\left|f(z)\right|\leq C_{K}\left\|f\right\|_{2}\,,$$

was wiederum aus der Cauchy'schen Integralformel folgt. So impliziert die Konvergenz einer Folge holomorpher Funktionen in L²(D) auch eine kompakte Konvergenz, so dass die Grenzfunktion ebenfalls holomorph ist. Eine weitere Konsequenz dieser Ungleichung ist, dass die lineare Funktion, die eine Funktion f in einem Punkt von D bewertet, tatsächlich kontinuierlich auf L^{2, h}(D) ist. Das Rieszsche Repräsentationstheorem impliziert, dass das Bewertungsfunktional als Element von L^{2, h}(D) dargestellt werden kann. Für jedes z ∈ D gibt es also eine Funktion ηz ∈ L^{2, h}(D), so dass

$$f(z)=\int _{D}f(\zeta ){\overline {\eta _{z}(\zeta )}}\,\mathrm {d} \mu (\zeta )$$

für alle f ∈ L^{2, h}(D). Der Integrand

$$K(\zeta ,z)={\overline {\eta _{z}(\zeta )}}$$

wird als Bergman-Kern von D bezeichnet. Dieser Integralkern erfüllt eine reproduzierende Eigenschaft

$$f(z)=\int _{D}f(\zeta )K(\zeta ,z)\,\mathrm {d} \mu (\zeta )\,.$$

ⓘ

Ein Bergman-Raum ist ein Beispiel für einen Hilbert-Raum mit reproduzierendem Kern, d. h. ein Hilbert-Raum von Funktionen mit einem Kern K(ζ, z), der eine analoge reproduzierende Eigenschaft erfüllt. Der Hardy-Raum H²(D) kennt ebenfalls einen reproduzierenden Kern, den sogenannten Szegő-Kernel. Reproduzierende Kerne sind auch in anderen Bereichen der Mathematik üblich. In der harmonischen Analysis ist beispielsweise der Poisson-Kernel ein reproduzierender Kern für den Hilbert-Raum der quadratisch-integrablen harmonischen Funktionen auf der Einheitskugel. Dass letzterer überhaupt ein Hilbert-Raum ist, ergibt sich aus dem Mittelwertsatz für harmonische Funktionen. ⓘ

Anwendungen

Viele der Anwendungen von Hilbert-Räumen machen sich die Tatsache zunutze, dass Hilbert-Räume Verallgemeinerungen einfacher geometrischer Konzepte wie Projektion und Basiswechsel aus ihrem üblichen endlichdimensionalen Umfeld unterstützen. Insbesondere die Spektraltheorie kontinuierlicher selbstadjungierter linearer Operatoren auf einem Hilbert-Raum verallgemeinert die übliche spektrale Zerlegung einer Matrix, und dies spielt oft eine wichtige Rolle bei Anwendungen der Theorie in anderen Bereichen der Mathematik und Physik. ⓘ

Sturm-Liouville-Theorie

Die Obertöne einer schwingenden Saite. Dies sind Eigenfunktionen eines zugehörigen Sturm-Liouville-Problems. Die Eigenwerte 1, 1/2, 1/3, ... bilden die (musikalische) harmonische Reihe. ⓘ

In der Theorie der gewöhnlichen Differentialgleichungen werden Spektralmethoden auf einem geeigneten Hilbert-Raum verwendet, um das Verhalten von Eigenwerten und Eigenfunktionen von Differentialgleichungen zu untersuchen. Das Sturm-Liouville-Problem beispielsweise taucht bei der Untersuchung der Oberschwingungen von Wellen in einer Geigensaite oder einer Trommel auf und ist ein zentrales Problem bei gewöhnlichen Differentialgleichungen. Das Problem ist eine Differentialgleichung der Form

$$-{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}}\right]+q(x)y=\lambda w(x)y$$

für eine unbekannte Funktion y auf einem Intervall [a, b], die allgemeinen homogenen Robin-Randbedingungen genügt

$${\begin{cases}\alpha y(a)+\alpha 'y'(a)&=0\\\beta y(b)+\beta 'y'(b)&=0\,.\end{cases}}$$

Die Funktionen p, q und w sind im Voraus gegeben, und das Problem besteht darin, die Funktion y und die Konstanten λ zu finden, für die die Gleichung eine Lösung hat. Das Problem hat nur Lösungen für bestimmte Werte von λ, die als Eigenwerte des Systems bezeichnet werden. Dies ist eine Folge des Spektralsatzes für kompakte Operatoren, der auf den Integraloperator angewendet wird, der durch die Greensche Funktion für das System definiert ist. Eine weitere Konsequenz dieses allgemeinen Ergebnisses ist, dass die Eigenwerte λ des Systems in einer zunehmenden, gegen unendlich tendierenden Folge angeordnet werden können. ⓘ

Partielle Differentialgleichungen

Hilbert-Räume sind ein grundlegendes Hilfsmittel bei der Untersuchung von partiellen Differentialgleichungen. Für viele Klassen von partiellen Differentialgleichungen, wie z. B. lineare elliptische Gleichungen, ist es möglich, eine verallgemeinerte Lösung (bekannt als schwache Lösung) zu betrachten, indem die Klasse der Funktionen erweitert wird. Viele schwache Formulierungen beziehen sich auf die Klasse der Sobolev-Funktionen, die ein Hilbert-Raum ist. Eine geeignete schwache Formulierung reduziert das analytische Problem, eine Lösung zu finden oder, was oft noch wichtiger ist, zu zeigen, dass eine Lösung existiert und für gegebene Randdaten eindeutig ist, auf ein geometrisches Problem. Für lineare elliptische Gleichungen ist das Lax-Milgram-Theorem ein geometrisches Ergebnis, das die eindeutige Lösbarkeit für eine große Klasse von Problemen gewährleistet. Diese Strategie bildet die Grundlage für die Galerkin-Methode (eine Finite-Elemente-Methode) zur numerischen Lösung von partiellen Differentialgleichungen. ⓘ

Ein typisches Beispiel ist die Poisson-Gleichung -Δu = g mit Dirichlet-Randbedingungen in einem begrenzten Gebiet Ω in R². Die schwache Formulierung besteht darin, eine solche Funktion u zu finden, die für alle kontinuierlich differenzierbaren Funktionen v in Ω auf dem Rand verschwindet:

$$\int _{\Omega }\nabla u\cdot \nabla v=\int _{\Omega }gv\,.$$

ⓘ

Dies kann in Form des Hilbert-Raums H¹
₀(Ω) umformuliert werden, der aus solchen Funktionen u besteht, die zusammen mit ihren schwachen partiellen Ableitungen auf Ω quadratisch integrierbar sind und auf dem Rand verschwinden. Die Frage reduziert sich dann darauf, u in diesem Raum so zu finden, dass für alle v in diesem Raum

$$a(u,v)=b(v)$$

ⓘ

wobei a eine kontinuierliche bilineare Form und b eine kontinuierliche lineare Funktion ist, die jeweils durch

$$a(u,v)=\int _{\Omega }\nabla u\cdot \nabla v,\quad b(v)=\int _{\Omega }gv\,.$$

ⓘ

Da die Poisson-Gleichung elliptisch ist, folgt aus der Poincaréschen Ungleichung, dass die bilineare Form a zwingend ist. Das Lax-Milgram-Theorem gewährleistet dann die Existenz und Eindeutigkeit von Lösungen dieser Gleichung. ⓘ

Hilbert-Räume erlauben es, viele elliptische partielle Differentialgleichungen auf ähnliche Weise zu formulieren, und der Lax-Milgram-Satz ist dann ein grundlegendes Werkzeug für ihre Analyse. Mit geeigneten Modifikationen können ähnliche Techniken auf parabolische partielle Differentialgleichungen und bestimmte hyperbolische partielle Differentialgleichungen angewendet werden. ⓘ

Ergodische Theorie

Der Weg einer Billardkugel im Bunimovich-Stadion wird durch ein ergodisches dynamisches System beschrieben. ⓘ

Das Gebiet der Ergodentheorie ist die Untersuchung des langfristigen Verhaltens chaotischer dynamischer Systeme. Der prototypische Fall eines Fachgebiets, auf das die ergodische Theorie anwendbar ist, ist die Thermodynamik, in der - obwohl der mikroskopische Zustand eines Systems extrem kompliziert ist (es ist unmöglich, das Ensemble der einzelnen Kollisionen zwischen Materieteilchen zu verstehen) - das durchschnittliche Verhalten über ausreichend lange Zeitintervalle nachvollziehbar ist. Die Gesetze der Thermodynamik sind Behauptungen über ein solches Durchschnittsverhalten. Insbesondere besagt eine Formulierung des nullten Hauptsatzes der Thermodynamik, dass über ausreichend lange Zeiträume die einzige funktionell unabhängige Messung, die man an einem thermodynamischen System im Gleichgewicht vornehmen kann, seine Gesamtenergie in Form der Temperatur ist. ⓘ

Ein ergodisches dynamisches System ist ein System, für das es außer der Energie - die durch den Hamiltonian gemessen wird - keine anderen funktionell unabhängigen erhaltenen Größen im Phasenraum gibt. Genauer gesagt, nehmen wir an, dass die Energie E fest ist, und lassen wir ΩE die Teilmenge des Phasenraums sein, die aus allen Zuständen der Energie E besteht (eine Energieoberfläche), und lassen wir Tt den Evolutionsoperator im Phasenraum bezeichnen. Das dynamische System ist ergodisch, wenn es keine kontinuierlichen, nicht konstanten Funktionen auf ΩE gibt, so dass

$$f(T_{t}w)=f(w)$$

ⓘ

für alle w auf ΩE und alle Zeiten t. Das Theorem von Liouville impliziert, dass es ein Maß μ auf der Energiefläche gibt, das unter der Zeittranslation invariant ist. Folglich ist die Zeittranslation eine unitäre Transformation des Hilbert-Raums L²(ΩE, μ), die aus quadratisch-integrablen Funktionen auf der Energiefläche ΩE in Bezug auf das innere Produkt

$$\left\langle f,g\right\rangle _{L^{2}\left(\Omega _{E},\mu \right)}=\int _{E}f{\bar {g}}\,\mathrm {d} \mu \,.$$

ⓘ

Der Satz der mittleren Ergodie von Neumann besagt folgendes:

• Wenn Ut eine (stark stetige) einparametrige Halbgruppe von unitären Operatoren auf einem Hilbert-Raum H ist und P die orthogonale Projektion auf den Raum der gemeinsamen Fixpunkte von Ut, {x ∈H | Utx = x, ∀t > 0} ist, dann
  $$Px=\lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}U_{t}x\,\mathrm {d} t\,.$$
  ⓘ

Für ein ergodisches System besteht die feste Menge der zeitlichen Entwicklung nur aus den konstanten Funktionen, so dass das ergodische Theorem Folgendes impliziert: für jede Funktion f ∈ L²(ΩE, μ),

$${\underset {T\to \infty }{L^{2}-\lim }}{\frac {1}{T}}\int _{0}^{T}f(T_{t}w)\,\mathrm {d} t=\int _{\Omega _{E}}f(y)\,\mathrm {d} \mu (y)\,.$$

ⓘ

Das heißt, der Langzeitmittelwert einer Beobachtungsgröße f ist gleich ihrem Erwartungswert über einer Energiefläche. ⓘ

Fourier-Analyse

Überlagerung von Sinuswellen-Basisfunktionen (unten) zur Bildung einer Sägezahnwelle (oben) ⓘ

Sphärische Harmonische, eine orthonormale Basis für den Hilbert-Raum der quadratisch-integrablen Funktionen auf der Kugel, dargestellt in radialer Richtung ⓘ

Eines der grundlegenden Ziele der Fourier-Analyse besteht darin, eine Funktion in eine (möglicherweise unendliche) Linearkombination gegebener Basisfunktionen zu zerlegen: die zugehörige Fourier-Reihe. Die klassische Fourier-Reihe, die zu einer auf dem Intervall [0, 1] definierten Funktion f gehört, ist eine Reihe der Form

$$\sum _{n=-\infty }^{\infty }a_{n}e^{2\pi in\theta }$$

wobei

$$a_{n}=\int _{0}^{1}f(\theta )e^{-2\pi in\theta }\,\mathrm {d} \theta \,.$$

ⓘ

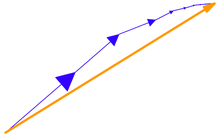
Das Beispiel der Addition der ersten Terme einer Fourier-Reihe für eine Sägezahnfunktion ist in der Abbildung dargestellt. Die Basisfunktionen sind Sinuswellen mit Wellenlängen λ/n (für ganzzahliges n), die kürzer sind als die Wellenlänge λ des Sägezahns selbst (außer für n = 1, die Grundwelle). Alle Basisfunktionen haben Knotenpunkte an den Knotenpunkten des Sägezahns, aber alle außer der Grundwelle haben zusätzliche Knotenpunkte. Die Oszillation der summierten Terme um den Sägezahn wird als Gibbs-Phänomen bezeichnet. ⓘ

Ein wichtiges Problem der klassischen Fourier-Reihen ist die Frage, in welchem Sinne die Fourier-Reihe, wenn überhaupt, gegen die Funktion f konvergiert. Die Funktionen en(θ) = e^2πinθ bilden eine orthogonale Basis des Hilbertraums L²([0, 1]). Folglich lässt sich jede quadratisch integrierbare Funktion als Reihe

$$f(\theta )=\sum _{n}a_{n}e_{n}(\theta )\,,\quad a_{n}=\langle f,e_{n}\rangle$$

ⓘ

ausgedrückt werden, und diese Reihe konvergiert im Sinne des Hilbert-Raums (d. h. im L²-Mittelwert). ⓘ

Das Problem kann auch von einem abstrakten Standpunkt aus untersucht werden: Jeder Hilbert-Raum hat eine orthonormale Basis, und jedes Element des Hilbert-Raums kann auf eindeutige Weise als Summe von Vielfachen dieser Basiselemente geschrieben werden. Die Koeffizienten dieser Basiselemente werden manchmal abstrakt als Fourier-Koeffizienten des Elements des Raums bezeichnet. Diese Abstraktion ist besonders nützlich, wenn es natürlicher ist, verschiedene Basisfunktionen für einen Raum wie L²([0, 1]) zu verwenden. In vielen Fällen ist es wünschenswert, eine Funktion nicht in trigonometrische Funktionen zu zerlegen, sondern z. B. in orthogonale Polynome oder Wavelets, und in höheren Dimensionen in sphärische Harmonische. ⓘ

Wenn beispielsweise en beliebige orthonormale Basisfunktionen von L²[0, 1] sind, dann kann eine gegebene Funktion in L²[0, 1] als endliche Linearkombination approximiert werden

$$f(x)\approx f_{n}(x)=a_{1}e_{1}(x)+a_{2}e_{2}(x)+\cdots +a_{n}e_{n}(x)\,.$$

ⓘ

Die Koeffizienten {a_j} werden so gewählt, dass der Betrag der Differenz ||f - fn||² so klein wie möglich ist. Geometrisch gesehen ist die beste Approximation die orthogonale Projektion von f auf den Unterraum, der aus allen Linearkombinationen der {e_j} besteht, und lässt sich berechnen durch

$$a_{j}=\int _{0}^{1}{\overline {e_{j}(x)}}f(x)\,\mathrm {d} x\,.$$

ⓘ

Dass diese Formel die Differenz ||f - fn||² minimiert, ist eine Folge der Besselschen Ungleichung und der Parsevalschen Formel. ⓘ

In verschiedenen Anwendungen auf physikalische Probleme kann eine Funktion in physikalisch sinnvolle Eigenfunktionen eines Differentialoperators (typischerweise des Laplace-Operators) zerlegt werden: Dies bildet die Grundlage für die spektrale Untersuchung von Funktionen unter Bezugnahme auf das Spektrum des Differentialoperators. Eine konkrete physikalische Anwendung ist das Problem des Hörens der Form einer Trommel: Kann man angesichts der Grundschwingungsformen, die ein Trommelfell erzeugen kann, auf die Form der Trommel selbst schließen? Die mathematische Formulierung dieser Frage beinhaltet die Dirichlet-Eigenwerte der Laplace-Gleichung in der Ebene, die die Grundschwingungsformen in direkter Analogie zu den ganzen Zahlen darstellen, die die Grundschwingungsformen der Geigensaite darstellen. ⓘ

Die Spektraltheorie liegt auch bestimmten Aspekten der Fourier-Transformation einer Funktion zugrunde. Während die Fourier-Analyse eine auf einer kompakten Menge definierte Funktion in das diskrete Spektrum der Laplace-Figur zerlegt (was den Schwingungen einer Geigensaite oder einer Trommel entspricht), ist die Fourier-Transformation einer Funktion die Zerlegung einer auf dem gesamten euklidischen Raum definierten Funktion in ihre Komponenten im kontinuierlichen Spektrum der Laplace-Figur. Die Fourier-Transformation ist auch geometrisch, und zwar in einem Sinne, der durch das Plancherel-Theorem präzisiert wird, das besagt, dass sie eine Isometrie eines Hilbert-Raums (des "Zeitbereichs") mit einem anderen (dem "Frequenzbereich") ist. Diese Isometrieeigenschaft der Fourier-Transformation ist ein wiederkehrendes Thema in der abstrakten harmonischen Analyse (da sie die Energieerhaltung für die kontinuierliche Fourier-Transformation widerspiegelt), wie zum Beispiel das Plancherel-Theorem für sphärische Funktionen in der nichtkommutativen harmonischen Analyse beweist. ⓘ

Quantenmechanik

Die Orbitale eines Elektrons in einem Wasserstoffatom sind Eigenfunktionen der Energie. ⓘ

In der mathematisch strengen Formulierung der Quantenmechanik, die von John von Neumann entwickelt wurde, werden die möglichen Zustände (genauer gesagt, die reinen Zustände) eines quantenmechanischen Systems durch Einheitsvektoren (sogenannte Zustandsvektoren) dargestellt, die sich in einem komplexen separierbaren Hilbert-Raum befinden, der als Zustandsraum bezeichnet wird und bis zu einer komplexen Zahl der Norm 1 (dem Phasenfaktor) wohldefiniert ist. Mit anderen Worten: Die möglichen Zustände sind Punkte in der Projektivierung eines Hilbert-Raums, der gewöhnlich als komplexer projektiver Raum bezeichnet wird. Die genaue Beschaffenheit dieses Hilbert-Raums hängt vom System ab; so sind beispielsweise die Positions- und Impulszustände für ein einzelnes nichtrelativistisches Spin-Null-Teilchen der Raum aller quadratisch-integrablen Funktionen, während die Zustände für den Spin eines einzelnen Protons Einheitselemente des zweidimensionalen komplexen Hilbert-Raums der Spinoren sind. Jede Beobachtungsgröße wird durch einen selbstadjunkten linearen Operator dargestellt, der auf den Zustandsraum wirkt. Jeder Eigenzustand einer Beobachtungsgröße entspricht einem Eigenvektor des Operators, und der zugehörige Eigenwert entspricht dem Wert der Beobachtungsgröße in diesem Eigenzustand. ⓘ

Das innere Produkt zwischen zwei Zustandsvektoren ist eine komplexe Zahl, die als Wahrscheinlichkeitsamplitude bezeichnet wird. Bei einer idealen Messung eines quantenmechanischen Systems ist die Wahrscheinlichkeit, dass ein System von einem bestimmten Ausgangszustand in einen bestimmten Eigenzustand kollabiert, durch das Quadrat des Absolutwerts der Wahrscheinlichkeitsamplituden zwischen Ausgangs- und Endzustand gegeben. Die möglichen Ergebnisse einer Messung sind die Eigenwerte des Operators, was die Wahl selbstadjungierter Operatoren erklärt, da alle Eigenwerte real sein müssen. Die Wahrscheinlichkeitsverteilung einer Beobachtungsgröße in einem bestimmten Zustand kann durch Berechnung der Spektralzerlegung des entsprechenden Operators ermittelt werden. ⓘ

Für ein allgemeines System sind die Zustände in der Regel nicht rein, sondern werden als statistische Mischungen von reinen Zuständen oder gemischten Zuständen dargestellt, die durch Dichtematrizen gegeben sind: selbstadjungierte Operatoren der Spur 1 in einem Hilbert-Raum. Darüber hinaus können bei allgemeinen quantenmechanischen Systemen die Auswirkungen einer einzelnen Messung andere Teile eines Systems in einer Weise beeinflussen, die stattdessen durch ein positives, operatorbewertetes Maß beschrieben wird. Daher ist die Struktur sowohl der Zustände als auch der Observablen in der allgemeinen Theorie wesentlich komplizierter als die Idealisierung für reine Zustände. ⓘ

Beispiele sind

• die möglichen Wellenfunktionen eines freien Teilchens bilden den Hilbertraum $L^{2}$ aller quadratintegrablen Funktionen $\psi \colon \mathbb {R} ^{3}\rightarrow \mathbb {C}$ mit dem üblichen $L^{2}$-Skalarprodukt $\textstyle \langle \psi \,|\,\phi \rangle =\int _{\mathbb {R} ^{3}}\psi ^{*}({\vec {x}})\,\phi ({\vec {x}})\,{\rm {d}}{\vec {x}}$.
• die möglichen Spinzustände eines Elektrons spannen den Hilbertraum $\mathbb {C} ^{2}$ mit dem komplexen Standardskalarprodukt auf. ⓘ

Farbwahrnehmung

Jede echte physikalische Farbe kann durch eine Kombination von reinen Spektralfarben dargestellt werden. Da physikalische Farben aus einer beliebigen Anzahl von Spektralfarben zusammengesetzt sein können, lässt sich der Raum der physikalischen Farben treffend durch einen Hilbert-Raum über Spektralfarben darstellen. Der Mensch hat drei Arten von Zapfenzellen für die Farbwahrnehmung, so dass die wahrnehmbaren Farben durch einen dreidimensionalen euklidischen Raum dargestellt werden können. Die lineare Abbildung des Hilbert-Raums der physikalischen Farben auf den euklidischen Raum der vom Menschen wahrnehmbaren Farben erklärt, warum viele verschiedene physikalische Farben vom Menschen als identisch wahrgenommen werden können (z. B. reines gelbes Licht im Gegensatz zu einer Mischung aus rotem und grünem Licht, siehe Metamerie). ⓘ

Eigenschaften

Pythagoreische Identität

Zwei Vektoren u und v in einem Hilbert-Raum H sind orthogonal, wenn ⟨u, v⟩ = 0. Die Schreibweise dafür ist u ⊥ v. Allgemeiner ausgedrückt: Wenn S eine Teilmenge in H ist, bedeutet die Schreibweise u ⊥ S, dass u orthogonal zu jedem Element von S ist. ⓘ

Wenn u und v orthogonal sind, hat man

$$\|u+v\|^{2}=\langle u+v,u+v\rangle =\langle u,u\rangle +2\,\operatorname {Re} \langle u,v\rangle +\langle v,v\rangle =\|u\|^{2}+\|v\|^{2}\,.$$

ⓘ

Durch Induktion auf n wird dies auf jede Familie u₁, ..., un von n orthogo_nalen Vektoren erweitert,

$$\left\|u_{1}+\cdots +u_{n}\right\|^{2}=\left\|u_{1}\right\|^{2}+\cdots +\left\|u_{n}\right\|^{2}.$$

ⓘ

Während die pythagoräische Identität in dieser Form in jedem inneren Produktraum gültig ist, ist für die Erweiterung der pythagoräischen Identität auf Reihen Vollständigkeit erforderlich. Eine Reihe Σuk orthogonaler Vektoren konvergiert in H nur dann, wenn die Reihe der Quadrate der Normen konvergiert, und

$$\left\|\sum _{k=0}^{\infty }u_{k}\right\|^{2}=\sum _{k=0}^{\infty }\left\|u_{k}\right\|^{2}\,.$$

Außerdem ist die Summe einer Reihe von orthogonalen Vektoren unabhängig von der Reihenfolge, in der sie gebildet wird. ⓘ

Parallelogrammidentität und Polarisation

Geometrisch gesehen besagt die Parallelogrammidentität, dass AC² + BD² = 2(AB² + AD²). Mit anderen Worten: Die Summe der Quadrate der Diagonalen ist doppelt so groß wie die Summe der Quadrate zweier beliebiger benachbarter Seiten. ⓘ

Per Definition ist jeder Hilbert-Raum auch ein Banach-Raum. Außerdem gilt in jedem Hilbert-Raum die folgende Parallelogramm-Identität:

$$\left\|u+v\right\|^{2}+\left\|u-v\right\|^{2}=2\left(\left\|u\right\|^{2}+\left\|v\right\|^{2}\right)\,.$$

ⓘ

Umgekehrt ist jeder Banach-Raum, in dem die Parallelogramm-Identität gilt, ein Hilbert-Raum, und das innere Produkt ist durch die Norm eindeutig durch die Polarisationsidentität bestimmt. Für reelle Hilbert-Räume ist die Polarisationsidentität

$$\langle u,v\rangle ={\frac {1}{4}}\left(\left\|u+v\right\|^{2}-\left\|u-v\right\|^{2}\right)\,.$$

ⓘ

Für komplexe Hilbert-Räume lautet sie

$$\langle u,v\rangle ={\tfrac {1}{4}}\left(\left\|u+v\right\|^{2}-\left\|u-v\right\|^{2}+i\left\|u+iv\right\|^{2}-i\left\|u-iv\right\|^{2}\right)\,.$$

ⓘ

Das Parallelogrammgesetz impliziert, dass jeder Hilbert-Raum ein gleichmäßig konvexer Banach-Raum ist. ⓘ

Beste Approximation

In diesem Unterabschnitt wird das Hilbertsche Projektionstheorem angewandt. Ist C eine nichtleere geschlossene konvexe Teilmenge eines Hilbert-Raums H und x ein Punkt in H, so gibt es einen einzigen Punkt y ∈ C, der den Abstand zwischen x und den Punkten in C minimiert,

$$y\in C\,,\quad \|x-y\|=\operatorname {dist} (x,C)=\min\{\|x-z\|:z\in C\}\,.$$

ⓘ

Dies ist äquivalent zu der Aussage, dass es einen Punkt mit minimaler Norm in der übersetzten konvexen Menge D = C - x gibt. Der Beweis besteht darin zu zeigen, dass jede minimierende Folge (dn) ⊂ D Cauchy ist (unter Verwendung der Parallelogramm-Identität) und daher (unter Verwendung der Vollständigkeit) zu einem Punkt in D konvergiert, der minimale Norm hat. Allgemeiner ausgedrückt gilt dies für jeden gleichmäßig konvexen Banach-Raum. ⓘ

Wendet man dieses Ergebnis auf einen geschlossenen Unterraum F von H an, so lässt sich zeigen, dass der Punkt y ∈ F, der x am nächsten liegt, gekennzeichnet ist durch

$$y\in F\,,\quad x-y\perp F\,.$$

ⓘ

Dieser Punkt y ist die orthogonale Projektion von x auf F, und die Abbildung P_F : x → y ist linear (siehe Orthogonale Ergänzungen und Projektionen). Dieses Ergebnis ist vor allem in der angewandten Mathematik von Bedeutung, insbesondere in der numerischen Analyse, wo es die Grundlage der Methoden der kleinsten Quadrate bildet. ⓘ

Insbesondere, wenn F nicht gleich H ist, kann man einen von Null verschiedenen Vektor v finden, der orthogonal zu F ist (wählen Sie x ∉ F und v = x - y). Ein sehr nützliches Kriterium erhält man, wenn man diese Beobachtung auf den geschlossenen Unterraum F anwendet, der durch eine Teilmenge S von H erzeugt wird.

Eine Teilmenge S von H überspannt einen dichten Vektorunterraum, wenn (und nur wenn) der Vektor 0 der einzige Vektor v ∈ H ist, der orthogonal zu S ist. ⓘ

Dualität

Der Dualraum H* ist der Raum aller stetigen linearen Funktionen aus dem Raum H in das Basisfeld. Er besitzt eine natürliche Norm, definiert durch

$$\|\varphi \|=\sup _{\|x\|=1,x\in H}|\varphi (x)|\,.$$

Diese Norm erfüllt das Parallelogrammgesetz, so dass der duale Raum auch ein Raum mit innerem Produkt ist, wobei das innere Produkt mit Hilfe der Polarisationsidentität durch diese duale Norm definiert werden kann. Der duale Raum ist auch vollständig, so dass er ein eigenständiger Hilbert-Raum ist. Wenn e- = (ei)_{i ∈ I} eine vollständige Orthonormalbasis für H ist, dann ist das innere Produkt auf dem Dualraum von zwei beliebigen $f,g\in H^{*}$ ist

$$\langle f,g\rangle _{H^{*}}=\sum _{i\in I}f(e_{i}){\overline {g(e_{i})}}$$

wobei alle bis auf abzählbar viele der Terme in dieser Reihe Null sind. ⓘ

Das Rieszsche Repräsentationstheorem bietet eine bequeme Beschreibung des Dualraums. Zu jedem Element u von H gibt es ein eindeutiges Element φu von H*, definiert durch

$$\varphi _{u}(x)=\langle x,u\rangle$$

wobei darüber hinaus, $\left\|\varphi _{u}\right\|=\left\|u\right\|.$ ⓘ

Das Rieszsche Repräsentationstheorem besagt, dass die durch u ↦ φu definierte Karte von H nach H* surjektiv ist, was diese Karte zu einem isometrischen antilinearen Isomorphismus macht. Zu jedem Element φ des Duals H* gibt es also ein und nur ein u_φ in H, so dass

$$\langle x,u_{\varphi }\rangle =\varphi (x)$$

für alle x ∈ H. Das innere Produkt auf dem dualen Raum H* erfüllt

$$\langle \varphi ,\psi \rangle =\langle u_{\psi },u_{\varphi }\rangle \,.$$

ⓘ

Die Umkehrung der Ordnung auf der rechten Seite stellt die Linearität von φ durch die Antilinearität von u_φ wieder her. Im reellen Fall ist der antilineare Isomorphismus von H zu seinem Dual tatsächlich ein Isomorphismus, und so sind reelle Hilbert-Räume natürlich isomorph zu ihren eigenen Dualen. ⓘ

Der repräsentierende Vektor u_φ wird auf folgende Weise erhalten. Wenn φ ≠ 0 ist, ist der Kern F = Ker(φ) ein geschlossener Vektorunterraum von H, der nicht gleich H ist, daher gibt es einen zu F orthogonalen Vektor v ungleich Null. Der Vektor u ist ein geeignetes skalares Vielfaches λv von v. Die Bedingung, dass φ(v) = ⟨v, u⟩ ist, ergibt

$$u=\langle v,v\rangle ^{-1}\,{\overline {\varphi (v)}}\,v\,.$$

ⓘ

Diese Korrespondenz φ ↔ u wird durch die in der Physik beliebte Bra-Ket-Schreibweise ausgenutzt. Es ist in der Physik üblich, anzunehmen, dass das innere Produkt, bezeichnet mit ⟨x|y⟩, rechts linear ist,

$$\langle x|y\rangle =\langle y,x\rangle \,.$$

ⓘ

Das Ergebnis ⟨x|y⟩ kann als die Wirkung des linearen Funktionals ⟨x| (der BH) auf den Vektor |y⟩ (das Ket) betrachtet werden. ⓘ

Der Rieszsche Repräsentationssatz beruht im Wesentlichen nicht nur auf dem Vorhandensein eines inneren Produkts, sondern auch auf der Vollständigkeit des Raums. Das Theorem impliziert nämlich, dass das topologische Dual eines jeden Raums mit innerem Produkt mit dessen Vollständigkeit identifiziert werden kann. Eine unmittelbare Folge des Riesz-Darstellungssatzes ist auch, dass ein Hilbert-Raum H reflexiv ist, was bedeutet, dass die natürliche Abbildung von H in seinen doppelten Dualraum ein Isomorphismus ist. ⓘ

Schwach-konvergente Folgen

In einem Hilbert-Raum H ist eine Folge {xn} schwach konvergent zu einem Vektor x ∈ H, wenn

$$\lim _{n}\langle x_{n},v\rangle =\langle x,v\rangle$$

für jedes v ∈ H. ⓘ

Zum Beispiel konvergiert jede orthonormale Folge {fn} schwach gegen 0, als Folge der Besselschen Ungleichung. Jede schwach konvergente Folge {xn} ist nach dem Prinzip der einheitlichen Begrenztheit beschränkt. ⓘ

Umgekehrt lässt jede beschränkte Folge in einem Hilbert-Raum schwach konvergente Teilfolgen zu (Alaoglus Theorem). Diese Tatsache kann verwendet werden, um Minimierungsergebnisse für stetige konvexe Funktionen zu beweisen, so wie der Satz von Bolzano-Weierstraß für stetige Funktionen auf Rd verwendet wird. Unter mehreren Varianten lautet eine einfache Aussage wie folgt:

Wenn f : H → R eine konvexe stetige Funktion ist, so dass f(x) gegen +∞ tendiert, wenn ||x|| gegen ∞ tendiert, dann besitzt f ein Minimum in einem Punkt x₀ ∈ H. ⓘ

Diese Tatsache (und ihre verschiedenen Verallgemeinerungen) sind für direkte Methoden in der Variationsrechnung von grundlegender Bedeutung. Minimierungsergebnisse für konvexe Funktionale sind auch eine direkte Folge der etwas abstrakteren Tatsache, dass geschlossene begrenzte konvexe Teilmengen in einem Hilbert-Raum H schwach kompakt sind, da H reflexiv ist. Die Existenz schwach konvergenter Teilfolgen ist ein Spezialfall des Eberlein-Šmulschen Satzes. ⓘ

Eigenschaften von Banach-Räumen

Jede allgemeine Eigenschaft von Banach-Räumen gilt auch für Hilbert-Räume. Der Satz von der offenen Abbildung besagt, dass eine kontinuierliche surjektive lineare Transformation von einem Banach-Raum in einen anderen eine offene Abbildung ist, d. h., dass sie offene Mengen in offene Mengen überführt. Ein Korollar ist der Satz von der begrenzten Umkehrung, der besagt, dass eine kontinuierliche und bijektive lineare Funktion von einem Banach-Raum zu einem anderen ein Isomorphismus ist (d. h. eine kontinuierliche lineare Abbildung, deren Umkehrung ebenfalls kontinuierlich ist). Dieser Satz ist im Fall von Hilbert-Räumen wesentlich einfacher zu beweisen als in allgemeinen Banach-Räumen. Der Satz von der offenen Abbildung ist äquivalent zum Satz vom geschlossenen Graphen, der besagt, dass eine lineare Funktion von einem Banach-Raum zu einem anderen dann und nur dann stetig ist, wenn ihr Graph eine geschlossene Menge ist. Im Falle von Hilbert-Räumen ist dies grundlegend für die Untersuchung unbeschränkter Operatoren (siehe geschlossener Operator). ⓘ

Das (geometrische) Hahn-Banach-Theorem besagt, dass eine geschlossene konvexe Menge durch eine Hyperebene des Hilbert-Raums von jedem Punkt außerhalb dieser Menge getrennt werden kann. Dies ist eine unmittelbare Folge der Eigenschaft der besten Annäherung: Wenn y das Element einer geschlossenen konvexen Menge F ist, das x am nächsten liegt, dann ist die trennende Hyperebene die Ebene, die senkrecht auf dem Segment xy steht, das durch seinen Mittelpunkt geht. ⓘ

Operatoren auf Hilbert-Räumen

Begrenzte Operatoren

Die stetigen linearen Operatoren A : H₁ → H₂ aus einem Hilbert-Raum H₁ in einen zweiten Hilbert-Raum H₂ sind beschränkt in dem Sinne, dass sie beschränkte Mengen auf beschränkte Mengen abbilden. Umgekehrt gilt: Wenn ein Operator beschränkt ist, dann ist er kontinuierlich. Der Raum solcher beschränkter linearer Operatoren hat eine Norm, die Operatornorm, die durch

$$\lVert A\rVert =\sup \left\{\,\lVert Ax\rVert :\lVert x\rVert \leq 1\,\right\}\,.$$

ⓘ

Die Summe und das Kompositum von zwei begrenzten linearen Operatoren sind ebenfalls begrenzt und linear. Für y in H₂ ist die Karte, die x ∈ H₁ nach ⟨Ax, y⟩ schickt, linear und stetig und kann daher gemäß dem Rieszschen Repräsentationssatz in der folgenden Form dargestellt werden

$$\left\langle x,A^{*}y\right\rangle =\langle Ax,y\rangle$$

für einen Vektor A*y in H₁. Dies definiert einen weiteren beschränkten linearen Operator A* : H₂ → H₁, den Adjungierten von A. Der Adjungierte erfüllt die Bedingung A** = A. Wenn der Rieszsche Repräsentationssatz verwendet wird, um jeden Hilbert-Raum mit seinem kontinuierlichen Dualraum zu identifizieren, kann gezeigt werden, dass der Adjungierte von A identisch ist mit der Transponierten tA : H₂* → H₁* von A, die per Definition $\psi \in H_{2}^{*}$ an das Funktional $\psi \circ A\in H_{1}^{*}.$ ⓘ

Die Menge B(H) aller beschränkten linearen Operatoren auf H (d. h. Operatoren H → H) ist zusammen mit den Additions- und Kompositionsoperationen, der Norm und der adjungierten Operation eine C*-Algebra, die eine Art von Operatoralgebra ist. ⓘ

Ein Element A von B(H) heißt "selbstadjungiert" oder "hermitisch", wenn A* = A. Wenn A hermitisch ist und ⟨Ax, x⟩ ≥ 0 für jedes x, dann heißt A "nicht-negativ", geschrieben A ≥ 0; wenn Gleichheit nur gilt, wenn x = 0, dann heißt A "positiv". Die Menge der selbstadjungierten Operatoren lässt eine partielle Ordnung zu, in der A ≥ B ist, wenn A - B ≥ 0. Wenn A die Form B*B für irgendein B hat, dann ist A nichtnegativ; wenn B invertierbar ist, dann ist A positiv. Umgekehrt gilt auch, dass es für einen nichtnegativen Operator A eine einzige nichtnegative Quadratwurzel B gibt, so dass

$$A=B^{2}=B^{*}B\,.$$

ⓘ

In einem Sinne, der durch den Spektralsatz präzisiert wird, können selbstadjungierte Operatoren sinnvollerweise als Operatoren betrachtet werden, die "real" sind. Ein Element A von B(H) wird als normal bezeichnet, wenn A*A = AA*. Normale Operatoren zerfallen in die Summe aus einem selbstadjungierten Operator und einem imaginären Vielfachen eines selbstadjungierten Operators

$$A={\frac {A+A^{*}}{2}}+i{\frac {A-A^{*}}{2i}}$$

die miteinander kommutieren. Normale Operatoren können auch in Form ihrer Real- und Imaginärteile betrachtet werden. ⓘ

Ein Element U von B(H) wird als unitär bezeichnet, wenn U invertierbar ist und seine Inverse durch U* gegeben ist. Dies kann auch dadurch ausgedrückt werden, dass U onto ist und ⟨Ux, Uy⟩ = ⟨x, y⟩ für alle x, y ∈ H. Die unitären Operatoren bilden eine Gruppe unter Komposition, die die Isometriegruppe von H ist. ⓘ

Ein Element von B(H) ist kompakt, wenn es begrenzte Mengen in relativ kompakte Mengen überführt. Äquivalent dazu ist ein beschränkter Operator T kompakt, wenn für jede beschränkte Folge {xk} die Folge {Txk} eine konvergente Teilfolge hat. Viele Integraloperatoren sind kompakt und definieren eine spezielle Klasse von Operatoren, die als Hilbert-Schmidt-Operatoren bekannt sind und für die Untersuchung von Integralgleichungen besonders wichtig sind. Fredholm-Operatoren unterscheiden sich von einem kompakten Operator durch ein Vielfaches der Identität und werden entsprechend als Operatoren mit einem endlich dimensionalen Kernel und Kokernel charakterisiert. Der Index eines Fredholm-Operators T ist definiert durch

$$\operatorname {index} T=\dim \ker T-\dim \operatorname {coker} T\,.$$

ⓘ

Der Index ist homotopieinvariant und spielt in der Differentialgeometrie über den Atiyah-Singer-Index-Satz eine wichtige Rolle. ⓘ

Unbeschränkte Operatoren

Unbeschränkte Operatoren sind auch in Hilbert-Räumen berechenbar und haben wichtige Anwendungen in der Quantenmechanik. Ein unbeschränkter Operator T auf einem Hilbert-Raum H ist definiert als ein linearer Operator, dessen Domäne D(T) ein linearer Unterraum von H ist. Oft ist die Domäne D(T) ein dichter Unterraum von H, in diesem Fall ist T als dicht definierter Operator bekannt. ⓘ

Der Adjungierte eines dicht definierten unbeschränkten Operators ist im Wesentlichen auf die gleiche Weise definiert wie bei beschränkten Operatoren. Selbstadjungierte unbeschränkte Operatoren spielen die Rolle der Observablen in der mathematischen Formulierung der Quantenmechanik. Beispiele für selbstadjungierte unbeschränkte Operatoren auf dem Hilbert-Raum L²(R) sind:

• Eine geeignete Erweiterung des Differentialoperators
  $$(Af)(x)=-i{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)\,,$$
  wobei i die imaginäre Einheit und f eine differenzierbare Funktion mit kompakter Unterstützung ist.
• Der Multiplikations-x-Operator:
  $$(Bf)(x)=xf(x)\,.$$
  ⓘ

Diese entsprechen den Impuls- bzw. Positionsobservablen. Man beachte, dass weder A noch B auf ganz H definiert sind, da im Fall von A die Ableitung nicht zu existieren braucht und im Fall von B die Produktfunktion nicht quadratisch integrierbar sein muss. In beiden Fällen bildet die Menge der möglichen Argumente dichte Unterräume von L²(R). ⓘ

Konstruktionen

Direkte Summen

Zwei Hilbert-Räume H₁ und H₂ lassen sich zu einem weiteren Hilbert-Raum zusammenfassen, der als (orthogonale) direkte Summe bezeichnet wird, und der

$$H_{1}\oplus H_{2}\,,$$

ⓘ

bestehend aus der Menge aller geordneten Paare (x₁, x₂) mit xi ∈ Hi, i = 1, 2, und dem inneren Produkt definiert durch

$${\bigl \langle }(x_{1},x_{2}),(y_{1},y_{2}){\bigr \rangle }_{H_{1}\oplus H_{2}}=\left\langle x_{1},y_{1}\right\rangle _{H_{1}}+\left\langle x_{2},y_{2}\right\rangle _{H_{2}}\,.$$

ⓘ

Allgemeiner ausgedrückt: Wenn Hi eine Familie von Hilberträumen ist, die durch i ∈ I indiziert sind, dann besteht die direkte Summe der Hi, bezeichnet als

$$\bigoplus _{i\in I}H_{i}$$

besteht aus der Menge aller indizierten Familien

$$x=(x_{i}\in H_{i}|i\in I)\in \prod _{i\in I}H_{i}$$

im kartesischen Produkt der H_i so, dass

$$\sum _{i\in I}\|x_{i}\|^{2}<\infty \,.$$

ⓘ

Das innere Produkt ist definiert durch

$$\langle x,y\rangle =\sum _{i\in I}\left\langle x_{i},y_{i}\right\rangle _{H_{i}}\,.$$

ⓘ

Jeder der Hi ist als geschlossener Unterraum in der direkten Summe aller Hi enthalten. Außerdem sind die Hi paarweise orthogonal. Gibt es umgekehrt in einem Hilbert-Raum H ein System geschlossener Unterräume Vi, i ∈ I, die paarweise orthogonal sind und deren Vereinigung in H dicht ist, dann ist H kanonisch isomorph zur direkten Summe von Vi. In diesem Fall wird H die interne direkte Summe von Vi genannt. Eine direkte Summe (intern oder extern) ist auch mit einer Familie von orthogonalen Projektionen Ei auf den i-ten direkten Summanden Hi ausgestattet. Diese Projektionen sind beschränkte, selbstadjungierte, idempotente Operatoren, die die Orthogonalitätsbedingung erfüllen

$$E_{i}E_{j}=0,\quad i\neq j\,.$$

ⓘ

Der Spektralsatz für kompakte selbstadjungierte Operatoren auf einem Hilbert-Raum H besagt, dass sich H in eine orthogonale direkte Summe der Eigenräume eines Operators aufspaltet, und gibt auch eine explizite Zerlegung des Operators als Summe von Projektionen auf die Eigenräume an. Die direkte Summe von Hilbert-Räumen erscheint auch in der Quantenmechanik als Fock-Raum eines Systems mit einer variablen Anzahl von Teilchen, wobei jeder Hilbert-Raum in der direkten Summe einem zusätzlichen Freiheitsgrad des quantenmechanischen Systems entspricht. In der Darstellungstheorie garantiert das Peter-Weyl-Theorem, dass sich jede unitäre Darstellung einer kompakten Gruppe auf einem Hilbert-Raum als direkte Summe von endlich-dimensionalen Darstellungen aufspaltet. ⓘ

Tensor-Produkte

Ist x₁, y₁ ∊ H₁ und x₂, y₂ ∊ H₂, so definiert man ein inneres Produkt auf dem (gewöhnlichen) Tensorprodukt wie folgt. Für einfache Tensoren sei

$$\langle x_{1}\otimes x_{2},\,y_{1}\otimes y_{2}\rangle =\langle x_{1},y_{1}\rangle \,\langle x_{2},y_{2}\rangle \,.$$

ⓘ

Diese Formel erstreckt sich dann durch Sesquilinearität auf ein inneres Produkt auf H₁ ⊗ H₂. Das Hilbertsche Tensorprodukt von H₁ und H₂, manchmal mit H₁ ${\widehat {\otimes }}$ H₂, ist der Hilbert-Raum, den man durch Vervollständigung von H₁ ⊗ H₂ für die mit diesem inneren Produkt verbundene Metrik erhält. ⓘ

Ein Beispiel hierfür ist der Hilbert-Raum L²([0, 1]). Das Hilbertsche Tensorprodukt von zwei Kopien von L²([0, 1]) ist isometrisch und linear isomorph zum Raum L²([0, 1]²) der quadratisch-integrablen Funktionen auf dem Quadrat [0, 1]². Dieser Isomorphismus schickt einen einfachen Tensor f₁ ⊗ f₂ zu der Funktion

$$(s,t)\mapsto f_{1}(s)\,f_{2}(t)$$

auf dem Quadrat. ⓘ

Dieses Beispiel ist in folgendem Sinne typisch. Zu jedem einfachen Tensorprodukt x₁ ⊗ x₂ gehört der Operator vom Rang eins von H^∗
₁ nach H₂, der ein gegebenes x* ∈ H^∗
₁ als

$$x^{*}\mapsto x^{*}(x_{1})x_{2}\,.$$

ⓘ

Diese auf einfachen Tensoren definierte Abbildung führt zu einer linearen Identifikation zwischen H₁ ⊗ H₂ und dem Raum der Operatoren endlichen Ranges von H^∗
₁ nach H₂. Dies führt zu einer linearen Isometrie des Hilbertschen Tensorprodukts H₁ ${\widehat {\otimes }}$ H₂ mit dem Hilbert-Raum HS(H^∗
₁, H₂) der Hilbert-Schmidt-Operatoren von H^∗
₁ nach H₂. ⓘ

Orthonormalbasen

Der Begriff der Orthonormalbasis aus der linearen Algebra lässt sich auf Hilbert-Räume übertragen. In einem Hilbert-Raum H ist eine Orthonormalbasis eine Familie {e_k}_{k ∈ B} von Elementen von H, die die Bedingungen erfüllen:

1. Orthogonalität: Je zwei verschiedene Elemente von B sind orthogonal: ⟨e_k, e_j⟩ = 0 für alle k, j ∈ B mit k ≠ j.
2. Normalisierung: Jedes Element der Familie hat die Norm 1: ||e_k|| = 1 für alle k ∈ B.
3. Vollständigkeit: Die lineare Spannweite der Familie ek, k ∈ B, ist dicht in H. ⓘ

Ein System von Vektoren, das die ersten beiden Grundbedingungen erfüllt, heißt orthonormales System oder orthonormale Menge (oder orthonormale Folge, wenn B abzählbar ist). Ein solches System ist immer linear unabhängig. Die Vollständigkeit eines orthonormalen Systems von Vektoren eines Hilbert-Raums kann äquivalent umformuliert werden als:

Wenn ⟨v, ek⟩ = 0 für alle k ∈ B und einige v ∈ H, dann ist v = 0. ⓘ

Dies hängt mit der Tatsache zusammen, dass der einzige Vektor, der orthogonal zu einem dichten linearen Unterraum ist, der Nullvektor ist, denn wenn S eine beliebige orthonormale Menge ist und v orthogonal zu S ist, dann ist v orthogonal zur Schließung der linearen Spanne von S, die der gesamte Raum ist. ⓘ

Beispiele für orthonormale Basen sind:

• Die Menge {(1, 0, 0), (0, 1, 0), (0, 0, 1)} bildet eine orthonormale Basis von R³ mit dem Punktprodukt;
• die Folge {fn : n ∈ Z} mit fn(x) = exp(2πinx) bildet eine Orthonormalbasis des komplexen Raums L²([0, 1]); ⓘ

Im unendlichdimensionalen Fall ist eine Orthonormalbasis keine Basis im Sinne der linearen Algebra; zur Unterscheidung wird die letztgenannte Basis auch Hamelbasis genannt. Dass die Spannweite der Basisvektoren dicht ist, bedeutet, dass jeder Vektor im Raum als Summe einer unendlichen Reihe geschrieben werden kann, und die Orthogonalität impliziert, dass diese Zerlegung eindeutig ist. ⓘ

Zwei Elemente des Hilbertraumes heißen orthogonal zueinander, wenn ihr Skalarprodukt 0 ergibt. Eine Familie von paarweise orthogonalen Vektoren heißt Orthogonalsystem. Unter den Orthogonalsystemen spielen die Orthogonalbasen eine besondere Rolle: das sind Orthogonalsysteme, die nicht mehr durch Hinzufügen eines weiteren Vektors vergrößert werden können, also bezüglich Inklusion maximal sind. Äquivalent dazu ist, dass die lineare Hülle im Hilbertraum dicht ist. Außer im Falle von endlichdimensionalen Räumen bilden Orthogonalbasen keine Basis im üblichen Sinn der linearen Algebra (Hamelbasis). Sind diese Basisvektoren darüber hinaus so normiert, dass das Skalarprodukt eines Vektors mit sich selbst 1 ergibt, so spricht man von einem Orthonormalsystem bzw. einer Orthonormalbasis. Die Vektoren $v_{i}$ bilden also genau dann ein Orthonormalsystem, wenn $\langle v_{i},v_{j}\rangle =\delta _{ij}$ für alle $i,j$. Dabei ist $\delta _{ij}$ das Kronecker-Delta. ⓘ

Mittels des Lemmas von Zorn lässt sich zeigen, dass jeder Hilbertraum eine Orthonormalbasis besitzt (es kann sogar jedes Orthonormalsystem zu einer Orthonormalbasis ergänzt werden). ⓘ

Eine Orthonormalbasis ist ein mächtiges Hilfsmittel bei der Untersuchung von Hilberträumen über $\mathbb {R}$ bzw. $\mathbb {C}$ und ihren Elementen. Insbesondere bietet eine Orthonormalbasis eine einfache Möglichkeit, die Darstellung eines Vektors durch die Elemente der Orthonormalbasis zu bestimmen. Sei $B=(b_{1},b_{2},\dots )$ eine Orthonormalbasis und $v$ ein Vektor aus dem Hilbertraum. Da $B$ eine Hilbertraumbasis des Raumes bildet, gibt es Koeffizienten $\alpha _{k}\in \mathbb {R}$ bzw. $\mathbb {C}$, so dass ⓘ

$v=\sum _{k}\alpha _{k}b_{k}$ ⓘ

ist. Diese Koeffizienten bestimmt man unter Ausnutzung der speziellen Eigenschaften der Orthonormalbasis als ⓘ

$\langle b_{n},v\rangle =\left\langle b_{n},\sum _{k}\alpha _{k}b_{k}\right\rangle =\sum _{k}\alpha _{k}\langle b_{n},b_{k}\rangle =\alpha _{n}$, ⓘ

da das Skalarprodukt von unterschiedlichen Basisvektoren 0 und von gleichen Basisvektoren 1 ist. Der $n$-te Basiskoeffizient der Darstellung eines Vektors in einer Orthonormalbasis kann also durch Skalarproduktbildung ermittelt werden. Diese Koeffizienten werden auch Fourierkoeffizienten genannt, da sie eine Verallgemeinerung des Konzeptes der Fourieranalyse darstellen. ⓘ

Sequenzräume

Der Raum $\ell _{2}$ der quadratsummierbaren Folgen der komplexen Zahlen ist die Menge der unendlichen Folgen

$$(c_{1},c_{2},c_{3},\dots )$$

von reellen oder komplexen Zahlen, die so beschaffen sind, dass

$$\left|c_{1}\right|^{2}+\left|c_{2}\right|^{2}+\left|c_{3}\right|^{2}+\cdots <\infty \,.$$

ⓘ

Dieser Raum hat eine orthonormale Basis:

$${\begin{aligned}e_{1}&=(1,0,0,\dots )\\e_{2}&=(0,1,0,\dots )\\&\ \ \vdots \end{aligned}}$$

ⓘ

Dieser Raum ist die unendlich-dimensionale Verallgemeinerung des $\ell _{2}^{n}$ Raums der endlich-dimensionalen Vektoren. Er ist in der Regel das erste Beispiel, mit dem gezeigt wird, dass in unendlichdimensionalen Räumen eine geschlossene und begrenzte Menge nicht notwendigerweise (sequentiell) kompakt ist (wie dies in allen endlichdimensionalen Räumen der Fall ist). Die obige Menge orthonormaler Vektoren zeigt dies in der Tat: Es handelt sich um eine unendliche Folge von Vektoren in der Einheitskugel (d. h. der Kugel der Punkte mit einer Norm kleiner oder gleich eins). Diese Menge ist eindeutig begrenzt und geschlossen; dennoch konvergiert keine Teilfolge dieser Vektoren zu irgendetwas und folglich ist die Einheitskugel in $\ell _{2}$ nicht kompakt ist. Intuitiv liegt dies daran, dass es immer eine andere Koordinatenrichtung gibt, in die die nächsten Elemente der Folge ausweichen können. ⓘ

Man kann den Raum verallgemeinern $\ell _{2}$ auf viele Arten verallgemeinern. Wenn beispielsweise B eine beliebige (unendliche) Menge ist, kann man einen Hilbert-Raum von Folgen mit der Indexmenge B bilden, definiert durch

$$\ell ^{2}(B)=\left\{x:B{\xrightarrow {x}}\mathbb {C} \,\left|\,\sum _{b\in B}\left|x(b)\right|^{2}<\infty \right.\right\}\,.$$

ⓘ

Die Summation über B ist hier definiert durch

$$\sum _{b\in B}\left|x(b)\right|^{2}=\sup \sum _{n=1}^{N}\left|x(b_{n})\right|^{2}$$

Das Supremum wird über alle endlichen Teilmengen von B gebildet. Daraus folgt, dass jedes Element von l²(B) nur abzählbar viele Terme ungleich Null hat, damit diese Summe endlich ist. Dieser Raum wird ein Hilbert-Raum mit dem inneren Produkt

$$\langle x,y\rangle =\sum _{b\in B}x(b){\overline {y(b)}}$$

ⓘ

für alle x, y ∈ l²(B). Auch hier hat die Summe nur abzählbar viele Terme ungleich Null und ist nach der Cauchy-Schwarz-Ungleichung bedingungslos konvergent. ⓘ

Eine Orthonormalbasis von l²(B) wird durch die Menge B indiziert, gegeben durch

$$e_{b}(b')={\begin{cases}1&{\text{if }}b=b'\\0&{\text{otherwise.}}\end{cases}}$$

ⓘ

Besselsche Ungleichung und Parsevalsche Formel

Sei f₁, ..., fn ein endliches orthonormales System in H. Für einen beliebigen Vektor x ∈ H sei

$$y=\sum _{j=1}^{n}\langle x,f_{j}\rangle \,f_{j}\,.$$

ⓘ

Dann sei ⟨x, f_k⟩ = ⟨y, f_k⟩ für jedes k = 1, ..., n. Daraus folgt, dass x - y orthogonal zu jedem f_k ist, also ist x - y orthogonal zu y. Unter zweifacher Anwendung der Pythagoräischen Identität ergibt sich

$$\|x\|^{2}=\|x-y\|^{2}+\|y\|^{2}\geq \|y\|^{2}=\sum _{j=1}^{n}{\bigl |}\langle x,f_{j}\rangle {\bigr |}^{2}\,.$$

ⓘ

Sei {fi}, i ∈ I, ein beliebiges orthonormales System in H. Die Anwendung der obigen Ungleichung auf jede endliche Teilmenge J von I ergibt die Besselsche Ungleichung:

$$\sum _{i\in I}{\bigl |}\langle x,f_{i}\rangle {\bigr |}^{2}\leq \|x\|^{2},\quad x\in H$$

(gemäß der Definition der Summe einer beliebigen Familie von nichtnegativen reellen Zahlen). ⓘ

Geometrisch gesehen impliziert die Besselsche Ungleichung, dass die orthogonale Projektion von x auf den linearen Unterraum, der von fi aufgespannt wird, eine Norm hat, die nicht größer ist als die von x. In zwei Dimensionen ist dies die Behauptung, dass die Länge der Schenkel eines rechtwinkligen Dreiecks nicht größer sein darf als die Länge der Hypotenuse. ⓘ

Die Besselsche Ungleichung ist ein Sprungbrett zu einem stärkeren Ergebnis, der Parsevalschen Identität, die den Fall regelt, dass die Besselsche Ungleichung tatsächlich eine Gleichheit ist. Wenn {ek}_{k ∈ B} eine orthonormale Basis von H ist, kann jedes Element x von H per Definition geschrieben werden als

$$x=\sum _{k\in B}\left\langle x,e_{k}\right\rangle \,e_{k}\,.$$

ⓘ

Selbst wenn B nicht abzählbar ist, garantiert die Besselsche Ungleichung, dass der Ausdruck wohldefiniert ist und nur aus abzählbar vielen Termen ungleich Null besteht. Diese Summe wird Fourier-Entwicklung von x genannt, und die einzelnen Koeffizienten ⟨x, ek⟩ sind die Fourier-Koeffizienten von x. Die Parseval-Identität besagt dann, dass

$$\|x\|^{2}=\sum _{k\in B}|\langle x,e_{k}\rangle |^{2}\,.$$

ⓘ

Umgekehrt gilt: Wenn {ek} eine orthonormale Menge ist, so dass die Parsevalsche Identität für jedes x gilt, dann ist {ek} eine orthonormale Basis. ⓘ

Hilbert-Dimension

Aus dem Zornschen Lemma folgt, dass jeder Hilbert-Raum eine orthonormale Basis hat; außerdem haben zwei orthonormale Basen desselben Raums die gleiche Kardinalität, die Hilbert-Dimension des Raums. Da zum Beispiel l²(B) eine Orthonormalbasis hat, die durch B indiziert ist, ist seine Hilbert-Dimension die Kardinalität von B (die eine endliche ganze Zahl oder eine abzählbare oder nicht abzählbare Kardinalzahl sein kann). ⓘ

Wenn {ek}_{k ∈ B} eine Orthonormalbasis von H ist, dann ist die Abbildung Φ : H → l²(B), die durch Φ(x) = ⟨x, ek⟩_k∈B definiert ist, ein isometrischer Isomorphismus von Hilbert-Räumen: Sie ist eine bijektive lineare Abbildung, die

$${\bigl \langle }\Phi (x),\Phi (y){\bigr \rangle }_{l^{2}(B)}=\left\langle x,y\right\rangle _{H}$$

für alle x, y ∈ H. Die Kardinalzahl von B ist die Hilbert-Dimension von H. Somit ist jeder Hilbert-Raum isometrisch isomorph zu einem Sequenzraum l²(B) für eine Menge B. ⓘ

Trennbare Räume

Per Definition ist ein Hilbert-Raum separabel, wenn er eine dichte abzählbare Teilmenge enthält. Zusammen mit dem Zornschen Lemma bedeutet dies, dass ein Hilbert-Raum dann und nur dann separabel ist, wenn er eine abzählbare Orthonormalbasis zulässt. Alle unendlich-dimensionalen separierbaren Hilbert-Räume sind daher isometrisch isomorph zu l². ⓘ

In der Vergangenheit wurde oft verlangt, dass Hilbert-Räume als Teil der Definition separabel sein müssen. Die meisten in der Physik verwendeten Räume sind trennbar, und da diese alle isomorph zueinander sind, wird jeder unendlich-dimensionale trennbare Hilbert-Raum oft als "Hilbert-Raum" oder einfach als "Hilbert-Raum" bezeichnet. Selbst in der Quantenfeldtheorie sind die meisten Hilbert-Räume tatsächlich trennbar, wie es die Wightman-Axiome vorschreiben. Es wird jedoch manchmal argumentiert, dass auch nicht-trennbare Hilbert-Räume in der Quantenfeldtheorie wichtig sind, etwa weil die Systeme in der Theorie eine unendliche Anzahl von Freiheitsgraden besitzen und jedes unendliche Hilbert-Tensorprodukt (von Räumen mit einer Dimension größer als eins) nicht-trennbar ist. Ein bosonisches Feld kann beispielsweise als Element eines Tensorprodukts betrachtet werden, dessen Faktoren harmonische Oszillatoren in jedem Punkt des Raums darstellen. Aus dieser Perspektive könnte der natürliche Zustandsraum eines Bosons als ein nicht-trennbarer Raum erscheinen. Er ist jedoch nur ein kleiner trennbarer Unterraum des vollständigen Tensorprodukts, der physikalisch sinnvolle Felder enthalten kann (auf denen die Observablen definiert werden können). Ein anderer nicht-trennbarer Hilbert-Raum modelliert den Zustand einer unendlichen Ansammlung von Teilchen in einem unbeschränkten Bereich des Raums. Eine Orthonormalbasis des Raums wird durch die Dichte der Teilchen, einen kontinuierlichen Parameter, indiziert, und da die Menge der möglichen Dichten nicht abzählbar ist, ist die Basis nicht abzählbar. ⓘ

Orthogonale Ergänzungen und Projektionen

Ist S eine Teilmenge eines Hilbert-Raums H, so ist die Menge der zu S orthogonalen Vektoren definiert durch

$$S^{\perp }=\left\{x\in H:\langle x,s\rangle =0\ {\text{ for all }}s\in S\right\}\,.$$

ⓘ

Die Menge S^⊥ ist ein geschlossener Unterraum von H (kann mit Hilfe der Linearität und Stetigkeit des inneren Produkts leicht bewiesen werden) und bildet somit selbst einen Hilbert-Raum. Wenn V ein geschlossener Unterraum von H ist, dann heißt V^⊥ das orthogonales Komplement von V. Tatsächlich kann dann jedes x ∈ H eindeutig als x = v + w geschrieben werden, mit v ∈ V und w ∈ V^⊥. Daher ist H die interne Hilbertsche direkte Summe von V und V^⊥. ⓘ

Der lineare Operator P_V : H → H, der x auf v abbildet, heißt orthogonale Projektion auf V. Es gibt eine natürliche Eins-zu-Eins-Entsprechung zwischen der Menge aller geschlossenen Unterräume von H und der Menge aller beschränkten selbstadjunkten Operatoren P, so dass P² = P ist. Konkret, ⓘ

Theorem - Die orthogonale Projektion P_V ist ein selbstadjungierter linearer Operator auf H von Norm ≤ 1 mit der Eigenschaft P²
_V = P_V. Darüber hinaus hat jeder selbstadjungierte lineare Operator E, so dass E² = E ist, die Form P_V, wobei V der Bereich von E ist. Für jedes x in H ist P_V(x) das einzige Element v von V, das den Abstand ||x - v|| minimiert. ⓘ

Dies liefert die geometrische Interpretation von P_V(x): es ist die beste Annäherung an x durch Elemente von V. ⓘ

Projektionen PU und P_V heißen zueinander orthogonal, wenn PUP_V = 0. Dies ist äquivalent dazu, dass U und V als Unterräume von H orthogonal sind. Die Summe der beiden Projektionen PU und P_V ist nur dann eine Projektion, wenn U und V zueinander orthogonal sind, und in diesem Fall ist PU + P_V = P_U+V. Das Kompositum PUP_V ist im Allgemeinen keine Projektion; vielmehr ist das Kompositum nur dann eine Projektion, wenn die beiden Projektionen kommutieren, und in diesem Fall ist PUP_V = P_U∩V. ⓘ

Durch die Einschränkung der Kodomäne auf den Hilbert-Raum V führt die orthogonale Projektion P_V zu einer Projektionsabbildung π : H → V; sie ist das Adjungierte der Einschlussabbildung

$$i:V\to H\,,$$

was bedeutet, dass

$$\left\langle ix,y\right\rangle _{H}=\left\langle x,\pi y\right\rangle _{V}$$

für alle x ∈ V und y ∈ H. ⓘ

Die Operatornorm der orthogonalen Projektion P_V auf einen geschlossenen Unterraum V ungleich Null ist gleich 1:

$$\|P_{V}\|=\sup _{x\in H,x\neq 0}{\frac {\|P_{V}x\|}{\|x\|}}=1\,.$$

ⓘ

Jeder geschlossene Unterraum V eines Hilbert-Raums ist also das Bild eines Operators P mit der Norm eins, so dass P² = P. Die Eigenschaft, geeignete Projektionsoperatoren zu besitzen, charakterisiert Hilbert-Räume:

• Ein Banach-Raum der Dimension größer als 2 ist (isometrisch) ein Hilbert-Raum, wenn und nur wenn es für jeden geschlossenen Unterraum V einen Operator P_V der Norm 1 gibt, dessen Bild V ist, so dass P²
  V = PV. ⓘ

Während dieses Ergebnis die metrische Struktur eines Hilbert-Raums charakterisiert, kann die Struktur eines Hilbert-Raums als topologischer Vektorraum selbst durch das Vorhandensein von komplementären Unterräumen charakterisiert werden:

• Ein Banach-Raum X ist topologisch und linear isomorph zu einem Hilbert-Raum, wenn und nur wenn es zu jedem geschlossenen Unterraum V einen geschlossenen Unterraum W gibt, so dass X gleich der internen direkten Summe V ⊕ W ist. ⓘ

Das orthogonale Komplement erfüllt einige weitere elementare Ergebnisse. Es ist eine monotone Funktion in dem Sinne, dass wenn U ⊂ V, dann V^⊥ ⊆ U^⊥ mit Gleichheit nur dann gilt, wenn V in der Schließung von U enthalten ist. Dieses Ergebnis ist ein Spezialfall des Hahn-Banach-Satzes. Der Abschluss eines Unterraums kann vollständig durch das orthogonale Komplement charakterisiert werden: Wenn V ein Unterraum von H ist, dann ist der Abschluss von V gleich V^⊥⊥. Das orthogonale Komplement ist also eine Galoisverbindung auf der partiellen Ordnung der Unterräume eines Hilbert-Raums. Im Allgemeinen ist das orthogonale Komplement einer Summe von Unterräumen die Schnittmenge der orthogonalen Komplemente:

$$\left(\sum _{i}V_{i}\right)^{\perp }=\bigcap _{i}V_{i}^{\perp }\,.$$

ⓘ

Wenn d_ie Vi zusätzlich geschlossen sind, dann

$${\overline {\sum _{i}V_{i}^{\perp }}}=\left(\bigcap _{i}V_{i}\right)^{\perp }\,.$$

ⓘ

Spektraltheorie

Es gibt eine gut entwickelte Spektraltheorie für selbstadjungierte Operatoren in einem Hilbert-Raum, die in etwa der Untersuchung von symmetrischen Matrizen über den reellen Zahlen oder selbstadjungierten Matrizen über den komplexen Zahlen entspricht. Im gleichen Sinne kann man eine "Diagonalisierung" eines selbstadjungierten Operators als eine geeignete Summe (eigentlich ein Integral) orthogonaler Projektionsoperatoren erhalten. ⓘ

Das Spektrum eines Operators T, bezeichnet mit σ(T), ist die Menge der komplexen Zahlen λ, so dass T - λ keine kontinuierliche Inverse hat. Wenn T begrenzt ist, ist das Spektrum immer eine kompakte Menge in der komplexen Ebene und liegt innerhalb der Scheibe |z| ≤ ||T||. Wenn T selbstadjungiert ist, dann ist das Spektrum reell. In der Tat ist es im Intervall [m, M] enthalten, wobei

$$m=\inf _{\|x\|=1}\langle Tx,x\rangle \,,\quad M=\sup _{\|x\|=1}\langle Tx,x\rangle \,.$$

ⓘ

Außerdem sind m und M beide tatsächlich im Spektrum enthalten. ⓘ

Die Eigenräume eines Operators T sind gegeben durch

$$H_{\lambda }=\ker(T-\lambda )\,.$$

ⓘ

Anders als bei endlichen Matrizen muss nicht jedes Element des Spektrums von T ein Eigenwert sein: dem linearen Operator T - λ darf nur eine Inverse fehlen, weil er nicht surjektiv ist. Die Elemente des Spektrums eines Operators im allgemeinen Sinne werden als Spektralwerte bezeichnet. Da die Spektralwerte keine Eigenwerte sein müssen, ist die spektrale Zerlegung oft subtiler als in endlichen Dimensionen. ⓘ

Der Spektralsatz eines selbstadjungierten Operators T nimmt jedoch eine besonders einfache Form an, wenn zusätzlich angenommen wird, dass T ein kompakter Operator ist. Der Spektralsatz für kompakte selbstadjungierte Operatoren besagt:

• Ein kompakter selbstadjungierter Operator T hat nur abzählbar (oder endlich) viele Spektralwerte. Das Spektrum von T hat keinen Grenzpunkt in der komplexen Ebene außer möglicherweise Null. Die Eigenräume von T zerlegen H in eine orthogonale direkte Summe:
  $$H=\bigoplus _{\lambda \in \sigma (T)}H_{\lambda }\,.$$
  Wenn E_λ die orthogonale Projektion auf den Eigenraum H_λ bezeichnet, dann gilt außerdem
  $$T=\sum _{\lambda \in \sigma (T)}\lambda E_{\lambda }\,,$$
  wobei die Summe in Bezug auf die Norm von B(H) konvergiert. ⓘ

Dieser Satz spielt eine grundlegende Rolle in der Theorie der Integralgleichungen, da viele Integraloperatoren kompakt sind, insbesondere solche, die aus Hilbert-Schmidt-Operatoren hervorgehen. ⓘ

Der allgemeine Spektralsatz für selbstadjungierte Operatoren beinhaltet eine Art von Operator-bewertetem Riemann-Stieltjes-Integral, anstatt einer unendlichen Summation. Die mit T assoziierte Spektralfamilie ordnet jeder reellen Zahl λ einen Operator E_λ zu, der die Projektion auf den Nullraum des Operators (T - λ)⁺ ist, wobei der positive Teil eines selbstadjungierten Operators definiert ist durch

$$A^{+}={\tfrac {1}{2}}\left({\sqrt {A^{2}}}+A\right)\,.$$

ⓘ

Die Operatoren E_λ sind monoton steigend in Bezug auf die partielle Ordnung, die für selbstadjungierte Operatoren definiert ist; die Eigenwerte entsprechen genau den Sprungdiskontinuitäten. Man hat den Spektralsatz, der behauptet

$$T=\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{\lambda }\,.$$

ⓘ

Das Integral wird als Riemann-Stieltjes-Integral verstanden, das bezüglich der Norm auf B(H) konvergent ist. Insbesondere hat man die gewöhnliche skalarwertige Integraldarstellung

$$\langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} \langle E_{\lambda }x,y\rangle \,.$$

ⓘ

Eine ähnliche spektrale Zerlegung gilt auch für normale Operatoren, doch da das Spektrum nun nicht-reelle komplexe Zahlen enthalten kann, muss das operatorwertige Stieltjes-Maß dE_λ durch eine Auflösung der Identität ersetzt werden. ⓘ

Eine wichtige Anwendung spektraler Methoden ist der Satz der spektralen Abbildung, der es erlaubt, auf einen selbstadjungierten Operator T jede kontinuierliche komplexe Funktion f anzuwenden, die auf dem Spektrum von T definiert ist, indem man das Integral

$$f(T)=\int _{\sigma (T)}f(\lambda )\,\mathrm {d} E_{\lambda }\,.$$

ⓘ

Die sich daraus ergebende kontinuierliche Funktionsrechnung findet insbesondere bei Pseudodifferentialoperatoren Anwendung. ⓘ

Die Spektraltheorie für unbeschränkte selbstadjungierte Operatoren ist nur unwesentlich schwieriger als für beschränkte Operatoren. Das Spektrum eines unbeschränkten Operators ist genau so definiert wie das von beschränkten Operatoren: λ ist ein Spektralwert, wenn der Resolventenoperator

$$R_{\lambda }=(T-\lambda )^{-1}$$

ⓘ

kein wohldefinierter kontinuierlicher Operator ist. Die Selbstadjungiertheit von T garantiert immer noch, dass das Spektrum real ist. Der wesentliche Gedanke bei der Arbeit mit unbeschränkten Operatoren besteht also darin, stattdessen das Resolvent R_λ zu betrachten, bei dem λ nicht reell ist. Dies ist ein beschränkter normaler Operator, der eine spektrale Darstellung zulässt, die dann auf eine spektrale Darstellung von T selbst übertragen werden kann. Eine ähnliche Strategie wird beispielsweise bei der Untersuchung des Spektrums des Laplace-Operators angewandt: Anstatt den Operator direkt zu betrachten, sucht man nach einem zugehörigen Resolventen wie einem Riesz- oder Bessel-Potential. ⓘ

Eine genaue Version des Spektralsatzes lautet in diesem Fall wie folgt:

Theorem - Einem dicht definierten selbstadjungierten Operator T auf einem Hilbert-Raum H entspricht eine eindeutige Auflösung der Identität E auf den Borel-Mengen von R, so dass

$$\langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{x,y}(\lambda )$$

für alle x ∈ D(T) und y ∈ H. Das Spektralmaß E ist auf das Spektrum von T konzentriert.

Es gibt auch eine Version des Spektralsatzes, die für unbeschränkte normale Operatoren gilt. ⓘ

In der Populärkultur

Thomas Pynchon führte die fiktive Figur Sammy Hilbert-Spaess (ein Wortspiel mit "Hilbert Space") in seinem Roman Gravity's Rainbow von 1973 ein. Hilbert-Spaess wird zunächst als "allgegenwärtiger Doppelagent" und später als "mindestens ein Doppelagent" beschrieben. Der Roman hatte sich zuvor auf die Unvollständigkeitssätze des deutschen Mathematikers Kurt Gödel bezogen, die zeigten, dass Hilberts Programm, Hilberts formalisierter Plan zur Vereinheitlichung der Mathematik in einem einzigen Satz von Axiomen, nicht möglich war. ⓘ

Unterräume

Ein Unterhilbertraum oder Teilhilbertraum eines Hilbertraums ist eine Teilmenge, die mit der Skalarmultiplikation, Addition und Skalarprodukt eingeschränkt auf diese Teilmenge wiederum einen Hilbertraum bildet. Konkret heißt das, dass die Teilmenge die Null enthält und abgeschlossen unter Skalarmultiplikation und Addition ist, das heißt ein Untervektorraum ist, und bezüglich des Skalarprodukts immer noch vollständig ist. Dies ist äquivalent dazu, dass die Teilmenge im topologischen Sinne abgeschlossen ist. Daher bezeichnet man Unterhilberträume auch als abgeschlossene Unterräume bzw. abgeschlossene Teilräume und bezeichnet im Gegensatz dazu beliebige Untervektorräume einfach nur als Unterräume bzw. Teilräume. Ein Solcher ist im Allgemeinen nur ein Prähilbertraum. Jeder Prähilbertraum ist in einem Hilbertraum als dichter Untervektorraum enthalten, nämlich in seiner Vervollständigung. Auch ist es möglich einen Quotientenraum bezüglich eines Unterhilbertraums zu bilden, der wiederum ein Hilbertraum ist. ⓘ

Dies alles gilt im Wesentlichen analog für beliebige Banachräume, wobei deren Untervektorräume dann nicht unbedingt Prähilberträume, wohl aber normierte Räume sind. Eine Besonderheit dagegen ist die Gültigkeit des Projektionssatzes: Für jeden Unterhilbertraum und jedes beliebige Element des Hilbertraums gibt es ein Element des Unterhilbertraums mit minimalem Abstand. Dies gilt für Banachräume dagegen schon im Endlichdimensionalen im Allgemeinen nicht. Dies erlaubt eine kanonische Identifikation des Quotientenraums bezüglich eines Unterhilbertraums mit einem Unterhilbertraum, das orthogonale Komplement, und das Konzept der Orthogonalprojektion. Das orthogonale Komplement eines Unterhilbertraums ist ein komplementärer Unterhilbertraum, für Banachräume dagegen existiert zu einem Unterbanachraum im Allgemeinen kein komplementärer Unterbanachraum. ⓘ

Konjugierter Hilbertraum

Im Falle eines komplexen Hilbertraums besteht eine gewisse Asymmetrie zwischen den beiden Komponenten des Skalarproduktes; das Skalarprodukt ist linear in der zweiten Komponente und konjugiert linear in der ersten. Man kann daher zu einem komplexen Hilbertraum $H$ wie folgt einen weiteren Hilbertraum ${\overline {H}}$ definieren. Als Menge ist ${\overline {H}}=H$, auch die Addition auf ${\overline {H}}$ wird von $H$ übernommen. Die skalare Multiplikation und das Skalarprodukt für ${\overline {H}}$ werden wie folgt erklärt:

skalare Multiplikation: $\lambda \cdot _{\overline {H}}u:={\overline {\lambda }}u$

Skalarprodukt: $\langle u,v\rangle _{\overline {H}}:={\overline {\langle u,v\rangle }}=\langle v,u\rangle$.

Man prüft nach, dass ${\overline {H}}$ mit diesen Definitionen wieder ein Hilbertraum ist, man nennt ihn den konjugierten Hilbertraum. Der zu ${\overline {H}}$ konjugierte Hilbertraum ist offenbar wieder $H$. ⓘ

Dualraum

Der topologische Dualraum $H^{\prime }$ der stetigen, linearen Funktionale auf einem Hilbertraum $H$ ist wie bei jedem Banachraum selbst wieder ein Banachraum. Eine Besonderheit bei Hilberträumen ist der Satz von Fréchet-Riesz: Jeder reelle Hilbertraum $H$ ist mittels des isometrischen Vektorraumisomorphismus $H\rightarrow H^{\prime },\,v\mapsto \langle v,\cdot \rangle$ isomorph zu seinem Dualraum. Die Norm auf dem Dualraum ist daher ebenfalls von einem Skalarprodukt induziert, er ist somit ebenfalls ein Hilbertraum. Im Falle eines komplexen Hilbertraums gilt der Satz analog, allerdings ist jene Abbildung nur semilinear, das heißt ein antiunitärer Operator. In beiden Fällen ist der Hilbertraum isomorph zu seinem Dualraum (ein antiunitärer Operator $H\to H^{\prime }$ lässt sich nämlich in einen unitären Operator $H\to H^{\prime }$ und einen antiunitären Operator $H^{\prime }\to H^{\prime }$ zerlegen), und somit erst recht zu seinem Bidualraum, jeder Hilbertraum ist also reflexiv. ⓘ

Trivia

An mehreren Universitäten des deutschsprachigen Raumes gibt es als „Hilbertraum“ bezeichnete Räumlichkeiten. ⓘ