Noether-Theorem

Erste Seite von Emmy Noethers Artikel "Invariante Variationsprobleme" (1918), in dem sie ihr Theorem bewies. ⓘ

Das Noether-Theorem oder Noethers erster Satz besagt, dass jede differenzierbare Symmetrie der Wirkung eines physikalischen Systems mit konservativen Kräften ein entsprechendes Erhaltungsgesetz hat. Das Theorem wurde 1915 von der Mathematikerin Emmy Noether bewiesen und 1918 veröffentlicht. Die Wirkung eines physikalischen Systems ist das Integral einer Lagrangeschen Funktion über die Zeit, aus der das Verhalten des Systems nach dem Prinzip der kleinsten Wirkung bestimmt werden kann. Dieses Theorem gilt nur für kontinuierliche und glatte Symmetrien im physikalischen Raum. ⓘ

Das Noethersche Theorem wird in der theoretischen Physik und der Variationsrechnung verwendet. Er ist eine Verallgemeinerung der Formulierungen zu den Bewegungskonstanten in der Lagrangeschen und der Hamiltonschen Mechanik (entwickelt 1788 bzw. 1833) und gilt nicht für Systeme, die nicht allein mit einer Lagrangeschen Formel modelliert werden können (z. B. Systeme mit einer Rayleigh-Dissipationsfunktion). Insbesondere brauchen dissipative Systeme mit kontinuierlichen Symmetrien kein entsprechendes Erhaltungsgesetz zu haben. ⓘ

Eine Erhaltungsgröße eines Systems von Teilchen ist eine Funktion der Zeit $t$, der Orte $x$ und der Geschwindigkeiten $v$ der Teilchen, deren Wert sich auf jeder von ihnen im Laufe der Zeit durchlaufenen Bahn $x(t)$ nicht ändert. So ist die Energie $E(t,x,v)={\tfrac {1}{2}}\,m\,v^{2}+V(x)$ eines nichtrelativistischen Teilchens der Masse $m$, das sich im Potential $V$ bewegt, eine Erhaltungsgröße. Das heißt, für jede Bahn $x(t)$, die der Bewegungsgleichung $m{\tfrac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}+\mathrm {grad} \,V(x)=0$ genügt, gilt zu jeder Zeit $t$:

$E{\bigl (}t,x(t),{\tfrac {\mathrm {d} x}{\mathrm {d} t}}(t){\bigr )}=E{\bigl (}0,x(0),{\tfrac {\mathrm {d} x}{\mathrm {d} t}}(0){\bigr )}$. ⓘ

Grundlegende Illustrationen und Hintergrund

Zur Veranschaulichung: Wenn sich ein physikalisches System unabhängig von seiner Ausrichtung im Raum gleich verhält, ist seine Lagrange unter kontinuierlichen Rotationen symmetrisch: Aus dieser Symmetrie ergibt sich nach dem Noether-Theorem, dass der Drehimpuls des Systems als Folge seiner Bewegungsgesetze erhalten bleibt. Das physikalische System selbst muss nicht symmetrisch sein; ein zerklüfteter Asteroid, der im Weltraum taumelt, behält trotz seiner Asymmetrie den Drehimpuls bei. Es sind die Gesetze seiner Bewegung, die symmetrisch sind. ⓘ

Ein weiteres Beispiel: Wenn ein physikalischer Prozess unabhängig von Ort und Zeit zu den gleichen Ergebnissen führt, dann ist seine Lagrange bei kontinuierlichen Translationen im Raum bzw. in der Zeit symmetrisch: Nach dem Satz von Noether erklären diese Symmetrien die Erhaltungssätze für den linearen Impuls und die Energie in diesem System. ⓘ

Das Noether-Theorem ist sowohl wegen der Einblicke, die es in die Erhaltungssätze gewährt, als auch als praktisches Berechnungsinstrument wichtig. Er ermöglicht es den Forschern, aus den beobachteten Symmetrien eines physikalischen Systems die erhaltenen Größen (Invarianten) zu bestimmen. Umgekehrt können Forscher ganze Klassen hypothetischer Lagrangescher mit gegebenen Invarianten betrachten, um ein physikalisches System zu beschreiben. Zur Veranschaulichung: Nehmen wir an, es wird eine physikalische Theorie vorgeschlagen, in der eine Größe X erhalten bleibt. Ein Forscher kann die Arten von Lagrangeschen berechnen, in denen X durch eine kontinuierliche Symmetrie erhalten bleibt. Aufgrund des Noether-Theorems liefern die Eigenschaften dieser Lagrangeschen weitere Kriterien, um die Auswirkungen zu verstehen und die Eignung der neuen Theorie zu beurteilen. ⓘ

Es gibt zahlreiche Versionen des Noether-Theorems mit unterschiedlichem Grad an Allgemeinheit. Es gibt natürliche Quantengegenstücke zu diesem Satz, die in den Ward-Takahashi-Identitäten ausgedrückt sind. Es gibt auch Verallgemeinerungen des Noether-Theorems auf Überräume. ⓘ

Informelle Aussage des Satzes

Abgesehen von den technischen Feinheiten lässt sich der Satz von Noether auch informell formulieren:

Wenn ein System eine kontinuierliche Symmetrieeigenschaft hat, dann gibt es entsprechende Größen, deren Werte in der Zeit erhalten bleiben. ⓘ

Eine anspruchsvollere Version des Satzes, die Felder einbezieht, besagt Folgendes:

Jeder differenzierbaren Symmetrie, die durch lokale Aktionen erzeugt wird, entspricht ein konservierter Strom. ⓘ

Das Wort "Symmetrie" in der obigen Aussage bezieht sich genauer gesagt auf die Kovarianz der Form, die ein physikalisches Gesetz in Bezug auf eine eindimensionale Lie-Gruppe von Transformationen annimmt, die bestimmte technische Kriterien erfüllen. Das Erhaltungsgesetz einer physikalischen Größe wird gewöhnlich als Kontinuitätsgleichung ausgedrückt. ⓘ

Der formale Beweis des Theorems nutzt die Bedingung der Invarianz, um einen Ausdruck für einen Strom abzuleiten, der mit einer erhaltenen physikalischen Größe verbunden ist. In der modernen (seit ca. 1980) Terminologie wird die erhaltene Größe als Noether-Ladung bezeichnet, während der Strom, der diese Ladung trägt, Noether-Strom genannt wird. Der Noether-Strom ist bis zu einem solenoidalen (divergenzfreien) Vektorfeld definiert. ⓘ

Im Zusammenhang mit der Gravitation gilt Felix Kleins Aussage des Noether-Theorems für die Wirkung I als Voraussetzung für die Invarianten:

Wenn ein Integral I unter einer stetigen Gruppe G_ρ mit ρ Parametern invariant ist, dann sind ρ linear unabhängige Kombinationen der Lagrange-Ausdrücke Divergenzen. ⓘ

Kurze Illustration und Überblick über das Konzept

Diagramm zur Veranschaulichung des Noether-Theorems für eine koordinatenweise Symmetrie. ⓘ

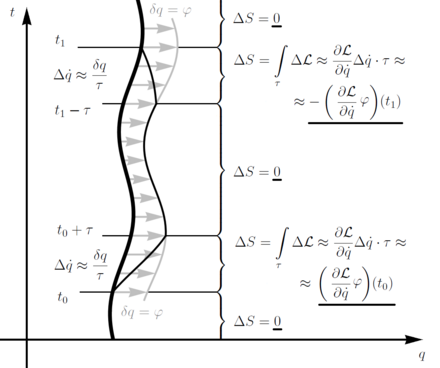
Die Grundidee des Noether-Theorems lässt sich am einfachsten anhand eines Systems mit einer Koordinate $q$ und einer kontinuierlichen Symmetrie $\varphi :q\mapsto q+\delta q$ (graue Pfeile im Diagramm). Betrachten Sie eine beliebige Trajektorie $q(t)$ (im Diagramm fett gedruckt), die die Bewegungsgesetze des Systems erfüllt. Das heißt, die Aktion $S$ die dieses System steuert, ist auf dieser Bahn stationär, d. h. sie ändert sich nicht bei einer lokalen Variation der Bahn. Insbesondere ändert sie sich nicht bei einer Variation, die den Symmetriefluss $\varphi$ auf ein Zeitsegment [t₀, t₁] anwendet und außerhalb dieses Segments bewegungslos ist. Um die Flugbahn kontinuierlich zu halten, verwenden wir "Puffer"-Perioden von geringer Dauer $\tau$ um allmählich zwischen den Segmenten zu wechseln. ⓘ

Die Gesamtänderung der Aktion $S$ umfasst nun die Veränderungen, die durch jedes Intervall im Spiel hervorgerufen werden. Teile, in denen die Veränderung selbst verschwindet, bringen keine $\Delta S$. Auch der mittlere Teil ändert die Wirkung nicht, da seine Transformation $\varphi$ ist eine Symmetrie und erhält somit die Lagrange $L$ und die Wirkung ${\textstyle S=\int L}$. Die einzigen verbleibenden Teile sind die "puffernden" Teile. Grob gesagt, tragen sie vor allem durch ihre "Schrägstellung" bei ${\dot {q}}\rightarrow {\dot {q}}\pm \delta q/\tau$. ⓘ

Das ändert die Lagrange um $\Delta L\approx {\bigl (}\partial L/\partial {\dot {q}}{\bigr )}\Delta {\dot {q}}$, die sich integriert zu

$$\Delta S=\int \Delta L\approx \int {\frac {\partial L}{\partial {\dot {q}}}}\Delta {\dot {q}}\approx \int {\frac {\partial L}{\partial {\dot {q}}}}\left(\pm {\frac {\delta q}{\tau }}\right)\approx \ \pm {\frac {\partial L}{\partial {\dot {q}}}}\delta q=\pm {\frac {\partial L}{\partial {\dot {q}}}}\varphi .$$

ⓘ

Diese letzten Terme, ausgewertet um die Endpunkte $t_{0}$ und $t_{1}$ausgewertet werden, sollten sich gegenseitig aufheben, so dass die Gesamtänderung der Wirkung $\Delta S$ gleich Null ist, wie es zu erwarten wäre, wenn die Trajektorie eine Lösung ist. Das bedeutet

$$\left({\frac {\partial L}{\partial {\dot {q}}}}\varphi \right)(t_{0})=\left({\frac {\partial L}{\partial {\dot {q}}}}\varphi \right)(t_{1}),$$

was bedeutet, dass die Größe $\left(\partial L/\partial {\dot {q}}\right)\varphi$ erhalten bleibt, was die Schlussfolgerung des Noether-Theorems ist. Wenn zum Beispiel reine Translationen von $q$ durch eine Konstante die Symmetrie ist, dann wird die erhaltene Größe einfach $\left(\partial L/\partial {\dot {q}}\right)=p$der kanonische Impuls. ⓘ

Allgemeinere Fälle folgen der gleichen Idee:

• Wenn mehrere Koordinaten $q_{r}$ eine Symmetrietransformation erfahren $q_{r}\mapsto q_{r}+\varphi _{r}$so addieren sich ihre Wirkungen durch Linearität zu einer Erhaltungsgröße ${\textstyle \sum _{r}\left(\partial L/\partial {\dot {q}}_{r}\right)\varphi _{r}}$.
• Wenn es Zeittransformationen gibt $t\mapsto t+T$bewirken sie, dass die "puffernden" Segmente die beiden folgenden Terme beitragen zu $\Delta S$:
  $$\Delta S\approx \pm \left(TL+\int {\frac {\partial L}{\partial {\dot {q}}_{r}}}\Delta {\dot {q}}_{r}\right)\approx \pm T\left(L-{\frac {\partial L}{\partial {\dot {q}}_{r}}}{\dot {q}}_{r}\right),$$
  Der erste Term ist auf die Streckung der zeitlichen Dimension des "puffernden" Segments zurückzuführen (wodurch sich die Größe des Integrationsbereichs ändert), der zweite auf seine "Schrägstellung" wie im Beispielsfall. Zusammen fügen sie einen Summanden ${\textstyle T\left(L-\sum _{r}\left(\partial L/\partial {\dot {q}}_{r}\right){\dot {q}}_{r}\right)}$ zur Erhaltungsgröße hinzu.
• Schließlich, wenn anstelle einer Trajektorie $q(t)$ ganze Felder $\psi (q_{r},t)$ betrachtet werden, ersetzt das Argument
  • das Intervall $[t_{0},t_{1}]$ durch eine begrenzte Region $U$ des $(q_{r},t)$-Bereichs,
  • die Endpunkte $t_{0}$ und $t_{1}$ mit der Begrenzung $\partial U$ der Region,
  • und sein Beitrag zu $\Delta S$ wird als Fluss einer Erhaltungsgröße interpretiert $j_{r}$die analog zu der vorherigen Definition einer konservierten Größe aufgebaut ist.
  Nun wird der Nullbeitrag des "puffernden" $\partial U$ zu $\Delta S$ wird als Verschwinden des Gesamtstroms $j_{r}$ durch den $\partial U$. Das ist der Sinn, in dem er erhalten bleibt: Wie viel hinein "fließt", so viel "fließt" auch heraus. ⓘ

Historischer Kontext

Ein Erhaltungssatz besagt, dass eine bestimmte Größe X in der mathematischen Beschreibung der Entwicklung eines Systems während seiner gesamten Bewegung konstant bleibt - sie ist eine Invariante. Mathematisch gesehen ist die Änderungsrate von X (seine Ableitung nach der Zeit) gleich Null, ⓘ

${\frac {dX}{dt}}={\dot {X}}=0~.$ ⓘ

Solche Größen gelten als konserviert; sie werden oft als Bewegungskonstanten bezeichnet (obwohl es sich nicht um Bewegung an sich handeln muss, sondern nur um die zeitliche Entwicklung). Wenn z. B. die Energie eines Systems erhalten bleibt, ist seine Energie zu jedem Zeitpunkt unveränderlich, was eine Beschränkung für die Bewegung des Systems darstellt und bei der Lösung des Problems helfen kann. Abgesehen von den Einblicken, die solche Bewegungskonstanten in die Natur eines Systems geben, sind sie ein nützliches Berechnungsinstrument; beispielsweise kann eine Näherungslösung korrigiert werden, indem der nächstgelegene Zustand gefunden wird, der die geeigneten Erhaltungssätze erfüllt. ⓘ

Die ersten entdeckten Bewegungskonstanten waren Impuls und kinetische Energie, die im 17. Jahrhundert von René Descartes und Gottfried Leibniz auf der Grundlage von Kollisionsexperimenten vorgeschlagen und von späteren Forschern verfeinert wurden. Isaac Newton war der erste, der den Impulserhaltungssatz in seiner modernen Form formulierte und zeigte, dass er eine Folge des dritten Newtonschen Gesetzes ist. Nach der allgemeinen Relativitätstheorie sind die Erhaltungssätze für den linearen Impuls, die Energie und den Drehimpuls nur dann global korrekt, wenn sie durch die Summe des Spannungs-Energie-Tensors (nichtgravitative Spannungsenergie) und des Landau-Lifshitz-Spannungs-Energie-Impuls-Pseudotensors (gravitative Spannungsenergie) ausgedrückt werden. Die lokale Erhaltung des linearen Impulses und der Energie ohne Gravitation in einem frei fallenden Bezugssystem wird durch das Verschwinden der kovarianten Divergenz des Spannungs-Energie-Tensors ausgedrückt. Eine weitere wichtige konservierte Größe, die bei Studien zur Himmelsmechanik astronomischer Körper entdeckt wurde, ist der Laplace-Runge-Lenz-Vektor. ⓘ

Im späten 18. und frühen 19. Jahrhundert entwickelten die Physiker systematischere Methoden zur Entdeckung von Invarianten. Ein großer Fortschritt wurde 1788 mit der Entwicklung der Lagrangeschen Mechanik erzielt, die mit dem Prinzip der kleinsten Wirkung zusammenhängt. Bei diesem Ansatz kann der Zustand des Systems durch jede Art von verallgemeinerten Koordinaten q beschrieben werden; die Bewegungsgesetze müssen nicht in einem kartesischen Koordinatensystem ausgedrückt werden, wie es in der Newtonschen Mechanik üblich war. Die Wirkung ist definiert als das Zeitintegral I einer Funktion, die als Lagrangesche L ⓘ

$I=\int L(\mathbf {q} ,{\dot {\mathbf {q} }},t)\,dt~,$ ⓘ

wobei der Punkt über q die Änderungsrate der Koordinaten q angibt, ⓘ

${\dot {\mathbf {q} }}={\frac {d\mathbf {q} }{dt}}~.$ ⓘ

Das Hamilton-Prinzip besagt, dass der physikalische Pfad q(t) - derjenige, den das System tatsächlich durchläuft - ein Pfad ist, für den infinitesimale Variationen dieses Pfades keine Änderung von I verursachen, zumindest bis zur ersten Ordnung. Dieser Grundsatz führt zu den Euler-Lagrange-Gleichungen, ⓘ

${\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right)={\frac {\partial L}{\partial \mathbf {q} }}~.$ ⓘ

Wenn also eine der Koordinaten, z. B. qk, nicht in der Lagrange-Gleichung vorkommt, ist die rechte Seite der Gleichung Null, und die linke Seite erfordert, dass ⓘ

${\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {q}}_{k}}}\right)={\frac {dp_{k}}{dt}}=0~,$ ⓘ

wobei der Impuls ⓘ

$p_{k}={\frac {\partial L}{\partial {\dot {q}}_{k}}}$ ⓘ

während der gesamten Bewegung (auf dem physikalischen Weg) erhalten bleibt. ⓘ

Das Fehlen der ignorierbaren Koordinate qk in der Lagrange bedeutet also, dass die Lagrange von Änderungen oder Transformationen von qk unberührt bleibt; die Lagrange ist invariant und weist unter solchen Transformationen eine Symmetrie auf. Dies ist die Grundidee, die im Noether-Theorem verallgemeinert wird. ⓘ

Im 19. Jahrhundert wurden mehrere alternative Methoden zur Bestimmung konservierter Größen entwickelt, insbesondere von William Rowan Hamilton. So entwickelte er beispielsweise eine Theorie der kanonischen Transformationen, die es ermöglichte, die Koordinaten so zu verändern, dass einige Koordinaten aus der Lagrange verschwanden, wie oben beschrieben, was zu konservierten kanonischen Momenten führte. Ein anderer Ansatz, und vielleicht der effizienteste, um erhaltene Größen zu finden, ist die Hamilton-Jacobi-Gleichung. ⓘ

Mathematischer Ausdruck

Einfache Form mit Störung

Der Kern des Noether-Theorems ist die Verallgemeinerung der skizzierten ignorierbaren Koordinaten. ⓘ

Man kann davon ausgehen, dass die oben definierte Lagrange L unter kleinen Störungen (Warpings) der Zeitvariablen t und der verallgemeinerten Koordinaten q invariant ist. ⓘ

${\begin{aligned}t&\rightarrow t^{\prime }=t+\delta t\\\mathbf {q} &\rightarrow \mathbf {q} ^{\prime }=\mathbf {q} +\delta \mathbf {q} ~,\end{aligned}}$ ⓘ

wobei die Störungen δt und δq beide klein, aber variabel sind. Der Allgemeinheit halber nehmen wir an, dass es (sagen wir) N solcher Symmetrietransformationen der Wirkung gibt, d.h. Transformationen, die die Wirkung unverändert lassen; gekennzeichnet durch einen Index r = 1, 2, 3, ..., N. ⓘ

Dann kann die resultierende Störung als lineare Summe der einzelnen Störungsarten geschrieben werden,

${\begin{aligned}\delta t&=\sum _{r}\varepsilon _{r}T_{r}\\\delta \mathbf {q} &=\sum _{r}\varepsilon _{r}\mathbf {Q} _{r}~,\end{aligned}}$ ⓘ

wobei εr infinitesimale Parameterkoeffizienten sind, die den einzelnen:

• dem Generator Tr der Zeitentwicklung und
• Generators Qr der verallgemeinerten Koordinaten.

Für Translationen ist Qr eine Konstante mit Längeneinheiten; für Rotationen ist es ein Ausdruck, der linear in den Komponenten von q ist, und die Parameter bilden einen Winkel. ⓘ

Anhand dieser Definitionen zeigte Noether, dass die N Größen ⓘ

$\left({\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\cdot {\dot {\mathbf {q} }}-L\right)T_{r}-{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\cdot \mathbf {Q} _{r}$ ⓘ

konserviert sind (Bewegungskonstanten). ⓘ

Beispiele

I. Zeitinvarianz ⓘ

Zur Veranschaulichung betrachten wir eine Lagrange, die nicht von der Zeit abhängt, d. h. die bei Änderungen t → t + δt invariant (symmetrisch) ist, ohne dass sich die Koordinaten q ändern. In diesem Fall ist N = 1, T = 1 und Q = 0; die entsprechende erhaltene Größe ist die Gesamtenergie H ⓘ

$H={\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\cdot {\dot {\mathbf {q} }}-L.$ ⓘ

II. Translationsinvarianz ⓘ

Betrachten wir eine Lagrange, die nicht von einer ("ignorierbaren", wie oben) Koordinate q_k abhängt; sie ist also invariant (symmetrisch) unter Änderungen q_k → q_k + δq_k. In diesem Fall ist N = 1, T = 0 und Q_k = 1; die erhaltene Größe ist der entsprechende lineare Impuls p_{k ⓘ}

$p_{k}={\frac {\partial L}{\partial {\dot {q_{k}}}}}.$ ⓘ

In der speziellen und allgemeinen Relativitätstheorie sind diese scheinbar getrennten Erhaltungssätze Aspekte eines einzigen Erhaltungssatzes, nämlich des Spannungs-Energie-Tensors, der im nächsten Abschnitt abgeleitet wird. ⓘ

III. Rotationsinvarianz ⓘ

Die Erhaltung des Drehimpulses L = r × p ist analog zu seinem linearen Gegenstück, dem Drehimpuls. Es wird angenommen, dass die Lagrange rotationssymmetrisch ist, d. h. dass die Lagrange nicht von der absoluten Orientierung des physikalischen Systems im Raum abhängt. Nehmen wir zur Konkretisierung an, dass sich die Lagrange bei kleinen Drehungen um einen Winkel δθ um eine Achse n nicht ändert; eine solche Drehung transformiert die kartesischen Koordinaten durch die Gleichung ⓘ

$\mathbf {r} \rightarrow \mathbf {r} +\delta \theta \,\mathbf {n} \times \mathbf {r} .$ ⓘ

Da die Zeit nicht transformiert wird, ist T = 0, und N = 1. Nimmt man δθ als ε-Parameter und die kartesischen Koordinaten r als verallgemeinerte Koordinaten q, so sind die entsprechenden Q-Variablen gegeben durch ⓘ

$\mathbf {Q} =\mathbf {n} \times \mathbf {r} .$ ⓘ

Das Noether-Theorem besagt, dass die folgende Größe erhalten bleibt,

${\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\cdot \mathbf {Q} =\mathbf {p} \cdot \left(\mathbf {n} \times \mathbf {r} \right)=\mathbf {n} \cdot \left(\mathbf {r} \times \mathbf {p} \right)=\mathbf {n} \cdot \mathbf {L} .$ ⓘ

Mit anderen Worten, die Komponente des Drehimpulses L entlang der n-Achse ist konserviert. Und wenn n beliebig ist, d.h. wenn das System unempfindlich gegen jede Drehung ist, dann ist jede Komponente von L erhalten; kurz gesagt, der Drehimpuls ist erhalten. ⓘ

Version der Feldtheorie

Die soeben dargestellte Version des Noether-Satzes ist ein Spezialfall der 1915 abgeleiteten allgemeinen Version, auch wenn sie für sich genommen nützlich ist. Um den Geschmack des allgemeinen Satzes zu vermitteln, wird nun eine Version des Noether-Satzes für kontinuierliche Felder in einer vierdimensionalen Raumzeit gegeben. Da feldtheoretische Probleme in der modernen Physik häufiger vorkommen als mechanische Probleme, ist diese feldtheoretische Version die am häufigsten verwendete (oder am häufigsten implementierte) Version des Noether-Satzes. ⓘ

Es sei eine Menge von differenzierbaren Feldern $\varphi$ die über den gesamten Raum und die gesamte Zeit definiert sind; zum Beispiel wäre die Temperatur $T(\mathbf {x} ,t)$ wäre ein solches Feld, da sie eine an jedem Ort und zu jeder Zeit definierte Zahl ist. Das Prinzip der kleinsten Wirkung kann auf solche Felder angewendet werden, aber die Wirkung ist nun ein Integral über Raum und Zeit ⓘ

${\mathcal {S}}=\int {\mathcal {L}}\left(\varphi ,\partial _{\mu }\varphi ,x^{\mu }\right)\,d^{4}x$ ⓘ

(der Satz kann weiter verallgemeinert werden für den Fall, dass die Lagrange bis zur n-ten Ableitung abhängt, und kann auch mit Hilfe von Strahlbündeln formuliert werden). ⓘ

Eine kontinuierliche Transformation der Felder $\varphi$ kann infinitesimal geschrieben werden als ⓘ

$\varphi \mapsto \varphi +\varepsilon \Psi ,$ ⓘ

wobei $\Psi$ im Allgemeinen eine Funktion ist, die sowohl von $x^{\mu }$ und $\varphi$. Die Bedingung für $\Psi$ eine physikalische Symmetrie erzeugen kann, ist, dass die Wirkung ${\mathcal {S}}$ linksinvariant ist. Dies ist sicherlich der Fall, wenn die Lagrangesche Dichte ${\mathcal {L}}$ linksinvariant ist, aber auch, wenn sich die Lagrange durch eine Divergenz ändert, ⓘ

${\mathcal {L}}\mapsto {\mathcal {L}}+\varepsilon \partial _{\mu }\Lambda ^{\mu },$ ⓘ

denn das Integral einer Divergenz wird nach dem Divergenztheorem zu einem Randterm. Ein System, das durch eine bestimmte Aktion beschrieben wird, kann mehrere unabhängige Symmetrien dieser Art aufweisen, die durch $r=1,2,\ldots ,N,$ so dass die allgemeinste Symmetrietransformation wie folgt geschrieben werden kann ⓘ

$\varphi \mapsto \varphi +\varepsilon _{r}\Psi _{r},$ ⓘ

mit der Folge ⓘ

${\mathcal {L}}\mapsto {\mathcal {L}}+\varepsilon _{r}\partial _{\mu }\Lambda _{r}^{\mu }.$ ⓘ

Für solche Systeme besagt das Noether-Theorem, dass es Folgendes gibt $N$ konservierte Stromdichten ⓘ

$j_{r}^{\nu }=\Lambda _{r}^{\nu }-{\frac {\partial {\mathcal {L}}}{\partial \varphi _{,\nu }}}\cdot \Psi _{r}$ ⓘ

(wobei das Punktprodukt so verstanden wird, dass es die Feldindizes kontrahiert, nicht den $\nu$ Index oder $r$ Index). ⓘ

In solchen Fällen wird der Erhaltungssatz auf vierdimensionale Weise ausgedrückt ⓘ

$\partial _{\nu }j^{\nu }=0,$ ⓘ

was zum Ausdruck bringt, dass sich die Menge einer erhaltenen Menge innerhalb einer Kugel nicht ändern kann, wenn nicht etwas davon aus der Kugel herausfließt. Zum Beispiel ist die elektrische Ladung konserviert; die Menge der Ladung innerhalb einer Kugel kann sich nicht ändern, wenn nicht ein Teil der Ladung die Kugel verlässt. ⓘ

Betrachten wir zur Veranschaulichung ein physikalisches System von Feldern, das sich bei Translationen in Zeit und Raum, wie oben betrachtet, gleich verhält; mit anderen Worten, $L\left({\boldsymbol {\varphi }},\partial _{\mu }{\boldsymbol {\varphi }},x^{\mu }\right)$ ist in seinem dritten Argument konstant. In diesem Fall ist N = 4, eine für jede Dimension von Raum und Zeit. Eine infinitesimale Translation im Raum, $x^{\mu }\mapsto x^{\mu }+\varepsilon _{r}\delta _{r}^{\mu }$ (wobei $\delta$ bezeichnet das Kronecker-Delta), wirkt sich auf die Felder wie folgt aus $\varphi (x^{\mu })\mapsto \varphi \left(x^{\mu }-\varepsilon _{r}\delta _{r}^{\mu }\right)$Das heißt, die Umbenennung der Koordinaten ist gleichbedeutend mit der Beibehaltung der Koordinaten bei gleichzeitiger Verschiebung des Feldes selbst, was wiederum gleichbedeutend mit einer Transformation des Feldes ist, indem sein Wert in jedem Punkt $x^{\mu }$ durch den Wert des Punktes $x^{\mu }-\varepsilon X^{\mu }$ "dahinter" ersetzt wird, der auf $x^{\mu }$ durch die betrachtete infinitesimale Verschiebung. Da es sich um eine infinitesimale Verschiebung handelt, können wir diese Transformation wie folgt schreiben ⓘ

$\Psi _{r}=-\delta _{r}^{\mu }\partial _{\mu }\varphi .$ ⓘ

Die Lagrangesche Dichte transformiert sich auf die gleiche Weise, ${\mathcal {L}}\left(x^{\mu }\right)\mapsto {\mathcal {L}}\left(x^{\mu }-\varepsilon _{r}\delta _{r}^{\mu }\right)$also ⓘ

$\Lambda _{r}^{\mu }=-\delta _{r}^{\mu }{\mathcal {L}}$ ⓘ

und somit entspricht der Satz von Noether dem Erhaltungssatz für den Spannungs-Energie-Tensor T_μ^ν, wobei wir $\mu$ anstelle von $r$. Indem wir also den oben genannten Ausdruck verwenden und die vier erhaltenen Ströme (einen für jeden $\mu$) in einen Tensor $T$ergibt sich nach dem Noether-Theorem ⓘ

$T_{\mu }{}^{\nu }=-\delta _{\mu }^{\nu }{\mathcal {L}}+\delta _{\mu }^{\sigma }\partial _{\sigma }\varphi {\frac {\partial {\mathcal {L}}}{\partial \varphi _{,\nu }}}=\left({\frac {\partial {\mathcal {L}}}{\partial \varphi _{,\nu }}}\right)\cdot \varphi _{,\mu }-\delta _{\mu }^{\nu }{\mathcal {L}}$ ⓘ

mit ⓘ

$T_{\mu }{}^{\nu }{}_{,\nu }=0$ ⓘ

(wir umbenannt $\mu$ als $\sigma$ in einem Zwischenschritt, um Konflikte zu vermeiden). (Allerdings kann der $T$ kann sich jedoch von dem symmetrischen Tensor unterscheiden, der in der allgemeinen Relativitätstheorie als Quellterm verwendet wird; siehe Kanonischer Spannungs-Energie-Tensor.) ⓘ

Die Erhaltung der elektrischen Ladung kann dagegen abgeleitet werden, indem Ψ als linear in den Feldern φ und nicht in den Ableitungen betrachtet wird. In der Quantenmechanik ist die Wahrscheinlichkeitsamplitude ψ(x), ein Teilchen an einem Punkt x zu finden, ein komplexes Feld φ, weil es jedem Punkt in Raum und Zeit eine komplexe Zahl zuordnet. Die Wahrscheinlichkeitsamplitude selbst ist physikalisch nicht messbar; nur die Wahrscheinlichkeit p = |ψ|² kann aus einer Reihe von Messungen abgeleitet werden. Daher ist das System invariant gegenüber Transformationen des ψ-Feldes und seines konjugierten komplexen Feldes ψ^*, die |ψ|² unverändert lassen, wie z. B. ⓘ

$\psi \rightarrow e^{i\theta }\psi \ ,\ \psi ^{*}\rightarrow e^{-i\theta }\psi ^{*}~,$ ⓘ

eine komplexe Drehung. Im Grenzfall, wenn die Phase θ unendlich klein wird, δθ, kann sie als Parameter ε genommen werden, während die Ψ gleich iψ bzw. -iψ* sind. Ein konkretes Beispiel ist die Klein-Gordon-Gleichung, die relativistisch korrekte Version der Schrödinger-Gleichung für spinlose Teilchen, die die Lagrangedichte ⓘ

$L=\partial _{\nu }\psi \partial _{\mu }\psi ^{*}\eta ^{\nu \mu }+m^{2}\psi \psi ^{*}.$ ⓘ

In diesem Fall besagt das Noether-Theorem, dass der konservierte (∂ ⋅ j = 0) Strom gleich ist ⓘ

$j^{\nu }=i\left({\frac {\partial \psi }{\partial x^{\mu }}}\psi ^{*}-{\frac {\partial \psi ^{*}}{\partial x^{\mu }}}\psi \right)\eta ^{\nu \mu }~,$ ⓘ

was, multipliziert mit der Ladung dieser Teilchenart, die elektrische Stromdichte aufgrund dieser Teilchenart ergibt. Diese "Eichinvarianz" wurde erstmals von Hermann Weyl festgestellt und ist eine der prototypischen Eichsymmetrien der Physik. ⓘ

Ableitungen

Man sagt, dass eine Differentialgleichung eine Symmetrie besitzt, wenn es eine Transformation des Raumes der Kurven gibt, die die Lösungen der Differentialgleichungen auf Lösungen abbildet. Für variationell selbstadjungierte Differentialgleichungen erhält man eine solche Transformation, wenn die Transformation das Wirkungsfunktional bis auf Randterme invariant lässt. Das Noether-Theorem besagt, dass die Invarianz des Wirkungsfunktionals gegenüber einer einparametrigen stetigen Transformationsgruppe die Existenz einer Erhaltungsgröße zur Folge hat und dass umgekehrt jede Erhaltungsgröße die Existenz einer (mindestens infinitesimalen) Symmetrie der Wirkung zur Folge hat. ⓘ

Wir beschränken uns hier auf Symmetrien in der klassischen Mechanik. ⓘ

Sei $\Phi _{s}$ eine einparametrige, differenzierbare Gruppe von Transformationen, die (genügend differenzierbare) Kurven $\Gamma \colon t\mapsto x(t)$ auf Kurven $\Gamma _{s}\colon t\mapsto x(s,t,\Gamma )$ abbildet, und gehöre der Parameterwert $s=0$ zur identischen Abbildung, $\Phi _{0}\Gamma \colon t\mapsto x(t)$. ⓘ

Beispielsweise bildet $\Phi _{s}\Gamma =\Gamma _{s}$ mit $\Gamma _{s}\colon t\mapsto x(t+s)$ jede Kurve $\Gamma$ auf die um $s$ früher durchlaufene Kurve ab. Die Transformation $\Phi _{s}\Gamma =\Gamma _{s}$ mit $\Gamma _{s}\colon t\mapsto x(t)+s\,c$ verschiebt jede Kurve um eine Konstante $s\,c$. ⓘ

Die Transformationen $\Phi _{s}$ heißen lokal, wenn sich die Ableitung bei der identischen Abbildung, die infinitesimale Transformation ⓘ

${\frac {\partial }{\partial s}}_{|_{s=0}}x(s,t,\Gamma )\ ,$ ⓘ

für alle Kurven $\Gamma$ als Funktion $\delta x(t,x,v)$ der Zeit, des Ortes $x$ und der Geschwindigkeit $v$, ausgewertet auf der Kurve $\Gamma$, schreiben lässt, ⓘ

$\delta x\left(t,x(t),{\frac {\mathrm {d} x}{\mathrm {d} t}}\right)={\frac {\partial }{\partial s}}_{|_{s=0}}x(s,t,\Gamma )$. ⓘ

Beispielsweise sind die Verschiebungen von Zeit und Ort lokal und gehören zur infinitesimalen Transformation $\delta x=v$ beziehungsweise zu $\delta x=c$. ⓘ

Sei nun ${\mathcal {L}}(t,x,v)$ die Lagrangefunktion des mechanischen Systems. Dann heißen die lokalen Transformationen $\Phi _{s}$ Symmetrien der Wirkung, wenn sich für alle Kurven $\Gamma$ die Lagrangefunktion bei infinitesimalen Transformationen nur um die Zeitableitung einer Funktion $K(t,x)$, ausgewertet auf $\Gamma$, ändert:

${\frac {\partial }{\partial s}}_{|_{s=0}}{\mathcal {L}}\left(t,x(s,t),{\frac {\partial x}{\partial t}}(s,t)\right)={\frac {\mathrm {d} }{\mathrm {d} t}}K\left(t,x(t),{\frac {\partial x}{\partial t}}(t)\right)$ ⓘ

Denn dann ändert sich die Wirkung nur um Randterme ⓘ

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} s}}S[\Gamma _{s}]_{|_{s=0}}&=\int _{t_{1}}^{t_{2}}\mathrm {d} t\,{\frac {\partial }{\partial s}}_{|_{s=0}}{\mathcal {L}}\left(t,x(s,t),{\frac {\partial x}{\partial t}}(s,t)\right)\\&=\int _{t_{1}}^{t_{2}}\mathrm {d} t\,{\frac {\mathrm {d} }{\mathrm {d} t}}K\left(t,x(t)\right)=K\left(t_{2},x(t_{2})\right)-K\left(t_{1},x(t_{1})\right)\end{aligned}}$. ⓘ

Der Zusammenhang dieser Definition der Symmetrie der Wirkung mit der Erhaltungsgröße wird klar, wenn man die partiellen Ableitungen der Lagrangefunktion nach $s$ ausführt, und dabei als Kurzschrift die Definition der infinitesimalen Transformation verwendet ⓘ

${\begin{aligned}{\frac {\partial }{\partial s}}_{|_{s=0}}{\mathcal {L}}(t,x(s,t),{\frac {\partial x}{\partial t}}(s,t))&={\frac {\partial x(s,t)}{\partial s}}_{|_{s=0}}{\frac {\partial }{\partial x}}{\mathcal {L}}(t,x,v)+{\frac {\partial ^{2}x(s,t)}{\partial s\partial t}}_{|_{s=0}}{\frac {\partial }{\partial v}}{\mathcal {L}}(t,x,v)\\&=\delta x{\frac {\partial }{\partial x}}{\mathcal {L}}(t,x,v)+{\frac {\mathrm {d} \delta x}{\mathrm {d} t}}{\frac {\partial }{\partial v}}{\mathcal {L}}(t,x,v)\end{aligned}}$ ⓘ

Ergänzt man den ersten Term zu einem Vielfachen der Bewegungsgleichung und zieht man die Ergänzung beim zweiten Term ab, entsteht ⓘ

${\frac {\partial }{\partial s}}_{|_{s=0}}{\mathcal {L}}\left(t,x(s,t),{\frac {\partial x}{\partial t}}(s,t)\right)=\delta x\left({\frac {\partial }{\partial x}}{\mathcal {L}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial }{\partial v}}{\mathcal {L}}\right)+{\frac {\mathrm {d} }{\mathrm {d} t}}\left(\delta x{\frac {\partial }{\partial v}}{\mathcal {L}}\right)$ ⓘ

und die Definitionsgleichung einer infinitesimalen Symmetrie einer Wirkung lautet ⓘ

$\delta x\left({\frac {\partial }{\partial x}}{\mathcal {L}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial }{\partial v}}{\mathcal {L}}\right)+{\frac {\mathrm {d} }{\mathrm {d} t}}\left(\delta x{\frac {\partial }{\partial v}}{\mathcal {L}}-K\right)=0$. ⓘ

Da aber das $\delta x$-Fache der Bewegungsgleichungen auf den physikalisch durchlaufenen Bahnen verschwindet, besagt diese Gleichung, dass die Funktion ⓘ

$Q=\delta x{\frac {\partial }{\partial v}}{\mathcal {L}}-K$, ⓘ

die zur Symmetrie gehörige Noetherladung, sich auf den physikalisch durchlaufenen Bahnen nicht ändert:

${\frac {\mathrm {d} }{\mathrm {d} t}}Q\left(t,x_{\mathrm {phys} }(t),{\frac {\mathrm {d} x_{\mathrm {phys} }(t)}{\mathrm {d} t}}\right)=0$ ⓘ

Umgekehrt ist jede Erhaltungsgröße definitionsgemäß eine Funktion $Q(t,x,v)$, deren Zeitableitung auf physikalischen Bahnen verschwindet, also ein Vielfaches (von Ableitungen) der Bewegungsgleichungen ist. Dieses Vielfache definiert die infinitesimale Symmetrie $\delta x$. ⓘ

Eine unabhängige Variable

Betrachten wir den einfachsten Fall, ein System mit einer unabhängigen Variablen, der Zeit. Angenommen, die abhängigen Variablen q sind so beschaffen, dass das Wirkungsintegral ⓘ

$$I=\int _{t_{1}}^{t_{2}}L[\mathbf {q} [t],{\dot {\mathbf {q} }}[t],t]\,dt$$

ⓘ

bei kurzen infinitesimalen Änderungen der abhängigen Variablen invariant ist. Mit anderen Worten, sie erfüllen die Euler-Lagrange-Gleichungen ⓘ

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}[t]={\frac {\partial L}{\partial \mathbf {q} }}[t].$ ⓘ

Und nehmen wir an, dass das Integral unter einer kontinuierlichen Symmetrie invariant ist. Mathematisch wird eine solche Symmetrie als ein Fluss φ dargestellt, der auf die Variablen wie folgt wirkt ⓘ

${\begin{aligned}t&\rightarrow t'=t+\varepsilon T\\\mathbf {q} [t]&\rightarrow \mathbf {q} '[t']=\varphi [\mathbf {q} [t],\varepsilon ]=\varphi [\mathbf {q} [t'-\varepsilon T],\varepsilon ]\end{aligned}}$ ⓘ

wobei ε eine reelle Variable ist, die den Betrag des Flusses angibt, und T eine reelle Konstante ist (die Null sein kann), die angibt, wie sehr der Fluss die Zeit verschiebt. ⓘ

${\dot {\mathbf {q} }}[t]\rightarrow {\dot {\mathbf {q} }}'[t']={\frac {d}{dt}}\varphi [\mathbf {q} [t],\varepsilon ]={\frac {\partial \varphi }{\partial \mathbf {q} }}[\mathbf {q} [t'-\varepsilon T],\varepsilon ]{\dot {\mathbf {q} }}[t'-\varepsilon T].$ ⓘ

Das Wirkungsintegral fließt zu ⓘ

${\begin{aligned}I'[\varepsilon ]&=\int _{t_{1}+\varepsilon T}^{t_{2}+\varepsilon T}L[\mathbf {q} '[t'],{\dot {\mathbf {q} }}'[t'],t']\,dt'\\[6pt]&=\int _{t_{1}+\varepsilon T}^{t_{2}+\varepsilon T}L[\varphi [\mathbf {q} [t'-\varepsilon T],\varepsilon ],{\frac {\partial \varphi }{\partial \mathbf {q} }}[\mathbf {q} [t'-\varepsilon T],\varepsilon ]{\dot {\mathbf {q} }}[t'-\varepsilon T],t']\,dt'\end{aligned}}$ ⓘ

das als eine Funktion von ε betrachtet werden kann. Berechnet man die Ableitung bei ε = 0 und verwendet die Leibnizsche Regel, so erhält man ⓘ

${\begin{aligned}0={\frac {dI'}{d\varepsilon }}[0]={}&L[\mathbf {q} [t_{2}],{\dot {\mathbf {q} }}[t_{2}],t_{2}]T-L[\mathbf {q} [t_{1}],{\dot {\mathbf {q} }}[t_{1}],t_{1}]T\\[6pt]&{}+\int _{t_{1}}^{t_{2}}{\frac {\partial L}{\partial \mathbf {q} }}\left(-{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}T+{\frac {\partial \varphi }{\partial \varepsilon }}\right)+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\left(-{\frac {\partial ^{2}\varphi }{(\partial \mathbf {q} )^{2}}}{\dot {\mathbf {q} }}^{2}T+{\frac {\partial ^{2}\varphi }{\partial \varepsilon \partial \mathbf {q} }}{\dot {\mathbf {q} }}-{\frac {\partial \varphi }{\partial \mathbf {q} }}{\ddot {\mathbf {q} }}T\right)\,dt.\end{aligned}}$ ⓘ

Beachten Sie, dass die Euler-Lagrange-Gleichungen Folgendes implizieren ⓘ

${\begin{aligned}{\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}T\right)&=\left({\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right){\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}T+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\left({\frac {d}{dt}}{\frac {\partial \varphi }{\partial \mathbf {q} }}\right){\dot {\mathbf {q} }}T+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\ddot {\mathbf {q} }}\,T\\[6pt]&={\frac {\partial L}{\partial \mathbf {q} }}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}T+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\left({\frac {\partial ^{2}\varphi }{(\partial \mathbf {q} )^{2}}}{\dot {\mathbf {q} }}\right){\dot {\mathbf {q} }}T+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\ddot {\mathbf {q} }}\,T.\end{aligned}}$ ⓘ

Setzt man dies in die vorherige Gleichung ein, erhält man ⓘ

${\begin{aligned}0={\frac {dI'}{d\varepsilon }}[0]={}&L[\mathbf {q} [t_{2}],{\dot {\mathbf {q} }}[t_{2}],t_{2}]T-L[\mathbf {q} [t_{1}],{\dot {\mathbf {q} }}[t_{1}],t_{1}]T-{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}[t_{2}]T+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}[t_{1}]T\\[6pt]&{}+\int _{t_{1}}^{t_{2}}{\frac {\partial L}{\partial \mathbf {q} }}{\frac {\partial \varphi }{\partial \varepsilon }}+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial ^{2}\varphi }{\partial \varepsilon \partial \mathbf {q} }}{\dot {\mathbf {q} }}\,dt.\end{aligned}}$ ⓘ

Wiederum unter Verwendung der Euler-Lagrange-Gleichungen erhalten wir ⓘ

${\frac {d}{dt}}\left({\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \varepsilon }}\right)=\left({\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}\right){\frac {\partial \varphi }{\partial \varepsilon }}+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial ^{2}\varphi }{\partial \varepsilon \partial \mathbf {q} }}{\dot {\mathbf {q} }}={\frac {\partial L}{\partial \mathbf {q} }}{\frac {\partial \varphi }{\partial \varepsilon }}+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial ^{2}\varphi }{\partial \varepsilon \partial \mathbf {q} }}{\dot {\mathbf {q} }}.$ ⓘ

Setzt man dies in die vorherige Gleichung ein, erhält man ⓘ

${\begin{aligned}0={}&L[\mathbf {q} [t_{2}],{\dot {\mathbf {q} }}[t_{2}],t_{2}]T-L[\mathbf {q} [t_{1}],{\dot {\mathbf {q} }}[t_{1}],t_{1}]T-{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}[t_{2}]T+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}[t_{1}]T\\[6pt]&{}+{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \varepsilon }}[t_{2}]-{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \varepsilon }}[t_{1}].\end{aligned}}$ ⓘ

Daraus kann man ersehen, dass ⓘ

$\left({\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \mathbf {q} }}{\dot {\mathbf {q} }}-L\right)T-{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \varepsilon }}$ ⓘ

eine Konstante der Bewegung ist, d. h. sie ist eine konservierte Größe. Da φ[q, 0] = q ist, erhalten wir ${\frac {\partial \varphi }{\partial \mathbf {q} }}=1$ und somit vereinfacht sich die Erhaltungsgröße zu ⓘ

$\left({\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\dot {\mathbf {q} }}-L\right)T-{\frac {\partial L}{\partial {\dot {\mathbf {q} }}}}{\frac {\partial \varphi }{\partial \varepsilon }}.$ ⓘ

Um die Formeln nicht zu sehr zu verkomplizieren, wurde bei dieser Herleitung davon ausgegangen, dass sich der Fluss im Laufe der Zeit nicht ändert. Das gleiche Ergebnis kann im allgemeineren Fall erzielt werden. ⓘ

Feldtheoretische Herleitung

Der Satz von Noether kann auch für Tensorfelder φ^A abgeleitet werden, wobei der Index A die verschiedenen Komponenten der verschiedenen Tensorfelder umfasst. Diese Feldgrößen sind Funktionen, die über einen vierdimensionalen Raum definiert sind, dessen Punkte durch Koordinaten x^μ gekennzeichnet sind, wobei der Index μ für die Zeit (μ = 0) und drei räumliche Dimensionen (μ = 1, 2, 3) gilt. Diese vier Koordinaten sind die unabhängigen Variablen, und die Werte der Felder bei jedem Ereignis sind die abhängigen Variablen. Bei einer infinitesimalen Transformation wird die Veränderung der Koordinaten wie folgt geschrieben ⓘ

$x^{\mu }\rightarrow \xi ^{\mu }=x^{\mu }+\delta x^{\mu }$ ⓘ

während die Transformation der Feldvariablen wie folgt ausgedrückt wird ⓘ

$\varphi ^{A}\rightarrow \alpha ^{A}\left(\xi ^{\mu }\right)=\varphi ^{A}\left(x^{\mu }\right)+\delta \varphi ^{A}\left(x^{\mu }\right)\,.$ ⓘ

Nach dieser Definition ergeben sich die Feldänderungen δφ^A aus zwei Faktoren: intrinsische Änderungen des Feldes selbst und Änderungen der Koordinaten, da das transformierte Feld α^A von den transformierten Koordinaten ξ^μ abhängt. Um die intrinsischen Änderungen zu isolieren, kann die Feldänderung an einem einzelnen Punkt x^μ definiert werden ⓘ

$\alpha ^{A}\left(x^{\mu }\right)=\varphi ^{A}\left(x^{\mu }\right)+{\bar {\delta }}\varphi ^{A}\left(x^{\mu }\right)\,.$ ⓘ

Werden die Koordinaten geändert, so ändert sich auch die Grenze des Raum-Zeit-Bereichs, über den die Lagrange integriert wird; die ursprüngliche Grenze und ihre transformierte Version werden mit Ω bzw. Ω' bezeichnet. ⓘ

Der Satz von Noether geht von der Annahme aus, dass eine bestimmte Transformation der Koordinaten und Feldvariablen die Wirkung nicht verändert, die als Integral der Lagrangeschen Dichte über die gegebene Raumzeitregion definiert ist. Mathematisch ausgedrückt kann diese Annahme wie folgt formuliert werden ⓘ

$\int _{\Omega ^{\prime }}L\left(\alpha ^{A},{\alpha ^{A}}_{,\nu },\xi ^{\mu }\right)d^{4}\xi -\int _{\Omega }L\left(\varphi ^{A},{\varphi ^{A}}_{,\nu },x^{\mu }\right)d^{4}x=0$ ⓘ

wobei das tiefgestellte Komma eine partielle Ableitung in Bezug auf die Koordinate(n) nach dem Komma angibt, z. B. ⓘ

${\varphi ^{A}}_{,\sigma }={\frac {\partial \varphi ^{A}}{\partial x^{\sigma }}}\,.$ ⓘ

Da ξ eine Dummy-Variable der Integration ist und die Änderung der Grenze Ω per Annahme infinitesimal ist, können die beiden Integrale unter Verwendung der vierdimensionalen Version des Divergenztheorems in der folgenden Form kombiniert werden ⓘ

$\int _{\Omega }\left\{\left[L\left(\alpha ^{A},{\alpha ^{A}}_{,\nu },x^{\mu }\right)-L\left(\varphi ^{A},{\varphi ^{A}}_{,\nu },x^{\mu }\right)\right]+{\frac {\partial }{\partial x^{\sigma }}}\left[L\left(\varphi ^{A},{\varphi ^{A}}_{,\nu },x^{\mu }\right)\delta x^{\sigma }\right]\right\}d^{4}x=0\,.$ ⓘ

Die Differenz der Lagrangeschen kann in den infinitesimalen Variationen erster Ordnung geschrieben werden als ⓘ

$\left[L\left(\alpha ^{A},{\alpha ^{A}}_{,\nu },x^{\mu }\right)-L\left(\varphi ^{A},{\varphi ^{A}}_{,\nu },x^{\mu }\right)\right]={\frac {\partial L}{\partial \varphi ^{A}}}{\bar {\delta }}\varphi ^{A}+{\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}{\bar {\delta }}{\varphi ^{A}}_{,\sigma }\,.$ ⓘ

Da die Variationen jedoch, wie oben beschrieben, am selben Punkt definiert sind, können die Variation und die Ableitung in umgekehrter Reihenfolge durchgeführt werden; sie sind kommutativ ⓘ

${\bar {\delta }}{\varphi ^{A}}_{,\sigma }={\bar {\delta }}{\frac {\partial \varphi ^{A}}{\partial x^{\sigma }}}={\frac {\partial }{\partial x^{\sigma }}}\left({\bar {\delta }}\varphi ^{A}\right)\,.$ ⓘ

Unter Verwendung der Euler-Lagrange-Feldgleichungen ⓘ

${\frac {\partial }{\partial x^{\sigma }}}\left({\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}\right)={\frac {\partial L}{\partial \varphi ^{A}}}$ ⓘ

kann die Differenz der Lagrangeschen Gleichungen wie folgt geschrieben werden ⓘ

${\begin{aligned}&\left[L\left(\alpha ^{A},{\alpha ^{A}}_{,\nu },x^{\mu }\right)-L\left(\varphi ^{A},{\varphi ^{A}}_{,\nu },x^{\mu }\right)\right]\\[4pt]={}&{\frac {\partial }{\partial x^{\sigma }}}\left({\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}\right){\bar {\delta }}\varphi ^{A}+{\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}{\bar {\delta }}{\varphi ^{A}}_{,\sigma }={\frac {\partial }{\partial x^{\sigma }}}\left({\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}{\bar {\delta }}\varphi ^{A}\right).\end{aligned}}$ ⓘ

Die Änderung der Wirkung kann also wie folgt geschrieben werden ⓘ

$\int _{\Omega }{\frac {\partial }{\partial x^{\sigma }}}\left\{{\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}{\bar {\delta }}\varphi ^{A}+L\left(\varphi ^{A},{\varphi ^{A}}_{,\nu },x^{\mu }\right)\delta x^{\sigma }\right\}d^{4}x=0\,.$ ⓘ

Da dies für jede Region Ω gilt, muss der Integrand gleich Null sein ⓘ

${\frac {\partial }{\partial x^{\sigma }}}\left\{{\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}{\bar {\delta }}\varphi ^{A}+L\left(\varphi ^{A},{\varphi ^{A}}_{,\nu },x^{\mu }\right)\delta x^{\sigma }\right\}=0\,.$ ⓘ

Für jede Kombination der verschiedenen Symmetrietransformationen kann die Störung wie folgt geschrieben werden ⓘ

${\begin{aligned}\delta x^{\mu }&=\varepsilon X^{\mu }\\\delta \varphi ^{A}&=\varepsilon \Psi ^{A}={\bar {\delta }}\varphi ^{A}+\varepsilon {\mathcal {L}}_{X}\varphi ^{A}\end{aligned}}$ ⓘ

wobei ${\mathcal {L}}_{X}\varphi ^{A}$ ist die Lie-Ableitung von φA in X^μ-Richtung. Wenn φA ein Skalar ist oder ${X^{\mu }}_{,\nu }=0$, ⓘ

${\mathcal {L}}_{X}\varphi ^{A}={\frac {\partial \varphi ^{A}}{\partial x^{\mu }}}X^{\mu }\,.$ ⓘ

Diese Gleichungen implizieren, dass die Feldvariation in einem Punkt gleich ist ⓘ

${\bar {\delta }}\varphi ^{A}=\varepsilon \Psi ^{A}-\varepsilon {\mathcal {L}}_{X}\varphi ^{A}\,.$ ⓘ

Differenziert man die obige Divergenz nach ε bei ε = 0 und ändert das Vorzeichen, so erhält man den Erhaltungssatz ⓘ

${\frac {\partial }{\partial x^{\sigma }}}j^{\sigma }=0$ ⓘ

wobei der Erhaltungsstrom gleich ist ⓘ

$j^{\sigma }=\left[{\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}{\mathcal {L}}_{X}\varphi ^{A}-L\,X^{\sigma }\right]-\left({\frac {\partial L}{\partial {\varphi ^{A}}_{,\sigma }}}\right)\Psi ^{A}\,.$ ⓘ

Ableitung der Mannigfaltigkeit/Faserbündel

Angenommen, wir haben eine n-dimensionale orientierte Riemannsche Mannigfaltigkeit M und eine Zielmannigfaltigkeit T. Sei ${\mathcal {C}}$ sei der Konfigurationsraum der glatten Funktionen von M nach T. (Allgemeiner ausgedrückt, können wir glatte Abschnitte eines Faserbündels über M haben.) ⓘ

Beispiele für dieses M in der Physik sind:

• In der klassischen Mechanik ist M in der Hamilton-Formulierung die eindimensionale Mannigfaltigkeit $\mathbb {R}$die die Zeit darstellt, und der Zielraum ist das Kotangensbündel des Raums der verallgemeinerten Positionen.
• In der Feldtheorie ist M die Mannigfaltigkeit der Raumzeit und der Zielraum ist die Menge der Werte, die die Felder an jedem beliebigen Punkt annehmen können. Wenn es zum Beispiel m reelle Skalarfelder gibt, $\varphi _{1},\ldots ,\varphi _{m}$dann ist die Ziel-Mannigfaltigkeit $\mathbb {R} ^{m}$. Wenn das Feld ein reelles Vektorfeld ist, dann ist die Zielmannigfaltigkeit isomorph zu $\mathbb {R} ^{3}$. ⓘ

Nehmen wir nun an, es gibt ein Funktional ⓘ

${\mathcal {S}}:{\mathcal {C}}\rightarrow \mathbb {R} ,$ ⓘ

genannt die Aktion. (Es nimmt Werte in $\mathbb {R}$und nicht $\mathbb {C}$ein; dies hat physikalische Gründe und ist für diesen Beweis unwichtig.) ⓘ

Um die übliche Version des Noether-Satzes zu erhalten, brauchen wir zusätzliche Einschränkungen für die Wirkung. Wir nehmen an ${\mathcal {S}}[\varphi ]$ ist das Integral über M einer Funktion ⓘ

${\mathcal {L}}(\varphi ,\partial _{\mu }\varphi ,x)$ ⓘ

genannt Lagrangesche Dichte, abhängig von φ, ihrer Ableitung und der Position. Mit anderen Worten, für φ in ${\mathcal {C}}$ ⓘ

${\mathcal {S}}[\varphi ]\,=\,\int _{M}{\mathcal {L}}[\varphi (x),\partial _{\mu }\varphi (x),x]\,d^{n}x.$ ⓘ

Nehmen wir an, es sind Randbedingungen gegeben, d. h. eine Spezifikation des Wertes von φ am Rand, wenn M kompakt ist, oder ein Grenzwert für φ, wenn x sich ∞ nähert. Dann ist der Unterraum von ${\mathcal {C}}$ der aus solchen Funktionen φ besteht, dass alle funktionalen Ableitungen von ${\mathcal {S}}$ bei φ gleich Null sind, d. h:

${\frac {\delta {\mathcal {S}}[\varphi ]}{\delta \varphi (x)}}\approx 0$ ⓘ

und dass φ die gegebenen Randbedingungen erfüllt, ist der Unterraum von on shell solutions. (Siehe Prinzip der stationären Wirkung) ⓘ

Nehmen wir nun an, wir haben eine infinitesimale Transformation auf ${\mathcal {C}}$, erzeugt durch eine funktionale Ableitung, Q, so dass ⓘ

$Q\left[\int _{N}{\mathcal {L}}\,\mathrm {d} ^{n}x\right]\approx \int _{\partial N}f^{\mu }[\varphi (x),\partial \varphi ,\partial \partial \varphi ,\ldots ]\,ds_{\mu }$ ⓘ

für alle kompakten Untermannigfaltigkeiten N oder mit anderen Worten, ⓘ

$Q[{\mathcal {L}}(x)]\approx \partial _{\mu }f^{\mu }(x)$ ⓘ

für alle x, wobei wir setzen ⓘ

${\mathcal {L}}(x)={\mathcal {L}}[\varphi (x),\partial _{\mu }\varphi (x),x].$ ⓘ

Wenn dies auf der Schale und außerhalb der Schale gilt, sagen wir, dass Q eine Symmetrie außerhalb der Schale erzeugt. Wenn dies nur auf der Schale gilt, sagen wir, Q erzeugt eine On-Shell-Symmetrie. Dann sagen wir, dass Q ein Generator einer Ein-Parameter-Symmetrie-Lie-Gruppe ist. ⓘ

Aufgrund des Euler-Lagrange-Theorems gilt nun für jedes N auf der Schale (und nur auf der Schale) ⓘ

${\begin{aligned}Q\left[\int _{N}{\mathcal {L}}\,\mathrm {d} ^{n}x\right]&=\int _{N}\left[{\frac {\partial {\mathcal {L}}}{\partial \varphi }}-\partial _{\mu }{\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\varphi )}}\right]Q[\varphi ]\,\mathrm {d} ^{n}x+\int _{\partial N}{\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\varphi )}}Q[\varphi ]\,\mathrm {d} s_{\mu }\\&\approx \int _{\partial N}f^{\mu }\,\mathrm {d} s_{\mu }.\end{aligned}}$ ⓘ

Da dies für jedes N gilt, haben wir ⓘ

$\partial _{\mu }\left[{\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\varphi )}}Q[\varphi ]-f^{\mu }\right]\approx 0.$ ⓘ

Dies ist jedoch die Kontinuitätsgleichung für den Strom $J^{\mu }$ definiert durch:

$J^{\mu }\,=\,{\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\varphi )}}Q[\varphi ]-f^{\mu },$ ⓘ

Diese wird als die mit der Symmetrie verbundene Noether-Strömung" bezeichnet. Die Kontinuitätsgleichung besagt, dass die Integration dieses Stroms über eine raumähnliche Scheibe eine konservierte Größe, die Noether-Ladung, ergibt (vorausgesetzt natürlich, dass die Ströme im Unendlichen hinreichend schnell abfallen, wenn M nicht kompakt ist). ⓘ

Verallgemeinerung auf Lie-Algebren

Angenommen, wir haben zwei Symmetrieableitungen Q₁ und Q₂. Dann ist [Q₁, Q₂] auch eine Symmetrieableitung. Wir wollen dies explizit sehen. Sagen wir

$$Q_{1}[{\mathcal {L}}]\approx \partial _{\mu }f_{1}^{\mu }$$

und

$$Q_{2}[{\mathcal {L}}]\approx \partial _{\mu }f_{2}^{\mu }$$

ⓘ

dann,

$$[Q_{1},Q_{2}][{\mathcal {L}}]=Q_{1}[Q_{2}[{\mathcal {L}}]]-Q_{2}[Q_{1}[{\mathcal {L}}]]\approx \partial _{\mu }f_{12}^{\mu }$$

wobei f₁₂ = Q₁[f₂^μ] - Q₂[f₁^μ]. So,

$$j_{12}^{\mu }=\left({\frac {\partial }{\partial (\partial _{\mu }\varphi )}}{\mathcal {L}}\right)(Q_{1}[Q_{2}[\varphi ]]-Q_{2}[Q_{1}[\varphi ]])-f_{12}^{\mu }.$$

ⓘ

Dies zeigt, dass wir den Satz von Noether auf natürliche Weise auf größere Lie-Algebren erweitern können. ⓘ

Verallgemeinerung des Beweises

Dies gilt für jede lokale Symmetrieableitung Q, die QS ≈ 0 erfüllt, und auch für allgemeinere lokale funktional differenzierbare Aktionen, einschließlich solcher, bei denen die Lagrange von höheren Ableitungen der Felder abhängt. Sei ε eine beliebige glatte Funktion der Raumzeit- (oder Zeit-) Mannigfaltigkeit, so dass der Abschluss ihres Trägers disjunkt vom Rand ist. ε ist eine Testfunktion. Aufgrund des Variationsprinzips (das übrigens nicht für den Rand gilt) erfüllt die durch q[ε][Φ(x)] = ε(x)Q[Φ(x)] erzeugte Ableitungsverteilung q die Bedingung q[ε][S] ≈ 0 für jedes ε, oder kompakter: q(x)[S] ≈ 0 für alle x, die nicht auf dem Rand liegen (aber denken Sie daran, dass q(x) eine Abkürzung für eine Ableitungs-Verteilung ist, nicht für eine durch x parametrisierte Ableitung im Allgemeinen). Dies ist die Verallgemeinerung des Noetherschen Satzes. ⓘ

Um zu sehen, wie die Verallgemeinerung mit der obigen Version zusammenhängt, nehmen wir an, dass die Wirkung das Raumzeitintegral einer Lagrange ist, die nur von φ und ihren ersten Ableitungen abhängt. Nehmen Sie außerdem an ⓘ

$Q[{\mathcal {L}}]\approx \partial _{\mu }f^{\mu }$ ⓘ

dann, ⓘ

${\begin{aligned}q[\varepsilon ][{\mathcal {S}}]&=\int q[\varepsilon ][{\mathcal {L}}]d^{n}x\\[6pt]&=\int \left\{\left({\frac {\partial }{\partial \varphi }}{\mathcal {L}}\right)\varepsilon Q[\varphi ]+\left[{\frac {\partial }{\partial (\partial _{\mu }\varphi )}}{\mathcal {L}}\right]\partial _{\mu }(\varepsilon Q[\varphi ])\right\}d^{n}x\\[6pt]&=\int \left\{\varepsilon Q[{\mathcal {L}}]+\partial _{\mu }\varepsilon \left[{\frac {\partial }{\partial \left(\partial _{\mu }\varphi \right)}}{\mathcal {L}}\right]Q[\varphi ]\right\}\,d^{n}x\\[6pt]&\approx \int \varepsilon \partial _{\mu }\left\{f^{\mu }-\left[{\frac {\partial }{\partial (\partial _{\mu }\varphi )}}{\mathcal {L}}\right]Q[\varphi ]\right\}\,d^{n}x\end{aligned}}$ ⓘ

für alle $\varepsilon$. ⓘ

Allgemeiner ausgedrückt, wenn die Lagrange von höheren Ableitungen abhängt, dann ⓘ

$\partial _{\mu }\left[f^{\mu }-\left[{\frac {\partial }{\partial (\partial _{\mu }\varphi )}}{\mathcal {L}}\right]Q[\varphi ]-2\left[{\frac {\partial }{\partial (\partial _{\mu }\partial _{\nu }\varphi )}}{\mathcal {L}}\right]\partial _{\nu }Q[\varphi ]+\partial _{\nu }\left[\left[{\frac {\partial }{\partial (\partial _{\mu }\partial _{\nu }\varphi )}}{\mathcal {L}}\right]Q[\varphi ]\right]-\,\dotsm \right]\approx 0.$ ⓘ

Beispiele

Beispiel 1: Energieerhaltung

Betrachten wir den speziellen Fall eines Newtonschen Teilchens der Masse m, Koordinate x, das sich unter dem Einfluss eines Potentials V bewegt, koordiniert durch die Zeit t. Die Wirkung S ist:

${\begin{aligned}{\mathcal {S}}[x]&=\int L\left[x(t),{\dot {x}}(t)\right]\,dt\\&=\int \left({\frac {m}{2}}\sum _{i=1}^{3}{\dot {x}}_{i}^{2}-V(x(t))\right)\,dt.\end{aligned}}$ ⓘ

Der erste Term in den Klammern ist die kinetische Energie des Teilchens, der zweite ist seine potentielle Energie. Betrachten wir den Generator der Zeitverschiebungen Q = d/dt. Mit anderen Worten, $Q[x(t)]={\dot {x}}(t)$. Die Koordinate x hat eine explizite Abhängigkeit von der Zeit, während V keine hat; folglich:

$Q[L]={\frac {d}{dt}}\left[{\frac {m}{2}}\sum _{i}{\dot {x}}_{i}^{2}-V(x)\right]=m\sum _{i}{\dot {x}}_{i}{\ddot {x}}_{i}-\sum _{i}{\frac {\partial V(x)}{\partial x_{i}}}{\dot {x}}_{i}$ ⓘ

Wir können also setzen ⓘ

$L={\frac {m}{2}}\sum _{i}{\dot {x}}_{i}^{2}-V(x).$ ⓘ

dann, ⓘ

${\begin{aligned}j&=\sum _{i=1}^{3}{\frac {\partial L}{\partial {\dot {x}}_{i}}}Q[x_{i}]-L\\&=m\sum _{i}{\dot {x}}_{i}^{2}-\left[{\frac {m}{2}}\sum _{i}{\dot {x}}_{i}^{2}-V(x)\right]\\[3pt]&={\frac {m}{2}}\sum _{i}{\dot {x}}_{i}^{2}+V(x).\end{aligned}}$ ⓘ

Die rechte Seite ist die Energie, und das Noether-Theorem besagt, dass $dj/dt=0$ (d.h. der Grundsatz der Energieerhaltung ist eine Folge der Invarianz unter Zeittranslation). ⓘ

Allgemeiner ausgedrückt: Wenn die Lagrange nicht explizit von der Zeit abhängt, ist die Größe ⓘ

$\sum _{i=1}^{3}{\frac {\partial L}{\partial {\dot {x}}_{i}}}{\dot {x_{i}}}-L$ ⓘ

(der so genannte Hamiltonian) konserviert. ⓘ

Beispiel 2: Erhaltung des Schwerpunkts des Impulses

Betrachten wir weiterhin die 1-dimensionale Zeit, so sei ⓘ

${\begin{aligned}{\mathcal {S}}\left[{\vec {x}}\right]&=\int {\mathcal {L}}\left[{\vec {x}}(t),{\dot {\vec {x}}}(t)\right]dt\\[3pt]&=\int \left[\sum _{\alpha =1}^{N}{\frac {m_{\alpha }}{2}}\left({\dot {\vec {x}}}_{\alpha }\right)^{2}-\sum _{\alpha <\beta }V_{\alpha \beta }\left({\vec {x}}_{\beta }-{\vec {x}}_{\alpha }\right)\right]dt,\end{aligned}}$ ⓘ

oder $N$ Newtonsche Teilchen, bei denen das Potenzial nur paarweise von der relativen Verschiebung abhängt. ⓘ

Für ${\vec {Q}}$betrachten wir den Generator der Galilei-Transformationen (d. h. eine Änderung des Bezugssystems). Mit anderen Worten, ⓘ

$Q_{i}\left[x_{\alpha }^{j}(t)\right]=t\delta _{i}^{j}.$ ⓘ

Und ⓘ

${\begin{aligned}Q_{i}[{\mathcal {L}}]&=\sum _{\alpha }m_{\alpha }{\dot {x}}_{\alpha }^{i}-\sum _{\alpha <\beta }t\partial _{i}V_{\alpha \beta }\left({\vec {x}}_{\beta }-{\vec {x}}_{\alpha }\right)\\&=\sum _{\alpha }m_{\alpha }{\dot {x}}_{\alpha }^{i}.\end{aligned}}$ ⓘ

Dies hat die Form von ${\textstyle {\frac {d}{dt}}\sum _{\alpha }m_{\alpha }x_{\alpha }^{i}}$ Wir können also setzen ⓘ

${\vec {f}}=\sum _{\alpha }m_{\alpha }{\vec {x}}_{\alpha }.$ ⓘ

dann, ⓘ

${\begin{aligned}{\vec {j}}&=\sum _{\alpha }\left({\frac {\partial }{\partial {\dot {\vec {x}}}_{\alpha }}}{\mathcal {L}}\right)\cdot {\vec {Q}}\left[{\vec {x}}_{\alpha }\right]-{\vec {f}}\\[6pt]&=\sum _{\alpha }\left(m_{\alpha }{\dot {\vec {x}}}_{\alpha }t-m_{\alpha }{\vec {x}}_{\alpha }\right)\\[3pt]&={\vec {P}}t-M{\vec {x}}_{CM}\end{aligned}}$ ⓘ

wobei ${\vec {P}}$ ist der Gesamtimpuls, M ist die Gesamtmasse und ${\vec {x}}_{CM}$ ist der Massenschwerpunkt. Das Noethersche Theorem besagt:

${\frac {d{\vec {j}}}{dt}}=0\Rightarrow {\vec {P}}-M{\dot {\vec {x}}}_{CM}=0.$ ⓘ

Beispiel 3: Konforme Transformation

Die beiden Beispiele 1 und 2 beziehen sich auf eine 1-dimensionale Mannigfaltigkeit (Zeit). Ein Beispiel, das die Raumzeit betrifft, ist eine konforme Transformation eines masselosen reellen Skalarfeldes mit einem quartischen Potential in der (3 + 1)-Minkowski-Raumzeit. ⓘ

${\begin{aligned}{\mathcal {S}}[\varphi ]&=\int {\mathcal {L}}\left[\varphi (x),\partial _{\mu }\varphi (x)\right]d^{4}x\\[3pt]&=\int \left({\frac {1}{2}}\partial ^{\mu }\varphi \partial _{\mu }\varphi -\lambda \varphi ^{4}\right)d^{4}x\end{aligned}}$ ⓘ

Betrachten Sie für Q den Generator einer Raumzeit-Reskalierung. Mit anderen Worten, ⓘ

$Q[\varphi (x)]=x^{\mu }\partial _{\mu }\varphi (x)+\varphi (x).$ ⓘ

Der zweite Term auf der rechten Seite ergibt sich aus dem "konformen Gewicht" von $\varphi$. Und ⓘ

$Q[{\mathcal {L}}]=\partial ^{\mu }\varphi \left(\partial _{\mu }\varphi +x^{\nu }\partial _{\mu }\partial _{\nu }\varphi +\partial _{\mu }\varphi \right)-4\lambda \varphi ^{3}\left(x^{\mu }\partial _{\mu }\varphi +\varphi \right).$ ⓘ

Dies hat die Form von ⓘ

$\partial _{\mu }\left[{\frac {1}{2}}x^{\mu }\partial ^{\nu }\varphi \partial _{\nu }\varphi -\lambda x^{\mu }\varphi ^{4}\right]=\partial _{\mu }\left(x^{\mu }{\mathcal {L}}\right)$ ⓘ

(wo wir eine Änderung der Dummy-Indizes vorgenommen haben), also setze ⓘ

$f^{\mu }=x^{\mu }{\mathcal {L}}.$ ⓘ

Dann ⓘ

${\begin{aligned}j^{\mu }&=\left[{\frac {\partial }{\partial (\partial _{\mu }\varphi )}}{\mathcal {L}}\right]Q[\varphi ]-f^{\mu }\\&=\partial ^{\mu }\varphi \left(x^{\nu }\partial _{\nu }\varphi +\varphi \right)-x^{\mu }\left({\frac {1}{2}}\partial ^{\nu }\varphi \partial _{\nu }\varphi -\lambda \varphi ^{4}\right).\end{aligned}}$ ⓘ

Noethers Theorem besagt, dass $\partial _{\mu }j^{\mu }=0$ (was man explizit überprüfen kann, indem man die Euler-Lagrange-Gleichungen auf der linken Seite einsetzt). ⓘ

Versucht man, das Ward-Takahashi-Analogon dieser Gleichung zu finden, stößt man aufgrund von Anomalien auf ein Problem. ⓘ

Anwendungen

Die Anwendung des Noether-Theorems ermöglicht es Physikern, durch die Analyse der verschiedenen Transformationen, die die Form der beteiligten Gesetze invariant machen würden, tiefgreifende Einblicke in jede allgemeine Theorie der Physik zu gewinnen. Ein Beispiel:

• Die Invarianz physikalischer Systeme in Bezug auf die räumliche Verschiebung (mit anderen Worten, dass sich die physikalischen Gesetze nicht mit dem Ort im Raum ändern) ergibt den Satz der Erhaltung des linearen Impulses;
• die Invarianz in Bezug auf die Rotation ergibt das Gesetz der Erhaltung des Drehimpulses;
• Invarianz in Bezug auf die Zeitverschiebung ergibt den bekannten Energieerhaltungssatz. ⓘ

In der Quantenfeldtheorie liefert das Analogon zum Noether-Theorem, die Ward-Takahashi-Identität, weitere Erhaltungssätze, wie z. B. die Erhaltung der elektrischen Ladung aufgrund der Invarianz gegenüber einer Änderung des Phasenfaktors des komplexen Feldes des geladenen Teilchens und der zugehörigen Eichung des elektrischen Potentials und des Vektorpotentials. ⓘ

Die Noether-Ladung wird auch bei der Berechnung der Entropie stationärer Schwarzer Löcher verwendet. ⓘ