Raumzeit
| Teil einer Serie über ⓘ |
| Raumzeit |
|---|
 |
|
|
In der Physik ist die Raumzeit ein mathematisches Modell, das die drei Dimensionen des Raums und eine Dimension der Zeit zu einer einzigen vierdimensionalen Mannigfaltigkeit verbindet. Mit Hilfe von Raumzeitdiagrammen lassen sich relativistische Effekte veranschaulichen, z. B. warum verschiedene Beobachter unterschiedlich wahrnehmen, wo und wann Ereignisse stattfinden. ⓘ
Bis zum 20. Jahrhundert ging man davon aus, dass die dreidimensionale Geometrie des Universums (ihr räumlicher Ausdruck in Form von Koordinaten, Abständen und Richtungen) unabhängig von der eindimensionalen Zeit ist. Der Physiker Albert Einstein hat die Idee der Raumzeit im Rahmen seiner Relativitätstheorie mitentwickelt. Vor seiner bahnbrechenden Arbeit hatten Wissenschaftler zwei getrennte Theorien zur Erklärung physikalischer Phänomene: Isaac Newtons physikalische Gesetze beschrieben die Bewegung massiver Objekte, während James Clerk Maxwells elektromagnetische Modelle die Eigenschaften des Lichts erklärten. Im Jahr 1905 stützte sich Einstein in seiner Arbeit über die spezielle Relativitätstheorie jedoch auf zwei Postulate:
- Die physikalischen Gesetze sind in allen Inertialsystemen (d. h. nichtbeschleunigenden Bezugssystemen) invariant (d. h. identisch)
- Die Lichtgeschwindigkeit in einem Vakuum ist für alle Beobachter gleich, unabhängig von der Bewegung der Lichtquelle. ⓘ
Die logische Konsequenz aus diesen Postulaten ist die untrennbare Verbindung der vier Dimensionen Raum und Zeit, die bisher als unabhängig galten. Daraus ergeben sich viele kontraintuitive Konsequenzen: Die Lichtgeschwindigkeit ist nicht nur unabhängig von der Bewegung der Lichtquelle, sondern auch konstant, unabhängig davon, in welchem Bezugssystem sie gemessen wird; die Abstände und sogar die zeitliche Anordnung von Ereignispaaren ändern sich, wenn sie in verschiedenen Inertialsystemen gemessen werden (dies ist die Relativität der Gleichzeitigkeit); und die lineare Additivität der Geschwindigkeiten gilt nicht mehr. ⓘ
Einstein formulierte seine Theorie auf der Grundlage der Kinematik (der Lehre von den bewegten Körpern). Seine Theorie war ein Fortschritt gegenüber der Theorie der elektromagnetischen Phänomene von Lorentz (1904) und der elektrodynamischen Theorie von Poincaré. Diese Theorien enthielten zwar Gleichungen, die mit denen von Einstein identisch waren (d. h. die Lorentz-Transformation), aber es handelte sich im Wesentlichen um Ad-hoc-Modelle, die vorgeschlagen wurden, um die Ergebnisse verschiedener Experimente zu erklären - darunter das berühmte Michelson-Morley-Interferometerexperiment -, die sich nur schwer in bestehende Paradigmen einfügen ließen. ⓘ
1908 stellte Hermann Minkowski - einst einer der Mathematikprofessoren des jungen Einstein in Zürich - eine geometrische Interpretation der speziellen Relativitätstheorie vor, die die Zeit und die drei räumlichen Dimensionen des Raums zu einem einzigen vierdimensionalen Kontinuum verschmolz, das heute als Minkowski-Raum bekannt ist. Ein wesentliches Merkmal dieser Interpretation ist die formale Definition des Raumzeitintervalls. Obwohl sich die Messungen von Entfernung und Zeit zwischen Ereignissen bei Messungen in verschiedenen Bezugssystemen unterscheiden, ist das Raumzeitintervall unabhängig von dem Inertialsystem, in dem sie aufgezeichnet werden. ⓘ
Minkowskis geometrische Interpretation der Relativitätstheorie erwies sich als entscheidend für Einsteins Entwicklung seiner allgemeinen Relativitätstheorie von 1915, in der er zeigte, wie Masse und Energie die flache Raumzeit zu einer pseudo-Riemannschen Mannigfaltigkeit krümmen. ⓘ
Raumzeit oder Raum-Zeit-Kontinuum bezeichnet die gemeinsame Darstellung des dreidimensionalen Raums und der eindimensionalen Zeit in einer vierdimensionalen mathematischen Struktur. Diese Darstellung wird in der Relativitätstheorie benutzt. ⓘ
Der Mensch erlebt Ort und Zeit als zwei verschiedene Gegebenheiten, unter anderem wegen der mit der Zeit verbundenen Kausalität (eine Wirkung kann nicht früher als ihre Ursache eintreten). In der klassischen Physik und größtenteils in der Technik werden Ort und Zeit als voneinander unabhängige Größen behandelt. Bei Geschwindigkeiten von der Größenordnung der Lichtgeschwindigkeit zeigt sich jedoch, dass sich Zeit und Ort eines Ereignisses gegenseitig bedingen. Zum Beispiel hängt der zeitliche Abstand zweier Ereignisse, wie er von einem bewegten Beobachter festgestellt wird, auch von ihrem räumlichen Abstand ab. Mit der Entwicklung der speziellen Relativitätstheorie wurde erkannt, dass es vorteilhaft ist, die beiden Größen als Koordinaten in einem gemeinsamen vierdimensionalen Raum, dem Minkowski-Raum, zu betrachten. ⓘ
Im Zusammenhang der klassischen Mechanik ist der Raumzeitbegriff von Penrose und Arnold diskutiert worden. ⓘ
Einführung
Definitionen
In der nichtrelativistischen klassischen Mechanik wird die Zeit als eine universelle Messgröße betrachtet, die im gesamten Raum gleichförmig und vom Raum getrennt ist. Die klassische Mechanik geht davon aus, dass die Zeit eine konstante Durchlaufgeschwindigkeit hat, unabhängig vom Bewegungszustand des Beobachters oder von äußeren Faktoren. Außerdem geht sie davon aus, dass der Raum euklidisch ist; sie nimmt an, dass der Raum der Geometrie des gesunden Menschenverstands folgt. ⓘ
Im Rahmen der speziellen Relativitätstheorie kann die Zeit nicht von den drei Dimensionen des Raums getrennt werden, da die beobachtete Geschwindigkeit, mit der die Zeit für ein Objekt vergeht, von der Geschwindigkeit des Objekts relativ zum Beobachter abhängt. Die allgemeine Relativitätstheorie erklärt auch, wie Gravitationsfelder den Lauf der Zeit für ein Objekt aus der Sicht eines Beobachters außerhalb des Feldes verlangsamen können. ⓘ
Im gewöhnlichen Raum wird eine Position durch drei Zahlen angegeben, die als Dimensionen bezeichnet werden. Im kartesischen Koordinatensystem heißen diese x, y und z. Eine Position in der Raumzeit wird als Ereignis bezeichnet und erfordert die Angabe von vier Zahlen: die dreidimensionale Position im Raum sowie die Position in der Zeit (Abb. 1). Ein Ereignis wird durch eine Reihe von Koordinaten x, y, z und t dargestellt. Die Raumzeit ist also vierdimensional. Mathematische Ereignisse haben die Dauer Null und stellen einen einzigen Punkt in der Raumzeit dar. ⓘ
Der Weg eines Teilchens durch die Raumzeit kann als eine Folge von Ereignissen betrachtet werden. Die Reihe von Ereignissen kann miteinander verbunden werden, um eine Linie zu bilden, die den Weg eines Teilchens durch die Raumzeit darstellt. Diese Linie wird die Weltlinie des Teilchens genannt. ⓘ
Mathematisch gesehen ist die Raumzeit eine Mannigfaltigkeit, d. h. sie erscheint in der Nähe eines jeden Punktes lokal "flach", so wie eine Weltkugel in einem ausreichend kleinen Maßstab flach erscheint. Ein extrem großer Skalenfaktor, (üblicherweise als Lichtgeschwindigkeit bezeichnet) setzt die im Raum gemessenen Entfernungen in Beziehung zu den in der Zeit gemessenen Entfernungen. Die Größe dieses Skalenfaktors (fast 300.000 Kilometer oder 190.000 Meilen im Raum entsprechen einer Sekunde in der Zeit) und die Tatsache, dass die Raumzeit eine Mannigfaltigkeit ist, impliziert, dass es bei gewöhnlichen, nicht-relativistischen Geschwindigkeiten und bei gewöhnlichen Entfernungen in menschlichem Maßstab wenig gibt, was der Mensch beobachten könnte, das sich merklich von dem unterscheidet, was er beobachten könnte, wenn die Welt euklidisch wäre. Erst mit dem Aufkommen empfindlicher wissenschaftlicher Messungen in der Mitte des 18. Jahrhunderts, wie dem Fizeau-Experiment und dem Michelson-Morley-Experiment, wurden rätselhafte Diskrepanzen zwischen Beobachtungen und Vorhersagen festgestellt, die auf der impliziten Annahme eines euklidischen Raums beruhten. ⓘ

In der speziellen Relativitätstheorie bezeichnet ein Beobachter in den meisten Fällen einen Bezugsrahmen, von dem aus eine Reihe von Objekten oder Ereignissen gemessen wird. Diese Verwendung unterscheidet sich erheblich von der gewöhnlichen englischen Bedeutung des Begriffs. Bezugsrahmen sind von Natur aus nichtlokale Konstrukte, und nach dieser Verwendung des Begriffs macht es keinen Sinn, von einem Beobachter zu sprechen, der einen Ort hat. In Abb. 1-1 stellen wir uns vor, dass der betrachtete Rahmen mit einem dichten Gitter von Uhren ausgestattet ist, die innerhalb dieses Bezugsrahmens synchronisiert sind und sich unbegrenzt über die drei Dimensionen des Raums erstrecken. Ein bestimmter Ort innerhalb des Gitters ist nicht wichtig. Das Uhrengitter dient dazu, die Zeit und die Position von Ereignissen zu bestimmen, die innerhalb des gesamten Bezugssystems stattfinden. Der Begriff Beobachter bezieht sich auf das gesamte Ensemble von Uhren, die mit einem Inertialsystem verbunden sind. In diesem idealisierten Fall ist jedem Punkt im Raum eine Uhr zugeordnet, und so registrieren die Uhren jedes Ereignis sofort, ohne Zeitverzögerung zwischen einem Ereignis und seiner Aufzeichnung. Ein realer Beobachter wird jedoch aufgrund der Lichtgeschwindigkeit eine Verzögerung zwischen der Aussendung eines Signals und seiner Erfassung feststellen. Um die Uhren zu synchronisieren, wird bei der Datenreduktion im Anschluss an ein Experiment der Zeitpunkt des Empfangs eines Signals so korrigiert, dass er die tatsächliche Zeit widerspiegelt, wenn es von einem idealisierten Uhrengitter aufgezeichnet worden wäre. ⓘ
In vielen Büchern über die spezielle Relativitätstheorie, vor allem in älteren, wird das Wort "Beobachter" in der gewöhnlichen Bedeutung des Wortes verwendet. Aus dem Kontext geht in der Regel hervor, welche Bedeutung angenommen wurde. ⓘ
Physiker unterscheiden zwischen dem, was man misst oder beobachtet (nachdem man Signallaufzeiten herausgerechnet hat), und dem, was man visuell ohne solche Korrekturen sieht. Die Unkenntnis des Unterschieds zwischen dem, was man misst/beobachtet, und dem, was man sieht, ist die Ursache für viele Fehler bei den Anfängern der Relativitätstheorie. ⓘ
Geschichte
Mitte des 18. Jahrhunderts galten verschiedene Experimente wie die Beobachtung des Arago-Flecks und unterschiedliche Messungen der Lichtgeschwindigkeit in Luft und Wasser als Beweis für die Wellennatur des Lichts im Gegensatz zu einer Korpuskular-Theorie. Man ging davon aus, dass die Ausbreitung von Wellen die Existenz eines wellenförmigen Mediums voraussetzt; im Falle der Lichtwellen wurde dies als ein hypothetischer leuchtender Äther angesehen. Die verschiedenen Versuche, die Eigenschaften dieses hypothetischen Mediums zu bestimmen, ergaben jedoch widersprüchliche Ergebnisse. So zeigte das Fizeau-Experiment von 1851, dass die Lichtgeschwindigkeit in fließendem Wasser um einen vom Brechungsindex des Wassers abhängigen Betrag geringer ist als die Summe aus der Lichtgeschwindigkeit in Luft und der Geschwindigkeit des Wassers. Unter anderem führte die Abhängigkeit der in diesem Experiment festgestellten partiellen Ätherverzögerung vom Brechungsindex (der von der Wellenlänge abhängt) zu der unangenehmen Schlussfolgerung, dass der Äther für verschiedene Lichtfarben gleichzeitig mit unterschiedlichen Geschwindigkeiten fließt. Das berühmte Michelson-Morley-Experiment von 1887 (Abb. 1-2) zeigte keinen unterschiedlichen Einfluss der Erdbewegungen durch den hypothetischen Äther auf die Lichtgeschwindigkeit, und die wahrscheinlichste Erklärung, die vollständige Mitnahme des Äthers, stand im Widerspruch zu den Beobachtungen der stellaren Aberration. ⓘ
George Francis FitzGerald (1889) und Hendrik Lorentz (1892) schlugen unabhängig voneinander vor, dass materielle Körper, die sich durch den festen Äther bewegen, bei ihrer Passage physikalisch beeinflusst werden und sich in der Bewegungsrichtung um genau den Betrag zusammenziehen, der notwendig war, um die negativen Ergebnisse des Michelson-Morley-Experiments zu erklären. (In Richtungen quer zur Bewegungsrichtung treten keine Längenänderungen auf.) ⓘ
Bis 1904 hatte Lorentz seine Theorie so erweitert, dass er zu Gleichungen gelangte, die formal mit denen identisch waren, die Einstein später ableiten sollte (d. h. die Lorentz-Transformation), jedoch mit einer grundlegend anderen Interpretation. Als Theorie der Dynamik (die Untersuchung von Kräften und Drehmomenten und ihrer Wirkung auf die Bewegung) ging seine Theorie von tatsächlichen physikalischen Verformungen der physikalischen Bestandteile der Materie aus. Die Gleichungen von Lorentz sagten eine Größe voraus, die er als Ortszeit bezeichnete und mit der er die Aberration des Lichts, das Fizeau-Experiment und andere Phänomene erklären konnte. Lorentz betrachtete die Ortszeit jedoch nur als ein mathematisches Hilfsmittel, sozusagen als einen Trick, um die Transformation von einem System in ein anderes zu vereinfachen. ⓘ
Andere Physiker und Mathematiker kamen um die Jahrhundertwende dem nahe, was heute als Raumzeit bekannt ist. Einstein selbst stellte fest, dass die spezielle Relativitätstheorie, wenn wir ihre Entwicklung rückblickend betrachten, 1905 reif für die Entdeckung war, da so viele Leute einzelne Teile des Puzzles enträtselten". ⓘ
Ein wichtiges Beispiel ist Henri Poincaré, der 1898 argumentierte, dass die Gleichzeitigkeit von zwei Ereignissen eine Frage der Konvention ist. Im Jahr 1900 erkannte er, dass die Lorentz'sche "Ortszeit" in Wirklichkeit das ist, was durch sich bewegende Uhren angezeigt wird, indem er eine explizit operative Definition der Uhrensynchronisation unter der Annahme einer konstanten Lichtgeschwindigkeit anwandte. In den Jahren 1900 und 1904 wies er auf die inhärente Unauffindbarkeit des Äthers hin, indem er die Gültigkeit des von ihm so genannten Relativitätsprinzips betonte, und 1905/1906 vervollkommnete er die Lorentzsche Elektronentheorie mathematisch, um sie mit dem Relativitätspostulat in Einklang zu bringen. Während er verschiedene Hypothesen über die Lorentz-invariante Gravitation diskutierte, führte er das innovative Konzept einer vierdimensionalen Raumzeit ein, indem er verschiedene vier Vektoren definierte, nämlich Vier-Position, Vier-Geschwindigkeit und Vier-Kraft. Er verfolgte den vierdimensionalen Formalismus in späteren Arbeiten jedoch nicht weiter, da er der Meinung war, dass diese Forschungsrichtung "große Schmerzen für begrenzten Nutzen" mit sich bringe, und kam schließlich zu dem Schluss, "dass die dreidimensionale Sprache für die Beschreibung unserer Welt am besten geeignet zu sein scheint". Außerdem glaubte Poincaré noch 1909 an die dynamische Interpretation der Lorentz-Transformation. Aus diesen und anderen Gründen vertreten die meisten Wissenschaftshistoriker die Auffassung, dass Poincaré die heutige Spezielle Relativitätstheorie nicht erfunden hat. ⓘ
1905 führte Einstein die spezielle Relativitätstheorie (wenn auch ohne Verwendung der Techniken des Raumzeitformalismus) in ihrem modernen Verständnis als Theorie von Raum und Zeit ein. Seine Ergebnisse sind zwar mathematisch äquivalent zu denen von Lorentz und Poincaré, aber Einstein zeigte, dass die Lorentz-Transformationen nicht das Ergebnis von Wechselwirkungen zwischen Materie und Äther sind, sondern vielmehr die Natur von Raum und Zeit selbst betreffen. Er erhielt alle seine Ergebnisse, indem er erkannte, dass die gesamte Theorie auf zwei Postulaten aufgebaut werden kann: Das Relativitätsprinzip und das Prinzip der Konstanz der Lichtgeschwindigkeit. ⓘ
Einstein führte seine Analyse in Bezug auf die Kinematik (die Untersuchung von sich bewegenden Körpern ohne Bezug auf Kräfte) und nicht auf die Dynamik durch. Seine Arbeit zur Einführung in das Thema war voller anschaulicher Bilder, die den Austausch von Lichtsignalen zwischen sich bewegenden Uhren, sorgfältige Messungen der Längen von sich bewegenden Stäben und andere Beispiele dieser Art beinhalteten. ⓘ
Darüber hinaus ersetzte Einstein 1905 frühere Versuche einer elektromagnetischen Masse-Energie-Relation, indem er die allgemeine Äquivalenz von Masse und Energie einführte, die für seine spätere Formulierung des Äquivalenzprinzips im Jahr 1907 entscheidend war, das die Äquivalenz von Trägheits- und Gravitationsmasse erklärt. Mit Hilfe der Masse-Energie-Äquivalenz zeigte Einstein außerdem, dass die Gravitationsmasse eines Körpers proportional zu seinem Energiegehalt ist, was eines der ersten Ergebnisse bei der Entwicklung der allgemeinen Relativitätstheorie war. Obwohl es den Anschein hat, dass er anfangs nicht geometrisch über die Raumzeit nachdachte, hat Einstein bei der weiteren Entwicklung der allgemeinen Relativitätstheorie den Raumzeitformalismus vollständig einbezogen. ⓘ
Als Einstein 1905 veröffentlichte, hatte ein anderer seiner Konkurrenten, sein ehemaliger Mathematikprofessor Hermann Minkowski, ebenfalls die meisten Grundelemente der speziellen Relativitätstheorie gefunden. Max Born erzählte von einem Treffen mit Minkowski, bei dem er sich darum bemühte, Minkowskis Schüler/Kollaborateur zu werden:
Ich fuhr nach Köln, traf Minkowski und hörte seine berühmte Vorlesung 'Raum und Zeit' vom 2. September 1908. [...] Er erzählte mir später, dass es für ihn ein großer Schock war, als Einstein seine Arbeit veröffentlichte, in der er die Äquivalenz der verschiedenen Ortszeiten von Beobachtern, die sich relativ zueinander bewegen, feststellte; denn er war unabhängig davon zu den gleichen Schlussfolgerungen gekommen, hatte sie aber nicht veröffentlicht, weil er zuerst die mathematische Struktur in ihrer ganzen Pracht ausarbeiten wollte. Er erhob nie einen Prioritätsanspruch und gab Einstein stets seinen vollen Anteil an der großen Entdeckung. ⓘ
Minkowski hatte sich mindestens seit dem Sommer 1905 mit dem Stand der Elektrodynamik nach Michelsons störenden Experimenten befasst, als Minkowski und David Hilbert ein Seminar für Fortgeschrittene leiteten, an dem namhafte Physiker der Zeit teilnahmen, um die Arbeiten von Lorentz, Poincaré und anderen zu studieren. Es ist jedoch überhaupt nicht klar, wann Minkowski begann, die geometrische Formulierung der Speziellen Relativitätstheorie zu formulieren, die seinen Namen tragen sollte, oder inwieweit er von Poincarés vierdimensionaler Interpretation der Lorentz-Transformation beeinflusst wurde. Es ist auch nicht klar, ob er Einsteins entscheidenden Beitrag zum Verständnis der Lorentz-Transformationen jemals in vollem Umfang gewürdigt hat, da er Einsteins Arbeit als eine Erweiterung von Lorentz' Arbeit betrachtete. ⓘ
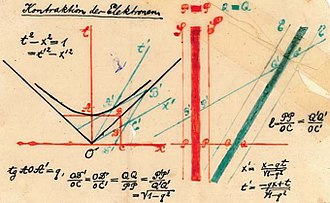
Am 5. November 1907 (etwas mehr als ein Jahr vor seinem Tod) stellte Minkowski seine geometrische Interpretation der Raumzeit in einem Vortrag vor der Mathematischen Gesellschaft zu Göttingen mit dem Titel Das Relativitätsprinzip vor. Am 21. September 1908 hielt Minkowski seinen berühmten Vortrag "Raum und Zeit" vor der Deutschen Gesellschaft der Naturforscher und Ärzte. Zu den einleitenden Worten von Raum und Zeit gehört Minkowskis berühmte Aussage, dass "von nun an der Raum für sich selbst und die Zeit für sich selbst völlig zu einem bloßen Schatten schrumpfen werden, und nur eine Art von Vereinigung der beiden wird die Unabhängigkeit bewahren." Raum und Zeit enthielt die erste öffentliche Präsentation von Raumzeitdiagrammen (Abb. 1-4) und eine bemerkenswerte Demonstration, dass das Konzept des invarianten Intervalls (siehe unten) zusammen mit der empirischen Beobachtung, dass die Lichtgeschwindigkeit endlich ist, die Ableitung der gesamten Speziellen Relativitätstheorie ermöglicht. ⓘ
Das Raumzeitkonzept und die Lorentz-Gruppe sind eng mit bestimmten Arten von Kugel-, hyperbolischen oder konformen Geometrien und ihren Transformationsgruppen verbunden, die bereits im 19. Jahrhundert entwickelt wurden und in denen invariante Intervalle analog zum Raumzeitintervall verwendet werden. ⓘ
Einstein seinerseits lehnte Minkowskis geometrische Interpretation der Speziellen Relativitätstheorie zunächst ab und betrachtete sie als überflüssige Gelehrsamkeit. Für die Vollendung seiner 1907 begonnenen Suche nach der allgemeinen Relativitätstheorie erwies sich die geometrische Interpretation der Relativitätstheorie jedoch als unerlässlich, und 1916 bekannte sich Einstein voll und ganz zu Minkowski, dessen Interpretation den Übergang zur allgemeinen Relativitätstheorie erheblich erleichterte. Da es noch andere Arten von Raumzeiten gibt, wie die gekrümmte Raumzeit der allgemeinen Relativitätstheorie, wird die Raumzeit der speziellen Relativitätstheorie heute als Minkowski-Raumzeit bezeichnet. ⓘ
Raumzeit in der Speziellen Relativitätstheorie
Intervall der Raumzeit
In drei Dimensionen kann der Abstand zwischen zwei Punkten mit Hilfe des Satzes von Pythagoras definiert werden:
Auch wenn zwei Betrachter die x-, y- und z-Position der beiden Punkte mit unterschiedlichen Koordinatensystemen messen, ist der Abstand zwischen den Punkten für beide gleich (vorausgesetzt, sie messen mit denselben Einheiten). Der Abstand ist "unveränderlich". ⓘ
In der Speziellen Relativitätstheorie ist der Abstand zwischen zwei Punkten jedoch nicht mehr derselbe, wenn er von zwei verschiedenen Beobachtern gemessen wird und sich einer der Beobachter aufgrund der Lorentzkontraktion bewegt. Noch komplizierter wird die Situation, wenn die beiden Punkte nicht nur räumlich, sondern auch zeitlich voneinander getrennt sind. Wenn zum Beispiel ein Beobachter zwei Ereignisse am gleichen Ort, aber zu unterschiedlichen Zeiten sieht, wird eine Person, die sich in Bezug auf den ersten Beobachter bewegt, die beiden Ereignisse an unterschiedlichen Orten sehen, weil sie (von ihrem Standpunkt aus) stationär ist und sich die Position des Ereignisses entfernt oder nähert. Daher muss ein anderes Maß verwendet werden, um die effektive "Entfernung" zwischen zwei Ereignissen zu messen. ⓘ
In der vierdimensionalen Raumzeit ist das Analogon zur Entfernung das Intervall. Obwohl die Zeit als vierte Dimension hinzukommt, wird sie anders behandelt als die räumlichen Dimensionen. Der Minkowski-Raum unterscheidet sich daher in wichtigen Aspekten vom vierdimensionalen euklidischen Raum. Der Hauptgrund für die Verschmelzung von Raum und Zeit zu einer Raumzeit ist, dass Raum und Zeit für sich genommen nicht invariant sind, d. h., dass verschiedene Beobachter unter den richtigen Bedingungen nicht über die Länge der Zeit zwischen zwei Ereignissen (wegen der Zeitdilatation) oder die Entfernung zwischen den beiden Ereignissen (wegen der Längenkontraktion) übereinstimmen werden. Die spezielle Relativitätstheorie bietet jedoch eine neue Invariante, das so genannte Raumzeitintervall, das Entfernungen im Raum und in der Zeit kombiniert. Alle Beobachter, die die Zeit und den Abstand zwischen zwei Ereignissen messen, berechnen am Ende dasselbe Raumzeitintervall. Angenommen, ein Beobachter misst zwei Ereignisse, die in der Zeit durch und einen räumlichen Abstand Dann ist das Raumzeitintervall zwischen den beiden Ereignissen, die durch einen Abstand im Raum und um in der -Koordinate trennen, ist:
oder für drei Raumdimensionen, ⓘ
Die Konstante die Lichtgeschwindigkeit, wandelt Zeiteinheiten (wie Sekunden) in Raumeinheiten (wie Meter) um. Das quadrierte Intervall ist ein Maß für den Abstand zwischen den Ereignissen A und B, die zeitlich und zusätzlich räumlich voneinander getrennt sind, entweder weil es zwei getrennte Objekte gibt, die Ereignisse durchlaufen, oder weil sich ein einzelnes Objekt im Raum träge zwischen seinen Ereignissen bewegt. Das Trennungsintervall wird abgeleitet, indem man den räumlichen Abstand, der das Ereignis B vom Ereignis A trennt, quadriert und vom Quadrat des räumlichen Abstands subtrahiert, den ein Lichtsignal in demselben Zeitintervall zurücklegt . Wenn die Trennung der Ereignisse durch ein Lichtsignal erfolgt, verschwindet diese Differenz und . ⓘ
Wenn die betrachteten Ereignisse unendlich nahe beieinander liegen, dann können wir schreiben ⓘ
In einem anderen Inertialsystem, beispielsweise mit den Koordinaten kann das Raumzeitintervall in der gleichen Form wie oben geschrieben werden. Wegen der Konstanz der Lichtgeschwindigkeit gehören die Lichtereignisse in allen Inertialsystemen zum Intervall Null, . Für jedes andere infinitesimale Ereignis, bei dem , kann man beweisen, dass was wiederum durch Integration zu folgenden Ergebnissen führt . Die Invarianz des Intervalls eines beliebigen Ereignisses zwischen allen intertialen Bezugssystemen ist eines der grundlegenden Ergebnisse der speziellen Relativitätstheorie. ⓘ
Obwohl der Kürze halber häufig Intervallausdrücke ohne Deltas verwendet werden, so auch in den meisten der folgenden Erörterungen, sollte man wissen, dass im Allgemeinen, bedeutet , usw. Wir beschäftigen uns immer mit Differenzen von räumlichen oder zeitlichen Koordinatenwerten, die zu zwei Ereignissen gehören, und da es keinen bevorzugten Ursprung gibt, haben einzelne Koordinatenwerte keine wesentliche Bedeutung. ⓘ

Die obige Gleichung ähnelt dem Satz des Pythagoras, allerdings mit einem Minuszeichen zwischen dem und den Terme. Das Raumzeitintervall ist die Menge nicht selbst. Der Grund dafür ist, dass Intervalle in der Minkowski-Raumzeit, anders als Abstände in der euklidischen Geometrie, negativ sein können. Anstatt sich mit Quadratwurzeln negativer Zahlen zu befassen, betrachten Physiker üblicherweise als ein eigenständiges Symbol und nicht als das Quadrat von etwas. ⓘ
Im Allgemeinen kann beliebige Werte der reellen Zahl annehmen. Wenn positiv ist, wird das Raumzeitintervall als zeitähnlich bezeichnet. Da die räumliche Entfernung, die ein massives Objekt zurücklegt, immer kleiner ist als die Entfernung, die das Licht im gleichen Zeitintervall zurücklegt, sind reelle Intervalle immer zeitlich gleich. Wenn negativ ist, wird das Raumzeitintervall als raumzeitlich bezeichnet, wobei das Raumzeitintervall imaginär ist. Raumzeitintervalle sind gleich Null, wenn Mit anderen Worten: Das Raumzeitintervall zwischen zwei Ereignissen auf der Weltlinie von etwas, das sich mit Lichtgeschwindigkeit bewegt, ist Null. Ein solches Intervall wird als lichtartig oder Null bezeichnet. Ein Photon, das von einem weit entfernten Stern in unserem Auge ankommt, ist nicht gealtert, obwohl es (aus unserer Perspektive) Jahre auf seinem Weg zurückgelegt hat. ⓘ
Ein Raumzeitdiagramm wird in der Regel nur mit einer einzigen Raum- und einer einzigen Zeitkoordinate gezeichnet. Abb. 2-1 zeigt ein Raumzeitdiagramm, in dem die Weltlinien (d. h. die Wege in der Raumzeit) zweier Photonen A und B dargestellt sind, die vom selben Ereignis ausgehen und sich in entgegengesetzte Richtungen bewegen. Darüber hinaus zeigt C die Weltlinie eines Objekts, das langsamer als das Licht ist. Die vertikale Zeitkoordinate ist um skaliert, so dass sie die gleichen Einheiten (Meter) hat wie die horizontale Raumkoordinate. Da sich Photonen mit Lichtgeschwindigkeit fortbewegen, haben ihre Weltlinien eine Steigung von ±1, d. h. jeder Meter, den ein Photon nach links oder rechts zurücklegt, benötigt etwa 3,3 Nanosekunden Zeit. ⓘ
In der Literatur zur Relativitätstheorie sind zwei Vorzeichenkonventionen gebräuchlich:
und .
Diese Vorzeichenkonventionen sind mit den metrischen Signaturen (+---) und (-+++) verbunden. Eine geringfügige Abwandlung besteht darin, die Zeitkoordinate an die letzte statt an die erste Stelle zu setzen. Beide Konventionen sind auf dem Gebiet der Relativitätstheorie weit verbreitet. ⓘ
Bezugsrahmen


Um einen Einblick zu erhalten, wie Raumzeitkoordinaten, die von Beobachtern in verschiedenen Bezugsrahmen gemessen werden, miteinander verglichen werden können, ist es nützlich, mit einem vereinfachten Aufbau zu arbeiten, bei dem sich die Rahmen in einer Standardkonfiguration befinden. Dies ermöglicht eine Vereinfachung der Mathematik, ohne dass die Schlussfolgerungen an Allgemeinheit verlieren. In Abb. 2-2 sind zwei galileische Bezugsrahmen (d. h. konventionelle 3-Raum-Rahmen) in relativer Bewegung dargestellt. Der Rahmen S gehört zu einem ersten Beobachter O, und der Rahmen S′ (sprich: "S prime") gehört zu einem zweiten Beobachter O′.
- Die x-, y- und z-Achsen des Bildes S sind parallel zu den jeweiligen Primärachsen des Bildes S′ ausgerichtet.
- Das Bild S′ bewegt sich in x-Richtung des Bildes S mit einer konstanten Geschwindigkeit v, gemessen im Bild S.
- Die Ursprünge der Rahmen S und S′ sind deckungsgleich, wenn die Zeit t = 0 für Rahmen S und t′ = 0 für Rahmen S′ ist. ⓘ
In Abb. 2-3a ist Abb. 2-2 in einer anderen Ausrichtung wiedergegeben. Abb. 2-3b zeigt ein Raumzeitdiagramm aus der Sicht des Beobachters O. Da sich S und S′ in der Standardkonfiguration befinden, fallen ihre Ursprünge zu den Zeitpunkten t = 0 im Rahmen S und t′ = 0 im Rahmen S′ zusammen. Die ct′-Achse verläuft durch die Ereignisse im Einzelbild S′, die x′ = 0 haben. Aber die Punkte mit x′ = 0 bewegen sich in x-Richtung des Einzelbildes S mit der Geschwindigkeit v, so dass sie zu keinem anderen Zeitpunkt als Null mit der ct-Achse zusammenfallen. Daher ist die ct′-Achse in Bezug auf die ct-Achse um einen Winkel θ geneigt, der durch ⓘ
Die x′-Achse ist ebenfalls gegenüber der x-Achse gekippt. Um den Winkel dieser Neigung zu bestimmen, sei daran erinnert, dass die Neigung der Weltlinie eines Lichtimpulses immer ±1 ist. Abb. 2-3c zeigt ein Raumzeitdiagramm aus der Sicht des Beobachters O′. Das Ereignis P stellt die Aussendung eines Lichtimpulses bei x′ = 0, ct′ = -a dar. Der Impuls wird von einem Spiegel reflektiert, der sich in einem Abstand a von der Lichtquelle befindet (Ereignis Q), und kehrt bei x′ = 0, ct′ = a zur Lichtquelle zurück (Ereignis R). ⓘ
Die gleichen Ereignisse P, Q, R sind in Abb. 2-3b im Bild des Beobachters O eingezeichnet. Die Lichtwege haben Steigungen = 1 und -1, so dass △PQR ein rechtwinkliges Dreieck bildet, bei dem PQ und QR jeweils 45 Grad zur x- und ct-Achse stehen. Da OP = OQ = OR ist, muss der Winkel zwischen x′ und x ebenfalls θ sein. ⓘ
Während im Ruhezustand die Raum- und Zeitachsen rechtwinklig aufeinandertreffen, sind die Achsen des sich bewegenden Rahmens in einem spitzen Winkel zueinander gezeichnet. Die Rahmen sind eigentlich gleichwertig. Die Asymmetrie ist auf unvermeidliche Verzerrungen bei der Abbildung von Raum-Zeit-Koordinaten auf eine kartesische Ebene zurückzuführen und sollte nicht anders betrachtet werden als die Art und Weise, in der auf einer Mercator-Projektion der Erde die relative Größe von Landmassen in Polnähe (Grönland und Antarktis) im Vergleich zu Landmassen in Äquatornähe stark übertrieben ist. ⓘ
Lichtkegel

In Abbildung 2-4 befindet sich das Ereignis O im Ursprung eines Raumzeitdiagramms, und die beiden diagonalen Linien stellen alle Ereignisse dar, die in Bezug auf das Ursprungsereignis keinen Raumzeitabstand haben. Diese beiden Linien bilden den so genannten Lichtkegel des Ereignisses O, denn wenn man eine zweite räumliche Dimension hinzufügt (Abb. 2-5), entsteht das Bild von zwei rechtwinkligen Kreiskegeln, deren Spitzen sich bei O treffen. ⓘ

Ein Lichtkegel (Doppelkegel) teilt die Raumzeit in Bezug auf seine Spitze in verschiedene Bereiche auf. Das Innere des Zukunftslichtkegels besteht aus allen Ereignissen, die vom Scheitelpunkt durch mehr Zeit (zeitliche Distanz) getrennt sind, als nötig ist, um ihre räumliche Distanz mit Lichtgeschwindigkeit zu überwinden; diese Ereignisse bilden die zeitliche Zukunft des Ereignisses O. Ebenso umfasst die zeitliche Vergangenheit die inneren Ereignisse des Vergangenheitslichtkegels. In den zeitlichen Intervallen ist also Δct größer als Δx, so dass die zeitlichen Intervalle positiv sind. Der Bereich außerhalb des Lichtkegels besteht aus Ereignissen, die vom Ereignis O durch mehr Raum getrennt sind, als mit Lichtgeschwindigkeit in der gegebenen Zeit durchquert werden kann. Diese Ereignisse bilden den so genannten raumartigen Bereich des Ereignisses O, der in Abb. 2-4 mit "Anderswo" bezeichnet ist. Aufgrund der Invarianz des Raumzeitintervalls ordnen alle Beobachter jedem Ereignis denselben Lichtkegel zu und sind sich somit über diese Aufteilung der Raumzeit einig. ⓘ
Der Lichtkegel spielt eine wesentliche Rolle im Konzept der Kausalität. Es ist möglich, dass sich ein Signal, das nicht schneller als das Licht ist, von Ort und Zeit von O zu Ort und Zeit von D bewegt (Abb. 2-4). Es ist also möglich, dass das Ereignis O einen kausalen Einfluss auf das Ereignis D hat. Der Zukunftslichtkegel enthält alle Ereignisse, die von O kausal beeinflusst werden könnten. Ebenso ist es möglich, dass sich ein nicht-lichtschnelles Signal von Ort und Zeit von A zu Ort und Zeit von O bewegt. Der vergangene Lichtkegel enthält alle Ereignisse, die einen kausalen Einfluss auf O haben könnten. Nimmt man dagegen an, dass sich Signale nicht schneller als mit Lichtgeschwindigkeit fortbewegen können, so kann jedes Ereignis, wie z. B. B oder C, in der raumähnlichen Region (Elsewhere) weder das Ereignis O beeinflussen, noch können sie von dem Ereignis O mit Hilfe eines solchen Signals beeinflusst werden. Unter dieser Annahme ist jede kausale Beziehung zwischen dem Ereignis O und den Ereignissen in der raumähnlichen Region eines Lichtkegels ausgeschlossen. ⓘ
Relativität der Gleichzeitigkeit

Alle Beobachter stimmen darin überein, dass für ein beliebiges Ereignis ein Ereignis innerhalb des zukünftigen Lichtkegels des Ereignisses nach dem Ereignis eintritt. Ebenso tritt für ein bestimmtes Ereignis ein Ereignis innerhalb des Lichtkegels der Vergangenheit vor diesem Ereignis ein. Die Vorher-Nachher-Beziehung, die für zeitlich getrennte Ereignisse beobachtet wird, bleibt unverändert, unabhängig vom Bezugssystem des Beobachters, d. h. unabhängig davon, wie sich der Beobachter bewegt. Ganz anders verhält es sich bei räumlich getrennten Ereignissen. Abb. 2-4 wurde vom Bezugssystem eines Beobachters gezeichnet, der sich mit v = 0 bewegt. Von diesem Bezugssystem aus wird beobachtet, dass das Ereignis C nach dem Ereignis O eintritt und das Ereignis B vor dem Ereignis O. Von einem anderen Bezugssystem aus kann die Reihenfolge dieser nicht kausal zusammenhängenden Ereignisse umgekehrt werden. Insbesondere ist festzustellen, dass zwei Ereignisse, die in einem bestimmten Bezugssystem gleichzeitig auftreten, notwendigerweise durch ein raumähnliches Intervall voneinander getrennt sind und somit nicht kausal zusammenhängen. Die Feststellung, dass die Gleichzeitigkeit nicht absolut ist, sondern vom Bezugsrahmen des Beobachters abhängt, wird als Relativität der Gleichzeitigkeit bezeichnet. ⓘ
Abb. 2-6 veranschaulicht die Verwendung von Raumzeitdiagrammen bei der Analyse der Relativität der Gleichzeitigkeit. Die Ereignisse in der Raumzeit sind unveränderlich, aber die Koordinatensysteme transformieren sich, wie oben für Abb. 2-3 beschrieben. Im Bezugssystem eines Beobachters, der sich mit v = 0 bewegt, sind die drei Ereignisse (A, B, C) gleichzeitig. Im Bezugssystem eines Beobachters, der sich mit v = 0,3c bewegt, erscheinen die Ereignisse in der Reihenfolge C, B, A. Im Bezugssystem eines Beobachters, der sich mit v = -0,5c bewegt, erscheinen die Ereignisse in der Reihenfolge A, B, C. Die weiße Linie stellt eine Gleichzeitigkeitsebene dar, die von der Vergangenheit des Beobachters in die Zukunft des Beobachters verschoben wird und die Ereignisse hervorhebt, die sich auf ihr befinden. Die graue Fläche ist der Lichtkegel des Beobachters, der unveränderlich bleibt. ⓘ
Ein raumgleiches Raumzeitintervall gibt die gleiche Entfernung an, die ein Beobachter messen würde, wenn die gemessenen Ereignisse für den Beobachter gleichzeitig stattfinden würden. Ein raumähnliches Raumzeitintervall liefert daher ein Maß für die richtige Entfernung, d. h. die wahre Entfernung = Ebenso liefert ein zeitgleiches Raumzeitintervall dasselbe Maß an Zeit, das durch das kumulative Ticken einer Uhr, die sich entlang einer bestimmten Weltlinie bewegt, dargestellt wird. Ein zeitgleiches Raumzeitintervall liefert also ein Maß für die Eigenzeit = ⓘ
Unveränderliche Hyperbel

Im euklidischen Raum (der nur räumliche Dimensionen hat) bildet die Menge der Punkte, die (unter Verwendung der euklidischen Metrik) von einem bestimmten Punkt äquidistant sind, einen Kreis (in zwei Dimensionen) oder eine Kugel (in drei Dimensionen). In der (1+1)-dimensionalen Minkowski-Raumzeit (mit einer zeitlichen und einer räumlichen Dimension) bilden die Punkte in einem konstanten Raumzeitintervall vom Ursprung entfernt (unter Verwendung der Minkowski-Metrik) Kurven, die durch die beiden Gleichungen ⓘ
mit eine positive reelle Konstante. Diese Gleichungen beschreiben zwei Familien von Hyperbeln in einem x-ct-Raumzeitdiagramm, die als invariante Hyperbeln bezeichnet werden. ⓘ
In Abb. 2-7a verbindet jede magentafarbene Hyperbel alle Ereignisse, die einen festen räumlichen Abstand vom Ursprung haben, während die grünen Hyperbeln Ereignisse mit gleichem zeitlichen Abstand verbinden. ⓘ
Die magentafarbenen Hyperbeln, die die x-Achse kreuzen, sind zeitliche Kurven, d. h. diese Hyperbeln stellen tatsächliche Pfade dar, die von (ständig beschleunigten) Teilchen in der Raumzeit durchlaufen werden können: Zwischen zwei beliebigen Ereignissen auf einer Hyperbel ist eine Kausalitätsbeziehung möglich, weil der Kehrwert der Steigung - der die notwendige Geschwindigkeit darstellt - für alle Sekanten kleiner ist als . Andererseits sind die grünen Hyperbeln, die die ct-Achse kreuzen, raumähnliche Kurven, weil alle Intervalle entlang dieser Hyperbeln raumähnliche Intervalle sind: Zwischen zwei beliebigen Punkten auf einer dieser Hyperbeln ist keine Kausalität möglich, da alle Sekanten Geschwindigkeiten größer als . ⓘ
Abb. 2-7b zeigt die Situation in der (1+2)-dimensionalen Minkowski-Raumzeit (eine zeitliche und zwei räumliche Dimensionen) mit den entsprechenden Hyperboloiden. Die invarianten Hyperbeln, die um raumzeitliche Intervalle vom Ursprung verschoben werden, erzeugen Hyperboloide von einem Blatt, während die invarianten Hyperbeln, die um zeitliche Intervalle vom Ursprung verschoben werden, Hyperboloide von zwei Blättern erzeugen. ⓘ
Die (1+2)-dimensionale Grenze zwischen raum- und zeitgleichen Hyperboloiden, die durch die Ereignisse gebildet wird, die ein Null-Raumzeit-Intervall zum Ursprung bilden, wird durch die Entartung der Hyperboloide zum Lichtkegel gebildet. In (1+1)-Dimensionen entarten die Hyperbeln zu den beiden grauen 45°-Linien, die in Abb. 2-7a dargestellt sind. ⓘ
Zeitdilatation und Längenkontraktion
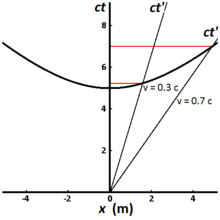
Abb. 2-8 zeigt die invariante Hyperbel für alle Ereignisse, die vom Ursprung aus in einer Eigenzeit von 5 Metern (etwa 1,67×10-8 s) erreicht werden können. Die verschiedenen Weltlinien stehen für Uhren, die sich mit unterschiedlichen Geschwindigkeiten bewegen. Eine Uhr, die in Bezug auf den Beobachter stillsteht, hat eine vertikale Weltlinie, und die vom Beobachter gemessene verstrichene Zeit ist gleich der Eigenzeit. Bei einer Uhr mit einer Geschwindigkeit von 0,3 c beträgt die vom Beobachter gemessene verstrichene Zeit 5,24 Meter (1,75×10-8 s), während bei einer Uhr mit einer Geschwindigkeit von 0,7 c die vom Beobachter gemessene verstrichene Zeit 7,00 Meter (2,34×10-8 s) beträgt. Dies veranschaulicht das als Zeitdilatation bekannte Phänomen. Uhren, die sich schneller bewegen, brauchen (im Beobachterrahmen) länger, um dieselbe Menge an Eigenzeit zu vergehen, und sie bewegen sich innerhalb dieser Eigenzeit weiter entlang der x-Achse, als sie es ohne Zeitdilatation tun würden. Die Messung der Zeitdilatation durch zwei Beobachter in unterschiedlichen Inertialsystemen beruht auf Gegenseitigkeit. Wenn Beobachter O die Uhren von Beobachter O′ als langsamer laufend in seinem Bezugssystem misst, misst Beobachter O′ seinerseits die Uhren von Beobachter O als langsamer laufend. ⓘ

Die Längenkontraktion ist wie die Zeitdilatation eine Erscheinung der Relativitätstheorie der Gleichzeitigkeit. Die Messung der Länge erfordert die Messung des Raumzeitintervalls zwischen zwei Ereignissen, die im eigenen Bezugssystem gleichzeitig stattfinden. Aber Ereignisse, die in einem Bezugssystem gleichzeitig sind, sind im Allgemeinen in anderen Bezugssystemen nicht gleichzeitig. ⓘ
Abb. 2-9 zeigt die Bewegungen eines 1 m langen Stabes, der sich mit 0,5 c auf der x-Achse bewegt. Die Kanten des blauen Bandes stellen die Weltlinien der beiden Endpunkte des Stabes dar. Die invariante Hyperbel veranschaulicht Ereignisse, die vom Ursprung durch ein raumartiges Intervall von 1 m getrennt sind. Die Endpunkte O und B, die bei t′ = 0 gemessen werden, sind im Bezugssystem S′ gleichzeitige Ereignisse. Aber für einen Beobachter im Rahmen S sind die Ereignisse O und B nicht gleichzeitig. Um die Länge zu messen, misst der Beobachter im Körper S die Endpunkte des Stabes in der Projektion auf die x-Achse entlang ihrer Weltlinien. Die Projektion der Weltlinie des Stabes auf die x-Achse ergibt die verkürzte Länge OC. ⓘ
(nicht abgebildet) Zieht man eine senkrechte Linie durch A, so dass sie die x′-Achse schneidet, so zeigt sich, dass, auch wenn OB aus der Sicht des Beobachters O verkürzt ist, OA aus der Sicht des Beobachters O′ ebenfalls verkürzt ist. So wie jeder Beobachter die Uhren des anderen als langsam laufend misst, so misst jeder Beobachter die Lineale des anderen als verkürzt. ⓘ
Was die gegenseitige Längenkontraktion betrifft, so zeigt Abb. 2-9, dass die geprimten und ungeprimten Rahmen um einen hyperbolischen Winkel (analog zu den gewöhnlichen Winkeln in der euklidischen Geometrie) zueinander gedreht sind. Aufgrund dieser Drehung ist die Projektion eines geprimten Meterstabs auf die ungeprimte x-Achse verkürzt, während die Projektion eines ungeprimten Meterstabs auf die geprimte x′-Achse ebenfalls verkürzt ist. ⓘ
Gegenseitige Zeitdilatation und das Zwillingsparadoxon
Wechselseitige Zeitdilatation
Gegenseitige Zeitdilatation und Längenkontraktion erscheinen Anfängern als in sich selbst widersprüchliche Konzepte. Wenn ein Beobachter im Körper S eine Uhr im ruhenden Körper S' als langsamer laufend als seine Uhr misst, während sich S' mit der Geschwindigkeit v in S bewegt, dann verlangt das Relativitätsprinzip, dass ein Beobachter im Körper S' ebenfalls eine Uhr im Körper S, die sich mit der Geschwindigkeit -v in S' bewegt, als langsamer laufend als seine Uhr misst. Wie zwei Uhren langsamer laufen können als die andere, ist eine wichtige Frage, die "zum Kern des Verständnisses der Speziellen Relativitätstheorie führt." ⓘ
Dieser scheinbare Widerspruch rührt daher, dass die unterschiedlichen Einstellungen der notwendigen, miteinander verbundenen Messungen nicht korrekt berücksichtigt werden. Diese Einstellungen ermöglichen eine konsistente Erklärung des nur scheinbaren Widerspruchs. Es geht nicht um das abstrakte Ticken zweier identischer Uhren, sondern darum, wie man den zeitlichen Abstand zweier Ticks einer sich bewegenden Uhr in einem Rahmen messen kann. Es stellt sich heraus, dass bei der gegenseitigen Beobachtung der Dauer zwischen den Ticks von Uhren, die sich jeweils in dem entsprechenden Rahmen bewegen, verschiedene Sätze von Uhren beteiligt sein müssen. Um die Tickdauer einer bewegten Uhr W′ (in S′ ruhend) im Rahmen S zu messen, verwendet man zwei zusätzliche, synchronisierte Uhren W1 und W2, die in zwei beliebig festen Punkten in S mit dem räumlichen Abstand d ruhen.
- Zwei Ereignisse können durch die Bedingung "zwei Uhren sind gleichzeitig an einem Ort" definiert werden, d. h. wenn W′ jeweils W1 und W2 passiert. Für beide Ereignisse werden die beiden Ablesungen der kollokierten Uhren aufgezeichnet. Die Differenz der beiden Ablesungen von W1 und W2 ist der zeitliche Abstand der beiden Ereignisse in S, und ihr räumlicher Abstand ist d. Die Differenz der beiden Ablesungen von W′ ist der zeitliche Abstand der beiden Ereignisse in S′. In S′ sind diese Ereignisse nur zeitlich voneinander getrennt, sie finden am selben Ort in S′ statt. Aufgrund der Invarianz des von diesen beiden Ereignissen aufgespannten Raumzeitintervalls und des räumlichen Abstands d ungleich Null in S muss der zeitliche Abstand in S′ kleiner sein als der in S: Der kleinere zeitliche Abstand zwischen den beiden Ereignissen, der sich aus den Ablesungen der beweglichen Uhr W′ ergibt, gehört zur langsamer laufenden Uhr W′. ⓘ
Umgekehrt benötigt man zur Beurteilung des zeitlichen Abstands zweier Ereignisse auf einer bewegten Uhr W (die in S ruht) im Rahmen S′ zwei ruhende Uhren in S′.
- Bei diesem Vergleich bewegt sich die Uhr W mit der Geschwindigkeit -v vorbei. Die erneute Aufzeichnung der vier Ablesungen für die Ereignisse, definiert durch "zwei Uhren gleichzeitig an einem Ort", ergibt die analogen zeitlichen Abstände der beiden Ereignisse, nun zeitlich und räumlich getrennt in S′, und nur zeitlich getrennt, aber zusammen in S. Um das Raumzeitintervall invariant zu halten, muss der zeitliche Abstand in S kleiner sein als in S′, wegen der räumlichen Trennung der Ereignisse in S′: nun wird beobachtet, dass die Uhr W langsamer läuft. ⓘ
Die notwendigen Aufzeichnungen für die beiden Urteile, mit "einer bewegten Uhr" und "zwei ruhenden Uhren" in S bzw. S′, beinhalten zwei verschiedene Sätze mit jeweils drei Uhren. Da an den Messungen verschiedene Uhrensätze beteiligt sind, besteht keine inhärente Notwendigkeit, dass die Messungen wechselseitig "konsistent" sind, so dass, wenn ein Beobachter die bewegte Uhr als langsam misst, der andere Beobachter die Uhr des einen als schnell misst. ⓘ
Abb. 2-10 veranschaulicht die vorangegangene Diskussion über die gegenseitige Zeitdilatation mit Minkowski-Diagrammen. Das obere Bild zeigt die Messungen aus der Sicht des "ruhenden" Bildes S mit ungeprimten, rechtwinkligen Achsen und des "sich mit v > 0 bewegenden" Bildes S′, koordiniert durch geprimte, schräge Achsen, schräg nach rechts; das untere Bild zeigt das "ruhende" Bild S′ mit geprimten, rechtwinkligen Koordinaten und das "sich mit -v < 0 bewegende" Bild S, mit ungeprimten, schrägen Achsen, schräg nach links. ⓘ
Jede parallel zu einer Raumachse (x, x′) gezogene Linie stellt eine Gleichzeitigkeitslinie dar. Alle Ereignisse auf einer solchen Linie haben den gleichen Zeitwert (ct, ct′). Ebenso stellt jede parallel zu einer zeitlichen Achse gezogene Linie (ct, ct′) eine Linie gleicher räumlicher Koordinatenwerte (x, x′) dar. ⓘ
- Man kann in beiden Bildern den Ursprung O (= O′) als das Ereignis bezeichnen, bei dem die jeweilige "bewegte Uhr" in beiden Vergleichen mit der "ersten ruhenden Uhr" zusammenfällt. Offensichtlich sind für dieses Ereignis die Ablesungen an beiden Uhren in beiden Vergleichen gleich Null. Infolgedessen sind die Weltlinien der beweglichen Uhren die schräg nach rechts verlaufende ct′-Achse (obere Bilder, Uhr W′) und die schräg nach links verlaufende ct-Achse (untere Bilder, Uhr W). Die Weltlinien von W1 und W′1 sind die entsprechenden vertikalen Zeitachsen (ct in den oberen Bildern, und ct′ in den unteren Bildern). ⓘ
- Im oberen Bild wird der Ort für W2 als Ax > 0 angenommen, und somit schneidet die (in den Bildern nicht gezeigte) Weltlinie dieser Uhr die Weltlinie der sich bewegenden Uhr (die ct′-Achse) in dem mit A bezeichneten Ereignis, bei dem "zwei Uhren gleichzeitig an einem Ort sind". Im unteren Bild wird der Ort für W′2 als Cx′ < 0 angenommen, und so passiert die bewegliche Uhr W bei dieser Messung W′2 im Ereignis C. ⓘ
- Im oberen Bild ist die ct-Koordinate At des Ereignisses A (die Ablesung von W2) mit B bezeichnet, so dass die verstrichene Zeit zwischen den beiden Ereignissen, gemessen mit W1 und W2, als OB angegeben wird. Für einen Vergleich muss die Länge des mit W′ gemessenen Zeitintervalls OA auf den Maßstab der ct-Achse transformiert werden. Dies geschieht durch die invariante Hyperbel (siehe auch Abb. 2-8) durch A, die alle Ereignisse mit dem gleichen Raumzeitintervall vom Ursprung wie A verbindet, und ergibt das Ereignis C auf der ct-Achse, und offensichtlich: OC < OB, die "bewegte" Uhr W′ läuft langsamer. ⓘ
Um die gegenseitige Zeitdilatation unmittelbar im oberen Bild zu zeigen, kann das Ereignis D als das Ereignis bei x′ = 0 (der Ort der Uhr W′ in S′) konstruiert werden, das gleichzeitig mit C (OC hat das gleiche Raumzeitintervall wie OA) in S′ stattfindet. Dies zeigt, dass das Zeitintervall OD länger ist als OA, was bedeutet, dass die "laufende" Uhr langsamer läuft. ⓘ
Im unteren Bild bewegt sich der Rahmen S mit der Geschwindigkeit -v im Rahmen S′ in Ruhe. Die Weltlinie der Uhr W ist die ct-Achse (schräg nach links), die Weltlinie von W′1 ist die vertikale ct′-Achse, und die Weltlinie von W′2 ist die Vertikale durch das Ereignis C, mit ct′-Koordinate D. Die invariante Hyperbel durch das Ereignis C skaliert das Zeitintervall OC auf OA, das kürzer ist als OD; außerdem wird B (ähnlich wie D in den oberen Bildern) als simultan zu A in S konstruiert, bei x = 0. Das Ergebnis OB > OC entspricht wieder dem obigen. ⓘ
Das Wort "messen" ist wichtig. In der klassischen Physik kann ein Beobachter ein beobachtetes Objekt nicht beeinflussen, aber der Bewegungszustand des Objekts kann die Beobachtungen des Beobachters an dem Objekt beeinflussen. ⓘ
Zwillingsparadoxon
In vielen Einführungen zur Speziellen Relativitätstheorie werden die Unterschiede zwischen der Galileischen Relativitätstheorie und der Speziellen Relativitätstheorie durch eine Reihe von "Paradoxien" veranschaulicht. Bei diesen Paradoxien handelt es sich in Wirklichkeit um ungelöste Probleme, die sich daraus ergeben, dass wir mit Geschwindigkeiten, die mit der Lichtgeschwindigkeit vergleichbar sind, nicht vertraut sind. Die Abhilfe besteht darin, viele Probleme der speziellen Relativitätstheorie zu lösen und sich mit ihren sogenannten kontraintuitiven Vorhersagen vertraut zu machen. Der geometrische Ansatz zur Untersuchung der Raumzeit gilt als eine der besten Methoden, um eine moderne Intuition zu entwickeln. ⓘ
Das Zwillingsparadoxon ist ein Gedankenexperiment mit eineiigen Zwillingen, von denen einer in einer Hochgeschwindigkeitsrakete ins All fliegt und bei seiner Rückkehr feststellt, dass der auf der Erde gebliebene Zwilling stärker gealtert ist. Dieses Ergebnis erscheint rätselhaft, da jeder Zwilling den anderen Zwilling als sich bewegend wahrnimmt, so dass es auf den ersten Blick den Anschein hat, dass jeder den anderen weniger gealtert sieht. Das Zwillingsparadoxon umgeht die oben dargelegte Rechtfertigung für die gegenseitige Zeitdilatation, indem es die Notwendigkeit einer dritten Uhr vermeidet. Dennoch ist das Zwillingsparadoxon kein echtes Paradoxon, da es im Rahmen der speziellen Relativitätstheorie leicht zu verstehen ist. ⓘ
Der Eindruck, dass es sich um ein Paradoxon handelt, rührt von einem Missverständnis dessen her, was die spezielle Relativitätstheorie aussagt. Die Spezielle Relativitätstheorie erklärt nicht alle Bezugssysteme für gleichwertig, sondern nur die Inertialsysteme. Der Rahmen des reisenden Zwillings ist in den Zeiten, in denen er beschleunigt, nicht träge. Außerdem ist der Unterschied zwischen den Zwillingen beobachtbar: Der reisende Zwilling muss seine Raketen abfeuern, um nach Hause zurückkehren zu können, während der zu Hause gebliebene Zwilling dies nicht tut. ⓘ
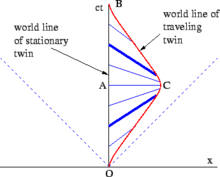
Diese Unterschiede sollten sich in einem unterschiedlichen Alter der Zwillinge niederschlagen. Das Raum-Zeit-Diagramm in Abb. 2-11 zeigt den einfachen Fall eines Zwillings, der auf der x-Achse geradeaus geht und sofort wieder zurückkehrt. Vom Standpunkt des zu Hause gebliebenen Zwillings aus gesehen, ist das Zwillingsparadoxon überhaupt nicht rätselhaft. Die entlang der Weltlinie des reisenden Zwillings von O nach C gemessene Eigenzeit plus die von C nach B gemessene Eigenzeit ist geringer als die Eigenzeit des zu Hause gebliebenen Zwillings, die von O nach A nach B gemessen wird. Komplexere Trajektorien erfordern die Integration der Eigenzeit zwischen den jeweiligen Ereignissen entlang der Kurve (d. h. das Wegintegral), um den Gesamtbetrag der vom reisenden Zwilling erlebten Eigenzeit zu berechnen. ⓘ
Komplikationen ergeben sich, wenn das Zwillingsparadoxon aus der Sicht des reisenden Zwillings analysiert wird. ⓘ
Im Folgenden wird die Nomenklatur von Weiss verwendet, die den zu Hause gebliebenen Zwilling als Terence und den reisenden Zwilling als Stella bezeichnet. ⓘ
Stella befindet sich nicht in einem Inertialsystem. Angesichts dieser Tatsache wird manchmal fälschlicherweise behauptet, die vollständige Auflösung des Zwillingsparadoxons erfordere die allgemeine Relativitätstheorie:
Eine reine SR-Analyse würde folgendermaßen aussehen: Analysiert man Stellas Ruhezustand, so ist sie während der gesamten Reise unbeweglich. Wenn sie ihre Raketen für die Umkehr zündet, erfährt sie eine Pseudokraft, die einer Gravitationskraft ähnelt. Die Abbildungen 2-6 und 2-11 veranschaulichen das Konzept der Geraden (Ebenen) der Gleichzeitigkeit: Linien, die parallel zur x-Achse des Beobachters verlaufen (xy-Ebene), stellen eine Reihe von Ereignissen dar, die im Beobachterrahmen simultan sind. In Abb. 2-11 verbinden die blauen Linien Ereignisse auf der Weltlinie von Terence, die aus der Sicht von Stella gleichzeitig mit Ereignissen auf ihrer Weltlinie sind. (Terence wiederum würde eine Reihe von horizontalen Gleichzeitigkeitslinien beobachten.) Während der gesamten Hin- und Rückreise misst Stella, dass die Uhren von Terence langsamer gehen als ihre eigenen. Doch während der Wende (d. h. zwischen den fettgedruckten blauen Linien in der Abbildung) kommt es zu einer Verschiebung des Winkels ihrer Gleichzeitigkeitslinien, was einem schnellen Überspringen der Ereignisse in Terence' Weltlinie entspricht, die Stella als gleichzeitig mit ihren eigenen betrachtet. Daher stellt Stella am Ende ihrer Reise fest, dass Terence mehr gealtert ist als sie selbst. ⓘ
Obwohl die allgemeine Relativitätstheorie nicht erforderlich ist, um das Zwillingsparadoxon zu analysieren, bietet die Anwendung des Äquivalenzprinzips der allgemeinen Relativitätstheorie einige zusätzliche Einblicke in dieses Thema. Stella ist nicht in einem Inertialsystem stationär. Analysiert man Stellas Ruhezustand, so ist sie während der gesamten Reise unbeweglich. Wenn sie rollt, ist ihr Ruhezustand inertial, und Terence' Uhr scheint langsam zu laufen. Wenn sie jedoch ihre Raketen für die Wende abfeuert, ist ihr Ruhezustand ein beschleunigter Zustand, und sie erfährt eine Kraft, die sie antreibt, als befände sie sich in einem Gravitationsfeld. Terence befindet sich scheinbar hoch oben in diesem Feld, und aufgrund der gravitativen Zeitdilatation scheint seine Uhr schneller zu laufen, so dass Terence unter dem Strich mehr gealtert ist als Stella, wenn sie wieder zusammen sind. Die theoretischen Argumente, die die gravitative Zeitdilatation vorhersagen, sind nicht auf die allgemeine Relativitätstheorie beschränkt. Jede Theorie der Schwerkraft wird die gravitative Zeitdilatation vorhersagen, wenn sie das Äquivalenzprinzip respektiert, einschließlich der Newtonschen Theorie. ⓘ
Gravitation
In diesem einführenden Abschnitt haben wir uns auf die Raumzeit der speziellen Relativitätstheorie konzentriert, da sie am einfachsten zu beschreiben ist. Die Minkowski-Raumzeit ist flach, berücksichtigt die Gravitation nicht, ist überall gleichförmig und dient lediglich als statischer Hintergrund für die Ereignisse, die in ihr stattfinden. Das Vorhandensein der Schwerkraft erschwert die Beschreibung der Raumzeit erheblich. In der allgemeinen Relativitätstheorie ist die Raumzeit nicht länger ein statischer Hintergrund, sondern interagiert aktiv mit den physikalischen Systemen, die sie enthält. Die Raumzeit krümmt sich bei Vorhandensein von Materie, kann Wellen ausbreiten, Licht krümmen und weist eine Vielzahl anderer Phänomene auf. Einige dieser Phänomene werden in den späteren Abschnitten dieses Artikels beschrieben. ⓘ
Mathematische Grundlagen der Raumzeit
Galileische Transformationen
Ein grundlegendes Ziel ist es, Messungen von Beobachtern in relativer Bewegung vergleichen zu können. Ein Beobachter O, der sich im Raum S befindet, hat die Zeit- und Raumkoordinaten eines Ereignisses gemessen und diesem Ereignis drei kartesische Koordinaten und die Zeit zugewiesen, wie sie auf seinem Gitter aus synchronisierten Uhren (x, y, z, t) gemessen wurden (siehe Abb. 1-1). Ein zweiter Beobachter O′ in einem anderen Rahmen S′ misst dasselbe Ereignis in seinem Koordinatensystem und seinem Gitter synchronisierter Uhren (x′, y′, z′, t′). Bei Inertialsystemen ist keiner der beiden Beobachter einer Beschleunigung ausgesetzt, und eine einfache Reihe von Gleichungen ermöglicht es uns, die Koordinaten (x, y, z, t) mit (x′, y′, z′, t′) in Beziehung zu setzen. Unter der Voraussetzung, dass sich die beiden Koordinatensysteme in der Standardkonfiguration befinden, d. h. dass sie mit parallelen (x, y, z)-Koordinaten ausgerichtet sind und dass t = 0 ist, wenn t′ = 0 ist, lautet die Koordinatentransformation wie folgt:

Abb. 3-1 veranschaulicht, dass in Newtons Theorie die Zeit universell ist, nicht die Lichtgeschwindigkeit. Betrachten Sie das folgende Gedankenexperiment: Der rote Pfeil zeigt einen Zug, der sich mit 0,4 c in Bezug auf den Bahnsteig bewegt. Innerhalb des Zuges schießt ein Fahrgast eine Kugel mit einer Geschwindigkeit von 0,4 c im Rahmen des Zuges ab. Der blaue Pfeil veranschaulicht, dass eine Person, die auf den Gleisen des Zuges steht, die Geschwindigkeit der Kugel mit 0,8 c misst. Dies entspricht unseren naiven Erwartungen. ⓘ
Allgemeiner ausgedrückt: Angenommen, der Rahmen S′ bewegt sich mit der Geschwindigkeit v in Bezug auf den Rahmen S, dann misst der Beobachter O′ im Rahmen S′ ein Objekt, das sich mit der Geschwindigkeit u′ bewegt. Da x = ut, x′ = x - vt und t = t′ ist, kann die Geschwindigkeit u in Bezug auf den Rahmen S als x′ = ut - vt = (u - v)t = (u - v)t′ geschrieben werden. Dies führt zu u′ = x′/t′ und schließlich
- oder ⓘ
was das allgemein gültige Galilei-Gesetz für die Addition von Geschwindigkeiten ist. ⓘ
Relativistische Zusammensetzung von Geschwindigkeiten

Die Zusammensetzung der Geschwindigkeiten ist in der relativistischen Raumzeit ganz anders. Um die Komplexität der Gleichungen etwas zu reduzieren, führen wir eine gemeinsame Kurzform für das Verhältnis der Geschwindigkeit eines Objekts relativ zum Licht ein, ⓘ
Abb. 3-2a zeigt einen roten Zug, der sich mit einer Geschwindigkeit von v/c = β = s/a vorwärts bewegt. Ein Passagier schießt aus dem ursprünglichen Rahmen des Zuges eine Kugel mit einer Geschwindigkeit ab, die durch u′/c = β′ = n/m gegeben ist, wobei die Entfernung entlang einer Linie parallel zur roten x′-Achse und nicht parallel zur schwarzen x-Achse gemessen wird. Wie hoch ist die zusammengesetzte Geschwindigkeit u des Geschosses relativ zur Plattform, die durch den blauen Pfeil dargestellt ist? Bezugnehmend auf Abb. 3-2b:
- Von der Plattform aus betrachtet, ist die zusammengesetzte Geschwindigkeit des Geschosses gegeben durch u = c(s + r)/(a + b).
- Die beiden gelben Dreiecke sind ähnlich, weil sie rechtwinklige Dreiecke sind, die einen gemeinsamen Winkel α haben. Im großen gelben Dreieck ist das Verhältnis s/a = v/c = β.
- Die Verhältnisse der entsprechenden Seiten der beiden gelben Dreiecke sind konstant, so dass r/a = b/s = n/m = β′. Also b = u′s/c und r = u′a/c.
- Setzen Sie die Ausdrücke für b und r in den Ausdruck für u aus Schritt 1 ein, um die Einsteinsche Formel für die Addition von Geschwindigkeiten zu erhalten:
Die oben dargestellte relativistische Formel für die Addition von Geschwindigkeiten weist mehrere wichtige Merkmale auf:
- Wenn u′ und v beide sehr klein im Vergleich zur Lichtgeschwindigkeit sind, dann wird das Produkt vu′/c2 verschwindend klein, und das Gesamtergebnis unterscheidet sich nicht mehr von der Galileischen Formel (Newtons Formel) für die Addition von Geschwindigkeiten: u = u′ + v. Die Galileische Formel ist ein Spezialfall der relativistischen Formel, die für kleine Geschwindigkeiten gilt.
- Wenn u′ gleich c gesetzt wird, dann ergibt die Formel u = c, unabhängig vom Ausgangswert von v. Die Lichtgeschwindigkeit ist für alle Beobachter gleich, unabhängig von ihrer Bewegung relativ zur emittierenden Quelle. ⓘ
Zeitdilatation und Längenkontraktion - eine neue Betrachtung

Die quantitativen Ausdrücke für Zeitdilatation und Längenkontraktion lassen sich leicht ermitteln. Abb. 3-3 ist ein zusammengesetztes Bild, das Einzelbilder aus zwei früheren Animationen enthält, die für die Zwecke dieses Abschnitts vereinfacht und neu beschriftet wurden. ⓘ
Um die Komplexität der Gleichungen etwas zu reduzieren, gibt es eine Reihe von verschiedenen Kurzschreibweisen für ct:
- und . sind üblich.
- Man sieht auch sehr häufig die Verwendung der Konvention ⓘ

In Abb. 3-3a stellen die Segmente OA und OK gleiche Raumzeitintervalle dar. Die Zeitdilatation wird durch das Verhältnis OB/OK dargestellt. Die invariante Hyperbel hat die Gleichung w = √x2 + k2 mit k = OK, und die rote Linie, die die Weltlinie eines bewegten Teilchens darstellt, hat die Gleichung w = x/β = xc/v. Mit ein wenig algebraischer Manipulation erhält man ⓘ
Der Ausdruck mit dem Quadratwurzel-Symbol kommt in der Relativitätstheorie sehr häufig vor, und einer der Ausdrücke wird Lorentz-Faktor genannt, der mit dem griechischen Buchstaben gamma bezeichnet wird :
Wenn v größer oder gleich c ist, wird der Ausdruck für physikalisch bedeutungslos, was bedeutet, dass c die maximal mögliche Geschwindigkeit in der Natur ist. Für jedes v, das größer als Null ist, ist der Lorentz-Faktor größer als eins, obwohl die Form der Kurve so beschaffen ist, dass der Lorentz-Faktor für niedrige Geschwindigkeiten extrem nahe bei eins liegt. ⓘ
In Abb. 3-3b stellen die Segmente OA und OK gleiche Raumzeitintervalle dar. Die Längenkontraktion wird durch das Verhältnis OB/OK dargestellt. Die invariante Hyperbel hat die Gleichung x = √w2 + k2, wobei k = OK ist, und die Kanten des blauen Bandes, das die Weltlinien der Endpunkte eines bewegten Stabes darstellt, haben die Steigung 1/β = c/v. Das Ereignis A hat die Koordinaten (x, w) = (γk, γβk). Da die Tangente durch A und B die Gleichung w = (x - OB)/β hat, haben wir γβk = (γk - OB)/β und
Lorentz-Transformationen
Die Galilei-Transformationen und das sich daraus ergebende Gesetz der Addition der Geschwindigkeiten funktionieren gut in unserer gewöhnlichen Welt der niedrigen Geschwindigkeiten von Flugzeugen, Autos und Bällen. Ab Mitte des 18. Jahrhunderts begannen jedoch empfindliche wissenschaftliche Instrumente, Anomalien zu entdecken, die nicht mit der gewöhnlichen Addition von Geschwindigkeiten übereinstimmten. ⓘ
Lorentz-Transformationen werden in der Speziellen Relativitätstheorie verwendet, um die Koordinaten eines Ereignisses von einem Koordinatensystem in ein anderes zu übertragen. ⓘ
Der Lorentz-Faktor erscheint in den Lorentz-Transformationen:
Die inversen Lorentztransformationen sind:
Wenn v ≪ c und x klein genug ist, gehen die Terme v2/c2 und vx/c2 gegen Null, und die Lorentz-Transformationen nähern sich den Galilei-Transformationen an. ⓘ
usw., bedeuten meist wirklich usw. Obwohl die Lorentztransformationsgleichungen der Kürze halber ohne Deltas geschrieben werden, bedeutet x Δx usw. Im Allgemeinen geht es immer um die räumlichen und zeitlichen Unterschiede zwischen den Ereignissen. ⓘ
Eine Gruppe von Transformationen als normale Lorentz-Transformationen und die andere als inverse Transformationen zu bezeichnen, ist irreführend, da es keinen wesentlichen Unterschied zwischen den beiden Rahmen gibt. Verschiedene Autoren bezeichnen die eine oder die andere Gruppe von Transformationen als "inverse" Gruppe. Die Vorwärts- und Rückwärtstransformationen stehen in einem trivialen Verhältnis zueinander, da sich das S-Frame nur vorwärts oder rückwärts in Bezug auf S′ bewegen kann. Die Umkehrung der Gleichungen bedeutet also einfach, dass man die primed und unprimed Variablen vertauscht und v durch -v ersetzt. ⓘ
Beispiel: Terence und Stella nehmen an einem Weltraumrennen von der Erde zum Mars teil. Terence ist ein Offizieller an der Startlinie, während Stella eine Teilnehmerin ist. Zum Zeitpunkt t = t′ = 0 beschleunigt Stellas Raumschiff augenblicklich auf eine Geschwindigkeit von 0,5 c. Die Entfernung von der Erde zum Mars beträgt 300 Lichtsekunden (etwa 90,0×106 km). Terence beobachtet Stella beim Überqueren der Ziellinie mit t = 600,00 s. Stella beobachtet jedoch, dass die Zeit auf ihrem Schiffschronometer als sie die Ziellinie passiert, und sie berechnet die Entfernung zwischen der Start- und der Ziellinie, gemessen in ihrem Rahmen, auf 259,81 Lichtsekunden (etwa 77,9×106 km). 1). ⓘ
Ableitung der Lorentz-Transformationen

Seit Einsteins ursprünglicher Arbeit aus dem Jahr 1905 gab es viele Dutzend Ableitungen der Lorentz-Transformationen, jede mit ihrem eigenen Schwerpunkt. Obwohl Einsteins Ableitung auf der Invarianz der Lichtgeschwindigkeit beruhte, gibt es andere physikalische Prinzipien, die als Ausgangspunkt dienen können. Letztlich können diese alternativen Ausgangspunkte als verschiedene Ausprägungen des zugrundeliegenden Lokalitätsprinzips betrachtet werden, das besagt, dass der Einfluss, den ein Teilchen auf ein anderes ausübt, nicht augenblicklich übertragen werden kann. ⓘ
Die hier dargestellte und in Abb. 3-5 illustrierte Herleitung basiert auf einer von Bais vorgestellten und nutzt frühere Ergebnisse aus den Abschnitten Relativistische Zusammensetzung von Geschwindigkeiten, Zeitdilatation und Längenkontraktion. Das Ereignis P hat Koordinaten (w, x) im schwarzen "Ruhesystem" und Koordinaten (w′, x′) im roten Rahmen, der sich mit dem Geschwindigkeitsparameter β = v/c bewegt. Um w′ und x′ in Bezug auf w und x (oder umgekehrt) zu bestimmen, ist es zunächst einfacher, die inverse Lorentztransformation herzuleiten.
- Eine Längenausdehnung bzw. -kontraktion in den Querrichtungen kann es nicht geben. y' muss gleich y und z′ muss gleich z sein, sonst würde es vom Beobachter abhängen, ob eine schnell bewegte 1-m-Kugel durch ein 1-m-Kreisloch passt. Das erste Postulat der Relativitätstheorie besagt, dass alle Inertialsysteme gleichwertig sind, und eine transversale Expansion/Kontraktion würde dieses Gesetz verletzen.
- Aus der Zeichnung: w = a + b und x = r + s
- Aus früheren Ergebnissen mit ähnlichen Dreiecken wissen wir, dass s/a = b/r = v/c = β.
- Aufgrund der Zeitdilatation ist a = γw′.
- Setzt man Gleichung (4) in s/a = β ein, ergibt sich s = γw′β.
- Die Längenkontraktion und ähnliche Dreiecke liefern uns r = γx′ und b = βr = βγx′.
- Setzt man die Ausdrücke für s, a, r und b in die Gleichungen in Schritt 2 ein, erhält man sofort
Die obigen Gleichungen sind alternative Ausdrücke für die t- und x-Gleichungen der inversen Lorentz-Transformation, wie man sieht, wenn man ct für w, ct′ für w′ und v/c für β einsetzt. Aus der inversen Transformation können die Gleichungen der Vorwärtstransformation abgeleitet werden, indem man für t′ und x′ löst. ⓘ
Linearität der Lorentz-Transformationen
Die Lorentz-Transformationen haben eine mathematische Eigenschaft, die Linearität genannt wird, da x′ und t′ als Linearkombinationen von x und t erhalten werden, ohne dass höhere Potenzen beteiligt sind. Die Linearität der Transformation spiegelt eine grundlegende Eigenschaft der Raumzeit wider, die bei der Herleitung stillschweigend vorausgesetzt wurde, nämlich, dass die Eigenschaften von Inertialsystemen unabhängig von Ort und Zeit sind. Bei fehlender Gravitation sieht die Raumzeit überall gleich aus. Alle Inertialbeobachter sind sich einig darüber, was eine beschleunigte und was eine nichtbeschleunigte Bewegung ist. Jeder Beobachter kann seine eigenen Messungen von Raum und Zeit verwenden, die jedoch nicht absolut sind. Die Konventionen eines anderen Beobachters sind genauso gut geeignet. ⓘ
Ein Ergebnis der Linearität ist, dass, wenn zwei Lorentz-Transformationen nacheinander angewendet werden, das Ergebnis auch eine Lorentz-Transformation ist. ⓘ
Beispiel: Terence beobachtet Stella, die sich mit 0,500 c von ihm entfernt, und er kann die Lorentztransformationen mit β = 0,500 verwenden, um Stellas Messungen mit seinen eigenen in Beziehung zu setzen. Stella beobachtet in ihrem Körper Ursula, die sich mit 0,250 c von ihr wegbewegt, und sie kann die Lorentz-Transformationen mit β = 0,250 verwenden, um Ursulas Messungen mit ihren eigenen in Beziehung zu setzen. Aufgrund der Linearität der Transformationen und der relativistischen Zusammensetzung der Geschwindigkeiten kann Terence die Lorentztransformationen mit β = 0,666 verwenden, um Ursulas Messungen mit seinen eigenen in Beziehung zu setzen. ⓘ
Doppler-Effekt
Der Dopplereffekt ist die Änderung der Frequenz oder Wellenlänge einer Welle für einen Empfänger und eine Quelle in relativer Bewegung. Der Einfachheit halber betrachten wir hier zwei grundlegende Szenarien: (1) Die Bewegungen der Quelle und/oder des Empfängers verlaufen genau entlang der Linie, die sie verbindet (longitudinaler Dopplereffekt), und (2) die Bewegungen verlaufen im rechten Winkel zu dieser Linie (transversaler Dopplereffekt). Wir ignorieren Szenarien, in denen sie sich entlang von Zwischenwinkeln bewegen. ⓘ
Longitudinaler Dopplereffekt
Die klassische Doppler-Analyse befasst sich mit Wellen, die sich in einem Medium ausbreiten, wie z. B. Schallwellen oder Wasserwellen, und die zwischen Quellen und Empfängern übertragen werden, die sich aufeinander zu oder voneinander weg bewegen. Die Analyse solcher Wellen hängt davon ab, ob sich die Quelle, der Empfänger oder beide relativ zum Medium bewegen. Unter der Annahme, dass der Empfänger in Bezug auf das Medium stationär ist und die Quelle sich mit einer Geschwindigkeit von vs bei einem Geschwindigkeitsparameter von βs direkt vom Empfänger wegbewegt, wird die Wellenlänge vergrößert und die beobachtete Frequenz f ist gegeben durch
Wenn die Quelle stationär ist und der Empfänger sich mit einer Geschwindigkeit von vr direkt von der Quelle wegbewegt (Geschwindigkeitsparameter βr), ändert sich die Wellenlänge nicht, aber die Übertragungsgeschwindigkeit der Wellen relativ zum Empfänger wird verringert, und die beobachtete Frequenz f ist gegeben durch

Licht breitet sich, anders als Schall oder Wasserwellen, nicht durch ein Medium aus, und es gibt keinen Unterschied zwischen einer Quelle, die sich vom Empfänger entfernt, und einem Empfänger, der sich von der Quelle entfernt. Abb. 3-6 zeigt ein relativistisches Raumzeitdiagramm, in dem sich eine Quelle mit einem Geschwindigkeitsparameter β vom Empfänger entfernt, so dass der Abstand zwischen Quelle und Empfänger zur Zeit w βw beträgt. Aufgrund der Zeitdilatation, . Da die Steigung des grünen Lichtstrahls -1 ist, . Der relativistische Dopplereffekt ist also gegeben durch
Transversaler Dopplereffekt

Nehmen wir an, dass sich eine Quelle und ein Empfänger, die sich beide in gleichförmiger Trägheitsbewegung entlang von sich nicht schneidenden Linien nähern, am nächsten zueinander stehen. Es scheint, dass die klassische Analyse vorhersagt, dass der Empfänger keine Dopplerverschiebung feststellt. Aufgrund von Feinheiten in der Analyse ist diese Erwartung nicht unbedingt zutreffend. Dennoch ist die transversale Dopplerverschiebung, wenn sie richtig definiert ist, ein relativistischer Effekt, für den es kein klassisches Analogon gibt. Die Feinheiten sind die folgenden:
- Abb. 3-7a. Wie sieht die Frequenzmessung aus, wenn sich der Empfänger geometrisch am nächsten an der Quelle befindet? Dieses Szenario lässt sich am einfachsten aus dem Bild S' der Quelle analysieren.
- Abb. 3-7b. Wie hoch ist die gemessene Frequenz, wenn der Empfänger die Quelle als am nächsten zu ihm stehend betrachtet? Dieses Szenario lässt sich am einfachsten aus dem Bild S des Empfängers analysieren.
Zwei andere Szenarien werden üblicherweise in Diskussionen über die transversale Dopplerverschiebung untersucht:
- Abb. 3-7c. Wenn sich der Empfänger in einem Kreis um die Quelle bewegt, welche Frequenz misst der Empfänger?
- Abb. 3-7d. Wenn sich die Quelle im Kreis um den Empfänger bewegt, welche Frequenz misst der Empfänger?
In Szenario (a) ist der Punkt der größten Annäherung rahmenunabhängig und stellt den Moment dar, in dem es keine Abstandsänderung gegenüber der Zeit gibt (d. h. dr/dt = 0, wobei r der Abstand zwischen Empfänger und Quelle ist) und somit keine longitudinale Dopplerverschiebung. Die Quelle beobachtet, dass der Empfänger von Licht der Frequenz f′ beleuchtet wird, aber sie beobachtet auch, dass der Empfänger eine zeitverzögerte Uhr hat. Im Bild S wird der Empfänger daher von blauverschobenem Licht mit der Frequenz
In Szenario (b) zeigt die Abbildung, dass der Empfänger von dem Licht beleuchtet wird, das aus der Zeit stammt, als die Quelle dem Empfänger am nächsten war, obwohl sich die Quelle weiterbewegt hat. Da die Uhren der Quelle im Bild S zeitlich gedehnt sind und dr/dt an diesem Punkt gleich Null war, ist das Licht der Quelle, das von diesem nächstgelegenen Punkt ausgesendet wurde, mit der Frequenz rotverschoben
Die Szenarien (c) und (d) können durch einfache Zeitdilatationsargumente analysiert werden. In (c) beobachtet der Empfänger das Licht der Quelle mit einer Blauverschiebung um den Faktor In (b) ist das Licht rotverschoben, und in (d) ist das Licht rotverschoben. Die einzige scheinbare Komplikation besteht darin, dass sich die umlaufenden Objekte in einer beschleunigten Bewegung befinden. Wenn jedoch ein Inertialbeobachter auf eine beschleunigte Uhr blickt, ist für die Berechnung der Zeitdilatation nur die momentane Geschwindigkeit der Uhr wichtig. (Der umgekehrte Fall trifft jedoch nicht zu.) Die meisten Berichte über die transversale Dopplerverschiebung bezeichnen den Effekt als Rotverschiebung und analysieren ihn anhand der Szenarien (b) oder (d). ⓘ
Energie und Impuls
Ausdehnung des Impulses auf vier Dimensionen

In der klassischen Mechanik wird der Bewegungszustand eines Teilchens durch seine Masse und seine Geschwindigkeit charakterisiert. Der lineare Impuls, das Produkt aus Masse und Geschwindigkeit eines Teilchens, ist eine vektorielle Größe, die die gleiche Richtung wie die Geschwindigkeit hat: p = mv. Er ist eine konservierte Größe, d. h., wenn ein geschlossenes System nicht durch äußere Kräfte beeinflusst wird, kann sich sein Gesamtimpuls nicht ändern. ⓘ
In der relativistischen Mechanik wird der Impulsvektor auf vier Dimensionen erweitert. Dem Impulsvektor wird eine Zeitkomponente hinzugefügt, die es ermöglicht, den Raumzeit-Impulsvektor wie den Raumzeit-Positionsvektor zu transformieren . Bei der Untersuchung der Eigenschaften des Raumzeit-Impulses beginnen wir in Abb. 3-8a mit der Betrachtung des Zustands eines Teilchens im Ruhezustand. Im Ruhezustand ist die räumliche Komponente des Impulses gleich Null, d. h. p = 0, aber die zeitliche Komponente ist gleich mc. ⓘ
Wir können die transformierten Komponenten dieses Vektors im bewegten System mit Hilfe der Lorentz-Transformationen erhalten, oder wir können sie direkt aus der Abbildung ablesen, da wir wissen, dass und . da die roten Achsen mit Gamma skaliert sind. Abb. 3-8b veranschaulicht die Situation, wie sie sich im bewegten Bild darstellt. Es ist ersichtlich, dass die Raum- und Zeitkomponenten des Viermoments ins Unendliche gehen, wenn sich die Geschwindigkeit des bewegten Rahmens c nähert. ⓘ
Wir werden diese Information in Kürze verwenden, um einen Ausdruck für den Viererimpuls zu erhalten. ⓘ
Impuls des Lichts

Lichtteilchen oder Photonen bewegen sich mit der Geschwindigkeit c, der Konstante, die gemeinhin als Lichtgeschwindigkeit bekannt ist. Diese Aussage ist keine Tautologie, denn viele moderne Formulierungen der Relativitätstheorie gehen nicht von einer konstanten Lichtgeschwindigkeit aus. Photonen breiten sich also entlang einer lichtähnlichen Weltlinie aus und haben in geeigneten Einheiten für jeden Beobachter gleiche Raum- und Zeitkomponenten. ⓘ
Eine Folge der Maxwellschen Theorie des Elektromagnetismus ist, dass Licht Energie und Impuls trägt und dass ihr Verhältnis eine Konstante ist: . Umstellen, und da für Photonen die Raum- und die Zeitkomponente gleich sind, muss E/c mit der Zeitkomponente des Raum-Zeit-Impulsvektors gleichgesetzt werden. ⓘ
Photonen bewegen sich mit Lichtgeschwindigkeit, haben aber einen endlichen Impuls und eine endliche Energie. Damit dies der Fall ist, muss der Massetermin in γmc gleich Null sein, was bedeutet, dass Photonen masselose Teilchen sind. Unendlich mal Null ist eine unbestimmte Größe, aber E/c ist wohldefiniert. ⓘ
Nach dieser Analyse ist die Energie eines Photons, wenn sie im ruhenden System gleich E ist, gleich in einem bewegten System. Dieses Ergebnis lässt sich durch Betrachtung von Abb. 3-9 oder durch Anwendung der Lorentz-Transformationen ableiten und steht im Einklang mit der zuvor gegebenen Analyse des Dopplereffekts. ⓘ
Masse-Energie-Beziehung
Die Betrachtung der Zusammenhänge zwischen den verschiedenen Komponenten des relativistischen Impulsvektors führte Einstein zu mehreren berühmten Schlussfolgerungen. ⓘ
- Im Grenzfall niedriger Geschwindigkeit, wenn β = v/c gegen Null geht, nähert sich γ 1, so dass die räumliche Komponente des relativistischen Impulses nähert sich mv, dem klassischen Begriff für den Impuls. Nach dieser Sichtweise kann γm als relativistische Verallgemeinerung von m interpretiert werden. Einstein schlug vor, dass die relativistische Masse eines Objekts mit der Geschwindigkeit gemäß der folgenden Formel zunimmt .
- Vergleicht man die Zeitkomponente des relativistischen Impulses mit der des Photons, so dass Einstein zu folgender Beziehung gelangte . Vereinfacht auf den Fall der Geschwindigkeit Null ist dies Einsteins berühmte Gleichung für den Zusammenhang zwischen Energie und Masse. ⓘ
Eine andere Möglichkeit, die Beziehung zwischen Masse und Energie zu betrachten, ist eine Reihenentwicklung von γmc2 bei niedrigen Geschwindigkeiten:
Der zweite Term ist lediglich ein Ausdruck für die kinetische Energie des Teilchens. Die Masse scheint in der Tat eine andere Form der Energie zu sein. ⓘ
Das von Einstein 1905 eingeführte Konzept der relativistischen Masse, mrel, hat sich, obwohl es in den Teilchenbeschleunigern rund um den Globus (oder in allen Instrumenten, deren Einsatz von Hochgeschwindigkeitsteilchen abhängt, wie Elektronenmikroskope, altmodische Farbfernsehgeräte usw.) jeden Tag aufs Neue bestätigt wird, in der Physik nicht als fruchtbares Konzept erwiesen, da es nicht als Grundlage für andere theoretische Entwicklungen gedient hat. Die relativistische Masse zum Beispiel spielt in der allgemeinen Relativitätstheorie keine Rolle. ⓘ
Aus diesem Grund und auch aus pädagogischen Gründen bevorzugen die meisten Physiker derzeit eine andere Terminologie, wenn sie sich auf die Beziehung zwischen Masse und Energie beziehen. "Relativistische Masse" ist ein veralteter Begriff. Der Begriff "Masse" an sich bezieht sich auf die Ruhemasse oder invariante Masse und ist gleich der invarianten Länge des relativistischen Impulsvektors. In einer Formel ausgedrückt,
Diese Formel gilt für alle Teilchen, sowohl für masselose als auch für massive. Für Photonen, bei denen mrest gleich Null ist, ergibt sie sich, . ⓘ
Vierfaches Moment
Aufgrund der engen Beziehung zwischen Masse und Energie wird das Viermoment (auch 4-Moment genannt) auch als Energie-Moment-4-Vektor bezeichnet. Mit einem großen P für den Vierer-Impuls und einem kleinen p für den Raumimpuls kann der Vierer-Impuls geschrieben werden als
- oder alternativ,
- unter Verwendung der Konvention, dass ⓘ
Erhaltungssätze
In der Physik besagen Erhaltungssätze, dass sich bestimmte messbare Eigenschaften eines isolierten physikalischen Systems nicht ändern, wenn sich das System im Laufe der Zeit weiterentwickelt. Im Jahr 1915 entdeckte Emmy Noether, dass jedem Erhaltungssatz eine grundlegende Symmetrie der Natur zugrunde liegt. Die Tatsache, dass es bei physikalischen Prozessen keine Rolle spielt, wo im Raum sie stattfinden (Raumtranslationssymmetrie), führt zur Impulserhaltung, die Tatsache, dass es bei solchen Prozessen keine Rolle spielt, wann sie stattfinden (Zeittranslationssymmetrie), führt zur Energieerhaltung usw. In diesem Abschnitt werden die Newton'schen Ansichten über die Erhaltung von Masse, Impuls und Energie aus einer relativistischen Perspektive betrachtet. ⓘ
Gesamtimpuls
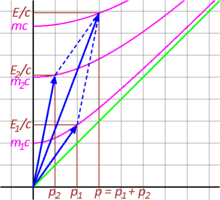
Um zu verstehen, wie die Newtonsche Sichtweise der Impulserhaltung in einem relativistischen Kontext modifiziert werden muss, untersuchen wir das Problem zweier kollidierender Körper, die auf eine einzige Dimension beschränkt sind. ⓘ
In der Newtonschen Mechanik können zwei Extremfälle dieses Problems unterschieden werden, die eine Mathematik von minimaler Komplexität ergeben:
- (1) Die beiden Körper prallen in einem vollständig elastischen Stoß voneinander ab.
- (2) Die beiden Körper haften aneinander und bewegen sich als ein einziges Teilchen weiter. Dieser zweite Fall ist der Fall eines völlig unelastischen Zusammenstoßes.
In beiden Fällen, (1) und (2), bleiben Impuls, Masse und Gesamtenergie erhalten. Die kinetische Energie bleibt jedoch beim inelastischen Zusammenstoß nicht erhalten. Ein bestimmter Anteil der ursprünglichen kinetischen Energie wird in Wärme umgewandelt. ⓘ
Im Fall (2) stoßen zwei Massen mit den Impulsen und . kollidieren und erzeugen ein einzelnes Teilchen mit erhaltener Masse das sich mit der Schwerpunktsgeschwindigkeit des ursprünglichen Systems bewegt, . Der Gesamtimpuls ist konserviert. ⓘ
Abb. 3-10 zeigt den inelastischen Zusammenstoß zweier Teilchen aus relativistischer Sicht. Die Zeitkomponenten und . addieren sich zur Summe E/c des resultierenden Vektors, was bedeutet, dass die Energie erhalten bleibt. Ebenso addieren sich die Raumkomponenten und . addieren sich zu p des resultierenden Vektors. Der Vierfachimpuls ist, wie erwartet, eine erhaltene Größe. Die invariante Masse des verschmolzenen Teilchens, die durch den Schnittpunkt der invarianten Hyperbel des Gesamtimpulses mit der Energieachse gegeben ist, ist jedoch nicht gleich der Summe der invarianten Massen der einzelnen Teilchen, die zusammengestoßen sind. Vielmehr ist sie größer als die Summe der Einzelmassen: . ⓘ
Betrachtet man die Ereignisse dieses Szenarios in umgekehrter Reihenfolge, so stellt man fest, dass die Nichterhaltung der Masse ein häufiges Phänomen ist: Wenn ein instabiles Elementarteilchen spontan in zwei leichtere Teilchen zerfällt, bleibt zwar die Gesamtenergie erhalten, nicht aber die Masse. Ein Teil der Masse wird in kinetische Energie umgewandelt. ⓘ
Wahl des Bezugssystems
Die Freiheit, ein beliebiges Bezugssystem für die Durchführung einer Analyse zu wählen, ermöglicht es uns, ein besonders geeignetes zu wählen. Für die Analyse von Impuls- und Energieproblemen ist der "Schwerpunktrahmen" (auch Nullimpulsrahmen oder COM-Rahmen genannt) in der Regel am besten geeignet. Dies ist der Rahmen, in dem die Raumkomponente des Gesamtimpulses des Systems Null ist. Abb. 3-11 zeigt den Zerfall eines Hochgeschwindigkeitsteilchens in zwei Tochterteilchen. Im Laborrahmen werden die Tochterteilchen bevorzugt in eine Richtung emittiert, die entlang der Flugbahn des ursprünglichen Teilchens verläuft. Im COM-Frame hingegen werden die beiden Tochterteilchen in entgegengesetzte Richtungen emittiert, obwohl ihre Massen und die Größe ihrer Geschwindigkeiten im Allgemeinen nicht gleich sind. ⓘ
Energie- und Impulserhaltung
In einer Newton'schen Analyse von wechselwirkenden Teilchen ist die Umwandlung zwischen Rahmen einfach, da es genügt, die Galilei-Transformation auf alle Geschwindigkeiten anzuwenden. Da ist der Impuls . Wenn der Gesamtimpuls eines wechselwirkenden Systems von Teilchen in einem Rahmen als erhalten gilt, wird er auch in jedem anderen Rahmen als erhalten angesehen. ⓘ
Die Impulserhaltung im COM-Rahmen läuft auf die Forderung hinaus, dass p = 0 sowohl vor als auch nach der Kollision ist. In der Newton'schen Analyse schreibt die Erhaltung der Masse vor, dass . In den vereinfachten, eindimensionalen Szenarien, die wir betrachtet haben, ist nur eine zusätzliche Bedingung erforderlich, bevor die Ausgangsimpulse der Teilchen bestimmt werden können - eine Energiebedingung. Im eindimensionalen Fall eines vollständig elastischen Zusammenstoßes ohne Verlust an kinetischer Energie sind die Ausgangsgeschwindigkeiten der zurückprallenden Teilchen im COM-Rahmen genau gleich und entgegengesetzt zu ihren Eingangsgeschwindigkeiten. Im Falle eines völlig unelastischen Stoßes mit vollständigem Verlust an kinetischer Energie sind die Ausgangsgeschwindigkeiten der zurückprallenden Teilchen gleich Null. ⓘ
Newtonsche Impulse, berechnet als berechnen, verhalten sich bei der Lorentz-Transformation nicht korrekt. Die lineare Transformation der Geschwindigkeiten wird ersetzt durch die stark nichtlineare Die lineare Transformation der Geschwindigkeiten führt dazu, dass eine Berechnung, die die Impulserhaltung in einem System zeigt, in anderen Systemen ungültig ist. Einstein stand vor der Wahl, entweder die Impulserhaltung aufzugeben oder die Definition des Impulses zu ändern. Er entschied sich für die zweite Möglichkeit. ⓘ
Der relativistische Erhaltungssatz für Energie und Impuls ersetzt die drei klassischen Erhaltungssätze für Energie, Impuls und Masse. Die Masse wird nicht mehr eigenständig erhalten, da sie in der relativistischen Gesamtenergie aufgegangen ist. Dies macht die relativistische Energieerhaltung zu einem einfacheren Konzept als in der nichtrelativistischen Mechanik, da die Gesamtenergie ohne jegliche Einschränkungen erhalten bleibt. Kinetische Energie, die in Wärme oder innere potentielle Energie umgewandelt wird, zeigt sich als Massenzunahme. ⓘ
Beispiel: Wegen der Äquivalenz von Masse und Energie werden die Massen der Elementarteilchen üblicherweise in Energieeinheiten angegeben, wobei 1 MeV = 106 Elektronenvolt. Ein geladenes Pion ist ein Teilchen mit einer Masse von 139,57 MeV (ca. das 273-fache der Elektronenmasse). Es ist instabil und zerfällt in ein Myon mit einer Masse von 105,66 MeV (ca. das 207-fache der Elektronenmasse) und ein Antineutrino, das eine fast vernachlässigbare Masse hat. Die Differenz zwischen der Pionenmasse und der Myonmasse beträgt 33,91 MeV.
π−
→
μ−
+
ν
μ ⓘ
Abb. 3-12a zeigt das Energie-Impuls-Diagramm für diese Zerfallsreaktion im Ruhezustand des Pions. Aufgrund seiner vernachlässigbaren Masse bewegt sich ein Neutrino mit nahezu Lichtgeschwindigkeit. Der relativistische Ausdruck für seine Energie lautet wie der des Photons was auch der Wert der Raumkomponente seines Impulses ist. Um den Impuls zu erhalten, hat das Myon den gleichen Wert der Raumkomponente des Impulses des Neutrinos, allerdings in der entgegengesetzten Richtung. ⓘ
Algebraische Analysen der Energetik dieser Zerfallsreaktion sind online verfügbar, daher zeigt Abb. 3-12b stattdessen eine Lösung mit dem Grafikrechner. Die Energie des Neutrinos beträgt 29,79 MeV, und die Energie des Myons beträgt 33,91 MeV - 29,79 MeV = 4,12 MeV. Der größte Teil der Energie wird von dem Neutrino mit der Masse von fast null abgeführt. ⓘ
Über die Grundlagen hinaus
Die Themen in diesem Abschnitt sind technisch wesentlich schwieriger als die in den vorangegangenen Abschnitten und sind für das Verständnis der Einführung in die gekrümmte Raumzeit nicht unbedingt erforderlich. ⓘ
Schnelligkeit

Lorentz-Transformationen setzen die Koordinaten von Ereignissen in einem Bezugsrahmen in Beziehung zu denen eines anderen Rahmens. Die relativistische Komposition von Geschwindigkeiten wird verwendet, um zwei Geschwindigkeiten zu addieren. Die Formeln zur Durchführung der letztgenannten Berechnungen sind nichtlinear und damit komplexer als die entsprechenden Galilei-Formeln. ⓘ
Diese Nichtlinearität ist ein Artefakt der von uns gewählten Parameter. Wir haben bereits festgestellt, dass in einem x-ct-Raumzeitdiagramm die Punkte in einem konstanten Raumzeitintervall vom Ursprung eine unveränderliche Hyperbel bilden. Wir haben auch festgestellt, dass die Koordinatensysteme zweier Raumzeit-Bezugsrahmen in Standardkonfiguration hyperbolisch zueinander gedreht sind. ⓘ
Die natürlichen Funktionen zur Darstellung dieser Beziehungen sind die hyperbolischen Entsprechungen der trigonometrischen Funktionen. Abb. 4-1a zeigt einen Einheitskreis mit sin(a) und cos(a). Der einzige Unterschied zwischen diesem Diagramm und dem bekannten Einheitskreis der elementaren Trigonometrie besteht darin, dass a nicht als der Winkel zwischen dem Strahl und der x-Achse, sondern als die doppelte Fläche des Sektors interpretiert wird, den der Strahl von der x-Achse aus überstreicht. (Numerisch sind die Winkel- und 2 × Flächenmaße für den Einheitskreis identisch.) Abb. 4-1b zeigt eine Einheitshyperbel mit sinh(a) und cosh(a), wobei a ebenfalls als doppelte gefärbte Fläche interpretiert wird. Abb. 4-2 zeigt die Darstellungen der Funktionen sinh, cosh und tanh. ⓘ
Für den Einheitskreis ist die Steigung des Strahls gegeben durch ⓘ
In der kartesischen Ebene ist die Drehung des Punktes (x, y) in den Punkt (x', y') um den Winkel θ gegeben durch
In einem Raumzeitdiagramm ist der Geschwindigkeitsparameter ist das Analogon der Steigung. Die Geschwindigkeit φ ist definiert durch ⓘ
wobei ⓘ
Die oben definierte Geschwindigkeit ist in der Speziellen Relativitätstheorie sehr nützlich, da viele Ausdrücke eine wesentlich einfachere Form annehmen, wenn sie durch sie ausgedrückt werden. Zum Beispiel ist die Geschwindigkeit in der Formel für die kollineare Geschwindigkeitsaddition einfach additiv; ⓘ
oder mit anderen Worten, ⓘ
Die Lorentz-Transformationen nehmen eine einfache Form an, wenn sie in Form der Geschwindigkeit ausgedrückt werden. Der γ-Faktor kann geschrieben werden als ⓘ
Transformationen, die eine Relativbewegung mit gleichförmiger Geschwindigkeit und ohne Drehung der Raumkoordinatenachsen beschreiben, werden als Boosts bezeichnet. ⓘ
Setzt man γ und γβ in die zuvor dargestellten Transformationen ein und schreibt sie in Matrixform um, so kann der Lorentz-Boost in x-Richtung wie folgt geschrieben werden
und der inverse Lorentz-Boost in x-Richtung kann geschrieben werden als
Mit anderen Worten: Lorentz-Boosts stellen hyperbolische Rotationen in der Minkowski-Raumzeit dar. ⓘ
Die Vorteile der Verwendung von hyperbolischen Funktionen sind so groß, dass sie in einigen Lehrbüchern, wie z. B. in den klassischen Büchern von Taylor und Wheeler, bereits zu einem sehr frühen Zeitpunkt eingeführt werden. ⓘ
4-Vektoren
Vier Vektoren wurden bereits im Zusammenhang mit dem Energie-Impuls-4-Vektor erwähnt, jedoch ohne große Betonung. In der Tat werden sie in keiner der elementaren Ableitungen der speziellen Relativitätstheorie benötigt. Wenn man sie aber einmal verstanden hat, vereinfachen 4-Vektoren und allgemeiner Tensoren die Mathematik und das begriffliche Verständnis der Speziellen Relativitätstheorie erheblich. Wenn man ausschließlich mit solchen Objekten arbeitet, erhält man Formeln, die offensichtlich relativistisch invariant sind, was in nicht-trivialen Zusammenhängen einen erheblichen Vorteil darstellt. So ist beispielsweise der Nachweis der relativistischen Invarianz der Maxwellschen Gleichungen in ihrer üblichen Form nicht trivial, während es sich bei der Verwendung der Feldstärketensor-Formulierung lediglich um eine Routineberechnung (eigentlich nicht mehr als eine Beobachtung) handelt. Andererseits stützt sich die allgemeine Relativitätstheorie von Anfang an stark auf 4-Vektoren und allgemeiner auf Tensoren, die physikalisch relevante Einheiten darstellen. Um diese durch Gleichungen in Beziehung zu setzen, die nicht auf spezifischen Koordinaten beruhen, werden Tensoren benötigt, die in der Lage sind, solche 4-Vektoren auch in einer gekrümmten Raumzeit zu verbinden, und nicht nur in einer flachen wie in der speziellen Relativitätstheorie. Die Untersuchung von Tensoren liegt außerhalb des Rahmens dieses Artikels, der nur eine grundlegende Diskussion der Raumzeit bietet. ⓘ
Definition von 4-Vektoren
Ein 4-Tupel, ist ein "4-Vektor", wenn sich seine Komponenten Ai gemäß der Lorentz-Transformation zwischen den Rahmen transformieren. ⓘ
Wenn man Koordinaten ist A ein 4-Vektor, wenn er (in x-Richtung) transformiert gemäß
was sich daraus ergibt, dass in der früheren Darstellung der Lorentz-Transformation ct einfach durch A0 und x durch A1 ersetzt wurde. ⓘ
Wenn wir x, t usw. schreiben, meinen wir wie üblich Δx, Δt usw. ⓘ
Die letzten drei Komponenten eines 4-Vektors müssen ein Standardvektor im dreidimensionalen Raum sein. Daher muss sich ein 4-Vektor wie sowohl unter Lorentz-Transformationen als auch unter Drehungen. ⓘ
Eigenschaften von 4-Vektoren
- Abschluss unter Linearkombination: Wenn A und B 4-Vektoren sind, dann auch ein 4-Vektor.
- Invarianz des Innenprodukts: Wenn A und B 4-Vektoren sind, dann ist ihr inneres Produkt (Skalarprodukt) invariant, d. h. ihr inneres Produkt ist unabhängig von dem Rahmen, in dem es berechnet wird. Man beachte, dass sich die Berechnung des inneren Produkts von der Berechnung des inneren Produkts eines 3-Vektors unterscheidet. Im Folgenden, und . sind 3-Vektoren:
- Das obige innere Produkt ist nicht nur invariant unter der Lorentz-Transformation, sondern auch invariant unter der Rotation im 3-Raum.
- Zwei Vektoren werden als orthogonal bezeichnet, wenn Anders als bei 3-Vektoren stehen orthogonale 4-Vektoren nicht unbedingt im rechten Winkel zueinander. Die Regel besagt, dass zwei 4-Vektoren orthogonal sind, wenn sie um gleiche und entgegengesetzte Winkel von der 45°-Linie abweichen, die die Weltlinie eines Lichtstrahls ist. Dies bedeutet, dass ein lichtartiger 4-Vektor zu sich selbst orthogonal ist.
- Invarianz des Betrags eines Vektors: Der Betrag eines Vektors ist das innere Produkt eines 4-Vektors mit sich selbst, und ist eine rahmenunabhängige Eigenschaft. Wie bei Intervallen kann der Betrag positiv, negativ oder null sein, so dass die Vektoren als zeitlich, räumlich oder null (lichtartig) bezeichnet werden. Beachten Sie, dass ein Nullvektor nicht dasselbe ist wie ein Nullvektor. Ein Nullvektor ist ein Vektor, für den während ein Nullvektor ein Vektor ist, dessen Komponenten alle gleich Null sind. Zu den Spezialfällen, die die Invarianz der Norm veranschaulichen, gehören das invariante Intervall und die invariante Länge des relativistischen Impulsvektors ⓘ
Beispiele für 4-Vektoren
- Verschiebungs-4-Vektor: Auch bekannt als die Raumzeitseparation, ist dies (Δt, Δx, Δy, Δz), oder für infinitesimale Separationen, (dt, dx, dy, dz).
- Geschwindigkeits-4-Vektor: Dieser ergibt sich, wenn der 4-Vektor der Verschiebung geteilt wird durch geteilt wird, wobei die Eigenzeit zwischen den beiden Ereignissen ist, die dt, dx, dy und dz ergeben.
- Die 4-Geschwindigkeit ist tangential zur Weltlinie eines Teilchens und hat eine Länge, die einer Zeiteinheit im Rahmen des Teilchens entspricht.
- Ein beschleunigtes Teilchen hat kein Inertialsystem, in dem es sich immer in Ruhe befindet. Es kann jedoch immer ein Inertialsystem gefunden werden, das sich im Moment mit dem Teilchen in Bewegung befindet. Dieser Rahmen, der momentane kreisende Bezugsrahmen (MCRF), ermöglicht die Anwendung der Speziellen Relativitätstheorie auf die Analyse von beschleunigten Teilchen.
- Da sich Photonen auf Null-Linien bewegen, für ein Photon und eine 4-Geschwindigkeit nicht definiert werden. Es gibt keinen Rahmen, in dem sich ein Photon in Ruhe befindet, und es kann kein MCRF entlang des Weges eines Photons bestimmt werden.
- Energie-Impuls-4-Vektor:
- Wie bereits angedeutet, gibt es verschiedene Behandlungen für den Energie-Impuls-4-Vektor, so dass man ihn auch wie folgt ausdrücken kann oder Die erste Komponente ist die Gesamtenergie (einschließlich der Masse) des Teilchens (oder des Systems von Teilchen) in einem gegebenen Rahmen, während die übrigen Komponenten sein Raumimpuls sind. Der Energie-Impuls-4-Vektor ist eine konservierte Größe.
- 4-Vektor der Beschleunigung: Dieser ergibt sich aus der Ableitung des Geschwindigkeits-4-Vektors nach
- Kraft 4-Vektor: Dies ist die Ableitung des Impuls-4-Vektors nach
Wie erwartet, sind die Endkomponenten der obigen 4-Vektoren alle Standard-3-Vektoren, die dem räumlichen 3-Moment, der 3-Kraft usw. entsprechen. ⓘ
4-Vektoren und physikalisches Gesetz
Das erste Postulat der speziellen Relativitätstheorie besagt, dass alle Inertialsysteme gleichwertig sind. Ein physikalisches Gesetz, das in einem Rahmen gilt, muss in allen Rahmen gelten, da es sonst möglich wäre, zwischen den Rahmen zu unterscheiden. Die Newton'schen Impulse verhalten sich bei der Lorentz'schen Transformation nicht richtig, und Einstein zog es vor, die Definition des Impulses in eine Definition mit 4-Vektoren zu ändern, anstatt die Impulserhaltung aufzugeben. ⓘ
Physikalische Gesetze müssen auf Konstrukten beruhen, die rahmenunabhängig sind. Dies bedeutet, dass physikalische Gesetze die Form von Gleichungen annehmen können, die Skalare verbinden, die immer rahmenunabhängig sind. Gleichungen, die 4-Vektoren einbeziehen, erfordern jedoch die Verwendung von Tensoren mit entsprechendem Rang, die ihrerseits aus 4-Vektoren aufgebaut sein können. ⓘ
Beschleunigung
Es ist ein weit verbreiteter Irrtum, dass die Spezielle Relativitätstheorie nur auf Inertialsysteme anwendbar ist und dass sie nicht in der Lage ist, mit beschleunigten Objekten oder beschleunigenden Bezugssystemen umzugehen. Tatsächlich können beschleunigte Objekte im Allgemeinen analysiert werden, ohne dass man sich mit beschleunigenden Rahmen befassen muss. Nur wenn die Gravitation eine Rolle spielt, ist die allgemeine Relativitätstheorie erforderlich. ⓘ
Der richtige Umgang mit beschleunigten Bezugssystemen erfordert jedoch eine gewisse Sorgfalt. Der Unterschied zwischen der speziellen und der allgemeinen Relativitätstheorie besteht darin, dass (1) in der speziellen Relativitätstheorie alle Geschwindigkeiten relativ sind, die Beschleunigung jedoch absolut. (2) In der allgemeinen Relativitätstheorie ist jede Bewegung relativ, egal ob sie träge, beschleunigt oder rotierend ist. Um diesen Unterschied auszugleichen, verwendet die allgemeine Relativitätstheorie eine gekrümmte Raumzeit. ⓘ
In diesem Abschnitt werden mehrere Szenarien mit beschleunigten Bezugssystemen analysiert. ⓘ
Dewan-Beran-Bell-Raumschiff-Paradoxon
Das Dewan-Beran-Bell-Raumschiff-Paradoxon (Bell's spaceship paradox) ist ein gutes Beispiel für ein Problem, bei dem intuitives Denken ohne die geometrische Einsicht des Raumzeitansatzes zu Problemen führen kann. ⓘ

In Abb. 4-4 schweben zwei identische Raumschiffe im Weltraum und befinden sich im Verhältnis zueinander in Ruhe. Sie sind durch eine Schnur verbunden, die nur eine begrenzte Dehnung zulässt, bevor sie reißt. Zu einem bestimmten Zeitpunkt beschleunigen beide Raumschiffe in unserem Beobachterrahmen mit der gleichen konstanten Eigenbeschleunigung in die gleiche Richtung entlang der Linie zwischen ihnen. Wird die Schnur reißen? ⓘ
Als das Paradoxon neu und relativ unbekannt war, hatten selbst professionelle Physiker Schwierigkeiten, die Lösung zu finden. Zwei Argumentationsstränge führen zu entgegengesetzten Schlussfolgerungen. Beide Argumente, die im Folgenden vorgestellt werden, sind fehlerhaft, auch wenn eines von ihnen die richtige Antwort liefert.
- Für Beobachter im Ruhezustand haben die Raumschiffe zu Beginn einen Abstand L und bleiben während der Beschleunigung gleich weit voneinander entfernt. Während der Beschleunigung ist L eine längenkontrahierte Strecke des Abstands L' = γL im Rahmen der beschleunigenden Raumschiffe. Nach einer ausreichend langen Zeit wird γ auf einen ausreichend großen Faktor anwachsen, so dass die Schnur reißen muss.
- A und B seien die hinteren und vorderen Raumschiffe. Jedes Raumschiff sieht das andere Raumschiff, das dasselbe tut wie es selbst. A sagt, dass B die gleiche Beschleunigung hat wie er, und B sieht, dass A jede seiner Bewegungen mitmacht. Die Raumschiffe bleiben also gleich weit voneinander entfernt, und die Schnur reißt nicht. ⓘ
Das Problem mit dem ersten Argument ist, dass es keinen "Rahmen der Raumschiffe" gibt. Das kann es nicht geben, denn die beiden Raumschiffe messen einen wachsenden Abstand zwischen ihnen. Da es keinen gemeinsamen Rahmen der Raumschiffe gibt, ist die Länge des Fadens unbestimmt. Dennoch ist die Schlussfolgerung richtig, und das Argument ist größtenteils richtig. Das zweite Argument ignoriert jedoch völlig die Relativität der Gleichzeitigkeit. ⓘ

Ein Raumzeitdiagramm (Abb. 4-5) macht die korrekte Lösung dieses Paradoxons fast sofort deutlich. Zwei Beobachter in der Minkowski-Raumzeit beschleunigen mit konstanter Größe Beschleunigung für die Eigenzeit (Beschleunigung und verstrichene Zeit werden von den Beobachtern selbst gemessen, nicht von einem Inertialbeobachter). Sie befinden sich vor und nach dieser Phase im Gleichgewicht und sind träge. In der Minkowski-Geometrie ist die Länge entlang der Gleichzeitigkeitslinie größer als die Länge entlang der Geraden der Gleichzeitigkeit . ⓘ
Die Längenzunahme kann mit Hilfe der Lorentztransformation berechnet werden. Wenn, wie in Abb. 4-5 dargestellt, die Beschleunigung beendet ist, bleiben die Schiffe in einem konstanten Versatz in einem Rahmen Wenn und . sind die Positionen der Schiffe in sind, sind die Positionen im Rahmen sind:
Das "Paradoxon" ergibt sich sozusagen aus der Art und Weise, wie Bell sein Beispiel konstruiert hat. In der üblichen Diskussion über die Lorentz-Kontraktion ist die Ruhelänge fixiert und die bewegte Länge verkürzt sich, gemessen im Rahmen . Wie in Abb. 4-5 gezeigt, behauptet Bells Beispiel, dass die bewegten Längen und . gemessen im Rahmen als fest, wodurch die Länge des ruhenden Rahmens im Rahmen zu vergrößern. ⓘ
Beschleunigter Beobachter mit Horizont
Bestimmte Problemstellungen der Speziellen Relativitätstheorie können zu Erkenntnissen über Phänomene führen, die normalerweise mit der Allgemeinen Relativitätstheorie in Verbindung gebracht werden, wie z. B. Ereignishorizonte. Im Text zu Abb. 2-7 stellen die magentafarbenen Hyperbeln tatsächliche Bahnen dar, die von einem ständig beschleunigten Reisenden in der Raumzeit zurückgelegt werden. In Perioden positiver Beschleunigung nähert sich die Geschwindigkeit des Reisenden gerade der Lichtgeschwindigkeit an, während die Beschleunigung des Reisenden, gemessen in unserem Bezugssystem, ständig abnimmt. ⓘ
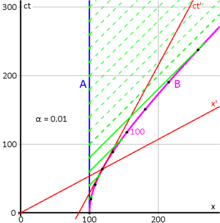
In Abb. 4-6 sind verschiedene Merkmale der Bewegungen des Reisenden genauer dargestellt. Zu jedem beliebigen Zeitpunkt wird ihre Raumachse durch eine Linie gebildet, die durch den Ursprung und ihre aktuelle Position auf der Hyperbel verläuft, während ihre Zeitachse die Tangente an die Hyperbel an ihrer Position ist. Der Geschwindigkeitsparameter nähert sich einem Grenzwert von eins, wenn zunimmt. Gleichermaßen, gegen unendlich. ⓘ
Die Form der unveränderlichen Hyperbel entspricht einer Bahn mit konstanter Eigenbeschleunigung. Dies lässt sich wie folgt nachweisen:
- Wir erinnern uns, dass
- Da folgern wir, dass
- Aus dem relativistischen Kraftgesetz,
- Durch Einsetzen von aus Schritt 2 und dem Ausdruck für aus Schritt 3 ergibt die ein konstanter Ausdruck ist. ⓘ
Abb. 4-6 veranschaulicht ein konkretes berechnetes Szenario. Terence (A) und Stella (B) stehen zunächst gemeinsam 100 Lichtstunden vom Ursprung entfernt. Stella hebt zum Zeitpunkt 0 ab, wobei ihr Raumschiff mit 0,01 c pro Stunde beschleunigt wird. Alle zwanzig Stunden sendet Terence per Funk aktuelle Informationen über die Situation zu Hause an Stella (durchgezogene grüne Linien). Stella empfängt diese regelmäßigen Übertragungen, aber die zunehmende Entfernung (die zum Teil durch die Zeitdilatation kompensiert wird) führt dazu, dass sie die Mitteilungen von Terence immer später empfängt, gemessen an ihrer Uhr, und dass sie nach 100 Stunden an seiner Uhr keine Mitteilungen mehr von Terence erhält (gestrichelte grüne Linien). ⓘ
Nach 100 Stunden nach Terence' Uhr betritt Stella eine dunkle Region. Sie ist außerhalb von Terence' zeitgleicher Zukunft gereist. Andererseits kann Terence weiterhin Stellas Botschaften an ihn empfangen, und zwar auf unbestimmte Zeit. Er muss nur lange genug warten. Die Raumzeit wurde in verschiedene Regionen aufgeteilt, die durch einen scheinbaren Ereignishorizont getrennt sind. Solange Stella weiter beschleunigt, kann sie nie erfahren, was sich hinter diesem Horizont abspielt. ⓘ
Einführung in die gekrümmte Raumzeit
Grundlegende Thesen
Newtons Theorien gingen davon aus, dass die Bewegung vor dem Hintergrund eines starren euklidischen Bezugssystems stattfindet, das sich über den gesamten Raum und die gesamte Zeit erstreckt. Die Schwerkraft wird durch eine geheimnisvolle Kraft vermittelt, die augenblicklich über eine Entfernung hinweg wirkt und deren Wirkung unabhängig vom dazwischen liegenden Raum ist. Im Gegensatz dazu leugnete Einstein, dass es einen euklidischen Bezugsrahmen im Hintergrund gibt, der sich über den gesamten Raum erstreckt. Auch gibt es keine Gravitationskraft, sondern nur die Struktur der Raumzeit selbst. ⓘ

In der Raumzeit wird die Bahn eines Satelliten, der die Erde umkreist, nicht durch die entfernten Einflüsse von Erde, Mond und Sonne bestimmt. Stattdessen bewegt sich der Satellit nur als Reaktion auf lokale Bedingungen durch den Raum. Da die Raumzeit überall lokal flach ist, wenn man sie in einem ausreichend kleinen Maßstab betrachtet, folgt der Satellit in seinem lokalen Inertialsystem immer einer geraden Linie. Wir sagen, dass der Satellit immer der Bahn einer Geodäte folgt. Wenn man die Bewegungen eines einzelnen Teilchens verfolgt, kann man keinen Beweis für Gravitation entdecken. ⓘ
Bei jeder Analyse der Raumzeit muss man zum Nachweis der Gravitation die relativen Beschleunigungen von zwei Körpern oder zwei getrennten Teilchen beobachten. In Abb. 5-1 zeigen zwei getrennte Teilchen, die sich im freien Fall im Gravitationsfeld der Erde befinden, Gezeitenbeschleunigungen, die auf lokale Inhomogenitäten im Gravitationsfeld zurückzuführen sind, so dass jedes Teilchen einem anderen Weg durch die Raumzeit folgt. Die Gezeitenbeschleunigungen, die diese Teilchen im Verhältnis zueinander aufweisen, bedürfen zu ihrer Erklärung keiner Kräfte. Vielmehr beschrieb Einstein sie durch die Geometrie der Raumzeit, d. h. die Krümmung der Raumzeit. Diese Gezeitenbeschleunigungen sind rein lokal. Es ist die kumulative Gesamtwirkung vieler lokaler Manifestationen der Krümmung, die zum Auftreten einer Gravitationskraft führt, die in großer Entfernung von der Erde wirkt. ⓘ
Der allgemeinen Relativitätstheorie liegen zwei zentrale Aussagen zugrunde.
- Das erste entscheidende Konzept ist die Koordinatenunabhängigkeit: Die physikalischen Gesetze können nicht davon abhängen, welches Koordinatensystem man verwendet. Dies ist eine wesentliche Erweiterung des Relativitätsprinzips gegenüber der speziellen Relativitätstheorie, die besagt, dass die physikalischen Gesetze für jeden Beobachter, der sich in einem nicht beschleunigten (Inertial-)Bezugssystem bewegt, gleich sein müssen. In der allgemeinen Relativitätstheorie, um Einsteins eigene (übersetzte) Worte zu verwenden, "müssen die physikalischen Gesetze so beschaffen sein, dass sie für Bezugssysteme in jeder Art von Bewegung gelten". Dies führt zu einem unmittelbaren Problem: In beschleunigten Systemen spürt man Kräfte, die es scheinbar ermöglichen würden, den eigenen Beschleunigungszustand absolut zu beurteilen. Einstein löste dieses Problem durch das Äquivalenzprinzip. ⓘ

- Das Äquivalenzprinzip besagt, dass in jedem hinreichend kleinen Bereich des Raumes die Auswirkungen der Gravitation die gleichen sind wie die der Beschleunigung.
- In Abb. 5-2 befindet sich Person A in einem Raumschiff, das weit von massiven Objekten entfernt ist und eine gleichmäßige Beschleunigung von g erfährt, während Person B sich in einem auf der Erde ruhenden Kasten befindet. Unter der Voraussetzung, dass das Raumschiff so klein ist, dass Gezeiteneffekte nicht messbar sind (angesichts der Empfindlichkeit heutiger Schwerkraftmessgeräte dürften A und B Liliputaner sein), gibt es keine Experimente, die A und B durchführen können, um festzustellen, in welcher Umgebung sie sich befinden.
- Ein alternativer Ausdruck des Äquivalenzprinzips ist die Feststellung, dass es in Newtons universellem Gravitationsgesetz, F = GMmg/r2 = mgg, und in Newtons zweitem Gesetz, F = mia, a priori keinen Grund gibt, warum die Gravitationsmasse mg gleich der Trägheitsmasse mi sein sollte. Das Äquivalenzprinzip besagt, dass diese beiden Massen identisch sind. ⓘ
Um von der obigen elementaren Beschreibung der gekrümmten Raumzeit zu einer vollständigen Beschreibung der Gravitation zu gelangen, sind Tensorkalkül und Differentialgeometrie erforderlich, beides Themen, die ein umfangreiches Studium erfordern. Ohne diese mathematischen Hilfsmittel ist es zwar möglich, über die allgemeine Relativitätstheorie zu schreiben, aber es ist nicht möglich, nicht-triviale Ableitungen zu demonstrieren. ⓘ
Krümmung der Zeit

Bei der Diskussion der speziellen Relativitätstheorie spielten die Kräfte nur eine untergeordnete Rolle. Die spezielle Relativitätstheorie geht davon aus, dass es möglich ist, Trägheitsrahmen zu definieren, die die gesamte Raumzeit ausfüllen und deren Uhren alle im gleichen Takt laufen wie die Uhr am Ursprung. Ist dies wirklich möglich? In einem ungleichmäßigen Gravitationsfeld lautet die Antwort laut Experiment: Nein. Gravitationsfelder machen es unmöglich, ein globales Inertialsystem zu konstruieren. In ausreichend kleinen Bereichen der Raumzeit sind lokale Inertialsysteme jedoch möglich. Bei der allgemeinen Relativitätstheorie geht es darum, diese lokalen Bezugssysteme systematisch zu einem allgemeineren Bild der Raumzeit zusammenzufügen. ⓘ
Jahre vor der Veröffentlichung der Allgemeinen Relativitätstheorie im Jahr 1916 nutzte Einstein das Äquivalenzprinzip, um die Existenz der Gravitationsrotverschiebung in folgendem Gedankenexperiment vorherzusagen: (i) Nehmen wir an, ein Turm der Höhe h (Abb. 5-3) sei gebaut worden. (ii) Man lässt ein Teilchen der Ruhemasse m von der Spitze des Turms fallen. Es fällt frei mit der Beschleunigung g und erreicht den Boden mit der Geschwindigkeit v = (2gh)1/2, so dass seine Gesamtenergie E, gemessen von einem Beobachter am Boden, beträgt (iii) Ein Masse-Energie-Wandler wandelt die Gesamtenergie des Teilchens in ein einziges hochenergetisches Photon um, das er nach oben richtet. (iv) An der Spitze des Turms wandelt ein Energie-Masse-Wandler die Energie des Photons E' wieder in ein Teilchen der Ruhemasse m' um. ⓘ
Es muss sein, dass m = m' ist, da man sonst ein Perpetuum Mobile konstruieren könnte. Wir sagen also voraus, dass E' = m ist, so dass
Ein Photon, das im Gravitationsfeld der Erde aufsteigt, verliert an Energie und wird rotverschoben. Frühe Versuche, diese Rotverschiebung durch astronomische Beobachtungen zu messen, waren nicht sehr überzeugend, aber endgültige Laborbeobachtungen wurden von Pound & Rebka (1959) und später von Pound & Snider (1964) durchgeführt. ⓘ
Das Licht hat eine Frequenz, und diese Frequenz kann zum Antrieb einer Uhr verwendet werden. Die Rotverschiebung durch die Gravitation führt zu einer wichtigen Schlussfolgerung über die Zeit selbst: Die Schwerkraft lässt die Zeit langsamer laufen. Nehmen wir an, wir bauen zwei identische Uhren, deren Gang durch einen stabilen atomaren Übergang gesteuert wird. Wir stellen eine Uhr auf die Spitze des Turms, während die andere Uhr auf dem Boden bleibt. Ein Experimentator, der sich auf dem Turm befindet, beobachtet, dass die Signale der Bodenuhr eine niedrigere Frequenz haben als die der Uhr neben ihm auf dem Turm. Das Licht, das den Turm hinaufsteigt, ist nur eine Welle, und es ist unmöglich, dass die Wellenberge auf dem Weg nach oben verschwinden. An der Spitze des Turms kommen genau so viele Lichtschwingungen an, wie unten ausgesendet wurden. Der Experimentator kommt zu dem Schluss, dass die Bodenuhr zu langsam geht, und kann dies bestätigen, indem er die Turmuhr herunterholt, um sie mit der Bodenuhr zu vergleichen. Bei einem 1 km hohen Turm würde die Diskrepanz etwa 9,4 Nanosekunden pro Tag betragen, was mit modernen Instrumenten leicht messbar ist. ⓘ
Die Uhren in einem Gravitationsfeld gehen nicht alle gleich schnell. Experimente wie das Pound-Rebka-Experiment haben die Krümmung der Zeitkomponente der Raumzeit eindeutig nachgewiesen. Das Pound-Rebka-Experiment sagt nichts über die Krümmung der Raumkomponente der Raumzeit aus. Die theoretischen Argumente zur Vorhersage der gravitativen Zeitdilatation hängen jedoch überhaupt nicht von den Details der allgemeinen Relativitätstheorie ab. Jede Theorie der Schwerkraft sagt eine gravitative Zeitdilatation voraus, wenn sie das Äquivalenzprinzip beachtet. Dies gilt auch für die Newtonsche Gravitation. Eine Standarddemonstration der allgemeinen Relativitätstheorie besteht darin, zu zeigen, dass im "Newtonschen Limit" (d. h. die Teilchen bewegen sich langsam, das Gravitationsfeld ist schwach und das Feld ist statisch) die Krümmung der Zeit allein ausreicht, um das Newtonsche Gravitationsgesetz abzuleiten. ⓘ
Die Newtonsche Gravitation ist eine Theorie der gekrümmten Zeit. Die allgemeine Relativitätstheorie ist eine Theorie der gekrümmten Zeit und des gekrümmten Raums. Bei G als Gravitationskonstante, M als Masse eines Newtonschen Sterns und umlaufenden Körpern unbedeutender Masse im Abstand r vom Stern ist das Raumzeitintervall für die Newtonsche Gravitation eines, bei dem nur der Zeitkoeffizient variabel ist:
Krümmung des Raums
Der Koeffizient vor beschreibt die Krümmung der Zeit in der Newtonschen Gravitation, und diese Krümmung trägt vollständig zu allen Newtonschen Gravitationseffekten bei. Wie erwartet, ist dieser Korrekturfaktor direkt proportional zu und . und wegen des Wertes im Nenner steigt der Korrekturfaktor mit der Annäherung an den gravitierenden Körper, was bedeutet, dass die Zeit gekrümmt ist. ⓘ
Aber die allgemeine Relativitätstheorie ist eine Theorie des gekrümmten Raums und der gekrümmten Zeit. Wenn es also Terme gibt, die die räumlichen Komponenten des oben dargestellten Raumzeitintervalls verändern, sollte man ihre Auswirkungen dann nicht z. B. auf Planeten- und Satellitenbahnen aufgrund von Krümmungskorrekturfaktoren sehen, die auf die räumlichen Terme angewendet werden? ⓘ
Die Antwort ist, dass man sie sieht, aber die Auswirkungen sind winzig. Der Grund dafür ist, dass die Planetengeschwindigkeiten im Vergleich zur Lichtgeschwindigkeit extrem klein sind, so dass für Planeten und Satelliten des Sonnensystems der Der Zeitkoeffizient ist kleiner als der Raumkoeffizient. ⓘ
Trotz der Winzigkeit der räumlichen Terme wurden die ersten Hinweise darauf, dass mit der Newtonschen Gravitation etwas nicht stimmt, bereits vor über anderthalb Jahrhunderten entdeckt. Im Jahr 1859 berichtete Urbain Le Verrier in einer Analyse der verfügbaren zeitlichen Beobachtungen von Merkurumläufen über die Sonnenscheibe von 1697 bis 1848, dass die bekannte Physik die Merkurbahn nicht erklären könne, es sei denn, es gäbe möglicherweise einen Planeten oder Asteroidengürtel innerhalb der Merkurbahn. Das Perihel der Merkurbahn wies eine höhere Präzessionsrate auf als die, die durch die Anziehungskräfte der anderen Planeten erklärt werden konnte. Die Fähigkeit, den winzigen Wert dieser anomalen Präzession (nur 43 Bogensekunden pro tropisches Jahrhundert) zu erkennen und genau zu messen, ist ein Zeugnis für die Raffinesse der Astrometrie des 19.Jahrhunderts. ⓘ

Als der berühmte Astronom, der zuvor die Existenz des Neptun "mit der Spitze seiner Feder" entdeckt hatte, indem er die Schwankungen in der Umlaufbahn des Uranus analysierte, löste Le Verriers Ankündigung eine zwei Jahrzehnte andauernde "Vulkan-Manie" aus, als Berufs- und Amateurastronomen gleichermaßen nach dem hypothetischen neuen Planeten suchten. Bei dieser Suche wurde Vulkan mehrmals falsch gesichtet. Schließlich wurde festgestellt, dass es weder einen solchen Planeten noch einen Asteroidengürtel gab. ⓘ
1916 zeigte Einstein, dass die anomale Präzession des Merkurs durch die räumlichen Terme der Krümmung der Raumzeit erklärt werden kann. Die zeitliche Krümmung, die lediglich Ausdruck der Newtonschen Gravitation ist, spielt bei der Erklärung der anomalen Präzession keine Rolle. Der Erfolg seiner Berechnung war für Einsteins Fachkollegen ein deutlicher Hinweis darauf, dass die allgemeine Relativitätstheorie richtig sein könnte. ⓘ
Die spektakulärste von Einsteins Vorhersagen war seine Berechnung, dass die Krümmungsterme in den räumlichen Komponenten des Raumzeitintervalls in der Biegung des Lichts um einen massiven Körper gemessen werden können. Licht hat in einem Raumzeitdiagramm eine Neigung von ±1. Seine Bewegung im Raum ist gleich seiner Bewegung in der Zeit. Für den schwachen Feldausdruck des invarianten Intervalls berechnete Einstein eine Krümmung mit exakt gleichem, aber entgegengesetztem Vorzeichen in den räumlichen Komponenten.
In der Newtonschen Gravitation wird die Koeffizient vor die Krümmung des Lichts um einen Stern voraus. In der allgemeinen Relativitätstheorie sagt die Koeffizient vor sagt eine Verdoppelung der Gesamtkrümmung voraus. ⓘ
Die Geschichte der Eddington-Finsternis-Expedition von 1919 und Einsteins Aufstieg zu Ruhm ist an anderer Stelle gut erzählt. ⓘ
Quellen der Raumzeitkrümmung
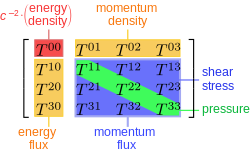
In der Newtonschen Gravitationstheorie ist die einzige Quelle der Gravitationskraft die Masse. ⓘ
Im Gegensatz dazu identifiziert die allgemeine Relativitätstheorie neben der Masse mehrere Quellen der Raumzeitkrümmung. In den Einsteinschen Feldgleichungen, werden die Quellen der Gravitation auf der rechten Seite in dem Spannungs-Energie-Tensor. ⓘ
Abb. 5-5 klassifiziert die verschiedenen Quellen der Gravitation im Spannungs-Energie-Tensor:
- (rot): Die gesamte Masse-Energie-Dichte, einschließlich aller Beiträge zur potenziellen Energie aus Kräften zwischen den Teilchen sowie der kinetischen Energie aus zufälligen thermischen Bewegungen.
- und . (orange): Dies sind die Terme der Impulsdichte. Auch wenn es keine Massenbewegung gibt, kann Energie durch Wärmeleitung übertragen werden, und die übertragene Energie trägt Impuls.
- sind die Flussraten der i-Komponente des Impulses pro Flächeneinheit in j-Richtung. Selbst wenn es keine Massenbewegung gibt, führen zufällige thermische Bewegungen der Teilchen zu einem Impulsfluss, so dass die Terme i = j (grün) den isotropen Druck und die Terme i ≠ j (blau) die Schubspannungen darstellen. ⓘ
Eine wichtige Schlussfolgerung, die sich aus den Gleichungen ableiten lässt, ist, dass, umgangssprachlich gesagt, die Schwerkraft selbst Schwerkraft erzeugt. Energie hat Masse. Auch in der Newtonschen Gravitation ist das Gravitationsfeld mit einer Energie verbunden, der so genannten potenziellen Gravitationsenergie. In der allgemeinen Relativitätstheorie fließt die Energie des Gravitationsfeldes in die Erzeugung des Gravitationsfeldes zurück. Dadurch sind die Gleichungen nichtlinear und nur in Fällen mit schwachem Feld zu lösen. Die numerische Relativitätstheorie ist ein Teilgebiet der allgemeinen Relativitätstheorie, bei dem numerische Methoden zur Lösung und Analyse von Problemen eingesetzt werden, häufig unter Verwendung von Supercomputern zur Untersuchung von schwarzen Löchern, Gravitationswellen, Neutronensternen und anderen Phänomenen im Bereich des starken Feldes. ⓘ
Energie-Momentum
In der Speziellen Relativitätstheorie ist die Masse-Energie eng mit dem Impuls verbunden. So wie Raum und Zeit verschiedene Aspekte einer umfassenderen Einheit namens Raumzeit sind, so sind Masse-Energie und Impuls lediglich verschiedene Aspekte einer einheitlichen, vierdimensionalen Größe namens Vier-Impuls. Wenn die Masse-Energie eine Quelle der Schwerkraft ist, muss folglich auch der Impuls eine Quelle sein. Die Einbeziehung des Impulses als Quelle der Schwerkraft führt zu der Vorhersage, dass sich bewegende oder rotierende Massen Felder erzeugen können, die den von bewegten Ladungen erzeugten Magnetfeldern entsprechen, ein Phänomen, das als Gravitationsmagnetismus bekannt ist. ⓘ

Es ist bekannt, dass sich die Kraft des Magnetismus durch Anwendung der Regeln der speziellen Relativitätstheorie auf bewegte Ladungen herleiten lässt. (Eine beredte Demonstration dessen wurde von Feynman in Band II, Kapitel 13-6 seiner Vorlesungen über Physik, online verfügbar, gegeben). Eine analoge Logik kann verwendet werden, um den Ursprung des Gravitationsmagnetismus zu demonstrieren. In Abb. 5-7a haben zwei parallele, unendlich lange Ströme massiver Teilchen die gleichen und entgegengesetzten Geschwindigkeiten -v und +v relativ zu einem Testteilchen, das sich in Ruhe befindet und zwischen den beiden zentriert ist. Aufgrund der Symmetrie des Aufbaus ist die Nettokraft auf das zentrale Teilchen gleich Null. Angenommen, so dass die Geschwindigkeiten einfach additiv sind. Abb. 5-7b zeigt genau denselben Aufbau, jedoch im Rahmen des oberen Stroms. Das Testteilchen hat eine Geschwindigkeit von +v, und der untere Strom hat eine Geschwindigkeit von +2v. Da sich die physikalische Situation nicht geändert hat, sondern nur der Rahmen, in dem die Dinge beobachtet werden, sollte das Testteilchen von keiner der beiden Strömungen angezogen werden. Es ist jedoch keineswegs klar, dass die auf das Testteilchen ausgeübten Kräfte gleich sind. (1) Da sich der untere Strom schneller bewegt als der obere, hat jedes Teilchen im unteren Strom eine größere Massenenergie als ein Teilchen im oberen Strom. (2) Aufgrund der Lorentz-Kontraktion gibt es im unteren Strom mehr Teilchen pro Längeneinheit als im oberen Strom. (3) Ein weiterer Beitrag zur aktiven Gravitationsmasse des unteren Stroms ergibt sich aus einem zusätzlichen Druckterm, über den wir an dieser Stelle nicht genügend Hintergrundwissen haben, um ihn zu diskutieren. Alle diese Effekte zusammengenommen würden scheinbar erfordern, dass das Testteilchen in Richtung des unteren Stroms gezogen wird. ⓘ
Das Testteilchen wird aufgrund einer geschwindigkeitsabhängigen Kraft, die dazu dient, ein Teilchen, das sich in dieselbe Richtung wie der Bodenstrom bewegt, abzustoßen, nicht zum Bodenstrom gezogen. Dieser geschwindigkeitsabhängige Gravitationseffekt ist der Gravitomagnetismus. ⓘ
Materie, die sich durch ein gravitomagnetisches Feld bewegt, unterliegt daher den so genannten Frame-Dragging-Effekten, die der elektromagnetischen Induktion entsprechen. Es wurde vorgeschlagen, dass solche gravitomagnetischen Kräfte der Erzeugung der relativistischen Jets (Abb. 5-8) zugrunde liegen, die von einigen rotierenden supermassiven Schwarzen Löchern ausgestoßen werden. ⓘ
Druck und Spannung
Auch Größen, die direkt mit Energie und Impuls zusammenhängen, sollten Quellen der Schwerkraft sein, nämlich innerer Druck und Spannung. Zusammengenommen dienen Masse/Energie, Impuls, Druck und Spannung als Quellen der Schwerkraft: In ihrer Gesamtheit geben sie der Raumzeit vor, wie sie sich krümmen soll. ⓘ
Die allgemeine Relativitätstheorie sagt voraus, dass Druck als Gravitationsquelle mit genau der gleichen Stärke wie die Masse-Energie-Dichte wirkt. Die Einbeziehung des Drucks als Quelle der Schwerkraft führt zu dramatischen Unterschieden zwischen den Vorhersagen der allgemeinen Relativitätstheorie und denen der Newtonschen Gravitation. Zum Beispiel setzt der Druckterm eine Höchstgrenze für die Masse eines Neutronensterns. Je massereicher ein Neutronenstern ist, desto mehr Druck ist erforderlich, um sein Gewicht gegen die Schwerkraft zu halten. Der erhöhte Druck trägt jedoch zur Schwerkraft bei, die auf die Masse des Sterns wirkt. Ab einer bestimmten Masse, die durch die Tolman-Oppenheimer-Volkoff-Grenze bestimmt wird, läuft der Prozess aus dem Ruder und der Neutronenstern kollabiert zu einem Schwarzen Loch. ⓘ
Bei Berechnungen wie hydrodynamischen Simulationen von Kernkollaps-Supernovae sind die Spannungsterme von großer Bedeutung. ⓘ
Diese Vorhersagen über die Rolle von Druck, Impuls und Spannung als Quellen der Raumzeitkrümmung sind elegant und spielen eine wichtige Rolle in der Theorie. Was den Druck betrifft, so wurde das frühe Universum von Strahlung dominiert, und es ist höchst unwahrscheinlich, dass die relevanten kosmologischen Daten (z. B. die Häufigkeit der Nukleosynthese usw.) reproduziert werden könnten, wenn der Druck nicht zur Schwerkraft beitragen würde oder wenn er als Quelle der Schwerkraft nicht die gleiche Stärke hätte wie die Massenenergie. Ebenso wäre die mathematische Konsistenz der Einsteinschen Feldgleichungen gebrochen, wenn die Spannungsterme nicht als Quelle der Schwerkraft beitragen würden. ⓘ
Experimenteller Test der Quellen der Raumzeitkrümmung
Definitionen: Aktive, passive und träge Masse
Bondi unterscheidet zwischen verschiedenen möglichen Arten von Masse: (1) aktive Masse () ist die Masse, die als Quelle eines Gravitationsfeldes wirkt; (2) passive Masse () ist die Masse, die auf ein Gravitationsfeld reagiert; (3) Trägheitsmasse () ist die Masse, die auf die Beschleunigung reagiert. ⓘ
- ist dasselbe wie die Gravitationsmasse () in der Diskussion um das Äquivalenzprinzip. ⓘ
In der Newtonschen Theorie,
- Das dritte Gesetz von Aktion und Reaktion besagt, dass und . gleich sein muss.
- Andererseits ist die Frage, ob und . gleich sind, ist ein empirisches Ergebnis. ⓘ
In der allgemeinen Relativitätstheorie,
- Die Gleichheit von und . wird durch das Äquivalenzprinzip diktiert.
- Es gibt kein "Aktions- und Reaktionsprinzip", das eine notwendige Beziehung zwischen und . . ⓘ
Druck als Gravitationsquelle

Das klassische Experiment zur Messung der Stärke einer Gravitationsquelle (d. h. ihrer aktiven Masse) wurde erstmals 1797 von Henry Cavendish durchgeführt (Abb. 5-9a). Zwei kleine, aber dichte Kugeln sind an einem feinen Draht aufgehängt und bilden eine Torsionswaage. Bringt man zwei große Testmassen in die Nähe der Kugeln, so entsteht ein spürbares Drehmoment. Mit den Abmessungen der Apparatur und der messbaren Federkonstante des Torsionsdrahtes kann die Gravitationskonstante G bestimmt werden. ⓘ
Die Untersuchung von Druckeffekten durch Zusammendrücken der Testmassen ist aussichtslos, da die im Labor erreichbaren Drücke im Vergleich zur Masseenergie einer Metallkugel unbedeutend sind. ⓘ
Die elektromagnetischen Abstoßungsdrücke, die dadurch entstehen, dass Protonen im Inneren von Atomkernen fest zusammengepresst werden, liegen jedoch in der Größenordnung von 1028 atm ≈ 1033 Pa ≈ 1033 kg-s-2m-1. Dies entspricht etwa 1 % der Kernmassendichte von etwa 1018 kg/m3 (nach Berücksichtigung von c2 ≈ 9×1016m2s-2). ⓘ
Wenn der Druck nicht als Gravitationsquelle wirkt, dann sollte das Verhältnis für Kerne mit höherer Ordnungszahl Z, bei denen die elektrostatischen Drücke höher sind, niedriger sein. L. B. Kreuzer (1968) führte ein Cavendish-Experiment mit einer Teflonmasse durch, die in einem Gemisch aus den Flüssigkeiten Trichlorethylen und Dibromethan schwebte, die die gleiche Auftriebsdichte wie das Teflon hatten (Abb. 5-9b). Fluor hat die Ordnungszahl Z = 9, während Brom Z = 35 hat. Kreuzer stellte fest, dass die Verlagerung der Teflonmasse keine unterschiedliche Auslenkung des Torsionsstabs verursachte, so dass die aktive Masse und die passive Masse mit einer Genauigkeit von 5×10-5 gleichwertig waren. ⓘ
Obwohl Kreuzer dieses Experiment ursprünglich nur als einen Test des Verhältnisses von aktiver und passiver Masse betrachtete, deutete Clifford Will (1976) das Experiment als einen grundlegenden Test der Kopplung von Quellen an Gravitationsfelder um. ⓘ
1986 stellten Bartlett und Van Buren fest, dass die Laser-Entfernungsmessung auf dem Mond einen Versatz von 2 km zwischen dem Figurenzentrum des Mondes und seinem Massenzentrum festgestellt hatte. Dies deutet auf eine Asymmetrie in der Verteilung von Fe (reichlich im Mondkern vorhanden) und Al (reichlich in der Kruste und im Mantel vorhanden) hin. Wenn der Druck nicht in gleichem Maße zur Krümmung der Raumzeit beiträgt wie die Masse-Energie, würde sich der Mond nicht auf der von der klassischen Mechanik vorhergesagten Umlaufbahn befinden. Sie nutzten ihre Messungen, um die Diskrepanzen zwischen aktiver und passiver Masse auf etwa 10-12 zu begrenzen. ⓘ
Gravitomagnetismus

Die Existenz des Gravitationsmagnetismus wurde von Gravity Probe B (GP-B) bewiesen, einer satellitengestützten Mission, die am 20. April 2004 startete. Die Raumfahrtphase dauerte bis . Ziel der Mission war es, die Krümmung der Raumzeit in Erdnähe zu messen, wobei der Schwerpunkt auf dem Gravitomagnetismus lag. ⓘ
Erste Ergebnisse bestätigten den relativ großen geodätischen Effekt (der auf die einfache Raumzeitkrümmung zurückzuführen ist und auch als de-Sitter-Präzession bezeichnet wird) mit einer Genauigkeit von etwa 1 %. Der weitaus geringere Frame-Dragging-Effekt (der auf den Gravitationsmagnetismus zurückzuführen ist und auch als Lense-Thirring-Präzession bezeichnet wird) war aufgrund unerwarteter Ladungseffekte, die zu einer variablen Drift in den Gyroskopen führten, schwer zu messen. Dennoch konnten bis zum wurde der Frame-Dragging-Effekt mit einer Genauigkeit von 15 % des erwarteten Ergebnisses bestätigt, während der geodätische Effekt mit mehr als 0,5 % bestätigt wurde. ⓘ
Spätere Messungen des Frame-Dragging-Effekts durch Laser-Ranging-Beobachtungen der LARES-, LAGEOS-1- und LAGEOS-2-Satelliten haben die GP-B-Messung verbessert, wobei die Ergebnisse (Stand 2016) den Effekt auf weniger als 5 % des theoretischen Werts begrenzen, auch wenn die Genauigkeit dieses Ergebnisses nicht ganz unumstritten ist. ⓘ
Ein weiteres Projekt, das Gyroscopes in General Relativity (GINGER) Experiment, versucht, diesen Effekt mit drei 6 m langen Ringlasern zu messen, die 1400 m unter der Erdoberfläche im rechten Winkel zueinander angebracht sind. ⓘ
Technische Themen
Ist die Raumzeit wirklich gekrümmt?
Nach Poincarés konventionalistischer Auffassung wären die wesentlichen Kriterien für die Wahl einer euklidischen Geometrie gegenüber einer nicht-euklidischen Geometrie die Wirtschaftlichkeit und Einfachheit. Ein Realist würde sagen, dass Einstein entdeckt hat, dass die Raumzeit nicht-euklidisch ist. Ein Konventionalist würde sagen, dass Einstein es lediglich bequemer fand, eine nicht-euklidische Geometrie zu verwenden. Der Konventionalist würde behaupten, dass Einsteins Analyse nichts darüber aussagt, was die Geometrie der Raumzeit wirklich ist. ⓘ
Dies sei gesagt,
- 1. Ist es möglich, die allgemeine Relativitätstheorie in Form einer flachen Raumzeit darzustellen?
- 2. Gibt es Situationen, in denen eine Interpretation der allgemeinen Relativitätstheorie mit einer flachen Raumzeit zweckmäßiger ist als die übliche Interpretation mit einer gekrümmten Raumzeit? ⓘ
Als Antwort auf die erste Frage haben eine Reihe von Autoren, darunter Deser, Grishchuk, Rosen, Weinberg usw., verschiedene Formulierungen der Gravitation als ein Feld in einer flachen Mannigfaltigkeit vorgelegt. Diese Theorien werden als "bimetrische Gravitation", "feldtheoretischer Ansatz zur allgemeinen Relativitätstheorie" usw. bezeichnet. Kip Thorne hat einen populären Überblick über diese Theorien gegeben. ⓘ
Das Paradigma der flachen Raumzeit geht davon aus, dass die Materie ein Gravitationsfeld erzeugt, das die Lineale schrumpfen lässt, wenn sie von der Umfangsrichtung in die Radialrichtung gedreht werden, und das das Ticken der Uhren beschleunigt. Das Paradigma der flachen Raumzeit ist dem Paradigma der gekrümmten Raumzeit völlig gleichwertig, da beide die gleichen physikalischen Phänomene darstellen. Ihre mathematischen Formulierungen sind jedoch völlig unterschiedlich. Berufstätige Physiker wechseln routinemäßig zwischen den Techniken der gekrümmten und der flachen Raumzeit, je nach den Anforderungen des jeweiligen Problems. Das Paradigma der flachen Raumzeit erweist sich als besonders praktisch bei der Durchführung von Näherungsrechnungen in schwachen Feldern. Daher werden die Techniken der flachen Raumzeit bei der Lösung von Gravitationswellenproblemen verwendet, während die Techniken der gekrümmten Raumzeit bei der Analyse von Schwarzen Löchern zum Einsatz kommen. ⓘ
Asymptotische Symmetrien
Die Raumzeitsymmetriegruppe der Speziellen Relativitätstheorie ist die Poincaré-Gruppe, eine zehndimensionale Gruppe mit drei Lorentzverstärkungen, drei Rotationen und vier Raumzeittranslationen. Es ist logisch zu fragen, welche Symmetrien, wenn überhaupt, in der Allgemeinen Relativitätstheorie gelten könnten. Ein nachvollziehbarer Fall wäre die Betrachtung der Symmetrien der Raumzeit aus der Sicht von Beobachtern, die sich weit entfernt von allen Quellen des Gravitationsfeldes befinden. Die naive Erwartung für asymptotisch flache Raumzeitsymmetrien könnte einfach darin bestehen, die Symmetrien der flachen Raumzeit der Speziellen Relativitätstheorie zu erweitern und zu reproduzieren, d. h. die Poincaré-Gruppe. ⓘ
1962 nahmen sich Hermann Bondi, M. G. van der Burg, A. W. Metzner und Rainer K. Sachs dieses asymptotischen Symmetrieproblems an, um den Energiefluss im Unendlichen aufgrund sich ausbreitender Gravitationswellen zu untersuchen. Ihr erster Schritt bestand darin, einige physikalisch sinnvolle Randbedingungen für das Gravitationsfeld im lichtähnlichen Unendlichen festzulegen, um zu charakterisieren, was es bedeutet, dass eine Metrik asymptotisch flach ist, ohne a priori Annahmen über die Natur der asymptotischen Symmetriegruppe zu treffen - nicht einmal die Annahme, dass eine solche Gruppe existiert. Nachdem sie dann die ihrer Meinung nach sinnvollsten Randbedingungen entworfen hatten, untersuchten sie die Art der sich ergebenden asymptotischen Symmetrietransformationen, die die Form der für asymptotisch flache Gravitationsfelder geeigneten Randbedingungen unverändert lassen. Sie fanden heraus, dass die asymptotischen Symmetrietransformationen tatsächlich eine Gruppe bilden und die Struktur dieser Gruppe nicht von dem jeweiligen Gravitationsfeld abhängt. Das bedeutet, dass man, wie erwartet, die Kinematik der Raumzeit von der Dynamik des Gravitationsfeldes trennen kann, zumindest bei räumlicher Unendlichkeit. Die rätselhafte Überraschung im Jahr 1962 war die Entdeckung einer reichen unendlich-dimensionalen Gruppe (der so genannten BMS-Gruppe) als asymptotische Symmetriegruppe anstelle der endlich-dimensionalen Poincaré-Gruppe, die eine Untergruppe der BMS-Gruppe ist. Nicht nur die Lorentz-Transformationen sind asymptotische Symmetrietransformationen, sondern es gibt auch zusätzliche Transformationen, die keine Lorentz-Transformationen sind, aber asymptotische Symmetrietransformationen sind. Tatsächlich fanden sie eine zusätzliche Unendlichkeit von Transformationsgeneratoren, die als Supertranslationen bekannt sind. Daraus ergibt sich die Schlussfolgerung, dass sich die Allgemeine Relativitätstheorie (GR) im Falle schwacher Felder in großen Entfernungen nicht auf die Spezielle Relativitätstheorie reduzieren lässt. ⓘ
Gekrümmte Mannigfaltigkeiten
Aus physikalischen Gründen ist ein Raumzeitkontinuum mathematisch definiert als eine vierdimensionale, glatte, zusammenhängende Lorentzsche Mannigfaltigkeit . Das bedeutet, dass die glatte Lorentz-Metrik hat die Signatur . Die Metrik bestimmt die Geometrie der Raumzeit sowie die Geodäten von Teilchen und Lichtstrahlen. Zu jedem Punkt (Ereignis) auf dieser Mannigfaltigkeit werden Koordinatendiagramme verwendet, um Beobachter in Bezugsrahmen darzustellen. Normalerweise werden kartesische Koordinaten verwendet. Außerdem werden der Einfachheit halber die Maßeinheiten meist so gewählt, dass die Lichtgeschwindigkeit gleich 1 ist. ⓘ
Ein Bezugsrahmen (Beobachter) kann mit einem dieser Koordinatendiagramme identifiziert werden; ein solcher Beobachter kann jedes Ereignis beschreiben . Ein anderer Bezugsrahmen kann durch ein zweites Koordinatendiagramm über . Zwei Beobachter (einer in jedem Bezugssystem) können dasselbe Ereignis beschreiben aber unterschiedliche Beschreibungen erhalten. ⓘ
In der Regel sind viele sich überschneidende Koordinatendiagramme erforderlich, um eine Mannigfaltigkeit abzudecken. Gegeben sind zwei Koordinatendiagramme, eines mit (für einen Beobachter) und ein anderes mit (stellvertretend für einen anderen Beobachter), so stellt der Schnittpunkt der beiden Karten den Bereich der Raumzeit dar, in dem beide Beobachter physikalische Größen messen und somit die Ergebnisse vergleichen können. Die Beziehung zwischen den beiden Messreihen ist durch eine nicht-singuläre Koordinatentransformation an diesem Schnittpunkt gegeben. Die Vorstellung von Koordinatendiagrammen als lokalen Beobachtern, die in ihrer Umgebung Messungen durchführen können, ist auch physikalisch sinnvoll, da man auf diese Weise tatsächlich physikalische Daten sammelt - lokal. ⓘ
Zwei Beobachter, von denen sich einer auf der Erde befindet, der andere aber in einer schnellen Rakete zum Jupiter fliegt, können zum Beispiel den Einschlag eines Kometen in den Jupiter beobachten (dies ist das Ereignis ). Im Allgemeinen werden sie sich über den genauen Ort und Zeitpunkt des Einschlags nicht einig sein, d. h. sie werden unterschiedliche 4-Tupel haben (da sie unterschiedliche Koordinatensysteme verwenden). Auch wenn sich ihre kinematischen Beschreibungen unterscheiden, gelten die dynamischen (physikalischen) Gesetze, wie die Impulserhaltung und der erste Hauptsatz der Thermodynamik, weiterhin. Die Relativitätstheorie verlangt sogar mehr als das, denn sie schreibt vor, dass diese (und alle anderen physikalischen) Gesetze in allen Koordinatensystemen die gleiche Form haben müssen. Dies führt Tensoren in die Relativitätstheorie ein, durch die alle physikalischen Größen dargestellt werden. ⓘ
Geodäten werden als zeitähnlich, null oder raumähnlich bezeichnet, wenn der Tangentenvektor zu einem Punkt der Geodäte von dieser Art ist. Die Bahnen von Teilchen und Lichtstrahlen in der Raumzeit werden durch zeitähnliche bzw. nullähnliche (lichtähnliche) Geodäten dargestellt. ⓘ
Raumzeit in der speziellen Relativitätstheorie
Mathematische Motivation der Minkowski-Metrik
- Betrachtet man den D’Alembert-Operator mit ⓘ
- so ist zu erkennen, dass man auch abkürzend ⓘ
- schreiben kann, wenn folgende zwei Vierervektoren eingeführt werden:
- ⓘ
- In diesem Fall tritt die Zeit als vierte Dimension auf, die Metrik muss also von einer -Matrix induziert sein. ⓘ
- Da die vier Dimensionen linear unabhängig sind, lässt sich auf Diagonalform bringen (Hauptachsentransformation). ⓘ
- Aufgrund der Forderung, dass es keine ausgezeichneten Raumzeit-Koordinaten gibt, können die Diagonalelemente nur den Wert besitzen. Für die Raumkoordinaten wird hier gewählt. Dies ist aber eine Konvention, die nicht einheitlich verwendet wird. ⓘ
- Die Zeitkomponente kann nicht dasselbe Vorzeichen haben wie die Raumkomponenten. Hierzu betrachtet man wieder den D’Alembert-Operator :
- Daraus ergäbe sich als homogene Wellengleichung für eine Welle ⓘ
- Setzt man nun für eine ebene Welle an, d. h. , so ergäbe sich eine komplexe Frequenz, und damit wäre exponentiell gedämpft. In diesem Fall gäbe es also keine dauerhaften ebenen Wellen, was im Widerspruch zur Beobachtung steht. Folglich muss die Zeitkomponente ein anderes Vorzeichen haben:
- ⓘ
- Daraus ergibt sich die korrekte homogene Wellengleichung ⓘ
Minkowski-Diagramm
Im Minkowski-Diagramm können die Verhältnisse geometrisch dargestellt und analysiert werden. Wegen der komplexen Eigenschaft der Zeitkomponente wird dort die Drehung der Zeitachse mit umgekehrtem Vorzeichen wie die Drehung der Koordinatenachse dargestellt. ⓘ
Raumzeit in der allgemeinen Relativitätstheorie
Nichteuklidische Geometrien
Grundlage zur Beschreibung der Raumzeit in der allgemeinen Relativitätstheorie ist die pseudo-riemannsche Geometrie. Die Koordinatenachsen sind hier nichtlinear, was als Raumkrümmung interpretiert werden kann. Für die vierdimensionale Raumzeit werden die gleichen mathematischen Hilfsmittel wie zur Beschreibung einer zweidimensionalen Kugeloberfläche oder für Sattelflächen herangezogen. Als unumstößlich angesehene Aussagen der euklidischen Geometrie, insbesondere das Parallelenaxiom, müssen in diesen Theorien aufgegeben und durch allgemeinere Beziehungen ersetzt werden. Die kürzeste Verbindung zwischen zwei Punkten ist hier beispielsweise kein Geradenteilstück mehr. Einer Geraden in der euklidischen Geometrie entspricht die Geodäte in der nicht-euklidischen Welt; im Falle einer Kugeloberfläche sind die Geodäten die Großkreise. Die Winkelsumme im – aus Geodätenabschnitten bestehenden – Dreieck ist auch nicht mehr 180 Grad. Im Falle der Kugeloberfläche ist sie größer als 180 Grad, im Falle von Sattelflächen dagegen kleiner. ⓘ
Raumzeit-Krümmung
Die Krümmung von Raum und Zeit wird durch jede Form von Energie, wie etwa Masse, Strahlung oder Druck, verursacht. Diese Größen bilden zusammen den Energie-Impuls-Tensor und gehen in die Einsteingleichungen als Quelle des Gravitationsfeldes ein. Die daraus resultierende krummlinige Bewegung von kräftefreien Körpern entlang von Geodäten wird der Gravitationsbeschleunigung zugeschrieben – in diesem Modell existiert so etwas wie eine Gravitationskraft nicht mehr. In einem infinitesimalen Raumabschnitt (lokale Karte) besitzt das erzeugte Gravitationsfeld stets die flache Metrik der speziellen Relativitätstheorie. Dies wird durch eine konstante Raumkrümmung mit dem Faktor beschrieben. Die Krümmung der Weltlinien (Bewegungskurven in der Raumzeit) aller kräftefreien Körper in diesem Raumabschnitt ist gleich. ⓘ
In vielen populären Darstellungen der allgemeinen Relativitätstheorie wird häufig nicht beachtet, dass nicht nur der Raum, sondern auch die Zeit gekrümmt sein muss, um ein Gravitationsfeld zu erzeugen. Dass stets Raum und Zeit gekrümmt sein müssen, ist anschaulich leicht zu verstehen: Wäre nur der Raum gekrümmt, so wäre die Trajektorie eines geworfenen Steines immer dieselbe, egal welche Anfangsgeschwindigkeit der Stein besäße, da er stets nur dem gekrümmten Raum folgen würde. Nur durch die zusätzliche Krümmung der Zeit können die verschiedenen Trajektorien zustande kommen. Im Rahmen der ART kann dies auch mathematisch gezeigt werden. ⓘ
Im normalen, dreidimensionalen Raum ist nur die Projektion der Weltlinien auf die Bewegungsebene sichtbar. Hat der Körper die Geschwindigkeit , so ist die Weltlinie gegenüber der Zeitachse geneigt, und zwar um den Winkel α mit . Die Projektion der Bahn wird mit steigendem um den Faktor länger, der Krümmungsradius um den gleichen Faktor größer, die Winkeländerung also kleiner. Die Krümmung (Winkeländerung pro Längenabschnitt) ist daher um den Faktor kleiner. ⓘ
Mit ⓘ
folgt dann aus der Weltlinienkrümmung für die beobachtete Bahnkrümmung im dreidimensionalen Raum ⓘ
- . ⓘ
Raumkrümmung und Zentrifugalbeschleunigung
Für kleine Geschwindigkeiten v≪c ist die Bahnkrümmung g/v2 und entspricht damit dem Wert bei einer klassischen Zentrifugalbeschleunigung. Für Lichtstrahlen mit v=c hat der Faktor (1 + v2/c2) den Wert 2, die Krümmung 2g/c2 entspricht also dem doppelten Wert der klassischen Betrachtung g/c2. Die Winkelabweichung von Sternenlicht der Fixsterne in Sonnennähe sollte also doppelt so groß sein wie im klassischen Fall. Dies wurde von Arthur Eddington im Rahmen einer Afrikaexpedition zur Beobachtung der Sonnenfinsternis von 1919 erstmals verifiziert, was große Aufmerksamkeit fand und zur Durchsetzung der Allgemeinen Relativitätstheorie wesentlich beitrug. Seine Beobachtungen erwiesen sich in späteren Analysen zwar als ungenau, nachfolgende Beobachtungen bei Sonnenfinsternissen bestätigten aber die Vorhersagen der Allgemeinen Relativitätstheorie. ⓘ
Wegen dieser kleinen Abweichung vom klassischen Wert sind die Planetenbahnen auch keine exakten Ellipsen mehr, sondern unterliegen einer Apsidendrehung. Eine solche bis dahin in der Himmelsmechanik nicht erklärbare Apsidendrehung war zuvor beim Planeten Merkur beobachtet worden und fand durch die Allgemeine Relativitätstheorie eine Erklärung. ⓘ
Symmetrien
Die Raumzeit ist charakterisiert durch eine Anzahl von Symmetrien, die sehr wichtig für die darin geltende Physik sind. Zu diesen Symmetrien zählen neben den Symmetrien des Raumes (Translation, Rotation) auch die Symmetrien unter Lorentztransformationen (Wechsel zwischen Bezugssystemen verschiedener Geschwindigkeit). Letzteres stellt das Relativitätsprinzip sicher. ⓘ








































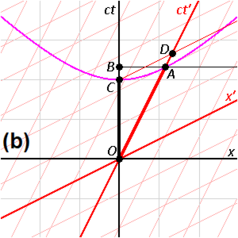






































































































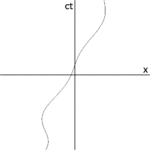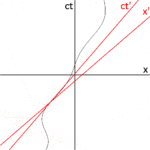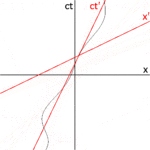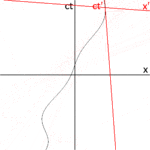









































![{\displaystyle -\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)

![{\displaystyle \left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)














































