Laplace-Transformation

Die Laplace-Transformation, benannt nach Pierre-Simon Laplace, ist eine einseitige Integraltransformation, die eine gegebene Funktion $f$ vom reellen Zeitbereich in eine Funktion $F$ im komplexen Spektralbereich (Frequenzbereich; Bildbereich) überführt. Diese Funktion $F$ wird Laplace-Transformierte oder Spektralfunktion genannt. ⓘ

Die Laplace-Transformation hat Gemeinsamkeiten mit der Fourier-Transformation, vermeidet aber die dort auftretenden Konvergenzprobleme bei nicht absolut integrierbaren, aber praktisch wichtigen Signalen. ⓘ

Sie ist auf kausale Signale mit kontinuierlichem Zeitbereich anwendbar und verwandt mit der Z-Transformation, einer entsprechenden Transformation für Signale mit diskretem Zeitbereich. ⓘ

Vergleich der Z-Transformation und der Laplace-Transformation ⓘ

Geschichte

Pierre-Simon, Marquis de Laplace ⓘ

Die Laplace-Transformation ist nach dem Mathematiker und Astronomen Pierre-Simon, marquis de Laplace, benannt, der eine ähnliche Transformation in seinen Arbeiten zur Wahrscheinlichkeitstheorie verwendete. Laplace schrieb ausführlich über die Verwendung von Erzeugungsfunktionen in Essai philosophique sur les probabilités (1814), und die Integralform der Laplace-Transformation entwickelte sich auf natürliche Weise als Ergebnis. ⓘ

Laplaces Verwendung von Erzeugungsfunktionen ähnelte dem, was heute als z-Transformation bekannt ist, und er schenkte dem Fall der kontinuierlichen Variablen, der von Niels Henrik Abel diskutiert wurde, wenig Aufmerksamkeit. Die Theorie wurde im 19. und frühen 20. Jahrhundert von Mathias Lerch, Oliver Heaviside und Thomas Bromwich weiter entwickelt. ⓘ

Die heute weit verbreitete Anwendung der Transformation (hauptsächlich in der Technik) entstand während und kurz nach dem Zweiten Weltkrieg und ersetzte die frühere Heaviside-Operationsrechnung. Die Vorteile der Laplace-Transformation wurden von Gustav Doetsch hervorgehoben, dem der Name Laplace-Transformation offenbar zu verdanken ist. ⓘ

Ab 1744 untersuchte Leonhard Euler Integrale der Form

$$z=\int X(x)e^{ax}\,dx\quad {\text{ and }}\quad z=\int X(x)x^{A}\,dx$$

als Lösungen von Differentialgleichungen, verfolgte das Thema aber nicht sehr weit. Joseph Louis Lagrange war ein Bewunderer von Euler und untersuchte in seiner Arbeit über die Integration von Wahrscheinlichkeitsdichtefunktionen Ausdrücke der Form

$$\int X(x)e^{-ax}a^{x}\,dx,$$

die einige moderne Historiker im Rahmen der modernen Laplace-Transformationstheorie interpretiert haben. ⓘ

Diese Art von Integralen scheint erstmals 1782 die Aufmerksamkeit von Laplace auf sich gezogen zu haben, da er im Geiste Eulers die Integrale selbst als Lösungen von Gleichungen verwendete. Doch im Jahre 1785 machte Laplace den entscheidenden Schritt nach vorn, als er nicht einfach nach einer Lösung in Form eines Integrals suchte, sondern begann, die Transformationen in dem Sinne anzuwenden, der später populär werden sollte. Er verwendete ein Integral der Form

$$\int x^{s}\varphi (x)\,dx,$$

das einer Mellin-Transformation ähnelt, um die gesamte Differenzgleichung zu transformieren und nach Lösungen der transformierten Gleichung zu suchen. Anschließend wandte er die Laplace-Transformation auf die gleiche Weise an und begann, einige ihrer Eigenschaften abzuleiten, wobei er ihre potenzielle Leistungsfähigkeit zu schätzen begann. ⓘ

Laplace erkannte auch, dass Joseph Fouriers Methode der Fourier-Reihen zur Lösung der Diffusionsgleichung nur auf einen begrenzten Bereich des Raums anwendbar war, da diese Lösungen periodisch waren. Im Jahr 1809 wandte Laplace seine Transformation an, um Lösungen zu finden, die sich unbegrenzt im Raum ausbreiten. ⓘ

Formale Definition

Die Laplace-Transformation einer Funktion f(t), die für alle reellen Zahlen t ≥ 0 definiert ist, ist die Funktion F(s), die eine einseitige Transformation ist, definiert durch

$F(s)=\int _{0}^{\infty }f(t)e^{-st}\,dt$

(Gl.1)

wobei s ein komplexzahliger Frequenzparameter ist

$$s=\sigma +i\omega ,$$

mit reellen Zahlen σ und ω. ⓘ

Eine alternative Schreibweise für die Laplace-Transformation ist ${\mathcal {L}}\{f\}$ anstelle von F. ⓘ

Die Bedeutung des Integrals hängt von der Art der interessierenden Funktionen ab. Eine notwendige Bedingung für die Existenz des Integrals ist, dass f auf [0, ∞) lokal integrierbar sein muss. Für lokal integrierbare Funktionen, die im Unendlichen abklingen oder vom Exponentialtyp sind ($|f(t)|\leq Ae^{B|t|}$), kann das Integral als ein (echtes) Lebesgue-Integral verstanden werden. Für viele Anwendungen ist es jedoch notwendig, es als ein bedingt konvergentes unechtes Integral bei ∞ zu betrachten. Noch allgemeiner kann das Integral in einem schwachen Sinn verstanden werden, worauf weiter unten eingegangen wird. ⓘ

Man kann die Laplace-Transformation eines endlichen Borel-Maßes μ durch das Lebesgue-Integral definieren

$${\mathcal {L}}\{\mu \}(s)=\int _{[0,\infty )}e^{-st}\,d\mu (t).$$

ⓘ

Ein wichtiger Spezialfall ist, wenn μ ein Wahrscheinlichkeitsmaß ist, zum Beispiel die Dirac-Delta-Funktion. In der Operationsrechnung wird die Laplace-Transformation eines Maßes oft so behandelt, als ob das Maß von einer Wahrscheinlichkeitsdichtefunktion f abstammt. In diesem Fall schreibt man, um mögliche Verwechslungen zu vermeiden, oft

$${\mathcal {L}}\{f\}(s)=\int _{0^{-}}^{\infty }f(t)e^{-st}\,dt,$$

wobei die untere Grenze von 0- eine Kurzschreibweise für

$$\lim _{\varepsilon \rightarrow 0^{+}}\int _{-\varepsilon }^{\infty }.$$

ⓘ

Dieser Grenzwert unterstreicht, dass jede Punktmasse, die bei 0 liegt, vollständig von der Laplace-Transformation erfasst wird. Obwohl es beim Lebesgue-Integral nicht notwendig ist, einen solchen Grenzwert zu nehmen, erscheint er natürlicher im Zusammenhang mit der Laplace-Stieltjes-Transformation. ⓘ

Bilaterale Laplace-Transformation

Wenn man von der Laplace-Transformation spricht, ist in der Regel die unilaterale oder einseitige Transformation gemeint. Die Laplace-Transformation kann alternativ auch als zweiseitige Laplace-Transformation oder zweiseitige Laplace-Transformation definiert werden, indem die Grenzen der Integration auf die gesamte reelle Achse ausgedehnt werden. In diesem Fall wird die gewöhnliche einseitige Transformation einfach zu einem Spezialfall der zweiseitigen Transformation, bei der die Definition der zu transformierenden Funktion mit der Heaviside-Stufenfunktion multipliziert wird. ⓘ

Die bilaterale Laplace-Transformation F(s) ist wie folgt definiert:

$F(s)=\int _{-\infty }^{\infty }e^{-st}f(t)\,dt$

(Gl.2)

Eine alternative Schreibweise für die bilaterale Laplace-Transformation ist ${\mathcal {B}}\{f\}$anstelle von $F$. ⓘ

Inverse Laplace-Transformation

Zwei integrierbare Funktionen haben nur dann dieselbe Laplace-Transformation, wenn sie sich auf einer Menge mit Lebesgue-Maß Null unterscheiden. Das bedeutet, dass es im Bereich der Transformation eine inverse Transformation gibt. Tatsächlich ist die Laplace-Transformation nicht nur für integrierbare Funktionen, sondern auch für viele andere Funktionsräume eine Eins-zu-Eins-Abbildung von einem Funktionsraum in einen anderen, auch wenn es normalerweise keine einfache Charakterisierung des Bereichs gibt. ⓘ

Typische Funktionsräume, in denen dies zutrifft, sind die Räume der beschränkten stetigen Funktionen, der Raum L^∞(0, ∞) oder allgemeiner die temperierten Verteilungen auf (0, ∞). Die Laplace-Transformation ist ebenfalls definiert und injektiv für geeignete Räume von temperierten Verteilungen. ⓘ

In diesen Fällen befindet sich das Bild der Laplace-Transformation in einem Raum analytischer Funktionen im Konvergenzbereich. Die inverse Laplace-Transformation ist durch das folgende komplexe Integral gegeben, das unter verschiedenen Namen bekannt ist (Bromwich-Integral, Fourier-Mellin-Integral und Mellinsche Umkehrformel):

$f(t)={\mathcal {L}}^{-1}\{F\}(t)={\frac {1}{2\pi i}}\lim _{T\to \infty }\int _{\gamma -iT}^{\gamma +iT}e^{st}F(s)\,ds$

(Gl.3)

wobei γ eine reelle Zahl ist, so dass der Konturpfad der Integration im Konvergenzbereich von F(s) liegt. In den meisten Anwendungen kann die Kontur geschlossen werden, was die Anwendung des Restwertsatzes ermöglicht. Eine alternative Formel für die inverse Laplace-Transformation wird durch die Post'sche Inversionsformel gegeben. Der Grenzwert wird hier in der schwachen *-Topologie interpretiert. ⓘ

In der Praxis ist es in der Regel bequemer, eine Laplace-Transformation in bekannte, aus einer Tabelle gewonnene Funktionstransformationen zu zerlegen und die Inverse durch Überprüfung zu konstruieren. ⓘ

Wahrscheinlichkeitsrechnung

In der reinen und angewandten Wahrscheinlichkeitsrechnung ist die Laplace-Transformation als Erwartungswert definiert. Wenn X eine Zufallsvariable mit der Wahrscheinlichkeitsdichtefunktion f ist, dann ist die Laplace-Transformation von f durch den Erwartungswert gegeben

$${\mathcal {L}}\{f\}(s)=\operatorname {E} \!\left[e^{-sX}\right]\!.$$

ⓘ

Vereinbarungsgemäß wird dies als die Laplace-Transformation der Zufallsvariablen X selbst bezeichnet. Ersetzt man hier s durch -t, so erhält man die momenterzeugende Funktion von X. Die Laplace-Transformation findet in der gesamten Wahrscheinlichkeitstheorie Anwendung, einschließlich der ersten Durchgangszeiten von stochastischen Prozessen wie Markov-Ketten und der Erneuerungstheorie. ⓘ

Von besonderem Nutzen ist die Möglichkeit, die kumulative Verteilungsfunktion einer kontinuierlichen Zufallsvariablen X mit Hilfe der Laplace-Transformation wie folgt wiederherzustellen:

$$F_{X}(x)={\mathcal {L}}^{-1}\!\left\{{\frac {1}{s}}\operatorname {E} \left[e^{-sX}\right]\right\}\!(x)={\mathcal {L}}^{-1}\!\left\{{\frac {1}{s}}{\mathcal {L}}\{f\}(s)\right\}\!(x).$$

ⓘ

Bereich der Konvergenz

Wenn f eine lokal integrierbare Funktion (oder allgemeiner ein Borel-Maß mit lokal beschränkter Variation) ist, dann konvergiert die Laplace-Transformation F(s) von f, sofern der Grenzwert

$$\lim _{R\to \infty }\int _{0}^{R}f(t)e^{-st}\,dt$$

existiert. ⓘ

Die Laplace-Transformation konvergiert absolut, wenn das Integral

$$\int _{0}^{\infty }\left|f(t)e^{-st}\right|\,dt$$

als echtes Lebesgue-Integral existiert. Die Laplace-Transformation wird in der Regel als bedingt konvergent verstanden, d. h. sie konvergiert im ersten, aber nicht im zweiten Sinne. ⓘ

Die Menge der Werte, für die F(s) absolut konvergiert, hat entweder die Form Re(s) > a oder Re(s) ≥ a, wobei a eine erweiterte reelle Konstante mit -∞ ≤ a ≤ ∞ ist (eine Folge des Theorems der dominierten Konvergenz). Die Konstante a ist als Abszisse der absoluten Konvergenz bekannt und hängt vom Wachstumsverhalten von f(t) ab. Analog dazu konvergiert die zweiseitige Transformation absolut in einem Streifen der Form a < Re(s) < b, der möglicherweise die Linien Re(s) = a oder Re(s) = b einschließt. Die Teilmenge der Werte von s, für die die Laplace-Transformation absolut konvergiert, wird als Bereich der absoluten Konvergenz oder als Domäne der absoluten Konvergenz bezeichnet. Im zweiseitigen Fall wird sie manchmal auch als Streifen der absoluten Konvergenz bezeichnet. Die Laplace-Transformation ist im Bereich der absoluten Konvergenz analytisch: Dies ist eine Folge des Satzes von Fubini und des Satzes von Morera. ⓘ

In ähnlicher Weise wird die Menge der Werte, für die F(s) (bedingt oder absolut) konvergiert, als Bereich der bedingten Konvergenz oder einfach als Konvergenzbereich (ROC) bezeichnet. Wenn die Laplace-Transformation (bedingt) bei s = s₀ konvergiert, dann konvergiert sie automatisch für alle s mit Re(s) > Re(s₀). Daher ist das Konvergenzgebiet eine Halbebene der Form Re(s) > a, die möglicherweise einige Punkte der Grenzlinie Re(s) = a einschließt. ⓘ

Im Konvergenzbereich Re(s) > Re(s₀) kann die Laplace-Transformation von f durch Integration nach Teilen als Integral ausgedrückt werden

$$F(s)=(s-s_{0})\int _{0}^{\infty }e^{-(s-s_{0})t}\beta (t)\,dt,\quad \beta (u)=\int _{0}^{u}e^{-s_{0}t}f(t)\,dt.$$

ⓘ

Das heißt, F(s) kann im Konvergenzbereich tatsächlich als absolut konvergente Laplace-Transformation einer anderen Funktion ausgedrückt werden. Insbesondere ist sie analytisch. ⓘ

Es gibt mehrere Paley-Wiener-Theoreme über die Beziehung zwischen den Zerfallseigenschaften von f und den Eigenschaften der Laplace-Transformation im Konvergenzbereich. ⓘ

In technischen Anwendungen ist eine Funktion, die einem linearen zeitinvarianten System (LTI) entspricht, stabil, wenn jede begrenzte Eingabe eine begrenzte Ausgabe erzeugt. Dies entspricht der absoluten Konvergenz der Laplace-Transformierten der Impulsantwortfunktion im Bereich Re(s) ≥ 0. Folglich sind LTI-Systeme stabil, sofern die Pole der Laplace-Transformierten der Impulsantwortfunktion einen negativen Realteil haben. ⓘ

Diese ROC wird verwendet, um die Kausalität und Stabilität eines Systems zu bestimmen. ⓘ

Eigenschaften und Theoreme

Die Laplace-Transformation hat eine Reihe von Eigenschaften, die sie für die Analyse linearer dynamischer Systeme nützlich machen. Der wichtigste Vorteil ist, dass die Differenzierung durch s zur Multiplikation und die Integration zur Division wird (was an die Art und Weise erinnert, wie Logarithmen die Multiplikation zur Addition von Logarithmen machen). ⓘ

Aufgrund dieser Eigenschaft wird die Laplace-Variable s auch als Operatorvariable im Bereich L bezeichnet: entweder Ableitungsoperator oder (für s-1) Integrationsoperator. Die Umformung verwandelt Integral- und Differentialgleichungen in Polynomgleichungen, die viel einfacher zu lösen sind. Nach der Lösung kehrt man mit der inversen Laplace-Transformation in den ursprünglichen Bereich zurück. ⓘ

Bei den Funktionen f(t) und g(t) und ihren jeweiligen Laplace-Transformationen F(s) und G(s),

$${\begin{aligned}f(t)&={\mathcal {L}}^{-1}\{F\}(s),\\g(t)&={\mathcal {L}}^{-1}\{G\}(s),\end{aligned}}$$

ⓘ

enthält die folgende Tabelle eine Liste der Eigenschaften der einseitigen Laplace-Transformation:

Eigenschaften der einseitigen Laplace-Transformation ⓘ

Eigenschaft	Zeitbereich	s-Bereich	Anmerkung
Linearität	$af(t)+bg(t)\$	$aF(s)+bG(s)\$	Kann mit den Grundregeln der Integration bewiesen werden.
Ableitung im Frequenzbereich	$tf(t)\$	$-F'(s)\$	F′ ist die erste Ableitung von F nach s.
Allgemeine Ableitung im Frequenzbereich	$t^{n}f(t)\$	$(-1)^{n}F^{(n)}(s)\$	Allgemeinere Form, n-te Ableitung von F(s).
Ableitung	$f'(t)\$	$sF(s)-f(0^{+})\$	Es wird angenommen, dass f eine differenzierbare Funktion ist und dass ihre Ableitung vom Exponentialtyp ist. Diese kann dann durch Integration nach Teilen erhalten werden
Zweite Ableitung	$f(t)\$	${\textstyle s^{2}F(s)-sf(0^{+})-f'(0^{+})\ }$	Es wird angenommen, dass f zweimal differenzierbar ist und die zweite Ableitung vom Exponentialtyp ist. Dies ergibt sich aus der Anwendung der Eigenschaft der Differenzierung auf f′(t).
Allgemeine Ableitung	$f^{(n)}(t)\$	$s^{n}F(s)-\sum _{k=1}^{n}s^{n-k}f^{(k-1)}(0^{+})\$	f wird als n-fach differenzierbar angenommen, wobei die n-te Ableitung vom Exponentialtyp ist. Ergibt sich durch mathematische Induktion.
Integration im Frequenzbereich	${\frac {1}{t}}f(t)\$	$\int _{s}^{\infty }F(\sigma )\,d\sigma \$	Dies wird aus der Natur der Frequenzdifferenzierung und der bedingten Konvergenz abgeleitet.
Integration im Zeitbereich	$\int _{0}^{t}f(\tau )\,d\tau =(u*f)(t)$	${1 \over s}F(s)$	u(t) ist die Heaviside-Schrittfunktion und (u ∗ f)(t) ist die Faltung von u(t) und f(t).
Frequenzverschiebung	$e^{at}f(t)\$	$F(s-a)\$
Zeitverschiebung	$f(t-a)u(t-a)\$	$e^{-as}F(s)\$	$a>0\$u(t) ist die Heaviside-Schrittfunktion
Zeitliche Skalierung	$f(at)$	${\frac {1}{a}}F\left({s \over a}\right)$	$a>0\$
Multiplikation	$f(t)g(t)$	${\frac {1}{2\pi i}}\lim _{T\to \infty }\int _{c-iT}^{c+iT}F(\sigma )G(s-\sigma )\,d\sigma \$	Die Integration erfolgt entlang der vertikalen Linie Re(σ) = c, die vollständig innerhalb des Konvergenzbereichs von F liegt.
Faltung	$(f*g)(t)=\int _{0}^{t}f(\tau )g(t-\tau )\,d\tau$	$F(s)\cdot G(s)\$
Kreisförmige Faltung	$(f*g)(t)=\int _{0}^{T}f(\tau )g(t-\tau )\,d\tau$	$F(s)\cdot G(s)\$	Für periodische Funktionen mit Periode T.
Komplexe Konjugation	$f^{*}(t)$	$F^{*}(s^{*})$
Kreuzkorrelation	$(f\star g)(t)=\int _{0}^{\infty }f(\tau )^{*}\,g(t+\tau )\,d\tau$	$F^{*}(-s^{*})\cdot G(s)$
Periodische Funktion	$f(t)$	${1 \over 1-e^{-Ts}}\int _{0}^{T}e^{-st}f(t)\,dt$	f(t) ist eine periodische Funktion der Periode T, so dass f(t) = f(t + T), für alle t ≥ 0. Dies ist das Ergebnis der Eigenschaft der Zeitverschiebung und der geometrischen Reihe.
Periodische Summierung	$\sum _{n=0}^{\infty }f(t-Tn)u(t-Tn)$ $\sum _{n=0}^{\infty }(-1)^{n}f(t-Tn)u(t-Tn)$	${\frac {1}{1-e^{-Ts}}}F(s)$ ${\frac {1}{1+e^{-Ts}}}F(s)$

Anfangswert-Theorem

$f(0^{+})=\lim _{s\to \infty }{sF(s)}.$

Endwertsatz

$f(\infty )=\lim _{s\to 0}{sF(s)}$, wenn alle Pole von $sF(s)$ in der linken Halbebene liegen.

Der Endwertsatz ist nützlich, weil er das Langzeitverhalten angibt, ohne dass partielle Bruchzerlegungen (oder andere schwierige Algebra) durchgeführt werden müssen. Wenn F(s) einen Pol in der rechten Ebene oder Pole auf der imaginären Achse hat (z. B., wenn $f(t)=e^{t}$ oder $f(t)=\sin(t)$), dann ist das Verhalten dieser Formel undefiniert. ⓘ

mit $f(0)=f_{0}$. Unter Ausnutzung der Linearität der Laplace-Transformation und des Verhaltens bei Ableitung im Ursprungsbereich (s. Tabelle der allgemeinen Eigenschaften) ist die Transformierte gegeben durch ⓘ

mit $F(s)={\mathcal {L}}\{f(t)\}$. Die Rücktransformation in den Ursprungsbereich ist in obiger Korrespondenztabelle aufgeführt (s. Exponentialfunktion), ⓘ

Obige Differentialgleichung beschreibt also einfache Wachstums- und Abnahmeprozesse und findet sich demnach in vielen Bereichen, u. a. in Natur-, Wirtschafts- und Sozialwissenschaften. ⓘ

Beziehung zu Potenzreihen

Die Laplace-Transformation kann als ein kontinuierliches Analogon einer Potenzreihe betrachtet werden. Wenn a(n) eine diskrete Funktion einer positiven ganzen Zahl n ist, dann ist die zu a(n) gehörende Potenzreihe die Reihe

$$\sum _{n=0}^{\infty }a(n)x^{n}$$

wobei x eine reelle Variable ist (siehe Z-Transformation). Ersetzt man die Summation über n durch Integration über t, so ergibt sich eine kontinuierliche Version der Potenzreihe

$$\int _{0}^{\infty }f(t)x^{t}\,dt$$

wobei die diskrete Funktion a(n) durch die kontinuierliche Funktion f(t) ersetzt wird. ⓘ

Ändert man die Basis der Potenz von x auf e, so erhält man

$$\int _{0}^{\infty }f(t)\left(e^{\ln {x}}\right)^{t}\,dt$$

ⓘ

Damit dies für alle beschränkten Funktionen f konvergiert, muss ln x < 0 sein. Die Substitution -s = ln x ergibt nur die Laplace-Transformation:

$$\int _{0}^{\infty }f(t)e^{-st}\,dt$$

ⓘ

Mit anderen Worten: Die Laplace-Transformation ist ein kontinuierliches Analogon einer Potenzreihe, bei der der diskrete Parameter n durch den kontinuierlichen Parameter t und x durch e-s ersetzt wird. ⓘ

Die Laplace-Transformation bildet eine endliche Zeitfunktion ⓘ

$f(t)=0$ für ${\begin{cases}t<0\\t>T\end{cases}}$ ⓘ

auf eine ganze Funktion ab. Dies bedeutet, dass die Bildfunktion ⓘ

in der ganzen komplexen Frequenzebene analytisch ist, also keine Singularitäten besitzt. ⓘ

Beziehung zu Momenten

Die Größen

$$\mu _{n}=\int _{0}^{\infty }t^{n}f(t)\,dt$$

ⓘ

sind die Momente der Funktion f. Wenn die ersten n Momente von f absolut konvergieren, dann durch wiederholte Differenzierung unter dem Integral,

$$(-1)^{n}({\mathcal {L}}f)^{(n)}(0)=\mu _{n}.$$

Dies ist von besonderer Bedeutung in der Wahrscheinlichkeitstheorie, wo die Momente einer Zufallsvariablen X durch die Erwartungswerte gegeben sind $\mu _{n}=\operatorname {E} [X^{n}]$. Dann gilt die Beziehung

$$\mu _{n}=(-1)^{n}{\frac {d^{n}}{ds^{n}}}\operatorname {E} \left[e^{-sX}\right](0).$$

ⓘ

Berechnung der Laplace-Transformation der Ableitung einer Funktion

Oft ist es sinnvoll, die Differenzierungseigenschaft der Laplace-Transformation zu nutzen, um die Transformation der Ableitung einer Funktion zu finden. Dies lässt sich aus dem grundlegenden Ausdruck für eine Laplace-Transformation wie folgt ableiten:

$${\begin{aligned}{\mathcal {L}}\left\{f(t)\right\}&=\int _{0^{-}}^{\infty }e^{-st}f(t)\,dt\\[6pt]&=\left[{\frac {f(t)e^{-st}}{-s}}\right]_{0^{-}}^{\infty }-\int _{0^{-}}^{\infty }{\frac {e^{-st}}{-s}}f'(t)\,dt\quad {\text{(by parts)}}\\[6pt]&=\left[-{\frac {f(0^{-})}{-s}}\right]+{\frac {1}{s}}{\mathcal {L}}\left\{f'(t)\right\},\end{aligned}}$$

ⓘ

und ergibt ⓘ

$${\mathcal {L}}\{f'(t)\}=s\cdot {\mathcal {L}}\{f(t)\}-f(0^{-}),$$

ⓘ

und im zweiseitigen Fall, ⓘ

$${\mathcal {L}}\{f'(t)\}=s\int _{-\infty }^{\infty }e^{-st}f(t)\,dt=s\cdot {\mathcal {L}}\{f(t)\}.$$

ⓘ

Das allgemeine Ergebnis ⓘ

$${\mathcal {L}}\left\{f^{(n)}(t)\right\}=s^{n}\cdot {\mathcal {L}}\{f(t)\}-s^{n-1}f(0^{-})-\cdots -f^{(n-1)}(0^{-}),$$

ⓘ

wobei $f^{(n)}$ die n-te Ableitung von f bezeichnet, kann dann mit einem induktiven Argument ermittelt werden. ⓘ

Auswerten von Integralen über die positive reelle Achse

Eine nützliche Eigenschaft der Laplace-Transformation ist die folgende:

$$\int _{0}^{\infty }f(x)g(x)\,dx=\int _{0}^{\infty }({\mathcal {L}}f)(s)\cdot ({\mathcal {L}}^{-1}g)(s)\,ds$$

ⓘ

Unter geeigneten Annahmen über das Verhalten von $f,g$ in einer rechten Nachbarschaft von $0$ und für die Abklingrate von $f,g$ in einer linken Nachbarschaft von $\infty$. Die obige Formel ist eine Variation der Integration durch Teile, mit den Operatoren ${\frac {d}{dx}}$ und $\int \,dx$ ersetzt werden durch ${\mathcal {L}}$ und ${\mathcal {L}}^{-1}$. Wir wollen die äquivalente Formulierung beweisen:

$$\int _{0}^{\infty }({\mathcal {L}}f)(x)g(x)\,dx=\int _{0}^{\infty }f(s)({\mathcal {L}}g)(s)\,ds.$$

ⓘ

Durch Einsetzen von $({\mathcal {L}}f)(x)=\int _{0}^{\infty }f(s)e^{-sx}\,ds$ wird die linke Seite zu:

$$\int _{0}^{\infty }\int _{0}^{\infty }f(s)g(x)e^{-sx}\,ds\,dx,$$

ⓘ

aber unter der Annahme, dass der Satz von Fubini gilt, erhalten wir durch Umkehrung der Integrationsreihenfolge die gewünschte rechte Seite. ⓘ

Mit dieser Methode lassen sich Integrale berechnen, die mit den elementaren Methoden der Realrechnung sonst nur schwer zu berechnen wären. Ein Beispiel, ⓘ

$$\int _{0}^{\infty }{\frac {\sin x}{x}}dx=\int _{0}^{\infty }{\mathcal {L}}(1)(x)\sin xdx=\int _{0}^{\infty }1\cdot {\mathcal {L}}(\sin )(x)dx=\int _{0}^{\infty }{\frac {dx}{x^{2}+1}}={\frac {\pi }{2}}.$$

ⓘ

Analytizität

Die Laplace-Transformierte ist infolge der Existenz ihrer Ableitungen nach der komplexen Frequenz $s$ im Bildbereich ⓘ

$F^{(n)}(s)={\mathcal {L}}\{(-t)^{n}f(t)\}\qquad (n=1,2,3,\dots )$ ⓘ

im Innern der Konvergenzhalbebene beliebig oft komplex differenzierbar, das heißt analytisch (beziehungsweise regulär oder holomorph). Somit kann $F(s)$ mit den Mitteln der Funktionentheorie untersucht werden. Die Funktion $F(s)$ kann in die linke Halbebene analytisch fortsetzbar sein, aber nicht zwingend. Eine solche analytische Fortsetzung lässt sich dann aber nicht mehr als Laplace-Transformierte schreiben. ⓘ

Konjugierte Symmetrie

Eine weitere wichtige Eigenschaft der Laplace-Transformierten reeller Zeitfunktionen ist die konjugierte Symmetrie im komplexen Bildbereich ⓘ

$F({\bar {s}})={\bar {F}}(s)$ ⓘ

oder separiert in Real- und Imaginärteil

$\operatorname {Re} (F({\bar {s}}))=\operatorname {Re} (F(s))$

$\operatorname {Im} (F({\bar {s}}))=-\operatorname {Im} (F(s))$ ⓘ

wobei der Überstrich die komplex konjugierte Größe kennzeichnet. Aufgrund dieser Eigenschaft genügt es, die Bildfunktion in der oberen Halbebene $\operatorname {Im} (s)\geq 0$ zu studieren. ⓘ

Beziehung zu anderen Transformationen

Laplace-Stieltjes-Transformation

Die (einseitige) Laplace-Stieltjes-Transformation einer Funktion g : ℝ → ℝ ist durch das Lebesgue-Stieltjes-Integral definiert ⓘ

$$\{{\mathcal {L}}^{*}g\}(s)=\int _{0}^{\infty }e^{-st}\,d\,g(t)~.$$

ⓘ

Es wird angenommen, dass die Funktion g von beschränkter Variation ist. Wenn g die Antiderivative von f ist:

$$g(x)=\int _{0}^{x}f(t)\,d\,t$$

ⓘ

dann stimmen die Laplace-Stieltjes-Transformation von g und die Laplace-Transformation von f überein. Im Allgemeinen ist die Laplace-Stieltjes-Transformation die Laplace-Transformation des Stieltjes-Maßes, das zu g gehört. In der Praxis besteht der einzige Unterschied zwischen den beiden Transformationen darin, dass die Laplace-Transformation als Funktion der Dichtefunktion des Maßes betrachtet wird, während die Laplace-Stieltjes-Transformation als Funktion der kumulativen Verteilungsfunktion betrachtet wird. ⓘ

Fourier-Transformation

Die Fourier-Transformation ist (unter bestimmten Bedingungen) ein Spezialfall der bilateralen Laplace-Transformation. Während die Fourier-Transformation einer Funktion eine komplexe Funktion einer reellen Variablen (Frequenz) ist, ist die Laplace-Transformation einer Funktion eine komplexe Funktion einer komplexen Variablen. Die Laplace-Transformation ist in der Regel auf die Transformation von Funktionen von t mit t ≥ 0 beschränkt. Eine Folge dieser Beschränkung ist, dass die Laplace-Transformation einer Funktion eine holomorphe Funktion der Variablen s ist. Im Gegensatz zur Fourier-Transformation ist die Laplace-Transformation einer Verteilung im Allgemeinen eine wohlbehaltene Funktion. Techniken für komplexe Variablen können auch zur direkten Untersuchung von Laplace-Transformationen verwendet werden. Als holomorphe Funktion hat die Laplace-Transformation eine Potenzreihendarstellung. Diese Potenzreihe drückt eine Funktion als eine lineare Überlagerung von Momenten der Funktion aus. Diese Sichtweise findet in der Wahrscheinlichkeitstheorie Anwendung. ⓘ

Die Fourier-Transformation ist äquivalent zur Auswertung der zweiseitigen Laplace-Transformation mit dem imaginären Argument s = iω oder s = 2πiξ, wenn die unten erläuterte Bedingung erfüllt ist, ⓘ

$${\begin{aligned}{\hat {f}}(\omega )&={\mathcal {F}}\{f(t)\}\\[4pt]&={\mathcal {L}}\{f(t)\}|_{s=i\omega }=F(s)|_{s=i\omega }\\[4pt]&=\int _{-\infty }^{\infty }e^{-i\omega t}f(t)\,dt~.\end{aligned}}$$

ⓘ

Diese Konvention der Fourier-Transformation (${\hat {f}}_{3}(\omega )$ in Fourier-Transformation § Andere Konventionen) erfordert einen Faktor von 1/2π bei der inversen Fourier-Transformation. Diese Beziehung zwischen der Laplace- und der Fourier-Transformation wird häufig verwendet, um das Frequenzspektrum eines Signals oder eines dynamischen Systems zu bestimmen. ⓘ

Die obige Beziehung ist nur dann gültig, wenn der Konvergenzbereich (ROC) von F(s) die imaginäre Achse σ = 0 enthält. ⓘ

Zum Beispiel hat die Funktion f(t) = cos(ω₀t) eine Laplace-Transformation F(s) = s/(s² + ω₀²), deren ROC Re(s) > 0 ist. Da s = iω₀ ein Pol von F(s) ist, ergibt die Substitution von s = iω in F(s) nicht die Fourier-Transformation von f(t)u(t), die proportional zur Dirac-Delta-Funktion δ(ω - ω₀) ist. ⓘ

Es gilt jedoch eine Beziehung der Form

$$\lim _{\sigma \to 0^{+}}F(\sigma +i\omega )={\hat {f}}(\omega )$$

gilt jedoch unter viel schwächeren Bedingungen. Dies gilt beispielsweise für das obige Beispiel, sofern der Grenzwert als schwacher Grenzwert von Maßen verstanden wird (siehe vage Topologie). Allgemeine Bedingungen, die den Grenzwert der Laplace-Transformation einer Funktion auf dem Rand mit der Fourier-Transformation verbinden, haben die Form von Paley-Wiener-Theoremen. ⓘ

Mellin-Transformation

Die Mellin-Transformation und ihre Umkehrung sind mit der zweiseitigen Laplace-Transformation durch einen einfachen Variablenwechsel verbunden. ⓘ

Wenn bei der Mellin-Transformation

$$G(s)={\mathcal {M}}\{g(\theta )\}=\int _{0}^{\infty }\theta ^{s}g(\theta )\,{\frac {d\theta }{\theta }}$$

θ = e-t gesetzt wird, erhält man eine zweiseitige Laplace-Transformation. ⓘ

Z-Transformation

Die einseitige Z-Transformation ist einfach die Laplace-Transformation eines ideal abgetasteten Signals mit der Ersetzung von

$$z{\stackrel {\mathrm {def} }{{}={}}}e^{sT},$$

wobei T = 1/fs das Abtastintervall (in Zeiteinheiten, z. B. Sekunden) und fs die Abtastrate (in Proben pro Sekunde oder Hertz) ist. ⓘ

Sei

$$\Delta _{T}(t)\ {\stackrel {\mathrm {def} }{=}}\ \sum _{n=0}^{\infty }\delta (t-nT)$$

eine Abtastimpulsfolge (auch Dirac-Kamm genannt) und

$${\begin{aligned}x_{q}(t)&{\stackrel {\mathrm {def} }{{}={}}}x(t)\Delta _{T}(t)=x(t)\sum _{n=0}^{\infty }\delta (t-nT)\\&=\sum _{n=0}^{\infty }x(nT)\delta (t-nT)=\sum _{n=0}^{\infty }x[n]\delta (t-nT)\end{aligned}}$$

die abgetastete Darstellung des zeitkontinuierlichen x(t)

$$x[n]{\stackrel {\mathrm {def} }{{}={}}}x(nT)~.$$

ⓘ

Die Laplace-Transformation des abgetasteten Signals x_q(t) ist

$${\begin{aligned}X_{q}(s)&=\int _{0^{-}}^{\infty }x_{q}(t)e^{-st}\,dt\\&=\int _{0^{-}}^{\infty }\sum _{n=0}^{\infty }x[n]\delta (t-nT)e^{-st}\,dt\\&=\sum _{n=0}^{\infty }x[n]\int _{0^{-}}^{\infty }\delta (t-nT)e^{-st}\,dt\\&=\sum _{n=0}^{\infty }x[n]e^{-nsT}~.\end{aligned}}$$

ⓘ

Dies ist die genaue Definition der einseitigen Z-Transformation der diskreten Funktion x[n] ⓘ

$$X(z)=\sum _{n=0}^{\infty }x[n]z^{-n}$$

mit der Ersetzung von z → e^sT. ⓘ

Vergleicht man die letzten beiden Gleichungen, so findet man die Beziehung zwischen der einseitigen Z-Transformation und der Laplace-Transformation des abgetasteten Signals,

$$X_{q}(s)=X(z){\Big |}_{z=e^{sT}}.$$

ⓘ

Die Ähnlichkeit zwischen der Z-Transformation und der Laplace-Transformation wird in der Theorie der Zeitskalenberechnung weiter ausgeführt. ⓘ

Borel-Transformation

Die Integralform der Borel-Transformation ⓘ

$$F(s)=\int _{0}^{\infty }f(z)e^{-sz}\,dz$$

ⓘ

ist ein Spezialfall der Laplace-Transformation für f eine ganze Funktion vom Exponentialtyp, was bedeutet, dass ⓘ

$$|f(z)|\leq Ae^{B|z|}$$

ⓘ

für einige Konstanten A und B. Die verallgemeinerte Borel-Transformation ermöglicht die Verwendung einer anderen Gewichtungsfunktion anstelle der Exponentialfunktion, um Funktionen zu transformieren, die nicht vom Exponentialtyp sind. Der Satz von Nachbin enthält notwendige und hinreichende Bedingungen dafür, dass die Borel-Transformation wohldefiniert ist. ⓘ

Grundlegende Beziehungen

Da eine gewöhnliche Laplace-Transformation als Spezialfall einer zweiseitigen Transformation geschrieben werden kann, und da die zweiseitige Transformation als Summe zweier einseitiger Transformationen geschrieben werden kann, sind die Theorie der Laplace-, Fourier-, Mellin- und Z-Transformationen im Grunde dasselbe Thema. Allerdings sind mit jeder dieser vier großen Integraltransformationen eine andere Sichtweise und andere charakteristische Probleme verbunden. ⓘ

Tabelle mit ausgewählten Laplace-Transformationen

Die folgende Tabelle enthält Laplace-Transformationen für viele gängige Funktionen einer einzelnen Variablen. Definitionen und Erklärungen finden Sie in den Erläuterungen am Ende der Tabelle. ⓘ

Weil die Laplace-Transformation ein linearer Operator ist, ⓘ

• Die Laplace-Transformierte einer Summe ist die Summe der Laplace-Transformierten der einzelnen Terme.
  $${\mathcal {L}}\{f(t)+g(t)\}={\mathcal {L}}\{f(t)\}+{\mathcal {L}}\{g(t)\}$$
  ⓘ

• Die Laplace-Transformierte eines Vielfachen einer Funktion ist dieses Vielfache mal die Laplace-Transformierte dieser Funktion.
  $${\mathcal {L}}\{af(t)\}=a{\mathcal {L}}\{f(t)\}$$
  ⓘ

Unter Verwendung dieser Linearität und verschiedener trigonometrischer, hyperbolischer und komplexer Zahleneigenschaften (usw.) und/oder Identitäten können einige Laplace-Transformationen schneller aus anderen gewonnen werden, als wenn man die Definition direkt verwendet. ⓘ

Die einseitige Laplace-Transformation benötigt als Eingabe eine Funktion, deren Zeitbereich die nichtnegativen reellen Zahlen sind, weshalb alle Zeitbereichsfunktionen in der folgenden Tabelle Vielfache der Heaviside-Schrittfunktion u(t) sind. ⓘ

Die Einträge in der Tabelle, die eine Zeitverzögerung τ beinhalten, müssen kausal sein (was bedeutet, dass τ > 0 ist). Ein kausales System ist ein System, bei dem die Impulsantwort h(t) für alle Zeiten t vor t = 0 gleich Null ist. Im Allgemeinen ist der Konvergenzbereich für kausale Systeme nicht derselbe wie der für antikausale Systeme. ⓘ

Ausgewählte Laplace-Transformationen ⓘ

Funktion	Zeitbereich $f(t)={\mathcal {L}}^{-1}\{F(s)\}$	Laplace s-Domäne $F(s)={\mathcal {L}}\{f(t)\}$	Bereich der Konvergenz	Referenz
Einheitsimpuls	$\delta (t)\$	$1$	alle s	Prüfung
verzögerter Impuls	$\delta (t-\tau )\$	$e^{-\tau s}\$		Zeitverschiebung von Einheitsimpuls
Einheitsschritt	$u(t)\$	${1 \over s}$	${\mathcal {R_{e}}}(s)>0$	Einheitsimpuls integrieren
verzögerter Einheitsschritt	$u(t-\tau )\$	${\frac {1}{s}}e^{-\tau s}$	${\mathcal {R_{e}}}(s)>0$	Zeitverschiebung von Einheitsschritt
Rechteckimpuls	$u(t)-u(t-\tau )$	${\frac {1}{s}}(1-e^{-\tau s})$	${\mathcal {R_{e}}}(s)>0$
Rampe	$t\cdot u(t)\$	${\frac {1}{s^{2}}}$	${\mathcal {R_{e}}}(s)>0$	Einheit integrieren Impuls zweimal
n-te Potenz (für ganzzahliges n)	$t^{n}\cdot u(t)$	${n! \over s^{n+1}}$	${\mathcal {R_{e}}}(s)>0$ (n > -1)	Einheit integrieren Schritt n-mal
q-te Potenz (für komplexes q)	$t^{q}\cdot u(t)$	${\operatorname {\Gamma } (q+1) \over s^{q+1}}$	${\mathcal {R_{e}}}(s)>0$ ${\mathcal {R_{e}}}(q)>-1$
n-te Wurzel	${\sqrt[{n}]{t}}\cdot u(t)$	${1 \over s^{{\frac {1}{n}}+1}}\operatorname {\Gamma } \left({\frac {1}{n}}+1\right)$	${\mathcal {R_{e}}}(s)>0$	Setzen Sie q = 1/n oben.
n-te Potenz mit Frequenzverschiebung	$t^{n}e^{-\alpha t}\cdot u(t)$	${\frac {n!}{(s+\alpha )^{n+1}}}$	${\mathcal {R_{e}}}(s)>-\alpha$	Integriere Einheitsschritt, Frequenzverschiebung anwenden
verzögerte n-te Potenz mit Frequenzverschiebung	$(t-\tau )^{n}e^{-\alpha (t-\tau )}\cdot u(t-\tau )$	${\frac {n!\cdot e^{-\tau s}}{(s+\alpha )^{n+1}}}$	${\mathcal {R_{e}}}(s)>-\alpha$	Einheitsschritt integrieren, Frequenzverschiebung anwenden, Zeitverschiebung anwenden
exponentieller Zerfall	$e^{-\alpha t}\cdot u(t)$	${1 \over s+\alpha }$	${\mathcal {R_{e}}}(s)>-\alpha$	Frequenzverschiebung von Einheitsschritt
zweiseitigem exponentiellem Abklingen (nur bei zweiseitiger Transformation)	$e^{-\alpha |t|}\$	${2\alpha \over \alpha ^{2}-s^{2}}$	$-\alpha <{\mathcal {R_{e}}}(s)<\alpha$	Frequenzverschiebung von Einheitsschritt
exponentieller Ansatz	$(1-e^{-\alpha t})\cdot u(t)\$	${\frac {\alpha }{s(s+\alpha )}}$	${\mathcal {R_{e}}}(s)>0$	Einheitsschritt minus exponentieller Zerfall
Sinus	$\sin(\omega t)\cdot u(t)\$	${\omega \over s^{2}+\omega ^{2}}$	${\mathcal {R_{e}}}(s)>0$
Kosinus	$\cos(\omega t)\cdot u(t)\$	${s \over s^{2}+\omega ^{2}}$	${\mathcal {R_{e}}}(s)>0$
hyperbolischer Sinus	$\sinh(\alpha t)\cdot u(t)\$	${\alpha \over s^{2}-\alpha ^{2}}$	${\mathcal {R_{e}}}(s)>\left|\alpha \right|$
hyperbolischer Kosinus	$\cosh(\alpha t)\cdot u(t)\$	${s \over s^{2}-\alpha ^{2}}$	${\mathcal {R_{e}}}(s)>\left|\alpha \right|$
exponentiell abklingende Sinuswelle	$e^{-\alpha t}\sin(\omega t)\cdot u(t)\$	${\omega \over (s+\alpha )^{2}+\omega ^{2}}$	${\mathcal {R_{e}}}(s)>-\alpha$
exponentiell abklingende Kosinuswelle	$e^{-\alpha t}\cos(\omega t)\cdot u(t)\$	${s+\alpha \over (s+\alpha )^{2}+\omega ^{2}}$	${\mathcal {R_{e}}}(s)>-\alpha$
natürlicher Logarithmus	$\ln(t)\cdot u(t)$	$-{1 \over s}\left[\ln(s)+\gamma \right]$	${\mathcal {R_{e}}}(s)>0$
Bessel-Funktion der ersten Art, der Ordnung n	$J_{n}(\omega t)\cdot u(t)$	${\frac {\left({\sqrt {s^{2}+\omega ^{2}}}-s\right)^{\!n}}{\omega ^{n}{\sqrt {s^{2}+\omega ^{2}}}}}$	${\mathcal {R_{e}}}(s)>0$ (n > -1)
Fehlerfunktion	$\operatorname {erf} (t)\cdot u(t)$	${\frac {1}{s}}e^{(1/4)s^{2}}\!\left(1-\operatorname {erf} {\frac {s}{2}}\right)$	${\mathcal {R_{e}}}(s)>0$
Erklärende Anmerkungen: u(t) steht für die Heaviside-Stufenfunktion. δ steht für die Dirac-Delta-Funktion. Γ(z) steht für die Gammafunktion. γ ist die Euler-Mascheroni-Konstante. t, eine reelle Zahl, steht in der Regel für die Zeit, kann aber auch für jede andere unabhängige Dimension stehen. s ist der komplexe Frequenzbereichsparameter, und Re(s) ist sein Realteil. α, β, τ, und ω sind reelle Zahlen. n ist eine ganze Zahl.

Ersatzschaltbilder und Impedanzen im s-Bereich

Die Laplace-Transformation wird häufig in der Schaltungsanalyse verwendet, und es können einfache Konvertierungen in die s-Domäne von Schaltungselementen vorgenommen werden. Schaltungselemente können in Impedanzen umgewandelt werden, die den Phasenimpedanzen sehr ähnlich sind. ⓘ

Hier finden Sie eine Zusammenfassung der Äquivalente:

Beachten Sie, dass der Widerstand im Zeitbereich und im s-Bereich genau derselbe ist. Die Quellen werden eingefügt, wenn es Anfangsbedingungen für die Schaltungselemente gibt. Liegt beispielsweise an einem Kondensator eine Anfangsspannung an oder fließt durch die Induktivität ein Anfangsstrom, so berücksichtigen die im s-Bereich eingefügten Quellen dies. ⓘ

Die Entsprechungen für Strom- und Spannungsquellen werden einfach aus den Transformationen in der obigen Tabelle abgeleitet. ⓘ

Beispiele und Anwendungen

Die Laplace-Transformation wird häufig in Technik und Physik verwendet; der Ausgang eines linearen, zeitinvarianten Systems kann durch Faltung seiner Einheitsimpulsantwort mit dem Eingangssignal berechnet werden. Wird diese Berechnung im Laplace-Raum durchgeführt, wird die Faltung zu einer Multiplikation, die aufgrund ihrer algebraischen Form leichter zu lösen ist. Weitere Informationen finden Sie unter Steuerungstheorie. Die Laplace-Transformation ist für eine große Klasse von Funktionen invertierbar. Bei einer einfachen mathematischen oder funktionalen Beschreibung eines Eingangs oder Ausgangs eines Systems liefert die Laplace-Transformation eine alternative funktionale Beschreibung, die häufig den Prozess der Analyse des Systemverhaltens oder der Synthese eines neuen Systems auf der Grundlage einer Reihe von Spezifikationen vereinfacht. ⓘ

Die Laplace-Transformation kann auch zur Lösung von Differentialgleichungen verwendet werden und findet im Maschinenbau und in der Elektrotechnik breite Anwendung. Die Laplace-Transformation reduziert eine lineare Differentialgleichung auf eine algebraische Gleichung, die dann nach den formalen Regeln der Algebra gelöst werden kann. Die ursprüngliche Differentialgleichung kann dann durch Anwendung der inversen Laplace-Transformation gelöst werden. Der englische Elektroingenieur Oliver Heaviside schlug zuerst ein ähnliches Verfahren vor, allerdings ohne die Laplace-Transformation zu verwenden; die daraus resultierende Operationsrechnung wird als Heaviside-Kalkül bezeichnet. ⓘ

Auswertung unechter Integrale

Sei ${\mathcal {L}}\left\{f(t)\right\}=F(s)$. Dann (siehe die Tabelle oben) ⓘ

$${\mathcal {L}}\left\{{\frac {f(t)}{t}}\right\}=\int _{0}^{\infty }{\frac {f(t)}{t}}e^{-st}\,dt=\int _{s}^{\infty }F(p)\,dp.$$

ⓘ

Im Grenzwert $s\rightarrow 0$erhält man ⓘ

$$\int _{0}^{\infty }{\frac {f(t)}{t}}\,dt=\int _{0}^{\infty }F(p)\,dp,$$

ⓘ

vorausgesetzt, die Vertauschung der Grenzwerte kann begründet werden. Dies ist oft als Folge des Endwertsatzes möglich. Auch wenn die Vertauschung nicht zu rechtfertigen ist, kann die Berechnung aufschlussreich sein. Beispielsweise erhält man mit a ≠ 0 ≠ b, formal betrachtet ⓘ

$${\begin{aligned}\int _{0}^{\infty }{\frac {\cos(at)-\cos(bt)}{t}}\,dt&=\int _{0}^{\infty }\left({\frac {p}{p^{2}+a^{2}}}-{\frac {p}{p^{2}+b^{2}}}\right)\,dp\\[6pt]&=\left[{\frac {1}{2}}\ln {\frac {p^{2}+a^{2}}{p^{2}+b^{2}}}\right]_{0}^{\infty }={\frac {1}{2}}\ln {\frac {b^{2}}{a^{2}}}=\ln \left|{\frac {b}{a}}\right|.\end{aligned}}$$

ⓘ

Die Gültigkeit dieser Identität kann auf andere Weise bewiesen werden. Sie ist ein Beispiel für ein Frullani-Integral. ⓘ

Ein weiteres Beispiel ist das Dirichlet-Integral. ⓘ

Komplexe Impedanz eines Kondensators

In der Theorie der elektrischen Schaltungen ist der Stromfluss in einem Kondensator proportional zur Kapazität und zur Änderungsrate des elektrischen Potenzials (in SI-Einheiten). Symbolisch wird dies durch die folgende Differentialgleichung ausgedrückt ⓘ

$$i=C{dv \over dt},$$

ⓘ

wobei C die Kapazität (in Farad) des Kondensators ist, i = i(t) der elektrische Strom (in Ampere) durch den Kondensator in Abhängigkeit von der Zeit und v = v(t) die Spannung (in Volt) an den Anschlüssen des Kondensators, ebenfalls in Abhängigkeit von der Zeit. ⓘ

Nimmt man die Laplace-Transformation dieser Gleichung, so erhält man ⓘ

$$I(s)=C(sV(s)-V_{0}),$$

ⓘ

wobei ⓘ

$${\begin{aligned}I(s)&={\mathcal {L}}\{i(t)\},\\V(s)&={\mathcal {L}}\{v(t)\},\end{aligned}}$$

ⓘ

und ⓘ

$$V_{0}=v(0).$$

ⓘ

Löst man V(s), so erhält man ⓘ

$$V(s)={I(s) \over sC}+{V_{0} \over s}.$$

ⓘ

Die Definition der komplexen Impedanz Z (in Ohm) ist das Verhältnis der komplexen Spannung V geteilt durch den komplexen Strom I, wobei der Ausgangszustand V₀ auf Null gehalten wird:

$$Z(s)=\left.{V(s) \over I(s)}\right|_{V_{0}=0}.$$

ⓘ

Unter Verwendung dieser Definition und der vorherigen Gleichung finden wir:

$$Z(s)={\frac {1}{sC}},$$

ⓘ

Dies ist der korrekte Ausdruck für die komplexe Impedanz eines Kondensators. Darüber hinaus findet die Laplace-Transformation breite Anwendung in der Kontrolltheorie. ⓘ

Partielle Bruchentwicklung

Betrachten wir ein lineares zeitinvariantes System mit der Übertragungsfunktion

$$H(s)={\frac {1}{(s+\alpha )(s+\beta )}}.$$

ⓘ

Die Impulsantwort ist einfach die inverse Laplace-Transformation dieser Übertragungsfunktion:

$$h(t)={\mathcal {L}}^{-1}\{H(s)\}.$$

ⓘ

Zur Auswertung dieser inversen Transformation wird zunächst H(s) mit der Methode der Partialbruchentwicklung erweitert, ⓘ

$${\frac {1}{(s+\alpha )(s+\beta )}}={P \over s+\alpha }+{R \over s+\beta }.$$

ⓘ

Die unbekannten Konstanten P und R sind die Residuen, die an den entsprechenden Polen der Übertragungsfunktion liegen. Jedes Residuum stellt den relativen Beitrag dieser Singularität zur Gesamtform der Übertragungsfunktion dar. ⓘ

Nach dem Residuensatz hängt die inverse Laplace-Transformation nur von den Polen und ihren Residuen ab. Um den Rest P zu finden, multiplizieren wir beide Seiten der Gleichung mit s + α und erhalten

$${\frac {1}{s+\beta }}=P+{R(s+\alpha ) \over s+\beta }.$$

ⓘ

Wenn man dann s = -α setzt, verschwindet der Beitrag von R und es bleibt nur noch

$$P=\left.{1 \over s+\beta }\right|_{s=-\alpha }={1 \over \beta -\alpha }.$$

ⓘ

In ähnlicher Weise ist der Rest R gegeben durch

$$R=\left.{1 \over s+\alpha }\right|_{s=-\beta }={1 \over \alpha -\beta }.$$

ⓘ

Man beachte, dass

$$R={-1 \over \beta -\alpha }=-P$$

und so ergibt die Substitution von R und P in den erweiterten Ausdruck für H(s)

$$H(s)=\left({\frac {1}{\beta -\alpha }}\right)\cdot \left({1 \over s+\alpha }-{1 \over s+\beta }\right).$$

ⓘ

Unter Verwendung der Linearitätseigenschaft und der bekannten Transformation für exponentiellen Zerfall (siehe Punkt 3 in der Tabelle der Laplace-Transformationen oben) können wir schließlich die inverse Laplace-Transformation von H(s) verwenden, um Folgendes zu erhalten

$$h(t)={\mathcal {L}}^{-1}\{H(s)\}={\frac {1}{\beta -\alpha }}\left(e^{-\alpha t}-e^{-\beta t}\right),$$

was die Impulsantwort des Systems ist. ⓘ

Faltung

Mit Hilfe der Faltungseigenschaft kann dasselbe Ergebnis erzielt werden, als ob das System eine Reihe von Filtern mit Übertragungsfunktionen von 1/(s + a) und 1/(s + b) wäre. Das heißt, die Umkehrung von ⓘ

$$H(s)={\frac {1}{(s+a)(s+b)}}={\frac {1}{s+a}}\cdot {\frac {1}{s+b}}$$

ⓘ

ist ⓘ

$${\mathcal {L}}^{-1}\!\left\{{\frac {1}{s+a}}\right\}*{\mathcal {L}}^{-1}\!\left\{{\frac {1}{s+b}}\right\}=e^{-at}*e^{-bt}=\int _{0}^{t}e^{-ax}e^{-b(t-x)}\,dx={\frac {e^{-at}-e^{-bt}}{b-a}}.$$

ⓘ

Phasenverzögerung

Zeitfunktion	Laplace-Transformation ⓘ
$\sin {(\omega t+\varphi )}$	${\frac {s\sin(\varphi )+\omega \cos(\varphi )}{s^{2}+\omega ^{2}}}$
$\cos {(\omega t+\varphi )}$	${\frac {s\cos(\varphi )-\omega \sin(\varphi )}{s^{2}+\omega ^{2}}}.$

Wir beginnen mit der Laplace-Transformation, ⓘ

$$X(s)={\frac {s\sin(\varphi )+\omega \cos(\varphi )}{s^{2}+\omega ^{2}}}$$

ⓘ

finden wir die Umkehrung, indem wir zunächst die Terme im Bruch umordnen:

$${\begin{aligned}X(s)&={\frac {s\sin(\varphi )}{s^{2}+\omega ^{2}}}+{\frac {\omega \cos(\varphi )}{s^{2}+\omega ^{2}}}\\&=\sin(\varphi )\left({\frac {s}{s^{2}+\omega ^{2}}}\right)+\cos(\varphi )\left({\frac {\omega }{s^{2}+\omega ^{2}}}\right).\end{aligned}}$$

ⓘ

Wir können nun die inverse Laplace-Transformation unserer Terme berechnen:

$${\begin{aligned}x(t)&=\sin(\varphi ){\mathcal {L}}^{-1}\left\{{\frac {s}{s^{2}+\omega ^{2}}}\right\}+\cos(\varphi ){\mathcal {L}}^{-1}\left\{{\frac {\omega }{s^{2}+\omega ^{2}}}\right\}\\&=\sin(\varphi )\cos(\omega t)+\cos(\varphi )\sin(\omega t).\end{aligned}}$$

ⓘ

Dies ist einfach der Sinus der Summe der Argumente und ergibt:

$$x(t)=\sin(\omega t+\varphi ).$$

ⓘ

Wir können eine ähnliche Logik anwenden, um herauszufinden, dass ⓘ

$${\mathcal {L}}^{-1}\left\{{\frac {s\cos \varphi -\omega \sin \varphi }{s^{2}+\omega ^{2}}}\right\}=\cos {(\omega t+\varphi )}.$$

ⓘ

Statistische Mechanik

In der statistischen Mechanik definiert die Laplace-Transformation der Zustandsdichte $g(E)$ die Partitionsfunktion definiert. Das heißt, die kanonische Partitionsfunktion $Z(\beta )$ ist gegeben durch

$$Z(\beta )=\int _{0}^{\infty }e^{-\beta E}g(E)\,dE$$

und die Umkehrung ist gegeben durch

$$g(E)={\frac {1}{2\pi i}}\int _{\beta _{0}-i\infty }^{\beta _{0}+i\infty }e^{\beta E}Z(\beta )\,d\beta$$

ⓘ

Räumliche (nicht zeitliche) Struktur des astronomischen Spektrums

Die breite und allgemeine Anwendbarkeit der Laplace-Transformation und ihrer Umkehrung wird durch eine Anwendung in der Astronomie veranschaulicht, die einige Informationen über die räumliche Verteilung der Materie einer astronomischen Quelle hochfrequenter Wärmestrahlung liefert, die zu weit entfernt ist, um sie als mehr als einen Punkt aufzulösen, und zwar anhand ihres Flussdichtespektrums, anstatt den Zeitbereich mit dem Spektrum (Frequenzbereich) in Beziehung zu setzen. ⓘ

Unter der Annahme bestimmter Eigenschaften des Objekts, z. B. Kugelform und konstante Temperatur, können Berechnungen, die auf der Durchführung einer inversen Laplace-Transformation des Spektrums des Objekts beruhen, das einzig mögliche Modell für die Verteilung der Materie im Objekt (Dichte als Funktion der Entfernung vom Zentrum) ergeben, das mit dem Spektrum übereinstimmt. Wenn unabhängige Informationen über die Struktur eines Objekts verfügbar sind, hat sich die Methode der inversen Laplace-Transformation als gut geeignet erwiesen. ⓘ

Galerie

• 

  Eine Beispielkurve von et cos(10t), die zusammen mit ähnlichen Kurven zu einer Laplace-Transformation addiert wird.

• 

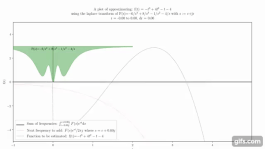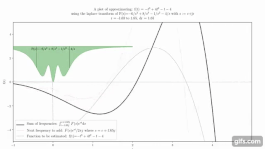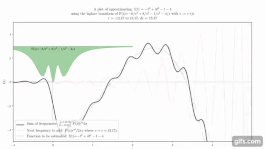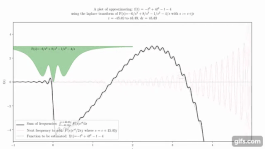
  Animation, die zeigt, wie das Zusammenfügen von Kurven eine Funktion annähern kann. ⓘ

Laplace-Rücktransformation

Zur Laplace-Transformation gibt es auch eine Rücktransformation, also einen Operator der zu einer gegebenen Spektralfunktion $F(s)$ die entsprechende Zeitfunktion $f(t)$ zuordnet. Dieser Integraloperator wird auch Bromwich-Integral genannt und ist nach dem Mathematiker und Physiker Thomas John I’Anson Bromwich benannt. ⓘ

Aussage

Die Zeitfunktion $f(t)$ kann durch die Umkehrformel ⓘ

${\mathcal {L}}^{-1}\left\{F(s)\right\}={\frac {1}{2\pi \mathrm {i} }}\int _{\gamma -\mathrm {i} \infty }^{\gamma +\mathrm {i} \infty }\mathrm {e} ^{st}F(s)\,\mathrm {d} s={\begin{cases}f(t)&{\text{für }}t\geq 0\\0&{\text{für }}t<0\end{cases}}\qquad {\text{mit }}\gamma >s_{0},$ ⓘ

aus der Spektralfunktion $F(s)$ bestimmt werden, dabei ist $s_{0}$ der größte Realteil einer Singularität von $F$. ⓘ

Eigenschaften

Grenzwertsätze

$\lim _{s\to 0+}sF(s)=\lim _{t\to \infty }f(t)$ ⓘ

$\lim _{s\to \infty }sF(s)=\lim _{t\to 0+}f(t)$ ⓘ

Insbesondere strebt jede Laplace-Transformierte gegen $0$, wenn $\operatorname {Re} s$ gegen $+\infty$ strebt. Der erste Grenzwertsatz gilt nur, wenn $F(s)$ außer einem einfachen Pol bei $s=0$ keine weiteren Singularitäten in der Halbebene $\operatorname {Re} s\geq 0$ besitzt. ⓘ

Eindeutigkeit

Wenn für zwei Zeitfunktionen $f(t)$ und $g(t)$ die Voraussetzungen gelten:

• $f(t)$ und $g(t)$ sind stückweise stetig
• $f(t)$ und $g(t)$ sind von exponentieller Ordnung für $t\to \infty$
• die Laplace-Transformierten $F(s)={\mathcal {L}}\{f(t)\}$ und $G(s)={\mathcal {L}}\{g(t)\}$ existieren
• $F(s)=G(s)$ im Konvergenzbereich ⓘ

dann ist $f(t)=g(t)$ überall dort, wo $f$ und $g$ stetig sind. ⓘ

Vergleiche: Eindeutigkeitssatz von Lerch ⓘ

Physikalische Dimension

Bei Anwendungen der Laplace-Transformation ist auch die Dimension der Laplace-Transformierten

$F(s)={\mathcal {L}}\left\{f(t)\right\}=\int _{0}^{\infty }\mathrm {e} ^{-st}f(t)\,\mathrm {d} t\qquad ({\textrm {mit:}}\quad s=\sigma +\mathrm {i} \omega ;\quad \sigma >0;\quad t\geq 0)$

von Interesse. Meist hat $t$ die Dimension $\mathrm {Zeit}$, dann besitzt die komplexe Frequenz $s$ die Dimension $\mathrm {Zeit} ^{-1}$. Der Ausdruck $\mathrm {e} ^{-st}$ im Integranden ist somit dimensionslos. Durch die Integration über den Zeitbereich wird die Dimension der Zeitfunktion $f(t)$ mit der Dimension des Zeitdifferentials $\mathrm {d} t$ multipliziert:

$[F(s)]=[f(t)][t]=[f(t)]s$. ⓘ

Beispielsweise besitzt die Laplace-Transformierte eines elektrischen Stroms $i(t)$ (gemessen in Ampere)

$I(s)={\mathcal {L}}\left\{i(t)\right\}=\int _{0}^{\infty }\mathrm {e} ^{-st}i(t)\,\mathrm {d} t$

die Dimension einer Ladung As = C, also Coulomb. ⓘ