Fourierreihe
Eine Fourier-Reihe () ist eine Summe, die eine periodische Funktion als eine Summe von Sinus- und Cosinuswellen darstellt. Die Frequenz jeder Welle in der Summe, oder Oberschwingung, ist ein ganzzahliges Vielfaches der Grundfrequenz der periodischen Funktion. Die Phase und die Amplitude jeder Oberschwingung können mit Hilfe der Oberschwingungsanalyse bestimmt werden. Eine Fourier-Reihe kann potenziell eine unendliche Anzahl von Oberschwingungen enthalten. Die Summierung eines Teils, aber nicht aller Oberschwingungen in der Fourier-Reihe einer Funktion ergibt eine Annäherung an diese Funktion. Wenn man zum Beispiel die ersten Oberschwingungen der Fourier-Reihe für eine Rechteckwelle verwendet, erhält man eine Annäherung an eine Rechteckwelle. ⓘ
Eine Rechteckwelle (dargestellt als blauer Punkt) wird durch ihre sechste Teilsumme (dargestellt als violetter Punkt) angenähert, die durch Summierung der ersten sechs Terme (dargestellt als Pfeile) der Fourier-Reihe der Rechteckwelle gebildet wird. Jeder Pfeil beginnt bei der vertikalen Summe aller Pfeile zu seiner Linken (d. h. bei der vorherigen Teilsumme).
Funktion (in rot) ist eine Fourier-Serien-Summe von 6 harmonisch verbundenen Sinuswellen (in blau). Ihre Fourier-Transformierte ist eine Darstellung im Frequenzbereich, die die Amplituden der summierten Sinuswellen zeigt. ⓘ
Fast jede periodische Funktion kann durch eine konvergierende Fourier-Reihe dargestellt werden. Konvergenz von Fourier-Reihen bedeutet, dass jede aufeinanderfolgende partielle Fourier-Summe die Funktion besser annähert und der Funktion mit einer potenziell unendlichen Anzahl von Oberschwingungen entspricht, wenn immer mehr Oberschwingungen der Reihe summiert werden. Die mathematischen Beweise hierfür werden unter dem Begriff Fourier-Theorem zusammengefasst (siehe ). ⓘ
Fourier-Reihen können nur Funktionen darstellen, die periodisch sind. Nicht-periodische Funktionen können jedoch mit einer Erweiterung der Fourier-Reihe, der so genannten Fourier-Transformation, behandelt werden, die nicht-periodische Funktionen als periodische Funktionen mit unendlicher Periode behandelt. Diese Transformation kann also Frequenzbereichsdarstellungen von nichtperiodischen Funktionen sowie von periodischen Funktionen erzeugen, so dass eine Wellenform zwischen ihrer Zeitbereichsdarstellung und ihrer Frequenzbereichsdarstellung umgewandelt werden kann. ⓘ
Seit der Zeit von Fourier wurden viele verschiedene Ansätze zur Definition und zum Verständnis des Konzepts der Fourier-Reihe entdeckt, die alle miteinander übereinstimmen, aber jeweils unterschiedliche Aspekte des Themas betonen. Einige der leistungsfähigeren und eleganteren Ansätze beruhen auf mathematischen Ideen und Werkzeugen, die zu Fouriers Zeiten noch nicht verfügbar waren. Fourier definierte die Fourier-Reihe ursprünglich für reellwertige Funktionen mit reellen Argumenten und verwendete die Sinus- und Kosinusfunktionen als Basis für die Zerlegung. Seitdem wurden viele andere Fourier-Transformationen definiert, die seine ursprüngliche Idee auf viele Anwendungen ausdehnten und ein Gebiet der Mathematik namens Fourier-Analyse ins Leben riefen. ⓘ

Als Fourierreihe, nach Joseph Fourier (1768–1830), bezeichnet man die Reihenentwicklung einer periodischen, abschnittsweise stetigen Funktion in eine Funktionenreihe aus Sinus- und Kosinusfunktionen. Die Basisfunktionen der Fourierreihe bilden ein bekanntes Beispiel für eine Orthonormalbasis. Im Rahmen der Theorie der Hilberträume werden auch Entwicklungen nach einem beliebigen vollständigen Orthonormalsystem als Fourierreihe bezeichnet. Eine Verallgemeinerung ist die Fourier-Transformation. Die Lehre der Fourierreihen ist Teil der Fourier-Analyse (klassische harmonische Analysis). ⓘ
Definition
Die Funktion
welche die Koeffizienten der Fourierreihe einer -periodischen Funktion liefert, nennen wir die Fourier-Transformierte von . Die nennen wir Fourier-Koeffizienten. Die Funktionen bilden einen -Vektorraum bzgl. punktweiser Addition und Multiplikation. ⓘ
Allgemeine Formen
Die Fourier-Reihe kann in verschiedenen Formen dargestellt werden. Die Amplituden-Phasen-Form, die Sinus-Cosinus-Form und die Exponentialform sind gebräuchlich und werden hier für eine reellwertige Funktion dargestellt . (Siehe und für alternative Formen). ⓘ
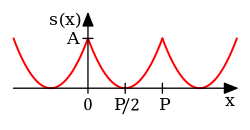
Die Anzahl der summierten Terme, ist eine potenziell unendliche ganze Zahl. Trotzdem kann es sein, dass die Reihe nicht konvergiert oder bei allen Werten von bei allen Werten von (z. B. bei einer Ein-Punkt-Diskontinuität) im Analyseintervall. Für die für physikalische Prozesse typischen, wohlbehaltenen Funktionen wird üblicherweise Gleichheit angenommen, und die Dirichlet-Bedingungen liefern ausreichende Bedingungen. ⓘ
Der ganzzahlige Index, ist auch die Anzahl der Zyklen der Harmonische in der Periode der Funktion durchläuft . Deshalb:
- Die Wellenlänge der Harmonischen ist und in Einheiten von .
- Die ist die Frequenz der Oberschwingung und in reziproken Einheiten von . ⓘ

Amplituden-Phasen-Form
Die Fourier-Reihe in Amplituden-Phasen-Form ist:
- Ihre Harmonische ist .
- ist die die Amplitude der Harmonischen und ist ihre Phasenverschiebung.
- Die Grundfrequenz von ist der Begriff für den Fall, dass gleich 1 ist, und kann bezeichnet werden als Harmonische bezeichnet werden.
- wird manchmal als die Harmonische oder Gleichstromkomponente genannt. Sie ist der Mittelwert von . ⓘ
Er kann eindeutig Funktionen darstellen, die nur eine Summe aus einer oder mehreren harmonischen Frequenzen sind. F{³"u}r diejenigen, die mit diesem Konzept noch nicht vertraut sind, ist bemerkenswert, dass es aufgrund der potenziell unendlichen Anzahl von Termen auch die Zwischenfrequenzen und/oder nicht-sinusf{³"u}rmige Funktionen darstellen kann (). ⓘ

Die Koeffizienten und können durch ein Verfahren der harmonischen Analyse bestimmt werden. Man betrachte eine reellwertige Funktion die auf einem Intervall integrabel ist, das bei einem beliebigen beginnt und die Länge . Die Kreuzkorrelationsfunktion: ist im Wesentlichen ein angepasster Filter, mit Vorlage . Das Maximum von ist ein Maß für die Amplitude der Frequenz in der Funktion und der Wert von beim Maximum bestimmt die Phase für diese Frequenz. Abbildung 2 ist ein Beispiel, bei dem eine Rechteckwelle ist (nicht dargestellt) und die Frequenz ist die Harmonische bezeichnet werden. ⓘ
Anstelle der rechenintensiven Kreuzkorrelation, bei der jede Phase ausgewertet werden muss, nutzt die Fourier-Analyse eine trigonometrische Identität: Substituiert man diese, erhält man: Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} \Chi_n(\varphi) &= \tfrac{2}{P} \int_P s(x) \cdot \cos\left(\tfrac{2\pi}{P} n x-\varphi \right)\, dx ; \quad \varphi \in [0, 2\pi]\\ &=\cos(\varphi)\cdot \underbrace{\tfrac{2}{P}\int_P s(x) \cdot \cos\left(\tfrac{2\pi}{P} n x\right)\, dx}_{\triangleq\ a_n} +\sin(\varphi)\cdot \underbrace{\tfrac{2}{P}\int_P s(x) \cdot \sin\left(\tfrac{2\pi}{P} n x\right)\, dx}_{\triangleq\ b_n}\ &=\cos(\varphi)\cdot a_n + \sin(\varphi)\cdot b_n \end{align} } ⓘ
Man beachte die Definitionen von und und dass und vereinfacht werden kann:
- Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \begin{align} A_n \Dreieckq \Chi_n(\varphi_n)\ &= \cos(\varphi_n)\cdot a_n + \sin(\varphi_n)\cdot b_n \\ &=\frac{a_n}{\sqrt{a_n^2+b_n^2}}\cdot a_n + \frac{b_n}{\sqrt{a_n^2+b_n^2}}\cdot b_n =\frac{a_n^2+b_n^2}{\sqrt{a_n^2+b_n^2}} &= \sqrt{a_n^2+b_n^2}. \end{align} } ⓘ
und sind die kartesischen Koordinaten eines Vektors mit Polarkoordinaten und Abbildung 2 ist ein Beispiel für diese Beziehungen. ⓘ
Sinus-Cosinus-Form
Die Substitution in ergibt:
In Bezug auf die leicht zu berechnenden Größen, und erinnern wir daran, dass:
Eine alternative Form der Fourier-Reihe, die kartesische Koordinaten verwendet, ist daher die Sinus-Cosinus-Form: ⓘ
Exponentialform
Eine weitere anwendbare Identität ist die Eulersche Formel:
- Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} \cos\left( \tfrac {2\pi } P nx - \varphi_n \right) &{}\equiv \tfrac{1}{2} e^{ i \left(2\pi nx/P - \varphi_n \right)} + \tfrac{1}{2} e^{-i \left(2\pi nx/P - \varphi_n \right)} \\\[6pt] & = \left(\tfrac{1}{2} e^{-i \varphi_n}\right) \cdot e^{i 2\pi(+n)x/P} +left(\tfrac{1}{2} e^{-i \varphi_n}\right)^* \cdot e^{i 2\pi(-n)x/P} \end{align} }
(Anmerkung: Das ∗ steht für die komplexe Konjugation). ⓘ
Also mit den Definitionen:
- Fehler beim Parsen (Unbekannte Funktion „\begin{array}“): {\displaystyle c_n \triangleq \left\{ \begin{array}{lll} A_0/2 &= a_0/2, \quad & n = 0\\ \tfrac{A_n}{2} e^{-i \varphi_n} &= \tfrac{1}{2}(a_n -i b_n), \quad & n > 0\\\ c_{|n|}^*, \quad && n < 0 \end{array} \right\} = \tfrac{1}{P} \int_P s(x) \cdot e^{-i 2\pi nx/P} \, dx, } ⓘ
ist das Endergebnis: Dies ist die übliche Form für die Verallgemeinerung auf . Negative Werte von entsprechen einer negativen Frequenz (erklärt in ). ⓘ
Beispiel


Betrachten wir eine Sägezahnfunktion:
In diesem Fall sind die Fourier-Koeffizienten gegeben durch
- Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_n & = \frac{1}{\pi}\int_{-\pi}^{\pi}s(x) \cos(nx)\,dx = 0, \quad n \ge 0. \\\[4pt] b_n & = \frac{1}{\pi}\int_{-\pi}^{\pi}s(x) \sin(nx)\, dx\\[4pt] &= -\frac{2}{\pi n}\cos(n\pi) + \frac{2}{\pi^2 n^2}\sin(n\pi)\\[4pt] &= \frac{2\,(-1)^{n+1}}{\pi n}, \quad n \ge 1.\end{align}}
Es kann gezeigt werden, dass die Fourier-Reihe in jedem Punkt gegen in jedem Punkt wobei differenzierbar ist, und daher: Wenn konvergiert die Fourier-Reihe gegen 0, das ist die Halbsumme der linken und rechten Grenze von s bei . Dies ist ein besonderer Fall des Dirichlet-Theorems für Fourier-Reihen. ⓘ
Dieses Beispiel führt zu einer Lösung des Basler Problems. ⓘ
Konvergenz
Ein Beweis dafür, dass eine Fourier-Reihe eine gültige Darstellung einer beliebigen periodischen Funktion ist (die die Dirichlet-Bedingungen erfüllt), wird in zusammengefasst. ⓘ
Bei technischen Anwendungen wird im Allgemeinen davon ausgegangen, dass die Fourier-Reihe fast überall konvergiert (Ausnahmen sind diskrete Unstetigkeiten), da die in der Technik vorkommenden Funktionen sich besser verhalten als die Funktionen, die Mathematiker als Gegenbeispiele für diese Annahme liefern können. Insbesondere, wenn stetig ist und die Ableitung von (die möglicherweise nicht überall existiert) quadratisch integrierbar ist, dann konvergiert die Fourier-Reihe von absolut und gleichförmig konvergiert zu . Wenn eine Funktion auf dem Intervall quadratisch integrierbar ist , dann konvergiert die Fourier-Reihe in fast jedem Punkt gegen die Funktion. Es ist möglich, Fourier-Koeffizienten für allgemeinere Funktionen oder Verteilungen zu definieren; in solchen Fällen ist die Konvergenz in der Norm oder die schwache Konvergenz gewöhnlich von Interesse. ⓘ
Beispiel für die Konvergenz zu einer etwas beliebigen Funktion. Beachten Sie die Entwicklung des "Klingelns" (Gibbs-Phänomen) an den Übergängen zu/von den vertikalen Abschnitten. ⓘ
Komplexe Funktionen
Wenn ist eine komplexwertige Funktion einer reellen Variablen sind beide Komponenten (Real- und Imaginärteil) reellwertige Funktionen, die durch eine Fourier-Reihe dargestellt werden können. Die beiden Koeffizientensätze und die Partialsumme sind gegeben durch: ⓘ
- und ⓘ
Definition von Fehler beim Parsen (Unbekannte Funktion „\Dreieckq“): {\displaystyle c_n \Dreieckq c_{_{Rn}}+i\cdot c_{_{In}}} ergibt: Dies ist identisch mit außer und nicht mehr komplex konjugiert sind. Die Formel für ist ebenfalls unverändert:
Andere gebräuchliche Notationen
Die Notation ist unzureichend, um die Fourier-Koeffizienten mehrerer verschiedener Funktionen zu beschreiben. Daher wird sie üblicherweise durch eine modifizierte Form der Funktion ersetzt (, in diesem Fall) ersetzt, wie z. B. oder , und die funktionale Notation ersetzt häufig die tiefgestellte Schreibweise:
In der Technik, insbesondere wenn die Variable die Zeit darstellt, wird die Koeffizientenfolge als Darstellung im Frequenzbereich bezeichnet. Eckige Klammern werden häufig verwendet, um zu betonen, dass der Bereich dieser Funktion eine diskrete Menge von Frequenzen ist. ⓘ
Eine andere häufig verwendete Frequenzbereichsdarstellung verwendet die Koeffizienten der Fourier-Reihe, um einen Dirac-Kamm zu modulieren:
wobei stellt einen kontinuierlichen Frequenzbereich dar. Wenn die Variable hat Einheiten von Sekunden, hat die Einheit Hertz. Die "Zähne" des Kammes sind in Abständen von Vielfachen (d. h. Harmonischen) von , die als Grundfrequenz bezeichnet wird. kann aus dieser Darstellung durch eine inverse Fourier-Transformation zurückgewonnen werden:
- Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} \mathcal{F}^{-1}\{S(f)\} &= \int_{-\infty}^\infty \left( \sum_{n=-\infty}^\infty S[n]\cdot \delta \left(f-\frac{n}{P}\right)\right) e^{i 2 \pi f x}\,df, \\\[6pt] &= \sum_{n=-\infty}^\infty S[n]\cdot \int_{-\infty}^\infty \delta\left(f-\frac{n}{P}\right) e^{i 2 \pi f x}\,df, \\\[6pt] &= \sum_{n=-\infty}^\infty S[n]\cdot e^{i\,2\pi nx/P} \ s_\infty(x) \triangleq \ \end{align}} ⓘ
Die konstruierte Funktion wird daher gemeinhin als Fourier-Transformation bezeichnet, auch wenn das Fourier-Integral einer periodischen Funktion bei den harmonischen Frequenzen nicht konvergent ist. ⓘ
Geschichte
Die Fourier-Reihe wurde zu Ehren von Jean-Baptiste Joseph Fourier (1768-1830) benannt, der nach Vorarbeiten von Leonhard Euler, Jean le Rond d'Alembert und Daniel Bernoulli wichtige Beiträge zur Untersuchung trigonometrischer Reihen leistete. Fourier führte die Reihen zur Lösung der Wärmegleichung in einer Metallplatte ein und veröffentlichte seine ersten Ergebnisse 1807 in seiner Mémoire sur la propagation de la chaleur dans les corps solides (Abhandlung über die Ausbreitung der Wärme in festen Körpern) und 1822 in seiner Théorie analytique de la chaleur (Analytische Theorie der Wärme). Das Mémoire führte die Fourier-Analyse ein, insbesondere die Fourier-Reihen. Durch die Forschungen von Fourier wurde die Tatsache festgestellt, dass eine beliebige (zunächst kontinuierliche und später auf jede stückweise glatte) Funktion durch eine trigonometrische Reihe dargestellt werden kann. Die erste Bekanntgabe dieser großen Entdeckung erfolgte 1807 durch Fourier vor der französischen Akademie. Frühe Ideen zur Zerlegung einer periodischen Funktion in die Summe einfacher oszillierender Funktionen gehen auf das 3. Jahrhundert v. Chr. zurück, als antike Astronomen ein empirisches Modell der Planetenbewegungen vorschlugen, das auf Deferenten und Epizyklen beruhte. ⓘ
Die Wärmegleichung ist eine partielle Differentialgleichung. Vor der Arbeit von Fourier war keine Lösung der Wärmegleichung im allgemeinen Fall bekannt, obwohl bestimmte Lösungen bekannt waren, wenn sich die Wärmequelle auf einfache Weise verhielt, insbesondere wenn die Wärmequelle eine Sinus- oder Kosinuswelle war. Diese einfachen Lösungen werden heute manchmal als Eigenlösungen bezeichnet. Fouriers Idee war es, eine komplizierte Wärmequelle als Überlagerung (oder Linearkombination) von einfachen Sinus- und Kosinuswellen zu modellieren und die Lösung als Überlagerung der entsprechenden Eigenlösungen zu schreiben. Diese Überlagerung oder Linearkombination wird als Fourier-Reihe bezeichnet. ⓘ
Aus heutiger Sicht sind die Ergebnisse von Fourier eher informell, da es im frühen neunzehnten Jahrhundert noch keinen genauen Begriff von Funktion und Integral gab. Später drückten Peter Gustav Lejeune Dirichlet und Bernhard Riemann die Ergebnisse von Fourier mit größerer Präzision und Formalität aus. ⓘ
Obwohl die ursprüngliche Motivation darin bestand, die Wärmegleichung zu lösen, wurde später deutlich, dass dieselben Techniken auf eine Vielzahl mathematischer und physikalischer Probleme angewandt werden können, insbesondere auf lineare Differentialgleichungen mit konstanten Koeffizienten, deren Eigenlösungen Sinuskurven sind. Die Fourier-Reihe hat viele solcher Anwendungen in der Elektrotechnik, der Schwingungsanalyse, der Akustik, der Optik, der Signalverarbeitung, der Bildverarbeitung, der Quantenmechanik, der Ökonometrie, der Schalentheorie usw. ⓘ
Dirichlet konnte 1829 beweisen, dass Fouriers Behauptung zumindest für Lipschitz-stetige Funktionen zutrifft. Du Bois-Reymond fand 1876 eine stetige Funktion, deren Fourierreihe divergiert. Im 20. Jahrhundert gelangte man schließlich zur Erkenntnis, dass es auch für stetige oder stückweise stetige Funktionen konvergente Fourierreihen gibt, wenn der Konvergenzbegriff geeignet abgeschwächt wird (Lennart Carleson). ⓘ
Als eine frühe geometrische Vorform der Approximation durch eine Fourierreihe kann die Epizykeltheorie betrachtet werden. ⓘ
Anfänge
Joseph Fourier schrieb: Dies gibt sofort jeden Koeffizienten ak der trigonometrischen Reihe für φ(y) für jede Funktion, die eine solche Expansion hat. Es funktioniert, weil, wenn φ eine solche Entwicklung hat, dann (unter geeigneten Konvergenzannahmen) das Integral Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_k&=\int_{-1}^1\varphi(y)\cos(2k+1)\frac{\pi y}{2}\,dy \\\ &= \int_{-1}^1\left(a\cos\frac{\pi y}{2}\cos(2k+1)\frac{\pi y}{2}+a'\cos 3\frac{\pi y}{2}\cos(2k+1)\frac{\pi y}{2}+\cdots\right)\,dy \end{align}} kann Term für Term durchgeführt werden. Aber alle Terme, die bei der Integration von -1 bis 1 verschwinden, so dass nur die Term übrig. ⓘ
Mit diesen wenigen Zeilen, die dem modernen Formalismus der Fourier-Reihen sehr nahe kommen, hat Fourier sowohl die Mathematik als auch die Physik revolutioniert. Obwohl ähnliche trigonometrische Reihen bereits von Euler, d'Alembert, Daniel Bernoulli und Gauß verwendet wurden, glaubte Fourier, dass solche trigonometrischen Reihen jede beliebige Funktion darstellen könnten. Inwieweit dies tatsächlich zutrifft, ist eine etwas heikle Frage, und die langjährigen Versuche, diese Idee zu klären, haben zu wichtigen Entdeckungen in den Theorien der Konvergenz, der Funktionsräume und der harmonischen Analyse geführt. ⓘ
Als Fourier 1811 einen späteren Wettbewerbsbeitrag einreichte, kam das Komitee (dem unter anderem Lagrange, Laplace, Malus und Legendre angehörten) zu dem Schluss: ...die Art und Weise, wie der Autor zu diesen Gleichungen gelangt, ist nicht frei von Schwierigkeiten und...seine Analyse, um sie zu integrieren, lässt noch etwas zu wünschen übrig, was die Allgemeinheit und sogar die Strenge betrifft. ⓘ
Fourier's Motivation

Die Fourier'sche Reihenentwicklung der Sägezahnfunktion (oben) sieht komplizierter aus als die einfache Formel Daher ist nicht sofort ersichtlich, wozu man die Fourier-Reihe benötigt. Es gibt zwar viele Anwendungen, aber die Motivation von Fourier war die Lösung der Wärmegleichung. Betrachten wir zum Beispiel eine Metallplatte in Form eines Quadrats, dessen Seiten messen Meter messen, mit den Koordinaten Fehler beim Parsen (Unbekannte Funktion „\mal“): {\displaystyle (x,y) \in [0,\pi] \mal [0,\pi]} . Wenn es innerhalb der Platte keine Wärmequelle gibt und drei der vier Seiten auf 0 Grad Celsius gehalten werden, während die vierte Seite, gegeben durch auf dem Temperaturgradienten gehalten wird Grad Celsius, für in , dann kann man zeigen, dass die stationäre Wärmeverteilung (oder die Wärmeverteilung nach Ablauf einer langen Zeitspanne) gegeben ist durch
- Fehler beim Parsen (Syntaxfehler): {\displaystyle T(x,y) = 2\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} \sin(nx) {\sinh(ny) \über \sinh(n\pi)}.}
Dabei ist sinh die hyperbolische Sinusfunktion. Diese Lösung der Wärmegleichung erhält man durch Multiplikation jedes Terms von mit . Während unsere Beispielfunktion eine unnötig komplizierte Fourier-Reihe zu haben scheint, ist die Wärmeverteilung ist nicht trivial. Die Funktion kann nicht in einer geschlossenen Form geschrieben werden. Diese Methode zur Lösung des Wärmeproblems wurde durch die Arbeit von Fourier ermöglicht. ⓘ
Komplexe Fourier-Reihen-Animation
thumb|Komplexe Fourier-Reihe, die den Buchstaben "e" nachzeichnet (Der Julia-Quellcode, der die Bilder dieser Animation erzeugt, befindet sich in Anhang B). ⓘ
Ein Beispiel für die Fähigkeit der komplexen Fourier-Reihe, jede beliebige zweidimensionale geschlossene Figur abzubilden, zeigt die nebenstehende Animation der komplexen Fourier-Reihe, die den Buchstaben "e" (für Exponential) abbildet. Beachten Sie, dass die Animation die Variable "t" verwendet, um den Buchstaben "e" in der komplexen Ebene zu parametrisieren, was der Verwendung des Parameters "x" im Unterabschnitt über komplexwertige Funktionen in diesem Artikel entspricht. ⓘ
In der hinteren Ebene der Animation werden die rotierenden Vektoren in einer Reihenfolge zusammengefasst, die zwischen einem Vektor, der sich in positiver Richtung (gegen den Uhrzeigersinn) dreht, und einem Vektor, der sich mit der gleichen Frequenz, aber in negativer Richtung (im Uhrzeigersinn) dreht, abwechselt, was zu einem einzigen Abtastarm mit vielen Zickzacklinien führt. Diese Perspektive zeigt, wie die Addition der beiden rotierenden Vektoren (einer in positiver und einer in negativer Richtung) die vorherige Kurve (als hellgraue gepunktete Linie dargestellt) näher an die Form des Buchstabens "e" heranführt. ⓘ
In der vorderen Ebene der Animation werden die rotierenden Vektoren in zwei Gruppen zusammengefasst, die Gruppe aller positiv rotierenden Vektoren und die Gruppe aller negativ rotierenden Vektoren (die nicht rotierende Komponente wird gleichmäßig auf die beiden aufgeteilt), was zu zwei in entgegengesetzte Richtungen rotierenden Abtastarmen führt. Der kleine Kreis in der Animation kennzeichnet den Mittelpunkt zwischen den beiden Armen und auch den Mittelpunkt zwischen dem Ursprung und dem aktuellen Abtastpunkt, der mit "+" bezeichnet ist. Diese Perspektive zeigt, dass die komplexe Fourier-Reihe eine Erweiterung (Hinzufügen eines Arms) der komplexen geometrischen Reihe ist, die nur einen Arm hat. Sie zeigt auch, wie die beiden Arme miteinander koordiniert werden. Wenn sich zum Beispiel der Abtastpunkt in positiver Richtung dreht, bleibt der Arm in negativer Richtung geparkt. Wenn sich der Abtastpunkt in die negative Richtung dreht, bleibt der Arm in positiver Richtung geparkt. ⓘ
Zwischen der hinteren und der vorderen Ebene der Animation befinden sich rotierende Trapeze, deren Flächen die Werte der komplexen Fourier-Serien-Terme darstellen. Diese Perspektive zeigt die Amplitude, die Frequenz und die Phase der einzelnen Terme der komplexen Fourier-Reihe in Bezug auf die Reihensumme, die in der hinteren und vorderen Ebene räumlich zum Buchstaben "e" konvergiert. Der linke und der rechte Kanal der Tonspur entsprechen den realen bzw. imaginären Komponenten des aktuellen Abtastpunkts "+", jedoch mit einer um den Faktor 3536 erhöhten Frequenz, so dass die Grundfrequenz der Animation (n=1) ein 220-Hz-Ton (A220) ist. ⓘ
Andere Anwendungen
Die zeitdiskrete Fourier-Transformation ist ein Beispiel für eine Fourier-Reihe. ⓘ
Eine weitere Anwendung ist die Lösung des Basler Problems mit Hilfe des Satzes von Parseval. Das Beispiel lässt sich verallgemeinern und man kann ζ(2n) für jede positive ganze Zahl berechnen. ⓘ
Tabelle der allgemeinen Fourier-Reihen
Einige gängige Paare von periodischen Funktionen und ihre Fourier-Reihenkoeffizienten sind in der folgenden Tabelle aufgeführt. ⓘ
- bezeichnet eine periodische Funktion, die auf .
- bezeichnet die Fourier-Reihenkoeffizienten (Sinus-Cosinus-Form) der periodischen Funktion . ⓘ
| Zeitbereich |
Plot | Frequenzbereich (Sinus-Cosinus-Form) |
Bemerkungen | Referenz ⓘ |
|---|---|---|---|---|
| Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_0 = & \frac{4A}{\pi}\ a_n = & \begin{cases} \frac{-4A}{\pi}\frac{1}{n^2-1} & \quad n \text{ even} \\ 0 & \quad n \text{ ungerade} \end{cases}\\ b_n = & 0\\ \end{align}} | Vollwellengleichgerichteter Sinus | |||
| Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_0 = & \frac{2A}{\pi}\ a_n = & \begin{cases} \frac{-2A}{\pi}\frac{1}{n^2-1} & \quad n \text{ even} \\ 0 & \quad n \text{ ungerade} \end{cases}\\ b_n = & \begin{cases} \frac{A}{2} & \quad n=1 \\\ 0 & \quad n > 1 \end{cases}\ \end{align}} | Einweg-gleichgerichteter Sinus | |||
| Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_0 = & 2AD\\ a_n = & \frac{A}{n \pi} \sin \left( 2 \pi n D \right)\\ b_n = & \frac{2A}{n \pi} \left( \sin \left( \pi n D \right) \right) ^2\ \end{align}} | ||||
| Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_0 = & A\\ a_n = & 0\\ b_n = & \frac{-A}{n \pi}\ \end{align}} | ||||
| Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_0 = & A\\ a_n = & 0\\ b_n = & \frac{A}{n \pi}\ \end{align}} | ||||
| Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} a_0 = & \frac{2A}{3}\ a_n = & \frac{4A}{\pi^2 n^2}\\ b_n = & 0\\ \end{align}} |
Tabelle der grundlegenden Eigenschaften
Diese Tabelle zeigt einige mathematische Operationen im Zeitbereich und die entsprechenden Auswirkungen auf die Koeffizienten der Fourier-Reihe. Notation:
- Komplexe Konjugation wird durch ein Sternchen gekennzeichnet.
- bezeichnen -periodische Funktionen oder Funktionen, die nur für
- bezeichnen die Fourier-Reihenkoeffizienten (Exponentialform) von und ⓘ
| Eigenschaft | Zeitbereich | Frequenzbereich (Exponentialform) | Bemerkungen | Referenz ⓘ |
|---|---|---|---|---|
| Linearität | ||||
| Zeitumkehr / Frequenzumkehr | ||||
| Zeitkonjugation | ||||
| Zeitumkehr & Konjugation | ||||
| Realteil in der Zeit | ||||
| Imaginärteil in der Zeit | ||||
| Realteil in der Frequenz | ||||
| Imaginärteil in der Frequenz | ||||
| Verschiebung in der Zeit / Modulation in der Frequenz | ||||
| Verschiebung in der Frequenz / Modulation in der Zeit |
Symmetrieeigenschaften
Wenn die Real- und Imaginärteile einer komplexen Funktion in ihre geraden und ungeraden Teile zerlegt werden, gibt es vier Komponenten, die im Folgenden mit den Indizes RE, RO, IE und IO bezeichnet werden. Und es gibt eine Eins-zu-Eins-Abbildung zwischen den vier Komponenten einer komplexen Zeitfunktion und den vier Komponenten ihrer komplexen Frequenztransformation:
- Fehler beim Parsen (Unbekannte Funktion „\begin{array}“): {\displaystyle \begin{array}{rccccccccccc} \text{Zeitbereich} & s & = & s_{_{\text{RE}} & + & s_{_{\text{RO}} & + & i s_{_{\text{IE}} & + & \underbrace{i\ s_{_{\text{IO}}}} \\ \Bigg\Updownarrow\mathcal{F} & &\Bigg\Updownarrow\mathcal{F} & & \ \ \Bigg\Updownarrow\mathcal{F} & & \ \ \Bigg\Updownarrow\mathcal{F} & & \ \ \ \text{Frequenzbereich} & S & = & S_\text{RE} & + & \overbrace{\,i\ S_\text{IO}\,} & + & i S_\text{IE} & + & S_\text{RO} \end{array} } ⓘ
Daraus ergeben sich verschiedene Zusammenhänge, zum Beispiel:
- Die Transformation einer reellwertigen Funktion () ist die gerade symmetrische Funktion . Umgekehrt impliziert eine geradzahlig-symmetrische Transformation einen reell-wertigen Zeitbereich.
- Die Transformierte einer imaginärwertigen Funktion () ist die ungerade symmetrische Funktion, und umgekehrt.
- Die Transformation einer geradzahlig-symmetrischen Funktion () ist die reellwertige Funktion , und das Umgekehrte ist wahr.
- Die Transformation einer ungeradzahligen symmetrischen Funktion () ist die imaginärwertige Funktion, und die Umkehrung ist wahr. ⓘ
Andere Eigenschaften
Riemann-Lebesgue-Lemma
Wenn ist integrabel, Fehler beim Parsen (Unbekannte Funktion „\zu“): {\textstyle \lim_{|n| \zu \infty} S[n]=0} , Fehler beim Parsen (Unbekannte Funktion „\bis“): {\textstyle \lim_{n \bis +\infty} a_n=0} und Fehler beim Parsen (Unbekannte Funktion „\bis“): {\textstyle \lim_{n \bis +\infty} b_n=0.} Dieses Ergebnis ist als Riemann-Lebesgue-Lemma bekannt. ⓘ
Das Parsevalsche Theorem
Wenn gehört zu (ein Intervall der Länge ) dann: ⓘ
Theorem von Plancherel
Wenn sind Koeffizienten und dann gibt es eine eindeutige Funktion so dass für jede . ⓘ
Faltungstheoreme
Gegeben -periodische Funktionen, und mit Fourierreihenkoeffizienten und ⓘ
- Das punktweise Produkt: ist auch -periodisch, und seine Fourier-Reihenkoeffizienten sind gegeben durch die diskrete Faltung der und Folgen gegeben:
- Die periodische Faltung: ist auch -periodisch, mit Fourier-Reihenkoeffizienten:
- Eine zweifach unendliche Folge Fehler beim Parsen (Unbekannte Funktion „\links“): {\displaystyle \links \{c_n \rechts \}_{n \in Z}} in ist die Folge der Fourier-Koeffizienten einer Funktion in wenn und nur wenn sie eine Faltung von zwei Folgen in . Siehe . ⓘ
Abgeleitete Eigenschaft
Wir sagen, dass gehört zu wenn eine 2-periodische Funktion ist auf die ist mal differenzierbar ist, und ihre Ableitung ist stetig.
- Wenn , dann sind die Fourier-Koeffizienten der Ableitung in Form der Fourier-Koeffizienten ausgedrückt werden der Funktion ausgedrückt werden, und zwar über die Formel .
- Wenn , dann . Insbesondere, da für einen festen haben wir Fehler beim Parsen (Unbekannte Funktion „\zu“): {\displaystyle \widehat{s^{(k)}}[n]\zu 0} als Fehler beim Parsen (Unbekannte Funktion „\zu“): {\displaystyle n\zu\infty} folgt, dass gegen Null tendiert, was bedeutet, dass die Fourier-Koeffizienten schneller gegen Null konvergieren als die k-te Potenz von n für jede . ⓘ
Kompakte Gruppen
Eine der interessanten Eigenschaften der Fourier-Transformation, die wir erwähnt haben, ist, dass sie Faltungen in punktweise Produkte überführt. Wenn dies die Eigenschaft ist, die wir erhalten wollen, kann man Fourier-Reihen auf jeder kompakten Gruppe erzeugen. Typische Beispiele sind die klassischen kompakten Gruppen. Dadurch wird die Fourier-Transformation auf alle Räume der Form L2(G) verallgemeinert, wobei G eine kompakte Gruppe ist, und zwar so, dass die Fourier-Transformation Faltungen in punktweise Produkte umsetzt. Die Fourier-Reihe existiert und konvergiert in ähnlicher Weise wie in diesem Fall. ⓘ
Eine alternative Erweiterung auf kompakte Gruppen ist das Peter-Weyl-Theorem, das Ergebnisse über Darstellungen kompakter Gruppen analog zu denen über endliche Gruppen beweist. ⓘ

Sei ein Hilbertraum mit einer Orthonormalbasis . Dann kann man jedes Element des Hilbertraums durch
darstellen. Diese Reihendarstellung wird auch (verallgemeinerte) Fourier-Reihe genannt. ⓘ
Riemannsche Mannigfaltigkeiten
Wenn der Bereich keine Gruppe ist, gibt es keine inhärent definierte Faltung. Wenn jedoch eine kompakte riemannsche Mannigfaltigkeit ist, hat sie einen Laplace-Beltrami-Operator. Der Laplace-Beltrami-Operator ist der Differentialoperator, der dem Laplace-Operator für die riemannsche Mannigfaltigkeit entspricht . In Analogie dazu kann man die Wärmegleichungen auf . Da Fourier zu seiner Basis kam, indem er versuchte, die Wärmegleichung zu lösen, besteht die natürliche Verallgemeinerung darin, die Eigenlösungen des Laplace-Beltrami-Operators als Basis zu verwenden. Dies verallgemeinert Fourier-Reihen auf Räume des Typs , wobei eine Riemannsche Mannigfaltigkeit ist. Die Fourier-Reihen konvergieren auf ähnliche Weise wie die Fall. Ein typisches Beispiel ist die Annahme, dass als Kugel mit der üblichen Metrik anzunehmen; in diesem Fall besteht die Fourier-Basis aus sphärischen Harmonischen. ⓘ
Örtlich kompakte abelsche Gruppen
Die oben beschriebene Verallgemeinerung auf kompakte Gruppen lässt sich nicht auf nicht kompakte, nicht-abelsche Gruppen übertragen. Es gibt jedoch eine unkomplizierte Verallgemeinerung auf lokal kompakte abelsche Gruppen (LCA). ⓘ
Diese verallgemeinert die Fourier-Transformation auf oder , wobei ist eine LCA-Gruppe. Wenn kompakt ist, erhält man ebenfalls eine Fourier-Reihe, die ähnlich konvergiert wie im Fall Fall konvergiert, aber wenn nicht kompakt ist, erhält man stattdessen ein Fourier-Integral. Diese Verallgemeinerung ergibt die übliche Fourier-Transformation, wenn die zugrunde liegende lokal kompakte abelsche Gruppe . ⓘ
Die oben beschriebene Darstellung der Fourierreihe als Summe von komplexen Exponentialfunktionen ist zwar in gewissem Sinne die mathematisch kompakteste Darstellung, hat jedoch den Nachteil, dass im Allgemeinen auch für reellwertige Funktionen komplexwertige Fourier-Koeffizienten auftreten. Man kann die Fourierreihe aber auch anders darstellen. ⓘ
Erweiterungen
Fourier-Reihen auf einem Quadrat
Wir können auch die Fourier-Reihe für Funktionen zweier Variablen definieren und im Quadrat : Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} f(x,y) & = \sum_{j,k \in \Z} c_{j,k}e^{ijx}e^{iky},\\\[5pt] c_{j,k} & = \frac{1}{4 \pi^2} \int_{-\pi}^\pi \int_{-\pi}^\pi f(x,y) e^{-ijx}e^{-iky}\, dx \, dy. \end{align}} ⓘ
Abgesehen davon, dass sie für die Lösung partieller Differentialgleichungen wie der Wärmegleichung nützlich sind, ist eine bemerkenswerte Anwendung von Fourier-Reihen auf dem Quadrat die Bildkompression. Insbesondere der jpeg-Bildkompressionsstandard verwendet die zweidimensionale diskrete Kosinustransformation, eine diskrete Form der Fourier-Kosinustransformation, die nur den Kosinus als Basisfunktion verwendet. ⓘ
Bei zweidimensionalen Arrays mit gestaffeltem Aussehen verschwindet die Hälfte der Fourier-Reihenkoeffizienten aufgrund zusätzlicher Symmetrie. ⓘ
Fourier-Reihe der Bravais-Gitterperiodenfunktion
Ein dreidimensionales Bravais-Gitter ist definiert als die Menge der Vektoren der Form:
Wir können also eine neue Funktion definieren, Fehler beim Parsen (Unbekannte Funktion „\links“): {\displaystyle g(x_1,x_2,x_3) \triangleq f(\mathbf{r}) = f \links (x_1\frac{\mathbf{a}_{1}}{a_1}+x_2\frac{\mathbf{a}_{2}}{a_2}+x_3\frac{\mathbf{a}_{3}}{a_3} \right ).} ⓘ
Diese neue Funktion, ist nun eine Funktion von drei Variablen, von denen jede eine Periodizität hat , und hat:
Auf diese Weise können wir einen Satz von Fourier-Koeffizienten bilden, die jeweils durch drei unabhängige ganze Zahlen indiziert sind . Im Folgenden verwenden wir die Funktionsschreibweise, um diese Koeffizienten zu bezeichnen, während wir früher tiefgestellte Zahlen verwendet haben. Wenn wir eine Reihe schreiben für auf dem Intervall für schreiben, können wir folgendes definieren:
Und dann können wir schreiben:
Weiteres Definieren: Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} h^\mathrm{two}(m_1, m_2, x_3) & \triangleq \frac{1}{a_2}\int_0^{a_2} h^\mathrm{one}(m_1, x_2, x_3)\cdot e^{-i 2\pi \frac{m_2}{a_2} x_2}\, dx_2 \\\[12pt] & = \frac{1}{a_2}\int_0^{a_2} dx_2 \frac{1}{a_1}\int_0^{a_1} dx_1 g(x_1, x_2, x_3)\cdot e^{-i 2\pi \left(\frac{m_1}{a_1} x_1+\frac{m_2}{a_2} x_2\right)} \end{align}} ⓘ
Wir können schreiben noch einmal als:
Schließlich wenden wir das Gleiche für die dritte Koordinate an und definieren: Fehler beim Parsen (Unbekannte Funktion „\begin{align}“): {\displaystyle \begin{align} h^\mathrm{drei}(m_1, m_2, m_3) & \triangleq \frac{1}{a_3}\int_0^{a_3} h^\mathrm{zwei}(m_1, m_2, x_3)\cdot e^{-i 2\pi \frac{m_3}{a_3} x_3}\, dx_3 \\\[12pt] & = \frac{1}{a_3}\int_0^{a_3} dx_3 \frac{1}{a_2}\int_0^{a_2} dx_2 \frac{1}{a_1}\int_0^{a_1} dx_1 g(x_1, x_2, x_3)\cdot e^{-i 2\pi \left(\frac{m_1}{a_1} x_1+\frac{m_2}{a_2} x_2 + \frac{m_3}{a_3} x_3\right)} \end{align}} ⓘ
Wir schreiben als:
Umformulierung:
Nun kann jeder reziproke Gittervektor geschrieben werden (was aber nicht bedeutet, dass dies die einzige Schreibweise ist) als , wobei sind ganze Zahlen und sind reziproke Gittervektoren, die folgende Bedingungen erfüllen ( für und für ). Dann gilt für jeden beliebigen reziproken Gittervektor und ein beliebiger Positionsvektor im ursprünglichen Bravais-Gitterraum ihr Skalarprodukt: Fehler beim Parsen (Unbekannte Funktion „\rechts“): {\displaystyle \mathbf{G} \cdot \mathbf{r} = \left ( m_1\mathbf{g}_1 + m_2\mathbf{g}_2 + m_3\mathbf{g}_3 \right ) \cdot \left (x_1\frac{\mathbf{a}_1}{a_1}+ x_2\frac{\mathbf{a}_2}{a_2} +x_3\frac{\mathbf{a}_3}{a_3} \rechts ) = 2\pi \left( x_1\frac{m_1}{a_1}+x_2\frac{m_2}{a_2}+x_3\frac{m_3}{a_3} \rechts ).} ⓘ
Es ist also klar, dass in unserer Expansion von die Summe tatsächlich über reziproke Gittervektoren geht:
wobei
Unter der Annahme
(es kann zur Vereinfachung der Berechnungen von Vorteil sein, in einem solchen kartesischen Koordinatensystem zu arbeiten, in dem zufällig parallel zur x-Achse liegt, in der xy-Ebene liegt und hat Komponenten auf allen drei Achsen). Der Nenner ist genau das Volumen der primitiven Einheitszelle, die von den drei primitiven Vektoren eingeschlossen wird , und . Insbesondere wissen wir nun, dass
Wir können nun schreiben als ein Integral mit dem traditionellen Koordinatensystem über das Volumen der primitiven Zelle schreiben, anstatt mit den , und Variablen:
Hilbert-Raum-Interpretation
In der Sprache der Hilbert-Räume ist die Menge der Funktionen ist eine Orthonormalbasis für den Raum der quadratisch-integrablen Funktionen auf . Dieser Raum ist eigentlich ein Hilbert-Raum mit einem inneren Produkt, das für zwei beliebige Elemente und durch:
- wobei die komplex Konjugierte von
Das grundlegende Fourier-Reihenergebnis für Hilbert-Räume kann wie folgt geschrieben werden

Dies entspricht genau der oben angegebenen komplexen Exponentialformel. Die Version mit Sinus und Kosinus ist auch mit der Hilbert-Raum-Interpretation gerechtfertigt. Die Sinus- und Kosinusfunktionen bilden nämlich eine orthogonale Menge:
Fourier-Theorem zum Nachweis der Konvergenz von Fourier-Reihen
Diese Theoreme und informelle Variationen davon, die die Konvergenzbedingungen nicht spezifizieren, werden manchmal allgemein als Fourier-Theorem oder Fourier-Theorem bezeichnet. ⓘ
Das frühere
Eigenschaft der kleinsten Quadrate
Das Theorem von Parseval impliziert dies: ⓘ
Konvergenztheoreme
Aufgrund der Eigenschaft der kleinsten Quadrate und der Vollständigkeit der Fourier-Basis erhalten wir ein elementares Konvergenzergebnis. ⓘ
Wir haben bereits erwähnt, dass, wenn kontinuierlich differenzierbar ist, dann ist die Fourier-Koeffizient der Ableitung . Im Wesentlichen folgt aus der Cauchy-Schwarz-Ungleichung, dass absolut summierbar ist. Die Summe dieser Reihe ist eine stetige Funktion, gleich , da die Fourier-Reihe im Mittelwert konvergiert zu : Dieses Ergebnis kann leicht bewiesen werden, wenn weiter angenommen wird als ist, da in diesem Fall gegen Null tendiert, wenn Fehler beim Parsen (Unbekannte Funktion „\rechtsPfeil“): {\displaystyle n \rechtsPfeil \infty} . Allgemeiner ausgedrückt: Die Fourier-Reihe ist absolut summierbar und konvergiert daher gleichmäßig zu , vorausgesetzt, dass eine Hölder-Bedingung der Ordnung . Im absolut summierbaren Fall gilt die Ungleichung:
beweist gleichmäßige Konvergenz. ⓘ
Es sind noch viele andere Ergebnisse zur Konvergenz von Fourier-Reihen bekannt, angefangen bei dem einfachen Ergebnis, dass die Reihe konvergiert bei wenn differenzierbar ist bei konvergiert, bis hin zu Lennart Carlesons viel anspruchsvollerem Ergebnis, dass die Fourier-Reihe einer Funktion tatsächlich fast überall konvergiert. ⓘ
Divergenz
Da Fourier-Reihen so gute Konvergenzeigenschaften haben, sind viele von einigen der negativen Ergebnisse überrascht. Zum Beispiel muss die Fourier-Reihe einer kontinuierlichen T-periodischen Funktion nicht punktweise konvergieren. Das Prinzip der einheitlichen Begrenztheit liefert einen einfachen, nicht-konstruktiven Beweis für diese Tatsache. ⓘ
1922 veröffentlichte Andrey Kolmogorov einen Artikel mit dem Titel Une série de Fourier-Lebesgue divergente presque partout, in dem er ein Beispiel für eine Lebesgue-integrable Funktion gab, deren Fourier-Reihe fast überall divergiert. Er später konstruiert ein Beispiel für eine integrierbare Funktion, deren Fourier-Reihe divergiert überall. ⓘ
Mathematische Hintergründe


2π-periodische Funktionen
Orthonormalsystem
Betrachten wir nun die Menge . (Diese Menge ist wohldefiniert, weil die Funktion bzgl. für alle -periodisch ist.) Da offensichtlich gilt, erzeugt einen Untervektorraum von . Da die Vektoren in linear unabhängig sind, ist eine Basis von . hat daher Dimension . ⓘ
Für zwei beliebige Vektoren gilt:
Bezüglich des inneren Produkts ist somit eine Orthonormalbasis von . ⓘ
Darstellung in Amplituden-Phasen-Form
Für reellwertige Funktionen ist des Weiteren eine Darstellung der Fourierreihe in der Form
mit möglich. Wegen
folgt
mit
Es folgt daher
Der Winkel ergibt sich zu
(Hinweis: In der Literatur findet man den Winkel oftmals in Form des Arkustangens angegeben. Da die Tangensfunktion nur -periodisch ist, muss man bei einer solchen Darstellung Fallunterscheidungen vornehmen. Wenn man den Winkel jedoch über den Arkuskosinus oder Arkussinus berechnet, hat man den Vorteil, dass man keine Fallunterscheidungen vornehmen muss, weil die Sinus- und Kosinusfunktion -periodisch sind!) ⓘ
Verallgemeinerungen
Zusammenhang mit der Fourier-Transformation für nicht-periodische Funktionen
Mit Fourierreihen lassen sich nur periodische Funktionen und ihr Spektrum beschreiben. Um auch nichtperiodische Funktionen spektral beschreiben zu können, führt man einen Grenzübergang der Periode durch. Dadurch wird die Frequenzauflösung beliebig fein, was in einem Verschwinden des komplexen Amplitudenspektrums resultiert. Aus diesem Grund führt man das komplexe Amplitudendichtespektrum ein, ausgehend von der komplexen Fourierreihe zunächst für die diskreten Argumente :
Durch Bildung des Grenzwertes (wobei gleichzeitig ) folgt damit unmittelbar die Fourier-Transformation:
Beispiele
Dreieckpuls

Die Dreieckfunktion lässt sich je nach gewünschter Phasenlage mit Sinus- und Kosinustermen approximieren. Mit dem Scheitelwert lauten die Fourierreihen:
Rechteckpuls

Die Rechteckschwingung ist definiert durch
Die Fourierreihe dazu lautet
Anhand dieser Funktion erkennt man, dass man eine Rechteckschwingung durch unendlich viele Harmonische darstellen kann. Sie enthält jeweils die ungeraden harmonischen Oberschwingungen, wobei die Amplitude mit steigender Frequenz abnimmt. Aufgrund dessen wird ein Rechtecksignal auch häufig zum Testen elektronischer Schaltungen genommen, da so das Frequenzverhalten dieser Schaltung erkannt wird. ⓘ
Allgemein enthalten alle periodischen Schwingungen mit der Periodendauer der Grundschwingung und beliebigem Verlauf innerhalb der Periode nur ungeradzahlige Oberschwingungen, wenn gilt:

Im rechten Bild ist die Fourier-Synthese einer Rechteckschwingung dargestellt. Die Diagramme der ersten Spalte zeigen diejenige Schwingung, die in der jeweiligen Zeile hinzugefügt wird. Die Diagramme in der zweiten Spalte zeigen alle bisher berücksichtigten Schwingungen, die dann in den Diagrammen der dritten Spalte addiert werden, um dem zu erzeugenden Signal möglichst nahezukommen. Die Schwingung aus der ersten Zeile nennt sich Fundamentalschwingung, alle weiteren, die hinzugefügt werden, sind Oberschwingungen (Harmonische). Je mehr solcher Vielfache der Grundfrequenz berücksichtigt werden, umso näher kommt man einem idealen Rechtecksignal. An den unstetigen Stellen des Rechtecksignals bildet sich durch die Fourier-Synthese bedingt ein so genannter Überschwinger, der auch bei größerer Approximation nicht verschwindet. Diese Erscheinung wird Gibbssches Phänomen genannt, sie weist eine konstante und von der Bandbreite unabhängige Überschwingung von etwa 18 % des vollen Sprungs auf. Die vierte Spalte zeigt das Amplitudenspektrum normiert auf die Grundschwingung. ⓘ
Sägezahnpuls (steigend)

Ebenso lassen sich punktsymmetrische Funktionen aus Sinustermen approximieren. Hier erreicht man eine Phasenverschiebung durch alternierende Vorzeichen:
Sinuspuls

Konvergenzaussagen zur Fourierreihe
Satz von Carleson
Der Satz von Carleson ist ein tiefliegendes Resultat zur Konvergenz einer Fourierreihe. ⓘ
Sei eine quadratintegrierbare Funktion, dann konvergiert die Fourierreihe von fast überall. ⓘ
Diese Aussage ist sogar für alle -Räume mit richtig und heißt in dieser allgemeinen Form Satz von Carleson–Hunt. Dass die Aussage für falsch ist, konnte Kolmogorov 1923 durch ein Gegenbeispiel zeigen. Nikolai Nikolajewitsch Lusin vermutete schon 1915 die Richtigkeit des Satzes von Carleson, konnte sie jedoch nicht beweisen. Der Beweis gelang erst Lennart Carleson im Jahr 1966. ⓘ
Gibbssches Phänomen

In der Umgebung von Sprungstellen entstehen dort in der Fourierreihe typische Über- und Unterschwinger von etwa 9 % der halben Sprunghöhe. Dieser Effekt hat weitreichende Auswirkungen in der Signalverarbeitung. ⓘ
Mathematische Ursache dafür ist, dass für nicht stetige Funktionen und
zwar Konvergenz im Sinne der -Norm vorliegt, jedoch die Folge im Allgemeinen nicht gleichmäßig konvergiert. ⓘ









































![{\displaystyle {displaystyles_{\scriptscriptstyle N}(x)={\frac {A_{0}}{2}}+\sum _{n=1}^{N}\left[A_{n}\cos(\varphi _{n})\cdot \cos \left({\tfrac {2\pi }{P}}nx\right)+A_{n}\sin(\varphi _{n})\cdot \sin \left({\tfrac {2\pi }{P}}nx\right)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4282eaf0585a9c565e95dc07a71a67b1e9a96213)




![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)




![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)
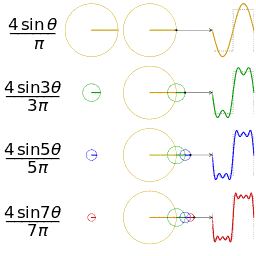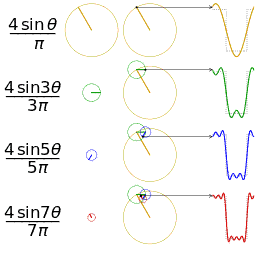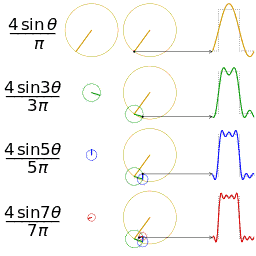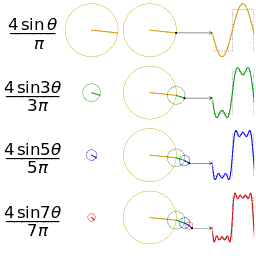








![{\displaystyle {\begin{aligned}c_{n}&={\tfrac {1}{P}}\int _{P}\operatorname {Re} \{s(x)\}\cdot e^{-i{\frac {2\pi }{P}}nx}\ dx+i\cdot {\tfrac {1}{P}}\int _{P}\operatorname {Im} \{s(x)\}\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\\[4pt]&={\tfrac {1}{P}}\int _{P}\left(\operatorname {Re} \{s(x)\}+i\cdot \operatorname {Im} \{s(x)\}\right)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\ =\ {\tfrac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2f3a7cab08bd95f922c1fbc2f921addb4edfcd3)
![{\displaystyle {\hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}[n]\cdot e^{i\,2\pi nx/P}\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}&&\scriptstyle {\mathsf {common\ engineeringnotation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bca229d9a26677b0282e7552b1a637cddeadd2ac)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)




























![{\displaystyle x\in [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \operatorname {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i{\frac {2\pi x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb7150e991a2642dc0c62cdee40602d99227420)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)



![{\textstyle \sum _{n=-\infty }^{\infty }{\Bigl |}S[n]{\Bigr |}^{2}={\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45449c99cf90bed698c4b3797561759081fc2e5)



![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)


![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)

![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





![{\displaystyle {\widehat {s'}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a50845d25c79fe9547d0194fce67a390efc1a4ed)

![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b)
![{\displaystyle {\widehat {s'}}[n]=in{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d281471757291b705a757faa55af0f1cebf8a0b6)

![{\displaystyle {\widehat {s^{(k)}}}[n]=(in)^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0120eafbcb1c02b4c2f81f5589fdc328c28bd20)

![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c)





![{\displaystyle [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




![{\displaystyle [-\pi ,\pi ]\times [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)


















![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)






















![{\displaystyle {\begin{vmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[12pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[12pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)












![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)











![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i{\tfrac {2\pi }{P}}nx},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b030eaf773387de3787b4a003ef7599624be959)
![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i{\tfrac {2\pi }{P}}nx}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a29c02020f3c186b790b680deabe8e985ebcd700)
![{\displaystyle (i\cdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762)


![{\displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)

![{\displaystyle \sup _{x}|s(x)-s_{_{N}}(x)|\leq \sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)





























![{\displaystyle {\begin{array}{rl}f(t)=&-{\frac {8h}{\pi ^{2}}}\left[{\cos {\omega t}+{\frac {1}{3^{2}}}\cos {3\omega t}+{\frac {1}{5^{2}}}\cos {5\omega t}+\cdots }\right]\\[.6em]=&-{\frac {8h}{\pi ^{2}}}\sum \limits _{k=1}^{\infty }{\dfrac {\cos((2k-1)\omega t)}{(2k-1)^{2}}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac0816328465e723a3eb49acb738691a2257a182)
![{\displaystyle {\begin{array}{rl}f(t)=&{\frac {8h}{\pi ^{2}}}\left[{\sin {\omega t}-{\frac {1}{3^{2}}}\sin {3\omega t}+{\frac {1}{5^{2}}}\sin {5\omega t}\mp \cdots }\right]\\[.6em]=&{\frac {8h}{\pi ^{2}}}\sum \limits _{k=1}^{\infty }(-1)^{k-1}{\dfrac {\sin((2k-1)\omega t)}{(2k-1)^{2}}}\;.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb728294d5b8476de7705fabbfbad598c13f44cf)

![{\displaystyle {\begin{aligned}f(t)=&{\tfrac {4h}{\pi }}\left[\sin \omega t+{\tfrac {1}{3}}\sin 3\omega t+{\tfrac {1}{5}}\sin 5\omega t+{\tfrac {1}{7}}\sin 7\omega t+\cdots \right]\\=&{\tfrac {4h}{\pi }}\sum _{k=1}^{\infty }{\dfrac {\sin \left((2k-1)\omega t\right)}{2k-1}}\;.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62d0dedb9d52eca0c9da658b80b18a4f62ab7274)

![{\displaystyle {\begin{array}{rl}f(t)=&-{\frac {2h}{\pi }}\left[{\sin {\omega t}-{\frac {1}{2}}\sin {2\omega t}+{\frac {1}{3}}\sin {3\omega t}\mp \cdots }\right]\\[.6em]=&-{\frac {2h}{\pi }}\sum \limits _{k=1}^{\infty }(-1)^{k-1}{\dfrac {\sin k\omega t}{k}}\;.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fff4313085a939d2ed07550f435e5109fed5d03)
![{\displaystyle {\begin{array}{rl}f(t)=&h\left|\sin {\omega t}\right|\\[.6em]=&{\frac {4h}{\pi }}\left[{\frac {1}{2}}-{\frac {\cos {2\omega t}}{3}}-{\frac {\cos {4\omega t}}{15}}-{\frac {\cos {6\omega t}}{35}}-\cdots \right]\\[.6em]=&{\frac {2h}{\pi }}-{\frac {4h}{\pi }}\sum \limits _{k=1}^{\infty }{\dfrac {\cos {2k\omega t}}{(2k)^{2}-1}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca2d08cf24b2982d1690b70ba440305e35245738)
![{\displaystyle f\in L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)

![{\displaystyle p\in {}]1,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3e7df94c446864bfffa5ab1e63d19c10693c581)



