Banachraum

In der Mathematik, genauer gesagt in der Funktionalanalysis, ist ein Banach-Raum (ausgesprochen [ˈbanax]) ein vollständiger normierter Vektorraum. Ein Banach-Raum ist also ein Vektorraum mit einer Metrik, die die Berechnung der Vektorlänge und des Abstands zwischen Vektoren ermöglicht, und er ist vollständig in dem Sinne, dass eine Cauchy-Folge von Vektoren immer zu einem wohldefinierten Grenzwert konvergiert, der innerhalb des Raums liegt. ⓘ

Banach-Räume sind nach dem polnischen Mathematiker Stefan Banach benannt, der dieses Konzept einführte und es 1920-1922 zusammen mit Hans Hahn und Eduard Helly systematisch untersuchte. Maurice René Fréchet war der erste, der den Begriff "Banach-Raum" verwendete, und Banach wiederum prägte dann den Begriff "Fréchet-Raum". Banach-Räume sind ursprünglich aus dem Studium der Funktionsräume von Hilbert, Fréchet und Riesz Anfang des Jahrhunderts hervorgegangen. Banach-Räume spielen eine zentrale Rolle in der Funktionalanalysis. In anderen Bereichen der Analysis sind die untersuchten Räume oft Banach-Räume. ⓘ

Definition

Ein Banach-Raum ist ein vollständiger normierter Raum $(X,\|\cdot \|).$ Ein normierter Raum ist ein Paar $(X,\|\cdot \|)$ bestehend aus einem Vektorraum $X$ über einem Skalarfeld $\mathbb {K}$ (wobei $\mathbb {K}$ ist üblicherweise $\mathbb {R}$ oder $\mathbb {C}$) zusammen mit einer unterschiedenen Norm $\|\cdot \|:X\to \mathbb {R} .$ Wie alle Normen induziert auch diese Norm eine translationsinvariante Abstandsfunktion, die als kanonische oder (norm)induzierte Metrik bezeichnet wird und definiert ist durch

$$d(x,y):=\|y-x\|=\|x-y\|$$

für alle Vektoren $x,y\in X.$ Dies macht $X$ zu einem metrischen Raum $(X,d).$ Eine Folge $x_{\bullet }=\left(x_{n}\right)_{n=1}^{\infty }$ wird genannt $d$-Cauchy oder Cauchy in $(X,d)$ oder $\|\cdot \|$-Cauchy wenn für jede reelle $r>0,$ ein Index existiert $N$ derart, dass

$$d\left(x_{n},x_{m}\right)=\left\|x_{n}-x_{m}\right\|<r$$

wenn $m$ und $n$ größer sind als $N.$ Die kanonische Metrik $d$ wird als eine vollständige Metrik wenn das Paar $(X,d)$ ist ein vollständiger metrischer Raumist, was per Definition bedeutet, dass für jede Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} -Cauchy-Folge Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x_{\bull} = \left(x_n\right)_{n=1}^{\infty}} in Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (X, d),} gibt es einige $x\in X$ derart, dass Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \lim_{n \to \infty} \left\|x_n - x\right\| = 0} wo, weil Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle \left\|x_n - x\right\| = d\left(x_n, x\right),} die Konvergenz dieser Folge zu Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle x} äquivalent ausgedrückt werden kann als:

$$\lim _{n\to \infty }x_{n}=x\;{\text{ in }}(X,d).$$

ⓘ

Per Definition ist der normierte Raum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (X, \| \cdot \|)} ein Banach-Raum wenn die norminduzierte Metrik Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle d} eine vollständige Metrik ist, oder anders ausgedrückt, wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (X, d)} ein vollständiger metrischer Raum ist. Die Norm $\|\cdot \|$ eines normierten Raums Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (X, \| \cdot \|)} wird als eine vollständige Norm wenn Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (X, \| \cdot \|)} ein Banach-Raum ist. ⓘ

L-Semi-Innenprodukt ⓘ

Für jeden normierten Raum Fehler beim Parsen (MathML mit SVG- oder PNG-Rückgriff (empfohlen für moderne Browser und Barrierefreiheitswerkzeuge): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://wikimedia.org/api/rest_v1/“:): {\displaystyle (X, \| \cdot \|),} gibt es ein L-Semi-Innenprodukt $\langle \cdot ,\cdot \rangle$ auf $X$ derart, dass ${\textstyle \|x\|={\sqrt {\langle x,x\rangle }}}$ für alle $x\in X$Im Allgemeinen kann es unendlich viele L-Semi-Innenprodukte geben, die diese Bedingung erfüllen. L-Semi-Innenprodukte sind eine Verallgemeinerung der inneren Produkte, die Hilbert-Räume grundlegend von allen anderen Banach-Räumen unterscheiden. Dies zeigt, dass alle normierten Räume (und damit alle Banachräume) als Verallgemeinerungen von (Prä-)Hilberträumen betrachtet werden können. ⓘ

Charakterisierung in Form von Reihen ⓘ

Die Vektorraumstruktur erlaubt es, das Verhalten von Cauchy-Folgen mit dem von konvergierenden Reihen von Vektoren in Beziehung zu setzen. Ein normierter Raum $X$ ist dann und nur dann ein Banach-Raum, wenn jede absolut konvergente Reihe in $X$ konvergiert in $X,$

$$\sum _{n=1}^{\infty }\|v_{n}\|<\infty \quad {\text{ implies that }}\quad \sum _{n=1}^{\infty }v_{n}\ \ {\text{ converges in }}\ \ X.$$

ⓘ

Topologie

Die kanonische Metrik $d$ eines normierten Raums $(X,\|\cdot \|)$ induziert die übliche metrische Topologie $\tau _{d}$ auf $X,$ wobei diese Topologie, die als kanonische oder norminduzierte Topologie bezeichnet wird. Bei jedem normierten Raum wird automatisch davon ausgegangen, dass er diese Hausdorff-Topologie trägt, sofern nicht anders angegeben. Mit dieser Topologie ist jeder Banach-Raum ein Baire-Raum, obwohl es normierte Räume gibt, die Baire, aber nicht Banach sind. Die Norm $\|\,\cdot \,\|:\left(X,\tau _{d}\right)\to \mathbb {R}$ ist immer eine kontinuierliche Funktion in Bezug auf die Topologie, die sie induziert. ⓘ

Die offenen und geschlossenen Kugeln mit dem Radius $r>0$ mit dem Mittelpunkt in einem Punkt $x\in X$ sind jeweils die Mengen

$$B_{r}(x):=\{z\in X:\|z-x\|<r\}\qquad {\text{ and }}\qquad C_{r}(x):=\{z\in X:\|z-x\|\leq r\}.$$

Jede dieser Kugeln ist eine konvexe und begrenzte Teilmenge von $X,$ aber eine kompakte Kugel/Nachbarschaft existiert nur dann, wenn $X$ ein endlich-dimensionaler Vektorraum ist. Insbesondere kann kein unendlich-dimensionaler normierter Raum lokal kompakt sein oder die Heine-Borel-Eigenschaft besitzen. Wenn $x_{0}$ ein Vektor ist und $s\neq 0$ ein Skalar ist, dann

$$x_{0}+sB_{r}(x)=B_{|s|r}\left(x_{0}+sx\right)\qquad {\text{ and }}\qquad x_{0}+sC_{r}(x)=C_{|s|r}\left(x_{0}+sx\right).$$

Mit $s:=1$ zeigt, dass diese norminduzierte Topologie translationsinvariant ist, was bedeutet, dass für jede $x\in X$ und $S\subseteq X,$ die Teilmenge $S$ offen (bzw. geschlossen) ist in $X$ nur dann offen (bzw. geschlossen) ist, wenn dies auch für ihre Translation gilt $x+S:=\{x+s:s\in S\}.$ Folglich ist die norminduzierte Topologie vollständig durch eine beliebige Nachbarschaftsbasis am Ursprung bestimmt. Einige übliche Nachbarschaftsbasen am Ursprung sind:

$$\left\{B_{r}(0):r>0\right\},\qquad \left\{C_{r}(0):r>0\right\},\qquad \left\{B_{r_{n}}(0):n\in \mathbb {N} \right\},\qquad {\text{ or }}\qquad \left\{C_{r_{n}}(0):n\in \mathbb {N} \right\}$$

wobei $\left(r_{n}\right)_{n=1}^{\infty }$ eine Folge in von positiven reellen Zahlen ist, die zu $0$ in $\mathbb {R}$ konvergiert (z. B. $r_{n}:=1/n$ oder $r_{n}:=1/2^{n}$ zum Beispiel). So kann zum Beispiel jede offene Teilmenge $U$ von $X$ kann als Vereinigung geschrieben werden

$$U=\bigcup _{x\in I}B_{r_{x}}(x)=\bigcup _{x\in I}x+B_{r_{x}}(0)=\bigcup _{x\in I}x+r_{x}B_{1}(0)$$

geschrieben werden, die durch eine Teilmenge $I\subseteq U,$ wobei jede $r_{x}$ von der Form $r_{x}={\tfrac {1}{n_{x}}}$ für eine ganze Zahl $n_{x}>0$ (die geschlossene Kugel kann auch anstelle der offenen Kugel verwendet werden, obwohl die Indizierungsmenge $I$ und Radien $r_{x}$ möglicherweise geändert werden müssen). Zusätzlich, $I$ immer als abzählbar gewählt werden, wenn $X$ ist ein teilbarer Raumist, was per Definition bedeutet, dass $X$ eine abzählbare dichte Teilmenge enthält. Das Anderson-Kadec-Theorem besagt, dass jeder unendlich-dimensionale trennbare Fréchet-Raum homöomorph ist zum Produktraum ${\textstyle \prod _{i\in \mathbb {N} }\mathbb {R} }$ von abzählbar vielen Kopien von $\mathbb {R}$ (dieser Homöomorphismus muss keine lineare Abbildung sein). Da jeder Banach-Raum ein Fréchet-Raum ist, gilt dies auch für alle unendlich-dimensionalen trennbaren Banach-Räume, einschließlich des trennbaren Hilbert $\ell$²-Folge-Raum $\ell ^{2}(\mathbb {N} )$ mit seiner üblichen Norm $\|\cdot \|_{2},$ wo (in scharfem Gegensatz zu endlich-dimensionalen Räumen) $\ell ^{2}(\mathbb {N} )$ auch homöomorph zu seiner Einheit ist Kugel $\left\{x\in \ell ^{2}(\mathbb {N} ):\|x\|_{2}=1\right\}.$ ⓘ

Diese norm-induzierte Topologie macht auch $\left(X,\tau _{d}\right)$ zu einem so genannten topologischen Vektorraum (TVS), der per Definition ein Vektorraum ist, der mit einer Topologie ausgestattet ist, die die Operationen der Addition und der skalaren Multiplikation kontinuierlich macht. Es wird betont, dass der TVS $\left(X,\tau _{d}\right)$ ist nur ein Vektorraum in Verbindung mit einer bestimmten Art von Topologie ist; das heißt, als TVS betrachtet, ist er nicht verbunden mit irgendeiner Norm oder Metrik verbunden (die beide "vergessen" werden). ⓘ

Vergleich vollständiger metrisierbarer Vektortopologien ⓘ

Das Theorem der offenen Abbildung impliziert, dass, wenn $\tau {\text{ and }}\tau _{2}$ Topologien sind auf $X$ sind, die beide $(X,\tau )$ und $\left(X,\tau _{2}\right)$ zu vollständigen metrisierbaren TVS machen (z. B. Banach- oder Fréchet-Räume) und wenn eine Topologie feiner oder gröber ist als die andere, dann müssen sie gleich sein (d. h. wenn $\tau \subseteq \tau _{2}{\text{ or }}\tau _{2}\subseteq \tau {\text{ then }}\tau =\tau _{2}$). Wenn also zum Beispiel $(X,p){\text{ and }}(X,q)$ Banach-Räume mit Topologien $\tau _{p}{\text{ and }}\tau _{q}$ sind und einer dieser Räume eine offene Kugel hat, die auch eine offene Teilmenge des anderen Raums ist (oder, äquivalent, wenn einer von $p:\left(X,\tau _{q}\right)\to \mathbb {R}$ oder $q:\left(X,\tau _{p}\right)\to \mathbb {R}$ kontinuierlich ist), dann sind ihre Topologien identisch und ihre Normen sind äquivalent. ⓘ

Vollkommenheit

Vollständige Normen und äquivalente Normen ⓘ

Zwei Normen auf einem Vektorraum werden als äquivalent wenn sie die gleiche Topologie induzieren. Wenn $p$ und $q$ sind zwei äquivalente Normen auf einem Vektorraum $X$ dann ist $(X,p)$ ein Banachraum, wenn und nur wenn $(X,q)$ ein Banach-Raum ist. In dieser Fußnote finden Sie ein Beispiel für eine kontinuierliche Norm auf einem Banach-Raum, die nicht äquivalent zu der gegebenen Norm des Banach-Raums ist. Alle Normen auf einem endlich-dimensionalen Vektorraum sind äquivalent und jeder endlich-dimensionale normierte Raum ist ein Banach-Raum. ⓘ

Vollständige Normen vs. vollständige Metriken ⓘ

Eine Metrik $D$ auf einem Vektorraum $X$ ist induziert durch eine Norm auf $X$ wenn und nur wenn $D$ translationsinvariant ist und absolut homogenist, was bedeutet, dass $D(sx,sy)=|s|D(x,y)$ für alle Skalare $s$ und alle $x,y\in X,$ in diesem Fall die Funktion $\|x\|:=D(x,0)$ eine Norm auf $X$ und die kanonische Metrik, induziert durch $\|\cdot \|$ ist gleich $D.$ ⓘ

Angenommen, dass $(X,\|\cdot \|)$ ein normierter Raum ist und dass $\tau$ die Normtopologie ist, die induziert wird durch $X.$ Angenommen, dass $D$ ist irgendeiner Metrik auf $X$ so dass die Topologie, die $D$ induziert auf $X$ ist gleich $\tau .$ Wenn $D$ translationsinvariant ist, dann $(X,\|\cdot \|)$ ein Banachraum, wenn und nur wenn $(X,D)$ ein vollständiger metrischer Raum. Wenn $D$ ist nicht translationsinvariant, dann kann es möglich sein, dass $(X,\|\cdot \|)$ ein Banach-Raum sein, aber für $(X,D)$ zu nicht ein vollständiger metrischer Raum sein (siehe diese Fußnote für ein Beispiel). Im Gegensatz dazu impliziert ein Satz von Klee, der auch für alle metrisierbaren topologischen Vektorräume gilt, dass, wenn es eine irgendeiner vollständige Metrik $D$ auf $X$ die die Normtopologie induziert $\tau$ auf $X,$ dann ist $(X,\|\cdot \|)$ ein Banach-Raum ist. ⓘ

Ein Fréchet-Raum ist ein lokal konvexer topologischer Vektorraum, dessen Topologie durch eine translationsinvariante vollständige Metrik induziert ist. Jeder Banach-Raum ist ein Fréchet-Raum, aber nicht umgekehrt; es gibt sogar Fréchet-Räume, auf denen keine Norm eine stetige Funktion ist (z. B. der Raum der reellen Folgen ${\textstyle \mathbb {R} ^{\mathbb {N} }=\prod _{i\in \mathbb {N} }\mathbb {R} }$ mit der Produkttopologie). Die Topologie jedes Fréchet-Raums wird jedoch durch eine abzählbare Familie von reellwertigen (notwendigerweise stetigen) Abbildungen induziert, die man als Seminarmen bezeichnet und die Verallgemeinerungen von Normen sind. Es ist sogar möglich, dass ein Fréchet-Raum eine Topologie hat, die durch eine abzählbare Familie von Normen (solche Normen wären notwendigerweise kontinuierlich) aber kein Banach/normbarer Raum ist, weil seine Topologie nicht durch eine einzelne Norm definiert werden kann. Ein Beispiel für einen solchen Raum ist der Fréchet-Raum $C^{\infty }(K),$ dessen Definition in dem Artikel über Räume von Testfunktionen und Verteilungen zu finden ist. ⓘ

Vollständige Normen vs. vollständige topologische Vektorräume ⓘ

Neben der metrischen Vollständigkeit gibt es noch einen weiteren Begriff der Vollständigkeit, und zwar den Begriff des vollständigen topologischen Vektorraums (TVS) oder der TVS-Vollständigkeit, der auf der Theorie der einheitlichen Räume beruht. Insbesondere verwendet der Begriff der TVS-Vollständigkeit eine eindeutige translationsinvariante Uniformität, die so genannte kanonische Uniformität, die abhängt von nur von der Vektorsubtraktion und der Topologie $\tau$ abhängt, mit der der Vektorraum ausgestattet ist, und so ist dieser Begriff der TVS-Vollständigkeit insbesondere unabhängig von der Norm, die die Topologie $\tau$ (und gilt sogar für TVSs, die nicht sogar metrisierbar sind). Jeder Banach-Raum ist eine vollständige TVS. Außerdem ist ein normierter Raum dann und nur dann ein Banach-Raum (d. h. seine norminduzierte Metrik ist vollständig), wenn er als topologischer Vektorraum vollständig ist. Wenn $(X,\tau )$ ein metrisierbarer topologischer Vektorraum ist (wie z. B. jede norminduzierte Topologie), dann ist $(X,\tau )$ ein vollständiger TVS, wenn und nur wenn er ein sequenziell vollständige TVS ist, d. h., es genügt zu prüfen, dass jede Cauchy Folge in $(X,\tau )$ konvergiert in $(X,\tau )$ zu irgendeinem Punkt von $X$ (d.h. es besteht keine Notwendigkeit, den allgemeineren Begriff der beliebigen Cauchy-Netze zu betrachten). ⓘ

Wenn $(X,\tau )$ ist ein topologischer Vektorraum, dessen Topologie induziert ist durch eine (möglicherweise unbekannte) Norm induziert ist (solche Räume werden als normierbar und sie sind dadurch gekennzeichnet, dass sie Hausdorff sind und eine begrenzte konvexe Nachbarschaft des Ursprungs haben), dann $(X,\tau )$ ein vollständiger topologischer Vektorraum, wenn und nur wenn $X$ eine Norm zugeordnet werden kann $\|\cdot \|$ zugewiesen werden kann, die auf $X$ die Topologie $\tau$ induziert und außerdem $(X,\|\cdot \|)$ zu einem Banach-Raum macht. Ein lokal konvexer topologischer Hausdorff-Vektorraum $X$ ist dann und nur dann normierbar, wenn sein starker Dualraum $X_{b}^{\prime }$ normierbar ist, wobei in diesem Fall $X_{b}^{\prime }$ ein Banach-Raum ist ($X_{b}^{\prime }$ bezeichnet den starken Dualraum von $X,$ dessen Topologie eine Verallgemeinerung der dualen norminduzierten Topologie auf dem kontinuierlichen dualen Raum $X^{\prime }$; siehe diese Fußnote für weitere Einzelheiten). Wenn $X$ eine metrisierbare lokal konvexe TVS ist, dann ist $X$ normierbar, wenn und nur wenn $X_{b}^{\prime }$ ein Fréchet-Urysohn-Raum ist. Dies zeigt, dass Banach-Räume in der Kategorie der lokal konvexen TVSs genau die vollständigen Räume sind, die sowohl metrifizierbar sind als auch metrifizierbare starke Dualräume haben. ⓘ

Vervollständigungen

Jeder normierte Raum lässt sich isometrisch auf einen dichten Vektorunterraum des eine Banach-Raums eingebettet werden, wobei dieser Banach-Raum als eine Vervollständigung des normierten Raums genannt wird. Diese Hausdorff-Vervollständigung ist bis zur isometrischen Isomorphie eindeutig. ⓘ

Genauer gesagt, für jeden normierten Raum $X,$ gibt es einen Banachraum $Y$ und eine Abbildung $T:X\to Y$ derart, dass $T$ ist eine isometrische Abbildung und $T(X)$ dicht ist in $Y.$ Wenn $Z$ ein anderer Banachraum ist, so dass es einen isometrischen Isomorphismus von $X$ auf eine dichte Teilmenge von $Z,$ dann ist $Z$ ist isometrisch isomorph zu $Y.$ Dieser Banach-Raum $Y$ ist der Hausdorff Vervollständigung des normierten Raums $X.$ Der zugrunde liegende metrische Raum für $Y$ ist derselbe wie die metrische Vervollständigung von $X,$ mit den erweiterten Vektorraumoperationen von $X$ zu $Y.$ Die Vervollständigung von $X$ wird manchmal bezeichnet durch ${\widehat {X}}.$ ⓘ

Allgemeine Theorie

Lineare Operatoren, Isomorphismen

Wenn $X$ und $Y$ sind normierte Räume über demselben Grundfeld $\mathbb {K} ,$ die Menge aller kontinuierlichen $\mathbb {K}$-linearen Abbildungen $T:X\to Y$ wird bezeichnet durch $B(X,Y).$ In unendlich-dimensionalen Räumen sind nicht alle linearen Abbildungen stetig. Eine lineare Abbildung von einem normierten Raum $X$ auf einen anderen normierten Raum ist dann und nur dann stetig, wenn sie auf der geschlossenen Einheitskugel von $X.$ So kann dem Vektorraum $B(X,Y)$ kann die Operatornorm

$$\|T\|=\sup \left\{\|Tx\|_{Y}\mid x\in X,\ \|x\|_{X}\leq 1\right\}.$$

ⓘ

Für $Y$ einen Banach-Raum, ist der Raum $B(X,Y)$ ein Banach-Raum in Bezug auf diese Norm. ⓘ

Wenn $X$ ist ein Banach-Raum, der Raum $B(X)=B(X,X)$ bildet eine unitale Banach-Algebra; die Multiplikationsoperation ist durch die Komposition linearer Abbildungen gegeben. ⓘ

Wenn $X$ und $Y$ sind genormte Räume, sie sind isomorphe genormte Räume, wenn es eine lineare Bijektion $T:X\to Y$ derart, dass $T$ und ihre Inverse $T^{-1}$ stetig sind. Wenn einer der beiden Räume $X$ oder $Y$ vollständig (oder reflexiv, trennbar usw.) ist, dann ist es auch der andere Raum. Zwei normierte Räume $X$ und $Y$ sind isometrisch isomorph, wenn darüber hinaus, $T$ eine Isometrie ist, d. h, $\|T(x)\|=\|x\|$ für jeden $x$ in $X.$ Der Banach-Mazur-Abstand $d(X,Y)$ zwischen zwei isomorphen, aber nicht isometrischen Räumen $X$ und $Y$ ist ein Maß dafür, wie sehr sich die beiden Räume $X$ und $Y$ unterscheiden. ⓘ

Stetige und beschränkte lineare Funktionen und Semiformen

Jeder kontinuierliche lineare Operator ist ein beschränkter linearer Operator, und wenn man sich nur mit normierten Räumen befasst, gilt auch das Umgekehrte. Das heißt, ein linearer Operator zwischen zwei normierten Räumen ist dann und nur dann beschränkt, wenn er eine stetige Funktion ist. Da also insbesondere das Skalarfeld (das ist $\mathbb {R}$ oder $\mathbb {C}$) ein normierter Raum ist, ist ein lineares Funktional auf einem normierten Raum dann und nur dann ein beschränktes lineares Funktional, wenn es ein stetiges lineares Funktional ist. Dies ermöglicht die Anwendung von Ergebnissen, die sich auf Stetigkeit beziehen (wie die folgenden), auf Banach-Räume. Obwohl Beschränktheit dasselbe ist wie Stetigkeit für lineare Abbildungen zwischen normierten Räumen, wird der Begriff "beschränkt" üblicherweise verwendet, wenn man sich hauptsächlich mit Banach-Räumen beschäftigt. ⓘ

Wenn $f:X\to \mathbb {R}$ ist eine subadditive Funktion (wie eine Norm, eine sublineare Funktion oder ein reelles lineares Funktional), dann $f$ im Ursprung stetig, wenn und nur wenn $f$ gleichmäßig stetig auf allen von $X$; und wenn darüber hinaus $f(0)=0$ dann ist $f$ nur dann stetig ist, wenn ihr Absolutwert $|f|:X\to [0,\infty )$ stetig ist, was nur dann der Fall ist, wenn $\{x\in X:|f(x)|<1\}$ eine offene Teilmenge von $X.$ Und, was für die Anwendung des Hahn-Banach-Satzes sehr wichtig ist, ein lineares Funktional $f$ dann und nur dann stetig ist, wenn dies auch für seinen Realteil gilt $\operatorname {Re} f$ und darüber hinaus, $\|\operatorname {Re} f\|=\|f\|$ und der Realteil $\operatorname {Re} f$ vollständig bestimmt $f,$ weshalb das Hahn-Banach-Theorem oft nur für reelle lineare Funktionale angegeben wird. Außerdem ist ein lineares Funktional $f$ auf $X$ ist dann und nur dann stetig, wenn die Seminorm $|f|$ stetig ist, was nur dann der Fall ist, wenn es eine stetige Seminorm $p:X\to \mathbb {R}$ derart, dass $|f|\leq p$Diese letzte Aussage über das lineare Funktional $f$ und Seminorm $p$ findet sich in vielen Versionen des Hahn-Banach-Satzes. ⓘ

Grundlegende Begriffe

Das kartesische Produkt $X\times Y$ von zwei normierten Räumen ist nicht kanonisch mit einer Norm ausgestattet. Es werden jedoch häufig mehrere äquivalente Normen verwendet, wie z. B.

$$\|(x,y)\|_{1}=\|x\|+\|y\|,\qquad \|(x,y)\|_{\infty }=\max(\|x\|,\|y\|)$$

und führen zu isomorphen normierten Räumen. In diesem Sinne ist das Produkt $X\times Y$ (oder die direkte Summe $X\oplus Y$) dann und nur dann vollständig, wenn die beiden Faktoren vollständig sind. ⓘ

Wenn $M$ ist ein geschlossener linearer Unterraum eines normierten Raums $X,$ gibt es eine natürliche Norm für den Quotientenraum $X/M,$

$$\|x+M\|=\inf \limits _{m\in M}\|x+m\|.$$

ⓘ

Der Quotient $X/M$ ist ein Banach-Raum, wenn $X$ vollständig ist. Die Quotientenkarte von $X$ auf $X/M,$ sendet $x\in X$ in seine Klasse $x+M,$ ist linear, onto und hat die Norm $1,$ außer wenn $M=X,$ in diesem Fall ist der Quotient der Nullraum. ⓘ

Der geschlossene lineare Unterraum $M$ von $X$ wird als ein komplementärer Unterraum von $X$ wenn $M$ der Bereich einer surjektiven beschränkten linearen Projektion ist $P:X\to M.$ In diesem Fall ist der Raum $X$ isomorph zu der direkten Summe von $M$ und $\ker P,$ der Kernel der Projektion $P.$ ⓘ

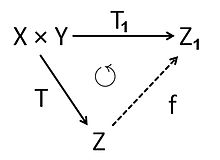
Angenommen, dass $X$ und $Y$ Banachräume sind und dass $T\in B(X,Y).$ Es existiert eine kanonische Faktorisierung von $T$ als

$$T=T_{1}\circ \pi ,\ \ \ T:X\ {\overset {\pi }{\longrightarrow }}\ X/ker(T)\ {\overset {T_{1}}{\longrightarrow }}\ Y$$

wobei die erste Abbildung $\pi$ die Quotientenkarte ist, und die zweite Karte $T_{1}$ sendet jede Klasse $x+\ker T$ im Quotienten in das Bild $T(x)$ in $Y.,$ Dies ist gut definiert, da alle Elemente derselben Klasse dasselbe Bild haben. Die Abbildung $T_{1}$ ist eine lineare Bijektion von $X/\ker T$ auf den Bereich $T(X),$ deren Inverse nicht begrenzt sein muss. ⓘ

Klassische Räume

Grundlegende Beispiele für Banach-Räume sind: die Lp-Räume $L^{p}$ und ihre Spezialfälle, die Sequenzräume $\ell ^{p}$ die aus skalaren Folgen bestehen, die durch natürliche Zahlen indiziert sind $\mathbb {N}$darunter der Raum $\ell ^{1}$ der absolut summierbaren Folgen und der Raum $\ell ^{2}$ der quadratisch summierbaren Folgen; der Raum $c_{0}$ der gegen Null tendierenden Folgen und der Raum $\ell ^{\infty }$ der beschränkten Folgen; der Raum $C(K)$ der kontinuierlichen skalaren Funktionen auf einem kompakten Hausdorff-Raum $K,$ ausgestattet mit der Max-Norm,

$$\|f\|_{C(K)}=\max\{|f(x)|:x\in K\},\quad f\in C(K).$$

ⓘ

Nach dem Banach-Mazur-Theorem ist jeder Banach-Raum isometrisch isomorph zu einem Unterraum von irgendeinem $C(K).$ Für jeden trennbaren Banach-Raum $X,$ gibt es einen geschlossenen Unterraum $M$ von $\ell ^{1}$ derart, dass $X:=\ell ^{1}/M.$ ⓘ

Jeder Hilbert-Raum dient als Beispiel für einen Banach-Raum. Ein Hilbert-Raum $H$ auf $\mathbb {K} =\mathbb {R} ,\mathbb {C}$ ist vollständig für eine Norm der Form

$$\|x\|_{H}={\sqrt {\langle x,x\rangle }},$$

wobei

$$\langle \cdot ,\cdot \rangle :H\times H\to \mathbb {K}$$

ist das innere Produkt, linear in seinem ersten Argument, das die folgenden Bedingungen erfüllt:

$${\begin{aligned}\langle y,x\rangle &={\overline {\langle x,y\rangle }},\quad {\text{ for all }}x,y\in H\\\langle x,x\rangle &\geq 0,\quad {\text{ for all }}x\in H\\\langle x,x\rangle =0{\text{ if and only if }}x&=0.\end{aligned}}$$

ⓘ

Zum Beispiel ist der Raum $L^{2}$ ist ein Hilbert-Raum. ⓘ

Die Hardy-Räume, die Sobolev-Räume sind Beispiele für Banach-Räume, die mit $L^{p}$ Räumen verwandt sind und eine zusätzliche Struktur haben. Sie sind unter anderem in verschiedenen Bereichen der Analysis, der Harmonischen Analyse und der partiellen Differentialgleichungen von Bedeutung. ⓘ

Banach-Algebren

Eine Banach-Algebra ist ein Banach-Raum $A$ über $\mathbb {K} =\mathbb {R}$ oder $\mathbb {C} ,$ zusammen mit einer Struktur der Algebra über $\mathbb {K}$, so dass die Produktabbildung $A\times A\ni (a,b)\mapsto ab\in A$ stetig ist. Eine äquivalente Norm auf $A$ kann so gefunden werden, dass $\|ab\|\leq \|a\|\|b\|$ für alle $a,b\in A.$ ⓘ

Beispiele

• Der Banach-Raum $C(K)$ mit dem punktweisen Produkt, ist eine Banach-Algebra.
• Die Scheibenalgebra $A(\mathbf {D} )$ besteht aus Funktionen, die holomorph auf der offenen Einheitsscheibe $D\subseteq \mathbb {C}$ und stetig auf ihrem Abschluss: ${\overline {\mathbf {D} }}.$ Ausgestattet mit der maximalen Norm auf ${\overline {\mathbf {D} }},$ ist die Scheibenalgebra $A(\mathbf {D} )$ ist eine geschlossene Unteralgebra von $C\left({\overline {\mathbf {D} }}\right).$
• Die Wiener Algebra $A(\mathbf {T} )$ ist die Algebra der Funktionen auf dem Einheitskreis $\mathbf {T}$ mit absolut konvergenten Fourierreihen. Über die Abbildung, die eine Funktion auf $\mathbf {T}$ mit der Folge ihrer Fourier-Koeffizienten verbindet, ist diese Algebra isomorph zur Banach-Algebra $\ell ^{1}(Z),$ wobei das Produkt die Faltung von Folgen ist.
• Für jeden Banach-Raum $X,$ der Raum $B(X)$ der beschränkten linearen Operatoren auf $X,$ mit der Komposition von Karten als Produkt, eine Banach-Algebra ist.
• Eine C*-Algebra ist eine komplexe Banach-Algebra $A$ mit einer antilinearen Involution $a\mapsto a^{*}$ derart, dass $\left\|a^{*}a\right\|=\|a\|^{2}.$ Der Raum $B(H)$ von gebundenen linearen Operatoren auf einem Hilbert-Raum $H$ ist ein grundlegendes Beispiel für eine C*-Algebra. Das Gelfand-Naimark-Theorem besagt, dass jede C*-Algebra isometrisch isomorph zu einer C*-Unteralgebra von einigen $B(H).$ Der Raum $C(K)$ von komplexen stetigen Funktionen auf einem kompakten Hausdorff-Raum $K$ ist ein Beispiel für eine kommutative C*-Algebra, bei der die Involution jeder Funktion $f$ ihre komplexe Konjugierte ${\overline {f}}.$ ⓘ

Dualer Raum

Wenn $X$ ist ein normierter Raum und $\mathbb {K}$ das zugrundeliegende Feld (entweder die reellen oder die komplexen Zahlen), der kontinuierliche Dualraum ist der Raum der kontinuierlichen linearen Abbildungen von $X$ in $\mathbb {K} ,$ oder kontinuierliche lineare Funktionale. Die Notation für den kontinuierlichen Dualraum ist $X^{\prime }=B(X,\mathbb {K} )$ in diesem Artikel. Da $\mathbb {K}$ ein Banachraum ist (mit dem Absolutwert als Norm), ist das Dual $X^{\prime }$ ein Banach-Raum, für jeden normierten Raum $X.$ ⓘ

Das Hauptwerkzeug zum Nachweis der Existenz kontinuierlicher linearer Funktionale ist der Hahn-Banach-Satz. ⓘ

Hahn-Banach-Theorem - Sei $X$ sei ein Vektorraum über dem Feld $\mathbb {K} =\mathbb {R} ,\mathbb {C} .$ Ferner sei

• $Y\subseteq X$ ein linearer Unterraum sein,
• $p:X\to \mathbb {R}$ sei eine unterlineare Funktion und
• $f:Y\to \mathbb {K}$ sei ein lineares Funktional, so daß $\operatorname {Re} (f(y))\leq p(y)$ für alle $y\in Y.$

Dann gibt es ein lineares Funktional $F:X\to \mathbb {K}$} , so dass

$$F{\big \vert }_{Y}=f,\quad {\text{ and }}\quad {\text{ for all }}x\in X,\ \ \operatorname {Re} (F(x))\leq p(x).$$

ⓘ

Insbesondere kann jedes kontinuierliche lineare Funktional auf einem Unterraum eines normierten Raumes kontinuierlich auf den gesamten Raum ausgedehnt werden, ohne die Norm des Funktionals zu erhöhen. Ein wichtiger Spezialfall ist der folgende: Für jeden Vektor $x$ in einem normierten Raum $X,$ gibt es ein stetiges lineares Funktional $f$ auf $X$ derart, dass

$$f(x)=\|x\|_{X},\quad \|f\|_{X^{\prime }}\leq 1.$$

ⓘ

Wenn $x$ nicht gleich dem $\mathbf {0}$ Vektor ist, muss das Funktional $f$ die Norm Eins haben und wird als normierendes Funktional für $x.$ ⓘ

Das Hahn-Banach-Separations-Theorem besagt, dass zwei disjunkte, nicht leere konvexe Mengen in einem reellen Banach-Raum, von denen eine offen ist, durch eine geschlossene affine Hyperebene getrennt werden können. Die offene konvexe Menge liegt streng auf einer Seite der Hyperebene, die zweite konvexe Menge liegt auf der anderen Seite, kann aber die Hyperebene berühren. ⓘ

Eine Teilmenge $S$ in einem Banach-Raum $X$ ist total, wenn die lineare Spannweite von $S$ dicht ist in $X.$ Die Teilmenge $S$ ist total in $X$ dann und nur dann, wenn das einzige kontinuierliche lineare Funktional, das auf $S$ ist das $\mathbf {0}$ Funktional ist: Diese Äquivalenz folgt aus dem Hahn-Banach-Theorem. ⓘ

Wenn $X$ ist die direkte Summe zweier geschlossener linearer Teilräume $M$ und $N,$ dann ist das Dual $X^{\prime }$ von $X$ isomorph zur direkten Summe der Duale von $M$ und $N.$ Wenn $M$ ist ein geschlossener linearer Unterraum in $X,$ kann man die orthogonal zu $M$ dem Dual zuordnen,

$$M^{bot}=\left\{x^{\prime }\in X:x^{\prime }(m)=0,\ {\text{ for all }}m\in M\right\}.$$

ⓘ

Das Orthogonale $M^{\bot }$ ist ein geschlossener linearer Unterraum des Duals. Der Dual von $M$ ist isometrisch isomorph zu $X'/M^{\bot }.$ Der Dual von $X/M$ ist isometrisch isomorph zu $M^{\bot }.$ ⓘ

Das Dual eines trennbaren Banach-Raums muss nicht trennbar sein, aber:

Theorem - Sei $X$ ein normierter Raum sein. Wenn $X'$ trennbar ist, dann ist $X$ trennbar sein. ⓘ

Wenn $X'$ ist, kann das obige Kriterium für die Totalität verwendet werden, um die Existenz einer abzählbaren totalen Teilmenge zu beweisen in $X.$ ⓘ

Schwache Topologien

Die schwache Topologie auf einem Banach-Raum $X$ ist die gröbste Topologie auf $X$ für die alle Elemente $x^{\prime }$ im stetigen Dualraum $X^{\prime }$ stetig sind. Die Normtopologie ist also feiner als die schwache Topologie. Aus dem Hahn-Banach-Trennungssatz folgt, dass die schwache Topologie Hausdorff ist, und dass eine normgeschlossene konvexe Teilmenge eines Banach-Raums auch schwach geschlossen ist. Eine normkontinuierliche lineare Abbildung zwischen zwei Banachräumen $X$ und $Y$ ist ebenfalls schwach stetig, d. h. sie ist stetig von der schwachen Topologie von $X$ zu der von $Y.$ ⓘ

Wenn $X$ unendlich-dimensional ist, gibt es lineare Abbildungen, die nicht stetig sind. Der Raum $X^{*}$ aller linearen Abbildungen von $X$ auf das zugrundeliegende Feld $\mathbb {K}$ (dieser Raum $X^{*}$ wird der algebraische Dualraum genannt, um ihn zu unterscheiden von $X^{\prime }$ induziert auch eine Topologie auf $X$ die feiner ist als die schwache Topologie und in der Funktionalanalysis viel weniger verwendet wird. ⓘ

Auf einem dualen Raum $X^{\prime },$ gibt es eine Topologie, die schwächer ist als die schwache Topologie von $X^{\prime },$ genannt schwache* Topologie. Sie ist die gröbste Topologie auf $X^{\prime }$ für die alle Auswertungskarten $x^{\prime }\in X^{\prime }\mapsto x^{\prime }(x),$ wobei $x$ Bereiche über $X,$ stetig sind. Ihre Bedeutung ergibt sich aus dem Banach-Alaoglu-Theorem. ⓘ

Banach-Alaoglu-Theorem - Sei $X$ sei ein normierter Vektorraum. Dann ist die geschlossene Einheitskugel $B=\left\{x\in X:\|x\|\leq 1\right\}$ des Dualraums in der schwachen* Topologie kompakt. ⓘ

Der Banach-Alaoglu-Satz kann mit Hilfe des Satzes von Tychonoff über unendliche Produkte kompakter Hausdorff-Räume bewiesen werden. Wenn $X$ trennbar ist, ist die Einheitskugel $B^{\prime }$ des Duals ein metrisierbarer kompakter Raum in der schwachen* Topologie. ⓘ

Beispiele für duale Räume

Der Dual von $c_{0}$ ist isometrisch isomorph zu $\ell ^{1}$: Für jedes beschränkte lineare Funktional $f$ auf $c_{0},$ gibt es ein eindeutiges Element $y=\left\{y_{n}\right\}\in \ell ^{1}$ derart, dass

$$f(x)=\sum _{n\in \mathbb {N} }x_{n}y_{n},\qquad x=\{x_{n}\}\in c_{0},\ \ {\text{and}}\ \ \|f\|_{(c_{0})'}=\|y\|_{\ell _{1}}.$$

ⓘ

Der Dual von $\ell ^{1}$ ist isometrisch isomorph zu $\ell ^{\infty }$. Der Dual des Lebesgue-Raums $L^{p}([0,1])$ ist isometrisch isomorph zu $L^{q}([0,1])$ wenn $1\leq p<\infty$ und ${\frac {1}{p}}+{\frac {1}{q}}=1.$ ⓘ

Für jeden Vektor $y$ in einem Hilbert-Raum $H,$ die Abbildung

$$x\in H\to f_{y}(x)=\langle x,y\rangle$$

ⓘ

ein stetiges lineares Funktional definiert $f_{y}$ auf $H.$Das Rieszsche Repräsentationstheorem besagt, dass jedes stetige lineare Funktional auf $H$ von der Form $f_{y}$ für einen eindeutig definierten Vektor $y$ in $H.$ Die Abbildung $y\in H\to f_{y}$ ist eine antilineare isometrische Bijektion von $H$ auf ihr Dual $H'.$ Wenn die Skalare reell sind, ist diese Abbildung ein isometrischer Isomorphismus. ⓘ

Wenn $K$ ist ein kompakter topologischer Hausdorff-Raum, der Dual $M(K)$ von $C(K)$ ist der Raum der Radonmaße im Sinne von Bourbaki. Die Teilmenge $P(K)$ von $M(K)$ bestehend aus nichtnegativen Maßen der Masse 1 (Wahrscheinlichkeitsmaße) ist eine konvexe w*-geschlossene Teilmenge der Einheitskugel von $M(K).$ Die Extrempunkte von $P(K)$ sind die Dirac-Maße auf $K.$ Die Menge der Dirac-Maße auf $K,$ ausgestattet mit der w*-Topologie, ist homöomorph zu $K.$ ⓘ

Banach-Stein-Theorem - Wenn $K$ und $L$ kompakte Hausdorff-Räume sind und wenn $C(K)$ und $C(L)$ isometrisch isomorph sind, dann sind die topologischen Räume $K$ und $L$ homöomorph. ⓘ

Das Ergebnis wurde von Amir und Cambern auf den Fall erweitert, dass der multiplikative Banach-Mazur-Abstand zwischen $C(K)$ und $C(L)$ ist $<2.$ Das Theorem ist nicht mehr wahr, wenn der Abstand $=2.$ ⓘ

In der kommutativen Banach-Algebra $C(K),$ sind die Maximalideale genau Kerne von Dirac-Maßen auf $K,$

$$I_{x}=\ker \delta _{x}=\{f\in C(K):f(x)=0\},\quad x\in K.$$

ⓘ

Allgemeiner ausgedrückt, können die Maximalideale einer unitalen kommutativen Banach-Algebra nach dem Gelfand-Mazur-Theorem mit ihren Charakteren identifiziert werden - nicht nur als Mengen, sondern als topologische Räume: Erstere mit der Hull-Kernel-Topologie und letztere mit der w*-Topologie. In dieser Identifikation kann der maximale Idealraum als eine w*-kompakte Teilmenge der Einheitskugel im Dual betrachtet werden $A'.$ ⓘ

Theorem - Wenn $K$ ein kompakter Hausdorff-Raum ist, dann ist der maximale Idealraum $\Xi$ der Banach-Algebra $C(K)$ homöomorph zu $K.$ ⓘ

Nicht jede unitale kommutative Banach-Algebra ist von der Form $C(K)$ für einen kompakten Hausdorff-Raum $K.$ Diese Aussage gilt jedoch, wenn man $C(K)$ in die kleinere Kategorie der kommutativen C*-Algebren einordnet. Das Gelfandsche Repräsentationstheorem für kommutative C*-Algebren besagt, dass jede kommutative unitale C*-Algebra $A$ isometrisch isomorph zu einem $C(K)$ Raum. Der kompakte Hausdorff-Raum $K$ ist hier wiederum der maximale Idealraum, der im Kontext der C*-Algebra auch als das Spektrum von $A$ im Kontext der C*-Algebra genannt. ⓘ

Bidual

Wenn $X$ ist ein normierter Raum, das (kontinuierliche) Dual $X$ des Duals $X'$ wird Bidual genannt, oder zweites Dual von $X.$ Für jeden normierten Raum $X,$ gibt es eine natürliche Abbildung,

$${\begin{cases}F_{X}:X\to X\\F_{X}(x)(f)=f(x)&{\text{ for all }}x\in X,{\text{ and for all }}f\in X'\end{cases}}$$

ⓘ

Diese definiert $F_{X}(x)$ als ein kontinuierliches lineares Funktional auf $X^{\prime },$ d.h. ein Element von $X^{\prime \prime }.$ Die Abbildung $F_{X}:x\to F_{X}(x)$ ist eine lineare Abbildung von $X$ zu $X^{\prime \prime }.$ Als Folge der Existenz eines Normierungsfunktionals $f$ für jeden $x\in X,$ ist diese Karte $F_{X}$ isometrisch, also injektiv. ⓘ

Zum Beispiel ist das Dual von $X=c_{0}$ identifiziert mit $\ell ^{1},$ und das Dual von $\ell ^{1}$ identifiziert mit $\ell ^{\infty },$ dem Raum der beschränkten Skalarfolgen. Unter diesen Identifikationen, $F_{X}$ die Einschlusskarte von $c_{0}$ zu $\ell ^{\infty }.$ Sie ist zwar isometrisch, aber nicht onto. ⓘ

Wenn $F_{X}$ surjektiv ist, dann heißt der normierte Raum $X$ reflexiv genannt (siehe unten). Als Dual eines normierten Raums ist das Bidual $X$ vollständig, daher ist jeder reflexiv genormte Raum ein Banach-Raum. ⓘ

Unter Verwendung der isometrischen Einbettung $F_{X},$ ist es üblich, einen normierten Raum $X$ als eine Teilmenge seines Biduals zu betrachten. Wenn $X$ ein Banach-Raum ist, betrachtet man ihn als geschlossenen linearen Unterraum von $X^{\prime \prime }.$ Wenn $X$ nicht reflexiv ist, ist die Einheitskugel von $X$ eine echte Teilmenge der Einheitskugel von $X^{\prime \prime }.$ Das Goldstine-Theorem besagt, dass die Einheitskugel eines normierten Raums in der Einheitskugel des Biduals schwach*-verdichtet ist. Mit anderen Worten: Für jede $x$ im Bidual gibt es ein Netz $\left(x_{i}\right)_{i\in I}$ in $X$ so dass

$$\sup _{i\in I}\left\|x_{i}\right\|\leq \|x\|,\ \ x(f)=\lim _{i}f\left(x_{i}\right),\quad f\in X'.$$

ⓘ

Das Netz kann durch eine schwach*-konvergente Folge ersetzt werden, wenn das Dual $X'$ trennbar ist. Andererseits können die Elemente des Biduals von $\ell ^{1}$ die nicht in $\ell ^{1}$ können nicht schwach*-konvergente Folgen in $\ell ^{1},$ da $\ell ^{1}$ schwach sequentiell vollständig ist. ⓘ

Banachsche Theoreme

Hier sind die wichtigsten allgemeinen Ergebnisse über Banach-Räume, die auf die Zeit von Banachs Buch (Banach (1932)) zurückgehen und mit dem Satz über die Baire-Kategorie zusammenhängen. Diesem Satz zufolge kann ein vollständiger metrischer Raum (wie ein Banach-Raum, ein Fréchet-Raum oder ein F-Raum) nicht gleich einer Vereinigung von abzählbar vielen geschlossenen Teilmengen mit leeren Innenräumen sein. Daher kann ein Banach-Raum nicht die Vereinigung von abzählbar vielen geschlossenen Unterräumen sein, es sei denn, er ist bereits gleich einem von ihnen; ein Banach-Raum mit abzählbarer Hamel-Basis ist endlich-dimensional. ⓘ

Banach-Steinhaus-Theorem - Sei $X$ sei ein Banach-Raum und $Y$ sei ein normierter Vektorraum. Angenommen, dass $F$ sei eine Sammlung von kontinuierlichen linearen Operatoren aus $X$ zu $Y.$ Das Prinzip der gleichmäßigen Begrenztheit besagt, dass, wenn für alle $x$ in $X$ haben wir $\sup _{T\in F}\|T(x)\|_{Y}<\infty ,$ dann ist $\sup _{T\in F}\|T\|_{Y}<\infty .$ ⓘ

Das Banach-Steinhaus-Theorem ist nicht auf Banach-Räume beschränkt. Er kann zum Beispiel auf den Fall ausgedehnt werden, dass $X$ ein Fréchet-Raum ist, sofern die Schlussfolgerung wie folgt modifiziert wird: Unter der gleichen Hypothese gibt es eine Nachbarschaft $U$ von $\mathbf {0}$ in $X$ so dass alle $T$ in $F$ gleichmäßig begrenzt sind auf $U,$

$$\sup _{T\in F}\sup _{x\in U}\;\|T(x)\|_{Y}<\infty .$$

ⓘ

Der Satz von der offenen Abbildung - Sei $X$ und $Y$ seien Banach-Räume und $T:X\to Y$ sei ein surjektiver kontinuierlicher linearer Operator, dann $T$ eine offene Abbildung. ⓘ

Korollar - Jeder eineindeutige beschränkte lineare Operator von einem Banachraum auf einen Banachraum ist ein Isomorphismus. ⓘ

Der erste Isomorphiesatz für Banachräume - Angenommen, dass $X$ und $Y$ Banachräume sind und dass $T\in B(X,Y).$ Nehmen wir weiter an, dass der Bereich von $T$ geschlossen ist in $Y.$ Dann ist $X/\ker T$ isomorph zu $T(X).$ ⓘ

Dieses Ergebnis ist eine direkte Folge des vorangegangenen Banach-Isomorphiesatzes und der kanonischen Faktorisierung beschränkter linearer Abbildungen. ⓘ

Korollar - Wenn ein Banach-Raum $X$ die interne direkte Summe von geschlossenen Unterräumen ist $M_{1},\ldots ,M_{n},$ dann ist $X$ isomorph zu $M_{1}\oplus \cdots \oplus M_{n}.$ ⓘ

Dies ist eine weitere Konsequenz des Banachschen Isomorphiesatzes, angewandt auf die kontinuierliche Bijektion von $M_{1}\oplus \cdots \oplus M_{n}$ auf $X$ sendet $m_{1},\cdots ,m_{n}$ auf die Summe $m_{1}+\cdots +m_{n}.$ ⓘ

Der Satz vom geschlossenen Graphen - Sei $T:X\to Y$ sei eine lineare Abbildung zwischen Banach-Räumen. Der Graph von $T$ geschlossen ist in $X\times Y$ wenn und nur wenn $T$ ist stetig. ⓘ

Reflexivität

Der normierte Raum $X$ wird reflexiv genannt, wenn die natürliche Abbildung

$${\begin{cases}F_{X}:X\to X\\F_{X}(x)(f)=f(x)&{\text{ for all }}x\in X,{\text{ and for all }}f\in X'\end{cases}}$$

surjektiv ist. Reflexiv genormte Räume sind Banachräume. ⓘ

Theorem - Wenn $X$ ist ein reflexiver Banachraum, jeder geschlossene Unterraum von $X$ und jeder Quotientenraum von $X$ sind reflexiv. ⓘ

Dies ist eine Folge des Hahn-Banach-Satzes. Ferner gilt nach dem Satz der offenen Abbildung: Gibt es einen beschränkten linearen Operator vom Banachraum $X$ auf den Banach-Raum $Y,$ dann ist $Y$ reflexiv ist. ⓘ

Theorem - Wenn $X$ ist ein Banach-Raum, dann ist $X$ reflexiv, wenn und nur wenn $X^{\prime }$ reflexiv ist. ⓘ

Korollar - Sei $X$ sei ein reflexiver Banach-Raum. Dann ist $X$ trennbar, wenn und nur wenn $X^{\prime }$ trennbar sein. ⓘ

In der Tat, wenn der Dual $Y^{\prime }$ eines Banach-Raums $Y$ trennbar ist, dann ist $Y$ trennbar ist. Wenn $X$ reflexiv und trennbar ist, dann ist der Dual von $X^{\prime }$ trennbar, also sind $X^{\prime }$ trennbar sein. ⓘ

Theorem - Angenommen, dass $X_{1},\ldots ,X_{n}$ normierte Räume sind und dass $X=X_{1}\oplus \cdots \oplus X_{n}.$ Dann ist $X$ reflexiv ist, wenn und nur wenn jeder $X_{j}$ reflexiv ist. ⓘ

Hilbert-Räume reflexiv sind. Die $L^{p}$ Räume sind reflexiv, wenn $1<p<\infty .$ Ganz allgemein sind gleichmäßig konvexe Räume nach dem Milman-Pettis-Theorem reflexiv. Die Räume $c_{0},\ell ^{1},L^{1}([0,1]),C([0,1])$ sind nicht reflexiv. In diesen Beispielen für nicht-reflexive Räume $X,$ ist das Bidual $X$ "viel größer" als $X.$ Nämlich unter der natürlichen isometrischen Einbettung von $X$ in $X$ gemäß dem Hahn-Banach-Theorem ist der Quotient $X^{\prime \prime }/X$ unendlich-dimensional und sogar untrennbar. Robert C. James hat jedoch ein Beispiel für einen nicht-reflexiven Raum konstruiert, der üblicherweise "James-Raum" genannt und mit $J,$ so dass der Quotient $J^{\prime \prime }/J$ eindimensional ist. Außerdem ist dieser Raum $J$ isometrisch isomorph zu seinem Bidual. ⓘ

Theorem - Ein Banach-Raum $X$ ist dann und nur dann reflexiv, wenn seine Einheitskugel in der schwachen Topologie kompakt ist. ⓘ

Wenn $X$ reflexiv ist, folgt, dass alle geschlossenen und beschränkten konvexen Teilmengen von $X$ schwach kompakt sind. In einem Hilbert-Raum $H,$ wird die schwache Kompaktheit der Einheitskugel sehr oft auf folgende Weise verwendet: Jede beschränkte Folge in $H$ hat schwach konvergente Teilsequenzen. ⓘ

Die schwache Kompaktheit der Einheitskugel ist ein Hilfsmittel, um in reflexiven Räumen Lösungen für bestimmte Optimierungsprobleme zu finden. Zum Beispiel kann jede konvexe stetige Funktion auf der Einheitskugel $B$ eines reflexiven Raums erreicht ihr Minimum an einem Punkt in $B.$ ⓘ

Ein Spezialfall des vorangegangenen Ergebnisses liegt vor, wenn $X$ ein reflexiver Raum über $\mathbb {R} ,$ jede stetige lineare Funktion $f$ in $X^{\prime }$ sein Maximum erreicht $\|f\|$ auf der Einheitskugel von $X.$ Das folgende Theorem von Robert C. James liefert eine umgekehrte Aussage. ⓘ

James' Theorem - Für einen Banach-Raum sind die beiden folgenden Eigenschaften äquivalent:

• $X$ reflexiv ist.
• für alle $f$ in $X^{\prime }$ Es gibt $x\in X$ mit $\|x\|\leq 1,$ so dass $f(x)=\|f\|.$ ⓘ

Das Theorem kann erweitert werden, um eine Charakterisierung schwach kompakter konvexer Mengen zu geben. ⓘ

Auf jedem nicht-reflexiven Banach-Raum $X,$ gibt es kontinuierliche lineare Funktionale, die nicht normiert sind. Das Bishop-Phelps-Theorem besagt jedoch, dass normhaltige Funktionale im Dualen normdicht sind. $X^{\prime }$ von $X.$ ⓘ

Schwache Konvergenzen von Folgen

Eine Folge $\left\{x_{n}\right\}$ in einem Banach-Raum $X$ ist schwach konvergent zu einem Vektor $x\in X$ wenn $\left\{f\left(x_{n}\right)\right\}$ konvergiert zu $f(x)$ für jede stetige lineare Funktion $f$ im Dual $X^{\prime }.$ Die Folge $\left\{x_{n}\right\}$ ist eine schwache Cauchy-Folge, wenn $\left\{f\left(x_{n}\right)\right\}$ zu einer skalaren Grenze konvergiert $L(f),,$ für jeden $f$ in $X^{\prime }.$ Eine Folge $\left\{f_{n}\right\}$ im Dual $X^{\prime }$ ist schwach* konvergent zu einem Funktional $f\in X^{\prime }$ wenn $f_{n}(x)$ konvergiert zu $f(x)$ für jeden $x$ in $X.$ Schwach Cauchy-Sequenzen, schwach konvergente und schwach* konvergente Sequenzen sind normbeschränkt, als Folge des Banach-Steinhaus-Theorems. ⓘ

Wenn die Folge $\left\{x_{n}\right\}$ in $X$ eine schwach Cauchy-Folge ist, definiert der Grenzwert $L$ oben ein beschränktes lineares Funktional auf dem Dual $X^{\prime },$ das heißt, ein Element $L$ des Biduals von $X,$ und $L$ ist der Grenzwert von $\left\{x_{n}\right\}$ in der schwachen*-Topologie des Biduals. Der Banach-Raum $X$ ist schwach sequentiell vollständig, wenn jede schwache Cauchy-Folge schwach konvergent ist in $X.$ Aus der vorangegangenen Diskussion folgt, dass reflexive Räume schwach sequentiell vollständig sind. ⓘ

Theorem  - Für jedes Maß $\mu ,$ der Raum $L^{1}(\mu )$ schwach sequentiell vollständig ist. ⓘ

Eine orthonormale Folge in einem Hilbert-Raum ist ein einfaches Beispiel für eine schwach konvergente Folge, deren Grenze gleich dem $\mathbf {0}$ Vektor. Die Einheitsvektorbasis von $\ell ^{p}$ für $1<p<\infty ,$ oder von $c_{0},$ ist ein weiteres Beispiel für eine schwach konvergente Folge, d. h. eine Folge, die schwach konvergiert zu $\mathbf {0} .$ Für jede schwach ungültige Folge in einem Banach-Raum gibt es eine Folge von konvexen Kombinationen von Vektoren aus der gegebenen Folge, die normkonvergent ist zu $\mathbf {0} .$ ⓘ

Die Einheitsvektorbasis von $\ell ^{1}$ ist nicht schwach Cauchy. Schwach Cauchy-Folgen in $\ell ^{1}$ sind schwach konvergent, da $L^{1}$-Räume schwach sequentiell vollständig sind. Tatsächlich sind schwach konvergente Folgen in $\ell ^{1}$ sind normkonvergent. Dies bedeutet, dass $\ell ^{1}$ die Schur'sche Eigenschaft erfüllt. ⓘ

Ergebnisse, die die ℓ¹ Basis

Schwache Cauchy-Folgen und die $\ell ^{1}$ Basis sind die umgekehrten Fälle der Dichotomie, die in dem folgenden tiefen Ergebnis von H. P. Rosenthal aufgestellt wurde. ⓘ

Theorem - Sei $\left\{x_{n}\right\}_{n\in \mathbb {N} }$ Sei eine beschränkte Folge in einem Banach-Raum. Entweder $\left\{x_{n}\right\}_{n\in \mathbb {N} }$ eine schwache Cauchy-Teilfolge, oder sie hat eine Teilfolge, die der Standard-Einheitsvektorbasis von $\ell ^{1}.$ ⓘ

Ein Komplement zu diesem Ergebnis stammt von Odell und Rosenthal (1975). ⓘ

Theorem - Sei $X$ sei ein trennbarer Banach-Raum. Die folgenden Aussagen sind äquivalent:

• Der Raum $X$ enthält keinen geschlossenen Unterraum, der isomorph zu $\ell ^{1}.$
• Jedes Element des Biduals $X$ ist der schwache*-Grenzwert einer Folge $\left\{x_{n}\right\}$ in $X.$ ⓘ

Nach dem Goldstine-Theorem ist jedes Element der Einheitskugel $B^{\prime \prime }$ von $X^{\prime \prime }$ die schwache* Grenze eines Netzes in der Einheitskugel von $X.$ Wenn $X$ enthält nicht $\ell ^{1},$ jedes Element von $B^{\prime \prime }$ ist schwach*-Grenze eines Folge in der Einheitskugel von $X.$ ⓘ

Wenn der Banach-Raum $X$ trennbar ist, ist die Einheitskugel des Duals $X^{\prime },$ die mit der schwachen*-Topologie ausgestattet ist, ein metrisierbarer kompakter Raum $K,$ und jedes Element $x^{\prime \prime }$ des Duals $X^{\prime \prime }$ definiert eine beschränkte Funktion auf $K$:

$$x'\in K\mapsto x(x'),\quad \left|x(x')\right|\leq \left\|x\right\|.$$

ⓘ

Diese Funktion ist kontinuierlich für die kompakte Topologie von $K$ wenn und nur wenn $x^{\prime \prime }$ ist tatsächlich in $X,$ als Teilmenge von $X^{\prime \prime }.$ Für den Rest des Absatzes wird zusätzlich angenommen, dass $X$ enthält nicht $\ell ^{1}.$ Nach dem vorhergehenden Ergebnis von Odell und Rosenthal ist die Funktion $x^{\prime \prime }$ der punktweise Grenzwert auf $K$ einer Folge $\left\{x_{n}\right\}\subseteq X$ von stetigen Funktionen auf $K,$ und ist daher eine Funktion der ersten Baire-Klasse auf $K.$ Die Einheitskugel des Biduals ist eine punktweise kompakte Teilmenge der ersten Baire-Klasse auf $K.$ ⓘ

Sequenzen, schwache und schwache* Kompaktheit

Wenn $X$ trennbar ist, ist die Einheitskugel des Duals nach dem Banach-Alaoglu-Theorem schwach*-kompakt und für die schwache*-Topologie metrisierbar, so dass jede beschränkte Folge im Dual schwach*-konvergente Teilfolgen hat. Dies gilt für trennbare reflexive Räume, aber in diesem Fall gilt noch mehr, wie im Folgenden erklärt wird. ⓘ

Die schwache Topologie eines Banach-Raums $X$ ist metrisierbar, wenn und nur wenn $X$ endlich-dimensional ist. Wenn der Dual $X'$ separabel ist, ist die schwache Topologie der Einheitskugel von $X$ metrifizierbar. Dies gilt insbesondere für trennbare reflexive Banach-Räume. Obwohl die schwache Topologie der Einheitskugel im Allgemeinen nicht metrifizierbar ist, kann man die schwache Kompaktheit durch Sequenzen charakterisieren. ⓘ

Eberlein-Šmulisches Theorem - Eine Menge $A$ in einem Banach-Raum ist dann und nur dann relativ schwach kompakt, wenn jede Folge $\left\{a_{n}\right\}$ in $A$ eine schwach konvergente Teilsequenz hat. ⓘ

Ein Banach-Raum $X$ ist dann und nur dann reflexiv, wenn jede beschränkte Folge in $X$ eine schwach konvergente Teilsequenz hat. ⓘ

Eine schwach kompakte Teilmenge $A$ in $\ell ^{1}$ norm-kompakt ist. In der Tat hat jede Folge in $A$ hat schwach konvergente Teilfolgen nach Eberlein-Šmulian, die nach der Schur-Eigenschaft von $\ell ^{1}.$ ⓘ

Schauder-Basen

Eine Schauder-Basis in einem Banach-Raum $X$ ist eine Folge $\left\{e_{n}\right\}_{n\geq 0}$ von Vektoren in $X$ mit der Eigenschaft, dass für jeden Vektor $x\in X,$ gibt es eindeutig definierte Skalare $\left\{x_{n}\right\}_{n\geq 0}$ in Abhängigkeit von $x,$ derart, dass

$$x=\sum _{n=0}^{\infty }x_{n}e_{n},\quad {\textit {i.e.,}}\quad x=\lim _{n}P_{n}(x),\ P_{n}(x):=\sum _{k=0}^{n}x_{k}e_{k}.$$

ⓘ

Banach-Räume mit Schauder-Basis sind notwendigerweise trennbar, da die abzählbare Menge der endlichen Linearkombinationen mit rationalen Koeffizienten (z. B.) dicht ist. ⓘ

Aus dem Banach-Steinhaus-Theorem folgt, dass die linearen Zuordnungen $\left\{P_{n}\right\}$ einheitlich durch eine Konstante begrenzt sind $C.$ Sei $\left\{e_{n}^{*}\right\}$ die Koordinatenfunktionale bezeichnen, die jeder Koordinate $x$ in $X$ die Koordinate $x_{n}$ von $x$ in der obigen Erweiterung zuordnen. Sie werden biorthogonale Funktionale genannt. Wenn die Basisvektoren die Norm $1,$ haben, haben die Koordinatenfunktionale $\left\{e_{n}^{*}\right\}$ die Norm $\,\leq 2C$ in dem Dual von $X.$ ⓘ

Die meisten klassischen trennbaren Räume haben explizite Basen. Das Haar-System $\left\{h_{n}\right\}$ ist eine Basis für $L^{p}([0,1]),1\leq p<\infty .$ Das trigonometrische System ist eine Basis in $L^{p}(\mathbf {T} )$ wenn $1<p<\infty .$ Das Schauder-System ist eine Basis im Raum $C([0,1]).$ Die Frage, ob die Scheibenalgebra $A(\mathbf {D} )$ eine Basis hat, blieb mehr als vierzig Jahre lang offen, bis Bočkarev 1974 zeigte, dass $A(\mathbf {D} )$ eine Basis zulässt, die aus dem Franklin-System konstruiert ist. ⓘ

Da jeder Vektor $x$ in einem Banach-Raum $X$ mit einer Basis ist der Grenzwert von $P_{n}(x),$ mit $P_{n}$ von endlichem Rang und gleichmäßig begrenzt ist, erfüllt der Raum $X$ die Eigenschaft der begrenzten Approximation. Das erste Beispiel von Enflo für einen Raum, der die Approximationseigenschaft nicht erfüllt, war gleichzeitig das erste Beispiel für einen separablen Banach-Raum ohne Schauder-Basis. ⓘ

Robert C. James charakterisierte die Reflexivität in Banachräumen mit einer Basis: der Raum $X$ mit einer Schauder-Basis ist dann und nur dann reflexiv, wenn die Basis sowohl schrumpfend als auch begrenzt vollständig ist. In diesem Fall bilden die biorthogonalen Funktionale eine Basis des Duals von $X.$ ⓘ

Tensorprodukt

Sei $X$ und $Y$ seien zwei $\mathbb {K}$-Vektorräume. Das Tensorprodukt $X\otimes Y$ von $X$ und $Y$ ist ein $\mathbb {K}$-Vektorraum $Z$ mit einer bilinearen Abbildung $T:X\times Y\to Z$ die die folgende universelle Eigenschaft hat:

Wenn $T_{1}:X\times Y\to Z_{1}$ Ist eine beliebige bilineare Abbildung in einen $\mathbb {K}$-Vektorraum $Z_{1},$ dann gibt es eine eindeutige lineare Abbildung $f:Z\to Z_{1}$ derart, dass $T_{1}=f\circ T.$ ⓘ

Das Bild unter $T$ eines Paares $(x,y)$ in $X\times Y$ wird bezeichnet durch $x\otimes y,$ und wird einfacher Tensor genannt. Jedes Element $z$ in $X\otimes Y$ ist eine endliche Summe von solchen einfachen Tensoren. ⓘ

Es gibt verschiedene Normen, die auf das Tensorprodukt der zugrundeliegenden Vektorräume gelegt werden können, unter anderem die projektive Kreuznorm und die injektive Kreuznorm, die 1955 von A. Grothendieck eingeführt wurden. ⓘ

Im Allgemeinen ist das Tensorprodukt von vollständigen Räumen nicht wieder vollständig. Wenn man mit Banachräumen arbeitet, ist es üblich zu sagen, dass das projektive Tensorprodukt zweier Banachräume $X$ und $Y$ ist das Vervollständigung $X{\widehat {\otimes }}_{\pi }Y$ des algebraischen Tensorprodukts $X\otimes Y$ mit der projektiven Tensornorm ausgestattet ist, und in ähnlicher Weise für das injektive Tensorprodukt $X{\widehat {\otimes }}_{\varepsilon }Y.$ Grothendieck bewies insbesondere, dass ⓘ

$${\begin{aligned}C(K){\widehat {\otimes }}_{\varepsilon }Y&\simeq C(K,Y),\\L^{1}([0,1]){\widehat {\otimes }}_{\pi }Y&\simeq L^{1}([0,1],Y),\end{aligned}}$$

wobei $K$ ein kompakter Hausdorff-Raum ist, $C(K,Y)$ der Banach-Raum der stetigen Funktionen von $K$ zu $Y$ und $L^{1}([0,1],Y)$ der Raum der Bochner-meßbaren und integrablen Funktionen von $[0,1]$ zu $Y,$ ist und wo die Isomorphismen isometrisch sind. Die beiden obigen Isomorphismen sind die jeweiligen Erweiterungen der Karte, die den Tensor $f\otimes y$ zu der vektorwertigen Funktion $s\in K\to f(s)y\in Y.$ ⓘ

Tensorprodukte und die Approximationseigenschaft

Sei $X$ sei ein Banach-Raum. Das Tensorprodukt $X'{\widehat {\otimes }}_{\varepsilon }X$ ist isometrisch identifiziert mit der Schließung in $B(X)$ der Menge der Operatoren endlichen Ranges. Wenn $X$ die Approximationseigenschaft hat, fällt diese Schließung mit dem Raum der kompakten Operatoren auf $X.$ ⓘ

Für jeden Banach-Raum $Y,$ gibt es eine natürliche Norm $1$ lineare Karte

$$Y{\widehat {\otimes }}_{\pi }X\to Y{\widehat {\otimes }}_{\varepsilon }X$$

die man durch Erweiterung der Identitätskarte des algebraischen Tensorprodukts erhält. Grothendieck verband das Approximationsproblem mit der Frage, ob diese Karte eineindeutig ist, wenn $Y$ das Dual von $X.$ Genauer gesagt, für jeden Banach-Raum $X,$ die Abbildung

$$X'{\widehat {\otimes }}_{\pi }X\ \longrightarrow X'{\widehat {\otimes }}_{\varepsilon }X$$

dann und nur dann eineindeutig, wenn $X$ die Eigenschaft der Annäherung hat. ⓘ

Grothendieck vermutete, dass $X{\widehat {\otimes }}_{\pi }Y$ und $X{\widehat {\otimes }}_{\varepsilon }Y$ unterschiedlich sein muss, wenn $X$ und $Y$ unendlich-dimensionale Banach-Räume sind. Dies wurde 1983 von Gilles Pisier widerlegt. Pisier konstruierte einen unendlich-dimensionalen Banach-Raum $X$ derart, dass $X{\widehat {\otimes }}_{\pi }X$ und $X{\widehat {\otimes }}_{\varepsilon }X$ gleich sind. Außerdem ist dieser Raum, genau wie Enflo's Beispiel, ein $X$ ein "handgemachter" Raum, der nicht die Eigenschaft der Annäherung besitzt. Auf der anderen Seite bewies Szankowski, dass der klassische Raum $B\left(\ell ^{2}\right)$ nicht die Eigenschaft der Annäherung hat. ⓘ

Einige Klassifizierungsergebnisse

Charakterisierungen des Hilbert-Raums unter den Banach-Räumen

Eine notwendige und hinreichende Bedingung dafür, dass die Norm eines Banach-Raums $X$ einem inneren Produkt zugeordnet werden kann, ist die Parallelogrammidentität:

Parallelogramm-Identität - für alle $x,y\in X:\qquad \|x+y\|^{2}+\|x-y\|^{2}=2\left(\|x\|^{2}+\|y\|^{2}\right).$ ⓘ

Daraus folgt z.B., dass der Lebesgue-Raum $L^{p}([0,1])$ nur dann ein Hilbert-Raum ist, wenn $p=2.$ Wenn diese Identität erfüllt ist, ist das zugehörige innere Produkt durch die Polarisationsidentität gegeben. Im Fall von reellen Skalaren ergibt sich dies:

$$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}\right).$$

ⓘ

Für komplexe Skalare definiert man das innere Produkt so, dass es $\mathbb {C}$-linear in $x,$ antilinear in $y,$ die Polarisationsidentität ergibt:

$$\langle x,y\rangle ={\tfrac {1}{4}}\left(\|x+y\|^{2}-\|x-y\|^{2}+i\left(\|x+iy\|^{2}-\|x-iy\|^{2}\right)\right).$$

ⓘ

Um zu sehen, dass das Parallelogrammgesetz ausreichend ist, muss man im reellen Fall beachten, dass $\langle x,y\rangle$ symmetrisch ist und im komplexen Fall die hermitesche Symmetrieeigenschaft erfüllt und $\langle ix,y\rangle =i\langle x,y\rangle .$ Das Parallelogrammgesetz impliziert, dass $\langle x,y\rangle$ additiv ist in $x.$ Daraus folgt, dass sie linear über den rationalen Zahlen ist, also linear durch Stetigkeit. ⓘ

Es gibt mehrere Charakterisierungen von Räumen, die isomorph (und nicht isometrisch) zu Hilbert-Räumen sind. Das Parallelogrammgesetz kann auf mehr als zwei Vektoren ausgedehnt und durch die Einführung einer zweiseitigen Ungleichung mit einer Konstante abgeschwächt werden $c\geq 1$: Kwapień bewies, dass wenn

$$c^{-2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}\leq \operatorname {Ave} _{\pm }\left\|\sum _{k=1}^{n}\pm x_{k}\right\|^{2}\leq c^{2}\sum _{k=1}^{n}\left\|x_{k}\right\|^{2}$$

für jede ganze Zahl $n$ und alle Familien von Vektoren$\left\{x_{1},\ldots ,x_{n}\right\}\subseteq X,$ dann ist der Banach-Raum $X$ isomorph zu einem Hilbert-Raum ist. Hier, $\operatorname {Ave} _{\pm }$ den Durchschnitt über die $2^{n}$ mögliche Wahl der Vorzeichen $\pm 1.$ Im selben Artikel bewies Kwapień, dass die Gültigkeit eines Banach-bewerteten Parseval-Satzes für die Fourier-Transformation Banach-Räume charakterisiert, die zu Hilbert-Räumen isomorph sind. ⓘ

Lindenstrauss und Tzafriri bewiesen, dass ein Banach-Raum, in dem jeder geschlossene lineare Unterraum komplementär ist (d.h. der Bereich einer begrenzten linearen Projektion ist), zu einem Hilbert-Raum isomorph ist. Der Beweis beruht auf Dvoretzkys Theorem über euklidische Schnitte hochdimensionaler zentralsymmetrischer konvexer Körper. Mit anderen Worten besagt der Satz von Dvoretzky, dass für jede ganze Zahl $n,$ jeder endlich-dimensionale normierte Raum, dessen Dimension ausreichend groß ist im Vergleich zu $n,$ Unterräume enthält, die nahezu isometrisch zu dem $n$-dimensionalen euklidischen Raum. ⓘ

Das nächste Ergebnis liefert die Lösung des so genannten homogenen Raumproblems. Ein unendlich-dimensionaler Banach-Raum $X$ gilt als homogen, wenn er zu allen seinen unendlich-dimensionalen geschlossenen Unterräumen isomorph ist. Ein Banach-Raum, der isomorph zu $\ell ^{2}$ ist homogen, und Banach fragt nach der Umkehrung. ⓘ

Theorem - Ein Banach-Raum, der zu allen seinen unendlich-dimensionalen geschlossenen Unterräumen isomorph ist, ist isomorph zu einem separablen Hilbert-Raum. ⓘ

Ein unendlich-dimensionaler Banach-Raum ist hereditär unzerlegbar, wenn kein Unterraum von ihm isomorph zu der direkten Summe zweier unendlich-dimensionaler Banach-Räume sein kann. Der Gowers-Dichotomiesatz besagt, dass jeder unendlich-dimensionale Banach-Raum $X$ entweder einen Unterraum $Y$ mit unbedingter Basis oder einen hereditär unzerlegbaren Unterraum $Z,$ und insbesondere, $Z$ nicht isomorph zu seinen geschlossenen Hyperebenen ist. Wenn $X$ homogen ist, muss er also eine unbedingte Basis haben. Aus der von Komorowski und Tomczak-Jaegermann erhaltenen Teillösung für Räume mit einer unbedingten Basis folgt, dass $X$ isomorph zu $\ell ^{2}.$ ⓘ

Metrische Klassifikation

Wenn $T:X\to Y$ eine Isometrie des Banach-Raums $X$ auf den Banach-Raum $Y$ (wobei beide $X$ und $Y$ sind Vektorräume über $\mathbb {R}$), dann besagt das Mazur-Ulam-Theorem, dass $T$ eine affine Transformation sein muss. Insbesondere, wenn $T(0_{X})=0_{Y},$ dies ist $T$ bildet die Nullstelle von $X$ auf die Nullstelle von $Y,$ dann ist $T$ linear sein muss. Dieses Ergebnis impliziert, dass die Metrik in Banach-Räumen, und allgemeiner in normierten Räumen, deren lineare Struktur vollständig abbildet. ⓘ

Topologische Klassifizierung

Endlich dimensionale Banach-Räume sind als topologische Räume nur dann homöomorph, wenn sie die gleiche Dimension wie reelle Vektorräume haben. ⓘ

Das Anderson-Kadec-Theorem (1965-66) beweist, dass zwei beliebige unendlich-dimensionale trennbare Banachräume als topologische Räume homöomorph sind. Das Kadec-Theorem wurde von Torunczyk erweitert, der bewies, dass zwei beliebige Banach-Räume nur dann homöomorph sind, wenn sie denselben Dichtecharakter haben, d. h. die minimale Kardinalität einer dichten Teilmenge. ⓘ

Räume mit kontinuierlichen Funktionen

Wenn zwei kompakte Hausdorff-Räume $K_{1}$ und $K_{2}$ homöomorph sind, sind die Banach-Räume $C\left(K_{1}\right)$ und $C\left(K_{2}\right)$ isometrisch. Umgekehrt, wenn $K_{1}$ nicht homöomorph ist zu $K_{2},$ ist, muss der (multiplikative) Banach-Mazur-Abstand zwischen $C\left(K_{1}\right)$ und $C\left(K_{2}\right)$ größer oder gleich sein als $2,$ siehe oben die Ergebnisse von Amir und Cambern. Obwohl nicht abzählbare kompakte metrische Räume verschiedene Homöomorphie-Typen haben können, hat man das folgende Ergebnis von Milutin:

Theorem - Sei $K$ Sei ein nicht abzählbarer kompakter metrischer Raum. Dann $C(K)$ isomorph zu $C([0,1]).$ ⓘ

Die Situation ist anders für abzählbar unendliche kompakte Hausdorff-Räume. Jeder abzählbar unendliche kompakte $K$ ist homöomorph zu einem geschlossenen Intervall von Ordnungszahlen

$$\langle 1,\alpha \rangle =\{\gamma \ :\ 1\leq \gamma \leq \alpha \}$$

ausgestattet mit der Ordnungstopologie, wobei $\alpha$ eine abzählbar unendliche Ordnungszahl ist. Der Banach-Raum $C(K)$ ist dann isometrisch zu C(⟨1, α⟩). Wenn $\alpha ,\beta$ zwei abzählbar unendliche Ordinalzahlen sind, und unter der Annahme $\alpha \leq \beta ,$ sind die Räume C(⟨1, α⟩) und C(⟨1, β⟩) isomorph, wenn und nur wenn β < α^ω. Zum Beispiel sind die Banach-Räume

$$C(\langle 1,\omega \rangle ),\ C(\langle 1,\omega ^{\omega }\rangle ),\ C(\langle 1,\omega ^{\omega ^{2}}\rangle ),\ C(\langle 1,\omega ^{\omega ^{3}}\rangle ),\cdots ,C(\langle 1,\omega ^{\omega ^{\omega }}\rangle ),\cdots$$

nicht isomorph zueinander. ⓘ

Beispiele

Glossar der Symbole für die folgende Tabelle:

• $\mathbb {F}$ bezeichnet den Bereich der reellen Zahlen $\mathbb {R}$ oder komplexe Zahlen $\mathbb {C} .$
• $K$ ist ein kompakter Hausdorff-Raum.
• $p,q\in \mathbb {R}$ sind reelle Zahlen mit $1<p,q<\infty$ die Hölder-Konjugierte sind, d.h. sie erfüllen ${\frac {1}{q}}+{\frac {1}{p}}=1$ und somit auch $q={\frac {p}{p-1}}.$
• $\Sigma$ ist ein $\sigma$-Algebra der Mengen.
• $\Xi$ ist eine Algebra von Mengen (für Räume, die nur endliche Additivität erfordern, wie der ba-Raum).
• $\mu$ ist ein Maß mit Variation $|\mu |.$ Ein positives Maß ist eine reell-wertige positive Mengenfunktion, die auf einer $\sigma$-Algebra, die abzählbar additiv ist. ⓘ

Klassische Banach-Räume ⓘ
	Dualer Raum	Reflexiv	Schwach sequentiell vollständig	Norm		Anmerkungen
$\mathbb {F} ^{n}$	$\mathbb {F} ^{n}$	Ja	Ja	$\|x\|_{2}$	$=\left(\sum _{i=1}^{n}|x_{i}|^{2}\right)^{1/2}$	Euklidischer Raum
$\ell _{p}^{n}$	$\ell _{q}^{n}$	Ja	Ja	$\|x\|_{p}$	$=\left(\sum _{i=1}^{n}|x_{i}|^{p}\right)^{\frac {1}{p}}$
$\ell _{\infty }^{n}$	$\ell _{1}^{n}$	Ja	Ja	$\|x\|_{\infty }$	$=\max \nolimits _{1\leq i\leq n}|x_{i}|$
$\ell ^{p}$	$\ell ^{q}$	Ja	Ja	$\|x\|_{p}$	$=\left(\sum _{i=1}^{\infty }|x_{i}|^{p}\right)^{\frac {1}{p}}$
$\ell ^{1}$	$\ell ^{\infty }$	Nein	Ja	$\|x\|_{1}$	$=\sum _{i=1}^{\infty }\left|x_{i}\right|$
$\ell ^{\infty }$	$\operatorname {ba}$	Nein	Nein	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$
$\operatorname {c}$	$\ell ^{1}$	Nein	Nein	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$
$c_{0}$	$\ell ^{1}$	Nein	Nein	$\|x\|_{\infty }$	$=\sup \nolimits _{i}\left|x_{i}\right|$	Isomorph, aber nicht isometrisch zu $c.$
$\operatorname {bv}$	$\ell ^{\infty }$	Nein	Ja	$\|x\|_{bv}$	$=\left|x_{1}\right|+\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|$	Isometrisch isomorph zu $\ell ^{1}.$
$\operatorname {bv} _{0}$	$\ell ^{\infty }$	Nein	Ja	$\|x\|_{bv_{0}}$	$=\sum _{i=1}^{\infty }\left|x_{i+1}-x_{i}\right|$	Isometrisch isomorph zu $\ell ^{1}.$
$\operatorname {bs}$	$\operatorname {ba}$	Nein	Nein	$\|x\|_{bs}$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|$	Isometrisch isomorph zu $\ell ^{\infty }.$
$\operatorname {cs}$	$\ell ^{1}$	Nein	Nein	$\|x\|_{bs}$	$=\sup \nolimits _{n}\left|\sum _{i=1}^{n}x_{i}\right|$	Isometrisch isomorph zu $c.$
$B(K,\Xi )$	$\operatorname {ba} (\Xi )$	Nein	Nein	$\|f\|_{B}$	$=\sup \nolimits _{k\in K}|f(k)|$
$C(K)$	$\operatorname {rca} (K)$	Nein	Nein	$\|x\|_{C(K)}$	$=\max \nolimits _{k\in K}|f(k)|$
$\operatorname {ba} (\Xi )$	?	Nein	Ja	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$
$\operatorname {ca} (\Sigma )$	?	Nein	Ja	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$	Ein geschlossener Unterraum von $\operatorname {ba} (\Sigma ).$
$\operatorname {rca} (\Sigma )$	?	Nein	Ja	$\|\mu \|_{ba}$	$=\sup \nolimits _{S\in \Sigma }|\mu |(S)$	Ein geschlossener Unterraum von $\operatorname {ca} (\Sigma ).$
$L^{p}(\mu )$	$L^{q}(\mu )$	Ja	Ja	$\|f\|_{p}$	$=\left(\int |f|^{p}\,d\mu \right)^{\frac {1}{p}}$
$L^{1}(\mu )$	$L^{\infty }(\mu )$	Nein	Ja	$\|f\|_{1}$	$=\int |f|\,d\mu$	Der Dual ist $L^{\infty }(\mu )$ wenn $\mu$ ist $\sigma$-unendlich.
$\operatorname {BV} ([a,b])$	?	Nein	Ja	$\|f\|_{BV}$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)$	$V_{f}([a,b]).$ ist die Gesamtvariation von $f$
$\operatorname {NBV} ([a,b])$	?	Nein	Ja	$\|f\|_{BV}$	$=V_{f}([a,b])$	$\operatorname {NBV} ([a,b])$ besteht aus $\operatorname {BV} ([a,b])$ Funktionen, so dass $\lim \nolimits _{x\to a^{+}}f(x)=0$
$\operatorname {AC} ([a,b])$	$\mathbb {F} +L^{\infty }([a,b])$	Nein	Ja	$\|f\|_{BV}$	$=V_{f}([a,b])+\lim \nolimits _{x\to a^{+}}f(x)$	Isomorph zum Sobolev-Raum $W^{1,1}([a,b]).$
$C^{n}([a,b])$	$\operatorname {rca} ([a,b])$	Nein	Nein	$\|f\|$	$=\sum _{i=0}^{n}\sup \nolimits _{x\in [a,b]}\left|f^{(i)}(x)\right|$	Isomorph zu $\mathbb {R} ^{n}\oplus C([a,b]),$ im Wesentlichen durch den Taylor'schen Lehrsatz.

Fréchet-Ableitung

Es ist möglich, die Ableitung einer Funktion $f\colon V\to W$ zwischen zwei Banachräumen zu definieren. Intuitiv sieht man, dass, falls $x$ ein Element von $V$ ist, die Ableitung von $f$ im Punkt $x$ eine stetige lineare Abbildung ist, die $f$ nahe $x$ in der Ordnung des Abstandes $\vert h\vert$ approximiert. ⓘ

Man nennt $f$ (Fréchet)-differenzierbar in $x$, falls eine stetige lineare Abbildung $A\colon V\to W$ existiert, so dass

$\lim _{h\to 0}{\|f(x+h)-f(x)-A(h)\| \over \|h\|}=0$

gilt. Der Grenzwert wird hier über alle Folgen mit nicht-Null-Element aus $V$ gebildet, die gegen 0 konvergieren. Falls der Grenzwert existiert, schreibt man $Df(x)=A$ und nennt es die (Fréchet)-Ableitung von $f$ in $x$. Weitere Verallgemeinerungen der Ableitung ergeben sich analog zur Analysis auf endlichdimensionalen Räumen. Gemeinsam für alle Ableitungsbegriffe ist aber die Frage nach der Stetigkeit der linearen Abbildung $Df(x)$ ⓘ

Dieser Begriff der Ableitung ist eine Verallgemeinerung der gewöhnlichen Ableitung von Funktionen $\mathbb {R} \to \mathbb {R}$, da die linearen Abbildungen von $\mathbb {R}$ auf $\mathbb {R}$ einfach Multiplikationen mit reellen Zahlen sind. ⓘ

Falls $f$ differenzierbar ist in jedem Punkt $x$ aus $V$, dann ist $Df\colon V\to L(V,W)$ eine weitere Abbildung zwischen Banachräumen (im Allgemeinen keine lineare Abbildung!) und kann möglicherweise erneut differenziert werden, wodurch die höheren Ableitungen von $f$ definiert werden. Die $n$-te Ableitung im Punkt $x$ kann somit als multilineare Abbildung $V_{n}\to W$ gesehen werden. ⓘ

Differentiation ist eine lineare Operation im folgenden Sinne: Sind $f$ und $g$ zwei Abbildungen $V\to W$, die in $x$ differenzierbar sind, und sind $r$ und $s$ Skalare aus $\mathbb {K}$, dann ist $rf+sg$ differenzierbar in $x$ und es gilt

$D(rf+sg)(x)=rD(f)(x)+sD(g)(x)$. ⓘ

Die Kettenregel ist in diesem Zusammenhang ebenfalls gültig. Wenn $f\colon V\to W$ eine in $x\in V$ und $g\colon W\to X$ eine in $f(x)$ differenzierbare Funktion ist, dann ist die Komposition $g\circ f$ in $x$ differenzierbar und die Ableitung ist die Komposition der Ableitungen

$D(g\circ f)(x)=D(g)(f(x))\circ D(f)(x).$ ⓘ

Auch Richtungsableitungen können auf unendlichdimensionale Vektorräume erweitert werden, an dieser Stelle sei auf das Gâteaux-Differential verwiesen. ⓘ

Auf einem Banach-Raum können mehrere Konzepte einer Ableitung definiert werden. Siehe die Artikel über die Fréchet-Ableitung und die Gateaux-Ableitung für Details. Die Fréchet-Ableitung ermöglicht eine Erweiterung des Konzepts der Gesamtableitung auf Banachräume. Die Gateaux-Ableitung ermöglicht die Erweiterung einer gerichteten Ableitung auf lokal konvexe topologische Vektorräume. Die Fréchet-Differenzierbarkeit ist eine stärkere Bedingung als die Gateaux-Differenzierbarkeit. Die Quasi-Ableitung ist eine weitere Verallgemeinerung der Richtungsableitung, die eine stärkere Bedingung als Gateaux-Differenzierbarkeit, aber eine schwächere Bedingung als Fréchet-Differenzierbarkeit impliziert. ⓘ

Verallgemeinerungen

Mehrere wichtige Räume in der Funktionalanalysis, zum Beispiel der Raum aller unendlich oft differenzierbaren Funktionen $\mathbb {R} \to \mathbb {R} ,$ oder der Raum aller Verteilungen auf $\mathbb {R} ,$ sind vollständig, aber keine normierten Vektorräume und daher keine Banach-Räume. In Fréchet-Räumen hat man immer noch eine vollständige Metrik, während LF-Räume vollständige einheitliche Vektorräume sind, die als Grenzen von Fréchet-Räumen entstehen. ⓘ

Integration Banachraum-wertiger Funktionen

Unter bestimmten Bedingungen ist es möglich Banachraum-wertige Funktionen zu integrieren. Im zwanzigsten Jahrhundert wurden viele verschiedene Zugänge zu einer Integrationstheorie von Banachraum-wertigen Funktionen vorgestellt. Beispiele sind das Bochner-Integral, das Birkhoff-Integral und das Pettis-Integral. In endlichdimensionalen Banachräumen führen diese drei verschiedenen Zugänge zur Integration letztendlich zum selben Integral. Für unendlichdimensionale Banachräume ist dies jedoch im Allgemeinen nicht mehr der Fall. Ferner kann man von gewöhnlichen Maßen zu vektoriellen Maßen, die ihre Werte in Banachräumen annehmen, übergehen und ein Integral bezüglich solcher Maße definieren. ⓘ