Flächeninhalt
| Bereich ⓘ | |
|---|---|
Gemeinsame Symbole | A |
| SI-Einheit | Quadratmeter [m2] |
| In SI-Basiseinheiten | 1 m2 |

Der Flächeninhalt ist die Größe, die die Ausdehnung eines Bereichs in der Ebene oder auf einer gekrümmten Fläche ausdrückt. Der Flächeninhalt eines ebenen Bereichs oder einer ebenen Fläche bezieht sich auf die Fläche einer Form oder einer ebenen Lamelle, während sich der Flächeninhalt auf die Fläche einer offenen Oberfläche oder die Begrenzung eines dreidimensionalen Objekts bezieht. Die Fläche kann als die Menge an Material mit einer bestimmten Dicke verstanden werden, die erforderlich wäre, um ein Modell der Form herzustellen, oder als die Menge an Farbe, die erforderlich ist, um die Oberfläche mit einer einzigen Schicht zu bedecken. Sie ist das zweidimensionale Analogon der Länge einer Kurve (ein eindimensionales Konzept) oder des Volumens eines Körpers (ein dreidimensionales Konzept). ⓘ
Die Fläche einer Form kann gemessen werden, indem die Form mit Quadraten einer bestimmten Größe verglichen wird. Im Internationalen Einheitensystem (SI) ist die Standardeinheit der Fläche der Quadratmeter (m2), also die Fläche eines Quadrats mit einer Seitenlänge von einem Meter. Eine Form mit einer Fläche von drei Quadratmetern hätte die gleiche Fläche wie drei solcher Quadrate. In der Mathematik hat das Einheitsquadrat den Flächeninhalt 1, und der Flächeninhalt jeder anderen Form oder Fläche ist eine dimensionslose reelle Zahl. ⓘ

Es gibt mehrere bekannte Formeln für die Flächeninhalte einfacher Formen wie Dreiecke, Rechtecke und Kreise. Mit Hilfe dieser Formeln kann der Flächeninhalt eines beliebigen Polygons ermittelt werden, indem das Polygon in Dreiecke unterteilt wird. Für Formen mit gekrümmten Begrenzungen ist in der Regel die Infinitesimalrechnung erforderlich, um den Flächeninhalt zu berechnen. In der Tat war das Problem der Bestimmung des Flächeninhalts von ebenen Figuren eine wichtige Motivation für die historische Entwicklung der Infinitesimalrechnung. ⓘ
Bei einer festen Form wie einer Kugel, einem Kegel oder einem Zylinder wird der Bereich der Begrenzungsfläche als Flächeninhalt bezeichnet. Formeln für den Flächeninhalt einfacher Formen wurden bereits von den alten Griechen berechnet, aber die Berechnung des Flächeninhalts einer komplizierteren Form erfordert in der Regel eine multivariable Kalkulation. ⓘ
Der Flächeninhalt spielt in der modernen Mathematik eine wichtige Rolle. Neben seiner offensichtlichen Bedeutung in der Geometrie und der Infinitesimalrechnung ist der Flächeninhalt mit der Definition von Determinanten in der linearen Algebra verbunden und ist eine grundlegende Eigenschaft von Oberflächen in der Differentialgeometrie. In der Analysis wird der Flächeninhalt einer Teilmenge der Ebene mit Hilfe des Lebesgue-Maßes definiert, obwohl nicht jede Teilmenge messbar ist. Im Allgemeinen wird der Flächeninhalt in der höheren Mathematik als ein Spezialfall des Volumens für zweidimensionale Regionen betrachtet. ⓘ
Der Flächeninhalt kann mit Hilfe von Axiomen definiert werden, die ihn als eine Funktion einer Sammlung bestimmter ebener Figuren auf die Menge der reellen Zahlen definieren. Es kann bewiesen werden, dass eine solche Funktion existiert. ⓘ
| Physikalische Größe ⓘ | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Flächeninhalt Oberfläche Querschnittsfläche | ||||||||||||
| Formelzeichen | (area) | ||||||||||||
| Abgeleitet von | Länge | ||||||||||||
| |||||||||||||

Die Ausmessung von Flächeninhalten geschieht in der Regel nicht direkt. Stattdessen werden bestimmte Längen gemessen, woraus dann der Flächeninhalt berechnet wird. Zur Messung des Flächeninhalts eines Rechtecks oder einer Kugeloberfläche misst man üblicherweise die Seitenlängen des Rechtecks bzw. den Durchmesser der Kugel und erhält den gewünschten Flächeninhalt mittels geometrischer Formeln, wie sie unten aufgelistet werden. ⓘ
In der Technik benutzt man zur näherungsweisen Flächenbestimmung mechanische Planimeter, bei denen bei Umfahren der Fläche die Summierung der Flächenelemente kontinuierlich erfolgt. Das Ergebnis kann an einer Skala abgelesen werden. Chemiker pflegten früher den Inhalt einer beliebigen Fläche mit Hilfe einer Analysenwaage oder Mikrowaage zu bestimmen: Die Fläche wurde sorgfältig aus Papier ausgeschnitten und gewogen, ebenso ein Stück des gleichen Papiers mit genau bekannter Fläche; eine Dreisatzrechnung führte zum Ergebnis. ⓘ
Formale Definition
Ein Ansatz zur Definition des Begriffs "Fläche" ist die Verwendung von Axiomen. Der "Flächeninhalt" kann definiert werden als eine Funktion von einer Sammlung M einer speziellen Art von ebenen Figuren (die als messbare Mengen bezeichnet werden) zur Menge der reellen Zahlen, die die folgenden Eigenschaften erfüllt:
- Für alle S in M ist a(S) ≥ 0.
- Wenn S und T in M sind, dann sind auch S ∪ T und S ∩ T, und auch a(S∪T) = a(S) + a(T) - a(S∩T).
- Sind S und T in M mit S ⊆ T, dann ist T - S in M und a(T-S) = a(T) - a(S).
- Wenn eine Menge S in M ist und S kongruent zu T ist, dann ist auch T in M und a(S) = a(T).
- Jedes Rechteck R ist in M. Wenn das Rechteck die Länge h und die Breite k hat, dann ist a(R) = hk.
- Ein Stufenbereich wird aus einer endlichen Vereinigung benachbarter Rechtecke gebildet, die auf einer gemeinsamen Basis ruhen, d. h. S ⊆ Q ⊆ T. Wenn es eine eindeutige Zahl c gibt, so dass a(S) ≤ c ≤ a(T) für alle solchen Stufenbereiche S und T ist, dann ist a(Q) = c. ⓘ
Es kann bewiesen werden, dass eine solche Flächenfunktion tatsächlich existiert. ⓘ
Einheiten

Jede Längeneinheit hat eine entsprechende Flächeneinheit, nämlich die Fläche eines Quadrats mit der gegebenen Seitenlänge. Flächen können also in Quadratmetern (m2), Quadratzentimetern (cm2), Quadratmillimetern (mm2), Quadratkilometern (km2), Quadratfuß (ft2), Quadratyard (yd2), Quadratmeilen (mi2) und so weiter gemessen werden. Algebraisch kann man sich diese Einheiten als die Quadrate der entsprechenden Längeneinheiten vorstellen. ⓘ
Die SI-Einheit der Fläche ist der Quadratmeter, der als abgeleitete SI-Einheit gilt. ⓘ
Umrechnungen

Die Berechnung der Fläche eines Quadrats, dessen Länge und Breite 1 Meter beträgt, wäre wie folgt: 1 Meter × 1 Meter = 1 m2 ⓘ
Ein Rechteck mit unterschiedlichen Seiten (z. B. 3 m lang und 2 m breit) hätte also eine Fläche in Quadrateinheiten, die sich wie folgt berechnen lässt: 3 Meter × 2 Meter = 6 m2. Dies entspricht 6 Millionen Quadratmillimetern. Andere nützliche Umrechnungen sind:
- 1 Quadratkilometer = 1.000.000 Quadratmeter
- 1 Quadratmeter = 10.000 Quadratzentimeter = 1.000.000 Quadratmillimeter
- 1 Quadratzentimeter = 100 Quadratmillimeter. ⓘ
Nicht-metrische Einheiten
Bei nicht-metrischen Einheiten ist die Umrechnung zwischen zwei Quadrateinheiten das Quadrat der Umrechnung zwischen den entsprechenden Längeneinheiten.
- 1 Fuß = 12 Zoll,
das Verhältnis zwischen Quadratfuß und Quadratzoll ist
- 1 Quadratfuß = 144 Quadratzoll,
wobei 144 = 122 = 12 × 12. Ähnlich:
- 1 Quadratyard = 9 Quadratfuß
- 1 Quadratmeile = 3.097.600 Quadrat-Yards = 27.878.400 Quadratfuß
Darüber hinaus gibt es folgende Umrechnungsfaktoren:
- 1 Quadratzoll = 6,4516 Quadratzentimeter
- 1 Quadratfuß = 0,09290304 Quadratmeter
- 1 Quadratyard = 0,83612736 Quadratmeter
- 1 Quadratmeile = 2,589988110336 Quadratkilometer ⓘ
Andere Einheiten einschließlich historischer Einheiten
Es gibt mehrere andere gebräuchliche Einheiten für die Fläche. Das Are war die ursprüngliche Flächeneinheit im metrischen System, mit:
- 1 are = 100 Quadratmeter
Obwohl das Are nicht mehr gebräuchlich ist, wird der Hektar immer noch häufig zur Messung von Land verwendet:
- 1 Hektar = 100 Ar = 10.000 Quadratmeter = 0,01 Quadratkilometer
Weitere ungebräuchliche metrische Flächeneinheiten sind das Tetrade, das Hektar und das Myriade. ⓘ
Der Acre wird ebenfalls häufig zur Messung von Landflächen verwendet, wobei
- 1 acre = 4.840 square yards = 43.560 square feet.
Ein Acre entspricht etwa 40 % eines Hektars. ⓘ
Auf der atomaren Skala wird die Fläche in Einheiten von Scheunen gemessen, d. h.:
- 1 Scheune = 10-28 Quadratmeter.
Die Scheune wird üblicherweise zur Beschreibung der Querschnittsfläche von Wechselwirkungen in der Kernphysik verwendet. ⓘ
In Indien,
- 20 dhurki = 1 dhur
- 20 dhur = 1 khatha
- 20 khata = 1 bigha
- 32 khata = 1 Acker ⓘ
Geschichte
Kreisgebiet
Im 5. Jahrhundert v. Chr. wies Hippokrates von Chios im Rahmen seiner Quadratur der Lune des Hippokrates als Erster nach, dass die Fläche einer Scheibe (der von einem Kreis umschlossene Bereich) proportional zum Quadrat des Durchmessers ist, ohne jedoch die Proportionalitätskonstante zu bestimmen. Eudoxus von Cnidus, ebenfalls im 5. Jahrhundert v. Chr., fand ebenfalls heraus, dass die Fläche einer Scheibe proportional zum Quadrat des Radius ist. ⓘ
Später befasste sich Buch I der Elemente von Euklid mit der Gleichheit von Flächen zwischen zweidimensionalen Figuren. Der Mathematiker Archimedes wandte die Werkzeuge der euklidischen Geometrie an, um in seinem Buch Messung eines Kreises zu zeigen, dass die Fläche im Inneren eines Kreises gleich der Fläche eines rechtwinkligen Dreiecks ist, dessen Basis die Länge des Kreisumfangs hat und dessen Höhe dem Radius des Kreises entspricht. (Der Umfang ist 2πr, und die Fläche eines Dreiecks ist die Hälfte der Grundfläche mal der Höhe, was die Fläche πr2 für die Scheibe ergibt). Archimedes näherte sich dem Wert von π (und damit der Fläche eines Kreises mit Einheitsradius) mit seiner Verdoppelungsmethode an, bei der er ein regelmäßiges Dreieck in einen Kreis einschrieb und dessen Fläche notierte, dann die Anzahl der Seiten verdoppelte, um ein regelmäßiges Sechseck zu erhalten, und dann wiederholt die Anzahl der Seiten verdoppelte, während sich die Fläche des Polygons der des Kreises immer mehr annäherte (und dasselbe mit umschriebenen Polygonen tat). ⓘ
Der Schweizer Wissenschaftler Johann Heinrich Lambert bewies 1761, dass π, das Verhältnis der Fläche eines Kreises zu seinem quadrierten Radius, irrational ist, d. h. es ist nicht gleich dem Quotienten zweier ganzer Zahlen. Im Jahr 1794 bewies der französische Mathematiker Adrien-Marie Legendre, dass π2 irrational ist; damit ist auch bewiesen, dass π irrational ist. 1882 bewies der deutsche Mathematiker Ferdinand von Lindemann, dass π transzendental ist (nicht die Lösung einer Polynomgleichung mit rationalen Koeffizienten) und bestätigte damit eine Vermutung von Legendre und Euler. ⓘ
Fläche des Dreiecks
Heron (oder Hero) von Alexandria fand die so genannte Heron-Formel für den Flächeninhalt eines Dreiecks in Abhängigkeit von seinen Seiten, und ein Beweis findet sich in seinem Buch Metrica, das um 60 n. Chr. geschrieben wurde. Es wird vermutet, dass Archimedes die Formel schon über zwei Jahrhunderte früher kannte, und da Metrica eine Sammlung des in der Antike vorhandenen mathematischen Wissens ist, ist es möglich, dass die Formel schon vor der Erwähnung in diesem Werk existierte. ⓘ
Im Jahr 499 drückte Aryabhata, ein großer Mathematiker und Astronom aus dem klassischen Zeitalter der indischen Mathematik und Astronomie, im Aryabhatiya (Abschnitt 2.6) die Fläche eines Dreiecks als die Hälfte der Basis mal der Höhe aus. ⓘ
Eine Formel, die der von Heron entspricht, wurde von den Chinesen unabhängig von den Griechen entdeckt. Sie wurde 1247 im Shushu Jiuzhang ("Mathematische Abhandlung in neun Abschnitten") von Qin Jiushao veröffentlicht. ⓘ
Viereckige Fläche
Im 7. Jahrhundert n. Chr. entwickelte Brahmagupta eine Formel, die heute als Brahmagupta-Formel bekannt ist, um die Fläche eines zyklischen Vierecks (ein in einen Kreis eingeschriebenes Viereck) in Abhängigkeit von seinen Seiten zu bestimmen. Im Jahr 1842 fanden die deutschen Mathematiker Carl Anton Bretschneider und Karl Georg Christian von Staudt unabhängig voneinander eine Formel für den Flächeninhalt beliebiger Vierecke, die als Bretschneidersche Formel bekannt ist. ⓘ
Allgemeine Polygonfläche
Die Entwicklung der kartesischen Koordinaten durch René Descartes im 17. Jahrhundert ermöglichte die Entwicklung der Vermessungsformel für den Flächeninhalt beliebiger Polygone mit bekannten Scheitelpunkten durch Gauß im 19. ⓘ
Mit der Infinitesimalrechnung ermittelte Flächen
Mit der Entwicklung der Integralrechnung im späten 17. Jahrhundert wurden Werkzeuge zur Verfügung gestellt, die in der Folge zur Berechnung komplizierterer Flächeninhalte verwendet werden konnten, z. B. zur Berechnung des Flächeninhalts einer Ellipse und der Flächeninhalte verschiedener gekrümmter dreidimensionaler Objekte. ⓘ
Formeln zur Flächenberechnung
Formeln für Polygone
Für ein sich nicht selbst schneidendes (einfaches) Polygon sind die kartesischen Koordinaten (i=0, 1, ..., n-1), deren n Scheitelpunkte bekannt sind, wird der Flächeninhalt durch die Vermessungsformel angegeben:
Wenn i=n-1 ist, dann wird i+1 als Modul n ausgedrückt und bezieht sich somit auf 0. ⓘ
Rechtecke
Die grundlegendste Flächenformel ist die Formel für den Flächeninhalt eines Rechtecks. Bei einem Rechteck mit der Länge l und der Breite w lautet die Formel für den Flächeninhalt:
- A = lw (Rechteck).
Das heißt, der Flächeninhalt des Rechtecks ist die Länge multipliziert mit der Breite. Als Sonderfall, da l = w im Falle eines Quadrats, ist der Flächeninhalt eines Quadrats mit der Seitenlänge s durch die Formel gegeben:
- A = s2 (Quadrat). ⓘ
Die Formel für den Flächeninhalt eines Rechtecks ergibt sich direkt aus den grundlegenden Eigenschaften des Flächeninhalts und wird manchmal als Definition oder Axiom betrachtet. Wird hingegen die Geometrie vor der Arithmetik entwickelt, kann diese Formel zur Definition der Multiplikation der reellen Zahlen verwendet werden. ⓘ
Zerlegung, Parallelogramme und Dreiecke
Die meisten anderen einfachen Formeln für den Flächeninhalt ergeben sich aus der Methode des Zerschneidens. Dabei wird eine Form in Teile zerlegt, deren Flächeninhalt die Summe des Flächeninhalts der ursprünglichen Form ergeben muss. ⓘ

Ein Beispiel: Jedes Parallelogramm kann in ein Trapez und ein rechtwinkliges Dreieck unterteilt werden, wie in der Abbildung links dargestellt. Wenn das Dreieck auf die andere Seite des Trapezes verschoben wird, entsteht ein Rechteck. Daraus folgt, dass die Fläche des Parallelogramms gleich der Fläche des Rechtecks ist:
- A = bh (Parallelogramm). ⓘ

Dasselbe Parallelogramm kann jedoch auch entlang einer Diagonale in zwei kongruente Dreiecke zerlegt werden, wie in der Abbildung rechts dargestellt. Daraus folgt, dass die Fläche eines jeden Dreiecks die Hälfte der Fläche des Parallelogramms ist:
- (Dreieck).
Mit ähnlichen Argumenten lassen sich auch Flächenformeln für das Trapez sowie für kompliziertere Vielecke finden. ⓘ
Flächeninhalt von gekrümmten Formen
Kreise
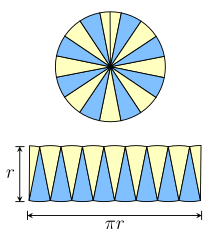
Die Formel für den Flächeninhalt eines Kreises (richtiger: der von einem Kreis eingeschlossene Bereich oder der Bereich einer Scheibe) basiert auf einer ähnlichen Methode. Bei einem Kreis mit dem Radius r kann man den Kreis in Sektoren unterteilen, wie in der Abbildung rechts dargestellt. Jeder Sektor hat annähernd die Form eines Dreiecks, und die Sektoren können so angeordnet werden, dass sie annähernd ein Parallelogramm bilden. Die Höhe dieses Parallelogramms ist r, und die Breite ist die Hälfte des Kreisumfangs, also πr. Die Gesamtfläche des Kreises ist also πr2:
- A = πr2 (Kreis).
Obwohl die in dieser Formel verwendete Zerlegung nur annähernd ist, wird der Fehler immer kleiner, je mehr Sektoren der Kreis zerlegt wird. Der Grenzwert der Flächen der angenäherten Parallelogramme ist genau πr2, was der Fläche des Kreises entspricht. ⓘ
Dieses Argument ist eigentlich eine einfache Anwendung der Ideen der Infinitesimalrechnung. In der Antike wurde die Methode der Erschöpfung in ähnlicher Weise verwendet, um den Flächeninhalt des Kreises zu bestimmen, und diese Methode ist heute als Vorläufer der Integralrechnung anerkannt. Mit modernen Methoden kann der Flächeninhalt eines Kreises durch ein bestimmtes Integral berechnet werden:
Ellipsen
Die Formel für den von einer Ellipse eingeschlossenen Flächeninhalt ist mit der Formel für einen Kreis verwandt; für eine Ellipse mit Haupt- und Nebenachse x und y lautet die Formel:
Nicht planarer Flächeninhalt

Die meisten grundlegenden Formeln für den Flächeninhalt lassen sich durch Zerschneiden und Abflachen von Flächen erhalten (siehe: abwickelbare Flächen). Schneidet man beispielsweise die Seitenfläche eines Zylinders (oder eines Prismas) der Länge nach ein, so kann die Fläche zu einem Rechteck abgeflacht werden. In ähnlicher Weise kann die Seitenfläche eines Kegels durch einen Schnitt entlang der Seite zu einem Kreissektor abgeflacht und die resultierende Fläche berechnet werden. ⓘ
Die Formel für den Flächeninhalt einer Kugel ist schwieriger herzuleiten: Da eine Kugel eine Gaußsche Krümmung ungleich Null hat, kann sie nicht abgeflacht werden. Die Formel für den Flächeninhalt einer Kugel wurde erstmals von Archimedes in seinem Werk Über die Kugel und den Zylinder aufgestellt. Die Formel lautet:
- A = 4πr2 (Kugel),
wobei r der Radius der Kugel ist. Wie bei der Formel für den Flächeninhalt eines Kreises werden bei der Ableitung dieser Formel Methoden verwendet, die der Infinitesimalrechnung ähneln. ⓘ
Allgemeine Formeln
Flächeninhalte von 2-dimensionalen Figuren
- Ein Dreieck: (wobei B eine beliebige Seite und h der Abstand zwischen der Linie, auf der B liegt, und dem anderen Scheitelpunkt des Dreiecks ist). Diese Formel kann verwendet werden, wenn die Höhe h bekannt ist. Wenn die Längen der drei Seiten bekannt sind, kann die Formel von Heron verwendet werden: wobei a, b, c die Seiten des Dreiecks sind, und die Hälfte des Umfangs ist. Wenn ein Winkel und seine beiden eingeschlossenen Seiten gegeben sind, ist die Fläche wobei C der gegebene Winkel ist und a und b die eingeschlossenen Seiten sind. Wird das Dreieck in eine Koordinatenebene eingezeichnet, kann eine Matrix verwendet werden, die sich auf den Absolutwert von vereinfacht . Diese Formel ist auch als Schnürsenkelformel bekannt und stellt eine einfache Möglichkeit dar, den Flächeninhalt eines Koordinatendreiecks durch Einsetzen der drei Punkte (x1,y1), (x2,y2) und (x3,y3) zu bestimmen. Die Schnürsenkelformel kann auch verwendet werden, um die Flächen anderer Polygone zu bestimmen, wenn deren Eckpunkte bekannt sind. Ein anderer Ansatz für ein Koordinatendreieck ist die Anwendung der Infinitesimalrechnung, um den Flächeninhalt zu bestimmen.
- Ein einfaches Polygon, das auf einem Gitter aus Punkten mit gleichem Abstand (d. h. Punkten mit ganzzahligen Koordinaten) so konstruiert ist, dass alle Eckpunkte des Polygons Gitterpunkte sind: Dabei ist i die Anzahl der Gitterpunkte innerhalb des Polygons und b die Anzahl der Randpunkte. Dieses Ergebnis ist als Picks Theorem bekannt. ⓘ
Fläche in der Infinitesimalrechnung

Die Integralrechnung wurde unter anderem zur Ermittlung von Flächeninhalten unter Kurven, das heißt unter Funktionsgraphen, entwickelt. Die Idee besteht darin, die Fläche zwischen Kurve und -Achse durch eine Reihe schmaler Rechtecke zu approximieren und dann die Breite dieser Rechtecke in einem Grenzprozess gegen 0 gehen zu lassen. Die Konvergenz dieses Grenzübergangs hängt von der verwendeten Kurve ab. Betrachtet man einen beschränkten Bereich, etwa die Kurve über einem beschränkten Intervall wie in nebenstehender Zeichnung, so zeigen Sätze der Analysis, dass die Stetigkeit der Kurve bereits ausreicht, um die Konvergenz des Grenzprozesses zu sichern. Dabei tritt das Phänomen auf, dass Flächen unterhalb der -Achse negativ werden, was bei der Bestimmung von Flächeninhalten unerwünscht sein kann. Will man dies vermeiden, muss man zum Betrag der Funktion übergehen. ⓘ

Will man auch die Intervallgrenzen und zulassen, so ermittelt man zunächst die Flächen für endliche Grenzen und wie gerade beschrieben und lässt dann in einem weiteren Grenzprozess , oder beides streben. Hier kann es vorkommen, dass dieser Grenzprozess nicht konvergiert, zum Beispiel bei oszillierenden Funktionen wie der Sinusfunktion. Beschränkt man sich auf Funktionen, die ihren Funktionsgraphen in der oberen Halbebene haben, so können diese Oszillationseffekte zwar nicht mehr auftreten, aber es kommt durchaus vor, dass der Flächeninhalt zwischen Kurve und -Achse unendlich wird. Da die Gesamtfläche eine unendliche Ausdehnung hat, ist das sogar ein plausibles und letztlich auch erwartetes Ergebnis. Wenn die Kurve sich allerdings für weit von 0 entfernte Stellen hinreichend schnell der -Achse nähert, so kann das Phänomen eintreten, dass auch einer unendlich ausgedehnten Fläche ein endlicher Flächeninhalt zukommt. Ein bekanntes und für die Wahrscheinlichkeitstheorie wichtiges Beispiel ist die Fläche zwischen der gaußschen Glockenkurve
und der -Achse. Obwohl die Fläche von bis reicht, ist der Flächeninhalt gleich 1. ⓘ
Bei dem Versuch, weitere Flächen, etwa auch unter unstetigen Kurven, zu berechnen, stößt man schließlich auf die Frage, welchen Mengen in der Ebene denn überhaupt ein sinnvoller Flächeninhalt zukommen soll. Diese Frage erweist sich als schwierig, wie im Artikel zum Maßproblem ausgeführt wird. Es stellt sich heraus, dass der hier verwendete intuitive Flächeninhaltsbegriff nicht sinnvoll auf alle Teilmengen der Ebene ausgedehnt werden kann. ⓘ
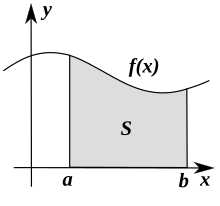
- Die Fläche zwischen einer Kurve mit positivem Wert und der horizontalen Achse, gemessen zwischen zwei Werten a und b (b ist definiert als der größere der beiden Werte) auf der horizontalen Achse, ist gegeben durch das Integral von a nach b der Funktion, die die Kurve darstellt:
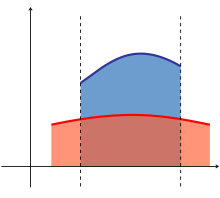
- Die Fläche zwischen den Graphen zweier Funktionen ist gleich dem Integral der einen Funktion, f(x), minus dem Integral der anderen Funktion, g(x):
- wobei die Kurve mit dem größeren y-Wert ist.
- Eine durch eine Funktion begrenzte Fläche in Polarkoordinaten ausgedrückt ist:
- Die Fläche, die von einer parametrischen Kurve mit Endpunkten ist durch die Linienintegrale gegeben:
- oder die z-Komponente von
- (Einzelheiten siehe Green'scher Satz § Flächenberechnung.) Dies ist das Prinzip des mechanischen Geräts Planimeter. ⓘ
Begrenzte Fläche zwischen zwei quadratischen Funktionen
Um die begrenzte Fläche zwischen zwei quadratischen Funktionen zu bestimmen, subtrahieren wir die eine von der anderen und schreiben die Differenz als
wobei f(x) die quadratische Obergrenze und g(x) die quadratische Untergrenze ist. Definieren Sie die Diskriminante von f(x)-g(x) als
Durch Vereinfachung der Integralformel zwischen den Graphen zweier Funktionen (wie im obigen Abschnitt angegeben) und Anwendung der Vieta-Formel erhält man
Die obige Formel bleibt gültig, wenn eine der begrenzenden Funktionen linear statt quadratisch ist. ⓘ
Flächeninhalt von 3-dimensionalen Figuren
- Kegel: wobei r der Radius der kreisförmigen Grundfläche und h die Höhe ist. Dies kann auch umgeschrieben werden als oder wobei r der Radius und l die schräge Höhe des Kegels ist. ist die Grundfläche und die Seitenfläche des Kegels ist.
- Würfel: , wobei s die Länge einer Kante ist.
- Zylinder: , wobei r der Radius einer Grundfläche und h die Höhe ist. Die kann auch umgeschrieben werden als , wobei d der Durchmesser ist.
- Prisma: , wobei B die Fläche einer Grundfläche, P der Umfang einer Grundfläche und h die Höhe des Prismas ist.
- Pyramide: , wobei B die Grundfläche, P der Umfang der Grundfläche und L die Länge der Schräge ist.
- Rechtwinkliges Prisma: , wobei für die Länge, w für die Breite und h für die Höhe steht. ⓘ
Allgemeine Formel für den Flächeninhalt
Die allgemeine Formel für den Flächeninhalt des Graphen einer stetig differenzierbaren Funktion wobei und ist ein Bereich in der xy-Ebene mit glattem Rand:
Eine noch allgemeinere Formel für den Flächeninhalt des Graphen einer parametrischen Fläche in der Vektorform wobei ist eine stetig differenzierbare Vektorfunktion von ist:
Liste der Formeln
In nachfolgender Tabelle sind einige Figuren aus der ebenen Geometrie zusammen mit Formeln zur Berechnung ihres Flächeninhaltes aufgelistet. ⓘ
| Figur/Objekt | Flächeninhalt | Bezeichnungen ⓘ |
|---|---|---|
| Rechteck | 
| |
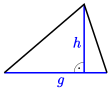
| Dreieck |
|
|
| gleichsch. Dreieck | 
| |
| gleichseit. Dreieck | 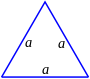
| |
| Trapez | 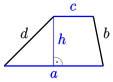
| |
| Raute | 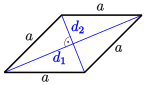
| |
| Parallelogramm | 
| |
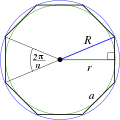
| regul. Sechseck | 
| |
| regul. Polygon ( Seiten) |
|
(Umfang) |
| Kreis | 
| |
| Ellipse | 
| |
| Integral | 
| |
| Leibniz-Formel | 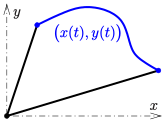
|
Zur Ermittlung des Flächeninhaltes eines Polygons kann man dieses triangulieren, das heißt, es durch Ziehen von Diagonalen in Dreiecke zerlegen, dann die Flächeninhalte der Dreiecke ermitteln und diese Teilflächen schließlich addieren. Sind die Koordinaten , , der Eckpunkte des Polygons in einem kartesischen Koordinatensystem bekannt, kann die Fläche mit der Gaußschen Trapezformel berechnet werden:
Dabei gilt hier für die Indizes: Mit ist und mit ist gemeint. Die Summe ist positiv, wenn die Eckpunkte entsprechend dem Drehsinn des Koordinatensystems durchlaufen werden. Eventuell ist bei negativen Ergebnissen der Betrag zu wählen. Speziell für polygonale Flächen mit Gitterpunkten als Ecken lässt sich der Satz von Pick anwenden. Andere Flächen lassen sich in der Regel leicht durch Polygone approximieren, so dass man leicht an einen Näherungswert kommen kann. ⓘ
Die obigen Berechnungen zeigen, wie man die Flächeninhalte vieler gängiger Formen ermitteln kann. ⓘ
Die Flächeninhalte unregelmäßiger (und damit beliebiger) Vielecke lassen sich mit der "Surveyor's formula" (Schnürsenkelformel) berechnen. ⓘ
Verhältnis von Flächeninhalt und Umfang
Die isoperimetrische Ungleichung besagt, dass für eine geschlossene Kurve der Länge L (der von ihr umschlossene Bereich hat also den Umfang L) und für den Flächeninhalt A des von ihr umschlossenen Bereichs, ⓘ
und die Gleichheit gilt nur dann, wenn die Kurve ein Kreis ist. Ein Kreis hat also den größten Flächeninhalt aller geschlossenen Figuren mit einem bestimmten Umfang. ⓘ
Im anderen Extremfall kann eine Figur mit gegebenem Umfang L einen beliebig kleinen Flächeninhalt haben, wie ein Rhombus, der beliebig weit "gekippt" ist, so dass zwei seiner Winkel beliebig nahe bei 0° und die beiden anderen beliebig nahe bei 180° liegen. ⓘ
Bei einem Kreis ist das Verhältnis von Fläche zu Umfang (der Begriff für den Umfang eines Kreises) gleich der Hälfte des Radius r. Dies geht aus der Flächenformel πr2 und der Umfangsformel 2πr hervor. ⓘ
Der Flächeninhalt eines regelmäßigen Polygons ist die Hälfte des Umfangs mal der Apotheme (wobei die Apotheme der Abstand zwischen dem Mittelpunkt und dem nächstgelegenen Punkt auf einer beliebigen Seite ist). ⓘ
Fraktale
Die Verdopplung der Kantenlängen eines Polygons multipliziert dessen Fläche mit vier, was zwei (das Verhältnis der neuen zur alten Seitenlänge) hoch zwei (die Dimension des Raums, in dem das Polygon liegt) ist. Wenn jedoch die eindimensionalen Längen eines in zwei Dimensionen gezeichneten Fraktals alle verdoppelt werden, skaliert der räumliche Inhalt des Fraktals um eine Zweierpotenz, die nicht unbedingt eine ganze Zahl ist. Diese Potenz wird die fraktale Dimension des Fraktals genannt. ⓘ
Flächenhalbierende
Es gibt unendlich viele Linien, die die Fläche eines Dreiecks halbieren. Drei davon sind die Mediane des Dreiecks (die die Mittelpunkte der Seiten mit den gegenüberliegenden Scheitelpunkten verbinden), und diese fallen im Schwerpunkt des Dreiecks zusammen; sie sind die einzigen Flächenhalbierenden, die durch den Schwerpunkt gehen. Jede Linie durch ein Dreieck, die sowohl den Flächeninhalt als auch den Umfang des Dreiecks in zwei Hälften teilt, geht durch den Mittelpunkt des Dreiecks (den Mittelpunkt des Inkreises). Für jedes beliebige Dreieck gibt es entweder eine, zwei oder drei dieser Linien. ⓘ
Jede Linie durch den Mittelpunkt eines Parallelogramms halbiert den Flächeninhalt. ⓘ
Alle Flächenhalbierenden eines Kreises oder einer anderen Ellipse gehen durch den Mittelpunkt, und alle Sehnen durch den Mittelpunkt halbieren die Fläche. Im Falle eines Kreises sind dies die Durchmesser des Kreises. ⓘ
Optimierung
Bei einer Drahtkontur ist die Fläche mit der geringsten Fläche, die sie aufspannt ("füllt"), eine Minimalfläche. Bekannte Beispiele sind Seifenblasen. ⓘ
Die Frage nach der Füllfläche des Riemannschen Kreises bleibt offen. ⓘ
Der Kreis hat die größte Fläche aller zweidimensionalen Objekte mit demselben Umfang. ⓘ
Ein zyklisches Polygon (ein in einen Kreis eingeschriebenes Polygon) hat den größten Flächeninhalt aller Polygone mit einer gegebenen Anzahl von gleich langen Seiten. ⓘ
Eine Version der isoperimetrischen Ungleichung für Dreiecke besagt, dass das Dreieck mit dem größten Flächeninhalt unter allen Dreiecken mit einem bestimmten Umfang gleichseitig ist. ⓘ
Das Dreieck mit dem größten Flächeninhalt aller Dreiecke, die in einen gegebenen Kreis eingeschrieben sind, ist gleichseitig; und das Dreieck mit dem kleinsten Flächeninhalt aller Dreiecke, die einen gegebenen Kreis umschreiben, ist gleichseitig. ⓘ
Das Verhältnis zwischen der Fläche des Inkreises und der Fläche eines gleichseitigen Dreiecks ist größer als das eines nicht-gleichseitigen Dreiecks. ⓘ
Das Verhältnis zwischen der Fläche und dem Quadrat des Umfangs eines gleichseitigen Dreiecks ist größer als das eines jeden anderen Dreiecks. ⓘ
Differentialgeometrie
In der Differentialgeometrie wird der Flächeninhalt einer ebenen oder gekrümmten Fläche mit den Koordinaten als Flächenintegral berechnet:
Dabei entspricht das Flächenelement der Intervallbreite in der eindimensionalen Integralrechnung. Es gibt den Flächeninhalt des durch die Tangenten an die Koordinatenlinien aufgespannten Parallelogramms mit den Seitenlängen und an. Das Flächenelement ist abhängig vom Koordinatensystem und der Gaußschen Krümmung der Fläche. ⓘ
In kartesischen Koordinaten ist das Flächenelement . Auf der Kugeloberfläche mit dem Radius und der Länge sowie der Breite als Koordinatenparametern gilt . Für die Oberfläche einer Kugel () erhält man damit den Flächeninhalt:
Zur Berechnung des Flächenelements ist es nicht zwingend erforderlich, die Lage einer räumlichen Fläche im Raum zu kennen. Das Flächenelement kann allein aus solchen Maßen abgeleitet werden, die innerhalb der Fläche gemessen werden können, und zählt damit zur inneren Geometrie der Fläche. Dies ist auch der Grund dafür, dass sich der Flächeninhalt einer (abwickelbaren) Fläche beim Abwickeln nicht ändert und damit durch Abwickeln in eine Ebene bestimmt werden kann. ⓘ
Flächen in der Physik
Flächen treten naturgemäß auch in der Physik als zu messende Größe auf. Flächen werden in der Regel indirekt unter Verwendung obiger Formeln gemessen. Typische Größen, bei denen Flächen auftreten, sind:
- Druck = Kraft pro Fläche
- Intensität = Energie pro Zeit und Fläche
- Magnetisches Moment einer Leiterschleife = Strom mal umflossene Fläche
- Oberflächenspannung = Zur Flächenvergrößerung geleistete Arbeit pro zusätzlich entstandene Fläche
- Oberflächenladungsdichte = Ladung pro Fläche
- Stromdichte = Strom pro durchflossene Fläche ⓘ

Oft wird der Fläche auch eine Richtung, die senkrecht zur Fläche verläuft, zugewiesen, was die Fläche zu einem Vektor macht und ihr wegen der zwei möglichen Wahlen der senkrechten Richtung eine Orientierung verleiht. Die Länge des Vektors ist dabei ein Maß für den Flächeninhalt. Bei einem durch Vektoren und begrenzten Parallelogramm ist dieser das Vektorprodukt
- .
Sind es Oberflächen, verwendet man in der Regel das Normalenvektorfeld, um ihnen an jeder Stelle lokal eine Richtung zuweisen zu können. Dies führt zu Fluss-Größen, die man als Skalarprodukt aus betrachtetem Vektorfeld und Fläche (als Vektor) definiert. So errechnet sich der Strom aus der Stromdichte gemäß
- ,
wobei im Integral das Skalarprodukt
gebildet wird. Zur Auswertung derartiger Integrale sind Formeln zur Berechnung von Oberflächen hilfreich. ⓘ
Es treten in der Physik daneben auch Flächengrößen auf, die tatsächlich experimentell bestimmt werden, etwa Streuquerschnitte. Hierbei geht man von der Vorstellung aus, ein Teilchenstrom treffe auf ein festes Zielobjekt, auf das sogenannte Target, und die Teilchen des Teilchenstroms treffen mit gewisser Wahrscheinlichkeit auf die Teilchen des Targets. Das makroskopisch gemessene Streuverhalten lässt dann Rückschlüsse auf die Querschnittsflächen zu, welche die Targetteilchen den Stromteilchen entgegenhalten. Die so ermittelte Größe hat die Dimension einer Fläche. Da das Streuverhalten nicht nur von geometrischen Größen, sondern auch von anderen Wechselwirkungen der Streupartner untereinander abhängt, ist die gemessene Fläche nicht immer direkt mit dem geometrischen Querschnitt der Streupartner gleichzusetzen. Man spricht dann allgemeiner vom Wirkungsquerschnitt, der ebenfalls die Dimension einer Fläche hat. ⓘ
















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
























































































![{\displaystyle A=r^{2}\int _{-\pi }^{\pi }\int _{-\pi /2}^{\pi /2}\cos B\,\mathrm {d} B\,\mathrm {d} L=r^{2}\int _{-\pi }^{\pi }\left[\sin B\right]_{-\pi /2}^{\pi /2}\,\mathrm {d} L=2r^{2}\int _{-\pi }^{\pi }\mathrm {d} L=4\pi r^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee1ae4c7efe499849c71c6f32661778c239a1b0b)






