Gravitationskonstante

Notationen für die Gravitationskonstante

Werte von G	Einheiten ⓘ
6.67430(15)×10−11	N m2⋅kg-2
6.67430(15)×10−8	dyne cm2⋅gramm-2
4.30091(25)×10−3	pc⋅M⊙-1⋅(km/s)2

Die Gravitationskonstante G ist eine Schlüsselgröße im Newtonschen Gesetz der universellen Gravitation. ⓘ

Die Gravitationskonstante (auch bekannt als universelle Gravitationskonstante, Newtonsche Gravitationskonstante oder Cavendish-Gravitationskonstante), die mit dem Großbuchstaben G bezeichnet wird, ist eine empirische physikalische Konstante, die in die Berechnung der Gravitationswirkungen in Sir Isaac Newtons Gesetz der universellen Gravitation und in Albert Einsteins Allgemeiner Relativitätstheorie eingeht. ⓘ

Im Newtonschen Gesetz ist sie die Proportionalitätskonstante, die die Gravitationskraft zwischen zwei Körpern mit dem Produkt ihrer Massen und dem inversen Quadrat ihres Abstands verbindet. In den Einsteinschen Feldgleichungen quantifiziert sie die Beziehung zwischen der Geometrie der Raumzeit und dem Energie-Momententensor (auch als Spannungs-Energie-Tensor bezeichnet). ⓘ

Der gemessene Wert der Konstante ist mit einiger Sicherheit auf vier signifikante Stellen genau bekannt. In SI-Einheiten beträgt ihr Wert etwa 6,674×10-11 m³⋅kg-1⋅s-2. ⓘ

Die moderne Schreibweise des Newtonschen Gesetzes, die G einschließt, wurde in den 1890er Jahren von C. V. Boys eingeführt. Die erste implizite Messung mit einer Genauigkeit von etwa 1 % wird Henry Cavendish in einem Experiment von 1798 zugeschrieben. ⓘ

wobei bereits die vierte Dezimalstelle unsicher ist. ⓘ

Definition

Nach dem Newtonschen Gesetz der universellen Gravitation ist die Anziehungskraft (F) zwischen zwei punktförmigen Körpern direkt proportional zum Produkt ihrer Massen (m₁ und m₂) und umgekehrt proportional zum Quadrat des Abstands r zwischen ihren Massenschwerpunkten:

$$F=G{\frac {m_{1}m_{2}}{r^{2}}}.$$

Die Proportionalitätskonstante, G, ist die Gravitationskonstante. Umgangssprachlich wird die Gravitationskonstante auch als "Big G" bezeichnet, im Unterschied zum "kleinen g" (g), das das lokale Gravitationsfeld der Erde darstellt (entspricht der Beschleunigung im freien Fall). Wobei $M_{\oplus }$ die Masse der Erde ist und $r_{\oplus }$ der Radius der Erde ist, sind die beiden Größen durch miteinander verbunden:

$$g={\frac {GM_{\oplus }}{r_{\oplus }^{2}}}.$$

ⓘ

Die Gravitationskonstante erscheint in den Einsteinschen Feldgleichungen der allgemeinen Relativitätstheorie,

$$G_{\mu \nu }+\Lambda g_{\mu \nu }=\kappa T_{\mu \nu }\,,$$

wobei G_μν der Einstein-Tensor, Λ die kosmologische Konstante, g_μν der metrische Tensor, T_μν der Spannungs-Energie-Tensor und κ die Einsteinsche Konstante ist, eine ursprünglich von Einstein eingeführte Konstante, die direkt mit der Newtonschen Gravitationskonstante zusammenhängt:

$$\kappa ={\frac {8\pi G}{c^{4}}}\approx 2.077\times 10^{-43}\mathrm {\,m{\cdot }J^{-1}} .$$

ⓘ

Diese Form des Gesetzes wurde 1873, 200 Jahre nach Newton, durch Alfred Cornu und Jean-Baptistin Baille eingeführt. Newton schrieb sein Gesetz ohne Nennung der Konstante in Form der Proportionalitäten $F\propto m_{1}\ ,\ F\propto m_{2}\ ,\ F\propto r^{-2}$, wie es damals in der wissenschaftlichen Literatur üblich war. ⓘ

Um die Formulierung eines rationalisierten Einheitensystems zu erhalten, hätte man eine Definition über ${\textstyle F=G\,{\frac {m_{1}\,m_{2}}{4\pi r^{2}}}}$ wählen müssen, also mit einer 4π-mal so großen Proportionalitätskonstanten. ⓘ

Wert und Unsicherheit

Die Gravitationskonstante ist eine physikalische Konstante, die nur schwer mit hoher Genauigkeit zu messen ist. Dies liegt daran, dass die Gravitationskraft im Vergleich zu anderen fundamentalen Kräften eine extrem schwache Kraft ist. ⓘ

Der vom Committee on Data for Science and Technology (CODATA) 2018 empfohlene Wert der Gravitationskonstante (mit Standardunsicherheit in Klammern) lautet in SI-Einheiten:

$$G=6.67430(15)\times 10^{-11}{\rm {\ m^{3}{\cdot }kg^{-1}{\cdot }s^{-2}}}$$

ⓘ

Dies entspricht einer relativen Standardunsicherheit von 2,2×10-5 (22 ppm). ⓘ

Natürliche Einheiten

Die Gravitationskonstante ist eine definierende Konstante in einigen Systemen natürlicher Einheiten, insbesondere in geometrischen Einheitensystemen wie den Planck-Einheiten und den Stoney-Einheiten. Wenn sie in solchen Einheiten ausgedrückt wird, hat der Wert der Gravitationskonstante im Allgemeinen den numerischen Wert 1 oder einen Wert in der Nähe davon. Da der gemessene Wert von G in Bezug auf andere bekannte fundamentale Konstanten mit erheblichen Unsicherheiten behaftet ist, zeigt sich ein ähnliches Maß an Unsicherheit in den Werten vieler Größen, wenn sie in einem solchen Einheitensystem ausgedrückt werden. ⓘ

Orbitalmechanik

In der Astrophysik ist es üblich, Entfernungen in Parsecs (pc), Geschwindigkeiten in Kilometern pro Sekunde (km/s) und Massen in Sonneneinheiten M_⊙ zu messen. In diesen Einheiten ist die Gravitationskonstante:

$$G\approx 4.3009\times 10^{-3}{\rm {}}{\frac {pc}{M_{\odot }}}{\rm {\ (km/s)^{2}}}.\,$$

In Situationen, in denen Gezeiten eine Rolle spielen, sind die relevanten Längenskalen Sonnenradien und nicht Parsecs. In diesen Einheiten ist die Gravitationskonstante gleich:

$$G\approx 1.90809\times 10^{5}R_{\odot }M_{\odot }^{-1}{\rm {\ (km/s)^{2}}}.\,$$

In der Orbitalmechanik gilt für die Periode P eines Objekts auf einer Kreisbahn um ein kugelförmiges Objekt die Gleichung

$$GM={\frac {3\pi V}{P^{2}}}$$

wobei V das Volumen innerhalb des Radius der Umlaufbahn ist. Daraus folgt, dass

$P^{2}={\frac {3\pi }{G}}{\frac {V}{M}}\approx 10.896\ \mathrm {h^{2}{\cdot }g{\cdot }cm^{-3}} {\frac {V}{M}}.$

Diese Art, G auszudrücken, zeigt die Beziehung zwischen der durchschnittlichen Dichte eines Planeten und der Periode eines Satelliten, der ihn knapp über seiner Oberfläche umkreist. ⓘ

Für elliptische Bahnen gilt das 3. Kepler'sche Gesetz, ausgedrückt in den für die Erdbahn charakteristischen Einheiten:

$G=4\pi ^{2}{\rm {\ AU^{3}{\cdot }yr^{-2}}}\ M^{-1}\approx 39.478{\rm {\ AU^{3}{\cdot }yr^{-2}}}\ M_{\odot }^{-1},$

Dabei wird die Entfernung in Form der Halbachse der Erdbahn (der Astronomischen Einheit, AE), die Zeit in Jahren und die Masse in der Gesamtmasse des umlaufenden Systems (M = M_☉ + MErde + M_☾). ⓘ

Die obige Gleichung ist nur innerhalb der Näherung der Erdbahn um die Sonne als Zweikörperproblem in der Newtonschen Mechanik exakt, die gemessenen Größen enthalten Korrekturen aus den Störungen durch andere Körper im Sonnensystem und aus der allgemeinen Relativitätstheorie. ⓘ

Von 1964 bis 2012 wurde sie jedoch als Definition der astronomischen Einheit verwendet und galt somit per Definition:

$$1\ \mathrm {AU} =\left({\frac {GM}{4\pi ^{2}}}{\rm {yr}}^{2}\right)^{\frac {1}{3}}\approx 1.495979\times 10^{11}{\rm {m}}.$$

Seit 2012 ist AU genau mit 1,495978707×10¹¹ m definiert, und die Gleichung kann nicht mehr als exakt gültig angesehen werden. ⓘ

Die Größe GM - das Produkt aus der Gravitationskonstante und der Masse eines bestimmten astronomischen Körpers wie der Sonne oder der Erde - wird als Standardgravitationsparameter (auch μ genannt) bezeichnet. Der Standardgravitationsparameter GM erscheint wie oben in Newtons Gesetz der universellen Gravitation sowie in Formeln für die Ablenkung von Licht durch Gravitationslinsen, in Keplers Gesetzen der Planetenbewegung und in der Formel für die Fluchtgeschwindigkeit. ⓘ

Diese Größe dient zur Vereinfachung verschiedener Formeln, die mit der Schwerkraft zusammenhängen. Das Produkt GM ist viel genauer bekannt als die beiden Faktoren. ⓘ

Werte für GM

Körper	μ = GM	Wert	Relative Unsicherheit ⓘ
Sonne	GM☉	1,32712440018(8)×1020 m3⋅s-2	6×10−11
Erde	GMErde	3,986004418(8)×1014 m3⋅s-2	2×10−9

Berechnungen in der Himmelsmechanik können auch mit den Einheiten der Sonnenmassen, der mittleren Sonnentage und der astronomischen Einheiten anstelle der SI-Standardeinheiten durchgeführt werden. Zu diesem Zweck wurde in der Vergangenheit häufig die Gaußsche Gravitationskonstante k = 0,01720209895 verwendet, die die mittlere Winkelgeschwindigkeit des Systems Sonne-Erde, gemessen in Radiant pro Tag, ausdrückt. Die Verwendung dieser Konstante und die damit verbundene Definition der oben erwähnten astronomischen Einheit wird von der IAU seit 2012 nicht mehr empfohlen. ⓘ

Geschichte der Messung

Frühe Geschichte

Die Existenz der Konstante wird in Newtons Gesetz der universellen Gravitation, das in den 1680er Jahren veröffentlicht wurde, angedeutet (obwohl die Notation als G aus den 1890er Jahren stammt), wird aber nicht in seiner Philosophiæ Naturalis Principia Mathematica berechnet, in der er das Gesetz der Gravitation im Quadrat postuliert. In der Principia zog Newton die Möglichkeit in Betracht, die Stärke der Schwerkraft durch Messung der Auslenkung eines Pendels in der Nähe eines großen Hügels zu messen, war aber der Meinung, dass der Effekt zu gering wäre, um messbar zu sein. Dennoch hatte er die Möglichkeit, die Größenordnung der Konstante abzuschätzen, als er vermutete, dass "die mittlere Dichte der Erde fünf- oder sechsmal so groß sein könnte wie die Dichte von Wasser", was einer Gravitationskonstante in der Größenordnung entspricht:

G ≈ (6,7±0,6)×10-11 m³⋅kg-1⋅s-2 ⓘ

Eine Messung wurde 1738 von Pierre Bouguer und Charles Marie de La Condamine im Rahmen ihrer "Peruanischen Expedition" versucht. Bouguer spielte die Bedeutung ihrer Ergebnisse 1740 herunter und meinte, das Experiment habe zumindest bewiesen, dass die Erde keine hohle Schale sein könne, wie einige Denker der damaligen Zeit, darunter Edmond Halley, behauptet hatten. ⓘ

Das 1772 vorgeschlagene und 1776 abgeschlossene Schiehallion-Experiment war die erste erfolgreiche Messung der mittleren Dichte der Erde und damit indirekt auch der Gravitationskonstante. Das von Charles Hutton (1778) gemeldete Ergebnis ergab eine Dichte von 4,5 g/cm³ (das 4+1/2-fache der Dichte von Wasser), was etwa 20 % unter dem heutigen Wert liegt. Dies führte sofort zu Schätzungen der Dichten und Massen von Sonne, Mond und Planeten, die Hutton an Jérôme Lalande schickte, um sie in seine Planetentafeln aufzunehmen. Wie bereits erwähnt, ist die Bestimmung der durchschnittlichen Dichte der Erde gleichbedeutend mit der Messung der Gravitationskonstante, wenn man den mittleren Radius der Erde und die mittlere Gravitationsbeschleunigung an der Erdoberfläche annimmt, indem man

$$G=g{\frac {R_{\oplus }^{2}}{M_{\oplus }}}={\frac {3g}{4\pi R_{\oplus }\rho _{\oplus }}}.$$

Auf dieser Grundlage entspricht Huttons Ergebnis von 1778 G ≈ 8×10-11 m³⋅kg-1⋅s-2. ⓘ

Schema der Torsionswaage, die im Cavendish-Experiment verwendet wurde, das Henry Cavendish 1798 durchführte, um G zu messen. Mit Hilfe eines Flaschenzugs wurden große Kugeln, die an einem Gestell hingen, neben den kleinen Kugeln in Rotation versetzt. ⓘ

Die erste direkte Messung der Gravitationskraft zwischen zwei Körpern im Labor wurde 1798, einundsiebzig Jahre nach Newtons Tod, von Henry Cavendish durchgeführt. Er ermittelte den Wert für G implizit mit Hilfe einer Torsionswaage, die von dem Geologen Rev. John Michell (1753) erfunden wurde. Er verwendete einen horizontalen Torsionsbalken mit Bleikugeln, deren Trägheit (im Verhältnis zur Torsionskonstante) er durch die Zeitmessung der Balkenschwingung bestimmen konnte. Die schwache Anziehungskraft der Kugeln auf andere Kugeln, die neben dem Balken platziert waren, ließ sich an der dadurch verursachten Ablenkung erkennen. Obwohl der Versuchsplan auf Michell zurückgeht, ist das Experiment heute als Cavendish-Experiment bekannt, da es erstmals von Cavendish erfolgreich durchgeführt wurde. ⓘ

Cavendishs erklärtes Ziel war das "Wiegen der Erde", d. h. die Bestimmung der durchschnittlichen Dichte der Erde und der Erdmasse. Sein Ergebnis, ρ_🜨 = 5,448(33) g-cm-3, entspricht dem Wert von G = 6,74(4)×10-11 m³⋅kg-1⋅s-2. Er ist erstaunlich genau und liegt etwa 1 % über dem modernen Wert (vergleichbar mit der angegebenen Standardunsicherheit von 0,6 %). ⓘ

19. Jahrhundert

Die Genauigkeit des gemessenen Werts von G hat sich seit dem ursprünglichen Cavendish-Experiment nur geringfügig verbessert. G ist recht schwierig zu messen, da die Schwerkraft viel schwächer ist als andere fundamentale Kräfte und ein Versuchsgerät nicht vom Gravitationseinfluss anderer Körper getrennt werden kann. ⓘ

Messungen mit Pendeln wurden von Francesco Carlini (1821, 4,39 g/cm³), Edward Sabine (1827, 4,77 g/cm³), Carlo Ignazio Giulio (1841, 4,95 g/cm³) und George Biddell Airy (1854, 6,6 g/cm³) durchgeführt. ⓘ

Das Experiment von Cavendish wurde erstmals von Ferdinand Reich (1838, 1842, 1853) wiederholt, der einen Wert von 5,5832(149) g-cm-3 ermittelte, der sogar noch schlechter ist als Cavendishs Ergebnis und um 1,5 % vom heutigen Wert abweicht. Cornu und Baille (1873) fanden 5,56 g-cm-3. ⓘ

Cavendishs Experiment erwies sich als zuverlässiger als Pendelversuche vom Typ "Schiehallion" (Auslenkung) oder "Peruvian" (Periode in Abhängigkeit von der Höhe). Pendelversuche wurden weiterhin durchgeführt, von Robert von Sterneck (1883, Ergebnisse zwischen 5,0 und 6,3 g/cm³) und Thomas Corwin Mendenhall (1880, 5,77 g/cm³). ⓘ

Cavendishs Ergebnis wurde erstmals von John Henry Poynting (1891) verbessert, der einen Wert von 5,49(3) g-cm-3 veröffentlichte, der vom heutigen Wert um 0,2 % abweicht, aber mit dem heutigen Wert innerhalb der angegebenen Standardunsicherheit von 0,55 % vereinbar ist. Zusätzlich zu Poynting wurden Messungen von C. V. Boys (1895) und Carl Braun (1897) durchgeführt, deren Ergebnisse mit dem heutigen Wert G = 6,66(1)×10-11 m³⋅kg-1⋅s-2 übereinstimmen. Die moderne Notation mit der Konstante G wurde von Boys 1894 eingeführt und wurde Ende der 1890er Jahre zum Standard, wobei die Werte gewöhnlich im cgs-System angegeben wurden. Richarz und Krigar-Menzel (1898) versuchten eine Wiederholung des Cavendish-Experiments mit 100.000 kg Blei als anziehender Masse. Die Genauigkeit ihres Ergebnisses von 6,683(11)×10-11 m³⋅kg-1⋅s-2 lag jedoch in der gleichen Größenordnung wie die anderen Ergebnisse zu dieser Zeit. ⓘ

Arthur Stanley Mackenzie gibt in The Laws of Gravitation (1899) einen Überblick über die Arbeiten des 19. Poynting ist der Autor des Artikels "Gravitation" in der Encyclopædia Britannica Eleventh Edition (1911). Hier gibt er einen Wert von G = 6,66×10-11 m³⋅kg-1⋅s-2 mit einer Unsicherheit von 0,2 % an. ⓘ

Moderner Wert

Paul R. Heyl (1930) veröffentlichte den Wert von 6,670(5)×10-11 m³⋅kg-1⋅s-2 (relative Unsicherheit 0,1%), der 1942 auf 6,673(3)×10-11 m³⋅kg-1⋅s-2 (relative Unsicherheit 0,045% = 450 ppm) verbessert wurde. ⓘ

Veröffentlichte Werte von G, die aus hochpräzisen Messungen seit den 1950er Jahren abgeleitet wurden, sind weiterhin mit Heyl (1930) kompatibel, schwanken aber innerhalb der relativen Unsicherheit von etwa 0,1 % (oder 1.000 ppm) ziemlich stark, und es ist nicht ganz klar, ob die Unsicherheit seit der Messung von 1942 überhaupt verringert wurde. Einige in den 1980er bis 2000er Jahren veröffentlichte Messungen schlossen sich sogar gegenseitig aus. Die Festlegung eines Standardwerts für G mit einer Standardunsicherheit von mehr als 0,1 % bleibt daher eher spekulativ. ⓘ

Bis 1969 wurde der vom National Institute of Standards and Technology (NIST) empfohlene Wert mit einer Standardunsicherheit von 0,046 % (460 ppm) angegeben, die bis 1986 auf 0,012 % (120 ppm) gesenkt wurde. Die fortgesetzte Veröffentlichung widersprüchlicher Messungen veranlasste das NIST jedoch, die Standardunsicherheit des 1998 empfohlenen Wertes erheblich zu erhöhen, und zwar um den Faktor 12 auf eine Standardunsicherheit von 0,15 %, die größer ist als die von Heyl (1930) angegebene. ⓘ

In den Jahren 2002 und 2006 wurde die Unsicherheit erneut gesenkt, aber 2010 noch einmal um konservativere 20 % angehoben, so dass der 1986 veröffentlichte Standardunsicherheitswert von 120 ppm erreicht wurde. Für die Aktualisierung 2014 reduzierte CODATA die Unsicherheit auf 46 ppm, weniger als die Hälfte des Wertes von 2010 und eine Größenordnung unter der Empfehlung von 1969. ⓘ

Die folgende Tabelle zeigt die vom NIST empfohlenen Werte, die seit 1969 veröffentlicht wurden:

Zeitleiste der Messungen und empfohlenen Werte für G seit 1900: Empfohlene Werte, die auf einer Literaturübersicht basieren, sind in rot dargestellt, einzelne Torsionswaagenexperimente in blau, andere Arten von Experimenten in grün. ⓘ

Empfohlene Werte für G

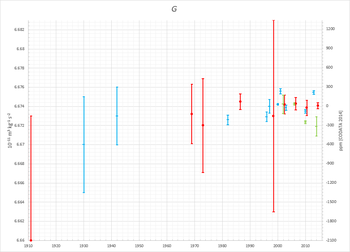
Jahr	G (10-11-m3⋅kg-1⋅s-2)	Standardunsicherheit	Ref. ⓘ
1969	6.6732(31)	460 ppm
1973	6.6720(49)	730 ppm
1986	6.67449(81)	120 ppm
1998	6.673(10)	1.500 ppm
2002	6.6742(10)	150 ppm
2006	6.67428(67)	100 ppm
2010	6.67384(80)	120 ppm
2014	6.67408(31)	46 ppm
2018	6.67430(15)	22 ppm

In der Januarausgabe 2007 von Science beschrieben Fixler et al. eine Messung der Gravitationskonstante mit einer neuen Technik, der Atominterferometrie, und gaben einen Wert von G = 6,693(34)×10-11 m³⋅kg-1⋅s-2 an, der 0,28 % (2800 ppm) über dem CODATA-Wert von 2006 liegt. Eine verbesserte Messung der kalten Atome durch Rosi et al. wurde 2014 mit G = 6,67191(99)×10-11 m³⋅kg-1⋅s-2 veröffentlicht. Obwohl dieses Ergebnis viel näher am akzeptierten Wert liegt (was darauf hindeutet, dass die Messung von Fixler et al. fehlerhaft war), lag es 325 ppm unter dem empfohlenen CODATA-Wert von 2014, wobei sich die Standardunsicherheitsintervalle nicht überschnitten. ⓘ

Seit 2018 laufen Bemühungen zur Neubewertung der widersprüchlichen Messergebnisse, die vom NIST koordiniert werden, insbesondere eine Wiederholung der von Quinn et al. (2013) berichteten Experimente. ⓘ

Im August 2018 gab eine chinesische Forschergruppe neue Messungen auf der Grundlage von Torsionswaagen bekannt, 6,674184(78)×10-11 m³⋅kg-1⋅s-2 und 6,674484(78)×10-11 m³⋅kg-1⋅s-2, die auf zwei verschiedenen Methoden basieren. Es wird behauptet, dass dies die genauesten Messungen sind, die jemals gemacht wurden, mit einer Standardunsicherheit, die mit 12 ppm angegeben wird. Die Differenz von 2,7σ zwischen den beiden Ergebnissen deutet darauf hin, dass es Fehlerquellen geben könnte, die nicht berücksichtigt wurden. ⓘ

Vorgeschlagene Zeitabweichung

Eine umstrittene Studie von Anderson et al. aus dem Jahr 2015 über einige frühere Messungen von G legt nahe, dass die meisten der sich gegenseitig ausschließenden Werte in hochpräzisen Messungen von G durch eine periodische Variation erklärt werden können. Die Schwankung wurde mit einer Periode von 5,9 Jahren gemessen, ähnlich wie bei Tageslängenmessungen (LOD), was auf eine gemeinsame physikalische Ursache hindeutet, die nicht unbedingt eine Schwankung von G ist. Eine Antwort wurde von einigen der ursprünglichen Autoren der G-Messungen, die in Anderson et al. verwendet wurden, verfasst. Ein Diagramm mit geschätzten Messzeitpunkten, die von den ursprünglichen Autoren angegeben wurden, verschlechtert die Tageslängenkorrelation erheblich. Auch die Betrachtung der von Karagioz und Izmailov über ein Jahrzehnt gesammelten Daten zeigt keine Korrelation mit den Messungen der Tageslänge. Die Schwankungen von G sind also höchstwahrscheinlich auf systematische Messfehler zurückzuführen, die nicht richtig berücksichtigt wurden. Unter der Annahme, dass die Physik von Supernovae des Typs Ia universell ist, hat die Analyse der Beobachtungen von 580 Supernovae gezeigt, dass sich die Gravitationskonstante in den letzten neun Milliarden Jahren um weniger als einen Teil von zehn Milliarden pro Jahr verändert hat (Mould et al., 2014). ⓘ

Messungen

Die Gravitationskraft zwischen der Erde und einem anderen Objekt, d. h., sein Gewicht, lässt sich zwar sehr genau messen, allerdings müsste man, um daraus die Gravitationskonstante mit gleicher Genauigkeit zu bestimmen, die Erdmasse oder besser die ganze Massenverteilung in der Erde zuverlässig kennen. Das ist aber nicht gegeben, sodass zur Messung von $G$ die überaus geringe Anziehungskraft zwischen Körpern bekannter Masse im Labor bestimmt werden muss. Beispielsweise beträgt die Anziehungskraft zwischen zwei Körpern von je 100 kg Masse in 1 m Abstand weniger als 10⁻⁹ (ein Milliardstel) ihrer Gewichtskraft, und alle andere Materie im Labor oder außerhalb davon übt auf die Testkörper ebenfalls Gravitation aus. Diese Messungen gestalten sich daher schwierig. Schon kleinste Temperaturunterschiede, Luftströmungen, Ungleichmäßigkeiten im Material oder Kriechen des Materials, sogar die Anzahl der Fahrzeuge auf dem Parkplatz vor dem Institutsgebäude, verfälschen die Ergebnisse. ⓘ