Determinante

In der linearen Algebra ist die Determinante eine Zahl (ein Skalar), die einer quadratischen Matrix zugeordnet wird und aus ihren Einträgen berechnet werden kann. Sie gibt an, wie sich das Volumen bei der durch die Matrix beschriebenen linearen Abbildung ändert, und ist ein nützliches Hilfsmittel bei der Lösung linearer Gleichungssysteme. Allgemeiner kann man jeder linearen Selbstabbildung (Endomorphismus) eine Determinante zuordnen. Übliche Schreibweisen für die Determinante einer quadratischen Matrix $A$ sind $\det(A)$, $\det A$ oder $|A|$. ⓘ

Die 2x2-Determinante ist gleich dem orientierten Flächeninhalt des von ihren Spaltenvektoren aufgespannten Parallelogramms ⓘ

Zum Beispiel kann die Determinante einer $2\times 2$-Matrix

$A={\begin{pmatrix}a&c\\b&d\end{pmatrix}}$

mit der Formel

$\det A={\begin{vmatrix}a&c\\b&d\end{vmatrix}}=ad-bc$

berechnet werden. ⓘ

Mit Hilfe von Determinanten kann man beispielsweise feststellen, ob ein lineares Gleichungssystem eindeutig lösbar ist, und kann die Lösung mit Hilfe der Cramerschen Regel explizit angeben. Das Gleichungssystem ist genau dann eindeutig lösbar, wenn die Determinante der Koeffizientenmatrix ungleich null ist. Entsprechend ist eine quadratische Matrix mit Einträgen aus einem Körper genau dann invertierbar, wenn ihre Determinante ungleich null ist. ⓘ

Schreibt man $n$ Vektoren im $\mathbb {R} ^{n}$ als Spalten einer quadratischen Matrix, so kann die Determinante dieser Matrix gebildet werden. Bilden bei dieser Festlegung die $n$ Vektoren eine Basis, so kann das Vorzeichen der Determinante dazu verwendet werden, die Orientierung von euklidischen Räumen zu definieren. Der Absolutbetrag dieser Determinante entspricht zugleich dem Volumen des n-Parallelotops (auch Spat genannt), das durch diese Vektoren aufgespannt wird. ⓘ

Wird die lineare Abbildung $f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{n}$ durch die Matrix $A$ repräsentiert und ist $S\subseteq \mathbb {R} ^{n}$ eine beliebige messbare Teilmenge, dann folgt, dass das Volumen von $f(S)$ durch $\left|\det A\right|\cdot \operatorname {Volumen} (S)$ gegeben ist. ⓘ

Wird die lineare Abbildung $f\colon \mathbb {R} ^{n}\to \mathbb {R} ^{m}$ durch die $m\times n$-Matrix $A$ repräsentiert und ist $S\subseteq \mathbb {R} ^{n}$ eine beliebige messbare Teilmenge, so gilt im Allgemeinen, dass das $m$-dimensionale Volumen von $f(S)$ durch $\textstyle {\sqrt {\det(A^{T}A)}}\cdot \operatorname {Volumen} (S)$ gegeben ist, siehe Gramsche Determinante ⓘ

Das Konzept der Determinante ist von Interesse für $(n\times n)$-Matrizen mit $n>1$. Für $n=1$ verkommt es zur Trivialität $\det a=a$: So besteht ein lineares Gleichungssystem für den Fall $n=1$ aus einer Gleichung $ax=b$. Lösbarkeitskriterium und -strategie für diese Gleichung sind bekannt: Falls $a\neq 0$, setze $x:=a^{-1}b$. ⓘ

Für eine 3 × 3-Matrix A lautet die Determinante entsprechend

${\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}$ ⓘ

Jede Determinante einer 2 × 2-Matrix in dieser Gleichung wird als Minor der Matrix A bezeichnet. Dieses Verfahren kann erweitert werden, um eine rekursive Definition für die Determinante einer n × n-Matrix zu erhalten, die als Laplace-Erweiterung bekannt ist. ⓘ

Determinanten kommen überall in der Mathematik vor. So wird beispielsweise eine Matrix häufig verwendet, um die Koeffizienten in einem System linearer Gleichungen darzustellen, und Determinanten können zur Lösung dieser Gleichungen verwendet werden (Cramersche Regel), obwohl andere Lösungsmethoden rechnerisch viel effizienter sind. Determinanten werden verwendet, um das charakteristische Polynom einer Matrix zu definieren, dessen Wurzeln die Eigenwerte sind. In der Geometrie wird das vorzeichenbehaftete n-dimensionale Volumen eines n-dimensionalen Parallelepipeds durch eine Determinante ausgedrückt. Diese wird in der Infinitesimalrechnung mit äußeren Differentialformen und der Jacobi-Determinante verwendet, insbesondere bei Variablenwechseln in Mehrfachintegralen. ⓘ

2 × 2-Matrizen

Die Determinante einer 2 × 2-Matrix ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ wird entweder durch "det" oder durch senkrechte Balken um die Matrix herum bezeichnet und ist definiert als

$\det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}={\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc.$

Zum Beispiel,

$\det {\begin{pmatrix}3&7\\1&-4\end{pmatrix}}={\begin{vmatrix}3&7\\1&{-4}\end{vmatrix}}=3\cdot (-4)-7\cdot 1=-19.$ ⓘ

Erste Eigenschaften

Die Determinante hat mehrere Schlüsseleigenschaften, die sich durch direkte Auswertung der Definition für $2\times 2$-Matrizen bewiesen werden können, und die auch für Determinanten größerer Matrizen gelten. Sie lauten wie folgt: Erstens ist die Determinante der Einheitsmatrix ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ ist 1. Zweitens: Die Determinante ist Null, wenn zwei Zeilen gleich sind:

${\begin{vmatrix}a&b\\a&b\end{vmatrix}}=ab-ba=0.$

Dies gilt auch, wenn die beiden Spalten gleich sind. Außerdem,

${\begin{vmatrix}a&b+b'\\c&d+d'\end{vmatrix}}=a(d+d')-(b+b')c={\begin{vmatrix}a&b\\c&d\end{vmatrix}}+{\begin{vmatrix}a&b'\\c&d'\end{vmatrix}}.$

Wenn schließlich eine beliebige Spalte mit einer bestimmten Zahl multipliziert wird $r$ multipliziert wird (d. h. alle Einträge in dieser Spalte werden mit dieser Zahl multipliziert), wird auch die Determinante mit dieser Zahl multipliziert:

${\begin{vmatrix}r\cdot a&b\\r\cdot c&d\end{vmatrix}}=rad-brc=r(ad-bc)=r\cdot {\begin{vmatrix}a&b\\c&d\end{vmatrix}}.$ ⓘ

Geometrische Bedeutung

Der Flächeninhalt des Parallelogramms ist der Absolutwert der Determinante der Matrix, die aus den Vektoren gebildet wird, die die Seiten des Parallelogramms darstellen. ⓘ

Wenn die Matrixeinträge reelle Zahlen sind, kann die Matrix A dazu verwendet werden, zwei lineare Abbildungen darzustellen: eine, die die Standardbasisvektoren auf die Zeilen von A abbildet, und eine, die sie auf die Spalten von A abbildet. In beiden Fällen bilden die Bilder der Basisvektoren ein Parallelogramm, das das Bild des Einheitsquadrats unter der Abbildung darstellt. Das Parallelogramm, das durch die Zeilen der obigen Matrix definiert ist, hat die Eckpunkte (0, 0), (a, b), (a + c, b + d) und (c, d), wie in der nebenstehenden Abbildung gezeigt. ⓘ

Der Absolutwert von ad - bc ist der Flächeninhalt des Parallelogramms und stellt somit den Skalierungsfaktor dar, um den die Flächen durch A transformiert werden. (Das Parallelogramm, das durch die Spalten von A gebildet wird, ist im Allgemeinen ein anderes Parallelogramm, aber da die Determinante symmetrisch in Bezug auf Zeilen und Spalten ist, ist der Flächeninhalt derselbe). ⓘ

Der Absolutwert der Determinante ergibt zusammen mit dem Vorzeichen die orientierte Fläche des Parallelogramms. Die orientierte Fläche ist dieselbe wie die gewöhnliche Fläche, nur dass sie negativ ist, wenn der Winkel zwischen dem ersten und dem zweiten Vektor, der das Parallelogramm definiert, im Uhrzeigersinn verläuft (was der Richtung entgegengesetzt ist, die man für die Identitätsmatrix erhalten würde). ⓘ

Um zu zeigen, dass ad - bc der vorzeichenbehaftete Flächeninhalt ist, kann man eine Matrix mit zwei Vektoren u ≡ (a, b) und v ≡ (c, d) betrachten, die die Seiten des Parallelogramms darstellen. Die vorzeichenbehaftete Fläche kann als |u| |v| sin θ für den Winkel θ zwischen den Vektoren ausgedrückt werden, was einfach Basis mal Höhe ist, die Länge des einen Vektors mal die senkrechte Komponente des anderen. Wegen des Sinus ist dies bereits die vorzeichenbehaftete Fläche, doch lässt sie sich bequemer durch den Kosinus des Komplementärwinkels zu einem senkrechten Vektor ausdrücken, z. B. u^⊥ = (-b, a), so dass |u^⊥| |v| cos θ′, was nach dem Muster des Skalarprodukts gleich ad - bc ist:

${\text{Signed area}}=|{\boldsymbol {u}}|\,|{\boldsymbol {v}}|\,\sin \,\theta =\left|{\boldsymbol {u}}^{\perp }\right|\,\left|{\boldsymbol {v}}\right|\,\cos \,\theta '={\begin{pmatrix}-b\\a\end{pmatrix}}\cdot {\begin{pmatrix}c\\d\end{pmatrix}}=ad-bc.$ ⓘ

Das Volumen dieses Parallelepipeds ist der Absolutwert der Determinante der Matrix, die durch die aus den Vektoren r1, r2 und r3 gebildeten Spalten gebildet wird. ⓘ

Die Determinante gibt also den Skalierungsfaktor und die Orientierung an, die durch die durch A dargestellte Abbildung induziert werden. Wenn die Determinante gleich 1 ist, ist die durch die Matrix definierte lineare Abbildung gleichwichtig und orientierungserhaltend. ⓘ

Das Objekt, das als Bivektor bekannt ist, ist mit diesen Ideen verbunden. In 2D kann er als ein orientiertes Ebenensegment interpretiert werden, das durch die Vorstellung von zwei Vektoren mit dem Ursprung (0, 0) und den Koordinaten (a, b) und (c, d) gebildet wird. Der Betrag des Bivektors (bezeichnet durch (a, b) ∧ (c, d)) ist die vorzeichenbehaftete Fläche, die auch die Determinante ad - bc ist. ⓘ

Wird eine n × n reelle Matrix A in Form ihrer Spaltenvektoren geschrieben $A=\left[{\begin{array}{c|c|c|c}\mathbf {a} _{1}&\mathbf {a} _{2}&\cdots &\mathbf {a} _{n}\end{array}}\right]$, dann

$A{\begin{pmatrix}1\\0\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{1},\quad A{\begin{pmatrix}0\\1\\\vdots \\0\end{pmatrix}}=\mathbf {a} _{2},\quad \ldots ,\quad A{\begin{pmatrix}0\\0\\\vdots \\1\end{pmatrix}}=\mathbf {a} _{n}.$ ⓘ

Dies bedeutet, dass $A$ den Einheitswürfel n auf das n-dimensionale Parallelotop abbildet, das durch die Vektoren $\mathbf {a} _{1},\mathbf {a} _{2},\ldots ,\mathbf {a} _{n},$ den Bereich $P=\left\{c_{1}\mathbf {a} _{1}+\cdots +c_{n}\mathbf {a} _{n}\mid 0\leq c_{i}\leq 1\ \forall i\right\}.$ ⓘ

Die Determinante gibt das vorzeichenbehaftete n-dimensionale Volumen dieses Parallelotops an, $\det(A)=\pm {\text{vol}}(P),$ und beschreibt somit ganz allgemein den n-dimensionalen Volumenskalierungsfaktor der von A erzeugten linearen Transformation. (Das Vorzeichen gibt an, ob die Transformation die Orientierung beibehält oder umkehrt.) Insbesondere, wenn die Determinante Null ist, hat dieses Parallelotop ein Volumen von Null und ist nicht vollständig n-dimensional, was bedeutet, dass die Dimension des Bildes von A kleiner als n ist. Das bedeutet, dass A eine lineare Transformation erzeugt, die weder onto noch eineindeutig und somit nicht invertierbar ist. ⓘ

Definition

In der Folge ist A eine quadratische Matrix mit n Zeilen und n Spalten, so dass sie wie folgt geschrieben werden kann

$A={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{bmatrix}}.$ ⓘ

Die Einträge $a_{1,1}$ usw. sind für viele Zwecke reelle oder komplexe Zahlen. Wie weiter unten erläutert, ist die Determinante auch für Matrizen definiert, deren Einträge Elemente in abstrakteren algebraischen Strukturen sind, die als kommutative Ringe bezeichnet werden. ⓘ

Die Determinante von A wird mit det(A) bezeichnet, oder sie kann direkt in Bezug auf die Matrixeinträge angegeben werden, indem man statt Klammern umschließende Balken schreibt:

${\begin{vmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,n}\\a_{2,1}&a_{2,2}&\cdots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{n,1}&a_{n,2}&\cdots &a_{n,n}\end{vmatrix}}.$ ⓘ

Es gibt verschiedene äquivalente Möglichkeiten, die Determinante einer quadratischen Matrix A zu definieren, d. h. einer Matrix mit der gleichen Anzahl von Zeilen und Spalten: Die Determinante kann über die Leibniz-Formel definiert werden, eine explizite Formel, die Summen von Produkten bestimmter Einträge der Matrix beinhaltet. Die Determinante kann auch als die einzige Funktion charakterisiert werden, die von den Einträgen der Matrix abhängt, die bestimmte Eigenschaften erfüllen. Dieser Ansatz kann auch zur Berechnung von Determinanten durch Vereinfachung der betreffenden Matrizen verwendet werden. ⓘ

Leibniz-Formel

Die Leibniz-Formel für die Determinante einer 3 × 3-Matrix lautet wie folgt:

${\begin{aligned}{\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a(ei-fh)-b(di-fg)+c(dh-eg)\\&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}$ ⓘ

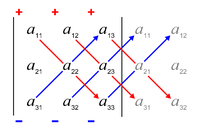
Die Regel von Sarrus ist eine Gedächtnisstütze für diese Formel: die Summe der Produkte der drei diagonalen Zeilen der Matrixelemente von Nordwest nach Südost minus die Summe der Produkte der drei diagonalen Zeilen der Elemente von Südwest nach Nordost, wenn die Kopien der ersten beiden Spalten der Matrix wie in der Abbildung daneben geschrieben werden:

Dieses Schema zur Berechnung der Determinante einer 3 × 3-Matrix lässt sich nicht auf höhere Dimensionen übertragen. ⓘ

n × n-Matrizen

Die Leibniz-Formel drückt die Determinante einer $n\times n$-Matrix auf eine Weise, die in höheren Dimensionen konsistent ist. ⓘ

Sie ist ein Ausdruck, der den Begriff der Permutationen und deren Signatur beinhaltet. Eine Permutation der Menge $\{1,2,\dots ,n\}$ ist eine Funktion $\sigma$ die diese Menge ganzer Zahlen neu ordnet. Der Wert an der $i$-Stelle nach der Umordnung $\sigma$ wird bezeichnet mit $\sigma _{i}$. Die Menge aller solcher Permutationen, die so genannte symmetrische Gruppe, wird als $S_{n}$. Die Signatur von $\sigma$ ist definiert als $+1$ wenn die Umordnung, die durch $\sigma$ durch das aufeinanderfolgende Vertauschen von zwei Einträgen mit einer geraden Anzahl von Vertauschungen erreicht werden kann, und $-1$ immer dann, wenn sie durch eine ungerade Anzahl solcher Vertauschungen erreicht werden kann. ⓘ

Gegeben eine Permutation $\sigma$ und einer $n\times n$-Matrix $A$, wobei $a_{i,j}$ das Element in der $i$-ten Zeile und $j$-Spalte von $A$bezeichnet, das Produkt

$a_{1,\sigma _{1}}\cdot a_{2,\sigma _{2}}\cdot \dots \cdot a_{n,\sigma _{n}}$,

auch kürzer geschrieben in der Pi-Notation als

$\prod _{i=1}^{n}a_{i,\sigma _{i}}$,

wird verwendet, um die Determinante mit Hilfe der Leibniz-Formel zu definieren:

$\det(A)=\sum _{\sigma \in S_{n}}\left(\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}\right)$. ⓘ

Die folgende Tabelle wickelt diese Terme für den Fall $n=3$. In der ersten Spalte ist eine Permutation nach ihren Werten aufgelistet. In der zweiten Zeile ist zum Beispiel die Permutation $\sigma$ erfüllt $\sigma _{1}=1,\sigma _{2}=3,\sigma _{3}=2$. Sie kann aus der Standardordnung (1, 2, 3) durch einen einzigen Austausch (Vertauschen des zweiten und dritten Eintrags) erhalten werden, so dass ihre Signatur lautet $\operatorname {sgn}(\sigma )=-1$. ⓘ

Permutationen von $\{1,2,3\}$ und ihr Beitrag zur Determinante ⓘ

Permutation $\sigma$	$\operatorname {sgn}(\sigma )$	$\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}$
1, 2, 3	$+1$	$+a_{1,1}a_{2,2}a_{3,3}$
1, 3, 2	$-1$	$-a_{1,1}a_{2,3}a_{3,2}$
3, 1, 2	$+1$	$+a_{1,3}a_{2,1}a_{3,2}$
3, 2, 1	$-1$	$-a_{1,3}a_{2,2}a_{3,1}$
2, 3, 1	$+1$	$+a_{1,2}a_{2,3}a_{3,1}$
2, 1, 3	$-1$	$-a_{1,2}a_{2,1}a_{3,3}$

Die Summe der sechs Terme in der dritten Spalte lautet dann ⓘ

$\sum _{\sigma \in S_{3}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}=a_{1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}+a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}+a_{1,2}a_{2,3}a_{3,1}-a_{1,2}a_{2,1}a_{3,3}.$

Dies ergibt die Formel für $3\times 3$-Matrizen zurück. Für eine allgemeine $n\times n$-Matrix enthält die Leibniz-Formel $n!$ (n faktorielle) Summanden, von denen jeder ein Produkt von n Einträgen der Matrix ist. ⓘ

Die Leibniz-Formel kann auch durch eine Summation ausgedrückt werden, bei der nicht nur Permutationen, sondern alle Folgen von $n$ Indizes im Bereich $1,\dots ,n$ vorkommen. Dazu verwendet man das Levi-Civita-Symbol $\varepsilon _{i_{1},\cdots ,i_{n}}$ anstelle des Vorzeichens einer Permutation

$\det(A)=\sum _{i_{1},i_{2},\ldots ,i_{n}=1}^{n}\varepsilon _{i_{1}\cdots i_{n}}a_{1,i_{1}}\cdots a_{n,i_{n}},$

Damit erhält man die obige Formel zurück, da das Levi-Civita-Symbol Null ist, wenn die Indizes $i_{1},\dots ,i_{n}$ keine Permutation bilden. ⓘ

Eigenschaften der Determinante

Charakterisierung der Determinante

Die Determinante kann durch die folgenden drei Schlüsseleigenschaften charakterisiert werden. Um diese anzugeben, ist es zweckmäßig, eine $n\times n$-Matrix A als bestehend aus ihren $n$ Spalten zu betrachten, also bezeichnet als

$A={\big (}a_{1},\dots ,a_{n}{\big )},$

wobei der Spaltenvektor $a_{i}$ (für jedes i) aus den Einträgen der Matrix in der i-ten Spalte zusammengesetzt ist. ⓘ

2. $\det \left(I\right)=1$, wobei $I$ ist eine Identitätsmatrix.
4. Die Determinante ist multilinear: Wenn die j-te Spalte einer Matrix $A$ als Linearkombination geschrieben wird $a_{j}=r\cdot v+w$ von zwei Spaltenvektoren v und w und einer Zahl r geschrieben wird, dann ist die Determinante von A als eine ähnliche Linearkombination ausdrückbar:

   ${\begin{aligned}|A|&={\big |}a_{1},\dots ,a_{j-1},r\cdot v+w,a_{j+1},\dots ,a_{n}|\\&=r\cdot |a_{1},\dots ,v,\dots a_{n}|+|a_{1},\dots ,w,\dots ,a_{n}|\end{aligned}}$

6. Die Determinante ist alternierend: Immer wenn zwei Spalten einer Matrix identisch sind, ist ihre Determinante 0:

   $|a_{1},\dots ,v,\dots ,v,\dots ,a_{n}|=0.$ ⓘ

Wenn die Determinante wie oben durch die Leibniz-Formel definiert ist, können diese drei Eigenschaften durch direkte Betrachtung der Formel bewiesen werden. Einige Autoren nähern sich der Determinante auch direkt über diese drei Eigenschaften: Es kann gezeigt werden, dass es genau eine Funktion gibt, die einer beliebigen $n\times n$-Matrix A eine Zahl zuweist, die diese drei Eigenschaften erfüllt. Dies zeigt auch, dass diese abstraktere Herangehensweise an die Determinante die gleiche Definition liefert wie diejenige, die die Leibniz-Formel verwendet. ⓘ

Um dies zu sehen, genügt es, die Determinante durch Multilinearität in den Spalten zu einer (großen) Linearkombination von Determinanten von Matrizen zu erweitern, bei denen jede Spalte ein Standard-Basisvektor ist. Diese Determinanten sind entweder 0 (durch Eigenschaft 9) oder ±1 (durch Eigenschaften 1 und 12 unten), so dass die Linearkombination den obigen Ausdruck in Form des Levi-Civita-Symbols ergibt. Obwohl diese Charakterisierung weniger technisch aussieht, kann sie die Leibniz-Formel bei der Definition der Determinante nicht vollständig ersetzen, da ohne sie die Existenz einer geeigneten Funktion nicht klar ist. ⓘ

Unmittelbare Konsequenzen

Aus diesen Regeln ergeben sich mehrere weitere Konsequenzen:

• Die Determinante ist eine homogene Funktion, d.h.,
  $$\det(cA)=c^{n}\det(A)$$
  (für eine $n\times n$ Matrix $A$).
• Das Vertauschen eines beliebigen Paares von Spalten einer Matrix multipliziert deren Determinante mit -1. Dies folgt daraus, dass die Determinante multilinear und alternierend ist (Eigenschaften 2 und 3 oben):
  $$|a_{1},\dots ,a_{j},\dots a_{i},\dots ,a_{n}|=-|a_{1},\dots ,a_{i},\dots ,a_{j},\dots ,a_{n}|.$$
  Diese Formel kann iterativ angewandt werden, wenn mehrere Spalten vertauscht werden. Zum Beispiel
  $$|a_{3},a_{1},a_{2},a_{4}\dots ,a_{n}|=-|a_{1},a_{3},a_{2},a_{4},\dots ,a_{n}|=|a_{1},a_{2},a_{3},a_{4},\dots ,a_{n}|.$$
  Noch allgemeiner ausgedrückt: Jede Permutation der Spalten multipliziert die Determinante mit dem Vorzeichen der Permutation.
• Wenn eine Spalte als Linearkombination der anderen Spalten ausgedrückt werden kann (d. h. die Spalten der Matrix bilden eine linear abhängige Menge), ist die Determinante 0. Als Sonderfall gilt: Wenn eine Spalte so beschaffen ist, dass alle ihre Einträge Null sind, dann ist die Determinante dieser Matrix 0.
• Addiert man ein skalares Vielfaches einer Spalte zu einer anderen Spalte, ändert sich der Wert der Determinante nicht. Dies ist eine Folge der Multilinearität und des Alternierens: Durch die Multilinearität ändert sich die Determinante um ein Vielfaches der Determinante einer Matrix mit zwei gleichen Spalten, deren Determinante 0 ist, da die Determinante alternierend ist.
• Wenn $A$ eine Dreiecksmatrix ist, d.h. $a_{ij}=0$wenn $i>j$ oder, alternativ, wenn $i<j$ist, dann ist ihre Determinante gleich dem Produkt der Diagonaleinträge:
  $$\det(A)=a_{11}a_{22}\cdots a_{nn}=\prod _{i=1}^{n}a_{ii}.$$
  In der Tat kann eine solche Matrix durch geeignete Addition von Vielfachen der Spalten mit weniger Nicht-Null-Einträgen zu denen mit mehr Einträgen zu einer Diagonalmatrix reduziert werden (ohne Änderung der Determinante). Für eine solche Matrix reduziert sich die Linearität in jeder Spalte auf die Identitätsmatrix, und in diesem Fall gilt die angegebene Formel durch die allererste charakterisierende Eigenschaft der Determinanten. Alternativ kann diese Formel auch aus der Leibniz-Formel abgeleitet werden, da die einzige Permutation $\sigma$ die einen Beitrag ungleich Null liefert, die Identitätspermutation ist. ⓘ

Beispiel

Diese oben aufgeführten charakterisierenden Eigenschaften und ihre Konsequenzen sind nicht nur theoretisch von Bedeutung, sondern können auch zur Berechnung von Determinanten für konkrete Matrizen verwendet werden. Die Gaußsche Eliminierung kann nämlich angewandt werden, um eine beliebige Matrix in die obere Dreiecksform zu bringen, wobei die Schritte dieses Algorithmus die Determinante auf kontrollierte Weise beeinflussen. Das folgende konkrete Beispiel veranschaulicht die Berechnung der Determinante der Matrix $A$ unter Verwendung dieser Methode:

$A={\begin{bmatrix}-2&-1&2\\2&1&4\\-3&3&-1\end{bmatrix}}.$ ⓘ

Berechnung der Determinante der Matrix $A$ ⓘ

Matrix	$B={\begin{bmatrix}-3&-1&2\\3&1&4\\0&3&-1\end{bmatrix}}$	$C={\begin{bmatrix}-3&5&2\\3&13&4\\0&0&-1\end{bmatrix}}$	$D={\begin{bmatrix}5&-3&2\\13&3&4\\0&0&-1\end{bmatrix}}$	$E={\begin{bmatrix}18&-3&2\\0&3&4\\0&0&-1\end{bmatrix}}$
Erhält man durch	Addieren der zweiten Spalte zur ersten	3 mal die dritte Spalte zur zweiten addiert	Vertauschen der ersten beiden Spalten	Hinzufügen von $-{\frac {13}{3}}$ mal die zweite Spalte zur ersten
Determinante	$|A|=|B|$	$|B|=|C|$	$|D|=-|C|$	$|E|=|D|$

Die Kombination dieser Gleichungen ergibt $|A|=-|E|=-(18\cdot 3\cdot (-1))=54.$ ⓘ

Transponieren

Die Determinante der Transponierten von $A$ ist gleich der Determinante von A:

$\det \left(A^{\textsf {T}}\right)=\det(A)$.

Dies kann durch Einsichtnahme in die Leibniz-Formel bewiesen werden. Dies impliziert, dass in allen oben genannten Eigenschaften das Wort "Spalte" durchgehend durch "Zeile" ersetzt werden kann. Betrachtet man zum Beispiel eine n × n-Matrix als aus n Zeilen zusammengesetzt, so ist die Determinante eine n-lineare Funktion. ⓘ

Multiplikativität und Matrixgruppen

Die Determinante ist also eine multiplikative Abbildung, d. h. für quadratische Matrizen $A$ und $B$ gleicher Größe ist die Determinante eines Matrixprodukts gleich dem Produkt ihrer Determinanten:

$\det(AB)=\det(A)\det(B)$ ⓘ

Diese wichtige Tatsache kann durch die Beobachtung bewiesen werden, dass für eine feste Matrix $B$beide Seiten der Gleichung alternierend und multilinear sind, und zwar als Funktion in Abhängigkeit von den Spalten von $A$. Außerdem nehmen sie beide den Wert $\det B$ wenn $A$ die Identitätsmatrix ist. Die oben erwähnte eindeutige Charakterisierung alternierender multilinearer Karten zeigt also diese Behauptung. ⓘ

Eine Matrix $A$ ist genau dann invertierbar, wenn ihre Determinante ungleich Null ist. Dies folgt aus der Multiplikativität von $\det$ und der unten erwähnten Formel für die Inverse mit der adjungierten Matrix. In diesem Fall ist die Determinante der inversen Matrix gegeben durch

$\det \left(A^{-1}\right)={\frac {1}{\det(A)}}=[\det(A)]^{-1}$. ⓘ

Insbesondere haben Produkte und Umkehrungen von Matrizen mit einer Determinante ungleich Null (bzw. Determinante Eins) diese Eigenschaft. Daher bildet die Menge solcher Matrizen (mit fester Größe $n$) eine Gruppe, die als allgemeine lineare Gruppe $\operatorname {GL} _{n}$ (bzw. eine Untergruppe, die spezielle lineare Gruppe $\operatorname {SL} _{n}\subset \operatorname {GL} _{n}$. Allgemeiner ausgedrückt, bezeichnet das Wort "speziell" die Untergruppe einer anderen Matrixgruppe von Matrizen der Determinante eins. Beispiele sind die spezielle orthogonale Gruppe (die, wenn n 2 oder 3 ist, aus allen Rotationsmatrizen besteht) und die spezielle unitäre Gruppe. ⓘ

Die Cauchy-Binet-Formel ist eine Verallgemeinerung dieser Produktformel für rechteckige Matrizen. Diese Formel kann auch in eine multiplikative Formel für zusammengesetzte Matrizen umgewandelt werden, deren Einträge die Determinanten aller quadratischen Untermatrizen einer gegebenen Matrix sind. ⓘ

Laplace-Erweiterung

Die Laplace-Erweiterung drückt die Determinante einer Matrix $A$ in Form von Determinanten kleinerer Matrizen ausgedrückt, die als ihre Minoren bezeichnet werden. Der Minor $M_{i,j}$ ist definiert als die Determinante der $(n-1)\times (n-1)$-Matrix, die sich aus $A$ durch Entfernen der $i$-Zeile und der $j$-Spalte ergibt. Der Ausdruck $(-1)^{i+j}M_{i,j}$ wird als Kofaktor bezeichnet. Für jede $i$hat man die Gleichheit

$\det(A)=\sum _{j=1}^{n}(-1)^{i+j}a_{ij}M_{ij},$

was als Laplace-Entwicklung entlang der i-ten Zeile bezeichnet wird. Zum Beispiel ergibt die Laplace-Entwicklung entlang der ersten Zeile ($i=1$) die folgende Formel:

${\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=a{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c{\begin{vmatrix}d&e\\g&h\end{vmatrix}}$

Durch Abspulen der Determinanten dieser $2\times 2$-Matrizen erhält man die oben erwähnte Leibniz-Formel zurück. In ähnlicher Weise ergibt die Laplace-Entwicklung entlang der $j$-Spalte die Gleichheit

$\det(A)=\sum _{i=1}^{n}(-1)^{i+j}a_{ij}M_{ij}.$

Die Laplace-Erweiterung kann iterativ zur Berechnung der Determinanten verwendet werden, aber dieser Ansatz ist für große Matrizen ineffizient. Sie ist jedoch nützlich für die Berechnung der Determinanten hochsymmetrischer Matrizen wie der Vandermonde-Matrix

$${\begin{vmatrix}1&1&1&\cdots &1\\x_{1}&x_{2}&x_{3}&\cdots &x_{n}\\x_{1}^{2}&x_{2}^{2}&x_{3}^{2}&\cdots &x_{n}^{2}\\\vdots &\vdots &\vdots &\ddots &\vdots \\x_{1}^{n-1}&x_{2}^{n-1}&x_{3}^{n-1}&\cdots &x_{n}^{n-1}\end{vmatrix}}=\prod _{1\leq i<j\leq n}\left(x_{j}-x_{i}\right).$$

Diese Determinante wurde z. B. beim Beweis des Satzes von Baker in der Theorie der transzendenten Zahlen verwendet. ⓘ

Adjugierte Matrix

Die adjugierte Matrix $\operatorname {adj} (A)$ ist die Transponierte der Matrix der Kofaktoren, d.h.,

$(\operatorname {adj} (A))_{ij}=(-1)^{i+j}M_{ji}.$ ⓘ

Für jede Matrix gilt

$(\det A)I=A\operatorname {adj} A=(\operatorname {adj} A)\,A.$ ⓘ

Die Adjugationsmatrix kann also verwendet werden, um die Inverse einer nichtsingulären Matrix auszudrücken:

$A^{-1}={\frac {1}{\det A}}\operatorname {adj} A.$ ⓘ

Blockmatrizen

Die Formel für die Determinante einer $2\times 2$-Matrix gilt unter geeigneten weiteren Annahmen auch für eine Blockmatrix, d.h. eine Matrix, die aus vier Submatrizen $A,B,C,D$ der Dimension $n\times n$, $n\times m$, $m\times n$ und $m\times m$zusammensetzt. Die einfachste solche Formel, die entweder mit der Leibniz-Formel oder einer Faktorisierung mit dem Schur-Komplement bewiesen werden kann, ist

$\det {\begin{pmatrix}A&0\\C&D\end{pmatrix}}=\det(A)\det(D)=\det {\begin{pmatrix}A&B\\0&D\end{pmatrix}}.$

Wenn $A$ invertierbar ist (und in ähnlicher Weise, wenn $D$ invertierbar ist), hat man ⓘ

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(A)\det \left(D-CA^{-1}B\right).$

Wenn $D$ ist eine $1\times 1$-Matrix ist, vereinfacht sich dies zu $\det(A)(D-CA^{-1}B)$. ⓘ

Wenn die Blöcke quadratische Matrizen der gleichen Größe sind, gelten weitere Formeln. Zum Beispiel, wenn $C$ und $D$ kommutieren (d.h., $CD=DC$), dann gilt ⓘ

$\det {\begin{pmatrix}A&B\\C&D\end{pmatrix}}=\det(AD-BC).$

Diese Formel wurde auf Matrizen verallgemeinert, die aus mehr als $2\times 2$ Blöcken zusammengesetzten Matrizen verallgemeinert, wiederum unter geeigneten Kommutativitätsbedingungen zwischen den einzelnen Blöcken. ⓘ

Für $A=D$ und $B=C$gilt die folgende Formel (auch wenn $A$ und $B$ nicht kommutativ sind)

$\det {\begin{pmatrix}A&B\\B&A\end{pmatrix}}=\det(A-B)\det(A+B).$ ⓘ

Sylvesters Determinanten-Theorem

Das Sylvestersche Determinantensatz besagt, dass für A, eine m × n-Matrix, und B, eine n × m-Matrix (so dass A und B Dimensionen haben, die es erlauben, sie in beliebiger Reihenfolge zu multiplizieren und eine quadratische Matrix zu bilden):

$\det \left(I_{\mathit {m}}+AB\right)=\det \left(I_{\mathit {n}}+BA\right),$ ⓘ

wobei Im und In die m × m bzw. n × n Identitätsmatrizen sind. ⓘ

Aus diesem allgemeinen Ergebnis ergeben sich mehrere Konsequenzen.

1. Für den Fall eines Spaltenvektors c und eines Zeilenvektors r mit jeweils m Komponenten ermöglicht die Formel die schnelle Berechnung der Determinante einer Matrix, die sich von der Identitätsmatrix durch eine Matrix vom Rang 1 unterscheidet:

   $\det \left(I_{\mathit {m}}+cr\right)=1+rc.$

2. Allgemeiner ausgedrückt, für jede invertierbare m × m-Matrix X,
   $\det(X+AB)=\det(X)\det \left(I_{\mathit {n}}+BX^{-1}A\right),$
3. Für einen Spalten- und Zeilenvektor wie oben:
   $\det(X+cr)=\det(X)\det \left(1+rX^{-1}c\right)=\det(X)+r\,\operatorname {adj} (X)\,c.$
4. Für quadratische Matrizen $A$ und $B$ der gleichen Größe haben die Matrizen $AB$ und $BA$ die gleichen charakteristischen Polynome (also die gleichen Eigenwerte). ⓘ

Summe

Die Determinante der Summe $A+B$ zweier gleich großer quadratischer Matrizen lässt sich im Allgemeinen nicht durch die Determinanten von A und B ausdrücken. Für positiv semidefinite Matrizen $A$, $B$ und $C$ von gleicher Größe,

$$\det(A+B+C)+\det(C)\geq \det(A+C)+\det(B+C){\text{,}}$$

mit der Korollarie

$$\det(A+B)\geq \det(A)+\det(B){\text{.}}$$

Umgekehrt, wenn $A$ und $B$ hermitesch sind, positiv-unendlich und die Größe $n\times n$sind, dann hat die Determinante eine konkave $n$Wurzel; dies impliziert

$${\sqrt[{n}]{\det {\!(A+B)}}}\leq {\sqrt[{n}]{\det {\!(A)}}}+{\sqrt[{n}]{\det {\!(B)}}}$$

durch Homogenität. ⓘ

Summenidentität für 2×2-Matrizen

Für den speziellen Fall von $2\times 2$ Matrizen mit komplexen Einträgen kann die Determinante der Summe in Form von Determinanten und Spuren in der folgenden Identität geschrieben werden:

$\det(A+B)=\det(A)+\det(B)+{\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$ ⓘ

Beweis der Identität

Dies lässt sich zeigen, indem man jeden Term in Komponenten ausschreibt $A_{ij},B_{ij}$. Die linke Seite ist

$(A_{11}+B_{11})(A_{22}+B_{22})-(A_{12}+B_{12})(A_{21}+B_{21}).$

Durch Expandieren erhält man

$A_{11}A_{22}+B_{11}A_{22}+A_{11}B_{22}+B_{11}B_{22}-A_{12}A_{21}-B_{12}A_{21}-A_{12}B_{21}-B_{12}B_{21}.$

Die Terme, die quadratisch sind in $A$ sind, werden gesehen als $\det(A)$und in ähnlicher Weise für $B$, so dass der Ausdruck geschrieben werden kann

$\det(A)+\det(B)+A_{11}B_{22}+B_{11}A_{22}-A_{12}B_{21}-B_{12}A_{21}.$

Wir können dann die Querterme schreiben als

$(A_{11}+A_{22})(B_{11}+B_{22})-(A_{11}B_{11}+A_{12}B_{21}+A_{21}B_{12}+A_{22}B_{22})$

die man erkennen kann als

${\text{tr}}(A){\text{tr}}(B)-{\text{tr}}(AB).$

was den Beweis vervollständigt. ⓘ

Dies hat eine Anwendung auf $2\times 2$ Matrixalgebren. Betrachten wir zum Beispiel die komplexen Zahlen als Matrixalgebra. Die komplexen Zahlen haben eine Darstellung als Matrizen der Form

$$aI+b\mathbf {i} :=a{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+b{\begin{pmatrix}0&-1\\1&0\end{pmatrix}}$$

mit $a$ und $b$ real. Da ${\text{tr}}(\mathbf {i} )=0$nimmt man $A=aI$ und $B=b\mathbf {i}$ in der obigen Identität ergibt

$\det(aI+b\mathbf {i} )=a^{2}\det(I)+b^{2}\det(\mathbf {i} )=a^{2}+b^{2}.$

Dieses Ergebnis folgt einfach aus ${\text{tr}}(\mathbf {i} )=0$ und $\det(I)=\det(\mathbf {i} )=1$. ⓘ

Eigenschaften der Determinante im Verhältnis zu anderen Begriffen

Eigenwerte und charakteristisches Polynom

Die Determinante steht in enger Beziehung zu zwei anderen zentralen Begriffen der linearen Algebra, den Eigenwerten und dem charakteristischen Polynom einer Matrix. Sei $A$ sei eine $n\times n$-Matrix mit komplexen Einträgen und Eigenwerten $\lambda _{1},\lambda _{2},\ldots ,\lambda _{n}$. (Darunter ist zu verstehen, dass ein Eigenwert mit der algebraischen Vielfachheit μ mal in dieser Liste vorkommt.) Dann ist die Determinante von A das Produkt aller Eigenwerte,

$\det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.$

Das Produkt aller Eigenwerte, die nicht Null sind, wird als Pseudodeterminante bezeichnet. ⓘ

Das charakteristische Polynom ist definiert als

$\chi _{A}(t)=\det(t\cdot I-A).$

hier, $t$ die Unbestimmtheit des Polynoms und $I$ ist die Identitätsmatrix mit der gleichen Größe wie $A$. Mit Hilfe dieses Polynoms lassen sich mit Hilfe der Determinanten die Eigenwerte der Matrix $A$zu finden: Sie sind genau die Wurzeln dieses Polynoms, d.h. die komplexen Zahlen $\lambda$ derart, dass

$\chi _{A}(\lambda )=0.$ ⓘ

Eine hermitesche Matrix ist positiv definit, wenn alle ihre Eigenwerte positiv sind. Das Sylvester-Kriterium besagt, dass dies gleichbedeutend damit ist, dass die Determinanten der Submatrizen

$A_{k}:={\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots &a_{1,k}\\a_{2,1}&a_{2,2}&\cdots &a_{2,k}\\\vdots &\vdots &\ddots &\vdots \\a_{k,1}&a_{k,2}&\cdots &a_{k,k}\end{bmatrix}}$ ⓘ

positiv sind, für alle $k$ zwischen $1$ und $n$. ⓘ

Trace

Die Spur tr(A) ist per Definition die Summe der Diagonaleinträge von A und entspricht ebenfalls der Summe der Eigenwerte. Daher gilt für komplexe Matrizen A,

$\det(\exp(A))=\exp(\operatorname {tr} (A))$ ⓘ

oder für reelle Matrizen A,

$\operatorname {tr} (A)=\log(\det(\exp(A))).$ ⓘ

Hier bezeichnet exp(A) das Matrixexponential von A, denn jeder Eigenwert λ von A entspricht dem Eigenwert exp(λ) von exp(A). Insbesondere ist bei einem beliebigen Logarithmus von A, d. h. einer beliebigen Matrix L, die folgende Bedingungen erfüllt

$\exp(L)=A$ ⓘ

ist die Determinante von A gegeben durch

$\det(A)=\exp(\operatorname {tr} (L)).$ ⓘ

Zum Beispiel für n = 2, n = 3 bzw. n = 4,

${\begin{aligned}\det(A)&={\frac {1}{2}}\left(\left(\operatorname {tr} (A)\right)^{2}-\operatorname {tr} \left(A^{2}\right)\right),\\\det(A)&={\frac {1}{6}}\left(\left(\operatorname {tr} (A)\right)^{3}-3\operatorname {tr} (A)~\operatorname {tr} \left(A^{2}\right)+2\operatorname {tr} \left(A^{3}\right)\right),\\\det(A)&={\frac {1}{24}}\left(\left(\operatorname {tr} (A)\right)^{4}-6\operatorname {tr} \left(A^{2}\right)\left(\operatorname {tr} (A)\right)^{2}+3\left(\operatorname {tr} \left(A^{2}\right)\right)^{2}+8\operatorname {tr} \left(A^{3}\right)~\operatorname {tr} (A)-6\operatorname {tr} \left(A^{4}\right)\right).\end{aligned}}$ ⓘ

vgl. Cayley-Hamilton-Theorem. Solche Ausdrücke lassen sich aus kombinatorischen Argumenten, den Newtonschen Identitäten oder dem Faddeev-LeVerrier-Algorithmus ableiten. Das heißt, für generisches n ist detA = (-1)nc₀ der vorzeichenbehaftete konstante Term des charakteristischen Polynoms, bestimmt rekursiv aus

$c_{n}=1;~~~c_{n-m}=-{\frac {1}{m}}\sum _{k=1}^{m}c_{n-m+k}\operatorname {tr} \left(A^{k}\right)~~(1\leq m\leq n)~.$ ⓘ

Im allgemeinen Fall lässt sich dies auch aus

$\det(A)=\sum _{\begin{array}{c}k_{1},k_{2},\ldots ,k_{n}\geq 0\\k_{1}+2k_{2}+\cdots +nk_{n}=n\end{array}}\prod _{l=1}^{n}{\frac {(-1)^{k_{l}+1}}{l^{k_{l}}k_{l}!}}\operatorname {tr} \left(A^{l}\right)^{k_{l}},$ ⓘ

wobei die Summe über die Menge aller ganzen Zahlen kl ≥ 0 genommen wird, die die Gleichung

$\sum _{l=1}^{n}lk_{l}=n.$ ⓘ

Die Formel kann in Form des vollständigen exponentiellen Bell-Polynoms mit n Argumenten sl = -(l - 1)! tr(Al) ausgedrückt werden als

$\det(A)={\frac {(-1)^{n}}{n!}}B_{n}(s_{1},s_{2},\ldots ,s_{n}).$ ⓘ

Diese Formel kann auch verwendet werden, um die Determinante einer Matrix AI_J mit mehrdimensionalen Indizes I = (i₁, i₂, ..., ir) und J = (j₁, j₂, ..., jr) zu bestimmen. Das Produkt und die Spur solcher Matrizen sind auf natürliche Weise definiert als

$(AB)_{J}^{I}=\sum _{K}A_{K}^{I}B_{J}^{K},\operatorname {tr} (A)=\sum _{I}A_{I}^{I}.$ ⓘ

Eine wichtige Identität beliebiger Dimension n lässt sich aus der Mercatorreihenentwicklung des Logarithmus ableiten, wenn die Entwicklung konvergiert. Wenn jeder Eigenwert von A im Absolutwert kleiner als 1 ist,

$\det(I+A)=\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$ ⓘ

wobei I die Identitätsmatrix ist. Allgemeiner ausgedrückt, wenn

$\sum _{k=0}^{\infty }{\frac {1}{k!}}\left(-\sum _{j=1}^{\infty }{\frac {(-1)^{j}s^{j}}{j}}\operatorname {tr} \left(A^{j}\right)\right)^{k}\,,$ ⓘ

als formale Potenzreihe in s expandiert wird, dann sind alle Koeffizienten von sm für m > n Null und das verbleibende Polynom ist det(I + sA). ⓘ

Obere und untere Schranken

Für eine positiv definite Matrix A liefert der Spuroperator die folgenden engen unteren und oberen Schranken für die logarithmische Determinante

$\operatorname {tr} \left(I-A^{-1}\right)\leq \log \det(A)\leq \operatorname {tr} (A-I)$ ⓘ

Diese Beziehung kann über die Formel für die KL-Divergenz zwischen zwei multivariaten Normalverteilungen abgeleitet werden. ⓘ

Außerdem,

${\frac {n}{\operatorname {tr} \left(A^{-1}\right)}}\leq \det(A)^{\frac {1}{n}}\leq {\frac {1}{n}}\operatorname {tr} (A)\leq {\sqrt {{\frac {1}{n}}\operatorname {tr} \left(A^{2}\right)}}.$ ⓘ

Diese Ungleichungen können bewiesen werden, indem man die Spuren und die Determinante in Form von Eigenwerten ausdrückt. Sie entsprechen der bekannten Tatsache, dass das harmonische Mittel kleiner ist als das geometrische Mittel, das wiederum kleiner ist als das arithmetische Mittel, das wiederum kleiner ist als der quadratische Mittelwert. ⓘ

Ableitung

Die Leibniz-Formel zeigt, dass die Determinante von reellen (oder analog für komplexe) quadratischen Matrizen eine Polynomfunktion von $\mathbf {R} ^{n\times n}$ zu $\mathbf {R}$. Insbesondere ist sie überall differenzierbar. Ihre Ableitung kann mit der Jacobi-Formel ausgedrückt werden:

${\frac {d\det(A)}{d\alpha }}=\operatorname {tr} \left(\operatorname {adj} (A){\frac {dA}{d\alpha }}\right).$ ⓘ

wobei $\operatorname {adj} (A)$ die Adjugierte von $A$. Insbesondere, wenn $A$ invertierbar ist, haben wir ⓘ

${\frac {d\det(A)}{d\alpha }}=\det(A)\operatorname {tr} \left(A^{-1}{\frac {dA}{d\alpha }}\right).$ ⓘ

Ausgedrückt in Form der Einträge von $A$ausgedrückt, sind dies ⓘ

${\frac {\partial \det(A)}{\partial A_{ij}}}=\operatorname {adj} (A)_{ji}=\det(A)\left(A^{-1}\right)_{ji}.$ ⓘ

Eine weitere äquivalente Formulierung ist ⓘ

$\det(A+\epsilon X)-\det(A)=\operatorname {tr} (\operatorname {adj} (A)X)\epsilon +O\left(\epsilon ^{2}\right)=\det(A)\operatorname {tr} \left(A^{-1}X\right)\epsilon +O\left(\epsilon ^{2}\right)$, ⓘ

unter Verwendung der Big-O-Schreibweise. Der Spezialfall, in dem $A=I$, die Identitätsmatrix, ergibt ⓘ

$\det(I+\epsilon X)=1+\operatorname {tr} (X)\epsilon +O\left(\epsilon ^{2}\right).$ ⓘ

Diese Identität wird bei der Beschreibung von Lie-Algebren verwendet, die mit bestimmten Matrix-Lie-Gruppen verbunden sind. Zum Beispiel ist die spezielle lineare Gruppe $\operatorname {SL} _{n}$ ist definiert durch die Gleichung $\det A=1$. Die obige Formel zeigt, dass ihre Lie-Algebra die spezielle lineare Lie-Algebra ${\mathfrak {sl}}_{n}$ ist, die aus den Matrizen mit der Spur Null besteht. ⓘ

Schreibt man eine $3\times 3$-Matrix als $A={\begin{bmatrix}a&b&c\end{bmatrix}}$ wobei $a,b,c$ sind Spaltenvektoren der Länge 3, dann kann der Gradient über einen der drei Vektoren als das Kreuzprodukt der beiden anderen geschrieben werden:

${\begin{aligned}\nabla _{\mathbf {a} }\det(A)&=\mathbf {b} \times \mathbf {c} \\\nabla _{\mathbf {b} }\det(A)&=\mathbf {c} \times \mathbf {a} \\\nabla _{\mathbf {c} }\det(A)&=\mathbf {a} \times \mathbf {b} .\end{aligned}}$ ⓘ

Geschichte

Historisch gesehen wurden Determinanten schon lange vor Matrizen verwendet: Eine Determinante wurde ursprünglich als eine Eigenschaft eines Systems linearer Gleichungen definiert. Die Determinante "bestimmt", ob das System eine eindeutige Lösung hat (was genau dann der Fall ist, wenn die Determinante ungleich Null ist). In diesem Sinne wurden Determinanten erstmals im chinesischen Mathematiklehrbuch Die neun Kapitel über die mathematische Kunst (九章算術, chinesische Gelehrte, um das 3. Jahrhundert v. Chr.) verwendet. In Europa wurden die Lösungen von linearen Systemen aus zwei Gleichungen von Cardano im Jahr 1545 durch eine determinantenähnliche Einheit ausgedrückt. ⓘ

Die Determinanten selbst stammen aus den Arbeiten von Seki Takakazu (1683) in Japan und parallel dazu von Leibniz (1693). Cramer (1750) stellte die Cramersche Regel auf, ohne sie zu beweisen. Sowohl Cramer als auch Bezout (1779) wurden durch die Frage nach ebenen Kurven, die durch eine gegebene Menge von Punkten verlaufen, zu Determinanten geführt. ⓘ

Vandermonde (1771) erkannte Determinanten erstmals als unabhängige Funktionen. Laplace (1772) gab die allgemeine Methode der Erweiterung einer Determinante in Bezug auf ihre komplementären Minoren: Vandermonde hatte bereits einen Spezialfall angegeben. Unmittelbar danach behandelte Lagrange (1773) Determinanten zweiter und dritter Ordnung und wandte sie auf Fragen der Eliminierungstheorie an; er bewies viele Spezialfälle der allgemeinen Identitäten. ⓘ

Gauß (1801) machte den nächsten Schritt. Wie Lagrange machte er viel Gebrauch von Determinanten in der Zahlentheorie. Er führte das Wort "Determinante" ein (Laplace hatte "Resultante" verwendet), wenn auch nicht in der heutigen Bedeutung, sondern eher als Anwendung auf die Diskriminante eines Quants. Gauß führte auch den Begriff der reziproken (inversen) Determinanten ein und kam dem Multiplikationssatz sehr nahe. ⓘ

Der nächste wichtige Beitrag stammt von Binet (1811, 1812), der den Satz über das Produkt zweier Matrizen mit m Spalten und n Zeilen formell formulierte, der für den Spezialfall m = n auf den Multiplikationssatz zurückgeht. Am selben Tag (30. November 1812), an dem Binet seine Arbeit der Akademie vorstellte, legte auch Cauchy eine Arbeit zu diesem Thema vor. (Siehe Cauchy-Binet-Formel.) Darin verwendet er das Wort "Determinante" in seiner heutigen Bedeutung, fasst zusammen und vereinfacht, was damals zu diesem Thema bekannt war, verbessert die Notation und gibt das Multiplikationstheorem mit einem Beweis, der zufriedenstellender ist als der von Binet. Mit ihm beginnt die Theorie in ihrer Allgemeinheit. ⓘ

(Jacobi 1841) verwendet die funktionale Determinante, die Sylvester später Jacobian nennt. In seinen Erinnerungen in Crelle's Journal für 1841 behandelt er speziell dieses Thema, sowie die Klasse der alternierenden Funktionen der Sylvester hat als alternants. Über die Zeit der Jacobi's letzten Erinnerungen, Sylvester (1839) und Cayley begann ihre Arbeit. Cayley führte 1841 die moderne Notation für die Determinante mit vertikalen Balken ein. ⓘ

Die Untersuchung spezieller Formen von Determinanten war das natürliche Ergebnis der Vervollständigung der allgemeinen Theorie. Achsensymmetrische Determinanten wurden von Lebesgue, Hesse und Sylvester untersucht; persymmetrische Determinanten von Sylvester und Hankel; Zirkulanten von Catalan, Spottiswoode, Glaisher und Scott; schiefe Determinanten und Pfaffianer, in Verbindung mit der Theorie der orthogonalen Transformation, von Cayley; Kontinuitäten von Sylvester; Wronskianer (von Muir so genannt) von Christoffel und Frobenius; zusammengesetzte Determinanten von Sylvester, Reiss und Picquet; Jacobianer und Hessianer von Sylvester; und symmetrische Gauche-Determinanten von Trudi. Von den Lehrbüchern zu diesem Thema war das von Spottiswoode das erste. In Amerika veröffentlichten Hanus (1886), Weld (1893) und Muir/Metzler (1933) Abhandlungen. ⓘ

Anwendungen

Die Cramersche Regel

Determinanten können verwendet werden, um die Lösungen eines linearen Gleichungssystems zu beschreiben, das in Matrixform geschrieben wird als $Ax=b$. Diese Gleichung hat eine eindeutige Lösung $x$ wenn und nur wenn $\det(A)$ ungleich Null ist. In diesem Fall ist die Lösung durch die Cramersche Regel gegeben:

$x_{i}={\frac {\det(A_{i})}{\det(A)}}\qquad i=1,2,3,\ldots ,n$ ⓘ

wobei $A_{i}$ ist die Matrix, die durch Ersetzen der $i$-Spalte von $A$ durch den Spaltenvektor $b$. Dies folgt unmittelbar aus der Spaltenerweiterung der Determinante, d.h.

$\det(A_{i})=\det {\begin{bmatrix}a_{1}&\ldots &b&\ldots &a_{n}\end{bmatrix}}=\sum _{j=1}^{n}x_{j}\det {\begin{bmatrix}a_{1}&\ldots &a_{i-1}&a_{j}&a_{i+1}&\ldots &a_{n}\end{bmatrix}}=x_{i}\det(A)$

wobei die Vektoren $a_{j}$ die Spalten von A sind. Die Regel wird auch durch die Identität impliziert ⓘ

$A\,\operatorname {adj} (A)=\operatorname {adj} (A)\,A=\det(A)\,I_{n}.$ ⓘ

Die Cramersche Regel kann implementiert werden in $\operatorname {O} (n^{3})$ Zeit implementiert werden, was vergleichbar ist mit gebräuchlicheren Methoden zur Lösung von linearen Gleichungssystemen, wie LU, QR oder Singulärwertzerlegung. ⓘ

Lineare Unabhängigkeit

Determinanten können verwendet werden, um linear abhängige Vektoren zu charakterisieren: $\det A$ Die Determinante ist nur dann Null, wenn die Spaltenvektoren (oder, äquivalent dazu, die Zeilenvektoren) der Matrix $A$ linear abhängig sind. Bei zwei linear unabhängigen Vektoren zum Beispiel $v_{1},v_{2}\in \mathbf {R} ^{3}$ein dritter Vektor $v_{3}$ genau dann in der Ebene, die von den beiden erstgenannten Vektoren aufgespannt wird, wenn die Determinante der $3\times 3$-Matrix, die aus den drei Vektoren besteht, Null ist. Der gleiche Gedanke wird auch in der Theorie der Differentialgleichungen verwendet: gegebene Funktionen $f_{1}(x),\dots ,f_{n}(x)$ (angenommen, sie sind $n-1$ mal differenzierbar), ist die Wronskianer definiert als

$W(f_{1},\ldots ,f_{n})(x)={\begin{vmatrix}f_{1}(x)&f_{2}(x)&\cdots &f_{n}(x)\\f_{1}'(x)&f_{2}'(x)&\cdots &f_{n}'(x)\\\vdots &\vdots &\ddots &\vdots \\f_{1}^{(n-1)}(x)&f_{2}^{(n-1)}(x)&\cdots &f_{n}^{(n-1)}(x)\end{vmatrix}}.$ ⓘ

Sie ist ungleich Null (für einige $x$) in einem bestimmten Intervall, wenn und nur wenn die gegebenen Funktionen und alle ihre Ableitungen bis zur Ordnung $n-1$ linear unabhängig sind. Wenn gezeigt werden kann, dass die Wronskianer überall in einem Intervall Null ist, dann bedeutet dies im Fall von analytischen Funktionen, dass die gegebenen Funktionen linear abhängig sind. Siehe die Wronskianer und lineare Unabhängigkeit. Eine weitere Anwendung der Determinante ist die Resultante, die ein Kriterium dafür liefert, wann zwei Polynome eine gemeinsame Wurzel haben. ⓘ

Orientierung einer Basis

Man kann sich die Determinante so vorstellen, dass sie jeder Folge von n Vektoren in Rn eine Zahl zuordnet, indem sie die quadratische Matrix verwendet, deren Spalten die gegebenen Vektoren sind. So stellt beispielsweise eine orthogonale Matrix mit Einträgen in Rn eine orthonormale Basis im euklidischen Raum dar. Die Determinante einer solchen Matrix bestimmt, ob die Orientierung der Basis mit der Orientierung der Standardbasis übereinstimmt oder ihr entgegengesetzt ist. Ist die Determinante +1, hat die Basis die gleiche Orientierung. Ist sie -1, so hat die Basis die entgegengesetzte Ausrichtung. ⓘ

Allgemeiner ausgedrückt: Wenn die Determinante von A positiv ist, stellt A eine orientierungserhaltende lineare Transformation dar (wenn A eine orthogonale 2 × 2- oder 3 × 3-Matrix ist, handelt es sich um eine Drehung), während A, wenn sie negativ ist, die Orientierung der Basis ändert. ⓘ

Volumen und Jacobi-Determinante

Wie bereits erwähnt, ist der Absolutwert der Determinante von reellen Vektoren gleich dem Volumen des von diesen Vektoren aufgespannten Parallelepipeds. Daraus folgt, dass, wenn $f:\mathbf {R} ^{n}\to \mathbf {R} ^{n}$ die lineare Abbildung ist, die durch Multiplikation mit einer Matrix $A$, und $S\subset \mathbf {R} ^{n}$ eine beliebige messbare Teilmenge ist, dann ist das Volumen von $f(S)$ ist gegeben durch $|\det(A)|$ mal dem Volumen von $S$. Allgemeiner ausgedrückt: Wenn die lineare Abbildung $f:\mathbf {R} ^{n}\to \mathbf {R} ^{m}$ dargestellt wird durch die $m\times n$-Matrix $A$dargestellt wird, dann ist das $n$-dimensionale Volumen von $f(S)$ gegeben durch:

$\operatorname {volume} (f(S))={\sqrt {\det \left(A^{\textsf {T}}A\right)}}\operatorname {volume} (S).$ ⓘ

Durch die Berechnung des Volumens des Tetraeders, das durch vier Punkte begrenzt wird, können sie zur Identifizierung schiefer Linien verwendet werden. Das Volumen eines beliebigen Tetraeders mit seinen Eckpunkten $a,b,c,d$, ${\frac {1}{6}}\cdot |\det(a-b,b-c,c-d)|$oder jede andere Kombination von Paaren von Scheitelpunkten, die einen spannenden Baum über die Scheitelpunkte bilden. ⓘ

Eine nichtlineare Karte $f\colon \mathbf {R} ^{2}\to \mathbf {R} ^{2}$ verwandelt ein kleines Quadrat (links, in rot) in ein verzerrtes Parallelogramm (rechts, in rot). Die Jacobi an einem Punkt ergibt die beste lineare Approximation des verzerrten Parallelogramms in der Nähe dieses Punktes (rechts, in durchscheinendem Weiß), und die Jacobi-Determinante gibt das Verhältnis der Fläche des approximierenden Parallelogramms zu der des ursprünglichen Quadrats an. ⓘ

Für eine allgemeine differenzierbare Funktion lässt sich vieles von dem oben Gesagten übertragen, wenn man die Jacobimatrix von f betrachtet.

$f:\mathbf {R} ^{n}\rightarrow \mathbf {R} ^{n},$ ⓘ

ist die Jacobimatrix die n × n-Matrix, deren Einträge durch die partiellen Ableitungen gegeben sind

$D(f)=\left({\frac {\partial f_{i}}{\partial x_{j}}}\right)_{1\leq i,j\leq n}.$ ⓘ

Ihre Determinante, die Jacobische Determinante, erscheint in der höherdimensionalen Version der Integration durch Substitution: Für geeignete Funktionen f und eine offene Teilmenge U von Rn (das Gebiet von f) ist das Integral über f(U) einer anderen Funktion φ : Rn → Rm gegeben durch

$\int _{f(U)}\phi (\mathbf {v} )\,d\mathbf {v} =\int _{U}\phi (f(\mathbf {u} ))\left|\det(\operatorname {D} f)(\mathbf {u} )\right|\,d\mathbf {u} .$ ⓘ

Der Jacobi kommt auch im Satz von der umgekehrten Funktion vor. ⓘ

Im Bereich der Kartographie kann die Determinante verwendet werden, um die Expansionsrate einer Karte in der Nähe der Pole zu messen. ⓘ

Abstrakte algebraische Aspekte

Determinante eines Endomorphismus

Die oben genannten Identitäten bezüglich der Determinante von Produkten und Inversen von Matrizen implizieren, dass ähnliche Matrizen die gleiche Determinante haben: Zwei Matrizen A und B sind ähnlich, wenn es eine invertierbare Matrix X gibt, so dass A = X-1BX ist. Die wiederholte Anwendung der obigen Identitäten ergibt in der Tat ⓘ

$\det(A)=\det(X)^{-1}\det(B)\det(X)=\det(B)\det(X)^{-1}\det(X)=\det(B).$ ⓘ

Die Determinante wird daher auch als Ähnlichkeitsinvariante bezeichnet. Die Determinante einer linearen Transformation

$T:V\to V$

für einen endlichdimensionalen Vektorraum V ist definiert als die Determinante der Matrix, die sie beschreibt, in Bezug auf eine beliebige Wahl der Basis in V. Durch die Ähnlichkeitsinvarianz ist diese Determinante unabhängig von der Wahl der Basis für V und hängt daher nur vom Endomorphismus T ab. ⓘ

Falls $A$ und $B$ ähnlich sind, das heißt, falls eine invertierbare Matrix $X$ existiert, sodass $A=X^{-1}BX$, dann stimmen ihre Determinanten überein, denn ⓘ

Quadratische Matrizen über kommutativen Ringen

Die obige Definition der Determinante unter Verwendung der Leibniz-Regel gilt allgemeiner, wenn die Einträge der Matrix Elemente eines kommutativen Rings sind $R$sind, wie z.B. die ganzen Zahlen $\mathbf {Z}$sind, im Gegensatz zum Feld der reellen oder komplexen Zahlen. Darüber hinaus gilt die Charakterisierung der Determinante als die einzige alternierende multilineare Abbildung, die folgende Bedingungen erfüllt $\det(I)=1$ erfüllt, immer noch gültig, ebenso wie alle Eigenschaften, die sich aus dieser Charakterisierung ergeben. ⓘ

Eine Matrix $A\in \operatorname {Mat} _{n\times n}(R)$ ist invertierbar (in dem Sinne, dass es eine inverse Matrix gibt, deren Einträge in $R$), wenn und nur wenn ihre Determinante ein invertierbares Element in $R$. Für $R=\mathbf {Z}$bedeutet dies, dass die Determinante +1 oder -1 ist. Eine solche Matrix wird unimodular genannt. ⓘ

Da die Determinante multiplikativ ist, definiert sie einen Gruppenhomomorphismus

$\operatorname {GL} _{n}(R)\rightarrow R^{\times },$

zwischen der allgemeinen linearen Gruppe (der Gruppe der invertierbaren $n\times n$-Matrizen mit Einträgen in $R$) und der multiplikativen Gruppe der Einheiten in $R$. Da sie die Multiplikation in beiden Gruppen respektiert, ist diese Abbildung ein Gruppenhomomorphismus. ⓘ

Die Determinante ist eine natürliche Transformation. ⓘ

Gegeben ein Ringhomomorphismus $f:R\to S$gibt es eine Abbildung $\operatorname {GL} _{n}(f):\operatorname {GL} _{n}(R)\to \operatorname {GL} _{n}(S)$ die durch Ersetzen aller Einträge in $R$ durch ihre Bilder unter $f$. Die Determinante respektiert diese Abbildungen, d. h. die Identität

$f(\det((a_{i,j})))=\det((f(a_{i,j})))$

gilt. Mit anderen Worten: Das dargestellte Kommutativdiagramm ist kommutativ. ⓘ

Zum Beispiel ist die Determinante der komplex Konjugierten einer komplexen Matrix (die auch die Determinante ihrer konjugierten Transponierten ist) die komplex Konjugierte ihrer Determinante, und für ganzzahlige Matrizen: die Reduktion modulo $m$ der Determinante einer solchen Matrix ist gleich der Determinante der Matrix, die modulo $m$ (letztere Determinante wird durch modulare Arithmetik berechnet). In der Sprache der Kategorientheorie ist die Determinante eine natürliche Transformation zwischen den beiden Funktoren $\operatorname {GL} _{n}$ und $(-)^{\times }$. Um eine weitere Abstraktionsebene hinzuzufügen, kann man sagen, dass die Determinante ein Morphismus algebraischer Gruppen ist, von der allgemeinen linearen Gruppe zur multiplikativen Gruppe,

$\det :\operatorname {GL} _{n}\to \mathbb {G} _{m}.$ ⓘ

Äußere Algebra

Eine Abbildung $\det \colon K^{n\times n}\to K$ vom Raum der quadratischen Matrizen in den zugrunde liegenden Körper $K$ bildet jede Matrix auf ihre Determinante ab, wenn sie folgende drei Eigenschaften (Axiome nach Karl Weierstraß) erfüllt, wobei eine quadratische Matrix spaltenweise als $A=(v_{1},\dotsc ,v_{n})$ geschrieben wird:

• Sie ist multilinear, d. h. linear in jeder Spalte:

Für alle $v_{1},\ldots ,v_{n},w\in K^{n}$ gilt:

${\begin{aligned}&\det(v_{1},\ldots ,v_{i-1},v_{i}+w,v_{i+1},\ldots ,v_{n})\\&=\det(v_{1},\ldots ,v_{i-1},v_{i},v_{i+1},\ldots ,v_{n})+\det(v_{1},\ldots ,v_{i-1},w,v_{i+1},\ldots ,v_{n})\end{aligned}}$

Für alle $v_{1},\ldots ,v_{n}\in K^{n}$ und alle $r\in K$ gilt:

$\det(v_{1},\ldots ,v_{i-1},r\cdot v_{i},v_{i+1},\ldots ,v_{n})=r\cdot \det(v_{1},\ldots ,v_{i-1},v_{i},v_{i+1},\ldots ,v_{n})$

• Sie ist alternierend, d. h., wenn in zwei Spalten das gleiche Argument steht, ist die Determinante gleich 0:

Für alle $v_{1},\ldots ,v_{n}\in K^{n}$ und alle $i,j\in \{1,\ldots ,n\},i\neq j$ gilt:

$\det(v_{1},\ldots ,v_{i-1},v_{i},v_{i+1},\ldots ,v_{j-1},v_{i},v_{j+1}\ldots ,v_{n})=0$

Hieraus folgt, dass sich das Vorzeichen ändert, wenn man zwei Spalten vertauscht:

Für alle $v_{1},\ldots ,v_{n}\in K^{n}$ und alle $i,j\in \{1,\ldots ,n\},i\neq j$ gilt:

$\det(v_{1},\ldots ,v_{i},\ldots ,v_{j},\ldots ,v_{n})=-\det(v_{1},\ldots ,v_{j},\ldots ,v_{i},\ldots ,v_{n})$

Oft wird diese Folgerung zur Definition von alternierend verwendet. Im Allgemeinen ist diese jedoch nicht zur obigen äquivalent. Wird alternierend nämlich auf die zweite Weise definiert, gibt es keine eindeutige Determinantenform, wenn der Körper, über dem der Vektorraum gebildet wird, ein von 0 verschiedenes Element $x$ mit $x=-x$ besitzt (Charakteristik 2).

• Sie ist normiert, d. h., die Einheitsmatrix hat die Determinante 1:

$\det E_{n}=1$ ⓘ

Es lässt sich beweisen (und Karl Weierstraß hat dies 1864 oder sogar früher getan), dass es eine und nur eine solche normierte alternierende Multilinearform auf der Algebra der $n\times n$-Matrizen über dem zugrundeliegenden Körper gibt – nämlich diese Determinantenfunktion $\det$ (Weierstraßsche Determinantenkennzeichnung). Auch die schon erwähnte geometrische Interpretation (Volumeneigenschaft und Orientierung) folgt daraus. ⓘ

Die Determinante einer linearen Transformation $T:V\to V$ eines $n$-dimensionalen Vektorraums $V$ oder, allgemeiner, eines freien Moduls vom (endlichen) Rang $n$ über einem kommutativen Ring $R$ kann auf koordinatenfreie Weise formuliert werden, indem man die $n$-ten äußeren Potenz $\bigwedge ^{n}V$ von $V$. Die Karte $T$ induziert eine lineare Abbildung

${\begin{aligned}\bigwedge ^{n}T:\bigwedge ^{n}V&\rightarrow \bigwedge ^{n}V\\v_{1}\wedge v_{2}\wedge \dots \wedge v_{n}&\mapsto Tv_{1}\wedge Tv_{2}\wedge \dots \wedge Tv_{n}.\end{aligned}}$ ⓘ

Diese Definition stimmt mit der konkreteren, koordinatenabhängigen Definition überein. Dies kann mit Hilfe der Eindeutigkeit einer multilinearen alternierenden Form auf $n$-Tupel von Vektoren in $R^{n}$. Aus diesem Grund ist die höchste von Null verschiedene äußere Potenz $\bigwedge ^{n}V$ (im Gegensatz zur Determinante, die einem Endomorphismus zugeordnet ist) manchmal auch als Determinante von $V$ bezeichnet und ähnlich für komplexere Objekte wie Vektorbündel oder Kettenkomplexe von Vektorräumen. Die Minoren einer Matrix können auch in diesem Rahmen betrachtet werden, indem man niedrigere alternierende Formen betrachtet $\bigwedge ^{k}V$ mit $k<n$. ⓘ

Verallgemeinerungen und verwandte Begriffe

Determinanten, wie sie oben behandelt wurden, lassen mehrere Varianten zu: Die Permanenz einer Matrix ist definiert als die Determinante, mit der Ausnahme, dass die Faktoren $\operatorname {sgn}(\sigma )$ die in der Leibnizschen Regel vorkommen, weggelassen werden. Die Immanante verallgemeinert beide durch die Einführung eines Charakters der symmetrischen Gruppe $S_{n}$ in die Leibnizsche Regel einführt. ⓘ

Determinanten für endlich-dimensionale Algebren

Für jede assoziative Algebra $A$ die als Vektorraum über einem Feld endlich-dimensional ist $F$, gibt es eine Determinantenabbildung ⓘ

$\det :A\to F.$

Diese Definition geht davon aus, dass das charakteristische Polynom unabhängig von der Determinante ist, und definiert die Determinante als den Term niedrigster Ordnung dieses Polynoms. Diese allgemeine Definition liefert die Determinante für die Matrixalgebra $A=\operatorname {Mat} _{n\times n}(F)$Sie umfasst aber auch mehrere andere Fälle, darunter die Determinante eines Quaternions,

$\det(a+ib+jc+kd)=a^{2}+b^{2}+c^{2}+d^{2}$,

die Norm $N_{L/F}:L\to F$ einer Felderweiterung sowie die Pfaffsche Norm einer schiefsymmetrischen Matrix und die reduzierte Norm einer zentralen einfachen Algebra sind ebenfalls Spezialfälle dieser Konstruktion. ⓘ

Unendliche Matrizen

Für Matrizen mit einer unendlichen Anzahl von Zeilen und Spalten lassen sich die obigen Definitionen der Determinante nicht direkt übernehmen. In der Leibniz-Formel müsste zum Beispiel eine unendliche Summe (deren Terme alle unendliche Produkte sind) berechnet werden. Die Funktionalanalysis bietet verschiedene Erweiterungen der Determinante für solche unendlich-dimensionalen Situationen, die jedoch nur für bestimmte Arten von Operatoren funktionieren. ⓘ

Die Fredholm-Determinante definiert die Determinante für Operatoren, die als Spurklassenoperatoren bekannt sind, durch eine geeignete Verallgemeinerung der Formel

$\det(I+A)=\exp(\operatorname {tr} (\log(I+A))).$ ⓘ

Ein weiterer unendlich-dimensionaler Begriff der Determinante ist die funktionale Determinante. ⓘ

Operatoren in von-Neumann-Algebren

Für Operatoren in einem endlichen Faktor kann man eine positive reellwertige Determinante definieren, die Fuglede-Kadison-Determinante, die die kanonische Spur verwendet. In der Tat gibt es für jeden Trace-Zustand auf einer von-Neumann-Algebra einen Begriff der Fuglede-Kadison-Determinante. ⓘ

Verwandte Begriffe für nicht-kommutative Ringe

Für Matrizen über nicht-kommutativen Ringen sind Multilinearität und alternierende Eigenschaften für n ≥ 2 unvereinbar, so dass es keine gute Definition der Determinante in diesem Bereich gibt. ⓘ

Für quadratische Matrizen mit Einträgen in einem nicht-kommutativen Ring gibt es verschiedene Schwierigkeiten bei der Definition von Determinanten analog zu denen für kommutative Ringe. Der Leibniz-Formel kann eine Bedeutung gegeben werden, sofern die Reihenfolge für das Produkt angegeben wird, und ähnlich verhält es sich mit anderen Definitionen der Determinante, aber die Nicht-Kommutativität führt dann zum Verlust vieler grundlegender Eigenschaften der Determinante, wie der multiplikativen Eigenschaft oder der Tatsache, dass die Determinante bei Transposition der Matrix unverändert bleibt. Für nicht-kommutative Ringe gibt es keinen vernünftigen Begriff einer Multilinearform (das Vorhandensein einer bilinearen Form ungleich Null mit einem regulären Element von R als Wert auf einem Paar von Argumenten impliziert, dass R kommutativ ist). Dennoch wurden verschiedene Begriffe der nicht-kommutativen Determinante formuliert, die einige der Eigenschaften von Determinanten bewahren, insbesondere Quasideterminanten und die Dieudonné-Determinante. Für einige Klassen von Matrizen mit nicht-kommutativen Elementen kann man die Determinante definieren und Theoreme der linearen Algebra beweisen, die ihren kommutativen Entsprechungen sehr ähnlich sind. Beispiele sind die q-Determinante für Quantengruppen, die Capelli-Determinante für Capelli-Matrizen und die Berezinsche Determinante für Supermatrizen (d. h. Matrizen, deren Einträge Elemente von $\mathbb {Z} _{2}$-gradierten Ringen sind). Manin-Matrizen bilden die Klasse, die den Matrizen mit kommutativen Elementen am nächsten kommt. ⓘ

Berechnung

Determinanten werden hauptsächlich als theoretisches Werkzeug verwendet. In der numerischen linearen Algebra werden sie nur selten explizit berechnet, da die Determinante für Anwendungen wie die Überprüfung der Invertierbarkeit und die Ermittlung von Eigenwerten weitgehend durch andere Techniken ersetzt wurde. In der numerischen Geometrie werden jedoch häufig Berechnungen im Zusammenhang mit Determinanten durchgeführt. ⓘ

Während die Determinante direkt mit der Leibniz-Regel berechnet werden kann, ist dieser Ansatz für große Matrizen extrem ineffizient, da diese Formel die Berechnung von $n!$ ($n$ Faktorielle) Produkte für eine $n\times n$-Matrix erfordert. Die Anzahl der erforderlichen Operationen wächst daher sehr schnell: Sie liegt in der Größenordnung $n!$. Die Laplace-Erweiterung ist ähnlich ineffizient. Daher wurden aufwändigere Verfahren zur Berechnung von Determinanten entwickelt. ⓘ

Zersetzungsmethoden

Einige Methoden berechnen $\det(A)$ indem die Matrix als Produkt von Matrizen geschrieben wird, deren Determinanten leichter berechnet werden können. Solche Techniken werden als Zerlegungsmethoden bezeichnet. Beispiele sind die LU-Zerlegung, die QR-Zerlegung oder die Cholesky-Zerlegung (für positiv definite Matrizen). Diese Methoden sind von der Ordnung $\operatorname {O} (n^{3})$was eine erhebliche Verbesserung gegenüber $\operatorname {O} (n!)$. ⓘ

Zum Beispiel drückt die LU-Zerlegung $A$ als ein Produkt

$A=PLU.$

einer Permutationsmatrix $P$ (die genau eine einzige $1$ in jeder Spalte und ansonsten Nullen hat), einer unteren Dreiecksmatrix $L$ und einer oberen Dreiecksmatrix $U$. Die Determinanten der beiden Dreiecksmatrizen $L$ und $U$ lassen sich schnell berechnen, da sie die Produkte der jeweiligen Diagonaleinträge sind. Die Determinante von $P$ ist einfach das Vorzeichen $\varepsilon$ der entsprechenden Permutation (das ist $+1$ für eine gerade Anzahl von Permutationen und ist $-1$ für eine ungerade Anzahl von Permutationen). Sobald eine solche LU-Zerlegung bekannt ist für $A$bekannt ist, lässt sich ihre Determinante leicht wie folgt berechnen ⓘ

$\det(A)=\varepsilon \det(L)\cdot \det(U).$ ⓘ

Weitere Methoden

Die Ordnung $\operatorname {O} (n^{3})$ die durch Zerlegungsmethoden erreicht wird, wurde durch verschiedene Methoden verbessert. Wenn zwei Matrizen der Ordnung $n$ in der Zeit multipliziert werden können $M(n)$, wobei $M(n)\geq n^{a}$ für einige $a>2$multipliziert werden, dann gibt es einen Algorithmus, der die Determinante in der Zeit $O(M(n))$. Das bedeutet zum Beispiel, dass ein $\operatorname {O} (n^{2.376})$ Algorithmus existiert, der auf dem Coppersmith-Winograd-Algorithmus basiert. Dieser Exponent wurde 2016 weiter auf 2,373 gesenkt. ⓘ

Neben der Komplexität des Algorithmus können weitere Kriterien zum Vergleich von Algorithmen herangezogen werden. Insbesondere für Anwendungen, die Matrizen über Ringe betreffen, gibt es Algorithmen, die die Determinante ohne Divisionen berechnen. (Im Gegensatz dazu erfordert die Gauß-Elimination Divisionen.) Ein solcher Algorithmus, dessen Komplexität $\operatorname {O} (n^{4})$ basiert auf der folgenden Idee: Man ersetzt Permutationen (wie in der Leibniz-Regel) durch so genannte geschlossene geordnete Spaziergänge, in denen mehrere Elemente wiederholt werden können. Die sich daraus ergebende Summe hat mehr Terme als bei der Leibniz-Regel, aber dabei können mehrere dieser Produkte wiederverwendet werden, was das Verfahren effizienter macht als das naive Rechnen mit der Leibniz-Regel. Algorithmen können auch nach ihrer Bitkomplexität bewertet werden, d. h. danach, wie viele Bits an Genauigkeit benötigt werden, um die bei der Berechnung auftretenden Zwischenwerte zu speichern. Die Gaußsche Eliminationsmethode (oder LU-Zerlegung) hat zum Beispiel die Ordnung $\operatorname {O} (n^{3})$, aber die Bitlänge der Zwischenwerte kann exponentiell lang werden. Im Vergleich dazu hat der Bareiss-Algorithmus, eine Methode der exakten Division (d. h. er verwendet zwar Divisionen, aber nur in Fällen, in denen diese Divisionen ohne Rest durchgeführt werden können), dieselbe Ordnung, aber die Bitkomplexität entspricht ungefähr der Bitgröße der ursprünglichen Einträge in der Matrix mal $n$. ⓘ

Wenn die Determinante von A und die Inverse von A bereits berechnet wurden, ermöglicht das Determinantenlemmas der Matrix die schnelle Berechnung der Determinante von A + uv^T, wobei u und v Spaltenvektoren sind. ⓘ

Charles Dodgson (d. h. Lewis Carroll, bekannt durch Alices Abenteuer im Wunderland) erfand eine Methode zur Berechnung von Determinanten, die Dodgson-Kondensation. Leider funktioniert diese interessante Methode nicht immer in ihrer ursprünglichen Form. ⓘ

Permanente

Die Permanente ist ein „vorzeichenloses“ Analogon zur Determinante, wird allerdings viel seltener verwendet. ⓘ

Spezielle Determinanten

• Wronski-Determinante
• Pfaffsche Determinante
• Vandermonde-Determinante
• Gramsche Determinante
• Funktionaldeterminante (auch Jacobi-Determinante genannt)
• Determinante (Knotentheorie) ⓘ