Volumen
| Volumen ⓘ | |
|---|---|
 Mit einem Messbecher kann man das Volumen von Flüssigkeiten messen. Dieser Becher misst das Volumen in Einheiten von Tassen, Unzen und Millilitern. | |
Gebräuchliche Symbole | V |
| SI-Einheit | Kubikmeter [m3] |
Andere Einheiten | Liter, flüssige Unze, Gallone, Quart, Pint, tsp, flüssiges Dram, in3, yd3, Barrel |
| In SI-Basiseinheiten | 1 m3 |
| Abmessung | L3 |
Das Volumen ist eine skalare Größe, die den dreidimensionalen Raum angibt, der von einer geschlossenen Fläche umschlossen wird. Zum Beispiel der Raum, den ein Stoff (fest, flüssig, gasförmig oder Plasma) oder eine 3D-Form einnimmt oder enthält. Das Volumen wird häufig numerisch mit der abgeleiteten SI-Einheit, dem Kubikmeter, quantifiziert. Unter dem Volumen eines Behälters wird im Allgemeinen das Fassungsvermögen des Behälters verstanden, d. h. die Menge an Fluid (Gas oder Flüssigkeit), die der Behälter aufnehmen kann, und nicht die Menge an Raum, die der Behälter selbst verdrängt. Dreidimensionalen mathematischen Formen werden ebenfalls Volumina zugewiesen. Die Volumina einiger einfacher Formen, wie z. B. regelmäßiger, geradliniger und kreisförmiger Formen, lassen sich leicht mit Hilfe arithmetischer Formeln berechnen. Volumina komplizierter Formen können mit der Integralrechnung berechnet werden, wenn eine Formel für die Begrenzung der Form existiert. Eindimensionalen Figuren (z. B. Linien) und zweidimensionalen Formen (z. B. Quadraten) wird im dreidimensionalen Raum ein Volumen von Null zugewiesen. ⓘ
Das Volumen eines Festkörpers (ob regelmäßig oder unregelmäßig geformt) kann durch die Verdrängung einer Flüssigkeit bestimmt werden. Die Verdrängung einer Flüssigkeit kann auch zur Bestimmung des Volumens eines Gases verwendet werden. Das kombinierte Volumen zweier Stoffe ist in der Regel größer als das Volumen nur eines der beiden Stoffe. Es kommt jedoch vor, dass sich eine Substanz in der anderen auflöst, und in solchen Fällen ist das kombinierte Volumen nicht additiv. ⓘ
In der Differentialgeometrie wird das Volumen mit Hilfe der Volumenform ausgedrückt und ist eine wichtige globale Riemannsche Invariante. In der Thermodynamik ist das Volumen ein grundlegender Parameter und eine konjugierte Variable zum Druck. ⓘ
| Physikalische Größe ⓘ | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Volumen Rauminhalt | ||||||||||||
| Formelzeichen | |||||||||||||
| Abgeleitet von | Länge | ||||||||||||
| |||||||||||||
Das Volumen (Pl. Volumen oder Volumina; von lat. volumen „Windung, Krümmung“, aus volvere „wälzen, rollen“), auch: Raum- oder Kubikinhalt, ist der räumliche Inhalt eines geometrischen Körpers. Übliches Formelzeichen ist V. ⓘ
Technisch muss unterschieden werden:
- Hohlvolumen, der freie Raum innerhalb gewisser Grenzen, etwa das Fassungsvermögen eines Behälters
- Rauminhalt, das Volumen fester Körper, von Flüssigkeiten oder Gasen ⓘ
Einheiten
Für jede Längeneinheit gibt es eine entsprechende Volumeneinheit: das Volumen eines Würfels, dessen Seiten die angegebene Länge haben. Zum Beispiel ist ein Kubikzentimeter (cm3) das Volumen eines Würfels, dessen Seiten einen Zentimeter (1 cm) lang sind. ⓘ
Im Internationalen Einheitensystem (SI) ist die Standardeinheit des Volumens der Kubikmeter (m3). Das metrische System enthält auch den Liter (L) als Volumeneinheit, wobei ein Liter dem Volumen eines Würfels von 10 cm entspricht. Also
- 1 Liter = (10 cm)3 = 1000 Kubikzentimeter = 0,001 Kubikmeter, ⓘ
also
- 1 Kubikmeter = 1000 Liter.
Kleine Flüssigkeitsmengen werden oft in Millilitern gemessen, wobei
- 1 Milliliter = 0,001 Liter = 1 Kubikzentimeter.
Ebenso können große Mengen in Megaliter gemessen werden, wobei
- 1 Million Liter = 1000 Kubikmeter = 1 Megaliter. ⓘ
Darüber hinaus werden verschiedene andere traditionelle Volumeneinheiten verwendet, darunter der Kubikzoll, der Kubikfuß, der Kubikyard, die Kubikmeile, der Teelöffel, der Esslöffel, die Flüssigunze, das Flüssigdram, der Gill, das Pint, das Quart, die Gallone, das Minim, das Barrel, das Cord, der Peck, der Bushel, der Hogshead, der Acre-foot und der Board-foot. Dies sind alles Volumeneinheiten. ⓘ
Verwandte Begriffe
Das Oxford English Dictionary definiert das Fassungsvermögen als "das Maß für den Inhalt eines Gefäßes und für Flüssigkeiten, Getreide oder Ähnliches, das die Form des Gefäßes annimmt, in dem es sich befindet". (Das Wort Kapazität hat auch andere, nicht verwandte Bedeutungen, wie z. B. Kapazitätsmanagement). Das Fassungsvermögen ist nicht identisch mit dem Volumen, obwohl es eng damit verbunden ist; das Fassungsvermögen eines Behälters ist immer das Volumen in seinem Inneren. Einheiten des Fassungsvermögens sind der SI-Liter und seine abgeleiteten Einheiten sowie imperiale Einheiten wie Gill, Pint, Gallone und andere. Volumeneinheiten sind die Kuben der Längeneinheiten. Im metrischen System sind die Einheiten für Fassungsvermögen und Volumen eng miteinander verbunden: Ein Liter entspricht genau 1 Kubikdezimeter, dem Fassungsvermögen eines Würfels mit einer Seitenlänge von 10 cm. In anderen Systemen ist die Umrechnung nicht trivial; das Fassungsvermögen des Kraftstofftanks eines Fahrzeugs wird beispielsweise selten in Kubikfuß, sondern in Gallonen angegeben (eine imperiale Gallone füllt ein Volumen von 0,1605 cu ft). ⓘ
Die Dichte eines Objekts ist definiert als das Verhältnis von Masse zu Volumen. Der Kehrwert der Dichte ist das spezifische Volumen, das als Volumen geteilt durch die Masse definiert ist. Das spezifische Volumen ist ein wichtiges Konzept in der Thermodynamik, wo das Volumen einer Arbeitsflüssigkeit oft ein wichtiger Parameter eines untersuchten Systems ist. ⓘ
Die volumetrische Durchflussrate in der Fluiddynamik ist das Flüssigkeitsvolumen, das pro Zeiteinheit durch eine bestimmte Oberfläche fließt (z. B. Kubikmeter pro Sekunde [m3 s-1]). ⓘ
Der volumetrische Raum ist eine 3D-Region, die neben der Kapazität oder dem Volumen auch eine Form hat. ⓘ
Kalkül
In der Infinitesimalrechnung, einem Teilgebiet der Mathematik, wird das Volumen einer Region D in R3 durch ein dreifaches Integral der konstanten Funktion über den Bereich und wird gewöhnlich wie folgt geschrieben:
In Zylinderkoordinaten ist das Volumenintegral ⓘ
In sphärischen Koordinaten (unter Verwendung der Konvention für Winkel mit als Azimut und gemessen von der Polarachse; siehe mehr zu den Konventionen), ist das Volumenintegral ⓘ
Formeln
Mathematisch gesehen ist das Volumen (der Rauminhalt) ein Maß für eine messbare Teilmenge des gewöhnlichen dreidimensionalen Raums. Im Allgemeinen lässt sich das Volumen eines Körpers (Bereich im ) durch ein 3-fach-Integral beschreiben. Solche Integrale können sehr schwierig oder nur numerisch lösbar sein. Bei vielen einfachen Fällen (Polyeder) lässt sich das Volumen ohne Integrale bestimmen. Bei Rotationskörper und solchen mit stetigen Querschnittsflächen (s. Tabelle) kommt man mit einfachen Integralen aus. Hier die Volumina einiger häufig vorkommender Körper:
| Körper | Volumen | Parameter ⓘ |
|---|---|---|
| Würfel | 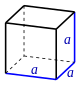
| |
| Quader | 
| |
| Prisma (Grundfläche G) |
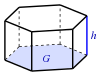
| |
| Pyramide (Grundfläche G) |

| |
| Kugel | 
| |
| Ellipsoid | 
| |
| senkrechter Kreiszylinder | 
| |
| senkrechter Kreiskegel | 
| |
| Torus | 
| |
| Rotationskörper | 
| |
| Körper mit stetiger
Querschnittsfläche |
Für den Rotationskörper ist
|
Verhältnis der Volumina eines Kegels, einer Kugel und eines Zylinders mit gleichem Radius und gleicher Höhe

Mit den obigen Formeln lässt sich zeigen, dass die Volumina eines Kegels, einer Kugel und eines Zylinders mit gleichem Radius und gleicher Höhe im Verhältnis 1 : 2 : 3 stehen, und zwar wie folgt ⓘ
Der Radius des Kegels, des Zylinders und der Kugel sei r und die Höhe sei h (oder 2r) für den Kegel und den Zylinder. ⓘ
Dann: Volumen des Kegels:
Volumen der Kugel:
Volumen des Zylinders:
Die Entdeckung des Verhältnisses 2 : 3 zwischen dem Volumen der Kugel und dem des Zylinders wird Archimedes zugeschrieben. ⓘ
Herleitung der Formeln
Kugel
Das Volumen einer Kugel ist das Integral einer unendlichen Anzahl von unendlich kleinen Kreisscheiben mit der Dicke dx. Die Berechnung des Volumens einer Kugel mit dem Mittelpunkt 0 und dem Radius r lautet wie folgt. ⓘ
Der Flächeninhalt der Kreisscheibe ist . ⓘ
Der Radius der Kreisscheiben, die so definiert sind, dass die x-Achse sie senkrecht durchschneidet, beträgt
oder
wobei y oder z für den Radius einer Scheibe bei einem bestimmten x-Wert stehen kann. ⓘ
Unter Verwendung von y als Radius der Scheibe kann das Volumen der Kugel wie folgt berechnet werden
Jetzt
Kombinieren ergibt ⓘ
Diese Formel lässt sich schneller ableiten, wenn man die Formel für den Oberflächeninhalt der Kugel verwendet, die lautet . Das Volumen der Kugel besteht aus Schichten von unendlich dünnen Kugelschalen, und das Kugelvolumen ist gleich ⓘ
Kegel
Der Kegel ist eine Art Pyramidenform. Die Grundgleichung für Pyramiden, ein Drittel mal Basis mal Höhe, gilt auch für Kegel. ⓘ
Mit Hilfe der Infinitesimalrechnung ist das Volumen eines Kegels jedoch das Integral einer unendlichen Anzahl von unendlich dünnen Kreisscheiben mit der Dicke dx. Die Berechnung des Volumens eines Kegels mit der Höhe h, dessen Basis in (0, 0, 0) mit dem Radius r zentriert ist, lautet wie folgt. ⓘ
Der Radius jeder Kreisscheibe ist r, wenn x = 0 und 0, wenn x = h, und variiert dazwischen linear,
Der Flächeninhalt der Kreisscheibe ist dann
Das Volumen des Kegels kann dann berechnet werden als
und nach Extraktion der Konstanten
Durch Integrieren erhält man
Differentialgeometrie
In der Differentialgeometrie, einem Teilgebiet der Mathematik, ist eine Volumenform auf einer differenzierbaren Mannigfaltigkeit eine Differentialform höchsten Grades (d. h., deren Grad gleich der Dimension der Mannigfaltigkeit ist), die nirgendwo gleich Null ist. Eine Mannigfaltigkeit hat dann und nur dann eine Volumenform, wenn sie orientierbar ist. Eine orientierbare Mannigfaltigkeit hat unendlich viele Volumenformen, da die Multiplikation einer Volumenform mit einer nicht verschwindenden Funktion eine andere Volumenform ergibt. Bei nicht orientierbaren Mannigfaltigkeiten kann man stattdessen den schwächeren Begriff der Dichte definieren. Die Integration der Volumenform ergibt das Volumen der Mannigfaltigkeit entsprechend dieser Form. ⓘ
Eine orientierte pseudo-Riemannsche Mannigfaltigkeit hat eine natürliche Volumenform. In lokalen Koordinaten kann sie ausgedrückt werden als
wobei die 1-Formen sind, die eine positiv orientierte Basis für das Kotangentenbündel der Mannigfaltigkeit bilden, und die Determinante der Matrixdarstellung des metrischen Tensors auf der Mannigfaltigkeit in Form der gleichen Basis ist. ⓘ
Man kann ein Volumen auch über mehrdimensionale Mannigfaltigkeiten definieren, siehe dazu auch Volumenform. Nach dieser Verallgemeinerung ist das Volumen eines Teilraumes des zweidimensionalen euklidischen Raumes sein Flächeninhalt und Entsprechendes gilt auch in höherdimensionalen euklidischen Räumen. Beispielsweise hat ein n-dimensionaler Hyperwürfel mit Kantenlänge ein Volumen von . ⓘ
Thermodynamik
In der Thermodynamik ist das Volumen eines Systems ein wichtiger extensiver Parameter für die Beschreibung seines thermodynamischen Zustands. Das spezifische Volumen, eine intensive Eigenschaft, ist das Volumen des Systems pro Masseneinheit. Das Volumen ist eine Funktion des Zustands und steht in Wechselwirkung mit anderen thermodynamischen Eigenschaften wie Druck und Temperatur. So ist das Volumen beispielsweise durch das ideale Gasgesetz mit dem Druck und der Temperatur eines idealen Gases verknüpft. ⓘ
Berechnung
Die Aufgabe der numerischen Berechnung des Volumens von Objekten wird im Bereich der Computergeometrie in der Informatik untersucht, wobei effiziente Algorithmen zur annähernden oder genauen Durchführung dieser Berechnung für verschiedene Arten von Objekten erforscht werden. Die Technik der konvexen Volumenapproximation zeigt beispielsweise, wie man das Volumen eines beliebigen konvexen Körpers mithilfe eines Zugehörigkeitsorakels approximieren kann. ⓘ
Geschichte
Die ersten bekannten Formeln zur Volumenbestimmung (auch Stereometrie) stammen schon aus dem frühen Ägypten. Das Moskauer Papyrus ist eine Sammlung von Rechenaufgaben und ist etwa auf das Jahr 1850 v. Chr. datiert. Unter anderem sind hier die Formeln für die Bestimmung der Volumina für Rechteckkegel beschrieben. Die Bestimmung wurde durch Analyse und anschließender Synthese erreicht. Das heißt, der Körper wurde in mehrere bekannte Körper zerlegt und die Einzelvolumina addiert. ⓘ
Messmethoden
Im Laufe der Zeit haben sich ganz unterschiedliche Methoden zur Bestimmung von Volumina entwickelt:
- Auslitern: Der Körper wird mit Sand oder Wasser gefüllt, dessen Menge anschließend in einem bekannten Gefäß bestimmt wird; somit lässt sich bei Gefäßen das Volumen ihres Innenraumes bestimmen.
- Wasserverdrängung: Der Körper wird in ein vollständig mit Wasser gefülltes Gefäß eingetaucht. Das Volumen des übertretenden Wassers wird anschließend in einem geometrisch einfachen Gefäß (z. B. Zylinder) vermessen. Infolge möglicher Wechselwirkungen zwischen Probekörper und Wasser kann es zu Messfehlern kommen, weshalb auch andere Flüssigkeiten eingesetzt werden können.
- Bei einem Körper mit einer bekannten Dichte lässt sich das Volumen auch erwiegen. ⓘ
Hohlraum
Ein Hohlraum ist ein mathematisches, ein physikalisches oder ein natürliches Objekt. Sein Volumen wird als Hohlvolumen bezeichnet. Ein in einer Struktur eingeschlossenes Volumen kann ein Hohlraum sein. Dabei verändert die Existenz von Hohlräumen oft die umliegende Struktur, z. B. in Hinsicht auf Festigkeit oder Elastizität (Siehe Porosität). ⓘ
Ein natürlicher Hohlraum enthält ein Vakuum oder ist mit Gasen, Flüssigkeiten oder anderen Stoffen gefüllt, was wiederum die umschließende Struktur beeinflussen kann. Insbesondere kann die Grenzfläche zwischen Hohlraum und Struktur sich verändern, schwer zu erkennen sein oder auch nur auf gedanklicher Ebene existieren. Auch ein Hohlraum, der eine oder mehrere Öffnungen hat, also nicht vollständig von der umschließenden Struktur umgeben ist, wird umgangssprachlich so bezeichnet. ⓘ
Die Größe des umschlossenen Volumens kann oft errechnet oder experimentell bestimmt werden. In manchen Fällen ist das allerdings prinzipiell nicht möglich. ⓘ
Hohlraumbildung ist ein oft auftretendes Phänomen bei geologischen und sonstigen physikalischen und chemischen Prozessen. ⓘ
Evakuierte Hohlräume haben mehrere universelle Eigenschaften, eine davon ist die Hohlraumstrahlung. ⓘ
Beispiele: Hohlraum ⓘ
- … als Gefäß: Flasche, Tank, Verdauungssystem, Schwamm
- … als Aufenthaltsort: Wohnung, Höhle
- … als Ergebnis chemischer oder physikalischer Vorgänge: Luftblase, Seifenblase, „Löcher“ im Käse, Lunker ⓘ













































