Dreieck

Gleichseitiges Dreieck ⓘ
Ein regelmäßiges Dreieck
Typ	Regelmäßiges Vieleck
Kanten und Scheitelpunkte	3
Schläfli-Symbol	{3}
Coxeter-Dynkin-Diagramme
Symmetrie-Gruppe	Zweiflächig (D3), Ordnung 2×3
Innenwinkel (Grad)	60°
Eigenschaften	Konvex, zyklisch, gleichseitig, isogonal, isotoxisch

Dreieck ⓘ
Ein Dreieck
Kanten und Scheitelpunkte	3
Schläfli-Symbol	{3} (für gleichseitige Dreiecke)
Fläche	verschiedene Methoden; siehe unten
Innenwinkel (Grad)	60° (für gleichseitige Dreiecke)

Dreieck = Tri (drei) + Winkel ⓘ

Ein Dreieck ist ein Vieleck mit drei Kanten und drei Scheitelpunkten. Es ist eine der Grundformen der Geometrie. Ein Dreieck mit den Eckpunkten A, B und C hat die Bezeichnung $\triangle ABC$. ⓘ

In der euklidischen Geometrie bestimmen drei beliebige Punkte, wenn sie nicht kollinear sind, ein eindeutiges Dreieck und gleichzeitig eine eindeutige Ebene (d. h. einen zweidimensionalen euklidischen Raum). Mit anderen Worten: Es gibt nur eine Ebene, die dieses Dreieck enthält, und jedes Dreieck ist in einer Ebene enthalten. Wenn die gesamte Geometrie nur aus der euklidischen Ebene besteht, gibt es nur eine Ebene, in der alle Dreiecke enthalten sind; in höherdimensionalen euklidischen Räumen ist dies jedoch nicht mehr der Fall. In diesem Artikel geht es um Dreiecke in der euklidischen Geometrie, insbesondere in der euklidischen Ebene, sofern nicht anders angegeben. ⓘ

allgemeines Dreieck ⓘ

In der Trigonometrie, einem Teilgebiet der Mathematik, spielen Dreiecke die wesentliche Rolle. Siehe dazu insbesondere Dreiecksgeometrie. ⓘ

Arten von Dreiecken

Euler-Diagramm der Dreieckstypen, unter Verwendung der Definition, dass gleichschenklige Dreiecke mindestens 2 gleiche Seiten haben (d. h. gleichseitige Dreiecke sind gleichschenklig). ⓘ

Die Terminologie zur Kategorisierung von Dreiecken ist mehr als zweitausend Jahre alt und wurde bereits auf der ersten Seite von Euklids Elementen definiert. Die Namen, die für die moderne Klassifizierung verwendet werden, sind entweder eine direkte Transkription von Euklids Griechisch oder ihre lateinischen Übersetzungen. ⓘ

Nach Seitenlängen

Der antike griechische Mathematiker Euklid definierte drei Arten von Dreiecken nach der Länge ihrer Seiten:

Griechisch: τῶν δὲ τριπλεύρων σχημάτων ἰσόπλευρον μὲν τρίγωνόν ἐστι τὸ τὰς τρεῖς ἴσας ἔχον πλευράς, ἰσοσκελὲς δὲ τὸ τὰς δύο μόνας ἴσας ἔχον πλευράς, σκαληνὸν δὲ τὸ τὰς τρεῖς ἀνίσους ἔχον πλευράς, Lit. 'Von den dreiseitigen Figuren ist ein isopleuronisches [gleichseitiges] Dreieck dasjenige, dessen drei Seiten gleich sind, ein gleichschenkliges dasjenige, dessen zwei Seiten allein gleich sind, und ein skalenförmiges dasjenige, dessen drei Seiten ungleich sind. ⓘ

• Ein gleichseitiges Dreieck (griechisch: ἰσόπλευρον, romanisiert: isópleuron, wörtlich: "gleiche Seiten") hat drei gleich lange Seiten. Ein gleichseitiges Dreieck ist auch ein regelmäßiges Vieleck, bei dem alle Winkel 60° messen.
• Ein gleichschenkliges Dreieck (griechisch: ἰσοσκελὲς, romanisiert: isoskelés, wörtlich: "gleiche Schenkel") hat zwei gleich lange Seiten. Ein gleichschenkliges Dreieck hat auch zwei Winkel mit dem gleichen Maß, nämlich die Winkel, die den beiden gleich langen Seiten gegenüberliegen. Diese Tatsache ist der Inhalt des Satzes vom gleichschenkligen Dreieck, der schon Euklid bekannt war. Einige Mathematiker definieren ein gleichschenkliges Dreieck als ein Dreieck mit genau zwei gleichen Seiten, während andere ein gleichschenkliges Dreieck als ein Dreieck mit mindestens zwei gleichen Seiten definieren. Nach der letztgenannten Definition wären alle gleichseitigen Dreiecke gleichschenklige Dreiecke. Das rechtwinklige Dreieck 45-45-90, das im Tetrakis-Quadrat auftaucht, ist gleichschenklig.
• Bei einem skalaren Dreieck (griechisch: σκαληνὸν, romanisiert: skalinón, wörtlich: "ungleich") sind alle Seiten unterschiedlich lang. Gleichermaßen sind alle Winkel unterschiedlich lang. ⓘ

• 

  Gleichseitiges Dreieck

• 

  Gleichschenkliges Dreieck

• 

  Scalene-Dreieck ⓘ

Schraffuren, auch Häkchen genannt, werden in Diagrammen von Dreiecken und anderen geometrischen Figuren verwendet, um Seiten mit gleichen Längen zu kennzeichnen. Eine Seite kann mit einem Muster von "Häkchen", kurzen Liniensegmenten in Form von Strichmännchen, markiert werden; zwei Seiten sind gleich lang, wenn sie beide mit demselben Muster markiert sind. In einem Dreieck besteht das Muster normalerweise aus nicht mehr als 3 Strichen. Ein gleichseitiges Dreieck hat auf allen drei Seiten das gleiche Muster, ein gleichschenkliges Dreieck hat nur auf zwei Seiten das gleiche Muster, und ein ungleichseitiges Dreieck hat auf allen Seiten unterschiedliche Muster, da keine Seiten gleich sind. ⓘ

In ähnlicher Weise werden Muster von 1, 2 oder 3 konzentrischen Bögen innerhalb der Winkel verwendet, um gleiche Winkel anzuzeigen: Ein gleichseitiges Dreieck hat das gleiche Muster auf allen 3 Winkeln, ein gleichschenkliges Dreieck hat das gleiche Muster auf nur 2 Winkeln, und ein ungleichseitiges Dreieck hat unterschiedliche Muster auf allen Winkeln, da keine Winkel gleich sind. ⓘ

Nach Innenwinkeln

Die erste Seite von Euklids Elementen, aus der weltweit ersten gedruckten Version (1482), zeigt den Abschnitt "Definitionen" von Buch I. Das rechtwinklige Dreieck ist mit "orthogonius" beschriftet, und die beiden abgebildeten Winkel sind "acutus" und "angulus obtusus". ⓘ

Dreiecke können auch nach ihren Innenwinkeln klassifiziert werden, die hier in Grad gemessen werden.

• Bei einem rechtwinkligen Dreieck (oder rechtwinkligen Dreieck) beträgt einer der Innenwinkel 90° (rechter Winkel). Die dem rechten Winkel gegenüberliegende Seite ist die Hypotenuse, die längste Seite des Dreiecks. Die beiden anderen Seiten werden als Schenkel oder Katheten (Singular: Katheten) des Dreiecks bezeichnet. Für rechtwinklige Dreiecke gilt der Satz des Pythagoras: Die Summe der Quadrate der Längen der beiden Schenkel ist gleich dem Quadrat der Länge der Hypotenuse: a² + b² = c², wobei a und b die Längen der Schenkel sind und c die Länge der Hypotenuse ist. Spezielle rechtwinklige Dreiecke sind rechtwinklige Dreiecke mit zusätzlichen Eigenschaften, die die Berechnungen mit ihnen erleichtern. Eines der beiden bekanntesten ist das rechtwinklige Dreieck 3-4-5, bei dem 3² + 4² = 5² ist. Das 3-4-5-Dreieck ist auch als ägyptisches Dreieck bekannt. In diesem Fall sind 3, 4 und 5 ein pythagoräisches Tripel. Das andere ist ein gleichschenkliges Dreieck mit 2 Winkeln von 45 Grad (45-45-90-Dreieck).
  • Dreiecke, die keinen Winkel von 90° haben, nennt man schiefe Dreiecke.
• Ein Dreieck, bei dem alle Innenwinkel kleiner als 90° sind, ist ein spitzwinkliges Dreieck oder spitzwinkliges Dreieck. Wenn c die Länge der längsten Seite ist, dann ist a² + b² > c², wobei a und b die Längen der anderen Seiten sind.
• Ein Dreieck, bei dem ein Innenwinkel mehr als 90° beträgt, ist ein stumpfwinkliges Dreieck oder ein stumpfwinkliges Dreieck. Wenn c die Länge der längsten Seite ist, dann ist a² + b² < c², wobei a und b die Längen der anderen Seiten sind.
• Ein Dreieck mit einem Innenwinkel von 180° (und kollinearen Eckpunkten) ist entartet. Ein rechtwinkliges entartetes Dreieck hat kollineare Eckpunkte, von denen zwei zusammenfallen. ⓘ

Ein Dreieck, das zwei Winkel mit dem gleichen Maß hat, hat auch zwei Seiten mit der gleichen Länge und ist daher ein gleichschenkliges Dreieck. Daraus folgt, dass in einem Dreieck, in dem alle Winkel das gleiche Maß haben, alle drei Seiten die gleiche Länge haben und es daher gleichseitig ist. ⓘ

Rechts	Stumpf	Akut
	$\underbrace {\qquad \qquad \qquad \qquad \qquad \qquad } _{}$
	Schräg

Grundlegende Fakten

Ein Dreieck, das den Außenwinkel d zeigt. ⓘ

Bei Dreiecken wird davon ausgegangen, dass es sich um zweidimensionale ebene Figuren handelt, es sei denn, aus dem Kontext ergibt sich etwas anderes (siehe Nicht-ebene Dreiecke, unten). In strengen Abhandlungen wird ein Dreieck daher als 2-Simplex bezeichnet (siehe auch Polytop). Grundlegende Fakten über Dreiecke wurden von Euklid in den Büchern 1-4 seiner um 300 v. Chr. verfassten Elemente dargestellt. ⓘ

Die Maße der Innenwinkel des Dreiecks ergeben immer 180 Grad (gleiche Farbe, um anzuzeigen, dass sie gleich sind). ⓘ

Die Summe der Maße der Innenwinkel eines Dreiecks im euklidischen Raum beträgt immer 180 Grad. Diese Tatsache ist gleichbedeutend mit dem Parallelitätspostulat von Euklid. Auf diese Weise lässt sich das Maß des dritten Winkels eines beliebigen Dreiecks bestimmen, wenn man das Maß zweier Winkel kennt. Ein Außenwinkel eines Dreiecks ist ein Winkel, der ein lineares Paar (und somit ergänzend) zu einem Innenwinkel ist. Das Maß eines Außenwinkels eines Dreiecks ist gleich der Summe der Maße der beiden Innenwinkel, die nicht an ihn angrenzen; dies ist der Satz vom Außenwinkel. Die Summe der Maße der drei Außenwinkel (einer für jeden Scheitelpunkt) eines beliebigen Dreiecks beträgt 360 Grad. ⓘ

Ähnlichkeit und Kongruenz

Zwei Dreiecke gelten als ähnlich, wenn jeder Winkel des einen Dreiecks das gleiche Maß hat wie der entsprechende Winkel im anderen Dreieck. Die entsprechenden Seiten ähnlicher Dreiecke haben Längen, die im gleichen Verhältnis zueinander stehen, und auch diese Eigenschaft reicht aus, um Ähnlichkeit zu begründen. ⓘ

Einige grundlegende Theoreme über ähnliche Dreiecke lauten:

• Nur wenn ein Paar von Innenwinkeln zweier Dreiecke das gleiche Maß hat und ein anderes Paar ebenfalls das gleiche Maß hat, sind die Dreiecke ähnlich.
• Nur wenn ein Paar korrespondierender Seiten zweier Dreiecke im gleichen Verhältnis wie ein anderes Paar korrespondierender Seiten steht und ihre eingeschlossenen Winkel das gleiche Maß haben, sind die Dreiecke ähnlich. (Der eingeschlossene Winkel für zwei beliebige Seiten eines Polygons ist der Innenwinkel zwischen diesen beiden Seiten).
• Nur wenn drei Paare korrespondierender Seiten zweier Dreiecke alle im gleichen Verhältnis stehen, sind die Dreiecke ähnlich. ⓘ

Zwei kongruente Dreiecke haben genau die gleiche Größe und Form: Alle Paare von korrespondierenden Innenwinkeln sind gleich groß, und alle Paare von korrespondierenden Seiten haben die gleiche Länge. (Das sind insgesamt sechs Gleichheiten, aber drei reichen oft aus, um Kongruenz zu beweisen). ⓘ

Einige individuell notwendige und hinreichende Bedingungen für die Kongruenz eines Dreieckspaares sind:

• SAS-Postulat: Zwei Seiten eines Dreiecks haben die gleiche Länge wie zwei Seiten des anderen Dreiecks, und die eingeschlossenen Winkel haben das gleiche Maß.
• ASA: Zwei Innenwinkel und die eingeschlossene Seite eines Dreiecks haben das gleiche Maß bzw. die gleiche Länge wie die des anderen Dreiecks. (Die eingeschlossene Seite eines Winkelpaares ist die Seite, die ihnen gemeinsam ist).
• SSS: Jede Seite eines Dreiecks hat die gleiche Länge wie eine entsprechende Seite des anderen Dreiecks.
• AAS: Zwei Winkel und eine entsprechende (nicht eingeschlossene) Seite eines Dreiecks haben das gleiche Maß bzw. die gleiche Länge wie die des anderen Dreiecks. (Dies wird manchmal als AAcorrS bezeichnet und schließt dann ASA oben ein.) ⓘ

Einige individuell ausreichende Bedingungen sind:

• Hypotenusen-Schenkel (HL) Theorem: Die Hypotenuse und ein Schenkel in einem rechtwinkligen Dreieck haben die gleiche Länge wie die in einem anderen rechtwinkligen Dreieck. Dies wird auch als RHS (rechtwinkliges Dreieck, Hypotenuse, Seite) bezeichnet.
• Hypotenusen-Winkel-Theorem: Die Hypotenuse und der spitze Winkel des einen rechtwinkligen Dreiecks haben die gleiche Länge bzw. das gleiche Maß wie die des anderen rechtwinkligen Dreiecks. Dies ist nur ein Sonderfall des AAS-Satzes.

Eine wichtige Bedingung ist:

• Seite-Seite-Winkel (oder Winkel-Seite-Seite) Bedingung: Wenn zwei Seiten und ein dazugehöriger, nicht eingeschlossener Winkel eines Dreiecks die gleiche Länge bzw. das gleiche Maß wie in einem anderen Dreieck haben, reicht dies nicht aus, um die Kongruenz zu beweisen; wenn aber der gegebene Winkel der längeren Seite der beiden Seiten gegenüberliegt, dann sind die Dreiecke kongruent. Der Hypotenusen-Bein-Satz ist ein Sonderfall dieses Kriteriums. Die Seite-Seite-Winkel-Bedingung allein garantiert noch nicht, dass die Dreiecke kongruent sind, da ein Dreieck stumpfwinklig und das andere spitzwinklig sein könnte. ⓘ

Mit Hilfe von rechtwinkligen Dreiecken und dem Konzept der Ähnlichkeit lassen sich die trigonometrischen Funktionen Sinus und Kosinus definieren. Dies sind Funktionen eines Winkels, die in der Trigonometrie untersucht werden. ⓘ

Rechtwinklige Dreiecke

Der Satz des Pythagoras ⓘ

Ein zentraler Satz ist der Satz des Pythagoras, der besagt, dass in jedem rechtwinkligen Dreieck das Quadrat der Länge der Hypotenuse gleich der Summe der Quadrate der Längen der beiden anderen Seiten ist. Wenn die Hypotenuse die Länge c und die Schenkel die Längen a und b haben, dann besagt der Satz

$a^{2}+b^{2}=c^{2}.$ ⓘ

Umgekehrt gilt: Erfüllen die Seitenlängen eines Dreiecks die obige Gleichung, dann hat das Dreieck einen rechten Winkel gegenüber der Seite c. ⓘ

Einige andere Fakten über rechtwinklige Dreiecke:

• Die spitzen Winkel eines rechtwinkligen Dreiecks sind komplementär.

$a+b+90^{\circ }=180^{\circ }\Rightarrow a+b=90^{\circ }\Rightarrow a=90^{\circ }-b.$

• Wenn die Schenkel eines rechtwinkligen Dreiecks gleich lang sind, dann haben die Winkel, die diesen Schenkeln gegenüberliegen, das gleiche Maß. Da diese Winkel komplementär sind, ergibt sich, dass jeder Winkel 45 Grad misst. Nach dem Satz des Pythagoras ist die Länge der Hypotenuse gleich der Länge eines Schenkels mal √2.
• In einem rechtwinkligen Dreieck mit spitzen Winkeln von 30 und 60 Grad ist die Hypotenuse doppelt so lang wie die kürzere Seite, und die längere Seite ist gleich der Länge der kürzeren Seite mal √3:

$c=2a\,$

$b=a\times {\sqrt {3}}.$ ⓘ

Bei allen Dreiecken sind Winkel und Seiten durch das Kosinus- und das Sinusgesetz (auch Kosinusregel und Sinusregel genannt) miteinander verbunden. ⓘ

Das Vorhandensein eines Dreiecks

Bedingung für die Seiten

Die Dreiecksungleichung besagt, dass die Summe der Längen zweier beliebiger Seiten eines Dreiecks größer als oder gleich der Länge der dritten Seite sein muss. Diese Summe kann nur im Falle eines entarteten Dreiecks, d. h. eines Dreiecks mit kollinearen Eckpunkten, gleich der Länge der dritten Seite sein. Es ist nicht möglich, dass diese Summe kleiner ist als die Länge der dritten Seite. Ein Dreieck mit drei gegebenen positiven Seitenlängen existiert nur dann, wenn diese Seitenlängen die Dreiecksungleichung erfüllen. ⓘ

Bedingungen für die Winkel

Drei gegebene Winkel bilden nur dann ein nicht entartetes Dreieck (und zwar unendlich viele), wenn beide Bedingungen erfüllt sind: (a) jeder der Winkel ist positiv, und (b) die Summe der Winkel beträgt 180°. Wenn entartete Dreiecke zulässig sind, sind auch Winkel von 0° zulässig. ⓘ

Trigonometrische Bedingungen

Drei positive Winkel α, β und γ, die jeweils kleiner als 180° sind, sind die Winkel eines Dreiecks, wenn und nur wenn eine der folgenden Bedingungen gilt

$\tan {\frac {\alpha }{2}}\tan {\frac {\beta }{2}}+\tan {\frac {\beta }{2}}\tan {\frac {\gamma }{2}}+\tan {\frac {\gamma }{2}}\tan {\frac {\alpha }{2}}=1,$ ⓘ

$\sin ^{2}{\frac {\alpha }{2}}+\sin ^{2}{\frac {\beta }{2}}+\sin ^{2}{\frac {\gamma }{2}}+2\sin {\frac {\alpha }{2}}\sin {\frac {\beta }{2}}\sin {\frac {\gamma }{2}}=1,$ ⓘ

$\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )=4\sin(\alpha )\sin(\beta )\sin(\gamma ),$ ⓘ

$\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma +2\cos(\alpha )\cos(\beta )\cos(\gamma )=1,$ ⓘ

$\tan(\alpha )+\tan(\beta )+\tan(\gamma )=\tan(\alpha )\tan(\beta )\tan(\gamma ),$ ⓘ

Die letzte Gleichheit gilt nur, wenn keiner der Winkel 90° ist (der Wert der Tangensfunktion ist also immer endlich). ⓘ

Punkte, Linien und Kreise, die zu einem Dreieck gehören

Es gibt Tausende verschiedener Konstruktionen, die einen speziellen Punkt finden, der mit einem Dreieck assoziiert ist (und oft innerhalb eines Dreiecks liegt) und eine einzigartige Eigenschaft erfüllt: siehe den Artikel Enzyklopädie der Dreiecksmittelpunkte für einen Katalog dieser Konstruktionen. Oft werden sie konstruiert, indem man drei Linien findet, die auf symmetrische Weise mit den drei Seiten (oder Scheitelpunkten) verbunden sind, und dann beweist, dass sich die drei Linien in einem einzigen Punkt treffen: ein wichtiges Werkzeug zum Nachweis der Existenz dieser Linien ist das Ceva-Theorem, das ein Kriterium dafür liefert, wann drei solcher Linien zusammenfallen. In ähnlicher Weise werden Linien, die mit einem Dreieck verbunden sind, oft konstruiert, indem man beweist, dass drei symmetrisch konstruierte Punkte kollinear sind: Hier bietet der Satz des Menelaos ein nützliches allgemeines Kriterium. In diesem Abschnitt werden nur einige der am häufigsten vorkommenden Konstruktionen erläutert. ⓘ

Der Kreismittelpunkt ist der Mittelpunkt eines Kreises, der durch die drei Scheitelpunkte des Dreiecks verläuft. ⓘ

Eine rechtwinklige Winkelhalbierende einer Dreiecksseite ist eine Gerade, die durch den Mittelpunkt der Seite geht und senkrecht zu ihr steht, d. h. einen rechten Winkel mit ihr bildet. Die drei Mittelsenkrechten treffen sich in einem Punkt, dem Umkreismittelpunkt des Dreiecks, der gewöhnlich mit O bezeichnet wird; dieser Punkt ist der Mittelpunkt des Umkreises, des Kreises, der durch alle drei Scheitelpunkte verläuft. Der Durchmesser dieses Kreises, der so genannte Zirkumdiameter, lässt sich aus dem oben genannten Sinusgesetz ableiten. Der Radius des Kreises wird als Umfangsradius bezeichnet. ⓘ

Der Satz von Thales besagt, dass, wenn der Mittelpunkt des Kreises auf einer Seite des Dreiecks liegt, der gegenüberliegende Winkel ein rechter Winkel ist. Liegt der Umkreismittelpunkt innerhalb des Dreiecks, so ist das Dreieck spitz; liegt der Umkreismittelpunkt außerhalb des Dreiecks, so ist das Dreieck stumpf. ⓘ

Der Schnittpunkt der Höhenlagen ist das Orthozentrum. ⓘ

Eine Höhe eines Dreiecks ist eine Gerade, die durch einen Scheitelpunkt verläuft und senkrecht zur gegenüberliegenden Seite steht (d. h. einen rechten Winkel mit ihr bildet). Diese gegenüberliegende Seite wird als Basis der Höhe bezeichnet, und der Punkt, an dem die Höhe die Basis (oder ihre Verlängerung) schneidet, wird als Fuß der Höhe bezeichnet. Die Länge der Höhe ist der Abstand zwischen der Basis und dem Scheitelpunkt. Die drei Höhen schneiden sich in einem einzigen Punkt, dem so genannten Orthozentrum des Dreiecks, das in der Regel mit H bezeichnet wird. Das Orthozentrum liegt nur dann im Inneren des Dreiecks, wenn das Dreieck spitzwinklig ist. ⓘ

Der Schnittpunkt der Winkelhalbierenden ist der Mittelpunkt des Inkreises. ⓘ

Eine Winkelhalbierende eines Dreiecks ist eine gerade Linie durch einen Scheitelpunkt, die den entsprechenden Winkel halbiert. Die drei Winkelhalbierenden schneiden sich in einem einzigen Punkt, dem Mittelpunkt, der in der Regel mit I bezeichnet wird, dem Mittelpunkt des Inkreises des Dreiecks. Der Inkreis ist der Kreis, der im Inneren des Dreiecks liegt und alle drei Seiten berührt. Sein Radius wird Inradius genannt. Es gibt drei weitere wichtige Kreise, die Exkreise; sie liegen außerhalb des Dreiecks und berühren eine Seite sowie die Verlängerungen der beiden anderen. Die Mittelpunkte der Innen- und Außenkreise bilden ein orthozentrisches System. ⓘ

Der Schnittpunkt der Mediane ist der Flächenschwerpunkt. ⓘ

Ein Median eines Dreiecks ist eine gerade Linie durch einen Scheitelpunkt und den Mittelpunkt der gegenüberliegenden Seite und teilt das Dreieck in zwei gleiche Flächen. Die drei Mediane schneiden sich in einem einzigen Punkt, dem geometrischen Schwerpunkt des Dreiecks, der in der Regel mit G bezeichnet wird. Der Schwerpunkt eines starren dreieckigen Objekts (das aus einer dünnen Platte mit gleichmäßiger Dichte ausgeschnitten wurde) ist auch sein Massenschwerpunkt: Das Objekt kann in einem gleichmäßigen Gravitationsfeld auf seinem Schwerpunkt balanciert werden. Der Schwerpunkt schneidet jeden Median im Verhältnis 2:1, d. h. der Abstand zwischen einem Scheitelpunkt und dem Schwerpunkt ist doppelt so groß wie der Abstand zwischen dem Schwerpunkt und dem Mittelpunkt der gegenüberliegenden Seite. ⓘ

Der Neun-Punkte-Kreis weist eine Symmetrie auf, bei der sechs Punkte auf der Kante des Dreiecks liegen. ⓘ

Die Mittelpunkte der drei Seiten und die Füße der drei Höhen liegen alle auf einem einzigen Kreis, dem Neun-Punkte-Kreis des Dreiecks. Die übrigen drei Punkte, nach denen das Dreieck benannt ist, sind die Mittelpunkte des Höhenabschnitts zwischen den Scheitelpunkten und dem Orthozentrum. Der Radius des Neun-Punkte-Kreises ist halb so groß wie der des Umkreises. Er berührt den Inkreis (im Feuerbachpunkt) und die drei Außenkreise. ⓘ

Die Eulersche Linie ist eine Gerade durch das Orthozentrum (blau), den Mittelpunkt des Neun-Punkte-Kreises (rot), den Schwerpunkt (orange) und den Umkreismittelpunkt (grün) ⓘ

Das Orthozentrum (blauer Punkt), der Mittelpunkt des Neun-Punkte-Kreises (rot), der Schwerpunkt (orange) und der Umkreismittelpunkt (grün) liegen alle auf einer einzigen Linie, der so genannten Eulerschen Linie (rote Linie). Der Mittelpunkt des Neun-Punkte-Kreises liegt in der Mitte zwischen dem Orthozentrum und dem Zirkumzentrum, und der Abstand zwischen dem Schwerpunkt und dem Zirkumzentrum ist halb so groß wie der zwischen dem Schwerpunkt und dem Orthozentrum. ⓘ

Der Mittelpunkt des Inkreises liegt im Allgemeinen nicht auf der Eulerschen Linie. ⓘ

Spiegelt man einen Median an der Winkelhalbierenden, die durch denselben Scheitelpunkt geht, erhält man einen Symmedian. Die drei Symmediane schneiden sich in einem einzigen Punkt, dem Symmedianpunkt des Dreiecks. ⓘ

Berechnung von Seiten und Winkeln

Es gibt verschiedene Standardmethoden, um die Länge einer Seite oder das Maß eines Winkels zu berechnen. Bestimmte Methoden eignen sich für die Berechnung von Werten in einem rechtwinkligen Dreieck; in anderen Situationen können komplexere Methoden erforderlich sein. ⓘ

Trigonometrische Verhältnisse in rechtwinkligen Dreiecken

Ein rechtwinkliges Dreieck enthält immer einen Winkel von 90° (π/2 Bogenmaß), hier mit der Bezeichnung C. Die Winkel A und B können variieren. Trigonometrische Funktionen geben die Beziehungen zwischen den Seitenlängen und Innenwinkeln eines rechtwinkligen Dreiecks an. ⓘ

In rechtwinkligen Dreiecken können die trigonometrischen Verhältnisse von Sinus, Kosinus und Tangens verwendet werden, um unbekannte Winkel und die Längen unbekannter Seiten zu ermitteln. Die Seiten des Dreiecks sind wie folgt bekannt:

• Die Hypotenuse ist die Seite, die dem rechten Winkel gegenüberliegt oder als längste Seite eines rechtwinkligen Dreiecks definiert ist, in diesem Fall h.
• Die Gegenseite ist die Seite, die dem gesuchten Winkel gegenüberliegt, in diesem Fall a.
• Die angrenzende Seite ist die Seite, die mit dem interessierenden Winkel und dem rechten Winkel in Berührung kommt, daher ihr Name. In diesem Fall ist die angrenzende Seite b. ⓘ

Sinus, Kosinus und Tangens

Der Sinus eines Winkels ist das Verhältnis zwischen der Länge der gegenüberliegenden Seite und der Länge der Hypotenuse. In unserem Fall

$\sin A={\frac {\text{opposite side}}{\text{hypotenuse}}}={\frac {a}{h}}\,.$ ⓘ

Dieses Verhältnis hängt nicht von dem gewählten rechtwinkligen Dreieck ab, solange es den Winkel A enthält, da alle diese Dreiecke ähnlich sind. ⓘ

Der Kosinus eines Winkels ist das Verhältnis zwischen der Länge der angrenzenden Seite und der Länge der Hypotenuse. In unserem Fall

$\cos A={\frac {\text{adjacent side}}{\text{hypotenuse}}}={\frac {b}{h}}\,.$ ⓘ

Der Tangens eines Winkels ist das Verhältnis zwischen der Länge der gegenüberliegenden Seite und der Länge der angrenzenden Seite. In unserem Fall

$\tan A={\frac {\text{opposite side}}{\text{adjacent side}}}={\frac {a}{b}}={\frac {\sin A}{\cos A}}\,.$ ⓘ

Das Akronym "SOH-CAH-TOA" ist eine nützliche Gedächtnisstütze für diese Verhältnisse. ⓘ

Inverse Funktionen

Mit den inversen trigonometrischen Funktionen lassen sich die Innenwinkel eines rechtwinkligen Dreiecks mit der Länge zweier beliebiger Seiten berechnen. ⓘ

Arcsin kann verwendet werden, um einen Winkel aus der Länge der gegenüberliegenden Seite und der Länge der Hypotenuse zu berechnen.

$\theta =\arcsin \left({\frac {\text{opposite side}}{\text{hypotenuse}}}\right)$ ⓘ

Arccos kann verwendet werden, um einen Winkel aus der Länge der angrenzenden Seite und der Länge der Hypotenuse zu berechnen.

$\theta =\arccos \left({\frac {\text{adjacent side}}{\text{hypotenuse}}}\right)$ ⓘ

Arctan kann verwendet werden, um einen Winkel aus der Länge der gegenüberliegenden Seite und der Länge der angrenzenden Seite zu berechnen.

$\theta =\arctan \left({\frac {\text{opposite side}}{\text{adjacent side}}}\right)$ ⓘ

In Einführungskursen in Geometrie und Trigonometrie wird häufig die Notation sin-1, cos-1 usw. anstelle von arcsin, arccos usw. verwendet. In der höheren Mathematik, in der trigonometrische Funktionen üblicherweise auf Potenzen erhöht werden, ist die Schreibweise arcsin, arccos usw. jedoch Standard, da so die Verwechslung zwischen multiplikativer Umkehrung und kompositioneller Umkehrung vermieden wird. ⓘ

Regeln für Sinus, Kosinus und Tangens

Ein Dreieck mit den Seitenlängen a, b und c und Winkeln von α, β bzw. γ. ⓘ

Das Sinusgesetz besagt, dass das Verhältnis zwischen der Länge einer Seite und dem Sinus des entsprechenden gegenüberliegenden Winkels konstant ist, d. h.

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}.$ ⓘ

Dieses Verhältnis ist gleich dem Durchmesser des Umkreises des gegebenen Dreiecks. Eine andere Interpretation dieses Satzes ist, dass jedes Dreieck mit den Winkeln α, β und γ einem Dreieck ähnelt, dessen Seitenlängen gleich sin α, sin β und sin γ sind. Dieses Dreieck kann konstruiert werden, indem man zunächst einen Kreis mit dem Durchmesser 1 konstruiert und in diesen zwei der Winkel des Dreiecks einschreibt. Die Länge der Seiten dieses Dreiecks ist dann sin α, sin β und sin γ. Die Seite, deren Länge sin α ist, liegt dem Winkel gegenüber, dessen Maß α ist, usw. ⓘ

Das Kosinusgesetz oder die Kosinusregel verbindet die Länge einer unbekannten Seite eines Dreiecks mit den Längen der anderen Seiten und dem Winkel, der der unbekannten Seite gegenüberliegt. Das Gesetz besagt Folgendes: Für ein Dreieck mit den Seitenlängen a, b, c und den Winkeln α, β, γ kann bei zwei bekannten Längen des Dreiecks a und b und dem Winkel zwischen den beiden bekannten Seiten γ (bzw. dem Winkel gegenüber der unbekannten Seite c) folgende Formel zur Berechnung der dritten Seite c verwendet werden:

$c^{2}\ =a^{2}+b^{2}-2ab\cos(\gamma )$

$b^{2}\ =a^{2}+c^{2}-2ac\cos(\beta )$

$a^{2}\ =b^{2}+c^{2}-2bc\cos(\alpha )$ ⓘ

Wenn die Längen aller drei Seiten eines beliebigen Dreiecks bekannt sind, können die drei Winkel berechnet werden:

$\alpha =\arccos \left({\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)$

$\beta =\arccos \left({\frac {a^{2}+c^{2}-b^{2}}{2ac}}\right)$

$\gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)$ ⓘ

Das Tangentengesetz oder die Tangentenregel kann verwendet werden, um eine Seite oder einen Winkel zu finden, wenn zwei Seiten und ein Winkel oder zwei Winkel und eine Seite bekannt sind. Es besagt Folgendes:

${\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}.$ ⓘ

Lösung von Dreiecken

Die "Lösung von Dreiecken" ist das wichtigste trigonometrische Problem: die fehlenden Merkmale eines Dreiecks (drei Winkel, die Längen der drei Seiten usw.) zu finden, wenn mindestens drei dieser Merkmale gegeben sind. Das Dreieck kann in einer Ebene oder auf einer Kugel liegen. Dieses Problem taucht häufig in verschiedenen trigonometrischen Anwendungen auf, z. B. in der Geodäsie, Astronomie, im Bauwesen, in der Navigation usw. ⓘ

Berechnung des Flächeninhalts eines Dreiecks

Der Flächeninhalt eines Dreiecks lässt sich z. B. mit Hilfe der Kongruenz der Dreiecke als die Hälfte des Flächeninhalts eines Parallelogramms mit gleicher Basislänge und Höhe darstellen. ⓘ

Eine grafische Herleitung der Formel $T={\frac {h}{2}}b$ die das übliche Verfahren der Verdopplung und anschließenden Halbierung des Flächeninhalts des Dreiecks vermeidet. ⓘ

Die Berechnung des Flächeninhalts T eines Dreiecks ist ein elementares Problem, das in vielen verschiedenen Situationen auftritt. Die bekannteste und einfachste Formel lautet:

$T={\frac {1}{2}}bh,$

wobei b die Länge der Basis des Dreiecks und h die Höhe des Dreiecks ist. Der Begriff "Basis" bezeichnet eine beliebige Seite, und "Höhe" bezeichnet die Länge einer Senkrechten vom Scheitelpunkt gegenüber der Basis auf die Linie, die die Basis enthält. Im Jahr 499 n. Chr. verwendete Aryabhata diese illustrierte Methode in der Aryabhatiya (Abschnitt 2.6). ⓘ

Obwohl diese Formel einfach ist, ist sie nur dann nützlich, wenn die Höhe ohne weiteres ermittelt werden kann, was nicht immer der Fall ist. So könnte es für den Vermesser eines dreieckigen Feldes relativ einfach sein, die Länge jeder Seite zu messen, aber relativ schwierig, eine "Höhe" zu ermitteln. Je nachdem, was über das Dreieck bekannt ist, können in der Praxis verschiedene Methoden verwendet werden. Im Folgenden finden Sie eine Auswahl häufig verwendeter Formeln für den Flächeninhalt eines Dreiecks. ⓘ

Anwendung der Trigonometrie

Anwendung der Trigonometrie zur Bestimmung der Höhe h. ⓘ

Die Höhe eines Dreiecks kann durch die Anwendung der Trigonometrie ermittelt werden. ⓘ

SAS-Wissen: Unter Verwendung der Beschriftungen in der Abbildung rechts ist die Höhe h = a sin $\gamma$. Setzt man dies in die Formel $T={\frac {1}{2}}bh$ einsetzen, kann der Flächeninhalt des Dreiecks wie folgt ausgedrückt werden:

$T={\frac {1}{2}}ab\sin \gamma ={\frac {1}{2}}bc\sin \alpha ={\frac {1}{2}}ca\sin \beta$ ⓘ

(wobei α der Innenwinkel bei A ist, β der Innenwinkel bei B ist, $\gamma$ der Innenwinkel bei C ist und c die Linie AB ist). ⓘ

Da außerdem sin α = sin (π - α) = sin (β + $\gamma$), und das Gleiche gilt für die beiden anderen Winkel:

$T={\frac {1}{2}}ab\sin(\alpha +\beta )={\frac {1}{2}}bc\sin(\beta +\gamma )={\frac {1}{2}}ca\sin(\gamma +\alpha ).$ ⓘ

Wenn man AAS kennt:

$T={\frac {b^{2}(\sin \alpha )(\sin(\alpha +\beta ))}{2\sin \beta }},$ ⓘ

und sinngemäß, wenn die bekannte Seite a oder c ist. ⓘ

Kenntnis von ASA:

$T={\frac {a^{2}}{2(\cot \beta +\cot \gamma )}}={\frac {a^{2}(\sin \beta )(\sin \gamma )}{2\sin(\beta +\gamma )}},$ ⓘ

und sinngemäß, wenn die bekannte Seite b oder c ist. ⓘ

Verwendung der Heronschen Formel

Die Form des Dreiecks wird durch die Längen der Seiten bestimmt. Daher kann der Flächeninhalt auch aus den Seitenlängen abgeleitet werden. Mit der Heronschen Formel:

$T={\sqrt {s(s-a)(s-b)(s-c)}}$ ⓘ

wobei $s={\tfrac {a+b+c}{2}}$ der Halbmesser oder die Hälfte des Umfangs des Dreiecks ist. ⓘ

Drei weitere äquivalente Möglichkeiten, die Heronsche Formel zu schreiben, sind

$T={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}$

$T={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}$

$T={\frac {1}{4}}{\sqrt {(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}.$ ⓘ

Verwendung von Vektoren

Der Flächeninhalt eines Parallelogramms in einem dreidimensionalen euklidischen Raum kann mit Hilfe von Vektoren berechnet werden. Die Vektoren AB und AC zeigen von A nach B bzw. von A nach C. Der Flächeninhalt des Parallelogramms ABDC ist dann

$|\mathbf {AB} \times \mathbf {AC} |,$ ⓘ

das ist der Betrag des Kreuzprodukts der Vektoren AB und AC. Der Flächeninhalt des Dreiecks ABC ist die Hälfte davon,

${\frac {1}{2}}|\mathbf {AB} \times \mathbf {AC} |.$ ⓘ

Der Flächeninhalt des Dreiecks ABC kann auch wie folgt durch Punktprodukte ausgedrückt werden:

${\frac {1}{2}}{\sqrt {(\mathbf {AB} \cdot \mathbf {AB} )(\mathbf {AC} \cdot \mathbf {AC} )-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}}={\frac {1}{2}}{\sqrt {|\mathbf {AB} |^{2}|\mathbf {AC} |^{2}-(\mathbf {AB} \cdot \mathbf {AC} )^{2}}}.\,$ ⓘ

Im zweidimensionalen euklidischen Raum kann der Vektor AB als freier Vektor im kartesischen Raum gleich (x₁,y₁) und AC als (x₂,y₂) ausgedrückt werden:

${\frac {1}{2}}\,|x_{1}y_{2}-x_{2}y_{1}|.\,$ ⓘ

Verwendung von Koordinaten

Wenn der Scheitelpunkt A im Ursprung (0, 0) eines kartesischen Koordinatensystems liegt und die Koordinaten der beiden anderen Scheitelpunkte durch B = (x_B, y_B) und C = (xC, yC) gegeben sind, kann die Fläche als 1⁄2 mal der Absolutwert der Determinante berechnet werden

$T={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{B}&x_{C}\\y_{B}&y_{C}\end{pmatrix}}\right|={\frac {1}{2}}|x_{B}y_{C}-x_{C}y_{B}|.$ ⓘ

Für drei allgemeine Scheitelpunkte lautet die Gleichung:

$T={\frac {1}{2}}\left|\det {\begin{pmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{pmatrix}}\right|={\frac {1}{2}}{\big |}x_{A}y_{B}-x_{A}y_{C}+x_{B}y_{C}-x_{B}y_{A}+x_{C}y_{A}-x_{C}y_{B}{\big |},$ ⓘ

die geschrieben werden kann als

$T={\frac {1}{2}}{\big |}(x_{A}-x_{C})(y_{B}-y_{A})-(x_{A}-x_{B})(y_{C}-y_{A}){\big |}.$ ⓘ

Wenn die Punkte entgegen dem Uhrzeigersinn nacheinander beschriftet werden, sind die obigen Determinantenausdrücke positiv und die Vorzeichen für den Absolutwert können weggelassen werden. Die obige Formel ist als Schnürsenkelformel oder Vermessungsformel bekannt. ⓘ

Wenn wir die Scheitelpunkte in der komplexen Ebene lokalisieren und sie in der Reihenfolge gegen den Uhrzeigersinn als a = xA + yAi, b = x_B + y_Bi und c = x_C + y_Ci bezeichnen und ihre komplex Konjugierten als ${\bar {a}}$, ${\bar {b}}$und ${\bar {c}}$, dann ist die Formel

$T={\frac {i}{4}}{\begin{vmatrix}a&{\bar {a}}&1\\b&{\bar {b}}&1\\c&{\bar {c}}&1\end{vmatrix}}$ ⓘ

äquivalent zur Schnürsenkelformel. ⓘ

In drei Dimensionen ist der Flächeninhalt eines allgemeinen Dreiecks A = (x_A, y_A, z_A), B = (x_B, y_B, z_B) und C = (x_C, y_C, z_C) die pythagoreische Summe der Flächeninhalte der jeweiligen Projektionen auf die drei Hauptebenen (d. h. x = 0, y = 0 und z = 0):

$T={\frac {1}{2}}{\sqrt {{\begin{vmatrix}x_{A}&x_{B}&x_{C}\\y_{A}&y_{B}&y_{C}\\1&1&1\end{vmatrix}}^{2}+{\begin{vmatrix}y_{A}&y_{B}&y_{C}\\z_{A}&z_{B}&z_{C}\\1&1&1\end{vmatrix}}^{2}+{\begin{vmatrix}z_{A}&z_{B}&z_{C}\\x_{A}&x_{B}&x_{C}\\1&1&1\end{vmatrix}}^{2}}}.$ ⓘ

Verwendung von Linienintegralen

Der Flächeninhalt einer geschlossenen Kurve, z. B. eines Dreiecks, wird durch das Linienintegral des algebraischen oder vorzeichenbehafteten Abstands eines Punktes auf der Kurve von einer beliebig orientierten geraden Linie L um die Kurve bestimmt. ⓘ

Diese Methode eignet sich gut zur Berechnung der Fläche eines beliebigen Polygons. Nimmt man L als x-Achse, so ist das Linienintegral zwischen aufeinanderfolgenden Scheitelpunkten (xi,yi) und (x_i+1,y_i+1) durch die Basis mal die mittlere Höhe gegeben, nämlich (x_i+1 - xi)(yi + y_i+1)/2. Das Vorzeichen der Fläche ist ein allgemeiner Indikator für die Richtung der Durchquerung, wobei eine negative Fläche eine Durchquerung gegen den Uhrzeigersinn anzeigt. Die Fläche eines Dreiecks fällt dann als der Fall eines Polygons mit drei Seiten aus. ⓘ

Die Linienintegralmethode hat zwar mit anderen koordinatenbasierten Methoden die willkürliche Wahl eines Koordinatensystems gemeinsam, doch im Gegensatz zu den anderen Methoden wird weder der Scheitelpunkt des Dreiecks als Ursprung noch die Seite als Basis willkürlich gewählt. Außerdem bindet die Wahl des Koordinatensystems, das durch L definiert ist, nur zwei Freiheitsgrade anstelle der üblichen drei, da das Gewicht ein lokaler Abstand ist (z. B. x_i+1 - xi in der obigen Darstellung), so dass die Methode nicht die Wahl einer zu L normalen Achse erfordert. ⓘ

Wenn man in Polarkoordinaten arbeitet, ist es nicht notwendig, in kartesische Koordinaten umzurechnen, um die Linienintegration zu verwenden, da das Linienintegral zwischen aufeinanderfolgenden Scheitelpunkten (ri,θi) und (r_i+1,θ_i+1) eines Polygons direkt durch rir_i+1sin(θ_i+1 - θi)/2 gegeben ist. Dies gilt für alle Werte von θ, wobei die numerische Genauigkeit etwas abnimmt, wenn |θ| um viele Größenordnungen größer ist als π. Bei dieser Formulierung zeigt eine negative Fläche eine Traversierung im Uhrzeigersinn an, was beim Mischen von polaren und kartesischen Koordinaten beachtet werden sollte. So wie die Wahl der y-Achse (x = 0) für die Linienintegration in kartesischen Koordinaten unerheblich ist, so ist auch die Wahl des Nullpunkts (θ = 0) hier unerheblich. ⓘ

Formeln, die der Heronschen Formel ähneln

Drei Formeln haben die gleiche Struktur wie die Heronsche Formel, werden aber in Form von anderen Variablen ausgedrückt. Bezeichnet man zunächst die Mediane der Seiten a, b und c als ma, mb bzw. mc und ihre Halbsumme (ma + mb + mc)/2 als σ, so erhält man

$T={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}}.$ ⓘ

Bezeichnet man dann die Höhen der Seiten a, b und c als ha, hb bzw. hc und die Halbsumme der Kehrwerte der Höhen als $H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2$ haben wir

$T^{-1}=4{\sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}.$ ⓘ

Bezeichnet man die Halbsumme der Sinusse der Winkel als S = [(sin α) + (sin β) + (sin γ)]/2, so erhält man

$T=D^{2}{\sqrt {S(S-\sin \alpha )(S-\sin \beta )(S-\sin \gamma )}}$ ⓘ

wobei D der Durchmesser des Umkreises ist: $D={\tfrac {a}{\sin \alpha }}={\tfrac {b}{\sin \beta }}={\tfrac {c}{\sin \gamma }}.$ ⓘ

Mit Hilfe des Satzes von Pick

Das Pick'sche Theorem ist ein Verfahren zur Bestimmung des Flächeninhalts eines beliebigen Gitterpolygons (das auf einem Gitter mit vertikal und horizontal benachbarten Gitterpunkten in gleichem Abstand und mit Scheitelpunkten auf Gitterpunkten gezeichnet ist). ⓘ

Das Theorem besagt:

$T=I+{\frac {1}{2}}B-1$ ⓘ

wobei $I$ die Anzahl der inneren Gitterpunkte und B die Anzahl der Gitterpunkte am Rande des Polygons ist. ⓘ

Andere Flächenformeln

Es gibt zahlreiche weitere Flächenformeln, wie z. B.

$T=r\cdot s,$ ⓘ

wobei r der Inradius und s der Halbmesser ist (diese Formel gilt für alle tangentialen Polygone), und ⓘ

$T=r_{a}(s-a)=r_{b}(s-b)=r_{c}(s-c)$ ⓘ

wobei $r_{a},\,r_{b},\,r_{c}$ die Radien der Exzirkel sind, die die Seiten a, b bzw. c tangieren. ⓘ

Wir haben auch ⓘ

$T={\frac {1}{2}}D^{2}(\sin \alpha )(\sin \beta )(\sin \gamma )$ ⓘ

und

$T={\frac {abc}{2D}}={\frac {abc}{4R}}$ ⓘ

für den Umfang D; und

$T={\frac {\tan \alpha }{4}}(b^{2}+c^{2}-a^{2})$ ⓘ

für den Winkel α ≠ 90°. ⓘ

Die Fläche kann auch ausgedrückt werden als

$T={\sqrt {rr_{a}r_{b}r_{c}}}.$ ⓘ

Im Jahr 1885 gab Baker eine Sammlung von über hundert verschiedenen Flächenformeln für das Dreieck heraus. Dazu gehören:

$T={\frac {1}{2}}[abch_{a}h_{b}h_{c}]^{1/3},$

$T={\frac {1}{2}}{\sqrt {abh_{a}h_{b}}},$

$T={\frac {a+b}{2(h_{a}^{-1}+h_{b}^{-1})}},$

$T={\frac {Rh_{b}h_{c}}{a}}$ ⓘ

für den Umfangsradius (Radius des Umkreises) R, und

$T={\frac {h_{a}h_{b}}{2\sin \gamma }}.$ ⓘ

Obere Schranke für den Flächeninhalt

Der Flächeninhalt T eines beliebigen Dreiecks mit dem Umfang p erfüllt ⓘ

$T\leq {\tfrac {p^{2}}{12{\sqrt {3}}}},$ ⓘ

wobei die Gleichheit nur dann gilt, wenn das Dreieck gleichseitig ist. ⓘ

Andere obere Schranken für den Flächeninhalt T sind gegeben durch ⓘ

$4{\sqrt {3}}T\leq a^{2}+b^{2}+c^{2}$ ⓘ

und ⓘ

$4{\sqrt {3}}T\leq {\frac {9abc}{a+b+c}},$ ⓘ

beide gelten wiederum nur, wenn das Dreieck gleichseitig ist. ⓘ

Halbierung der Fläche

Es gibt unendlich viele Linien, die den Flächeninhalt eines Dreiecks halbieren. Drei davon sind die Mediane, die als einzige Flächenhalbierende durch den Schwerpunkt gehen. Drei weitere Flächenhalbierende sind parallel zu den Seiten des Dreiecks. ⓘ

Jede Linie durch ein Dreieck, die sowohl die Fläche als auch den Umfang des Dreiecks halbiert, geht durch den Mittelpunkt des Dreiecks. Für jedes beliebige Dreieck kann es eine, zwei oder drei dieser Linien geben. ⓘ

Weitere Formeln für allgemeine euklidische Dreiecke

Die Formeln in diesem Abschnitt gelten für alle euklidischen Dreiecke. ⓘ

Mediane, Winkelhalbierende, rechtwinklige Seitenhalbierende und Höhenlagen

Die Mediane und die Seiten stehen in folgender Beziehung

${\frac {3}{4}}(a^{2}+b^{2}+c^{2})=m_{a}^{2}+m_{b}^{2}+m_{c}^{2}$ ⓘ

und

$m_{a}={\frac {1}{2}}{\sqrt {2b^{2}+2c^{2}-a^{2}}}={\sqrt {{\frac {1}{2}}(a^{2}+b^{2}+c^{2})-{\frac {3}{4}}a^{2}}}$, ⓘ

und äquivalent für mb und m_c. ⓘ

Für den Winkel A, der der Seite a gegenüberliegt, ist die Länge der inneren Winkelhalbierenden gegeben durch

$w_{A}={\frac {2{\sqrt {bcs(s-a)}}}{b+c}}={\sqrt {bc\left[1-{\frac {a^{2}}{(b+c)^{2}}}\right]}}={\frac {2bc}{b+c}}\cos {\frac {A}{2}},$ ⓘ

für den Halbmesser s, wobei die Länge der Winkelhalbierenden vom Scheitelpunkt bis zum Schnittpunkt mit der gegenüberliegenden Seite gemessen wird. ⓘ

Die inneren Mittelsenkrechten sind gegeben durch ⓘ

$p_{a}={\frac {2aT}{a^{2}+b^{2}-c^{2}}},$

$p_{b}={\frac {2bT}{a^{2}+b^{2}-c^{2}}},$

$p_{c}={\frac {2cT}{a^{2}-b^{2}+c^{2}}},$ ⓘ

wobei die Seitenlänge $a\geq b\geq c$ und der Flächeninhalt ist $T.$ ⓘ

Die Höhe von z.B. der Seite der Länge a ist ⓘ

$h_{a}={\frac {2T}{a}}.$ ⓘ

Umfangsradius und Inradius

Die folgenden Formeln beziehen sich auf den Umfangsradius R und den Innenradius r:

$R={\sqrt {\frac {a^{2}b^{2}c^{2}}{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}};$

$r={\sqrt {\frac {(-a+b+c)(a-b+c)(a+b-c)}{4(a+b+c)}}};$

${\frac {1}{r}}={\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}$ ⓘ

wobei h_a usw. die Höhen zu den tiefgestellten Seiten sind;

${\frac {r}{R}}={\frac {4T^{2}}{sabc}}=\cos \alpha +\cos \beta +\cos \gamma -1;$ ⓘ

und

$2Rr={\frac {abc}{a+b+c}}$. ⓘ

Das Produkt aus zwei Seiten eines Dreiecks ist gleich der Höhe der dritten Seite mal dem Durchmesser D des Umkreises:

$ab=h_{c}D,\quad \quad bc=h_{a}D,\quad ca=h_{b}D.$ ⓘ

Benachbarte Dreiecke

Angenommen, zwei benachbarte, aber nicht überlappende Dreiecke haben dieselbe Seite der Länge f und teilen sich denselben Umkreis, so dass die Seite der Länge f eine Sehne des Umkreises ist und die Dreiecke die Seitenlängen (a, b, f) und (c, d, f) haben, wobei die beiden Dreiecke zusammen ein zyklisches Viereck mit den Seitenlängen (a, b, c, d) bilden. Dann

$f^{2}={\frac {(ac+bd)(ad+bc)}{(ab+cd)}}.\,$ ⓘ

Schwerpunkt

Sei G der Schwerpunkt eines Dreiecks mit den Eckpunkten A, B und C, und sei P ein beliebiger innerer Punkt. Dann sind die Abstände zwischen den Punkten verbunden durch

$(PA)^{2}+(PB)^{2}+(PC)^{2}=(GA)^{2}+(GB)^{2}+(GC)^{2}+3(PG)^{2}.\,$ ⓘ

Die Summe der Quadrate der Seiten des Dreiecks ist gleich dem Dreifachen der Summe der quadrierten Abstände des Schwerpunkts von den Scheitelpunkten:

$AB^{2}+BC^{2}+CA^{2}=3(GA^{2}+GB^{2}+GC^{2}).$ ⓘ

Seien qa, qb und qc die Entfernungen vom Schwerpunkt zu den Seiten der Längen a, b und c. Dann gilt

${\frac {q_{a}}{q_{b}}}={\frac {b}{a}},\quad \quad {\frac {q_{b}}{q_{c}}}={\frac {c}{b}},\quad \quad {\frac {q_{a}}{q_{c}}}={\frac {c}{a}}\,$ ⓘ

und

$q_{a}\cdot a=q_{b}\cdot b=q_{c}\cdot c={\frac {2}{3}}T\,$ ⓘ

für die Fläche T. ⓘ

Zirkumzentrum, Inzentrum und Orthozentrum

Das Carnotsche Theorem besagt, dass die Summe der Abstände vom Mittelpunkt zu den drei Seiten gleich der Summe von Umfangsradius und Innenradius ist. Dabei wird die Länge eines Segments nur dann als negativ angesehen, wenn das Segment vollständig außerhalb des Dreiecks liegt. Diese Methode ist besonders nützlich, um die Eigenschaften von abstrakteren Formen von Dreiecken abzuleiten, wie z. B. die durch Lie-Algebren induzierten Dreiecke, die ansonsten die gleichen Eigenschaften wie gewöhnliche Dreiecke haben. ⓘ

Der Satz von Euler besagt, dass der Abstand d zwischen dem Kreismittelpunkt und dem Mittelpunkt gegeben ist durch

$\displaystyle d^{2}=R(R-2r)$ ⓘ

oder äquivalent

${\frac {1}{R-d}}+{\frac {1}{R+d}}={\frac {1}{r}},$ ⓘ

wobei R der Umfangsradius und r der Innenradius ist. Für alle Dreiecke gilt also R ≥ 2r, wobei Gleichheit für gleichseitige Dreiecke gilt. ⓘ

Wenn wir angeben, dass das Orthozentrum eine Höhe in Segmente der Längen u und v, eine andere Höhe in die Segmentlängen w und x und die dritte Höhe in die Segmentlängen y und z unterteilt, dann ist uv = wx = yz. ⓘ

Der Abstand einer Seite zum Zirkumzentrum ist gleich der Hälfte des Abstands des gegenüberliegenden Scheitelpunkts zum Orthozentrum. ⓘ

Die Summe der Quadrate der Entfernungen von den Scheitelpunkten zum Orthozentrum H plus die Summe der Quadrate der Seiten ist gleich dem Zwölffachen des Quadrats des Umfangsradius:

$AH^{2}+BH^{2}+CH^{2}+a^{2}+b^{2}+c^{2}=12R^{2}.$ ⓘ

Winkel

Zusätzlich zu dem Sinusgesetz, dem Kosinusgesetz, dem Tangentengesetz und den oben genannten trigonometrischen Existenzbedingungen gilt für jedes Dreieck ⓘ

$a=b\cos C+c\cos B,\quad b=c\cos A+a\cos C,\quad c=a\cos B+b\cos A.$ ⓘ

Morley's Trisektorsatz

Das Morley-Dreieck, das sich aus der Dreiteilung jedes Innenwinkels ergibt. Dies ist ein Beispiel für eine endliche Unterteilungsregel. ⓘ

Der Satz von Morley besagt, dass in jedem Dreieck die drei Schnittpunkte der benachbarten Winkeldreiecke ein gleichseitiges Dreieck bilden, das so genannte Morley-Dreieck. ⓘ

In ein Dreieck eingeschriebene Figuren

Kegelschnitte

Wie bereits erwähnt, hat jedes Dreieck einen einzigen Inkreis, der im Inneren des Dreiecks liegt und alle drei Seiten tangiert. ⓘ

Jedes Dreieck hat eine eindeutige Steinersche Inellipse, die im Inneren des Dreiecks liegt und die Mittelpunkte der Seiten tangiert. Der Satz von Marden zeigt, wie man die Brennpunkte dieser Ellipse findet. Diese Ellipse hat den größten Flächeninhalt von allen Ellipsen, die alle drei Seiten des Dreiecks tangieren. ⓘ

Die Mandart-Ellipse eines Dreiecks ist die Ellipse, die in das Dreieck eingeschrieben ist und die Seiten des Dreiecks an den Berührungspunkten der Außenkreise tangiert. ⓘ

Für jede Ellipse, die in ein Dreieck ABC eingeschrieben ist, seien die Brennpunkte P und Q. Dann ⓘ

${\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.$ ⓘ

Konvexes Polygon

Jedes konvexe Polygon mit dem Flächeninhalt T kann in ein Dreieck mit einem Flächeninhalt von höchstens 2T eingeschrieben werden. Die Gleichheit gilt (ausschließlich) für ein Parallelogramm. ⓘ

Sechseck

Das Lemoine-Sechseck ist ein zyklisches Sechseck, dessen Eckpunkte durch die sechs Schnittpunkte der Seiten eines Dreiecks mit den drei Geraden gegeben sind, die parallel zu den Seiten verlaufen und durch seinen Symmetriepunkt gehen. Sowohl in der einfachen als auch in der sich selbst schneidenden Form befindet sich das Lemoine-Hexagon im Inneren des Dreiecks mit zwei Eckpunkten auf jeder Seite des Dreiecks. ⓘ

Quadrate

Jedes spitzwinklige Dreieck hat drei eingeschriebene Quadrate (Quadrate im Inneren des Dreiecks, bei denen alle vier Eckpunkte eines Quadrats auf einer Seite des Dreiecks liegen, so dass zwei von ihnen auf derselben Seite liegen und somit eine Seite des Quadrats mit einem Teil einer Seite des Dreiecks zusammenfällt). In einem rechtwinkligen Dreieck fallen zwei der Quadrate zusammen und haben einen Scheitelpunkt im rechten Winkel des Dreiecks, so dass ein rechtwinkliges Dreieck nur zwei verschiedene einbeschriebene Quadrate hat. Ein stumpfwinkliges Dreieck hat nur ein einbeschriebenes Quadrat, dessen eine Seite mit einem Teil der längsten Seite des Dreiecks zusammenfällt. Innerhalb eines bestimmten Dreiecks ist eine längere gemeinsame Seite mit einem kleineren Inkreisquadrat verbunden. Wenn ein Inskriptionsquadrat eine Seite der Länge qa und das Dreieck eine Seite der Länge a hat, von der ein Teil mit einer Seite des Quadrats zusammenfällt, dann stehen qa, a, die Höhe ha der Seite a und der Flächeninhalt T des Dreiecks in folgender Beziehung

$q_{a}={\frac {2Ta}{a^{2}+2T}}={\frac {ah_{a}}{a+h_{a}}}.$ ⓘ

Das größtmögliche Verhältnis zwischen dem Flächeninhalt des einbeschriebenen Quadrats und dem Flächeninhalt des Dreiecks ist 1/2, was eintritt, wenn a² = 2T, q = a/2 und die Höhe des Dreiecks von der Basis der Länge a gleich a ist. $2{\sqrt {2}}/3=0.94....$ Diese beiden Extremfälle treten beim gleichschenkligen rechtwinkligen Dreieck auf. ⓘ

Dreiecke

Von einem inneren Punkt eines Bezugsdreiecks aus dienen die nächstgelegenen Punkte auf den drei Seiten als Scheitelpunkte des Pedaldreiecks dieses Punktes. Wenn der innere Punkt der Mittelpunkt des Bezugsdreiecks ist, sind die Scheitelpunkte des Pedaldreiecks die Mittelpunkte der Seiten des Bezugsdreiecks, so dass das Pedaldreieck als Mittelpunktsdreieck oder Mitteldreieck bezeichnet wird. Das Mitteldreieck unterteilt das Bezugsdreieck in vier kongruente Dreiecke, die dem Bezugsdreieck ähnlich sind. ⓘ

Das Gergonne-Dreieck oder Berührungsdreieck eines Bezugsdreiecks hat seine Eckpunkte in den drei Berührungspunkten der Seiten des Bezugsdreiecks mit dessen Inkreis. Das Extouch-Dreieck eines Bezugsdreiecks hat seine Scheitelpunkte in den Berührungspunkten der Außenkreise des Bezugsdreiecks mit dessen Seiten (nicht verlängert). ⓘ

Figuren, die von einem Dreieck umschrieben werden

Das tangentiale Dreieck eines Bezugsdreiecks (außer einem rechtwinkligen Dreieck) ist das Dreieck, dessen Seiten an seinen Scheitelpunkten auf den Tangenten des Umkreises des Bezugsdreiecks liegen. ⓘ

Wie bereits erwähnt, hat jedes Dreieck einen eindeutigen Umkreis, einen Kreis, der durch alle drei Scheitelpunkte verläuft und dessen Mittelpunkt der Schnittpunkt der rechtwinkligen Winkelhalbierenden der Dreiecksseiten ist. ⓘ

Außerdem hat jedes Dreieck eine eindeutige Steiner-Ellipse, die durch die Eckpunkte des Dreiecks geht und deren Mittelpunkt im Schwerpunkt des Dreiecks liegt. Von allen Ellipsen, die durch die Scheitelpunkte des Dreiecks gehen, hat sie die kleinste Fläche. ⓘ

Die Kiepert-Hyperbel ist die einzige Kegelform, die durch die drei Scheitelpunkte des Dreiecks, seinen Schwerpunkt und seinen Mittelpunkt geht. ⓘ

Von allen Dreiecken, die in einem gegebenen konvexen Polygon enthalten sind, gibt es ein Dreieck mit maximalem Flächeninhalt, dessen Eckpunkte alle Eckpunkte des gegebenen Polygons sind. ⓘ

Bestimmung der Lage eines Punktes in einem Dreieck

Eine Möglichkeit, die Lage von Punkten in (oder außerhalb) eines Dreiecks zu bestimmen, besteht darin, das Dreieck an einem beliebigen Ort und mit beliebiger Orientierung in der kartesischen Ebene zu platzieren und kartesische Koordinaten zu verwenden. Dieser Ansatz ist zwar für viele Zwecke praktisch, hat aber den Nachteil, dass die Koordinatenwerte aller Punkte von der willkürlichen Platzierung in der Ebene abhängig sind. ⓘ

Zwei Systeme vermeiden diese Eigenschaft, so dass die Koordinaten eines Punktes nicht durch Verschieben, Drehen oder Spiegeln des Dreiecks beeinträchtigt werden, die alle ein kongruentes Dreieck ergeben, oder sogar durch Skalierung, um ein ähnliches Dreieck zu erhalten:

• Trilineare Koordinaten geben die relativen Abstände eines Punktes von den Seiten an, so dass die Koordinaten $x:y:z$ angeben, dass das Verhältnis der Entfernung des Punktes von der ersten Seite zu seiner Entfernung von der zweiten Seite $x:y$ usw.
• Baryzentrische Koordinaten der Form $\alpha :\beta :\gamma$ geben die Lage des Punktes durch die relativen Gewichte an, die auf die drei Scheitelpunkte gelegt werden müssten, um das ansonsten gewichtslose Dreieck auf dem gegebenen Punkt auszugleichen. ⓘ

Nicht-planare Dreiecke

Ein nicht-ebenes Dreieck ist ein Dreieck, das nicht in einer (ebenen) Ebene enthalten ist. Einige Beispiele für nicht-planare Dreiecke in nicht-euklidischen Geometrien sind sphärische Dreiecke in der sphärischen Geometrie und hyperbolische Dreiecke in der hyperbolischen Geometrie. ⓘ

Während die Winkelmaße der Innenwinkel in ebenen Dreiecken immer 180° ergeben, hat ein hyperbolisches Dreieck Winkelmaße, die weniger als 180° ergeben, und ein sphärisches Dreieck hat Winkelmaße, die mehr als 180° ergeben. Ein hyperbolisches Dreieck erhält man durch Zeichnen auf einer negativ gekrümmten Fläche, z. B. einer Sattelfläche, und ein sphärisches Dreieck erhält man durch Zeichnen auf einer positiv gekrümmten Fläche, z. B. einer Kugel. Zeichnet man also ein riesiges Dreieck auf der Erdoberfläche, so wird man feststellen, dass die Summe der Winkelmaße größer als 180° ist; sie liegt nämlich zwischen 180° und 540°. Insbesondere ist es möglich, ein Dreieck auf einer Kugel so zu zeichnen, dass das Maß jedes seiner Innenwinkel gleich 90° ist, so dass sich eine Gesamtsumme von 270° ergibt. ⓘ

Auf einer Kugel ist die Summe der Winkel eines Dreiecks also

180° × (1 + 4f), ⓘ

wobei f der Bruchteil der Kugelfläche ist, der von dem Dreieck eingeschlossen wird. Nehmen wir zum Beispiel an, wir zeichnen ein Dreieck auf der Erdoberfläche, dessen Eckpunkte am Nordpol, an einem Punkt auf dem Äquator bei 0° Länge und an einem Punkt auf dem Äquator bei 90° westlicher Länge liegen. Die Großkreislinie zwischen den beiden letztgenannten Punkten ist der Äquator, und die Großkreislinie zwischen einem der beiden Punkte und dem Nordpol ist eine Längengradlinie; an den beiden Punkten auf dem Äquator liegen also rechte Winkel vor. Außerdem beträgt der Winkel am Nordpol ebenfalls 90°, weil die beiden anderen Scheitelpunkte sich um 90° des Längengrades unterscheiden. Die Summe der Winkel in diesem Dreieck ist also 90° + 90° + 90° = 270°. Das Dreieck umschließt 1/4 der nördlichen Hemisphäre (90°/360° vom Nordpol aus gesehen) und damit 1/8 der Erdoberfläche, so dass in der Formel f = 1/8 ist; somit gibt die Formel die Winkelsumme des Dreiecks korrekt mit 270° an. ⓘ

Aus der obigen Winkelsummenformel können wir auch ersehen, dass die Erdoberfläche lokal flach ist: Wenn wir ein beliebig kleines Dreieck in der Nähe eines Punktes auf der Erdoberfläche zeichnen, wird der Bruchteil f der Erdoberfläche, der von dem Dreieck eingeschlossen wird, beliebig nahe bei Null liegen. In diesem Fall vereinfacht sich die Winkelsummenformel auf 180°, was, wie wir wissen, der euklidischen Geometrie für Dreiecke auf einer ebenen Fläche entspricht. ⓘ

Sattelfläche und geodätisches Dreieck ⓘ

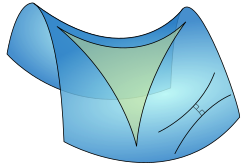
Zur nichteuklidischen Geometrie – in der das Parallelenaxiom nicht gilt – zählen auch Dreiecke auf einer Sattelfläche. Während eine Kugel überall konvex gekrümmt ist, haben Sattel- und andere hyperbolische Flächen sowohl konvexe als auch konkave Krümmung (ihr Produkt, das Krümmungsmaß, ist negativ). ⓘ

Entsprechend ist auch der Exzess negativ – d. h. die Winkelsumme eines Dreiecks auf einer Sattelfläche ist kleiner als 180°. Die Kongruenzsätze machen Aussagen über die Dreiecksgrößen (Seitenlänge, Winkel), die notwendig sind, um ein Dreieck eindeutig zu bestimmen. ⓘ

Dreiecke im Bauwesen

Das Flatiron Building in New York ist wie ein dreieckiges Prisma geformt. ⓘ

Das Rechteck ist die beliebteste und gebräuchlichste geometrische Form für Gebäude, da es leicht zu stapeln und zu organisieren ist. Aber Dreiecke sind zwar konzeptionell schwieriger zu handhaben, bieten aber eine große Stärke. Da die Computertechnologie den Architekten hilft, kreative neue Gebäude zu entwerfen, werden dreieckige Formen als Gebäudeteile und als Hauptform für einige Arten von Wolkenkratzern sowie für Baumaterialien immer häufiger verwendet. In Tokio fragten sich Architekten 1989, ob es möglich sei, einen 500-stöckigen Turm zu bauen, um erschwinglichen Büroraum für diese dicht gedrängte Stadt zu schaffen, aber angesichts der Erdbebengefahr für die Gebäude waren die Architekten der Ansicht, dass eine dreieckige Form notwendig wäre, wenn ein solches Gebäude gebaut werden sollte. ⓘ

In New York City, wo der Broadway die Hauptstraßen kreuzt, sind die entstehenden Blöcke wie Dreiecke geschnitten, und Gebäude wurden auf diesen Formen errichtet; ein solches Gebäude ist das dreieckig geformte Flatiron Building, von dem Immobilienmakler zugeben, dass es ein "Gewirr von unbeholfenen Räumen hat, die nicht leicht moderne Büromöbel aufnehmen können", was aber nicht verhindert hat, dass das Gebäude zu einem Wahrzeichen wurde. In Norwegen haben Designer Häuser mit dreieckigen Motiven entworfen. Dreiecksformen finden sich in Kirchen und öffentlichen Gebäuden, einschließlich Hochschulen, sowie als Stützen für innovative Hausentwürfe. ⓘ

Dreiecke sind stabil; während ein Rechteck durch Druck auf einen seiner Punkte zu einem Parallelogramm zusammenfallen kann, haben Dreiecke eine natürliche Stärke, die Strukturen gegen seitlichen Druck stützt. Ein Dreieck verändert seine Form nicht, solange seine Seiten nicht gebogen, verlängert oder gebrochen werden oder seine Gelenke brechen; im Wesentlichen unterstützt jede der drei Seiten die beiden anderen. Ein Rechteck hingegen ist in struktureller Hinsicht stärker von der Festigkeit seiner Verbindungen abhängig. Einige innovative Designer haben vorgeschlagen, Ziegel nicht aus Rechtecken, sondern aus dreieckigen Formen herzustellen, die sich dreidimensional kombinieren lassen. Es ist wahrscheinlich, dass Dreiecke mit zunehmender Komplexität der Architektur immer häufiger auf neue Weise verwendet werden. Es ist wichtig, sich daran zu erinnern, dass Dreiecke in Bezug auf ihre Steifigkeit stark sind, aber wenn sie in einer mosaikartigen Anordnung gepackt sind, sind sie unter Druck nicht so stark wie Sechsecke (daher sind sechseckige Formen in der Natur weit verbreitet). Mosaikartige Dreiecke haben jedoch immer noch eine höhere Festigkeit als freitragende Dreiecke, und dies ist die Grundlage für eine der stärksten vom Menschen geschaffenen Strukturen, das tetraedrische Fachwerk. ⓘ

Einteilung

Einteilung der Dreiecke:
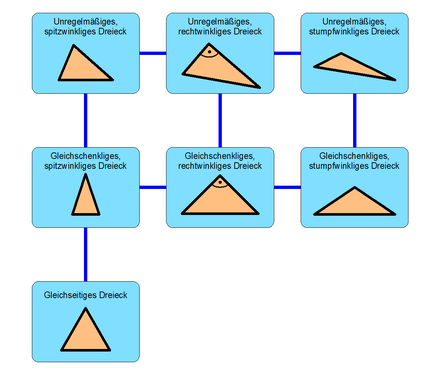
Von links nach rechts: spitzwinklig, rechtwinklig, stumpfwinklig
Von oben nach unten: unregelmäßig, gleichschenklig, gleichseitig ⓘ

Das allgemeine Dreieck

Berechnung eines beliebigen Dreiecks

WWS- oder SWW-Fall

Der WWS- oder SWW-Fall kann (wie nebenstehender Abbildung zu entnehmen) auf zweierlei Weise gelöst werden: Entweder man berechnet mittels des Sinussatzes zunächst einmal eine der beiden noch fehlenden Seiten und rechnet dann weiter wie im SSW-Fall, oder aber man bestimmt, was wesentlich bequemer ist, mittels der Winkelsumme im Dreieck den noch fehlenden dritten Winkel und verfährt dann weiter wie im WSW-Fall. ⓘ

WWW-Fall

Der WWW-Fall ist bei ebenen Dreiecken überhaupt nicht eindeutig lösbar, weil in diesem Fall in Wirklichkeit nur zwei voneinander unabhängige Angaben vorliegen, die Größe des dritten Winkels dagegen stets zwangsläufig aus der Größe der beiden anderen resultiert. Ohne eine gegebene Seite ist zwar die Form des gesuchten Dreiecks gegeben, seine Größe aber bleibt unbestimmt. ⓘ

Dreieck als Symbol

Das Dreieck wird als Symbol verwendet, zum Beispiel in der Theologie, als ideologisches Symbol, als mathematisches Symbol und auch in Schildern. ⓘ