Hawking-Strahlung

Hawking-Strahlung ist eine Wärmestrahlung, die aufgrund von relativistischen Quanteneffekten außerhalb des Ereignishorizonts eines Schwarzen Lochs freigesetzt werden soll. Sie ist nach dem Physiker Stephen Hawking benannt, der 1974 ein theoretisches Argument für ihre Existenz entwickelte. Die Hawking-Strahlung ist ein rein kinematischer Effekt, der für Lorentz-Geometrien mit Ereignishorizonten oder lokalen scheinbaren Horizonten typisch ist. ⓘ

Die Hawking-Strahlung verringert die Masse und Rotationsenergie von Schwarzen Löchern und soll daher auch zur Verdampfung von Schwarzen Löchern führen. Aus diesem Grund wird erwartet, dass Schwarze Löcher, die nicht auf andere Weise an Masse gewinnen, schrumpfen und schließlich verschwinden. Bei allen außer den kleinsten Schwarzen Löchern würde dies extrem langsam geschehen. Die Strahlungstemperatur ist umgekehrt proportional zur Masse des Schwarzen Lochs, so dass man davon ausgeht, dass kleine Schwarze Löcher eine stärkere Strahlung abgeben als größere Schwarze Löcher und sich daher schneller auflösen sollten. ⓘ

Die Hawking-Strahlung ist auch für die aktuelle Forschung von Interesse, weil sie als potenzielles Testfeld für eine Theorie der Quantengravitation dienen könnte. ⓘ

Ähnliche Phänomene wie in der Hawking-Strahlung treten in der Kosmologie auf (Gibbons-Hawking-Effekt) und bei beschleunigten Bezugssystemen (Unruh-Effekt). ⓘ

Es wurden auch Experimente durchgeführt, Analoga von Hawking-Strahlung in anderen physikalischen Systemen zum Beispiel in Optik und Akustik mit Schwarze-Loch-Analoga nachzuweisen. ⓘ

Überblick

Schwarze Löcher sind astrophysikalische Objekte, die vor allem wegen ihrer kompakten Größe und ihrer immensen Anziehungskraft von Interesse sind. Sie wurden erstmals in Einsteins allgemeiner Relativitätstheorie von 1915 vorhergesagt, bevor ein halbes Jahrhundert später die ersten astrophysikalischen Beweise erbracht wurden. ⓘ

Ein Schwarzes Loch kann entstehen, wenn genügend Materie und/oder Energie auf ein Volumen komprimiert wird, das so klein ist, dass die Fluchtgeschwindigkeit größer als die Lichtgeschwindigkeit ist. Nichts kann sich so schnell fortbewegen, also kann nichts innerhalb einer Entfernung, die proportional zur Masse des Schwarzen Lochs ist, über diese Entfernung hinaus entkommen. Der Bereich, über den hinaus nicht einmal Licht entkommen kann, ist der Ereignishorizont; ein Beobachter außerhalb dieses Bereichs kann die Ereignisse innerhalb des Ereignishorizonts nicht beobachten, wahrnehmen oder von ihnen beeinflusst werden. Das Wesen eines Schwarzen Lochs ist sein Ereignishorizont, eine theoretische Abgrenzung zwischen Ereignissen und deren kausalen Beziehungen. ⓘ

Bild des Raums, der mit der Newtonschen Fluchtgeschwindigkeit in ein Schwarzschild-Schwarzes Loch einfällt. Außerhalb/innerhalb des Horizonts (rot) ist die Einfallgeschwindigkeit kleiner/größer als die Lichtgeschwindigkeit. Am Ereignishorizont ist die Einfallgeschwindigkeit gleich der Lichtgeschwindigkeit. Bildnachweis: Andrew Hamilton, JILA ⓘ

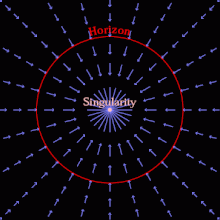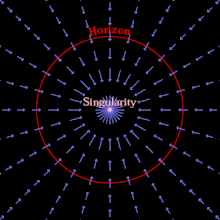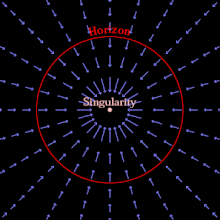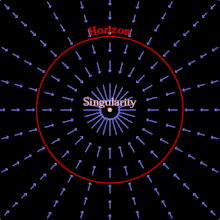
Alternativ kann man sich den Ereignishorizont unter Verwendung der Fallkoordinaten der allgemeinen Relativitätstheorie als die Region vorstellen, jenseits derer der Raum schneller fällt als die Lichtgeschwindigkeit. (Obwohl sich nichts schneller als das Licht durch den Raum bewegen kann, kann der Raum selbst mit beliebiger Geschwindigkeit einfallen.) Sobald sich Materie innerhalb des Ereignishorizonts befindet, fällt die gesamte Materie im Inneren unaufhaltsam in eine Gravitationssingularität, einen Ort mit unendlicher Krümmung und null Größe, und hinterlässt eine verzerrte Raumzeit ohne jegliche Materie. Ein klassisches Schwarzes Loch ist reine leere Raumzeit, und das einfachste (nicht rotierende und ungeladene) ist nur durch seine Masse und seinen Ereignishorizont gekennzeichnet. ⓘ

Mit unserem derzeitigen Verständnis der Quantenphysik können wir untersuchen, was in der Region um den Ereignishorizont passieren könnte. 1974 wandte der britische Physiker Stephen Hawking die Quantenfeldtheorie in einer gekrümmten Raumzeit an, um zu zeigen, dass die Schwerkraft am Ereignishorizont theoretisch stark genug ist, um Wärmestrahlung zu emittieren und Energie aus einer winzigen Entfernung um den Ereignishorizont herum in das weitere Universum "entweichen" zu lassen. Diese Energie wirkte so, als würde das Schwarze Loch selbst langsam verdampfen (obwohl sie eigentlich von außen kam). ⓘ

Ein wichtiger Unterschied zwischen der von Hawking berechneten Strahlung des Schwarzen Lochs und der von einem Schwarzen Körper ausgehenden Wärmestrahlung besteht darin, dass letztere statistischer Natur ist und nur ihr Durchschnitt das so genannte Plancksche Gesetz der Strahlung Schwarzer Körper erfüllt, während erstere besser zu den Daten passt. Die Wärmestrahlung enthält also Informationen über den Körper, von dem sie ausgeht, während die Hawking-Strahlung keine solchen Informationen zu enthalten scheint und nur von der Masse, dem Drehimpuls und der Ladung des Schwarzen Lochs abhängt (das No-Hair-Theorem). Dies führt zu dem Informationsparadoxon des Schwarzen Lochs. ⓘ

Gemäß der vermuteten Eichtheorie-Gravitation-Dualität (auch bekannt als AdS/CFT-Korrespondenz) sind Schwarze Löcher in bestimmten Fällen (und vielleicht auch generell) äquivalent zu Lösungen der Quantenfeldtheorie bei einer Temperatur ungleich Null. Das bedeutet, dass bei schwarzen Löchern kein Informationsverlust zu erwarten ist (da die Theorie keinen solchen Verlust zulässt) und die von einem schwarzen Loch ausgehende Strahlung wahrscheinlich die übliche Wärmestrahlung ist. Wenn dies zutrifft, müsste Hawkings ursprüngliche Berechnung korrigiert werden, obwohl nicht bekannt ist, wie (siehe unten). ⓘ

Ein Schwarzes Loch von einer Sonnenmasse (M_☉) hat eine Temperatur von nur 60 Nanokelvin (60 Milliardstel Kelvin); tatsächlich würde ein solches Schwarzes Loch weit mehr kosmische Mikrowellenhintergrundstrahlung absorbieren als es aussendet. Ein Schwarzes Loch von 4,5×10²² kg (etwa die Masse des Mondes oder etwa 133 μm Durchmesser) würde sich bei 2,7 K im Gleichgewicht befinden und so viel Strahlung absorbieren, wie es aussendet. ⓘ

Entdeckung

Hawkings Entdeckung folgte auf einen Besuch in Moskau im Jahr 1973, wo ihn die sowjetischen Wissenschaftler Jakow Zel'dowitsch und Alexej Starobinskij davon überzeugten, dass rotierende Schwarze Löcher Teilchen erzeugen und aussenden sollten, während der russische Physiker Wladimir Gribow der Meinung war, dass auch ein nicht rotierendes Schwarzes Loch Strahlung aussenden sollte. Als Hawking die Berechnung durchführte, stellte er zu seiner Überraschung fest, dass dies stimmte. 1972 vermutete Jacob Bekenstein, dass Schwarze Löcher eine Entropie haben sollten, und im selben Jahr stellte er einen Satz auf, der kein Haar in der Suppe findet. Bekensteins Entdeckung und Ergebnisse werden von Stephen Hawking gewürdigt, der aufgrund dieses Formalismus auch über Strahlung nachdachte. ⓘ

Dem Physiker Dmitri Diakonov zufolge gab es auf dem Zeldovich-Seminar in Moskau 1972-1973 einen Streit zwischen Zeldovich und Vladimir Gribov. Zeldovich war der Ansicht, dass nur ein rotierendes Schwarzes Loch Strahlung aussenden kann, während Gribov glaubte, dass auch ein nicht rotierendes Schwarzes Loch aufgrund der Gesetze der Quantenmechanik Strahlung aussendet. Diese Darstellung wird durch Gribovs Nachruf in der Physik-Uspekhi von Vitaly Ginzburg und anderen bestätigt. ⓘ

Prozess der Emission

Die Hawking-Strahlung wird durch den Unruh-Effekt und das Äquivalenzprinzip für die Horizonte Schwarzer Löcher bedingt. In der Nähe des Ereignishorizonts eines Schwarzen Lochs muss ein lokaler Beobachter beschleunigen, um nicht hineinzufallen. Ein beschleunigter Beobachter sieht ein thermisches Bad von Teilchen, die aus dem lokalen Beschleunigungshorizont herausspringen, sich umdrehen und im freien Fall wieder hineinfallen. Die Bedingung des lokalen thermischen Gleichgewichts impliziert, dass die konsistente Ausdehnung dieses lokalen thermischen Bades im Unendlichen eine endliche Temperatur hat, was bedeutet, dass einige dieser vom Horizont ausgesandten Teilchen nicht wieder absorbiert werden und zu ausgehender Hawking-Strahlung werden. ⓘ

Ein Schwarzschild-Schwarzes Loch hat eine Metrik:

$\left(\mathrm {d} s\right)^{2}=-\left(1-{\tfrac {2M}{r}}\right)\,\left(\mathrm {d} t\right)^{2}+{\frac {1}{\left(1-{\frac {2M}{r}}\right)}}\,\left(\mathrm {d} r\right)^{2}+r^{2}\,\left(\mathrm {d} \Omega \right)^{2}\,$. ⓘ

Das Schwarze Loch ist die Hintergrundraumzeit für eine Quantenfeldtheorie. ⓘ

Die Feldtheorie ist durch ein lokales Pfadintegral definiert. Wenn also die Randbedingungen am Horizont bestimmt werden, ist der Zustand des Feldes außerhalb des Lochs festgelegt. Um die geeigneten Randbedingungen zu finden, betrachten wir einen stationären Beobachter knapp außerhalb des Horizonts an der Position

$r=2M+{\frac {\rho ^{2}}{8M}}\,.$ ⓘ

Die lokale Metrik niedrigster Ordnung ist

$\left(\mathrm {d} s\right)^{2}\;=\;-\left({\frac {\rho }{4M}}\right)^{2}\,\left(\mathrm {d} t\right)^{2}+\left(\mathrm {d} \rho \right)^{2}+\left(\mathrm {d} X_{\perp }\right)^{2}\;=\;-\rho ^{2}\,\left(\mathrm {d} \tau \right)^{2}+\left(\mathrm {d} \rho \right)^{2}+\left(\mathrm {d} X_{\perp }\right)^{2}$, ⓘ

das ist Rindler in Form von τ = t/4M. Die Metrik beschreibt einen Rahmen, der beschleunigt wird, um nicht in das Schwarze Loch zu fallen. Die lokale Beschleunigung, α = 1/ρ, divergiert mit ρ → 0. ⓘ

Der Horizont ist keine besondere Grenze, und Objekte können hineinfallen. Daher sollte sich der lokale Beobachter im gewöhnlichen Minkowski-Raum nach dem Äquivalenzprinzip beschleunigt fühlen. Der Beobachter in der Nähe des Horizonts muss das Feld mit einer lokalen Temperatur angeregt sehen

$T\;=\;{\frac {\alpha }{2\pi }}\;=\;{\frac {1}{2\pi \rho }}\;=\;{\frac {1}{4\pi {\sqrt {2Mr\left(1-{\frac {2M}{r}}\right)\,}}\,}}\,$; ⓘ

das ist der Unruh-Effekt. ⓘ

Die Rotverschiebung der Gravitation ist durch die Quadratwurzel der Zeitkomponente der Metrik gegeben. Damit sich der Zustand der Feldtheorie konsistent ausdehnen kann, muss also überall ein thermischer Hintergrund vorhanden sein, dessen lokale Temperatur mit der Temperatur des nahen Horizonts rotverschoben ist:

$T(r')\;=\;{\frac {1}{\,4\pi {\sqrt {2Mr\left(1-{\frac {2M}{r}}\right)\,}}\,}}{\sqrt {\frac {1-{\frac {2M}{r}}}{\,1-{\frac {2M}{r'}}\,}}}\;=\;{\frac {1}{4\pi {\sqrt {2Mr\left(1-{\frac {2M}{r'}}\right)}}}}\,$. ⓘ

Die inverse Temperatur, die im Unendlichen auf r′ rotverschoben ist, beträgt ⓘ

$T(\infty )={\frac {1}{4\pi {\sqrt {2Mr}}}}$ ⓘ

und r ist die Position in der Nähe des Horizonts, in der Nähe von 2M, also ist dies wirklich:

$T(\infty )={\frac {1}{8\pi M}}$. ⓘ

Eine Feldtheorie, die auf dem Hintergrund eines Schwarzen Lochs definiert ist, befindet sich also in einem thermischen Zustand, dessen Temperatur im Unendlichen gleich ist:

$T_{\text{H}}={\frac {1}{8\pi M}}$. ⓘ

Aus der Temperatur des Schwarzen Lochs lässt sich leicht die Entropie S des Schwarzen Lochs berechnen. Die Änderung der Entropie, wenn eine Wärmemenge dQ hinzugefügt wird, beträgt:

$\mathrm {d} S\;=\;{\frac {\mathrm {d} Q}{T}}\;=\;8\pi M\,\mathrm {d} Q\,$. ⓘ

Die zugeführte Wärmeenergie dient dazu, die Gesamtmasse zu erhöhen, also:

$\mathrm {d} S\;=\;8\pi M\,\mathrm {d} M\;=\;\mathrm {d} \left(4\pi M^{2}\right)\,$. ⓘ

Der Radius eines Schwarzen Lochs ist das Doppelte seiner Masse in Planck-Einheiten, so dass die Entropie eines Schwarzen Lochs proportional zu seiner Oberfläche ist:

$S=\pi R^{2}={\frac {A}{4}}$. ⓘ

Unter der Annahme, dass ein kleines Schwarzes Loch eine Entropie von Null hat, ist die Integrationskonstante Null. Die Bildung eines schwarzen Lochs ist der effizienteste Weg, um Masse in einer Region zu komprimieren, und diese Entropie ist auch eine Grenze für den Informationsgehalt einer beliebigen Kugel in der Raumzeit. Die Form des Ergebnisses deutet stark darauf hin, dass die physikalische Beschreibung einer Gravitationstheorie irgendwie auf einer begrenzten Fläche kodiert werden kann. ⓘ

mit der Sonnenmasse $M_{\odot }$. ⓘ

Auf ähnliche Weise lässt sich die Strahlungsleistung nach dem Stefan-Boltzmann-Gesetz abschätzen:

$P\approx c{\frac {{(k_{\mathrm {B} }T)}^{4}}{{(\hbar c)}^{3}}}A\approx c{\frac {\hbar c}{{r_{\mathrm {S} }}^{4}}}{r_{\mathrm {S} }}^{2}\approx {\frac {\hbar c^{6}}{G^{2}M^{2}}}$ ⓘ

Oder bei Angabe mit MKS-Einheiten:

$\tau /\mathrm {s} \approx 10^{-20}(M/\mathrm {kg} )^{3}$ ⓘ

Verdampfung des Schwarzen Lochs

Wenn Teilchen entweichen, verliert das Schwarze Loch einen kleinen Teil seiner Energie und damit auch einen Teil seiner Masse (Masse und Energie sind durch Einsteins Gleichung E = mc² miteinander verbunden). Folglich hat ein verdampfendes Schwarzes Loch eine endliche Lebensdauer. Durch Dimensionsanalyse lässt sich zeigen, dass die Lebensdauer eines Schwarzen Lochs mit der Kubikzahl seiner ursprünglichen Masse skaliert, und Hawking schätzte, dass jedes Schwarze Loch, das sich im frühen Universum mit einer Masse von weniger als etwa 10¹⁵ g gebildet hat, bis zum heutigen Tag vollständig verdampft sein würde. ⓘ

Im Jahr 1976 verfeinerte Don Page diese Schätzung, indem er die erzeugte Energie und die Zeit bis zur Verdampfung für ein nicht rotierendes, nicht geladenes Schwarzschild-Schwarzes Loch der Masse M berechnete. Die Berechnungen werden durch die Tatsache erschwert, dass ein Schwarzes Loch aufgrund seiner endlichen Größe kein perfekter Schwarzer Körper ist; der Absorptionsquerschnitt nimmt auf komplizierte, spinabhängige Weise mit abnehmender Frequenz ab, insbesondere wenn die Wellenlänge mit der Größe des Ereignishorizonts vergleichbar wird. Page kam zu dem Schluss, dass ursprüngliche schwarze Löcher nur dann bis heute überleben können, wenn ihre ursprüngliche Masse etwa 4×10¹¹ kg oder mehr beträgt. Als Page 1976 schrieb, ging er mit dem damaligen Verständnis von Neutrinos fälschlicherweise davon aus, dass Neutrinos keine Masse haben und nur zwei Neutrino-Varianten existieren, weshalb seine Ergebnisse zur Lebensdauer schwarzer Löcher nicht mit den modernen Ergebnissen übereinstimmen, die drei Neutrino-Varianten mit Massen ungleich Null berücksichtigen. Eine Berechnung aus dem Jahr 2008, bei der der Teilchengehalt des Standardmodells und der WMAP-Wert für das Alter des Universums verwendet wurden, ergab eine Massengrenze von (5,00±0,04)×10¹¹ kg. ⓘ

Wenn Schwarze Löcher unter Hawking-Strahlung verdampfen, wird ein Schwarzes Loch mit der Masse einer Sonne in 10⁶⁴ Jahren verdampfen, was weitaus länger ist als das Alter des Universums. Ein supermassives Schwarzes Loch mit einer Masse von 10¹¹ (100 Milliarden) M_☉ wird in etwa 2×10¹⁰⁰ Jahren verdampfen. Es wird vorhergesagt, dass einige Monster-Schwarze Löcher im Universum weiter wachsen werden, vielleicht bis zu 10¹⁴ M_☉ während des Zusammenbruchs von Superhaufen von Galaxien. Selbst diese würden in einer Zeitspanne von bis zu 10¹⁰⁶ Jahren verdampfen. ⓘ

Die von einem Schwarzen Loch in Form von Hawking-Strahlung ausgestrahlte Energie lässt sich für den einfachsten Fall eines nicht rotierenden, ungeladenen Schwarzschild-Schwarzlochs der Masse M leicht abschätzen. Kombiniert man die Formeln für den Schwarzschild-Radius des Schwarzen Lochs, das Stefan-Boltzmann-Gesetz für Schwarzkörperstrahlung, die obige Formel für die Temperatur der Strahlung und die Formel für die Oberfläche einer Kugel (den Ereignishorizont des Schwarzen Lochs), lassen sich mehrere Gleichungen ableiten. ⓘ

Die Temperatur der Hawking-Strahlung ist:

$T_{\mathrm {H} }={\frac {\hbar c^{3}}{8\pi GMk_{\mathrm {B} }}}$ ⓘ

Die Bekenstein-Hawking-Leuchtkraft eines Schwarzen Lochs unter der Annahme reiner Photonenemission (d. h., dass keine anderen Teilchen emittiert werden) und unter der Annahme, dass der Horizont die strahlende Fläche ist, ist:

$P={\frac {\hbar c^{6}}{15360\pi G^{2}M^{2}}}$ ⓘ

wobei P die Leuchtkraft, d.h. die abgestrahlte Leistung, ħ die reduzierte Planck-Konstante, c die Lichtgeschwindigkeit, G die Gravitationskonstante und M die Masse des Schwarzen Lochs ist. Es ist erwähnenswert, dass die obige Formel noch nicht im Rahmen der semiklassischen Gravitation abgeleitet wurde. ⓘ

Die Zeit, die das Schwarze Loch braucht, um sich aufzulösen, beträgt:

$t_{\mathrm {ev} }={\frac {5120\pi G^{2}M^{3}}{\hbar c^{4}}}={\frac {480c^{2}V}{\hbar G}}\approx 2.1\times 10^{67}\,{\text{years}}\ \left({\frac {M}{M_{\odot }}}\right)^{3},$ ⓘ

wobei M und V die Masse und das (Schwarzschild-)Volumen des schwarzen Lochs sind. Ein Schwarzes Loch von einer Sonnenmasse (M_☉ = 2,0×10³⁰ kg) braucht mehr als 10⁶⁷ Jahre, um zu verdampfen - viel länger als das derzeitige Alter des Universums von 1,4×10¹⁰ Jahren. Für ein schwarzes Loch von 10¹¹ kg beträgt die Verdampfungszeit jedoch 2,6×10⁹ Jahre. Aus diesem Grund suchen einige Astronomen nach Anzeichen für explodierende primordiale schwarze Löcher. ⓘ

Da das Universum jedoch die kosmische Mikrowellen-Hintergrundstrahlung enthält, muss das Schwarze Loch eine Temperatur haben, die höher ist als die der heutigen Schwarzkörperstrahlung des Universums von 2,7 K. Eine Studie legt nahe, dass M weniger als 0,8 % der Masse der Erde betragen muss - das entspricht etwa der Masse des Mondes - damit sich das Schwarze Loch auflösen kann. ⓘ

Die Verdampfung Schwarzer Löcher hat mehrere wichtige Konsequenzen:

• Die Verdampfung Schwarzer Löcher führt zu einer konsistenteren Sichtweise der Thermodynamik Schwarzer Löcher, da sie zeigt, wie Schwarze Löcher thermisch mit dem Rest des Universums wechselwirken.
• Im Gegensatz zu den meisten Objekten nimmt die Temperatur eines Schwarzen Lochs zu, wenn es Masse abstrahlt. Die Geschwindigkeit des Temperaturanstiegs ist exponentiell, wobei der wahrscheinlichste Endpunkt die Auflösung des Schwarzen Lochs in einem heftigen Ausbruch von Gammastrahlen ist. Eine vollständige Beschreibung dieser Auflösung erfordert jedoch ein Modell der Quantengravitation, da sie eintritt, wenn sich die Masse des Schwarzen Lochs einer Planck-Masse nähert und sein Radius sich ebenfalls zwei Planck-Längen nähert.
• Die einfachsten Modelle der Verdampfung Schwarzer Löcher führen zu dem Informationsparadoxon der Schwarzen Löcher. Der Informationsgehalt eines Schwarzen Lochs scheint verloren zu gehen, wenn es sich auflöst, da die Hawking-Strahlung in diesen Modellen zufällig ist (sie hat keinen Bezug zur ursprünglichen Information). Es wurde eine Reihe von Lösungen für dieses Problem vorgeschlagen, darunter die, dass die Hawking-Strahlung so gestört wird, dass sie die fehlende Information enthält, dass die Hawking-Verdampfung eine Art Restteilchen hinterlässt, das die fehlende Information enthält, und dass die Information unter diesen Bedingungen verloren gehen kann. ⓘ

Probleme und Erweiterungen

Trans-Plancksches Problem

Das transplancksche Problem besteht darin, dass Hawkings ursprüngliche Berechnung Quantenteilchen einschließt, deren Wellenlänge in der Nähe des Horizonts des Schwarzen Lochs kürzer als die Planck-Länge wird. Dies ist auf das besondere Verhalten in diesem Bereich zurückzuführen, in dem die Zeit aus der Ferne gemessen stehen bleibt. Ein Teilchen, das von einem Schwarzen Loch mit einer endlichen Frequenz ausgesandt wird, muss, wenn es bis zum Horizont zurückverfolgt wird, eine unendliche Frequenz und damit eine transplancksche Wellenlänge haben. ⓘ

Der Unruh-Effekt und der Hawking-Effekt sprechen beide von Feldmoden in der oberflächlich stationären Raumzeit, die ihre Frequenz relativ zu anderen Koordinaten ändern, die über den Horizont hinweg regelmäßig sind. Dies ist zwangsläufig der Fall, denn um außerhalb eines Horizonts zu bleiben, ist eine Beschleunigung erforderlich, die die Moden ständig dopplerverschiebt. ⓘ

Ein ausgehendes Photon der Hawking-Strahlung hat, wenn der Modus in der Zeit zurückverfolgt wird, eine Frequenz, die von derjenigen, die es in großer Entfernung hat, abweicht, wenn es sich dem Horizont nähert, was erfordert, dass die Wellenlänge des Photons am Horizont des Schwarzen Lochs unendlich "knirscht". In einer maximal ausgedehnten externen Schwarzschild-Lösung bleibt die Frequenz des Photons nur dann regulär, wenn der Modus in die vergangene Region verlängert wird, in die sich kein Beobachter begeben kann. Diese Region scheint unbeobachtbar und physikalisch verdächtig zu sein, so dass Hawking eine Schwarzes-Loch-Lösung ohne eine Vergangenheitsregion verwendete, die sich zu einem endlichen Zeitpunkt in der Vergangenheit bildet. In diesem Fall kann die Quelle aller ausgehenden Photonen identifiziert werden: ein mikroskopischer Punkt genau in dem Moment, in dem sich das Schwarze Loch erstmals bildete. ⓘ

Die Quantenfluktuationen an diesem winzigen Punkt enthalten nach Hawkings ursprünglicher Berechnung die gesamte ausgehende Strahlung. Die Moden, die schließlich die ausgehende Strahlung enthalten, sind durch ihren langen Aufenthalt in der Nähe des Ereignishorizonts so stark rotverschoben, dass sie als Moden mit einer Wellenlänge beginnen, die viel kürzer als die Plancklänge ist. Da die physikalischen Gesetze bei so kurzen Entfernungen unbekannt sind, finden manche Hawkings ursprüngliche Berechnung nicht überzeugend. ⓘ

Das transplancksche Problem wird heute meist als mathematisches Artefakt der Horizontberechnungen angesehen. Derselbe Effekt tritt bei gewöhnlicher Materie auf, die auf ein Weißes Loch fällt. Materie, die auf das Weiße Loch fällt, sammelt sich dort an, hat aber keine zukünftige Region, in die sie gehen kann. Verfolgt man die Zukunft dieser Materie, so wird sie auf den letzten singulären Endpunkt der Entwicklung des Weißen Lochs komprimiert, in eine transplancksche Region. Der Grund für diese Art von Divergenzen ist, dass Moden, die aus Sicht der äußeren Koordinaten am Horizont enden, dort eine singuläre Frequenz haben. Der einzige Weg, um herauszufinden, was klassischerweise passiert, ist die Ausdehnung in andere Koordinaten, die den Horizont überschreiten. ⓘ

Es gibt alternative physikalische Bilder der Hawking-Strahlung, in denen das transplancksche Problem behandelt wird. Der springende Punkt ist, dass ähnliche transplancksche Probleme auftreten, wenn die mit der Unruh-Strahlung belegten Moden in der Zeit zurückverfolgt werden. Beim Unruh-Effekt kann die Größe der Temperatur aus der gewöhnlichen Minkowski-Feldtheorie berechnet werden und ist nicht umstritten. ⓘ

Große Extradimensionen

Die Formeln aus dem vorigen Abschnitt sind nur anwendbar, wenn die Gravitationsgesetze bis hinunter zur Planck-Skala annähernd gültig sind. Insbesondere für Schwarze Löcher mit Massen unterhalb der Planck-Masse (~10-8 kg) führen sie zu unmöglichen Lebensdauern unterhalb der Planck-Zeit (~10-43 s). Dies wird normalerweise als Hinweis darauf gewertet, dass die Planck-Masse die untere Grenze für die Masse eines Schwarzen Lochs darstellt. ⓘ

In einem Modell mit großen zusätzlichen Dimensionen (10 oder 11) können die Werte der Planck-Konstanten radikal anders sein, und die Formeln für die Hawking-Strahlung müssen ebenfalls geändert werden. Insbesondere wird die Lebensdauer eines mikroschwarzen Lochs mit einem Radius unterhalb der Skala der Extradimensionen durch Gleichung 9 in Cheung (2002) und die Gleichungen 25 und 26 in Carr (2005) angegeben. ⓘ

$\tau \sim {\frac {1}{M_{*}}}\left({\frac {M_{\mathrm {BH} }}{M_{*}}}\right)^{\frac {n+3}{n+1}}\,,$ ⓘ

wobei M_∗ die niedrige Energieskala ist, die bis zu einigen TeV reichen kann, und n die Anzahl der großen Extradimensionen ist. Diese Formel ist nun mit schwarzen Löchern vereinbar, die nur wenige TeV leicht sind und eine Lebensdauer in der Größenordnung der "neuen Planck-Zeit" ~10-26 s haben. ⓘ

Quantengravitation in Schleifen

Die Quantengeometrie des Ereignishorizonts eines Schwarzen Lochs wurde mit Hilfe der Schleifenquantengravitation eingehend untersucht. Die Schleifenquantisierung reproduziert nicht das ursprünglich von Bekenstein und Hawking entdeckte Ergebnis für die Entropie Schwarzer Löcher, es sei denn, der Wert eines freien Parameters wird so eingestellt, dass verschiedene Konstanten aufgehoben werden, so dass die Bekenstein-Hawking-Entropieformel reproduziert wird. Auf der Grundlage der Theorie wurden jedoch Quantengravitationskorrekturen für die Entropie und die Strahlung von Schwarzen Löchern errechnet. ⓘ

Basierend auf den Fluktuationen der Horizontfläche weist ein Quantenschwarzes Loch Abweichungen vom Hawking-Spektrum auf, die beobachtbar wären, wenn man die Röntgenstrahlung der Hawking-Strahlung von verdampfenden primordialen Schwarzen Löchern beobachten würde. Die Quanteneffekte konzentrieren sich auf eine Reihe von diskreten und unvermischten Frequenzen, die über dem Spektrum der Hawking-Strahlung liegen und stark ausgeprägt sind. ⓘ

Experimentelle Beobachtung

Astronomische Suche

Im Juni 2008 startete die NASA das Fermi-Weltraumteleskop, das nach den endlichen Gammastrahlenblitzen sucht, die von verdampfenden primordialen Schwarzen Löchern erwartet werden. ⓘ

Physik mit Schwerionenbeschleunigern

Wenn die spekulativen Theorien über große Extradimensionen richtig sind, dann könnte der Large Hadron Collider des CERN in der Lage sein, Mikro-Schwarze Löcher zu erzeugen und deren Verdampfung zu beobachten. Am CERN wurde noch kein solches Mikro-Schwarzes Loch beobachtet. ⓘ

Experimentelles

Unter experimentell erreichbaren Bedingungen für Gravitationssysteme ist dieser Effekt zu klein, um direkt beobachtet zu werden. Es wurde vorhergesagt, dass die Hawking-Strahlung in Analogie zu schwarzen Löchern mit Schall untersucht werden könnte, bei denen Schallstörungen analog zum Licht in einem gravitativen schwarzen Loch und die Strömung einer annähernd perfekten Flüssigkeit analog zur Gravitation sind (siehe Analoge Modelle der Gravitation). Es wurden Beobachtungen von Hawking-Strahlung in sonischen Schwarzen Löchern mit Bose-Einstein-Kondensaten gemeldet. ⓘ

Im September 2010 wurde in einem Versuchsaufbau ein Labor-Ereignishorizont eines Weißen Lochs" erzeugt, von dem die Experimentatoren behaupteten, dass er ein optisches Analogon zur Hawking-Strahlung ausstrahlt. Die Ergebnisse bleiben jedoch unbestätigt und umstritten, und ihr Status als echte Bestätigung bleibt zweifelhaft. ⓘ

Erläuterungen zu Hawkings Originalarbeit

Erläuterungen

Hawking arbeitet in einer semiklassischen Näherung, d. h., er betrachtet eine freie Quantenfeldtheorie auf einer klassischen, schwach gekrümmten Raumzeit. Relevant ist im Wesentlichen die globale Struktur der Raumzeit sowie insbesondere die Existenz eines Ereignishorizontes. ⓘ

Hawking setzt einen sphärisch-symmetrischen Kollaps einer Masse $M$ voraus, d. h., er geht nicht von einer rein statischen Schwarzschild-Metrik aus. Letztere gilt jedoch aufgrund des Birkhoff-Theorem im Außenraum des Kollaps exakt. Die Details der Innenraumlösung sind für die Argumentation irrelevant. ⓘ

Hawking beginnt mit der kanonischen Quantisierung freier Felder auf Basis einer verallgemeinerten Fourierentwicklung. Diese Fouriermoden sind dabei speziell Lösungen der Klein-Gordon-Gleichung für masselose Skalarfelder auf der Raumzeit-Geometrie. Die dabei notwendige Zerlegung der Fouriermoden nach positiven und negativen Frequenzen sowie die daraus folgende Klassifizierung von Teilchen und Antiteilchen ist aufgrund der Raumzeitgeometrie nicht eindeutig. Im Zuge der Quantisierung kann ein Beobachter mathematisch jeweils für ihn gültige Erzeugungs- und Vernichtungsoperatoren sowie einen für ihn gültigen Vakuumzustand (Fock-Zustand) definieren, in dem entsprechend seiner Klassifizierung keine Teilchen und Antiteilchen existieren. Während diese Beobachterabhängigkeit in der Minkowski-Raumzeit für die Erzeugungs- und Vernichtungsoperatoren sowie für den Vakuumzustand letztlich irrelevant ist, führt sie bei Anwesenheit eines Ereignishorizontes zu inäquivalenten Vakuumzuständen. ⓘ

Mathematisch existiert eine Transformation, die sogenannte Bogoljubov-Transformation, die die Erzeugungs- und Vernichtungsoperatoren beider Beobachter ineinander überführt. Hawking fixiert zunächst einen Vakuumzustand sowie die Erzeugungs- und Vernichtungsoperatoren für die ferne Vergangenheit. In diesem Zustand verschwindet der Erwartungswert des Teilchenzahloperators (definiert für die ferne Vergangenheit). Anschließend bestimmt er die Bogoljubov-Transformation für die Erzeugungs- und Vernichtungsoperatoren für die ferne Zukunft. Dazu wird im Wesentlichen die Streuung der Fouriermoden am kollabierenden Schwarzen Loch berechnet. Der für die Hawking-Strahlung relevante Anteil stammt dabei aus der Streuung der Moden innerhalb des kollabierenden Körpers. Damit kann nun der Erwartungswert des Teilchenzahloperators (definiert für die ferne Zukunft) im ursprünglichen Vakuumzustand (definiert für die ferne Vergangenheit) berechnet werden. Es zeigt sich, dass dieser Erwartungswert nicht verschwindet! Der Beobachter in der fernen Zukunft sieht demnach nicht den für ihn gültigen Vakuumzustand, sondern einen Zustand, in dem tatsächlich Teilchen und Antiteilchen (bzgl. seiner Definition) enthalten sind. Die thermische Natur des Spektrums folgt aus der genauen Form der Bogoljubov-Transformation. ⓘ

Der physikalische Kern von Hawkings Argumentation lautet demnach wie folgt: Der Kollaps sowie die Anwesenheit eines Horizontes führt zu inäquivalenten Vakuumzuständen. Während in einer flachen Raumzeit die Zeitentwicklung das Vakuum invariant lässt, ist dieses in einer Raumzeit mit Schwarzem Loch einem „Streuprozess“ unterworfen, der das initiale Vakuum in einen thermischen Zustand überführt. ⓘ

Details

Hawking betrachtet die freie Klein-Gordon-Gleichung ⓘ

$-g^{ab}\nabla _{a}\nabla _{b}\phi =0$ ⓘ

eines masselosen Skalarfeldes. ⓘ

Er führt nun die beiden Hyperflächen ${\mathcal {I}}^{-}$ und ${\mathcal {I}}^{+}$ ein, welche den Außenraum des Schwarzen Loches in der fernen, asymptotischen Vergangenheit (-) und der fernen Zukunft (+) darstellen. Auf diesen Hyperflächen gibt es vollständige Funktionensysteme $f_{i}$ und $p_{i}$, mittels derer der Feldoperator $\phi$ als Fouriersumme von Erzeugern und Vernichtern dargestellt werden kann:

$\phi =\sum _{i}[f_{i}a_{i}+{\bar {f}}_{i}a_{i}^{\dagger }]$ ⓘ

$\phi =\sum _{i}[p_{i}b_{i}+{\bar {p}}_{i}b_{i}^{\dagger }]+\ldots$ ⓘ

“…” steht dabei für ein weiteres Funktionensystem auf der lichtartigen Hyperfläche des Ereignishorizontes. Das ist zwar prinzipiell notwendig, um ein eindeutig lösbares Anfangswertproblem zu erhalten, aber für die weitere Rechnung nicht weiter wichtig. ⓘ

Hawking definiert dann den Vakuumzustand ⓘ

$a_{i}|0_{-}\rangle =0$ ⓘ

bezüglich der von ${\mathcal {I}}^{-}$ einlaufenden Teilchen. ⓘ

Der allgemeine Zusammenhang zwischen den beiden Familien von Erzeugern und Vernichtern besteht nun in der Bogoljubov-Transformation ⓘ

$p_{i}=\sum _{j}\left[\alpha _{ij}f_{j}+\beta _{ij}{\bar {f}}_{j}\right]$ ⓘ

$b_{i}=\sum _{j}\left[{\bar {\alpha }}_{ij}a_{j}-{\bar {\beta }}_{ij}a_{j}^{\dagger }\right]$ ⓘ

Hawking zeigt im Folgenden, dass die Streuung der aus ${\mathcal {I}}^{-}$ einlaufenden Moden am Schwarzen Loch dazu führt, dass ein Beobachter auf ${\mathcal {I}}^{+}$ dem Zustand $|0_{-}\rangle$ einen nicht-verschwindenden Teilcheninhalt ⓘ

$\langle 0_{-}|b_{i}^{\dagger }b_{i}|0_{-}\rangle =\sum _{ij}|\beta _{ij}|^{2}>0$ ⓘ

zuschreibt. Die Erzeugungsrate der Teilchen folgt dabei direkt aus den Koeffizienten $\beta _{ij}$ der Bogoljubov-Transformation. Diese mischen den Vernichtern auf ${\mathcal {I}}^{-}$ einen Anteil von Erzeugern auf ${\mathcal {I}}^{+}$ bei. ⓘ

Die Streuung der Moden erfolgt dabei sowohl an der äußeren Schwarzschildgeometrie als auch an der Geometrie des Innenraums des kollabierenden Sterns. Letztere ergibt einen nicht-trivialen Beitrag zu den $p_{i}$-Moden, die dann die spezielle Form der Bogoljubov-Koeffizienten bewirken. ⓘ

Der Beitrag einer Mode mit Radialfrequenz $\omega$ ist dabei ⓘ

$p_{i}\sim {\frac {1}{e^{2\pi \omega /\kappa }-1}}$ ⓘ

mit $\kappa =1/4M$. D. h., es liegt thermische Strahlung mit Temperatur $T_{H}=1/8\pi M$ (in natürlichen Einheiten) entsprechend der Bose-Einstein-Statistik vor. ⓘ

Hawking erläutert grob, dass für Fermionen ein Verlauf ⓘ

$p_{i}\sim {\frac {1}{e^{2\pi \omega /\kappa }+1}}$ ⓘ

entsprechend der Fermi-Dirac-Statistik zu erwarten ist. ⓘ

Der Beitrag massebehafteter Teilchen ist exponentiell unterdrückt, da in diesem Fall in der Frequenz bzw. der die Masse entsprechend $\omega ^{2}\sim E^{2}=m^{2}+p^{2}$ zu berücksichtigen ist. ⓘ