Drehimpuls

Drehimpuls ⓘ
Dieser Kreisel bleibt aufrecht stehen, während er sich dreht, da sein Drehimpuls erhalten bleibt.
Gebräuchliche Symbole	L
In SI-Basiseinheiten	kg m2 s-1
Erhalten?	ja
Ableitungen von anderen Größen	L = Iω = r × p
Dimension	M L2T-1

In der Physik ist der Drehimpuls (seltener auch Drehimpuls oder Rotationsimpuls) das rotatorische Analogon des linearen Impulses. Er ist eine wichtige Größe in der Physik, weil er eine konservierte Größe ist - der Gesamtdrehimpuls eines geschlossenen Systems bleibt konstant. Der Drehimpuls hat sowohl eine Richtung als auch einen Betrag, und beide bleiben erhalten. Fahrräder und Motorräder, Frisbees, Gewehrkugeln und Gyroskope verdanken ihre nützlichen Eigenschaften der Erhaltung des Drehimpulses. Die Erhaltung des Drehimpulses ist auch der Grund dafür, dass Wirbelstürme Spiralen bilden und Neutronensterne hohe Rotationsgeschwindigkeiten aufweisen. Im Allgemeinen schränkt die Drehimpulserhaltung die mögliche Bewegung eines Systems ein, legt sie aber nicht eindeutig fest. ⓘ

Der dreidimensionale Drehimpuls eines Punktteilchens wird klassischerweise als Pseudovektor r × p dargestellt, dem Kreuzprodukt aus dem Ortsvektor r des Teilchens (relativ zu einem Ursprung) und seinem Impulsvektor; letzterer ist p = mv in der Newtonschen Mechanik. Im Gegensatz zum Impuls hängt der Drehimpuls davon ab, wo dieser Ursprung gewählt wird, da die Position des Teilchens von dort aus gemessen wird. ⓘ

Der Drehimpuls ist eine extensive Größe, d. h. der Gesamtdrehimpuls eines beliebigen zusammengesetzten Systems ist die Summe der Drehimpulse seiner Bestandteile. Für einen kontinuierlichen starren Körper oder eine Flüssigkeit ist der Gesamtdrehimpuls das Volumenintegral der Drehimpulsdichte (Drehimpuls pro Volumeneinheit im Grenzfall, wenn das Volumen auf Null schrumpft) über den gesamten Körper. ⓘ

Ähnlich wie bei der Erhaltung des linearen Impulses, der erhalten bleibt, wenn keine äußere Kraft wirkt, bleibt der Drehimpuls erhalten, wenn kein äußeres Drehmoment auftritt. Das Drehmoment kann als die Änderungsrate des Drehimpulses definiert werden, analog zur Kraft. Das externe Nettodrehmoment eines Systems ist immer gleich dem Gesamtdrehmoment des Systems; mit anderen Worten, die Summe aller internen Drehmomente eines Systems ist immer gleich 0 (dies ist das Analogon des dritten Newtonschen Bewegungsgesetzes). Für ein geschlossenes System (in dem es kein externes Nettodrehmoment gibt) muss daher das Gesamtdrehmoment des Systems 0 sein, was bedeutet, dass der Gesamtdrehimpuls des Systems konstant ist. Die Änderung des Drehimpulses bei einer bestimmten Wechselwirkung wird manchmal als Drall bezeichnet, was aber eher unüblich ist. Der Drall ist das winkelmäßige Analogon des Impulses. ⓘ

Demonstrationsexperiment zur Drehimpulserhaltung (Video, 18 s). Indem die Person ein Drehmoment aufbringt, ändert der Drehimpuls des Rades seine Richtung in die Senkrechte (roter Pfeil). Nach dem Prinzip Actio gleich Reactio bekommt der Drehstuhl durch das Reaktionsmoment einen entgegengesetzten Drehimpuls (gelber Pfeil). Der vertikale Drehimpuls von null bleibt dabei erhalten. ⓘ

Der Drehimpuls (in der Mechanik auch Drall oder veraltet Schwung oder Impulsmoment, in der Quantenmechanik in manchen Fällen auch Spin) ist eine physikalische Erhaltungsgröße. Ein System hat beispielsweise dann einen Drehimpuls, wenn es sich um seinen Massenschwerpunkt dreht, wie bspw. ein Kreisel, ein Sportler bei einer Pirouette oder ein Planetensystem. ⓘ

Der Drehimpuls ist eine vektorielle Größe, und zwar – wie das Drehmoment und die Winkelgeschwindigkeit – ein Pseudovektor. Seine Dimension ist das Produkt aus Masse, Länge und Geschwindigkeit. Im SI-Einheitensystem wird er in Newtonmetersekunden ($\mathrm {N\,m\,s}$) gemessen. Sein Formelzeichen ist ${\vec {L}}$ oder ${\vec {J}}$. ⓘ

Der Drehimpuls bezieht sich immer auf den Punkt im Raum, der als Bezugspunkt der Drehbewegung gewählt wird. Bei einem frei rotierenden System wird als Bezugspunkt oft der Schwerpunkt festgelegt, in der Astronomie meist der Schwerpunkt des Zentralgestirns. Wenn die Rotation durch ein Lager vorgegeben ist, wird meist ein Punkt auf der Achse gewählt. ⓘ

Der Drehimpuls lässt sich allgemein als Vektorprodukt aus dem Ortsvektor ${\vec {r}}$ und dem Impuls ${\vec {p}}$ des Körpers berechnen:

${\vec {L}}={\vec {r}}\times {\vec {p}},$

oder mit Hilfe des Trägheitstensors $\mathbf {\Theta }$ und der Winkelgeschwindigkeit $\omega$ zu:

${\vec {L}}=\mathbf {\Theta } \cdot {\vec {\omega }}.$ ⓘ

In der Quantenmechanik wird der Drehimpuls durch den Drehimpulsoperator beschrieben. Dabei zeigt sich, dass er eine quantisierte Größe ist. Der Betrag des Drehimpulses ist stets ein ganz- oder halbzahliges Vielfaches des reduzierten Planckschen Wirkungsquantums. Die Ausrichtung des Drehimpulses ist ebenfalls gequantelt. Sie unterliegt der Richtungsquantelung in Bezug auf die Quantisierungsachse. Die Rolle des Eigendrehimpulses wird vom Spin wahrgenommen, der nicht mit einer räumlichen Bewegung verbunden ist. Somit setzt sich der Drehimpulsoperator aus den Komponenten Bahndrehimpulsoperator ${\hat {\mathbf {L} }}={\hat {\mathbf {r} }}\times {\hat {\mathbf {p} }}$ und Spinoperator zusammen. ⓘ

Leonhard Euler führte 1775 den Drallsatz als ein fundamentales von den Newton’schen Gesetzen unabhängiges Prinzip in der Mechanik ein. Er besagt, dass ein Drehmoment auf das System einwirken muss, um den Drehimpuls zu ändern. Die Drehimpulserhaltung lässt sich im Alltag an vielen Stellen erfahren (siehe Video, oder Pirouetteneffekt). ⓘ

Definition in der klassischen Mechanik

Ebenso wie bei der Winkelgeschwindigkeit gibt es zwei spezielle Arten von Drehimpulsen eines Objekts: Der Drehimpuls ist der Drehimpuls um den Massenschwerpunkt des Objekts, während der Bahndrehimpuls der Drehimpuls um einen gewählten Drehpunkt ist. Die Erde hat einen Bahndrehimpuls, weil sie sich um die Sonne dreht, und einen Dralldrehimpuls, weil sie sich täglich um die Polachse dreht. Der Gesamtdrehimpuls ist die Summe aus Drehimpuls und Bahndrehimpuls. Im Fall der Erde ist die primär erhaltene Größe der Gesamtdrehimpuls des Sonnensystems, da der Drehimpuls in geringem, aber bedeutendem Umfang zwischen den Planeten und der Sonne ausgetauscht wird. Der Bahndrehimpulsvektor eines Punktteilchens ist immer parallel und direkt proportional zu seinem Bahndrehgeschwindigkeitsvektor ω, wobei die Proportionalitätskonstante sowohl von der Masse des Teilchens als auch von seinem Abstand vom Ursprung abhängt. Der Drehimpulsvektor eines starren Körpers ist proportional, aber nicht immer parallel zum Drehgeschwindigkeitsvektor Ω, so dass die Proportionalitätskonstante eher ein Tensor zweiten Ranges als ein Skalar ist. ⓘ

Bahndrehimpuls in zwei Dimensionen

Die Geschwindigkeit des Teilchens m in Bezug auf den Ursprung O lässt sich in Komponenten auflösen, die parallel (v_∥) und senkrecht (v_⊥) zum Radiusvektor r verlaufen. Der Drehimpuls von m ist proportional zur senkrechten Komponente v_⊥ der Geschwindigkeit oder, anders ausgedrückt, zum senkrechten Abstand r_⊥ vom Ursprung. ⓘ

Der Drehimpuls ist eine Vektorgröße (genauer gesagt, ein Pseudovektor), die das Produkt aus der Rotationsträgheit eines Körpers und der Rotationsgeschwindigkeit (in Radiant/Sekunde) um eine bestimmte Achse darstellt. Liegt die Flugbahn des Teilchens jedoch in einer einzigen Ebene, reicht es aus, den Drehimpuls nicht als Vektor, sondern als Skalar (genauer gesagt als Pseudoskalar) zu betrachten. Der Drehimpuls kann als Rotationsanalogon des linearen Impulses betrachtet werden. Wenn also der lineare Impuls p proportional zur Masse m und zur linearen Geschwindigkeit v ist

$p=mv,$ ⓘ

ist der Drehimpuls L proportional zum Trägheitsmoment I und der in Radiant pro Sekunde gemessenen Winkelgeschwindigkeit ω.

$L=I\omega .$ ⓘ

Im Gegensatz zur Masse, die nur von der Menge der Materie abhängt, ist das Trägheitsmoment auch von der Lage der Drehachse und der Form der Materie abhängig. Im Gegensatz zur linearen Geschwindigkeit, die nicht von der Wahl des Ursprungs abhängt, wird die Winkelgeschwindigkeit auf einer Umlaufbahn immer in Bezug auf einen festen Ursprung gemessen. Daher sollte L streng genommen als der Drehimpuls relativ zu diesem Zentrum bezeichnet werden. ⓘ

Da $I=r^{2}m$ für ein einzelnes Teilchen und $\omega ={\frac {v}{r}}$ für eine Kreisbewegung kann der Drehimpuls erweitert werden, $L=r^{2}m\cdot {\frac {v}{r}},$ und reduziert werden auf,

$L=rmv,$ ⓘ

das Produkt aus dem Rotationsradius r und dem linearen Impuls des Teilchens $p=mv$, wobei $v$ in diesem Fall die äquivalente lineare (tangentiale) Geschwindigkeit am Radius ist ($=r\omega$). ⓘ

Diese einfache Analyse lässt sich auch auf nicht kreisförmige Bewegungen anwenden, wenn nur die Komponente der Bewegung betrachtet wird, die senkrecht zum Radiusvektor steht. In diesem Fall,

$L=rmv_{\perp },$ ⓘ

wobei $v_{\perp }=v\sin(\theta )$ die senkrechte Komponente der Bewegung ist. Erweitern, $L=rmv\sin(\theta ),$ Umordnen, $L=r\sin(\theta )mv,$ und Reduktion kann auch der Drehimpuls ausgedrückt werden,

$L=r_{\perp }mv,$ ⓘ

wobei $r_{\perp }=r\sin(\theta )$ ist die Länge des Impulsarms, einer Linie, die senkrecht vom Ursprung auf die Bahn des Teilchens fällt. Auf diese Definition (Länge des Impulsarms)×(linearer Impuls) bezieht sich der Begriff Impulsmoment. ⓘ

Skalar-Drehimpuls aus der Lagrangeschen Mechanik

Ein anderer Ansatz besteht darin, den Drehimpuls als den konjugierten Impuls (auch kanonischer Impuls genannt) der Drehkoordinate $\phi$ ausgedrückt in der Lagrange des mechanischen Systems. Betrachten wir ein mechanisches System mit einer Masse $m$ das sich zwangsweise auf einem Kreis mit dem Radius $a$ zu bewegen, ohne dass ein äußeres Kraftfeld vorhanden ist. Die kinetische Energie des Systems ist

$T={\frac {1}{2}}ma^{2}\omega ^{2}={\frac {1}{2}}ma^{2}{\dot {\phi }}^{2}.$ ⓘ

und die potentielle Energie ist

$U=0.$ ⓘ

Dann lautet die Lagrange

${\mathcal {L}}\left(\phi ,{\dot {\phi }}\right)=T-U={\frac {1}{2}}ma^{2}{\dot {\phi }}^{2}.$ ⓘ

Der verallgemeinerte Impuls "kanonisch konjugiert zu" der Koordinate $\phi$ ist definiert durch

$p_{\phi }={\frac {\partial {\mathcal {L}}}{\partial {\dot {\phi }}}}=ma^{2}{\dot {\phi }}=I\omega =L.$ ⓘ

Bahndrehimpuls in drei Dimensionen

Beziehung zwischen Kraft- (F), Drehmoment- (τ), Impuls- (p) und Drehimpuls- (L) Vektoren in einem rotierenden System. r ist der Positionsvektor. ⓘ

Um den Bahndrehimpuls in drei Dimensionen vollständig zu definieren, muss man die Geschwindigkeit kennen, mit der der Positionsvektor den Winkel überstreicht, die Richtung, die senkrecht zur momentanen Ebene der Winkelverschiebung steht, sowie die beteiligte Masse und die Verteilung dieser Masse im Raum. Durch die Beibehaltung des Vektorcharakters des Drehimpulses bleibt auch der allgemeine Charakter der Gleichungen erhalten, die jede Art von dreidimensionaler Bewegung um den Drehpunkt - kreisförmig, linear oder anders - beschreiben können. In Vektorschreibweise kann der Bahndrehimpuls eines Punktteilchens, das sich um den Ursprung bewegt, wie folgt ausgedrückt werden:

$\mathbf {L} =I{\boldsymbol {\omega }},$ ⓘ

wobei

• $I=r^{2}m$ ist das Trägheitsmoment für eine Punktmasse,
• ${\boldsymbol {\omega }}={\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}$ ist die Bahnwinkelgeschwindigkeit des Teilchens um den Ursprung in Radiant/Sekunde (Einheit 1/Sekunde),
• $\mathbf {r}$ ist der Positionsvektor des Teilchens relativ zum Ursprung, $r=\left\vert \mathbf {r} \right\vert$,
• $\mathbf {v}$ ist die lineare Geschwindigkeit des Teilchens relativ zum Ursprung und
• $m$ ist die Masse des Teilchens. ⓘ

Dies kann erweitert, reduziert und nach den Regeln der Vektoralgebra umgeordnet werden:

${\begin{aligned}\mathbf {L} &=\left(r^{2}m\right)\left({\frac {\mathbf {r} \times \mathbf {v} }{r^{2}}}\right)\\&=m\left(\mathbf {r} \times \mathbf {v} \right)\\&=\mathbf {r} \times m\mathbf {v} \\&=\mathbf {r} \times \mathbf {p} ,\end{aligned}}$ ⓘ

das ist das Kreuzprodukt aus dem Ortsvektor $\mathbf {r}$ und des linearen Impulses $\mathbf {p} =m\mathbf {v}$ des Teilchens. Nach der Definition des Kreuzprodukts steht der $\mathbf {L}$ Vektor sowohl senkrecht zu $\mathbf {r}$ und $\mathbf {p}$. Er ist senkrecht zur Ebene der Winkelverschiebung gerichtet, wie die Rechtsregel besagt, so dass die Winkelgeschwindigkeit gegen den Uhrzeigersinn vom Kopf des Vektors aus gesehen wird. Umgekehrt definiert der $\mathbf {L}$ Vektor die Ebene, in der $\mathbf {r}$ und $\mathbf {p}$ liegen. ⓘ

Durch die Definition eines Einheitsvektors $\mathbf {\hat {u}}$ senkrecht zur Ebene der Winkelverschiebung, ergibt sich eine skalare Winkelgeschwindigkeit $\omega$ resultiert, wobei

$\omega \mathbf {\hat {u}} ={\boldsymbol {\omega }},$ und

$\omega ={\frac {v_{\perp }}{r}},$ wobei $v_{\perp }$ die senkrechte Komponente der Bewegung ist, wie oben beschrieben. ⓘ

Die zweidimensionalen skalaren Gleichungen des vorigen Abschnitts können somit eine Richtung erhalten:

${\begin{aligned}\mathbf {L} &=I{\boldsymbol {\omega }}\\&=I\omega \mathbf {\hat {u}} \\&=\left(r^{2}m\right)\omega \mathbf {\hat {u}} \\&=rmv_{\perp }\mathbf {\hat {u}} \\&=r_{\perp }mv\mathbf {\hat {u}} ,\end{aligned}}$

und $\mathbf {L} =rmv\mathbf {\hat {u}}$ für eine Kreisbewegung, bei der die gesamte Bewegung senkrecht zum Radius verläuft $r$. ⓘ

Im sphärischen Koordinatensystem wird der Drehimpulsvektor wie folgt ausgedrückt

$\mathbf {L} =m\mathbf {r} \times \mathbf {v} =mr^{2}\left({\dot {\theta }}\,{\hat {\boldsymbol {\varphi }}}-{\dot {\varphi }}\sin \theta \,\mathbf {\hat {\boldsymbol {\theta }}} \right).$ ⓘ

Drehimpuls in einer beliebigen Anzahl von Dimensionen

Die Definition des Drehimpulses mit Hilfe des Kreuzprodukts gilt nur für drei Dimensionen. Die Definition als Bivektor L = r ∧ p, wobei ∧ das äußere Produkt ist, ist in beliebig vielen Dimensionen gültig. ⓘ

Analogie zum linearen Impuls

Der Drehimpuls kann als das rotatorische Analogon des linearen Impulses beschrieben werden. Wie der lineare Impuls beinhaltet er Elemente der Masse und der Verschiebung. Im Gegensatz zum linearen Impuls umfasst er auch Elemente der Position und der Form. ⓘ

Bei vielen Problemen in der Physik geht es um Materie, die sich um einen bestimmten Punkt im Raum bewegt, sei es in tatsächlicher Rotation um diesen Punkt oder einfach in der Vorbeibewegung, wobei man wissen möchte, welche Wirkung die sich bewegende Materie auf den Punkt hat - kann sie Energie auf ihn ausüben oder Arbeit an ihm verrichten? Energie, d. h. die Fähigkeit, Arbeit zu verrichten, kann in Materie gespeichert werden, indem sie in Bewegung versetzt wird - eine Kombination aus Trägheit und Verschiebung. Die Trägheit wird durch die Masse und die Verschiebung durch die Geschwindigkeit gemessen. Ihr Produkt, ⓘ

${\begin{aligned}({\text{amount of inertia}})\times ({\text{amount of displacement}})&={\text{amount of (inertia⋅displacement)}}\\{\text{mass}}\times {\text{velocity}}&={\text{momentum}}\\m\times v&=p\\\end{aligned}}$ ⓘ

ist der Impuls der Materie. Bezieht man diesen Impuls auf einen zentralen Punkt, ergibt sich eine Komplikation: Der Impuls wird nicht direkt auf den Punkt angewendet. So befindet sich beispielsweise ein Materieteilchen am äußeren Rand eines Rades am Ende eines Hebels, der genauso lang ist wie der Radius des Rades, und sein Impuls dreht den Hebel um den Mittelpunkt. Dieser imaginäre Hebel wird als Momentarm bezeichnet. Er bewirkt eine Vervielfachung der Kraft des Impulses im Verhältnis zu seiner Länge, was als Moment bezeichnet wird. Der Impuls des Teilchens bezieht sich also auf einen bestimmten Punkt, ⓘ

${\begin{aligned}({\text{moment arm}})\times ({\text{amount of inertia}})\times ({\text{amount of displacement}})&={\text{moment of (inertia⋅displacement)}}\\{\text{length}}\times {\text{mass}}\times {\text{velocity}}&={\text{moment of momentum}}\\r\times m\times v&=L\\\end{aligned}}$ ⓘ

der Drehimpuls, manchmal auch, wie hier, das Drehmoment des Teilchens gegenüber diesem bestimmten Mittelpunkt genannt. Die Gleichung $L=rmv$ kombiniert ein Moment (eine Masse $m$ Drehimpulsarm $r$) mit einer linearen (geradlinig äquivalenten) Geschwindigkeit $v$. Die lineare Geschwindigkeit bezogen auf den Mittelpunkt ist einfach das Produkt aus dem Abstand $r$ und der Winkelgeschwindigkeit $\omega$ gegenüber dem Punkt: $v=r\omega ,$ ein weiteres Moment. Der Drehimpuls enthält also ein doppeltes Moment: $L=rmr\omega .$ Leicht vereinfachend, $L=r^{2}m\omega ,$ die Größe $r^{2}m$ ist das Trägheitsmoment des Teilchens, das manchmal auch als zweites Moment der Masse bezeichnet wird. Es ist ein Maß für die Rotationsträgheit. ⓘ

Das Trägheitsmoment (hier dargestellt) und damit der Drehimpuls ist für jede mögliche Konfiguration von Masse und Drehachse unterschiedlich. ⓘ

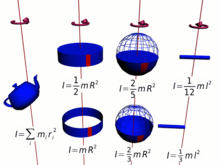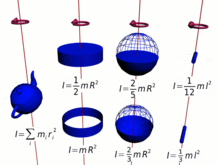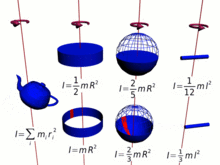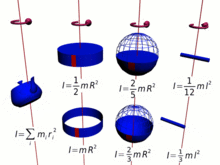
Da das Trägheitsmoment ein entscheidender Teil des Drehimpulses ist, beinhaltet dieser notwendigerweise alle Komplikationen des ersten, der durch Multiplikation der elementaren Bits der Masse mit den Quadraten ihrer Abstände vom Rotationszentrum berechnet wird. Das gesamte Trägheitsmoment und der Drehimpuls sind daher eine komplexe Funktion der Konfiguration der Materie um das Rotationszentrum und der Ausrichtung der Rotation für die verschiedenen Teile. ⓘ

Bei einem starren Körper, z. B. einem Rad oder einem Asteroiden, ist die Ausrichtung der Rotation einfach die Position der Rotationsachse gegenüber der Masse des Körpers. Sie kann durch den Massenschwerpunkt verlaufen oder nicht, oder sie kann vollständig außerhalb des Körpers liegen. Für ein und denselben Körper kann der Drehimpuls für jede mögliche Achse, um die eine Drehung stattfinden kann, einen anderen Wert annehmen. Er erreicht ein Minimum, wenn die Achse durch den Massenschwerpunkt verläuft. ⓘ

Bei einer Ansammlung von Objekten, die sich um ein Zentrum drehen, z. B. bei allen Körpern des Sonnensystems, können die Ausrichtungen einigermaßen geordnet sein, so wie es beim Sonnensystem der Fall ist, wobei die meisten Achsen der Körper in der Nähe der Achse des Systems liegen. Ihre Ausrichtung kann aber auch völlig zufällig sein. ⓘ

Je größer die Masse und je weiter sie vom Rotationszentrum entfernt ist (je länger der Hebelarm), desto größer ist das Trägheitsmoment und damit der Drehimpuls bei einer bestimmten Winkelgeschwindigkeit. In vielen Fällen kann das Trägheitsmoment und damit der Drehimpuls vereinfacht werden durch,

$I=k^{2}m,$

wobei $k$ ist der Trägheitsradius, also der Abstand von der Achse, in dem die gesamte Masse $m$ kann als konzentriert betrachtet werden.

In ähnlicher Weise gilt für eine Punktmasse $m$ ist das Trägheitsmoment definiert als,

$I=r^{2}m$

wobei $r$ der Radius der Punktmasse vom Rotationszentrum,

und für eine beliebige Ansammlung von Teilchen $m_{i}$ als die Summe,

$\sum _{i}I_{i}=\sum _{i}r_{i}^{2}m_{i}$ ⓘ

Die Abhängigkeit des Drehimpulses von Position und Form spiegelt sich in seinen Einheiten gegenüber dem linearen Impuls wider: kg⋅m²/s, N⋅m⋅s oder J⋅s für den Drehimpuls gegenüber kg⋅m/s oder N⋅s für den linearen Impuls. Bei der Berechnung des Drehimpulses als Produkt des Trägheitsmoments mal der Winkelgeschwindigkeit muss die Winkelgeschwindigkeit in Bogenmaß pro Sekunde ausgedrückt werden, wobei das Bogenmaß den dimensionslosen Wert 1 annimmt. (Bei der Dimensionsanalyse kann es sinnvoll sein, die Orientierungsanalyse zu verwenden, bei der das Bogenmaß als Basiseinheit verwendet wird, was jedoch nicht in den Anwendungsbereich des internationalen Einheitensystems fällt). Die Einheiten des Drehimpulses können als Drehmoment⋅Zeit oder als Energie⋅Zeit pro Winkel interpretiert werden. Ein Objekt mit einem Drehimpuls von L N⋅m⋅s kann durch einen Drehimpuls von L N⋅m⋅s auf Nullrotation gebracht werden (die gesamte Rotationsenergie kann aus ihm herausgeholt werden), oder gleichwertig durch ein Drehmoment oder eine Arbeit von L N⋅m für eine Sekunde oder eine Energie von L J für eine Sekunde. ⓘ

Die Ebene, die senkrecht zur Drehimpulsachse durch den Massenschwerpunkt verläuft, wird manchmal als unveränderliche Ebene bezeichnet, weil die Richtung der Achse fest bleibt, wenn nur die Wechselwirkungen der Körper innerhalb des Systems, frei von äußeren Einflüssen, betrachtet werden. Eine solche Ebene ist die unveränderliche Ebene des Sonnensystems. ⓘ

Drehimpuls und Drehmoment

Das zweite Newtonsche Bewegungsgesetz lässt sich mathematisch ausdrücken,

$\mathbf {F} =m\mathbf {a} ,$

oder Kraft = Masse × Beschleunigung. Das Rotationsäquivalent für Punktteilchen lässt sich wie folgt herleiten:

$\mathbf {L} =I{\boldsymbol {\omega }}$

Das bedeutet, dass das Drehmoment (d. h. die zeitliche Ableitung des Drehimpulses) gleich

${\boldsymbol {\tau }}={\frac {dI}{dt}}{\boldsymbol {\omega }}+I{\frac {d{\boldsymbol {\omega }}}{dt}}.$ ⓘ

Da das Trägheitsmoment gleich $mr^{2}$ist, folgt daraus, dass ${\frac {dI}{dt}}=2mr{\frac {dr}{dt}}=2rp_{||}$, und ${\frac {d\mathbf {L} }{dt}}=I{\frac {d{\boldsymbol {\omega }}}{dt}}+2rp_{||}{\boldsymbol {\omega }},$ was sich reduziert auf ⓘ

${\boldsymbol {\tau }}=I{\boldsymbol {\alpha }}+2rp_{||}{\boldsymbol {\omega }}.$

Dies ist das rotatorische Analogon des zweiten Newtonschen Gesetzes. Beachten Sie, dass das Drehmoment nicht unbedingt proportional oder parallel zur Winkelbeschleunigung ist (wie man erwarten könnte). Der Grund dafür ist, dass sich das Trägheitsmoment eines Teilchens mit der Zeit ändern kann, was bei einer gewöhnlichen Masse nicht der Fall ist. ⓘ

Erhaltung des Drehimpulses

Der Drehimpuls eines Körpers ist die Summe der Drehimpulse seiner Komponenten:

${\vec {L}}=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {x}}}_{n}$

bzw. für einen Körper mit kontinuierlicher Masseverteilung das Integral:

${\vec {L}}=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times {{\vec {v}}({\vec {x}})}$ ⓘ

• $m_{1\ldots N}$ … die Massen der Massepunkte des Körpers mit diskreter Masserverteilung
• $\rho ({\vec {x}})$ … die Massendichte der kontinuierlichen Masseverteilung
• ${\vec {x}}_{1\ldots N}$ und ${\dot {\vec {x}}}_{1\ldots N}$ … die Orte und Geschwindigkeiten der Massepunkte des Körpers mit diskreter Masseverteilung
• ${\vec {v}}({\vec {x}})$ … das Geschwindigkeitsfeld, das angibt, mit welcher Geschwindigkeit sich die Masse am Ort ${\vec {x}}$ bewegt ⓘ

Mit Hilfe des Massenmittelpunkts eines Körpers und dessen Ortskoordinate ${\vec {s}}$ sowie seiner Schwerpunktsgeschwindigkeit ${\dot {\vec {s}}}$ können darauf bezogene Ortskoordinaten ${\vec {\chi }}:={\vec {x}}-{\vec {s}}$ und die Winkelgeschwindigkeiten der Massepunkte ${\vec {\omega }}_{n}$ definiert werden. Dann lassen sich die Geschwindigkeiten ausdrücken als:

${\begin{aligned}{\dot {\vec {x}}}_{n}&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}_{n}\\{{\vec {v}}({\vec {x}}})&={\dot {\vec {s}}}+{\vec {\omega }}_{n}\times {\vec {\chi }}.\end{aligned}}$ ⓘ

Bei einem starren Körper, dessen Ausrichtung zum Bezugspunkt konstant ist, sind zudem alle Winkelgeschwindigkeiten gleich groß $(\forall n:{\vec {\omega }}_{n}\equiv {\vec {\omega }})$. Damit ergibt sich der Drehimpuls zu:

${\begin{aligned}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right){\text{ bzw.}}\\{\vec {L}}&=\int \mathrm {d} ^{3}x\,\rho ({\vec {x}})\,{\vec {x}}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}\right)\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\int \mathrm {d} ^{3}\chi \rho ({\vec {\chi }})\,{\vec {\chi }}\times \left({\vec {\omega }}\times {\vec {\chi }}\right){\text{ oder verallgemeinert}}\\&=M{\vec {s}}\times {\dot {\vec {s}}}+\mathbf {\Theta } _{s}\cdot {\vec {\omega }}.\end{aligned}}$ ⓘ

Hier sind zusätzlich

• $M=\sum _{n}m_{n}$ die Gesamtmasse des Körpers und
• $\mathbf {\Theta } _{s}=\int \mathrm {d} ^{3}x\rho ({\vec {x}})\,[({\vec {x}}\cdot {\vec {x}})\,\mathbf {1} -{\vec {x}}\otimes {\vec {x}}]$ der Trägheitstensor des Körpers bezogen auf seinen Massenmittelpunkt. ⓘ

Herleitung

---

ⓘ

Eine Eiskunstläuferin, die sich im Trudeln befindet, nutzt die Drehimpulserhaltung - die Verringerung ihres Trägheitsmoments durch das Einziehen ihrer Arme und Beine erhöht ihre Drehgeschwindigkeit. ⓘ

Allgemeine Überlegungen

Eine Analogie zum dritten Newtonschen Bewegungsgesetz könnte lauten: "In einem geschlossenen System kann auf keinen Gegenstand ein Drehmoment ausgeübt werden, ohne dass auf einen anderen Gegenstand ein gleiches und entgegengesetztes Drehmoment ausgeübt wird." Daher kann der Drehimpuls zwischen Objekten in einem geschlossenen System ausgetauscht werden, aber der Gesamtdrehimpuls vor und nach dem Austausch bleibt konstant (wird erhalten). ⓘ

Anders ausgedrückt: Ein starrer Körper befindet sich in gleichmäßiger Rotation, solange kein äußerer Einfluss auf ihn einwirkt. Wenn also kein äußerer Einfluss auf ihn einwirkt, bleibt der ursprüngliche Drehimpuls des Systems konstant. ⓘ

Der Drehimpulserhaltungssatz wird bei der Analyse von Bewegungen mit zentraler Kraft verwendet. Wenn die Nettokraft auf einen Körper immer auf einen Punkt, den Mittelpunkt, gerichtet ist, dann gibt es kein Drehmoment auf den Körper in Bezug auf den Mittelpunkt, da die gesamte Kraft entlang des Radiusvektors gerichtet ist und keine senkrecht zum Radius. Mathematisch gesehen ist das Drehmoment ${\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} =\mathbf {0} ,$ denn in diesem Fall $\mathbf {r}$ und $\mathbf {F}$ sind parallele Vektoren. Daher ist der Drehimpuls des Körpers um den Mittelpunkt konstant. Dies ist der Fall bei der Gravitationsanziehung in den Bahnen von Planeten und Satelliten, wo die Gravitationskraft immer auf den primären Körper gerichtet ist und die umlaufenden Körper ihren Drehimpuls durch den Austausch von Abstand und Geschwindigkeit bei ihrer Bewegung um den primären Körper erhalten. Die Bewegung der Zentralkraft wird auch bei der Analyse des Bohrschen Atommodells verwendet. ⓘ

Bei einem Planeten verteilt sich der Drehimpuls auf die Drehung des Planeten und seine Umdrehung in der Umlaufbahn, und diese werden häufig durch verschiedene Mechanismen ausgetauscht. Die Drehimpulserhaltung im Erde-Mond-System führt zu einer Übertragung von Drehimpulsen von der Erde auf den Mond aufgrund des Gezeitendrehmoments, das der Mond auf die Erde ausübt. Dies wiederum führt zu einer Verlangsamung der Rotationsrate der Erde (etwa 65,7 Nanosekunden pro Tag) und zu einer allmählichen Vergrößerung des Radius der Mondbahn (etwa 3,82 Zentimeter pro Jahr). ⓘ

Das von den beiden entgegengesetzten Kräften Fg und -Fg verursachte Drehmoment bewirkt eine Änderung des Drehimpulses L in Richtung dieses Drehmoments (da das Drehmoment die zeitliche Ableitung des Drehimpulses ist). Dies führt zu einer Präzessionsbewegung des Kreisels. ⓘ

Der Drehimpulserhaltungssatz erklärt die Winkelbeschleunigung einer Schlittschuhläuferin, die ihre Arme und Beine nahe an die vertikale Drehachse bringt. Indem sie einen Teil ihrer Körpermasse näher an die Achse bringt, verringert sie das Trägheitsmoment ihres Körpers. Da der Drehimpuls das Produkt aus Trägheitsmoment und Winkelgeschwindigkeit ist, muss die Winkelgeschwindigkeit (Drehgeschwindigkeit) der Läuferin zunehmen, wenn der Drehimpuls konstant bleibt (erhalten bleibt). ⓘ

Dasselbe Phänomen führt dazu, dass kompakte Sterne (wie Weiße Zwerge, Neutronensterne und Schwarze Löcher) extrem schnell rotieren, wenn sie sich aus viel größeren und langsamer rotierenden Sternen bilden. Verringert sich die Größe eines Objekts um das n-fache, so erhöht sich seine Winkelgeschwindigkeit um den Faktor n². ⓘ

Die Energieerhaltung ist nicht immer eine vollständige Erklärung für die Dynamik eines Systems, aber sie ist eine wichtige Einschränkung. Ein Kreisel zum Beispiel unterliegt einem Gravitationsdrehmoment, das ihn zum Umkippen bringt und den Drehimpuls um die Nutationsachse verändert. Vernachlässigt man jedoch die Reibung am Berührungspunkt des Kreisels, so bleibt der Drehimpuls um die Kreiselachse und um die Präzessionsachse erhalten. Außerdem können sich in jedem Planetensystem die Planeten, Sterne, Kometen und Asteroiden auf zahlreiche komplizierte Arten bewegen, aber nur so, dass der Drehimpuls des Systems erhalten bleibt. ⓘ

Das Noether-Theorem besagt, dass jedes Erhaltungsgesetz mit einer Symmetrie (Invariante) der zugrunde liegenden Physik verbunden ist. Die Symmetrie, die mit der Erhaltung des Drehimpulses verbunden ist, ist die Rotationsinvarianz. Die Tatsache, dass die Physik eines Systems unverändert bleibt, wenn es um einen beliebigen Winkel um eine Achse gedreht wird, bedeutet, dass der Drehimpuls erhalten bleibt. ⓘ

Beziehung zum zweiten Newton'schen Gesetz der Bewegung

Die Drehimpulserhaltung kann zwar getrennt von den Newton'schen Bewegungsgesetzen als Folge des Noether'schen Satzes für rotationssymmetrische Systeme verstanden werden, sie kann aber auch einfach als effiziente Berechnungsmethode für Ergebnisse verstanden werden, die sich auch sonst direkt aus dem zweiten Newton'schen Gesetz und den Gesetzen über die Naturkräfte (wie dem dritten Newton'schen Gesetz, den Maxwell'schen Gleichungen und der Lorentz-Kraft) ableiten lassen. Bei gegebenen Anfangsbedingungen von Position und Geschwindigkeit für jeden Punkt und den Kräften bei einer solchen Bedingung kann man das zweite Newtonsche Gesetz zur Berechnung der zweiten Ableitung der Position verwenden, und die Lösung dieser Ableitung gibt vollständige Informationen über die Entwicklung des physikalischen Systems mit der Zeit. In der Quantenmechanik ist dies jedoch nicht mehr der Fall, da es einen Teilchenspin gibt, d. h. einen Drehimpuls, der nicht durch die kumulative Wirkung punktförmiger Bewegungen im Raum beschrieben werden kann. ⓘ

Ein Beispiel dafür ist die Abnahme des Trägheitsmoments, z. B. wenn ein Eiskunstläufer seine Hände einzieht und damit die Kreisbewegung beschleunigt. Im Sinne der Drehimpulserhaltung gelten für den Drehimpuls L, das Trägheitsmoment I und die Winkelgeschwindigkeit ω:

$0=dL=d(I\cdot \omega )=dI\cdot \omega +I\cdot d\omega$ ⓘ

Daraus ergibt sich, dass die Änderung eine Energie von:

$dE=d\left({\frac {1}{2}}I\cdot \omega ^{2}\right)={\frac {1}{2}}dI\cdot \omega ^{2}+I\cdot \omega \cdot d\omega =-{\frac {1}{2}}dI\cdot \omega ^{2}$

Eine Abnahme des Trägheitsmoments erfordert also eine investierte Energie. ⓘ

Dies kann mit der Arbeit verglichen werden, die mit den Newtonschen Gesetzen berechnet wird. Jeder Punkt des rotierenden Körpers wird zu jedem Zeitpunkt mit einer Radialbeschleunigung von beschleunigt:

$-r\cdot \omega ^{2}$ ⓘ

Betrachten wir einen Punkt der Masse m, dessen Ortsvektor relativ zum Bewegungszentrum zu einem gegebenen Zeitpunkt senkrecht zur z-Achse steht und sich in einem Abstand z befindet:

$-m\cdot z\cdot \omega ^{2}$ ⓘ

Die Arbeit, die erforderlich ist, um diesen Punkt in eine vom Bewegungszentrum entfernte Entfernung dz zu bringen, beträgt also:

$dW=-m\cdot z\cdot \omega ^{2}\cdot dz=-m\cdot \omega ^{2}\cdot d\left({\frac {1}{2}}z^{2}\right)$ ⓘ

Für einen nicht punktförmigen Körper muss man darüber integrieren, wobei m durch die Massendichte pro Einheit z ersetzt wird:

$dW=-{\frac {1}{2}}dI\cdot \omega ^{2}$ ⓘ

was genau der Energie entspricht, die für die Erhaltung des Drehimpulses erforderlich ist. ⓘ

Man beachte, dass die obige Berechnung auch pro Masse durchgeführt werden kann, wenn man nur die Kinematik verwendet. Das Phänomen, dass ein Eiskunstläufer die Tangentialgeschwindigkeit beschleunigt, während er seine Hände nach innen zieht, lässt sich also in Laiensprache wie folgt verstehen: Die Handflächen des Eiskunstläufers bewegen sich nicht in einer geraden Linie, so dass sie ständig nach innen beschleunigt werden, aber keine zusätzliche Geschwindigkeit gewinnen, weil die Beschleunigung immer dann erfolgt, wenn ihre Bewegung nach innen gleich Null ist. Dies ist jedoch anders, wenn die Handflächen näher an den Körper gezogen werden: Die Beschleunigung durch die Rotation erhöht nun die Geschwindigkeit; aber wegen der Rotation führt die Zunahme der Geschwindigkeit nicht zu einer signifikanten Geschwindigkeit nach innen, sondern zu einer Zunahme der Rotationsgeschwindigkeit. ⓘ

Im Lagrangeschen Formalismus

In der Lagrangeschen Mechanik ist der Drehimpuls für die Rotation um eine bestimmte Achse der konjugierte Impuls der verallgemeinerten Koordinate des Winkels um dieselbe Achse. Zum Beispiel, $L_{z}$der Drehimpuls um die z-Achse, ist:

$L_{z}={\frac {\partial {\cal {L}}}{\partial {\dot {\theta }}_{z}}}$

wobei ${\cal {L}}$ ist die Lagrange und $\theta _{z}$ ist der Winkel um die z-Achse. ⓘ

Beachten Sie, dass ${\dot {\theta }}_{z}$die zeitliche Ableitung des Winkels ist, die Winkelgeschwindigkeit $\omega _{z}$. Normalerweise hängt die Lagrange von der Winkelgeschwindigkeit durch die kinetische Energie ab: Letztere kann geschrieben werden, indem man die Geschwindigkeit in ihren radialen und tangentialen Teil zerlegt, wobei der tangentiale Teil in der x-y-Ebene um die z-Achse gleich ist:

$\sum _{i}{\frac {1}{2}}m_{i}{v_{T}}_{i}^{2}=\sum _{i}{\frac {1}{2}}m_{i}(x_{i}^{2}+y_{i}^{2}){{\omega _{z}}_{i}}^{2}$

Dabei steht der Index i für den i-ten Körper, und m, vT und ωz stehen für die Masse, die Tangentialgeschwindigkeit um die z-Achse bzw. die Winkelgeschwindigkeit um diese Achse. ⓘ

Für einen nicht punktförmigen Körper mit der Dichte ρ haben wir stattdessen:

${\frac {1}{2}}\int \rho (x,y,z)(x_{i}^{2}+y_{i}^{2}){{\omega _{z}}_{i}}^{2}\,dx\,dy={\frac {1}{2}}{I_{z}}_{i}{{\omega _{z}}_{i}}^{2}$

wobei die Integration über die Fläche des Körpers erfolgt und Iz das Trägheitsmoment um die z-Achse ist. ⓘ

Unter der Annahme, dass die potenzielle Energie nicht von ωz abhängt (diese Annahme kann bei elektromagnetischen Systemen fehlschlagen), haben wir also den Drehimpuls des i-ten Objekts:

${\begin{aligned}{L_{z}}_{i}&={\frac {\partial {\cal {L}}}{\partial {{\omega _{z}}_{i}}}}={\frac {\partial E_{k}}{\partial {{\omega _{z}}_{i}}}}\\&={I_{z}}_{i}\cdot {\omega _{z}}_{i}\end{aligned}}$ ⓘ

Wir haben bisher jedes Objekt um einen separaten Winkel gedreht; wir können auch einen Gesamtwinkel θz definieren, um den wir das ganze System drehen, also auch jedes Objekt um die z-Achse, und haben den Gesamtdrehimpuls:

$L_{z}=\sum _{i}{I_{z}}_{i}\cdot {\omega _{z}}_{i}$ ⓘ

Aus den Euler-Lagrange-Gleichungen ergibt sich dann folgendes:

$0={\frac {\partial {\cal {L}}}{\partial {{\theta _{z}}_{i}}}}-{\frac {d}{dt}}\left({\frac {\partial {\cal {L}}}{\partial {{{\dot {\theta }}_{z}}_{i}}}}\right)={\frac {\partial {\cal {L}}}{\partial {{\theta _{z}}_{i}}}}-{\frac {d{L_{z}}_{i}}{dt}}$ ⓘ

Da die Lagrange-Gleichung nur durch das Potential von den Winkeln des Objekts abhängig ist, haben wir:

${\frac {d{L_{z}}_{i}}{dt}}={\frac {\partial {\cal {L}}}{\partial {{\theta _{z}}_{i}}}}=-{\frac {\partial V}{\partial {{\theta _{z}}_{i}}}}$

das ist das Drehmoment auf das i-te Objekt. ⓘ

Angenommen, das System ist drehungsinvariant, so dass das Potenzial unabhängig von einer Gesamtdrehung um den Winkel θz ist (es kann also von den Winkeln der Objekte nur durch deren Differenzen abhängen, in der Form $V({\theta _{z}}_{i},{\theta _{z}}_{j})=V({\theta _{z}}_{i}-{\theta _{z}}_{j})$). Wir erhalten also für den Gesamtdrehimpuls:

${\frac {dL_{z}}{dt}}=-{\frac {\partial V}{\partial {\theta _{z}}}}=0$

Und somit ist der Drehimpuls um die z-Achse erhalten. ⓘ

Diese Analyse lässt sich für jede Achse getrennt wiederholen, so dass der Drehimpulsvektor erhalten bleibt. Die Winkel um die drei Achsen können jedoch nicht gleichzeitig als verallgemeinerte Koordinaten behandelt werden, da sie nicht unabhängig sind; insbesondere genügen zwei Winkel pro Punkt, um seine Position zu bestimmen. Es stimmt zwar, dass die vollständige Beschreibung eines starren Körpers neben drei translatorischen Freiheitsgraden auch die Angabe von drei rotatorischen Freiheitsgraden erfordert; diese können jedoch nicht als Drehungen um die kartesischen Achsen definiert werden (siehe Euler-Winkel). Dieser Vorbehalt spiegelt sich in der Quantenmechanik in den nicht-trivialen Kommutationsbeziehungen der verschiedenen Komponenten des Drehimpulsoperators wider. ⓘ

Im Hamiltonschen Formalismus

In der Hamiltonschen Mechanik kann der Hamiltonian als Funktion des Drehimpulses beschrieben werden. Wie zuvor ist der Teil der kinetischen Energie, der sich auf die Drehung um die z-Achse für das i-te Objekt bezieht, gleich:

${\frac {1}{2}}{I_{z}}_{i}{{\omega _{z}}_{i}}^{2}={\frac {{{L_{z}}_{i}}^{2}}{2{I_{z}}_{i}}}$ ⓘ

Dies entspricht der Energieabhängigkeit des Impulses entlang der z-Achse, ${\frac {{{p_{z}}_{i}}^{2}}{{2m}_{i}}}$. ⓘ

Die Hamilton-Gleichungen setzen den Winkel um die z-Achse in Beziehung zu seinem konjugierten Impuls, dem Drehimpuls um dieselbe Achse:

${\begin{aligned}{\frac {d{\theta _{z}}_{i}}{dt}}&={\frac {\partial {\cal {H}}}{\partial {L_{z}}_{i}}}={\frac {{L_{z}}_{i}}{{I_{z}}_{i}}}\\{\frac {d{L_{z}}_{i}}{dt}}&=-{\frac {\partial {\cal {H}}}{\partial {\theta _{z}}_{i}}}=-{\frac {\partial V}{\partial {\theta _{z}}_{i}}}\end{aligned}}$ ⓘ

Die erste Gleichung ergibt

${L_{z}}_{i}={I_{z}}_{i}\cdot {{{\dot {\theta }}_{z}}_{i}}={I_{z}}_{i}\cdot {\omega _{z}}_{i}$ ⓘ

Damit erhalten wir die gleichen Ergebnisse wie im Lagrangeschen Formalismus. ⓘ

Beachten Sie, dass wir die kinetische Energie für die Kombination aller Achsen zusammen wie folgt schreiben

$E_{k}={\frac {1}{2}}\sum _{i}{\frac {|{\bf {{p}_{i}|^{2}}}}{2m_{i}}}=\sum _{i}\left({\frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{\frac {1}{2}}{\bf {{L}_{i}}}^{\textsf {T}}{I_{i}}^{-1}{\bf {{L}_{i}}}\right)$ ⓘ

wobei pr der Impuls in radialer Richtung ist und das Trägheitsmoment eine 3-dimensionale Matrix ist; fette Buchstaben stehen für 3-dimensionale Vektoren. ⓘ

Für punktförmige Körper haben wir:

$E_{k}=\sum _{i}\left({\frac {{{p_{r}}_{i}}^{2}}{2m_{i}}}+{\frac {|{\bf {{L}_{i}}}|^{2}}{2m_{i}{r_{i}}^{2}}}\right)$ ⓘ

Diese Form des kinetischen Energieteils des Hamiltonian ist nützlich bei der Analyse zentraler Potentialprobleme und lässt sich leicht in ein quantenmechanisches Arbeitssystem umwandeln (z. B. beim Problem des Wasserstoffatoms). ⓘ

Herleitung

Bei der Herleitung kommen verschiedene Umstellungen, die Graßmann-Identität (BAC-CAB-Formel), und die Definition des Massenmittelpunkts zum Einsatz:

${\begin{array}{lllll}{\vec {L}}&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\dot {\vec {s}}}+{\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {x}}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|+{\vec {0}}={\vec {s}}-{\vec {s}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}+{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Ausklammern}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left({\vec {x}}_{n}-{\vec {s}}\right)\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\vec {x}}_{n}-{\vec {s}}={\vec {\chi }}_{n}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,{\vec {s}}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&\left|{\text{Graßmann-Identität}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+\sum _{n}m_{n}\,\left({\vec {\omega }}\left({\vec {s}}\cdot {\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)\right)&\left|{\text{Summe in die Klammer}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+{\vec {\omega }}\left({\vec {s}}\cdot \sum _{n}m_{n}{\vec {\chi }}_{n}\right)-\sum _{n}m_{n}{\vec {\chi }}_{n}\left({\vec {s}}\cdot {\vec {\omega }}\right)&\left|\sum _{n}m_{n}\chi _{n}={\vec {0}}\right.\\&=\sum _{n}m_{n}\,{\vec {x}}_{n}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&+0\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\chi }}_{n}\times \left({\vec {\omega }}\times {\vec {\chi }}_{n}\right)&&\left|{\text{Graßmann-Identität}}\right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,{\vec {\omega }}\left({\vec {\chi }}_{n}{\vec {\chi }}_{n}\right)-{\vec {\chi }}_{n}\left({\vec {\omega }}{\vec {\chi }}_{n}\right)&&\left|{\text{Dyadisches Produkt}}\otimes \right.\\&=M{\vec {s}}\times {\dot {\vec {s}}}&+\sum _{n}m_{n}\,\left(({\vec {\chi }}_{n}{\vec {\chi }}_{n})\mathbf {1} -{\vec {\chi }}_{n}\otimes {\vec {\chi }}_{n}\right){\vec {\omega }}\end{array}}$ ⓘ

Der erste Term $M{\vec {s}}\times {\dot {\vec {s}}}$ wird Bahndrehimpuls genannt, der zweite Term ist der Eigendrehimpuls. ⓘ

Der Eigendrehimpuls

Der Eigendrehimpuls eines starren Körpers ist der Anteil seines Drehimpulses, der durch die Rotation um seinen Massenmittelpunkt ${\vec {s}}$ darstellbar ist. Mit Hilfe der Winkelgeschwindigkeit ${\vec {\omega }}_{s}$ und des Trägheitstensors $\mathbf {\Theta } _{s}$, jeweils auf den Massenmittelpunkt ${\vec {s}}$ bezogen, lässt er sich als deren Matrixprodukt berechnen:

${\vec {L}}_{s}=\mathbf {\Theta } _{s}\cdot {\vec {\omega }}_{s}.$ ⓘ

Im Allgemeinen zeigen ${\vec {\omega }}$ und ${\vec {L}}_{s}$ nicht in die gleiche Richtung – ein rotierender Körper „eiert“, wenn er sich frei bewegen kann, oder zeigt Unwucht, wenn die Richtung der Achse festgehalten wird. Nur bei Rotation um eine der Hauptträgheitsachsen des Körpers sind ${\vec {\omega }}$ und ${\vec {L}}_{s}$ parallel, sodass die Erhaltung des Drehimpulses auch gleichbleibende Richtung der Drehachse und damit die Konstanz des Trägheitsmoments bewirkt. Der Trägheitstensor ist symmetrisch und deshalb sind die Hauptträgheitsachsen paarweise orthogonal. Aus dem Trägheitstensor kann man zu jeder beliebigen Drehachse das Trägheitsmoment und die Hauptträgheitsachsen durch Lösung des Eigenwertproblems berechnen. ⓘ

Drehimpuls in der Orbitalmechanik

Während in der klassischen Mechanik die Sprache des Drehimpulses durch die Newtonschen Bewegungsgesetze ersetzt werden kann, ist sie besonders nützlich für Bewegungen in einem zentralen Potential wie die Planetenbewegung im Sonnensystem. So wird die Bahn eines Planeten im Sonnensystem durch seine Energie, seinen Drehimpuls und die Winkel der Hauptachse der Bahn relativ zu einem Koordinatensystem definiert. ⓘ

In der Astrodynamik und Himmelsmechanik wird eine eng mit dem Drehimpuls verwandte Größe definiert als

$\mathbf {h} =\mathbf {r} \times \mathbf {v} ,$

als spezifischer Drehimpuls bezeichnet. Beachten Sie, dass $\mathbf {L} =m\mathbf {h} .$ Die Masse spielt bei Berechnungen in der Orbitalmechanik oft keine Rolle, da die Bewegung eines Körpers durch die Schwerkraft bestimmt wird. Der Hauptkörper des Systems ist oft so viel größer als alle Körper, die sich um ihn herum bewegen, dass die Gravitationswirkung der kleineren Körper auf ihn vernachlässigt werden kann; er behält im Grunde genommen eine konstante Geschwindigkeit bei. Die Bewegung aller Körper wird unabhängig von ihrer Masse in gleicher Weise von der Schwerkraft beeinflusst, und daher bewegen sich alle unter den gleichen Bedingungen in etwa gleich. ⓘ

Feste Körper

Der Drehimpuls ist auch ein äußerst nützliches Konzept zur Beschreibung rotierender starrer Körper wie eines Kreisels oder eines Gesteinsplaneten. Für eine kontinuierliche Massenverteilung mit der Dichtefunktion ρ(r) hat ein differentielles Volumenelement dV mit dem Ortsvektor r innerhalb der Masse ein Massenelement dm = ρ(r)dV. Daher ist der infinitesimale Drehimpuls dieses Elements:

$d\mathbf {L} =\mathbf {r} \times dm\mathbf {v} =\mathbf {r} \times \rho (\mathbf {r} )dV\mathbf {v} =dV\mathbf {r} \times \rho (\mathbf {r} )\mathbf {v}$ ⓘ

und die Integration dieses Differentials über das Volumen der gesamten Masse ergibt ihren Gesamtdrehimpuls:

$\mathbf {L} =\int _{V}dV\mathbf {r} \times \rho (\mathbf {r} )\mathbf {v}$ ⓘ

In der folgenden Ableitung können ähnliche Integrale die Summen für den Fall einer kontinuierlichen Masse ersetzen. ⓘ

Sammlung von Teilchen

Der Drehimpuls der Teilchen i ist die Summe der Kreuzprodukte R × MV + Σri × mivi. ⓘ

Für eine Ansammlung von Teilchen, die sich um einen beliebigen Ursprung bewegen, ist es aufschlussreich, die Drehimpulsgleichung zu entwickeln, indem man ihre Bewegung in Komponenten um ihren eigenen Massenschwerpunkt und um den Ursprung auflöst. Gegeben,

• $m_{i}$ ist die Masse des Teilchens $i$,
• $\mathbf {R} _{i}$ ist der Positionsvektor des Teilchens $i$ in Bezug auf den Ursprung,
• $\mathbf {V} _{i}$ ist die Geschwindigkeit des Teilchens $i$ in Bezug auf den Ursprung,
• $\mathbf {R}$ ist der Positionsvektor des Massenschwerpunkts im Verhältnis zum Ursprung,
• $\mathbf {V}$ ist die Geschwindigkeit des Massenmittelpunkts im Verhältnis zum Ursprung,
• $\mathbf {r} _{i}$ ist der Positionsvektor des Teilchens $i$ bezogen auf den Massenschwerpunkt,
• $\mathbf {v} _{i}$ ist die Geschwindigkeit des Teilchens $i$ bezogen auf den Massenschwerpunkt, ⓘ

Die Gesamtmasse der Teilchen ist einfach ihre Summe,

$M=\sum _{i}m_{i}.$ ⓘ

Der Positionsvektor des Massenschwerpunkts ist definiert durch,

$M\mathbf {R} =\sum _{i}m_{i}\mathbf {R} _{i}.$ ⓘ

Durch Betrachtung,

$\mathbf {R} _{i}=\mathbf {R} +\mathbf {r} _{i}$ und $\mathbf {V} _{i}=\mathbf {V} +\mathbf {v} _{i}.$ ⓘ

Der Gesamtdrehimpuls der Gesamtheit der Teilchen ist die Summe der Drehimpulse der einzelnen Teilchen,

$\mathbf {L} =\sum _{i}\left(\mathbf {R} _{i}\times m_{i}\mathbf {V} _{i}\right)$     (1) ⓘ

Erweitern von $\mathbf {R} _{i}$,

${\begin{aligned}\mathbf {L} &=\sum _{i}\left[\left(\mathbf {R} +\mathbf {r} _{i}\right)\times m_{i}\mathbf {V} _{i}\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} _{i}\right]\end{aligned}}$ ⓘ

Erweitern von $\mathbf {V} _{i}$,

${\begin{aligned}\mathbf {L} &=\sum _{i}\left[\mathbf {R} \times m_{i}\left(\mathbf {V} +\mathbf {v} _{i}\right)+\mathbf {r} _{i}\times m_{i}(\mathbf {V} +\mathbf {v} _{i})\right]\\&=\sum _{i}\left[\mathbf {R} \times m_{i}\mathbf {V} +\mathbf {R} \times m_{i}\mathbf {v} _{i}+\mathbf {r} _{i}\times m_{i}\mathbf {V} +\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\right]\\&=\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} +\sum _{i}\mathbf {R} \times m_{i}\mathbf {v} _{i}+\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\end{aligned}}$ ⓘ

Es kann gezeigt werden, dass (siehe Seitenleiste), ⓘ

Beweisen Sie, dass $\sum _{i}m_{i}\mathbf {r} _{i}=\mathbf {0}$ ${\begin{aligned}\mathbf {r} _{i}&=\mathbf {R} _{i}-\mathbf {R} \\m_{i}\mathbf {r} _{i}&=m_{i}\left(\mathbf {R} _{i}-\mathbf {R} \right)\\\sum _{i}m_{i}\mathbf {r} _{i}&=\sum _{i}m_{i}\left(\mathbf {R} _{i}-\mathbf {R} \right)\\&=\sum _{i}(m_{i}\mathbf {R} _{i}-m_{i}\mathbf {R} )\\&=\sum _{i}m_{i}\mathbf {R} _{i}-\sum _{i}m_{i}\mathbf {R} \\&=\sum _{i}m_{i}\mathbf {R} _{i}-\left(\sum _{i}m_{i}\right)\mathbf {R} \\&=\sum _{i}m_{i}\mathbf {R} _{i}-M\mathbf {R} \end{aligned}}$ was nach der Definition des Massenschwerpunkts $\mathbf {0} ,$ und in ähnlicher Weise für $\sum _{i}m_{i}\mathbf {v} _{i}.$ ⓘ

$\sum _{i}m_{i}\mathbf {r} _{i}=\mathbf {0}$ und $\sum _{i}m_{i}\mathbf {v} _{i}=\mathbf {0} ,$

Daher verschwinden der zweite und dritte Term,

$\mathbf {L} =\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}.$ ⓘ

Der erste Term kann umformuliert werden,

$\sum _{i}\mathbf {R} \times m_{i}\mathbf {V} =\mathbf {R} \times \sum _{i}m_{i}\mathbf {V} =\mathbf {R} \times M\mathbf {V} ,$ ⓘ

und der Gesamtdrehimpuls für die Ansammlung von Teilchen ist schließlich,

$\mathbf {L} =\mathbf {R} \times M\mathbf {V} +\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}$     (2) ⓘ

Der erste Term ist der Drehimpuls des Massenschwerpunkts relativ zum Ursprung. Ähnlich wie bei Einzelteilchen, unten, ist es der Drehimpuls eines Teilchens der Masse M im Massenschwerpunkt, das sich mit der Geschwindigkeit V bewegt. Der zweite Term ist der Drehimpuls der Teilchen, die sich relativ zum Massenschwerpunkt bewegen, ähnlich wie bei Fester Massenschwerpunkt, unten. Das Ergebnis ist allgemein - die Bewegung der Teilchen ist nicht auf die Rotation oder Drehung um den Ursprung oder den Massenschwerpunkt beschränkt. Die Teilchen müssen keine Einzelmassen sein, sondern können Elemente einer kontinuierlichen Verteilung sein, wie z. B. ein fester Körper. ⓘ

Wenn man die Gleichung (2) mit Hilfe von Vektoridentitäten umstellt, beide Terme mit "eins" multipliziert und entsprechend gruppiert, ⓘ

${\begin{aligned}\mathbf {L} &=M(\mathbf {R} \times \mathbf {V} )+\sum _{i}\left[m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&={\frac {R^{2}}{R^{2}}}M\left(\mathbf {R} \times \mathbf {V} \right)+\sum _{i}\left[{\frac {r_{i}^{2}}{r_{i}^{2}}}m_{i}\left(\mathbf {r} _{i}\times \mathbf {v} _{i}\right)\right],\\&=R^{2}M\left({\frac {\mathbf {R} \times \mathbf {V} }{R^{2}}}\right)+\sum _{i}\left[r_{i}^{2}m_{i}\left({\frac {\mathbf {r} _{i}\times \mathbf {v} _{i}}{r_{i}^{2}}}\right)\right],\\\end{aligned}}$ ⓘ

ergibt den Gesamtdrehimpuls des Teilchensystems in Form des Trägheitsmoments $I$ und der Winkelgeschwindigkeit ${\boldsymbol {\omega }}$, ⓘ

$\mathbf {L} =I_{R}{\boldsymbol {\omega }}_{R}+\sum _{i}I_{i}{\boldsymbol {\omega }}_{i}.$     (3) ⓘ

Fall eines einzelnen Teilchens

Im Fall eines einzelnen Teilchens, das sich um einen willkürlichen Ursprung bewegt,

${\begin{aligned}\mathbf {r} _{i}&=\mathbf {v} _{i}=\mathbf {0} ,\\\mathbf {r} &=\mathbf {R} ,\\\mathbf {v} &=\mathbf {V} ,\\m&=M,\end{aligned}}$

$\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}=\mathbf {0} ,$

$\sum _{i}I_{i}{\boldsymbol {\omega }}_{i}=\mathbf {0} ,$ und die Gleichungen (2) und (3) für den Gesamtdrehimpuls reduzieren sich auf,

$\mathbf {L} =\mathbf {R} \times m\mathbf {V} =I_{R}{\boldsymbol {\omega }}_{R}.$ ⓘ

Fall eines festen Massenschwerpunkts

Für den Fall, dass der Massenschwerpunkt im Raum in Bezug auf den Ursprung fixiert ist,

$\mathbf {V} =\mathbf {0} ,$

$\mathbf {R} \times M\mathbf {V} =\mathbf {0} ,$

$I_{R}{\boldsymbol {\omega }}_{R}=\mathbf {0} ,$ und die Gleichungen (2) und (3) für den Gesamtdrehimpuls reduzieren sich auf,

$\mathbf {L} =\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}=\sum _{i}I_{i}{\boldsymbol {\omega }}_{i}.$ ⓘ

Drehimpuls in der allgemeinen Relativitätstheorie

Der 3-Drehimpuls als Bivektor (ebenes Element) und Achsenvektor eines Teilchens der Masse m mit momentaner 3-Position x und 3-Impuls p. ⓘ

In der modernen (20. Jahrhundert) theoretischen Physik wird der Drehimpuls (ohne Eigendrehimpuls - siehe unten) mit einem anderen Formalismus beschrieben, anstelle eines klassischen Pseudovektors. In diesem Formalismus ist der Drehimpuls die mit der Rotationsinvarianz verbundene 2-Form-Noether-Ladung. Infolgedessen ist der Drehimpuls für allgemeine gekrümmte Raumzeiten nicht erhalten, es sei denn, er ist asymptotisch rotationsinvariant. ⓘ

In der klassischen Mechanik kann der Drehimpuls eines Teilchens in ein Flächenelement umgedeutet werden:

$\mathbf {L} =\mathbf {r} \wedge \mathbf {p} \,,$ ⓘ

in dem das äußere Produkt ∧ das Kreuzprodukt × ersetzt (diese Produkte haben ähnliche Eigenschaften, sind aber nicht äquivalent). Dies hat den Vorteil einer klareren geometrischen Interpretation als ebenes Element, das aus den Vektoren x und p definiert wird, und der Ausdruck gilt für eine beliebige Anzahl von Dimensionen (zwei oder mehr). In kartesischen Koordinaten:

${\begin{aligned}\mathbf {L} &=\left(xp_{y}-yp_{x}\right)\mathbf {e} _{x}\wedge \mathbf {e} _{y}+\left(yp_{z}-zp_{y}\right)\mathbf {e} _{y}\wedge \mathbf {e} _{z}+\left(zp_{x}-xp_{z}\right)\mathbf {e} _{z}\wedge \mathbf {e} _{x}\\&=L_{xy}\mathbf {e} _{x}\wedge \mathbf {e} _{y}+L_{yz}\mathbf {e} _{y}\wedge \mathbf {e} _{z}+L_{zx}\mathbf {e} _{z}\wedge \mathbf {e} _{x}\,,\end{aligned}}$ ⓘ

oder kompakter in Indexschreibweise:

$L_{ij}=x_{i}p_{j}-x_{j}p_{i}\,.$ ⓘ

Die Winkelgeschwindigkeit kann auch als ein antisymmetrischer Tensor zweiter Ordnung mit den Komponenten ω_ij definiert werden. Die Beziehung zwischen den beiden antisymmetrischen Tensoren ist durch das Trägheitsmoment gegeben, das nun ein Tensor vierter Ordnung sein muss:

$L_{ij}=I_{ijk\ell }\omega _{k\ell }\,.$ ⓘ

Auch diese Gleichung mit L und ω als Tensoren gilt für eine beliebige Anzahl von Dimensionen. Diese Gleichung erscheint auch im Formalismus der geometrischen Algebra, in dem L und ω Bivektoren sind und das Trägheitsmoment eine Abbildung zwischen ihnen ist. ⓘ

In der relativistischen Mechanik wird der relativistische Drehimpuls eines Teilchens als ein antisymmetrischer Tensor zweiter Ordnung ausgedrückt:

$M_{\alpha \beta }=X_{\alpha }P_{\beta }-X_{\beta }P_{\alpha }$ ⓘ

Er wird in der Sprache der Vierervektoren, nämlich der vier Positionen X und der vier Impulse P, ausgedrückt und absorbiert das oben genannte L zusammen mit der Bewegung des Massenschwerpunkts des Teilchens. ⓘ

In jedem der oben genannten Fälle ist der Gesamtdrehimpuls für ein System von Teilchen nur die Summe der Drehimpulse der einzelnen Teilchen, und der Massenschwerpunkt ist für das System. ⓘ

Drehimpuls in der Quantenmechanik

In der Quantenmechanik wird der Drehimpuls (wie andere Größen) als Operator ausgedrückt, und seine eindimensionalen Projektionen haben quantisierte Eigenwerte. Der Drehimpuls unterliegt der Heisenbergschen Unschärferelation, die besagt, dass zu jedem Zeitpunkt nur eine Projektion (auch "Komponente" genannt) mit bestimmter Genauigkeit gemessen werden kann; die beiden anderen bleiben unbestimmt. Aus diesem Grund ist die Drehachse eines Quantenteilchens undefiniert. Quanten-Teilchen besitzen zwar eine Art nicht-orbitalen Drehimpuls, den sogenannten "Spin", aber dieser Drehimpuls entspricht nicht einer Drehbewegung. In der relativistischen Quantenmechanik wird die obige relativistische Definition zu einem tensoriellen Operator. ⓘ

Spin, Orbital- und Gesamtdrehimpuls

Drehimpulse eines klassischen Objekts.

• Links: Der "Spin"-Drehimpuls S ist in Wirklichkeit der Bahndrehimpuls des Objekts in jedem Punkt.
• Rechts: Extrinsischer Bahndrehimpuls L um eine Achse.
• Oben: der Trägheitstensor I und die Winkelgeschwindigkeit ω (L ist nicht immer parallel zu ω).
• Unten: Drehimpuls p und seine radiale Position r von der Achse. Der Gesamtdrehimpuls (Spin plus Orbital) ist J. Für ein Quantenteilchen sind die Interpretationen unterschiedlich; der Teilchenspin hat nicht die obige Interpretation. ⓘ

Die klassische Definition des Drehimpulses als $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ kann auf die Quantenmechanik übertragen werden, indem r als Quantenpositionsoperator und p als Quantenimpulsoperator neu interpretiert werden. L ist dann ein Operator, der speziell als Bahndrehimpulsoperator bezeichnet wird. Die Komponenten des Drehimpulsoperators erfüllen die Kommutationsbeziehungen der Lie-Algebra so(3). In der Tat sind diese Operatoren genau die infinitesimale Wirkung der Rotationsgruppe auf den Quanten-Hilbert-Raum. (Siehe auch die nachstehende Diskussion über die Drehimpulsoperatoren als Generatoren von Rotationen). ⓘ

In der Quantenphysik gibt es jedoch noch eine andere Art von Drehimpuls, den so genannten Spin-Drehimpuls, der durch den Spin-Operator S dargestellt wird. Der Spin wird oft als ein Teilchen dargestellt, das sich buchstäblich um eine Achse dreht, aber das ist ein irreführendes und ungenaues Bild: Der Spin ist eine intrinsische Eigenschaft eines Teilchens, die nichts mit irgendeiner Art von Bewegung im Raum zu tun hat und sich grundlegend vom Bahndrehimpuls unterscheidet. Alle Elementarteilchen haben einen charakteristischen Spin (möglicherweise Null), und fast alle Elementarteilchen haben einen Spin ungleich Null. Zum Beispiel haben Elektronen "Spin 1/2" (was eigentlich "Spin ħ/2" bedeutet), Photonen haben "Spin 1" (was eigentlich "Spin ħ" bedeutet) und Pi-Mesonen haben Spin 0. ⓘ

Schließlich gibt es noch den Gesamtdrehimpuls J, der sowohl den Spin als auch den Bahndrehimpuls aller Teilchen und Felder zusammenfasst. (Für ein Teilchen ist J = L + S.) Der Drehimpulserhaltungssatz gilt für J, aber nicht für L oder S. So kann beispielsweise durch die Spin-Bahn-Wechselwirkung Drehimpuls zwischen L und S hin und her übertragen werden, wobei der Gesamtdrehimpuls konstant bleibt. Elektronen und Photonen müssen keine ganzzahligen Werte für den Gesamtdrehimpuls haben, sondern können auch halbzahlige Werte haben. ⓘ

In Molekülen ist der Gesamtdrehimpuls F die Summe des rovibronischen (orbitalen) Drehimpulses N, des Elektronenspindrehimpulses S und des Kernspindrehimpulses I. Für elektronische Singulett-Zustände wird der rovibronische Drehimpuls mit J statt mit N bezeichnet. Wie von Van Vleck erläutert, haben die Komponenten des molekularen rovibronischen Drehimpulses, die sich auf molekülfeste Achsen beziehen, andere Kommutationsbeziehungen als die Komponenten um raumfeste Achsen. ⓘ

Quantisierung

In der Quantenmechanik ist der Drehimpuls quantisiert, d. h. er kann nicht kontinuierlich variieren, sondern nur in "Quantensprüngen" zwischen bestimmten zulässigen Werten. Für jedes System gelten die folgenden Einschränkungen für Messergebnisse, wobei $\hbar$ die reduzierte Planck-Konstante ist und ${\hat {n}}$ ein beliebiger euklidischer Vektor wie x, y oder z ist:

Wenn man misst...	Das Ergebnis kann sein... ⓘ
$L_{\hat {n}}$	$\ldots ,-2\hbar ,-\hbar ,0,\hbar ,2\hbar ,\ldots$
$S_{\hat {n}}$ oder $J_{\hat {n}}$	$\ldots ,-{\frac {3}{2}}\hbar ,-\hbar ,-{\frac {1}{2}}\hbar ,0,{\frac {1}{2}}\hbar ,\hbar ,{\frac {3}{2}}\hbar ,\ldots$
${\begin{aligned}&L^{2}\\={}&L_{x}^{2}+L_{y}^{2}+L_{z}^{2}\end{aligned}}$	$\left[\hbar ^{2}n(n+1)\right]$, wobei $n=0,1,2,\ldots$
$S^{2}$ oder $J^{2}$	$\left[\hbar ^{2}n(n+1)\right]$, wobei $n=0,{\frac {1}{2}},1,{\frac {3}{2}},\ldots$

Bei dieser stehenden Welle auf einer kreisförmigen Saite ist der Kreis in genau 8 Wellenlängen unterteilt. Eine stehende Welle wie diese kann 0, 1, 2 oder eine beliebige ganzzahlige Anzahl von Wellenlängen auf dem Kreis haben, aber sie kann keine nicht ganzzahlige Anzahl von Wellenlängen wie 8,3 haben. In der Quantenmechanik wird der Drehimpuls aus einem ähnlichen Grund quantisiert. ⓘ

Die reduzierte Planck-Konstante $\hbar$ ist nach alltäglichen Maßstäben winzig, etwa 10-34 J s, und daher hat diese Quantisierung keinen merklichen Einfluss auf den Drehimpuls makroskopischer Objekte. In der mikroskopischen Welt ist sie jedoch sehr wichtig. So wird beispielsweise die Struktur der Elektronenschalen und -unterschalen in der Chemie durch die Quantisierung des Drehimpulses erheblich beeinflusst. ⓘ

Die Quantisierung des Drehimpulses wurde erstmals von Niels Bohr in seinem Atommodell postuliert und später von Erwin Schrödinger in seiner Schrödinger-Gleichung vorhergesagt. ⓘ

Unschärfe

An der Definition $\mathbf {L} =\mathbf {r} \times \mathbf {p}$sind sechs Operatoren beteiligt: Die Ortsoperatoren $r_{x}$, $r_{y}$, $r_{z}$. und die Impulsoperatoren $p_{x}$, $p_{y}$, $p_{z}$. Die Heisenbergsche Unschärferelation besagt jedoch, dass es nicht möglich ist, alle sechs dieser Größen gleichzeitig mit beliebiger Genauigkeit zu kennen. Daher gibt es Grenzen für das, was man über den Drehimpuls eines Teilchens wissen oder messen kann. Das Beste, was man tun kann, ist, gleichzeitig sowohl den Betrag des Drehimpulsvektors als auch seine Komponente entlang einer Achse zu messen. ⓘ

Die Unschärfe hängt eng mit der Tatsache zusammen, dass die verschiedenen Komponenten eines Drehimpulsoperators nicht kommutieren, zum Beispiel $L_{x}L_{y}\neq L_{y}L_{x}$. (Zu den genauen Kommutationsbeziehungen siehe Drehimpulsoperator). ⓘ

Gesamtdrehimpuls als Generator von Rotationen

Wie oben erwähnt, ist der Bahndrehimpuls L wie in der klassischen Mechanik definiert: $\mathbf {L} =\mathbf {r} \times \mathbf {p}$Der Gesamtdrehimpuls J wird jedoch auf eine andere, grundlegendere Weise definiert: J ist als "Generator von Rotationen" definiert. Genauer gesagt, ist J so definiert, dass der Operator

$R({\hat {n}},\phi )\equiv \exp \left(-{\frac {i}{\hbar }}\phi \,\mathbf {J} \cdot {\hat {\mathbf {n} }}\right)$

der Rotationsoperator ist, der ein beliebiges System um den Winkel $\phi$ um die Achse ${\hat {\mathbf {n} }}$. (Das "exp" in der Formel bezieht sich auf den exponentiellen Operator) Um es andersherum auszudrücken: Was auch immer unser Quanten-Hilbert-Raum ist, wir erwarten, dass die Rotationsgruppe SO(3) auf ihn wirkt. Es gibt dann eine zugehörige Wirkung der Lie-Algebra so(3) von SO(3); die Operatoren, die die Wirkung von so(3) auf unseren Hilbert-Raum beschreiben, sind die (gesamten) Drehimpulsoperatoren. ⓘ

Die Beziehung zwischen dem Drehimpulsoperator und den Rotationsoperatoren ist die gleiche wie die Beziehung zwischen Lie-Algebren und Lie-Gruppen in der Mathematik. Die enge Beziehung zwischen Drehimpuls und Rotationen spiegelt sich im Noether-Theorem wider, das beweist, dass der Drehimpuls erhalten bleibt, wenn die physikalischen Gesetze rotationsinvariant sind. ⓘ

Drehimpuls in der Elektrodynamik

Bei der Beschreibung der Bewegung eines geladenen Teilchens in einem elektromagnetischen Feld ist der kanonische Impuls P (abgeleitet aus der Lagrange für dieses System) nicht eichinvariant. Infolgedessen ist auch der kanonische Drehimpuls L = r × P nicht eichinvariant. Stattdessen ist der physikalische Impuls, der so genannte kinetische Impuls (der in diesem Artikel durchgehend verwendet wird), (in SI-Einheiten) ⓘ

$\mathbf {p} =m\mathbf {v} =\mathbf {P} -e\mathbf {A}$ ⓘ

wobei e die elektrische Ladung des Teilchens und A das magnetische Vektorpotential des elektromagnetischen Feldes ist. Der eichinvariante Drehimpuls, also der kinetische Drehimpuls, ist gegeben durch ⓘ

$\mathbf {K} =\mathbf {r} \times (\mathbf {P} -e\mathbf {A} )$ ⓘ

Die Wechselwirkung mit der Quantenmechanik wird in dem Artikel über kanonische Kommutationsbeziehungen näher erläutert. ⓘ

Drehimpuls in der Optik

In der klassischen Maxwellschen Elektrodynamik ist der Poynting-Vektor eine lineare Impulsdichte des elektromagnetischen Feldes. ⓘ

$\mathbf {S} (\mathbf {r} ,t)=\epsilon _{0}c^{2}\mathbf {E} (\mathbf {r} ,t)\times \mathbf {B} (\mathbf {r} ,t).$ ⓘ

Der Vektor der Drehimpulsdichte $\mathbf {L} (\mathbf {r} ,t)$ ist gegeben durch ein Vektorprodukt wie in der klassischen Mechanik:

$\mathbf {l} (\mathbf {r} ,t)=\epsilon _{0}\mu _{0}\mathbf {r} \times \mathbf {S} (\mathbf {r} ,t).$ ⓘ

Die obigen Identitäten sind lokal gültig, d. h. in jedem Raumpunkt $\mathbf {r}$ zu einem bestimmten Zeitpunkt $t$. ⓘ

Drehimpuls in der Natur und im Kosmos

Tropische Wirbelstürme und andere verwandte Wetterphänomene erfordern die Erhaltung des Drehimpulses, um die Dynamik zu erklären. Die Winde drehen sich langsam um Tiefdruckgebiete, was hauptsächlich auf den Coriolis-Effekt zurückzuführen ist. Wenn sich das Tiefdruckgebiet verstärkt und die langsam zirkulierende Luft zum Zentrum gezogen wird, müssen die Moleküle schneller werden, um den Drehimpuls zu erhalten. Wenn sie das Zentrum erreichen, werden die Geschwindigkeiten zerstörerisch. ⓘ

Johannes Kepler bestimmte die Gesetze der Planetenbewegung ohne Kenntnis der Impulserhaltung. Doch nicht lange nach seiner Entdeckung wurde ihre Ableitung aus der Drehimpulserhaltung bestimmt. Planeten bewegen sich umso langsamer, je weiter sie sich auf ihren elliptischen Bahnen befinden, was sich intuitiv dadurch erklären lässt, dass der Bahndrehimpuls proportional zum Radius der Bahn ist. Da sich die Masse nicht ändert und der Drehimpuls erhalten bleibt, nimmt die Geschwindigkeit ab. ⓘ

Die Gezeitenbeschleunigung ist ein Effekt der Gezeitenkräfte zwischen einem umlaufenden natürlichen Satelliten (z. B. dem Mond) und dem primären Planeten, den er umkreist (z. B. die Erde). Das Gravitationsmoment zwischen dem Mond und dem Gezeitenwulst der Erde bewirkt, dass der Mond ständig auf eine etwas höhere Umlaufbahn befördert und die Erde in ihrer Rotation abgebremst wird. Die Erde verliert einen Drehimpuls, der auf den Mond übertragen wird, so dass der Drehimpuls insgesamt erhalten bleibt. ⓘ

Drehimpuls in Technik und Technologie

Video: Ein gyroskopisches Trainingsgerät ist eine Anwendung des Drehimpulserhaltungssatzes zur Muskelstärkung. Eine Masse, die sich in einer kugelförmigen Vorrichtung schnell um ihre Achse dreht, definiert einen Drehimpuls. Wenn der Trainierende die Kugel kippt, entsteht eine Kraft, die die Drehgeschwindigkeit noch erhöht, wenn der Trainierende gezielt darauf reagiert. ⓘ

Beispiele für die Nutzung der Drehimpulserhaltung zu praktischen Zwecken gibt es viele. In Motoren wie Dampfmaschinen oder Verbrennungsmotoren wird ein Schwungrad benötigt, um die seitliche Bewegung der Kolben effizient in eine Drehbewegung umzuwandeln. ⓘ

Trägheitsnavigationssysteme nutzen ausdrücklich die Tatsache, dass der Drehimpuls in Bezug auf den Inertialrahmen des Raums erhalten bleibt. Die Trägheitsnavigation ermöglicht U-Boot-Fahrten unter der Polkappe, ist aber auch für alle Formen der modernen Navigation entscheidend. ⓘ

Gewehrkugeln nutzen die durch die Drehimpulserhaltung gegebene Stabilität, um ihre Flugbahn genauer zu gestalten. Die Erfindung der gezogenen Feuerwaffen und Kanonen verschaffte ihren Benutzern einen bedeutenden strategischen Vorteil in der Schlacht und stellte somit einen technologischen Wendepunkt in der Geschichte dar. ⓘ

Geschichte

Isaac Newton wies in seinen Principia auf den Drehimpuls in seinen Beispielen für das erste Bewegungsgesetz hin,

Ein Kreisel, dessen Teile durch ihren Zusammenhalt fortwährend aus der geradlinigen Bewegung herausgezogen werden, hört nicht auf, sich zu drehen, es sei denn, er wird durch die Luft gebremst. Die größeren Körper der Planeten und Kometen, die in freierem Raum auf weniger Widerstand stoßen, behalten ihre fortschreitenden und kreisförmigen Bewegungen viel länger bei.

Er untersuchte den Drehimpuls nicht weiter direkt in den Principia, sondern sagte:

Aus solcher Art von Reflexionen entstehen manchmal auch die Kreisbewegungen von Körpern um ihre eigenen Zentren. Aber das sind Fälle, die ich im Folgenden nicht betrachte; und es wäre zu mühsam, jede Einzelheit zu demonstrieren, die sich auf dieses Thema bezieht.

Sein geometrischer Beweis des Flächengesetzes ist jedoch ein herausragendes Beispiel für Newtons Genialität und beweist indirekt die Drehimpulserhaltung im Falle einer zentralen Kraft. ⓘ

Das Gesetz der Flächeninhalte

Newtons Herleitung

Newtons Herleitung des Flächengesetzes mit geometrischen Mitteln ⓘ

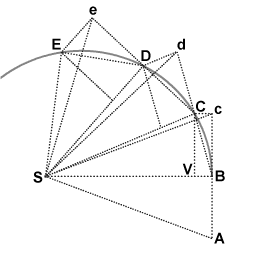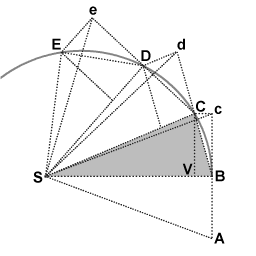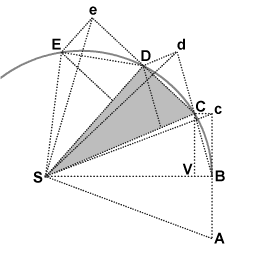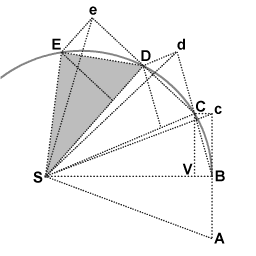
Wenn ein Planet die Sonne umkreist, überstreicht die Linie zwischen der Sonne und dem Planeten in gleichen Zeitabständen gleiche Flächen. Dies war bekannt, seit Kepler sein zweites Gesetz der Planetenbewegung dargelegt hatte. Newton leitete einen einzigartigen geometrischen Beweis ab und zeigte, dass die Anziehungskraft der Schwerkraft der Sonne die Ursache für alle Keplerschen Gesetze ist. ⓘ

Während des ersten Zeitintervalls bewegt sich ein Objekt von Punkt A zu Punkt B. Ungestört würde es sich während des zweiten Intervalls zu Punkt c bewegen. Wenn das Objekt in B ankommt, erhält es einen Impuls, der auf den Punkt S gerichtet ist. Der Impuls verleiht ihm eine kleine zusätzliche Geschwindigkeit in Richtung S, so dass es sich während des zweiten Intervalls von B nach V bewegen würde, wenn dies seine einzige Geschwindigkeit wäre. Nach den Regeln der Geschwindigkeitskomposition addieren sich diese beiden Geschwindigkeiten, und der Punkt C wird durch die Konstruktion des Parallelogramms BcCV gefunden. Die Bahn des Objekts wird also durch den Impuls so abgelenkt, dass es am Ende des zweiten Intervalls im Punkt C ankommt. Da die Dreiecke SBc und SBC die gleiche Basis SB und die gleiche Höhe Bc oder VC haben, haben sie den gleichen Flächeninhalt. Aufgrund der Symmetrie hat das Dreieck SBc auch die gleiche Fläche wie das Dreieck SAB, so dass das Objekt die gleichen Flächen SAB und SBC in gleicher Zeit ausgefegt hat. ⓘ

Am Punkt C erhält das Objekt einen weiteren Impuls in Richtung S, der seine Bahn während des dritten Intervalls von d nach D erneut ablenkt. So geht es weiter bis E und darüber hinaus, wobei die Dreiecke SAB, SBc, SBC, SCd, SCD, SDe, SDE alle die gleiche Fläche haben. Wenn man die Zeitintervalle immer kleiner werden lässt, nähert sich der Pfad ABCDE auf unbestimmte Zeit einer kontinuierlichen Kurve an. ⓘ

Da diese Herleitung geometrisch ist und keine spezifische Kraft angewendet wird, beweist sie ein allgemeineres Gesetz als Keplers zweites Gesetz der Planetenbewegung. Es zeigt, dass das Flächengesetz für jede zentrale Kraft gilt, ob sie nun anziehend oder abstoßend, kontinuierlich oder nicht kontinuierlich oder null ist. ⓘ

Drehimpulserhaltung im Flächengesetz

Die Proportionalität des Drehimpulses zur Fläche, die von einem bewegten Objekt durchlaufen wird, lässt sich verstehen, wenn man sich vergegenwärtigt, dass die Basen der Dreiecke, d. h. die Linien von S zum Objekt, dem Radius entsprechen rentsprechen, und dass die Höhen der Dreiecke proportional zur senkrechten Komponente der Geschwindigkeit sind v_⊥. Wenn also die pro Zeiteinheit überstrichene Fläche konstant ist, dann ergibt sich nach der Formel für die Dreiecksfläche 1/2(Basis)(Höhe) das Produkt (Basis)(Höhe) und damit das Produkt rv_⊥ konstant sind: wenn r und die Basislänge verringert werden, vmüssen _⊥ und Höhe proportional zunehmen. Die Masse ist konstant, daher ist der Drehimpuls rmv_⊥ durch diesen Austausch von Abstand und Geschwindigkeit erhalten bleibt. ⓘ

Im Falle des Dreiecks SBC ist die Fläche gleich 1/2(SB)(VC). Wo immer sich C aufgrund des Impulses bei B befindet, ist das Produkt (SB)(VC) und damit rmv_⊥ konstant bleiben. Ähnlich verhält es sich für jedes der Dreiecke. ⓘ

Nach Newton

Leonhard Euler, Daniel Bernoulli und Patrick d'Arcy verstanden alle den Drehimpuls im Sinne der Erhaltung der Flächengeschwindigkeit, ein Ergebnis ihrer Analyse von Keplers zweitem Gesetz der Planetenbewegung. Es ist unwahrscheinlich, dass sie die Auswirkungen auf gewöhnliche rotierende Materie erkannten. ⓘ

Wie Newton berührte auch Euler 1736 in seiner Mechanica einige der Drehimpulsgleichungen, ohne sie weiter zu entwickeln. ⓘ

Bernoulli schrieb 1744 in einem Brief von einem "Moment der Rotationsbewegung", möglicherweise die erste Konzeption des Drehimpulses, wie wir ihn heute verstehen. ⓘ

1799 erkannte Pierre-Simon Laplace zum ersten Mal, dass eine feste Ebene mit der Rotation verbunden war - seine unveränderliche Ebene. ⓘ

Louis Poinsot begann 1803, Drehungen als Liniensegment senkrecht zur Drehung darzustellen, und entwickelte die "Erhaltung der Momente" weiter. ⓘ

1852 verwendete Léon Foucault in einem Experiment ein Gyroskop, um die Erdrotation anzuzeigen. ⓘ

Im Manual of Applied Mechanics von William J. M. Rankine aus dem Jahr 1858 wurde der Drehimpuls erstmals im modernen Sinne definiert:

...eine Linie, deren Länge proportional zur Größe des Drehimpulses ist und deren Richtung senkrecht zur Bewegungsebene des Körpers und des Fixpunkts verläuft, und zwar so, dass, wenn die Bewegung des Körpers vom Ende der Linie aus betrachtet wird, der Radiusvektor des Körpers eine rechtshändige Drehung zu haben scheint.

In einer Ausgabe desselben Buches von 1872 erklärte Rankine, dass "der Begriff Drehimpuls von Mr. Hayward eingeführt wurde", womit er sich wahrscheinlich auf R.B. Haywards Artikel On a Direct Method of estimating Velocities, Accelerations, and all similar Quantities with respect to Axes moveable in any manner in Space with Applications bezog, der 1856 eingeführt und 1864 veröffentlicht wurde. Rankine irrte sich, denn der Begriff taucht in zahlreichen Veröffentlichungen ab dem späten 18. bis frühen 19. Der Artikel von Hayward war jedoch offensichtlich die erste Verwendung des Begriffs und des Konzepts, das von einem Großteil der englischsprachigen Welt wahrgenommen wurde. Davor wurde der Drehimpuls im Englischen in der Regel als "momentum of rotation" bezeichnet. ⓘ

Verschiebung, Drehung, Spiegelung

Während Ortsvektor ${\vec {r}}$ und Impuls ${\vec {p}}=m{\vec {v}}$ bei einer Punktspiegelung um den Koordinatenursprung ihre Richtung umkehren, bleibt die des Drehimpulses bezüglich der Scheibenmitte ${\vec {L}}=m{\vec {r}}\times {\vec {v}}$ unverändert. (Im Bild sind die Vektoren in Fettdruck und nicht mit Pfeil gezeichnet.) ⓘ

Betrag und Richtung des Drehimpulses einer Punktmasse hängen davon ab, welchen Punkt man als Bezugspunkt wählt. Bei Verschiebung des Bezugspunkts ändert sich der Vektor jedes Ortes in ${\vec {x}}^{\,\prime }={\vec {x}}+{\vec {a}}$ und der Drehimpuls in ⓘ

${\vec {L}}^{\prime }={\vec {L}}+{\vec {a}}\times {\vec {p}}.$ ⓘ

Oft wählt man als Bezugspunkt den Massenmittelpunkt oder einen Punkt, der bei den betrachteten Drehungen ruht, also auf der Drehachse liegt. ⓘ

Das Kreuzprodukt zweier Vektoren steht stets senkrecht auf der von ihnen aufgespannten Ebene, eine Drehung des betrachteten Systems aber dreht sowohl die Ortsvektoren als auch die Bahngeschwindigkeiten um denselben Betrag, wodurch auch der Drehimpuls in gleicher Weise mitgedreht wird. ⓘ

Bei einer Punktspiegelung am Bezugspunkt geht der Ort in den gegenüber liegenden Ort über. Auch das Vorzeichen der Geschwindigkeit in Bezug auf diesen Punkt kehrt sich um. Bei der Bildung des Kreuzprodukts kompensieren sich diese beiden Vorzeichenwechsel, sodass sich bei einer Punktspiegelung der Drehimpuls nicht ändert. Damit unterscheidet er sich vom Verhalten der Geschwindigkeit oder des Ortsvektors: Der Drehimpuls gehört zur Klasse der Pseudovektoren. ⓘ