Ereignishorizont
| Allgemeine Relativitätstheorie ⓘ |
|---|
 |
|
|
In der Astrophysik ist ein Ereignishorizont eine Grenze, jenseits derer Ereignisse einen Beobachter nicht beeinflussen können. Wolfgang Rindler prägte den Begriff in den 1950er Jahren. ⓘ
Im Jahr 1784 schlug John Michell vor, dass die Schwerkraft in der Nähe massereicher kompakter Objekte so stark sein kann, dass nicht einmal das Licht entkommen kann. Zu dieser Zeit waren die Newtonsche Gravitationstheorie und die so genannte Korpuskeltheorie des Lichts vorherrschend. Wenn die Fluchtgeschwindigkeit des Gravitationseinflusses eines massiven Objekts die Lichtgeschwindigkeit übersteigt, kann nach diesen Theorien Licht, das aus dem Inneren des Objekts oder von ihm stammt, vorübergehend entkommen, kehrt aber zurück. 1958 führte David Finkelstein auf der Grundlage der allgemeinen Relativitätstheorie eine strengere Definition des lokalen Ereignishorizonts eines Schwarzen Lochs ein, d. h. einer Grenze, jenseits derer Ereignisse jeglicher Art keinen Einfluss auf einen außenstehenden Beobachter haben können, was zu Informations- und Firewall-Paradoxien führte und eine erneute Überprüfung des Konzepts lokaler Ereignishorizonte und des Begriffs Schwarzer Löcher zur Folge hatte. In der Folge wurden mehrere Theorien entwickelt, einige mit, andere ohne Ereignishorizonte. Stephen Hawking, einer der führenden Entwickler von Theorien zur Beschreibung Schwarzer Löcher, schlug vor, anstelle eines Ereignishorizonts einen scheinbaren Horizont zu verwenden: "Der Gravitationskollaps erzeugt scheinbare Horizonte, aber keine Ereignishorizonte". Schließlich kam er zu dem Schluss, dass "das Fehlen von Ereignishorizonten bedeutet, dass es keine schwarzen Löcher gibt - im Sinne von Zuständen, aus denen das Licht nicht ins Unendliche entweichen kann." ⓘ
Jedes Objekt, das sich dem Horizont von der Seite des Beobachters aus nähert, scheint langsamer zu werden und den Horizont nie ganz zu überqueren. Aufgrund der Rotverschiebung durch die Schwerkraft wird sein Bild mit der Zeit röter, je weiter sich das Objekt vom Beobachter entfernt. ⓘ
In einem expandierenden Universum erreicht die Expansionsgeschwindigkeit die Lichtgeschwindigkeit und übersteigt sie sogar, so dass Signale nicht mehr in bestimmte Regionen gelangen können. Ein kosmischer Ereignishorizont ist ein echter Ereignishorizont, da er alle Arten von Signalen beeinflusst, einschließlich Gravitationswellen, die sich mit Lichtgeschwindigkeit ausbreiten. ⓘ
Zu den spezifischeren Arten von Horizonten gehören die verwandten, aber unterschiedlichen absoluten und scheinbaren Horizonte, die um ein Schwarzes Loch herum zu finden sind. Weitere unterschiedliche Typen sind:
- Der Cauchy-Horizont und der Killing-Horizont.
- Die Photonensphären und Ergosphären der Kerr-Lösung.
- Teilchenhorizonte und kosmologische Horizonte, die für die Kosmologie relevant sind.
- Isolierte und dynamische Horizonte, die in der aktuellen Forschung zu Schwarzen Löchern von Bedeutung sind. ⓘ
| statisch | rotierend | |
|---|---|---|
| ungeladen | Schwarzschild-Metrik | Kerr-Metrik |
| geladen | Reissner-Nordström-Metrik | Kerr-Newman-Metrik |
| : Elektrische Ladung; : Drehimpuls | ||
Ein Ereignishorizont ist in der allgemeinen Relativitätstheorie eine Grenzfläche in der Raumzeit, für die gilt, dass Ereignisse jenseits dieser Grenzfläche prinzipiell nicht sichtbar für Beobachter sind, die sich diesseits der Grenzfläche befinden. Mit „Ereignissen“ sind Punkte in der Raumzeit gemeint, die durch Ort und Zeit festgelegt sind. Der Ereignishorizont bildet eine Grenze für Informationen und kausale Zusammenhänge, die sich aus der Struktur der Raumzeit und den Gesetzen der Physik, insbesondere in Bezug auf die Lichtgeschwindigkeit, ergeben. Bei statischen Schwarzen Löchern ist der Ereignishorizont eine Kugeloberfläche, deren Radius Schwarzschild-Radius genannt wird. ⓘ
Für jede Masse ab der Planckmasse (ca. 22 µg) gibt es einen Schwarzschild-Radius: Wenn ein Objekt auf ein Kugelvolumen mit einem kleineren Radius als seinem Schwarzschild-Radius komprimiert wird, so wird es ein Schwarzes Loch. Masseärmere Objekte haben eine zu große Ortsunschärfe und können deshalb nicht ausreichend komprimiert werden. Zum Beispiel liegt die Ortsunschärfe eines viel masseärmeren Protons bei etwa 10−15 m, während der Ereignishorizont bei 10−54 m läge. ⓘ
Form und Größe des Ereignishorizontes hängen nur von der Masse, dem Drehimpuls und der Ladung des Schwarzen Lochs in seinem Innern ab. Im Allgemeinen hat der Ereignishorizont die Form eines Rotationsellipsoids. Bei einem nicht rotierenden, elektrisch ungeladenen Schwarzen Loch ist er kugelförmig. ⓘ
Kosmischer Ereignishorizont
In der Kosmologie ist der Ereignishorizont des beobachtbaren Universums die größte Entfernung, aus der Licht, das heute ausgesendet wird, den Beobachter in der Zukunft erreichen kann. Dies unterscheidet sich von dem Konzept des Teilchenhorizonts, der die größte Entfernung darstellt, aus der in der Vergangenheit ausgesandtes Licht den Beobachter zu einem bestimmten Zeitpunkt erreichen kann. Für Ereignisse, die jenseits dieser Entfernung stattfinden, hatte das Licht nicht genug Zeit, um unseren Standort zu erreichen, selbst wenn es zu Beginn des Universums ausgesendet wurde. Die Entwicklung des Teilchenhorizonts mit der Zeit hängt von der Art der Expansion des Universums ab. Wenn die Expansion bestimmte Merkmale aufweist, werden Teile des Universums niemals beobachtbar sein, egal wie lange der Beobachter darauf wartet, dass das Licht aus diesen Regionen eintrifft. Die Grenze, jenseits derer Ereignisse niemals beobachtet werden können, ist ein Ereignishorizont und stellt die maximale Ausdehnung des Teilchenhorizonts dar. ⓘ
Das Kriterium für die Feststellung, ob ein Teilchenhorizont für das Universum existiert, lautet wie folgt. Definieren Sie eine bewegliche Entfernung dp als
In dieser Gleichung ist a der Skalenfaktor, c ist die Lichtgeschwindigkeit und t0 ist das Alter des Universums. Wenn dp → ∞ (d. h. Punkte, die beliebig weit entfernt sind), dann existiert kein Ereignishorizont. Wenn dp ≠ ∞, ist ein Horizont vorhanden. ⓘ
Beispiele für kosmologische Modelle ohne Ereignishorizont sind Universen, die von Materie oder Strahlung dominiert werden. Ein Beispiel für ein kosmologisches Modell mit Ereignishorizont ist ein Universum, in dem die kosmologische Konstante vorherrscht (ein de-Sitter-Universum). ⓘ
Eine Berechnung der Geschwindigkeiten des kosmologischen Ereignishorizonts und der Teilchenhorizonte wurde in einer Arbeit über das kosmologische FLRW-Modell vorgenommen, das das Universum als aus nicht wechselwirkenden Bestandteilen zusammengesetzt annähert, wobei jeder Bestandteil eine perfekte Flüssigkeit ist. ⓘ
Scheinbarer Horizont eines beschleunigten Teilchens

Bewegt sich ein Teilchen mit konstanter Geschwindigkeit in einem sich nicht ausdehnenden Universum, das frei von Gravitationsfeldern ist, wird jedes Ereignis, das sich in diesem Universum ereignet, schließlich von dem Teilchen beobachtet werden können, da die vorderen Lichtkegel dieser Ereignisse die Weltlinie des Teilchens schneiden. Wenn das Teilchen jedoch beschleunigt wird, schneiden die Lichtkegel einiger Ereignisse die Weltlinie des Teilchens in manchen Situationen nie. Unter diesen Bedingungen gibt es im (beschleunigten) Bezugssystem des Teilchens einen scheinbaren Horizont, der eine Grenze darstellt, jenseits derer Ereignisse nicht mehr beobachtbar sind. ⓘ
Dies ist zum Beispiel bei einem gleichmäßig beschleunigten Teilchen der Fall. Ein Raumzeitdiagramm dieser Situation ist in der Abbildung rechts zu sehen. Während das Teilchen beschleunigt, nähert es sich der Lichtgeschwindigkeit in Bezug auf sein ursprüngliches Bezugssystem, erreicht sie aber nie. Im Raum-Zeit-Diagramm ist seine Bahn eine Hyperbel, die sich asymptotisch einer 45-Grad-Linie (der Bahn eines Lichtstrahls) nähert. Ein Ereignis, dessen Lichtkegelrand diese Asymptote ist oder weiter als diese Asymptote entfernt ist, kann von dem beschleunigenden Teilchen niemals beobachtet werden. Im Bezugssystem des Teilchens befindet sich hinter ihm eine Grenze, aus der keine Signale entweichen können (ein scheinbarer Horizont). Der Abstand zu dieser Grenze ist gegeben durch , wobei a die konstante Eigenbeschleunigung des Teilchens ist. ⓘ
Während in der realen Welt (z. B. in Teilchenbeschleunigern) Annäherungen an diese Art von Situation vorkommen können, ist ein echter Ereignishorizont niemals vorhanden, da dies voraussetzt, dass das Teilchen unbegrenzt beschleunigt wird (was beliebig große Energiemengen und einen beliebig großen Apparat erfordert). ⓘ
Wechselwirkung mit einem kosmischen Horizont
Im Falle eines Horizonts, der von einem gleichmäßig beschleunigten Beobachter im leeren Raum wahrgenommen wird, scheint der Horizont in einem festen Abstand zum Beobachter zu bleiben, unabhängig davon, wie sich seine Umgebung bewegt. Eine Änderung der Beschleunigung des Beobachters kann dazu führen, dass sich der Horizont mit der Zeit zu bewegen scheint oder dass es keinen Ereignishorizont gibt, je nach der gewählten Beschleunigungsfunktion. Der Beobachter berührt nie den Horizont und passiert nie einen Ort, an dem er zu sein schien. ⓘ
Im Falle eines Horizonts, der von einem Bewohner eines De-Sitter-Universums wahrgenommen wird, scheint der Horizont für einen nichtbeschleunigenden Beobachter immer in einer festen Entfernung zu liegen. Er wird nie berührt, auch nicht von einem beschleunigten Beobachter. ⓘ
Ereignishorizont eines Schwarzen Lochs
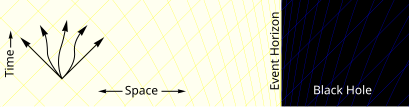 Weit entfernt vom Schwarzen Loch kann sich ein Teilchen in jede beliebige Richtung bewegen. Es ist nur durch die Lichtgeschwindigkeit eingeschränkt. ⓘ |
 Näher am Schwarzen Loch beginnt sich die Raumzeit zu verformen. In einigen geeigneten Koordinatensystemen gibt es mehr Pfade, die auf das Schwarze Loch zugehen, als Pfade, die sich davon entfernen. |
 Innerhalb des Ereignishorizonts führen alle zukünftigen Zeitpfade das Teilchen näher an das Zentrum des Schwarzen Lochs heran. Ein Entkommen des Teilchens ist nicht mehr möglich, egal in welche Richtung es sich bewegt. |
Eines der bekanntesten Beispiele für einen Ereignishorizont stammt aus der Beschreibung der allgemeinen Relativitätstheorie für ein Schwarzes Loch, ein Himmelsobjekt, das so dicht ist, dass keine Materie oder Strahlung in der Nähe seinem Gravitationsfeld entkommen kann. Häufig wird dies als die Grenze beschrieben, innerhalb derer die Fluchtgeschwindigkeit des Schwarzen Lochs größer als die Lichtgeschwindigkeit ist. Eine detailliertere Beschreibung ist jedoch, dass innerhalb dieses Horizonts alle lichtähnlichen Pfade (Pfade, die das Licht nehmen könnte) (und somit alle Pfade in den vorderen Lichtkegeln der Teilchen innerhalb des Horizonts) so verzerrt werden, dass sie weiter in das Loch fallen. Sobald sich ein Teilchen innerhalb des Horizonts befindet, ist die Bewegung in das Loch so unvermeidlich wie eine Vorwärtsbewegung in der Zeit - unabhängig davon, in welche Richtung sich das Teilchen bewegt - und kann je nach dem verwendeten Raumzeit-Koordinatensystem als äquivalent zu dieser Bewegung angesehen werden. ⓘ
Die Oberfläche am Schwarzschild-Radius wirkt bei einem nicht rotierenden Körper, der in diesen Radius passt, wie ein Ereignishorizont (bei einem rotierenden Schwarzen Loch verhält es sich allerdings etwas anders). Der Schwarzschild-Radius eines Objekts ist proportional zu seiner Masse. Theoretisch wird jede Menge Materie zu einem Schwarzen Loch, wenn sie in einen Raum komprimiert wird, der in den entsprechenden Schwarzschild-Radius passt. Für die Masse der Sonne beträgt dieser Radius etwa 3 Kilometer, für die Erde etwa 9 Millimeter (0,35 Zoll). In der Praxis haben jedoch weder die Erde noch die Sonne die erforderliche Masse (und damit die erforderliche Gravitationskraft), um den Druck der Elektronen- und Neutronenentartung zu überwinden. Die minimale Masse, die erforderlich ist, damit ein Stern über diese Drücke hinaus kollabiert, ist die Tolman-Oppenheimer-Volkoff-Grenze, die bei etwa drei Sonnenmassen liegt. ⓘ
Nach den grundlegenden Gravitationskollapsmodellen bildet sich vor der Singularität eines Schwarzen Lochs ein Ereignishorizont. Würden sich alle Sterne in der Milchstraße unter Beibehaltung ihrer proportionalen Abstände zum galaktischen Zentrum allmählich zusammenballen, würden sie alle in ihren gemeinsamen Schwarzschild-Radius fallen, lange bevor sie zur Kollision gezwungen werden. Bis zum Kollaps in ferner Zukunft würden die Beobachter in einer Galaxie, die von einem Ereignishorizont umgeben ist, ihr Leben normal weiterführen. ⓘ
Ereignishorizonte schwarzer Löcher werden weithin missverstanden. Weit verbreitet, wenn auch falsch, ist die Vorstellung, dass Schwarze Löcher die Materie in ihrer Umgebung "aufsaugen", obwohl sie in Wirklichkeit genauso wenig in der Lage sind, nach Material zu suchen, das sie verzehren können, wie jeder andere Gravitationsanzieher. Wie bei jeder Masse im Universum muss die Materie in ihren Gravitationsbereich kommen, damit die Möglichkeit besteht, sie einzufangen oder mit einer anderen Masse zu vereinigen. Ebenso verbreitet ist die Vorstellung, dass man beobachten kann, wie Materie in ein schwarzes Loch fällt. Dies ist jedoch nicht möglich. Astronomen können nur Akkretionsscheiben um Schwarze Löcher nachweisen, in denen sich Materie mit einer solchen Geschwindigkeit bewegt, dass durch Reibung hochenergetische Strahlung entsteht, die nachgewiesen werden kann (ebenso wird ein Teil der Materie aus diesen Akkretionsscheiben entlang der Rotationsachse des Schwarzen Lochs herausgedrückt, wodurch sichtbare Strahlen entstehen, wenn diese Ströme mit Materie wie interstellarem Gas interagieren oder wenn sie zufällig direkt auf die Erde gerichtet sind). Darüber hinaus wird ein entfernter Beobachter niemals sehen, dass etwas den Horizont erreicht. Stattdessen scheint das Objekt bei seiner Annäherung an das Loch immer langsamer zu werden, während das von ihm ausgesandte Licht immer weiter rotverschoben wird. ⓘ
Topologisch ist der Ereignishorizont von der Kausalstruktur her als der vergangene Nullkegel der zukünftigen konformen zeitlichen Unendlichkeit definiert. ⓘ
Der Ereignishorizont des Schwarzen Lochs ist teleologischer Natur, was bedeutet, dass wir die gesamte zukünftige Raumzeit des Universums kennen müssten, um die aktuelle Position des Horizonts zu bestimmen, was im Grunde unmöglich ist. Aufgrund des rein theoretischen Charakters der Grenze des Ereignishorizonts erfährt das reisende Objekt nicht notwendigerweise seltsame Effekte und durchquert die berechnete Grenze tatsächlich in einer endlichen Eigenzeit. ⓘ
Wechselwirkung mit Horizonten Schwarzer Löcher
Ein Missverständnis im Zusammenhang mit Ereignishorizonten, insbesondere mit Ereignishorizonten von Schwarzen Löchern, besteht darin, dass sie eine unveränderliche Oberfläche darstellen, die Objekte, die sich ihnen nähern, vernichtet. In der Praxis scheinen alle Ereignishorizonte in einiger Entfernung von jedem Beobachter zu liegen, und Objekte, die in Richtung eines Ereignishorizonts geschickt werden, scheinen diesen aus der Sicht des sendenden Beobachters nie zu durchqueren (da der Lichtkegel des Ereignisses, das den Horizont durchquert, die Weltlinie des Beobachters nie schneidet). Der Versuch, ein Objekt in der Nähe des Horizonts in Bezug auf einen Beobachter zum Stillstand zu bringen, erfordert die Anwendung einer Kraft, deren Größe unbegrenzt zunimmt (und unendlich wird), je näher sie kommt. ⓘ
Im Falle des Horizonts um ein schwarzes Loch sind sich alle Beobachter, die sich in Bezug auf ein entferntes Objekt nicht bewegen, einig, wo sich der Horizont befindet. Dies scheint es einem Beobachter, der an einem Seil (oder Stab) zum Loch hinuntergelassen wird, zwar zu ermöglichen, den Horizont zu berühren, in der Praxis ist dies jedoch nicht möglich. Wird das Seil jedoch langsam herabgelassen (so dass sich jeder Punkt auf dem Seil in Schwarzschild-Koordinaten annähernd in Ruhe befindet), so nähert sich die Eigenbeschleunigung (G-Kraft), die die Punkte auf dem Seil erfahren, die sich dem Horizont immer mehr nähern, der Unendlichkeit an, so dass das Seil zerreißen würde. Wenn das Seil schnell herabgelassen wird (vielleicht sogar im freien Fall), dann kann der Beobachter am unteren Ende des Seils tatsächlich den Ereignishorizont berühren und sogar überschreiten. Sobald dies jedoch geschieht, ist es unmöglich, das untere Ende des Seils wieder aus dem Ereignishorizont herauszuziehen, denn wenn das Seil straff gezogen wird, nehmen die Kräfte entlang des Seils bei Annäherung an den Ereignishorizont unbegrenzt zu, und irgendwann muss das Seil reißen. Außerdem darf der Bruch nicht am Ereignishorizont erfolgen, sondern muss an einem Punkt auftreten, an dem der zweite Beobachter ihn beobachten kann. ⓘ
Unter der Annahme, dass der mögliche scheinbare Horizont weit innerhalb des Ereignishorizonts liegt oder dass es keinen gibt, würden Beobachter, die einen Ereignishorizont eines Schwarzen Lochs durchqueren, in diesem Moment nichts Besonderes sehen oder spüren. Visuell gesehen nehmen Beobachter, die in das Loch fallen, den möglichen scheinbaren Horizont als einen schwarzen, undurchlässigen Bereich wahr, der die Singularität umschließt. Andere Objekte, die auf demselben radialen Weg, aber zu einem früheren Zeitpunkt in den Bereich des Horizonts eingetreten sind, würden unter dem Beobachter erscheinen, solange sie nicht in den scheinbaren Horizont eingetreten sind, und sie könnten Nachrichten austauschen. Zunehmende Gezeitenkräfte sind ebenfalls lokal spürbare Effekte, die von der Masse des Schwarzen Lochs abhängen. In realistischen stellaren Schwarzen Löchern tritt die Spaghettifizierung früh auf: Die Gezeitenkräfte reißen die Materie weit vor dem Ereignishorizont auseinander. Bei supermassiven Schwarzen Löchern, die sich in den Zentren von Galaxien befinden, tritt die Spaghettifizierung jedoch innerhalb des Ereignishorizonts auf. Ein menschlicher Astronaut würde den Fall durch einen Ereignishorizont nur in einem Schwarzen Loch mit einer Masse von etwa 10 000 Sonnenmassen oder mehr überleben. ⓘ
Jenseits der allgemeinen Relativitätstheorie
Ein kosmischer Ereignishorizont wird gemeinhin als realer Ereignishorizont akzeptiert, während die Beschreibung eines lokalen Ereignishorizonts eines Schwarzen Lochs durch die allgemeine Relativitätstheorie als unvollständig und umstritten gilt. Wenn die Bedingungen, unter denen lokale Ereignishorizonte auftreten, mit Hilfe eines umfassenderen Bildes von der Funktionsweise des Universums modelliert werden, das sowohl die Relativitätstheorie als auch die Quantenmechanik einschließt, wird erwartet, dass lokale Ereignishorizonte andere Eigenschaften haben als die, die mit der allgemeinen Relativitätstheorie allein vorhergesagt werden. ⓘ
Gegenwärtig geht man davon aus, dass der Hawking-Strahlungsmechanismus die primäre Auswirkung von Quanteneffekten darin besteht, dass Ereignishorizonte eine Temperatur besitzen und daher Strahlung aussenden. Bei Schwarzen Löchern äußert sich dies als Hawking-Strahlung, und die umfassendere Frage, wie das Schwarze Loch eine Temperatur erhält, ist Teil des Themas der Thermodynamik Schwarzer Löcher. Bei beschleunigten Teilchen äußert sich dies in Form des Unruh-Effekts, durch den der Raum um das Teilchen herum mit Materie und Strahlung gefüllt zu sein scheint. ⓘ
Nach der umstrittenen Firewall-Hypothese für Schwarze Löcher würde Materie, die in ein Schwarzes Loch fällt, durch eine hochenergetische "Firewall" am Ereignishorizont verbrannt werden. ⓘ
Eine Alternative bietet das Komplementaritätsprinzip, demzufolge im Horoskop des fernen Beobachters die einfallende Materie am Horizont thermalisiert und als Hawking-Strahlung reemittiert wird, während im Horoskop eines einfallenden Beobachters die Materie ungestört durch den inneren Bereich weiterläuft und an der Singularität zerstört wird. Diese Hypothese verstößt nicht gegen das No-Cloning-Theorem, da es für jeden Beobachter nur eine einzige Kopie der Information gibt. Die Komplementarität von Schwarzen Löchern wird durch die Skalierungsgesetze von Strings nahe dem Ereignishorizont nahegelegt, die darauf hindeuten, dass sie sich im Schwarzschild-Diagramm so ausdehnen, dass sie den Horizont bedecken und sich zu einer Plancklängen dicken Membran thermisieren. ⓘ
Für eine vollständige Beschreibung lokaler Ereignishorizonte, die durch die Schwerkraft erzeugt werden, dürfte zumindest eine Theorie der Quantengravitation erforderlich sein. Eine solche Theorie könnte die M-Theorie sein. Ein weiterer Kandidat ist die Schleifenquantengravitation. ⓘ
Geschichte
John Michell war der Erste, der sich mit der Frage auseinandersetzte, wie groß die Anziehungskraft eines Himmelskörpers sein muss, damit Licht nicht mehr von seiner Oberfläche entweichen kann. Unter Benutzung der Newtonschen Gravitationstheorie und der Korpuskeltheorie fand er 1783 eine Beziehung zwischen dem Radius und der Masse eines Himmelskörpers, bei dem dieser Effekt auftritt. Diesen Radius hat Karl Schwarzschild 1916 in einer allgemeinrelativistischen Rechnung wiedergefunden, daher wurde er ihm zu Ehren als Schwarzschild-Radius bezeichnet. ⓘ
Schwarzschild-Radius
Der Schwarzschild-Radius eines Körpers der Masse ist gegeben durch:
Häufig wird die Masse von Objekten in der Astronomie in Sonnenmassen angegeben, mit . Für den Schwarzschild-Radius der Sonne ergibt sich damit:
oder allgemein:
- . ⓘ
Für die Masse der Erde beträgt der Schwarzschild-Radius 9 mm und für den Mount Everest 1 nm. ⓘ
Das Schwarzschild-Volumen beträgt ⓘ
womit sich eine kritische Dichte durch ⓘ
definieren lässt. Sobald ein Körper diese Dichte überschreitet, entsteht ein Schwarzes Loch. Man beachte, dass die kritische Dichte mit zunehmender Masse abnimmt. ⓘ
| Objekt | Masse | Schwarzschild- radius |
Volumen | Dichte ⓘ |
|---|---|---|---|---|
| Deimos-Masse (Schwarzschildradius ~1500 Protonenradien) |
1,8 · 1015 kg | 2,6 pm | ||
| Mondmasse (1/81 Erdmasse) | 7,346 · 1022 kg | 0,109 mm | 0,005 43 mm3 | |
| Erdmasse | 5,969 · 1024 kg | 8,86 mm | 2,917 cm3 | 2,046 · 1030 kg/m3 |
| Sonnenmasse (333000 Erdmassen) | 1,988 · 1030 kg | 2952 m | 107,8 km3 | 1,845 · 1019 kg/m3 |
| Sagittarius A* (4,3 Mill. Sonnenmassen) |
8,5 · 1036 kg | 12,7 Mill. km 0,085 AE |
106 kg/m3 51-fache Dichte von Gold | |
| Masse der Milchstraße (2 Bill. Sonnenmassen) |
~4 · 1042 kg | ~6,4 Bill. km ~40.000 AE |
~4,5 mg/m3 Dichte von H2 bei 300 K/5 Pa | |
| Radius des beobachtbaren Universums |
2,97 · 1053 kg | 46,6 Mrd. Lj. |
Ereignishorizont in der Schwarzschild-Metrik
Bei nichtrotierenden, ungeladenen Schwarzen Löchern gilt die Schwarzschild-Metrik, und der Ereignishorizont ist mit dem Schwarzschild-Radius identisch. ⓘ
Zu beachten ist ferner, dass der Radius des Ereignishorizonts in der allgemeinen Relativitätstheorie nicht den Abstand vom Mittelpunkt angibt, sondern über die Oberfläche von Kugeln definiert ist. Ein kugelförmiger Ereignishorizont mit Radius hat dieselbe Fläche wie eine Sphäre gleichen Radius im euklidischen Raum, nämlich . Aufgrund der Raumzeitkrümmung sind die radialen Abstände im Gravitationsfeld vergrößert (das heißt, der Abstand zweier Kugelschalen mit – über die Kugelfläche definierten – Radialkoordinaten und ist größer als die Differenz dieser Radien). ⓘ
Bedeutung und Eigenschaften des Ereignishorizonts eines Schwarzen Lochs
Gravitative Rotverschiebung
Die Frequenz eines Photons, das aus einem Gravitationsfeld zu einem entfernten Beobachter gelangt, wird zum roten (energiearmen) Teil des Lichtspektrums verschoben, da dem Photon die entsprechende potentielle Energie verloren geht. Die Rotverschiebung ist umso größer, je näher sich die Lichtquelle am Schwarzen Loch befindet. Am Ereignishorizont wird die Rotverschiebung unendlich groß. ⓘ
Einfallzeit für einen außenstehenden Beobachter
Für einen außenstehenden Beobachter, der aus sicherer Entfernung zusieht, wie ein Teilchen auf ein Schwarzes Loch zufällt, hat es den Anschein, als würde es sich asymptotisch dem Ereignishorizont annähern. Das bedeutet, ein außenstehender Beobachter sieht niemals, wie es den Ereignishorizont erreicht, da aus seiner Sicht dazu unendlich viel Zeit benötigt wird. Das gilt nicht für makroskopische Objekte, die selbst die Raumzeit verformen. Insbesondere lassen sich Supernovae beobachten. ⓘ
Drehimpuls und elektrische Ladung
Elektrisch geladene Schwarze Löcher
Elektrisch geladene, nichtrotierende Schwarze Löcher werden durch die Reissner-Nordström-Metrik beschrieben, elektrisch geladene, rotierende Schwarze Löcher durch die Kerr-Newman-Metrik. ⓘ





















