Thales
Thales von Milet ⓘ | |
|---|---|
 Posthumes Porträt von Thales von Wilhelm Meyer, nach einer Büste aus dem 4. | |
| Geboren | c. 626/623 V. CHR. Antike griechische Stadt Milet (heute: Balat, Didim, Aydın, Türkei) |
| Gestorben | c. 548/545 v. Chr. (im Alter von 78 Jahren) |
| Zeitalter | Vorsokratische Philosophie |
| Region | Westliche Philosophie |
| Schule |
|
Hauptinteressen | |
Bemerkenswerte Ideen |
|
Einflüsse
| |
Beeinflusst
| |
Thales von Milet (/ˈθeɪliːz/ THAY-leez; griechisch: Θαλῆς; ca. 624/623 - ca. 548/545 v. Chr.) war ein griechischer Mathematiker, Astronom und vorsokratischer Philosoph aus Milet in Ionien, Kleinasien. Er war einer der Sieben Weisen Griechenlands. Viele, vor allem Aristoteles, betrachteten ihn als den ersten Philosophen der griechischen Tradition, und auch sonst gilt er historisch als die erste Person, von der bekannt ist, dass sie sich mit wissenschaftlicher Philosophie befasst hat. Er wird oft als der Vater der Wissenschaft bezeichnet. ⓘ
Thales ist dafür bekannt, dass er die Welt und das Universum nicht mehr mit Hilfe der Mythologie erklärte, sondern natürliche Objekte und Phänomene durch naturalistische Theorien und Hypothesen erklärte. Fast alle anderen vorsokratischen Philosophen folgten ihm, indem sie die Natur aus einer Einheit von allem erklärten, die auf der Existenz einer einzigen ultimativen Substanz beruht, anstatt mythologische Erklärungen zu verwenden. Aristoteles betrachtete ihn als den Begründer der Ionischen Schule der Philosophie und berichtete über Thales' Hypothese, dass das Ursprungsprinzip der Natur und die Natur der Materie eine einzige materielle Substanz sei: Wasser. ⓘ
In der Mathematik nutzte Thales die Geometrie, um die Höhe von Pyramiden und die Entfernung von Schiffen vom Ufer zu berechnen. Er ist der erste bekannte Mensch, der das deduktive Denken in der Geometrie anwendet, indem er vier Folgesätze zum Thales-Theorem ableitet. Er ist auch der erste bekannte Mensch, dem eine mathematische Entdeckung zugeschrieben wird. ⓘ

Thales hat wahrscheinlich keine Schriften hinterlassen. Die Überlieferung fand durch andere Autoren der Antike statt. Da sich schon früh Legenden um ihn gebildet haben, kann man sich auf über ihn bekannte Details meist nicht verlassen. Es lässt sich jedoch ein grobes Bild zeichnen. ⓘ
Demnach hat er sich in seiner Heimatstadt Milet politisch betätigt und war jemand, der für seine große Weisheit bewundert wurde. So erachtete man ihn als einen der Sieben Weisen und als Begründer der griechischen Naturphilosophie, Astronomie und Geometrie. ⓘ
Leben

Die Lebensdaten von Thales sind nicht genau bekannt, werden aber durch einige in den Quellen erwähnte datierbare Ereignisse grob festgelegt. Laut Herodot sagte Thales die Sonnenfinsternis vom 28. Mai 585 v. Chr. voraus. Diogenes Laërtius zitiert die Chronik des Apollodorus von Athen, wonach Thales im Alter von 78 Jahren während der 58. Olympiade (548-545 v. Chr.) starb, und führt seinen Tod auf einen Hitzschlag beim Zuschauen der Spiele zurück. ⓘ
Thales wurde wahrscheinlich um die Mitte der 620er Jahre v. Chr. in der Stadt Milet geboren. Der antike Schriftsteller Apollodoros aus Athen, der im 2. Jahrhundert v. Chr. schrieb, nahm an, dass Thales um das Jahr 625 v. Chr. geboren wurde. Herodot, der im fünften Jahrhundert v. Chr. schrieb, beschrieb Thales als "einen Phönizier mit entfernter Abstammung". Es ist jedoch wahrscheinlich, dass er genauso griechisch war wie die meisten Milesier, da seine Vorfahren Kadmäer aus Böotien und keine Semiten waren. Tim Whitmarsh schrieb, dass Thales Wasser als Urstoff ansah, und da thal das phönizische Wort für Feuchtigkeit ist, könnte sein Name von diesem Umstand abgeleitet sein. Dies scheint jedoch eine Minderheitsmeinung zu sein, da die meisten Wörterbücher behaupten, dass sein Name von dem griechischen Wort "θᾰ́λλω" (thállō, "gedeihen") + -ης (-ēs) stammt, was in diesem Fall "einer, der gedeiht" bedeutet. ⓘ
Der spätere Historiker Diogenes Laërtius verweist in seinem "Leben der Philosophen" aus dem dritten Jahrhundert n. Chr. auf Herodot, Duris und Demokrit, die alle darin übereinstimmen, "dass Thales der Sohn von Examyas und Kleobulina war und zu den Theliden gehörte, die Phönizier sind und zu den edelsten Nachkommen von Cadmus und Agenor gehören". Ihre Namen sind karischen bzw. griechischen Ursprungs. Friedrich Nietzsche betont, dass seine Vorfahren nur in dem Sinne "phönizisch" waren, dass sie ihre fiktive Herkunft auf das Seefahrervolk des mythologischen Helden Cadmus zurückführen konnten. Seine Familie wanderte also von Theben in Mittelgriechenland nach Ionien in Kleinasien. Diogenes stellt dann fest, dass "die meisten Schriftsteller ihn jedoch als gebürtig aus Milet und aus einer angesehenen Familie darstellen". Seine angebliche Mutter, Kleobulina, wurde auch als seine Gefährtin und nicht als seine Mutter beschrieben. Dennoch sind sich die Gelehrten einig, dass er, auch wenn einige antike Autoren behaupten, er sei phönizischer Abstammung gewesen, höchstwahrscheinlich ein gebürtiger Milesier von adliger Geburt und mit Sicherheit ein Grieche war. Diogenes fährt fort, indem er weitere widersprüchliche Berichte liefert: den einen, dass Thales heiratete und entweder einen Sohn zeugte (Cybisthus oder Cybisthon) oder seinen gleichnamigen Neffen adoptierte; den zweiten, dass er nie heiratete, da er seiner Mutter als junger Mann sagte, es sei zu früh zum Heiraten, und als älterer Mann, es sei zu spät. Plutarch hatte diese Version schon früher erzählt: Solon besuchte Thales und fragte ihn, warum er ledig geblieben sei; Thales antwortete, dass ihm der Gedanke, sich um Kinder kümmern zu müssen, nicht gefalle. Dennoch adoptierte er einige Jahre später aus Sehnsucht nach einer Familie seinen Neffen Cybisthus. ⓘ
Es wird angenommen, dass Thales irgendwann in seinem Leben Ägypten besuchte, wo er etwas über Geometrie lernte. Es ist nicht unmöglich, dass Thales Ägypten besuchte, da Milet dort eine ständige Kolonie hatte (nämlich Naucratis), doch Besuche in Ägypten wurden von späteren Schriftstellern häufig verschiedenen Philosophen zugeschrieben, insbesondere wenn diese versuchten, mathematische Kenntnisse zu erklären. Thales kann Ägypten aus Berichten anderer gekannt haben, ohne es tatsächlich besucht zu haben. Diogenes Laërtius schrieb, dass Thales Milet als athenische Kolonie identifiziert. ⓘ
Thales (der etwa 30 Jahre vor Pythagoras und 300 Jahre vor Euklid, Eudoxus von Knidos und Eudemus von Rhodos starb) wird oft als "der erste griechische Mathematiker" gefeiert. Zwar weisen einige Historiker wie Colin R. Fletcher darauf hin, dass es einen Vorgänger von Thales gegeben haben könnte, der in Eudemus' verlorenem Buch Geschichte der Geometrie genannt wird, doch ohne das Werk "wird die Frage zur reinen Spekulation". Fletcher vertritt die Ansicht, dass es keinen brauchbaren Vorgänger für den Titel des ersten griechischen Mathematikers gibt, die einzige Frage ist, ob Thales sich als Praktiker auf diesem Gebiet qualifiziert; er ist der Meinung, dass "Thales die Techniken der Beobachtung, des Experimentierens, der Superposition und der Deduktion beherrschte ... er hat sich als Mathematiker erwiesen." ⓘ
Aristoteles schrieb in der Metaphysik: "Thales, der Begründer dieser Philosophenschule, sagt, dass die permanente Einheit das Wasser ist (weshalb er auch behauptete, dass die Erde auf dem Wasser schwimmt). Vermutlich leitete er diese Annahme daraus ab, dass die Nahrung von allem feucht ist, und dass die Wärme selbst aus der Feuchtigkeit entsteht und für ihre Existenz von ihr abhängt (und das, woraus ein Ding entsteht, ist immer sein erstes Prinzip). Daraus leitete er seine Annahme ab; und auch aus der Tatsache, dass die Samen von allem eine feuchte Natur haben, während Wasser das erste Prinzip der Natur von feuchten Dingen ist." ⓘ
Tätigkeiten
Thales betätigte sich in vielen Bereichen, darunter auch im Ingenieurwesen. Manche sagen, dass er keine Schriften hinterlassen hat. Andere sagen, er habe "Über die Sonnenwende" und "Über die Tagundnachtgleiche" geschrieben. Der nautische Sternenführer wird ihm zugeschrieben, aber das war in der Antike umstritten. Keine ihm zugeschriebene Schrift ist erhalten geblieben. Diogenes Laërtius zitiert zwei Briefe von Thales: einen an Pherecydes von Syros, in dem er ihm anbietet, sein Buch über die Religion zu rezensieren, und einen an Solon, in dem er ihm anbietet, ihm bei seinem Aufenthalt in Athen Gesellschaft zu leisten. ⓘ
Die Geschichte der Olive als Beispiel für einen Optionshandel

Eine Geschichte mit verschiedenen Versionen erzählt, wie Thales durch die Vorhersage des Wetters eine reiche Olivenernte erzielte. In einer Version kaufte er alle Olivenpressen in Milet, nachdem er das Wetter und eine gute Ernte für ein bestimmtes Jahr vorausgesagt hatte. In einer anderen Version der Geschichte erklärt Aristoteles, dass Thales die Pressen im Voraus mit einem Preisnachlass reserviert hatte und sie zu einem hohen Preis vermieten konnte, wenn die Nachfrage auf dem Höhepunkt war, nachdem er eine besonders gute Ernte vorausgesagt hatte. Diese erste Version der Geschichte wäre die erste historisch bekannte Schaffung und Verwendung von Termingeschäften, während die zweite Version die erste historisch bekannte Schaffung und Verwendung von Optionen wäre. ⓘ
Aristoteles erklärt, dass Thales damit nicht das Ziel verfolgte, sich selbst zu bereichern, sondern seinen Mitmenschen in Miles zu beweisen, dass die Philosophie im Gegensatz zu ihrer Meinung nützlich sein kann. Oder aber Thales hatte seinen Ausflug ins Unternehmertum aufgrund einer persönlichen Herausforderung unternommen, die ihm von einer Person gestellt wurde, die ihn gefragt hatte, warum er als intelligenter und berühmter Philosoph noch keinen Reichtum erlangt habe. ⓘ
Die Rolle des Beraters
Diogenes Laërtius berichtet, dass Thales als Berater berühmt wurde, als er den Milesiern riet, sich nicht auf eine Symmachia, einen "gemeinsamen Kampf", mit den Lydiern einzulassen. Dies wurde manchmal als ein Bündnis gedeutet. Eine andere Geschichte von Herodot besagt, dass Krösus seine Armee in das persische Gebiet sandte. Er wurde durch den Fluss Halys aufgehalten, der damals unüberwindbar war. Thales brachte das Heer über den Fluss, indem er flussaufwärts eine Umleitung grub, um die Strömung zu verringern und die Überquerung des Flusses zu ermöglichen. Während Herodot berichtet, dass die meisten seiner griechischen Landsleute glauben, Thales habe den Fluss Halys umgeleitet, um die militärischen Bemühungen von König Krösus zu unterstützen, hält er selbst dies für zweifelhaft. ⓘ
Krösus wurde vor der Stadt Sardes von Kyros besiegt, der anschließend Milet verschonte, weil es nichts unternommen hatte. Kyrus war von Krösus' Weisheit und seiner Verbindung zu den Weisen so beeindruckt, dass er ihn verschonte und seinen Rat in verschiedenen Angelegenheiten annahm. Die ionischen Städte sollten demoi, also "Bezirke", sein.
Er riet ihnen, einen einzigen Regierungssitz zu errichten, und wies auf Teos als den geeignetsten Ort dafür hin; "denn das", so sagte er, "war der Mittelpunkt Ioniens. Die anderen Städte könnten weiterhin ihre eigenen Gesetze haben, als ob sie unabhängige Staaten wären". ⓘ
Milet jedoch erhielt von Kyros günstige Bedingungen. Die anderen Städte blieben in einem Ionischen Bund von zwölf Städten (außer Milet) und wurden von den Persern unterworfen. ⓘ
Astronomie
Laut Herodot sagte Thales die Sonnenfinsternis vom 28. Mai 585 v. Chr. voraus. Thales beschrieb auch die Position von Ursa Minor und war der Meinung, dass das Sternbild als Orientierungshilfe für die Navigation auf See nützlich sein könnte. Er berechnete die Dauer des Jahres und die Zeitpunkte der Tagundnachtgleichen und Sonnenwenden. Außerdem wird ihm die erste Beobachtung der Hyaden und die Berechnung der Position der Plejaden zugeschrieben. Plutarch weist darauf hin, dass zu seiner Zeit (um 100 n. Chr.) ein in Versen verfasstes Werk, die Astronomie, existierte, das Thales zugeschrieben wird. ⓘ
Herodot schreibt, dass im sechsten Jahr des Krieges die Lydier unter König Alyattes und die Meder unter Kyaxares in eine unentschiedene Schlacht verwickelt waren, als plötzlich der Tag zur Nacht wurde, was dazu führte, dass beide Parteien die Kämpfe einstellten und einen Friedensvertrag aushandelten. Herodot erwähnt auch, dass der Verlust des Tageslichts von Thales vorhergesagt worden war. Er erwähnt jedoch nicht den Ort der Schlacht. ⓘ
Als Alyattes sich weigerte, seine Anhänger aufzugeben, als Kyaxares ihn dazu aufforderte, brach ein Krieg zwischen den Lydiern und den Medern aus, der fünf Jahre lang mit unterschiedlichem Erfolg andauerte. Im Laufe des Krieges errangen die Meder viele Siege über die Lydier, und die Lydier errangen ebenfalls viele Siege über die Meder. Unter ihren anderen Schlachten gab es auch eine Nachtschlacht. Da jedoch das Gleichgewicht nicht zugunsten eines der beiden Völker ausfiel, kam es im sechsten Jahr zu einem weiteren Kampf, in dessen Verlauf, gerade als die Schlacht warm wurde, plötzlich der Tag zur Nacht wurde. Dieses Ereignis war von Thales, dem Milesier, vorhergesagt worden, der die Ionier vorwarnte und das Jahr festlegte, in dem es tatsächlich stattfand. Als die Meder und Lydier die Veränderung bemerkten, stellten sie ihre Kämpfe ein und waren gleichermaßen bestrebt, sich auf Friedensbedingungen zu einigen. ⓘ
Ausgehend von der Liste der medischen Könige und der Dauer ihrer Herrschaft, die Herodot an anderer Stelle angibt, starb Kyaxares jedoch 10 Jahre vor der Sonnenfinsternis. ⓘ
Folgendes hat Diogenes Laertios zur Astronomie des Thales überliefert:
„Manche Autoren geben an, er habe als erster Astronomie getrieben, Sonnenfinsternisse vorhergesagt und die Sonnenwenden festgelegt.“
„Auch bestimmte er zuerst die Sonnenbahn von Wende zu Wende, nach anderen auch das Verhältnis von Sonnen- und Monddurchmesser zum jeweiligen Bahnumfang als 1:720. Als erster hat er den monatsletzten Tag mit „der Dreißigste“ bezeichnet und naturtheoretische Probleme erörtert.“
„Er soll die Jahreszeiten eingeführt und das Jahr in 365 Tage geteilt haben.“
Der Mondkrater Thales ist nach ihm benannt. ⓘ
Sagacity

Diogenes Laërtius erzählt uns, dass die Sieben Weisen um 582 v. Chr. unter dem Archonten Damasius in Athen gegründet wurden und dass Thales der erste Weise war. In derselben Geschichte wird jedoch behauptet, dass Thales nach Milet ausgewandert sei. Es wird auch berichtet, dass er sich erst nach seiner politischen Karriere mit der Natur beschäftigte. So gerne wir die sieben Weisen datieren würden, müssen wir diese Geschichten und das verlockende Datum verwerfen, wenn wir glauben wollen, dass Thales aus Milet stammte, die Sonnenfinsternis vorhersagte und mit Krösus am Feldzug gegen Kyrus teilnahm. ⓘ
Thales erhielt Unterricht von einem ägyptischen Priester und soll enge Kontakte zu den Priestern von Theben und ihrer linearen Geometrie gehabt haben. ⓘ
Es ist ziemlich sicher, dass er aus einer wohlhabenden, etablierten Familie stammte, die ihren Kindern üblicherweise eine höhere Ausbildung ermöglichte. Außerdem konnte sich der einfache Bürger, sofern er kein Seefahrer oder Kaufmann war, die große Reise nach Ägypten nicht leisten und verkehrte nicht mit adligen Gesetzgebern wie Solon. ⓘ
In Diogenes Laërtius' Leben der bedeutenden Philosophen, Kapitel 1.39, erzählt Laërtius mehrere Geschichten über einen teuren Gegenstand, der an den Weisesten gehen soll. In einer Version (die Laërtius Callimachus in seinen Iambics zuschreibt) bestimmt Bathykles von Arkadien in seinem Testament, dass eine teure Schale "'demjenigen gegeben werden sollte, der durch seine Weisheit am meisten Gutes getan hatte.' So wurde sie Thales gegeben, ging bei allen Weisen umher und kam wieder zu Thales zurück. Und er schickte sie an Apollon in Didyma, mit dieser Widmung: "Thales, der Milesier, Sohn des Examyas, [widmet sie] dem delphinischen Apollon, nachdem er zweimal den Preis von allen Griechen gewonnen hat." ⓘ
Theorien
Die frühen Griechen und andere Zivilisationen vor ihnen beriefen sich bei der Erklärung von Naturphänomenen oft auf den Willen anthropomorpher Götter und Heroen. Thales hingegen versuchte, Naturphänomene durch rationale Hypothesen zu erklären, die sich auf die natürlichen Prozesse selbst bezogen. Anstatt zum Beispiel anzunehmen, dass Erdbeben das Ergebnis übernatürlicher Launen sind, erklärte Thales sie mit der Hypothese, dass die Erde auf Wasser schwimmt und Erdbeben entstehen, wenn die Erde von Wellen geschüttelt wird. ⓘ
Thales war ein Hylozoist (jemand, der glaubt, dass die Materie lebendig ist, d. h. Seele(n) enthält). Aristoteles schrieb (De Anima 411 a7-8) über Thales: ...Thales dachte, dass alle Dinge voller Götter sind. Aristoteles führt den Ursprung des Denkens von Thales darüber, dass Materie im Allgemeinen Seelen enthält, darauf zurück, dass Thales zunächst davon ausging, dass, weil Magnete Eisen bewegen, das Vorhandensein von Bewegung in der Materie darauf hinweist, dass diese Materie Leben enthält. ⓘ
Thales fragte nach Aristoteles, was die Natur (griech. arche) des Gegenstandes sei, damit er sich auf seine charakteristische Weise verhalte. Physis (φύσις) kommt von phyein (φύειν), "wachsen", verwandt mit unserem Wort "sein". (G)natura ist die Art und Weise, wie ein Ding "geboren" wird, wiederum mit dem Stempel dessen, was es in sich selbst ist. ⓘ
Aristoteles charakterisiert die meisten Philosophen als "zunächst" (πρῶτον) denkend, dass die "Prinzipien in Form der Materie die einzigen Prinzipien aller Dinge" seien, wobei "Prinzip" arche, "Materie" hyle ("Holz" oder "Stoff", "Material") und "Form" eidos ist. ⓘ
Arche wird mit "Prinzip" übersetzt, aber die beiden Wörter haben nicht genau dieselbe Bedeutung. Ein Prinzip von etwas ist lediglich zeitlich oder logisch vorgeordnet (verwandt mit pro-). Eine Arche (von ἄρχειν, "herrschen") beherrscht ein Objekt in irgendeiner Weise. Wird die arche als Ursprung aufgefasst, dann ist eine spezifische Kausalität impliziert, d.h. B soll nur deshalb charakteristisch B sein, weil es von A kommt, das es beherrscht. ⓘ
Die archai, die Aristoteles in seiner bekannten Passage über die ersten griechischen Wissenschaftler im Sinn hatte, sind nicht notwendigerweise zeitlich vor ihren Objekten angesiedelt, sondern sind Bestandteile von ihnen. Im Pluralismus bestehen die Objekte beispielsweise aus Erde, Luft, Feuer und Wasser, aber diese Elemente verschwinden nicht mit der Herstellung des Objekts. Sie bleiben als archai in ihm, wie die Atome der Atomisten. ⓘ
Was Aristoteles damit sagen will, ist, dass die ersten Philosophen versuchten, die Substanz(en) zu definieren, aus denen alle materiellen Objekte bestehen. Das ist übrigens genau das, was moderne Wissenschaftler in der Kernphysik zu erreichen versuchen, was ein weiterer Grund ist, warum Thales als erster westlicher Wissenschaftler bezeichnet wird, aber einige zeitgenössische Wissenschaftler lehnen diese Interpretation ab. ⓘ
Geometrie
Thales war für seine theoretische und praktische Anwendung der Geometrie bekannt und wird oft als der erste Mensch in der westlichen Welt angesehen, der deduktives Denken auf die Geometrie anwandte (und wird daher oft als der erste westliche Mathematiker betrachtet). Sein Verständnis war sowohl theoretisch als auch praktisch. Zum Beispiel sagte er:
Megiston topos: apanta gar chorei (Μέγιστον τόπος- ἄπαντα γὰρ χωρεῖ.) ⓘ
Das Größte ist der Raum, denn er enthält alle Dinge.
Der Topos befindet sich im Newtonschen Raum, da das Verb chorei die Bedeutung hat, vor den Dingen zu weichen oder sich auszubreiten, um ihnen Platz zu machen, was Ausdehnung bedeutet. Innerhalb dieser Ausdehnung haben die Dinge eine Position. Punkte, Linien, Flächen und Körper, die durch Abstände und Winkel miteinander verbunden sind, ergeben sich aus dieser Annahme. ⓘ
Thales verstand ähnliche Dreiecke und rechtwinklige Dreiecke und nutzte dieses Wissen auf praktische Weise. Bei Diogenes Laërtius (a.a.O.) wird erzählt, dass er die Höhe der Pyramiden anhand ihres Schattens in dem Augenblick maß, in dem sein eigener Schatten seiner Höhe entsprach. Ein rechtwinkliges Dreieck mit zwei gleichen Schenkeln ist ein rechtwinkliges 45-Grad-Dreieck, das alle gleich sind. Die Länge des Schattens der Pyramide, gemessen von der Mitte der Pyramide, muss in diesem Moment gleich der Höhe der Pyramide gewesen sein. ⓘ
Diese Geschichte deutet darauf hin, dass er mit dem ägyptischen Seked oder Seqed vertraut war, dem Verhältnis zwischen der Steigung und dem Gefälle eines Abhangs (Kotangens). Das Seked findet sich in den Problemen 56, 57, 58, 59 und 60 des Rhind-Papyrus - einem altägyptischen mathematischen Dokument. ⓘ
Praktischerweise benutzte Thales die gleiche Methode, um die Entfernungen von Schiffen auf See zu messen, so Eudemus, wie von Proclus ("in Euclidem") berichtet. Laut Kirk & Raven braucht man für dieses Kunststück nur drei gerade Stöcke, die an einem Ende befestigt sind, und die Kenntnis der eigenen Höhe. Ein Stock wird senkrecht in den Boden gesteckt. Ein zweiter wird waagerecht ausgerichtet. Mit dem dritten visiert man das Schiff an und berechnet das Seked aus der Höhe des Stocks und seiner Entfernung vom Einsteckpunkt zur Sichtlinie (Proclus, In Euclidem, 352). ⓘ
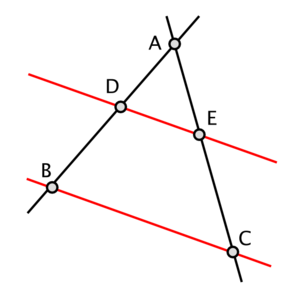
Thales' Theoreme
In der Elementargeometrie gibt es zwei Thales-Theoreme, von denen das eine als Thales-Theorem bekannt ist und sich auf ein Dreieck bezieht, das in einen Kreis eingeschrieben ist und den Durchmesser des Kreises als einen Schenkel hat; das andere Theorem wird auch als Abschnittssatz bezeichnet. Darüber hinaus schrieb Eudemus ihm die Entdeckung zu, dass ein Kreis durch seinen Durchmesser halbiert wird, dass die Basiswinkel eines gleichschenkligen Dreiecks gleich sind und dass die vertikalen Winkel gleich sind. Einer historischen Notiz zufolge beobachtete Thales bei einem Besuch in Ägypten, dass die Ägypter, wann immer sie zwei sich schneidende Linien zeichneten, die vertikalen Winkel maßen, um sicherzustellen, dass sie gleich waren. Thales kam zu dem Schluss, dass man beweisen kann, dass alle vertikalen Winkel gleich sind, wenn man einige allgemeine Begriffe akzeptiert, wie z. B.: alle geraden Winkel sind gleich, Gleiche, die zu Gleichen addiert werden, sind gleich, und Gleiche, die von Gleichen subtrahiert werden, sind gleich. ⓘ
Den Beweis für die Vorrangstellung von Thales finden wir in einem Buch von Proklos, der tausend Jahre nach Thales schrieb, aber vermutlich eine Kopie von Eudemus' Buch besaß. Proklos schrieb: "Thales war der erste, der nach Ägypten ging und diese Studie nach Griechenland zurückbrachte." Er fährt fort, dass er nicht nur das in Ägypten erworbene Wissen anwandte, sondern auch "selbst viele Sätze entdeckte und die zugrundeliegenden Prinzipien vieler anderer seinen Nachfolgern offenbarte, wobei seine Methode in einigen Fällen allgemeiner, in anderen mehr empirisch war." ⓘ
Andere Zitate von Proclus listen weitere mathematische Errungenschaften von Thales auf:
Es heißt, Thales habe als erster gezeigt, dass der Kreis durch den Durchmesser halbiert wird, wobei die Ursache der Halbierung der ungehinderte Durchgang der Geraden durch den Mittelpunkt ist. ⓘ
[Thales] soll als erster gewusst und dargelegt haben, dass die Winkel an der Basis eines gleichschenkligen Dreiecks gleich sind, obwohl er die gleichen Winkel auf archaische Weise als ähnlich bezeichnete. ⓘ
Dieses Theorem, dass, wenn zwei gerade Linien einander schneiden, die vertikalen und gegenüberliegenden Winkel gleich sind, wurde, wie Eudemus sagt, zuerst von Thales entdeckt, obwohl die wissenschaftliche Demonstration durch den Verfasser der Elemente verbessert wurde. ⓘ
Eudemus schreibt in seiner Geschichte der Geometrie dieses Theorem [die Gleichheit von Dreiecken mit zwei Winkeln und einer Seite gleich] Thales zu. Denn er sagt, dass die Methode, mit der Thales zeigte, wie man die Entfernung von Schiffen auf dem Meer findet, notwendigerweise diese Methode beinhaltet. ⓘ
Pamphila sagt, dass er [Thales], nachdem er die Geometrie von den Ägyptern gelernt hatte, als erster ein rechtwinkliges Dreieck in einen Kreis einzeichnete, woraufhin er einen Ochsen opferte. ⓘ
Neben Proklos führt auch Hieronymus von Rhodos Thales als ersten griechischen Mathematiker an. Hieronymus behauptet, dass Thales die Höhe der Pyramiden mit Hilfe eines Theorems der Geometrie, das heute als Schnittpunkttheorem bekannt ist, messen konnte (nachdem er Daten mit seinem Spazierstock gesammelt und dessen Schatten mit denen der Pyramiden verglichen hatte). Abwandlungen der Geschichte von Hieronymus finden wir bei Diogenes Laërtius, Plinius dem Älteren und Plutarch. Nach Hieronymus, der historisch von Diogenes Laërtius zitiert wird, fand Thales die Höhe der Pyramiden durch den Vergleich der Länge des Schattens, den eine Person und die Pyramiden warfen. ⓘ
Aufgrund der Abweichungen zwischen den Zeugnissen, wie z. B. der "Geschichte vom Opfer eines Ochsen anlässlich der Entdeckung, dass der Winkel am Durchmesser eines Kreises ein rechter Winkel ist", die in der von Diogenes Laërtius überlieferten Version eher Pythagoras als Thales zugeschrieben wird, bezweifeln einige Historiker (wie z. B. D. R. Dicks), dass solche Anekdoten überhaupt einen historischen Wert haben. ⓘ
Wasser als erstes Prinzip
Die berühmteste philosophische Position von Thales war seine kosmologische These, die uns durch eine Passage aus Aristoteles' Metaphysik überliefert ist. In diesem Werk gab Aristoteles unmissverständlich Thales' Hypothese über die Natur aller Materie wieder - dass das Ursprungsprinzip der Natur eine einzige materielle Substanz sei: Wasser. Anschließend stellte Aristoteles eine Reihe von Vermutungen an, die auf seinen eigenen Beobachtungen beruhten, um zu begründen, warum Thales diese Idee vertreten haben könnte (auch wenn Aristoteles sie selbst nicht vertrat). ⓘ
Aristoteles legte in Metaphysik 983 b6 8-11, 17-21 seine eigenen Überlegungen zu Materie und Form dar, die möglicherweise etwas Licht auf die Ideen von Thales werfen. (Die Passage enthält Worte, die später von der Wissenschaft mit ganz anderen Bedeutungen übernommen wurden.) ⓘ
Dasjenige, aus dem alles Seiende ist und aus dem es zuerst wird und in das es zuletzt verwandelt wird, wobei seine Substanz unter ihm bleibt, sich aber in Eigenschaften verwandelt, das, so sagen sie, ist das Element und Prinzip der Dinge, die sind. ...Denn es ist notwendig, dass es irgendeine Natur (φύσις) gibt, entweder eine oder mehrere, aus der die anderen Dinge des Gegenstandes werden, der gerettet wird... Thales, der Begründer dieser Art von Philosophie, sagt, es sei das Wasser. ⓘ
In diesem Zitat sehen wir Aristoteles' Darstellung des Problems der Veränderung und der Definition der Substanz. Er fragte, wenn sich ein Gegenstand verändert, ist er dann derselbe oder ein anderer? Wie kann es in beiden Fällen eine Veränderung von einem zum anderen geben? Die Antwort lautet, dass die Substanz "erhalten bleibt", aber verschiedene Eigenschaften (πάθη, die Dinge, die man "erfährt") erwirbt oder verliert. ⓘ
Aristoteles vermutete, dass Thales zu seiner Schlussfolgerung kam, indem er überlegte, dass die "Nahrung aller Dinge feucht ist und dass sogar das Heiße aus dem Feuchten entsteht und davon lebt." Während Aristoteles' Vermutung, warum Thales das Wasser als Ursprungsprinzip der Materie ansah, sein eigenes Denken ist, wird seine Aussage, dass Thales es als Wasser ansah, allgemein als wirklich von Thales stammend akzeptiert, und er wird als ein beginnender Materie- und Formist angesehen. ⓘ
Thales glaubte, die Erde müsse eine flache Scheibe sein, die in einer Wasserfläche schwimmt. ⓘ
Heraklit Homericus sagt, dass Thales seine Schlussfolgerung daraus zog, dass er sah, wie sich feuchte Substanz in Luft, Schleim und Erde verwandelte. Wahrscheinlich war Thales der Ansicht, dass sich die Erde aus dem Wasser, auf dem sie schwamm, und den sie umgebenden Ozeanen verfestigte. ⓘ
Der Jahrhunderte später schreibende Diogenes Laërtius stellt ebenfalls fest, dass Thales lehrte: "Das Wasser bildete (ὑπεστήσατο, 'stand unter') das Prinzip aller Dinge." ⓘ
Aristoteles betrachtete die Position von Thales als ungefähres Äquivalent zu den späteren Ideen von Anaximenes, der meinte, dass alles aus Luft bestehe. In dem 1870 erschienenen Buch Dictionary of Greek and Roman Biography and Mythology heißt es dazu:
In seinem Dogma, dass das Wasser der Ursprung der Dinge ist, das heißt, dass es dasjenige ist, aus dem alles entsteht und in das sich alles auflöst, mag Thales den orphischen Kosmogonien gefolgt sein, während er im Gegensatz zu ihnen versuchte, die Wahrheit der Behauptung zu beweisen. Daher bringt Aristoteles, gleich nachdem er ihn den Begründer der Philosophie genannt hat, die Gründe vor, die Thales zur Bestätigung dieser Behauptung angeführt haben soll; denn dass keine schriftliche Ausarbeitung oder gar ein Buch von Thales erhalten war, beweisen die Ausdrücke, die Aristoteles verwendet, wenn er die Lehren und Beweise des Milesianers vorbringt. (p. 1016) ⓘ
Der Glaube an die Göttlichkeit
Aristoteles zufolge glaubte Thales, dass die Magnetsteine eine Seele hätten, weil Eisen von ihnen angezogen werde (durch die Kraft des Magnetismus). ⓘ
Aristoteles definierte die Seele als das Prinzip des Lebens, das die Materie durchdringt und lebendig macht, indem es ihr die Animation oder die Kraft zum Handeln verleiht. Die Idee stammt nicht von ihm, da die Griechen im Allgemeinen an die Unterscheidung zwischen Geist und Materie glaubten, die schließlich nicht nur zu einer Unterscheidung zwischen Körper und Seele, sondern auch zwischen Materie und Energie führen sollte. Wenn Dinge lebendig waren, mussten sie eine Seele haben. Dieser Glaube war keine Neuerung, denn die gewöhnliche antike Bevölkerung des Mittelmeerraums glaubte, dass natürliche Handlungen von Göttern verursacht wurden. Dementsprechend behaupten Aristoteles und andere antike Autoren, dass Thales glaubte, dass "alle Dinge voller Götter" waren. In ihrem Eifer, ihn zum Ersten in allem zu machen, sagten einige, er sei der Erste gewesen, der diesen Glauben vertrat, von dem weithin bekannt gewesen sein muss, dass er falsch war. Thales suchte jedoch nach etwas Allgemeinerem, einer universellen Substanz des Geistes. Das war auch im Polytheismus der damaligen Zeit der Fall. Zeus war die Verkörperung des höchsten Geistes, der über alle untergeordneten Erscheinungen herrschte. Seit Thales neigten die Philosophen jedoch dazu, den Geist zu entpersönlichen oder zu objektivieren, als wäre er die Substanz der Beseelung an sich und nicht tatsächlich ein Gott wie die anderen Götter. Das Ergebnis war eine völlige Entkopplung des Geistes von der Substanz, was die Tür zu einem nicht-göttlichen Handlungsprinzip öffnete. ⓘ
Das klassische Denken war jedoch nur ein Stück weit auf diesem Weg vorangekommen. Anstatt sich auf die Person Zeus zu beziehen, sprach man von dem großen Geist:
"Thales", so Cicero, "versichert, dass das Wasser das Prinzip aller Dinge ist, und dass Gott jener Geist ist, der alle Dinge aus dem Wasser geformt und geschaffen hat." ⓘ
Der universelle Geist erscheint als römischer Glaube auch bei Virgil:
Am Anfang stärkt der innere GEIST (spiritus intus) Himmel und Erde,
die wässrigen Felder und die lichte Kugel der Luna, und dann -
Titanensterne; und der Geist (mens), der durch die Glieder fließt
Erregt die ganze Masse, und vermischt sich mit GROSSER MATERIE (magno corpore) ⓘ
Nach Henry Fielding (1775) bekräftigt Diogenes Laërtius (1.35), dass Thales "die unabhängige Präexistenz Gottes von Ewigkeit her" postulierte, indem er erklärte, "dass Gott das älteste aller Wesen sei, denn er existiere ohne eine vorherige Ursache, selbst in der Art der Zeugung; dass die Welt das schönste aller Dinge sei, denn sie sei von Gott erschaffen worden." ⓘ
Einflüsse

Aufgrund des Mangels an Quellen über Thales und der Diskrepanzen zwischen den Berichten in den erhaltenen Quellen gibt es eine wissenschaftliche Debatte über mögliche Einflüsse auf Thales und die griechischen Mathematiker, die nach ihm kamen. Der Historiker Roger L. Cooke weist darauf hin, dass Proclus den mesopotamischen Einfluss auf Thales oder die griechische Geometrie nicht erwähnt, dass er aber "in der griechischen Astronomie, in der Verwendung des sexagesimalen Systems zur Messung von Winkeln und in Ptolemäus' ausdrücklicher Verwendung mesopotamischer astronomischer Beobachtungen deutlich wird". Cooke stellt fest, dass sie möglicherweise auch im zweiten Buch von Euklids Elementen vorkommt, "das geometrische Konstruktionen enthält, die bestimmten algebraischen Beziehungen entsprechen, die häufig in den Keilschrifttafeln zu finden sind". Cooke stellt fest: "Diese Beziehung ist jedoch umstritten." ⓘ
Der Historiker B.L. Van der Waerden gehört zu den Befürwortern des mesopotamischen Einflusses und schreibt: "Daraus folgt, dass wir den traditionellen Glauben aufgeben müssen, dass die ältesten griechischen Mathematiker die Geometrie ganz allein entdeckt haben ... ein Glaube, der nur so lange haltbar war, wie nichts über die babylonische Mathematik bekannt war. Dies schmälert in keiner Weise die Bedeutung von Thales; im Gegenteil, sein Genie erhält erst jetzt die Ehre, die ihm gebührt, die Ehre, eine logische Struktur für die Geometrie entwickelt zu haben, den Beweis in die Geometrie eingeführt zu haben." ⓘ
Einige Historiker wie D. R. Dicks bezweifeln, dass wir anhand der fragwürdigen Quellen, die uns zur Verfügung stehen, feststellen können, wie sehr Thales von babylonischen Quellen beeinflusst war. Er weist darauf hin, dass Thales zwar in der Lage gewesen sein soll, eine Sonnenfinsternis mit Hilfe eines Zyklus namens "Saros" zu berechnen, der "von den Babyloniern entlehnt" worden sein soll, "die Babylonier verwendeten jedoch keine Zyklen zur Vorhersage von Sonnenfinsternissen, sondern berechneten sie anhand von Beobachtungen des Breitengrades des Mondes, die kurz vor der erwarteten Syzygie gemacht wurden." Dicks zitiert den Historiker O. Neugebauer, der berichtet, dass "600 v. Chr. keine babylonische Theorie zur Vorhersage von Sonnenfinsternissen existierte, wie man an der sehr unbefriedigenden Situation 400 Jahre später sehen kann; auch entwickelten die Babylonier nie eine Theorie, die den Einfluss der geografischen Breite berücksichtigte." Dicks untersucht den als "Saros" bezeichneten Zyklus, den Thales verwendet haben soll und von dem man annimmt, dass er von den Babyloniern stammt. Er weist darauf hin, dass Ptolemäus diesen und einen anderen Zyklus in seinem Buch Mathematical Syntaxis verwendet, ihn aber griechischen Astronomen vor Hipparchus und nicht den Babyloniern zuschreibt. Dicks stellt fest, dass Herodot berichtet, dass Thales einen Zyklus zur Vorhersage der Sonnenfinsternis nutzte, aber er behauptet, dass "wenn dies der Fall war, die Erfüllung der 'Vorhersage' ein reiner Glücksfall und keine Wissenschaft war". Er geht noch weiter und schließt sich anderen Historikern (F. Martini, J.L. E. Dreyer, O. Neugebauer) an, indem er die Historizität der Finsternisgeschichte gänzlich ablehnt. Dicks verbindet die Geschichte von Thales, der die Ursache für eine Sonnenfinsternis entdeckt hat, mit der Behauptung von Herodot, Thales habe den Zyklus der Sonne in Bezug auf die Sonnenwenden entdeckt, und kommt zu dem Schluss, dass er dieses Wissen, das weder die Ägypter noch die Babylonier noch seine unmittelbaren Nachfolger besaßen, unmöglich besessen haben kann". Josephus ist der einzige antike Historiker, der behauptet, Thales habe Babylonien besucht. ⓘ
Herodot schrieb, dass die Griechen die Praxis der Einteilung des Tages in 12 Teile, den Polos und den Gnomon von den Babyloniern lernten. (Die genaue Bedeutung des von ihm verwendeten Wortes polos ist unbekannt, gängige Theorien lauten: "die Himmelskuppel", "die Spitze der Achse der Himmelskugel" oder eine sphärische, konkave Sonnenuhr.) Doch selbst Herodots Behauptungen über den babylonischen Einfluss werden von einigen modernen Historikern angezweifelt, wie z. B. von L. Zhmud, der darauf hinweist, dass die Einteilung des Tages in zwölf Teile (und analog dazu des Jahres) den Ägyptern bereits im zweiten Jahrtausend bekannt war, dass der Gnomon sowohl den Ägyptern als auch den Babyloniern bekannt war und dass die Idee der "Himmelskugel" zu dieser Zeit außerhalb Griechenlands nicht verwendet wurde. ⓘ
Weniger umstritten als die Behauptung, Thales habe die babylonische Mathematik erlernt, ist die Behauptung, er sei von den Ägyptern beeinflusst worden. Der Historiker S. N. Bychkov vertritt die Ansicht, dass die Idee, dass die Grundwinkel eines gleichschenkligen Dreiecks gleich sind, wahrscheinlich aus Ägypten stammt. Das liegt daran, dass es beim Bau eines Hausdaches nicht darauf ankommt, dass der Querschnitt genau ein gleichschenkliges Dreieck ist (da der First des Daches genau passen muss), während eine symmetrische quadratische Pyramide keine Fehler in den Basiswinkeln der Flächen haben darf, da sie sonst nicht genau zusammenpassen. Der Historiker D.R. Dicks stimmt zu, dass die Mathematik bei den Babyloniern und vor allem bei den Ägyptern im Vergleich zu den Griechen zur Zeit des Thales fortgeschrittener war - "beide Kulturen kannten die richtigen Formeln zur Bestimmung der Flächen und Volumina einfacher geometrischer Figuren wie Dreiecke, Rechtecke, Trapezoide usw. Die Ägypter konnten auch das Volumen des Kegelstumpfes einer Pyramide mit quadratischer Grundfläche korrekt berechnen (die Babylonier verwendeten dafür eine falsche Formel) und benutzten eine Formel für den Flächeninhalt eines Kreises ... die einen Wert für π von 3,1605 ergibt - eine gute Annäherung." Dicks stimmt auch zu, dass dies einen Einfluss auf Thales gehabt hätte (von dem die ältesten Quellen übereinstimmend sagen, dass er sich für Mathematik und Astronomie interessierte), aber er ist der Meinung, dass die Erzählungen über Thales' Reisen in diese Länder reine Mythen sind. ⓘ
Die antike Zivilisation und die gewaltigen Monumente Ägyptens hatten "einen tiefen und unauslöschlichen Eindruck auf die Griechen". Sie schrieben den Ägyptern "ein uraltes Wissen über bestimmte Themen" zu (einschließlich der Geometrie) und behaupteten, dass einige ihrer eigenen Ideen ägyptischen Ursprungs seien, um ihnen "ein respektables Alter" zu verleihen (z. B. die "hermetische" Literatur der alexandrinischen Zeit). ⓘ
Dicks ist der Ansicht, dass Thales zur Zeit des Eudämon zwar eine prominente Figur in der griechischen Geschichte war, aber "nichts Sicheres bekannt war, außer dass er in Milet lebte". Es entwickelte sich die Tradition, dass Thales nach Ägypten gegangen sein muss, da "die Milesier in der Lage waren, weit zu reisen". Da Herodot sagt, Ägypten sei der Geburtsort der Geometrie, muss er diese dort gelernt haben. Da er dort gewesen sein muss, muss eine der Theorien über die Nilüberschwemmung, die Herodot aufgestellt hat, von Thales stammen. Da er in Ägypten gewesen sein muss, muss er auch etwas mit den Pyramiden zu tun gehabt haben - daher die Erzählung von der Vermessung derselben. Ähnliche apokryphe Geschichten gibt es von Pythagoras und Platon, die nach Ägypten reisten, ohne dass es dafür Belege gibt. ⓘ
Da die ägyptische und babylonische Geometrie zu jener Zeit "im Wesentlichen arithmetisch" war, also tatsächliche Zahlen verwendete und "das Verfahren dann mit ausdrücklichen Anweisungen beschrieben wird, was mit diesen Zahlen zu tun ist", gab es keinen Hinweis darauf, wie die Verfahrensregeln zustande kamen, und nichts in Richtung eines logisch geordneten Korpus von verallgemeinertem geometrischen Wissen mit analytischen 'Beweisen', wie wir sie in den Worten von Euklid, Archimedes und Apollonius finden. Selbst wenn Thales also dorthin gereist wäre, hätte er nichts über die Theoreme lernen können, die er dort aufgeschnappt haben soll (vor allem, weil es keine Beweise dafür gibt, dass die Griechen dieser Zeit ägyptische Hieroglyphen verwenden konnten). ⓘ
Jahrhundert v. Chr. und zur Zeit des Hipparchos (ca. 190-120 v. Chr.) waren auch die allgemeine babylonische Einteilung des Kreises in 360 Grad und das Sexagesimalsystem unbekannt. Herodot sagt fast nichts über die babylonische Literatur und Wissenschaft und sehr wenig über ihre Geschichte. Einige Historiker, wie z. B. P. Schnabel, sind der Ansicht, dass die Griechen nur durch Berossus, einen babylonischen Priester, der um 270 v. Chr. in Kos eine Schule gegründet haben soll, mehr über die babylonische Kultur erfahren haben (inwieweit diese jedoch auf dem Gebiet der Geometrie tätig war, ist umstritten). ⓘ
Dicks weist darauf hin, dass der primitive Zustand der griechischen Mathematik und astronomischen Ideen, den die eigentümlichen Vorstellungen von Thales' Nachfolgern (wie Anaximander, Anaximenes, Xenophanes und Heraklit) zeigen, die der Historiker J. L. Heiberg als "eine Mischung aus brillanter Intuition und kindlichen Analogien" bezeichnet, gegen die Behauptungen spätantiker Schriftsteller spricht, Thales habe fortschrittliche Konzepte auf diesen Gebieten entdeckt und gelehrt. ⓘ
John Burnet (1892) bemerkte
Schließlich haben wir ein einziges anerkanntes Beispiel für eine philosophische Gilde, nämlich die der Pythagoräer. Und es wird sich zeigen, dass die Hypothese einer regelmäßigen Organisation wissenschaftlicher Tätigkeit, wenn man sie denn so nennen will, die einzige Erklärung für alle Fakten ist. Die Entwicklung der Lehre in den Händen von Thales, Anaximander und Anaximenes beispielsweise kann nur als Ausarbeitung einer einzigen Idee in einer Schule mit einer kontinuierlichen Tradition verstanden werden.
Laut der byzantinischen Enzyklopädie Suda aus dem 10. Jahrhundert war Thales der "Lehrer und Verwandter" von Anaximander. ⓘ
Nicholas Molinari hat kürzlich einen wichtigen griechischen Einfluss auf Thales' Idee der archai nachgewiesen, nämlich die archaische Wassergottheit Acheloios, die mit Wasser gleichgesetzt und zu Thales' Lebzeiten in Milet verehrt wurde. Er argumentiert, dass Thales als Weiser und Weltreisender mit vielen Mythologien und Religionen in Berührung kam, und während sie alle einen gewissen Einfluss hatten, war seine Heimatstadt Acheloios die wesentlichste. Als Beweis führt er die Tatsache an, dass Hydor speziell "frisches Wasser" bedeutete und dass Acheloios in Mythos und Kunst als Gestaltwandler angesehen wurde, der sich in alles verwandeln konnte. Er weist auch darauf hin, dass die Flüsse der Welt in der Antike als die "Sehnen des Acheloios" angesehen wurden, und dass sich diese Vielzahl von Gottheiten in Thales' Vorstellung widerspiegelt, dass "alle Dinge voller Götter sind". ⓘ
Interpretationen
In der langen Geschichte der Philosophie hat es kaum einen Philosophen oder Philosophiehistoriker gegeben, der Thales nicht erwähnt und versucht hat, ihn in irgendeiner Weise zu charakterisieren. Es ist allgemein anerkannt, dass er dem menschlichen Denken etwas Neues gebracht hat. Mathematik, Astronomie und Medizin gab es bereits. Thales fügte diesen verschiedenen Wissenssammlungen etwas hinzu, um eine Allgemeingültigkeit zu schaffen, die, soweit uns die Schrift überliefert, vorher nicht überliefert war, sondern ein neues Gebiet schuf. ⓘ
Seither fragen sich Interessierte, was dieses neue Etwas ist. Die Antworten fallen in (mindestens) zwei Kategorien: die Theorie und die Methode. Hat man eine Antwort gefunden, ist der nächste logische Schritt die Frage, wie Thales im Vergleich zu anderen Philosophen einzuordnen ist, was zu seiner Klassifizierung (zu Recht oder zu Unrecht) führt. ⓘ
Theorie
Die natürlichsten Beinamen von Thales sind "Materialist" und "Naturalist", die auf ousia und physis beruhen. Die katholische Enzyklopädie stellt fest, dass Aristoteles ihn einen Physiologen nannte, was so viel bedeutet wie "Student der Natur". Andererseits wäre er, wie Aristoteles, ein früher Physiker gewesen. Sie untersuchten Korpora, "Körper", die mittelalterlichen Abkömmlinge von Substanzen. ⓘ
Russell
Die meisten sind sich einig, dass Thales' Denkweise von der Einheit der Substanz geprägt ist, so auch Bertrand Russell:
Die Ansicht, dass alle Materie eins ist, ist eine recht seriöse wissenschaftliche Hypothese. ⓘ ...Aber es ist immer noch eine beachtliche Leistung, entdeckt zu haben, dass eine Substanz in verschiedenen Aggregatzuständen dieselbe bleibt.
Russell spiegelte nur eine etablierte Tradition wider; zum Beispiel: Nietzsche schrieb in seiner Philosophie im tragischen Zeitalter der Griechen:
Die griechische Philosophie scheint mit einer absurden Vorstellung zu beginnen, mit der Behauptung, das Wasser sei der Urgrund und der Schoß aller Dinge. Ist es wirklich notwendig, dass wir diesen Satz ernsthaft zur Kenntnis nehmen? Ja, und zwar aus drei Gründen. Erstens, weil er etwas über den Urgrund aller Dinge aussagt; zweitens, weil er dies in einer Sprache tut, die frei von Bildern und Fabeln ist, und schließlich, weil in ihm, wenn auch nur ansatzweise, der Gedanke enthalten ist, dass "alle Dinge eins sind". ⓘ
Diese Art von Materialismus sollte jedoch nicht mit dem deterministischen Materialismus verwechselt werden. Thales versuchte lediglich, die Einheit zu erklären, die im freien Spiel der Eigenschaften zu beobachten ist. Die Ankunft der Ungewissheit in der modernen Welt ermöglichte eine Rückkehr zu Thales; so schreibt John Elof Boodin ("Gott und die Schöpfung"):
Wir können das Universum nicht aus der Vergangenheit ablesen... ⓘ
Boodin
Boodin definiert einen "emergenten" Materialismus, bei dem die Sinnesobjekte ungewiss aus dem Substrat hervorgehen. Thales ist der Begründer dieser Art von Materialismus. ⓘ
Feldman
Spätere scholastische Denker behaupteten, dass Thales bei der Wahl des Wassers von der babylonischen oder chaldäischen Religion beeinflusst war, die davon ausging, dass ein Gott die Schöpfung durch Einwirkung auf das bereits vorhandene Wasser begonnen hatte. Der Historiker Abraham Feldman ist der Ansicht, dass dies bei näherer Betrachtung nicht zutrifft. In der babylonischen Religion ist das Wasser leblos und unfruchtbar, bis ein Gott auf es einwirkt, aber für Thales war das Wasser selbst göttlich und schöpferisch. Er behauptete, dass "alle Dinge voller Götter sind", und die Natur der Dinge zu verstehen bedeute, die Geheimnisse der Götter zu entdecken und durch dieses Wissen die Möglichkeit zu eröffnen, dass man größer sein könne als der größte Olympier. ⓘ
Feldman weist darauf hin, dass andere Denker zwar die Nässe der Welt erkannten, "aber keiner von ihnen zu dem Schluss kam, dass alles letztlich aus Wasser besteht." Er weist ferner darauf hin, dass Thales "ein wohlhabender Bürger der sagenhaft reichen orientalischen Hafenstadt Milet war ... ein Händler mit den Grundnahrungsmitteln der Antike, Wein und Öl ... Er hatte sicherlich mit den Muscheln der Phönizier zu tun, die den Farbstoff des kaiserlichen Purpurs absondern." Feldman erinnert an die Geschichten von Thales, der die Entfernung von Booten im Hafen maß, mechanische Verbesserungen für die Schiffsnavigation entwickelte, eine Erklärung für die Überschwemmung des Nils gab (lebenswichtig für die ägyptische Landwirtschaft und den griechischen Handel) und den Lauf des Flusses Halys änderte, so dass eine Armee ihn durchqueren konnte. Anstatt das Wasser als Hindernis zu betrachten, dachte Thales über die jährliche religiöse Versammlung der Ionier für sportliche Rituale nach (die auf der Landzunge von Mykale abgehalten wurde und von der man glaubte, dass sie von der Ahnenverwandtschaft von Poseidon, dem Gott des Meeres, angeordnet wurde). Er rief die an diesem Ritual teilnehmenden ionischen Handelsstaaten dazu auf, es in eine demokratische Föderation unter dem Schutz Poseidons umzuwandeln, die die Kräfte der persischen Hirtenvölker abwehren würde. Feldman kommt zu dem Schluss, dass Thales erkannte, "dass das Wasser ein revolutionärer Gleichmacher und der elementare Faktor war, der den Lebensunterhalt und die Geschäfte der Welt bestimmte" und "der gemeinsame Kanal der Staaten". ⓘ
Feldman betrachtet das Umfeld von Thales und geht davon aus, dass Thales Tränen, Schweiß und Blut als Wert für die Arbeit eines Menschen und als Mittel zur Beförderung lebenswichtiger Güter (sei es auf Gewässern oder durch den Schweiß von Sklaven und Lasttieren) angesehen hätte. Er hätte gesehen, dass Mineralien aus Wasser verarbeitet werden können, wie lebenserhaltendes Salz und Gold aus Flüssen. Er hätte gesehen, wie Fische und andere Nahrungsmittel aus dem Wasser gewonnen werden. Feldman weist darauf hin, dass Thales die Ansicht vertrat, der lodestone sei lebendig, da er Metalle an sich ziehe. Er behauptet, dass Thales, der "immer in Sichtweite seines geliebten Meeres lebte", sah, wie das Wasser scheinbar den gesamten "Verkehr mit Wein und Öl, Milch und Honig, Säften und Farbstoffen" an sich zog, was ihn zu "einer Vision des Universums führte, das zu einer einzigen Substanz verschmolz, die an sich wertlos und dennoch die Quelle des Reichtums war." Feldman kommt zu dem Schluss, dass für Thales "...das Wasser alle Dinge vereinte. Die soziale Bedeutung des Wassers in der Zeit von Thales veranlasste ihn, durch Eisenwaren und Trockenwaren, durch Erde und Sperma, Blut, Schweiß und Tränen hindurch einen grundlegenden flüssigen Stoff zu erkennen ... das Wasser, das alltäglichste und mächtigste Material, das ihm bekannt war." In Verbindung mit der Vorstellung seines Zeitgenossen von der "spontanen Erzeugung" wird deutlich, wie Thales der Meinung sein konnte, dass Wasser göttlich und schöpferisch sein könnte. ⓘ
Feldman verweist auf die dauerhafte Verbindung der Theorie, dass "alles, was ist, Nässe ist", mit Thales selbst, indem er darauf hinweist, dass Diogenes Laërtius von einem Gedicht, wahrscheinlich einer Satire, spricht, in dem Thales von der Sonne in den Himmel entführt wird. ⓘ
Aufschwung der theoretischen Forschung
Im Westen steht Thales auch für eine neue Art von Forschergemeinschaft. Edmund Husserl versucht, die neue Bewegung wie folgt zu beschreiben. Der philosophische Mensch ist eine "neue kulturelle Konfiguration", die darauf beruht, von der "vorgegebenen Tradition" zurückzutreten und eine rationale "Untersuchung dessen, was an sich selbst wahr ist", d. h. ein Ideal der Wahrheit, in Angriff zu nehmen. Es beginnt mit isolierten Individuen wie Thales, die jedoch im Laufe der Zeit unterstützt werden und mit denen zusammengearbeitet wird. Schließlich verwandelt das Ideal die Normen der Gesellschaft und sprengt die nationalen Grenzen. ⓘ
Klassifizierung
Der Begriff "Vorsokratiker" geht letztlich auf den Philosophen Aristoteles zurück, der die frühen Philosophen als solche bezeichnete, die sich mit der Substanz beschäftigen. ⓘ
Diogenes Laërtius hingegen verfolgte einen streng geografischen und ethnischen Ansatz. Die Philosophen waren entweder Ionier oder Italiener. Er verwendet den Begriff "Ionier" in einem weiteren Sinne, der auch die athenischen Akademiker einschließt, die keine Vorsokratiker waren. Vom philosophischen Standpunkt aus gesehen wäre jede Gruppierung genauso effektiv gewesen. Es gibt keine Grundlage für eine ionische oder italienische Einheit. Einige Gelehrte geben jedoch dem Schema des Diogenes insofern recht, als sie von einer "ionischen" Schule sprechen. Eine solche Schule gab es jedoch nicht. ⓘ
Der populärste Ansatz bezieht sich auf eine milesianische Schule, was gesellschaftlich und philosophisch eher zu rechtfertigen ist. Sie suchten nach der Substanz der Phänomene und mögen miteinander studiert haben. Einige antike Autoren bezeichnen sie als Milesioi, "von Milet". ⓘ
Einfluss auf andere

Thales hatte einen tiefgreifenden Einfluss auf andere griechische Denker und damit auf die westliche Geschichte. Manche glauben, Anaximander sei ein Schüler von Thales gewesen. Frühe Quellen berichten, dass einer von Anaximanders berühmteren Schülern, Pythagoras, Thales als junger Mann besuchte und dass Thales ihm riet, nach Ägypten zu reisen, um seine philosophischen und mathematischen Studien zu vertiefen. ⓘ
Viele Philosophen folgten dem Beispiel von Thales und suchten nach Erklärungen in der Natur und nicht im Übernatürlichen; andere kehrten zu übernatürlichen Erklärungen zurück, formulierten sie aber in der Sprache der Philosophie und nicht in der des Mythos oder der Religion. ⓘ
Betrachtet man speziell den Einfluss von Thales in der vorsokratischen Ära, so wird deutlich, dass er einer der ersten Denker war, der mehr in Richtung logos als mythos dachte. Der Unterschied zwischen diesen beiden tiefgründigeren Arten, die Welt zu sehen, besteht darin, dass der Mythos sich auf die Geschichten des heiligen Ursprungs konzentriert, während der Logos sich auf die Argumentation konzentriert. Wenn der mythische Mensch die Welt so erklären will, wie er sie sieht, erklärt er sie anhand von Göttern und Mächten. Das mythische Denken unterscheidet nicht zwischen Dingen und Personen und es unterscheidet auch nicht zwischen Natur und Kultur. Die Art und Weise, wie ein Denker des Logos ein Weltbild präsentiert, unterscheidet sich radikal von der des mythischen Denkers. In seiner konkreten Form ist der Logos eine Denkweise, die nicht nur den Individualismus, sondern auch das Abstrakte berücksichtigt. Außerdem setzt er auf eine vernünftige und kontinuierliche Argumentation. Dies ist die Grundlage der Philosophie und ihrer Art, die Welt durch abstrakte Argumente zu erklären, und nicht durch Götter und mythische Geschichten. ⓘ
Verlässlichkeit der Quellen

Aufgrund des hohen Stellenwerts, den Thales in der griechischen Kultur einnahm, wurde sein Ruf mit großem Interesse und Bewunderung verfolgt. Aufgrund dieser Anhängerschaft waren die mündlich überlieferten Geschichten über sein Leben offen für Erweiterungen und historische Fälschungen, noch bevor sie Generationen später aufgeschrieben wurden. Die meisten modernen Meinungsverschiedenheiten rühren von dem Versuch her, das, was wir wissen, zu interpretieren, insbesondere bei der Unterscheidung zwischen Legende und Tatsache. ⓘ
Chronologische Einordnung
Der Historiker D.R. Dicks und andere Historiker unterteilen die antiken Quellen über Thales in solche vor 320 v. Chr. und solche nach diesem Jahr (einige wie Proclus, der im 5. Jahrhundert n. Chr. schrieb, und Simplicius von Kilikien im 6.) Zur ersten Kategorie gehören unter anderem Herodot, Platon, Aristoteles, Aristophanes und Theophrastus. Zur zweiten Kategorie gehören unter anderem Plautus, Aetius, Eusebius, Plutarch, Josephus, Iamblichus, Diogenes Laërtius, Theon von Smyrna, Apuleius, Clemens von Alexandria, Plinius der Ältere und Johannes Tzetzes. ⓘ
Früheste Quellen
Die frühesten Quellen über Thales (der vor 320 v. Chr. lebte) sind oft die gleichen wie für die anderen milesischen Philosophen (Anaximander und Anaximenes). Diese Quellen waren entweder ungefähr zeitgleich (wie Herodot) oder lebten nur wenige hundert Jahre nach seinem Tod. Außerdem schrieben sie auf der Grundlage einer mündlichen Tradition, die im Griechenland ihrer Zeit weit verbreitet und gut bekannt war. ⓘ
Spätere Quellen
Bei den letzten Quellen über Thales handelt es sich um mehrere "Zuschreibungen von Kommentatoren und Kompilatoren, die zwischen 700 und 1000 Jahren nach seinem Tod lebten", die "Anekdoten von unterschiedlicher Plausibilität" enthalten und nach Ansicht einiger Historiker (wie D. R. Dicks) "keinerlei historischen Wert" haben. Dicks weist darauf hin, dass "die 'Autoritäten' sich nicht einmal über die grundlegendsten Fakten seines Lebens einig sind - z. B. ob er Milesier oder Phönizier war, ob er Schriften hinterlassen hat oder nicht, ob er verheiratet oder ledig war -, geschweige denn über die eigentlichen Ideen und Leistungen, die ihm zugeschrieben werden." ⓘ
Vergleich der beiden Quellengruppen
Im Vergleich zwischen den Werken der älteren und der jüngeren Autoren weist Dicks darauf hin, dass Thales und die anderen Männer, die als "die sieben Weisen Griechenlands" bezeichnet werden, in den Werken der frühen Autoren einen anderen Ruf genießen als in denen der späteren Autoren. Näher an ihrer eigenen Zeit wurden Thales, Solon, Bias von Priene, Pittacus von Mytilene und andere als "im Wesentlichen praktische Männer, die in den Angelegenheiten ihrer jeweiligen Staaten eine führende Rolle spielten und den früheren Griechen als Gesetzgeber und Staatsmänner weitaus besser bekannt waren als als tiefgründige Denker und Philosophen" gepriesen. So preist Platon ihn (zusammen mit Anacharsis) als den Erfinder der Töpferscheibe und des Ankers. ⓘ
Erst in den Schriften der zweiten Gruppe von Autoren (die nach 320 v. Chr. arbeiteten) "erhalten wir das Bild von Thales als dem Pionier des griechischen wissenschaftlichen Denkens, insbesondere in Bezug auf Mathematik und Astronomie, die er in Babylonien und Ägypten kennengelernt haben soll". Anstelle "der früheren Tradition, [in der] er ein beliebtes Beispiel für einen intelligenten Mann ist, der über ein gewisses technisches 'Know-how' verfügt... schieben ihm die späteren Doxographen [wie Dicaearchus in der zweiten Hälfte des vierten Jahrhunderts v. Chr.] eine beliebige Anzahl von Entdeckungen und Errungenschaften zu, um ihn zu einer Figur übermenschlicher Weisheit aufzubauen". ⓘ
Von Dicks vorgeschlagenes Problem
Dicks weist auf ein weiteres Problem hin, das sich bei den überlieferten Informationen über Thales ergibt, denn anstatt antike Quellen zu verwenden, die näher an der Zeit von Thales liegen, zogen es die Autoren der Spätantike ("Epitomaten, Exzerpteure und Kompilatoren") tatsächlich vor, "einen oder mehrere Vermittler zu benutzen, so dass wir das, was wir tatsächlich in ihnen lesen, nicht einmal aus zweiter, sondern aus dritter, vierter oder fünfter Hand erhalten. Es liegt auf der Hand, dass diese Verwendung von Zwischenquellen, die von Jahrhundert zu Jahrhundert kopiert und wieder abgeschrieben wurden, wobei jeder Autor zusätzliche Informationen von mehr oder weniger großer Plausibilität aus seinem eigenen Wissen hinzufügte, ein fruchtbares Feld für Überlieferungsfehler, falsche Zuschreibungen und fiktive Zuschreibungen bot". Dicks weist darauf hin, dass "bestimmte Lehren, die spätere Kommentatoren für Thales erfanden ... dann in die biographische Tradition aufgenommen wurden", von späteren Autoren kopiert wurden, die dann von denen zitiert wurden, die nach ihnen kamen, "und so, weil sie von verschiedenen Autoren wiederholt werden können, die sich auf verschiedene Quellen stützen, einen illusorischen Eindruck von Echtheit erzeugen können." ⓘ
Aristoteles
Zweifel bestehen auch bei den philosophischen Positionen, die Thales zugeschrieben werden: "In Wirklichkeit stammen sie direkt von Aristoteles' eigenen Interpretationen, die dann als falsche Zuschreibungen an Thales in die doxographische Tradition eingegangen sind". (Die gleiche Behandlung erfuhr Anaxagoras durch Aristoteles.) ⓘ
Die meisten philosophischen Analysen der Philosophie von Thales stammen von Aristoteles, einem Berufsphilosophen und Schüler Alexanders des Großen, der 200 Jahre nach Thales' Tod schrieb. Aristoteles scheint, seinen überlieferten Büchern nach zu urteilen, keinen Zugang zu den Werken von Thales gehabt zu haben, obwohl er wahrscheinlich Zugang zu den Werken anderer Autoren über Thales hatte, wie Herodot, Hekataeus, Platon usw., sowie zu anderen, deren Werke heute ausgestorben sind. Es war Aristoteles' ausdrückliches Ziel, das Werk von Thales darzustellen, und zwar nicht, weil es an sich bedeutsam war, sondern als Auftakt zu seinen eigenen naturphilosophischen Arbeiten. Geoffrey Kirk und John Raven, die englischen Kompilatoren der Fragmente der Vorsokratiker, behaupten, dass Aristoteles' "Urteile oft durch seine Sichtweise der früheren Philosophie als stolpernder Fortschritt auf dem Weg zur Wahrheit, die Aristoteles selbst in seinen physikalischen Lehren offenbart hat, verzerrt sind". Es gab auch eine umfangreiche mündliche Tradition. Sowohl die mündliche als auch die schriftliche Überlieferung wurde von allen gebildeten Menschen in der Region gelesen oder war ihnen bekannt. ⓘ
Die Philosophie des Aristoteles trug eine besondere Handschrift: Sie vertrat die Theorie der Materie und der Form, die die modernen Scholastiker als Hylomorphismus bezeichnet haben. Obwohl sie einst weit verbreitet war, wurde sie von der rationalistischen und modernen Wissenschaft nicht allgemein übernommen, da sie hauptsächlich für metaphysische Analysen nützlich ist, sich aber nicht für die Details eignet, die für die moderne Wissenschaft von Interesse sind. Es ist nicht klar, ob die Theorie von Materie und Form bereits bei Thales existierte, und wenn ja, ob Thales sie vertrat. ⓘ
Einige Historiker wie B. Snell behaupten zwar, dass Aristoteles sich auf eine vorplatonische schriftliche Aufzeichnung von Hippias und nicht auf eine mündliche Überlieferung stützte, doch ist dies eine umstrittene Position. Stellvertretend für den wissenschaftlichen Konsens stellt Dicks fest, dass "die Überlieferung über ihn schon im fünften Jahrhundert v. Chr. offensichtlich ausschließlich auf Hörensagen beruhte.... Es scheint, dass die frühen Ionier schon zu Aristoteles' Zeiten weitgehend nur noch Namen waren, denen die volkstümliche Überlieferung verschiedene Ideen oder Errungenschaften mit mehr oder weniger Plausibilität zuordnete". Er weist darauf hin, dass Werke, deren Existenz im sechsten Jahrhundert v. Chr. von Anaximander und Xenophanes bestätigt wurde, bereits im vierten Jahrhundert v. Chr. verschwunden waren, so dass die Wahrscheinlichkeit, dass vorsokratisches Material bis in die Zeit des Aristoteles überlebt hat, fast gleich Null ist (noch unwahrscheinlicher für Aristoteles' Schüler Theophrastus und Eudemus und noch unwahrscheinlicher für die nach ihnen folgenden). ⓘ
Diogenes Laërtius
Die wichtigste Sekundärquelle zu den Einzelheiten von Thales' Leben und Werdegang ist Diogenes Laërtius, "Leben der großen Philosophen". Wie der Name schon sagt, handelt es sich dabei in erster Linie um ein biografisches Werk. Im Vergleich zu Aristoteles ist Diogenes kein großer Philosoph. Er ist derjenige, der im Prolog dieses Werks die Einteilung der frühen Philosophen in "Ionier" und "Italiener" vornimmt, aber er ordnet die Akademiker der ionischen Schule zu und weist ansonsten erhebliche Unordnung und Widersprüche auf, insbesondere in dem langen Abschnitt über die Vorläufer der "ionischen Schule". Diogenes zitiert zwei Briefe, die Thales zugeschrieben werden, aber Diogenes schrieb etwa acht Jahrhunderte nach Thales' Tod, und seine Quellen enthielten oft "unzuverlässige oder sogar gefälschte Informationen", daher die Sorge um die Trennung von Fakten und Legenden in den Berichten über Thales. ⓘ
Diese Verwendung von Hörensagen und das Fehlen von Originalquellen veranlasst einige Historiker wie Dicks und Werner Jaeger dazu, den späten Ursprung des traditionellen Bildes der vorsokratischen Philosophie zu betrachten und die gesamte Idee als ein Konstrukt aus einem späteren Zeitalter anzusehen: "Das gesamte Bild, das uns von der Geschichte der frühen Philosophie überliefert ist, wurde in den zwei oder drei Generationen von Platon bis zu den unmittelbaren Schülern des Aristoteles gestaltet". ⓘ
Philosophie und Wissenschaft
Naturphilosophie
Sonstiges
Aristoteles berichtet, Thales habe die Ruhelage der Erde damit erklärt, dass die Erde auf Wasser schwimme. ⓘ
Als Grund für die jährliche Überschwemmung des Nils soll Thales die Etesien genannt haben, denn diese Sommerwinde, die der nördlichen Fließrichtung des Nils entgegengesetzt sind, würden das Abfließen ins Mittelmeer verhindern. ⓘ
Anekdoten
Bekannt geworden sind vor allem zwei Anekdoten über Thales. Nach der ersten soll er aufgrund seiner astronomischen Kenntnisse eine große Olivenernte prognostiziert und daraufhin gewinnbringend in Ölpressen investiert haben:
„Man hielt ihm […] aufgrund seiner Armut vor, dass die Philosophie eine nutzlose Beschäftigung sei. Da er nun infolge seiner Sternbeobachtung erkannt hatte, dass es eine reiche Olivenernte geben werde, soll er noch im Winter […] für alle Ölpressen in Milet und Chios Anzahlungen hinterlegt und sie, da niemand dagegenhielt, für einen geringen Betrag gemietet haben. Als aber der rechte Augenblick gekommen war, und gleichzeitig und plötzlich ein hoher Bedarf an Ölpressen entstand, habe er sie zu seinen Bedingungen vermietet und viel Geld dabei gemacht. Er habe damit bewiesen, dass es für Philosophen leicht sei, reich zu werden, wenn sie nur wollten, es jedoch dies nicht sei, wonach sie strebten.“
Nach der zweiten soll er von einer Magd verspottet worden sein, weil er beim Sterneschauen in einen Brunnen gefallen sei:
„Thales […] fiel, als er sich mit den Sternen beschäftigte und nach oben blickte, in einen Brunnen. Da soll ihn eine witzige und reizende thrakische Magd verspottet haben, weil er zwar die Dinge am Himmel zu erkennen begehre, ihm aber, was ihm vor den Füßen liege, entgehe.“
Eine häufig rezipierte Anekdote ist, dass Thales einen Dreifuß erhalten habe, welcher als Preis für den weisesten aller Menschen gedacht gewesen sei. Es existieren einige widersprüchliche Fassungen dieser Geschichte. ⓘ
Ehrung
Nach Thales ist die Pflanzengattung Thalesia Bronner aus der Familie der Weinrebengewächse (Vitaceae) benannt. ⓘ
Quellensammlungen
- Hermann Diels, Walther Kranz (Hrsg.): Die Fragmente der Vorsokratiker. 6. Auflage. Band 1, Berlin 1951, S. 67–81 (nur teilweise mit deutscher Übersetzung; zahlreiche Neuauflagen).
- M. Laura Gemelli Marciano (Hrsg.): Die Vorsokratiker. Band 1, Artemis & Winkler, Mannheim 2007, ISBN 978-3-7608-1735-4, S. 6–31 (mit deutscher Übersetzung, Erläuterungen sowie Einführung zu Leben und Werk).
- Jaap Mansfeld (Hrsg.): Die Vorsokratiker. Band 1, Reclam, Stuttgart 1983, S. 44–55 (nur deutsche Übersetzung; zahlreiche Neuauflagen).
- Georg Wöhrle (Hrsg.): Thales (= Traditio Praesocratica. Die Milesier. Band 1). De Gruyter, Berlin 2009 (mit deutscher Übersetzung). ⓘ