Kontinuitätsgleichung

Eine Kontinuitätsgleichung oder Transportgleichung ist eine Gleichung, die den Transport einer bestimmten Menge beschreibt. Sie ist besonders einfach und aussagekräftig, wenn sie auf eine konservierte Größe angewandt wird, kann aber verallgemeinert werden, um sie auf jede umfangreiche Größe anzuwenden. Da Masse, Energie, Impuls, elektrische Ladung und andere natürliche Größen unter ihren jeweiligen Bedingungen erhalten bleiben, kann eine Vielzahl von physikalischen Phänomenen mit Hilfe von Kontinuitätsgleichungen beschrieben werden. ⓘ

Kontinuitätsgleichungen sind eine stärkere, lokale Form der Erhaltungssätze. Eine schwache Version des Energieerhaltungssatzes besagt beispielsweise, dass Energie weder erzeugt noch vernichtet werden kann, d. h. die Gesamtenergiemenge im Universum ist festgelegt. Diese Aussage schließt nicht aus, dass eine Energiemenge an einem Punkt verschwindet und gleichzeitig an einem anderen Punkt wieder auftaucht. Eine stärkere Aussage ist, dass Energie lokal konserviert ist: Energie kann weder geschaffen noch zerstört werden, noch kann sie sich von einem Ort zum anderen "teleportieren" - sie kann sich nur durch einen kontinuierlichen Fluss bewegen. Eine Kontinuitätsgleichung ist der mathematische Weg, um diese Art von Aussage auszudrücken. Die Kontinuitätsgleichung für elektrische Ladung besagt beispielsweise, dass sich die Menge der elektrischen Ladung in einem beliebigen Raumvolumen nur durch die Menge des elektrischen Stroms ändern kann, der durch die Grenzen dieses Volumens hinein- oder hinausfließt. ⓘ

Kontinuitätsgleichungen können ganz allgemein "Quellen"- und "Senken"-Terme enthalten, die es ihnen ermöglichen, Mengen zu beschreiben, die oft, aber nicht immer erhalten bleiben, wie z. B. die Dichte einer Molekülart, die durch chemische Reaktionen erzeugt oder zerstört werden kann. In einem alltäglichen Beispiel gibt es eine Kontinuitätsgleichung für die Anzahl der lebenden Menschen; sie hat einen "Quellterm", um die Geburt von Menschen zu berücksichtigen, und einen "Sinkterm", um das Sterben von Menschen zu berücksichtigen. ⓘ

Jede Kontinuitätsgleichung kann in einer "integralen Form" (in Form eines Flussintegrals) ausgedrückt werden, die für jede endliche Region gilt, oder in einer "differentiellen Form" (in Form des Divergenzoperators), die für einen Punkt gilt. ⓘ

Kontinuitätsgleichungen liegen spezielleren Transportgleichungen wie der Konvektions-Diffusionsgleichung, der Boltzmann-Transportgleichung und den Navier-Stokes-Gleichungen zugrunde. ⓘ

Strömungen, die durch Kontinuitätsgleichungen geregelt werden, können mit Hilfe eines Sankey-Diagramms veranschaulicht werden. ⓘ

Eine Kontinuitätsgleichung ist eine bestimmte partielle Differentialgleichung, die zu einer Erhaltungsgröße (s. u.) gehört. Sie verknüpft die zeitliche Änderung ${\frac {\partial }{\partial t}}$ der räumlichen Dichte $\rho$, mit der diese Erhaltungsgröße an einem Punkt vorliegt, mit der räumlichen Änderung ihrer Stromdichte ${\vec {j}}$:

${\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\cdot {\vec {j}}=0$ ⓘ

Zur mathematischen Definition von ${\vec {\nabla }}\cdot$ siehe Divergenz eines Vektorfeldes. ⓘ

Allgemeine Gleichung

Definition der Strömung

Eine Kontinuitätsgleichung ist nützlich, wenn eine Strömung definiert werden kann. Um eine Strömung zu definieren, muss es zunächst eine Größe q geben, die fließen oder sich bewegen kann, wie Masse, Energie, elektrische Ladung, Impuls, Anzahl der Moleküle usw. ρ sei die Volumendichte dieser Menge, d. h. die Menge von q pro Volumeneinheit. ⓘ

Die Art und Weise, wie diese Menge q fließt, wird durch ihren Fluss beschrieben. Der Fluss von q ist ein Vektorfeld, das wir mit j bezeichnen. Hier sind einige Beispiele und Eigenschaften des Flusses:

• Die Dimension des Flusses ist "die Menge von q, die pro Zeiteinheit durch eine Flächeneinheit fließt". Wenn zum Beispiel in der Massenkontinuitätsgleichung für fließendes Wasser 1 Gramm Wasser pro Sekunde durch ein Rohr mit einer Querschnittsfläche von 1 cm² fließt, dann ist der durchschnittliche Massenfluss j innerhalb des Rohrs (1 g/s) / cm², und seine Richtung ist entlang des Rohrs in der Richtung, in die das Wasser fließt. Außerhalb des Rohrs, wo sich kein Wasser befindet, ist der Fluss gleich Null.
• Wenn es ein Geschwindigkeitsfeld u gibt, das die betreffende Strömung beschreibt - mit anderen Worten, wenn sich die gesamte Menge q an einem Punkt x mit der Geschwindigkeit u(x) bewegt -, dann ist der Fluss per Definition gleich der Dichte mal dem Geschwindigkeitsfeld:
  $$\mathbf {j} =\rho \mathbf {u}$$
  Wenn z. B. in der Gleichung der Massenkontinuität für fließendes Wasser u die Geschwindigkeit des Wassers an jedem Punkt und ρ die Dichte des Wassers an jedem Punkt ist, dann ist j der Massenstrom.
• In einem bekannten Beispiel ist der Fluss der elektrischen Ladung die elektrische Stromdichte.
  

  Veranschaulichung, wie der Fluss j einer Menge q durch eine offene Fläche S fließt (dS ist der Differentialvektorbereich).
• Wenn es eine imaginäre Fläche S gibt, dann ist das Oberflächenintegral des Flusses über S gleich der Menge von q, die pro Zeiteinheit durch die Fläche S fließt:

  $({\text{Rate that }}q{\text{ is flowing through the imaginary surface }}S)=\iint _{S}\mathbf {j} \cdot d\mathbf {S}$

  wobei ${\textstyle \iint _{S}d\mathbf {S} }$ ein Oberflächenintegral ist. ⓘ

(Man beachte, dass das Konzept, das hier als "Fluss" bezeichnet wird, in der Literatur teilweise auch als "Flussdichte" bezeichnet wird, wobei "Fluss" das Oberflächenintegral der Flussdichte bezeichnet. Siehe den Hauptartikel über Fluss für weitere Einzelheiten). ⓘ

Integralform

Die Integralform der Kontinuitätsgleichung besagt, dass:

• Die Menge von q in einer Region nimmt zu, wenn zusätzliches q durch die Oberfläche der Region nach innen fließt, und nimmt ab, wenn es nach außen fließt;
• Die Menge von q in einer Region nimmt zu, wenn neues q innerhalb der Region entsteht, und sie nimmt ab, wenn q zerstört wird;
• Abgesehen von diesen beiden Prozessen gibt es keine andere Möglichkeit, wie sich die Menge von q in einer Region ändern kann. ⓘ

Mathematisch gesehen lautet die Integralform der Kontinuitätsgleichung, die die Steigerungsrate von q innerhalb eines Volumens V ausdrückt:

${\frac {dq}{dt}}+$ $\scriptstyle S$ $\mathbf {j} \cdot d\mathbf {S} =\Sigma$ ⓘ

In der Integralform der Kontinuitätsgleichung ist S eine beliebige geschlossene Fläche, die ein Volumen V vollständig umschließt, wie eine der Flächen auf der linken Seite. S kann keine Fläche mit Begrenzungen sein, wie die Flächen auf der rechten Seite. (Flächen sind blau, Begrenzungen sind rot.) ⓘ

wobei

• S ist eine beliebige gedachte geschlossene Fläche, die ein Volumen V einschließt,
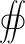• S dS ein Oberflächenintegral über diese geschlossene Fläche bezeichnet,
• q ist die Gesamtmenge der Menge im Volumen V,
• j der Fluß von q ist,
• t ist die Zeit,
• Σ ist die Nettorate, mit der q im Volumen V pro Zeiteinheit erzeugt wird. Wenn q erzeugt wird, nennt man es eine Quelle von q, und Σ wird dadurch positiver. Wenn q vernichtet wird, spricht man von einer Senke von q, und Σ wird dadurch negativer. Dieser Term wird manchmal geschrieben als $dq/dt|_{\text{gen}}$ oder die gesamte Veränderung von q durch seine Erzeugung oder Zerstörung innerhalb des Kontrollvolumens. ⓘ

In einem einfachen Beispiel könnte V ein Gebäude sein und q die Anzahl der Personen im Gebäude. Die Oberfläche S würde aus den Wänden, Türen, dem Dach und dem Fundament des Gebäudes bestehen. Die Kontinuitätsgleichung besagt dann, dass die Anzahl der Personen im Gebäude zunimmt, wenn Personen das Gebäude betreten (ein Fluss durch die Oberfläche nach innen), abnimmt, wenn Personen das Gebäude verlassen (ein Fluss durch die Oberfläche nach außen), zunimmt, wenn jemand im Gebäude ein Kind bekommt (eine Quelle, Σ > 0), und abnimmt, wenn jemand im Gebäude stirbt (eine Senke, Σ < 0). ⓘ

Differentialform

Nach dem Divergenztheorem kann eine allgemeine Kontinuitätsgleichung auch in einer "Differentialform" geschrieben werden:

${\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =\sigma$

wobei

• ∇⋅ ist die Divergenz,
• ρ ist die Menge der Menge q pro Volumeneinheit,
• j der Fluß von q ist,
• t ist die Zeit,
• σ ist die Erzeugung von q pro Volumeneinheit pro Zeiteinheit. Terme, die q erzeugen (d. h., σ > 0) oder entfernen (d. h., σ < 0), werden als "Quellen" bzw. "Senken" bezeichnet. ⓘ

Aus dieser allgemeinen Gleichung lässt sich jede beliebige Kontinuitätsgleichung ableiten, von der einfachen Volumenkontinuitätsgleichung bis zu den komplizierten Navier-Stokes-Gleichungen. Diese Gleichung verallgemeinert auch die Advektionsgleichung. Andere Gleichungen in der Physik, wie das Gaußsche Gesetz für das elektrische Feld und das Gaußsche Gesetz für die Schwerkraft, haben eine ähnliche mathematische Form wie die Kontinuitätsgleichung, werden aber in der Regel nicht als "Kontinuitätsgleichung" bezeichnet, da j in diesen Fällen nicht den Fluss einer realen physikalischen Größe darstellt. ⓘ

Wenn q eine konservierte Größe ist, die weder erzeugt noch zerstört werden kann (wie z. B. Energie), ist σ = 0 und die Gleichungen lauten:

$${\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0$$

ⓘ

Elektromagnetismus

In der elektromagnetischen Theorie ist die Kontinuitätsgleichung ein empirisches Gesetz, das die (lokale) Ladungserhaltung ausdrückt. Mathematisch gesehen ist sie eine automatische Folge der Maxwellschen Gleichungen, obwohl die Ladungserhaltung grundlegender ist als die Maxwellschen Gleichungen. Es besagt, dass die Divergenz der Stromdichte J (in Ampere pro Quadratmeter) gleich der negativen Änderungsrate der Ladungsdichte ρ (in Coulomb pro Kubikmeter) ist,

$$\nabla \cdot \mathbf {J} =-{\frac {\partial \rho }{\partial t}}$$

ⓘ

Konsistenz mit den Maxwellschen Gleichungen

Eine der Maxwell'schen Gleichungen, das Ampère'sche Gesetz (mit Maxwell'scher Korrektur), besagt

$$\nabla \times \mathbf {H} =\mathbf {J} +{\frac {\partial \mathbf {D} }{\partial t}}.$$

Die Divergenz beider Seiten (die Divergenz und die partielle Ableitung nach der Zeit gehen ineinander über) ergibt

$$\nabla \cdot (\nabla \times \mathbf {H} )=\nabla \cdot \mathbf {J} +{\frac {\partial (\nabla \cdot \mathbf {D} )}{\partial t}},$$

aber die Divergenz einer Krümmung ist Null, so dass

$$\nabla \cdot \mathbf {J} +{\frac {\partial (\nabla \cdot \mathbf {D} )}{\partial t}}=0.$$

Das Gaußsche Gesetz (eine weitere Maxwell-Gleichung) besagt jedoch, dass

$$\nabla \cdot \mathbf {D} =\rho ,$$

das in die vorherige Gleichung eingesetzt werden kann, um die Kontinuitätsgleichung zu erhalten

$$\nabla \cdot \mathbf {J} +{\frac {\partial \rho }{\partial t}}=0.$$

ⓘ

Strom ist die Bewegung von Ladung. Die Kontinuitätsgleichung besagt, dass, wenn sich Ladung aus einem Differenzvolumen herausbewegt (d. h. die Divergenz der Stromdichte ist positiv), die Ladungsmenge innerhalb dieses Volumens abnimmt, so dass die Änderungsrate der Ladungsdichte negativ ist. Daher läuft die Kontinuitätsgleichung auf die Erhaltung der Ladung hinaus. ⓘ

Wenn es magnetische Monopole gibt, würde es auch eine Kontinuitätsgleichung für Monopolströme geben, siehe den Artikel über Monopole für Hintergrundinformationen und die Dualität zwischen elektrischen und magnetischen Strömen. ⓘ

Fluiddynamik

In der Fluiddynamik besagt die Kontinuitätsgleichung, dass die Geschwindigkeit, mit der Masse in ein System eintritt, gleich der Geschwindigkeit ist, mit der Masse das System verlässt, zuzüglich der Akkumulation von Masse innerhalb des Systems. Die Differentialform der Kontinuitätsgleichung lautet:

$${\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0$$

wobei

• ρ ist die Flüssigkeitsdichte,
• t ist die Zeit,
• u ist das Geschwindigkeitsvektorfeld der Strömung. ⓘ

Die zeitliche Ableitung kann als die Akkumulation (oder der Verlust) von Masse im System verstanden werden, während der Divergenzterm die Differenz zwischen dem Einstrom und dem Ausstrom darstellt. In diesem Zusammenhang ist diese Gleichung auch eine der Euler-Gleichungen (Strömungslehre). Die Navier-Stokes-Gleichungen bilden eine vektorielle Kontinuitätsgleichung, die die Erhaltung des linearen Impulses beschreibt. ⓘ

Wenn das Fluid inkompressibel ist (die volumetrische Dehnungsrate ist Null), vereinfacht sich die Massenkontinuitätsgleichung zu einer Volumenkontinuitätsgleichung:

$$\nabla \cdot \mathbf {u} =0,$$

Das bedeutet, dass die Divergenz des Geschwindigkeitsfeldes überall gleich Null ist. Physikalisch gesehen ist dies gleichbedeutend mit der Aussage, dass die lokale Volumendilatationsrate gleich Null ist, so dass sich ein Wasserstrom durch ein konvergierendes Rohr nur durch eine Erhöhung seiner Geschwindigkeit anpassen wird, da Wasser weitgehend inkompressibel ist. ⓘ

Computer Vision

Beim Computersehen ist der optische Fluss das Muster der scheinbaren Bewegung von Objekten in einer visuellen Szene. Unter der Annahme, dass sich die Helligkeit des sich bewegenden Objekts zwischen zwei Einzelbildern nicht ändert, lässt sich die Gleichung für den optischen Fluss wie folgt herleiten:

$${\frac {\partial I}{\partial x}}V_{x}+{\frac {\partial I}{\partial y}}V_{y}+{\frac {\partial I}{\partial t}}=\nabla I\cdot \mathbf {V} +{\frac {\partial I}{\partial t}}=0$$

wobei

• t ist die Zeit,
• x, y Koordinaten im Bild,
• I ist die Bildintensität an der Bildkoordinate (x, y) und zum Zeitpunkt t,
• V ist der Geschwindigkeitsvektor des optischen Flusses $(V_{x},V_{y})$ an der Bildkoordinate (x, y) und zum Zeitpunkt t ⓘ

Energie und Wärme

Der Energieerhaltungssatz besagt, dass Energie weder erzeugt noch zerstört werden kann. (Zu den Besonderheiten der allgemeinen Relativitätstheorie siehe unten.) Daher gibt es eine Kontinuitätsgleichung für den Energiefluss:

$${\frac {\partial u}{\partial t}}+\nabla \cdot \mathbf {q} =0$$

wobei

• u, lokale Energiedichte (Energie pro Volumeneinheit),
• q, Energiefluss (Energietransfer pro Querschnittsfläche und Zeiteinheit) als Vektor, ⓘ

Ein wichtiges praktisches Beispiel ist der Fluss von Wärme. Wenn Wärme in einem Festkörper fließt, kann die Kontinuitätsgleichung mit dem Fourierschen Gesetz (der Wärmestrom ist proportional zum Temperaturgradienten) kombiniert werden, um die Wärmegleichung zu erhalten. Die Gleichung des Wärmestroms kann auch Quellenterme enthalten: Obwohl Energie weder erzeugt noch vernichtet werden kann, kann Wärme aus anderen Energiearten erzeugt werden, z. B. durch Reibung oder Joulesche Wärme. ⓘ

Wahrscheinlichkeitsverteilungen

Wenn es eine Größe gibt, die sich kontinuierlich gemäß einem stochastischen (zufälligen) Prozess bewegt, wie der Ort eines einzelnen gelösten Moleküls mit Brownscher Bewegung, dann gibt es eine Kontinuitätsgleichung für ihre Wahrscheinlichkeitsverteilung. Der Fluss ist in diesem Fall die Wahrscheinlichkeit pro Flächeneinheit und pro Zeiteinheit, dass das Teilchen eine Oberfläche durchquert. Gemäß der Kontinuitätsgleichung ist die negative Divergenz dieses Flusses gleich der Änderungsrate der Wahrscheinlichkeitsdichte. Die Kontinuitätsgleichung spiegelt die Tatsache wider, dass sich das Molekül immer irgendwo befindet - das Integral seiner Wahrscheinlichkeitsverteilung ist immer gleich 1 - und dass es sich in einer kontinuierlichen Bewegung bewegt (kein Teleportieren). ⓘ

Quantenmechanik

Die Quantenmechanik ist ein weiterer Bereich, in dem es eine Kontinuitätsgleichung gibt, die mit der Erhaltung der Wahrscheinlichkeit zusammenhängt. Die Begriffe in der Gleichung erfordern die folgenden Definitionen und sind etwas weniger offensichtlich als die anderen Beispiele oben, weshalb sie hier kurz erläutert werden:

• Die Wellenfunktion Ψ für ein einzelnes Teilchen im Ortsraum (und nicht im Impulsraum), d. h. eine Funktion von Ort r und Zeit t, Ψ = Ψ(r, t).
• Die Wahrscheinlichkeitsdichtefunktion lautet
  $$\rho (\mathbf {r} ,t)=\Psi ^{*}(\mathbf {r} ,t)\Psi (\mathbf {r} ,t)=|\Psi (\mathbf {r} ,t)|^{2}.$$
• Die Wahrscheinlichkeit, das Teilchen innerhalb von V zum Zeitpunkt t zu finden, wird wie folgt bezeichnet und definiert
  $$P=P_{\mathbf {r} \in V}(t)=\int _{V}\Psi ^{*}\Psi dV=\int _{V}|\Psi |^{2}dV.$$
• Der Wahrscheinlichkeitsstrom (auch Wahrscheinlichkeitsfluss genannt) ist
  $$\mathbf {j} (\mathbf {r} ,t)={\frac {\hbar }{2mi}}\left[\Psi ^{*}\left(\nabla \Psi \right)-\Psi \left(\nabla \Psi ^{*}\right)\right].$$
  ⓘ

Mit diesen Definitionen lautet die Kontinuitätsgleichung:

$$\nabla \cdot \mathbf {j} +{\frac {\partial \rho }{\partial t}}=0\mathrel {\rightleftharpoons } \nabla \cdot \mathbf {j} +{\frac {\partial |\Psi |^{2}}{\partial t}}=0.$$

ⓘ

Jede der beiden Formen kann angegeben werden. Intuitiv zeigen die obigen Größen, dass es sich um einen Wahrscheinlichkeitsstrom handelt. Die Wahrscheinlichkeit, das Teilchen an einer bestimmten Position r und zu einem bestimmten Zeitpunkt t zu finden, fließt wie eine Flüssigkeit; daher der Begriff Wahrscheinlichkeitsstrom, ein Vektorfeld. Das Teilchen selbst fließt nicht deterministisch in diesem Vektorfeld. ⓘ

Konsistenz mit der Schrödinger-Gleichung

Die zeitabhängige 3-d-Schrödinger-Gleichung und ihre komplexe Konjugierte (i → -i durchgehend) lauten wie folgt:

$${\begin{aligned}-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi +U\Psi &=i\hbar {\frac {\partial \Psi }{\partial t}},\\-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\Psi ^{*}+U\Psi ^{*}&=-i\hbar {\frac {\partial \Psi ^{*}}{\partial t}},\\\end{aligned}}$$

wobei U die Potentialfunktion ist. Die partielle Ableitung von ρ nach t ist:

$${\frac {\partial \rho }{\partial t}}={\frac {\partial |\Psi |^{2}}{\partial t}}={\frac {\partial }{\partial t}}\left(\Psi ^{*}\Psi \right)=\Psi ^{*}{\frac {\partial \Psi }{\partial t}}+\Psi {\frac {\partial \Psi ^{*}}{\partial t}}.$$

Multiplikation der Schrödingergleichung mit Ψ* und anschließende Lösung für Ψ* ∂Ψ/∂t, und in ähnlicher Weise Multiplikation der komplex konjugierten Schrödingergleichung mit Ψ und anschließende Lösung für Ψ ∂Ψ*/∂t;

$${\begin{aligned}\Psi ^{*}{\frac {\partial \Psi }{\partial t}}&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right],\\\Psi {\frac {\partial \Psi ^{*}}{\partial t}}&=-{\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}+U\Psi \Psi ^{*}\right],\\\end{aligned}}$$

Einsetzen der zeitlichen Ableitung von ρ:

$${\begin{aligned}{\frac {\partial \rho }{\partial t}}&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right]-{\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}+U\Psi \Psi ^{*}\right]\\&={\frac {1}{i\hbar }}\left[-{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +U\Psi ^{*}\Psi \right]+{\frac {1}{i\hbar }}\left[+{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}-U\Psi ^{*}\Psi \right]\\[2pt]&=-{\frac {1}{i\hbar }}{\frac {\hbar ^{2}\Psi ^{*}}{2m}}\nabla ^{2}\Psi +{\frac {1}{i\hbar }}{\frac {\hbar ^{2}\Psi }{2m}}\nabla ^{2}\Psi ^{*}\\[2pt]&={\frac {\hbar }{2im}}\left[\Psi \nabla ^{2}\Psi ^{*}-\Psi ^{*}\nabla ^{2}\Psi \right]\\\end{aligned}}$$

Die Laplacian-Operatoren (∇²) im obigen Ergebnis deuten darauf hin, dass die rechte Seite die Divergenz von j ist, und die umgekehrte Reihenfolge der Terme impliziert, dass es sich insgesamt um das Negativ von j handelt:

$${\begin{aligned}\nabla \cdot \mathbf {j} &=\nabla \cdot \left[{\frac {\hbar }{2mi}}\left(\Psi ^{*}\left(\nabla \Psi \right)-\Psi \left(\nabla \Psi ^{*}\right)\right)\right]\\&={\frac {\hbar }{2mi}}\left[\Psi ^{*}\left(\nabla ^{2}\Psi \right)-\Psi \left(\nabla ^{2}\Psi ^{*}\right)\right]\\&=-{\frac {\hbar }{2mi}}\left[\Psi \left(\nabla ^{2}\Psi ^{*}\right)-\Psi ^{*}\left(\nabla ^{2}\Psi \right)\right]\\\end{aligned}}$$

Die Kontinuitätsgleichung lautet also:

$${\begin{aligned}&{\frac {\partial \rho }{\partial t}}=-\nabla \cdot \mathbf {j} \\[3pt]{}\Rightarrow {}&{\frac {\partial \rho }{\partial t}}+\nabla \cdot \mathbf {j} =0\\\end{aligned}}$$

Die Integralform folgt wie bei der allgemeinen Gleichung. ⓘ

Halbleiter

Der gesamte Stromfluss im Halbleiter setzt sich aus dem Driftstrom und dem Diffusionsstrom sowohl der Elektronen im Leitungsband als auch der Löcher im Valenzband zusammen. ⓘ

Allgemeine Form für Elektronen in einer Dimension:

$${\frac {\partial n}{\partial t}}=n\mu _{n}{\frac {\partial E}{\partial x}}+\mu _{n}E{\frac {\partial n}{\partial x}}+D_{n}{\frac {\partial ^{2}n}{\partial x^{2}}}+(G_{n}-R_{n})$$

wobei:

• n die lokale Konzentration der Elektronen ist
• $\mu _{n}$ die Mobilität der Elektronen
• E das elektrische Feld in der Verarmungszone ist
• Dn ist der Diffusionskoeffizient für Elektronen
• G_n die Erzeugungsrate der Elektronen
• Rn ist die Rekombinationsrate der Elektronen ⓘ

Ähnliches gilt für Löcher:

$${\frac {\partial p}{\partial t}}=-p\mu _{p}{\frac {\partial E}{\partial x}}-\mu _{p}E{\frac {\partial p}{\partial x}}+D_{p}{\frac {\partial ^{2}p}{\partial x^{2}}}+(G_{p}-R_{p})$$

wobei:

• p ist die lokale Konzentration der Löcher
• $\mu _{p}$ die Mobilität der Löcher
• E das elektrische Feld in der Verarmungszone ist
• D_p ist der Diffusionskoeffizient für Löcher
• G_p ist die Rate der Erzeugung von Löchern
• R_p ist die Rekombinationsrate von Löchern ⓘ

Ableitung

In diesem Abschnitt wird die Ableitung der obigen Gleichung für Elektronen dargestellt. Eine ähnliche Herleitung kann für die Gleichung für Löcher gefunden werden. ⓘ

Betrachten wir die Tatsache, dass die Anzahl der Elektronen in einem Volumen aus Halbleitermaterial mit der Querschnittsfläche A und der Länge dx entlang der x-Achse erhalten bleibt. Genauer gesagt, kann man sagen:

$${\text{Rate of change of electron density}}=({\text{Electron flux in}}-{\text{Electron flux out}})+{\text{Net generation inside a volume}}$$

ⓘ

Mathematisch kann diese Gleichheit geschrieben werden:

$${\begin{aligned}{\frac {dn}{dt}}A\,dx&=[J(x+dx)-J(x)]{\frac {A}{e}}+(G_{n}-R_{n})A\,dx\\[3pt]{\frac {dn}{dt}}A\,dx&=[J(x)+{\frac {dJ}{dx}}dx-J(x)]{\frac {A}{e}}+(G_{n}-R_{n})A\,dx\\[3pt]{\frac {dn}{dt}}&={\frac {1}{e}}{\frac {dJ}{dx}}+(G_{n}-R_{n})\end{aligned}}$$

Hier bezeichnet J die Stromdichte (deren Richtung vereinbarungsgemäß gegen den Elektronenfluss gerichtet ist) aufgrund des Elektronenflusses innerhalb des betrachteten Volumens des Halbleiters. Sie wird auch Elektronenstromdichte genannt. ⓘ

Die Gesamtelektronenstromdichte ist die Summe der Driftstrom- und Diffusionsstromdichten:

$$J_{n}=en\mu _{n}E+eD_{n}{\frac {dn}{dx}}$$

ⓘ

Wir haben also

$${\frac {dn}{dt}}={\frac {1}{e}}{\frac {d}{dx}}\left(en\mu _{n}E+eD_{n}{\frac {dn}{dx}}\right)+(G_{n}-R_{n})$$

ⓘ

Die Anwendung der Produktregel führt zu dem endgültigen Ausdruck:

$${\frac {dn}{dt}}=\mu _{n}E{\frac {dn}{dx}}+\mu _{n}n{\frac {dE}{dx}}+D_{n}{\frac {d^{2}n}{dx^{2}}}+(G_{n}-R_{n})$$

ⓘ

Lösung

Der Schlüssel zur Lösung dieser Gleichungen in realen Geräten besteht darin, wann immer möglich Bereiche zu wählen, in denen die meisten Mechanismen vernachlässigbar sind, so dass sich die Gleichungen auf eine viel einfachere Form reduzieren. ⓘ

Relativistische Version

Spezielle Relativitätstheorie

Die Notation und die Hilfsmittel der speziellen Relativitätstheorie, insbesondere 4-Vektoren und 4-Gradienten, bieten eine bequeme Möglichkeit, jede Kontinuitätsgleichung zu schreiben. ⓘ

Die Dichte einer Größe ρ und ihr Strom j können zu einem 4-Vektor, dem 4-Strom, zusammengefasst werden:

$$J=\left(c\rho ,j_{x},j_{y},j_{z}\right)$$

Dabei ist c die Lichtgeschwindigkeit. Die 4-Divergenz dieses Stroms ist:

$$\partial _{\mu }J^{\mu }=c{\frac {\partial \rho }{\partial ct}}+\nabla \cdot \mathbf {j}$$

wobei ∂_μ der 4-Gradient und μ ein Index ist, der die Raumzeitdimension bezeichnet. Dann lautet die Kontinuitätsgleichung:

$$\partial _{\mu }J^{\mu }=0$$

für den üblichen Fall, dass es keine Quellen oder Senken gibt, d. h. für perfekt erhaltene Größen wie Energie oder Ladung. Diese Kontinuitätsgleichung ist offenkundig ("offensichtlich") Lorentz-invariant. ⓘ

Beispiele für Kontinuitätsgleichungen, die häufig in dieser Form formuliert werden, sind die elektrische Ladungserhaltung

$$\partial _{\mu }J^{\mu }=0$$

wobei J der elektrische 4-Strom ist; und die Energie-Impuls-Erhaltung

$$\partial _{\nu }T^{\mu \nu }=0$$

wobei T der Spannungs-Energie-Tensor ist. ⓘ

Allgemeine Relativitätstheorie

In der allgemeinen Relativitätstheorie, wo die Raumzeit gekrümmt ist, beinhaltet die Kontinuitätsgleichung (in Differentialform) für Energie, Ladung oder andere erhaltene Größen die kovariante Divergenz anstelle der gewöhnlichen Divergenz. ⓘ

So ist beispielsweise der Spannungs-Energie-Tensor ein Tensorfeld zweiter Ordnung, das Energie-Impuls-Dichten, Energie-Impuls-Flüsse und Schubspannungen einer Masse-Energie-Verteilung enthält. Die differentielle Form der Energie-Impuls-Erhaltung in der allgemeinen Relativitätstheorie besagt, dass die kovariante Divergenz des Spannungs-Energie-Tensors Null ist:

$${T^{\mu }}_{\nu ;\mu }=0.$$

ⓘ

Dies ist eine wichtige Einschränkung für die Form der Einsteinschen Feldgleichungen in der allgemeinen Relativitätstheorie. ⓘ

Die gewöhnliche Divergenz des Spannungs-Energie-Tensors muss jedoch nicht verschwinden:

$$\partial _{\mu }T^{\mu \nu }=-\Gamma _{\mu \lambda }^{\mu }T^{\lambda \nu }-\Gamma _{\mu \lambda }^{\nu }T^{\mu \lambda },$$

ⓘ

Die rechte Seite verschwindet nur für eine flache Geometrie. ⓘ

Infolgedessen ist die Integralform der Kontinuitätsgleichung schwer zu definieren und nicht unbedingt für eine Region gültig, in der die Raumzeit stark gekrümmt ist (z. B. um ein Schwarzes Loch oder im gesamten Universum). ⓘ

Teilchenphysik

Quarks und Gluonen haben eine Farbladung, die wie die elektrische Ladung immer erhalten bleibt, und es gibt eine Kontinuitätsgleichung für solche Farbladungsströme (explizite Ausdrücke für Ströme sind im Gluonen-Feldstärketensor enthalten). ⓘ

Es gibt viele andere Größen in der Teilchenphysik, die oft oder immer erhalten bleiben: Baryonenzahl (proportional zur Anzahl der Quarks abzüglich der Anzahl der Antiquarks), Elektronenzahl, mu-Zahl, tau-Zahl, Isospin und andere. Für jedes dieser Elemente gibt es eine entsprechende Kontinuitätsgleichung, die möglicherweise Quellen-/Senkenterme enthält. ⓘ

Noethers Theorem

Ein Grund dafür, dass Erhaltungsgleichungen in der Physik häufig vorkommen, ist das Noether-Theorem. Dieser besagt, dass es immer dann, wenn die physikalischen Gesetze eine kontinuierliche Symmetrie aufweisen, eine Kontinuitätsgleichung für eine erhaltene physikalische Größe gibt. Die drei berühmtesten Beispiele sind:

• Die physikalischen Gesetze sind in Bezug auf die Zeittranslation invariant, d. h., die physikalischen Gesetze sind heute noch dieselben wie gestern. Diese Symmetrie führt zu der Kontinuitätsgleichung für die Erhaltung der Energie.
• Die physikalischen Gesetze sind in Bezug auf die Raumtranslation invariant - so sind beispielsweise die physikalischen Gesetze in Brasilien dieselben wie in Argentinien. Diese Symmetrie führt zu der Kontinuitätsgleichung für die Impulserhaltung.
• Die physikalischen Gesetze sind invariant in Bezug auf die Orientierung - wenn man beispielsweise im Weltraum schwebt, gibt es keine Messung, mit der man feststellen könnte, in welcher Richtung man sich befindet; die physikalischen Gesetze sind dieselben, unabhängig von der Orientierung. Diese Symmetrie führt zu der Kontinuitätsgleichung für die Erhaltung des Drehimpulses. ⓘ

Spezielle Kontinuitätsgleichungen

Hydrodynamik

Verändert sich in der Hydrodynamik die Massendichte $\rho (t,{\vec {x}})$, weil die Flüssigkeit mit der Geschwindigkeit ${\vec {u}}={\tfrac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}$ längs der Bahnkurven ${\vec {x}}(t)$ strömt, so ist die zugehörige Stromdichte ⓘ

${\vec {j}}=\rho \,{\vec {u}}$ ⓘ

und die Kontinuitätsgleichung lautet ⓘ

${\begin{alignedat}{2}&{\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\cdot (\rho {\vec {u}})&&=0\\\Leftrightarrow &{\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\rho \cdot {\vec {u}}+\rho {\vec {\nabla }}\cdot {\vec {u}}&&=0\end{alignedat}}$ (Begründung: Produktregel) ⓘ

Für die zeitliche Änderung der Dichte bei einem Teilchen, das die Bahn ${\vec {x}}(t)$ durchläuft, besagt dies:

${\begin{alignedat}{2}&{\frac {\partial \rho }{\partial t}}+{\vec {\nabla }}\rho \cdot {\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} t}}&&=-\rho \cdot {\vec {\nabla }}\cdot {\vec {u}}\\\Leftrightarrow &{\frac {\mathrm {d} }{\mathrm {d} t}}\rho (t,{\vec {x}}(t))&&=-\rho \cdot {\vec {\nabla }}\cdot \,{\vec {u}}\end{alignedat}}$ (Begründung: totales Differential). ⓘ

Entlang einer Trajektorie ändert sich also die Dichte mit der Divergenz der Strömung ${\vec {u}}.$ ⓘ

Die Strömung ist inkompressibel, wenn die Dichte entlang einer Trajektorie konstant bleibt:

${\frac {\mathrm {d} }{\mathrm {d} t}}\rho (t,{\vec {x}}(t))=0$ ⓘ

Daraus folgt, dass in diesem Fall die Divergenz der Strömung Null ist:

$\Rightarrow {\vec {\nabla }}\cdot {\vec {u}}={\frac {\partial u}{\partial x}}+{\frac {\partial v}{\partial y}}+{\frac {\partial w}{\partial z}}=0$ ⓘ

Quantenmechanik

In der nichtrelativistischen Quantenmechanik wird der Zustand eines Teilchens, etwa eines einzelnen Elektrons, durch eine Wellenfunktion $\Psi ({\vec {x}},t)$ beschrieben. ⓘ

Das Betragsquadrat

$\rho ({\vec {x}},t)=|\Psi ({\vec {x}},t)|^{2}$

gibt die Wahrscheinlichkeitsdichte dafür an, ein Teilchen zur Zeit $t$ am Ort ${\vec {x}}$ vorzufinden. Mit der zugehörigen Wahrscheinlichkeitsstromdichte

${\vec {j}}=-{\frac {i\hbar }{2m}}(\Psi ^{*}{\vec {\nabla }}\Psi -\Psi {\vec {\nabla }}\Psi ^{*})$

gilt ohne äußeres Magnetfeld als Folge der Schrödingergleichung die Kontinuitätsgleichung

${\frac {\partial }{\partial t}}\rho +{\vec {\nabla }}\cdot {\vec {j}}=0\,$.

Ist ein äußeres Magnetfeld vorhanden, muss auf die Pauli-Gleichung zurückgegriffen werden und es ergibt sich

${\vec {j}}=-{\frac {i\hbar }{2m}}(\Psi ^{\dagger }{\vec {\nabla }}\Psi -({\vec {\nabla }}\Psi ^{\dagger })\Psi )-{\frac {q}{m}}{\vec {A}}\Psi ^{\dagger }\Psi +{\frac {\hbar }{2m}}{\vec {\nabla }}\times (\Psi ^{\dagger }{\vec {\sigma }}\Psi )$

wobei $\sigma$ für die Pauli-Matrizen stehen. Der letzte Term verschwindet zwar bei der Divergenzbildung und ist nicht direkt aus der Pauli-Gleichung ableitbar, ergibt sich aber aus dem nichtrelativistischen Grenzfall der Dirac-Gleichung. ⓘ

Im Rahmen der relativistischen Quantenmechanik gehorchen Teilchen der Klein-Gordon-Gleichung (für Skalarbosonen) beziehungsweise der Dirac-Gleichung (für Fermionen). Da die Gleichungen der Speziellen Relativitätstheorie gehorchen, können die Kontinuitätsgleichungen für diese Fälle in manifest kovarianter Form

$\partial _{\mu }j^{\mu }=\partial _{t}\rho +{\vec {\nabla }}\cdot {\vec {j}}=0$

geschrieben werden und es ergibt sich

$j_{\text{KG}}^{\mu }=\mathrm {i} \left(\phi ^{*}\partial ^{\mu }\phi -\phi \partial ^{\mu }\phi ^{*}\right)$

$j_{\text{Dirac}}^{\mu }=\psi ^{\dagger }\gamma ^{0}\gamma ^{\mu }\psi$

wobei $\phi$ beziehungsweise $\psi$ für die skalare bosonische/vektorwertige fermionische Wellenfunktion stehen und $\gamma$ die Dirac-Matrizen sind. ⓘ

Im Rahmen der Klein-Gordon-Kontinuitätsgleichung kann – im Gegensatz zum nichtrelativistischen oder fermionen Fall – die Größe $j^{0}={\frac {1}{c}}\mathrm {i} \left(\phi ^{*}\partial _{t}\phi -\phi \partial _{t}\phi ^{*}\right)$ nicht als Wahrscheinlichkeitsdichte gedeutet werden, da diese Größe nicht positiv semidefinit ist. ⓘ

Weitere Anwendungen: Allgemeine Erhaltungsgrößen

Man erkennt an der Analogie zum „elektrischen“ Fall, dass Kontinuitätsgleichungen immer dann gelten müssen, wenn eine ladungsartige Größe und eine stromartige Größe wie oben angegeben zusammenhängen. Als weiteres konkretes Beispiel könnte man etwa den in der Thermodynamik wichtigen Wärmestrom angeben. Die „Ladungsdichte“ muss bei Integration über den Gesamtraum eine Erhaltungsgröße ergeben, z. B. die elektrische Gesamtladung, bzw. – im Falle der Quantenmechanik – die Gesamtwahrscheinlichkeit, 1, oder im dritten Fall, die gesamte zugeführte Wärme, bei Systemen, deren Wärmeinhalt als „erhalten“ angesehen werden kann (z. B. Wärmediffusion). ⓘ

In der Strömungsmechanik folgt aus der Kontinuitätsgleichung das Kontinuitätsgesetz für (inkompressible) Fluide. ⓘ

Literatur

• Batchelor, G.K.: An introduction to fluid dynamics, Cambridge university press, 2000, ISBN 0-521-66396-2 ⓘ

Weblinks

• Video: Kontinuitätsgleichung. Institut für den Wissenschaftlichen Film (IWF) 2004, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.3203/IWF/C-14818. ⓘ