Delta-Distribution

Schematische Darstellung des Dirac-Deltas durch eine Linie, die von einem Pfeil überragt wird. Die Höhe des Pfeils gibt normalerweise den Wert einer multiplikativen Konstante an, die die Fläche unter der Funktion ergibt. Die andere Konvention besteht darin, die Fläche neben die Pfeilspitze zu schreiben. ⓘ

Das Dirac-Delta als der Grenzwert von $a\to 0$ (im Sinne von Verteilungen) der Folge von nullpunktzentrierten Normalverteilungen $\delta _{a}(x)={\frac {1}{\left|a\right|{\sqrt {\pi }}}}e^{-(x/a)^{2}}$ ⓘ

In der Mathematik ist die Dirac-Delta-Verteilung (δ-Verteilung), auch bekannt als Einheitsimpuls, eine verallgemeinerte Funktion oder Verteilung über den reellen Zahlen, deren Wert überall außer bei Null gleich Null ist und deren Integral über die gesamte reelle Linie gleich Eins ist. ⓘ

Nach heutigem Verständnis ist der Impuls eine lineare Funktion, die jede kontinuierliche Funktion auf ihren Wert bei Null abbildet, oder der schwache Grenzwert einer Folge von Höckerfunktionen, die über den größten Teil der reellen Linie Null sind, mit einer hohen Spitze am Ursprung. Bump-Funktionen werden daher manchmal als "ungefähre" oder "entstehende" Delta-Verteilungen bezeichnet. ⓘ

Die Deltafunktion wurde von dem Physiker Paul Dirac als Hilfsmittel für die Normalisierung von Zustandsvektoren eingeführt. Sie wird auch in der Wahrscheinlichkeitstheorie und der Signalverarbeitung verwendet. Ihre Gültigkeit war umstritten, bis Laurent Schwartz die Theorie der Verteilungen entwickelte, in der sie als eine lineare Form definiert ist, die auf Funktionen wirkt. ⓘ

Die Kronecker-Delta-Funktion, die in der Regel auf einem diskreten Gebiet definiert ist und die Werte 0 und 1 annimmt, ist das diskrete Analogon der Dirac-Delta-Funktion. ⓘ

Die Delta-Distribution (auch δ-Funktion; Dirac-Funktion, -Impuls, -Puls, -Stoß (nach Paul Dirac), Stoßfunktion, Nadelimpuls, Impulsfunktion oder Einheitsimpulsfunktion genannt) als mathematischer Begriff ist eine spezielle irreguläre Distribution mit kompaktem Träger. Sie hat in der Mathematik und Physik grundlegende Bedeutung. Ihr übliches Formelsymbol ist δ (kleines Delta). ⓘ

Motivation und Überblick

Die Kurve des Dirac-Deltas wird in der Regel als eine Kurve entlang der gesamten x-Achse und der positiven y-Achse betrachtet. Das Dirac-Delta wird zur Modellierung einer hohen schmalen Spike-Funktion (eines Impulses) und anderer ähnlicher Abstraktionen wie einer Punktladung, Punktmasse oder eines Elektronenpunktes verwendet. Um zum Beispiel die Dynamik einer Billardkugel zu berechnen, die gestoßen wird, kann man die Kraft des Stoßes durch ein Dirac-Delta annähern. Dadurch werden nicht nur die Gleichungen vereinfacht, sondern man kann auch die Bewegung der Kugel berechnen, indem man nur den Gesamtimpuls des Aufpralls berücksichtigt, ohne ein detailliertes Modell der gesamten elastischen Energieübertragung auf subatomarer Ebene (zum Beispiel). ⓘ

Nehmen wir an, eine Billardkugel befindet sich im Ruhezustand. Zum Zeitpunkt $t=0$ wird sie von einer anderen Kugel gestoßen, die ihr einen Impuls $P$, in ${\text{kg m s}}^{-1}$. Der Impulsaustausch erfolgt zwar nicht sofort, da er durch elastische Prozesse auf molekularer und subatomarer Ebene vermittelt wird, doch für praktische Zwecke ist es zweckmäßig, diese Energieübertragung als tatsächlich sofort zu betrachten. Die Kraft ist daher $P\,\delta (t)$. (Die Einheiten von $\delta (t)$ sind $\mathrm {s} ^{-1}$.) ⓘ

Um diese Situation strenger zu modellieren, nehmen wir an, dass die Kraft stattdessen gleichmäßig über ein kleines Zeitintervall verteilt ist $\Delta t=[0,T]$. Das bedeutet, ⓘ

$F_{\Delta t}(t)={\begin{cases}P/\Delta t&0<t\leq T,\\0&{\text{otherwise}}.\end{cases}}$ ⓘ

Dann wird der Impuls zu jedem Zeitpunkt t durch Integration ermittelt:

$p(t)=\int _{0}^{t}F_{\Delta t}(\tau )\,\mathrm {d} \tau ={\begin{cases}P&t\geq T\\P\,t/\Delta t&0\leq t\leq T\\0&{\text{otherwise.}}\end{cases}}$ ⓘ

Die Modellsituation einer momentanen Impulsübertragung erfordert nun, dass man den Grenzwert als $\Delta t\to 0$, was überall ein Ergebnis außer bei 0 ergibt:

$p(t)={\begin{cases}P&t>0\\0&t<0.\end{cases}}$ ⓘ

Hier sind die Funktionen $F_{\Delta t}$ als nützliche Annäherungen an die Idee der momentanen Impulsübertragung betrachtet werden. ⓘ

Die Deltafunktion ermöglicht es uns, einen idealisierten Grenzwert dieser Annäherungen zu konstruieren. Leider ist der tatsächliche Grenzwert der Funktionen (im Sinne der punktweisen Konvergenz) ${\textstyle \lim _{\Delta t\to 0}F_{\Delta t}}$ überall gleich Null, außer an einem einzigen Punkt, wo er unendlich ist. Um dem Dirac-Delta einen angemessenen Sinn zu geben, sollten wir stattdessen darauf bestehen, dass die Eigenschaft ⓘ

$\int _{-\infty }^{\infty }F_{\Delta t}(t)\,\mathrm {d} t=P,$ ⓘ

die für alle $\Delta t>0$gilt, auch im Grenzwert gelten sollte. So wird in der Gleichung ${\textstyle F(t)=P\,\delta (t)=\lim _{\Delta t\to 0}F_{\Delta t}(t)}$wird davon ausgegangen, dass der Grenzwert immer außerhalb des Integrals liegt. ⓘ

In der angewandten Mathematik, wie wir es hier getan haben, wird die Deltafunktion oft als eine Art Grenzwert (schwacher Grenzwert) einer Folge von Funktionen behandelt, von denen jedes Mitglied eine hohe Spitze am Ursprung hat: zum Beispiel eine Folge von Gaußschen Verteilungen, die im Ursprung zentriert sind und deren Varianz gegen Null tendiert. ⓘ

Das Dirac-Delta ist keine echte Funktion, zumindest keine gewöhnliche mit Bereich und Reichweite in reellen Zahlen. Zum Beispiel sind die Objekte f(x) = δ(x) und g(x) = 0 überall gleich, außer bei x = 0, haben aber unterschiedliche Integrale. Nach der Lebesgue-Integrationstheorie ist f nur dann integrierbar, wenn g integrierbar ist und die Integrale von f und g identisch sind, wenn f und g solche Funktionen sind, dass f = g fast überall ist. Ein rigoroser Ansatz zur Betrachtung der Dirac-Delta-Funktion als eigenständiges mathematisches Objekt erfordert die Maßtheorie oder die Theorie der Verteilungen. ⓘ

Geschichte

Joseph Fourier stellte in seiner Abhandlung Théorie analytique de la chaleur den so genannten Fourier-Integralsatz in der Form:

$f(x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\ \ d\alpha \,f(\alpha )\ \int _{-\infty }^{\infty }dp\ \cos(px-p\alpha )\ ,$ ⓘ

was gleichbedeutend ist mit der Einführung der δ-Funktion in der Form:

$\delta (x-\alpha )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }dp\ \cos(px-p\alpha )\ .$ ⓘ

Später drückte Augustin Cauchy das Theorem mit Hilfe von Exponentialen aus:

$f(x)={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\ e^{ipx}\left(\int _{-\infty }^{\infty }e^{-ip\alpha }f(\alpha )\,d\alpha \right)\,dp.$ ⓘ

Cauchy wies darauf hin, dass die Reihenfolge der Integration in diesem Ergebnis unter bestimmten Umständen von Bedeutung ist (vgl. Fubinis Theorem). ⓘ

Wie mit der Verteilungstheorie begründet, kann die Cauchy-Gleichung so umgestellt werden, dass sie der ursprünglichen Formulierung von Fourier ähnelt und die δ-Funktion wie folgt dargestellt wird ⓘ

${\begin{aligned}f(x)&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{ipx}\left(\int _{-\infty }^{\infty }e^{-ip\alpha }f(\alpha )\,d\alpha \right)\,dp\\[4pt]&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\left(\int _{-\infty }^{\infty }e^{ipx}e^{-ip\alpha }\,dp\right)f(\alpha )\,d\alpha =\int _{-\infty }^{\infty }\delta (x-\alpha )f(\alpha )\,d\alpha ,\end{aligned}}$ ⓘ

wobei die δ-Funktion wie folgt ausgedrückt wird ⓘ

$\delta (x-\alpha )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{ip(x-\alpha )}\,dp\ .$ ⓘ

Eine strenge Interpretation der Exponentialform und die verschiedenen Einschränkungen der Funktion f, die für ihre Anwendung notwendig sind, erstreckten sich über mehrere Jahrhunderte. Die Probleme mit einer klassischen Interpretation werden im Folgenden erläutert:

Der größte Nachteil der klassischen Fourier-Transformation ist eine recht enge Klasse von Funktionen (Originalen), für die sie effektiv berechnet werden kann. Diese Funktionen müssen nämlich hinreichend schnell (in der Nähe des Unendlichen) gegen Null abfallen, um die Existenz des Fourier-Integrals zu gewährleisten. Zum Beispiel existiert die Fourier-Transformation von so einfachen Funktionen wie Polynomen nicht im klassischen Sinne. Durch die Erweiterung der klassischen Fourier-Transformation auf Verteilungen wurde die Klasse der zu transformierenden Funktionen erheblich vergrößert, wodurch viele Hindernisse beseitigt wurden. ⓘ

Zu den weiteren Entwicklungen gehörte die Verallgemeinerung des Fourier-Integrals, "beginnend mit Plancherels bahnbrechender L²-Theorie (1910), fortgesetzt mit den Arbeiten von Wiener und Bochner (um 1930) und gipfelnd in der Verschmelzung mit L. Schwartz' Theorie der Verteilungen (1945) ...", und führte zur formalen Entwicklung der Dirac-Delta-Funktion. ⓘ

Eine Infinitesimalformel für eine unendlich hohe Einheitsimpuls-Deltafunktion (infinitesimale Version der Cauchy-Verteilung) erscheint ausdrücklich in einem Text von Augustin Louis Cauchy aus dem Jahr 1827. Siméon Denis Poisson betrachtete das Thema im Zusammenhang mit der Untersuchung der Wellenausbreitung, ebenso wie Gustav Kirchhoff etwas später. Kirchhoff und Hermann von Helmholtz führten auch den Einheitsimpuls als Grenzwert von Gaußschen Kräften ein, der auch Lord Kelvins Vorstellung von einer punktförmigen Wärmequelle entsprach. Ende des 19. Jahrhunderts verwendete Oliver Heaviside formale Fourier-Reihen, um den Einheitsimpuls zu manipulieren. Die Dirac-Deltafunktion als solche wurde von Paul Dirac 1927 in seinem Aufsatz The Physical Interpretation of the Quantum Dynamics eingeführt und in seinem Lehrbuch The Principles of Quantum Mechanics verwendet. Er nannte sie "Deltafunktion", da er sie als kontinuierliches Analogon des diskreten Kronecker-Deltas verwendete. ⓘ

Definitionen

Die Funktion $\delta _{k}$ kann man nun mit einer regulären Distribution

$\delta _{k}(f):=\langle \delta _{k},f\rangle :=\int _{\mathbb {R} ^{n}}\delta _{k}(x)\,f(x)\,\mathrm {d} x$

identifizieren. Nur im Limes $k\to \infty$ erhält man das ungewöhnliche Verhalten der Delta-Distribution ⓘ

$\lim _{k\to \infty }\delta _{k}(f)=\lim _{k\to \infty }\langle \delta _{k},f\rangle =f(0)=\langle \delta ,f\rangle$ ⓘ

wobei zu beachten ist, dass die Limes-Bildung nicht unter dem Integral, sondern davor erfolgt. Würde man den Limes unter das Integral ziehen, so wäre $\delta _{\epsilon }$ fast überall Null, nur nicht bei $x=0$. Ein einzelner Punkt hat jedoch das Lebesgue-Maß Null und das ganze Integral würde verschwinden. ⓘ

Anschaulich stellt man sich die Delta-Distribution als eine beliebig hohe und beliebig schmale Funktion vor, die über der x-Achse eine Fläche mit Größe 1 Flächeneinheit einschließt. Man lässt nun die Funktion immer schmaler und dafür immer höher werden – die Fläche darunter muss konstant 1 bleiben. Es existieren auch mehrdimensionale Dirac-Distributionen, diese werden anschaulich zu mehrdimensionalen „Keulen“ mit dem Volumen 1. ⓘ

Das Dirac-Delta kann man sich grob als eine Funktion auf der reellen Linie vorstellen, die überall Null ist, außer am Ursprung, wo sie unendlich ist, ⓘ

$\delta (x)={\begin{cases}+\infty ,&x=0\\0,&x\neq 0\end{cases}}$ ⓘ

und die außerdem die Identität erfüllen muss ⓘ

$\int _{-\infty }^{\infty }\delta (x)\,dx=1.$ ⓘ

Dies ist lediglich eine heuristische Charakterisierung. Das Dirac-Delta ist keine Funktion im herkömmlichen Sinne, da keine auf den reellen Zahlen definierte Funktion diese Eigenschaften hat. Die Dirac-Delta-Funktion kann entweder als eine Verteilung oder als ein Maß definiert werden. ⓘ

Als Maß

Eine Möglichkeit, den Begriff der Dirac-Deltafunktion genau zu erfassen, ist die Definition eines Maßes, des so genannten Dirac-Maßes, das eine Teilmenge A der reellen Linie R als Argument akzeptiert und δ(A) = 1 liefert, wenn 0 ∈ A, und δ(A) = 0 andernfalls. Wenn man sich die Deltafunktion als Modell einer idealisierten Punktmasse bei 0 vorstellt, dann repräsentiert δ(A) die in der Menge A enthaltene Masse. Man kann dann das Integral gegen δ als das Integral einer Funktion gegen diese Massenverteilung definieren. Formal liefert das Lebesgue-Integral das notwendige analytische Mittel. Das Lebesgue-Integral in Bezug auf das Maß δ erfüllt ⓘ

$\int _{-\infty }^{\infty }f(x)\,\delta \{dx\}=f(0)$ ⓘ

für alle stetigen, kompakten Funktionen f. Das Maß δ ist nicht absolut stetig in Bezug auf das Lebesgue-Maß - es ist sogar ein singuläres Maß. Folglich hat das Deltamaß keine Radon-Nikodym-Ableitung (in Bezug auf das Lebesgue-Maß) - keine echte Funktion, für die die Eigenschaft ⓘ

$\int _{-\infty }^{\infty }f(x)\delta (x)\,dx=f(0)$ ⓘ

gilt. Folglich ist die letztgenannte Schreibweise ein bequemer Missbrauch der Schreibweise und kein Standardintegral (Riemann- oder Lebesgue-Integral). ⓘ

Als Wahrscheinlichkeitsmaß auf R ist das Deltamaß durch seine kumulative Verteilungsfunktion charakterisiert, die die Einheitsschrittfunktion ist. ⓘ

$H(x)={\begin{cases}1&{\text{if }}x\geq 0\\0&{\text{if }}x<0.\end{cases}}$ ⓘ

Das bedeutet, dass H(x) das Integral der kumulativen Indikatorfunktion 1(-∞, x] in Bezug auf das Maß δ ist; d.h., ⓘ

$H(x)=\int _{\mathbf {R} }\mathbf {1} _{(-\infty ,x]}(t)\,\delta \{dt\}=\delta (-\infty ,x],$ ⓘ

wobei letzteres das Maß dieses Intervalls ist, genauer gesagt, δ((-∞, x]). So kann insbesondere die Integration der Deltafunktion gegen eine stetige Funktion richtig als Riemann-Stieltjes-Integral verstanden werden:

$\int _{-\infty }^{\infty }f(x)\delta \{dx\}=\int _{-\infty }^{\infty }f(x)\,dH(x).$ ⓘ

Alle höheren Momente von δ sind Null. Insbesondere sind die charakteristische Funktion und die momenterzeugende Funktion beide gleich eins. ⓘ

Als eine Verteilung

In der Verteilungstheorie wird eine verallgemeinerte Funktion nicht als Funktion an sich betrachtet, sondern nur in Bezug darauf, wie sie sich auf andere Funktionen auswirkt, wenn sie gegen diese "integriert" wird. Um die Deltafunktion richtig zu definieren, genügt es, zu sagen, was das "Integral" der Deltafunktion gegen eine hinreichend "gute" Testfunktion φ ist, die auch als Bump-Funktion bezeichnet wird. Wenn die Deltafunktion bereits als Maß verstanden wird, dann liefert das Lebesgue-Integral einer Testfunktion gegen dieses Maß das notwendige Integral. ⓘ

Ein typischer Raum von Testfunktionen besteht aus allen glatten Funktionen auf R mit kompakter Unterstützung, die so viele Ableitungen wie nötig haben. Als Verteilung ist das Dirac-Delta ein lineares Funktional auf dem Raum der Testfunktionen und ist definiert durch ⓘ

$\delta [\varphi ]=\varphi (0)$

(1) ⓘ

für jede Testfunktion $\varphi$. ⓘ

Damit δ eine richtige Verteilung ist, muss sie in einer geeigneten Topologie auf dem Raum der Testfunktionen stetig sein. Damit eine lineare Funktion S auf dem Raum der Testfunktionen eine Verteilung definiert, ist es im Allgemeinen notwendig und ausreichend, dass es für jede positive ganze Zahl N eine ganze Zahl M_N und eine Konstante C_N gibt, so dass für jede Testfunktion φ die Ungleichung gilt ⓘ

$\left|S[\varphi ]\right|\leq C_{N}\sum _{k=0}^{M_{N}}\sup _{x\in [-N,N]}\left|\varphi ^{(k)}(x)\right|.$ ⓘ

Bei der δ-Verteilung hat man eine solche Ungleichung (mit CN = 1) mit MN = 0 für alle N. Somit ist δ eine Verteilung der Ordnung Null. Sie ist außerdem eine Verteilung mit kompakter Unterstützung (die Unterstützung ist {0}). ⓘ

Die Delta-Verteilung kann auch auf mehrere gleichwertige Arten definiert werden. Zum Beispiel ist sie die verteilungsmäßige Ableitung der Heaviside-Stufenfunktion. Das bedeutet, dass für jede Testfunktion φ gilt ⓘ

$\delta [\varphi ]=-\int _{-\infty }^{\infty }\varphi '(x)H(x)\,dx.$ ⓘ

Intuitiv, wenn die Integration durch Teile erlaubt wäre, dann müsste sich das letztgenannte Integral vereinfachen zu ⓘ

$\int _{-\infty }^{\infty }\varphi (x)H'(x)\,dx=\int _{-\infty }^{\infty }\varphi (x)\delta (x)\,dx,$ ⓘ

und tatsächlich ist eine Form der Integration durch Teile für das Stieltjes-Integral erlaubt, und in diesem Fall hat man ⓘ

$-\int _{-\infty }^{\infty }\varphi '(x)H(x)\,dx=\int _{-\infty }^{\infty }\varphi (x)\,dH(x).$ ⓘ

Im Rahmen der Maßtheorie führt das Dirac-Maß zu einer Verteilung durch Integration. Umgekehrt definiert Gleichung (1) ein Daniell-Integral auf dem Raum aller kompakt unterstützten stetigen Funktionen φ, das durch den Riesz-Darstellungssatz als das Lebesgue-Integral von φ über ein Radon-Maß dargestellt werden kann. ⓘ

Im Allgemeinen wird der Begriff "Dirac-Deltafunktion" im Sinne von Verteilungen und nicht von Maßen verwendet, wobei das Dirac-Maß einer von mehreren Begriffen für den entsprechenden Begriff in der Maßtheorie ist. In einigen Quellen wird auch der Begriff Dirac-Delta-Verteilung verwendet. ⓘ

Verallgemeinerungen

Die Deltafunktion kann im n-dimensionalen euklidischen Raum Rn als das Maß definiert werden, für das gilt ⓘ

$\int _{\mathbf {R} ^{n}}f(\mathbf {x} )\delta \{d\mathbf {x} \}=f(\mathbf {0} )$ ⓘ

für jede kompakt unterstützte stetige Funktion f. Als Maß ist die n-dimensionale Deltafunktion das Produktmaß der 1-dimensionalen Deltafunktionen in jeder Variablen einzeln. Formal hat man also für x = (x₁, x₂, ..., xn) ⓘ

$\delta (\mathbf {x} )=\delta (x_{1})\delta (x_{2})\cdots \delta (x_{n}).$

(2) ⓘ

Die Deltafunktion kann auch im Sinne von Verteilungen genau wie oben im eindimensionalen Fall definiert werden. Trotz der weit verbreiteten Verwendung in technischen Zusammenhängen sollte (2) jedoch mit Vorsicht behandelt werden, da das Produkt von Verteilungen nur unter recht engen Bedingungen definiert werden kann. ⓘ

Der Begriff des Dirac-Maßes ist für jede Menge sinnvoll. Wenn also X eine Menge ist, x₀ ∈ X ein markierter Punkt ist und Σ eine beliebige Sigma-Algebra von Teilmengen von X ist, dann ist das Maß, das auf den Mengen A ∈ Σ durch ⓘ

$\delta _{x_{0}}(A)={\begin{cases}1&{\text{if }}x_{0}\in A\\0&{\text{if }}x_{0}\notin A\end{cases}}$ ⓘ

definiert ist, das Deltamaß oder die auf x₀ konzentrierte Einheitsmasse. ⓘ

Eine weitere gängige Verallgemeinerung der Deltafunktion ist die auf eine differenzierbare Mannigfaltigkeit, wo die meisten ihrer Eigenschaften als Verteilung aufgrund der differenzierbaren Struktur ebenfalls genutzt werden können. Die Deltafunktion auf einer Mannigfaltigkeit M, die im Punkt x₀ ∈ M zentriert ist, ist als die folgende Verteilung definiert:

$\delta _{x_{0}}[\varphi ]=\varphi (x_{0})$

(3) ⓘ

für alle kompakten glatten reellwertigen Funktionen φ auf M. Ein üblicher Spezialfall dieser Konstruktion ist der, bei dem M eine offene Menge im euklidischen Raum Rn ist. ⓘ

Auf einem lokal kompakten Hausdorff-Raum X ist das Dirac-Delta-Maß, das auf einen Punkt x konzentriert ist, das Radon-Maß, das mit dem Daniell-Integral (3) auf kompakt unterstützten stetigen Funktionen φ assoziiert ist. Auf dieser Ebene der Allgemeinheit ist die Infinitesimalrechnung als solche nicht mehr möglich, es stehen jedoch eine Reihe von Techniken aus der abstrakten Analysis zur Verfügung. Zum Beispiel ist die Abbildung $x_{0}\mapsto \delta _{x_{0}}$ eine kontinuierliche Einbettung von X in den Raum der endlichen Radon-Maße auf X, ausgestattet mit ihrer vagen Topologie. Außerdem ist die konvexe Hülle des Bildes von X unter dieser Einbettung dicht im Raum der Wahrscheinlichkeitsmaße auf X. ⓘ

Eigenschaften

• Definierende Eigenschaft der Delta-Distribution: Faltungseigenschaft, auch Ausblendeigenschaft, Siebeigenschaft genannt

$\langle \delta ,f\rangle =\int _{-\infty }^{\infty }\delta (x)\,f(x)\,\mathrm {d} x=f(0)$

bzw. mit den Eigenschaften Translation und Skalierung (siehe unten) folgt:

$\int _{-\infty }^{\infty }f(x)\,\delta (x-a)\,\mathrm {d} x=\int _{-\infty }^{\infty }f(x)\,\delta (a-x)\,\mathrm {d} x=f(a),$

speziell für den Fall der konstanten Funktion 1:

$\int _{-\infty }^{\infty }\delta (x-a)\,\mathrm {d} x=1$ ⓘ

• Linearität:

$\langle \delta ,f+g\rangle =\langle \delta ,f\rangle +\langle \delta ,g\rangle =f(0)+g(0)$ ⓘ

• Translation:

$\langle \delta (\cdot -a),f\rangle =\langle \delta ,f(\cdot +a)\rangle =f(a)$

für $\delta (\cdot -a)$ ist auch die Bezeichnung $\delta _{a}$ gebräuchlich. ⓘ

• Skalierung:

$\langle \delta (a\cdot ),f\rangle ={\frac {1}{|a|}}\langle \delta ,f({\tfrac {\cdot }{a}})\rangle ={\frac {1}{|a|}}f(0)$

und

$\delta (\alpha x)={\frac {1}{|\alpha |}}\delta (x)$

das heißt die Delta-Distribution ist positiv homogen vom Grad −1. ⓘ

• Dimension

Eine direkte Folgerung aus der Skalierungseigenschaft ist die Dimension bzw. Maßeinheit der Delta-Distribution. Sie entspricht genau der reziproken Dimension ihres Arguments. Hat $x$ beispielsweise die Dimension einer Länge, so hat $\delta (x)$ die Dimension (1/Länge). ⓘ

• Hintereinanderausführung:

$\int _{-\infty }^{\infty }\phi (x)\,\delta (g(x))\,\mathrm {d} x=\sum _{i=1}^{n}\int _{-\infty }^{\infty }\phi (x){\frac {\delta (x-x_{i})}{|g'(x_{i})|}}\,\mathrm {d} x=\sum _{i=1}^{n}{\frac {\phi (x_{i})}{|g'(x_{i})|}},$

$\delta (g(x))=\sum _{i=1}^{n}{\frac {\delta (x-x_{i})}{|g^{\prime }(x_{i})|}}$

wobei $x_{i}$ die einfachen Nullstellen von $g(x)$ sind (sofern $g(x)$ nur endlich viele und nur einfache Nullstellen hat). Damit folgt als ein Spezialfall die Rechenregel

$\delta (x^{2}-\alpha ^{2})={\frac {1}{2|\alpha |}}[\delta (x-\alpha )+\delta (x+\alpha )].$ ⓘ

Skalierung und Symmetrie

Die Deltafunktion erfüllt die folgende Skalierungseigenschaft für einen von Null verschiedenen Skalar α:

$\int _{-\infty }^{\infty }\delta (\alpha x)\,dx=\int _{-\infty }^{\infty }\delta (u)\,{\frac {du}{|\alpha |}}={\frac {1}{|\alpha |}}$ ⓘ

Und so

$\delta (\alpha x)={\frac {\delta (x)}{|\alpha |}}.$

(4) ⓘ

Beweis:

$${\begin{aligned}\delta (\alpha x)&=\lim _{a\to 0}{\frac {1}{|a|{\sqrt {\pi }}}}e^{-(\alpha x/a)^{2}}\qquad {\text{since }}a{\text{ is a dummy variable, we set }}a=\alpha b\\&=\lim _{b\to 0}{\frac {1}{|\alpha b|{\sqrt {\pi }}}}e^{-(\alpha x/(\alpha b))^{2}}\\&=\lim _{b\to 0}{\frac {1}{|\alpha |}}{\frac {1}{|b|{\sqrt {\pi }}}}e^{-(x/b)^{2}}={\frac {1}{|\alpha |}}\delta (x)\end{aligned}}$$

ⓘ

Insbesondere ist die Deltafunktion eine gerade Verteilung, in dem Sinne, dass ⓘ

$\delta (-x)=\delta (x)$ ⓘ

die homogen vom Grad -1 ist. ⓘ

Algebraische Eigenschaften

Das Verteilungsprodukt von δ mit x ist gleich Null:

$x\delta (x)=0.$ ⓘ

Umgekehrt, wenn xf(x) = xg(x), wobei f und g Verteilungen sind, dann ⓘ

$f(x)=g(x)+c\delta (x)$ ⓘ

für eine Konstante c. ⓘ

Übersetzung

Das Integral des zeitverzögerten Dirac-Deltas ist ⓘ

$\int _{-\infty }^{\infty }f(t)\delta (t-T)\,dt=f(T).$ ⓘ

Dies wird manchmal auch als Siebeigenschaft oder Sampling-Eigenschaft bezeichnet. Man sagt, dass die Deltafunktion den Wert bei t = T "heraussiebt". ⓘ

Daraus folgt, dass die Wirkung der Faltung einer Funktion f(t) mit dem zeitverzögerten Dirac-Delta $\delta _{T}(t)=\delta (t-T)$ eine Zeitverzögerung von f(t) um den gleichen Betrag bewirkt:

${\begin{aligned}(f*\delta _{T})(t)\ &{\stackrel {\mathrm {def} }{=}}\ \int _{-\infty }^{\infty }f(\tau )\delta (t-T-\tau )\,d\tau \\&=\int _{-\infty }^{\infty }f(\tau )\delta (\tau -(t-T))\,d\tau \qquad {\text{since}}~\delta (-x)=\delta (x)~~{\text{by (4)}}\\&=f(t-T).\end{aligned}}$ ⓘ

Dies gilt unter der genauen Bedingung, dass f eine temperierte Verteilung ist (siehe die Diskussion der Fourier-Transformation weiter unten). Als Spezialfall haben wir zum Beispiel die Identität (verstanden im Sinne der Verteilung) ⓘ

$\int _{-\infty }^{\infty }\delta (\xi -x)\delta (x-\eta )\,dx=\delta (\eta -\xi ).$ ⓘ

Komposition mit einer Funktion

Ganz allgemein kann die Delta-Verteilung mit einer glatten Funktion g(x) so zusammengesetzt werden, dass die bekannte Formel für den Variablenwechsel gilt, nämlich ⓘ

$\int _{\mathbb {R} }\delta {\bigl (}g(x){\bigr )}f{\bigl (}g(x){\bigr )}\left|g'(x)\right|dx=\int _{g(\mathbb {R} )}\delta (u)f(u)\,du$ ⓘ

vorausgesetzt, g ist eine stetig differenzierbare Funktion mit g′ nirgendwo Null. Das heißt, es gibt eine eindeutige Möglichkeit, der Verteilung eine Bedeutung zuzuweisen $\delta \circ g$ so dass diese Identität für alle kompakt unterstützten Testfunktionen f gilt. Daher muss der Bereich aufgebrochen werden, um den Punkt g′ = 0 auszuschließen. Diese Verteilung erfüllt δ(g(x)) = 0, wenn g nirgendwo Null ist, und andernfalls, wenn g eine reelle Wurzel bei x₀ hat, dann ⓘ

$\delta (g(x))={\frac {\delta (x-x_{0})}{|g'(x_{0})|}}.$ ⓘ

Es ist daher natürlich, die Zusammensetzung δ(g(x)) für kontinuierlich differenzierbare Funktionen g zu definieren durch ⓘ

$\delta (g(x))=\sum _{i}{\frac {\delta (x-x_{i})}{|g'(x_{i})|}}$ ⓘ

wobei sich die Summe über alle Wurzeln (d.h. alle verschiedenen) von g(x) erstreckt, die als einfach angenommen werden. Also zum Beispiel ⓘ

$\delta \left(x^{2}-\alpha ^{2}\right)={\frac {1}{2|\alpha |}}{\Big [}\delta \left(x+\alpha \right)+\delta \left(x-\alpha \right){\Big ]}.$ ⓘ

In der Integralform kann die verallgemeinerte Skalierungseigenschaft geschrieben werden als ⓘ

$\int _{-\infty }^{\infty }f(x)\,\delta (g(x))\,dx=\sum _{i}{\frac {f(x_{i})}{|g'(x_{i})|}}.$ ⓘ

Eigenschaften in n Dimensionen

Die Delta-Verteilung in einem n-dimensionalen Raum erfüllt stattdessen die folgende Skalierungseigenschaft,

$\delta (\alpha \mathbf {x} )=|\alpha |^{-n}\delta (\mathbf {x} )~,$

so dass δ eine homogene Verteilung vom Grad -n ist. ⓘ

Unter jeder Spiegelung oder Drehung ρ ist die Deltafunktion invariant,

$\delta (\rho \mathbf {x} )=\delta (\mathbf {x} )~.$ ⓘ

Wie im einvariablen Fall ist es möglich, die Zusammensetzung von δ mit einer Bi-Lipschitz-Funktion g: Rn → Rn eindeutig zu definieren, so dass die Identität

$\int _{\mathbb {R} ^{n}}\delta (g(\mathbf {x} ))\,f(g(\mathbf {x} ))\left|\det g'(\mathbf {x} )\right|\,d\mathbf {x} =\int _{g(\mathbb {R} ^{n})}\delta (\mathbf {u} )f(\mathbf {u} )\,d\mathbf {u}$

für alle kompakt unterstützten Funktionen f. ⓘ

Mit Hilfe der Coarea-Formel aus der geometrischen Maßtheorie kann man auch die Komposition der Deltafunktion mit einer Submersion von einem euklidischen Raum in einen anderen mit anderer Dimension definieren; das Ergebnis ist eine Art von Strom. Im Spezialfall einer kontinuierlich differenzierbaren Funktion g : Rn → R, so dass der Gradient von g nirgendwo Null ist, gilt die folgende Identität

$\int _{\mathbb {R} ^{n}}f(\mathbf {x} )\,\delta (g(\mathbf {x} ))\,d\mathbf {x} =\int _{g^{-1}(0)}{\frac {f(\mathbf {x} )}{|\mathbf {\nabla } g|}}\,d\sigma (\mathbf {x} )$

wobei das Integral auf der rechten Seite über g-1(0) gilt, der (n - 1)-dimensionalen Fläche, die durch g(x) = 0 in Bezug auf das Minkowski-Inhaltsmaß definiert ist. Dies wird als einfaches Schichtintegral bezeichnet. ⓘ

Allgemeiner ausgedrückt: Wenn S eine glatte Hypersurface von Rn ist, dann können wir S die Verteilung zuordnen, die jede kompakt unterstützte glatte Funktion g über S integriert:

$\delta _{S}[g]=\int _{S}g(\mathbf {s} )\,d\sigma (\mathbf {s} )$ ⓘ

Dabei ist σ das zu S gehörende Hypersurface-Maß. Diese Verallgemeinerung steht im Zusammenhang mit der Potentialtheorie der einfachen Schichtpotentiale auf S. Wenn D ein Gebiet in Rn mit glattem Rand S ist, dann ist δS gleich der normalen Ableitung der Indikatorfunktion von D im Verteilungssinn,

$-\int _{\mathbb {R} ^{n}}g(\mathbf {x} )\,{\frac {\partial 1_{D}(\mathbf {x} )}{\partial n}}\,d\mathbf {x} =\int _{S}\,g(\mathbf {s} )\,d\sigma (\mathbf {s} ),$

wobei n die äußere Normale ist. Für einen Beweis siehe z.B. den Artikel über die Oberflächen-Deltafunktion. ⓘ

Ableitungen

Ableitung der Delta-Distribution

Die Delta-Distribution kann wie jede Distribution beliebig oft distributiv differenziert werden:

$\langle \delta ',f\rangle =-\langle \delta ,f'\rangle =-f'(0).$ ⓘ

Dies gilt auch für die $n$-te distributive Ableitung:

$\langle \delta ^{(n)},f\rangle =(-1)^{n}\langle \delta ,f^{(n)}\rangle =(-1)^{n}f^{(n)}(0).$ ⓘ

Fourier-Laplace-Transformation

Da die Delta-Distribution einen kompakten Träger hat, ist es möglich, die Fourier-Laplace-Transformation dieser zu bilden. Für diese gilt

${\hat {\delta }}=1\,.$ ⓘ

Fourier-Transformation

Die Fourier-Laplace-Transformation ist ein Spezialfall der Fourier-Transformation und somit gilt auch

${\mathcal {F}}(\delta )(\phi )=\delta ({\mathcal {F}}(\phi ))=\delta \left(\int _{-\infty }^{\infty }e^{-ix\xi }\phi (x)\mathrm {d} x\right)=\langle 1,\phi \rangle \,.$ ⓘ

Es gibt auch die Konvention, den Faktor ${\tfrac {1}{\sqrt {2\pi }}}$ mit der Fourier-Transformation zu multiplizieren. In dem Fall ist ${\tfrac {1}{\sqrt {2\pi }}}$ ebenfalls das Ergebnis der Fourier-Transformation der Delta-Distribution. Anschaulich bedeutet das Resultat der Transformation, dass in der Delta-Distribution alle Frequenzen enthalten sind, und zwar mit gleicher Stärke. Die Darstellung $\delta (x)={\mathcal {F}}^{-1}(1)$ (beziehungsweise $\delta (x)={\mathcal {F}}^{-1}({\tfrac {1}{\sqrt {2\pi }}})$ bei der anderen Konvention für den Vorfaktor) ist eine in der Physik wichtige Darstellung der Delta-Distribution. ⓘ

Laplace-Transformation

Die Laplace-Transformation ${\mathcal {L}}$ der Delta-Distribution erhält man als Spezialfall der Fourier-Laplace-Transformation. Es gilt nämlich auch hier

${\mathcal {L}}(\delta )=1\,.$ ⓘ

Im Gegensatz zur Fourier-Transformation gibt es hier keine anderen Konventionen. ⓘ

Transformation der verschobenen Delta-Distribution

Es ist ebenfalls möglich die Fourier-Transformation beziehungsweise die Laplace-Transformation für die um $a>0$ verschobene Delta-Distribution $\delta _{a}$ zu berechnen. Es gilt

${\begin{aligned}{\mathcal {F}}(\delta _{a})&=e^{-i\xi a}\\{\mathcal {L}}(\delta _{a})&=e^{-\xi a}.\end{aligned}}$ ⓘ

Fourier-Transformation

Die Deltafunktion ist eine temperierte Verteilung und hat daher eine wohldefinierte Fouriertransformation. Formal findet man ⓘ

${\widehat {\delta }}(\xi )=\int _{-\infty }^{\infty }e^{-2\pi ix\xi }\delta (x)\,dx=1.$ ⓘ

Genau genommen ist die Fourier-Transformierte einer Verteilung definiert, indem man die Selbstadjungiertheit der Fourier-Transformierten unter der Dualitätspaarung $\langle \cdot ,\cdot \rangle$ von temperierten Verteilungen mit Schwartz-Funktionen. Somit ist ${\widehat {\delta }}$ als die einzige temperierte Verteilung definiert, die folgende Bedingungen erfüllt ⓘ

$\langle {\widehat {\delta }},\varphi \rangle =\langle \delta ,{\widehat {\varphi }}\rangle$ ⓘ

für alle Schwartz-Funktionen $\varphi$. Und in der Tat folgt hieraus, dass ${\widehat {\delta }}=1.$ ⓘ

Aus dieser Identität folgt, dass die Faltung der Deltafunktion mit jeder anderen temperierten Verteilung S einfach S ist:

$S*\delta =S.$ ⓘ

Das heißt, dass δ ein Identitätselement für die Faltung auf temperierten Verteilungen ist, und tatsächlich ist der Raum der kompakt unterstützten Verteilungen unter Faltung eine assoziative Algebra mit der Identität der Deltafunktion. Diese Eigenschaft ist in der Signalverarbeitung von grundlegender Bedeutung, da die Faltung mit einer temperierten Verteilung ein lineares zeitinvariantes System darstellt, und die Anwendung des linearen zeitinvarianten Systems misst seine Impulsantwort. Die Impulsantwort kann mit einem beliebigen Genauigkeitsgrad berechnet werden, indem eine geeignete Näherung für δ gewählt wird. Siehe LTI-Systemtheorie § Impulsantwort und Faltung. ⓘ

Die inverse Fourier-Transformation der temperierten Verteilung f(ξ) = 1 ist die Deltafunktion. Formal wird sie wie folgt ausgedrückt ⓘ

$\int _{-\infty }^{\infty }1\cdot e^{2\pi ix\xi }\,d\xi =\delta (x)$ ⓘ

und strenger ausgedrückt folgt daraus, dass ⓘ

$\langle 1,{\widehat {f}}\rangle =f(0)=\langle \delta ,f\rangle$ ⓘ

für alle Schwartz-Funktionen f. ⓘ

In diesen Begriffen liefert die Deltafunktion eine suggestive Aussage über die Orthogonalitätseigenschaft des Fourier-Kerns auf R. Formal hat man ⓘ

$\int _{-\infty }^{\infty }e^{i2\pi \xi _{1}t}\left[e^{i2\pi \xi _{2}t}\right]^{*}\,dt=\int _{-\infty }^{\infty }e^{-i2\pi (\xi _{2}-\xi _{1})t}\,dt=\delta (\xi _{2}-\xi _{1}).$ ⓘ

Dies ist natürlich eine Kurzform für die Behauptung, dass die Fourier-Transformierte der temperierten Verteilung ⓘ

$f(t)=e^{i2\pi \xi _{1}t}$ ⓘ

ist. ⓘ

${\widehat {f}}(\xi _{2})=\delta (\xi _{1}-\xi _{2})$ ⓘ

was wiederum aus der Selbstadjungiertheit der Fouriertransformation folgt. ⓘ

Durch analytische Fortsetzung der Fourier-Transformierten ergibt sich die Laplace-Transformierte der Deltafunktion wie folgt ⓘ

$\int _{0}^{\infty }\delta (t-a)e^{-st}\,dt=e^{-sa}.$ ⓘ

Ableitungen der Dirac-Deltafunktion

Die Ableitung der Dirac-Delta-Verteilung, bezeichnet mit $\delta ^{\prime }$ und auch als Dirac-Delta-Primzahl oder Dirac-Delta-Ableitung bezeichnet, wie in Laplacian des Indikators beschrieben, ist für kompakt unterstützte glatte Testfunktionen definiert $\varphi$ durch definiert. ⓘ

$\delta '[\varphi ]=-\delta [\varphi ']=-\varphi '(0).$ ⓘ

Die erste Gleichung hier ist eine Art Integration durch Teile, denn wenn $\delta$ eine wahre Funktion wäre, dann ⓘ

$\int _{-\infty }^{\infty }\delta '(x)\varphi (x)\,dx=-\int _{-\infty }^{\infty }\delta (x)\varphi '(x)\,dx.$ ⓘ

Die $k$-te Ableitung von $\delta$ ist in ähnlicher Weise definiert wie die Verteilung, die für Testfunktionen durch ⓘ

$\delta ^{(k)}[\varphi ]=(-1)^{k}\varphi ^{(k)}(0).$ ⓘ

Insbesondere ist $\delta$ ist eine unendlich differenzierbare Verteilung. ⓘ

Die erste Ableitung der Deltafunktion ist der Verteilungsgrenzwert des Differenzenquotienten:

$\delta '(x)=\lim _{h\to 0}{\frac {\delta (x+h)-\delta (x)}{h}}.$ ⓘ

Genauer gesagt, man hat ⓘ

$\delta '=\lim _{h\to 0}{\frac {1}{h}}(\tau _{h}\delta -\delta )$ ⓘ

wobei $\tau _{h}$ der Translationsoperator ist, definiert auf Funktionen durch $\tau _{h}\varphi (x)=\varphi (x+h)$definiert ist, und auf einer Verteilung $S$ durch definiert. ⓘ

$(\tau _{h}S)[\varphi ]=S[\tau _{-h}\varphi ].$ ⓘ

In der Theorie des Elektromagnetismus stellt die erste Ableitung der Deltafunktion einen punktförmigen magnetischen Dipol dar, der sich im Ursprung befindet. Sie wird daher auch als Dipol oder Dublettfunktion bezeichnet. ⓘ

Die Ableitung der Deltafunktion erfüllt eine Reihe von grundlegenden Eigenschaften, darunter:

${\begin{aligned}&\delta '(-x)=-\delta '(x)\\&x\delta '(x)=-\delta (x)\end{aligned}}$ ⓘ

Die Ableitung der Deltafunktion erfüllt eine Reihe grundlegender Eigenschaften, die durch Anwendung einer Testfunktion und Integration durch Teile gezeigt werden können. ⓘ

Die letztgenannte Eigenschaft kann auch durch Anwendung der Definition der Verteilungsableitung, des Liebnitzschen Satzes und der Linearität des inneren Produkts nachgewiesen werden:

$${\begin{aligned}\langle x\delta ',\varphi \rangle \,&=\,\langle \delta ',x\varphi \rangle \,=\,-\langle \delta ,(x\varphi )'\rangle \,=\,-\langle \delta ,x'\varphi +x\varphi '\rangle \,=\,-\langle \delta ,x'\varphi \rangle -\langle \delta ,x\varphi '\rangle \,=\,-x'(0)\varphi (0)-x(0)\varphi '(0)\\&=\,-x'(0)\langle \delta ,\varphi \rangle -x(0)\langle \delta ,\varphi '\rangle \,=\,-x'(0)\langle \delta ,\varphi \rangle +x(0)\langle \delta ',\varphi \rangle \,=\,\langle x(0)\delta '-x'(0)\delta ,\varphi \rangle \\\Longrightarrow x(t)\delta '(t)&=x(0)\delta '(t)-x'(0)\delta (t)=-x'(0)\delta (t)=-\delta (t)\end{aligned}}$$

ⓘ

Außerdem ist die Faltung von $\delta '$ mit einer kompakt gestützten, glatten Funktion $f$ ist. ⓘ

$\delta '*f=\delta *f'=f',$ ⓘ

was aus den Eigenschaften der Verteilungsableitung einer Faltung folgt. ⓘ

Höhere Dimensionen

Allgemeiner ausgedrückt, auf einer offenen Menge $U$ im $n$-dimensionalen euklidischen Raum $\mathbb {R} ^{n}$ist die Dirac-Delta-Verteilung mit dem Zentrum in einem Punkt $a\in U$ ist definiert durch ⓘ

$\delta _{a}[\varphi ]=\varphi (a)$ ⓘ

für alle $\varphi \in C_{c}^{\infty }(U)$den Raum aller glatten Funktionen mit kompakter Unterstützung auf $U$. Wenn $\alpha =(\alpha _{1},\ldots ,\alpha _{n})$ ist ein beliebiger Multi-Index mit $|\alpha |=\alpha _{1}+\cdots +\alpha _{n}$ und $\partial ^{\alpha }$ den zugehörigen Operator der gemischten partiellen Ableitung bezeichnet, dann ist die $\alpha$-te Ableitung $\partial ^{\alpha }\delta _{a}$ von $\delta _{a}$ gegeben durch ⓘ

$\left\langle \partial ^{\alpha }\delta _{a},\,\varphi \right\rangle =(-1)^{|\alpha |}\left\langle \delta _{a},\partial ^{\alpha }\varphi \right\rangle =(-1)^{|\alpha |}\partial ^{\alpha }\varphi (x){\Big |}_{x=a}\quad {\text{ for all }}\varphi \in C_{c}^{\infty }(U).$ ⓘ

Das heißt, die $\alpha$-te Ableitung von $\delta _{a}$ ist die Verteilung, deren Wert für jede Testfunktion $\varphi$ ist die $\alpha$-te Ableitung von $\varphi$ bei $a$ (mit dem entsprechenden positiven oder negativen Vorzeichen). ⓘ

Die ersten partiellen Ableitungen der Deltafunktion werden als Doppelschichten entlang der Koordinatenebenen betrachtet. Allgemeiner ausgedrückt: Die normale Ableitung einer einfachen Schicht, die auf einer Oberfläche aufliegt, ist eine Doppelschicht, die auf dieser Oberfläche aufliegt und einen laminaren magnetischen Monopol darstellt. Höhere Ableitungen der Deltafunktion sind in der Physik als Multipole bekannt. ⓘ

Höhere Ableitungen kommen in der Mathematik natürlich als Bausteine für die vollständige Struktur von Verteilungen mit Punktauflage vor. Wenn $S$ ist eine beliebige Verteilung auf $U$ unterstützt auf der Menge $\{a\}$ die aus einem einzigen Punkt besteht, dann gibt es eine ganze Zahl $m$ und Koeffizienten $c_{\alpha }$ so dass ⓘ

$S=\sum _{|\alpha |\leq m}c_{\alpha }\partial ^{\alpha }\delta _{a}.$ ⓘ

Darstellungen der Deltafunktion

Die Deltafunktion kann als der Grenzwert einer Folge von Funktionen betrachtet werden ⓘ

$\delta (x)=\lim _{\varepsilon \to 0^{+}}\eta _{\varepsilon }(x),$ ⓘ

wobei η_ε(x) manchmal als entstehende Deltafunktion bezeichnet wird. Dieser Grenzwert ist in einem schwachen Sinne zu verstehen: entweder, dass ⓘ

$\lim _{\varepsilon \to 0^{+}}\int _{-\infty }^{\infty }\eta _{\varepsilon }(x)f(x)\,dx=f(0)$

(5) ⓘ

für alle stetigen Funktionen f mit kompakter Unterstützung gilt, oder dass dieser Grenzwert für alle glatten Funktionen f mit kompakter Unterstützung gilt. Der Unterschied zwischen diesen beiden leicht unterschiedlichen Arten der schwachen Konvergenz ist oft subtil: Erstere ist Konvergenz im Sinne der vagen Topologie von Maßen, letztere ist Konvergenz im Sinne von Verteilungen. ⓘ

Annäherungen an die Identität

Typischerweise kann eine naszierende Deltafunktion η_ε auf folgende Weise konstruiert werden. Sei η eine absolut integrierbare Funktion auf R mit dem Gesamtintegral 1, und definiere ⓘ

$\eta _{\varepsilon }(x)=\varepsilon ^{-1}\eta \left({\frac {x}{\varepsilon }}\right).$ ⓘ

In n Dimensionen verwendet man stattdessen die Skalierung ⓘ

$\eta _{\varepsilon }(x)=\varepsilon ^{-n}\eta \left({\frac {x}{\varepsilon }}\right).$ ⓘ

Dann zeigt ein einfacher Variablenwechsel, dass η_ε ebenfalls das Integral 1 hat. Man kann zeigen, dass (5) für alle stetigen, kompakt unterstützten Funktionen f gilt, und somit konvergiert η_ε schwach gegen δ im Sinne der Maße. ⓘ

Die auf diese Weise konstruierten η_ε werden als Annäherung an die Identität bezeichnet. Diese Terminologie kommt daher, dass der Raum L¹(R) der absolut integrierbaren Funktionen unter der Operation der Faltung von Funktionen geschlossen ist: f ∗ g ∈ L¹(R), wenn f und g in L¹(R) liegen. Es gibt jedoch keine Identität in L¹(R) für das Faltungsprodukt: kein Element h, so dass f ∗ h = f für alle f. Dennoch approximiert die Folge η_ε eine solche Identität in dem Sinne, dass ⓘ

$f*\eta _{\varepsilon }\to f\quad {\text{as }}\varepsilon \to 0.$ ⓘ

Dieser Grenzwert gilt im Sinne der mittleren Konvergenz (Konvergenz in L¹). Weitere Bedingungen für η_ε, z. B. dass es sich um einen Mollifikator handelt, der mit einer kompakt unterstützten Funktion assoziiert ist, sind erforderlich, um die punktweise Konvergenz fast überall sicherzustellen. ⓘ

Wenn die Anfangsfunktion η = η₁ selbst glatt und kompakt unterstützt ist, wird die Folge als Mollifier bezeichnet. Den Standard-Mollifier erhält man, indem man η als eine geeignet normalisierte Höckerfunktion wählt, z. B. ⓘ

$\eta (x)={\begin{cases}e^{-{\frac {1}{1-|x|^{2}}}}&{\text{if }}|x|<1\\0&{\text{if }}|x|\geq 1.\end{cases}}$ ⓘ

In manchen Situationen, z. B. in der numerischen Analyse, ist eine stückweise lineare Annäherung an die Identität wünschenswert. Dies kann erreicht werden, indem man η₁ als Hutfunktion wählt. Mit dieser Wahl von η₁ erhält man ⓘ

$\eta _{\varepsilon }(x)=\varepsilon ^{-1}\max \left(1-\left|{\frac {x}{\varepsilon }}\right|,0\right)$ ⓘ

die alle stetig und kompakt unterstützt sind, obwohl sie nicht glatt sind und somit kein Mollifikator. ⓘ

Probabilistische Überlegungen

Im Zusammenhang mit der Wahrscheinlichkeitstheorie ist es naheliegend, die zusätzliche Bedingung aufzustellen, dass die anfängliche η₁ in einer Annäherung an die Identität positiv sein sollte, da eine solche Funktion dann eine Wahrscheinlichkeitsverteilung darstellt. Die Faltung mit einer Wahrscheinlichkeitsverteilung ist manchmal vorteilhaft, weil sie nicht zu Über- oder Unterschreitungen führt, da die Ausgabe eine konvexe Kombination der Eingabewerte ist und somit zwischen dem Maximum und dem Minimum der Eingabefunktion liegt. Nimmt man η₁ als eine beliebige Wahrscheinlichkeitsverteilung an und lässt η_ε(x) = η₁(x/ε)/ε gelten, so erhält man eine Annäherung an die Identität. Im Allgemeinen konvergiert diese schneller zu einer Deltafunktion, wenn η zusätzlich den Mittelwert 0 und kleine höhere Momente hat. Wenn η₁ zum Beispiel die Gleichverteilung auf [-1/2, 1/2] ist, die auch als Rechteckfunktion bekannt ist, dann:

$\eta _{\varepsilon }(x)={\frac {1}{\varepsilon }}\operatorname {rect} \left({\frac {x}{\varepsilon }}\right)={\begin{cases}{\frac {1}{\varepsilon }},&-{\frac {\varepsilon }{2}}<x<{\frac {\varepsilon }{2}}\\0,&{\text{otherwise}}.\end{cases}}$ ⓘ

Ein weiteres Beispiel ist die Wigner-Halbkreisverteilung ⓘ

$\eta _{\varepsilon }(x)={\begin{cases}{\frac {2}{\pi \varepsilon ^{2}}}{\sqrt {\varepsilon ^{2}-x^{2}}},&-\varepsilon <x<\varepsilon \\0,&{\text{otherwise}}\end{cases}}$ ⓘ

Diese ist kontinuierlich und kompakt unterstützt, aber kein Mollifikator, weil sie nicht glatt ist. ⓘ

Halbgruppen

Naszierende Deltafunktionen treten oft als Faltungshalbgruppen auf. Dies läuft auf die weitere Bedingung hinaus, dass die Faltung von η_ε mit η_δ Folgendes erfüllen muss ⓘ

$\eta _{\varepsilon }*\eta _{\delta }=\eta _{\varepsilon +\delta }$ ⓘ

für alle ε, δ > 0. Faltungshalbgruppen in L¹, die eine naszierende Deltafunktion bilden, sind immer eine Annäherung an die Identität im obigen Sinne, aber die Halbgruppenbedingung ist eine ziemlich starke Einschränkung. ⓘ

In der Praxis treten Halbgruppen, die die Deltafunktion approximieren, als fundamentale Lösungen oder Green'sche Funktionen für physikalisch motivierte elliptische oder parabolische partielle Differentialgleichungen auf. Im Kontext der angewandten Mathematik treten Halbgruppen als Ausgang eines linearen zeitinvarianten Systems auf. Abstrakt ausgedrückt: Wenn A ein linearer Operator ist, der auf Funktionen von x wirkt, dann ergibt sich eine Faltungshalbgruppe durch die Lösung des Anfangswertproblems ⓘ

${\begin{cases}{\dfrac {\partial }{\partial t}}\eta (t,x)=A\eta (t,x),\quad t>0\\[5pt]\displaystyle \lim _{t\to 0^{+}}\eta (t,x)=\delta (x)\end{cases}}$ ⓘ

wobei der Grenzwert wie üblich im schwachen Sinne zu verstehen ist. Setzt man η_ε(x) = η(ε, x), so erhält man die zugehörige naszierende Deltafunktion. ⓘ

Einige Beispiele für physikalisch wichtige Faltungshalbgruppen, die sich aus einer solchen fundamentalen Lösung ergeben, sind die folgenden. ⓘ

Der Wärmekern

Der Wärmekern, definiert durch ⓘ

$\eta _{\varepsilon }(x)={\frac {1}{\sqrt {2\pi \varepsilon }}}\mathrm {e} ^{-{\frac {x^{2}}{2\varepsilon }}}$ ⓘ

definiert ist, stellt die Temperatur in einem unendlichen Draht zum Zeitpunkt t > 0 dar, wenn zum Zeitpunkt t = 0 eine Einheit Wärmeenergie am Ursprung des Drahtes gespeichert ist. Diese Halbgruppe entwickelt sich gemäß der eindimensionalen Wärmegleichung:

${\frac {\partial u}{\partial t}}={\frac {1}{2}}{\frac {\partial ^{2}u}{\partial x^{2}}}.$ ⓘ

In der Wahrscheinlichkeitstheorie ist η_ε(x) eine Normalverteilung mit der Varianz ε und dem Mittelwert 0. Sie stellt die Wahrscheinlichkeitsdichte der Position eines Teilchens zum Zeitpunkt t = ε dar, das vom Ursprung ausgeht und einer standardmäßigen Brownschen Bewegung folgt. In diesem Zusammenhang ist die Halbgruppenbedingung dann ein Ausdruck der Markov-Eigenschaft der Brownschen Bewegung. ⓘ

Im höherdimensionalen euklidischen Raum Rn ist der Wärmekern ⓘ

$\eta _{\varepsilon }={\frac {1}{(2\pi \varepsilon )^{n/2}}}\mathrm {e} ^{-{\frac {x\cdot x}{2\varepsilon }}},$ ⓘ

und hat mutatis mutandis die gleiche physikalische Interpretation. Er stellt auch eine entstehende Deltafunktion in dem Sinne dar, dass η_ε → δ im Verteilungssinn als ε → 0. ⓘ

Der Poisson-Kern

Der Poisson-Kernel ⓘ

$\eta _{\varepsilon }(x)={\frac {1}{\pi }}\mathrm {Im} \left\{{\frac {1}{x-\mathrm {i} \varepsilon }}\right\}={\frac {1}{\pi }}{\frac {\varepsilon }{\varepsilon ^{2}+x^{2}}}={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\mathrm {e} ^{\mathrm {i} \xi x-|\varepsilon \xi |}\,d\xi$ ⓘ

ist die fundamentale Lösung der Laplace-Gleichung in der oberen Halbebene. Er stellt das elektrostatische Potenzial in einer halbunendlichen Platte dar, deren Potenzial entlang des Randes durch die Deltafunktion fixiert wird. Der Poisson-Kern ist auch eng mit der Cauchy-Verteilung und den Epanechnikov- und Gauß-Kernfunktionen verwandt. Diese Halbgruppe entwickelt sich gemäß der Gleichung ⓘ

${\frac {\partial u}{\partial t}}=-\left(-{\frac {\partial ^{2}}{\partial x^{2}}}\right)^{\frac {1}{2}}u(t,x)$ ⓘ

wobei der Operator streng genommen als Fourier-Multiplikator definiert ist ⓘ

${\mathcal {F}}\left[\left(-{\frac {\partial ^{2}}{\partial x^{2}}}\right)^{\frac {1}{2}}f\right](\xi )=|2\pi \xi |{\mathcal {F}}f(\xi ).$ ⓘ

Oszillatorische Integrale

In Bereichen der Physik wie der Wellenausbreitung und der Wellenmechanik sind die betreffenden Gleichungen hyperbolisch und können daher mehr singuläre Lösungen aufweisen. Daher sind die entstehenden Deltafunktionen, die als fundamentale Lösungen der zugehörigen Cauchy-Probleme auftreten, im Allgemeinen oszillierende Integrale. Ein Beispiel, das aus einer Lösung der Euler-Tricomi-Gleichung der transsonischen Gasdynamik stammt, ist die umskalierte Airy-Funktion ⓘ

$\varepsilon ^{-1/3}\operatorname {Ai} \left(x\varepsilon ^{-1/3}\right).$ ⓘ

Obwohl die Fourier-Transformation verwendet wird, ist es leicht zu erkennen, dass diese Funktion in gewissem Sinne eine Halbgruppe erzeugt - sie ist nicht absolut integrierbar und kann daher keine Halbgruppe im oben genannten starken Sinne definieren. Viele entstehende Delta-Funktionen, die als oszillierende Integrale konstruiert sind, konvergieren nur im Sinne von Verteilungen (ein Beispiel ist der Dirichlet-Kernel unten) und nicht im Sinne von Maßen. ⓘ

Ein weiteres Beispiel ist das Cauchy-Problem für die Wellengleichung in R¹⁺¹:

${\begin{aligned}c^{-2}{\frac {\partial ^{2}u}{\partial t^{2}}}-\Delta u&=0\\u=0,\quad {\frac {\partial u}{\partial t}}=\delta &\qquad {\text{for }}t=0.\end{aligned}}$ ⓘ

Die Lösung u stellt die Verschiebung einer unendlichen elastischen Saite aus dem Gleichgewicht dar, mit einer anfänglichen Störung im Ursprung. ⓘ

Andere Annäherungen an die Identität dieser Art sind die sinc-Funktion (die in der Elektronik und Telekommunikation weit verbreitet ist) ⓘ

$\eta _{\varepsilon }(x)={\frac {1}{\pi x}}\sin \left({\frac {x}{\varepsilon }}\right)={\frac {1}{2\pi }}\int _{-{\frac {1}{\varepsilon }}}^{\frac {1}{\varepsilon }}\cos(kx)\,dk$ ⓘ

und die Bessel-Funktion ⓘ

$\eta _{\varepsilon }(x)={\frac {1}{\varepsilon }}J_{\frac {1}{\varepsilon }}\left({\frac {x+1}{\varepsilon }}\right).$ ⓘ

Zerlegung von ebenen Wellen

Ein Ansatz zur Untersuchung einer linearen partiellen Differentialgleichung ⓘ

$L[u]=f,$ ⓘ

in der L ein Differentialoperator auf Rn ist, besteht darin, zunächst eine Fundamentallösung zu suchen, d. h. eine Lösung der Gleichung ⓘ

$L[u]=\delta .$ ⓘ

Wenn L besonders einfach ist, kann dieses Problem oft direkt mit Hilfe der Fourier-Transformation gelöst werden (wie im Fall des bereits erwähnten Poisson-Kerns und des Wärmekerns). Bei komplizierteren Operatoren ist es manchmal einfacher, zunächst eine Gleichung der Form ⓘ

$L[u]=h$ ⓘ

wobei h eine ebene Wellenfunktion ist, d. h. sie hat die Form ⓘ

$h=h(x\cdot \xi )$ ⓘ

für einen Vektor ξ. Eine solche Gleichung kann (wenn die Koeffizienten von L analytische Funktionen sind) durch das Cauchy-Kovalevskaya-Theorem oder (wenn die Koeffizienten von L konstant sind) durch Quadratur aufgelöst werden. Wenn also die Deltafunktion in ebene Wellen zerlegt werden kann, dann kann man im Prinzip lineare partielle Differentialgleichungen lösen. ⓘ

Eine solche Zerlegung der Deltafunktion in ebene Wellen war Teil einer allgemeinen Technik, die im Wesentlichen von Johann Radon eingeführt und dann in dieser Form von Fritz John (1955) weiterentwickelt wurde. Wählen Sie k so, dass n + k eine gerade ganze Zahl ist, und setzen Sie für eine reelle Zahl s ⓘ

$g(s)=\operatorname {Re} \left[{\frac {-s^{k}\log(-is)}{k!(2\pi i)^{n}}}\right]={\begin{cases}{\frac {|s|^{k}}{4k!(2\pi i)^{n-1}}}&n{\text{ odd}}\\[5pt]-{\frac {|s|^{k}\log |s|}{k!(2\pi i)^{n}}}&n{\text{ even.}}\end{cases}}$ ⓘ

Dann erhält man δ durch Anwendung einer Potenz des Laplacian auf das Integral von g(x - ξ) für ξ in der Einheitskugel Sn-1 in Bezug auf das Einheitsmaß dω:

$\delta (x)=\Delta _{x}^{(n+k)/2}\int _{S^{n-1}}g(x\cdot \xi )\,d\omega _{\xi }.$ ⓘ

Der Laplacian wird hier als schwache Ableitung interpretiert, so dass diese Gleichung bedeutet, dass für jede Testfunktion φ, ⓘ

$\varphi (x)=\int _{\mathbf {R} ^{n}}\varphi (y)\,dy\,\Delta _{x}^{\frac {n+k}{2}}\int _{S^{n-1}}g((x-y)\cdot \xi )\,d\omega _{\xi }.$ ⓘ

Das Ergebnis ergibt sich aus der Formel für das Newtonsche Potential (die fundamentale Lösung der Poissonschen Gleichung). Dies ist im Wesentlichen eine Form der Inversionsformel für die Radon-Transformation, da sie den Wert von φ(x) aus seinen Integralen über Hyperebenen wiederherstellt. Wenn zum Beispiel n ungerade ist und k = 1, dann lautet das Integral auf der rechten Seite ⓘ

${\begin{aligned}&c_{n}\Delta _{x}^{\frac {n+1}{2}}\iint _{S^{n-1}}\varphi (y)|(y-x)\cdot \xi |\,d\omega _{\xi }\,dy\\[5pt]={}&c_{n}\Delta _{x}^{(n+1)/2}\int _{S^{n-1}}\,d\omega _{\xi }\int _{-\infty }^{\infty }|p|R\varphi (\xi ,p+x\cdot \xi )\,dp\end{aligned}}$ ⓘ

wobei Rφ(ξ, p) die Radontransformation von φ ist:

$R\varphi (\xi ,p)=\int _{x\cdot \xi =p}f(x)\,d^{n-1}x.$ ⓘ

Ein alternativer äquivalenter Ausdruck der ebenen Wellenzerlegung, aus Gelfand & Shilov (1966-1968, I, §3.10), ist ⓘ

$\delta (x)={\frac {(n-1)!}{(2\pi i)^{n}}}\int _{S^{n-1}}(x\cdot \xi )^{-n}\,d\omega _{\xi }$ ⓘ

für n gerade, und ⓘ

$\delta (x)={\frac {1}{2(2\pi i)^{n-1}}}\int _{S^{n-1}}\delta ^{(n-1)}(x\cdot \xi )\,d\omega _{\xi }$ ⓘ

für n ungerade. ⓘ

Fourier-Kerne

Bei der Untersuchung von Fourier-Reihen besteht eine wichtige Frage darin, ob und in welchem Sinne die mit einer periodischen Funktion verbundene Fourier-Reihe gegen die Funktion konvergiert. Die n-te Partialsumme der Fourier-Reihe einer Funktion f mit der Periode 2π ist durch Faltung (im Intervall [-π,π]) mit dem Dirichlet-Kernel definiert:

$D_{N}(x)=\sum _{n=-N}^{N}e^{inx}={\frac {\sin \left(\left(N+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}.$

Daraus folgt,

$s_{N}(f)(x)=D_{N}*f(x)=\sum _{n=-N}^{N}a_{n}e^{inx}$

wobei

$a_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(y)e^{-iny}\,dy.$

Ein grundlegendes Ergebnis der elementaren Fourier-Reihen besagt, dass der Dirichlet-Kernel zu einem Vielfachen der Deltafunktion tendiert, wenn N → ∞. Dies wird im Sinne der Verteilung so interpretiert, dass

$s_{N}(f)(0)=\int _{\mathbf {R} }D_{N}(x)f(x)\,dx\to 2\pi f(0)$

für jede kompakt unterstützte glatte Funktion f. Formal hat man also

$\delta (x)={\frac {1}{2\pi }}\sum _{n=-\infty }^{\infty }e^{inx}$

auf dem Intervall [-π,π]. ⓘ

Trotzdem gilt das Ergebnis nicht für alle kompakt gestützten stetigen Funktionen, d.h. D_N konvergiert nicht schwach im Sinne der Maße. Die mangelnde Konvergenz der Fourier-Reihen hat zur Einführung einer Reihe von Summierbarkeitsmethoden geführt, um Konvergenz zu erreichen. Die Methode der Cesàro-Summation führt zum Fejér-Kernel ⓘ

$F_{N}(x)={\frac {1}{N}}\sum _{n=0}^{N-1}D_{n}(x)={\frac {1}{N}}\left({\frac {\sin {\frac {Nx}{2}}}{\sin {\frac {x}{2}}}}\right)^{2}.$ ⓘ

Die Fejér-Kerne tendieren zur Deltafunktion in einem stärkeren Sinne, nämlich ⓘ

$\int _{\mathbf {R} }F_{N}(x)f(x)\,dx\to 2\pi f(0)$ ⓘ

für jede kompakt unterstützte kontinuierliche Funktion f. Daraus folgt, dass die Fourier-Reihe jeder kontinuierlichen Funktion in jedem Punkt zum Wert der Funktion Cesàro-summierbar ist. ⓘ

Hilbert-Raum-Theorie

Die Dirac-Delta-Verteilung ist ein dicht definiertes unbeschränktes lineares Funktional auf dem Hilbert-Raum L² der quadratisch-integrablen Funktionen. In der Tat sind glatte, kompakt unterstützte Funktionen dicht in L², und die Wirkung der Delta-Verteilung auf solche Funktionen ist wohldefiniert. In vielen Anwendungen ist es möglich, Unterräume von L² zu identifizieren und eine stärkere Topologie anzugeben, auf der die Delta-Funktion ein beschränktes lineares Funktional definiert. ⓘ

Sobolev-Räume

Der Sobolev-Einbettungssatz für Sobolev-Räume auf der reellen Geraden R besagt, dass jede quadratisch integrierbare Funktion f, für die gilt ⓘ

$\|f\|_{H^{1}}^{2}=\int _{-\infty }^{\infty }|{\widehat {f}}(\xi )|^{2}(1+|\xi |^{2})\,d\xi <\infty$ ⓘ

automatisch stetig ist und insbesondere folgende Bedingungen erfüllt ⓘ

$\delta [f]=|f(0)|<C\|f\|_{H^{1}}.$ ⓘ

Somit ist δ ein beschränktes lineares Funktional auf dem Sobolev-Raum H¹. Äquivalent dazu ist δ ein Element des kontinuierlichen Dualraums H-1 von H¹. Allgemeiner, in n Dimensionen, hat man δ ∈ H-s(Rn) vorausgesetzt s > n / 2. ⓘ

Räume der holomorphen Funktionen

In der komplexen Analysis kommt die Deltafunktion über die Cauchysche Integralformel ins Spiel, die besagt, dass, wenn D ein Gebiet in der komplexen Ebene mit glattem Rand ist, dann ⓘ

$f(z)={\frac {1}{2\pi i}}\oint _{\partial D}{\frac {f(\zeta )\,d\zeta }{\zeta -z}},\quad z\in D$ ⓘ

für alle holomorphen Funktionen f in D, die auf dem Abschluss von D stetig sind. Folglich wird die Deltafunktion δ_z in dieser Klasse holomorpher Funktionen durch das Cauchy-Integral dargestellt:

$\delta _{z}[f]=f(z)={\frac {1}{2\pi i}}\oint _{\partial D}{\frac {f(\zeta )\,d\zeta }{\zeta -z}}.$ ⓘ

Außerdem sei H²(∂D) der Hardy-Raum, der aus der Schließung in L²(∂D) aller holomorphen Funktionen in D besteht, die bis zum Rand von D stetig sind. Dann dehnen sich Funktionen in H²(∂D) eindeutig zu holomorphen Funktionen in D aus, und die Cauchy-Integralformel gilt weiterhin. Insbesondere für z ∈ D ist die Deltafunktion δz eine stetige lineare Funktion auf H²(∂D). Dies ist ein Spezialfall der Situation in mehreren komplexen Variablen, in der für glatte Gebiete D der Szegő-Kernel die Rolle des Cauchy-Integrals spielt. ⓘ

Auflösungen der Identität

Bei einer vollständigen orthonormalen Basismenge von Funktionen {φn} in einem separablen Hilbert-Raum, zum Beispiel den normalisierten Eigenvektoren eines kompakten selbstadjungierten Operators, kann jeder Vektor f ausgedrückt werden als

$f=\sum _{n=1}^{\infty }\alpha _{n}\varphi _{n}.$

Die Koeffizienten {αn} werden gefunden als

$\alpha _{n}=\langle \varphi _{n},f\rangle ,$

was durch die Notation dargestellt werden kann:

$\alpha _{n}=\varphi _{n}^{\dagger }f,$

eine Form der Bra-Ket-Notation von Dirac. Mit dieser Notation nimmt die Entwicklung von f die dyadische Form an:

$f=\sum _{n=1}^{\infty }\varphi _{n}\left(\varphi _{n}^{\dagger }f\right).$ ⓘ

Wenn I den Identitätsoperator im Hilbert-Raum bezeichnet, wird der Ausdruck ⓘ

$I=\sum _{n=1}^{\infty }\varphi _{n}\varphi _{n}^{\dagger },$ ⓘ

als eine Auflösung der Identität bezeichnet. Wenn der Hilbert-Raum der Raum L²(D) der quadratisch-integrablen Funktionen auf einer Domäne D ist, ist die Menge:

$\varphi _{n}\varphi _{n}^{\dagger },$ ⓘ

ist ein Integraloperator, und der Ausdruck für f kann wie folgt umgeschrieben werden ⓘ

$f(x)=\sum _{n=1}^{\infty }\int _{D}\,\left(\varphi _{n}(x)\varphi _{n}^{*}(\xi )\right)f(\xi )\,d\xi .$ ⓘ

Die rechte Seite konvergiert zu f im Sinne von L². Sie muss nicht punktweise gelten, selbst wenn f eine stetige Funktion ist. Dennoch ist es üblich, die Notation zu missbrauchen und zu schreiben ⓘ

$f(x)=\int \,\delta (x-\xi )f(\xi )\,d\xi ,$ ⓘ

zu schreiben, was zur Darstellung der Deltafunktion führt:

$\delta (x-\xi )=\sum _{n=1}^{\infty }\varphi _{n}(x)\varphi _{n}^{*}(\xi ).$ ⓘ

Mit einem geeigneten starren Hilbert-Raum (Φ, L²(D), Φ*), in dem Φ ⊂ L²(D) alle kompakt unterstützten glatten Funktionen enthält, kann diese Summation in Φ* konvergieren, abhängig von den Eigenschaften der Basis φn. In den meisten Fällen, die von praktischem Interesse sind, stammt die orthonormale Basis von einem Integral- oder Differentialoperator; in diesem Fall konvergiert die Reihe im Sinne der Verteilung. ⓘ

Infinitesimal-Delta-Funktionen

Cauchy benutzte ein Infinitesimal α, um eine unendlich hohe und schmale Dirac-Deltafunktion δ_α mit einem Einheitsimpuls aufzuschreiben, die ${\textstyle \int F(x)\delta _{\alpha }(x)=F(0)}$ in einer Reihe von Artikeln im Jahr 1827. Cauchy definierte in Cours d'Analyse (1827) ein Infinitesimal im Sinne einer gegen Null tendierenden Folge. Eine solche Nullfolge wird nämlich in der Terminologie von Cauchy und Lazare Carnot zu einem Infinitesimal. ⓘ

Die Nicht-Standard-Analyse ermöglicht eine rigorose Behandlung von Infinitesimalen. Der Artikel von Yamashita (2007) enthält eine Bibliographie über moderne Dirac-Delta-Funktionen im Zusammenhang mit einem infinitesimal angereicherten Kontinuum, das durch die Hyperrealen bereitgestellt wird. Hier kann das Dirac-Delta durch eine tatsächliche Funktion gegeben sein, die die Eigenschaft hat, dass für jede reelle Funktion F gilt ${\textstyle \int F(x)\delta _{\alpha }(x)=F(0)}$ wie von Fourier und Cauchy vorausgesehen. ⓘ

Dirac-Kamm

Ein Dirac-Kamm ist eine unendliche Reihe von Dirac-Delta-Funktionen, die in Abständen von T ⓘ

Ein so genannter gleichmäßiger "Impulszug" von Dirac-Delta-Maßen, der als Dirac-Kamm oder als Shah-Verteilung bekannt ist, erzeugt eine Abtastfunktion, die häufig in der digitalen Signalverarbeitung (DSP) und der diskreten Zeitsignalanalyse verwendet wird. Der Dirac-Kamm ist als unendliche Summe gegeben, deren Grenze im Sinne der Verteilung verstanden wird, ⓘ

$\operatorname {III} (x)=\sum _{n=-\infty }^{\infty }\delta (x-n),$ ⓘ

die eine Folge von Punktmassen bei jeder der ganzen Zahlen ist. ⓘ

Bis zu einer allgemeinen Normalisierungskonstante ist der Dirac-Kamm gleich seiner eigenen Fourier-Transformation. Dies ist von Bedeutung, denn wenn $f$ eine beliebige Schwartz-Funktion ist, dann ist die Periodisierung von $f$ durch die Faltung gegeben ist

$(f*\operatorname {III} )(x)=\sum _{n=-\infty }^{\infty }f(x-n).$

Insbesondere ist

$(f*\operatorname {III} )^{\wedge }={\widehat {f}}{\widehat {\operatorname {III} }}={\widehat {f}}\operatorname {III}$

ist genau die Poisson-Summenformel. Allgemeiner ausgedrückt, bleibt diese Formel wahr, wenn $f$ eine temperierte Verteilung mit schnellem Abstieg ist oder, äquivalent dazu, wenn ${\widehat {f}}$ eine langsam wachsende, gewöhnliche Funktion im Raum der temperierten Verteilungen ist. ⓘ

Sokhotski-Plemelj-Theorem

Das Sokhotski-Plemelj-Theorem, das in der Quantenmechanik von Bedeutung ist, setzt die Deltafunktion in Beziehung zur Verteilung p.v. 1/x, dem Cauchy-Hauptwert der Funktion 1/x, definiert durch ⓘ

$\left\langle \operatorname {p.v.} {\frac {1}{x}},\varphi \right\rangle =\lim _{\varepsilon \to 0^{+}}\int _{|x|>\varepsilon }{\frac {\varphi (x)}{x}}\,dx.$ ⓘ

Die Formel von Sokhotsky besagt, dass ⓘ

$\lim _{\varepsilon \to 0^{+}}{\frac {1}{x\pm i\varepsilon }}=\operatorname {p.v.} {\frac {1}{x}}\mp i\pi \delta (x),$ ⓘ

Hier ist der Grenzwert im Sinne der Verteilung zu verstehen, d. h. für alle kompakten, glatten Funktionen f, ⓘ

$\lim _{\varepsilon \to 0^{+}}\int _{-\infty }^{\infty }{\frac {f(x)}{x\pm i\varepsilon }}\,dx=\mp i\pi f(0)+\lim _{\varepsilon \to 0^{+}}\int _{|x|>\varepsilon }{\frac {f(x)}{x}}\,dx.$ ⓘ

Beziehung zum Kronecker-Delta

Das Kronecker-Delta δ_ij ist die Größe, die durch ⓘ

$\delta _{ij}={\begin{cases}1&i=j\\0&i\not =j\end{cases}}$ ⓘ

für alle ganzen Zahlen i, j. Diese Funktion erfüllt dann das folgende Analogon der Sichtereigenschaft: Wenn $(a_{i})_{i\in \mathbf {Z} }$ eine beliebige zweifach unendliche Folge ist, dann ⓘ

$\sum _{i=-\infty }^{\infty }a_{i}\delta _{ik}=a_{k}.$ ⓘ

In ähnlicher Weise erfüllt das Dirac-Delta für jede reelle oder komplexwertige stetige Funktion f auf R die Sichtereigenschaft ⓘ

$\int _{-\infty }^{\infty }f(x)\delta (x-x_{0})\,dx=f(x_{0}).$ ⓘ

Dies zeigt, dass die Kronecker-Delta-Funktion ein diskretes Analogon der Dirac-Delta-Funktion ist. ⓘ

Anwendungen

Wahrscheinlichkeitsrechnung

In der Wahrscheinlichkeitstheorie und der Statistik wird die Dirac-Delta-Funktion häufig verwendet, um eine diskrete Verteilung oder eine teilweise diskrete, teilweise kontinuierliche Verteilung mit Hilfe einer Wahrscheinlichkeitsdichtefunktion (die normalerweise zur Darstellung absolut kontinuierlicher Verteilungen verwendet wird) darzustellen. Die Wahrscheinlichkeitsdichtefunktion f(x) einer diskreten Verteilung, die aus Punkten x = {x₁, ..., xn} mit den entsprechenden Wahrscheinlichkeiten p₁, ..., pn besteht, kann beispielsweise wie folgt geschrieben werden ⓘ

$f(x)=\sum _{i=1}^{n}p_{i}\delta (x-x_{i}).$ ⓘ

Betrachten wir als weiteres Beispiel eine Verteilung, bei der 6/10 der Zeit eine Standardnormalverteilung und 4/10 der Zeit genau den Wert 3,5 ergibt (d. h. eine teils kontinuierliche, teils diskrete Mischverteilung). Die Dichtefunktion dieser Verteilung kann geschrieben werden als ⓘ

$f(x)=0.6\,{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}+0.4\,\delta (x-3.5).$ ⓘ

Die Deltafunktion wird auch verwendet, um die resultierende Wahrscheinlichkeitsdichtefunktion einer Zufallsvariablen darzustellen, die durch eine kontinuierlich differenzierbare Funktion transformiert wird. Wenn Y = g(X) eine stetig differenzierbare Funktion ist, dann kann die Dichte von Y wie folgt geschrieben werden ⓘ

$f_{Y}(y)=\int _{-\infty }^{+\infty }f_{X}(x)\delta (y-g(x))dx.$ ⓘ

Die Deltafunktion wird auch auf eine ganz andere Weise verwendet, um die lokale Zeit eines Diffusionsprozesses (wie die Brownsche Bewegung) darzustellen. Die lokale Zeit eines stochastischen Prozesses B(t) ist gegeben durch

$\ell (x,t)=\int _{0}^{t}\delta (x-B(s))\,ds$

und stellt die Zeit dar, die der Prozess an einem Punkt x im Bereich des Prozesses verbringt. Genauer gesagt, kann dieses Integral in einer Dimension wie folgt geschrieben werden

$\ell (x,t)=\lim _{\varepsilon \to 0^{+}}{\frac {1}{2\varepsilon }}\int _{0}^{t}\mathbf {1} _{[x-\varepsilon ,x+\varepsilon ]}(B(s))\,ds$

wobei 1[x-ε, x+ε] die Indikatorfunktion des Intervalls [x-ε, x+ε] ist. ⓘ

Quantenmechanik

Die Deltafunktion ist in der Quantenmechanik von Nutzen. Die Wellenfunktion eines Teilchens gibt die Amplitudenwahrscheinlichkeit an, mit der ein Teilchen in einem bestimmten Bereich des Raums gefunden wird. Man nimmt an, dass Wellenfunktionen Elemente des Hilbert-Raums L² von quadratisch-integrablen Funktionen sind, und die Gesamtwahrscheinlichkeit, ein Teilchen innerhalb eines bestimmten Intervalls zu finden, ist das Integral des Betrags der Wellenfunktion zum Quadrat über das Intervall. Eine Menge {$|\varphi _{n}\rangle$} von Wellenfunktionen ist orthonormal, wenn sie normalisiert sind durch ⓘ

$\langle \varphi _{n}\mid \varphi _{m}\rangle =\delta _{nm}$ ⓘ

wobei $\delta$ das Kronecker-Delta ist. Eine Menge von orthonormalen Wellenfunktionen ist vollständig im Raum der quadratisch-integrablen Funktionen, wenn jede Wellenfunktion $|\psi \rangle$ sich als Linearkombination der {$|\varphi _{n}\rangle$} mit komplexen Koeffizienten ausgedrückt werden kann:

$\psi =\sum c_{n}\varphi _{n},$ ⓘ

mit $c_{n}=\langle \varphi _{n}|\psi \rangle$. Vollständige orthonormale Systeme von Wellenfunktionen erscheinen natürlich als die Eigenfunktionen des Hamiltonian (eines gebundenen Systems) in der Quantenmechanik, der die Energieniveaus misst, die Eigenwerte genannt werden. Die Menge der Eigenwerte wird in diesem Fall als Spektrum der Hamiltonfunktion bezeichnet. In der Braket-Schreibweise, wie oben, impliziert diese Gleichheit die Auflösung der Identität:

$I=\sum |\varphi _{n}\rangle \langle \varphi _{n}|.$ ⓘ

Hier wird angenommen, dass die Eigenwerte diskret sind, aber die Menge der Eigenwerte einer Beobachtungsgröße kann auch kontinuierlich und nicht diskret sein. Ein Beispiel ist die Positionsmessgröße Qψ(x) = xψ(x). Das Spektrum der Position (in einer Dimension) ist die gesamte reelle Linie und wird als kontinuierliches Spektrum bezeichnet. Anders als der Hamilton-Operator hat der Positionsoperator jedoch keine Eigenfunktionen. Der herkömmliche Weg, diesen Mangel zu beheben, besteht darin, die Klasse der verfügbaren Funktionen zu erweitern, indem man auch Verteilungen zulässt, d. h. den Hilbert-Raum der Quantenmechanik durch einen geeigneten manipulierten Hilbert-Raum zu ersetzen. In diesem Zusammenhang verfügt der Positionsoperator über einen vollständigen Satz von Eigenverteilungen, die durch die Punkte y der reellen Linie gekennzeichnet sind und wie folgt lauten ⓘ

$\varphi _{y}(x)=\delta (x-y).$ ⓘ

Die Eigenfunktionen der Position werden mit $\varphi _{y}=|y\rangle$ in Dirac-Schreibweise bezeichnet und sind als Lageeigenzustände bekannt. ⓘ

Ähnliche Überlegungen gelten für die Eigenzustände des Impulsoperators oder jedes anderen selbstadjunkten unbeschränkten Operators P im Hilbert-Raum, sofern das Spektrum von P stetig ist und es keine entarteten Eigenwerte gibt. In diesem Fall gibt es eine Menge Ω von reellen Zahlen (das Spektrum) und eine Sammlung φ_y von Verteilungen, die durch die Elemente von Ω indiziert sind, so dass ⓘ

$P\varphi _{y}=y\varphi _{y}.$ ⓘ

Das heißt, φ_y sind die Eigenvektoren von P. Wenn die Eigenvektoren so normalisiert werden, dass ⓘ

$\langle \varphi _{y},\varphi _{y'}\rangle =\delta (y-y')$ ⓘ

im Sinne der Verteilung, dann gilt für jede Testfunktion ψ, ⓘ

$\psi (x)=\int _{\Omega }c(y)\varphi _{y}(x)\,dy$ ⓘ

wobei ⓘ

$c(y)=\langle \psi ,\varphi _{y}\rangle .$ ⓘ

Das heißt, wie im diskreten Fall, gibt es eine Auflösung der Identität ⓘ

$I=\int _{\Omega }|\varphi _{y}\rangle \,\langle \varphi _{y}|\,dy$ ⓘ

wobei das Operator-bewertete Integral wieder im schwachen Sinne zu verstehen ist. Wenn das Spektrum von P sowohl kontinuierliche als auch diskrete Teile hat, dann beinhaltet die Auflösung der Identität eine Summation über das diskrete Spektrum und ein Integral über das kontinuierliche Spektrum. ⓘ

Die Deltafunktion hat auch viele speziellere Anwendungen in der Quantenmechanik, wie z. B. die Deltapotentialmodelle für ein einfaches und ein doppeltes Potentialtopf. ⓘ

Strukturelle Mechanik

Die Deltafunktion kann in der Strukturmechanik verwendet werden, um transiente Lasten oder Punktlasten zu beschreiben, die auf Strukturen wirken. Die Gleichung für ein einfaches Masse-Feder-System, das durch einen plötzlichen Kraftimpuls I zum Zeitpunkt t = 0 angeregt wird, kann wie folgt geschrieben werden ⓘ

$m{\frac {\mathrm {d} ^{2}\xi }{\mathrm {d} t^{2}}}+k\xi =I\delta (t),$ ⓘ

wobei m die Masse, ξ die Durchbiegung und k die Federkonstante ist. ⓘ

Ein weiteres Beispiel: Die Gleichung für die statische Durchbiegung eines schlanken Balkens lautet nach der Euler-Bernoulli-Theorie, ⓘ

$EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=q(x),$ ⓘ

wobei EI die Biegesteifigkeit des Trägers, w die Durchbiegung, x die Raumkoordinate und q(x) die Lastverteilung ist. Wird ein Balken durch eine Punktkraft F bei x = x₀ belastet, wird die Lastverteilung wie folgt geschrieben ⓘ

$q(x)=F\delta (x-x_{0}).$ ⓘ

Da die Integration der Deltafunktion zur Heaviside-Stufenfunktion führt, folgt daraus, dass die statische Durchbiegung eines schlanken Trägers, der mehreren Punktlasten ausgesetzt ist, durch eine Reihe von stückweisen Polynomen beschrieben wird. ⓘ

Auch ein auf einen Balken wirkendes Punktmoment kann durch Deltafunktionen beschrieben werden. Betrachten wir zwei entgegengesetzte Punktkräfte F im Abstand d. Sie erzeugen dann ein Moment M = Fd, das auf den Balken wirkt. Lassen Sie nun den Abstand d gegen den Grenzwert Null gehen, während M konstant gehalten wird. Die Lastverteilung unter der Annahme eines im Uhrzeigersinn wirkenden Moments bei x = 0 wird wie folgt beschrieben ⓘ

${\begin{aligned}q(x)&=\lim _{d\to 0}{\Big (}F\delta (x)-F\delta (x-d){\Big )}\\[4pt]&=\lim _{d\to 0}\left({\frac {M}{d}}\delta (x)-{\frac {M}{d}}\delta (x-d)\right)\\[4pt]&=M\lim _{d\to 0}{\frac {\delta (x)-\delta (x-d)}{d}}\\[4pt]&=M\delta '(x).\end{aligned}}$ ⓘ

Die Punktmomente können also durch die Ableitung der Deltafunktion dargestellt werden. Die Integration der Balkengleichung führt wiederum zu einer stückweisen polynomialen Durchbiegung. ⓘ

Definition über Dirac-Maß

Das durch ein positives Radon-Maß $\mu$ erzeugte Funktional $\textstyle \langle \mu ,f\rangle =\int f(x)\,\mathrm {d} \mu$ (für $f\in {\mathcal {D}}$) ist eine Distribution. Die Delta-Distribution wird von folgendem Radon-Maß – man spricht hier speziell vom Diracmaß – erzeugt:

$\delta (A)={\begin{cases}1,\ &{\text{ falls }}0\in A,\\0,\ &{\text{ sonst,}}\end{cases}}$ ⓘ

wobei $A\subseteq \mathbb {R}$. Ein Maß lässt sich physikalisch interpretieren, z. B. als Massenverteilung oder Ladungsverteilung des Raums. Dann entspricht die Delta-Distribution einem Massenpunkt der Masse 1 oder einer Punktladung der Ladung 1 im Ursprung. ⓘ

$\langle \delta ,f\rangle =\int f(x)\,\mathrm {d} \delta =f(0).$ ⓘ

Befinden sich an den Stellen $x_{i}\in \mathbb {R}$ Punktladungen $q_{i}$, wobei die Summe über alle Ladungen endlich bleibt, dann wird für $A\subset \mathbb {R}$ ein Maß auf der $\sigma$-Algebra aller Teilmengen von $\mathbb {R}$ definiert, das der Ladungsverteilung entspricht ($i_{A}$ durchlaufe alle $i$ mit $x_{i}\in A$):

$\rho (A):=\sum _{i_{A}}q_{i}.$ ⓘ

Für dieses Maß ist dann die zugehörige Distribution:

$\langle \rho ,f\rangle =\int f(x)\,\mathrm {d} \rho =\sum _{i_{A}}f(x_{i})q_{i}.$ ⓘ

Beispiele für Dirac-Folgen

Im Folgenden werden verschiedene Approximationen (Dirac-Folgen) $\delta _{\epsilon }(x)$ angegeben, zunächst stetig differenzierbare:

• Glockenfunktionen (Normalverteilungen)

$\delta _{\epsilon }(x)={\frac {1}{\sqrt {2\pi \epsilon }}}\,\exp \left(-{\frac {x^{2}}{2\epsilon }}\right)$

Die angegebenen Funktionen besitzen ein sehr schmales und sehr hohes Maximum bei x=0, die Breite ist etwa ${\sqrt {\epsilon }}\to 0$ und die Höhe etwa $1/{\sqrt {\epsilon }}\to \infty$. Für alle $\epsilon$ ist der Flächeninhalt unter der Funktion 1. ⓘ

• Lorentzkurven

$\delta _{\epsilon }(x)={\frac {1}{\pi }}{\frac {\epsilon }{x^{2}+\epsilon ^{2}}}$ ⓘ

• Fresnel-Darstellung

$\delta _{\epsilon }(x)={\frac {1}{\sqrt {i\pi \epsilon }}}\,\exp \left({\frac {ix^{2}}{\epsilon }}\right)$

die man sich vorstellen kann als eine Linie, die auf einen Zylinder gewickelt ist, und deren Wicklungen durch das $x^{2}$ immer enger werden; die Grundfläche (in $x$-$y$-Ausrichtung) des Zylinders wird aus dem Imaginär- und Realteil der Funktion gebildet, die Funktion entwickelt sich dann in $z$-Richtung. ⓘ

Es sind aber auch Approximationen möglich, die nur stückweise stetig differenzierbar sind:

• Rechteckfunktion

$\delta _{\epsilon }(x)={\frac {\operatorname {rect} (x/\epsilon )}{\epsilon }}={\begin{cases}{\frac {1}{\epsilon }}&\ |x|\leq {\frac {\epsilon }{2}}\\0&\ {\text{sonst}}\end{cases}}$ ⓘ

• Dreiecksfunktion

$\delta _{\epsilon }(x)={\begin{cases}{\frac {\epsilon +x}{\epsilon ^{2}}}&\ -\epsilon \leq x\leq 0\\{\frac {\epsilon -x}{\epsilon ^{2}}}&\ 0<x\leq \epsilon \\0&\ {\text{sonst}}\end{cases}}$ ⓘ

• Exponentialfunktion um Ursprung abfallend

$\delta _{\epsilon }(x)={\frac {1}{2\epsilon }}\exp \left(-{\frac {|x|}{\epsilon }}\right)$ ⓘ

Weitere Beispiele

Approximation durch die Sincfunktion ⓘ

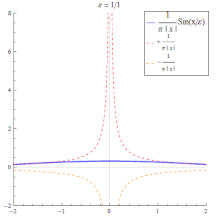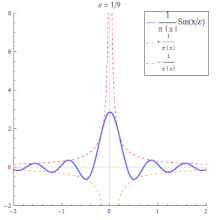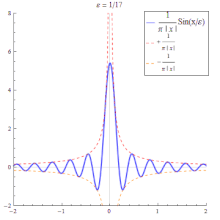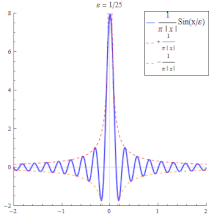
• Die Funktionenfolge der Sinc-Funktionen

$\delta _{\epsilon }(x)={\frac {1}{\pi x}}\sin \left({\frac {x}{\epsilon }}\right)$
ist keine Dirac-Folge, da ihre Folgenglieder auch negative Werte annehmen. Betrachtet man allerdings den Ausdruck

$\lim _{\epsilon \to 0}\int _{-\infty }^{\infty }{\frac {1}{\pi x}}\sin \left({\frac {x}{\epsilon }}\right)\phi (x)\mathrm {d} x$

so konvergiert für alle $\phi \in {\mathcal {D}}$ diese Folge im distributionellen Sinn gegen die Delta-Distribution. ⓘ

Praktische Anwendung

Praktische Bedeutung hat der Dirac-Stoß bei der Ermittlung der Impulsantwort in der Akustik (in anderen Sparten der Physik spricht man auch von einer $\delta$-Größe, wenn man meint, dass die betreffende Größe einer schmalst-möglichen Verteilung genügt). So hat jeder Raum ein eigenes Schallverhalten. Mit einem Dirac-Impuls (angenähert durch ein Klatschen mit den Händen) kann dieses Verhalten (durch Messen des „Echos“, also der Systemantwort) ermittelt werden. ⓘ

Typische, technisch realisierbare Dirac-Werte:

• Hochspannungstechnik ca. 1–100 ns Halbwertsbreite
• Hochfrequenztechnik ca. 10–100 ps Halbwertsbreite
• Pulslasertechnik ca. 10–100 fs Halbwertsbreite ⓘ

Eine wichtige Anwendung der Delta-Distribution ist die Lösung inhomogener linearer Differentialgleichungen mit der Methode der Greenschen Funktion. ⓘ

Mehrdimensionale Delta-Distribution

Definition

Im Mehrdimensionalen ist der Raum der Testfunktionen ${\mathcal {E}}$ gleich $C^{\infty }(\mathbb {R} ^{n})$, der Raum der beliebig oft total differenzierbaren Funktionen $f\colon \,\mathbb {R} ^{n}\to \mathbb {R}$. ⓘ

Die Delta-Distribution hat auf die Testfunktion $f\colon \,\mathbb {R} ^{n}\to \mathbb {R}$ die folgende Wirkung:

$\delta \colon \,{\mathcal {E}}\to \mathbb {R} \,,\ f\mapsto f({\vec {0}})$ ⓘ

In der informellen Integralschreibweise unter Verwendung von Translation und Skalierung:

$\int f({\vec {x}})\,\delta ({\vec {x}}-{\vec {a}})\,\mathrm {d} ^{n}x=\int f({\vec {x}})\,\delta ({\vec {a}}-{\vec {x}})\,\mathrm {d} ^{n}x=f({\vec {a}})$. ⓘ

Eigenschaften

Die „mehrdimensionale“ Delta-Distribution lässt sich als Produkt von „eindimensionalen“ Delta-Distributionen schreiben:

$\delta ({\vec {x}}-{\vec {a}})=\delta (x_{1}-a_{1})\,\delta (x_{2}-a_{2})\,\dots \,\delta (x_{n}-a_{n})$. ⓘ

Speziell im Dreidimensionalen gibt es eine Darstellung der Delta-Distribution, die häufig in der Elektrodynamik eingesetzt wird, um Punktladungen darzustellen:

$\delta ({\vec {x}}-{\vec {a}})=-{\frac {1}{4\pi }}\Delta {\frac {1}{\|{\vec {x}}-{\vec {a}}\|_{2}}}$. ⓘ

Delta-Distribution in krummlinigen Koordinatensystemen

In krummlinigen Koordinatensystemen muss die Funktionaldeterminante

$\mathrm {d} ^{3}r=\mathrm {d} x~\mathrm {d} y~\mathrm {d} z=\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}~\mathrm {d} a~\mathrm {d} b~\mathrm {d} c$

berücksichtigt werden. ⓘ

Der Ansatz ⓘ

$\delta ({{\vec {r}}-{\vec {r}}_{0}})=\gamma (a,b,c)~\delta (a-a_{0})~\delta (b-b_{0})~\delta (c-c_{0})$ ⓘ

mit ${\vec {r}}=(a,b,c)$ und ${\vec {r}}_{0}=(a_{0},b_{0},c_{0})$ führt dabei auf die Gleichung ⓘ

$\int _{V}\delta ({\vec {r}}-{\vec {r}}_{0})~\mathrm {d} ^{3}r=\iiint _{V}\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}~\gamma (a,b,c)~\delta (a-a_{0})~\delta (b-b_{0})~\delta (c-c_{0})~\mathrm {d} a~\mathrm {d} b~\mathrm {d} c~{\stackrel {!}{=}}~1$, falls ${\vec {r}}_{0}\in V$. ⓘ

Daran lässt sich ablesen, dass gelten muss

$\gamma =\left(\left.\det {\frac {\partial (x,y,z)}{\partial (a,b,c)}}\right|_{{\vec {r}}_{0}}\right)^{-1}$. ⓘ

In krummlinigen Koordinatensystem muss die Delta-Distribution also mit einem Vorfaktor versehen werden, der dem Kehrwert der Funktionaldeterminante entspricht. ⓘ

Beispiele

In Kugelkoordinaten mit ${\vec {r}}=(r,\theta ,\phi )$ und ${\vec {r}}_{0}=(r_{0},\theta _{0},\phi _{0})$ gilt:

$\delta ({\vec {r}}-{\vec {r}}_{0})={\frac {1}{r^{2}\sin \theta }}~\delta (r-r_{0})~\delta (\theta -\theta _{0})~\delta (\phi -\phi _{0})$ ⓘ

In Zylinderkoordinaten mit ${\vec {r}}=(\rho ,\phi ,z)$ und ${\vec {r}}_{0}=(\rho _{0},\phi _{0},z_{0})$ gilt:

$\delta ({\vec {r}}-{\vec {r}}_{0})={\frac {1}{\rho }}~\delta (\rho -\rho _{0})~\delta (\phi -\phi _{0})~\delta (z-z_{0})$ ⓘ